1 Introduction and statement of the results
The main objective in this article is to study the
![]() $L^p$
boundedness of oscillating multipliers on symmetric spaces of arbitrary rank and locally symmetric spaces. Our aim is to find the corresponding analogues of the classical Euclidean assumptions on the abovementioned geometries and to generalize the results obtained in the rank one case by Giulini and Meda in [Reference Giulini and Meda13]. The ingredients we shall use were already known, however, their present use allows us to overcome the rank obstacle in a uniform manner.
$L^p$
boundedness of oscillating multipliers on symmetric spaces of arbitrary rank and locally symmetric spaces. Our aim is to find the corresponding analogues of the classical Euclidean assumptions on the abovementioned geometries and to generalize the results obtained in the rank one case by Giulini and Meda in [Reference Giulini and Meda13]. The ingredients we shall use were already known, however, their present use allows us to overcome the rank obstacle in a uniform manner.
To put the result in perspective, let us discuss the background. On
![]() $\mathbb {R}^{n}$
, consider the function
$\mathbb {R}^{n}$
, consider the function
where
![]() $\theta $
is a smooth function, vanishing near zero and equal to
$\theta $
is a smooth function, vanishing near zero and equal to
![]() $1$
outside the unit ball. As usual, denote by
$1$
outside the unit ball. As usual, denote by
![]() $C_0^{\infty }(\mathbb {R}^n)$
the set of smooth, compactly supported functions on
$C_0^{\infty }(\mathbb {R}^n)$
the set of smooth, compactly supported functions on
![]() $\mathbb {R}^n$
. Let
$\mathbb {R}^n$
. Let
![]() $\widetilde {T}_{\alpha ,\beta }$
be the operator which in the Fourier transform variables is given by
$\widetilde {T}_{\alpha ,\beta }$
be the operator which in the Fourier transform variables is given by
In other words,
![]() $\widetilde {T}_{\alpha ,\beta }$
is a convolution operator with kernel the inverse Fourier transform of
$\widetilde {T}_{\alpha ,\beta }$
is a convolution operator with kernel the inverse Fourier transform of
![]() $\widetilde {m}_{\alpha ,\beta }$
. This family provides examples of operators that do not fall under the scope of Calderón–Zygmund theory, but rather are given by “strongly singular kernels,” [Reference Fefferman11]. They are also interesting because of their intimate connection with the Cauchy problem for the wave and the Schrödinger equation, for
$\widetilde {m}_{\alpha ,\beta }$
. This family provides examples of operators that do not fall under the scope of Calderón–Zygmund theory, but rather are given by “strongly singular kernels,” [Reference Fefferman11]. They are also interesting because of their intimate connection with the Cauchy problem for the wave and the Schrödinger equation, for
![]() $\alpha =1$
and
$\alpha =1$
and
![]() $\alpha =2$
, respectively. In the euclidean setting, these operators have been extensively studied, see for example [Reference Fefferman and Stein10, Reference Fefferman11, Reference Hirschman17, Reference Schonbek25, Reference Stein26, Reference Wainger27]. The
$\alpha =2$
, respectively. In the euclidean setting, these operators have been extensively studied, see for example [Reference Fefferman and Stein10, Reference Fefferman11, Reference Hirschman17, Reference Schonbek25, Reference Stein26, Reference Wainger27]. The
![]() $L^{p}$
-boundedness of oscillating multipliers has been studied also in various geometric settings as Riemannian manifolds, Lie groups and symmetric spaces, see for instance [Reference Alexopoulos1, Reference Georgiadis12, Reference Giulini and Meda13, Reference Marias21] and the references therein. In particular, for the rank one case of symmetric spaces (which include hyperbolic space) and locally symmetric spaces, see [Reference Cowling, Giulini and Meda8, Reference Giulini and Meda13, Reference Ionescu18, Reference Papageorgiou24].
$L^{p}$
-boundedness of oscillating multipliers has been studied also in various geometric settings as Riemannian manifolds, Lie groups and symmetric spaces, see for instance [Reference Alexopoulos1, Reference Georgiadis12, Reference Giulini and Meda13, Reference Marias21] and the references therein. In particular, for the rank one case of symmetric spaces (which include hyperbolic space) and locally symmetric spaces, see [Reference Cowling, Giulini and Meda8, Reference Giulini and Meda13, Reference Ionescu18, Reference Papageorgiou24].
In the present paper, we deal with oscillating multipliers in the setting of noncompact symmetric spaces of arbitrary rank. These are Riemannian, nonpositively curved manifolds, with a structure that induces a Fourier-like analysis. In more detail, let G be a semi-simple, noncompact, connected Lie group with finite center and take K be a maximal compact subgroup of G. We consider the symmetric space of noncompact type
![]() $X=G/K$
, with
$X=G/K$
, with
![]() $\operatorname {dim}X=n$
. Denote by
$\operatorname {dim}X=n$
. Denote by
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $ \mathfrak {k}$
the Lie algebras of G and K, respectively. We have the Cartan decomposition
$ \mathfrak {k}$
the Lie algebras of G and K, respectively. We have the Cartan decomposition
![]() $\mathfrak {g}=\mathfrak {p} \oplus \mathfrak {k}$
. Let
$\mathfrak {g}=\mathfrak {p} \oplus \mathfrak {k}$
. Let
![]() $ \mathfrak {a}$
be a maximal abelian subspace of
$ \mathfrak {a}$
be a maximal abelian subspace of
![]() $\mathfrak {p}$
and denote its dual by
$\mathfrak {p}$
and denote its dual by
![]() $\mathfrak { a}^*$
. If
$\mathfrak { a}^*$
. If
![]() $\operatorname {dim}\mathfrak {a}=d$
, then we say that X has rank d. The Killing form of
$\operatorname {dim}\mathfrak {a}=d$
, then we say that X has rank d. The Killing form of
![]() $\mathfrak {g}$
induces a scalar product on
$\mathfrak {g}$
induces a scalar product on
![]() $\mathfrak {a}$
, hence on
$\mathfrak {a}$
, hence on
![]() $\mathfrak {a}^*$
. The norm induced by the corresponding product on
$\mathfrak {a}^*$
. The norm induced by the corresponding product on
![]() $\mathfrak {a}^*$
will be denoted by
$\mathfrak {a}^*$
will be denoted by
![]() $\|\cdot \|$
.
$\|\cdot \|$
.
Let X be a symmetric space of noncompact type. Consider the function
where
![]() $\rho $
is the half sum of positive roots counted with their multiplicity. This multiplier is the analogue of (1) in the present setting, but since it remains bounded for all
$\rho $
is the half sum of positive roots counted with their multiplicity. This multiplier is the analogue of (1) in the present setting, but since it remains bounded for all
![]() $\lambda \in \mathfrak {a}^{\ast }$
, as in [Reference Giulini and Meda13], the cut-off function in (1) is no longer necessary. Denote by
$\lambda \in \mathfrak {a}^{\ast }$
, as in [Reference Giulini and Meda13], the cut-off function in (1) is no longer necessary. Denote by
![]() $\kappa _{\alpha ,\beta }$
the inverse spherical Fourier transform of
$\kappa _{\alpha ,\beta }$
the inverse spherical Fourier transform of
![]() $m_{\alpha ,\beta }$
in the sense of distributions. Consider the convolution operator
$m_{\alpha ,\beta }$
in the sense of distributions. Consider the convolution operator
![]() $T_{\alpha ,\beta }$
, where
$T_{\alpha ,\beta }$
, where
Let
![]() $\Gamma $
be a discrete and torsion free subgroup of G and let us consider the locally symmetric space
$\Gamma $
be a discrete and torsion free subgroup of G and let us consider the locally symmetric space
![]() $M=\Gamma \backslash X$
, which equipped with the projection of the canonical Riemannian structure of X, becomes a Riemannian manifold.
$M=\Gamma \backslash X$
, which equipped with the projection of the canonical Riemannian structure of X, becomes a Riemannian manifold.
To define oscillating multipliers on M, we first observe that if
![]() $f\in C_{0}^{\infty }(M)$
, then the function
$f\in C_{0}^{\infty }(M)$
, then the function
![]() $T_{\alpha ,\beta }f$
defined by (3) is right K-invariant and left
$T_{\alpha ,\beta }f$
defined by (3) is right K-invariant and left
![]() $\Gamma $
-invariant. So,
$\Gamma $
-invariant. So,
![]() $ T_{\alpha ,\beta }$
can be considered as an operator acting on functions on
$ T_{\alpha ,\beta }$
can be considered as an operator acting on functions on
![]() $ M$
, which we shall denote by
$ M$
, which we shall denote by
![]() $\widehat {T}_{\alpha ,\beta }$
.
$\widehat {T}_{\alpha ,\beta }$
.
Let
![]() $\kappa $
be a K-bi-invariant function and denote by
$\kappa $
be a K-bi-invariant function and denote by
![]() $\ast |\kappa |$
the convolution operator whose kernel is
$\ast |\kappa |$
the convolution operator whose kernel is
![]() $|\kappa |$
. Let
$|\kappa |$
. Let
![]() $p\in (1,\infty )$
, denote by
$p\in (1,\infty )$
, denote by
![]() $p^{\prime }$
its conjugate and set
$p^{\prime }$
its conjugate and set
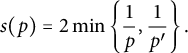 $$ \begin{align*} s(p)=2\min \left\{ \frac{1}{p},\frac{1}{p^{\prime }}\right\} . \end{align*} $$
$$ \begin{align*} s(p)=2\min \left\{ \frac{1}{p},\frac{1}{p^{\prime }}\right\} . \end{align*} $$
We shall assume that the following version of the Kunze and Stein phenomenon holds,
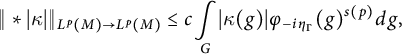 $$ \begin{align} \Vert \ast |\kappa |\Vert _{L^{p}(M)\rightarrow L^{p}(M)}\leq c\underset{G}{ \int }|\kappa (g)|\varphi _{-i\eta _{\Gamma }}(g)^{s(p)}{dg}, \end{align} $$
$$ \begin{align} \Vert \ast |\kappa |\Vert _{L^{p}(M)\rightarrow L^{p}(M)}\leq c\underset{G}{ \int }|\kappa (g)|\varphi _{-i\eta _{\Gamma }}(g)^{s(p)}{dg}, \end{align} $$
where
![]() $\varphi _{\lambda }$
are the elementary spherical functions,
$\varphi _{\lambda }$
are the elementary spherical functions,
![]() $\eta _{\Gamma }$
is a vector of the euclidean sphere
$\eta _{\Gamma }$
is a vector of the euclidean sphere
![]() $S(0,(\left \Vert \rho \right \Vert {}^{2}-\lambda _{0})^{1/2})$
of
$S(0,(\left \Vert \rho \right \Vert {}^{2}-\lambda _{0})^{1/2})$
of
![]() $\mathfrak {a}^{\ast }$
and
$\mathfrak {a}^{\ast }$
and
![]() $\lambda _{0}$
is the bottom of the spectrum of the Laplacian
$\lambda _{0}$
is the bottom of the spectrum of the Laplacian
![]() $\Delta _{M}$
. For example, this is the case for
$\Delta _{M}$
. For example, this is the case for
![]() $M=\Gamma \backslash G/K$
, when (i)
$M=\Gamma \backslash G/K$
, when (i)
![]() $\Gamma $
is a lattice, or (ii) G possesses Kazhdan’s property (T) or (iii)
$\Gamma $
is a lattice, or (ii) G possesses Kazhdan’s property (T) or (iii)
![]() $\Gamma \backslash G$
is nonamenable, see [Reference Lohoué and Marias20] for more details. We say that M belongs in the class (KS) if (4), is valid on it. Note that X belongs in (KS), [Reference Herz14, Reference Lohoué and Marias20].
$\Gamma \backslash G$
is nonamenable, see [Reference Lohoué and Marias20] for more details. We say that M belongs in the class (KS) if (4), is valid on it. Note that X belongs in (KS), [Reference Herz14, Reference Lohoué and Marias20].
Our main result is the following theorem.
Theorem 1 Assume that
![]() $\alpha \in (0,1)$
and that
$\alpha \in (0,1)$
and that
![]() $M=\Gamma \backslash X$
belongs in the class (KS).
$M=\Gamma \backslash X$
belongs in the class (KS).
-
(i) If
 $\beta>n\alpha /2$
, then
$\beta>n\alpha /2$
, then
 ${T}_{\alpha ,\beta }$
(resp.
${T}_{\alpha ,\beta }$
(resp.
 $\widehat {T} _{\alpha ,\beta }$
) is bounded on
$\widehat {T} _{\alpha ,\beta }$
) is bounded on
 $L^{p}(X)$
(resp. on
$L^{p}(X)$
(resp. on
 $L^{p}(M)$
) for all
$L^{p}(M)$
) for all
 $ p\in (1,\infty )$
.
$ p\in (1,\infty )$
. -
(ii) If
 $\beta \leq n\alpha /2$
, then
$\beta \leq n\alpha /2$
, then
 ${T}_{\alpha ,\beta }$
(resp.
${T}_{\alpha ,\beta }$
(resp.
 $\widehat { T}_{\alpha ,\beta }$
) is bounded on
$\widehat { T}_{\alpha ,\beta }$
) is bounded on
 $L^{p}(X)$
(resp. on
$L^{p}(X)$
(resp. on
 $L^{p}(M)$
) for all
$L^{p}(M)$
) for all
 $p\in (1,\infty )$
, provided that
$p\in (1,\infty )$
, provided that
 $\beta>\alpha n|1/p-1/2|.$
$\beta>\alpha n|1/p-1/2|.$
The above theorem was proved in [Reference Giulini and Meda13, Reference Papageorgiou24] for the rank one case, taking
![]() $\beta \in \mathbb {C}$
with
$\beta \in \mathbb {C}$
with
![]() $\text {Re}\beta>0$
, but we will consider
$\text {Re}\beta>0$
, but we will consider
![]() $\beta>0$
for simplicity. Our proof treats symmetric and locally symmetric spaces of arbitrary rank in a uniform way.
$\beta>0$
for simplicity. Our proof treats symmetric and locally symmetric spaces of arbitrary rank in a uniform way.
Let us make a few remarks about the symmetric space case. First, the operator
![]() $T_{\alpha , \beta }$
is bounded on
$T_{\alpha , \beta }$
is bounded on
![]() $L^2(X)$
since the multiplier is bounded for all
$L^2(X)$
since the multiplier is bounded for all
![]() $\alpha , \beta>0$
. But for
$\alpha , \beta>0$
. But for
![]() $p\neq 2$
, there is a certain necessary condition (see [Reference Clerc and Stein7, Theorem 1] or [Reference Anker3, p.604]), first observed by Clerc and Stein, which has no Euclidean analogue: every multiplier that yields an
$p\neq 2$
, there is a certain necessary condition (see [Reference Clerc and Stein7, Theorem 1] or [Reference Anker3, p.604]), first observed by Clerc and Stein, which has no Euclidean analogue: every multiplier that yields an
![]() $L^p(X)$
bounded operator, for some
$L^p(X)$
bounded operator, for some
![]() $p\in (1, \infty )$
,
$p\in (1, \infty )$
,
![]() $p\neq 2$
, extends to an invariant by the Weyl group, bounded, holomorphic function inside the tube
$p\neq 2$
, extends to an invariant by the Weyl group, bounded, holomorphic function inside the tube
![]() $\mathcal {T}^p=\mathfrak {a^{\ast }}+i|2/p-1|C_{\rho }$
. Here,
$\mathcal {T}^p=\mathfrak {a^{\ast }}+i|2/p-1|C_{\rho }$
. Here,
![]() $C_{\rho }$
denotes the convex hull of the images of
$C_{\rho }$
denotes the convex hull of the images of
![]() $\rho $
under the Weyl group. In the rank one case, the interior of the tube reduces to the strip
$\rho $
under the Weyl group. In the rank one case, the interior of the tube reduces to the strip
![]() $\{\lambda \in \mathbb {C}: |\text {Im}\lambda |<|2/p-1|\rho \}$
. Moreover, when
$\{\lambda \in \mathbb {C}: |\text {Im}\lambda |<|2/p-1|\rho \}$
. Moreover, when
![]() $p = 1$
, the multiplier should even extend to a bounded continuous function on the closed tube
$p = 1$
, the multiplier should even extend to a bounded continuous function on the closed tube
![]() $\mathcal {T}^1$
. Denote by
$\mathcal {T}^1$
. Denote by
![]() $\langle \cdot , \cdot \rangle $
the
$\langle \cdot , \cdot \rangle $
the
![]() $\mathbb {C}$
-bilinear extension of the inner product of
$\mathbb {C}$
-bilinear extension of the inner product of
![]() $\mathfrak {a}^{\ast }$
to
$\mathfrak {a}^{\ast }$
to
![]() $\mathfrak {a}_{\mathbb {C}}^{\ast }$
and observe that at
$\mathfrak {a}_{\mathbb {C}}^{\ast }$
and observe that at
![]() $\lambda = i\rho $
, the quantity
$\lambda = i\rho $
, the quantity
![]() $\langle \lambda , \lambda \rangle +\|\rho \|^2$
vanishes. Thus,
$\langle \lambda , \lambda \rangle +\|\rho \|^2$
vanishes. Thus,
![]() $m_{\alpha , \beta }$
is not defined for
$m_{\alpha , \beta }$
is not defined for
![]() $\lambda = i\rho $
, for any
$\lambda = i\rho $
, for any
![]() $\beta>0$
and the
$\beta>0$
and the
![]() $L^1(X)$
problem is ill-posed.
$L^1(X)$
problem is ill-posed.
The critical index concerning the size of
![]() $\beta $
appearing in Theorem 1 is the same as in the euclidean case. This is due to the following observation: the part of the operator “at infinity,” which is related to the large-frequencies’ part of the kernel, is bounded on all
$\beta $
appearing in Theorem 1 is the same as in the euclidean case. This is due to the following observation: the part of the operator “at infinity,” which is related to the large-frequencies’ part of the kernel, is bounded on all
![]() $L^p(X)$
,
$L^p(X)$
,
![]() $p\in (1, \infty )$
, without any restrictions on the size of the parameter
$p\in (1, \infty )$
, without any restrictions on the size of the parameter
![]() $\beta $
; on the other hand, the remaining “local part” is essentially euclidean, thus inducing the condition between parameters
$\beta $
; on the other hand, the remaining “local part” is essentially euclidean, thus inducing the condition between parameters
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
on Theorem 1. However, the result for
$\beta $
on Theorem 1. However, the result for
![]() $\alpha =1$
, cannot be obtained as a limit case of
$\alpha =1$
, cannot be obtained as a limit case of
![]() $\alpha \in (0,1)$
,
$\alpha \in (0,1)$
,
![]() $\alpha \rightarrow 1^{-}$
. Indeed, for
$\alpha \rightarrow 1^{-}$
. Indeed, for
![]() $\alpha =1$
the critical index for
$\alpha =1$
the critical index for
![]() $\beta $
is
$\beta $
is
![]() $(n-1)\left | 1/p-1/2\right |$
, rather than
$(n-1)\left | 1/p-1/2\right |$
, rather than
![]() $n \left | 1/p-1/2\right |$
, so a different approach is required, see for instance [Reference Cowling, Giulini and Meda8].
$n \left | 1/p-1/2\right |$
, so a different approach is required, see for instance [Reference Cowling, Giulini and Meda8].
The case
![]() $\alpha>1$
differs considerably from the corresponding Euclidean result or, for instance, the case of Riemannian manifolds of nonnegative Ricci curvature [Reference Alexopoulos1, Theorem 1]. In fact, for
$\alpha>1$
differs considerably from the corresponding Euclidean result or, for instance, the case of Riemannian manifolds of nonnegative Ricci curvature [Reference Alexopoulos1, Theorem 1]. In fact, for
![]() $\alpha>1$
, the operator is bounded only on
$\alpha>1$
, the operator is bounded only on
![]() $L^2(X)$
. This is once again due to the necessary condition of Clerc and Stein. Indeed, writing the complex number
$L^2(X)$
. This is once again due to the necessary condition of Clerc and Stein. Indeed, writing the complex number
![]() $\langle \lambda , \lambda \rangle +\|\rho \|^2$
in polar form, it is easy to see that the multiplier
$\langle \lambda , \lambda \rangle +\|\rho \|^2$
in polar form, it is easy to see that the multiplier
![]() $m_{\alpha , \beta }(\lambda )$
is not bounded in any tube domain
$m_{\alpha , \beta }(\lambda )$
is not bounded in any tube domain
![]() $\mathcal {T}^p$
,
$\mathcal {T}^p$
,
![]() $p\neq 2$
(see also [Reference Giulini and Meda13, p.97]).
$p\neq 2$
(see also [Reference Giulini and Meda13, p.97]).
As usual, we perform a splitting of the kernel
![]() $\kappa _{\alpha ,\beta }$
:
$\kappa _{\alpha ,\beta }$
:
where
![]() $\zeta \in C^{\infty }(K\backslash G/K)$
is a cut-off function such that
$\zeta \in C^{\infty }(K\backslash G/K)$
is a cut-off function such that
 $$ \begin{align} \zeta (x)= \begin{cases} 1, & \text{if }|x|\leq 1/2, \\ 0, & \text{if }|x|\geq 1. \end{cases} \end{align} $$
$$ \begin{align} \zeta (x)= \begin{cases} 1, & \text{if }|x|\leq 1/2, \\ 0, & \text{if }|x|\geq 1. \end{cases} \end{align} $$
Denote by
![]() ${T}_{\alpha ,\beta }^{0}$
(resp.
${T}_{\alpha ,\beta }^{0}$
(resp.
![]() ${T}_{\alpha ,\beta }^{\infty }$
) the convolution operators on X with kernel
${T}_{\alpha ,\beta }^{\infty }$
) the convolution operators on X with kernel
![]() $\kappa _{\alpha ,\beta }^{0}$
(resp.
$\kappa _{\alpha ,\beta }^{0}$
(resp.
![]() $\kappa _{\alpha ,\beta }^{\infty })$
. Let
$\kappa _{\alpha ,\beta }^{\infty })$
. Let
![]() $\widehat {T} _{\alpha ,\beta }^{0}$
and
$\widehat {T} _{\alpha ,\beta }^{0}$
and
![]() $\widehat {T}_{\alpha ,\beta }^{\infty }$
be the corresponding convolution operators on M. To prove the
$\widehat {T}_{\alpha ,\beta }^{\infty }$
be the corresponding convolution operators on M. To prove the
![]() $L^{p}$
boundedness of the local part
$L^{p}$
boundedness of the local part
![]() $T_{\alpha ,\beta }^{0}$
on X, we follow the spectral multiplier approach of [Reference Alexopoulos2] (see also [Reference Georgiadis12, Reference Marias22]) and then use the spherical Fourier transform in order to adapt these ideas to the symmetric space setting. Then, the result on M for
$T_{\alpha ,\beta }^{0}$
on X, we follow the spectral multiplier approach of [Reference Alexopoulos2] (see also [Reference Georgiadis12, Reference Marias22]) and then use the spherical Fourier transform in order to adapt these ideas to the symmetric space setting. Then, the result on M for
![]() $\widehat {T}_{\alpha ,\beta }^{0}$
will follow. To prove the
$\widehat {T}_{\alpha ,\beta }^{0}$
will follow. To prove the
![]() $L^{p}$
boundedness of the parts at infinity
$L^{p}$
boundedness of the parts at infinity
![]() $T_{\alpha ,\beta }^{\infty }$
,
$T_{\alpha ,\beta }^{\infty }$
,
![]() $\widehat {T}_{\alpha ,\beta }^{\infty }$
, we shall make use as in [Reference Anker3, Reference Lohoué and Marias20, Reference Papageorgiou24] of Kunze and Stein phenomenon. We modify the proof of the main multiplier theorem in [Reference Anker3, Reference Lohoué and Marias20] in order to exploit the decay rate of the derivatives of
$\widehat {T}_{\alpha ,\beta }^{\infty }$
, we shall make use as in [Reference Anker3, Reference Lohoué and Marias20, Reference Papageorgiou24] of Kunze and Stein phenomenon. We modify the proof of the main multiplier theorem in [Reference Anker3, Reference Lohoué and Marias20] in order to exploit the decay rate of the derivatives of
![]() $m_{\alpha , \beta }$
.
$m_{\alpha , \beta }$
.
The paper is organized as follows. In Section 2, we present the necessary tools we need for our proofs. In Section 3, we study the
![]() $L^{p}$
boundedness of the part of the operator near the origin. In Section 4, we treat the part at infinity and we finish the proof of Theorem 1.
$L^{p}$
boundedness of the part of the operator near the origin. In Section 4, we treat the part at infinity and we finish the proof of Theorem 1.
Throughout this article, the different constants will always be denoted by the same letter c.
2 Preliminaries
In this section, we recall some basic facts about symmetric and locally symmetric spaces, which we will use for the proof of our results. For details see [Reference Anker3, Reference Helgason15, Reference Helgason16, Reference Lohoué and Marias20].
Let G be a semisimple Lie group, connected, noncompact, with finite center and let K be a maximal compact subgroup of G. We denote by X the noncompact symmetric space
![]() $G/K$
. The group G acts naturally on X by left translations. Denote by
$G/K$
. The group G acts naturally on X by left translations. Denote by
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $\mathfrak {k}$
the Lie algebras of G and
$\mathfrak {k}$
the Lie algebras of G and
![]() $K $
, respectively. If X, Y are two elements of
$K $
, respectively. If X, Y are two elements of
![]() $\mathfrak {g}$
, then
$\mathfrak {g}$
, then
![]() $\text {ad}(X)(Y)=[X,Y]$
is a linear transformation of
$\text {ad}(X)(Y)=[X,Y]$
is a linear transformation of
![]() $\mathfrak {g}$
to itself. Thus, we may define the Killing form by
$\mathfrak {g}$
to itself. Thus, we may define the Killing form by
![]() $B(X,Y)=\text {tr}(\text {ad}X\text {ad}Y)$
, which is symmetric and bilinear. Let also
$B(X,Y)=\text {tr}(\text {ad}X\text {ad}Y)$
, which is symmetric and bilinear. Let also
![]() $\mathfrak {p}$
be the subspace of
$\mathfrak {p}$
be the subspace of
![]() $\mathfrak {g}$
which is orthogonal to
$\mathfrak {g}$
which is orthogonal to
![]() $\mathfrak {k}$
with respect to the Killing form. We identify
$\mathfrak {k}$
with respect to the Killing form. We identify
![]() $\mathfrak {p}$
with the tangent space at the origin
$\mathfrak {p}$
with the tangent space at the origin
![]() $o=K$
on X.
$o=K$
on X.
Fix
![]() $ \mathfrak {a} $
a maximal abelian subspace of
$ \mathfrak {a} $
a maximal abelian subspace of
![]() $\mathfrak {p}$
and denote by
$\mathfrak {p}$
and denote by
![]() $ \mathfrak {a}^{\ast }$
the real dual of
$ \mathfrak {a}^{\ast }$
the real dual of
![]() $\mathfrak {a}$
. The Killing form on
$\mathfrak {a}$
. The Killing form on
![]() $\mathfrak {g}$
restricts to a positive definite form on
$\mathfrak {g}$
restricts to a positive definite form on
![]() $\mathfrak {a}$
. This in turn induces a positive inner product, hence a norm
$\mathfrak {a}$
. This in turn induces a positive inner product, hence a norm
![]() $\|\cdot \|$
on
$\|\cdot \|$
on
![]() $\mathfrak {a}$
, and by duality, on
$\mathfrak {a}$
, and by duality, on
![]() $\mathfrak {a^{\ast }}$
as well (we will use the same notation for the norms). If
$\mathfrak {a^{\ast }}$
as well (we will use the same notation for the norms). If
![]() $\operatorname {dim} \mathfrak {a}=d$
, we say that X has rank d.
$\operatorname {dim} \mathfrak {a}=d$
, we say that X has rank d.
The Killing form endows X with both a natural Riemannian metric and a corresponding G-invariant measure (denoted
![]() $dx$
). Therefore, we can define the Laplace–Beltrami operator
$dx$
). Therefore, we can define the Laplace–Beltrami operator
![]() $\Delta _{X}$
on X. If
$\Delta _{X}$
on X. If
![]() $\Gamma $
is a discrete, torsion-free subgroup of G, then the locally symmetric space
$\Gamma $
is a discrete, torsion-free subgroup of G, then the locally symmetric space
![]() $M=\Gamma \backslash X$
, equipped with the projection of the canonical Riemannian structure of X, becomes a Riemannian manifold. In the sequel, we assume that
$M=\Gamma \backslash X$
, equipped with the projection of the canonical Riemannian structure of X, becomes a Riemannian manifold. In the sequel, we assume that
![]() $\operatorname {dim} X=n $
.
$\operatorname {dim} X=n $
.
We say that
![]() $\alpha \in \mathfrak {a}^{\ast }\backslash \{0\}$
is a root vector, if the space
$\alpha \in \mathfrak {a}^{\ast }\backslash \{0\}$
is a root vector, if the space
is nontrivial. We shall denote by
![]() $m_{\alpha }=\text {dim}\mathfrak {g}^{\alpha }$
the multiplicity of the root
$m_{\alpha }=\text {dim}\mathfrak {g}^{\alpha }$
the multiplicity of the root
![]() $\alpha $
and by
$\alpha $
and by
![]() $\Sigma \subset \mathfrak {a^{\ast }}$
the root system associated to
$\Sigma \subset \mathfrak {a^{\ast }}$
the root system associated to
![]() $(\mathfrak {g}, \mathfrak {a})$
, containing all roots. Let W be the Weyl group associated to
$(\mathfrak {g}, \mathfrak {a})$
, containing all roots. Let W be the Weyl group associated to
![]() $\Sigma $
, that is, the finite subgroup of isometries of
$\Sigma $
, that is, the finite subgroup of isometries of
![]() $\Sigma $
, generated by reflections orthogonal to the walls (the hyperplanes orthogonal to the roots of
$\Sigma $
, generated by reflections orthogonal to the walls (the hyperplanes orthogonal to the roots of
![]() $\Sigma $
). The roots divide
$\Sigma $
). The roots divide
![]() $\mathfrak {a}$
into Weyl chambers, maximal connected regions where no root vanishes. Choose a Weyl chamber
$\mathfrak {a}$
into Weyl chambers, maximal connected regions where no root vanishes. Choose a Weyl chamber
![]() $\mathfrak {a}_{+}$
, to be called positive, and say that a root
$\mathfrak {a}_{+}$
, to be called positive, and say that a root
![]() $\alpha $
is positive if
$\alpha $
is positive if
![]() $\alpha (H)$
is positive for H in
$\alpha (H)$
is positive for H in
![]() $\mathfrak {a}_{+}$
. The set
$\mathfrak {a}_{+}$
. The set
![]() $\Sigma ^+$
contains all positive roots and
$\Sigma ^+$
contains all positive roots and
![]() $\Sigma _0^+\subset \Sigma ^+$
all
$\Sigma _0^+\subset \Sigma ^+$
all
![]() $\alpha $
that are indivisible, meaning that
$\alpha $
that are indivisible, meaning that
![]() $\alpha /2$
is not a root. Denote by
$\alpha /2$
is not a root. Denote by
![]() $\rho $
the half sum of positive roots counted with their multiplicities:
$\rho $
the half sum of positive roots counted with their multiplicities:
Thus the norm
![]() $\|\rho \|$
is defined, and the
$\|\rho \|$
is defined, and the
![]() $L^2$
spectrum of the Laplace-Beltrami operator
$L^2$
spectrum of the Laplace-Beltrami operator
![]() $\Delta _{X}$
consists of the half line
$\Delta _{X}$
consists of the half line
![]() $[\|\rho \|^2, \infty )$
.
$[\|\rho \|^2, \infty )$
.
We have the Cartan decomposition on the group level by
where
![]() $\overline {\mathfrak {a}_{+}}$
is the closure of the cone
$\overline {\mathfrak {a}_{+}}$
is the closure of the cone
![]() $\mathfrak {a}_{+}$
. Let H be the (unique, contrarily to the K components)
$\mathfrak {a}_{+}$
. Let H be the (unique, contrarily to the K components)
![]() $\overline {\mathfrak {a}_{+}}$
component of
$\overline {\mathfrak {a}_{+}}$
component of
![]() $x \in G$
in the decomposition (7) and define
$x \in G$
in the decomposition (7) and define
![]() $|x|=\|H\|$
. Viewed on
$|x|=\|H\|$
. Viewed on
![]() $G/K$
,
$G/K$
,
![]() $|x|$
is the distance of
$|x|$
is the distance of
![]() $xK$
to the origin
$xK$
to the origin
![]() $o=K$
. Functions on X are identified with the right K-invariant functions on G and vice versa. Similarly, left K-invariant functions on X can be viewed as K-bi-invariant functions on G. Normalize the Haar measure
$o=K$
. Functions on X are identified with the right K-invariant functions on G and vice versa. Similarly, left K-invariant functions on X can be viewed as K-bi-invariant functions on G. Normalize the Haar measure
![]() $dk$
of K such that
$dk$
of K such that
![]() $\int _{K}dk=1$
. Then, from the Cartan decomposition, it follows that
$\int _{K}dk=1$
. Then, from the Cartan decomposition, it follows that
where the Jacobian density
![]() $\delta (H)$
satisfies
$\delta (H)$
satisfies
 $$ \begin{align} \delta(H)=\prod_{\alpha \in \Sigma^+}\sinh^{m_{\alpha}}\alpha(H)\asymp \left\{ \prod_{\alpha \in \Sigma^+} \left(\frac{\alpha(H)}{1+\alpha(H)}\right)^{m_{\alpha}} \right\}e^{2\rho(H)}, \end{align} $$
$$ \begin{align} \delta(H)=\prod_{\alpha \in \Sigma^+}\sinh^{m_{\alpha}}\alpha(H)\asymp \left\{ \prod_{\alpha \in \Sigma^+} \left(\frac{\alpha(H)}{1+\alpha(H)}\right)^{m_{\alpha}} \right\}e^{2\rho(H)}, \end{align} $$
where
![]() $f(x)\asymp g(x)$
means that there exist finite positive constants
$f(x)\asymp g(x)$
means that there exist finite positive constants
![]() $C_1\leq C_2$
such that
$C_1\leq C_2$
such that
![]() $C_1g(x)\leq f(x)\leq C_2g(x)$
. Note that if f is K-bi invariant [Reference Anker and Ji4, p. 1038], then
$C_1g(x)\leq f(x)\leq C_2g(x)$
. Note that if f is K-bi invariant [Reference Anker and Ji4, p. 1038], then
The role played by exponentials in euclidean Fourier analysis is played by the (elementary) spherical functions in the Fourier analysis of K-bi-invariant functions on G. They are K-bi-invariant and given by the integral representation
We then have
for some constants
![]() $c, a>0$
, [Reference Anker and Ji4, p. 1046]. Denote by
$c, a>0$
, [Reference Anker and Ji4, p. 1046]. Denote by
![]() $S(K\backslash G/K)$
the Schwartz space of K-bi-invariant functions on G. Then, the spherical Fourier transform
$S(K\backslash G/K)$
the Schwartz space of K-bi-invariant functions on G. Then, the spherical Fourier transform
![]() $\mathcal {H}$
is defined by
$\mathcal {H}$
is defined by
Let
![]() $S(\mathfrak {a^{\ast }})$
be the usual Schwartz space on the euclidean space
$S(\mathfrak {a^{\ast }})$
be the usual Schwartz space on the euclidean space
![]() $\mathfrak {a^{\ast }}$
and
$\mathfrak {a^{\ast }}$
and
![]() $S(\mathfrak {a^{\ast }})^{W}$
the subspace of Weyl-invariant functions in
$S(\mathfrak {a^{\ast }})^{W}$
the subspace of Weyl-invariant functions in
![]() $S(\mathfrak {a^{\ast }})$
(e.g., radial:
$S(\mathfrak {a^{\ast }})$
(e.g., radial:
![]() $m(\lambda )=m_0(\|\lambda \|)$
). Then, by a celebrated theorem of Harish-Chandra,
$m(\lambda )=m_0(\|\lambda \|)$
). Then, by a celebrated theorem of Harish-Chandra,
![]() $\mathcal {H}$
is an isomorphism between
$\mathcal {H}$
is an isomorphism between
![]() $S(K\backslash G/K)$
and
$S(K\backslash G/K)$
and
![]() $S(\mathfrak {a^{\ast }})^W$
and its inverse is given by
$S(\mathfrak {a^{\ast }})^W$
and its inverse is given by
where
![]() $\mathbf {c}(\lambda )$
is the Harish-Chandra function. It is explicitly known, but we shall only need the following rough estimate:
$\mathbf {c}(\lambda )$
is the Harish-Chandra function. It is explicitly known, but we shall only need the following rough estimate:
for some constants
![]() $c, b> 0$
, [Reference Anker3, p. 601].
$c, b> 0$
, [Reference Anker3, p. 601].
Set
Then the heat kernel
![]() $ p_{t}(x)$
on X is given by
$ p_{t}(x)$
on X is given by
![]() $(\mathcal {H}^{-1}m_{t})(x)$
[Reference Anker and Ji4]. The heat kernel on symmetric spaces has been extensively studied, see for example [Reference Anker and Ji4, Reference Anker and Ostellari6]. Sharp estimates of the heat kernel have been obtained by Davies and Mandouvalos in [Reference Davies and Mandouvalos9] for the case of real hyperbolic space, while Anker and Ji [Reference Anker and Ji4] and later Anker and Ostellari [Reference Anker and Ostellari6], generalized the results of [Reference Davies and Mandouvalos9] to all symmetric spaces of noncompact type. Recall also a few fundamental properties of the heat kernel, [Reference Anker and Ostellari6]: it is a bi-K-invariant function on G, thus determined by its restriction to the positive Weyl chamber. Moreover it is symmetric and positive:
$(\mathcal {H}^{-1}m_{t})(x)$
[Reference Anker and Ji4]. The heat kernel on symmetric spaces has been extensively studied, see for example [Reference Anker and Ji4, Reference Anker and Ostellari6]. Sharp estimates of the heat kernel have been obtained by Davies and Mandouvalos in [Reference Davies and Mandouvalos9] for the case of real hyperbolic space, while Anker and Ji [Reference Anker and Ji4] and later Anker and Ostellari [Reference Anker and Ostellari6], generalized the results of [Reference Davies and Mandouvalos9] to all symmetric spaces of noncompact type. Recall also a few fundamental properties of the heat kernel, [Reference Anker and Ostellari6]: it is a bi-K-invariant function on G, thus determined by its restriction to the positive Weyl chamber. Moreover it is symmetric and positive:
![]() $p_t(x, y) = p_t(y, x)> 0$
, for every
$p_t(x, y) = p_t(y, x)> 0$
, for every
![]() $x, y\in X$
, where
$x, y\in X$
, where
The heat operator
![]() $e^{t\Delta }$
is given by
$e^{t\Delta }$
is given by
Finally, the semigroup property holds:
Recall that
![]() $\Sigma _{0}^{+}$
is the set of positive indivisible roots
$\Sigma _{0}^{+}$
is the set of positive indivisible roots
![]() $\alpha $
and by
$\alpha $
and by
![]() $m_{\alpha }$
the dimension of the root space
$m_{\alpha }$
the dimension of the root space
![]() $\mathfrak {g}^{\alpha }$
. In [Reference Anker and Ostellari6, Main Theorem] it is proved the following sharp estimate:
$\mathfrak {g}^{\alpha }$
. In [Reference Anker and Ostellari6, Main Theorem] it is proved the following sharp estimate:
 $$ \begin{align} p_{t}(\exp {H})&\asymp ct^{-n/2}\left( \underset{\alpha \in \Sigma _{0}^{+}}{ \prod }(1+\alpha(H) )(1+t+\alpha(H) )^{\frac{ m_{\alpha }+m_{2\alpha }}{2}-1}\right) \nonumber \\ & \quad \times e^{-\left\Vert \rho \right\Vert ^{2}t-\rho(H) -\left\Vert H\right\Vert ^{2}/4t},\quad t>0, \;H\in \overline{\mathfrak{a} _{+}}, \end{align} $$
$$ \begin{align} p_{t}(\exp {H})&\asymp ct^{-n/2}\left( \underset{\alpha \in \Sigma _{0}^{+}}{ \prod }(1+\alpha(H) )(1+t+\alpha(H) )^{\frac{ m_{\alpha }+m_{2\alpha }}{2}-1}\right) \nonumber \\ & \quad \times e^{-\left\Vert \rho \right\Vert ^{2}t-\rho(H) -\left\Vert H\right\Vert ^{2}/4t},\quad t>0, \;H\in \overline{\mathfrak{a} _{+}}, \end{align} $$
where
![]() $n=$
dimX.
$n=$
dimX.
From (17), we deduce the following crude estimate
which is sufficient for our purposes.
3
 $L^p$
boundedness of the local part
$L^p$
boundedness of the local part
In this section, we shall prove the following proposition.
Proposition 2 Assume that
![]() $\alpha \in (0,1)$
.
$\alpha \in (0,1)$
.
-
(i) If
 $\beta>n\alpha /2$
, then
$\beta>n\alpha /2$
, then
 ${T}_{\alpha ,\beta }^{0}$
(resp.
${T}_{\alpha ,\beta }^{0}$
(resp.
 $ \widehat {T}_{\alpha ,\beta }^{0}$
) is bounded on
$ \widehat {T}_{\alpha ,\beta }^{0}$
) is bounded on
 $L^{p}(X)$
(resp. on
$L^{p}(X)$
(resp. on
 $ L^{p}(M)$
) for every
$ L^{p}(M)$
) for every
 $p\in [1,\infty ]$
.
$p\in [1,\infty ]$
. -
(ii) If
 $\beta \leq n\alpha /2$
, then
$\beta \leq n\alpha /2$
, then
 ${T}_{\alpha ,\beta }^{0}$
(resp.
${T}_{\alpha ,\beta }^{0}$
(resp.
 $\widehat {T}_{\alpha ,\beta }^{0}$
) is bounded on
$\widehat {T}_{\alpha ,\beta }^{0}$
) is bounded on
 $L^{p}(X)$
(resp. on
$L^{p}(X)$
(resp. on
 $L^{p}(M)$
),
$L^{p}(M)$
),
 $p\in (1,\infty )$
, provided that
$p\in (1,\infty )$
, provided that
 $\beta>\alpha n\left \vert 1/p-1/2\right \vert $
.
$\beta>\alpha n\left \vert 1/p-1/2\right \vert $
.
To prove the
![]() $L^{p}$
boundedness of the local part
$L^{p}$
boundedness of the local part
![]() $T_{\alpha ,\beta }^{0}$
of the operator
$T_{\alpha ,\beta }^{0}$
of the operator
![]() $T_{\alpha ,\beta }$
on X we shall follow the approach of [Reference Alexopoulos2] (see also [Reference Georgiadis12, Reference Marias22]), and express the kernel
$T_{\alpha ,\beta }$
on X we shall follow the approach of [Reference Alexopoulos2] (see also [Reference Georgiadis12, Reference Marias22]), and express the kernel
![]() $\kappa _{\alpha ,\beta }$
of the operator
$\kappa _{\alpha ,\beta }$
of the operator
![]() $T_{\alpha ,\beta }$
via the heat kernel
$T_{\alpha ,\beta }$
via the heat kernel
![]() $ p_{t}$
of the symmetric space X.
$ p_{t}$
of the symmetric space X.
As in [Reference Giulini and Meda13], we may write
and observe that
Consider the functions
![]() $\omega _0, \omega \in C_{0}^{\infty }(\mathbb {R}_+)$
, such that
$\omega _0, \omega \in C_{0}^{\infty }(\mathbb {R}_+)$
, such that
and take
Then, as in [Reference Alexopoulos1], for
![]() $j\geq 0$
, we write
$j\geq 0$
, we write
where
Define the operators
![]() $T_j=\mu _j(\Delta _X)$
and note that by (19) and (21), we have
$T_j=\mu _j(\Delta _X)$
and note that by (19) and (21), we have
![]() $T_{\alpha , \beta }=\sum_{j\geq 0}T_j.$
Using the group structure, we may also write
$T_{\alpha , \beta }=\sum_{j\geq 0}T_j.$
Using the group structure, we may also write
where
 $$ \begin{align} m_j(\lambda)&=\mu_j(\|\lambda\|^2+\|\rho\|^2)=\mu_{\alpha, \beta}(\|\lambda\|^2+\|\rho\|^2)\omega_j(\|\lambda\|^2+\|\rho\|^2)\nonumber\\ &=m_{\alpha, \beta}(\lambda)\omega_j(\|\lambda\|^2+\|\rho\|^2), \quad \lambda\in \mathfrak{a}^{\ast}.\end{align} $$
$$ \begin{align} m_j(\lambda)&=\mu_j(\|\lambda\|^2+\|\rho\|^2)=\mu_{\alpha, \beta}(\|\lambda\|^2+\|\rho\|^2)\omega_j(\|\lambda\|^2+\|\rho\|^2)\nonumber\\ &=m_{\alpha, \beta}(\lambda)\omega_j(\|\lambda\|^2+\|\rho\|^2), \quad \lambda\in \mathfrak{a}^{\ast}.\end{align} $$
Observe that
![]() $m_j$
are Weyl-invariant as radial functions, so the kernels
$m_j$
are Weyl-invariant as radial functions, so the kernels
![]() $\kappa _j$
are K-bi-invariant. By (22) and (24), we have
$\kappa _j$
are K-bi-invariant. By (22) and (24), we have
 $$ \begin{align*} \operatorname{supp}m_0 &\subset \{\lambda:0\leq\|\lambda\|^2+\|\rho\|^2\leq 2\} \text{ and } \\ \operatorname{supp}m_j &\subset \{\lambda: 2^{j-1}\leq\|\lambda\|^2+\|\rho\|^2\leq 2^{j+1}\}, \;j\in \mathbb{N}. \end{align*} $$
$$ \begin{align*} \operatorname{supp}m_0 &\subset \{\lambda:0\leq\|\lambda\|^2+\|\rho\|^2\leq 2\} \text{ and } \\ \operatorname{supp}m_j &\subset \{\lambda: 2^{j-1}\leq\|\lambda\|^2+\|\rho\|^2\leq 2^{j+1}\}, \;j\in \mathbb{N}. \end{align*} $$
Depending on the size of
![]() $\|\rho \|$
, finitely many of the above sets may be empty. To simplify the presentation, let us assume from now on that
$\|\rho \|$
, finitely many of the above sets may be empty. To simplify the presentation, let us assume from now on that
![]() $\|\rho \|=1$
, so that
$\|\rho \|=1$
, so that
Set
and observe that
and that
 $$ \begin{align} h_{j}(e^{2^{-j}\Delta _{X}})e^{2^{-j}\Delta _{X}}& = {\mu}_{j}(2^{j}\ln e^{2^{-j}\Delta _{X}})e^{-2^{-j}\Delta _{X}}e^{2^{-j}\Delta _{X}} \nonumber\\ & = {\mu}_{j}(\Delta _{X}). \end{align} $$
$$ \begin{align} h_{j}(e^{2^{-j}\Delta _{X}})e^{2^{-j}\Delta _{X}}& = {\mu}_{j}(2^{j}\ln e^{2^{-j}\Delta _{X}})e^{-2^{-j}\Delta _{X}}e^{2^{-j}\Delta _{X}} \nonumber\\ & = {\mu}_{j}(\Delta _{X}). \end{align} $$
Recall that we denoted by
![]() $p_{t}$
the heat kernel of X and by
$p_{t}$
the heat kernel of X and by
![]() $\kappa _{j}$
the kernel of the operator
$\kappa _{j}$
the kernel of the operator
![]() $T_{j}= {\mu }_{j}(\Delta _{X})$
. Then, from (29) it follows that
$T_{j}= {\mu }_{j}(\Delta _{X})$
. Then, from (29) it follows that
 $$ \begin{align} \kappa _{j}(x)& = {\mu}_{j}(\Delta _{X})\delta _{0}(x)=h_{j}(e^{2^{-j}\Delta _{X}})e^{2^{-j}\Delta _{X}}\delta _{0}(x) \nonumber\\ & =h_{j}(e^{2^{-j}\Delta _{X}})p_{2^{-j}}(x). \end{align} $$
$$ \begin{align} \kappa _{j}(x)& = {\mu}_{j}(\Delta _{X})\delta _{0}(x)=h_{j}(e^{2^{-j}\Delta _{X}})e^{2^{-j}\Delta _{X}}\delta _{0}(x) \nonumber\\ & =h_{j}(e^{2^{-j}\Delta _{X}})p_{2^{-j}}(x). \end{align} $$
Note that
 $$ \begin{align} \sum_{j\geq 0}\kappa _{j}(x) &=\sum_{j\geq 0} {\mu}_{j}(\Delta _{X})\delta _{0}(x) \nonumber \\ &= {\mu}_{\alpha ,\beta }(\Delta _{X})\delta _{0}(x)=\kappa _{\alpha ,\beta }(x). \end{align} $$
$$ \begin{align} \sum_{j\geq 0}\kappa _{j}(x) &=\sum_{j\geq 0} {\mu}_{j}(\Delta _{X})\delta _{0}(x) \nonumber \\ &= {\mu}_{\alpha ,\beta }(\Delta _{X})\delta _{0}(x)=\kappa _{\alpha ,\beta }(x). \end{align} $$
Our proof will be based on the following lemma, the proof of which is postponed until the end of this section.
Lemma 3 For every
![]() $j\geq 0$
,
$j\geq 0$
,
Here,
![]() $B_1$
denotes the geodesic unit ball on X, which is a homogeneous space in the sense of Coifman and Weiss, see [Reference Anker and Lohoué5].
$B_1$
denotes the geodesic unit ball on X, which is a homogeneous space in the sense of Coifman and Weiss, see [Reference Anker and Lohoué5].
3.1 Proof of Proposition 2
We treat first the case of symmetric spaces. It suffices to interpolate between the
![]() $L^{\infty }$
and
$L^{\infty }$
and
![]() $L^2$
result, and then use duality. In our proof, the properties of the spherical Fourier transform on K-bi-invariant functions are central. For locally symmetric spaces, the required
$L^2$
result, and then use duality. In our proof, the properties of the spherical Fourier transform on K-bi-invariant functions are central. For locally symmetric spaces, the required
![]() $L^p$
boundedness for
$L^p$
boundedness for
![]() $\widehat {T}_{\alpha ,\beta }^{0}$
will follow as a consequence of the
$\widehat {T}_{\alpha ,\beta }^{0}$
will follow as a consequence of the
![]() $L^p$
result for
$L^p$
result for
![]() $T_{\alpha , \beta }^0$
on symmetric spaces.
$T_{\alpha , \beta }^0$
on symmetric spaces.
(i) Let
![]() $\beta>\alpha n/2$
. Recall that
$\beta>\alpha n/2$
. Recall that
![]() $\kappa _{\alpha ,\beta }=\sum_{j\geq 0}\kappa _{j}$
. We shall show that
$\kappa _{\alpha ,\beta }=\sum_{j\geq 0}\kappa _{j}$
. We shall show that
![]() $\kappa _{\alpha ,\beta }^0\in L^1(X)$
, using the fact that it is compactly supported. Indeed, by (5) and Lemma 3, we have
$\kappa _{\alpha ,\beta }^0\in L^1(X)$
, using the fact that it is compactly supported. Indeed, by (5) and Lemma 3, we have
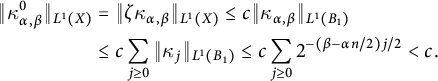 $$ \begin{align*} \Vert \kappa _{\alpha ,\beta }^{0}\Vert _{L^{1}(X)} &=\Vert \zeta \kappa _{\alpha ,\beta }\Vert _{L^{1}(X)}\leq c\Vert \kappa _{\alpha ,\beta }\Vert _{L^{1}(B_1)} \\ &\leq c\sum_{j\geq 0}\Vert \kappa _{j}\Vert _{L^{1}(B_1)}\leq c\sum_{j\geq 0}2^{-(\beta -\alpha n/2)j/2} < c. \end{align*} $$
$$ \begin{align*} \Vert \kappa _{\alpha ,\beta }^{0}\Vert _{L^{1}(X)} &=\Vert \zeta \kappa _{\alpha ,\beta }\Vert _{L^{1}(X)}\leq c\Vert \kappa _{\alpha ,\beta }\Vert _{L^{1}(B_1)} \\ &\leq c\sum_{j\geq 0}\Vert \kappa _{j}\Vert _{L^{1}(B_1)}\leq c\sum_{j\geq 0}2^{-(\beta -\alpha n/2)j/2} < c. \end{align*} $$
This implies that
It remains to show the
![]() $L^2$
result for
$L^2$
result for
![]() $T_{\alpha , \beta }^0$
by summing over
$T_{\alpha , \beta }^0$
by summing over
![]() $T_j^0$
. The spherical Fourier transform properties will allow us to estimate
$T_j^0$
. The spherical Fourier transform properties will allow us to estimate
![]() $m_j^0$
by the known estimates of
$m_j^0$
by the known estimates of
![]() $m_j$
. By Plancherel theorem, the K-bi-invariance of
$m_j$
. By Plancherel theorem, the K-bi-invariance of
![]() $\zeta $
and
$\zeta $
and
![]() $\kappa _{j}$
, and (5), we get that
$\kappa _{j}$
, and (5), we get that
 $$ \begin{align} \Vert T_{j}^{0}\Vert _{L^{2}(X)\rightarrow L^{2}(X)}& \leq \Vert m_{j}^{0}\Vert _{L^{\infty }(\mathfrak{a^{\ast }})}=\Vert \mathcal{H}(\kappa _{j}^{0})\Vert _{L^{\infty }(\mathfrak{a^{\ast }})} \nonumber \\ & =\Vert \mathcal{H}(\zeta \kappa _{j})\Vert _{L^{\infty }(\mathfrak{a^{\ast }})}=\Vert \mathcal{H}(\zeta )\ast \mathcal{H}(\kappa _{j})\Vert _{L^{\infty }(\mathfrak{a^{\ast }})} \nonumber \\ & =\Vert \mathcal{H}(\zeta )\ast m_{j}\Vert _{L^{\infty }(\mathfrak{a^{\ast } })}\leq \Vert \mathcal{H}(\zeta )\Vert _{L^{1}(\mathfrak{a^{\ast }})}\Vert m_{j}\Vert _{L^{\infty }(\mathfrak{a^{\ast }})}. \end{align} $$
$$ \begin{align} \Vert T_{j}^{0}\Vert _{L^{2}(X)\rightarrow L^{2}(X)}& \leq \Vert m_{j}^{0}\Vert _{L^{\infty }(\mathfrak{a^{\ast }})}=\Vert \mathcal{H}(\kappa _{j}^{0})\Vert _{L^{\infty }(\mathfrak{a^{\ast }})} \nonumber \\ & =\Vert \mathcal{H}(\zeta \kappa _{j})\Vert _{L^{\infty }(\mathfrak{a^{\ast }})}=\Vert \mathcal{H}(\zeta )\ast \mathcal{H}(\kappa _{j})\Vert _{L^{\infty }(\mathfrak{a^{\ast }})} \nonumber \\ & =\Vert \mathcal{H}(\zeta )\ast m_{j}\Vert _{L^{\infty }(\mathfrak{a^{\ast } })}\leq \Vert \mathcal{H}(\zeta )\Vert _{L^{1}(\mathfrak{a^{\ast }})}\Vert m_{j}\Vert _{L^{\infty }(\mathfrak{a^{\ast }})}. \end{align} $$
But
![]() $\zeta \in S(K\backslash G/K)$
. So, as it is mentioned in Section 2, its spherical Fourier transform
$\zeta \in S(K\backslash G/K)$
. So, as it is mentioned in Section 2, its spherical Fourier transform
![]() $\mathcal {H}(\zeta )$
, belongs in
$\mathcal {H}(\zeta )$
, belongs in
![]() $S(\mathfrak { a^{\ast }})^{W}\subset L^{1}(\mathfrak {a^{\ast }})$
. So,
$S(\mathfrak { a^{\ast }})^{W}\subset L^{1}(\mathfrak {a^{\ast }})$
. So,
From (33), (26) and (2) it follows that
 $$ \begin{align*} \Vert T_{j}^{0}\Vert _{L^{2}(X)\rightarrow L^{2}(X)}& \leq c(\zeta )\Vert m_{j}\Vert _{L^{\infty }(\mathfrak{a^{\ast }})} \\ & =c(\zeta )\mathop{\mathrm{sup}}\limits_{2^{^{(j- {2})/2}}\leq \Vert \lambda \Vert \leq 2^{^{(j+1)/2}}}\left\vert m_{\alpha ,\beta }\left( \lambda \right) \omega (2^{-j}\lambda )\right\vert \\ & \leq c(\zeta )2^{-\beta j/2},\; {j\geq 2.} \end{align*} $$
$$ \begin{align*} \Vert T_{j}^{0}\Vert _{L^{2}(X)\rightarrow L^{2}(X)}& \leq c(\zeta )\Vert m_{j}\Vert _{L^{\infty }(\mathfrak{a^{\ast }})} \\ & =c(\zeta )\mathop{\mathrm{sup}}\limits_{2^{^{(j- {2})/2}}\leq \Vert \lambda \Vert \leq 2^{^{(j+1)/2}}}\left\vert m_{\alpha ,\beta }\left( \lambda \right) \omega (2^{-j}\lambda )\right\vert \\ & \leq c(\zeta )2^{-\beta j/2},\; {j\geq 2.} \end{align*} $$
It is easy to see that using the same arguments for the remaining cases
![]() $j=0,1$
, an inequality of the form above is also satisfied. Further, by the fact that
$j=0,1$
, an inequality of the form above is also satisfied. Further, by the fact that
![]() $T_{\alpha ,\beta }^{0}=\sum_{j\geq 0}T_{j}^{0}$
, it follows that
$T_{\alpha ,\beta }^{0}=\sum_{j\geq 0}T_{j}^{0}$
, it follows that
 $$ \begin{align} \Vert T_{\alpha ,\beta }^{0}\Vert _{L^{2}(X)\rightarrow L^{2}(X)} &\leq \sum_{j\geq 0}\Vert T_{j}^{0}\Vert _{L^{2}(X)\rightarrow L^{2}(X)} \nonumber \\ &\leq c\sum_{j\geq 0}2^{-\beta j/2}\leq c<\infty . \end{align} $$
$$ \begin{align} \Vert T_{\alpha ,\beta }^{0}\Vert _{L^{2}(X)\rightarrow L^{2}(X)} &\leq \sum_{j\geq 0}\Vert T_{j}^{0}\Vert _{L^{2}(X)\rightarrow L^{2}(X)} \nonumber \\ &\leq c\sum_{j\geq 0}2^{-\beta j/2}\leq c<\infty . \end{align} $$
By interpolation and duality, it follows from (32) and (34) that
![]() $T_{\alpha ,\beta }^{0}$
is bounded on
$T_{\alpha ,\beta }^{0}$
is bounded on
![]() $L^{p}(X)$
, for all
$L^{p}(X)$
, for all
![]() $p\in [1,\infty ]$
.
$p\in [1,\infty ]$
.
(ii) Let
![]() $\beta \leq \alpha n/2$
. Once again, we shall interpolate between the
$\beta \leq \alpha n/2$
. Once again, we shall interpolate between the
![]() $L^{\infty }$
and
$L^{\infty }$
and
![]() $L^2$
result. Recall that
$L^2$
result. Recall that
![]() $T_{j}^{0}=\ast \kappa _{j}^{0}$
and that
$T_{j}^{0}=\ast \kappa _{j}^{0}$
and that
![]() $\kappa _{j}^{0}=\zeta \kappa _{j}$
. So, from Lemma 3 we get that
$\kappa _{j}^{0}=\zeta \kappa _{j}$
. So, from Lemma 3 we get that
 $$ \begin{align} \Vert T_{j}^{0}\Vert _{L^{\infty }(X)\rightarrow L^{\infty }(X)} &\leq \Vert \kappa _{j}^{0}\Vert _{L^{1}(X)}=\Vert \zeta \kappa _{j}\Vert _{L^{1}(X)} \nonumber \\ &\leq c\Vert \kappa _{j}\Vert _{L^{1}(B_1)}\leq c2^{-(\beta -\alpha n/2)j/2}. \end{align} $$
$$ \begin{align} \Vert T_{j}^{0}\Vert _{L^{\infty }(X)\rightarrow L^{\infty }(X)} &\leq \Vert \kappa _{j}^{0}\Vert _{L^{1}(X)}=\Vert \zeta \kappa _{j}\Vert _{L^{1}(X)} \nonumber \\ &\leq c\Vert \kappa _{j}\Vert _{L^{1}(B_1)}\leq c2^{-(\beta -\alpha n/2)j/2}. \end{align} $$
Also, we have that
Interpolating between (35) and (36) we get that for
![]() $p\geq 2$
$p\geq 2$
 $$ \begin{align*} \Vert T_{j}^{0}\Vert _{L^{p}(X)\rightarrow L^{p}(X)}& \leq c\Vert T_{j}^{0}\Vert _{L^{\infty }(X)\rightarrow L^{\infty }(X)}^{1-2/p}\Vert T_{j}^{0}\Vert _{L^{2}(X)\rightarrow L^{2}(X)}^{2/p} \\ & \leq c2^{-(1-2/p)(\beta -\alpha n/2)j/2}2^{-(2/p)\beta j/2} \\ & \leq c2^{-\left( \beta -\alpha n\left( \frac{1}{2}-\frac{1}{p}\right) \right) j/2}. \end{align*} $$
$$ \begin{align*} \Vert T_{j}^{0}\Vert _{L^{p}(X)\rightarrow L^{p}(X)}& \leq c\Vert T_{j}^{0}\Vert _{L^{\infty }(X)\rightarrow L^{\infty }(X)}^{1-2/p}\Vert T_{j}^{0}\Vert _{L^{2}(X)\rightarrow L^{2}(X)}^{2/p} \\ & \leq c2^{-(1-2/p)(\beta -\alpha n/2)j/2}2^{-(2/p)\beta j/2} \\ & \leq c2^{-\left( \beta -\alpha n\left( \frac{1}{2}-\frac{1}{p}\right) \right) j/2}. \end{align*} $$
Thus,
 $$ \begin{align*} \Vert T_{\alpha ,\beta }^{0}\Vert _{L^{p}(X)\rightarrow L^{p}(X)} &\leq \sum_{j\geq 0}\Vert T_{j}^{0}\Vert _{L^{p}(X)\rightarrow L^{p}(X)} \\ &\leq c\sum_{j\geq 0}2^{-\left( \beta -\alpha n\left( \frac{1}{2}-\frac{1}{p }\right) \right) j/2}<\infty , \end{align*} $$
$$ \begin{align*} \Vert T_{\alpha ,\beta }^{0}\Vert _{L^{p}(X)\rightarrow L^{p}(X)} &\leq \sum_{j\geq 0}\Vert T_{j}^{0}\Vert _{L^{p}(X)\rightarrow L^{p}(X)} \\ &\leq c\sum_{j\geq 0}2^{-\left( \beta -\alpha n\left( \frac{1}{2}-\frac{1}{p }\right) \right) j/2}<\infty , \end{align*} $$
provided that
![]() $\beta>\alpha n\left ( \frac {1}{2}-\frac {1}{p}\right ) $
. The
$\beta>\alpha n\left ( \frac {1}{2}-\frac {1}{p}\right ) $
. The
![]() $ L^{p}$
-boundedness of
$ L^{p}$
-boundedness of
![]() $T_{\alpha ,\beta }^{0}$
for
$T_{\alpha ,\beta }^{0}$
for
![]() $p\in (1,2)$
, follows by duality.
$p\in (1,2)$
, follows by duality.
To prove the
![]() $L^{p}$
boundedness of the local part
$L^{p}$
boundedness of the local part
![]() $\widehat {T}_{\alpha ,\beta }^{0}$
of the operator on the locally symmetric space M, we need the following result [Reference Lohoué and Marias19, Proposition 13].
$\widehat {T}_{\alpha ,\beta }^{0}$
of the operator on the locally symmetric space M, we need the following result [Reference Lohoué and Marias19, Proposition 13].
Proposition 4 Assume that
![]() $p\in (1, \infty )$
. If the operator
$p\in (1, \infty )$
. If the operator
![]() $T^0=\ast \kappa ^0$
is
$T^0=\ast \kappa ^0$
is
![]() $L^p(X)$
-bounded, then the operator
$L^p(X)$
-bounded, then the operator
![]() $\widehat {T^0}=\ast \kappa ^0$
is
$\widehat {T^0}=\ast \kappa ^0$
is
![]() $L^p(M)$
-bounded.
$L^p(M)$
-bounded.
So, for the
![]() $L^p$
result on M, observe first that
$L^p$
result on M, observe first that
![]() $\widehat {T} _{\alpha ,\beta }^{0}$
can be defined as an operator on the group G, and then, apply the local result of Proposition 2 to conclude its boundedness on
$\widehat {T} _{\alpha ,\beta }^{0}$
can be defined as an operator on the group G, and then, apply the local result of Proposition 2 to conclude its boundedness on
![]() $L^{p}(X)$
. Consequently, the continuity of
$L^{p}(X)$
. Consequently, the continuity of
![]() $\widehat {T}_{\alpha ,\beta }^{0}$
on
$\widehat {T}_{\alpha ,\beta }^{0}$
on
![]() $L^{p}(M)$
follows by Proposition 4. Note that the
$L^{p}(M)$
follows by Proposition 4. Note that the
![]() $L^p$
boundeness of
$L^p$
boundeness of
![]() $\widehat {T} _{\alpha ,\beta }^{0}$
holds without any restrictions on the group
$\widehat {T} _{\alpha ,\beta }^{0}$
holds without any restrictions on the group
![]() $\Gamma $
.
$\Gamma $
.
3.2 Proof of Lemma 3
In this section, our aim is to prove estimates of the
![]() $L^{2}$
-norm of the kernels
$L^{2}$
-norm of the kernels
![]() $\kappa _{j}$
, which will allow us to prove Lemma 3 by using the Cauchy–Schwartz inequality.
$\kappa _{j}$
, which will allow us to prove Lemma 3 by using the Cauchy–Schwartz inequality.
For
![]() $r>0$
, set
$r>0$
, set
Set also
The set
![]() $B_r$
consists of all points on X at distance at most r from the origin K, [Reference Anker and Ji4, p. 1066]. For small radii, observe the following euclidean upper bound for volume growth: using (8), (9) and the fact that
$B_r$
consists of all points on X at distance at most r from the origin K, [Reference Anker and Ji4, p. 1066]. For small radii, observe the following euclidean upper bound for volume growth: using (8), (9) and the fact that
![]() $\sum_{\alpha \in \Sigma ^+}m_{\alpha }=n-d$
, [Reference Anker and Ji4, p. 1037], we have
$\sum_{\alpha \in \Sigma ^+}m_{\alpha }=n-d$
, [Reference Anker and Ji4, p. 1037], we have
By G-invariance, the same upper bound would hold for small balls of any center (and in fact, a lower bound of the same form is true, see [Reference Anker and Lohoué5, p. 1317]). Finally, consider the annulus
The following lemma is technical but important for the proof of Lemma 7.
Lemma 5 There are constants
![]() $c>0$
and
$c>0$
and
![]() $\delta \in (0,1/8)$
such that for all
$\delta \in (0,1/8)$
such that for all
![]() $j \in \mathbb {N}, q \geq -j$
and
$j \in \mathbb {N}, q \geq -j$
and
![]() $|t|\leq \delta 2^{(q+j)/2}$
,
$|t|\leq \delta 2^{(q+j)/2}$
,
Proof By (15) and (16), we have that
 $$ \begin{align} e^{ite^{2^{-j}\Delta _{X}}}p_{2^{-j}}(x)=\sum_{m\geq 0}\frac{(it)^{m}}{m!} e^{m2^{-j}\Delta _{X}}p_{2^{-j}}(x)=\sum_{m\geq 0}\frac{(it)^{m}}{m!} p_{(m+1)2^{-j}}(x). \end{align} $$
$$ \begin{align} e^{ite^{2^{-j}\Delta _{X}}}p_{2^{-j}}(x)=\sum_{m\geq 0}\frac{(it)^{m}}{m!} e^{m2^{-j}\Delta _{X}}p_{2^{-j}}(x)=\sum_{m\geq 0}\frac{(it)^{m}}{m!} p_{(m+1)2^{-j}}(x). \end{align} $$
Since
![]() $p_t$
is a K-bi-invariant function, the same is true for
$p_t$
is a K-bi-invariant function, the same is true for
![]() $ e^{ite^{2^{-j}\Delta _{X}}}p_{2^{-j}}$
. Bearing in mind that if
$ e^{ite^{2^{-j}\Delta _{X}}}p_{2^{-j}}$
. Bearing in mind that if
![]() $x=k(\exp H)k^{\prime }\in A_{q}$
, then
$x=k(\exp H)k^{\prime }\in A_{q}$
, then
![]() $\Vert H\Vert \geq 2^{q/2}$
, it follows from (40) and the estimate (18) of
$\Vert H\Vert \geq 2^{q/2}$
, it follows from (40) and the estimate (18) of
![]() $p_{t}(\exp H)$
that
$p_{t}(\exp H)$
that
 $$ \begin{align} \left\vert e^{ite^{2^{-j}\Delta _{X}}}p_{2^{-j}}(\exp H)\right\vert & \leq c\sum_{m\geq 0}\frac{|t|^{m}}{m!}p_{(m+1)2^{-j}}(\exp H) \nonumber \\ & \leq c\sum_{m\in \mathbb{N}}\frac{|t|^{m}}{m!} ((m+1)2^{-j})^{-n/2}e^{-2^{q}/4(m+1)2^{-j}} \nonumber\\ & \leq c2^{jn/2}\sum_{m\in \mathbb{N}}m^{-n/2}\frac{|t|^{m}}{m!} e^{-2^{q+j}/4\left( m+1\right) } \nonumber \\ & \leq c2^{jn/2}\sum_{m\in \mathbb{N}}\frac{|t|^{m}}{m!}e^{-2^{q+j}/4\left( m+1\right) }. \end{align} $$
$$ \begin{align} \left\vert e^{ite^{2^{-j}\Delta _{X}}}p_{2^{-j}}(\exp H)\right\vert & \leq c\sum_{m\geq 0}\frac{|t|^{m}}{m!}p_{(m+1)2^{-j}}(\exp H) \nonumber \\ & \leq c\sum_{m\in \mathbb{N}}\frac{|t|^{m}}{m!} ((m+1)2^{-j})^{-n/2}e^{-2^{q}/4(m+1)2^{-j}} \nonumber\\ & \leq c2^{jn/2}\sum_{m\in \mathbb{N}}m^{-n/2}\frac{|t|^{m}}{m!} e^{-2^{q+j}/4\left( m+1\right) } \nonumber \\ & \leq c2^{jn/2}\sum_{m\in \mathbb{N}}\frac{|t|^{m}}{m!}e^{-2^{q+j}/4\left( m+1\right) }. \end{align} $$
Set
and
 $$ \begin{align*} S_{k}=\sum_{m\in N_{k}}\frac{|t|^{m}}{m!}e^{-2^{q+j}/4\left( m+1\right) },\quad k=1,2. \end{align*} $$
$$ \begin{align*} S_{k}=\sum_{m\in N_{k}}\frac{|t|^{m}}{m!}e^{-2^{q+j}/4\left( m+1\right) },\quad k=1,2. \end{align*} $$
From (41), we have that
We shall first estimate
![]() $S_{1}$
. If
$S_{1}$
. If
![]() $m\in N_1$
, then
$m\in N_1$
, then
![]() $m\leq 2^{(q+j)/2}$
. So,
$m\leq 2^{(q+j)/2}$
. So,
and
 $$ \begin{align*} S_{1}\leq ce^{-2^{(q+j)/2}/8}\sum_{m\in N_{1}}\frac{|t|^{m}}{m!} =ce^{-2^{(q+j)/2}/8}e^{|t|}. \end{align*} $$
$$ \begin{align*} S_{1}\leq ce^{-2^{(q+j)/2}/8}\sum_{m\in N_{1}}\frac{|t|^{m}}{m!} =ce^{-2^{(q+j)/2}/8}e^{|t|}. \end{align*} $$
But
![]() $|t|\leq \delta 2^{(q+j)/2},$
and consequently
$|t|\leq \delta 2^{(q+j)/2},$
and consequently
since
![]() $\delta <1/8$
.
$\delta <1/8$
.
To estimate
![]() $S_{2}$
, we make use of Stirling’s formula:
$S_{2}$
, we make use of Stirling’s formula:
![]() $\frac {1}{m!}\leq c\left ( \frac {e}{m}\right ) ^{m}$
. By the estimate (18) of
$\frac {1}{m!}\leq c\left ( \frac {e}{m}\right ) ^{m}$
. By the estimate (18) of
![]() $ p_{t}(\exp H)$
, and the facts that
$ p_{t}(\exp H)$
, and the facts that
![]() $|t|\leq \delta 2^{(q+j)/2}$
and
$|t|\leq \delta 2^{(q+j)/2}$
and
![]() $ m>2^{(q+j)/2}$
, we have
$ m>2^{(q+j)/2}$
, we have
 $$ \begin{align*} S_{2} &=\sum_{m\in N_{2}}\frac{|t|^{m}}{m!}e^{-2^{q+j}/4(m+1)}\leq \sum_{m\in N_{2}}\frac{|t|^{m}}{m!}\leq c\sum_{m\in N_{2}}(\delta 2^{(q+j)/2})^{m}\left( \frac{e}{m}\right) ^{m} \\ &\leq c\sum_{m\in N_{2}}(\delta 2^{(q+j)/2})^{m}\left( \frac{e}{2^{(q+j)/2}} \right) ^{m}\leq c\sum_{m\in N_{2}}(\delta e)^{m}. \end{align*} $$
$$ \begin{align*} S_{2} &=\sum_{m\in N_{2}}\frac{|t|^{m}}{m!}e^{-2^{q+j}/4(m+1)}\leq \sum_{m\in N_{2}}\frac{|t|^{m}}{m!}\leq c\sum_{m\in N_{2}}(\delta 2^{(q+j)/2})^{m}\left( \frac{e}{m}\right) ^{m} \\ &\leq c\sum_{m\in N_{2}}(\delta 2^{(q+j)/2})^{m}\left( \frac{e}{2^{(q+j)/2}} \right) ^{m}\leq c\sum_{m\in N_{2}}(\delta e)^{m}. \end{align*} $$
But
![]() $\delta < 1/8 < e^{-2}$
. So,
$\delta < 1/8 < e^{-2}$
. So,
Putting together (42–44), the estimate (39) follows, and the proof of the lemma is complete.▪
We also need the following approximation lemma, [Reference Alexopoulos1, Reference Natanson23].
For
![]() $f\in C_{0}^{k}(\mathbb {R})$
,
$f\in C_{0}^{k}(\mathbb {R})$
,
![]() $k\in \mathbb {N}$
, consider the norm
$k\in \mathbb {N}$
, consider the norm
Lemma 6 Let
![]() $f\in C_{0}^{k}(\mathbb {R})$
,
$f\in C_{0}^{k}(\mathbb {R})$
,
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $s>0$
. Then there exist a continuous and integrable function
$s>0$
. Then there exist a continuous and integrable function
![]() $\psi $
and a constant
$\psi $
and a constant
![]() $c>0$
, independent of
$c>0$
, independent of
![]() $s $
and f, such that
$s $
and f, such that
Finally, we need the following estimates of the functions
![]() $h_{j}$
defined in ( 27):
$h_{j}$
defined in ( 27):
and
The proofs of (45) and (46) are straightforward, thus omitted.
We shall now prove the following lemma, which will allow us to prove Lemma 3 by using the Cauchy–Schwartz inequality.
Lemma 7 Assume that
![]() $q\leq 0$
. Then, there are constants
$q\leq 0$
. Then, there are constants
![]() $c, c_k>0$
such that for all
$c, c_k>0$
such that for all
![]() $j, k\in \mathbb {N}, q\geq -j $
,
$j, k\in \mathbb {N}, q\geq -j $
,
-
(i)
 $\Vert \kappa _{j}\Vert _{L^{2}(X)}\leq c2^{-\left ( \beta -\frac {n }{2} \right )j/2}$
.
$\Vert \kappa _{j}\Vert _{L^{2}(X)}\leq c2^{-\left ( \beta -\frac {n }{2} \right )j/2}$
. -
(ii)
 $\Vert \kappa _{j}\Vert _{L^{2}(A_{q})}\leq c_k2^{-\left ( \beta - \frac {n}{2}+k(1-\alpha )\right )j/2}2^{-kq/2} $
.
$\Vert \kappa _{j}\Vert _{L^{2}(A_{q})}\leq c_k2^{-\left ( \beta - \frac {n}{2}+k(1-\alpha )\right )j/2}2^{-kq/2} $
.
Proof (i) By the semigroup property of the heat operator and the estimate (18) of
![]() $p_{t}(x,y)$
, we have that
$p_{t}(x,y)$
, we have that
 $$ \begin{align*} \Vert p_{t}(\cdot ,y)\Vert _{L^{2}(X)}^{2}& =\int_{X}p_{t}^{2}(x,y)dx=\int_{X}p_{t}(x,y)p_{t}(y,x)dx \\ & =p_{2t}(y,y)=p_{2t}(o)\leq ct^{-n/2}. \end{align*} $$
$$ \begin{align*} \Vert p_{t}(\cdot ,y)\Vert _{L^{2}(X)}^{2}& =\int_{X}p_{t}^{2}(x,y)dx=\int_{X}p_{t}(x,y)p_{t}(y,x)dx \\ & =p_{2t}(y,y)=p_{2t}(o)\leq ct^{-n/2}. \end{align*} $$
It follows that
for any
![]() $y\in X$
.
$y\in X$
.
Recall now that
![]() $\kappa _{j}(x)=h_{j}(e^{2^{-j}\Delta _{X}})p_{2^{-j}}(x)$
. So, combining (47) and (45), we get that
$\kappa _{j}(x)=h_{j}(e^{2^{-j}\Delta _{X}})p_{2^{-j}}(x)$
. So, combining (47) and (45), we get that
(ii) Let us consider a function
![]() $\psi _{j,q}$
, satisfying Lemma 6, i.e.,
$\psi _{j,q}$
, satisfying Lemma 6, i.e.,
and
where the constant c in (49) is independent of j and q. Combining (46) with (49), it follows that
Write
 $$ \begin{align} \kappa _{j}(x)& =h_{j}\left( e^{2^{-j}\Delta _{X}}\right) p_{2^{-j}}(x) \nonumber\\ & =\left( \left( h_{j}-h_{j}\ast {\psi }_{j,q}\right) +h_{j}\ast {\psi } _{j,q}\right) (e^{2^{-j}\Delta _{X}})p_{2^{-j}}(x). \end{align} $$
$$ \begin{align} \kappa _{j}(x)& =h_{j}\left( e^{2^{-j}\Delta _{X}}\right) p_{2^{-j}}(x) \nonumber\\ & =\left( \left( h_{j}-h_{j}\ast {\psi }_{j,q}\right) +h_{j}\ast {\psi } _{j,q}\right) (e^{2^{-j}\Delta _{X}})p_{2^{-j}}(x). \end{align} $$
Thus
 $$ \begin{align} \Vert \kappa _{j}\Vert _{L^{2}(A_{q})}& \leq \Vert \left( h_{j}-h_{j}\ast { \psi }_{j,q}\right) \left( e^{2^{-j}\Delta _{X}}\right) p_{2^{-j}}(x)\Vert _{L^{2}(A_{q})} \nonumber \\ & \quad +\Vert (h_{j}\ast {\psi }_{j,q})(e^{2^{-j}\Delta _{X}})p_{2^{-j}}(x)\Vert _{L^{2}(A_{q})}:=I_{1}+I_{2}. \end{align} $$
$$ \begin{align} \Vert \kappa _{j}\Vert _{L^{2}(A_{q})}& \leq \Vert \left( h_{j}-h_{j}\ast { \psi }_{j,q}\right) \left( e^{2^{-j}\Delta _{X}}\right) p_{2^{-j}}(x)\Vert _{L^{2}(A_{q})} \nonumber \\ & \quad +\Vert (h_{j}\ast {\psi }_{j,q})(e^{2^{-j}\Delta _{X}})p_{2^{-j}}(x)\Vert _{L^{2}(A_{q})}:=I_{1}+I_{2}. \end{align} $$
From (47), it follows that
 $$ \begin{align*} I_{1} & \leq \Vert h_{j}-h_{j}\ast {\psi }_{j,q}\Vert _{\infty }\Vert p_{2^{-j}}\Vert _{L^{2}(X)} \\ & \leq \Vert h_{j}-h_{j}\ast {\psi }_{j,q}\Vert _{\infty }2^{jn/4}. \end{align*} $$
$$ \begin{align*} I_{1} & \leq \Vert h_{j}-h_{j}\ast {\psi }_{j,q}\Vert _{\infty }\Vert p_{2^{-j}}\Vert _{L^{2}(X)} \\ & \leq \Vert h_{j}-h_{j}\ast {\psi }_{j,q}\Vert _{\infty }2^{jn/4}. \end{align*} $$
But, by (50),
So,
Let us now estimate
![]() $I_{2}$
. By the inversion formula of the euclidean Fourier transform, we have that
$I_{2}$
. By the inversion formula of the euclidean Fourier transform, we have that
 $$ \begin{align} (h_{j}\ast {\psi }_{j,q})(e^{2^{-j}\Delta _{X}})& =c\int_{\mathbb{R}} \widehat{(h_{j}\ast {\psi }_{j,q})}(t)e^{ite^{2^{-j}\Delta _{X}}}dt \nonumber \\ & =c\int_{\mathbb{R}}\hat{h}_{j}(t)\hat{\psi}_{j,q}(t)e^{ite^{2^{-j}\Delta _{X}}}dt. \end{align} $$
$$ \begin{align} (h_{j}\ast {\psi }_{j,q})(e^{2^{-j}\Delta _{X}})& =c\int_{\mathbb{R}} \widehat{(h_{j}\ast {\psi }_{j,q})}(t)e^{ite^{2^{-j}\Delta _{X}}}dt \nonumber \\ & =c\int_{\mathbb{R}}\hat{h}_{j}(t)\hat{\psi}_{j,q}(t)e^{ite^{2^{-j}\Delta _{X}}}dt. \end{align} $$
Bearing in mind that
![]() $\operatorname {supp}\hat {\psi }_{j,q}\subset \left [ -\delta 2^{(q+j)/2},\delta 2^{(q+j)/2}\right ] $
, we get that
$\operatorname {supp}\hat {\psi }_{j,q}\subset \left [ -\delta 2^{(q+j)/2},\delta 2^{(q+j)/2}\right ] $
, we get that
 $$ \begin{align*} \left\vert (h_{j}\ast {\psi }_{j,q})(e^{2^{-j}\Delta _{X}})p_{2^{-j}}(x)\right\vert &\leq c\int\limits_{{|t|\leq\delta 2^{(q+j)/2}}}|\hat{h}_{j}(t)||\hat{\psi}_{j,q}(t)| \left\vert e^{ite^{2^{-j}\Delta _{X}}}p_{2^{-j}}(x)\right\vert dt \nonumber \\ & \leq c\Vert \hat{h}_{j}\Vert _{\infty }\Vert \hat{\psi}_{j,q}\Vert _{\infty }\int\limits_{{|t|\leq\delta 2^{(q+j)/2}}}\left\vert e^{ite^{2^{-j}\Delta _{X}}}p_{2^{-j}}(x)\right\vert dt. \nonumber \end{align*} $$
$$ \begin{align*} \left\vert (h_{j}\ast {\psi }_{j,q})(e^{2^{-j}\Delta _{X}})p_{2^{-j}}(x)\right\vert &\leq c\int\limits_{{|t|\leq\delta 2^{(q+j)/2}}}|\hat{h}_{j}(t)||\hat{\psi}_{j,q}(t)| \left\vert e^{ite^{2^{-j}\Delta _{X}}}p_{2^{-j}}(x)\right\vert dt \nonumber \\ & \leq c\Vert \hat{h}_{j}\Vert _{\infty }\Vert \hat{\psi}_{j,q}\Vert _{\infty }\int\limits_{{|t|\leq\delta 2^{(q+j)/2}}}\left\vert e^{ite^{2^{-j}\Delta _{X}}}p_{2^{-j}}(x)\right\vert dt. \nonumber \end{align*} $$
But from Lemma 5, we have that
So,
 $$ \begin{align} \left\vert (h_{j}\ast {\psi }_{j,q})(e^{2^{-j}\Delta _{X}})p_{2^{-j}}(x)\right\vert & \leq c\Vert \hat{h}_{j}\Vert _{\infty }\Vert \hat{\psi}_{j,q}\Vert _{\infty }\int\limits_{{|t|\leq \delta 2^{(q+j)/2}}}e^{-c2^{(q+j)/2}}2^{jn/2}dt \nonumber \\ & \leq c\Vert \hat{h}_{j}\Vert _{\infty }\Vert \hat{\psi}_{j,q}\Vert _{\infty }\delta 2^{(q+j)/2}e^{-c2^{(q+j)/2}}2^{jn/2} \nonumber \\ & \leq c\Vert {h}_{j}\Vert _{1}\Vert \hat{\psi}_{j,q}\Vert _{\infty }e^{-c2^{(q+j)/2}}2^{jn/2}, \end{align} $$
$$ \begin{align} \left\vert (h_{j}\ast {\psi }_{j,q})(e^{2^{-j}\Delta _{X}})p_{2^{-j}}(x)\right\vert & \leq c\Vert \hat{h}_{j}\Vert _{\infty }\Vert \hat{\psi}_{j,q}\Vert _{\infty }\int\limits_{{|t|\leq \delta 2^{(q+j)/2}}}e^{-c2^{(q+j)/2}}2^{jn/2}dt \nonumber \\ & \leq c\Vert \hat{h}_{j}\Vert _{\infty }\Vert \hat{\psi}_{j,q}\Vert _{\infty }\delta 2^{(q+j)/2}e^{-c2^{(q+j)/2}}2^{jn/2} \nonumber \\ & \leq c\Vert {h}_{j}\Vert _{1}\Vert \hat{\psi}_{j,q}\Vert _{\infty }e^{-c2^{(q+j)/2}}2^{jn/2}, \end{align} $$
where in the last step we used the inequality
![]() $\Vert \hat {h}_{j}\Vert _{\infty }\leq \Vert {h}_{j}\Vert _{1}$
.
$\Vert \hat {h}_{j}\Vert _{\infty }\leq \Vert {h}_{j}\Vert _{1}$
.
Next, recall that from (45), we have that
![]() $\Vert {h}_{j}\Vert _{\infty }\leq c2^{-\beta j/2}$
. Also, by (28),
$\Vert {h}_{j}\Vert _{\infty }\leq c2^{-\beta j/2}$
. Also, by (28),
![]() $\operatorname {supp} h_{j}\subset (e^{1/2},e^{2})$
. These yield that
$\operatorname {supp} h_{j}\subset (e^{1/2},e^{2})$
. These yield that
Also, from (49), we have that
![]() $\Vert \hat {\psi }_{j,q}\Vert _{\infty } < c$
. Combining this with (56) and (55) we deduce that
$\Vert \hat {\psi }_{j,q}\Vert _{\infty } < c$
. Combining this with (56) and (55) we deduce that
Finally, note that if
![]() $q\leq 0$
, then by (38),
$q\leq 0$
, then by (38),
So, by (57), it follows that
 $$ \begin{align*} \Vert (h_{j}\ast {\psi }_{j,q})(e^{2^{-j}\Delta _{X}})p_{2^{-j}}\Vert _{L^{2}(A_{q})}& \leq |A_{q}|^{1/2}\Vert (h_{j}\ast {\psi } _{j,q})(e^{2^{-j}\Delta _{X}})p_{2^{-j}}\Vert _{\infty } \\ & \leq c|B_{2^{(q+1)/2}}|^{1/2}2^{-\beta j/2}e^{-c2^{(q+j)/2}}2^{jn/2} \\ & \leq c2^{qn/4}2^{-\beta j/2}e^{-c2^{(q+j)/2}}2^{jn/2} \\ & \leq c2^{(q+j)n/4}2^{-\beta j/2}e^{-c2^{(q+j)/2}}2^{jn/4}. \end{align*} $$
$$ \begin{align*} \Vert (h_{j}\ast {\psi }_{j,q})(e^{2^{-j}\Delta _{X}})p_{2^{-j}}\Vert _{L^{2}(A_{q})}& \leq |A_{q}|^{1/2}\Vert (h_{j}\ast {\psi } _{j,q})(e^{2^{-j}\Delta _{X}})p_{2^{-j}}\Vert _{\infty } \\ & \leq c|B_{2^{(q+1)/2}}|^{1/2}2^{-\beta j/2}e^{-c2^{(q+j)/2}}2^{jn/2} \\ & \leq c2^{qn/4}2^{-\beta j/2}e^{-c2^{(q+j)/2}}2^{jn/2} \\ & \leq c2^{(q+j)n/4}2^{-\beta j/2}e^{-c2^{(q+j)/2}}2^{jn/4}. \end{align*} $$
Using that
we obtain that
 $$ \begin{align} I_{2}& =\Vert (h_{j}\ast {\psi }_{j,q})(e^{2^{-j}\Delta _{X}})p_{2^{-j}}\Vert _{L^{2}(A_{q})} \leq c_k2^{-\beta j/2}2^{-k(q+j)/2}2^{jn/4} \nonumber \\ &=c_k2^{-(\beta -n/2+k)j/2}2^{-kq/2} \nonumber \\ & \leq c_k2^{-(\beta -n/2+k(1-\alpha ))j/2}2^{-kq/2}. \end{align} $$
$$ \begin{align} I_{2}& =\Vert (h_{j}\ast {\psi }_{j,q})(e^{2^{-j}\Delta _{X}})p_{2^{-j}}\Vert _{L^{2}(A_{q})} \leq c_k2^{-\beta j/2}2^{-k(q+j)/2}2^{jn/4} \nonumber \\ &=c_k2^{-(\beta -n/2+k)j/2}2^{-kq/2} \nonumber \\ & \leq c_k2^{-(\beta -n/2+k(1-\alpha ))j/2}2^{-kq/2}. \end{align} $$
From (58) and (53), it follows that
and the proof of the lemma is complete.▪
3.2.1 Proof of Lemma 3
Recall that by (23), we have
![]() $\kappa _0=\mathcal {H}^{-1}m_0$
. So, by (24), (25) and the inversion formula (12), we have
$\kappa _0=\mathcal {H}^{-1}m_0$
. So, by (24), (25) and the inversion formula (12), we have
Using (11) and (13), we immediately obtain the trivial estimate
Thus,
![]() $\kappa _0$
is integrable in
$\kappa _0$
is integrable in
![]() $B_1$
, with
$B_1$
, with
For
![]() $j\geq 1$
write
$j\geq 1$
write
Using Lemma 7 and the fact that by (38),
![]() $|B_r|\leq cr^{n},\;r\leq 1$
, the Cauchy–Schwartz inequality implies that
$|B_r|\leq cr^{n},\;r\leq 1$
, the Cauchy–Schwartz inequality implies that
 $$ \begin{align} \int_{|x|\leq 2^{-(1-\alpha )j/2}}|\kappa _{j}(x)|dx& \leq |B_{2^{-(1-\alpha )j/2}}|^{1/2}\Vert \kappa _{j}\Vert _{L^{2}(X)} \nonumber\\ & \leq c2^{-(1-\alpha )jn/4}2^{-\beta j/2}2^{jn/4} \nonumber \\ & \leq c2^{-(\beta -\alpha n/2)j/2}. \end{align} $$
$$ \begin{align} \int_{|x|\leq 2^{-(1-\alpha )j/2}}|\kappa _{j}(x)|dx& \leq |B_{2^{-(1-\alpha )j/2}}|^{1/2}\Vert \kappa _{j}\Vert _{L^{2}(X)} \nonumber\\ & \leq c2^{-(1-\alpha )jn/4}2^{-\beta j/2}2^{jn/4} \nonumber \\ & \leq c2^{-(\beta -\alpha n/2)j/2}. \end{align} $$
Set
and note that
Note also that if
![]() $q=-(1-\alpha )(\ell +1)$
,
$q=-(1-\alpha )(\ell +1)$
,
![]() $\ell =0,1,...,j-1$
, then,
$\ell =0,1,...,j-1$
, then,
![]() $ 0\geq q\geq -j$
.
$ 0\geq q\geq -j$
.
It follows that
 $$ \begin{align} \int_{2^{-(1-\alpha )j/2}\leq |x|\leq 1}|\kappa _{j}(x)|dx& \leq \sum_{\ell =0}^{j-1}\int_{{A}_{\ell }}|\kappa _{j}(x)|dx \nonumber \\ & \leq \sum_{\ell =0}^{j-1}|{A}_{\ell }|^{1/2}\Vert \kappa _{j}\Vert _{L^{2}( {A}_{\ell })} \nonumber \\ & \leq \sum_{\ell =0}^{j-1}|{B}_{2^{-(1-\alpha )\ell /2}} |^{1/2}\Vert \kappa _{j}\Vert _{L^{2}({A}_{\ell })} \nonumber\\ & \leq c\sum_{\ell =0}^{j-1}2^{-(1-\alpha )\ell n/4}\Vert \kappa _{j}\Vert _{L^{2}({A}_{\ell })}. \end{align} $$
$$ \begin{align} \int_{2^{-(1-\alpha )j/2}\leq |x|\leq 1}|\kappa _{j}(x)|dx& \leq \sum_{\ell =0}^{j-1}\int_{{A}_{\ell }}|\kappa _{j}(x)|dx \nonumber \\ & \leq \sum_{\ell =0}^{j-1}|{A}_{\ell }|^{1/2}\Vert \kappa _{j}\Vert _{L^{2}( {A}_{\ell })} \nonumber \\ & \leq \sum_{\ell =0}^{j-1}|{B}_{2^{-(1-\alpha )\ell /2}} |^{1/2}\Vert \kappa _{j}\Vert _{L^{2}({A}_{\ell })} \nonumber\\ & \leq c\sum_{\ell =0}^{j-1}2^{-(1-\alpha )\ell n/4}\Vert \kappa _{j}\Vert _{L^{2}({A}_{\ell })}. \end{align} $$
But, from Lemma 7,
for all
![]() $j,k\in \mathbb {N},$
and
$j,k\in \mathbb {N},$
and
![]() $q\in \left [ -j,0\right ] $
.
$q\in \left [ -j,0\right ] $
.
Choosing
![]() $k>n/2$
, from (62) and (63), it follows that
$k>n/2$
, from (62) and (63), it follows that
 $$ \begin{align} \int_{2^{-(1-\alpha )j/2}\leq |x|\leq 1}|\kappa _{j}(x)|dx& \leq c\sum_{\ell =0}^{j-1}2^{-(1-\alpha )\ell n/4}2^{-(\beta -n/2+k(1-\alpha ))j/2}2^{k(1-\alpha )\ell /2} \nonumber \\ & \leq c2^{-(\beta -n/2+k(1-\alpha ))j/2}\sum_{\ell =0}^{j-1}2^{(k-n/2)(1-\alpha )\ell /2} \nonumber \\ & \leq c2^{-(\beta -n/2+k(1-\alpha ))j/2}2^{(k-n/2)(1-\alpha )j/2} \nonumber \\ & \leq c2^{-j\beta /2}2^{jn/4}2^{-nj/4}2^{nj\alpha /4} \nonumber\\ & \leq c2^{-(\beta -\alpha n/2)j/2}. \end{align} $$
$$ \begin{align} \int_{2^{-(1-\alpha )j/2}\leq |x|\leq 1}|\kappa _{j}(x)|dx& \leq c\sum_{\ell =0}^{j-1}2^{-(1-\alpha )\ell n/4}2^{-(\beta -n/2+k(1-\alpha ))j/2}2^{k(1-\alpha )\ell /2} \nonumber \\ & \leq c2^{-(\beta -n/2+k(1-\alpha ))j/2}\sum_{\ell =0}^{j-1}2^{(k-n/2)(1-\alpha )\ell /2} \nonumber \\ & \leq c2^{-(\beta -n/2+k(1-\alpha ))j/2}2^{(k-n/2)(1-\alpha )j/2} \nonumber \\ & \leq c2^{-j\beta /2}2^{jn/4}2^{-nj/4}2^{nj\alpha /4} \nonumber\\ & \leq c2^{-(\beta -\alpha n/2)j/2}. \end{align} $$
Combining (61) and (64), we obtain that
and the proof of the lemma is complete.
4 The part at infinity
In this section, we prove the
![]() $L^{p}$
-boundedness of
$L^{p}$
-boundedness of
![]() $T_{\alpha ,\beta }^{\infty }$
(resp.
$T_{\alpha ,\beta }^{\infty }$
(resp.
![]() $\widehat {T}_{\alpha ,\beta }^{\infty }$
), which combined with the
$\widehat {T}_{\alpha ,\beta }^{\infty }$
), which combined with the
![]() $L^{p}$
-boundedness of
$L^{p}$
-boundedness of
![]() $T_{\alpha ,\beta }^{0}$
(resp.
$T_{\alpha ,\beta }^{0}$
(resp.
![]() $ \widehat {T}_{\alpha ,\beta }^{0}$
) proved in Section 3, finish the proof of Theorem 1.
$ \widehat {T}_{\alpha ,\beta }^{0}$
) proved in Section 3, finish the proof of Theorem 1.
Proposition 8 Assume that
![]() $\alpha \in \left ( 0,1\right ) $
and that M belongs in the class (KS). Then the operator
$\alpha \in \left ( 0,1\right ) $
and that M belongs in the class (KS). Then the operator
![]() ${T}_{\alpha ,\beta }^{\infty }$
(resp.
${T}_{\alpha ,\beta }^{\infty }$
(resp.
![]() $\widehat {T}_{\alpha ,\beta }^{\infty }$
) is bounded on
$\widehat {T}_{\alpha ,\beta }^{\infty }$
) is bounded on
![]() $L^{p}(X)$
(resp. on
$L^{p}(X)$
(resp. on
![]() $L^{p}(M)$
) for all
$L^{p}(M)$
) for all
![]() $p\in \left ( 1,\infty \right ) $
.
$p\in \left ( 1,\infty \right ) $
.
For the proof of the proposition above we shall make use, as in [Reference Anker3, Reference Lohoué and Marias20, Reference Papageorgiou24], of the Kunze and Stein phenomenon. We shall give the proof of the
![]() $L^{p}$
-boundedness only for
$L^{p}$
-boundedness only for
![]() $\widehat {T}_{\alpha ,\beta }^{\infty }$
. The case of
$\widehat {T}_{\alpha ,\beta }^{\infty }$
. The case of
![]() $T_{\alpha ,\beta }^{\infty }$
is similar, thus omitted. For that we need to introduce some notation.
$T_{\alpha ,\beta }^{\infty }$
is similar, thus omitted. For that we need to introduce some notation.
For
![]() $p\in (1,\infty )$
, set
$p\in (1,\infty )$
, set
 $$ \begin{align} v_{\Gamma }(p)=2\min \{(1/p),(1/p^{\prime })\}\frac{\|\eta _{\Gamma }\|}{ \|\rho\| }+|(2/p)-1|, \end{align} $$
$$ \begin{align} v_{\Gamma }(p)=2\min \{(1/p),(1/p^{\prime })\}\frac{\|\eta _{\Gamma }\|}{ \|\rho\| }+|(2/p)-1|, \end{align} $$
where
![]() $p^{\prime }$
is the conjugate of p and
$p^{\prime }$
is the conjugate of p and
![]() $\eta _{\Gamma }\in \mathfrak {a^{\ast }}$
is the vector appearing in (4). Recall that
$\eta _{\Gamma }\in \mathfrak {a^{\ast }}$
is the vector appearing in (4). Recall that
![]() $\|\eta _{\Gamma }\|=(\|\rho \|^2-\lambda _{0})^{1/2}$
, where
$\|\eta _{\Gamma }\|=(\|\rho \|^2-\lambda _{0})^{1/2}$
, where
![]() $\lambda _{0}$
the bottom of the spectrum of the Laplacian
$\lambda _{0}$
the bottom of the spectrum of the Laplacian
![]() $\Delta _{M}$
. Note that
$\Delta _{M}$
. Note that
![]() $v_{\Gamma }(p)\leq 1$
.
$v_{\Gamma }(p)\leq 1$
.
Consider a bounded, Weyl invariant function
![]() $m(\lambda )$
,
$m(\lambda )$
,
![]() $\lambda \in \mathfrak {a}^{\ast }$
. For
$\lambda \in \mathfrak {a}^{\ast }$
. For
![]() $N\in \mathbb {N}$
,
$N\in \mathbb {N}$
,
![]() $v\in \mathbb {R}$
and
$v\in \mathbb {R}$
and
![]() $\theta>0 $
, we say that a multiplier
$\theta>0 $
, we say that a multiplier
![]() $m(\lambda )$
,
$m(\lambda )$
,
![]() $\lambda \in \mathfrak {a^*}$
, belongs in the class
$\lambda \in \mathfrak {a^*}$
, belongs in the class
![]() $\mathcal {M} (v,N,\theta )$
, if
$\mathcal {M} (v,N,\theta )$
, if
-
• m is analytic inside the tube
 $\mathcal {T}^v=\mathfrak {a^*} +ivC_{\rho }$
and
$\mathcal {T}^v=\mathfrak {a^*} +ivC_{\rho }$
and -
• for all multi-indices
 $k\in \mathbb {N}$
with
$k\in \mathbb {N}$
with
 $|k|\leq N$
,
$|k|\leq N$
,
 $\partial ^{k}m(\lambda )$
extends continuously to the whole of
$\partial ^{k}m(\lambda )$
extends continuously to the whole of
 $\mathcal {T}^{v}$
with (66)
$\mathcal {T}^{v}$
with (66) $$ \begin{align} |\partial ^{k}m(\lambda )|\leq c(1+\|\lambda\| ^{2})^{-|k|\theta /2}:=\langle\lambda \rangle^{-|k|\theta }. \end{align} $$
$$ \begin{align} |\partial ^{k}m(\lambda )|\leq c(1+\|\lambda\| ^{2})^{-|k|\theta /2}:=\langle\lambda \rangle^{-|k|\theta }. \end{align} $$
Let
![]() $\kappa =\mathcal {H}^{-1}m $
, and denote by
$\kappa =\mathcal {H}^{-1}m $
, and denote by
![]() $\kappa ^{\infty }$
its part away from the origin. Consider the convolution operator
$\kappa ^{\infty }$
its part away from the origin. Consider the convolution operator
![]() $\widehat {T}_{\kappa }^{\infty }$
. The following result will be applied to prove Proposition 8.
$\widehat {T}_{\kappa }^{\infty }$
. The following result will be applied to prove Proposition 8.
Proposition 9 Fix
![]() $p\in (1,\infty )$
and consider a Weyl-invariant function
$p\in (1,\infty )$
and consider a Weyl-invariant function
![]() $m\in \mathcal {M}(v,N,\theta )$
,
$m\in \mathcal {M}(v,N,\theta )$
,
![]() $\theta \in (0,1)$
, with
$\theta \in (0,1)$
, with
![]() $v>v_{\Gamma }(p)$
and
$v>v_{\Gamma }(p)$
and
![]() $N=\left [ \frac {n+1}{ 2\theta }\right ] +1$
. Then,
$N=\left [ \frac {n+1}{ 2\theta }\right ] +1$
. Then,
![]() $\widehat {T}_{\kappa }^{\infty }$
is bounded on
$\widehat {T}_{\kappa }^{\infty }$
is bounded on
![]() $L^{p}(M).$
$L^{p}(M).$
Let us assume for the moment that this result is valid. Then, note that the multiplier
![]() $m_{\alpha ,\beta }$
belongs in the class
$m_{\alpha ,\beta }$
belongs in the class
![]() $\mathcal {M}(v,N, \theta )$
, for
$\mathcal {M}(v,N, \theta )$
, for
![]() $\theta =1-\alpha $
. Indeed,
$\theta =1-\alpha $
. Indeed,
![]() $m_{\alpha ,\beta }\left ( \lambda \right ) $
has poles only at
$m_{\alpha ,\beta }\left ( \lambda \right ) $
has poles only at
![]() $\lambda =i\rho $
and the points in its Weyl orbit. So, the function
$\lambda =i\rho $
and the points in its Weyl orbit. So, the function
![]() $\lambda \longrightarrow m_{\alpha ,\beta }\left ( \lambda \right ) $
is analytic in the tube
$\lambda \longrightarrow m_{\alpha ,\beta }\left ( \lambda \right ) $
is analytic in the tube
![]() $\mathcal {T}^v=\mathfrak { a^{\ast }}+ivC_{\rho }$
,
$\mathcal {T}^v=\mathfrak { a^{\ast }}+ivC_{\rho }$
,
![]() $v\in (v_{\Gamma }(p),1)$
. Secondly, for
$v\in (v_{\Gamma }(p),1)$
. Secondly, for
![]() $\lambda \in \mathcal {T}^v$
, it is straightforward to see that
$\lambda \in \mathcal {T}^v$
, it is straightforward to see that
for every multi-index k. Thus, it follows from Proposition 9 that
![]() $\widehat {T}^{\infty }_{\alpha , \beta }$
is bounded on
$\widehat {T}^{\infty }_{\alpha , \beta }$
is bounded on
![]() $L^p(M)$
, for all
$L^p(M)$
, for all
![]() $p\in (1, \infty )$
, and the proof of Theorem 1 is complete.
$p\in (1, \infty )$
, and the proof of Theorem 1 is complete.
It remains to prove Proposition 9. Since M belongs in the class (KS), then, according to Kunze and Stein phenomenon, we have that
 $$ \begin{align*} ||\widehat{T}^{\infty }||_{L^{p}(M)\rightarrow L^{p}(M)} &\leq \int_{G}\left\vert \kappa ^{\infty }(x)\right\vert \varphi _{-i\eta _{\Gamma }}(x)^{s(p)}dx \\ &\leq c\int_{|x|\geq 1/2}\left\vert \kappa(x)\right\vert \varphi _{-i\eta _{\Gamma }}(x)^{s(p)}dx. \end{align*} $$
$$ \begin{align*} ||\widehat{T}^{\infty }||_{L^{p}(M)\rightarrow L^{p}(M)} &\leq \int_{G}\left\vert \kappa ^{\infty }(x)\right\vert \varphi _{-i\eta _{\Gamma }}(x)^{s(p)}dx \\ &\leq c\int_{|x|\geq 1/2}\left\vert \kappa(x)\right\vert \varphi _{-i\eta _{\Gamma }}(x)^{s(p)}dx. \end{align*} $$
We shall deal only with the integral for
![]() $|x|\geq 1$
; the case for
$|x|\geq 1$
; the case for
![]() $1/2\leq |x|\leq 1$
is trivial due to compactness. To estimate the integral for
$1/2\leq |x|\leq 1$
is trivial due to compactness. To estimate the integral for
![]() $ \left \vert x\right \vert \geq 1$
, we proceed as in the proof of Theorem 1 in [Reference Lohoué and Marias20], which is based on Proposition 5 of [Reference Anker3]. Using (37), we have
$ \left \vert x\right \vert \geq 1$
, we proceed as in the proof of Theorem 1 in [Reference Lohoué and Marias20], which is based on Proposition 5 of [Reference Anker3]. Using (37), we have
 $$ \begin{align} \int_{|x|\geq 1}|\kappa(x)|\varphi _{-i\eta _{\Gamma }}(x)^{s(p)}dx& =\sum_{j\geq 1}\int_{B_{j+1}\backslash B_{j}}|\kappa(x)|\varphi _{-i\eta _{\Gamma }}(x)^{s(p)}dx\nonumber\\ &:=\sum_{j\geq 1} I_j. \end{align} $$
$$ \begin{align} \int_{|x|\geq 1}|\kappa(x)|\varphi _{-i\eta _{\Gamma }}(x)^{s(p)}dx& =\sum_{j\geq 1}\int_{B_{j+1}\backslash B_{j}}|\kappa(x)|\varphi _{-i\eta _{\Gamma }}(x)^{s(p)}dx\nonumber\\ &:=\sum_{j\geq 1} I_j. \end{align} $$
Thus, it is sufficient to estimate the integrals in these annuli (actually the proof in [Reference Anker3] uses a polyhedral variant of the balls
![]() $B_j$
). Set
$B_j$
). Set
![]() $b=n-d$
,
$b=n-d$
,
![]() $d=\dim \mathfrak {a^{\ast }}=\operatorname {rank}X$
and let
$d=\dim \mathfrak {a^{\ast }}=\operatorname {rank}X$
and let
![]() $b^{\prime }$
be the smallest integer
$b^{\prime }$
be the smallest integer
![]() $\geq b/2$
. In [Reference Lohoué and Marias20, p. 645], using [Reference Anker3, p. 608], it is proved that for any
$\geq b/2$
. In [Reference Lohoué and Marias20, p. 645], using [Reference Anker3, p. 608], it is proved that for any
![]() $\theta>0$
, if
$\theta>0$
, if
![]() $m\in \mathcal {M}(v, N, \theta )$
, then for
$m\in \mathcal {M}(v, N, \theta )$
, then for
![]() $j\geq 1$
and every multi-index k with
$j\geq 1$
and every multi-index k with
![]() $|k|\leq N$
, we have
$|k|\leq N$
, we have
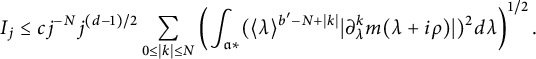 $$\begin{align*} I_j \leq cj^{-N}j^{(d-1)/2} \sum_{0\leq |k|\leq N}\left( \int_{\mathfrak{a\ast }}(\langle \lambda \rangle^{b^{\prime }-N+|k|}|\partial _{\lambda }^{k}m(\lambda +i\rho)|)^{2}d\lambda \right)^{1/2}. \end{align*}$$
$$\begin{align*} I_j \leq cj^{-N}j^{(d-1)/2} \sum_{0\leq |k|\leq N}\left( \int_{\mathfrak{a\ast }}(\langle \lambda \rangle^{b^{\prime }-N+|k|}|\partial _{\lambda }^{k}m(\lambda +i\rho)|)^{2}d\lambda \right)^{1/2}. \end{align*}$$
We shall now modify the arguments used in the proof of [Reference Lohoué and Marias20, Theorem 1] to control
![]() $I_j$
. There, it is assumed that the decay rate of the multiplier derivatives (66) holds true for
$I_j$
. There, it is assumed that the decay rate of the multiplier derivatives (66) holds true for
![]() $\theta =1$
. We show that the result is still valid for
$\theta =1$
. We show that the result is still valid for
![]() $\theta \in (0,1)$
(increasing the number of derivatives we have to control). Let m satisfy
$\theta \in (0,1)$
(increasing the number of derivatives we have to control). Let m satisfy
for some fixed
![]() $\theta \in (0,1)$
. If N is large enough, say
$\theta \in (0,1)$
. If N is large enough, say
![]() $N>\frac {n+1}{2\theta }\geq \frac {2b^{\prime }+d}{2\theta }$
, using (69) it follows that
$N>\frac {n+1}{2\theta }\geq \frac {2b^{\prime }+d}{2\theta }$
, using (69) it follows that
 $$ \begin{align} I_{j}& \leq cj^{-N}j^{(d-1)/2}\sum_{0\leq |k|\leq N}\left( \int_{\mathfrak{ a\ast }}(\langle \lambda \rangle^{b^{\prime }-N+|k|}\langle \lambda \rangle^{-|k|\theta })^{2}d\lambda \right) ^{1/2}\nonumber \\ & \leq cj^{-N}j^{(d-1)/2}\left( \int_{\mathfrak{a\ast }}\langle\lambda \rangle^{2(b^{\prime }-\theta N)}d\lambda \right) ^{1/2}\nonumber \\ & \leq cj^{-N}j^{(d-1)/2}. \end{align} $$
$$ \begin{align} I_{j}& \leq cj^{-N}j^{(d-1)/2}\sum_{0\leq |k|\leq N}\left( \int_{\mathfrak{ a\ast }}(\langle \lambda \rangle^{b^{\prime }-N+|k|}\langle \lambda \rangle^{-|k|\theta })^{2}d\lambda \right) ^{1/2}\nonumber \\ & \leq cj^{-N}j^{(d-1)/2}\left( \int_{\mathfrak{a\ast }}\langle\lambda \rangle^{2(b^{\prime }-\theta N)}d\lambda \right) ^{1/2}\nonumber \\ & \leq cj^{-N}j^{(d-1)/2}. \end{align} $$
Combining (68) and (70), we conclude that
 $$ \begin{align*} \int_{|x|\geq 1}\left\vert \kappa(x)\right\vert \varphi _{-i\eta _{\Gamma }}(x)^{s(p)}dx=\sum_{j\geq 1}I_{j}\leq c\sum_{j\geq 1}j^{-N}j^{(d-1)/2}<\infty , \end{align*} $$
$$ \begin{align*} \int_{|x|\geq 1}\left\vert \kappa(x)\right\vert \varphi _{-i\eta _{\Gamma }}(x)^{s(p)}dx=\sum_{j\geq 1}I_{j}\leq c\sum_{j\geq 1}j^{-N}j^{(d-1)/2}<\infty , \end{align*} $$
since
![]() $N-\frac {d-1}{2}>1$
, and the proof of Proposition 9 is complete.
$N-\frac {d-1}{2}>1$
, and the proof of Proposition 9 is complete.
Acknowledgment
The author would like to thank Professor Anestis Fotiadis for stimulating discussions and support, as well as the anonymous referee for valuable comments and suggestions.