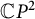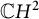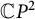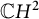1 Introduction
Let
![]() $\bar {M}^n(c)$
, for an integer
$\bar {M}^n(c)$
, for an integer
![]() $n\ge 2$
and a real number
$n\ge 2$
and a real number
![]() $c\not =0$
, be a nonflat complex space form of complex dimension n with constant holomorphic sectional curvature c. A complete and simply connected complex space form is complex analytically isometric to the complex projective space
$c\not =0$
, be a nonflat complex space form of complex dimension n with constant holomorphic sectional curvature c. A complete and simply connected complex space form is complex analytically isometric to the complex projective space
![]() $\mathbb {C}P^n$
if
$\mathbb {C}P^n$
if
![]() $c>0$
, or the complex hyperbolic space
$c>0$
, or the complex hyperbolic space
![]() $\mathbb {C}H^n$
if
$\mathbb {C}H^n$
if
![]() $c<0$
.
$c<0$
.
There are a great many of studies on real hypersurfaces of
![]() $\bar {M}^n(c)$
(see, e.g., [Reference Cecil and Ryan3, Reference Niebergall and Ryan16] and the references therein). In particular, it is known that there do not exist real hypersurfaces with parallel Ricci tensor in nonflat complex space forms
$\bar {M}^n(c)$
(see, e.g., [Reference Cecil and Ryan3, Reference Niebergall and Ryan16] and the references therein). In particular, it is known that there do not exist real hypersurfaces with parallel Ricci tensor in nonflat complex space forms
![]() $\bar {M}^{n}(c)$
for
$\bar {M}^{n}(c)$
for
![]() $n\geq 2$
(see [Reference Ki8, Reference Kim10, Reference Ryan19]). Moreover, it was further shown in [Reference Ki, Nakagawa and Suh9, Reference Kimura and Maeda12, Reference Niebergall and Ryan17] (cf. also Theorem 6.29 in [Reference Niebergall and Ryan16]) that there do not exist Ricci-semisymmetric real hypersurfaces in
$n\geq 2$
(see [Reference Ki8, Reference Kim10, Reference Ryan19]). Moreover, it was further shown in [Reference Ki, Nakagawa and Suh9, Reference Kimura and Maeda12, Reference Niebergall and Ryan17] (cf. also Theorem 6.29 in [Reference Niebergall and Ryan16]) that there do not exist Ricci-semisymmetric real hypersurfaces in
![]() $\bar {M}^{n}(c)$
for
$\bar {M}^{n}(c)$
for
![]() $n\geq 3$
, and there do not exist Hopf Ricci-semisymmetric hypersurfaces in
$n\geq 3$
, and there do not exist Hopf Ricci-semisymmetric hypersurfaces in
![]() $\bar {M}^{2}(c)$
. Based on these results, in their wonderful book [Reference Cecil and Ryan3], Cecil and Ryan stated in Remark 8.70 of [Reference Cecil and Ryan3] that “The existence of non-Hopf Ricci-semisymmetric hypersurfaces in
$\bar {M}^{2}(c)$
. Based on these results, in their wonderful book [Reference Cecil and Ryan3], Cecil and Ryan stated in Remark 8.70 of [Reference Cecil and Ryan3] that “The existence of non-Hopf Ricci-semisymmetric hypersurfaces in
![]() $\mathbb {C}P^{2}$
and
$\mathbb {C}P^{2}$
and
![]() $\mathbb {C}H^{2}$
is an open question,” and then they further raised the following interesting problem.
$\mathbb {C}H^{2}$
is an open question,” and then they further raised the following interesting problem.
Problem 1.1 (cf. page 531 of [Reference Cecil and Ryan3])
Do there exist non-Hopf Ricci-semisymmetric hypersurfaces in
![]() $\mathbb {C}P^{2}$
and
$\mathbb {C}P^{2}$
and
![]() $\mathbb {C}H^{2}$
?
$\mathbb {C}H^{2}$
?
In this paper, we shall solve the above problem by proving the following theorem.
Theorem 1.1 There do not exist non-Hopf Ricci-semisymmetric hypersurfaces in both
![]() $\mathbb {C}P^{2}$
and
$\mathbb {C}P^{2}$
and
![]() $\mathbb {C}H^{2}$
.
$\mathbb {C}H^{2}$
.
To introduce the related notions, we recall that every connected orientable real hypersurface M of an almost Hermitian manifold
![]() $(\bar {M}, J)$
is associated with a Reeb vector field, called also the structure vector field, defined by
$(\bar {M}, J)$
is associated with a Reeb vector field, called also the structure vector field, defined by
![]() $\xi :=-JN$
, where N is the unit normal vector field of
$\xi :=-JN$
, where N is the unit normal vector field of
![]() $M\hookrightarrow \bar {M}$
. M is called a Hopf hypersurface if the integral curves of
$M\hookrightarrow \bar {M}$
. M is called a Hopf hypersurface if the integral curves of
![]() $\xi $
are geodesics. In particular, by Berndt, Bolton, and Woodward [Reference Berndt, Bolton and Woodward2], a real hypersurface of any nearly Kähler manifold is Hopf if and only if its Reeb vector field is a principal vector field. As is well known, Takagi [Reference Takagi20] investigated homogeneous real hypersurfaces in
$\xi $
are geodesics. In particular, by Berndt, Bolton, and Woodward [Reference Berndt, Bolton and Woodward2], a real hypersurface of any nearly Kähler manifold is Hopf if and only if its Reeb vector field is a principal vector field. As is well known, Takagi [Reference Takagi20] investigated homogeneous real hypersurfaces in
![]() $\mathbb {C}P^{n}$
and gave a well-known list, which is often referred to as Takagi’s list:
$\mathbb {C}P^{n}$
and gave a well-known list, which is often referred to as Takagi’s list:
![]() $(A_{1})$
,
$(A_{1})$
,
![]() $(A_{2})$
,
$(A_{2})$
,
![]() $(B)$
,
$(B)$
,
![]() $(C)$
,
$(C)$
,
![]() $(D)$
,
$(D)$
,
![]() $(E)$
. Then, Montiel [Reference Montiel15] provided a similar list of the real hypersurfaces in
$(E)$
. Then, Montiel [Reference Montiel15] provided a similar list of the real hypersurfaces in
![]() $\mathbb {C}H^{n}$
, which is often referred to as Montiel’s list:
$\mathbb {C}H^{n}$
, which is often referred to as Montiel’s list:
![]() $(A_{0})$
,
$(A_{0})$
,
![]() $(A_{1})$
,
$(A_{1})$
,
![]() $(A_{2})$
,
$(A_{2})$
,
![]() $(B)$
. Kimura [Reference Kimura11] proved that a Hopf hypersurface of
$(B)$
. Kimura [Reference Kimura11] proved that a Hopf hypersurface of
![]() $\mathbb {C}P^{n}$
with constant principal curvatures is locally congruent to one of the Takagi’s list, whereas Berndt [Reference Berndt1] proved that a Hopf hypersurface of
$\mathbb {C}P^{n}$
with constant principal curvatures is locally congruent to one of the Takagi’s list, whereas Berndt [Reference Berndt1] proved that a Hopf hypersurface of
![]() $\mathbb {C}H^{n}$
with constant principal curvatures is locally congruent to one of the Montiel’s list. These hypersurfaces can be seen as the tubes over a submanifold of the ambient spaces.
$\mathbb {C}H^{n}$
with constant principal curvatures is locally congruent to one of the Montiel’s list. These hypersurfaces can be seen as the tubes over a submanifold of the ambient spaces.
To study the Ricci-semisymmetric real hypersurfaces in
![]() $\mathbb {C}P^{2}$
and
$\mathbb {C}P^{2}$
and
![]() $\mathbb {C}H^{2}$
, we recall that a Riemannian manifold M is called Ricci-semisymmetric (or Ricci-semiparallel) if
$\mathbb {C}H^{2}$
, we recall that a Riemannian manifold M is called Ricci-semisymmetric (or Ricci-semiparallel) if
or simply write
![]() $R\cdot S=0$
. Here, R and S are the curvature tensor and the Ricci operator of M, respectively.
$R\cdot S=0$
. Here, R and S are the curvature tensor and the Ricci operator of M, respectively.
The study of Ricci-semisymmetric real hypersurfaces in
![]() $\bar {M}^n(c)$
has a long history. First, Kimura and Maeda [Reference Kimura and Maeda12] proved that the Hopf hypersurfaces of
$\bar {M}^n(c)$
has a long history. First, Kimura and Maeda [Reference Kimura and Maeda12] proved that the Hopf hypersurfaces of
![]() $\mathbb {C}P^n,n\geq 2$
, cannot be Ricci-semisymmetric. Ki, Nakagawa, and Suh [Reference Ki, Nakagawa and Suh9] classified cyclic Ricci-semisymmetric (or cyclic Ryan) hypersurfaces of the nonflat complex space forms
$\mathbb {C}P^n,n\geq 2$
, cannot be Ricci-semisymmetric. Ki, Nakagawa, and Suh [Reference Ki, Nakagawa and Suh9] classified cyclic Ricci-semisymmetric (or cyclic Ryan) hypersurfaces of the nonflat complex space forms
![]() $\bar {M}^{n}(c),n\geq 3$
. Moreover, we know from the results of [Reference Ki, Nakagawa and Suh9] that all the cyclic Ricci-semisymmetric hypersurfaces are not Ricci-semisymmetric. Hence, there do not exist Ricci-semisymmetric real hypersurfaces in
$\bar {M}^{n}(c),n\geq 3$
. Moreover, we know from the results of [Reference Ki, Nakagawa and Suh9] that all the cyclic Ricci-semisymmetric hypersurfaces are not Ricci-semisymmetric. Hence, there do not exist Ricci-semisymmetric real hypersurfaces in
![]() $\bar {M}^{n}(c)$
for
$\bar {M}^{n}(c)$
for
![]() $n\geq 3$
. Niebergall and Ryan [Reference Niebergall and Ryan17] proved that the Hopf hypersurfaces in
$n\geq 3$
. Niebergall and Ryan [Reference Niebergall and Ryan17] proved that the Hopf hypersurfaces in
![]() $\bar {M}^{2}(c)$
cannot be semisymmetric, i.e.,
$\bar {M}^{2}(c)$
cannot be semisymmetric, i.e.,
![]() $R\cdot R=0$
. As a Riemannian
$R\cdot R=0$
. As a Riemannian
![]() $3$
-manifold is semisymmetric if and only if
$3$
-manifold is semisymmetric if and only if
![]() $R\cdot S=0$
, we see that Hopf hypersurfaces of
$R\cdot S=0$
, we see that Hopf hypersurfaces of
![]() $\bar {M}^{2}(c)$
cannot be Ricci-semisymmetric. In summary, we have the following.
$\bar {M}^{2}(c)$
cannot be Ricci-semisymmetric. In summary, we have the following.
Theorem 1.2 (Theorem 6.29 of [Reference Niebergall and Ryan16])
In a complex space form of constant holomorphic sectional curvature
![]() $4c, c\neq 0$
, there exists no real hypersurface
$4c, c\neq 0$
, there exists no real hypersurface
![]() $M^{2n-1}, n\geq 3$
, satisfying
$M^{2n-1}, n\geq 3$
, satisfying
![]() $R\cdot S = 0$
. For
$R\cdot S = 0$
. For
![]() $n = 2$
, there are no Hopf hypersurfaces satisfying
$n = 2$
, there are no Hopf hypersurfaces satisfying
![]() $R\cdot S=0$
.
$R\cdot S=0$
.
Combining Theorems 1.1 and 1.2, we have the following.
Corollary 1.1 There do not exist Ricci-semisymmetric hypersurfaces in nonflat complex space forms
![]() $\bar {M}^{n}(c),n\geq 2$
. In particular, there do not exist non-Hopf semisymmetric hypersurfaces in both
$\bar {M}^{n}(c),n\geq 2$
. In particular, there do not exist non-Hopf semisymmetric hypersurfaces in both
![]() $\mathbb {C}P^{2}$
and
$\mathbb {C}P^{2}$
and
![]() $\mathbb {C}H^{2}$
.
$\mathbb {C}H^{2}$
.
Remark 1.1 In contrast to Corollary 1.1, we know by Theorem 6.30 of [Reference Niebergall and Ryan16] and Theorem 8 of [Reference Ivey and Ryan7] that there exist real hypersurfaces in the nonflat complex space forms
![]() $\bar {M}^{n}(c)\ (n\geq 2)$
satisfying
$\bar {M}^{n}(c)\ (n\geq 2)$
satisfying
A real hypersurface of
![]() $\bar {M}^{n}(c)$
satisfying (1.2) is said to be pseudo-Ryan, whereas Hopf pseudo-Ryan hypersurfaces in
$\bar {M}^{n}(c)$
satisfying (1.2) is said to be pseudo-Ryan, whereas Hopf pseudo-Ryan hypersurfaces in
![]() $\bar {M}^{n}(c)$
coincide with the pseudo-Einstein ones for all
$\bar {M}^{n}(c)$
coincide with the pseudo-Einstein ones for all
![]() $n\ge 2$
. See Remark 8.70 of [Reference Cecil and Ryan3] for details.
$n\ge 2$
. See Remark 8.70 of [Reference Cecil and Ryan3] for details.
Remark 1.2 As related results, we would mention some nice researches about real hypersurfaces of an almost Hermitian manifold with recurrent Ricci tensor (see [Reference Hamada4–Reference Hu, Yao and Zhang6, Reference Loo13, Reference Loo14]). Recall that a Riemannian manifold M is called having recurrent Ricci tensor S if there exists a one-form
![]() $\omega $
on M such that
$\omega $
on M such that
![]() $(\nabla _{X}S)Y=\omega (X)S(Y)$
for all
$(\nabla _{X}S)Y=\omega (X)S(Y)$
for all
![]() $X,Y \in TM$
. Loo [Reference Loo13] and Hamada [Reference Hamada5] proved independently that there are no real hypersurfaces with recurrent Ricci tensor in
$X,Y \in TM$
. Loo [Reference Loo13] and Hamada [Reference Hamada5] proved independently that there are no real hypersurfaces with recurrent Ricci tensor in
![]() $\bar {M}^{n}(c)$
for
$\bar {M}^{n}(c)$
for
![]() $n\ge 3$
, and then in Theorem 20 of [Reference Loo14], Loo further proved that the Ricci operator S being recurrent implies that S is semiparallel. Thus, combining with Theorem 1.1, we have shown that there do not exist non-Hopf hypersurfaces in
$n\ge 3$
, and then in Theorem 20 of [Reference Loo14], Loo further proved that the Ricci operator S being recurrent implies that S is semiparallel. Thus, combining with Theorem 1.1, we have shown that there do not exist non-Hopf hypersurfaces in
![]() $\bar {M}^2(c)$
with recurrent Ricci tensor. Finally, we noticed that very recently Wang [Reference Wang21] studied Ricci
$\bar {M}^2(c)$
with recurrent Ricci tensor. Finally, we noticed that very recently Wang [Reference Wang21] studied Ricci
![]() $\eta $
-recurrent real hypersurfaces in
$\eta $
-recurrent real hypersurfaces in
![]() $\bar {M}^2(c)$
.
$\bar {M}^2(c)$
.
This paper is organized as follows. In Section 2, we review the necessary materials about real hypersurfaces of the nonflat complex space forms. In Section 3, we establish three basic lemmas about the non-Hopf Ricci-semisymmetric hypersurfaces in the nonflat complex planes
![]() $\bar {M}^{2}(c)$
. In Section 4, we complete the proof of Theorem 1.1.
$\bar {M}^{2}(c)$
. In Section 4, we complete the proof of Theorem 1.1.
2 Preliminaries
2.1 Geometry of hypersurfaces in nonflat complex space forms
Let
![]() $\bar {M}^{n}(c)$
be the nonflat complex space form with the constant holomorphic sectional curvature c, the complex structure J, and the Kähler metric
$\bar {M}^{n}(c)$
be the nonflat complex space form with the constant holomorphic sectional curvature c, the complex structure J, and the Kähler metric
![]() $\bar {g}$
, respectively. Let M be a connected real hypersurface of
$\bar {g}$
, respectively. Let M be a connected real hypersurface of
![]() $\bar {M}^{n}(c)$
with unit normal vector field N. Denote by
$\bar {M}^{n}(c)$
with unit normal vector field N. Denote by
![]() $\bar \nabla $
the Levi–Civita connection of the metric
$\bar \nabla $
the Levi–Civita connection of the metric
![]() $\bar {g}$
, and g the induced metric on M. Put
$\bar {g}$
, and g the induced metric on M. Put
where
![]() $\phi X$
and
$\phi X$
and
![]() $\eta (X)N$
are the tangential and normal parts of
$\eta (X)N$
are the tangential and normal parts of
![]() $JX$
, respectively.
$JX$
, respectively.
![]() $\xi $
is called the Reeb vector field or the structure vector field,
$\xi $
is called the Reeb vector field or the structure vector field,
![]() $\phi $
is a tensor field of type
$\phi $
is a tensor field of type
![]() $(1,1)$
, and
$(1,1)$
, and
![]() $\eta $
is a
$\eta $
is a
![]() $1$
-form on M. By definition, for any
$1$
-form on M. By definition, for any
![]() $X,Y\in TM$
, the following relations hold:
$X,Y\in TM$
, the following relations hold:
 $$ \begin{align} \left\{ \begin{aligned} &\eta(X)=g(X,\xi),\ \phi^{2}(X)=-X+\eta(X)\xi,\ \eta(\phi X)=0, \\ &g(\phi X, Y)=-g(X,\phi Y), \ g(\phi X,\phi Y)=g(X,Y)-\eta(X)\eta(Y). \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &\eta(X)=g(X,\xi),\ \phi^{2}(X)=-X+\eta(X)\xi,\ \eta(\phi X)=0, \\ &g(\phi X, Y)=-g(X,\phi Y), \ g(\phi X,\phi Y)=g(X,Y)-\eta(X)\eta(Y). \end{aligned} \right. \end{align} $$
Let
![]() $\nabla $
be the induced Levi–Civita connection on M, and let R be its Riemannian curvature tensor. The formulas of Gauss and Weingarten are given by
$\nabla $
be the induced Levi–Civita connection on M, and let R be its Riemannian curvature tensor. The formulas of Gauss and Weingarten are given by
where h is the second fundamental form and A is the shape operator of M, which are related by
![]() $h(X,Y)=g(AX,Y)N$
. From (2.1) and
$h(X,Y)=g(AX,Y)N$
. From (2.1) and
![]() $\bar {\nabla }J=0$
, we obtain
$\bar {\nabla }J=0$
, we obtain
The Gauss and Codazzi equations of M are given, for any
![]() $X, Y, Z\in TM$
, by
$X, Y, Z\in TM$
, by
 $$ \begin{align} \begin{aligned} R(X,Y)Z=&\tfrac{c}{4}\big\{g(Y,Z)X-g(X,Z)Y +g(\phi Y,Z)\phi X-g(\phi X,Z)\phi Y\\ &-2g(\phi X, Y)\phi Z \big\}+g(AY,Z)AX-g(AX,Z)AY, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} R(X,Y)Z=&\tfrac{c}{4}\big\{g(Y,Z)X-g(X,Z)Y +g(\phi Y,Z)\phi X-g(\phi X,Z)\phi Y\\ &-2g(\phi X, Y)\phi Z \big\}+g(AY,Z)AX-g(AX,Z)AY, \end{aligned} \end{align} $$
By the Gauss equation (2.5), we have
where
![]() $m=\mathrm {trace}A$
is the mean curvature, and S is the Ricci operator.
$m=\mathrm {trace}A$
is the mean curvature, and S is the Ricci operator.
2.2 The standard non-Hopf frame and their connections
From this subsection on, we shall restrict to the nonflat complex planes
![]() $\bar {M}^2(c)$
. For a non-Hopf hypersurface M of
$\bar {M}^2(c)$
. For a non-Hopf hypersurface M of
![]() $\bar {M}^2(c)$
, there exists nonempty open subset
$\bar {M}^2(c)$
, there exists nonempty open subset
As our study is of local in nature, we shall assume
![]() $\Omega =M$
in the sequel. Then, as
$\Omega =M$
in the sequel. Then, as
![]() $\phi \nabla _{\xi }\xi =\phi ^{2}A\xi =-A\xi +\eta (A\xi )\xi $
, we get
$\phi \nabla _{\xi }\xi =\phi ^{2}A\xi =-A\xi +\eta (A\xi )\xi $
, we get
where
![]() $\alpha =\eta (A\xi )$
,
$\alpha =\eta (A\xi )$
,
![]() $\beta = |\phi \nabla _{\xi }\xi |\not =0$
, and
$\beta = |\phi \nabla _{\xi }\xi |\not =0$
, and
![]() $U=-\frac {1}{\beta }\phi \nabla _{\xi }\xi $
. It is clear that
$U=-\frac {1}{\beta }\phi \nabla _{\xi }\xi $
. It is clear that
![]() $\{\xi , U,\phi U\}$
is an orthonormal frame field of M which, following that in [Reference Cecil and Ryan3], is called the “standard non-Hopf frame” of M. Then, there are smooth functions
$\{\xi , U,\phi U\}$
is an orthonormal frame field of M which, following that in [Reference Cecil and Ryan3], is called the “standard non-Hopf frame” of M. Then, there are smooth functions
![]() $\gamma , \delta $
, and
$\gamma , \delta $
, and
![]() $\mu $
on M such that
$\mu $
on M such that
By using (2.4), (2.8), and (2.9), direct calculations give the following.
Lemma 2.1 (cf. [Reference Panagiotidou and Xenos18])
With respect to the standard non-Hopf frame, there are smooth functions
![]() $\kappa _{i}\ (1\le i\le 3)$
such that the following relations hold:
$\kappa _{i}\ (1\le i\le 3)$
such that the following relations hold:
 $$ \begin{align} &\nabla_U\xi=-\delta U+\gamma\phi U,\ \nabla_{\phi U}\xi=-\mu U+\delta\phi U,\ \nabla_\xi\xi=\beta\phi U,\nonumber\\ &\nabla_UU=\kappa_{1}\phi U+\delta\xi,\ \nabla_{\phi U}U=\kappa_{2}\phi U+\mu\xi,\ \nabla_{\xi}U=\kappa_{3}\phi U,\\ &\nabla_{U}\phi U=-\kappa_{1}U-\gamma\xi,\ \nabla_{\phi U}\phi U=-\kappa_{2}U-\delta\xi,\ \nabla_{\xi}\phi U=-\kappa_{3}U-\beta\xi.\nonumber \end{align} $$
$$ \begin{align} &\nabla_U\xi=-\delta U+\gamma\phi U,\ \nabla_{\phi U}\xi=-\mu U+\delta\phi U,\ \nabla_\xi\xi=\beta\phi U,\nonumber\\ &\nabla_UU=\kappa_{1}\phi U+\delta\xi,\ \nabla_{\phi U}U=\kappa_{2}\phi U+\mu\xi,\ \nabla_{\xi}U=\kappa_{3}\phi U,\\ &\nabla_{U}\phi U=-\kappa_{1}U-\gamma\xi,\ \nabla_{\phi U}\phi U=-\kappa_{2}U-\delta\xi,\ \nabla_{\xi}\phi U=-\kappa_{3}U-\beta\xi.\nonumber \end{align} $$
Moreover, substituting
![]() $X=\xi , U, \phi U$
in (2.7), respectively, together with the use of (2.8) and (2.9), we obtain
$X=\xi , U, \phi U$
in (2.7), respectively, together with the use of (2.8) and (2.9), we obtain
 $$ \begin{align} &S\xi=(\tfrac{c}{2}+\alpha\gamma+\alpha\mu-\beta^{2})\xi +\beta\mu U-\beta\delta \phi U, \nonumber\\ &SU=\beta\mu \xi+(\tfrac{5}{4}c+\alpha\gamma+\gamma\mu -\beta^{2}-\delta^{2})U+\alpha\delta \phi U,\\ &S\phi U=-\beta\delta \xi+\alpha\delta U +(\tfrac{5}{4}c+\alpha\mu+\gamma\mu-\delta^{2})\phi U.\nonumber \end{align} $$
$$ \begin{align} &S\xi=(\tfrac{c}{2}+\alpha\gamma+\alpha\mu-\beta^{2})\xi +\beta\mu U-\beta\delta \phi U, \nonumber\\ &SU=\beta\mu \xi+(\tfrac{5}{4}c+\alpha\gamma+\gamma\mu -\beta^{2}-\delta^{2})U+\alpha\delta \phi U,\\ &S\phi U=-\beta\delta \xi+\alpha\delta U +(\tfrac{5}{4}c+\alpha\mu+\gamma\mu-\delta^{2})\phi U.\nonumber \end{align} $$
3 Basic lemmas on non-Hopf Ricci-semisymmetric real hypersurfaces
In this section, we establish three basic lemmas on non-Hopf Ricci-semisymmetric real hypersurfaces in
![]() $\bar {M}^{2}(c)$
. To begin with, we have the following lemma.
$\bar {M}^{2}(c)$
. To begin with, we have the following lemma.
Lemma 3.1 Let M be a non-Hopf Ricci-semisymmetric hypersurface in the nonflat complex planes
![]() $\bar {M}^{2}(c)$
, and
$\bar {M}^{2}(c)$
, and
![]() $\{\xi ,U,\phi U\}$
is the standard non-Hopf frame such that (2.8)–(2.10) hold. Then we have the following equations:
$\{\xi ,U,\phi U\}$
is the standard non-Hopf frame such that (2.8)–(2.10) hold. Then we have the following equations:
Proof First of all, substituting
![]() $(X,Y,Z,W)=(\xi ,U,\phi U,U)$
in (1.1), then by direct calculations with the use of (2.11) and Gauss equation (2.5), we can obtain
$(X,Y,Z,W)=(\xi ,U,\phi U,U)$
in (1.1), then by direct calculations with the use of (2.11) and Gauss equation (2.5), we can obtain
As
![]() $\beta \neq 0$
and
$\beta \neq 0$
and
![]() $c\not =0$
, we have
$c\not =0$
, we have
![]() $\delta =0$
as claimed.
$\delta =0$
as claimed.
Next, substituting in (1.1),
respectively, with the use of (3.1), (2.11), and (2.5), we obtain
Now, we claim that
![]() $\mu \neq 0$
. Indeed, if
$\mu \neq 0$
. Indeed, if
![]() $\mu =0$
, from (3.6), we shall get
$\mu =0$
, from (3.6), we shall get
![]() $\alpha \gamma -\beta ^2=0$
. Then, from (3.5), we obtain
$\alpha \gamma -\beta ^2=0$
. Then, from (3.5), we obtain
![]() $c=0$
. This is a contradiction to the assumption.
$c=0$
. This is a contradiction to the assumption.
From (3.4) and
![]() $\mu \neq 0$
, we obtain (3.2).
$\mu \neq 0$
, we obtain (3.2).
Finally, substituting (3.2) into (3.5) or (3.6), we get (3.3).
Next, applying Lemma 3.1, the Gauss–Codazzi equations and some techniques, we have the following basic lemma.
Lemma 3.2 Let M be a non-Hopf Ricci-semisymmetric hypersurface in the nonflat complex planes
![]() $\bar {M}^{2}(c)$
, and
$\bar {M}^{2}(c)$
, and
![]() $\{\xi ,U,\phi U\}$
is the standard non-Hopf frame such that (2.8)–(2.10) hold. Then we have the following equations:
$\{\xi ,U,\phi U\}$
is the standard non-Hopf frame such that (2.8)–(2.10) hold. Then we have the following equations:
Proof Substituting
![]() $(X,Y)=(\xi , U)$
in Codazzi equation (2.6) and using (3.1), we obtain
$(X,Y)=(\xi , U)$
in Codazzi equation (2.6) and using (3.1), we obtain
Then, from (3.2) and (3.22), we obtain (3.8).
Similarly, substituting in (2.6),
![]() $(X,Y)=(\xi , \phi U), (U, \phi U)$
, respectively, with the use of (3.1), we can obtain (3.10)–(3.14).
$(X,Y)=(\xi , \phi U), (U, \phi U)$
, respectively, with the use of (3.1), we can obtain (3.10)–(3.14).
Next, substituting in Gauss equation (2.5),
respectively, and using (3.1), we can calculate to obtain (3.15)–(3.17).
To prove the remaining equations (3.7), (3.9), (3.18), and (3.19), more computations are needed.
![]() $\bullet $
Substituting the derivative of (3.2) with respect to
$\bullet $
Substituting the derivative of (3.2) with respect to
![]() $\phi U$
and using (3.11)–(3.13), we obtain
$\phi U$
and using (3.11)–(3.13), we obtain
 $$ \begin{align} 0&=\phi U(\alpha)\gamma+\phi U(\gamma)\alpha-2\beta\phi U(\beta)\\ &=\beta\gamma\kappa_3+\beta\gamma\mu-\alpha\mu\kappa_1+\alpha\gamma\kappa_1 -\beta c-2\beta^2\kappa_1.\nonumber \end{align} $$
$$ \begin{align} 0&=\phi U(\alpha)\gamma+\phi U(\gamma)\alpha-2\beta\phi U(\beta)\\ &=\beta\gamma\kappa_3+\beta\gamma\mu-\alpha\mu\kappa_1+\alpha\gamma\kappa_1 -\beta c-2\beta^2\kappa_1.\nonumber \end{align} $$
From (3.8), we have
![]() $\gamma \mu +\gamma \kappa _3= \beta \kappa _1+\mu \kappa _3$
. Substituting it into (3.23), we have
$\gamma \mu +\gamma \kappa _3= \beta \kappa _1+\mu \kappa _3$
. Substituting it into (3.23), we have
 $$ \begin{align*} 0&=\beta(\beta\kappa_1+\mu\kappa_3)-\alpha\mu\kappa_1 +\alpha\gamma\kappa_1-\beta c-2\beta^2\kappa_1\\ &=\kappa_1(\alpha\gamma-\beta^2)+\beta\mu\kappa_3-\alpha\mu\kappa_1-\beta c. \end{align*} $$
$$ \begin{align*} 0&=\beta(\beta\kappa_1+\mu\kappa_3)-\alpha\mu\kappa_1 +\alpha\gamma\kappa_1-\beta c-2\beta^2\kappa_1\\ &=\kappa_1(\alpha\gamma-\beta^2)+\beta\mu\kappa_3-\alpha\mu\kappa_1-\beta c. \end{align*} $$
By using (3.2), the above equation can be rewritten as
Substituting (3.2) into (3.5), we have
As
![]() $\beta \mu \neq 0$
, we get from (3.25) that
$\beta \mu \neq 0$
, we get from (3.25) that
![]() $\alpha \mu +\tfrac {c}{4}\neq 0$
. It follows from (3.24) and (3.25) that
$\alpha \mu +\tfrac {c}{4}\neq 0$
. It follows from (3.24) and (3.25) that
 $$ \begin{align*} \left| \begin{array}{cc} -\kappa_1 & \mu\kappa_3-c \\ c+\gamma\mu & -\beta\mu^2 \end{array} \right| =0. \end{align*} $$
$$ \begin{align*} \left| \begin{array}{cc} -\kappa_1 & \mu\kappa_3-c \\ c+\gamma\mu & -\beta\mu^2 \end{array} \right| =0. \end{align*} $$
That is,
By (3.8), we have
![]() $\beta \kappa _1-\gamma \kappa _3 =\gamma \mu -\kappa _3\mu $
. Substituting it into the above equation, we have
$\beta \kappa _1-\gamma \kappa _3 =\gamma \mu -\kappa _3\mu $
. Substituting it into the above equation, we have
which implies that
![]() $\bullet $
Substituting the derivative of (3.3) along
$\bullet $
Substituting the derivative of (3.3) along
![]() $\xi $
and using (3.10), we have
$\xi $
and using (3.10), we have
It follows that
![]() $\bullet $
Substituting the derivative of (3.3) along U and using (3.14) and (3.21), we obtain
$\bullet $
Substituting the derivative of (3.3) along U and using (3.14) and (3.21), we obtain
 $$ \begin{align*} \begin{split} 0&=\mu(4U(\alpha)+U(\gamma)-U(\mu))+(4\alpha+\gamma-\mu)U(\mu)\\ &=\mu(4\xi(\beta)+U(\gamma))+\kappa_2(\gamma-\mu)(4\alpha+\gamma-2\mu). \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} 0&=\mu(4U(\alpha)+U(\gamma)-U(\mu))+(4\alpha+\gamma-\mu)U(\mu)\\ &=\mu(4\xi(\beta)+U(\gamma))+\kappa_2(\gamma-\mu)(4\alpha+\gamma-2\mu). \end{split} \end{align*} $$
It follows that
![]() $\bullet $
Substituting the derivative of (3.2) along
$\bullet $
Substituting the derivative of (3.2) along
![]() $\xi $
, we have
$\xi $
, we have
![]() $\bullet $
Substituting the derivative of (3.2) along U, and using (3.20) and (3.21), we obtain
$\bullet $
Substituting the derivative of (3.2) along U, and using (3.20) and (3.21), we obtain
Substituting (3.28) into (3.30), and (3.29) into (3.31), we have
 $$ \begin{align} \left\{ \begin{aligned} &-2\beta\xi(\beta)+(-\tfrac{\gamma}{4}+\alpha)\xi(\gamma) =\tfrac{\gamma\beta\kappa_2(4\alpha+\gamma-2\mu)}{4\mu},\\ &(\gamma-4\alpha)\xi(\beta)-2\beta\xi(\gamma) =\tfrac{\alpha(\gamma-\mu)\kappa_2(4\alpha+\gamma-2\mu)}{\mu}. \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &-2\beta\xi(\beta)+(-\tfrac{\gamma}{4}+\alpha)\xi(\gamma) =\tfrac{\gamma\beta\kappa_2(4\alpha+\gamma-2\mu)}{4\mu},\\ &(\gamma-4\alpha)\xi(\beta)-2\beta\xi(\gamma) =\tfrac{\alpha(\gamma-\mu)\kappa_2(4\alpha+\gamma-2\mu)}{\mu}. \end{aligned} \right. \end{align} $$
Since
 $$ \begin{align*} \left| \begin{array}{cc} -2\beta & -\frac{\gamma}{4}+\alpha \\ \gamma-4\alpha & -2\beta \end{array} \right|=4\beta^{2}+\tfrac{(\gamma-4\alpha)^2}{4}> 0, \end{align*} $$
$$ \begin{align*} \left| \begin{array}{cc} -2\beta & -\frac{\gamma}{4}+\alpha \\ \gamma-4\alpha & -2\beta \end{array} \right|=4\beta^{2}+\tfrac{(\gamma-4\alpha)^2}{4}> 0, \end{align*} $$
we can solve (3.32) to obtain
 $$ \begin{align*} \left\{ \begin{aligned} &\xi(\beta)=\tfrac{\kappa_2(4\alpha+\gamma-2\mu)}{\mu(4\beta^2 +\tfrac{(\gamma-4\alpha)^2}{4})}\big[-\tfrac{\beta^2\gamma}{2} -\alpha(\gamma-\mu)(-\tfrac{\gamma}{4}+\alpha)\big],\\ &\xi(\gamma)= \tfrac{\beta\kappa_2(4\alpha+\gamma-2\mu)}{\mu(4\beta^2 +\tfrac{(\gamma-4\alpha)^2}{4})}(-\alpha\gamma+2\alpha\mu-\tfrac{\gamma^2}{4}). \end{aligned} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{aligned} &\xi(\beta)=\tfrac{\kappa_2(4\alpha+\gamma-2\mu)}{\mu(4\beta^2 +\tfrac{(\gamma-4\alpha)^2}{4})}\big[-\tfrac{\beta^2\gamma}{2} -\alpha(\gamma-\mu)(-\tfrac{\gamma}{4}+\alpha)\big],\\ &\xi(\gamma)= \tfrac{\beta\kappa_2(4\alpha+\gamma-2\mu)}{\mu(4\beta^2 +\tfrac{(\gamma-4\alpha)^2}{4})}(-\alpha\gamma+2\alpha\mu-\tfrac{\gamma^2}{4}). \end{aligned} \right. \end{align*} $$
From (3.2), we have
From (3.3) and the fact that
![]() $\mu \neq 0$
, we have
$\mu \neq 0$
, we have
Thus, we obtain
 $$ \begin{align} \tfrac{4\alpha+\gamma-2\mu}{\mu(4\beta^{2}+\tfrac{(\gamma-4\alpha)^2}{4})} =\tfrac{4(4\alpha+\gamma-2\mu)}{\mu(4c+(\gamma+4\alpha)^2)} =\tfrac{-4(c+\mu^2)}{\mu^2(4c+(\mu-\tfrac{c}{\mu})^2)} =-\tfrac{4}{\mu^2+c}. \end{align} $$
$$ \begin{align} \tfrac{4\alpha+\gamma-2\mu}{\mu(4\beta^{2}+\tfrac{(\gamma-4\alpha)^2}{4})} =\tfrac{4(4\alpha+\gamma-2\mu)}{\mu(4c+(\gamma+4\alpha)^2)} =\tfrac{-4(c+\mu^2)}{\mu^2(4c+(\mu-\tfrac{c}{\mu})^2)} =-\tfrac{4}{\mu^2+c}. \end{align} $$
Then, with the use of (3.33)–(3.35),
![]() $\xi (\beta )$
and
$\xi (\beta )$
and
![]() $\xi (\gamma )$
can be rewritten as
$\xi (\gamma )$
can be rewritten as
 $$ \begin{align} \xi(\beta)=&-\tfrac{4\kappa_2}{\mu^2+c}\big[-\tfrac12(\alpha\gamma+\tfrac{c}{4})\gamma -\alpha(\gamma-\mu)(-\tfrac{\gamma}{4}+\alpha)\big] \nonumber\\ =&\tfrac{\kappa_2(\gamma-\mu)}{\mu^2+c}(\alpha\gamma+4\alpha^2 -\tfrac{\gamma\mu}{2}) \end{align} $$
$$ \begin{align} \xi(\beta)=&-\tfrac{4\kappa_2}{\mu^2+c}\big[-\tfrac12(\alpha\gamma+\tfrac{c}{4})\gamma -\alpha(\gamma-\mu)(-\tfrac{\gamma}{4}+\alpha)\big] \nonumber\\ =&\tfrac{\kappa_2(\gamma-\mu)}{\mu^2+c}(\alpha\gamma+4\alpha^2 -\tfrac{\gamma\mu}{2}) \end{align} $$
and
From (3.20) and (3.37), we obtain (3.7). From (3.21) and (3.36), we obtain (3.9).
Next, substituting (3.37) into (3.28), we obtain
 $$ \begin{align*} \xi(\alpha)=&-\tfrac{\beta\kappa_2(4\alpha+\gamma-2\mu)}{4\mu} -\tfrac{\beta\kappa_2}{\mu^2+c} \left(\alpha\gamma-2\alpha\mu+\tfrac{\gamma^2}{4}\right)\\ =&-\tfrac{\beta\kappa_2}{(\mu^2+c)} \left[\tfrac{(4\alpha+\gamma-2\mu)}{4}\tfrac{\mu^2+c}{\mu}+\alpha\gamma -2\alpha\mu+\tfrac{\gamma^2}{4}\right]. \end{align*} $$
$$ \begin{align*} \xi(\alpha)=&-\tfrac{\beta\kappa_2(4\alpha+\gamma-2\mu)}{4\mu} -\tfrac{\beta\kappa_2}{\mu^2+c} \left(\alpha\gamma-2\alpha\mu+\tfrac{\gamma^2}{4}\right)\\ =&-\tfrac{\beta\kappa_2}{(\mu^2+c)} \left[\tfrac{(4\alpha+\gamma-2\mu)}{4}\tfrac{\mu^2+c}{\mu}+\alpha\gamma -2\alpha\mu+\tfrac{\gamma^2}{4}\right]. \end{align*} $$
By using (3.3), we have
So (3.18) is obtained.
Substituting (3.36) into (3.29), we obtain
 $$ \begin{align*} \begin{split} U(\gamma)=& -\tfrac{\kappa_2(\gamma-\mu)(4\alpha+\gamma-2\mu)}{\mu} -4\tfrac{\kappa_2(\gamma-\mu)}{\mu^2+c}(\alpha\gamma+4\alpha^2 -\tfrac{\gamma\mu}{2})\\ =&-\tfrac{\kappa_2(\gamma-\mu)}{\mu^2+c} [(4\alpha+\gamma-2\mu)\tfrac{\mu^2+c}{\mu} +4(\alpha\gamma+4\alpha^2-\tfrac{\gamma\mu}{2})]. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} U(\gamma)=& -\tfrac{\kappa_2(\gamma-\mu)(4\alpha+\gamma-2\mu)}{\mu} -4\tfrac{\kappa_2(\gamma-\mu)}{\mu^2+c}(\alpha\gamma+4\alpha^2 -\tfrac{\gamma\mu}{2})\\ =&-\tfrac{\kappa_2(\gamma-\mu)}{\mu^2+c} [(4\alpha+\gamma-2\mu)\tfrac{\mu^2+c}{\mu} +4(\alpha\gamma+4\alpha^2-\tfrac{\gamma\mu}{2})]. \end{split} \end{align*} $$
By using (3.3), we have
So (3.19) is obtained. We have completed the proof of Lemma 3.2.
Lemma 3.3 Let M be a non-Hopf Ricci-semisymmetric hypersurface in
![]() $\bar {M}^{2}(c)$
, and
$\bar {M}^{2}(c)$
, and
![]() $\{\xi ,U,\phi U\}$
is the standard non-Hopf frame such that (2.8)–(2.10) hold. Then there exists at least one point
$\{\xi ,U,\phi U\}$
is the standard non-Hopf frame such that (2.8)–(2.10) hold. Then there exists at least one point
![]() $p\in M$
such that
$p\in M$
such that
![]() $\kappa _{2}\neq 0$
at p.
$\kappa _{2}\neq 0$
at p.
Proof In fact, if
![]() $\kappa _{2}\equiv 0$
on M, by (3.10) and (3.14), we have
$\kappa _{2}\equiv 0$
on M, by (3.10) and (3.14), we have
![]() $\xi (\mu )=U(\mu )=0$
. Thus, we have
$\xi (\mu )=U(\mu )=0$
. Thus, we have
From (3.27), we have
![]() $\phi U(\mu )=0$
. Thus, we obtain that
$\phi U(\mu )=0$
. Thus, we obtain that
![]() $\mu $
is a constant. It follows from (3.26) that
$\mu $
is a constant. It follows from (3.26) that
![]() $\gamma -\kappa _3$
is a constant. Then, substituting the derivative of
$\gamma -\kappa _3$
is a constant. Then, substituting the derivative of
![]() $\gamma -\kappa _3$
with respect to
$\gamma -\kappa _3$
with respect to
![]() $\phi U$
and using (3.13), (3.15), and the fact that
$\phi U$
and using (3.13), (3.15), and the fact that
![]() $\kappa _2=0$
, we obtain
$\kappa _2=0$
, we obtain
 $$ \begin{align*} \begin{split} 0&=-\mu\kappa_{1}+\gamma\kappa_{1} +\beta\gamma+2\beta\mu+(-2\beta\mu-\beta\kappa_{3}-\kappa_{3}\kappa_{1} +\mu\kappa_{1})\\ &=(\beta+\kappa_1)(\gamma-\kappa_3). \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} 0&=-\mu\kappa_{1}+\gamma\kappa_{1} +\beta\gamma+2\beta\mu+(-2\beta\mu-\beta\kappa_{3}-\kappa_{3}\kappa_{1} +\mu\kappa_{1})\\ &=(\beta+\kappa_1)(\gamma-\kappa_3). \end{split} \end{align*} $$
As
![]() $\kappa _3\neq \gamma $
, we have
$\kappa _3\neq \gamma $
, we have
![]() $\beta =-\kappa _1$
.
$\beta =-\kappa _1$
.
Next, by
![]() $\kappa _2=0$
, (3.7), and (3.19), we have
$\kappa _2=0$
, (3.7), and (3.19), we have
![]() $\xi (\gamma )=U(\gamma )=0$
. Thus,
$\xi (\gamma )=U(\gamma )=0$
. Thus,
As
![]() $\kappa _3\neq \gamma $
, from (3.38),
$\kappa _3\neq \gamma $
, from (3.38),
![]() $\beta =-\kappa _1$
, and (3.13), we obtain
$\beta =-\kappa _1$
, and (3.13), we obtain
which is a contradiction to
![]() $\beta \neq 0$
and
$\beta \neq 0$
and
![]() $\mu \neq 0$
. This completes the proof of Lemma 3.3.
$\mu \neq 0$
. This completes the proof of Lemma 3.3.
4 Proof of Theorem 1.1
Now, we are ready to complete the proof of Theorem 1.1.
Suppose on the contrary that
![]() $\bar {M}^{2}(c)$
admits a non-Hopf Ricci-semisymmetric hypersurface M, and
$\bar {M}^{2}(c)$
admits a non-Hopf Ricci-semisymmetric hypersurface M, and
![]() $\{\xi ,U,\phi U\}$
is the standard non-Hopf frame on M such that (2.8)–(2.10) hold. Then, from (3.3), we have
$\{\xi ,U,\phi U\}$
is the standard non-Hopf frame on M such that (2.8)–(2.10) hold. Then, from (3.3), we have
![]() $c=\mu ^2-\gamma \mu -4\alpha \mu $
. Substituting it into (3.24), we obtain
$c=\mu ^2-\gamma \mu -4\alpha \mu $
. Substituting it into (3.24), we obtain
 $$ \begin{align*} \begin{split} 0=&-\kappa_1(\alpha\mu+\tfrac{\mu^2-\gamma\mu-4\alpha\mu}{4}) +\beta(\mu\kappa_3+4\alpha\mu+\gamma\mu-\mu^2)\\ =&\mu[\tfrac{\kappa_1(\gamma-\mu)}{4}+\beta(\kappa_3+4\alpha+\gamma-\mu)]. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} 0=&-\kappa_1(\alpha\mu+\tfrac{\mu^2-\gamma\mu-4\alpha\mu}{4}) +\beta(\mu\kappa_3+4\alpha\mu+\gamma\mu-\mu^2)\\ =&\mu[\tfrac{\kappa_1(\gamma-\mu)}{4}+\beta(\kappa_3+4\alpha+\gamma-\mu)]. \end{split} \end{align*} $$
As
![]() $\mu \neq 0$
, we have
$\mu \neq 0$
, we have
From (3.26), we have
Now, we claim that
In fact, if
![]() $\gamma =\mu $
, from (3.3), we get
$\gamma =\mu $
, from (3.3), we get
![]() $4\alpha \gamma +c=0$
. This combining with (3.2) implies that
$4\alpha \gamma +c=0$
. This combining with (3.2) implies that
![]() $\beta ^2=0$
. This is a contradiction, which verifies the claim.
$\beta ^2=0$
. This is a contradiction, which verifies the claim.
Then, substituting (4.2) into (4.1) and applying (3.34), we obtain
![]() $\bullet $
Substituting the derivative of (4.2) along U and applying (3.14) and (3.19), we obtain
$\bullet $
Substituting the derivative of (4.2) along U and applying (3.14) and (3.19), we obtain
![]() $\bullet $
Substituting the derivative of (4.3) along
$\bullet $
Substituting the derivative of (4.3) along
![]() $\xi $
, then applying (3.7), (3.9), and (3.10), we obtain
$\xi $
, then applying (3.7), (3.9), and (3.10), we obtain
 $$ \begin{align} \xi(\kappa_1)=&\tfrac{4\xi(\beta)(\mu-\gamma) -4\beta(\xi(\mu)-\xi(\gamma))}{(\mu-\gamma)^2}\Big(\gamma-\tfrac{c\mu}{\mu^2+c}\Big) \nonumber\\ &+\tfrac{4\beta}{\mu-\gamma}\Big[\xi(\gamma)-\tfrac{c\xi(\mu)(\mu^2+c) -c\mu(2\mu\xi(\mu))}{(\mu^2+c)^2}\Big]\nonumber\\ =&\tfrac{1}{(\mu-\gamma)^2} \Big[\tfrac{-4\kappa_2(\mu-\gamma)^2}{\mu^2+c}\Big(\alpha\gamma+4\alpha^2-\tfrac{\gamma\mu}{2}\Big)\nonumber\\ &\qquad\qquad -4\beta\Big(\beta\kappa_2-\tfrac{\beta\kappa_2}{\mu^2+c}\Big(4\alpha\gamma-8\alpha\mu+\gamma^2\Big)\Big)\Big] \Big(\gamma-\tfrac{c\mu}{\mu^2+c}\Big)\nonumber\\ &+\tfrac{4\beta}{\mu-\gamma}\Big[\tfrac{\beta\kappa_2}{\mu^2+c}(4\alpha\gamma-8\alpha\mu+\gamma^2) -\tfrac{c(c-\mu^2)\beta\kappa_2}{(\mu^2+c)^2}\Big]\\ =&\tfrac{\kappa_2}{\mu^2+c}\Big\{\tfrac{1}{(\mu-\gamma)^2}\Big[-4(\mu-\gamma)^2\Big(\alpha\gamma +4\alpha^2-\tfrac{\gamma\mu}{2}\Big)\nonumber\\ &\qquad\qquad\qquad-4\beta^2\Big(\mu^2+c-\Big(4\alpha\gamma-8\alpha\mu+\gamma^2\Big)\Big)\Big]\Big(\gamma-\tfrac{c\mu}{\mu^2+c}\Big)\nonumber\\ &\qquad+\tfrac{4\beta^2}{\mu-\gamma}\Big[4\alpha\gamma-8\alpha\mu+\gamma^2 -\tfrac{c(c-\mu^2)}{\mu^2+c}\Big]\Big\}.\nonumber \end{align} $$
$$ \begin{align} \xi(\kappa_1)=&\tfrac{4\xi(\beta)(\mu-\gamma) -4\beta(\xi(\mu)-\xi(\gamma))}{(\mu-\gamma)^2}\Big(\gamma-\tfrac{c\mu}{\mu^2+c}\Big) \nonumber\\ &+\tfrac{4\beta}{\mu-\gamma}\Big[\xi(\gamma)-\tfrac{c\xi(\mu)(\mu^2+c) -c\mu(2\mu\xi(\mu))}{(\mu^2+c)^2}\Big]\nonumber\\ =&\tfrac{1}{(\mu-\gamma)^2} \Big[\tfrac{-4\kappa_2(\mu-\gamma)^2}{\mu^2+c}\Big(\alpha\gamma+4\alpha^2-\tfrac{\gamma\mu}{2}\Big)\nonumber\\ &\qquad\qquad -4\beta\Big(\beta\kappa_2-\tfrac{\beta\kappa_2}{\mu^2+c}\Big(4\alpha\gamma-8\alpha\mu+\gamma^2\Big)\Big)\Big] \Big(\gamma-\tfrac{c\mu}{\mu^2+c}\Big)\nonumber\\ &+\tfrac{4\beta}{\mu-\gamma}\Big[\tfrac{\beta\kappa_2}{\mu^2+c}(4\alpha\gamma-8\alpha\mu+\gamma^2) -\tfrac{c(c-\mu^2)\beta\kappa_2}{(\mu^2+c)^2}\Big]\\ =&\tfrac{\kappa_2}{\mu^2+c}\Big\{\tfrac{1}{(\mu-\gamma)^2}\Big[-4(\mu-\gamma)^2\Big(\alpha\gamma +4\alpha^2-\tfrac{\gamma\mu}{2}\Big)\nonumber\\ &\qquad\qquad\qquad-4\beta^2\Big(\mu^2+c-\Big(4\alpha\gamma-8\alpha\mu+\gamma^2\Big)\Big)\Big]\Big(\gamma-\tfrac{c\mu}{\mu^2+c}\Big)\nonumber\\ &\qquad+\tfrac{4\beta^2}{\mu-\gamma}\Big[4\alpha\gamma-8\alpha\mu+\gamma^2 -\tfrac{c(c-\mu^2)}{\mu^2+c}\Big]\Big\}.\nonumber \end{align} $$
Substituting (4.6) into (4.5) and applying (3.3), we obtain
 $$ \begin{align} \xi(\kappa_1) =&\tfrac{\kappa_2}{\mu^2+c}\Big\{\Big[-4\Big(\alpha\gamma+4\alpha^2-\tfrac{\gamma\mu}{2}\Big) -\tfrac{\mu-4\alpha}{\mu-\gamma}\Big(2\mu^2-\gamma\mu-4\alpha\gamma+4\alpha\mu-\gamma^2\Big)\Big] \nonumber\\ &\qquad\times\Big(\gamma-\tfrac{c\mu}{\mu^2+c}\Big)+\Big(\mu-4\alpha\Big)\Big[4\alpha\gamma-8\alpha\mu+\gamma^2 -\tfrac{c(c-\mu^2)}{\mu^2+c}\Big]\Big\} \nonumber\\ =&\tfrac{\kappa_2}{\mu^2+c}\Big\{\mu(4\alpha+\gamma-2\mu)\Big(\gamma-\tfrac{c\mu}{\mu^2+c}\Big) +(\mu-4\alpha)\Big[4\alpha\gamma-8\alpha\mu+\gamma^2\\ &\qquad-\tfrac{c(c-\mu^2)}{\mu^2+c}\Big]\Big\}.\nonumber \end{align} $$
$$ \begin{align} \xi(\kappa_1) =&\tfrac{\kappa_2}{\mu^2+c}\Big\{\Big[-4\Big(\alpha\gamma+4\alpha^2-\tfrac{\gamma\mu}{2}\Big) -\tfrac{\mu-4\alpha}{\mu-\gamma}\Big(2\mu^2-\gamma\mu-4\alpha\gamma+4\alpha\mu-\gamma^2\Big)\Big] \nonumber\\ &\qquad\times\Big(\gamma-\tfrac{c\mu}{\mu^2+c}\Big)+\Big(\mu-4\alpha\Big)\Big[4\alpha\gamma-8\alpha\mu+\gamma^2 -\tfrac{c(c-\mu^2)}{\mu^2+c}\Big]\Big\} \nonumber\\ =&\tfrac{\kappa_2}{\mu^2+c}\Big\{\mu(4\alpha+\gamma-2\mu)\Big(\gamma-\tfrac{c\mu}{\mu^2+c}\Big) +(\mu-4\alpha)\Big[4\alpha\gamma-8\alpha\mu+\gamma^2\\ &\qquad-\tfrac{c(c-\mu^2)}{\mu^2+c}\Big]\Big\}.\nonumber \end{align} $$
In the following, we shall calculate the expression of
![]() $\xi (\kappa _1)-U(\kappa _3)$
in two different ways. On the one hand, from (4.4) and (4.7), we have
$\xi (\kappa _1)-U(\kappa _3)$
in two different ways. On the one hand, from (4.4) and (4.7), we have
 $$ \begin{align} \xi(\kappa_1)-U(\kappa_3) =\tfrac{\kappa_2}{\mu^2+c}&\Big\{\mu(4\alpha+\gamma-2\mu)\Big(\gamma-\tfrac{c\mu}{\mu^2+c}\Big) \nonumber\\ &+(\mu-4\alpha)\Big[4\alpha\gamma-8\alpha\mu+\gamma^2-\tfrac{c(c-\mu^2)}{\mu^2+c}\Big] \nonumber\\ &-(\gamma-\mu)\Big[4c+\gamma^2+4\alpha\gamma+2\gamma\mu -\tfrac{c^2(c+3\mu^2)}{\mu^2(\mu^2+c)}\Big]\Big\}\\ =\tfrac{\kappa_2}{\mu^2+c}&\Big\{\gamma\mu(4\alpha+\gamma-2\mu) +(\mu-4\alpha)\Big(4\alpha\gamma-8\alpha\mu+\gamma^2\Big) \nonumber\\ &+(\mu-\gamma)( 4c+\gamma^2+4\alpha\gamma+2\gamma\mu) \nonumber\\ &+(\mu-\gamma)\tfrac{c\mu^4-c^2(c+3\mu^2)}{\mu^2(\mu^2+c)} +(\mu-4\alpha)\tfrac{c\mu^4-c\mu^2(c-\mu^2)}{\mu^2(\mu^2+c)}\Big\}.\nonumber \end{align} $$
$$ \begin{align} \xi(\kappa_1)-U(\kappa_3) =\tfrac{\kappa_2}{\mu^2+c}&\Big\{\mu(4\alpha+\gamma-2\mu)\Big(\gamma-\tfrac{c\mu}{\mu^2+c}\Big) \nonumber\\ &+(\mu-4\alpha)\Big[4\alpha\gamma-8\alpha\mu+\gamma^2-\tfrac{c(c-\mu^2)}{\mu^2+c}\Big] \nonumber\\ &-(\gamma-\mu)\Big[4c+\gamma^2+4\alpha\gamma+2\gamma\mu -\tfrac{c^2(c+3\mu^2)}{\mu^2(\mu^2+c)}\Big]\Big\}\\ =\tfrac{\kappa_2}{\mu^2+c}&\Big\{\gamma\mu(4\alpha+\gamma-2\mu) +(\mu-4\alpha)\Big(4\alpha\gamma-8\alpha\mu+\gamma^2\Big) \nonumber\\ &+(\mu-\gamma)( 4c+\gamma^2+4\alpha\gamma+2\gamma\mu) \nonumber\\ &+(\mu-\gamma)\tfrac{c\mu^4-c^2(c+3\mu^2)}{\mu^2(\mu^2+c)} +(\mu-4\alpha)\tfrac{c\mu^4-c\mu^2(c-\mu^2)}{\mu^2(\mu^2+c)}\Big\}.\nonumber \end{align} $$
By using (3.3), we have
 $$ \begin{align} \gamma\mu&(4\alpha+\gamma-2\mu)+(\mu-4\alpha)(4\alpha\gamma-8\alpha\mu+\gamma^2)\nonumber\\ &+(\mu-\gamma)( 4c+\gamma^2+4\alpha\gamma+2\gamma\mu) \nonumber\\ &=12\alpha\gamma\mu+\gamma^2\mu-8\alpha\mu^2-16\alpha^2\gamma+32\alpha^2\mu -8\alpha\gamma^2+4(\mu-\gamma)c-\gamma^3\\ &=8\alpha(4\alpha\mu+\gamma\mu-\mu^2)+\gamma(4\alpha\mu+\gamma\mu-\mu^2) +\mu^2\gamma+4(\mu-\gamma)c-\gamma(\gamma+4\alpha)^2\nonumber\\ &=-8\alpha c-5\gamma c+4\mu c+\mu^2\gamma-\gamma(\gamma+4\alpha)^2\nonumber \end{align} $$
$$ \begin{align} \gamma\mu&(4\alpha+\gamma-2\mu)+(\mu-4\alpha)(4\alpha\gamma-8\alpha\mu+\gamma^2)\nonumber\\ &+(\mu-\gamma)( 4c+\gamma^2+4\alpha\gamma+2\gamma\mu) \nonumber\\ &=12\alpha\gamma\mu+\gamma^2\mu-8\alpha\mu^2-16\alpha^2\gamma+32\alpha^2\mu -8\alpha\gamma^2+4(\mu-\gamma)c-\gamma^3\\ &=8\alpha(4\alpha\mu+\gamma\mu-\mu^2)+\gamma(4\alpha\mu+\gamma\mu-\mu^2) +\mu^2\gamma+4(\mu-\gamma)c-\gamma(\gamma+4\alpha)^2\nonumber\\ &=-8\alpha c-5\gamma c+4\mu c+\mu^2\gamma-\gamma(\gamma+4\alpha)^2\nonumber \end{align} $$
and
 $$ \begin{align} (\mu-\gamma)&\tfrac{c\mu^4-c^2(c+3\mu^2)}{\mu^2(\mu^2+c)} +(\mu-4\alpha)\tfrac{c\mu^4-c\mu^2(c-\mu^2)}{\mu^2(\mu^2+c)} \nonumber\\ =&\tfrac{c}{\mu^2(\mu^2+c)}\Big[3\mu^5-(\mu-\gamma)c^2-4c\mu^3-\gamma\mu^4 +3c\gamma\mu^2-8\alpha\mu^4+4\alpha\mu^2c\Big] \nonumber\\ =&\tfrac{c}{(\mu^2+c)}\Big[3\mu^3-(\mu-\gamma)(\mu-\gamma-4\alpha)^2 -4c\mu-\gamma\mu^2+3c\gamma-8\alpha\mu^2 \nonumber\\ &+4\alpha c\Big]\\ =&\tfrac{c}{(\mu^2+c)}\Big[\mu^3-4\alpha(4\alpha\mu+\gamma\mu-\mu^2) -\mu(4\alpha\mu+\gamma\mu-\mu^2)\nonumber\\ &-3\gamma(4\alpha\mu+\gamma\mu-\mu^2) +\gamma(\gamma+4\alpha)^2-4c\mu+3c\gamma+4\alpha c\Big]\nonumber\\ =&\tfrac{c}{(\mu^2+c)}\Big[\mu^3+8\alpha c-3\mu c+6\gamma c+\gamma(\gamma+4\alpha)^2\Big].\nonumber \end{align} $$
$$ \begin{align} (\mu-\gamma)&\tfrac{c\mu^4-c^2(c+3\mu^2)}{\mu^2(\mu^2+c)} +(\mu-4\alpha)\tfrac{c\mu^4-c\mu^2(c-\mu^2)}{\mu^2(\mu^2+c)} \nonumber\\ =&\tfrac{c}{\mu^2(\mu^2+c)}\Big[3\mu^5-(\mu-\gamma)c^2-4c\mu^3-\gamma\mu^4 +3c\gamma\mu^2-8\alpha\mu^4+4\alpha\mu^2c\Big] \nonumber\\ =&\tfrac{c}{(\mu^2+c)}\Big[3\mu^3-(\mu-\gamma)(\mu-\gamma-4\alpha)^2 -4c\mu-\gamma\mu^2+3c\gamma-8\alpha\mu^2 \nonumber\\ &+4\alpha c\Big]\\ =&\tfrac{c}{(\mu^2+c)}\Big[\mu^3-4\alpha(4\alpha\mu+\gamma\mu-\mu^2) -\mu(4\alpha\mu+\gamma\mu-\mu^2)\nonumber\\ &-3\gamma(4\alpha\mu+\gamma\mu-\mu^2) +\gamma(\gamma+4\alpha)^2-4c\mu+3c\gamma+4\alpha c\Big]\nonumber\\ =&\tfrac{c}{(\mu^2+c)}\Big[\mu^3+8\alpha c-3\mu c+6\gamma c+\gamma(\gamma+4\alpha)^2\Big].\nonumber \end{align} $$
Substituting (4.9) and (4.10) into (4.8), we obtain
 $$ \begin{align} \xi(\kappa_1)-U(\kappa_3)=&\tfrac{\kappa_2}{\mu^2+c} \big\{4\mu c-5\gamma c-8\alpha c+\gamma\mu^2-\gamma(\gamma+4\alpha)^2 \nonumber\\ &+\tfrac{c}{\mu^2+c}\big[\mu^3+8c\alpha -3c\mu+6c\gamma+\gamma(\gamma+4\alpha)^2\big]\big\}\nonumber\\ =&\tfrac{\kappa_2}{\mu^2+c}\big\{5\mu c-5\gamma c-8\alpha c+\gamma\mu^2 -\gamma(\gamma+4\alpha)^2\\ &+\tfrac{c}{\mu^2+c}\big[8c\alpha-4c\mu+6c\gamma+\gamma(\gamma+4\alpha)^2\big]\big\}.\nonumber \end{align} $$
$$ \begin{align} \xi(\kappa_1)-U(\kappa_3)=&\tfrac{\kappa_2}{\mu^2+c} \big\{4\mu c-5\gamma c-8\alpha c+\gamma\mu^2-\gamma(\gamma+4\alpha)^2 \nonumber\\ &+\tfrac{c}{\mu^2+c}\big[\mu^3+8c\alpha -3c\mu+6c\gamma+\gamma(\gamma+4\alpha)^2\big]\big\}\nonumber\\ =&\tfrac{\kappa_2}{\mu^2+c}\big\{5\mu c-5\gamma c-8\alpha c+\gamma\mu^2 -\gamma(\gamma+4\alpha)^2\\ &+\tfrac{c}{\mu^2+c}\big[8c\alpha-4c\mu+6c\gamma+\gamma(\gamma+4\alpha)^2\big]\big\}.\nonumber \end{align} $$
On the other hand, substituting (4.2) into (3.17) and applying (3.3), we obtain
From (4.11) and (4.12), we obtain
 $$ \begin{align*} \begin{split} 0=\tfrac{\kappa_2}{\mu^2+c}&\big\{5\mu c-5\gamma c-8\alpha c+\gamma\mu^2 -\gamma(\gamma+4\alpha)^2\\ &+\tfrac{c}{\mu^2+c}(8c\alpha-4c\mu+6c\gamma+\gamma(\gamma+4\alpha)^2) -c(\mu-\gamma-4\alpha)\big\}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} 0=\tfrac{\kappa_2}{\mu^2+c}&\big\{5\mu c-5\gamma c-8\alpha c+\gamma\mu^2 -\gamma(\gamma+4\alpha)^2\\ &+\tfrac{c}{\mu^2+c}(8c\alpha-4c\mu+6c\gamma+\gamma(\gamma+4\alpha)^2) -c(\mu-\gamma-4\alpha)\big\}. \end{split} \end{align*} $$
Since
![]() $\tfrac {\kappa _2}{\mu ^2+c}\neq 0$
, we obtain
$\tfrac {\kappa _2}{\mu ^2+c}\neq 0$
, we obtain
 $$ \begin{align} 0=&4\mu c-4\gamma c-4\alpha c+\gamma\mu^2-\gamma(\gamma+4\alpha)^2 \\ &+\tfrac{c}{\mu^2+c}\big[8c\alpha-4c\mu+6c\gamma+\gamma(\gamma+4\alpha)^2\big].\nonumber \end{align} $$
$$ \begin{align} 0=&4\mu c-4\gamma c-4\alpha c+\gamma\mu^2-\gamma(\gamma+4\alpha)^2 \\ &+\tfrac{c}{\mu^2+c}\big[8c\alpha-4c\mu+6c\gamma+\gamma(\gamma+4\alpha)^2\big].\nonumber \end{align} $$
By using (3.34), we can rewrite (4.13) to obtain
 $$ \begin{align} 0=&4\mu c-3\gamma c-c\Big(\mu-\tfrac{c}{\mu}\Big)+\gamma\mu^2-\gamma\Big(\mu-\tfrac{c}{\mu}\Big)^2 \nonumber\\ &+\tfrac{c}{\mu^2+c}\Big[8c\alpha-4c\mu+6c\gamma+\gamma\Big(\mu-\tfrac{c}{\mu}\Big)^2\Big]. \end{align} $$
$$ \begin{align} 0=&4\mu c-3\gamma c-c\Big(\mu-\tfrac{c}{\mu}\Big)+\gamma\mu^2-\gamma\Big(\mu-\tfrac{c}{\mu}\Big)^2 \nonumber\\ &+\tfrac{c}{\mu^2+c}\Big[8c\alpha-4c\mu+6c\gamma+\gamma\Big(\mu-\tfrac{c}{\mu}\Big)^2\Big]. \end{align} $$
Multiplying both sides of (4.14) by
![]() $\mu ^2(\mu ^2+c)$
, we shall obtain
$\mu ^2(\mu ^2+c)$
, we shall obtain
Since
![]() $c\mu \neq 0$
, we have
$c\mu \neq 0$
, we have
By using (3.3), we can rewrite (4.15) to obtain that
It follows from (3.27) that
![]() $\bullet $
Substituting the derivative of (4.17) along
$\bullet $
Substituting the derivative of (4.17) along
![]() $\xi $
and using (3.10), we obtain
$\xi $
and using (3.10), we obtain
Since
![]() $\beta \neq 0$
and
$\beta \neq 0$
and
![]() $\mu \neq 0$
, we obtain that
$\mu \neq 0$
, we obtain that
![]() $\kappa _2\equiv 0$
, a contradiction to Lemma 3.3.
$\kappa _2\equiv 0$
, a contradiction to Lemma 3.3.
We have completed the proof of Theorem 1.1.
Acknowledgment
The authors would like to express their heartfelt thanks to the referee for his/her carefully reading of the submitted version and made valuable comments.