Hostname: page-component-f554764f5-sl7kg Total loading time: 0 Render date: 2025-04-23T07:29:48.072Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasi-steady transitions in confined convection

Published online by Cambridge University Press:  26 November 2024

Takatoshi Yanagisawa Open the ORCID record for Takatoshi Yanagisawa [Opens in a new window] ,
Sota Takano ,
Daisuke Noto Open the ORCID record for Daisuke Noto [Opens in a new window] ,
Masanori Kameyama Open the ORCID record for Masanori Kameyama [Opens in a new window]  and
Yuji Tasaka Open the ORCID record for Yuji Tasaka [Opens in a new window]
Takatoshi Yanagisawa
Affiliation:
Japan Agency for Marine-Earth Science and Technology (JAMSTEC), 237-0061 Yokosuka, Japan Laboratory for Flow Control, Faculty of Engineering, Hokkaido University, 060-8628 Sapporo, Japan
Sota Takano
Affiliation:
Laboratory for Flow Control, Faculty of Engineering, Hokkaido University, 060-8628 Sapporo, Japan
Daisuke Noto
Affiliation:
Department of Earth and Environmental Science, University of Pennsylvania, Philadelphia, PA 19104, USA
Masanori Kameyama
Affiliation:
Japan Agency for Marine-Earth Science and Technology (JAMSTEC), 237-0061 Yokosuka, Japan Geodynamics Research Center, Ehime University, 790-8577 Matsuyama, Japan
Yuji Tasaka*
Affiliation:
Japan Agency for Marine-Earth Science and Technology (JAMSTEC), 237-0061 Yokosuka, Japan Laboratory for Flow Control, Faculty of Engineering, Hokkaido University, 060-8628 Sapporo, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

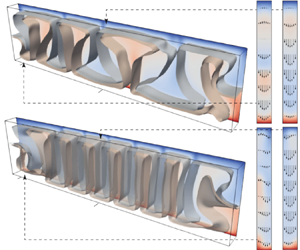
We study the effect of geometrical confinement on thermal convection by laboratory experiments and direct numerical simulations using Hele-Shaw geometries (typically the gap-to-height aspect ratio $0.12$) for the Prandtl number $Pr \geq 40$ and the Rayleigh number $Ra \leq 6 \times 10^7$. Under such strong unidirectional confinement, the convective flows are forced to squeeze within the narrow gap and exhibit unique spatiotemporal signatures, which contrast those in unconfined systems. With the increase of $Ra$, we identify that the system experiences five convective regimes that can be classified from two aspects, time dependency and flow dimensionality: (I) quasi-two-dimensional (quasi-2-D) steady flow; (II) quasi-2-D flow with oscillatory corner rolls; (III) three-dimensional (3-D) flow with oscillatory corner rolls; (IV) 3-D steady flow; and (V) 3-D time-dependent motion of plumes around sidewalls. Notably, unsteadiness does not emerge globally, but is localised near the sidewalls as oscillatory corner rolls, resulting in the regime transitions happening in a quasi-steady manner. We confirm that these regime transitions show less dependence on both $Pr$ and the other (wider) horizontal scale of the geometry. Moreover, we find that a recently proposed criterion ‘degree of confinement’ (Noto et al., Proc. Natl Acad. Sci. USA, vol. 121, issue 28, 2024, e2403699121) successfully explains the emergence of 3-D structures, expanding its applicable range to smaller $Ra$. This study deepens the comprehension of the thermal convection emerging in tight geometries, impacting across disciplines, such as Earth and planetary science, and thermal engineering.

JFM classification

Low-Reynolds-number flows: Hele-Shaw flows Convection: Buoyancy-driven instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , A44
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503.CrossRefGoogle Scholar
Atkinson, B.W. & Wu Zhang, J. 1996 Mesoscale shallow convection in the atmosphere. Rev. Geophys. 34 (4), 403–431.CrossRefGoogle Scholar
Babushkin, I.A., Glazkin, I.V., Demin, V.A., Platonova, A.N. & Putin, G.F. 2009 Variability of a typical flow in a Hele-Shaw cell. Fluid Dyn. 44 (5), 631–640.CrossRefGoogle Scholar
Backhaus, S., Turitsyn, K. & Ecke, R.E. 2011 Convective instability and mass transport of diffusion layers in a Hele-Shaw geometry. Phys. Rev. Lett. 106 (10), 104501.CrossRefGoogle Scholar
Benn, D., Gulley, J., Luckman, A., Adamek, A. & Glowacki, P.S. 2009 Englacial drainage systems formed by hydrologically driven crevasse propagation. J. Glaciol. 55 (191), 513–523.CrossRefGoogle Scholar
Bouffard, D. & Wüest, A. 2019 Convection in lakes. Annu. Rev. Fluid Mech. 51 (1), 189–215.CrossRefGoogle Scholar
Cheng, J.S., Stellmach, S., Ribeiro, A., Grannan, A., King, E.M. & Aurnou, J.M. 2015 Laboratory-numerical models of rapidly rotating convection in planetary cores. Geophys. J. Intl 201 (1), 1–17.CrossRefGoogle Scholar
Cherkaoui, A.S.M. & Wilcock, W.S.D. 2001 Laboratory studies of high Rayleigh number circulation in an open-top Hele-Shaw cell: an analog to mid-ocean ridge hydrothermal systems. J. Geophys. Res. Solid Earth 106 (B6), 10983–11000.CrossRefGoogle Scholar
Chong, K.L., Huang, S.-D., Kaczorowski, M. & Xia, K.-Q. 2015 Condensation of coherent structures in turbulent flows. Phys. Rev. Lett. 115 (26), 264503.CrossRefGoogle ScholarPubMed
Chong, K.L., Wagner, S., Kaczorowski, M., Shishkina, O. & Xia, K.-Q. 2018 Effect of Prandtl number on heat transport enhancement in Rayleigh–Bénard convection under geometrical confinement. Phys. Rev. Fluids 3 (1), 013501.CrossRefGoogle Scholar
Chong, K.L. & Xia, K.-Q. 2016 Exploring the severely confined regime in Rayleigh–Bénard convection. J. Fluid Mech. 805, R4.CrossRefGoogle Scholar
Chorin, A.J. 1967 A numerical method for solving incompressible viscous flow problems. J. Comput. Phys. 2 (1), 12–26.CrossRefGoogle Scholar
De Paoli, M. 2023 Convective mixing in porous media: a review of Darcy, pore-scale and Hele-Shaw studies. Eur. Phys. J. E 46 (12), 129.CrossRefGoogle ScholarPubMed
Doering, C.R. 2020 Turning up the heat in turbulent thermal convection. Proc. Natl Acad. Sci. USA 117 (18), 9671–9673.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Hartlep, T., Tilgner, A. & Busse, F.H. 2003 Large scale structures in Rayleigh–Bénard convection at high Rayleigh numbers. Phys. Rev. Lett. 91 (6), 064501.CrossRefGoogle ScholarPubMed
Hewitt, D.R., Neufeld, J.A. & Lister, J.R. 2012 Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 108 (22), 224503.CrossRefGoogle Scholar
Horn, S., Shishkina, O. & Wagner, C. 2013 On non-Oberbeck–Boussinesq effects in three-dimensional Rayleigh–Bénard convection in glycerol. J. Fluid Mech. 724, 175–202.CrossRefGoogle Scholar
Huang, S.-D., Kaczorowski, M., Ni, R. & Xia, K.-Q. 2013 Confinement-induced heat-transport enhancement in turbulent thermal convection. Phys. Rev. Lett. 111 (10), 104501.CrossRefGoogle ScholarPubMed
Jha, B., Cueto-Felgueroso, L. & Juanes, R. 2011 Fluid mixing from viscous fingering. Phys. Rev. Lett. 106 (19), 194502.CrossRefGoogle ScholarPubMed
Jones, T.J. & Llewellin, E.W. 2021 Convective tipping point initiates localization of basaltic fissure eruptions. Earth Planet. Sci. Lett. 553, 116637.CrossRefGoogle Scholar
Kameyama, M. 2005 ACuTEMan: a multigrid-based mantle convection simulation code and its optimization to the Earth Simulator. J. Earth Simulator 4, 2–10.Google Scholar
Kameyama, M., Kageyama, A. & Sato, T. 2005 Multigrid iterative algorithm using pseudo- compressibility for three-dimensional mantle convection with strongly variable viscosity. J. Comput. Phys. 206 (1), 162–181.CrossRefGoogle Scholar
Kameyama, M., Kageyama, A. & Sato, T. 2008 Multigrid-based simulation code for mantle convection in spherical shell using yin-yang grid. Phys. Earth Planet. Inter. 171 (1–4), 19–32.CrossRefGoogle Scholar
Koschmieder, E.L. 1993 Bénard Cells and Taylor Vortices, chap. 6.1. Cambridge University Press.Google Scholar
Koster, J.N., Ehrhard, P. & Müller, U. 1986 Nonsteady end effects in Hele-Shaw cells. Phys. Rev. Lett. 56 (17), 1802–1804.CrossRefGoogle ScholarPubMed
Krishnamurti, R. 1970 a On the transition to turbulent convection. Part 1. The transition from two- to three-dimensional flow. J. Fluid Mech. 42 (2), 295–307.CrossRefGoogle Scholar
Krishnamurti, R. 1970 b On the transition to turbulent convection. Part 2. The transition to time-dependent flow. J. Fluid Mech. 42 (2), 309–320.CrossRefGoogle Scholar
Kuo, J.S. & Chiu, D.T. 2011 Controlling mass transport in microfluidic devices. Annu. Rev. Anal. Chem. 4, 275–296.CrossRefGoogle ScholarPubMed
Letelier, J.A., Mujica, N. & Ortega, J.H. 2019 Perturbative corrections for the scaling of heat transport in a Hele-Shaw geometry and its application to geological vertical fractures. J. Fluid Mech. 864, 746–767.CrossRefGoogle Scholar
Letelier, J.A., Ulloa, H.N., Leyrer, J. & Ortega, J.H. 2023 Scaling CO$_2$–brine mixing in permeable media via analogue models. J. Fluid Mech. 962, A8.CrossRefGoogle Scholar
Liang, Y., Wen, B., Hesse, M.A. & DiCarlo, D. 2018 Effect of dispersion on solutal convection in porous media. Geophys. Res. Lett. 45 (18), 9690–9698.CrossRefGoogle Scholar
Marshall, J. & Schott, F. 1999 Open-ocean convection: observations, theory, and models. Rev. Geophys. 37 (1), 1–64.CrossRefGoogle Scholar
Noto, D., Letelier, J.A. & Ulloa, H.N. 2024 Plume-scale confinement on thermal convection. Proc. Natl Acad. Sci. USA 121 (28), e2403699121.CrossRefGoogle ScholarPubMed
Noto, D., Ohie, K., Yoshida, T. & Tasaka, Y. 2023 a Optical spinning rheometry test on viscosity curves of less viscous fluids at low shear rate range. Exp. Fluids 64 (1), 18.CrossRefGoogle Scholar
Noto, D., Tasaka, Y. & Murai, Y. 2023 b Low-cost 3D color particle tracking velocimetry: application to thermal turbulence in water. Exp. Fluids 64 (5), 92.CrossRefGoogle Scholar
Noto, D., Ulloa, H.N. & Letelier, J.A. 2023 c Reconstructing temperature fields for thermally-driven flows under quasi-steady state. Exp. Fluids 64 (4), 74.CrossRefGoogle Scholar
Nsengiyumva, E.M. & Alexandridis, P. 2022 Xanthan gum in aqueous solutions: fundamentals and applications. Intl J. Biol. Macromol. 216, 583–604.CrossRefGoogle ScholarPubMed
Ozawa, M., Müller, U., Kimura, I. & Takamori, T. 1992 Flow and temperature measurement of natural convection in a Hele-Shaw cell using a thermo-sensitive liquid-crystal tracer. Exp. Fluids 12 (4-5), 213–222.CrossRefGoogle Scholar
Pandey, A., Verma, M.K. & Mishra, P.K. 2014 Scaling of heat flux and energy spectrum for very large Prandtl number convection. Phys. Rev. E 89 (2), 023006.CrossRefGoogle ScholarPubMed
Patterson, J.W., Driesner, T., Matthai, S. & Tomlinson, R. 2018 Heat and fluid transport induced by convective fluid circulation within a fracture or fault. J. Geophys. Res. Solid Earth 123 (4), 2658–2673.CrossRefGoogle Scholar
Plumley, M. & Julien, K. 2019 Scaling laws in Rayleigh–Bénard convection. Earth Space Sci. 6 (9), 1580–1592.CrossRefGoogle Scholar
Schmalzl, J., Breuer, M. & Hansen, U. 2002 The influence of the Prandtl number on the style of vigorous thermal convection. Geophys. Astrophys. Fluid Dyn. 96 (5), 381–403.CrossRefGoogle Scholar
Schubert, G. 1992 Numerical models of mantle convection. Annu. Rev. Fluid Mech. 24, 359–394.CrossRefGoogle Scholar
Shishkina, O. 2021 Rayleigh–Bénard convection: the container shape matters. Phys. Rev. Fluids 6, 090502.CrossRefGoogle Scholar
Stone, H.A., Stroock, A.D. & Ajdari, A. 2004 Engineering flows in small devices: microfluidics toward a lab-on-a-chip. Annu. Rev. Fluid Mech. 36, 381–411.CrossRefGoogle Scholar
Ulloa, H.N. & Letelier, J.A. 2022 Energetics and mixing of thermally driven flows in Hele-Shaw cells. J. Fluid Mech. 930, A16.CrossRefGoogle Scholar
Vera, M. & Linan, A. 2010 Laminar counterflow parallel-plate heat exchangers: exact and approximate solutions. Intl J. Heat Mass Transfer 53 (21–22), 4885–4898.CrossRefGoogle Scholar
Weiss, S., He, X., Ahlers, G., Bodenschatz, E. & Shishkina, O. 2018 Bulk temperature and heat transport in turbulent Rayleigh–Bénard convection of fluids with temperature-dependent properties. J. Fluid Mech. 851, 374–390.CrossRefGoogle Scholar
Whitcomb, P.J. & Macosko, C.W. 1978 Rheology of xanthan gum. J. Rheol. 22 (5), 493–505.CrossRefGoogle Scholar
Xia, K.-Q., Lam, S. & Zhou, S.-Q. 2002 Heat-flux measurement in high-Prandtl-number turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 88 (6), 064501.CrossRefGoogle ScholarPubMed
Zhang, L. & Xia, K.-Q. 2023 Heat transfer in a quasi-one-dimensional Rayleigh–Bénard convection cell. J. Fluid Mech. 973, R5.CrossRefGoogle Scholar
Zocchi, G., Moses, E. & Libchaber, A. 1990 Coherent structures in turbulent convection, an experimental study. Physica A 166 (3), 387–407.CrossRefGoogle Scholar