1 THE GALACTIC BULGE
The bar-like shape and boxy/peanut structure of the Galactic bulge, found also in a large number of external galaxies (Lütticke, Dettmar, & Pohlen Reference Lütticke, Dettmar and Pohlen2000; Kormendy & Kennicutt Reference Kormendy and Kennicutt2004), have been known for long time (Okuda et al. Reference Okuda, Maihara, Oda and Sugiyama1977; Maihara et al. Reference Maihara, Oda, Sugiyama and Okuda1978; Weiland et al. Reference Weiland1994; Dwek et al. Reference Dwek1995; Binney, Gerhard, & Spergel Reference Binney, Gerhard and Spergel1997; Babusiaux & Gilmore Reference Babusiaux and Gilmore2005; López-Corredoira et al. Reference López-Corredoira, Cabrera-Lavers and Gerhard2005; Rattenbury et al. Reference Rattenbury, Mao, Sumi and Smith2007; Cao et al. Reference Cao, Mao, Nataf, Rattenbury and Gould2013). This structure constitutes the innermost thick part of a longer and flatter bar, extending up to about 4–5 kpc from the Galaxy centre (Benjamin et al. Reference Benjamin2005; Cabrera-Lavers et al. Reference Cabrera-Lavers, Hammersley, González-Fernández, López-Corredoira, Garzón and Mahoney2007; Wegg, Gerhard, & Portail Reference Wegg, Gerhard and Portail2015). Its orientation is between 20° and 30° with respect to the Sun–Galaxy centre direction (Bissantz & Gerhard Reference Bissantz and Gerhard2002; Shen et al. Reference Shen, Rich, Kormendy, Howard, De Propris and Kunder2010; Wegg & Gerhard Reference Wegg and Gerhard2013), and at vertical distances from the plane of about 400 pc, a prominent X-shape becomes visible in the data (McWilliam & Zoccali Reference McWilliam and Zoccali2010; Nataf et al. Reference Nataf, Udalski, Gould, Fouqué and Stanek2010; Wegg & Gerhard Reference Wegg and Gerhard2013; Gonzalez et al. Reference Gonzalez, Zoccali, Debattista, Valenti and Minniti2015a), indicative of a stellar bar evolving secularly after buckling (Combes & Sanders Reference Combes and Sanders1981; Athanassoula Reference Athanassoula2005; Debattista et al. Reference Debattista, Mayer, Carollo, Moore, Wadsley and Quinn2006; Martinez-Valpuesta, Shlosman, & Heller Reference Martinez-Valpuesta, Shlosman and Heller2006; Ness et al. Reference Ness2012; Di Matteo et al. Reference Di Matteo2014).
Studies of the bulge kinematics also support its bar-like nature and thus ultimately its link to the disc. The bulge shows indeed cylindrical rotation (Howard et al. Reference Howard, Rich, Reitzel, Koch, De Propris and Zhao2008, Reference Howard2009; Kunder et al. Reference Kunder2012), as predicted by N-body models where the bulge is formed via the buckling of a pre-existing thin stellar bar formed in a cold stellar disc (Shen et al. Reference Shen, Rich, Kormendy, Howard, De Propris and Kunder2010; Saha, Martinez-Valpuesta, & Gerhard Reference Saha, Martinez-Valpuesta and Gerhard2012; Ness et al. Reference Ness2013b; Di Matteo et al. Reference Matteo2015). The vertex deviation observed in the stellar velocities (Zhao, Spergel, & Rich Reference Zhao, Spergel and Rich1994; Soto, Rich, & Kuijken Reference Soto, Rich and Kuijken2007; Babusiaux et al. Reference Babusiaux2010), especially for its metal-rich population (Babusiaux et al. Reference Babusiaux2010), is also an indication of its asymmetric structure.
Bulge stars span a large range in [Fe/H] and [α/Fe] values (with
![]() $-3\text{dex} \le \text{[Fe/H]} \le \text{0.6dex and 0dex} \le \text{[$\alpha $/Fe]} \le \text{0.4dex}$
, see Rich Reference Rich1988; McWilliam & Rich Reference McWilliam and Rich2004; Zoccali et al. Reference Zoccali2003; Ness et al. Reference Ness2013a; Gonzalez et al. Reference Gonzalez2015b), and several recent works show that their chemical patterns strikingly resemble those of stars at the solar vicinity (Meléndez et al. Reference Meléndez2008; Alves-Brito et al. Reference Alves-Brito, Meléndez, Asplund, Ramírez and Yong2010; Bensby et al. Reference Bensby2010; Ryde et al. Reference Ryde2010; Gonzalez et al. Reference Gonzalez2011c, Reference Gonzalez2015b; Ryde et al. Reference Ryde, Schultheis, Grieco, Matteucci, Rich and Uttenthaler2016; Ness & Freeman Reference Ness and Freeman2016), once the outer disc sequence—present at the solar vicinity and not in the inner disc (see next Section)—is removed from the comparison. It is important here to note that previous works (McWilliam & Rich Reference McWilliam and Rich1994; Rich & Origlia Reference Rich and Origlia2005; Zoccali et al. Reference Zoccali2006; Lecureur et al. Reference Lecureur, Hill, Zoccali, Barbuy, Gómez, Minniti, Ortolani and Renzini2007; Hill et al. Reference Hill2011; Johnson et al. Reference Johnson, Rich, Fulbright, Valenti and McWilliam2011) have pointed out a difference between the chemistry of the bulge and that of the thick disc at the solar vicinity, with bulge stars being more α-enhanced than thick disc stars of the same metallicity. This argument naturally led to exclude that the α-enhanced population of the bulge could be the result of the secular evolution of the disc, via bar formation (see for example Zoccali et al. Reference Zoccali2006), as suggested also by chemical evolution models (Matteucci & Brocato Reference Matteucci and Brocato1990; Matteucci & Romano Reference Matteucci and Romano1999; Ballero et al. Reference Ballero, Matteucci, Origlia and Rich2007). However, in more recent studies, these differences appear much less dramatic than previous findings. Quoting Johnson et al. (Reference Johnson, Rich, Fulbright, Valenti and McWilliam2011), for example: “While [. . .] the [Si/Fe], [Ca/Fe], and [α/Fe] ratios are generally enhanced by ~ 0.2 dex in bulge giants compared to thick disk giants (and dwarfs), this enhancement is not extraordinarily different than the combined measurement uncertainty and choice of abundance normalization scale [. . .]. Interestingly, both the thick disk and bulge appear to show similar declines in the [α/Fe] ratio at [Fe/H] ≈ −0.3.” Indeed, the current data show that the offset between the chemistry of bulge stars and that of discs stars at the solar vicinity (see Bensby et al. Reference Bensby2010; Gonzalez et al. Reference Gonzalez2011c; Adibekyan et al. Reference Adibekyan, Sousa, Santos, Mena, González Hernández, Israelian, Mayor and Khachatryan2012; Johnson et al. Reference Johnson, Rich, Kobayashi, Kunder and Koch2014; Ryde et al. Reference Ryde, Schultheis, Grieco, Matteucci, Rich and Uttenthaler2016) is comparable to the existing systematics between spectroscopic studies of stars in the solar neighbourhood (compare, for example, Alves-Brito et al. Reference Alves-Brito, Meléndez, Asplund, Ramírez and Yong2010; Gonzalez et al. Reference Gonzalez2011c; Adibekyan et al. Reference Adibekyan, Sousa, Santos, Mena, González Hernández, Israelian, Mayor and Khachatryan2012; Bensby, Feltzing, & Oey Reference Bensby, Feltzing and Oey2014) or between the differences among different bulge studies (Gonzalez et al. Reference Gonzalez2011c; Bensby et al. Reference Bensby2010; Johnson et al. Reference Johnson, Rich, Kobayashi and Fulbright2012, Reference Johnson, Rich, Kobayashi, Kunder and Koch2014; Van der Swaelmen et al. Reference Van der Swaelmen, Barbuy, Hill, Zoccali, Minniti, Ortolani and Gómez2016).
$-3\text{dex} \le \text{[Fe/H]} \le \text{0.6dex and 0dex} \le \text{[$\alpha $/Fe]} \le \text{0.4dex}$
, see Rich Reference Rich1988; McWilliam & Rich Reference McWilliam and Rich2004; Zoccali et al. Reference Zoccali2003; Ness et al. Reference Ness2013a; Gonzalez et al. Reference Gonzalez2015b), and several recent works show that their chemical patterns strikingly resemble those of stars at the solar vicinity (Meléndez et al. Reference Meléndez2008; Alves-Brito et al. Reference Alves-Brito, Meléndez, Asplund, Ramírez and Yong2010; Bensby et al. Reference Bensby2010; Ryde et al. Reference Ryde2010; Gonzalez et al. Reference Gonzalez2011c, Reference Gonzalez2015b; Ryde et al. Reference Ryde, Schultheis, Grieco, Matteucci, Rich and Uttenthaler2016; Ness & Freeman Reference Ness and Freeman2016), once the outer disc sequence—present at the solar vicinity and not in the inner disc (see next Section)—is removed from the comparison. It is important here to note that previous works (McWilliam & Rich Reference McWilliam and Rich1994; Rich & Origlia Reference Rich and Origlia2005; Zoccali et al. Reference Zoccali2006; Lecureur et al. Reference Lecureur, Hill, Zoccali, Barbuy, Gómez, Minniti, Ortolani and Renzini2007; Hill et al. Reference Hill2011; Johnson et al. Reference Johnson, Rich, Fulbright, Valenti and McWilliam2011) have pointed out a difference between the chemistry of the bulge and that of the thick disc at the solar vicinity, with bulge stars being more α-enhanced than thick disc stars of the same metallicity. This argument naturally led to exclude that the α-enhanced population of the bulge could be the result of the secular evolution of the disc, via bar formation (see for example Zoccali et al. Reference Zoccali2006), as suggested also by chemical evolution models (Matteucci & Brocato Reference Matteucci and Brocato1990; Matteucci & Romano Reference Matteucci and Romano1999; Ballero et al. Reference Ballero, Matteucci, Origlia and Rich2007). However, in more recent studies, these differences appear much less dramatic than previous findings. Quoting Johnson et al. (Reference Johnson, Rich, Fulbright, Valenti and McWilliam2011), for example: “While [. . .] the [Si/Fe], [Ca/Fe], and [α/Fe] ratios are generally enhanced by ~ 0.2 dex in bulge giants compared to thick disk giants (and dwarfs), this enhancement is not extraordinarily different than the combined measurement uncertainty and choice of abundance normalization scale [. . .]. Interestingly, both the thick disk and bulge appear to show similar declines in the [α/Fe] ratio at [Fe/H] ≈ −0.3.” Indeed, the current data show that the offset between the chemistry of bulge stars and that of discs stars at the solar vicinity (see Bensby et al. Reference Bensby2010; Gonzalez et al. Reference Gonzalez2011c; Adibekyan et al. Reference Adibekyan, Sousa, Santos, Mena, González Hernández, Israelian, Mayor and Khachatryan2012; Johnson et al. Reference Johnson, Rich, Kobayashi, Kunder and Koch2014; Ryde et al. Reference Ryde, Schultheis, Grieco, Matteucci, Rich and Uttenthaler2016) is comparable to the existing systematics between spectroscopic studies of stars in the solar neighbourhood (compare, for example, Alves-Brito et al. Reference Alves-Brito, Meléndez, Asplund, Ramírez and Yong2010; Gonzalez et al. Reference Gonzalez2011c; Adibekyan et al. Reference Adibekyan, Sousa, Santos, Mena, González Hernández, Israelian, Mayor and Khachatryan2012; Bensby, Feltzing, & Oey Reference Bensby, Feltzing and Oey2014) or between the differences among different bulge studies (Gonzalez et al. Reference Gonzalez2011c; Bensby et al. Reference Bensby2010; Johnson et al. Reference Johnson, Rich, Kobayashi and Fulbright2012, Reference Johnson, Rich, Kobayashi, Kunder and Koch2014; Van der Swaelmen et al. Reference Van der Swaelmen, Barbuy, Hill, Zoccali, Minniti, Ortolani and Gómez2016).
Evidence about the presence of multiple components, or populations, in the bulge comes from the investigation of its metallicity distribution function (hereafter MDF), at different latitudes and longitudes (Babusiaux et al. Reference Babusiaux2010; Hill et al. Reference Hill2011; Uttenthaler et al. Reference Uttenthaler, Schultheis, Nataf, Robin, Lebzelter and Chen2012; Ness et al. Reference Ness2013a; Rojas-Arriagada et al. Reference Rojas-Arriagada2014; Gonzalez et al. Reference Gonzalez2015b). In the largest spectroscopic study of the bulge conducted so far, the ARGOS survey (Freeman et al. Reference Freeman2013), Ness et al. (Reference Ness2013a) decomposed the global MDFs found at latitudes b = −5°, −7.5°, −10° (integrated over the whole range of longitudes − 15° ⩽ l ⩽ 15°) into five gaussian components, called A, B, C, D, and E, whose metallicities peak at about [Fe/H] = 0.1 dex, − 0.3 dex, − 0.7 dex, − 1.2 dex, and − 1.7 dex, respectively. Of those five components, D and E are negligible in the fields considered, representing 6% at most of the whole sample, while the proportion of populations A, B, and C has been shown to vary with the height from the plane: A represents about 40% of the sample at b = −5°, and decreases to 16 and 12%, respectively, at b = −7.5° and b = −10°; the C component, on the opposite, increases with the height from the plane, passing from 20% at b = −5° to 30% at b = −7.5° and to roughly 40% at b = −10°; B shows the smallest variations, and its fractional contribution to the bulge is significant at all latitudes considered in this study (40% at b = −5°, 50% at b = −7.5°, 44% at b = −10°). The different proportion of these components with height above the plane naturally explains the existence of a vertical metallicity gradient in the bulge, as reported by Ness et al. (Reference Ness2013a) and even before in the studies of Zoccali et al. (Reference Zoccali, Hill, Lecureur, Barbuy, Renzini, Minniti, Gómez and Ortolani2008), Gonzalez et al. (Reference Gonzalez, Rejkuba, Zoccali, Valenti and Minniti2011b), and Gonzalez et al. (Reference Gonzalez, Rejkuba, Zoccali, Valent, Minniti and Tobar2013). Interestingly, it has been shown that the structural and kinematic properties change from one component to the other (Ness et al. Reference Ness2013b, Reference Ness2013a). The most metal-rich components A and B, characterised by [Fe/H] ⩾ −0.5 dex, show a split in the distribution of K-magnitudes of their red clump stars. This distribution is particularly suitable to understand the underlying morphology. The density of a peanut-shaped bulge indeed shows some minimum in the centre, on its minor axis, minimum which is more accentuated at higher latitudes. On the line of sight, this produces a bimodal distribution, or a split, in the apparent K-magnitude of the red clump. In particular, it appears that in the Milky Way bulge, the deepest minima between peaks in the K-magnitude distribution are found in the most metal-rich population (i.e. population A, see Figure 1 reproduced from Ness et al. Reference Ness2013a). At the latitudes covered by ARGOS, component C does not show any split. Interestingly, however, the maximum in the K-magnitude distribution of its stars is not located at K = 12.9, as would be expected from a population which reaches its maximum density in the Galaxy centre, but rather it seems to peak where the far lobe of the peanut of populations A and B is found (again, see Figure 1 here reproduced from Ness et al. Reference Ness2013a). I will comment more on this point in Section 3.

Figure 1. From Ness et al. (Reference Ness2013a): Magnitude distribution of red clump stars along the bulge minor axis, at latitudes
![]() $\rm b=-5^\circ , -7.5^\circ \rm {and} -10^\circ$
. The clump stars are splitter into three different metallicity bins:
$\rm b=-5^\circ , -7.5^\circ \rm {and} -10^\circ$
. The clump stars are splitter into three different metallicity bins:
![]() $\text{[Fe/H]} > 0$
(red curve),
$\text{[Fe/H]} > 0$
(red curve),
![]() $-0.5\text{dex}\break < \text{[Fe/H]}< 0$
, and
$-0.5\text{dex}\break < \text{[Fe/H]}< 0$
, and
![]() $\text{[Fe/H]} < -0.5\text{dex}$
.
$\text{[Fe/H]} < -0.5\text{dex}$
.
At any given latitude, populations A, B, and C also show different kinematics (Ness et al. Reference Ness2013b). In particular, while the rotation curve, as deduced from radial velocities, is very similar in the three populations at all latitudesFootnote 1 , showing that the cylindrical rotation observed globally is also reproduced by each component individually, the velocity dispersions change with latitude and depend on the population examined. Component B has velocity dispersion profiles similar to A (but with higher absolute values), while component C shows dispersions constant both with longitude and latitude (see Figure 6 in Ness et al. Reference Ness2013b). As previously said, other studies have shown that the bulge MDF can be decomposed in multiple components. Depending on the number of components found (two in Babusiaux et al. Reference Babusiaux2010; Hill et al. Reference Hill2011; Bensby et al. Reference Bensby, Alves-Brito, Oey, Yong and Meléndez2011; Uttenthaler et al. Reference Uttenthaler, Schultheis, Nataf, Robin, Lebzelter and Chen2012; Rojas-Arriagada et al. Reference Rojas-Arriagada2014; Gonzalez et al. Reference Gonzalez2015b, and five in Ness et al. Reference Ness2013a), the fraction of stars attributed to the metal-rich and metal-poor component(s) change, and accordingly their structural and kinematic properties.
Finally, few words on the ages of stars in the bulge. Isochrone fitting of main-sequence turnoff stars in the bulge have led to the general conclusion that the majority of the stars in the bulge are old, typically ≳ 10 Gyr (Terndrup Reference Terndrup1988; Holtzman et al. Reference Holtzman1993; Ortolani et al. Reference Ortolani, Renzini, Gilmozzi, Marconi, Barbuy, Bica and Rich1995; Feltzing & Gilmore Reference Feltzing and Gilmore2000; Zoccali et al. Reference Zoccali2003; Clarkson et al. Reference Clarkson2008; Brown et al. Reference Brown2010; Valenti et al. Reference Valenti, Zoccali, Renzini, Brown, Gonzalez, Minniti, Debattista and Mayer2013). Such old ages have been interpreted as evidence that the bulge is a classical spheroid, that is a structure formed by mergers in the early phases of the Milky Way evolution (Ortolani et al. Reference Ortolani, Renzini, Gilmozzi, Marconi, Barbuy, Bica and Rich1995; Zoccali et al. Reference Zoccali2003; Brown et al. Reference Brown2010). However, some findings are questioning this picture. The dating of microlensed dwarf stars in the bulge at latitudes − 5° ⩽ b ⩽ −2° has shown, indeed, that the most metal-rich stars ([Fe/H] > −0.4 dex) show a range in stellar ages from 3 to 12 Gyr (Bensby et al. Reference Bensby2013, see also Figure 1 in Ness et al. Reference Ness, Debattista, Bensby, Feltzing, Cole, Johnson and Freeman2014). Young stars are not expected to be present in a classical spheroid, formed at early times, but are a natural outcome of a bulge formed secularly, through the bar (Ness et al. Reference Ness, Debattista, Bensby, Feltzing, Cole, Johnson and Freeman2014). Moreover, very recently, the VVV survey (Minniti et al. Reference Minniti2010) has reported the presence of numerous classical Cepheids (ages ⩽ 100 Myr) close to the Galaxy mid-plane (latitudes − 1.7° ⩽ b ⩽ 2°) and distributed along the whole bulge longitudinal extent (Dékány et al. Reference Dékány2015). The recent findings about the ages of stars in the bulge strengthen the global picture traced so far about the composite nature of this structure.
Overall, the bulge shows a very well-defined vertical structuring: the coldest, most metal-rich, and youngest components are preferentially found at low latitudes and the weight of the dynamically hottest and most metal-poor components ( − 1 ⩽ [Fe/H] ⩽ −0.5 dex) increases with height from the plane. A population with intermediate metallicity [ − 0.5 ⩽ [Fe/H] ⩽ 0 dex, population B in Ness et al. (Reference Ness2013a)] is however found at all latitudes in similar proportions. In the following of this review, I will discuss how it is possible to explain the trends observed for the main populations of the Galactic bulge—those with [Fe/H] ≳ −1 dex—in a scenario where these populations originate from the thin and thick discs of the Milky Way. I will not discuss further about stars with [Fe/H] ≲ −1 dex, whose origin is very likely linked to the Galactic halo and/or the very early phases of Galactic formation (Diemand, Madau, & Moore Reference Diemand, Madau and Moore2005; Tumlinson Reference Tumlinson2010; García Pérez et al. Reference Pérez2013; Ness et al. Reference Ness2013a; Howes et al. Reference Howes2014, Reference Howes2015).
2 THE GALACTIC DISC(S)
To understand the nature and origin of the Milky Way bulge, it is necessary to locate it in its environment: the Galaxy, and in particular its stellar disc(s). To present our most recent view of the Galactic discs, I have chosen to maintain the classical nomenclature adopted in the literature.
The thick disc belongs to a sequence which extends from high [α/Fe] and low metallicities until it joins the metal-rich thin disc, at solar [α/Fe] and super-solar metallicities. Because of the reasons recalled in the following of this section, I will refer to this sequence—running from the metal-poor thick disc to the metal-rich thin disc—also as the ‘inner disc sequence’. It is useful to remind at this point that this sequence shows a continuity in chemical patterns, with stellar ages decreasing with increasing metallicities from about 13 Gyr—for the oldest thick disc—to ages of about 9–10 Gyr—for the young thick disc—to ages younger than 8 Gyr for the metal-rich thin disc (see Figure 2 and Haywood et al. Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013). However, this continuity in chemical patterns hides a halt in the star-formation history of the inner disc, which took place at the transition from the thick to the thin disc formation (Haywood et al. Reference Haywood, Lehnert, Di Matteo, Snaith, Schultheis, Katz and Gomez2016). In the following, I use also the nomenclature ‘inner thin disc’: this is essentially equivalent to the metal-rich thin disc, since—as we will see in Section 2.2—the thin disc in the inner regions reduces to the metal-rich thin disc sequence only.

Figure 2. [α/Fe] versus [Fe/H] for the stars at solar vicinity in the sample of Adibekyan et al. (Reference Adibekyan, Sousa, Santos, Mena, González Hernández, Israelian, Mayor and Khachatryan2012) for which a robust age could be derived by Haywood et al. (Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013). The colours and the sizes of the symbols code the age of the stars. In this plot, the thick disc appears as the sequence which extends from high [α/Fe] and low metallicities until it joins the metal-rich thin disc, at solar [α/Fe] and super-solar metallicities. In the text, this sequence is also called the ‘inner disc sequence’. The metal-poor thin disc extends from [Fe/H] ~ − 0.7 dex and super-solar [α/Fe] to higher metallicities ([Fe/H] ~ −0.3 dex), but with the caveat that especially the upper limit in metallicity of this sequence is very uncertain. This sequence represents that of the ‘outer thin disc’. See Haywood et al. (Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013) and discussion in the text for the reasons behind the use of this nomenclature.
The metal-poor thin disc extends from [Fe/H] ~ −0.7 dex and super-solar [α/Fe] to higher metallicities ([Fe/H] ~ −0.3 dex), but with the caveat that especially the upper limit in metallicity of this sequence is very uncertain. I will refer to this sequence also as that of the ‘outer thin disc’.
The Sun is at the interface of the inner and outer thin discs, in a ~ 3 kpc wide region that shares chemical properties of both the inner and outer discs.
The ‘inner/outer disc’ nomenclature used in this paper has been already adopted in Haywood et al. (Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013), where we emphasised that “there is perhaps more continuity between the thin and thick discs than between the inner thin disc and outer thin disc. The inner thin disc and the thick disc seem to be more like the same structure [. . .] while the outer disc appears more like a separate component” (see also Figure 2). In the following, I will review the main reasons behind this vision, and explain why the most recent discoveries about the stellar populations of the Milky Way discs and their mutual links are of fundamental importance also for our understanding of the bulge, and its main components.
2.1. The thick disc
The thick disc, the last component discovered in the Milky Way in the early 80s (Gilmore & Reid Reference Gilmore and Reid1983) has been for longtime seen as a population formed in a short-lived ( ~ 1 Gyr) starburst episode produced at early epochs (Burkert, Truran, & Hensler Reference Burkert, Truran and Hensler1992; Chiappini, Matteucci, & Gratton Reference Chiappini, Matteucci and Gratton1997; Chiappini et al. Reference Chiappini, Matteucci, Beers and Nomoto1999; Mashonkina & Gehren Reference Mashonkina and Gehren2001; Fuhrmann Reference Fuhrmann2004; Reid Reference Reid2005; Bernkopf & Fuhrmann Reference Bernkopf and Fuhrmann2006), chemically separated from the stellar thin disc (Fuhrmann Reference Fuhrmann1998), and with a rotational lag with respect to thin disc stars between 50 and 100 km s−1 (Norris Reference Norris1986; Wyse & Gilmore Reference Wyse and Gilmore1986; Freeman Reference Freeman1987; Ojha et al. Reference Ojha, Bienayme, Robin and Mohan1994; Chiba & Beers Reference Chiba and Beers2000; Fuhrmann Reference Fuhrmann2008; Bensby et al. Reference Bensby, Feltzing and Oey2014). With a scale length estimated to be similar or greater than that of the thin disc (Ojha Reference Ojha2001; Robin et al. Reference Robin, Reylé, Derrière and Picaud2003; Jurić et al. Reference Jurić2008; de Jong et al. Reference de Jong, Yanny, Rix, Dolphin, Martin and Beers2010) on the basis of colour-selection studies, and with a thick-to-thin disc volume density normalisation at the solar vicinity of 10% at most (Robin et al. Reference Robin, Reylé, Derrière and Picaud2003; Jurić et al. Reference Jurić2008), it has been long considered as a minor contributor to the mass budget of the Galaxy, constituting about 20% of the thin disc mass (Robin et al. Reference Robin, Reylé, Derrière and Picaud2003). We will see in the following that the estimates of thick disc scale lengths and mass have been significantly revised. But before moving to discuss these new estimates, I will recall the main processes proposed for the formation of thick discs in galaxies.
Many different scenarios have been indeed suggested to explain thick discs formation. N-body models have shown that accretion of satellites can heat a kinematically cold disc and form, in few Gyrs, thick discs with vertical sizes, rotational lags, stellar eccentricities, and masses similar to those observed for the Milky Way for appropriate orbital parameters, mass ratios, and gas fractions of the progenitor galaxies (Quinn, Hernquist, & Fullagar Reference Quinn, Hernquist and Fullagar1993; Walker, Mihos, & Hernquist Reference Walker, Mihos and Hernquist1996; Huang & Carlberg Reference Huang and Carlberg1997; Sellwood, Nelson, & Tremaine Reference Sellwood, Nelson and Tremaine1998; Velazquez & White Reference Velazquez and White1999; Bekki & Chiba Reference Bekki and Chiba2001; Hänninen & Flynn Reference Hänninen and Flynn2002; Read et al. Reference Read, Lake, Agertz and Debattista2008; Villalobos & Helmi Reference Villalobos and Helmi2008, Reference Villalobos and Helmi2009; Purcell, Kazantzidis, & Bullock Reference Purcell, Kazantzidis and Bullock2009; Moster et al. Reference Moster, Macciò, Somerville, Johansson and Naab2010; Qu et al. Reference Qu, Di Matteo, Lehnert, van Driel and Jog2010, Reference Qu, Di Matteo, Lehnert and van Driel2011; House et al. Reference House2011; Bekki & Tsujimoto Reference Bekki and Tsujimoto2011; Di Matteo et al. Reference Di Matteo, Lehnert, Qu and van Driel2011; Moster et al. Reference Moster, Macciò, Somerville, Naab and Cox2012). One of the main objection to this scenario is that it should lead to a flaring of the disc (Bournaud, Elmegreen, & Martig Reference Bournaud, Elmegreen and Martig2009), while usually these structures are not observed to flare (van der Kruit & Searle Reference van der Kruit and Searle1982; de Grijs Reference de Grijs1998; Comerón et al. Reference Comerón2011). Note however that recently it has been shown that it is possible to reconcile an apparent lack of flaring with thick disc formed via satellite heating (Minchev et al. Reference Minchev, Martig, Streich, Scannapieco, de Jong and Steinmetz2015).
Mergers of gas rich subunits, in which discs form thick ab initio, are also a viable mechanism of formation (Brook et al. Reference Brook, Kawata, Gibson and Freeman2004, Reference Brook, Richard, Kawata, Martel and Gibson2007; Richard et al. Reference Richard, Brook, Martel, Kawata, Gibson and Sanchez-Blazquez2010).
Clumpy disc galaxies, where massive gas and stellar over densities scatter stars in a pre-existing thin disc, making the overall disc thicker, have also been shown to be able to form thick structures in about 1 Gyr (Bournaud et al. Reference Bournaud, Elmegreen and Martig2009), as suggested by Noguchi (Reference Noguchi1996). However, this scenario may have difficulties in explaining the chemo-kinematic relations satisfied by thick disc stars in the Milky Way (see Inoue & Saitoh Reference Inoue and Saitoh2014).
Finally, secular evolution processes, like radial migration, have been suggested to be able to explain the characteristics of the thick disc at the solar vicinity, namely its structure, kinematic, and chemical properties (Schönrich & Binney Reference Schönrich and Binney2009b; Loebman et al. Reference Loebman, Roškar, Debattista, Ivezić, Quinn and Wadsley2011). However, the effectiveness of this process in heating the disc has been repeatedly questioned (Minchev et al. Reference Minchev, Famaey, Quillen, Dehnen, Martig and Siebert2012; Vera-Ciro et al. Reference Vera-Ciro, D’Onghia, Navarro and Abadi2014; Halle et al. Reference Halle, Di Matteo, Haywood and Combes2015).
These ‘classical’ picture and scenarios have been recently challenged by a number of findings.
-
• Large scale spectroscopic surveys, like SEGUE and APOGEE, have shown the existence of a structural continuity between the thick and thin discs (Bovy, Rix, & Hogg Reference Bovy, Rix and Hogg2012a; Bovy et al. Reference Bovy, Rix, Liu, Hogg, Beers and Lee2012c, Reference Bovy, Rix, Schlafly, Nidever, Holtzman, Shetrone and Beers2015), and inside the thick disc itself. The morphological-chemical structuring of the thick disc can be appreciated in Figure 3 reproduced from Bovy et al. (Reference Bovy, Rix, Liu, Hogg, Beers and Lee2012c), where the vertical and radial scale lengths of disc stars grouped in bins of ([α/Fe]–[Fe/H])—the so-called ‘mono-abundance populations’ in Bovy et al. studies—are plotted, with colours coding the [α/Fe] and [Fe/H], respectively. Alpha-abundant [i.e. [α/Fe] > ~ 0.2–0.3 dex in the Bovy et al. (Reference Bovy, Rix, Liu, Hogg, Beers and Lee2012c) scale], thick disc stars are characterised by short scale lengths, and have scale heights that diminish with decreasing [α/Fe] and increasing [Fe/H]Footnote 2 . Overall, the α-enhanced thick disc has a scale length significantly shorter than that of the thin disc as a whole ( ~ 2 kpc for the thick disc, and about 3.6 kpc for the thin; see Bovy et al. Reference Bovy, Rix, Liu, Hogg, Beers and Lee2012c; Cheng et al. Reference Cheng2012). This scale length is about a factor of two smaller than previous estimates (Ojha Reference Ojha2001; Jurić et al. Reference Jurić2008; de Jong et al. Reference de Jong, Yanny, Rix, Dolphin, Martin and Beers2010). That the thick disc had a shorter scale length than the thin disc was also found by means of high-resolution spectroscopic studies, which suggest a scale length for this population similar to that found by APOGEE and SEGUE (see Bensby et al. Reference Bensby, Alves-Brito, Oey, Yong and Meléndez2011).

Figure 3. From Bovy et al. (Reference Bovy, Rix, Liu, Hogg, Beers and Lee2012c): vertical scale heights versus radial scale lengths for disc mono-abundance populations. In the top panel, points are colour-coded by [α/Fe], in the bottom panel by [Fe/H]. Alpha-abundant [i.e. [α/Fe] > ~ 0.2–0.3 dex in the Bovy et al. (Reference Bovy, Rix, Liu, Hogg, Beers and Lee2012c) scale], thick disc stars are characterised by short scale lengths, and have scale heights that diminish with decreasing [α/Fe] and increasing [Fe/H].
-
• The analysis and dating of high spectroscopic data for stars at the solar vicinity have shown that the stars in the Galactic disc(s) satisfy a very well defined [α/Fe]—age relation and that the α-enhanced thick disc formed in a prolonged burst of star formation (lasting 3–4 Gyr, see Haywood et al. Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013). Note that since those stars span a wide range of pericentre and apocentre distances, up to 1–2 kiloparsecs from the Galactic centre, this relation is not local but should apply to the whole thick disc (see discussion in Haywood, et al. Reference Haywood, Di Matteo, Snaith and Lehnert2015).
-
• The imprint left on the chemical abundances of long-lived stars at the solar vicinity coupled with a chemical evolution model, allowed to derive a robust measurement of the Milky Way star-formation history and to recognise that, in the Milky Way, the thick disc stellar population is as massive as its thin disc counterpart, suggesting a fundamental role of this component in the genesis of our Galaxy (Snaith et al. Reference Snaith, Haywood, Di Matteo, Lehnert, Combes, Katz and Gómez2014, Reference Snaith, Haywood, Di Matteo, Lehnert, Combes, Katz and Gómez2015).
That the thick disc is massive finds two independent confirmations.
-
1. In the most recent thick disc scale length measurements: as discussed in Snaith et al. (Reference Snaith, Haywood, Di Matteo, Lehnert, Combes, Katz and Gómez2014), from the stellar surface densities derived from SEGUE (Bovy et al. Reference Bovy, Rix, Hogg, Beers, Lee and Zhang2012b, Reference Bovy, Rix, Liu, Hogg, Beers and Lee2012c) and assuming that the thick and thin discs separate at [α/Fe] = 0.25 dex (on the SEGUE scale Bovy et al. Reference Bovy, Rix, Liu, Hogg, Beers and Lee2012c), the thin disc contributes
 ${\sim }21\,\rm {M_\odot }\,\rm pc^{-2}$
to the local stellar surface density, and the thick disc
${\sim }21\,\rm {M_\odot }\,\rm pc^{-2}$
to the local stellar surface density, and the thick disc
 ${\sim }8\,\rm M_\odot \,\rm pc^{-2}$
. Correcting for the scale length effect, the thick disc represents ~ 47% of the stellar mass within 10 kpc of the galactic centre, in accordance with the estimates derived from the star-formation history and chemical modelling.
${\sim }8\,\rm M_\odot \,\rm pc^{-2}$
. Correcting for the scale length effect, the thick disc represents ~ 47% of the stellar mass within 10 kpc of the galactic centre, in accordance with the estimates derived from the star-formation history and chemical modelling. -
2. In the census of white dwarf stars at the solar vicinity: Fuhrmann et al. (Reference Fuhrmann, Chini, Hoffmeister and Bernkopf2012) revised the fraction of local white dwarfs belonging to the thin and thick discs, respectively, finding a larger fraction of thick disc white dwarfs than what suggested by previous estimates. This finding, coupled with the different scale lengths and heights of the two populations, lead Fuhrmann et al. (Reference Fuhrmann, Chini, Hoffmeister and Bernkopf2012) to the conclusion that the thin disc is not dominant in the Milky Way, and that very likely the two populations have equal masses.
The most recent findings thus point to the presence of a massive thick disc, as massive as the thin counterpart, whose density at the solar vicinity is not representative of the global thick-to-thin mass ratio, and which is mainly concentrated in the inner disc. Explaining the formation of such a massive and centrally concentrated component is of course challenging for any evolutionary model: it would require high mass fractions already in place at high-redshift to sustain the prolonged star formation (Snaith et al. Reference Snaith, Haywood, Di Matteo, Lehnert, Combes, Katz and Gómez2014, Reference Snaith, Haywood, Di Matteo, Lehnert, Combes, Katz and Gómez2015; Haywood, et al. Reference Haywood, Di Matteo, Snaith and Lehnert2015), it is at odds with secular evolution models which only predict a marginal contribution of the thick disc to the overall mass budget of the Galaxy (Minchev et al. Reference Minchev, Famaey, Quillen, Dehnen, Martig and Siebert2012), it requires mergers and accretion events to be fine tuned enough to generate (or preserve?) kinematics–chemistry(-age) relations as those observed today on local and kpc-scale data [see Haywood et al. (Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013), Bovy et al. (Reference Bovy, Rix and Hogg2012a), Bovy et al. (Reference Bovy, Rix, Liu, Hogg, Beers and Lee2012c), Bovy et al. (Reference Bovy, Rix, Hogg, Beers, Lee and Zhang2012b), and Bird et al. (Reference Bird, Kazantzidis, Weinberg, Guedes, Mayer and Madau2013); Stinson et al. (Reference Stinson2013) for predictions from cosmological models].
2.2. The thin disc
In the ‘classical’ picture, the thin disc is the dominant and most massive stellar component of the Galaxy. Until few years ago, its kinematic and chemical properties were mostly known for stars at the solar vicinity. From kinematics studies, it has been inferred that the stars at the solar radius are significantly affected by the stellar Galactic bar: the Sun seems indeed to be located just outside the outer Lindblad resonance (hereafter OLR, see Dehnen Reference Dehnen1999, Reference Dehnen2000; Fux Reference Fux2001; Minchev, Nordhaus, & Quillen Reference Minchev, Nordhaus and Quillen2007), and several moving groups in the solar vicinity have been ascribed to the effect of bar resonances (Dehnen Reference Dehnen2000; Chakrabarty Reference Chakrabarty2007; Famaey et al. Reference Famaey, Pont, Luri, Udry, Mayor and Jorissen2007; Famaey, Siebert, & Jorissen Reference Famaey, Siebert and Jorissen2008; Antoja et al. Reference Antoja, Valenzuela, Pichardo, Moreno, Figueras and Fernández2009). For stars confined at about a 100 parsecs from the Sun, where ages have been determined with sufficient accuracy, data show the existence of velocity dispersions—age relations for disc stars, with the older the stars the higher their dispersions (Wielen Reference Wielen1977; Dehnen & Binney Reference Dehnen and Binney1998; Binney, Dehnen, & Bertelli Reference Binney, Dehnen and Bertelli2000; Nordström et al. Reference Nordström2004; Seabroke & Gilmore Reference Seabroke and Gilmore2007), but note that some studies suggest a possible saturation for stars older than few Gyrs (Freeman Reference Freeman and Sundelius1991; Edvardsson et al. Reference Edvardsson, Andersen, Gustafsson, Lambert, Nissen and Tomkin1993; Gomez et al. Reference Gomez, Grenier, Udry, Haywood, Meillon, Sabas, Sellier, Morin and Bonnet1997; Quillen & Garnett Reference Quillen, Garnett, Funes and Corsini2001; Soubiran et al. Reference Soubiran, Bienaymé, Mishenina and Kovtyukh2008). These trends may be the signature of internal processes which kinematically heat stars over time (e.g. Spitzer & Schwarzschild Reference Spitzer and Schwarzschild1951; Lacey Reference Lacey1984; Carlberg & Sellwood Reference Carlberg and Sellwood1985; Kroupa Reference Kroupa2002). But they may also reflect a much more global trend observed in all disc stars, belonging to the thin as well as to the thick disc population. These two populations, examined as a whole, show a continuous decrease of velocity dispersions with age, from the oldest thick disc stars to the youngest thin disc objects (Haywood et al. Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013). However, it is not clear how representative this relation is of the initial formation of the disc(s) and how much internal processes (heating by spiral arms, bar formation and buckling, etc.) and accretion events may have changed it over time, also because different evolutionary scenarios may be able to produce similar relations at the present epoch (House et al. Reference House2011).
From the chemical point of view, the thin disc shows signatures of a complex formation history. Stars at the solar vicinity have a metallicity distribution which peaks around [Fe/H] ~ 0 (Haywood Reference Haywood2001), with the tails of the distribution extending from [Fe/H] ~ −0.8 dex to super solar values. The large spread in metallicities of stars at the solar vicinity may be appreciated also looking at the age-metallicity relation: at any age, the dispersion is too significant to be explained simply by inhomogeneities in the interstellar medium at the time of formation of the different generations of stars (Haywood Reference Haywood2008; Haywood et al. Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013). Some other processes have been thus invoked. Radial migration (Roškar et al. Reference Roškar, Debattista, Stinson, Quinn, Kaufmann and Wadsley2008; Brunetti, Chiappini, & Pfenniger Reference Brunetti, Chiappini and Pfenniger2011; Minchev et al. Reference Minchev, Famaey, Combes, Di Matteo, Mouhcine and Wozniak2011; Brook et al. Reference Brook2012; Minchev, Chiappini, & Martig Reference Minchev, Chiappini and Martig2013; Miranda et al. Reference Miranda2016) has been, over the last 10 yrs, the most popular scenario to explain the metallicity and abundance distributions of stars at the solar vicinity, starting from the early suggestion by Sellwood & Binney (Reference Sellwood and Binney2002). N-body models have repeatedly found that radial migration (both blurring and churning, following the terminology of Schönrich & Binney Reference Schönrich and Binney2009a) is a global process, stimulated by the presence of one or multiple stellar asymmetries, and as such it should have naturally affected the whole disc. However, this seems at odds with a number of more recent findings (see, for example, Haywood et al. Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013; Halle et al. Reference Halle, Di Matteo, Haywood and Combes2015, and the following of this section) that question the strength of radial migration and the spatial extent over which it is able to operate in our Galaxy. Many studies are indeed revealing that the thin disc appears radially structured, with little contamination between the inner thin disc (R GC ⩽ 6 − 7 kpc, with R GC being the in-plane distance from the Galactic centre) and the outer thin disc (R GC ⩾ 10 kpc). It is only in an intermediate region containing the solar radius (6 − 7 kpc ⩽ R GC ⩽ 10 kpc) that the chemical patterns of the inner and outer disc coexist. This result is fundamental not only because it questions the borders of radial migration, but also for the comprehension of the bulge components. For this reason, I will devote the rest of the section in revising the evidence of this inner–outer disc dycothomy.
A first indication comes from the work of Haywood (Reference Haywood2008), who shows that thin disc stars at the solar vicinity do not all share the same orbital properties: most of the metal-rich thin disc stars ([Fe/H] ⩾ 0.1 dex) found at the solar vicinity tend to have pericentres inside the solar radius, up to few kpc from the Galactic centre, and apocentres at or just outside the solar position, while metal-poor thin disc stars ([Fe/H] ⩽ −0.4 dex) have orbits which do not penetrate so much in the inner disc (their pericentres are usually above 6 kpc) and their apocentres extend much further out in the outer disc, up to 12 kpc from the Galaxy centre (see Figure 4).

Figure 4. From Haywood (Reference Haywood2008): The different distribution of pericentres and apocentres for stars at the solar vicinity kinematically selected as thin disc stars in the Geneva Copenhagen survey (Nordström et al. Reference Nordström2004), for different metallicity intervals. As evidenced by Haywood (Reference Haywood2008), thin disc stars at the solar vicinity do not all share the same orbital properties: most of the metal-rich thin disc stars ([Fe/H] ⩾ 0.1 dex) tend to have pericentres inside the solar radius, up to few kpc from the Galactic centre, and apocentres at or just outside the solar position, while metal-poor thin disc stars ([Fe/H] ⩽ −0.4 dex) have orbits with pericentres above 6 kpc and with apocentres which extend much further out in the disc, up to ~ 12 kpc from the Galaxy centre.
A second indication comes from the work of Bensby et al. (Reference Bensby, Alves-Brito, Oey, Yong and Meléndez2011): this study reveals that the (thin+thick discs) chemical patterns found at the solar radius are not representative of the whole disc. Only at the solar vicinity the two patterns—the one going from [α/Fe] ~ 0.4 dex and [Fe/H] ~ −1 dex to solar values, and the one going from [α/Fe] ~ 0.2 dex and [Fe/H] ~ −0.7 dex (red and blue lines, respectively, in Figure 2 of their work)—coexist. In their inner disc sample, made of stars with distances from the galactic centre between 4 and 7 kpc, the second pattern is not present, while it is the only pattern that appears in the outer disc (distances between 9 and 13 kpc). In particular, it is striking to observe that metal-rich thin disc stars, present at the solar vicinity, are not found in the outer disc, at distances greater than ~ 9 kpc from the galaxy centre. In Haywood et al. (Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013), we have re-investigated the question, calculating the ages of a high-resolution spectroscopic sample of stars at the solar vicinity (from Adibekyan et al. Reference Adibekyan, Sousa, Santos, Mena, González Hernández, Israelian, Mayor and Khachatryan2012). From this study, we concluded that the inner (R GC ⩽ 6 − 7 kpc) and outer (R GC ⩾ 10 kpc) discs did not follow the same chemical evolution: at a given age, outer disc stars are more α-enriched than co-eval inner disc stars, and have metallicities up to ~ 0.4 dex lower. Having detailed chemical abundances and ages, in Snaith et al. (Reference Snaith, Haywood, Di Matteo, Lehnert, Combes, Katz and Gómez2014, Reference Snaith, Haywood, Di Matteo, Lehnert, Combes, Katz and Gómez2015), we reconstructed the star-formation histories of the inner and outer discs, showing that the outer disc started to form about 10 Gyr ago, from an interstellar medium whose metallicity was diluted by 0.3–0.4 dex with respect to the metallicity of the interstellar medium present in the inner disc at the same time. In Haywood et al. (Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013), we proposed that the outer regions of the Milky Way possibly formed from a mixture of enriched material expelled from the thick disc, and of accreted, metal-poor gas. Afterwards, the evolution of the outer disc remained essentially disconnected from that of the inner disc. All these studies, except that of Bensby et al. (Reference Bensby, Alves-Brito, Oey, Yong and Meléndez2011), have been based on the analysis of stars at the solar vicinity. The definite confirmation that this picture is correct, and that the chemical patterns of the inner and outer discs are different and co-exist only in the solar region comes from APOGEE. The distribution in the [α-Fe]–[Fe/H] plane of about 70 000 stars in the APOGEE survey, spanning a large range of distances from the Sun, is shown in Hayden et al. (Reference Hayden2015) and here reproduced in Figure 5. This figure perfectly summarises the points made in this section:
-
• the α-enhanced thick disc is centrally concentrated—very few thick disc stars are indeed observed at distances greater than 10–11 kpc from the Galaxy centre;

Figure 5. From Hayden et al. (Reference Hayden2015): Distribution of stars in the [α/Fe] versus [Fe/H] plane as a function of R and
 $|\text{z}|$
as revealed by APOGEE. The black line in each panel shows the similarity of the shape of the α-abundant sequence with R. Different rows correspond to stars at different heights above the Galactic plane, different columns to stars in different radial bins.
$|\text{z}|$
as revealed by APOGEE. The black line in each panel shows the similarity of the shape of the α-abundant sequence with R. Different rows correspond to stars at different heights above the Galactic plane, different columns to stars in different radial bins. -
• in a 2-kpc wide region around the Sun, two chemical patterns are observed: one going from α-enhanced, metal-poor thick disc stars to solar [α/Fe] and supersolar [Fe/H] values, the second pattern starting at [α/Fe] ~ 0.1 dex and [Fe/H] ~ −0.5 dex with [Fe/H] increasing up to solar values. These two patterns co-exist only in a few kpc region around the Sun: in the outer disc the α-enhanced pattern disappears, while in the inner disc, it is the low-α sequence which is not present.
There are at least two implications of these results which are of interest for our study:
-
• Radial migration by churning (Sellwood & Binney Reference Sellwood and Binney2002; Schönrich & Binney Reference Schönrich and Binney2009a; Roškar et al. Reference Roškar, Debattista, Stinson, Quinn, Kaufmann and Wadsley2008; Minchev et al. Reference Minchev, Chiappini and Martig2013), that is the change of guiding radii of stars caused by the presence of one or multiple asymmetries in the stellar disc, has not been efficient in mixing stars of the inner (R GC ⩽ 6 − 7 kpc) and outer Milky Way disc (R GC ⩾ 9–10 kpc). The difference of chemical patterns of these two regions of the Galaxy, with an overlap only in a few-kpc zone around the Sun, implies that no siginificant migration of stars has occurred between these two regions. Whatever the formation scenario for the outer disc of the Milky Way is (gas/satellites accretion with a possible role of winds from the inner disc), and whatever the process that ignited star formation in those outer regions about 10 Gyr ago, some mechanism has prevented stars from migrating afterwards. In Halle et al. (Reference Halle, Di Matteo, Haywood and Combes2015), we propose that the mechanism that inhibited migration is dynamical and is related to the position of the bar OLR, position that is currently estimated to be just inside the solar radius. By using N-body models, we show indeed that the bar OLR limits the exchange of angular momentum, separating the disc in two distinct parts with minimal or null exchange, except in the transition zone, which is delimited by the position of the OLR at the epoch of the formation of the bar, and at the final epoch. This also implies that stars migrated in the bar/bulge region from the outer disc can originate in a region whose maximal extent is given by the final (i.e. current) position of the OLR (Di Matteo et al. Reference Di Matteo2014). Unless the Galaxy, over time, has experienced the formation of several bars, and/or strong spiral waves, with different pattern speeds (in that case the scenario would become much more complex), the picture is simple: only stars inside the solar region, where the OLR should be currently located, can have migrated in the inner disc and contributed to the bulge populations.
-
• The chemical patterns of the inner disc are only part of the chemical patterns observed at the solar radius. When one compares the chemistry of bulge stars to those of disc stars, it is fundamental to take this result into account. In particular, if the comparison is done with the chemical patterns observed at the solar vicinity, the low-α pattern of the metal-poor thin disc must not be taken into account in the comparison, simply because this pattern is typical of the outer disc and not of the region inside 6–7 kpc from the Galaxy centre. The chemical patterns of the bulge differ from those of the stellar disc at the solar vicinity as much as the latter differs from the chemical patterns of the inner disc. The difference in chemical patterns of the bulge and of the thin disc at the solar radius arises because the solar radius is not representative of the chemistry of the inner thin disc, not because the metal-rich bulge is a different population from the inner thin disc. In this respect, the α-enhancement of the bulge with respect to the thin disc found, for example, by Johnson et al. (Reference Johnson, Rich, Fulbright, Valenti and McWilliam2011) and Gonzalez et al. (Reference Gonzalez2015b) arises because the whole thin disc is included in the comparison, while the metal-poor thin disc present at the solar vicinity should be removed. Once this is done, the filiation between the inner thin disc and the metal-rich bulge becomes evident.
3 THE BULGE/BAR/DISC(S) CONNECTION IN N-BODY SIMULATIONS
The observational evidences recalled in the previous sections suggest to investigate the nature of the bulge and its stellar components in view of the recent discoveries about the disc(s) populations (Sections 1 and 2). It is by quantifying and understanding the response of a thin+thick disc to bar formation and instabilities that we can solve the puzzle of the main (i.e. [Fe/H] ⩾ −1) populations of the Galactic bulge.
In the following of this section, I will discuss three points, that are fundamental to me to understand why our current modelling of the Milky Way bulge is incomplete.
-
1. N-body simulations which try to interpret the Milky Way bulge as the result of a bar instability in a pure thin disc galaxy fail in reproducing the chemo-kinematic relations, as found in the most recent surveys. They are successful in reproducing global trends, but not the trends satisfied by the individual bulge components. This failure has been evidenced in Di Matteo et al. (Reference Matteo2015), and I will summarise here the main points made in that paper, after recalling the successes of the bulge/bar/thin disc scenario.
-
2. If the Milky Way contains any classical bulge, its mass must be small (not more than 10%). Several independent N-body models have now reached this same conclusion, and this also means that the origin of the metal-poor populations which are significant in the bulge—60% and more, depending on latitude, for stars with [Fe/H] ⩽ 0 dex; up to 40% for stars with [Fe/H] ⩽ −0.5 dex only; according to Ness et al. (Reference Ness2013a)—cannot be ascribed to the presence of a classical bulge, which makes 10% at most of the thin disc mass.
-
3. Neither a pure thin disc model nor the inclusion of a low-mass classical bulge can explain the properties of the metal-poor component present in the bulge. It is only by adding the thick disc to the picture that we can naturally understand the vertical structuring of the bulge, the variation of metal-rich and metal-poor components with height, their relative weight, and the absence of a boxy-/peanut-shaped structure for the metal-poor ( − 1 dex ⩽ [Fe/H] ⩽ −0.5 dex) stars at latitudes b ⩾ −10°. I will show this, by presenting the first results of N-body simulations which include a massive thick disc, and that have high enough resolution to allow to study in detail the mapping of a thin+thick disc into a boxy bulge.
3.1. The bar/bulge/thin disc connection: successes and failures
3.1.1. Successes
Because of the boxy-/peanut-shaped nature of the Milky Way bulge and because of the marginal role that the thick disc was considered to play in the mass budget of the Galaxy until recently, all N-body models so far—except those of Bekki & Tsujimoto (Reference Bekki and Tsujimoto2011)—have modelled the visible Galaxy as a pure thin disc, with the possible inclusion of a classical bulge. These models, which I will refer to also as ‘pure thin disc’ models—even in the case they contain a small ( ~ 10%) classical bulge, as in Shen et al. (Reference Shen, Rich, Kormendy, Howard, De Propris and Kunder2010) and Di Matteo et al. (Reference Matteo2015)—have been successful in reproducing a number of global characteristics of the Milky Way bulge, as its structure and X-shape, its kinematics and metallicity trends.
Martinez-Valpuesta & Gerhard (Reference Martinez-Valpuesta and Gerhard2011) and Gerhard & Martinez-Valpuesta (Reference Gerhard and Martinez-Valpuesta2012), for example, showed how a pure thin disc model can be able to reproduce star counts observations in the Galactic plane, for the long bar, and in the inner regions of the boxy bulge ( − 10° ⩽ l ⩽ 10° and b = ±1°), where a sudden change in the structure of the bulge is observed at |l| ~ 4° (Nishiyama et al. Reference Nishiyama2005; Gonzalez et al. Reference Gonzalez, Rejkuba, Minniti, Zoccali, Valenti and Saito2011a). By means of a N-body model of a stellar bar grown from a thin disc, Ness et al. (Reference Ness2012) were able to explain the split in the distribution of red giant clump stars along the bar minor axis, as observed by ARGOS.
The pure thin disc model developed by Shen et al. (Reference Shen, Rich, Kormendy, Howard, De Propris and Kunder2010) has been successful in explaining the stellar kinematics of the bulge region from the BRAVA bulge survey (Howard et al. Reference Howard, Rich, Reitzel, Koch, De Propris and Zhao2008), at latitudes b = −4°, −6°, and − 8° and longitudes − 10° ⩽ b ⩽ +10°. In particular, this N-body simulation reproduces the cylindrical rotation observed all over the analysed fields and the corresponding trends in velocity dispersions. Kunder et al. (Reference Kunder2012) confirmed this agreement, by comparing Shen et al. (Reference Shen, Rich, Kormendy, Howard, De Propris and Kunder2010) model to a more extended sample of stars from BRAVA at similar latitudes and longitudes. Similar results were obtained by Gardner et al. (Reference Gardner, Debattista, Robin, Vásquez and Zoccali2014), in their comparison with BRAVA, and by Zoccali et al. (Reference Zoccali2014), who used the pure thin disc N-body model presented in Martinez-Valpuesta & Gerhard (Reference Martinez-Valpuesta and Gerhard2011) and compared it with the bulge kinematics from the GIBS survey, extending the comparison between data and models also closer to the Galaxy mid-plane, at latitude b = −2°. That a ‘pure thin disc’ model is able to reproduce the global kinematics of the bulge has been also shown by Ness et al. (Reference Ness2013b), in their comparison with the ARGOS kinematics at latitudes b = −5°, −7.5°, and − 10° and by Di Matteo et al. (Reference Matteo2015), who compared their N-body model to ARGOS and BRAVA data.
Such models have been shown to be able to reproduce also the vertical metallicity gradient, similar to those observed (Zoccali et al. Reference Zoccali, Hill, Lecureur, Barbuy, Renzini, Minniti, Gómez and Ortolani2008; Gonzalez et al. Reference Gonzalez, Rejkuba, Zoccali, Valenti and Minniti2011b, Reference Gonzalez, Rejkuba, Zoccali, Valent, Minniti and Tobar2013; Ness et al. Reference Ness2013a). Martinez-Valpuesta & Gerhard (Reference Martinez-Valpuesta and Gerhard2013) indeed showed how an initial steep ( ~ − 0.4 dex kpc−1) radial metallicity gradient in the thin disc can be mapped into a comparable vertical metallicity gradient in the bulge: the most loosely bound stars, in the disc outskirts, are indeed preferentially redistributed at large heights from the plane, while more bound stars tend to be found at low latitudes (see also Di Matteo et al. Reference Di Matteo2014). This explain why, in a pure thin disc which has initially—before bar formation—a steep enough metallicity gradient, models predict also longitude–latitude metallicity maps remarkably similar to observations (see Figure 6 and Martinez-Valpuesta & Gerhard Reference Martinez-Valpuesta and Gerhard2013). I will comment in the following on the limitations of this scenario.

Figure 6. From Martinez-Valpuesta & Gerhard (Reference Martinez-Valpuesta and Gerhard2013): Bulge metallicity maps of a simulated thin disc galaxy in galactic coordinates (l, b). The modelled galaxy has initially a steep radial metallicity gradient in the disc, that is mapped into a vertical metallicity gradient in the bulge, when the bar buckles. The trends found are remarkably similar to observations (Gonzalez et al. Reference Gonzalez, Rejkuba, Zoccali, Valent, Minniti and Tobar2013). However, even if successful in reproducing global bulge properties, a pure thin disc model for the Galactic bulge—as the one presented here—fails in reproducing the detailed chemo-kinematic relations of its stars (see Figure 8 and Di Matteo et al. Reference Matteo2015).

Figure 7. From Di Matteo et al. (Reference Matteo2015): Rotation curve (top panel) and velocity dispersions (bottom panel) of bulge stars in the pure thin disc N-body model discussed in Di Matteo et al. (Reference Matteo2015). Four different latitudes are shown for the modelled galaxy: b = −4° (yellow squares), b = −6° (red squares), b = −8° (pale blue squares), b = −10° (dark blue squares). For comparison, BRAVA fields at b = −4° (yellow, solid curve), b = −6° (red, dashed curve), and b = −8° (pale blue, dotted curve), and ARGOS fields at b = −10° (dark blue, dash-dotted curve) are also given. The thickness of the curves corresponds to the ± 1σ error in the observational data. See also Shen et al. (Reference Shen, Rich, Kormendy, Howard, De Propris and Kunder2010), Kunder et al. (Reference Kunder2012), and Zoccali et al. (Reference Zoccali2014) for similar global kinematic trends. However, even if successful in reproducing global kinematic properties, a pure thin disc model—as the one presented here—for the Galactic bulge fails in reproducing the detailed chemo-kinematic relations of its stars (see Figure 8 and Di Matteo et al. Reference Matteo2015).
Finally, even if we are only starting to discover the spatial redistribution of stars with different ages in the Galactic bulge, the most recent findings (Bensby et al. Reference Bensby2013; Dékány et al. Reference Dékány2015) seem in agreement with models predictions about the presence of young stars close to the Galaxy mid-plane, as a consequence of the continuous star formation in the galactic thin disc (Ness et al. Reference Ness, Debattista, Bensby, Feltzing, Cole, Johnson and Freeman2014).
3.1.2. Failures
In the scenario where the bulge formed from a pure thin disc, through the intermediate of a bar, it is fundamental that initially—i.e. before bar formation—the thin disc has a steep radial metallicity gradient [ ~ − 0.4 dex kpc−1 as found by Martinez-Valpuesta & Gerhard (Reference Martinez-Valpuesta and Gerhard2013) and Di Matteo et al. (Reference Matteo2015)]. In this way, metal-poor stars originating at large radii in the thin disc are preferentially mapped at high latitudes in the Galactic bulge and give rise to a vertical gradient of about − 0.04 dex deg−1, similar to the findings of Gonzalez et al. (Reference Gonzalez, Rejkuba, Zoccali, Valent, Minniti and Tobar2013). In this scenario, because all bulge stars have a thin disc origin, at a given latitude they should be all part of the boxy-/peanut-shaped structure, independently on their metallicities. This fact has two consequences, which enter in conflict with the detailed structure and chemo-kinematic relations currently known for the bulge components:
-
1. at a given latitude, all red clump stars in the Milky Way's bulge with [Fe/H] > −1 dex should show a split in the distribution of their K-magnitudes, which is not observed;
-
2. the metal-poor population ( − 1 dex < [Fe/H] ⩽ −0.5 dex) should be a kinematically warm replica of the more metal rich ones ( − 0.5 dex < [Fe/H]), which is not.
These failures have been presented and discussed in Di Matteo et al. (Reference Matteo2015), where we have indeed shown how a ‘pure thin disc’ model can reproduce the global kinematics and chemistry of the bulge, without reproducing the detailed chemo-kinematic and structural properties of its components. The problem is essentially related to the fact that, in such a scenario, metal-poor stars at any given latitude would contribute to the external part of the peanut and that they would have an angular momentum greater than that of more metal-rich stars (whose origin would be in the inner galaxy, given the initial radial metallicity gradient). A higher angular momentum for metal-poor stars would break the cylindrical rotation observed for this component, and would imply also a rotation curve different from that of the most metal-rich populations. This is not observed in the data, which on the contrary show that populations A, B, and C all show cylindrical rotation and similar rotation curves. Moreover, because in this scenario metal-poor stars would have a thin disc origin, their velocity dispersion profiles would have a shape similar to those of the most metal-rich components, only shifted at higher absolute values. This again is not observed. As shown in Figures 6–8, even if successful in explaining global properties of the bulge, the ‘pure thin disc’ model fails in reproducing the properties of its stellar components (Figure 8). For a more extensive discussion on these points, I refer the reader to Di Matteo et al. (Reference Di Matteo2014) and Di Matteo et al. (Reference Matteo2015).

Figure 8. From Di Matteo et al. (Reference Matteo2015): Rotation curves (left panels) and velocity dispersions (right panels) of a boxy bulge formed from a thin stellar disc (square symbols) compared to ARGOS data (coloured curves). In the N-body model, only bulge stars are shown. An initial radial metallicity profile [Fe/H] = 0.5-0.4R in the disc is assumed, similar to Martinez-Valpuesta & Gerhard (Reference Martinez-Valpuesta and Gerhard2013). Three different metallicity bins are shown, from top to bottom in decreasing [Fe/H], corresponding to the populations A, B, and C, as defined by Ness et al. (Reference Ness2013a). For each plot, four different latitudes are shown for the modeled galaxy: b = −4° (yellow squares), b = −6° (red squares), b = −8° (pale blue squares), b = −10° (dark blue squares). For comparison, ARGOS fields at b = −5° (orange, solid curve), b = −7.5° (pale blue, dashed curve), b = −10° (dark blue, dotted curve) for populations A, B, and C are also given. The thickness of the curves corresponds to the ± 1σ error in the observational data. Note that such model does not reproduce both the cylindrical rotation observed for all the three populations, and the constancy with latitude and longitude of the velocity dispersion of population C.
3.2. On the marginal role of any classical bulge in the Milky Way
If the metal-poor stars in the Milky Way bulge cannot have a thin disc origin, can they belong to a classical bulge? Several N-body models, starting from those presented by Shen et al. (Reference Shen, Rich, Kormendy, Howard, De Propris and Kunder2010), and then Kunder et al. (Reference Kunder2012), Di Matteo et al. (Reference Di Matteo2014) and Zoccali et al. (Reference Zoccali2014), show that this is not a viable possibility. They all agree indeed in finding that the mass of any classical bulge present in the Galaxy must be small (10% at most). Shen et al. (Reference Shen, Rich, Kormendy, Howard, De Propris and Kunder2010), for example, showed that for higher mass ratios, the classical bulge would determine signatures in the global velocity dispersion profiles of stars in the bulge not compatible with BRAVA observations (see Figure 4 in Shen et al. Reference Shen, Rich, Kormendy, Howard, De Propris and Kunder2010). Subsequent works arrived to similar conclusions. Such a small classical bulge can explain neither the large fraction of metal-poor stars observed in the bulge, nor their increasing fraction with latitude. In Di Matteo et al. (Reference Di Matteo2014, Figure 11), we have indeed shown that the contribution of a low-mass classical bulge to the total stellar density is maximal in the innermost regions of the bulge (typically inside 0.5 kpc, where it can account for 20% at most of the total local stellar density) and this fraction decreases with increasing latitude. The weight of such a classical bulge, and its trends with latitude, are significantly different from those observed for components B and/or C by Ness et al. (Reference Ness2013a), excluding that a low-mass classical bulge can represent the bulk of these populations.
Moreover, a classical component would leave signatures in the kinematics of stars in the bulge. Even if stars in the classical bulge can acquire some angular momentum during the bar formation and evolution (see, for example Saha et al. Reference Saha, Martinez-Valpuesta and Gerhard2012; Saha & Gerhard Reference Saha and Gerhard2013), these stars do not attain rotational velocities comparable to those of disc stars, whatever their location in the boxy structure. This is shown, for example, in Figure 12 in Di Matteo et al. (Reference Di Matteo2014), but also in Fux (Reference Fux1997): in this latter model, the galactocentric radial velocity of the spheroidal component—whose mass is about 50% of that of the stellar disc—is about half the value found for disc stars in all bulge fields (see their Table 5 and their Figure 16). This rules out the possibility that the bulk of the metal-poor stars in the Galactic bulge can be associated to a spheroid like that modelled by Fux (Reference Fux1997): if this was the case, metal-poor and metal-rich stars should show a significantly different amount of rotation, something excluded by the data (Ness et al. Reference Ness2013b, Reference Ness2016).
3.3. On the bulge/bar/thin+thick disc connection: towards the solution?
The previous discussion has shown that neither metal-poor thin disc stars trapped in the bar instability nor a classical bulge can explain the relative weight, fraction as a function of latitude, structure, and kinematics of the metal-poor populations observed in the Galactic bulge. At the same time, we have learned from the evidences recalled in Section 2 that a thick disc is massively present in the inner regions of the Milky Way, and that is has [α/Fe] and [Fe/H] compatible with those of stars in the bulge. This lead us to suggest in Di Matteo et al. (Reference Di Matteo2014, Reference Matteo2015) that the Milky Way bulge is the result of the mapping of the thin+thick disc of the Galaxy into the boxy-/peanut-shaped structure. In this scenario, we can understand the chemical patterns present in the Galactic bulge already in terms of the chemical patterns of stars at the solar vicinity: the inner disc sequence is mapped into the boxy bulge, while the outer disc sequence, which—as we have seen—contains stars with pericentres slightly inside the solar radius, is not. More in details, we suggest that components A, B, and C as defined by Ness et al. (Reference Ness2013a) correspond, respectively, to the metal-rich thin disc, the young thick disc and the old thick disc, adopting the nomenclature of Haywood et al. (Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013) and following the scheme presented here in Figure 9, and already discussed in Di Matteo et al. (Reference Di Matteo2014, Reference Matteo2015). Note that this scenario is somehow different from the one presented in Ness et al. (Reference Ness2013a): they indeed associate component C only with the thick disc, while in their interpretation component B should represent the early thin disc.

Figure 9. The scenario proposed in Di Matteo et al. (Reference Di Matteo2014, Reference Matteo2015) for the origin of the bulge components A, B, and C (Ness et al. Reference Ness2013a). In this scenario, the chemical patterns present in the Galactic bulge can be understood in terms of the chemical patterns of stars at the solar vicinity: the inner (thin+thick) disc sequence is mapped into the boxy bulge, with components A, B, and C that correspond, respectively, to the metal-rich thin disc, the young thick disc and the old thick disc, adopting the nomenclature in Haywood et al. (Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013). Note that in this scenario, the outer disc sequence, visible at the solar vicinity, is not present in the boxy bulge. This latter is indeed representative of the outer disc, not of the inner disc (see Section 2.2), and as a consequence it is not mapped into the boxy bulge.
How to test the validity of this scheme with N-body simulations? The recent observational results pose a challenge for idealised models, which have generally represented the stellar content of a Milky Way-type galaxy with a thin stellar disc and an optional bulge. The vertical structuring observed in the data, with a continuous sequence of ‘mono-abundance’ populations, whose scale height depends on their [α/Fe] and [Fe/H], needs to be captured somehow. A solution may be to use, as initial conditions, snapshots of Milky Way-like galaxies taken from cosmological simulations, where ‘mono-abundance’ sequences have been indeed reproduced (Bird et al. Reference Bird, Kazantzidis, Weinberg, Guedes, Mayer and Madau2013; Stinson et al. Reference Stinson2013). The limit of this approach is in the difficulty of investigating a large number of initial conditions, varying thin-to-thick disc ratios, for example, or disc(s) scale lengths and heights. To guarantee to have controlled sequences of (thin+thick) disc models, we have decided to follow a different approach, by constructing idealised galaxies, containing stellar discs of different scale heights and lengths, with masses and sizes in agreement with the most recent estimates for the Milky Way. In the following, I will show how the mapping of a thin+thick disc into a boxy-/peanut-shaped bulge is done in one of these simulations, and the kind of trends it predicts. The disc galaxy modelled here is made of 25 million particles, redistributed among stars and dark matter. The stellar disc, made of 20 million particles, is structured in three components (hereafter called ‘thin,’ ‘’intermediate’, and ‘thick’ discs, respectively) with scale heights varying from 0.3 kpc, to 0.6 and 0.9 kpc, and with velocity dispersions at the solar vicinity similar to those observed for the thin, young thick, and old thick disc, respectively (Haywood et al. Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013). The intermediate and thick disc together constitute 50% of the stellar mass in the modelled galaxy, with the remaining 50% being in the thin disc. I would like to highlight here that we chose to model only three disc components simply to identify three phases of an otherwise probably continuous chemical evolution. The same is valid for the Galactic bulge: components A, B, and C have been found by fitting the bulge MDF with multiple gaussians (Ness et al. Reference Ness2013a). But the existence of several components in the bulge MDF does not indicate necessarily that these components are really distinct. And indeed, the [α/Fe] versus [Fe/H] plot of the ARGOS stars presented in Ness et al. (Reference Ness2013a) shows a continuity between the three components.
The modelled galaxy is evolved in isolation for 5 Gyr. It rapidly develops a stellar bar which buckles after a couple of Gyrs and forms a boxy-/peanut-shaped bulge. A couple of results of this simulation seem worth mentioning in this context:
-
1. Stars of all components contribute to the stellar bar and to the boxy-/peanut-shaped structure, but their relative weight depends on the characteristics of the initial stellar disc (i.e. kinematically cold or warm) and on the height above the plane (see Figure 10). In particular, in our experiment, by integrating over the whole bulge extent, thin disc stars constitute 40% of the total stellar densities at |z| ⩽ 0.25 kpc, but this fraction diminishes to about 25% at 1 kpc ⩽ z ⩽ 1.5 kpc. Thick disc stars show the opposite trend: they represent less than 20% of the total stellar density at |z| ⩽ 0.25 kpc, but their fraction rises to more than 40% at 1 kpc ⩽ z ⩽ 1.5 kpc. Finally, the intermediate disc—which in our experiment should mimic the young thick disc following Haywood et al. (Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013) nomenclature—has a weight which is nearly independent on the vertical distance from the plane: 40% at |z| ⩽ 0.25 kpc, 35% at 1 kpc ⩽ z ⩽ 1.5 kpc. Note that at the highest distances from the plane, intermediate plus thick disc stars—which should mimic the young plus old thick disc, that is components B plus C in our scenario—constitute the great majority (75%) of the local stellar density. Even with the uncertainties still present in the model (thin-to-thick discs mass ratios, and in particular, the fraction of young and old thick disc stars to the total thick disc mass; initial velocity dispersion profiles in the inner galaxy, etc), it is striking to see the similarity with the findings of Ness et al. (Reference Ness2013a). In particular, the trends found for our thin and thick discs are reminiscent of those of populations A and C in Ness et al. (Reference Ness2013a), while our intermediate disc shows a weight whose nearly independence on the height above the plane is reminiscent of population B.
-
2. At a given height above the plane, the boxy/peanut shape is more pronounced in the kinematically cold populations than in the hottest one (see Figure 11). In particular, in our experiment, a clear peanut shape in the thick disc is only visible at large heights above the plane, greater than 1 kpc. This has two interesting implications.
Ness et al. (Reference Ness2013a) found that population C does not show any split in the K-magnitude distribution of stars at latitudes b = −5°, −7.5°, and − 10°, but interestingly at b = −10°, the maximum of the K-magnitude distribution of component C does not coincide with the Galaxy centre, but is shifted towards K-magnitude values similar to those where one of the two maxima of the peanut-shaped populations A and B is found (see Figure 1 here reproduced from Ness et al. Reference Ness2013a, and the previous discussion in Section 1). This may indicate the presence of a weak peanut shape also in population C, but possibly visible only at larger distances from the Galactic plane than those explored by bulge surveys so far. A mapping of the outer bulge, at |b| > 10°, would greatly help in understanding the morphology of the metal-poor bulge populations, and to clarify to what extent the characteristics that we have deduced for these stars from fields at |b| ⩽ 10° are really representative of their ensemble.
The second implication has to do with the spatial distribution of bulge RR Lyrae stars. Dékány et al. (Reference Dékány, Minniti, Catelan, Zoccali, Saito, Hempel and Gonzalez2013) found that, at latitudes b > −5°, bulge RR Lyrae in the VVV survey do not show a strong barred distribution, as the one traced by metal-rich red clump stars at similar latitudes, but a more spherical shape (note however that, at similar latitudes, Pietrukowicz et al. (Reference Pietrukowicz2012) found different results: their sample of RR Lyrae stars from the OGLE-III experiment shows a barred distribution similar to that of bulge red clump giants). It may be tempting to use these findings as indicative of the presence of a classical spheroid in the bulge. However, our model predicts that a different strength in the elongation of the bar in thick and thin disc stars is expected, especially at small heights above the plane. Thus, if a different spatial distribution was found between RR Lyrae with [Fe/H] ≳ −1 dex—i.e. the RR Lyrae population with metallicities compatible with the thick disc—and metal-rich red clump giants in the bulge, this should not be taken as an indication of the presence of a classical spheroid in the bulge. As we show in Figure 11, indeed, the thicker and kinematically warmer the disc is, the weaker and rounder its stellar bar. Also the absence of a clear bimodal distribution in RR Lyrae at b > −5° can be understood in a scenario where the metal-rich (i.e. [Fe/H] ≳ −1 dex) RR Lyrae component is related to the thick disc: indeed, as discussed in the previous point, the peanut-shaped morphology of thick disc stars appears only at large heights above the plane, and is not present at low latitudes, where not even the more metal-rich components of the bulge (A and B) show any split.
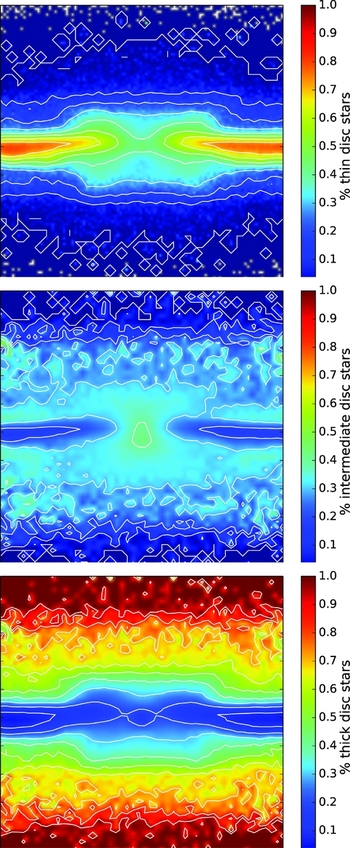
Figure 10. The fraction of thin (top panel), intermediate (middle panel), and thick disc (bottom panel) stars in the boxy-/peanut-shaped bulge of a simulated Milky Way-type galaxy, seen edge-on. In this simulation, the three discs components are intended to model the thin disc, young thick disc, and old thick disc, respectively, accordingly to the nomenclature adopted in Haywood et al. (Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013) and summarised here in Figure 2. Note that the fraction of thin disc stars decreases with height above the plane, that of thick disc stars increases with height above the plane, and that of intermediate stars stays nearly constant, with proportions similar to those found for populations A, B and C by Ness et al. (Reference Ness2013a). Each frame is 5 kpc × 5 kpc in size.

Figure 11. Face-on view of the simulated thin+thick disc galaxy for four different slices in z. From left to right: |z| < 0.25 kpc, 0.25kpc < z < 0.5kpc, 0.75kpc < z < 1kpc, 1kpc < z < 1.5kpc. For each of these slices, all stars in the selected z-range are shown in the first row. The second, third, and last row correspond, respectively, to the distribution of thin, intermediate, and thick disc stars only. I recall that in this simulation the three discs components are intended to model the thin disc, young thick disc, and old thick disc, respectively, accordingly to the nomenclature adopted in Haywood et al. (Reference Haywood, Di Matteo, Lehnert, Katz and Gómez2013) and summarised here in Figure 2. Each frame is 5 kpc × 5 kpc in size.
4 CONCLUSIONS
To understand the properties of the Galactic bulge and the way these properties change with metallicity, we need to place this structure in its environment, that is the Galactic stellar disc, and take into account the most recent findings about the latter. The stellar disc is vertically structured, with an α-enhanced, metal-poor, and kinematically warm disc (the so-called thick disc) at least as massive as the thin counterpart, and mostly concentrated in the inner regions of the Galaxy. The disc is also radially structured, with chemical patterns that differ in the inner (R ≲ 6 kpc) and outer (R ≳ 10 kpc) regions. When this radial and vertical structuring are taken into account, the chemical similarity between the bulge and the disc becomes evident, and little room is left for the presence of any classical spheroid. N-body modelling aiming at understanding and explaining the chemo-kinematic and morphological properties of the different bulge components need to implement the new vision we have acquired of the Galactic disc(s) populations. First results about the modelling of a composite disc galaxy and its mapping into the bulge are presented and support the hypothesis of a pure (thin+thick) disc scenario for the origin of the vast majority (i.e. for stars with [Fe/H] ≳ −1 dex) of the Milky Way bulge.
ACKNOWLEDGEMENTS
These pages are the results of the work done in the last years with many collaborators, and I take this opportunity to thank all of them: F. Combes, A. Gómez, A. Halle, M. Haywood, D. Katz, M. Lehnert, B. Semelin, and O. Snaith. In particular, I need to thank M. Haywood for introducing me to the universe of the Galactic stellar populations, pushing me to look at the data from a new and fascinating perspective. A. Gómez is warmly thanked for the long time spent in producing Milky Way analogues from the simulations. Our science is always the results of many enriching discussions, and the ideas developed in this paper have benefited of the support and criticism of a number of colleagues that I wish to acknowledge: O. Gerhard, V. Hill, I. Martinez-Valpuesta, M.Ness, L. Origlia, A. Recio-Blanco, M. Schultheis, M. Zoccali. A special thank to F. Matteucci and C. Morossi, for organising some of the most enriching meetings I have attended in the last years, and which have deeply contributed to shape the ideas presented in this paper. The ANR (Agence Nationale de la Recherche) is acknowledged for its financial support through the GalHis grant (P. I.: A. Robin) till 2013, and now by funding the MOD4Gaia project (ANR-15-CE31-0007). I am grateful to the Editor of this Special Issue on the Galactic bulge, B. Barbuy, for inviting me to write this contribution.
















