Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-14T02:32:20.072Z Has data issue: false hasContentIssue false
  • English
  • Français

Conformally invariant complete metrics

Part of: Geometric function theory

Published online by Cambridge University Press:  30 May 2022

TOSHIYUKI SUGAWA ,
MATTI VUORINEN  and
TANRAN ZHANG
TOSHIYUKI SUGAWA
Affiliation:
Graduate School of Information Sciences, Tohoku University, Aoba-ku, Sendai 980-8579, Japan. e-mail: [email protected]
MATTI VUORINEN
Affiliation:
Department of Mathematics and Statistics, University of Turku, FI-20014 Turku, Finland. e-mail: [email protected]
TANRAN ZHANG
Affiliation:
Department of Mathematics, Soochow University, No.1 Shizi Street, Suzhou 215006, China. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

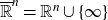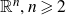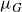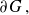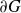For a domain G in the one-point compactification $\overline{\mathbb{R}}^n = {\mathbb{R}}^n \cup \{ \infty\}$ of ${\mathbb{R}}^n, n \geqslant 2$ , we characterise the completeness of the modulus metric $\mu_G$ in terms of a potential-theoretic thickness condition of $\partial G\,,$ Martio’s M-condition [ 35 ]. Next, we prove that $\partial G$ is uniformly perfect if and only if 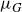$\mu_G$ admits a minorant in terms of a Möbius invariant metric. Several applications to quasiconformal maps are given.

MSC classification

Primary: 30C35: General theory of conformal mappings
Secondary: 30C55: General theory of univalent and multivalent functions
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 2 , March 2023 , pp. 273 - 300
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

The authors were supported in part by JSPS KAKENHI Grant Number JP17H02847 and NSF of the Higher Education Institutions of Jiangsu Province, China, Grant Number 17KJB110015, and NSFC Grant Number 12001391.

References

Ahlfors, L. V.. Conformal invariants: Topics in Geometric Function Theory (McGraw-Hill, New York, 1973).Google Scholar
Anderson, G. D., Vamanamurthy, M. K. and Vuorinen, M. K.. Conformal Invariants, Inequalities and Quasiconformal Maps (Wiley-Interscience, 1997).Google Scholar
Avkhadiev, F. G. and Wirths, K. J.. Schwarz–Pick type inequalities. Frontiers in Mathematics (Birkhäuser Verlag, Basel 2009).CrossRefGoogle Scholar
Beardon, A. F.. The geometry of discrete groups. Graduate Texts in Math. 91 (Springer-Verlag, New York, 1983).CrossRefGoogle Scholar
Beardon, A. F.. The Apollonian metric of a domain in ${\mathbb{R}}^n$ . Quasiconformal mappings and analysis (Ann Arbor, MI, 1995), (Springer, New York, 1998), 91–108.Google Scholar
Beardon, A. F. and Minda, D.. The Schwarz–Pick Lemma and the hyperbolic metric (Bookms 2018).Google Scholar
Beardon, A. F. and Pommerenke, Ch. The Poincaré metric of plane domains. J. London Math. Soc. 18 (1978), 475–483.CrossRefGoogle Scholar
Betsakos, D. and Pouliasis, S.. Isometries for the modulus metric are quasiconformal mappings. Trans. Amer. Math. Soc. 372 (2019), 2735–2752.CrossRefGoogle Scholar
Bridgeman, M. and Canary, R. D.. Uniformly perfect domains and convex hulls: improved bounds in a generalization of a theorem of Sullivan. Pure Appl. Math. Q. 9 (2013), 49–71.CrossRefGoogle Scholar
Bridson, M. R. and Haefliger, A.. Metric spaces of non-positive curvature. Fundamental Principles of Mathematical Sciences, 319 (Springer-Verlag, Berlin, 1999).CrossRefGoogle Scholar
Buckley, S.M. and Herron, D. A.. Quasihyperbolic geodesics are hyperbolic quasi-geodesics. J. Eur. Math. Soc. 22 (2020), 1917–1970.Google Scholar
Ferrand, J.. A characterisation of quasiconformal mappings by the behaviour of a function of three points. Complex analysis. Lecture Notes in Math. 1351 (Springer, Berlin, 1988), 110–123.Google Scholar
Ferrand, J.. Conformal capacities and conformally invariant functions on Riemannian manifolds. Geom. Dedicata 61 (1996), 103–120.CrossRefGoogle Scholar
Ferrand, J.. Conformal capacities and extremal metrics. Pacific J. Math. 180 (1997), 41–49.CrossRefGoogle Scholar
Ferrand, J., Martin, G. J. and Vuorinen, M. K.. Lipschitz conditions in conformally invariant metrics. J. Analyse Math. 56 (1991), 187–210.CrossRefGoogle Scholar
Garnett, J. B. and Marshall, D. E.. Harmonic Measure (Cambridge University Press, 2005).CrossRefGoogle Scholar
Gaussier, H.. Metric properties of domains in $\mathbb C^n$ . In Geometric Function Theory in Higher Dimension, Springer INdAM Ser. 26 (Springer, Cham, 2017), 143–155.CrossRefGoogle Scholar
Gehring, F. W. and Hag, K.. The ubiquitous quasidisk. With contributions by Ole Jacob Broch. Mathematical Surveys and Monographs, 184 (American Mathematical Society, Providence, RI, 2012).CrossRefGoogle Scholar
Gehring, F. W., Martin, G. J. and Palka, B.. An introduction to the theory of higher-dimensional quasiconformal mappings. Math. Surveys Monogr. 216 (American Mathematical Society, Providence, RI, 2017).CrossRefGoogle Scholar
Gehring, F. W. and Osgood, B. G.. Uniform domains and the quasihyperbolic metric. J. Analyse Math. 36 (1979), 50–74.CrossRefGoogle Scholar
Gehring, F. W. and Palka, B. P.. Quasiconformally homogeneous domains. J. Analyse Math. 30 (1976), 172–199.CrossRefGoogle Scholar
Golberg, A., Sugawa, T. and Vuorinen, M.. Teichmüller’s lemma in higher dimensions and its applications. Comput. Methods Funct. Theory, 20 (2020), 539–558.CrossRefGoogle Scholar
Hariri, P., Klén, R. and Vuorinen, M.. Conformally invariant metrics and quasiconformal mappings. Springer Monogr. Math. (Springer, 2020).CrossRefGoogle Scholar
Herron, D. A.. Uniform domains and hyperbolic distance. J. Anal. Math. 143 (2021), 349–400.CrossRefGoogle Scholar
Herron, D. A., Ibragimov, Z. and Minda, D.. Geodesics and curvature of Möbius invariant metrics. Rocky Mountain J. Math. 38 (2008), 891–921.CrossRefGoogle Scholar
Herron, D. A. and Julian, P. K.. Ferrand’s Möbius invariant metric. J. Anal. 21 (2013), 101–121.Google Scholar
Herron, D. A., Ma, W. and Minda, D.. Möbius invariant metrics bilipschitz equivalent to the hyperbolic metric. Conform. Geom. Dyn. 12 (2008), 67–96.CrossRefGoogle Scholar
Jarnicki, M. and Pflug, P.. Invariant Distances and Metrics in Complex Analysis. Second extended edition. De Gruyter Expositions in Mathematics, 9 (Walter de Gruyter GmbH & Co. KG, Berlin, 2013).CrossRefGoogle Scholar
Järvi, P. and Vuorinen, M.. Uniformly perfect sets and quasiregular mappings. J. London Math. Soc. 54 (1996), 515–529.CrossRefGoogle Scholar
Keen, L. and Lakic, N.. Hyperbolic Geometry from a Local Viewpoint (Cambridge University Press, Cambridge, 2007).CrossRefGoogle Scholar
Lelong–Ferrand, J.. Invariants conformes globaux sur les variétés riemanniennes (French). J. Differential Geometry 8 (1973), 487–510.CrossRefGoogle Scholar
Lewis, J. L.. Uniformly fat sets. Trans. Amer. Math. Soc. 308 (1988), 177–196.CrossRefGoogle Scholar
Ma, W. and Minda, D.. The hyperbolic metric and uniformly perfect regions. J. Anal. 20 (2012), 59–70.Google Scholar
Marden, A. and Markovic, V.. Characterisation of plane regions that support quasiconformal mappings to their domes. Bull. Lond. Math. Soc. 39 (2007), no. 6, 962–972.Google Scholar
Martio, O.. Equicontinuity theorem with an application to variational integrals. Duke Math. J. 42 (1975), no. 3, 569–581.Google Scholar
Martio, O. and Sarvas, J.. Density conditions in the n-capacity. Indiana Univ. Math. J. 26 (1977), no. 3, 761–776.Google Scholar
Martio, O. and Sarvas, J.. Injectivity theorems in plane and space. Ann. Acad. Sci. Fenn. Ser. A I Math. 4 (1978/79), 383–401.CrossRefGoogle Scholar
Pansu, P.. Quasiconformal mappings and manifolds of negative curvature. Curvature and topology of Riemannian manifolds. Lecture Notes in Math. 1201 (Springer, Berlin, 1986), 212–229.Google Scholar
Pansu, P.. Jacqueline Ferrand and her oeuvre. Notices Amer. Math. Soc. 65 (2018), no. 2, 201–205.Google Scholar
A. Papadopoulos. Metric spaces, convexity and non-positive curvature . IRMA Lectures in Mathematics and Theoretical Physics 6 (European Mathematical Society, Zürich, 2014).Google Scholar
Pflug, P.. Invariant metrics and completeness. J. Korean Math. Soc. 37 (2000), 269–284.Google Scholar
Pommerenke, Ch. Uniformly perfect sets and the Poincaré metric. Arch. Math. 32 (1979), 192–199.CrossRefGoogle Scholar
Pommerenke, Ch. On uniformly perfect sets and Fuchsian groups. Analysis 4 (1984), 299–321.CrossRefGoogle Scholar
Pouliasis, S. and Yu, A.. Solynin. Infinitesimally small spheres and conformally invariant metrics. J. Anal. Math. 143 (2021), no. 1, 179–205.Google Scholar
Reshetnyak, Yu. G.. Space mappings with bounded distortion. Trans. Math. Monogr. 73 (American Mathematical Society, Providence, RI, 1989).Google Scholar
Rickman, S.. Quasiregular mappings. Ergeb. Math. Grenzgeb. (3) 26 (Springer-Verlag, Berlin, 1993).Google Scholar
Seittenranta, P.. Möbius-invariant metrics. Math. Proc. Camb. Phil. Soc. 125 (1999), 511–533.CrossRefGoogle Scholar
Sugawa, T.. Uniformly perfect sets: analytic and geometric aspects (Japanese). Sugaku 53 (2001), 387–402. (English trans: Sugaku Expo. 16 (2003), 225–242)Google Scholar
Sugawa, T., Vuorinen, M. and Zhang, T.. On the hyperbolic distance of n-times punctured spheres. J. Analyse Math. 141 (2020), no. 2, 663–687.Google Scholar
Sugawa, T. and Zhang, T.. Construction of nearly hyperbolic distance on punctured spheres. Bull. Math. Sci. 8 (2018), 307–323.CrossRefGoogle Scholar
Tukia, P. and Väisälä, J.. Quasisymmetric embeddings of metric spaces. Ann. Acad. Sci. Fenn. Ser. A I Math. 5 (1980), no. 1, 97–114.Google Scholar
Väisälä, J.. Lectures on n-dimensional quasiconformal mappings. Lecture Notes in Math. 229 (Springer-Verlag, Berlin-New York, 1971).CrossRefGoogle Scholar
Vuorinen, M.. Conformal invariants and quasiregular mappings. J. Analyse Math. 45 (1985), 69–115.CrossRefGoogle Scholar
Vuorinen, M.. On quasiregular mappings and domains with a complete conformal metric. Math. Z. 194 (1987), no. 4, 459–470.Google Scholar
Vuorinen, M.. Conformal geometry and quasiregular mappings. Lecture Notes in Math. 1319 (Springer-Verlag, 1988).CrossRefGoogle Scholar
Zhang, X.. Isometries for the modulus metric in higher dimensions are conformal mappings. Sci. China Math. 64 (2021), no. 9, 1951–1958.CrossRefGoogle Scholar