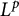1 Introduction
The theory of maximal monotone operators
![]() ${\boldsymbol {A}}:\mathcal {X}\rightrightarrows \mathcal {X}^{*}$
in Hilbert and reflexive Banach spaces provides a very powerful framework to solve nonlinear equations (see, e.g., the review [Reference Borwein11]). We recall that an operator
${\boldsymbol {A}}:\mathcal {X}\rightrightarrows \mathcal {X}^{*}$
in Hilbert and reflexive Banach spaces provides a very powerful framework to solve nonlinear equations (see, e.g., the review [Reference Borwein11]). We recall that an operator
![]() ${\boldsymbol {A}}\subset \mathcal {X}\times \mathcal {X}^{*}$
(which we identify with its graph) is said to be monotone if
${\boldsymbol {A}}\subset \mathcal {X}\times \mathcal {X}^{*}$
(which we identify with its graph) is said to be monotone if
while
![]() ${\boldsymbol {A}}$
is said to be maximal monotone if every proper extension of
${\boldsymbol {A}}$
is said to be maximal monotone if every proper extension of
![]() ${\boldsymbol {A}}$
fails to be monotone.
${\boldsymbol {A}}$
fails to be monotone.
In the Hilbertian case, the theory can also be applied to differential inclusions of the form
driven by a maximal monotone operator
![]() ${\boldsymbol {A}}$
and to prove the generation of a semigroup of contractions (see, e.g., [Reference Barbu6, Reference Brézis13]).
${\boldsymbol {A}}$
and to prove the generation of a semigroup of contractions (see, e.g., [Reference Barbu6, Reference Brézis13]).
The notion of maximality of the (multivalued) operator
![]() ${\boldsymbol {A}}$
plays a crucial role, since by the Minty–Browder theorem it is equivalent to the solvability of the resolvent equation
${\boldsymbol {A}}$
plays a crucial role, since by the Minty–Browder theorem it is equivalent to the solvability of the resolvent equation
where J is the duality map from
![]() $\mathcal {X}$
to
$\mathcal {X}$
to
![]() $\mathcal {X}^{*}$
[Reference Barbu6, Theorem 2.2]. In the Hilbertian framework, the solution to (1.2) corresponds to the solvability of the Implicit Euler Scheme associated with (1.1) and provides a general condition for the existence of a solution to (1.1). In this respect, an essential tool is the well-known fact that every monotone operator
$\mathcal {X}^{*}$
[Reference Barbu6, Theorem 2.2]. In the Hilbertian framework, the solution to (1.2) corresponds to the solvability of the Implicit Euler Scheme associated with (1.1) and provides a general condition for the existence of a solution to (1.1). In this respect, an essential tool is the well-known fact that every monotone operator
![]() ${\boldsymbol {A}}$
admits a maximal extension [Reference Brézis13, Reference Debrunner and Flor18], whose domain is contained in the closed convex hull of the domain of
${\boldsymbol {A}}$
admits a maximal extension [Reference Brézis13, Reference Debrunner and Flor18], whose domain is contained in the closed convex hull of the domain of
![]() ${\boldsymbol {A}}.$
${\boldsymbol {A}}.$
Motivated by the study of operators in Bochner-
![]() $L^{p}$
spaces
$L^{p}$
spaces
![]() $\mathcal {X}=L^{p}(\Omega ,{\mathcal {B}},\mathbb {P};\mathsf {X})$
(here
$\mathcal {X}=L^{p}(\Omega ,{\mathcal {B}},\mathbb {P};\mathsf {X})$
(here
![]() $(\Omega , {\mathcal {B}})$
is a standard Borel space endowed with a nonatomic probability measure
$(\Omega , {\mathcal {B}})$
is a standard Borel space endowed with a nonatomic probability measure
![]() $\mathbb {P}$
and
$\mathbb {P}$
and
![]() $\mathsf {X}$
is a reflexive and separable Banach space) which are invariant by measure-preserving transformations of
$\mathsf {X}$
is a reflexive and separable Banach space) which are invariant by measure-preserving transformations of
![]() $\Omega $
, in this paper we address the general problem of finding maximal extensions of monotone operators which are invariant by a group
$\Omega $
, in this paper we address the general problem of finding maximal extensions of monotone operators which are invariant by a group
![]() $\mathsf {G}$
of suitable transformations of
$\mathsf {G}$
of suitable transformations of
![]() $\mathcal {X}\times \mathcal {X}^{*}$
. More precisely, let us consider a group
$\mathcal {X}\times \mathcal {X}^{*}$
. More precisely, let us consider a group
![]() $\mathsf {G}$
of linear isomorphisms acting on
$\mathsf {G}$
of linear isomorphisms acting on
![]() $\mathcal {X}\times \mathcal {X}^{*}$
whose elements
$\mathcal {X}\times \mathcal {X}^{*}$
whose elements
![]() $\mathsf {U}=(U,U')$
preserve the duality pairing and the norms in
$\mathsf {U}=(U,U')$
preserve the duality pairing and the norms in
![]() $\mathcal {X}\times \mathcal {X}^{*}$
, i.e., for every
$\mathcal {X}\times \mathcal {X}^{*}$
, i.e., for every
![]() $(U,U')\in \mathsf {G}$
and every
$(U,U')\in \mathsf {G}$
and every
![]() $z=(x,v)\in \mathcal {X}\times \mathcal {X}^{*}$
, we have
$z=(x,v)\in \mathcal {X}\times \mathcal {X}^{*}$
, we have
Given a monotone operator
![]() ${\boldsymbol {A}}\subset \mathcal {X}\times \mathcal {X}^{*}$
which is
${\boldsymbol {A}}\subset \mathcal {X}\times \mathcal {X}^{*}$
which is
![]() $\mathsf {G}$
-invariant, i.e.,
$\mathsf {G}$
-invariant, i.e.,
we will prove (see Theorem 2.5) that there exists a maximal extension
![]() ${\boldsymbol {\hat A}}$
of
${\boldsymbol {\hat A}}$
of
![]() ${\boldsymbol {A}}$
preserving the
${\boldsymbol {A}}$
preserving the
![]() $\mathsf {G}$
-invariance; we will also find
$\mathsf {G}$
-invariance; we will also find
![]() ${\boldsymbol {\hat A}}$
so that its proper domain
${\boldsymbol {\hat A}}$
so that its proper domain
![]() $\mathrm {D}({\boldsymbol {\hat {A}}})$
does not exceed the closed convex hull of
$\mathrm {D}({\boldsymbol {\hat {A}}})$
does not exceed the closed convex hull of
![]() $\mathrm {D}({\boldsymbol {A}}).$
$\mathrm {D}({\boldsymbol {A}}).$
Since it is not clear how to adapt to this context the classical proof based on the Debrunner–Flor and Zorn lemma (see, e.g., [Reference Brézis13, Theorem 2.1 and Corollary 2.1, Chapter II]), we will use the powerful explicit construction of [Reference Bauschke and Wang8]. This is based on kernel averages of convex functionals and on the characterization of monotone and maximal monotone operators via suitable convex Lagrangians on
![]() $\mathcal {X}\times \mathcal {X}^{*}$
, a deep theory started with the seminal paper [Reference Fitzpatrick19] (where the so-called Fitzpatrick’s function is introduced for the first time) and further developed in a more recent series of relevant contributions (see, e.g., [Reference Burachik and Svaiter14, Reference Ghoussoub22, Reference Martinez-Legaz and Théra24–Reference Penot26, Reference Visintin35] and the references therein).
$\mathcal {X}\times \mathcal {X}^{*}$
, a deep theory started with the seminal paper [Reference Fitzpatrick19] (where the so-called Fitzpatrick’s function is introduced for the first time) and further developed in a more recent series of relevant contributions (see, e.g., [Reference Burachik and Svaiter14, Reference Ghoussoub22, Reference Martinez-Legaz and Théra24–Reference Penot26, Reference Visintin35] and the references therein).
The advantage of this direct approach is that it provides an explicit formula for the extension of
![]() ${\boldsymbol {A}}$
which behaves quite well with respect to the action of the group
${\boldsymbol {A}}$
which behaves quite well with respect to the action of the group
![]() $\mathsf {G}$
. As an intermediate step, which can be relevant also in other applications independently of
$\mathsf {G}$
. As an intermediate step, which can be relevant also in other applications independently of
![]() $\mathsf {G}$
-invariance, we will also show (Theorem 2.3) how to modify the construction of [Reference Bauschke and Wang8] in order to confine the domain of the extension
$\mathsf {G}$
-invariance, we will also show (Theorem 2.3) how to modify the construction of [Reference Bauschke and Wang8] in order to confine the domain of the extension
![]() ${\boldsymbol {\hat {A}}}$
to the closed convex hull of
${\boldsymbol {\hat {A}}}$
to the closed convex hull of
![]() $\mathrm {D}({\boldsymbol {A}})$
(see also [Reference Bauschke and Wang9, Theorem 2.13] for a partial result in this direction).
$\mathrm {D}({\boldsymbol {A}})$
(see also [Reference Bauschke and Wang9, Theorem 2.13] for a partial result in this direction).
As a byproduct, we can adapt the same strategy of [Reference Bauschke and Wang9] to prove a version of the Kirszbraun–Valentine extension theorem (see [Reference Kirszbraun23, Reference Valentine33, Reference Valentine34]) for
![]() $\mathsf {G}$
-invariant Lipschitz maps in Hilbert spaces (Theorem 2.11): it states that every L-Lipschitz map
$\mathsf {G}$
-invariant Lipschitz maps in Hilbert spaces (Theorem 2.11): it states that every L-Lipschitz map
![]() $f:D\to \mathcal {H}$
defined in a subset D of an Hilbert space
$f:D\to \mathcal {H}$
defined in a subset D of an Hilbert space
![]() $\mathcal {H}$
, whose graph is invariant with respect to the action of a group
$\mathcal {H}$
, whose graph is invariant with respect to the action of a group
![]() $\mathsf {G}$
of isometries of
$\mathsf {G}$
of isometries of
![]() $\mathcal {H}$
, can be extended to an L-Lipschitz function
$\mathcal {H}$
, can be extended to an L-Lipschitz function
![]() $\hat f:\mathcal {H}\to \mathcal {H}$
which is
$\hat f:\mathcal {H}\to \mathcal {H}$
which is
![]() $\mathsf {G}$
-invariant as well. The basic idea here still goes back to Minty: the graphs of nonexpansive maps in Hilbert spaces are in one-to-one correspondence with graphs of monotone maps via the Cayley transformation
$\mathsf {G}$
-invariant as well. The basic idea here still goes back to Minty: the graphs of nonexpansive maps in Hilbert spaces are in one-to-one correspondence with graphs of monotone maps via the Cayley transformation
![]() $T:\mathcal {H}\times \mathcal {H}\to \mathcal {H}\times \mathcal {H}$
defined as
$T:\mathcal {H}\times \mathcal {H}\to \mathcal {H}\times \mathcal {H}$
defined as
It is worth noticing that such a correspondence allowed the authors of [Reference Reich and Simons28] to use for the first time the Fitzpatrick’s function to prove the Kirszbraun–Valentine theorem (see [Reference Kirszbraun23, Reference Valentine33, Reference Valentine34]), which states that every
![]() $1$
-Lipschitz continuous map can be extended to the whole
$1$
-Lipschitz continuous map can be extended to the whole
![]() $\mathcal {H}$
(see also [Reference Bauschke7] where this approach is improved in order to obtain an extension with an optimal range). The same correspondence, together with the explicit construction of a maximal extension of a monotone operator
$\mathcal {H}$
(see also [Reference Bauschke7] where this approach is improved in order to obtain an extension with an optimal range). The same correspondence, together with the explicit construction of a maximal extension of a monotone operator
![]() ${\boldsymbol {A}}$
in [Reference Bauschke and Wang8], is used in [Reference Bauschke and Wang9] to provide the first constructive proof of the Kirszbraun–Valentine theorem.
${\boldsymbol {A}}$
in [Reference Bauschke and Wang8], is used in [Reference Bauschke and Wang9] to provide the first constructive proof of the Kirszbraun–Valentine theorem.
We will also provide in the Appendix an alternative proof based on another more recent explicit formula for such kind of extension given by [Reference Azagra, Le Gruyer and Mudarra5] (see also [Reference Azagra, Le Gruyer and Mudarra4]).
These results, besides being interesting by themselves, find interesting applications in the case when
![]() $\mathcal {X}$
is the
$\mathcal {X}$
is the
![]() $L^{p}$
-space of random variables
$L^{p}$
-space of random variables
over a space of parametrizations
![]() $(\Omega ,{\mathcal {B}},\mathbb {P})$
, where
$(\Omega ,{\mathcal {B}},\mathbb {P})$
, where
![]() $(\Omega ,{\mathcal {B}})$
is a standard Borel space,
$(\Omega ,{\mathcal {B}})$
is a standard Borel space,
![]() $\mathbb {P}$
is a nonatomic probability measure, and
$\mathbb {P}$
is a nonatomic probability measure, and
![]() $\mathsf {X}$
is a separable and reflexive Banach space, while
$\mathsf {X}$
is a separable and reflexive Banach space, while
![]() $\mathsf {G}$
is a group of isomorphisms generated by measure-preserving maps, i.e.,
$\mathsf {G}$
is a group of isomorphisms generated by measure-preserving maps, i.e.,
![]() ${\mathcal {B}}-{\mathcal {B}}$
measurable maps
${\mathcal {B}}-{\mathcal {B}}$
measurable maps
![]() $g:\Omega \to \Omega $
which are essentially injective and such that
$g:\Omega \to \Omega $
which are essentially injective and such that
![]() $g_{\sharp}\mathbb {P}=\mathbb {P}$
, where
$g_{\sharp}\mathbb {P}=\mathbb {P}$
, where
![]() $g_{\sharp}\mathbb {P}$
denotes the push-forward of
$g_{\sharp}\mathbb {P}$
denotes the push-forward of
![]() $\mathbb {P}$
by g. Every measure-preserving isomorphism g induces an element
$\mathbb {P}$
by g. Every measure-preserving isomorphism g induces an element
![]() $\mathsf {U}_{g}$
of
$\mathsf {U}_{g}$
of
![]() $\mathsf {G}$
whose action on
$\mathsf {G}$
whose action on
![]() $(X,X')\in \mathcal {X}\times \mathcal {X}^{*}$
is simply given by
$(X,X')\in \mathcal {X}\times \mathcal {X}^{*}$
is simply given by
![]() $\mathsf {U}_{g}(X,X')= (X\circ g,X'\circ g)$
.
$\mathsf {U}_{g}(X,X')= (X\circ g,X'\circ g)$
.
The interest for invariance by measure-preserving isomorphisms in
![]() $\mathcal {X}\times \mathcal {X}^{*}$
is justified by its link with the stronger property of law invariance: a set
$\mathcal {X}\times \mathcal {X}^{*}$
is justified by its link with the stronger property of law invariance: a set
![]() ${\boldsymbol {A}}\subset \mathcal {X}\times \mathcal {X}^{*}$
is law invariant if whenever
${\boldsymbol {A}}\subset \mathcal {X}\times \mathcal {X}^{*}$
is law invariant if whenever
![]() $(X,X')\in {\boldsymbol {A}}$
, then
$(X,X')\in {\boldsymbol {A}}$
, then
![]() ${\boldsymbol {A}}$
also contains all the pairs
${\boldsymbol {A}}$
also contains all the pairs
![]() $(Y,Y')\in \mathcal {X}\times \mathcal {X}^{*}$
with the same law of
$(Y,Y')\in \mathcal {X}\times \mathcal {X}^{*}$
with the same law of
![]() $(X,X')$
, i.e.,
$(X,X')$
, i.e.,
![]() $(Y,Y')_{\sharp}\mathbb {P}=(X,X')_{\sharp}\mathbb {P}.$
It is clear that law invariant subsets of
$(Y,Y')_{\sharp}\mathbb {P}=(X,X')_{\sharp}\mathbb {P}.$
It is clear that law invariant subsets of
![]() $\mathcal {X}\times \mathcal {X}^{*}$
are also invariant by measure-preserving isomorphisms; using the results of [Reference Brenier and Gangbo12], we will show that the converse implication holds for closed sets: therefore, for closed sets, these two properties are in fact equivalent. Since the graph of a maximal monotone operator is closed, we obtain that a monotone operator in
$\mathcal {X}\times \mathcal {X}^{*}$
are also invariant by measure-preserving isomorphisms; using the results of [Reference Brenier and Gangbo12], we will show that the converse implication holds for closed sets: therefore, for closed sets, these two properties are in fact equivalent. Since the graph of a maximal monotone operator is closed, we obtain that a monotone operator in
![]() $\mathcal {X}\times \mathcal {X}^{*}$
whose graph is invariant by the action of measure-preserving isomorphisms admits a maximal monotone extension which is law invariant (Theorem 4.4).
$\mathcal {X}\times \mathcal {X}^{*}$
whose graph is invariant by the action of measure-preserving isomorphisms admits a maximal monotone extension which is law invariant (Theorem 4.4).
This framework is exploited in Section 3 (where we study the approximation of transport maps and plans by various classes of measure-preserving isomorphisms) and Section 4.
The Hilbertian setting when
![]() $p=p^{*}=2$
and
$p=p^{*}=2$
and
![]() $\mathsf {X}$
is an Hilbert space (so that
$\mathsf {X}$
is an Hilbert space (so that
![]() $\mathcal {X}=L^{2}(\Omega ,{\mathcal {B}},\mathbb {P};\mathsf {X})$
is a Hilbert space as well that can be identified with its dual
$\mathcal {X}=L^{2}(\Omega ,{\mathcal {B}},\mathbb {P};\mathsf {X})$
is a Hilbert space as well that can be identified with its dual
![]() $\mathcal {X}^{*}$
) provides an important case, which we will further exploit in [Reference Cavagnari, Savaré and Sodini17]. It turns out that maximal dissipative operators
$\mathcal {X}^{*}$
) provides an important case, which we will further exploit in [Reference Cavagnari, Savaré and Sodini17]. It turns out that maximal dissipative operators
![]() $\boldsymbol {B}$
on
$\boldsymbol {B}$
on
![]() $L^{2}(\Omega ,{\mathcal {B}},\mathbb {P};\mathsf {X})$
, invariant by measure-preserving isomorphisms, are the Hilbertian counterparts of maximal totally dissipative operators on the Wasserstein space
$L^{2}(\Omega ,{\mathcal {B}},\mathbb {P};\mathsf {X})$
, invariant by measure-preserving isomorphisms, are the Hilbertian counterparts of maximal totally dissipative operators on the Wasserstein space
![]() $\mathcal {P}_{2}(\mathsf {X})$
of laws, where
$\mathcal {P}_{2}(\mathsf {X})$
of laws, where
![]() $\mathcal {P}_{2}(\mathsf {X})$
denotes the space of Borel probability measures with finite second moment endowed with the so-called Kantorovich–Rubinstein–Wasserstein distance
$\mathcal {P}_{2}(\mathsf {X})$
denotes the space of Borel probability measures with finite second moment endowed with the so-called Kantorovich–Rubinstein–Wasserstein distance
![]() $W_{2}$
. The results obtained in Section 4 in the framework (1.6) are used in [Reference Cavagnari, Savaré and Sodini17] to develop a well-posedness theory for dissipative evolution equations in the metric space
$W_{2}$
. The results obtained in Section 4 in the framework (1.6) are used in [Reference Cavagnari, Savaré and Sodini17] to develop a well-posedness theory for dissipative evolution equations in the metric space
![]() $(\mathcal {P}_{2}(\mathsf {X}),W_{2})$
, together with a Lagrangian characterization for the solution of the corresponding Cauchy problem.
$(\mathcal {P}_{2}(\mathsf {X}),W_{2})$
, together with a Lagrangian characterization for the solution of the corresponding Cauchy problem.
Besides the direct application of the general invariance extension result provided in Section 2, in Section 4, we also analyze further properties of Lipschitz functions and maximal dissipative operators on
![]() $\mathcal {X}= L^{2}(\Omega ,{\mathcal {B}},\mathbb {P};\mathsf {X})$
, which are invariant by measure-preserving isomorphisms. In particular, we prove that the effect of a Lipschitz invariant map
$\mathcal {X}= L^{2}(\Omega ,{\mathcal {B}},\mathbb {P};\mathsf {X})$
, which are invariant by measure-preserving isomorphisms. In particular, we prove that the effect of a Lipschitz invariant map
![]() ${\boldsymbol {L}}:\mathcal {X}\to \mathcal {X}$
on an element
${\boldsymbol {L}}:\mathcal {X}\to \mathcal {X}$
on an element
![]() $X\in \mathcal {X}$
can always be represented as
$X\in \mathcal {X}$
can always be represented as
where
![]() $l:\mathcal {S}(\mathsf {X})\to \mathsf {X}$
is a (uniquely determined) continuous map defined in
$l:\mathcal {S}(\mathsf {X})\to \mathsf {X}$
is a (uniquely determined) continuous map defined in
whose sections
![]() $l(\cdot ,\mu )$
are Lipschitz as well, for every
$l(\cdot ,\mu )$
are Lipschitz as well, for every
![]() $\mu \in \mathcal {P}_{2}(\mathsf {X}).$
$\mu \in \mathcal {P}_{2}(\mathsf {X}).$
An important application of these results concerns the resolvent operator, the Moreau–Yosida approximation, and the semigroup associated with a maximal dissipative invariant operator
![]() $\boldsymbol {B}$
in
$\boldsymbol {B}$
in
![]() $L^{2}(\Omega ,{\mathcal {B}},\mathbb {P}; \mathsf {X})$
, for which we obtain new relevant representation formulae (Theorem 4.12).
$L^{2}(\Omega ,{\mathcal {B}},\mathbb {P}; \mathsf {X})$
, for which we obtain new relevant representation formulae (Theorem 4.12).
The above structural characterizations rely on various approximation properties for couplings between probability measures in terms of maps and measure-preserving transformations. We collect them in Section 3, with the aim to present many important results available in the literature (cf. [Reference Brenier and Gangbo12, Reference Carmona and Delarue16, Reference Gangbo and Tudorascu21, Reference Pratelli27]) in a unified framework and (in some cases) a slightly more general setting adapted to Section 4.
2 Extension of monotone operators and Lipschitz maps invariant by a group of isometries
Let
![]() $\mathcal {X}$
be a reflexive Banach space with norm
$\mathcal {X}$
be a reflexive Banach space with norm
![]() $|\cdot |$
, and let
$|\cdot |$
, and let
![]() $\mathcal {X}^{*}$
be its dual endowed with the dual norm
$\mathcal {X}^{*}$
be its dual endowed with the dual norm
![]() $|\cdot |_{*}$
.
$|\cdot |_{*}$
.
We denote by
![]() $\mathsf {c}:\mathcal {X}^{*}\times \mathcal {X}\to \mathbb {R}$
, the duality pairing
$\mathsf {c}:\mathcal {X}^{*}\times \mathcal {X}\to \mathbb {R}$
, the duality pairing
![]() $\langle \cdot , \cdot \rangle $
between
$\langle \cdot , \cdot \rangle $
between
![]() $\mathcal {X}^{*}$
and
$\mathcal {X}^{*}$
and
![]() $\mathcal {X}$
and by
$\mathcal {X}$
and by
![]() $\mathcal {Z}$
the product space
$\mathcal {Z}$
the product space
![]() $\mathcal {X}\times \mathcal {X}^{*}$
with dual
$\mathcal {X}\times \mathcal {X}^{*}$
with dual
![]() $\mathcal {Z}^{*}:=\mathcal {X}^{*}\times \mathcal {X}$
.
$\mathcal {Z}^{*}:=\mathcal {X}^{*}\times \mathcal {X}$
.
A (multivalued) operator
![]() ${\boldsymbol {A}}:\mathcal {X}\rightrightarrows \mathcal {X}^{*}$
(which we identify with its graph, a subset of
${\boldsymbol {A}}:\mathcal {X}\rightrightarrows \mathcal {X}^{*}$
(which we identify with its graph, a subset of
![]() $ \mathcal {X} \times \mathcal {X}^{*}$
) is monotone if it satisfies
$ \mathcal {X} \times \mathcal {X}^{*}$
) is monotone if it satisfies
The proper domain
![]() $\mathrm {D}({\boldsymbol {A}})\subset \mathcal {X}$
of
$\mathrm {D}({\boldsymbol {A}})\subset \mathcal {X}$
of
![]() ${\boldsymbol {A}}$
is just the projection on the first component of (the graph of)
${\boldsymbol {A}}$
is just the projection on the first component of (the graph of)
![]() ${\boldsymbol {A}}.$
A monotone operator
${\boldsymbol {A}}.$
A monotone operator
![]() ${\boldsymbol {A}}$
is maximal if any monotone operator in
${\boldsymbol {A}}$
is maximal if any monotone operator in
![]() $\mathcal {X}\times \mathcal {X}^{*}$
containing
$\mathcal {X}\times \mathcal {X}^{*}$
containing
![]() ${\boldsymbol {A}}$
coincides with
${\boldsymbol {A}}$
coincides with
![]() ${\boldsymbol {A}}.$
${\boldsymbol {A}}.$
In order to address the extension problem of monotone operators
![]() ${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
invariant by the action of a group of isometric isomorphisms, it is crucial to have some explicit formula providing a maximal extension of
${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
invariant by the action of a group of isometric isomorphisms, it is crucial to have some explicit formula providing a maximal extension of
![]() ${\boldsymbol {A}}$
. In this respect, the characterization of monotone and maximal monotone operators by means of suitable “contact sets” of convex functionals in
${\boldsymbol {A}}$
. In this respect, the characterization of monotone and maximal monotone operators by means of suitable “contact sets” of convex functionals in
![]() $\mathcal {X}\times \mathcal {X}^{*},$
started with the seminal paper [Reference Fitzpatrick19] and further developed in a more recent series of relevant contributions (see, e.g., [Reference Burachik and Svaiter14, Reference Ghoussoub22, Reference Martinez-Legaz and Théra24–Reference Penot26, Reference Visintin35] and the references therein), and the kernel averaging operation developed by [Reference Bauschke and Wang8] provide extremely powerful tools, that we are going to quickly recall in the next section. We will also show how to slightly improve this construction in order to obtain an explicit formula providing a maximal extension of
$\mathcal {X}\times \mathcal {X}^{*},$
started with the seminal paper [Reference Fitzpatrick19] and further developed in a more recent series of relevant contributions (see, e.g., [Reference Burachik and Svaiter14, Reference Ghoussoub22, Reference Martinez-Legaz and Théra24–Reference Penot26, Reference Visintin35] and the references therein), and the kernel averaging operation developed by [Reference Bauschke and Wang8] provide extremely powerful tools, that we are going to quickly recall in the next section. We will also show how to slightly improve this construction in order to obtain an explicit formula providing a maximal extension of
![]() ${\boldsymbol {A}}$
whose domain is contained in the closed convex hull of
${\boldsymbol {A}}$
whose domain is contained in the closed convex hull of
![]() $\mathrm {D}({\boldsymbol {A}})$
. In this connection, we mention that the existence of a maximal extension of
$\mathrm {D}({\boldsymbol {A}})$
. In this connection, we mention that the existence of a maximal extension of
![]() ${\boldsymbol {A}}$
with the desired abovementioned optimality for the domain can be deduced by [Reference Bauschke7], thanks to the correspondence revealed by Minty between monotone operators and firmly nonexpansive mappings. Indeed, [Reference Bauschke7] uses the Fitzpatrick function to prove the Kirszbraun–Valentine extension theorem for firmly nonexpansive mappings with optimal range localization. However, part of the proof still relies on Zorn’s lemma and it is not entirely constructive.
${\boldsymbol {A}}$
with the desired abovementioned optimality for the domain can be deduced by [Reference Bauschke7], thanks to the correspondence revealed by Minty between monotone operators and firmly nonexpansive mappings. Indeed, [Reference Bauschke7] uses the Fitzpatrick function to prove the Kirszbraun–Valentine extension theorem for firmly nonexpansive mappings with optimal range localization. However, part of the proof still relies on Zorn’s lemma and it is not entirely constructive.
2.1 Maximal extensions of monotone operators by self-dual Lagrangians
Following the presentation of [Reference Bauschke and Wang8, Reference Penot26], given a set
![]() ${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
and its indicator function
${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
and its indicator function
![]() $\mathrm {I}_{\boldsymbol {A}}$
, we consider the proper function
$\mathrm {I}_{\boldsymbol {A}}$
, we consider the proper function
![]() $\mathsf {c}_{{\boldsymbol {A}}}: \mathcal {X}^{*} \times \mathcal {X} \to (-\infty , +\infty ]$
defined as
$\mathsf {c}_{{\boldsymbol {A}}}: \mathcal {X}^{*} \times \mathcal {X} \to (-\infty , +\infty ]$
defined as
 $$\begin{align*}\mathsf{c}_{{\boldsymbol{A}}}(v,x):= \mathsf{c}(v,x)+\mathrm{I}_{\boldsymbol{A}}(x,v)= \begin{cases} \langle v, x \rangle, \quad &\text{ if } (x,v) \in {\boldsymbol{A}}, \\ + \infty, \quad &\text{ else}.\end{cases}\end{align*}$$
$$\begin{align*}\mathsf{c}_{{\boldsymbol{A}}}(v,x):= \mathsf{c}(v,x)+\mathrm{I}_{\boldsymbol{A}}(x,v)= \begin{cases} \langle v, x \rangle, \quad &\text{ if } (x,v) \in {\boldsymbol{A}}, \\ + \infty, \quad &\text{ else}.\end{cases}\end{align*}$$
Notice that
![]() $\mathsf {c}_{{\boldsymbol {A}}}$
has an affine minorant if
$\mathsf {c}_{{\boldsymbol {A}}}$
has an affine minorant if
![]() ${\boldsymbol {A}}$
is monotone, in the sense that
${\boldsymbol {A}}$
is monotone, in the sense that
where
![]() $(x_{0},v_{0})\in {\boldsymbol {A}}$
is an arbitrary given point.
$(x_{0},v_{0})\in {\boldsymbol {A}}$
is an arbitrary given point.
Recalling that the convex conjugate
![]() $g^{*}:\mathcal {Z}^{*} \to (-\infty ,+\infty ]$
of a proper function
$g^{*}:\mathcal {Z}^{*} \to (-\infty ,+\infty ]$
of a proper function
![]() $g: \mathcal {Z} \to (-\infty , +\infty ]$
with an affine minorant is defined as
$g: \mathcal {Z} \to (-\infty , +\infty ]$
with an affine minorant is defined as
with an analogous definition in the case of a function
![]() $h:\mathcal {Z}^{*} \to (-\infty ,+\infty ]$
, we can introduce the Fitzpatrick function
$h:\mathcal {Z}^{*} \to (-\infty ,+\infty ]$
, we can introduce the Fitzpatrick function
![]() $\mathsf {f}_{\boldsymbol {A}}:\mathcal {Z}\to (-\infty ,+\infty ]$
and the convex l.s.c. relaxation
$\mathsf {f}_{\boldsymbol {A}}:\mathcal {Z}\to (-\infty ,+\infty ]$
and the convex l.s.c. relaxation
![]() $\mathsf {p}_{\boldsymbol {A}}:\mathcal {Z}^{*}\to (-\infty ,+\infty ]$
of
$\mathsf {p}_{\boldsymbol {A}}:\mathcal {Z}^{*}\to (-\infty ,+\infty ]$
of
![]() $\mathsf {c}_{{\boldsymbol {A}}}$
:
$\mathsf {c}_{{\boldsymbol {A}}}$
:
It will be often useful to switch the order of the components of elements in
![]() $\mathcal {X}\times \mathcal {X}^{*}$
: we will denote by
$\mathcal {X}\times \mathcal {X}^{*}$
: we will denote by
![]() ${\mathfrak {s}}:{\mathcal {X}}\times {\mathcal {X}}^{*} \to \mathcal {X}^{*}\times \mathcal {X}$
the switch map
${\mathfrak {s}}:{\mathcal {X}}\times {\mathcal {X}}^{*} \to \mathcal {X}^{*}\times \mathcal {X}$
the switch map
If g is any function defined in
![]() $\mathcal {X} \times \mathcal {X}^{*}$
(resp. in
$\mathcal {X} \times \mathcal {X}^{*}$
(resp. in
![]() $\mathcal {X}^{*}\times \mathcal {X}$
), we set
$\mathcal {X}^{*}\times \mathcal {X}$
), we set
![]() $g^{\top }:=g\circ \mathfrak {s}$
(resp.
$g^{\top }:=g\circ \mathfrak {s}$
(resp.
![]() $g^{\top }:=g\circ \mathfrak {s}^{-1}$
). In particular,
$g^{\top }:=g\circ \mathfrak {s}^{-1}$
). In particular,
![]() $\mathsf {c}^{\top }$
is the duality pairing between
$\mathsf {c}^{\top }$
is the duality pairing between
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {X}^{*}$
.
$\mathcal {X}^{*}$
.
We collect in the following statement some useful properties.
Theorem 2.1 (Representation of monotone operators)
-
(1) If
 $f:\mathcal {Z}\to (-\infty ,+\infty ]$
is a convex l.s.c. function satisfying
$f:\mathcal {Z}\to (-\infty ,+\infty ]$
is a convex l.s.c. function satisfying
 $f\ge \mathsf {c}^{\top }$
, then (2.4)and
$f\ge \mathsf {c}^{\top }$
, then (2.4)and $$ \begin{align} \text{the contact set } {\boldsymbol{A}}_f:=\Big\{(x,v)\in \mathcal{Z}: f(x,v)=\langle v,x\rangle \Big\} \text{ is monotone, } f^{*}\ge \mathsf{f}_{{\boldsymbol{A}}_{f}}^{\top}, \end{align} $$
(2.5)where
$$ \begin{align} \text{the contact set } {\boldsymbol{A}}_f:=\Big\{(x,v)\in \mathcal{Z}: f(x,v)=\langle v,x\rangle \Big\} \text{ is monotone, } f^{*}\ge \mathsf{f}_{{\boldsymbol{A}}_{f}}^{\top}, \end{align} $$
(2.5)where $$ \begin{align} {\boldsymbol{A}}_f\subset \boldsymbol{T}_f:=\Big\{(x,v)\in \mathcal{Z}: (v,x)\in \partial f(x,v)\Big\}, \end{align} $$
$$ \begin{align} {\boldsymbol{A}}_f\subset \boldsymbol{T}_f:=\Big\{(x,v)\in \mathcal{Z}: (v,x)\in \partial f(x,v)\Big\}, \end{align} $$
 $\partial f$
denotes the subdifferential of f. An analogous statement holds for
$\partial f$
denotes the subdifferential of f. An analogous statement holds for
 $g:\mathcal {Z}^{*}\to (-\infty ,+\infty ]$
satisfying
$g:\mathcal {Z}^{*}\to (-\infty ,+\infty ]$
satisfying
 $g\ge \mathsf {c}$
, by setting
$g\ge \mathsf {c}$
, by setting
 ${\boldsymbol {A}}_g:={\boldsymbol {A}}_{g^{\top }}.$
${\boldsymbol {A}}_g:={\boldsymbol {A}}_{g^{\top }}.$
-
(2) If
 ${\boldsymbol {A}}$
is monotone, then (2.6)
${\boldsymbol {A}}$
is monotone, then (2.6) $$ \begin{align} \mathsf{f}_{\boldsymbol{A}}^{\top}\le \mathsf{p}_{\boldsymbol{A}}\le \mathsf{c}_{\boldsymbol{A}}; \end{align} $$
(2.7)i.e.,
$$ \begin{align} \mathsf{f}_{\boldsymbol{A}}^{\top}\le \mathsf{p}_{\boldsymbol{A}}\le \mathsf{c}_{\boldsymbol{A}}; \end{align} $$
(2.7)i.e., $$ \begin{align} \mathsf{p}_{\boldsymbol{A}}\ge \mathsf{c};\quad \mathsf{p}_{\boldsymbol{A}}=\mathsf{c}\quad \text{on }{\boldsymbol{A}}, \end{align} $$
$$ \begin{align} \mathsf{p}_{\boldsymbol{A}}\ge \mathsf{c};\quad \mathsf{p}_{\boldsymbol{A}}=\mathsf{c}\quad \text{on }{\boldsymbol{A}}, \end{align} $$
 ${\boldsymbol {A}}\subset {\boldsymbol {A}}_{\mathsf {p}_{\boldsymbol {A}}}.$
${\boldsymbol {A}}\subset {\boldsymbol {A}}_{\mathsf {p}_{\boldsymbol {A}}}.$
-
(3) If
 ${\boldsymbol {A}}$
is a monotone operator and
${\boldsymbol {A}}$
is a monotone operator and
 $f:\mathcal {Z}\to (-\infty ,+\infty ]$
is a convex l.s.c. function satisfying
$f:\mathcal {Z}\to (-\infty ,+\infty ]$
is a convex l.s.c. function satisfying
 $\mathsf {c}^{\top }\le f\le \mathsf {p}_{\boldsymbol {A}}^{\top }$
, then the contact set
$\mathsf {c}^{\top }\le f\le \mathsf {p}_{\boldsymbol {A}}^{\top }$
, then the contact set
 ${\boldsymbol {A}}_f$
is a monotone extension of
${\boldsymbol {A}}_f$
is a monotone extension of
 ${\boldsymbol {A}}.$
${\boldsymbol {A}}.$
-
(4) If
 ${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
is maximal monotone, then
${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
is maximal monotone, then
 $\mathsf {f}_{\boldsymbol {A}}\ge \mathsf {c}^{\top }$
. Conversely, if
$\mathsf {f}_{\boldsymbol {A}}\ge \mathsf {c}^{\top }$
. Conversely, if
 ${\boldsymbol {A}}$
is monotone and
${\boldsymbol {A}}$
is monotone and
 $\mathsf {f}_{\boldsymbol {A}}\ge \mathsf {c}^{\top }$
, then (2.8)provides a maximal monotone extension of
$\mathsf {f}_{\boldsymbol {A}}\ge \mathsf {c}^{\top }$
, then (2.8)provides a maximal monotone extension of $$ \begin{align} {\boldsymbol{\hat{A}}}:= \Big\{z\in \mathcal{Z}:\mathsf{f}_{\boldsymbol{A}}(z)= \mathsf{c}^{\top} (z)\Big\} = \Big\{z\in \mathcal{Z}: \mathsf{p}_{\boldsymbol{A}}(z)= \mathsf{c} (z)\Big\} \end{align} $$
$$ \begin{align} {\boldsymbol{\hat{A}}}:= \Big\{z\in \mathcal{Z}:\mathsf{f}_{\boldsymbol{A}}(z)= \mathsf{c}^{\top} (z)\Big\} = \Big\{z\in \mathcal{Z}: \mathsf{p}_{\boldsymbol{A}}(z)= \mathsf{c} (z)\Big\} \end{align} $$
 ${\boldsymbol {A}}$
.
${\boldsymbol {A}}$
.
-
(5) If
 $f:\mathcal {Z}\to (-\infty ,+\infty ]$
is a convex l.s.c. function satisfying
$f:\mathcal {Z}\to (-\infty ,+\infty ]$
is a convex l.s.c. function satisfying
 $f\ge \mathsf {c}^{\top }$
, then
$f\ge \mathsf {c}^{\top }$
, then
 ${\boldsymbol {A}}_f$
is maximal monotone if and only if
${\boldsymbol {A}}_f$
is maximal monotone if and only if
 $f^{*}\ge \mathsf {c}$
and in this case
$f^{*}\ge \mathsf {c}$
and in this case
 ${\boldsymbol {A}}_f= {\boldsymbol {A}}_{(f^{*})^{\top }}.$
${\boldsymbol {A}}_f= {\boldsymbol {A}}_{(f^{*})^{\top }}.$
-
(6) If
 $f:\mathcal {Z}\to (-\infty ,+\infty ]$
is a convex l.s.c. function satisfying the self-duality property (2.9)then
$f:\mathcal {Z}\to (-\infty ,+\infty ]$
is a convex l.s.c. function satisfying the self-duality property (2.9)then $$ \begin{align} f^{*}=f^{\top}, \end{align} $$
$$ \begin{align} f^{*}=f^{\top}, \end{align} $$
 $f\ge \mathsf {c}^{\top }$
and the contact set
$f\ge \mathsf {c}^{\top }$
and the contact set
 ${\boldsymbol {A}}_f$
is maximal monotone.
${\boldsymbol {A}}_f$
is maximal monotone.
Proof We give a few references and sketches for the proof.
(1) The inclusion in (2.5) follows by [Reference Fitzpatrick19, Theorem 2.4] and shows in particular that
![]() ${\boldsymbol {A}}_f$
is monotone since
${\boldsymbol {A}}_f$
is monotone since
![]() $\mathbf {T}_f$
is monotone by [Reference Fitzpatrick19, Proposition 2.2]. Clearly,
$\mathbf {T}_f$
is monotone by [Reference Fitzpatrick19, Proposition 2.2]. Clearly,
![]() $f^{\top } \le \mathsf {c}_{{\boldsymbol {A}}_f}$
so that, passing to the conjugates, the reverse inequality follows.
$f^{\top } \le \mathsf {c}_{{\boldsymbol {A}}_f}$
so that, passing to the conjugates, the reverse inequality follows.
(2) The result in (2.6) is [Reference Penot26, Proposition 4(c)], while (2.7) is [Reference Penot26, Proposition 4(f)].
(3) This follows by (1) and (2).
(4) The first implication follows by [Reference Penot26, Theorem 5]. The second implication follows by [Reference Penot26, Theorem 6] choosing
![]() $g:=f_{\boldsymbol {A}}$
and [Reference Burachik and Svaiter14, Theorem 3.1].
$g:=f_{\boldsymbol {A}}$
and [Reference Burachik and Svaiter14, Theorem 3.1].
(5) The first part of the sentence is [Reference Penot26, Theorem 6], while the equality
![]() ${\boldsymbol {A}}_f={\boldsymbol {A}}_{(f^{*})^{\top }}$
can be found, e.g., in [Reference Burachik and Svaiter14, Theorem 3.1].
${\boldsymbol {A}}_f={\boldsymbol {A}}_{(f^{*})^{\top }}$
can be found, e.g., in [Reference Burachik and Svaiter14, Theorem 3.1].
(6) This is contained in the statement and in the proof of [Reference Bauschke and Wang8, Fact 5.6].
The previous result suggests a strategy (cf. Theorem 2.2 below) to construct a maximal extension of a given monotone operator
![]() ${\boldsymbol {A}}$
starting from a convex and l.s.c. function
${\boldsymbol {A}}$
starting from a convex and l.s.c. function
![]() $f:\mathcal {Z}\to (-\infty ,+\infty ]$
satisfying
$f:\mathcal {Z}\to (-\infty ,+\infty ]$
satisfying
Using the kernel average introduced in [Reference Bauschke and Wang8], one obtains a self-dual Lagrangian
![]() $R_f$
which satisfies
$R_f$
which satisfies
![]() $\mathsf {f}_{\boldsymbol {A}}\le R_f\le \mathsf {p}_{\boldsymbol {A}}^{\top }$
, so that the contact set of
$\mathsf {f}_{\boldsymbol {A}}\le R_f\le \mathsf {p}_{\boldsymbol {A}}^{\top }$
, so that the contact set of
![]() $R_f$
is a maximal monotone extension of
$R_f$
is a maximal monotone extension of
![]() ${\boldsymbol {A}}.$
We introduce a function
${\boldsymbol {A}}.$
We introduce a function
where
![]() $\psi ^\vee (z):=\psi (-z)$
for every
$\psi ^\vee (z):=\psi (-z)$
for every
![]() $z \in \mathcal {Z}.$
The assumption in (2.11), in particular, implies that
$z \in \mathcal {Z}.$
The assumption in (2.11), in particular, implies that
since
A typical example is given by
The following result is an immediate consequence of [Reference Bauschke and Wang8, Fact 5.6, Theorem 5.7, and Remark 5.8].
Theorem 2.2 (Kernel averages and maximal monotone extensions [Reference Bauschke and Wang8])
Let
![]() ${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
be a monotone operator, and let
${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
be a monotone operator, and let
![]() $\mathsf {f}_{\boldsymbol {A}}:=\mathsf {c}_{{\boldsymbol {A}}}^{*}, \mathsf {p}_{\boldsymbol {A}}:=\mathsf {c}_{{\boldsymbol {A}}}^{**}$
be defined as above and
$\mathsf {f}_{\boldsymbol {A}}:=\mathsf {c}_{{\boldsymbol {A}}}^{*}, \mathsf {p}_{\boldsymbol {A}}:=\mathsf {c}_{{\boldsymbol {A}}}^{**}$
be defined as above and
![]() $\psi :\mathcal {Z}\to [0,+\infty )$
a self-dual function as in (2.11). Let
$\psi :\mathcal {Z}\to [0,+\infty )$
a self-dual function as in (2.11). Let
![]() $f: \mathcal {Z} \to (-\infty ,+\infty ]$
be a lower semicontinuous and convex function satisfying (2.10).
$f: \mathcal {Z} \to (-\infty ,+\infty ]$
be a lower semicontinuous and convex function satisfying (2.10).
-
(1) The function
 $R_f: \mathcal {Z} \to (-\infty ,+\infty ]$
defined as (2.14)is self-dual and satisfies the bound (2.10), i.e.,
$R_f: \mathcal {Z} \to (-\infty ,+\infty ]$
defined as (2.14)is self-dual and satisfies the bound (2.10), i.e., $$ \begin{align} R_f(x,v):= \min_{(x,v)=\frac{1}{2}(x_1+x_{2},v_1+v_{2})} \left \{ \frac{1}{2}f(x_1,v_1) + \frac{1}{2}f^{*}(v_{2},x_{2})+\frac{1}{4} \psi(x_1-x_{2},v_1-v_{2}) \right \} \end{align} $$
$$ \begin{align} R_f(x,v):= \min_{(x,v)=\frac{1}{2}(x_1+x_{2},v_1+v_{2})} \left \{ \frac{1}{2}f(x_1,v_1) + \frac{1}{2}f^{*}(v_{2},x_{2})+\frac{1}{4} \psi(x_1-x_{2},v_1-v_{2}) \right \} \end{align} $$
 $\mathsf {f}_{\boldsymbol {A}}\le R_f\le \mathsf {p}_{\boldsymbol {A}}^{\top }.$
$\mathsf {f}_{\boldsymbol {A}}\le R_f\le \mathsf {p}_{\boldsymbol {A}}^{\top }.$
-
(2) The operator
 $\tilde {{\boldsymbol {A}}}$
defined as the contact set of
$\tilde {{\boldsymbol {A}}}$
defined as the contact set of
 $R_f$
(2.15)is a maximal monotone extension of
$R_f$
(2.15)is a maximal monotone extension of $$ \begin{align} \tilde{{\boldsymbol{A}}} := \left \{ (x,v) \in \mathcal{Z} : R_f(x,v)=\langle v,x\rangle\right \} \end{align} $$
$$ \begin{align} \tilde{{\boldsymbol{A}}} := \left \{ (x,v) \in \mathcal{Z} : R_f(x,v)=\langle v,x\rangle\right \} \end{align} $$
 ${\boldsymbol {A}}$
.
${\boldsymbol {A}}$
.
We want to show that, for a suitable choice of f as in the previous theorem, we can produce a maximal monotone extension of
![]() ${\boldsymbol {A}}$
with domain included in
${\boldsymbol {A}}$
with domain included in
![]() $ D:=\overline {\operatorname {co}}\left (\mathrm {D}({\boldsymbol {A}})\right )$
. We claim that such f can be defined as
$ D:=\overline {\operatorname {co}}\left (\mathrm {D}({\boldsymbol {A}})\right )$
. We claim that such f can be defined as
where
![]() $\mathrm {I}_C$
is the indicator function of
$\mathrm {I}_C$
is the indicator function of
![]() $C=D\times \mathcal {X}^{*}$
, i.e.,
$C=D\times \mathcal {X}^{*}$
, i.e.,
![]() $\mathrm {I}_C(x,v)=0$
if
$\mathrm {I}_C(x,v)=0$
if
![]() $x \in D$
and
$x \in D$
and
![]() $\mathrm {I}_C(x,v)=+\infty $
if
$\mathrm {I}_C(x,v)=+\infty $
if
![]() $x \notin D$
.
$x \notin D$
.
Theorem 2.3 (A maximal monotone extension with minimal domain)
Let
![]() ${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
be a monotone operator, and let
${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
be a monotone operator, and let
![]() $f:\mathcal {Z}\to (-\infty , + \infty ]$
be as in (2.16). The following hold:
$f:\mathcal {Z}\to (-\infty , + \infty ]$
be as in (2.16). The following hold:
-
(1) f is a l.s.c. and convex function such that
 $\mathsf {f}_{\boldsymbol {A}} \le f \le \mathsf {p}_{\boldsymbol {A}}^{\top } $
.
$\mathsf {f}_{\boldsymbol {A}} \le f \le \mathsf {p}_{\boldsymbol {A}}^{\top } $
. -
(2)
 $\mathrm {D}(f)\subset C=D\times \mathcal {X}^{*}$
and
$\mathrm {D}(f)\subset C=D\times \mathcal {X}^{*}$
and
 $ \mathrm {D}(f^{*}) \subset \mathfrak {s}(C)=\mathcal {X}^{*}\times D$
.
$ \mathrm {D}(f^{*}) \subset \mathfrak {s}(C)=\mathcal {X}^{*}\times D$
. -
(3) Defining
 $R_f$
as in (2.14) and its contact set
$R_f$
as in (2.14) and its contact set
 $\tilde {\boldsymbol {A}}$
as in (2.15),
$\tilde {\boldsymbol {A}}$
as in (2.15),
 $\mathrm {D}(R_f)\subset C=D\times \mathcal {X}^{*}$
and
$\mathrm {D}(R_f)\subset C=D\times \mathcal {X}^{*}$
and
 $\tilde {\boldsymbol {A}}$
provides a maximal extension of
$\tilde {\boldsymbol {A}}$
provides a maximal extension of
 ${\boldsymbol {A}}$
with domain
${\boldsymbol {A}}$
with domain
 $\mathrm {D}(\tilde {\boldsymbol {A}})\subset D.$
$\mathrm {D}(\tilde {\boldsymbol {A}})\subset D.$
Proof (1) It is clear that f is convex and lower semicontinuous and
![]() $f \ge \mathsf {f}_{\boldsymbol {A}}$
. On the other hand,
$f \ge \mathsf {f}_{\boldsymbol {A}}$
. On the other hand,
![]() $f^{\top }\le \mathsf {c}_{\boldsymbol {A}}$
by (2.6) and since
$f^{\top }\le \mathsf {c}_{\boldsymbol {A}}$
by (2.6) and since
![]() $\mathrm {I}_C=0$
on
$\mathrm {I}_C=0$
on
![]() ${\boldsymbol {A}}$
. It follows that
${\boldsymbol {A}}$
. It follows that
![]() $f^{\top }\le \mathsf {c}_{\boldsymbol {A}}^{**}=\mathsf {p}_{\boldsymbol {A}}.$
$f^{\top }\le \mathsf {c}_{\boldsymbol {A}}^{**}=\mathsf {p}_{\boldsymbol {A}}.$
(2) It is clear from the definition of f that
![]() $f(x,v)=+\infty $
if
$f(x,v)=+\infty $
if
![]() $x \notin D$
. Let us compute the conjugate
$x \notin D$
. Let us compute the conjugate
![]() $f^{*}$
of f: by the Fenchel–Rockafellar duality theorem (see, e.g., [Reference Rockafellar29, Theorem 16.4]), we have that
$f^{*}$
of f: by the Fenchel–Rockafellar duality theorem (see, e.g., [Reference Rockafellar29, Theorem 16.4]), we have that
where
![]() $\operatorname {\mathrm {cl}}$
denotes the lower semicontinuous envelope of a given function (i.e.,
$\operatorname {\mathrm {cl}}$
denotes the lower semicontinuous envelope of a given function (i.e.,
![]() $\operatorname {\mathrm {cl}}(h)$
is the largest lower semicontinuous function staying below h) and
$\operatorname {\mathrm {cl}}(h)$
is the largest lower semicontinuous function staying below h) and
![]() $\mathbin \Box $
denotes the inf-convolution (or epigraphical sum) of two functions: if
$\mathbin \Box $
denotes the inf-convolution (or epigraphical sum) of two functions: if
![]() $k,j:\mathcal {Z}^{*} \to (-\infty , + \infty ]$
, then
$k,j:\mathcal {Z}^{*} \to (-\infty , + \infty ]$
, then
![]() $k\mathbin \Box j$
is defined as
$k\mathbin \Box j$
is defined as
Since
![]() $\mathrm {I}_C(x,v)=\mathrm {I}_D(x)$
, we can easily compute its dual for every
$\mathrm {I}_C(x,v)=\mathrm {I}_D(x)$
, we can easily compute its dual for every
![]() $z=(v,x)\in \mathcal {X}^{*} \times \mathcal {X}$
$z=(v,x)\in \mathcal {X}^{*} \times \mathcal {X}$
 $$ \begin{align*} \mathrm{I}_C^{*}(v,x)&= \sup_{(x_{0},v_{0}) \in \mathcal{X}^{*} \times \mathcal{X}} \langle v,x_{0} \rangle + \langle v_{0},x\rangle -\mathrm{I}_D(x_{0}) = \sup_{x_{0}\in D, v_{0} \in \mathcal{X}^{*}} \langle v_{0},x \rangle + \langle v,x_{0}\rangle\\ &= \mathrm{I}_{0}(x)+\sigma_D(v), \end{align*} $$
$$ \begin{align*} \mathrm{I}_C^{*}(v,x)&= \sup_{(x_{0},v_{0}) \in \mathcal{X}^{*} \times \mathcal{X}} \langle v,x_{0} \rangle + \langle v_{0},x\rangle -\mathrm{I}_D(x_{0}) = \sup_{x_{0}\in D, v_{0} \in \mathcal{X}^{*}} \langle v_{0},x \rangle + \langle v,x_{0}\rangle\\ &= \mathrm{I}_{0}(x)+\sigma_D(v), \end{align*} $$
where
![]() $\mathrm {I}_{0}$
is the indicator function of the singleton
$\mathrm {I}_{0}$
is the indicator function of the singleton
![]() $\{0\}$
and
$\{0\}$
and
![]() $\sigma _D$
is the support function of D defined by
$\sigma _D$
is the support function of D defined by
We thus have
 $$ \begin{align*} (\mathsf{p}_{\boldsymbol{A}} \mathbin\Box \mathrm{I}^{*}_C)(v,x) &= \inf_{x_1+x_{2}=x,v_1+v_{2}=v} \mathsf{p}_{\boldsymbol{A}}(v_1,x_1)+\mathrm{I}_{0}(x_{2}) +\sigma_D(v_{2}) \\ &= \inf_{v_1+v_{2}=v} \mathsf{p}_{\boldsymbol{A}}(v_1,x)+\sigma_D(v_{2}). \end{align*} $$
$$ \begin{align*} (\mathsf{p}_{\boldsymbol{A}} \mathbin\Box \mathrm{I}^{*}_C)(v,x) &= \inf_{x_1+x_{2}=x,v_1+v_{2}=v} \mathsf{p}_{\boldsymbol{A}}(v_1,x_1)+\mathrm{I}_{0}(x_{2}) +\sigma_D(v_{2}) \\ &= \inf_{v_1+v_{2}=v} \mathsf{p}_{\boldsymbol{A}}(v_1,x)+\sigma_D(v_{2}). \end{align*} $$
Since
![]() $\mathsf {p}_{\boldsymbol {A}} =\mathsf {c}_{\boldsymbol {A}}^{**}$
and
$\mathsf {p}_{\boldsymbol {A}} =\mathsf {c}_{\boldsymbol {A}}^{**}$
and
![]() $\mathsf {c}_{{\boldsymbol {A}}}(v,x)=+\infty $
, if
$\mathsf {c}_{{\boldsymbol {A}}}(v,x)=+\infty $
, if
![]() $x\not \in D$
, we deduce that
$x\not \in D$
, we deduce that
![]() $\mathsf {p}_{\boldsymbol {A}}(v,x)=+\infty $
if
$\mathsf {p}_{\boldsymbol {A}}(v,x)=+\infty $
if
![]() $x\not \in D$
,
$x\not \in D$
,
![]() $\mathrm {D}(\mathsf {p}_{\boldsymbol {A}} \mathbin \Box \mathrm {I}^{*}_C)\subset \mathfrak {s}(C)= \mathcal {X}^{*}\times D$
, and therefore that
$\mathrm {D}(\mathsf {p}_{\boldsymbol {A}} \mathbin \Box \mathrm {I}^{*}_C)\subset \mathfrak {s}(C)= \mathcal {X}^{*}\times D$
, and therefore that
![]() $\mathrm {D}(f^{*})\subset \operatorname {\mathrm {cl}}( \mathcal {X}^{*}\times D)=\mathcal {X}^{*} \times D$
.
$\mathrm {D}(f^{*})\subset \operatorname {\mathrm {cl}}( \mathcal {X}^{*}\times D)=\mathcal {X}^{*} \times D$
.
(3) By the first claim and Theorem 2.2 with f as in (2.16), we obtain that
![]() $\tilde {{\boldsymbol {A}}}$
is a maximal monotone extension of
$\tilde {{\boldsymbol {A}}}$
is a maximal monotone extension of
![]() ${\boldsymbol {A}}$
. We only need to check that
${\boldsymbol {A}}$
. We only need to check that
![]() $\mathrm {D}(\tilde {{\boldsymbol {A}}}) \subset D=\overline {\operatorname {co}}\left (\mathrm {D}({\boldsymbol {A}})\right )$
. Since it is clear from the definition of contact set that
$\mathrm {D}(\tilde {{\boldsymbol {A}}}) \subset D=\overline {\operatorname {co}}\left (\mathrm {D}({\boldsymbol {A}})\right )$
. Since it is clear from the definition of contact set that
![]() $\mathrm {D}(\tilde {\boldsymbol {A}})\subset \pi ^{\mathcal {X}}(\mathrm {D}(R_f))$
, it is sufficient to check that
$\mathrm {D}(\tilde {\boldsymbol {A}})\subset \pi ^{\mathcal {X}}(\mathrm {D}(R_f))$
, it is sufficient to check that
![]() $\mathrm {D}(R_f)\subset C$
.
$\mathrm {D}(R_f)\subset C$
.
Let
![]() $(x,v) \in \mathrm {D}(R_f)$
, then by (2.14) we can find
$(x,v) \in \mathrm {D}(R_f)$
, then by (2.14) we can find
![]() $x_1,x_{2} \in \mathcal {X}$
and
$x_1,x_{2} \in \mathcal {X}$
and
![]() $v_1,v_{2} \in \mathcal {X}^{*}$
such that
$v_1,v_{2} \in \mathcal {X}^{*}$
such that
![]() $(x,v)=\frac {1}{2}(x_1+x_{2},v_1+v_{2})$
and
$(x,v)=\frac {1}{2}(x_1+x_{2},v_1+v_{2})$
and
![]() $(x_1,v_1)\in \mathrm {D}(f)$
,
$(x_1,v_1)\in \mathrm {D}(f)$
,
![]() $(v_{2},x_{2})\in \mathrm {D} (f^{*})$
: in particular,
$(v_{2},x_{2})\in \mathrm {D} (f^{*})$
: in particular,
![]() $x_1,x_{2}$
belong to the convex set D by (2) and therefore
$x_1,x_{2}$
belong to the convex set D by (2) and therefore
![]() $x\in D$
as well.
$x\in D$
as well.
2.2 Extension of monotone operators invariant w.r.t. the action of a group of linear isomorphisms of
 $\mathcal {X}\times \mathcal {X}^{*}$
$\mathcal {X}\times \mathcal {X}^{*}$
We will now focus on operators which are invariant with respect to a group
![]() $\mathsf {G}$
of bounded linear isomorphisms of
$\mathsf {G}$
of bounded linear isomorphisms of
![]() $\mathcal {Z}$
of the form
$\mathcal {Z}$
of the form
![]() $\mathsf {U}=(U,U'):\mathcal {Z} \to \mathcal {Z}$
. For every
$\mathsf {U}=(U,U'):\mathcal {Z} \to \mathcal {Z}$
. For every
![]() $z=(x,v)\in \mathcal {Z}$
, we thus have
$z=(x,v)\in \mathcal {Z}$
, we thus have
and we assume that all the maps
![]() $\mathsf {U}\in \mathsf {G}$
satisfy the following properties:
$\mathsf {U}\in \mathsf {G}$
satisfy the following properties:
for a fixed self-dual function
![]() $\psi :\mathcal {Z}\to [0,+\infty )$
as in (2.11). Notice that the first identity in (2.18) implies
$\psi :\mathcal {Z}\to [0,+\infty )$
as in (2.11). Notice that the first identity in (2.18) implies
so that
![]() $U^{*}\circ U'$
(resp.
$U^{*}\circ U'$
(resp.
![]() $(U')^{*}\circ U$
) is the identity in
$(U')^{*}\circ U$
) is the identity in
![]() $\mathcal {X}^{*}$
(resp. in
$\mathcal {X}^{*}$
(resp. in
![]() $\mathcal {X}$
), i.e.,
$\mathcal {X}$
), i.e.,
![]() $U'=(U^{*})^{-1}=(U^{-1})^{*}$
is the transpose inverse of U.
$U'=(U^{*})^{-1}=(U^{-1})^{*}$
is the transpose inverse of U.
Given
![]() $\mathsf {U}=(U,U') \in \mathsf {G}$
, we define as usual
$\mathsf {U}=(U,U') \in \mathsf {G}$
, we define as usual
![]() $\mathsf {U}^{\top }:=\mathfrak {s} \circ \mathsf {U}\circ \mathfrak {s}^{-1}=(U',U):\mathcal {Z}^{*}\to \mathcal {Z}^{*}$
observing that
$\mathsf {U}^{\top }:=\mathfrak {s} \circ \mathsf {U}\circ \mathfrak {s}^{-1}=(U',U):\mathcal {Z}^{*}\to \mathcal {Z}^{*}$
observing that
![]() $\mathsf {U}^{\top }$
coincides with the inverse transpose of
$\mathsf {U}^{\top }$
coincides with the inverse transpose of
![]() $\mathsf {U}$
with respect to the duality paring between
$\mathsf {U}$
with respect to the duality paring between
![]() $z^{*}=(v^{*},x^{*})\in \mathcal {Z}^{*}$
and
$z^{*}=(v^{*},x^{*})\in \mathcal {Z}^{*}$
and
![]() $z=(x,v)\in \mathcal {Z}$
given by
$z=(x,v)\in \mathcal {Z}$
given by
since
 $$ \begin{align*} \langle \mathsf{U}^{\top} z^{*},\mathsf{U}z\rangle &= \langle (U'v^{*},Ux^{*}), (Ux,U'v)\rangle= \langle U'v^{*},Ux\rangle +\langle U'v,Ux^{*}\rangle = \langle v^{*},x\rangle +\langle v,x^{*}\rangle \\&= \langle z^{*},z\rangle. \end{align*} $$
$$ \begin{align*} \langle \mathsf{U}^{\top} z^{*},\mathsf{U}z\rangle &= \langle (U'v^{*},Ux^{*}), (Ux,U'v)\rangle= \langle U'v^{*},Ux\rangle +\langle U'v,Ux^{*}\rangle = \langle v^{*},x\rangle +\langle v,x^{*}\rangle \\&= \langle z^{*},z\rangle. \end{align*} $$
In particular, we have the formula
Definition 2.1 [
![]() $\mathsf {G}$
-invariance] We say that a set
$\mathsf {G}$
-invariance] We say that a set
![]() ${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
is
${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
is
![]() $\mathsf {G}$
-invariant if
$\mathsf {G}$
-invariant if
![]() $\mathsf {U} {\boldsymbol {A}}\subset {\boldsymbol {A}}$
for every
$\mathsf {U} {\boldsymbol {A}}\subset {\boldsymbol {A}}$
for every
![]() $\mathsf {U}\in \mathsf {G}$
(i.e.,
$\mathsf {U}\in \mathsf {G}$
(i.e.,
![]() $(Ux,U'v)\in {\boldsymbol {A}}$
for every
$(Ux,U'v)\in {\boldsymbol {A}}$
for every
![]() $(x,v) \in {\boldsymbol {A}}$
and
$(x,v) \in {\boldsymbol {A}}$
and
![]() $(U,U')\in \mathsf {G}$
). A function g defined in
$(U,U')\in \mathsf {G}$
). A function g defined in
![]() $ \mathcal {X} \times \mathcal {X}^{*}$
(resp. in
$ \mathcal {X} \times \mathcal {X}^{*}$
(resp. in
![]() $\mathcal {X}^{*}\times \mathcal {X}$
) is said to be
$\mathcal {X}^{*}\times \mathcal {X}$
) is said to be
![]() $\mathsf {G}$
-invariant if
$\mathsf {G}$
-invariant if
![]() $g \circ \mathsf {U}=g$
(resp.
$g \circ \mathsf {U}=g$
(resp.
![]() $g\circ \mathsf {U}^{\top }=g$
) for every
$g\circ \mathsf {U}^{\top }=g$
) for every
![]() $\mathsf {U}\in \mathsf {G}$
. A function
$\mathsf {U}\in \mathsf {G}$
. A function
![]() $h: \mathcal {X} \to \mathcal {X}^{*}$
is
$h: \mathcal {X} \to \mathcal {X}^{*}$
is
![]() $\mathsf {G}$
-invariant if its graph is
$\mathsf {G}$
-invariant if its graph is
![]() $\mathsf {G}$
-invariant as a subset of
$\mathsf {G}$
-invariant as a subset of
![]() $\mathcal {X} \times \mathcal {X}^{*}$
.
$\mathcal {X} \times \mathcal {X}^{*}$
.
The following simple result clarifies the relation between
![]() $\mathsf {G}$
-invariance of monotone operators and
$\mathsf {G}$
-invariance of monotone operators and
![]() $\mathsf {G}$
-invariance of the corresponding Lagrangian functions.
$\mathsf {G}$
-invariance of the corresponding Lagrangian functions.
Proposition 2.4
-
(1) If
 $f:\mathcal {Z}\to (-\infty ,+\infty ]$
is
$f:\mathcal {Z}\to (-\infty ,+\infty ]$
is
 $\mathsf {G}$
-invariant, then
$\mathsf {G}$
-invariant, then
 $f^{*}$
is
$f^{*}$
is
 $\mathsf {G}$
-invariant.
$\mathsf {G}$
-invariant. -
(2) If
 ${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
is a
${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
is a
 $\mathsf {G}$
-invariant monotone operator, then the functions
$\mathsf {G}$
-invariant monotone operator, then the functions
 $\mathsf {c}_{\boldsymbol {A}}, \mathsf {f}_{\boldsymbol {A}}, \mathsf {p}_{\boldsymbol {A}}$
defined in Section 2.1 are
$\mathsf {c}_{\boldsymbol {A}}, \mathsf {f}_{\boldsymbol {A}}, \mathsf {p}_{\boldsymbol {A}}$
defined in Section 2.1 are
 $\mathsf {G}$
-invariant.
$\mathsf {G}$
-invariant. -
(3) If
 $f:\mathcal {Z}\to (-\infty ,+\infty ]$
is a
$f:\mathcal {Z}\to (-\infty ,+\infty ]$
is a
 $\mathsf {G}$
-invariant, l.s.c., and convex function satisfying
$\mathsf {G}$
-invariant, l.s.c., and convex function satisfying
 $f\ge \mathsf {c}^{\top }$
, then the contact set
$f\ge \mathsf {c}^{\top }$
, then the contact set
 ${\boldsymbol {A}}_f$
defined as in (2.4) is
${\boldsymbol {A}}_f$
defined as in (2.4) is
 $\mathsf {G}$
-invariant.
$\mathsf {G}$
-invariant. -
(4) If
 $f:\mathcal {Z}\to (-\infty ,+\infty ]$
is
$f:\mathcal {Z}\to (-\infty ,+\infty ]$
is
 $\mathsf {G}$
-invariant, then the kernel average
$\mathsf {G}$
-invariant, then the kernel average
 $R_f$
defined as in (2.14) is
$R_f$
defined as in (2.14) is
 $\mathsf {G}$
-invariant as well.
$\mathsf {G}$
-invariant as well.
Proof (1) We simply have, for every
![]() $\mathsf {U}\in \mathsf {G}$
,
$\mathsf {U}\in \mathsf {G}$
,
 $$ \begin{align*} f^{*}(\mathsf{U}^{\top} z^{*}) &= \sup_{z\in \mathcal{Z}}\left\{ \langle \mathsf{U}^{\top} z^{*},z\rangle -f(z)\right\}= \sup_{z\in \mathcal{Z}}\left\{ \langle z^{*},\mathsf{U}^{-1} z\rangle -f(z)\right\} \\& = \sup_{z\in \mathcal{Z}}\left\{ \langle z^{*},\mathsf{U}^{-1} z\rangle -f(\mathsf{U}^{-1} z)\right\}= \sup_{\tilde z\in \mathcal{Z}}\left\{ \langle z^{*},\tilde z\rangle -f(\tilde z)\right\} =f^{*}(z^{*}), \end{align*} $$
$$ \begin{align*} f^{*}(\mathsf{U}^{\top} z^{*}) &= \sup_{z\in \mathcal{Z}}\left\{ \langle \mathsf{U}^{\top} z^{*},z\rangle -f(z)\right\}= \sup_{z\in \mathcal{Z}}\left\{ \langle z^{*},\mathsf{U}^{-1} z\rangle -f(z)\right\} \\& = \sup_{z\in \mathcal{Z}}\left\{ \langle z^{*},\mathsf{U}^{-1} z\rangle -f(\mathsf{U}^{-1} z)\right\}= \sup_{\tilde z\in \mathcal{Z}}\left\{ \langle z^{*},\tilde z\rangle -f(\tilde z)\right\} =f^{*}(z^{*}), \end{align*} $$
where we applied (2.20), the fact that
![]() $\mathsf {U}^{-1}\in \mathsf {G}$
, the
$\mathsf {U}^{-1}\in \mathsf {G}$
, the
![]() $\mathsf {G}$
-invariance of f, and the fact that
$\mathsf {G}$
-invariance of f, and the fact that
![]() $\{\tilde z=\mathsf {U}^{-1}z:z\in \mathcal {Z}\}=\mathcal {Z}.$
$\{\tilde z=\mathsf {U}^{-1}z:z\in \mathcal {Z}\}=\mathcal {Z}.$
(2) One immediately sees that
![]() $\mathsf {c}_{\boldsymbol {A}}$
is
$\mathsf {c}_{\boldsymbol {A}}$
is
![]() $\mathsf {G}$
invariant thanks to the
$\mathsf {G}$
invariant thanks to the
![]() $\mathsf {G}$
-invariance of
$\mathsf {G}$
-invariance of
![]() ${\boldsymbol {A}}$
and (2.18). The invariance of
${\boldsymbol {A}}$
and (2.18). The invariance of
![]() $\mathsf {f}_{\boldsymbol {A}}$
and of
$\mathsf {f}_{\boldsymbol {A}}$
and of
![]() $\mathsf {p}_{\boldsymbol {A}}$
then follows by the previous claim.
$\mathsf {p}_{\boldsymbol {A}}$
then follows by the previous claim.
(3) If
![]() $z=(x,v)\in {\boldsymbol {A}}_f$
, we know that
$z=(x,v)\in {\boldsymbol {A}}_f$
, we know that
![]() $f(z)=\mathsf {c}^{\top }(z)$
. Since f is
$f(z)=\mathsf {c}^{\top }(z)$
. Since f is
![]() $\mathsf {G}$
-invariant, (2.18) yields, for every
$\mathsf {G}$
-invariant, (2.18) yields, for every
![]() $\mathsf {U}\in \mathsf {G}$
,
$\mathsf {U}\in \mathsf {G}$
,
so that
![]() $\mathsf {U}z\in {\boldsymbol {A}}_f.$
$\mathsf {U}z\in {\boldsymbol {A}}_f.$
(4) We first observe that the function
satisfies
thanks to the invariance of f, the invariance of
![]() $f^{*}$
from claim (1), and the invariance property of
$f^{*}$
from claim (1), and the invariance property of
![]() $\psi $
stated in (2.18).
$\psi $
stated in (2.18).
Since
![]() $\mathsf {U}$
is a linear isomorphism, we also have
$\mathsf {U}$
is a linear isomorphism, we also have
Combining the above identities, we immediately get
![]() $R_f(\mathsf {U}z)= R_f(z).$
$R_f(\mathsf {U}z)= R_f(z).$
We can now obtain our main result.
Theorem 2.5 (
 $\mathsf {G}$
-invariant maximal monotone extensions)
$\mathsf {G}$
-invariant maximal monotone extensions)
Let
![]() ${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
be a
${\boldsymbol {A}} \subset \mathcal {X} \times \mathcal {X}^{*}$
be a
![]() $\mathsf {G}$
-invariant monotone operator with
$\mathsf {G}$
-invariant monotone operator with
![]() $D:=\overline {\operatorname {co}}\left (\mathrm {D}({\boldsymbol {A}})\right ).$
Then the function f given by (2.16) is
$D:=\overline {\operatorname {co}}\left (\mathrm {D}({\boldsymbol {A}})\right ).$
Then the function f given by (2.16) is
![]() $\mathsf {G}$
-invariant and, defining
$\mathsf {G}$
-invariant and, defining
![]() $R_f$
as in (2.14) and its contact set
$R_f$
as in (2.14) and its contact set
![]() $\tilde {{\boldsymbol {A}}}$
as in (2.15), then
$\tilde {{\boldsymbol {A}}}$
as in (2.15), then
![]() $\tilde {\boldsymbol {A}}$
is a
$\tilde {\boldsymbol {A}}$
is a
![]() $\mathsf {G}$
-invariant maximal monotone extension of
$\mathsf {G}$
-invariant maximal monotone extension of
![]() ${\boldsymbol {A}}$
with domain included in
${\boldsymbol {A}}$
with domain included in
![]() $\overline {\operatorname {co}}\left (\mathrm {D}({\boldsymbol {A}})\right )$
.
$\overline {\operatorname {co}}\left (\mathrm {D}({\boldsymbol {A}})\right )$
.
Proof Let us first observe that
![]() $C':=\mathrm {D}({\boldsymbol {A}})\times \mathcal {X}^{*}$
is
$C':=\mathrm {D}({\boldsymbol {A}})\times \mathcal {X}^{*}$
is
![]() $\mathsf {G}$
-invariant, thanks to the invariance of
$\mathsf {G}$
-invariant, thanks to the invariance of
![]() ${\boldsymbol {A}}.$
Since every element of
${\boldsymbol {A}}.$
Since every element of
![]() $\mathsf {G}$
is linear, also
$\mathsf {G}$
is linear, also
![]() $\operatorname {co}(C')$
is
$\operatorname {co}(C')$
is
![]() $\mathsf {G}$
-invariant. Eventually, since every element of
$\mathsf {G}$
-invariant. Eventually, since every element of
![]() $\mathsf {G}$
is continuous,
$\mathsf {G}$
is continuous,
![]() $C:=\operatorname {\mathrm {cl}}(\operatorname {co}(C'))$
is
$C:=\operatorname {\mathrm {cl}}(\operatorname {co}(C'))$
is
![]() $\mathsf {G}$
-invariant as well.
$\mathsf {G}$
-invariant as well.
By claim (2) of Proposition 2.4, we deduce that the function f given by (2.16) is
![]() $\mathsf {G}$
-invariant. The invariance of
$\mathsf {G}$
-invariant. The invariance of
![]() $\tilde {\boldsymbol {A}}$
then follows by applying Claims (4) and (3) of Proposition 2.4, recalling that
$\tilde {\boldsymbol {A}}$
then follows by applying Claims (4) and (3) of Proposition 2.4, recalling that
![]() $R_f\ge \mathsf {c}^{\top }$
by Theorem 2.1(6). We conclude by Theorem 2.3.
$R_f\ge \mathsf {c}^{\top }$
by Theorem 2.1(6). We conclude by Theorem 2.3.
2.3 Extension of invariant dissipative operators in Hilbert spaces
We now quickly apply the results of the previous Section 2.2 to the particular case of dissipative operators in Hilbert spaces. We adopt the dissipative viewpoint in view of applications to differential equations, but clearly all our statements apply to monotone operators as well. The main reference is [Reference Brézis13].
We consider a Hilbert space
![]() $\mathcal {H}$
with norm
$\mathcal {H}$
with norm
![]() $|\cdot |$
, scalar product
$|\cdot |$
, scalar product
![]() $\langle \cdot , \cdot \rangle $
, and dual
$\langle \cdot , \cdot \rangle $
, and dual
![]() $\mathcal {H}^{*}$
which we identify with
$\mathcal {H}^{*}$
which we identify with
![]() $\mathcal {H}$
. A multivalued operator
$\mathcal {H}$
. A multivalued operator
![]() $\boldsymbol {B}\subset \mathcal {H}\times \mathcal {H}$
is dissipative if the operator
$\boldsymbol {B}\subset \mathcal {H}\times \mathcal {H}$
is dissipative if the operator
is monotone. More generally,
![]() $\boldsymbol {B}$
is said to be
$\boldsymbol {B}$
is said to be
![]() $\lambda $
-dissipative (
$\lambda $
-dissipative (
![]() $\lambda \in \mathbb {R}$
) if
$\lambda \in \mathbb {R}$
) if
Remark 2.6 (
 $\lambda $
-transformation)
$\lambda $
-transformation)
Denoting by
![]() $\boldsymbol {i}(\cdot )$
the identity function on
$\boldsymbol {i}(\cdot )$
the identity function on
![]() $\mathcal {H}$
, it is easy to check that
$\mathcal {H}$
, it is easy to check that
![]() $\boldsymbol {B}$
is
$\boldsymbol {B}$
is
![]() $\lambda $
-dissipative if and only if
$\lambda $
-dissipative if and only if
![]() $\boldsymbol {B}^{\lambda }:= \boldsymbol {B}-\lambda \boldsymbol {i}$
is dissipative, or, equivalently,
$\boldsymbol {B}^{\lambda }:= \boldsymbol {B}-\lambda \boldsymbol {i}$
is dissipative, or, equivalently,
![]() $-\boldsymbol {B}^\lambda =\lambda \boldsymbol {i}-\boldsymbol {B}$
is monotone. Notice that
$-\boldsymbol {B}^\lambda =\lambda \boldsymbol {i}-\boldsymbol {B}$
is monotone. Notice that
![]() $\mathrm {D}(\boldsymbol {B})=\mathrm {D}(\boldsymbol {B}^\lambda )=\mathrm {D}(-\boldsymbol {B}^\lambda )$
.
$\mathrm {D}(\boldsymbol {B})=\mathrm {D}(\boldsymbol {B}^\lambda )=\mathrm {D}(-\boldsymbol {B}^\lambda )$
.
We say that a
![]() $\lambda $
-dissipative operator
$\lambda $
-dissipative operator
![]() $\boldsymbol {B}$
is maximal if
$\boldsymbol {B}$
is maximal if
![]() $\boldsymbol {B}$
is maximal w.r.t. inclusion in the class of
$\boldsymbol {B}$
is maximal w.r.t. inclusion in the class of
![]() $\lambda $
-dissipative operators or, equivalently, if
$\lambda $
-dissipative operators or, equivalently, if
![]() $-\boldsymbol {B}^\lambda $
is a maximal monotone operator.
$-\boldsymbol {B}^\lambda $
is a maximal monotone operator.
If
![]() $\boldsymbol {B}\subset \mathcal {H}\times \mathcal {H}$
is a
$\boldsymbol {B}\subset \mathcal {H}\times \mathcal {H}$
is a
![]() $\lambda $
-dissipative operator, a maximal
$\lambda $
-dissipative operator, a maximal
![]() $\lambda $
-dissipative extension of
$\lambda $
-dissipative extension of
![]() $\boldsymbol {B}$
is any set
$\boldsymbol {B}$
is any set
![]() $\boldsymbol {C} \subset \mathcal {H} \times \mathcal {H}$
such that
$\boldsymbol {C} \subset \mathcal {H} \times \mathcal {H}$
such that
![]() $\boldsymbol {B} \subset \boldsymbol {C}$
and
$\boldsymbol {B} \subset \boldsymbol {C}$
and
![]() $\boldsymbol {C}$
is maximal
$\boldsymbol {C}$
is maximal
![]() $\lambda $
-dissipative.
$\lambda $
-dissipative.
As an immediate application of Theorem 2.5, we obtain an important result for dissipative operators which are invariant with respect to the action of a group
![]() $\mathsf {G}$
of isometries.
$\mathsf {G}$
of isometries.
Theorem 2.7 (Extension of invariant
 $\lambda $
-dissipative operators)
$\lambda $
-dissipative operators)
Let
![]() $\mathsf {G}_{\mathcal {H}}$
be a group of linear isometries of
$\mathsf {G}_{\mathcal {H}}$
be a group of linear isometries of
![]() $\mathcal {H}$
, and let
$\mathcal {H}$
, and let
![]() $\mathsf {G}:=\{(U,U):U\in \mathsf {G}_{\mathcal {H}}\}$
be the induced group of linear isometries in
$\mathsf {G}:=\{(U,U):U\in \mathsf {G}_{\mathcal {H}}\}$
be the induced group of linear isometries in
![]() $\mathcal {H}\times \mathcal {H}$
. Let
$\mathcal {H}\times \mathcal {H}$
. Let
![]() $\boldsymbol {B}\subset \mathcal {H}\times \mathcal {H}$
be a
$\boldsymbol {B}\subset \mathcal {H}\times \mathcal {H}$
be a
![]() $\lambda $
-dissipative operator which is
$\lambda $
-dissipative operator which is
![]() $\mathsf {G}$
-invariant (as a subset of
$\mathsf {G}$
-invariant (as a subset of
![]() $\mathcal {H}\times \mathcal {H}$
). Then there exists a maximal
$\mathcal {H}\times \mathcal {H}$
). Then there exists a maximal
![]() $\lambda $
-dissipative extension
$\lambda $
-dissipative extension
![]() $\hat {\boldsymbol {B}}$
of
$\hat {\boldsymbol {B}}$
of
![]() $\boldsymbol {B}$
with
$\boldsymbol {B}$
with
![]() $\mathrm {D}(\hat {\boldsymbol {B}})\subset \overline {\operatorname {co}}\left (\mathrm {D}(\boldsymbol {B})\right )$
which is
$\mathrm {D}(\hat {\boldsymbol {B}})\subset \overline {\operatorname {co}}\left (\mathrm {D}(\boldsymbol {B})\right )$
which is
![]() $\mathsf {G}$
-invariant as well.
$\mathsf {G}$
-invariant as well.
Proof We can choose the self-dual kernel
and we immediately get that
![]() $\mathsf {G}$
satisfies (2.18). The statement is then an immediate application of Theorem 2.5 to the
$\mathsf {G}$
satisfies (2.18). The statement is then an immediate application of Theorem 2.5 to the
![]() $\mathsf {G}$
-invariant monotone operator
$\mathsf {G}$
-invariant monotone operator
![]() ${\boldsymbol {A}}:=-\boldsymbol {B}^\lambda .$
${\boldsymbol {A}}:=-\boldsymbol {B}^\lambda .$
Remark 2.8 If
![]() $\boldsymbol {B}$
is a
$\boldsymbol {B}$
is a
![]() $\mathsf {G}$
-invariant
$\mathsf {G}$
-invariant
![]() $\lambda $
-dissipative operator which is maximal (with respect to inclusion) in the collection of
$\lambda $
-dissipative operator which is maximal (with respect to inclusion) in the collection of
![]() $\mathsf {G}$
-invariant
$\mathsf {G}$
-invariant
![]() $\lambda $
-dissipative operators, then
$\lambda $
-dissipative operators, then
![]() $\boldsymbol {B}$
is maximal
$\boldsymbol {B}$
is maximal
![]() $\lambda $
-dissipative.
$\lambda $
-dissipative.
We now derive a few more properties concerning the resolvent, the Yosida regularization and the minimal selection of a maximal
![]() $\lambda $
-dissipative and
$\lambda $
-dissipative and
![]() $\mathsf {G}$
-invariant operator
$\mathsf {G}$
-invariant operator
![]() $\boldsymbol {B}\subset \mathcal {H}\times \mathcal {H}$
. For references on the corresponding definitions and properties, we refer to [Reference Brézis13], where the theory is developed in detail for the case
$\boldsymbol {B}\subset \mathcal {H}\times \mathcal {H}$
. For references on the corresponding definitions and properties, we refer to [Reference Brézis13], where the theory is developed in detail for the case
![]() $\lambda =0$
. If
$\lambda =0$
. If
![]() $\lambda \ne 0$
, analogous statements can be obtained and we refer the interested reader to [Reference Cavagnari, Savaré and Sodini17, Appendix A].
$\lambda \ne 0$
, analogous statements can be obtained and we refer the interested reader to [Reference Cavagnari, Savaré and Sodini17, Appendix A].
In the following, we use the notation
![]() $\lambda ^+:= \lambda \vee 0$
and we set
$\lambda ^+:= \lambda \vee 0$
and we set
![]() $1/\lambda ^+=+\infty $
if
$1/\lambda ^+=+\infty $
if
![]() $\lambda ^+=0$
. We denote by
$\lambda ^+=0$
. We denote by
![]() $\boldsymbol {B} x\equiv \boldsymbol {B}(x):=\{v\in \mathcal {H}:(x,v)\in \boldsymbol {B}\}$
the sections of
$\boldsymbol {B} x\equiv \boldsymbol {B}(x):=\{v\in \mathcal {H}:(x,v)\in \boldsymbol {B}\}$
the sections of
![]() $\boldsymbol {B}$
, with
$\boldsymbol {B}$
, with
![]() $x\in \mathcal {H}$
.
$x\in \mathcal {H}$
.
Recall that for every
![]() $0<\tau <1/\lambda ^+$
, the resolvent
$0<\tau <1/\lambda ^+$
, the resolvent
![]() ${\boldsymbol {J}_{\tau }}:=(\boldsymbol {i}-\tau \boldsymbol {B})^{-1}$
of
${\boldsymbol {J}_{\tau }}:=(\boldsymbol {i}-\tau \boldsymbol {B})^{-1}$
of
![]() $\boldsymbol {B}$
is a
$\boldsymbol {B}$
is a
![]() $(1-\lambda \tau )^{-1}$
-Lipschitz map defined on the whole
$(1-\lambda \tau )^{-1}$
-Lipschitz map defined on the whole
![]() $\mathcal {H}$
. The minimal selection
$\mathcal {H}$
. The minimal selection
![]() $\boldsymbol {B}^\circ :\mathrm {D}(\boldsymbol {B})\to \mathcal {H}$
of
$\boldsymbol {B}^\circ :\mathrm {D}(\boldsymbol {B})\to \mathcal {H}$
of
![]() $\boldsymbol {B}$
is also characterized by
$\boldsymbol {B}$
is also characterized by
The Yosida approximation of
![]() $\boldsymbol {B}$
is defined by
$\boldsymbol {B}$
is defined by
![]() $\boldsymbol {B}_{\tau }:=\frac {{\boldsymbol {J}_{\tau }}-\boldsymbol {i}}{\tau }$
. For every
$\boldsymbol {B}_{\tau }:=\frac {{\boldsymbol {J}_{\tau }}-\boldsymbol {i}}{\tau }$
. For every
![]() $0<\tau <1/\lambda ^+$
,
$0<\tau <1/\lambda ^+$
,
![]() $\boldsymbol {B}_{\tau }$
is maximal
$\boldsymbol {B}_{\tau }$
is maximal
![]() $\frac {\lambda }{1-\lambda \tau }$
-dissipative and
$\frac {\lambda }{1-\lambda \tau }$
-dissipative and
![]() $\frac {2-\lambda \tau }{\tau (1-\lambda \tau )}$
-Lipschitz continuous.
$\frac {2-\lambda \tau }{\tau (1-\lambda \tau )}$
-Lipschitz continuous.
Moreover (cf. [Reference Brézis13, Proposition 2.6] or [Reference Cavagnari, Savaré and Sodini17, Appendix A]), the following hold:
Since
![]() $\boldsymbol {B}$
is a maximal
$\boldsymbol {B}$
is a maximal
![]() $\lambda $
-dissipative operator, there exists a semigroup of
$\lambda $
-dissipative operator, there exists a semigroup of
![]() $e^{\lambda t}$
-Lipschitz transformations
$e^{\lambda t}$
-Lipschitz transformations
![]() $(\boldsymbol {S}_t)_{t \ge 0}$
with
$(\boldsymbol {S}_t)_{t \ge 0}$
with
![]() $\boldsymbol {S}_t: \overline {\mathrm {D}(\boldsymbol {B})} \to \overline {\mathrm {D}(\boldsymbol {B})}$
s.t. for every
$\boldsymbol {S}_t: \overline {\mathrm {D}(\boldsymbol {B})} \to \overline {\mathrm {D}(\boldsymbol {B})}$
s.t. for every
![]() $x_{0}\in \mathrm {D}(\boldsymbol {B})$
the curve
$x_{0}\in \mathrm {D}(\boldsymbol {B})$
the curve
![]() $t \mapsto \boldsymbol {S}_t x_{0}$
is included in
$t \mapsto \boldsymbol {S}_t x_{0}$
is included in
![]() $\mathrm {D}(\boldsymbol {B})$
and it is the unique locally Lipschitz continuous solution of the differential inclusion
$\mathrm {D}(\boldsymbol {B})$
and it is the unique locally Lipschitz continuous solution of the differential inclusion
 $$ \begin{align} \begin{cases} \dot{x}_t \in \boldsymbol{B} x_t, \quad \text{ a.e. } t>0, \\ x {|_{t=0}} = x_{0}. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \dot{x}_t \in \boldsymbol{B} x_t, \quad \text{ a.e. } t>0, \\ x {|_{t=0}} = x_{0}. \end{cases} \end{align} $$
We also have
and
Proposition 2.9 (Invariance of resolvents, Yosida regularizations, semigroups, and minimal selections)
Let
![]() $\boldsymbol {B} \subset \mathcal {H} \times \mathcal {H}$
be a maximal
$\boldsymbol {B} \subset \mathcal {H} \times \mathcal {H}$
be a maximal
![]() $\lambda $
-dissipative operator which is
$\lambda $
-dissipative operator which is
![]() $\mathsf {G}$
-invariant. Then, for every
$\mathsf {G}$
-invariant. Then, for every
![]() $0<\tau <1/\lambda ^+,\,t\ge 0$
, the operators
$0<\tau <1/\lambda ^+,\,t\ge 0$
, the operators
![]() ${\boldsymbol {J}_{\tau }}$
,
${\boldsymbol {J}_{\tau }}$
,
![]() $\boldsymbol {B}_{\tau }$
,
$\boldsymbol {B}_{\tau }$
,
![]() $\boldsymbol {S}_t$
,
$\boldsymbol {S}_t$
,
![]() $\boldsymbol {B}^\circ $
are
$\boldsymbol {B}^\circ $
are
![]() $\mathsf {G}$
-invariant.
$\mathsf {G}$
-invariant.
Proof The identities
![]() ${\boldsymbol {J}_{\tau }} (Ux)=U({\boldsymbol {J}_{\tau }} x)$
and
${\boldsymbol {J}_{\tau }} (Ux)=U({\boldsymbol {J}_{\tau }} x)$
and
![]() $\boldsymbol {B}^\circ (Ux) = U(\boldsymbol {B}^\circ x)$
come from the
$\boldsymbol {B}^\circ (Ux) = U(\boldsymbol {B}^\circ x)$
come from the
![]() $\mathsf {G}$
-invariance of
$\mathsf {G}$
-invariance of
![]() $\boldsymbol {B}$
and the uniqueness property of the resolvent operator. The exponential formula (cf. (2.28))
$\boldsymbol {B}$
and the uniqueness property of the resolvent operator. The exponential formula (cf. (2.28))
yields the
![]() $\mathsf {G}$
-invariance of
$\mathsf {G}$
-invariance of
![]() $\boldsymbol {S}_t$
.
$\boldsymbol {S}_t$
.
2.4 Extension of invariant Lipschitz maps in Hilbert spaces
We conclude this general discussion concerning
![]() $\mathsf {G}$
-invariant sets and maps addressing the problem of the global extension of a
$\mathsf {G}$
-invariant sets and maps addressing the problem of the global extension of a
![]() $\mathsf {G}$
-invariant Lipschitz map defined in a subset of a separable Hilbert space
$\mathsf {G}$
-invariant Lipschitz map defined in a subset of a separable Hilbert space
![]() $\mathcal {H}.$
$\mathcal {H}.$
As in Theorem 2.7, we consider a group
![]() $\mathsf {G}_{\mathcal {H}}$
of isometric isomorphisms of
$\mathsf {G}_{\mathcal {H}}$
of isometric isomorphisms of
![]() $\mathcal {H}$
inducing the group
$\mathcal {H}$
inducing the group
![]() $\mathsf {G}:=\{(U,U):U\in \mathsf {G}_{\mathcal {H}}\}$
in
$\mathsf {G}:=\{(U,U):U\in \mathsf {G}_{\mathcal {H}}\}$
in
![]() $\mathcal {H}\times \mathcal {H}.$
$\mathcal {H}\times \mathcal {H}.$
In addition to Definition 2.1, we also give the following definition.
Definition 2.2 [
![]() $\mathsf {G}_{\mathcal {H}}$
-invariance for
$\mathsf {G}_{\mathcal {H}}$
-invariance for
![]() $\mathcal {H}$
-valued maps] We say that a function
$\mathcal {H}$
-valued maps] We say that a function
![]() $f:D\to \mathcal {H}$
, where
$f:D\to \mathcal {H}$
, where
![]() $D\subset \mathcal {H}$
, is
$D\subset \mathcal {H}$
, is
![]() $\mathsf {G}_{\mathcal {H}}$
-invariant if its graph is
$\mathsf {G}_{\mathcal {H}}$
-invariant if its graph is
![]() $\mathsf {G}$
-invariant:
$\mathsf {G}$
-invariant:
The Kirszbraun–Valentine theorem [Reference Kirszbraun23, Reference Valentine34] states that every Lipschitz function
![]() $f:D\to \mathcal {H}$
defined in a subset D of
$f:D\to \mathcal {H}$
defined in a subset D of
![]() $\mathcal {H}$
with Lipschitz constant
$\mathcal {H}$
with Lipschitz constant
![]() $L\ge 0$
admits a Lipschitz extension
$L\ge 0$
admits a Lipschitz extension
![]() $F:\mathcal {H}\to \mathcal {H}$
whose Lipschitz constant coincides with L. We want to prove that it is possible to find such an extension preserving
$F:\mathcal {H}\to \mathcal {H}$
whose Lipschitz constant coincides with L. We want to prove that it is possible to find such an extension preserving
![]() $\mathsf {G}$
-invariance.
$\mathsf {G}$
-invariance.
Our starting point is the following well-known fact, going back to Minty (see also [Reference Alberti and Ambrosio1]). We introduce the isometric Cayley transforms
![]() $T, T^{-1}:\mathcal {H}\times \mathcal {H}\to \mathcal {H}\times \mathcal {H}$
$T, T^{-1}:\mathcal {H}\times \mathcal {H}\to \mathcal {H}\times \mathcal {H}$
Lemma 2.10 (Lipschitz and monotone graphs)
Let
![]() $\boldsymbol {F},{\boldsymbol {A}}$
be two subsets of
$\boldsymbol {F},{\boldsymbol {A}}$
be two subsets of
![]() $\mathcal {H}\times \mathcal {H}$
such that
$\mathcal {H}\times \mathcal {H}$
such that
![]() ${\boldsymbol {A}}=T(\boldsymbol {F})$
. The following two properties are equivalent:
${\boldsymbol {A}}=T(\boldsymbol {F})$
. The following two properties are equivalent:
-
(1)
 $\boldsymbol {F}$
is the graph of a nonexpansive map f defined on the set D given by
$\boldsymbol {F}$
is the graph of a nonexpansive map f defined on the set D given by  $$\begin{align*}D:=\pi^1(\boldsymbol{F}) =\big\{y\in\mathcal{H}:(y,w)\in\boldsymbol{F} \text{ for some }w\in \mathcal{H}\big\};\end{align*}$$
$$\begin{align*}D:=\pi^1(\boldsymbol{F}) =\big\{y\in\mathcal{H}:(y,w)\in\boldsymbol{F} \text{ for some }w\in \mathcal{H}\big\};\end{align*}$$
-
(2)
 ${\boldsymbol {A}}$
is monotone.
${\boldsymbol {A}}$
is monotone.
Moreover, assuming that
![]() ${\boldsymbol {A}}$
is monotone, the following hold:
${\boldsymbol {A}}$
is monotone, the following hold:
-
(i)
 ${\boldsymbol {A}}$
is maximal monotone if and only if
${\boldsymbol {A}}$
is maximal monotone if and only if
 $D=\mathcal {H}.$
$D=\mathcal {H}.$
-
(ii)
 ${\boldsymbol {A}}$
is
${\boldsymbol {A}}$
is
 $\mathsf {G}$
-invariant if and only if
$\mathsf {G}$
-invariant if and only if
 $\boldsymbol {F}$
is
$\boldsymbol {F}$
is
 $\mathsf {G}$
-invariant (or, equivalently, f is
$\mathsf {G}$
-invariant (or, equivalently, f is
 $\mathsf {G}_{\mathcal {H}}$
-invariant).
$\mathsf {G}_{\mathcal {H}}$
-invariant). -
(iii) If
 ${\boldsymbol {A}}'$
is a monotone extension of
${\boldsymbol {A}}'$
is a monotone extension of
 ${\boldsymbol {A}}$
and
${\boldsymbol {A}}$
and
 $f':D'\to \mathcal {H}$
is the nonexpansive map associated with
$f':D'\to \mathcal {H}$
is the nonexpansive map associated with
 $ \boldsymbol {F}':=T^{-1}({\boldsymbol {A}}')$
, then
$ \boldsymbol {F}':=T^{-1}({\boldsymbol {A}}')$
, then
 $D':=\pi ^1(\boldsymbol {F}')\supset D$
and
$D':=\pi ^1(\boldsymbol {F}')\supset D$
and
 $f'$
is an extension of
$f'$
is an extension of
 $f.$
$f.$
Proof Let us take a pair of elements
![]() $(x_i,v_i)=T(y_i,w_i)\in {\boldsymbol {A}}$
,
$(x_i,v_i)=T(y_i,w_i)\in {\boldsymbol {A}}$
,
![]() $i=1,2$
; we have
$i=1,2$
; we have
![]() $y_i=\frac 1{\sqrt 2} (x_i+v_i)$
,
$y_i=\frac 1{\sqrt 2} (x_i+v_i)$
,
![]() $w_i=\frac 1{\sqrt 2}(-x_i+v_i)$
so that
$w_i=\frac 1{\sqrt 2}(-x_i+v_i)$
so that
and then
This proves the first statement.
Concerning (i), it is sufficient to recall that the domain D of f coincides with the image of
![]() $h({\boldsymbol {A}})$
where
$h({\boldsymbol {A}})$
where
![]() $h(x,v):=\frac 1{\sqrt 2}(x+v)$
and we know that
$h(x,v):=\frac 1{\sqrt 2}(x+v)$
and we know that
![]() ${\boldsymbol {A}}$
is maximal monotone if and only if such an image coincides with
${\boldsymbol {A}}$
is maximal monotone if and only if such an image coincides with
![]() $\mathcal {H}$
(cf. [Reference Brézis13, Proposition 2.2(ii)]).
$\mathcal {H}$
(cf. [Reference Brézis13, Proposition 2.2(ii)]).
The second property (ii) is an immediate consequence of the invertibility of T and of the linearity of the transformations of
![]() $\mathsf {G}$
so that for every
$\mathsf {G}$
so that for every
![]() $\mathsf {U}=(U,U)\in \mathsf {G}$
, we have
$\mathsf {U}=(U,U)\in \mathsf {G}$
, we have
![]() $T\circ \mathsf {U}= \mathsf {U}\circ T$
.
$T\circ \mathsf {U}= \mathsf {U}\circ T$
.
Let us eventually consider claim (iii): we clearly have
![]() $\boldsymbol {F}'= T^{-1}({\boldsymbol {A}}')\supset T^{-1}({\boldsymbol {A}}) = \boldsymbol {F}$
and therefore
$\boldsymbol {F}'= T^{-1}({\boldsymbol {A}}')\supset T^{-1}({\boldsymbol {A}}) = \boldsymbol {F}$
and therefore
![]() $D'=\pi ^1(\boldsymbol {F}')\supset \pi ^1(\boldsymbol {F})=D$
. On the other hand, since both
$D'=\pi ^1(\boldsymbol {F}')\supset \pi ^1(\boldsymbol {F})=D$
. On the other hand, since both
![]() $\boldsymbol {F}'$
and
$\boldsymbol {F}'$
and
![]() $\boldsymbol {F}$
are the graph of a nonexpansive map,
$\boldsymbol {F}$
are the graph of a nonexpansive map,
![]() $\boldsymbol {F}'\cap (D\times \mathcal {H})= \boldsymbol {F}\cap (D\times \mathcal {H})$
and therefore the restriction of
$\boldsymbol {F}'\cap (D\times \mathcal {H})= \boldsymbol {F}\cap (D\times \mathcal {H})$
and therefore the restriction of
![]() $f'$
to D coincides with f.
$f'$
to D coincides with f.
We can now state our result concerning the extension of
![]() $\mathsf {G}$
-invariant Lipschitz maps.
$\mathsf {G}$
-invariant Lipschitz maps.
Theorem 2.11 (Extension of
 $\mathsf {G}$
-invariant Lipschitz maps)
$\mathsf {G}$
-invariant Lipschitz maps)
Let us suppose that
![]() $f:D\to \mathcal {H}$
is L-Lipschitz and
$f:D\to \mathcal {H}$
is L-Lipschitz and
![]() $\mathsf {G}_{\mathcal {H}}$
-invariant according to (2.29). Then there exists a L-Lipschitz map
$\mathsf {G}_{\mathcal {H}}$
-invariant according to (2.29). Then there exists a L-Lipschitz map
![]() $\hat f:\mathcal {H}\to \mathcal {H}$
extending f which is
$\hat f:\mathcal {H}\to \mathcal {H}$
extending f which is
![]() $\mathsf {G}_{\mathcal {H}}$
-invariant as well.
$\mathsf {G}_{\mathcal {H}}$
-invariant as well.
Proof Up to a rescaling, it is not restrictive to assume that
![]() $L=1$
so that f is nonexpansive.
$L=1$
so that f is nonexpansive.
Let
![]() $\boldsymbol {F}\subset \mathcal {H}\times \mathcal {H}$
be the graph of f, and let
$\boldsymbol {F}\subset \mathcal {H}\times \mathcal {H}$
be the graph of f, and let
![]() ${\boldsymbol {A}}:=T(\boldsymbol {F})$
. By Lemma 2.10, we know that
${\boldsymbol {A}}:=T(\boldsymbol {F})$
. By Lemma 2.10, we know that
![]() ${\boldsymbol {A}}$
is a monotone
${\boldsymbol {A}}$
is a monotone
![]() $\mathsf {G}$
-invariant operator
$\mathsf {G}$
-invariant operator
We can now apply Theorem 2.7 to find a maximal monotone extension
![]() ${\boldsymbol {\hat {A}}}$
of
${\boldsymbol {\hat {A}}}$
of
![]() ${\boldsymbol {A}}$
which is still
${\boldsymbol {A}}$
which is still
![]() $\mathsf {G}$
-invariant.
$\mathsf {G}$
-invariant.
Setting
![]() $\boldsymbol {\hat F}:= T^{-1}({\boldsymbol {\hat {A}}})$
, we can eventually apply Lemma 2.10 to obtain that
$\boldsymbol {\hat F}:= T^{-1}({\boldsymbol {\hat {A}}})$
, we can eventually apply Lemma 2.10 to obtain that
![]() $\boldsymbol {\hat F}$
is the graph of a nonexpansive map
$\boldsymbol {\hat F}$
is the graph of a nonexpansive map
![]() $\hat f:\hat D\to \mathcal {H}.$
Moreover, Claim (i) shows that
$\hat f:\hat D\to \mathcal {H}.$
Moreover, Claim (i) shows that
![]() $\hat D=\mathcal {H}$
so that
$\hat D=\mathcal {H}$
so that
![]() $\hat f$
is globally defined, Claim (ii) shows that
$\hat f$
is globally defined, Claim (ii) shows that
![]() $\hat f$
is
$\hat f$
is
![]() $\mathsf {G}_{\mathcal {H}}$
-invariant, and Claim (iii) ensures that
$\mathsf {G}_{\mathcal {H}}$
-invariant, and Claim (iii) ensures that
![]() $\hat f$
is an extension of f.
$\hat f$
is an extension of f.
3 Borel partitions and almost optimal couplings
In this section, we collect some useful results concerning Borel isomorphisms and partitions of standard Borel spaces. These results, besides being interesting by themselves, will also turn out to be useful in Section 4, where we will deal with a particular group of isometric isomorphisms on Banach spaces of
![]() $L^{p}$
-type.
$L^{p}$
-type.
We start by fixing the fundamental definitions and notations involved in the statements of the main theorems of this section, which are presented in Section 3.2. These results concern the approximation of arbitrary couplings between probability measures by couplings which are concentrated on maps, through the action of measure-preserving transformations. In particular, Corollary 3.15 concerns the approximation of bistochastic measures by the graph of measure-preserving maps and it is written here in the general context of a standard Borel space
![]() $(\Omega , {\mathcal {B}})$
endowed with a nonatomic probability measure
$(\Omega , {\mathcal {B}})$
endowed with a nonatomic probability measure
![]() $\mathbb {P}$
. This result relies on the analogous property stated for the d-dimensional Lebesgue measure in [Reference Brenier and Gangbo12, Theorem 1.1]. In the same spirit of Corollary 3.15, Corollary 3.16 provides an approximation result for the law of a pair of measurable random variables defined on
$\mathbb {P}$
. This result relies on the analogous property stated for the d-dimensional Lebesgue measure in [Reference Brenier and Gangbo12, Theorem 1.1]. In the same spirit of Corollary 3.15, Corollary 3.16 provides an approximation result for the law of a pair of measurable random variables defined on
![]() $(\Omega , {\mathcal {B}},\mathbb {P})$
with values in a pair of separable Banach spaces. A consequence of this result is the key lemma [Reference Cardaliaguet15, Lemma 6.4] (cf. also [Reference Carmona and Delarue16, Lemma 5.23, p. 379]), which states that if X and Y are random variables with the same law, then X can be approximated by Y through the action of a sequence of measure-preserving transformations. Finally, we reported a fundamental result in Optimal Transportation Theory, concerning the equivalence between the Monge and the Kantorovich formulations (see [Reference Pratelli27, Theorem B]). This is the content of Proposition 3.18 where the result is written using the language of random variables (cf. also [Reference Gangbo and Tudorascu21, Lemma 3.13]), so as to be easily recalled in Section 4.
$(\Omega , {\mathcal {B}},\mathbb {P})$
with values in a pair of separable Banach spaces. A consequence of this result is the key lemma [Reference Cardaliaguet15, Lemma 6.4] (cf. also [Reference Carmona and Delarue16, Lemma 5.23, p. 379]), which states that if X and Y are random variables with the same law, then X can be approximated by Y through the action of a sequence of measure-preserving transformations. Finally, we reported a fundamental result in Optimal Transportation Theory, concerning the equivalence between the Monge and the Kantorovich formulations (see [Reference Pratelli27, Theorem B]). This is the content of Proposition 3.18 where the result is written using the language of random variables (cf. also [Reference Gangbo and Tudorascu21, Lemma 3.13]), so as to be easily recalled in Section 4.
In order to introduce all the technical tools used to state and prove all these properties, in Section 3.1, we list some well-known facts about standard Borel spaces.
Definition 3.1 (Standard Borel spaces and nonatomic measures)
A standard Borel space
![]() $(\Omega , {\mathcal {B}})$
is a measurable space that is isomorphic (as a measure space) to a Polish space. Equivalently, there exists a Polish topology
$(\Omega , {\mathcal {B}})$
is a measurable space that is isomorphic (as a measure space) to a Polish space. Equivalently, there exists a Polish topology
![]() $\tau $
on
$\tau $
on
![]() $\Omega $
such that the Borel sigma algebra generated by
$\Omega $
such that the Borel sigma algebra generated by
![]() $\tau $
coincides with
$\tau $
coincides with
![]() ${\mathcal {B}}$
. We say that a positive finite measure
${\mathcal {B}}$
. We say that a positive finite measure
![]() $\mathfrak {m}$
on
$\mathfrak {m}$
on
![]() $(\Omega , {\mathcal {B}})$
is nonatomic (also called atomless or diffuse) if
$(\Omega , {\mathcal {B}})$
is nonatomic (also called atomless or diffuse) if
![]() $\mathfrak {m}(\{\omega \}) = 0$
for every
$\mathfrak {m}(\{\omega \}) = 0$
for every
![]() $\omega \in \Omega $
(notice that
$\omega \in \Omega $
(notice that
![]() $\{\omega \} \in {\mathcal {B}}$
since it is compact in any Polish topology on
$\{\omega \} \in {\mathcal {B}}$
since it is compact in any Polish topology on
![]() $\Omega $
).
$\Omega $
).
We notice that, being
![]() $(\Omega ,{\mathcal {B}})$
standard Borel,
$(\Omega ,{\mathcal {B}})$
standard Borel,
![]() $\mathfrak {m}$
is nonatomic if and only if for every
$\mathfrak {m}$
is nonatomic if and only if for every
![]() $B\in {\mathcal {B}}$
with
$B\in {\mathcal {B}}$
with
![]() $\mathfrak {m}(B)>0$
, there exists
$\mathfrak {m}(B)>0$
, there exists
![]() $B'\in {\mathcal {B}},\ B'\subset B$
, such that
$B'\in {\mathcal {B}},\ B'\subset B$
, such that
![]() $0<\mathfrak {m}(B')<\mathfrak {m}(B).$
$0<\mathfrak {m}(B')<\mathfrak {m}(B).$
Definition 3.2 (Partitions)
If
![]() $(\Omega , {\mathcal {B}})$
is a standard Borel space and
$(\Omega , {\mathcal {B}})$
is a standard Borel space and
![]() $N \in \mathbb {N}$
, a family of subsets
$N \in \mathbb {N}$
, a family of subsets
![]() $\mathfrak {P}_N=\{\Omega _{N,k}\}_{k \in I_N} \subset {\mathcal {B}}$
, where
$\mathfrak {P}_N=\{\Omega _{N,k}\}_{k \in I_N} \subset {\mathcal {B}}$
, where
![]() $I_N:=\{0, \dots , N-1\}$
, is called an N-partition of
$I_N:=\{0, \dots , N-1\}$
, is called an N-partition of
![]() $(\Omega , {\mathcal {B}})$
if
$(\Omega , {\mathcal {B}})$
if
If
![]() $(\Omega , {\mathcal {B}})$
is a standard Borel space endowed with a nonatomic, positive finite measure
$(\Omega , {\mathcal {B}})$
is a standard Borel space endowed with a nonatomic, positive finite measure
![]() $\mathfrak {m}$
, we denote by
$\mathfrak {m}$
, we denote by
![]() $\mathrm {S}(\Omega , {\mathcal {B}}, \mathfrak {m})$
the class of
$\mathrm {S}(\Omega , {\mathcal {B}}, \mathfrak {m})$
the class of
![]() ${\mathcal {B}}$
-
${\mathcal {B}}$
-
![]() ${\mathcal {B}}$
-measurable maps
${\mathcal {B}}$
-measurable maps
![]() $g:\Omega \to \Omega $
which are essentially injective and measure-preserving, meaning that there exists a full
$g:\Omega \to \Omega $
which are essentially injective and measure-preserving, meaning that there exists a full
![]() $\mathfrak {m}$
-measure set
$\mathfrak {m}$
-measure set
![]() $\Omega _{0} \in {\mathcal {B}}$
such that g is injective on
$\Omega _{0} \in {\mathcal {B}}$
such that g is injective on
![]() $\Omega _{0}$
and
$\Omega _{0}$
and
![]() $g_\sharp \mathfrak {m}=\mathfrak {m}$
, where
$g_\sharp \mathfrak {m}=\mathfrak {m}$
, where
![]() $g_\sharp \mathfrak {m}$
is the push forward of
$g_\sharp \mathfrak {m}$
is the push forward of
![]() $\mathfrak {m}$
through g. We recall that, if X and Y are Polish spaces,
$\mathfrak {m}$
through g. We recall that, if X and Y are Polish spaces,
![]() $f: X \to Y$
is a Borel map, and
$f: X \to Y$
is a Borel map, and
![]() $\mu $
is a nonnegative and finite measure on X, then
$\mu $
is a nonnegative and finite measure on X, then
![]() $f_\sharp \mu $
is defined by
$f_\sharp \mu $
is defined by
for every
![]() $\varphi :Y\to \mathbb {R}$
bounded (or nonnegative) Borel function.
$\varphi :Y\to \mathbb {R}$
bounded (or nonnegative) Borel function.
If
![]() $\mathcal {A} \subset {\mathcal {B}}$
is a sigma algebra on
$\mathcal {A} \subset {\mathcal {B}}$
is a sigma algebra on
![]() $\Omega $
, we denote by
$\Omega $
, we denote by
![]() $\mathrm {S}(\Omega , {\mathcal {B}}, \mathfrak {m}; \mathcal {A})$
the subset of
$\mathrm {S}(\Omega , {\mathcal {B}}, \mathfrak {m}; \mathcal {A})$
the subset of
![]() $\mathrm {S}(\Omega , {\mathcal {B}}, \mathfrak {m})$
of
$\mathrm {S}(\Omega , {\mathcal {B}}, \mathfrak {m})$
of
![]() $\mathcal {A}-\mathcal {A}$
measurable maps. Finally,
$\mathcal {A}-\mathcal {A}$
measurable maps. Finally,
![]() ${\mathrm {Sym}(I_N)}$
denotes the set of permutations of
${\mathrm {Sym}(I_N)}$
denotes the set of permutations of
![]() $I_N$
, i.e., bijective maps
$I_N$
, i.e., bijective maps
![]() $\sigma : I_N \to I_N$
.
$\sigma : I_N \to I_N$
.
We consider the partial order on
![]() $\mathbb {N}$
given by
$\mathbb {N}$
given by
where
![]() $m\mid n$
means that
$m\mid n$
means that
![]() $n/m\in \mathbb {N}$
. We write
$n/m\in \mathbb {N}$
. We write ![]() if
if
![]() $m \prec n$
and
$m \prec n$
and
![]() $m \ne n$
.
$m \ne n$
.
Definition 3.3 (Segmentations)
Let
![]() $(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic, positive finite measure
$(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic, positive finite measure
![]() $\mathfrak {m}$
, and let
$\mathfrak {m}$
, and let
![]() ${\mathfrak {N}} \subset \mathbb {N}$
be an unbounded directed set w.r.t.
${\mathfrak {N}} \subset \mathbb {N}$
be an unbounded directed set w.r.t.
![]() $\prec $
. We say that a collection of partitions
$\prec $
. We say that a collection of partitions
![]() $(\mathfrak {P}_N)_{N \in {\mathfrak {N}}}$
of
$(\mathfrak {P}_N)_{N \in {\mathfrak {N}}}$
of
![]() $\Omega $
, with corresponding sigma algebras
$\Omega $
, with corresponding sigma algebras
![]() ${\mathcal {B}}_N:= \sigma (\mathfrak {P}_N)$
, is an
${\mathcal {B}}_N:= \sigma (\mathfrak {P}_N)$
, is an
![]() ${\mathfrak {N}}$
-segmentation of
${\mathfrak {N}}$
-segmentation of
![]() $(\Omega , {\mathcal {B}}, \mathfrak {m})$
if:
$(\Omega , {\mathcal {B}}, \mathfrak {m})$
if:
-
(1)
 $\mathfrak {P}_N= \{\Omega _{N,k}\}_{k \in I_N}$
is an N-partition of
$\mathfrak {P}_N= \{\Omega _{N,k}\}_{k \in I_N}$
is an N-partition of
 $(\Omega , {\mathcal {B}})$
for every
$(\Omega , {\mathcal {B}})$
for every
 $N \in {\mathfrak {N}}$
,
$N \in {\mathfrak {N}}$
, -
(2)
 $\mathfrak {m}(\Omega _{N,k})=\mathfrak {m}(\Omega )/N$
for every
$\mathfrak {m}(\Omega _{N,k})=\mathfrak {m}(\Omega )/N$
for every
 $k\in I_N$
and every
$k\in I_N$
and every
 $N \in {\mathfrak {N}}$
,
$N \in {\mathfrak {N}}$
, -
(3) if
 $M\mid N=KM$
, then
$M\mid N=KM$
, then
 $\bigcup _{k=0}^{K-1}\Omega _{N,mK+k}=\Omega _{M,m}$
,
$\bigcup _{k=0}^{K-1}\Omega _{N,mK+k}=\Omega _{M,m}$
,
 $m\in I_{M}$
,
$m\in I_{M}$
, -
(4)
 $\sigma \left ( \left \{ {\mathcal {B}}_N \mid N \in {\mathfrak {N}} \right \} \right ) = {\mathcal {B}}$
.
$\sigma \left ( \left \{ {\mathcal {B}}_N \mid N \in {\mathfrak {N}} \right \} \right ) = {\mathcal {B}}$
.
In this case, we call
![]() $(\Omega , {\mathcal {B}}, \mathfrak {m}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
an
$(\Omega , {\mathcal {B}}, \mathfrak {m}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
an
![]() ${\mathfrak {N}}$
-refined standard Borel measure space.
${\mathfrak {N}}$
-refined standard Borel measure space.
Remark 3.1 It is clear that
![]() ${\mathcal {B}}_M \subset {\mathcal {B}}_N$
if and only if
${\mathcal {B}}_M \subset {\mathcal {B}}_N$
if and only if
![]() $M \mid N$
.
$M \mid N$
.
Example 3.2 The canonical example of
![]() ${\mathfrak {N}}$
-refined standard Borel measure space is
${\mathfrak {N}}$
-refined standard Borel measure space is
where
![]() $\lambda ^c$
is the one-dimensional Lebesgue measure restricted to
$\lambda ^c$
is the one-dimensional Lebesgue measure restricted to
![]() $[0,1)$
and weighted by a constant
$[0,1)$
and weighted by a constant
![]() $c>0$
and
$c>0$
and
![]() $\mathfrak {I}_N=(I_{N,k})_{k \in I_N}$
with
$\mathfrak {I}_N=(I_{N,k})_{k \in I_N}$
with
![]() $I_{N,k}:=[k/N,(k+1)/N)$
,
$I_{N,k}:=[k/N,(k+1)/N)$
,
![]() $k \in I_N$
and
$k \in I_N$
and
![]() $N \in {\mathfrak {N}}$
.
$N \in {\mathfrak {N}}$
.
3.1 Technical tools on standard Borel spaces and measure-preserving isomorphisms
We start with the following fundamental result that follows by, e.g., [Reference Royden30, Theorem 9, Chapter 15].
Theorem 3.3 (Isomorphisms of standard Borel spaces)
Let
![]() $(\Omega , {\mathcal {B}})$
and
$(\Omega , {\mathcal {B}})$
and
![]() $(\Omega ', {\mathcal {B}}',)$
be standard Borel spaces endowed with nonatomic, positive finite measures
$(\Omega ', {\mathcal {B}}',)$
be standard Borel spaces endowed with nonatomic, positive finite measures
![]() $\mathfrak {m}$
and
$\mathfrak {m}$
and
![]() $\mathfrak {m}'$
, respectively, such that
$\mathfrak {m}'$
, respectively, such that
![]() $\mathfrak {m}(\Omega ) = \mathfrak {m}'(\Omega ')$
. Then there exist two measurable functions
$\mathfrak {m}(\Omega ) = \mathfrak {m}'(\Omega ')$
. Then there exist two measurable functions
![]() $\varphi : \Omega \to \Omega '$
and
$\varphi : \Omega \to \Omega '$
and
![]() $\psi : \Omega '\to \Omega $
such that
$\psi : \Omega '\to \Omega $
such that
Corollary 3.4 Let
![]() $(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic, positive finite measure
$(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic, positive finite measure
![]() $\mathfrak {m}$
, and let
$\mathfrak {m}$
, and let
![]() $(\Omega ', {\mathcal {B}}')$
be a standard Borel space. Then, for every nonatomic, positive measure
$(\Omega ', {\mathcal {B}}')$
be a standard Borel space. Then, for every nonatomic, positive measure
![]() $\mu $
on
$\mu $
on
![]() $(\Omega ', {\mathcal {B}}')$
such that
$(\Omega ', {\mathcal {B}}')$
such that
![]() $\mu (\Omega ')= \mathfrak {m}(\Omega )$
, there exists a measurable map
$\mu (\Omega ')= \mathfrak {m}(\Omega )$
, there exists a measurable map
![]() $X: \Omega \to \Omega '$
such that
$X: \Omega \to \Omega '$
such that
![]() $X_\sharp \mathfrak {m} = \mu $
.
$X_\sharp \mathfrak {m} = \mu $
.
Lemma 3.5 (Existence of
 ${\mathfrak {N}}$
-segmentations)
${\mathfrak {N}}$
-segmentations)
For any standard Borel space
![]() $(\Omega , {\mathcal {B}})$
endowed with a nonatomic, positive finite measure
$(\Omega , {\mathcal {B}})$
endowed with a nonatomic, positive finite measure
![]() $\mathfrak {m}$
and any unbounded directed set
$\mathfrak {m}$
and any unbounded directed set
![]() ${\mathfrak {N}} \subset \mathbb {N}$
w.r.t.
${\mathfrak {N}} \subset \mathbb {N}$
w.r.t.
![]() $\prec $
, there exists an
$\prec $
, there exists an
![]() ${\mathfrak {N}}$
-segmentation of
${\mathfrak {N}}$
-segmentation of
![]() $(\Omega , {\mathcal {B}}, \mathfrak {m})$
.
$(\Omega , {\mathcal {B}}, \mathfrak {m})$
.
Proof Let
![]() $([0,1), \mathcal {B}([0,1)), \lambda ^c, (\mathfrak {I}_N)_{N \in {\mathfrak {N}}})$
be the
$([0,1), \mathcal {B}([0,1)), \lambda ^c, (\mathfrak {I}_N)_{N \in {\mathfrak {N}}})$
be the
![]() ${\mathfrak {N}}$
-refined standard Borel space of Example 3.2 with
${\mathfrak {N}}$
-refined standard Borel space of Example 3.2 with
![]() $c=\mathfrak {m}(\Omega )$
. Since
$c=\mathfrak {m}(\Omega )$
. Since
![]() $([0,1), \mathcal {B}([0,1)))$
is a standard Borel space endowed with the nonatomic, positive finite measure
$([0,1), \mathcal {B}([0,1)))$
is a standard Borel space endowed with the nonatomic, positive finite measure
![]() $\lambda ^c$
such that
$\lambda ^c$
such that
![]() $\mathfrak {m}(\Omega ) = \lambda ^c([0,1))$
, by Theorem 3.3, we can find measurable maps
$\mathfrak {m}(\Omega ) = \lambda ^c([0,1))$
, by Theorem 3.3, we can find measurable maps
![]() $\varphi :[0,1) \to \Omega $
,
$\varphi :[0,1) \to \Omega $
,
![]() $\psi : \Omega \to [0,1)$
and two subsets
$\psi : \Omega \to [0,1)$
and two subsets
![]() $\Omega _{0} \in {\mathcal {B}}$
,
$\Omega _{0} \in {\mathcal {B}}$
,
![]() $U \in \mathcal {B}([0,1))$
such that
$U \in \mathcal {B}([0,1))$
such that
![]() $\mathfrak {m}(\Omega _{0})=\lambda ^c(U)=0$
,
$\mathfrak {m}(\Omega _{0})=\lambda ^c(U)=0$
,
![]() $\varphi \circ \psi = \boldsymbol {i}_{\Omega \setminus \Omega _{0}}$
,
$\varphi \circ \psi = \boldsymbol {i}_{\Omega \setminus \Omega _{0}}$
,
![]() $\psi \circ \varphi = \boldsymbol {i}_{[0,1)\setminus U}$
,
$\psi \circ \varphi = \boldsymbol {i}_{[0,1)\setminus U}$
,
![]() $\varphi _\sharp \lambda ^c=\mathfrak {m}$
and
$\varphi _\sharp \lambda ^c=\mathfrak {m}$
and
![]() $\psi _\sharp \mathfrak {m}=\lambda ^c$
. We can thus define
$\psi _\sharp \mathfrak {m}=\lambda ^c$
. We can thus define
Setting
![]() $\mathfrak {P}_N := \{\Omega _{N,k}\}_{k \in I_N}$
for every
$\mathfrak {P}_N := \{\Omega _{N,k}\}_{k \in I_N}$
for every
![]() $N \in {\mathfrak {N}}$
, it is easy to check that
$N \in {\mathfrak {N}}$
, it is easy to check that
![]() $(\mathfrak {P}_N)_{N \in {\mathfrak {N}}}$
is a
$(\mathfrak {P}_N)_{N \in {\mathfrak {N}}}$
is a
![]() ${\mathfrak {N}}$
-segmentation of
${\mathfrak {N}}$
-segmentation of
![]() $(\Omega , {\mathcal {B}}, \mathfrak {m})$
.
$(\Omega , {\mathcal {B}}, \mathfrak {m})$
.
Definition 3.4 (Compatible partitions)
If
![]() $(\Omega , {\mathcal {B}})$
and
$(\Omega , {\mathcal {B}})$
and
![]() $(\Omega ', {\mathcal {B}}')$
are standard Borel spaces endowed with nonatomic, positive finite measures
$(\Omega ', {\mathcal {B}}')$
are standard Borel spaces endowed with nonatomic, positive finite measures
![]() $\mathfrak {m}$
and
$\mathfrak {m}$
and
![]() $\mathfrak {m}'$
, respectively, such that
$\mathfrak {m}'$
, respectively, such that
![]() $\mathfrak {m}(\Omega )=\mathfrak {m}'(\Omega ')$
and
$\mathfrak {m}(\Omega )=\mathfrak {m}'(\Omega ')$
and
![]() $\mathfrak {P}_N =\{\Omega _{N,k}\}_{k \in I_N}$
and
$\mathfrak {P}_N =\{\Omega _{N,k}\}_{k \in I_N}$
and
![]() $\mathfrak {P}^{\prime }_N =\{\Omega ^{\prime }_{N,k}\}_{k \in I_N}$
are N-partitions of
$\mathfrak {P}^{\prime }_N =\{\Omega ^{\prime }_{N,k}\}_{k \in I_N}$
are N-partitions of
![]() $(\Omega , {\mathcal {B}})$
and
$(\Omega , {\mathcal {B}})$
and
![]() $(\Omega ', {\mathcal {B}}')$
, respectively, we say that
$(\Omega ', {\mathcal {B}}')$
, respectively, we say that
![]() $\mathfrak {P}_N$
and
$\mathfrak {P}_N$
and
![]() $\mathfrak {P}^{\prime }_N$
are
$\mathfrak {P}^{\prime }_N$
are
![]() $\mathfrak {m}-\mathfrak {m}'$
compatible if
$\mathfrak {m}-\mathfrak {m}'$
compatible if
Lemma 3.6 (Isomorphisms preserving compatible partitions)
Let
![]() $(\Omega , {\mathcal {B}})$
and
$(\Omega , {\mathcal {B}})$
and
![]() $(\Omega ', {\mathcal {B}}')$
be standard Borel spaces endowed with nonatomic, positive finite measures
$(\Omega ', {\mathcal {B}}')$
be standard Borel spaces endowed with nonatomic, positive finite measures
![]() $\mathfrak {m}$
and
$\mathfrak {m}$
and
![]() $\mathfrak {m}'$
, respectively, such that
$\mathfrak {m}'$
, respectively, such that
![]() $\mathfrak {m}(\Omega )= \mathfrak {m}'(\Omega ')$
, and let
$\mathfrak {m}(\Omega )= \mathfrak {m}'(\Omega ')$
, and let
![]() $\mathfrak {P}_N=\{\Omega _{N,k}\}_{k \in I_N}$
and
$\mathfrak {P}_N=\{\Omega _{N,k}\}_{k \in I_N}$
and
![]() $\mathfrak {P}^{\prime }_N=\{\Omega ^{\prime }_{N,k}\}_{k \in I_N}$
be two
$\mathfrak {P}^{\prime }_N=\{\Omega ^{\prime }_{N,k}\}_{k \in I_N}$
be two
![]() $\mathfrak {m}-\mathfrak {m}'$
compatible N-partitions of
$\mathfrak {m}-\mathfrak {m}'$
compatible N-partitions of
![]() $(\Omega , {\mathcal {B}})$
and
$(\Omega , {\mathcal {B}})$
and
![]() $(\Omega ', {\mathcal {B}}')$
, respectively, for some
$(\Omega ', {\mathcal {B}}')$
, respectively, for some
![]() $N \in \mathbb {N}$
. Then there exist two functions
$N \in \mathbb {N}$
. Then there exist two functions
![]() $\varphi : \Omega \to \Omega '$
and
$\varphi : \Omega \to \Omega '$
and
![]() $\psi : \Omega '\to \Omega $
such that:
$\psi : \Omega '\to \Omega $
such that:
-
(1)
 $\varphi $
is
$\varphi $
is
 ${\mathcal {B}}$
-
${\mathcal {B}}$
-
 ${\mathcal {B}}'$
measurable and
${\mathcal {B}}'$
measurable and
 $\sigma (\mathfrak {P}_N)$
-
$\sigma (\mathfrak {P}_N)$
-
 $\sigma (\mathfrak {P}^{\prime }_N)$
measurable;
$\sigma (\mathfrak {P}^{\prime }_N)$
measurable; -
(2)
 $\psi $
is
$\psi $
is
 ${\mathcal {B}}'$
-
${\mathcal {B}}'$
-
 ${\mathcal {B}}$
measurable and
${\mathcal {B}}$
measurable and
 $\sigma (\mathfrak {P}^{\prime }_N)$
-
$\sigma (\mathfrak {P}^{\prime }_N)$
-
 $\sigma (\mathfrak {P}_N)$
measurable;
$\sigma (\mathfrak {P}_N)$
measurable; -
(3) for every
 $k \in I_N$
, it holds (3.4)
$k \in I_N$
, it holds (3.4) $$ \begin{align} \varphi(\Omega_{N,k}) \subset \Omega^{\prime}_{N, k}, \quad \psi(\Omega^{\prime}_{N,k}) \subset \Omega_{N, k}; \end{align} $$
$$ \begin{align} \varphi(\Omega_{N,k}) \subset \Omega^{\prime}_{N, k}, \quad \psi(\Omega^{\prime}_{N,k}) \subset \Omega_{N, k}; \end{align} $$
-
(4) for every
 $I \subset I_N$
, it holds where the subscript I denotes the restriction to
$I \subset I_N$
, it holds where the subscript I denotes the restriction to $$ \begin{align*} \psi_I \circ \varphi_I &= \boldsymbol{i}_{\Omega_I} \mathfrak{m}_I-\text{ a.e. in}\ \Omega_I,\\ \varphi_I \circ \psi_I &= \boldsymbol{i}_{\Omega^{\prime}_I} \mathfrak{m}_I'-\text{a.e. in}\ \Omega_I',\\ (\varphi_I)_\sharp \mathfrak{m}_I &= \mathfrak{m}_I',\\ (\psi_I)_\sharp \mathfrak{m}_I'&=\mathfrak{m}_I, \end{align*} $$
$$ \begin{align*} \psi_I \circ \varphi_I &= \boldsymbol{i}_{\Omega_I} \mathfrak{m}_I-\text{ a.e. in}\ \Omega_I,\\ \varphi_I \circ \psi_I &= \boldsymbol{i}_{\Omega^{\prime}_I} \mathfrak{m}_I'-\text{a.e. in}\ \Omega_I',\\ (\varphi_I)_\sharp \mathfrak{m}_I &= \mathfrak{m}_I',\\ (\psi_I)_\sharp \mathfrak{m}_I'&=\mathfrak{m}_I, \end{align*} $$
 $\cup _{k \in I} \Omega _{N,k}$
or
$\cup _{k \in I} \Omega _{N,k}$
or
 $\cup _{k \in I} \Omega ^{\prime }_{N,k}$
.
$\cup _{k \in I} \Omega ^{\prime }_{N,k}$
.
Proof Applying Theorem 3.3 to the standard Borel spaces
![]() $(\Omega _{\{k\}}, {\mathcal {B}}_{\{k\}})$
and
$(\Omega _{\{k\}}, {\mathcal {B}}_{\{k\}})$
and
![]() $(\Omega ^{\prime }_{\{k\}}, {\mathcal {B}}^{\prime }_{\{k\}})$
endowed, respectively, with the nonatomic, positive finite measures
$(\Omega ^{\prime }_{\{k\}}, {\mathcal {B}}^{\prime }_{\{k\}})$
endowed, respectively, with the nonatomic, positive finite measures
![]() $\mathfrak {m}_{\{k\}}$
and
$\mathfrak {m}_{\{k\}}$
and
![]() $\mathfrak {m}^{\prime }_{\{k\}}$
for every
$\mathfrak {m}^{\prime }_{\{k\}}$
for every
![]() $k \in I_N$
, we obtain the existence of measurable functions
$k \in I_N$
, we obtain the existence of measurable functions
![]() $\varphi _{k}, \psi _{k}$
satisfying (3.3) for each couple
$\varphi _{k}, \psi _{k}$
satisfying (3.3) for each couple
![]() $\Omega _{N,k}$
,
$\Omega _{N,k}$
,
![]() $\Omega ^{\prime }_{N,k}$
. It is then enough to define
$\Omega ^{\prime }_{N,k}$
. It is then enough to define
Notice that (3.4) is satisfied by construction.
Corollary 3.7 (Lifting permutations to isomorphisms)
Let
![]() $(\Omega , {\mathcal {B}}, \mathfrak {m})$
be a standard Borel space endowed with a nonatomic, positive finite measure
$(\Omega , {\mathcal {B}}, \mathfrak {m})$
be a standard Borel space endowed with a nonatomic, positive finite measure
![]() $\mathfrak {m}$
, and let
$\mathfrak {m}$
, and let
![]() $\mathfrak {P}_N=\{\Omega _{N,k}\}_{k \in I_N}$
be an N-partition of
$\mathfrak {P}_N=\{\Omega _{N,k}\}_{k \in I_N}$
be an N-partition of
![]() $(\Omega , {\mathcal {B}})$
for some
$(\Omega , {\mathcal {B}})$
for some
![]() $N \in \mathbb {N}$
such that
$N \in \mathbb {N}$
such that
![]() $\mathfrak {m}(\Omega _{N,k})= \mathfrak {m}(\Omega )/N$
for every
$\mathfrak {m}(\Omega _{N,k})= \mathfrak {m}(\Omega )/N$
for every
![]() $k \in I_N$
. If
$k \in I_N$
. If
![]() $\sigma \in {\mathrm {Sym}(I_N)}$
, there exists a measure-preserving isomorphism
$\sigma \in {\mathrm {Sym}(I_N)}$
, there exists a measure-preserving isomorphism
![]() $g \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathfrak {m}; \sigma (\mathfrak {P}_N))$
such that
$g \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathfrak {m}; \sigma (\mathfrak {P}_N))$
such that
where
![]() $g_{k}$
is the restriction of g to
$g_{k}$
is the restriction of g to
![]() $\Omega _{N,k}$
.
$\Omega _{N,k}$
.
Proof It is enough to apply Lemma 3.6 to the standard Borel spaces
![]() $(\Omega , {\mathcal {B}})$
and
$(\Omega , {\mathcal {B}})$
and
![]() $(\Omega ', {\mathcal {B}}')$
=
$(\Omega ', {\mathcal {B}}')$
=
![]() $(\Omega , {\mathcal {B}})$
endowed with the nonatomic, positive finite measures
$(\Omega , {\mathcal {B}})$
endowed with the nonatomic, positive finite measures
![]() $\mathfrak {m}$
and
$\mathfrak {m}$
and
![]() $\mathfrak {m}'=\mathfrak {m}$
, respectively, with the N-partitions
$\mathfrak {m}'=\mathfrak {m}$
, respectively, with the N-partitions
![]() $\mathfrak {P}_N$
and
$\mathfrak {P}_N$
and
![]() $\mathfrak {P}^{\prime }_N=\{\Omega _{N,\sigma (k)}\}_{k \in I_N}$
, respectively.
$\mathfrak {P}^{\prime }_N=\{\Omega _{N,\sigma (k)}\}_{k \in I_N}$
, respectively.
Corollary 3.8 Let
![]() $(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic, positive finite measure
$(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic, positive finite measure
![]() $\mathfrak {m}$
, and let
$\mathfrak {m}$
, and let
![]() $\Omega _{0}, \Omega _1 \in {\mathcal {B}}$
be such that
$\Omega _{0}, \Omega _1 \in {\mathcal {B}}$
be such that
![]() $\mathfrak {m}(\Omega _{0})=\mathfrak {m}(\Omega _1)>0$
and
$\mathfrak {m}(\Omega _{0})=\mathfrak {m}(\Omega _1)>0$
and
![]() $\Omega _{0} \cap \Omega _1 = \emptyset $
. Then there exists a measure-preserving isomorphism
$\Omega _{0} \cap \Omega _1 = \emptyset $
. Then there exists a measure-preserving isomorphism
![]() $g \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathfrak {m})$
such that
$g \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathfrak {m})$
such that
where
![]() $g_i$
is the restriction of g to
$g_i$
is the restriction of g to
![]() $\Omega _{k}$
,
$\Omega _{k}$
,
![]() $k=0,1$
.
$k=0,1$
.
Proof Applying Corollary 3.7 to the standard Borel space
![]() $(\Omega _{0} \cup \Omega _1,{\mathcal {B}}|_{\Omega _{0} \cup \Omega _1})$
endowed with the nonatomic, positive finite measure
$(\Omega _{0} \cup \Omega _1,{\mathcal {B}}|_{\Omega _{0} \cup \Omega _1})$
endowed with the nonatomic, positive finite measure
![]() $ \mathfrak {m}|_{\Omega _{0} \cup \Omega _1}$
with the
$ \mathfrak {m}|_{\Omega _{0} \cup \Omega _1}$
with the
![]() $2$
-Borel partition
$2$
-Borel partition
![]() $\mathfrak {P}_{2}= \{\Omega _{k}\}_{k=0,1}$
and
$\mathfrak {P}_{2}= \{\Omega _{k}\}_{k=0,1}$
and
![]() $\sigma $
sending
$\sigma $
sending
![]() $0$
to
$0$
to
![]() $1$
, we obtain the existence of a measure-preserving isomorphism
$1$
, we obtain the existence of a measure-preserving isomorphism
![]() $\tilde {g} \in \mathrm {S}(\Omega _{0} \cup \Omega _1,{\mathcal {B}}|_{\Omega _{0} \cup \Omega _1}, \mathfrak {m}|_{\Omega _{0} \cup \Omega _1})$
such that
$\tilde {g} \in \mathrm {S}(\Omega _{0} \cup \Omega _1,{\mathcal {B}}|_{\Omega _{0} \cup \Omega _1}, \mathfrak {m}|_{\Omega _{0} \cup \Omega _1})$
such that
where
![]() $\tilde {g}_i$
is the restriction of
$\tilde {g}_i$
is the restriction of
![]() $\tilde {g}$
to
$\tilde {g}$
to
![]() $\Omega _{k}$
,
$\Omega _{k}$
,
![]() $k=0,1$
. It is then enough to define
$k=0,1$
. It is then enough to define
![]() $g: \Omega \to \Omega $
as
$g: \Omega \to \Omega $
as
 $$\begin{align*}g(\omega) = \begin{cases} \tilde{g}(\omega), \quad &\text{ if } \omega \in \Omega_{0} \cup \Omega_1, \\ \omega, \quad &\text{ if } \omega \in \Omega \setminus (\Omega_{0} \cup \Omega_1). \end{cases}\\[-34pt] \end{align*}$$
$$\begin{align*}g(\omega) = \begin{cases} \tilde{g}(\omega), \quad &\text{ if } \omega \in \Omega_{0} \cup \Omega_1, \\ \omega, \quad &\text{ if } \omega \in \Omega \setminus (\Omega_{0} \cup \Omega_1). \end{cases}\\[-34pt] \end{align*}$$
The next result is a particular case of Doob’s Martingale Convergence Theorem for Banach-valued maps (see [Reference Stroock32, Theorem 6.1.12]). We recall that a filtration on
![]() $(\Omega , {\mathcal {B}})$
is a sequence
$(\Omega , {\mathcal {B}})$
is a sequence
![]() $(\mathcal {F}_n)_{n \in \mathbb {N}}$
of sub-sigma algebras of
$(\mathcal {F}_n)_{n \in \mathbb {N}}$
of sub-sigma algebras of
![]() ${\mathcal {B}}$
such that
${\mathcal {B}}$
such that
![]() $\mathcal {F}_n \subset \mathcal {F}_{n+1}$
.
$\mathcal {F}_n \subset \mathcal {F}_{n+1}$
.
Theorem 3.9 Let
![]() $(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic, positive finite measure
$(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic, positive finite measure
![]() $\mathfrak {m}$
, let
$\mathfrak {m}$
, let
![]() $(\mathcal {F}_n)_{n \in \mathbb {N}}$
be a filtration on
$(\mathcal {F}_n)_{n \in \mathbb {N}}$
be a filtration on
![]() $(\Omega , {\mathcal {B}})$
such that
$(\Omega , {\mathcal {B}})$
such that
![]() $ \sigma \left ( \left \{ \mathcal {F}_n \mid n \in \mathbb {N} \right \} \right ) = {\mathcal {B}}$
, let
$ \sigma \left ( \left \{ \mathcal {F}_n \mid n \in \mathbb {N} \right \} \right ) = {\mathcal {B}}$
, let
![]() $\mathsf {X}$
be a separable Banach space, and let
$\mathsf {X}$
be a separable Banach space, and let
![]() $p\in [1,\infty ).$
Then, given
$p\in [1,\infty ).$
Then, given
![]() $X \in L^{p}(\Omega , {\mathcal {B}}, \mathfrak {m};\mathsf {X})$
, the
$X \in L^{p}(\Omega , {\mathcal {B}}, \mathfrak {m};\mathsf {X})$
, the
![]() $\mathsf {X}$
-valued martingale
$\mathsf {X}$
-valued martingale
satisfies
both
![]() $\mathfrak {m}$
-a.e. and in
$\mathfrak {m}$
-a.e. and in
![]() $L^{p}(\Omega , {\mathcal {B}}, \mathfrak {m};\mathsf {X})$
.
$L^{p}(\Omega , {\mathcal {B}}, \mathfrak {m};\mathsf {X})$
.
In general, the collection of sigma algebras
![]() $(\mathcal {B}_N)_{N \in {\mathfrak {N}}}$
associated with a segmentation according to Definition 3.3 is not a filtration since it fails to be ordered by inclusion (recall Remark 3.1). However, it is always possible to extract from
$(\mathcal {B}_N)_{N \in {\mathfrak {N}}}$
associated with a segmentation according to Definition 3.3 is not a filtration since it fails to be ordered by inclusion (recall Remark 3.1). However, it is always possible to extract from
![]() $(\mathcal {B}_N)_{N \in {\mathfrak {N}}}$
a filtration still satisfying item (4) in Definition 3.3. More precisely, we have the following result.
$(\mathcal {B}_N)_{N \in {\mathfrak {N}}}$
a filtration still satisfying item (4) in Definition 3.3. More precisely, we have the following result.
Lemma 3.10 (Cofinal filtrations)
Let
![]() ${\mathfrak {N}} \subset \mathbb {N}$
be an unbounded directed subset w.r.t.
${\mathfrak {N}} \subset \mathbb {N}$
be an unbounded directed subset w.r.t.
![]() $\prec $
. Then there exists a totally ordered cofinal sequence
$\prec $
. Then there exists a totally ordered cofinal sequence
![]() $(b_n)_n \subset {\mathfrak {N}}$
satisfying:
$(b_n)_n \subset {\mathfrak {N}}$
satisfying:
-
•
 for every
for every
 $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
, -
• for every
 $N\in \mathbb {N}$
, there exists
$N\in \mathbb {N}$
, there exists
 $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
 $N\mid b_n.$
$N\mid b_n.$
In particular, for every
![]() ${\mathfrak {N}}$
-refined standard Borel measure space
${\mathfrak {N}}$
-refined standard Borel measure space
![]() $(\Omega , {\mathcal {B}}, \mathfrak {m}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
, it holds that
$(\Omega , {\mathcal {B}}, \mathfrak {m}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
, it holds that
![]() $({\mathcal {B}}_{b_n})_{n \in \mathbb {N}}$
is a filtration on
$({\mathcal {B}}_{b_n})_{n \in \mathbb {N}}$
is a filtration on
![]() $(\Omega , {\mathcal {B}})$
,
$(\Omega , {\mathcal {B}})$
,
and
![]() $\sigma \left ( \left \{ {\mathcal {B}}_{b_n} \mid n \in \mathbb {N} \right \} \right ) = {\mathcal {B}}$
.
$\sigma \left ( \left \{ {\mathcal {B}}_{b_n} \mid n \in \mathbb {N} \right \} \right ) = {\mathcal {B}}$
.
For every
![]() $p \in [1,+\infty )$
and every separable Banach space
$p \in [1,+\infty )$
and every separable Banach space
![]() $\mathsf {X}$
, we thus have that
$\mathsf {X}$
, we thus have that
Proof Since
![]() ${\mathfrak {N}}$
is unbounded and directed, for every finite subset
${\mathfrak {N}}$
is unbounded and directed, for every finite subset
![]() $\mathfrak {M} \subset {\mathfrak {N}}$
, the quantity
$\mathfrak {M} \subset {\mathfrak {N}}$
, the quantity
is well defined. Let
![]() $(a_n)_n \subset \mathbb {N}$
be an enumeration of
$(a_n)_n \subset \mathbb {N}$
be an enumeration of
![]() ${\mathfrak {N}}$
and consider the following sequence defined by induction
${\mathfrak {N}}$
and consider the following sequence defined by induction
Then ![]() for every
for every
![]() $n \in \mathbb {N}$
and (3.6) holds for
$n \in \mathbb {N}$
and (3.6) holds for
![]() $(b_n)_n$
and any
$(b_n)_n$
and any
![]() ${\mathfrak {N}}$
-refined standard Borel measure space
${\mathfrak {N}}$
-refined standard Borel measure space
![]() $(\Omega , {\mathcal {B}}, \mathfrak {m}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
.
$(\Omega , {\mathcal {B}}, \mathfrak {m}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
.
In the next lemma, we show that, given two distinct points
![]() $\omega , \omega "$
, they can always be separated by some partition
$\omega , \omega "$
, they can always be separated by some partition
![]() $\mathfrak {P}_N$
for
$\mathfrak {P}_N$
for
![]() $N \in {\mathfrak {N}}$
sufficiently large.
$N \in {\mathfrak {N}}$
sufficiently large.
Lemma 3.11 (Separation property)
Let
![]() $(\Omega , {\mathcal {B}}, \mathfrak {m}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
be an
$(\Omega , {\mathcal {B}}, \mathfrak {m}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
be an
![]() ${\mathfrak {N}}$
-refined standard Borel measure space. Then there exists
${\mathfrak {N}}$
-refined standard Borel measure space. Then there exists
![]() $\Omega _{0} \in {\mathcal {B}}$
with
$\Omega _{0} \in {\mathcal {B}}$
with
![]() $\mathfrak {m}(\Omega _{0})=0$
such that for every
$\mathfrak {m}(\Omega _{0})=0$
such that for every
![]() $\omega ', \omega " \in \Omega \setminus \Omega _{0}$
,
$\omega ', \omega " \in \Omega \setminus \Omega _{0}$
,
![]() $\omega ' \ne \omega "$
, there exists
$\omega ' \ne \omega "$
, there exists
![]() $M \in {\mathfrak {N}}$
such that for every
$M \in {\mathfrak {N}}$
such that for every
![]() $N\in {\mathfrak {N}}$
,
$N\in {\mathfrak {N}}$
,
![]() $M\mid N$
, there exist
$M\mid N$
, there exist
![]() $k', k" \in I_{N}$
,
$k', k" \in I_{N}$
,
![]() $k' \ne k"$
with
$k' \ne k"$
with
![]() $\omega ' \in \Omega _{N, k'}$
and
$\omega ' \in \Omega _{N, k'}$
and
![]() $\omega " \in \Omega _{N,k"}$
.
$\omega " \in \Omega _{N,k"}$
.
Proof Let
![]() $(b_n)_n\subset {\mathfrak {N}}$
be a totally ordered cofinal sequence as in Lemma 3.10, and let
$(b_n)_n\subset {\mathfrak {N}}$
be a totally ordered cofinal sequence as in Lemma 3.10, and let
![]() $\tau $
be a Polish topology on
$\tau $
be a Polish topology on
![]() $\Omega $
such that
$\Omega $
such that
![]() ${\mathcal {B}}$
coincides with the Borel sigma algebra generated by
${\mathcal {B}}$
coincides with the Borel sigma algebra generated by
![]() $\tau $
. By [Reference Bogachev10, Proposition 6.5.4], there exists a countable family
$\tau $
. By [Reference Bogachev10, Proposition 6.5.4], there exists a countable family
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() $\tau $
-continuous functions
$\tau $
-continuous functions
![]() $f: \Omega \to [0,1]$
separating the points of
$f: \Omega \to [0,1]$
separating the points of
![]() $\Omega $
, meaning that for every
$\Omega $
, meaning that for every
![]() $\omega ', \omega " \in \Omega $
,
$\omega ', \omega " \in \Omega $
,
![]() $\omega ' \ne \omega "$
, there exists
$\omega ' \ne \omega "$
, there exists
![]() $f \in \mathcal {F}$
such that
$f \in \mathcal {F}$
such that
![]() $f(\omega ') \ne f(\omega ")$
. Since
$f(\omega ') \ne f(\omega ")$
. Since
![]() $\mathcal {F} \subset L^{2}(\Omega , {\mathcal {B}}, \mathfrak {m}; \mathbb {R})$
, by Theorem 3.9 with
$\mathcal {F} \subset L^{2}(\Omega , {\mathcal {B}}, \mathfrak {m}; \mathbb {R})$
, by Theorem 3.9 with
![]() $\mathcal {F}_n:={\mathcal {B}}_{b_n}$
, for every
$\mathcal {F}_n:={\mathcal {B}}_{b_n}$
, for every
![]() $f \in \mathcal {F}$
, there exists an
$f \in \mathcal {F}$
, there exists an
![]() $\mathfrak {m}$
-negligible set
$\mathfrak {m}$
-negligible set
![]() $\Omega _f$
such that
$\Omega _f$
such that
Let
![]() $\Omega _{0} := \cup _{f \in \mathcal {F}} \Omega _f$
, and let
$\Omega _{0} := \cup _{f \in \mathcal {F}} \Omega _f$
, and let
![]() $\omega ', \omega " \in \Omega \setminus \Omega _{0}$
,
$\omega ', \omega " \in \Omega \setminus \Omega _{0}$
,
![]() $\omega ' \ne \omega "$
. We can find
$\omega ' \ne \omega "$
. We can find
![]() $f \in \mathcal {F}$
such that
$f \in \mathcal {F}$
such that
![]() $f(\omega ') \ne f(\omega ")$
. Thus, there exists
$f(\omega ') \ne f(\omega ")$
. Thus, there exists
![]() $M=b_m \in {\mathfrak {N}}$
such that
$M=b_m \in {\mathfrak {N}}$
such that
Since
![]() ${\mathbb {E}}_{\mathfrak {m}} \left [ f \mid \sigma \left ( \mathfrak {P}_{M} \right ) \right ]$
is constant on every
${\mathbb {E}}_{\mathfrak {m}} \left [ f \mid \sigma \left ( \mathfrak {P}_{M} \right ) \right ]$
is constant on every
![]() $\Omega _{M,k}$
,
$\Omega _{M,k}$
,
![]() $k \in I_{M}$
, we conclude that the points
$k \in I_{M}$
, we conclude that the points
![]() $\omega '$
and
$\omega '$
and
![]() $\omega "$
belong to different elements of
$\omega "$
belong to different elements of
![]() $\mathfrak {P}_{M}$
, and therefore they also belong to different elements of
$\mathfrak {P}_{M}$
, and therefore they also belong to different elements of
![]() $\mathfrak {P}_{N}$
for every
$\mathfrak {P}_{N}$
for every
![]() $N\in {\mathfrak {N}}$
multiple of M.
$N\in {\mathfrak {N}}$
multiple of M.
Proposition 3.12 (Segmentation preserving isomorphisms)
Let
![]() $(\Omega , {\mathcal {B}}, \mathfrak {m}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
and
$(\Omega , {\mathcal {B}}, \mathfrak {m}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
and
![]() $(\Omega ', {\mathcal {B}}', \mathfrak {m}', (\mathfrak {P}^{\prime }_N)_{N \in {\mathfrak {N}}})$
be
$(\Omega ', {\mathcal {B}}', \mathfrak {m}', (\mathfrak {P}^{\prime }_N)_{N \in {\mathfrak {N}}})$
be
![]() ${\mathfrak {N}}$
-refined standard Borel measure spaces such that
${\mathfrak {N}}$
-refined standard Borel measure spaces such that
![]() $\mathfrak {m}(\Omega ) = \mathfrak {m}'(\Omega ')$
. Then there exist two measurable functions
$\mathfrak {m}(\Omega ) = \mathfrak {m}'(\Omega ')$
. Then there exist two measurable functions
![]() $\varphi : \Omega \to \Omega '$
and
$\varphi : \Omega \to \Omega '$
and
![]() $\psi : \Omega '\to \Omega $
such that for every
$\psi : \Omega '\to \Omega $
such that for every
![]() $N \in {\mathfrak {N}}$
and every
$N \in {\mathfrak {N}}$
and every
![]() $I \subset I_N$
, it holds
$I \subset I_N$
, it holds
 $$ \begin{align*} \psi_I \circ \varphi_I &= \boldsymbol{i}_{\Omega_I} \mathfrak{m}_I-\text{a.e. in}\ \Omega_I, \quad \varphi_I \circ \psi_I = \boldsymbol{i}_{\Omega^{\prime}_I}\ \mathfrak{m}_I'-\text{ a.e. in}\ \Omega_I',\\ (\varphi_I)_\sharp \mathfrak{m}_I &= \mathfrak{m}_I', \quad (\psi_I)_\sharp \mathfrak{m}_I'=\mathfrak{m}_I, \end{align*} $$
$$ \begin{align*} \psi_I \circ \varphi_I &= \boldsymbol{i}_{\Omega_I} \mathfrak{m}_I-\text{a.e. in}\ \Omega_I, \quad \varphi_I \circ \psi_I = \boldsymbol{i}_{\Omega^{\prime}_I}\ \mathfrak{m}_I'-\text{ a.e. in}\ \Omega_I',\\ (\varphi_I)_\sharp \mathfrak{m}_I &= \mathfrak{m}_I', \quad (\psi_I)_\sharp \mathfrak{m}_I'=\mathfrak{m}_I, \end{align*} $$
where the subscript I denotes the restriction to
![]() $\cup _{k \in I} \Omega _{N,k}$
or
$\cup _{k \in I} \Omega _{N,k}$
or
![]() $\cup _{k \in I} \Omega ^{\prime }_{N,k}$
.
$\cup _{k \in I} \Omega ^{\prime }_{N,k}$
.
Proof By Lemma 3.10, it is enough to prove the statement in case
![]() ${\mathfrak {N}} = (b_n)_n$
, where
${\mathfrak {N}} = (b_n)_n$
, where
![]() $(b_n)_n \subset \mathbb {N}$
is strictly
$(b_n)_n \subset \mathbb {N}$
is strictly
![]() $\prec $
-increasing sequence and
$\prec $
-increasing sequence and
![]() $(\Omega ', {\mathcal {B}}', \mathfrak {m}', (\mathfrak {P}^{\prime }_N)_{N \in {\mathfrak {N}}})$
is
$(\Omega ', {\mathcal {B}}', \mathfrak {m}', (\mathfrak {P}^{\prime }_N)_{N \in {\mathfrak {N}}})$
is
![]() $([0,1), \mathcal {B}([0,1)), \lambda ^c, (\mathfrak {I}_N)_{N \in {\mathfrak {N}}})$
as in Example 3.2 with
$([0,1), \mathcal {B}([0,1)), \lambda ^c, (\mathfrak {I}_N)_{N \in {\mathfrak {N}}})$
as in Example 3.2 with
![]() $c= \mathfrak {m}(\Omega )$
. By Lemma 3.6, we can find for every
$c= \mathfrak {m}(\Omega )$
. By Lemma 3.6, we can find for every
![]() $n \in \mathbb {N}$
two measurable maps
$n \in \mathbb {N}$
two measurable maps
![]() $\varphi _n: \Omega \to [0,1)$
and
$\varphi _n: \Omega \to [0,1)$
and
![]() $\psi _n:[0,1) \to \Omega $
satisfying the thesis of Lemma 3.6 for the standard Borel spaces
$\psi _n:[0,1) \to \Omega $
satisfying the thesis of Lemma 3.6 for the standard Borel spaces
![]() $(\Omega , {\mathcal {B}})$
and
$(\Omega , {\mathcal {B}})$
and
![]() $([0,1), \mathcal {B}([0,1))$
endowed with nonatomic, positive, and finite measures
$([0,1), \mathcal {B}([0,1))$
endowed with nonatomic, positive, and finite measures
![]() $\mathfrak {m}$
and
$\mathfrak {m}$
and
![]() $\lambda ^c$
, respectively, and the
$\lambda ^c$
, respectively, and the
![]() $\mathfrak {m}-\lambda ^c$
compatible
$\mathfrak {m}-\lambda ^c$
compatible
![]() $b_n$
-partitions of
$b_n$
-partitions of
![]() $(\Omega , {\mathcal {B}})$
and
$(\Omega , {\mathcal {B}})$
and
![]() $([0,1), \mathcal {B}([0,1)))$
given by
$([0,1), \mathcal {B}([0,1)))$
given by
![]() $\mathfrak {P}_{b_n}$
and
$\mathfrak {P}_{b_n}$
and
![]() $\mathfrak {I}_{b_n}$
, where we recall from Example 3.2 that
$\mathfrak {I}_{b_n}$
, where we recall from Example 3.2 that
![]() $\mathfrak {I}_{b_n}= (I_{b_n,k})_{k \in I_{b_n}}$
with
$\mathfrak {I}_{b_n}= (I_{b_n,k})_{k \in I_{b_n}}$
with
![]() $I_{b_n,k}=[k/b_n, (k+1)/b_n)$
. Since
$I_{b_n,k}=[k/b_n, (k+1)/b_n)$
. Since
![]() $\sum _n b_n^{-1} < + \infty $
, for every
$\sum _n b_n^{-1} < + \infty $
, for every
![]() $\omega \in \Omega $
, the sequence
$\omega \in \Omega $
, the sequence
![]() $(\varphi _n(\omega ))_n \subset [0,1)$
is Cauchy, hence converges. We thus have the existence of a measurable map
$(\varphi _n(\omega ))_n \subset [0,1)$
is Cauchy, hence converges. We thus have the existence of a measurable map
![]() $\varphi : \Omega \to [0,1)$
such that
$\varphi : \Omega \to [0,1)$
such that
If
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $k \in I_{b_n}$
, and
$k \in I_{b_n}$
, and
![]() $ \xi \in \mathrm {C}_b(I_{b_n,k})$
, then
$ \xi \in \mathrm {C}_b(I_{b_n,k})$
, then
 $$ \begin{align*} \int_{I_{b_n, k}} \xi \,\mathrm{d} \varphi_\sharp \mathfrak{m} &= \int_{\Omega_{b_n,k}} \xi(\varphi(\omega)) \,\mathrm{d} \mathfrak{m}(\omega) = \lim_m \int_{\Omega_{b_n,k}} \xi(\varphi_m(\omega)) \,\mathrm{d} \mathfrak{m}(\omega) \\ & = \lim_m \int_{I_{b_n,k}} \xi \,\mathrm{d} \lambda^c = \int_{I_{b_n,k}} \xi\,\mathrm{d} \lambda^c, \end{align*} $$
$$ \begin{align*} \int_{I_{b_n, k}} \xi \,\mathrm{d} \varphi_\sharp \mathfrak{m} &= \int_{\Omega_{b_n,k}} \xi(\varphi(\omega)) \,\mathrm{d} \mathfrak{m}(\omega) = \lim_m \int_{\Omega_{b_n,k}} \xi(\varphi_m(\omega)) \,\mathrm{d} \mathfrak{m}(\omega) \\ & = \lim_m \int_{I_{b_n,k}} \xi \,\mathrm{d} \lambda^c = \int_{I_{b_n,k}} \xi\,\mathrm{d} \lambda^c, \end{align*} $$
since for m sufficiently large
![]() $(\varphi _m)_\sharp \mathfrak {m}|_{\Omega _{b_n,k}}=\lambda ^c|_{I_{b_n,k}}$
by Lemma 3.6. This shows that
$(\varphi _m)_\sharp \mathfrak {m}|_{\Omega _{b_n,k}}=\lambda ^c|_{I_{b_n,k}}$
by Lemma 3.6. This shows that
![]() $\varphi _\sharp \mathfrak {m} |_{\Omega _{b_n,k}} = \lambda ^c|_{I_{b_n,k}}$
for every
$\varphi _\sharp \mathfrak {m} |_{\Omega _{b_n,k}} = \lambda ^c|_{I_{b_n,k}}$
for every
![]() $k \in I_{b_n}$
and every
$k \in I_{b_n}$
and every
![]() $n \in \mathbb {N}$
. To conclude, it is enough to show that
$n \in \mathbb {N}$
. To conclude, it is enough to show that
![]() $\varphi $
is
$\varphi $
is
![]() $\mathfrak {m}$
-essentially injective. Let
$\mathfrak {m}$
-essentially injective. Let
![]() $\Omega _{0} \subset \Omega $
be the
$\Omega _{0} \subset \Omega $
be the
![]() $\mathfrak {m}$
-negligible subset of
$\mathfrak {m}$
-negligible subset of
![]() $\Omega $
given by Lemma 3.11, and let
$\Omega $
given by Lemma 3.11, and let
![]() $\Omega _1:= \varphi ^{-1}(J)$
, where
$\Omega _1:= \varphi ^{-1}(J)$
, where
Since
![]() $\lambda ^c(J)=0$
, then
$\lambda ^c(J)=0$
, then
![]() $\mathfrak {m}(\Omega _1)=0$
; let
$\mathfrak {m}(\Omega _1)=0$
; let
![]() $\omega ', \omega " \in \Omega \setminus (\Omega _{0} \cup \Omega _1)$
. Then there exists
$\omega ', \omega " \in \Omega \setminus (\Omega _{0} \cup \Omega _1)$
. Then there exists
![]() $M \in \mathbb {N}$
such that
$M \in \mathbb {N}$
such that
![]() $\omega '$
and
$\omega '$
and
![]() $\omega "$
belong to different elements of
$\omega "$
belong to different elements of
![]() $\mathfrak {P}_{b_n}$
for every
$\mathfrak {P}_{b_n}$
for every
![]() $n \ge M$
. By (3.4) and Lemma 3.11, we can find
$n \ge M$
. By (3.4) and Lemma 3.11, we can find
![]() $k',k" \in I_{b_M}$
with
$k',k" \in I_{b_M}$
with
![]() $k \ne k'$
such that
$k \ne k'$
such that
![]() $\varphi _n(\omega ') \in I_{b_{M}, k'}$
and
$\varphi _n(\omega ') \in I_{b_{M}, k'}$
and
![]() $\varphi _n(\omega ") \in I_{b_{M}, k"}$
for every
$\varphi _n(\omega ") \in I_{b_{M}, k"}$
for every
![]() $n \ge M$
. Thus,
$n \ge M$
. Thus,
![]() $\varphi (\omega ') \in \overline {I_{b_{M}, k'}}$
and
$\varphi (\omega ') \in \overline {I_{b_{M}, k'}}$
and
![]() $\varphi (\omega ') \in \overline {I_{b_{M}, k"}}$
; however, since
$\varphi (\omega ') \in \overline {I_{b_{M}, k"}}$
; however, since
it must be that
![]() $\varphi (\omega ') \ne \varphi (\omega ").$
$\varphi (\omega ') \ne \varphi (\omega ").$
3.2 Approximation of couplings by using measure-preserving isomorphisms
If X is a Polish space, we denote by
![]() $\mathcal {P}(X)$
the space of Borel probability measures on X which is endowed with the weak (or narrow) topology: a sequence
$\mathcal {P}(X)$
the space of Borel probability measures on X which is endowed with the weak (or narrow) topology: a sequence
![]() $(\mu _n)_n \subset \mathcal {P}(X)$
converges to
$(\mu _n)_n \subset \mathcal {P}(X)$
converges to
![]() $\mu \in \mathcal {P}(X)$
if
$\mu \in \mathcal {P}(X)$
if
for every
![]() $\varphi :X \to \mathbb {R}$
continuous and bounded. In this case, we write
$\varphi :X \to \mathbb {R}$
continuous and bounded. In this case, we write
![]() $\mu _n \to \mu $
in
$\mu _n \to \mu $
in
![]() $\mathcal {P}(X)$
.
$\mathcal {P}(X)$
.
If
![]() $X,Y$
are Polish spaces and
$X,Y$
are Polish spaces and
![]() $(\mu ,\nu )\in \mathcal {P}(X)\times \mathcal {P}(Y)$
, we define the set of admissible transport plans
$(\mu ,\nu )\in \mathcal {P}(X)\times \mathcal {P}(Y)$
, we define the set of admissible transport plans
where
![]() $\pi ^i$
,
$\pi ^i$
,
![]() $i=1,2$
, denotes the projection on the ith component and we call
$i=1,2$
, denotes the projection on the ith component and we call
![]() $\pi ^{i}_{\sharp }\boldsymbol {\gamma }$
the ith marginal of
$\pi ^{i}_{\sharp }\boldsymbol {\gamma }$
the ith marginal of
![]() $\boldsymbol {\gamma }$
.
$\boldsymbol {\gamma }$
.
Definition 3.5 (Wasserstein spaces)
Let
![]() $\mathsf {X}$
be a separable Banach space,
$\mathsf {X}$
be a separable Banach space,
![]() $\mu \in \mathcal {P}(\mathsf {X})$
, and
$\mu \in \mathcal {P}(\mathsf {X})$
, and
![]() $p\ge 1$
. We define the space
$p\ge 1$
. We define the space
Given
![]() $\mu ,\nu \in \mathcal {P}_p(\mathsf {X})$
, we define the
$\mu ,\nu \in \mathcal {P}_p(\mathsf {X})$
, we define the
![]() $L^{p}$
-Wasserstein distance
$L^{p}$
-Wasserstein distance
![]() $W_p$
by
$W_p$
by
We denote by
![]() $\Gamma _o(\mu , \nu )$
the (nonempty, compact, and convex) subset of admissible plans in
$\Gamma _o(\mu , \nu )$
the (nonempty, compact, and convex) subset of admissible plans in
![]() $\Gamma (\mu , \nu )$
realizing the infimum in (3.10).
$\Gamma (\mu , \nu )$
realizing the infimum in (3.10).
We recall that
![]() $(\mathcal {P}_p(\mathsf {X}), W_p)$
is a complete and separable metric space. Moreover, if
$(\mathcal {P}_p(\mathsf {X}), W_p)$
is a complete and separable metric space. Moreover, if
![]() $(\mu _n)_{n\in \mathbb {N}}\subset \mathcal {P}_p(\mathsf {X})$
and
$(\mu _n)_{n\in \mathbb {N}}\subset \mathcal {P}_p(\mathsf {X})$
and
![]() $\mu \in \mathcal {P}_p(\mathsf {X})$
, the following holds (see [Reference Ambrosio, Gigli and Savaré3, Proposition 7.1.5 and Lemma 5.1.7]):
$\mu \in \mathcal {P}_p(\mathsf {X})$
, the following holds (see [Reference Ambrosio, Gigli and Savaré3, Proposition 7.1.5 and Lemma 5.1.7]):
 $$ \begin{align} \mu_n\to\mu\text{ in }\mathcal{P}_p(\mathsf{X}),\text{ as }n\to+\infty \quad\Longleftrightarrow\quad\begin{cases}\mu_n\to\mu \text{ in }\mathcal{P}(\mathsf{X}),\\ \int_{\mathsf{X}} |x|^{p} \,\mathrm{d} \mu_n\to\int_{\mathsf{X}} |x|^{p} \,\mathrm{d} \mu, \end{cases} \text{ as }n\to+\infty. \end{align} $$
$$ \begin{align} \mu_n\to\mu\text{ in }\mathcal{P}_p(\mathsf{X}),\text{ as }n\to+\infty \quad\Longleftrightarrow\quad\begin{cases}\mu_n\to\mu \text{ in }\mathcal{P}(\mathsf{X}),\\ \int_{\mathsf{X}} |x|^{p} \,\mathrm{d} \mu_n\to\int_{\mathsf{X}} |x|^{p} \,\mathrm{d} \mu, \end{cases} \text{ as }n\to+\infty. \end{align} $$
We refer, e.g., to [Reference Ambrosio, Gigli and Savaré3, Chapter 7] for a more comprehensive introduction to Wasserstein distances.
The following result is an application of [Reference Brenier and Gangbo12, Theorem 1.1]. We will use the following notation: if
![]() $\mathsf {X}_1$
and
$\mathsf {X}_1$
and
![]() $\mathsf {X}_{2}$
are sets and
$\mathsf {X}_{2}$
are sets and
![]() $X_1:\mathsf {X}_1\to \mathsf {X}_1$
,
$X_1:\mathsf {X}_1\to \mathsf {X}_1$
,
![]() $X_{2}:\mathsf {X}_{2}\to \mathsf {X}_{2}$
, we denote by
$X_{2}:\mathsf {X}_{2}\to \mathsf {X}_{2}$
, we denote by
![]() $X_1\otimes X_{2}:\mathsf {X}_1\times \mathsf {X}_{2}\to \mathsf {X}_1\times \mathsf {X}_{2}$
the map
$X_1\otimes X_{2}:\mathsf {X}_1\times \mathsf {X}_{2}\to \mathsf {X}_1\times \mathsf {X}_{2}$
the map
![]() $(x_1,x_{2})\mapsto (X_1(x_1),X_{2}(x_{2}))$
.
$(x_1,x_{2})\mapsto (X_1(x_1),X_{2}(x_{2}))$
.
Theorem 3.13 (Approximation of bistochastic couplings)
Let
![]() $(\Omega , {\mathcal {B}}, \mathbb {P}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
be a
$(\Omega , {\mathcal {B}}, \mathbb {P}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
be a
![]() ${\mathfrak {N}}$
-refined standard Borel probability space. Then, for every
${\mathfrak {N}}$
-refined standard Borel probability space. Then, for every
![]() $\boldsymbol {\gamma } \in \Gamma (\mathbb {P}, \mathbb {P})$
, there exist a totally ordered strictly increasing sequence
$\boldsymbol {\gamma } \in \Gamma (\mathbb {P}, \mathbb {P})$
, there exist a totally ordered strictly increasing sequence
![]() $(N_n)_n \subset {\mathfrak {N}}$
and maps
$(N_n)_n \subset {\mathfrak {N}}$
and maps
![]() $g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{N_n})$
such that, for every separable Banach spaces
$g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{N_n})$
such that, for every separable Banach spaces
![]() $\mathsf {Z}, \mathsf {Z}'$
and every
$\mathsf {Z}, \mathsf {Z}'$
and every
![]() $Z \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z})$
,
$Z \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z})$
,
![]() $Z' \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z}')$
, it holds
$Z' \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z}')$
, it holds
Proof By Lemma 3.10, it is not restrictive to assume that
![]() ${\mathfrak {N}}=(b_n)_n$
for a totally ordered strictly increasing sequence
${\mathfrak {N}}=(b_n)_n$
for a totally ordered strictly increasing sequence
![]() $(b_n)_n$
,
$(b_n)_n$
,
![]() $n\in \mathbb {N}$
. We divide the proof in several steps.
$n\in \mathbb {N}$
. We divide the proof in several steps.
(1) Let
![]() $([0,1), \mathcal {B}([0,1)), \lambda ^1, (\mathfrak {I}_N)_{N \in {\mathfrak {N}}})$
be the
$([0,1), \mathcal {B}([0,1)), \lambda ^1, (\mathfrak {I}_N)_{N \in {\mathfrak {N}}})$
be the
![]() ${\mathfrak {N}}$
-refined standard Borel probability space of Example 3.2 with
${\mathfrak {N}}$
-refined standard Borel probability space of Example 3.2 with
![]() $c=1$
. Then, for every
$c=1$
. Then, for every
![]() $\boldsymbol {\gamma } \in \Gamma (\lambda ^1, \lambda ^1)$
, there exist a strictly increasing sequence
$\boldsymbol {\gamma } \in \Gamma (\lambda ^1, \lambda ^1)$
, there exist a strictly increasing sequence
![]() $(N_n)_n \subset \mathbb {N}$
and maps
$(N_n)_n \subset \mathbb {N}$
and maps
![]() $g_n \in \mathrm {S}([0,1), \mathcal {B}([0,1)), \lambda ^1; \sigma (\mathfrak {I}_{b_{N_n}}))$
such that
$g_n \in \mathrm {S}([0,1), \mathcal {B}([0,1)), \lambda ^1; \sigma (\mathfrak {I}_{b_{N_n}}))$
such that
Let
![]() $\bar {\mathcal {L}}$
be the one-dimensional Lebesgue measure restricted to
$\bar {\mathcal {L}}$
be the one-dimensional Lebesgue measure restricted to
![]() $[0,1]$
, and let
$[0,1]$
, and let
![]() $\boldsymbol {\gamma } \in \Gamma (\lambda ^1, \lambda ^1)$
. Let
$\boldsymbol {\gamma } \in \Gamma (\lambda ^1, \lambda ^1)$
. Let
![]() $\boldsymbol {\mu } \in \mathcal {P}([0,1] \times [0,1]) $
be an extension of
$\boldsymbol {\mu } \in \mathcal {P}([0,1] \times [0,1]) $
be an extension of
![]() $\boldsymbol {\gamma }$
to
$\boldsymbol {\gamma }$
to
![]() $[0,1] \times [0,1]$
such that
$[0,1] \times [0,1]$
such that
![]() $\boldsymbol {\mu } \in \Gamma (\bar {\mathcal {L}}, \bar {\mathcal {L}})$
. In [Reference Brenier and Gangbo12, Theorem 1.1], it is proven that it is possible to find a strictly increasing sequence
$\boldsymbol {\mu } \in \Gamma (\bar {\mathcal {L}}, \bar {\mathcal {L}})$
. In [Reference Brenier and Gangbo12, Theorem 1.1], it is proven that it is possible to find a strictly increasing sequence
![]() $(N_n)_n \subset \mathbb {N}$
and maps
$(N_n)_n \subset \mathbb {N}$
and maps
![]() $(f_n)_n \subset \mathrm {S}([0,1], \mathcal {B}([0,1]), \bar {\mathcal {L}})$
such that for every
$(f_n)_n \subset \mathrm {S}([0,1], \mathcal {B}([0,1]), \bar {\mathcal {L}})$
such that for every
![]() $n \in \mathbb {N}$
, there exists
$n \in \mathbb {N}$
, there exists
![]() $\sigma _n \in {\mathrm {Sym}(I_{2^{N_n}})}$
such that
$\sigma _n \in {\mathrm {Sym}(I_{2^{N_n}})}$
such that
with
![]() $x_{m,j}$
being the center of
$x_{m,j}$
being the center of
![]() $I_{2^m, j}$
, and satisfying
$I_{2^m, j}$
, and satisfying
If we call
![]() $g_n$
the restriction of
$g_n$
the restriction of
![]() $f_n$
to
$f_n$
to
![]() $[0,1)$
,
$[0,1)$
,
![]() $n \in \mathbb {N}$
, we get that
$n \in \mathbb {N}$
, we get that
![]() $g_n \in \mathrm {S}([0,1), \mathcal {B}([0,1)), \lambda ^1; \sigma (\mathfrak {I}_{b_{N_n}}))$
for every
$g_n \in \mathrm {S}([0,1), \mathcal {B}([0,1)), \lambda ^1; \sigma (\mathfrak {I}_{b_{N_n}}))$
for every
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
This proves the first step only in case
![]() $b_n=2^n$
. However, it can be easily checked that the proof of [Reference Brenier and Gangbo12, Theorem 1.1] does not depend on the specific choice of the sequence
$b_n=2^n$
. However, it can be easily checked that the proof of [Reference Brenier and Gangbo12, Theorem 1.1] does not depend on the specific choice of the sequence
![]() $b_n$
, but it is enough that
$b_n$
, but it is enough that ![]() for every
for every
![]() $n \in \mathbb {N}$
so that the length of the interval
$n \in \mathbb {N}$
so that the length of the interval
![]() $[k/b_n, (k+1)/b_n]$
goes to
$[k/b_n, (k+1)/b_n]$
goes to
![]() $0$
faster than
$0$
faster than
![]() $2^{-n}$
as
$2^{-n}$
as
![]() $n \to + \infty $
. This concludes the proof of the first claim.
$n \to + \infty $
. This concludes the proof of the first claim.
(2) Let
![]() $([0,1), \mathcal {B}([0,1)), \lambda ^1, (\mathfrak {I}_N)_{N \in {\mathfrak {N}}})$
be the
$([0,1), \mathcal {B}([0,1)), \lambda ^1, (\mathfrak {I}_N)_{N \in {\mathfrak {N}}})$
be the
![]() ${\mathfrak {N}}$
-refined standard Borel probability space of Example 3.2 with
${\mathfrak {N}}$
-refined standard Borel probability space of Example 3.2 with
![]() $c=1$
. Then, for every
$c=1$
. Then, for every
![]() $\boldsymbol {\gamma } \in \Gamma (\lambda ^1, \lambda ^1)$
, there exist a strictly increasing sequence
$\boldsymbol {\gamma } \in \Gamma (\lambda ^1, \lambda ^1)$
, there exist a strictly increasing sequence
![]() $(N_n)_n \subset \mathbb {N}$
and maps
$(N_n)_n \subset \mathbb {N}$
and maps
![]() $g_n \in \mathrm {S}([0,1), \mathcal {B}([0,1)), \lambda ^1; \sigma (\mathfrak {I}_{b_{N_n}}))$
such that, for every separable Banach spaces
$g_n \in \mathrm {S}([0,1), \mathcal {B}([0,1)), \lambda ^1; \sigma (\mathfrak {I}_{b_{N_n}}))$
such that, for every separable Banach spaces
![]() $\mathsf {Z}, \mathsf {Z}'$
and every
$\mathsf {Z}, \mathsf {Z}'$
and every
![]() $Z \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1; \mathsf {Z})$
,
$Z \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1; \mathsf {Z})$
,
![]() $Z' \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1; \mathsf {Z}')$
, it holds
$Z' \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1; \mathsf {Z}')$
, it holds
Let
![]() $\boldsymbol {\gamma } \in \Gamma (\lambda ^1, \lambda ^1)$
, and let
$\boldsymbol {\gamma } \in \Gamma (\lambda ^1, \lambda ^1)$
, and let
![]() $(g_n)_n$
be the sequence given by claim (1) for
$(g_n)_n$
be the sequence given by claim (1) for
![]() $\boldsymbol {\gamma }$
. Let
$\boldsymbol {\gamma }$
. Let
![]() $\mathsf {Z}$
and
$\mathsf {Z}$
and
![]() $\mathsf {Z}'$
be separable Banach spaces, and let
$\mathsf {Z}'$
be separable Banach spaces, and let
![]() $Z \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1; \mathsf {Z})$
,
$Z \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1; \mathsf {Z})$
,
![]() $Z' \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1; \mathsf {Z}')$
. Observe that for every
$Z' \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1; \mathsf {Z}')$
. Observe that for every
![]() $\varepsilon>0$
, there exists a compact set
$\varepsilon>0$
, there exists a compact set
![]() $K_\varepsilon \subset [0,1)$
such that the restrictions of Z and
$K_\varepsilon \subset [0,1)$
such that the restrictions of Z and
![]() $Z'$
to
$Z'$
to
![]() $K_\varepsilon $
are continuous in
$K_\varepsilon $
are continuous in
![]() $K_\varepsilon $
and
$K_\varepsilon $
and
![]() $\lambda ^1([0,1)\setminus K_\varepsilon )<\varepsilon $
, so that, setting
$\lambda ^1([0,1)\setminus K_\varepsilon )<\varepsilon $
, so that, setting
![]() $\gamma _n:=(\boldsymbol {i}_{[0,1)}, g_n)_\sharp \lambda ^1$
,
$\gamma _n:=(\boldsymbol {i}_{[0,1)}, g_n)_\sharp \lambda ^1$
,
![]() $n \in \mathbb {N}$
, we have that
$n \in \mathbb {N}$
, we have that
![]() $\gamma _n([0,1)^{2}\setminus K_\varepsilon ^{2})\le 2\varepsilon $
for every
$\gamma _n([0,1)^{2}\setminus K_\varepsilon ^{2})\le 2\varepsilon $
for every
![]() $n\in \mathbb {N}$
. By [Reference Ambrosio, Gigli and Savaré3, Proposition 5.1.10] and claim (1),
$n\in \mathbb {N}$
. By [Reference Ambrosio, Gigli and Savaré3, Proposition 5.1.10] and claim (1),
![]() $(Z\otimes Z')_\sharp (\boldsymbol {i}_{[0,1)}, g_n)_\sharp \lambda ^1 \to (Z\otimes Z')_\sharp \boldsymbol {\gamma } \text { in } \mathcal {P}(\mathsf {Z}\times \mathsf {Z}')$
.
$(Z\otimes Z')_\sharp (\boldsymbol {i}_{[0,1)}, g_n)_\sharp \lambda ^1 \to (Z\otimes Z')_\sharp \boldsymbol {\gamma } \text { in } \mathcal {P}(\mathsf {Z}\times \mathsf {Z}')$
.
(3) Conclusion. Let
![]() $\boldsymbol {\gamma } \in \Gamma (\mathbb {P}, \mathbb {P})$
, and let
$\boldsymbol {\gamma } \in \Gamma (\mathbb {P}, \mathbb {P})$
, and let
![]() $\varphi :\Omega \to [0,1)$
and
$\varphi :\Omega \to [0,1)$
and
![]() $\psi : [0,1) \to \Omega $
be the maps given by Proposition 3.12 for the
$\psi : [0,1) \to \Omega $
be the maps given by Proposition 3.12 for the
![]() ${\mathfrak {N}}$
-refined standard Borel probability spaces
${\mathfrak {N}}$
-refined standard Borel probability spaces
![]() $(\Omega , {\mathcal {B}}, \mathbb {P}, (\mathfrak P_N)_{N \in {\mathfrak {N}}})$
and
$(\Omega , {\mathcal {B}}, \mathbb {P}, (\mathfrak P_N)_{N \in {\mathfrak {N}}})$
and
![]() $([0,1), \mathcal {B}([0,1)), \lambda ^1, (\mathfrak {I}_N)_{N \in {\mathfrak {N}}})$
, where the latter is as in Example 3.2 with
$([0,1), \mathcal {B}([0,1)), \lambda ^1, (\mathfrak {I}_N)_{N \in {\mathfrak {N}}})$
, where the latter is as in Example 3.2 with
![]() $c=1$
. If we define
$c=1$
. If we define
![]() $\boldsymbol {\gamma }':=(\varphi \otimes \varphi )_\sharp \boldsymbol {\gamma }$
, we have that
$\boldsymbol {\gamma }':=(\varphi \otimes \varphi )_\sharp \boldsymbol {\gamma }$
, we have that
![]() $\boldsymbol {\gamma }' \in \Gamma (\lambda ^1, \lambda ^1)$
so that we can find a strictly increasing sequence
$\boldsymbol {\gamma }' \in \Gamma (\lambda ^1, \lambda ^1)$
so that we can find a strictly increasing sequence
![]() $(N_n)_n \subset \mathbb {N}$
and maps
$(N_n)_n \subset \mathbb {N}$
and maps
![]() $g^{\prime }_n \in \mathrm {S}([0,1), \mathcal {B}([0,1)), \lambda ^1; \sigma (\mathfrak {I}_{b_{N_n}}))$
as in step (2). Let us define
$g^{\prime }_n \in \mathrm {S}([0,1), \mathcal {B}([0,1)), \lambda ^1; \sigma (\mathfrak {I}_{b_{N_n}}))$
as in step (2). Let us define
Then, up to change each
![]() $g_n$
on a
$g_n$
on a
![]() $\mathbb {P}$
-negligible set of points, we can assume that
$\mathbb {P}$
-negligible set of points, we can assume that
![]() $g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{b_{N_n}})$
. Let
$g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{b_{N_n}})$
. Let
![]() $\mathsf {Z}$
and
$\mathsf {Z}$
and
![]() $\mathsf {Z}'$
be separable Banach spaces, and let
$\mathsf {Z}'$
be separable Banach spaces, and let
![]() $Z \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z})$
,
$Z \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z})$
,
![]() $Z' \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z}')$
. If we define
$Z' \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z}')$
. If we define
![]() $Z_{0}:=Z \circ \psi $
and
$Z_{0}:=Z \circ \psi $
and
![]() $Z^{\prime }_{0}:=Z' \circ \psi $
, we get that
$Z^{\prime }_{0}:=Z' \circ \psi $
, we get that
![]() $Z_{0} \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1); \mathsf {Z})$
,
$Z_{0} \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1); \mathsf {Z})$
,
![]() $Z_{0}' \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1); \mathsf {Z}')$
. By step (2), we thus get
$Z_{0}' \in L^0([0,1), \mathcal {B}([0,1)), \lambda ^1); \mathsf {Z}')$
. By step (2), we thus get
which is equivalent to (3.12).
Remark 3.14 In the setting of Theorem 3.13, let
![]() $\varphi :\mathsf {Z}\to [0,+\infty )$
,
$\varphi :\mathsf {Z}\to [0,+\infty )$
,
![]() $\varphi ':\mathsf {Z}'\to [0,+\infty )$
be Borel functions.
$\varphi ':\mathsf {Z}'\to [0,+\infty )$
be Borel functions.
Setting
then we have for every
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
 $$ \begin{align*} \int \psi \,\mathrm{d} (Z \otimes Z')_\sharp (\boldsymbol{i}_{\Omega}, g_n)_{\sharp}\mathbb{P} &= \int \psi(Z,Z'\circ g_n)\,\mathrm{d} \mathbb{P}= \int \Big(\varphi(Z)+\varphi'(Z'\circ g_n)\Big)\,\,\mathrm{d} \mathbb{P} \\&= \int \varphi(Z)\,\mathrm{d}\mathbb{P}+ \int \varphi'(Z')\,\mathrm{d}\mathbb{P} \\&= \int \varphi(Z(x_1))\,\mathrm{d}\boldsymbol{\gamma}(x_1,x_{2})+ \int \varphi'(Z'(x_{2}))\,\mathrm{d}\boldsymbol{\gamma}(x_1,x_{2}) \\&= \int \psi(Z(x_1),Z'(x_{2}))\, \mathrm{d}\boldsymbol{\gamma}(x_1,x_{2})= \int \psi \,\mathrm{d} (Z\otimes Z')_\sharp \boldsymbol{\gamma}. \end{align*} $$
$$ \begin{align*} \int \psi \,\mathrm{d} (Z \otimes Z')_\sharp (\boldsymbol{i}_{\Omega}, g_n)_{\sharp}\mathbb{P} &= \int \psi(Z,Z'\circ g_n)\,\mathrm{d} \mathbb{P}= \int \Big(\varphi(Z)+\varphi'(Z'\circ g_n)\Big)\,\,\mathrm{d} \mathbb{P} \\&= \int \varphi(Z)\,\mathrm{d}\mathbb{P}+ \int \varphi'(Z')\,\mathrm{d}\mathbb{P} \\&= \int \varphi(Z(x_1))\,\mathrm{d}\boldsymbol{\gamma}(x_1,x_{2})+ \int \varphi'(Z'(x_{2}))\,\mathrm{d}\boldsymbol{\gamma}(x_1,x_{2}) \\&= \int \psi(Z(x_1),Z'(x_{2}))\, \mathrm{d}\boldsymbol{\gamma}(x_1,x_{2})= \int \psi \,\mathrm{d} (Z\otimes Z')_\sharp \boldsymbol{\gamma}. \end{align*} $$
As a consequence, if
![]() $\mathsf {Z}=\mathsf {Z}'=\mathsf {X}$
for a separable Banach space
$\mathsf {Z}=\mathsf {Z}'=\mathsf {X}$
for a separable Banach space
![]() $\mathsf {X}$
and
$\mathsf {X}$
and
![]() $Z,Z' \in L^{p}(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {X})$
,
$Z,Z' \in L^{p}(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {X})$
,
![]() $p \in [1,+\infty )$
, then the convergence in (3.12) holds in
$p \in [1,+\infty )$
, then the convergence in (3.12) holds in
![]() $\mathcal {P}_p(\mathsf {X}^{2})$
. To prove this, it suffices to apply (3.11) and choose
$\mathcal {P}_p(\mathsf {X}^{2})$
. To prove this, it suffices to apply (3.11) and choose
![]() $\psi (z,z'):= |z|_{\mathsf {X}}^{p} + |z'|_{\mathsf {X}}^{p}$
,
$\psi (z,z'):= |z|_{\mathsf {X}}^{p} + |z'|_{\mathsf {X}}^{p}$
,
![]() $z,z' \in \mathsf {X}$
, in the above identity.
$z,z' \in \mathsf {X}$
, in the above identity.
We deduce two important applications.
Corollary 3.15 Let
![]() $(\Omega , {\mathcal {B}}, \mathbb {P}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
be an
$(\Omega , {\mathcal {B}}, \mathbb {P}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
be an
![]() ${\mathfrak {N}}$
-refined standard Borel probability space. Then, for every
${\mathfrak {N}}$
-refined standard Borel probability space. Then, for every
![]() $\boldsymbol {\gamma } \in \Gamma (\mathbb {P}, \mathbb {P})$
, there exist a totally ordered strictly increasing sequence
$\boldsymbol {\gamma } \in \Gamma (\mathbb {P}, \mathbb {P})$
, there exist a totally ordered strictly increasing sequence
![]() $(N_n)_n \subset {\mathfrak {N}}$
and maps
$(N_n)_n \subset {\mathfrak {N}}$
and maps
![]() $g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{{N_n}})$
such that, for every Polish topology
$g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{{N_n}})$
such that, for every Polish topology
![]() $\tau $
on
$\tau $
on
![]() $\Omega $
generating
$\Omega $
generating
![]() ${\mathcal {B}}$
, it holds
${\mathcal {B}}$
, it holds
where
![]() $\tau \otimes \tau $
is the product topology on
$\tau \otimes \tau $
is the product topology on
![]() $\Omega \times \Omega $
.
$\Omega \times \Omega $
.
Proof By Theorem 3.13 and Remark 3.14, we have the existence of a strictly increasing sequence
![]() $(N_n)_n \subset \mathbb {N}$
and maps
$(N_n)_n \subset \mathbb {N}$
and maps
![]() $g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{{N_n}})$
such that, choosing the separable Hilbert space
$g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{{N_n}})$
such that, choosing the separable Hilbert space
![]() $\mathbb {R}$
, we get
$\mathbb {R}$
, we get
for every
![]() $\varphi _1, \varphi _{2} \in \mathrm {C}_b(\Omega , \tau ) \subset L^{2}(\Omega ,{\mathcal {B}}, \mathbb {P}; \mathbb {R})$
. Since the range of
$\varphi _1, \varphi _{2} \in \mathrm {C}_b(\Omega , \tau ) \subset L^{2}(\Omega ,{\mathcal {B}}, \mathbb {P}; \mathbb {R})$
. Since the range of
![]() $\varphi _i$
is bounded and thus relatively compact, by the
$\varphi _i$
is bounded and thus relatively compact, by the
![]() $\mathcal {P}(\mathbb {R}^{2})$
convergence, we get that
$\mathcal {P}(\mathbb {R}^{2})$
convergence, we get that
for every continuous function
![]() $h: \mathbb {R}^{2} \to \mathbb {R}$
where
$h: \mathbb {R}^{2} \to \mathbb {R}$
where
![]() $\boldsymbol {\gamma }_n = (\boldsymbol {i}_{\Omega }, g_n)_{\sharp}\mathbb {P}$
,
$\boldsymbol {\gamma }_n = (\boldsymbol {i}_{\Omega }, g_n)_{\sharp}\mathbb {P}$
,
![]() $n \in \mathbb {N}$
. Choosing
$n \in \mathbb {N}$
. Choosing
![]() $h(x,y):= xy$
, we get that
$h(x,y):= xy$
, we get that
Let
![]() $\mathcal {A} \subset \mathrm {C}_b(\Omega , \tau )$
be a unital subalgebra whose induced initial topology on
$\mathcal {A} \subset \mathrm {C}_b(\Omega , \tau )$
be a unital subalgebra whose induced initial topology on
![]() $\Omega $
coincides with
$\Omega $
coincides with
![]() $\tau $
(e.g., the subset of
$\tau $
(e.g., the subset of
![]() $\mathsf {d}$
-Lipschitz continuous and bounded functions for a complete distance
$\mathsf {d}$
-Lipschitz continuous and bounded functions for a complete distance
![]() $\mathsf {d}$
inducing
$\mathsf {d}$
inducing
![]() $\tau $
). It is easy to check that
$\tau $
). It is easy to check that
 $$\begin{align*}\mathcal{A} \otimes \mathcal{A} := \left \{ \sum_{i=1}^n \varphi_1^i \otimes \varphi_{2}^i \mid (\varphi_1^i)_{i=1}^n, (\varphi_{2}^i)_{i=1}^n \subset \mathcal{A}, \, n \in \mathbb{N} \right \} \subset \mathrm{C}_b(\Omega \times \Omega, \tau \otimes \tau) \end{align*}$$
$$\begin{align*}\mathcal{A} \otimes \mathcal{A} := \left \{ \sum_{i=1}^n \varphi_1^i \otimes \varphi_{2}^i \mid (\varphi_1^i)_{i=1}^n, (\varphi_{2}^i)_{i=1}^n \subset \mathcal{A}, \, n \in \mathbb{N} \right \} \subset \mathrm{C}_b(\Omega \times \Omega, \tau \otimes \tau) \end{align*}$$
is a unital subalgebra whose induced initial topology on
![]() $\Omega \times \Omega $
coincides with
$\Omega \times \Omega $
coincides with
![]() $\tau \otimes \tau $
. By (3.15), we thus have that
$\tau \otimes \tau $
. By (3.15), we thus have that
We conclude by [Reference Savaré and Sodini31, Lemma 2.3].
The second part of the following corollary represents a sort of extension of the known result in [Reference Cardaliaguet15, Lemma 6.4] (cf. also [Reference Carmona and Delarue16, Lemma 5.23, p. 379]) to the class of pairs
![]() $(X,Y)$
of random variables, where X and Y take values on possibly different separable Banach spaces, with possibly different p-integrability. Whenever the joint distribution of two pairs
$(X,Y)$
of random variables, where X and Y take values on possibly different separable Banach spaces, with possibly different p-integrability. Whenever the joint distribution of two pairs
![]() $(X,Y),(X',Y')$
belonging to such a class is equal, we are able to prove the existence of a sequence of measure-preserving maps giving the desired strong approximation result for both the components.
$(X,Y),(X',Y')$
belonging to such a class is equal, we are able to prove the existence of a sequence of measure-preserving maps giving the desired strong approximation result for both the components.
Corollary 3.16 Let
![]() $(\Omega , {\mathcal {B}}, \mathbb {P}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
be an
$(\Omega , {\mathcal {B}}, \mathbb {P}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
be an
![]() ${\mathfrak {N}}$
-refined standard Borel probability space, let
${\mathfrak {N}}$
-refined standard Borel probability space, let
![]() $\mathsf {Z}$
and
$\mathsf {Z}$
and
![]() $\mathsf {Z}'$
be separable Banach spaces, and let
$\mathsf {Z}'$
be separable Banach spaces, and let
![]() $Z \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z})$
,
$Z \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z})$
,
![]() $Z' \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z}')$
. Then, for every
$Z' \in L^0(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Z}')$
. Then, for every
![]() $\boldsymbol {\mu }\in \Gamma (Z_{\sharp}\mathbb {P},Z^{\prime }_{\sharp}\mathbb {P})$
, there exist a totally ordered strictly increasing sequence
$\boldsymbol {\mu }\in \Gamma (Z_{\sharp}\mathbb {P},Z^{\prime }_{\sharp}\mathbb {P})$
, there exist a totally ordered strictly increasing sequence
![]() $(N_n)_n \subset {\mathfrak {N}}$
and maps
$(N_n)_n \subset {\mathfrak {N}}$
and maps
![]() $g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{{N_n}})$
such that
$g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{{N_n}})$
such that
In particular, if
![]() $\mathsf {X}$
and
$\mathsf {X}$
and
![]() $\mathsf {Y}$
are separable Banach spaces,
$\mathsf {Y}$
are separable Banach spaces,
![]() $X,X' \in L^{p}(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {X})$
,
$X,X' \in L^{p}(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {X})$
,
![]() $Y,Y' \in L^q(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Y})$
,
$Y,Y' \in L^q(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Y})$
,
![]() $p,q \in [1,+\infty )$
, and
$p,q \in [1,+\infty )$
, and
![]() $(X,Y)_{\sharp}\mathbb {P}=(X',Y')_{\sharp}\mathbb {P}$
, then there exist a totally ordered strictly increasing sequence
$(X,Y)_{\sharp}\mathbb {P}=(X',Y')_{\sharp}\mathbb {P}$
, then there exist a totally ordered strictly increasing sequence
![]() $(N_n)_n \subset {\mathfrak {N}}$
and maps
$(N_n)_n \subset {\mathfrak {N}}$
and maps
![]() $g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{{N_n}})$
such that
$g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{{N_n}})$
such that
![]() $X'\circ g_n\to X$
in
$X'\circ g_n\to X$
in
![]() $L^{p}(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {X})$
and
$L^{p}(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {X})$
and
![]() $Y'\circ g_n\to Y$
in
$Y'\circ g_n\to Y$
in
![]() $L^q(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Y})$
as
$L^q(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {Y})$
as
![]() $n\to \infty $
.
$n\to \infty $
.
Proof Let
![]() $\mu :=Z_{\sharp}\mathbb {P}$
and
$\mu :=Z_{\sharp}\mathbb {P}$
and
![]() $\mu ':=Z^{\prime }_{\sharp}\mathbb {P}$
; let us first observe that there exists
$\mu ':=Z^{\prime }_{\sharp}\mathbb {P}$
; let us first observe that there exists
![]() $\boldsymbol {\gamma }\in \Gamma ({\mathbb {P}},{\mathbb {P}})$
such that
$\boldsymbol {\gamma }\in \Gamma ({\mathbb {P}},{\mathbb {P}})$
such that
![]() $(Z\otimes Z')_\sharp \boldsymbol {\gamma }=\boldsymbol {\mu }$
. In fact, we can disintegrate
$(Z\otimes Z')_\sharp \boldsymbol {\gamma }=\boldsymbol {\mu }$
. In fact, we can disintegrate
![]() $\mathbb {P}$
w.r.t. Z and
$\mathbb {P}$
w.r.t. Z and
![]() $\mu $
(see, e.g., [Reference Ambrosio, Gigli and Savaré3, Theorem 5.3.1] for details on the disintegration theorem), obtaining a Borel family of measures
$\mu $
(see, e.g., [Reference Ambrosio, Gigli and Savaré3, Theorem 5.3.1] for details on the disintegration theorem), obtaining a Borel family of measures
![]() $(\theta _z)_{z\in \mathsf {Z}}\subset \mathcal {P}(\Omega )$
such that
$(\theta _z)_{z\in \mathsf {Z}}\subset \mathcal {P}(\Omega )$
such that
![]() $\theta _z$
is concentrated on
$\theta _z$
is concentrated on
![]() $Z^{-1}(z)$
for
$Z^{-1}(z)$
for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $z \in \mathsf {Z}$
and
$z \in \mathsf {Z}$
and
![]() $\mathbb {P}=\int \theta _z \,\mathrm {d}\mu (z)$
; similarly, we can also find
$\mathbb {P}=\int \theta _z \,\mathrm {d}\mu (z)$
; similarly, we can also find
![]() $(\theta ^{\prime }_{z'})_{z'\in \mathsf {Z}'}\subset \mathcal {P}(\Omega )$
such that
$(\theta ^{\prime }_{z'})_{z'\in \mathsf {Z}'}\subset \mathcal {P}(\Omega )$
such that
![]() $\theta _{z'}^{\prime }$
is concentrated on
$\theta _{z'}^{\prime }$
is concentrated on
![]() $(Z')^{-1}(z')$
for
$(Z')^{-1}(z')$
for
![]() $\mu '$
-a.e.
$\mu '$
-a.e.
![]() $z' \in \mathsf {Z}'$
and
$z' \in \mathsf {Z}'$
and
![]() $\mathbb {P} = \int \theta ^{\prime }_{z'}\,\mathrm {d}\mu '(z')$
. We can thus define
$\mathbb {P} = \int \theta ^{\prime }_{z'}\,\mathrm {d}\mu '(z')$
. We can thus define
![]() $\boldsymbol {\gamma }:=\int (\theta _{z}\otimes \theta ^{\prime }_{z'})\,{\mathrm {d}} \boldsymbol {\mu }(z,z')\in {\mathcal {P}}({\Omega }\times {\Omega })$
, and it is immediate to check that
$\boldsymbol {\gamma }:=\int (\theta _{z}\otimes \theta ^{\prime }_{z'})\,{\mathrm {d}} \boldsymbol {\mu }(z,z')\in {\mathcal {P}}({\Omega }\times {\Omega })$
, and it is immediate to check that
![]() $(Z\otimes Z')_\sharp \boldsymbol {\gamma }=\boldsymbol {\mu }$
since for every function
$(Z\otimes Z')_\sharp \boldsymbol {\gamma }=\boldsymbol {\mu }$
since for every function
![]() $\varphi _1\in \mathrm {C}_b(\mathsf {Z})$
,
$\varphi _1\in \mathrm {C}_b(\mathsf {Z})$
,
![]() $\varphi _{2}\in \mathrm {C}_b(\mathsf {Z'})$
,
$\varphi _{2}\in \mathrm {C}_b(\mathsf {Z'})$
,
 $$ \begin{align*} &\int \varphi_1(Z(\omega))\varphi_{2}(Z'(\omega'))\,\mathrm{d}\boldsymbol{\gamma}(\omega,\omega')\\ &= \int \bigg(\int \varphi_1(Z(\omega))\varphi_{2}(Z'(\omega'))\,\mathrm{d}\theta_{z}(\omega)\,\mathrm{d}\theta^{\prime}_{z'}(\omega') \bigg)\,\mathrm{d} \boldsymbol{\mu}(z,z') \\&= \int \int \varphi_1(Z(\omega))\,\mathrm{d}\theta_z(\omega) \int\varphi_{2}(Z'(\omega'))\,\mathrm{d}\theta^{\prime}_{z'}(\omega') \,\mathrm{d} \boldsymbol{\mu}(z,z') \\&= \int \Big( \varphi_1(z) \varphi_{2}(z')\Big) \,\mathrm{d} \boldsymbol{\mu}(z,z'). \end{align*} $$
$$ \begin{align*} &\int \varphi_1(Z(\omega))\varphi_{2}(Z'(\omega'))\,\mathrm{d}\boldsymbol{\gamma}(\omega,\omega')\\ &= \int \bigg(\int \varphi_1(Z(\omega))\varphi_{2}(Z'(\omega'))\,\mathrm{d}\theta_{z}(\omega)\,\mathrm{d}\theta^{\prime}_{z'}(\omega') \bigg)\,\mathrm{d} \boldsymbol{\mu}(z,z') \\&= \int \int \varphi_1(Z(\omega))\,\mathrm{d}\theta_z(\omega) \int\varphi_{2}(Z'(\omega'))\,\mathrm{d}\theta^{\prime}_{z'}(\omega') \,\mathrm{d} \boldsymbol{\mu}(z,z') \\&= \int \Big( \varphi_1(z) \varphi_{2}(z')\Big) \,\mathrm{d} \boldsymbol{\mu}(z,z'). \end{align*} $$
Notice also that it is enough to verify that
![]() $(Z,Z')_{\sharp}\mathbb {P}$
and
$(Z,Z')_{\sharp}\mathbb {P}$
and
![]() $\boldsymbol {\gamma }$
have the same integral for every function of the form
$\boldsymbol {\gamma }$
have the same integral for every function of the form
![]() $\varphi _1 \otimes \varphi _{2}$
as above to conclude that the two measures coincide (see, e.g., the proof of the above Corollary 3.15). We can then apply (3.12) and obtain (3.16).
$\varphi _1 \otimes \varphi _{2}$
as above to conclude that the two measures coincide (see, e.g., the proof of the above Corollary 3.15). We can then apply (3.12) and obtain (3.16).
Let us show the last part of the statement: we take
![]() $\mathsf {Z}=\mathsf {Z}':=\mathsf {X} \times \mathsf {Y}$
and, by (3.16) with
$\mathsf {Z}=\mathsf {Z}':=\mathsf {X} \times \mathsf {Y}$
and, by (3.16) with
![]() $Z:=(X,Y)$
,
$Z:=(X,Y)$
,
![]() $Z':=(X',Y')$
and
$Z':=(X',Y')$
and
![]() $\boldsymbol {\mu }:=(\boldsymbol {i}_{\mathsf {X} \times \mathsf {Y}},\boldsymbol {i}_{\mathsf {X} \times \mathsf {Y}})_\sharp (X,Y)_{\sharp}\mathbb {P}$
, we have that
$\boldsymbol {\mu }:=(\boldsymbol {i}_{\mathsf {X} \times \mathsf {Y}},\boldsymbol {i}_{\mathsf {X} \times \mathsf {Y}})_\sharp (X,Y)_{\sharp}\mathbb {P}$
, we have that
We thus have that
![]() $(X,X'\circ g_n)_{\sharp}\mathbb {P} \to (\boldsymbol {i}_{\mathsf {X}},\boldsymbol {i}_{\mathsf {X}})_\sharp X_{\sharp}\mathbb {P}$
in
$(X,X'\circ g_n)_{\sharp}\mathbb {P} \to (\boldsymbol {i}_{\mathsf {X}},\boldsymbol {i}_{\mathsf {X}})_\sharp X_{\sharp}\mathbb {P}$
in
![]() $\mathcal {P}(\mathsf {X}^{2})$
. By Remark 3.14 with
$\mathcal {P}(\mathsf {X}^{2})$
. By Remark 3.14 with
![]() $\psi ((x,y),(x',y'))= |x|_{\mathsf {X}}^{p} + |x'|_{\mathsf {X}}^{p}$
,
$\psi ((x,y),(x',y'))= |x|_{\mathsf {X}}^{p} + |x'|_{\mathsf {X}}^{p}$
,
![]() $x,x \in \mathsf {X}, y,y' \in \mathsf {Y}$
, we get, also using (3.11), that
$x,x \in \mathsf {X}, y,y' \in \mathsf {Y}$
, we get, also using (3.11), that
![]() $(X,X'\circ g_n)_{\sharp}\mathbb {P} \to (\boldsymbol {i}_{\mathsf {X}},\boldsymbol {i}_{\mathsf {X}})_\sharp X_{\sharp}\mathbb {P}$
in
$(X,X'\circ g_n)_{\sharp}\mathbb {P} \to (\boldsymbol {i}_{\mathsf {X}},\boldsymbol {i}_{\mathsf {X}})_\sharp X_{\sharp}\mathbb {P}$
in
![]() $\mathcal {P}_p(\mathsf {X}^{2})$
. As a consequence (see, e.g., [Reference Ambrosio, Gigli and Savaré3, Proposition 7.1.5 and Lemma 5.1.7]), we get
$\mathcal {P}_p(\mathsf {X}^{2})$
. As a consequence (see, e.g., [Reference Ambrosio, Gigli and Savaré3, Proposition 7.1.5 and Lemma 5.1.7]), we get
 $$ \begin{align*} \lim_{n\to\infty} \int |X-X'\circ g_n|^{p}\,\mathrm{d}\mathbb{P} &= \lim_{n\to\infty} \int |x-x'|^{p}\,\mathrm{d}\big((X,X'\circ g_n)_{\sharp}\mathbb{P})(x,x')\\ &= \int |x-x'|^{p}\,\mathrm{d}((\boldsymbol{i}_{\mathsf{X}},\boldsymbol{i}_{\mathsf{X}})_\sharp X_{\sharp}\mathbb{P})(x,x')\\ &=0. \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty} \int |X-X'\circ g_n|^{p}\,\mathrm{d}\mathbb{P} &= \lim_{n\to\infty} \int |x-x'|^{p}\,\mathrm{d}\big((X,X'\circ g_n)_{\sharp}\mathbb{P})(x,x')\\ &= \int |x-x'|^{p}\,\mathrm{d}((\boldsymbol{i}_{\mathsf{X}},\boldsymbol{i}_{\mathsf{X}})_\sharp X_{\sharp}\mathbb{P})(x,x')\\ &=0. \end{align*} $$
The proof for Y and
![]() $Y'$
is identical.
$Y'$
is identical.
Remark 3.17 In the same setting of Corollary 3.16 and similarly to Remark 3.14, if
![]() $\mathsf {Z}=\mathsf {Z}'=\mathsf {X}$
for a separable Banach space
$\mathsf {Z}=\mathsf {Z}'=\mathsf {X}$
for a separable Banach space
![]() $\mathsf {X}$
and
$\mathsf {X}$
and
![]() $X,X' \in L^{p}(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {X})$
,
$X,X' \in L^{p}(\Omega , {\mathcal {B}}, \mathbb {P}; \mathsf {X})$
,
![]() $p \in [1,+\infty )$
, then (3.11) gives that the convergence in (3.16) holds in
$p \in [1,+\infty )$
, then (3.11) gives that the convergence in (3.16) holds in
![]() $\mathcal {P}_p(\mathsf {X}^{2})$
,
$\mathcal {P}_p(\mathsf {X}^{2})$
,
As a byproduct, we recover the following important result (see, e.g., [Reference Gangbo and Tudorascu21, Lemma 3.13] for a statement in case
![]() $p=2$
and
$p=2$
and
![]() $\mathsf {X}=\mathbb {R}^d$
), which is also related to the equivalence between the Monge and the Kantorovich formulations of Optimal Transport problems [Reference Ambrosio2, Theorems 2.1 and 9.3], [Reference Pratelli27, Theorem B].
$\mathsf {X}=\mathbb {R}^d$
), which is also related to the equivalence between the Monge and the Kantorovich formulations of Optimal Transport problems [Reference Ambrosio2, Theorems 2.1 and 9.3], [Reference Pratelli27, Theorem B].
Proposition 3.18 Let
![]() $(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic probability measure
$(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic probability measure
![]() $\mathbb {P}$
, let
$\mathbb {P}$
, let
![]() $\mathsf {X}$
be a separable Banach space, and let
$\mathsf {X}$
be a separable Banach space, and let
![]() $p\in [1,+\infty )$
. If
$p\in [1,+\infty )$
. If
![]() $\mu , \nu \in \mathcal {P}_p(\mathsf {X})$
and
$\mu , \nu \in \mathcal {P}_p(\mathsf {X})$
and
![]() $X \in L^{p}(\Omega , {\mathcal {B}},\mathbb {P}; \mathsf {X})$
is s.t.
$X \in L^{p}(\Omega , {\mathcal {B}},\mathbb {P}; \mathsf {X})$
is s.t.
![]() $X_{\sharp}\mathbb {P} = \mu $
, then, for every
$X_{\sharp}\mathbb {P} = \mu $
, then, for every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $Y \in L^{p}(\Omega , {\mathcal {B}},\mathbb {P}; \mathsf {X})$
s.t.
$Y \in L^{p}(\Omega , {\mathcal {B}},\mathbb {P}; \mathsf {X})$
s.t.
![]() $Y_{\sharp}\mathbb {P} = \nu $
and
$Y_{\sharp}\mathbb {P} = \nu $
and
Proof Let us consider the
![]() ${\mathfrak {N}}$
-refined standard Borel probability space
${\mathfrak {N}}$
-refined standard Borel probability space
![]() $(\Omega , {\mathcal {B}}, \mathbb {P}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
with
$(\Omega , {\mathcal {B}}, \mathbb {P}, (\mathfrak {P}_N)_{N \in {\mathfrak {N}}})$
with
![]() ${\mathfrak {N}} =(2^k)_{k \in \mathbb {N}}$
; let
${\mathfrak {N}} =(2^k)_{k \in \mathbb {N}}$
; let
![]() $\boldsymbol {\mu } \in \Gamma _o(\mu , \nu )$
and let
$\boldsymbol {\mu } \in \Gamma _o(\mu , \nu )$
and let
![]() $X'\in L^{p}(\Omega ,{\mathcal {B}},\mathbb {P}; \mathsf {X})$
be such that
$X'\in L^{p}(\Omega ,{\mathcal {B}},\mathbb {P}; \mathsf {X})$
be such that
![]() $X^{\prime }_{\sharp}\mathbb {P}=\nu $
. By Corollary 3.16 and Remark 3.17, there exist a strictly increasing sequence
$X^{\prime }_{\sharp}\mathbb {P}=\nu $
. By Corollary 3.16 and Remark 3.17, there exist a strictly increasing sequence
![]() $(N_n)_n \subset {\mathfrak {N}}$
and maps
$(N_n)_n \subset {\mathfrak {N}}$
and maps
![]() $g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{{N_n}})$
such that
$g_n \in \mathrm {S}(\Omega , {\mathcal {B}}, \mathbb {P}; {\mathcal {B}}_{{N_n}})$
such that
We have
 $$ \begin{align*} \lim_{n\to\infty} \int |X-X'\circ g_n|^{p}\,\mathrm{d}\mathbb{P} &= \lim_{n\to\infty} \int |x-y|^{p}\,\mathrm{d}\big((X,X'\circ g_n)_{\sharp}\mathbb{P})(x,y)\\&=\int |x-y|^{p}\,\mathrm{d}\boldsymbol{\mu}(x,y) =W_p^{p}(\mu,\nu). \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty} \int |X-X'\circ g_n|^{p}\,\mathrm{d}\mathbb{P} &= \lim_{n\to\infty} \int |x-y|^{p}\,\mathrm{d}\big((X,X'\circ g_n)_{\sharp}\mathbb{P})(x,y)\\&=\int |x-y|^{p}\,\mathrm{d}\boldsymbol{\mu}(x,y) =W_p^{p}(\mu,\nu). \end{align*} $$
Thus, given
![]() $\varepsilon>0$
, it is always possible to find
$\varepsilon>0$
, it is always possible to find
![]() $n \in \mathbb {N}$
sufficiently large such that
$n \in \mathbb {N}$
sufficiently large such that
![]() $Y:=X' \circ g_n$
satisfies the thesis.
$Y:=X' \circ g_n$
satisfies the thesis.
4 Monotone-dissipative operators and Lipschitz maps in
 $L^{p}$
-spaces invariant by measure-preserving transformations
$L^{p}$
-spaces invariant by measure-preserving transformations
Let
![]() $(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic probability measure
$(\Omega , {\mathcal {B}})$
be a standard Borel space endowed with a nonatomic probability measure
![]() $\mathbb {P}$
(see Definition 3.1). We denote by
$\mathbb {P}$
(see Definition 3.1). We denote by
![]() $\mathrm {S}(\Omega )$
the class of
$\mathrm {S}(\Omega )$
the class of
![]() ${\mathcal {B}}$
-
${\mathcal {B}}$
-
![]() ${\mathcal {B}}$
-measurable maps
${\mathcal {B}}$
-measurable maps
![]() $g:\Omega \to \Omega $
which are essentially injective and measure-preserving, i.e., there exists a full
$g:\Omega \to \Omega $
which are essentially injective and measure-preserving, i.e., there exists a full
![]() $\mathbb {P}$
-measure set
$\mathbb {P}$
-measure set
![]() $\Omega _{0} \in {\mathcal {B}}$
such that g is injective on
$\Omega _{0} \in {\mathcal {B}}$
such that g is injective on
![]() $\Omega _{0}$
and
$\Omega _{0}$
and
![]() $g_{\sharp}\mathbb {P}=\mathbb {P}$
. If
$g_{\sharp}\mathbb {P}=\mathbb {P}$
. If
![]() $g\in \mathrm {S}(\Omega )$
, there exists
$g\in \mathrm {S}(\Omega )$
, there exists
![]() $g^{-1}\in \mathrm {S}(\Omega )$
(defined up to a
$g^{-1}\in \mathrm {S}(\Omega )$
(defined up to a
![]() $\mathbb {P}$
-negligible set) such that
$\mathbb {P}$
-negligible set) such that
![]() $g^{-1}\circ g=g\circ g^{-1}=\boldsymbol {i}_\Omega \mathbb {P}$
-a.e. in
$g^{-1}\circ g=g\circ g^{-1}=\boldsymbol {i}_\Omega \mathbb {P}$
-a.e. in
![]() $\Omega $
.
$\Omega $
.
Consider two separable Banach spaces
![]() $\mathsf {X},\mathsf {Y}$
and fix exponents
$\mathsf {X},\mathsf {Y}$
and fix exponents
![]() $p,q\in [1,+\infty )$
. We set
$p,q\in [1,+\infty )$
. We set
Notice that for every
![]() $g\in \mathrm {S}(\Omega )$
, the pullback transformation
$g\in \mathrm {S}(\Omega )$
, the pullback transformation
![]() $g^{*}:\mathcal {X}\mapsto \mathcal {X}$
sending X to
$g^{*}:\mathcal {X}\mapsto \mathcal {X}$
sending X to
![]() $X \circ g$
is a linear isometry of
$X \circ g$
is a linear isometry of
![]() $\mathcal {X}$
: in particular,
$\mathcal {X}$
: in particular,
The aim of this section is to study properties of maps and sets/operators, defined on these particular spaces, which are invariant by measure-preserving transformations. We will also apply the results of Section 2 to this particular setting. The interest on such kinds of properties is made evident by the implications in the study of dissipative evolutions in Wasserstein spaces via Lagrangian representations (cf. [Reference Cavagnari, Savaré and Sodini17]).
Definition 4.1 (Invariant sets and maps)
We say that a set
![]() $\boldsymbol {B}\subset \mathcal {X}\times \mathcal {Y}$
is invariant by measure-preserving isomorphisms if for every
$\boldsymbol {B}\subset \mathcal {X}\times \mathcal {Y}$
is invariant by measure-preserving isomorphisms if for every
![]() $g \in \mathrm {S}(\Omega )$
it holds
$g \in \mathrm {S}(\Omega )$
it holds
where, with a slight abuse of notation, we denote with the same symbol
![]() $g^{*}$
both the pullback transformation induced by g on
$g^{*}$
both the pullback transformation induced by g on
![]() $\mathcal {X}$
and on
$\mathcal {X}$
and on
![]() $\mathcal {Y}$
. A set
$\mathcal {Y}$
. A set
![]() $\boldsymbol {B} \subset \mathcal {X}\times \mathcal {Y}$
is law invariant if it holds
$\boldsymbol {B} \subset \mathcal {X}\times \mathcal {Y}$
is law invariant if it holds
A (single valued) operator
![]() ${\boldsymbol {L}}:\mathrm {D}({\boldsymbol {L}})\subset \mathcal {X}\to \mathcal {Y}$
is invariant by measure-preserving isomorphisms (resp. law invariant) if its graph in
${\boldsymbol {L}}:\mathrm {D}({\boldsymbol {L}})\subset \mathcal {X}\to \mathcal {Y}$
is invariant by measure-preserving isomorphisms (resp. law invariant) if its graph in
![]() $\mathcal {X}\times \mathcal {Y}$
is invariant by measure preserving isomorphisms (resp. law invariant).
$\mathcal {X}\times \mathcal {Y}$
is invariant by measure preserving isomorphisms (resp. law invariant).
It is easy to check that a law invariant set or operator is also invariant by measure-preserving isomorphisms. It is also immediate to check that an operator
![]() ${\boldsymbol {L}}:\mathrm {D}({\boldsymbol {L}})\subset \mathcal {X}\to \mathcal {Y}$
is invariant by measure-preserving isomorphisms if for every
${\boldsymbol {L}}:\mathrm {D}({\boldsymbol {L}})\subset \mathcal {X}\to \mathcal {Y}$
is invariant by measure-preserving isomorphisms if for every
![]() $g\in \mathrm {S}(\Omega )$
and every
$g\in \mathrm {S}(\Omega )$
and every
![]() $X\in \mathrm {D}({\boldsymbol {L}})$
it holds
$X\in \mathrm {D}({\boldsymbol {L}})$
it holds
Similarly,
![]() ${\boldsymbol {L}}$
is law invariant if for every
${\boldsymbol {L}}$
is law invariant if for every
![]() $X\in \mathrm {D}({\boldsymbol {L}}),\ X'\in \mathcal {X},\ Y'\in \mathcal {Y}$
,
$X\in \mathrm {D}({\boldsymbol {L}}),\ X'\in \mathcal {X},\ Y'\in \mathcal {Y}$
,
Remark 4.1 Notice that, when
![]() $\mathsf {Y}=\mathsf {X}^{*}$
are reflexive,
$\mathsf {Y}=\mathsf {X}^{*}$
are reflexive,
![]() $p>1$
, and
$p>1$
, and
![]() $q=p^{*}$
is the conjugate exponent of p, then
$q=p^{*}$
is the conjugate exponent of p, then
![]() $\mathcal {Y}=\mathcal {X}^{*}$
and the notion of invariance by measure-preserving isomorphisms for
$\mathcal {Y}=\mathcal {X}^{*}$
and the notion of invariance by measure-preserving isomorphisms for
![]() $\boldsymbol {B}\subset \mathcal {X}\times \mathcal {Y}$
coincides with the
$\boldsymbol {B}\subset \mathcal {X}\times \mathcal {Y}$
coincides with the
![]() $\mathsf {G}$
-invariance of Definition 2.1,
$\mathsf {G}$
-invariance of Definition 2.1,
![]() $\mathsf {G}$
being the group of isometric isomorphisms induced by
$\mathsf {G}$
being the group of isometric isomorphisms induced by
![]() $\mathrm {S}(\Omega )$
via
$\mathrm {S}(\Omega )$
via
![]() $g^{*}:\mathcal {X}\times \mathcal {X}^{*} \to \mathcal {X}\times \mathcal {X}^{*}$
with
$g^{*}:\mathcal {X}\times \mathcal {X}^{*} \to \mathcal {X}\times \mathcal {X}^{*}$
with
![]() $g^{*}(X,V) = (X\circ g,V\circ g)$
for every
$g^{*}(X,V) = (X\circ g,V\circ g)$
for every
![]() $(X,V) \in \mathcal {X}\times \mathcal {X}^{*}$
and every
$(X,V) \in \mathcal {X}\times \mathcal {X}^{*}$
and every
![]() $g \in \mathrm {S}(\Omega )$
.
$g \in \mathrm {S}(\Omega )$
.
Let us denote by
![]() $\iota :\mathcal {X}\to \mathcal {P}_p(\mathsf {X})$
the push-forward operator,
$\iota :\mathcal {X}\to \mathcal {P}_p(\mathsf {X})$
the push-forward operator,
![]() $\iota (X):=X_{\sharp}\mathbb {P}$
(cf. (3.1)). We frequently use the notation
$\iota (X):=X_{\sharp}\mathbb {P}$
(cf. (3.1)). We frequently use the notation
![]() $\iota _X=\iota (X)$
. The map
$\iota _X=\iota (X)$
. The map
![]() $\iota $
induces a one-to-one correspondence between subsets in
$\iota $
induces a one-to-one correspondence between subsets in
![]() $\mathcal {P}_p(\mathsf {X})$
(see (3.9)) and law invariant subsets of
$\mathcal {P}_p(\mathsf {X})$
(see (3.9)) and law invariant subsets of
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
As a first result, we show that for closed sets and continuous operators the two notions of invariance are in fact equivalent.
Proposition 4.2 (Closed sets invariant by m.p.i. are law invariant)
If
![]() $\boldsymbol {B}\subset \mathcal {X}\times \mathcal {Y}$
is invariant by measure-preserving isomorphisms, then its closure
$\boldsymbol {B}\subset \mathcal {X}\times \mathcal {Y}$
is invariant by measure-preserving isomorphisms, then its closure
![]() $\overline {\boldsymbol {B}}$
is also law invariant. In particular, a closed set of
$\overline {\boldsymbol {B}}$
is also law invariant. In particular, a closed set of
![]() $\mathcal {X}\times \mathcal {Y}$
is law invariant if and only if it is invariant by measure-preserving isomorphisms and if
$\mathcal {X}\times \mathcal {Y}$
is law invariant if and only if it is invariant by measure-preserving isomorphisms and if
![]() ${\boldsymbol {L}}:\mathrm {D}({\boldsymbol {L}})\subset \mathcal {X}\to {\mathcal {Y}}$
is a continuous operator invariant by measure-preserving isomorphisms and
${\boldsymbol {L}}:\mathrm {D}({\boldsymbol {L}})\subset \mathcal {X}\to {\mathcal {Y}}$
is a continuous operator invariant by measure-preserving isomorphisms and
![]() $\mathrm {D}({\boldsymbol {L}})$
is closed, then
$\mathrm {D}({\boldsymbol {L}})$
is closed, then
![]() ${\boldsymbol {L}}$
is also law invariant.
${\boldsymbol {L}}$
is also law invariant.
Proof Let us first observe that if
![]() $\boldsymbol {B}$
is invariant by measure-preserving isomorphisms, then
$\boldsymbol {B}$
is invariant by measure-preserving isomorphisms, then
![]() $\overline {\boldsymbol {B}}$
has the same property, since for every
$\overline {\boldsymbol {B}}$
has the same property, since for every
![]() $g\in \mathrm {S}(\Omega )$
the pullback transformation
$g\in \mathrm {S}(\Omega )$
the pullback transformation
![]() $g^{*}$
is an isometry in
$g^{*}$
is an isometry in
![]() $\mathcal {X}$
and in
$\mathcal {X}$
and in
![]() $\mathcal {Y}$
. Let us now suppose that
$\mathcal {Y}$
. Let us now suppose that
![]() $\boldsymbol {B}$
is closed and invariant by measure-preserving isomorphisms,
$\boldsymbol {B}$
is closed and invariant by measure-preserving isomorphisms,
![]() $(X,Y)\in \boldsymbol {B}$
,
$(X,Y)\in \boldsymbol {B}$
,
![]() $(X',Y')\in \mathcal {X}\times \mathcal {Y}$
with
$(X',Y')\in \mathcal {X}\times \mathcal {Y}$
with
![]() $(X,Y)_{\sharp}\mathbb {P}=(X',Y')_{\sharp}\mathbb {P}$
. We can apply Corollary 3.16 and find a sequence of measure-preserving isomorphisms
$(X,Y)_{\sharp}\mathbb {P}=(X',Y')_{\sharp}\mathbb {P}$
. We can apply Corollary 3.16 and find a sequence of measure-preserving isomorphisms
![]() $g_n\in \mathrm {S}(\Omega )$
such that
$g_n\in \mathrm {S}(\Omega )$
such that
![]() $(X,Y)\circ g_n\to (X',Y')$
in
$(X,Y)\circ g_n\to (X',Y')$
in
![]() $\mathcal {X}\times \mathcal {Y}$
. Since
$\mathcal {X}\times \mathcal {Y}$
. Since
![]() $(X,Y)\circ g_n\in \boldsymbol {B}$
and
$(X,Y)\circ g_n\in \boldsymbol {B}$
and
![]() $\boldsymbol {B}$
is closed, we deduce that
$\boldsymbol {B}$
is closed, we deduce that
![]() $(X',Y')\in \boldsymbol {B}$
as well.
$(X',Y')\in \boldsymbol {B}$
as well.
The case of continuous operators then follows by the fact that the graph of a continuous operator is closed.
Remark 4.3 In light of Proposition 4.2, if a subset
![]() $\boldsymbol {B} \subset \mathcal {X}\times \mathcal {Y}$
(resp. an operator
$\boldsymbol {B} \subset \mathcal {X}\times \mathcal {Y}$
(resp. an operator
![]() ${\boldsymbol {L}}:\mathrm {D}({\boldsymbol {L}})\subset \mathcal {X}\to \mathcal {Y}$
) is closed (resp. continuous and
${\boldsymbol {L}}:\mathrm {D}({\boldsymbol {L}})\subset \mathcal {X}\to \mathcal {Y}$
) is closed (resp. continuous and
![]() $\mathrm {D}({\boldsymbol {L}})$
is closed), we use the simplified terminology invariant, whenever
$\mathrm {D}({\boldsymbol {L}})$
is closed), we use the simplified terminology invariant, whenever
![]() $\boldsymbol {B}$
(resp.
$\boldsymbol {B}$
(resp.
![]() ${\boldsymbol {L}}$
) is law invariant or invariant by measure-preserving isomorphisms, being these two notions equivalent.
${\boldsymbol {L}}$
) is law invariant or invariant by measure-preserving isomorphisms, being these two notions equivalent.
As an application of the results in Section 2, we obtain the following extension results.
Theorem 4.4 (Maximal extensions of monotone operators invariant by measure-preserving isomorphisms)
Let
![]() $\mathsf {X}$
be a separable and reflexive Banach space,
$\mathsf {X}$
be a separable and reflexive Banach space,
![]() $p\in (1,\infty )$
, and
$p\in (1,\infty )$
, and
![]() $\mathcal {X}:=L^{p}(\Omega ,{\mathcal {B}}, \mathbb {P};\mathsf {X})$
. If
$\mathcal {X}:=L^{p}(\Omega ,{\mathcal {B}}, \mathbb {P};\mathsf {X})$
. If
![]() ${\boldsymbol {A}}\subset \mathcal {X}\times \mathcal {X}^{*}$
is a monotone operator invariant by measure-preserving isomorphisms, then there exists a maximal monotone extension of
${\boldsymbol {A}}\subset \mathcal {X}\times \mathcal {X}^{*}$
is a monotone operator invariant by measure-preserving isomorphisms, then there exists a maximal monotone extension of
![]() ${\boldsymbol {A}}$
which is invariant by measure-preserving isomorphisms (and therefore also law invariant) whose domain is contained in
${\boldsymbol {A}}$
which is invariant by measure-preserving isomorphisms (and therefore also law invariant) whose domain is contained in
![]() $\overline {\operatorname {co}}\left (\mathrm {D}({\boldsymbol {A}})\right ).$
$\overline {\operatorname {co}}\left (\mathrm {D}({\boldsymbol {A}})\right ).$
Proof The thesis follows by applying Theorem 2.5 and Remark 4.1. Recall also that if
![]() ${\boldsymbol {A}}$
is maximal monotone, then it is closed (see, e.g., [Reference Barbu6, Proposition 2.1]); hence, we can apply Proposition 4.2.
${\boldsymbol {A}}$
is maximal monotone, then it is closed (see, e.g., [Reference Barbu6, Proposition 2.1]); hence, we can apply Proposition 4.2.
Theorem 4.5 (Extension of Lipschitz and
 $\lambda $
-dissipative invariant graphs)
$\lambda $
-dissipative invariant graphs)
Assume
![]() ${p=2}$
, and let
${p=2}$
, and let
![]() $\mathsf {X}$
be a separable and Hilbert space. The following hold:
$\mathsf {X}$
be a separable and Hilbert space. The following hold:
-
(1) If
 ${\boldsymbol {L}}:\mathrm {D}({\boldsymbol {L}})\subset \mathcal {X}\to \mathcal {X}$
is an L-Lipschitz function invariant by measure-preserving isomorphisms, then there exists an L-Lipschitz extension
${\boldsymbol {L}}:\mathrm {D}({\boldsymbol {L}})\subset \mathcal {X}\to \mathcal {X}$
is an L-Lipschitz function invariant by measure-preserving isomorphisms, then there exists an L-Lipschitz extension
 $ {\hat {\boldsymbol {L}}}:\mathcal {X}\to \mathcal {X}$
, defined on the whole
$ {\hat {\boldsymbol {L}}}:\mathcal {X}\to \mathcal {X}$
, defined on the whole
 $\mathcal {X}$
which is invariant by measure-preserving isomorphisms.
$\mathcal {X}$
which is invariant by measure-preserving isomorphisms. -
(2) If
 $\boldsymbol {B} \subset \mathcal {X} \times \mathcal {X}$
is a
$\boldsymbol {B} \subset \mathcal {X} \times \mathcal {X}$
is a
 $\lambda $
-dissipative operator which is invariant by measure-preserving isomorphisms, then there exists a maximal
$\lambda $
-dissipative operator which is invariant by measure-preserving isomorphisms, then there exists a maximal
 $\lambda $
-dissipative extension
$\lambda $
-dissipative extension
 $\hat {\boldsymbol {B}}$
of
$\hat {\boldsymbol {B}}$
of
 $\boldsymbol {B}$
which is invariant by measure-preserving isomorphisms (and therefore also law invariant) whose domain is contained in
$\boldsymbol {B}$
which is invariant by measure-preserving isomorphisms (and therefore also law invariant) whose domain is contained in
 $\overline {\operatorname {co}}\left (\mathrm {D}(\boldsymbol {B})\right ).$
$\overline {\operatorname {co}}\left (\mathrm {D}(\boldsymbol {B})\right ).$
Proof The assertion is an immediate application of Theorems 2.11 and 2.7, choosing
![]() $\mathcal {H}:=\mathcal {X}$
and
$\mathcal {H}:=\mathcal {X}$
and
![]() $\mathsf {G}_{\mathcal {H}}$
as the group of isometric isomorphisms induced by
$\mathsf {G}_{\mathcal {H}}$
as the group of isometric isomorphisms induced by
![]() $\mathrm {S}(\Omega )$
via
$\mathrm {S}(\Omega )$
via
![]() $g^{*}:\mathcal {X} \to \mathcal {X}$
with
$g^{*}:\mathcal {X} \to \mathcal {X}$
with
![]() $g^{*}X = X\circ g$
for every
$g^{*}X = X\circ g$
for every
![]() $X \in \mathcal {X}$
and every
$X \in \mathcal {X}$
and every
![]() $g \in \mathrm {S}(\Omega )$
(cf. Remark 4.1). Notice that
$g \in \mathrm {S}(\Omega )$
(cf. Remark 4.1). Notice that
![]() $\boldsymbol {B}$
is closed being maximal dissipative, hence law invariant by Proposition 4.2.
$\boldsymbol {B}$
is closed being maximal dissipative, hence law invariant by Proposition 4.2.
We conclude this section with some useful representation results for various classes of law invariant transformations.
Given a set
![]() $D\subset \mathcal {P}_p(\mathsf {X})$
, we set
$D\subset \mathcal {P}_p(\mathsf {X})$
, we set
and we just write
![]() $\mathcal {S}(\mathsf {X})=\mathcal {S}(\mathsf {X},\mathcal {P}_p(\mathsf {X}))$
. The set
$\mathcal {S}(\mathsf {X})=\mathcal {S}(\mathsf {X},\mathcal {P}_p(\mathsf {X}))$
. The set
![]() $\mathcal {S}(\mathsf {X})$
is of
$\mathcal {S}(\mathsf {X})$
is of
![]() $G_\delta $
type (see [Reference Fornasier, Savaré and Sodini20, Formula (4.3)]) so that
$G_\delta $
type (see [Reference Fornasier, Savaré and Sodini20, Formula (4.3)]) so that
![]() $\mathcal {S}(\mathsf {X},D)$
is a Borel set, if D is Borel.
$\mathcal {S}(\mathsf {X},D)$
is a Borel set, if D is Borel.
We state a first result on uniqueness of a representation of a single-valued operator
![]() ${\boldsymbol {L}}:\mathcal {X}\to \mathcal {Y}$
by a map from
${\boldsymbol {L}}:\mathcal {X}\to \mathcal {Y}$
by a map from
![]() $\mathcal {S}(\mathsf {X})$
to
$\mathcal {S}(\mathsf {X})$
to
![]() $\mathsf {Y}$
. We then state existence (and uniqueness) of such map-representation when
$\mathsf {Y}$
. We then state existence (and uniqueness) of such map-representation when
![]() ${\boldsymbol {L}}$
is Lipschitz continuous and invariant, showing also further properties inherited by such map representation. Finally, we will go back to the case of (possibly multivalued) maximal
${\boldsymbol {L}}$
is Lipschitz continuous and invariant, showing also further properties inherited by such map representation. Finally, we will go back to the case of (possibly multivalued) maximal
![]() $\lambda $
-dissipative operators in the final Theorem 4.12.
$\lambda $
-dissipative operators in the final Theorem 4.12.
Lemma 4.6 Let
![]() ${\boldsymbol {L}}: \mathrm {D}({\boldsymbol {L}}) \to \mathcal {Y}$
be a map defined in
${\boldsymbol {L}}: \mathrm {D}({\boldsymbol {L}}) \to \mathcal {Y}$
be a map defined in
![]() $\mathrm {D}({\boldsymbol {L}}) \subset \mathcal {X}$
. If
$\mathrm {D}({\boldsymbol {L}}) \subset \mathcal {X}$
. If
![]() $\boldsymbol {f}_i: \mathcal {S}(\mathsf {X}, \iota (\mathrm {D}({\boldsymbol {L}})) \to \mathsf {Y}$
,
$\boldsymbol {f}_i: \mathcal {S}(\mathsf {X}, \iota (\mathrm {D}({\boldsymbol {L}})) \to \mathsf {Y}$
,
![]() $i=1,2$
, satisfy
$i=1,2$
, satisfy
-
•
 $\boldsymbol {f}_i(\cdot , \mu )$
is continuous for every
$\boldsymbol {f}_i(\cdot , \mu )$
is continuous for every
 $\mu \in \iota (\mathrm {D}({\boldsymbol {L}}))$
,
$\mu \in \iota (\mathrm {D}({\boldsymbol {L}}))$
, -
• for every
 $X\in \mathrm {D}({\boldsymbol {L}})$
$X\in \mathrm {D}({\boldsymbol {L}})$
 ${\boldsymbol {L}} X(w)=\boldsymbol {f}_i(X(w),X_{\sharp}\mathbb {P})$
for a.e.
${\boldsymbol {L}} X(w)=\boldsymbol {f}_i(X(w),X_{\sharp}\mathbb {P})$
for a.e.
 $\omega \in \Omega $
,
$\omega \in \Omega $
,
then
![]() $\boldsymbol {f}_1=\boldsymbol {f}_{2}$
.
$\boldsymbol {f}_1=\boldsymbol {f}_{2}$
.
Proof Let
![]() $(x,\mu ) \in \mathcal {S}(\mathsf {X}, \iota (\mathrm {D}({\boldsymbol {L}}))$
. Since
$(x,\mu ) \in \mathcal {S}(\mathsf {X}, \iota (\mathrm {D}({\boldsymbol {L}}))$
. Since
![]() $\mu \in \iota (\mathrm {D}({\boldsymbol {L}}))$
, we can find (a representative of)
$\mu \in \iota (\mathrm {D}({\boldsymbol {L}}))$
, we can find (a representative of)
![]() $X \in \mathrm {D}({\boldsymbol {L}})$
such that
$X \in \mathrm {D}({\boldsymbol {L}})$
such that
![]() $X_{\sharp}\mathbb {P}= \mu $
and a full
$X_{\sharp}\mathbb {P}= \mu $
and a full
![]() $\mathbb {P}$
-measure set
$\mathbb {P}$
-measure set
![]() $\Omega _{0} \subset \Omega $
such that
$\Omega _{0} \subset \Omega $
such that
Since
![]() $X(\Omega _{0})$
is dense in
$X(\Omega _{0})$
is dense in
![]() $\operatorname {\mathrm {supp}}(\mu )$
, we can find
$\operatorname {\mathrm {supp}}(\mu )$
, we can find
![]() $(\omega _n)_n \subset \Omega _{0}$
such that
$(\omega _n)_n \subset \Omega _{0}$
such that
![]() $X(\omega _n) \to x$
. Using the continuity of
$X(\omega _n) \to x$
. Using the continuity of
![]() $\boldsymbol {f}_i(\cdot , \mu )$
, we can write the above equality for
$\boldsymbol {f}_i(\cdot , \mu )$
, we can write the above equality for
![]() $\omega =\omega _n$
and then pass to the limit as
$\omega =\omega _n$
and then pass to the limit as
![]() $n \to + \infty $
obtaining that
$n \to + \infty $
obtaining that
![]() $\boldsymbol {f}_1(x,\mu )=\boldsymbol {f}_{2}(x,\mu )$
.
$\boldsymbol {f}_1(x,\mu )=\boldsymbol {f}_{2}(x,\mu )$
.
In the following Theorem 4.7, we provide an important structural representation of invariant Lipschitz maps from
![]() $\mathcal {X}$
to
$\mathcal {X}$
to
![]() $\mathcal {Y}$
. Similar kinds of problems have been considered in [Reference Carmona and Delarue16, Proposition 5.36].
$\mathcal {Y}$
. Similar kinds of problems have been considered in [Reference Carmona and Delarue16, Proposition 5.36].
Theorem 4.7 (Structure of invariant Lipschitz maps)
Let
![]() $\mathsf {X},\mathsf {Y}$
be separable Banach spaces, and let
$\mathsf {X},\mathsf {Y}$
be separable Banach spaces, and let
![]() $\mathcal {X},\mathcal {Y}$
be as in (4.1).
$\mathcal {X},\mathcal {Y}$
be as in (4.1).
-
(1) Let
 ${\boldsymbol {L}}: \mathcal {X} \to \mathcal {Y}$
be an L-Lipschitz map, invariant by measure-preserving isomorphisms. Then there exists a unique continuous map
${\boldsymbol {L}}: \mathcal {X} \to \mathcal {Y}$
be an L-Lipschitz map, invariant by measure-preserving isomorphisms. Then there exists a unique continuous map
 ${\boldsymbol {f}}_{{\boldsymbol {L}}}:\mathcal {S}(\mathsf {X}) \to \mathsf {Y}$
such that (4.9)
${\boldsymbol {f}}_{{\boldsymbol {L}}}:\mathcal {S}(\mathsf {X}) \to \mathsf {Y}$
such that (4.9) $$ \begin{align} \text{for every}\ X\in \mathcal{X},\quad {\boldsymbol{L}} X(\omega)={\boldsymbol{f}}_{{\boldsymbol{L}}}(X(\omega),X_{\sharp}\mathbb{P})\ \text{for a.e}.~\omega\in \Omega. \end{align} $$
$$ \begin{align} \text{for every}\ X\in \mathcal{X},\quad {\boldsymbol{L}} X(\omega)={\boldsymbol{f}}_{{\boldsymbol{L}}}(X(\omega),X_{\sharp}\mathbb{P})\ \text{for a.e}.~\omega\in \Omega. \end{align} $$
Moreover,
 ${\boldsymbol {f}}_{{\boldsymbol {L}}} (\cdot , \mu ): \operatorname {\mathrm {supp}}(\mu ) \to \mathsf {Y}$
is L-Lipschitz.
${\boldsymbol {f}}_{{\boldsymbol {L}}} (\cdot , \mu ): \operatorname {\mathrm {supp}}(\mu ) \to \mathsf {Y}$
is L-Lipschitz. -
(2) Let
 $\mathsf {X}$
be a Hilbert space and
$\mathsf {X}$
be a Hilbert space and
 $p=2$
, let
$p=2$
, let
 $\mathrm {D}({\boldsymbol {L}}) \subset \mathcal {X}$
, and let
$\mathrm {D}({\boldsymbol {L}}) \subset \mathcal {X}$
, and let
 ${\boldsymbol {L}}: \mathrm {D}({\boldsymbol {L}}) \to \mathcal {X}$
be an L-Lipschitz map, invariant by measure-preserving isomorphisms. Then there exists a unique continuous map
${\boldsymbol {L}}: \mathrm {D}({\boldsymbol {L}}) \to \mathcal {X}$
be an L-Lipschitz map, invariant by measure-preserving isomorphisms. Then there exists a unique continuous map
 ${\boldsymbol {f}}_{{\boldsymbol {L}}}:\mathcal {S}(\mathsf {X}, \iota (\mathrm {D}({\boldsymbol {L}}))\to \mathsf {X}$
such that (4.10)
${\boldsymbol {f}}_{{\boldsymbol {L}}}:\mathcal {S}(\mathsf {X}, \iota (\mathrm {D}({\boldsymbol {L}}))\to \mathsf {X}$
such that (4.10) $$ \begin{align} \text{for every}\ X\in \mathrm{D}({\boldsymbol{L}}),\quad {\boldsymbol{L}} X(\omega)={\boldsymbol{f}}_{{\boldsymbol{L}}}(X(\omega),X_{\sharp}\mathbb{P})\ \text{for a.e}.~\omega\in \Omega. \end{align} $$
$$ \begin{align} \text{for every}\ X\in \mathrm{D}({\boldsymbol{L}}),\quad {\boldsymbol{L}} X(\omega)={\boldsymbol{f}}_{{\boldsymbol{L}}}(X(\omega),X_{\sharp}\mathbb{P})\ \text{for a.e}.~\omega\in \Omega. \end{align} $$
Moreover,
 ${\boldsymbol {f}}_{{\boldsymbol {L}}} (\cdot , \mu ): \operatorname {\mathrm {supp}}(\mu ) \to \mathsf {X}$
is L-Lipschitz.
${\boldsymbol {f}}_{{\boldsymbol {L}}} (\cdot , \mu ): \operatorname {\mathrm {supp}}(\mu ) \to \mathsf {X}$
is L-Lipschitz.
Proof We prove item (1). Let
![]() ${\mathfrak {N}}:= \{2^n \mid n \in \mathbb {N}\}$
, and let
${\mathfrak {N}}:= \{2^n \mid n \in \mathbb {N}\}$
, and let
![]() $(\mathfrak {P}_N)_{N \in {\mathfrak {N}}}$
be an
$(\mathfrak {P}_N)_{N \in {\mathfrak {N}}}$
be an
![]() ${\mathfrak {N}}$
-segmentation of
${\mathfrak {N}}$
-segmentation of
![]() $(\Omega , {\mathcal {B}}, \mathbb {P})$
as in Definition 3.3, whose existence is granted by Lemma 3.5. Let us define
$(\Omega , {\mathcal {B}}, \mathbb {P})$
as in Definition 3.3, whose existence is granted by Lemma 3.5. Let us define
We divide the proof in several steps.
(a) If
![]() $X \in \mathcal {X}_m$
for some
$X \in \mathcal {X}_m$
for some
![]() $m \in \mathbb {N}$
, then (there exists a unique representative of)
$m \in \mathbb {N}$
, then (there exists a unique representative of)
![]() ${\boldsymbol {L}} X$
(that) belongs to
${\boldsymbol {L}} X$
(that) belongs to
![]() $\mathcal {Y}_m$
and
$\mathcal {Y}_m$
and
Let
![]() $\Omega ' \subset \Omega $
be a full
$\Omega ' \subset \Omega $
be a full
![]() $\mathbb {P}$
-measure subset of
$\mathbb {P}$
-measure subset of
![]() $\Omega $
where both (3.5) and Lemma 3.11 hold for the
$\Omega $
where both (3.5) and Lemma 3.11 hold for the
![]() $L^q(\Omega , {\mathcal {B}}, \mathbb {P};\mathsf {Y})$
function
$L^q(\Omega , {\mathcal {B}}, \mathbb {P};\mathsf {Y})$
function
![]() ${\boldsymbol {L}} X$
.
${\boldsymbol {L}} X$
.
Let us fix
![]() $k \in I_m:=\{0,\dots ,2^m-1\}$
and show that (a representative of)
$k \in I_m:=\{0,\dots ,2^m-1\}$
and show that (a representative of)
![]() ${\boldsymbol {L}} X $
is constant on
${\boldsymbol {L}} X $
is constant on
![]() $\Omega ^{\prime }_{m,k}:= \Omega _{m,k} \cap \Omega '$
, where
$\Omega ^{\prime }_{m,k}:= \Omega _{m,k} \cap \Omega '$
, where
![]() $\mathfrak {P}_{2^m} := \{\Omega _{m,k}\}_{k \in I_m}$
.
$\mathfrak {P}_{2^m} := \{\Omega _{m,k}\}_{k \in I_m}$
.
Let
![]() $\omega ', \omega " \in \Omega ^{\prime }_{m,k}$
with
$\omega ', \omega " \in \Omega ^{\prime }_{m,k}$
with
![]() $\omega '\ne \omega "$
. For every
$\omega '\ne \omega "$
. For every
![]() $n \in \mathbb {N}$
, there exist
$n \in \mathbb {N}$
, there exist
![]() $k(n;\omega '), k(n;\omega ") \in I_{n}$
such that
$k(n;\omega '), k(n;\omega ") \in I_{n}$
such that
![]() $\omega ' \in \Omega _{n,k(n;\omega ')}$
and
$\omega ' \in \Omega _{n,k(n;\omega ')}$
and
![]() $\omega " \in \Omega _{n,k(n;\omega ")}$
. By Lemma 3.11, we know that for
$\omega " \in \Omega _{n,k(n;\omega ")}$
. By Lemma 3.11, we know that for
![]() $n \in \mathbb {N}$
sufficiently large
$n \in \mathbb {N}$
sufficiently large
![]() $\Omega _{n,k(n;\omega ')}, \Omega _{n,k(n;\omega ")} \subset \Omega _{m,k}$
and
$\Omega _{n,k(n;\omega ')}, \Omega _{n,k(n;\omega ")} \subset \Omega _{m,k}$
and
![]() $\Omega _{n,k(n;\omega ')} \cap \Omega _{n,k(n;\omega ")} = \emptyset $
. Thus, since
$\Omega _{n,k(n;\omega ')} \cap \Omega _{n,k(n;\omega ")} = \emptyset $
. Thus, since
![]() $\mathbb {P}(\Omega _{n,k(n;\omega ')})= \mathbb {P}(\Omega _{n,k(n;\omega ")})=2^{-n}$
for every
$\mathbb {P}(\Omega _{n,k(n;\omega ')})= \mathbb {P}(\Omega _{n,k(n;\omega ")})=2^{-n}$
for every
![]() $n \in \mathbb {N}$
(see Definition 3.3), by Corollary 3.8, we can find a measure-preserving isomorphism
$n \in \mathbb {N}$
(see Definition 3.3), by Corollary 3.8, we can find a measure-preserving isomorphism
![]() $g_n \in \mathrm {S}(\Omega )$
such that
$g_n \in \mathrm {S}(\Omega )$
such that
and
![]() $g_n$
is the identity outside
$g_n$
is the identity outside
![]() $\Omega _{n,k(n;\omega ')} \cup \Omega _{n,k(n;\omega ")}$
. By (4.6) and by Lipschitz continuity of
$\Omega _{n,k(n;\omega ')} \cup \Omega _{n,k(n;\omega ")}$
. By (4.6) and by Lipschitz continuity of
![]() ${\boldsymbol {L}}$
, we have
${\boldsymbol {L}}$
, we have
since X is constant on the whole
![]() $\Omega _{m,k}$
. This implies that
$\Omega _{m,k}$
. This implies that
By definition of conditional expectation, this means that
Passing to the limit as
![]() $n \to + \infty $
, we get by (3.5) that
$n \to + \infty $
, we get by (3.5) that
![]() ${\boldsymbol {L}} X(\omega ')={\boldsymbol {L}} X(\omega ")$
. This proves that
${\boldsymbol {L}} X(\omega ')={\boldsymbol {L}} X(\omega ")$
. This proves that
![]() ${\boldsymbol {L}} X$
is
${\boldsymbol {L}} X$
is
![]() $\mathbb {P}$
-almost everywhere constant on
$\mathbb {P}$
-almost everywhere constant on
![]() $\Omega _{m,k}$
; being
$\Omega _{m,k}$
; being
![]() $k \in I_m$
arbitrary, we can find a representative of
$k \in I_m$
arbitrary, we can find a representative of
![]() ${\boldsymbol {L}} X$
belonging to
${\boldsymbol {L}} X$
belonging to
![]() $\mathcal {Y}_m$
. If
$\mathcal {Y}_m$
. If
![]() $\omega ', \omega " \in \Omega $
and
$\omega ', \omega " \in \Omega $
and
![]() $\omega ' \in \Omega _{m,i}$
,
$\omega ' \in \Omega _{m,i}$
,
![]() $\omega "\in \Omega _{m,j}$
,
$\omega "\in \Omega _{m,j}$
,
![]() $i,j\in I_m$
, we choose as
$i,j\in I_m$
, we choose as
![]() $g \in \mathrm {S}(\Omega )$
a measure-preserving isomorphism induced by the permutation
$g \in \mathrm {S}(\Omega )$
a measure-preserving isomorphism induced by the permutation
![]() $\sigma \in {\mathrm {Sym}(I_m)}$
that swaps i and j (see Corollary 3.7), so that we get by Lipschitz continuity of
$\sigma \in {\mathrm {Sym}(I_m)}$
that swaps i and j (see Corollary 3.7), so that we get by Lipschitz continuity of
![]() ${\boldsymbol {L}}$
that
${\boldsymbol {L}}$
that
which yields (4.11).
(b) For every
![]() $X\in \mathcal {X}$
, there exists a unique L-Lipschitz map
$X\in \mathcal {X}$
, there exists a unique L-Lipschitz map
![]() $\boldsymbol {f}_X:\operatorname {\mathrm {supp}}(X_{\sharp}\mathbb {P})\to \mathsf {Y}$
such that
$\boldsymbol {f}_X:\operatorname {\mathrm {supp}}(X_{\sharp}\mathbb {P})\to \mathsf {Y}$
such that
![]() ${\boldsymbol {L}} X(\omega ) = \boldsymbol {f}_{X}(X(\omega ))$
for
${\boldsymbol {L}} X(\omega ) = \boldsymbol {f}_{X}(X(\omega ))$
for
![]() $\mathbb {P}$
-a.e.
$\mathbb {P}$
-a.e.
![]() $\omega $
.
$\omega $
.
Let
![]() $X \in \mathcal {X}$
; setting
$X \in \mathcal {X}$
; setting
![]() $X_n:=\mathbb {E}[X|{\mathcal {B}}_n]\in \mathcal {X}_n$
, by Theorem 3.9, we have
$X_n:=\mathbb {E}[X|{\mathcal {B}}_n]\in \mathcal {X}_n$
, by Theorem 3.9, we have
![]() $X_n \to X$
(hence also
$X_n \to X$
(hence also
![]() ${\boldsymbol {L}} X_n \to {\boldsymbol {L}} X$
). Let us consider two representatives of
${\boldsymbol {L}} X_n \to {\boldsymbol {L}} X$
). Let us consider two representatives of
![]() ${\boldsymbol {L}} X$
and X, a full measure set
${\boldsymbol {L}} X$
and X, a full measure set
![]() $\Omega _{0} \subset \Omega $
and a subsequence
$\Omega _{0} \subset \Omega $
and a subsequence
![]() $(X_{n_{k}})_{k}$
s.t.
$(X_{n_{k}})_{k}$
s.t.
![]() $X_{n_{k}}(\omega ) \to X(\omega )$
and
$X_{n_{k}}(\omega ) \to X(\omega )$
and
![]() ${\boldsymbol {L}} X_{n_{k}}(\omega ) \to {\boldsymbol {L}} X (\omega )$
for every
${\boldsymbol {L}} X_{n_{k}}(\omega ) \to {\boldsymbol {L}} X (\omega )$
for every
![]() $\omega \in \Omega _{0}$
. By (4.11), we have
$\omega \in \Omega _{0}$
. By (4.11), we have
Passing to the limit in the above inequality for every couple
![]() $(\omega , \omega ') \in \Omega _{0}^{2}$
, we obtain that
$(\omega , \omega ') \in \Omega _{0}^{2}$
, we obtain that
This gives the existence of a (unique) L-Lipschitz function
![]() $\boldsymbol {f}_X: \overline {X(\Omega _{0})}\to \mathsf {Y}$
s.t.
$\boldsymbol {f}_X: \overline {X(\Omega _{0})}\to \mathsf {Y}$
s.t.
![]() ${\boldsymbol {L}} X(\omega ) = \boldsymbol {f}_{X}(X(\omega ))$
for every
${\boldsymbol {L}} X(\omega ) = \boldsymbol {f}_{X}(X(\omega ))$
for every
![]() $\omega \in \Omega _{0}$
. Notice that
$\omega \in \Omega _{0}$
. Notice that
![]() $\overline {X(\Omega _{0})}\supset \operatorname {\mathrm {supp}}(X_{\sharp}\mathbb {P})$
.
$\overline {X(\Omega _{0})}\supset \operatorname {\mathrm {supp}}(X_{\sharp}\mathbb {P})$
.
(c) If
![]() $X, X'\in \mathcal {X}$
with
$X, X'\in \mathcal {X}$
with
![]() $\mu =X_{\sharp}\mathbb {P}=X^{\prime }_{\sharp}\mathbb {P}$
, then
$\mu =X_{\sharp}\mathbb {P}=X^{\prime }_{\sharp}\mathbb {P}$
, then
![]() $\boldsymbol {f}_X=\boldsymbol {f}_{X'}$
on
$\boldsymbol {f}_X=\boldsymbol {f}_{X'}$
on
![]() $\operatorname {\mathrm {supp}}(\mu )$
. In particular, we can define
$\operatorname {\mathrm {supp}}(\mu )$
. In particular, we can define
![]() ${\boldsymbol {f}}_{{\boldsymbol {L}}} (\cdot ,\mu ):=\boldsymbol {f}_X(\cdot )$
whenever
${\boldsymbol {f}}_{{\boldsymbol {L}}} (\cdot ,\mu ):=\boldsymbol {f}_X(\cdot )$
whenever
![]() $\mu =X_{\sharp}\mathbb {P}$
.
$\mu =X_{\sharp}\mathbb {P}$
.
By hypothesis, we have
By the previous claim, the disintegration (see, e.g., [Reference Ambrosio, Gigli and Savaré3, Theorem 5.3.1] for details on the disintegration theorem) of the common measure
![]() $\boldsymbol {\mu }:= (X, {\boldsymbol {L}} X)_{\sharp}\mathbb {P} $
with respect to its first marginal
$\boldsymbol {\mu }:= (X, {\boldsymbol {L}} X)_{\sharp}\mathbb {P} $
with respect to its first marginal
![]() $\mu $
is given by
$\mu $
is given by
![]() $\delta _{\boldsymbol {f}_X(\cdot )}$
which should coincide with
$\delta _{\boldsymbol {f}_X(\cdot )}$
which should coincide with
![]() $\delta _{\boldsymbol {f}_X'(\cdot )}\ \mu $
-a.e. in
$\delta _{\boldsymbol {f}_X'(\cdot )}\ \mu $
-a.e. in
![]() $\mathsf {X}$
. Since
$\mathsf {X}$
. Since
![]() $\boldsymbol {f}_X$
and
$\boldsymbol {f}_X$
and
![]() $\boldsymbol {f}_{X'}$
are both Lipschitz continuous and coincide
$\boldsymbol {f}_{X'}$
are both Lipschitz continuous and coincide
![]() $\mu $
-a.e., they coincide on
$\mu $
-a.e., they coincide on
![]() $\operatorname {\mathrm {supp}}(\mu )$
.
$\operatorname {\mathrm {supp}}(\mu )$
.
(d) The map
![]() ${\boldsymbol {f}}_{{\boldsymbol {L}}}$
is continuous on
${\boldsymbol {f}}_{{\boldsymbol {L}}}$
is continuous on
![]() $\mathcal {S}(\mathsf {X})$
.
$\mathcal {S}(\mathsf {X})$
.
Let us consider a sequence
![]() $(x_n,\mu _n)_n$
in
$(x_n,\mu _n)_n$
in
![]() $\mathcal {S}(\mathsf {X})$
converging to
$\mathcal {S}(\mathsf {X})$
converging to
![]() $(x,\mu )\in \mathcal {S}(\mathsf {X})$
, and let us prove that there exists an increasing subsequence
$(x,\mu )\in \mathcal {S}(\mathsf {X})$
, and let us prove that there exists an increasing subsequence
![]() $k\mapsto n(k)$
such that
$k\mapsto n(k)$
such that
![]() ${\boldsymbol {f}}_{{\boldsymbol {L}}}(x_{n(k)},\mu _{n(k)})\to {\boldsymbol {f}}_{{\boldsymbol {L}}}(x,\mu )$
as
${\boldsymbol {f}}_{{\boldsymbol {L}}}(x_{n(k)},\mu _{n(k)})\to {\boldsymbol {f}}_{{\boldsymbol {L}}}(x,\mu )$
as
![]() $k\to \infty $
.
$k\to \infty $
.
By Proposition 3.18, we can find a limit map
![]() $X\in \mathcal {X}$
and a sequence
$X\in \mathcal {X}$
and a sequence
![]() $X_n\in \mathcal {X}$
converging to X such that
$X_n\in \mathcal {X}$
converging to X such that
![]() $(X_n)_{\sharp}\mathbb {P}=\mu _n,\ X_{\sharp}\mathbb {P}=\mu $
. Since
$(X_n)_{\sharp}\mathbb {P}=\mu _n,\ X_{\sharp}\mathbb {P}=\mu $
. Since
![]() ${\boldsymbol {L}} X_n\to {\boldsymbol {L}} X$
, we can then extract a subsequence
${\boldsymbol {L}} X_n\to {\boldsymbol {L}} X$
, we can then extract a subsequence
![]() $k\mapsto n(k)$
and find a set of full measure
$k\mapsto n(k)$
and find a set of full measure
![]() $\Omega _{0}\subset \Omega $
such that
$\Omega _{0}\subset \Omega $
such that
![]() $X_{n(k)}(\omega )\to X(\omega )$
and
$X_{n(k)}(\omega )\to X(\omega )$
and
![]() $Y_{n(k)}(\omega )\to Y(\omega )$
as
$Y_{n(k)}(\omega )\to Y(\omega )$
as
![]() $k\to \infty $
for every
$k\to \infty $
for every
![]() $\omega \in \Omega _{0}$
, where
$\omega \in \Omega _{0}$
, where
![]() $Y_n:={\boldsymbol {L}} X_n,\ Y:={\boldsymbol {L}} X$
.
$Y_n:={\boldsymbol {L}} X_n,\ Y:={\boldsymbol {L}} X$
.
Let us fix
![]() $\varepsilon>0$
; since
$\varepsilon>0$
; since
![]() $x\in \operatorname {\mathrm {supp}}(\mu )$
and
$x\in \operatorname {\mathrm {supp}}(\mu )$
and
![]() $X(\Omega _{0})\cap \operatorname {\mathrm {supp}}(\mu )$
is dense in
$X(\Omega _{0})\cap \operatorname {\mathrm {supp}}(\mu )$
is dense in
![]() $\operatorname {\mathrm {supp}}(\mu )$
, we can find
$\operatorname {\mathrm {supp}}(\mu )$
, we can find
![]() $\omega \in \Omega _{0}$
such that
$\omega \in \Omega _{0}$
such that
![]() $|X(\omega )-x|_{\mathsf {X}}\le \varepsilon $
. We then obtain
$|X(\omega )-x|_{\mathsf {X}}\le \varepsilon $
. We then obtain
 $$ \begin{align*} |{\boldsymbol{f}}_{{\boldsymbol{L}}}(x_{n(k)},\mu_{n(k)})-{\boldsymbol{f}}_{{\boldsymbol{L}}}(x,\mu)|_{\mathsf{Y}} &\le |{\boldsymbol{f}}_{{\boldsymbol{L}}}(x_{n(k)},\mu_{n(k)})- {\boldsymbol{f}}_{{\boldsymbol{L}}}(X_{n(k)}(\omega),\mu_{n(k)})|_{\mathsf{Y}} \\&\quad + |{\boldsymbol{f}}_{{\boldsymbol{L}}}(X_{n(k)}(\omega),\mu_{n(k)})- {\boldsymbol{f}}_{{\boldsymbol{L}}}(X(\omega),\mu)|_{\mathsf{Y}} \\&\quad+ |{\boldsymbol{f}}_{{\boldsymbol{L}}}(X(\omega),\mu)-{\boldsymbol{f}}_{{\boldsymbol{L}}}(x,\mu)|_{\mathsf{Y}} \\&\le L| x_{n(k)}-X_{n(k)}(\omega)|_{\mathsf{X}}+|Y_{n(k)}(\omega)-Y(\omega)|_{\mathsf{Y}}\\ &\quad+ L|X(\omega)-x|_{\mathsf{X}}. \end{align*} $$
$$ \begin{align*} |{\boldsymbol{f}}_{{\boldsymbol{L}}}(x_{n(k)},\mu_{n(k)})-{\boldsymbol{f}}_{{\boldsymbol{L}}}(x,\mu)|_{\mathsf{Y}} &\le |{\boldsymbol{f}}_{{\boldsymbol{L}}}(x_{n(k)},\mu_{n(k)})- {\boldsymbol{f}}_{{\boldsymbol{L}}}(X_{n(k)}(\omega),\mu_{n(k)})|_{\mathsf{Y}} \\&\quad + |{\boldsymbol{f}}_{{\boldsymbol{L}}}(X_{n(k)}(\omega),\mu_{n(k)})- {\boldsymbol{f}}_{{\boldsymbol{L}}}(X(\omega),\mu)|_{\mathsf{Y}} \\&\quad+ |{\boldsymbol{f}}_{{\boldsymbol{L}}}(X(\omega),\mu)-{\boldsymbol{f}}_{{\boldsymbol{L}}}(x,\mu)|_{\mathsf{Y}} \\&\le L| x_{n(k)}-X_{n(k)}(\omega)|_{\mathsf{X}}+|Y_{n(k)}(\omega)-Y(\omega)|_{\mathsf{Y}}\\ &\quad+ L|X(\omega)-x|_{\mathsf{X}}. \end{align*} $$
Taking the
![]() $\limsup $
as
$\limsup $
as
![]() $k\to \infty $
, we get
$k\to \infty $
, we get
and, since
![]() $\varepsilon>0$
is arbitrary, we obtain the convergence.
$\varepsilon>0$
is arbitrary, we obtain the convergence.
We prove item (2): by Theorem 4.5, it is enough to prove the statement in case the map
![]() ${\boldsymbol {L}}$
is defined on the whole
${\boldsymbol {L}}$
is defined on the whole
![]() $\mathcal {X}$
. We can then apply the previous claim with
$\mathcal {X}$
. We can then apply the previous claim with
![]() $\mathsf {Y}=\mathsf {X}$
and
$\mathsf {Y}=\mathsf {X}$
and
![]() $p=q=2.$
$p=q=2.$
In the particular case, when
![]() $p=q=2$
and
$p=q=2$
and
![]() $\mathsf {X}=\mathsf {Y}$
is a Hilbert space, also
$\mathsf {X}=\mathsf {Y}$
is a Hilbert space, also
![]() $\lambda $
-dissipativity (2.23) is inherited from
$\lambda $
-dissipativity (2.23) is inherited from
![]() ${\boldsymbol {L}}$
to its representative map
${\boldsymbol {L}}$
to its representative map
![]() ${\boldsymbol {f}}_{{\boldsymbol {L}}}$
.
${\boldsymbol {f}}_{{\boldsymbol {L}}}$
.
Proposition 4.8 (
 $\lambda $
-dissipative representations)
$\lambda $
-dissipative representations)
Let us suppose that
![]() $p=2$
,
$p=2$
,
![]() $\mathsf {X}$
is a separable Hilbert space, and
$\mathsf {X}$
is a separable Hilbert space, and
![]() ${\boldsymbol {L}}:\mathcal {X}\to \mathcal {X}$
is an invariant Lipschitz
${\boldsymbol {L}}:\mathcal {X}\to \mathcal {X}$
is an invariant Lipschitz
![]() $\lambda $
-dissipative operator. Then, for every
$\lambda $
-dissipative operator. Then, for every
![]() $\mu \in \mathcal {P}_{2}(\mathsf {X})$
, the map
$\mu \in \mathcal {P}_{2}(\mathsf {X})$
, the map
![]() ${\boldsymbol {f}}_{{\boldsymbol {L}}}(\cdot ,\mu )$
of Theorem 4.7 is (pointwise)
${\boldsymbol {f}}_{{\boldsymbol {L}}}(\cdot ,\mu )$
of Theorem 4.7 is (pointwise)
![]() $\lambda $
-dissipative, i.e.,
$\lambda $
-dissipative, i.e.,
Remark 4.9 Recalling Remark 2.6,
![]() ${\boldsymbol {L}}:\mathcal {X}\to \mathcal {X}$
is an invariant Lipschitz
${\boldsymbol {L}}:\mathcal {X}\to \mathcal {X}$
is an invariant Lipschitz
![]() $\lambda $
-dissipative operator if and only if its
$\lambda $
-dissipative operator if and only if its
![]() $\lambda $
-transformation
$\lambda $
-transformation
![]() ${\boldsymbol {L}}^\lambda :={\boldsymbol {L}}-\lambda \boldsymbol {i}_{\mathcal {X}}$
is an invariant Lipschitz dissipative operator. Moreover, by applying Theorem 4.7 to both
${\boldsymbol {L}}^\lambda :={\boldsymbol {L}}-\lambda \boldsymbol {i}_{\mathcal {X}}$
is an invariant Lipschitz dissipative operator. Moreover, by applying Theorem 4.7 to both
![]() ${\boldsymbol {L}}$
and
${\boldsymbol {L}}$
and
![]() ${\boldsymbol {L}}^\lambda $
, we can identify
${\boldsymbol {L}}^\lambda $
, we can identify
so that both
![]() ${\boldsymbol {f}}_{{\boldsymbol {L}}}$
and
${\boldsymbol {f}}_{{\boldsymbol {L}}}$
and
![]() ${\boldsymbol {f}}_{{\boldsymbol {L}}^\lambda }$
satisfy (4.10) with
${\boldsymbol {f}}_{{\boldsymbol {L}}^\lambda }$
satisfy (4.10) with
![]() ${\boldsymbol {L}}$
and
${\boldsymbol {L}}$
and
![]() ${\boldsymbol {L}}^\lambda $
, respectively.
${\boldsymbol {L}}^\lambda $
, respectively.
Proof Thanks to Remark 4.9, proving the
![]() $\lambda $
-dissipativity in (4.13) for
$\lambda $
-dissipativity in (4.13) for
![]() ${\boldsymbol {L}}$
is equivalent to prove the
${\boldsymbol {L}}$
is equivalent to prove the
![]() $0$
-dissipativity result in (4.13) for
$0$
-dissipativity result in (4.13) for
![]() ${\boldsymbol {L}}^\lambda $
.
${\boldsymbol {L}}^\lambda $
.
We keep the same notation of the proof of Theorem 4.7 applied to
![]() ${\boldsymbol {L}}^\lambda $
. The case when
${\boldsymbol {L}}^\lambda $
. The case when
![]() $\mu =X_{\sharp}\mathbb {P}$
, with
$\mu =X_{\sharp}\mathbb {P}$
, with
![]() $X\in \mathcal {X}_m$
for some
$X\in \mathcal {X}_m$
for some
![]() $m\in \mathbb {N}$
, follows as in claim (a) of the proof of Theorem 4.7: we can assume that
$m\in \mathbb {N}$
, follows as in claim (a) of the proof of Theorem 4.7: we can assume that
![]() ${\boldsymbol {L}}^\lambda X$
is constant on every
${\boldsymbol {L}}^\lambda X$
is constant on every
![]() $\Omega _{m,k}$
. If
$\Omega _{m,k}$
. If
![]() $\omega ',\omega "\in \Omega $
and
$\omega ',\omega "\in \Omega $
and
![]() $\omega '\in \Omega _{m,i}$
,
$\omega '\in \Omega _{m,i}$
,
![]() $\omega " \in \Omega _{m,j}$
,
$\omega " \in \Omega _{m,j}$
,
![]() $i,j\in I_m$
and
$i,j\in I_m$
and
![]() $g\in \mathrm {S}(\Omega )$
is a measure-preserving isomorphism induced by the permutation that swaps i and j as in Corollary 3.7, we get
$g\in \mathrm {S}(\Omega )$
is a measure-preserving isomorphism induced by the permutation that swaps i and j as in Corollary 3.7, we get
We can eventually argue by approximation, as in claim (b) of the proof of Theorem 4.7, and using the representation of
![]() ${\boldsymbol {L}}^\lambda X$
in terms of
${\boldsymbol {L}}^\lambda X$
in terms of
![]() ${\boldsymbol {f}}_{{\boldsymbol {L}}^\lambda }$
to get
${\boldsymbol {f}}_{{\boldsymbol {L}}^\lambda }$
to get
Proposition 4.10 (Stability of Lipschitz representations)
If
![]() ${\boldsymbol {L}}_n, {\boldsymbol {L}}:\mathcal {X}\to \mathcal {Y}$
are L-Lipschitz invariant maps and
${\boldsymbol {L}}_n, {\boldsymbol {L}}:\mathcal {X}\to \mathcal {Y}$
are L-Lipschitz invariant maps and
![]() $D\subset \mathcal {X}$
is an invariant closed set, such that
$D\subset \mathcal {X}$
is an invariant closed set, such that
then setting
![]() $\tilde D:=\big \{X_{\sharp}\mathbb {P}:X\in D\big \}$
, we have
$\tilde D:=\big \{X_{\sharp}\mathbb {P}:X\in D\big \}$
, we have
![]() ${\boldsymbol {f}}_{{\boldsymbol {L}}_n}\to {\boldsymbol {f}}_{{\boldsymbol {L}}}$
pointwise in
${\boldsymbol {f}}_{{\boldsymbol {L}}_n}\to {\boldsymbol {f}}_{{\boldsymbol {L}}}$
pointwise in
![]() $\mathcal {S}(\mathsf {X},\tilde D)$
, where
$\mathcal {S}(\mathsf {X},\tilde D)$
, where
![]() ${\boldsymbol {f}}_{{\boldsymbol {L}}}$
is as in Theorem 4.7.
${\boldsymbol {f}}_{{\boldsymbol {L}}}$
is as in Theorem 4.7.
Proof We fix
![]() $\mu \in \tilde D$
and we set
$\mu \in \tilde D$
and we set
![]() $\boldsymbol {f}_n:={\boldsymbol {f}}_{{\boldsymbol {L}}_n}(\cdot ,\mu ):\operatorname {\mathrm {supp}}(\mu )\to \mathsf {Y}$
. We observe that
$\boldsymbol {f}_n:={\boldsymbol {f}}_{{\boldsymbol {L}}_n}(\cdot ,\mu ):\operatorname {\mathrm {supp}}(\mu )\to \mathsf {Y}$
. We observe that
![]() $\boldsymbol {f}_n$
are L-Lipschitz and form a Cauchy sequence in
$\boldsymbol {f}_n$
are L-Lipschitz and form a Cauchy sequence in
![]() $L^q(\mathsf {X},\mu ;\mathsf {Y})$
: we denote by
$L^q(\mathsf {X},\mu ;\mathsf {Y})$
: we denote by
![]() $\tilde {\boldsymbol {f}}$
its limit. For every
$\tilde {\boldsymbol {f}}$
its limit. For every
![]() $x\in \operatorname {\mathrm {supp}}(\mu )$
and
$x\in \operatorname {\mathrm {supp}}(\mu )$
and
![]() $\rho>0$
, we can set
$\rho>0$
, we can set
We have
![]() $\boldsymbol {f}_{n,\rho }(x)\to \boldsymbol {f}_\rho (x)$
for every
$\boldsymbol {f}_{n,\rho }(x)\to \boldsymbol {f}_\rho (x)$
for every
![]() $x\in \operatorname {\mathrm {supp}}(\mu )$
and every
$x\in \operatorname {\mathrm {supp}}(\mu )$
and every
![]() $\rho>0$
. On the other hand,
$\rho>0$
. On the other hand,
so that a simple argument using the triangle inequality shows that the sequence
![]() $(\boldsymbol {f}_n(x))_{n\in \mathbb {N}}$
is Cauchy in
$(\boldsymbol {f}_n(x))_{n\in \mathbb {N}}$
is Cauchy in
![]() $\mathsf {Y}$
for every
$\mathsf {Y}$
for every
![]() $x\in \operatorname {\mathrm {supp}}(\mu )$
and its pointwise limit
$x\in \operatorname {\mathrm {supp}}(\mu )$
and its pointwise limit
![]() $\boldsymbol {g}(\cdot ,\mu )$
is L-Lipschitz and represents
$\boldsymbol {g}(\cdot ,\mu )$
is L-Lipschitz and represents
![]() ${\boldsymbol {L}}$
as in (4.10) for every
${\boldsymbol {L}}$
as in (4.10) for every
![]() $X \in D$
. Arguing as in claim (d) in the proof of Theorem 4.7 and using the continuity of
$X \in D$
. Arguing as in claim (d) in the proof of Theorem 4.7 and using the continuity of
![]() ${\boldsymbol {L}}$
, we can eventually deduce that
${\boldsymbol {L}}$
, we can eventually deduce that
![]() $\boldsymbol {g}$
is continuous in
$\boldsymbol {g}$
is continuous in
![]() $\mathcal {S}(\mathsf {X},\tilde D)$
. The fact that
$\mathcal {S}(\mathsf {X},\tilde D)$
. The fact that
![]() $\boldsymbol {g}={\boldsymbol {f}}_{{\boldsymbol {L}}}$
comes from Lemma 4.6.
$\boldsymbol {g}={\boldsymbol {f}}_{{\boldsymbol {L}}}$
comes from Lemma 4.6.
When the maps
![]() ${\boldsymbol {L}}_n$
are not uniformly Lipschitz, we can still obtain a limiting representation.
${\boldsymbol {L}}_n$
are not uniformly Lipschitz, we can still obtain a limiting representation.
Lemma 4.11 Let
![]() $D \subset \mathcal {X}$
and
$D \subset \mathcal {X}$
and
![]() ${\boldsymbol {L}}_n, {\boldsymbol {L}}: D \to \mathcal {Y}$
be maps such that
${\boldsymbol {L}}_n, {\boldsymbol {L}}: D \to \mathcal {Y}$
be maps such that
![]() ${\boldsymbol {L}}_n$
are law invariant,
${\boldsymbol {L}}_n$
are law invariant,
![]() ${\boldsymbol {L}}_n$
converge pointwise to
${\boldsymbol {L}}_n$
converge pointwise to
![]() ${\boldsymbol {L}}$
on D as
${\boldsymbol {L}}$
on D as
![]() $n\to \infty $
and there exist Borel functions
$n\to \infty $
and there exist Borel functions
![]() $\boldsymbol {f}_n: \mathcal {S}(\mathsf {X}, \iota (D)) \to \mathsf {Y}$
such that
$\boldsymbol {f}_n: \mathcal {S}(\mathsf {X}, \iota (D)) \to \mathsf {Y}$
such that
Then
![]() ${\boldsymbol {L}}$
is law invariant and, for every
${\boldsymbol {L}}$
is law invariant and, for every
![]() $\mu \in \iota (D)$
, there exists a map
$\mu \in \iota (D)$
, there exists a map
![]() $\boldsymbol {f}[\mu ] \in L^q(\mathsf {X}, \mu; \mathsf {Y})$
such that, for every
$\boldsymbol {f}[\mu ] \in L^q(\mathsf {X}, \mu; \mathsf {Y})$
such that, for every
![]() $X \in D$
, there exists an increasing subsequence
$X \in D$
, there exists an increasing subsequence
![]() $k \mapsto n_{k}$
such that
$k \mapsto n_{k}$
such that
Proof First of all, notice that
![]() ${\boldsymbol {L}}$
is law invariant, being pointwise limit of law invariant maps. Let
${\boldsymbol {L}}$
is law invariant, being pointwise limit of law invariant maps. Let
![]() $\mu \in \iota (D)$
be fixed. If
$\mu \in \iota (D)$
be fixed. If
![]() $X\in D$
is such that
$X\in D$
is such that
![]() $X_{\sharp}\mathbb {P}=\mu $
, we can find an increasing subsequence
$X_{\sharp}\mathbb {P}=\mu $
, we can find an increasing subsequence
![]() $k \mapsto n_{k}$
such that
$k \mapsto n_{k}$
such that
![]() ${\boldsymbol {L}}_{n_{k}} X \to {\boldsymbol {L}} X\ \mathbb {P}$
-a.e. in
${\boldsymbol {L}}_{n_{k}} X \to {\boldsymbol {L}} X\ \mathbb {P}$
-a.e. in
![]() $\Omega $
and define
$\Omega $
and define
 $$\begin{align*}\boldsymbol{f}_X(x):= \begin{cases} \lim_{k \to + \infty}\boldsymbol{f}_{n_{k}}(x, \mu), \quad &\text{ if } x \in E, \\ 0, \quad &\text{ else}, \end{cases}\end{align*}$$
$$\begin{align*}\boldsymbol{f}_X(x):= \begin{cases} \lim_{k \to + \infty}\boldsymbol{f}_{n_{k}}(x, \mu), \quad &\text{ if } x \in E, \\ 0, \quad &\text{ else}, \end{cases}\end{align*}$$
where
![]() $E \subset \mathsf {X}$
is the Borel set of points in
$E \subset \mathsf {X}$
is the Borel set of points in
![]() $\mathsf {X}$
where
$\mathsf {X}$
where
![]() $\lim _{k \to + \infty }\boldsymbol {f}_{n_{k}}(x, \mu )$
exists. Let us now show that
$\lim _{k \to + \infty }\boldsymbol {f}_{n_{k}}(x, \mu )$
exists. Let us now show that
![]() $\boldsymbol {f}_X$
represents
$\boldsymbol {f}_X$
represents
![]() ${\boldsymbol {L}}$
, i.e.,
${\boldsymbol {L}}$
, i.e.,
We know that
so that, choosing representatives of X,
![]() ${\boldsymbol {L}} X$
,
${\boldsymbol {L}} X$
,
![]() ${\boldsymbol {L}}_{n_{k}}X$
, we can find a full
${\boldsymbol {L}}_{n_{k}}X$
, we can find a full
![]() $\mathbb {P}$
-measure set
$\mathbb {P}$
-measure set
![]() $\Omega _{0} \subset \Omega $
such that
$\Omega _{0} \subset \Omega $
such that
Thus, for every
![]() $\omega \in \Omega _{0}$
,
$\omega \in \Omega _{0}$
,
![]() $X(\omega ) \in E$
and then
$X(\omega ) \in E$
and then
![]() ${\boldsymbol {L}} X(\omega ) = f_X(X(\omega ))$
. If now
${\boldsymbol {L}} X(\omega ) = f_X(X(\omega ))$
. If now
![]() $X' \in D$
is such that
$X' \in D$
is such that
![]() ${X'}_{\sharp}\mathbb {P}=\mu $
, arguing as in claim (c) of the proof of Theorem 4.7, it is easy to see that
${X'}_{\sharp}\mathbb {P}=\mu $
, arguing as in claim (c) of the proof of Theorem 4.7, it is easy to see that
![]() $\boldsymbol {f}_X=\boldsymbol {f}_{X'}\ \mu $
-almost everywhere.
$\boldsymbol {f}_X=\boldsymbol {f}_{X'}\ \mu $
-almost everywhere.
We eventually apply the previous results to (possibly multivalued) maximal
![]() $\lambda $
-dissipative operators
$\lambda $
-dissipative operators
![]() $\boldsymbol {B}\subset \mathcal {X}\times \mathcal {X}$
(with
$\boldsymbol {B}\subset \mathcal {X}\times \mathcal {X}$
(with
![]() $p=q=2$
and
$p=q=2$
and
![]() $\mathsf {X}=\mathsf {Y}$
) which are invariant by measure-preserving isomorphisms. We show that the invariance property is inherited by the associated resolvent operator, Yosida approximation, minimal selection, and semigroup which also enjoy a map-representation property.
$\mathsf {X}=\mathsf {Y}$
) which are invariant by measure-preserving isomorphisms. We show that the invariance property is inherited by the associated resolvent operator, Yosida approximation, minimal selection, and semigroup which also enjoy a map-representation property.
We denote by
![]() $\iota \big (D(\boldsymbol {B})\big ):=\Big \{X_{\sharp}\mathbb {P}:X\in \mathrm {D}(\boldsymbol {B})\Big \}$
the image in
$\iota \big (D(\boldsymbol {B})\big ):=\Big \{X_{\sharp}\mathbb {P}:X\in \mathrm {D}(\boldsymbol {B})\Big \}$
the image in
![]() $\mathcal {P}_{2}(\mathsf {X})$
of the domain of
$\mathcal {P}_{2}(\mathsf {X})$
of the domain of
![]() $\boldsymbol {B}$
.
$\boldsymbol {B}$
.
Theorem 4.12 (Structure of resolvents, Yosida approximations, and semigroups)
Let
![]() $\mathsf {X}$
be a separable Hilbert space, and let
$\mathsf {X}$
be a separable Hilbert space, and let
![]() $p=2$
. Let
$p=2$
. Let
![]() $\boldsymbol {B} \subset \mathcal {X} \times \mathcal {X}$
be a maximal
$\boldsymbol {B} \subset \mathcal {X} \times \mathcal {X}$
be a maximal
![]() $\lambda $
-dissipative operator which is invariant by measure-preserving isomorphisms. Then, for every
$\lambda $
-dissipative operator which is invariant by measure-preserving isomorphisms. Then, for every
![]() $0<\tau <1/\lambda ^+,\ t\ge 0$
, the operators
$0<\tau <1/\lambda ^+,\ t\ge 0$
, the operators
![]() $ \boldsymbol {B}, \boldsymbol {B}_{\tau }, {\boldsymbol {J}_{\tau }},\boldsymbol {S}_t,\boldsymbol {B}^\circ $
are law invariant. Moreover, there exist (uniquely defined) continuous maps
$ \boldsymbol {B}, \boldsymbol {B}_{\tau }, {\boldsymbol {J}_{\tau }},\boldsymbol {S}_t,\boldsymbol {B}^\circ $
are law invariant. Moreover, there exist (uniquely defined) continuous maps
![]() $\boldsymbol {j}_{\tau }:\mathcal {S}(\mathsf {X})\to \mathsf {X}$
,
$\boldsymbol {j}_{\tau }:\mathcal {S}(\mathsf {X})\to \mathsf {X}$
,
![]() $\boldsymbol {b}_{\tau }: \mathcal {S}(\mathsf {X}) \to \mathsf {X}$
, and
$\boldsymbol {b}_{\tau }: \mathcal {S}(\mathsf {X}) \to \mathsf {X}$
, and
![]() $ \boldsymbol {s}_t:\mathcal {S}(\mathsf {X},\overline {\iota \big (D(\boldsymbol {B})\big )})\to \mathsf {X}$
such that:
$ \boldsymbol {s}_t:\mathcal {S}(\mathsf {X},\overline {\iota \big (D(\boldsymbol {B})\big )})\to \mathsf {X}$
such that:
-
(1) for every
 $\mu \in \mathcal {P}_{2}(\mathsf {X})$
, the map
$\mu \in \mathcal {P}_{2}(\mathsf {X})$
, the map
 $\boldsymbol {j}_{\tau }(\cdot ,\mu ): \operatorname {\mathrm {supp}}(\mu ) \to \mathsf {X}$
is
$\boldsymbol {j}_{\tau }(\cdot ,\mu ): \operatorname {\mathrm {supp}}(\mu ) \to \mathsf {X}$
is
 $(1-\lambda \tau )^{-1}$
-Lipschitz continuous, for
$(1-\lambda \tau )^{-1}$
-Lipschitz continuous, for
 $0<\tau < 1/\lambda ^+$
,
$0<\tau < 1/\lambda ^+$
, -
(2) for every
 $\mu \in \mathcal {P}_{2}(\mathsf {X})$
, the map
$\mu \in \mathcal {P}_{2}(\mathsf {X})$
, the map
 $\boldsymbol {b}_{\tau }(\cdot ,\mu ): \operatorname {\mathrm {supp}}(\mu ) \to \mathsf {X}$
is
$\boldsymbol {b}_{\tau }(\cdot ,\mu ): \operatorname {\mathrm {supp}}(\mu ) \to \mathsf {X}$
is
 $\frac {2-\lambda \tau }{\tau (1-\lambda \tau )}$
-Lipschitz continuous, for
$\frac {2-\lambda \tau }{\tau (1-\lambda \tau )}$
-Lipschitz continuous, for
 $0<\tau < 1/\lambda ^+$
,
$0<\tau < 1/\lambda ^+$
, -
(3) for every
 $\mu \in \overline {\iota \big (D(\boldsymbol {B})\big )}$
, the map
$\mu \in \overline {\iota \big (D(\boldsymbol {B})\big )}$
, the map
 $\boldsymbol {s}_t(\cdot ,\mu ): \operatorname {\mathrm {supp}}(\mu ) \to \mathsf {X}$
is
$\boldsymbol {s}_t(\cdot ,\mu ): \operatorname {\mathrm {supp}}(\mu ) \to \mathsf {X}$
is
 $e^{\lambda t}$
-Lipschitz continuous,
$e^{\lambda t}$
-Lipschitz continuous,
and
together with the invariance and semigroup properties
 $$ \begin{align} \begin{aligned} \mu\in \overline{\iota\big(D(\boldsymbol{B})\big)}&\quad\Rightarrow\quad \boldsymbol{s}_t(\cdot,\mu)_\sharp\mu\in \overline{\iota\big(D(\boldsymbol{B})\big)};\\ \mu\in {\iota\big(D(\boldsymbol{B})\big)}&\quad\Rightarrow\quad \boldsymbol{s}_t(\cdot,\mu)_\sharp\mu\in {\iota\big(D(\boldsymbol{B})\big)},\\ \boldsymbol{s}_{t+h}(x,\mu)=\boldsymbol{s}_h(\boldsymbol{s}_t(x,\mu),\boldsymbol{s}_t(\cdot,\mu)_\sharp\mu)&\quad \text{for every }(x,\mu) \in \mathcal{S}(\mathsf{X},\overline{\iota\big(D(\boldsymbol{B})\big)}),\quad t,h\ge0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mu\in \overline{\iota\big(D(\boldsymbol{B})\big)}&\quad\Rightarrow\quad \boldsymbol{s}_t(\cdot,\mu)_\sharp\mu\in \overline{\iota\big(D(\boldsymbol{B})\big)};\\ \mu\in {\iota\big(D(\boldsymbol{B})\big)}&\quad\Rightarrow\quad \boldsymbol{s}_t(\cdot,\mu)_\sharp\mu\in {\iota\big(D(\boldsymbol{B})\big)},\\ \boldsymbol{s}_{t+h}(x,\mu)=\boldsymbol{s}_h(\boldsymbol{s}_t(x,\mu),\boldsymbol{s}_t(\cdot,\mu)_\sharp\mu)&\quad \text{for every }(x,\mu) \in \mathcal{S}(\mathsf{X},\overline{\iota\big(D(\boldsymbol{B})\big)}),\quad t,h\ge0. \end{aligned} \end{align} $$
Finally, for every
![]() $\mu \in \iota \big (D(\boldsymbol {B})\big )$
, there exists a map
$\mu \in \iota \big (D(\boldsymbol {B})\big )$
, there exists a map
![]() $\boldsymbol {b}^\circ (\cdot ,\mu ) \in L^{2}(\mathsf {X}, \mu; \mathsf {X})$
such that for every
$\boldsymbol {b}^\circ (\cdot ,\mu ) \in L^{2}(\mathsf {X}, \mu; \mathsf {X})$
such that for every
![]() $X\in \mathcal {X}$
,
$X\in \mathcal {X}$
,
For every
![]() $\mu \in \iota \big (D(\boldsymbol {B})\big )$
, the map
$\mu \in \iota \big (D(\boldsymbol {B})\big )$
, the map
![]() $\boldsymbol {b}^\circ (\cdot ,\mu )$
is
$\boldsymbol {b}^\circ (\cdot ,\mu )$
is
![]() $\lambda $
-dissipative in a set
$\lambda $
-dissipative in a set
![]() $\mathsf {X}_{0}\subset \mathsf {X}$
of full
$\mathsf {X}_{0}\subset \mathsf {X}$
of full
![]() $\mu $
-measure and satisfies
$\mu $
-measure and satisfies
 $$ \begin{align} \lim_{h\downarrow0}\int\bigg|\frac 1h(\boldsymbol{s}_{t+h}(x,\mu)-\boldsymbol{s}_t(x,\mu))- \boldsymbol{b}^\circ(\boldsymbol{s}_t(x,\mu),\boldsymbol{s}_t(\cdot,\mu)_\sharp \mu)\bigg|^{2}\,\mathrm{d}\mu(x)=0\quad t\ge0. \end{align} $$
$$ \begin{align} \lim_{h\downarrow0}\int\bigg|\frac 1h(\boldsymbol{s}_{t+h}(x,\mu)-\boldsymbol{s}_t(x,\mu))- \boldsymbol{b}^\circ(\boldsymbol{s}_t(x,\mu),\boldsymbol{s}_t(\cdot,\mu)_\sharp \mu)\bigg|^{2}\,\mathrm{d}\mu(x)=0\quad t\ge0. \end{align} $$
Remark 4.13 By Theorem 4.12, a maximal
![]() $\lambda $
-dissipative operator
$\lambda $
-dissipative operator
![]() $\boldsymbol {B} \subset \mathcal {X} \times \mathcal {X}$
,
$\boldsymbol {B} \subset \mathcal {X} \times \mathcal {X}$
,
![]() $\lambda \in \mathbb {R}$
, is law invariant if and only if it is invariant by measure-preserving isomorphisms. Thanks to (4.21), also
$\lambda \in \mathbb {R}$
, is law invariant if and only if it is invariant by measure-preserving isomorphisms. Thanks to (4.21), also
![]() $D(\boldsymbol {B})$
is law invariant, i.e., if
$D(\boldsymbol {B})$
is law invariant, i.e., if
![]() $X\in D(\boldsymbol {B})$
and
$X\in D(\boldsymbol {B})$
and
![]() $Y\in \mathcal {X}$
is such that
$Y\in \mathcal {X}$
is such that
![]() $Y_{\sharp}\mathbb {P}=X_{\sharp}\mathbb {P}$
, then
$Y_{\sharp}\mathbb {P}=X_{\sharp}\mathbb {P}$
, then
![]() $Y\in D(\boldsymbol {B})$
.
$Y\in D(\boldsymbol {B})$
.
Proof First, notice that
![]() $\boldsymbol {B}$
is closed being maximal
$\boldsymbol {B}$
is closed being maximal
![]() $\lambda $
-dissipative; hence, it is law invariant by Proposition 4.2. Recall that
$\lambda $
-dissipative; hence, it is law invariant by Proposition 4.2. Recall that
![]() ${\boldsymbol {J}_{\tau }}$
is everywhere defined,
${\boldsymbol {J}_{\tau }}$
is everywhere defined,
![]() $(1-\lambda \tau )^{-1}$
-Lipschitz continuous for every
$(1-\lambda \tau )^{-1}$
-Lipschitz continuous for every
![]() $0<\tau <1/\lambda ^+$
(see Section 2.3) and invariant by measure-preserving isomorphisms by Proposition 2.9. Fixed
$0<\tau <1/\lambda ^+$
(see Section 2.3) and invariant by measure-preserving isomorphisms by Proposition 2.9. Fixed
![]() $0<\tau <1/\lambda ^+$
, we can thus apply Proposition 4.2 and Theorem 4.7(1) and get that
$0<\tau <1/\lambda ^+$
, we can thus apply Proposition 4.2 and Theorem 4.7(1) and get that
![]() ${\boldsymbol {J}_{\tau }}$
is law invariant together with property (1) in Theorem 4.12 and (4.17). Similarly,
${\boldsymbol {J}_{\tau }}$
is law invariant together with property (1) in Theorem 4.12 and (4.17). Similarly,
![]() $\boldsymbol {S}_t$
is defined on the closed set
$\boldsymbol {S}_t$
is defined on the closed set
![]() $\overline {\mathrm {D}(\boldsymbol {B})}$
, and it is
$\overline {\mathrm {D}(\boldsymbol {B})}$
, and it is
![]() $e^{\lambda t}$
-Lipschitz continuous (cf. Section 2.3) and invariant by measure-preserving isomorphisms by Proposition 2.9, so that we can apply Proposition 4.2 and Theorem 4.7(1) and get that it is law invariant together with property (3) of Theorem 4.12 and (4.19). The content of (4.20) immediately follows by the semigroup and invariance properties of
$e^{\lambda t}$
-Lipschitz continuous (cf. Section 2.3) and invariant by measure-preserving isomorphisms by Proposition 2.9, so that we can apply Proposition 4.2 and Theorem 4.7(1) and get that it is law invariant together with property (3) of Theorem 4.12 and (4.19). The content of (4.20) immediately follows by the semigroup and invariance properties of
![]() $\boldsymbol {S}_t$
(cf. Section 2.3), also using that
$\boldsymbol {S}_t$
(cf. Section 2.3), also using that
![]() $\overline {\iota (\mathrm {D}(\boldsymbol {B}))}=\iota (\overline {\mathrm {D}(\boldsymbol {B})})$
.
$\overline {\iota (\mathrm {D}(\boldsymbol {B}))}=\iota (\overline {\mathrm {D}(\boldsymbol {B})})$
.
We now prove (4.21). If
![]() $X \in \mathrm {D}(\boldsymbol {B})$
, we have that
$X \in \mathrm {D}(\boldsymbol {B})$
, we have that
![]() $\boldsymbol {B}_{\tau } X \to \boldsymbol {B}^\circ X$
as
$\boldsymbol {B}_{\tau } X \to \boldsymbol {B}^\circ X$
as
![]() $\tau \downarrow 0$
; moreover,
$\tau \downarrow 0$
; moreover,
![]() $\boldsymbol {B}_{\tau }$
is law invariant, everywhere defined and, for every
$\boldsymbol {B}_{\tau }$
is law invariant, everywhere defined and, for every
![]() $0<\tau < 1/\lambda ^+$
,
$0<\tau < 1/\lambda ^+$
,
![]() $\boldsymbol {B}_{\tau }$
is
$\boldsymbol {B}_{\tau }$
is
![]() $\lambda /(1-\lambda \tau )$
-dissipative and
$\lambda /(1-\lambda \tau )$
-dissipative and
![]() $\frac {2-\lambda \tau }{\tau (1-\lambda \tau )}$
-Lipschitz continuous (cf. Section 2.3). Hence, we can apply Theorem 4.7(2) and get that
$\frac {2-\lambda \tau }{\tau (1-\lambda \tau )}$
-Lipschitz continuous (cf. Section 2.3). Hence, we can apply Theorem 4.7(2) and get that
![]() $\boldsymbol {B}^\circ $
is law invariant and that there exists, for every
$\boldsymbol {B}^\circ $
is law invariant and that there exists, for every
![]() $\mu \in \iota \big (D(\boldsymbol {B})\big )$
, a map
$\mu \in \iota \big (D(\boldsymbol {B})\big )$
, a map
![]() $\boldsymbol {b}^\circ [\mu ]\equiv \boldsymbol {b}^\circ (\cdot ,\mu )\in L^{2}(\mathsf {X},\mu; \mathsf {X})$
such that for every
$\boldsymbol {b}^\circ [\mu ]\equiv \boldsymbol {b}^\circ (\cdot ,\mu )\in L^{2}(\mathsf {X},\mu; \mathsf {X})$
such that for every
![]() $X \in \mathrm {D}(\boldsymbol {B}),$
$X \in \mathrm {D}(\boldsymbol {B}),$
where
![]() $\boldsymbol {b}_{\tau }$
is the (unique) continuous map that represents
$\boldsymbol {b}_{\tau }$
is the (unique) continuous map that represents
![]() $\boldsymbol {B}_{\tau }$
coming from Theorem 4.7(1),
$\boldsymbol {B}_{\tau }$
coming from Theorem 4.7(1),
![]() $0<\tau < 1/\lambda ^+$
. To complete the proof of (4.21), we have to check that, if
$0<\tau < 1/\lambda ^+$
. To complete the proof of (4.21), we have to check that, if
![]() $\mu \in \iota \big (D(\boldsymbol {B})\big )$
and
$\mu \in \iota \big (D(\boldsymbol {B})\big )$
and
![]() $X\in \mathcal {X}$
is such that
$X\in \mathcal {X}$
is such that
![]() $X_{\sharp}\mathbb {P}=\mu $
, then
$X_{\sharp}\mathbb {P}=\mu $
, then
![]() $X\in \mathrm {D}(\boldsymbol {B})$
. Since
$X\in \mathrm {D}(\boldsymbol {B})$
. Since
![]() $\mu \in \iota \big (D(\boldsymbol {B})\big )$
, there exists
$\mu \in \iota \big (D(\boldsymbol {B})\big )$
, there exists
![]() $Y\in \mathrm {D}(\boldsymbol {B})$
such that
$Y\in \mathrm {D}(\boldsymbol {B})$
such that
![]() $Y_{\sharp}\mathbb {P}=X_{\sharp}\mathbb {P}=\mu $
. By (4.18), we have
$Y_{\sharp}\mathbb {P}=X_{\sharp}\mathbb {P}=\mu $
. By (4.18), we have
 $$ \begin{align*} |\boldsymbol{B}_{\tau} Y|^{2}_{\mathcal{X}}&=\int |b_{\tau}(Y(\omega),\mu)|^{2}\mathrm{d}\mathbb{P}(\omega)=\int |b_{\tau}(x,\mu)|^{2}\mathrm{d}\mu(x)\\ &=\int |b_{\tau}(X(\omega),\mu)|^{2}\mathrm{d}\mathbb{P}(\omega)=|\boldsymbol{B}_{\tau} X|_{\mathcal{X}}^{2}. \end{align*} $$
$$ \begin{align*} |\boldsymbol{B}_{\tau} Y|^{2}_{\mathcal{X}}&=\int |b_{\tau}(Y(\omega),\mu)|^{2}\mathrm{d}\mathbb{P}(\omega)=\int |b_{\tau}(x,\mu)|^{2}\mathrm{d}\mu(x)\\ &=\int |b_{\tau}(X(\omega),\mu)|^{2}\mathrm{d}\mathbb{P}(\omega)=|\boldsymbol{B}_{\tau} X|_{\mathcal{X}}^{2}. \end{align*} $$
Hence, since
![]() $Y\in \mathrm {D}(\boldsymbol {B})$
, by (2.24), we have
$Y\in \mathrm {D}(\boldsymbol {B})$
, by (2.24), we have
Recalling (2.25), we get
![]() $X\in \mathrm {D}(\boldsymbol {B})$
. Finally, (4.22) follows by (2.27) using (4.19) and (4.21).
$X\in \mathrm {D}(\boldsymbol {B})$
. Finally, (4.22) follows by (2.27) using (4.19) and (4.21).
It only remains to show that, for every
![]() $\mu \in \iota \big (D(\boldsymbol {B})\big )$
, the map
$\mu \in \iota \big (D(\boldsymbol {B})\big )$
, the map
![]() $\boldsymbol {b}^\circ [\mu ]$
is
$\boldsymbol {b}^\circ [\mu ]$
is
![]() $\lambda $
-dissipative in a full
$\lambda $
-dissipative in a full
![]() $\mu $
-measure set. To this aim, observe that we can apply Theorem 4.7(1) to
$\mu $
-measure set. To this aim, observe that we can apply Theorem 4.7(1) to
![]() $\boldsymbol {B}_{\tau }$
,
$\boldsymbol {B}_{\tau }$
,
![]() $0<\tau <1/\lambda ^+$
, so that for every
$0<\tau <1/\lambda ^+$
, so that for every
![]() $\mu \in \mathcal {P}_{2}(\mathsf {X})$
, we have
$\mu \in \mathcal {P}_{2}(\mathsf {X})$
, we have
Let
![]() $\mu \in \iota \big (D(\boldsymbol {B})\big )$
, and let us consider a representative of
$\mu \in \iota \big (D(\boldsymbol {B})\big )$
, and let us consider a representative of
![]() $X \in \mathrm {D}(\boldsymbol {B})$
such that
$X \in \mathrm {D}(\boldsymbol {B})$
such that
![]() $X_{\sharp}\mathbb {P}=\mu $
; let
$X_{\sharp}\mathbb {P}=\mu $
; let
![]() $\tau _{k}$
be a sequence as in (4.24) and let
$\tau _{k}$
be a sequence as in (4.24) and let
![]() $\Omega _{0}$
be a full
$\Omega _{0}$
be a full
![]() $\mathbb {P}$
-measure set where the convergence in (4.24) takes place. If we take
$\mathbb {P}$
-measure set where the convergence in (4.24) takes place. If we take
![]() $y,y' \in X(\Omega _{0}) \cap \operatorname {\mathrm {supp}}(\mu )$
, then we can find
$y,y' \in X(\Omega _{0}) \cap \operatorname {\mathrm {supp}}(\mu )$
, then we can find
![]() $\omega , \omega ' \in \Omega _{0}$
such that
$\omega , \omega ' \in \Omega _{0}$
such that
![]() $X(\omega )=y$
and
$X(\omega )=y$
and
![]() $X(\omega ')=y'$
so that, passing to the limit as
$X(\omega ')=y'$
so that, passing to the limit as
![]() $k \to + \infty $
in (4.25) written for
$k \to + \infty $
in (4.25) written for
![]() $\tau =\tau _{k}$
, we get that
$\tau =\tau _{k}$
, we get that
It is then enough to observe that
![]() $X(\Omega _{0}) \cap \operatorname {\mathrm {supp}}(\mu )$
contains a Borel set
$X(\Omega _{0}) \cap \operatorname {\mathrm {supp}}(\mu )$
contains a Borel set
![]() $\mathsf {X}_{0}$
of full
$\mathsf {X}_{0}$
of full
![]() $\mu $
-measure to conclude: in fact, being
$\mu $
-measure to conclude: in fact, being
![]() $X(\Omega _{0})$
a Suslin set, we can find two Borel sets
$X(\Omega _{0})$
a Suslin set, we can find two Borel sets
![]() $E_{0}, E_1$
such that
$E_{0}, E_1$
such that
![]() $E_{0} \subset X(\Omega _{0}) \subset E_1$
and
$E_{0} \subset X(\Omega _{0}) \subset E_1$
and
![]() $\mu (E_1 \setminus E_{0})=0$
. Since
$\mu (E_1 \setminus E_{0})=0$
. Since
![]() $\mu (E_1)=X_{\sharp}\mathbb {P} (E_1) \ge \mathbb {P}(\Omega _{0})=1$
, we conclude that we can take
$\mu (E_1)=X_{\sharp}\mathbb {P} (E_1) \ge \mathbb {P}(\Omega _{0})=1$
, we conclude that we can take
![]() $\mathsf {X}_{0}:=E_{0} \cap \operatorname {\mathrm {supp}}(\mu )$
.
$\mathsf {X}_{0}:=E_{0} \cap \operatorname {\mathrm {supp}}(\mu )$
.
A An alternative proof of the extension theorem for
 $\textsf {G}$
-invariant Lipschitz maps
$\textsf {G}$
-invariant Lipschitz maps
We provide an alternative proof to the extension result for invariant Lipschitz maps stated in Theorem 2.11. Here, we use a recent and beautiful explicit construction of a Lipschitz extension provided by [Reference Azagra, Le Gruyer and Mudarra5] (see also [Reference Azagra, Le Gruyer and Mudarra4]) and we show that it preserves the invariance. We consider a Hilbert space
![]() $\mathcal {H}$
with norm
$\mathcal {H}$
with norm
![]() $|\cdot |$
and scalar product
$|\cdot |$
and scalar product
![]() $\langle \cdot , \cdot \rangle $
as in Section 2.4.
$\langle \cdot , \cdot \rangle $
as in Section 2.4.
Recall that if
![]() $g:\mathsf {W}\to \mathbb {R}$
is a function defined in a Hilbert space
$g:\mathsf {W}\to \mathbb {R}$
is a function defined in a Hilbert space
![]() $\mathsf {W}$
, then its convex envelope is defined by
$\mathsf {W}$
, then its convex envelope is defined by
 $$ \begin{align} \operatorname{co}(g)(w):= \inf\left\{\sum_{i=1}^N \alpha_i g(w_i): \alpha_i\ge0,\ \sum_{i=1}^N\alpha_i=1,\ w_i\in \mathsf{W},\ \sum_{i=1}^N \alpha_i w_i=w,\ N\in \mathbb{N}\right\}. \end{align} $$
$$ \begin{align} \operatorname{co}(g)(w):= \inf\left\{\sum_{i=1}^N \alpha_i g(w_i): \alpha_i\ge0,\ \sum_{i=1}^N\alpha_i=1,\ w_i\in \mathsf{W},\ \sum_{i=1}^N \alpha_i w_i=w,\ N\in \mathbb{N}\right\}. \end{align} $$
If g is locally bounded from above, then also
![]() $\operatorname {co}(g)$
is locally bounded from above and it is therefore locally Lipschitz.
$\operatorname {co}(g)$
is locally bounded from above and it is therefore locally Lipschitz.
Theorem A.1 [Reference Azagra, Le Gruyer and Mudarra5]
Let
![]() $f:D\to \mathcal {H}$
be an L-Lipschitz map defined in
$f:D\to \mathcal {H}$
be an L-Lipschitz map defined in
![]() $D\subset \mathcal {H}$
. Setting for every
$D\subset \mathcal {H}$
. Setting for every
![]() $x,y\in \mathcal {H}$
$x,y\in \mathcal {H}$
 $$ \begin{align} \begin{aligned} g(x,y):={}& \inf_{x'\in D} \Big\{\langle f(x'),y\rangle+ \frac L2 |(x-x',y)|_{\mathcal{H}\times \mathcal{H}}^{2}\Big\}+ \frac L2 |(x,y)|_{\mathcal{H}\times \mathcal{H}}^{2},\\ \tilde g:={}&\operatorname{co}(g), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} g(x,y):={}& \inf_{x'\in D} \Big\{\langle f(x'),y\rangle+ \frac L2 |(x-x',y)|_{\mathcal{H}\times \mathcal{H}}^{2}\Big\}+ \frac L2 |(x,y)|_{\mathcal{H}\times \mathcal{H}}^{2},\\ \tilde g:={}&\operatorname{co}(g), \end{aligned} \end{align} $$
then
![]() $\tilde g$
is a convex function of class
$\tilde g$
is a convex function of class
![]() $\mathrm {C}^{1,1}$
in
$\mathrm {C}^{1,1}$
in
![]() $\mathcal {H}\times \mathcal {H}$
and its partial differential with respect to the second variable in
$\mathcal {H}\times \mathcal {H}$
and its partial differential with respect to the second variable in
![]() $\mathcal {H}$
$\mathcal {H}$
is an L-Lipschitz extension of f.
We state our first result concerning the extension of
![]() $\mathsf {G}_{\mathcal {H}}$
-invariant Lipschitz maps.
$\mathsf {G}_{\mathcal {H}}$
-invariant Lipschitz maps.
Theorem A.2 Under the same assumption of Theorem A.1, let us also suppose that f is
![]() $\mathsf {G}_{\mathcal {H}}$
-invariant according to (2.29). Then F is
$\mathsf {G}_{\mathcal {H}}$
-invariant according to (2.29). Then F is
![]() $\mathsf {G}_{\mathcal {H}}$
-invariant as well. In particular, any
$\mathsf {G}_{\mathcal {H}}$
-invariant as well. In particular, any
![]() $\mathsf {G}_{\mathcal {H}}$
-invariant L-Lipschitz function
$\mathsf {G}_{\mathcal {H}}$
-invariant L-Lipschitz function
![]() $f:D\to \mathcal {H}$
defined in a subset D of
$f:D\to \mathcal {H}$
defined in a subset D of
![]() $\mathcal {H}$
admits a
$\mathcal {H}$
admits a
![]() $\mathsf {G}_{\mathcal {H}}$
-invariant L-Lipschitz extension
$\mathsf {G}_{\mathcal {H}}$
-invariant L-Lipschitz extension
![]() $F:\mathcal {H}\to \mathcal {H}.$
$F:\mathcal {H}\to \mathcal {H}.$
Proof We divide the proof in several claims.
Claim 1: the map g is
![]() $\mathsf {G}_{\mathcal {H}}$
-invariant, i.e.,
$\mathsf {G}_{\mathcal {H}}$
-invariant, i.e.,
![]() $g(Ux,Uy)=g(x,y)$
for every
$g(Ux,Uy)=g(x,y)$
for every
![]() $(x,y)\in \mathcal {H}\times \mathcal {H}$
and
$(x,y)\in \mathcal {H}\times \mathcal {H}$
and
![]() $U\in \mathsf {G}_{\mathcal {H}}.$
$U\in \mathsf {G}_{\mathcal {H}}.$
Every element
![]() $x'\in D$
can be written as
$x'\in D$
can be written as
![]() $x'=Ux"$
with
$x'=Ux"$
with
![]() $x"=U^{-1}x'\in D$
, so that for every
$x"=U^{-1}x'\in D$
, so that for every
![]() $U\in \mathsf {G}_{\mathcal {H}}$
and
$U\in \mathsf {G}_{\mathcal {H}}$
and
![]() $(x,y)\in \mathcal {H}\times \mathcal {H}$
,
$(x,y)\in \mathcal {H}\times \mathcal {H}$
,
 $$ \begin{align*} g(Ux,Uy)&= \inf_{x'\in D} \Big\{\langle f(x'),Uy\rangle+ \frac L2 |(Ux-x',Uy)|_{\mathcal{H}\times \mathcal{H}}^{2}\Big\}+ \frac L2 |(Ux,Uy)|_{\mathcal{H}\times \mathcal{H}}^{2} \\&= \inf_{x"\in D} \Big\{\langle f(Ux"),Uy\rangle+ \frac L2 |(U(x-x"),Uy)|_{\mathcal{H}\times \mathcal{H}}^{2}\Big\}+ \frac L2 |(Ux,Uy)|_{\mathcal{H}\times \mathcal{H}}^{2} \\&= \inf_{x"\in D} \Big\{\langle f(x"),y\rangle+ \frac L2 |(x-x",y)|_{\mathcal{H}\times \mathcal{H}}^{2}\Big\}+ \frac L2 |(x,y)|_{\mathcal{H}\times \mathcal{H}}^{2} \\&=g(x,y), \end{align*} $$
$$ \begin{align*} g(Ux,Uy)&= \inf_{x'\in D} \Big\{\langle f(x'),Uy\rangle+ \frac L2 |(Ux-x',Uy)|_{\mathcal{H}\times \mathcal{H}}^{2}\Big\}+ \frac L2 |(Ux,Uy)|_{\mathcal{H}\times \mathcal{H}}^{2} \\&= \inf_{x"\in D} \Big\{\langle f(Ux"),Uy\rangle+ \frac L2 |(U(x-x"),Uy)|_{\mathcal{H}\times \mathcal{H}}^{2}\Big\}+ \frac L2 |(Ux,Uy)|_{\mathcal{H}\times \mathcal{H}}^{2} \\&= \inf_{x"\in D} \Big\{\langle f(x"),y\rangle+ \frac L2 |(x-x",y)|_{\mathcal{H}\times \mathcal{H}}^{2}\Big\}+ \frac L2 |(x,y)|_{\mathcal{H}\times \mathcal{H}}^{2} \\&=g(x,y), \end{align*} $$
where we used (2.29) and the isometric character of U to get
![]() $\langle f(Ux"),Uy\rangle = \langle Uf(x"),Uy\rangle = \langle f(x"),y\rangle $
.
$\langle f(Ux"),Uy\rangle = \langle Uf(x"),Uy\rangle = \langle f(x"),y\rangle $
.
Claim 2: the map
![]() $\tilde g:=\operatorname {co}(g)$
is
$\tilde g:=\operatorname {co}(g)$
is
![]() $\mathsf {G}_{\mathcal {H}}$
-invariant as well.
$\mathsf {G}_{\mathcal {H}}$
-invariant as well.
It is sufficient to observe that for every
![]() $U\in \mathsf {G}_{\mathcal {H}},\ N\in \mathbb {N}$
, and
$U\in \mathsf {G}_{\mathcal {H}},\ N\in \mathbb {N}$
, and
![]() $\alpha _i\ge 0$
with
$\alpha _i\ge 0$
with
![]() $\sum _{i=1}^N\alpha _i=1$
, a collection
$\sum _{i=1}^N\alpha _i=1$
, a collection
![]() $\{(x_i,y_i)\}_{i=1}^N \in (\mathcal {H}\times \mathcal {H})^N$
satisfies
$\{(x_i,y_i)\}_{i=1}^N \in (\mathcal {H}\times \mathcal {H})^N$
satisfies
![]() $\sum _{i=1}^N \alpha _i (x_i,y_i)=(x,y)$
if and only if
$\sum _{i=1}^N \alpha _i (x_i,y_i)=(x,y)$
if and only if
![]() $\sum _{i=1}^N \alpha _i (U x_i,Uy_i)=(Ux,Uy)$
. Using (A.1) and the invariance of g, we thus obtain
$\sum _{i=1}^N \alpha _i (U x_i,Uy_i)=(Ux,Uy)$
. Using (A.1) and the invariance of g, we thus obtain
![]() $\tilde g(Ux,Uy)=\tilde g(x,y)$
for every
$\tilde g(Ux,Uy)=\tilde g(x,y)$
for every
![]() $x,y \in \mathcal {H}$
.
$x,y \in \mathcal {H}$
.
Claim 3: the map
![]() $F:=\nabla _y \tilde {g}(\cdot ,0)$
is
$F:=\nabla _y \tilde {g}(\cdot ,0)$
is
![]() $\mathsf {G}_{\mathcal {H}}$
-invariant.
$\mathsf {G}_{\mathcal {H}}$
-invariant.
Since we know that
![]() $\tilde g$
is Frechét differentiable, we observe that
$\tilde g$
is Frechét differentiable, we observe that
![]() $z= F(x)$
if and only if
$z= F(x)$
if and only if
Being
![]() $\tilde g$
invariant, for every
$\tilde g$
invariant, for every
![]() $U\in \mathsf {G}_{\mathcal {H}}$
and
$U\in \mathsf {G}_{\mathcal {H}}$
and
![]() $x\in \mathcal {H}$
, the above formula immediately yields
$x\in \mathcal {H}$
, the above formula immediately yields
 $$ \begin{align*} \tilde g(Ux,y)&= \tilde g(Ux,UU^{-1}y)= \tilde g(x,U^{-1}y) \\&= \tilde g(x,0)+\langle z,U^{-1}y\rangle +o(|U^{-1}y|) \\&= \tilde g(Ux,0)+\langle Uz,y\rangle +o(|y|) \quad \text{as }y\to 0, \end{align*} $$
$$ \begin{align*} \tilde g(Ux,y)&= \tilde g(Ux,UU^{-1}y)= \tilde g(x,U^{-1}y) \\&= \tilde g(x,0)+\langle z,U^{-1}y\rangle +o(|U^{-1}y|) \\&= \tilde g(Ux,0)+\langle Uz,y\rangle +o(|y|) \quad \text{as }y\to 0, \end{align*} $$
so that
![]() $F(Ux)=Uz=UF(x)$
.
$F(Ux)=Uz=UF(x)$
.