Energy measurement system of a large-aperture high power laser experiment platform

Abstract

An energy measurement system in a Large-aperture high power laser experiment platform is introduced. The entire measurement system includes five calorimeters, which carry out the energy measurement of the fundamental frequency before the frequency conversion unit, remaining fundamental frequency, remain second-harmonics, third harmonics, as well as the energy balance measurement after the frequency conversion unit. Combinational indirect calibration and direct calibration are employed to calibrate the sampling coefficients of the calorimeters. The analysis of the data showed that, regarding the energy balance coefficients, combinational calibration approach gives a higher precision, and leads to an energy balance with 1%; and regarding the energy sampling coefficients for the various wavelengths after the frequency conversion, the results from direct and combinational calibration are consistent. The uncertainties for all energy sampling coefficients are within 3%, which guarantees the reliability of the energy measurement for the laser facility.

1. Introduction

The maximum output performance of the traditional high power laser facility^[1–4] is often limited by the damage of the optical units, components and the entire system under high energy flux level. This is especially so for ultraviolet optical components. Various studies show that, not only the third-harmonics, but the remaining fundamental frequency, and the second harmonics also have a serious impact on the optical component damages^[4–6]. Therefore, in order to systematically study the load capacity of the optical equipment, component and system under high intensity, it is necessary to have a high-precision measurement platform^[7–9]. Not only does this platform have to have the sophisticated capabilities for laser parameter diagnosis, online damage detection for optical components, but it must also be able to comprehensively measure energy, which can obtain the energy of the remaining fundamental frequency, remaining second-harmonics, and third-harmonics entering the optical components.

This article introduces an energy measurement system for Large-aperture High Power Laser Experiment Platform^{[10, 11]}. This system is composed of the sampling optical path and energy calorimeters, which are used to measure the energy of a single wavelength before and after the frequency conversion. We also show how to calibrate the calorimeter sampling coefficients.

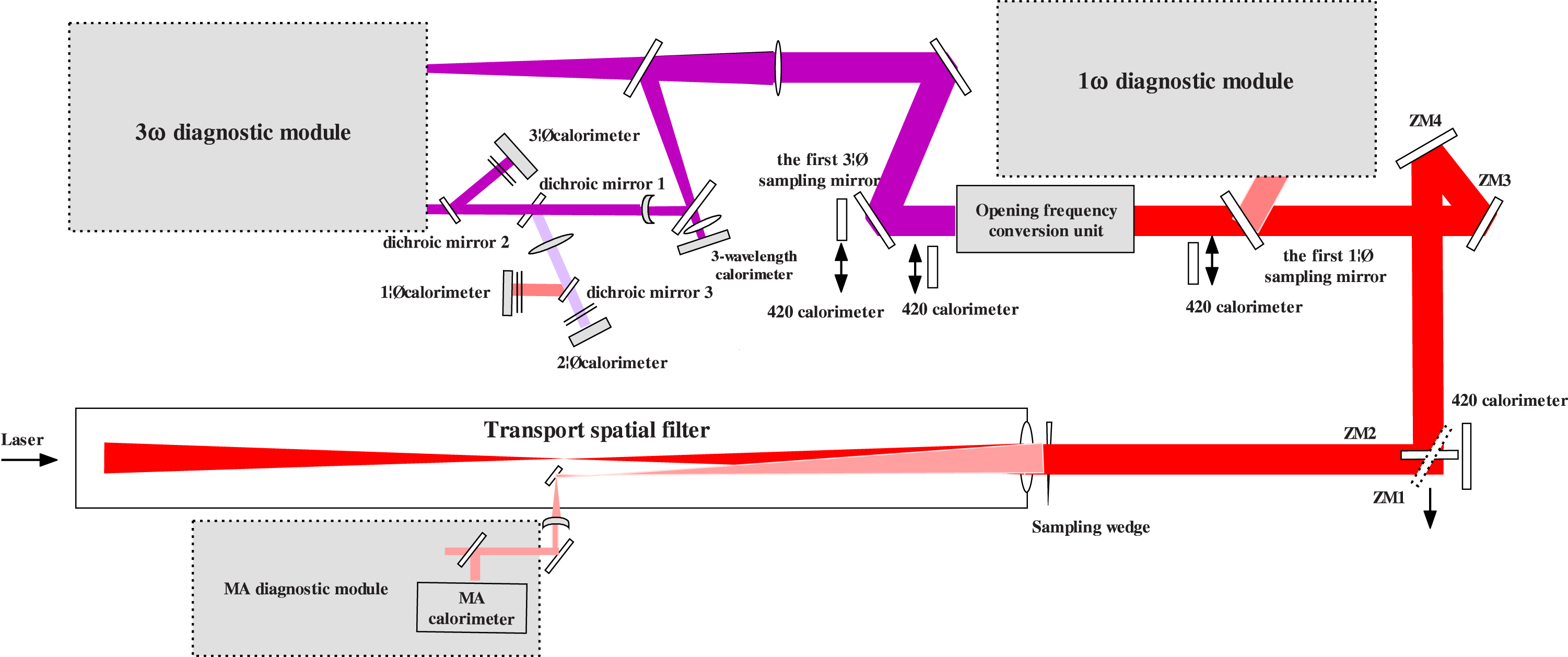
Figure 1. Schematic view of the energy diagnostic system of the large-aperture High Power Laser Experiment Platform.

2. System optical paths

Our Large-aperture High Power Laser Experiment Platform is a comprehensive experiment verification platform that can output more than tens of thousands of joules. It can be used for comprehensively evaluating the load capacity of the optical equipment, component and system under high energy flux level. The optical paths of its energy measurement system are listed as in figure 1. The laser from the last lens of the transmission spatial filter is divided into two paths: about 0.2% goes back the same optical path by sampling wedge as reflected light. Around the filtering holes in the spatial filter, the negative lens changes the beam aperture from 400 mm $\times $ 400 mm to 50 mm $\times $ 50 mm parallel light. Then it enters the calorimeter in the main amplifier diagnostic module, where the fundamental frequency laser energy is measured. After the main laser transmitted from the sampling wedge passes the vertically placed reflection mirrors ZM1 and ZM2, the height of the laser beam was lowered down to about 1.2 m above the ground. At the same time, the optical path is rotated for $90^\circ $. And then it enters the ZM3 and ZM4 both at an angle of incidence of $22.5^\circ $, where the laser is turned to go parallel with the transport spatial filter. After being transmitted by the fundamental frequency sampling mirror 1, the light goes into the frequency conversion unit. The mixed parallel laser beams after the crystal conversion (remaining fundamental frequency, remaining second-harmonics, third-harmonics) enters the third-harmonics sampling mirror 1. After the reflected light is reflected and sampled by the third-harmonics sampling mirror 2, it enters the large-aperture beam shrink optical path, where the light beam is transformed into a 50 mm $\times $ 50 mm parallel light to complete the relevant parameter diagnosis of the third-harmonics. Its transmitted light is then absorbed by the absorber. An interface to a large-aperture calorimeter is placed in front of the absorber, so it can calibrate the total energy when needed.

There are two reflection mirrors in the third-harmonics system to turn the optical path. After being transmitted from the second reflection mirror, and being collimated by the three-wavelength collimation lens, it enters the three-wavelength calorimeter. That accomplishes the sampling of all three wavelengths.

The light through the third-harmonics beam shrink system is a mixture of fundamental frequency, second-harmonics and third-harmonics. After being reflected by dichroic mirror 1 and dichroic mirror 2, the light enters third-harmonics calorimeter. The purpose of dichroic mirror 1 is to only transmit third-harmonics light, and only reflect fundamental frequency and second-harmonics light; dichroic mirror 2 is a half-transmission-half-reflection mirror. At the same time, it serves as a wave aberration compensation for any measurement that follows.

After the mixed light is reflected by dichroic mirror 1, it becomes a mixture of fundamental frequency and second-harmonics. Due to the chromatic aberration, it needs to be collimated. After being converged by the energy convergence lens, the light was projected on dichroic mirror 3. Its reflected light enters the fundamental frequency calorimeter, and the transmitted light enters the second-harmonics calorimeter.

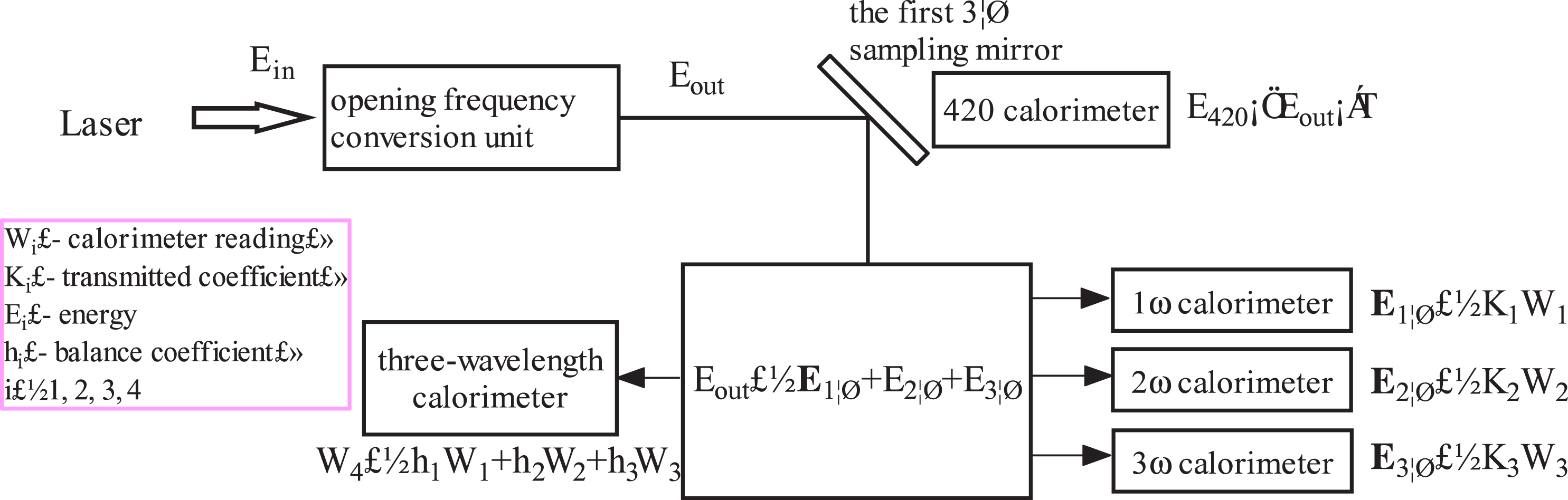
Figure 2. After-crystal energy relationship diagram.

A filter was placed in front of each single-wavelength calorimeter, to ensure that the light entering the calorimeter is actually of a single wavelength.

Based on the modularization design requirement, all the calorimeters in the system use uniform calibers, and are composed of energy sensors, amplifiers, and display modules. The entire energy measurement system is centrally sampled and processed through remote control^{[12, 13]}.

3. System calibration

For the fundamental frequency part of the main optical path, the energy values of two key points need to be known: the main amplifier output energy $E$ (after the sampling wedge in figure 1), and the energy before the crystal in the frequency conversion unit $E_{\mathrm{in}}$. They can both be given by the main amplifier calorimeter. Therefore it is necessary to calibrate based on the sampling coefficients^[14]. First, we take the light guide ZM1 out of the optical path, and replace it with a standard calorimeter with a caliber of 420 mm $\times $ 420 mm, (420 standard calorimeter), to calibrate the main amplifier output energy. The sampling coefficient of the main amplifier calorimeter is given by: $k_{\mathrm{MA}}=E_{420}/W_{\mathrm{MA}}$, where $E_{420}$ is the energy given by the 420 calorimeter; $W_{\mathrm{MA}}$ is the main amplifier calorimeter readings. Then we place the 420 calorimeter in front of the frequency conversion unit. The same approach is used on the main amplifier calorimeter to calculate the energy sampling coefficient, $k_{\mathrm{in}}$, before the frequency conversion unit. Therefore the main amplifier output energy, $E_{\mathrm{MA}}$, as well as the energy before the crystal in the frequency conversion unit, $E_{\mathrm{in}}$, are both given by the main amplifier calorimeter: $E_{\mathrm{MA}}=k_{\mathrm{MA}}\, W_{\mathrm{MA}}$, $E_{\mathrm{in}}=k_{\mathrm{in}}\, E_{\mathrm{MA}}$.

Here are four calorimeters after the frequency conversion unit. They are used to measure the energy of the remaining fundamental frequency, remaining second-harmonics, third-harmonics, and to sample the total energy for the purpose of energy balance. Their relationship can be shown in figure 2. Here the single wavelength calorimeter readings are from after the crystal. Energy balance refers to that the sampling coefficients of the single-wavelength calorimeters maintain a constant quantitative relationship, which can be used to monitor the reliability of various sampling coefficients. Since there is no target focusing lens in the frequency conversion unit, it is difficult to achieve harmonic separation^{[3, 4]}. Therefore they cannot be calibrated using traditional perforation method. Two different methods are employed here: direction and combinational calibration.

3.1. Direct calibration

We place the 420 standard calorimeter after the third-harmonics sampling mirror 1, and insert an absorbing glass element between the frequency conversion unit and the mirror 1, (two $1\omega $- and one $2\omega $- absorbing glass), to let only third-harmonics light pass for the main laser shot. That makes only third-harmonics calorimeter and the three-wavelength calorimeter have readings, and leads to the sampling coefficient of the third-harmonics ${K}'_{3} (E_{420} ={K}'_{3} W_{3})$, as well as the energy balancing coefficient $h_{3}(W_{4}=h_{3}W_{3})$. Then we adjust the third-harmonics crystal, and only let fundamental frequency and second-harmonics pass the frequency conversion. Then we remove the $2\omega $ absorbing glass, and only let second-harmonics pass. That leads to the sampling coefficient of the second-harmonics ${K}'_{2}(E_{420}={K}'_{2} W_{2})$, and its energy balancing coefficient, $h_{2}(W_{4}=h_{2}W_{2})$. Last we disable the second-harmonics, only the fundamental frequency can pass the frequency conversion unit. After taking down all the absorbing glass components, we use the main laser shot to obtain the sampling coefficient of the fundamental frequency, ${K}'_{1} (E_{420} ={K}'_{1} W_{1})$, and the energy balancing coefficient, $h_{1}(W_{4}=h_{1}W_{1})$.

Then, based on the energy transmission-reflection rate of different wavelengths from the online calibration of the third-harmonics sampling mirror 1, we get the single-wavelength sampling coefficients, $K_{1}, K_{2}$, and $K_{3}$ after the third-harmonics crystal, and before the third-harmonics sampling mirror 1.

3.2. Combinational calibration

In the direct calibration approach, often we have a small number of calibrated laser shot missions. Also because the inserted absorbing glass element is difficult to guarantee a single-wavelength output, it results in a fair amount of dispersion in the sampling coefficient. Therefore we can also employ combinational calibration approach. There is no need to insert additional filters. The steps to calibrate the sampling coefficients are as follows: first, we place the 420 calorimeter after the third-harmonics sampling mirror 1. Within the range of $0.8\sim 4\ {\rm kJ}$ (the valid measurement range of the 420 calorimeter), we take incident fundamental frequency at different energy levels. We record the total energy from three wavelengths, and use the other four calorimeters to record the readings from the remaining fundamental frequency, remaining second-harmonics and third-harmonics. Then the relationship between the calorimeter readings can be expressed as follows:

(1)$$\begin {eqnarray}E_{420i}=K'_{1}W_{1i}+{K}'_{2}W_{2i}+{K}'_{3}W_{3i}\label {eq1} \end {eqnarray}$$

(2)$$\begin {eqnarray}W_{4i}=h_{1}W_{1i}+h_{2}W_{2i}+h_{3}W_{3i}\label {eq2} \end {eqnarray}$$

where $i=1,2,\ldots $ are the different laser shot index number. Then the total sampling coefficients and the energy balancing coefficients satisfy the following matrix relationship:

(3)$$\begin {eqnarray} \left ({\begin {array}{@{}l@{}} {K}'_{1} \\ {K}'_{2} \\ {K}'_{3} \end {array}}\right ) &=& \left ({\begin {array}{@{}lll@{}} W_{1i} & W_{2i} & W_{3i} \\ W_{1j} & W_{2j} & W_{3j} \\ W_{1k} & W_{2k} & W_{3k} \end {array}}\right )^{-1}\ast \left ({\begin {array}{@{}l@{}} E_{420i} \\ E_{420j} \\ E_{420k} \end {array}}\right )\quad \left ({\begin {array}{@{}l@{}} h_{1} \\ h_{2} \\ h_{3} \end {array}}\right ) \\ &=& \left ({\begin {array}{@{}lll@{}} W_{1i} & W_{2i} & W_{3i} \\ W_{1j} & W_{2j} & W_{3j} \\ W_{1k} & W_{2k} & W_{3k} \end {array}}\right )^{-1}\ast \left ({\begin {array}{@{}l@{}} W_{4i} \\ W_{4j} \\ W_{4k} \end {array}}\right )\label {eq3} \end {eqnarray}$$

where $i$, $j$, and $k$ are the numbering of any single laser shot. Then we use linear square to run linear regression, and give average coefficients and errors. Lastly, we process the obtained the energy sampling coefficient, $K_{1}$, $K_{2}$ and $K_{3}$ using the same approach.

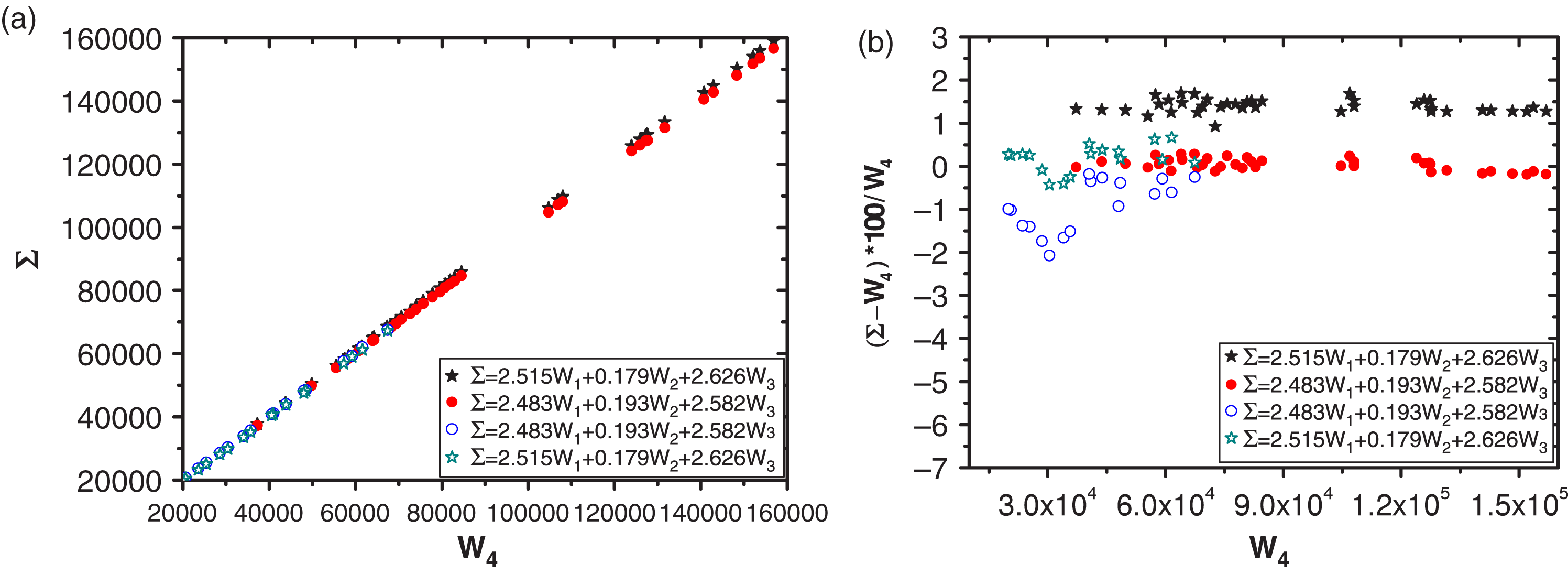
Figure 3. Comparison of the energy balancing relationship between the two approaches. (a) the relationship curve between $\Sigma =h_{1}W_{1}+h_{2}W_{2}+h_{3}W_{3}$ and energy reading from three-wavelength calorimeter reading $W_{4}$ and (b) their corresponding relative errors.

4. Results and analysis

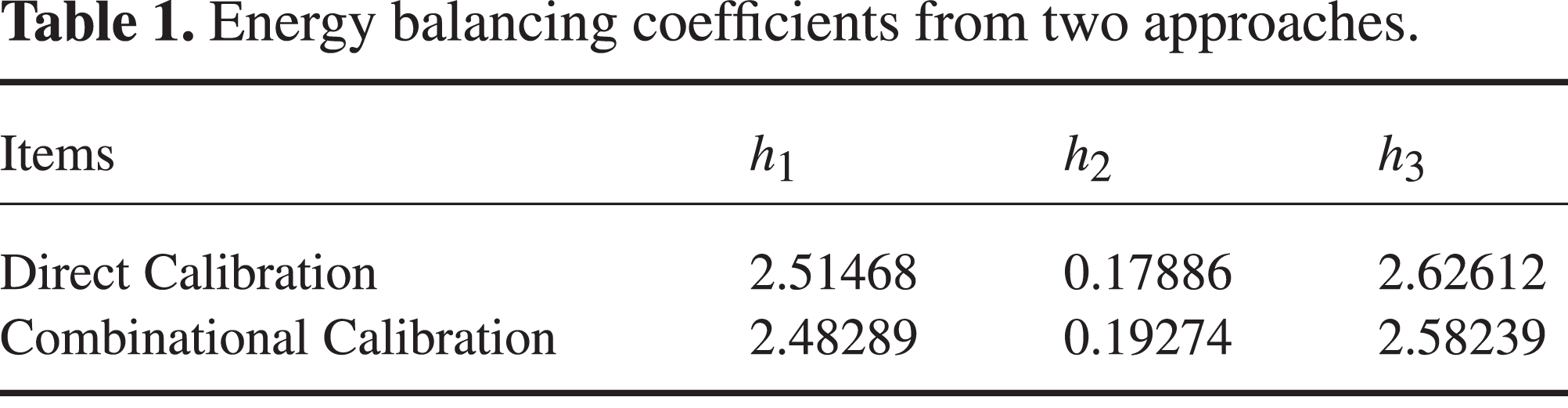
Table 1 shows the energy balancing coefficients from two calibration approaches. Figure 3 shows the corresponding energy balancing relationship. The hollow star in the figure means the energy balancing relationship obtained through direct calibration, and their relative errors. And the laser energy for only one wavelength exists after the frequency conversion at each laser shot. A solid star means the energy balancing coefficients are obtained through indirection calibration applied on mixed light. Here at each laser shot, the energy of all three wavelengths exists after the frequency conversion (remaining fundamental frequency, remaining second harmonics and third harmonics). A solid dot means to apply indirection combinational calibration on the raw data corresponding to the solid star to get the energy balancing relationship. A hollow dot means to apply the combinational calibration results on the raw data from hallow star to obtain the energy balancing relationship.

We can see from figure 3 that, with each calibration shot mission, for the direct calibration marked by the hollow star and the combinational calibration marked by solid dot, their obtained energy balancing relationship $h_{1}W_{1}+h_{2}W_{2}+h_{3}W_{3}$ and their three-wavelength calorimeter reading $W_{4}$ match very well. All relative errors are within 1%. But if we apply the coefficients from the direct calibration on a normal laser shot mission, where all remaining fundamental frequency, second-harmonics and third harmonics exist, the combinational result $h_{1}W_{1}+h_{2}W_{2}+h_{3}W_{3}$ and $W_{4}$ have a systematic error, and the relative error is about 1.4%. And if we apply the energy balancing relationship from the combinational calibration on the single-wavelength output, we also see systematic errors, in an opposite direction.

Table 1. Energy balancing coefficients from two approaches.

There are two areas of reasons for this situation. First there is a sensitivity difference in the calorimeters themselves. Since under the normal phase matching condition, the second-harmonics light from the harmonics crystal are almost all converted into third-harmonics with the crystal, the remaining second-harmonics light is far less than the remaining fundamental frequency and third-harmonics light. The design of the diagnosis system takes many factors into consideration, so that the energy sampling coefficients have a relatively smaller difference before entering the photosensitive surface in the calorimeter. Therefore, in order to guarantee the measurement precision of the second-harmonics energy, the sensitivity to the second-harmonics is about 10 times of that in the remaining fundamental frequency, third-harmonics, three-wavelength calorimeters, all of which have similar sensitivities. So during direct calibration, taking the measurement range of the 420 calorimeter into consideration, the actual energy value that enters the second-harmonics calorimeter is at the center of the linear region of this calorimeter^[15]. But that is at the bottom of the three-wavelength calorimeter linear region. Therefore this leads to higher changes in $h_{2}$ and higher dispersions from different laser shot. Another reason is that even though absorbing glass is inserted into the optical path, it is difficult to get clean third-harmonics. Also we only have limited number of shot missions, these leads to a system error in the obtained average coefficients.

Based on the analysis above, the error from combinational calibration approach is smaller. The obtained energy balance relationship is with 1%. We can use it as the guidance on the accuracy of the energy measurement. Once the deviation exceeds this value, the reason is either the measured energy values are not within the linear regions of the calorimeters, or there is a change in the energy balancing relationship. For the latter, we need to check the optical component damage in optical path.

In the process of energy balancing coefficient calibration, only the readings from four calorimeters need to be recorded. There is no need to record the input energy levels. In order to obtain the input energy level, we need to calibrate the energy sampling coefficients of the optical path. Due to the limited number of laser shot missions, we only apply one group of calibration data, that from the direct calibration, in both groups of results. The result can be seen in table 2 and figure 4. Both approaches give out similar results.

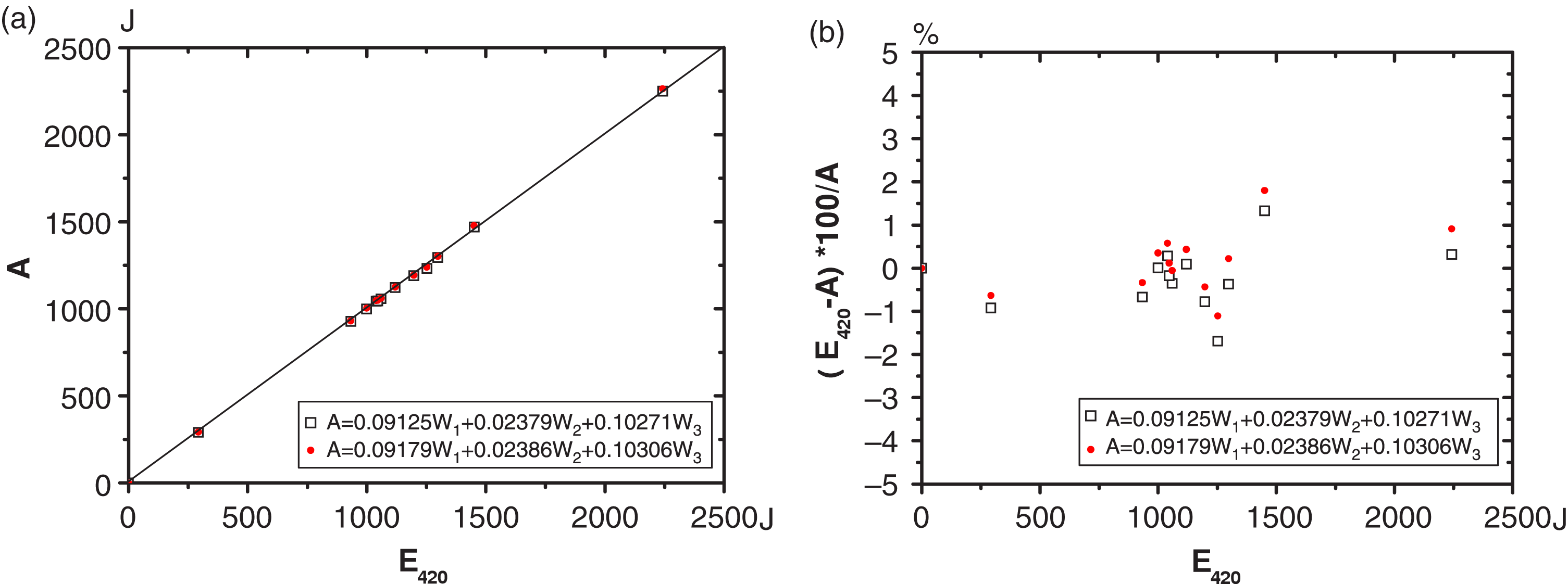
Figure 4. Comparison between the energy balancing relationships from two approaches. (a) The relationship curve between $A={K}'_{1} W_{1}+{K}'_{2} W_{2}+{K}'_{3}W_{3}$ and energy reading from the 420 calorimeter, $E_{420}$, in back of the third-harmonics sampling mirror 1 and (b) their corresponding relative errors.

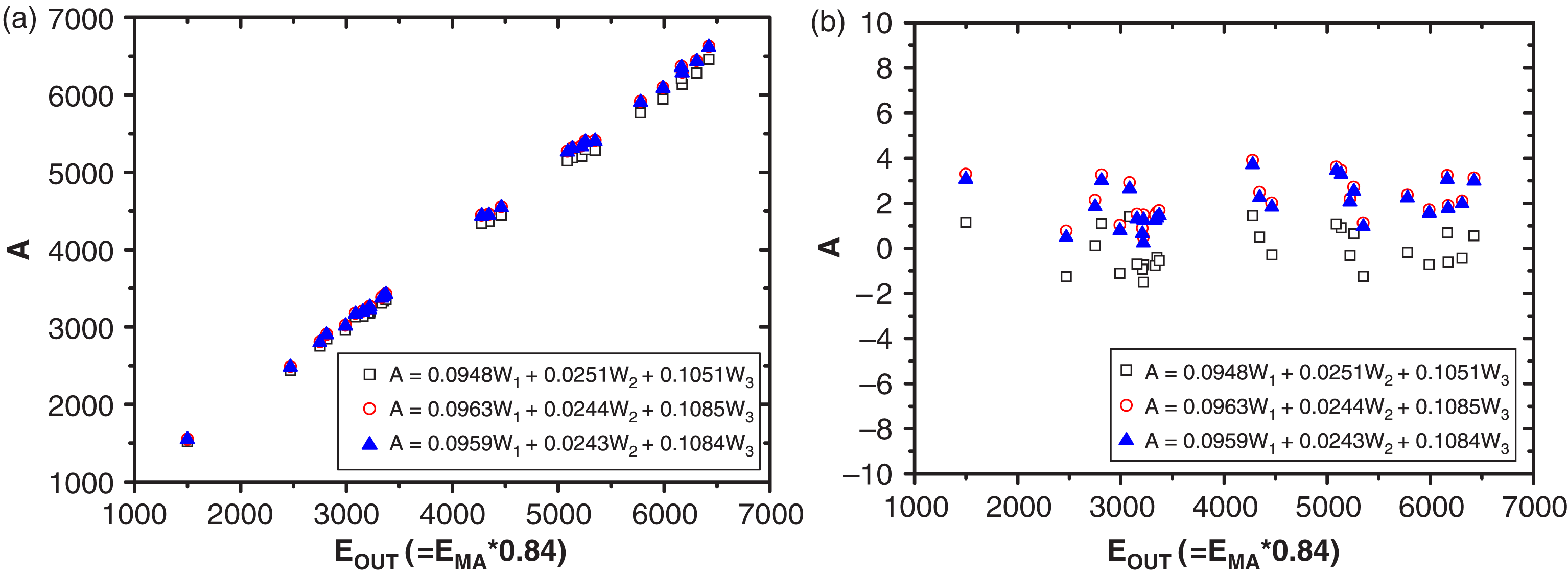
Figure 5. The relationship curve (a) between the total output energy from calibration and that derived from the main amplifier, and (b) their corresponding relative errors.

Table 2. The energy sampling coefficients from two approaches.

In order to verify the accuracy of the calibration data, we accumulate the laser shot results that follow. More specifically, we use the main amplifier energy to backward calculate the total energy after the crystal, $E_{\mathrm{out}}$. After comparing it to the after-crystal energy values from the sampling coefficient combination, we observe the consistency between the two results. The energy transmission coefficient between the main amplifier and the frequency conversion unit is $k_{\mathrm{in}}=0.95$. The transmission coefficient of the frequency conversion unit is $T=88{\%}$. We assume the transmission rate under different frequencies conversion efficiency stay the same, then the after-crystal energy, $E_{\mathrm{out}}$, can be approximated as: $E_{\mathrm{out}}=TE_{\mathrm{in}}=Tk_{\mathrm{in}}E_{\mathrm{MA}} \approx 0.84E_{\mathrm{MA}}$.

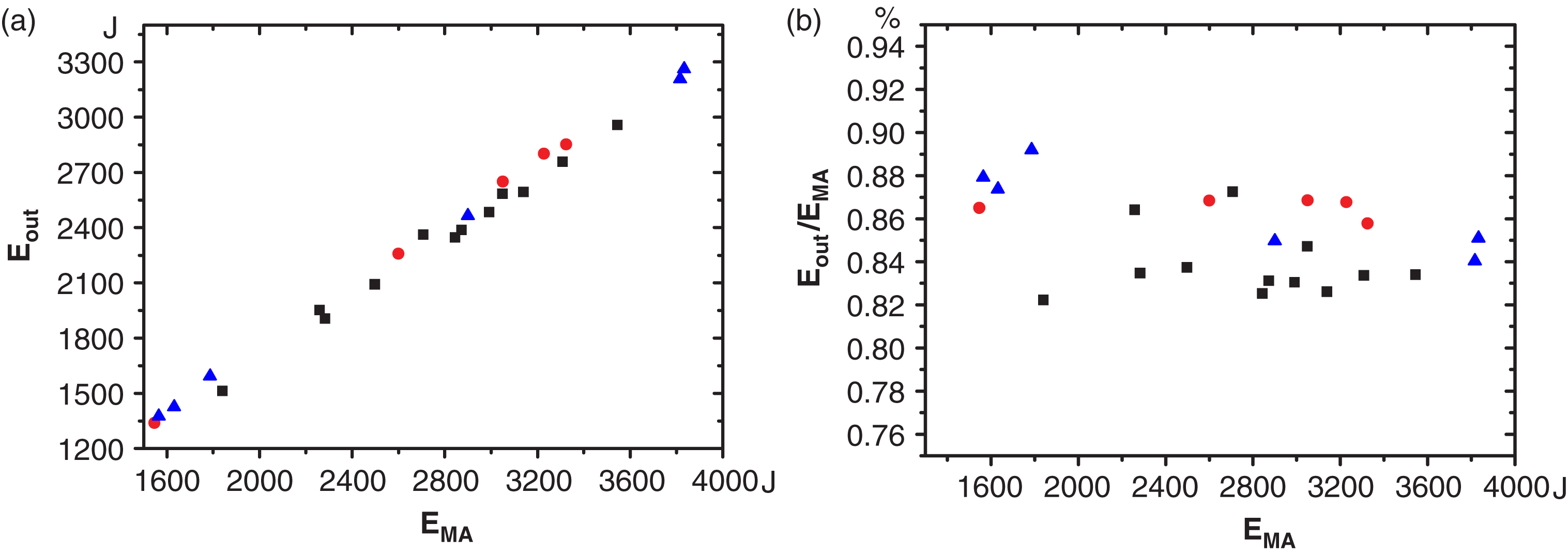
Figure 6. Under different harmonics conversion efficiencies, the relationship curve between (a) the main amplifier energy and the total output energy from the crystal, and (b) their corresponding relative errors.

The experiment results can be seen in figure 5. The hollow squares show that relationship between the derived energy from the main amplifier energy $E_{\mathrm{out}}$, and combined energy from three-single wavelength calorimeter readings using the combination approach. Hollow circles represent the energy sampling coefficients from the direct calibration, and solid triangles represent the results from the combinational calibration.

We can see from figure 5 that, there is a 2% system error between the output energy of the frequency conversion unit using the calibration, and the total output energy derived from the main amplifier. The dispersion of the average deviation is about 2%.

To explain such dispersions, besides the size of our data, also lies within the fact that the derived energy from main amplifier $E_{\mathrm{out}}$ is approximate. Since the crystal has a rather large absorption to the fundamental frequency light, there are some differences in the transmission rate from the crystal in the frequency conversion unit for different harmonics conversion efficiencies. figure 6 shows the relationship curve between the main amplifier energy, $E_{\mathrm{MA}}$, representing the total input energy $E_{\mathrm{in}}$, and the actual measured total energy output, $E_{\mathrm{out}}$, under various conversion efficiencies. The different marks in the graph represent only the measurement results at different shot period. Apparently, under different conversion efficiencies, the transmission coefficients in the frequency conversion component have variations. The deviation is around $\pm $3%. Therefore the dispersion in figure 5 only represents the deviations in $E_{\mathrm{out}}$. It is also the error introduced by the transmission coefficients of the frequency conversion unit.

Regarding the system error, the main reason lies in that the fundamental frequency transmission rate in the frequency conversion unit is 88%, (no frequency conversion), in place of the total transmission rate of the frequency conversion unit. When there is significant harmonics conversion efficiency, the total transmission rate increases. That is also the reason why the third-harmonics sampling coefficients derived from the main amplifier is relatively smaller.

5. Conclusions

This article introduces the energy measurement system in a Large-aperture high power laser experiment platform, and its calibration process. The data analysis shows that, regarding the energy balancing coefficients, results obtained from the combinational approach has a higher precision. The energy balance can be controlled within 1%. It can accurately monitor the reliability of the energy sampling efficiency. Regarding the energy sampling coefficients to all the wavelengths after the frequency conversion, the results from direct and the combinational calibration approaches are consistent. But due to the limited number of laser shot missions, there is about 2% system error in the total output energy, along with 2% dispersion. However, the results are guaranteed to ensure the single wavelength energy measurement controlled within the 4.7% uncertainty range. To further improve the energy measurement accuracy of the third-harmonics, it is necessary to have a large number of laser shot statistics. This will be the focus of our future work.