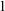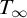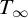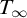1 Introduction
In the past years, we observed a rapid development of geometric tools and techniques related to model-theoretic stability theory. After a successful use of these techniques in the context of stable theories and remarkable applications in algebraic geometry, studies went beyond the class of stable theories. One of the main tools of a geometric nature in model theory is the notion of an independence relation (cf. [Reference Adler2]), which plays a key role in the description of simple theories (cf. [Reference Kim and Pillay24]). Another important geometric tool in model theory is the notion of a rank, which also can be used to characterize dividing lines in the stability hierarchy. For example, a theory is simple if and only if the local rank
![]() $D(x=x,\varphi ,k)$
is finite for every choice of a formula
$D(x=x,\varphi ,k)$
is finite for every choice of a formula
![]() $\varphi $
and every natural number k (cf. Proposition 3.13 in [Reference Casanovas4]). Actually, in the case of simple theories there is an elegant connection between the local rank D and forking independence
$\varphi $
and every natural number k (cf. Proposition 3.13 in [Reference Casanovas4]). Actually, in the case of simple theories there is an elegant connection between the local rank D and forking independence ![]() , in short: the rank decreases in an extension of types if and only if this extension is a forking extension (Proposition 5.22 in [Reference Casanovas4]). On top of that, the local rank in simple theories was used to develop the theory of generics there (see [Reference Pillay25]).
, in short: the rank decreases in an extension of types if and only if this extension is a forking extension (Proposition 5.22 in [Reference Casanovas4]). On top of that, the local rank in simple theories was used to develop the theory of generics there (see [Reference Pillay25]).
Independence relations and ranks behave less nicely in the case of non-simple NSOP
![]() $_1$
theories. The NSOP
$_1$
theories. The NSOP
![]() $_1$
theories were defined in [Reference Džamonja and Shelah17], then studied more intensively in [Reference Chernikov and Ramsey11] and in [Reference Kaplan and Ramsey20], where also the ideas from Kim’s talk (see [Reference Kim23]) came to the picture (roughly speaking: Kim proposed a notion of independence corresponding to non-dividing along Morley sequences). Further studies on NSOP
$_1$
theories were defined in [Reference Džamonja and Shelah17], then studied more intensively in [Reference Chernikov and Ramsey11] and in [Reference Kaplan and Ramsey20], where also the ideas from Kim’s talk (see [Reference Kim23]) came to the picture (roughly speaking: Kim proposed a notion of independence corresponding to non-dividing along Morley sequences). Further studies on NSOP
![]() $_1$
focused on proving desired properties of the notion of independence related to the notion of Kim-forking as defined in [Reference Kaplan and Ramsey20] (where Kim-dividing and Kim-forking were defined with the use of global invariant types), e.g., [Reference Kaplan and Ramsey21, Reference Kaplan, Ramsey and Shelah22]. A limitation of this approach is that sometimes there are no invariant global types extending a given type (however, everything is fine if we work only over models). Then, in [Reference Dobrowolski, Kim and Ramsey15], the authors redefined the notions of Kim-dividing, Kim-forking, and Kim-independence to avoid this obstacle and worked with definitions more in the spirit of [Reference Kim23]. However, they needed an extra assumption, i.e., they were working in NSOP
$_1$
focused on proving desired properties of the notion of independence related to the notion of Kim-forking as defined in [Reference Kaplan and Ramsey20] (where Kim-dividing and Kim-forking were defined with the use of global invariant types), e.g., [Reference Kaplan and Ramsey21, Reference Kaplan, Ramsey and Shelah22]. A limitation of this approach is that sometimes there are no invariant global types extending a given type (however, everything is fine if we work only over models). Then, in [Reference Dobrowolski, Kim and Ramsey15], the authors redefined the notions of Kim-dividing, Kim-forking, and Kim-independence to avoid this obstacle and worked with definitions more in the spirit of [Reference Kim23]. However, they needed an extra assumption, i.e., they were working in NSOP
![]() $_1$
theories enjoying the existence axiom for forking independence. The NSOP
$_1$
theories enjoying the existence axiom for forking independence. The NSOP
![]() $_1$
theories enjoying the existence axiom were also studied in [Reference Chernikov, Byungham and Ramsey10], where, e.g., transitivity of Kim-independence (as defined in [Reference Dobrowolski, Kim and Ramsey15]) was obtained over arbitrary sets. The important question, whether every NSOP
$_1$
theories enjoying the existence axiom were also studied in [Reference Chernikov, Byungham and Ramsey10], where, e.g., transitivity of Kim-independence (as defined in [Reference Dobrowolski, Kim and Ramsey15]) was obtained over arbitrary sets. The important question, whether every NSOP
![]() $_1$
theory automatically enjoys the existence axiom for forking independence remains open.
$_1$
theory automatically enjoys the existence axiom for forking independence remains open.
Similarly as forking independence in the case of simple theories, Kim-independence was used to describe the class of NSOP
![]() $_1$
theories (see [Reference Kaplan and Ramsey20]). Therefore one could expect that there should also exists a good notion of a rank, which, similarly to the situation in simple theories, is related to Kim-independence in the context of NSOP
$_1$
theories (see [Reference Kaplan and Ramsey20]). Therefore one could expect that there should also exists a good notion of a rank, which, similarly to the situation in simple theories, is related to Kim-independence in the context of NSOP
![]() $_1$
theories and which also describes the class of NSOP
$_1$
theories and which also describes the class of NSOP
![]() $_1$
theories (i.e., the rank is finite if and only if the theory is NSOP
$_1$
theories (i.e., the rank is finite if and only if the theory is NSOP
![]() $_1$
). Some attempts to define such a rank for NSOP
$_1$
). Some attempts to define such a rank for NSOP
![]() $_1$
theories were made in [Reference Chernikov, Byungham and Ramsey10], however they were not fully successful in relating the rank to Kim-independence (see Question 4.9 in [Reference Chernikov, Byungham and Ramsey10]). On the other hand, the rank defined in [Reference Chernikov, Byungham and Ramsey10] is finite provided T is NSOP
$_1$
theories were made in [Reference Chernikov, Byungham and Ramsey10], however they were not fully successful in relating the rank to Kim-independence (see Question 4.9 in [Reference Chernikov, Byungham and Ramsey10]). On the other hand, the rank defined in [Reference Chernikov, Byungham and Ramsey10] is finite provided T is NSOP
![]() $_1$
with existence and, in a private communication, Byunghan Kim informed us that SOP
$_1$
with existence and, in a private communication, Byunghan Kim informed us that SOP
![]() $_1$
implies that this rank is not finite (for some formula
$_1$
implies that this rank is not finite (for some formula
![]() $\varphi $
, natural number k and some type q). Thus finiteness of the rank from [Reference Chernikov, Byungham and Ramsey10] characterizes the class of NSOP
$\varphi $
, natural number k and some type q). Thus finiteness of the rank from [Reference Chernikov, Byungham and Ramsey10] characterizes the class of NSOP
![]() $_1$
theories.
$_1$
theories.
Let us mention here that also the situation with generics in NSOP
![]() $_1$
groups is more difficult than in groups with simple theory. For example, the theory of vector spaces with a generic bilinear form with values in an algebraically closed field, does not have Kim-forking generics for the additive group of vector space (see [Reference Dobrowolski14]). The theory of generics in NSOP
$_1$
groups is more difficult than in groups with simple theory. For example, the theory of vector spaces with a generic bilinear form with values in an algebraically closed field, does not have Kim-forking generics for the additive group of vector space (see [Reference Dobrowolski14]). The theory of generics in NSOP
![]() $_1$
groups is currently under development and a suitable notion of rank could be very useful in that context.
$_1$
groups is currently under development and a suitable notion of rank could be very useful in that context.
To summarize, for us, there were three main properties expected from the new notion of rank: being finite if and only if the theory is NSOP
![]() $_1$
, being related to Kim-independence, and having a prospective use in the development of generics in NSOP
$_1$
, being related to Kim-independence, and having a prospective use in the development of generics in NSOP
![]() $_1$
groups. Here is what we managed to obtain so far. Our notion of rank (Definition 3.1) is local and depends on pairs consisting of a formula and a global type. It has all the usual properties of a rank and it is finite, provided the theory T is NSOP
$_1$
groups. Here is what we managed to obtain so far. Our notion of rank (Definition 3.1) is local and depends on pairs consisting of a formula and a global type. It has all the usual properties of a rank and it is finite, provided the theory T is NSOP
![]() $_1$
. Nevertheless, it is also finite outside the class of NSOP
$_1$
. Nevertheless, it is also finite outside the class of NSOP
![]() $_1$
theories (e.g., in DLO, see Example 3.6), which was not expected, but makes the rank more interesting outside of the class of NSOP
$_1$
theories (e.g., in DLO, see Example 3.6), which was not expected, but makes the rank more interesting outside of the class of NSOP
![]() $_1$
theories (more on that in Section 6). To obtain a rank which is related to the notion of Kim-independence, we follow some ideas from the doctoral thesis of Hans Adler (see Section 2.4 in [Reference Adler2]). More precisely, our rank is not a foundation rank (i.e., defined recursively), but a rank which is witnessed by our account on dividing patterns (see [Reference Adler2]) related to Kim-dividing given as in [Reference Kaplan and Ramsey20]. In Section 3.2, we explain the connection between our rank and Kim-independence, which depends on some notions of stationarity.
$_1$
theories (more on that in Section 6). To obtain a rank which is related to the notion of Kim-independence, we follow some ideas from the doctoral thesis of Hans Adler (see Section 2.4 in [Reference Adler2]). More precisely, our rank is not a foundation rank (i.e., defined recursively), but a rank which is witnessed by our account on dividing patterns (see [Reference Adler2]) related to Kim-dividing given as in [Reference Kaplan and Ramsey20]. In Section 3.2, we explain the connection between our rank and Kim-independence, which depends on some notions of stationarity.
After noticing that our notion of rank might be finite outside of NSOP
![]() $_1$
, we investigated behaviour of the rank in the case of NTP
$_1$
, we investigated behaviour of the rank in the case of NTP
![]() $_2$
theories. It turned out that a slight modification of the main definition (compare Definition 3.1 and Definition 6.11) results in finiteness of the rank in any theory of finite dp-rank. Moreover, the modified rank is bounded by the inp-rank and hence by the dp-rank. On top of that, the aforementioned modification does not affect the notion of our rank in the case of NSOP
$_2$
theories. It turned out that a slight modification of the main definition (compare Definition 3.1 and Definition 6.11) results in finiteness of the rank in any theory of finite dp-rank. Moreover, the modified rank is bounded by the inp-rank and hence by the dp-rank. On top of that, the aforementioned modification does not affect the notion of our rank in the case of NSOP
![]() $_1$
theories. Therefore, in this paper, we provide a notion of local rank which shares finiteness in two opposite corners of the stability hierarchy, which seems to be quite intriguing. Perhaps, a good notion of rank will be more suitable to work across different dividing lines in the neo-stability hierarchy than a notion of independence (like, for example, thorn-independence). On top of that, to provide the definition of ranks in Section 6, we introduce semi-global types and show Kim’s lemma for Kim-dividing witnessed via sequences in semi-global types.
$_1$
theories. Therefore, in this paper, we provide a notion of local rank which shares finiteness in two opposite corners of the stability hierarchy, which seems to be quite intriguing. Perhaps, a good notion of rank will be more suitable to work across different dividing lines in the neo-stability hierarchy than a notion of independence (like, for example, thorn-independence). On top of that, to provide the definition of ranks in Section 6, we introduce semi-global types and show Kim’s lemma for Kim-dividing witnessed via sequences in semi-global types.
In Section 4 we study forking in the theory
![]() $T_\infty $
of infinite-dimensional vector spaces over an algebraically closed field with a generic bilinear form, which is one of the main algebraic examples of a non-simple NSOP
$T_\infty $
of infinite-dimensional vector spaces over an algebraically closed field with a generic bilinear form, which is one of the main algebraic examples of a non-simple NSOP
![]() $_1$
theory. We describe forking of formulae in
$_1$
theory. We describe forking of formulae in
![]() $T_\infty $
, answering in particular a question from [Reference Granger18] about equivalence of dividing and dividing finitely, and yielding, to the best of our knowledge, first example of a non-simple NSOP
$T_\infty $
, answering in particular a question from [Reference Granger18] about equivalence of dividing and dividing finitely, and yielding, to the best of our knowledge, first example of a non-simple NSOP
![]() $_1$
theory in which forking and dividing coincide for formulae.
$_1$
theory in which forking and dividing coincide for formulae.
The paper is organized as follows. In Section 2, we recall definitions and several facts needed later. Section 3 contains the definition and some basic properties of the new rank; then the new rank is related to the notion of Kim-independence. Section 4 is focused on forking in the theory
![]() $T_{\infty }$
and verifies auxiliary notions introduced in the previous section. In Section 5, we collect more examples of NSOP
$T_{\infty }$
and verifies auxiliary notions introduced in the previous section. In Section 5, we collect more examples of NSOP
![]() $_1$
theories and we discuss the three relevant notions of independence. Finally, in Section 6, we go with our rank beyond the class of NSOP
$_1$
theories and we discuss the three relevant notions of independence. Finally, in Section 6, we go with our rank beyond the class of NSOP
![]() $_1$
theories.
$_1$
theories.
2 Basics about NSOP
 $_1$
$_1$
As usual, we work with a complete
![]() $\mathcal {L}$
-theory T and with a monster model
$\mathcal {L}$
-theory T and with a monster model
![]() $\mathfrak {C}$
of T, i.e., a
$\mathfrak {C}$
of T, i.e., a
![]() $\kappa $
-strongly homogeneous and
$\kappa $
-strongly homogeneous and
![]() $\kappa $
-saturated model of T for some big cardinal
$\kappa $
-saturated model of T for some big cardinal
![]() $\kappa $
. By a small tuple/subset/substructure we mean some tuple/subset/substructure of size strictly smaller than
$\kappa $
. By a small tuple/subset/substructure we mean some tuple/subset/substructure of size strictly smaller than
![]() $\kappa $
. Unless stated otherwise, all considered tuples/subsets/substructures will be small. For example,
$\kappa $
. Unless stated otherwise, all considered tuples/subsets/substructures will be small. For example,
![]() $A\subseteq \mathfrak {C}$
tacitly implies that
$A\subseteq \mathfrak {C}$
tacitly implies that
![]() $|A|<\kappa $
. In short, we follow conventions being standard in model theory, e.g., outlined in [Reference Casanovas4, Reference Tent and Ziegler26].
$|A|<\kappa $
. In short, we follow conventions being standard in model theory, e.g., outlined in [Reference Casanovas4, Reference Tent and Ziegler26].
At the beginning, we need to evoke several definitions and facts about Kim-dividing and NSOP
![]() $_1$
theories. A reader unfamiliar with the subject may consult, e.g., [Reference Chernikov, Byungham and Ramsey10, Reference Dobrowolski, Kim and Ramsey15, Reference Kaplan and Ramsey20].
$_1$
theories. A reader unfamiliar with the subject may consult, e.g., [Reference Chernikov, Byungham and Ramsey10, Reference Dobrowolski, Kim and Ramsey15, Reference Kaplan and Ramsey20].
Definition 2.1. A formula
![]() $\varphi (x;y)$
has SOP
$\varphi (x;y)$
has SOP
![]() $_1$
(Strict Order Property of the first kind) if there exists a collection of tuples
$_1$
(Strict Order Property of the first kind) if there exists a collection of tuples
![]() $(a_{\eta })_{\eta \in 2^{<\omega }}$
such that:
$(a_{\eta })_{\eta \in 2^{<\omega }}$
such that:
-
(1)
 $\{\varphi (x;a_{\eta |_{\alpha }})\;|\;\alpha <\omega \}$
is consistent for every
$\{\varphi (x;a_{\eta |_{\alpha }})\;|\;\alpha <\omega \}$
is consistent for every
 $\eta \in 2^\omega $
,
$\eta \in 2^\omega $
, -
(2) if
 $\eta \in 2^{<\omega }$
and
$\eta \in 2^{<\omega }$
and
 $\nu \trianglerighteq \eta \smallfrown \langle 0\rangle $
, then
$\nu \trianglerighteq \eta \smallfrown \langle 0\rangle $
, then
 $\{\varphi (x;a_{\nu }),\,\varphi (x;a_{\eta \smallfrown \langle 1\rangle })\}$
is inconsistent,
$\{\varphi (x;a_{\nu }),\,\varphi (x;a_{\eta \smallfrown \langle 1\rangle })\}$
is inconsistent,
where
![]() $\trianglelefteq $
denotes the tree partial order on
$\trianglelefteq $
denotes the tree partial order on
![]() $2^{<\omega }$
. The theory T has SOP
$2^{<\omega }$
. The theory T has SOP
![]() $_1$
if there is a formula which has SOP
$_1$
if there is a formula which has SOP
![]() $_1$
. Otherwise we say that T is NSOP
$_1$
. Otherwise we say that T is NSOP
![]() $_1$
.
$_1$
.
Definition 2.2. We say that T enjoys the existence axiom for forking independence if for each set A and each tuple b we have that ![]() . If T is NSOP
. If T is NSOP
![]() $_1$
and enjoys the existence axiom for forking independence, then we say that T is NSOP
$_1$
and enjoys the existence axiom for forking independence, then we say that T is NSOP
![]() $_1$
with existence.
$_1$
with existence.
Definition 2.3 (Morley sequence in a type).
Let
![]() $A\subseteq \mathfrak {C}$
,
$A\subseteq \mathfrak {C}$
,
![]() $p(y)\in S(A)$
, and let
$p(y)\in S(A)$
, and let
![]() $(I,<)$
be a linearly ordered set. We call a sequence
$(I,<)$
be a linearly ordered set. We call a sequence
![]() $(b_i)_{i\in I}$
a Morley sequence in p if:
$(b_i)_{i\in I}$
a Morley sequence in p if:
-
(1)
 for each
for each
 $i\in I$
,
$i\in I$
, -
(2)
 $(b_i)_{i\in I}$
is A-indiscernible,
$(b_i)_{i\in I}$
is A-indiscernible, -
(3)
 $b_i\models p$
for each
$b_i\models p$
for each
 $i\in I$
.
$i\in I$
.
Definition 2.4 (Morley sequence in an invariant global type).
Assume that
![]() $q(y)\in S(\mathfrak {C})$
(i.e., q is a global type) is A-invariant and let
$q(y)\in S(\mathfrak {C})$
(i.e., q is a global type) is A-invariant and let
![]() $(I,<)$
be a linearly ordered set. By a Morley sequence in q over A (of order type I) we understand a sequence
$(I,<)$
be a linearly ordered set. By a Morley sequence in q over A (of order type I) we understand a sequence
![]() $\bar {b}=(b_i)_{i\in I}$
such that
$\bar {b}=(b_i)_{i\in I}$
such that
![]() $b_i\models q|_{Ab_{<i}}$
for each
$b_i\models q|_{Ab_{<i}}$
for each
![]() $i\in I$
. By
$i\in I$
. By
![]() $q^{\otimes I}$
we indicate the global A-invariant type in variables
$q^{\otimes I}$
we indicate the global A-invariant type in variables
![]() $(x_i)_{i\in I}$
such that for any
$(x_i)_{i\in I}$
such that for any
![]() $B\supseteq A$
, if
$B\supseteq A$
, if
![]() $\bar {b}\models q^{\otimes I}|_B$
then then
$\bar {b}\models q^{\otimes I}|_B$
then then
![]() $b_i\models q|_{Bb_{<i}}$
for all
$b_i\models q|_{Bb_{<i}}$
for all
![]() $i\in I$
.
$i\in I$
.
Therefore, if
![]() $q(y)\in S(\mathfrak {C})$
is A-invariant, we have two possible notions of a Morley sequence: a Morley sequence in
$q(y)\in S(\mathfrak {C})$
is A-invariant, we have two possible notions of a Morley sequence: a Morley sequence in
![]() $q|_A$
and a Morley sequence in q over A. Of course, a Morley sequence in q over A is a Morley sequence in
$q|_A$
and a Morley sequence in q over A. Of course, a Morley sequence in q over A is a Morley sequence in
![]() $q|_A$
. The converse does not hold in general.
$q|_A$
. The converse does not hold in general.
Definition 2.5. Let
![]() $q(y)$
be an A-invariant global type. We say that a formula
$q(y)$
be an A-invariant global type. We say that a formula
![]() $\varphi (x;y)\ q$
-divides over A if for some (equivalently: any) Morley sequence
$\varphi (x;y)\ q$
-divides over A if for some (equivalently: any) Morley sequence
![]() $(b_i)_{i<\omega }$
in q over A, the set
$(b_i)_{i<\omega }$
in q over A, the set
![]() $\{\varphi (x,b_i)\;|\;i<\omega \}$
is inconsistent.
$\{\varphi (x,b_i)\;|\;i<\omega \}$
is inconsistent.
We have the following two notions of Kim-dividing, (A) appears in [Reference Dobrowolski, Kim and Ramsey15] and (B) appear in [Reference Kaplan and Ramsey20]. For us notion (A) is the one which we will use here. However, Theorem 7.7 from [Reference Kaplan and Ramsey20] implies that (A) and (B) coincide over a model (i.e., if
![]() $A=M\preceq \mathfrak {C}$
) provided T is NSOP
$A=M\preceq \mathfrak {C}$
) provided T is NSOP
![]() $_1$
, and therefore we will switch very often to notion (B) if the situation is placed over a model.
$_1$
, and therefore we will switch very often to notion (B) if the situation is placed over a model.
Definition 2.6. Let
![]() $A\subseteq \mathfrak {C}$
.
$A\subseteq \mathfrak {C}$
.
-
(A) Assume that
 $k\in \mathbb {N}\setminus \{0\}$
. We say that
$k\in \mathbb {N}\setminus \{0\}$
. We say that
 $\varphi (x,b)\ k$
-Kim-divides over A if there exists a Morley sequence
$\varphi (x,b)\ k$
-Kim-divides over A if there exists a Morley sequence
 $(b_i)_{i<\omega }$
in
$(b_i)_{i<\omega }$
in
 $\operatorname {tp}(b/A)$
such that
$\operatorname {tp}(b/A)$
such that
 $\{\varphi (x,b_i)\;|\;i<\omega \}$
is k-inconsistent. We say that
$\{\varphi (x,b_i)\;|\;i<\omega \}$
is k-inconsistent. We say that
 $\varphi (x,b)$
Kim-divides over A if there exists
$\varphi (x,b)$
Kim-divides over A if there exists
 $k\in \mathbb {N}\setminus \{0\}$
such that
$k\in \mathbb {N}\setminus \{0\}$
such that
 $\varphi (x,b)\ k$
-Kim-divides over A.
$\varphi (x,b)\ k$
-Kim-divides over A. -
(B) We say that
 $\varphi (x;b)$
Kim-divides over A if there exists an A-invariant global type
$\varphi (x;b)$
Kim-divides over A if there exists an A-invariant global type
 $q(y)\supseteq \operatorname {tp}(b/A)$
such that
$q(y)\supseteq \operatorname {tp}(b/A)$
such that
 $\varphi (x;y)\ q$
-divides over A. Equivalently, we say that
$\varphi (x;y)\ q$
-divides over A. Equivalently, we say that
 $\varphi (x;b)$
Kim-divides over A if there exists an A-invariant global type
$\varphi (x;b)$
Kim-divides over A if there exists an A-invariant global type
 $q(y)\supseteq \operatorname {tp}(b/A)$
and a Morley sequence
$q(y)\supseteq \operatorname {tp}(b/A)$
and a Morley sequence
 $(b_i)_{i<\omega }\models q^{\otimes \omega }|_A$
such that
$(b_i)_{i<\omega }\models q^{\otimes \omega }|_A$
such that
 $b_0=b$
and the set
$b_0=b$
and the set
 $\{\varphi (x,b_i)\;|\;i<\omega \}$
is inconsistent.
$\{\varphi (x,b_i)\;|\;i<\omega \}$
is inconsistent.
Fact 2.7 (Kim’s lemma over models).
Assume that T has NSOP
![]() $_1$
and let
$_1$
and let
![]() $M\preceq \mathfrak {C}$
. The following are equivalent:
$M\preceq \mathfrak {C}$
. The following are equivalent:
-
(1)
 $\varphi (x;b)$
Kim-divides over M,
$\varphi (x;b)$
Kim-divides over M, -
(2) for any M-invariant global type
 $q(y)\supseteq \operatorname {tp}(b/M)$
and any Morley sequence
$q(y)\supseteq \operatorname {tp}(b/M)$
and any Morley sequence
 $(b_i)_{i<\omega }\models q^{\otimes \omega }|_M$
we have that the set
$(b_i)_{i<\omega }\models q^{\otimes \omega }|_M$
we have that the set
 $\{\varphi (x,b_i)\;|\;i<\omega \}$
is inconsistent.
$\{\varphi (x,b_i)\;|\;i<\omega \}$
is inconsistent.
Later on, we will define a local rank related to the notion of Kim-dividing. Our rank will focus on Kim-dividing over models, so one could ask how much of the picture is lost if we restrict our attention only to Kim-dividing over models. First, let us make an observation easily following from the definition: if
![]() $\varphi (x,b)$
Kim-divides over A with respect to definition (B) and
$\varphi (x,b)$
Kim-divides over A with respect to definition (B) and
![]() $A\subseteq B$
then there exists
$A\subseteq B$
then there exists
![]() $c\equiv _A b$
such that
$c\equiv _A b$
such that ![]() and such that
and such that
![]() $\varphi (x,c)$
Kim-divides over B with respect to definition (B). This means that passing to Kim-dividing over models is not so harmful if we decide to work with the definition (B). The following lemma shows the same for the notion of Kim-dividing from the definition (A). The proof is not a surprise in any meaning, but let us follow the argument for a little warm-up.
$\varphi (x,c)$
Kim-divides over B with respect to definition (B). This means that passing to Kim-dividing over models is not so harmful if we decide to work with the definition (B). The following lemma shows the same for the notion of Kim-dividing from the definition (A). The proof is not a surprise in any meaning, but let us follow the argument for a little warm-up.
Lemma 2.8 (any T).
Let
![]() $A\subseteq B$
,
$A\subseteq B$
,
![]() $\varphi (x;y)\in \mathcal {L}(A)$
. If
$\varphi (x;y)\in \mathcal {L}(A)$
. If
![]() $\varphi (x,a)\ k$
-Kim-divides over A, then there exists
$\varphi (x,a)\ k$
-Kim-divides over A, then there exists
![]() $c\equiv _A a$
such that
$c\equiv _A a$
such that ![]() and
and
![]() $\varphi (x,c)\ k$
-Kim-divides over B.
$\varphi (x,c)\ k$
-Kim-divides over B.
Proof By the definition of k-Kim-dividing, there exists an A-indiscernible sequence
![]() $(a_i)_{i<\omega }$
such that
$(a_i)_{i<\omega }$
such that
![]() $a_0=a$
, for each
$a_0=a$
, for each
![]() $i<\omega $
we have
$i<\omega $
we have ![]() and
and
![]() $\{\varphi (x,a_i)\;|\;i<\omega \}$
is k-inconsistent. We will use several properties of
$\{\varphi (x,a_i)\;|\;i<\omega \}$
is k-inconsistent. We will use several properties of ![]() , which hold in any theory T, these are listed, e.g., in Remark 5.3 in [Reference Casanovas4].
, which hold in any theory T, these are listed, e.g., in Remark 5.3 in [Reference Casanovas4].
Step 1: Increase the length of
![]() $(a_i)_{i<\omega }$
to a big cardinal
$(a_i)_{i<\omega }$
to a big cardinal
![]() $\lambda $
(big enough for the use of Erdős–Rado theorem for B-indiscernibility, see, e.g., Proposition 1.6 in [Reference Casanovas4]). To do it, consider:
$\lambda $
(big enough for the use of Erdős–Rado theorem for B-indiscernibility, see, e.g., Proposition 1.6 in [Reference Casanovas4]). To do it, consider:
 $$ \begin{align*}p(\bar{x})=p\big((x_{\alpha})_{\alpha<\lambda} \big):=\bigcup\limits_{\substack{ n<\omega \\ \alpha_0<\dots<\alpha_n<\lambda}}\operatorname{tp}(a_0\ldots a_n/Aa_0)[x_{\alpha_0},\ldots,x_{\alpha_n}].\end{align*} $$
$$ \begin{align*}p(\bar{x})=p\big((x_{\alpha})_{\alpha<\lambda} \big):=\bigcup\limits_{\substack{ n<\omega \\ \alpha_0<\dots<\alpha_n<\lambda}}\operatorname{tp}(a_0\ldots a_n/Aa_0)[x_{\alpha_0},\ldots,x_{\alpha_n}].\end{align*} $$
Let
![]() $\bar {b}=(b_{\alpha })_{\alpha <\lambda }\models p(\bar {x})$
, then
$\bar {b}=(b_{\alpha })_{\alpha <\lambda }\models p(\bar {x})$
, then
![]() $\bar {b}$
is A-indiscernible,
$\bar {b}$
is A-indiscernible,
![]() $b_0=a_0=a$
,
$b_0=a_0=a$
,
![]() $\{\varphi (x,b_{\alpha })\;|\;\alpha <\lambda \}$
is k-inconsistent. Invariance and finite character of
$\{\varphi (x,b_{\alpha })\;|\;\alpha <\lambda \}$
is k-inconsistent. Invariance and finite character of ![]() imply that also
imply that also ![]() for each
for each
![]() $\alpha <\lambda $
.
$\alpha <\lambda $
.
Step 2: Force ![]() -independence over B. We define recursively partial elementary over A maps
-independence over B. We define recursively partial elementary over A maps
![]() $f_{\alpha }:\operatorname {dcl}(Ab_{\leqslant \alpha })\to \mathfrak {C}$
, where
$f_{\alpha }:\operatorname {dcl}(Ab_{\leqslant \alpha })\to \mathfrak {C}$
, where
![]() $\alpha <\lambda $
, such that:
$\alpha <\lambda $
, such that:
-
•
 $f_{\alpha +1}|_{\operatorname {dcl}(Ab_{\leqslant \alpha })}=f_{\alpha }|_{\operatorname {dcl}({Ab_{\leqslant \alpha })}}$
,
$f_{\alpha +1}|_{\operatorname {dcl}(Ab_{\leqslant \alpha })}=f_{\alpha }|_{\operatorname {dcl}({Ab_{\leqslant \alpha })}}$
, -
•
 ,
,
for each
![]() $\alpha <\lambda $
. We start with obtaining
$\alpha <\lambda $
. We start with obtaining
![]() $f_0$
. Since
$f_0$
. Since ![]() ,
,
![]() $\operatorname {tp}(b_0/A)$
does not fork over A and so there exists a non-forking extension:
$\operatorname {tp}(b_0/A)$
does not fork over A and so there exists a non-forking extension:
Let
![]() $f_0$
be determined by
$f_0$
be determined by
![]() $f_0(b_0)=b_0'$
and
$f_0(b_0)=b_0'$
and
![]() $f_0|_A=\operatorname {id}_A$
. Now, we deal with the successor step
$f_0|_A=\operatorname {id}_A$
. Now, we deal with the successor step
![]() $\alpha \rightsquigarrow \alpha +1$
. Let
$\alpha \rightsquigarrow \alpha +1$
. Let
![]() $f_{\alpha }'\in \operatorname {Aut}(\mathfrak {C})$
extend
$f_{\alpha }'\in \operatorname {Aut}(\mathfrak {C})$
extend
![]() $f_{\alpha }$
. Because
$f_{\alpha }$
. Because ![]() , we have that
, we have that ![]() . There exists an extension
. There exists an extension
which does not fork over A, i.e., ![]() . Let
. Let
![]() $f_{\alpha +1}$
be determined by
$f_{\alpha +1}$
be determined by
![]() $f_{\alpha +1}(b_{\alpha +1})=b_{\alpha +1}'$
and
$f_{\alpha +1}(b_{\alpha +1})=b_{\alpha +1}'$
and
![]() $f_{\alpha +1}|_{\operatorname {dcl}(Ab_{\leqslant \alpha })}=f_{\alpha }|_{\operatorname {dcl}(Ab_{\leqslant \alpha })}$
. We move on to the limit ordinal step:
$f_{\alpha +1}|_{\operatorname {dcl}(Ab_{\leqslant \alpha })}=f_{\alpha }|_{\operatorname {dcl}(Ab_{\leqslant \alpha })}$
. We move on to the limit ordinal step:
![]() $\beta <\lambda $
and
$\beta <\lambda $
and
![]() $\beta \in \operatorname {Lim}$
. Let
$\beta \in \operatorname {Lim}$
. Let
![]() $f^-_{\beta }\in \operatorname {Aut}(\mathfrak {C})$
extend
$f^-_{\beta }\in \operatorname {Aut}(\mathfrak {C})$
extend
![]() $\bigcup _{\alpha <\beta }f_{\alpha }$
. From
$\bigcup _{\alpha <\beta }f_{\alpha }$
. From ![]() we obtain
we obtain ![]() , so, again, we can find an extension
, so, again, we can find an extension
which does not fork over A, i.e., ![]() . Let
. Let
![]() $f_{\beta }$
be determined by
$f_{\beta }$
be determined by
![]() $f_{\beta }(b_{\beta })=b^{\prime }_{\beta }$
and
$f_{\beta }(b_{\beta })=b^{\prime }_{\beta }$
and
![]() $f_{\beta }|_{\operatorname {dcl}(Ab_{<\beta })}=f^-_{\beta }|_{\operatorname {dcl}(Ab_{<\beta })}$
. After the recursion is done, we take
$f_{\beta }|_{\operatorname {dcl}(Ab_{<\beta })}=f^-_{\beta }|_{\operatorname {dcl}(Ab_{<\beta })}$
. After the recursion is done, we take
![]() $f\in \operatorname {Aut}(\mathfrak {C})$
which extends
$f\in \operatorname {Aut}(\mathfrak {C})$
which extends
![]() $\bigcup _{\alpha <\lambda }f_{\alpha }$
and set
$\bigcup _{\alpha <\lambda }f_{\alpha }$
and set
![]() $(b^{\prime }_{\alpha })_{\alpha <\lambda }=(f(b_{\alpha }))_{\alpha <\lambda }$
.
$(b^{\prime }_{\alpha })_{\alpha <\lambda }=(f(b_{\alpha }))_{\alpha <\lambda }$
.
Step 3: Erdős–Rado. By Erdős–Rado theorem (e.g., Proposition 1.6 in [Reference Casanovas4]), there exists a B-indiscernible sequence
![]() $(c_i)_{i<\omega }$
such that for each
$(c_i)_{i<\omega }$
such that for each
![]() $n<\omega $
there exist
$n<\omega $
there exist
![]() $\alpha _0<\dots <\alpha _n<\lambda $
satisfying
$\alpha _0<\dots <\alpha _n<\lambda $
satisfying
Thus:
-
•
 $c_0\equiv _B b^{\prime }_{\alpha _0}\equiv _A b^{\prime }_0\equiv _A b_0=a$
,
$c_0\equiv _B b^{\prime }_{\alpha _0}\equiv _A b^{\prime }_0\equiv _A b_0=a$
, -
•
 $\{\varphi (x,c_i)\;|\;i<\omega \}$
is k-inconsistent (since
$\{\varphi (x,c_i)\;|\;i<\omega \}$
is k-inconsistent (since
 $\bar {b}'\equiv _A\bar {b}$
and
$\bar {b}'\equiv _A\bar {b}$
and
 $\{\varphi (x,b_{\alpha })\;|\;\alpha <\lambda \}$
is k-inconsistent),
$\{\varphi (x,b_{\alpha })\;|\;\alpha <\lambda \}$
is k-inconsistent), -
•
 (because
(because
 $c_0\ldots c_n\equiv _B b^{\prime }_{\alpha _0}\ldots b^{\prime }_{\alpha _n}$
and
$c_0\ldots c_n\equiv _B b^{\prime }_{\alpha _0}\ldots b^{\prime }_{\alpha _n}$
and  , and
, and  satisfies monotonicity, base-monotonicity, and invariance).
satisfies monotonicity, base-monotonicity, and invariance).
Therefore
![]() $\varphi (x,c_0)\ k$
-Kim-divides over B and
$\varphi (x,c_0)\ k$
-Kim-divides over B and
![]() $c_0\equiv _A a$
.
$c_0\equiv _A a$
.
For some
![]() $\alpha _0<\lambda $
we have that
$\alpha _0<\lambda $
we have that
![]() $c_0\equiv _B b^{\prime }_{\alpha _0}$
. Then, because
$c_0\equiv _B b^{\prime }_{\alpha _0}$
. Then, because ![]() and because
and because ![]() satisfies monotonicity and invariance, we obtain that also
satisfies monotonicity and invariance, we obtain that also ![]() .
.
Definition 2.9.
-
(1) A partial type
 $\pi (x)$
Kim-forks over A if for some
$\pi (x)$
Kim-forks over A if for some $$ \begin{align*}\pi(x)\vdash\bigvee\limits_{j\leqslant n}\psi_j(x;b_j)\end{align*} $$
$$ \begin{align*}\pi(x)\vdash\bigvee\limits_{j\leqslant n}\psi_j(x;b_j)\end{align*} $$
 $n<\omega $
and
$n<\omega $
and
 $\psi _j(x;b_j)$
Kim-divides over A for each
$\psi _j(x;b_j)$
Kim-divides over A for each
 $j\leqslant n$
.
$j\leqslant n$
.
-
(2) Let a be a tuple from
 $\mathfrak {C}$
and let
$\mathfrak {C}$
and let
 $A,B\subseteq \mathfrak {C}$
. We say that a is Kim-independent from B over A, denoted by
$A,B\subseteq \mathfrak {C}$
. We say that a is Kim-independent from B over A, denoted by  , if
, if
 $\operatorname {tp}(a/AB)$
does not Kim-fork over A.
$\operatorname {tp}(a/AB)$
does not Kim-fork over A.
One could redefine the notions of Kim-forking and Kim-independence using Kim-dividing with respect to definition (B). In such a case, we will always indicate that we work with Kim-forking with respect to definition (B) or use ![]() to denote Kim-independence defined with Kim-dividing with respect to definition (B).
to denote Kim-independence defined with Kim-dividing with respect to definition (B).
The previous lemma easily leads to the following.
Corollary 2.10. Let
![]() $A\subseteq B$
,
$A\subseteq B$
,
![]() $a,d\in \mathfrak {C}$
.
$a,d\in \mathfrak {C}$
.
-
(1) If
 $\varphi (x,a)$
Kim-divides over A, then there exists
$\varphi (x,a)$
Kim-divides over A, then there exists
 $c\equiv _A a$
such that
$c\equiv _A a$
such that  and
and
 $\varphi (x,c)$
Kim-divides over B.
$\varphi (x,c)$
Kim-divides over B. -
(2) If for all
 $c\equiv _A a$
such that
$c\equiv _A a$
such that  , the formula
, the formula
 $\varphi (x,c)$
does not Kim-divide over B, then
$\varphi (x,c)$
does not Kim-divide over B, then
 $\varphi (x,a)$
does not Kim-divide over A.
$\varphi (x,a)$
does not Kim-divide over A. -
(3) If for all
 $d'\equiv _A d$
and all
$d'\equiv _A d$
and all
 $c\equiv _A a$
such that
$c\equiv _A a$
such that  we have
we have  then
then  .
.
The following characterization of NSOP
![]() $_1$
proved much more useful in studying Kim-independence than the original definition of NSOP
$_1$
proved much more useful in studying Kim-independence than the original definition of NSOP
![]() $_1$
introduced in [Reference Džamonja and Shelah17].
$_1$
introduced in [Reference Džamonja and Shelah17].
Theorem 2.11 (Theorem 8.1 in [Reference Kaplan and Ramsey20]).
The following are equivalent:
-
(1) T is NSOP
 $_1$
.
$_1$
. -
(2) Kim’s lemma for Kim-dividing: For any
 $M\preceq \mathfrak {C}$
and any
$M\preceq \mathfrak {C}$
and any
 $\varphi (x;b)$
, if
$\varphi (x;b)$
, if
 $\varphi (x;y)\ q$
-divides over M for some M-invariant
$\varphi (x;y)\ q$
-divides over M for some M-invariant
 $q(y)\in S(\mathfrak {C})$
with
$q(y)\in S(\mathfrak {C})$
with
 $\operatorname {tp}(b/M)\subseteq q(y)$
, then
$\operatorname {tp}(b/M)\subseteq q(y)$
, then
 $\varphi (x;y)\ q$
-divides over M for any M-invariant
$\varphi (x;y)\ q$
-divides over M for any M-invariant
 $q(y)\in S(\mathfrak {C})$
with
$q(y)\in S(\mathfrak {C})$
with
 $\operatorname {tp}(b/M)\subseteq q(y)$
.
$\operatorname {tp}(b/M)\subseteq q(y)$
.
Fact 2.7 has a generalization to Kim-dividing over arbitrary sets:
Theorem 2.12 (Theorem 3.5 in [Reference Dobrowolski, Kim and Ramsey15]).
Let T be NSOP
![]() $_1$
with existence. Then T satisfies Kim’s lemma for Kim-dividing over arbitrary sets: if a formula
$_1$
with existence. Then T satisfies Kim’s lemma for Kim-dividing over arbitrary sets: if a formula
![]() $\varphi (x,b)$
Kim-divides over A with respect to some Morley sequence in
$\varphi (x,b)$
Kim-divides over A with respect to some Morley sequence in
![]() $\operatorname {tp}(b/A)$
then the formula
$\operatorname {tp}(b/A)$
then the formula
![]() $\varphi (x,b)$
Kim-divides over A with respect to any Morley sequence in
$\varphi (x,b)$
Kim-divides over A with respect to any Morley sequence in
![]() $\operatorname {tp}(b/A)$
.
$\operatorname {tp}(b/A)$
.
As we will notice in a moment, Kim’s lemma for Kim-dividing (over models) will be the main reason behind the fact that our local rank is finite in the context of NSOP
![]() $_1$
theories.
$_1$
theories.
3 Rank
3.1 Definition and basic properties
In this section, we are interested in defining a local rank depending on pairs consisting of an
![]() $\mathcal {L}$
-formula and a global type. We will prove several properties of this new rank. Our idea for the rank was in some way motivated by Hans Adler’s doctoral dissertation (see [Reference Adler2]). More precisely, in Section 2 of his dissertation, Adler defines so called dividing patterns and then defines a local rank measuring the length of a maximal dividing pattern. In our case, we could not simply reuse his idea, since we are trying to “domesticate” Kim-dividing, and instead of that we propose our own variation on Kim-dividing patterns.
$\mathcal {L}$
-formula and a global type. We will prove several properties of this new rank. Our idea for the rank was in some way motivated by Hans Adler’s doctoral dissertation (see [Reference Adler2]). More precisely, in Section 2 of his dissertation, Adler defines so called dividing patterns and then defines a local rank measuring the length of a maximal dividing pattern. In our case, we could not simply reuse his idea, since we are trying to “domesticate” Kim-dividing, and instead of that we propose our own variation on Kim-dividing patterns.
Let
![]() $Q:=\big ((\varphi _0(x;y_0),q_0(y_0)),\ldots ,(\varphi _{n-1}(x;y_{n-1}),q_{n-1}(y_{n-1}) )\big )$
, where
$Q:=\big ((\varphi _0(x;y_0),q_0(y_0)),\ldots ,(\varphi _{n-1}(x;y_{n-1}),q_{n-1}(y_{n-1}) )\big )$
, where
![]() $\varphi _0,\ldots $
$\varphi _0,\ldots $
![]() $\dots ,\varphi _{n-1}\in \mathcal {L}$
and
$\dots ,\varphi _{n-1}\in \mathcal {L}$
and
![]() $q_0,\ldots ,q_{n-1}$
are global types.
$q_0,\ldots ,q_{n-1}$
are global types.
Definition 3.1. We define a local rank, called Q-rank,
For any set of
![]() $\mathcal {L}$
-formulae
$\mathcal {L}$
-formulae
![]() $\pi (x)$
we have
$\pi (x)$
we have
![]() $D_Q(\pi (x))\geqslant \lambda $
if and only if there exists
$D_Q(\pi (x))\geqslant \lambda $
if and only if there exists
![]() $\eta \in n^{\lambda }$
and
$\eta \in n^{\lambda }$
and
![]() $(b^{\alpha },M^{\alpha })_{\alpha <\lambda }$
such that:
$(b^{\alpha },M^{\alpha })_{\alpha <\lambda }$
such that:
-
(1)
 $\operatorname {dom}(\pi (x))\subseteq M^0$
,
$\operatorname {dom}(\pi (x))\subseteq M^0$
, -
(2)
 $q_0,\ldots ,q_{n-1}$
are
$q_0,\ldots ,q_{n-1}$
are
 $M^0$
-invariant,
$M^0$
-invariant, -
(3)
 $M^{\alpha }\preceq \mathfrak {C}$
for each
$M^{\alpha }\preceq \mathfrak {C}$
for each
 $\alpha <\lambda $
and
$\alpha <\lambda $
and
 $(M^{\alpha })_{\alpha <\lambda }$
is increasing and continuous,
$(M^{\alpha })_{\alpha <\lambda }$
is increasing and continuous, -
(4)
 $b^{\alpha }M^{\alpha }\subseteq M^{\alpha +1}$
for each
$b^{\alpha }M^{\alpha }\subseteq M^{\alpha +1}$
for each
 $\alpha +1<\lambda $
,
$\alpha +1<\lambda $
, -
(5)
 $b^{\alpha }\models q_{\eta (\alpha )}|_{M^{\alpha }}$
for each
$b^{\alpha }\models q_{\eta (\alpha )}|_{M^{\alpha }}$
for each
 $\alpha <\lambda $
,
$\alpha <\lambda $
, -
(6)
 $\pi (x)\cup \{\varphi _{\eta (\alpha )}(x;b^{\alpha })\;|\;\alpha <\lambda \}$
is consistent,
$\pi (x)\cup \{\varphi _{\eta (\alpha )}(x;b^{\alpha })\;|\;\alpha <\lambda \}$
is consistent, -
(7) each
 $\varphi _{\eta (\alpha )}(x;b^{\alpha })$
Kim-divides over
$\varphi _{\eta (\alpha )}(x;b^{\alpha })$
Kim-divides over
 $M^{\alpha }$
with respect to definition (B), i.e., for each
$M^{\alpha }$
with respect to definition (B), i.e., for each
 $\alpha <\lambda $
there exists an
$\alpha <\lambda $
there exists an
 $M^{\alpha }$
-invariant global type
$M^{\alpha }$
-invariant global type
 $r_{\alpha }(y_{\eta (\alpha )})$
extending
$r_{\alpha }(y_{\eta (\alpha )})$
extending
 $\operatorname {tp}(b^{\alpha }/M^{\alpha })$
and
$\operatorname {tp}(b^{\alpha }/M^{\alpha })$
and
 $\bar {b}^{\alpha }=(b^{\alpha }_i)_{i<\omega }\models r_{\alpha }^{\otimes \omega }|_{M^{\alpha }}$
such that
$\bar {b}^{\alpha }=(b^{\alpha }_i)_{i<\omega }\models r_{\alpha }^{\otimes \omega }|_{M^{\alpha }}$
such that
 $b^{\alpha }_0=b^{\alpha }$
and
$b^{\alpha }_0=b^{\alpha }$
and
 $\{\varphi _{\eta (\alpha )}(x;b^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent.
$\{\varphi _{\eta (\alpha )}(x;b^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent.
If
![]() $D_Q(\pi )\geqslant \lambda $
for each
$D_Q(\pi )\geqslant \lambda $
for each
![]() $\lambda \in \operatorname {Ord}$
, then we set
$\lambda \in \operatorname {Ord}$
, then we set
![]() $D_Q(\pi )=\infty $
. Otherwise
$D_Q(\pi )=\infty $
. Otherwise
![]() $D_Q(\pi )$
is the maximal
$D_Q(\pi )$
is the maximal
![]() $\lambda \in \operatorname {Ord}$
such that
$\lambda \in \operatorname {Ord}$
such that
![]() $D_Q(\pi )\geqslant \lambda $
.
$D_Q(\pi )\geqslant \lambda $
.
Remark 3.2. If T is NSOP
![]() $_1$
, then Definition 3.1 is equivalent to the same definition but with the condition (3) replaced by
$_1$
, then Definition 3.1 is equivalent to the same definition but with the condition (3) replaced by
-
(3*)
 $M^{\alpha }\preceq \mathfrak {C}$
for each
$M^{\alpha }\preceq \mathfrak {C}$
for each
 $\alpha <\lambda $
,
$\alpha <\lambda $
,
 $(M^{\alpha })_{\alpha <\lambda }$
is continuous, and each
$(M^{\alpha })_{\alpha <\lambda }$
is continuous, and each
 $M^{\alpha +1}$
is
$M^{\alpha +1}$
is
 $|M^{\alpha }|^+$
-saturated,
$|M^{\alpha }|^+$
-saturated,
or even by
-
(3**)
 $M^{\alpha }\preceq \mathfrak {C}$
for each
$M^{\alpha }\preceq \mathfrak {C}$
for each
 $\alpha <\lambda $
,
$\alpha <\lambda $
,
 $(M^{\alpha })_{\alpha <\lambda }$
is continuous, and each
$(M^{\alpha })_{\alpha <\lambda }$
is continuous, and each
 $M^{\alpha +1}$
is
$M^{\alpha +1}$
is
 $|M^{\alpha }|^+$
-saturated and strongly
$|M^{\alpha }|^+$
-saturated and strongly
 $|M^{\alpha }|^+$
-homogeneous.
$|M^{\alpha }|^+$
-homogeneous.
The proof is a quite standard and long recursion, which uses transitivity and symmetry of ![]() over models. Thus we omit it. If we refer to Definition 3.1 in the case of T being NSOP
over models. Thus we omit it. If we refer to Definition 3.1 in the case of T being NSOP
![]() $_1$
, we usually have in mind its equivalent formulation with the condition (3
$_1$
, we usually have in mind its equivalent formulation with the condition (3
![]() $^\ast $
).
$^\ast $
).
Let us explain a little bit the concept behind this rank. For simplicity we assume that
![]() $Q=( (\varphi ,q) )$
. Then the witnesses from the definition of
$Q=( (\varphi ,q) )$
. Then the witnesses from the definition of
![]() $D_Q(\pi )\geqslant \lambda $
,
$D_Q(\pi )\geqslant \lambda $
,
![]() $(M^{\alpha },b^{\alpha }_i)_{\alpha <\lambda ,i<\omega }$
, may be used to draw the following tree:
$(M^{\alpha },b^{\alpha }_i)_{\alpha <\lambda ,i<\omega }$
, may be used to draw the following tree:

Each horizontal sequence of
![]() $b^{\alpha }_i$
’s is a Morley sequence in some global
$b^{\alpha }_i$
’s is a Morley sequence in some global
![]() $M^{\alpha }$
-invariant type and so witnesses Kim-dividing of
$M^{\alpha }$
-invariant type and so witnesses Kim-dividing of
![]() $\varphi (x;b^{\alpha }_0)$
over
$\varphi (x;b^{\alpha }_0)$
over
![]() $M^{\alpha }$
. This is nothing new.
$M^{\alpha }$
. This is nothing new.
The first new ingredient in our rank is that we require that also the leftmost branch in our tree forms a Morley sequence, this time in the previously fixed global type q (which is
![]() $M^0$
-invariant). In other words, we focus only on Morley sequences —and that is in accordance with the intuition that all the essential data in a NSOP
$M^0$
-invariant). In other words, we focus only on Morley sequences —and that is in accordance with the intuition that all the essential data in a NSOP
![]() $_1$
theory is coded by Morley sequences.
$_1$
theory is coded by Morley sequences.
The second new ingredient in our rank is that we allow “jumps” in the extension of the base parameters between levels. More precisely, instead of the sequence
![]() $\operatorname {dom}(\pi )\subseteq M^0\preceq M^1\preceq \ldots $
, we could consider a more standard sequence
$\operatorname {dom}(\pi )\subseteq M^0\preceq M^1\preceq \ldots $
, we could consider a more standard sequence
![]() $\operatorname {dom}(\pi )\subseteq \operatorname {dom}(\pi )b^0_0\subseteq \operatorname {dom}(\pi )b^0_0b^1_0\subseteq \ldots $
. However, let us recall that
$\operatorname {dom}(\pi )\subseteq \operatorname {dom}(\pi )b^0_0\subseteq \operatorname {dom}(\pi )b^0_0b^1_0\subseteq \ldots $
. However, let us recall that ![]() does not necessarily satisfy the base monotonicity axiom, thus we allow in our rank some freedom in choosing the parameters over which each next level Kim-divides.
does not necessarily satisfy the base monotonicity axiom, thus we allow in our rank some freedom in choosing the parameters over which each next level Kim-divides.
Remark 3.3. Because in NSOP
![]() $_1$
theories the both notions of Kim-dividing ( (A) and (B) from Definition 2.6) coincide over a model and in our rank we consider only Kim-dividing over models, our rank is suitable to work with both notions of Kim-dividing in the NSOP
$_1$
theories the both notions of Kim-dividing ( (A) and (B) from Definition 2.6) coincide over a model and in our rank we consider only Kim-dividing over models, our rank is suitable to work with both notions of Kim-dividing in the NSOP
![]() $_1$
environment.
$_1$
environment.
In the following lines, we will make use of our intuition and show several nice properties of the Q-rank, we also refine the definition of Q-rank, so it will become more technical, but it will allow us to prove a few more facts. We start with something completely trivial.
Fact 3.4.
-
(1)
 $D_Q(\pi )\geqslant \lambda $
,
$D_Q(\pi )\geqslant \lambda $
,
 $f\in \operatorname {Aut}(\mathfrak {C})\ \Rightarrow \ D_{f(Q)}(f(\pi ))\geqslant \lambda $
.
$f\in \operatorname {Aut}(\mathfrak {C})\ \Rightarrow \ D_{f(Q)}(f(\pi ))\geqslant \lambda $
. -
(2) If
 $\pi '\subseteq \pi $
then
$\pi '\subseteq \pi $
then
 $D_Q(\pi )\leqslant D_{Q}(\pi ')$
.
$D_Q(\pi )\leqslant D_{Q}(\pi ')$
. -
(3)
 $D_Q(\pi )\leqslant \oplus _{j<n}D_{((\varphi _j,q_j))}(\pi )$
, where
$D_Q(\pi )\leqslant \oplus _{j<n}D_{((\varphi _j,q_j))}(\pi )$
, where
 $\oplus $
denotes the Cantor sum.
$\oplus $
denotes the Cantor sum.
Proof Items (1) and (2) follow by the definition. Item (3) follows from the following fact, which can be proven by a straightforward induction on
![]() $\alpha $
: for any ordinal
$\alpha $
: for any ordinal
![]() $\alpha =A_0\dot \cup A_1\dot \cup \cdots \dot \cup A_{n-1}$
, if
$\alpha =A_0\dot \cup A_1\dot \cup \cdots \dot \cup A_{n-1}$
, if
![]() $\alpha _i$
is the order type of
$\alpha _i$
is the order type of
![]() $A_i$
for
$A_i$
for
![]() $i<n$
, then
$i<n$
, then
![]() $\alpha \leqslant \alpha _0\oplus \alpha _1\oplus \dots \oplus \alpha _{n-1}$
.
$\alpha \leqslant \alpha _0\oplus \alpha _1\oplus \dots \oplus \alpha _{n-1}$
.
Corollary 3.5. There exists finite Q such that
![]() $D_Q(x=x)\geqslant \omega $
if and only if there exists Q such that
$D_Q(x=x)\geqslant \omega $
if and only if there exists Q such that
![]() $|Q|=1$
and
$|Q|=1$
and
![]() $D_Q(x=x)\geqslant \omega $
.
$D_Q(x=x)\geqslant \omega $
.
As we will see in a moment, the Q-rank is finite in the case of NSOP
![]() $_1$
theories, which is a desired property of our rank. It also happens that outside of NSOP
$_1$
theories, which is a desired property of our rank. It also happens that outside of NSOP
![]() $_1$
the rank may be finite, e.g., in the case of T being DLO. In the following example we work with Definition 3.1, however a more general result on finiteness of our rank in the context of NIP theories is provided in Section 6, where we work with a slightly modified definition of Q-rank (see Definition 6.11).
$_1$
the rank may be finite, e.g., in the case of T being DLO. In the following example we work with Definition 3.1, however a more general result on finiteness of our rank in the context of NIP theories is provided in Section 6, where we work with a slightly modified definition of Q-rank (see Definition 6.11).
Example 3.6. Let T be the theory of dense linear orders without endpoints, DLO. First, we will show that
![]() $D_Q(x=x)\leq 1$
for
$D_Q(x=x)\leq 1$
for
![]() $Q=(\phi (x,yz),q)$
, where q is an arbitrary invariant type and
$Q=(\phi (x,yz),q)$
, where q is an arbitrary invariant type and
![]() $ \phi (x,yz)=(y<x<z)$
. Suppose
$ \phi (x,yz)=(y<x<z)$
. Suppose
![]() $M^i, b^i_j, i< 2$
,
$M^i, b^i_j, i< 2$
,
![]() $j<\omega $
with
$j<\omega $
with
![]() $b^i_j=(a^i_j,c^i_j)$
witness that
$b^i_j=(a^i_j,c^i_j)$
witness that
![]() $D_Q(x=x)\geq 2$
. As
$D_Q(x=x)\geq 2$
. As
![]() $\phi (x;a^1_0,c^1_0)$
divides over
$\phi (x;a^1_0,c^1_0)$
divides over
![]() $a^0_0c^0_0$
(i.e., over
$a^0_0c^0_0$
(i.e., over
![]() $b^0_0$
),
$b^0_0$
),
![]() $a^0_0,c^0_0$
cannot lie in
$a^0_0,c^0_0$
cannot lie in
![]() $(a^1_0,c^1_0)$
, hence by the consistency condition we must have
$(a^1_0,c^1_0)$
, hence by the consistency condition we must have
![]() $a^0_0<a^1_0<c^1_0<c^0_0$
. But then an automorphism over
$a^0_0<a^1_0<c^1_0<c^0_0$
. But then an automorphism over
![]() $M_0$
moving
$M_0$
moving
![]() $b^0_0$
to
$b^0_0$
to
![]() $b^0_1$
will move
$b^0_1$
will move
![]() $\phi (x;a^1_0,c^1_0)$
to a formula inconsistent with it. This contradicts
$\phi (x;a^1_0,c^1_0)$
to a formula inconsistent with it. This contradicts
![]() $M_0$
-invariance of the restriction
$M_0$
-invariance of the restriction
![]() $q'$
of q to the first variable as
$q'$
of q to the first variable as
![]() $a^1_0\models q'|M_1$
.
$a^1_0\models q'|M_1$
.
Note also that if
![]() $\phi (x,y)$
is of the form
$\phi (x,y)$
is of the form
![]() $x>y$
or
$x>y$
or
![]() $x<y$
or
$x<y$
or
![]() $x=x$
, then
$x=x$
, then
![]() $D_{(\phi ,q)}(x=x)=0$
, as in that case no instance of
$D_{(\phi ,q)}(x=x)=0$
, as in that case no instance of
![]() $\phi (x,y)$
Kim-divides over any set. Also, it is easy to see that if
$\phi (x,y)$
Kim-divides over any set. Also, it is easy to see that if
![]() $\phi (x,y)=(x=y)$
then
$\phi (x,y)=(x=y)$
then
![]() $D_{(\phi ,q)}(x=x)=1$
.
$D_{(\phi ,q)}(x=x)=1$
.
Now let
![]() $Q=(\phi (x,y),q(y))$
with
$Q=(\phi (x,y),q(y))$
with
![]() $x=x_0\dots x_{n-1}$
be a variable of length n,
$x=x_0\dots x_{n-1}$
be a variable of length n,
![]() $\phi (x,y)$
a formula and
$\phi (x,y)$
a formula and
![]() $q(y)$
a global invariant type. By quantifier elimination and completeness of
$q(y)$
a global invariant type. By quantifier elimination and completeness of
![]() $q(y)$
we have that
$q(y)$
we have that
![]() $q(y)\wedge \phi (x,y)\equiv q(y)\wedge \bigvee _{i<k} \phi _i(x,y)$
where each
$q(y)\wedge \phi (x,y)\equiv q(y)\wedge \bigvee _{i<k} \phi _i(x,y)$
where each
![]() $\phi _i(x,y)$
defines a product of intervals with endpoints in the set
$\phi _i(x,y)$
defines a product of intervals with endpoints in the set
![]() $y\cup \{+\infty , -\infty \}$
.
$y\cup \{+\infty , -\infty \}$
.
We claim that
![]() $D_Q(x=x)\leq nk$
. Suppose for a contradiction that
$D_Q(x=x)\leq nk$
. Suppose for a contradiction that
![]() $D_Q(x=x)> nk$
. Then by pigeonhole principle one easily gets that
$D_Q(x=x)> nk$
. Then by pigeonhole principle one easily gets that
![]() $D_{Q'}(x=x)> n$
where
$D_{Q'}(x=x)> n$
where
![]() $Q'=(\phi _l,q)$
for some
$Q'=(\phi _l,q)$
for some
![]() $l<k$
. Let
$l<k$
. Let
![]() $(b^i,M^i)_{i<n+1}$
witness that
$(b^i,M^i)_{i<n+1}$
witness that
![]() $D_{Q'}(x=x)\geq n+1$
. Choose
$D_{Q'}(x=x)\geq n+1$
. Choose
![]() $c\models \{\phi (x,b^i):i<N\}$
and let
$c\models \{\phi (x,b^i):i<N\}$
and let
![]() $\psi (x)$
be a formula equivalent to
$\psi (x)$
be a formula equivalent to
![]() $\operatorname {qftp}(c/\emptyset )$
. By replacing
$\operatorname {qftp}(c/\emptyset )$
. By replacing
![]() $\phi _l(x,y)$
with
$\phi _l(x,y)$
with
![]() $\psi (x)\wedge \phi _l(x,y)$
we may assume
$\psi (x)\wedge \phi _l(x,y)$
we may assume
![]() $\phi _l(x,y)$
is of the form
$\phi _l(x,y)$
is of the form
![]() $\psi (x)\wedge \bigwedge _{j<n} \chi _j(x_j,y)$
, where each
$\psi (x)\wedge \bigwedge _{j<n} \chi _j(x_j,y)$
, where each
![]() $\chi _j(x_j,y)$
defines an interval with endpoints in
$\chi _j(x_j,y)$
defines an interval with endpoints in
![]() $y\cup \{+\infty , -\infty \}$
. Again by pigeonhole principle we must have that
$y\cup \{+\infty , -\infty \}$
. Again by pigeonhole principle we must have that
![]() $D_{Q"}(x=x)\geq 2$
with
$D_{Q"}(x=x)\geq 2$
with
![]() $Q"=(\psi (x)\wedge \chi _j(x_j,y))$
for some
$Q"=(\psi (x)\wedge \chi _j(x_j,y))$
for some
![]() $j<n$
. As
$j<n$
. As
![]() $\psi (x)$
is over
$\psi (x)$
is over
![]() $\emptyset $
and is consistent, we get that, for any j, any family of instances of
$\emptyset $
and is consistent, we get that, for any j, any family of instances of
![]() $\psi (x)\wedge \chi _j(x_j,y)$
is consistent if and only if the corresponding family of instances of
$\psi (x)\wedge \chi _j(x_j,y)$
is consistent if and only if the corresponding family of instances of
![]() $\chi _j(x_j,y)$
is consistent (any realisation of the latter can be extended to a realisation of
$\chi _j(x_j,y)$
is consistent (any realisation of the latter can be extended to a realisation of
![]() $\psi (x)$
, since there is a unique 1-type in DLO). Hence
$\psi (x)$
, since there is a unique 1-type in DLO). Hence
![]() $D_{Q"}(x=x)=D_{(\chi _j(x_j,y),q)}(x_j=x_j)$
. But
$D_{Q"}(x=x)=D_{(\chi _j(x_j,y),q)}(x_j=x_j)$
. But
![]() $D_{(\chi _j(x_j,y),q)}(x_j=x_j)\leq 1$
by the first two paragraphs, a contradiction.
$D_{(\chi _j(x_j,y),q)}(x_j=x_j)\leq 1$
by the first two paragraphs, a contradiction.
Definition 3.7. Let
![]() $\varphi (x;y)\in \mathcal {L}$
and let
$\varphi (x;y)\in \mathcal {L}$
and let
![]() $q(y)\in S(\mathfrak {C})$
. We define
$q(y)\in S(\mathfrak {C})$
. We define
![]() $C_{\varphi ,q}\leqslant \omega $
as
$C_{\varphi ,q}\leqslant \omega $
as
 $$ \begin{align*} C_{\varphi,q} &:= \max\{k\;|\;(\exists M\preceq\mathfrak{C},\,M\text{ is}\ M-\text{invariant}) \\ & (\exists (a_i)_{i<\omega}\models q^{\otimes\omega}|_M)(\{\varphi(x;a_i)\;|\;i<k\}\text{ is consistent})\}. \end{align*} $$
$$ \begin{align*} C_{\varphi,q} &:= \max\{k\;|\;(\exists M\preceq\mathfrak{C},\,M\text{ is}\ M-\text{invariant}) \\ & (\exists (a_i)_{i<\omega}\models q^{\otimes\omega}|_M)(\{\varphi(x;a_i)\;|\;i<k\}\text{ is consistent})\}. \end{align*} $$
Remark 3.8. Let
![]() $M,N\preceq \mathfrak {C}$
. Assume that:
$M,N\preceq \mathfrak {C}$
. Assume that:
-
• q is M-invariant,
 $(a_i)_{i<\omega }\models q^{\otimes \omega }|_M$
and
$(a_i)_{i<\omega }\models q^{\otimes \omega }|_M$
and
 $k_M$
is the maximal number (or
$k_M$
is the maximal number (or
 $\omega $
) such that
$\omega $
) such that
 $\{\varphi (x;a_i)\;|\;i<k_M\}$
is consistent.
$\{\varphi (x;a_i)\;|\;i<k_M\}$
is consistent. -
• q is N-invariant,
 $(b_i)_{i<\omega }\models q^{\otimes \omega }|_N$
and
$(b_i)_{i<\omega }\models q^{\otimes \omega }|_N$
and
 $k_N$
is the maximal number (or
$k_N$
is the maximal number (or
 $\omega $
) such that
$\omega $
) such that
 $\{\varphi (x;b_i)\;|\;i<k_M\}$
is consistent.
$\{\varphi (x;b_i)\;|\;i<k_M\}$
is consistent.
Then
![]() $k_N=k_M$
. To see this we introduce auxiliary
$k_N=k_M$
. To see this we introduce auxiliary
![]() $\bar {N}\preceq \mathfrak {C}$
which contains M and N, and a Morley sequence
$\bar {N}\preceq \mathfrak {C}$
which contains M and N, and a Morley sequence
![]() $(c_i)_{i<\omega }\models q^{\otimes \omega }|_{\bar {N}}$
. We have that
$(c_i)_{i<\omega }\models q^{\otimes \omega }|_{\bar {N}}$
. We have that
![]() $(a_i)_{i<\omega }\equiv _M (c_i)_{i<\omega }\equiv _N (b_i)_{i<\omega }$
. This remark says that
$(a_i)_{i<\omega }\equiv _M (c_i)_{i<\omega }\equiv _N (b_i)_{i<\omega }$
. This remark says that
![]() $C_{\varphi ,q}$
is in some sense a uniform bound and it can not happen that for each
$C_{\varphi ,q}$
is in some sense a uniform bound and it can not happen that for each
![]() $M\preceq \mathfrak {C}$
and each corresponding Morley sequence
$M\preceq \mathfrak {C}$
and each corresponding Morley sequence
![]() $(a_i)_{i<\omega }$
,
$(a_i)_{i<\omega }$
,
![]() $\max \{k\;|\;\{\varphi (x;a_i)\;|\;i<k\}\}$
is finite, but
$\max \{k\;|\;\{\varphi (x;a_i)\;|\;i<k\}\}$
is finite, but
![]() $C_{\varphi ,q}=\omega $
.
$C_{\varphi ,q}=\omega $
.
From now on (if not stated otherwise), we assume that T has NSOP
![]() $_1$
.
$_1$
.
Lemma 3.9. Then
![]() $D_Q(\pi )\geqslant \lambda $
if and only if there exist
$D_Q(\pi )\geqslant \lambda $
if and only if there exist
![]() $\eta \in n^\lambda $
and
$\eta \in n^\lambda $
and
![]() $\big ((b^{\alpha }_i)_{i<\omega },M^{\alpha }\big )_{\alpha <\lambda }$
such that:
$\big ((b^{\alpha }_i)_{i<\omega },M^{\alpha }\big )_{\alpha <\lambda }$
such that:
-
(1)
 $\operatorname {dom}(\pi (x))\subseteq M^0$
,
$\operatorname {dom}(\pi (x))\subseteq M^0$
, -
(2)
 $q_0,\ldots ,q_{n-1}$
are
$q_0,\ldots ,q_{n-1}$
are
 $M^0$
-invariant,
$M^0$
-invariant, -
(3)
 $M^{\alpha }\preceq \mathfrak {C}$
for each
$M^{\alpha }\preceq \mathfrak {C}$
for each
 $\alpha <\lambda $
,
$\alpha <\lambda $
,
 $(M^{\alpha })_{\alpha <\lambda }$
is continuous, and each
$(M^{\alpha })_{\alpha <\lambda }$
is continuous, and each
 $M^{\alpha +1}$
is
$M^{\alpha +1}$
is
 $|M^{\alpha }|^+$
-saturated,
$|M^{\alpha }|^+$
-saturated, -
(4)
 $(b^{\alpha }_i)_{i<\omega } M^{\alpha }\subseteq M^{\alpha +1}$
for each
$(b^{\alpha }_i)_{i<\omega } M^{\alpha }\subseteq M^{\alpha +1}$
for each
 $\alpha +1<\lambda $
,
$\alpha +1<\lambda $
, -
(5)
 $\pi (x)\cup \{\varphi _{\eta (\alpha )}(x;b^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent,
$\pi (x)\cup \{\varphi _{\eta (\alpha )}(x;b^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent, -
(6) for each
 $\alpha <\lambda $
, we have
$\alpha <\lambda $
, we have
 $(b^{\alpha }_i)_{i<\omega }\models q^{\otimes \omega }_{\eta (\alpha )}|_{M^{\alpha }}$
and
$(b^{\alpha }_i)_{i<\omega }\models q^{\otimes \omega }_{\eta (\alpha )}|_{M^{\alpha }}$
and
 $\{\varphi _{\eta (\alpha )}(x;b^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent.
$\{\varphi _{\eta (\alpha )}(x;b^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent.
Proof The implication right-to-left is straightforward and holds even without the assumption about NSOP
![]() $_1$
. Let us show the implication left-to-right.
$_1$
. Let us show the implication left-to-right.
By Remark 3.2, there is a configuration satisfying conditions (1)–(7) from Definition 3.1 such that each
![]() $M^{\alpha +1}$
is
$M^{\alpha +1}$
is
![]() $|M^{\alpha }|^+$
-saturated. By Kim’s lemma (Fact 2.7), we can replace the condition (7) from Definition 3.1, by: for each
$|M^{\alpha }|^+$
-saturated. By Kim’s lemma (Fact 2.7), we can replace the condition (7) from Definition 3.1, by: for each
![]() $\alpha <\lambda $
there exists
$\alpha <\lambda $
there exists
![]() $\bar {c}^{\alpha }=(c^{\alpha }_i)_{i<\omega }\models q^{\otimes \omega }_{\eta (\alpha )}|_{M^{\alpha }}$
such that
$\bar {c}^{\alpha }=(c^{\alpha }_i)_{i<\omega }\models q^{\otimes \omega }_{\eta (\alpha )}|_{M^{\alpha }}$
such that
![]() $c^{\alpha }_0=b^{\alpha }$
and
$c^{\alpha }_0=b^{\alpha }$
and
![]() $\{\varphi _{\eta (\alpha )}(x;c^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent. By saturation of
$\{\varphi _{\eta (\alpha )}(x;c^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent. By saturation of
![]() $M^{\alpha +1}$
, we find
$M^{\alpha +1}$
, we find
![]() $(b^{\alpha }_i)_{i<\omega }\subseteq M^{\alpha +1}$
such that
$(b^{\alpha }_i)_{i<\omega }\subseteq M^{\alpha +1}$
such that
![]() $(b^{\alpha }_i)_{i<\omega }\equiv _{M^{\alpha }b^{\alpha }}(c^{\alpha }_i)_{i<\omega }$
which is the desired sequence to finish the proof.
$(b^{\alpha }_i)_{i<\omega }\equiv _{M^{\alpha }b^{\alpha }}(c^{\alpha }_i)_{i<\omega }$
which is the desired sequence to finish the proof.
Lemma 3.10.
![]() $D_Q(\{x=x\})\leqslant \sum \limits _{j\in J}C_{\varphi _j,q_j}<\omega $
, where
$D_Q(\{x=x\})\leqslant \sum \limits _{j\in J}C_{\varphi _j,q_j}<\omega $
, where
![]() $J=\{j< n\;|\;C_{\varphi _j,q_j}<\omega \}$
.
$J=\{j< n\;|\;C_{\varphi _j,q_j}<\omega \}$
.
Proof Let us deal first with the case when
![]() $Q=((\varphi (x;y),q(y)))$
. Assume that
$Q=((\varphi (x;y),q(y)))$
. Assume that
![]() $D_Q(\pi )\geqslant \lambda>0$
and let
$D_Q(\pi )\geqslant \lambda>0$
and let
![]() $(b^{\alpha },M^{\alpha })_{\alpha <\lambda }$
be as in Definition 3.1 (
$(b^{\alpha },M^{\alpha })_{\alpha <\lambda }$
be as in Definition 3.1 (
![]() $\eta $
is constant, so we skip it).
$\eta $
is constant, so we skip it).
We have that
![]() $b^{\alpha }\models q|_{M^{\alpha }}$
and since
$b^{\alpha }\models q|_{M^{\alpha }}$
and since
![]() $b^{\alpha }M^{\alpha }\subseteq M^{\alpha +1}$
, it is
$b^{\alpha }M^{\alpha }\subseteq M^{\alpha +1}$
, it is
![]() $b^{\alpha }\models q|_{M^0b^{<\alpha }}$
. We know also that q is
$b^{\alpha }\models q|_{M^0b^{<\alpha }}$
. We know also that q is
![]() $M^0$
-invariant and that
$M^0$
-invariant and that
![]() $\{\varphi (x;b^{\alpha })\;|\;\alpha <\lambda \}$
is consistent. On the other hand, by Lemma 3.9, there exists a Morley sequence
$\{\varphi (x;b^{\alpha })\;|\;\alpha <\lambda \}$
is consistent. On the other hand, by Lemma 3.9, there exists a Morley sequence
![]() $(b^0_i)_{i<\omega }\models q^{\otimes \omega }|_{M^0}$
such that
$(b^0_i)_{i<\omega }\models q^{\otimes \omega }|_{M^0}$
such that
![]() $b^0_0=b^0$
and
$b^0_0=b^0$
and
![]() $\{\varphi (x;b^0_i)\;|\;i<\omega \}$
is inconsistent. Therefore
$\{\varphi (x;b^0_i)\;|\;i<\omega \}$
is inconsistent. Therefore
![]() $C_{\varphi ,q}<\omega $
and so
$C_{\varphi ,q}<\omega $
and so
![]() $\lambda \leqslant C_{\varphi ,q}<\omega $
.
$\lambda \leqslant C_{\varphi ,q}<\omega $
.
We switch to the general case where
Now, the function
![]() $\eta \in n^{\lambda }$
becomes important. We have that
$\eta \in n^{\lambda }$
becomes important. We have that
![]() $\lambda =\bigcup _{j< n}\eta ^{-1}[j]$
, so we are done if we can show that
$\lambda =\bigcup _{j< n}\eta ^{-1}[j]$
, so we are done if we can show that
![]() $|\eta ^{-1}[j]|=0$
or
$|\eta ^{-1}[j]|=0$
or
![]() $|\eta ^{-1}[j]|\leqslant C_{\varphi _j,k_j}<\omega $
for each
$|\eta ^{-1}[j]|\leqslant C_{\varphi _j,k_j}<\omega $
for each
![]() $j< n$
. Fix some
$j< n$
. Fix some
![]() $j< n$
and assume that
$j< n$
and assume that
![]() $|\eta ^{-1}[j]|>0$
. Let
$|\eta ^{-1}[j]|>0$
. Let
![]() $\alpha <\lambda $
be the first index such that
$\alpha <\lambda $
be the first index such that
![]() $\eta (\alpha )=j$
. Repeating the first part of this proof for
$\eta (\alpha )=j$
. Repeating the first part of this proof for
![]() $q_j$
we obtain what we need.
$q_j$
we obtain what we need.
Corollary 3.11.
![]() $D_Q(\pi )\leqslant \sum \limits _{j\in J}C_{\varphi _j,q_j}<\omega $
, where
$D_Q(\pi )\leqslant \sum \limits _{j\in J}C_{\varphi _j,q_j}<\omega $
, where
![]() $J=\{j< n\;|\;C_{\varphi _j,q_j}<\omega \}$
.
$J=\{j< n\;|\;C_{\varphi _j,q_j}<\omega \}$
.
Lemma 3.12.
![]() $D_Q(\pi )\geqslant \lambda $
if and only there exist
$D_Q(\pi )\geqslant \lambda $
if and only there exist
![]() $\eta \in n^{\lambda }$
,
$\eta \in n^{\lambda }$
,
![]() $(b^{\alpha }_i)_{\alpha <\lambda ,i<\omega }$
, and
$(b^{\alpha }_i)_{\alpha <\lambda ,i<\omega }$
, and
![]() $M\preceq \mathfrak {C}$
such that
$M\preceq \mathfrak {C}$
such that
-
(1)
 $\operatorname {dom}(\pi )\subseteq M$
,
$\operatorname {dom}(\pi )\subseteq M$
, -
(2)
 $q_0,\ldots ,q_{n-1}$
are M-invariant,
$q_0,\ldots ,q_{n-1}$
are M-invariant, -
(3)
 $\pi (x)\cup \{\varphi _{\eta (\alpha )}(x;b^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent,
$\pi (x)\cup \{\varphi _{\eta (\alpha )}(x;b^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent, -
(4)
 $\{\varphi _{\eta (\alpha )}(x;b^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent for each
$\{\varphi _{\eta (\alpha )}(x;b^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent for each
 $\alpha <\lambda $
,
$\alpha <\lambda $
, -
(5)
 $$ \begin{align*}(b^{\lambda-1}_i)_{i<\omega}^\smallfrown\ldots^\smallfrown(b^0_i)_{i<\omega}\models q_{\eta(\lambda-1)}^{\otimes\omega}\otimes\cdots\otimes q_{\eta(0)}^{\otimes\omega}|_{M}.\end{align*} $$
$$ \begin{align*}(b^{\lambda-1}_i)_{i<\omega}^\smallfrown\ldots^\smallfrown(b^0_i)_{i<\omega}\models q_{\eta(\lambda-1)}^{\otimes\omega}\otimes\cdots\otimes q_{\eta(0)}^{\otimes\omega}|_{M}.\end{align*} $$
Proof The left-to-right implication is straightforward: by Lemma 3.9 there are proper
![]() $\eta \in n^\lambda $
and
$\eta \in n^\lambda $
and
![]() $\big ((b^{\alpha }_i)_{i<\omega },M^{\alpha }\big )_{\alpha <\lambda }$
, we set
$\big ((b^{\alpha }_i)_{i<\omega },M^{\alpha }\big )_{\alpha <\lambda }$
, we set
![]() $M:=M^0$
and reuse
$M:=M^0$
and reuse
![]() $(b^{\alpha }_i)_{\alpha <\lambda ,i<\omega }$
.
$(b^{\alpha }_i)_{\alpha <\lambda ,i<\omega }$
.
Let us take care of the right-to-left implication. We will recursively define a sequence
![]() $((e^{\alpha }_i)_{i<\omega },M^{\alpha })_{\alpha <\lambda }$
satisfying all the six conditions from Lemma 3.9. Because we do not want to get lost in a notational madness, instead of introducing new subscripts, we will sketch a few first steps.
$((e^{\alpha }_i)_{i<\omega },M^{\alpha })_{\alpha <\lambda }$
satisfying all the six conditions from Lemma 3.9. Because we do not want to get lost in a notational madness, instead of introducing new subscripts, we will sketch a few first steps.
We set
![]() $M^0:=M$
and take
$M^0:=M$
and take
![]() $M^1\preceq \mathfrak {C}$
which is a
$M^1\preceq \mathfrak {C}$
which is a
![]() $|M^0|^+$
-saturated, and which contains
$|M^0|^+$
-saturated, and which contains
![]() $M^0$
and
$M^0$
and
![]() $(b^0_i)_{i<\omega }$
. Consider a Morley sequence
$(b^0_i)_{i<\omega }$
. Consider a Morley sequence
We have
Now, let
![]() $M^2\preceq \mathfrak {C}$
be
$M^2\preceq \mathfrak {C}$
be
![]() $|M^1|^+$
-saturated such that
$|M^1|^+$
-saturated such that
![]() $M^1(c^1_i)_{i<\omega }\subseteq M^2$
and let us choose one more Morley sequence
$M^1(c^1_i)_{i<\omega }\subseteq M^2$
and let us choose one more Morley sequence
We see that
and so
 $$ \begin{align*} (d^{\lambda-1}_i)_{i<\omega}^\smallfrown\ldots^\smallfrown(d^2_i)_{i<\omega}^\smallfrown(c^1_i)_{i<\omega}^\smallfrown(b^0_i)_{i<\omega} &\equiv_{M^0} (c^{\lambda-1}_i)_{i<\omega}^\smallfrown\ldots^\smallfrown(c^1_i)_{i<\omega}^\smallfrown(b^0_i)_{i<\omega} \\ &\equiv_{M^0} (b^{\lambda-1}_i)_{i<\omega}^\smallfrown\ldots^\smallfrown(b^0_i)_{i<\omega}. \end{align*} $$
$$ \begin{align*} (d^{\lambda-1}_i)_{i<\omega}^\smallfrown\ldots^\smallfrown(d^2_i)_{i<\omega}^\smallfrown(c^1_i)_{i<\omega}^\smallfrown(b^0_i)_{i<\omega} &\equiv_{M^0} (c^{\lambda-1}_i)_{i<\omega}^\smallfrown\ldots^\smallfrown(c^1_i)_{i<\omega}^\smallfrown(b^0_i)_{i<\omega} \\ &\equiv_{M^0} (b^{\lambda-1}_i)_{i<\omega}^\smallfrown\ldots^\smallfrown(b^0_i)_{i<\omega}. \end{align*} $$
Set
![]() $(e^2_i)_{i<\omega }:=(d^2_i)_{i<\omega }$
,
$(e^2_i)_{i<\omega }:=(d^2_i)_{i<\omega }$
,
![]() $(e^1_i)_{i<\omega }:=(c^1_i)_{i<\omega }$
and
$(e^1_i)_{i<\omega }:=(c^1_i)_{i<\omega }$
and
![]() $(e^0_i)_{i<\omega }:=(b^0_i)_{i<\omega }$
.
$(e^0_i)_{i<\omega }:=(b^0_i)_{i<\omega }$
.
Continuing this process we will obtain a sequence of models
![]() $M^0\preceq M^1\preceq \cdots \preceq M^{\lambda -1}$
and Morley sequences
$M^0\preceq M^1\preceq \cdots \preceq M^{\lambda -1}$
and Morley sequences
![]() $(e^{\alpha }_i)_{i<\omega }\models q_{\eta (\alpha )}^{\otimes \omega }|_{M^{\alpha }}$
, where
$(e^{\alpha }_i)_{i<\omega }\models q_{\eta (\alpha )}^{\otimes \omega }|_{M^{\alpha }}$
, where
![]() $\alpha <\lambda $
, such that
$\alpha <\lambda $
, such that
![]() $M^{\alpha }(e^{\alpha }_i)_{i<\omega }\subseteq M^{\alpha +1}$
and
$M^{\alpha }(e^{\alpha }_i)_{i<\omega }\subseteq M^{\alpha +1}$
and
Since
![]() $\operatorname {dom}(\pi (x))\subseteq M=M^0$
, we have also that
$\operatorname {dom}(\pi (x))\subseteq M=M^0$
, we have also that
![]() $\pi (x)\,\cup \,\{\varphi _{\eta (\alpha )}(x;e^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent and that
$\pi (x)\,\cup \,\{\varphi _{\eta (\alpha )}(x;e^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent and that
![]() $\{\varphi _{\eta (\alpha )}(x;e^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent for each
$\{\varphi _{\eta (\alpha )}(x;e^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent for each
![]() $\alpha <\lambda $
. Therefore all the conditions of Lemma 3.9 are satisfied for
$\alpha <\lambda $
. Therefore all the conditions of Lemma 3.9 are satisfied for
![]() $((e^{\alpha }_i)_{i<\omega },M^{\alpha })_{\alpha <\lambda }$
.
$((e^{\alpha }_i)_{i<\omega },M^{\alpha })_{\alpha <\lambda }$
.
Example 3.13. Let us provide an example of a situation when the rank of the home sort is finite, but strictly bigger than
![]() $1$
. Let k be any natural number greater than
$1$
. Let k be any natural number greater than
![]() $1$
and let p be equal to zero or to a prime number distinct from 2. Consider the 2-sorted theory
$1$
and let p be equal to zero or to a prime number distinct from 2. Consider the 2-sorted theory
![]() $T_k$
of k-dimensional vector spaces over an algebraically closed field of characteristic p, equipped with a non-degenerate symmetric bilinear form (see [Reference Dobrowolski14, Chapter 10]). Let x and y be single vector variables,
$T_k$
of k-dimensional vector spaces over an algebraically closed field of characteristic p, equipped with a non-degenerate symmetric bilinear form (see [Reference Dobrowolski14, Chapter 10]). Let x and y be single vector variables,
![]() $\phi (x,y)=(x\perp y\wedge x\neq 0)$
, and let
$\phi (x,y)=(x\perp y\wedge x\neq 0)$
, and let
![]() $q(y)$
be the generic type in the vector sort V (so q is
$q(y)$
be the generic type in the vector sort V (so q is
![]() $\emptyset $
-invariant). Put
$\emptyset $
-invariant). Put
![]() $Q=((\phi (x,y),q(y)))$
. We will show that
$Q=((\phi (x,y),q(y)))$
. We will show that
![]() $D_Q(\{x=x\})=k-1$
.
$D_Q(\{x=x\})=k-1$
.
Let
![]() $(v_i)_{i<\omega }$
be a Morley sequence in
$(v_i)_{i<\omega }$
be a Morley sequence in
![]() $q(y)$
. Then in particular
$q(y)$
. Then in particular
![]() $v_0,\dots ,v_{k-1}$
are linearly independent, which easily implies that
$v_0,\dots ,v_{k-1}$
are linearly independent, which easily implies that
![]() $\bigwedge _{i<k}\phi (x,v_i)$
is inconsistent. Thus
$\bigwedge _{i<k}\phi (x,v_i)$
is inconsistent. Thus
![]() $D_Q(\{x=x\})\leq k-1$
. For the other inequality, put
$D_Q(\{x=x\})\leq k-1$
. For the other inequality, put
![]() $M_i=\operatorname {acl}(a_{0},a_{1},\dots ,a_{k-1+i})$
for
$M_i=\operatorname {acl}(a_{0},a_{1},\dots ,a_{k-1+i})$
for
![]() $i<k$
and note that
$i<k$
and note that
![]() $b^i:=v_{k+i}\models q|_{M_i}$
(as
$b^i:=v_{k+i}\models q|_{M_i}$
(as ![]() and
and
![]() $b^i\models q|_{\emptyset }$
), and each
$b^i\models q|_{\emptyset }$
), and each
![]() $M_i$
is an elementary submodel by quantifier elimination. Also, the sequence
$M_i$
is an elementary submodel by quantifier elimination. Also, the sequence
![]() $(v_{k+i},v_{k+i+1},\dots )$
is Morley over
$(v_{k+i},v_{k+i+1},\dots )$
is Morley over
![]() $M_i$
, and it witnesses that
$M_i$
, and it witnesses that
![]() $\phi (x,b^i)$
Kim-divides over
$\phi (x,b^i)$
Kim-divides over
![]() $M_i$
for each
$M_i$
for each
![]() $i<k$
. Finally,
$i<k$
. Finally,
![]() $\bigwedge _{i<k-1} \phi (x,b^i)$
is consistent, as there is a non-zero vector orthogonal to
$\bigwedge _{i<k-1} \phi (x,b^i)$
is consistent, as there is a non-zero vector orthogonal to
![]() $b^0,\dots ,b^{i-2}$
. This shows that
$b^0,\dots ,b^{i-2}$
. This shows that
![]() $D_Q(\{x=x\})=k-1$
.
$D_Q(\{x=x\})=k-1$
.
Remark 3.14. Note that if T is an NSOP
![]() $_1$
theory (as we assume here) and for some
$_1$
theory (as we assume here) and for some
![]() $k<\omega $
, a formula
$k<\omega $
, a formula
![]() $\varphi (x,y)$
,
$\varphi (x,y)$
,
![]() $M\preceq \mathfrak {C}$
, some M-invariant
$M\preceq \mathfrak {C}$
, some M-invariant
![]() $q(y)\in S(\mathfrak {C})$
and some
$q(y)\in S(\mathfrak {C})$
and some
![]() $(b_i)_{i<\omega }\models q^{\otimes \omega }|_M$
, the set
$(b_i)_{i<\omega }\models q^{\otimes \omega }|_M$
, the set
![]() $\{\varphi (x,b_i)\;|\;i<\omega \}$
is k-inconsistent but not
$\{\varphi (x,b_i)\;|\;i<\omega \}$
is k-inconsistent but not
![]() $(k-1)$
-inconsistent, then
$(k-1)$
-inconsistent, then
![]() $D_{((\varphi ,q))}(x=x)=k-1$
(as in Example 3.13). To see this, consider a linear order I being
$D_{((\varphi ,q))}(x=x)=k-1$
(as in Example 3.13). To see this, consider a linear order I being
![]() $(k-1)$
-many copies of
$(k-1)$
-many copies of
![]() $\omega $
(one after another one) and
$\omega $
(one after another one) and
![]() $(c_i)_{i\in I}\models q^{\otimes I}|_M$
and use Lemma 3.12. In other words, for
$(c_i)_{i\in I}\models q^{\otimes I}|_M$
and use Lemma 3.12. In other words, for
![]() $\pi (x):=\{x=x\}$
the situation is quite simple and either
$\pi (x):=\{x=x\}$
the situation is quite simple and either
![]() $D_{((\varphi ,q))}(\pi )=0$
or
$D_{((\varphi ,q))}(\pi )=0$
or
![]() $D_{((\varphi ,q))}(\pi )=C_{\varphi ,q}$
provided
$D_{((\varphi ,q))}(\pi )=C_{\varphi ,q}$
provided
![]() $C_{\varphi ,q}<\omega $
.
$C_{\varphi ,q}<\omega $
.
Lemma 3.15. If
![]() $\pi \vdash \pi '$
then
$\pi \vdash \pi '$
then
Proof Assume that
![]() $D_Q(\pi )\geqslant \lambda \in \mathbb {N}_{>0}$
, then by Lemma 3.12 there exist
$D_Q(\pi )\geqslant \lambda \in \mathbb {N}_{>0}$
, then by Lemma 3.12 there exist
![]() $\eta \in n^{\lambda }$
,
$\eta \in n^{\lambda }$
,
![]() $(b^{\alpha }_i)_{\alpha <\lambda ,i<\omega }$
, and
$(b^{\alpha }_i)_{\alpha <\lambda ,i<\omega }$
, and
![]() $M\preceq \mathfrak {C}$
such that:
$M\preceq \mathfrak {C}$
such that:
-
(1)
 $\operatorname {dom}(\pi )\subseteq M$
,
$\operatorname {dom}(\pi )\subseteq M$
, -
(2)
 $q_0,\ldots ,q_{n-1}$
are M-invariant,
$q_0,\ldots ,q_{n-1}$
are M-invariant, -
(3)
 $\pi (x)\cup \{\varphi _{\eta (\alpha )}(x;b^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent,
$\pi (x)\cup \{\varphi _{\eta (\alpha )}(x;b^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent, -
(4)
 $\{\varphi _{\eta (\alpha )}(x;b^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent for each
$\{\varphi _{\eta (\alpha )}(x;b^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent for each
 $\alpha <\lambda $
,
$\alpha <\lambda $
, -
(5)
 $$ \begin{align*}(b^{\lambda-1}_i)_{i<\omega}^\smallfrown\ldots^\smallfrown(b^0_i)_{i<\omega}\models q_{\eta(\lambda-1)}^{\otimes\omega}\otimes\dots\otimes q_{\eta(0)}^{\otimes\omega}|_{M}.\end{align*} $$
$$ \begin{align*}(b^{\lambda-1}_i)_{i<\omega}^\smallfrown\ldots^\smallfrown(b^0_i)_{i<\omega}\models q_{\eta(\lambda-1)}^{\otimes\omega}\otimes\dots\otimes q_{\eta(0)}^{\otimes\omega}|_{M}.\end{align*} $$
Let
![]() $N\preceq \mathfrak {C}$
contain M and
$N\preceq \mathfrak {C}$
contain M and
![]() $\operatorname {dom}(\pi ')$
, and let
$\operatorname {dom}(\pi ')$
, and let
Then naturally
![]() $\operatorname {dom}(\pi ')\subseteq N$
and
$\operatorname {dom}(\pi ')\subseteq N$
and
![]() $q_1,\ldots ,q_n$
are N-invariant. Because
$q_1,\ldots ,q_n$
are N-invariant. Because
we have also that
![]() $\{\varphi _{\eta (\alpha )}(x;c^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent for each
$\{\varphi _{\eta (\alpha )}(x;c^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent for each
![]() $\alpha <\lambda $
, and that
$\alpha <\lambda $
, and that
![]() $\pi (x)\cup \{\varphi _{\eta (\alpha )}(x;c^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent. Moreover,
$\pi (x)\cup \{\varphi _{\eta (\alpha )}(x;c^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent. Moreover,
![]() $\pi \vdash \pi '$
implies that
$\pi \vdash \pi '$
implies that
![]() $\pi '(x)\cup \{\varphi _{\eta (\alpha )}(x;c^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent. Hence, Lemma 3.12 gives us
$\pi '(x)\cup \{\varphi _{\eta (\alpha )}(x;c^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent. Hence, Lemma 3.12 gives us
![]() $D_Q(\pi ')\geqslant \lambda $
.
$D_Q(\pi ')\geqslant \lambda $
.
Lemma 3.16.
![]() $D_Q\Big(\pi \cup \Big\{\bigvee \limits _{j\leqslant m}\psi _j\Big\}\Big)=\max \limits _{j\leqslant m} D_Q(\pi \cup \{\psi _j\})$
.
$D_Q\Big(\pi \cup \Big\{\bigvee \limits _{j\leqslant m}\psi _j\Big\}\Big)=\max \limits _{j\leqslant m} D_Q(\pi \cup \{\psi _j\})$
.
Proof Because
![]() $\pi \cup \{\psi _i\}\vdash \pi \cup \{\bigvee _{j}\psi _j\}$
for each
$\pi \cup \{\psi _i\}\vdash \pi \cup \{\bigvee _{j}\psi _j\}$
for each
![]() $i\leqslant m$
, Lemma 3.15 gives us that
$i\leqslant m$
, Lemma 3.15 gives us that
 $$ \begin{align*}\max\limits_{j\leqslant m} D_Q(\pi\cup\{\psi_j\})\leqslant D_Q\Big(\pi\cup\Big\{\bigvee\limits_{j\leqslant m}\psi_j\Big\}\Big).\end{align*} $$
$$ \begin{align*}\max\limits_{j\leqslant m} D_Q(\pi\cup\{\psi_j\})\leqslant D_Q\Big(\pi\cup\Big\{\bigvee\limits_{j\leqslant m}\psi_j\Big\}\Big).\end{align*} $$
Hence it is enough to show that
 $$ \begin{align*}D_Q\Big(\pi\cup\Big\{\bigvee\limits_{j\leqslant m}\psi_j\Big\}\Big)\geqslant\lambda\quad\Rightarrow\quad \max\limits_{j\leqslant m} D_Q(\pi\cup\{\psi_j\})\geqslant\lambda.\end{align*} $$
$$ \begin{align*}D_Q\Big(\pi\cup\Big\{\bigvee\limits_{j\leqslant m}\psi_j\Big\}\Big)\geqslant\lambda\quad\Rightarrow\quad \max\limits_{j\leqslant m} D_Q(\pi\cup\{\psi_j\})\geqslant\lambda.\end{align*} $$
Let
![]() $D_Q(\pi \cup \{\bigvee _{j}\psi _j\})\geqslant \lambda $
, i.e., there exists
$D_Q(\pi \cup \{\bigvee _{j}\psi _j\})\geqslant \lambda $
, i.e., there exists
![]() $\eta \in n^\lambda $
and
$\eta \in n^\lambda $
and
![]() $(b^{\alpha },M^{\alpha })_{\alpha <\lambda }$
as in Definition 3.1, in particular,
$(b^{\alpha },M^{\alpha })_{\alpha <\lambda }$
as in Definition 3.1, in particular,
-
•
 $\operatorname {dom}(\pi \cup \{\bigvee _{j}\psi _j\})\subseteq M^0$
,
$\operatorname {dom}(\pi \cup \{\bigvee _{j}\psi _j\})\subseteq M^0$
, -
•
 $\pi \cup \{\bigvee _j\psi _j\}\cup \{\varphi _{\eta (\alpha )}(x;b^{\alpha })\;|\;\alpha <\lambda \}$
is consistent.
$\pi \cup \{\bigvee _j\psi _j\}\cup \{\varphi _{\eta (\alpha )}(x;b^{\alpha })\;|\;\alpha <\lambda \}$
is consistent.
Thus there is
![]() $i_0\leqslant m$
such that
$i_0\leqslant m$
such that
![]() $\pi \cup \{\psi _{i_0}\}\cup \{\varphi _{\eta (\alpha )}(x;b^{\alpha })\;|\;\alpha <\lambda \}$
is consistent. Because
$\pi \cup \{\psi _{i_0}\}\cup \{\varphi _{\eta (\alpha )}(x;b^{\alpha })\;|\;\alpha <\lambda \}$
is consistent. Because
![]() $\operatorname {dom}(\pi \cup \{\psi _{i_0}\})\subseteq \operatorname {dom}(\pi \cup \{\bigvee _j\psi _j\})\subseteq M^0$
, we have that
$\operatorname {dom}(\pi \cup \{\psi _{i_0}\})\subseteq \operatorname {dom}(\pi \cup \{\bigvee _j\psi _j\})\subseteq M^0$
, we have that
![]() $D_Q(\pi \cup \{\psi _{i_0}\})\geqslant \lambda $
and so also
$D_Q(\pi \cup \{\psi _{i_0}\})\geqslant \lambda $
and so also
![]() $\max _{j} D_Q(\pi \cup \{\psi _j\})\geqslant \lambda $
.
$\max _{j} D_Q(\pi \cup \{\psi _j\})\geqslant \lambda $
.
Let us recall that we are working in a theory T which is NSOP
![]() $_1$
.
$_1$
.
Lemma 3.17. Assume that
![]() $q_0(y_0)=\dots =q_{n-1}(y_{n-1})=q(y)$
(in Q).
$q_0(y_0)=\dots =q_{n-1}(y_{n-1})=q(y)$
(in Q).
-
(1) Let
 $\{\pi _{\beta }\}$
lists all finite subsets of
$\{\pi _{\beta }\}$
lists all finite subsets of
 $\pi $
. If for each
$\pi $
. If for each
 $\beta $
we have that
$\beta $
we have that
 $D_Q(\pi _{\beta })\geqslant \lambda <\omega $
, then
$D_Q(\pi _{\beta })\geqslant \lambda <\omega $
, then
 $D_Q(\pi )\geqslant \lambda $
.
$D_Q(\pi )\geqslant \lambda $
. -
(2) We can always find a finite
 $\pi _0\subseteq \pi $
such that
$\pi _0\subseteq \pi $
such that
 $D_Q(\pi _0)=D_Q(\pi )$
.
$D_Q(\pi _0)=D_Q(\pi )$
.
Proof Because for each
![]() $\beta $
we have
$\beta $
we have
![]() $D_Q(\pi _{\beta })\geqslant \lambda $
, by Lemma 3.12, for each
$D_Q(\pi _{\beta })\geqslant \lambda $
, by Lemma 3.12, for each
![]() $\beta $
there exists a function
$\beta $
there exists a function
![]() $\eta _{\beta }\in n^{\lambda }$
, a sequence of sequences
$\eta _{\beta }\in n^{\lambda }$
, a sequence of sequences
![]() $(b^{\beta ,\alpha }_i)_{\alpha <\lambda ,i<\omega }$
and a model
$(b^{\beta ,\alpha }_i)_{\alpha <\lambda ,i<\omega }$
and a model
![]() $M^{\beta }\preceq \mathfrak {C}$
such that:
$M^{\beta }\preceq \mathfrak {C}$
such that:
-
(1)
 $\operatorname {dom}(\pi _{\beta })\subseteq M^{\beta }$
,
$\operatorname {dom}(\pi _{\beta })\subseteq M^{\beta }$
, -
(2) q is
 $M^{\beta }$
-invariant,
$M^{\beta }$
-invariant, -
(3)
 $\pi _{\beta }(x)\cup \{\varphi _{\eta _{\beta }(\alpha )}(x;b^{\beta ,\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent,
$\pi _{\beta }(x)\cup \{\varphi _{\eta _{\beta }(\alpha )}(x;b^{\beta ,\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent, -
(4)
 $\{\varphi _{\eta _{\beta }(\alpha )}(x;b^{\beta ,\alpha }_i)\;|\;i<\omega \}$
is inconsistent for each
$\{\varphi _{\eta _{\beta }(\alpha )}(x;b^{\beta ,\alpha }_i)\;|\;i<\omega \}$
is inconsistent for each
 $\alpha <\lambda $
,
$\alpha <\lambda $
, -
(5)
 $$ \begin{align*}(b^{\beta,\lambda-1}_i)_{i<\omega}^\smallfrown\ldots^\smallfrown(b^{\beta,0}_i)_{i<\omega}\models q^{\otimes\omega}\otimes\dots\otimes q^{\otimes\omega}|_{M^{\beta}}.\end{align*} $$
$$ \begin{align*}(b^{\beta,\lambda-1}_i)_{i<\omega}^\smallfrown\ldots^\smallfrown(b^{\beta,0}_i)_{i<\omega}\models q^{\otimes\omega}\otimes\dots\otimes q^{\otimes\omega}|_{M^{\beta}}.\end{align*} $$
Let
![]() $N\preceq \mathfrak {C}$
be such that
$N\preceq \mathfrak {C}$
be such that
![]() $\bigcup \limits _{\beta }M^{\beta }\subseteq N$
. Moreover, let us pick up the following Morley sequences:
$\bigcup \limits _{\beta }M^{\beta }\subseteq N$
. Moreover, let us pick up the following Morley sequences:
and, without loss of generality, let
![]() $\{\varphi _{\eta _{\beta }(\alpha )}(x;y)\;|\;\beta ,\alpha <\lambda \}=\{\varphi _0(x;y),\ldots ,\varphi _{r-1} (x;y)\}$
for some
$\{\varphi _{\eta _{\beta }(\alpha )}(x;y)\;|\;\beta ,\alpha <\lambda \}=\{\varphi _0(x;y),\ldots ,\varphi _{r-1} (x;y)\}$
for some
![]() $r\leqslant n$
. We introduce
$r\leqslant n$
. We introduce
![]() $\psi (x;y):=\bigvee \limits _{i<r}\varphi _i(x;y)$
, and note that
$\psi (x;y):=\bigvee \limits _{i<r}\varphi _i(x;y)$
, and note that
is consistent (otherwise, by compactness,
![]() $\pi _{\beta }(x)\,\cup \,\{\psi (x;c^{\alpha }_0)\;|\;\alpha <\lambda \}$
is inconsistent for some
$\pi _{\beta }(x)\,\cup \,\{\psi (x;c^{\alpha }_0)\;|\;\alpha <\lambda \}$
is inconsistent for some
![]() $\beta $
, which is impossible, since
$\beta $
, which is impossible, since
and
![]() $\pi _{\beta }(x)\cup \{\varphi _{\eta _{\beta }(\alpha )}(x;b^{\beta ,\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent). Consider
$\pi _{\beta }(x)\cup \{\varphi _{\eta _{\beta }(\alpha )}(x;b^{\beta ,\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent). Consider
![]() $d\models \pi (x)\,\cup \,\{\psi (x;c^{\alpha }_0)\;|\;\alpha <\lambda \}$
, then for each
$d\models \pi (x)\,\cup \,\{\psi (x;c^{\alpha }_0)\;|\;\alpha <\lambda \}$
, then for each
![]() $\alpha <\lambda $
there is
$\alpha <\lambda $
there is
![]() $i_{\alpha }<r$
such that
$i_{\alpha }<r$
such that
![]() $\models \varphi _{i_{\alpha }}(d,c^{\alpha }_0)$
. Let
$\models \varphi _{i_{\alpha }}(d,c^{\alpha }_0)$
. Let
![]() $\eta \in n^{\lambda }$
be given by
$\eta \in n^{\lambda }$
be given by
![]() $\eta :\alpha \mapsto i_{\alpha }$
.
$\eta :\alpha \mapsto i_{\alpha }$
.
As we want to use Lemma 3.12 to show that
![]() $D_Q(\pi )\geqslant \lambda $
, and we have already defined
$D_Q(\pi )\geqslant \lambda $
, and we have already defined
![]() $\eta $
,
$\eta $
,
![]() $N\preceq \mathfrak {C}$
and
$N\preceq \mathfrak {C}$
and
![]() $(c^{\alpha }_i)_{\alpha <\lambda ,i<\omega }$
, we need to verify whether all the five conditions from Lemma 3.12 hold. Obviously,
$(c^{\alpha }_i)_{\alpha <\lambda ,i<\omega }$
, we need to verify whether all the five conditions from Lemma 3.12 hold. Obviously,
![]() $\operatorname {dom}(\pi )\subseteq N$
and q is N-invariant, so we have the first and the second condition. The fifth condition is naturally satisfied by the choice of
$\operatorname {dom}(\pi )\subseteq N$
and q is N-invariant, so we have the first and the second condition. The fifth condition is naturally satisfied by the choice of
![]() $(c^{\alpha }_i)_{\alpha <\lambda ,i<\omega }$
. The third condition says that
$(c^{\alpha }_i)_{\alpha <\lambda ,i<\omega }$
. The third condition says that
![]() $\pi (x)\,\cup \,\{\varphi _{\eta (\alpha }(x,c^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent, which is witnessed by element d. For the fourth condition, we need to note that
$\pi (x)\,\cup \,\{\varphi _{\eta (\alpha }(x,c^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent, which is witnessed by element d. For the fourth condition, we need to note that
![]() $\{\varphi _{\eta (\alpha )}(x,c^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent for every
$\{\varphi _{\eta (\alpha )}(x,c^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent for every
![]() $\alpha <\lambda $
. Because
$\alpha <\lambda $
. Because
![]() $\eta (\alpha )< r$
, there exist
$\eta (\alpha )< r$
, there exist
![]() $\beta $
and
$\beta $
and
![]() $\alpha '<\lambda $
such that
$\alpha '<\lambda $
such that
![]() $\eta (\alpha )=\eta _{\beta }(\alpha ')$
. We know that
$\eta (\alpha )=\eta _{\beta }(\alpha ')$
. We know that
![]() $\{\varphi _{\eta _{\beta }(\alpha ')}(x,b^{\beta ,\alpha '}_i)\;|\;i<\omega \}$
is inconsistent, that
$\{\varphi _{\eta _{\beta }(\alpha ')}(x,b^{\beta ,\alpha '}_i)\;|\;i<\omega \}$
is inconsistent, that
![]() $(b^{\beta ,\alpha '}_i)_{i<\omega }\models q^{\otimes \omega }|_{M^{\beta }}$
and that
$(b^{\beta ,\alpha '}_i)_{i<\omega }\models q^{\otimes \omega }|_{M^{\beta }}$
and that
![]() $(c^{\alpha }_i)_{i<\omega }\models q^{\otimes \omega }|_{M^{\beta }}$
. Thus also
$(c^{\alpha }_i)_{i<\omega }\models q^{\otimes \omega }|_{M^{\beta }}$
. Thus also
![]() $\{\varphi _{\eta (\alpha )}(x,c^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent.
$\{\varphi _{\eta (\alpha )}(x,c^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent.
Corollary 3.18. Let
![]() $q_0(y_0)=\dots =q_{n-1}(y_{n-1})=q(y)$
(in Q) and let
$q_0(y_0)=\dots =q_{n-1}(y_{n-1})=q(y)$
(in Q) and let
![]() $\pi (x)$
be a partial type over A. Then there exists
$\pi (x)$
be a partial type over A. Then there exists
![]() $p(x)\in S(A)$
extending
$p(x)\in S(A)$
extending
![]() $\pi (x)$
such that
$\pi (x)$
such that
![]() $D_Q(p)=D_Q(\pi )$
.
$D_Q(p)=D_Q(\pi )$
.
Proof The proof is completely standard, but let us sketch it anyway. Consider
By Lemmas 3.15 and 3.16, the set
![]() $\tilde {\pi }$
is a partial type over A. Let
$\tilde {\pi }$
is a partial type over A. Let
![]() $p(x)\in S(A)$
be any extension of
$p(x)\in S(A)$
be any extension of
![]() $\tilde {\pi }$
.
$\tilde {\pi }$
.
If
![]() $D_Q(p)<D_Q(\pi )$
then by Lemma 3.17 there exists a finite subset
$D_Q(p)<D_Q(\pi )$
then by Lemma 3.17 there exists a finite subset
![]() $p_0(x)\subseteq p(x)$
such that
$p_0(x)\subseteq p(x)$
such that
![]() $D_Q(p_0)<D_Q(\pi )$
. Let
$D_Q(p_0)<D_Q(\pi )$
. Let
![]() $\psi (x):=\bigwedge p_0(x)\in L(A)$
, we have that
$\psi (x):=\bigwedge p_0(x)\in L(A)$
, we have that
Thus
![]() $\neg \psi (x)\in \tilde {\pi }(x)\subseteq p(x)$
and we got a contradiction with
$\neg \psi (x)\in \tilde {\pi }(x)\subseteq p(x)$
and we got a contradiction with
![]() $\psi (x)\in p(x)$
.
$\psi (x)\in p(x)$
.
Let
![]() $\Delta =\{\varphi _1(x;y),\ldots ,\varphi _n(x;y)\}$
and
$\Delta =\{\varphi _1(x;y),\ldots ,\varphi _n(x;y)\}$
and
![]() $1<k<\omega $
. Recall that there is a local rank used in simple theories, denoted
$1<k<\omega $
. Recall that there is a local rank used in simple theories, denoted
![]() $D(\,\cdot \,,\Delta ,k)$
(cf. Chapter 3 in [Reference Casanovas4]). This local rank may be used to characterize simplicity as: T is simple if and only if
$D(\,\cdot \,,\Delta ,k)$
(cf. Chapter 3 in [Reference Casanovas4]). This local rank may be used to characterize simplicity as: T is simple if and only if
![]() $D(\{x=x\},\{\varphi \},k)<\omega $
for all
$D(\{x=x\},\{\varphi \},k)<\omega $
for all
![]() $\varphi $
and k (e.g., Proposition 3.13 in [Reference Casanovas4]). As our rank is also local, we can treat our rank as an analogon of the local rank
$\varphi $
and k (e.g., Proposition 3.13 in [Reference Casanovas4]). As our rank is also local, we can treat our rank as an analogon of the local rank
![]() $D(\,\cdot \,,\Delta ,k)$
. Let us compare now the both local ranks.
$D(\,\cdot \,,\Delta ,k)$
. Let us compare now the both local ranks.
Remark 3.19. For each
![]() $Q=((\varphi _0,q_0),\ldots ,(\varphi _{n-1},q_{n-1}))$
and any partial type
$Q=((\varphi _0,q_0),\ldots ,(\varphi _{n-1},q_{n-1}))$
and any partial type
![]() $\pi $
, there exists
$\pi $
, there exists
![]() $K<\omega $
such that for any
$K<\omega $
such that for any
![]() $k\geqslant K$
we have
$k\geqslant K$
we have
Proof As T is NSOP
![]() $_1$
, there is some
$_1$
, there is some
![]() $\lambda <\omega $
such that
$\lambda <\omega $
such that
![]() $D_Q(\pi )=\lambda $
. Let
$D_Q(\pi )=\lambda $
. Let
![]() $\eta $
and
$\eta $
and
![]() $(b^\alpha ,M^\alpha )_{\alpha <\lambda }$
be as in Definition 3.1. For each
$(b^\alpha ,M^\alpha )_{\alpha <\lambda }$
be as in Definition 3.1. For each
![]() $\alpha <\lambda $
there exists
$\alpha <\lambda $
there exists
![]() $k_{\alpha }<\omega $
such that
$k_{\alpha }<\omega $
such that
![]() $\varphi _{\eta (\alpha )}(x;b^{\alpha })$
$\varphi _{\eta (\alpha )}(x;b^{\alpha })$
![]() $k_{\alpha }$
-divides over
$k_{\alpha }$
-divides over
![]() $M^{\alpha }$
. Set
$M^{\alpha }$
. Set
![]() $K:=\max \{k_0,\ldots ,k_{\lambda -1}\}$
. Then, by definition,
$K:=\max \{k_0,\ldots ,k_{\lambda -1}\}$
. Then, by definition,
![]() $D(\pi ,\{\varphi _0,\ldots ,\varphi _{n-1}\},k)\geqslant \lambda $
, provided
$D(\pi ,\{\varphi _0,\ldots ,\varphi _{n-1}\},k)\geqslant \lambda $
, provided
![]() $k\geqslant K$
.
$k\geqslant K$
.
On the other hand, if T is NSOP
![]() $_1$
but not simple, then there must be a formula
$_1$
but not simple, then there must be a formula
![]() $\varphi $
and some
$\varphi $
and some
![]() $k_0<\omega $
such that
$k_0<\omega $
such that
![]() $D(\{x=x\},\{\varphi \},k_0)\geqslant \omega $
. Thus for every
$D(\{x=x\},\{\varphi \},k_0)\geqslant \omega $
. Thus for every
![]() $K<\omega $
there exists
$K<\omega $
there exists
![]() $k\geqslant K$
(e.g.,
$k\geqslant K$
(e.g.,
![]() $k=K+k_0$
) such that
$k=K+k_0$
) such that
![]() $D(\{x=x\},\{\varphi \},k)\geqslant \omega $
but,
$D(\{x=x\},\{\varphi \},k)\geqslant \omega $
but,
![]() $D_{((\varphi ,q))}(\{x=x\})<\omega $
for any choice of
$D_{((\varphi ,q))}(\{x=x\})<\omega $
for any choice of
![]() $q\in S(\mathfrak {C})$
. Therefore sharp inequality in Remark 3.19 happens outside of the class of simple theories. One could ask about equality under the assumption of simplicity. The following counterexample, which is even stable, leaves no doubt.
$q\in S(\mathfrak {C})$
. Therefore sharp inequality in Remark 3.19 happens outside of the class of simple theories. One could ask about equality under the assumption of simplicity. The following counterexample, which is even stable, leaves no doubt.
Example 3.20. Let T be the theory of an equivalence relation E with infinitely many classes all of which are infinite. It is well-known that T is
![]() $\omega $
-stable of Morley rank
$\omega $
-stable of Morley rank
![]() $2$
. Let
$2$
. Let
![]() $\varphi _0(x,y)=E(x,y)$
and
$\varphi _0(x,y)=E(x,y)$
and
![]() $\varphi _1(x,y)=(x=y)$
. Then it is easy to see that for any
$\varphi _1(x,y)=(x=y)$
. Then it is easy to see that for any
![]() $k>1$
we have that
$k>1$
we have that
![]() $D(\{x=x\},\{\varphi _0(x,y),\varphi _1(x,y)\},k)=2$
. Now, fix two arbitrary invariant global types
$D(\{x=x\},\{\varphi _0(x,y),\varphi _1(x,y)\},k)=2$
. Now, fix two arbitrary invariant global types
![]() $q_0(x),q_1(x)$
and put
$q_0(x),q_1(x)$
and put
![]() $Q=\{(\varphi _0,q_0),(\varphi _1,q_1)\}$
. We claim that
$Q=\{(\varphi _0,q_0),(\varphi _1,q_1)\}$
. We claim that
![]() $D_Q(\{x=x\})\leq 1$
. Suppose for a contradiction that
$D_Q(\{x=x\})\leq 1$
. Suppose for a contradiction that
![]() $D_Q(\{x=x\})\geqslant 2$
witnessed by
$D_Q(\{x=x\})\geqslant 2$
witnessed by
![]() $M^0,M^1,b^0,b^1$
and
$M^0,M^1,b^0,b^1$
and
![]() $\eta :2 \to 2$
. The case where
$\eta :2 \to 2$
. The case where
![]() $\eta (0)=1$
can be excluded immediately, so assume
$\eta (0)=1$
can be excluded immediately, so assume
![]() $\eta (0)=0$
. Observe that
$\eta (0)=0$
. Observe that
![]() $\models E(b^0,b^1)$
, as otherwise
$\models E(b^0,b^1)$
, as otherwise
![]() $\varphi _{\eta (0)}(x,b^0)\wedge \varphi _{\eta (1)}(x,b^1)$
would be inconsistent (note
$\varphi _{\eta (0)}(x,b^0)\wedge \varphi _{\eta (1)}(x,b^1)$
would be inconsistent (note
![]() $\varphi _i(x,y)\vdash E(x,y)$
for
$\varphi _i(x,y)\vdash E(x,y)$
for
![]() $i=0,1$
). On the other hand, as
$i=0,1$
). On the other hand, as
![]() $b^1\models q_{\eta (1)}|_{M^0b^0}$
, we have in particular that
$b^1\models q_{\eta (1)}|_{M^0b^0}$
, we have in particular that ![]() , so
, so
![]() $E(b^0,M^0)\neq \emptyset $
, which contradicts that
$E(b^0,M^0)\neq \emptyset $
, which contradicts that
![]() $\varphi _0(x,b^0)$
divides over
$\varphi _0(x,b^0)$
divides over
![]() $M^0$
.
$M^0$
.
3.2 Rank vs. Kim-independence
We know that Kim-generics do not exist in the theory of infinite-dimensional vector spaces with a bilinear form (see Proposition 8.15 in [Reference Dobrowolski14]), which is NSOP
![]() $_1$
. Since in the case of simple theories, a notion of finite local rank, which is compatible with forking and invariant under shifts by elements of a definable group (so-called stratified local rank, see, e.g., Fact 3.7 in [Reference Tent and Ziegler26]), would lead to the existence of forking generics (see Lemma 3.8 in [Reference Tent and Ziegler26]), we probably should not expect that a notion of finite local rank in the case of NSOP
$_1$
. Since in the case of simple theories, a notion of finite local rank, which is compatible with forking and invariant under shifts by elements of a definable group (so-called stratified local rank, see, e.g., Fact 3.7 in [Reference Tent and Ziegler26]), would lead to the existence of forking generics (see Lemma 3.8 in [Reference Tent and Ziegler26]), we probably should not expect that a notion of finite local rank in the case of NSOP
![]() $_1$
theories will be compatible with Kim-forking and invariant under shifts by group elements (otherwise one could try to prove existence of Kim-generics, which does not always hold). Anyway, it seems that our notion of rank does not behave well under shifts by elements of some definable group, so does not immediately exclude compatibility of the rank with Kim-forking. Here, we study this problem and relate our results to an important question from [Reference Chernikov, Byungham and Ramsey10].
$_1$
theories will be compatible with Kim-forking and invariant under shifts by group elements (otherwise one could try to prove existence of Kim-generics, which does not always hold). Anyway, it seems that our notion of rank does not behave well under shifts by elements of some definable group, so does not immediately exclude compatibility of the rank with Kim-forking. Here, we study this problem and relate our results to an important question from [Reference Chernikov, Byungham and Ramsey10].
Lemma 3.21. Let
![]() $M\preceq N\preceq \mathfrak {C}$
and
$M\preceq N\preceq \mathfrak {C}$
and
![]() $a\in \mathfrak {C}$
. If
$a\in \mathfrak {C}$
. If
![]() $D_Q(\operatorname {tp}(a/M))=D_Q(\operatorname {tp}(a/N))$
for each M-invariant Q such that
$D_Q(\operatorname {tp}(a/M))=D_Q(\operatorname {tp}(a/N))$
for each M-invariant Q such that
![]() $|Q|=1$
, then
$|Q|=1$
, then ![]() .
.
Proof Assume that ![]() , which means that
, which means that
![]() $\operatorname {tp}(a/N)$
Kim-divides over M. Let
$\operatorname {tp}(a/N)$
Kim-divides over M. Let
![]() $\varphi (x,b)\in \operatorname {tp}(a/N)$
Kim-divide over M. There exists an M-invariant
$\varphi (x,b)\in \operatorname {tp}(a/N)$
Kim-divide over M. There exists an M-invariant
![]() $q(y)\in S(\mathfrak {C})$
extending
$q(y)\in S(\mathfrak {C})$
extending
![]() $\operatorname {tp}(b/M)$
such that
$\operatorname {tp}(b/M)$
such that
![]() $\varphi (x,b)\ q$
-divides over M. We set
$\varphi (x,b)\ q$
-divides over M. We set
![]() $Q=\big ((\varphi (x;y),q(y))\big )$
. By Lemma 3.15 and Corollary 3.11, it follows that
$Q=\big ((\varphi (x;y),q(y))\big )$
. By Lemma 3.15 and Corollary 3.11, it follows that
Therefore there exists a sequence
![]() $(b^{\alpha },M^{\alpha })_{\alpha <\lambda }$
such that:
$(b^{\alpha },M^{\alpha })_{\alpha <\lambda }$
such that:
-
(1)
 $Mb\subseteq M^0$
,
$Mb\subseteq M^0$
, -
(2) q is
 $M^0$
-invariant,
$M^0$
-invariant, -
(3)
 $M^{\alpha }\preceq \mathfrak {C}$
and
$M^{\alpha }\preceq \mathfrak {C}$
and
 $M^{\alpha +1}$
is
$M^{\alpha +1}$
is
 $|M^{\alpha }|^+$
-saturated for each
$|M^{\alpha }|^+$
-saturated for each
 $\alpha <\lambda $
,
$\alpha <\lambda $
, -
(4)
 $b^{\alpha }M^{\alpha }\subseteq M^{\alpha +1}$
for each
$b^{\alpha }M^{\alpha }\subseteq M^{\alpha +1}$
for each
 $\alpha +1<\lambda $
,
$\alpha +1<\lambda $
, -
(5)
 $b^{\alpha }\models q|_{M^{\alpha }}$
for each
$b^{\alpha }\models q|_{M^{\alpha }}$
for each
 $\alpha <\lambda $
,
$\alpha <\lambda $
, -
(6)
 $\operatorname {tp}(a/M)\;\cup \;\{\varphi (x;b)\}\;\cup \;\{\varphi (x;b^{\alpha })\;|\;\alpha <\lambda \}$
is consistent,
$\operatorname {tp}(a/M)\;\cup \;\{\varphi (x;b)\}\;\cup \;\{\varphi (x;b^{\alpha })\;|\;\alpha <\lambda \}$
is consistent, -
(7)
 $\varphi (x;b^{\alpha })$
Kim-divides over
$\varphi (x;b^{\alpha })$
Kim-divides over
 $M^\alpha $
for each
$M^\alpha $
for each
 $\alpha <\lambda $
.
$\alpha <\lambda $
.
By Lemma 3.12, we can modify
![]() $M^0$
and so assume that
$M^0$
and so assume that
![]() $M^0$
is
$M^0$
is
![]() $|M|^+$
-saturated, which we do. We set
$|M|^+$
-saturated, which we do. We set
![]() $M^{-1}:=M$
and
$M^{-1}:=M$
and
![]() $b^{-1}:=b$
. Checking that
$b^{-1}:=b$
. Checking that
![]() $(b^{\alpha },M^{\alpha })_{-1\leqslant \alpha <\lambda }$
witnesses that
$(b^{\alpha },M^{\alpha })_{-1\leqslant \alpha <\lambda }$
witnesses that
![]() $D_Q(\operatorname {tp}(a/M))\geqslant \lambda +1$
is routine (note that, as
$D_Q(\operatorname {tp}(a/M))\geqslant \lambda +1$
is routine (note that, as
![]() $\lambda <\omega $
,
$\lambda <\omega $
,
![]() $(b^{\alpha },M^{\alpha })_{-1\leqslant \alpha <\lambda }$
can be naturally indexed by the elements of
$(b^{\alpha },M^{\alpha })_{-1\leqslant \alpha <\lambda }$
can be naturally indexed by the elements of
![]() $\lambda +1$
).
$\lambda +1$
).
Lemma 3.22. Let T be NSOP
![]() $_1$
with existence. Assume that
$_1$
with existence. Assume that
![]() $a\in \mathfrak {C}$
,
$a\in \mathfrak {C}$
,
![]() $M\preceq N\preceq \mathfrak {C}$
, N is
$M\preceq N\preceq \mathfrak {C}$
, N is
![]() $|M|^+$
-saturated,
$|M|^+$
-saturated,
![]() $q(y)\in S(\mathfrak {C})$
is M-invariant, and that
$q(y)\in S(\mathfrak {C})$
is M-invariant, and that
![]() $q^{\otimes \omega \cdot n}|_M$
is stationary for any
$q^{\otimes \omega \cdot n}|_M$
is stationary for any
![]() $n<\omega $
. Let
$n<\omega $
. Let
![]() $Q=\big ((\varphi (x;y),q(y))\big )$
. If
$Q=\big ((\varphi (x;y),q(y))\big )$
. If ![]() then
then
![]() $D_Q(a/M)=D_Q(a/N)$
.
$D_Q(a/M)=D_Q(a/N)$
.
Proof Let
![]() $D_Q(a/M)=:\lambda <\omega $
, it means by Lemma 3.9 that there exists
$D_Q(a/M)=:\lambda <\omega $
, it means by Lemma 3.9 that there exists
![]() $\big ( (b^{\alpha }_i)_{i<\omega }, M^{\alpha }\big )_{\alpha <\lambda }$
such that:
$\big ( (b^{\alpha }_i)_{i<\omega }, M^{\alpha }\big )_{\alpha <\lambda }$
such that:
-
(1)
 $M\subseteq M^0$
,
$M\subseteq M^0$
, -
(2) q is
 $M^0$
-invariant (which comes for free as q is M-invariant and
$M^0$
-invariant (which comes for free as q is M-invariant and
 $M\subseteq M^0$
),
$M\subseteq M^0$
), -
(3)
 $M^{\alpha }\preceq \mathfrak {C}$
for all
$M^{\alpha }\preceq \mathfrak {C}$
for all
 $\alpha <\lambda $
,
$\alpha <\lambda $
,
 $(M^{\alpha })_{\alpha <\lambda }$
is continuous, and
$(M^{\alpha })_{\alpha <\lambda }$
is continuous, and
 $M^{\alpha +1}$
is
$M^{\alpha +1}$
is
 $|M^{\alpha }|^+$
-saturated for all
$|M^{\alpha }|^+$
-saturated for all
 $\alpha +1<\lambda $
,
$\alpha +1<\lambda $
, -
(4)
 $b^{\alpha }_{<\omega }M^{\alpha }\subseteq M^{\alpha +1}$
for all
$b^{\alpha }_{<\omega }M^{\alpha }\subseteq M^{\alpha +1}$
for all
 $\alpha +1<\lambda $
,
$\alpha +1<\lambda $
, -
(5)
 $b^{\alpha }_{<\omega }\models q^{\otimes \omega }|_{M^{\alpha }}$
for all
$b^{\alpha }_{<\omega }\models q^{\otimes \omega }|_{M^{\alpha }}$
for all
 $\alpha <\lambda $
,
$\alpha <\lambda $
, -
(6)
 $\operatorname {tp}(a/M)\;\cup \;\{\varphi (x;b^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent,
$\operatorname {tp}(a/M)\;\cup \;\{\varphi (x;b^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent, -
(7)
 $\{\varphi (x;b^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent for all
$\{\varphi (x;b^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent for all
 $\alpha <\lambda $
.
$\alpha <\lambda $
.
Step 1. Let
![]() $d\models \operatorname {tp}(a/M)\;\cup \;\{\varphi (x;b^{\alpha }_0)\;|\;\alpha <\lambda \}$
and let
$d\models \operatorname {tp}(a/M)\;\cup \;\{\varphi (x;b^{\alpha }_0)\;|\;\alpha <\lambda \}$
and let
![]() $N"\preceq \mathfrak {C}$
be such that
$N"\preceq \mathfrak {C}$
be such that
![]() $aN\equiv _M dN"$
. By the existence axiom for forking independence, there exists
$aN\equiv _M dN"$
. By the existence axiom for forking independence, there exists
![]() $N'\equiv _{Md}N"$
such that
$N'\equiv _{Md}N"$
such that
Because ![]() , we have that
, we have that ![]() and then also that
and then also that ![]() . As
. As
![]() $N'$
is
$N'$
is
![]() $|M|^+$
-saturated, Proposition 5.4 from [Reference Casanovas4] assures us that
$|M|^+$
-saturated, Proposition 5.4 from [Reference Casanovas4] assures us that ![]() and
and ![]() combine into
combine into ![]() . Then monotonicity of
. Then monotonicity of ![]() gives us
gives us ![]() .
.
Step 2. Because
![]() $aN\equiv _M dN"\equiv _M dN'$
and
$aN\equiv _M dN"\equiv _M dN'$
and
![]() $q(y)$
is M-invariant, we have that
$q(y)$
is M-invariant, we have that
![]() $D_Q(a/N)=D_Q(d/N')$
, so it is enough to show that
$D_Q(a/N)=D_Q(d/N')$
, so it is enough to show that
![]() $D_Q(d/N')\geqslant \lambda $
. Note that
$D_Q(d/N')\geqslant \lambda $
. Note that
![]() $\operatorname {tp}(d/N')\;\cup \;\{\varphi (x;b^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent.
$\operatorname {tp}(d/N')\;\cup \;\{\varphi (x;b^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent.
Step 3. Note that
Since ![]() and the type
and the type
![]() $q^{\otimes \omega }\otimes \dots \otimes q^{\otimes \omega }|_M$
(
$q^{\otimes \omega }\otimes \dots \otimes q^{\otimes \omega }|_M$
(
![]() $\lambda $
-many repetitions) is stationary, we have that also
$\lambda $
-many repetitions) is stationary, we have that also
Step 4. Now, Lemma 3.12 gives us easily
![]() $D_Q(d/N')\geqslant \lambda $
.
$D_Q(d/N')\geqslant \lambda $
.
Definition 3.23. Consider
![]() $p(x)\in S(A)$
. We call
$p(x)\in S(A)$
. We call
![]() $p(x)$
Kim-stationary if for each
$p(x)$
Kim-stationary if for each
![]() $B\supseteq A$
there is a unique Kim-nonforking extension of p over B.
$B\supseteq A$
there is a unique Kim-nonforking extension of p over B.
Repeating the proof of [Reference Casanovas4, Lemma 11.6] we get:
Fact 3.24. (Arbitrary T) Let ![]() be any invariant ternary relation satisfying symmetry [over models] and extension [over models]. Then for any parameter set [any model] M and
be any invariant ternary relation satisfying symmetry [over models] and extension [over models]. Then for any parameter set [any model] M and
![]() $a,b$
, if
$a,b$
, if
![]() $\operatorname {tp}(ab/M)$
is
$\operatorname {tp}(ab/M)$
is ![]() -stationary then
-stationary then
![]() $tp(a/M)$
is
$tp(a/M)$
is ![]() -stationary.
-stationary.
Proof Let
![]() $N\succeq M$
and let
$N\succeq M$
and let
![]() $a'\equiv _M a"\equiv _M a$
be such that
$a'\equiv _M a"\equiv _M a$
be such that ![]() and
and ![]() . By extension, symmetry, and invariance, there are
. By extension, symmetry, and invariance, there are
![]() $b',b"$
such that
$b',b"$
such that
![]() $a'b'\equiv _M a"b"\equiv _M ab$
,
$a'b'\equiv _M a"b"\equiv _M ab$
, ![]() and
and ![]() . Then by
. Then by ![]() -stationarity of
-stationarity of
![]() $\operatorname {tp}(ab/M)$
we have that
$\operatorname {tp}(ab/M)$
we have that
![]() $a'b'\equiv _N a"b"$
, so in particular
$a'b'\equiv _N a"b"$
, so in particular
![]() $a'\equiv _N a"$
.
$a'\equiv _N a"$
.
Remark 3.25. Let
![]() $p(x)$
be a complete type over
$p(x)$
be a complete type over
![]() $M\subseteq \mathfrak {C}$
with x possibly infinite.
$M\subseteq \mathfrak {C}$
with x possibly infinite.
-
(1) Let T be simple, then
 $p(x)$
is stationary if and only if
$p(x)$
is stationary if and only if
 $p|_{x_0}$
is stationary for every finite subtuple
$p|_{x_0}$
is stationary for every finite subtuple
 $x_0$
of x.
$x_0$
of x. -
(2) (T being NSOP
 $_1$
) Let
$_1$
) Let
 $M\preceq \mathfrak {C}$
. We have that
$M\preceq \mathfrak {C}$
. We have that
 $p(x)$
Kim-stationary if and only if
$p(x)$
Kim-stationary if and only if
 $p|_{x_0}$
is Kim-stationary for every finite subtuple
$p|_{x_0}$
is Kim-stationary for every finite subtuple
 $x_0$
of x.
$x_0$
of x.
Proof We start with the proof of (1). The implication from left to right follows from Fact 3.24. Assume
![]() $p|_{x_0}$
is stationary for every finite subtuple
$p|_{x_0}$
is stationary for every finite subtuple
![]() $x_0$
of x and let
$x_0$
of x and let
![]() $q_0,q_1$
be global non-forking extensions of p. Then for every finite subtuple
$q_0,q_1$
be global non-forking extensions of p. Then for every finite subtuple
![]() $x_0$
of x we have that
$x_0$
of x we have that
![]() $q_0|_{x_0}$
and
$q_0|_{x_0}$
and
![]() $q_1|_{x_0}$
are non-forking extensions of
$q_1|_{x_0}$
are non-forking extensions of
![]() $p|_{x_0}$
, so by stationarity of
$p|_{x_0}$
, so by stationarity of
![]() $p|_{x_0}$
they are equal, hence
$p|_{x_0}$
they are equal, hence
![]() $q_0=q_1$
and p is stationary.
$q_0=q_1$
and p is stationary.
The argument for Kim-stationarity is exactly the same.
Lemma 3.26. Let
![]() $A\subseteq \mathfrak {C}$
, let
$A\subseteq \mathfrak {C}$
, let
![]() $(I,<)$
be an infinite linear ordering without a maximal element, and let
$(I,<)$
be an infinite linear ordering without a maximal element, and let
![]() $q(y)\in S(\mathfrak {C})$
be an A-invariant type.
$q(y)\in S(\mathfrak {C})$
be an A-invariant type.
-
(1) Let T be simple. If
 $q|_A$
is stationary then also
$q|_A$
is stationary then also
 $q^{\otimes \omega }|_A$
is stationary.
$q^{\otimes \omega }|_A$
is stationary. -
(2) (Any T) If
 $q^{\otimes \omega }|_A$
is stationary then
$q^{\otimes \omega }|_A$
is stationary then
 $q^{\otimes I}|_A$
is stationary.
$q^{\otimes I}|_A$
is stationary. -
(3) (Any T) If
 $q^{\otimes \omega }|_A$
is Kim-stationary then
$q^{\otimes \omega }|_A$
is Kim-stationary then
 $q^{\otimes I}|_A$
is Kim-stationary.
$q^{\otimes I}|_A$
is Kim-stationary.
Proof We start with the proof of (1). By Remark 3.25, it is enough to show that for each
![]() $n<\omega $
, the type
$n<\omega $
, the type
![]() $q^{\otimes n}|_A$
is stationary. This can be shown inductively by the use of the following claim:
$q^{\otimes n}|_A$
is stationary. This can be shown inductively by the use of the following claim:
Claim. If
![]() $p(x)\in S(\mathfrak {C})$
is A-invariant, such that
$p(x)\in S(\mathfrak {C})$
is A-invariant, such that
![]() $p|_A$
is stationary, then
$p|_A$
is stationary, then
![]() $q\otimes p|_A$
is stationary.
$q\otimes p|_A$
is stationary.
Proof of the claim
Let
![]() $B\supseteq A$
, let
$B\supseteq A$
, let
![]() $ab\models q\otimes p|_A$
be such that
$ab\models q\otimes p|_A$
be such that ![]() , and let
, and let
![]() $a'b'\models q\otimes p|_B$
. Our goal is
$a'b'\models q\otimes p|_B$
. Our goal is
![]() $ab\models q\otimes p|_B$
. As
$ab\models q\otimes p|_B$
. As ![]() , we have
, we have ![]() . Since
. Since
![]() $b'\models p|_B$
and p is A-invariant, also
$b'\models p|_B$
and p is A-invariant, also ![]() . Stationarity of
. Stationarity of
![]() $p|_A$
implies that there exists
$p|_A$
implies that there exists
![]() $f\in \operatorname {Aut}(\mathfrak {C}/B)$
such that
$f\in \operatorname {Aut}(\mathfrak {C}/B)$
such that
![]() $f(b)=b'$
, thus
$f(b)=b'$
, thus
![]() $b\models p|_B$
. Because
$b\models p|_B$
. Because
![]() $a\models q|_{Ab}$
, we have that
$a\models q|_{Ab}$
, we have that
![]() $f(a)\models q|_{Ab'}$
. Since q is A-invariant, we obtain that
$f(a)\models q|_{Ab'}$
. Since q is A-invariant, we obtain that ![]() . On the other hand,
. On the other hand, ![]() changes via f into
changes via f into ![]() , then symmetry, base monotonicity, normality and monotonicity of
, then symmetry, base monotonicity, normality and monotonicity of ![]() give us
give us ![]() . By transitivity of
. By transitivity of ![]() ,
, ![]() and
and ![]() imply that
imply that ![]() , which by the fact that
, which by the fact that
![]() $a'\models q|_{Bb'}$
(so
$a'\models q|_{Bb'}$
(so ![]() ) and by stationarity of
) and by stationarity of
![]() $q|A$
implies
$q|A$
implies
![]() $f(a)\equiv _{Bb'}a'$
. As
$f(a)\equiv _{Bb'}a'$
. As
![]() $f(a)\models q|_{Bb'}$
, we have that
$f(a)\models q|_{Bb'}$
, we have that
![]() $a\models q|_{Bb}$
, thus
$a\models q|_{Bb}$
, thus
![]() $ab\models q\otimes p|_B$
and we end the proof of the claim.
$ab\models q\otimes p|_B$
and we end the proof of the claim.
Now, we are moving to the proof of (2). Assume that
![]() $\bar {a}=(a_i)_{i\in I}\models q^{\otimes I}|_A$
and
$\bar {a}=(a_i)_{i\in I}\models q^{\otimes I}|_A$
and
![]() $\bar {b}=(b_i)_{i\in I}\models q^{\otimes I}|_A$
are such that
$\bar {b}=(b_i)_{i\in I}\models q^{\otimes I}|_A$
are such that ![]() and
and ![]() for some
for some
![]() $B\supseteq A$
. We need to show that
$B\supseteq A$
. We need to show that
![]() $\operatorname {tp}(\bar {a}/B)=\operatorname {tp}(\bar {b}/B)$
, which holds if and only if for each
$\operatorname {tp}(\bar {a}/B)=\operatorname {tp}(\bar {b}/B)$
, which holds if and only if for each
![]() $n<\omega $
and each
$n<\omega $
and each
![]() $i_1,\ldots ,i_n\in I$
, such that
$i_1,\ldots ,i_n\in I$
, such that
![]() $i_1<\cdots <i_n$
, we have
$i_1<\cdots <i_n$
, we have
![]() $\operatorname {tp}(a_{i_n}\ldots a_{i_1}/B)=\operatorname {tp}(b_{i_n}\ldots b_{i_1}/B)$
. Consider such
$\operatorname {tp}(a_{i_n}\ldots a_{i_1}/B)=\operatorname {tp}(b_{i_n}\ldots b_{i_1}/B)$
. Consider such
![]() $i_1,\ldots ,i_n\in I$
and choose any infinite sequence
$i_1,\ldots ,i_n\in I$
and choose any infinite sequence
![]() $I_0\subseteq I$
starting with
$I_0\subseteq I$
starting with
![]() $(i_1,\ldots ,i_n)$
which has the order type of
$(i_1,\ldots ,i_n)$
which has the order type of
![]() $(\omega ,<)$
. Let
$(\omega ,<)$
. Let
![]() $a_{I_0}:=(a_i)_{i\in I_0}$
and
$a_{I_0}:=(a_i)_{i\in I_0}$
and
![]() $b_{I_0}:=(b_i)_{i\in I_0}$
. Then
$b_{I_0}:=(b_i)_{i\in I_0}$
. Then
![]() $a_{I_0}\models q^{\otimes \omega }|_A$
,
$a_{I_0}\models q^{\otimes \omega }|_A$
,
![]() $b_{I_0}\models q^{\otimes \omega }|_A$
. Monotonicity of
$b_{I_0}\models q^{\otimes \omega }|_A$
. Monotonicity of ![]() gives us that
gives us that ![]() and
and ![]() . As
. As
![]() $q^{\otimes \omega }|_A$
is stationary we have that
$q^{\otimes \omega }|_A$
is stationary we have that
![]() $a_{I_0}\equiv _B b_{I_0}$
, so in particular
$a_{I_0}\equiv _B b_{I_0}$
, so in particular
![]() $\operatorname {tp}(a_{i_n}\ldots a_{i_1}/B)=\operatorname {tp}(b_{i_n}\ldots b_{i_1}/B)$
.
$\operatorname {tp}(a_{i_n}\ldots a_{i_1}/B)=\operatorname {tp}(b_{i_n}\ldots b_{i_1}/B)$
.
The proof of (3) is similar to the proof of (2), as the only property of ![]() used was monotonicity, which also holds for
used was monotonicity, which also holds for ![]() .
.
Definition 3.27. Let
![]() $A\subseteq \mathfrak {C}$
and let
$A\subseteq \mathfrak {C}$
and let
![]() $q(y)\in S(\mathfrak {C})$
be A-invariant.
$q(y)\in S(\mathfrak {C})$
be A-invariant.
-
(1) We call
 $q|_A$
strongly stationary if the type
$q|_A$
strongly stationary if the type
 $q^{\otimes \omega }|_A$
is stationary.
$q^{\otimes \omega }|_A$
is stationary. -
(2) We call
 $q|_A$
strongly Kim-stationary if the type
$q|_A$
strongly Kim-stationary if the type
 $q^{\otimes \omega }|_A$
is Kim-stationary.
$q^{\otimes \omega }|_A$
is Kim-stationary.
Remark 3.28. Let
![]() $A\subseteq \mathfrak {C}$
and let
$A\subseteq \mathfrak {C}$
and let
![]() $q(y)\in S(\mathfrak {C})$
be A-invariant, and let
$q(y)\in S(\mathfrak {C})$
be A-invariant, and let
![]() $(I,<)$
be an infinite linear ordering without a maximal element.
$(I,<)$
be an infinite linear ordering without a maximal element.
-
(1) If the type
 $q|_A$
is strongly stationary then
$q|_A$
is strongly stationary then
 $q^{\otimes I}|_A$
is stationary.
$q^{\otimes I}|_A$
is stationary. -
(2) If in addition T is simple, then the type
 $q|_A$
is strongly stationary if and only if
$q|_A$
is strongly stationary if and only if
 $q|_A$
is stationary.
$q|_A$
is stationary. -
(3) If the type
 $q|_A$
is strongly Kim-stationary then
$q|_A$
is strongly Kim-stationary then
 $q^{\otimes I}|_A$
is Kim-stationary.
$q^{\otimes I}|_A$
is Kim-stationary. -
(4) If in addition
 $A\subseteq M\preceq \mathfrak {C}$
, the type
$A\subseteq M\preceq \mathfrak {C}$
, the type
 $q^{\otimes \omega }|_M$
is Kim-stationary if and only if for each finite subtuple
$q^{\otimes \omega }|_M$
is Kim-stationary if and only if for each finite subtuple
 $\bar {x}$
of
$\bar {x}$
of
 $(x_i)_{i<\omega }$
, the type
$(x_i)_{i<\omega }$
, the type
 $\big (q^{\otimes \omega }|_M\big )_{\bar {x}}$
is Kim-stationary.
$\big (q^{\otimes \omega }|_M\big )_{\bar {x}}$
is Kim-stationary.
Question 3.29. Let
![]() $M\preceq \mathfrak {C}$
and let
$M\preceq \mathfrak {C}$
and let
![]() $q(y)\in S(\mathfrak {C})$
be M-invariant such that
$q(y)\in S(\mathfrak {C})$
be M-invariant such that
![]() $q|_M$
is Kim-stationary. Is the type
$q|_M$
is Kim-stationary. Is the type
![]() $q^{\otimes \omega }|_M$
Kim-stationary?
$q^{\otimes \omega }|_M$
Kim-stationary?
Corollary 3.30. Let T be NSOP
![]() $_1$
with existence. Assume that
$_1$
with existence. Assume that
![]() $a\in \mathfrak {C}$
,
$a\in \mathfrak {C}$
,
![]() $M\preceq N\preceq \mathfrak {C}$
, that
$M\preceq N\preceq \mathfrak {C}$
, that
![]() $q(y)\in S(\mathfrak {C})$
is M-invariant and let
$q(y)\in S(\mathfrak {C})$
is M-invariant and let
![]() $Q=\big ((\varphi (x;y),q(y))\big )$
.
$Q=\big ((\varphi (x;y),q(y))\big )$
.
-
(1) Assume that N is
 $|M|^+$
-saturated and
$|M|^+$
-saturated and
 $q|_M$
is strongly stationary, then
$q|_M$
is strongly stationary, then 
-
(2) Assume that T is simple and
 $q|_M$
is stationary, then
$q|_M$
is stationary, then 
-
(3) If
 $q|_M$
is strongly Kim-stationary, then
$q|_M$
is strongly Kim-stationary, then 
Proof (1) is exactly the content of Lemma 3.22. For (2), we use Lemma 3.26 and repeat the proof of Lemma 3.22, where in Step 1, instead of the saturation assumption we use transitivity, which naturally holds in simple theories.
(3) also uses a modification of the proof of Lemma 3.22. More precisely, in Step 1, we use that ![]() implies
implies ![]() and that transitivity (over arbitrary sets) holds in NSOP
and that transitivity (over arbitrary sets) holds in NSOP
![]() $_1$
with existence. We obtain
$_1$
with existence. We obtain ![]() and then
and then ![]() . Then, Step 3 follows by the definition of strong Kim-stationarity. The rest (Step 2 and Step 4) remains the same.
. Then, Step 3 follows by the definition of strong Kim-stationarity. The rest (Step 2 and Step 4) remains the same.
It is worth comparing (2) and (3) in the above corollary with Theorem 4.7(2) from [Reference Chernikov, Byungham and Ramsey10]. We are aware that we introduced a different notion of rank, but because of that, we were able to drop the assumption on simplicity from [Reference Chernikov, Byungham and Ramsey10, Theorem 4.7(2)] at the cost of assuming strong stationarity of the type q and so to provide partial answer to the counterpart to Question 4.9 from [Reference Chernikov, Byungham and Ramsey10] for our notion of rank.
In Example 4.1, we will observe that the stationarity assumption in Lemma 3.22 cannot be removed. Moreover, in Proposition 4.2, we will see that in the case of vector spaces with a bilinear form, being strongly Kim-stationary is equivalent to being Kim-stationary.
4 Forking in
 $T_{\infty }$
$T_{\infty }$
In this section we describe forking in the theory
![]() $T_\infty $
of vector spaces with a generic bilinear form, answering in particular a question about equivalence of dividing and dividing finitely stated in the first paragraph of Section 12.5 in [Reference Granger18]. Before that let us recall the basic definitions and provide some facts related to the previous sections.
$T_\infty $
of vector spaces with a generic bilinear form, answering in particular a question about equivalence of dividing and dividing finitely stated in the first paragraph of Section 12.5 in [Reference Granger18]. Before that let us recall the basic definitions and provide some facts related to the previous sections.
Let
![]() $T_{\infty }$
be the theory of two-sorted vector spaces over an algebraically closed field of a fixed characteristic p different from 2 (we allow
$T_{\infty }$
be the theory of two-sorted vector spaces over an algebraically closed field of a fixed characteristic p different from 2 (we allow
![]() $p=0$
), with a sort V for vectors and a sort K for scalars, equipped with a non-degenerate symmetric (or alternating) bilinear form, as studied in [Reference Granger18]. Then T is NSOP
$p=0$
), with a sort V for vectors and a sort K for scalars, equipped with a non-degenerate symmetric (or alternating) bilinear form, as studied in [Reference Granger18]. Then T is NSOP
![]() $_1$
by [Reference Chernikov and Ramsey11, Corollary 6.1] and it has existence by [Reference Dobrowolski14, Proposition 8.1]. Fix a monster model
$_1$
by [Reference Chernikov and Ramsey11, Corollary 6.1] and it has existence by [Reference Dobrowolski14, Proposition 8.1]. Fix a monster model
![]() $\mathfrak {C}=(V(\mathfrak {C}), K(\mathfrak {C}))$
of
$\mathfrak {C}=(V(\mathfrak {C}), K(\mathfrak {C}))$
of
![]() $T_{\infty }$
. If
$T_{\infty }$
. If
![]() $A\subseteq \mathfrak {C}\models T_\infty $
, put
$A\subseteq \mathfrak {C}\models T_\infty $
, put
![]() $\langle A \rangle :=\operatorname {Lin}_{K(\mathfrak {C})}(V(A))$
and let
$\langle A \rangle :=\operatorname {Lin}_{K(\mathfrak {C})}(V(A))$
and let
![]() $A_K:=A\cap K(\mathfrak {C})$
. By [Reference Dobrowolski14, Corollary 8.13], for any sets
$A_K:=A\cap K(\mathfrak {C})$
. By [Reference Dobrowolski14, Corollary 8.13], for any sets
![]() $A,B,C$
we have that
$A,B,C$
we have that ![]() if and only if:
if and only if:
-
•
 $\langle AC \rangle \cap \langle BC \rangle =\langle C \rangle $
and
$\langle AC \rangle \cap \langle BC \rangle =\langle C \rangle $
and -
•
 ,
,
where
![]() $\operatorname {dcl}(\ast )_K$
means
$\operatorname {dcl}(\ast )_K$
means
![]() $(\operatorname {dcl}(\ast ))_K$
(for an algebraic description of
$(\operatorname {dcl}(\ast ))_K$
(for an algebraic description of
![]() $\operatorname {dcl}(*),$
see [Reference Granger18, Proposition 9.5.1]). For a discussion about forking and dividing in
$\operatorname {dcl}(*),$
see [Reference Granger18, Proposition 9.5.1]). For a discussion about forking and dividing in
![]() $T_\infty $
, see [Reference Granger18, Section 12.3] and the rest of this section below. In all the proofs in this section we will assume the bilinear form is symmetric; the arguments in the alternating case are analogous.
$T_\infty $
, see [Reference Granger18, Section 12.3] and the rest of this section below. In all the proofs in this section we will assume the bilinear form is symmetric; the arguments in the alternating case are analogous.
Example 4.1. Let
![]() $M\models T_\infty $
and let
$M\models T_\infty $
and let
![]() $q_0$
be the unique global
$q_0$
be the unique global ![]() -generic (in the sense of [Reference Granger18, Definition 12.2.1]) type in V. Let
-generic (in the sense of [Reference Granger18, Definition 12.2.1]) type in V. Let
![]() $v\models q_0|_{M}$
and let
$v\models q_0|_{M}$
and let
![]() $N\succ M$
be a model containing v. Then
$N\succ M$
be a model containing v. Then
![]() $q_0|_M(x)\cup \{x\perp v\}$
does not Kim-fork over M so it has a realisation w with
$q_0|_M(x)\cup \{x\perp v\}$
does not Kim-fork over M so it has a realisation w with ![]() . Let
. Let
![]() $\varphi (x,y)$
express that
$\varphi (x,y)$
express that
![]() $x\in \langle y\rangle \setminus \{0\}$
with x and y being single vector variables, and
$x\in \langle y\rangle \setminus \{0\}$
with x and y being single vector variables, and
![]() $Q=((\varphi (x,y),q_0(y)))$
. We claim that
$Q=((\varphi (x,y),q_0(y)))$
. We claim that
![]() $D_Q(w/N)=0$
and
$D_Q(w/N)=0$
and
![]() $D_Q(w/M)\geq 1$
, which shows that the stationarity assumption in Lemma 3.22 cannot be removed. Indeed, note that if
$D_Q(w/M)\geq 1$
, which shows that the stationarity assumption in Lemma 3.22 cannot be removed. Indeed, note that if
![]() $N\prec N_0$
and
$N\prec N_0$
and
![]() $b\models q_0|_{N_0}$
then b is not orthogonal to v, so
$b\models q_0|_{N_0}$
then b is not orthogonal to v, so
![]() $\operatorname {tp}(w/N)\cup \varphi (x,b)$
is inconsistent, hence
$\operatorname {tp}(w/N)\cup \varphi (x,b)$
is inconsistent, hence
![]() $D_Q(w/N)=0$
. On the other hand,
$D_Q(w/N)=0$
. On the other hand,
![]() $\operatorname {tp}(w/M) \cup \varphi (x,b)$
is consistent and
$\operatorname {tp}(w/M) \cup \varphi (x,b)$
is consistent and
![]() $\varphi (x,b)\ q_0$
-forks over
$\varphi (x,b)\ q_0$
-forks over
![]() $N_0$
(as the sets
$N_0$
(as the sets
![]() $\langle b_i\rangle \setminus \{0\}$
are pairwise disjoint for a Morley sequence
$\langle b_i\rangle \setminus \{0\}$
are pairwise disjoint for a Morley sequence
![]() $(b_i)_{i<\omega }$
in
$(b_i)_{i<\omega }$
in
![]() $q_0$
over
$q_0$
over
![]() $N_0$
, since such a sequence is linearly independent). Thus
$N_0$
, since such a sequence is linearly independent). Thus
![]() $D_Q(w/M)\geq 1$
(and it is actually easy to see that
$D_Q(w/M)\geq 1$
(and it is actually easy to see that
![]() $D_Q(w/M)= 1$
).
$D_Q(w/M)= 1$
).
Proposition 4.2. Let
![]() $p(x)=\operatorname {tp}(a/M)$
be a complete type over
$p(x)=\operatorname {tp}(a/M)$
be a complete type over
![]() $M\models T_\infty $
. Then
$M\models T_\infty $
. Then
![]() $p(x)$
is Kim-stationary iff
$p(x)$
is Kim-stationary iff
![]() $a\subseteq K(\mathfrak {C})\cup \langle V(M)\rangle $
. Hence
$a\subseteq K(\mathfrak {C})\cup \langle V(M)\rangle $
. Hence
![]() $p(x)$
is Kim-stationary if and only if it is strongly Kim-stationary.
$p(x)$
is Kim-stationary if and only if it is strongly Kim-stationary.
Proof By Remark 3.25, we may assume x is a finite tuple of variables. Assume the right-hand side first. Then by compactness
![]() $p(x)\vdash x\subseteq V_0\cup K(\mathfrak {C})$
for some finite-dimensional subspace
$p(x)\vdash x\subseteq V_0\cup K(\mathfrak {C})$
for some finite-dimensional subspace
![]() $V_0\leq V(\mathfrak {C})$
. As
$V_0\leq V(\mathfrak {C})$
. As
![]() $V_0\cup K(\mathfrak {C})$
is stably embedded in
$V_0\cup K(\mathfrak {C})$
is stably embedded in
![]() $\mathfrak {C}$
and definable over M in the pure field K, we can view
$\mathfrak {C}$
and definable over M in the pure field K, we can view
![]() $p(x)$
as a complete type over
$p(x)$
as a complete type over
![]() $V_0(M)\cup K(M)$
in the finite Morley rank structure
$V_0(M)\cup K(M)$
in the finite Morley rank structure
![]() $V_0\cup K(\mathfrak {C})$
. Hence Kim-stationarity of
$V_0\cup K(\mathfrak {C})$
. Hence Kim-stationarity of
![]() $p(x)$
follows as in
$p(x)$
follows as in
![]() $V_0\cup K(\mathfrak {C})$
Kim-independence coincides with forking independence and
$V_0\cup K(\mathfrak {C})$
Kim-independence coincides with forking independence and
![]() $V_0(M)\cup K(M)\prec V_0\cup K(\mathfrak {C})$
.
$V_0(M)\cup K(M)\prec V_0\cup K(\mathfrak {C})$
.
Now assume that
![]() $p(x)$
is stationary and let
$p(x)$
is stationary and let
![]() $p'(x_0)$
be its restriction to a single vector variable
$p'(x_0)$
be its restriction to a single vector variable
![]() $x_0$
. By Fact 3.24,
$x_0$
. By Fact 3.24,
![]() $p'(x_0)$
is Kim-stationary. Let
$p'(x_0)$
is Kim-stationary. Let
![]() $a_0\models p'(x_0)$
be the coordinate of a corresponding to
$a_0\models p'(x_0)$
be the coordinate of a corresponding to
![]() $x_0$
. Suppose for a contradiction that
$x_0$
. Suppose for a contradiction that
![]() $a_0\notin \langle M \rangle $
. Let
$a_0\notin \langle M \rangle $
. Let
![]() $v\in V(\mathfrak {C})$
be orthogonal to M with
$v\in V(\mathfrak {C})$
be orthogonal to M with
![]() $[v,v]=1$
and let
$[v,v]=1$
and let
![]() $N\succ M$
be such that
$N\succ M$
be such that
![]() $v\in N$
. Then it is routine to check that
$v\in N$
. Then it is routine to check that
![]() $p'(x_0)\cup \{[x_0,v]=0\}$
does not Kim-fork over M, so it extends to a complete type
$p'(x_0)\cup \{[x_0,v]=0\}$
does not Kim-fork over M, so it extends to a complete type
![]() $s(x_0)$
over N which does not Kim-fork over M. Let
$s(x_0)$
over N which does not Kim-fork over M. Let
![]() $r(x_0)$
be the unique
$r(x_0)$
be the unique
![]() $\Gamma $
-independent extension of
$\Gamma $
-independent extension of
![]() $p'(x_0)$
over N. Then
$p'(x_0)$
over N. Then
![]() $r(x_0)$
and
$r(x_0)$
and
![]() $s(x_0)$
are two distinct Kim-independent extensions of
$s(x_0)$
are two distinct Kim-independent extensions of
![]() $p'(x_0)$
over N, which contradicts Kim-stationarity of
$p'(x_0)$
over N, which contradicts Kim-stationarity of
![]() $p'(x_0)$
.
$p'(x_0)$
.
For
![]() $m<\omega $
,
$m<\omega $
,
![]() $T_m$
denotes the theory of m-dimensional vector spaces over an algebraically closed field of characteristic p equipped with a non-degenerate symmetric bilinear form. The following are Definitions 12.3.8 and 12.3.11 in [Reference Granger18]. For the definition of dividing uniformly (which we will not use directly), see [Reference Granger18, Definition 12.3.4].
$T_m$
denotes the theory of m-dimensional vector spaces over an algebraically closed field of characteristic p equipped with a non-degenerate symmetric bilinear form. The following are Definitions 12.3.8 and 12.3.11 in [Reference Granger18]. For the definition of dividing uniformly (which we will not use directly), see [Reference Granger18, Definition 12.3.4].
Definition 4.3. Let
![]() $\phi (x,b)$
be a formula and let A be a countable set.
$\phi (x,b)$
be a formula and let A be a countable set.
-
(1)
 $\phi (x,b)$
divides finitely over A if there is an A-indiscernible sequence
$\phi (x,b)$
divides finitely over A if there is an A-indiscernible sequence
 $(b_i)_{i<\omega }$
of realisations of
$(b_i)_{i<\omega }$
of realisations of
 $\operatorname {tp}(b/A)$
such that
$\operatorname {tp}(b/A)$
such that
 $\{\phi (x; b_i):i<\omega \}$
is inconsistent and
$\{\phi (x; b_i):i<\omega \}$
is inconsistent and
 $\{b_i:i<\omega \}$
is contained in some finite-dimensional substructure
$\{b_i:i<\omega \}$
is contained in some finite-dimensional substructure
 $N\subseteq \mathfrak {C}$
.
$N\subseteq \mathfrak {C}$
. -
(2)
 $\phi (x;b)\ \Gamma $
MS-divides over A, if there is a
$\phi (x;b)\ \Gamma $
MS-divides over A, if there is a
 $\Gamma $
-Morley sequence
$\Gamma $
-Morley sequence
 $(b_i)_{i<\omega }$
in
$(b_i)_{i<\omega }$
in
 $\operatorname {tp}(b/A)$
(i.e., a
$\operatorname {tp}(b/A)$
(i.e., a  -independent A-indiscernible sequence or realisations of
-independent A-indiscernible sequence or realisations of
 $\operatorname {tp}(b/A)$
) such that the set
$\operatorname {tp}(b/A)$
) such that the set
 $\{\phi (x;b_i):i<\omega \}$
is inconsistent.
$\{\phi (x;b_i):i<\omega \}$
is inconsistent.
For the definition of ![]() , see [Reference Granger18, Definition 12.2.1]. As
, see [Reference Granger18, Definition 12.2.1]. As ![]() implies
implies ![]() (see [Reference Kaplan and Ramsey20, Proposition 9.38(1)]), every
(see [Reference Kaplan and Ramsey20, Proposition 9.38(1)]), every
![]() $\Gamma $
-Morley sequence is a Kim-Morley sequence. Hence, as Kim-dividing is witnessed by any Kim-Morley sequence (see [Reference Chernikov, Byungham and Ramsey10, Theorem 3.8]), it follows that
$\Gamma $
-Morley sequence is a Kim-Morley sequence. Hence, as Kim-dividing is witnessed by any Kim-Morley sequence (see [Reference Chernikov, Byungham and Ramsey10, Theorem 3.8]), it follows that
![]() $\Gamma $
MS-dividing is the same as Kim-dividing in
$\Gamma $
MS-dividing is the same as Kim-dividing in
![]() $T_\infty $
.
$T_\infty $
.
By
![]() $\omega ^*=\{i^*:i<\omega \}$
we will denote a copy of
$\omega ^*=\{i^*:i<\omega \}$
we will denote a copy of
![]() $\omega $
with the reversed order.
$\omega $
with the reversed order.
Proposition 4.4. Let A be a countable set of parameters and
![]() $\varphi (x,b)$
a formula which divides over A. Then
$\varphi (x,b)$
a formula which divides over A. Then
![]() $\varphi (x,b)$
divides finitely over A (so it divides uniformly over A by [Reference Granger18, Lemma 12.3.9]).
$\varphi (x,b)$
divides finitely over A (so it divides uniformly over A by [Reference Granger18, Lemma 12.3.9]).
Moreover, if k is such that
![]() $\varphi (x,b)\ k$
-divides over A, then there is an A-indiscernible sequence witnessing this contained in a model of
$\varphi (x,b)\ k$
-divides over A, then there is an A-indiscernible sequence witnessing this contained in a model of
![]() $T_{2k|V(b)|}$
.
$T_{2k|V(b)|}$
.
Proof Let k be such that
![]() $\varphi (x,b)\ k$
-divides over A. By compactness we can find an A-indiscernible sequence
$\varphi (x,b)\ k$
-divides over A. By compactness we can find an A-indiscernible sequence
![]() $(b_i)_{i<\omega \frown \omega ^*}$
with
$(b_i)_{i<\omega \frown \omega ^*}$
with
![]() $b_{0^*}=b$
such that the set
$b_{0^*}=b$
such that the set
![]() $\{\varphi (x,b_i):i<\omega \frown \omega ^*\}$
is k-inconsistent. Note that for any i the type
$\{\varphi (x,b_i):i<\omega \frown \omega ^*\}$
is k-inconsistent. Note that for any i the type
![]() $tp(b_{i^*}/Ab_{<\omega }b_{(<i)^*})$
is finitely satisfiable in
$tp(b_{i^*}/Ab_{<\omega }b_{(<i)^*})$
is finitely satisfiable in
![]() $b_{<\omega }$
, hence in particular, putting
$b_{<\omega }$
, hence in particular, putting
![]() $C:=Ab_{<\omega }$
we get that the sequence
$C:=Ab_{<\omega }$
we get that the sequence
![]() $I:=(b_{i^*})_{i<\omega }$
is Morley over C. Hence
$I:=(b_{i^*})_{i<\omega }$
is Morley over C. Hence
![]() $\varphi (x,b)$
Kim-divides over C, so (by Kim’s lemma), it
$\varphi (x,b)$
Kim-divides over C, so (by Kim’s lemma), it
![]() $\Gamma $
MS-divides over C. Thus, by [Reference Granger18, Lemma 12.3.12],
$\Gamma $
MS-divides over C. Thus, by [Reference Granger18, Lemma 12.3.12],
![]() $\varphi (x,b)$
divides finitely over C so, as
$\varphi (x,b)$
divides finitely over C so, as
![]() $A\subseteq C$
, it divides finitely over A.
$A\subseteq C$
, it divides finitely over A.
Moreover, the proof [Reference Granger18, Lemma 12.3.12] gives that a C-indiscernible sequence witnessing k-dividing of
![]() $\varphi (x,b)$
over C can be found in an R-dimensional subspace of
$\varphi (x,b)$
over C can be found in an R-dimensional subspace of
![]() $V(\mathfrak {C})$
provided that there is a model
$V(\mathfrak {C})$
provided that there is a model
![]() $N_R\models T_R$
containing k elements of a
$N_R\models T_R$
containing k elements of a
![]() $\Gamma $
-Morley sequence witnessing
$\Gamma $
-Morley sequence witnessing
![]() $\Gamma $
MS-dividing of
$\Gamma $
MS-dividing of
![]() $\varphi (x,b)$
over C. But such k elements contain at most
$\varphi (x,b)$
over C. But such k elements contain at most
![]() $k|V(b)|$
vectors, so there is a model of
$k|V(b)|$
vectors, so there is a model of
![]() $T_{2k|V(b)|}$
containing all of them (see, e.g., [Reference Dobrowolski14, Fact 3.2]). This gives the ‘moreover’ clause.
$T_{2k|V(b)|}$
containing all of them (see, e.g., [Reference Dobrowolski14, Fact 3.2]). This gives the ‘moreover’ clause.
By [Reference Granger18, Remark 12.3.14] we conclude:
Corollary 4.5. In
![]() $T_\infty $
, forking and dividing coincide: for any small set A and any formula
$T_\infty $
, forking and dividing coincide: for any small set A and any formula
![]() $\varphi (x,b)$
we have that
$\varphi (x,b)$
we have that
![]() $\varphi (x,b)$
forks over A if and only if
$\varphi (x,b)$
forks over A if and only if
![]() $\varphi (x,b)$
divides over A.
$\varphi (x,b)$
divides over A.
Next, we will describe dividing of formulae in
![]() $T_\infty $
in terms of dividing in the
$T_\infty $
in terms of dividing in the
![]() $\omega $
-stable theories
$\omega $
-stable theories
![]() $T_m$
(which are interpretable in
$T_m$
(which are interpretable in
![]() $ACF$
).
$ACF$
).
By quantifier elimination in
![]() $T_\infty $
(see [Reference Dobrowolski14, Fact 2.8], [Reference Granger18, 9.2.3]), we may (and will) restrict ourselves to considering only quantifier-free formulae.
$T_\infty $
(see [Reference Dobrowolski14, Fact 2.8], [Reference Granger18, 9.2.3]), we may (and will) restrict ourselves to considering only quantifier-free formulae.
Fact 4.6. Let
![]() $M\models T_m$
(with
$M\models T_m$
(with
![]() $M\subseteq \mathfrak {C}\models T_\infty $
) and let
$M\subseteq \mathfrak {C}\models T_\infty $
) and let
![]() $\varphi (x,a)$
be a (quantifier-free) formula with
$\varphi (x,a)$
be a (quantifier-free) formula with
![]() $a\subseteq M$
. Then if
$a\subseteq M$
. Then if
![]() $\varphi (x,a)$
is consistent in
$\varphi (x,a)$
is consistent in
![]() $T_\infty $
and
$T_\infty $
and
![]() $m\geq 2(|V(x)|+|V(a)|)$
, then
$m\geq 2(|V(x)|+|V(a)|)$
, then
![]() $\varphi (x,a)$
is consistent in M.
$\varphi (x,a)$
is consistent in M.
Proof Suppose
![]() $\mathfrak {C}\models \varphi (b,a)$
for some
$\mathfrak {C}\models \varphi (b,a)$
for some
![]() $b\subseteq \mathfrak {C}$
. Then, as
$b\subseteq \mathfrak {C}$
. Then, as
![]() $m\geq 2|V(ab)|$
, there is a model
$m\geq 2|V(ab)|$
, there is a model
![]() $N\models T_m$
containing
$N\models T_m$
containing
![]() $ba$
(see [Reference Dobrowolski14, Fact 3.2]). As
$ba$
(see [Reference Dobrowolski14, Fact 3.2]). As
![]() $\varphi (x,a)$
is quantifier-free, we have
$\varphi (x,a)$
is quantifier-free, we have
![]() $N\models \varphi (b,a)$
. By quantifier elimination in
$N\models \varphi (b,a)$
. By quantifier elimination in
![]() $T_m$
we conclude that
$T_m$
we conclude that
![]() $\varphi (x,a)$
is consistent in M.
$\varphi (x,a)$
is consistent in M.
Proposition 4.7. Suppose
![]() $A\subseteq \mathfrak {C}$
,
$A\subseteq \mathfrak {C}$
,
![]() $|A_V|<\omega $
,
$|A_V|<\omega $
,
![]() $\varphi (x,b)$
is a (quantifier-free) formula, and
$\varphi (x,b)$
is a (quantifier-free) formula, and
![]() $k<\omega $
. Let
$k<\omega $
. Let
![]() $M\subseteq \mathfrak {C}$
be a model of
$M\subseteq \mathfrak {C}$
be a model of
![]() $T_{m}$
with
$T_{m}$
with
![]() $m\geq 2k|V(b)|$
containing A and b. Then
$m\geq 2k|V(b)|$
containing A and b. Then
![]() $\varphi (x,b)\ k$
-divides over A in
$\varphi (x,b)\ k$
-divides over A in
![]() $T_\infty $
if and only if it k-divides over A in M.
$T_\infty $
if and only if it k-divides over A in M.
Proof Suppose first that
![]() $\varphi (x,b)\ k$
-divides over A in
$\varphi (x,b)\ k$
-divides over A in
![]() $T_\infty $
. By Proposition 4.4, we can find a sequence
$T_\infty $
. By Proposition 4.4, we can find a sequence
![]() $(b_i)_{i<\omega }$
contained in a model
$(b_i)_{i<\omega }$
contained in a model
![]() $N\models T_{m}$
witnessing this. Then, as
$N\models T_{m}$
witnessing this. Then, as
![]() $\{\varphi (x,b_i):i<\omega \}$
is k-inconsistent in
$\{\varphi (x,b_i):i<\omega \}$
is k-inconsistent in
![]() $T_\infty $
, it is k-inconsistent in N as well. Hence, by quantifier elimination in
$T_\infty $
, it is k-inconsistent in N as well. Hence, by quantifier elimination in
![]() $T_m$
,
$T_m$
,
![]() $\varphi (x,b)\ k$
-divides in M.
$\varphi (x,b)\ k$
-divides in M.
Conversely, suppose
![]() $\varphi (x,b)\ k$
-divides in M, and consider arbitrary
$\varphi (x,b)\ k$
-divides in M, and consider arbitrary
![]() $l<\omega $
and a finite subset
$l<\omega $
and a finite subset
![]() $p_0\subseteq \operatorname {qftp}(b/A)$
. Then there is a sequence
$p_0\subseteq \operatorname {qftp}(b/A)$
. Then there is a sequence
![]() $(b_i)_{i<l}$
of tuples in M such that for any
$(b_i)_{i<l}$
of tuples in M such that for any
![]() $i_1<\dots <i_k$
we have that
$i_1<\dots <i_k$
we have that
![]() $\bigwedge _{j<k} \varphi (x,b_{i_j})$
is inconsistent in M and
$\bigwedge _{j<k} \varphi (x,b_{i_j})$
is inconsistent in M and
![]() $b_i\models p_0$
for every
$b_i\models p_0$
for every
![]() $i<l$
. Then, as
$i<l$
. Then, as
![]() $b_{i_0}\dots b_{i_{k-1}}$
contains at most
$b_{i_0}\dots b_{i_{k-1}}$
contains at most
![]() $k|V(b)|$
vectors and
$k|V(b)|$
vectors and
![]() $m\geq 2k|V(b)|$
, we get by Fact 4.6 that
$m\geq 2k|V(b)|$
, we get by Fact 4.6 that
![]() $\bigwedge _{j<k} \varphi (x,b_{i_j})$
is inconsistent in
$\bigwedge _{j<k} \varphi (x,b_{i_j})$
is inconsistent in
![]() $T_\infty $
as well. So, by compactness,
$T_\infty $
as well. So, by compactness,
![]() $\varphi (x,b)\ k$
-divides in
$\varphi (x,b)\ k$
-divides in
![]() $T_\infty $
.
$T_\infty $
.
5 Further examples
In this section, we collect more examples of NSOP
![]() $_1$
theories with existence. In each of them, there exist at least three related notions of independence:
$_1$
theories with existence. In each of them, there exist at least three related notions of independence: ![]() ,
, ![]() and
and ![]() (recall that
(recall that ![]() denotes Kim-independence with respect to definition (B) of Kim-dividing). We would like to better understand what are the relations between these three notions of independence. Obviously:
denotes Kim-independence with respect to definition (B) of Kim-dividing). We would like to better understand what are the relations between these three notions of independence. Obviously: ![]() . The first natural question is: when
. The first natural question is: when ![]() and
and ![]() coincide?
coincide?
Remark 5.1. Let T be NSOP
![]() $_1$
with existence. Then
$_1$
with existence. Then ![]() if and only if for every C and every
if and only if for every C and every
![]() $p(x)\in S(C)$
we have that
$p(x)\in S(C)$
we have that
![]() $p(x)$
extends to a global C-invariant type. The implication “
$p(x)$
extends to a global C-invariant type. The implication “
![]() $\Rightarrow $
” holds for arbitrary T.
$\Rightarrow $
” holds for arbitrary T.
Proof “
![]() $\Leftarrow $
”: We only need to show that
$\Leftarrow $
”: We only need to show that ![]() for arbitrary
for arbitrary
![]() $a,B,C$
. By assumption
$a,B,C$
. By assumption
![]() $\operatorname {tp}(B/C)$
extends to a global C-invariant type
$\operatorname {tp}(B/C)$
extends to a global C-invariant type
![]() $r(x)$
. If
$r(x)$
. If ![]() , then there is an
, then there is an
![]() $aC$
-indiscernible Morley sequence in
$aC$
-indiscernible Morley sequence in
![]() $r(x)$
over C starting with B. As I is in particular
$r(x)$
over C starting with B. As I is in particular ![]() -Morley over C, by Kim’s lemma we get that
-Morley over C, by Kim’s lemma we get that ![]() . “
. “
![]() $\Rightarrow $
”: Suppose there exist B and C such that
$\Rightarrow $
”: Suppose there exist B and C such that
![]() $\operatorname {tp}(B/C)$
does not extend to a global C-invariant type. Then for any D we have that
$\operatorname {tp}(B/C)$
does not extend to a global C-invariant type. Then for any D we have that
![]() $\operatorname {tp}(BD/C)$
does not extend to a global C-invariant type, so, vacuously,
$\operatorname {tp}(BD/C)$
does not extend to a global C-invariant type, so, vacuously, ![]() for any
for any
![]() $D,E$
. But we can choose (assuming T has infinite models) D and E such that
$D,E$
. But we can choose (assuming T has infinite models) D and E such that
![]() $E\subseteq \operatorname {acl}(D)\setminus \operatorname {acl}(C)$
, in which case
$E\subseteq \operatorname {acl}(D)\setminus \operatorname {acl}(C)$
, in which case ![]() , hence
, hence ![]() does not imply
does not imply ![]() in T.
in T.
Remark 5.2.
-
(1) Note in particular that if there exists C with
 $\operatorname {acl}(C)\neq \operatorname {dcl}(C)$
then for any
$\operatorname {acl}(C)\neq \operatorname {dcl}(C)$
then for any
 $c\in \operatorname {acl}(C)\setminus \operatorname {dcl}(C)$
the type
$c\in \operatorname {acl}(C)\setminus \operatorname {dcl}(C)$
the type
 $\operatorname {tp}(c/C)$
does not extend to a global C-invariant type, so
$\operatorname {tp}(c/C)$
does not extend to a global C-invariant type, so  .
. -
(2) By exactly the same argument as above, if T is NSOP
 $_1$
with existence, then
$_1$
with existence, then  coincides with
coincides with  over algebraically closed sets if and only if for any algebraically closed C any
over algebraically closed sets if and only if for any algebraically closed C any
 $p(x)\in S(C)$
we have that
$p(x)\in S(C)$
we have that
 $p(x)$
extends to a global C-invariant type. In particular, if
$p(x)$
extends to a global C-invariant type. In particular, if
 $T=T^{eq}$
is stable then
$T=T^{eq}$
is stable then  coincides with
coincides with  over algebraically closed sets.
over algebraically closed sets.
Example 5.3. We are working in
![]() $T_{\infty }$
. As there are sets C with
$T_{\infty }$
. As there are sets C with
![]() $\operatorname {dcl}(C)\neq \operatorname {acl}(C)$
(for example, in the sort
$\operatorname {dcl}(C)\neq \operatorname {acl}(C)$
(for example, in the sort
![]() $K(\mathfrak {C})$
, on which the induced structure is just that of a pure algebraically closed field), we have that
$K(\mathfrak {C})$
, on which the induced structure is just that of a pure algebraically closed field), we have that ![]() in
in
![]() $T_\infty $
. We expect that
$T_\infty $
. We expect that ![]() over algebraically closed sets which however relies on Question 5.4 below: by the proof of [Reference Dobrowolski14, Proposition 8.1], any complete type over a finite set C extends to a global type
over algebraically closed sets which however relies on Question 5.4 below: by the proof of [Reference Dobrowolski14, Proposition 8.1], any complete type over a finite set C extends to a global type
![]() $p(x)$
which is invariant over
$p(x)$
which is invariant over
![]() $\operatorname {acl}^{eq}(C)$
. By compactness, the same is true for arbitrary C, as the existence of a global
$\operatorname {acl}^{eq}(C)$
. By compactness, the same is true for arbitrary C, as the existence of a global
![]() $\operatorname {acl}^{eq}(C)$
-invariant extension of
$\operatorname {acl}^{eq}(C)$
-invariant extension of
![]() $p(x)$
is equivalent to consistency of the type
$p(x)$
is equivalent to consistency of the type
![]() $p(x)\cup \{\varphi (x,d)\leftrightarrow \varphi (x,d'):\varphi (x,y)\in L, d,d'\in \mathfrak {C}^{eq}, d\equiv _{\operatorname {acl}^{eq}(C)}d'\}$
. So, if
$p(x)\cup \{\varphi (x,d)\leftrightarrow \varphi (x,d'):\varphi (x,y)\in L, d,d'\in \mathfrak {C}^{eq}, d\equiv _{\operatorname {acl}^{eq}(C)}d'\}$
. So, if
![]() $\operatorname {dcl}^{eq}(\operatorname {acl}(C))=\operatorname {acl}^{eq}(C)$
then
$\operatorname {dcl}^{eq}(\operatorname {acl}(C))=\operatorname {acl}^{eq}(C)$
then
![]() $p(x)$
extends to a global
$p(x)$
extends to a global
![]() $\operatorname {acl}(C)$
-invariant type in
$\operatorname {acl}(C)$
-invariant type in
![]() $T^{eq}_\infty $
, which restricts to a global
$T^{eq}_\infty $
, which restricts to a global
![]() $\operatorname {acl}(C)$
-invariant type in
$\operatorname {acl}(C)$
-invariant type in
![]() $T_\infty $
.
$T_\infty $
.
Question 5.4. Is it true in
![]() $T_\infty $
that for any set C we have
$T_\infty $
that for any set C we have
![]() $\operatorname {dcl}^{eq}(\operatorname {acl}(C))=\operatorname {acl}^{eq}(C)$
?
$\operatorname {dcl}^{eq}(\operatorname {acl}(C))=\operatorname {acl}^{eq}(C)$
?
Example 5.5. Assume that T is the theory of
![]() $\omega $
-free PAC fields, let
$\omega $
-free PAC fields, let
![]() $F^*$
be a monster model of T and let
$F^*$
be a monster model of T and let
![]() $\bar {F}:=(F^*)^{\operatorname{sep}}$
(so
$\bar {F}:=(F^*)^{\operatorname{sep}}$
(so
![]() $\bar {F}$
is a model of
$\bar {F}$
is a model of
![]() $\operatorname {\mathrm {SCF}}$
and in this example, if we refer to
$\operatorname {\mathrm {SCF}}$
and in this example, if we refer to
![]() $\operatorname {\mathrm {SCF}}$
, we actually refer to
$\operatorname {\mathrm {SCF}}$
, we actually refer to
![]() $\operatorname {Th}({\bar {F}})$
). Assume that
$\operatorname {Th}({\bar {F}})$
). Assume that
![]() $A=\operatorname {acl}(A)$
,
$A=\operatorname {acl}(A)$
,
![]() $B=\operatorname {acl}(B)$
,
$B=\operatorname {acl}(B)$
,
![]() $C=\operatorname {acl}(C)$
(by [Reference Chatzidakis and Pillay7], we know that
$C=\operatorname {acl}(C)$
(by [Reference Chatzidakis and Pillay7], we know that
![]() $\operatorname {acl}(\ast )$
is obtained by closing under
$\operatorname {acl}(\ast )$
is obtained by closing under
![]() $\lambda $
-functions and then taking the field-theoretic algebraic closure) and
$\lambda $
-functions and then taking the field-theoretic algebraic closure) and
![]() $C\subseteq A\cap B$
. By [Reference Chatzidakis6], we have
$C\subseteq A\cap B$
. By [Reference Chatzidakis6], we have ![]() if and only if:
if and only if:
-
•
 (forking independence in
(forking independence in
 $\operatorname {\mathrm {SCF}}$
) and
$\operatorname {\mathrm {SCF}}$
) and -
•
 $\operatorname {acl}(AB)\cap (AB_0)^{\operatorname{sep}}B^{\operatorname{sep}}=\operatorname {acl}(AB_0)B$
for each
$\operatorname {acl}(AB)\cap (AB_0)^{\operatorname{sep}}B^{\operatorname{sep}}=\operatorname {acl}(AB_0)B$
for each
 $B_0=\operatorname {acl}(B_0)\subseteq B$
.
$B_0=\operatorname {acl}(B_0)\subseteq B$
.
Let
![]() $A'$
be a small subset of
$A'$
be a small subset of
![]() $F^*$
and let
$F^*$
and let
![]() $B=\operatorname {acl}(B)$
. By the general properties of forking independence (e.g., Remark 5.3 in [Reference Casanovas4]),
$B=\operatorname {acl}(B)$
. By the general properties of forking independence (e.g., Remark 5.3 in [Reference Casanovas4]), ![]() holds if and only if
holds if and only if ![]() , where
, where
![]() $A:=\operatorname {acl}(A'B)$
. By the above description of forking independence in the theory of
$A:=\operatorname {acl}(A'B)$
. By the above description of forking independence in the theory of
![]() $\omega $
-free PAC fields, we have
$\omega $
-free PAC fields, we have ![]() (and so also
(and so also ![]() and
and ![]() ). So we see that the existence axiom for forking independence holds over algebraically closed sets. Actually, the existence axiom for forking independence holds over arbitrary sets (cf. Remarks 2.15 and 2.16 in [Reference Dobrowolski, Kim and Ramsey15]).
). So we see that the existence axiom for forking independence holds over algebraically closed sets. Actually, the existence axiom for forking independence holds over arbitrary sets (cf. Remarks 2.15 and 2.16 in [Reference Dobrowolski, Kim and Ramsey15]).
Let us recall what is ![]() and
and ![]() in the case of
in the case of
![]() $\omega $
-free PAC fields. Up to the best of our knowledge, there is no description of
$\omega $
-free PAC fields. Up to the best of our knowledge, there is no description of ![]() or
or ![]() over arbitrary sets, so we need to pick a model
over arbitrary sets, so we need to pick a model
![]() $F\preceq F^*$
. Assume that
$F\preceq F^*$
. Assume that
![]() $A=\operatorname {acl}(A)$
and
$A=\operatorname {acl}(A)$
and
![]() $B=\operatorname {acl}(B)$
, and
$B=\operatorname {acl}(B)$
, and
![]() $F\subseteq A\cap B$
. Then,
$F\subseteq A\cap B$
. Then, ![]() if and only if
if and only if ![]() (as both notions of Kim-dividing coincide over models in NSOP
(as both notions of Kim-dividing coincide over models in NSOP
![]() $_1$
), if and only if:
$_1$
), if and only if:
-
•
 and
and -
•
 ,
,
where (2) is considered in the so-called sorted system, which is a first-order structure build from all the quotients by open normal subgroups of the absolute Galois group (see, e.g., [Reference Chatzidakis5, Reference Cherlin, van den Dries and Macintyre8, Reference Hoffmann and Lee19]). In fact, as the absolute Galois group is the free profinite group on
![]() $\omega $
-many generators, this sorted system is stable (by [Reference Chatzidakis5]) and hence the second dot above can be replaced by “
$\omega $
-many generators, this sorted system is stable (by [Reference Chatzidakis5]) and hence the second dot above can be replaced by “![]() ”, i.e., the forking independence relation, which is described in Proposition 4.1 in [Reference Chatzidakis5].
”, i.e., the forking independence relation, which is described in Proposition 4.1 in [Reference Chatzidakis5].
Example 5.6. Let T be the theory ACFG, exposed in [Reference d’Elbée13]. More precisely, fix some prime number
![]() $p>0$
and let
$p>0$
and let
![]() $L_G$
be the language of rings extended by a symbol for a unary predicate G. Models of the
$L_G$
be the language of rings extended by a symbol for a unary predicate G. Models of the
![]() $L_G$
-theory ACF
$L_G$
-theory ACF
![]() $_G$
are algebraically closed fields of characteristic p with an additive subgroup under the predicate G. Now, the
$_G$
are algebraically closed fields of characteristic p with an additive subgroup under the predicate G. Now, the
![]() $L_G$
-theory ACFG is the model companion of ACF
$L_G$
-theory ACFG is the model companion of ACF
![]() $_G$
; let
$_G$
; let
![]() $(K,G)$
be its monster model. For
$(K,G)$
be its monster model. For
![]() $A\subseteq K$
, let
$A\subseteq K$
, let
![]() $\bar {A}$
denote the field-theoretic algebraic closure of A in K. Take
$\bar {A}$
denote the field-theoretic algebraic closure of A in K. Take
![]() $A,B,C\subseteq K$
and recall that the weak independence relation,
$A,B,C\subseteq K$
and recall that the weak independence relation, ![]() , is given as follows:
, is given as follows:
-
•
 and
and -
•
 $G(\overline {AC}+\overline {BC})=G(\overline {AC})+G(\overline {BC}),$
$G(\overline {AC}+\overline {BC})=G(\overline {AC})+G(\overline {BC}),$
where ![]() denotes the forking independence relation in ACF. By Corollary 3.16 from [Reference d’Elbée13], we have that
denotes the forking independence relation in ACF. By Corollary 3.16 from [Reference d’Elbée13], we have that ![]() is
is ![]() after forcing base monotonicity:
after forcing base monotonicity:

Therefore ACFG, which is a NSOP
![]() $_1$
theory, enjoys the existence axiom for forking independence. In a private communication with Christian d’Elbée, it was suggested to us to use Corollary 1.7 from [Reference d’Elbée13] and Theorem 2.12, to show that
$_1$
theory, enjoys the existence axiom for forking independence. In a private communication with Christian d’Elbée, it was suggested to us to use Corollary 1.7 from [Reference d’Elbée13] and Theorem 2.12, to show that ![]() coincides with
coincides with ![]() over algebraically closed sets. As the proof is standard, we omit it here. Therefore
over algebraically closed sets. As the proof is standard, we omit it here. Therefore ![]() coincides with
coincides with ![]() over algebraically closed subsets and
over algebraically closed subsets and ![]() coincides with
coincides with ![]() over models. In ACFG, there exist sets C such that
over models. In ACFG, there exist sets C such that
![]() $\operatorname {dcl}(C)\neq \operatorname {acl}(C)$
, thus
$\operatorname {dcl}(C)\neq \operatorname {acl}(C)$
, thus ![]() in general (by Remark 5.2). One could ask whether
in general (by Remark 5.2). One could ask whether ![]() and
and ![]() coincide over algebraically closed sets (similarly as in
coincide over algebraically closed sets (similarly as in
![]() $T_{\infty }$
)?
$T_{\infty }$
)?
Example 5.7. In [Reference Conant and Kruckman12], another example of an NSOP
![]() $_1$
theory with existence was studied. More precisely,
$_1$
theory with existence was studied. More precisely,
![]() $T_{m,n}$
denotes the theory of existentially closed incidence structures omitting the complete incidence structure
$T_{m,n}$
denotes the theory of existentially closed incidence structures omitting the complete incidence structure
![]() $K_{m,n}$
. In other words,
$K_{m,n}$
. In other words,
![]() $T_{m,n}$
is the theory of a generic
$T_{m,n}$
is the theory of a generic
![]() $K_{m,n}$
-free bipartite graph. Theorem 4.11 from [Reference Conant and Kruckman12] gives us that
$K_{m,n}$
-free bipartite graph. Theorem 4.11 from [Reference Conant and Kruckman12] gives us that
![]() $T_{m,n}$
is NSOP
$T_{m,n}$
is NSOP
![]() $_1$
and Corollary 4.24 from [Reference Conant and Kruckman12] implies that
$_1$
and Corollary 4.24 from [Reference Conant and Kruckman12] implies that
![]() $T_{m,n}$
satisfies the existence axiom for forking independence. Actually, the aforementioned corollary gives us also a nice description of forking independence, thus let us evoke it: for any
$T_{m,n}$
satisfies the existence axiom for forking independence. Actually, the aforementioned corollary gives us also a nice description of forking independence, thus let us evoke it: for any
![]() $A,B,C\subseteq \mathfrak {C}\models T_{m,n}$
we have
$A,B,C\subseteq \mathfrak {C}\models T_{m,n}$
we have

and ![]() is a ternary relation coinciding with
is a ternary relation coinciding with ![]() over models. Thus, again, forking independence is induced by forcing base monotonicity on a ternary relation related to
over models. Thus, again, forking independence is induced by forcing base monotonicity on a ternary relation related to ![]() .
.
The above examples motivate asking the following question:
Question 5.8. Assume that T is NSOP
![]() $_1$
with existence. Is it true that
$_1$
with existence. Is it true that ![]() is
is ![]() after forcing base monotonicity, i.e.,
after forcing base monotonicity, i.e.,

We know that in any theory T (not necessarily an NSOP
![]() $_1$
theory), for each a and A it holds that
$_1$
theory), for each a and A it holds that ![]() Footnote
1
. Assuming that Question 5.8 has an affirmative answer and assuming that
Footnote
1
. Assuming that Question 5.8 has an affirmative answer and assuming that ![]() coincide with
coincide with ![]() over algebraically closed sets, we would obtain the forking existence axiom over algebraically closed sets.
over algebraically closed sets, we would obtain the forking existence axiom over algebraically closed sets.
6 Beyond NSOP
 $_1$
$_1$
Now, let us consider arbitrary theory T (not necessarily NSOP
![]() $_1$
). Instead of Definition 3.1, one could define the rank by the conditions from Lemma 3.12. Such a rank would be always finite (indeed, by the consistency condition and pigeonhole principle applied to
$_1$
). Instead of Definition 3.1, one could define the rank by the conditions from Lemma 3.12. Such a rank would be always finite (indeed, by the consistency condition and pigeonhole principle applied to
![]() $\eta $
, rank of any type
$\eta $
, rank of any type
![]() $\pi $
would be bounded by
$\pi $
would be bounded by
![]() $\sum _{i\in \eta (\lambda )}C_{\phi _i,q_i}<\omega $
) and satisfy the standard properties (Lemmas 3.15–3.17 and Corollary 3.18). This is some strategy, however it seems that we require too much here. Thus, let us derive yet another notion of rank and show its finiteness in an important class of theories. The new rank is a slight modification of Q-rank and, as we will see in a moment, the new rank coincides with the Q-rank in NSOP
$\sum _{i\in \eta (\lambda )}C_{\phi _i,q_i}<\omega $
) and satisfy the standard properties (Lemmas 3.15–3.17 and Corollary 3.18). This is some strategy, however it seems that we require too much here. Thus, let us derive yet another notion of rank and show its finiteness in an important class of theories. The new rank is a slight modification of Q-rank and, as we will see in a moment, the new rank coincides with the Q-rank in NSOP
![]() $_1$
theories.
$_1$
theories.
6.1 Refining notions
We start with introducing a refined notion of an invariant type and a notion of a surrogate of a global type. These notions are used in Definition 6.11 and came out from studying examples similar to the one in Section 6.3.
Definition 6.1. Let
![]() $A,B$
be small subsets of
$A,B$
be small subsets of
![]() $\mathfrak {C}$
and let
$\mathfrak {C}$
and let
![]() $C\subseteq \mathfrak {C}$
. A type
$C\subseteq \mathfrak {C}$
. A type
![]() $q(y)\in S(C)$
is
$q(y)\in S(C)$
is
![]() $B/A$
-invariant if
$B/A$
-invariant if
![]() $f(q)=q$
for every
$f(q)=q$
for every
![]() $f\in \operatorname {Aut}(\mathfrak {C}/A)$
such that
$f\in \operatorname {Aut}(\mathfrak {C}/A)$
such that
![]() $f(B)=B$
. (Note that this implies C is invariant under all such f.)
$f(B)=B$
. (Note that this implies C is invariant under all such f.)
Remark 6.2. Let
![]() $A\subseteq B$
be small subsets of
$A\subseteq B$
be small subsets of
![]() $\mathfrak {C}$
, let
$\mathfrak {C}$
, let
![]() $C\subseteq \mathfrak {C}$
, and let
$C\subseteq \mathfrak {C}$
, and let
![]() $q(y)\in S(C)$
. We have: q is A-invariant
$q(y)\in S(C)$
. We have: q is A-invariant
![]() $\Rightarrow \ q$
is
$\Rightarrow \ q$
is
![]() $B/A$
-invariant
$B/A$
-invariant
![]() $\Rightarrow \ q$
is B-invariant.
$\Rightarrow \ q$
is B-invariant.
Definition 6.3. A type
![]() $q(y)$
is a semi-global type over A if there exists
$q(y)$
is a semi-global type over A if there exists
![]() $\pi (y)\in S(A)$
such that
$\pi (y)\in S(A)$
such that
![]() $q(y)\in S(A\,\cup \,\pi (\mathfrak {C}))$
and
$q(y)\in S(A\,\cup \,\pi (\mathfrak {C}))$
and
![]() $\pi \subseteq q$
.
$\pi \subseteq q$
.
Definition 6.4 (Morley in semi-global type).
Let q be an A-invariant semi-global type over A and let
![]() $(I,<)$
be a linearly ordered set. By a Morley sequence in q over A (of order type I) we understand a sequence
$(I,<)$
be a linearly ordered set. By a Morley sequence in q over A (of order type I) we understand a sequence
![]() $b_I=(b_i)_{i\in I}$
such that
$b_I=(b_i)_{i\in I}$
such that
![]() $b_i\models q|_{Ab_{<i}}$
.
$b_i\models q|_{Ab_{<i}}$
.
Remark 6.5. Assume that
![]() $A\subseteq B$
are small subsets of
$A\subseteq B$
are small subsets of
![]() $\mathfrak {C}$
, and q is an
$\mathfrak {C}$
, and q is an
![]() $B/A$
-invariant semi-global type over B and
$B/A$
-invariant semi-global type over B and
![]() $(I,<)$
is a linearly ordered set.
$(I,<)$
is a linearly ordered set.
-
(1) For each
 $f\in \operatorname {Aut}(\mathfrak {C}/A)$
with
$f\in \operatorname {Aut}(\mathfrak {C}/A)$
with
 $f(B)=B$
, we have
$f(B)=B$
, we have
 $f(q)=q\in S(B\,\cup \,\pi (\mathfrak {C}))$
for some
$f(q)=q\in S(B\,\cup \,\pi (\mathfrak {C}))$
for some
 $\pi (y)\in S(B)$
. More precisely,
$\pi (y)\in S(B)$
. More precisely,
 $f(\pi )=\pi \in S(B)$
(B is fixed setwise), so
$f(\pi )=\pi \in S(B)$
(B is fixed setwise), so
 $f(B\,\cup \,\pi (\mathfrak {C}))=B\,\cup \,\pi (\mathfrak {C})$
, and so we do not need to add new parameters to the domain of q (to satisfy
$f(B\,\cup \,\pi (\mathfrak {C}))=B\,\cup \,\pi (\mathfrak {C})$
, and so we do not need to add new parameters to the domain of q (to satisfy
 $B/A$
-invariance of q) and being a
$B/A$
-invariance of q) and being a
 $B/A$
-invariant semi-global type over B is well-defined.
$B/A$
-invariant semi-global type over B is well-defined. -
(2) If
 $b_I=(b_i)_{i\in I}$
and
$b_I=(b_i)_{i\in I}$
and
 $c_I=(c_i)_{i\in I}$
are Morley sequences in q over B, then
$c_I=(c_i)_{i\in I}$
are Morley sequences in q over B, then
 $b_I\equiv _B c_I$
. Thus we see that
$b_I\equiv _B c_I$
. Thus we see that
 $b_I$
and
$b_I$
and
 $c_I$
realize a common type over B, which we denote
$c_I$
realize a common type over B, which we denote
 $q^{\otimes I}|_B$
. Moreover,
$q^{\otimes I}|_B$
. Moreover,
 $b_I$
is B-indiscernible and
$b_I$
is B-indiscernible and  for all
for all
 $i\in I$
.
$i\in I$
.
Lemma 6.6. Suppose q is a
![]() $B/A$
-invariant semi-global type over B and
$B/A$
-invariant semi-global type over B and
![]() $c_I=(c_i)_{i\in I}\models q^{\otimes I}|_B$
for some linearly ordered set I. Let
$c_I=(c_i)_{i\in I}\models q^{\otimes I}|_B$
for some linearly ordered set I. Let
![]() $f\in \operatorname {Aut}(\mathfrak {C}/A)$
with
$f\in \operatorname {Aut}(\mathfrak {C}/A)$
with
![]() $f(B)=B$
and let b be an enumeration of B. Then
$f(B)=B$
and let b be an enumeration of B. Then
![]() $bc_I\equiv f(b)c_I$
.
$bc_I\equiv f(b)c_I$
.
Proof By compactness, we may assume that
![]() $I=\{i_1,\dots ,i_{n}\}$
is finite. Assume by induction that
$I=\{i_1,\dots ,i_{n}\}$
is finite. Assume by induction that
![]() $bc_1\dots c_{n-1}\equiv f(b)c_1\dots c_{n-1}$
. Pick
$bc_1\dots c_{n-1}\equiv f(b)c_1\dots c_{n-1}$
. Pick
![]() $\tilde f\in \operatorname {Aut}(\mathfrak {C})$
sending
$\tilde f\in \operatorname {Aut}(\mathfrak {C})$
sending
![]() $bc_1\dots c_{n-1}$
to
$bc_1\dots c_{n-1}$
to
![]() $f(b)c_1\dots c_{n-1}$
. Then, as
$f(b)c_1\dots c_{n-1}$
. Then, as
![]() $\tilde f(q)=q$
by
$\tilde f(q)=q$
by
![]() $B/A$
-invariance, we have
$B/A$
-invariance, we have
which shows that
![]() $f(b)c_1\dots c_n\equiv f(b)c_1\dots c_{n-1} \tilde f(c_n)=\tilde f(bc_1\dots c_n)\equiv bc_1\dots c_n$
.
$f(b)c_1\dots c_n\equiv f(b)c_1\dots c_{n-1} \tilde f(c_n)=\tilde f(bc_1\dots c_n)\equiv bc_1\dots c_n$
.
Lemma 6.7. Assume that q and r are A-invariant semi-global types over A,
![]() $tp(b/A)=r|_A=q|_A$
. If for a formula
$tp(b/A)=r|_A=q|_A$
. If for a formula
![]() $\varphi (x,b)$
there is
$\varphi (x,b)$
there is
![]() $b_{<\omega }\models q^{\otimes \omega }|_A$
and
$b_{<\omega }\models q^{\otimes \omega }|_A$
and
![]() $c_{<\omega }\models r^{\otimes \omega }|_A$
such that
$c_{<\omega }\models r^{\otimes \omega }|_A$
such that
![]() $\{\varphi (x,b_i)\;|\;i<\omega \}$
is consistent and
$\{\varphi (x,b_i)\;|\;i<\omega \}$
is consistent and
![]() $\{\varphi (x,c_i)\;|\;i<\omega \}$
is inconsistent, then T has SOP
$\{\varphi (x,c_i)\;|\;i<\omega \}$
is inconsistent, then T has SOP
![]() $_1$
.
$_1$
.
Proof As
![]() $tp(b/A)=r|_A=q|_A$
, we have that
$tp(b/A)=r|_A=q|_A$
, we have that
![]() $q,r\in S(A\,\cup \,\operatorname {tp}(b/A)(\mathfrak {C}))$
and we can repeat the proof of Proposition 3.15 from [Reference Kaplan and Ramsey20].
$q,r\in S(A\,\cup \,\operatorname {tp}(b/A)(\mathfrak {C}))$
and we can repeat the proof of Proposition 3.15 from [Reference Kaplan and Ramsey20].
Corollary 6.8. If T is NSOP
![]() $_1$
then we have Kim’s lemma for semi-global type dividing: for any small set
$_1$
then we have Kim’s lemma for semi-global type dividing: for any small set
![]() $A\subseteq \mathfrak {C}$
, any formula
$A\subseteq \mathfrak {C}$
, any formula
![]() $\varphi (x,b)$
, if there is an A-invariant semi-global type
$\varphi (x,b)$
, if there is an A-invariant semi-global type
![]() $q\supseteq \operatorname {tp}(b/A)$
over A and a sequence
$q\supseteq \operatorname {tp}(b/A)$
over A and a sequence
![]() $b_{<\omega }\models q^{\otimes \omega }|_A$
such that
$b_{<\omega }\models q^{\otimes \omega }|_A$
such that
![]() $\{\varphi (x,b_i)\;|\;i<\omega \}$
is inconsistent, then
$\{\varphi (x,b_i)\;|\;i<\omega \}$
is inconsistent, then
![]() $\{\varphi (x,c_i)\;|\;i<\omega \}$
is inconsistent for any A-invariant semi-global type
$\{\varphi (x,c_i)\;|\;i<\omega \}$
is inconsistent for any A-invariant semi-global type
![]() $r\supseteq \operatorname {tp}(b/A)$
over A and any sequence
$r\supseteq \operatorname {tp}(b/A)$
over A and any sequence
![]() $c_{<\omega }\models r^{\otimes \omega }|_A$
.
$c_{<\omega }\models r^{\otimes \omega }|_A$
.
Proposition 6.9. The following are equivalent for the complete theory T:
-
(1) T is NSOP
 $_1$
.
$_1$
. -
(2) (Kim’s lemma for semi-global types dividing) For any small
 $M\preceq \mathfrak {C}$
, any formula
$M\preceq \mathfrak {C}$
, any formula
 $\varphi (x,b)$
, if there is an M-invariant semi-global type
$\varphi (x,b)$
, if there is an M-invariant semi-global type
 $q\supseteq \operatorname {tp}(b/M)$
over M and a sequence
$q\supseteq \operatorname {tp}(b/M)$
over M and a sequence
 $b_{<\omega }\models q^{\otimes \omega }|_M$
such that
$b_{<\omega }\models q^{\otimes \omega }|_M$
such that
 $\{\varphi (x,b_i)\;|\;i<\omega \}$
is inconsistent, then
$\{\varphi (x,b_i)\;|\;i<\omega \}$
is inconsistent, then
 $\{\varphi (x,c_i)\;|\;i<\omega \}$
is inconsistent for any M-invariant semi-global type
$\{\varphi (x,c_i)\;|\;i<\omega \}$
is inconsistent for any M-invariant semi-global type
 $r\supseteq \operatorname {tp}(b/M)$
over M and any sequence
$r\supseteq \operatorname {tp}(b/M)$
over M and any sequence
 $c_{<\omega }\models r^{\otimes \omega }|_M$
.
$c_{<\omega }\models r^{\otimes \omega }|_M$
. -
(3) (Kim’s lemma for Kim-dividing) For any small
 $M\preceq \mathfrak {C}$
, any formula
$M\preceq \mathfrak {C}$
, any formula
 $\varphi (x,b)$
, if there is an M-invariant global type
$\varphi (x,b)$
, if there is an M-invariant global type
 $q\supseteq \operatorname {tp}(b/M)$
and a sequence
$q\supseteq \operatorname {tp}(b/M)$
and a sequence
 $b_{<\omega }\models q^{\otimes \omega }|_M$
such that
$b_{<\omega }\models q^{\otimes \omega }|_M$
such that
 $\{\varphi (x,b_i)\;|\;i<\omega \}$
is inconsistent, then
$\{\varphi (x,b_i)\;|\;i<\omega \}$
is inconsistent, then
 $\{\varphi (x,c_i)\;|\;i<\omega \}$
is inconsistent for any M-invariant global type
$\{\varphi (x,c_i)\;|\;i<\omega \}$
is inconsistent for any M-invariant global type
 $r\supseteq \operatorname {tp}(b/M)$
and any sequence
$r\supseteq \operatorname {tp}(b/M)$
and any sequence
 $c_{<\omega }\models r^{\otimes \omega }|_M$
.
$c_{<\omega }\models r^{\otimes \omega }|_M$
.
Proof (1)
![]() $\Rightarrow $
(2) follows by Corollary 6.8. If q and r are M-invariant global types extending
$\Rightarrow $
(2) follows by Corollary 6.8. If q and r are M-invariant global types extending
![]() $\operatorname {tp}(b/M)$
then
$\operatorname {tp}(b/M)$
then
![]() $q|_B$
and
$q|_B$
and
![]() $r|_B$
, where
$r|_B$
, where
![]() $B:=M\,\cup \,\operatorname {tp}(b/M)(\mathfrak {C})$
, are M-invariant semi-global types over M and thus (3) is implied by (2). Finally, (3)
$B:=M\,\cup \,\operatorname {tp}(b/M)(\mathfrak {C})$
, are M-invariant semi-global types over M and thus (3) is implied by (2). Finally, (3)
![]() $\Rightarrow $
(1) is contained in Theorem 3.16 from [Reference Kaplan and Ramsey20].
$\Rightarrow $
(1) is contained in Theorem 3.16 from [Reference Kaplan and Ramsey20].
Remark 6.10. Say that we are interested in the notion of Kim-dividing (over A) of a formula
![]() $\varphi (x,b)$
. As it was earlier pointed out, the main issue with the definition of Kim-dividing from [Reference Kaplan and Ramsey20] is that there might be not enough many A-invariant global extensions of
$\varphi (x,b)$
. As it was earlier pointed out, the main issue with the definition of Kim-dividing from [Reference Kaplan and Ramsey20] is that there might be not enough many A-invariant global extensions of
![]() $\operatorname {tp}(b/A)$
to witness Kim-dividing. Perhaps there are situations, where it is easier to find an A-invariant semi-global extension (over A) of
$\operatorname {tp}(b/A)$
to witness Kim-dividing. Perhaps there are situations, where it is easier to find an A-invariant semi-global extension (over A) of
![]() $\operatorname {tp}(b/A)$
and so working with semi-global types (instead of global types) in the definition of Kim-dividing from [Reference Kaplan and Ramsey20] might give better results.
$\operatorname {tp}(b/A)$
and so working with semi-global types (instead of global types) in the definition of Kim-dividing from [Reference Kaplan and Ramsey20] might give better results.
6.2 Modifying rank
Again, let
where
![]() $\varphi _0,\ldots ,\varphi _{n-1}\in \mathcal {L}$
and
$\varphi _0,\ldots ,\varphi _{n-1}\in \mathcal {L}$
and
![]() $q_0,\ldots ,q_{n-1}$
are global types.
$q_0,\ldots ,q_{n-1}$
are global types.
Definition 6.11. We define a local rank, called
![]() $\tilde{Q}$
-rank,
$\tilde{Q}$
-rank,
For any set of
![]() $\mathcal {L}$
-formulae
$\mathcal {L}$
-formulae
![]() $\pi (x)$
we have
$\pi (x)$
we have
![]() $\tilde {D}_Q(\pi (x))\geqslant \lambda $
if and only if there exist
$\tilde {D}_Q(\pi (x))\geqslant \lambda $
if and only if there exist
![]() $\eta \in n^{\lambda }$
and
$\eta \in n^{\lambda }$
and
![]() $\big (b^{\alpha }_{\mathbb {Z}},M^{\alpha }\big )_{\alpha <\lambda }$
, where
$\big (b^{\alpha }_{\mathbb {Z}},M^{\alpha }\big )_{\alpha <\lambda }$
, where
![]() $b^{\alpha }_{\mathbb {Z}}=(b^{\alpha }_i)_{i\in \mathbb {Z}}$
, such that:
$b^{\alpha }_{\mathbb {Z}}=(b^{\alpha }_i)_{i\in \mathbb {Z}}$
, such that:
-
(1)
 $\operatorname {dom}(\pi (x))\subseteq M^0$
,
$\operatorname {dom}(\pi (x))\subseteq M^0$
, -
(2)
 $q_0,\ldots ,q_{n-1}$
are
$q_0,\ldots ,q_{n-1}$
are
 $M^0$
-invariant,
$M^0$
-invariant, -
(3)
 $M^{\alpha }\preceq \mathfrak {C}$
for each
$M^{\alpha }\preceq \mathfrak {C}$
for each
 $\alpha <\lambda $
,
$\alpha <\lambda $
,
 $(M^{\alpha })_{\alpha <\lambda }$
is increasing and continuous, and each
$(M^{\alpha })_{\alpha <\lambda }$
is increasing and continuous, and each
 $M^{\alpha +1}$
is
$M^{\alpha +1}$
is
 $|M^{\alpha }|^+$
-saturated and strongly
$|M^{\alpha }|^+$
-saturated and strongly
 $|M^{\alpha }|^+$
-homogeneous,
$|M^{\alpha }|^+$
-homogeneous, -
(4)
 $b^{\alpha }_{\mathbb {Z}}M^{\alpha }\subseteq M^{\alpha +1}$
for each
$b^{\alpha }_{\mathbb {Z}}M^{\alpha }\subseteq M^{\alpha +1}$
for each
 $\alpha +1<\lambda $
,
$\alpha +1<\lambda $
, -
(5)
 $b^{\alpha }_0\models q_{\eta (\alpha )}|_{M^{\alpha }}$
for each
$b^{\alpha }_0\models q_{\eta (\alpha )}|_{M^{\alpha }}$
for each
 $\alpha <\lambda $
,
$\alpha <\lambda $
, -
(6)
 $\pi (x)\cup \{\varphi _{\eta (\alpha )}(x;b^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent,
$\pi (x)\cup \{\varphi _{\eta (\alpha )}(x;b^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent, -
(7) for each
 $\alpha <\lambda $
there exists an
$\alpha <\lambda $
there exists an
 $M^{\alpha }/M^0$
-invariant semi-global type
$M^{\alpha }/M^0$
-invariant semi-global type
 $r_{\alpha }(y_{\eta (\alpha )})$
over
$r_{\alpha }(y_{\eta (\alpha )})$
over
 $M^{\alpha }$
such that
$M^{\alpha }$
such that
 $b^{\alpha }_{\mathbb {Z}}\models r_{\alpha }^{\otimes \mathbb {Z}}|_{M^{\alpha }}$
and
$b^{\alpha }_{\mathbb {Z}}\models r_{\alpha }^{\otimes \mathbb {Z}}|_{M^{\alpha }}$
and
 $\{\varphi _{\eta (\alpha )}(x;b^{\alpha }_i)\;|\;i\in \mathbb {Z}\}$
is inconsistent.
$\{\varphi _{\eta (\alpha )}(x;b^{\alpha }_i)\;|\;i\in \mathbb {Z}\}$
is inconsistent.
If
![]() $\tilde {D}_Q(\pi )\geqslant \lambda $
for each
$\tilde {D}_Q(\pi )\geqslant \lambda $
for each
![]() $\lambda \in \operatorname {Ord}$
, then we set
$\lambda \in \operatorname {Ord}$
, then we set
![]() $\tilde {D}_Q(\pi )=\infty $
. Otherwise
$\tilde {D}_Q(\pi )=\infty $
. Otherwise
![]() $\tilde {D}_Q(\pi )$
is the maximal
$\tilde {D}_Q(\pi )$
is the maximal
![]() $\lambda \in \operatorname {Ord}$
such that
$\lambda \in \operatorname {Ord}$
such that
![]() $\tilde {D}_Q(\pi )\geqslant \lambda $
.
$\tilde {D}_Q(\pi )\geqslant \lambda $
.
Proposition 6.12. If T is NSOP
![]() $_1$
then
$_1$
then
![]() $D_Q=\tilde {D}_Q$
.
$D_Q=\tilde {D}_Q$
.
Proof If
![]() $D_Q(\pi )\geqslant \lambda $
then there exist
$D_Q(\pi )\geqslant \lambda $
then there exist
![]() $\eta \in n^{\lambda }$
and
$\eta \in n^{\lambda }$
and
![]() $(b^{\alpha },M^{\alpha })_{\alpha <\lambda }$
as in Definition 3.1. By Remark 3.2, we may assume that each
$(b^{\alpha },M^{\alpha })_{\alpha <\lambda }$
as in Definition 3.1. By Remark 3.2, we may assume that each
![]() $M^{\alpha +1}$
is
$M^{\alpha +1}$
is
![]() $|M^{\alpha }|^+$
-saturated and strongly
$|M^{\alpha }|^+$
-saturated and strongly
![]() $|M^{\alpha }|^+$
-homogeneous. Then, as in Lemma 3.9, we may assume that each
$|M^{\alpha }|^+$
-homogeneous. Then, as in Lemma 3.9, we may assume that each
![]() $r_{\alpha }\in S(\mathfrak {C})$
from the condition (7) of Definition 3.1 is equal to
$r_{\alpha }\in S(\mathfrak {C})$
from the condition (7) of Definition 3.1 is equal to
![]() $q_{\eta (\alpha )}$
and that we have
$q_{\eta (\alpha )}$
and that we have
![]() $b^{\alpha }_{<\omega }\subseteq M^{\alpha +1}$
satisfying
$b^{\alpha }_{<\omega }\subseteq M^{\alpha +1}$
satisfying
![]() $q_{\eta (\alpha )}^{\otimes \omega }|_{M^{\alpha }}$
and such that
$q_{\eta (\alpha )}^{\otimes \omega }|_{M^{\alpha }}$
and such that
![]() $\{\varphi _{\eta (\alpha )}(x,b^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent. By saturation of
$\{\varphi _{\eta (\alpha )}(x,b^{\alpha }_i)\;|\;i<\omega \}$
is inconsistent. By saturation of
![]() $M^{\alpha +1}$
, we can extend each
$M^{\alpha +1}$
, we can extend each
![]() $b^{\alpha }_{<\omega }$
to
$b^{\alpha }_{<\omega }$
to
![]() $b^{\alpha }_{\mathbb {Z}}\models q_{\eta (\alpha )}^{\otimes \mathbb {Z}}|_{M^{\alpha }}$
contained in
$b^{\alpha }_{\mathbb {Z}}\models q_{\eta (\alpha )}^{\otimes \mathbb {Z}}|_{M^{\alpha }}$
contained in
![]() $M^{\alpha +1}$
such that
$M^{\alpha +1}$
such that
![]() $\{\varphi _{\eta (\alpha )}(x,b^{\alpha }_i)\;|\;i\in \mathbb {Z}\}$
is inconsistent. Finally,
$\{\varphi _{\eta (\alpha )}(x,b^{\alpha }_i)\;|\;i\in \mathbb {Z}\}$
is inconsistent. Finally,
![]() $q_{\eta (\alpha )}|_{B^{\alpha }}$
, where
$q_{\eta (\alpha )}|_{B^{\alpha }}$
, where
![]() $B^{\alpha }:=M^{\alpha }\,\cup \,q_{\eta (\alpha )}|_{M^{\alpha }}(\mathfrak {C})$
, is an
$B^{\alpha }:=M^{\alpha }\,\cup \,q_{\eta (\alpha )}|_{M^{\alpha }}(\mathfrak {C})$
, is an
![]() $M^{\alpha }/M^0$
-invariant semi-global type over
$M^{\alpha }/M^0$
-invariant semi-global type over
![]() $M^{\alpha }$
. Therefore we fulfill all the conditions of Definition 6.11 and we see that
$M^{\alpha }$
. Therefore we fulfill all the conditions of Definition 6.11 and we see that
![]() $\tilde {D}_Q(\pi )\geqslant \lambda $
.
$\tilde {D}_Q(\pi )\geqslant \lambda $
.
Now, assume that
![]() $\tilde {D}_Q(\pi )\geqslant \lambda $
. There exists
$\tilde {D}_Q(\pi )\geqslant \lambda $
. There exists
![]() $\eta \in n^{\lambda }$
and
$\eta \in n^{\lambda }$
and
![]() $\big (b^{\alpha }_{\mathbb {Z}}=(b^{\alpha }_i)_{i\in \mathbb {Z}},M^{\alpha }\big )_{\alpha <\lambda }$
as in Definition 6.11. All the first six conditions from Definition 3.1 are naturally satisfied by
$\big (b^{\alpha }_{\mathbb {Z}}=(b^{\alpha }_i)_{i\in \mathbb {Z}},M^{\alpha }\big )_{\alpha <\lambda }$
as in Definition 6.11. All the first six conditions from Definition 3.1 are naturally satisfied by
![]() $\eta $
,
$\eta $
,
![]() $M^{\alpha }$
, and
$M^{\alpha }$
, and
![]() $b^{\alpha }_{<\omega }$
, where
$b^{\alpha }_{<\omega }$
, where
![]() $\alpha <\lambda $
. To see that also the condition (7) of Definition 3.1 is satisfied, we argue as follows. Let
$\alpha <\lambda $
. To see that also the condition (7) of Definition 3.1 is satisfied, we argue as follows. Let
![]() $\alpha <\lambda $
, let
$\alpha <\lambda $
, let
![]() $c^{\alpha }_{<\omega }\models q_{\eta (\alpha )}^{\otimes \omega }|_{M^{\alpha }}$
be contained in
$c^{\alpha }_{<\omega }\models q_{\eta (\alpha )}^{\otimes \omega }|_{M^{\alpha }}$
be contained in
![]() $M^{\alpha +1}$
and such that
$M^{\alpha +1}$
and such that
![]() $c^{\alpha }_0=b^{\alpha }_0$
. We know that
$c^{\alpha }_0=b^{\alpha }_0$
. We know that
![]() $q_{\eta (\alpha )}$
is
$q_{\eta (\alpha )}$
is
![]() $M^0$
-invariant, so in particular also
$M^0$
-invariant, so in particular also
![]() $M^{\alpha }$
-invariant. Moreover, as
$M^{\alpha }$
-invariant. Moreover, as
![]() $q_{\eta (\alpha )}|_{B^{\alpha }}$
, where
$q_{\eta (\alpha )}|_{B^{\alpha }}$
, where
![]() $B^{\alpha }:=M^{\alpha }\,\cup \,q_{\eta (\alpha )}|_{M^{\alpha }}(\mathfrak {C})$
, is an
$B^{\alpha }:=M^{\alpha }\,\cup \,q_{\eta (\alpha )}|_{M^{\alpha }}(\mathfrak {C})$
, is an
![]() $M^{\alpha }$
-invariant semi-global type over
$M^{\alpha }$
-invariant semi-global type over
![]() $M^{\alpha }$
, and there exists an
$M^{\alpha }$
, and there exists an
![]() $M^{\alpha }/M^0$
-invariant semi-global type
$M^{\alpha }/M^0$
-invariant semi-global type
![]() $r_{\alpha }(y_{\eta (\alpha )})$
over
$r_{\alpha }(y_{\eta (\alpha )})$
over
![]() $M^{\alpha }$
such that
$M^{\alpha }$
such that
![]() $b^{\alpha }_{\mathbb {Z}}\models r_{\alpha }^{\otimes \mathbb {Z}}|_{M^{\alpha }}$
and we have that
$b^{\alpha }_{\mathbb {Z}}\models r_{\alpha }^{\otimes \mathbb {Z}}|_{M^{\alpha }}$
and we have that
![]() $\{\varphi _{\eta (\alpha )}(x;b^{\alpha }_i)\;|\;i\in \mathbb {Z}\}$
is inconsistent (by the condition (7) of Definition 6.11), Corollary 6.8 implies that
$\{\varphi _{\eta (\alpha )}(x;b^{\alpha }_i)\;|\;i\in \mathbb {Z}\}$
is inconsistent (by the condition (7) of Definition 6.11), Corollary 6.8 implies that
![]() $\{\varphi _{\eta (\alpha )}(x;c^{\alpha }_i)\;|\;i\in \mathbb {Z}\}$
is inconsistent.
$\{\varphi _{\eta (\alpha )}(x;c^{\alpha }_i)\;|\;i\in \mathbb {Z}\}$
is inconsistent.
Corollary 6.13. If T is NSOP
![]() $_1$
then
$_1$
then
![]() $\tilde {D}_Q(\pi )<\omega $
for any choice of
$\tilde {D}_Q(\pi )<\omega $
for any choice of
![]() $\pi $
and finite Q.
$\pi $
and finite Q.
The following easily follows by the definition.
Fact 6.14.
-
(1)
 $\tilde {D}_Q(\pi ))\geqslant \lambda $
,
$\tilde {D}_Q(\pi ))\geqslant \lambda $
,
 $f\in \operatorname {Aut}(\mathfrak {C})\ \Rightarrow \ \tilde {D}_{f(Q)}(f(\pi ))\geqslant \lambda $
.
$f\in \operatorname {Aut}(\mathfrak {C})\ \Rightarrow \ \tilde {D}_{f(Q)}(f(\pi ))\geqslant \lambda $
. -
(2) If
 $\operatorname {dom}(\pi ')\subseteq \operatorname {dom}(\pi )$
and
$\operatorname {dom}(\pi ')\subseteq \operatorname {dom}(\pi )$
and
 $\pi \vdash \pi '$
then
$\pi \vdash \pi '$
then
 $\tilde {D}_Q(\pi )\leqslant \tilde {D}_Q(\pi ')$
.
$\tilde {D}_Q(\pi )\leqslant \tilde {D}_Q(\pi ')$
. -
(3)
 $\tilde {D}_Q(\pi )\leqslant \sum \limits _{j<n}\tilde {D}_{((\varphi _j,q_j))}(\pi )$
.
$\tilde {D}_Q(\pi )\leqslant \sum \limits _{j<n}\tilde {D}_{((\varphi _j,q_j))}(\pi )$
. -
(4) We have
 $$ \begin{align*}\tilde{D}_Q\Big(\pi\,\cup\,\Big\{\bigvee\limits_{j\leqslant m}\psi_j\Big\}\Big)\leqslant\max\limits_{j\leqslant m}\tilde{D}_Q(\pi\,\cup\,\{\psi_j\}).\end{align*} $$
$$ \begin{align*}\tilde{D}_Q\Big(\pi\,\cup\,\Big\{\bigvee\limits_{j\leqslant m}\psi_j\Big\}\Big)\leqslant\max\limits_{j\leqslant m}\tilde{D}_Q(\pi\,\cup\,\{\psi_j\}).\end{align*} $$
Question 6.15. Working outside of NSOP
![]() $_1$
, can we improve statements (2) and (4) in Fact 6.14 so they will get theses as in Lemma 3.15 and Lemma 3.16?
$_1$
, can we improve statements (2) and (4) in Fact 6.14 so they will get theses as in Lemma 3.15 and Lemma 3.16?
Proposition 6.16. If
![]() $\tilde {D}_Q(\pi (x))\geqslant \lambda $
then there exist natural numbers
$\tilde {D}_Q(\pi (x))\geqslant \lambda $
then there exist natural numbers
![]() $l_{\alpha }$
, formulae
$l_{\alpha }$
, formulae
![]() $\psi _{\alpha }(x,y_{\alpha }),$
and sequences
$\psi _{\alpha }(x,y_{\alpha }),$
and sequences
![]() $c^{\alpha }_{\mathbb {Z}}:=(c^{\alpha }_i)_{i\in \mathbb {Z}}$
, where
$c^{\alpha }_{\mathbb {Z}}:=(c^{\alpha }_i)_{i\in \mathbb {Z}}$
, where
![]() $\alpha <\lambda $
such that:
$\alpha <\lambda $
such that:
-
• for each
 $\sigma :\lambda \to \mathbb {Z}$
the set is consistent,
$\sigma :\lambda \to \mathbb {Z}$
the set is consistent, $$ \begin{align*}\pi(x)\,\cup\,\bigcup\limits_{\alpha<\lambda}\{\psi_{\alpha}(x,c^{\alpha}_{\sigma(\alpha)}),\,\neg\psi_{\alpha}(x,c^{\alpha}_l)\;|\;l\neq\sigma(\alpha)\}\end{align*} $$
$$ \begin{align*}\pi(x)\,\cup\,\bigcup\limits_{\alpha<\lambda}\{\psi_{\alpha}(x,c^{\alpha}_{\sigma(\alpha)}),\,\neg\psi_{\alpha}(x,c^{\alpha}_l)\;|\;l\neq\sigma(\alpha)\}\end{align*} $$
-
• for each
 $\alpha <\lambda $
the set is
$\alpha <\lambda $
the set is $$ \begin{align*}\{\psi_{\alpha}(x,c^{\alpha}_l)\;|\;l\in\mathbb{Z}\}\end{align*} $$
$$ \begin{align*}\{\psi_{\alpha}(x,c^{\alpha}_l)\;|\;l\in\mathbb{Z}\}\end{align*} $$
 $l_{\alpha }$
-inconsistent.
$l_{\alpha }$
-inconsistent.
Proof Consider
![]() $((b^{\alpha }_{\mathbb {Z}}),M^{\alpha })_{\alpha <\lambda }$
as in Definition 6.11. For simpler notation, let us introduce small
$((b^{\alpha }_{\mathbb {Z}}),M^{\alpha })_{\alpha <\lambda }$
as in Definition 6.11. For simpler notation, let us introduce small
![]() $M^{\lambda }\preceq \mathfrak {C}$
which contains all
$M^{\lambda }\preceq \mathfrak {C}$
which contains all
![]() $M^{\alpha }$
’s, all
$M^{\alpha }$
’s, all
![]() $b^{\alpha }_{\mathbb {Z}}$
’s and is
$b^{\alpha }_{\mathbb {Z}}$
’s and is
![]() $|\bigcup _{\alpha }M^{\alpha }|^+$
-saturated and strongly
$|\bigcup _{\alpha }M^{\alpha }|^+$
-saturated and strongly
![]() $|\bigcup _{\alpha }M^{\alpha }|^+$
-homogeneous. We know that
$|\bigcup _{\alpha }M^{\alpha }|^+$
-homogeneous. We know that
![]() $\pi (x)\,\cup \,\{\varphi _{\eta (\alpha )}(x,b^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent.
$\pi (x)\,\cup \,\{\varphi _{\eta (\alpha )}(x,b^{\alpha }_0)\;|\;\alpha <\lambda \}$
is consistent.
Claim 1. There are natural numbers
![]() $(k_{\alpha })_{\alpha <\lambda }$
such that
$(k_{\alpha })_{\alpha <\lambda }$
such that
 $$ \begin{align*}\pi(x)\,\cup\,\bigcup\limits_{\alpha<\lambda}\Big(\{\varphi_{\eta(\alpha)}(x,b^{\alpha}_l)\;|\;0\leqslant l<k_{\alpha}\}\,\cup\,\{\neg\varphi_{\eta(\alpha)}(x,b^{\alpha}_l)\;|\;l<0\text{ or }l\geqslant k_{\alpha}\}\Big)\end{align*} $$
$$ \begin{align*}\pi(x)\,\cup\,\bigcup\limits_{\alpha<\lambda}\Big(\{\varphi_{\eta(\alpha)}(x,b^{\alpha}_l)\;|\;0\leqslant l<k_{\alpha}\}\,\cup\,\{\neg\varphi_{\eta(\alpha)}(x,b^{\alpha}_l)\;|\;l<0\text{ or }l\geqslant k_{\alpha}\}\Big)\end{align*} $$
is consistent.
Proof of Claim 1
We will choose
![]() $k_{\alpha }$
’s recursively. Let
$k_{\alpha }$
’s recursively. Let
![]() $k_0<\omega $
be maximal such that
$k_0<\omega $
be maximal such that
is consistent. Then also
 $$ \begin{align*} \pi(x) & \cup \{\varphi_{\eta(0)}(x,b^{0}_l)\;|\;0\leqslant l<k_0\} \\ &\cup \{\neg\varphi_{\eta(0)}(x,b^{0}_l)\;|\;l<0\text{ or }l\geqslant k_{0}\} \\ & \cup \{\varphi_{\eta(\alpha)}(x,b^{\alpha}_0)\;|\;0<\alpha<\lambda\} \end{align*} $$
$$ \begin{align*} \pi(x) & \cup \{\varphi_{\eta(0)}(x,b^{0}_l)\;|\;0\leqslant l<k_0\} \\ &\cup \{\neg\varphi_{\eta(0)}(x,b^{0}_l)\;|\;l<0\text{ or }l\geqslant k_{0}\} \\ & \cup \{\varphi_{\eta(\alpha)}(x,b^{\alpha}_0)\;|\;0<\alpha<\lambda\} \end{align*} $$
is consistent. If not then, by compactness,
is consistent for some
![]() $s<0$
or
$s<0$
or
![]() $s\geqslant k_0$
. Assume
$s\geqslant k_0$
. Assume
![]() $s<0$
. Because
$s<0$
. Because
![]() $b^0_s b^0_0\ldots b^0_{k_0-1}\equiv _{M^0}b^0_0\ldots b^0_{k_0}$
and
$b^0_s b^0_0\ldots b^0_{k_0-1}\equiv _{M^0}b^0_0\ldots b^0_{k_0}$
and
![]() $b^0_{\mathbb {Z}}\subseteq M^1$
, and
$b^0_{\mathbb {Z}}\subseteq M^1$
, and
![]() $M^1$
is
$M^1$
is
![]() $|M^0|^+$
-saturated and strongly
$|M^0|^+$
-saturated and strongly
![]() $|M^0|^+$
-homogeneous, there exists
$|M^0|^+$
-homogeneous, there exists
![]() $f_1\in \operatorname {Aut}(M^1/M^0)$
such that such that
$f_1\in \operatorname {Aut}(M^1/M^0)$
such that such that
![]() $f^0_1(b^0_s b^0_0\ldots b^0_{k_0-1})=b^0_0\ldots b^0_{k_0}$
.
$f^0_1(b^0_s b^0_0\ldots b^0_{k_0-1})=b^0_0\ldots b^0_{k_0}$
.
We recursively construct an increasing sequence
![]() $f_{\alpha }\in \operatorname {Aut}(M^{\alpha }/M^0)$
for
$f_{\alpha }\in \operatorname {Aut}(M^{\alpha }/M^0)$
for
![]() $1\leqslant \alpha \leqslant \lambda $
. Assume that we have
$1\leqslant \alpha \leqslant \lambda $
. Assume that we have
![]() $f_{\alpha }\in \operatorname {Aut}(M^{\alpha }/M^0)$
and we need to define
$f_{\alpha }\in \operatorname {Aut}(M^{\alpha }/M^0)$
and we need to define
![]() $f_{\alpha +1}$
. Consider any extension
$f_{\alpha +1}$
. Consider any extension
![]() $f_{\alpha }\subseteq f_{\alpha }'\in \operatorname {Aut}(M^{\alpha +1}/M^0)$
. As
$f_{\alpha }\subseteq f_{\alpha }'\in \operatorname {Aut}(M^{\alpha +1}/M^0)$
. As
![]() $b^{\alpha }_{\mathbb {Z}}\models r_{\alpha }^{\otimes \mathbb {Z}}|_{M^{\alpha }}$
(
$b^{\alpha }_{\mathbb {Z}}\models r_{\alpha }^{\otimes \mathbb {Z}}|_{M^{\alpha }}$
(
![]() $r_{\alpha }$
as in the condition (7) of Definition 6.11), we have
$r_{\alpha }$
as in the condition (7) of Definition 6.11), we have
![]() $f^{\prime }_{\alpha }(b^{\alpha }_{\mathbb {Z}})\models f^{\prime }_{\alpha }(r_{\alpha })^{\otimes \mathbb {Z}}|_{f^{\prime }_{\alpha }(M^{\alpha })}$
. We know that
$f^{\prime }_{\alpha }(b^{\alpha }_{\mathbb {Z}})\models f^{\prime }_{\alpha }(r_{\alpha })^{\otimes \mathbb {Z}}|_{f^{\prime }_{\alpha }(M^{\alpha })}$
. We know that
![]() $f^{\prime }_{\alpha }(M^{\alpha })=M^{\alpha }$
,
$f^{\prime }_{\alpha }(M^{\alpha })=M^{\alpha }$
,
![]() $f^{\prime }_{\alpha }|_{M^0}=\operatorname {id}_{M^0}$
and that
$f^{\prime }_{\alpha }|_{M^0}=\operatorname {id}_{M^0}$
and that
![]() $r_{\alpha }$
is
$r_{\alpha }$
is
![]() $M^{\alpha }/M^0$
-invariant. Thus
$M^{\alpha }/M^0$
-invariant. Thus
![]() $f^{\prime }_{\alpha }(b^{\alpha }_{\mathbb {Z}})\models r_{\alpha }^{\otimes \mathbb {Z}}|_{M^{\alpha }}$
and
$f^{\prime }_{\alpha }(b^{\alpha }_{\mathbb {Z}})\models r_{\alpha }^{\otimes \mathbb {Z}}|_{M^{\alpha }}$
and
![]() $f^{\prime }_{\alpha }(b^{\alpha }_{\mathbb {Z}})\equiv _{M^{\alpha }}b^{\alpha }_{\mathbb {Z}}$
. There exists
$f^{\prime }_{\alpha }(b^{\alpha }_{\mathbb {Z}})\equiv _{M^{\alpha }}b^{\alpha }_{\mathbb {Z}}$
. There exists
![]() $f^{\prime \prime }_{\alpha }\in \operatorname {Aut}(M^{\alpha +1}/M^{\alpha })$
such that
$f^{\prime \prime }_{\alpha }\in \operatorname {Aut}(M^{\alpha +1}/M^{\alpha })$
such that
![]() $f^{\prime \prime }_{\alpha }f^{\prime }_{\alpha }(b^{\alpha }_{\mathbb {Z}})=b^{\alpha }_{\mathbb {Z}}$
. Set
$f^{\prime \prime }_{\alpha }f^{\prime }_{\alpha }(b^{\alpha }_{\mathbb {Z}})=b^{\alpha }_{\mathbb {Z}}$
. Set
![]() $f_{\alpha +1}:=f^{\prime \prime }_{\alpha }\circ f^{\prime }_{\alpha }\in \operatorname {Aut}(M^{\alpha +1}/M^0)$
and note that
$f_{\alpha +1}:=f^{\prime \prime }_{\alpha }\circ f^{\prime }_{\alpha }\in \operatorname {Aut}(M^{\alpha +1}/M^0)$
and note that
![]() $f_{\alpha }\subseteq f_{\alpha +1}$
. If
$f_{\alpha }\subseteq f_{\alpha +1}$
. If
![]() $\delta \leqslant \lambda $
is a limit ordinal, then simply put
$\delta \leqslant \lambda $
is a limit ordinal, then simply put
![]() $f_{\delta }:=\bigcup \limits _{1\leqslant \alpha <\delta }f_{\alpha }\in \operatorname {Aut}(M^{\delta }/M^0)$
.
$f_{\delta }:=\bigcup \limits _{1\leqslant \alpha <\delta }f_{\alpha }\in \operatorname {Aut}(M^{\delta }/M^0)$
.
After applying
![]() $f_{\lambda }$
to the set of formulae from (1), we obtain that
$f_{\lambda }$
to the set of formulae from (1), we obtain that
is consistent which contradicts the maximality of
![]() $k_0$
.
$k_0$
.
Now, assume that there are
![]() $(k_{\beta })_{\beta <\gamma }$
such that
$(k_{\beta })_{\beta <\gamma }$
such that
 $$ \begin{align*} \pi(x) & \cup \bigcup\limits_{\beta<\gamma} \{\varphi_{\eta(\beta)}(x,b^{\beta}_l)\;|\;0\leqslant l<k_{\beta}\} \\ & \cup \bigcup\limits_{\beta<\gamma} \{\neg\varphi_{\eta(\beta)}(x,b^{\beta}_l)\;|\;l<0\text{ or }l\geqslant k_{\beta}\} \\ & \cup \{\varphi_{\eta(\alpha)}(x,b^{\alpha}_0)\;|\;\gamma\leqslant\alpha<\lambda\} \end{align*} $$
$$ \begin{align*} \pi(x) & \cup \bigcup\limits_{\beta<\gamma} \{\varphi_{\eta(\beta)}(x,b^{\beta}_l)\;|\;0\leqslant l<k_{\beta}\} \\ & \cup \bigcup\limits_{\beta<\gamma} \{\neg\varphi_{\eta(\beta)}(x,b^{\beta}_l)\;|\;l<0\text{ or }l\geqslant k_{\beta}\} \\ & \cup \{\varphi_{\eta(\alpha)}(x,b^{\alpha}_0)\;|\;\gamma\leqslant\alpha<\lambda\} \end{align*} $$
is consistent. Let
![]() $k_{\gamma }<\omega $
be maximal such that
$k_{\gamma }<\omega $
be maximal such that
 $$ \begin{align*} \pi(x) & \cup \bigcup\limits_{\beta<\gamma} \{\varphi_{\eta(\beta)}(x,b^{\beta}_l)\;|\;0\leqslant l<k_{\beta}\} \\ & \cup \bigcup\limits_{\beta<\gamma} \{\neg\varphi_{\eta(\beta)}(x,b^{\beta}_l)\;|\;l<0\text{ or }l\geqslant k_{\beta}\} \\ & \cup \{\varphi_{\eta(\gamma)}(x,b^{\gamma}_l)\;|\;0\leqslant l<k_{\gamma}\} \\ & \cup \{\varphi_{\eta(\alpha)}(x,b^{\alpha}_0)\;|\;\gamma<\alpha<\lambda\} \end{align*} $$
$$ \begin{align*} \pi(x) & \cup \bigcup\limits_{\beta<\gamma} \{\varphi_{\eta(\beta)}(x,b^{\beta}_l)\;|\;0\leqslant l<k_{\beta}\} \\ & \cup \bigcup\limits_{\beta<\gamma} \{\neg\varphi_{\eta(\beta)}(x,b^{\beta}_l)\;|\;l<0\text{ or }l\geqslant k_{\beta}\} \\ & \cup \{\varphi_{\eta(\gamma)}(x,b^{\gamma}_l)\;|\;0\leqslant l<k_{\gamma}\} \\ & \cup \{\varphi_{\eta(\alpha)}(x,b^{\alpha}_0)\;|\;\gamma<\alpha<\lambda\} \end{align*} $$
is consistent. Repeating the argument from the case of
![]() $\gamma =0$
, we will obtain that also
$\gamma =0$
, we will obtain that also
 $$ \begin{align*} \pi(x) & \cup \bigcup\limits_{\beta\leqslant\gamma} \{\varphi_{\eta(\beta)}(x,b^{\beta}_l)\;|\;0\leqslant l<k_{\beta}\} \\ & \cup \bigcup\limits_{\beta\leqslant\gamma} \{\neg\varphi_{\eta(\beta)}(x,b^{\beta}_l)\;|\;l<0\text{ or }l\geqslant k_{\beta}\} \\ & \cup \{\varphi_{\eta(\alpha)}(x,b^{\alpha}_0)\;|\;\gamma<\alpha<\lambda\} \end{align*} $$
$$ \begin{align*} \pi(x) & \cup \bigcup\limits_{\beta\leqslant\gamma} \{\varphi_{\eta(\beta)}(x,b^{\beta}_l)\;|\;0\leqslant l<k_{\beta}\} \\ & \cup \bigcup\limits_{\beta\leqslant\gamma} \{\neg\varphi_{\eta(\beta)}(x,b^{\beta}_l)\;|\;l<0\text{ or }l\geqslant k_{\beta}\} \\ & \cup \{\varphi_{\eta(\alpha)}(x,b^{\alpha}_0)\;|\;\gamma<\alpha<\lambda\} \end{align*} $$
is consistent. Here ends the proof of Claim 1.
Claim 2. The array
![]() $(b^\alpha _i)^{\alpha <\lambda }_{i\in \mathbb {Z}}$
is mutually indiscernible over
$(b^\alpha _i)^{\alpha <\lambda }_{i\in \mathbb {Z}}$
is mutually indiscernible over
![]() $M_0$
, i.e., for every
$M_0$
, i.e., for every
![]() $\alpha _0<\lambda $
we have that
$\alpha _0<\lambda $
we have that
![]() $(b^{\alpha _0}_i)_{i\in \mathbb {Z}}$
is indiscernible over
$(b^{\alpha _0}_i)_{i\in \mathbb {Z}}$
is indiscernible over
![]() $(b^{\alpha }_i)_{\alpha \neq \alpha _0,i\in \mathbb {Z}}$
.
$(b^{\alpha }_i)_{\alpha \neq \alpha _0,i\in \mathbb {Z}}$
.
Proof of Claim 2
Let
![]() $\bar {i},\bar {j}\subseteq \mathbb {Z}$
be increasing tuples of the same length m. As
$\bar {i},\bar {j}\subseteq \mathbb {Z}$
be increasing tuples of the same length m. As
![]() $b^{\alpha _0}_{\bar {i}}$
and
$b^{\alpha _0}_{\bar {i}}$
and
![]() $b^{\alpha _0}_{\bar {j}}$
both satisfy
$b^{\alpha _0}_{\bar {j}}$
both satisfy
![]() $r_{\alpha _0}^{\otimes m}|_{M_{\alpha _0}}$
, we have
$r_{\alpha _0}^{\otimes m}|_{M_{\alpha _0}}$
, we have
![]() $b^\alpha _{\bar {i}}\equiv _{M_\alpha } b^\alpha _{\bar {j}}$
, so there is some
$b^\alpha _{\bar {i}}\equiv _{M_\alpha } b^\alpha _{\bar {j}}$
, so there is some
![]() $f_{\alpha _0+1}\in \operatorname {Aut}(M_{\alpha _0+1}/M_{\alpha _0})$
with
$f_{\alpha _0+1}\in \operatorname {Aut}(M_{\alpha _0+1}/M_{\alpha _0})$
with
![]() $f_{\alpha _0+1}(b^{\alpha _0}_{\bar i})=f_{\alpha _0+1}(b^{\alpha _0}_{\bar j})$
. By Lemma 6.6 we have that
$f_{\alpha _0+1}(b^{\alpha _0}_{\bar i})=f_{\alpha _0+1}(b^{\alpha _0}_{\bar j})$
. By Lemma 6.6 we have that
![]() $f_{\alpha _0+1}\cup \operatorname {id}_{b^{\alpha _0+1}_{\mathbb Z}}$
is an elementary map, so it extends to an automorphism
$f_{\alpha _0+1}\cup \operatorname {id}_{b^{\alpha _0+1}_{\mathbb Z}}$
is an elementary map, so it extends to an automorphism
![]() $f_{\alpha _0+2}$
of
$f_{\alpha _0+2}$
of
![]() $M_{\alpha _0+2}$
. Continuing inductively, we obtain a compatible sequence of automorphisms
$M_{\alpha _0+2}$
. Continuing inductively, we obtain a compatible sequence of automorphisms
![]() $f_{\alpha }\in \operatorname {Aut}(M_{\alpha }/M_{\alpha _0})\supseteq f_{\alpha _0+1}$
for
$f_{\alpha }\in \operatorname {Aut}(M_{\alpha }/M_{\alpha _0})\supseteq f_{\alpha _0+1}$
for
![]() $\alpha _0<\alpha \leq \lambda $
with
$\alpha _0<\alpha \leq \lambda $
with
![]() $f_{\alpha }(b^{\beta }_{\mathbb Z})=b^{\beta }_{\mathbb Z}$
for every
$f_{\alpha }(b^{\beta }_{\mathbb Z})=b^{\beta }_{\mathbb Z}$
for every
![]() $\beta <\alpha $
(at limit steps we take unions). Then
$\beta <\alpha $
(at limit steps we take unions). Then
![]() $f_\lambda $
witnesses that
$f_\lambda $
witnesses that
![]() $b^{\alpha _0}_{\bar i}\equiv _{(b^{\alpha }_i)_{\alpha \neq \alpha _0,i\in \mathbb {Z}}} b^{\alpha _0}_{\bar j}$
. Here ends the proof of Claim 2.
$b^{\alpha _0}_{\bar i}\equiv _{(b^{\alpha }_i)_{\alpha \neq \alpha _0,i\in \mathbb {Z}}} b^{\alpha _0}_{\bar j}$
. Here ends the proof of Claim 2.
Let
where
![]() $\alpha <\lambda $
and
$\alpha <\lambda $
and
![]() $n\in \mathbb {Z}$
.
$n\in \mathbb {Z}$
.
By Claim 2, the array
![]() $(c^\alpha _i)^{\alpha <\lambda }_{i\in \mathbb {Z}}$
is also mutually indiscernible over
$(c^\alpha _i)^{\alpha <\lambda }_{i\in \mathbb {Z}}$
is also mutually indiscernible over
![]() $M_0$
. Hence, the first item from the thesis of the proposition follows from consistency of
$M_0$
. Hence, the first item from the thesis of the proposition follows from consistency of
![]() $\pi (x)\,\cup \,\bigcup \limits _{\alpha <\lambda }\{\psi _{\alpha }(x,c^{\alpha }_{0}),\,\neg \psi _{\alpha }(x,c^{\alpha }_l)\;|\;l\neq 0\}$
.
$\pi (x)\,\cup \,\bigcup \limits _{\alpha <\lambda }\{\psi _{\alpha }(x,c^{\alpha }_{0}),\,\neg \psi _{\alpha }(x,c^{\alpha }_l)\;|\;l\neq 0\}$
.
For the second item of the thesis, we argue shortly as follows. Because of the condition (7) in Definition 6.11, for each
![]() $\alpha <\lambda $
there exists
$\alpha <\lambda $
there exists
![]() $l_{\alpha }<\omega $
such that
$l_{\alpha }<\omega $
such that
![]() $\{\varphi _{\eta (\alpha )}(x,b^{\alpha }_i)\;|\;i\in \mathbb {Z}\}$
is
$\{\varphi _{\eta (\alpha )}(x,b^{\alpha }_i)\;|\;i\in \mathbb {Z}\}$
is
![]() $l_{\alpha }$
-inconsistent. In particular for each
$l_{\alpha }$
-inconsistent. In particular for each
![]() $\alpha <\lambda $
, we have that
$\alpha <\lambda $
, we have that
![]() $\{\psi _{\alpha }(x,c^{\alpha }_n)\;|\;n\in \mathbb {Z}\}$
is
$\{\psi _{\alpha }(x,c^{\alpha }_n)\;|\;n\in \mathbb {Z}\}$
is
![]() $l_{\alpha }$
-inconsistent.
$l_{\alpha }$
-inconsistent.
Fact 6.17 (Fact 2.11 in [Reference Dolich, Goodrick and Lippel16]).
For any theory T the following are equivalent.
-
(1) T is dp-minimal.
-
(2) There is no sequence of formulae
 $\psi _1(x,y), \dots , \psi _{2^n}(x,y)$
with
$\psi _1(x,y), \dots , \psi _{2^n}(x,y)$
with
 $|x|=n$
and sequences
$|x|=n$
and sequences
 $(a^j_i)_{i\in \omega }$
with
$(a^j_i)_{i\in \omega }$
with
 $1 \leqslant j \leqslant 2^n$
so that for any
$1 \leqslant j \leqslant 2^n$
so that for any
 $\sigma : \{1, \dots , 2^n\} \to \omega $
, the set is consistent.
$\sigma : \{1, \dots , 2^n\} \to \omega $
, the set is consistent. $$\begin{align*}\bigwedge_{1 \leqslant k \leqslant 2^n} \psi_k(x, a^k_{\sigma(k)}) \wedge \bigwedge_{1 \leqslant k \leqslant 2^n} \bigwedge_{l\neq\sigma(k)}\neg\psi_k(x, a^k_l)\end{align*}$$
$$\begin{align*}\bigwedge_{1 \leqslant k \leqslant 2^n} \psi_k(x, a^k_{\sigma(k)}) \wedge \bigwedge_{1 \leqslant k \leqslant 2^n} \bigwedge_{l\neq\sigma(k)}\neg\psi_k(x, a^k_l)\end{align*}$$
Corollary 6.18. If T is dp-minimal then
![]() $\tilde {D}_Q(\pi (x))<2^{|x|}$
.
$\tilde {D}_Q(\pi (x))<2^{|x|}$
.
Question 6.19. What other properties does
![]() $\tilde {D}_Q$
satisfy in the dp-minimal context? For example, do we have a counterpart of Lemma 3.17 in the dp-minimal context?
$\tilde {D}_Q$
satisfy in the dp-minimal context? For example, do we have a counterpart of Lemma 3.17 in the dp-minimal context?
The following definitions may be found in [Reference Chernikov9].
Definition 6.20.
-
(1) An inp-pattern in
 $\pi (x)$
of depth
$\pi (x)$
of depth
 $\lambda $
is
$\lambda $
is
 $(l_{\alpha },\varphi _{\alpha }(x,y_{\alpha }),(b^{\alpha }_i)_{i<\omega })_{\alpha <\lambda }$
such that:
$(l_{\alpha },\varphi _{\alpha }(x,y_{\alpha }),(b^{\alpha }_i)_{i<\omega })_{\alpha <\lambda }$
such that:-
•
 $\{\varphi _{\alpha }(x,b^{\alpha }_i)\;|\;i<\omega \}$
is
$\{\varphi _{\alpha }(x,b^{\alpha }_i)\;|\;i<\omega \}$
is
 $l_{\alpha }$
-inconsistent for each
$l_{\alpha }$
-inconsistent for each
 $\alpha <\lambda $
,
$\alpha <\lambda $
, -
•
 $\pi (x)\,\cup \,\{\varphi _{\alpha }(x,b^{\alpha }_{\sigma (\alpha )})\;|\;\alpha <\lambda \}$
is consistent for each
$\pi (x)\,\cup \,\{\varphi _{\alpha }(x,b^{\alpha }_{\sigma (\alpha )})\;|\;\alpha <\lambda \}$
is consistent for each
 $\sigma :\lambda \to \omega $
.
$\sigma :\lambda \to \omega $
.
-
-
(2) The burden of
 $\pi (x)$
, denoted
$\pi (x)$
, denoted
 , is the the supremum of the depths of all inp-patterns in
, is the the supremum of the depths of all inp-patterns in
 $\pi (x)$
.
$\pi (x)$
. -
(3) We let the dp-rank of
 $\pi (x)$
, denoted
$\pi (x)$
, denoted
 , be the supremum of
, be the supremum of
 $\lambda $
for which there are
$\lambda $
for which there are
 $a\models \pi $
and mutually indiscernible over
$a\models \pi $
and mutually indiscernible over
 $C:=\operatorname {dom}(\pi )$
sequences
$C:=\operatorname {dom}(\pi )$
sequences
 $(b^{\alpha }_i)_{i<\omega }$
, where
$(b^{\alpha }_i)_{i<\omega }$
, where
 $\alpha <\lambda $
, such that none of them is indiscernible over
$\alpha <\lambda $
, such that none of them is indiscernible over
 $aC$
.
$aC$
.
Fact 6.21.
-
(1)
 (Fact 3.8 in [Reference Chernikov9]).
(Fact 3.8 in [Reference Chernikov9]). -
(2) If T is NIP then
 for every partial type
for every partial type
 $\pi (x)$
(Fact 3.8 in [Reference Chernikov9]).
$\pi (x)$
(Fact 3.8 in [Reference Chernikov9]). -
(3) T is NTP
 $_2$
iff
$_2$
iff
 for every partial type
for every partial type
 $\pi (x)$
(Fact 3.2 in [Reference Chernikov9]).
$\pi (x)$
(Fact 3.2 in [Reference Chernikov9]). -
(4) T is NIP iff
 for every partial type
for every partial type
 $\pi (x)$
(Proposition 10 in [Reference Adler1]).
$\pi (x)$
(Proposition 10 in [Reference Adler1]).
Corollary 6.22.
-
(1) For every Q and partial type
 $\pi $
, we have
$\pi $
, we have 
-
(2) If T is NTP
 $_2$
then for every Q and partial type
$_2$
then for every Q and partial type
 $\pi $
, we have
$\pi $
, we have  $$ \begin{align*}\tilde{D}_Q(\pi)<\infty.\end{align*} $$
$$ \begin{align*}\tilde{D}_Q(\pi)<\infty.\end{align*} $$
As we see above,
![]() $\tilde {Q}$
-rank is finite in NSOP
$\tilde {Q}$
-rank is finite in NSOP
![]() $_1$
and finite dp-rank theories. There is a natural question: what is the class of theories for which
$_1$
and finite dp-rank theories. There is a natural question: what is the class of theories for which
![]() $\tilde {Q}$
-rank is finite. We need to look for a class of theories which generalizes finite dp-rank theories and NSOP
$\tilde {Q}$
-rank is finite. We need to look for a class of theories which generalizes finite dp-rank theories and NSOP
![]() $_1$
theories at the same time. In their recent work, authors of [Reference Ahn, Kim and Lee3] provide a new dividing line in the stability hierarchy, called the antichain tree property and show that theories without the antichain tree property (NATP) generalize NTP
$_1$
theories at the same time. In their recent work, authors of [Reference Ahn, Kim and Lee3] provide a new dividing line in the stability hierarchy, called the antichain tree property and show that theories without the antichain tree property (NATP) generalize NTP
![]() $_2$
and NSOP
$_2$
and NSOP
![]() $_1$
.
$_1$
.
Question 6.23. Is
![]() $\tilde {D}_Q$
finite in NATP? Is
$\tilde {D}_Q$
finite in NATP? Is
![]() $\tilde {D}_Q$
infinite in ATP?
$\tilde {D}_Q$
infinite in ATP?
A prospective approach to answer the second above question above, could be by considering the
![]() $\tilde {Q}$
-rank in the context of NSOP theories with SOP
$\tilde {Q}$
-rank in the context of NSOP theories with SOP
![]() $_1$
.
$_1$
.
Moreover, one could use finiteness of the
![]() $\tilde {Q}$
-rank to indicate that a given theory is placed among an extension of the current known boundary of the combinatorially tame universe [Reference Tran27]. For example, the author of [Reference Tran27] notes that his theory ACFO of algebraically closed fields with multiplicative circular orders has TP
$\tilde {Q}$
-rank to indicate that a given theory is placed among an extension of the current known boundary of the combinatorially tame universe [Reference Tran27]. For example, the author of [Reference Tran27] notes that his theory ACFO of algebraically closed fields with multiplicative circular orders has TP
![]() $_2$
(Proposition 3.25 in [Reference Tran27]), but on the other hand his theory is a quite natural expansion of the theory of the algebraic closure of a finite field. For sure it is worth checking whether the
$_2$
(Proposition 3.25 in [Reference Tran27]), but on the other hand his theory is a quite natural expansion of the theory of the algebraic closure of a finite field. For sure it is worth checking whether the
![]() $\tilde {Q}$
-rank is finite (or ordinal-valued) in the case of ACFO.
$\tilde {Q}$
-rank is finite (or ordinal-valued) in the case of ACFO.
6.3 An example where the rank is infinite: valued Boolean algebras
Let B be a Boolean algebra considered in language
![]() $L_{BA}=\{\wedge ,\vee ,^c, 0,1\}$
and
$L_{BA}=\{\wedge ,\vee ,^c, 0,1\}$
and
![]() $(P,\leqslant ,0_P,1_P)$
a linearly ordered set with minimal element
$(P,\leqslant ,0_P,1_P)$
a linearly ordered set with minimal element
![]() $0_P$
and maximal element
$0_P$
and maximal element
![]() $1_P$
. We call a function
$1_P$
. We call a function
![]() $v:B\to P$
a valuation, if
$v:B\to P$
a valuation, if
![]() $v(x)=0_P$
iff
$v(x)=0_P$
iff
![]() $x=0$
,
$x=0$
,
![]() $V(1)=1_P$
, and
$V(1)=1_P$
, and
![]() $v(x\vee y)=\max (v(x),x(y))$
for all
$v(x\vee y)=\max (v(x),x(y))$
for all
![]() $x,y\in B$
. Now let
$x,y\in B$
. Now let
![]() $L_{VBA}=L_{BA}\cup \{v,0_P,1_P\}$
be a two-sorted language on sorts B and P, where v is a symbol of a unary function from B to P. Let
$L_{VBA}=L_{BA}\cup \{v,0_P,1_P\}$
be a two-sorted language on sorts B and P, where v is a symbol of a unary function from B to P. Let
![]() $DVBA_0$
be the
$DVBA_0$
be the
![]() $L_{VBA}$
-theory expressing that
$L_{VBA}$
-theory expressing that
![]() $(B,\vee ,\wedge ,^c,0,1)$
is an atomless Boolean algebra,
$(B,\vee ,\wedge ,^c,0,1)$
is an atomless Boolean algebra,
![]() $v:B\to P$
is a valuation, and for all
$v:B\to P$
is a valuation, and for all
![]() $x\leqslant y$
in B (here, “
$x\leqslant y$
in B (here, “
![]() $\leqslant $
” indicates the canonical ordering in Boolean algebras) and any
$\leqslant $
” indicates the canonical ordering in Boolean algebras) and any
![]() $p\in P$
such that
$p\in P$
such that
![]() $v(x)<p<v(y)$
there exists
$v(x)<p<v(y)$
there exists
![]() $z\in B$
with
$z\in B$
with
![]() $x\leqslant z\leqslant y$
and
$x\leqslant z\leqslant y$
and
![]() $v(z)=p$
(density) and there are disjoint
$v(z)=p$
(density) and there are disjoint
![]() $y_1,y_2\leqslant y$
with
$y_1,y_2\leqslant y$
with
![]() $v(y_1)=v(y_2)=v(y)$
(no valuation-atoms).
$v(y_1)=v(y_2)=v(y)$
(no valuation-atoms).
It is easy to see that
![]() $DVBA_0$
is consistent. By Example 4.33 from [Reference Ahn, Kim and Lee3],
$DVBA_0$
is consistent. By Example 4.33 from [Reference Ahn, Kim and Lee3],
![]() $DVBA_0$
has ATP, so intuitively one may expect that the
$DVBA_0$
has ATP, so intuitively one may expect that the
![]() $\tilde {Q}$
-rank is infinite in
$\tilde {Q}$
-rank is infinite in
![]() $DVBA_0$
. Let us argue on that.
$DVBA_0$
. Let us argue on that.
Proposition 6.24.
![]() $DVBA_0$
is complete and admits QE in
$DVBA_0$
is complete and admits QE in
![]() $L_{VBA}$
.
$L_{VBA}$
.
Proof Let
![]() $M,N\models DVBA_0$
and let
$M,N\models DVBA_0$
and let
![]() $f:A\to B$
be an isomorphism with
$f:A\to B$
be an isomorphism with
![]() $A,B$
finitely generated substructures of M and N, respectively. Since M and N are locally finite, A and B are finite. Let
$A,B$
finitely generated substructures of M and N, respectively. Since M and N are locally finite, A and B are finite. Let
![]() $a\in M$
be an element. By a standard back-and-forth argument, it is enough to find
$a\in M$
be an element. By a standard back-and-forth argument, it is enough to find
![]() $b\in B$
such that f extends to an isomorphism of the substructures generated by
$b\in B$
such that f extends to an isomorphism of the substructures generated by
![]() $Aa$
and
$Aa$
and
![]() $Bb$
. Let
$Bb$
. Let
![]() $(a_1,\dots ,a_k)$
be all the atoms in A and
$(a_1,\dots ,a_k)$
be all the atoms in A and
![]() $(b_1,\dots ,b_k)$
all the atoms in B. Let
$(b_1,\dots ,b_k)$
all the atoms in B. Let
![]() $P(A)=\{p_1,\dots ,p_l\}$
and
$P(A)=\{p_1,\dots ,p_l\}$
and
![]() $P(B)=\{q_1,\dots ,q_l\}$
be ascending enumerations in sort P. Assume
$P(B)=\{q_1,\dots ,q_l\}$
be ascending enumerations in sort P. Assume
![]() $a\in B(M)$
(the argument in case
$a\in B(M)$
(the argument in case
![]() $a\in P(M)$
is very similar). By the quantifier elimination in
$a\in P(M)$
is very similar). By the quantifier elimination in
![]() $(P,\leqslant , 0_P, 1_P)$
, we can find
$(P,\leqslant , 0_P, 1_P)$
, we can find
![]() $q^{\prime }_1,\dots ,q^{\prime }_k,q^{\prime \prime }_1,\dots ,q^{\prime \prime }_k\in P(N)$
such that
$q^{\prime }_1,\dots ,q^{\prime }_k,q^{\prime \prime }_1,\dots ,q^{\prime \prime }_k\in P(N)$
such that
![]() $(q_1,\dots ,q_l,q^{\prime }_1,\dots ,q^{\prime }_k,q^{\prime \prime }_1,\dots ,q^{\prime \prime }_k)$
has the same quantifier-free type as
$(q_1,\dots ,q_l,q^{\prime }_1,\dots ,q^{\prime }_k,q^{\prime \prime }_1,\dots ,q^{\prime \prime }_k)$
has the same quantifier-free type as
By the density axiom, for every
![]() $i\leqslant k$
we can find
$i\leqslant k$
we can find
![]() $b^{\prime }_i\leqslant b_i$
such that
$b^{\prime }_i\leqslant b_i$
such that
![]() $v(b^{\prime }_i)=q^{\prime }_i$
and
$v(b^{\prime }_i)=q^{\prime }_i$
and
![]() $v(b_i\wedge b_i^{\prime c})=q^{\prime \prime }_i$
. Put
$v(b_i\wedge b_i^{\prime c})=q^{\prime \prime }_i$
. Put
![]() $b:=\bigvee \limits _{i\leqslant k} b^{\prime }_i$
. Define
$b:=\bigvee \limits _{i\leqslant k} b^{\prime }_i$
. Define
![]() $f'(a\wedge a_i)=b^{\prime }_i$
for all
$f'(a\wedge a_i)=b^{\prime }_i$
for all
![]() $i\leqslant k$
and
$i\leqslant k$
and
Then
![]() $f\cup f'$
uniquely extends to an isomorphism of the substructures generated by
$f\cup f'$
uniquely extends to an isomorphism of the substructures generated by
![]() $Aa$
and
$Aa$
and
![]() $Bb$
which sends a to b, as required.
$Bb$
which sends a to b, as required.
Let
![]() $q(y)=\{0_P<v(y\wedge m)=v(y)<v(m')\;|\;m,m'\in B\setminus \{0\}\}$
. We claim that
$q(y)=\{0_P<v(y\wedge m)=v(y)<v(m')\;|\;m,m'\in B\setminus \{0\}\}$
. We claim that
![]() $q(y)$
determines a complete global type (note it will obviously be
$q(y)$
determines a complete global type (note it will obviously be
![]() $\emptyset $
-invariant). Clearly
$\emptyset $
-invariant). Clearly
![]() $q(y)$
determines a complete type of y in the Boolean algebra B. Hence, by the quantifier elimination, it is enough to prove that for any
$q(y)$
determines a complete type of y in the Boolean algebra B. Hence, by the quantifier elimination, it is enough to prove that for any
![]() $x,y\models q$
and any
$x,y\models q$
and any
![]() $a,b,c,d\in B$
we have
$a,b,c,d\in B$
we have
![]() $v((x\wedge a )\vee (x^c\wedge b))<v((x\wedge c )\vee (x^c\wedge d))$
if and only if
$v((x\wedge a )\vee (x^c\wedge b))<v((x\wedge c )\vee (x^c\wedge d))$
if and only if
![]() $v((y\wedge a )\vee (y^c\wedge b))<v((y\wedge c )\vee (y\wedge d))$
, and likewise for equality in place of inequality. Note that if
$v((y\wedge a )\vee (y^c\wedge b))<v((y\wedge c )\vee (y\wedge d))$
, and likewise for equality in place of inequality. Note that if
![]() $b\neq 0$
then
$b\neq 0$
then
![]() $v(x^c\wedge b)=v(b)>v(x\wedge a )$
, so
$v(x^c\wedge b)=v(b)>v(x\wedge a )$
, so
![]() $v((x\wedge a )\vee (x^c\wedge b))=v(b)$
. On the other hand, if
$v((x\wedge a )\vee (x^c\wedge b))=v(b)$
. On the other hand, if
![]() $b=0$
then
$b=0$
then
![]() $v((x\wedge a )\vee (x^c\wedge b))=v(x\wedge a)=v(x)$
. Hence, the equivalences easily follow by inspection.
$v((x\wedge a )\vee (x^c\wedge b))=v(x\wedge a)=v(x)$
. Hence, the equivalences easily follow by inspection.
Now, for any model M define
![]() $r_M(y)=\{0_P<v(y\wedge m)=v(y)<v(m')\;|\;m,m'\in B, v(m)\in conv(v[B(M)\setminus \{0\}])\}\cup \{y\wedge c=0\;|\;v(c)<v[B(M)\setminus \{0\}]\}$
, where
$r_M(y)=\{0_P<v(y\wedge m)=v(y)<v(m')\;|\;m,m'\in B, v(m)\in conv(v[B(M)\setminus \{0\}])\}\cup \{y\wedge c=0\;|\;v(c)<v[B(M)\setminus \{0\}]\}$
, where
![]() $conv$
denotes the convex hull operation in
$conv$
denotes the convex hull operation in
![]() $(P,\leqslant )$
. Note
$(P,\leqslant )$
. Note
![]() $q|_M\subseteq r_M$
. Again, by quantifier elimination
$q|_M\subseteq r_M$
. Again, by quantifier elimination
![]() $r_M(y)$
determines a complete global type. Moreover, as
$r_M(y)$
determines a complete global type. Moreover, as
![]() $v[B(M)\setminus 0]$
and its convex hull are invariant under automorphisms preserving M setwise, we get that
$v[B(M)\setminus 0]$
and its convex hull are invariant under automorphisms preserving M setwise, we get that
![]() $r_M(y)$
is
$r_M(y)$
is
![]() $M/M_0$
-invariant for any
$M/M_0$
-invariant for any
![]() $M_0\prec M$
.
$M_0\prec M$
.
Let
![]() $\varphi (x,y)=(x\neq 0\wedge x\leqslant y)$
and
$\varphi (x,y)=(x\neq 0\wedge x\leqslant y)$
and
![]() $Q=(\varphi (x,y),q(y))$
. We claim that
$Q=(\varphi (x,y),q(y))$
. We claim that
![]() $\tilde {D}_Q(x=x)=\infty $
for x a variable of the sort B. Fix any ordinal
$\tilde {D}_Q(x=x)=\infty $
for x a variable of the sort B. Fix any ordinal
![]() $\lambda $
. Choose
$\lambda $
. Choose
![]() $(M^\alpha , b^\alpha )_{\alpha <\lambda }$
with
$(M^\alpha , b^\alpha )_{\alpha <\lambda }$
with
![]() $(M^\alpha )_{\alpha <\lambda }$
continuous so that
$(M^\alpha )_{\alpha <\lambda }$
continuous so that
![]() $b^\alpha \models q|_{M^\alpha }$
and
$b^\alpha \models q|_{M^\alpha }$
and
![]() $b^{\alpha }M^{\alpha }\subseteq M^{\alpha +1}$
for every
$b^{\alpha }M^{\alpha }\subseteq M^{\alpha +1}$
for every
![]() $\alpha <\lambda $
, and each
$\alpha <\lambda $
, and each
![]() $M^{\alpha +1}$
is
$M^{\alpha +1}$
is
![]() $|M^{\alpha }|^+$
-saturated and strongly
$|M^{\alpha }|^+$
-saturated and strongly
![]() $|M^{\alpha }|^+$
-homogeneous. Then
$|M^{\alpha }|^+$
-homogeneous. Then
![]() $r|_{M^\alpha }$
witnesses that
$r|_{M^\alpha }$
witnesses that
![]() $\varphi (x,b^\alpha )$
Kim-divides (with respect to a semi-global type) over
$\varphi (x,b^\alpha )$
Kim-divides (with respect to a semi-global type) over
![]() $M^\alpha $
for every
$M^\alpha $
for every
![]() $\alpha <\lambda $
(this is because for any Morley sequence
$\alpha <\lambda $
(this is because for any Morley sequence
![]() $(m_i)_{i<\omega }$
in r we have that
$(m_i)_{i<\omega }$
in r we have that
![]() $m_i\wedge m_j=0$
for all
$m_i\wedge m_j=0$
for all
![]() $i\neq j$
). On the other hand,
$i\neq j$
). On the other hand,
![]() $\{\varphi (x,b^\alpha )\;|\;\alpha <\lambda \}$
is consistent by compactness and the choice of q. This shows that
$\{\varphi (x,b^\alpha )\;|\;\alpha <\lambda \}$
is consistent by compactness and the choice of q. This shows that
![]() $\tilde {D}_Q(x=x)\geqslant \lambda $
, so
$\tilde {D}_Q(x=x)\geqslant \lambda $
, so
![]() $\tilde {D}_Q(x=x)=\infty $
.
$\tilde {D}_Q(x=x)=\infty $
.
Acknowledgments
We thank Zoé Chatzidakis, Itay Kaplan, Byughan Kim, Nick Ramsey, and Tomasz Rzepecki for helpful discussions and comments, and the anonymous referee for careful reading of the paper and many helpful suggestions.
Funding
The first author is supported by DFG project BA 6785/2-1 and by EPSRC Grant EP/V03619X/1. The second author is supported by the European Union’s Horizon research and innovation programme under the MSCA project no. 101063183, by the National Science Centre (Narodowe Centrum Nauki, Poland) (Grant No. 2021/43/B/ST1/00405). SDG.





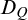
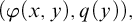
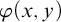
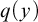
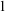
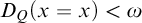
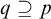
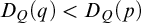
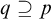
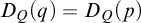
 -stationary. We give natural examples of families of invariant types satisfying this property in some NSOP
-stationary. We give natural examples of families of invariant types satisfying this property in some NSOP