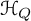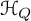1. Introduction
Cohomological Hall algebras (abbreviated as CoHAs) were introduced in [Reference Kontsevich and Soibelman36] as a mathematical interpretation of the notion of algebra of (closed) BPS states in string theory [Reference Harvey and Moore30]. In a nutshell, the definition of CoHA goes through the same lines as the definition of the usual Hall algebra [Reference Lusztig45, Reference Ringel55], but it uses cohomology of moduli stacks of objects instead of constructible functions on those stacks. As a consequence, the underlying vector space of CoHA is easier to describe explicitly. In particular, for the category of quiver representations, one can obtain [Reference Kontsevich and Soibelman36] an explicit description of the product of CoHA using the Feigin–Odesskii shuffle product.
However, one is also interested in representations of BPS algebras, modeled by spaces of open BPS states. In mathematical terms, this corresponds to CoHA-module structures constructed on cohomology of moduli spaces of stable framed quiver representations [Reference Franzen17, Reference Franzen18, Reference Soibelman62]. This approach is reminiscent of the construction of Heisenberg algebra action on the cohomology (or K-theory) of Hilbert schemes on surfaces [Reference Grojnowski26, Reference Lehn38, Reference Lehn and Sorger39, Reference Li, Qin and Wang43, Reference Nakajima49, Reference Schiffmann and Vasserot61] or quantum group actions on equivariant cohomology (or K-theory) of Nakajima quiver varieties [Reference Nakajima50]. Explicit description of CoHA-modules, using shuffle products, was obtained in [Reference Franzen18].
Poincaré series of CoHAs provide one of the possible approaches to the refined Donaldson–Thomas (DT) invariants, also called the BPS invariants [Reference Kontsevich and Soibelman35]. As a result, one can think about CoHAs as a categorification of DT invariants. Unraveling new intrinsic structures of CoHAs (say, that of a Hopf algebra or that of a vertex algebra) leads to a better understanding of properties of DT invariants.
Vertex algebras were introduced in [Reference Borcherds4] in order to formalise the machinery behind some remarkable constructions in representation theory of infinite-dimensional Lie algebras [Reference Frenkel and Kac21, Reference Frenkel, Lepowsky and Meurman22]. In modern language, those constructions are instances of lattice vertex algebras. More general vertex algebras provide a mathematical apparatus to work with operator product expansions (OPEs) in quantum field theory [Reference Wilson63, Reference Wilson and Zimmermann64]. For us, a special role will be played by the principal subalgebras of lattice vertex algebras [Reference Feĭgin and Stoyanovskiĭ16, Reference Milas and Penn47] that give explicit realisations of the so-called free vertex algebras [Reference Roitman57, Reference Roitman58].
Operator product expansions
![]() $A(z)B(w)=\sum _{n\in \mathbb {Z}}(z-w)^n O_n(w)$
have a regular part (corresponding to non-negative n) and a singular part. If one is only interested in the singular parts of OPEs, this leads to the notion of vertex Lie algebras, also known as Lie conformal algebras [Reference Kac34, Reference Primc51]. By contrast to vertex algebras, these structures only use n-products for
$A(z)B(w)=\sum _{n\in \mathbb {Z}}(z-w)^n O_n(w)$
have a regular part (corresponding to non-negative n) and a singular part. If one is only interested in the singular parts of OPEs, this leads to the notion of vertex Lie algebras, also known as Lie conformal algebras [Reference Kac34, Reference Primc51]. By contrast to vertex algebras, these structures only use n-products for
![]() $n\ge 0$
. The relationship between vertex Lie algebras and vertex algebras is closely resembling that between Lie algebras and associative algebras. Notably, many important vertex algebras, and, in particular, free vertex algebras mentioned earlier, arise as universal envelopes of vertex Lie algebras. These universal enveloping vertex algebras are cocommutative vertex bialgebras (meaning vertex algebras with a compatible coalgebra structure) and are automatically universal enveloping algebras of Lie algebras. Thus, they possess a Hopf algebra structure, and this is where their relationship to CoHAs manifests itself.
$n\ge 0$
. The relationship between vertex Lie algebras and vertex algebras is closely resembling that between Lie algebras and associative algebras. Notably, many important vertex algebras, and, in particular, free vertex algebras mentioned earlier, arise as universal envelopes of vertex Lie algebras. These universal enveloping vertex algebras are cocommutative vertex bialgebras (meaning vertex algebras with a compatible coalgebra structure) and are automatically universal enveloping algebras of Lie algebras. Thus, they possess a Hopf algebra structure, and this is where their relationship to CoHAs manifests itself.
Exploring the relationship between CoHAs and vertex algebras is the main topic of this paper. This relationship is not entirely new, and there seem to be some physical reasons for it [Reference Rapčák, Soibelman, Yang and Zhao53]. For example, in [Reference Schiffmann and Vasserot60, Theorem B] (see also [Reference Rapčák, Soibelman, Yang and Zhao53]), a relationship between an equivariant spherical CoHA of a
![]() $3$
-loop quiver and the current algebra [Reference Arakawa1, §3.11] of some vertex algebra was established. However, in [Reference Joyce33], there was given a very general construction of vertex algebra structures on homology groups of various moduli stacks, which leads to a vertex algebra structure on the duals of cohomological Hall algebras.
$3$
-loop quiver and the current algebra [Reference Arakawa1, §3.11] of some vertex algebra was established. However, in [Reference Joyce33], there was given a very general construction of vertex algebra structures on homology groups of various moduli stacks, which leads to a vertex algebra structure on the duals of cohomological Hall algebras.
In this paper, we traverse the path between CoHAs and vertex algebras in a different direction. Namely, given a symmetric quiver Q, we show that, for the principal free vertex algebra corresponding to the Euler form of Q, the shuffle product formula of CoHA emerges ‘for free’, since these free vertex algebras are universal envelopes of appropriate vertex Lie algebras.
In [Reference Kontsevich and Soibelman36, §6.2], it was asked if CoHA can be identified with a Hopf algebra of the form
![]() $U({\mathfrak {g}})$
, where
$U({\mathfrak {g}})$
, where
![]() ${\mathfrak {g}}$
is a graded Lie algebra. In physics terms, this Lie algebra should correspond to the space of single-particle BPS states [Reference Harvey and Moore30, Reference Rapčák, Soibelman, Yang and Zhao53]. Of course, in view of Milnor–Moore theorem, one just needs to find a suitable cocommutative bialgebra structure on CoHA. A bialgebra structure for usual Hall algebras is guaranteed by Green’s theorem [Reference Green25] and appropriate twists from [Reference Xiao65]. A cohomological incarnation of Green’s theorem was proved in [Reference Davison8] for some localisation of CoHAs for quivers with potential (see also [Reference Yang and Zhao66] for a purely algebraic approach to a similar problem). It is unclear, however, what are the implications of this result for a bialgebra structure on the CoHA itself. For a different cocommutative coproduct for usual Hall algebras, see [Reference Bridgeland and Laredo5, Reference Joyce32 Reference Ringel56].
${\mathfrak {g}}$
is a graded Lie algebra. In physics terms, this Lie algebra should correspond to the space of single-particle BPS states [Reference Harvey and Moore30, Reference Rapčák, Soibelman, Yang and Zhao53]. Of course, in view of Milnor–Moore theorem, one just needs to find a suitable cocommutative bialgebra structure on CoHA. A bialgebra structure for usual Hall algebras is guaranteed by Green’s theorem [Reference Green25] and appropriate twists from [Reference Xiao65]. A cohomological incarnation of Green’s theorem was proved in [Reference Davison8] for some localisation of CoHAs for quivers with potential (see also [Reference Yang and Zhao66] for a purely algebraic approach to a similar problem). It is unclear, however, what are the implications of this result for a bialgebra structure on the CoHA itself. For a different cocommutative coproduct for usual Hall algebras, see [Reference Bridgeland and Laredo5, Reference Joyce32 Reference Ringel56].
For a symmetric quiver Q, the algebra
![]() ${\mathcal {H}}_Q$
is supercommutative (once certain sign twists are implemented), and thus, the required Lie algebra
${\mathcal {H}}_Q$
is supercommutative (once certain sign twists are implemented), and thus, the required Lie algebra
![]() ${\mathfrak {g}}$
has to be abelian. In this case, it was conjectured in [Reference Kontsevich and Soibelman36, §2.6] and proved in [Reference Efimov14] that there exists an abelian Lie algebra
${\mathfrak {g}}$
has to be abelian. In this case, it was conjectured in [Reference Kontsevich and Soibelman36, §2.6] and proved in [Reference Efimov14] that there exists an abelian Lie algebra
![]() ${\mathfrak {g}}$
such that
${\mathfrak {g}}$
such that
![]() ${\mathcal {H}}_Q\simeq U({\mathfrak {g}})$
and
${\mathcal {H}}_Q\simeq U({\mathfrak {g}})$
and
![]() ${\mathfrak {g}}$
is of the form
${\mathfrak {g}}$
is of the form
![]() ${\mathfrak {g}}^{\mathrm {prim}}[x]$
with x of cohomological degree
${\mathfrak {g}}^{\mathrm {prim}}[x]$
with x of cohomological degree
![]() $2$
. Further generalisations for quivers with potentials were obtained in [Reference Davison and Meinhardt9].
$2$
. Further generalisations for quivers with potentials were obtained in [Reference Davison and Meinhardt9].
In our approach to the above question, we change the setting, and we argue that the graded dual
![]() ${\mathcal {H}}{_Q^{\vee }}$
, which is a (super) cocommutative coalgebra, has a vertex bialgebra structure and can be represented as the universal enveloping algebra of a canonical Lie algebra (non-abelian in general). More precisely, we establish the following result.
${\mathcal {H}}{_Q^{\vee }}$
, which is a (super) cocommutative coalgebra, has a vertex bialgebra structure and can be represented as the universal enveloping algebra of a canonical Lie algebra (non-abelian in general). More precisely, we establish the following result.
Theorem 1.1 (Theorem 5.7)
Let Q be a symmetric quiver, let
![]() $L=\mathbb {Z}^{Q_0}$
and let
$L=\mathbb {Z}^{Q_0}$
and let
![]() $\chi $
be the Euler form of Q. Then the coalgebra
$\chi $
be the Euler form of Q. Then the coalgebra
![]() ${\mathcal {H}}{_Q^{\vee }}$
has a canonical structure of a cocommutative connected vertex bialgebra. The space of primitive elements
${\mathcal {H}}{_Q^{\vee }}$
has a canonical structure of a cocommutative connected vertex bialgebra. The space of primitive elements
is a vertex Lie algebra (also having a structure of a Lie algebra) such that
![]() ${\mathcal {H}}{_Q^{\vee }}$
is isomorphic to the universal enveloping vertex algebra of C (as vertex bialgebras). The canonical derivation
${\mathcal {H}}{_Q^{\vee }}$
is isomorphic to the universal enveloping vertex algebra of C (as vertex bialgebras). The canonical derivation
![]() $\partial $
on C has L-degree zero and cohomological degree
$\partial $
on C has L-degree zero and cohomological degree
![]() $-2$
, and C is a free
$-2$
, and C is a free
![]() ${\mathbb {Q}}[\partial ]$
-module such that the space of generators
${\mathbb {Q}}[\partial ]$
-module such that the space of generators
has finite-dimensional components
![]() $W_{\mathbf {d}}$
and
$W_{\mathbf {d}}$
and
![]() $k\equiv \chi ({\mathbf {d}},{\mathbf {d}})\pmod 2$
whenever
$k\equiv \chi ({\mathbf {d}},{\mathbf {d}})\pmod 2$
whenever
![]() $W_{\mathbf {d}}^k\ne 0$
.
$W_{\mathbf {d}}^k\ne 0$
.
The coalgebra
![]() ${\mathcal {H}}{_Q^{\vee }}$
is isomorphic to the universal enveloping algebra
${\mathcal {H}}{_Q^{\vee }}$
is isomorphic to the universal enveloping algebra
![]() $U(C)$
, where we interpret C as a Lie algebra. Consequently, the refined Donaldson–Thomas invariants of Q are the characters of the components of
$U(C)$
, where we interpret C as a Lie algebra. Consequently, the refined Donaldson–Thomas invariants of Q are the characters of the components of
![]() $C/\partial C$
and are contained in
$C/\partial C$
and are contained in
![]() ${\mathbb {N}}[q^{\pm {\frac 12}}]$
; hence, we obtain a new proof of positivity of DT invariants for symmetric quivers, originally proved in [Reference Efimov14]. Note that the quotient
${\mathbb {N}}[q^{\pm {\frac 12}}]$
; hence, we obtain a new proof of positivity of DT invariants for symmetric quivers, originally proved in [Reference Efimov14]. Note that the quotient
![]() $C/\partial C$
has a canonical Lie algebra structure; see §4.2.3. The Lie algebra
$C/\partial C$
has a canonical Lie algebra structure; see §4.2.3. The Lie algebra
![]() $C/\partial C$
is different from the BPS Lie algebra introduced in [Reference Davison and Meinhardt9] (although the characters of both algebras compute DT invariants), which is a Lie subalgebra of
$C/\partial C$
is different from the BPS Lie algebra introduced in [Reference Davison and Meinhardt9] (although the characters of both algebras compute DT invariants), which is a Lie subalgebra of
![]() ${\mathcal {H}}_Q$
and has, in particular, the trivial bracket. We conjecture that our results can be generalised to CoHAs associated to (symmetric) quivers with potential.
${\mathcal {H}}_Q$
and has, in particular, the trivial bracket. We conjecture that our results can be generalised to CoHAs associated to (symmetric) quivers with potential.
Our approach also allows one to re-interpret the CoHA-modules
![]() ${\mathcal {M}}_{\mathbf {w}}$
arising from moduli spaces of stable framed representations (also known as non-commutative Hilbert schemes). In particular, we construct combinatorial spanning sets for duals of those modules; this result is a substantial generalisation (and a conceptual interpretation) of the main theorem of [Reference Dotsenko10].
${\mathcal {M}}_{\mathbf {w}}$
arising from moduli spaces of stable framed representations (also known as non-commutative Hilbert schemes). In particular, we construct combinatorial spanning sets for duals of those modules; this result is a substantial generalisation (and a conceptual interpretation) of the main theorem of [Reference Dotsenko10].
Let us mention that all vertex Lie algebras that we consider naturally lead to Lie algebras with quadratic relations. Moreover, principal free vertex algebras are modules with quadratic relations over these Lie algebras, so one may wish to study them in the context of the Koszul duality theory. This approach is taken in the paper [Reference Dotsenko, Feigin and Reineke11].
Structure of the paper
In §2, we summarise various conventions used throughout the paper. In particular, for a free abelian group L equipped with an integer-valued symmetric bilinear form, we introduce in §2.2 a special braiding for the monoidal category of L-graded vector spaces; in this way, we completely avoid any non-canonical choices of sign twists needed both to ensure super-commutativity of CoHA [Reference Kontsevich and Soibelman36, §2.6] and mutual locality of vertex operators in lattice vertex algebras [Reference Kac34, §5.4]. In §3, we recall the necessary definitions and results of the theory of cohomological Hall algebras and their modules. In §4, we recall the necessary definitions and results of the theory of vertex algebras and conformal algebras, adapted to the symmetric monoidal category of L-graded vector spaces with the braiding arising from a symmetric bilinear form. In §5, we prove the main result of this paper: a new interpretation of CoHA
![]() ${\mathcal {H}}_Q$
as the graded dual of the principal free vertex algebra
${\mathcal {H}}_Q$
as the graded dual of the principal free vertex algebra
![]() ${\mathcal {P}}_Q$
. To that end, we obtain a natural isomorphism of graded vector spaces
${\mathcal {P}}_Q$
. To that end, we obtain a natural isomorphism of graded vector spaces
![]() ${\mathcal {P}}{_Q^{\vee }}\simeq {\mathcal {H}}_Q$
(Proposition 5.3) and then show that the canonical coalgebra structure on
${\mathcal {P}}{_Q^{\vee }}\simeq {\mathcal {H}}_Q$
(Proposition 5.3) and then show that the canonical coalgebra structure on
![]() ${\mathcal {P}}_Q$
leads to the shuffle product of CoHA (Theorem 5.6). As a consequence, we show that the dual of CoHA is identified with the universal envelope of a Lie algebra with a freely acting derivation (Theorem 5.7), leading to a new proof of positivity of DT invariants (Corollary 5.10). In §6, we give two new descriptions of the dual space of the CoHA-module
${\mathcal {P}}_Q$
leads to the shuffle product of CoHA (Theorem 5.6). As a consequence, we show that the dual of CoHA is identified with the universal envelope of a Lie algebra with a freely acting derivation (Theorem 5.7), leading to a new proof of positivity of DT invariants (Corollary 5.10). In §6, we give two new descriptions of the dual space of the CoHA-module
![]() ${\mathcal {M}}_{\mathbf {w}}$
: as the kernel of the appropriate reduced coaction map (Theorem 6.3) and via an explicit combinatorial spanning set inside
${\mathcal {M}}_{\mathbf {w}}$
: as the kernel of the appropriate reduced coaction map (Theorem 6.3) and via an explicit combinatorial spanning set inside
![]() ${\mathcal {P}}_Q$
(Theorem 6.4). We also use those results to establish a surprising symmetry result for the positive and the negative halves of the coefficient Lie algebra, which may be interpreted as strong evidence for the Koszulness conjecture of [Reference Dotsenko, Feigin and Reineke11].
${\mathcal {P}}_Q$
(Theorem 6.4). We also use those results to establish a surprising symmetry result for the positive and the negative halves of the coefficient Lie algebra, which may be interpreted as strong evidence for the Koszulness conjecture of [Reference Dotsenko, Feigin and Reineke11].
2. Conventions
Unless specified otherwise, all vector spaces and (co)chain complexes in this article are defined over the ground field of rational numbers. We use cohomological degrees and view homologically graded complexes as cohomologically graded ones: for a chain complex
![]() $C_*$
, we consider the cochain complex
$C_*$
, we consider the cochain complex
![]() $C^*$
with
$C^*$
with
![]() $C^{n}=C_{-n}$
(note that
$C^{n}=C_{-n}$
(note that
![]() $C[k]^n=C^{n+k}=C_{-n-k}=C[k]_{-n}$
). Throughout the paper, L denotes a free abelian group equipped with an integer-valued symmetric bilinear form
$C[k]^n=C^{n+k}=C_{-n-k}=C[k]_{-n}$
). Throughout the paper, L denotes a free abelian group equipped with an integer-valued symmetric bilinear form
![]() $(\cdot ,\cdot )$
.
$(\cdot ,\cdot )$
.
Our work brings together two different worlds: that of cohomological Hall algebras and that of vertex operator algebras. The former operates within the derived category
![]() $D(\operatorname {\mathrm {Vect}})$
, which we identify with
$D(\operatorname {\mathrm {Vect}})$
, which we identify with
![]() $\operatorname {\mathrm {Vect}}^{\mathbb {Z}}$
; the latter uses half-integer conformal weights and thus operates within the category
$\operatorname {\mathrm {Vect}}^{\mathbb {Z}}$
; the latter uses half-integer conformal weights and thus operates within the category
![]() $\operatorname {\mathrm {Vect}}^{{\frac 12}\mathbb {Z}}$
. Both traditions are well established, so we decided to not break either of them, but rather make the necessary effort to carefully translate results from one language to another.
$\operatorname {\mathrm {Vect}}^{{\frac 12}\mathbb {Z}}$
. Both traditions are well established, so we decided to not break either of them, but rather make the necessary effort to carefully translate results from one language to another.
2.1. Borel–Moore homology
For an introduction to Borel–Moore homology, see, for example, [Reference Chriss and Ginzburg7], and for an introduction to equivariant Borel–Moore homology, see, for example, [Reference Edidin and Graham13]. Given an algebraic variety X over
![]() ${\mathbb {C}}$
, we define its Borel–Moore homology
${\mathbb {C}}$
, we define its Borel–Moore homology
![]() $H^{\mathrm {BM}}(X)$
as
$H^{\mathrm {BM}}(X)$
as
where
![]() $H^n_c(X)$
denotes the cohomology with compact support and coefficients in
$H^n_c(X)$
denotes the cohomology with compact support and coefficients in
![]() ${\mathbb {Q}}$
. If X is smooth and has dimension
${\mathbb {Q}}$
. If X is smooth and has dimension
![]() $d_X$
, then the Poincaré duality implies that
$d_X$
, then the Poincaré duality implies that
Given an algebraic group G acting on X, we define the equivariant Borel–Moore homology
![]() $H^{\mathrm {BM}}_G(X)=H^{\mathrm {BM}}([X/G])$
as
$H^{\mathrm {BM}}_G(X)=H^{\mathrm {BM}}([X/G])$
as
where
![]() $H^n_{c,G}(X)$
denotes G-equivariant cohomology with compact support and coefficients in
$H^n_{c,G}(X)$
denotes G-equivariant cohomology with compact support and coefficients in
![]() ${\mathbb {Q}}$
. If X is smooth and
${\mathbb {Q}}$
. If X is smooth and
![]() $X,G$
have dimensions
$X,G$
have dimensions
![]() $d_X,d_G$
, respectively, then
$d_X,d_G$
, respectively, then
2.2. Graded vector spaces
Let us consider the category
![]() $\operatorname {\mathrm {Vect}}^L$
of L-graded vector spaces
$\operatorname {\mathrm {Vect}}^L$
of L-graded vector spaces
![]() $V=\bigoplus _{\alpha \in L}V_\alpha $
, with morphisms of degree zero. It has a structure of a closed monoidal category with tensor products and internal
$V=\bigoplus _{\alpha \in L}V_\alpha $
, with morphisms of degree zero. It has a structure of a closed monoidal category with tensor products and internal
![]() $\operatorname {\mathrm {Hom}}$
-objects defined by
$\operatorname {\mathrm {Hom}}$
-objects defined by
We equip
![]() $\operatorname {\mathrm {Vect}}^L$
with a symmetric monoidal category structure, where the braiding morphism is defined using the symmetric bilinear form
$\operatorname {\mathrm {Vect}}^L$
with a symmetric monoidal category structure, where the braiding morphism is defined using the symmetric bilinear form
![]() $(\cdot ,\cdot )$
on L:
$(\cdot ,\cdot )$
on L:
In what follows, we shall often use
![]() ${\mathcal {C}}$
to denote
${\mathcal {C}}$
to denote
![]() $\operatorname {\mathrm {Vect}}^L$
equipped with the thus defined symmetric closed monoidal category structure.
$\operatorname {\mathrm {Vect}}^L$
equipped with the thus defined symmetric closed monoidal category structure.
We define associative algebras in
![]() ${\mathcal {C}}$
as monoid objects in this category; in particular, for each
${\mathcal {C}}$
as monoid objects in this category; in particular, for each
![]() $V\in {\mathcal {C}}$
, the object
$V\in {\mathcal {C}}$
, the object
![]() $\underline {\textrm {End}}(V)={\underline {\textrm {Hom}}}(V,V)\in {\mathcal {C}}$
is an associative algebra. Using the braiding
$\underline {\textrm {End}}(V)={\underline {\textrm {Hom}}}(V,V)\in {\mathcal {C}}$
is an associative algebra. Using the braiding
![]() $\sigma $
, one may also define commutative algebras and Lie algebras, and their modules. (Alternatively, one may note that the category
$\sigma $
, one may also define commutative algebras and Lie algebras, and their modules. (Alternatively, one may note that the category
![]() ${\mathcal {C}}$
contains the category
${\mathcal {C}}$
contains the category
![]() $\operatorname {\mathrm {Vect}}$
as a full symmetric monoidal subcategory of objects of degree zero, and so one may consider objects in
$\operatorname {\mathrm {Vect}}$
as a full symmetric monoidal subcategory of objects of degree zero, and so one may consider objects in
![]() ${\mathcal {C}}$
, which are algebras over the classical operads
${\mathcal {C}}$
, which are algebras over the classical operads
![]() $\mathsf {Ass}$
,
$\mathsf {Ass}$
,
![]() $\mathsf {Com}$
and
$\mathsf {Com}$
and
![]() $\mathsf {Lie}$
in
$\mathsf {Lie}$
in
![]() $\operatorname {\mathrm {Vect}}$
.) In particular, as in the case of
$\operatorname {\mathrm {Vect}}$
.) In particular, as in the case of
![]() $\operatorname {\mathrm {Vect}}$
, the free associative algebra generated by an object X of
$\operatorname {\mathrm {Vect}}$
, the free associative algebra generated by an object X of
![]() ${\mathcal {C}}$
is the tensor algebra
${\mathcal {C}}$
is the tensor algebra
![]() $\mathsf {T}(X)=\coprod _{n\ge 0} X^{\otimes n}$
, and the free commutative algebra generated by an object X of
$\mathsf {T}(X)=\coprod _{n\ge 0} X^{\otimes n}$
, and the free commutative algebra generated by an object X of
![]() ${\mathcal {C}}$
is the symmetric algebra
${\mathcal {C}}$
is the symmetric algebra
![]() $S(X)=\coprod _{n\ge 0} (X^{\otimes n})_{\Sigma _n}$
.
$S(X)=\coprod _{n\ge 0} (X^{\otimes n})_{\Sigma _n}$
.
Given an associative algebra
![]() $A\in {\mathcal {C}}$
, we may equip it with the bracket
$A\in {\mathcal {C}}$
, we may equip it with the bracket
this defines a functor from the category of associative algebras in
![]() ${\mathcal {C}}$
to the category of Lie algebras in
${\mathcal {C}}$
to the category of Lie algebras in
![]() ${\mathcal {C}}$
. This functor has a left adjoint functor, the functor of the universal enveloping algebra
${\mathcal {C}}$
. This functor has a left adjoint functor, the functor of the universal enveloping algebra
![]() $U({\mathfrak {g}})$
of a Lie algebra
$U({\mathfrak {g}})$
of a Lie algebra
![]() ${\mathfrak {g}}$
. We shall use two different versions of the Poincaré–Birkhoff–Witt theorem for universal enveloping algebras. The first of them asserts that if
${\mathfrak {g}}$
. We shall use two different versions of the Poincaré–Birkhoff–Witt theorem for universal enveloping algebras. The first of them asserts that if
![]() ${\mathfrak {g}}$
is a Lie algebra and
${\mathfrak {g}}$
is a Lie algebra and
![]() ${\mathfrak {h}}\subset {\mathfrak {g}}$
is a Lie subalgebra, the universal enveloping algebra
${\mathfrak {h}}\subset {\mathfrak {g}}$
is a Lie subalgebra, the universal enveloping algebra
![]() $U({\mathfrak {g}})$
is a free
$U({\mathfrak {g}})$
is a free
![]() $U({\mathfrak {h}})$
-module, and the vector space of generators of this module is isomorphic to
$U({\mathfrak {h}})$
-module, and the vector space of generators of this module is isomorphic to
![]() $S({\mathfrak {g}}/{\mathfrak {h}})$
; moreover, if there exists a Lie subalgebra
$S({\mathfrak {g}}/{\mathfrak {h}})$
; moreover, if there exists a Lie subalgebra
![]() ${\mathfrak {h}}'$
such that
${\mathfrak {h}}'$
such that
![]() ${\mathfrak {g}}={\mathfrak {h}}\oplus {\mathfrak {h}}'$
, we may take
${\mathfrak {g}}={\mathfrak {h}}\oplus {\mathfrak {h}}'$
, we may take
![]() $U({\mathfrak {h}}')\subset U({\mathfrak {g}})$
as the space of generators. The second version uses the fact that
$U({\mathfrak {h}}')\subset U({\mathfrak {g}})$
as the space of generators. The second version uses the fact that
![]() $U({\mathfrak {g}})$
has a canonical coproduct
$U({\mathfrak {g}})$
has a canonical coproduct
![]() $\Delta $
for which elements of
$\Delta $
for which elements of
![]() ${\mathfrak {g}}$
are primitive, and this coproduct makes
${\mathfrak {g}}$
are primitive, and this coproduct makes
![]() $U({\mathfrak {g}})$
a cocommutative coassociative coalgebra. The theorem asserts that as a coalgebra,
$U({\mathfrak {g}})$
a cocommutative coassociative coalgebra. The theorem asserts that as a coalgebra,
![]() $U({\mathfrak {g}})$
is isomorphic to
$U({\mathfrak {g}})$
is isomorphic to
![]() $S^c({\mathfrak {g}})$
, the cofree cocommutative coassociative conilpotent coalgebra generated by
$S^c({\mathfrak {g}})$
, the cofree cocommutative coassociative conilpotent coalgebra generated by
![]() ${\mathfrak {g}}$
(note that since we work over
${\mathfrak {g}}$
(note that since we work over
![]() ${\mathbb {Q}}$
, the underlying object of
${\mathbb {Q}}$
, the underlying object of
![]() $S^c(X)$
is the same as that of
$S^c(X)$
is the same as that of
![]() $S(X)$
for all X in
$S(X)$
for all X in
![]() ${\mathcal {C}}$
). To prove the Poincaré–Birkhoff–Witt theorem in
${\mathcal {C}}$
). To prove the Poincaré–Birkhoff–Witt theorem in
![]() ${\mathcal {C}}$
, one may use the methods of [Reference Bergman2] or [Reference Dotsenko and Tamaroff12] for the first version and the methods of [Reference Quillen52, Appendix B] or [Reference Loday44] for the second version.
${\mathcal {C}}$
, one may use the methods of [Reference Bergman2] or [Reference Dotsenko and Tamaroff12] for the first version and the methods of [Reference Quillen52, Appendix B] or [Reference Loday44] for the second version.
We note that for an abelian group L equipped with a homomorphism
![]() $p\colon L\to \mathbb {Z}_2$
(for example, the parity
$p\colon L\to \mathbb {Z}_2$
(for example, the parity
![]() $\mathbb {Z}\to \mathbb {Z}_2$
), one normally thinks of the category of L-graded vector spaces with the braiding morphism (the Koszul sign rule)
$\mathbb {Z}\to \mathbb {Z}_2$
), one normally thinks of the category of L-graded vector spaces with the braiding morphism (the Koszul sign rule)
and refers to the corresponding commutative (or Lie) algebras as super-commutative algebras (or Lie superalgebras). In this paper, we mostly encounter the more general setting discussed above and suppress the qualifier ‘super’.
2.3. Laurent series
Let V be a vector space. Let
![]() $V{[\![{z^{\pm 1}}]\!]}$
be the vector space of doubly infinite Laurent series with coefficients in V and
$V{[\![{z^{\pm 1}}]\!]}$
be the vector space of doubly infinite Laurent series with coefficients in V and
![]() $V{(\;\!\!\!({z})\!\!\!\;)}\subset V{[\![{z^{\pm 1}}]\!]}$
be the subspace of formal Laurent series (that is, series for which only finitely many negative components are non-zero). For a series
$V{(\;\!\!\!({z})\!\!\!\;)}\subset V{[\![{z^{\pm 1}}]\!]}$
be the subspace of formal Laurent series (that is, series for which only finitely many negative components are non-zero). For a series
![]() $v=\sum _{n\in \mathbb {Z}} v_nz^n \in V{[\![{z^{\pm 1}}]\!]}$
, we denote the coefficient
$v=\sum _{n\in \mathbb {Z}} v_nz^n \in V{[\![{z^{\pm 1}}]\!]}$
, we denote the coefficient
![]() $v_{-1}$
by
$v_{-1}$
by
![]() $\operatorname {\mathrm {Res}}_z v$
.
$\operatorname {\mathrm {Res}}_z v$
.
Formal Laurent series with coefficients in an algebra do themselves form an algebra. It is important to note that doubly infinite Laurent series in several variables contain several different subspaces of formal Laurent series in those variables: for instance, the subspaces
![]() ${\mathbb {Q}}{(\;\!\!\!({z})\!\!\!\;)}{(\;\!\!\!({w})\!\!\!\;)}$
and
${\mathbb {Q}}{(\;\!\!\!({z})\!\!\!\;)}{(\;\!\!\!({w})\!\!\!\;)}$
and
![]() $\mathbb {Q}{(\;\!\!\!({w})\!\!\!\;)}{(\;\!\!\!({z})\!\!\!\;)}$
of
$\mathbb {Q}{(\;\!\!\!({w})\!\!\!\;)}{(\;\!\!\!({z})\!\!\!\;)}$
of
![]() ${\mathbb {Q}}{[\![{z^{\pm 1},w^{\pm 1}}]\!]}$
are different. A lot of formulas in the theory of vertex algebras use the fact that rational functions like
${\mathbb {Q}}{[\![{z^{\pm 1},w^{\pm 1}}]\!]}$
are different. A lot of formulas in the theory of vertex algebras use the fact that rational functions like
![]() $\frac 1{z-w}$
can be expanded as elements of both of these rings. To avoid unnecessarily heavy formulas, we shall frequently use the binomial expansion convention for such expansion; see for example, [Reference Lepowsky and Li40, §2.2]: for
$\frac 1{z-w}$
can be expanded as elements of both of these rings. To avoid unnecessarily heavy formulas, we shall frequently use the binomial expansion convention for such expansion; see for example, [Reference Lepowsky and Li40, §2.2]: for
![]() $n\in \mathbb {Z}$
, we define the formal Laurent series
$n\in \mathbb {Z}$
, we define the formal Laurent series
![]() $(z+w)^n$
by the formula
$(z+w)^n$
by the formula
 $$ \begin{align*}(z+w)^n =\sum_{k\ge 0}\binom{n}{k}z^{n-k}w^k.\end{align*} $$
$$ \begin{align*}(z+w)^n =\sum_{k\ge 0}\binom{n}{k}z^{n-k}w^k.\end{align*} $$
In plain words, we expand powers of binomials as power series in the second summand. Thus, for example,
![]() $(z-w)^n=(-1)^n(-z+w)^n$
for all
$(z-w)^n=(-1)^n(-z+w)^n$
for all
![]() $n\in \mathbb {Z}$
, but it is equal to
$n\in \mathbb {Z}$
, but it is equal to
![]() $(-1)^n(w-z)^n$
only for
$(-1)^n(w-z)^n$
only for
![]() $n\ge 0$
. An important doubly infinite Laurent series in
$n\ge 0$
. An important doubly infinite Laurent series in
![]() ${\mathbb {Q}}{[\![{z^{\pm 1}}]\!]}$
is the ‘delta function’
${\mathbb {Q}}{[\![{z^{\pm 1}}]\!]}$
is the ‘delta function’
Doubly infinite Laurent series cannot be multiplied, but in the instances where we use the above series, we shall use the following version, which can be multiplied by any formal Laurent series in w:
 $$ \begin{align*}\delta{\left({\frac{z-w}u}\right)}=\sum_{n\in\mathbb{Z}}\sum_{k\ge0}(-1)^k\binom nk u^{-n}z^{n-k}w^k.\end{align*} $$
$$ \begin{align*}\delta{\left({\frac{z-w}u}\right)}=\sum_{n\in\mathbb{Z}}\sum_{k\ge0}(-1)^k\binom nk u^{-n}z^{n-k}w^k.\end{align*} $$
A useful formula involving this expression is
![]() $\operatorname {\mathrm {Res}}_z \delta {\left ({\frac {z-w}u}\right )}=u$
.
$\operatorname {\mathrm {Res}}_z \delta {\left ({\frac {z-w}u}\right )}=u$
.
2.4. Characters and Poincaré series
Given an object
![]() $M\in \operatorname {\mathrm {Vect}}^{\mathbb {Z}}$
with finite-dimensional components, we define its character
$M\in \operatorname {\mathrm {Vect}}^{\mathbb {Z}}$
with finite-dimensional components, we define its character
![]() $\operatorname {\mathrm {ch}}(M)$
by the formula
$\operatorname {\mathrm {ch}}(M)$
by the formula
The number
![]() $-{\frac 12} k$
will be called the weight of the component
$-{\frac 12} k$
will be called the weight of the component
![]() $M^k$
(it may be convenient to view
$M^k$
(it may be convenient to view
![]() $-k$
as a homological degree). Note that
$-k$
as a homological degree). Note that
In particular, for an algebraic variety X, we have
the Poincaré polynomial (with compact support) of X.
More generally, given an object
![]() $M\in (\operatorname {\mathrm {Vect}}^{L})^{\mathbb {Z}}\simeq \operatorname {\mathrm {Vect}}^{L\times \mathbb {Z}}$
with finite-dimensional components
$M\in (\operatorname {\mathrm {Vect}}^{L})^{\mathbb {Z}}\simeq \operatorname {\mathrm {Vect}}^{L\times \mathbb {Z}}$
with finite-dimensional components
![]() $M_{\mathbf {d}}^k$
, for
$M_{\mathbf {d}}^k$
, for
![]() ${\mathbf {d}}\in L$
and
${\mathbf {d}}\in L$
and
![]() $k\in \mathbb {Z}$
, we define its Poincaré series
$k\in \mathbb {Z}$
, we define its Poincaré series
![]() $Z(M,x,q)$
by the formula
$Z(M,x,q)$
by the formula
2.5. Plethystic exponential
For more information on
![]() $\lambda $
-rings and plethystic exponentials, see, for example, [Reference Getzler24, Reference Mozgovoy48]. Consider the ring
$\lambda $
-rings and plethystic exponentials, see, for example, [Reference Getzler24, Reference Mozgovoy48]. Consider the ring
and its unique maximal ideal
![]() ${\mathfrak {m}}$
. We equip R with the
${\mathfrak {m}}$
. We equip R with the
![]() ${\mathfrak {m}}$
-adic topology. We define plethystic exponential to be the continuous group isomorphism
${\mathfrak {m}}$
-adic topology. We define plethystic exponential to be the continuous group isomorphism
defined on monomials by
Let us assume now that
![]() $L=\mathbb {Z}^I$
is equipped with a symmetric bilinear form
$L=\mathbb {Z}^I$
is equipped with a symmetric bilinear form
![]() $(\cdot ,\cdot )$
and let
$(\cdot ,\cdot )$
and let
![]() $\operatorname {\mathrm {Vect}}^{L\times \mathbb {Z}}$
be the corresponding symmetric monoidal category (with the signs in the braiding depending just on L-degrees). We consider a subcategory
$\operatorname {\mathrm {Vect}}^{L\times \mathbb {Z}}$
be the corresponding symmetric monoidal category (with the signs in the braiding depending just on L-degrees). We consider a subcategory
![]() ${\mathcal {A}}\subset \operatorname {\mathrm {Vect}}^{L\times \mathbb {Z}}$
consisting of objects
${\mathcal {A}}\subset \operatorname {\mathrm {Vect}}^{L\times \mathbb {Z}}$
consisting of objects
such that
![]() $M_{\mathbf {d}}^k$
are finite-dimensional and
$M_{\mathbf {d}}^k$
are finite-dimensional and
![]() $M_{\mathbf {d}}^k=0$
for
$M_{\mathbf {d}}^k=0$
for
![]() $k\gg 0$
. Then the Poincaré series (4) induces a ring homomorphism
$k\gg 0$
. Then the Poincaré series (4) induces a ring homomorphism
This homomorphism is actually a
![]() $\lambda $
-ring homomorphism (with the
$\lambda $
-ring homomorphism (with the
![]() $\lambda $
-ring structure on
$\lambda $
-ring structure on
![]() $K_0({\mathcal {A}})$
induced by the symmetric monoidal category structure on
$K_0({\mathcal {A}})$
induced by the symmetric monoidal category structure on
![]() ${\mathcal {A}}$
that we defined earlier see, for example, [Reference Getzler24, Reference Heinloth31]). We will formulate this fact in the following way.
${\mathcal {A}}$
that we defined earlier see, for example, [Reference Getzler24, Reference Heinloth31]). We will formulate this fact in the following way.
Theorem 2.1. For any graded space
![]() $M\in {\mathcal {A}}$
with
$M\in {\mathcal {A}}$
with
![]() $M_0=0$
, we have
$M_0=0$
, we have
Proof. It is enough to prove the statement for a one-dimensional space
![]() $M=M_{\mathbf {d}}^k$
. If
$M=M_{\mathbf {d}}^k$
. If
![]() $({\mathbf {d}},{\mathbf {d}})$
is odd, then
$({\mathbf {d}},{\mathbf {d}})$
is odd, then
![]() $Z(M)=-q^{-{\frac 12} k}x^{\mathbf {d}}$
. However,
$Z(M)=-q^{-{\frac 12} k}x^{\mathbf {d}}$
. However,
![]() $S(M)={\mathbb {Q}}\oplus M$
; hence,
$S(M)={\mathbb {Q}}\oplus M$
; hence,
If
![]() $({\mathbf {d}},{\mathbf {d}})$
is even, then
$({\mathbf {d}},{\mathbf {d}})$
is even, then
![]() $Z(M)=q^{-{\frac 12} k}x^{\mathbf {d}}$
. On the other hand,
$Z(M)=q^{-{\frac 12} k}x^{\mathbf {d}}$
. On the other hand,
![]() $S(M) =\coprod _{n\ge 0}(M^{\otimes n})_{\Sigma _n} =\coprod _{n\ge 0}M^{\otimes n}$
, hence
$S(M) =\coprod _{n\ge 0}(M^{\otimes n})_{\Sigma _n} =\coprod _{n\ge 0}M^{\otimes n}$
, hence
 $$ \begin{align*}Z(S(M))=\sum_{n\ge0}q^{-n{\frac12} k}x^{n{\mathbf{d}}} =\operatorname{\mathrm{Exp}}{\left({q^{-{\frac12} k}x^{\mathbf{d}}}\right)} =\operatorname{\mathrm{Exp}}(Z(M)).\\[-37pt] \end{align*} $$
$$ \begin{align*}Z(S(M))=\sum_{n\ge0}q^{-n{\frac12} k}x^{n{\mathbf{d}}} =\operatorname{\mathrm{Exp}}{\left({q^{-{\frac12} k}x^{\mathbf{d}}}\right)} =\operatorname{\mathrm{Exp}}(Z(M)).\\[-37pt] \end{align*} $$
3. CoHA and CoHA-modules
Let Q be a symmetric quiver with the set of vertices I. In this section, we consider the abelian group
![]() $L=\mathbb {Z}^{I}$
equipped with the Euler form
$L=\mathbb {Z}^{I}$
equipped with the Euler form
 $$\begin{align*}\chi({\mathbf{d}},{\mathbf{e}}) =\sum_{i\in Q_0}{\mathbf{d}}_i{\mathbf{e}}_i-\sum_{(a:i\to j)\in Q_1} {\mathbf{d}}_i{\mathbf{e}}_j, \end{align*}$$
$$\begin{align*}\chi({\mathbf{d}},{\mathbf{e}}) =\sum_{i\in Q_0}{\mathbf{d}}_i{\mathbf{e}}_i-\sum_{(a:i\to j)\in Q_1} {\mathbf{d}}_i{\mathbf{e}}_j, \end{align*}$$
which is a symmetric bilinear form.
3.1. Definition of CoHA
For more details on the results of this section, see [Reference Kontsevich and Soibelman36]. For any
![]() ${\mathbf {d}}\in {\mathbb {N}}^{I}$
, we define the space of representations
${\mathbf {d}}\in {\mathbb {N}}^{I}$
, we define the space of representations
which has the standard action of
![]() $G_{\mathbf {d}}=\prod _{i\in I}\operatorname {\mathrm {GL}}_{{\mathbf {d}}_i}({\mathbb {C}})$
. We define the cohomological Hall algebra (CoHA) with the underlying L-graded object in
$G_{\mathbf {d}}=\prod _{i\in I}\operatorname {\mathrm {GL}}_{{\mathbf {d}}_i}({\mathbb {C}})$
. We define the cohomological Hall algebra (CoHA) with the underlying L-graded object in
![]() $D(\operatorname {\mathrm {Vect}})\simeq \operatorname {\mathrm {Vect}}^{\mathbb {Z}}$
equal
$D(\operatorname {\mathrm {Vect}})\simeq \operatorname {\mathrm {Vect}}^{\mathbb {Z}}$
equal
where
is considered as an object of
![]() $D(\operatorname {\mathrm {Vect}})$
(note that the stack
$D(\operatorname {\mathrm {Vect}})$
(note that the stack
![]() $[R_{\mathbf {d}}/G_{\mathbf {d}}]$
has dimension
$[R_{\mathbf {d}}/G_{\mathbf {d}}]$
has dimension
![]() $-\chi ({\mathbf {d}},{\mathbf {d}})$
). Multiplication in this algebra is constructed as follows. Given
$-\chi ({\mathbf {d}},{\mathbf {d}})$
). Multiplication in this algebra is constructed as follows. Given
![]() ${\mathbf {d}},{\mathbf {e}}\in {\mathbb {N}}^I$
, consider
${\mathbf {d}},{\mathbf {e}}\in {\mathbb {N}}^I$
, consider
and let
![]() $R_{{\mathbf {d}},{\mathbf {e}}}\subset R_{{\mathbf {d}}+{\mathbf {e}}}$
be the subspace of representations that preserve
$R_{{\mathbf {d}},{\mathbf {e}}}\subset R_{{\mathbf {d}}+{\mathbf {e}}}$
be the subspace of representations that preserve
![]() $V_{\mathbf {d}}$
. It is equipped with an action of the parabolic subgroup
$V_{\mathbf {d}}$
. It is equipped with an action of the parabolic subgroup
![]() $G_{{\mathbf {d}},{\mathbf {e}}}\subset G_{{\mathbf {d}}+{\mathbf {e}}}$
consisting of maps that preserve
$G_{{\mathbf {d}},{\mathbf {e}}}\subset G_{{\mathbf {d}}+{\mathbf {e}}}$
consisting of maps that preserve
![]() $V_{\mathbf {d}}$
. We have morphisms of stacks
$V_{\mathbf {d}}$
. We have morphisms of stacks
where q has dimension
![]() $-\chi ({\mathbf {e}},{\mathbf {d}})$
. These maps induce morphisms in
$-\chi ({\mathbf {e}},{\mathbf {d}})$
. These maps induce morphisms in
![]() $D(\operatorname {\mathrm {Vect}})$
$D(\operatorname {\mathrm {Vect}})$
Taking the composition, we obtain the multiplication map
in
![]() $D(\operatorname {\mathrm {Vect}})$
. It was proved in [Reference Kontsevich and Soibelman36] that this multiplication is associative.
$D(\operatorname {\mathrm {Vect}})$
. It was proved in [Reference Kontsevich and Soibelman36] that this multiplication is associative.
3.2. Shuffle algebra description
For any
![]() $n\ge 0$
, define the graded algebra
$n\ge 0$
, define the graded algebra
where
![]() $x_i$
has degree
$x_i$
has degree
![]() $2$
and
$2$
and
![]() $\Sigma _n$
is the symmetric group on n elements. Similarly, for any
$\Sigma _n$
is the symmetric group on n elements. Similarly, for any
![]() ${\mathbf {d}}\in {\mathbb {N}}^{I}$
, define
${\mathbf {d}}\in {\mathbb {N}}^{I}$
, define
Then
This implies that
It was proved in [Reference Kontsevich and Soibelman36] that the product
![]() ${\mathcal {H}}_{Q,{\mathbf {d}}}\otimes {\mathcal {H}}_{Q,{\mathbf {e}}}\to {\mathcal {H}}_{Q,{\mathbf {d}}+{\mathbf {e}}}$
is given by the shuffle product
${\mathcal {H}}_{Q,{\mathbf {d}}}\otimes {\mathcal {H}}_{Q,{\mathbf {e}}}\to {\mathcal {H}}_{Q,{\mathbf {d}}+{\mathbf {e}}}$
is given by the shuffle product
 $$ \begin{align} f*g=\sum_{\sigma\in\operatorname{\mathrm{Sh}}({\mathbf{d}},{\mathbf{e}})}\sigma(fgK), \end{align} $$
$$ \begin{align} f*g=\sum_{\sigma\in\operatorname{\mathrm{Sh}}({\mathbf{d}},{\mathbf{e}})}\sigma(fgK), \end{align} $$
where the sum runs over all
![]() $({\mathbf {d}},{\mathbf {e}})$
-shuffles, meaning
$({\mathbf {d}},{\mathbf {e}})$
-shuffles, meaning
![]() $\sigma \in \Sigma _{{\mathbf {d}}+{\mathbf {e}}}$
satisfying
$\sigma \in \Sigma _{{\mathbf {d}}+{\mathbf {e}}}$
satisfying
and the kernel K is a function in the localisation of
![]() $\Lambda _{\mathbf {d}}\otimes \Lambda _{\mathbf {e}}$
defined by
$\Lambda _{\mathbf {d}}\otimes \Lambda _{\mathbf {e}}$
defined by
 $$ \begin{align} K(x,y) =\frac {\prod_{a:i\to j}\prod_{k=1}^{{\mathbf{d}}_i}\prod_{\ell=1}^{{\mathbf{e}}_j} (y_{j,\ell}-x_{i,k})} {\prod_{i\in I}\prod_{k=1}^{{\mathbf{d}}_i}\prod_{\ell=1}^{{\mathbf{e}}_i} (y_{i,\ell}-x_{i,k})} =\prod_{i,j\in I} \prod_{k=1}^{{\mathbf{d}}_i}\prod_{\ell=1}^{{\mathbf{e}}_j} (y_{j,\ell}-x_{i,k})^{-\chi(i,j)}. \end{align} $$
$$ \begin{align} K(x,y) =\frac {\prod_{a:i\to j}\prod_{k=1}^{{\mathbf{d}}_i}\prod_{\ell=1}^{{\mathbf{e}}_j} (y_{j,\ell}-x_{i,k})} {\prod_{i\in I}\prod_{k=1}^{{\mathbf{d}}_i}\prod_{\ell=1}^{{\mathbf{e}}_i} (y_{i,\ell}-x_{i,k})} =\prod_{i,j\in I} \prod_{k=1}^{{\mathbf{d}}_i}\prod_{\ell=1}^{{\mathbf{e}}_j} (y_{j,\ell}-x_{i,k})^{-\chi(i,j)}. \end{align} $$
The above formula for the shuffle product implies that
This formula implies that
![]() ${\mathcal {H}}_Q$
is a commutative algebra in the symmetric monoidal category
${\mathcal {H}}_Q$
is a commutative algebra in the symmetric monoidal category
![]() $\operatorname {\mathrm {Vect}}^{L\times \mathbb {Z}}\simeq (\operatorname {\mathrm {Vect}}^{\mathbb {Z}})^L$
with the braiding arising from the Euler form
$\operatorname {\mathrm {Vect}}^{L\times \mathbb {Z}}\simeq (\operatorname {\mathrm {Vect}}^{\mathbb {Z}})^L$
with the braiding arising from the Euler form
![]() $\chi $
.
$\chi $
.
Remark 3.1. It was observed in [Reference Kontsevich and Soibelman36, §2.6] that it is possible to modify multiplication in
![]() ${\mathcal {H}}_Q$
(non-canonically) to make it super-commutative. For that, one defines the parity map
${\mathcal {H}}_Q$
(non-canonically) to make it super-commutative. For that, one defines the parity map
![]() $p\colon L\to \mathbb {Z}_2$
,
$p\colon L\to \mathbb {Z}_2$
,
![]() ${\mathbf {d}}\mapsto \chi ({\mathbf {d}},{\mathbf {d}})\pmod 2$
and chooses a group homomorphism
${\mathbf {d}}\mapsto \chi ({\mathbf {d}},{\mathbf {d}})\pmod 2$
and chooses a group homomorphism
![]() $\varepsilon \colon L\times L\to \mu _2={{\left \{{\pm 1}\right \}}}$
such that
$\varepsilon \colon L\times L\to \mu _2={{\left \{{\pm 1}\right \}}}$
such that
Then the product on
![]() ${\mathcal {H}}_Q$
defined by
${\mathcal {H}}_Q$
defined by
is super-commutative:
![]() $f\star g=(-1)^{p({\mathbf {d}})p({\mathbf {e}})}g\star f$
for all
$f\star g=(-1)^{p({\mathbf {d}})p({\mathbf {e}})}g\star f$
for all
![]() $f\in {\mathcal {H}}_{Q,{\mathbf {d}}}$
,
$f\in {\mathcal {H}}_{Q,{\mathbf {d}}}$
,
![]() $g\in {\mathcal {H}}_{Q,{\mathbf {e}}}$
. We shall avoid non-canonical choices and not use this sign twist. Instead, we shall interpret
$g\in {\mathcal {H}}_{Q,{\mathbf {e}}}$
. We shall avoid non-canonical choices and not use this sign twist. Instead, we shall interpret
![]() ${\mathcal {H}}_Q$
as a commutative algebra in
${\mathcal {H}}_Q$
as a commutative algebra in
![]() $\operatorname {\mathrm {Vect}}^{L\times \mathbb {Z}}$
or
$\operatorname {\mathrm {Vect}}^{L\times \mathbb {Z}}$
or
![]() $\operatorname {\mathrm {Vect}}^L$
with the symmetric monoidal category structure arising from
$\operatorname {\mathrm {Vect}}^L$
with the symmetric monoidal category structure arising from
![]() $\chi $
.
$\chi $
.
3.3. Modules over CoHA
For more details about modules over CoHAs, see for example, [Reference Franzen18, Reference Soibelman62]. Let
![]() ${\mathbf {w}}\in {\mathbb {N}}^{I}$
be a vector, called a framing vector. We may consider a new (framed) quiver
${\mathbf {w}}\in {\mathbb {N}}^{I}$
be a vector, called a framing vector. We may consider a new (framed) quiver
![]() $Q^{{\mathbf {w}}}$
by adding a new vertex
$Q^{{\mathbf {w}}}$
by adding a new vertex
![]() $\infty $
and
$\infty $
and
![]() ${\mathbf {w}}_i$
arrows
${\mathbf {w}}_i$
arrows
![]() $\infty \to i$
for all
$\infty \to i$
for all
![]() $i\in I$
. For any
$i\in I$
. For any
![]() ${\mathbf {d}}\in {\mathbb {N}}^{I}$
, let
${\mathbf {d}}\in {\mathbb {N}}^{I}$
, let
![]() $\bar {\mathbf {d}}=({\mathbf {d}},1)\in {\mathbb {N}}^{Q_0^{\mathbf {w}}}$
and
$\bar {\mathbf {d}}=({\mathbf {d}},1)\in {\mathbb {N}}^{Q_0^{\mathbf {w}}}$
and
Let
![]() $R^{{\mathsf {f}},\mathrm {st}}_{{\mathbf {d}},{\mathbf {w}}}\subset R^{\mathsf {f}}_{{\mathbf {d}},{\mathbf {w}}}$
be the open subset of stable representations, consisting of representations M generated by
$R^{{\mathsf {f}},\mathrm {st}}_{{\mathbf {d}},{\mathbf {w}}}\subset R^{\mathsf {f}}_{{\mathbf {d}},{\mathbf {w}}}$
be the open subset of stable representations, consisting of representations M generated by
![]() $M_\infty $
. Then
$M_\infty $
. Then
![]() $G_{\mathbf {d}}$
acts freely on
$G_{\mathbf {d}}$
acts freely on
![]() $R^{{\mathsf {f}},\mathrm {st}}_{{\mathbf {d}},{\mathbf {w}}}$
, and we consider the moduli space
$R^{{\mathsf {f}},\mathrm {st}}_{{\mathbf {d}},{\mathbf {w}}}$
, and we consider the moduli space
called the non-commutative Hilbert scheme. Using this moduli space, one can define a module over CoHA, denoted by
![]() ${\mathcal {M}}_{\mathbf {w}}$
. Its underlying L-graded object in
${\mathcal {M}}_{\mathbf {w}}$
. Its underlying L-graded object in
![]() $D(\operatorname {\mathrm {Vect}})\simeq \operatorname {\mathrm {Vect}}^{\mathbb {Z}}$
is
$D(\operatorname {\mathrm {Vect}})\simeq \operatorname {\mathrm {Vect}}^{\mathbb {Z}}$
is
The CoHA-action is defined as follows. Let
![]() $R^{\mathsf {f}}_{{\mathbf {d}},{\mathbf {e}},{\mathbf {w}}}\subset R^{\mathsf {f}}_{{\mathbf {d}}+{\mathbf {e}},{\mathbf {w}}}$
be the subspace of framed representations that preserve
$R^{\mathsf {f}}_{{\mathbf {d}},{\mathbf {e}},{\mathbf {w}}}\subset R^{\mathsf {f}}_{{\mathbf {d}}+{\mathbf {e}},{\mathbf {w}}}$
be the subspace of framed representations that preserve
![]() $V_{\mathbf {d}}=\bigoplus _{i\in I}{\mathbb {C}}^{{\mathbf {d}}_i}$
, and let
$V_{\mathbf {d}}=\bigoplus _{i\in I}{\mathbb {C}}^{{\mathbf {d}}_i}$
, and let
![]() $R^{{\mathsf {f}},\mathrm {st}}_{{\mathbf {d}},{\mathbf {e}},{\mathbf {w}}}\subset R^{\mathsf {f}}_{{\mathbf {d}},{\mathbf {e}},{\mathbf {w}}}$
be the open subset of stable representations. It is equipped with a free action of the group
$R^{{\mathsf {f}},\mathrm {st}}_{{\mathbf {d}},{\mathbf {e}},{\mathbf {w}}}\subset R^{\mathsf {f}}_{{\mathbf {d}},{\mathbf {e}},{\mathbf {w}}}$
be the open subset of stable representations. It is equipped with a free action of the group
![]() $G_{{\mathbf {d}},{\mathbf {e}}}$
, and we define
$G_{{\mathbf {d}},{\mathbf {e}}}$
, and we define
![]() $\operatorname {\mathrm {Hilb}}_{{\mathbf {d}},{\mathbf {e}},{\mathbf {w}}}=R^{{\mathsf {f}},\mathrm {st}}_{{\mathbf {d}},{\mathbf {e}},{\mathbf {w}}}/G_{{\mathbf {d}},{\mathbf {e}}}$
. We have morphisms of stacks and algebraic varieties
$\operatorname {\mathrm {Hilb}}_{{\mathbf {d}},{\mathbf {e}},{\mathbf {w}}}=R^{{\mathsf {f}},\mathrm {st}}_{{\mathbf {d}},{\mathbf {e}},{\mathbf {w}}}/G_{{\mathbf {d}},{\mathbf {e}}}$
. We have morphisms of stacks and algebraic varieties
where q has dimension
![]() $n=-\chi ({\mathbf {e}},{\mathbf {d}})+{\mathbf {w}}\cdot {\mathbf {d}}$
. These maps induce morphisms in
$n=-\chi ({\mathbf {e}},{\mathbf {d}})+{\mathbf {w}}\cdot {\mathbf {d}}$
. These maps induce morphisms in
![]() $D(\operatorname {\mathrm {Vect}})$
$D(\operatorname {\mathrm {Vect}})$
Taking the composition, we obtain the action map
in
![]() $D(\operatorname {\mathrm {Vect}}).$
The compatibility with the product of CoHA is proved in the same way as the associativity of that product.
$D(\operatorname {\mathrm {Vect}}).$
The compatibility with the product of CoHA is proved in the same way as the associativity of that product.
The module
![]() ${\mathcal {M}}_{\mathbf {w}}$
can be also described using shuffle algebras [Reference Franzen17, Reference Franzen18]. Consider the forgetful map
${\mathcal {M}}_{\mathbf {w}}$
can be also described using shuffle algebras [Reference Franzen17, Reference Franzen18]. Consider the forgetful map
![]() $j\colon R^{{\mathsf {f}},\mathrm {st}}_{{\mathbf {d}},{\mathbf {w}}}\to R_{\mathbf {d}}$
and the corresponding map of stacks
$j\colon R^{{\mathsf {f}},\mathrm {st}}_{{\mathbf {d}},{\mathbf {w}}}\to R_{\mathbf {d}}$
and the corresponding map of stacks
having dimension
![]() ${\mathbf {w}}\cdot {\mathbf {d}}$
. It induces a map
${\mathbf {w}}\cdot {\mathbf {d}}$
. It induces a map
which induces a map of L-graded objects in
![]() $D(\operatorname {\mathrm {Vect}})$
$D(\operatorname {\mathrm {Vect}})$
It was proved in [Reference Franzen17, Theorem 5.2.1] that this map is an epimorphism of
![]() ${\mathcal {H}}_Q$
-modules and that its kernel is equal to
${\mathcal {H}}_Q$
-modules and that its kernel is equal to
where the last expression means the ideal with respect to the product in
![]() ${\mathcal {H}}_Q$
${\mathcal {H}}_Q$
 $$ \begin{align*}e_{{\mathbf{d}}}^{{\mathbf{w}}}=\prod_{i\in I}\prod_{k=1}^{{\mathbf{d}}_i}x_{i,k}^{{\mathbf{w}}_i}\in\Lambda_{\mathbf{d}}\end{align*} $$
$$ \begin{align*}e_{{\mathbf{d}}}^{{\mathbf{w}}}=\prod_{i\in I}\prod_{k=1}^{{\mathbf{d}}_i}x_{i,k}^{{\mathbf{w}}_i}\in\Lambda_{\mathbf{d}}\end{align*} $$
is the product of appropriate powers of elementary symmetric functions and
![]() $e_{\mathbf {d}}^{\mathbf {w}}{\mathcal {H}}_{Q,{\mathbf {d}}}$
means the product in
$e_{\mathbf {d}}^{\mathbf {w}}{\mathcal {H}}_{Q,{\mathbf {d}}}$
means the product in
![]() $\Lambda _{\mathbf {d}}$
(corresponding to the cup product in cohomology).
$\Lambda _{\mathbf {d}}$
(corresponding to the cup product in cohomology).
3.4. Characters of CoHA and CoHA modules
Let us collect some well-known formulas for the Poincaré series (4) of our objects of interest. We begin with the Poincaré series of CoHA.
Proposition 3.2. We have
 $$ \begin{align*}Z({\mathcal{H}}_Q,x,q) =A_Q(x,q) :=\sum_{{\mathbf{d}}\in{\mathbb{N}}^I} \frac{(-q^{\frac12})^{-\chi({\mathbf{d}},{\mathbf{d}})}}{(q{^{-1}})_{\mathbf{d}}}x^{\mathbf{d}}, \end{align*} $$
$$ \begin{align*}Z({\mathcal{H}}_Q,x,q) =A_Q(x,q) :=\sum_{{\mathbf{d}}\in{\mathbb{N}}^I} \frac{(-q^{\frac12})^{-\chi({\mathbf{d}},{\mathbf{d}})}}{(q{^{-1}})_{\mathbf{d}}}x^{\mathbf{d}}, \end{align*} $$
where
![]() $(q)_{\mathbf {d}}=\prod _{i\in I} (q)_{{\mathbf {d}}_i}$
and
$(q)_{\mathbf {d}}=\prod _{i\in I} (q)_{{\mathbf {d}}_i}$
and
![]() $(q)_n=\prod _{k=1}^n(1-q^k)$
.
$(q)_n=\prod _{k=1}^n(1-q^k)$
.
Proof. Consider
![]() $\Lambda _n={\mathbb {Q}}[x_1,\dots ,x_n]^{\Sigma _n}\simeq {\mathbb {Q}}[e_1,\dots ,e_n]$
, where
$\Lambda _n={\mathbb {Q}}[x_1,\dots ,x_n]^{\Sigma _n}\simeq {\mathbb {Q}}[e_1,\dots ,e_n]$
, where
![]() $\deg x_i=2$
and
$\deg x_i=2$
and
![]() $\deg e_i=2i$
. Then
$\deg e_i=2i$
. Then
 $$ \begin{align*}\operatorname{\mathrm{ch}}(\Lambda_n)=\prod_{k=1}^n\frac1{1-q^{-k}}=\frac1{(q{^{-1}})_n}.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{ch}}(\Lambda_n)=\prod_{k=1}^n\frac1{1-q^{-k}}=\frac1{(q{^{-1}})_n}.\end{align*} $$
This implies that
![]() $\operatorname {\mathrm {ch}}(\Lambda _{\mathbf {d}})=\frac 1{(q{^{-1}})_{\mathbf {d}}}$
, and therefore,
$\operatorname {\mathrm {ch}}(\Lambda _{\mathbf {d}})=\frac 1{(q{^{-1}})_{\mathbf {d}}}$
, and therefore,
![]() ${\mathcal {H}}_{Q,{\mathbf {d}}}=\Lambda _{\mathbf {d}}[-\chi ({\mathbf {d}},{\mathbf {d}})]$
has the character
${\mathcal {H}}_{Q,{\mathbf {d}}}=\Lambda _{\mathbf {d}}[-\chi ({\mathbf {d}},{\mathbf {d}})]$
has the character
 $$ \begin{align*}\operatorname{\mathrm{ch}}({\mathcal{H}}_{Q,{\mathbf{d}}}) =\sum_k\dim\Lambda_{\mathbf{d}}^{k-\chi({\mathbf{d}},{\mathbf{d}})}q^{-{\frac12} k} =q^{-{\frac12}\chi({\mathbf{d}},{\mathbf{d}})}\operatorname{\mathrm{ch}}(\Lambda_{\mathbf{d}}) =\frac{q^{-{\frac12}\chi({\mathbf{d}},{\mathbf{d}})}}{(q{^{-1}})_{\mathbf{d}}}.\\[-37pt] \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{ch}}({\mathcal{H}}_{Q,{\mathbf{d}}}) =\sum_k\dim\Lambda_{\mathbf{d}}^{k-\chi({\mathbf{d}},{\mathbf{d}})}q^{-{\frac12} k} =q^{-{\frac12}\chi({\mathbf{d}},{\mathbf{d}})}\operatorname{\mathrm{ch}}(\Lambda_{\mathbf{d}}) =\frac{q^{-{\frac12}\chi({\mathbf{d}},{\mathbf{d}})}}{(q{^{-1}})_{\mathbf{d}}}.\\[-37pt] \end{align*} $$
Remark 3.3. We also have
 $$ \begin{align*}A_Q(x,q) =\sum_{\mathbf{d}} \frac{(-q^{\frac12})^{-\chi({\mathbf{d}},{\mathbf{d}})}}{(q{^{-1}})_{\mathbf{d}}}x^{\mathbf{d}} =\sum_{\mathbf{d}} (-q^{\frac12})^{\chi({\mathbf{d}},{\mathbf{d}})} \frac{P_c(R_{\mathbf{d}},q)}{P_c(G_{\mathbf{d}},q)}x^{\mathbf{d}}, \end{align*} $$
$$ \begin{align*}A_Q(x,q) =\sum_{\mathbf{d}} \frac{(-q^{\frac12})^{-\chi({\mathbf{d}},{\mathbf{d}})}}{(q{^{-1}})_{\mathbf{d}}}x^{\mathbf{d}} =\sum_{\mathbf{d}} (-q^{\frac12})^{\chi({\mathbf{d}},{\mathbf{d}})} \frac{P_c(R_{\mathbf{d}},q)}{P_c(G_{\mathbf{d}},q)}x^{\mathbf{d}}, \end{align*} $$
where we used the fact that
![]() $P_c({\mathbb {C}}^n,q)=q^n$
and
$P_c({\mathbb {C}}^n,q)=q^n$
and
![]() $P_c(\operatorname {\mathrm {GL}}_n({\mathbb {C}}),q)=q^{n^2}(q{^{-1}})_n$
.
$P_c(\operatorname {\mathrm {GL}}_n({\mathbb {C}}),q)=q^{n^2}(q{^{-1}})_n$
.
Let us now determine the Poincaré series of the CoHA module
![]() ${\mathcal {M}}_{\mathbf {w}}$
.
${\mathcal {M}}_{\mathbf {w}}$
.
Proposition 3.4. We have
where
![]() $S_{{\mathbf {w}}}(x^{\mathbf {d}})=q^{{\frac 12}{\mathbf {w}}\cdot {\mathbf {d}}}x^{\mathbf {d}}$
.
$S_{{\mathbf {w}}}(x^{\mathbf {d}})=q^{{\frac 12}{\mathbf {w}}\cdot {\mathbf {d}}}x^{\mathbf {d}}$
.
Proof. It follows from [Reference Engel and Reineke15, Theorem 5.2] that
As
![]() $\mathcal M_{{\mathbf {w}},{\mathbf {d}}}=H^{\mathrm {BM}}(\operatorname {\mathrm {Hilb}}_{{\mathbf {d}},{\mathbf {w}}})[\chi ({\mathbf {d}},{\mathbf {d}})-2{\mathbf {w}}\cdot {\mathbf {d}}]$
, we obtain
$\mathcal M_{{\mathbf {w}},{\mathbf {d}}}=H^{\mathrm {BM}}(\operatorname {\mathrm {Hilb}}_{{\mathbf {d}},{\mathbf {w}}})[\chi ({\mathbf {d}},{\mathbf {d}})-2{\mathbf {w}}\cdot {\mathbf {d}}]$
, we obtain
We define (refined) DT invariants
![]() $\Omega _{\mathbf {d}}(q)$
of the quiver Q by the formula
$\Omega _{\mathbf {d}}(q)$
of the quiver Q by the formula
 $$ \begin{align} Z({\mathcal{H}}_Q,x,q{^{-1}})=A_Q(x,q{^{-1}})=\operatorname{\mathrm{Exp}}{\left({\frac{\sum_{\mathbf{d}} (-1)^{\chi({\mathbf{d}},{\mathbf{d}})}\Omega_{\mathbf{d}}(q{^{-1}}) x^{\mathbf{d}}}{1-q}}\right)}. \end{align} $$
$$ \begin{align} Z({\mathcal{H}}_Q,x,q{^{-1}})=A_Q(x,q{^{-1}})=\operatorname{\mathrm{Exp}}{\left({\frac{\sum_{\mathbf{d}} (-1)^{\chi({\mathbf{d}},{\mathbf{d}})}\Omega_{\mathbf{d}}(q{^{-1}}) x^{\mathbf{d}}}{1-q}}\right)}. \end{align} $$
By a theorem of Efimov [Reference Efimov14], we have
![]() $\Omega _{\mathbf {d}}(q)\in {\mathbb {N}}[q^{\pm {\frac 12}}]$
. We shall give a new proof of this result in Theorem 5.7. The above formula for the Poincaré series of the CoHA module can be written in the form
$\Omega _{\mathbf {d}}(q)\in {\mathbb {N}}[q^{\pm {\frac 12}}]$
. We shall give a new proof of this result in Theorem 5.7. The above formula for the Poincaré series of the CoHA module can be written in the form
 $$ \begin{align} Z(\mathcal M_{{\mathbf{w}}},x,q{^{-1}})= \operatorname{\mathrm{Exp}}{\left({\sum_{\mathbf{d}}\frac{1-q^{{\mathbf{w}}\cdot {\mathbf{d}}}}{1-q}(-1)^{\chi({\mathbf{d}},{\mathbf{d}})}\Omega_{\mathbf{d}}(q{^{-1}})x^{\mathbf{d}}}\right)}. \end{align} $$
$$ \begin{align} Z(\mathcal M_{{\mathbf{w}}},x,q{^{-1}})= \operatorname{\mathrm{Exp}}{\left({\sum_{\mathbf{d}}\frac{1-q^{{\mathbf{w}}\cdot {\mathbf{d}}}}{1-q}(-1)^{\chi({\mathbf{d}},{\mathbf{d}})}\Omega_{\mathbf{d}}(q{^{-1}})x^{\mathbf{d}}}\right)}. \end{align} $$
4. Vertex algebras and conformal algebras
Our goal in this section is to offer a detailed recollection of necessary definitions and results from the theory of vertex algebras and vertex Lie algebras, adapted to the closed symmetric monoidal category
![]() ${\mathcal {C}} = \operatorname {\mathrm {Vect}}^L$
of L-graded vector spaces with the braiding arising from a symmetric bilinear form, as defined in §2.2. In particular, we define vertex Lie algebras as a particular case of the general framework of conformal algebras. We, however, choose to not use the terminology ‘Lie conformal algebras’ since for some readers this would hint at the presence of important conformal symmetries (such as the Virasoro algebra) included as a subalgebra, which is not the case for algebras we consider. Our exposition merges material from many different sources, and, in particular, is inspired by the textbooks [Reference Frenkel and Ben-Zvi20, Reference Kac34, Reference Rosellen59].
${\mathcal {C}} = \operatorname {\mathrm {Vect}}^L$
of L-graded vector spaces with the braiding arising from a symmetric bilinear form, as defined in §2.2. In particular, we define vertex Lie algebras as a particular case of the general framework of conformal algebras. We, however, choose to not use the terminology ‘Lie conformal algebras’ since for some readers this would hint at the presence of important conformal symmetries (such as the Virasoro algebra) included as a subalgebra, which is not the case for algebras we consider. Our exposition merges material from many different sources, and, in particular, is inspired by the textbooks [Reference Frenkel and Ben-Zvi20, Reference Kac34, Reference Rosellen59].
4.1. Graded vertex algebras
In this section, we will introduce L-graded vertex algebras. We start with recalling the classical definition of a vertex superalgebra and then explain its generalisation to the L-graded case.
4.1.1. Classical vertex (super)algebras
Let
![]() $\operatorname {\mathrm {Vect}}^{\mathbb {Z}_2}$
be the category of
$\operatorname {\mathrm {Vect}}^{\mathbb {Z}_2}$
be the category of
![]() $\mathbb {Z}_2$
-graded vector spaces (also called super vector spaces), equipped with a symmetric monoidal category structure using the Koszul sign rule (2). Given a
$\mathbb {Z}_2$
-graded vector spaces (also called super vector spaces), equipped with a symmetric monoidal category structure using the Koszul sign rule (2). Given a
![]() $\mathbb {Z}_2$
-graded vector space
$\mathbb {Z}_2$
-graded vector space
![]() $V=V_0\oplus V_1$
and
$V=V_0\oplus V_1$
and
![]() $a\in V_p$
, we call
$a\in V_p$
, we call
![]() $p(a)=p\in \mathbb {Z}_2$
the parity of a. The
$p(a)=p\in \mathbb {Z}_2$
the parity of a. The
![]() $\mathbb {Z}_2$
-graded vector space
$\mathbb {Z}_2$
-graded vector space
![]() $\underline {\textrm {End}}(V)=\underline {\textrm {Hom}}(V,V)$
is equipped with the Lie bracket
$\underline {\textrm {End}}(V)=\underline {\textrm {Hom}}(V,V)$
is equipped with the Lie bracket
Define the space of fields
 $$ \begin{align*}{\mathcal{F}}(V)={\left\{\left.{\sum_{n\in\mathbb{Z}} a(n)z^{-n-1}\in\underline{\textrm{End}}(V){[\![{z^{\pm1}}]\!]}}\ \right\vert{\forall v\in V,\, a(n)v=0\text{ for }n\gg0}\right\}}. \end{align*} $$
$$ \begin{align*}{\mathcal{F}}(V)={\left\{\left.{\sum_{n\in\mathbb{Z}} a(n)z^{-n-1}\in\underline{\textrm{End}}(V){[\![{z^{\pm1}}]\!]}}\ \right\vert{\forall v\in V,\, a(n)v=0\text{ for }n\gg0}\right\}}. \end{align*} $$
This means that, for every
![]() $\mathfrak {a}(z)\in {\mathcal {F}}(V)$
and
$\mathfrak {a}(z)\in {\mathcal {F}}(V)$
and
![]() $v\in V$
, we have
$v\in V$
, we have
![]() $\mathfrak {a}(z)v\in V{(\;\!\!\!(z)\!\!\!\;)} $
. We equip
$\mathfrak {a}(z)v\in V{(\;\!\!\!(z)\!\!\!\;)} $
. We equip
![]() ${\mathcal {F}}(V)$
with the
${\mathcal {F}}(V)$
with the
![]() $\mathbb {Z}_2$
-grading, where
$\mathbb {Z}_2$
-grading, where
![]() $\mathfrak {a}(z)=\sum _n a(n)z^{-n-1}$
has parity p if
$\mathfrak {a}(z)=\sum _n a(n)z^{-n-1}$
has parity p if
![]() $a(n)$
has parity p for all
$a(n)$
has parity p for all
![]() $n\in \mathbb {Z}$
. We say that two fields
$n\in \mathbb {Z}$
. We say that two fields
![]() $\mathfrak {a}(z),\mathfrak {b}(z)\in {\mathcal {F}}(V)$
are (mutually) local if
$\mathfrak {a}(z),\mathfrak {b}(z)\in {\mathcal {F}}(V)$
are (mutually) local if
A vertex (super)algebra is a triple ![]() , where V is a
, where V is a
![]() $\mathbb {Z}_2$
-graded vector space,
$\mathbb {Z}_2$
-graded vector space,
![]() $Y\colon V\to {\mathcal {F}}(V)$
is a linear map, and
$Y\colon V\to {\mathcal {F}}(V)$
is a linear map, and ![]() is an element called vacuum, such that, for all
is an element called vacuum, such that, for all
![]() $a,b\in V$
,
$a,b\in V$
,
-
(1)
 $Y(a,z)=\sum _{n}a(n)z^{-n-1}$
has the same parity as a.
$Y(a,z)=\sum _{n}a(n)z^{-n-1}$
has the same parity as a. -
(2)
 , the identity operator.
, the identity operator. -
(3)
 for
for
 $n\ge 0$
and
$n\ge 0$
and  .
. -
(4)
 $[T,Y(a,z)]=\partial _z Y(a,z)$
, where
$[T,Y(a,z)]=\partial _z Y(a,z)$
, where
 $T\in \operatorname {\mathrm {End}}(V)$
is defined by
$T\in \operatorname {\mathrm {End}}(V)$
is defined by  and
and
 $\partial _z=\frac {\partial }{\partial z}$
.
$\partial _z=\frac {\partial }{\partial z}$
. -
(5)
 $Y(a,z)$
and
$Y(a,z)$
and
 $Y(b,z)$
are local.
$Y(b,z)$
are local.
Remark 4.1. One can show that, for any
![]() $a\in V$
,
$a\in V$
,
Therefore,
4.1.2. Graded vertex algebras
In the remaining part of section of §4, we shall mostly work in the category
![]() ${\mathcal {C}}^{{\frac 12}\mathbb {Z}}\simeq \operatorname {\mathrm {Vect}}^{L\times {\frac 12}\mathbb {Z}}$
(the corresponding
${\mathcal {C}}^{{\frac 12}\mathbb {Z}}\simeq \operatorname {\mathrm {Vect}}^{L\times {\frac 12}\mathbb {Z}}$
(the corresponding
![]() ${\frac 12}\mathbb {Z}$
-degrees will be called weights). It has a symmetric monoidal category structure induced from that of
${\frac 12}\mathbb {Z}$
-degrees will be called weights). It has a symmetric monoidal category structure induced from that of
![]() ${\mathcal {C}}$
(without any additional signs coming from weights). Consider an object
${\mathcal {C}}$
(without any additional signs coming from weights). Consider an object
![]() $V=\bigoplus _{n\in {\frac 12}\mathbb {Z}}V_n\in {\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
bounded below, meaning that
$V=\bigoplus _{n\in {\frac 12}\mathbb {Z}}V_n\in {\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
bounded below, meaning that
![]() $V_n=0$
for
$V_n=0$
for
![]() $n\ll 0$
. We define the space of fields
$n\ll 0$
. We define the space of fields
where z has L-degree zero and weight
![]() $-1$
. Note that if
$-1$
. Note that if
![]() $\sum _n a(n)z^{-n-1}\in {\mathcal {F}}(V)$
has weight k, then
$\sum _n a(n)z^{-n-1}\in {\mathcal {F}}(V)$
has weight k, then
![]() $a(n)$
has weight
$a(n)$
has weight
![]() $k-n-1$
. This implies that, for any
$k-n-1$
. This implies that, for any
![]() $b\in V$
, we have
$b\in V$
, we have
by the assumption on V. Locality of fields is defined in the same way as in (18), using the bracket on
![]() $\underline {\textrm {End}}(V)$
. We define an L-graded vertex algebra to be a triple
$\underline {\textrm {End}}(V)$
. We define an L-graded vertex algebra to be a triple ![]() , where
, where
![]() $V\in {\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
is bounded below,
$V\in {\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
is bounded below,
![]() $Y\colon V\to {\mathcal {F}}(V)$
is a linear map, and
$Y\colon V\to {\mathcal {F}}(V)$
is a linear map, and ![]() , such that, for all
, such that, for all
![]() $a,b\in V$
,
$a,b\in V$
,
-
(1) Y preserves degrees, meaning that, for
 $Y(a,z)=\sum _na(n)z^{-n-1}$
, the operator
$Y(a,z)=\sum _na(n)z^{-n-1}$
, the operator
 $a(n)$
has the same L-degree as a and the weight
$a(n)$
has the same L-degree as a and the weight
 $\operatorname {\mathrm {wt}}(a)-n-1$
.
$\operatorname {\mathrm {wt}}(a)-n-1$
. -
(2)
 .
. -
(3)
 for
for
 $n\ge 0$
and
$n\ge 0$
and  .
. -
(4)
 $[T,Y(a,z)]=\partial _z Y(a,z)$
, where
$[T,Y(a,z)]=\partial _z Y(a,z)$
, where
 $T\in \underline {\textrm {End}}(V)$
is defined by
$T\in \underline {\textrm {End}}(V)$
is defined by  .
. -
(5)
 $Y(a,z)$
and
$Y(a,z)$
and
 $Y(b,z)$
are local.
$Y(b,z)$
are local.
Note that the map
![]() $T\colon V\to V$
has L-degree zero and weight
$T\colon V\to V$
has L-degree zero and weight
![]() $1$
. Note also that the map
$1$
. Note also that the map
![]() $Y\colon V\to {\mathcal {F}}(V)$
is encoded by the products
$Y\colon V\to {\mathcal {F}}(V)$
is encoded by the products
By definition, a morphism
![]() $f\colon V\to W$
between two graded vertex algebras is a degree zero linear map that preserves the vacuum and all these products. A module over a graded vertex algebra V is a graded vector space M equipped with a degree zero linear map
$f\colon V\to W$
between two graded vertex algebras is a degree zero linear map that preserves the vacuum and all these products. A module over a graded vertex algebra V is a graded vector space M equipped with a degree zero linear map
![]() $Y_M\colon V\to {\mathcal {F}}(M)$
that preserves products, maps
$Y_M\colon V\to {\mathcal {F}}(M)$
that preserves products, maps ![]() to
to
![]() $\operatorname {\mathrm {id}}_M$
and maps V to a subspace of mutually local fields.
$\operatorname {\mathrm {id}}_M$
and maps V to a subspace of mutually local fields.
Remark 4.2. For a lattice L equipped with a symmetric bilinear form
![]() $(\cdot ,\cdot )$
, it is conventional to use the braiding on
$(\cdot ,\cdot )$
, it is conventional to use the braiding on
![]() $\operatorname {\mathrm {Vect}}^{L}$
given by the Koszul signs
$\operatorname {\mathrm {Vect}}^{L}$
given by the Koszul signs
![]() $(-1)^{p(\alpha )p(\beta )}$
, where
$(-1)^{p(\alpha )p(\beta )}$
, where
![]() $p(\alpha ) = (\alpha ,\alpha )\pmod 2$
. This is justified by the desire to work in the familiar setting of vertex (super)algebras. However, this convention requires one to introduce certain non-canonical sign twists [Reference Kac34, §5.4] (needed to ensure mutual locality of vertex operators in lattice vertex algebras), very similar to the sign twists from Remark 3.1. Our convention for the braiding in
$p(\alpha ) = (\alpha ,\alpha )\pmod 2$
. This is justified by the desire to work in the familiar setting of vertex (super)algebras. However, this convention requires one to introduce certain non-canonical sign twists [Reference Kac34, §5.4] (needed to ensure mutual locality of vertex operators in lattice vertex algebras), very similar to the sign twists from Remark 3.1. Our convention for the braiding in
![]() $\operatorname {\mathrm {Vect}}^L$
(see §2.2) allows one to avoid any non-canonical choices both in the case of CoHAs and in the case of vertex algebras.
$\operatorname {\mathrm {Vect}}^L$
(see §2.2) allows one to avoid any non-canonical choices both in the case of CoHAs and in the case of vertex algebras.
4.1.3. External products
Let
![]() $V\in {\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
be bounded below, and let
$V\in {\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
be bounded below, and let
![]() $\mathfrak {a}\in {\mathcal {F}}(V)_\alpha $
,
$\mathfrak {a}\in {\mathcal {F}}(V)_\alpha $
,
![]() $\mathfrak {b}\in {\mathcal {F}}(V)_\beta $
be two fields (here
$\mathfrak {b}\in {\mathcal {F}}(V)_\beta $
be two fields (here
![]() $\alpha ,\beta \in L$
). For any
$\alpha ,\beta \in L$
). For any
![]() $n\in \mathbb {Z}$
, we define
$n\in \mathbb {Z}$
, we define
and consider the binary operation ![]() on
on
![]() ${\mathcal {F}}(V)$
defined by
${\mathcal {F}}(V)$
defined by
We have ![]() by [Reference Li41, Lemma 3.1.4]. By Dong’s lemma [Reference Li41, Proposition 3.2.7], if
by [Reference Li41, Lemma 3.1.4]. By Dong’s lemma [Reference Li41, Proposition 3.2.7], if
![]() $\mathfrak {a},\mathfrak {b},\mathfrak {c}\in {\mathcal {F}}(V)$
and
$\mathfrak {a},\mathfrak {b},\mathfrak {c}\in {\mathcal {F}}(V)$
and
![]() $\mathfrak {a},\mathfrak {b}$
are local with
$\mathfrak {a},\mathfrak {b}$
are local with
![]() $\mathfrak {c}$
, then
$\mathfrak {c}$
, then ![]() is local with
is local with
![]() $\mathfrak {c}$
, for all
$\mathfrak {c}$
, for all
![]() $n\in \mathbb {Z}$
.
$n\in \mathbb {Z}$
.
The coefficients of the field ![]() can be written explicitly as
can be written explicitly as

In particular, for
![]() $m\ge 0$
, we have
$m\ge 0$
, we have

For
![]() $m=-1$
, we obtain
$m=-1$
, we obtain

Remark 4.3. The field
is the so-called normally ordered product
![]() $:{\mathfrak {a}}(z){\mathfrak {b}}(z)):$
of the fields
$:{\mathfrak {a}}(z){\mathfrak {b}}(z)):$
of the fields
![]() $\mathfrak {a}$
and
$\mathfrak {a}$
and
![]() $\mathfrak {b}$
. Here,
$\mathfrak {b}$
. Here,
![]() $f_+(z)=\sum _{n\ge 0}f_nz^n$
and
$f_+(z)=\sum _{n\ge 0}f_nz^n$
and
![]() $f_-(z)=\sum _{n<0}f_nz^n$
, for
$f_-(z)=\sum _{n<0}f_nz^n$
, for
![]() $f(z)=\sum _n f_nz^n$
.
$f(z)=\sum _n f_nz^n$
.
Lemma 4.4. If V is a vertex algebra, then
![]() $Y\colon V\to {\mathcal {F}}(V)$
preserves the products (19), meaning that
$Y\colon V\to {\mathcal {F}}(V)$
preserves the products (19), meaning that
![]() $a(n)b$
is mapped to
$a(n)b$
is mapped to ![]() for all
for all
![]() $a,b\in V$
and
$a,b\in V$
and
![]() $n\in \mathbb {Z}$
.
$n\in \mathbb {Z}$
.
Proof. By the Jacobi identity [Reference Frenkel, Lepowsky and Meurman23], for any
![]() $a,b\in V$
, we have
$a,b\in V$
, we have
 $$ \begin{align} [Y(a,z)\times_n Y(b,w)]=\operatorname{\mathrm{Res}}_u u^nw{^{-1}} Y(Y(a,u)b,w) \delta{\left({\frac{z-u}{w}}\right)}. \end{align} $$
$$ \begin{align} [Y(a,z)\times_n Y(b,w)]=\operatorname{\mathrm{Res}}_u u^nw{^{-1}} Y(Y(a,u)b,w) \delta{\left({\frac{z-u}{w}}\right)}. \end{align} $$
Applying
![]() $\operatorname {\mathrm {Res}}_z\delta {\left ({\frac {z-u}{w}}\right )}=w$
, we obtain
$\operatorname {\mathrm {Res}}_z\delta {\left ({\frac {z-u}{w}}\right )}=w$
, we obtain
This implies the statement.
For any
![]() $\mathfrak {a}\in {\mathcal {F}}(V)$
and
$\mathfrak {a}\in {\mathcal {F}}(V)$
and
![]() $n\in \mathbb {Z}$
, we obtain
$n\in \mathbb {Z}$
, we obtain ![]() , and we define
, and we define
Let
![]() $\operatorname {\mathrm {id}}_V\in \underline {\textrm {End}}(V)\subset {\mathcal {F}}(V)$
be the identity operator and
$\operatorname {\mathrm {id}}_V\in \underline {\textrm {End}}(V)\subset {\mathcal {F}}(V)$
be the identity operator and
![]() $T=\partial _z\in \underline {\textrm {End}}({\mathcal {F}}(V))$
. Then, for any
$T=\partial _z\in \underline {\textrm {End}}({\mathcal {F}}(V))$
. Then, for any
![]() $\mathfrak {a}\in {\mathcal {F}}(V)$
, we have [Reference Li41, Lemmas 3.1.6-3.1.7]
$\mathfrak {a}\in {\mathcal {F}}(V)$
, we have [Reference Li41, Lemmas 3.1.6-3.1.7]
-
(1)
 $Y(\operatorname {\mathrm {id}}_V,u)\mathfrak {a}=\mathfrak {a}$
.
$Y(\operatorname {\mathrm {id}}_V,u)\mathfrak {a}=\mathfrak {a}$
. -
(2)
 $Y(\mathfrak {a},u)\operatorname {\mathrm {id}}_V=e^{uT}\mathfrak {a}$
.
$Y(\mathfrak {a},u)\operatorname {\mathrm {id}}_V=e^{uT}\mathfrak {a}$
. -
(3)
 $Y(T\mathfrak {a},u)=[T,Y(\mathfrak {a},u)]=\partial _u Y(\mathfrak {a},u)$
.
$Y(T\mathfrak {a},u)=[T,Y(\mathfrak {a},u)]=\partial _u Y(\mathfrak {a},u)$
.
The last property implies ![]() . In particular,
. In particular,
A subspace
![]() $W\subset {\mathcal {F}}(V)$
is called a field algebra if it is closed under products
$W\subset {\mathcal {F}}(V)$
is called a field algebra if it is closed under products ![]() and contains
and contains
![]() $\operatorname {\mathrm {id}}_V$
. It is called a local field algebra if it consists of mutually local fields. In this case, consider the restriction
$\operatorname {\mathrm {id}}_V$
. It is called a local field algebra if it consists of mutually local fields. In this case, consider the restriction
By the locality assumption, we have
![]() $[\mathfrak {a}(z)\times _n\mathfrak {b}(w)]=0$
; hence,
$[\mathfrak {a}(z)\times _n\mathfrak {b}(w)]=0$
; hence, ![]() , for
, for
![]() $\mathfrak {a},\mathfrak {b}\in W$
and
$\mathfrak {a},\mathfrak {b}\in W$
and
![]() $n\gg 0$
. Therefore,
$n\gg 0$
. Therefore,
![]() $Y(\mathfrak {a},u)$
is a field, and we obtain a linear map
$Y(\mathfrak {a},u)$
is a field, and we obtain a linear map
![]() $Y:W\to {\mathcal {F}}(W)$
. The triple
$Y:W\to {\mathcal {F}}(W)$
. The triple
![]() $(W,Y,\operatorname {\mathrm {id}}_V)$
is a vertex algebra by [Reference Li41, Theorem 3.2.10]. For any subset
$(W,Y,\operatorname {\mathrm {id}}_V)$
is a vertex algebra by [Reference Li41, Theorem 3.2.10]. For any subset
![]() $S\subset {\mathcal {F}}(V)$
, consisting of mutually local (homogeneous) fields, let
$S\subset {\mathcal {F}}(V)$
, consisting of mutually local (homogeneous) fields, let
![]() ${{\left \langle S\right \rangle }} $
be the smallest subspace of
${{\left \langle S\right \rangle }} $
be the smallest subspace of
![]() ${\mathcal {F}}(V)$
containing
${\mathcal {F}}(V)$
containing
![]() $S\cup {{\left \{{\operatorname {\mathrm {id}}_V}\right \}}}$
and closed under all products
$S\cup {{\left \{{\operatorname {\mathrm {id}}_V}\right \}}}$
and closed under all products ![]() . Then by Dong’s lemma,
. Then by Dong’s lemma,
![]() ${{\left \langle {S}\right \rangle }}$
is a local field algebra, and we conclude that it is a vertex algebra.
${{\left \langle {S}\right \rangle }}$
is a local field algebra, and we conclude that it is a vertex algebra.
In particular, assume that ![]() is a vertex algebra. The map
is a vertex algebra. The map
![]() $Y\colon V\to {\mathcal {F}}(V)$
is injective as
$Y\colon V\to {\mathcal {F}}(V)$
is injective as ![]() . Let
. Let
![]() $W=Y(V)\subset {\mathcal {F}}(V)$
. Then W consists of mutually local fields by the definition of a vertex algebra. It is closed with respect to products by Lemma 4.4, and it contains
$W=Y(V)\subset {\mathcal {F}}(V)$
. Then W consists of mutually local fields by the definition of a vertex algebra. It is closed with respect to products by Lemma 4.4, and it contains ![]() . Therefore, W is a vertex algebra and
. Therefore, W is a vertex algebra and
![]() $Y\colon V\to W$
is an isomorphism of vertex algebras.
$Y\colon V\to W$
is an isomorphism of vertex algebras.
4.2. Conformal algebras
In this section, we will introduce the notion of conformal algebras, closely related to the notion of vertex algebras. For more details on this subject, see, for example, [Reference Primc51, Reference Roitman57].
4.2.1. Definition of conformal algebras
We define a conformal algebra to be an object
![]() $C\in {\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
equipped with a linear map
$C\in {\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
equipped with a linear map
![]() $\partial \colon {\mathfrak {C}}\to {\mathfrak {C}}$
(of L-degree zero and weight
$\partial \colon {\mathfrak {C}}\to {\mathfrak {C}}$
(of L-degree zero and weight
![]() $1$
) and bilinear operations
$1$
) and bilinear operations ![]() (of L-degree zero and weight
(of L-degree zero and weight
![]() $-n-1$
), for
$-n-1$
), for
![]() $n\in {\mathbb {N}}$
, such that for all
$n\in {\mathbb {N}}$
, such that for all
![]() $a,b\in {\mathfrak {C}}$
, we have
$a,b\in {\mathfrak {C}}$
, we have
-
(1)
 for
for
 $n\gg 0$
.
$n\gg 0$
. -
(2)
 .
. -
(3)
 .
.
Let us recall a fundamental class of examples of conformal algebras obtained via a procedure reminiscent of the construction of external products ![]() in §4.1.3. Suppose that
in §4.1.3. Suppose that
![]() ${\mathfrak {L}}\in {\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
is an algebra, by which we mean a graded vector space equipped with a bilinear operation
${\mathfrak {L}}\in {\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
is an algebra, by which we mean a graded vector space equipped with a bilinear operation
(despite the suggestive notation, we do not assume this operation to satisfy any of the properties of a Lie bracket). We define external products ![]() on the space
on the space
![]() ${\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
(where z has L-degree zero and weight
${\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
(where z has L-degree zero and weight
![]() $-1$
) by the formula (cf. (21))
$-1$
) by the formula (cf. (21))
for
![]() $\mathfrak {a}(z)=\sum _{n\in \mathbb {Z}}a(n)z^{-n-1}$
and
$\mathfrak {a}(z)=\sum _{n\in \mathbb {Z}}a(n)z^{-n-1}$
and
![]() $\mathfrak {b}(z)=\sum _{n\in \mathbb {Z}}b(n)z^{-n-1}$
in
$\mathfrak {b}(z)=\sum _{n\in \mathbb {Z}}b(n)z^{-n-1}$
in
![]() ${\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
. The coefficient of
${\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
. The coefficient of
![]() $z^{-m-1}$
in this series equals (cf. (23))
$z^{-m-1}$
in this series equals (cf. (23))

We also define
![]() $\partial =\frac {\partial }{\partial z}\colon {\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}\to {\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
, so that the map
$\partial =\frac {\partial }{\partial z}\colon {\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}\to {\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
, so that the map
![]() $\partial $
and the products
$\partial $
and the products ![]() satisfy the axioms (2) and (3) above. Note that the axiom (1) is satisfied by the fields
satisfy the axioms (2) and (3) above. Note that the axiom (1) is satisfied by the fields
![]() $\mathfrak {a},\mathfrak {b}\in {\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
if they are (mutually) local, meaning that
$\mathfrak {a},\mathfrak {b}\in {\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
if they are (mutually) local, meaning that
In this case, we have [Reference Kac34, §2.2]

We see that if
![]() ${\mathfrak {C}}\subset {\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
is a subspace consisting of pairwise mutually local elements which is closed under all external products and the map
${\mathfrak {C}}\subset {\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
is a subspace consisting of pairwise mutually local elements which is closed under all external products and the map
![]() $\partial $
, then
$\partial $
, then
![]() ${\mathfrak {C}}$
is a conformal algebra.
${\mathfrak {C}}$
is a conformal algebra.
4.2.2. Coefficient algebras of conformal algebras
For a conformal algebra ![]() , we shall now define the coefficient algebra
, we shall now define the coefficient algebra
![]() $\operatorname {\mathrm {Coeff}}( )$
. Note that we have
$\operatorname {\mathrm {Coeff}}( )$
. Note that we have
hence,
![]() $\partial C\subset C$
is an ideal with respect to the product
$\partial C\subset C$
is an ideal with respect to the product ![]() , and we can equip
, and we can equip
![]() $C/\partial C$
with the bracket
$C/\partial C$
with the bracket
In particular, we can apply this construction to the affinization of C [Reference Kac34, §2.7], which is defined to be
![]() $\tilde C=C[t^{\pm 1}]$
equipped with the derivation
$\tilde C=C[t^{\pm 1}]$
equipped with the derivation
![]() $\tilde \partial =\partial \otimes 1+1\otimes \partial _t$
and the products
$\tilde \partial =\partial \otimes 1+1\otimes \partial _t$
and the products

where
![]() ${\partial _t^{(k)}} =\frac 1{k!}\partial _t^k$
. Now we define the algebra of coefficients
${\partial _t^{(k)}} =\frac 1{k!}\partial _t^k$
. Now we define the algebra of coefficients
with the bracket given by ![]() . More explicitly, let us write
. More explicitly, let us write
![]() $C(n)=Ct^n\subset \tilde C$
and
$C(n)=Ct^n\subset \tilde C$
and
![]() $a(n)=at^n\in C(n)$
, for
$a(n)=at^n\in C(n)$
, for
![]() $a\in C$
,
$a\in C$
,
![]() $n\in \mathbb {Z}$
. Then
$n\in \mathbb {Z}$
. Then
![]() ${\mathfrak {L}}$
is equal to the quotient of
${\mathfrak {L}}$
is equal to the quotient of
![]() $\tilde C=\bigoplus _{n\in \mathbb {Z}}C(n)$
by the subspace generated by
$\tilde C=\bigoplus _{n\in \mathbb {Z}}C(n)$
by the subspace generated by
The operation
![]() $[-,-]$
given by (cf. (28))
$[-,-]$
given by (cf. (28))

descends from
![]() $\tilde C$
to
$\tilde C$
to
![]() ${\mathfrak {L}}$
. We will usually denote the image of
${\mathfrak {L}}$
. We will usually denote the image of
![]() $a(n)\in \tilde C$
in
$a(n)\in \tilde C$
in
![]() ${\mathfrak {L}}$
by
${\mathfrak {L}}$
by
![]() $a(n)$
. The map
$a(n)$
. The map
is a derivation of the algebra
![]() ${\mathfrak {L}}$
. Let
${\mathfrak {L}}$
. Let
From (31), we obtain that
![]() ${\mathfrak {L}}(n-1)$
embeds into
${\mathfrak {L}}(n-1)$
embeds into
![]() ${\mathfrak {L}}(n)$
for
${\mathfrak {L}}(n)$
for
![]() $n\ne 0$
. Therefore, we have increasing filtrations
$n\ne 0$
. Therefore, we have increasing filtrations
All of these subspaces are preserved by the derivation
![]() $\partial $
. It is clear from (32) that
$\partial $
. It is clear from (32) that
for
![]() $m,n\ge 0$
or
$m,n\ge 0$
or
![]() $m,n<0$
. In particular,
$m,n<0$
. In particular,
![]() ${\mathfrak {L}}_\pm $
are subalgebras of
${\mathfrak {L}}_\pm $
are subalgebras of
![]() ${\mathfrak {L}}$
. Moreover, we have an internal direct sum decomposition [Reference Primc51, Reference Roitman57]
${\mathfrak {L}}$
. Moreover, we have an internal direct sum decomposition [Reference Primc51, Reference Roitman57]
of the vector space
![]() ${\mathfrak {L}}$
, and an isomorphism of vector spaces
${\mathfrak {L}}$
, and an isomorphism of vector spaces
Under the isomorphism
![]() $C\simeq {\mathfrak {L}}_-$
, the bracket on C is given by [Reference Primc51, p. 4.14]
$C\simeq {\mathfrak {L}}_-$
, the bracket on C is given by [Reference Primc51, p. 4.14]
Note that the map
![]() $C\to \tilde C$
,
$C\to \tilde C$
,
![]() $a\mapsto a(0)$
, is a homomorphism of conformal algebras; hence, it induces a morphism of algebras
$a\mapsto a(0)$
, is a homomorphism of conformal algebras; hence, it induces a morphism of algebras
By [Reference Roitman57, Prop. P 1.3], the map
![]() $C\to {\mathfrak {L}}(0),\,a\mapsto a(0)$
has the kernel
$C\to {\mathfrak {L}}(0),\,a\mapsto a(0)$
has the kernel
![]() $\partial C+\sum _{k\ge 1}{\ker \partial ^k}$
; hence,
$\partial C+\sum _{k\ge 1}{\ker \partial ^k}$
; hence,
![]() $C/\partial C\to {\mathfrak {L}}(0)$
is an isomorphism if
$C/\partial C\to {\mathfrak {L}}(0)$
is an isomorphism if
![]() $\partial $
is injective. It is important to note that the brackets on C and
$\partial $
is injective. It is important to note that the brackets on C and
![]() $C/\partial C$
are not related.
$C/\partial C$
are not related.
The map
is a homomorphism of conformal algebras (meaning that it preserves the products and the derivation). Since
![]() $a\mapsto a(-1)$
is an isomorphism between
$a\mapsto a(-1)$
is an isomorphism between
![]() ${\mathfrak {C}}$
and
${\mathfrak {C}}$
and
![]() ${\mathfrak {L}}(-1)$
, this map is injective.
${\mathfrak {L}}(-1)$
, this map is injective.
The coefficient algebra
![]() ${\mathfrak {L}}=\operatorname {\mathrm {Coeff}}({\mathfrak {C}})$
satisfies the following universal property: if
${\mathfrak {L}}=\operatorname {\mathrm {Coeff}}({\mathfrak {C}})$
satisfies the following universal property: if
![]() ${\mathfrak {A}}$
is an algebra and
${\mathfrak {A}}$
is an algebra and
![]() $\psi \colon {\mathfrak {C}}\to {\mathfrak {A}}{[\![{z^{\pm 1}}]\!]}$
is a morphism of conformal algebras, then there exists a unique algebra morphism
$\psi \colon {\mathfrak {C}}\to {\mathfrak {A}}{[\![{z^{\pm 1}}]\!]}$
is a morphism of conformal algebras, then there exists a unique algebra morphism
![]() $\varrho \colon {\mathfrak {L}}\to {\mathfrak {A}}$
(given by
$\varrho \colon {\mathfrak {L}}\to {\mathfrak {A}}$
(given by
![]() $a(n)\mapsto \operatorname {\mathrm {Res}}_z z^n\psi (a)$
) such that the diagram
$a(n)\mapsto \operatorname {\mathrm {Res}}_z z^n\psi (a)$
) such that the diagram

is commutative.
4.2.3. Vertex Lie algebras and their enveloping vertex algebras
Using coefficient algebras, one can define particular types of conformal algebras. In particular, a conformal algebra
![]() ${\mathfrak {C}}$
is called a vertex Lie algebra (or Lie conformal algebra) if the algebra
${\mathfrak {C}}$
is called a vertex Lie algebra (or Lie conformal algebra) if the algebra
![]() $\operatorname {\mathrm {Coeff}}({\mathfrak {C}})$
is a Lie algebra. Equivalently, this means that, for
$\operatorname {\mathrm {Coeff}}({\mathfrak {C}})$
is a Lie algebra. Equivalently, this means that, for
![]() $a,b\in {\mathfrak {C}}$
and
$a,b\in {\mathfrak {C}}$
and
![]() $m,n\in {\mathbb {N}}$
, we have
$m,n\in {\mathbb {N}}$
, we have
-
(1)
 (Jacobi identity), or equivalently,
(Jacobi identity), or equivalently, .
. -
(2)
 , for
, for
 $a{\kern-1pt}\in{\kern-1pt} {\mathfrak {C}}_\alpha ,b{\kern-1pt}\in{\kern-1pt} {\mathfrak {C}}_\beta $
(anti-commutativity).
$a{\kern-1pt}\in{\kern-1pt} {\mathfrak {C}}_\alpha ,b{\kern-1pt}\in{\kern-1pt} {\mathfrak {C}}_\beta $
(anti-commutativity).
Under these conditions, the bracket (29) defined on
![]() $C/\partial C$
is a Lie bracket; see, for example, [Reference Kac34, Rem. 2.7a]. Let
$C/\partial C$
is a Lie bracket; see, for example, [Reference Kac34, Rem. 2.7a]. Let
![]() ${\mathfrak {C}}$
be a vertex Lie algebra and
${\mathfrak {C}}$
be a vertex Lie algebra and
![]() ${\mathfrak {L}}=\operatorname {\mathrm {Coeff}}({\mathfrak {C}})$
be its coefficient algebra. We define the Verma module
${\mathfrak {L}}=\operatorname {\mathrm {Coeff}}({\mathfrak {C}})$
be its coefficient algebra. We define the Verma module
where
![]() ${\mathbb {Q}}$
is equipped with the trivial
${\mathbb {Q}}$
is equipped with the trivial
![]() ${\mathfrak {L}}_+$
-module structure. Let
${\mathfrak {L}}_+$
-module structure. Let ![]() be the cyclic vector of this module. One can show that, for any
be the cyclic vector of this module. One can show that, for any
![]() $a\in {\mathfrak {C}}$
and
$a\in {\mathfrak {C}}$
and
![]() $v\in V$
, we have
$v\in V$
, we have
![]() $a(n)v=0$
for
$a(n)v=0$
for
![]() $n\gg 0$
. This implies that
$n\gg 0$
. This implies that
![]() $\phi (a)=\sum _n a(n)z^{-n-1}\in {\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
induces a field
$\phi (a)=\sum _n a(n)z^{-n-1}\in {\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
induces a field
![]() $\psi (a)\in {\mathcal {F}}(V)$
. The map
$\psi (a)\in {\mathcal {F}}(V)$
. The map
![]() $\psi :{\mathfrak {C}}\to {\mathcal {F}}(V)$
is injective as the map
$\psi :{\mathfrak {C}}\to {\mathcal {F}}(V)$
is injective as the map
![]() ${\mathfrak {C}}\simeq {\mathfrak {L}}_-\to \underline {\textrm {End}}(V)$
is injective.
${\mathfrak {C}}\simeq {\mathfrak {L}}_-\to \underline {\textrm {End}}(V)$
is injective.
The image of
![]() $\psi \colon {\mathfrak {C}}\to {\mathcal {F}}(V)$
consists of mutually local fields and generates a vertex algebra
$\psi \colon {\mathfrak {C}}\to {\mathcal {F}}(V)$
consists of mutually local fields and generates a vertex algebra
![]() $W\subset {\mathcal {F}}(V)$
. By [Reference Roitman57, §2.4], the vertex algebra W has a structure of an
$W\subset {\mathcal {F}}(V)$
. By [Reference Roitman57, §2.4], the vertex algebra W has a structure of an
![]() ${\mathfrak {L}}$
-module, and the map
${\mathfrak {L}}$
-module, and the map
![]() $W\to V$
,
$W\to V$
, ![]() is an isomorphism of
is an isomorphism of
![]() ${\mathfrak {L}}$
-modules. We shall call the vertex algebra
${\mathfrak {L}}$
-modules. We shall call the vertex algebra
![]() $W\simeq V$
the universal enveloping vertex algebra of
$W\simeq V$
the universal enveloping vertex algebra of
![]() ${\mathfrak {C}}$
and denote it by
${\mathfrak {C}}$
and denote it by
![]() ${\mathcal {U}}(C)$
. Note that we have a commutative diagram of graded vector spaces
${\mathcal {U}}(C)$
. Note that we have a commutative diagram of graded vector spaces

If V is a vertex algebra, then V equipped with the products
![]() $(n)\colon V\otimes V\to V$
,
$(n)\colon V\otimes V\to V$
,
![]() $n\ge 0$
, and the map
$n\ge 0$
, and the map
![]() $\partial =T\colon V\to V$
is a vertex Lie algebra. By [Reference Primc51, Theorem 5.5], the corresponding forgetful functor from the category of vertex algebras to the category of vertex Lie algebras has a left adjoint functor which is precisely the universal enveloping algebra functor
$\partial =T\colon V\to V$
is a vertex Lie algebra. By [Reference Primc51, Theorem 5.5], the corresponding forgetful functor from the category of vertex algebras to the category of vertex Lie algebras has a left adjoint functor which is precisely the universal enveloping algebra functor
![]() $C\mapsto {\mathcal {U}}(C)$
.
$C\mapsto {\mathcal {U}}(C)$
.
4.3. Vertex bialgebras
Let
![]() ${\mathcal {C}}$
be a symmetric monoidal category and
${\mathcal {C}}$
be a symmetric monoidal category and
![]() $(V,\Delta ,\varepsilon )$
be a (counital) coalgebra in
$(V,\Delta ,\varepsilon )$
be a (counital) coalgebra in
![]() ${\mathcal {C}}$
. We define the set of group-like elements
${\mathcal {C}}$
. We define the set of group-like elements
where ![]() is the unit object equipped with the canonical structure of a counital coalgebra. We say that V is connected if
is the unit object equipped with the canonical structure of a counital coalgebra. We say that V is connected if
![]() $G(V)$
contains exactly one element.
$G(V)$
contains exactly one element.
For example, let
![]() $L=\mathbb {Z}^I$
be equipped with a symmetric bilinear form and let
$L=\mathbb {Z}^I$
be equipped with a symmetric bilinear form and let
![]() ${\mathcal {C}}=\operatorname {\mathrm {Vect}}^L$
be the corresponding symmetric monoidal category. Let
${\mathcal {C}}=\operatorname {\mathrm {Vect}}^L$
be the corresponding symmetric monoidal category. Let
![]() $V\in {\mathcal {C}}$
be a coalgebra with degrees concentrated in
$V\in {\mathcal {C}}$
be a coalgebra with degrees concentrated in
![]() ${\mathbb {N}}^I\subset L$
and
${\mathbb {N}}^I\subset L$
and
![]() $\dim V_0=1$
. Then V is connected.
$\dim V_0=1$
. Then V is connected.
Following [Reference Li42, §4], we define a (local) vertex bialgebra to be a vertex algebra V equipped with a coalgebra structure
![]() $(V,\Delta ,\varepsilon )$
such that
$(V,\Delta ,\varepsilon )$
such that
![]() $\Delta :V\to V\otimes V$
and
$\Delta :V\to V\otimes V$
and
![]() $\varepsilon :V\to {\mathbb {Q}}$
are homomorphisms of vertex algebras. We say that a vertex bialgebra V is cocommutative if its coproduct is cocommutative. We define the subspace of primitive elements
$\varepsilon :V\to {\mathbb {Q}}$
are homomorphisms of vertex algebras. We say that a vertex bialgebra V is cocommutative if its coproduct is cocommutative. We define the subspace of primitive elements
An important family of cocommutative connected vertex bialgebras arises from vertex Lie algebras [Reference Han, Li and Xiao29, Reference Li42].
Proposition 4.5. [Reference Li42, §4] Let C be a vertex Lie algebra and
![]() $V={\mathcal {U}}(C)$
be its universal enveloping vertex algebra. Then there exists vertex algebra homomorphisms
$V={\mathcal {U}}(C)$
be its universal enveloping vertex algebra. Then there exists vertex algebra homomorphisms
uniquely determined by

The vertex algebra V equipped with
![]() $\Delta $
and
$\Delta $
and
![]() $\varepsilon $
is a cocommutative vertex bialgebra.
$\varepsilon $
is a cocommutative vertex bialgebra.
Proposition 4.6 [Reference Han, Li and Xiao29, Prop. 3.9]
Let C be a vertex Lie algebra,
![]() ${\mathfrak {L}}={\mathfrak {L}}_-\oplus {\mathfrak {L}}_+$
be its algebra of coefficients and
${\mathfrak {L}}={\mathfrak {L}}_-\oplus {\mathfrak {L}}_+$
be its algebra of coefficients and
![]() $V={\mathcal {U}}(C)=U({\mathfrak {L}})\otimes _{U({\mathfrak {L}}_+)}{\mathbb {Q}}$
be its universal enveloping vertex algebra. Then the canonical isomorphism
$V={\mathcal {U}}(C)=U({\mathfrak {L}})\otimes _{U({\mathfrak {L}}_+)}{\mathbb {Q}}$
be its universal enveloping vertex algebra. Then the canonical isomorphism
![]() $V\simeq U({\mathfrak {L}}_-)$
is an isomorphism of coalgebras. Moreover, the coalgebra V is connected and
$V\simeq U({\mathfrak {L}}_-)$
is an isomorphism of coalgebras. Moreover, the coalgebra V is connected and
![]() $P(V)=C$
.
$P(V)=C$
.
Conversely, we can associate a vertex Lie algebra with a vertex bialgebra.
Proposition 4.7 [Reference Han, Li and Xiao29, Prop. 4.8]
Let V be a vertex bialgebra. Then
![]() $P(V)$
is a vertex Lie subalgebra of V.
$P(V)$
is a vertex Lie subalgebra of V.
The next result is an analogue of the Milnor-Moore theorem for vertex bialgebras.
Theorem 4.8 [Reference Han, Li and Xiao29, Theorem 4.13]
Let V be a cocommutative connected vertex bialgebra. Then there is a canonical isomorphism
![]() ${\mathcal {U}}(P(V))\simeq V$
of vertex bialgebras.
${\mathcal {U}}(P(V))\simeq V$
of vertex bialgebras.
4.4. Free vertex algebras
As was observed already in [Reference Borcherds4, §4], the locality axiom contains a quantifier that does not allow one to define the free vertex algebra on a given set of generators, but if one restricts to some specific orders of locality, it is possible to define such a universal object; this has been done in [Reference Roitman57]. In this section, we recall the definition of the locality order and explain how free vertex algebras of given non-negative locality are constructed.
4.4.1. Locality order
Definition 4.9. Let
![]() $V\in {\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
be a bounded below object. We say that two fields
$V\in {\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
be a bounded below object. We say that two fields
![]() $\mathfrak {a}\in {\mathcal {F}}(V)_\alpha $
and
$\mathfrak {a}\in {\mathcal {F}}(V)_\alpha $
and
![]() $\mathfrak {b}\in {\mathcal {F}}(V)_\beta $
are (mutually) local of order
$\mathfrak {b}\in {\mathcal {F}}(V)_\beta $
are (mutually) local of order
![]() $N\in \mathbb {Z}$
if
$N\in \mathbb {Z}$
if
where the binomial expansion convention is used. Note that this condition means that
![]() $[\mathfrak {a}(z)\times _N\mathfrak {b}(w)]=0$
; see (20).
$[\mathfrak {a}(z)\times _N\mathfrak {b}(w)]=0$
; see (20).
We note that for
![]() $N\ge 0$
, the binomial expansion is finite and the locality condition becomes simply
$N\ge 0$
, the binomial expansion is finite and the locality condition becomes simply
being in agreement with the definition of locality (of unspecified order) in §4.1.1.
Lemma 4.10. Let V be a vertex algebra and
![]() $a,b\in V$
. Then
$a,b\in V$
. Then
![]() $Y(a,z),Y(b,z)$
are local of order N if and only if
$Y(a,z),Y(b,z)$
are local of order N if and only if
![]() $a(n)b=0$
for all
$a(n)b=0$
for all
![]() $n\ge N$
.
$n\ge N$
.
Proof. Let
![]() $\mathfrak {a}(z)=Y(a,z)$
and
$\mathfrak {a}(z)=Y(a,z)$
and
![]() $\mathfrak {b}(z)=Y(b,z)$
. If
$\mathfrak {b}(z)=Y(b,z)$
. If
![]() $[\mathfrak {a}(z)\times _N \mathfrak {b}(w)]=0$
, then
$[\mathfrak {a}(z)\times _N \mathfrak {b}(w)]=0$
, then
![]() $[\mathfrak {a}(z)\times _n \mathfrak {b}(w)]=0$
for all
$[\mathfrak {a}(z)\times _n \mathfrak {b}(w)]=0$
for all
![]() $n\ge N$
. This implies that
$n\ge N$
. This implies that ![]() . As
. As
![]() $Y\colon V\to {\mathcal {F}}(V)$
is injective and preserves products, we conclude that
$Y\colon V\to {\mathcal {F}}(V)$
is injective and preserves products, we conclude that
![]() $a(n)b=0$
for all
$a(n)b=0$
for all
![]() $n\ge N$
. Conversely, assume that
$n\ge N$
. Conversely, assume that
![]() $a(n)b=0$
for all
$a(n)b=0$
for all
![]() $n\ge N$
. By the Jacobi identity (25),
$n\ge N$
. By the Jacobi identity (25),
 $$ \begin{align*}[\mathfrak{a}(z)\times_N \mathfrak{b}(w)] =\operatorname{\mathrm{Res}}_u u^Nw{^{-1}} Y(\mathfrak{a}(u)b,w)\delta{\left({\frac{z-u}{w}}\right)} .\end{align*} $$
$$ \begin{align*}[\mathfrak{a}(z)\times_N \mathfrak{b}(w)] =\operatorname{\mathrm{Res}}_u u^Nw{^{-1}} Y(\mathfrak{a}(u)b,w)\delta{\left({\frac{z-u}{w}}\right)} .\end{align*} $$
Under our assumption, all powers of u on the right are non-negative, and we conclude that
![]() $[\mathfrak {a}(z)\times _N\mathfrak {b}(w)]=0$
.
$[\mathfrak {a}(z)\times _N\mathfrak {b}(w)]=0$
.
Using the binomial expansion convention in Equation (38) and extracting the coefficient of
![]() $z^{N-m-1}w^{-n-1}$
, one can obtain an equivalent collection of equations
$z^{N-m-1}w^{-n-1}$
, one can obtain an equivalent collection of equations
 $$ \begin{align} \sum_{k\ge0}(-1)^k\binom Nk & a(m-k)b(n+k)-\\ \nonumber & (-1)^{(\alpha,\beta)}\sum_{k\le N}(-1)^{k}\binom N{N-k} b(n+k)a(m-k)=0 \end{align} $$
$$ \begin{align} \sum_{k\ge0}(-1)^k\binom Nk & a(m-k)b(n+k)-\\ \nonumber & (-1)^{(\alpha,\beta)}\sum_{k\le N}(-1)^{k}\binom N{N-k} b(n+k)a(m-k)=0 \end{align} $$
for all
![]() $m,n\in \mathbb {Z}$
. If
$m,n\in \mathbb {Z}$
. If
![]() $N\ge 0$
, then the locality conditions can be written in the form
$N\ge 0$
, then the locality conditions can be written in the form
 $$ \begin{align} \sum_{k=0}^N(-1)^k\binom Nk[a(m-k),b(n+k)]=0. \end{align} $$
$$ \begin{align} \sum_{k=0}^N(-1)^k\binom Nk[a(m-k),b(n+k)]=0. \end{align} $$
4.4.2. Free vertex algebras
Let I be a set equipped with a symmetric function
![]() ${\mathcal {N}}\colon I\times I\to \mathbb {Z}$
called the locality function or just locality and a map
${\mathcal {N}}\colon I\times I\to \mathbb {Z}$
called the locality function or just locality and a map
![]() $\deg =(\deg _L,\operatorname {\mathrm {wt}}):I\to L\times {\frac 12}\mathbb {Z}$
. We consider the category
$\deg =(\deg _L,\operatorname {\mathrm {wt}}):I\to L\times {\frac 12}\mathbb {Z}$
. We consider the category
![]() $\operatorname {\mathrm {Ver}}_{{\mathcal {N}},\deg }$
of graded vertex algebras
$\operatorname {\mathrm {Ver}}_{{\mathcal {N}},\deg }$
of graded vertex algebras
![]() $V\in {\mathcal {C}}^{{\frac 12}\mathbb {Z}}=\operatorname {\mathrm {Vect}}^{L\times {\frac 12}\mathbb {Z}}$
equipped with a map
$V\in {\mathcal {C}}^{{\frac 12}\mathbb {Z}}=\operatorname {\mathrm {Vect}}^{L\times {\frac 12}\mathbb {Z}}$
equipped with a map
![]() $s\colon I\to V$
such that
$s\colon I\to V$
such that
-
(1) The image of s generates V (as a vertex algebra).
-
(2) For each
 $i\in I$
, the element
$i\in I$
, the element
 $s_i$
has degree
$s_i$
has degree
 $\deg (i)$
.
$\deg (i)$
. -
(3) For all
 $i,j\in I$
, the fields
$i,j\in I$
, the fields
 $Y(s_i,z)$
and
$Y(s_i,z)$
and
 $Y(s_j,z)$
are local of order
$Y(s_j,z)$
are local of order
 ${\mathcal {N}}(i,j)$
. Equivalently,
${\mathcal {N}}(i,j)$
. Equivalently,
 $s_i(n) s_j=0$
for all
$s_i(n) s_j=0$
for all
 $n\ge {\mathcal {N}}(i,j)$
.
$n\ge {\mathcal {N}}(i,j)$
.
Analogously to [Reference Roitman58], one proves that the category
![]() $\operatorname {\mathrm {Ver}}_{{\mathcal {N}},\deg }$
has an initial object, called the free vertex algebra with respect to locality
$\operatorname {\mathrm {Ver}}_{{\mathcal {N}},\deg }$
has an initial object, called the free vertex algebra with respect to locality
![]() ${\mathcal {N}}$
and degree
${\mathcal {N}}$
and degree
![]() $\deg $
. We shall now recall the construction of the free vertex algebra in the case of a non-negative locality function.
$\deg $
. We shall now recall the construction of the free vertex algebra in the case of a non-negative locality function.
4.4.3. Free vertex algebras of non-negative locality
Suppose that the locality function
![]() ${\mathcal {N}}$
is non-negative. We set
${\mathcal {N}}$
is non-negative. We set
The vector space
![]() ${\mathbb {Q}} X$
spanned by X can be viewed as an object of
${\mathbb {Q}} X$
spanned by X can be viewed as an object of
![]() ${\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
, where we set
${\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
, where we set
In the free associative algebra
![]() $\mathsf {T}({\mathbb {Q}} X)$
, we may consider the locality relations (40) with
$\mathsf {T}({\mathbb {Q}} X)$
, we may consider the locality relations (40) with
![]() $a,b\in I$
and
$a,b\in I$
and
![]() $N={\mathcal {N}}(a,b)$
. These relations are manifestly homogeneous, so they generate a homogeneous ideal
$N={\mathcal {N}}(a,b)$
. These relations are manifestly homogeneous, so they generate a homogeneous ideal
![]() ${\mathcal {I}}\subset \mathsf {T}({\mathbb {Q}} X)$
. The quotient
${\mathcal {I}}\subset \mathsf {T}({\mathbb {Q}} X)$
. The quotient
![]() ${\mathcal {B}} =\mathsf {T}({\mathbb {Q}} X)/{\mathcal {I}}$
by that ideal is an associative algebra in
${\mathcal {B}} =\mathsf {T}({\mathbb {Q}} X)/{\mathcal {I}}$
by that ideal is an associative algebra in
![]() ${\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
. Let us consider the subset
${\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
. Let us consider the subset
and the left
![]() ${\mathcal {B}}$
-module
${\mathcal {B}}$
-module
![]() ${\mathcal {P}}={\mathcal {B}} /{\mathcal {B}} X_+$
; we denote by
${\mathcal {P}}={\mathcal {B}} /{\mathcal {B}} X_+$
; we denote by ![]() the cyclic element of that module.
the cyclic element of that module.
Lemma 4.11. The module
![]() ${\mathcal {P}}$
is restricted, meaning that, for all
${\mathcal {P}}$
is restricted, meaning that, for all
![]() $i\in I$
and
$i\in I$
and
![]() $x\in {\mathcal {P}}$
, we have
$x\in {\mathcal {P}}$
, we have
![]() $i(n)x=0$
for
$i(n)x=0$
for
![]() $n\gg 0$
.
$n\gg 0$
.
Proof. Let
![]() $w=i_1(n_1)\dots i_p(n_p)$
be a monomial in
$w=i_1(n_1)\dots i_p(n_p)$
be a monomial in
![]() $\mathsf {T}({\mathbb {Q}} X)$
, and suppose that there exists
$\mathsf {T}({\mathbb {Q}} X)$
, and suppose that there exists
![]() $i\in I$
such that
$i\in I$
such that
![]() $i(n)w\notin {\mathcal {B}} X_+$
for arbitrary large n. We can assume that p is minimal possible. Then
$i(n)w\notin {\mathcal {B}} X_+$
for arbitrary large n. We can assume that p is minimal possible. Then
for
![]() $k\gg 0$
. Therefore, we can assume that for any
$k\gg 0$
. Therefore, we can assume that for any
![]() $k>n_1$
, we have
$k>n_1$
, we have
for
![]() $n\gg 0$
. Let
$n\gg 0$
. Let
![]() $N={\mathcal {N}}(i,i_1)$
. Then we have a locality relation
$N={\mathcal {N}}(i,i_1)$
. Then we have a locality relation
 $$ \begin{align*} \sum_{k=0}^N(-1)^k\binom Nk[i(n-k),i_1(n_1+k)]=0 \end{align*} $$
$$ \begin{align*} \sum_{k=0}^N(-1)^k\binom Nk[i(n-k),i_1(n_1+k)]=0 \end{align*} $$
in the algebra
![]() ${\mathcal {B}}$
. This relation implies that
${\mathcal {B}}$
. This relation implies that
![]() $i(n)w$
is contained in the left ideal generated by elements
$i(n)w$
is contained in the left ideal generated by elements
By our assumption, these elements are contained in
![]() ${\mathcal {B}} X_+$
for
${\mathcal {B}} X_+$
for
![]() $n\gg 0$
.
$n\gg 0$
.
This lemma implies that for every
![]() $i\in I$
, we have a field
$i\in I$
, we have a field
These fields are mutually local by construction. Let us define a derivation T of
![]() $\mathsf {T}({\mathbb {Q}} X)$
by the formula
$\mathsf {T}({\mathbb {Q}} X)$
by the formula
![]() $T i(n)=-ni(n-1)$
.
$T i(n)=-ni(n-1)$
.
Lemma 4.12. The derivation T preserves the ideal
![]() ${\mathcal {I}}$
. In particular, T induces endomorphisms of
${\mathcal {I}}$
. In particular, T induces endomorphisms of
![]() ${\mathcal {B}}$
and
${\mathcal {B}}$
and
![]() ${\mathcal {P}}$
.
${\mathcal {P}}$
.
Proof. Let us consider
![]() ${\mathbf i}(z)=\sum _{n\in \mathbb {Z}}i(n)z^{-n-1}$
as an element of
${\mathbf i}(z)=\sum _{n\in \mathbb {Z}}i(n)z^{-n-1}$
as an element of
![]() $\mathsf {T}({\mathbb {Q}} X){[\![{z^{\pm 1}}]\!]}$
. Using this notation, we see that the relations that generate
$\mathsf {T}({\mathbb {Q}} X){[\![{z^{\pm 1}}]\!]}$
. Using this notation, we see that the relations that generate
![]() ${\mathcal {I}}$
are coefficients of
${\mathcal {I}}$
are coefficients of
![]() $(z-w)^N[{\mathbf i}(z),\mathfrak {j}(w)]$
with
$(z-w)^N[{\mathbf i}(z),\mathfrak {j}(w)]$
with
![]() $N={\mathcal {N}}(i,j)$
. Since
$N={\mathcal {N}}(i,j)$
. Since
![]() $T{\mathbf i}(z)=\partial _z{\mathbf i}(z)$
, we have
$T{\mathbf i}(z)=\partial _z{\mathbf i}(z)$
, we have
and
Adding these equations, we obtain
which means that locality relations are preserved by T.
Applying the reconstruction theorem (see [Reference Kac34, Theorem 4.5] or [Reference Frenkel and Ben-Zvi20, §4.4]) to the fields
![]() ${\mathbf i}(z)\in {\mathcal {F}}({\mathcal {P}})$
and the endomorphism
${\mathbf i}(z)\in {\mathcal {F}}({\mathcal {P}})$
and the endomorphism
![]() $T\in \operatorname {\mathrm {End}}({\mathcal {P}})$
, we obtain a vertex algebra structure on
$T\in \operatorname {\mathrm {End}}({\mathcal {P}})$
, we obtain a vertex algebra structure on
![]() ${\mathcal {P}}$
with
${\mathcal {P}}$
with
The vertex algebra
![]() ${\mathcal {P}}$
is the free vertex algebra with respect to locality
${\mathcal {P}}$
is the free vertex algebra with respect to locality
![]() ${\mathcal {N}}$
and degree function
${\mathcal {N}}$
and degree function
![]() $\deg $
. We will sometimes denote the element
$\deg $
. We will sometimes denote the element ![]() by i.
by i.
4.4.4. Free vertex algebras as universal enveloping algebras
Next, we will show that the free vertex algebra
![]() ${\mathcal {P}}$
of non-negative locality can be identified with the universal enveloping algebra of a vertex Lie algebra. Let
${\mathcal {P}}$
of non-negative locality can be identified with the universal enveloping algebra of a vertex Lie algebra. Let
![]() ${\mathfrak {L}}$
be the Lie algebra with generators
${\mathfrak {L}}$
be the Lie algebra with generators
![]() $i(n)\in X$
subject to the locality relations (40) with
$i(n)\in X$
subject to the locality relations (40) with
![]() $a,b\in I$
and
$a,b\in I$
and
![]() $N={\mathcal {N}}(a,b)$
, and let
$N={\mathcal {N}}(a,b)$
, and let
![]() ${\mathfrak {L}}_+\subset {\mathfrak {L}}$
be the subalgebra generated by
${\mathfrak {L}}_+\subset {\mathfrak {L}}$
be the subalgebra generated by
![]() $X_+\subset X$
. Then we have
$X_+\subset X$
. Then we have
For every
![]() $i\in I$
, we consider
$i\in I$
, we consider
![]() ${\mathbf i}(z)=\sum _n i(n)z^{-n-1}\in {\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
. These elements are mutually local by definition; therefore, by Dong’s Lemma [Reference Li41, Prop. 3.2.7], they generate, under non-negative external products and the derivation
${\mathbf i}(z)=\sum _n i(n)z^{-n-1}\in {\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
. These elements are mutually local by definition; therefore, by Dong’s Lemma [Reference Li41, Prop. 3.2.7], they generate, under non-negative external products and the derivation
![]() $\partial _z$
, a conformal algebra
$\partial _z$
, a conformal algebra
which is a vertex Lie algebra as conditions from §4.2.3 are automatically satisfied.
Proposition 4.13. The free vertex algebra
![]() ${\mathcal {P}}$
of non-negative locality is isomorphic to the universal enveloping vertex algebra of the vertex Lie algebra C.
${\mathcal {P}}$
of non-negative locality is isomorphic to the universal enveloping vertex algebra of the vertex Lie algebra C.
Proof. First, let us show that the algebra morphism
is an isomorphism (cf. [Reference Roitman57, Prop. 3.1]). (In fact, this vertex Lie algebra is the free vertex Lie algebra with respect to locality
![]() ${\mathcal {N}}$
and degree function
${\mathcal {N}}$
and degree function
![]() $\deg $
.) To construct the inverse map, we need to show that elements
$\deg $
.) To construct the inverse map, we need to show that elements
![]() ${\mathbf i}(z)(n)$
satisfy the locality relations. This means that for
${\mathbf i}(z)(n)$
satisfy the locality relations. This means that for
![]() $N={\mathcal {N}}(i,j)$
, we have
$N={\mathcal {N}}(i,j)$
, we have
 $$ \begin{align*}\sum_{k=0}^N(-1)^k\binom Nk [{\mathbf i}(z)(m-k),\mathfrak{j}(z)(n+k)]=0\end{align*} $$
$$ \begin{align*}\sum_{k=0}^N(-1)^k\binom Nk [{\mathbf i}(z)(m-k),\mathfrak{j}(z)(n+k)]=0\end{align*} $$
in
![]() $\operatorname {\mathrm {Coeff}}(C)$
. Using the formula for the bracket in
$\operatorname {\mathrm {Coeff}}(C)$
. Using the formula for the bracket in
![]() $\operatorname {\mathrm {Coeff}}(C)$
, this equation can be written in the form
$\operatorname {\mathrm {Coeff}}(C)$
, this equation can be written in the form

Note that ![]() for
for
![]() $l\ge N$
by the locality relations. We claim that, however, for any
$l\ge N$
by the locality relations. We claim that, however, for any
![]() $0\le l<N$
, we have
$0\le l<N$
, we have
 $$ \begin{align*}\sum_{k=0}^N(-1)^k\binom Nk \binom{m-k}{l}=0. \end{align*} $$
$$ \begin{align*}\sum_{k=0}^N(-1)^k\binom Nk \binom{m-k}{l}=0. \end{align*} $$
This claim would imply the required statement. We have
 $$ \begin{align*} \sum_{k,l\ge0}\binom Nk \binom{m-k}{l}x^ky^l =\sum_{k\ge0}\binom Nk x^k(1+y)^{m-k} =(1+y)^m{\left({1+\frac x{1+y}}\right)}^N\\ =(1+x+y)^N(1+y)^{m-N}. \end{align*} $$
$$ \begin{align*} \sum_{k,l\ge0}\binom Nk \binom{m-k}{l}x^ky^l =\sum_{k\ge0}\binom Nk x^k(1+y)^{m-k} =(1+y)^m{\left({1+\frac x{1+y}}\right)}^N\\ =(1+x+y)^N(1+y)^{m-N}. \end{align*} $$
In particular, for
![]() $x=-1$
, we obtain
$x=-1$
, we obtain
 $$ \begin{align*}\sum_{k,l\ge0}(-1)^k\binom Nk \binom{m-k}{l}y^l =y^N(1+y)^{m-N}, \end{align*} $$
$$ \begin{align*}\sum_{k,l\ge0}(-1)^k\binom Nk \binom{m-k}{l}y^l =y^N(1+y)^{m-N}, \end{align*} $$
which has only powers of y that are
![]() $\ge N$
. This proves the claim.
$\ge N$
. This proves the claim.
The derivation
![]() $\partial $
on
$\partial $
on
![]() $\operatorname {\mathrm {Coeff}}(C)$
corresponds to the derivation T on
$\operatorname {\mathrm {Coeff}}(C)$
corresponds to the derivation T on
![]() ${\mathfrak {L}}\subset {\mathcal {B}}$
from Lemma 4.12. Using the isomorphism
${\mathfrak {L}}\subset {\mathcal {B}}$
from Lemma 4.12. Using the isomorphism
![]() $\varrho $
, we obtain the direct sum decomposition
$\varrho $
, we obtain the direct sum decomposition
where both subalgebras are preserved by T. By [Reference Roitman57, §3.2], the algebra
![]() ${\mathfrak {L}}_+\subset {\mathfrak {L}}$
is exactly the algebra generated by
${\mathfrak {L}}_+\subset {\mathfrak {L}}$
is exactly the algebra generated by
![]() $X_+={\left \{\left .{i(n)\in X}\ \right \vert {n\ge 0}\right \}}$
, which we introduced earlier.
$X_+={\left \{\left .{i(n)\in X}\ \right \vert {n\ge 0}\right \}}$
, which we introduced earlier.
This implies that
![]() ${\mathcal {P}}={\mathcal {B}}/{\mathcal {B}} X_+$
is isomorphic to the Verma module
${\mathcal {P}}={\mathcal {B}}/{\mathcal {B}} X_+$
is isomorphic to the Verma module
![]() $U({\mathfrak {L}})\otimes _{U({\mathfrak {L}}_+)}{\mathbb {Q}}$
as a
$U({\mathfrak {L}})\otimes _{U({\mathfrak {L}}_+)}{\mathbb {Q}}$
as a
![]() ${\mathcal {B}}$
-module, and therefore, the free vertex algebra
${\mathcal {B}}$
-module, and therefore, the free vertex algebra
![]() ${\mathcal {P}}$
is isomorphic to the universal enveloping vertex algebra
${\mathcal {P}}$
is isomorphic to the universal enveloping vertex algebra
![]() ${\mathcal {U}}({\mathfrak {C}})$
.
${\mathcal {U}}({\mathfrak {C}})$
.
4.5. Lattice vertex algebras
In this section, we recall an important class of vertex algebras called lattice vertex algebras. They play a prominent role in our work, for they can be used to construct convenient realisations of certain free vertex algebras.
4.5.1. Fock spaces
We consider the
![]() ${\mathbb {Q}}$
-vector space
${\mathbb {Q}}$
-vector space
![]() ${\mathfrak {h}}=L\otimes _{\mathbb {Z}}{\mathbb {Q}}$
associated to L and define the Heisenberg Lie algebra
${\mathfrak {h}}=L\otimes _{\mathbb {Z}}{\mathbb {Q}}$
associated to L and define the Heisenberg Lie algebra
![]() $\hat {\mathfrak {h}}$
as a one-dimensional extension
$\hat {\mathfrak {h}}$
as a one-dimensional extension
with central K and
Here and below, we define
![]() $h_n:=h\otimes t^n$
, for
$h_n:=h\otimes t^n$
, for
![]() $h\in {\mathfrak {h}}$
and
$h\in {\mathfrak {h}}$
and
![]() $n\in \mathbb {Z}$
. If we set weight degrees
$n\in \mathbb {Z}$
. If we set weight degrees
then
![]() $\hat {\mathfrak {h}}$
becomes a Lie algebra in
$\hat {\mathfrak {h}}$
becomes a Lie algebra in
![]() $\operatorname {\mathrm {Vect}}^{{\frac 12}\mathbb {Z}}$
.
$\operatorname {\mathrm {Vect}}^{{\frac 12}\mathbb {Z}}$
.
Let
![]() ${\mathsf {H}}$
be the associative Heisenberg algebra which is the quotient of the universal enveloping algebra of
${\mathsf {H}}$
be the associative Heisenberg algebra which is the quotient of the universal enveloping algebra of
![]() $\hat {\mathfrak {h}}$
modulo the ideal generated by
$\hat {\mathfrak {h}}$
modulo the ideal generated by
![]() $K-1$
. Consider the commutative subalgebra
$K-1$
. Consider the commutative subalgebra
For any
![]() $\lambda \in L{^{\vee }}=\operatorname {\mathrm {Hom}}(L,\mathbb {Z})$
, let
$\lambda \in L{^{\vee }}=\operatorname {\mathrm {Hom}}(L,\mathbb {Z})$
, let
![]() ${\mathbb {Q}}_\lambda $
be the
${\mathbb {Q}}_\lambda $
be the
![]() $1$
-dimensional module over
$1$
-dimensional module over
![]() ${\mathsf {H}}_+$
, where, for each
${\mathsf {H}}_+$
, where, for each
![]() $h\in {\mathfrak {h}}$
,
$h\in {\mathfrak {h}}$
,
![]() $h_0$
acts by multiplication with
$h_0$
acts by multiplication with
![]() $\lambda (h)$
and
$\lambda (h)$
and
![]() $h_n$
with
$h_n$
with
![]() $n>0$
acts trivially. We define the Fock space
$n>0$
acts trivially. We define the Fock space
![]() $V_\lambda $
to be the
$V_\lambda $
to be the
![]() ${\mathsf {H}}$
-module
${\mathsf {H}}$
-module
As a vector space, it is isomorphic to
![]() $S({\mathfrak {h}}\otimes t{^{-1}}{\mathbb {C}}[t{^{-1}}])$
. We denote the cyclic vector of
$S({\mathfrak {h}}\otimes t{^{-1}}{\mathbb {C}}[t{^{-1}}])$
. We denote the cyclic vector of
![]() $V_\lambda $
by
$V_\lambda $
by
![]() ${|\lambda \rangle }$
. In particular, for any
${|\lambda \rangle }$
. In particular, for any
![]() $\alpha \in L$
, we may consider the linear function
$\alpha \in L$
, we may consider the linear function
![]() $(\alpha ,\cdot )\in L{^{\vee }}$
, and by abuse of notation, we shall denote the corresponding Fock space by
$(\alpha ,\cdot )\in L{^{\vee }}$
, and by abuse of notation, we shall denote the corresponding Fock space by
![]() $V_\alpha $
and its generator by
$V_\alpha $
and its generator by
![]() ${|\alpha \rangle }$
.
${|\alpha \rangle }$
.
For any
![]() $\alpha \in L$
, we have a field
$\alpha \in L$
, we have a field
![]() $\alpha (z)=\sum _{n\in \mathbb {Z}}\alpha _nz^{-n-1}\in {\mathcal {F}}(V_0)$
. One knows that
$\alpha (z)=\sum _{n\in \mathbb {Z}}\alpha _nz^{-n-1}\in {\mathcal {F}}(V_0)$
. One knows that
![]() $V_0$
has a vertex algebra structure with the vacuum
$V_0$
has a vertex algebra structure with the vacuum
![]() ${| 0\rangle }$
and with
${| 0\rangle }$
and with
In particular,
![]() $Y(\alpha _{-1}{|0\rangle },z)=\alpha (z)$
. Similarly, using
$Y(\alpha _{-1}{|0\rangle },z)=\alpha (z)$
. Similarly, using
![]() $\operatorname {\mathrm {id}}_{V_\lambda }$
in the above formula, we can equip
$\operatorname {\mathrm {id}}_{V_\lambda }$
in the above formula, we can equip
![]() $V_\lambda $
with a module structure over the vertex algebra
$V_\lambda $
with a module structure over the vertex algebra
![]() $V_0$
.
$V_0$
.
4.5.2. Vertex operators and lattice vertex algebras
Let us consider the total Fock space
This space is automatically L-graded. We equip it with a weight grading for which
![]() $\operatorname {\mathrm {wt}}({|\beta \rangle })={\frac 12}(\beta ,\beta )$
, so that
$\operatorname {\mathrm {wt}}({|\beta \rangle })={\frac 12}(\beta ,\beta )$
, so that
 $$ \begin{align} \operatorname{\mathrm{wt}}(\alpha^{(1)}_{n_1}\dots \alpha^{(p)}_{n_p}{|\beta\rangle}) ={\frac12}(\beta,\beta)-\sum_{k=1}^p n_k\in{\frac12}\mathbb{Z}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{wt}}(\alpha^{(1)}_{n_1}\dots \alpha^{(p)}_{n_p}{|\beta\rangle}) ={\frac12}(\beta,\beta)-\sum_{k=1}^p n_k\in{\frac12}\mathbb{Z}. \end{align} $$
Thus,
![]() $V_L$
may be considered as an object in
$V_L$
may be considered as an object in
![]() ${\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
.
${\mathcal {C}}^{{\frac 12}\mathbb {Z}}$
.
Let
![]() $S_\alpha \colon V_L\to V_L$
be the unique linear map satisfying
$S_\alpha \colon V_L\to V_L$
be the unique linear map satisfying
-
(1)
 $S_\alpha {|\beta \rangle }={|{\alpha +\beta }\rangle }$
.
$S_\alpha {|\beta \rangle }={|{\alpha +\beta }\rangle }$
. -
(2)
 $[h_n,S_\alpha ]=0$
for
$[h_n,S_\alpha ]=0$
for
 $n\ne 0$
and
$n\ne 0$
and
 $h\in {\mathfrak {h}}$
.
$h\in {\mathfrak {h}}$
.
Let
![]() $z^{(\alpha ,-)}\colon V_L\to V_L{[\![{z^{\pm 1}}]\!]}$
be the map that acts on
$z^{(\alpha ,-)}\colon V_L\to V_L{[\![{z^{\pm 1}}]\!]}$
be the map that acts on
![]() $V_\beta $
by multiplication with
$V_\beta $
by multiplication with
![]() $z^{(\alpha ,\beta )}$
. Note that
$z^{(\alpha ,\beta )}$
. Note that
For any
![]() $\alpha \in L$
, we let
$\alpha \in L$
, we let
 $$ \begin{align*}\Gamma^-_\alpha(z)= \exp{\left({-\sum_{n<0}\frac{\alpha_n}nz^{-n}}\right)} ,\qquad \Gamma^+_\alpha(z)=\exp{\left({-\sum_{n>0}\frac{\alpha_n}nz^{-n}}\right)} .\end{align*} $$
$$ \begin{align*}\Gamma^-_\alpha(z)= \exp{\left({-\sum_{n<0}\frac{\alpha_n}nz^{-n}}\right)} ,\qquad \Gamma^+_\alpha(z)=\exp{\left({-\sum_{n>0}\frac{\alpha_n}nz^{-n}}\right)} .\end{align*} $$
Using these series, we now define the vertex operator (a field on
![]() $V_L$
)
$V_L$
)
Let us check that the operators
![]() $\Gamma _\alpha (z)$
are pairwise local.
$\Gamma _\alpha (z)$
are pairwise local.
Lemma 4.14. For any
![]() $\alpha ,\beta \in L$
, we have
$\alpha ,\beta \in L$
, we have
Equivalently,
![]() $\Gamma _\alpha (z)$
,
$\Gamma _\alpha (z)$
,
![]() $\Gamma _\beta (z)$
are local of order
$\Gamma _\beta (z)$
are local of order
![]() $-(\alpha ,\beta )$
.
$-(\alpha ,\beta )$
.
Proof. First of all, we have
which follows from the fact that
 $$ \begin{align*} &\exp{\left({ {\left[{\sum_{n>0}\frac{\alpha_n}nz^{-n}, \sum_{n<0}\frac{\beta_n}nw^{-n}}\right]} }\right)} =\\& \quad\exp{\left({(\alpha,\beta)\sum_{n>0}\frac{(w/z)^n}{-n}}\right)} ={\left({1-\frac wz}\right)}^{(\alpha,\beta)}. \end{align*} $$
$$ \begin{align*} &\exp{\left({ {\left[{\sum_{n>0}\frac{\alpha_n}nz^{-n}, \sum_{n<0}\frac{\beta_n}nw^{-n}}\right]} }\right)} =\\& \quad\exp{\left({(\alpha,\beta)\sum_{n>0}\frac{(w/z)^n}{-n}}\right)} ={\left({1-\frac wz}\right)}^{(\alpha,\beta)}. \end{align*} $$
Now we obtain
 $$ \begin{align} \Gamma_\alpha(z)\Gamma_\beta(w)& =S_\alpha \Gamma^-_\alpha(z)\Gamma^+_\alpha(z)z^{(\alpha,-)}\cdot S_\beta \Gamma^-_\beta(w)\Gamma^+_\beta(w)w^{(\beta,-)}\\\nonumber&=z^{(\alpha,\beta)}S_{\alpha+\beta} \Gamma^-_\alpha(z)\Gamma^+_\alpha(z)\Gamma^-_\beta(w)\Gamma^+_\beta(w) z^{(\alpha,-)} w^{(\beta,-)} \\\nonumber&=(z-w)^{(\alpha,\beta)}S_{\alpha+\beta} \Gamma^-_\alpha(z)\Gamma^-_\beta(w)\Gamma^+_\alpha(z)\Gamma^+_\beta(w) z^{(\alpha,-)} w^{(\beta,-)}, \end{align} $$
$$ \begin{align} \Gamma_\alpha(z)\Gamma_\beta(w)& =S_\alpha \Gamma^-_\alpha(z)\Gamma^+_\alpha(z)z^{(\alpha,-)}\cdot S_\beta \Gamma^-_\beta(w)\Gamma^+_\beta(w)w^{(\beta,-)}\\\nonumber&=z^{(\alpha,\beta)}S_{\alpha+\beta} \Gamma^-_\alpha(z)\Gamma^+_\alpha(z)\Gamma^-_\beta(w)\Gamma^+_\beta(w) z^{(\alpha,-)} w^{(\beta,-)} \\\nonumber&=(z-w)^{(\alpha,\beta)}S_{\alpha+\beta} \Gamma^-_\alpha(z)\Gamma^-_\beta(w)\Gamma^+_\alpha(z)\Gamma^+_\beta(w) z^{(\alpha,-)} w^{(\beta,-)}, \end{align} $$
and similarly for
![]() $\Gamma _\beta (w)\Gamma _\alpha (z)$
. This implies the first claim of the lemma. For the second claim, it is enough to note that
$\Gamma _\beta (w)\Gamma _\alpha (z)$
. This implies the first claim of the lemma. For the second claim, it is enough to note that
![]() $(w-z)^{-(\alpha ,\beta )}=(-1)^{(\alpha ,\beta )}(-w+z)^{-(\alpha ,\beta )}$
and recall Definition 4.9.
$(w-z)^{-(\alpha ,\beta )}=(-1)^{(\alpha ,\beta )}(-w+z)^{-(\alpha ,\beta )}$
and recall Definition 4.9.
Note that the weight of z is
![]() $-1$
and the weight of
$-1$
and the weight of
![]() $\alpha _n$
is
$\alpha _n$
is
![]() $-n$
. Therefore,
$-n$
. Therefore,
![]() $\alpha _n z^{-n}$
has weight zero, and the same is true for
$\alpha _n z^{-n}$
has weight zero, and the same is true for
![]() $\Gamma _\alpha ^{\pm }(z)$
. The element
$\Gamma _\alpha ^{\pm }(z)$
. The element
![]() $S_\alpha z^{(\alpha ,-)}{|\beta \rangle }=z^{(\alpha ,\beta )}{|{\alpha +\beta }\rangle }$
has weight
$S_\alpha z^{(\alpha ,-)}{|\beta \rangle }=z^{(\alpha ,\beta )}{|{\alpha +\beta }\rangle }$
has weight
![]() ${\frac 12}(\alpha ,\alpha )+{\frac 12}(\beta ,\beta )$
. We conclude that the operator
${\frac 12}(\alpha ,\alpha )+{\frac 12}(\beta ,\beta )$
. We conclude that the operator
![]() $\Gamma _\alpha (z)$
has weight
$\Gamma _\alpha (z)$
has weight
![]() ${\frac 12}(\alpha ,\alpha )$
, which is also the weight of
${\frac 12}(\alpha ,\alpha )$
, which is also the weight of
![]() ${|\alpha \rangle }$
. The total Fock space
${|\alpha \rangle }$
. The total Fock space
![]() $V_L$
has a structure of an L-graded vertex algebra, called the lattice vertex algebra, that extends the vertex algebra structure on
$V_L$
has a structure of an L-graded vertex algebra, called the lattice vertex algebra, that extends the vertex algebra structure on
![]() $V_0$
and satisfies
$V_0$
and satisfies
4.5.3. Principal free vertex algebras
Let
![]() $(e_i)_{i\in I}$
be a basis of the lattice L. Recall that, according to Lemma 4.14, the fields
$(e_i)_{i\in I}$
be a basis of the lattice L. Recall that, according to Lemma 4.14, the fields
![]() $\Gamma _i(z):=\Gamma _{e_i}(z)$
and
$\Gamma _i(z):=\Gamma _{e_i}(z)$
and
![]() $\Gamma _j(z):=\Gamma _{e_j}(z)$
on
$\Gamma _j(z):=\Gamma _{e_j}(z)$
on
![]() $V_L$
are local of order
$V_L$
are local of order
![]() $-(e_i,e_j)$
. We define the locality function
$-(e_i,e_j)$
. We define the locality function
and the degree map
 $$ \begin{align*}\deg:I\to L\times{\frac12}\mathbb{Z},\qquad \deg(i)={\left({e_i,{\frac12}(e_i,e_i)}\right)}.\end{align*} $$
$$ \begin{align*}\deg:I\to L\times{\frac12}\mathbb{Z},\qquad \deg(i)={\left({e_i,{\frac12}(e_i,e_i)}\right)}.\end{align*} $$
Let
![]() ${\mathcal {P}}$
be the free vertex algebra with respect to locality
${\mathcal {P}}$
be the free vertex algebra with respect to locality
![]() ${\mathcal {N}}$
and degree
${\mathcal {N}}$
and degree
![]() $\deg $
, which we shall also call the principal free vertex algebra. By the universality property of the free vertex algebra, there is a unique morphism of graded vertex algebras
$\deg $
, which we shall also call the principal free vertex algebra. By the universality property of the free vertex algebra, there is a unique morphism of graded vertex algebras
By [Reference Roitman58, Theorem 2], this morphism is injective. Therefore, the free vertex algebra
![]() ${\mathcal {P}}$
can be identified with the vertex subalgebra of
${\mathcal {P}}$
can be identified with the vertex subalgebra of
![]() $V_L$
generated by elements
$V_L$
generated by elements
![]() ${|{e_i}\rangle }$
,
${|{e_i}\rangle }$
,
![]() $i\in I$
. This subalgebra was studied in [Reference Milas and Penn47] under the name principal subalgebra.
$i\in I$
. This subalgebra was studied in [Reference Milas and Penn47] under the name principal subalgebra.
5. CoHA and the free vertex algebra
From now onwards, we restrict ourselves to the situation considered in §3, so that Q is a symmetric quiver with the set of vertices I, and
![]() $L=\mathbb {Z}^I$
is a lattice equipped with the Euler form
$L=\mathbb {Z}^I$
is a lattice equipped with the Euler form
![]() $\chi $
of the quiver Q. Then I parametrises the standard basis of L, and we can consider the corresponding principal free vertex algebra
$\chi $
of the quiver Q. Then I parametrises the standard basis of L, and we can consider the corresponding principal free vertex algebra
![]() ${\mathcal {P}}$
from §4.5.3, which we shall usually denote by
${\mathcal {P}}$
from §4.5.3, which we shall usually denote by
![]() ${\mathcal {P}}_Q$
. The locality function of that free vertex algebra is given by
${\mathcal {P}}_Q$
. The locality function of that free vertex algebra is given by
Hence, we see that
![]() ${\mathcal {N}}(i,j)\ge 0$
for
${\mathcal {N}}(i,j)\ge 0$
for
![]() $i\ne j$
and
$i\ne j$
and
![]() ${\mathcal {N}}(i,i)\ge -1$
. This property together with Lemma 5.1 implies that the construction of §4.4.3 for free vertex algebras of non-negative locality applies.
${\mathcal {N}}(i,i)\ge -1$
. This property together with Lemma 5.1 implies that the construction of §4.4.3 for free vertex algebras of non-negative locality applies.
In this section, we shall unravel a deep relationship between the principal free vertex algebra
![]() ${\mathcal {P}}_Q$
and the CoHA
${\mathcal {P}}_Q$
and the CoHA
![]() ${\mathcal {H}}_Q$
. In §5.2, we shall see that there is an isomorphism of vector spaces between the graded dual
${\mathcal {H}}_Q$
. In §5.2, we shall see that there is an isomorphism of vector spaces between the graded dual
![]() ${\mathcal {P}}{_Q^{\vee }}$
and
${\mathcal {P}}{_Q^{\vee }}$
and
![]() ${\mathcal {H}}_Q$
. In §5.3, we shall show that this isomorphism allows one to recover the algebra structure of
${\mathcal {H}}_Q$
. In §5.3, we shall show that this isomorphism allows one to recover the algebra structure of
![]() ${\mathcal {H}}_Q$
. Finally, in §5.4, we use our results to obtain a new proof of Efimov’s positivity theorem for Donaldson–Thomas invariants.
${\mathcal {H}}_Q$
. Finally, in §5.4, we use our results to obtain a new proof of Efimov’s positivity theorem for Donaldson–Thomas invariants.
5.1. Three incarnations
In this section, we shall discuss three different incarnations of the same vertex algebra
![]() ${\mathcal {P}}_Q$
: as a principal free algebra, as a free algebra of non-negative locality, and as the universal enveloping algebra of a vertex Lie algebra. From (40), we know that for
${\mathcal {P}}_Q$
: as a principal free algebra, as a free algebra of non-negative locality, and as the universal enveloping algebra of a vertex Lie algebra. From (40), we know that for
![]() ${\mathcal {N}}(i,j)\ge 0$
, the locality relation between
${\mathcal {N}}(i,j)\ge 0$
, the locality relation between
![]() $Y(i,z)$
and
$Y(i,z)$
and
![]() $Y(j,z)$
is a collection of ‘honest’ Lie algebra relations (finite combinations of Lie brackets). In our situation, the only possible negative value of the locality function is
$Y(j,z)$
is a collection of ‘honest’ Lie algebra relations (finite combinations of Lie brackets). In our situation, the only possible negative value of the locality function is
![]() ${\mathcal {N}}(i,j)=-1$
, in which case,
${\mathcal {N}}(i,j)=-1$
, in which case,
![]() $i=j$
and
$i=j$
and
![]() $\chi (e_i,e_i)=1$
.
$\chi (e_i,e_i)=1$
.
Lemma 5.1. Let V be a graded vertex algebra, and suppose that
![]() $\mathfrak {a}\in {\mathcal {F}}(V)_\alpha $
is a field with
$\mathfrak {a}\in {\mathcal {F}}(V)_\alpha $
is a field with
![]() $\chi (\alpha ,\alpha )\equiv 1\ \pmod {2}$
. Then
$\chi (\alpha ,\alpha )\equiv 1\ \pmod {2}$
. Then
![]() $\mathfrak {a}$
is local with itself of order
$\mathfrak {a}$
is local with itself of order
![]() $-1$
if and only if it is local with itself of order
$-1$
if and only if it is local with itself of order
![]() $0$
.
$0$
.
Proof. We already know that locality of order
![]() $-1$
implies locality of order
$-1$
implies locality of order
![]() $0$
, so we only need to prove the reverse implication. The locality of order
$0$
, so we only need to prove the reverse implication. The locality of order
![]() $-1$
is equivalent to the relations
$-1$
is equivalent to the relations
for all
![]() $m,n\in \mathbb {Z}$
. The locality of order
$m,n\in \mathbb {Z}$
. The locality of order
![]() $0$
is equivalent to
$0$
is equivalent to
It remains to note that, assuming that
![]() $m\ge n$
, Condition (45) can be rewritten as
$m\ge n$
, Condition (45) can be rewritten as
 $$ \begin{align*}\sum_{k=0}^{m-n}a(m-k)a(n+k)=0, \end{align*} $$
$$ \begin{align*}\sum_{k=0}^{m-n}a(m-k)a(n+k)=0, \end{align*} $$
which vanishes whenever (46) holds.
It follows from Lemma 5.1 that if
![]() ${\mathcal {N}}(i,i)=-1$
, then the field
${\mathcal {N}}(i,i)=-1$
, then the field
![]() $Y(i,z)$
is local of order
$Y(i,z)$
is local of order
![]() $0$
with itself, so the principal free vertex algebra
$0$
with itself, so the principal free vertex algebra
![]() ${\mathcal {P}}_Q$
coincides with the free vertex algebra for the non-negative locality function
${\mathcal {P}}_Q$
coincides with the free vertex algebra for the non-negative locality function
![]() ${\mathcal {N}}_+:=\max ({\mathcal {N}},0)$
. In particular, even though some values of the locality function for
${\mathcal {N}}_+:=\max ({\mathcal {N}},0)$
. In particular, even though some values of the locality function for
![]() ${\mathcal {P}}_Q$
can be negative, Proposition 4.13 implies that
${\mathcal {P}}_Q$
can be negative, Proposition 4.13 implies that
![]() ${\mathcal {P}}_Q$
is isomorphic to the universal enveloping vertex algebra
${\mathcal {P}}_Q$
is isomorphic to the universal enveloping vertex algebra
![]() ${\mathcal {U}}({\mathfrak {C}})$
of a vertex Lie algebra
${\mathcal {U}}({\mathfrak {C}})$
of a vertex Lie algebra
![]() ${\mathfrak {C}}$
.
${\mathfrak {C}}$
.
Let us recall some notation for future reference. We consider the sets
and define
![]() ${\mathfrak {L}}$
to be the Lie algebra generated by X subject to locality relations (40) with
${\mathfrak {L}}$
to be the Lie algebra generated by X subject to locality relations (40) with
![]() $a,b\in I$
and
$a,b\in I$
and
![]() $N={\mathcal {N}}_+(a,b)$
, and
$N={\mathcal {N}}_+(a,b)$
, and
![]() ${\mathfrak {L}}_+\subset {\mathfrak {L}}$
to be the subalgebra generated by
${\mathfrak {L}}_+\subset {\mathfrak {L}}$
to be the subalgebra generated by
![]() $X_+\subset X$
.
$X_+\subset X$
.
For every
![]() $i\in I$
, we consider
$i\in I$
, we consider
![]() ${\mathbf i}(z)=\sum _n i(n)z^{-n-1}\in {\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
, and we define
${\mathbf i}(z)=\sum _n i(n)z^{-n-1}\in {\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
, and we define
![]() ${\mathfrak {C}}\subset {\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
to be the vertex Lie algebra generated by these series. We know from Proposition 4.13 that
${\mathfrak {C}}\subset {\mathfrak {L}}{[\![{z^{\pm 1}}]\!]}$
to be the vertex Lie algebra generated by these series. We know from Proposition 4.13 that
![]() ${\mathfrak {L}}\simeq \operatorname {\mathrm {Coeff}}(C)$
and that we have a direct sum decomposition
${\mathfrak {L}}\simeq \operatorname {\mathrm {Coeff}}(C)$
and that we have a direct sum decomposition
where
![]() ${\mathfrak {L}}_{\pm }\subset {\mathfrak {L}}$
are Lie subalgebras closed under the derivation
${\mathfrak {L}}_{\pm }\subset {\mathfrak {L}}$
are Lie subalgebras closed under the derivation
We have an isomorphism of graded vector spaces (compatible with derivations)
Moreover, the principal free vertex algebra
![]() ${\mathcal {P}}_Q$
is isomorphic to the universal enveloping vertex algebra of the vertex Lie algebra C
${\mathcal {P}}_Q$
is isomorphic to the universal enveloping vertex algebra of the vertex Lie algebra C
We also have an isomorphism of graded vector spaces
5.2. The graded dual of the principal free vertex algebra
Our first goal is to exhibit a relationship between the underlying objects of
![]() ${\mathcal {P}}_Q$
and
${\mathcal {P}}_Q$
and
![]() ${\mathcal {H}}_Q$
. Recall from (41) that
${\mathcal {H}}_Q$
. Recall from (41) that
![]() ${\mathcal {P}}_Q$
is equipped with the L-degree as well as the weight
${\mathcal {P}}_Q$
is equipped with the L-degree as well as the weight

As we are aiming to relate vertex algebras to cohomological Hall algebras, we shall implement a relationship between half-integer weights and integer cohomological degrees, defining, for
![]() $u\in {\mathcal {P}}_Q$
, its (cohomological) degree to be
$u\in {\mathcal {P}}_Q$
, its (cohomological) degree to be
If we superpose the L-degree and the degree we just defined,
![]() ${\mathcal {P}}_Q$
becomes an object of
${\mathcal {P}}_Q$
becomes an object of
![]() $\operatorname {\mathrm {Vect}}^{L\times \mathbb {Z}}$
with finite-dimensional components
$\operatorname {\mathrm {Vect}}^{L\times \mathbb {Z}}$
with finite-dimensional components
![]() ${\mathcal {P}}_{Q,{\mathbf {d}}}^n$
, for
${\mathcal {P}}_{Q,{\mathbf {d}}}^n$
, for
![]() ${\mathbf {d}}\in {\mathbb {N}}^I$
and
${\mathbf {d}}\in {\mathbb {N}}^I$
and
![]() $n\in \mathbb {Z}$
; this immediately follows from the fact that the lattice realisation of free vertex algebras allows us to view
$n\in \mathbb {Z}$
; this immediately follows from the fact that the lattice realisation of free vertex algebras allows us to view
![]() ${\mathcal {P}}_Q$
as a subspace of the total Fock space
${\mathcal {P}}_Q$
as a subspace of the total Fock space
![]() $V_L$
. We define the graded dual space of
$V_L$
. We define the graded dual space of
![]() ${\mathcal {P}}_Q$
by the formula
${\mathcal {P}}_Q$
by the formula
Let us describe this graded dual directly. For a dimension vector
![]() ${\mathbf {d}}\in {\mathbb {N}}^I$
, let
${\mathbf {d}}\in {\mathbb {N}}^I$
, let
![]() $p={\left \lvert {\mathbf {d}}\right \rvert }$
and
$p={\left \lvert {\mathbf {d}}\right \rvert }$
and
![]() $\operatorname {\mathrm {Hom}} j=(j_1,\dots ,j_p)$
be any sequence of vertices with
$\operatorname {\mathrm {Hom}} j=(j_1,\dots ,j_p)$
be any sequence of vertices with
![]() $e_{j_1}+\cdots +e_{j_p}={\mathbf {d}}$
. We shall associate to such sequence
$e_{j_1}+\cdots +e_{j_p}={\mathbf {d}}$
. We shall associate to such sequence
![]() $\operatorname {\mathrm {Hom}} j$
and
$\operatorname {\mathrm {Hom}} j$
and
![]() $\xi \in {\mathcal {P}}{_{0,{\mathbf {d}}}^{\vee }}$
an element
$\xi \in {\mathcal {P}}{_{0,{\mathbf {d}}}^{\vee }}$
an element
![]() $F_{\xi ,\operatorname {\mathrm {Hom}} j}(z_1,\ldots ,z_p) \in {\mathbb {Q}}{(\;\!\!\!({z_1})\!\!\!\;)}\dots {(\;\!\!\!({z_p})\!\!\!\;)}$
given by the formula
$F_{\xi ,\operatorname {\mathrm {Hom}} j}(z_1,\ldots ,z_p) \in {\mathbb {Q}}{(\;\!\!\!({z_1})\!\!\!\;)}\dots {(\;\!\!\!({z_p})\!\!\!\;)}$
given by the formula
Lemma 5.2. For any
![]() $\xi \in {\mathcal {P}}{_{0,{\mathbf {d}}}^{\vee }}$
, the Laurent series
$\xi \in {\mathcal {P}}{_{0,{\mathbf {d}}}^{\vee }}$
, the Laurent series
![]() $F_{\xi ,\operatorname {\mathrm {Hom}} j}(z_1,\ldots ,z_p)$
is completely symmetric under the action of
$F_{\xi ,\operatorname {\mathrm {Hom}} j}(z_1,\ldots ,z_p)$
is completely symmetric under the action of
![]() $\Sigma _p$
permuting simultaneously the vertices
$\Sigma _p$
permuting simultaneously the vertices
![]() $j_k$
and the variables
$j_k$
and the variables
![]() $z_k$
. Moreover, this Laurent series is a polynomial in
$z_k$
. Moreover, this Laurent series is a polynomial in
![]() $z_1,\ldots , z_p$
.
$z_1,\ldots , z_p$
.
Proof. By the locality properties of the free vertex algebra
![]() ${\mathcal {P}}_Q$
, we have
${\mathcal {P}}_Q$
, we have
This shows that the Laurent series
is fully symmetric under the action of
![]() $\Sigma _p$
: the product
$\Sigma _p$
: the product
is multiplied by the exactly correct factors to make it completely symmetric.
To prove that
![]() $F_{\xi ,\operatorname {\mathrm {Hom}} j}(z_1,\ldots ,z_p)$
is a polynomial, we shall argue as follows. Note that
$F_{\xi ,\operatorname {\mathrm {Hom}} j}(z_1,\ldots ,z_p)$
is a polynomial, we shall argue as follows. Note that

Examining this formula, we immediately conclude that the Laurent series
![]() $F_{\xi ,\operatorname {\mathrm {Hom}} j} (z_1,\ldots ,z_p)$
does not contain any negative power of the last variable
$F_{\xi ,\operatorname {\mathrm {Hom}} j} (z_1,\ldots ,z_p)$
does not contain any negative power of the last variable
![]() $z_p$
: the vacuum vector
$z_p$
: the vacuum vector ![]() of
of
![]() ${\mathcal {P}}_Q$
is annihilated by all generators
${\mathcal {P}}_Q$
is annihilated by all generators
![]() $j_p(n)$
with
$j_p(n)$
with
![]() $n\ge 0$
, and multiplication by the product
$n\ge 0$
, and multiplication by the product
![]() $\prod _{k<l}(z_k-z_l)^{{\mathcal {N}}(j_k,j_l)}$
does not create negative powers of
$\prod _{k<l}(z_k-z_l)^{{\mathcal {N}}(j_k,j_l)}$
does not create negative powers of
![]() $z_p$
because of the convention for the geometric series expansion of
$z_p$
because of the convention for the geometric series expansion of
![]() $(z+w)^n$
. Since we already know that the result is symmetric, we conclude that (51) has no negative powers of any variable, and thus is a formal power series in
$(z+w)^n$
. Since we already know that the result is symmetric, we conclude that (51) has no negative powers of any variable, and thus is a formal power series in
![]() $z_1$
, …,
$z_1$
, …,
![]() $z_p$
. Finally, since we are dealing with the graded dual vector space, the linear functional
$z_p$
. Finally, since we are dealing with the graded dual vector space, the linear functional
![]() $\xi $
is supported at finitely many degrees, and so in
$\xi $
is supported at finitely many degrees, and so in
one ends up ignoring all coefficients of our formal power series but finitely many, and we obtain a polynomial.
We shall now state and prove the main result of this section. For a dimension vector
![]() ${\mathbf {d}}\in {\mathbb {N}}^I$
, we now make a choice of a concrete sequence of vertices
${\mathbf {d}}\in {\mathbb {N}}^I$
, we now make a choice of a concrete sequence of vertices
![]() $\operatorname {\mathrm {Hom}} i=(i_1,\dots ,i_p)$
with
$\operatorname {\mathrm {Hom}} i=(i_1,\dots ,i_p)$
with
![]() $e_{i_1}+\cdots +e_{i_p}={\mathbf {d}}$
. For that, we choose an order of I, use this order to identify I with
$e_{i_1}+\cdots +e_{i_p}={\mathbf {d}}$
. For that, we choose an order of I, use this order to identify I with
![]() ${{\left \{{1,\dots ,r}\right \}}}$
, where
${{\left \{{1,\dots ,r}\right \}}}$
, where
![]() $r=|I|$
, and put
$r=|I|$
, and put
We shall use formal variables
![]() $z_{{\mathbf {d}}_1+\dots +{\mathbf {d}}_{j-1}+k}=x_{j,k}$
associated to this sequence of vertices. Recall from §3.2 that
$z_{{\mathbf {d}}_1+\dots +{\mathbf {d}}_{j-1}+k}=x_{j,k}$
associated to this sequence of vertices. Recall from §3.2 that
is a graded algebra with
![]() $\deg (x_{j,k})=2$
(corresponding to weight
$\deg (x_{j,k})=2$
(corresponding to weight
![]() $-1$
, cf. §4.1.2).
$-1$
, cf. §4.1.2).
Proposition 5.3. We have an isomorphism of graded vector spaces
Specifically, for any dimension vector
![]() ${\mathbf {d}}$
, the isomorphism
${\mathbf {d}}$
, the isomorphism
![]() ${{\mathcal {P}}}{_{Q,\mathbf {d}}^{\vee }}\to {\mathcal {H}}_{Q,{\mathbf {d}}}=\Lambda _{\mathbf {d}}[-\chi ({\mathbf {d}},{\mathbf {d}})]$
is given by the formula
${{\mathcal {P}}}{_{Q,\mathbf {d}}^{\vee }}\to {\mathcal {H}}_{Q,{\mathbf {d}}}=\Lambda _{\mathbf {d}}[-\chi ({\mathbf {d}},{\mathbf {d}})]$
is given by the formula
Proof. We begin with noticing that, according to Lemma 5.2, the polynomial
![]() $F_\xi $
in variables
$F_\xi $
in variables
![]() $x_{j,k}$
is symmetric with respect to the action of the group
$x_{j,k}$
is symmetric with respect to the action of the group
![]() $\Sigma _{\mathbf {d}}=\prod _{i\in I}\Sigma _{{\mathbf {d}}_i}$
(the action of a permutation from
$\Sigma _{\mathbf {d}}=\prod _{i\in I}\Sigma _{{\mathbf {d}}_i}$
(the action of a permutation from
![]() $\Sigma _{\mathbf {d}}$
simultaneously on the vertices
$\Sigma _{\mathbf {d}}$
simultaneously on the vertices
![]() $i_k$
and the variables
$i_k$
and the variables
![]() $z_k$
is the same as the action on the variables only). Thus, F is a well-defined map into
$z_k$
is the same as the action on the variables only). Thus, F is a well-defined map into
![]() $\Lambda _{\mathbf {d}}[-\chi ({\mathbf {d}},{\mathbf {d}})]$
.
$\Lambda _{\mathbf {d}}[-\chi ({\mathbf {d}},{\mathbf {d}})]$
.
Let us first check that F is a map of degree zero. Recall that
![]() $Y(i,z)$
has weight
$Y(i,z)$
has weight
![]() ${\frac 12}\chi (e_i,e_i)$
, so by our convention
${\frac 12}\chi (e_i,e_i)$
, so by our convention
![]() $\deg (u)=-2\operatorname {\mathrm {wt}}(u)$
, the degree of
$\deg (u)=-2\operatorname {\mathrm {wt}}(u)$
, the degree of
![]() $Y(i,z)$
is equal to
$Y(i,z)$
is equal to
![]() $-\chi (e_i,e_i)$
. Therefore,
$-\chi (e_i,e_i)$
. Therefore,
![]() $F_\xi $
has degree
$F_\xi $
has degree
 $$ \begin{align*} \deg(\xi)+2\sum_{k<l}{\mathcal{N}}(i_k,i_l)-&\sum_k\chi(e_{i_k},e_{i_k}) =\\ &\deg(\xi)-\sum_{k,l}\chi(e_{i_k},e_{i_l}) =\deg(\xi)-\chi({\mathbf{d}},{\mathbf{d}}). \end{align*} $$
$$ \begin{align*} \deg(\xi)+2\sum_{k<l}{\mathcal{N}}(i_k,i_l)-&\sum_k\chi(e_{i_k},e_{i_k}) =\\ &\deg(\xi)-\sum_{k,l}\chi(e_{i_k},e_{i_l}) =\deg(\xi)-\chi({\mathbf{d}},{\mathbf{d}}). \end{align*} $$
This constant shift of degrees by
![]() $-\chi ({\mathbf {d}},{\mathbf {d}})$
means exactly that the map
$-\chi ({\mathbf {d}},{\mathbf {d}})$
means exactly that the map
has degree zero.
Let us show that F is injective. Suppose that for some
![]() $\xi \in {\mathcal {P}}{_{Q,{\mathbf {d}}}^{\vee }}$
, we have
$\xi \in {\mathcal {P}}{_{Q,{\mathbf {d}}}^{\vee }}$
, we have
![]() $F_\xi =0$
. According to Lemma 5.2, this implies that
$F_\xi =0$
. According to Lemma 5.2, this implies that
for any sequence of vertices with
![]() $e_{i_1}+\cdots +e_{i_p}={\mathbf {d}}$
. Since
$e_{i_1}+\cdots +e_{i_p}={\mathbf {d}}$
. Since
![]() $F_\xi $
is a polynomial, its product with
$F_\xi $
is a polynomial, its product with
![]() $\prod _{k<l}(z_k-z_l)^{-{\mathcal {N}}(j_k,j_l)}$
(expanded according to the binomial expansion convention) is well defined, so we may conclude that
$\prod _{k<l}(z_k-z_l)^{-{\mathcal {N}}(j_k,j_l)}$
(expanded according to the binomial expansion convention) is well defined, so we may conclude that
Extracting coefficients of individual monomials
![]() $z_1^{m_1}\cdots z_p^{m_p}$
, we see that
$z_1^{m_1}\cdots z_p^{m_p}$
, we see that
![]() $\xi $
vanishes on all vectors
$\xi $
vanishes on all vectors ![]() , so
, so
![]() $\xi =0$
.
$\xi =0$
.
Let us finally show that F is surjective. For that, we shall use the lattice vertex operator realisation, replacing
![]() $Y(i_k,z_k)$
by vertex operators
$Y(i_k,z_k)$
by vertex operators
![]() $\Gamma _{{i_k}}(z_k)=\Gamma _{e_{i_k}}(z_k)$
and
$\Gamma _{{i_k}}(z_k)=\Gamma _{e_{i_k}}(z_k)$
and ![]() by
by
![]() ${|0\rangle }$
. Recall that we established the equality (44)
${|0\rangle }$
. Recall that we established the equality (44)
This implies, more generally, that
 $$ \begin{align*} & \Gamma_{i_1}(z_1)\dots\Gamma_{i_p}(z_p)=\\ & \prod_{k<l}(z_k-z_l)^{\chi(e_{i_k},e_{i_l})}\Gamma^-_{i_1}(z_1)\dots\Gamma^-_{i_p}(z_p)\Gamma^+_{i_1}(z_1)\dots\Gamma^+_{i_p}(z_p) z_1^{(e_{i_1},-)}\cdots z_p^{(e_{i_p},-)}, \end{align*} $$
$$ \begin{align*} & \Gamma_{i_1}(z_1)\dots\Gamma_{i_p}(z_p)=\\ & \prod_{k<l}(z_k-z_l)^{\chi(e_{i_k},e_{i_l})}\Gamma^-_{i_1}(z_1)\dots\Gamma^-_{i_p}(z_p)\Gamma^+_{i_1}(z_1)\dots\Gamma^+_{i_p}(z_p) z_1^{(e_{i_1},-)}\cdots z_p^{(e_{i_p},-)}, \end{align*} $$
and therefore,

where the last equality uses the definition
![]() $\chi (e_{i_k},e_{i_l})=-{\mathcal {N}}(i_k,i_l)$
of the Euler form and the obvious fact that
$\chi (e_{i_k},e_{i_l})=-{\mathcal {N}}(i_k,i_l)$
of the Euler form and the obvious fact that
![]() $\Gamma ^+_{i}(z)|0\rangle =|0\rangle $
for all i. Thus, we may write
$\Gamma ^+_{i}(z)|0\rangle =|0\rangle $
for all i. Thus, we may write

If we now expand the exponentials, we obtain the formal infinite sum of all standard basis vectors
![]() $\prod _{j_s,n_s} e_{j_s,-n_s}^{a_s}$
of the Fock space
$\prod _{j_s,n_s} e_{j_s,-n_s}^{a_s}$
of the Fock space
![]() $V_{\mathbf {d}}$
with coefficients being scalar multiples of monomials in the power sum
$V_{\mathbf {d}}$
with coefficients being scalar multiples of monomials in the power sum
![]() $\Sigma _{\mathbf {d}}$
-symmetric functions [Reference Macdonald46]. Since every
$\Sigma _{\mathbf {d}}$
-symmetric functions [Reference Macdonald46]. Since every
![]() $\Sigma _{\mathbf {d}}$
-symmetric function is a polynomial in the power sum symmetric functions, we may obtain each
$\Sigma _{\mathbf {d}}$
-symmetric function is a polynomial in the power sum symmetric functions, we may obtain each
![]() $\Sigma _{\mathbf {d}}$
-symmetric function for a suitable choice of a linear functional on
$\Sigma _{\mathbf {d}}$
-symmetric function for a suitable choice of a linear functional on
![]() $V_{\mathbf {d}}$
, and the surjectivity claim follows.
$V_{\mathbf {d}}$
, and the surjectivity claim follows.
Using our result, we can immediately recover the formula for the Poincaré series
![]() $Z({\mathcal {P}}_Q,x,q)$
proved in [Reference Milas and Penn47, Theorem 5.3] using combinatorial bases for free vertex algebras.
$Z({\mathcal {P}}_Q,x,q)$
proved in [Reference Milas and Penn47, Theorem 5.3] using combinatorial bases for free vertex algebras.
Corollary 5.4. We have
 $$ \begin{align*}Z({\mathcal{P}}_Q,x,q) =\sum_{{\mathbf{d}}\in{\mathbb{N}}^I} \frac{(-q^{{\frac12}})^{\chi({\mathbf{d}},{\mathbf{d}})}}{(q)_{\mathbf{d}}}x^{\mathbf{d}}. \end{align*} $$
$$ \begin{align*}Z({\mathcal{P}}_Q,x,q) =\sum_{{\mathbf{d}}\in{\mathbb{N}}^I} \frac{(-q^{{\frac12}})^{\chi({\mathbf{d}},{\mathbf{d}})}}{(q)_{\mathbf{d}}}x^{\mathbf{d}}. \end{align*} $$
Proof. By Proposition 3.2, we have
 $$ \begin{align*}Z({\mathcal{H}}_Q,x,q) =\sum_{{\mathbf{d}}\in{\mathbb{N}}^I} \frac{(-q^{\frac12})^{-\chi({\mathbf{d}},{\mathbf{d}})}}{(q{^{-1}})_{\mathbf{d}}}x^{\mathbf{d}}.\end{align*} $$
$$ \begin{align*}Z({\mathcal{H}}_Q,x,q) =\sum_{{\mathbf{d}}\in{\mathbb{N}}^I} \frac{(-q^{\frac12})^{-\chi({\mathbf{d}},{\mathbf{d}})}}{(q{^{-1}})_{\mathbf{d}}}x^{\mathbf{d}}.\end{align*} $$
However, by the established isomorphism, we have
![]() $Z({\mathcal {P}}_Q,x,q)=Z({\mathcal {P}}{_Q^{\vee }},x,q{^{-1}})=Z({\mathcal {H}}_Q,x,q{^{-1}})$
.
$Z({\mathcal {P}}_Q,x,q)=Z({\mathcal {P}}{_Q^{\vee }},x,q{^{-1}})=Z({\mathcal {H}}_Q,x,q{^{-1}})$
.
5.3. The coalgebra structure of the principal free vertex algebra
Our next goal is to unravel a canonical coproduct on
![]() ${\mathcal {P}}_Q$
(cf. Proposition 4.5) and to relate it to the product on
${\mathcal {P}}_Q$
(cf. Proposition 4.5) and to relate it to the product on
![]() ${\mathcal {H}}_Q$
. The universal enveloping algebra
${\mathcal {H}}_Q$
. The universal enveloping algebra
![]() $U({\mathfrak {L}})$
is a bialgebra, with the canonical coproduct
$U({\mathfrak {L}})$
is a bialgebra, with the canonical coproduct
![]() $\Delta $
. Because of this coproduct, the tensor product
$\Delta $
. Because of this coproduct, the tensor product
![]() ${\mathcal {P}}_Q\otimes {\mathcal {P}}_Q$
acquires a
${\mathcal {P}}_Q\otimes {\mathcal {P}}_Q$
acquires a
![]() $U({\mathfrak {L}})$
-module structure; note that the action of
$U({\mathfrak {L}})$
-module structure; note that the action of
![]() $U({\mathfrak {L}})$
has obvious signs arising from the braiding.
$U({\mathfrak {L}})$
has obvious signs arising from the braiding.
Proposition 5.5. There exists a unique morphism of
![]() $U({\mathfrak {L}})$
-modules
$U({\mathfrak {L}})$
-modules
![]() $\delta \colon {\mathcal {P}}_Q\to {\mathcal {P}}_Q\otimes {\mathcal {P}}_Q$
for which
$\delta \colon {\mathcal {P}}_Q\to {\mathcal {P}}_Q\otimes {\mathcal {P}}_Q$
for which ![]() . This morphism makes
. This morphism makes
![]() ${\mathcal {P}}_Q$
a cocommutative coassociative coalgebra.
${\mathcal {P}}_Q$
a cocommutative coassociative coalgebra.
Proof. Recall that
![]() ${\mathcal {P}}_Q$
may also be described as
${\mathcal {P}}_Q$
may also be described as
![]() $U({\mathfrak {L}})/U({\mathfrak {L}})X_+$
, where
$U({\mathfrak {L}})/U({\mathfrak {L}})X_+$
, where
The
![]() $U({\mathfrak {L}})$
-module morphism condition implies that
$U({\mathfrak {L}})$
-module morphism condition implies that
for all
![]() $w\in {\mathcal {P}}_Q$
, and so it is clear that if the morphism
$w\in {\mathcal {P}}_Q$
, and so it is clear that if the morphism
![]() $\delta $
exists, then it is unique, and is induced by
$\delta $
exists, then it is unique, and is induced by
![]() $\Delta $
. Thus, all we have to show is that
$\Delta $
. Thus, all we have to show is that
![]() $\Delta $
descends to the quotient by the left ideal generated by
$\Delta $
descends to the quotient by the left ideal generated by
![]() $X_+$
, which follows from the property
$X_+$
, which follows from the property
Recall that we have an isomorphism of graded vector spaces (50)
The above coproduct on
![]() ${\mathcal {P}}_Q$
can be identified with the canonical coproduct on
${\mathcal {P}}_Q$
can be identified with the canonical coproduct on
![]() $U({\mathfrak {L}}_-)$
(cf. Proposition 4.6). We are now ready to state and prove the main result of this section.
$U({\mathfrak {L}}_-)$
(cf. Proposition 4.6). We are now ready to state and prove the main result of this section.
Theorem 5.6. The isomorphism
![]() $F\colon {\mathcal {P}}{_Q^{\vee }}\to {\mathcal {H}}_Q$
of Proposition 5.3 sends the product
$F\colon {\mathcal {P}}{_Q^{\vee }}\to {\mathcal {H}}_Q$
of Proposition 5.3 sends the product
![]() $\delta ^\vee $
of the commutative associative algebra
$\delta ^\vee $
of the commutative associative algebra
![]() ${\mathcal {P}}_Q^\vee $
to the shuffle product of
${\mathcal {P}}_Q^\vee $
to the shuffle product of
![]() ${\mathcal {H}}_Q$
.
${\mathcal {H}}_Q$
.
Proof. Suppose that
![]() $\zeta \in {\mathcal {P}}_{Q,{\mathbf {d}}}^\vee $
,
$\zeta \in {\mathcal {P}}_{Q,{\mathbf {d}}}^\vee $
,
![]() $\xi \in {\mathcal {P}}_{Q,{\mathbf {e}}}^\vee $
and
$\xi \in {\mathcal {P}}_{Q,{\mathbf {e}}}^\vee $
and
![]() $\operatorname {\mathrm {Hom}} i=(i_1,\dots ,i_p)$
is a sequence of vertices such that
$\operatorname {\mathrm {Hom}} i=(i_1,\dots ,i_p)$
is a sequence of vertices such that
![]() $\sum _{k}e_{i_k}={\mathbf {d}}+{\mathbf {e}}$
. According to the proof of Proposition 5.3,
$\sum _{k}e_{i_k}={\mathbf {d}}+{\mathbf {e}}$
. According to the proof of Proposition 5.3,
The map
![]() $\delta ^\vee $
is completely defined by
$\delta ^\vee $
is completely defined by
for all
![]() $u\in {\mathcal {P}}_Q$
. Note that
$u\in {\mathcal {P}}_Q$
. Note that

where
![]() $\kappa (A,B)=\sum _{a>b}\chi ({i_a},{i_b})$
, for
$\kappa (A,B)=\sum _{a>b}\chi ({i_a},{i_b})$
, for
![]() $A\sqcup B=[1,p]={{\left \{{1,\dots ,p}\right \}}}$
, and the products over A and B are taken in the increasing order. For the calculation of the symmetric polynomial (53), we need to consider only
$A\sqcup B=[1,p]={{\left \{{1,\dots ,p}\right \}}}$
, and the products over A and B are taken in the increasing order. For the calculation of the symmetric polynomial (53), we need to consider only
![]() $A,B$
with
$A,B$
with
![]() ${\mathbf {dim}}(A)=\sum _{a\in A}e_{i_a}={\mathbf {d}}$
and
${\mathbf {dim}}(A)=\sum _{a\in A}e_{i_a}={\mathbf {d}}$
and
![]() ${\mathbf {dim}}(B)={\mathbf {e}}$
. Recalling that the pairing of
${\mathbf {dim}}(B)={\mathbf {e}}$
. Recalling that the pairing of
![]() ${\mathcal {P}}_{Q,{\mathbf {d}}}^\vee \otimes {\mathcal {P}}_{Q,{\mathbf {e}}}^\vee $
with
${\mathcal {P}}_{Q,{\mathbf {d}}}^\vee \otimes {\mathcal {P}}_{Q,{\mathbf {e}}}^\vee $
with
![]() ${\mathcal {P}}_{Q,{\mathbf {d}}}\otimes {\mathcal {P}}_{Q,{\mathbf {e}}}$
produces an extra sign
${\mathcal {P}}_{Q,{\mathbf {d}}}\otimes {\mathcal {P}}_{Q,{\mathbf {e}}}$
produces an extra sign
![]() $(-1)^{\chi ({\mathbf {d}},{\mathbf {e}})}$
according to the braiding, we see that
$(-1)^{\chi ({\mathbf {d}},{\mathbf {e}})}$
according to the braiding, we see that
![]() $F_{\delta ^\vee (\zeta \otimes \xi )}$
is equal to
$F_{\delta ^\vee (\zeta \otimes \xi )}$
is equal to

The product
![]() $\prod _{k<l}(z_k-z_l)^{{\mathcal {N}}(i_k,i_l)}$
is equal to the product of four terms, according to whether each of the two elements k and l belongs to A or to B. Note that
$\prod _{k<l}(z_k-z_l)^{{\mathcal {N}}(i_k,i_l)}$
is equal to the product of four terms, according to whether each of the two elements k and l belongs to A or to B. Note that

is precisely
![]() $F_\zeta $
, and
$F_\zeta $
, and

is precisely
![]() $F_\xi $
, so we just need to investigate the factor by which their product is multiplied; that is,
$F_\xi $
, so we just need to investigate the factor by which their product is multiplied; that is,
 $$ \begin{align*} (-1)^{\kappa(A,B)+\chi({\mathbf{d}},{\mathbf{e}})} \prod_{{{\substack{{a<b}\\{a\in A,b\in B}}}}} (z_{a}-z_{b})^{{\mathcal{N}}(i_{a},i_{b})} \prod_{{{\substack{{b<a}\\{a\in A,b\in B}}}}} (z_{b}-z_{a})^{{\mathcal{N}}(i_{b},i_{a})} \\ =(-1)^{\kappa(A,B)+\chi({\mathbf{d}},{\mathbf{e}})} \prod_{{{\substack{{b<a}\\{a\in A,b\in B}}}}}(-1)^{{\mathcal{N}}(i_{a},i_{b})} \prod_{a\in A, b\in B} (z_{a}-z_{b})^{{\mathcal{N}}(i_a,i_b)}, \\ =(-1)^{\chi({\mathbf{d}},{\mathbf{e}})} \prod_{a\in A, b\in B}(z_{a}-z_{b})^{{\mathcal{N}}(i_a,i_b)} =\prod_{a\in A, b\in B} (z_{b}-z_{a})^{{\mathcal{N}}(i_a,i_b)}. \end{align*} $$
$$ \begin{align*} (-1)^{\kappa(A,B)+\chi({\mathbf{d}},{\mathbf{e}})} \prod_{{{\substack{{a<b}\\{a\in A,b\in B}}}}} (z_{a}-z_{b})^{{\mathcal{N}}(i_{a},i_{b})} \prod_{{{\substack{{b<a}\\{a\in A,b\in B}}}}} (z_{b}-z_{a})^{{\mathcal{N}}(i_{b},i_{a})} \\ =(-1)^{\kappa(A,B)+\chi({\mathbf{d}},{\mathbf{e}})} \prod_{{{\substack{{b<a}\\{a\in A,b\in B}}}}}(-1)^{{\mathcal{N}}(i_{a},i_{b})} \prod_{a\in A, b\in B} (z_{a}-z_{b})^{{\mathcal{N}}(i_a,i_b)}, \\ =(-1)^{\chi({\mathbf{d}},{\mathbf{e}})} \prod_{a\in A, b\in B}(z_{a}-z_{b})^{{\mathcal{N}}(i_a,i_b)} =\prod_{a\in A, b\in B} (z_{b}-z_{a})^{{\mathcal{N}}(i_a,i_b)}. \end{align*} $$
Recalling the shuffle product formula (8), we see that
so the isomorphism F recovers precisely the shuffle product of CoHA.
5.4. A new proof of positivity of Donaldson–Thomas invariants
The above results together with the isomorphism of graded vector spaces (50)
have an interesting consequence: another proof of Efimov’s positivity theorem for refined Donaldson–Thomas invariants [Reference Efimov14, Theorem 1.1]. To see that, we shall study the Lie algebra
![]() ${\mathfrak {L}}_-$
in more detail. Recall from §5.1 that
${\mathfrak {L}}_-$
in more detail. Recall from §5.1 that
![]() ${\mathfrak {L}}_-$
is stable under the derivation
${\mathfrak {L}}_-$
is stable under the derivation
![]() $\partial \colon {\mathfrak {L}}\to {\mathfrak {L}}$
.
$\partial \colon {\mathfrak {L}}\to {\mathfrak {L}}$
.
Theorem 5.7. Let Q be a symmetric quiver. Then the coalgebra
![]() ${\mathcal {H}}{_Q^{\vee }}$
has a canonical structure of a cocommutative connected vertex bialgebra. The space of primitive elements
${\mathcal {H}}{_Q^{\vee }}$
has a canonical structure of a cocommutative connected vertex bialgebra. The space of primitive elements
is a vertex Lie algebra (also having a structure of a Lie algebra) such that
![]() ${\mathcal {H}}{_Q^{\vee }}\simeq {\mathcal {U}}(C)$
as vertex bialgebras. The derivation
${\mathcal {H}}{_Q^{\vee }}\simeq {\mathcal {U}}(C)$
as vertex bialgebras. The derivation
![]() $\partial $
on C has L-degree zero and cohomological degree
$\partial $
on C has L-degree zero and cohomological degree
![]() $-2$
, and C is a free
$-2$
, and C is a free
![]() ${\mathbb {Q}}[\partial ]$
-module such that the space of generators
${\mathbb {Q}}[\partial ]$
-module such that the space of generators
has finite-dimensional components
![]() $W_{\mathbf {d}}$
and
$W_{\mathbf {d}}$
and
![]() $k\equiv \chi ({\mathbf {d}},{\mathbf {d}})\pmod 2$
whenever
$k\equiv \chi ({\mathbf {d}},{\mathbf {d}})\pmod 2$
whenever
![]() $W_{\mathbf {d}}^k\ne 0$
.
$W_{\mathbf {d}}^k\ne 0$
.
Proof. We have
![]() ${\mathcal {H}}{_Q^{\vee }}\simeq {\mathcal {P}}_Q\simeq {\mathcal {U}}(C)$
for the vertex Lie algebra C; see §5.1. Therefore,
${\mathcal {H}}{_Q^{\vee }}\simeq {\mathcal {P}}_Q\simeq {\mathcal {U}}(C)$
for the vertex Lie algebra C; see §5.1. Therefore,
![]() ${\mathcal {H}}{_Q^{\vee }}$
has a structure of a cocommutative connected vertex bialgebra and
${\mathcal {H}}{_Q^{\vee }}$
has a structure of a cocommutative connected vertex bialgebra and
![]() $P({\mathcal {H}}{_Q^{\vee }})\simeq C$
by Propositions 4.5 and 4.6. We can identify C with
$P({\mathcal {H}}{_Q^{\vee }})\simeq C$
by Propositions 4.5 and 4.6. We can identify C with
![]() ${\mathfrak {L}}_-$
, and we will show that
${\mathfrak {L}}_-$
, and we will show that
![]() ${\mathfrak {L}}_-$
satisfies the required properties. Theorem 5.6 implies that we have an isomorphism of coalgebras
${\mathfrak {L}}_-$
satisfies the required properties. Theorem 5.6 implies that we have an isomorphism of coalgebras
Let us define another derivation of
![]() ${\mathfrak {L}}$
, which we shall denote t; it acts on the generators of
${\mathfrak {L}}$
, which we shall denote t; it acts on the generators of
![]() ${\mathfrak {L}}$
by the formula
${\mathfrak {L}}$
by the formula
![]() $t(i(n))=-i(n+1)$
. By direct inspection, t preserves all relations of
$t(i(n))=-i(n+1)$
. By direct inspection, t preserves all relations of
![]() ${\mathfrak {L}}$
, and thus acts on this algebra. Moreover, this derivation preserves the subalgebra
${\mathfrak {L}}$
, and thus acts on this algebra. Moreover, this derivation preserves the subalgebra
![]() ${\mathfrak {L}}_+$
, and so acts on the vector space
${\mathfrak {L}}_+$
, and so acts on the vector space
![]() ${\mathfrak {L}}/{\mathfrak {L}}_+\simeq {\mathfrak {L}}_-$
. We note that
${\mathfrak {L}}/{\mathfrak {L}}_+\simeq {\mathfrak {L}}_-$
. We note that
![]() $[\partial ,t]=\operatorname {\mathrm {id}}$
on the space of generators; it follows that
$[\partial ,t]=\operatorname {\mathrm {id}}$
on the space of generators; it follows that
![]() $[\partial ,t]={\left \lvert {\mathbf {d}}\right \rvert }\cdot \operatorname {\mathrm {id}}$
on each graded component
$[\partial ,t]={\left \lvert {\mathbf {d}}\right \rvert }\cdot \operatorname {\mathrm {id}}$
on each graded component
![]() $({\mathfrak {L}}_-)_{\mathbf {d}}$
. Thus, each such component is a
$({\mathfrak {L}}_-)_{\mathbf {d}}$
. Thus, each such component is a
![]() $\mathbb {Z}$
-graded module over the Weyl algebra
$\mathbb {Z}$
-graded module over the Weyl algebra
![]() $A_1={\mathbb {Q}}[t,\partial ]$
of polynomial differential operators on the line (on which
$A_1={\mathbb {Q}}[t,\partial ]$
of polynomial differential operators on the line (on which
![]() $\partial $
acts by an endomorphism of weight
$\partial $
acts by an endomorphism of weight
![]() $1$
and t acts by an endomorphism of weight
$1$
and t acts by an endomorphism of weight
![]() $-1$
). Since we can embed
$-1$
). Since we can embed
![]() $({\mathfrak {L}}_-)_{\mathbf {d}}\subset {\mathcal {P}}_{0,{\mathbf {d}}}\subset V_{\mathbf {d}}$
(the Fock space), weights of
$({\mathfrak {L}}_-)_{\mathbf {d}}\subset {\mathcal {P}}_{0,{\mathbf {d}}}\subset V_{\mathbf {d}}$
(the Fock space), weights of
![]() $({\mathfrak {L}}_-)_{\mathbf {d}}$
are bounded from below. Therefore, by Lemma 5.8, we obtain
$({\mathfrak {L}}_-)_{\mathbf {d}}$
are bounded from below. Therefore, by Lemma 5.8, we obtain
![]() ${\mathfrak {L}}_-\simeq W\otimes {\mathbb {Q}}[\partial ]$
, for
${\mathfrak {L}}_-\simeq W\otimes {\mathbb {Q}}[\partial ]$
, for
![]() $W\simeq {\mathfrak {L}}_-/\partial {\mathfrak {L}}_-$
.
$W\simeq {\mathfrak {L}}_-/\partial {\mathfrak {L}}_-$
.
The Fock space
![]() $V_{\mathbf {d}}$
has finite-dimensional weight components, and its weights are bounded below. Moreover, each vector of
$V_{\mathbf {d}}$
has finite-dimensional weight components, and its weights are bounded below. Moreover, each vector of
![]() $V_{\mathbf {d}}$
is obtained from
$V_{\mathbf {d}}$
is obtained from
![]() ${|{\mathbf {d}}\rangle }$
by action of elements of integer weights; hence, all weights of
${|{\mathbf {d}}\rangle }$
by action of elements of integer weights; hence, all weights of
![]() $V_{\mathbf {d}}$
are of the form
$V_{\mathbf {d}}$
are of the form
![]() ${\frac 12}\chi ({\mathbf {d}},{\mathbf {d}})+n$
, for some
${\frac 12}\chi ({\mathbf {d}},{\mathbf {d}})+n$
, for some
![]() $n\in \mathbb {Z}$
. The corresponding degree is congruent to
$n\in \mathbb {Z}$
. The corresponding degree is congruent to
![]() $\chi ({\mathbf {d}},{\mathbf {d}})\pmod 2$
. The same applies to
$\chi ({\mathbf {d}},{\mathbf {d}})\pmod 2$
. The same applies to
![]() $W_{\mathbf {d}}\subset V_{\mathbf {d}}$
, and we conclude that
$W_{\mathbf {d}}\subset V_{\mathbf {d}}$
, and we conclude that
![]() $\operatorname {\mathrm {ch}}(W_{\mathbf {d}})\in {\mathbb {N}}{(\;\!\!\!({q^{\frac 12}})\!\!\!\;)}$
. It remains to establish that
$\operatorname {\mathrm {ch}}(W_{\mathbf {d}})\in {\mathbb {N}}{(\;\!\!\!({q^{\frac 12}})\!\!\!\;)}$
. It remains to establish that
![]() $W_{\mathbf {d}}$
is finite-dimensional, and for this, we will show that
$W_{\mathbf {d}}$
is finite-dimensional, and for this, we will show that
![]() $\operatorname {\mathrm {ch}}(W_{\mathbf {d}})\in {\mathbb {N}}[q^{\pm {\frac 12}}]$
.
$\operatorname {\mathrm {ch}}(W_{\mathbf {d}})\in {\mathbb {N}}[q^{\pm {\frac 12}}]$
.
Since
![]() ${\mathcal {H}}{_Q^{\vee }}\simeq U({\mathcal {L}}_-)$
and
${\mathcal {H}}{_Q^{\vee }}\simeq U({\mathcal {L}}_-)$
and
![]() ${\mathfrak {L}}_-\simeq W\otimes {\mathbb {Q}}[\partial ]$
, we obtain
${\mathfrak {L}}_-\simeq W\otimes {\mathbb {Q}}[\partial ]$
, we obtain
 $$ \begin{align*}Z({\mathcal{H}}_Q,x,q{^{-1}})=\operatorname{\mathrm{Exp}}{\left({Z({\mathfrak{L}}_-,x,q)}\right)} =\operatorname{\mathrm{Exp}}{\left({\frac{Z(W,x,q)}{1-q}}\right)}. \end{align*} $$
$$ \begin{align*}Z({\mathcal{H}}_Q,x,q{^{-1}})=\operatorname{\mathrm{Exp}}{\left({Z({\mathfrak{L}}_-,x,q)}\right)} =\operatorname{\mathrm{Exp}}{\left({\frac{Z(W,x,q)}{1-q}}\right)}. \end{align*} $$
Applying formula (15) for DT invariants, we obtain
meaning that
![]() $\operatorname {\mathrm {ch}}(W_{\mathbf {d}})=\Omega _{\mathbf {d}}(q{^{-1}})$
. Let us now use characters of CoHA-modules. According to (16), for any
$\operatorname {\mathrm {ch}}(W_{\mathbf {d}})=\Omega _{\mathbf {d}}(q{^{-1}})$
. Let us now use characters of CoHA-modules. According to (16), for any
![]() ${\mathbf {w}}\in {\mathbb {N}}^I$
, we have
${\mathbf {w}}\in {\mathbb {N}}^I$
, we have
 $$ \begin{align*}Z(\mathcal M_{{\mathbf{w}}},x,q{^{-1}})= \operatorname{\mathrm{Exp}}{\left({\sum_{\mathbf{d}}\frac{q^{{\mathbf{w}}\cdot {\mathbf{d}}}-1}{q-1}(-1)^{\chi({\mathbf{d}},{\mathbf{d}})}\Omega_{\mathbf{d}}(q{^{-1}})x^{\mathbf{d}}}\right)}. \end{align*} $$
$$ \begin{align*}Z(\mathcal M_{{\mathbf{w}}},x,q{^{-1}})= \operatorname{\mathrm{Exp}}{\left({\sum_{\mathbf{d}}\frac{q^{{\mathbf{w}}\cdot {\mathbf{d}}}-1}{q-1}(-1)^{\chi({\mathbf{d}},{\mathbf{d}})}\Omega_{\mathbf{d}}(q{^{-1}})x^{\mathbf{d}}}\right)}. \end{align*} $$
All components
![]() $\mathcal M_{{\mathbf {w}},{\mathbf {d}}}$
of the CoHA module
$\mathcal M_{{\mathbf {w}},{\mathbf {d}}}$
of the CoHA module
![]() $\mathcal M_{\mathbf {w}}$
are finite-dimensional (as the cohomology of an algebraic variety); hence,
$\mathcal M_{\mathbf {w}}$
are finite-dimensional (as the cohomology of an algebraic variety); hence,
![]() $Z(\mathcal M{_{{\mathbf {w}}},x,q^{-1}})\in \mathbb {Z}[q^{\pm {\frac 12}}]{[\![{x_i{\colon } i\in I}]\!]}$
. This implies that for all
$Z(\mathcal M{_{{\mathbf {w}}},x,q^{-1}})\in \mathbb {Z}[q^{\pm {\frac 12}}]{[\![{x_i{\colon } i\in I}]\!]}$
. This implies that for all
![]() ${\mathbf {d}}$
,
${\mathbf {d}}$
,
 $$ \begin{align*}\frac{q^{{\mathbf{w}}\cdot {\mathbf{d}}}-1}{q-1}\operatorname{\mathrm{ch}}(W_{\mathbf{d}}) =\frac{q^{{\mathbf{w}}\cdot {\mathbf{d}}}-1}{q-1}\Omega_{\mathbf{d}}(q{^{-1}})\end{align*} $$
$$ \begin{align*}\frac{q^{{\mathbf{w}}\cdot {\mathbf{d}}}-1}{q-1}\operatorname{\mathrm{ch}}(W_{\mathbf{d}}) =\frac{q^{{\mathbf{w}}\cdot {\mathbf{d}}}-1}{q-1}\Omega_{\mathbf{d}}(q{^{-1}})\end{align*} $$
is an element of
![]() ${\mathbb {Q}}[q^{\pm {\frac 12}}]$
(actually
${\mathbb {Q}}[q^{\pm {\frac 12}}]$
(actually
![]() $\mathbb {Z}[q^{\pm {\frac 12}}]$
, but we do not need this). We can choose
$\mathbb {Z}[q^{\pm {\frac 12}}]$
, but we do not need this). We can choose
![]() ${\mathbf {w}}\in {\mathbb {N}}^I$
such that
${\mathbf {w}}\in {\mathbb {N}}^I$
such that
![]() ${\mathbf {w}}\cdot {\mathbf {d}}>0$
. We have just shown that the product of the polynomial
${\mathbf {w}}\cdot {\mathbf {d}}>0$
. We have just shown that the product of the polynomial
![]() $\frac {q^{{\mathbf {w}}\cdot {\mathbf {d}}}-1}{q-1}\in {\mathbb {N}}[q]$
and the series
$\frac {q^{{\mathbf {w}}\cdot {\mathbf {d}}}-1}{q-1}\in {\mathbb {N}}[q]$
and the series
![]() $\operatorname {\mathrm {ch}}(W_{\mathbf {d}})\in {\mathbb {N}}{(\;\!\!\!({q^{{\frac 12}}})\!\!\!\;)}$
is a Laurent polynomial. This implies that
$\operatorname {\mathrm {ch}}(W_{\mathbf {d}})\in {\mathbb {N}}{(\;\!\!\!({q^{{\frac 12}}})\!\!\!\;)}$
is a Laurent polynomial. This implies that
![]() $\operatorname {\mathrm {ch}}(W_{\mathbf {d}})\in {\mathbb {N}}[q^{\pm {\frac 12}}]$
, as required.
$\operatorname {\mathrm {ch}}(W_{\mathbf {d}})\in {\mathbb {N}}[q^{\pm {\frac 12}}]$
, as required.
Lemma 5.8. Let
![]() $A_1={\mathbb {Q}}[t,\partial ]$
be the Weyl algebra (with
$A_1={\mathbb {Q}}[t,\partial ]$
be the Weyl algebra (with
![]() $\partial t-t\partial =1$
) equipped with the weight grading
$\partial t-t\partial =1$
) equipped with the weight grading
![]() $\operatorname {\mathrm {wt}}(\partial )=1$
,
$\operatorname {\mathrm {wt}}(\partial )=1$
,
![]() $\operatorname {\mathrm {wt}}(t)=-1$
, and let
$\operatorname {\mathrm {wt}}(t)=-1$
, and let
![]() $M=\bigoplus _{n\in \mathbb {Z}}M_n$
be a bounded below graded
$M=\bigoplus _{n\in \mathbb {Z}}M_n$
be a bounded below graded
![]() $A_1$
-module. Then M is a free module over
$A_1$
-module. Then M is a free module over
![]() ${\mathbb {Q}}[\partial ]$
. More precisely,
${\mathbb {Q}}[\partial ]$
. More precisely,
![]() $\partial \colon M\to M$
is injective, and we have
$\partial \colon M\to M$
is injective, and we have
![]() $M=\bigoplus _{n\ge 0}\partial ^n(V)$
, for any graded subspace
$M=\bigoplus _{n\ge 0}\partial ^n(V)$
, for any graded subspace
![]() $V\subset M$
such that
$V\subset M$
such that
![]() $M=V\oplus \operatorname {\mathrm {im}}(\partial )$
.
$M=V\oplus \operatorname {\mathrm {im}}(\partial )$
.
Proof. Assume that
![]() $\partial v=0$
for some (homogeneous)
$\partial v=0$
for some (homogeneous)
![]() $v\in M$
. Then the subspace
$v\in M$
. Then the subspace
![]() ${{\left \langle t^nv{\colon } n\ge 0\right \rangle }}$
is an
${{\left \langle t^nv{\colon } n\ge 0\right \rangle }}$
is an
![]() $A_1$
- submodule. It is finite-dimensional as
$A_1$
- submodule. It is finite-dimensional as
![]() $t^nv=0$
, for
$t^nv=0$
, for
![]() $n\gg 0$
, by degree reasons. But there are no nonzero finite-dimensional
$n\gg 0$
, by degree reasons. But there are no nonzero finite-dimensional
![]() $A_1$
-modules; hence, we conclude that
$A_1$
-modules; hence, we conclude that
![]() $v=0$
.
$v=0$
.
Let
![]() $V\subset M$
be a graded subspace such that
$V\subset M$
be a graded subspace such that
![]() $M=V\oplus \operatorname {\mathrm {im}}(\partial )$
. If the sum
$M=V\oplus \operatorname {\mathrm {im}}(\partial )$
. If the sum
![]() $\sum _{n\ge 0}\partial ^n(V)$
is not direct, we can find
$\sum _{n\ge 0}\partial ^n(V)$
is not direct, we can find
![]() $v_k\in V$
such that
$v_k\in V$
such that
![]() $\sum _{k=0}^n\partial ^k(v_k)=0$
and
$\sum _{k=0}^n\partial ^k(v_k)=0$
and
![]() $v_n\ne 0$
. As
$v_n\ne 0$
. As
![]() $\partial $
is injective, we can assume that
$\partial $
is injective, we can assume that
![]() $v_0\ne 0$
. But
$v_0\ne 0$
. But
![]() $v_0\in V\cap \operatorname {\mathrm {im}}(\partial )=0$
, which is a contradiction. To show that
$v_0\in V\cap \operatorname {\mathrm {im}}(\partial )=0$
, which is a contradiction. To show that
![]() $x\in M_k$
is contained in
$x\in M_k$
is contained in
![]() $\sum _{n\ge 0}\partial ^n(V)$
, we proceed by induction on k. We can decompose
$\sum _{n\ge 0}\partial ^n(V)$
, we proceed by induction on k. We can decompose
![]() $x=v+\partial (y)$
, where
$x=v+\partial (y)$
, where
![]() $v\in V_k$
and
$v\in V_k$
and
![]() $y\in M_{k-1}$
. By induction,
$y\in M_{k-1}$
. By induction,
![]() $y\in \sum _{n\ge 0}\partial ^n(V)$
; hence,
$y\in \sum _{n\ge 0}\partial ^n(V)$
; hence,
![]() $\partial (y)\in \sum _{n\ge 1}\partial ^n(V)$
. We conclude that
$\partial (y)\in \sum _{n\ge 1}\partial ^n(V)$
. We conclude that
![]() $x=v+\partial (y)\in \sum _{n\ge 0}\partial ^n(V)$
.
$x=v+\partial (y)\in \sum _{n\ge 0}\partial ^n(V)$
.
Remark 5.9. In the proof of [Reference Efimov14, Theorem 1.1], a free action of the polynomial ring in one variable on
![]() ${\mathcal {H}}_{Q,{\mathbf {d}}}$
is used to find a space of free generators of
${\mathcal {H}}_{Q,{\mathbf {d}}}$
is used to find a space of free generators of
![]() ${\mathcal {H}}_Q$
. This action on
${\mathcal {H}}_Q$
. This action on
![]() ${\mathcal {H}}_{Q,{\mathbf {d}}}$
is given by multiplication with
${\mathcal {H}}_{Q,{\mathbf {d}}}$
is given by multiplication with
and it can also be obtained as a by-product of our argument. Recall the derivation t from the proof of Theorem 5.7 that acts on the generators by the formula
![]() $t(i(n))=-i(n+1)$
. This means that
$t(i(n))=-i(n+1)$
. This means that
 $$ \begin{align*} t(Y(i,z))&=t\left(\sum_ni(n)z^{-n-1}\right)=\\&\quad -\sum_ni(n+1)z^{-n-1}=-\sum_ni(n)z^{-n-2}z=-zY(i,z). \end{align*} $$
$$ \begin{align*} t(Y(i,z))&=t\left(\sum_ni(n)z^{-n-1}\right)=\\&\quad -\sum_ni(n+1)z^{-n-1}=-\sum_ni(n)z^{-n-2}z=-zY(i,z). \end{align*} $$
Since t is a derivation, this implies that
 $$ \begin{align*} &\left.t(Y(i_1,z_1)Y(i_2,z_2)\cdots Y(i_p,z_p))\right|{}_{z_{{\mathbf{d}}_1+\dots+{\mathbf{d}}_{j-1}+k}=x_{j,k}}=\\ &-\left(\sum_{j\in I, 1\le k\le {\mathbf{d}}_j} x_{j,k}\right)\cdot \left.Y(i_1,z_1)Y(i_2,z_2)\cdots Y(i_p,z_p)\right|{}_{z_{{\mathbf{d}}_1+\dots+{\mathbf{d}}_{j-1}+k}=x_{j,k}}. \end{align*} $$
$$ \begin{align*} &\left.t(Y(i_1,z_1)Y(i_2,z_2)\cdots Y(i_p,z_p))\right|{}_{z_{{\mathbf{d}}_1+\dots+{\mathbf{d}}_{j-1}+k}=x_{j,k}}=\\ &-\left(\sum_{j\in I, 1\le k\le {\mathbf{d}}_j} x_{j,k}\right)\cdot \left.Y(i_1,z_1)Y(i_2,z_2)\cdots Y(i_p,z_p)\right|{}_{z_{{\mathbf{d}}_1+\dots+{\mathbf{d}}_{j-1}+k}=x_{j,k}}. \end{align*} $$
We see that up to a sign the multiplication by (54) is precisely the action of the endomorphism
![]() $t{^{\vee }}$
on
$t{^{\vee }}$
on
![]() ${\mathcal {P}}{_{Q,\mathbf {d}}^{\vee }}$
. We saw that
${\mathcal {P}}{_{Q,\mathbf {d}}^{\vee }}$
. We saw that
![]() ${\mathcal {P}}_Q$
is isomorphic to
${\mathcal {P}}_Q$
is isomorphic to
![]() $U({\mathfrak {L}}_-)\simeq S^c(W\otimes {\mathbb {Q}}[\partial ])$
as a coalgebra; after taking graded duals (which can be implemented by doing the Fourier transform for differential operators), the modules become
$U({\mathfrak {L}}_-)\simeq S^c(W\otimes {\mathbb {Q}}[\partial ])$
as a coalgebra; after taking graded duals (which can be implemented by doing the Fourier transform for differential operators), the modules become
![]() ${\mathbb {Q}}[t{^{\vee }}]$
-free.
${\mathbb {Q}}[t{^{\vee }}]$
-free.
Let us record a simple consequence of Theorem 5.7.
Corollary 5.10. For any symmetric quiver Q, consider the graded vertex bialgebra
![]() ${\mathcal {H}}{_Q^{\vee }}$
and its space of primitive elements
${\mathcal {H}}{_Q^{\vee }}$
and its space of primitive elements
![]() $C=P({\mathcal {H}}{_Q^{\vee }})$
, which is a vertex Lie algebra. Then the corresponding Donaldson–Thomas invariants satisfy
$C=P({\mathcal {H}}{_Q^{\vee }})$
, which is a vertex Lie algebra. Then the corresponding Donaldson–Thomas invariants satisfy
Proof. We established that
![]() ${\mathcal {H}}{_Q^{\vee }}\simeq {\mathcal {P}}_Q$
and that the principal free vertex algebra
${\mathcal {H}}{_Q^{\vee }}\simeq {\mathcal {P}}_Q$
and that the principal free vertex algebra
![]() ${\mathcal {P}}_Q$
is isomorphic to universal enveloping vertex algebra of a vertex Lie algebra C. We have seen in the proof of Theorem 5.7 that
${\mathcal {P}}_Q$
is isomorphic to universal enveloping vertex algebra of a vertex Lie algebra C. We have seen in the proof of Theorem 5.7 that
![]() $\Omega _{\mathbf {d}}(q{^{-1}})=\operatorname {\mathrm {ch}}(W_{\mathbf {d}})$
, where
$\Omega _{\mathbf {d}}(q{^{-1}})=\operatorname {\mathrm {ch}}(W_{\mathbf {d}})$
, where
![]() ${\mathfrak {L}}_-=W\otimes {\mathbb {Q}}[\partial ]$
, so that
${\mathfrak {L}}_-=W\otimes {\mathbb {Q}}[\partial ]$
, so that
![]() $W\simeq {\mathfrak {L}}_-/\partial {\mathfrak {L}}_-$
. Recall that for any vertex Lie algebra C, its coefficient algebra
$W\simeq {\mathfrak {L}}_-/\partial {\mathfrak {L}}_-$
. Recall that for any vertex Lie algebra C, its coefficient algebra
![]() ${\mathfrak {L}}$
has a decomposition
${\mathfrak {L}}$
has a decomposition
![]() ${\mathfrak {L}}={\mathfrak {L}}_-\oplus {\mathfrak {L}}_+$
such that
${\mathfrak {L}}={\mathfrak {L}}_-\oplus {\mathfrak {L}}_+$
such that
![]() $C\simeq {\mathfrak {L}}_-$
(as a graded vector space). Moreover, we have
$C\simeq {\mathfrak {L}}_-$
(as a graded vector space). Moreover, we have
which completes the proof.
This statement is easily generalisable to the following appealing conjecture suggesting a relationship between vertex algebras and more general DT invariants.
Conjecture 5.11. For each CoHA
![]() ${\mathcal {H}}$
associated to a (symmetric) quiver with potential, its dual
${\mathcal {H}}$
associated to a (symmetric) quiver with potential, its dual
![]() ${\mathcal {H}}{^{\vee }}$
can be equipped with a vertex bialgebra algebra structure (cf. [Reference Joyce33]) such that the corresponding perverse graded object is isomorphic to the universal enveloping vertex algebra of some vertex Lie algebra C. The corresponding DT invariants are equal to the characters of the components of
${\mathcal {H}}{^{\vee }}$
can be equipped with a vertex bialgebra algebra structure (cf. [Reference Joyce33]) such that the corresponding perverse graded object is isomorphic to the universal enveloping vertex algebra of some vertex Lie algebra C. The corresponding DT invariants are equal to the characters of the components of
![]() $C/\partial C$
.
$C/\partial C$
.
5.5. Relationship to the vertex algebras of Joyce
In this section, we will briefly explain the relationship of our results to the geometric construction of vertex algebras proposed in [Reference Joyce33] (see also [Reference Bojko3, Reference Gross27, Reference Gross, Joyce and Tanaka28, Reference Latyntsev37]). In order to do this, we will need to formulate a minor generalisation of that construction. Let us assume that we have the following data
-
(1) A lattice L equipped with a symmetric bilinear form
 $\chi $
.
$\chi $
. -
(2) An abelian category
 ${\mathcal {A}}$
and a linear map
${\mathcal {A}}$
and a linear map
 $\operatorname {\mathrm {cl}}:K_0({\mathcal {A}})\to L$
.
$\operatorname {\mathrm {cl}}:K_0({\mathcal {A}})\to L$
. -
(3) A moduli stack
 ${\mathcal {M}}$
of object in
${\mathcal {M}}$
of object in
 ${\mathcal {A}}$
such that the substack
${\mathcal {A}}$
such that the substack
 ${\mathcal {M}}_{\mathbf {d}}$
of objects
${\mathcal {M}}_{\mathbf {d}}$
of objects
 $E\in {\mathcal {M}}$
with
$E\in {\mathcal {M}}$
with
 $\operatorname {\mathrm {cl}}(E)={\mathbf {d}}$
is open and closed and there exist natural morphisms of stacks
$\operatorname {\mathrm {cl}}(E)={\mathbf {d}}$
is open and closed and there exist natural morphisms of stacks-
(a)
 $\Phi :{\mathcal {M}}\times {\mathcal {M}}\to {\mathcal {M}}$
that maps
$\Phi :{\mathcal {M}}\times {\mathcal {M}}\to {\mathcal {M}}$
that maps
 $(E,F)\mapsto E\oplus F$
.
$(E,F)\mapsto E\oplus F$
. -
(b)
 $\Psi :B{\mathbb {G}_{\mathrm {m}}}\times {\mathcal {M}}\to {\mathcal {M}}$
that maps
$\Psi :B{\mathbb {G}_{\mathrm {m}}}\times {\mathcal {M}}\to {\mathcal {M}}$
that maps
 ${\mathbb {G}_{\mathrm {m}}}\times \operatorname {\mathrm {Aut}} (E)\ni (t,f)\mapsto tf\in \operatorname {\mathrm {Aut}}(E)$
, for
${\mathbb {G}_{\mathrm {m}}}\times \operatorname {\mathrm {Aut}} (E)\ni (t,f)\mapsto tf\in \operatorname {\mathrm {Aut}}(E)$
, for
 $E\in {\mathcal {A}}$
.
$E\in {\mathcal {A}}$
.
-
-
(4) A perfect complex
 ${\Theta }$
on
${\Theta }$
on
 ${\mathcal {M}}\times {\mathcal {M}}$
such that
${\mathcal {M}}\times {\mathcal {M}}$
such that-
(a)
 ${\Theta }$
is weakly-symmetric, meaning that (56)in the Grothendieck group of
${\Theta }$
is weakly-symmetric, meaning that (56)in the Grothendieck group of $$ \begin{align} [\sigma^*{\Theta}{^{\vee}}]=[{\Theta}] \end{align} $$
$$ \begin{align} [\sigma^*{\Theta}{^{\vee}}]=[{\Theta}] \end{align} $$
 ${\mathcal {M}}\times {\mathcal {M}}$
, where
${\mathcal {M}}\times {\mathcal {M}}$
, where
 $\sigma :{\mathcal {M}}\times {\mathcal {M}}\to {\mathcal {M}}\times {\mathcal {M}}$
is the permutation of factors.
$\sigma :{\mathcal {M}}\times {\mathcal {M}}\to {\mathcal {M}}\times {\mathcal {M}}$
is the permutation of factors.
-
(b) The restriction
 ${\Theta }_{{\mathbf {d}},{\mathbf {e}}}={\Theta }|_{{\mathcal {M}}_{\mathbf {d}}\times {\mathcal {M}}_{\mathbf {e}}}$
has constant rank
${\Theta }_{{\mathbf {d}},{\mathbf {e}}}={\Theta }|_{{\mathcal {M}}_{\mathbf {d}}\times {\mathcal {M}}_{\mathbf {e}}}$
has constant rank
 $\chi ({\mathbf {d}},{\mathbf {e}})$
for all
$\chi ({\mathbf {d}},{\mathbf {e}})$
for all
 ${\mathbf {d}},{\mathbf {e}}\in L$
.
${\mathbf {d}},{\mathbf {e}}\in L$
. -
(c) We have
 $$ \begin{align*}(\Phi\times\operatorname{\mathrm{id}}_{\mathcal{M}})^*{\Theta}\simeq \pi_{13}^*{\Theta}\oplus\pi_{23}^*{\Theta},\qquad (\operatorname{\mathrm{id}}_{\mathcal{M}}\times\Phi)^*{\Theta}\simeq \pi_{12}^*{\Theta}\oplus\pi_{13}^*{\Theta}, \end{align*} $$
where
$$ \begin{align*}(\Phi\times\operatorname{\mathrm{id}}_{\mathcal{M}})^*{\Theta}\simeq \pi_{13}^*{\Theta}\oplus\pi_{23}^*{\Theta},\qquad (\operatorname{\mathrm{id}}_{\mathcal{M}}\times\Phi)^*{\Theta}\simeq \pi_{12}^*{\Theta}\oplus\pi_{13}^*{\Theta}, \end{align*} $$
where $$ \begin{align*}(\Psi\times\operatorname{\mathrm{id}}_{\mathcal{M}})^*{\Theta}\simeq {\mathcal{U}}\boxtimes{\Theta},\qquad (\operatorname{\mathrm{id}}_{\mathcal{M}}\times\Psi)^*{\Theta}\simeq {\mathcal{U}}{^{\vee}}\boxtimes{\Theta}, \end{align*} $$
$$ \begin{align*}(\Psi\times\operatorname{\mathrm{id}}_{\mathcal{M}})^*{\Theta}\simeq {\mathcal{U}}\boxtimes{\Theta},\qquad (\operatorname{\mathrm{id}}_{\mathcal{M}}\times\Psi)^*{\Theta}\simeq {\mathcal{U}}{^{\vee}}\boxtimes{\Theta}, \end{align*} $$
 $\pi _{ij}:{\mathcal {M}}^3\to {\mathcal {M}}^2$
is the projection to the corresponding factors and
$\pi _{ij}:{\mathcal {M}}^3\to {\mathcal {M}}^2$
is the projection to the corresponding factors and
 ${\mathcal {U}}$
is the universal line bundle over
${\mathcal {U}}$
is the universal line bundle over
 $B{\mathbb {G}_{\mathrm {m}}}$
.
$B{\mathbb {G}_{\mathrm {m}}}$
.
-
The proof of the following result goes through the same lines as in [Reference Joyce33].
Theorem 5.12. Consider the
![]() $L\times \mathbb {Z}$
-graded vector space
$L\times \mathbb {Z}$
-graded vector space
so that the component of
![]() $V_{\mathbf {d}}$
of homological degree k (and weight
$V_{\mathbf {d}}$
of homological degree k (and weight
![]() ${\frac 12} k$
) is
${\frac 12} k$
) is
![]() $H_{k-\chi ({\mathbf {d}},{\mathbf {d}})}({\mathcal {M}}_{\mathbf {d}})$
. Then V has a structure of a graded vertex algebra (in the symmetric monoidal category
$H_{k-\chi ({\mathbf {d}},{\mathbf {d}})}({\mathcal {M}}_{\mathbf {d}})$
. Then V has a structure of a graded vertex algebra (in the symmetric monoidal category
![]() $\operatorname {\mathrm {Vect}}^{L\times \mathbb {Z}}$
with the braiding induced by
$\operatorname {\mathrm {Vect}}^{L\times \mathbb {Z}}$
with the braiding induced by
![]() $\chi $
) defined by
$\chi $
) defined by
-
(1)
 , where
, where
 $\eta :{\mathbf {pt}}\to {\mathcal {M}}$
is the inclusion of the zero object.
$\eta :{\mathbf {pt}}\to {\mathcal {M}}$
is the inclusion of the zero object. -
(2) The operator
 $T:V\to V$
of homological degree
$T:V\to V$
of homological degree
 $2$
(and weight
$2$
(and weight
 $1$
) is defined by
$1$
) is defined by
 $T(v)=\Psi _*(t\boxtimes v)$
, where
$T(v)=\Psi _*(t\boxtimes v)$
, where
 $t\in H_2(B{\mathbb {G}_{\mathrm {m}}})=H_2({\mathbb {P}}^\infty )$
is the canonical generator.
$t\in H_2(B{\mathbb {G}_{\mathrm {m}}})=H_2({\mathbb {P}}^\infty )$
is the canonical generator. -
(3) For
 $u\in H_k({\mathcal {M}}_{\mathbf {d}})$
,
$u\in H_k({\mathcal {M}}_{\mathbf {d}})$
,
 $v\in H_*({\mathcal {M}}_{\mathbf {e}})$
, we define
$v\in H_*({\mathcal {M}}_{\mathbf {e}})$
, we define  $$ \begin{align*}Y(u,z)v= (-1)^{k\chi({\mathbf{d}},{\mathbf{d}})}z^{\chi({\mathbf{d}},{\mathbf{e}})} \Phi_*{\left({(e^{zT}\otimes\operatorname{\mathrm{id}})\left({(u\boxtimes v)\cap c_{z{^{-1}}}({\Theta}_{{\mathbf{d}},{\mathbf{e}}})}\right) }\right)}.\end{align*} $$
$$ \begin{align*}Y(u,z)v= (-1)^{k\chi({\mathbf{d}},{\mathbf{d}})}z^{\chi({\mathbf{d}},{\mathbf{e}})} \Phi_*{\left({(e^{zT}\otimes\operatorname{\mathrm{id}})\left({(u\boxtimes v)\cap c_{z{^{-1}}}({\Theta}_{{\mathbf{d}},{\mathbf{e}}})}\right) }\right)}.\end{align*} $$
Let us show that the above vertex algebra construction can be applied in the case of the moduli stack of representations of a symmetric quiver. Let Q be a symmetric quiver with the set of vertices I. Let
![]() $L=\mathbb {Z}^I$
and
$L=\mathbb {Z}^I$
and
![]() $\chi $
be the Euler form of Q. Let
$\chi $
be the Euler form of Q. Let
![]() ${\mathcal {A}}$
be the category of representations of Q and
${\mathcal {A}}$
be the category of representations of Q and
![]() ${\mathcal {M}}$
be the stack of representations of Q. We have a linear map
${\mathcal {M}}$
be the stack of representations of Q. We have a linear map
![]() ${\mathbf {dim}}:K_0({\mathcal {A}})\to L$
. We define the perfect complex
${\mathbf {dim}}:K_0({\mathcal {A}})\to L$
. We define the perfect complex
![]() ${\Theta }=\operatorname {\mathrm {RHom}}$
over
${\Theta }=\operatorname {\mathrm {RHom}}$
over
![]() ${\mathcal {M}}\times {\mathcal {M}}$
such that its fiber over
${\mathcal {M}}\times {\mathcal {M}}$
such that its fiber over
![]() $(M,N)\in {\mathcal {M}}\times {\mathcal {M}}$
is isomorphic to
$(M,N)\in {\mathcal {M}}\times {\mathcal {M}}$
is isomorphic to
![]() $\operatorname {\mathrm {RHom}}(M,N)\in D^b(\operatorname {\mathrm {Vect}})$
. The rank of
$\operatorname {\mathrm {RHom}}(M,N)\in D^b(\operatorname {\mathrm {Vect}})$
. The rank of
![]() ${\Theta }$
over
${\Theta }$
over
![]() ${\mathcal {M}}_{\mathbf {d}}\times {\mathcal {M}}_{\mathbf {e}}$
is equal to
${\mathcal {M}}_{\mathbf {d}}\times {\mathcal {M}}_{\mathbf {e}}$
is equal to
![]() $\chi ({\mathbf {d}},{\mathbf {e}})$
. In order to apply Theorem 5.12, we need to prove that
$\chi ({\mathbf {d}},{\mathbf {e}})$
. In order to apply Theorem 5.12, we need to prove that
![]() ${\Theta }$
is weakly-symmetric (56).
${\Theta }$
is weakly-symmetric (56).
Lemma 5.13. We have
in the Grothendieck group of
![]() ${\mathcal {M}}\times {\mathcal {M}}$
.
${\mathcal {M}}\times {\mathcal {M}}$
.
Proof. Let
![]() $A={\mathbb {C}} Q$
be the path algebra of Q. For every
$A={\mathbb {C}} Q$
be the path algebra of Q. For every
![]() $i\in I$
, let
$i\in I$
, let
![]() $e_i\in A$
be the corresponding idempotent and
$e_i\in A$
be the corresponding idempotent and
![]() $P=Ae_i$
be the corresponding projective A-module. For any representation M, we have the standard projective resolution
$P=Ae_i$
be the corresponding projective A-module. For any representation M, we have the standard projective resolution
Therefore,
![]() $\operatorname {\mathrm {RHom}}(M,N)$
can be written as a complex
$\operatorname {\mathrm {RHom}}(M,N)$
can be written as a complex
Similarly,
![]() $\operatorname {\mathrm {RHom}}(N,M)$
can be written as a complex
$\operatorname {\mathrm {RHom}}(N,M)$
can be written as a complex
Using the fact that Q is symmetric and that
![]() $\operatorname {\mathrm {Hom}}(N_i,M_j)\simeq \operatorname {\mathrm {Hom}}(M_j,N_i){^{\vee }}$
, we can rewrite this complex in the form
$\operatorname {\mathrm {Hom}}(N_i,M_j)\simeq \operatorname {\mathrm {Hom}}(M_j,N_i){^{\vee }}$
, we can rewrite this complex in the form
This implies that
![]() $[\operatorname {\mathrm {RHom}}(M,N){^{\vee }}]=[\operatorname {\mathrm {RHom}}(N,M)]$
. The statement of the lemma is a global version of this observation.
$[\operatorname {\mathrm {RHom}}(M,N){^{\vee }}]=[\operatorname {\mathrm {RHom}}(N,M)]$
. The statement of the lemma is a global version of this observation.
Applying the previous lemma and the construction of Theorem 5.12, we obtain a vertex algebra structure on
![]() $H_*({\mathcal {M}})\simeq {\mathcal {H}}{_Q^{\vee }}$
.
$H_*({\mathcal {M}})\simeq {\mathcal {H}}{_Q^{\vee }}$
.
Conjecture 5.14. The vertex algebra structure on
![]() $H_*({\mathcal {M}})\simeq {\mathcal {H}}{_Q^{\vee }}$
coincides with the vertex algebra structure constructed earlier on
$H_*({\mathcal {M}})\simeq {\mathcal {H}}{_Q^{\vee }}$
coincides with the vertex algebra structure constructed earlier on
![]() ${\mathcal {P}}_Q\simeq {\mathcal {H}}{_Q^{\vee }}$
; see Proposition 5.3 and Theorem 5.7.
${\mathcal {P}}_Q\simeq {\mathcal {H}}{_Q^{\vee }}$
; see Proposition 5.3 and Theorem 5.7.
However, in [Reference Latyntsev37], one constructed a quantum vertex bialgebra structure on
![]() $H_*({\mathcal {M}})$
associated with a complex
$H_*({\mathcal {M}})$
associated with a complex
![]() ${\Theta }$
which is not necessarily weakly-symmetric. In the case of symmetric quivers and
${\Theta }$
which is not necessarily weakly-symmetric. In the case of symmetric quivers and
![]() ${\Theta }=\operatorname {\mathrm {RHom}}$
, the resulting quantum vertex algebra structure on
${\Theta }=\operatorname {\mathrm {RHom}}$
, the resulting quantum vertex algebra structure on
![]() $H_*({\mathcal {M}})\simeq {\mathcal {H}}{_Q^{\vee }}$
is actually a vertex algebra (in an appropriate symmetric monoidal category) because of Lemma 5.13. Therefore, by the results of [Reference Latyntsev37], one has a vertex bialgebra structure on
$H_*({\mathcal {M}})\simeq {\mathcal {H}}{_Q^{\vee }}$
is actually a vertex algebra (in an appropriate symmetric monoidal category) because of Lemma 5.13. Therefore, by the results of [Reference Latyntsev37], one has a vertex bialgebra structure on
![]() $H_*({\mathcal {M}})\simeq {\mathcal {H}}{_Q^{\vee }}$
. We expect that Conjecture 5.14 can be lifted to the level of vertex bialgebras, where
$H_*({\mathcal {M}})\simeq {\mathcal {H}}{_Q^{\vee }}$
. We expect that Conjecture 5.14 can be lifted to the level of vertex bialgebras, where
![]() ${\mathcal {P}}_Q\simeq {\mathcal {H}}{_Q^{\vee }}$
is equipped with a vertex bialgebra structure by Theorem 5.7.
${\mathcal {P}}_Q\simeq {\mathcal {H}}{_Q^{\vee }}$
is equipped with a vertex bialgebra structure by Theorem 5.7.
6. CoHA-modules and free vertex algebras
In this section, we shall use previously obtained identification
![]() ${\mathcal {H}}{_Q^{\vee }}\cong {\mathcal {P}}_Q$
to give a new interpretation of the CoHA modules
${\mathcal {H}}{_Q^{\vee }}\cong {\mathcal {P}}_Q$
to give a new interpretation of the CoHA modules
considered in Section 3.3. Since
![]() ${\mathcal {M}}_{\mathbf {w}}$
is a quotient of
${\mathcal {M}}_{\mathbf {w}}$
is a quotient of
![]() ${\mathcal {H}}_Q$
, it is natural to seek for a description of
${\mathcal {H}}_Q$
, it is natural to seek for a description of
![]() ${\mathcal {M}}{_{{\mathbf {w}}}^{\vee }}$
as a subspace of
${\mathcal {M}}{_{{\mathbf {w}}}^{\vee }}$
as a subspace of
![]() ${\mathcal {P}}_Q$
. In this section, we give two such descriptions. In §6.1, we interpret
${\mathcal {P}}_Q$
. In this section, we give two such descriptions. In §6.1, we interpret
![]() ${\mathcal {M}}{_{{\mathbf {w}}}^{\vee }}$
in terms of the coproduct generalising the coproduct
${\mathcal {M}}{_{{\mathbf {w}}}^{\vee }}$
in terms of the coproduct generalising the coproduct
![]() ${\mathcal {P}}_Q\to {\mathcal {P}}_Q\otimes {\mathcal {P}}_Q$
considered earlier. In §6.2, we exhibit a combinatorially defined spanning set of
${\mathcal {P}}_Q\to {\mathcal {P}}_Q\otimes {\mathcal {P}}_Q$
considered earlier. In §6.2, we exhibit a combinatorially defined spanning set of
![]() ${\mathcal {M}}{_{{\mathbf {w}}}^{\vee }}\subset {\mathcal {P}}_Q$
.
${\mathcal {M}}{_{{\mathbf {w}}}^{\vee }}\subset {\mathcal {P}}_Q$
.
6.1. Modified coproduct
For each
![]() ${\mathbf {w}}\in {\mathbb {N}}^I$
, let us consider the subset
${\mathbf {w}}\in {\mathbb {N}}^I$
, let us consider the subset
of the set of generators of the Lie algebra
![]() ${\mathfrak {L}}$
, and the corresponding
${\mathfrak {L}}$
, and the corresponding
![]() $U({\mathfrak {L}})$
-module
$U({\mathfrak {L}})$
-module
![]() ${\mathcal {P}}_{\mathbf {w}}=U({\mathfrak {L}})/U({\mathfrak {L}})X_{\mathbf {w}}$
with the cyclic vector
${\mathcal {P}}_{\mathbf {w}}=U({\mathfrak {L}})/U({\mathfrak {L}})X_{\mathbf {w}}$
with the cyclic vector ![]() . For each
. For each
![]() $i\in I$
, the series
$i\in I$
, the series
![]() $\mathbf {i}(z)=\sum _{n\in \mathbb {Z}}i(n)z^{-n-1}$
defines a field on
$\mathbf {i}(z)=\sum _{n\in \mathbb {Z}}i(n)z^{-n-1}$
defines a field on
![]() ${\mathcal {P}}_{\mathbf {w}}$
. These series can be used to equip
${\mathcal {P}}_{\mathbf {w}}$
. These series can be used to equip
![]() ${\mathcal {P}}_{\mathbf {w}}$
with a structure of a module over the vertex algebra
${\mathcal {P}}_{\mathbf {w}}$
with a structure of a module over the vertex algebra
![]() ${\mathcal {P}}_Q$
; clearly,
${\mathcal {P}}_Q$
; clearly,
![]() ${\mathcal {P}}_Q$
itself is a particular case of this construction for
${\mathcal {P}}_Q$
itself is a particular case of this construction for
![]() ${\mathbf {w}}=0$
.
${\mathbf {w}}=0$
.
Note that since
![]() ${\mathbf {w}}\in {\mathbb {N}}^I$
, we have
${\mathbf {w}}\in {\mathbb {N}}^I$
, we have
![]() $X_+\subset X_{\mathbf {w}}$
, and therefore, there is a canonical surjection of
$X_+\subset X_{\mathbf {w}}$
, and therefore, there is a canonical surjection of
![]() $U({\mathfrak {L}})$
-modules
$U({\mathfrak {L}})$
-modules
![]() $\pi \colon {\mathcal {P}}_Q\to {\mathcal {P}}_{\mathbf {w}}$
. We shall now see how the graded dual
$\pi \colon {\mathcal {P}}_Q\to {\mathcal {P}}_{\mathbf {w}}$
. We shall now see how the graded dual
of
![]() ${\mathcal {P}}_{\mathbf {w}}$
is included in
${\mathcal {P}}_{\mathbf {w}}$
is included in
![]() ${\mathcal {P}}{_Q^{\vee }}$
. As before, we fix a dimension vector
${\mathcal {P}}{_Q^{\vee }}$
. As before, we fix a dimension vector
![]() ${\mathbf {d}}\in {\mathbb {N}}^I$
and let
${\mathbf {d}}\in {\mathbb {N}}^I$
and let
![]() $p={\left \lvert {\mathbf {d}}\right \rvert }$
and
$p={\left \lvert {\mathbf {d}}\right \rvert }$
and
![]() $\operatorname {\mathrm {Hom}} j=(j_1,\dots ,j_p)$
be any sequence of vertices with
$\operatorname {\mathrm {Hom}} j=(j_1,\dots ,j_p)$
be any sequence of vertices with
![]() $e_{j_1}+\cdots +e_{j_p}={\mathbf {d}}$
.
$e_{j_1}+\cdots +e_{j_p}={\mathbf {d}}$
.
Lemma 6.1. For any
![]() $\xi \in {\mathcal {P}}{_{{\mathbf {w}},{\mathbf {d}}}^{\vee }}$
, the Laurent series
$\xi \in {\mathcal {P}}{_{{\mathbf {w}},{\mathbf {d}}}^{\vee }}$
, the Laurent series
is completely symmetric under the action of
![]() $\Sigma _p$
permuting simultaneously the vertices
$\Sigma _p$
permuting simultaneously the vertices
![]() $j_p$
and the variables
$j_p$
and the variables
![]() $z_p$
. Moreover, it is a polynomial divisible by the product
$z_p$
. Moreover, it is a polynomial divisible by the product
![]() $z_1^{{\mathbf {w}}_{j_1}}\cdots z_p^{{\mathbf {w}}_{j_p}}$
.
$z_1^{{\mathbf {w}}_{j_1}}\cdots z_p^{{\mathbf {w}}_{j_p}}$
.
Proof. The proof is analogous to that of Lemma 5.2; the only difference is that
![]() $X_+$
is replaced by
$X_+$
is replaced by
![]() $X_{\mathbf {w}}$
, which has the effect of replacing the property of absence of negative powers by the property of absence of powers of
$X_{\mathbf {w}}$
, which has the effect of replacing the property of absence of negative powers by the property of absence of powers of
![]() $z_p$
that are less than
$z_p$
that are less than
![]() ${\mathbf {w}}_{j_p}$
.
${\mathbf {w}}_{j_p}$
.
Proposition 6.2. For any
![]() ${\mathbf {d}}\in {\mathbb {N}}^I$
, we have an isomorphism of graded vector spaces
${\mathbf {d}}\in {\mathbb {N}}^I$
, we have an isomorphism of graded vector spaces
 $$ \begin{align*}F\colon {\mathcal{P}}{_{{\mathbf{w}},{\mathbf{d}}}^{\vee}}\to e_{{\mathbf{d}}}^{\mathbf{w}}\Lambda_{\mathbf{d}}[-\chi({\mathbf{d}},{\mathbf{d}})],\qquad e_{{\mathbf{d}}}^{\mathbf{w}} =\prod_{i\in I}\prod_{k=1}^{{\mathbf{d}}_i}x_{i,k}^{{\mathbf{w}}_i}, \end{align*} $$
$$ \begin{align*}F\colon {\mathcal{P}}{_{{\mathbf{w}},{\mathbf{d}}}^{\vee}}\to e_{{\mathbf{d}}}^{\mathbf{w}}\Lambda_{\mathbf{d}}[-\chi({\mathbf{d}},{\mathbf{d}})],\qquad e_{{\mathbf{d}}}^{\mathbf{w}} =\prod_{i\in I}\prod_{k=1}^{{\mathbf{d}}_i}x_{i,k}^{{\mathbf{w}}_i}, \end{align*} $$
defined by the formula
where
![]() $p={\left \lvert {\mathbf {d}}\right \rvert }$
,
$p={\left \lvert {\mathbf {d}}\right \rvert }$
,
![]() $i_{{\mathbf {d}}_1+\dots +{\mathbf {d}}_{j-1}+k}=j$
and
$i_{{\mathbf {d}}_1+\dots +{\mathbf {d}}_{j-1}+k}=j$
and
![]() $z_{{\mathbf {d}}_1+\dots +{\mathbf {d}}_{j-1}+k}=x_{j,k}$
, for
$z_{{\mathbf {d}}_1+\dots +{\mathbf {d}}_{j-1}+k}=x_{j,k}$
, for
![]() $j\in I$
and
$j\in I$
and
![]() $1\le k\le {\mathbf {d}}_j$
.
$1\le k\le {\mathbf {d}}_j$
.
Proof. Completely analogous to that of Proposition 5.3.
We note that
![]() $e_{{\mathbf {d}}}^{\mathbf {w}}\Lambda _{\mathbf {d}}[-\chi ({\mathbf {d}},{\mathbf {d}})]\simeq e_{{\mathbf {d}}}^{\mathbf {w}}{\mathcal {H}}_{Q,{\mathbf {d}}}$
is precisely one of the vector spaces used in the shuffle algebra description (14) of the module
$e_{{\mathbf {d}}}^{\mathbf {w}}\Lambda _{\mathbf {d}}[-\chi ({\mathbf {d}},{\mathbf {d}})]\simeq e_{{\mathbf {d}}}^{\mathbf {w}}{\mathcal {H}}_{Q,{\mathbf {d}}}$
is precisely one of the vector spaces used in the shuffle algebra description (14) of the module
![]() ${\mathcal {M}}_{\mathbf {w}}$
. To use this observation, we consider the surjection
${\mathcal {M}}_{\mathbf {w}}$
. To use this observation, we consider the surjection
![]() $\pi :{\mathcal {P}}_Q\to {\mathcal {P}}_{\mathbf {w}}$
and define a
$\pi :{\mathcal {P}}_Q\to {\mathcal {P}}_{\mathbf {w}}$
and define a
![]() $U({\mathfrak {L}})$
-module map
$U({\mathfrak {L}})$
-module map
which can be interpreted as a coaction of the cocommutative coalgebra
![]() ${\mathcal {P}}_{\mathbf {w}}$
on its comodule
${\mathcal {P}}_{\mathbf {w}}$
on its comodule
![]() ${\mathcal {P}}_Q$
. Explicitly, we have
${\mathcal {P}}_Q$
. Explicitly, we have

where
![]() $\kappa (A,B)=\sum _{a>b}\chi ({i_a},{i_b})$
. Note that the projection of
$\kappa (A,B)=\sum _{a>b}\chi ({i_a},{i_b})$
. Note that the projection of
![]() $\rho _{\mathbf {w}}(v)$
to
$\rho _{\mathbf {w}}(v)$
to
![]() ${\mathcal {P}}_Q\otimes {\mathcal {P}}_{{\mathbf {w}},0}$
is equal to
${\mathcal {P}}_Q\otimes {\mathcal {P}}_{{\mathbf {w}},0}$
is equal to ![]() . Since the description of the module
. Since the description of the module
![]() ${\mathcal {M}}_{\mathbf {w}}$
uses the spaces
${\mathcal {M}}_{\mathbf {w}}$
uses the spaces
![]() $e_{{\mathbf {d}}}^{\mathbf {w}}{\mathcal {H}}_{Q,{\mathbf {d}}}$
with
$e_{{\mathbf {d}}}^{\mathbf {w}}{\mathcal {H}}_{Q,{\mathbf {d}}}$
with
![]() ${\mathbf {d}}>0$
, it will be useful to consider the reduced coaction
${\mathbf {d}}>0$
, it will be useful to consider the reduced coaction
Using the isomorphism
![]() $\bar {\mathcal {P}}_{\mathbf {w}}\simeq \bigoplus _{{\mathbf {d}}>0}{\mathcal {P}}_{{\mathbf {w}},{\mathbf {d}}}$
, we can write
$\bar {\mathcal {P}}_{\mathbf {w}}\simeq \bigoplus _{{\mathbf {d}}>0}{\mathcal {P}}_{{\mathbf {w}},{\mathbf {d}}}$
, we can write
![]() $\bar \rho _{\mathbf {w}}$
in the form
$\bar \rho _{\mathbf {w}}$
in the form
Theorem 6.3. The kernel of the map
![]() $\bar {\rho }_{\mathbf {w}}$
is isomorphic to the graded dual of the CoHA-module
$\bar {\rho }_{\mathbf {w}}$
is isomorphic to the graded dual of the CoHA-module
Proof. Note that we have an exact sequence
which, after passing to graded duals, becomes
Using the isomorphisms of Propositions 5.3, 6.2, we obtain the diagram

where the bottom right map is the shuffle product by Theorem 5.6. Its cokernel is isomorphic to the CoHA module
![]() ${\mathcal {M}}_{\mathbf {w}}$
by (14). Therefore, we obtain an isomorphism
${\mathcal {M}}_{\mathbf {w}}$
by (14). Therefore, we obtain an isomorphism
![]() $\ker (\bar {\rho }_{\mathbf {w}})^\vee \simeq {\mathcal {M}}_{\mathbf {w}}$
.
$\ker (\bar {\rho }_{\mathbf {w}})^\vee \simeq {\mathcal {M}}_{\mathbf {w}}$
.
6.2. Subspace construction
We shall now exhibit an explicit combinatorial spanning set of the subspace
![]() $\ker (\bar {\rho })\subset {\mathcal {P}}_Q$
. Let
$\ker (\bar {\rho })\subset {\mathcal {P}}_Q$
. Let
![]() $\mathcal Q_{\mathbf {w}}$
be the subspace of
$\mathcal Q_{\mathbf {w}}$
be the subspace of
![]() ${\mathcal {P}}_Q\simeq U({\mathfrak {L}})\otimes _{U({\mathfrak {L}}_+)}{\mathbb {Q}}$
obtained by applying elements of
${\mathcal {P}}_Q\simeq U({\mathfrak {L}})\otimes _{U({\mathfrak {L}}_+)}{\mathbb {Q}}$
obtained by applying elements of
![]() $X_{\mathbf {w}}={\left \{\left .{i(n)}\ \right \vert {n\ge -{\mathbf {w}}_i}\right \}}$
to the vacuum
$X_{\mathbf {w}}={\left \{\left .{i(n)}\ \right \vert {n\ge -{\mathbf {w}}_i}\right \}}$
to the vacuum ![]() .
.
We can also interpret this space as follows. Let
![]() ${\mathfrak {L}}^{\mathbf {w}}_+$
denote the Lie subalgebra of
${\mathfrak {L}}^{\mathbf {w}}_+$
denote the Lie subalgebra of
![]() ${\mathfrak {L}}$
generated by the set
${\mathfrak {L}}$
generated by the set
![]() $X_{\mathbf {w}}$
. As
$X_{\mathbf {w}}$
. As
![]() $X_+\subset X_{\mathbf {w}}$
, for
$X_+\subset X_{\mathbf {w}}$
, for
![]() ${\mathbf {w}}\in {\mathbb {N}}^I$
, we have
${\mathbf {w}}\in {\mathbb {N}}^I$
, we have
![]() ${\mathfrak {L}}_+\subset {\mathfrak {L}}^{\mathbf {w}}_+$
. Then
${\mathfrak {L}}_+\subset {\mathfrak {L}}^{\mathbf {w}}_+$
. Then
![]() $\mathcal Q_{\mathbf {w}}$
can be identified with
$\mathcal Q_{\mathbf {w}}$
can be identified with
where
![]() ${\mathbb {Q}}$
is equipped with the structure of the trivial
${\mathbb {Q}}$
is equipped with the structure of the trivial
![]() ${\mathfrak {L}}_+$
-module.
${\mathfrak {L}}_+$
-module.
We can actually identify
![]() $\mathcal Q_{\mathbf {w}}$
with the universal enveloping algebra of a certain Lie algebra as follows. Consider the Lie algebra isomorphism
$\mathcal Q_{\mathbf {w}}$
with the universal enveloping algebra of a certain Lie algebra as follows. Consider the Lie algebra isomorphism
which extends to the isomorphism
![]() $U({\mathfrak {L}})\to U({\mathfrak {L}})$
. Note that
$U({\mathfrak {L}})\to U({\mathfrak {L}})$
. Note that
![]() $\tau _{\mathbf {w}}$
maps
$\tau _{\mathbf {w}}$
maps
![]() ${\mathfrak {L}}_+$
to
${\mathfrak {L}}_+$
to
![]() ${\mathfrak {L}}^{\mathbf {w}}_+$
isomorphically; we also define a new Lie algebra
${\mathfrak {L}}^{\mathbf {w}}_+$
isomorphically; we also define a new Lie algebra
![]() ${\mathfrak {L}}^{\mathbf {w}}_-=\tau _{\mathbf {w}}({\mathfrak {L}}_-)$
, leading to the direct sum decomposition
${\mathfrak {L}}^{\mathbf {w}}_-=\tau _{\mathbf {w}}({\mathfrak {L}}_-)$
, leading to the direct sum decomposition
![]() ${\mathfrak {L}}={\mathfrak {L}}^{\mathbf {w}}_-\oplus {\mathfrak {L}}^{\mathbf {w}}_+$
. As
${\mathfrak {L}}={\mathfrak {L}}^{\mathbf {w}}_-\oplus {\mathfrak {L}}^{\mathbf {w}}_+$
. As
![]() ${\mathfrak {L}}_+\subset {\mathfrak {L}}^{\mathbf {w}}_+$
, we have direct sum decompositions
${\mathfrak {L}}_+\subset {\mathfrak {L}}^{\mathbf {w}}_+$
, we have direct sum decompositions
where
![]() ${\mathfrak {L}}^{{\mathbf {w}}}_\circ $
is a Lie algebra, being an intersection of two Lie algebras. We conclude that
${\mathfrak {L}}^{{\mathbf {w}}}_\circ $
is a Lie algebra, being an intersection of two Lie algebras. We conclude that
Theorem 6.4. For each
![]() ${\mathbf {w}}\in {\mathbb {N}}^I$
, we have a commutative diagram
${\mathbf {w}}\in {\mathbb {N}}^I$
, we have a commutative diagram

Proof. According to Theorem 6.3, we have
![]() $\mathcal M{_{{\mathbf {w}}}^{\vee }}\simeq \ker (\bar {\rho }_{\mathbf {w}})$
, so we need to show that
$\mathcal M{_{{\mathbf {w}}}^{\vee }}\simeq \ker (\bar {\rho }_{\mathbf {w}})$
, so we need to show that
![]() $\ker (\bar {\rho }_{\mathbf {w}})=\mathcal Q_{\mathbf {w}}$
. Let us first remark that
$\ker (\bar {\rho }_{\mathbf {w}})=\mathcal Q_{\mathbf {w}}$
. Let us first remark that
![]() $\mathcal Q_{\mathbf {w}}\subset \ker (\bar {\rho }_{\mathbf {w}})$
. Indeed, if
$\mathcal Q_{\mathbf {w}}\subset \ker (\bar {\rho }_{\mathbf {w}})$
. Indeed, if
with
![]() $i_k(n_k)\in X_{\mathbf {w}}$
for all k, then in Formula (57), we have
$i_k(n_k)\in X_{\mathbf {w}}$
for all k, then in Formula (57), we have ![]() whenever
whenever
![]() $B\ne \varnothing $
. Therefore,
$B\ne \varnothing $
. Therefore, ![]() and
and
![]() $\bar \rho (v)=0$
.
$\bar \rho (v)=0$
.
To establish that the inclusion
![]() $\mathcal Q_{\mathbf {w}}\subset \ker (\bar {\rho }_{\mathbf {w}})$
is an equality, it is sufficient to show that these two subspaces of
$\mathcal Q_{\mathbf {w}}\subset \ker (\bar {\rho }_{\mathbf {w}})$
is an equality, it is sufficient to show that these two subspaces of
![]() ${\mathcal {P}}_Q$
have the same Poincaré series; that is,
${\mathcal {P}}_Q$
have the same Poincaré series; that is,
We shall now prove this equality. The left-hand side computation will use various results about vertex Lie algebras. We have already seen that there is an isomorphism
![]() $\mathcal Q_{\mathbf {w}}\simeq U({\mathfrak {L}}^{{\mathbf {w}}}_\circ )$
. The decomposition (59) implies, together with the Poincaré–Birkhoff–Witt theorem, that we have an isomorphism of
$\mathcal Q_{\mathbf {w}}\simeq U({\mathfrak {L}}^{{\mathbf {w}}}_\circ )$
. The decomposition (59) implies, together with the Poincaré–Birkhoff–Witt theorem, that we have an isomorphism of
![]() $L\times \mathbb {Z}$
-graded vector spaces
$L\times \mathbb {Z}$
-graded vector spaces
and therefore,
or, equivalently,
According to Corollary 5.4, we have
This formula can be used to determine the Poincaré series of
![]() $U({\mathfrak {L}}^{\mathbf {w}}_-)=\tau _{\mathbf {w}}(U({\mathfrak {L}}_-))$
. Indeed, we have
$U({\mathfrak {L}}^{\mathbf {w}}_-)=\tau _{\mathbf {w}}(U({\mathfrak {L}}_-))$
. Indeed, we have
![]() $\operatorname {\mathrm {wt}}(\tau _{\mathbf {w}}(i(n))=\operatorname {\mathrm {wt}}(i(n))+{\mathbf {w}}_i$
. Therefore, for any graded subspace
$\operatorname {\mathrm {wt}}(\tau _{\mathbf {w}}(i(n))=\operatorname {\mathrm {wt}}(i(n))+{\mathbf {w}}_i$
. Therefore, for any graded subspace
![]() $M\subset U({\mathfrak {L}})_{\mathbf {d}}$
, we have
$M\subset U({\mathfrak {L}})_{\mathbf {d}}$
, we have
![]() $\operatorname {\mathrm {ch}}(\tau _{\mathbf {w}}(M))=q^{{\mathbf {w}}\cdot {\mathbf {d}}}\operatorname {\mathrm {ch}}(M)$
and, for any
$\operatorname {\mathrm {ch}}(\tau _{\mathbf {w}}(M))=q^{{\mathbf {w}}\cdot {\mathbf {d}}}\operatorname {\mathrm {ch}}(M)$
and, for any
![]() $L\times \mathbb {Z}$
-graded subspace
$L\times \mathbb {Z}$
-graded subspace
![]() $M\subset U({\mathfrak {L}})$
, we have
$M\subset U({\mathfrak {L}})$
, we have
where
![]() $S_{{\mathbf {w}}}(x^{\mathbf {d}})=q^{{\frac 12}{\mathbf {w}}\cdot {\mathbf {d}}}x^{\mathbf {d}}$
. This implies
$S_{{\mathbf {w}}}(x^{\mathbf {d}})=q^{{\frac 12}{\mathbf {w}}\cdot {\mathbf {d}}}x^{\mathbf {d}}$
. This implies
and so we may conclude that
At the same time, according to Theorem 6.3, we have
Since Proposition 3.4 asserts that
![]() $Z(\mathcal M_{{\mathbf {w}}},x,q)=A_Q(x,q)\cdot S_{-2{\mathbf {w}}}A_Q(x,q){^{-1}}$
, we conclude that
$Z(\mathcal M_{{\mathbf {w}}},x,q)=A_Q(x,q)\cdot S_{-2{\mathbf {w}}}A_Q(x,q){^{-1}}$
, we conclude that
which completes the proof.
Remark 6.5. Let us consider the quiver Q with one vertex
![]() $1$
and two loops. Its Euler form on
$1$
and two loops. Its Euler form on
![]() $\mathbb {Z}^I\simeq \mathbb {Z}$
is given by
$\mathbb {Z}^I\simeq \mathbb {Z}$
is given by
![]() $\chi (e_1,e_1)=-1$
, and the Lie algebra
$\chi (e_1,e_1)=-1$
, and the Lie algebra
![]() ${\mathfrak {L}}$
is the Lie superalgebra generated by odd elements
${\mathfrak {L}}$
is the Lie superalgebra generated by odd elements
![]() $a_n$
,
$a_n$
,
![]() $n\in \mathbb {Z}$
, such that
$n\in \mathbb {Z}$
, such that
This is precisely the algebra considered in [Reference Dotsenko10], where it was proved that for
![]() ${\mathbf {w}}=1$
and
${\mathbf {w}}=1$
and
![]() ${\mathbf {d}}=n$
, the dimension of
${\mathbf {d}}=n$
, the dimension of
![]() $\mathcal Q_{{\mathbf {w}},{\mathbf {d}}}$
is given by the n-th Catalan number, and incorporating the weight leads to the q-analogue of the Catalan numbers introduced by Carlitz and Riordan [Reference Carlitz and Riordan6]. We can recover this result using Theorem 6.4, which asserts that we should check the same for the dimension of
$\mathcal Q_{{\mathbf {w}},{\mathbf {d}}}$
is given by the n-th Catalan number, and incorporating the weight leads to the q-analogue of the Catalan numbers introduced by Carlitz and Riordan [Reference Carlitz and Riordan6]. We can recover this result using Theorem 6.4, which asserts that we should check the same for the dimension of
![]() ${\mathcal {M}}_{{\mathbf {w}},{\mathbf {d}}}$
. The latter vector space is, up to a degree shift, isomorphic to the cohomology of the non-commutative Hilbert scheme
${\mathcal {M}}_{{\mathbf {w}},{\mathbf {d}}}$
. The latter vector space is, up to a degree shift, isomorphic to the cohomology of the non-commutative Hilbert scheme
![]() ${\mathbb {H}}^{(2)}_{n,1}=\operatorname {\mathrm {Hilb}}_{n,1}$
. According to [Reference Reineke54], its dimension is indeed the n-th Catalan number. Moreover, the Poincaré polynomial of
${\mathbb {H}}^{(2)}_{n,1}=\operatorname {\mathrm {Hilb}}_{n,1}$
. According to [Reference Reineke54], its dimension is indeed the n-th Catalan number. Moreover, the Poincaré polynomial of
![]() ${\mathbb {H}}^{(2)}_{n,1}$
computed in [Reference Reineke54] is easily seen to produce the expected q-Catalan number.
${\mathbb {H}}^{(2)}_{n,1}$
computed in [Reference Reineke54] is easily seen to produce the expected q-Catalan number.
Recall that
![]() $\mathcal Q_{\mathbf {w}}$
is spanned by elements obtained by applying elements of
$\mathcal Q_{\mathbf {w}}$
is spanned by elements obtained by applying elements of
to the vacuum ![]() . Extracting from these elements a basis of
. Extracting from these elements a basis of
![]() $\mathcal Q_{\mathbf {w}}$
is far from obvious; for example, it does not seem that either of the two known combinatorial descriptions of a basis in
$\mathcal Q_{\mathbf {w}}$
is far from obvious; for example, it does not seem that either of the two known combinatorial descriptions of a basis in
![]() ${\mathcal {P}}_Q$
(obtained in [Reference Roitman58, Theorem 1] and in [Reference Milas and Penn47, Theorem 4.8]) is easy to use to describe a basis of
${\mathcal {P}}_Q$
(obtained in [Reference Roitman58, Theorem 1] and in [Reference Milas and Penn47, Theorem 4.8]) is easy to use to describe a basis of
![]() $\mathcal Q_{\mathbf {w}}$
. If one is in the situation for which the locality relations form a Gröbner basis (for the most obvious order of monomials, such quivers are classified in [Reference Dotsenko, Feigin and Reineke11]), such a description exists. For example, for each
$\mathcal Q_{\mathbf {w}}$
. If one is in the situation for which the locality relations form a Gröbner basis (for the most obvious order of monomials, such quivers are classified in [Reference Dotsenko, Feigin and Reineke11]), such a description exists. For example, for each
![]() $n\ge 1$
, if one considers the quiver on n vertices with two loops at each vertex and one arrow
$n\ge 1$
, if one considers the quiver on n vertices with two loops at each vertex and one arrow
![]() $i\to j$
for each
$i\to j$
for each
![]() $i\ne j$
, and the framing vector
$i\ne j$
, and the framing vector
![]() ${\mathbf {w}}=(1,1,\ldots ,1)$
, the locality relations form a Gröbner basis, and one recovers the result of [Reference Dotsenko10, Theorem 1] stating that the space
${\mathbf {w}}=(1,1,\ldots ,1)$
, the locality relations form a Gröbner basis, and one recovers the result of [Reference Dotsenko10, Theorem 1] stating that the space
![]() $\mathcal Q_{\mathbf {w}}$
has an explicit combinatorial basis labeled by parking functions on
$\mathcal Q_{\mathbf {w}}$
has an explicit combinatorial basis labeled by parking functions on
![]() $\{1,\ldots ,n\}$
.
$\{1,\ldots ,n\}$
.
However, one can describe an explicit basis of
![]() $\mathcal M_{\mathbf {w}}$
parametrised by subtrees of the tree of paths in the framed quiver [Reference Engel and Reineke15, Reference Reineke54] (this basis depends on some non-canonical choices). In the recent paper [Reference Franzen and Mozgovoy19], a canonical basis of
$\mathcal M_{\mathbf {w}}$
parametrised by subtrees of the tree of paths in the framed quiver [Reference Engel and Reineke15, Reference Reineke54] (this basis depends on some non-canonical choices). In the recent paper [Reference Franzen and Mozgovoy19], a canonical basis of
![]() $\mathcal M_{\mathbf {w}}$
was constructed. Taking the dual basis of
$\mathcal M_{\mathbf {w}}$
was constructed. Taking the dual basis of
![]() $\mathcal M{_{{\mathbf {w}}}^{\vee }}\simeq \mathcal Q_{\mathbf {w}}$
, we obtain a canonical combinatorial basis of
$\mathcal M{_{{\mathbf {w}}}^{\vee }}\simeq \mathcal Q_{\mathbf {w}}$
, we obtain a canonical combinatorial basis of
![]() $\mathcal Q_{\mathbf {w}}$
.
$\mathcal Q_{\mathbf {w}}$
.
6.3. Poincaré series of the Lie algebra
 ${\mathfrak {L}}_+$
${\mathfrak {L}}_+$
We shall now use our results on the Poincaré series of CoHA-modules to establish a surprising symmetry formula, showing that the Poincaré series of Lie algebras
![]() ${\mathfrak {L}}_-$
and
${\mathfrak {L}}_-$
and
![]() ${\mathfrak {L}}_+$
add up to zero. To the best of our knowledge, this result does not follow from the general principles. It would be interesting to determine the class of vertex Lie algebras for which such symmetry holds.
${\mathfrak {L}}_+$
add up to zero. To the best of our knowledge, this result does not follow from the general principles. It would be interesting to determine the class of vertex Lie algebras for which such symmetry holds.
Theorem 6.6. The Poincaré series
![]() $Z({\mathfrak {L}}_-,x,q)$
and
$Z({\mathfrak {L}}_-,x,q)$
and
![]() $Z({\mathfrak {L}}{_+^{\vee }},x,q)$
belong to the subring
$Z({\mathfrak {L}}{_+^{\vee }},x,q)$
belong to the subring
In that subring, we have the equality
Proof. We have
![]() ${\mathfrak {L}}={\mathfrak {L}}^{\mathbf {w}}_-\oplus {\mathfrak {L}}^{{\mathbf {w}}}_\circ \oplus {\mathfrak {L}}_+$
and
${\mathfrak {L}}={\mathfrak {L}}^{\mathbf {w}}_-\oplus {\mathfrak {L}}^{{\mathbf {w}}}_\circ \oplus {\mathfrak {L}}_+$
and
![]() ${\mathfrak {L}}^{\mathbf {w}}_+={\mathfrak {L}}^{{\mathbf {w}}}_\circ \oplus {\mathfrak {L}}_+$
by (59). Therefore,
${\mathfrak {L}}^{\mathbf {w}}_+={\mathfrak {L}}^{{\mathbf {w}}}_\circ \oplus {\mathfrak {L}}_+$
by (59). Therefore,
 $$ \begin{align*} Z({\mathfrak{L}}_-,x,q)&=Z({\mathfrak{L}}^{\mathbf{w}}_-,x,q)+Z({\mathfrak{L}}^{{\mathbf{w}}}_\circ,x,q),\\Z(({\mathfrak{L}}^{\mathbf{w}}_+){^{\vee}},x,q) &=Z(({\mathfrak{L}}^{{\mathbf{w}}}_\circ){^{\vee}},x,q)+Z({\mathfrak{L}}{_+^{\vee}},x,q). \end{align*} $$
$$ \begin{align*} Z({\mathfrak{L}}_-,x,q)&=Z({\mathfrak{L}}^{\mathbf{w}}_-,x,q)+Z({\mathfrak{L}}^{{\mathbf{w}}}_\circ,x,q),\\Z(({\mathfrak{L}}^{\mathbf{w}}_+){^{\vee}},x,q) &=Z(({\mathfrak{L}}^{{\mathbf{w}}}_\circ){^{\vee}},x,q)+Z({\mathfrak{L}}{_+^{\vee}},x,q). \end{align*} $$
Note that
 $$ \begin{align*}Z({\mathfrak{L}}^{\mathbf{w}}_-,x,q)&=Z(\tau_{\mathbf{w}}{\mathfrak{L}}_-,x,q) =S_{2{\mathbf{w}}}Z({\mathfrak{L}}_-,x,q),\\Z(({\mathfrak{L}}^{\mathbf{w}}_+){^{\vee}},x,q)&=Z((\tau_{\mathbf{w}}{\mathfrak{L}}_+){^{\vee}},x,q) =S_{-2{\mathbf{w}}}Z({\mathfrak{L}}{_+^{\vee}},x,q).\end{align*} $$
$$ \begin{align*}Z({\mathfrak{L}}^{\mathbf{w}}_-,x,q)&=Z(\tau_{\mathbf{w}}{\mathfrak{L}}_-,x,q) =S_{2{\mathbf{w}}}Z({\mathfrak{L}}_-,x,q),\\Z(({\mathfrak{L}}^{\mathbf{w}}_+){^{\vee}},x,q)&=Z((\tau_{\mathbf{w}}{\mathfrak{L}}_+){^{\vee}},x,q) =S_{-2{\mathbf{w}}}Z({\mathfrak{L}}{_+^{\vee}},x,q).\end{align*} $$
Hence,
By Corollary 5.4, we have
 $$ \begin{align*}\operatorname{\mathrm{Exp}}(Z({\mathfrak{L}}_-,x,q))=Z(U({\mathfrak{L}}_-),x,q)= \sum_{{\mathbf{d}}\in{\mathbb{N}}^I} \frac{(-q^{{\frac12}})^{\chi({\mathbf{d}},{\mathbf{d}})}}{(q)_{\mathbf{d}}}x^{\mathbf{d}}.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Exp}}(Z({\mathfrak{L}}_-,x,q))=Z(U({\mathfrak{L}}_-),x,q)= \sum_{{\mathbf{d}}\in{\mathbb{N}}^I} \frac{(-q^{{\frac12}})^{\chi({\mathbf{d}},{\mathbf{d}})}}{(q)_{\mathbf{d}}}x^{\mathbf{d}}.\end{align*} $$
Hence, this series as well as
![]() $Z({\mathfrak {L}}_-,x,q)$
are contained in
$Z({\mathfrak {L}}_-,x,q)$
are contained in
![]() ${\mathbb {Q}}(q^{\frac 12}){[\![{x_i{\colon } i\in I}]\!]}$
, and we can interpret (61) as an equality in this ring and obtain
${\mathbb {Q}}(q^{\frac 12}){[\![{x_i{\colon } i\in I}]\!]}$
, and we can interpret (61) as an equality in this ring and obtain
We have
![]() $U({\mathfrak {L}}^{{\mathbf {w}}}_\circ )\simeq \mathcal M{_{{\mathbf {w}}}^{\vee }}$
by Theorem 6.4 and (60). All components of the module
$U({\mathfrak {L}}^{{\mathbf {w}}}_\circ )\simeq \mathcal M{_{{\mathbf {w}}}^{\vee }}$
by Theorem 6.4 and (60). All components of the module
![]() $\mathcal M_{\mathbf {w}}$
are (degree shifted) cohomology of algebraic varieties, so they are finite-dimensional. Therefore, components of
$\mathcal M_{\mathbf {w}}$
are (degree shifted) cohomology of algebraic varieties, so they are finite-dimensional. Therefore, components of
![]() ${\mathfrak {L}}^{{\mathbf {w}}}_\circ $
are also finite-dimensional, meaning that the coefficients of the power series
${\mathfrak {L}}^{{\mathbf {w}}}_\circ $
are also finite-dimensional, meaning that the coefficients of the power series
![]() $Z({\mathfrak {L}}^{{\mathbf {w}}}_\circ ,x,q)$
are Laurent polynomials in
$Z({\mathfrak {L}}^{{\mathbf {w}}}_\circ ,x,q)$
are Laurent polynomials in
![]() $q^{{\frac 12}}$
and
$q^{{\frac 12}}$
and
![]() $Z({\mathfrak {L}}^{{\mathbf {w}}}_\circ ,x,q{^{-1}})=Z(({\mathfrak {L}}^{{\mathbf {w}}}_\circ ){^{\vee }},x,q)$
. Comparing (63) and (62), we obtain
$Z({\mathfrak {L}}^{{\mathbf {w}}}_\circ ,x,q{^{-1}})=Z(({\mathfrak {L}}^{{\mathbf {w}}}_\circ ){^{\vee }},x,q)$
. Comparing (63) and (62), we obtain
Letting
![]() ${\mathbf {w}}\to \infty $
(meaning that
${\mathbf {w}}\to \infty $
(meaning that
![]() ${\mathbf {w}}_i\to \infty $
for all
${\mathbf {w}}_i\to \infty $
for all
![]() $i\in I$
), we obtain the required equation.
$i\in I$
), we obtain the required equation.
This result implies that there exists a version of Corollary 5.10 where the action of
![]() $\partial $
on the Lie algebra
$\partial $
on the Lie algebra
![]() ${\mathfrak {L}}_+$
is used to determine the refined Donaldson–Thomas invariants. As a consequence, one obtains a strong supporting evidence for the Koszulness conjecture of [Reference Dotsenko, Feigin and Reineke11]. More precisely, in [Reference Dotsenko, Feigin and Reineke11], one constructed some explicit quadratic algebra
${\mathfrak {L}}_+$
is used to determine the refined Donaldson–Thomas invariants. As a consequence, one obtains a strong supporting evidence for the Koszulness conjecture of [Reference Dotsenko, Feigin and Reineke11]. More precisely, in [Reference Dotsenko, Feigin and Reineke11], one constructed some explicit quadratic algebra
![]() ${\mathcal {A}}_Q$
such that its Koszul dual algebra is isomorphic to
${\mathcal {A}}_Q$
such that its Koszul dual algebra is isomorphic to
![]() $U({\mathfrak {L}}_+)$
and
$U({\mathfrak {L}}_+)$
and
By Theorem 6.6, we have
Hence,
which is the ‘numerical Koszulness’ property of the algebra
![]() ${\mathcal {A}}_Q$
.
${\mathcal {A}}_Q$
.
Acknowledgements
The first author is grateful to Boris Feigin for introducing him to the beauty of principal subalgebras of lattice vertex algebras, and to Michael Finkelberg and Valery Lunts whose questions about a decade ago made him suspect that his work in [Reference Dotsenko10] may be related to non-commutative Hilbert schemes. The second author is grateful to Ben Davison, Hans Franzen, Boris Pioline, Markus Reineke, Olivier Schiffmann and Yan Soibelman for useful discussions. Both authors would like to thank Arkadij Bojko, Evgeny Feigin and Dominic Joyce for helpful feedback on a draft version of the paper.
This work has benefited from support provided by University of Strasbourg Institute for Advanced Study (USIAS) for the Fellowship USIAS-2021-061, within the French national program ‘Investment for the future’ (IdEx-Unistra), by the French national research agency project ANR-20-CE40-0016, and by Institut Universitaire de France.
Competing interest
The authors have no competing interest to declare.