Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-25T04:28:02.998Z Has data issue: false hasContentIssue false
  • English
  • Français

On the topology of the transversal slice of a quasi-homogeneous map germ

Part of: Local theory

Published online by Cambridge University Press:  06 October 2023

O. N. SILVA
O. N. SILVA*
Affiliation:
Universidade Federal da Paraíba, Departamento de Matemática, 58.051-900, João Pessoa-PB, Brazil. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a corank 1, finitely determined, quasi-homogeneous map germ f from 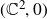$(\mathbb{C}^2,0)$ to 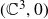$(\mathbb{C}^3,0)$. We describe the embedded topological type of a generic hyperplane section of 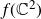$f(\mathbb{C}^2)$, denoted by 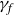$\gamma_f$, in terms of the weights and degrees of f. As a consequence, a necessary condition for a corank 1 finitely determined map germ 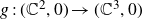$g\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$ to be quasi-homogeneous is that the plane curve 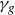$\gamma_g$ has either two or three characteristic exponents. As an application of our main result, we also show that any one-parameter unfolding 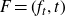$F=(f_t,t)$ of f which adds only terms of the same degrees as the degrees of f is Whitney equisingular.

MSC classification

Primary: 32B10: Germs of analytic sets, local parametrization 14B07: Deformations of singularities
Secondary: 32B15: Analytic subsets of affine space 14B05: Singularities
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 176 , Issue 2 , March 2024 , pp. 339 - 359
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Buchweitz, R.O. and Greuel, G.-M.. The milnor number and deformations of complex curve singularities. Invent. Math. 58 (1980), 241–281.Google Scholar
Callejas Bedregal, R., Houston, K. and Ruas, M.A.S.. Topological triviality of families of singular surfaces. Preprint (2006), arXiv:math/0611699v1.Google Scholar
Campillo, A.. Algebroid curves in positive characteristic. Lecture Notes in Math. 813 (Springer, 1980).CrossRefGoogle Scholar
Cohen, M.N.. Roots of formal power series and new theorems on riordan group elements. Preprint (2019), arXiv:1907.00116v1.Google Scholar
Damon, J.. Topological triviality and versality for subgroups of A and K II. Sufficient conditions and applications. Nonlinearity 5 (1992), 373–412.CrossRefGoogle Scholar
Decker, W., Greuel, G.-M., Pfister, G. and Schönemann, H.. Singular 4-0-2, A computer algebra system for polynomial computations. In: M. Kerber and M. Kohlhase (eds.), Symbolic Computation and Automated Reasoning. The Calculemus-2000 Symposium (2001), 227–233. Available at: http://www.singular.uni-kl.de.Google Scholar
Fernández de Bobadilla, J. and Pe Pereira, M.. Equisingularity at the normalisation. J. Topol. 88 (2008), 879–909.CrossRefGoogle Scholar
Gaffney, T.. Polar multiplicities and equisingularity of map germs. Topology 32 (1993), 185–223.CrossRefGoogle Scholar
Giles Flores, A., Silva, O.N. and Snoussi, J.. On tangency in equisingular families of curves and surfaces. Quart. J. Math. 71 (2020), 485–505.Google Scholar
Grauert, H. and Remmert, R.. Theory of stein spaces. Grundlehren Math. Wiss. 236 (Springer-Verlag, Berlin, 1979).CrossRefGoogle Scholar
Hernandes, M.E., Miranda, A.J. and Peñafort–Sanchis, G.. A presentation matrix algorithm for $f_{\ast}\mathcal{O}_{X,x}$ . Topology Appl. 234 (2018), 440–451.CrossRefGoogle Scholar
Marar, W.L. and Nuño–Ballesteros, J.J.. Slicing corank 1 map germs from $\mathbb{C}^2$ to $\mathbb{C}^3$ . Quart. J. Math. 65 (2014), 1375–1395.CrossRefGoogle Scholar
Marar, W.L., Nuño–Ballesteros, J.J. and Peñafort–Sanchis, G.. Double point curves for corank 2 map germs from $\mathbb{C}^2$ to $\mathbb{C}^3$ . Topology Appl. 159 (2012), 526–536.Google Scholar
Marar, W.L. and Mond, D.. Multiple point schemes for corank 1 maps. J. London Math. Soc. 39 (1989), 553–567.CrossRefGoogle Scholar
Mather, J.N.. Stability of $C^{\infty}$ mappings. VI: the nice dimensions. Lecture Notes in Math. 192 (Springer, Berlin, 1971), 207–253.CrossRefGoogle Scholar
Mond, D.. On the classification of germs of maps from $\mathbb{R}^2$ to $\mathbb{R}^3$ . Proc. London Math. Soc. 50 (3) (1985), 333–369.CrossRefGoogle Scholar
Mond, D.. Some remarks on the geometry and classification of germs of map from surfaces to 3-space. Topology 26 (1987), 361–383.CrossRefGoogle Scholar
Mond, D.. The number of vanishing cycles for a quasihomogeneous mapping from $\mathbb{C}^2$ to $\mathbb{C}^3$ . Quart. J. Math. 42 (2) (1991), 335–345.CrossRefGoogle Scholar
Mond, D. and Nuño–Ballesteros, J.J.. Singularities of mappings. Grundlehren Math. Wiss. 357 (Springer-Verlag, New York, 20202020), 335–345.Google Scholar
Mond, D. and Pellikaan, R.. Fitting ideals and multiple points of analytic mappings. Lecture Notes in Math. 1414 (1987), 107–161.Google Scholar
Niven, I.. Formal power series. Amer. Math. Monthly 76 (1969), 871–889.CrossRefGoogle Scholar
Pellikaan, R.. Hypersurface singularities and resolutions of Jacobi modules. Dissertation. Rijksuniversiteit te Utrecht (1985).Google Scholar
Peñafort–Sanchis, G.. Reflection maps. Math. Ann. 378 (2020), 559–598.CrossRefGoogle Scholar
Ruas, M.A.S. and Silva, O.N.. Whitney equisingularity of families of surfaces in $\mathbb{C}^3$ . Math. Proc. Camb. Phil. Soc. 166 (2019), 353–369.CrossRefGoogle Scholar
Saito, K.. Quasihomogene isolierte Singularitäten von Hyperflächen. Invent. Math. 14 (1971), 123–142.CrossRefGoogle Scholar
Silva, O.N.. On invariants of generic slices of weighted homogeneous corank 1 map germs from the plane to 3-space. Bull. Braz. Math. Soc. 52 (2021), 663–677.CrossRefGoogle Scholar
Silva, O.N.. Surfaces with non-isolated singularities. PhD. thesis. Universidade de São Paulo. Avalaible at http://www.teses.usp.br/teses/disponiveis/55/55135/tde-10052017-085440/pt-br.php (2017).Google Scholar
Surfer, https://imaginary.org/program/surfer Google Scholar
Wall, C.T.C.. Finite determinacy of smooth map germs. Bull. London Math. Soc. 13 (1981), 481–539.CrossRefGoogle Scholar