Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-24T15:53:59.571Z Has data issue: false hasContentIssue false
  • English
  • Français

Branching patterns of wave trains in mass-in-mass lattices

Part of: Functional-differential and differential-difference equations

Published online by Cambridge University Press:  11 January 2024

Ling Zhang  and
Shangjiang Guo
Ling Zhang
Affiliation:
School of Mathematics and Physics, China University of Geosciences, Wuhan, Hubei 430074, People's Republic of China ([email protected])
Shangjiang Guo
Affiliation:
School of Mathematics and Physics, China University of Geosciences, Wuhan, Hubei 430074, People's Republic of China Center for Mathematical Sciences, China University of Geosciences, Wuhan, Hubei 430074, People's Republic of China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the existence and branching patterns of wave trains in the mass-in-mass (MiM) lattice, which is a variant of the Fermi–Pasta–Ulam (FPU) lattice. In contrast to FPU lattice, we have to solve coupled advance-delay differential equations, which are reduced to a finite-dimensional bifurcation equation with an inherited Hamiltonian structure by applying a Lyapunov–Schmidt reduction and invariant theory. We establish a link between the MiM lattice and the monatomic FPU lattice. That is, the monochromatic and bichromatic wave trains persist near $\mu =0$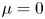 in the nonresonance case and in the resonance case $p:q$ 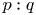where $q$ 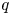is not an integer multiple of $p$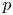. Furthermore, we obtain the multiplicity of bichromatic wave trains in $p:q$ 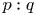resonance where $q$ 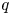is an integer multiple of $p$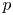, based on the singular theorem.

Keywords

Wave trainsbifurcationresonancesingularity theory

MSC classification

Secondary: 34K13: Periodic solutions 34K18: Bifurcation theory
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 27
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Betti, M. and Pelinovsky, D.. Periodic traveling waves in diatomic granular chains. J. Nonlinear Sci. 23 (2013), 689–730.CrossRefGoogle Scholar
Chen, F. and Herrmann, M.. KdV-like solitary waves in two-dimensional FPU-lattices. Discrete Contin. Dyn. Syst. 38 (2018), 2305–2332.CrossRefGoogle Scholar
Faver, T. E.. Small mass nanopteron traveling waves in mass-in-mass lattices with cubic FPUT potential. J. Dyn. Differ. Equ. 33 (2021), 1711–1752.CrossRefGoogle Scholar
Faver, T. E., Goodman, R. H. and Wright, J. D.. Solitary waves in mass-in-mass lattices. Z. Angew. Math. Phys. 71 (2020), 1–20.CrossRefGoogle Scholar
Fermi, E., Pasta, P., Ulam, S. and Tsingou, M., Studies of the nonlinear problems. (Los Alamos Document LA-1940,1955), 5 1955.CrossRefGoogle Scholar
Filip, A. and Venakides, S.. Existence and modulation of traveling waves in particle chains. Commun. Pure. Appl. Math. 52 (1999), 693–735.3.0.CO;2-9>CrossRefGoogle Scholar
Friesecke, G. and Wattis, J. A.. Existence theorem for solitary waves on lattices. Commun. Math. Phys. 161 (1994), 391–418.CrossRefGoogle Scholar
Golubitsky, M., Marsden, J. E., Stewart, I. and Dellnitz, M.. The constrained Liapunov-Schmidt procedure and periodic orbits. Fields Inst. Commun. 4 (1995), 81–127.Google Scholar
Golubitsky, M. and Schaeffer, D. G., Singularities and groups in bifurcation theory: Vol. I, Applied Math. Sciences, Vol. 51 (Springer-Verlag, New York, 1985).CrossRefGoogle Scholar
Guo, S., Lamb, J. S. and Rink, B. W.. Branching patterns of wave trains in the FPU lattice. Nonlinearity 22 (2009), 283–299.CrossRefGoogle Scholar
Hadadifard, F. and Wright, J. D.. Mass-in-mass lattices with small internal resonators. Stud. Appl. Math. 146 (2021), 81–98.CrossRefGoogle Scholar
Herrmann, M.. Unimodal wave trains and solitons in convex FPU chains. P. Roy. Soc. Edinb. A 140 (2010), 753–785.CrossRefGoogle Scholar
Iooss, G.. Travelling waves in the Fermi-Pasta-Ulam lattice. Nonlinearity 13 (2000), 849–866.CrossRefGoogle Scholar
James, G.. Periodic travelling waves and compactons in granular chains. J. Nonlinear Sci. 22 (2012), 813–848.CrossRefGoogle Scholar
Kevrekidis, P. G.. Non-linear waves in lattices: past, present, future. IMA J. Appl. Math. 76 (2011), 389–423.CrossRefGoogle Scholar
Kevrekidis, P. G., Stefanov, A. G. and Xu, H.. Traveling waves for the mass in mass model of granular chains. Lett. Math. Phys. 106 (2016), 1067–1088.CrossRefGoogle Scholar
Nesterenko, V. F.. Dynamics of heterogeneous materials (Springer Science & Business Media, New York, 2001).CrossRefGoogle Scholar
Pankov, A.. Travelling waves and periodic oscillations in Fermi-Pasta-Ulam lattices (Imperial College Press, London, 2005).CrossRefGoogle Scholar
Pankov, A. and Rothos, V. M.. Traveling waves in Fermi-Pasta-Ulam lattices with saturable nonlinearities. Discrete Contin. Dyn. Syst. 30 (2011), 835–849.CrossRefGoogle Scholar
Pelinovsky, D. E. and Schneider, G.. The monoatomic FPU system as a limit of a diatomic FPU system. Appl. Math. Lett. 107 (2020), 106387.CrossRefGoogle Scholar
Qin, W.. Modulation of uniform motion in diatomic Frenkel-Kontorova model. Discrete Contin. Dyn. Syst. 34 (2014), 3773–3788.CrossRefGoogle Scholar
Qin, W.. Wave propagation in diatomic lattices. SIAM J. Math. Anal. 47 (2015), 477–497.CrossRefGoogle Scholar
Smets, D. and Willem, M.. Solitary waves with prescribed speed on infinite lattices. J. Funct. Anal. 149 (1997), 266–275.CrossRefGoogle Scholar
Vainchtein, A.. Solitary waves in FPU-type lattices. Phys. D 434 (2022), 133252.CrossRefGoogle Scholar
Zabusky, N. J. and Kruskal, M. D.. Interaction of ‘solitons’ in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 15 (1965), 240–243.CrossRefGoogle Scholar
Zhang, L. and Guo, S.. Existence and multiplicity of wave trains in 2D lattices. J. Differ. Equ. 257 (2014), 759–783.CrossRefGoogle Scholar
Zhang, L. and Guo, S.. Existence and multiplicity of wave trains in a 2D diatomic face-centered lattice. J. Nonlinear Sci. 32 (2022), 1–38.CrossRefGoogle Scholar