1 Introduction
Automated planning is a prominent Artificial Intelligence (AI) challenge, which is concerned with the problem of finding a sequence of actions that can bring the agent into some goal state from a given initial condition. Automated planning is exploited in many real-world applications as it is a common capability requirement for intelligent autonomous agents (McCluskey et al., Reference McCluskey, Vaquero and Vallati2017). Example application domains include drilling (Fox et al., Reference Fox, Long, Tamboise and Isangulov2018), urban traffic control (McCluskey & Vallati, Reference McCluskey and Vallati2017), smart grid (Thiébaux et al., Reference Thiébaux, Coffrin, Hijazi and Slaney2013), UAV control (Ramírez et al., Reference Ramírez, Papasimeon, Lipovetzky, Benke, Miller, Pearce, Scala and Zamani2018; Kiam et al., Reference Kiam, Scala, Javega and Schulte2020), e-learning (Garrido et al., Reference Garrido, Morales and Serina2012), machine tool calibration (Parkinson et al., Reference Parkinson, Longstaff and Fletcher2014), human–robot interaction (Petrick & Foster, Reference Petrick and Foster2013), and mining (Lipovetzky et al., Reference Lipovetzky, Burt, Pearce and Stuckey2014).
The nature of real-world applications often necessitates the capability of expressing aspects of the environment with a high level of precision, and it is popular to do so through the exploitation of mixed representations providing both continuous and discrete variables along with changes that can be both instantaneous (turn on the motor) and/or continuous evolution of the system (a moving car). Following on from this, a dedicated language called PDDL+ (Planning Domain Definition Language +) was designed to support compact encoding of what are called hybrid models (Fox & Long, Reference Fox and Long2006).
The exploitation of AI planning in real-world applications is supported by the availability and continuous development of domain-independent planners providing ‘off the shelf’ technology that can be quickly used: since they accept the domain and problem description in a standardised interface language (PDDL+) and return plans using a standardised format, they can easily be exploited as embedded components within larger frameworks, as they can be interchanged without modifying the rest of the system. Automated planning can therefore be part of complex architectures, and the planning component—being modular itself—can immediately benefit from improvements in the field by swapping the corresponding internal modular components for a more advanced version of them.
Notably, hybrid PDDL+ models are amongst the most advanced models of systems, and the resulting problems are notoriously difficult for domain-independent planners to cope with due to non-linear behaviours and immense search spaces. To support the maintenance and readability by human experts, PDDL+ models allow the specification of the domain model using a lifted representation, therefore delegating to the planning engine the task of grounding the structures (actions, processes, and events) against a finite set of objects. More precisely, grounding is the task that, given some universe of objects, identifies lists of objects for each action/process/event that fully instantiate the structures. For non-toy problems, each given structure can be instantiated with millions of such lists, giving rise to an enormous amount of actions, processes, and events, which can make realistic problems impossible to tackle, even when just a handful of them is actually necessary to solve the problem.
Unfortunately, despite the importance and complexity of grounding for hybrid PDDL+ planning, there is a lack of studies focusing on investigating approaches that can limit the number of the generated structures. Most of the research on hybrid PDDL+ planning focuses on the design of domain-independent planning engines, such as DiNo (Piotrowski et al., Reference Piotrowski, Fox, Long, Magazzeni and Mercorio2016), UPMurphi (Della Penna et al., Reference Della Penna, Magazzeni, Mercorio and Intrigila2009), and CASP (Balduccini et al., Reference Balduccini, Magazzeni, Maratea and Leblanc2017), where the emphasis has been mostly given to the search module of such engines. The limited work available in the area of efficient PDDL+ grounding focused on reformulating the input models in order make them more amenable to planning engines (Franco et al., Reference Franco, Vallati, Lindsay and McCluskey2019), or on modifying the internal behaviour of planning engines to adapt them to the specific application domain (Vallati et al., Reference Vallati, Magazzeni, Schutter, Chrpa and McCluskey2016; McCluskey & Vallati, Reference McCluskey and Vallati2017), rather than on designing principled grounding modules for domain-independent planning engines. In several real-world hybrid PDDL+ applications, the grounding phase has to be done externally or manually. This not only produces a lengthy problem description but also complicates debugging and model reuse, basically invalidating some of the principles of knowledge engineering for planning (Biundo et al., Reference Biundo, Aylett, Beetz, Borrajo, Cesta, Grant, McCluskey, Milani and Verfaillie2003).
While grounding for PDDL+ has been scarcely investigated, a significant amount of work has been dedicated to designing efficient grounding approaches for classical planning. Classical planning provides a much less expressive formalism and has been studied for decades. Further, the International Planning Competition (Vallati et al., Reference Vallati, Chrpa and McCluskey2018) supported and fostered the development of highly engineered classical planning systems. In this context, the question that naturally arises is Can we leverage the extensive work on classical planning grounding to obtain efficient modular grounders for PDDL+ engines? To answer this question, in this paper, we investigate two grounding techniques for PDDL+ planning engines. The first grounding technique exploits a static analysis that is aimed at removing groundings that can never be reached because some conditions can never be satisfied. This is based on a first overapproximation of the problem. The second method deals with the above-mentioned question by constructing an abstracted, classical planning version of a PDDL+ model and feeds such a representation to off-the-shelf classical planning grounders. Also this technique exploits an overapproximation, but does so through approximations developed for classical planning. Both techniques have been designed in a modular fashion, to foster and support their integration into off-the-shelf planning engines, and, in particular for the second one, in a way that any advancement in classical planning can be reflected into PDDL+ planning. To assess the introduced grounding approaches, we consider two real-world hybrid planning applications, urban traffic control, and robotic manipulation, and we show empirically the impact that different grounding techniques can have in realistic conditions. Further, we consider two synthetic domains from the International Planning Competition (IPC), to provide an encompassing overview of the performance. Our findings show that it is possible to leverage the work done on classical planning grounding to obtain PDDL+ grounders that are more efficient and more modular than solutions at the state of the art. Last but not least, we observe that the adoption of the new technique enables the solving of several real-world problems whose resolution was not possible before this work.
Summarising, the main contributions of this work are as follows:
-
• the introduction and algorithmic specification of two modular grounders for PDDL+ hybrid planning;
-
• the deployment of such grounders as part of the state-of-the-art planning engine ENHSP (Scala et al., Reference Scala, Haslum, Thiébaux and Ramírez2016b);
-
• an empirical evaluation and validation of the proposed grounders on a range of real-world and synthetic benchmarks.Footnote 1
The remainder of this paper is organised as follows. First, in Section 2, we provide the necessary background. Then, in Section 3, we introduce and formalise the two grounding approaches. The experimental analysis is provided in Section 4. Then, in Section 5, we discuss related works. Finally, conclusions are given.
2 Background
Our work focuses on the language of hybrid planning with autonomous processes, also known as PDDL+, short for Planning Domain Definition Language Plus (Fox & Long, Reference Fox and Long2006). In this section, we report on the PDDL+ formalisation and define its semantics to provide only those accounts that are necessary to explain our contribution. A complete description of the language and its semantics is out of the scope of this paper, but can be found in the seminal work by Fox and Long (Reference Fox and Long2006) who define it via mapping into hybrid automata (Henzinger, Reference Henzinger1996).
2.1 Logical foundations
PDDL+ uses first-order logic to define formulae over a set of Boolean and numeric predicates called fluents Footnote 2. Boolean and numeric fluents are function symbols, each of which is accompanied with a list (possibly empty) of objects and/or typed variables. Objects are finite and typed entities modelling some aspect of interest. Variables are devices by which one can represent generic fluents. A fluent is said to be ground if the associated list does not contain variables; unground otherwise. A ground Boolean fluent can be true or false. A ground numeric fluent can instead take on any value from the set of real numbers
![]() $ \mathbb{R} $
plus the special symbol
$ \mathbb{R} $
plus the special symbol
![]() $ \bot $
. For instance, the Boolean fluent (on A B) can be used to model the fact that some object A is on object B; the numeric fluent (distance C D) can be used to model the numeric distance between city C and D. Or, alternatively, (distance C ?x) can be exploited to define a numeric property with the free variable ?x. Partially instantiated fluents are used as a means to compactly represent actions. Importantly, the value of a fluent can be determined only when it is ground.
$ \bot $
. For instance, the Boolean fluent (on A B) can be used to model the fact that some object A is on object B; the numeric fluent (distance C D) can be used to model the numeric distance between city C and D. Or, alternatively, (distance C ?x) can be exploited to define a numeric property with the free variable ?x. Partially instantiated fluents are used as a means to compactly represent actions. Importantly, the value of a fluent can be determined only when it is ground.
A first-order formula over some universe of fluents is defined recursively using the standard logical connectives:
-
•
 $p = \{\top,\bot\}$
where p is a Boolean fluent is a formula
$p = \{\top,\bot\}$
where p is a Boolean fluent is a formula -
•
 $ \ensuremath{\langle {\{\geq,>,=\},\xi,0} \rangle} $
where
$ \ensuremath{\langle {\{\geq,>,=\},\xi,0} \rangle} $
where
 $ \xi $
is an arithmetical expression over some numeric fluents is a formula
$ \xi $
is an arithmetical expression over some numeric fluents is a formula -
• if
 $ \psi $
is a formula, so is
$ \psi $
is a formula, so is
 $ \neg \psi $
$ \neg \psi $
-
• if
 $ \psi $
and
$ \psi $
and
 $ \phi $
are formulae, so is
$ \phi $
are formulae, so is
 $ \psi \wedge \phi$
$ \psi \wedge \phi$
-
• if
 $ \psi $
and
$ \psi $
and
 $ \phi $
are formulae, so is
$ \phi $
are formulae, so is
 $ \psi \vee \phi$
$ \psi \vee \phi$
We hereinafter call numeric condition the atomic formula of the form
![]() $ \ensuremath{\langle {\{\geq,>,=\},\xi,0} \rangle} $
. With a little abuse of notation, we use literals to refer to a Boolean fluent that is required true (i.e., the positive literal (on a b) for (on a b)
$ \ensuremath{\langle {\{\geq,>,=\},\xi,0} \rangle} $
. With a little abuse of notation, we use literals to refer to a Boolean fluent that is required true (i.e., the positive literal (on a b) for (on a b)
![]() $= \top$
) or false (i.e., the negative literal (not (on a b)) for (on a b)
$= \top$
) or false (i.e., the negative literal (not (on a b)) for (on a b)
![]() $= \bot$
); we also allow the notation
$= \bot$
); we also allow the notation
![]() $ v \in \xi $
to refer to some element v in the numeric expression
$ v \in \xi $
to refer to some element v in the numeric expression
![]() $ \xi $
. Finally, let f be a fluent, with
$ \xi $
. Finally, let f be a fluent, with
![]() $ \ensuremath{\overline{\sigma}}(\,f) $
we denote the list of typed objects and variables of f.
$ \ensuremath{\overline{\sigma}}(\,f) $
we denote the list of typed objects and variables of f.
PDDL+ uses formulae with the purpose of postulating constraints over assignments to Boolean or numeric fluents. For instance, we can use a formula
![]() $ \psi = $
(on A B) to express that (on A B) needs to hold true in order for a goal to be reached, or we can predicate that the battery level of some robot ((battery ?r)) has to be larger than 10 by a formula
$ \psi = $
(on A B) to express that (on A B) needs to hold true in order for a goal to be reached, or we can predicate that the battery level of some robot ((battery ?r)) has to be larger than 10 by a formula
![]() $\phi=$
(> (battery ?r) 10). As we will see next, this can be used in any precondition of transitions and in the goal specification.
$\phi=$
(> (battery ?r) 10). As we will see next, this can be used in any precondition of transitions and in the goal specification.
2.2 PDDL+ domain model and problem
Intuitively, A PDDL+ Domain Model defines the context of our planning problem, together with all the transitions that can happen.
Definition 1
Definition1 (PDDL+ Domain Model). A PDDL+ planning domain model is defined by the tuple
![]() $\langle T,C,F,X,A,E,P\rangle$
:
$\langle T,C,F,X,A,E,P\rangle$
:
-
• T (Types) is a set of types.
-
• C (Constants) is a set of typed objects, each of which is simply a name given to the object, and its type.
-
• F and X are sets of Boolean and numeric fluents, respectively.
-
• A (Actions), E (Events), and P (Processes) are sets of transition schemata. A transition schema is the tuple
 $\ensuremath{\langle {\ensuremath{\overline{\sigma}},pre,eff} \rangle}$
where:
$\ensuremath{\langle {\ensuremath{\overline{\sigma}},pre,eff} \rangle}$
where:-
–
 $ \bar{\sigma} $
is a sequence of objects from C or variables typed in T
$ \bar{\sigma} $
is a sequence of objects from C or variables typed in T
-
– pre is a first-order formula.
-
– eff is a set of Boolean and numeric effects. Boolean effects are assignments
 $ \ensuremath{\langle {p,\{\top,\bot\}} \rangle} $
with
$ \ensuremath{\langle {p,\{\top,\bot\}} \rangle} $
with
 $ p\in F $
where numeric effects are assignments
$ p\in F $
where numeric effects are assignments
 $ \ensuremath{\langle {p,\xi} \rangle} $
, with
$ \ensuremath{\langle {p,\xi} \rangle} $
, with
 $ \xi $
being an arithmetical expression.
$ \xi $
being an arithmetical expression. -
– Both pre and eff only mention fluents from
 $ \bar{\sigma} $
or objects from C.
$ \bar{\sigma} $
or objects from C.
-
Given some universe of typed Objects
![]() $ \Omega $
, we define the groundings of F, X and all transitions (actions, processes, and events).
$ \Omega $
, we define the groundings of F, X and all transitions (actions, processes, and events).
Definition 2
Definition2 (Grounding of
![]() $F$
and
$F$
and
![]() $X$
). The groundings of F(X) is the set of Boolean (numeric) fluents obtained by replacing, for each
$X$
). The groundings of F(X) is the set of Boolean (numeric) fluents obtained by replacing, for each
![]() $ f \in F $
(X), all variables in
$ f \in F $
(X), all variables in
![]() $ \ensuremath{\overline{\sigma}}(\,f) $
with concrete and suitable (with respect to their type) objects from
$ \ensuremath{\overline{\sigma}}(\,f) $
with concrete and suitable (with respect to their type) objects from
![]() $ \Omega $
.
$ \Omega $
.
Definition 3
Definition3 (Grounding of a Transition). A transition is ground if the parameters list only involves objects. The groundings of a transition schema
![]() $\texttt{a}$
over
$\texttt{a}$
over
![]() $ \Omega $
is denoted by
$ \Omega $
is denoted by
![]() $ \sigma(\texttt{a},\Omega) $
and corresponds to the set of all ground transitions obtained by substituting the parameter list
$ \sigma(\texttt{a},\Omega) $
and corresponds to the set of all ground transitions obtained by substituting the parameter list
![]() $\bar{\sigma}$
of a, with a list of compatible objects taken from
$\bar{\sigma}$
of a, with a list of compatible objects taken from
![]() $ \Omega $
, and then substituting each occurrence of the variables which were in
$ \Omega $
, and then substituting each occurrence of the variables which were in
![]() $\bar{\sigma}$
in the structure of a (preconditions and effects) with the newly introduced objects. Actions, processes, and events are all transitions; therefore, we will also talk about ground actions/processes/events when needed.
$\bar{\sigma}$
in the structure of a (preconditions and effects) with the newly introduced objects. Actions, processes, and events are all transitions; therefore, we will also talk about ground actions/processes/events when needed.
The set of atoms for a planning domain model is the set of all ground fluents obtained by grounding F and X using objects from
![]() $ \Omega $
. Such a set is referred by
$ \Omega $
. Such a set is referred by
![]() $ atoms(\Omega) $
. Analogously, the set of ground transitions obtained from
$ atoms(\Omega) $
. Analogously, the set of ground transitions obtained from
![]() $ \Omega $
is referred by
$ \Omega $
is referred by
![]() $ transitions(\Omega) = \bigcup\limits_{\substack{a \in A\cup E \cup P}} \sigma(\texttt{a},\Omega) $
.
$ transitions(\Omega) = \bigcup\limits_{\substack{a \in A\cup E \cup P}} \sigma(\texttt{a},\Omega) $
.
A PDDL+ planning problem is defined by combining a planning domain model D with a specific set of typed objects O, an initial state I, and a goal G. Intuitively, a planning problem asks whether, given a planning domain model, a set of objects, an initial state, and a goal there is a plan, that is, a set of actions allocated along a timeline that lets the agent achieves the goal from I considering the constraints imposed by D. We will see later what we mean by plan and what we mean by valid plan. More formally:
Definition 4
Definition4 (PDDL+ Planning Problem). Let D be a PDDL+ domain model, a planning problem is the tuple
![]() $ \Pi :$
$ \Pi :$
![]() $\langle$
D, O, I, G
$\langle$
D, O, I, G
![]() $\rangle$
where:
$\rangle$
where:
-
• is a set of typed objects.
-
• I is an assignment to all Boolean and numeric fluents that belong to
 $ atoms (O \cup C) $
$ atoms (O \cup C) $
-
• G is a first-order formula over ground Boolean and numeric fluents.
For the sake of compactness, the initial state can be specified in closed world assumption using the so-called set-theoretic formulation (Ghallab et al., Reference Ghallab, Nau and Traverso2004). That is, the initial state can be given as a set of literals for some subset of Boolean fluents and a set of assignments for some subset of numeric fluents. Everything that does not belong to this assignment is assumed to be false (for Boolean fluents) or undefined (for numeric fluents).
Hereinafter we subscript every conjunctive structure in the problem with B and N to isolate the components that deal only with Boolean (B) or numeric (N) fluents. This gets applied to the structure of formulae and in the initial state. As we will see, this is useful for mapping numeric into classical planning problems.
Figure 1 shows an example of a PDDL+ action, a process, and an event taken from the Urban Traffic Control domain model (McCluskey & Vallati, Reference McCluskey and Vallati2017) that will be considered in the experimental analysis. The action switchPhase allows to model the decision of the planning engine to stop early a traffic light phase; the continuous effects of the movement of traffic on a green light are modelled by the process flowrun_green. The shown triggerCatcher event is used for triggering a phase change.

Figure 1 An example of PDDL+ action, process, and event taken from the Urban Traffic Control domain model (McCluskey & Vallati, Reference McCluskey and Vallati2017; Antoniou et al., Reference Antoniou, Batsakis, Davies, Duke, McCluskey, Peytchev, Tachmazidis and Vallati2019)

Figure 2 An excerpt of a valid plan for a benchmark of the Urban Traffic Control domain
2.3 Semantics, plans, and validity
The semantics of a PDDL+ planning problem can be defined using the theory of hybrid automata (Henzinger, Reference Henzinger1996; Fox & Long, Reference Fox and Long2006). We will hereby report the basic semantics, the notion of a plan, and its validity. We say that a formula is satisfied in a state if such a state is a model for the formula. A ground action is applicable in a state if its precondition formula evaluates to true on that state. Events and processes are said to be active in a state if their preconditions are satisfied. Actions are decisions that can be taken by the agent. Processes and events are responses of the environment and cannot be controlled directly by the agent.
The application of an action in a state s instantaneously updates those numeric and Boolean fluents which are modified by its effects. Active processes initiate flows of continuous changes for subsets of numeric variables. The numeric effect of a process is to be understood as the time derivative of some variable x. Events trigger instantaneous changes on the state if their preconditions are satisfied.
A plan is a set of pairs
![]() $\ensuremath{\langle {t_i,a_i} \rangle}$
where
$\ensuremath{\langle {t_i,a_i} \rangle}$
where
![]() $ t_i \in \mathbb{R} $
and action
$ t_i \in \mathbb{R} $
and action
![]() $ a_i \in transitions(C \cup O)$
. A plan is valid if each action is applicable at its associated time. Plan validation corresponds to the task of evaluating whether each action precondition is satisfied in the trajectory of states induced by the active processes (that can change over time), the events that have been triggered, and the actions executed. A plan is a solution of the considered PDDL+ problem if the last state of the trajectory induced by all actions, processes, and events is a goal state for the problem, that is, a state in which the goal formula is satisfied.
$ a_i \in transitions(C \cup O)$
. A plan is valid if each action is applicable at its associated time. Plan validation corresponds to the task of evaluating whether each action precondition is satisfied in the trajectory of states induced by the active processes (that can change over time), the events that have been triggered, and the actions executed. A plan is a solution of the considered PDDL+ problem if the last state of the trajectory induced by all actions, processes, and events is a goal state for the problem, that is, a state in which the goal formula is satisfied.
An example excerpt of a valid plan for a benchmark from the Urban Traffic Control domain is provided in Figure 2. In this domain model, the only available action for the planning engine is to switch red the current traffic light phase. The action considers the current phase and the affected junctions. For instance, the first line of the strategy shown in Figure 2 means that the currently active phase 2 of intersection 6014 has to be stopped at time 130. Between each pair of actions, the system evolves for the effect of the active processes and events modelling the flow of vehicles and the switching of the traffic lights.
Several approaches have been investigated for solving hybrid planning problems; see, for instance (McDermott, Reference McDermott2003; Shin & Davis, Reference Shin and Davis2005; Della Penna et al., Reference Della Penna, Magazzeni, Mercorio and Intrigila2009; Bryce et al., Reference Bryce, Gao, Musliner and Goldman2015; Scala et al., Reference Scala, Haslum, Thiébaux and Ramírez2016b; Cashmore et al., Reference Cashmore, Magazzeni and Zehtabi2020). All these approaches have been conceived to work over representations that are variable-less. However, it is much more convenient to express the problem using the full power of the language of PDDL+. For instance, looking at our example of Figure 1, it is much more convenient to say that there is a generic switch phase among two types of objects and leave to the system the task of understanding which of the ground transitions need to be generated in order to get to the goal.
Albeit automatic grounding is desirable, this comes with the disadvantage that we move into the planning engine the burden for performing such an operation that, if not done with proper care, can represent an insurmountable barrier. Indeed, the naive grounding strategy requires blindly exploring each list of parameters of all open structures combinatorially, with a worst case that is exponential on the number of free variables in each such list (Helmert, Reference Helmert2009). A challenging aspect is that of understanding whether this can be limited by excluding from groundings all structures that are never reachable or irrelevant, whilst ensuring that the declarative representation and the desired semantics are kept consistent. In particular, we want to have a grounding mechanism that does not produce all ground transitions, but only those that are reachable. Note that, limiting the number of ground transitions directly translates into having to deal with a restricted number of ground atoms, too. Indeed, we will only need to track the atoms that are not left invariant by the actions; those which are unaffected by the actions can be removed and each formula that mentions them can be simplified with the value that such atoms have in the initial state. Because of this, in the next sections, we focus on limiting the number of ground transitions only.
In Section 3, we show two general methods aimed at performing this process. These methods exploit a relaxation principle, resulting in mechanisms that substantially depart from the naive approach of Definition 3. The second approach that we present, in particular, exploits an abstraction from PDDL+ to classical planning whose definition is necessary to understand the approach.
2.4 Classical planning
The classical planning problem differs from the PDDL+ problem in that:
-
• classical actions are not timed and are instantaneous; plans are just sequences of ground actions;
-
• there are no numeric fluents and therefore formulae cannot contain them;
-
• there are neither processes nor events that can change the state of the world autonomously; classical planning only models the agent’s decision.
Everything that is not touched by the action effects remains unchanged (frame axiom). A classical planning problem builds up on the logical foundations of the PDDL+ problem but for the absence of numeric variables. More formally:
Definition 5
Definition5. A classical planning problem
![]() $ \Pi $
is a tuple
$ \Pi $
is a tuple
![]() $ \ensuremath{\langle {T,C,F,A,O,I,G} \rangle} $
where:
$ \ensuremath{\langle {T,C,F,A,O,I,G} \rangle} $
where:
-
• T (Types) is a set of types
-
• C (Constants) is a set of typed objects, each of which is simply a name given to the object, and its type.
-
• O (Objects) is a set of typed objectsFootnote 3
-
• F is a set of Boolean fluents
-
• A (Actions) is a set of actions, each described by the pair
 $ \ensuremath{\langle {pre,eff} \rangle} $
where:
$ \ensuremath{\langle {pre,eff} \rangle} $
where:-
– pre is a logical formula across F over variables from
 $ \ensuremath{\overline{\sigma}}(a) $
and objects from
$ \ensuremath{\overline{\sigma}}(a) $
and objects from
 $ C \cup O $
$ C \cup O $
-
– eff is a set of Boolean assignments of the form
 $ \ensuremath{\langle {f,\{\top,\bot\}} \rangle} $
with f being a Boolean fluent.
$ \ensuremath{\langle {f,\{\top,\bot\}} \rangle} $
with f being a Boolean fluent.
-
-
• I is the initial assignment for ground Boolean fluents
-
• G is a logical formula
As it is possible to observe, a classical planning problem is a subclass of a PDDL+ problem; many of its components are indeed identical to PDDL+ (e.g., types, constants, and objects). Differently from a PDDL+ problem though, plans in classical planning are just sequences of actions. Valid plans are such that their sequence is a valid trajectory of states that transforms the given initial state I into a state in which the goal G is satisfied. A plan is said to be valid if all action preconditions are satisfied along the entire execution. For a more detailed description of classical planning, the interested reader is referred to Ghallab et al., (Reference Ghallab, Nau and Traverso2004).
3 Domain-independent PDDL+ grounding
This section is devoted to introduce two alternative routes for performing PDDL+ grounding in a domain-independent fashion.
3.1 Static analysis method
The first approach that we present is based on the idea of exploiting a static analysis of the domain model for focusing the generation of ground actions towards a reduced set of parameters. Such a subset of parameters is restricted leveraging from the necessary condition arising by looking at the static conjuncts belonging to the transition schema precondition, and the hidden preconditions emerging from numeric effects that need to be applied.
This idea has been already exploited in classical planning with great success since the earlier work by Hoffmann and Nebel (Reference Hoffmann and Nebel2001) in the FF planning system using the preprocessor of IPP (Koehler & Hoffmann, Reference Koehler and Hoffmann2000). As we will see in this section, it is possible to straightforwardly extend this approach to the case of hybrid PDDL+ planning. This boils down to (i) extending the static analysis to consider not only actions but also processes and events as possible transitions that can change the value of some predicate and/or fluent and (ii) consider the case of numeric condition separately to the case of literalsFootnote 4. In a nutshell, the idea is to consider events and processes just as a ‘traditional’ actions. Notice that, by doing so, we obtain a safe relaxation of our problem; indeed, we give to the agent the possibility of directly controlling the environment through processes and events as well. This change of semantics enlarges the set of possible solutions: if there is a problem solvable with the normal semantics, there always exists one trajectory of actions in which all processes and events are replaced by actions controllable by the agent. The contrary is not true: there may be a trajectory of actions that leads to the goal for which there is no mapping of such a trajectory into a valid sequencing of actions, processes, and eventsFootnote 5.
Our procedure implements this idea starting from the structure of the actions and is based on the notion of a static fluent. More formally, let
![]() $\Pi = \ensuremath{\langle {T,C,F,X,A,E,P,O,I,G} \rangle} $
be a PDDL+ planning domain model. We say that a Boolean or a numeric fluent v is static iff
$\Pi = \ensuremath{\langle {T,C,F,X,A,E,P,O,I,G} \rangle} $
be a PDDL+ planning domain model. We say that a Boolean or a numeric fluent v is static iff
![]() $\forall t \in A \cup E \cup P$
is such that
$\forall t \in A \cup E \cup P$
is such that
![]() $ abstract(v,t) \cap affected(t) = \emptyset$
where:
$ abstract(v,t) \cap affected(t) = \emptyset$
where:
-
• abstract(v, t) is the set of Boolean or numeric fluents (depending on whether v is a Boolean or numeric fluent) obtained by getting abstracted versions of such a fluent through some transition t. This abstraction amounts to substituting the variables in the parameters of v (if any) with compatible variables taken from the parameters of t. Note that there may be different substitutions also in this case, depending on which variables from the parameters list are taken.
-
• affected(t) is the set of Boolean or numeric fluents that are affected by the transition. That is
 $affected(t) = \{ v_1 \mid \ensuremath{\langle {v_1,\xi} \rangle} \in eff(t) \} \cup \{ v_1 \mid \ensuremath{\langle {v_1,\{\top,\bot\} \in eff(t)} \rangle} \}$
$affected(t) = \{ v_1 \mid \ensuremath{\langle {v_1,\xi} \rangle} \in eff(t) \} \cup \{ v_1 \mid \ensuremath{\langle {v_1,\{\top,\bot\} \in eff(t)} \rangle} \}$
Intuitively, given a set of static Boolean and numeric fluents, and an action t, the set of possible substitutions for the variables belonging to t parameters, that is,
![]() $\bar{\sigma}$
(t), can be constrained looking at the necessary static precondition conjuncts that need to be true for that transition to be applicable and looking at those numeric effects that need the evaluation of some numeric fluents to be applicable. We start from the universal substitution
$\bar{\sigma}$
(t), can be constrained looking at the necessary static precondition conjuncts that need to be true for that transition to be applicable and looking at those numeric effects that need the evaluation of some numeric fluents to be applicable. We start from the universal substitution
![]() $ Sub : V \to O\cup C $
that maps every variable to a set of objects by making sure to get only those which are compatible type wise. Then, we iterate over all conditions that involve static fluent (in case of numeric condition), or are themselves static (literals), and reduce the objects to be mapped only towards those generating conditions (numeric or literals) that are not statically unreachable.
$ Sub : V \to O\cup C $
that maps every variable to a set of objects by making sure to get only those which are compatible type wise. Then, we iterate over all conditions that involve static fluent (in case of numeric condition), or are themselves static (literals), and reduce the objects to be mapped only towards those generating conditions (numeric or literals) that are not statically unreachable.
Algorithm 1 Static Analysis-Based Grounding

The grounding reduction process for a transition is described in Algorithm 1. The main function of the algorithm is Reduce. This function takes the input of some transition and the initial state and produces a reduced set of substitutions for the transition parameters. As hinted at above, the procedure first sets each variable in the parameters of the action to the whole universe of objects and constants that are compatible with the variable at hand (Line 3). In this line, the function Con simply filters out those objects which are not consistent with the variable at hand. Then the algorithm iterates over all necessary numeric expressions and the precondition of the action. Notice that this algorithm here works under the assumption that the action precondition has been normalised to a conjunction of literals and numeric conditionsFootnote 6. The necessary numeric expressions (Necessary in the algorithm) are those expressions that need to be checked for being sure that none of its numeric fluent is irreversibly undefined.
Algorithm 2 Auxiliary Procedures

Algorithm 1 makes use of a number of auxiliary procedures, that is, ReduceExpression, ReduceSat, and ReduceNum whose descriptions are reported separately in Algorithm 2. The algorithm activates the appropriate function considering the type of precondition or necessary condition at hand, which can be either a numeric expression, a literal, or a numeric condition. These functions make use of the operator S v which is a way to access all the tuples where v is the first element. The intersection with some new tuples objs filters out those mappings that are not possible. Additional auxiliary procedures are presented in Algorithm 3 and are used in Algorithm 1 to check whether a considered fluent is static or not.
Algorithm 3 Checking for Static Fluent

Having defined what the reduction process is, the entire grounding process boils down to calling the reduce function for each action, event, and process and ground them only across the reduced set of objects that have been identified.
To explain the algorithm in practice, let us consider the situation of Figure 1. The (trigger ?i) Boolean fluent is not a static one because its truth value may depend on whether the action (switchPhase) (with compatible parameters) is applied or not. Different is the situation for the (turnrate ?p ?r1 ?r2) numeric fluent. The value of this fluent cannot be changed by any action in the problem, so whether this may ever be true or not, solely depends on the initial state of the problem. This is indeed a static numeric predicate. In particular, if some grounding of this predicate is less than (or equal to)
![]() $0.0$
, the parameters used for that grounding cannot be used in the flowrun_green parameters’ list. Our static analysis method will not even try to ground the actions associated to those parameters for which (turnrate ?p ?r1 ?r2) leads to (> (turnrate ?p ?r1 ?r2) 0.0) being unsatisfied. This indeed reduces the number of groundings to only those combinations of parameters that do satisfy (> (turnrate ?p ?r1 ?r2) 0.0); a brute force grounding will require the Cartesian product of all objects compatible with variables ?p ?r1 ?r2. In other words, assuming 100 objects of each kind, it will require 1 000 000 of groundings. As we will see in our real-world use cases, this situation is not rare and does happen due to the inherent weakness of relational representation in several benchmarks from the international planning competition, too Vallati et al. (Reference Vallati, Chrpa and McCluskey2018).
$0.0$
, the parameters used for that grounding cannot be used in the flowrun_green parameters’ list. Our static analysis method will not even try to ground the actions associated to those parameters for which (turnrate ?p ?r1 ?r2) leads to (> (turnrate ?p ?r1 ?r2) 0.0) being unsatisfied. This indeed reduces the number of groundings to only those combinations of parameters that do satisfy (> (turnrate ?p ?r1 ?r2) 0.0); a brute force grounding will require the Cartesian product of all objects compatible with variables ?p ?r1 ?r2. In other words, assuming 100 objects of each kind, it will require 1 000 000 of groundings. As we will see in our real-world use cases, this situation is not rare and does happen due to the inherent weakness of relational representation in several benchmarks from the international planning competition, too Vallati et al. (Reference Vallati, Chrpa and McCluskey2018).
This method may reduce the number of substitutions substantially, and therefore limit to some extent the combinatorial explosion of groundings caused by the cross-product of all universes of objects. Yet, it does not really exclude the groundings of some actions that could be easily detected as unreacheable. Let us come back to our example of Figure 1. Note that, although we do not know in general whether (trigger ?i) will ever be satisfied, we do know that only some of them can eventually be reached. Those are the ones obtained by applying the action swithcPhase with some parameter. Many of these actions are indeed not reachable, and this can be easily detected by noticing that the predicate (contains ?i ?p) is itself a static predicate.
To exploit this intuition in a systematic fashion, the next section shows how to make use of a classical planning abstraction, and therefore leverage on relaxed reachability grounding mechanisms present in state of the art classical planning engines.
3.2 Abstracting PDDL+ problems into classical problems
In this section, we show how to leverage on grounding systems developed for classical planning. Please refer to Section 2.4 for a discussion about the differences between hybrid PDDL+ planning and classical planning.
For the sake of clarity, let us omit names of structures (e.g., actions, events) when obvious from the context and refer to Boolean and numeric predicates using the simpler terms proposition and numeric. Let us further note that for convenience we have directly denoted the classical planning problem as the merge of an instance of a classical planning problem with the classical domain model.
We are now in the position to formalise the abstraction operation. Intuitively, we want to obtain a formulation of a classical planning problem that overestimates the behaviour of a given PDDL+ problem. We construct such an abstraction by means of a problem transformation. More precisely, we denote with
![]() $ \tau $
the abstraction from a PDDL+ problem to a classical planning problem.
$ \tau $
the abstraction from a PDDL+ problem to a classical planning problem.
![]() $ \tau $
is formally a mapping from a PDDL+ problem
$ \tau $
is formally a mapping from a PDDL+ problem
![]() $ \Pi : \ensuremath{\langle {T,C,F,X,A,E,P,O,I,G} \rangle} $
to the classical planning problem
$ \Pi : \ensuremath{\langle {T,C,F,X,A,E,P,O,I,G} \rangle} $
to the classical planning problem
![]() $ \Pi' : \ensuremath{\langle {T,C,F',A',O,I',G'} \rangle} $
where the primed components are defined in a way that the following holds:
$ \Pi' : \ensuremath{\langle {T,C,F',A',O,I',G'} \rangle} $
where the primed components are defined in a way that the following holds:
-
•
 $ F' = F \cup X$
$ F' = F \cup X$
-
•
 $ I' = I'_{B} \cup \bigcup\limits_{\ensuremath{\langle {f_i,k_i} \rangle} \in I_{N}}{f_i} $
$ I' = I'_{B} \cup \bigcup\limits_{\ensuremath{\langle {f_i,k_i} \rangle} \in I_{N}}{f_i} $
-
•
 $ A' = \bigcup\limits_{t \in A \cup E \cup P}\ensuremath{\langle {pre_{N \to F}(t),eff_{N \to F}(t)} \rangle}$
where
$ A' = \bigcup\limits_{t \in A \cup E \cup P}\ensuremath{\langle {pre_{N \to F}(t),eff_{N \to F}(t)} \rangle}$
where-
–
 $ pre_{N \to F}(t) = abs(pre(t)) \wedge \bigwedge\limits_{f_i \in \xi.\ensuremath{\langle {f_i,\xi} \rangle} \in eff_N(t)}f_i$
$ pre_{N \to F}(t) = abs(pre(t)) \wedge \bigwedge\limits_{f_i \in \xi.\ensuremath{\langle {f_i,\xi} \rangle} \in eff_N(t)}f_i$
-
–
 $ eff_{N \to F}(t) = eff_B(t) \cup \bigcup\limits_{f_i.\ensuremath{\langle {f_i,\xi} \rangle} \in eff_N(t)} f_i$
$ eff_{N \to F}(t) = eff_B(t) \cup \bigcup\limits_{f_i.\ensuremath{\langle {f_i,\xi} \rangle} \in eff_N(t)} f_i$
-
-
•
 $ G' = abs(G)$
$ G' = abs(G)$
where
![]() $ abs(\psi) $
is the abstraction of a general formula
$ abs(\psi) $
is the abstraction of a general formula
![]() $ \psi $
given in negation normal formFootnote 7, defined as follows:
$ \psi $
given in negation normal formFootnote 7, defined as follows:
 \begin{equation}abs(\psi) = \begin{cases} \psi & \text{if } \psi \text{ is a literal}\\ \bigwedge\limits_{f_i \in \xi. (\xi,\{\geq, >, =\},0) = \psi} f_i & \text{if } \psi \text{ is a numeric condition}\\ abs(\alpha) \wedge abs(\beta) & \text{if }\psi=\alpha \wedge \beta\\ abs(\alpha) \vee abs(\beta) & \text{if }\psi=\alpha \vee \beta\\ \neg abs(\alpha) & \text{if }\psi= \neg\alpha\\ \end{cases}\end{equation}
\begin{equation}abs(\psi) = \begin{cases} \psi & \text{if } \psi \text{ is a literal}\\ \bigwedge\limits_{f_i \in \xi. (\xi,\{\geq, >, =\},0) = \psi} f_i & \text{if } \psi \text{ is a numeric condition}\\ abs(\alpha) \wedge abs(\beta) & \text{if }\psi=\alpha \wedge \beta\\ abs(\alpha) \vee abs(\beta) & \text{if }\psi=\alpha \vee \beta\\ \neg abs(\alpha) & \text{if }\psi= \neg\alpha\\ \end{cases}\end{equation}
Coming back to our example of Figure 1, take for instance the formula (< (occupancy ?r2)(capacity ?r2)). This formula involves two numeric fluents, that is, (occupancy ?r2) and (capacity ?r2). These two numeric fluents will be reinterpreted as two new fresh Boolean predicates by Equation (1) with the same name. They will be made true only if some other action, process, or event use them somehow.
Ultimately, as we hinted at in the previous section, our approach focuses at identifying only those actions (processes, events in the case of PDDL+) that are reachable for the problem at hand. To precisely see how this is achieved through our mapping into classical planning, we need to define what a set of reachable ground actions is for classical planning more formally.
Definition 6
Definition6 (Reachable Ground Actions). The reachable ground actions set for a classical planning problem
![]() $ \Pi $
is the set of ground actions that can be eventually reached by iteratively applying actions starting from the initial state up-to saturation. That is, up to the point that no new state can be discovered.
$ \Pi $
is the set of ground actions that can be eventually reached by iteratively applying actions starting from the initial state up-to saturation. That is, up to the point that no new state can be discovered.
It can be proved that our transformation is complete in the sense that if an action, event, or process is reachable in the PDDL+ formulation, it is reachable in the generated classical planning problem, too.
Proposition 1
Proposition1 (Over-approximation of PDDL+ through
![]() $\tau$
). Let
$\tau$
). Let
![]() $ \Pi $
be a PDDL+ planning problem, the set of reachable ground actions, processes, and events is a subset of the ground actions reachable in
$ \Pi $
be a PDDL+ planning problem, the set of reachable ground actions, processes, and events is a subset of the ground actions reachable in
![]() $ \tau(\Pi) $
(with the proper transformation from actions to processes and events).
$ \tau(\Pi) $
(with the proper transformation from actions to processes and events).
Proof. We can prove this by observing that each atom in some formula of
![]() $\Pi$
that is achievable implies that the same atom, or its abstraction in case we are dealing with numeric condition, is achievable in
$\Pi$
that is achievable implies that the same atom, or its abstraction in case we are dealing with numeric condition, is achievable in
![]() $\tau(\Pi)$
. If the set of atoms that is reachable is the same, we can safely observe that all those actions in
$\tau(\Pi)$
. If the set of atoms that is reachable is the same, we can safely observe that all those actions in
![]() $\tau(\Pi)$
that have their precondition reachable will become themselves reachable. This observation is trivial for Boolean conditions, and only a bit more involved for numeric conditions. For this latter case indeed, if some numeric condition is reachable in
$\tau(\Pi)$
that have their precondition reachable will become themselves reachable. This observation is trivial for Boolean conditions, and only a bit more involved for numeric conditions. For this latter case indeed, if some numeric condition is reachable in
![]() $\Pi$
, this means that there is an action that can eventually satisfy its abstraction by interacting with some numeric variable in it. If we look at the abstraction operator of Equation (1), we observe that it suffices to have all numeric predicates evaluated in the numeric condition. And this is indeed the case if there is some action operating on it, or the initial state setting them to some value. Analogous is the consideration for the right-hand side of all effects in the transitions.
$\Pi$
, this means that there is an action that can eventually satisfy its abstraction by interacting with some numeric variable in it. If we look at the abstraction operator of Equation (1), we observe that it suffices to have all numeric predicates evaluated in the numeric condition. And this is indeed the case if there is some action operating on it, or the initial state setting them to some value. Analogous is the consideration for the right-hand side of all effects in the transitions.
Calculating the exact number of reachable ground actions is, however, unfeasible because it would require unrolling the complete transitions system, which, in the case of a PDDL+ problem may imply visiting an infinite transition system. Fortunately, thanks to the fact that we have a finite abstraction of the problem, we can limit this worst-case behaviour by adopting approximations that are used in classical planning problems. As matter of facts, in order to overcome the problem of detecting all reachable actions, modern classical planners use relaxed reachability grounding, based on ideas borrowed by Answer Set Programming (Helmert, Reference Helmert2009; Lifschitz, Reference Lifschitz2008)Footnote 8. This gives us a superset of reachable actions in that the transition system is itself approximated with one where the validity of conditions grows monotonically. Thanks to Proposition 1 then, we know that the set of reachable actions for the abstraction of a PDDL+ problem is a subset of the actions reachable in classical planning. By transitivity, we can hence use the classical ground actions as a way to overapproximate the reachable grounding for all events, actions, and processes for the concrete PDDL+ problem. Of course, once this approximation is done, we can use reachability analysis on numeric problems (such as Scala et al., Reference Scala, Haslum and Thiébaux2016a) and refine the set of ground action even further. Yet, this refinement is already done on a smaller set (the one computed by the classical planning abstraction), so it is expected to be done much faster. To some extent, this method can be seen as a two-level reachability analysis. The former is dealt with using classical planning. The latter using techniques that are aware of the numeric structure of the problem.
Algorithm 4 Classical Planning Abstraction-Based Grounding

Algorithm 4 summarises the main steps for grounding a whole PDDL+ problem using the abstraction mechanism as per above. As a first step, the algorithm calls transformation
![]() $ \tau $
, and then a classical grounder on the arising classical planning problem. Once a ground of the classical planning problem is generated, and actions are stored in
$ \tau $
, and then a classical grounder on the arising classical planning problem. Once a ground of the classical planning problem is generated, and actions are stored in
![]() $ A_{cg} $
, line 4, we iterate over all the generated actions and for each of them identify whether the action was an abstraction of a PDDL+ action, an event, or a process. For each of this, we then populate the new structures
$ A_{cg} $
, line 4, we iterate over all the generated actions and for each of them identify whether the action was an abstraction of a PDDL+ action, an event, or a process. For each of this, we then populate the new structures
![]() $ A_g $
,
$ A_g $
,
![]() $ E_g $
, and
$ E_g $
, and
![]() $ P_g $
that will only contain ground versions of the original transitions. Function ground accomplishes the task of substituting the objects found by grounding the classical planning action relative to each transition throughout the structure of the transition at hand.
$ P_g $
that will only contain ground versions of the original transitions. Function ground accomplishes the task of substituting the objects found by grounding the classical planning action relative to each transition throughout the structure of the transition at hand.
The abstraction-based mechanism has the obvious advantage of capturing deeper causal dependencies between actions. However, it introduces a bit of overhead. The system indeed needs to make use of an external classical planner, and there may be delays caused by encoding and decoding information from and to the PDDL+ representation. Next section studies this aspect empirically.
4 Experimental analysis
This section reports on an experimental analysis aimed at evaluating the impact and the importance of the proposed domain-independent PDDL+ grounding techniques for solving hybrid planning instances. In particular, we measure the size of the generated ground version of each benchmark instance with the methods presented in this paper (measured in terms of number of actions, processes, and events) and the computational time spent to perform the operation. We also measure the overall planning time to understand how (and if) grounding affects the search process as well. Our experiments use a variety of benchmarks took from standard benchmarks and real-world problems. More details below.
4.1 Experimental settings
For the sake of fairness, we implemented the considered grounding techniques as a modular component of the state-of-the-art planning engine ENHSP (Scala et al., Reference Scala, Haslum and Thiébaux2016a, Reference Scala, Haslum, Thiébaux and Ramírez2016b). This provides us a way for isolating the impact of the grounder on the overall planning process. ENHSP is a well-known Java-based planning engine that includes a wide range of domain-independent search techniques and heuristics for solving PDDL+ planning instances and is modular in nature. The results reported in this analysis have been obtained by running ENHSP tuned to maximise coverage. The classical planning abstraction of our PDDL+ problem is given to the Fast-Downward Grounding mechanism took from the last release of the plannerFootnote 9. Once the mechanism is done grounding the classical planning problem, we collect all the ground actions and remap them in the original actions/processes/events they have been generated from. Figure 3 reports the overall process and highlights the main modules of the ENHSP planning engine. Note that, in the figure, it is possible to go along with grounding using one from three different grounders: Naive, Static, and FDI. We use all of them for our experiments.
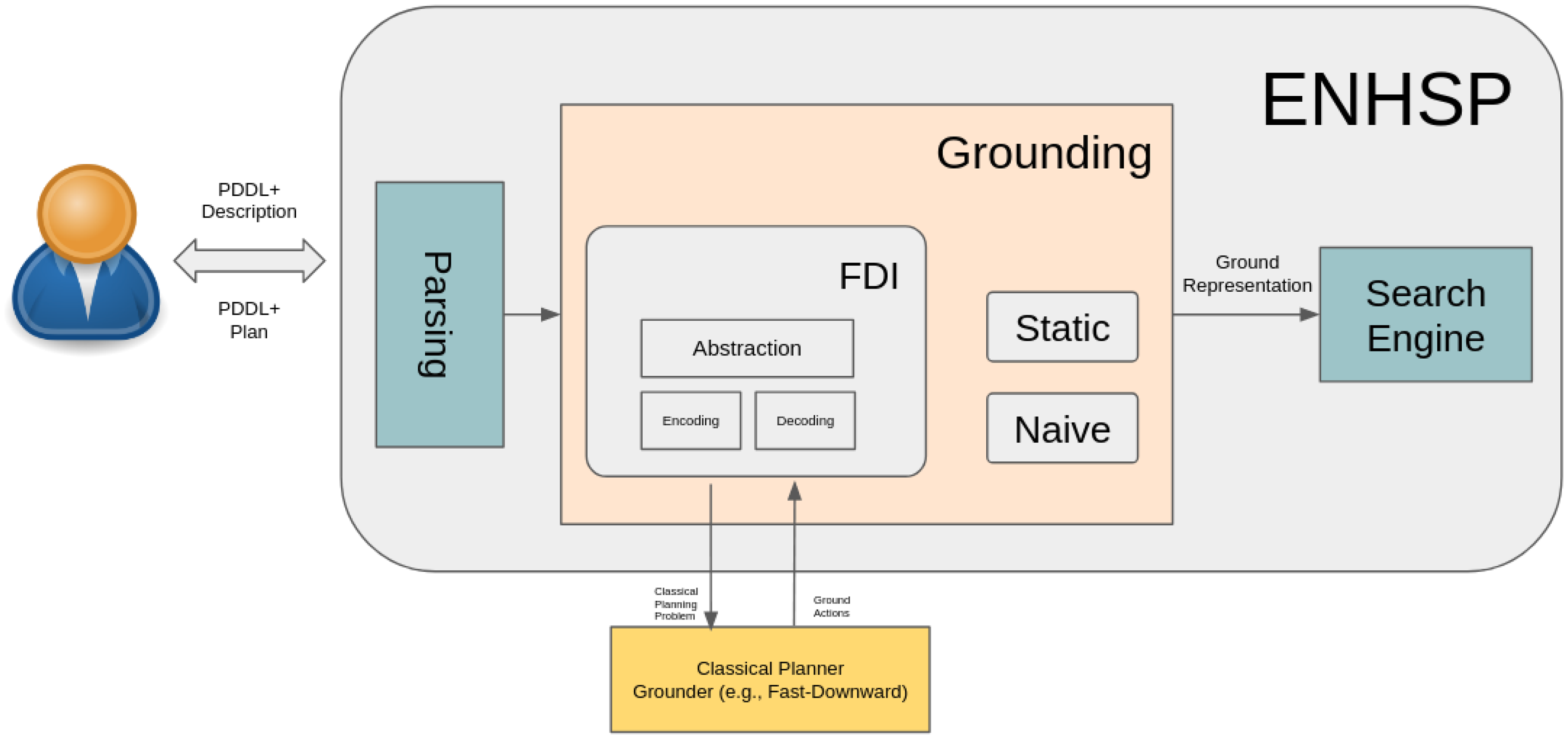
Figure 3 Grounding and Search Data flow in ENHSP. FDI, Static, and Naive represent the different grounding mechanisms implemented in ENHSP to evaluate our proposal. The module in yellow is the classical planning grounder, while the remaining modules are within the ENHSP planning system (parsing, grounding, and search)
The Naive grounder is our baseline: it naively grounds everything without any sort of pre-processing. The Static grounder refers to the approach introduced in Section 3.1, while FDI, short for Fast Downward Inference, is the term used to indicate the approach described in Section 3.2.
All the experiments were performed on an Intel i7-4750HQ CPU, 8 GB of RAM, and Linux operating system. A 15 CPU-time minutes cut-off time limit was enforced.
4.2 Considered benchmarks
We want to assess the importance of grounding on realistic and complex hybrid problems. For this reason, following the approach exploited by Franco et al. (Reference Franco, Vallati, Lindsay and McCluskey2019), the experimental evaluation is performed by considering four benchmark domains: two that have been used to models real-world applications, and two that are derived from well-known benchmarks exploited in past International Planning Competitions (Vallati et al., Reference Vallati, Chrpa and McCluskey2018).
As real-world benchmarks, we consider the Baxter and the Urban Traffic Control domains.
-
• The Baxter domain, recently introduced by Bertolucci et al. (Reference Bertolucci, Capitanelli, Maratea, Mastrogiovanni and Vallati2019), exploits planning for supporting robots in dealing with articulated objects manipulation tasks. The available domain model has been extended by adding events for preventing movements wider than 360 degrees. Problems consider articulated objects composed by between 5 and 15 links and between 2 and 10 grippers.
-
• The Urban Traffic Control (UTC) domain has been originally introduced by Vallati (2016). It models the use of planning for generating traffic light signal plans, in order to de-congest an area of a urban region. In this analysis, we considered the problems introduced by McCluskey and Vallati (Reference McCluskey and Vallati2017), which involved a large urban network of 10 junctions, part of the Manchester metropolitan area, and we extended it by considering problems with 20 and 30 junctions, obtained by connecting identical regions together. For stressing the grounding component, here we consider a slightly extended version of the domain. In particular, we make use of an event-driven mechanism to enable the processes tracking the traffic occupancy of the links. On benchmarks from this domain, ENHSP has been run with a delta (-d) value of
 $50.0$
and using the -s GBFS parameter (GBFS specifies the use of a Greedy Best First Search).
$50.0$
and using the -s GBFS parameter (GBFS specifies the use of a Greedy Best First Search).
As synthetic benchmarks, we considered the Rovers and Tetris domains, which appeared in past editions of the International Planning Competition.
-
• The Rovers domain is a well-known model introduced in IPC-3 (Long & Fox, Reference Long and Fox2003). Inspired by planetary rovers problems, this domain requires that a collection of rovers navigate a planet surface, finding samples and communicating them back to a lander. This was originally designed as a temporal domain model that extends classical planning by considering temporal aspects; we extended it using a PDDL+ formulation where continuous processes model the movements of the rovers and the energy generation via solar power. Each of the mentioned processes can be driven by the planning engine using two actions and is constrained, where appropriate, via dedicated events. On benchmarks from this domain, ENHSP has been run with the following configuration: -s GBFS -h hadd (the hadd option specifies the heuristic used by the planner, which corresponds to the
 $\hat{h}_{hbd}^{add}$
heuristic Scala et al., Reference Scala, Haslum and Thiébaux2016a).
$\hat{h}_{hbd}^{add}$
heuristic Scala et al., Reference Scala, Haslum and Thiébaux2016a). -
• Finally, we include the well-known Tetris domain model introduced in IPC-8 (Vallati et al., Reference Vallati, Chrpa and McCluskey2018). In this simplified version of the game, the goal is to clear an area of the grid, by moving pieces away. The original classical planning domain model has been extended in PDDL+ by modelling as continuous processes the movements of the pieces that consumes energy (that is limited) and requires a different amount of time to complete, according to the size and shape of the piece. The planning engine can decide when to start to move a piece, and in which direction; the actual movements are then modelled by processes. As in the Rovers case, processes are constrained, where appropriate, via events. On benchmarks from this domain, ENHSP has been run with the following configuration: -s GBFS -h hmrp (the hmrp option specifies the heuristic used by the planner, which corresponds to the
 $h_{\max}^{mrp}$
heuristic Scala et al., Reference Scala, Haslum, Thiébaux and Ramírez2016b).
$h_{\max}^{mrp}$
heuristic Scala et al., Reference Scala, Haslum, Thiébaux and Ramírez2016b).
For all domains, we collected a total of 10 instances, obtained by varying the number of objects, and the size of maps/boards.
4.3 Experimental results
Table 1 compares the results achieved by ENHSP using the three considered grounding techniques on benchmarks from the real-world domains. Results are presented in terms of grounding size, that is, the sum of instantiated actions + processes + events, the CPU-time needed by the grounding process, and the overall CPU-time needed by the planning engine to solve the considered planning problem. The overall CPU-time includes all the steps needed by the planning engine, and therefore includes parsing, grounding, pre-processing, search, and post-processing. The table also reports the averages obtained by the considered grounding techniques, in terms of ground size, ground CPU-time, and overall CPU-time. Averages are calculated by considering only instances for which all the 3 considered systems provided a value for the considered metric.
Table 1 Results, in terms of ground size, CPU-time needed by the grounding process, and runtime, achieved by ENHSP when using the three introduced grounders on the real-world benchmarks. ‘–’ indicates that the grounding process run out of memory. A runtime value of 900.0 indicates timeout. Avg indicates average values. Average Runtime (Grounding) is calculated by considering only instances solved (ground) by all the considered approaches. Bold is used to indicate best results with regard to the considered metric

It is easy to notice that the two domains have different characteristics in terms of ground size. Baxter instances tend to be more compact, in terms of naive ground size, but have a significant percentage of relevant actions, processes, and events. In other words, the ground instances are not huge, but in order to solve the encoded problem it is necessary to take into account a significant number of components. The UTC benchmarks are instead very different: the naive approach leads to a huge ground size that can even be too large to be generated at all, but the relevant elements that are identified by the FDI approach are very few. By no mean we are suggesting that this can be taken as an indicator of relative complexity of the problems; this is only a characteristic of the corresponding models, with no direct relation to complexity.
Naive is the technique that is consistently delivering the worst possible performance both in terms of ground size, and in terms of time needed to solve the planning instance. When compared to the other grounders, Naive can lead to a ground problem that is orders of magnitude larger: this is then reflected in the much higher CPU-time needed to solve the planning instances. Despite the fact that such results are quite intuitive, this analysis provides clear evidence of the detrimental impact that an inefficient grounder can have on the performance of an otherwise efficient planning system. In both UTC and Baxter domains, the use of the FDI grounder allows the planning engine to deliver the best runtime performance. In other words, the reduced grounding size is positively affecting also the subsequent steps. When analysing the provided output, we observed that the lower runtime is not only due to the reduced time needed by actually generating the ground problem, but the smaller grounding size is having an impact also on the search engine in general; we advocate this to the much larger size of the data structures needed to actually solve the problem in memory.
In a sense, the Naive results give a measure of how important grounding is for hybrid PDDL+ planning. The presented results suggest that the grounding approach can determine if a problem will be solved at all or not. Where this is a problem that happens often in classical planning (Corrêa et al., Reference Corrêa, Pommerening, Helmert and Francès2020), to the best of our knowledge, this is the first time that this aspect has been neatly assessed over PDDL+ problems, particularly on different real-world application benchmarks.
Table 2 shows the experimental results achieved on the considered synthetic benchmark domains: Rovers and Tetris. Instances from the Tetris domain provide a clear and coherent picture, that is, aligned with the observations made when considering the results achieved on the real-world benchmarks: FDI reduces by orders of magnitude the size of the ground problem, and is allowing the search step to find a solution within the 15 CPU-time minutes runtime. Both Static and Naive systematically provide much larger ground problem instances that do not allow the search engine to effectively explore the search space in order to find a solution. In fact, out of the considered instances, ENHSP has been able to solve only 3 (5) by using the Naive (Static) grounder. On the contrary, the use of FDI allows ENHSP to solve all the instances. Interestingly, FDI can lead to a longer grounding CPU-time, when compared to the other techniques: while this is not having a noticeable impact on the overall performance of the planner, it may be due to the additional pre-processing that is needed by this approach. Taking a different perspective, one may say that by investing a bit more CPU-time in pre-processing for grounding, a significant amount of CPU-time can be saved for the search step.
Table 2 Results, in terms of ground size, CPU-time needed by the grounding process, and runtime, achieved by ENHSP when using the three introduced grounders on the considered set of synthetic benchmarks. ‘–’ indicates that the grounding process run out of memory. A runtime value of 900.0 indicates timeout. Avg indicates average values. Average Runtime (Grounding) is calculated by considering only instances solved (ground) by all the considered approaches. Bold is used to indicate best results with regard to the considered metrics
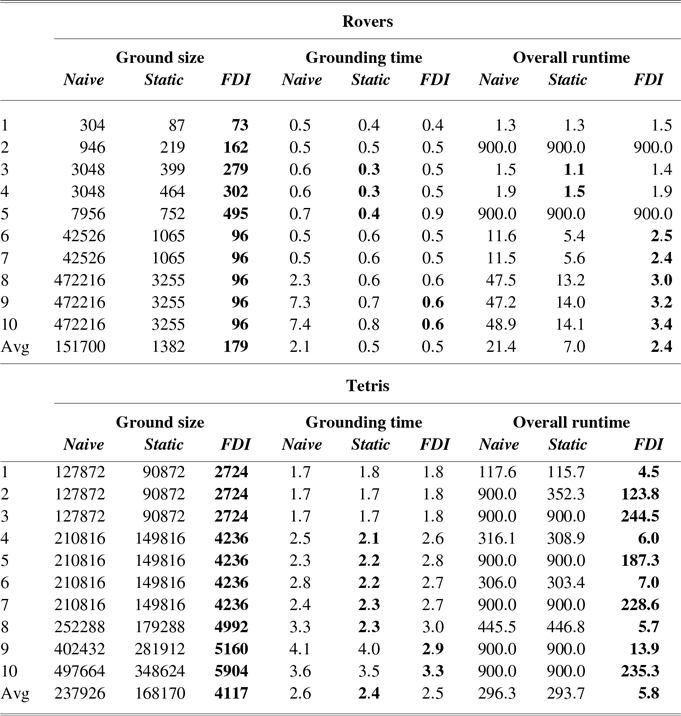
The Rovers benchmarks present some interesting aspects. In this domain, there is a huge difference in the ground size obtained by Naive and Static. This is particularly true for instances 6-10, where the number of objects is very large, but only a few of them are needed to solve the corresponding planning problem. Under such conditions, the benefits of using FDI are significant. In some other instances, Static and FDI are able to provide groundings of very similar size, even though this is limited to the smallest instances. Rovers is also the only domain among the considered where on easy instances—in terms of overall runtime—all the three grounding techniques allow ENHSP to deliver very similar performance. This seems to suggest that there is a trade-off to consider with regard to grounding: a more sophisticated grounding leads to a smaller ground size at the cost of a potentially higher CPU-time. This investment pays off only if either the obtained ground is significantly smaller than those achieved with less sophisticated techniques, or to find a goal space a large chunk of the search space has to be explored. In other cases, represented by problems
![]() $ 1$
, 3, and 4 of Rovers, the initial investment in pre-processing does not pay off.
$ 1$
, 3, and 4 of Rovers, the initial investment in pre-processing does not pay off.
With regard to quality and shape of the generated solutions, we observed no difference in the provided plans. On our set of benchmarks, the use of a grounder has an impact on runtime and coverage—as it can increase or reduce the number of options to consider and the size of each search state—but it does not affect the way in which search is performed. We cannot exclude that in very different domains the use of a grounder can also be reflected in a different shape of the provided solution, but our analysis suggests that this may not be usually the case.
Summarising, our experimental analysis indicates that the FDI grounder has a major positive impact on the performance of the state-of-the-art planning engine ENHSP, and the overhead coming from the machinery to abstract the problem and interfacing ENHSP with Fast-Downward planning system is largely compensated by the magnificent overall improvements. This behaviour is more marked in domain models where there is a potentially huge ground size, due to the presence of PDDL+ constructs with a large number of parameters, but the number of actually relevant ground constructs is limited.
4.4 Contextualisation of ENHSP’s performance
One may wonder about the performance of the selected ENHSP planning engine with regard to the other systems at the state of the art. To contextualise the results presented in the previous section and to some extent to justify the use of ENHSP only, we run two additional domain-independent PDDL+ planning engines on the considered benchmarks: UPMurphi (Della Penna et al., Reference Della Penna, Magazzeni, Mercorio and Intrigila2009) and DiNo (Piotrowski et al., Reference Piotrowski, Fox, Long, Magazzeni and Mercorio2016). Following some previous work where these planners have been employed (McCluskey & Vallati, Reference McCluskey and Vallati2017; Franco et al., Reference Franco, Vallati, Lindsay and McCluskey2019), we run them using the suggested parameter - -custom 5 4 4. Experiments were run using the same machine and the same settings described in Section 4.1.
Unfortunately, UPMurphi was not able to solve any of the considered benchmark instances. It either ran out of time or memory. Similarly, DiNo was able to solve only problem 1 from the Rovers domain, with a CPU-time of 140 seconds. As UPMurphi, in all the other cases, it ran out of either memory or time.
5 Related work
In this section, we position our work with regard to the wider research context.
Other approaches to grounding planning problems have been investigated in the last decade or so (for instance, Koehler & Hoffmann, Reference Koehler and Hoffmann2000; Helmert, Reference Helmert2009). The very first systematic approach to this problem has been proposed by Koehler and Hoffmann (Reference Koehler and Hoffmann2000). Very similarly to us, they present quite a sophisticated method that analyses those Boolean variables that are inertial and do so for the purpose of reducing the number of possible groundings for each operator. Their technique presents the same limits as our static analysis-based method, which has to do with not being able to look into the deeper dependencies between actions (see Section 3.1). In addition, their technique only focuses on classical planning problems, that is, on Boolean conditions with neither processes nor events. As observed by Helmert (Reference Helmert2009), this grounding mechanism can be very fast, but is not optimal memory-wise. Indeed, as in our case, it works by reducing some universe of groundings. Therefore, to make it fast enough, it relies on building into memory very large data structures. For many instances of the planning competitions, this results in having a planning system that cannot pass grounding even in problems that are actually simple to be solved. Helmert’s work (Helmert, Reference Helmert2009), to the best of our knowledge, is the first work that looked deeper into this problem and proposes a forward, marking procedure that establishes grounding on a relaxation-based schema. However, as for the work by Koehler and Hoffmann (Reference Koehler and Hoffmann2000), Helmert’s procedure only supports a classical planning representation. Our abstraction-based technique can exploit any classical planning grounder, and we did indeed exploit the relaxed reachability procedure presented by Helmert in our experiments. Note that in Helmert (Reference Helmert2009), Helmert grounds the development of the grounding phase into a Datalog program (Kaufmann et al., Reference Kaufmann, Leone, Perri and Schaub2016). Despite the proposed implementation is specific for planning problems, the same schema can likely be adopted to support more expressive formalism of planning by mapping them directly into more expressive Answer Set Problems. This is indeed an interesting line of research to pursue. More recently, Gnad et al. (Reference Gnad, Torralba, Domínguez, Areces and Bustos2019) introduced an approach for partial grounding of classical planning problems that takes advantage of machine learning techniques. The approach proposed by Gnad et al. is domain-specific, and the idea is to train a machine learning model on a large number of plans from a given domain, to capture the aspects that need to be ground to solve a classical planning problem from such a domain. This is a valuable and innovative approach to grounding, and it would be interesting to extend the approach to deal with more expressive planning formalisms.
Moving into more expressive representations we find the metric extension to Fast-Forward (Hoffman & Nebel, Reference Hoffmann and Nebel2001), Metric-FF (Hoffmann, Reference Hoffmann2003) that also supports an intelligent grounding mechanism as we do (many other systems use the Metric-FF baseline as a pre-processor for parsing and grounding and focus on documenting reasoning over ground representations instead, for example, Coles et al. (Reference Coles, Coles, Fox and Long2010), Coles and Coles (Reference Coles and Coles2011), Scala et al. (Reference Scala, Haslum, Thiébaux and Ramírez2016b). Metric-FF exploits an implementation that is similar to our static-based method. The seminal paper in which Metric-FF is described puts unfortunately most of the effort in describing the machinery for solving the resulting ground representation, leaving out many details on how the grounding is actually implemented. As a difference with regard to our work, from the description (Section 6.2), the grounding phase does not seem to support numeric variables that can take unknown variables and does not seem to be sensible to the problem of having indirect preconditions in the right-hand side of numeric effects. Moreover, as it builds on IPP implementation (Koehler & Hoffmann, Reference Koehler and Hoffmann2000), it does not leverage directly newly classical planning methods as we can do through our abstraction-based grounding. Moreover, Metric-FF schema does not support processes and events, and even if the extension to support them would not be a huge problem, it still suffers from the disadvantages of looking only over the static predicates, and therefore can blow up the memory. We argue that our abstraction-based procedure is more robust of direct extensions of a specific mechanism for numeric planning. We believe indeed that the price to pay in terms of overheard (calling different systems) is substantially dominated by the great modularity and flexibility given by the decomposition behind our abstraction method.
Grounding before planning is not the only way to initiate the solving of planning problems, even though is the most commonly exploited approach. Plan space planners in particular (either based on SAT, such as Robinson et al., Reference Robinson, Gretton, Pham and Sattar2008, SMT, like Bofill et al., Reference Bofill, Espasa and Villaret2016; Bit-Monnot, Reference Bit-Monnot2018, or more direct exploration of the plan space Younes & Simmons, Reference Younes and Simmons2003) indeed were built with the idea of combining search and grounding into a constraint satisfaction approach. Albeit this idea does not keep the pace with state-of-the-art planners based on heuristic search (probably for the difficulty of exploiting heuristics), there seems to be a revived interest in this direction that tries to combine lifted reasoning with heuristic forward search planner altogether (Ridder & Fox, Reference Ridder and Fox2014; Corrêa et al., Reference Corrêa, Pommerening, Helmert and Francès2020). In particular, the work by Corrêa et al. (Reference Corrêa, Pommerening, Helmert and Francès2020) proposes a novel planning engine that uses a lifted-successor generation to make practical the online generation of ground actions in a forward state space planners. The system shows interesting results on some set of benchmarks. Whether this line of research will lead to new generation planners is however still an open question, and so is the question of whether a similar mechanism can be adapted to problems over metric spaces with processes and events as PDDL+.
Finally, an approach that is orthogonal to the exploitation of efficient grounding techniques is model reformulation. Reformulation aims at making the problem model more amenable for automated solvers by changing part of the model provided as input. A large number of reformulation techniques have been introduced for classical planning models. Examples of reformulation techniques for classical PDDL models include macro-learning (Newton et al., Reference Newton, Levine, Fox and Long2007), entanglements (Chrpa et al., Reference Chrpa, Vallati and McCluskey2018), bagged representation (Riddle et al., Reference Riddle, Barley, Franco and Douglas2015), action schema splitting (Areces et al., Reference Areces, Bustos, Dominguez and Hoffmann2014), and configuration (Vallati et al., Reference Vallati, Hutter, Chrpa and McCluskey2015, Reference Vallati, Chrpa, McCluskey and Hutter2020). Limited work has been carried out on reformulation of non-classical PDDL models. Chrpa et al. (Reference Chrpa, Scala and Vallati2015) extended the notion of entanglements to numerical planning, and Franco et al. (Reference Franco, Vallati, Lindsay and McCluskey2019) focused on PDDL+ reformulation to reduce the arity of predicates and fluents to limit the exponential explosion of the ground problem size. A different line of work on reformulation investigated techniques to reduce the performance of automated solvers, to identify aspects of the models to which existing planning engines are sensitive to (Vallati and Chrpa, Reference Vallati and Chrpa2019).
6 Conclusions
Hybrid PDDL+ models are needed to correctly and accurately represent the dynamics of real-world applications. PDDL+ models are amongst the most advanced symbolic planning models and are notoriously difficult for planning engines to cope with. Complexity is exacerbated by the potentially huge size of the fully ground problems that are needed by planning engines in order to explore the search space. Despite the importance of the grounding step for any domain-independent PDDL+ planning engine, there is a lack of work devoted to the specific topic.
In this paper, we introduced two approaches for efficient and effective domain-independent PDDL+ grounding. In particular, we focused on investigating whether the vast amount of work done in the classical planning field could be exploited also for supporting PDDL+ grounding. The approaches have been developed in a modular fashion and can be easily plugged into existing planning systems based on forward search. Our experimental analysis, which includes large benchmarks derived from real-world applications, showed that (i) regardless of the efficiency of the search approach exploited, the grounding step alone can become so critical that it may determine whether a planning instance can be solved or not; (ii) grounding everything and hoping that the search component will efficiently navigate through the search space is the worst possible option, and (iii) it is indeed possible to fruitfully exploit grounding techniques that have been originally designed for classical planning.
We see several avenues for future work. First, we are interested in assessing whether a smart grounding approach can support the validation of complex scenarios, where the problems tackled are of significant size. Second, we plan to extend our methods by tailoring the grounding to some numeric aspect of the PDDL+ formalism. This may have the potential of further decreasing the number of ground actions at hand. Third, we envisage the exploitation of smart grounding techniques also in the context of knowledge engineering of PDDL+ models, in particular for providing support in terms of static and dynamic analysis and validation; this can be particularly interesting when a domain modeller is investigating different encoding of the problems and the impacts of such encoding on the size of the problem.
Acknowledgement
Mauro Vallati was supported by a UKRI Future Leaders Fellowship [grant number MR/T041196/1].












