Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-26T01:53:32.091Z Has data issue: false hasContentIssue false
  • English
  • Français

Li coefficients and the quadrilateral zeta function

Part of: Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  08 April 2024

Kajtaz H. Bllaca ,
Kamel Mazhouda  and
Takashi Nakamura Open the ORCID record for Takashi Nakamura [Opens in a new window]
Kajtaz H. Bllaca*
Affiliation:
Department of Mathematics, University of Prishtina, Mother Theresa, No. 5, 10000 Prishtina, Kosovo
Kamel Mazhouda
Affiliation:
Higher Institute of Applied Sciences and Technology, University of Sousse, Sousse 4003, Tunisia INSA Hauts-De-France, University Polytechnique Hauts-De-France, FR CNRS 2037, CERAMATHS, F-59313 Valenciennes, France e-mail: [email protected]
Takashi Nakamura
Affiliation:
Department of Liberal Arts, Faculty of Science and Technology, Tokyo University of Science, 2641 Yamazaki, Noda-shi, Chiba-ken 278-8510, Japan e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this note, we study the Li coefficients 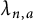$\lambda _{n,a}$ for the quadrilateral zeta function. Furthermore, we give an arithmetic and asymptotic formula for these coefficients. Especially, we show that for any fixed 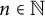$n \in {\mathbb {N}}$, there exists 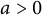$a>0$ such that 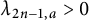$\lambda _{2n-1,a}> 0$ and 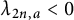$\lambda _{2n,a} < 0$.

Keywords

Li’s coefficientsthe quadrilateral zeta functionRiemann Hypothesis

MSC classification

Primary: 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses 11M35: Hurwitz and Lerch zeta functions
Type
Article
Information
Canadian Mathematical Bulletin , Volume 67 , Issue 3 , September 2024 , pp. 860 - 871
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The third author was partially supported by JSPS grant 22K03276.

References

Apostol, T. M., Introduction to analytic number theory, Undergraduate Texts in Mathematics, Springer, New York, 1976.Google Scholar
Apostol, T. M., Formulas for higher derivatives of the Riemann zeta function . Math. Comput. 44(1985), no. 169, 223–232.CrossRefGoogle Scholar
Berndt, B. C., On the Hurwitz zeta-function . Rocky Mountain J. Math. 2(1972), no. 1, 151–157.CrossRefGoogle Scholar
Bombieri, E. and Lagarias, J., Complements to Li’s criterion for the Riemann hypothesis . J. Number Theory 77(1999), 274–287.CrossRefGoogle Scholar
Brown, F., Li’s criterion and zero-free regions of $L$ -functions . J. Number Theory 111(2005), 1–32.CrossRefGoogle Scholar
Coffey, M. W., Series representations for the Stieltjes constants . Rocky Mountain J. Math. 44(2014), no. 2, 443–477.CrossRefGoogle Scholar
Flajolet, P. and Vepstas, L., On differences of zeta values . J. Comput. Appl. Math. 220(2008), nos. 1–2, 58–73.CrossRefGoogle Scholar
Lagarias, J. C., Li coefficients for automorphic $L$ -functions . Ann. Inst. Fourier (Grenoble) 57(2007), 1689–1740.CrossRefGoogle Scholar
Laurinčikas, A. and Garunkštis, R., The Lerch zeta-function, Kluwer Academic Publishers, Dordrecht, 2002.Google Scholar
Li, X.-J., The positivity of a sequence of numbers and the Riemann hypothesis . J. Number Theory 65(1997), 325–333.CrossRefGoogle Scholar
Mazhouda, K. and Smajlović, L., Evaluation of the Li coefficients on function fields and applications . Eur. J. Math. 5(2019), no. 2, 540–550.CrossRefGoogle Scholar
Mazhouda, K. and Sodaïgui, B., The Li–Sekatskii coefficients for the Selberg class . Int. J. Math. 33(2022), no. 12, Article no. 2250075, 23 pp.CrossRefGoogle Scholar
Nakamura, T., The functional equation and zeros on the critical line of the quadrilateral zeta function . J. Number Theory 233(2022), 432–455.CrossRefGoogle Scholar
Nakamura, T., On Lerch’s formula and zeros of the quadrilateral zeta function. Preprint, 2022, arXiv:2001.01981.Google Scholar
Nakamura, T., On zeros of bilateral Hurwitz and periodic zeta and zeta star functions . Rocky Mountain J. Math. 53(2023), no. 1, 157–176.CrossRefGoogle Scholar
Omar, S. and Mazhouda, K., The Li criterion and the Riemann hypothesis for the Selberg class II . J. Number Theory 130(2010), no. 4, 1109–1114.CrossRefGoogle Scholar
Smajlović, L., On Li’s criterion for the Riemann hypothesis for the Selberg class . J. Number Theory 130(2010), no. 4, 828–851.CrossRefGoogle Scholar
Titchmarsh, E. C., Theory of the Riemann zeta-function. 2nd ed., Clarendon Press, Oxford, 1986.Google Scholar
Voros, A., Sharpenings of Li’s criterion for the Riemann hypothesis . Math. Phys. Anal. Geom. 9(2006), 53–63.CrossRefGoogle Scholar