1. Introduction
Despite its ubiquity, turbulence continues to challenge mathematicians, physicists and engineers because of the complex hierarchy of eddies of fluid motion, which interact in a puzzling manner. Kolmogorov (Reference Kolmogorov1941a) was the first to hypothesize that, for asymptotically large Reynolds numbers, a clear separation is expected between the processes acting at large, intermediate and dissipative scales. The information conveyed by the large scales is likely to decline after the first nonlinear interactions so that there should exist a scale beyond which turbulence becomes universal and therefore locally isotropic. Under the same assumption of sufficiently large Reynolds numbers, Kolmogorov (Reference Kolmogorov1941b) carried out a statistical analysis of the velocity field by considering the turbulent kinetic energy probed at fixed scale defined as the distance between two points. His analysis showed that, for locally isotropic turbulence, the energy transfer between scales in the intermediate range is constant and proportional to the mean energy dissipation rate. This result, known as the 4/5th law, is often considered the only exact (yet asymptotic) theory of turbulence.
However, the Reynolds numbers achievable in laboratory experiments are far smaller than would be required for Kolmogorov's 4/5th law to apply. In such situations scale separation does not occur. The effect of finite Reynolds number, i.e. the combined influence of small-scale (viscous) and large-scale effects, has been accounted for in the generalized Kármán–Howarth–Kolmogorov equation, which is derived from first principles without the need to invoke any particular symmetry of the flow (e.g. Danaila et al. Reference Danaila, Anselmet, Zhou and Antonia2001; Hill Reference Hill2001). Extensive research on this theory in the last three decades (see, e.g. Qian Reference Qian1997; Danaila, Anselmet & Antonia Reference Danaila, Anselmet and Antonia2002; Marati, Casciola & Piva Reference Marati, Casciola and Piva2004; Antonia & Burattini Reference Antonia and Burattini2006; Valente & Vassilicos Reference Valente and Vassilicos2015) has demonstrated the predominant role of non-stationarity in decaying flows, statistical inhomogeneities, turbulent kinetic energy production, turbulent/pressure diffusion and the general concept of forcing.
To complicate matters further, the large scales sometimes reveal an identifiable and regular behaviour related to the type of hydrodynamical instability that has led to their creation. These are generally referred to as coherent structures (see, for example, Reynolds & Hussain Reference Reynolds and Hussain1972). They occur within most flows but they remain poorly understood because coherent motion possesses non-universal characteristics associated with initial and boundary conditions. Townsend (Reference Townsend1990) synthesized this conundrum in the following terms: ‘at this distance [50's] it may seem to be nearly the end of purely statistical approaches before concepts of eddy structure began to assume importance.’ Eighty years since Kolmogorov's theory open questions still remain such as the way coherent motion interacts with randomly fluctuating turbulent eddies and how the former can be incorporated into a statistical theory of turbulence. Does the organized motion influence the cascade process? Since coherent structures generally emerge from velocity shear, does the cascade process become sensitive to inhomogeneities? The recent work by Alves Portela, Papadakis & Vassilicos (Reference Alves Portela, Papadakis and Vassilicos2020) sheds new light on these long standing questions and proves that the effect of coherent motion needs to be explicitly accounted for.
2. Overview
The turbulence community owes a great deal to Reynolds & Hussain (Reference Reynolds and Hussain1972) who first highlighted the dynamical influence of coherent structures or ‘organized waves.’ They came up with the astute idea of decomposing the fluctuating field into mean, coherent and random components and found that a portion of the energy conveyed by the organized structures could be transferred to random motion. However, they considered one-point statistics and thus could not gain insight into the scales affected by the coherent motion.
This issue has been addressed more recently by Thiesset, Antonia & Danaila (Reference Thiesset, Antonia and Danaila2013) who showed that coherent motion may act to force the cascade between scales. They found that in contrast with classical decaying turbulence, the transfer of energy in wakes behind two-dimensional generators was systematically enhanced, and, therefore, closer to the asymptotic Kolmogorov scaling. This observation was further confirmed by invoking structure functions conditioned by the phase of the coherent motion (Thiesset, Danaila & Antonia Reference Thiesset, Danaila and Antonia2014), which is the two-point extension of the one-point phase-averaged statistics introduced by Reynolds & Hussain (Reference Reynolds and Hussain1972). Within this framework they showed that both the energy distribution and its transfer at a given scale are modulated (in amplitude) by the time-periodic dynamics of the coherent motion. Using two-point statistics, they derived the transport equations for the second-order structure functions of both coherent and random components of the velocity field to characterise the turbulent cascade process in the presence of coherent structures. They found that at a fixed location in the flow, energy transfer between scales is significantly enhanced when coherent motion is present, and diminished in its absence.
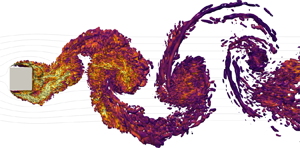
Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) apply a similar methodology to derive fully inhomogeneous and anisotropic Kármán–Howarth–Kolmogorov equations for the kinetic energy in the presence of quasi-periodic coherent structures, accounting for inhomogeneities of the mean flow. The novelty of their approach is to use this theoretical framework to explore the very near field of the wake behind a prism where the scale/space features remain largely unknown, in contrast with intermediate and far-field flows. They use direct numerical simulations (DNS) to calculate the contributions of all processes including turbulence decay and production, pressure/turbulent-diffusion and the forcing due to coherent structures.
The total ( $\text {coherent}+\text {random}$) energy transferred is restored, because all terms are computed from the first principles. Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) then discovered that there exists a reasonable portion of scales which surprisingly comply with the Kolmogorov constant energy transfer in the cascade. The authors qualify this result as ‘a clearly non-Kolmogorov yet Kolmogorov sounding [cascade].’ Indeed, Kolmogorov's theory should not apply for the Reynolds numbers investigated by Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) in the presence of the strong inhomogeneity and anisotropy of the flow. Could coherent motion and/or inhomogeneity be responsible for this apparent constant energy transfer? Using the previously introduced triple decomposition for the velocity structure functions, Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) showed that the constant total energy transfer hides a contribution of the forcing associated with the coherent motion. By further decomposing the total transfer term into an inhomogeneous and homogeneous contribution, they find that inhomogeneities also contribute directly to the energy transfer in addition to manifesting themselves through the appearance of additional terms in the generalized Kármán–Howarth–Kolmogorov equations.
$\text {coherent}+\text {random}$) energy transferred is restored, because all terms are computed from the first principles. Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) then discovered that there exists a reasonable portion of scales which surprisingly comply with the Kolmogorov constant energy transfer in the cascade. The authors qualify this result as ‘a clearly non-Kolmogorov yet Kolmogorov sounding [cascade].’ Indeed, Kolmogorov's theory should not apply for the Reynolds numbers investigated by Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) in the presence of the strong inhomogeneity and anisotropy of the flow. Could coherent motion and/or inhomogeneity be responsible for this apparent constant energy transfer? Using the previously introduced triple decomposition for the velocity structure functions, Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) showed that the constant total energy transfer hides a contribution of the forcing associated with the coherent motion. By further decomposing the total transfer term into an inhomogeneous and homogeneous contribution, they find that inhomogeneities also contribute directly to the energy transfer in addition to manifesting themselves through the appearance of additional terms in the generalized Kármán–Howarth–Kolmogorov equations.
Impressively, they characterise how energy is transferred from the injection, through the mean velocity gradients, to the coherent motion and finally to the random fluctuations. While this general picture is believed to apply to most flows, this is the first time that this complex process is unravelled in a quantitative way, enabled uniquely by the combination of theory and DNS. Moreover, the Kármán–Howarth–Kolmogorov equation for turbulent motion in the presence of coherent structures appears to be the most appropriate framework to quantify the extent and range of scales over which each effect influences the total energy transfer, including the forcing associated with the coherent motion. The work of Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) provides a significant step forward in characterising the effects of inlet/boundary conditions in a complex, inhomogeneous and anisotropic flow, with the ultimate aim of predicting them at Reynolds numbers typically encountered in the laboratory.
3. Future
The work by Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) opens new avenues of investigation of the intricate interactions between coherence and turbulence. Will the organized motion continue to influence the cascade process when the inlet velocity is increased, and/or when travelling through the intermediate and far field? How are each individual velocity components and cross-correlations affected? How do different directional components of energy flux perceive the coherent motion, beyond the circularly averaged transfer term considered by Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020)? How can this information be used to build physics-informed predictive tools such as large-eddy simulation models? Answers to these open questions may be provided by generalized Kármán–Howarth–Kolmogorov equations in the presence of periodic forcing.
In addition, the decomposition of the transfer term proposed by Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) into homogeneous and inhomogeneous contributions may help to ascertain the role of statistical inhomogeneity. The question of the uniqueness of such a decomposition, which is addressed in Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020), should be further examined.
Finally, it is worth stressing that in some flows, coherent structures do not possess a periodic signature or multiple periodic motions can be at play (e.g. farms of wind turbines). In such situations, phase averages are precluded and classical two-point statistics (correlation and structure functions) may not remain appropriate. One is then likely to rely on some other statistical tool such as low-pass or band-pass filters, proper orthogonal decomposition or dynamic mode decomposition, or wavelets to name a few. By pursuing work in this direction, one should be able to explicitly identify the different processes (transfer, production, dissipation) in such a new space of scales, flow positions and time.
Declaration of interests
The authors report no conflict of interest.




1. Introduction
Despite its ubiquity, turbulence continues to challenge mathematicians, physicists and engineers because of the complex hierarchy of eddies of fluid motion, which interact in a puzzling manner. Kolmogorov (Reference Kolmogorov1941a) was the first to hypothesize that, for asymptotically large Reynolds numbers, a clear separation is expected between the processes acting at large, intermediate and dissipative scales. The information conveyed by the large scales is likely to decline after the first nonlinear interactions so that there should exist a scale beyond which turbulence becomes universal and therefore locally isotropic. Under the same assumption of sufficiently large Reynolds numbers, Kolmogorov (Reference Kolmogorov1941b) carried out a statistical analysis of the velocity field by considering the turbulent kinetic energy probed at fixed scale defined as the distance between two points. His analysis showed that, for locally isotropic turbulence, the energy transfer between scales in the intermediate range is constant and proportional to the mean energy dissipation rate. This result, known as the 4/5th law, is often considered the only exact (yet asymptotic) theory of turbulence.
However, the Reynolds numbers achievable in laboratory experiments are far smaller than would be required for Kolmogorov's 4/5th law to apply. In such situations scale separation does not occur. The effect of finite Reynolds number, i.e. the combined influence of small-scale (viscous) and large-scale effects, has been accounted for in the generalized Kármán–Howarth–Kolmogorov equation, which is derived from first principles without the need to invoke any particular symmetry of the flow (e.g. Danaila et al. Reference Danaila, Anselmet, Zhou and Antonia2001; Hill Reference Hill2001). Extensive research on this theory in the last three decades (see, e.g. Qian Reference Qian1997; Danaila, Anselmet & Antonia Reference Danaila, Anselmet and Antonia2002; Marati, Casciola & Piva Reference Marati, Casciola and Piva2004; Antonia & Burattini Reference Antonia and Burattini2006; Valente & Vassilicos Reference Valente and Vassilicos2015) has demonstrated the predominant role of non-stationarity in decaying flows, statistical inhomogeneities, turbulent kinetic energy production, turbulent/pressure diffusion and the general concept of forcing.
To complicate matters further, the large scales sometimes reveal an identifiable and regular behaviour related to the type of hydrodynamical instability that has led to their creation. These are generally referred to as coherent structures (see, for example, Reynolds & Hussain Reference Reynolds and Hussain1972). They occur within most flows but they remain poorly understood because coherent motion possesses non-universal characteristics associated with initial and boundary conditions. Townsend (Reference Townsend1990) synthesized this conundrum in the following terms: ‘at this distance [50's] it may seem to be nearly the end of purely statistical approaches before concepts of eddy structure began to assume importance.’ Eighty years since Kolmogorov's theory open questions still remain such as the way coherent motion interacts with randomly fluctuating turbulent eddies and how the former can be incorporated into a statistical theory of turbulence. Does the organized motion influence the cascade process? Since coherent structures generally emerge from velocity shear, does the cascade process become sensitive to inhomogeneities? The recent work by Alves Portela, Papadakis & Vassilicos (Reference Alves Portela, Papadakis and Vassilicos2020) sheds new light on these long standing questions and proves that the effect of coherent motion needs to be explicitly accounted for.
2. Overview
The turbulence community owes a great deal to Reynolds & Hussain (Reference Reynolds and Hussain1972) who first highlighted the dynamical influence of coherent structures or ‘organized waves.’ They came up with the astute idea of decomposing the fluctuating field into mean, coherent and random components and found that a portion of the energy conveyed by the organized structures could be transferred to random motion. However, they considered one-point statistics and thus could not gain insight into the scales affected by the coherent motion.
This issue has been addressed more recently by Thiesset, Antonia & Danaila (Reference Thiesset, Antonia and Danaila2013) who showed that coherent motion may act to force the cascade between scales. They found that in contrast with classical decaying turbulence, the transfer of energy in wakes behind two-dimensional generators was systematically enhanced, and, therefore, closer to the asymptotic Kolmogorov scaling. This observation was further confirmed by invoking structure functions conditioned by the phase of the coherent motion (Thiesset, Danaila & Antonia Reference Thiesset, Danaila and Antonia2014), which is the two-point extension of the one-point phase-averaged statistics introduced by Reynolds & Hussain (Reference Reynolds and Hussain1972). Within this framework they showed that both the energy distribution and its transfer at a given scale are modulated (in amplitude) by the time-periodic dynamics of the coherent motion. Using two-point statistics, they derived the transport equations for the second-order structure functions of both coherent and random components of the velocity field to characterise the turbulent cascade process in the presence of coherent structures. They found that at a fixed location in the flow, energy transfer between scales is significantly enhanced when coherent motion is present, and diminished in its absence.
Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) apply a similar methodology to derive fully inhomogeneous and anisotropic Kármán–Howarth–Kolmogorov equations for the kinetic energy in the presence of quasi-periodic coherent structures, accounting for inhomogeneities of the mean flow. The novelty of their approach is to use this theoretical framework to explore the very near field of the wake behind a prism where the scale/space features remain largely unknown, in contrast with intermediate and far-field flows. They use direct numerical simulations (DNS) to calculate the contributions of all processes including turbulence decay and production, pressure/turbulent-diffusion and the forcing due to coherent structures.
The total ( $\text {coherent}+\text {random}$) energy transferred is restored, because all terms are computed from the first principles. Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) then discovered that there exists a reasonable portion of scales which surprisingly comply with the Kolmogorov constant energy transfer in the cascade. The authors qualify this result as ‘a clearly non-Kolmogorov yet Kolmogorov sounding [cascade].’ Indeed, Kolmogorov's theory should not apply for the Reynolds numbers investigated by Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) in the presence of the strong inhomogeneity and anisotropy of the flow. Could coherent motion and/or inhomogeneity be responsible for this apparent constant energy transfer? Using the previously introduced triple decomposition for the velocity structure functions, Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) showed that the constant total energy transfer hides a contribution of the forcing associated with the coherent motion. By further decomposing the total transfer term into an inhomogeneous and homogeneous contribution, they find that inhomogeneities also contribute directly to the energy transfer in addition to manifesting themselves through the appearance of additional terms in the generalized Kármán–Howarth–Kolmogorov equations.
$\text {coherent}+\text {random}$) energy transferred is restored, because all terms are computed from the first principles. Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) then discovered that there exists a reasonable portion of scales which surprisingly comply with the Kolmogorov constant energy transfer in the cascade. The authors qualify this result as ‘a clearly non-Kolmogorov yet Kolmogorov sounding [cascade].’ Indeed, Kolmogorov's theory should not apply for the Reynolds numbers investigated by Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) in the presence of the strong inhomogeneity and anisotropy of the flow. Could coherent motion and/or inhomogeneity be responsible for this apparent constant energy transfer? Using the previously introduced triple decomposition for the velocity structure functions, Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) showed that the constant total energy transfer hides a contribution of the forcing associated with the coherent motion. By further decomposing the total transfer term into an inhomogeneous and homogeneous contribution, they find that inhomogeneities also contribute directly to the energy transfer in addition to manifesting themselves through the appearance of additional terms in the generalized Kármán–Howarth–Kolmogorov equations.
Impressively, they characterise how energy is transferred from the injection, through the mean velocity gradients, to the coherent motion and finally to the random fluctuations. While this general picture is believed to apply to most flows, this is the first time that this complex process is unravelled in a quantitative way, enabled uniquely by the combination of theory and DNS. Moreover, the Kármán–Howarth–Kolmogorov equation for turbulent motion in the presence of coherent structures appears to be the most appropriate framework to quantify the extent and range of scales over which each effect influences the total energy transfer, including the forcing associated with the coherent motion. The work of Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) provides a significant step forward in characterising the effects of inlet/boundary conditions in a complex, inhomogeneous and anisotropic flow, with the ultimate aim of predicting them at Reynolds numbers typically encountered in the laboratory.
3. Future
The work by Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) opens new avenues of investigation of the intricate interactions between coherence and turbulence. Will the organized motion continue to influence the cascade process when the inlet velocity is increased, and/or when travelling through the intermediate and far field? How are each individual velocity components and cross-correlations affected? How do different directional components of energy flux perceive the coherent motion, beyond the circularly averaged transfer term considered by Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020)? How can this information be used to build physics-informed predictive tools such as large-eddy simulation models? Answers to these open questions may be provided by generalized Kármán–Howarth–Kolmogorov equations in the presence of periodic forcing.
In addition, the decomposition of the transfer term proposed by Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020) into homogeneous and inhomogeneous contributions may help to ascertain the role of statistical inhomogeneity. The question of the uniqueness of such a decomposition, which is addressed in Alves Portela et al. (Reference Alves Portela, Papadakis and Vassilicos2020), should be further examined.
Finally, it is worth stressing that in some flows, coherent structures do not possess a periodic signature or multiple periodic motions can be at play (e.g. farms of wind turbines). In such situations, phase averages are precluded and classical two-point statistics (correlation and structure functions) may not remain appropriate. One is then likely to rely on some other statistical tool such as low-pass or band-pass filters, proper orthogonal decomposition or dynamic mode decomposition, or wavelets to name a few. By pursuing work in this direction, one should be able to explicitly identify the different processes (transfer, production, dissipation) in such a new space of scales, flow positions and time.
Declaration of interests
The authors report no conflict of interest.