In a seminal contribution, Breunig and Jones (Reference Breunig and Jones2011) showcase the use of stochastic process methods in political science by applying them to budgetary data. Claiming that budget changes follow a power law distribution, they conclude to have found a general empirical law (cf. Jones et al. Reference Jones, Baumgartner, Breunig, Wlezien, Soroka, Foucault and Franc2009). Yet, their evidence is largely based on the analysis of frequency distributions using log–log plots: if size and frequencies of budget changes scale linearly on log scales, it is, according to their argumentation, evidence of a power law distribution.Footnote 1 But as Clauset, Shalizi, and Newman (Reference Clauset, Shalizi and Newman2009, 675) point out, “being roughly straight on a log–log plot is a necessary but not sufficient condition for power-law behavior.” Clauset, Shalizi, and Newman (Reference Clauset, Shalizi and Newman2009), in fact, demonstrate that several nonnormal, heavy-tailed distributions can appear as a straight line on log–log scales. Thus, “this method and other variations on the same theme generate significant systematic errors under relatively common conditions, […] and as a consequence the results they give cannot be trusted” (Clauset, Shalizi, and Newman Reference Clauset, Shalizi and Newman2009, 665).
In light of these challenges, this letter would like to revisit the claim of a power law distribution in budgetary data. To that end, I apply the principled statistical framework suggested by Clauset, Shalizi, and Newman (Reference Clauset, Shalizi and Newman2009), involving the following steps: first, we need to estimate the exponent via maximum likelihood, which is, however, conditional on knowing the lower tail. Having obtained estimates of the lower tail and, after that, of the exponent, we can then estimate the goodness of fit between the data and the presumed power law. Second, we can compare the power law fit to fits of other heavy-tailed distributions such as exponential, log-normal, and Weibull via likelihood ratio tests. The poweRlaw package by Gillespie (Reference Gillespie2015) offers an implementation of this procedure for R. The R code for this analysis is available at the Harvard Dataverse (Fatke, Breunig, and Jones Reference Fatke, Breunig and Jones2019).
The letter is structured according to these steps and applies them to the budgetary data by Breunig and Jones (Reference Breunig and Jones2011).Footnote 2 As the analysis does not reveal unambiguous support for a power law distribution in public budgets, the findings invite an empirical as well as theoretical refinement. Since, in a wider sense, the contribution intends to showcase the use of a more thorough, yet straight-forward approach to stochastic process methods in political science, the concluding section offers some more general remarks.
1 Parameter Estimation
This section details the estimation of the power law parameters and its goodness-of-fit measures using the budgetary data of Breunig and Jones (Reference Breunig and Jones2011). Results for overall, domestic, and defense outlays are shown in Table 1. (Note that the scaling differs from the original values, since absolute values of budgetary growth rates are used and linearly transformed to have a minimum of 1. Further below, I also report the results for separate analyses of positive and negative values.) Power law functions are defined as
![]() $f(x)=x^{-\unicode[STIX]{x1D6FC}}$
. Thus, we need to estimate the exponent
$f(x)=x^{-\unicode[STIX]{x1D6FC}}$
. Thus, we need to estimate the exponent
![]() $\unicode[STIX]{x1D6FC}$
(also called scaling parameter). However, power laws typically appear only above a threshold
$\unicode[STIX]{x1D6FC}$
(also called scaling parameter). However, power laws typically appear only above a threshold
![]() $x_{\text{min}}$
(also called lower bound). In other words, the estimate of
$x_{\text{min}}$
(also called lower bound). In other words, the estimate of
![]() $\unicode[STIX]{x1D6FC}$
is conditional on the value of
$\unicode[STIX]{x1D6FC}$
is conditional on the value of
![]() $x_{\text{min}}$
, which has to be estimated first. This should be done with care because a high threshold implies discarding valuable data points. Clauset, Shalizi, and Newman (Reference Clauset, Shalizi and Newman2009) propose to set
$x_{\text{min}}$
, which has to be estimated first. This should be done with care because a high threshold implies discarding valuable data points. Clauset, Shalizi, and Newman (Reference Clauset, Shalizi and Newman2009) propose to set
![]() $\hat{x}_{\text{min}}$
so that the remaining data is as similar as possible to a power law distribution. In practice, they advocate using the Kolmogorov–Smirnov (K–S) statistic to minimize the distance between the cumulative distribution functions (CDFs) of the data and the fitted model. To estimate the uncertainty of
$\hat{x}_{\text{min}}$
so that the remaining data is as similar as possible to a power law distribution. In practice, they advocate using the Kolmogorov–Smirnov (K–S) statistic to minimize the distance between the cumulative distribution functions (CDFs) of the data and the fitted model. To estimate the uncertainty of
![]() $\hat{x}_{\text{min}}$
a nonparametric bootstrap procedure can be applied that repeats the K–S statistic for randomly sampled values of the original data. In the transformed budgetary data
$\hat{x}_{\text{min}}$
a nonparametric bootstrap procedure can be applied that repeats the K–S statistic for randomly sampled values of the original data. In the transformed budgetary data
![]() $\hat{x}_{\text{min}}$
is estimated to be 1.12 leaving 60 observations as
$\hat{x}_{\text{min}}$
is estimated to be 1.12 leaving 60 observations as
![]() $n_{\text{tail}}$
. Clauset, Shalizi, and Newman (Reference Clauset, Shalizi and Newman2009, 669) suggest that at least 50 observations are necessary for reliable parameter estimation. With the lower bound set, we can calculate the maximum likelihood estimator for the scaling parameter
$n_{\text{tail}}$
. Clauset, Shalizi, and Newman (Reference Clauset, Shalizi and Newman2009, 669) suggest that at least 50 observations are necessary for reliable parameter estimation. With the lower bound set, we can calculate the maximum likelihood estimator for the scaling parameter
![]() $\hat{\unicode[STIX]{x1D6FC}}=1+n[\sum _{i=1}^{n}\ln \frac{x_{i}}{x_{\text{min}}}]^{-1}$
, which is asymptotically normal and consistent. The standard error can be computed analytically.Footnote
3
$\hat{\unicode[STIX]{x1D6FC}}=1+n[\sum _{i=1}^{n}\ln \frac{x_{i}}{x_{\text{min}}}]^{-1}$
, which is asymptotically normal and consistent. The standard error can be computed analytically.Footnote
3
Table 1. Statistics and parameter estimates (standard deviations in brackets) for budget changes (Breunig and Jones Reference Breunig and Jones2011).

Having estimated the most likely
![]() $\hat{\unicode[STIX]{x1D6FC}}$
and
$\hat{\unicode[STIX]{x1D6FC}}$
and
![]() $\hat{x}_{\text{min}}$
for our distribution, we can assess whether it indeed follows a power law. Alas, the challenge to conclusively identify power law behavior in empirical data is not trivial. Since a power law can be fitted to any empirical distribution, it is, in fact, only possible to test whether an empirical distribution of
$\hat{x}_{\text{min}}$
for our distribution, we can assess whether it indeed follows a power law. Alas, the challenge to conclusively identify power law behavior in empirical data is not trivial. Since a power law can be fitted to any empirical distribution, it is, in fact, only possible to test whether an empirical distribution of
![]() $x$
is consistent with the hypothesis that it is drawn from a distribution of the form
$x$
is consistent with the hypothesis that it is drawn from a distribution of the form
![]() $f(x)~=~x^{-\unicode[STIX]{x1D6FC}}$
rather than from (heavy-tailed) distributions of other forms. In contrast to qualitative appraisals using CDFs or log–log plots, which can only show a necessary but no sufficient condition, Clauset, Shalizi, and Newman (Reference Clauset, Shalizi and Newman2009) suggest a quantitative assessment using, again, the K–S statistic. To that end, multiple (typically between 1,000 and 10,000) synthetic data sets with the same parameters as estimated before are generated from the power law function. For each, we calculate the K–S statistic to assess its fit to the power law distribution, and compare it to the K–S statistic of the original distribution. The
$f(x)~=~x^{-\unicode[STIX]{x1D6FC}}$
rather than from (heavy-tailed) distributions of other forms. In contrast to qualitative appraisals using CDFs or log–log plots, which can only show a necessary but no sufficient condition, Clauset, Shalizi, and Newman (Reference Clauset, Shalizi and Newman2009) suggest a quantitative assessment using, again, the K–S statistic. To that end, multiple (typically between 1,000 and 10,000) synthetic data sets with the same parameters as estimated before are generated from the power law function. For each, we calculate the K–S statistic to assess its fit to the power law distribution, and compare it to the K–S statistic of the original distribution. The
![]() $p$
value corresponds to the fraction of synthetic data sets whose K–S statistic is larger (i.e., goodness of fit is poorer) than for the empirical data. Thus,
$p$
value corresponds to the fraction of synthetic data sets whose K–S statistic is larger (i.e., goodness of fit is poorer) than for the empirical data. Thus,
![]() $p$
values close to one suggest that differences between the empirical distribution and the power law model can be attributed to statistical fluctuations. If
$p$
values close to one suggest that differences between the empirical distribution and the power law model can be attributed to statistical fluctuations. If
![]() $p\leqslant 0.1$
, a power law is ruled out. In the case of budgetary changes,
$p\leqslant 0.1$
, a power law is ruled out. In the case of budgetary changes,
![]() $p$
values range above this cutoff between 0.25 and 0.62. Yet, this does not allow concluding that budgetary changes do follow a power law since other heavy-tailed distributions might describe the data equally well. The next section, therefore, presents likelihood ratio tests to compare the power law fit to fits of exponential, log-normal, and Weibull distributions.
$p$
values range above this cutoff between 0.25 and 0.62. Yet, this does not allow concluding that budgetary changes do follow a power law since other heavy-tailed distributions might describe the data equally well. The next section, therefore, presents likelihood ratio tests to compare the power law fit to fits of exponential, log-normal, and Weibull distributions.
2 Comparison to Other Distributions
Whereas the previous section assessed how well the data fits the power law function, comparing goodness of fits between several heavy-tailed functions can be insightful, too. Ideally, there are competitive theoretical expectations implying different distributions. But even if this is not the case, a comparative assessment is more conservative. It should be noted though that without alternative theoretical expectations the analysis is more explorative in nature. To assess, which function provides the best fit, we first fit several nonnormal and heavy-tailed functions to the data using the same
![]() $\hat{x}_{\text{min}}$
as found above for the power law distribution. Figure 1 illustrates CDFs for the three cases of budgetary changes and corresponding fits of exponential, log-normal, Weibull, and power law distributions. Log-normal and Weibull in particular deviate only marginally and seem to describe the empirical data equally well.
$\hat{x}_{\text{min}}$
as found above for the power law distribution. Figure 1 illustrates CDFs for the three cases of budgetary changes and corresponding fits of exponential, log-normal, Weibull, and power law distributions. Log-normal and Weibull in particular deviate only marginally and seem to describe the empirical data equally well.
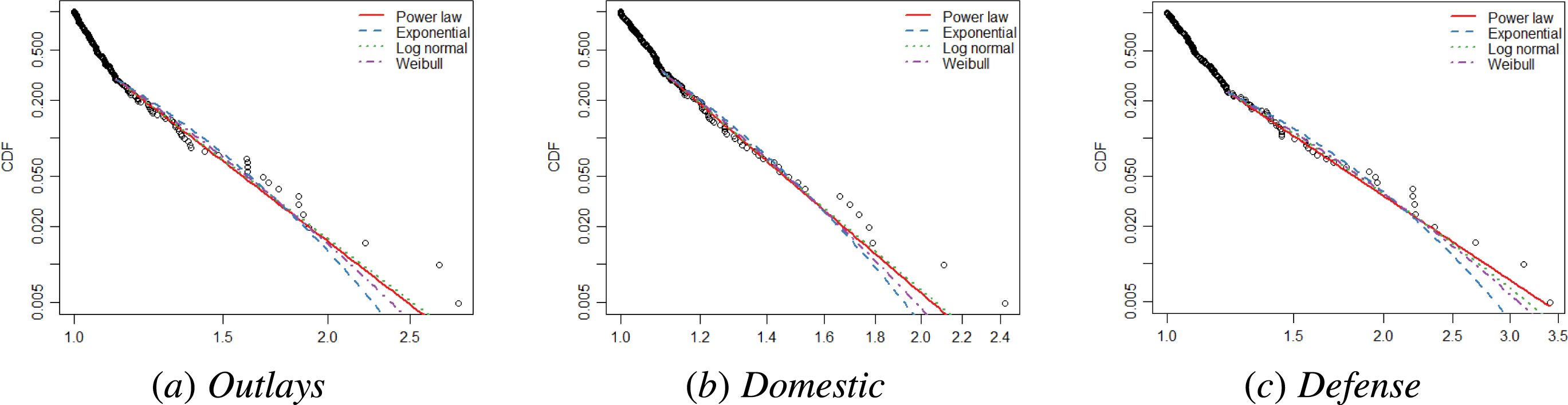
Figure 1. CDFs of budget changes (Breunig and Jones Reference Breunig and Jones2011) and corresponding fits.
Having fitted several distributions to the data, we can perform likelihood ratio tests to assess under which of two competing distributions the empirical distribution is more likely. Following Vuong’s method, we test H1 that one of the two distributions is closer to the empirical distribution by inspecting whether the ratio of the two estimated log-likelihoods is significantly different from zero. If that is the case, the sign of the ratio indicates whether the alternative distribution better describes the data than the power law distribution, or not. Table 2 displays log-likelihood ratios and
![]() $p$
values of two-sided tests of the log-likelihood ratio being significantly different from zero. As none of the
$p$
values of two-sided tests of the log-likelihood ratio being significantly different from zero. As none of the
![]() $p$
values indicates significant differences, we cannot reject H0 that both distributions are equally far from the empirical distribution.
$p$
values indicates significant differences, we cannot reject H0 that both distributions are equally far from the empirical distribution.
Table 2. Log-likelihood ratios and
![]() $p$
values (in brackets) for budget change data (Breunig and Jones Reference Breunig and Jones2011) compared to power law fits.
$p$
values (in brackets) for budget change data (Breunig and Jones Reference Breunig and Jones2011) compared to power law fits.

3 Further Analyses
The maximum likelihood estimator for the exponent
![]() $\unicode[STIX]{x1D6FC}$
, being equivalent to the Hill estimator, is potentially biased in small samples. An alternative procedure is to regress the logarithm of the values on the logarithm of their rank minus
$\unicode[STIX]{x1D6FC}$
, being equivalent to the Hill estimator, is potentially biased in small samples. An alternative procedure is to regress the logarithm of the values on the logarithm of their rank minus
![]() $1/2$
(Gabaix and Ibragimov Reference Gabaix and Ibragimov2011). These estimates, reported in Table A1 and Figure A1 in the supplementary material, are by and larger similar, but somewhat lower (4.603, 6.157, 3.820, respectively) for all three types of budget changes. Using the bias adjusted exponent estimates for the assessment of power law behavior, yields the same results. Again,
$1/2$
(Gabaix and Ibragimov Reference Gabaix and Ibragimov2011). These estimates, reported in Table A1 and Figure A1 in the supplementary material, are by and larger similar, but somewhat lower (4.603, 6.157, 3.820, respectively) for all three types of budget changes. Using the bias adjusted exponent estimates for the assessment of power law behavior, yields the same results. Again,
![]() $p$
values are too large to rule out power law behavior, while log-likelihood ratios do not indicate better fits of the power law distribution than of other heavy-tailed distributions.Footnote
4
$p$
values are too large to rule out power law behavior, while log-likelihood ratios do not indicate better fits of the power law distribution than of other heavy-tailed distributions.Footnote
4
When dealing with data on changes in public budgets, we should also consider the possibility that increases exhibit different behavior than decreases. For that reason, Jones et al. (Reference Jones, Baumgartner, Breunig, Wlezien, Soroka, Foucault and Franc2009) conduct their analysis separately for positive and negative values. Specifically, the “contagion of urgency” (Jones et al.
Reference Jones, Baumgartner, Breunig, Wlezien, Soroka, Foucault and Franc2009, 871) leading to power law distributed budget changes might apply when it comes to extending budgets. Cutting, in contrast, involves more negotiations and concessions, and thus makes extreme punctuation less likely. To that end, I repeat the analyses separately for positive and negative values. The results in Tables A2 and A3 as well as in Figure A2 in the supplementary material do not differ meaningfully from the previous results of the overall distribution. None of the
![]() $p$
values let us rule out power law behavior. At the same time, most of them are not as high as to attribute differences between the empirical distribution and the power law model only to statistical fluctuations (except in the case of cuts to domestic outlays). Comparing the fits to other distributions, we again cannot confidently favor one model over another. Given the low number of observations in the separate analyses, however, these estimates should be treated with care.
$p$
values let us rule out power law behavior. At the same time, most of them are not as high as to attribute differences between the empirical distribution and the power law model only to statistical fluctuations (except in the case of cuts to domestic outlays). Comparing the fits to other distributions, we again cannot confidently favor one model over another. Given the low number of observations in the separate analyses, however, these estimates should be treated with care.
In addition to formal likelihood ratios tests presented so far, it is also possible to infer graphically the distinctiveness of the empirical distribution. Figure A3 in the supplementary material includes multiple histograms of random data sets generated from various heavy-tailed distributions with the same parameters as estimated before. After reverting to the initial scaling and joining with the empirical values for
![]() $x<x_{\text{min}}$
, they are plotted along with the original one in Breunig and Jones (Reference Breunig and Jones2011, 107). The procedure can be reproduced using the provided R code. Evidently, it is challenging to pick the one histogram, which is based on empirical data, as all tails look rather similar and hardly any distribution seems to stand out clearly. While it is generally difficult to discern heavy-tailed distributions, this can be seen as further, and rather intuitive evidence that budget changes might just as well be described by another heavy-tailed function.
$x<x_{\text{min}}$
, they are plotted along with the original one in Breunig and Jones (Reference Breunig and Jones2011, 107). The procedure can be reproduced using the provided R code. Evidently, it is challenging to pick the one histogram, which is based on empirical data, as all tails look rather similar and hardly any distribution seems to stand out clearly. While it is generally difficult to discern heavy-tailed distributions, this can be seen as further, and rather intuitive evidence that budget changes might just as well be described by another heavy-tailed function.
4 Concluding Remarks
Power law distributions appear rather commonly in nature. Not only does the heavy tail of a power law allow for a higher frequency of extreme events than in Gaussian distributions, but its scale-free characteristic, moreover, imbues “them with a vague and mistakenly mystical sense of universality” (Stumpf and Porter Reference Stumpf and Porter2012, 666). It is thus understandable that they are sought after in data generated by social or political processes. However, the excitement should not come at the expense of a thorough assessment. This letter intends to draw the attention to what Clauset, Shalizi, and Newman (Reference Clauset, Shalizi and Newman2009) have proved: log–log plots are not an appropriate tool to establish empirical support, because the scaling property on log scales is a necessary, but no sufficient condition. Instead, researchers should follow the principled statistical framework suggested by Clauset, Shalizi, and Newman (Reference Clauset, Shalizi and Newman2009) and showcased in this letter with budgetary data by Breunig and Jones (Reference Breunig and Jones2011).
Several findings of supposed power laws have not fared well against this scrutiny (Clauset, Shalizi, and Newman Reference Clauset, Shalizi and Newman2009; Stumpf and Porter Reference Stumpf and Porter2012). A more thorough assessment will inevitably lead to more conservative estimates, and thus fewer startling results. On the one hand, a general empirical law of public budgets might be another case in point. For empirical analyses it is not necessarily inconvenient if a distribution does not follow a power law since it may become easier to calculate moments and conduct estimations. That does not imply it would not make sense to think about power laws in political data at all. There are many political phenomena with heavy tails covering several orders of magnitude. And finding evidence of power law behavior would indeed have implications for the data generating process as well as for applicable statistical methods. On the other hand, the result of applying the principled statistical framework did not rule out a power law distribution of budget changes either. As with many other political processes, data on budget changes, particularly regarding the tail of the distribution, are probably simply too sparse to confidently conclude power law behavior. This poses a general challenge because real systems are finite, whereas models of power law behavior assume infinite systems (Stumpf and Porter Reference Stumpf and Porter2012, 665).
This letter therefore seconds the note of caution expressed by Stumpf and Porter (Reference Stumpf and Porter2012). In addition to the application of the principled statistical framework, investigating power law behavior should comprise a theoretical aspect as well. Genuine insights can be gained when we are not only able to describe the data accurately, but also to formulate a model whose mechanism predicts a power law distribution. So far, there are no alternative models implying Weibull or log-normal distributions. But like distributions of income, explanations can evolve when more detailed evidence of the underlying functions becomes available. In that sense, the letter can be seen as invitation to revise and refine, empirically as well as theoretically, what has come to be known as punctuated equilibrium theory (PET) in policy analysis.
Supplementary Material
For supplementary material accompanying this paper, please visit https://doi.org/10.1017/pan.2019.33.





