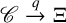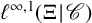A CRITERION FOR HYPERSYMMETRY ON DISCRETE GROUPOIDS

Abstract

Given a Fell bundle $\mathscr C\overset {q}{\to }\Xi $ over the discrete groupoid $\Xi $, we study the symmetry of the associated Hahn algebra $\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$ in terms of the isotropy subgroups of $\Xi $. We prove that $\Xi $ is symmetric (respectively hypersymmetric) if and only if all of the isotropy subgroups are symmetric (respectively hypersymmetric). We also characterise hypersymmetry using Fell bundles with constant fibres, showing that for discrete groupoids, ‘hypersymmetry’ equals ‘rigid symmetry’.

1 Introduction

This article treats the symmetry of certain Banach $^*$ -algebras connected with Fell bundles over discrete groupoids. The study of symmetry for groupoid algebras started not long ago, with Austad and Ortega [1]. They studied the Hahn algebra of a Hausdorff locally compact groupoid, gave necessary conditions for symmetry and even sufficient conditions in the case of transformation groupoids. This subject found a continuation in [2], where Jauré, Măntoiu and myself first treated the problem of symmetry for algebras related to Fell bundles over discrete groupoids. Among other things, in that paper, we proved a weaker form of Theorem 1.2 which is the main result of this paper.

Definition 1.1. A Banach $^*$ -algebra $\mathfrak B$ is called symmetric if the spectrum of $b^*b$ is positive for every $b\in \mathfrak B$ (this happens if and only if the spectrum of any self-adjoint element is real).

Theorem 1.2. Let $\Xi $ be a discrete groupoid. Then:

1. (1) the algebra $\ell ^{\infty ,1}(\Xi )$ is symmetric if and only if every isotropy group of $\Xi $ is symmetric;

2. (2) the algebra $\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$ is symmetric for every Fell bundle $\mathscr C$ over $\Xi $ if and only if every isotropy group of $\Xi $ is hypersymmetric.

This result is interesting as it reduces the question of the (hyper)symmetry of a given groupoid to the (hyper)symmetry of its isotropy subgroups and the study of group $\ell ^1$ -algebras is far more developed. For example, see [1, 2, 4, 5, 7–10, 13] and the references therein. Our results can be applied to get spectral $^*$ -subalgebras of $C^*$ -algebras associated with Fell bundles (a reduced Banach $^*$ -algebra is symmetric if and only if it is a spectral $^*$ -subalgebra of its enveloping $C^*$ -algebra [12, Theorem 11.4.1]).

The article is divided into 3 parts. Section 2 deals with preliminaries, where we introduce Fell bundles, the Hahn algebra of a Fell bundle and define what (hyper)symmetry for a groupoid means. In Section 3, we introduce a characterisation for hypersymmetry using only Fell bundles with constant fibres. It is analogous to the characterisation made for groups by Jauré and Măntoiu in [4]. Finally, Section 4 deals with the proof of Theorem 1.2. This is achieved by writing a general discrete groupoid as a disjoint union of transitive groupoids and proving that transitive groupoids are isomorphic to transitive transformation groups. Using the available theory for groups yields the desired result.

2 Preliminaries

Let $\Xi $ be a groupoid, with unit space $\mathcal U:=\Xi ^{(0)}$ , source map ${\mathrm {d}}$ and range map ${\mathrm {r}}$ . The ${\mathrm {d}}$ - and ${\mathrm {r}}$ -fibres are $\Xi _u=\{\xi \in \Xi \mid {\mathrm {d}}(\xi )=u\}$ and $\Xi ^u=\{\xi \in \Xi \mid {\mathrm {r}}(\xi )=u\}$ . The set of composable pairs is

$$ \begin{align*}\Xi^{(2)}\!:=\{(x,y)\mid{\mathrm{r}}(\,y)={\mathrm{d}}(x)\}. \end{align*} $$

The isotropy group associated with the unit $u\in \mathcal U$ is $\Xi _u^u=\Xi _u\cap \Xi ^u$ ; it is a subgroupoid of $\Xi $ , which happens to be a group. We endow the groupoid $\Xi $ with the discrete topology. Let us introduce an important class of groupoids which will be useful.

Definition 2.1. A groupoid $\Xi $ is called transitive if for any pair $u,v\in \mathcal U$ , there exists $x\in \Xi $ such that ${\mathrm {r}}(x)=u$ and ${\mathrm {d}}(x)=v$ .

The concept of transitivity is borrowed from the theory of dynamical systems. It comes from a natural but hidden action of the groupoid on its unit space. So the groupoid is transitive if and only if this action is transitive (see [3, Example 2.2, Corollary 7.8]).

In this article, we are going to work with Fell bundles $\mathscr C\overset {q}{\to }\Xi $ over the groupoid ${\Xi }$ (see [6, 11]). A Fell bundle is composed of fibres such that each fibre $\mathfrak C _x\!:=q^{-1}(\{x\})$ is a Banach space with norm $\parallel \!\cdot \!\parallel _{\mathfrak C_x}$ , the topology of $\mathscr C$ coincides with the norm topology on each fibre, there are antilinear continuous involutions

$$ \begin{align*} \mathfrak C _x\ni \!a\to a^{\bullet}\!\in\mathfrak C _{x^{-1}} \end{align*} $$

and for all $(x,y)\in \Xi ^{(2)}$ , there are continuous multiplications

$$ \begin{align*} \mathfrak C _x\times\mathfrak C _y\ni(a,b)\to a\bullet b\in\mathfrak C _{xy} \end{align*} $$

satisfying the following axioms valid for $a\in \mathfrak C_x, b\in \mathfrak C_y\,$ and $(x,y)\in \Xi ^{(2)}$ :

• • $\parallel \!ab\!\parallel _{\mathfrak C_{xy}}\,\le \,\parallel \!a\!\parallel _{\mathfrak C_{x}}\parallel \!b\!\parallel _{\mathfrak C_{y}}$ ;

• • $(ab)^\bullet =b^\bullet a^\bullet $ ;

• • $\parallel \!a^\bullet a\!\parallel _{\mathfrak C_{{\mathrm {d}}(x)}}=\,\parallel \!a\!\parallel _{\mathfrak C_{x}}^2$ ;

• • $a^\bullet a$ is positive in $\mathfrak C_{{\mathrm {d}}(x)}$ .

From these axioms, it follows that $\mathfrak C _x$ is a $C^*$ -algebra for every unit $x\in \mathcal U$ . Sometimes we simply write $\mathscr C=\bigsqcup _{x\in \Xi }\mathfrak C _x$ for the Fell bundle.

Our object of study is the Hahn algebra $\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$ adapted to Fell bundles [11]. In our case, it is formed by the sections $\Phi :\Xi \to \mathfrak C$ (thus satisfying $\Phi (x)\in \mathfrak C_x$ for every $x\in \Xi $ ) that can be obtained as a limit of finitely supported sections in the Hahn-type norm

It is a Banach $^*$ -algebra under the multiplication

$$ \begin{align*} (\Phi* \Psi)(x):=\sum_{yz=x}\Phi(\,y)\bullet\Psi(z) \end{align*} $$

and the involution

$$ \begin{align*} \Phi^*(x):=\Phi(x^{-1})^\bullet. \end{align*} $$

Remark 2.2. Let us point out some properties of the functions in $\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$ . If $\Phi _n\in \ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$ is a sequence of sections with finite support and $\Phi _n\to \Phi $ , then the convergence is uniform. Indeed, let $x\in \Xi $ and observe that

So

. This implies that the function $\Phi $ has countable support and vanishes at $\infty $ .

We denote by $C^*(\Xi \,\vert \,\mathscr C)$ the enveloping $C^*$ -algebra of the Hahn algebra $\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$ . It is a known fact that $\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$ is a dense $^*$ -subalgebra of $C^*(\Xi \!\mid \!\mathscr C)$ .

Definition 2.3

1. (i) The discrete groupoid $\Xi $ is called symmetric if the convolution Banach $^*$ -algebra $\ell ^{\infty ,1}(\Xi )$ is symmetric.

2. (ii) The discrete groupoid $\Xi $ is called hypersymmetric if given any Fell bundle $\mathscr C\!=\bigsqcup _{x\in \Xi }\mathfrak C _x$ , the Banach $^*$ -algebra $\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$ is symmetric.

Example 2.4. If $\Pi \subset X\times X$ is an equivalence relation on X, one can make $\Xi =\Pi $ a discrete groupoid by defining the operations

$$ \begin{align*} \begin{split} {\mathrm{d}}(x,y)=(\,y,y),\quad &{\mathrm{r}}(x,y)=(x,x),\quad (x,y)(\,y,z)=(x,z),\quad(x,y)^{-1}\!=(\,y,x). \end{split} \end{align*} $$

The unit space is $\,\mathcal U=\mathsf {Diag}(X)$ and it gets canonically identified with X, via the homeomorphism $(x,x)\mapsto x$ . In this case, all of the isotropy groups correspond to the trivial group $\Pi _u^u=\{(u,u)\}$ , so Theorem 4.9 will guarantee that $\Pi $ is hypersymmetric. A particular example is the so called pair groupoid, $\Pi =X\times X$ .

3 A characterisation of hypersymmetry for discrete groupoids

In [2], we introduced some special Fell bundles arising from Hilbert bundles to characterise the hypersymmetry of a discrete groupoid. However, in this paper, we will improve this characterisation. One can actually verify hypersymmetry by looking at much simpler algebras associated to Fell bundles with constant fibres. Let us make precise the Fell bundles of interest.

Definition 3.1. By a (left) groupoid action of a discrete groupoid $\Xi $ on the $C^*$ -bundle $\mathscr A\!:=\bigsqcup _{u\in \mathcal U}\mathfrak A_u\overset {p}{\to }\mathcal U$ over its unit space, we understand a continuous map

$$ \begin{align*} \mathscr A\rtimes\Xi:=\{(\alpha,x)\in\mathscr A\times\Xi\!\mid\!p(\alpha)={\mathrm{d}}(x)\}\ni(\alpha,x)\to \mathcal T(\alpha,x)\equiv\mathcal T_x(\alpha)\in\mathscr A \end{align*} $$

satisfying the axioms:

1. (a) $p[\mathcal T_x(\alpha )]={\mathrm {r}}(x)$ for all $x\in \Xi ,\,\alpha \in \mathfrak A_{{\mathrm {d}}(x)}$ ;

2. (b) each $\mathcal T_x$ is a $^*$ -isomorphism $:\mathfrak A_{{\mathrm {d}}(x)}\!\to \mathfrak A_{{\mathrm {r}}(x)}$ ;

3. (c) $\mathcal T_u={\mathrm {id}}_{\mathfrak A_u}$ for all $u\in \mathcal U$ ;

4. (d) if $(x,y)\in \Xi ^{(2)}$ and $(\alpha ,y)\in \mathscr A\rtimes \Xi $ , then $(\mathcal T_y(\alpha ),x)\in \mathscr A\rtimes \Xi $ and $\mathcal T_{xy}(\alpha )=\mathcal T_x[\mathcal T_y(\alpha )]$ .

Definition 3.2. Let $\mathcal T$ be a groupoid action of $\Xi $ on the $C^*$ -bundle $\mathscr A\!:=\bigsqcup _{u\in \mathcal U} \mathfrak A_u\overset {p}{\to }\mathcal U$ . We define its associated Fell bundle as follows. The underlying space is $\mathscr C_{\mathcal T}:=\mathscr A\rtimes \Xi $ with the topology inherited from the product topology and the obvious projection q. We endow it with the operations

$$ \begin{align*} (\alpha,x)\bullet(\,\beta,y):=(\alpha\mathcal T_x(\,\beta),xy)\quad \text{when } (x,y)\in\Xi^{(2)} \end{align*} $$

and

$$ \begin{align*} (\alpha,x)^\bullet:=(\mathcal T_{x^{-1}}(\alpha^*),x^{-1}) \end{align*} $$

to get a Fell bundle over $\Xi $ . A section is now a map $\Phi :\Xi \to \mathscr C_{\mathcal T}$ such that

$$ \begin{align*} \Phi(x)\equiv(\varphi(x),x)\in\mathfrak C_x=\mathfrak A_{{{\mathrm{r}}}(x)}\times\{x\}\quad\mbox{for all } x\in\Xi. \end{align*} $$

So we may identify every section $\Phi \in \ell ^{\infty ,1}(\Xi \,\vert \,\mathscr C_{\mathcal T})$ with a function $\Phi :\Xi \to \mathscr A$ (note the abuse of notation), such that $ \Phi (x)\in \mathfrak A_{{{\mathrm {r}}}(x)}$ .

We will also denote the algebra $\ell ^{\infty ,1}(\Xi \,\vert \,\mathscr C_{\mathcal T})$ by $\ell ^{\infty ,1}_{\mathcal T}(\Xi ,\mathscr A)$ to recall its particular nature. If the action $\mathcal T$ is trivial, meaning that $\mathfrak A_u\equiv \mathfrak A$ for all $u\in \mathcal U$ and $\mathcal T_x\equiv {\mathrm {id}}_{\mathfrak A}$ for all $x\in \Xi $ , then we denote the resulting algebra simply by $\ell ^{\infty ,1}(\Xi ,\mathfrak A)$ .

Remark 3.3. Let $\Phi ,\Psi \in \ell ^{\infty ,1}_{\mathcal T}(\Xi ,\mathscr A)$ . In this case, one may write the algebraic laws as

$$ \begin{align*} [\Phi*\Psi](x) & =\!\sum_{y\in\Xi^{{\mathrm{r}}(x)}}\!\Phi(\,y)\mathcal T_y[\Psi(\,y^{-1}x)], \\ \Phi^*(x) & =\mathcal T_{x}[\Phi(x^{-1})]^* \end{align*} $$

and the Hahn-type norm as

$$ \begin{align*} \parallel\!\Phi\!\parallel_{\ell^{\infty,1}_{\mathcal T}(\Xi,\mathscr A)}=\max\bigg\{\sup_{u\in \mathcal U}\sum_{{\mathrm{r}}(x)=u}\!\parallel\!\Phi(x)\!\parallel_{\mathfrak A_{{\mathrm{r}}(x)}},\,\sup_{u\in \mathcal U}\sum_{{\mathrm{d}}(x)=u}\!\parallel\!\Phi(x)\!\parallel_{\mathfrak A_{{\mathrm{r}}(x)}}\!\!\bigg\}. \end{align*} $$

Lemma 3.4. Let $\mathscr C\!=\bigsqcup _{x\in \Xi }\mathfrak C_x$ be a Fell bundle over the discrete groupoid $\Xi $ . Then there exists an isometric $^*$ -monomorphism

(3.1) $$\begin{align} \varphi:\ell^{\infty,1}(\Xi\,\vert\,\mathscr C)\to \ell^{\infty,1}(\Xi,C^*(\Xi\,\vert\,\mathscr C)). \end{align} $$

Proof. Set $\mathfrak A:=C^*(\Xi \,\vert \,\mathscr C)$ and, for every $x\in \Xi $ , embed $\mathfrak C_x$ into $\ell ^{\infty ,1}(\Xi \,\vert \,\mathscr C)\subset \mathfrak A$ by setting, for each $a\in \mathfrak C_x$ ,

$$ \begin{align*} (\theta_x a)(\,y):=a\ {\mathrm{if}}\ y=x,\quad(\theta_x a)(\,y):=0_{\mathfrak C_x}\ {\mathrm{if}}\ y\ne x. \end{align*} $$

It is not hard to prove that if $(x,y)\in \Xi ^{(2)}$ , then

$$ \begin{align*}\theta_xa*\theta_yb=\theta_{xy}(a\bullet b)\quad\text{and}\quad (\theta_xa)^*=\theta_{x^{-1}}a^{\bullet}\end{align*} $$

hold. However, one also has

. For, if $x\in \mathcal U$ , this equality holds because $\theta _x:\mathfrak C_x\to \mathfrak A$ is a $^*$ -monomorphism of $C^*$ -algebras and hence isometric, and if $x\in \Xi $ is not a unit, then one may apply the (now standard) trick

to conclude that $\theta _x$ preserves the mentioned norms. This allows us to successfully define

$$ \begin{align*} \varphi(\Phi)(x)=\theta_x \Phi(x) \quad\text{for }\Phi\in \ell^{\infty,1}(\Xi\,\vert\,\mathscr C) \end{align*} $$

and derive an isometry:

Now we check that $\varphi $ is a $^*$ -homomorphism,

$$ \begin{align*} [\varphi(\Phi)*\varphi(\Psi)](x)=\sum_{yz=x} \theta_y \Phi(\,y)*\theta_z\Psi(z) =\theta_x \sum_{yz=x} \Phi(\,y)\bullet\Psi(z) =\varphi(\Phi*\Psi)(x) \end{align*} $$

and

$$ \begin{align*} \varphi(\Phi^*)(x)=\theta_x \Phi^*(x)=\theta_x \Phi(x^{-1})^\bullet=[\theta_{x^{-1}}\Phi(x^{-1})]^*=\varphi(\Phi)(x^{-1})^*=\varphi(\Phi)^*(x). \end{align*} $$

This finishes the proof.

Remark 3.5. Observe that $\ell ^{\infty ,1}(\Xi ,\mathfrak A)\cong \ell ^{\infty ,1}(\Xi )\,\hat {\otimes }\,\mathfrak A$ , where $\hat {\otimes }$ denotes the projective tensor product. Indeed, given $(\varphi ,a)\in \ell ^{\infty ,1}(\Xi )\times \mathfrak A$ , define the function $\varphi \otimes a$ by

$$ \begin{align*}[\varphi\otimes a](x):=a\varphi(x) \quad\mbox{for all } x\in\Xi.\end{align*} $$

The map $(\varphi ,a)\mapsto \varphi \otimes a$ defined in $\ell ^{\infty ,1}(\Xi )\times \mathfrak A\to \ell ^{\infty ,1}(\Xi ,\mathfrak A)$ is bilinear, has norm $1$ (satisfies ) and it extends to a $^*$ -isomorphism

$$ \begin{align*} \iota: \ell^{\infty,1}(\Xi)\,\hat{\otimes}\,\mathfrak A\to \ell^{\infty,1}(\Xi,\mathfrak A). \end{align*} $$

The following corollary effectively reduces our concerns to the study of tensor products, just as in the group case (see [4, Theorem 2.4]).

Corollary 3.6. A discrete groupoid $\Xi $ is hypersymmetric if and only if the Banach $^*$ -algebra $\ell ^{\infty ,1}(\Xi ,\mathfrak A)\cong \ell ^{\infty ,1}(\Xi )\,\hat {\otimes }\,\mathfrak A$ is symmetric for every $C^*$ -algebra $\mathfrak A$ .

Proof. Every algebra of the form $\ell ^{\infty ,1}(\Xi ,\mathfrak A)$ comes from a Fell bundle (recall Definition 3.2), so it is symmetric if $\Xi $ is hypersymmetric. However, because of Lemma 3.4, given any Fell bundle $\mathscr C$ , the algebra $\ell ^{\infty ,1}(\Xi \,\vert \,\mathscr C)$ may be identified as a closed $^*$ -subalgebra of some algebra of the form $\ell ^{\infty ,1}(\Xi ,\mathfrak A)$ . So it will be symmetric if the latter is symmetric, by [12, Theorem 11.4.2].

Remark 3.7. In the group case, this condition has been called ‘rigid symmetry’ by many authors (including myself) and it was introduced by Leptin and Poguntke in [9]. It can also be seen in [1, 2, 4, 10, 13].

Before going into the following sections, let us simplify some notation. Let $\mathfrak A,\mathfrak B$ be Banach $^*$ -algebras. We will denote by $\mathfrak A\hookrightarrow \mathfrak B$ the fact that there exists an isometric $^*$ -monomorphism $\iota :\mathfrak A\to \mathfrak B$ . In this language, the conclusion of Lemma 3.4 can be written as $\ell ^{\infty ,1}(\Xi \,\vert \,\mathscr C)\hookrightarrow \ell ^{\infty ,1}(\Xi ,C^*(\Xi \,\vert \,\mathscr C))$ . However, the dual notation $\mathfrak A\twoheadrightarrow \mathfrak B$ means that there exists some contractive $^*$ -epimorphism $\pi :\mathfrak A\to \mathfrak B$ .

4 The result for discrete groupoids

The rest of the paper is devoted to proving Theorem 4.9. We will follow the strategy detailed in the introduction, starting with a complete (well-known) characterisation of discrete transitive groupoids as group transformation groupoids.

Definition 4.1. Let $\gamma $ be a continuous action of the (discrete) group $\mathsf {G}$ on the topological space X. We define the transformation groupoid $\Xi :=\mathsf {G}\ltimes _\gamma X$ associated to it as follows. As a topological space, $\mathsf {G}\ltimes _\gamma X$ is just $\mathsf {G}\times X$ and the maps ${\mathrm {r}},{\mathrm {d}}$ are given by ${\mathrm {d}}(a,x)=x$ and ${\mathrm {r}}(a,x)=\gamma _a(x)$ . The composition is $(b,\gamma _a(x))(a,x):=(ba,x)$ and inversion reads $(a,x)^{-1}:=(a^{-1}\!,\gamma _a(x))$ . The unit space is $\mathcal U=\{{\mathsf {e}}\}\times X\equiv X$ .

Proposition 4.2. Let $\Xi $ be a discrete transitive groupoid with isotropy group $\mathsf {G}$ . There is an abelian group structure on $\mathcal U$ and an action $\gamma $ of $\mathsf {G}'=\mathsf {G}\times \mathcal U$ on $\mathcal U$ such that $\Xi \cong \mathsf {G}'\ltimes _\gamma \mathcal U$ .

Proof. Let us give $\mathcal U$ some abelian group structure with additive notation and define the action of $\mathsf {G}'$ by $\gamma _{(\alpha ,w)}(v)=w+v$ . To construct an isomorphism $\varphi $ , fix some $u\in \mathcal U$ and realise $\mathsf {G}$ as $\Xi _u^u$ . Since $\Xi $ is transitive, for every $v\in \mathcal U$ , there exists an arrow $z_v\in \Xi $ such that ${\mathrm {d}}(z_v)=v$ and ${\mathrm {r}}(z_v)=u$ . Then,

$$ \begin{align*}\varphi: \mathsf{G}'\ltimes_\gamma \mathcal U\to \Xi \quad\text{defined by } \varphi((x,w),v)=z^{-1}_{w+v}x z_{v}\end{align*} $$

is the required isomorphism. Let us verify that $\varphi $ is indeed a groupoid isomorphism.

1. (i) If $((x_1,w_1),w_2+v)((x_2,w_2),v)=((x_1x_2,w_1+w_2),v)$ , then

   $$ \begin{align*} \varphi((x_1x_2,w_1+w_2),v)&=z^{-1}_{w_1+w_2+v}x_1x_2z_{v} \\ &=z^{-1}_{w_1+w_2+v}x_1z_{w_2+v}z_{w_2+v}^{-1}x_2z_{v} \\ &=\varphi((x_1,w_1),w_2+v)\varphi((x_2,w_2),v). \end{align*} $$

2. (ii) If $((x,w),v)\in \mathsf {G}'\ltimes _\gamma \mathcal U$ , then $((x,w),v)^{-1}=((x^{-1},-w),w+v)$ and

   $$ \begin{align*} \varphi((x^{-1},-w),w+v)=z^{-1}_v x^{-1}z_{w+v} =(z^{-1}_{w+v}x z_{v})^{-1}=\varphi((x,w),v)^{-1}. \end{align*} $$

3. (iii) The inverse function $\varphi ^{-1}$ is given by $\varphi ^{-1}(\xi )=((z_{{\mathrm {r}}(\xi )}\xi z_{{\mathrm {d}}(\xi )}^{-1},{\mathrm {r}}(\xi )-{\mathrm {d}}(\xi )),{\mathrm {d}}(\xi )).\\[-33pt] $

Remark 4.3. It follows from Proposition 4.2 that the pair groupoid ${\mathcal U}\times {\mathcal U}$ is isomorphic to ${\mathcal U}\ltimes _{\gamma |_{\mathcal U}} {\mathcal U}$ . (Here, $\mathsf {G}=\{\mathsf {e}\}$ is the trivial group.)

While the commutativity of $\mathcal U$ was not essential for the previous proof (any group structure would have worked out), it will be of vital importance in what follows (see the proof of Theorem 4.7). That is why it will be occasionally remarked in the following propositions.

The following lemma requires some notation. Given a $C^*$ -algebra $\mathfrak A$ and a group action $\gamma :\mathsf {G}\to {\mathrm {Bij}}(\mathcal U)$ , denote by $\Gamma $ the $\mathsf {G}$ -action on $\mathcal C_0(\mathcal U,\mathfrak A)$ satisfying $\Gamma _x(\,f)(u)=f(\gamma _{x^{-1}}(u))$ .

Lemma 4.4. Suppose that the discrete group $\mathsf {G}$ acts on $\mathcal U$ via $\gamma $ and $\mathfrak A$ is a $C^*$ -algebra. Then,

$$ \begin{align*} \ell^1_\Gamma(\mathsf{G},\mathcal C_0(\mathcal U,\mathfrak A))\twoheadrightarrow \ell^{\infty, 1}(\mathsf{G}\ltimes_\gamma \mathcal U,\mathfrak A). \end{align*} $$

Proof. Define $\pi :\ell ^1_\Gamma (\mathsf {G},\mathcal C_0(\mathcal U,\mathfrak A))\to \ell ^{\infty , 1}(\mathsf {G}\ltimes _\gamma \mathcal U,\mathfrak A)$ by the formula $\pi (\Phi )(x,u)=\Phi (x)(\gamma _{x}(u))$ . This map is well defined and clearly surjective, while it also satisfies

and

$$ \begin{align*} \pi(\Phi*\Psi)(x,u)&=[\Phi*\Psi](x)(\gamma_{x}(u)) \\ &=\bigg[\sum_{y\in \mathsf{G}}\Phi(\,y)\Gamma_y[\Psi(\,y^{-1}x)]\bigg](\gamma_{x}(u)) \\ &=\sum_{y\in \mathsf{G}}\Phi(\,y)(\gamma_{x}(u))\Psi(\,y^{-1}x)(\gamma_{y^{-1}x}(u)) \\ &=\sum_{y\in \mathsf{G}}\pi(\Phi)(\,y,\gamma_{y^{-1}x}(u))\pi(\Psi)(\,y^{-1}x,u) \\ &=[\pi(\Phi)*\pi(\Psi)](x,u). \end{align*} $$

Finally, we see that

$$ \begin{align*} \pi(\Phi^*)(x,u)&=\Phi^*(x)(\gamma_{x}(u)) \\ &=\Gamma_x[\Phi(x^{-1})^*](\gamma_{x}(u))=\Phi(x^{-1})(u)^*=[\pi(\Phi)(x^{-1},\gamma_{x}(u))]^*=\pi(\Phi)^*(x,u). \end{align*} $$

Hence, $\pi $ is a contractive $^*$ -epimorphism.

Lemma 4.4 will be used in the following form, which allows us to focus on the study of $\ell ^1$ -algebras arising from group $C^*$ -dynamical systems.

Corollary 4.5. If $\ell ^1_\Gamma (\mathsf {G},\mathcal C_0(\mathcal U,\mathfrak A))$ is a symmetric Banach $^*$ -algebra, then the algebra $\ell ^{\infty , 1}(\mathsf {G}\ltimes _\gamma \mathcal U,\mathfrak A)$ is also symmetric.

Proof. In Lemma 4.4, we showed that $\ell ^1_\Gamma (\mathsf {G},\mathcal C_0(\mathcal U,\mathfrak A))\twoheadrightarrow \ell ^{\infty , 1}(\mathsf {G}\ltimes _\gamma \mathcal U,\mathfrak A)$ , so the conclusion follows from [12, Theorem 11.4.2].

Proposition 4.6. Let $(\mathsf {G}\times \mathsf {H}, \Gamma , \mathfrak A)$ be a $C^*$ -dynamical system and assume that $\mathsf {G}$ acts trivially on $\mathfrak A$ . Then one has

(4.1) $$ \begin{align} \ell^1_\Gamma(\mathsf{G}',\mathfrak A)\cong \ell^1(\mathsf{G})\,\hat{\otimes}\,\ell^1_{\Gamma}(\mathsf{H},\mathfrak A), \end{align} $$

where $\mathsf {G}':=\mathsf {G}\times \mathsf {H}$ .

Proof. Observe that

$$ \begin{align*}\iota: \ell^1_\Gamma(\mathsf{G}',\mathfrak A)\to\ell^1(\mathsf{G},\ell^1_{\Gamma}(\mathsf{H},\mathfrak A))\quad\text{defined by }\iota(\Phi)(x)(\,y)=\Phi(x,y) \end{align*} $$

is an isometric $^*$ -isomorphism. Indeed, bijectivity is direct, while

and, identifying $(1_{\mathsf {G}},b)\in \mathsf {G}'$ with $b\in \mathsf {H}$ ,

$$ \begin{align*} [\iota(\Phi)*\iota(\Psi)](x)(\,y)&=\bigg[ \sum_{a\in \mathsf{G}} \iota(\Phi)(a)*\iota(\Psi)(a^{-1}x)\bigg](\,y) \\ &=\sum_{a\in \mathsf{G}}\sum_{b\in \mathsf{H}} \iota(\Phi)(a)(b)\Gamma_{b}[\iota(\Psi)(a^{-1}x)(b^{-1}y)] \\ &=\sum_{(a,b)\in \mathsf{G}\times\mathsf{H}}\Phi(a,b){\Gamma}_{(a,b)}[\Psi(a^{-1}x,b^{-1}y)] \\ &=\iota(\Phi*\Psi)(x)(\,y). \end{align*} $$

Finally,

$$ \begin{align*} \iota(\Phi^*)(x)(\,y)=\Phi^*(x,y)=\Gamma_{y}[\Phi(x^{-1},y^{-1})^*]=\iota(\Phi)(x^{-1})^*(\,y)=\iota(\Phi)^*(x)(\,y). \end{align*} $$

So $\ell ^1_\Gamma (\mathsf {G}',\mathfrak A)\cong \ell ^1(\mathsf {G},\ell ^1_{\Gamma }(\mathsf {H},\mathfrak A))\cong \ell ^1(\mathsf {G})\,\hat {\otimes }\,\ell ^1_{\Gamma }(\mathsf {H},\mathfrak A)$ .

We can put together the previous lemmas to obtain the following result, which is Theorem 1.2 for transitive groupoids.

Theorem 4.7. Let $\Xi $ be a discrete transitive groupoid with isotropy subgroup $\mathsf {G}$ . If $\mathsf {G}$ is symmetric (respectively hypersymmetric), then $\Xi $ is symmetric (respectively hypersymmetric).

Proof. Let us divide the proof into two cases, the first one being about hypersymmetry. Because of Proposition 4.2, we may assume that $\Xi =\mathsf {G}'\ltimes _\gamma \mathsf {H}$ , with $\mathsf {G}'=\mathsf {G}\times \mathsf {H}$ and $\gamma _{(g,h)}(k)=h+k$ .

First, suppose that $\mathsf {G}$ is hypersymmetric. Because of Corollaries 3.6 and 4.5, it is enough to show that $\mathsf {G}\times \mathsf {H}$ is hypersymmetric (or ‘rigidly symmetric’, see Remark 3.7). However, this follows from the fact that $\mathsf {H}$ is abelian and [9, Theorem 7].

Now suppose that $\mathsf {G}$ is only symmetric. Note that $\gamma |_{\mathsf {H}}$ coincides with the action of $\mathsf {H}$ on itself by left translation, so we will denote it by ${\mathrm {lt}}$ . Then,

$$ \begin{align*} \ell^1_\Gamma(\mathsf{G}',\mathcal C_0(\mathsf{H}))&\overset{(\scriptsize 4.1)}{\cong} \ell^1(\mathsf{G})\,\hat{\otimes}\,\ell^1_{\mathrm{lt}}(\mathsf{H},\mathcal C_0(\mathsf{H})) \\ &\overset{(3.1)}{\hookrightarrow} \ell^1(\mathsf{G})\,\hat{\otimes}\,\ell^1(\mathsf{H})\,\hat{\otimes}\,(\mathsf{H}\ltimes_{\mathrm{lt}}\mathcal C_0(\mathsf{H})) \\ &\cong \ell^1(\mathsf{H})\,\hat{\otimes}\,\ell^1(\mathsf{G},\mathcal K(\ell^2(\mathsf{H}))). \end{align*} $$

The final isomorphism holds because of the Stone–von Neumann theorem, that is, $\mathsf {H}\ltimes _{\mathrm {lt}}\kern-1.2pt \mathcal C_0(\mathsf {H})\kern-1.2pt\cong\kern-1.2pt \mathcal K(\ell ^2(\mathsf {H}))$ . Now, $\ell ^1(\mathsf {G},\kern-1.2pt \mathcal K(\ell ^2(\mathsf {H})\kern-0.5pt)\kern-0.5pt)$ is symmetric because of [5, Theorem 1], and hence $\ell ^1(\mathsf {H})\,\hat {\otimes }\,\ell ^1(\mathsf {G},\mathcal K(\ell ^2(\mathsf {H})))$ is symmetric because of [7, Theorem 5]. We conclude that $\ell ^1_\Gamma (\mathsf {G}',\mathcal C_0(\mathsf {H}))$ and thus $\ell ^{\infty ,1}(\Xi )$ are symmetric.

Corollary 4.8. The pair groupoid over a discrete set $\mathcal U$ is hypersymmetric.

Now we will proceed to upgrade Theorem 4.7 to the case of general discrete groupoids.

Theorem 4.9. A discrete groupoid $\Xi $ is symmetric (respectively hypersymmetric) if and only if its isotropy subgroups are symmetric (respectively hypersymmetric).

Proof. It is obvious that symmetry (respectively hypersymmetry) of $\Xi $ implies the symmetry (respectively hypersymmetry) of its isotropy groups ( $\ell ^{1}(\Xi _u^u,\mathfrak A)\hookrightarrow \ell ^{\infty ,1}(\Xi ,\mathfrak A)$ in a natural way). As the ‘only if’ part is clear, let us prove the ‘if’ part.

Let $\mathfrak A$ be a $C^*$ -algebra and $\Phi $ be an arbitrary section in $\ell ^{\infty ,1}(\Xi ,\mathfrak A)$ . The section $\Phi $ has a countable support (see Remark 2.2) and, since every discrete groupoid can be decomposed as a disjoint union of discrete transitive subgroupoids, we can find a countable number of disjoint transitive subgroupoids $\{\Xi (i)\}_{i\in \mathbb {N}}$ , such that ${\mathrm {supp}}(\Phi )\subset \bigcup _{i=1}^\infty \Xi (i) $ . Define $\Phi _n\in \ell ^{\infty ,1}(\Xi ,\mathfrak A)$ by

$$ \begin{align*}\Phi_n(x):=\begin{cases} \Phi(x) & \text{if\ } x\in \bigcup_{i=1}^{n} \Xi(i) , \\ 0_{\mathfrak A} & \text{if\ } x\not\in \bigcup_{i=1}^{n} \Xi(i). \\ \end{cases}\end{align*} $$

Then, $\lim _n\Phi _n= \Phi $ in $\ell ^{\infty ,1}(\Xi ,\mathfrak A)$ , but more importantly,

$$ \begin{align*} {\mathrm{Spec}}_{\ell^{\infty,1}(\Xi,\mathfrak A)}(\Phi)=\bigcup_{i=1}^\infty{\mathrm{Spec}}_{\ell^{\infty,1}(\Xi,\mathfrak A)}(\Phi_n). \end{align*} $$

So, to conclude, it is enough to prove that ${\mathrm {Spec}}_{\ell ^{\infty ,1}(\Xi ,\mathfrak A)}(\Phi _n)\subset \mathbb {R}$ , whenever $\Phi ^*=\Phi $ . Indeed, if $\Phi ^*=\Phi $ , after fixing n, we see that $\Phi _n^*=\Phi _n$ and $\ell ^{\infty ,1}(\Xi ,\mathfrak A)$ contains an isometric $^*$ -isomorphic copy of $\ell ^{\infty ,1}(\bigcup _{i=1}^n\Xi (i),\mathfrak A)$ , obtained by extending the sections in the latter algebra with zeros outside its original domain. So by definition, one has $\Phi _n\in \ell ^{\infty ,1}(\bigcup _{i=1}^n\Xi (i),\mathfrak A) \subset \ell ^{\infty ,1}(\Xi ,\mathfrak A)$ , which implies that

$$ \begin{align*} {\mathrm{Spec}}_{\ell^{\infty,1}(\Xi,\mathfrak A)}(\Phi_n)\subset{\mathrm{Spec}}_{\ell^{\infty,1}(\bigcup_{i=1}^n\Xi(i),\mathfrak A)}(\Phi_n). \end{align*} $$

However, $\ell ^{\infty ,1}(\bigcup _{i=1}^n\Xi (i),\mathfrak A)\cong \bigoplus _{i=1}^n \ell ^{\infty ,1}(\Xi (i),\mathfrak A)$ and since the (finite) direct sum of symmetric Banach $^*$ -algebras is symmetric, ${\mathrm {Spec}}_{\ell ^{\infty ,1}(\bigcup _{i=1}^n\Xi (i),\mathfrak A)}(\Phi _n)\subset \mathbb {R}$ and the result follows.

Example 4.10. Let $\Xi =\mathsf {G}\ltimes _\gamma X$ be a transformation groupoid (see Definition 4.1), where X is discrete. In this case, $\mathcal U=X$ and $\Xi _u^u=\{g\in G\mid \gamma _g(u)=u\}\times \{u\}$ , which can be identified with the stabiliser of u, namely ${\mathrm {Stab}}_\gamma (u)\leq \mathsf {G}$ .

Remark 4.11. We will finish this paper with a bit of wishful thinking. It is reasonable to believe that the groupoid analogue of [2, Theorem 3.3] could be true. For a general locally compact groupoid, one can define symmetry and hypersymmetry for $\Xi $ as the symmetry of the Hahn algebras $L^{\infty ,1}(\Xi )$ and $L^{\infty ,1}(\Xi \!\mid \!\mathscr C)$ , respectively. So we may pose two problems.

1. (i) Is the (hyper)symmetry of a Hausdorff locally compact groupoid $\Xi $ implied by the (hyper)symmetry of its discretisation $\Xi ^{\mathrm {dis}}$ ?

2. (ii) Is Corollary 3.6 still valid for étale groupoids?

In view of Theorem 1.2, problem (i) is equivalent to the following.

1. (i^′) Is the (hyper)symmetry of a Hausdorff locally compact groupoid $\Xi $ implied by the (hyper)symmetry of its discretised isotropy groups $(\Xi _u^u)^{\mathrm {dis}}$ ?