1. Introduction
Assessing the degree of multiple paternity in populations is important in behavioural ecology and evolution, population genetics and conservation biology (Chesser & Baker, Reference Chesser and Baker1996; Jennions & Petrie, Reference Jennions and Petrie2000; Bretman & Tregenza, Reference Bretman and Tregenza2005). Female promiscuity may lower extinction risk via its influence on effective population size (Sugg & Chesser, Reference Sugg and Chesser1994; Newman & Pilson, Reference Newman and Pilson1997; Martinez et al., Reference Martinez, Moran, Perez, de Gaudemar, Beall and Garcia-Vazquez2000), cause extreme sexual selection among males, even in species with socially monogamous mating systems (Griffith et al., Reference Griffith, Owens and Thuman2002) and lead to speciation via sexually antagonistic co-evolution (Arnqvist et al., Reference Arnqvist, Edvardsson, Friberg and Nilsson2000). Uncovering differences in the extent of polyandry, both within and among species, can help elucidate the complex relationship between ecological factors and mating system evolution (e.g. Emlen & Oring, Reference Emlen and Oring1977). Many such investigations require accurate estimates of the number of parents that produce progeny arrays (i.e. broods, clutches or litters). For example, studies of sexual selection, sperm competition and cryptic female choice require specific information about the number of males with which females mate (Birkhead & Moller, Reference Birkhead and Møller1998; Jones et al., Reference Jones, Arguello and Arnold2002a, Reference Jones, Arguello and Arnold2004).
Studying female mating behaviour has been simplified by the use of genetic data, which are frequently easier to obtain than observational data. Genetic analysis of sibling arrays often seeks to answer two main questions. First, what is the frequency of multiple mating (f mm) among females? Second, how many males fathered each clutch? The former question is easy to answer without complex analyses. For example, older studies classified broods as multiply sired if any locus yielded five or more alleles (e.g. Milkman & Zeitler, Reference Milkman and Zeitler1974; Kellogg et al., Reference Kellogg, Markert, Stauffer and Kocher1998). However, allele sharing and/or homozygosity among fathers potentially can obscure multiple paternity and cause low estimates of sire number, even when markers are highly polymorphic. To ameliorate this problem, Neff et al. (Reference Neff, Pitcher and Repka2002) developed a Bayesian model and computer program (FMM) for estimating f mm that incorporates population genetic parameters. Similarly, Kichler et al. (Reference Kichler, Holder, Davis, Marquez and Owens1999) created a likelihood-based computer program (LAMP) to estimate the frequency of multiple paternity, designed especially for instances when sample sizes are low.
Although the identification of broods or clutches of offspring that were sired by more than one male can be relatively simple and accurate when marker polymorphism and sample sizes are high, assessing the number of males that produced a sibship is analytically more challenging. This is especially true when sampling effort is limited and the distribution of paternity among competing males is highly skewed. Several different statistical approaches have been used to estimate the number of sires that produced a clutch. The easiest method, known as allele-counting (Bretman & Tregenza, Reference Bretman and Tregenza2005) or the single-locus minimum method (Myers & Zamudio, Reference Myers and Zamudio2004), results in the lowest estimates because it does not consider multilocus allele associations or population allele frequencies. Basically, the paternal alleles are tallied at each locus and the highest number is divided by two and rounded up. Emery et al. (Reference Emery, Wilson, Craig, Boyle and Noble2001) developed a more sophisticated technique that uses a Bayesian approach of modelling the probability that the data resulted from a range of sire numbers, given specified information about the population and mating system. Neff et al. (Reference Neff, Repka and Gross2000) independently developed probability models for estimating sire number, but they require knowledge of the genotypes of some putative parents. DeWoody et al. (Reference DeWoody, DeWoody, Fiumera and Avise2000a) wrote computer programs that simulate progeny arrays resulting from known parent combinations, allowing statistical evaluation of the estimates. Jones (Reference Jones2001, Reference Jones2005) developed a program (GERUD) that reconstructs parental genotypes from progeny data. This list is far from complete and the multitudes of analytical tools used to estimate sire number may continue to grow until relative performance has been evaluated thoroughly. Only then will it become more straightforward for researchers to choose the best way to analyse their parentage data.
Each of the numerous statistical approaches has unique strengths, weaknesses and limitations. Although some studies have evaluated the performance of certain techniques (e.g. DeWoody et al., Reference DeWoody, Walker and Avise2000b; Fiumera et al., Reference Fiumera, DeWoody, DeWoody, Asmussen and Avise2001; Jones, Reference Jones2005), rarely has this been done by independent researchers and very few have reported comparisons of results yielded by different statistical approaches to the same data, though this is beginning to change (Bretman & Tregenza, Reference Bretman and Tregenza2005; Jones et al., Reference Jones, Grossman, Walsh, Porter, Avise and Fiumera2007; Sefc et al., Reference Sefc, Mattersdorfer, Sturmbauer and Koblmuller2008). For example, Sefc & Koblmuller (Reference Sefc and Koblmuller2009) recently found that GERUD underestimated parent number, maximum-likelihood estimates in COLONY (Wang, Reference Wang2004) overestimated it, and Bayesian parental reconstruction in the program PARENTAGE (Emery et al., Reference Emery, Wilson, Craig, Boyle and Noble2001) did both. Using seven cricket broods, Bretman & Tregenza (Reference Bretman and Tregenza2005) compared estimates of sire number yielded by single-locus allele-counting, GERUD and PARENTAGE. For five multiply sired clutches with at least 3–7 sires, they found that estimates from allele-counting were 1–4 fathers lower than both GERUD and PARENTAGE. GERUD estimated 1–2 fewer fathers than PARENTAGE for some clutches. In a simulation study with a wide range of parent numbers, Fiumera et al. (Reference Fiumera, DeWoody, DeWoody, Asmussen and Avise2001) showed that the multilocus allele-counting method underestimated the true number of sires by 1–4 and that the estimates of their programs were more accurate. Clearly, choice of analytical technique has the potential to impact interpretation of data significantly.
Salamanders offer several advantages in studying mating system evolution. Because females completely control spermatophore transfer, the potentially confounding influence of male sexual coercion is nullified (Clutton-Brock & Parker, Reference Clutton-Brock and Parker1995). Most groups have internal fertilization and females possess spermathecae for storage of sperm from several males (Sever, Reference Sever2002). It already is known that several salamander species are polyandrous (e.g. Gabor & Halliday, Reference Gabor and Halliday1997; Gabor et al., Reference Gabor, Krenz and Jaeger2000; Garner & Schmidt, Reference Garner and Schmidt2002; Myers & Zamudio, Reference Myers and Zamudio2004; Adams et al., Reference Adams, Jones and Arnold2005; Steinfartz et al., Reference Steinfartz, Stemshorn, Kuesters and Tautz2006; Gopurenko et al., Reference Gopurenko, Williams, McCormick and DeWoody2006, Reference Gopurenko, Williams and DeWoody2007; Liebgold et al., Reference Liebgold, Cabe, Jaeger and Leberg2006; J. D. Krenz, personal communication), but some of these studies were performed in the laboratory and thus did not assess natural patterns of multiple mating. No detailed comparisons have been made among species to investigate the relationship between ecological variables and mating system parameters.
The primary purpose of this study is to compare several techniques for analysing genetic parentage data from half-sib progeny arrays, two of which have not been included in previous evaluations. We report analyses of one novel data set and reanalyses of three similar data sets from published papers. One of the papers (Jones et al., Reference Jones, Arguello and Arnold2004) reported data produced from small breeding groups in which parentage assignment allowed extreme confidence in estimates of parent number. This gave us the opportunity to test different statistical techniques against true (or extremely close to true) empirical assays. We evaluated five analytical approaches to genetic parentage data: (1) allele-counting, (2) parental reconstruction in GERUD, (3) a Bayesian probability model to estimate f mm (FMM), (4) computer simulations based on population allele frequencies (HAPLOTYPES) and (5) Bayesian parental reconstruction (PARENTAGE). We then use new data to elucidate female mating patterns in a previously unstudied salamander species. We collected marbled salamander (Ambystoma opacum) egg clutches and attendant females from a natural population and genotyped a sample of offspring from each brood with microsatellite DNA loci. We report estimates of the frequency of multiple paternity, the number of sires producing each clutch and reproductive skew among competing fathers. We observed a comparatively low multiple mating rate among marbled salamander females and tested whether this result was robust to changes in analytical technique. Finally, we discuss potential explanations for this mating system difference.
2. Materials and methods
(i) Data sets
In addition to a new data set collected from marbled salamander (A. opacum) clutches (see subsequent sections for details), we reanalysed three microsatellite data sets from published papers that investigated genetic mating systems in: (1) spotted salamanders (Ambystoma maculatum; Myers & Zamudio, Reference Myers and Zamudio2004), (2) rough-skinned newts (Taricha granulosa; Jones et al., Reference Jones, Arguello and Arnold2004) and (3) Ocoee salamanders (Desmognathus ocoee; Adams et al., Reference Adams, Jones and Arnold2005). The data from Jones et al. (Reference Jones, Arguello and Arnold2004) offer an excellent opportunity to evaluate the performance of different analytical techniques because the authors assigned paternity with extremely high confidence to each offspring in their sample, thereby allowing an accurate estimate of the true number of males that sired each brood. We took advantage of this in the evaluation process by comparing estimates garnered from different analytical techniques with the empirical assay. With all four data sets, we kept the analyses as straightforward as possible and did not use data from clutches or loci that could complicate the comparisons. For example, we did not consider several clutches that probably originated from multiple females and some loci that were incompatible with certain programs because of the presence of null alleles and/or what appeared to be mutations.
(ii) Analytical approaches
We analysed the data in five ways (Table 1). In single-locus allele-counting, maternal alleles were first excluded before tallying the number of remaining paternal alleles at each locus. Although identifying maternal alleles is problematic when offspring and mothers have identical heterozygous genotypes (Fiumera & Asmussen, Reference Fiumera and Asmussen2001), we employed the most conservative interpretation of such individuals, only counting one unique paternal allele even when identical individuals were common in an array. In this method, the number of sires is equal to half the number of paternal alleles at the most polymorphic locus, rounded up. Although this approach provides the minimum number of males that sired a brood, it does not consider the probability of allele sharing among sires, nor does it incorporate informative multilocus allele associations. Thus, the allele-counting method probably often underestimates the true extent of polyandry, especially when loci are not extraordinarily polymorphic.
Table 1. Summary of the five analysis techniques used in this study
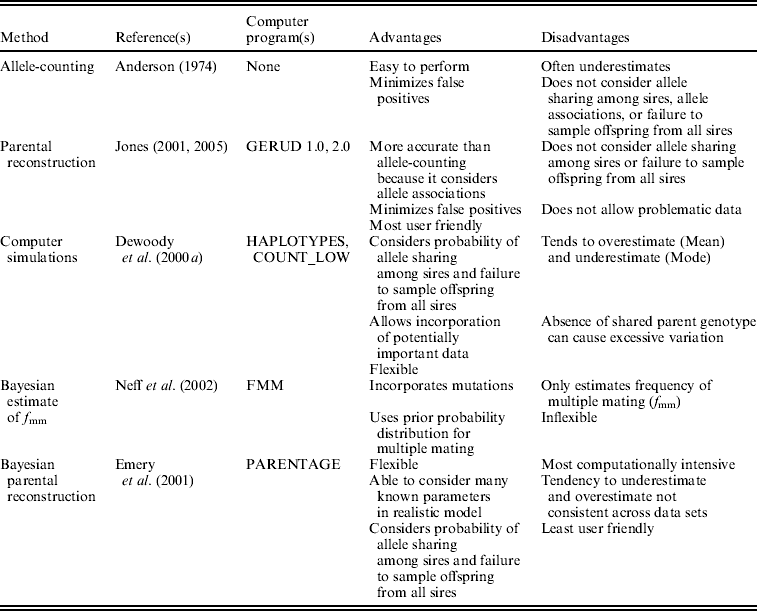
We also analysed the data with parental reconstruction in GERUD (Jones, Reference Jones2001, Reference Jones2005), which employs the multilocus genotypes of offspring in a brood to determine the genotypes of the parents. Although this technique does not incorporate the probability of allele-sharing among fathers of a clutch in its estimates of sire number, its estimates exceed those of the single-locus allele-counting method because it uses associations of alleles across loci. We also used GERUD to provide an estimate of the number of offspring sired by individual competing males for an assessment of reproductive skew within clutches. The program ranks the many potentially true combinations of parental genotypes by their probability of occurrence based on the rules of Mendelian inheritance and population allele frequencies. We averaged the parental contribution estimates of the most likely paternal combinations among all clutches within species.
We used the program FMM (Neff et al., Reference Neff, Pitcher and Repka2002) to estimate the frequency of multiple mating. This method uses a Bayesian model that incorporates the number of loci in the analysis, their allele frequencies, the maternal genotype, the number of paternal alleles in each clutch and the prior probability of multiple mating. It is limited by the need for assaying the shared parent of each brood, and it only calculates the overall f mm, not the number of individuals contributing genetically to each array, from information about the mating system and data set supplied by the user. However, it calculates confidence intervals of f mm and incorporates independent information about the probability of female polyandry. Because we had no such information available, we used a uniform prior probability distribution. The program also requires information about the number of sires contributing gametes to polyandrous broods and their relative fertilization success. Because it does not consider the potential for different numbers of sires, we analysed the data separately with all numbers of sires and observed skew estimates from GERUD (Table 2). We were forced to group alleles of similar size together for especially polymorphic loci because the program only allows 25 alleles per locus. We did not use this approach to analyse the spotted salamander data from Myers & Zamudio (Reference Myers and Zamudio2004) because it was problematic to determine the genotype of the shared parent for those clutches.
Table 2. Parameters used for simulations in HAPLOTYPES. We used exact sample sizes for all clutches, exact clutch sizes for D. ocoee, average clutch sizes for A. opacum and T. granulosa, and the estimated clutch sizes from Myers & Zamudio (Reference Myers and Zamudio2004) for A. maculatum. For population size in T. granulosa, we used the exact number of breeding adults present in tanks for rare sample sizes and the average number of adults for the most common sample size (N=24). Skew numbers are in percent, rounded to the nearest integer. Standard deviations of observed skew are in parentheses, calculated from Fig. 2 in Adams et al. (Reference Adams, Jones and Arnold2005) for D. ocoee. We modelled skew as a geometric distribution in which the most successful male sires a proportion of total offspring (α) and each subsequent male sires the same proportion of the remaining progeny
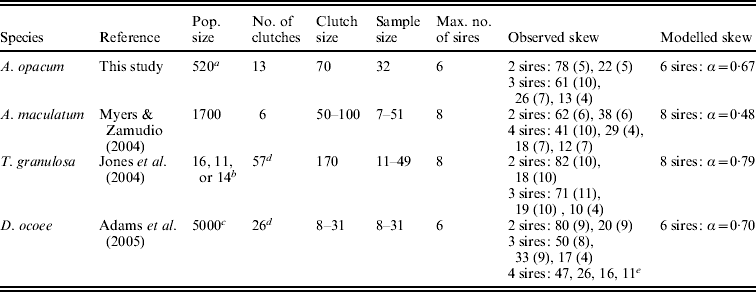
a Estimated from unpublished drift fence data.
b Exact or average size of breeding populations in experimental tanks (see table caption).
c Within the range of population size estimates of salamander species of similar size in the same region and habitat type.
d Did not analyse 1–2 clutches that were not clear in data files provided by original authors.
e Only data for one clutch reported.
We used the approach of DeWoody et al. (Reference DeWoody, DeWoody, Fiumera and Avise2000a) that incorporates computer simulations based on parameters specific to the sampling regime and population under study. Their computer program HAPLOTYPES randomly selects mating combinations from a simulated population based on these user-defined parameters, generates the resulting clutches of offspring and samples randomly from them before tallying the number of unique multilocus haplotypes in the sample. Repeated sampling generates a statistical distribution for the number of parents that is associated with the number of haplotypes detected. Researchers can then match the number of haplotypes detected in their real clutches to data from these simulated arrays. Output from the programs includes standard descriptive statistics such as mean, mode, standard deviation, range and confidence intervals of the true number of unshared parents in the simulated clutches. Because no previous study of which we are aware has evaluated the performance of mean and mode sire number from these simulations, we report and discuss both (denoted as HAPLOTYPES-Mean and HAPLOTYPES-Mode).
To determine the number of haplotypes represented in clutches, Fiumera et al. (Reference Fiumera, DeWoody, DeWoody, Asmussen and Avise2001) wrote three programs which differ in how they deal with the ambiguous situation when the shared parent and some offspring have identical heterozygous genotypes (Fiumera & Asmussen, Reference Fiumera and Asmussen2001). We used all three techniques and confirmed the results of Fiumera et al. (Reference Fiumera, DeWoody, DeWoody, Asmussen and Avise2001) that COUNT_MED and COUNT_HIGH generate extremely high estimates of sire number. Therefore, we only report results generated by COUNT_LOW, which treats problematic cases as missing data, making it possible for sire number estimates to be lower than those yielded by allele-counting.
Simulations in HAPLOTYPES require the user to define the maximum number of sires per clutch, population size and reproductive skew among competing sires. We relied on observed data and reproductive skew estimates calculated from GERUD analyses for specifying the parameters (Table 2). Choosing the maximum number of sires per clutch was somewhat arbitrary; we increased the highest sire number from GERUD analyses by a few sires for all species. Because unequal sharing of paternity among competing sires can impact estimates of sire number (Myers & Zamudio, Reference Myers and Zamudio2004), we incorporated reproductive skew in our simulations. Observed inequality estimates from the GERUD analysis (Table 2) indicated that skew roughly fit that expected from a geometric distribution defined by the following equation:
where α is the fraction sired by the first, i.e. most successful, male. For α in computer simulations, we used the weighted average among all clutches of the most successful sire's fertilization success. We report results gained from 1000 simulation runs.
Finally, we analysed the data with the Bayesian parental reconstruction program PARENTAGE written by Emery et al. (Reference Emery, Wilson, Craig, Boyle and Noble2001). The program uses observed offspring and parent genotypes (as well as several other parameters input by the user, if known) to estimate the probability distributions of parent numbers as well as their genotypes. We followed Sefc & Koblmuller (Reference Sefc and Koblmuller2009) in setting a low probability of more than one mother by using a prior distribution with a mean of 1 and standard deviation of 0·1. We modelled reproductive skew among competing fathers in the same way we did with HAPLOTYPES, as a geometric distribution with α defined as the weighted average among all clutches (Table 2). PARENTAGE uses one parameter that takes into account both the mutation and scoring error rates. We only report data yielded with this parameter set at 0·01, but we tested two other rates (0·05 and 0·002) and found the technique to be robust to this level of variance. The program is flexible and allows this parameter to be selected from a distribution with user-defined parameters, minimizing potential problems due to unknown mutation and error rates. We used 5000 iterations in the Markov Chain, burn-in of 5000 and thinning of 400 (Sefc & Koblmuller, Reference Sefc and Koblmuller2009).
(iii) Novel data collection
Marbled salamanders (A. opacum) breed in the fall when reproductive adults migrate to temporary wetlands during warm, rainy nights. Courtship is terrestrial and often occurs away from the breeding site (Krenz & Scott, Reference Krenz and Scott1994). Males deposit spermatophores on the ground as part of a stereotyped courtship ritual and females are free to choose whether they participate in courtship and accept spermatophores. After mating, females construct terrestrial nests under vegetative cover and remain with their eggs after oviposition for variable time periods. When nests are flooded during seasonal rains, hatchlings emerge from eggs and develop aquatically until metamorphosis. Because A. opacum sometimes breed on only a few nights during the fall season (D. A. Croshaw, unpublished data), they can be considered explosive breeders. To date, very few data concerning the mating system of A. opacum are available.
In November 2002, during the marbled salamander nesting season, we collected 15 egg clutches and their attendant females at Okie's Bay, a small Carolina bay on the U.S. Department of Energy's Savannah River Site in Aiken County, South Carolina. We held eggs in the laboratory for two to three weeks, while embryos developed to the point of hatching. We then submersed eggs in well water to induce hatching and collected a sample of hatchlings from each clutch for subsequent microsatellite genotyping.
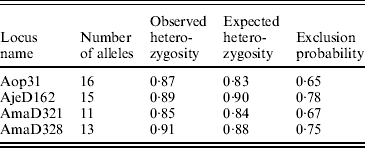
We genotyped 32 hatchlings and the attendant females from each of the 15 clutches at four microsatellite loci from Croshaw et al. (Reference Croshaw, Schable, Peters and Glenn2005). We have found no evidence of the presence of null alleles in these loci. The overall exclusion probability, with one parent known, and other basic properties of the loci were calculated with CERVUS 2.0 (Table 3; Marshall et al., Reference Marshall, Slate, Kruuk and Pemberton1998). Our PCR and genotyping protocols were described in detail in Croshaw et al. (Reference Croshaw, Schable, Peters and Glenn2005). Products from each of the four loci were run together in a single lane on an ABI 377-96 automated DNA sequencer. We scored alleles using Gensize Rox 500 ladder (Genetix) or CXR ladder (Promega) and GENESCAN 3.1.2 and GENOTYPER 2.5 software (PE Applied Biosystems).
Table 3. Basic properties of four microsatellite DNA loci for A. opacum used in this study (Croshaw et al., Reference Croshaw, Schable, Peters and Glenn2005). Data are based on a sample of 110 adults. Exclusion probabilities are with one parent known (total is 0·994)
We visually inspected each of the progeny arrays to determine their compatibility with the attendant female. In 2 of the 15 clutches, not all hatchlings were consistent with the genotype of the attendant female, indicating that they were most likely communal nests with offspring from one or more unsampled females. Because of the difficulty of analysing such broods, we did not consider these clutches further. For the other 13 clutches that were entirely full or half-siblings, we tallied the frequency of each paternal allele. To minimize the impact of potential scoring errors on our interpretation of the data, individuals that contained rare paternal alleles were assayed again for confirmation.
3. Results
Results from GERUD only, not any of the other analytical approaches, agreed exactly with paternity assignment of all sampled hatchlings with strict exclusion in the T. granulosa data set. In all species, the allele-counting method, FMM, and GERUD were similarly low in their estimates of the frequency of multiple paternity (Fig. 1) and the number of sires (Figs 2 and 3). Mode sire number from simulations (HAPLOTYPES-Mode) was the lowest estimate of all whereas mean sire number (HAPLOTYPES-Mean) yielded much higher estimates, substantially greater than the others for all species except A. maculatum. PARENTAGE estimates were generally lower than GERUD except for A. maculatum which was the least informative data set and the only one to use more than four loci. For that species, PARENTAGE exceeded all other techniques. We used analysis of variance (ANOVA) contrasts in SAS (SAS Institute, 2003) to test for within-species differences in estimated sire number among the five analysis techniques (Fig. 3). Overall, within-clutch effects were significant for three of four species (A. opacum: F=3·3, DF=4, 9, P=0·06; A. maculatum: F=19·3, DF=4, 2, P=0·05; D. ocoee: F=18·3, DF=4, 22, P<0·0001; T. granulosa: F=36·5, DF=4, 52, P<0·0001), indicating that the techniques included in the analysis yielded significantly different estimates of sire number.

Fig. 1. Frequencies of multiple mating for four salamander species estimated with six different analytical techniques: (1) allele-counting, (2) Bayesian probability model to estimate frequency of multiple mating (FMM), (3) parental reconstruction (GERUD), (4) computer simulations with mode (HAPS-Mode), (5) computer simulations with mean (HAPS-Mean) and (6) Bayesian parental reconstruction (PARENTAGE). Because there was no information about maternal genotype, we did not analyse the A. maculatum clutches with FMM. Neither HAPLOTYPES nor PARENTAGE relies solely on inference of paternal alleles, and it is possible for their estimates to be lower than those of allele-counting.
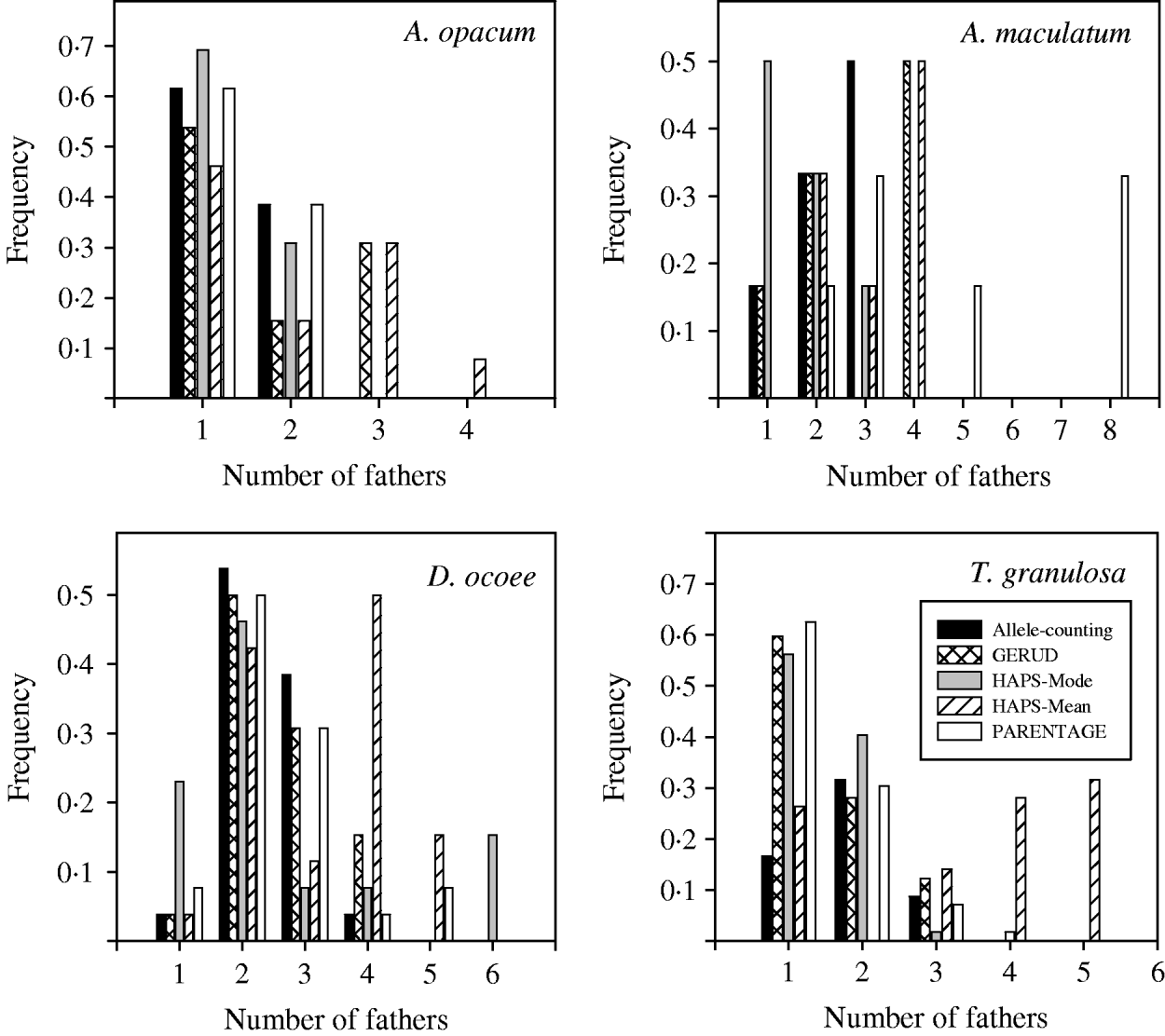
Fig. 2. Frequency histogram of sire number for four salamander species estimated with five different analytical techniques: (1) allele-counting, (2) parental reconstruction (GERUD), (3) computer simulations with mode (HAPS-Mode), (4) computer simulations with mean (HAPS-Mean) and (5) Bayesian parental reconstruction (PARENTAGE).
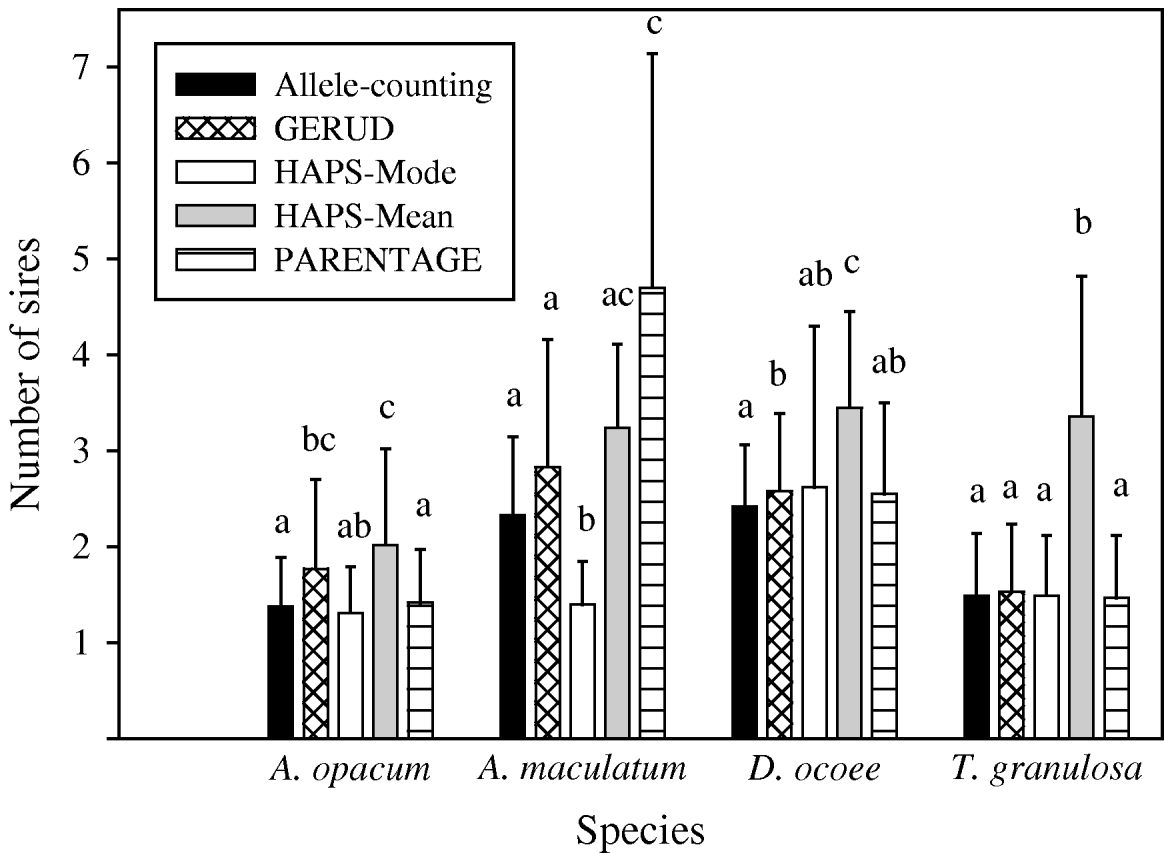
Fig. 3. Mean (+SD) number of sires per clutch for four species of salamander estimated by five analysis techniques: (1) allele-counting, (2) parental reconstruction (GERUD), (3) computer simulations with mode (HAPS-Mode), (4) computer simulations with mean (HAPS-Mean) and (5) Bayesian parental reconstruction (PARENTAGE). Letters above each bar indicate which estimates are significantly different from one another at the 0·05 level in within-species analyses. GERUD estimates for T. granulosa are identical to estimates garnered by highly reliable paternity exclusion of all but one male among a small group of candidate sires.
Frequency of multiple paternity was low in A. opacum clutches relative to the other species according to all analytical approaches (31–54%, Fig. 1). This general result was robust to changes in analysis technique, but details of the extent of differences and the significance level were affected (Table 4). Estimates from the reanalysed T. granulosa data set (36–74%) were similar to those for A. opacum, but the data were collected from experimental breeding tanks in which adults had limited mating opportunities. Thus, in analyses testing for interspecific differences in mating system, we used data inferred from Fig. 1 in Jones et al. (Reference Jones, Arguello and Arnold2002a) showing the number of mates for male and female T. granulosa in a natural habitat. We analysed sire number estimates and frequency of multiple paternity yielded by all techniques with ANOVA contrasts and simple logistic regressions, respectively, in SAS. Each of the logistic regression and ANOVA analyses were significant, but interspecific contrasts and odds ratios from the logistic regressions were variable (Table 4). HAPLOTYPES-Mode did not agree with the other techniques. The odds of a clutch having multiple paternity were much lower for A. opacum than for all other species (2·3–5·9 times greater for A. maculatum, 7·5–29·4 for D. ocoee and 2·1–5·6 for T. granulosa in natural habitat). D. ocoee always had significantly higher levels of multiple paternity than A. opacum, but only three of four techniques were significant for A. maculatum and one of four for T. granulosa. Thus, although the sample sizes for A. opacum and A. maculatum were very small, there is considerable evidence that A. opacum females mated with fewer males than in A. maculatum and D. ocoee. Evidence for a difference between A. opacum and T. granulosa is much more limited, however.
Table 4. Summary of analyses to test for interspecific differences in multiple paternity. Species columns are mean numbers of sires per clutch (standard deviation). Odds ratios (Odds) and contrasts are relative to A. opacum. The computer program FMM yielded only an estimate for the frequency of multiple mating (fmm), not the number of sires, making calculation of means and ANOVA analyses impossible. The strict exclusion in natural habitat method from Jones et al. (Reference Jones, Arguello and Arnold2002a) was used for T. granulosa in all analyses. For HAPLOTYPES-Mean and PARENTAGE, all A. maculatum clutches were determined to have multiple paternity, making calculation of a meaningful odds ratio impossible. We did not estimate fmm for A. maculatum. Tests that are significant at the 0·05 level are in bold. Species abbreviations: Aop, A. opacum; Ama, A. maculatum; Doc, D. ocoee; Tgr, T. granulosa

Relative fertilization success among competing males was significantly different from unity in doubly sired clutches of A. opacum (Chi-square goodness of fit tests: P<0·0001), A. maculatum (P=0·02) and T. granulosa (P<0·0001; Fig. 4, Table 2). Clutches sired by three males also showed significant skew in A. opacum (P<0·0001) and T. granulosa (P<0·0001), and those sired by four males were skewed in A. maculatum (P=0·0002). Patterns of fertilization success among competing males within three- and four-sire clutches of A. opacum and A. maculatum (Fig. 4) conformed to a geometric distribution in which the most successful male sires a certain proportion of the brood and each subsequent male sires the same proportion of the remaining progeny (P=0·36 and 0·84, respectively). Similar analyses in T. granulosa (P=0·21) and D. ocoee (Adams et al., Reference Adams, Jones and Arnold2005) were also consistent with this model (Table 2). However, there was considerable intra- and interspecific variation in the value of α.
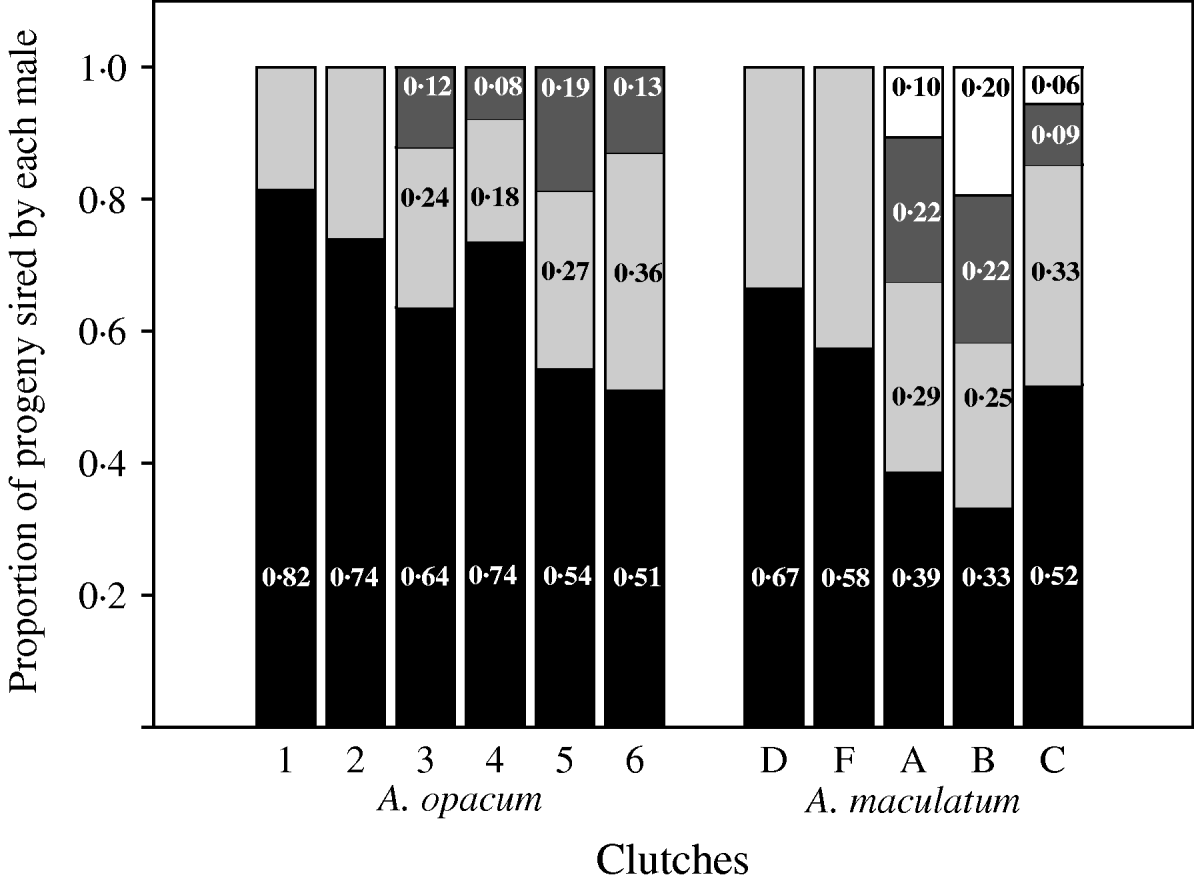
Fig. 4. Observed paternity distributions for six A. opacum clutches and five A. maculatum clutches with multiple fathers. Estimates were obtained with either GERUD 1.0 (A. opacum) or GERUD 2.0 (A. maculatum), which report potential parental genotypes and the number of progeny compatible with each sire. These observations are consistent with a geometric distribution of fertilizations among competing sires.
4. Discussion
(i) Analytical approaches to parentage data
This study shows that choice of statistical technique to estimate sire number can have substantial impacts on the interpretation of genetic parentage data. We analysed four similar data sets with allele-counting, GERUD, HAPLOTYPES, PARENTAGE and FMM (Table 1). Except for PARENTAGE, these techniques were consistently high or low relative to one another in their estimates. Estimated sire numbers yielded by these analytical methods were significantly different (sometimes exceeding 100% discrepancies). Had the original researchers used another analytical technique, they may have reported substantially different estimates of sire number. In tests for interspecific differences in levels of multiple paternity, our broad conclusion that A. opacum females mated with significantly fewer males than those of other species was robust to changes in analytical approach. However, the magnitude of differences among species was not consistent, showing further evidence for important discrepancies among these techniques. Our analyses underscore these differences and the need for further evaluation of techniques for estimating sire number.
Because we cannot know the true number of males that fathered these clutches, it is impossible to make a definitive ranking of the analytical approaches by accuracy. Analysis of the T. granulosa data, however, suggests that GERUD is the best choice because it agreed exactly with paternity assignment via strict exclusion. Although we cannot rule out the possibility that offspring from some males went unsampled, such an outcome is unlikely to equalize GERUD with HAPLOTYPES-Mean, which was very high in all estimates. Additionally, with the A. maculatum data set, HAPLOTYPES-Mode and PARENTAGE yielded estimates that were substantially lower or higher than GERUD, respectively. This was true despite the fact that PARENTAGE estimates were low in analysis of the other three data sets. GERUD was the only program that was consistent in its estimates relative to the allele-counting method. Therefore, of the techniques we used, we recommend GERUD because of its consistency across all data sets and accuracy with the T. granulosa data. A further important consideration is that GERUD is by far the most user-friendly of these programs, which maximizes the chances of performing analyses correctly.
Perhaps the most compelling situation in which to choose HAPLOTYPES or PARENTAGE over GERUD is when the data set is not highly informative because HAPLOTYPES and PARENTAGE account for the possibility of allele-sharing among fathers. However, our analyses suggest that these programs did not perform especially well with the least informative data set (A. maculatum, average exclusion probability with one parent known=0·974 compared with 0·990–0·998 for the other species). Another reason to choose PARENTAGE might be because Sefc & Koblmuller (Reference Sefc and Koblmuller2009) found that PARENTAGE was more accurate overall than their minimum method which is similar to the algorithm used in GERUD. However, when loci were highly variable, they found PARENTAGE to be less accurate than the minimum. Most genetic parentage data sets like the ones considered here contain a small number of highly variable loci. We know from the Sefc & Koblmuller (Reference Sefc and Koblmuller2009) study and our analyses that PARENTAGE tends to underestimate when marker number is low. Thus, for the most common situations, GERUD is likely to be a superior choice over PARENTAGE or HAPLOTYPES.
GERUD is not without its weaknesses, however. It cannot accommodate mutations, scoring errors, null alleles or missing data. Among the programs considered here, only PARENTAGE has good solutions to these problems. GERUD also is extremely computationally intensive with more than four or five loci (as is PARENTAGE; Sefc & Koblmuller, Reference Sefc and Koblmuller2009). Finally, GERUD will not include any data that cannot be reconciled with the presence of one shared parent, which is a primary reason why its estimates are low. Thus, PARENTAGE may be the best choice when researchers are unwilling to exclude loci with null alleles or individuals with missing data and/or do not wish to correct problems in their data manually.
As for the computer simulation programs, our analyses confirmed the conclusions of Fiumera et al. (Reference Fiumera, DeWoody, DeWoody, Asmussen and Avise2001) that HAPLOTYPES and GAMETES performed similarly (data from GAMETES not shown), and we agree that HAPLOTYPES should be used preferentially in nearly all situations. In a single phrase, Fiumera et al. (Reference Fiumera, DeWoody, DeWoody, Asmussen and Avise2001) seemed to advocate the use of mode rather than mean from the program output, but we are unaware of any previous report that explicitly discussed the performance of these measures. Several subsequent papers have reported the mean (Mackiewicz et al., Reference Mackiewicz, Fletcher, Wilkins, DeWoody and Avise2002, Reference Mackiewicz, Porter, Dakin and Avise2005; Walker et al., Reference Walker, Porter and Avise2002; Myers & Zamudio, Reference Myers and Zamudio2004), hence a comparison of mode and mean from HAPLOTYPES is warranted. Mode was very similar to GERUD and strict exclusion estimates with T. granulosa but often was lower in the other data sets. However, mean consistently yielded very high estimates, statistically greater than mode, and it probably should not be used when accurate estimates are desired. Although mode may generally perform similarly to GERUD, our analyses suggest that it is likely to underestimate, especially when the data set is less informative as in A. maculatum. An important result is that HAPLOTYPES-Mode did not agree with the other analysis techniques in its assessment of relative differences among species, suggesting that it is less robust to varying types of data sets. Thus, although mode is likely more accurate, mean sire number may be more precise and thus preferable when the primary purpose is to make relative comparisons among groups or species.
Although it is still unclear whether PARENTAGE or HAPLOTYPES is preferable, our analyses suggest that PARENTAGE is generally the better choice. It is probably more accurate than HAPLOTYPES-Mean and appears more robust to variance in marker number and polymorphism than HAPLOTYPES-Mode. HAPLOTYPES is less computationally intensive, but PARENTAGE exceeds it in flexibility. Additional evaluations of these two programs are needed.
FMM is limited because it does not estimate the number of sires that contributed to clutches, can only simultaneously consider one number of males for multiply sired clutches, cannot accommodate especially polymorphic loci, and does not easily incorporate missing data. Although estimates of FMM were similar to those of GERUD, we do not recommend it for most applications because GERUD can usually accomplish the same goals and is easier to use. The main advantage of FMM relative to GERUD is that it can incorporate the prior probability of multiple mating. However, PARENTAGE can also do this and is much more powerful and versatile. Thus, GERUD or PARENTAGE will nearly always be the better choice than FMM.
Our results generally agree with those from other studies that evaluated some of these analytical approaches. For example, Sefc & Koblmuller (Reference Sefc and Koblmuller2009) concluded from simulated data that PARENTAGE tends to underestimate when few loci are used but overestimate when marker number is greater. In this paper, the A. maculatum data set contained substantially more loci (mean of 6·7 per clutch) than in the other three data sets (mean of 3·1), and PARENTAGE estimates were extremely high. For the other three species that had few loci, PARENTAGE estimates were lower than GERUD. Like us, Bretman & Tregenza (Reference Bretman and Tregenza2005) also found that sire numbers from PARENTAGE were higher than GERUD when using six loci. Similarly, PARENTAGE estimates by Jones et al. (Reference Jones, Grossman, Walsh, Porter, Avise and Fiumera2007) with five loci resembled those from parental reconstruction but were slightly elevated. Our results are consistent with these findings, reinforcing the conclusion of Sefc & Koblmuller (Reference Sefc and Koblmuller2009) that PARENTAGE is affected considerably by marker number.
Our tests for interspecific differences in levels of multiple paternity provide a case study to assess the broader impacts of variant analytical approaches on biological conclusions. The general result that A. opacum females mate with significantly fewer males than other salamander species was robust to differences in analytical technique. However, details were affected meaningfully, making the more specific conclusions technique-dependent. HAPLOTYPES-Mode, likely in part because of its very low estimates for A. opacum and A. maculatum, did not agree with the other approaches. Thus, HAPLOTYPES-Mode may be the least likely of these methods to remain robust to substantial discrepancies among data sets in comparative analyses. However, the magnitude of interspecific differences also was affected when other techniques were used, as shown by as much as a 90% discrepancy in odds ratio.
This example underscores the importance of carefully considering properties and performance of analytical techniques for estimating sire number. Researchers should be aware that number and variability of loci are very important for accuracy of estimates (Sefc & Koblmuller, Reference Sefc and Koblmuller2009). Furthermore, effects of genetic marker properties are not necessarily consistent across different analytical techniques. Finally, we certainly agree with Sefc & Koblmuller (Reference Sefc and Koblmuller2009) that using multiple approaches should enhance the robustness of biological conclusions in most cases.
(ii) Comparing salamander mating systems
Our study is the first to investigate the extent and frequency of multiple mating by female A. opacum, although J. D. Krenz (personal communication) observed multiple paternity using allozyme markers. Because A. opacum likely do not have long-term sperm storage (Sever et al., Reference Sever, Krenz, Johnson and Rania1995), these results and those from semi-natural breeding groups (Croshaw, Reference Croshawin press) probably demonstrate polyandrous mating by females during a single breeding season. Although sample sizes for both Ambystoma species considered here are small, most analysis methods suggest that A. opacum females mated with significantly fewer males than A. maculatum and D. ocoee in natural mating situations, though similar evidence for T. granulosa was much more limited. A. opacum clutches were very rarely, if at all, sired by more than three males, unlike the other species that have been studied. Although our sampling regime may have been unable to detect paternity by more than four sires in a clutch, the same is true for that of A. maculatum and T. granulosa (Myers & Zamudio, Reference Myers and Zamudio2004; computer simulations in BROOD, DeWoody et al., Reference DeWoody, DeWoody, Fiumera and Avise2000a), and extremely few analyses estimated as many as four sires for A. opacum. Only the complete clutch sampling of D. ocoee by Adams et al. (Reference Adams, Jones and Arnold2005) was definitely sufficient to detect more than four sires. Thus, although differences in the extent of polyandry between A. opacum and D. ocoee could reflect discrepancies in ability to detect large numbers of sires, the same explanation cannot account for potential differences between A. opacum and the other two species.
Relating ecological factors to differences in mating systems among closely related species may be the most fruitful use of descriptive mating data. A. opacum and D. ocoee mate and oviposit in terrestrial habitats, whereas the other two species use aquatic breeding sites. A. opacum is an explosive breeder, whereas D. ocoee breeds over several months during summer. A. opacum females may not encounter many males during their receptive periods, especially if they occur while animals are in terrestrial woodland habitat surrounding the natal pond. Density of breeding aggregations could affect encounter rate and frequency of multiple paternity. Our breeding population at Okie's Bay was very sparsely populated, probably not more than 0·05 breeding adults per square metre of wetland. The other species were probably much more dense (as much as 25 animals per square metre for D. ocoee, Huheey & Brandon, Reference Huheey and Brandon1973; 0·79 breeders per square metre for T. granulosa, A. G. Jones, personal communication; and 1·83 breeders per square metre for A. maculatum, N. Ostman, personal communication). Of course, because only one population has been studied in each of these salamanders and sample sizes are small for two species, the available data are not sufficient to allow definitive conclusions about interspecific differences in mating system and their relationship to mating ecology. We hope that our data will stimulate further work assessing multiple paternity in many populations of these and other species of salamander for a thorough study of comparative mating ecology.
(iii) Reproductive skew in salamander clutches
This study is the first to report estimates of relative fertilization success among competing sires within A. opacum and A. maculatum clutches. Data from all species considered here (A. opacum, A. maculatum, T. granulosa and D. ocoee) fit a model of skew denoted by a geometric distribution (this study; Adams et al., Reference Adams, Jones and Arnold2005). However, a similar skew pattern probably does not reflect common means of storing sperm from different males within the female spermathecae. There are differences among salamander species in patterns of sperm precedence, and mating order is probably important in determining fertilization success of competing males. Evidence for first-male advantage exists for both T. granulosa and A. maculatum (Jones et al., Reference Jones, Adams and Arnold2002b; Tennessen & Zamudio, Reference Tennessen and Zamudio2003). However, D. ocoee and Notophthalmus viridescens have been reported to have mixed paternity with respect to mating order and members of the genus Triturus, closely related to Taricha, may have last-male precedence (Houck et al., Reference Houck, Tilley and Arnold1985; Gabor et al., Reference Gabor, Krenz and Jaeger2000; Sever, Reference Sever2002). Sever (Reference Sever2002) suggested that simple spermathecae, as presumably occurs in Taricha and Ambystoma, should favour last-male paternity. Desmognathus have complex spermathecae, facilitating interactions among ejaculates from different males and potentially confounding order effects. No explanations exist to account for the considerable variation in α that occurs both within and among species.
5. Conclusions
Our study highlights the differences among statistical techniques for analysing genetic parentage data from half-sib progeny arrays. Each technique has a unique set of strengths and weaknesses. HAPLOTYPES tends to yield very high or slightly low estimates depending on whether the mean or mode sire number is reported from the output. PARENTAGE probably both underestimates and overestimates in different situations, depending on the type of data set. Although these programs also are both difficult to implement, they do have the advantage of explicitly modelling the probability of allele-sharing among males and failure to assay at least one progeny of all unshared parents. For most purposes, however, we recommend GERUD because it was consistent relative to allele-counting across data sets, is by far the most user-friendly, and agreed completely with estimates of sire number based on strict exclusion of unrelated males in a controlled setting (the only data set for which accuracy could be assessed). Our reanalysis of three published data sets shows that interpretations can be affected by choice of analytical method. For consistency, future research intended to compare among mating systems and across studies should choose the same statistical technique or acquire the original raw data for new analyses. Although sample sizes were small for two of the four species in the analysis, A. opacum clutches had low levels of multiple paternity relative to at least two of the other three species, a possibility that invites further investigation of comparative mating ecology in salamanders.
E. Adams, A. Jones and E. Myers each kindly provided data sets for reanalysis. We also thank Y. DeWoody, A. DeWoody and E. Myers for help with HAPLOTYPES. W. Gibbons, J. Howard, S. Johnson, T. Mackay, J. Pechmann, P. Phillips and the reviewers provided valuable comments on an earlier draft. DAC was supported by a Board of Regents Superior Graduate Fellowship from the University of New Orleans. MBP was supported by the National Science Foundation Grant No. DBI-0139572. Other financial assistance was provided by award DE-FC09-96SR18546 from the U.S. Department of Energy to the University of Georgia Research Foundation.










