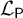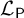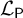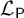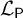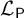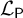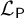1 Introduction
A body of recent work on the semantic paradoxes has focused on the patterns of sentential reference that do, or do not, generate paradoxes. One powerful tool for studying these inferential patterns is a graph-theoretic approach pioneered in [Reference Cook2] (hereafter referred to as the “Language of Paradox” or
![]() $\mathcal {L}_{\mathsf {P}}$
), which allows us to prove a number of interesting and important theorems regarding what sorts of patterns of reference give rise to paradoxes and other problematic semantic phenomena.Footnote
1
Three of the most powerful such results are:
$\mathcal {L}_{\mathsf {P}}$
), which allows us to prove a number of interesting and important theorems regarding what sorts of patterns of reference give rise to paradoxes and other problematic semantic phenomena.Footnote
1
Three of the most powerful such results are:
-
1. A transitivity theorem: This result shows that any pattern of sentential reference whose dependency graph within
 $\mathcal {L}_{\mathsf {P}}$
is transitive is paradoxical.
$\mathcal {L}_{\mathsf {P}}$
is transitive is paradoxical. -
2. The unwinding theorem [Reference Cook2]: This result allows us to transform any finite, circular pattern of sentential reference into a corresponding infinite, non-looping pattern with the exact same status vis-a-vis paradoxicality, determinacy, or indeterminacy.
-
3. The Duality Theorem [Reference Cook2]: This theorem states that the result of replacing conjunctions within an
 $\mathcal {L}_{\mathsf {P}}$
construction with disjunctions (obtaining a “dual”
$\mathcal {L}_{\mathsf {P}}$
construction with disjunctions (obtaining a “dual”
 $\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
construction) has exactly the same status vis-a-vis paradoxicality, determinacy, or indeterminacy as the original (and vice versa).
$\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
construction) has exactly the same status vis-a-vis paradoxicality, determinacy, or indeterminacy as the original (and vice versa).
While these results have provided deep insights into the structures that underlie semantic paradox and similar phenomena, they are limited. There remain a great many paradoxical constructions—including paradoxical infinitary constructions—that are neither transitive, nor unwindings of simpler finite structures within
![]() $\mathcal {L}_{\mathsf {P}}$
, nor duals of such finite structures or their unwindings, and hence resist explanation via these results. One such paradox is the
$\mathcal {L}_{\mathsf {P}}$
, nor duals of such finite structures or their unwindings, and hence resist explanation via these results. One such paradox is the
![]() $\mathcal {L}_{\mathsf {P}}$
version of the McGee paradox (and, more convenient for our purposes, the dual of this paradox).
$\mathcal {L}_{\mathsf {P}}$
version of the McGee paradox (and, more convenient for our purposes, the dual of this paradox).
Thus, one task that will be undertaken within this paper is providing an analysis of (the dual of) the McGee paradox, thus filling this lacuna. In order to carry out this task, however, we will need to introduce a new and powerful tool within the
![]() $\mathcal {L}_{\mathsf {P}}$
framework: strong
$\mathcal {L}_{\mathsf {P}}$
framework: strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphisms. The applications of strong
$\mathcal {L}_{\mathsf {P}}$
-homomorphisms. The applications of strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphisms are not limited to the study of this single paradox, however, and thus we will take the time to explore various ways that strong
$\mathcal {L}_{\mathsf {P}}$
-homomorphisms are not limited to the study of this single paradox, however, and thus we will take the time to explore various ways that strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphisms can be used to broaden our understanding of the patterns of sentential reference that generate paradoxes and other puzzles. In particular, we will see that we can give a very simple proof of a powerful theorem regarding
$\mathcal {L}_{\mathsf {P}}$
-homomorphisms can be used to broaden our understanding of the patterns of sentential reference that generate paradoxes and other puzzles. In particular, we will see that we can give a very simple proof of a powerful theorem regarding
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphisms by re-formulating parts of the
$\mathcal {L}_{\mathsf {P}}$
-homomorphisms by re-formulating parts of the
![]() $\mathcal {L}_{\mathsf { P}}$
framework within category theory, and this leads to the final task undertaken in the paper: to identify novel and potentially fruitful connections between existing methods for studying paradox such as
$\mathcal {L}_{\mathsf { P}}$
framework within category theory, and this leads to the final task undertaken in the paper: to identify novel and potentially fruitful connections between existing methods for studying paradox such as
![]() $\mathcal {L}_{\mathsf {P}}$
and the powerful methods and tools of contemporary category theory.
$\mathcal {L}_{\mathsf {P}}$
and the powerful methods and tools of contemporary category theory.
The essay will proceed as follows. In Section 2 we review the basics of the
![]() $\mathcal {L}_{\mathsf {P}}$
approach; we introduce strong
$\mathcal {L}_{\mathsf {P}}$
approach; we introduce strong
![]() $\mathcal {L}_{\mathsf { P}}$
-homomorphisms; and we state, but not prove, the main result of this paper—the strong
$\mathcal {L}_{\mathsf { P}}$
-homomorphisms; and we state, but not prove, the main result of this paper—the strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism theorem (hereafter the S
$\mathcal {L}_{\mathsf {P}}$
-homomorphism theorem (hereafter the S
![]() $\mathcal {L}_{\mathsf {P}}$
H theorem)—a result that entails that strong
$\mathcal {L}_{\mathsf {P}}$
H theorem)—a result that entails that strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphisms preserve paradoxicality. Then, in Section 3, we recast the central notions involved in the
$\mathcal {L}_{\mathsf {P}}$
-homomorphisms preserve paradoxicality. Then, in Section 3, we recast the central notions involved in the
![]() $\mathcal {L}_{\mathsf {P}}$
framework—including the notion of a strong
$\mathcal {L}_{\mathsf {P}}$
framework—including the notion of a strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism—in category-theoretic terms, and provide an extremely simple category theoretic proof of our main theorem. In this section we will also show how a number of extant results are now merely applications of the S
$\mathcal {L}_{\mathsf {P}}$
-homomorphism—in category-theoretic terms, and provide an extremely simple category theoretic proof of our main theorem. In this section we will also show how a number of extant results are now merely applications of the S
![]() $\mathcal {L}_{\mathsf {P}}$
H theorem. In Section 4 we will show how to represent (the dual of) the McGee paradox within
$\mathcal {L}_{\mathsf {P}}$
H theorem. In Section 4 we will show how to represent (the dual of) the McGee paradox within
![]() $\mathcal {L}_{\mathsf {P}}$
, and show that, although (the dual of) the McGee paradox is not transitive, it does exhibit another heretofore unrecognized condition that is sufficient for paradoxicality. In Section 5 we introduce a novel
$\mathcal {L}_{\mathsf {P}}$
, and show that, although (the dual of) the McGee paradox is not transitive, it does exhibit another heretofore unrecognized condition that is sufficient for paradoxicality. In Section 5 we introduce a novel
![]() $\mathcal {L}_{\mathsf {P}}$
construction—the Infinite Flower—that also exhibits this paradox-sufficient condition, but whose paradoxicality is much more obvious than that of (the dual of) the McGee construction, and we show how to apply the S
$\mathcal {L}_{\mathsf {P}}$
construction—the Infinite Flower—that also exhibits this paradox-sufficient condition, but whose paradoxicality is much more obvious than that of (the dual of) the McGee construction, and we show how to apply the S
![]() $\mathcal {L}_{\mathsf { P}}$
H theorem to give an extremely simple alternative proof of the paradoxicality of (the dual of) the McGee paradox. The Appendix extends the examination of the connections between
$\mathcal {L}_{\mathsf { P}}$
H theorem to give an extremely simple alternative proof of the paradoxicality of (the dual of) the McGee paradox. The Appendix extends the examination of the connections between
![]() $\mathcal {L}_{\mathsf {P}}$
and category theory via providing an alternative category-theoretic proof of the duality theorem.
$\mathcal {L}_{\mathsf {P}}$
and category theory via providing an alternative category-theoretic proof of the duality theorem.
2 The language of paradox
 $\mathcal {L}_{\mathsf {P}}$
$\mathcal {L}_{\mathsf {P}}$
Our first task is a brief review of a powerful framework for studying the patterns of sentential reference that generate semantic paradoxes: the language of paradox
![]() $\mathcal {L}_{\mathsf {P}}$
.
$\mathcal {L}_{\mathsf {P}}$
.
![]() $\mathcal {L}_{\mathsf {P}}$
contains conjunction
$\mathcal {L}_{\mathsf {P}}$
contains conjunction
![]() $\wedge $
, a proper class of sentence names
$\wedge $
, a proper class of sentence names
![]() $\mathsf { S}_\alpha , \alpha \in \mathsf {On}$
, and a falsity predicate
$\mathsf { S}_\alpha , \alpha \in \mathsf {On}$
, and a falsity predicate
![]() $\mathsf {F}$
.Footnote
2
We allow arbitrarily long infinitary conjunction—hence, given any non-empty class
$\mathsf {F}$
.Footnote
2
We allow arbitrarily long infinitary conjunction—hence, given any non-empty class
![]() $A \subseteq \mathsf {On}$
,
$A \subseteq \mathsf {On}$
,
is a well-formed formula. This follows the treatment in [Reference Cook2, Reference Cook3]. For present purposes, however, we will have no need for anything beyond countably infinite conjunctions. The well-formed formulas
![]() $\mathsf {WFF}_{\mathcal {L}_{\mathsf {P}}}$
are all and only the conjunctions of expressions of the form
$\mathsf {WFF}_{\mathcal {L}_{\mathsf {P}}}$
are all and only the conjunctions of expressions of the form
![]() $\mathsf {F}(\mathsf {S}_\alpha )$
, where a formula of the form
$\mathsf {F}(\mathsf {S}_\alpha )$
, where a formula of the form
![]() $\mathsf {F}(\mathsf {S}_\alpha )$
alone is a treated as a one-conjunct conjunction and hence is in
$\mathsf {F}(\mathsf {S}_\alpha )$
alone is a treated as a one-conjunct conjunction and hence is in
![]() $\mathsf {WFF}_{\mathcal {L}_{\mathsf {P}}}$
.
$\mathsf {WFF}_{\mathcal {L}_{\mathsf {P}}}$
.
A quick note on notation: Officially, only the
![]() $\mathsf {S}_\alpha $
s (
$\mathsf {S}_\alpha $
s (
![]() $\alpha \in \mathsf {On}$
) are sentence names in
$\alpha \in \mathsf {On}$
) are sentence names in
![]() $\mathcal {L}_{\mathsf {P}}$
. To improve clarity, however, we’ll sometimes use other letters in the same sans serif font for sentences letters (e.g.,
$\mathcal {L}_{\mathsf {P}}$
. To improve clarity, however, we’ll sometimes use other letters in the same sans serif font for sentences letters (e.g.,
![]() $\mathsf {L}$
for the sentence name in the Liar paradox,
$\mathsf {L}$
for the sentence name in the Liar paradox,
![]() $\mathsf {Y}_\alpha $
s for sentence names in the Yablo paradox, and
$\mathsf {Y}_\alpha $
s for sentence names in the Yablo paradox, and
![]() $\mathsf {M}_\alpha $
s and
$\mathsf {M}_\alpha $
s and
![]() $\mathsf {M}^{\mathsf { D}}_\alpha $
s for sentence names in the McGee construction and its dual), and we will also use ordered n-tuples and other convenient constructions for indexing sentence letters. These more convenient notations should be understood as merely abbreviations for official
$\mathsf {M}^{\mathsf { D}}_\alpha $
s for sentence names in the McGee construction and its dual), and we will also use ordered n-tuples and other convenient constructions for indexing sentence letters. These more convenient notations should be understood as merely abbreviations for official
![]() $\mathcal {L}_{\mathsf {P}}$
constructions.
$\mathcal {L}_{\mathsf {P}}$
constructions.
We obtain interesting (e.g., paradoxical) constructions within
![]() $\mathcal {L}_{\mathsf {P}}$
by applying a denotation function to
$\mathcal {L}_{\mathsf {P}}$
by applying a denotation function to
![]() $\mathcal {L}_{\mathsf {P}}$
. Denotation functions assign well-formed formulas to sentence names:
$\mathcal {L}_{\mathsf {P}}$
. Denotation functions assign well-formed formulas to sentence names:
Definition 2.1. A denotation function is any function
mapping each sentence name in
![]() $\mathcal {L}_{\mathsf {P}}$
to a well-formed formula of
$\mathcal {L}_{\mathsf {P}}$
to a well-formed formula of
![]() $\mathcal {L}_{\mathsf {P}}$
.
$\mathcal {L}_{\mathsf {P}}$
.
Denotation functions allow us to reconstruct familiar semantic puzzles within
![]() $\mathcal {L}_{\mathsf {P}}$
. For example, the Liar paradox is obtained via selecting any denotation function
$\mathcal {L}_{\mathsf {P}}$
. For example, the Liar paradox is obtained via selecting any denotation function
![]() $\delta _{\mathsf {L}}$
such that
$\delta _{\mathsf {L}}$
such that
Loosely put: Sentence name
![]() $\mathsf {L}$
names the sentence stating that (the sentence named by)
$\mathsf {L}$
names the sentence stating that (the sentence named by)
![]() $\mathsf {L}$
is false. We can express this more colloquially as
$\mathsf {L}$
is false. We can express this more colloquially as
Similarly, we can reconstruct the Yablo paradox by selecting a denotation function
![]() $\delta _{\mathsf {Y}}$
where, for all
$\delta _{\mathsf {Y}}$
where, for all
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
and we can express this a bit more informally as
 $$ \begin{align*} \mathsf{Y}_0: ~& \mathsf{F}(\mathsf{Y}_1) \wedge \mathsf{F}(\mathsf{Y}_2) \wedge \mathsf{F}(\mathsf{Y}_3) \wedge \cdots,\\ \mathsf{Y}_1: ~& \mathsf{F}(\mathsf{Y}_2) \wedge \mathsf{F}(\mathsf{Y}_3) \wedge \mathsf{F}(\mathsf{Y}_4) \wedge \cdots,\\ \mathsf{Y}_2: ~& \mathsf{F}(\mathsf{Y}_3) \wedge \mathsf{F}(\mathsf{Y}_4) \wedge \mathsf{F}(\mathsf{Y}_5) \wedge \cdots,\\ \text{etc.} \end{align*} $$
$$ \begin{align*} \mathsf{Y}_0: ~& \mathsf{F}(\mathsf{Y}_1) \wedge \mathsf{F}(\mathsf{Y}_2) \wedge \mathsf{F}(\mathsf{Y}_3) \wedge \cdots,\\ \mathsf{Y}_1: ~& \mathsf{F}(\mathsf{Y}_2) \wedge \mathsf{F}(\mathsf{Y}_3) \wedge \mathsf{F}(\mathsf{Y}_4) \wedge \cdots,\\ \mathsf{Y}_2: ~& \mathsf{F}(\mathsf{Y}_3) \wedge \mathsf{F}(\mathsf{Y}_4) \wedge \mathsf{F}(\mathsf{Y}_5) \wedge \cdots,\\ \text{etc.} \end{align*} $$
It will be useful to have some notation that tracks how a particular denotation function “behaves” with respect to a particular sentence or collection of sentences. Thus:
Definition 2.2. Given a denotation function
![]() $\delta $
, the dependency relation on
$\delta $
, the dependency relation on
![]() $\delta $
is:Footnote
3
$\delta $
is:Footnote
3
The dependency relation
![]() $\mathsf {Dep}_\delta $
tracks dependencies amongst the sentences in
$\mathsf {Dep}_\delta $
tracks dependencies amongst the sentences in
![]() $\mathcal {L}_{\mathsf {P}}$
induced by the denotation function
$\mathcal {L}_{\mathsf {P}}$
induced by the denotation function
![]() $\delta $
: if
$\delta $
: if
![]() $\langle \mathsf {S}_\alpha , \mathsf {S}_\beta \rangle \in \mathsf {Dep}_\delta $
, then the truth value of
$\langle \mathsf {S}_\alpha , \mathsf {S}_\beta \rangle \in \mathsf {Dep}_\delta $
, then the truth value of
![]() $\mathsf { S}_\alpha $
depends (in part) on the truth value of
$\mathsf { S}_\alpha $
depends (in part) on the truth value of
![]() $\mathsf {S}_\beta $
, since
$\mathsf {S}_\beta $
, since
![]() $\mathsf {S}_\alpha $
refers to a conjunction containing
$\mathsf {S}_\alpha $
refers to a conjunction containing
![]() $\mathsf {S}_\beta $
(according to
$\mathsf {S}_\beta $
(according to
![]() $\delta $
). We will write
$\delta $
). We will write
![]() $\mathsf {Dep}_\delta (\mathsf {S}_\alpha , \mathsf {S}_\beta )$
as shorthand for
$\mathsf {Dep}_\delta (\mathsf {S}_\alpha , \mathsf {S}_\beta )$
as shorthand for
![]() $\langle \mathsf { S}_\alpha , \mathsf {S}_\beta \rangle \in \mathsf {Dep}_\delta $
. Figure 1 depicts (an initial segment of) the dependency relation for the
$\langle \mathsf { S}_\alpha , \mathsf {S}_\beta \rangle \in \mathsf {Dep}_\delta $
. Figure 1 depicts (an initial segment of) the dependency relation for the
![]() $\mathcal {L}_{\mathsf {P}}$
version of the Yablo paradox (i.e.,
$\mathcal {L}_{\mathsf {P}}$
version of the Yablo paradox (i.e.,
![]() $\{ \mathsf {Y}_n\}_{ n \in \mathbb {N} }$
with
$\{ \mathsf {Y}_n\}_{ n \in \mathbb {N} }$
with
![]() $\delta _{\mathsf {Y}}$
).Footnote
4
$\delta _{\mathsf {Y}}$
).Footnote
4

Fig. 1 An initial segment of
![]() $\mathsf {Dep}_{\delta _{\mathsf {Y}}}$
.
$\mathsf {Dep}_{\delta _{\mathsf {Y}}}$
.
It will be convenient to restrict our attention to collections of sentence names (with a denotation function) that are closed in the following sense:
Definition 2.3. Given a denotation function
![]() $\delta $
and a class of ordinals A,
$\delta $
and a class of ordinals A,
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
is closed under
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
is closed under
![]() $\delta $
if and only if, for all
$\delta $
if and only if, for all
![]() $\alpha , \beta \in \mathsf {On}$
, if
$\alpha , \beta \in \mathsf {On}$
, if
![]() $\alpha \in A$
and
$\alpha \in A$
and
![]() $\mathsf {Dep}_\delta (\mathsf {S}_\alpha , \mathsf {S}_\beta )$
, then
$\mathsf {Dep}_\delta (\mathsf {S}_\alpha , \mathsf {S}_\beta )$
, then
![]() $\beta \in A$
.
$\beta \in A$
.
Informally: A class of sentence names (with a denotation function) is closed if, whenever it contains a sentence name
![]() $\mathsf {S}_\alpha $
, it contains all sentence names that
$\mathsf {S}_\alpha $
, it contains all sentence names that
![]() $\mathsf {S}_\alpha $
depends on. All examples discussed in the remainder of this essay are closed.
$\mathsf {S}_\alpha $
depends on. All examples discussed in the remainder of this essay are closed.
We evaluate the status of various (usually closed) collections of sentence names relative to a particular denotation function via considering assignments:
Definition 2.4. An assignment is any (total) function
![]() $\sigma $
mapping the sentence names to truth values:
$\sigma $
mapping the sentence names to truth values:
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptability of an assignment is straightforward:
$\mathcal {L}_{\mathsf {P}}$
-acceptability of an assignment is straightforward:
Definition 2.5. Given a denotation function
![]() $\delta $
, an assignment
$\delta $
, an assignment
![]() $\sigma $
, and a class of ordinals A,
$\sigma $
, and a class of ordinals A,
![]() $\sigma $
is
$\sigma $
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta $
if and only if, for any
$\delta $
if and only if, for any
![]() $\alpha \in A$
,
$\alpha \in A$
,
![]() $\sigma (\mathsf {S}_\alpha ) = \top $
if and only if, for all
$\sigma (\mathsf {S}_\alpha ) = \top $
if and only if, for all
![]() $\beta $
such that
$\beta $
such that
![]() $\mathsf {Dep}_\delta (\mathsf {S}_\alpha , \mathsf {S}_\beta )$
,
$\mathsf {Dep}_\delta (\mathsf {S}_\alpha , \mathsf {S}_\beta )$
,
![]() $\sigma (\mathsf {S}_\beta ) = \bot $
.
$\sigma (\mathsf {S}_\beta ) = \bot $
.
An assignment is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable when it assigns truth to a sentence name
$\mathcal {L}_{\mathsf {P}}$
-acceptable when it assigns truth to a sentence name
![]() $\mathsf {S}_\alpha $
if and only if it assigns falsity to every sentence name occurring in the conjunction denoted by
$\mathsf {S}_\alpha $
if and only if it assigns falsity to every sentence name occurring in the conjunction denoted by
![]() $\mathsf {S}_\alpha $
(and hence, intuitively, assigns truth to the conjunction itself).
$\mathsf {S}_\alpha $
(and hence, intuitively, assigns truth to the conjunction itself).
We can now define what it means to say that an
![]() $\mathcal {L}_{\mathsf {P}}$
construction is paradoxical, determinate, or indeterminate:
$\mathcal {L}_{\mathsf {P}}$
construction is paradoxical, determinate, or indeterminate:
Definition 2.6.
-
• A set of sentence names
 $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with denotation function
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with denotation function
 $\delta $
is paradoxical if there is no assignment
$\delta $
is paradoxical if there is no assignment
 $\sigma $
that is
$\sigma $
that is
 $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
 $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
 $\delta $
.
$\delta $
. -
• A set of sentence names
 $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with denotation function
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with denotation function
 $\delta $
is determinate if there is an assignment
$\delta $
is determinate if there is an assignment
 $\sigma $
that is
$\sigma $
that is
 $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
 $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
 $\delta $
, and every
$\delta $
, and every
 $\sigma $
that is
$\sigma $
that is
 $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
 $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
 $\delta $
agrees on the values assigned to each
$\delta $
agrees on the values assigned to each
 $\mathsf {S}_\beta \in \{\mathsf {S}_\alpha \}_{\alpha \in A}$
.
$\mathsf {S}_\beta \in \{\mathsf {S}_\alpha \}_{\alpha \in A}$
. -
• A set of sentence names
 $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with denotation function
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with denotation function
 $\delta $
is indeterminate if there exist assignments
$\delta $
is indeterminate if there exist assignments
 $\sigma _1, \sigma _2$
such that
$\sigma _1, \sigma _2$
such that
 $\sigma _1$
and
$\sigma _1$
and
 $\sigma _2$
are both
$\sigma _2$
are both
 $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
 $\{\mathsf { S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf { S}_\alpha \}_{\alpha \in A}$
with
 $\delta $
and there is an
$\delta $
and there is an
 $\mathsf {S}_\beta \in \{\mathsf {S}_\alpha \}_{\alpha \in A}$
such that
$\mathsf {S}_\beta \in \{\mathsf {S}_\alpha \}_{\alpha \in A}$
such that
 $\sigma _1(\mathsf { S}_\beta ) \not = \sigma _2(\mathsf {S}_\beta )$
.
$\sigma _1(\mathsf { S}_\beta ) \not = \sigma _2(\mathsf {S}_\beta )$
.
It is now straightforward to prove that the
![]() $\mathcal {L}_{\mathsf {P}}$
version of the Yablo paradox is paradoxical:
$\mathcal {L}_{\mathsf {P}}$
version of the Yablo paradox is paradoxical:
Theorem 2.7 [Reference Cook2].
![]() $\{{\mathsf {Y}_n }\}_{ n \in \mathbb {N}}$
with
$\{{\mathsf {Y}_n }\}_{ n \in \mathbb {N}}$
with
![]() $\delta _{\mathsf {Y}}$
is paradoxical.
$\delta _{\mathsf {Y}}$
is paradoxical.
Proof. Assume for reductio that there is an assignment function
![]() $\sigma $
that is
$\sigma $
that is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\{\mathsf {Y}_n \}_{n \in \mathbb {N}}$
with
$\{\mathsf {Y}_n \}_{n \in \mathbb {N}}$
with
![]() $\delta _{\mathsf {Y}}$
.
$\delta _{\mathsf {Y}}$
.
Let
![]() $n \in \mathbb {N}$
be arbitrary. Assume for reductio that
$n \in \mathbb {N}$
be arbitrary. Assume for reductio that
![]() $\sigma (\mathsf {Y}_n) = \top $
. Then, for all
$\sigma (\mathsf {Y}_n) = \top $
. Then, for all
![]() $\mathsf {Y}_m$
such that
$\mathsf {Y}_m$
such that
![]() $\mathsf { Dep}_{\delta _{\mathsf {Y}}}(\mathsf {Y}_n, \mathsf {Y}_m)$
,
$\mathsf { Dep}_{\delta _{\mathsf {Y}}}(\mathsf {Y}_n, \mathsf {Y}_m)$
,
![]() $\sigma (\mathsf {Y}_m) = \bot $
.
$\sigma (\mathsf {Y}_m) = \bot $
.
![]() $\mathsf {Dep}_{\delta _{\mathsf {Y}}}(\mathsf {Y}_n, \mathsf {Y}_m)$
if and only if
$\mathsf {Dep}_{\delta _{\mathsf {Y}}}(\mathsf {Y}_n, \mathsf {Y}_m)$
if and only if
![]() $n < m$
. Let
$n < m$
. Let
![]() $j> n$
. Then
$j> n$
. Then
![]() $\delta (\mathsf {Y}_j) = \bot $
. So, there is a
$\delta (\mathsf {Y}_j) = \bot $
. So, there is a
![]() $\mathsf {Y}_k$
such that
$\mathsf {Y}_k$
such that
![]() $\mathsf { Dep}_{\delta _{\mathsf {Y}}}(\mathsf {Y}_j, \mathsf {Y}_k)$
(i.e.,
$\mathsf { Dep}_{\delta _{\mathsf {Y}}}(\mathsf {Y}_j, \mathsf {Y}_k)$
(i.e.,
![]() $k> j$
) and
$k> j$
) and
![]() $\sigma (\mathsf {Y}_k) = \top $
. But then
$\sigma (\mathsf {Y}_k) = \top $
. But then
![]() $\mathsf {Dep}_{\delta _{\mathsf {Y}}}(\mathsf {Y}_n, \mathsf {Y}_k)$
. So
$\mathsf {Dep}_{\delta _{\mathsf {Y}}}(\mathsf {Y}_n, \mathsf {Y}_k)$
. So
![]() $\sigma (\mathsf {Y}_k) = \bot $
. Contradiction.
$\sigma (\mathsf {Y}_k) = \bot $
. Contradiction.
Since n was arbitrary, it follows that, for all
![]() $m \in \mathbb {N}$
,
$m \in \mathbb {N}$
,
![]() $\sigma (\mathsf {Y}_m) = \bot $
. Let
$\sigma (\mathsf {Y}_m) = \bot $
. Let
![]() $j \in \mathbb {N}$
be arbitrary. Then
$j \in \mathbb {N}$
be arbitrary. Then
![]() $\sigma (\mathsf {Y}_j) = \bot $
. Then there is a
$\sigma (\mathsf {Y}_j) = \bot $
. Then there is a
![]() $\mathsf {Y}_k$
such that
$\mathsf {Y}_k$
such that
![]() $\mathsf {Dep}_{\delta _{\mathsf {Y}}}(\mathsf {Y}_j, \mathsf {Y}_k)$
and
$\mathsf {Dep}_{\delta _{\mathsf {Y}}}(\mathsf {Y}_j, \mathsf {Y}_k)$
and
![]() $\sigma (\mathsf {Y}_k) = \top $
. Contradiction.
$\sigma (\mathsf {Y}_k) = \top $
. Contradiction.
Actually, the paradoxicality of the Yablo paradox is merely a special case of the following phenomenon:Footnote 5
Theorem 2.8 [Reference Cook3].
If
![]() $\ \mathsf {Dep_\delta }$
is transitive on
$\ \mathsf {Dep_\delta }$
is transitive on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
, then
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
, then
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
![]() $\delta $
) is paradoxical.
$\delta $
) is paradoxical.
Proof. Assume for reductio that there is an assignment function
![]() $\sigma $
that is
$\sigma $
that is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
.
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
.
Let
![]() $j \in A$
be arbitrary. Assume for reductio that
$j \in A$
be arbitrary. Assume for reductio that
![]() $\sigma (\mathsf {S}_j) = \top $
. Then, for all
$\sigma (\mathsf {S}_j) = \top $
. Then, for all
![]() $\mathsf {S}_k$
such that
$\mathsf {S}_k$
such that
![]() $\mathsf { Dep}_\delta (\mathsf {S}_j, \mathsf {S}_k)$
,
$\mathsf { Dep}_\delta (\mathsf {S}_j, \mathsf {S}_k)$
,
![]() $\sigma (\mathsf {S}_k) = \bot $
. Since
$\sigma (\mathsf {S}_k) = \bot $
. Since
![]() $\mathsf {Dep}_\delta $
is serial, there is a
$\mathsf {Dep}_\delta $
is serial, there is a
![]() $k \in A$
such that
$k \in A$
such that
![]() $\mathsf {Dep}_\delta (\mathsf {S}_j, \mathsf {S}_k)$
. So
$\mathsf {Dep}_\delta (\mathsf {S}_j, \mathsf {S}_k)$
. So
![]() $\sigma (\mathsf {S}_k) = \bot $
. Again, by seriality, there is an
$\sigma (\mathsf {S}_k) = \bot $
. Again, by seriality, there is an
![]() $m \in A$
such that
$m \in A$
such that
![]() $\mathsf { Dep}_\delta (\mathsf {S}_k, \mathsf {S}_m)$
and
$\mathsf { Dep}_\delta (\mathsf {S}_k, \mathsf {S}_m)$
and
![]() $\sigma (\mathsf {S}_m) = \top $
. By transitivity,
$\sigma (\mathsf {S}_m) = \top $
. By transitivity,
![]() $\mathsf {Dep}_\delta (\mathsf {S}_j, \mathsf {S}_m)$
. So
$\mathsf {Dep}_\delta (\mathsf {S}_j, \mathsf {S}_m)$
. So
![]() $\sigma (\mathsf {S}_m) = \bot $
. Contradiction.
$\sigma (\mathsf {S}_m) = \bot $
. Contradiction.
Since j was arbitrary, it follows that, for all
![]() $j \in A$
,
$j \in A$
,
![]() $\sigma (\mathsf {S}_j) = \bot $
. Let
$\sigma (\mathsf {S}_j) = \bot $
. Let
![]() $k \in A$
be arbitrary. Then
$k \in A$
be arbitrary. Then
![]() $\sigma (\mathsf {S}_k) = \bot $
. Then there is an
$\sigma (\mathsf {S}_k) = \bot $
. Then there is an
![]() $m \in A$
such that
$m \in A$
such that
![]() $\mathsf {Dep}_\delta (\mathsf {S}_k, \mathsf {S}_m)$
and
$\mathsf {Dep}_\delta (\mathsf {S}_k, \mathsf {S}_m)$
and
![]() $\sigma (\mathsf {S}_m) = \top $
. Contradiction.
$\sigma (\mathsf {S}_m) = \top $
. Contradiction.
Note that this result is unifying, in the sense that it identifies a property shared by many (but not all—see below!) paradoxes. For example, the
![]() $\mathcal {L}_{\mathsf {P}}$
version of the Liar paradox is also transitive. Thus,
$\mathcal {L}_{\mathsf {P}}$
version of the Liar paradox is also transitive. Thus,
![]() $\mathcal {L}_{\mathsf {P}}$
is a powerful tool for identifying general properties of paradoxes, allowing us to shift our attention away from isolated examples, and towards general types.
$\mathcal {L}_{\mathsf {P}}$
is a powerful tool for identifying general properties of paradoxes, allowing us to shift our attention away from isolated examples, and towards general types.
The connections between the Liar paradox and the Yablo paradox are actually much deeper than the mere fact that both are transitive, however, since the Yablo paradox is (isomorphic to) the “unwinding” of the Liar paradox. First, a definition:
Definition 2.9.
![]() $\ll $
is the lexicographic ordering on pairs of ordinals:
$\ll $
is the lexicographic ordering on pairs of ordinals:
 $$ \begin{align*} \langle \alpha_1, \alpha_2 \rangle \ll \langle \beta_1, \beta_2 \rangle \text{ iff } &\text{either: } & \alpha_1 < \beta_1,\\ & \ \ \ \ \ \ \text{or: } & \alpha_1 = \beta_1 \text{ and } \alpha_2 < \beta_2. \end{align*} $$
$$ \begin{align*} \langle \alpha_1, \alpha_2 \rangle \ll \langle \beta_1, \beta_2 \rangle \text{ iff } &\text{either: } & \alpha_1 < \beta_1,\\ & \ \ \ \ \ \ \text{or: } & \alpha_1 = \beta_1 \text{ and } \alpha_2 < \beta_2. \end{align*} $$
Given an
![]() $\mathcal {L}_{\mathsf {P}}$
construction, we can “unwind” it, obtaining an infinite analogue that contains no loops in its dependency relation:
$\mathcal {L}_{\mathsf {P}}$
construction, we can “unwind” it, obtaining an infinite analogue that contains no loops in its dependency relation:
Definition 2.10. The unwinding of
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta $
is
$\delta $
is
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}^{\mathsf {U}}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}^{\mathsf {U}}$
with
![]() $\delta ^{\mathsf { U}}$
where:
$\delta ^{\mathsf { U}}$
where:
and
Given an assignment
![]() $\sigma $
and a set of sentence names
$\sigma $
and a set of sentence names
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with denotation function
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with denotation function
![]() $\delta $
, the following construction provides us with a new assignment that treats each sentence name in
$\delta $
, the following construction provides us with a new assignment that treats each sentence name in
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}^{\mathsf {U}}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}^{\mathsf {U}}$
with
![]() $\delta ^{\mathsf {U}}$
analogously to the way
$\delta ^{\mathsf {U}}$
analogously to the way
![]() $\sigma $
treats its correlate in the original
$\sigma $
treats its correlate in the original
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta $
:
$\delta $
:
Definition 2.11. The
![]() $\mathbb {N}$
-image of an assignment
$\mathbb {N}$
-image of an assignment
![]() $\sigma $
is
$\sigma $
is
![]() $\sigma ^{\mathbb {N}}$
where (for any
$\sigma ^{\mathbb {N}}$
where (for any
![]() $\alpha \in \mathsf {On}, n \in \mathbb {N})$
:
$\alpha \in \mathsf {On}, n \in \mathbb {N})$
:
We now obtain the following striking result:Footnote 6
Theorem 2.12. For any
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta $
and assignment
$\delta $
and assignment
![]() $\sigma $
,
$\sigma $
,
![]() $\sigma $
is
$\sigma $
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\{\mathsf { S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf { S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta $
if and only if
$\delta $
if and only if
![]() $\sigma ^{\mathbb {N}}$
is
$\sigma ^{\mathbb {N}}$
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\{\mathsf { S}_\alpha \}_{\alpha \in A}^{\mathsf {U}}$
with
$\{\mathsf { S}_\alpha \}_{\alpha \in A}^{\mathsf {U}}$
with
![]() $\delta ^{\mathsf {U}}$
.
$\delta ^{\mathsf {U}}$
.
Proof. See [Reference Cook3, p. 143].
Further, it turns out that the assignments provided by Definition 2.11 are the only assignments (if any) that can be
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on any unwinding:
$\mathcal {L}_{\mathsf {P}}$
-acceptable on any unwinding:
Definition 2.13. An assignment
![]() $\sigma $
is recurrent on
$\sigma $
is recurrent on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}^{\mathsf {U}}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}^{\mathsf {U}}$
with
![]() $\delta ^{\mathsf {U}}$
if and only if, for any
$\delta ^{\mathsf {U}}$
if and only if, for any
![]() $\alpha \in A$
and
$\alpha \in A$
and
![]() $n, m \in \mathbb {N}$
:
$n, m \in \mathbb {N}$
:
Theorem 2.14. Any assignment
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}^{\mathsf {U}}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}^{\mathsf {U}}$
with
![]() $\delta ^{\mathsf {U}}$
is recurrent on
$\delta ^{\mathsf {U}}$
is recurrent on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}^{\mathsf {U}}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}^{\mathsf {U}}$
with
![]() $\delta ^{\mathsf {U}}$
.
$\delta ^{\mathsf {U}}$
.
Proof. See [Reference Cook3, p. 142].
Thus, the following corollary is immediate:Footnote 7
Corollary 2.15.
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta $
is paradoxical if and only if
$\delta $
is paradoxical if and only if
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}^{\mathsf {U}}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}^{\mathsf {U}}$
with
![]() $\delta ^{\mathsf {U}}$
is paradoxical.
$\delta ^{\mathsf {U}}$
is paradoxical.
This result allows us to further unify our explanation of at least some semantic paradoxes: Not only are the Liar and the Yablo paradox both instances of the transitivity-entails-paradoxicality phenomenon, but in addition, the latter is the unwinding of the former, and hence will have the same status vis-a-vis paradoxicality, determinacy, or indeterminacy. As we shall see, there are other well-known semantic paradoxes that can be easily re-formulated within
![]() $\mathcal {L}_{\mathsf {P}}$
, but which are neither transitive nor the unwindings of any simpler
$\mathcal {L}_{\mathsf {P}}$
, but which are neither transitive nor the unwindings of any simpler
![]() $\mathcal {L}_{\mathsf {P}}$
constructions.
$\mathcal {L}_{\mathsf {P}}$
constructions.
Our next result concerns
![]() $\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
—the dual of the language of paradox
$\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
—the dual of the language of paradox
![]() $\mathcal {L}_{\mathsf {P}}$
. We obtain
$\mathcal {L}_{\mathsf {P}}$
. We obtain
![]() $\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
by replacing the conjunctions in
$\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
by replacing the conjunctions in
![]() $\mathcal {L}_{\mathsf {P}}$
with disjunctions. The definitions of denotation function, dependency relation, closure, and assignments remain the same, and the only modification required is adopting the following definition of
$\mathcal {L}_{\mathsf {P}}$
with disjunctions. The definitions of denotation function, dependency relation, closure, and assignments remain the same, and the only modification required is adopting the following definition of
![]() $\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
-acceptability, which reverses the role of truth and falsity:
$\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
-acceptability, which reverses the role of truth and falsity:
Definition 2.16. Given a denotation function
![]() $\delta $
, an assignment
$\delta $
, an assignment
![]() $\sigma $
, and a class of ordinals A,
$\sigma $
, and a class of ordinals A,
![]() $\sigma $
is
$\sigma $
is
![]() $\mathcal {L}_{\mathsf {P}}^{\mathsf { D}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}^{\mathsf { D}}$
-acceptable on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta $
if and only if, for any
$\delta $
if and only if, for any
![]() $\alpha \in A$
,
$\alpha \in A$
,
![]() $\sigma (\mathsf {S}_\alpha ) = \bot $
if and only if, for all
$\sigma (\mathsf {S}_\alpha ) = \bot $
if and only if, for all
![]() $\beta $
such that
$\beta $
such that
![]() $\mathsf {Dep}_\delta (\mathsf {S}_\alpha , \mathsf {S}_\beta )$
,
$\mathsf {Dep}_\delta (\mathsf {S}_\alpha , \mathsf {S}_\beta )$
,
![]() $\sigma (\mathsf {S}_\beta ) = \top $
.
$\sigma (\mathsf {S}_\beta ) = \top $
.
Thus, an assignment is
![]() $\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
-acceptable when it assigns falsity to a sentence name
$\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
-acceptable when it assigns falsity to a sentence name
![]() $\mathsf {S}_\alpha $
if and only if it assigns truth to every sentence name occurring in the disjunction denoted by
$\mathsf {S}_\alpha $
if and only if it assigns truth to every sentence name occurring in the disjunction denoted by
![]() $\mathsf {S}_\alpha $
(and hence, intuitively, assigns falsity to the disjunction itself).
$\mathsf {S}_\alpha $
(and hence, intuitively, assigns falsity to the disjunction itself).
The following definition and theorem provide the connection between constructions in
![]() $\mathcal {L}_{\mathsf {P}}$
and constructions in
$\mathcal {L}_{\mathsf {P}}$
and constructions in
![]() $\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
.
$\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
.
Definition 2.17. Given an assignment
![]() $\sigma $
,
$\sigma $
,
![]() $\sigma ^{\mathsf {D}}$
is the assignment:
$\sigma ^{\mathsf {D}}$
is the assignment:
 $$ \begin{align*} \sigma^{\mathsf{D}}(\mathsf{S}_\alpha) & = \top, & \text{if } \sigma(\mathsf{S}_\alpha) = \bot,\\ & = \bot, & \text{if } \sigma(\mathsf{S}_\alpha) = \top. \end{align*} $$
$$ \begin{align*} \sigma^{\mathsf{D}}(\mathsf{S}_\alpha) & = \top, & \text{if } \sigma(\mathsf{S}_\alpha) = \bot,\\ & = \bot, & \text{if } \sigma(\mathsf{S}_\alpha) = \top. \end{align*} $$
Theorem 2.18. Given a denotation function
![]() $\delta $
and assignment
$\delta $
and assignment
![]() $\sigma $
,
$\sigma $
,
![]() $\sigma $
is
$\sigma $
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta $
if and only if
$\delta $
if and only if
![]() $\sigma ^{\mathsf {D}}$
is
$\sigma ^{\mathsf {D}}$
is
![]() $\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
-acceptable on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta $
.
$\delta $
.
Simply put, replacing the conjunctions in an
![]() $\mathcal {L}_{\mathsf {P}}$
construction with disjunctions (resulting in an
$\mathcal {L}_{\mathsf {P}}$
construction with disjunctions (resulting in an
![]() $\mathcal {L}_{\mathsf { P}}^{\mathsf {D}}$
construction) preserves the status of the construction with respect to the paradoxicality/determinacy/indeterminacy trichotomy (and vice versa).
$\mathcal {L}_{\mathsf { P}}^{\mathsf {D}}$
construction) preserves the status of the construction with respect to the paradoxicality/determinacy/indeterminacy trichotomy (and vice versa).
So far, we have only discussed results that are already well-known from the literature on
![]() $\mathcal {L}_{\mathsf {P}}$
. We now state a novel result, which we shall prove in the next section. First, some additional definitions:
$\mathcal {L}_{\mathsf {P}}$
. We now state a novel result, which we shall prove in the next section. First, some additional definitions:
Definition 2.19. A unary function:
is a strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism from
$\mathcal {L}_{\mathsf {P}}$
-homomorphism from
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta _1$
to
$\delta _1$
to
![]() $\{\mathsf { S}_\beta \}_{\beta \in B}$
with
$\{\mathsf { S}_\beta \}_{\beta \in B}$
with
![]() $\delta _2$
if and only if:
$\delta _2$
if and only if:
-
• Homo: For every
 $\mathsf {S}_{\alpha _1}, \mathsf {S}_{\alpha _2} \in \{\mathsf {S}_\alpha \}_{\alpha \in A}$
, if
$\mathsf {S}_{\alpha _1}, \mathsf {S}_{\alpha _2} \in \{\mathsf {S}_\alpha \}_{\alpha \in A}$
, if
 $\mathsf { Dep}_{\delta _1}(\mathsf {S}_{\alpha _1}, \mathsf {S}_{\alpha _2})$
, then
$\mathsf { Dep}_{\delta _1}(\mathsf {S}_{\alpha _1}, \mathsf {S}_{\alpha _2})$
, then
 $\mathsf {Dep}_{\delta _2}(f(\mathsf {S}_{\alpha _1}), f(\mathsf { S}_{\alpha _2}))$
.
$\mathsf {Dep}_{\delta _2}(f(\mathsf {S}_{\alpha _1}), f(\mathsf { S}_{\alpha _2}))$
. -
• Strong: For every
 $\mathsf {S}_{\alpha _1} \in \{\mathsf {S}_\alpha \}_{\alpha \in A}, \mathsf {S}_{\beta _1} \in \{\mathsf { S}_\beta \}_{\beta \in B}$
, if
$\mathsf {S}_{\alpha _1} \in \{\mathsf {S}_\alpha \}_{\alpha \in A}, \mathsf {S}_{\beta _1} \in \{\mathsf { S}_\beta \}_{\beta \in B}$
, if
 $\mathsf {Dep}_{\delta _2}(f(\mathsf {S}_{\alpha _1}), \mathsf {S}_{\beta _1})$
, then there is an
$\mathsf {Dep}_{\delta _2}(f(\mathsf {S}_{\alpha _1}), \mathsf {S}_{\beta _1})$
, then there is an
 $\mathsf { S}_{\alpha _2} \in \{\mathsf {S}_\alpha \}_{\alpha \in A}$
such that
$\mathsf { S}_{\alpha _2} \in \{\mathsf {S}_\alpha \}_{\alpha \in A}$
such that
 $\mathsf {Dep}_{\delta _1}(\mathsf {S}_{\alpha _1}, \mathsf {S}_{\alpha _2})$
and
$\mathsf {Dep}_{\delta _1}(\mathsf {S}_{\alpha _1}, \mathsf {S}_{\alpha _2})$
and
 $f(\mathsf {S}_{\alpha _2}) = \mathsf {S}_{\beta _1}$
.
$f(\mathsf {S}_{\alpha _2}) = \mathsf {S}_{\beta _1}$
.
Definition 2.20. A strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism f from
$\mathcal {L}_{\mathsf {P}}$
-homomorphism f from
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta _1$
to
$\delta _1$
to
![]() $\{\mathsf { S}_\beta \}_{\beta \in B}$
with
$\{\mathsf { S}_\beta \}_{\beta \in B}$
with
![]() $\delta _2$
is surjective if and only if:
$\delta _2$
is surjective if and only if:
-
• Surj: For every
 $\mathsf {S}_{\beta _1} \in \{\mathsf {S}_\beta \}_{\beta \in B}$
, there is an
$\mathsf {S}_{\beta _1} \in \{\mathsf {S}_\beta \}_{\beta \in B}$
, there is an
 $\mathsf {S}_{\alpha _1} \in \{\mathsf { S}_\alpha \}_{\alpha \in A}$
such that
$\mathsf {S}_{\alpha _1} \in \{\mathsf { S}_\alpha \}_{\alpha \in A}$
such that
 $f(\mathsf {S}_{\alpha _1}) = \mathsf {S}_{\beta _1}$
.
$f(\mathsf {S}_{\alpha _1}) = \mathsf {S}_{\beta _1}$
.
We will write:
if there is a strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism from
$\mathcal {L}_{\mathsf {P}}$
-homomorphism from
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta _1$
to
$\delta _1$
to
![]() $\{\mathsf {S}_\beta \}_{\beta \in B}$
with
$\{\mathsf {S}_\beta \}_{\beta \in B}$
with
![]() $\delta _2$
, and
$\delta _2$
, and
if there is a strong surjective
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism from
$\mathcal {L}_{\mathsf {P}}$
-homomorphism from
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta _1$
to
$\delta _1$
to
![]() $\{\mathsf { S}_\beta \}_{\beta \in B}$
with
$\{\mathsf { S}_\beta \}_{\beta \in B}$
with
![]() $\delta _2$
.Footnote
8
$\delta _2$
.Footnote
8
Given a strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism f from
$\mathcal {L}_{\mathsf {P}}$
-homomorphism f from
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta _1$
to
$\delta _1$
to
![]() $\{\mathsf {S}_\beta \}_{\beta \in B}$
with
$\{\mathsf {S}_\beta \}_{\beta \in B}$
with
![]() $\delta _2$
, any assignment
$\delta _2$
, any assignment
![]() $\sigma $
on
$\sigma $
on
![]() $\{\mathsf {S}_\beta \}_{\beta \in B}$
determines a corresponding assignment
$\{\mathsf {S}_\beta \}_{\beta \in B}$
determines a corresponding assignment
![]() $\sigma ^f$
on
$\sigma ^f$
on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
:
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
:
Definition 2.21. Given a strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism f from
$\mathcal {L}_{\mathsf {P}}$
-homomorphism f from
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta _1$
to
$\delta _1$
to
![]() $\{\mathsf {S}_\beta \}_{\beta \in A}$
with
$\{\mathsf {S}_\beta \}_{\beta \in A}$
with
![]() $\delta _2$
,
$\delta _2$
,
and any assignment
![]() $\sigma $
, the assignment induced by f on
$\sigma $
, the assignment induced by f on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
![]() $\sigma $
) is
$\sigma $
) is
![]() $\sigma ^f$
where:
$\sigma ^f$
where:
 $$ \begin{align*} \sigma^f(\mathsf{S}_\alpha) & = ~\sigma(f(\mathsf{S}_\alpha)), \quad \text{if } \alpha \in A,\\ & = ~\top, \qquad\qquad \text{ otherwise}. \end{align*} $$
$$ \begin{align*} \sigma^f(\mathsf{S}_\alpha) & = ~\sigma(f(\mathsf{S}_\alpha)), \quad \text{if } \alpha \in A,\\ & = ~\top, \qquad\qquad \text{ otherwise}. \end{align*} $$
We now state (but do not yet prove) what we shall call the strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism theorem (or S
$\mathcal {L}_{\mathsf {P}}$
-homomorphism theorem (or S
![]() $\mathcal {L}_{\mathsf {P}}$
H theorem):
$\mathcal {L}_{\mathsf {P}}$
H theorem):
Theorem 2.22. If
then (where f is any function witnessing the strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism), for any assignment
$\mathcal {L}_{\mathsf {P}}$
-homomorphism), for any assignment
![]() $\sigma $
, if
$\sigma $
, if
![]() $\sigma $
is
$\sigma $
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\{\mathsf {S}_\beta \}_{\beta \in B}$
with
$\{\mathsf {S}_\beta \}_{\beta \in B}$
with
![]() $\delta _2$
then
$\delta _2$
then
![]() $\sigma $
,
$\sigma $
,
![]() $\sigma ^f$
are
$\sigma ^f$
are
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta _1$
.
$\delta _1$
.
We can strengthen the conditional to a biconditional by requiring that the strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism be surjective:Footnote
9
$\mathcal {L}_{\mathsf {P}}$
-homomorphism be surjective:Footnote
9
Theorem 2.23. If
then (where f is any function witnessing the strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism), for any assignment
$\mathcal {L}_{\mathsf {P}}$
-homomorphism), for any assignment
![]() $\sigma $
,
$\sigma $
,
![]() $\sigma ^f$
is
$\sigma ^f$
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta _1$
if and only if
$\delta _1$
if and only if
![]() $\sigma $
is
$\sigma $
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\{\mathsf {S}_\beta \}_{\beta \in B}$
with
$\{\mathsf {S}_\beta \}_{\beta \in B}$
with
![]() $\delta _2$
.
$\delta _2$
.
We could prove the S
![]() $\mathcal {L}_{\mathsf {P}}$
H theorem (and its strengthening Theorem 2.23) within the framework just described.Footnote
10
Here we shall take a somewhat different path. It turns out that these theorems can be easily reformulated and proven with very basic category-theoretic tools. Doing so is the task of the next section.
$\mathcal {L}_{\mathsf {P}}$
H theorem (and its strengthening Theorem 2.23) within the framework just described.Footnote
10
Here we shall take a somewhat different path. It turns out that these theorems can be easily reformulated and proven with very basic category-theoretic tools. Doing so is the task of the next section.
3
 $\mathcal {L}_{\mathsf {P}}$
-homomorphisms and category theory
$\mathcal {L}_{\mathsf {P}}$
-homomorphisms and category theory
In this section we will reconstruct some of the machinery of the language of paradox
![]() $\mathcal {L}_{\mathsf {P}}$
within the category of sets Set, and use this reconstruction to prove the results given at the end of the previous section.
$\mathcal {L}_{\mathsf {P}}$
within the category of sets Set, and use this reconstruction to prove the results given at the end of the previous section.
Before doing so, a historical note is in order. The results given in this section, and applied in the sections that follow, are not the first time that investigations of paradoxicality and related phenomenon have mobilized category-theoretic tools. Of particular note, in this regard, is [Reference Lawvere, Mitchell, Roos, Ulmer, Brinkmann, Chase, Dedecker, Douglas, Hilton, Sigrist, Ehresmann, Gruenberg, Knus, William Lawvere and Mac Lane6], which proves a number of fixed-point theorems (including versions of Tarski’s Theorem and Cantor’s Theorem) within a category-theoretic setting. Thus, the idea that category theory has something to teach us about paradoxes is not new. The particular methods deployed below, however, are novel, and no doubt merely scratch the surface of what can be learned about semantic paradoxes via adopting a category-theoretic perspective.Footnote 11
Back to the mathematics! Understood category-theoretically, a denotation function
![]() $\delta $
is just a
$\delta $
is just a
![]() $\mathcal {P}$
-coalgebra from S to
$\mathcal {P}$
-coalgebra from S to
![]() $\mathcal {P}(S)$
(where
$\mathcal {P}(S)$
(where
![]() $\mathcal {P}$
is the (covariant) powerset functor
$\mathcal {P}$
is the (covariant) powerset functor
![]() $\mathcal {P}$
in Set) for some set S (understood as our set of sentence names).
$\mathcal {P}$
in Set) for some set S (understood as our set of sentence names).
Given this understanding of a denotation function, we can define acceptability as follows: Let
![]() $\Omega $
be the set of truth values (i.e.,
$\Omega $
be the set of truth values (i.e.,
![]() $\{\top , \bot \}$
), and
$\{\top , \bot \}$
), and
![]() $\downarrow{\kern-1pt}: \mathcal {P}(\Omega ) \rightarrow \Omega $
be the following morphism from
$\downarrow{\kern-1pt}: \mathcal {P}(\Omega ) \rightarrow \Omega $
be the following morphism from
![]() $\mathcal {P}(\Omega )$
to
$\mathcal {P}(\Omega )$
to
![]() $\Omega $
:
$\Omega $
:
 $$ \begin{align*} \downarrow\!(\{\bot\}) & =\ \downarrow\!(\varnothing) = \top,\\ \downarrow\!(\{\top\}) &= \ \downarrow\!(\{\top, \bot\} = \Omega) = \bot, \end{align*} $$
$$ \begin{align*} \downarrow\!(\{\bot\}) & =\ \downarrow\!(\varnothing) = \top,\\ \downarrow\!(\{\top\}) &= \ \downarrow\!(\{\top, \bot\} = \Omega) = \bot, \end{align*} $$
![]() $\downarrow $
is the category-theoretic analogue of the Pierce arrow expressing, in the present context (and put somewhat loosely), something like “all of the sentences are false.”Footnote
12
Then, given a denotation function
$\downarrow $
is the category-theoretic analogue of the Pierce arrow expressing, in the present context (and put somewhat loosely), something like “all of the sentences are false.”Footnote
12
Then, given a denotation function
![]() $\delta : S \rightarrow \mathcal {P}(S)$
, an assignment is just a morphism
$\delta : S \rightarrow \mathcal {P}(S)$
, an assignment is just a morphism
![]() $\sigma : S \rightarrow \Omega $
, and an assignment
$\sigma : S \rightarrow \Omega $
, and an assignment
![]() $\sigma $
is
$\sigma $
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable relative to a denotation function
$\mathcal {L}_{\mathsf {P}}$
-acceptable relative to a denotation function
![]() $\delta $
if and only if Figure 2 commutes.
$\delta $
if and only if Figure 2 commutes.

Fig. 2
![]() $\sigma $
is
$\sigma $
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\delta $
.
$\delta $
.
Next, a strong homomorphism between denotation functions
![]() $\delta _1$
and
$\delta _1$
and
![]() $\delta _2$
is, in the category-theoretic setting, just a coalgebra morphism between the
$\delta _2$
is, in the category-theoretic setting, just a coalgebra morphism between the
![]() $\mathcal {P}$
-coalgebras
$\mathcal {P}$
-coalgebras
![]() $\delta _1: S_1 \rightarrow \mathcal {P}(S_1)$
and
$\delta _1: S_1 \rightarrow \mathcal {P}(S_1)$
and
![]() $\delta _2: S_2 \rightarrow \mathcal {P}(S_2)$
.
$\delta _2: S_2 \rightarrow \mathcal {P}(S_2)$
.
![]() $f : S_1 \rightarrow S_2$
is a coalgebra morphism from
$f : S_1 \rightarrow S_2$
is a coalgebra morphism from
![]() $\delta _1$
to
$\delta _1$
to
![]() $\delta _2$
if and only if Figure 3 commutes.
$\delta _2$
if and only if Figure 3 commutes.

Fig. 3
f is a strong homomorphism from
![]() $\delta _1$
to
$\delta _1$
to
![]() $\delta _2$
.
$\delta _2$
.
Finally, the additional requirement that a strong homomorphism be surjective, needed for the strengthened version of the S
![]() $\mathcal {L}_{\mathsf { P}}$
H theorem (i.e., Theorem 2.23), becomes, in the present context, the requirement that the coalgebra morphism f is an epimorphism.
$\mathcal {L}_{\mathsf { P}}$
H theorem (i.e., Theorem 2.23), becomes, in the present context, the requirement that the coalgebra morphism f is an epimorphism.
We can now provide a very simple category-theoretic proof of the S
![]() $\mathcal {L}_{\mathsf {P}}$
H theorem:
$\mathcal {L}_{\mathsf {P}}$
H theorem:
Theorem 3.1. If
![]() $\delta _1 : S_1 \rightarrow \mathcal {P}(S_1)$
and
$\delta _1 : S_1 \rightarrow \mathcal {P}(S_1)$
and
![]() $\delta _2 : S_2 \rightarrow \mathcal {P}(S_2)$
are
$\delta _2 : S_2 \rightarrow \mathcal {P}(S_2)$
are
![]() $\mathcal {P}$
-coalgebras in Set, and
$\mathcal {P}$
-coalgebras in Set, and
![]() $f: S_1 \rightarrow S_2$
is a coalgebra morphism from
$f: S_1 \rightarrow S_2$
is a coalgebra morphism from
![]() $\delta _1$
to
$\delta _1$
to
![]() $\delta _2$
, then, for any
$\delta _2$
, then, for any
![]() $\sigma : S_2 \rightarrow \Omega $
, if
$\sigma : S_2 \rightarrow \Omega $
, if
![]() $\sigma $
is
$\sigma $
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\delta _2$
then
$\delta _2$
then
![]() $\sigma \circ f$
is
$\sigma \circ f$
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\delta _1$
.
$\delta _1$
.
Proof. Assume
![]() $f: S_1 \rightarrow S_2$
is a coalgebra morphism from
$f: S_1 \rightarrow S_2$
is a coalgebra morphism from
![]() $\delta : S_1 \rightarrow \mathcal {P}(S_1)$
to
$\delta : S_1 \rightarrow \mathcal {P}(S_1)$
to
![]() $\delta _2 : S_2 \rightarrow \mathcal {P}(S_2)$
, and hence
$\delta _2 : S_2 \rightarrow \mathcal {P}(S_2)$
, and hence

commutes. Now, assume
![]() $\sigma $
is acceptable on
$\sigma $
is acceptable on
![]() $\langle S_2, \delta _2 \rangle $
, and hence
$\langle S_2, \delta _2 \rangle $
, and hence

commutes. Then

commutes, and hence

commutes. Hence
![]() $\sigma \circ f$
is
$\sigma \circ f$
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\langle S_1, \delta _1 \rangle $
.
$\langle S_1, \delta _1 \rangle $
.
Adding in surjectivity, we obtain the following category-theoretic version of Theorem 2.23:
Theorem 3.2. If
![]() $\delta _1 : S_1 \rightarrow \mathcal {P}(S_1)$
and
$\delta _1 : S_1 \rightarrow \mathcal {P}(S_1)$
and
![]() $\delta _2 : S_2 \rightarrow \mathcal {P}(S_2)$
are
$\delta _2 : S_2 \rightarrow \mathcal {P}(S_2)$
are
![]() $\mathcal {P}$
-coalgebras in Set, and
$\mathcal {P}$
-coalgebras in Set, and
![]() $f: S_1 \rightarrow S_2$
is a coalgebra epimorphism from
$f: S_1 \rightarrow S_2$
is a coalgebra epimorphism from
![]() $\delta _1$
to
$\delta _1$
to
![]() $\delta _2$
, then, for any
$\delta _2$
, then, for any
![]() $\sigma : S_2 \rightarrow \Omega $
,
$\sigma : S_2 \rightarrow \Omega $
,
![]() $\sigma _2$
, if
$\sigma _2$
, if
![]() $\sigma \circ f$
is
$\sigma \circ f$
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\delta _1$
then
$\delta _1$
then
![]() $\sigma $
is
$\sigma $
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\delta _2$
.
$\delta _2$
.
Proof. Assume
![]() $f: S_1 \rightarrow S_2$
is a coalgebra morphism from
$f: S_1 \rightarrow S_2$
is a coalgebra morphism from
![]() $\delta : S_1 \rightarrow \mathcal {P}(S_1)$
to
$\delta : S_1 \rightarrow \mathcal {P}(S_1)$
to
![]() $\delta _2 : S_2 \rightarrow \mathcal {P}(S_2)$
, and hence
$\delta _2 : S_2 \rightarrow \mathcal {P}(S_2)$
, and hence

commutes, and assume further that f is an epimorphism, and hence, for any two
![]() $g, h : S_2 \rightarrow X$
, if
$g, h : S_2 \rightarrow X$
, if
![]() $gf = hf$
, then
$gf = hf$
, then
![]() $g = h$
. Assume
$g = h$
. Assume
![]() $\sigma \circ f$
is
$\sigma \circ f$
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\langle S_1, \delta _1 \rangle $
, and hence
$\langle S_1, \delta _1 \rangle $
, and hence

commutes. The second diagram gives us
while the first diagram provides
A simple substitution then gives us
which, since f is an epimorphism, provides
Hence,

commutes, and
![]() $\sigma $
is
$\sigma $
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\langle S_2, \delta _2 \rangle $
.
$\langle S_2, \delta _2 \rangle $
.
The following corollary is straightforward:
Corollary 3.3. If
![]() then
then
 $$ \begin{align*} &|\{\sigma : \sigma \text{ is } \mathcal{L}_{\mathsf{P}}\text{-acceptable on } \{\mathsf{S}_\alpha\}_{\alpha \in A} \text{ with } \delta_1\}| \\ \geq~& |\{\sigma : \sigma \text{ is } \mathcal{L}_{\mathsf{P}}\text{-acceptable on } \{\mathsf{S}_\beta\}_{\beta \in B} \text{ with } \delta_2\}|. \end{align*} $$
$$ \begin{align*} &|\{\sigma : \sigma \text{ is } \mathcal{L}_{\mathsf{P}}\text{-acceptable on } \{\mathsf{S}_\alpha\}_{\alpha \in A} \text{ with } \delta_1\}| \\ \geq~& |\{\sigma : \sigma \text{ is } \mathcal{L}_{\mathsf{P}}\text{-acceptable on } \{\mathsf{S}_\beta\}_{\beta \in B} \text{ with } \delta_2\}|. \end{align*} $$
Proof. Assume that
![]() , and let
, and let
be any
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism witnessing this fact. Then, if
$\mathcal {L}_{\mathsf {P}}$
-homomorphism witnessing this fact. Then, if
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\sigma _2$
are distinct assignments that are
$\sigma _2$
are distinct assignments that are
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\{\mathsf {S}_\beta \}_{\beta \in B}$
, then there is an
$\{\mathsf {S}_\beta \}_{\beta \in B}$
, then there is an
![]() $\mathsf {S}_{\beta _1} \in \{\mathsf {S}_\beta \}_{\beta \in B}$
such that
$\mathsf {S}_{\beta _1} \in \{\mathsf {S}_\beta \}_{\beta \in B}$
such that
But then, where
![]() $\mathsf {S}_{\alpha _1} \in \{\mathsf {S}_\alpha \}_{\alpha \in A}$
is such that
$\mathsf {S}_{\alpha _1} \in \{\mathsf {S}_\alpha \}_{\alpha \in A}$
is such that
![]() $f(\mathsf {S}_{\alpha _1}) = \mathsf {S}_{\beta _1}$
, we have:Footnote
13
$f(\mathsf {S}_{\alpha _1}) = \mathsf {S}_{\beta _1}$
, we have:Footnote
13
Thus, the mapping
![]() $(\xi )^f$
(induced by the strong
$(\xi )^f$
(induced by the strong
![]() $\mathcal {L}_{\mathsf {P}}$
homomorphism f) from
$\mathcal {L}_{\mathsf {P}}$
homomorphism f) from
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable assignments on
$\mathcal {L}_{\mathsf {P}}$
-acceptable assignments on
![]() $\{\mathsf {S}_\beta \}_{\beta \in B}$
with
$\{\mathsf {S}_\beta \}_{\beta \in B}$
with
![]() $\delta _2$
to
$\delta _2$
to
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable assignments on
$\mathcal {L}_{\mathsf {P}}$
-acceptable assignments on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta _1$
is one-to-one (but not necessarily onto).
$\delta _1$
is one-to-one (but not necessarily onto).
As hinted in the final line of this proof, the inequality between the cardinalities of the classes of
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable assignments cannot be strengthened to an identity, as the following simple example shows. Select a denotation function
$\mathcal {L}_{\mathsf {P}}$
-acceptable assignments cannot be strengthened to an identity, as the following simple example shows. Select a denotation function
![]() $\delta $
that provides an instance of the Liar
$\delta $
that provides an instance of the Liar
and an instance of the Open PairFootnote 14
then
![]() $f : \{\mathsf {OP}_1, \mathsf {OP}_2 \} \rightarrow \{\mathsf {L}\}$
where
$f : \{\mathsf {OP}_1, \mathsf {OP}_2 \} \rightarrow \{\mathsf {L}\}$
where
which is pictured in Figure 4, is a strong surjective
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism from
$\mathcal {L}_{\mathsf {P}}$
-homomorphism from
![]() $\{\mathsf {OP}_1, \mathsf {OP}_2 \}$
with
$\{\mathsf {OP}_1, \mathsf {OP}_2 \}$
with
![]() $\delta $
to
$\delta $
to
![]() $\{\mathsf {L}\}$
with
$\{\mathsf {L}\}$
with
![]() $\delta $
. But the Liar is paradoxical, while the Open Pair is not (it is indeterminate, with two
$\delta $
. But the Liar is paradoxical, while the Open Pair is not (it is indeterminate, with two
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable truth value assignments, each of which assigns
$\mathcal {L}_{\mathsf {P}}$
-acceptable truth value assignments, each of which assigns
![]() $\top $
to one sentence name and
$\top $
to one sentence name and
![]() $\bot $
to the other).
$\bot $
to the other).

Fig. 4 A simple strong (surjective)
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism.
$\mathcal {L}_{\mathsf {P}}$
-homomorphism.
This example of a strong surjective
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism from a non-paradoxical
$\mathcal {L}_{\mathsf {P}}$
-homomorphism from a non-paradoxical
![]() $\mathcal {L}_{\mathsf {P}}$
construction to a paradoxical one is an instance of the following fact:
$\mathcal {L}_{\mathsf {P}}$
construction to a paradoxical one is an instance of the following fact:
Theorem 3.4. For any
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with denotation function
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with denotation function
![]() $\delta $
,
$\delta $
,
Proof. Let
for any
![]() $\mathsf {S}_{\alpha _1} \in \{\mathsf {S}_\alpha \}_{\alpha \in A}$
.
$\mathsf {S}_{\alpha _1} \in \{\mathsf {S}_\alpha \}_{\alpha \in A}$
.
If
![]() $\mathsf {Dep}_{\delta }(\mathsf {S}_{\alpha _1}, \mathsf {S}_{\alpha _2})$
, then, since
$\mathsf {Dep}_{\delta }(\mathsf {S}_{\alpha _1}, \mathsf {S}_{\alpha _2})$
, then, since
![]() $f(\mathsf {S}_{\alpha _1}) = f(\mathsf {S}_{\alpha _2}) = \mathsf { L}$
, and
$f(\mathsf {S}_{\alpha _1}) = f(\mathsf {S}_{\alpha _2}) = \mathsf { L}$
, and
![]() $\mathsf {Dep}_{\delta _{\mathsf {L}}}(\mathsf {L}, \mathsf {L})$
, Homo is satisfied.
$\mathsf {Dep}_{\delta _{\mathsf {L}}}(\mathsf {L}, \mathsf {L})$
, Homo is satisfied.
For Strong, the only case is
![]() $\mathsf {Dep}_{\delta _{\mathsf {L}}}(f(\mathsf {S}_{\alpha _1}), \mathsf {L})$
for some
$\mathsf {Dep}_{\delta _{\mathsf {L}}}(f(\mathsf {S}_{\alpha _1}), \mathsf {L})$
for some
![]() $\mathsf {S}_{\alpha _1} \in \{\mathsf {S}_\alpha \}_{\alpha \in A}$
. Let
$\mathsf {S}_{\alpha _1} \in \{\mathsf {S}_\alpha \}_{\alpha \in A}$
. Let
![]() $\mathsf {S}_{\alpha _2} \in \{\mathsf {S}_\alpha \}_{\alpha \in A}$
be such that
$\mathsf {S}_{\alpha _2} \in \{\mathsf {S}_\alpha \}_{\alpha \in A}$
be such that
![]() $\mathsf {Dep}_\delta (\mathsf { S}_{\alpha _1}, \mathsf {S}_{\alpha _2})$
(the existence of such is guaranteed by the seriality of
$\mathsf {Dep}_\delta (\mathsf { S}_{\alpha _1}, \mathsf {S}_{\alpha _2})$
(the existence of such is guaranteed by the seriality of
![]() $\mathsf {Dep}_\delta $
and the non-emptiness of
$\mathsf {Dep}_\delta $
and the non-emptiness of
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
). Then
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
). Then
![]() $f(\mathsf {S}_{\alpha _2}) = \mathsf {L}$
.
$f(\mathsf {S}_{\alpha _2}) = \mathsf {L}$
.
f is clearly surjective.
Perhaps the simplest and most useful corollary of the S
![]() $\mathcal {L}_{\mathsf {P}}$
H theorem is the following corollary:Footnote
15
$\mathcal {L}_{\mathsf {P}}$
H theorem is the following corollary:Footnote
15
Corollary 3.5. If
![]() and
and
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta _1$
is paradoxical, then
$\delta _1$
is paradoxical, then
![]() $\{\mathsf { S}_\beta \}_{\beta \in B}$
with
$\{\mathsf { S}_\beta \}_{\beta \in B}$
with
![]() $\delta _2$
is paradoxical.
$\delta _2$
is paradoxical.
Given this, we can use strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphisms to categorize
$\mathcal {L}_{\mathsf {P}}$
-homomorphisms to categorize
![]() $\mathcal {L}_{\mathsf {P}}$
constructions in two (ultimately equivalent) ways:
$\mathcal {L}_{\mathsf {P}}$
constructions in two (ultimately equivalent) ways:
-
• We can show that
 $\langle \{\mathsf {S}_\alpha \}_{\alpha \in A}, \delta _1 \rangle $
is paradoxical by identifying an
$\langle \{\mathsf {S}_\alpha \}_{\alpha \in A}, \delta _1 \rangle $
is paradoxical by identifying an
 $\langle \{\mathsf { S}_\beta \}_{\beta \in B}, \delta _2 \rangle $
such that where
$\langle \{\mathsf { S}_\beta \}_{\beta \in B}, \delta _2 \rangle $
such that where
 $\langle \{\mathsf {S}_\beta \}_{\beta \in B}, \delta _2 \rangle $
is known to be paradoxical.
$\langle \{\mathsf {S}_\beta \}_{\beta \in B}, \delta _2 \rangle $
is known to be paradoxical.
-
• We can show that
 $\langle \{\mathsf {S}_\alpha \}_{\alpha \in A}, \delta _1 \rangle $
is non-paradoxical by identifying an
$\langle \{\mathsf {S}_\alpha \}_{\alpha \in A}, \delta _1 \rangle $
is non-paradoxical by identifying an
 $\langle \{\mathsf { S}_\beta \}_{\beta \in B}, \delta _2 \rangle $
such that where
$\langle \{\mathsf { S}_\beta \}_{\beta \in B}, \delta _2 \rangle $
such that where
 $\langle \{\mathsf {S}_\beta \}_{\beta \in B}, \delta _2 \rangle $
is known to be non-paradoxical.Footnote
16
$\langle \{\mathsf {S}_\beta \}_{\beta \in B}, \delta _2 \rangle $
is known to be non-paradoxical.Footnote
16
We can further demonstrate the usefulness of strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphisms by noting that we can re-construe part of the content of the unwinding theorem as a mere special case of the S
$\mathcal {L}_{\mathsf {P}}$
-homomorphisms by noting that we can re-construe part of the content of the unwinding theorem as a mere special case of the S
![]() $\mathcal {L}_{\mathsf {P}}$
H theorem. We begin with the following observation:
$\mathcal {L}_{\mathsf {P}}$
H theorem. We begin with the following observation:
Theorem 3.6. Given any
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta $
,
$\delta $
,
Proof. The reader is invited to verify that
where
is a strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism from
$\mathcal {L}_{\mathsf {P}}$
-homomorphism from
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}^{\mathsf {U}}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}^{\mathsf {U}}$
with
![]() $\delta ^{\mathsf {U}}$
to
$\delta ^{\mathsf {U}}$
to
![]() $\{\mathsf { S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf { S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta $
.
$\delta $
.
Thus, given any
![]() $\mathcal {L}_{\mathsf {P}}$
construction
$\mathcal {L}_{\mathsf {P}}$
construction
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
![]() $\delta $
), there is a strong
$\delta $
), there is a strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism from the unwinding of
$\mathcal {L}_{\mathsf {P}}$
-homomorphism from the unwinding of
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
![]() $\delta $
) to
$\delta $
) to
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
![]() $\delta $
) itself. As a result, the right-to-left direction of Corollary 2.15 is also an immediate corollary of the S
$\delta $
) itself. As a result, the right-to-left direction of Corollary 2.15 is also an immediate corollary of the S
![]() $\mathcal {L}_{\mathsf {P}}$
H theorem.Footnote
17
$\mathcal {L}_{\mathsf {P}}$
H theorem.Footnote
17
Before moving on to our examination of the McGee paradox (and its dual), we further strengthen the connections between the
![]() $\mathcal {L}_{\mathsf {P}}$
approach and category theory by noting that the Duality Theorem can also be given a simple category-theoretic proof. The proof is given in the Appendix.
$\mathcal {L}_{\mathsf {P}}$
approach and category theory by noting that the Duality Theorem can also be given a simple category-theoretic proof. The proof is given in the Appendix.
4 The McGee paradox in
 $\mathcal {L}_{\mathsf {P}}$
$\mathcal {L}_{\mathsf {P}}$
The McGee paradox was originally formulated within the language of arithmetic with a truth predicate [Reference McGee7], and in that context the main point of interest in the construction is that it was the central component in a proof that certain axiomatic theories of truth (in particular, FS; see [Reference Friedman and Sheard4]) are consistent but
![]() $\omega $
-inconsistent. Here our interests will be quite different, since we will be looking at the McGee Paradox in the context of
$\omega $
-inconsistent. Here our interests will be quite different, since we will be looking at the McGee Paradox in the context of
![]() $\mathcal {L}_{\mathsf {P}}$
, and we will, as a result, be implicitly assuming that we are working in the standard model of arithmetic (and hence that the McGee construction is genuinely paradoxical). Nevertheless, a quick reminder of McGee’s original construction is in order.
$\mathcal {L}_{\mathsf {P}}$
, and we will, as a result, be implicitly assuming that we are working in the standard model of arithmetic (and hence that the McGee construction is genuinely paradoxical). Nevertheless, a quick reminder of McGee’s original construction is in order.
Let
![]() $\mathcal {L}^{\mathsf {T}}$
be any language sufficient for Peano Arithmetic (PA) supplemented with a unary truth predicate
$\mathcal {L}^{\mathsf {T}}$
be any language sufficient for Peano Arithmetic (PA) supplemented with a unary truth predicate
![]() $\mathsf {T}(\xi )$
.
$\mathsf {T}(\xi )$
.
![]() $\ulcorner \Phi \urcorner $
is the name (or Gödel code) of
$\ulcorner \Phi \urcorner $
is the name (or Gödel code) of
![]() $\Phi $
. We abbreviate iterated applications of the truth predicate as follows:
$\Phi $
. We abbreviate iterated applications of the truth predicate as follows:
 $$ \begin{align*} \mathsf{T}^1(\xi) &=_{df} \mathsf{T}(\xi),\\ \mathsf{T}^{n+1}(\xi) &=_{df} \mathsf{T}(\ulcorner \mathsf{T}^n(\xi)\urcorner). \end{align*} $$
$$ \begin{align*} \mathsf{T}^1(\xi) &=_{df} \mathsf{T}(\xi),\\ \mathsf{T}^{n+1}(\xi) &=_{df} \mathsf{T}(\ulcorner \mathsf{T}^n(\xi)\urcorner). \end{align*} $$
We define falsity in terms of truth and negation:
And we abbreviate the iteration of falsity predicates along the same lines:
 $$ \begin{align*} \mathsf{F}^1(\xi) &=_{df} \mathsf{F}(\xi),\\ \mathsf{F}^{n+1}(\xi) &=_{df} \mathsf{F}(\ulcorner \mathsf{F}^n(\xi)\urcorner). \end{align*} $$
$$ \begin{align*} \mathsf{F}^1(\xi) &=_{df} \mathsf{F}(\xi),\\ \mathsf{F}^{n+1}(\xi) &=_{df} \mathsf{F}(\ulcorner \mathsf{F}^n(\xi)\urcorner). \end{align*} $$
We now obtain the McGee Paradox via an application of Gödel’s celebrated diagonalization theorem [Reference Gödel5] to the predicate
obtaining the McGee sentence
![]() $\mathsf {M}$
, where
$\mathsf {M}$
, where
Loosely put, the McGee Sentence M is true if and only if it is not the case that all sentences of the form:
It is true that …it is true that M
are true. Equivalently, M is true if and only if some sentence of that form is false—that is,
McGee’s construction has a dual version that will be more convenient for our purposes, since it can be reconstructed relatively straightforwardly within
![]() $\mathcal {L}_{\mathsf {P}}$
(McGee’s original construction is more naturally reconstructed in the
$\mathcal {L}_{\mathsf {P}}$
(McGee’s original construction is more naturally reconstructed in the
![]() $\mathcal {L}_{\mathsf {P}}^{\mathsf {D}})$
. The Dual McGee Sentence is
$\mathcal {L}_{\mathsf {P}}^{\mathsf {D}})$
. The Dual McGee Sentence is
![]() $\mathsf {M}^{\mathsf {D}}$
where (again via Gödelian diagonalization)
$\mathsf {M}^{\mathsf {D}}$
where (again via Gödelian diagonalization)
Loosely put, the Dual McGee Sentence
![]() $\mathsf {M}^{\mathsf {D}}$
is true if and only if all sentences of the form:
$\mathsf {M}^{\mathsf {D}}$
is true if and only if all sentences of the form:
It is true that …it is true that
![]() $\mathsf {M}^{\mathsf {D}}$
$\mathsf {M}^{\mathsf {D}}$
are false.
Calling this the “dual” of the original McGee construction is justified via noting that the above is equivalent to
In short, just as the move from
![]() $\mathcal {L}_{\mathsf {P}}$
to
$\mathcal {L}_{\mathsf {P}}$
to
![]() $\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
involves switching conjunctions and disjunctions, the move from the original McGee construction to its dual involves replacing a universal quantifier (akin to an infinitary conjunction) with an existential quantifier (akin to an infinitary disjunction).
$\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
involves switching conjunctions and disjunctions, the move from the original McGee construction to its dual involves replacing a universal quantifier (akin to an infinitary conjunction) with an existential quantifier (akin to an infinitary disjunction).
Given that we want to represent the McGee Paradox within
![]() $\mathcal {L}_{\mathsf {P}}$
, it will be somewhat more convenient to work with the Dual of the McGee Paradox formulated in terms of our (defined) falsity predicate, rather than the (primitive) truth predicate.Footnote
18
The following is equivalent to the formulation of the McGee Sentence given above:
$\mathcal {L}_{\mathsf {P}}$
, it will be somewhat more convenient to work with the Dual of the McGee Paradox formulated in terms of our (defined) falsity predicate, rather than the (primitive) truth predicate.Footnote
18
The following is equivalent to the formulation of the McGee Sentence given above:
Replacing each occurrence of
![]() $\mathsf {T}(\xi )$
with
$\mathsf {T}(\xi )$
with
![]() $\mathsf {F}(\ulcorner \mathsf {F} (\xi )\urcorner )$
, we obtain
$\mathsf {F}(\ulcorner \mathsf {F} (\xi )\urcorner )$
, we obtain
Commuting the initial negation and the quantifier, we obtain
Finally, we can simplify this a bit, via “cancelling out” the initial negation-falsity prefix, obtaining the following falsity variant of the Dual McGee Sentence:Footnote 19
Reconstructing the Dual of the McGee Paradox in
![]() $\mathcal {L}_{\mathsf {P}}$
is now straightforward: Our sentence names are
$\mathcal {L}_{\mathsf {P}}$
is now straightforward: Our sentence names are
![]() $\{\mathsf {M}^{\mathsf {D}}_n\}_{ n \in \mathbb {N}}$
, and our denotation function
$\{\mathsf {M}^{\mathsf {D}}_n\}_{ n \in \mathbb {N}}$
, and our denotation function
![]() $\delta _{\mathsf {M^{\mathsf {D}}}}$
is such that, for all
$\delta _{\mathsf {M^{\mathsf {D}}}}$
is such that, for all
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
 $$ \begin{align*} \delta_{\mathsf{M^{\mathsf{D}}}}(\mathsf{M}^{\mathsf{D}}_0) &= \wedge\{\mathsf{F}(\mathsf{M}^{\mathsf{D}}_{2m}) : m \in \mathbb{N}\},\\ \delta_{\mathsf{M^{\mathsf{D}}}}(\mathsf{M^{\mathsf{D}}_{n+1}}) &= \mathsf{F}(\mathsf{M}^{\mathsf{D}}_n). \end{align*} $$
$$ \begin{align*} \delta_{\mathsf{M^{\mathsf{D}}}}(\mathsf{M}^{\mathsf{D}}_0) &= \wedge\{\mathsf{F}(\mathsf{M}^{\mathsf{D}}_{2m}) : m \in \mathbb{N}\},\\ \delta_{\mathsf{M^{\mathsf{D}}}}(\mathsf{M^{\mathsf{D}}_{n+1}}) &= \mathsf{F}(\mathsf{M}^{\mathsf{D}}_n). \end{align*} $$
We can write this a bit more colloquially as
 $$ \begin{align*} \mathsf{M}^{\mathsf{D}}_0 &= \mathsf{F}(\mathsf{M}^{\mathsf{D}}_0) \wedge \mathsf{F}(\mathsf{M}^{\mathsf{D}}_2) \wedge \mathsf{F}(\mathsf{M}^{\mathsf{D}}_4) \wedge \mathsf{F}(\mathsf{M}^{\mathsf{D}}_6) \wedge \cdots,\\ \mathsf{M}^{\mathsf{D}}_1 &= \mathsf{F}(\mathsf{M}^{\mathsf{D}}_0), \\ \mathsf{M}^{\mathsf{D}}_2 &= \mathsf{F}(\mathsf{M}^{\mathsf{D}}_1), \\ \mathsf{M}^{\mathsf{D}}_3 &= \mathsf{F}(\mathsf{M}^{\mathsf{D}}_2), \\ \text{etc.} \end{align*} $$
$$ \begin{align*} \mathsf{M}^{\mathsf{D}}_0 &= \mathsf{F}(\mathsf{M}^{\mathsf{D}}_0) \wedge \mathsf{F}(\mathsf{M}^{\mathsf{D}}_2) \wedge \mathsf{F}(\mathsf{M}^{\mathsf{D}}_4) \wedge \mathsf{F}(\mathsf{M}^{\mathsf{D}}_6) \wedge \cdots,\\ \mathsf{M}^{\mathsf{D}}_1 &= \mathsf{F}(\mathsf{M}^{\mathsf{D}}_0), \\ \mathsf{M}^{\mathsf{D}}_2 &= \mathsf{F}(\mathsf{M}^{\mathsf{D}}_1), \\ \mathsf{M}^{\mathsf{D}}_3 &= \mathsf{F}(\mathsf{M}^{\mathsf{D}}_2), \\ \text{etc.} \end{align*} $$
Loosely speaking,
![]() $\mathsf {M}^{\mathsf {D}}_0$
“is”
$\mathsf {M}^{\mathsf {D}}_0$
“is”
![]() $\mathsf {M}^{\mathsf {D}}$
in the informal construction from Section 1, and (again, loosely speaking) each
$\mathsf {M}^{\mathsf {D}}$
in the informal construction from Section 1, and (again, loosely speaking) each
![]() $\mathsf {M}^{\mathsf {D}}_{n+1}$
“is”
$\mathsf {M}^{\mathsf {D}}_{n+1}$
“is”
![]() $\mathsf {F}(\mathsf {M}^{\mathsf {D}}_n)$
. Hence, for
$\mathsf {F}(\mathsf {M}^{\mathsf {D}}_n)$
. Hence, for
![]() $n \geq 1$
,
$n \geq 1$
,
and we can thus “rewrite”
![]() $\mathsf {M}^{\mathsf {D}}_0$
as
$\mathsf {M}^{\mathsf {D}}_0$
as
and hence as
This is just (modulo some unimportant notational changes, and replacing an infinite conjunction with the corresponding universal quantification) the Dual of the McGee Sentence given above:
Figure 5 depicts (an initial segment of) the dependency relation for the
![]() $\mathcal {L}_{\mathsf {P}}$
version of the Dual of the McGee paradox (i.e.,
$\mathcal {L}_{\mathsf {P}}$
version of the Dual of the McGee paradox (i.e.,
![]() $\{\mathsf {M}^{\mathsf {D}}_n\}_{n \in \mathbb {N}}$
with
$\{\mathsf {M}^{\mathsf {D}}_n\}_{n \in \mathbb {N}}$
with
![]() $\delta _{\mathsf {M}^{\mathsf {D}}}$
). Note that the dependency relation in the
$\delta _{\mathsf {M}^{\mathsf {D}}}$
). Note that the dependency relation in the
![]() $\mathcal {L}_{\mathsf {P}}$
version of the Dual of the McGee paradox is not transitive.
$\mathcal {L}_{\mathsf {P}}$
version of the Dual of the McGee paradox is not transitive.
![]() $\{\mathsf {M}^{\mathsf { D}}_n\}_{n \in \mathbb {N}}$
with
$\{\mathsf {M}^{\mathsf { D}}_n\}_{n \in \mathbb {N}}$
with
![]() $\delta _{\mathsf {M^{\mathsf {D}}}}$
is, however, paradoxical. In this section we give a direct proof of this fact—one that does not depend on the mobilization of strong
$\delta _{\mathsf {M^{\mathsf {D}}}}$
is, however, paradoxical. In this section we give a direct proof of this fact—one that does not depend on the mobilization of strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphisms:
$\mathcal {L}_{\mathsf {P}}$
-homomorphisms:
Lemma 4.1. For any assignment function
![]() $\sigma $
that is
$\sigma $
that is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\{\mathsf {M}^{\mathsf {D}}_n \}_{n \in \mathbb {N}}$
with
$\{\mathsf {M}^{\mathsf {D}}_n \}_{n \in \mathbb {N}}$
with
![]() $\delta _{\mathsf {M}^{\mathsf {D}}}$
, and any
$\delta _{\mathsf {M}^{\mathsf {D}}}$
, and any
![]() $n, m \in \mathbb {N}$
,
$n, m \in \mathbb {N}$
,
![]() $\sigma (\mathsf {M}^{\mathsf {D}}_{n}) = \sigma (\mathsf {M}^{\mathsf {D}}_{n + 2m})$
.
$\sigma (\mathsf {M}^{\mathsf {D}}_{n}) = \sigma (\mathsf {M}^{\mathsf {D}}_{n + 2m})$
.
Proof. Straightforward induction (or via direct inspection of Figure 5), left to the reader.
Theorem 4.2. {
![]() $\mathsf {M}^{\mathsf {D}}_n \}_{n \in \mathbb {N}}$
with
$\mathsf {M}^{\mathsf {D}}_n \}_{n \in \mathbb {N}}$
with
![]() $\delta _{\mathsf {\mathsf {M}^{\mathsf {D}}}}$
is paradoxical.
$\delta _{\mathsf {\mathsf {M}^{\mathsf {D}}}}$
is paradoxical.
Proof. Assume for reductio that there is an assignment
![]() $\sigma $
that is
$\sigma $
that is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\{\mathsf {M}^{\mathsf {D}}_n \}_{ n \in \mathbb {N}}$
with
$\{\mathsf {M}^{\mathsf {D}}_n \}_{ n \in \mathbb {N}}$
with
![]() $\delta _{\mathsf {M}^{\mathsf {D}}}$
.
$\delta _{\mathsf {M}^{\mathsf {D}}}$
.

Fig. 5 An initial segment of
![]() $\mathsf {Dep}_{\delta _{\mathsf {M}^{\mathsf {D}}}}$
.
$\mathsf {Dep}_{\delta _{\mathsf {M}^{\mathsf {D}}}}$
.
Assume that
![]() $\sigma (\mathsf {M}^{\mathsf {D}}_0) = \top $
. Then, for all
$\sigma (\mathsf {M}^{\mathsf {D}}_0) = \top $
. Then, for all
![]() $\mathsf {M}^{\mathsf {D}}_m$
such that
$\mathsf {M}^{\mathsf {D}}_m$
such that
![]() $\mathsf {Dep}_{\delta _{\mathsf {M^{\mathsf { D}}}}}(\mathsf {M}^{\mathsf {D}}_0, \mathsf {M}^{\mathsf {D}}_m)$
,
$\mathsf {Dep}_{\delta _{\mathsf {M^{\mathsf { D}}}}}(\mathsf {M}^{\mathsf {D}}_0, \mathsf {M}^{\mathsf {D}}_m)$
,
![]() $\sigma (\mathsf {M}^{\mathsf {D}}_m) = \bot $
. In particular,
$\sigma (\mathsf {M}^{\mathsf {D}}_m) = \bot $
. In particular,
![]() $\sigma (\mathsf {M}^{\mathsf {D}}_0) = \bot $
. Contradiction.
$\sigma (\mathsf {M}^{\mathsf {D}}_0) = \bot $
. Contradiction.
Thus,
![]() $\sigma (\mathsf {M}^{\mathsf {D}}_0) = \bot $
. So there is an
$\sigma (\mathsf {M}^{\mathsf {D}}_0) = \bot $
. So there is an
![]() $m \in \mathbb {N}$
such that
$m \in \mathbb {N}$
such that
![]() $\sigma (\mathsf {M}^{\mathsf {D}}_{2m}) = \top $
. This contradicts our lemma. Contradiction.
$\sigma (\mathsf {M}^{\mathsf {D}}_{2m}) = \top $
. This contradicts our lemma. Contradiction.
Hence there is no such assignment.
The paradoxicality of the Dual of the McGee paradox is, like the Yablo Paradox, a special case of a more general phenomenon. First, some additional definitions:Footnote 20
Definition 4.3. Given a denotation function
![]() $\delta $
, an infinite sequence of ordinals
$\delta $
, an infinite sequence of ordinals
is a
![]() $\delta $
-path if and only if, for all
$\delta $
-path if and only if, for all
![]() $m \in \mathbb {N}$
,
$m \in \mathbb {N}$
,
![]() $\mathsf {Dep}_\delta (\mathsf {S}_{\alpha _m}, \mathsf {S}_{\alpha _{m+1}})$
.
$\mathsf {Dep}_\delta (\mathsf {S}_{\alpha _m}, \mathsf {S}_{\alpha _{m+1}})$
.
Definition 4.4. A
![]() $\delta $
-path
$\delta $
-path
is an n-repeater if and only if
and there is no
![]() $m \in \mathbb {N}$
such that
$m \in \mathbb {N}$
such that
![]() $0 < m < n$
and
$0 < m < n$
and
Theorem 4.5. If
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
![]() $\delta $
) contains an
$\delta $
) contains an
![]() $\mathsf {S}_\beta $
such that every
$\mathsf {S}_\beta $
such that every
![]() $\delta $
-path beginning with
$\delta $
-path beginning with
![]() $\beta $
is an n-repeater for odd n, then
$\beta $
is an n-repeater for odd n, then
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
![]() $\delta $
) is paradoxical.
$\delta $
) is paradoxical.
Proof. Assume that
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
![]() $\delta $
) contains an
$\delta $
) contains an
![]() $\mathsf {S}_\beta $
such that every
$\mathsf {S}_\beta $
such that every
![]() $\delta $
-path beginning with
$\delta $
-path beginning with
![]() $\beta $
is an n-repeater for odd n. Assume for reductio
$\beta $
is an n-repeater for odd n. Assume for reductio
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
![]() $\delta $
) is not paradoxical. Then there is an assignment
$\delta $
) is not paradoxical. Then there is an assignment
![]() $\sigma $
that is
$\sigma $
that is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
![]() $\delta $
). If
$\delta $
). If
![]() $\sigma (\mathsf {S}_\beta ) = \top $
, then there is a
$\sigma (\mathsf {S}_\beta ) = \top $
, then there is a
![]() $\delta $
-path
$\delta $
-path
such that
 $$ \begin{align*} \sigma(\mathsf{S}_{\alpha_n}) & = \top, \quad \text{if } n \text{ is even,}\\ & = \bot, \quad \text{if } n \text{ is odd.} \end{align*} $$
$$ \begin{align*} \sigma(\mathsf{S}_{\alpha_n}) & = \top, \quad \text{if } n \text{ is even,}\\ & = \bot, \quad \text{if } n \text{ is odd.} \end{align*} $$
Since every
![]() $\delta $
-path beginning with
$\delta $
-path beginning with
![]() $\beta $
is an n-repeater for odd n, there is an m such that m is odd and
$\beta $
is an n-repeater for odd n, there is an m such that m is odd and
![]() $\mathsf {S}_\beta $
=
$\mathsf {S}_\beta $
=
![]() $\mathsf {S}_{\alpha _m}$
. But then
$\mathsf {S}_{\alpha _m}$
. But then
Contradiction. Hence
![]() $\sigma (\mathsf {S}_\beta ) \not = \top $
. A similar argument shows that
$\sigma (\mathsf {S}_\beta ) \not = \top $
. A similar argument shows that
![]() $\sigma (\mathsf {S}_\beta ) \not = \bot $
. Hence, there is no such
$\sigma (\mathsf {S}_\beta ) \not = \bot $
. Hence, there is no such
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable assignment.
$\mathcal {L}_{\mathsf {P}}$
-acceptable assignment.
This result, like the theorem regarding transitivity from the previous section, is also unifying, in the sense that it also identifies a property shared by many (but again, not all!) paradoxes. Note that the
![]() $\mathcal {L}_{\mathsf {P}}$
version of the Liar paradox is also a construction involving a sentence where every
$\mathcal {L}_{\mathsf {P}}$
version of the Liar paradox is also a construction involving a sentence where every
![]() $\delta $
-path beginning with that sentence is an n-repeater for odd n. But, just as the denotation relation on the Dual of the McGee paradox is not transitive, the dependency relation on the
$\delta $
-path beginning with that sentence is an n-repeater for odd n. But, just as the denotation relation on the Dual of the McGee paradox is not transitive, the dependency relation on the
![]() $\mathcal {L}_{\mathsf {P}}$
version of the Yablo paradox does not contain any such n-repeaters (since it contains no loops at all!).
$\mathcal {L}_{\mathsf {P}}$
version of the Yablo paradox does not contain any such n-repeaters (since it contains no loops at all!).
Now that we have given a proof of the paradoxicality of (the Dual of) the McGee paradox using methods mobilized in extant work within the
![]() $\mathcal {L}_{\mathsf {P}}$
framework, it is time to see what can be done using our new tool—strong
$\mathcal {L}_{\mathsf {P}}$
framework, it is time to see what can be done using our new tool—strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphisms.
$\mathcal {L}_{\mathsf {P}}$
-homomorphisms.
5 The infinite flower and
 $\mathcal {L}_{\mathsf {P}}$
-homomorphisms
$\mathcal {L}_{\mathsf {P}}$
-homomorphisms
We will begin this section by constructing a novel paradox: The Infinite Flower. First, we use the following pairs as indexes for the sentence names:
We now define the denotation function as follows (using IF rather than S merely for aesthetics—it’s a flower, after all):
 $$ \begin{align*} \delta_{\mathsf{IF}}(\mathsf{IF}_{\langle n, m \rangle}) = \begin{cases} \{\mathsf{IF}_{\langle j, 1 \rangle}: j \text{ odd}\}\cup\{\mathsf{IF}_{\langle 1, 0 \rangle}\}, & \text{if } n = 1 \text{ and } m = 0, \\ \{\mathsf{IF}_{\langle n, m+1 \rangle}: n \in \mathbb{N}\}, &\text{if } n \text{ odd} \text{ and } 0 < m < n - 1, \\ \{\mathsf{IF}_{\langle 1,0 \rangle}\}, &\text{if } n \text{ odd} \text{ and } m = n-1. \end{cases} \end{align*} $$
$$ \begin{align*} \delta_{\mathsf{IF}}(\mathsf{IF}_{\langle n, m \rangle}) = \begin{cases} \{\mathsf{IF}_{\langle j, 1 \rangle}: j \text{ odd}\}\cup\{\mathsf{IF}_{\langle 1, 0 \rangle}\}, & \text{if } n = 1 \text{ and } m = 0, \\ \{\mathsf{IF}_{\langle n, m+1 \rangle}: n \in \mathbb{N}\}, &\text{if } n \text{ odd} \text{ and } 0 < m < n - 1, \\ \{\mathsf{IF}_{\langle 1,0 \rangle}\}, &\text{if } n \text{ odd} \text{ and } m = n-1. \end{cases} \end{align*} $$
The structure of the Infinite Flower can be seen a bit more clearly in Figure 6, which represents its first four “petals.”

Fig. 6 An initial segment of
![]() $\mathsf {Dep}_{\delta _{\mathsf {IF}}}$
.
$\mathsf {Dep}_{\delta _{\mathsf {IF}}}$
.
Clearly, any path in the Infinite Flower beginning with
![]() $\mathsf {IF}_{\langle 0, 1 \rangle }$
is an n repeater for some odd n (the n is given by the first value of the pairs labeling the sentence names in the relevant “petal”). Hence the Infinite Flower is paradoxical, and is another instance of the sort of paradoxicality delineated by Theorem 4.5.
$\mathsf {IF}_{\langle 0, 1 \rangle }$
is an n repeater for some odd n (the n is given by the first value of the pairs labeling the sentence names in the relevant “petal”). Hence the Infinite Flower is paradoxical, and is another instance of the sort of paradoxicality delineated by Theorem 4.5.
But we don’t need all of the fancy machinery involved in Theorem 4.5 in order to see the paradoxicality of the Infinite Flower. There is a much more straightforward, rather obvious route to this knowledge. First, we merely need to note the familiar fact that any “cyclic”
![]() $\mathcal {L}_{\mathsf {P}}$
construction of odd length is paradoxical:
$\mathcal {L}_{\mathsf {P}}$
construction of odd length is paradoxical:
Definition 5.1. Given a denotation function
![]() $\delta $
, an finite sequence of n-many ordinals
$\delta $
, an finite sequence of n-many ordinals
is an n-cycle (with
![]() $\delta $
) if and only if:
$\delta $
) if and only if:
Theorem 5.2. [Reference Cook3] Given
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
![]() $\delta $
), if A (with
$\delta $
), if A (with
![]() $\delta $
) is an n-cycle for odd n, then
$\delta $
) is an n-cycle for odd n, then
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
![]() $\delta $
) is paradoxical.
$\delta $
) is paradoxical.
The Liar sentence L (with
![]() $\delta _{\mathsf {L}}$
) is a 1-repeater (hence paradoxical), while the Open Pair
$\delta _{\mathsf {L}}$
) is a 1-repeater (hence paradoxical), while the Open Pair
![]() $\mathsf {OP}_1, \mathsf {OP}_2$
(with
$\mathsf {OP}_1, \mathsf {OP}_2$
(with
![]() $\delta _{\mathsf {OP}}$
) is a 2-cycle, hence not covered by this result.Footnote
21
Examples of n-cycles for lengths 3, 5, and 7 are given by the respective “petals” in Figure 6.
$\delta _{\mathsf {OP}}$
) is a 2-cycle, hence not covered by this result.Footnote
21
Examples of n-cycles for lengths 3, 5, and 7 are given by the respective “petals” in Figure 6.
Now, once we have noted this very basic fact about odd cycles, the reader might fairly ask what it has to do with the topic at hand: the McGee paradox and strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphisms. The answer is simple: We can give an alternative argument to show that (the dual of) the McGee paradox is indeed paradoxical by noting two facts:
$\mathcal {L}_{\mathsf {P}}$
-homomorphisms. The answer is simple: We can give an alternative argument to show that (the dual of) the McGee paradox is indeed paradoxical by noting two facts:
-
1. The Infinite Flower is paradoxical.
-
2. There is a strong
 $\mathcal {L}_{\mathsf {P}}$
-homomorphism from the Infinite Flower to dual of the McGee paradox.
$\mathcal {L}_{\mathsf {P}}$
-homomorphism from the Infinite Flower to dual of the McGee paradox.
The first fact is easily verified once one notes that the Infinite Flower consists merely of a bunch of n-cycles pasted together (one for each odd n)—filling in the rather trivial details is left to the reader. For the second fact:Footnote 22
Theorem 5.3.
Proof. The reader is invited to verify that
is a strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism from the Infinite Flower to the Dual of the McGee paradox.
$\mathcal {L}_{\mathsf {P}}$
-homomorphism from the Infinite Flower to the Dual of the McGee paradox.
This result, plus the observation just made regarding the paradoxicality of the Infinite Flower, provide a simple proof of the paradoxicality of (the dual of) the McGee paradox via a quick application of the S
![]() $\mathcal {L}_{\mathsf {P}}$
H theorem (and, in particular, of Corollary 3.5). Further, this proof is arguably a good bit simpler than the more direct proofs given in the previous section (via either Theorem 4.2 or an application of Theorem 4.5).
$\mathcal {L}_{\mathsf {P}}$
H theorem (and, in particular, of Corollary 3.5). Further, this proof is arguably a good bit simpler than the more direct proofs given in the previous section (via either Theorem 4.2 or an application of Theorem 4.5).
Thus, strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphisms are a powerful tool for showing that novel
$\mathcal {L}_{\mathsf {P}}$
-homomorphisms are a powerful tool for showing that novel
![]() $\mathcal {L}_{\mathsf {P}}$
constructions are paradoxical, as advertised. In order to show that an
$\mathcal {L}_{\mathsf {P}}$
constructions are paradoxical, as advertised. In order to show that an
![]() $\mathcal {L}_{\mathsf {P}}$
construction
$\mathcal {L}_{\mathsf {P}}$
construction
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
(with
![]() $\delta $
) is paradoxical, we need only show some familiar or simpler construction whose paradoxicality has already been (or can easily be) established can be mapped to it by a strong
$\delta $
) is paradoxical, we need only show some familiar or simpler construction whose paradoxicality has already been (or can easily be) established can be mapped to it by a strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphism.
$\mathcal {L}_{\mathsf {P}}$
-homomorphism.
6 Conclusion
In this essay, we have demonstrated that strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homo morphisms are a powerful tool within the
$\mathcal {L}_{\mathsf {P}}$
-homo morphisms are a powerful tool within the
![]() $\mathcal {L}_{\mathsf {P}}$
framework. They have allowed us to identify straightforward characterizations of, and connections between, constructions that have not been dealt with previously within the
$\mathcal {L}_{\mathsf {P}}$
framework. They have allowed us to identify straightforward characterizations of, and connections between, constructions that have not been dealt with previously within the
![]() $\mathcal {L}_{\mathsf {P}}$
approach, such as (the dual of) the McGee paradox and the Infinite Flower. In addition, strong
$\mathcal {L}_{\mathsf {P}}$
approach, such as (the dual of) the McGee paradox and the Infinite Flower. In addition, strong
![]() $\mathcal {L}_{\mathsf {P}}$
-homomorphisms have illuminated new connections between various more familiar
$\mathcal {L}_{\mathsf {P}}$
-homomorphisms have illuminated new connections between various more familiar
![]() $\mathcal {L}_{\mathsf {P}}$
constructions, and have allowed us to generalize and unify extant results such as the unwinding theorem (and the duality theorem, handled in the Appendix). Finally, they have provided us with the tools to begin to draw important connections between the patterns of sentential reference that generate paradox and the methods and tools of category theory. No doubt, however, much more work remains to be done.
$\mathcal {L}_{\mathsf {P}}$
constructions, and have allowed us to generalize and unify extant results such as the unwinding theorem (and the duality theorem, handled in the Appendix). Finally, they have provided us with the tools to begin to draw important connections between the patterns of sentential reference that generate paradox and the methods and tools of category theory. No doubt, however, much more work remains to be done.
Appendix: Duality and category theory
Here, we give a novel category-theoretic proof of the Duality Theorem (Theorem 2.18). Recall that the only distinction between
![]() $\mathcal {L}_{\mathsf {P}}$
and
$\mathcal {L}_{\mathsf {P}}$
and
![]() $\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
is that the former uses conjunctions whereas the latter uses disjunctions, and hence
$\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
is that the former uses conjunctions whereas the latter uses disjunctions, and hence
![]() $\mathcal {L}_{\mathsf {L}}^{\mathsf {D}}$
mobilizes
$\mathcal {L}_{\mathsf {L}}^{\mathsf {D}}$
mobilizes
![]() $\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
-acceptability instead of
$\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
-acceptability instead of
![]() $\mathcal {L}_{\mathsf { P}}$
-acceptability. Thus, our first task is to formulate the notion of
$\mathcal {L}_{\mathsf { P}}$
-acceptability. Thus, our first task is to formulate the notion of
![]() $\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
in the category-theoretic setting. Let
$\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
in the category-theoretic setting. Let
![]() $|: \mathcal {P}(\Omega ) \rightarrow \Omega $
be the morphism
$|: \mathcal {P}(\Omega ) \rightarrow \Omega $
be the morphism
 $$ \begin{align*} |(\{\bot\}) &= |(\{\top, \bot\} = \Omega) = \top,\\ |(\{\top\}) &= |(\varnothing) = \bot. \end{align*} $$
$$ \begin{align*} |(\{\bot\}) &= |(\{\top, \bot\} = \Omega) = \top,\\ |(\{\top\}) &= |(\varnothing) = \bot. \end{align*} $$
![]() $|$
is the category-theoretic analogue of the Sheffer stroke (expressing something like “at least one of the sentences is false”). Thus, given a denotation function
$|$
is the category-theoretic analogue of the Sheffer stroke (expressing something like “at least one of the sentences is false”). Thus, given a denotation function
![]() $\delta $
(i.e., a coalgebra from S to
$\delta $
(i.e., a coalgebra from S to
![]() $\mathcal {P}(S)$
), an assignment
$\mathcal {P}(S)$
), an assignment
![]() $\sigma $
(i.e., a morphism from S to
$\sigma $
(i.e., a morphism from S to
![]() $\Omega $
) is
$\Omega $
) is
![]() $\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
acceptable on S relative to
$\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
acceptable on S relative to
![]() $\delta $
if and only if Figure 7 commutes.
$\delta $
if and only if Figure 7 commutes.

Fig. 7
![]() $\sigma ^{\mathsf {}}$
is
$\sigma ^{\mathsf {}}$
is
![]() $\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
-acceptable on
![]() $\delta $
.
$\delta $
.
Now, let
![]() $\neg : \Omega \rightarrow \Omega $
be the mapping:
$\neg : \Omega \rightarrow \Omega $
be the mapping:
 $$ \begin{align*} \neg(\top) = \bot,\\ \neg(\bot) = \top. \end{align*} $$
$$ \begin{align*} \neg(\top) = \bot,\\ \neg(\bot) = \top. \end{align*} $$
Note that
![]() $\neg \circ \neg = id_\Omega $
, and that
$\neg \circ \neg = id_\Omega $
, and that
![]() $\neg $
is a monomorphism.Footnote
23
Given an assignment
$\neg $
is a monomorphism.Footnote
23
Given an assignment
![]() $\sigma $
, the dual assignment
$\sigma $
, the dual assignment
![]() $\sigma ^{\mathsf {D}}$
given in Definition 2.17 is just
$\sigma ^{\mathsf {D}}$
given in Definition 2.17 is just
![]() $\neg \circ \sigma $
. Recall that we defined the functor
$\neg \circ \sigma $
. Recall that we defined the functor
![]() $\downarrow{\kern-1pt}: \mathcal {P}(\Omega ) \rightarrow \Omega $
as
$\downarrow{\kern-1pt}: \mathcal {P}(\Omega ) \rightarrow \Omega $
as
 $$ \begin{align*} \downarrow\!(\{\bot\}) & =\ \downarrow\!(\varnothing) = \top,\\ \downarrow\!(\{\top\}) &= \ \downarrow\!(\{\top, \bot\} = \Omega) = \bot. \end{align*} $$
$$ \begin{align*} \downarrow\!(\{\bot\}) & =\ \downarrow\!(\varnothing) = \top,\\ \downarrow\!(\{\top\}) &= \ \downarrow\!(\{\top, \bot\} = \Omega) = \bot. \end{align*} $$
The reader is invited to verify that
 $$ \begin{align*} \neg \circ \downarrow \circ \mathcal{P}\neg & = |,\\ \neg \circ | \circ \mathcal{P}\neg & =\, \downarrow, \end{align*} $$
$$ \begin{align*} \neg \circ \downarrow \circ \mathcal{P}\neg & = |,\\ \neg \circ | \circ \mathcal{P}\neg & =\, \downarrow, \end{align*} $$
that is, the following diagrams commute:

Now, in order to prove the duality theorem, we need to merely prove
Given a denotation function
![]() $\delta $
and assignment
$\delta $
and assignment
![]() $\sigma $
,
$\sigma $
,
![]() $\sigma $
is
$\sigma $
is
![]() $\mathcal {L}_{\mathsf {P}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}$
-acceptable on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta $
if and only if
$\delta $
if and only if
![]() $\sigma ^{\mathsf {D}}$
is
$\sigma ^{\mathsf {D}}$
is
![]() $\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
-acceptable on
$\mathcal {L}_{\mathsf {P}}^{\mathsf {D}}$
-acceptable on
![]() $\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
$\{\mathsf {S}_\alpha \}_{\alpha \in A}$
with
![]() $\delta $
.
$\delta $
.
Which, in the present context, amounts to proving that the diagram on the left commutes if and only if the diagram on the right commutes:

But the diagram on the left commutes if and only if

commutes (since
![]() $\neg $
is a monomorphism), which commutes if and only if
$\neg $
is a monomorphism), which commutes if and only if

commutes (since
![]() $\neg \circ | \circ \mathcal {P}\neg =\, \downarrow $
), which commutes if and only if
$\neg \circ | \circ \mathcal {P}\neg =\, \downarrow $
), which commutes if and only if

commutes (since
![]() $\neg \circ \neg = id_\Omega $
), which is just
$\neg \circ \neg = id_\Omega $
), which is just

Thus, the Duality Theorem is proven.
Acknowledgements
Thanks are owed to an anonymous referee whose comments and suggestions vastly improved this essay, and to the Undergraduate Research Opportunities Program (UROP) at the University of Minnesota—Twin Cities for providing funding to Jonathan Wolfgram to support his work on this project.