The race between offshoring and automation in explaining wage polarization

Abstract

Offshoring and automation are sources of wage polarization. We reassess these two determinants of wage polarization in a single directed technical change setup that encompasses routine and nonroutine production. We empirically establish the conditional positive relationship between automation and relocations on one side and wage polarization on the other. Theoretically, we show that wage polarization increases with automation and offshoring. In particular, wage polarization in favor of domestic (nonroutine) high(low)-skilled workers is positively affected by an increase in domestic (nonroutine) high(low)-skilled labor quantity and/or absolute productivity. Additionally, it is also positively influenced by a rise in foreign (routine) medium-skilled labor quantity and/or absolute productivity while negatively impacted by an increase in domestic (routine) medium-skilled labor quantity and/or absolute productivity. We show that the effect of offshoring on wage polarization diminishes with the degree of substitutability between routine and nonroutine sectors in the economy, with the share of machines in the production of intermediate goods, and with the scale effect. We quantitatively assess the impact through a thorough data-based calibration exercise, where the numerical results confirmed the theoretical findings.

1. Introduction

There is consensus in the literature that inequality has been increasing within most advanced economies since the 1980s [e.g., Alvaredo et al. (2018)]. Initially, the prevailing literature attributed this phenomenon to the bias of technological-knowledge progress in favor of high-skilled workers vis-à-vis low-skilled workers [e.g., Katz and Murphy (1992) and Acemoglu (1998, 2002)].¹ In the context of this directed technical change (DTC) literature, low-skilled and high-skilled workers are complemented by specific types of technologies. An increase in the supply of one type of labor causes an expansion of the market size of the technologies it complements (a market-size channel), which, given the associated profitability, creates additional incentives for R&D directed at those technologies. Consequently, technological-knowledge changes due to R&D activity are biased toward those technologies, that is, toward a specific sector. In turn, the bias increases the demand for the type of complementary labor that would supplement the supply. Thus, the proposed modeling explained the increased skill premium due to the increased relative supply of high-skilled labor.

Alternatively, considering three types of workers, as suggested by the finer analysis of the existing data, several authors have found that medium-skilled workers are employed in routine tasks, while low-skilled and high-skilled tasks are mainly employed in “purely manual” and “abstract/cognitive” nonroutine tasks, respectively [e.g., Acemoglu and Autor (2011), Autor and Dorn (2013), and Wang et al. (2021)]; for example, according to the World Bank Group (2016), around 57% of current jobs in the OECD are at risk of being replaced by robots or by relocations of tasks toward developing countries,² mainly at the level of complementary routine tasks for medium-skilled workers [Blanas et al. (2019)], since these tasks only require methodical repetitions [Autor et al. (2003)]. Both types of nonroutine tasks—purely manual and abstract/cognitive—are difficult to reduce to a specific set of instructions [Chui et al. (2016) and Acemoglu and Restrepo (2018a, b)]. Indeed, purely manual tasks require human and physical elements (e.g., service occupations), and abstract/cognitive tasks require complex cognitive processes (e.g., managers, technicians, accounting, consulting, planning, and even in various medical specialties, etc.).

There are two main (separately treated until now) explanations for the wage polarization observed in developed countries, which is described as a labor market phenomenon where earnings grow significantly at the tails of the distribution [Autor and Dorn (2013)]:

• • automation (or robotization), which, by leading to an increase in routine tasks performed by machines/robots, makes labor less productive in these tasks and decreases the relative demand for medium-skilled workers—for example, Autor et al. (2003), Acemoglu and Autor (2011), Autor and Dorn (2013), Acemoglu and Loebbing (2022), and Lankisch et al. (2019).³

• • offshoring/outsourcing/foreign direct investment (FDI) through which worldwide firms—that is, firms operating in developed/innovator countries and, directly or indirectly, in developing/follower countries—transfer production to countries with lower costs (hereinafter, relocations that promote international trade) that potentially benefit all workers in the world due to efficiency gains [e.g., Grossman and Rossi-Hansberg (2008) and Rodriguez-Clare (2010)] but also have strong distributional effects that can, for example, have negative implications on wages of medium-skilled workers in developed countries—for example, Feenstra and Hanson (1996, 1999), and Oldenski (2014).⁴ That is, greater imports of cheap medium-skilled inputs produced by worldwide firms in developing countries may lead to a decline in the medium-skilled wage and a rise in wage polarization in developed countries.

This paper focuses mainly on the explanation of wage polarization observed in many developed countries, based on the “race” between relocations and the automation of tasks.

Our main contribution is to simultaneously consider two different explanations of wage polarization that until now were treated separately (robotization and relocations) within the same DTC setup. First, our empirical analysis highlights the positive relationship between both automation and relocations on wage polarization, which is even stronger if taken as conditional in one another. Second, we show that the allocation of resources between tasks is such that automation is more important than offshoring if the level of domestic medium-skilled workers exceeds the number existing abroad—that is, if the “room” for automation exceeds the “room” for offshoring—and if the absolute advantage of domestic medium-skilled workers outweighs the absolute advantage of the same type of workers abroad. Moreover, after solving for the general equilibrium, we show unequivocally that wage polarization increases in both tails with automation and offshoring. In particular, wage polarization in favor of domestic (nonroutine) high(low)-skilled workers is positively affected by an increase in domestic (nonroutine) high(low)-skilled labor quantity and/or absolute productivity, although the latter relationship exhibits a downward effect beyond a certain threshold. It is also positively influenced by a rise in foreign (routine) medium-skilled labor quantity and/or absolute productivity while negatively impacted by an increase in domestic (routine) medium-skilled labor quantity and/or absolute productivity, with the latter exhibiting diminishing returns beyond a specific threshold. We show that the effect of offshoring on wage polarization diminishes with the degree of substitutability between routine and nonroutine sectors in the economy, with the share of machines in the production of intermediate goods and with the scale effect. Third, we thoroughly calibrate the model to assess its quantitative implications. By considering the USA as a domestic country, with a high degree of automation exposure and Mexico as a foreign country engaged in substantial cross-border relocations with the domestic nation, we quantify the behavior of crucial variables due to changes in parameters and exogenous variables. Thus, we graphically examine the impact of fluctuations in the values linked to the importance of the routine sector, which plays a crucial role in driving technical change or innovation, in the inter-sector technological-knowledge gap biased in favor of tasks produced by domestic (nonroutine) high- and low-skilled workers. Thereafter, we evaluate the repercussions of a change in the values associated with automation and relocations on the wage polarization in favor of domestic (nonroutine) high- and low-skilled workers. We will observe that the outcomes align with the theoretical findings.

After this Introduction, Section 2 analyzes empirically the relationship between relocation and automation with wage polarization using fixed effects estimations with several controls. In Section 3, the model is detailed; we start by modeling the preferences, which examines the demand side of the model (Section 3.1) and the productive side of the model (Sections 3.2–3.5). In Section 4, the model general equilibrium is solved, and the main theoretical results are derived. In Section 5, a calibration exercise is performed. Finally, in Section 6, the main conclusions are presented.

2. Empirical evidence

Empirical evidence of the impact of these two effects on wage inequality is still scarce, and to our knowledge, none is available that considers both phenomena simultaneously. Therefore, in order to tackle this issue, we begin our empirical analysis by plotting the wage polarization between high-and-medium-skilled, $\left (\frac{w_{H}}{w_{M}}\right )$ , and low-and-medium-skilled, $\left (\frac{w_{L}}{w_{M}}\right )$ , workers against measures of robot density and offshoring—see Figure 1.⁵ For this purpose, we have focused on examining 15 countries with large levels of operational industrial robots as well as high import rates of intermediate goods—Austria, Belgium, Denmark, France, Germany, Ireland, Italy, the Netherlands, Singapore, South Korea, Spain, Sweden, Switzerland, the UK, and the USA⁶— using data from 2002 to 2019.⁷ To measure the three variables linked to wage polarization ( $w_{H}$ , $w_{M}$ , $w_{L}$ ), we used the “average monthly earnings of employees by sex and occupation (in thousands)” dataset, based on the International Standard Classification of Occupations (ISCO) and the respective skill level, provided by the International Labor Organization (ILO). For the earnings of the most highly qualified workers, $w_{H}$ , we considered the average among the categories of occupations belonging to skill levels 3 and 4—(1) managers, senior officials, and legislators, (2) professionals, and (3) technicians and associate professionals—while for the wages of the medium qualified workers, $w_{M}$ , we took into account the average of the statistics reported among the categories falling within skill level 2—(4) clerks, (5) service and sales workers, (6) skilled agricultural and fishery workers, (7) craft and related trades workers, and (8) plant and machine operators, and assemblers. For the wages of low-skilled workers, $w_{L}$ , we included the data presented for the category belonging to skill level 1—(9) elementary occupations. Moreover, robot density was selected as the proxy to assess automation, calculated as the ratio between the number of operational industrial robots, retrieved from the International Federation of Robots, and the number of inhabitants, obtained from the World Bank database, in each country and each year. Finally, offshoring, targeted as a representative measure to analyze the trend in reallocations, was quantified as the intermediate goods imported from the world by the developed country, divided by the total quantity of intermediate goods imported and exported. The data were gathered by the World Integrated Trade Solution database.

Figure 1. Wage polarization, robot density, and offshoring, 2002–2019.

In Figure 1a and b, we plot the wage polarization among high-and-medium-skilled laborers on the vertical axis and the robot density and offshoring on the horizontal axis, respectively, as well as the fitted linear regression. Both slopes exhibit a significant and positive trend, indicating that advances in automation and reallocations correspond to higher earnings for high-skilled workers compared to medium-skilled employees. In Figure 1c and d, we instead plot the wage polarization among low-and-medium-skilled workers on the vertical axis and the robot density and offshoring on the horizontal axis, respectively, paired with the fitted line. In this case, while the plot in Figure 1d provides very similar findings to those above, indicating that progress in reallocations correlates with higher wages for low-skilled workers, the same cannot be said for the results presented in the graph in Figure 1c. In the latter chart, the plotted relationship between the two variables, together with the fitted regression line, does not exhibit strong statistical evidence of a significant correlation.

Furthermore, in order to clarify the findings presented in Figure 1, we implemented an empirical analysis by conducting unbalanced country-year-level panel data. Therefore, we specify the estimation equations for the wage polarization between high-medium-skilled and low-medium-skilled workers as:

(1) \begin{equation} \mathrm{log}\left (\frac{w_{H}}{w_{M}}\right )_{ct}=\beta _{0}+\beta _{1}\mathrm{log}\left (\textit{robot density}\right )_{ct}+\beta _{2}\left (\textit{offshoring}\right )_{ct}+\beta _{3}\left (\textit{controls}\right )_{ct}+\epsilon _{ct} \end{equation}

(2) \begin{equation} \mathrm{log}\left (\frac{w_{L}}{w_{M}}\right )_{ct}=\beta _{0}+\beta _{1}\mathrm{log}\left (robot\:density\right )_{ct}+\beta _{2}\!\left (offshoring\right )_{ct}+\beta _{3}\!\left (controls\right )_{ct}+\epsilon _{ct} \end{equation}

where $c$ indexes countries and $t$ is the time period. $\left (\frac{w_{H}}{w_{M}}\right )_{ct}$ and $\left (\frac{w_{L}}{w_{M}}\right )_{ct}$ are the outcomes of interest, denoting, following the same order, the ratio between the wages of high- and medium-skilled workers and the ratio between the wages of low- and medium-skilled workers. In its turn, $\left (\textit{robot density}\right )_{ct}$ and $\left (\textit{offshoring}\right )_{ct}$ are the measures adopted to assess the impact of automation and reallocations, respectively, as aforementioned. Lastly, both specifications include also $\left (\textit{controls}\right )_{ct}$ , which are country and year fixed effects and, following the same approach as education level ratios.⁸

Panels A and B of Table 1 show the estimates of wage polarization between the high- and medium-skilled workers equation (1) and wage polarization between the low- and medium-skilled workers equation (2). Both panels and columns incorporate country and year fixed effects, along with additional controls such as educational-level ratios. We find consistently significant positive estimates for automation and relocations in all other specifications. We focused our attention on columns (3) common to Panel A and Panel B, which are of greatest relevance to our analysis due to the fact that the effects are conditional to one another. Regarding Panel A, we noticed that a $1\%$ increase in robot density and a $1$ percentage point (pp) rise in offshoring ratio are associated, respectively, with a $0.0379\%$ and a $50.68\%$ average change in wage polarization between high-skilled and medium-skilled workers, ceteris paribus. We have also noted that a $1\%$ raise in robot density and a $1$ pp increase in the offshoring ratio lead, respectively, to an average variation of the wage polarization between low-skilled and medium-skilled workers of $0.0239\%$ and $31.48\%$ , ceteris paribus. Thus, according to the results presented, it should be noted that the reported positive coefficients imply both automation and relocation are possible conditional determinants of (two-sided) wage polarization, also conditional to one another. This constitutes sufficient empirical evidence to support a theoretical approach that considers both determinants together.

Table 1. Wage polarization estimates, 2002–2019

Notes: (i) HAC standard errors are in parentheses; (ii) ^*, ^**, and ^*** denote significant at 1%, 5%, and 10%, respectively.

3. The model

Based on an adaptation of the model proposed in Afonso and Pinho (2022), we develop a dynamic general equilibrium endogenous growth model where the aggregate output (i.e., the numeraire good) is produced by a continuum of nonroutine and routine tasks and is used in consumption and investment. The nonroutine sector is country-specific and is composed of tasks that require high-level abstract skills (nonroutine abstract/cognitive tasks) and others that require physical dexterity and proficiency in human interactions (nonroutine manual tasks). The routine sector, in turn, can be automated or relocated abroad by global firms (offshoring). Hence, routine tasks are performed by domestic high- and low-skilled workers, and nonroutine tasks are produced by medium-skilled workers in developed countries or by a mix of different types of workers in developing countries [Blanas et al. (2019)], where the representative worker in the developing country corresponds to the medium-skilled worker in the developed country. In either sector, nonroutine and routine, a continuum of competitive firms uses specific labor and specific quality-adjusted machines where quality is improved by vertical R&D. The machine sector consists of a continuum of monopolistic producers, each one using a specific design sold by the R&D sector. We intend to analyze the relative impact of automation and relocation (hence, trade) of routine tasks (offshoring) on competitiveness, wages, and economic growth. Relocations immediately affect the country’s competitiveness by decreasing the number of tasks produced in the developed country in contrast to automation. Both—offshoring and automation—provoked the emergence of some effects on wages—labor, market size, and price effects. The two last effects operate through the bias of technological-knowledge progress.⁹ Relocation and automation of tasks performed by medium-skilled workers immediately increase the relative labor supply—the labor effect—thus generating wage polarization. Furthermore, the technological-knowledge bias, generated by the dynamics of market size and price effects, also decisively affects wages, and the observed technological-knowledge progress affects economic growth. Economic growth frees up resources that become partially available for investment in R&D activities, thereby increasing the probability of successful research, which accelerates technological knowledge. The effects of aggregate technological knowledge affect firms’ productivity: when it increases, it generates higher demand and labor productivity. If technological-knowledge progress is biased toward the nonroutine sector, then it contributes to the emergence of wage polarization.

This section describes the economic setup of the closed economy in which infinitely lived households inelastically supply labor, maximize the utility of consumption from the aggregate final good, and invest in a firm’s equity. The inputs of the aggregate numeraire good, $Y$ , are two final goods, nonroutine ( $Y_{N}$ produced in the $N$ -sector) and routine ( $Y_{R}$ produced in the $R$ -sector), each one composed of many competitive firms that produce a continuum of tasks, that is, there are two sectors, $s=N$ and $s=R$ . In $s=N$ , there is a positive fixed level of high-skilled labor type, $L_{N}^{i}$ , and low-skilled labor type, $L_{N}^{h}$ . In $s=R$ , the production of the tasks can be carried out domestically by medium-skilled workers if automated, $L_{R}^{i}$ , or by foreign workers if relocated, $L_{R}^{h}$ . The continuum of tasks of each sector, $s=\{N,R\}$ , uses, in addition to the specific labor, a continuum of specific nondurable quality-adjusted machines,¹⁰ produced under monopolistic competition: the monopolist in industry $j$ uses a design, sold by the R&D sector and protected by a patent, and numeraire to produce at a price that maximizes profits. In the R&D sector, each potential entrant devotes numeraire to inventing successful vertical designs to be supplied to a new monopolist machine firm/industry, that is, R&D allows increasing (not the number, but) the quality of machines and, thus, the technological knowledge. Therefore, some endogenous technological knowledge complements high-skilled labor, low-skilled labor, medium-skilled labor, or foreign labor.

3.1. Preferences

Infinitely lived households obtain utility from the consumption, $C$ , of the unique aggregate final good, whose price we normalize to $1$ , and collect income from investments in financial assets (equity) and labor. They supply labor to both sectors, $s=\{N,R\}$ . Preferences are identical across workers $L_{N}^{i}$ , $L_{N}^{h}$ , $L_{R}^{i}$ , and $L_{R}^{h}$ . Thus, there is a representative household with preferences at time $t=0$ given by $U_{C}=\int _{0}^{\infty }\left (\frac{C(t)^{1-\theta }-1}{1-\theta }\right )e^{-\rho t}dt$ , where $\rho \gt 0$ is the subjective discount rate and $\theta \gt 0$ is the inverse of the inter-temporal elasticity of substitution. The flow budget constraint is

(3) \begin{equation} \dot{a}(t)=r(t)\cdot a(t)+\sum _{s=N,R}\left (w_{s}^{h}\cdot L_{s}^{h}+w_{s}^{i}\cdot L_{s}^{i}\right )-C(t), \end{equation}

where $a(t)=\sum _{s=N,R}\left [a_{s}^{h}(t)+a_{s}^{i}(t)\right ]$ denotes household’s real financial assets/wealth holdings (composed of equity of machine producers, considering the profits seized by the top-quality producers), $r$ is the real interest rate, and $w_{s}^{h}$ and $w_{s}^{i}$ are the wage for labor type $h$ and $i$ employed in sector $s=\{N,R\}$ , respectively. The initial level of wealth $a(0)$ is given, and the non-Ponzi games condition $\lim _{t\rightarrow \infty }e^{-\int _{0}^{t}r(s)ds}a(t)\geq 0$ is imposed. The representative household chooses the path of aggregate consumption $\left [C(t)\right ]_{t\geq 0}$ to maximize the discounted lifetime utility, resulting in the following optimal consumption path Euler equation:

(4) \begin{equation} \frac{\dot{C}(t)}{C(t)}=g=\frac{1}{\theta }\cdot \left [r(t)-\rho \right ]. \end{equation}

Moreover, the transversality condition is also standard: $\underset{t\rightarrow \infty }{lim}e^{-\rho t}\cdot C(t)^{-\theta }\cdot a(t)=0$ .

3.2. Technologies, output, and prices

3.2.1. Aggregate economy

The aggregate output $Y$ is produced with a CES aggregate production function of nonroutine and routine competitively produced final goods:

(5) \begin{equation} \begin{array}{ccc} Y(t) & =\left [\sum _{s=N,R}\chi _{s}\cdot Y_{s}(t)^{\frac{\varepsilon -1}{\varepsilon }}\right ]^{\frac{\varepsilon }{\varepsilon -1}} &,\end{array}\;\varepsilon \in \left (0,+\infty \right ), \end{equation}

where $Y_{N}$ and $Y_{R}$ are the total outputs of the $N$ - and the $R$ -sector, respectively, $\chi _{N}$ and $\chi _{R}$ , with $\sum _{s=N,R}\chi _{s}=1$ , are the distribution parameters, measuring the importance of the sectors, and $\varepsilon \geq 0$ is the elasticity of substitution between sectors, wherein $\varepsilon \gt 1$ $\left (\varepsilon \lt 1\right )$ means that they are gross substitutes (complements) in the production of $Y$ . The assumption of competitive final-good firms implies the following maximization problem: $\max _{Y_{s}}\,\Pi _{Y}=P_{Y}\cdot Y-\sum _{s=N,R}P_{s}\cdot Y_{s}$ . From the first-order conditions emerge the inverse demand for $Y_{s}$ :¹¹

(6) \begin{equation} \frac{P_{s}}{P_{Y}}=\chi _{s}\left (\frac{Y}{Y_{s}}\right )^{\frac{1}{\varepsilon }}\Leftrightarrow Y_{s}=\left (\frac{P_{s}}{P_{Y}\cdot \chi _{s}}\right )^{-\varepsilon }Y. \end{equation}

Thus, we obtain the following expression for relative demand for output from the $N$ -sector:

(7) \begin{equation} \frac{Y_{N}}{Y_{R}}=\left (\frac{\chi _{N}}{\chi _{R}}\right )^{\epsilon }\left (\frac{P_{N}}{P_{R}}\right )^{-\epsilon }, \end{equation}

which depends positively on the $N$ -sector relative weight parameter and negatively on the $N$ -sector relative price of output. Replacing (6) in (5), we have that $P_{Y}=\left [\sum _{s=N,R}\chi _{s}^{\varepsilon }\cdot P_{s}^{1-\varepsilon }\right ]^{\frac{1}{1-\varepsilon }}$ , where $P_{N}$ and $P_{R}$ are the prices of the outputs of, respectively, the $N$ - and the $R$ -sector, and thus the right-hand side of the expression is the unit production cost. Summing across sectors, from (6) we have that $P_{Y}\cdot Y=P_{N}\cdot Y_{N}+P_{R}\cdot Y_{R}$ .

3.2.2. Sectors of the economy

The output $Y_{s}$ of each sector $s=\{N,R\}$ is produced in perfect competition by the following production function with constant returns to scale $Y_{s}=\exp\! \left (\int _{0}^{1}\ln Y_{v_{s}}dv_{s}\right )$ , that is, $Y_{s}$ is a continuum of the output produced by tasks $Y_{v_{s}}$ indexed, respectively, by $v_{N}\in \left [0,1\right ]$ and $v_{R}\in \left [0,1\right ]$ . Tasks $v_{R}$ are routine tasks. The producer of $Y_{s}$ maximizes profits given by ${{\Pi _{s}}}=P_{s}\cdot Y_{s}-\int _{0}^{1}P_{v_{s}}\cdot Y_{v_{s}}dv_{s}$ , where $P_{v_{s}}$ is the price of output of task $v_{s}$ , subject to the restriction imposed by the functional form of the production function of $Y$ . Assuming perfect competition, the maximization problem results in the following first-order conditions: $\frac{\partial{\Pi }_{s}}{\partial Y_{v_{s}}}=0\Rightarrow Y_{v_{s}}=\frac{P_{s}\cdot Y_{s}}{P_{v_{s}}}$ . From here $P_{v_{s}}\cdot Y_{v_{s}}=P_{s}\cdot Y_{s}$ , which can be replaced in the profits function and the production function results, respectively, in ${\Pi _{s}}=P_{s}\cdot Y_{s}-\int _{0}^{1}P_{s}\cdot Y_{s}dv_{s}=0$ and also in

(8) \begin{equation} Y_{s}=\exp\! \left (\int _{0}^{1}\ln \frac{P_{s}\cdot Y_{s}}{P_{v_{s}}}dv_{s}\right )\Leftrightarrow P_{s}=\exp\! \left (\int _{0}^{1}\ln P_{v_{s}}dv_{s}\right ). \end{equation}

3.2.3. Tasks in each sector

Task producers in sector $s=N$ must choose to produce them either with domestic low-skilled labor type “ $h$ ” or with domestic high-skilled labor type “ $i$ ,” and task producers in sector $s=R$ must choose to produce them with foreign labor, relocating tasks in developing countries “ $h$ ” or with domestic medium-skilled labor employed in automated tasks “ $i$ ,” which implies choosing between the following two Cobb–Douglas production functions:

(9) \begin{eqnarray} Y_{v_{s}}^{h}(t) & = & \left [\int _{0}^{J}\left (q^{k(j,t)}{{\cdot }}x_{v_{s}}^{h}(k,j,t)\right )^{1-\alpha }dj\right ]\left [\left (1-v_{s}(t)\right )\cdot l_{s}^{h}\cdot L_{v_{s}}^{h}\right ]^{\alpha }, \end{eqnarray}

(10) \begin{eqnarray} Y_{v_{s}}^{i}(t) & = & \left [\int _{J}^{1}\left (q^{k(j,t)}{{\cdot }}x_{v_{s}}^{i}(k,j,t)\right )^{1-\alpha }dj\right ]\left [v_{s}(t)\cdot l_{s}^{i}\cdot L_{v_{s}}^{i}\right ]^{\alpha }. \end{eqnarray}

Each uses two factors: labor of type $L_{N}^{i},$ $L_{N}^{h}$ , and $L_{R}^{i}$ —domestic—or $L_{R}^{h}$ —foreign—(the second term on the right-hand side) and intermediate goods—machines/robots—(the first term on the right-hand side) with a share in the income of $\alpha$ and $1-\alpha$ , respectively. Each machine $j$ used in $v_{s}$ production is quality-adjusted: the constant quality upgrade is $q\gt 1$ , $k$ is the top-quality rung at $t$ , and $x_{v_{s}}^{h}(k,j,t)$ and $x_{v_{s}}^{i}(k,j,t)$ represent the units of machines or robots demanded for task $v_{s}$ if it is produced to be used by $L_{s}^{h}$ or by $L_{s}^{i}$ , respectively. The labor term includes the quantities employed in the production of $v_{s}$ , $L_{v_{s}}^{i}$ or $L_{v_{s}}^{h}$ , and two types of corrective factors accounting for productivity differentials such that workers are assigned to tasks according to location and the most efficient firm in production, that is, we take into account:

• • The absolute net advantage of labor. For $s=N$ , we consider $l_{N}^{i}\gt l_{N}^{h}$ since $L_{N}^{i}$ is more qualified than $L_{N}^{h}$ , implying that $L_{N}^{i}$ operates in increasingly abstract/cognitive nonroutine tasks, while $L_{N}^{h}$ operates in “purely manual” nonroutine tasks. In $s=R$ , the production can be performed by foreign workers if relocated, $L_{R}^{h}$ ,¹² or by domestic medium-skilled workers if automated, $L_{R}^{i}$ , and the quantities used should be corrected by the term $l_{R}^{h}$ and $l_{R}^{i}$ due to factors that are specific to automation and relocations; we consider that $l_{R}^{i}\gt l_{R}^{h}$ since domestic medium-skilled labor has an absolute productivity advantage over foreign labor in developing countries.¹³

• • The relative productivity advantage of labor. Following the point of view proposed by, for example, Acemoglu and Zilibotti (2001), through the terms $(1-v_{s})$ and $v_{s}$ in (9) and (10), $L^{i}$ is relatively more productive in tasks indexed by larger $v_{s}$ and vice versa.

In each sector $s$ , there is substitutability between tasks that use labor type $h$ and tasks that use labor type $i$ . On the other hand, it is assumed that, regardless of the labor type used by sector $s$ , there is complementarity between labor and a specific set of machines or robots. To determine the tasks that use labor type “ $h$ ” and labor type “ $i$ ” in each sector, firstly, we need to solve the respective maximization problems:

(11) \begin{eqnarray} \max _{x_{v_{s}}^{h}(k,j,t),L_{v_{s}}^{h}}{{\Pi _{v_{s}}^{h}}}(t) & = & P_{v_{s}}^{h}(t){\cdot }Y_{v_{s}}^{h}(t)-\int _{0}^{J}p(k,j,t){{\cdot }}x_{v_{s}}^{h}(k,j,t){\cdot }dj-w_{s}^{h}(t)\cdot L_{v_{s}}^{h}, \end{eqnarray}

(12) \begin{eqnarray} \max _{x_{v_{s}}^{i}(k,j,t),L_{v_{s}}^{i}}{{\Pi _{v_{s}}^{i}}}(t) & = & P_{v_{s}}^{i}(t){\cdot }Y_{v_{s}}^{i}(t)-\int _{J}^{1}p(k,j,t){{\cdot }}x_{v_{s}}^{i}(k,j,t){\cdot }dj-w_{s}^{i}(t)\cdot L_{v_{s}}^{i}, \end{eqnarray}

bearing in mind (9) and (10), where $P_{v_{s}}^{h}(t)$ and $P_{v_{s}}^{i}(t)$ are the price of task $v_{s}$ produced by labor type $h$ and $i$ , respectively, at time $t$ , $p(k,j,t)$ denotes the price paid for the machine $j$ with quality $k$ , at time $t$ , $w_{s}^{h}(t)$ and $w_{s}^{i}(t)$ are the price of each unit of labor type $h$ and $i$ , respectively, at time $t$ —these prices are given for the perfectly competitive producers of the tasks. From the first-order conditions with respect to machines/robots results:

(13) \begin{eqnarray} x_{v_{s}}^{h}(k,j,t) & = & \left [\frac{P_{v_{s}}^{h}(t)\cdot (1-\alpha )}{p(k,j,t)}\right ]^{\frac{1}{\alpha }}\cdot q^{k(j,t)\frac{1-\alpha }{\alpha }}\cdot \left (1-v_{s}(t)\right )\cdot l_{s}^{h}\cdot L_{v_{s}}^{h}, \end{eqnarray}

(14) \begin{eqnarray} x_{v_{s}}^{i}(k,j,t) & = & \left [\frac{P_{v_{s}}^{i}(t)\cdot (1-\alpha )}{p(k,j,t)}\right ]^{\frac{1}{\alpha }}\cdot q^{k(j,t)\frac{1-\alpha }{\alpha }}\cdot v_{s}(t)\cdot l_{s}^{i}\cdot L_{v_{s}}^{i}. \end{eqnarray}

Replacing (13) and (14) in the corresponding production functions (9) and (10), we have that:

(15) \begin{eqnarray} Y_{v_{s}}^{h}(t) & = & \left [\frac{P_{v_{s}}^{h}(t)\cdot (1-\alpha )}{p(k,j,t)}\right ]^{\frac{1-\alpha }{\alpha }}\cdot Q_{s}^{h}(t)\cdot \left (1-v_{s}(t)\right )\cdot l_{s}^{h}\cdot L_{v_{s}}^{h}, \end{eqnarray}

(16) \begin{eqnarray} Y_{v_{s}}^{i}(t) & = & \left [\frac{P_{v_{s}}^{i}(t)\cdot (1-\alpha )}{p(k,j,t)}\right ]^{\frac{1-\alpha }{\alpha }}\cdot Q_{s}^{i}(t)\cdot v_{s}(t)\cdot l_{s}^{i}\cdot L_{v_{s}}^{i} \end{eqnarray}

where $Q_{s}^{h}\equiv \int _{0}^{J}q^{k(j,t)\frac{1-\alpha }{\alpha }}dj$ and $Q_{s}^{i}\equiv \int _{J}^{1}q^{k(j,t)\frac{1-\alpha }{\alpha }}dj$ are measures of the quality level of machines/robots used in sector $s$ to be endogenously determined in Section 3, thereby originating the dynamic effects of the model.

3.2.4. Wages and threshold task in each sector

From the first-order conditions with respect to labor units results:

(17) \begin{eqnarray} w_{s}^{h}(t) & = & \left [P_{v_{s}}^{h}(t)\right ]^{\frac{1}{\alpha }}\cdot \left [\frac{1-\alpha }{p(k,j,t)}\right ]^{\frac{1-\alpha }{\alpha }}\cdot Q_{s}^{h}(t)\cdot \left (1-v_{s}(t)\right )\cdot l_{s}^{h}, \end{eqnarray}

(18) \begin{eqnarray} w_{s}^{i}(t) & = & \left [P_{v_{s}}^{i}(t)\right ]^{\frac{1}{\alpha }}\cdot \left [\frac{1-\alpha }{p(k,j,t)}\right ]^{\frac{1-\alpha }{\alpha }}\cdot Q_{s}^{i}(t)\cdot v_{s}(t)\cdot l_{s}^{i} \end{eqnarray}

In equilibrium, there is a threshold task $v_{s}$ , that ensures that each type of labor gets the same wage regardless of the task it is used for. To this end, we can define the following price indexes:

(19) \begin{equation} \left [P_{s}^{h}(t)\right ]^{\frac{1}{\alpha }}=\left [P_{v_{s}}^{h}(t)\right ]^{\frac{1}{\alpha }}\cdot \left (1-v_{s}(t)\right )\,{and}\,\left [P_{s}^{i}(t)\right ]^{\frac{1}{\alpha }}=\left [P_{v_{s}}^{i}(t)\right ]^{\frac{1}{\alpha }}\cdot v_{s}(t). \end{equation}

As shown in Appendix A.1, in sector $s=\{N,R\}$ (i) tasks with a very low (high) $v_{s}$ have a lower price if produced by $L_{s}^{h}$ ( $L_{s}^{i}$ ) rather than $L_{s}^{i}$ ( $L_{s}^{h}$ ), such that perfectly competitive producers use $L_{s}^{h}$ ( $L_{s}^{i}$ ) to avoid being driven out of the market, and (ii) there is a threshold task $v_{s},$ where prices are equal and is given by the following expression:

(20) \begin{equation} \overline{v}_{s}=\left [1+\left (\frac{Q_{s}^{i}}{Q_{s}^{h}}\frac{l_{s}^{i}}{l_{s}^{h}}\frac{L_{s}^{i}}{L_{s}^{h}}\right )^{\frac{1}{2}}\right ]^{-1}, \end{equation}

which assesses the “comparative advantage” of sector $s$ . Therefore, if $\overline{v}_{s}\lt v_{s}$ firms will be biased toward producing tasks using both labor type $h$ and the respective technological-knowledge level of each intermediate goods set, in sector $s$ , while if $\overline{v}_{s}\gt v_{s}$ firms will be biased toward producing tasks using both labor type $i$ and the respective technological-knowledge level of each intermediate goods set, in sector $s.$

In particular, whenever labor abroad becomes more productive,¹⁴ that is, $l_{R}^{h}$ increases, boosting the number of tasks relocated and promoting globalization. Automation, on the other hand, makes the use of domestic medium-skilled labor less advantageous, translating into a decrease of $l_{R}^{i}$ that negatively affects the production of routine tasks at home, thus favoring globalization. Finally, an increase in the technological-knowledge bias toward high-skilled workers decreases the incentive for automation and relocations. On the contrary, an increase in the technological-knowledge bias toward low-skilled workers increases the incentive for automation and relocations. Thus, improvements in the machines or robots’ technology that are biased toward low-skilled tasks would increase automation and relocations.

3.3. Machines sector

In the machines sector, producing the top quality $k$ of each $j$ needs an initial R&D cost to achieve the new prototype/design. This initial cost can only be recovered if, with the production of the new quality of the robot, profits are made over a certain time in the future. This is assured by a system of intellectual property rights that protect the leader firm’s monopoly. At the same time, this technological knowledge is accessible, practically free of charge, from other firms. Hence, each firm that holds the patent for the top quality $k$ of $j$ at $t$ supplies all respective tasks, $v_{s}$ , in sector $s=\{N,R\}$ . If we consider that each unit of robot $j$ requires one unit of final output $Y$ , since its price is 1 to 1 and the producer of $j$ gets profits $\pi _{s}(k,j,t)=\left [p(k,j,t)-1\right ]\cdot x_{s}(k,j,t)$ , where $x_{s}(k,j,t)=\int _{0}^{\overline{v}_{s}}x_{v_{s}}^{h}(k,j,t)\cdot dv_{s}+\int _{\overline{v}_{s}}^{1}x_{v_{s}}^{i}(k,j,t)\cdot dv_{s}$ is the demand for robot $j$ from all the producers of tasks $v_{s}$ that use such input, regardless of the labor type used in tasks.

Assuming that the monopolist charges the same price, $p(k,j,t)$ , for all these firms, we can find the optimal price by replacing $x_{s}(k,j,t)$ by the demand of the producer of a single task $v_{s}$ , that is, either by $x_{v_{s}}^{h}(k,j,t)$ or by $x_{v_{s}}^{i}(k,j,t)$ and then maximizing with respect to $p(k,j,t)$ . This can be seen by $\pi _{s}(k,j,t)=\int _{0}^{1}\pi _{v_{s}}(k,j,t)\cdot dv_{s}=\underbrace{\int _{0}^{\overline{v}_{s}}\pi _{v_{s}}^{h}(k,j,t)\cdot dv_{s}}_{\pi _{v_{s}}^{h}(k,j,t)}+\underbrace{\int _{\overline{v}_{s}}^{1}\pi _{v_{s}}^{i}(k,j,t)\cdot dv_{s}}_{\pi _{v_{s}}^{i}(k,j,t)}$ , where $\pi _{v_{s}}^{h}(k,j,t)$ and $\pi _{v_{s}}^{i}(k,j,t)$ denote the profits of the producer of $j$ for selling this robot to the producer of task $v_{s}$ . Therefore, we can find $p(k,j,t)$ by solving the following maximization problems $\max _{p(k,j,t)}\left [p(k,j,t)-1\right ]\cdot x_{v_{s}}^{h}(k,j,t)$ and $\max _{p(k,j,t)}\left [p(k,j,t)-1\right ]\cdot x_{v_{s}}^{i}(k,j,t)$ , where $x_{v_{s}}^{h}(k,j,t)$ and $x_{v_{s}}^{i}(k,j,t)$ can be done by (13) or (14). From the first-order condition $\frac{\partial \pi _{s}(k,j,t)}{\partial p(k,j,t)}$ , we have that $p(k,j,t)\equiv p=\frac{1}{1-\alpha }=q$ , assuming that the limit pricing strategy is binding.¹⁵ Taking also into account $p=q$ , (19), (13), and (14), the demand for the machine $j$ used in sector $s$ together with $L_{s}^{h}$ and $L_{s}^{i}$ is, respectively,

(21) \begin{eqnarray} x_{s}^{h}(t) & = & \int _{0}^{\overline{v}_{s}}x_{v_{s}}^{h}(k,j,t)\cdot dv_{s}=\left [\frac{P_{s}^{h}(t)\cdot (1-\alpha )}{q}\right ]^{\frac{1}{\alpha }}\cdot Q_{s}^{h}(t)\cdot l_{s}^{h}\cdot L_{s}^{h}, \end{eqnarray}

(22) \begin{eqnarray} x_{s}^{i}(t) & = & \int _{\overline{v}_{s}}^{1}x_{v_{s}}^{i}(k,j,t)\cdot dv_{s}=\left [\frac{P_{s}^{i}(t)\cdot (1-\alpha )}{q}\right ]^{\frac{1}{\alpha }}\cdot Q_{s}^{i}(t)\cdot l_{s}^{i}\cdot L_{s}^{i}. \end{eqnarray}

Total demand for robot $j$ used in sector $s$ is $X_{s}(j)=x_{s}^{h}(k,j,t)+x_{s}^{i}(k,j,t)$ , and the profits for the machines used in sector $s$ by labor type $h$ and $i$ are $\pi _{s}^{h}(t)=\left (q-1\right )\cdot x_{s}^{h}(t)$ and $\pi _{s}^{i}(k,j,t)=\left (q-1\right )\cdot x_{s}^{i}(t)$ , respectively.

3.4. Allocation of resources

Once determined the threshold task as in (20), we can start by determining absolute values for price indexes. To this end, we use the definition of the price of output underlying the producer’s output maximization problem in sector $s$ , $Y_{s}$ , which implies $P_{s}=\exp\! \left (\int _{0}^{1}\ln P_{v_{s}}dv_{s}\right )$ —see (8). We also make use of the result that the value of each task, $P_{v_{s}}Y_{v_{s}}$ , is a constant for all $v_{s}$ , and we use (19) and (20) to have $P_{s}^{i}=\left (\frac{\overline{v}_{s}}{1-\overline{v}_{s}}\right )^{\alpha }P_{s}^{h}$ . From this analysis, we obtain the following expressions—see Appendix A.2:

(23) \begin{equation} P_{s}^{h}=P_{s}\cdot \exp\! \!\left (-\alpha \right )\cdot \overline{v}_{s}^{-\alpha }\:\text{and}\:P_{s}^{i}=P_{s}\cdot \exp\! \left (-\alpha \right )\cdot \left (1-\overline{v}_{s}\right )^{-\alpha }\Rightarrow \frac{P_{s}^{i}}{P_{s}^{h}}=\left (\frac{Q_{s}^{i}}{Q_{s}^{h}}\frac{l_{s}^{i}}{l_{s}^{h}}\frac{L_{s}^{i}}{L_{s}^{h}}\right )^{-\frac{\alpha }{2}}, \end{equation}

where $P_{N}$ and $P_{R}$ are also determined in Appendix A.2. An increase in the labor level of sector $s$ has a market-size effect on the demand for machines through the term $\overline{v}_{s}$ . However, by affecting $\overline{v}_{s}$ the same effect has, in addition, a price effect since it increases the supply of output of sector $s$ that induces a decrease in the absolute price of this output and, therefore, a decrease in the price index of tasks in the sector. This decreases the output of each task, which decreases the demand for machines in the sector—see (21) and (22).

From the profit maximization problem of the producer of $Y$ and since in each sector some tasks are produced by labor $L_{s}^{h}$ and other parts are performed by labor $L_{s}^{i}$ , the aggregate output is the following: $P_{s}Y_{s}=\int _{0}^{1}P_{v_{s}}Y_{v_{s}}dv_{s}$ $=\int _{0}^{\overline{v}_{s}}P_{v_{s}}^{h}Y_{v_{s}}^{h}dv_{s}+\int _{\overline{v}_{s}}^{1}P_{v_{s}}^{i}Y_{v_{s}}^{i}dv_{s}$ $=P_{s}Y_{s}^{h}+P_{s}Y_{s}^{i}$ . On the basis of these definitions and taking into account (15), (16), (19), and (23), the outputs in sector $s$ performed by labor type $L_{s}^{h}$ , $Y_{s}^{h}$ , and labor type $L_{s}^{i}$ , $Y_{s}^{L_{s}^{i}}$ , are as follows:

(24) \begin{eqnarray} Y_{s}^{h} & = & \exp\! \left (-1\right )\cdot \left [\frac{P_{s}\cdot (1-\alpha )}{q}\right ]^{\frac{1-\alpha }{\alpha }}\cdot \frac{Q_{s}^{h}\cdot l_{s}^{h}\cdot L_{s}^{h}}{\overline{v}_{s}}, \end{eqnarray}

(25) \begin{eqnarray} Y_{s}^{i} & = & \exp\! \left (-1\right )\cdot \left [\frac{P_{s}\cdot (1-\alpha )}{q}\right ]^{\frac{1-\alpha }{\alpha }}\cdot \frac{Q_{s}^{i}\cdot l_{s}^{i}\cdot L_{s}^{i}}{1-\overline{v}_{s}}. \end{eqnarray}

We can use equations (24) and (25) to obtain the intra-country output ratio and the output of each sector as:

(26) \begin{equation} Y_{s}=\exp\! \left (-1\right )\cdot \left [\frac{P_{s}\cdot (1-\alpha )}{q}\right ]^{\frac{1-\alpha }{\alpha }}\cdot M_{s}, \end{equation}

where, bearing in mind (20), $M_{s}=\frac{Q_{s}\cdot l_{s}^{h}\cdot L_{s}^{h}}{\overline{v}_{s}}+\frac{Q_{s}\cdot l_{s}^{i}\cdot L_{s}^{i}}{1-\overline{v}_{s}}=$ $\left [\left (Q_{s}^{h}\cdot l_{s}^{h}\cdot L_{s}^{h}\right )^{\frac{1}{2}}+\left (Q_{s}^{i}\cdot l_{s}^{i}\cdot L_{s}^{i}\right )^{\frac{1}{2}}\right ]^{2}$ evaluates the market size. Similarly, we can obtain an expression for machines produced for each sector $s$ :

(27) \begin{equation} X_{s}=\exp\! (-1)\cdot \left [\frac{P_{s}\cdotp (1-\alpha )}{q}\right ]^{\frac{1}{\alpha }}\cdot M_{s}, \end{equation}

where the aggregate resources devoted to machines production in sector $s$ , $X_{s}$ , is also expressible as a function of the currently given technological knowledge in each sector $s$ .

The output performed by each labor type in each sector, $Y_{s}^{h}$ and $Y_{s}^{i}$ , and the output of sector $s$ , $Y_{s}$ , can increase in response to advancements in technological-knowledge levels. Moreover, a rise in the labor levels implies, (i) an increase in the output produced and, thereby, in the relative demand for machines, with an increase in the labor levels due to scale effects—through the terms $L_{s}^{h}$ or $L_{s}^{i}$ ; (ii) a decrease in the output produced and, thereby, in the relative demand for machines, due to price effects through the terms $\left (\overline{v}_{s}\right )^{-1}$ and $(1-\overline{v}_{s})^{-1}$ , since it increases the share of tasks produced by the respective labor type, which decreases the price index where such an increase took place.

Moreover, bearing in mind (26) the computed inter-sector output ratio is

(28) \begin{equation} \frac{Y_{N}}{Y_{R}}=\left (\frac{\chi _{N}}{\chi _{R}}\right )^{\frac{\epsilon -\alpha \epsilon }{1-\alpha +\epsilon \alpha }}\cdot \left (\frac{M_{N}}{M_{R}}\right )^{\frac{\epsilon \alpha }{1-\alpha +\epsilon \alpha }}. \end{equation}

Furthermore, from (7) and considering (26), the relative price of the output in the $N$ -sector is—see Appendix A.2:

(29) \begin{equation} \left (\frac{P_{N}}{P_{R}}\right )=\left (\frac{\chi _{R}}{\chi _{N}}\right )^{-\frac{\epsilon \alpha }{\epsilon \alpha +1-\alpha }}\cdot \left (\frac{M_{N}}{M_{R}}\right )^{-\frac{\alpha }{\epsilon \alpha +1-\alpha }}. \end{equation}

The intuition behind (29) can be grasped by taking into account that an increase in the relative relevance of the $N$ -sector in the production of the aggregate final good, $\frac{\chi _{N}}{\chi _{R}}$ , increases the relative demand for output in this sector which leads to an increase in relative prices. Hence, through $M_{N}$ and $M_{R}$ , (29) shows that if either the technological knowledge is highly $N$ -biased or if there is a large relative supply of $N$ , the output of the $N$ -sector is large—see (28), which implies a low relative price of the $N$ -sector. In this case, the demand for $N$ -machines is low, which discourages R&D activities aimed at improving their quality, as we will see below. Thus, labor structure affects the direction of R&D through the price channel and/or by the market-size channel. This latter channel may or may not be removed, eliminated, or not in conducting the economic mechanisms.

The question of wages for labor type $L_{s}^{i}$ and $L_{s}^{h}$ and the differences in wages that can be established still need to be addressed. From (19), the wages in (17) and (18) can be rewritten in the form:

(30) \begin{eqnarray} w_{s}^{h}(t) & = & \left [P_{s}^{h}(t)\right ]^{\frac{1}{\alpha }}\cdot \left (\frac{1-\alpha }{q}\right )^{\frac{1-\alpha }{\alpha }}\cdot Q_{s}^{h}(t)\cdot l_{s}^{h}, \end{eqnarray}

(31) \begin{eqnarray} w_{s}^{i}(t) & = & \left [P_{s}^{i}(t)\right ]^{\frac{1}{\alpha }}\cdot \left (\frac{1-\alpha }{q}\right )^{\frac{1-\alpha }{\alpha }}\cdot Q_{s}^{i}(t)\cdot l_{s}^{i}. \end{eqnarray}

Moreover, we can obtain wage differentials between types of labor in each sector $s$ , $\frac{w_{s}^{i}}{w_{s}^{h}}=\left (\frac{Q_{s}^{i}\cdot l_{s}^{i}}{Q_{s}^{h}\cdot l_{s}^{h}}\frac{L_{s}^{h}}{L_{s}^{i}}\right )^{\frac{1}{2}}$ , that allow us to obtain the (domestic) steady-state skill premium and the inter-country wage inequality in favor of the domestic country which are, respectively:

(32) \begin{equation} \frac{w_{N}^{i}}{w_{N}^{h}}=\left (\frac{Q_{N}^{i}\cdot l_{N}^{i}}{Q_{N}^{h}\cdot l_{N}^{h}}\frac{L_{N}^{h}}{L_{N}^{i}}\right )^{\frac{1}{2}}\:\text{and}\:\frac{w_{R}^{i}}{w_{R}^{h}}=\left (\frac{Q_{R}^{i}\cdot l_{R}^{i}}{Q_{R}^{h}\cdot l_{R}^{h}}\frac{L_{R}^{h}}{L_{R}^{i}}\right )^{\frac{1}{2}} \end{equation}

Finally, from (17), (18) [or (30) and (31)], (19), (20), and (23), we obtain the wage polarization in favor of domestic (nonroutine) high- and low-skilled workers:

(33) \begin{eqnarray} \frac{w_{N}^{i}}{w_{R}^{i}} & = & \left (\frac{\chi _{N}}{\chi _{R}}\right )^{\frac{\epsilon }{\epsilon \alpha +1-\alpha }}\cdot \left (\frac{M_{N}}{M_{R}}\right )^{-\frac{1}{\epsilon \alpha +1-\alpha }+\frac{1}{2}}\cdot \left (\frac{Q_{N}^{i}}{Q_{R}^{i}}\cdot \frac{l_{N}^{i}}{l_{R}^{i}}\cdot \frac{L_{R}^{i}}{L_{N}^{i}}\right )^{\frac{1}{2}}, \end{eqnarray}

(34) \begin{eqnarray} \frac{w_{N}^{h}}{w_{R}^{i}} & = & \left (\frac{\chi _{N}}{\chi _{R}}\right )^{\frac{\epsilon }{\epsilon \alpha +1-\alpha }}\cdot \left (\frac{M_{N}}{M_{R}}\right )^{-\frac{1}{\epsilon \alpha +1-\alpha }+\frac{1}{2}}\cdot \left (\frac{Q_{N}^{h}}{Q_{R}^{i}}\frac{l_{N}^{h}}{l_{R}^{i}}\frac{L_{R}^{i}}{L_{N}^{h}}\right )^{\frac{1}{2}}. \end{eqnarray}

Hence, from (32), both domestic skill premium and the inter-country wage inequality in favor of the domestic country are decreasing in the relative supply factor, since the more abundant factor is substituted for the less abundant one, given, respectively, by $\frac{L_{N}^{h}}{L_{N}^{i}}$ and $\frac{L_{R}^{h}}{L_{R}^{i}}$ , and, increasing, in the absolute productivity advantage given, respectively, by $l_{N}^{i}$ and $l_{R}^{i}$ . Moreover, a rise in technological-knowledge biased toward both $N^{i}$ , in the skill premium function, and $R^{i}$ , in the inter-country wage inequality in favor of the domestic country function positively impacts wages. This rise fosters competitiveness within their respective sectors and improves the workers’ relative productivity.

Furthermore, within the same context, from (33) and (34), the wage polarization in favor of domestic (nonroutine) high- and low-skilled workers, respectively, is positively affected by a rise in the relative relevance of the $N$ -sector since it augments the relative demand for output in this sector that leads to an increase in the wage polarization, biased to high- and low-skilled employees. Moreover, if $\frac{\epsilon }{\epsilon \alpha +1-\alpha }\gt \frac{1}{2}$ and the market size dominates the price of the price effect channel, an increase either in the technological-knowledge highly $N$ -biased, an increase in the relative supply factor of $R$ -sector, or a decrease in the absolute productivity in the $R$ -sector stimulates significant wages improvements at the tails of the distribution.

These results can be interpreted as short-run results, as R&D has not been considered yet. The exposition of the R&D sector closes the model and allows for the calculation of steady-state or long-run results. In fact, R&D is also responsible for the transitional dynamics of the model. The following subsection describes the R&D sector.

3.5. R&D sector

By producing innovative designs, R&D activities drive the rate and the direction of technological knowledge, and thus wages and economic growth. Innovative designs for the manufacture of new qualities of the machines are patented, and the leader firm in each industry—the one that produces according to the latest patent—uses limit pricing to assure monopoly. The value of the leading-edge patent relies on the profit yields accruing during each time $t$ to the monopolist and on the duration of the monopoly power. The duration, in turn, depends on the probability of a new innovation, which creatively destroys the current leading-edge design [e.g., Aghion and Howitt (1992), Grossman and Helpman (1991, ch. 12), and Barro and Sala-i-Martin (2004, ch. 7)]. The probability of successful innovation is, thus, at the heart of the R&D activity. Let $\mathcal{I}_{s}^{h}(k,j,t)$ and $\mathcal{I}_{s}^{i}(k,j,t)$ denote the instantaneous probability at time $t$ in sector $s$ for, respectively, $h$ and $i$ —a Poisson arrival rate—of successful innovation in the next higher quality $\left [k(j,t)+1\right ]$ in machine $j$ given current rung quality $k$ . We define it as follows:

(35) \begin{eqnarray} \mathcal{I}_{s}^{h}(k,j,t) & = & e_{s}^{h}(k,j,t)\cdot \beta q^{k(j,t)}\cdot \zeta ^{-1}q^{-\alpha ^{-1}k(j,t)}\cdot (L_{s}^{h})^{-\xi }, \end{eqnarray}

(36) \begin{eqnarray} \mathcal{I}_{s}^{i}(k,j,t) & = & e_{s}^{i}(k,j,t)\cdot \beta q^{k(j,t)}\cdot \zeta ^{-1}q^{-\alpha ^{-1}k(j,t)}\cdot (L_{s}^{i})^{-\xi }. \end{eqnarray}

where, for example, following Afonso and Sequeira (2023): (i) $e_{s}^{h}(k,j,t)$ and $e_{s}^{i}(k,j,t)$ are the flow of domestic final-good resources devoted to R&D in $j$ belonging to $s$ for, respectively, $h$ and $i$ , which define our framework as a lab equipment model; (ii) $\beta$ $q^{k(j,t)}$ , $\beta \gt 0$ , is the learning-by-past domestic R&D, as a positive learning effect of public knowledge accumulated from past successful R&D; (iii) $\zeta ^{-1}q^{-\alpha ^{-1}k(j,t)}$ , $\zeta \gt 0$ , is the adverse effect—the cost of complexity—caused by the increasing complexity of quality improvements;¹⁶ (iv) $(L_{s}^{h})^{-\xi }$ and $(L_{s}^{i})^{-\xi }$ , with $\xi \geq 0$ , are the adverse effects of market size, capturing the idea that the difficulty of introducing new quality machines and replacing old ones is proportional to the respective labor units in sector $s$ . The scale benefits on profits can be partially ( $0\lt \xi \lt 1$ ) or totally ( $\xi =1$ ) removed and thus allows us to remove (explicit) scale effects on the economic growth rate [e.g., Jones (1995) and Sequeira et al. (2018)]. However if $\xi \gt 1$ , we would have (negative) scale effects. That is, for reasons of simplicity, we reflect in R&D the costs of scale increasing, due to coordination among agents, processing of ideas, and informational, organizational, marketing, and transportation costs [e.g., Dinopoulos and Thompson (1999)].

We consider that the probability of innovation presented above is similar for incumbents and entrants. Thus, R&D is conducted by entrants, as shown in Appendix A.3. The value of the leading-edge patent for the producer of an intermediate good $j$ belonging to $s$ and used by, respectively, $h$ and $i$ , with quality level $k$ at time $t$ is the expected present value of the flow of profits given by the following equations:¹⁷ $V_{s}^{i}(j,k,t,T(k))=\int _{t}^{t+T(k)}\pi _{s}^{i}(j,s)\exp\! \left (-\int _{t}^{s}r(w)dw\right )ds$ and $V_{s}^{h}(j,k,t,T(k))=\int _{t}^{t+T(k)}\pi _{s}^{h}(j,s)\exp\! \left (-\int _{t}^{s}r(w)dw\right )ds$ , where $T(k)$ is the duration of the patent during which there is no innovation in the quality level of intermediate good $j$ by another entrant.¹⁸

Given the functional forms (35) and (36) of the probabilities of success in R&D, which rely on the resources—composite final goods—allocated to it, free-entry equilibrium is defined by the equality between expected revenue, $\mathcal{I}_{s}^{h}(j,t)\cdot V_{s}^{h}(j,t)$ and $\mathcal{I}_{s}^{i}(j,t)\cdot V_{s}^{i}(j,t)$ , and resources spent, $e_{s}^{h}(j,t)$ and $e_{s}^{i}(j,t)$ . By considering free entry in R&D activities, free access to the R&D technology, and a proportional relationship between successful R&D and the share of R&D effort, the R&D spending aimed at, for example, improving $j$ should equal the expected payoff generated by the innovation, that is,

(37) \begin{equation} \mathcal{I}_{s}^{h}(k,j,t)\cdot V_{s}^{h}(j,t)=e_{s}^{h}(j,t)\:and\:\mathcal{I}_{s}^{i}(k,j,t)\cdot V_{s}^{i}(j,t)=e_{s}^{i}(j,t). \end{equation}

Assuming that all the prices and quantities are fixed during the time in which there are no quality improvements [e.g., Aghion and Howitt (1992), Barro and Sala-i-Martin (2004), and Gil et al. (2013)], then we have that—see Appendix A.4:

(38) \begin{equation}{V_{s}^{h}(j,k,t)=\frac{\pi _{s}^{h}(j,k,t)}{r(t)+\mathcal{I}_{s}^{h}(j,t)}\:and\:V_{s}^{i}(j,k,t)=\frac{\pi _{s}^{i}(j,k,t)}{r(t)+\mathcal{I}_{s}^{i}(j,t)}}{,} \end{equation}

and can be seen as the no-arbitrage condition, where $V_{s}^{h}\left (k,j,t\right )\cdot r\left (t\right )$ and $V_{s}^{i}\left (k,j,t\right )\cdot r\left (t\right )$ , the expected income generated by a successful innovation at time $t$ on rung $k$ , equals the profit flow, $\pi _{s}^{h}(j,k,t)$ and $\pi _{s}^{i}(j,k,t)$ , minus the expected capital loss, $V_{s}^{h}\left (k,j,t\right )\cdot \mathcal{I}_{s}^{h}\left (j,\tau \right )$ and $V_{s}^{i}\left (k,j,t\right )\cdot \mathcal{I}_{s}^{i}\left (j,\tau \right )$ . Then plugging (38) into (37) and solving for $\mathcal{I}_{s}^{h}$ and $\mathcal{I}_{s}^{i}$ , the equilibrium probability of successful innovation in sector $s$ and for $h$ and $i$ are, respectively—given the interest rate and the price indexes of final goods:

(39) \begin{eqnarray} \mathcal{I}_{s}^{h}(t) & = & \frac{\beta }{\zeta }\cdot \left (\frac{q-1}{q}\right )\cdot \exp\! \left (-1\right )\cdot \left [\left (1-\alpha \right )\cdot P_{s}^{h}\right ]^{\frac{1}{\alpha }}\cdot l_{s}^{h}\cdot (L_{s}^{h})^{1-\xi }-r(t), \end{eqnarray}

(40) \begin{eqnarray} \mathcal{I}_{s}^{i}(t) & = & \frac{\beta }{\zeta }\cdot \left (\frac{q-1}{q}\right )\cdot \exp\! \left (-1\right )\cdot \left [\left (1-\alpha \right )\cdot P_{s}^{i}\right ]^{\frac{1}{\alpha }}\cdot l_{s}^{i}\cdot (L_{s}^{i})^{1-\xi }-r(t). \end{eqnarray}

The equilibrium $\mathcal{I}_{s}^{i}(t)$ and $\mathcal{I}_{s}^{h}(t)$ in (35) and (40) are, respectively, independent of $j$ and $k$ since the removal of the scale of technological-knowledge effects—see the exponents of $q$ in the demand of intermediate goods above, which impacts the expression of profits, and in equations (35) and (36).

Finally, from the definition of the probabilities of achieving higher quality rungs (35) and (40), and since, by definition, $\mathcal{I}_{s}^{h}(k,j,t)$ and $\mathcal{I}_{s}^{i}(k,j,t)$ do not differentiate between different machines belonging to the same sector, we have that:

(41) \begin{equation} E_{s}(t)=\underbrace{\int _{0}^{J}e_{s}^{h}(k,j,t)dj}_{E_{s}^{h}(t)}+\underbrace{\int _{J}^{1}e_{s}^{i}(k,j,t)dj}_{E_{s}^{i}(t)}=\mathcal{I}_{s}^{h}(k,j,t)\cdot \frac{\zeta }{\beta }\cdot Q_{s}^{h}\cdot (L_{s}^{h})^{\xi }+\mathcal{I}_{s}^{i}(k,j,t)\cdot \frac{\zeta }{\beta }\cdot Q_{s}^{i}\cdot (L_{s}^{i})^{\xi }, \end{equation}

and thus more resources devoted to R&D are needed as $Q_{s}^{h}$ and $Q_{s}^{i}$ rise to offset the greater difficulty of R&D when $Q_{s}^{h}$ and $Q_{s}^{i}$ increase.

The following section derives the general equilibrium of the model, as well as our main long-run results.

4. General equilibrium

As the economic structure has been characterized for given states of technological knowledge, $Q_{s}^{h}$ and $Q_{s}^{i}$ , we now proceed to characterize the general equilibrium, considering that firms, like households, are always rational and solve their problems, and markets clear. We derive the law of motion of the distinct technological-knowledge indexes, which drive the path of all macroeconomic aggregates—see (26), (27), and (41), including consumption, as will be clear after deriving the aggregate resource constraint. We also derive the technological-knowledge bias in the nonroutine sector $s=N$ , and the routine sector $s=R$ .

4.1. Technological-knowledge indexes and bias

If a new quality of machine $j$ is introduced, the rate of change in the quality index of sector $s$ used by, for example, labor type $h$ is the following: $\varDelta Q_{s}^{h}(t)=Q_{s}^{h}\left (k+1,t\right )-Q_{s}^{h}(k,t)=\int _{0}^{J}q^{\left [k(j,t)+1\right ]\left (\frac{1-\alpha }{\alpha }\right )}-\int _{0}^{J}q^{k(j,t)\left (\frac{1-\alpha }{\alpha }\right )}$ and thus $\frac{\varDelta Q_{s}^{h}}{Q_{s}^{h}}=\left [q^{\left (\frac{1-\alpha }{\alpha }\right )}-1\right ]$ . Since the probability of this occurring per unit of time is given by $\mathcal{I}_{s}^{h}(t)$ , we have that:

(42) \begin{align} \frac{\dot{Q_{s}^{h}}}{Q_{s}^{h}}&=\mathcal{I}_{s}^{h}(t)\cdot \left [q^{\left (\frac{1-\alpha }{\alpha }\right )}-1\right ]=\left [\frac{\beta }{\zeta }\cdot \left (\frac{q-1}{q}\right )\cdot \exp\! \left (-1\right )\cdot \left [\left (1-\alpha \right )\cdot P_{s}^{h}\right ]^{\frac{1}{\alpha }}\cdot l_{s}^{h}\cdot (L_{s}^{h})^{1-\xi }-r\right ]\nonumber\\&\qquad\cdot \left [q^{\left (\frac{1-\alpha }{\alpha }\right )}-1\right ] \end{align}

Thus, bearing in mind (42), from the emergence of a shock to a parameter or an exogenous variable to the steady state, the paths of the technological-knowledge bias in sector $s=N$ , which drives the skill premium and the inter-country wage inequality in (32), are as follows:

(43) \begin{eqnarray} \frac{\dot{Q_{N}^{i}}}{Q_{N}^{i}}-\frac{\dot{Q_{N}^{h}}}{Q_{N}^{h}} & = & \left [q^{\left (\frac{1-\alpha }{\alpha }\right )}-1\right ]\cdot \frac{\beta }{\zeta }\cdot \frac{q-1}{q}\cdot \exp\! \left (-1\right )\cdot \left (1-\alpha \right )^{\frac{1}{\alpha }}\nonumber\\&&\quad\cdot \left [\left (P_{N}^{i}\right )^{\frac{1}{\alpha }}\cdot l_{s}^{i}\cdot (L_{N}^{i})^{1-\xi }-\left (P_{N}^{h}\right )^{\frac{1}{\alpha }}\cdot l_{s}^{h}\cdot (L_{N}^{h})^{1-\xi }\right ], \end{eqnarray}

(44) \begin{eqnarray} \frac{\dot{Q_{R}^{i}}}{Q_{R}^{i}}-\frac{\dot{Q_{R}^{h}}}{Q_{R}^{h}} & = & \left [q^{\left (\frac{1-\alpha }{\alpha }\right )}-1\right ]\cdot \frac{\beta }{\zeta }\cdot \frac{q-1}{q}\cdot \exp\! \left (-1\right )\cdot \left (1-\alpha \right )^{\frac{1}{\alpha }}\nonumber\\ &&\qquad\cdot \left [\left (P_{R}^{i}\right )^{\frac{1}{\alpha }}\cdot l_{R}^{i}\cdot (L_{R}^{i})^{1-\xi }-\left (P_{R}^{h}\right )^{\frac{1}{\alpha }}\cdot l_{R}^{h}\cdot (L_{R}^{h})^{1-\xi }\right ]. \end{eqnarray}

In turn, the inter-sector technological knowledge, which drives the wage polarization in (33) and (34), are

(45) \begin{eqnarray} \frac{\dot{Q_{N}^{h}}}{Q_{N}^{h}}-\frac{\dot{Q_{R}^{h}}}{Q_{R}^{h}} & = & \left [q^{\left (\frac{1-\alpha }{\alpha }\right )}-1\right ]\frac{\beta }{\zeta }\cdot \left (\frac{q-1}{q}\right )\cdot \exp\! \left (-1\right )\nonumber\\ &&\qquad\cdot \left [\left (P_{N}^{h}\right )^{\frac{1}{\alpha }}\cdot l_{N}^{h}\cdot (L_{N}^{h})^{1-\xi }-\left (P_{R}^{h}\right )^{\frac{1}{\alpha }}\cdot l_{R}^{h}\cdot (L_{R}^{h})^{1-\xi }\right ], \end{eqnarray}

(46) \begin{eqnarray} \frac{\dot{Q_{N}^{i}}}{Q_{N}^{i}}-\frac{\dot{Q_{R}^{i}}}{Q_{R}^{i}} & = & \left [q^{\left (\frac{1-\alpha }{\alpha }\right )}-1\right ]\cdot \frac{\beta }{\zeta }\cdot \frac{q-1}{q}\cdot \exp\! \left (-1\right )\cdot \left (1-\alpha \right )^{\frac{1}{\alpha }}\nonumber\\ &&\quad\cdot \left [\left (P_{N}^{i}\right )^{\frac{1}{\alpha }}\cdot l_{N}^{i}\cdot (L_{N}^{i})^{1-\xi }-\left (P_{R}^{i}\right )^{\frac{1}{\alpha }}\cdot l_{R}^{i}\cdot (L_{R}^{i})^{1-\xi }\right ], \end{eqnarray}

(47) \begin{eqnarray} \frac{\dot{Q_{N}^{h}}}{Q_{N}^{h}}-\frac{\dot{Q_{R}^{h}}}{Q_{R}^{h}} & = & \left [q^{\left (\frac{1-\alpha }{\alpha }\right )}-1\right ]\cdot \frac{\beta }{\zeta }\cdot \frac{q-1}{q}\cdot \exp\! \left (-1\right )\cdot \left (1-\alpha \right )^{\frac{1}{\alpha }}\nonumber\\ &&\qquad\cdot \left [\left (P_{N}^{h}\right )^{\frac{1}{\alpha }}\cdot l_{N}^{h}\cdot (L_{N}^{h})^{1-\xi }-\left (P_{R}^{h}\right )^{\frac{1}{\alpha }}\cdot l_{R}^{h}\cdot (L_{R}^{h})^{1-\xi }\right ] \end{eqnarray}

4.2. Steady-state results

Taking into account, the aggregate expenditures in the final good are given by $Y=P_{N}Y_{N}+P_{R}Y_{R}$ from the profit maximization problem of the producer of aggregate output, considering that aggregate expenditures in machines and R&D activities are the sum of aggregates in both sectors already derived in equilibrium in the previous sections, $X\equiv X_{N}+X_{R}$ and $E\equiv E_{N}+E_{R}$ , and that assets in the economy are the present value of the patent of all producers of machines, that is, that $a=\sum _{s=N,R}\int _{0}^{J}V_{s}^{h}(k,j,t)dj+\int _{J}^{1}V_{s}^{i}(k,j,t)dj$ we can prove that in equilibrium the aggregate flow constraint of households can be expressed as $Y=C+X+E$ —see the respective proof in Appendix A.5. Since $Y$ , $X$ , and $E$ are all multiples of the quality indexes $Q_{N}^{h}$ , $Q_{N}^{i}$ , $Q_{R}^{h}$ , and $Q_{R}^{i}$ , the aggregate flow constraint implies that consumption $C$ is also a constant multiple of these variables, which implies that the path of all relevant variables outside the steady state depends on the path of the different quality indexes. At the end of transitional dynamics, the economy reaches the steady state, which is unique and stable, and all relevant macroeconomic variables grow at the same constant rate $g^{\ast }$ :

(48) \begin{equation} g^{\ast }\equiv \left (\frac{\dot{Q_{s}^{i}}}{Q_{s}^{i}}\right )^{*}=\left (\frac{\dot{Q_{s}^{h}}}{Q_{s}^{h}}\right )^{*}=\left (\frac{\dot{Y}}{Y}\right )^{*}=\left (\frac{\dot{X}}{X}\right )^{*}=\left (\frac{\dot{E}}{E}\right )^{*}=\left (\frac{\dot{C}}{C}\right )^{*}=\frac{r^{\ast }-\rho }{\theta }. \end{equation}

The uniqueness of the steady state is guaranteed by the uniqueness of the interest rate. To take into account the stability, it must be considered (42), (43), (44), (46), and (47). The dynamics of the Economy can be characterized by a two-dimensional dynamic system in detrended variables such as $\frac{Q_{s}^{i}}{Q_{s}^{h}}$ (or $\frac{Q_{N}^{i}}{Q_{R}^{i}}$ or $\frac{Q_{N}^{h}}{Q_{R}^{i}}$ or $\frac{Q_{N}^{i}}{Q_{R}^{h}}$ or $\frac{Q_{N}^{h}}{Q_{R}^{h}}$ ) and $\frac{C}{Q_{s}^{i}}$ (or $\frac{C}{Q_{s}^{h}}$ ) that has a recursive structure since the dynamics of $\frac{Q_{s}^{i}}{Q_{s}^{h}}$ depends, exclusively, on itself. For example, considering an economy starting out of the steady state, where $\frac{\dot{Q_{s}^{i}}}{Q_{s}^{i}}\gt \frac{\dot{Q_{s}^{h}}}{Q_{s}^{h}}$ , we will prove that, over $t$ , $\frac{\dot{Q_{s}^{i}}}{Q_{s}^{i}}\gt 0$ and $\frac{\dot{Q_{s}^{h}}}{Q_{s}^{h}}=0$ . Bearing in mind this situation, it is easy to perceive that $\overline{v}_{s}\gt \overline{v}_{s}^{*}$ which, in turn, implies $\frac{\dot{P}_{s}^{i}}{P_{s}^{I}}\lt \frac{\dot{P}_{s}^{h}}{P_{s}^{h}}$ . Thereby, $\frac{P_{s}^{i}}{P_{s}^{h}}$ is declining until

(49) \begin{equation} \left (\frac{P_{s}^{i}}{P_{s}^{h}}\right )^{*}=\left [\frac{l_{s}^{i}}{l_{s}^{h}}\cdot \left (\frac{L_{s}^{i}}{L_{s}^{h}}\right )^{1-\xi }\right ]^{-\alpha }\text{,} \end{equation}

attenuating the rate at which $\frac{Q_{s}^{i}}{Q_{s}^{h}}$ is increasing. In this sense, even with $\frac{\dot{Q_{s}^{i}}}{Q_{s}^{i}}\gt \frac{\dot{Q_{s}^{h}}}{Q_{s}^{h}}$ the difference between both equilibrium paths of technological knowledge, $\frac{\dot{Q_{s}^{i}}}{Q_{s}^{i}}-\frac{\dot{Q_{s}^{h}}}{Q_{s}^{h}}$ , is decreasing until approaches the steady state, where $\frac{\dot{Q_{s}^{i}}}{Q_{s}^{i}}=\frac{\dot{Q_{s}^{h}}}{Q_{s}^{h}}$ . The argument to exhibit the convergence to the steady state if $\frac{\dot{Q_{s}^{i}}}{Q_{s}^{i}}\lt \frac{\dot{Q_{s}^{h}}}{Q_{s}^{h}}$ is similar—see, for example, Acemoglu and Zilibotti (2001). Thus, the economy converges and remains in a steady state, if no other exogenous changes occur.

Lemma 1. A unique and stable steady state exists and along this growth path $Y$ , $C$ , $X$ , and $E$ growth at rate $g^{*}$ .

We now show the calculation of the variables of interest in the steady state and, for each one, a Proposition is presented in the face of an eventual “shock.”

From (23) and (49), we have that:

(50) \begin{equation} \left (\frac{Q_{s}^{i}}{Q_{s}^{h}}\right )^{*}=\frac{l_{s}^{i}}{l_{s}^{h}}\cdot \left (\frac{L_{s}^{i}}{L_{s}^{h}}\right )^{1-2\xi }\text{.} \end{equation}

Proposition 1. From (50), the steady-state intra-sector technological-knowledge gap increases when (i) the absolute advantages of a labor type $i$ , $l_{s}^{i}$ , over labor type, $h$ , $l_{s}^{h}$ , increases, (ii) the labor type $i$ , $L_{s}^{i}$ , over labor type $h$ , $L_{s}^{h}$ , increases and scale effects are strongly removed $\xi \gt \frac{1}{2}$ . By looking specifically at the routine sector, $s=R$ , ceteris paribus, an improvement in automation such that $\frac{l_{R}^{i}}{l_{R}^{h}}$ decreases redirects the intra-sector technological-knowledge bias that favors relocations.

Proof. Directly from (50).

In possession of (50), one can use (20) to determine

(51) \begin{equation} \overline{v}_{s}^{*}=\left [1+\frac{l_{s}^{i}}{l_{s}^{h}}\cdot \left (\frac{L_{s}^{i}}{L_{s}^{h}}\right )^{1-\xi }\right ]^{-1}\text{.} \end{equation}

Proposition 2. From (51), the steady-state threshold tasks $\overline{v}_{R}$ (threshold automated routine task with medium-skilled labor) and $\overline{v}_{N}$ (threshold nonroutine tasks produced with high-skilled labor) imply that: (i) the number of automated routine tasks produced is large when both the relative medium-skilled labor supply and the respective relative absolute advantage are high in the face of the foreign labor supply and the respective absolute advantage; in other words, relocations are more intense the higher the productivity and availability of labor abroad; (ii) the number of nonroutine tasks produced with high-skilled labor is large when both the relative high-skilled labor supply and the respective relative absolute advantage are high in the face of the low-skilled labor supply and the respective absolute advantage. Labor levels only cease to have an impact when scale effects are totally removed.

Proof. Directly from (51).

Hence, the “race” between automation and relocation is won by automation if the level of domestic medium-skilled workers exceeds the number existing abroad—that is, if the “room” for automation exceeds the “room” for relocations—and if the absolute advantage of domestic medium-skilled workers outweighs the absolute advantage of the same type of workers abroad.

Therefore, from (32) and (50), the (domestic) steady-state skill premium and the inter-country wage inequality in favor of the domestic country are, respectively:

(52) \begin{equation} \frac{w_{N}^{i}}{w_{N}^{h}}=\frac{l_{N}^{i}}{l_{N}^{h}}\cdot \left (\frac{L_{N}^{i}}{L_{N}^{h}}\right )^{-\xi }\:\textit{and}\:\frac{w_{R}^{i}}{w_{R}^{h}}=\frac{l_{R}^{i}}{l_{R}^{h}}\cdot \left (\frac{L_{R}^{i}}{L_{R}^{h}}\right )^{-\xi }. \end{equation}

Proposition 3. In the long run, provided there are some scale effects, unexpected changes in labor endowments have the following effects:

A. The skill premium is positively affected by an increase in low-skilled labor $L_{N}^{h}$ , over the high-skilled labor, $L_{N}^{i}$ —see (52).

B. The inter-country wage inequality in favor of the domestic country is positively affected by an increase in countries available to host relocations of routine production, reflected in $L_{R}^{h}$ , over the domestic medium-skilled labor $L_{R}^{i}$ , that is, inter-country wage inequality depends positively on relocation and negatively on automation—see (52).

Proof. A. and B. result directly from (52).

To compute the steady-state wage polarization, we start noting that in (46) and (47), $\left (\frac{\dot{Q_{N}^{i}}}{Q_{N}^{i}}\right )=\left (\frac{\dot{Q_{R}^{i}}}{Q_{R}^{i}}\right )$ and $\left (\frac{\dot{Q_{N}^{h}}}{Q_{N}^{h}}\right )=\left (\frac{\dot{Q_{R}^{i}}}{Q_{R}^{i}}\right )$ , which implies that

(53) \begin{equation} \left (\frac{P_{N}^{i}}{P_{R}^{i}}\right )^{*}=\left [\frac{l_{N}^{i}}{l_{R}^{i}}\cdot \left (\frac{L_{N}^{i}}{L_{R}^{i}}\right )^{1-\xi }\right ]^{-\alpha } \,\,\text{and}\,\,{\left (\frac{P_{N}^{h}}{P_{R}^{i}}\right )^{*}}={\left [\frac{l_{N}^{h}}{l_{R}^{i}}\cdot \left (\frac{L_{N}^{h}}{L_{R}^{i}}\right )^{1-\xi }\right ]^{-\alpha }}, \end{equation}

which, by equating, respectively, with the expressions that correspond to the relative price of $L_{s}^{i}$ task, obtained bearing in mind (23), that is, $\left (\frac{P_{N}^{i}}{P_{R}^{i}}\right )^{*}=\left (\frac{P_{N}^{i}}{P_{R}^{i}}\right )$ and $\left (\frac{P_{N}^{h}}{P_{R}^{i}}\right )^{*}=\left (\frac{P_{N}^{h}}{P_{R}^{i}}\right )$ , makes it possible to obtain $\left (\frac{Q_{N}^{h}}{Q_{R}^{h}}\right )^{*}$ , $\left (\frac{Q_{N}^{i}}{Q_{R}^{i}}\right )^{*}$ and $\left (\frac{Q_{N}^{h}}{Q_{R}^{i}}\right )^{*}$ which is given by:

(54) \begin{eqnarray} \left (\frac{Q_{N}^{i}}{Q_{R}^{i}}\right )^{*} & = & \left (\frac{\chi _{N}}{\chi _{R}}\right )^{\epsilon }\left (\frac{l_{N}^{i}}{l_{R}^{i}}\right )\left (\frac{L_{N}^{i}}{L_{R}^{i}}\right )^{1-2\xi }\left [\frac{l_{R}^{h}\cdot \left (L_{R}^{h}\right )^{1-\xi }+l_{R}^{i}\cdot \left (L_{R}^{i}\right )^{1-\xi }}{l_{N}^{h}\cdot \left (L_{N}^{h}\right )^{1-\xi }+l_{N}^{i}\cdot \left (L_{N}^{i}\right )^{1-\xi }}\right ]^{1-\epsilon \alpha +\alpha }, \end{eqnarray}

(55) \begin{eqnarray} \left (\frac{Q_{N}^{h}}{Q_{R}^{i}}\right )^{*} & = & \left (\frac{\chi _{N}}{\chi _{R}}\right )^{\epsilon }\left (\frac{l_{N}^{h}}{l_{R}^{i}}\right )\left (\frac{L_{N}^{h}}{L_{R}^{i}}\right )^{1-2\xi }\left [\frac{l_{R}^{h}\cdot \left (L_{R}^{h}\right )^{1-\xi }+l_{R}^{i}\cdot \left (L_{R}^{i}\right )^{1-\xi }}{l_{N}^{h}\cdot \left (L_{N}^{h}\right )^{1-\xi }+l_{N}^{i}\cdot \left (L_{N}^{i}\right )^{1-\xi }}\right ]^{1-\epsilon \alpha +\alpha }. \end{eqnarray}

Proposition 4. In the long term, unexpected changes in the importance of each sector and labor endowments have the following effects:

A. The inter-sector technological-knowledge gap biased in favor of tasks produced by domestic (nonroutine) high-skilled workers is positively affected by an: (i) increase (decrease) in the importance of the nonroutine (routine) sector $\chi _{N}$ $\left (\chi _{R}\right );$ (ii) increase in foreign (routine) medium-skilled labor, $L_{R}^{h},$ and domestic (nonroutine) high-skilled labor, $L_{N}^{i}$ , when $\frac{l_{N}^{h}\cdot \left (L_{N}^{h}\right )^{1-\xi }}{l_{N}^{i}\cdot \left (L_{N}^{i}\right )^{1-\xi }}\gt \frac{\alpha \left [1-\epsilon +\xi \left (\epsilon -1\right )\right ]+\xi }{\left (1-2\xi \right )}$ ; (iii) decrease in domestic (nonroutine) low-skilled labor, $L_{N}^{i}$ , and domestic (nonroutine) medium-skilled labor, $L_{R}^{i}$ , when $\frac{l_{R}^{h}\cdot \left (L_{R}^{h}\right )^{1-\xi }}{l_{R}^{i}\cdot \left (L_{R}^{i}\right )^{1-\xi }}\lt \frac{\alpha \left [1-\epsilon +\xi \left (\epsilon -1\right )\right ]-3\xi }{\left (1+2\xi \right )}$ ; (iv) increase in foreign (routine) medium-skilled absolute productivity, $l_{R}^{h},$ and domestic (nonroutine) high-skilled absolute productivity, $l_{N}^{i}$ , when $\frac{l_{N}^{h}\cdot \left (L_{N}^{h}\right )^{1-\xi }}{l_{N}^{i}\cdot \left (L_{N}^{i}\right )^{1-\xi }}\gt \alpha (1-\epsilon )$ ; (v) decrease in domestic (nonroutine) low-skilled absolute productivity, $l_{N}^{h},$ and domestic (nonroutine) medium-skilled absolute productivity, $l_{R}^{i}$ , when $\frac{l_{R}^{h}\cdot \left (L_{R}^{h}\right )^{1-\xi }}{l_{R}^{i}\cdot \left (L_{R}^{i}\right )^{1-\xi }}\gt \alpha (1-\epsilon )$ —see (54).

B. The inter-sector technological-knowledge gap biased in favor of tasks produced by domestic (nonroutine) low-skilled workers is positively affected by an: (i) increase (decrease) in the importance of the nonroutine (routine) sector $\chi _{N}$ $\left (\chi _{R}\right );$ (ii) increase in foreign (routine) medium-skilled labor, $L_{R}^{h},$ and domestic (nonroutine) low-skilled labor, $L_{N}^{h}$ , when $\frac{l_{N}^{i}\cdot \left (L_{N}^{i}\right )^{1-\xi }}{l_{N}^{h}\cdot \left (L_{N}^{h}\right )^{1-\xi }}\gt \frac{\alpha \left [1-\epsilon +\xi \left (\epsilon -1\right )\right ]+\xi }{\left (1-2\xi \right )}$ ; (iii) decrease in domestic (nonroutine) high-skilled labor, $L_{N}^{i}$ , and domestic (nonroutine) medium-skilled labor, $L_{R}^{i}$ , when $\frac{l_{R}^{h}\cdot \left (L_{R}^{h}\right )^{1-\xi }}{l_{R}^{i}\cdot \left (L_{R}^{i}\right )^{1-\xi }}\lt \frac{\alpha \left [1-\epsilon +\xi \left (\epsilon -1\right )\right ]-3\xi }{\left (1+2\xi \right )}$ ; (iv) increase in foreign (routine) medium-skilled absolute productivity, $l_{R}^{h},$ and domestic (nonroutine) low-skilled absolute productivity, $l_{N}^{h}$ , when $\frac{l_{N}^{i}\cdot \left (L_{N}^{i}\right )^{1-\xi }}{l_{N}^{h}\cdot \left (L_{N}^{h}\right )^{1-\xi }}\gt \alpha (1-\epsilon )$ ; (v) decrease in domestic (nonroutine) high-skilled absolute productivity, $l_{N}^{i},$ and domestic (nonroutine) medium-skilled absolute productivity, $l_{R}^{i}$ , when $\frac{l_{R}^{h}\cdot \left (L_{R}^{h}\right )^{1-\xi }}{l_{R}^{i}\cdot \left (L_{R}^{i}\right )^{1-\xi }}\gt \alpha (1-\epsilon )$ —see (55).

Proof. A. and B. result directly from (54) and (55), respectively.

Thus, bearing in mind (33) and (34) as well as (54) and (55) enable us to determine, respectively,

(56) \begin{eqnarray} \left (\frac{w_{N}^{i}}{w_{R}^{i}}\right )^{*} & = & \left (\frac{\chi _{N}}{\chi _{R}}\right )^{\epsilon }\left (\frac{l_{N}^{i}}{l_{R}^{i}}\right )\left (\frac{L_{R}^{i}}{L_{N}^{i}}\right )^{\xi }\left [\frac{l_{R}^{h}\cdot \left (L_{R}^{h}\right )^{1-\xi }+l_{R}^{i}\cdot \left (L_{R}^{i}\right )^{1-\xi }}{l_{N}^{h}\cdot \left (L_{N}^{h}\right )^{1-\xi }+l_{N}^{i}\cdot \left (L_{N}^{i}\right )^{1-\xi }}\right ]^{1-\epsilon \alpha +\alpha }, \end{eqnarray}

(57) \begin{eqnarray} \left (\frac{w_{N}^{h}}{w_{R}^{i}}\right )^{*} & = & \left (\frac{\chi _{N}}{\chi _{R}}\right )^{\epsilon }\left (\frac{l_{N}^{h}}{l_{R}^{i}}\right )\left (\frac{L_{R}^{i}}{L_{N}^{h}}\right )^{\xi }\left [\frac{l_{R}^{h}\cdot \left (L_{R}^{h}\right )^{1-\xi }+l_{R}^{i}\cdot \left (L_{R}^{i}\right )^{1-\xi }}{l_{N}^{h}\cdot \left (L_{N}^{h}\right )^{1-\xi }+l_{N}^{i}\cdot \left (L_{N}^{i}\right )^{1-\xi }}\right ]^{1-\epsilon \alpha +\alpha }. \end{eqnarray}

Proposition 5. In the long run, provided there are some scale effects, unexpected changes in labor endowments have the following effects:

A. The wage polarization in favor of domestic (nonroutine) high-skilled workers is positively affected by: (i) an increase (decrease) in the importance of the nonroutine (routine) sector $\chi _{N}$ $\left (\chi _{R}\right );$ (ii) an increase in domestic and foreign (routine) medium-skilled labor, reflected, respectively, in $L_{R}^{i}$ and $L_{R}^{h}$ , that is, wage polarization increases with automation and relocations; (iii) a decrease in domestic (nonroutine) high- and low-skilled labor, reflected in $L_{N}^{i}$ and $L_{N}^{h}$ ; (iv) an increase in foreign (routine) medium-skilled absolute productivity, $l_{R}^{h}$ , and domestic (nonroutine) high-skilled absolute productivity, $l_{N}^{i}$ , when $\frac{l_{N}^{h}\cdot \left (L_{N}^{h}\right )^{1-\xi }}{l_{N}^{i}\cdot \left (L_{N}^{i}\right )^{1-\xi }}\gt \alpha (1-\epsilon )$ ; (v) a decrease in domestic (nonroutine) low-skilled absolute productivity, $l_{N}^{h}$ , and domestic (routine) medium-skilled absolute productivity, $l_{R}^{i}$ , when $\frac{l_{R}^{h}\cdot \left (L_{R}^{h}\right )^{1-\xi }}{l_{R}^{i}\cdot \left (L_{R}^{i}\right )^{1-\xi }}\lt \alpha (1-\epsilon )$ —see (56).

B. The wage polarization in favor of domestic (nonroutine) low-skilled workers is positively affected by: (i) an increase (decrease) in the importance of the nonroutine (routine) sector $\chi _{N}$ $\left (\chi _{R}\right );$ (ii) an increase in domestic and foreign (routine) medium-skilled labor, reflected, respectively, in $L_{R}^{i}$ and $L_{R}^{h}$ , that is, wage polarization increases with automation and relocations; (iii) a decrease in domestic (nonroutine) high- and low-skilled labor, reflected in $L_{N}^{i}$ and $L_{N}^{h}$ ; (iv) an increase in foreign (routine) medium-skilled absolute productivity, $l_{R}^{h}$ , and domestic (nonroutine) low-skilled absolute productivity, $l_{N}^{h}$ , when $\frac{l_{N}^{i}\cdot \left (L_{N}^{i}\right )^{1-\xi }}{l_{N}^{h}\cdot \left (L_{N}^{h}\right )^{1-\xi }}\gt \alpha (1-\epsilon )$ ; (v) a decrease in domestic (nonroutine) high-skilled absolute productivity, $l_{N}^{h}$ , and domestic (routine) medium-skilled absolute productivity, $l_{R}^{i}$ , when $\frac{l_{R}^{h}\cdot \left (L_{R}^{h}\right )^{1-\xi }}{l_{R}^{i}\cdot \left (L_{R}^{i}\right )^{1-\xi }}\lt \alpha (1-\epsilon )$ —see (57).

Proof. A. and B. result directly from (56) and (57), respectively.

It is also worth noting that as $\epsilon \rightarrow 0$ (high complementarity) and $\alpha \rightarrow 1$ (low importance of machines in production), the lower would be the relevance of reallocations (offshoring) for wage polarization. Moreover, with low-scale effects $\xi \rightarrow 0$ , wage polarization would be greatly driven by productivity differences related both to reallocations and automation. In particular, in that case, wage polarization in favor of domestic (nonroutine) high(low)-skilled workers is positively affected by an increase in domestic (nonroutine) high(low)-skilled absolute productivity and decrease in domestic (routine) medium-skilled absolute productivity, $l_{N}^{i}$ . Moreover in the specific case when sectors are gross substitutes ( $\epsilon \geq 1$ ), wage polarization in favor of domestic (nonroutine) high-skilled workers is always positively affected an increase in foreign (routine) medium-skilled absolute productivity, $l_{R}^{h}$ , and domestic (nonroutine) high-skilled absolute productivity, $l_{N}^{i}$ , and never by a decrease in domestic (nonroutine) low-skilled absolute productivity, $l_{N}^{h}$ , and domestic (routine) medium-skilled absolute productivity, $l_{R}^{i}$ . Also wage polarization in favor of domestic (nonroutine) low-skilled workers is always positively affected by an increase in foreign (routine) medium-skilled absolute productivity, $l_{R}^{h}$ , and domestic (nonroutine) low-skilled absolute productivity, $l_{N}^{h}$ , and never by a decrease in domestic (nonroutine) high-skilled absolute productivity, $l_{N}^{h}$ , and domestic (routine) medium-skilled absolute productivity, $l_{R}^{i}$ .

Bearing in mind (42) and (48), the stable and unique steady-state economic growth rate is—considering, as example, the case in which labor is type $h$ :

(58) \begin{equation} g^{\ast }=\frac{\left [q^{\left (\frac{1-\alpha }{\alpha }\right )}-1\right ]\left \{ \left [\frac{\beta }{\zeta }\cdot \left (\frac{q-1}{q}\right )\cdot \exp\! \left (-1\right )\cdot \left [\left (1-\alpha \right )\cdot P_{s}^{h}\right ]^{\frac{1}{\alpha }}\cdot l_{s}^{h}\cdot (L_{s}^{h})^{1-\xi }\right ]-\rho \right \} }{\left [q^{\left (\frac{1-\alpha }{\alpha }\right )}-1\right ]\theta +1}\text{,} \end{equation}

where $\left (P_{s}^{h}\right )^{*}=\left (P_{s}\right )^{*}\cdot \exp\! \left (-\alpha \right )\cdot \left (\overline{v}_{s}^{-\alpha }\right )^{*}$ and $\left (P_{s}\right )^{*}$ is determined in Appendix A.6.

Proposition 6. From (58), the economic growth rate increases when the productive structure is improved—for example, $l_{s}^{h}$ , $l_{s}^{i}$ , $L_{s}^{h}$ , $L_{s}^{i}$ , $\beta$ increase, and $\varsigma$ decrease; hence, improvements in automation and relocations positively affect economic growth. An increase of $\alpha$ decreases the value of patents, making R&D less productive, thus penalizing the growth rate. Finally, the more patient—that is, the smaller the value of $\rho$ —and the less keen the individuals are on consumption—that is, the smaller the value of $\theta$ —the higher the growth rate.

Proof. Results directly from (58) and (66) and (67).

Hence, from (58), economic growth depends positively on automation—in line with, for example, Zeira (1998), Acemoglu and Restrepo (2017), and Graetz and Michaels (2018)—and also on relocations—in line with the empirical studies performed by, for example, Li and Liu (2005), Baharumshah and Almasaied (2009), Wang (2007), Krammer (2010), Cuadros and Alguacil (2014), and Su and Liu (2016).

5. Quantitative results

Throughout this section, we quantify the behavior of key variables, considering the USA as a domestic country and Mexico as a foreign country, such as the (i) inter-sector technological-knowledge gap biased in favor of tasks performed by domestic (nonroutine) high- and low-skilled workers, $\left (\frac{Q_{N}^{i}}{Q_{R}^{i}}\right )^{*}$ and $\left (\frac{Q_{N}^{h}}{Q_{R}^{i}}\right )^{*}$ , exhibited in (54) and (55), respectively, resulting from fluctuations in the values linked to the routine sector relevance, $\chi _{R}$ ; (ii) wage polarization in favor of domestic (nonroutine) high- and low-skilled workers, $\left (\frac{w_{N}^{i}}{w_{R}^{i}}\right )^{*}$ and $\left (\frac{w_{N}^{h}}{w_{R}^{i}}\right )^{*}$ ,—presented in (56) and (57), respectively—derived from a variation in the values associated with (a) automation, which is evidenced by the production of tasks that are carried out by domestic (routine) medium-skilled labor, $L_{N}^{i}$ , and by their absolute labor productivity, $l_{N}^{i}$ , and (b) reallocations, which is illustrated by the production of tasks that are performed by foreign (routine) medium-skilled labor, $L_{N}^{h}$ , that, in turn, reveals the willingness of developing countries to host relocations, and by their absolute labor productivity, $l_{N}^{h}$ .

Section 5.1 covers the calibration of necessary parameters and exogenous variables for implementing this approach, while Section 5.2 focuses on the analysis of the results obtained.

5.1. Data and calibration strategy

To carry out the quantitative exercises, it is required to calibrate several parameters and exogenous variables, previously exhibited on (56), (57), and (58). The values of most parameters were selected based on the literature on related models. However, crucial parameters and exogenous are data-based, following a thorough quantitative assessment.

First, we focus on the parameters based on the literature. In order to calibrate the elasticity of substitution between sectors, we followed Afonso, et al. (2022) where $\epsilon =0.50$ while for scale effects, the value of $\xi$ will be assumed to be $0.8$ , following the idea that in modern economies we may have positive but small-scale effects (e.g., Sequeira et al. 2018). For the labor share, the work carried out by Jones et al. (1993) was considered whereas $\alpha =0.64$ , which in turn allowed us to calculate the constant quality upgrade, $q=2.78$ , since $q=\frac{1}{1-\alpha }$ . Moreover, the value for the learning-by-past domestic R&D, measured by the obsolescence of (past) investments in R&D, was chosen to take into account Afonso (2012), $\beta =2$ , and the cost of complexity, measured through the Economic Complexity Index (ECI) developed by the Harvard Growth Lab’s Country Rankings, where, for the USA, $\zeta =1.64$ . Additionally, the rate time of preference and the inverse of the inter-temporal elasticity of substitution were attained based on Arrow (1999) and Croix and Delavallade (2009), respectively, where $\rho =0.015$ and $\theta =0.5$ .

Second, we focus on data-based exogenous variables. The relative importance of the routine sector was measured as a division between the gross value added of four manufacturing subsectors which account for more than 80% of all industrial robots—food products (C10–12), fossil fuels, chemicals and pharmaceuticals (C19–21), rubber, plastic and mineral products (C22–C23), metal products (C24–C25), computer, electronic and electrical equipment (C26–27), machinery and equipment (C28), and automotive (C29–C30)—and the gross value added of all industries.¹⁹ The average value for this specific period (2003–2020) was subsequently calculated, resulting in $\chi _{R}=0.087$ . Similarly, bearing in mind the remaining industries and manufacturing subsectors not mentioned previously as the numerator, the relative importance of the nonroutine sector was computed, leading to $\chi _{N}=0.913$ . Furthermore, the labor performed in both the domestic economy ( $L_{N}^{i}$ , $L_{N}^{h}$ , $L_{R}^{i}$ )—high-skilled, low-skilled, and medium-skilled in the USA—and foreign economy ( $L_{R}^{h}$ )—medium-skilled in Mexico—was measured by the number of employees in the respective skill level, through the “employment by sex, age and education (in thousands)” dataset, based on the ISCED, as previously detailed in Section 2.²⁰ Subsequently, an arithmetic average was computed, leading to $L_{N}^{i}=0.966$ , $L_{N}^{h}=1.502$ , $L_{R}^{i}=0.662$ , and $L_{R}^{h}=2.499$ . Lastly, we calculated the productivity by each labor type.²¹ Our purpose is to collect information regarding the level of education that is mostly employed in each occupation, rather than the minimum education required. We adopted the evidence produced by O^*NET that provides the level of schooling commonly undertaken in each job.²² When the occupations in the Bureau of Labor Statistics (BLS) database do not coincide with those in the O^*NET, we used the information available in the “typical education needed for entry.” Then, to categorize each detailed occupation by industry, we utilized the database released by the BLS “May 2021 National industry-specific occupational employment and wages estimates” to allocate the percentage of employees of each job in each industrial sector. In a later step, we retrieved the data, from the BLS (together with the Standard Occupational Classification system), for the number of employees by detailed occupation. Therefore, by obtaining the detailed jobs and employment data by detailed occupation, we were able to match both databases. It was possible to attain the amount and percentage of workers employed in each occupation, by education level in each industry. Consequently, bearing in mind the number of hours worked and value added by industry, it became feasible to obtain the corresponding hours worked and value added across each educational level within each sector.²³ That said, absolute productivity by skill level in the USA was measured using the ratio of the two aforementioned variables, yielding $l_{N}^{i}=82.339$ , $l_{N}^{h}=45.678$ , and $l_{R}^{i}=64.218$ . Lastly, to determine the absolute productivity of medium-skilled workers in Mexico, we decided to use the value of the parameters and variables indicated throughout the subsection in the expression (52) which refers to inter-country wage inequality in favor of the domestic country. Thus, in order to gather data on the wages of domestic and of foreign medium-skilled workers, we used the database “Average monthly earnings of employees by sex and occupation (in thousands),” based on the ISCO and the respective level of qualification, produced by the ILO, resulting in $\frac{w_{R}^{i}}{w_{R}^{h}}=7.942$ . Therefore, we acquired the value for absolute productivity foreign medium-skilled labor, which is given by $l_{R}^{h}=26.667.$ Table 2 presents each parameter and variable with its corresponding value, description, and source.

Table 2. Parameters and variables calibrated

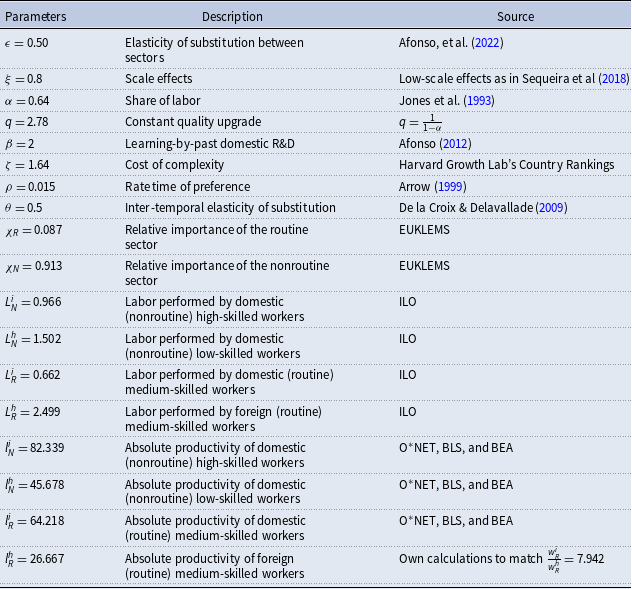
Moreover, given the values of the variables and parameters of interest,— $\chi _{R}$ , $L_{R}^{i}$ , $L_{R}^{h}$ , $l_{R}^{i}$ , and $l_{R}^{h}$ —we calculate the range of values for each will fall within an interval of $20\%$ below and $20\%$ above the mean, disposed in Table 3, which will be used for examining fluctuations in the mentioned key variables.

Table 3. Range of values for the variables and parameters of interest

5.2. Results and discussion

Bearing in mind the steady-state expressions for the crucial variables, —(54), (55), (56), and (57)—the calibration and the range of values, we visually analyze the behavior of each critical variable in order to confirm the theoretical conclusions.

The relative distribution parameters have the potential to contribute to biases inherent in the production process, which can interfere with technological-knowledge advances. Thus, if the relative distribution parameter tends in favor of the routine sector, it suggests that the economy attributes a higher importance to this sector, even before any technological changes. Nevertheless, as technology improves, it can reinforce this existing tendency. This specific impact on the technological-knowledge bias will depend on the values assigned to these parameters and their interaction with technological advances, expressed in the equations previously obtained in steady state, which ultimately lead to changes in the distribution of income and the allocation of resources.

Examining the effect of a shift in the relative importance of the routine sector on the key variables, $\left (\frac{Q_{N}^{i}}{Q_{R}^{i}}\right )^{*}$ and $\left (\frac{Q_{N}^{h}}{Q_{R}^{i}}\right )^{*}$ , a rise in this parameter conducts, in the first place, a decrease in the relative importance of the nonroutine sector and, results, subsequently, in an improvement in technological knowledge oriented toward tasks performed by medium-skilled domestic workers specialized in routine tasks.²⁴ In particular, a positive shift in the importance of the routine sector by $0.0348pp$ causes a bias of technological knowledge in favor of routine tasks performed by domestic medium-skilled workers, compared to nonroutine tasks carried out by high-skilled domestic workers, by $26.026\%$ —see Figure 2a. Similarly, the same fluctuation biases technological knowledge in favor of routine tasks undertaken by domestic medium-skilled workers, compared to nonroutine tasks performed by low-skilled domestic workers, by $24.825\%$ —see Figure 2b.

Figure 2. Effect of variations in the routine sector relevance, $\chi _{R}$ , on the inter-sector technological-knowledge gap biased in favor of tasks produced by domestic (nonroutine) high- and low-skilled workers, $\left(\frac{Q_{N}^{i}}{Q_{R}^{i}}\right)^{*},$ and $\left(\frac{Q_{N}^{h}}{Q_{R}^{i}}\right)^{*}$ .

Furthermore, variations in both automation, experienced through changes in the amount of domestic medium-skilled labor and its productivity in carrying out routine tasks, and offshoring, perceived as fluctuations in the supply of foreign medium-skilled labor and its productivity in carrying out relocated routine tasks, conduct significant transformations in technological progress. These modifications in turn lead to a transformation of the intermediate goods used by workers, causing changes in the competitiveness of each task and sector. As a result, these factors have a notable impact on economic growth²⁵ and wages variations.

Thus, an upward shift in the amount of the labor performed by both domestic and foreign (routine) medium-skilled employees on the key variables, $\big (\frac{w_{N}^{i}}{w_{R}^{i}}\big )^{*}$ and $\big (\frac{w_{N}^{h}}{w_{R}^{i}}\big )^{*}$ , induce a rise in the wage polarization in favor of domestic (nonroutine) high- and low-skilled workers.²⁶ More specifically, a positive fluctuation in the domestic and foreign (routine) medium-skilled labor amount by $0.2648pp$ and $0.9996pp$ generates a wage polarization increase toward domestic (nonroutine) high-skilled workers of $49.269\%$ and $3.8269\%$ , respectively—see Figure 3a and b. Along the same lines, the same variations induce a wage polarization rise in favor of domestic (nonroutine) low-skilled employees of $49.244\%$ and $3.8260\%$ , sequentially—see Figure 4a and b. Regarding the absolute productivity of domestic and foreign (routine) medium-skilled employees in both key variables, these changes lead, respectively, to a decline and a rise in the wage polarization toward domestic (nonroutine) high- and low-skilled laborers.²⁷ In particular, a positive change in the absolute productivity of domestic and foreign (routine) medium-skilled workers of $25.687pp$ and $10.667pp$ , respectively, causes a decrease and an increase of $5.920\%$ and $20.420\%$ in the wage polarization in the upper tail, that is, in the relative domestic (nonroutine) high-skilled workers—see Figure 3a and b. Additionally, a similar shift induces, respectively, a drop and growth of $5.918\%$ and $16.419\%$ in the wage polarization toward domestic (nonroutine) low-skilled employees—see Figures 4a and b.

Figure 3. Effect of variations in the exogenous variables that capture automation, $L_{N}^{i}$ and $l_{N}^{i}$ , and reallocations, $L_{N}^{h}$ and $l_{N}^{h}$ , on the wage polarization in favor of domestic (nonroutine) high-skilled workers, $\left(\frac{w_{N}^{i}}{w_{R}^{i}}\right)^{*}$ .

Figure 4. Effect of variations in the exogenous variables that capture automation, $L_{N}^{i}$ and $l_{N}^{i}$ , and reallocations, $L_{N}^{h}$ and $l_{N}^{h}$ , on the wage polarization in favor of domestic (nonroutine) low-skilled workers, $\left(\frac{w_{N}^{h}}{w_{R}^{i}}\right)^{*}$ .

In summary, as we have noticed, the “race” between automation and offshoring is won by automation if there are positive shocks in the supply of domestic and foreign medium-skilled labor. In other words, the earnings of high- and low-skilled employees are more susceptible to shifts in response to automation. In turn, the “race” between automation and offshoring is won by offshoring if there are improvements in the absolute productivity of domestic and foreign medium-skilled workers. In simpler terms, when the variables associated with offshoring are affected by fluctuations, both high- and low-skilled workers are more prone to experience shifts in their gains.

6. Concluding remarks

The rise of the skill premium since the 1980s was the main motivation for the development of the DTC literature. This literature links the increase in the relative supply of high-skilled workers with the technological-knowledge bias toward those workers, which induces a higher relative demand for this labor type. However, more recent and more detailed data point to a polarization of wages concerning the distribution of skills, requiring the literature to address modeling approaches that fit that data pattern.

In our theoretical model, we have considered three types of workers and, as suggested by the literature, it was assumed that medium-skilled workers are employed in routine tasks, which can be automated and relocated, while low- and high-skilled workers are employed mainly in, respectively, “purely manual” and “abstract/cognitive” nonroutine tasks. In this context, the impact of automation and relocations on technological-knowledge progress, competitiveness, wages, and economic growth was theoretically analyzed. Indeed, automation and relocations will impose a relative improvement in the absolute advantage of labor in the nonroutine sector over the routine sector, which increases the technological-knowledge advantage of the nonroutine sector over the routine sector. This technological-knowledge bias in favor of the nonroutine sector results in improved quality of the intermediate goods used by the routine sector, thus strengthening its competitiveness. Moreover, wages of workers in the nonroutine sector (particularly high-skilled labor, but also low-skilled labor) relative to workers in the routine sector (medium-skilled labor) increase, thus generating wage polarization. Moreover, while automation and relocations can yield benefits for workers across all categories, it is in the nonroutine sector that high-skilled workers experience a more pronounced wage advantage over low-skilled employees if there is an expansion in the number of the latter, resulting in an enhancement of the skill premium. Similarly, it is in the routine sector that foreign medium-skilled workers, affected by reallocations, experience a more pronounced wage advantage over domestic medium-skilled workers, impacted by automation, if there is an expansion in the number of the latter, resulting in an improvement of the inter-country wage inequality. In the same vein, the wages of workers in the nonroutine sector (high- and low-skilled labor) relative to workers in the routine sector (medium-skilled labor) increase when they face an improvement in automation and relocations, thus generating an augmentation in wage polarization. Lastly, also derived from the progress of technological knowledge, economic growth is also positively affected by both phenomena. Economic growth, in turn, frees up resources that become partially available for investment in R&D activities, thus increasing the probability of research success, which, in turn, accelerates technological knowledge.

In order to evaluate the main theoretical findings, we performed an exhaustive calibration of the model to assess its quantitative implications. Considering the USA as a domestic country, with a high degree of exposure to automation, and Mexico as a foreign country involved in substantial cross-border relocations with the domestic nation, we quantified the behavior of crucial variables, bearing in mind changes in parameters and exogenous variables. By analyzing the impact of fluctuations in the values associated with the significance of the routine sector, we observe that the inter-sector technological-knowledge gap, favoring tasks performed by both (nonroutine) high- and low-skilled domestic workers, significantly widens with the advancement of automation and relocations achievements. Moreover, by assessing the repercussions of a change in the values associated with both phenomena on wage polarization in favor of (nonroutine) high- and low-skilled domestic workers, we noticed that, on the one hand, the “race” between automation and offshoring is won by automation if there are enhancements in the supply of domestic and foreign medium-skilled labor. In other words, both earnings are more susceptible to shifts in response to automation. On the other hand, the “race” between automation and offshoring is won by offshoring if there are improvements in the absolute productivity of domestic and foreign medium-skilled workers. In other words, both earnings are more prone to fluctuations in response to offshoring.

The policy implications are also noteworthy. Both automation and relocations have several implications that influence the labor market for all classes of workers. These two events can lead to wage disparities, job displacement, and increased unemployment, particularly among the middle-skilled employees most exposed to these shifts. Therefore, to address the skills gap created by automation and offshoring, policymakers may be pressured to undertake interventions in labor and education markets, as well as international trade.