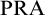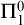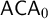ARROW’S THEOREM, ULTRAFILTERS, AND REVERSE MATHEMATICS

Abstract

This paper initiates the reverse mathematics of social choice theory, studying Arrow’s impossibility theorem and related results including Fishburn’s possibility theorem and the Kirman–Sondermann theorem within the framework of reverse mathematics. We formalise fundamental notions of social choice theory in second-order arithmetic, yielding a definition of countable society which is tractable in ${\mathsf {RCA}}_0$. We then show that the Kirman–Sondermann analysis of social welfare functions can be carried out in ${\mathsf {RCA}}_0$. This approach yields a proof of Arrow’s theorem in ${\mathsf {RCA}}_0$, and thus in $\mathrm {PRA}$, since Arrow’s theorem can be formalised as a $\Pi ^0_1$ sentence. Finally we show that Fishburn’s possibility theorem for countable societies is equivalent to ${\mathsf {ACA}}_0$ over ${\mathsf {RCA}}_0$.

1 Introduction

Arrow’s 1950 impossibility theorem [3, 4] is a foundational result in social choice theory. If a society contains only finitely many voters, then any aggregation of individual preference orderings (called a social welfare function) respecting Arrow’s conditions of unanimity and independence of irrelevant alternatives is dictated by a single voter. The theorem therefore appears to place substantial limits on the existence of methods for social decision-making that are fair, rational, and uniform. It has a wide range of applicability including the problems of selecting candidates in elections, deciding on public policies, and choosing between rival scientific theories. As such it has exerted a substantial influence on economics [19, 45], political science [41], and philosophy [25, 37].

Although Arrow’s theorem is essentially a result in finitary combinatorics, later developments in social choice theory in the 1970s brought in more powerful methods such as non-principal ultrafilters, which Fishburn [14] used to show that infinite societies have non-dictatorial social welfare functions. This result and others like it have led mathematical economists to grapple with non-constructivity and applications of the axiom of choice [33]. However, for economically and philosophically relevant models such as societies which are countable or continuous, reverse mathematics offers a more appropriate framework for gauging where (and what) non-constructive set existence axioms are actually necessary in social choice theory.

This paper initiates the reverse mathematics of social choice theory, studying Arrow’s impossibility theorem and related results including Fishburn’s possibility theorem within the framework of reverse mathematics. By defining fundamental notions of social choice theory in second-order arithmetic, we show that an influential analysis of social welfare functions in terms of ultrafilters by Kirman and Sondermann [29] can be carried out in ${\mathsf {RCA}}_0$ . This allows us to establish that Arrow’s theorem, when formalised as a statement of first-order arithmetic, is provable in primitive recursive arithmetic. Fishburn’s possibility theorem, on the other hand, uses non-constructive resources in an essential way, and we prove that its restriction to countable societies is equivalent to ${\mathsf {ACA}}_0$ .

In the classical Arrovian framework, a society $\mathcal {S}$ consists of a set V of voters, a set X of alternatives (or candidates), together with the set W of all weak orders of X (representing the different ways in which the set of alternatives can be rationally ordered), a set $\mathcal {A}$ of coalitions of voters, and a set $\mathcal {F}$ of profiles, i.e., functions ${f : V \to W}$ representing different elections or voting scenarios. In Arrow’s framework, $\mathcal {A}$ and $\mathcal {F}$ satisfy a condition known as unrestricted domain (or universal domain), meaning that $\mathcal {A} = {\mathcal {P}{(V)}}$ and $\mathcal {F} = W^V$ , the set of all functions $f : V \to W$ .

Given alternatives $x,y \in X$ , a profile $f : V \to W$ , and a voter $v \in V$ , we write

$$ \begin{align*} x \lesssim_{f(v)} y \end{align*} $$

to mean that voter v ranks x at least as highly y under profile f, and

$$ \begin{align*} x <_{f(v)} y \end{align*} $$

to mean that voter v strictly prefers x to y under profile f. A social welfare function $\sigma $ for a society $\mathcal {S}$ maps profiles in $\mathcal {F}$ to weak orders in W, and represents one way of consistently aggregating individual preference orderings into an overall social preference ordering. We write

$$ \begin{align*} x \lesssim_{\sigma(f)} y \end{align*} $$

to mean that the social welfare function $\sigma $ ranks x at least as highly as y under profile f, and similarly for $x <_{\sigma (f)} y$ . If R is a weak ordering and $Y \subseteq X$ , we write $R\mathpunct {\restriction _{Y}}$ to mean $R \cap Y^2$ . This lets us state Arrow’s conditions more precisely.

1. (1) Unanimity: If $x <_{f(v)} y$ for all $v \in V$ , then $x <_{\sigma (f)} y$ .

2. (2) Independence of irrelevant alternatives: If $f(v)\mathpunct {\restriction _{\{x,y\}}} = g(v)\mathpunct {\restriction _{\{x,y\}}}$ for all $v \in V$ then $\sigma (f)\mathpunct {\restriction _{\{x,y\}}} = \sigma (g)\mathpunct {\restriction _{\{x,y\}}}$ .

3. (3) Non-dictatoriality: There is no $d \in V$ such that for all $f \in \mathcal {F}$ , if $x <_{f(d)} y$ then $x <_{\sigma (f)} y$ .

Theorem 1.1 (Arrow’s impossibility theorem).

Suppose $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ is a society satisfying unrestricted domain such that V is a nonempty and finite set of voters, and X is a finite set of alternatives with $\left \lvert {X}\right \rvert \geq 3$ . Then there exists no social welfare function $\sigma : \mathcal {F} \to W$ satisfying unanimity, independence, and non-dictatoriality.

Fishburn [14] offered a way out of Arrow’s impossibility result, showing that Arrow’s conditions are consistent if we drop the requirement that V is finite. ¹

Theorem 1.2 (Fishburn’s possibility theorem).

Suppose $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ is a society satisfying unrestricted domain such that V is an infinite set of voters, and X is a finite set of alternatives with $\left \lvert {X}\right \rvert \geq 3$ . Then there exists a social welfare function $\sigma : \mathcal {F} \to W$ satisfying unanimity, independence, and non-dictatoriality.

Infinite societies are widely used in mathematical economics [5, 20–22]. ² Fishburn’s theorem is therefore of antecedent interest in its application domain, despite the prima facie implausibility of infinite ‘societies’.

On a mathematical level, Fishburn’s possibility theorem is best understood in the context of an influential analysis by Kirman and Sondermann [29] which shows that social welfare functions satisfying unanimity and independence correspond to ultrafilters. Arrow had already introduced the notion of a $\sigma $ -decisive coalition for a social welfare function $\sigma $ : a set $C \subseteq V$ such that if $x <_{f(v)} y$ for every $v \in C$ , then $x <_{\sigma (f)} y$ . Kirman and Sondermann established that the collection of all $\sigma $ -decisive coalitions forms an ultrafilter which is principal if and only if $\sigma $ is dictatorial.

Theorem 1.3 (Kirman–Sondermann theorem).

Suppose $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ is a society satisfying unrestricted domain such that V is a nonempty set of voters, and X is a finite set of alternatives with $\left \lvert {X}\right \rvert \geq 3$ . For any social welfare function $\sigma : \mathcal {F} \to W$ satisfying unanimity and independence, the set

$$ \begin{align*} \mathcal{U}_\sigma = \{ C \in \mathcal{A} : C\ \text{is}\ \sigma\text{-}decisive \}, \end{align*} $$

forms an ultrafilter on $\mathcal {A}$ which is principal if and only if $\sigma $ is dictatorial.

Arrow’s theorem is an immediate consequence of the Kirman–Sondermann theorem: as every ultrafilter on a finite set is principal and hence generated by a singleton $\{ d \}$ , any social welfare function for a society with a finite set V of voters must be dictatorial. The Kirman–Sondermann theorem also provides us with our first reverse mathematics-style result. Since it is provable in $\mathrm {ZF}$ , any non-dictatorial social welfare function $\sigma $ for a society with an infinite set V of voters will give rise to a non-principal ultrafilter $\mathcal {U}_\sigma $ on ${\mathcal {P}{(V)}}$ .

Theorem 1.4. Fishburn’s possibility theorem is equivalent over $\mathrm {ZF}$ to the statement that for every infinite set V there exists a non-principal ultrafilter on ${\mathcal {P}{(V)}}$ .

The existence of non-principal ultrafilters is unprovable in $\mathrm {ZF}$ [6], but is (strictly) implied by the axiom of choice [26, 40]. Many therefore consider Fishburn’s possibility theorem to be highly non-constructive [8–10, 36]. At least prima facie, this is a substantial problem for any genuine application of Fishburn’s possibility theorem in social choice theory, a field which is supposed to apply to everyday social decision-making processes such as national elections or votes in a hiring committee. ³ This kind of concern with applicability lies behind a wide range of studies of Arrow’s theorem using tools from computability theory and computational complexity theory. Amongst the former are the work of Lewis [32] in the 1980s and Mihara [35, 36] in the 1990s, while the latter is the preserve of the flourishing field of computational social choice theory [7, 11].

Lewis [32] worked principally with a notion of “recursively enumerable society” in which $V = \omega $ , the algebra of coalitions $\mathcal {A}$ is restricted to include only computably enumerable sets, and the set $\mathcal {F}$ of profiles is restricted to include only computable functions. The set X of alternatives must be have at least three elements, and be at most countably infinite. Lewis proved a weak version of Arrow’s theorem for such societies, showing that if $\sigma $ is a computable social welfare function for a recursively enumerable society $\mathcal {S}$ , then for each profile $f \in \mathcal {F}$ there exists a ‘dictator’ d such that for all $x,y \in X$ , if $x <_{f(d)} y$ , then $x <_{\sigma (f)} y$ . This ‘dictator’ is not necessarily unique across all profiles, and hence not a dictator in Arrow’s original sense. ⁴

Mihara’s approach in [35] is somewhat different, working with a single society $\mathcal {S}$ in which $V = \omega $ , and the coalition algebra $\mathcal {A}$ is precisely the set $\mathrm {REC}$ of all computable sets. Mihara allows a broader range of profiles in $\mathcal {F}$ , namely those which are measurable by sets in $\mathrm {REC}$ . ⁵ The set of alternatives X can be any set with at least three elements, although the computability requirements mean that only countably many alternatives will actually end up being considered by any given social welfare function. Unlike Lewis, Mihara defines a dictator as Arrow does: a single individual whose preferences determine the social ordering across all profiles. Mihara proves that any computable non-dictatorial social welfare function for the society based on the coalition algebra $\mathrm {REC}$ must compute ${0}'$ . The recursive counterexample which we give to Fishburn’s possibility theorem at the end of Section 5 improves on Mihara’s result by constructing a countable society which does not contain all computable sets as coalitions, and can be coded as a single computable set, but all of whose non-dictatorial social welfare functions compute ${0}'$ . In [36], Mihara shows that there exist non-dictatorial social welfare functions for this society which are computable relative to ${0}"$ . ⁶

The aim of this paper is to provide a more nuanced analysis of the situation regarding Arrow’s theorem, Fishburn’s theorem, and their relative (non-)constructivity in terms of the hierarchy of subsystems of second-order arithmetic studied in reverse mathematics. After briefly introducing the relevant background from reverse mathematics and social choice theory in Section 2, we present a canonical sequence of definitions in Section 3 for investigating the proof-theoretic strength of theorems in social choice theory. This investigation begins with Arrow’s impossibility theorem and Fishburn’s possibility theorem, but the framework is sufficiently general and flexible to accommodate future research on other landmark results in social choice theory such as the Gibbard–Satterthwaite theorem [17, 43].

The central definition is that of a countable society: a structure $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ in which $V \subseteq \mathbb {N}$ , and the algebra of coalitions $\mathcal {A} \subseteq {\mathcal {P}{(V)}}$ and the set of profiles $\mathcal {F} \subseteq W^V$ are both countable. Key to this definition and to the results in the paper are conditions on $\mathcal {A}$ and $\mathcal {F}$ called uniform measurability and quasi-partition embedding that ensure their richness and relative compatibility, and which are substantially weaker than previously proposed alternatives to Arrow’s unrestricted domain condition. Using this framework we prove the following results.

Theorem 1.5. Arrow’s impossibility theorem is provable in ${\mathsf {RCA}}_0$ .

In Section 4 we establish that the Kirman–Sondermann analysis of social welfare functions for countable (and hence finite) societies in terms of ultrafilters of decisive coalitions can be formalised in ${\mathsf {RCA}}_0$ . It follows that Arrow’s impossibility theorem is also provable in ${\mathsf {RCA}}_0$ . Moreover, by replacing finite sets with their codes, Arrow’s theorem can be formalised as a $\Pi ^0_1$ sentence which is provable in $\mathrm {PRA}$ .

Theorem 1.6. Fishburn’s possibility theorem for countable societies is equivalent over ${\mathsf {RCA}}_0$ to the axiom scheme of arithmetical comprehension.

This shows that Fishburn’s possibility theorem requires the same set existence principles for its proof as theorems of classical analysis like the Bolzano–Weierstrass theorem, and combinatorial principles like König’s infinity lemma or Ramsey’s theorem $\mathrm {RT}^n_k$ for $n \geq 2$ and $k \geq 3$ . Section 5 is devoted to proving this equivalence, which can be seen as an analogue in second-order arithmetic of theorem 1.4 above. This result can also be understood as generalising the results of Lewis and Mihara discussed above to the broader class of countable societies introduced in Section 3.

2 Preliminaries

This section provides a brief overview of subsystems of second-order arithmetic (Section 2.1), ultrafilters on countable algebras of sets (Section 2.2), and weak orders in social choice theory (Section 2.3).

2.1 Subsystems of second-order arithmetic

Reverse mathematics is a subfield of mathematical logic devoted to determining the set existence principles necessary to prove theorems of ordinary mathematics, including real and complex analysis, countable algebra, and countable infinitary combinatorics. This is done by formalising the theorems concerned in the language of second-order arithmetic, and proving equivalences between those formalisations and systems located in a well-understood hierarchy of set existence principles. The equivalence proofs are carried out in a weak base theory known as ${\mathsf {RCA}}_0$ , which roughly corresponds to computable mathematics and is briefly described below. For details of the material in this subsection, we refer readers to Simpson’s reference work Subsystems of Second Order Arithmetic [48], Dzhafarov and Mummert’s textbook Reverse Mathematics [12], and Hirschfeldt’s monograph Slicing the Truth [23].

Second-order arithmetic $\mathcal {L}_2$ is a two-sorted formal language, with number variables $x_1,x_2,\dotsc $ whose intended range is the natural numbers $\mathbb {N}$ , and set variables $X_1,X_2,\dotsc $ whose intended range is the powerset of the natural numbers ${\mathcal {P}{{(\mathbb {N})}}}$ . The non-logical symbols are those of Peano arithmetic ( $0,1,+,\times ,<$ ) plus the $\in $ symbol for set membership. The atomic formulas of $\mathcal {L}_2$ are those of the form $t_1 = t_2$ , $t_1 < t_2$ , and $t_1 \in X_1$ , where $t_1,t_2$ are number terms and $X_1$ is a set variable. As well as the usual logical connectives, it contains both number quantifiers (sometimes called first-order quantifiers) $\forall {x}$ and $\exists {x}$ , and set quantifiers (sometimes called second-order quantifiers) $\forall {X}$ and $\exists {X}$ . Formulas of $\mathcal {L}_2$ are built up from atomic formulas using logical connectives and set and number quantifiers.

The base theory ${\mathsf {RCA}}_0$ has three sets of axioms: the basic arithmetical axioms, the $\Sigma ^0_1$ induction scheme, and the recursive comprehension axiom scheme. The basic arithmetical axioms are those of Peano arithmetic, minus the induction scheme: in other words, the axioms of a commutative discrete ordered semiring. The $\Sigma ^0_1$ induction axiom scheme consists of the universal closures of all formulas of the form

(Σ₁ ⁰-Ind) $$\begin{align} (\varphi(0) \wedge \forall{n}(\varphi(n) \rightarrow \varphi(n+1))) \rightarrow \forall{n}\varphi(n), \end{align}$$

where $\varphi $ is a $\Sigma ^0_1$ formula, i.e., one of the form $\exists {k}\theta (n,k)$ where $\theta $ contains only bounded quantifiers. Finally, the recursive or $\Delta ^0_1$ comprehension axiom scheme consists of the universal closures of all formulas of the form

(Δ₁ ⁰-CA) $$\begin{align} (\varphi(n) \leftrightarrow \psi(n)) \rightarrow \exists{X}\forall{n}(n \in X \leftrightarrow \varphi(n)), \end{align}$$

where $\varphi $ is a $\Sigma ^0_1$ formula and $\psi $ is a $\Pi ^0_1$ formula, i.e., one of the form $\forall {k}\theta (n,k)$ where $\theta $ contains only bounded quantifiers.

Other subsystems of second-order arithmetic are obtained by extending ${\mathsf {RCA}}_0$ with additional axioms. The present paper is concerned only with one of these systems, ${\mathsf {ACA}}_0$ , which is obtained by augmenting the axioms of ${\mathsf {RCA}}_0$ with the arithmetical comprehension scheme, which consists of the universal closures of all formulas of the form

(ACA) $$\begin{align} \exists{X}\forall{n}(n \in X \leftrightarrow \varphi(n)), \end{align}$$

where $\varphi $ is an arithmetical formula, i.e., which may contain number quantifiers but no set quantifiers, although it may contain free set variables.

2.2 Countable algebras and ultrafilters

Our approach to ultrafilters on countable algebras of sets is based on that of Hirst [24]. We use the standard coding of a sequence of sets by a single sets using the primitive recursive pairing map $(m,n) = (m + n)^2 + m$ . $Y \subseteq \mathbb {N}$ is a sequence of sets, $Y = \mathopen {\langle }Y_i : i \in \mathbb {N}\mathclose {\rangle }$ , if

$$ \begin{align*} (i,v) \in Y \leftrightarrow v \in Y_i \end{align*} $$

for all $i,v \in \mathbb {N}$ .

Definition 2.1 (Countable algebras of sets).

Let $V \subseteq \mathbb {N}$ and let $\mathcal {A} = \mathopen {\langle }A_n : n \in \mathbb {N}\mathclose {\rangle }$ be a countable sequence of sets such that for every $i \in \mathbb {N}$ , $A_i \subseteq V$ . $\mathcal {A}$ is a countable algebra over V if it contains V and it is closed under unions, intersections, and complements relative to V. A countable algebra $\mathcal {A}$ over V is atomic if for all $v \in V$ , there exists $k \in \mathbb {N}$ such that $A_k = \{ v \}$ .

If $\mathcal {A}$ is a countable algebra over a set V, we write $A_i^c$ to denote its relative complement $V \setminus A_i$ . Repetitions are allowed, so given a countable algebra $\mathcal {A}$ we can computably construct an algebra $\mathcal {A}'$ which contains the same sets (typically in a different order) in which we can uniformly compute the operations of complementation, union, and intersection. We make this precise through the following definition.

Definition 2.2 (Boolean embeddings).

A boolean formation sequence is a finite sequence $s \in \mathrm {Seq}$ with $\left \lvert {s}\right \rvert \geq 1$ such that for all $j < \left \lvert {s}\right \rvert $ , one of the following obtains for some $n,m < j$ :

1. (1) $s(j) = (0,n,n)$ ,

2. (2) $s(j) = (1,n,n)$ and $n < j$ ,

3. (3) $s(j) = (2,n,m)$ and $n,m < j$ .

If s is a boolean formation sequence, then we write $s \in \mathrm {BFS}$ .

Fix a set $V \subseteq \mathbb {N}$ and suppose that $S = \mathopen {\langle } S_i : i \in \mathbb {N} \mathclose {\rangle }$ is a countable sequence of subsets of V and that $\mathcal {A} = \mathopen {\langle } A_i : i \in \mathbb {N} \mathclose {\rangle }$ is an algebra of sets over V. A function $e : \mathrm {BFS} \to \mathbb {N}$ is a boolean embedding of S into $\mathcal {A}$ if for all boolean formation sequences s with $k = \left \lvert {s}\right \rvert - 1$ , there exist $n,m < s$ such that:

1. (1) If $s(k) = (0,n,n),$ then $A_{e(s)} = S_n$ .

2. (2) If $s(k) = (1,n,n)$ and $n < k$ , then $A_{e(s)} = A_{e(s\mathpunct {\restriction _{n+1}})}^c$ .

3. (3) If $s(k) = (2,n,m)$ and $n,m < k$ , then $A_{e(s)} = A_{e(s\mathpunct {\restriction _{n+1}})} \cap A_{e(s\mathpunct {\restriction _{m+1}})}$ .

The following lemma is a straightforward exercise in primitive recursion.

Lemma 2.3. The following is provable in ${\mathsf {RCA}}_0$ . Suppose $S = \mathopen {\langle } S_i : i \in \mathbb {N} \mathclose {\rangle }$ is a sequence of subsets of $V \subseteq \mathbb {N}$ . Then there exists an algebra $\mathcal {A}$ over V, a boolean embedding e of S into $\mathcal {A}$ , and a boolean embedding $e^*$ from $\mathcal {A}$ into $\mathcal {A}$ .

Moreover, if S is already a countable algebra over V, then:

1. (1) For all $m \in \mathbb {N}$ , $S_m = A_{e(\mathopen {\langle }(0,m,m)\mathclose {\rangle })}$ .

2. (2) For all $n \in \mathbb {N}$ , there exists $k \in \mathbb {N}$ such that $A_n = S_k$ .

Definition 2.4 (Ultrafilters).

Suppose $\mathcal {A} = \mathopen {\langle }A_n : n \in N\mathclose {\rangle }$ is a countable algebra over $V \subseteq \mathbb {N}$ . $\mathcal {U} \subseteq \mathbb {N}$ is an ultrafilter on $\mathcal {A}$ if it obeys the following conditions for all $i,j,k \in \mathbb {N}$ .

1. (1) (Non-emptiness.) If $A_i = V$ , then $i \in \mathcal {U}$ .

2. (2) (Properness.) If $A_i = \emptyset $ , then $i \not \in \mathcal {U}$ .

3. (3) (Upwards closure.) If $i \in \mathcal {U}$ and $A_i \subseteq A_j$ , then $j \in \mathcal {U}$ .

4. (4) (Intersections.) If $i,j \in \mathcal {U}$ and $A_k = A_i \cap A_j$ , then $k \in \mathcal {U}$ .

5. (5) (Maximality.) If $A_j = A_i^c$ , then $i \in \mathcal {U}$ or $j \in \mathcal {U}$ .

An ultrafilter $\mathcal {U}$ is principal if it obeys the following condition, and non-principal otherwise.

1. (6) (Principality.) There exist $k,d \in \mathbb {N}$ such that $k \in \mathcal {U}$ and $A_k = \{ d \}$ .

The next lemma is elementary, but worth stating as it is used a number of times.

Lemma 2.5. The following is provable in ${\mathsf {RCA}}_0$ . Suppose $\mathcal {A}$ is a countable atomic algebra over $V \subseteq \mathbb {N}$ and $\mathcal {U} \subseteq \mathbb {N}$ is an ultrafilter on $\mathcal {A}$ . Then $\mathcal {U}$ has the following properties for all $i,j,k \in \mathbb {N}$ .

1. (1) If $i \in \mathcal {U}$ and $A_j = A_i^c$ , then $j \not \in \mathcal {U}$ .

2. (2) If $A_k = A_i \cup A_j$ and $k \in \mathcal {U}$ , then either $i \in \mathcal {U}$ or $j \in \mathcal {U}$ .

3. (3) Suppose $\mathopen {\langle }Y_i : i < k\mathclose {\rangle }$ is a finite sequence of sets and $s \in \mathrm {Seq}$ is such that $\left \lvert {s}\right \rvert = k + 1$ . If $Y_i = A_{s(i)}$ for all $i < k$ , $(\bigcup _{i<k} Y_i) = A_{s(k)}$ , and $s(k) \in \mathcal {U}$ , then there exists $j < k$ such that $s(j) \in \mathcal {U}$ .

4. (4) The following conditions are equivalent:

   1. (a) $\mathcal {U}$ is principal.

   2. (b) There exists $k \in \mathbb {N}$ such that $A_k$ is finite and $k \in \mathcal {U}$ .

   3. (c) There exists $d \in V$ such that for all $i \in \mathbb {N}$ , $i \in \mathcal {U}$ if and only if $d \in A_i$ .

When we come to consider Fishburn’s possibility theorem in Section 5, we will need the following well-known result: the existence of non-principal ultrafilters on countable algebras is equivalent to arithmetical comprehension. This equivalence appears in its present guise as theorem 9 of Kreuzer [31], but it has many antecedents. The proof of the forward direction presented here follows a partition construction from Kreuzer [30], although similar ideas have been used by others, going back to Kirby and Paris [28] and Solovay [49]. The reversal uses the fact that non-principal ultrafilters refine the Fréchet filter in order to code the jump, an idea drawn from Kirby [27, theorem 1.10].

Lemma 2.6. The following are equivalent over ${\mathsf {RCA}}_0$ .

1. (1) ${\mathsf {ACA}}_0$ .

2. (2) For every infinite set $V \subseteq \mathbb {N}$ and every atomic countable algebra $\mathcal {A}$ over V, there exists a non-principal ultrafilter $\mathcal {U}$ on $\mathcal {A}$ .

Proof. We first show that 1 implies 2. Working in ${\mathsf {ACA}}_0$ , let $V \subseteq \mathbb {N}$ be infinite and let $\mathcal {A}$ be a countable algebra over V; we do not need the additional assumption that $\mathcal {A}$ is atomic. Given $s \in 2^{<\mathbb {N}}$ , let

(1) $$ \begin{align} A^s = \bigcap_{i < \left\lvert{s}\right\rvert} \left\{\begin{array}{ll} A_i & \text{if } s(i) = 0, \\ (A_i)^c & \text{if } s(i) = 1. \end{array} \right. \end{align} $$

By $\Sigma ^0_0$ induction we have that for all $v \in V$ , $\forall {n}\exists {!s \in 2^n}(v \in A^s)$ . In other words, $\mathopen {\langle }A^s : s \in 2^n\mathclose {\rangle }$ is a partition of V. To see this, let $t \in 2^n$ be the unique sequence such that $z \in A^t$ . $v \in A^{t\operatorname {\mathrm {\smallfrown }}\mathopen {\langle }0\mathclose {\rangle }} \leftrightarrow v \in A_{n+1}$ , so if $v \in A_{n+1}$ we set $s = t\operatorname {\mathrm {\smallfrown }}\mathopen {\langle }0\mathclose {\rangle }$ and if $v \not \in A_{n+1}$ then we set $s = t\operatorname {\mathrm {\smallfrown }}\mathopen {\langle }1\mathclose {\rangle }$ . Since these possibilities are exclusive, either way $s \in 2^{n+1}$ is the unique sequence such that $v \in A^s$ as desired. Now let

(2) $$ \begin{align} T = \{ s \in 2^{<\mathbb{N}} : A^s \text{is infinite} \}. \end{align} $$

T exists by arithmetical comprehension. We claim that T is an infinite tree. Suppose not, so there is some n such that for all $s \in 2^n$ , $A^s$ is finite. Let $A' = \cup _{s \in 2^n} A^s$ . $A'$ is finite since every $A^s$ is, so let m bound the elements of $A'$ . By assumption V is infinite, so there exists $v \in V$ such that $v> m$ . $v \not \in A'$ so $v \not \in A^s$ for all $s \in 2^n$ , contradicting the fact that $\mathopen {\langle }A^s : s \in 2^n\mathclose {\rangle }$ partitions V. By weak König’s lemma that there exists an infinite path P in T, so let $\mathcal {U} = \{ k : P(k) = 0 \}$ , which exists by recursive comprehension in the parameter P. To complete the proof we show that $\mathcal {U}$ is a non-principal ultrafilter on $\mathcal {A}$ .

To establish non-principality, it suffices to note that every $A_i$ such that $i \in \mathcal {U}$ is infinite because $A^{P \mathpunct {\restriction _{i + 1}}}$ is an infinite subset of $A_i$ . To show maximality, let $i \in \mathcal {U}$ be arbitrary with $(A_i)^c = A_j$ , and suppose $j \in \mathcal {U}$ . Let $k = \max \{ i,j \} + 1$ . Since, by our assumption, $P(i) = P(j) = 0$ , we have that $A^{P \mathpunct {\restriction _{k}}} = \emptyset $ , contradicting the fact that ${P \mathpunct {\restriction _{k}} \in T}$ and so $A^{P \mathpunct {\restriction _{k}}}$ is infinite. To show that $\mathcal {U}$ is closed under intersections, let $i,j \in \mathcal {U}$ , let ${A_m = A_i \cap A_j}$ , and let $A_n = (A_m)^c$ . Suppose for a contradiction that $m \not \in \mathcal {U}$ , so by maximality $A_n \in \mathcal {U}$ . Let $k = \max \{ i,j,m,n \} + 1$ . Then $A^{P \mathpunct {\restriction _{k}}} = \emptyset $ , contradicting the fact that $P \mathpunct {\restriction _{k}} \in T$ . A similar argument establishes upwards closure. Take $i \in \mathcal {U}$ and suppose $A_i \subseteq A_j$ . Towards a contradiction assume that $j \in \mathcal {U}$ , so by maximality and intersections if $A_k = A_i \cap (A_j)^c = \emptyset $ then $k \in \mathcal {U}$ , contradicting non-principality.

Working now in ${\mathsf {RCA}}_0$ , we show that 2 implies 1. To prove arithmetical comprehension it suffices to prove that the range of any one-to-one function $h : \mathbb {N} \to \mathbb {N}$ exists [48, lemma III.1.3, pp. 105–106]. The sequence

(3) $$ \begin{align} B = \{ (2n, v) : v \in V \wedge (\exists{k < v})(h(k) = n) \} \cup \{ (2n+1,n) : n \in V \} \end{align} $$

exists by recursive comprehension since all quantifiers in its definition are bounded, and by Lemma 2.3 there exists a countable algebra $\mathcal {A} = \mathopen {\langle }A_i : i \in \mathbb {N}\mathclose {\rangle }$ over $\mathbb {N}$ and a boolean embedding $e : \mathrm {BFS} \to \mathbb {N}$ of B into $\mathcal {A}$ . The right-hand side of the union defining B ensures that $\mathcal {A}$ is atomic, i.e., it contains all singletons $\{v\}$ for $v \in V$ .

For convenience we write $n'$ to mean $e(\mathopen {\langle }(0,2n,2n)\mathclose {\rangle })$ , i.e., the index in $\mathcal {A}$ such that $A_{n'} = B_n$ .

By 2 there exists $\mathcal {U} \subseteq \mathbb {N}$ such that $\mathcal {U}$ is a non-principal ultrafilter on $\mathcal {A}$ , and by recursive comprehension, the set $Y = \{ n : n' \in \mathcal {U} \}$ exists. We show that $Y = \operatorname {\mathrm {ran}}(h) = \{ n : \exists {k}(h(k) = n) \}$ .

Suppose $n \in Y$ , so $n' \in \mathcal {U}$ and thus by non-principality $A_{n'}$ is non-empty, meaning there is some v such that $(\exists {k<v})(h(k) = n)$ . It follows that $\exists {k}(h(k) = n)$ , i.e., $n \in \operatorname {\mathrm {ran}}(h)$ . For the converse note that if $\exists {k}(h(k) = n)$ then $A_{n'}$ is cofinite. To see this, fix any $m \in A_{n'}$ and any $j \in \mathbb {N}$ . Assume $v + j \in A_{n'}$ , so there exists some $k < v + j$ such that $h(k) = n$ . $k < v + j + 1$ , so by $\Sigma ^0_0$ induction, for all j, $v + j \in A_{n'}$ . Consequently $A_{n'}$ is cofinite and so by maximality $n' \in \mathcal {U}$ , and thus $n \in Y$ .

2.3 Orderings in social choice theory

The paper aims to be self-contained where notions from social choice theory are concerned, but a good starting point for a deeper study is Taylor’s monograph Social Choice and the Mathematics of Manipulation [51]. In social choice theory, voters express their preferences as orders on the set of alternatives X (e.g., ranking candidates in an election). These orders are required to be transitive and strongly connected, but ties are permitted to express indifference between alternatives. This notion is standardly called a weak order in the social choice theory literature, and we follow this terminology here, noting that it is synonymous with the notion of a total preorder. In this paper we will be concerned exclusively with finite sets of alternatives X, and hence all our weak orders will be assumed to be coded by natural numbers.

Definition 2.7 (Weak orders).

Suppose $X \subseteq \mathbb {N}$ is nonempty and $R \subseteq X \times X$ . R is strongly connected if $(x,y) \in R$ or $(y,x) \in R$ for all $x,y \in X$ .

If R is a transitive and strongly connected relation then we call it a weak order and write $x \lesssim _R y$ to mean $(x,y) \in R$ , $x <_R y$ to mean $(x,y) \in R \wedge (y,x) \not \in R$ , and $x \sim _R y$ to mean $(x,y) \in R \wedge (y,x) \in R$ .

Many basic properties of weak orders can be established in ${\mathsf {RCA}}_0$ . For example, if R is a weak order then:

1. (1) $\lesssim _R$ is reflexive.

2. (2) $\sim _R$ is an equivalence relation on X.

3. (3) If $x <_R z$ then $x <_R y$ or $y <_R z$ (negative transitivity).

Given a set $V \subseteq \mathbb {N}$ of voters and a finite set $X \subseteq \mathbb {N}$ of alternatives, we let W be the set of all (codes for) weak orders on X. A profile is a function $f : V \to W$ . In practice we will always be concerned with countable sequences $\mathcal {F} = \mathopen {\langle } f_i : i \in \mathbb {N} \mathclose {\rangle }$ of profiles. If $f_i$ is a profile and $v \in V$ is a voter then we write $x \lesssim _{i(v)} y$ to mean that $x \lesssim _R y$ where $R = f_i(v)$ , i.e., that alternative x is preferred to y by voter v in the voting scenario represented by the profile $f_i$ . Similarly we write $x <_{i(v)} y$ to mean $x <_R y$ , and $x \sim _{i(v)} y$ to mean $x \sim _R y$ .

A coalition is simply a set $C \subseteq V$ of voters; by convention, we allow both the empty set and singleton sets containing only one voter to count as coalitions. Given a coalition C, we write $x \lesssim _{i[C]} y$ to mean that $x \lesssim _{i(v)} y$ for all $v \in C$ , and $x <_{i[C]} y$ and $x \sim _{i[C]} y$ have their obvious meanings.

If $Y \subseteq X$ , we write $f_i(v) = f_j(v)$ on Y to mean that $x \lesssim _{i(v)} y \leftrightarrow x \lesssim _{j(v)} y$ for all $x,y \in Y$ , i.e., that v’s preferences regarding all x and y in S are the same under both the voting scenarios represented by the profiles $f_i$ and $f_j$ . We write $f_i = f_j$ on Y to mean that $f_i(v) = f_j(v)$ on Y for all $v \in V$ .

3 Countable societies

In the classical social choice literature, the notion of a society has been generalised by Armstrong [1] to allow $\mathcal {A}$ to be any algebra of sets over V, rather than all of ${\mathcal {P}{(V)}}$ . In Armstrong’s generalisation $\mathcal {F}$ is always the set of all $\mathcal {A}$ -measurable profiles, i.e., those $f : V \to W$ such that for all $x,y \in X$ , $\{ v : x \lesssim _{f(v)} y \} \in \mathcal {A}$ . This paper only addresses the countable case, i.e., when not only V but also $\mathcal {A}$ and $\mathcal {F}$ are countable objects that can be coded by sets of natural numbers. ⁷

A countable society consists of a set of voters $V \subseteq \mathbb {N}$ , a finite set of alternatives $X \subseteq \mathbb {N}$ and the associated set W of weak orders on X, an atomic countable algebra of coalitions $\mathcal {A}$ , and a countable sequence of profiles $\mathcal {F} = \mathopen {\langle } f_i : i \in \mathbb {N} \mathclose {\rangle }$ over $V,X$ (i.e., for all i, $f_i$ is a function from V to W). However, in order for theorems about countable societies to continue to make sense in the way they do when $\mathcal {A} = {\mathcal {P}{(V)}}$ and $\mathcal {F} = W^V$ , we need to impose certain conditions on $\mathcal {A}$ and $\mathcal {F}$ . The first such condition is that profiles in $\mathcal {F}$ are measurable by coalitions in $\mathcal {A}$ . Measurability must also be uniform, to ensure that proofs using it can be carried out in ${\mathsf {RCA}}_0$ .

Definition 3.1 (Uniform measurability).

Suppose $V \subseteq \mathbb {N}$ is nonempty and $X \subseteq \mathbb {N}$ is finite, and that $\mathcal {A}$ is a countable algebra of sets over V and $\mathcal {F}$ is a countable sequence of profiles over $V,X$ . If there exists $\mu : \mathbb {N} \times X \times X \to \mathbb {N}$ such that for all $n \in \mathbb {N}$ , $x,y \in X$ , and $v \in V$ ,

$$ \begin{align*} x \lesssim_{n(v)} y \leftrightarrow v \in A_{\mu(n,x,y)}, \end{align*} $$

then we say $\mathcal {F}$ is uniformly $\mathcal {A}$ -measurable.

Lemma 3.2. The following is provable in ${\mathsf {RCA}}_0$ . Suppose $V \subseteq \mathbb {N}$ is nonempty and $X \subseteq \mathbb {N}$ is nonempty and finite, and that $\mathcal {A} = \mathopen {\langle } A_i : i \in \mathbb {N} \mathclose {\rangle }$ is a countable algebra of sets over V and $\mathcal {F} = \mathopen {\langle } f_i : i \in \mathbb {N} \mathclose {\rangle }$ is a countable sequence of profiles over $V,X$ . If $\mathcal {F}$ is uniformly $\mathcal {A}$ -measurable then there exist functions $\mu _{<}, \mu _{\sim } : \mathbb {N} \times X \times X \to \mathbb {N}$ such that for all $n \in \mathbb {N}$ , $x,y \in X$ , and $v \in V$ ,

$$ \begin{align*} x <_{n(v)} y \leftrightarrow v \in A_{\mu_{<}(n,x,y)} \end{align*} $$

and

$$ \begin{align*} x \sim_{n(v)} y \leftrightarrow v \in A_{\mu_{\sim}(n,x,y)}. \end{align*} $$

The second condition, quasi-partition embedding, ensures that finite sequences of coalitions in $\mathcal {A}$ can be recovered uniformly from profiles in $\mathcal {F}$ . This condition emerges naturally from the proofs of the Kirman–Sondermann theorem and Fishburn’s possibility theorem, although to the best of our knowledge it is isolated here for the first time. ⁸ Quasi-partitions of V, in which overlaps are allowed, are preferred to partitions since they are more computationally tractable. ⁹

Definition 3.3 (Quasi-partition embedding).

Suppose $V \subseteq \mathbb {N}$ is nonempty and $X \subseteq \mathbb {N}$ is finite with $|X| \geq 3$ , and that $\mathcal {A}$ is a countable algebra of sets over V and $\mathcal {F}$ is a countable profile algebra over $V,X$ . A permutation of a finite set W is a finite sequence $p \in \mathrm {Seq}$ such that for all (codes for) weak orders $R \in W$ there exists a unique i such that $p(i) = R$ . We write $p \in \mathrm {Perm}(W)$ to indicate that p is a permutation of W. A quasi-partition is a finite sequence $s \in \mathrm {Seq}$ such that $1 \leq \left \lvert {s}\right \rvert $ . We write $s \in \mathrm {QPart}(k)$ to indicate that s is a quasi-partition with $\left \lvert {s}\right \rvert \leq k$ . $\mathcal {A}$ is quasi-partition embedded into $\mathcal {F}$ if there exists a function $e : \mathrm {Perm}(W) \times \mathrm {QPart}(\left \lvert {W}\right \rvert ) \to \mathbb {N}$ such that for all $v \in V$ ,

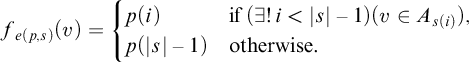$$ \begin{align*} f_{e(p,s)}(v) = \begin{cases} p(i) & \text{if }(\exists{!i < \left\lvert{s}\right\rvert-1}) (v \in A_{s(i)}), \\ p(\left\lvert{s}\right\rvert - 1) & \text{otherwise}. \end{cases} \end{align*} $$

Definition 3.4 (Countable societies).

A countable society $\mathcal {S}$ consists of a nonempty set $V \subseteq \mathbb {N}$ of voters, a finite set $X \subseteq \mathbb {N}$ of alternatives with $|X| \geq 3$ , an atomic countable algebra $\mathcal {A}$ over V, and a sequence $\mathcal {F} = \mathopen {\langle } f_i : i \in \mathbb {N} \mathclose {\rangle }$ of profiles over $V,X$ such that $\mathcal {F}$ is uniformly $\mathcal {A}$ -measurable and $\mathcal {A}$ is quasi-partition embedded into $\mathcal {F}$ .

A countable society $\mathcal {S}$ is finite if V is finite, and infinite otherwise.

Definition 3.5 (Social welfare functions).

Suppose that $\mathcal {S}$ is a countable society. $\sigma : \mathbb {N} \to W$ is a social welfare function for $\mathcal {S}$ if it obeys the following conditions.

1. (1) (Unanimity.) For all $x, y \in X$ and $i \in \mathbb {N}$ , if $x <_{i[V]} y$ then $x <_{\sigma (i)} y$ .

2. (2) (Independence.) For all $x,y \in X$ and all $i,j \in \mathbb {N}$ , if $f_i = f_j$ on $\{ x, y \}$ then $\sigma (i) = \sigma (j)$ on $\{ x, y \}$ .

If $\sigma $ obeys the following additional condition then it is non-dictatorial.

1. (3) (Non-dictatoriality.) For all $v \in V$ there exists $i \in \mathbb {N}$ and $x,y \in X$ such that $x <_{i(v)} y$ and $y \lesssim _{\sigma (i)} x$ .

Definition 3.6 (Decisive coalitions).

Suppose $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ is a countable society and that $\sigma $ is a social welfare function for $\mathcal {S}$ .

1. (1) $A_n$ is $\sigma $ -decisive for $x,y$ if for all i, $x <_{i[A_n]} y$ implies $x <_{\sigma (i)} y$ .

2. (2) $A_n$ is $\sigma $ -decisive if it is $\sigma $ -decisive for all $x,y \in X$ .

3. (3) $A_n$ is almost $\sigma $ -decisive for $x,y$ at i if $x <_{i[A_n]} y$ , $y <_{i[A_n^c]} x$ , and $x <_{\sigma (i)} y$ .

4. (4) $A_n$ is almost $\sigma $ -decisive for $x,y$ if

   $$ \begin{align*} \forall{i}( (x <_{i[A_n]} y \wedge y <_{i[A_n^c]} x) \rightarrow x <_{\sigma(i)} y ). \end{align*} $$

5. (5) $A_n$ is almost $\sigma $ -decisive if it is almost $\sigma $ -decisive for all $x,y \in X$ .

The notion of a decisive coalition is due to Arrow [4, definition 10, p. 52], while almost decisiveness was introduced by Sen [45, definition 3*2, p. 42]. The non-dictatoriality condition for social welfare functions can be rephrased in terms of decisive coalitions, namely by saying that no singleton $\{ d \} \subseteq V$ is $\sigma $ -decisive. This gives rise to some natural strengthenings of non-dictatoriality (Definition 5.1).

4 Arrow’s theorem via ultrafilters

In this section we show how the Kirman–Sondermann analysis of social welfare functions in terms of ultrafilters can be carried out in ${\mathsf {RCA}}_0$ (Theorem 4.4). This immediately gives a proof of Arrow’s theorem in ${\mathsf {RCA}}_0$ (Theorem 4.5).

Definition 4.1. The Kirman–Sondermann theorem for countable societies ( $\mathrm {KS}$ ) is the following statement: Suppose $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ is a countable society and that $\sigma $ is a social welfare function for $\mathcal {S}$ . Then there exists an ultrafilter

$$ \begin{align*} \mathcal{U}_\sigma = \{ i : A_i\ \text{is}\ \sigma\text{-decisive} \} \end{align*} $$

on $\mathcal {A}$ which is principal if and only if $\sigma $ is dictatorial.

Arrow’s theorem is the statement that if $\mathcal {S}$ is a finite society and $\sigma $ is a social welfare function for $\mathcal {S}$ , then $\sigma $ is dictatorial.

A crucial step in many proofs of Arrow’s theorem is sometimes known in the social choice literature as the “spread of decisiveness” [47, pp. 35–37] or the “contagion lemma” [9, pp. 44–45]. Kirman and Sondermann’s version of this is a lemma showing that there exists a profile f and a pair of alternatives $x,y \in X$ such that $C \subseteq V$ is almost $\sigma $ -decisive at f for $x,y$ if and only if C is almost $\sigma $ -decisive for every profile and every pair of alternatives [29, lemma A]. In our arithmetical setting, the corresponding versions of these two conditions are $\Sigma ^0_2$ and $\Pi ^0_2$ , respectively, so formalising Kirman and Sondermann’s lemma A establishes that the set $\{ i : A_i \text { is almost } \sigma \text {-decisive} \}$ is $\Delta ^0_2$ definable relative to $\mathcal {S}$ and $\sigma $ . However, the definition of a countable society in fact allows us to uniformly find witnesses for this last condition, and thereby obtain a $\Sigma ^0_0$ definition.

This and subsequent proofs are made easier by the use of some notation for weak orders. Given distinct alternatives $x,y,z \in X$ ,

$$ \begin{align*} R = x < y < z \sim \ast \end{align*} $$

means that R is a weak order such that $x <_R y$ and $y <_R z$ , and hence $x <_R z$ . We use the wildcard symbol $\ast $ to quantify over all $c \in X$ not explicitly mentioned, so in the example above, any other $c \in X$ is such that $y <_R c$ but $z \sim _R c$ . This notation thus denotes a unique weak order, or rather, the natural number coding it as a finite set.

Lemma 4.2. The following is provable in ${\mathsf {RCA}}_0$ . Suppose $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ is a countable society and $\sigma $ is a social welfare function for $\mathcal {S}$ . Then there exists a function $g : \mathbb {N} \to \mathbb {N}$ and alternatives $a,b \in X$ such that the following conditions are equivalent for all $n \in \mathbb {N}$ .

1. (1) $A_n$ is almost $\sigma $ -decisive.

2. (2) There exist $x,y \in X$ such that $A_n$ is almost $\sigma $ -decisive for $x,y$ .

3. (3) There exist $k \in \mathbb{N}$ and $x,y \in X$ such that $A_n$ is almost $\sigma $ -decisive for $x,y$ at k.

4. (4) $a <_{\sigma (g(i))} b$ .

Proof. It follows immediately from the statements that 1 implies 2, and 2 implies 3. We show that 3 implies 2. Let $f_m$ be arbitrary, let $A_n$ be almost $\sigma $ -decisive for $x,y$ at k, and assume that $x <_{m[A_n]} y$ and $y <_{m[A_n^c]} x$ . Given $v \in V$ , if $v \in A_n$ then $x <_{k(v)} y$ by almost $\sigma $ -decisiveness and $x <_{m(v)} y$ by assumption, while if $v \not \in A_n$ then $y <_{k(v)} x$ and $y <_{m(v)} x$ , so $f_m = f_k$ on $\{ x, y \}$ and thus $\sigma (m) = \sigma (k)$ on $\{ x, y \}$ by independence. Since $x <_{\sigma (k)} y$ it follows that $x <_{\sigma (m)} y$ , establishing that $A_n$ is almost $\sigma $ -decisive for $x,y$ .

Now we show that 2 implies 1. Let $A_n$ be almost $\sigma $ -decisive for $x,y$ and let $z \in X \setminus \{ x, y \}$ . Assume that $x <_{m[A_n]} z$ and $z <_{m[A_n^c]} x$ for some $f_m$ . Since $\mathcal {F}$ quasi-partition embeds $\mathcal {A}$ , there exists j such that

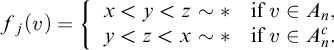$$ \begin{align*} f_j(v) = \left\{\begin{array}{ll} x < y < z \sim \ast & \text{if } v \in A_n, \\ y < z < x \sim \ast & \text{if } v \in A_n^c. \end{array} \right. \end{align*} $$

By the almost $\sigma $ -decisiveness of $A_n$ and the construction of $f_j$ , it follows that $x <_{\sigma (j)} y$ , and by unanimity, $y <_{\sigma (j)} z$ , so by transitivity we have that $x <_{\sigma (j)} z$ . By our initial assumption, and the construction of $f_j$ , $f_m = f_j$ on $\{ x, z \}$ , so by independence $x <_{\sigma (m)} z$ .

A similar argument yields that

$$ \begin{align*} \left(z \lesssim_{m[A_n]} y \wedge y \lesssim_{m[A_n^c]} z\right) \rightarrow z \lesssim_{\sigma(m)} y. \end{align*} $$

Now fix $w \in X$ . If $w \in \{ x, y, z \}$ we are done, so assume otherwise. Running the argument twice more we get that

$$ \begin{align*} \left(z \lesssim_{m[A_n]} w \wedge w \lesssim_{m[A_n^c]} z\right) \rightarrow z \lesssim_{\sigma(m)} w, \end{align*} $$

and since $w,z$ were arbitrary, we have established that $A_n$ is almost $\sigma $ -decisive.

Finally we show that g exists and that 1 and 4 are equivalent. Pick any $a,b \in X$ and let p be a permutation of W such that $p(0) = a < b < *$ and $p(1) = b < a < *$ . $\mathcal {A}$ is quasi-partition embedded into $\mathcal {F}$ by some $e : \mathbb {N} \to \mathbb {N}$ , so we have

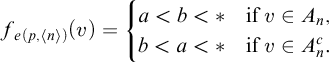$$ \begin{align*} f_{e(p,\mathopen{\langle}n\mathclose{\rangle})}(v) = \begin{cases} a < b < * & \text{if } v \in A_n, \\ b < a < * & \text{if } v \in A_n^c. \end{cases} \end{align*} $$

The function $g(n) = e(p,\mathopen {\langle }n\mathclose {\rangle })$ exists by recursive comprehension.

If $A_n$ is almost $\sigma $ -decisive then $a <_{\sigma (g(n))} b$ by the definition of g, so suppose for the converse implication that $a <_{\sigma (g(n))} b$ . $a <_{g(n)[A_n]} b$ and $b <_{g(n)[A_n^c]} a$ by the definition of g, meaning $A_n$ is almost $\sigma $ -decisive for $a,b$ at $g(n)$ . By the equivalence between 1 and 3, $A_n$ is almost $\sigma $ -decisive.

Lemma 4.3. The following is provable in ${\mathsf {RCA}}_0$ . Suppose $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ is a countable society and $\sigma $ is a social welfare function for $\mathcal {S}$ . Then the set

$$ \begin{align*} \mathcal{U}_\sigma = \{ i \in \mathbb{N} : A_i\ \text{is almost}\ \sigma\text{-decisive} \} \end{align*} $$

exists and forms an ultrafilter on $\mathcal {A}$ .

Proof. Working in ${\mathsf {RCA}}_0$ , fix a countable society $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ and a social welfare function $\sigma $ for $\mathcal {S}$ . For all of the arguments below we fix distinct $x,y,z \in X$ .

To show that $\mathcal {U}_\sigma $ exists, note that by Lemma 4.2 there exists a function $g : \mathbb {N} \to \mathbb {N}$ and $x,y \in X$ such that

$$ \begin{align*} x <_{\sigma(g(i))} y \leftrightarrow A_i\ \text{is\ almost}\ \sigma\text{-decisive}. \end{align*} $$

The left-hand side of this definition is $\Sigma ^0_0$ in the parameters $\mathcal {S},\sigma ,g$ , so $\mathcal {U}_\sigma $ exists by recursive comprehension in those parameters. In the remainder of the proof we show that $\mathcal {U}_\sigma $ is an ultrafilter on $\mathcal {A}$ .

That $\mathcal {U}_\sigma $ contains an index for V and no index for $\emptyset $ follows straightforwardly from unanimity, so we next prove upwards closure under the subset relation. Suppose $i \in \mathcal {U}_\sigma $ and $A_i \subseteq A_j$ , and partition V into

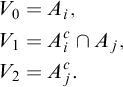$$ \begin{align*} V_0 &= A_i, \\ V_1 &= A_i^c \cap A_j, \\ V_2 &= A_j^c. \end{align*} $$

Since $\mathcal {A}$ is quasi-partition embedded into $\mathcal {F}$ , there exists some m such that

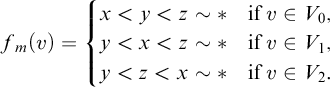$$ \begin{align*} f_m(v) = \begin{cases} x < y < z \sim \ast & \text{if } v \in V_0, \\ y < x < z \sim \ast & \text{if } v \in V_1, \\ y < z < x \sim \ast & \text{if } v \in V_2. \end{cases} \end{align*} $$

$x <_{m[A_i]} y$ by the definition of $f_m$ , so since $A_i$ is almost $\sigma $ -decisive we have that $x <_{\sigma (m)} y$ . The definition of $f_m$ also gives us that $y <_{m[V]} z$ , so by unanimity, $y <_{\sigma (m)} z$ , and by transitivity, $x <_{\sigma (m)} z$ , which suffices to establish that $j \in \mathcal {U}_\sigma $ by clause 3 of Lemma 4.2.

Next we prove that $\mathcal {U}_\sigma $ is closed under intersections. Suppose that $i,j \in \mathcal {U}_\sigma $ and that k is such that $A_k = A_i \cap A_j$ . Partition V into

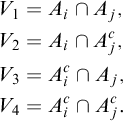$$ \begin{align*} V_1 &= A_i \cap A_j, \\ V_2 &= A_i \cap A_j^c, \\ V_3 &= A_i^c \cap A_j, \\ V_4 &= A_i^c \cap A_j^c. \end{align*} $$

By quasi-partition embedding let the profile $f_n$ be defined as follows:

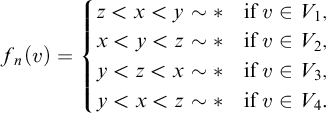$$ \begin{align*} f_n(v) = \begin{cases} z < x < y \sim \ast & \text{if } v \in V_1, \\ x < y < z \sim \ast & \text{if } v \in V_2, \\ y < z < x \sim \ast & \text{if } v \in V_3, \\ y < x < z \sim \ast & \text{if } v \in V_4. \end{cases} \end{align*} $$

Since $A_i = V_1 \cup V_2$ we have that $x <_{n[A_i]} y$ by the definition of $f_n$ . Similarly since $A_i^c = V_3 \cup V_4$ , $y <_{n[A_i^c]} x$ , so by the almost $\sigma $ -decisiveness of $A_i$ it follows that $x <_{\sigma (n)} y$ . By a parallel piece of reasoning we have that $z <_{\sigma (n)} x$ , and so by transitivity $z <_{\sigma (n)} y$ . It follows by clause 3 of Lemma 4.2 that $A_k$ is almost $\sigma $ -decisive.

Finally we prove that $\mathcal {U}_\sigma $ satisfies maximality. Suppose that $A_j = A_i^c$ . By quasi-partition embedding there exists some $m \in \mathbb {N}$ such that

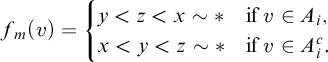$$ \begin{align*} f_m(v) = \begin{cases} y < z < x \sim \ast & \text{if } v \in A_i, \\ x < y < z \sim \ast & \text{if } v \in A_i^c. \end{cases} \end{align*} $$

By unanimity we have that $y <_{\sigma (m)} z$ , so either $y <_{\sigma (m)} x$ or $x <_{\sigma (m)} z$ . In the former case, $m,y,x$ witness that $A_i$ is almost $\sigma $ -decisive by clause 3 of Lemma 4.2, while in the latter case $m,x,z$ witness that $A_j$ is almost $\sigma $ -decisive.

Theorem 4.4. $\mathrm {KS}$ is provable in ${\mathsf {RCA}}_0$ .

Proof. We work in ${\mathsf {RCA}}_0$ . Let $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ be a countable society and let $\sigma : \mathbb {N} \to X$ be a social welfare function for $\mathcal {S}$ . By Lemma 4.3 there exists an ultrafilter $\mathcal {U}_\sigma \subseteq \mathbb {N}$ on $\mathcal {A}$ such that

$$ \begin{align*} \mathcal{U}_\sigma = \{ i \in \mathbb{N} : A_i\ \text{is almost}\ \sigma\text{-decisive} \}. \end{align*} $$

It only remains to be shown that (i) $i \in \mathcal {U}_\sigma $ if and only if $A_i$ is $\sigma $ -decisive, and (ii) $\mathcal {U}_\sigma $ is principal if and only if $\sigma $ is dictatorial.

For (i), the backwards direction is immediate from the definitions. For the forward direction fix $A_i$ such that $i \in \mathcal {U}_\sigma $ , i.e., $A_i$ is almost $\sigma $ -decisive. Let $f_m$ and $x,y$ be such that $x <_{m[A_i]} y$ ; we will establish that $x <_{\sigma (m)} y$ .

Start by partitioning V into the sets

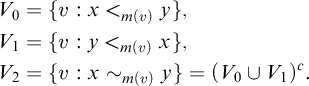$$ \begin{align*} V_0 &= \{ v : x <_{m(v)} y \}, \\ V_1 &= \{ v : y <_{m(v)} x \}, \\ V_2 &= \{ v : x \sim_{m(v)} y \} = (V_0 \cup V_1)^c. \end{align*} $$

By uniform $\mathcal {A}$ -measurability, there exist $e_0,e_1,e_2 \in \mathbb {N}$ such that $A_{e_j} = V_j$ for all $j \leq 2$ , and because $\mathcal {F}$ quasi-partition embeds $\mathcal {A}$ , there exists $n \in \mathbb {N}$ such that

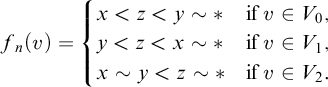$$ \begin{align*} f_n(v) = \begin{cases} x < z < y \sim \ast & \text{if } v \in V_0, \\ y < z < x \sim \ast & \text{if } v \in V_1, \\ x \sim y < z \sim \ast & \text{if } v \in V_2. \end{cases} \end{align*} $$

By hypothesis we have that $A_i$ is almost $\sigma $ -decisive and $A_i \subseteq V_0$ , so $V_0$ is almost $\sigma $ -decisive by upwards closure. $V_0^c = V_1 \cup V_2$ , so since $z <_{n[V_0]} y$ and $y <_{n[V_1 \cup V_2]} z$ , it follows from the almost $\sigma $ -decisiveness of $V_0$ that $z <_{\sigma (n)} y$ .

Let $e_3$ be such that $A_{e_3} = V_0 \cup V_2$ , and hence $A_{e_3}^c = V_1$ . By upwards closure again, $A_{e_3}$ is almost $\sigma $ -decisive, and so because $x <_{n[A_{e_3}]} z$ and $z <_{n[A_{e_3}^c]} x$ , $x <_{\sigma (n)} z$ . It follows by transitivity that $x <_{\sigma (n)} y$ . Finally, by definition $f_n = f_m$ on $\{ x, y \}$ , and so by independence $x <_{\sigma (m)} y$ as desired.

For the forward direction of (ii), assume that there exist $k,d$ such that $A_k = \{ d \}$ and $k \in \mathcal {U}_\sigma $ . It follows from (i) that $A_k$ is $\sigma $ -decisive, and so d is a dictator for $\sigma $ .

For the backwards direction of (ii), suppose that $\sigma $ has a dictator $d \in V$ . $\mathcal {A}$ is atomic, so let k be any index such that $A_k = \{ d \}$ . Since $\mathcal {F}$ quasi-partition embeds $\mathcal {A}$ , there exists an n such that $f_n$ is defined as follows:

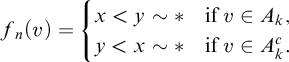$$ \begin{align*} f_n(v) = \begin{cases} x < y \sim \ast & \text{if } v \in A_k, \\ y < x \sim \ast & \text{if } v \in A_k^c. \end{cases} \end{align*} $$

By the definition of $f_n$ we have that $x <_{n[A_k]} y$ and $y <_{n[A_k^c]} x$ , and by the dictatoriality of d we have that $x <_{\sigma (n)} y$ , so by Lemma 4.2, $k \in \mathcal {U}_\sigma $ and hence $\mathcal {U}_\sigma $ is principal.

Theorem 4.5. Arrow’s theorem is provable in ${\mathsf {RCA}}_0$ .

Proof. We work in ${\mathsf {RCA}}_0$ . Suppose $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ is a finite society, and let $\sigma : \mathbb {N} \to W$ be any social welfare function for $\mathcal {S}$ . By $\mathrm {KS}$ (Theorem 4.4), there exists an ultrafilter $\mathcal {U}_\sigma $ on $\mathcal {A}$ which is principal if and only if $\sigma $ is dictatorial. Since V is finite, $\mathcal {U}_\sigma $ is principal by part 4 of Lemma 2.5. Therefore, $\sigma $ is dictatorial.

Since all the objects involved in Arrow’s theorem are finite, it can be formalised as a sentence $\theta $ in the language of first-order arithmetic, by replacing quantification over finite sets of natural numbers with quantification over the numbers that code them (for details see Section II.2 of [48] or Section 5.5.2 of [12]). The first-order sentence $\theta $ then follows in ${\mathsf {RCA}}_0$ from the second-order statement of Arrow’s theorem in virtue of the coding. As long as one is careful with writing down the relevant bounds, $\theta $ will be a $\Pi ^0_1$ statement, i.e., of the form $\forall {n}\psi (n)$ where $\psi (n)$ contains only bounded quantifiers. By results of Friedman [16] and Parsons [38], ${\mathsf {RCA}}_0$ is conservative over primitive recursive arithmetic ( $\mathrm {PRA}$ ) for all $\Pi ^0_2$ statements [48, sec. IX.1]. We therefore have that Arrow’s theorem (in the form of its first-order formalisation $\theta $ ) is provable in $\mathrm {PRA}$ , and hence it is finitarily provable in the sense of Tait’s analysis of Hilbert’s program [50]. Moreover, the bounds in $\theta $ are exponential, which suggests the following stronger result.

Conjecture 4.6. The first-order formalisation of Arrow’s theorem is provable in $\mathrm {I}\Delta _0 + \mathrm {exp}$ .

5 Fishburn’s possibility theorem

The main result of this section, Theorem 5.4 is that Fishburn’s possibility theorem for countable societies is equivalent to ${\mathsf {ACA}}_0$ over ${\mathsf {RCA}}_0$ . We also show that non-dictatorial social welfare functions actually satisfy more general non-dictatoriality conditions than Arrow’s original condition (Lemma 5.2).

Definition 5.1. Fishburn’s possibility theorem for countable societies ( $\mathrm {FPT}$ ) is the following statement: For all countable societies $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ where V is infinite, there exists a non-dictatorial social welfare function $\sigma $ for $\mathcal {S}$ .

A social welfare function $\sigma $ for $\mathcal {S}$ is k-non-dictatorial if for all $s \in \mathrm {Seq}(V)$ such that $\left \lvert {s}\right \rvert \leq k$ , there exists j and $x,y \in X$ such that for all $i < \left \lvert {s}\right \rvert $ , $x <_{j(s(i))} y$ and $y <_{\sigma (j)} x$ . $\mathrm {FPT}^k$ is the statement obtained by replacing non-dictatoriality in $\mathrm {FPT}$ with k-non-dictatoriality for some fixed $k \geq 1$ .

$\sigma $ is finitely non-dictatorial if for all $k \geq 1$ , $\sigma $ is k-non-dictatorial. $\mathrm {FPT}^{<\mathbb {N}}$ is the statement obtained by replacing non-dictatoriality in $\mathrm {FPT}$ with finite non-dictatoriality.

$\sigma $ has the cofinite coalitions property if for every profile $j \in \mathbb {N}$ , if cofinitely many $v \in V$ are such that $x <_{j(v)} y$ , then $x <_{\sigma (j)} y$ . $\mathrm {FPT}^+$ is the statement obtained by replacing non-dictatoriality in $\mathrm {FPT}$ with the cofinite coalitions property.

One concern with the interpretation of Fishburn’s possibility theorem has been that the choice of ultrafilter seems arbitrary. When faced with an infinite set with a complement of the same cardinality, there seems to be no reason to consider one to genuinely constitute a majority rather than the other. This is not the case for cofinite sets which, in an infinite society, clearly constitute a majority. A social welfare function with the cofinite coalitions property therefore satisfies a version of Condorcet consistency: if a majority (a cofinite set) of voters prefer x to y, then so does the social welfare function. Since an ultrafilter on a given algebra is non-principal exactly when it refines the Fréchet filter, the cofinite coalitions property is also the strongest non-dictatoriality property a social welfare function can have. We now show that all non-dictatorial social welfare functions have this property.

Lemma 5.2. The following is provable in ${\mathsf {RCA}}_0$ . Suppose $\mathcal {S}$ is a countable society and $\sigma $ is a social welfare function for $\mathcal {S}$ . Then the following conditions are equivalent.

1. (1) $\sigma $ is non-dictatorial.

2. (2) $\sigma $ is k-non-dictatorial for some fixed $k \geq 1$ .

3. (3) $\sigma $ is finitely non-dictatorial.

4. (4) $\sigma $ has the cofinite coalitions property.

Proof. The implications from 4 to 3, 3 to 2, and 2 to 1 are immediate. Working in ${\mathsf {RCA}}_0$ , we show that 1 implies 4. Let $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {S}\mathclose {\rangle }$ be a countable society and let $\sigma $ be a non-dictatorial social welfare function for $\mathcal {S}$ . By $\mathrm {KS}$ (Theorem 4.4) the ultrafilter $\mathcal {U}_\sigma $ of (indexes of) $\sigma $ -decisive coalitions exists and is non-principal. Moreover, V is infinite by Arrow’s theorem.

Fix an arbitrary profile $f_m$ and two alternatives $x, y \in X$ , and suppose that for some k, if $v \in V$ is such that $v \geq k$ then $x <_{m(v)} y$ . By the closure of $\mathcal {A}$ under finite unions and relative complements there exists a j such that $A_j = \{ v \in V : v \geq k \}$ , which is cofinite since V is infinite. Since $\mathcal {U}_\sigma $ is non-principal, $j \in \mathcal {U}_\sigma $ by part 4 of Lemma 2.5. Therefore, $A_j$ is $\sigma $ -decisive and $x <_{\sigma (m)} y$ .

The following Lemma 5.3 is a partial converse of the Kirman–Sondermann theorem for countable societies—partial because for any given ultrafilter $\mathcal {U}$ there may be distinct social welfare functions with $\mathcal {U}$ as their set of decisive coalitions. Various restrictions allow a one-to-one correspondence between ultrafilters and social welfare functions to be recovered, for example, by restricting to profiles and social welfare functions which output linear orders as in [51, theorem 6.1.3], or by imposing a monotonicity condition as in [2].

These restrictions are less interesting from a computability-theoretic point of view, since the resulting bijective functionals between ultrafilters and social welfare functions are themselves computable, while without these restrictions there are social welfare functions $\sigma $ such that $\mathcal {U}_\sigma <_{\mathrm {T}} \sigma $ . This can occur most strikingly when $\sigma $ is dictatorial, and hence $\mathcal {U}_\sigma $ is computable (since to compute membership in $\mathcal {U}_\sigma $ one simply needs to check for any given $A_i$ if $d \in A_i$ , where d is the dictator). There will remain infinitely many profiles $f_i$ and alternatives $x,y$ such that neither $\mu _<(i,x,y)$ nor $\mu _<(i,y,x)$ are in $\mathcal {U}_\sigma $ . Some of these gaps of indifference can be filled in by appealing to another, non-principal and non-computable ultrafilter, resulting in a social welfare function that is dictatorial but not computable. For details of this construction see proposition 1 of [35].

Lemma 5.3. The following statement is provable in ${\mathsf {RCA}}_0$ . Suppose $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ is a countable society. If $\mathcal {U}$ is an ultrafilter on $\mathcal {A}$ , then there exists a social welfare function $\sigma _{\mathcal {U}}$ for $\mathcal {S}$ with the following properties.

1. (1) For all $i \in \mathbb {N}$ , $i \in \mathcal {U}$ if and only if $A_i$ is $\sigma _{\mathcal {U}}$ -decisive.

2. (2) The following conditions are equivalent:

   1. (a) $\mathcal {U}$ is non-principal,

   2. (b) $\sigma _{\mathcal {U}}$ has the cofinite coalitions property.

Proof. Working in ${\mathsf {RCA}}_0$ , let $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ be a countable society and $\mathcal {U} \subseteq \mathbb {N}$ be an ultrafilter on $\mathcal {A}$ .

Let $\varphi (n,R)$ be the following $\Sigma ^0_0$ formula in the displayed free variables.

$$ \begin{align*} \varphi(n,R) \equiv (\forall{x,y} \in X)( (x,y) \in R \leftrightarrow \mu(n,x,y) \in \mathcal{U} ). \end{align*} $$

Note that here we are considering R as a natural number coding a finite set. Let b code the finite set $X \times X$ . Since our coding of finite sets by natural numbers is monotonic, $b \geq R'$ for all $R' \in W$ . By $\Sigma ^0_1$ induction, for all n there exists $R \leq b$ such that $\varphi (R,n)$ . This is just an application of comprehension for codes of finite sets; for details, see, e.g., [18].

We show that R is a weak order. To show strong connectedness, let $x,y \in X$ be arbitrary. If $x = y$ then since $x \lesssim _{n(v)} x$ for all $n \in \mathbb {N}$ and $v \in V$ , we have that $A_{\mu (n,x,x)} = V$ , so $\mu (n,x,x) \in \mathcal {U}$ by non-emptiness and thus $(x,x) \in R$ . Suppose instead that $x \neq y$ , let $i = \mu (n,x,y)$ and let j be such that $A_j = A_i^c$ . Since $\mathcal {U}$ is an ultrafilter, by maximality either $i \in \mathcal {U}$ or $j \in \mathcal {U}$ . If $i \in \mathcal {U}$ then $(x,y) \in R$ , so assume the latter. ${A_j = A_{\mu _<(n,y,x)} \subseteq A_{\mu (n,y,x)}}$ , so $\mu (n,y,x) \in \mathcal {U}$ by upwards closure, establishing that $(y,x) \in R$ .

For transitivity, suppose $(x,y) \in R$ and $(y,z) \in R$ , so ${\mu (n,x,y) \in \mathcal {U}}$ and $\mu (n,y,z) \in \mathcal {U}$ . Let j be such that $A_j = A_{\mu (n,x,y)} \cap A_{\mu (n,y,z)}$ , so $j \in \mathcal {U}$ by closure under intersections. Then $x \lesssim _{n[A_j]} y$ and $y \lesssim _{n[A_j]} z$ , so by transitivity we have that $x \lesssim _{n[A_j]} z$ . Thus, ${A_j \subseteq A_{\mu (n,x,z)}}$ and $\mu (n,x,z) \in \mathcal {U}$ by upwards closure.

This lets us define $\sigma \subseteq \mathbb {N}$ by

$$ \begin{align*} (n,R) \in \sigma \leftrightarrow R = \min R' \text{ such that } \varphi(R',n). \end{align*} $$

Since W is finite, the use of minimisation is bounded and so the definition of $\sigma $ is $\Sigma ^0_0$ in the parameters $\mu _<$ and $\mathcal {U}$ , meaning that $\sigma $ exists by recursive comprehension. By the claim, $\sigma \subseteq \mathbb {N} \times W$ and for all $n \in \mathbb {N}$ there exists $R \in W$ such that $(n,R) \in \sigma $ . Thus, since minimisation is a function, so is $\sigma $ , i.e., $\sigma : \mathbb {N} \to W$ .

We now show that $m \in \mathcal {U}$ if and only if $A_m$ is $\sigma $ -decisive. For the forwards direction, suppose $m \in \mathcal {U}$ and $x,y \in X$ and $n \in \mathbb {N}$ are such that $x <_{n[A_m]} y$ . By this hypothesis, $A_m \subseteq A_{\mu (n,x,y)}$ , so $\mu (n,x,y) \in \mathcal {U}$ by upwards closure. $A_{\mu (n,x,y)} = A_{\mu _<(n,x,y)} \cup A_{\mu _\sim (n,x,y)}$ , and thus either $\mu _<(n,x,y) \in \mathcal {U}$ or $\mu _\sim (n,x,y) \in \mathcal {U}$ by part 2 of Lemma 2.5. Suppose the latter. By hypothesis, $A_{\mu _\sim (n,x,y)} \cap A_m = \emptyset $ , and since $\mathcal {U}$ is closed under intersections it would have to contain an index for $\emptyset $ , contradicting properness. So $\mu _<(n,x,y) \in \mathcal {U}$ , $\mu _\sim (n,x,y) \not \in \mathcal {U}$ , and $\mu _<(n,y,x) \not \in \mathcal {U}$ , which establishes that $x <_{\sigma (n)} y$ by the definition of $\sigma $ . For the reverse direction, suppose $A_m$ is $\sigma $ -decisive and let $x,y \in X$ be arbitrary. By quasi-partition embedding there exists $f_k$ such that $x <_{k(v)} y$ if $v \in A_m$ , and $y <_{k(v)} x$ if $v \in A_m^c$ . By $\sigma $ -decisiveness, $x <_{\sigma (k)} y$ , so $\mu (k,x,y) \in \mathcal {U}$ . $A_m = A_{\mu (k,x,y)}$ , so $m \in \mathcal {U}$ by upwards closure.

To show that $\sigma $ satisfies unanimity, let $x,y \in X$ and $f_n$ be arbitrary, and suppose that $x <_{n[V]} y$ . Because $A_{\mu (n,x,y)} = V$ by uniform $\mathcal {A}$ -measurability, it follows by the non-emptiness condition for $\mathcal {U}$ that $\mu (n,x,y) \in \mathcal {U}$ . Moreover, we also have that $A_{\mu _<(n,y,x)} = A_{\mu _\sim (n,x,y)} = \emptyset $ , so $\mu _<(n,y,x) \not \in \mathcal {U}$ and $\mu _\sim (n,x,y) \not \in \mathcal {U}$ . It follows that by the construction of $\sigma $ , $x <_{\sigma (n)} y$ .

To show that $\sigma $ satisfies independence, let $x,y \in X$ and suppose $f_i = f_j$ on $\{ x, y \}$ . $A_{\mu (i,x,y)} = A_{\mu (j,x,y)}$ by uniform $\mathcal {A}$ -measurability. Upwards closure of $\mathcal {U}$ under $\subseteq $ then gives us that $\mu (i,x,y) \in \mathcal {U} \leftrightarrow \mu (j,x,y)$ . By the construction of $\sigma $ , $x \lesssim _{\sigma (i)} y \leftrightarrow x \lesssim _{\sigma (j)} y$ as desired.

Finally we prove that $\mathcal {U}$ is non-principal if and only if $\sigma $ has the cofinite coalitions property. For the forwards direction, suppose $\mathcal {U}$ is non-principal and let $A_i$ be cofinite, so $i \in \mathcal {U}$ by part 4 of Lemma 2.5. Suppose that $x <_{k[A_i]} y$ for some $x,y \in X$ and $k \in \mathbb {N}$ . Since $i \in \mathcal {U}$ , $A_i$ is $\sigma $ -decisive, and so $x <_{\sigma (k)} y$ . For the backwards direction, suppose $\sigma $ has the cofinite coalitions property and let $A_i$ be cofinite. By quasi-partition embedding, let j be such that $A_{\mu (j,x,y)} = \{ v : x <_{j(v)} y \} = A_i$ . $x <_{\sigma (j)} y$ by the cofinite coalitions property since $A_i$ is cofinite, so $\mu (j,x,y) \in \mathcal {U}$ , and hence $i \in \mathcal {U}$ by upwards closure under $\subseteq $ . Since i was arbitrary, $\mathcal {U}$ is non-principal by part 4 of Lemma 2.5.

Theorem 5.4. The following are equivalent over ${\mathsf {RCA}}_0$ .

1. (1) $\mathrm {FPT}$ .

2. (2) $\mathrm {FPT}^k$ for any $k \geq 1$ .

3. (3) $\mathrm {FPT}^{<\mathbb {N}}$ .

4. (4) $\mathrm {FPT}^+$ .

5. (5) Arithmetical comprehension.

Lemma 5.5. The following is provable in ${\mathsf {RCA}}_0$ . Suppose $V \subseteq \mathbb {N}$ is nonempty and $X \subseteq \mathbb {N}$ is finite with $\left \lvert {X}\right \rvert \geq 3$ and $\mathcal {A} = \mathopen {\langle } A_i : i \in \mathbb {N} \mathclose {\rangle }$ is a countable algebra over V. Then there exists a sequence $\mathcal {F} = \mathopen {\langle } f_i : i \in \mathbb {N} \mathclose {\rangle }$ of profiles over $V,X$ such that $\mathcal {F}$ is uniformly $\mathcal {A}$ -measurable and $\mathcal {A}$ is quasi-partition embedded into $\mathcal {F}$ .

Proof. We first apply Lemma 2.3 to replace $\mathcal {A}$ with an extensionally equivalent algebra $\mathcal {A}'$ in which we can uniformly compute boolean combinations via a boolean embedding. We abuse notation in the remainder of this proof by referring to $\mathcal {A}$ rather than $\mathcal {A}'$ .

The infinite set $\mathrm {Perm}(W) \times \mathrm {QPart}(\left \lvert {W}\right \rvert )$ exists by recursive comprehension, and by primitive recursion there exists a function $\mathit {en} : \mathbb {N} \to \mathrm {Perm}(W) \times \mathrm {QPart}(\left \lvert {W}\right \rvert )$ enumerating it. Let $\theta (n,v,w)$ be a $\Sigma ^0_0$ formula which says that $\mathit {en}(n) = (p,s)$ and either there exists a unique $j<\left \lvert {s}\right \rvert -1$ such that $v \in A_{s(j)}$ and $w = p(i)$ , or there exists no such unique j and $w = p(\left \lvert {s}\right \rvert -1)$ . The set $\mathcal {F} = \{ (n,v,w) : \theta (n,v,w) \}$ exists by recursive comprehension and codes a sequence of profiles $\mathopen {\langle } f_i : i \in \mathbb {N} \mathclose {\rangle }$ .

We now show that $e = \mathit {en}^{-1}$ is a quasi-partition embedding of $\mathcal {A}$ into $\mathcal {F}$ . Let p be a permutation of W, s a quasi-partition, and $k = e(p,s)$ . Suppose $v \in V$ . We reason by cases.

1. (1) Suppose there exists a unique $j<\left \lvert {s}\right \rvert -1$ such that $v \in A_{s(j)}$ . Then $(k,v,p(j)) \in \mathcal {F}$ by the construction of $\mathcal {F}$ , i.e., $f_k(v) = p(j)$ .

2. (2) Now suppose there is no such j. Then $(k,v,p(\left \lvert {s}\right \rvert -1)) \in \mathcal {F}$ by the construction of $\mathcal {F}$ , i.e., $f_k(v) = p(\left \lvert {s}\right \rvert -1)$ .

Finally we show that $\mathcal {F}$ is uniformly $\mathcal {A}$ -measurable. Fix $x,y \in X$ and a profile $f_n$ . By the construction of $\mathcal {F}$ , $\mathit {en}(n) = (s,p)$ for some quasi-partition s and permutation p of W. For all $j < \left \lvert {s}\right \rvert $ , let $t^j$ be a boolean formation sequence for the set

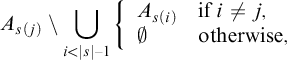$$ \begin{align*} A_{s(j)} \setminus \bigcup_{i < \left\lvert{s}\right\rvert-1} \left\{\begin{array}{ll} A_{s(i)} & \text{if } i \neq j, \\ \emptyset & \text{otherwise}, \end{array} \right. \end{align*} $$

and given boolean formation sequences $t_1$ and $t_2$ , let

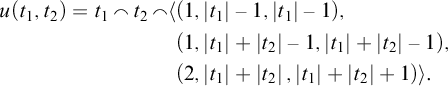$$ \begin{align*} u(t_1,t_2) = t_1 \operatorname{\mathrm{\smallfrown}} t_2 \operatorname{\mathrm{\smallfrown}} \mathopen{\langle}& (1,\left\lvert{t_1}\right\rvert-1,\left\lvert{t_1}\right\rvert-1), \\ & (1,\left\lvert{t_1}\right\rvert+\left\lvert{t_2}\right\rvert-1,\left\lvert{t_1}\right\rvert+\left\lvert{t_2}\right\rvert-1), \\ & (2,\left\lvert{t_1}\right\rvert+\left\lvert{t_2}\right\rvert,\left\lvert{t_1}\right\rvert+\left\lvert{t_2}\right\rvert+1) \mathclose{\rangle}. \end{align*} $$

Let $h_0(s,p,x,y) = \mathopen {\langle }\mathclose {\rangle }$ and

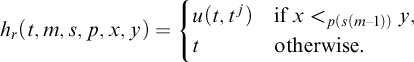$$ \begin{align*} h_r(t,m,s,p,x,y) = \begin{cases} u(t,t^j) & \text{if } x <_{p(s(m-1))} y, \\ t & \text{otherwise}. \end{cases} \end{align*} $$

Let h be the function defined by primitive recursion from $h_0$ and $h_r$ . Define $\mu : \mathbb {N} \times X \times X \to \mathbb {N}$ by $\mu (n,x,y) = e^*(h(\left \lvert {s}\right \rvert ,s,p,x,y))$ , where $e^* : \mathrm {BFS} \to \mathbb {N}$ is a boolean embedding of $\mathcal {A}$ into itself (this exists by Lemma 2.3). We can then verify by $\Sigma ^0_0$ induction that $\mathcal {F}$ is uniformly $\mathcal {A}$ -measurable via $\mu $ .

Proof of Theorem 5.4.

Statements 1–4 are equivalent by Lemma 5.2. To complete the proof it suffices to show that 5 implies 4 and 1 implies 5. To show that 5 implies 4, we work in ${\mathsf {ACA}}_0$ and suppose that $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ is a countable society and that V is infinite. By Lemma 2.6, there exists a non-principal ultrafilter $\mathcal {U}$ on $\mathcal {A}$ , and hence by Lemma 5.3 there exists a social welfare function $\sigma _{\mathcal {U}}$ for $\mathcal {S}$ with the cofinite coalitions property.

Finally we show that 1 implies 5. Working in ${\mathsf {RCA}}_0$ , let $V \subseteq \mathbb {N}$ be infinite and let $\mathcal {A}$ be a countable atomic algebra over V. Fix $X = \{ x, y, z \}$ . By Lemma 5.5 there exists a countable sequence of profiles $\mathcal {F}$ over $V,X$ such that $\mathcal {A}$ is quasi-partition embedded into $\mathcal {F}$ and $\mathcal {F}$ is uniformly $\mathcal {A}$ -measurable. $\mathcal {S} = \mathopen {\langle }V,X,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ is thus a countably infinite society, and so by $\mathrm {FPT}$ there exists a non-dictatorial social welfare function $\sigma $ for $\mathcal {S}$ . By $\mathrm {KS}$ (Theorem 4.4), there exists an ultrafilter $\mathcal {U}_\sigma $ on $\mathcal {A}$ which is non-principal since $\sigma $ is non-dictatorial. Since $\mathcal {A}$ is an arbitrary infinite atomic algebra, this implies arithmetical comprehension by Lemma 2.6.

We conclude this section with a few remarks on the computability-theoretic status of $\mathrm {FPT}$ . Early work in effectivising social choice theory emphasised the non-computability of non-dictatorial social welfare functions, and thus an extension of Arrow’s theorem from finite sets to computable sets. For example, Mihara [35] showed that when $V = \mathbb {N}$ , $\mathcal {A} = \mathrm {REC}$ , and $\mathcal {F}$ consists of all $\mathcal {A}$ -measurable profiles, any non-dictatorial social welfare function for this society is non-computable. In the present setting this is not automatic: there are countable societies with computable non-dictatorial social welfare functions. The natural minimal example of this is provided by a society based on a computable presentation of the finite–cofinite algebra. There is a single non-principal ultrafilter on this algebra, and both it and the non-dictatorial social welfare function derived from it via the construction in Lemma 5.3 are computable.

On the other hand, there are recursive counterexamples to Fishburn’s possibility theorem far less complex than the societies considered by Lewis [32] or Mihara [35] which we discussed in Section 1. The following argument is based on Kirby’s proof of the reverse direction of Lemma 2.6 [27, theorem 1.10]. Let $h : \mathbb {N} \to \mathbb {N}$ be a computable enumeration of the halting problem ${0}'$ . Using Lemma 2.3 we computably embed a sequence of sets $B = \mathopen {\langle } B_i : i \in \mathbb {N} \mathclose {\rangle }$ into a countable atomic algebra $\mathcal {A}$ , where B is defined by

$$ \begin{align*} B = \{ (2n, v) : (\exists{m < v})(h(m) = n) \} \cup \{ (2n+1, n) : n \in \mathbb{N} \}. \end{align*} $$

By Lemma 5.5 there exists a countable society $\mathcal {S} = \mathopen {\langle }\mathbb {N},3,\mathcal {A},\mathcal {F}\mathclose {\rangle }$ . We can then construct a primitive recursive function $g : \mathbb {N} \to \mathbb {N}$ that computes the indexes of a family of profiles such that $x <_{g(n)(v)} y$ if $v \in B_{2n}$ , and $y <_{g(n)(v)} x$ otherwise. If $\sigma $ is any non-dictatorial social welfare function for $\mathcal {S}$ , then ${0}' \leq _{\mathrm {T}} \sigma $ , since ${0}' = \operatorname {\mathrm {ran}}(h)$ is $\Sigma ^0_0$ definable in the parameter $\sigma $ by the formula $\varphi (n) \equiv x <_{\sigma (g(n))} y$ . There will only exist a v such that $v \in B_{2n}$ if $n \in \operatorname {\mathrm {ran}}(h)$ , but when there is, the cofinite coalitions property ensures that $x <_{f(v)} y$ . $\mathcal {S}$ is thus a computable society all of whose non-dictatorial social welfare functions compute ${0}'$ . Nevertheless, this non-computability result is ‘easy’ since it only requires coding a single jump. A natural question is thus whether we can obtain more precise degree-theoretic information about the complexity of non-dictatorial social welfare functions.

6 Conclusion and further work

The results presented in this paper initiate the reverse mathematics of social choice theory. In doing so, they demonstrate both the suitability of reverse mathematics as a framework in which to assess the effectivity of theorems from social choice theory, and the fruitfulness of social choice theory as a source for reverse mathematical results. It is straightforward within the present setting to define additional types of collective choice rules for countable societies, allowing further theorems like Sen’s liberal paradox [46] or the Gibbard–Satterthwaite theorem [17, 43] to be formalised in $\mathcal {L}_2$ , and their reverse mathematical status to be investigated. The latter theorem, which concerns strategic voting and the manipulability of elections, is a classical impossibility result from the 1970s. Like Arrow’s theorem, it has a corresponding possibility theorem when the set of voters is infinite [39]. Finally, the equivalence between $\mathrm {FPT}$ and arithmetical comprehension shows that the existence of non-computable sets is essential to proving the existence of non-dictatorial social welfare functions. On the one hand, this is a far weaker notion of non-constructivity than that measured by equivalences to choice principles over $\mathrm {ZF}$ . On the other, it shows that we cannot in general hope for computable rules for social decision-making in countably infinite societies, even for countable societies whose coalitions do not include all computable sets of voters.