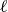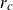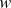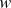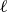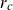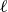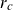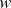1. Introduction
Over the last few decades, an increase in computational power has led to larger and larger direct numerical simulations of magnetohydrodynamic (MHD) turbulence (Biskamp Reference Biskamp2008; Beresnyak Reference Beresnyak2019; Schekochihin Reference Schekochihin2022). While these simulations generally support the theory of Goldreich & Sridhar (Reference Goldreich and Sridhar1995) for self-similar fluctuations in MHD turbulence, the same simulations also show the presence of transient coherent structures – spatiotemporal fluctuations known as the intermittency (see, e.g., Vlahos & Isliker (Reference Vlahos and Isliker2023), for a review). Among these coherent structures are current sheets, which are ribbon-shaped regions of high electric current density. Current sheets have also been identified in simulations of collisionless plasmas where the full kinetic equations are solved (e.g., Comisso & Sironi Reference Comisso and Sironi2018, Reference Comisso and Sironi2019).
Several groups have performed statistical studies of current sheets in MHD turbulence to categorize their geometric distributions (Servidio et al. Reference Servidio, Matthaeus, Shay, Dmitruk, Cassak and Wan2010; Uritsky et al. Reference Uritsky, Pouquet, Rosenberg, Mininni and Donovan2010; Zhdankin et al. Reference Zhdankin, Uzdensky, Perez and Boldyrev2013, Reference Zhdankin, Boldyrev, Perez and Tobias2014, Reference Zhdankin, Boldyrev and Uzdensky2016, Reference Zhdankin, Walker, Boldyrev and Lesur2017 Reference Zhdankin, Walker, Boldyrev and Lesura ; Ross & Latter Reference Ross and Latter2018). They measured the distribution of the width, length and thickness of the current sheets. The results revealed that the current sheets are indeed self-similar structures, and their geometric components obey power-law or exponential distributions. In addition, recent works have detected and analysed current sheets in collisionless regimes (Makwana et al. Reference Makwana, Zhdankin, Li, Daughton and Cattaneo2015; Azizabadi, Jain & Büchner Reference Azizabadi, Jain and Büchner2021; Sisti et al. Reference Sisti, Fadanelli, Cerri, Faganello, Califano and Agullo2021; Bussov & Nättilä, Reference Bussov and Nättilä2021). Others have also attempted to associate the properties of current sheets with the statistical distribution of turbulent field fluctuations, including recent works on relativistic MHD (Chernoglazov, Ripperda & Philippov Reference Chernoglazov, Ripperda and Philippov2021) and kinetic turbulence (Davis, Comisso & Giannios Reference Davis, Comisso and Giannios2024).
Here, we focus on current sheets in fully kinetic simulations of magnetically dominated (relativistic) plasma turbulence. In the magnetically dominated regime, a large reservoir of magnetic energy is available to cascade down and dissipate, leading to heating and acceleration of non-thermal particles. None of the previous studies have performed the geometric statistical analysis in this regime of turbulence, which has
![]() $v_{A} \approx c$
, where
$v_{A} \approx c$
, where
![]() $v_{A}$
is the Alfvén velocity and
$v_{A}$
is the Alfvén velocity and
![]() $c$
is the speed of light. Relativistic kinetic turbulence is an area of active study in recent years, spurred by progress with particle-in-cell (PIC) simulations (Zhdankin et al. Reference Zhdankin, Werner, Uzdensky and Begelman2017
Reference Zhdankin, Werner, Uzdensky and Begelmanb
; Comisso & Sironi Reference Comisso and Sironi2018; Nättilä & Beloborodov, Reference Nättilä and Beloborodov2021; Vega et al. Reference Vega, Boldyrev, Roytershteyn and Medvedev2022; Meringolo et al. Reference Meringolo, Cruz-Osorio, Rezzolla and Servidio2023; Singh et al. Reference Singh, French, Guo and Li2024). It is relevant for many high-energy astrophysical systems (e.g., compact objects and transients). The motivation of this study is to perform a two-dimensional (2-D) statistical analysis of current sheets and compare/contrast with previous results in the literature.
$c$
is the speed of light. Relativistic kinetic turbulence is an area of active study in recent years, spurred by progress with particle-in-cell (PIC) simulations (Zhdankin et al. Reference Zhdankin, Werner, Uzdensky and Begelman2017
Reference Zhdankin, Werner, Uzdensky and Begelmanb
; Comisso & Sironi Reference Comisso and Sironi2018; Nättilä & Beloborodov, Reference Nättilä and Beloborodov2021; Vega et al. Reference Vega, Boldyrev, Roytershteyn and Medvedev2022; Meringolo et al. Reference Meringolo, Cruz-Osorio, Rezzolla and Servidio2023; Singh et al. Reference Singh, French, Guo and Li2024). It is relevant for many high-energy astrophysical systems (e.g., compact objects and transients). The motivation of this study is to perform a two-dimensional (2-D) statistical analysis of current sheets and compare/contrast with previous results in the literature.
In this article, we apply the computer vision algorithm developed by Bussov & Nättilä (Reference Bussov and Nättilä2021) to 2-D fully kinetic (PIC) simulations of relativistic turbulence in pair plasmas. Notably, we measure the distributions of spatial scales of current sheets in the relativistic regime of kinetic turbulence. Section 2 describes the fundamental time scales and length scales and presents analytical expectations for the statistical scalings. In § 3, we discuss the numerical set-up of our PIC simulations, review the machine-learning segmentation algorithm and define our spatial scale measurements. In § 4, we present our measured distributions and their scaling indices. In § 5, we discuss the similarities between our scaling indices and previous studies and the implications for high-energy astrophysical plasmas.
2. Plasma length and time scales
We analyse the properties of current sheets in collisionless electron–positron pair plasmas. We consider pair plasma with an average temperature
![]() $\langle T \rangle$
(angular brackets
$\langle T \rangle$
(angular brackets
![]() $\langle \cdot \rangle$
indicate spatial averages in the remainder of the paper). Then, the average dimensionless temperature is given by
$\langle \cdot \rangle$
indicate spatial averages in the remainder of the paper). Then, the average dimensionless temperature is given by
where
![]() $k_{\mathrm {B}}$
is the Boltzmann constant,
$k_{\mathrm {B}}$
is the Boltzmann constant,
![]() $m_{\mathrm {e}}$
is the electron mass and
$m_{\mathrm {e}}$
is the electron mass and
![]() $c$
is the speed of light.
$c$
is the speed of light.
The plasma is magnetized by threading it with a uniform background field
![]() $\mathbf {B}_0 = B_{0} {\hat{\mathbf{z}}}$
. The dimensionless parameter quantifying the strength of the magnetic field is the magnetization, given by
$\mathbf {B}_0 = B_{0} {\hat{\mathbf{z}}}$
. The dimensionless parameter quantifying the strength of the magnetic field is the magnetization, given by
where
![]() $n_{\mathrm {0}}$
is the total particle number density.
$n_{\mathrm {0}}$
is the total particle number density.
The microscopic time scale of the plasma is characterized by the (cold) plasma frequency,
where
![]() $e$
is the electron charge. In relativistic plasmas, the plasma frequency also defines the microscopic length scale of the system, known as the plasma skin depth,
$e$
is the electron charge. In relativistic plasmas, the plasma frequency also defines the microscopic length scale of the system, known as the plasma skin depth,
The (non-relativistic) gyrofrequency is
The related gyroradius is
where
![]() $p$
is the momentum of the particle. In the following, we use the skin depth
$p$
is the momentum of the particle. In the following, we use the skin depth
![]() $c/\omega _{\mathrm {p}}$
as the reference scale when measuring sizes. This choice is made because
$c/\omega _{\mathrm {p}}$
as the reference scale when measuring sizes. This choice is made because
![]() $c/\omega _{\mathrm {p}}$
is the largest of the kinetic scales when
$c/\omega _{\mathrm {p}}$
is the largest of the kinetic scales when
![]() $\sigma _0 \gt 1$
, thus determining the characteristic width of structures.Footnote
1
$\sigma _0 \gt 1$
, thus determining the characteristic width of structures.Footnote
1
2.1. Current sheet distributions
The predominant intermittent structures in magnetically dominated plasma turbulence are current sheets.Footnote 2 In MHD turbulence, these structures are responsible for a large fraction of the overall resistive dissipation (e.g., Zhdankin, Boldyrev & Uzdensky Reference Zhdankin, Boldyrev and Uzdensky2016). In collisionless plasmas, they are likewise thought to be sites of energy dissipation through either magnetic reconnection or other kinetic damping mechanisms (e.g., Wan et al. Reference Wan, Matthaeus, Karimabadi, Roytershteyn, Shay, Wu, Daughton, Loring and Chapman2012; TenBarge & Howes Reference TenBarge and Howes2013; Howes Reference Howes2016; Parashar & Matthaeus Reference Parashar and Matthaeus2016; Loureiro & Boldyrev Reference Loureiro and Boldyrev2017; Mallet, Schekochihin & Chandran Reference Mallet, Schekochihin and Chandran2017; Ripperda et al. Reference Ripperda, Mahlmann, Chernoglazov, TenBarge, Most, Juno, Yuan, Philippov and Bhattacharjee2021; Nättilä & Beloborodov Reference Nättilä and Beloborodov2022; Borgogno et al. Reference Borgogno, Grasso, Achilli, Romé and Comisso2022; Chernoglazov, Hakobyan & Philippov Reference Chernoglazov, Hakobyan and Philippov2023; Comisso & Jiang Reference Comisso and Jiang2023; Davis et al. Reference Davis, Comisso and Giannios2024).
In domains with the full three spatial dimensions, current sheets have a ribbon-like morphology and, therefore, can be ideally characterized by three scales (ignoring curvature and finer structure). For 2-D simulations with an out-of-plane background magnetic field
![]() $\mathbf {B}_0$
, the largest scale is in the direction of
$\mathbf {B}_0$
, the largest scale is in the direction of
![]() $\mathbf {B}_0$
, which we will ignore. The remaining two scales are in the directions perpendicular to the background magnetic field; we use the terminology length
$\mathbf {B}_0$
, which we will ignore. The remaining two scales are in the directions perpendicular to the background magnetic field; we use the terminology length
![]() $\ell$
and width
$\ell$
and width
![]() $w$
to describe these two scales, ordered such that
$w$
to describe these two scales, ordered such that
![]() $\ell \gt w$
. See figure 1 for a schematic view of our general definitions. We emphasize that this differs from the terminology used in three-dimensional (3-D) studies.
$\ell \gt w$
. See figure 1 for a schematic view of our general definitions. We emphasize that this differs from the terminology used in three-dimensional (3-D) studies.

Figure 1. Schematic illustration of a 3-D current sheet along a background magnetic field
![]() $\mathbf {B}_0$
. The two directions perpendicular to the magnetic field are denoted with the 2-D plane. The length
$\mathbf {B}_0$
. The two directions perpendicular to the magnetic field are denoted with the 2-D plane. The length
![]() $\ell$
of a sheet (blue curved segment), followed by the width of the sheet
$\ell$
of a sheet (blue curved segment), followed by the width of the sheet
![]() $w$
(green line), and the radius of curvature
$w$
(green line), and the radius of curvature
![]() $r_c$
(orange line).
$r_c$
(orange line).
Numerical simulations of MHD turbulence exhibit current sheets that have a broad distribution of possible values of
![]() $\ell$
, spanning the turbulent inertial range; in particular, the data are well-described by a power-law distribution when
$\ell$
, spanning the turbulent inertial range; in particular, the data are well-described by a power-law distribution when
![]() $\ell$
is in the inertial range,
$\ell$
is in the inertial range,
where
![]() $N_{{sheets}} = \int P_\ell (\ell ) \, \mathrm {d} \ell$
is the number of sheets, and
$N_{{sheets}} = \int P_\ell (\ell ) \, \mathrm {d} \ell$
is the number of sheets, and
![]() $\alpha \approx 3.3$
is measured in MHD turbulence simulations (Zhdankin et al. Reference Zhdankin, Boldyrev and Uzdensky2016). We note that
$\alpha \approx 3.3$
is measured in MHD turbulence simulations (Zhdankin et al. Reference Zhdankin, Boldyrev and Uzdensky2016). We note that
![]() $\alpha$
is used as a general index for any power-law distribution in the following text. The widths, on the other hand, mainly reside near the dissipation scale
$\alpha$
is used as a general index for any power-law distribution in the following text. The widths, on the other hand, mainly reside near the dissipation scale
![]() $s$
, with a narrowly peaked distribution, which we will approximate as
$s$
, with a narrowly peaked distribution, which we will approximate as
where
![]() $s \sim c/\omega _{\mathrm {p}}$
. Furthermore, we measure the circular curvature of the current sheets,
$s \sim c/\omega _{\mathrm {p}}$
. Furthermore, we measure the circular curvature of the current sheets,
![]() $r_c$
, which may be expected to be a power-law distribution,
$r_c$
, which may be expected to be a power-law distribution,
because the structures are distorted by turbulent eddies spanning a broad range of scales. The power-law index for
![]() $P_{r_c}(r_c)$
is non-trivial to predict from theory. In addition, we will be analysing the joint 2-D distributions,
$P_{r_c}(r_c)$
is non-trivial to predict from theory. In addition, we will be analysing the joint 2-D distributions,
and
which capture the correlations between
![]() $\ell$
,
$\ell$
,
![]() $w$
and
$w$
and
![]() $r_c$
. The one-dimensional (1-D) distributions follow naturally from the marginalization of these distributions as, for example,
$r_c$
. The one-dimensional (1-D) distributions follow naturally from the marginalization of these distributions as, for example,
![]() $P_w(w)= \int P_{w,\ell }(w,\ell ) \, \mathrm {d} \ell$
. We anticipate that since
$P_w(w)= \int P_{w,\ell }(w,\ell ) \, \mathrm {d} \ell$
. We anticipate that since
![]() $w \sim s \sim c/\omega _{\mathrm {p}}$
, the width will be weakly correlated (if at all) with the other scales. The correlation between
$w \sim s \sim c/\omega _{\mathrm {p}}$
, the width will be weakly correlated (if at all) with the other scales. The correlation between
![]() $r_c$
and
$r_c$
and
![]() $\ell$
is non-trivial to predict, in general, since structures of varying lengths will be distorted by different populations of turbulent eddies. However, we note that
$\ell$
is non-trivial to predict, in general, since structures of varying lengths will be distorted by different populations of turbulent eddies. However, we note that
![]() $r_c \propto \ell$
if the relative curvature of the structure is scale independent (i.e., the typical shape of a curved structure is independent of its length).
$r_c \propto \ell$
if the relative curvature of the structure is scale independent (i.e., the typical shape of a curved structure is independent of its length).
3. Methods
3.1. Numerical methods and set-up
We analyse the 2-D freely evolving (decaying) turbulence simulations presented in Nättilä & Beloborodov (Reference Nättilä and Beloborodov2021). Here, we briefly review the simulation set-up, and initial conditions and refer the reader to the original paper for more details.
The simulations are initialized with a homogeneous pair plasma with a uniform density
![]() $n_{\pm, 0}$
and an initial temperature
$n_{\pm, 0}$
and an initial temperature
![]() $\theta _{\mathrm {0}} = 0.3$
. The plasma is threaded by a uniform out-of-plane magnetic field
$\theta _{\mathrm {0}} = 0.3$
. The plasma is threaded by a uniform out-of-plane magnetic field
![]() $\mathbf {B}_0 = B_0 {\hat{\mathbf{z}}}$
. To seed the turbulence, we perturb the magnetic field in the directions perpendicular to the magnetic field,
$\mathbf {B}_0 = B_0 {\hat{\mathbf{z}}}$
. To seed the turbulence, we perturb the magnetic field in the directions perpendicular to the magnetic field,
![]() $\mathbf {B}_{\perp } = (B_{\mathrm {x}}, B_{\mathrm {y}},0)$
with sinusoidal large-scale modes with wavelength
$\mathbf {B}_{\perp } = (B_{\mathrm {x}}, B_{\mathrm {y}},0)$
with sinusoidal large-scale modes with wavelength
![]() $l_0 = L/8$
(where
$l_0 = L/8$
(where
![]() $L$
is the size of the full simulation domain). The initial perturbation has amplitude
$L$
is the size of the full simulation domain). The initial perturbation has amplitude
![]() $\mathbf {B}^{{rms}}_{\perp }/\mathbf {B}_0 = 1$
, where
$\mathbf {B}^{{rms}}_{\perp }/\mathbf {B}_0 = 1$
, where
![]() $\mathbf {B}^{{rms}}_{\perp } = \sqrt {\langle \mathbf {B}^2_{\perp } \rangle }$
.
$\mathbf {B}^{{rms}}_{\perp } = \sqrt {\langle \mathbf {B}^2_{\perp } \rangle }$
.
The simulations use the relativistic PIC module in the Runko framework (Nättilä Reference Nättilä2022). The PIC algorithm evolves all three components of the electromagnetic fields using a second-order finite-difference scheme, while particles evolve in time using a relativistic Boris pusher. These simulations are 2.5D; i.e., all three components of the particle momenta and fields are retained, while there is variation in only two spatial coordinates. In addition, we impose doubly periodic boundary conditions on the domain and perform eight passes of digital current filtering at each time step. The current filtering is performed immediately after the particle’s current deposition using a three-point binomial filter to smooth out the numerical noise that results from a finite number of computational particles.
The 2-D domain in our simulations is a square in the x–y plane of size
![]() $L = 1024 c/\omega _{\mathrm {p}}$
, and it is covered with
$L = 1024 c/\omega _{\mathrm {p}}$
, and it is covered with
![]() $5120^{2}$
cell resolution. The (initial) plasma skin depth is resolved by five grid cells. In our 2-D simulations, we initialize fluctuations on a scale of
$5120^{2}$
cell resolution. The (initial) plasma skin depth is resolved by five grid cells. In our 2-D simulations, we initialize fluctuations on a scale of
![]() $l_{0} \approx 125 c/\omega _{\mathrm {p}}$
. We simulate the turbulence for
$l_{0} \approx 125 c/\omega _{\mathrm {p}}$
. We simulate the turbulence for
![]() $20 l_{0}/c$
. We focus on two simulations with
$20 l_{0}/c$
. We focus on two simulations with
![]() $\sigma _0 = 1$
and
$\sigma _0 = 1$
and
![]() $10$
, which correspond to the transrelativistic (magnetically dominated) regime. During the simulation, the plasma heats up and so
$10$
, which correspond to the transrelativistic (magnetically dominated) regime. During the simulation, the plasma heats up and so
![]() $\theta _{0}$
increases (see figure 6 in Nättilä & Beloborodov (Reference Nättilä and Beloborodov2021)). For our simulation with
$\theta _{0}$
increases (see figure 6 in Nättilä & Beloborodov (Reference Nättilä and Beloborodov2021)). For our simulation with
![]() $\sigma _0 = 1$
at
$\sigma _0 = 1$
at
![]() $t = l_{0}/c$
, we measure
$t = l_{0}/c$
, we measure
![]() $\theta \approx 0.45$
which then increases to
$\theta \approx 0.45$
which then increases to
![]() $\theta \approx 0.60$
at
$\theta \approx 0.60$
at
![]() $t = 15l_{0}/c$
. Similarly, for the case of
$t = 15l_{0}/c$
. Similarly, for the case of
![]() $\sigma _0 = 10$
, we first measure
$\sigma _0 = 10$
, we first measure
![]() $\theta \approx 0.50$
which then increases to
$\theta \approx 0.50$
which then increases to
![]() $\theta \approx 2.70$
. Thus, the temperatures become only mildly relativistic, and it is reasonable to use the non-relativistic expressions for kinetic scales from § 2.
$\theta \approx 2.70$
. Thus, the temperatures become only mildly relativistic, and it is reasonable to use the non-relativistic expressions for kinetic scales from § 2.
We present six visualizations of one of our simulations with
![]() $\sigma _0 = 10$
at
$\sigma _0 = 10$
at
![]() $t = 4.6\, l_0/c$
in figure 2. The magnetic eddies are visible for the fully developed turbulence as large plasma over-densities (figure 2
a). Secondly, we can visually trace out two types of structure in the out-of-the-plane current density component
$t = 4.6\, l_0/c$
in figure 2. The magnetic eddies are visible for the fully developed turbulence as large plasma over-densities (figure 2
a). Secondly, we can visually trace out two types of structure in the out-of-the-plane current density component
![]() $J_z$
(figure 2
b): elongated stripes (current sheets) and circular spots (plasmoids). These same structures are also visible as coherent structures in the (perpendicular) magnetic field
$J_z$
(figure 2
b): elongated stripes (current sheets) and circular spots (plasmoids). These same structures are also visible as coherent structures in the (perpendicular) magnetic field
![]() $\mathbf {B}_\perp$
(figure 2
c): the current sheets coincide with regions of alternating magnetic fields (in between colliding plasmoids). The plasmoids coincide with the location of magnetic loops. The regions with current sheets (with antiparallel fields) are prominent locations of energy dissipation. The sheet regions can be associated with areas of energy dissipation when visualizing the work done by the electric field
$\mathbf {B}_\perp$
(figure 2
c): the current sheets coincide with regions of alternating magnetic fields (in between colliding plasmoids). The plasmoids coincide with the location of magnetic loops. The regions with current sheets (with antiparallel fields) are prominent locations of energy dissipation. The sheet regions can be associated with areas of energy dissipation when visualizing the work done by the electric field
![]() $\propto \mathbf {J}\cdot \mathbf {E}$
(figure 2
d). We note that a significant fraction of the regions with high electric currents have magnetic fields that are parallel (rather than antiparallel) on both sides (Ha et al. Reference Ha, Nättilä, Davelaar and Sironi2024).
$\propto \mathbf {J}\cdot \mathbf {E}$
(figure 2
d). We note that a significant fraction of the regions with high electric currents have magnetic fields that are parallel (rather than antiparallel) on both sides (Ha et al. Reference Ha, Nättilä, Davelaar and Sironi2024).
A standard method to segment the current sheets into individual structures is to apply a threshold in the current density. To illustrate this method, we trace out the outlines of the sheets by applying a threshold of
![]() $J_{\mathrm {z}}/J_{{rms}} \gt 3$
(figure 2
e). In our case, however, we use the regions originating from a more advanced region-of-interest (ROI) detection (measured at a time
$J_{\mathrm {z}}/J_{{rms}} \gt 3$
(figure 2
e). In our case, however, we use the regions originating from a more advanced region-of-interest (ROI) detection (measured at a time
![]() $4l_0/c$
), relying on a computer vision segmentation algorithm presented in Bussov & Nättilä (Reference Bussov and Nättilä2021) (figure 2
f). Such segmentation method has the advantage that it clusters the sheets based on not only the electric current but also other features; this enables us to separate the current sheets and plasmoid cores from each other. The details of the method are given in the next section.
$4l_0/c$
), relying on a computer vision segmentation algorithm presented in Bussov & Nättilä (Reference Bussov and Nättilä2021) (figure 2
f). Such segmentation method has the advantage that it clusters the sheets based on not only the electric current but also other features; this enables us to separate the current sheets and plasmoid cores from each other. The details of the method are given in the next section.
3.2. Overview of the machine-learning algorithm
We employ the unsupervised ensemble machine-learning algorithm developed by Bussov & Nättilä (Reference Bussov and Nättilä2021) to segment the current sheets from fully kinetic plasma turbulence simulations. The algorithm is an ensemble extension of the self-organizing map (SOM) algorithm (Kohonen Reference Kohonen2001, Reference Kohonen2013) dubbed ‘statistically combined ensemble’ (SCE), which merges multiple (independent) SOM evaluations together, hence increasing the robustness of the ROI boundaries.
Briefly, we outline how the algorithm works. We apply the SOM algorithm to our simulation snapshots and cluster the data using three features:
![]() $\boldsymbol{B}_{\perp }$
,
$\boldsymbol{B}_{\perp }$
,
![]() $\boldsymbol{J}_{\boldsymbol{z}}$
and
$\boldsymbol{J}_{\boldsymbol{z}}$
and
![]() $\boldsymbol{J}_{\boldsymbol{z}} \cdot \boldsymbol{E}$
, where
$\boldsymbol{J}_{\boldsymbol{z}} \cdot \boldsymbol{E}$
, where
![]() $\boldsymbol{B}_{\perp}$
is the (in-plane) perpendicular magnetic field,
$\boldsymbol{B}_{\perp}$
is the (in-plane) perpendicular magnetic field,
![]() $\boldsymbol{J}_{\boldsymbol{z}}$
, is the (out-of-the-plane) parallel component of the current and
$\boldsymbol{J}_{\boldsymbol{z}}$
, is the (out-of-the-plane) parallel component of the current and
![]() $\boldsymbol{J}_{\boldsymbol{z}} \cdot \boldsymbol{E}$
is a measure of the work done by the electric field
$\boldsymbol{J}_{\boldsymbol{z}} \cdot \boldsymbol{E}$
is a measure of the work done by the electric field
![]() $\boldsymbol{E}$
. Each pixel on the image then defines a multidimensional feature-space data point.
$\boldsymbol{E}$
. Each pixel on the image then defines a multidimensional feature-space data point.

Figure 2. Visualization of the analysed turbulence data measured at time
![]() $t = 4.6 l_0/c$
: plasma density
$t = 4.6 l_0/c$
: plasma density
![]() $n/n_0$
, where
$n/n_0$
, where
![]() $n_0$
is the initial plasma density (a); out-of-the-plane current density
$n_0$
is the initial plasma density (a); out-of-the-plane current density
![]() $J_{z}/n_0 e c$
(b); strength of the in-plane magnetic field component
$J_{z}/n_0 e c$
(b); strength of the in-plane magnetic field component
![]() $\sqrt {B_x^2+B_y^2}/B_0$
, and the field lines (red curves), where
$\sqrt {B_x^2+B_y^2}/B_0$
, and the field lines (red curves), where
![]() $B_0$
is the initial guide field strength (c); a proxy of the work done by the parallel electric field
$B_0$
is the initial guide field strength (c); a proxy of the work done by the parallel electric field
![]() $\mathbf {J} \cdot \mathbf {E}/\sqrt {\langle (\mathbf {J} \cdot \mathbf {E})^2 \rangle }$
in units of the root mean square value (d); regions of the current density with
$\mathbf {J} \cdot \mathbf {E}/\sqrt {\langle (\mathbf {J} \cdot \mathbf {E})^2 \rangle }$
in units of the root mean square value (d); regions of the current density with
![]() $J/J_{{rms}} \gt 3$
, where
$J/J_{{rms}} \gt 3$
, where
![]() $J_{{rms}} = \sqrt {\langle J^2 \rangle }$
(e); and, current sheet regions from the SCE algorithm (f). The SCE algorithm is shown at
$J_{{rms}} = \sqrt {\langle J^2 \rangle }$
(e); and, current sheet regions from the SCE algorithm (f). The SCE algorithm is shown at
![]() $t = 4.0 l_0/c$
.
$t = 4.0 l_0/c$
.
The SOM algorithm is based on a 2-D network of neurons that are trained to approximate the multidimensional (feature-space) data. In practice, the map can be thought of as a (finite) surface that is fitted to the input data points. Conversely, each feature-space data point can be associated with a best-matching neuron on the map. The map defines a latent (reduced) data space for the input data.
The neural map is then used to cluster the feature-space data into different groups by associating a region on the map (i.e., a set of connected neurons) as one data cluster. The (feature-space) distance between the neurons defines a convenient cost function to separate the neurons into a finite number of clusters. In theory, the number of resulting clusters is arbitrary. Still, in practice, the map often has distinct regions of closely connected neurons that help set the number of resulting clusters from the analysis. In our case, the SOM algorithm results, on average, in four distinct clusters, one of which is the current sheets (see, Bussov & Nättilä (Reference Bussov and Nättilä2021) for more details).Footnote 3
In practice, we use an ensemble version of the SOM to segment the sheets. This so-called SCE method combines multiple SOM segmentations into one clustering realization to increase the signal-to-noise ratio of each ROI boundary. In general, our machine-learning-based segmentation method should be contrasted with the previously used threshold technique, where the boundaries of the current sheets are found by setting a threshold value for the magnitude of the electric current (see figure 2 f). We emphasize that our definition of a current sheet is more complex than what results, e.g., from segmenting the sheets with the threshold method: our definition of the current sheets is based on a combination of all three input features. The second reason, in addition to the more generic definition of the current sheet cluster, is that the SCE method is computationally faster, making it feasible to construct large structure catalogues. We note, however, that the algorithm is currently calibrated only on 2-D data, so we focus on that here.
3.3. Measurements
The following section presents our definitions of geometric length and width. Specifically, we analyse a time series of 2-D masks separated by
![]() $\Delta t = 1 l_0/c$
for two simulations with
$\Delta t = 1 l_0/c$
for two simulations with
![]() $\sigma _0 = 1$
and
$\sigma _0 = 1$
and
![]() $\sigma _0 = 10$
. We analyse a time interval,
$\sigma _0 = 10$
. We analyse a time interval,
![]() $l_0/c \leqslant t \leqslant 15 l_0/c$
when the turbulence is fully developed but still sustains large amplitude fluctuations. In practice, when analysing the structures, we use the open-source geometry library `Shapely’ (Gillies et al. Reference Gillies, van der Wel, Van den Bossche, Taves, Arnott and Ward2024) to automate the geometric analysis of the structures. First, we dissect each independent closed contour in a mask into
$l_0/c \leqslant t \leqslant 15 l_0/c$
when the turbulence is fully developed but still sustains large amplitude fluctuations. In practice, when analysing the structures, we use the open-source geometry library `Shapely’ (Gillies et al. Reference Gillies, van der Wel, Van den Bossche, Taves, Arnott and Ward2024) to automate the geometric analysis of the structures. First, we dissect each independent closed contour in a mask into
![]() $(x,y)$
coordinate lists that trace the element’s boundary. This procedure is repeated for every mask in the time series. Specifically, we use the Shapely.Polygon class, which takes a set of
$(x,y)$
coordinate lists that trace the element’s boundary. This procedure is repeated for every mask in the time series. Specifically, we use the Shapely.Polygon class, which takes a set of
![]() $N_p$
data points and connects the chain of coordinate points into a ‘ring’. We generate an instance of this polygon class for each structure in a given image. Once we generate the Polygon class to represent the current sheet, we measure its perimeter
$N_p$
data points and connects the chain of coordinate points into a ‘ring’. We generate an instance of this polygon class for each structure in a given image. Once we generate the Polygon class to represent the current sheet, we measure its perimeter
![]() $\mathcal {S}$
(
$\mathcal {S}$
(
![]() $=\oint \mathrm {d} s$
, where the line integral is performed along the closed curve around the polygon) and use it to define a robust estimator of the sheet length
$=\oint \mathrm {d} s$
, where the line integral is performed along the closed curve around the polygon) and use it to define a robust estimator of the sheet length
![]() $\ell$
as
$\ell$
as
so that
![]() $\ell \approx \mathcal {S}/2$
, where we assumed that
$\ell \approx \mathcal {S}/2$
, where we assumed that
![]() $w \ll \ell$
in the second part of the equation. We also tried measuring
$w \ll \ell$
in the second part of the equation. We also tried measuring
![]() $\ell$
by taking the pairwise distance between each coordinate point and identifying the largest distance as
$\ell$
by taking the pairwise distance between each coordinate point and identifying the largest distance as
![]() $\ell$
. However, we forgo this definition since we find it to be a noisier estimator of
$\ell$
. However, we forgo this definition since we find it to be a noisier estimator of
![]() $\ell$
. We also note that when accounting for the possible curvature of the structure, the natural length is the arclength of the structure, not the distance along the structure’s longest dimension; therefore, our definition
$\ell$
. We also note that when accounting for the possible curvature of the structure, the natural length is the arclength of the structure, not the distance along the structure’s longest dimension; therefore, our definition
![]() $\ell$
also naturally includes the curvature effects.
$\ell$
also naturally includes the curvature effects.
To measure the width (see appendix A for the full derivation), we take each structure and calculate the major axis of each sheet, which is defined as the largest distance between any set of points. Then, we rotate the structure such that its major axis lies on the
![]() $x$
axis. Then, we translate the structure to the origin. Once in this new reference frame, we measure the width using (B1).
$x$
axis. Then, we translate the structure to the origin. Once in this new reference frame, we measure the width using (B1).
Finally, we introduce a measurement of the curvature of the current sheet, dubbed ‘curvature radius’,
![]() $r_{c}$
. The radius of curvature is calculated by fitting a circle through the three points on the curve: leftmost point, centre point and rightmost point (in the new reference frame described above). Then, a circle with a radius
$r_{c}$
. The radius of curvature is calculated by fitting a circle through the three points on the curve: leftmost point, centre point and rightmost point (in the new reference frame described above). Then, a circle with a radius
![]() $r_c$
can be defined to pass through each point. In the limit that the curvature radius
$r_c$
can be defined to pass through each point. In the limit that the curvature radius
![]() $r_c \rightarrow 0$
, the structure is highly curved, and as
$r_c \rightarrow 0$
, the structure is highly curved, and as
![]() $r_c\rightarrow \infty$
, the structure becomes flat. We detail our simple circle fitting algorithm in appendix C.
$r_c\rightarrow \infty$
, the structure becomes flat. We detail our simple circle fitting algorithm in appendix C.

Figure 3. Examples of current sheets in our catalogue. Individual current sheets of varying length,
![]() $\ell$
, and radius of curvature,
$\ell$
, and radius of curvature,
![]() $r_{c}$
, are visualized in the transformed position space
$r_{c}$
, are visualized in the transformed position space
![]() $(x',y')$
using (A1) and (A2). The three red points mark the locations used to calculate the curvature radius using (C2). The green line shows the arc of the circle passing through the three points, with the centre calculated using (C6).
$(x',y')$
using (A1) and (A2). The three red points mark the locations used to calculate the curvature radius using (C2). The green line shows the arc of the circle passing through the three points, with the centre calculated using (C6).
In figure 3, we display representative examples from the resulting current sheet catalogue for the simulation with
![]() $\sigma _0 = 10$
. These examples show that most of the sheets have approximately constant width
$\sigma _0 = 10$
. These examples show that most of the sheets have approximately constant width
![]() $w$
.
$w$
.
Lastly, the approximation of the sheet curvature as part of a circle’s arc seems appropriate in almost all cases; in total, we find that only approximately
![]() $0.5\,\%$
of the sheets can not be adequately modelled as arcs (but are, e.g.,
$0.5\,\%$
of the sheets can not be adequately modelled as arcs (but are, e.g.,
![]() $S$
- or
$S$
- or
![]() $L$
-shaped). Such non-standard morphologies can sometimes result from the interactions and mergers of sheets.
$L$
-shaped). Such non-standard morphologies can sometimes result from the interactions and mergers of sheets.
4. Results
Our catalogue contains
![]() $\approx \!13\,000$
individual objects for
$\approx \!13\,000$
individual objects for
![]() $\sigma _0 = 1$
and
$\sigma _0 = 1$
and
![]() $\approx \!10\,000$
for
$\approx \!10\,000$
for
![]() $\sigma _0 = 10$
simulations. Each time snapshot contains, on average,
$\sigma _0 = 10$
simulations. Each time snapshot contains, on average,
![]() $\approx \!1\,000$
current sheets and provide detailed time-dependent statistics of the structures. The total volume-integrated magnitude of the electric current closely traces the evolution of the decaying turbulence: for
$\approx \!1\,000$
current sheets and provide detailed time-dependent statistics of the structures. The total volume-integrated magnitude of the electric current closely traces the evolution of the decaying turbulence: for
![]() $t = 0$
to
$t = 0$
to
![]() $\sim 3 \,l_0/c$
, we observe an initial transient period where the turbulent structures form and the magnitude of the electric current rapidly grows; for
$\sim 3 \,l_0/c$
, we observe an initial transient period where the turbulent structures form and the magnitude of the electric current rapidly grows; for
![]() $t \gtrsim 3 \,l_0/c$
, the turbulence decays and the magnitude of the current decreases slowly (see also, e.g., Nättilä & Beloborodov Reference Nättilä and Beloborodov2021). The analysed current sheets are long-lived intermittent structures and their time evolution is analysed and discussed in more detail, e.g., in Imbrogno et al. Reference Imbrogno, Meringolo, Servidio, Cruz-Osorio, Cerutti and Pegoraro2024.
$t \gtrsim 3 \,l_0/c$
, the turbulence decays and the magnitude of the current decreases slowly (see also, e.g., Nättilä & Beloborodov Reference Nättilä and Beloborodov2021). The analysed current sheets are long-lived intermittent structures and their time evolution is analysed and discussed in more detail, e.g., in Imbrogno et al. Reference Imbrogno, Meringolo, Servidio, Cruz-Osorio, Cerutti and Pegoraro2024.

Figure 4. The filling fraction of current sheets,
![]() $f$
, of our simulation of
$f$
, of our simulation of
![]() $\sigma _0 = 10$
measured at
$\sigma _0 = 10$
measured at
![]() $4.6l_0/c$
, as function of
$4.6l_0/c$
, as function of
![]() $J_{{thr}}/J_{{rms}}$
(blue line), where
$J_{{thr}}/J_{{rms}}$
(blue line), where
![]() $J_{{thr}}$
is the threshold factor, and where
$J_{{thr}}$
is the threshold factor, and where
![]() $J_{{rms}} = \sqrt {\langle J^2 \rangle }$
is the root mean square of the current density. The star symbol denotes the filling fraction measured using our machine-learning algorithm. We also fit the MHD data from Zhdankin et al. (Reference Zhdankin, Boldyrev and Uzdensky2016) (green line).
$J_{{rms}} = \sqrt {\langle J^2 \rangle }$
is the root mean square of the current density. The star symbol denotes the filling fraction measured using our machine-learning algorithm. We also fit the MHD data from Zhdankin et al. (Reference Zhdankin, Boldyrev and Uzdensky2016) (green line).
We calibrate our current sheet identification method with the previous method of ‘thresholding’ used in Zhdankin et al. (Reference Zhdankin, Boldyrev, Perez and Tobias2014) and Zhdankin et al. (Reference Zhdankin, Boldyrev and Uzdensky2016). In figure 4, we plot the volume filling fraction
![]() $f$
of the structures occupying pixels having current densities
$f$
of the structures occupying pixels having current densities
![]() $|\mathbf {J}| \gt J_{{rms}}$
, where
$|\mathbf {J}| \gt J_{{rms}}$
, where
![]() $J_{{rms}}$
is a threshold parameter that we vary. The filling fraction of the structures with current densities above the threshold exhibits a steep exponential decay at low
$J_{{rms}}$
is a threshold parameter that we vary. The filling fraction of the structures with current densities above the threshold exhibits a steep exponential decay at low
![]() $J_{{thr}}/J_{{rms}} \lt 3$
, which then flattens to a less steep decay for
$J_{{thr}}/J_{{rms}} \lt 3$
, which then flattens to a less steep decay for
![]() $J_{{thr}}/J_{{rms}} \gt 3$
. We also compare our results with the MHD analysis by Zhdankin et al. (Reference Zhdankin, Boldyrev and Uzdensky2016) which shows a very similar behaviour for
$J_{{thr}}/J_{{rms}} \gt 3$
. We also compare our results with the MHD analysis by Zhdankin et al. (Reference Zhdankin, Boldyrev and Uzdensky2016) which shows a very similar behaviour for
![]() $J_{{thr}}/J_{{rms}} \gt 3$
. We find that the filling fraction of structures detected by the SCE algorithm agrees with the thresholding method when
$J_{{thr}}/J_{{rms}} \gt 3$
. We find that the filling fraction of structures detected by the SCE algorithm agrees with the thresholding method when
![]() $J_{{thr}}/J_{{rms}} \approx 3$
(the red star in figure 4). This indicates the ‘effective’ threshold of the SCE algorithm.
$J_{{thr}}/J_{{rms}} \approx 3$
(the red star in figure 4). This indicates the ‘effective’ threshold of the SCE algorithm.

Figure 5. Width distributions,
![]() ${\rm d}N/{\rm d}w$
, for simulations with initial
${\rm d}N/{\rm d}w$
, for simulations with initial
![]() $\sigma _0 = (1, 10)$
. Two reference exponential fits with the corresponding index are shown in the legend.
$\sigma _0 = (1, 10)$
. Two reference exponential fits with the corresponding index are shown in the legend.

Figure 6. Length distribution,
![]() ${\rm d}N/{\rm d}\ell$
, for simulations with initial
${\rm d}N/{\rm d}\ell$
, for simulations with initial
![]() $\sigma _0 = (1, 10)$
. Three reference power laws with the corresponding index are shown in the legend.
$\sigma _0 = (1, 10)$
. Three reference power laws with the corresponding index are shown in the legend.

Figure 7. Radius of curvature distributions,
![]() ${\rm d}N/{\rm d}r_{c}$
, for simulations with initial
${\rm d}N/{\rm d}r_{c}$
, for simulations with initial
![]() $\sigma _0 = (1, 10)$
. Two reference power laws with the corresponding index are shown in the legend. This distribution is restricted to current sheets with
$\sigma _0 = (1, 10)$
. Two reference power laws with the corresponding index are shown in the legend. This distribution is restricted to current sheets with
![]() $\ell \gt 7.5 c/\omega _p$
, to avoid spurious measurements from small structures.
$\ell \gt 7.5 c/\omega _p$
, to avoid spurious measurements from small structures.
In figure 5, we plot the width distribution,
![]() $P_w(w)$
, of our current sheets for both values of
$P_w(w)$
, of our current sheets for both values of
![]() $\sigma _0 = 1$
and
$\sigma _0 = 1$
and
![]() $10$
. The distribution resembles an exponential distribution, peaking at around
$10$
. The distribution resembles an exponential distribution, peaking at around
![]() $3 \, c/\omega _{\mathrm {p}}$
. Qualitatively, the distributions are best modelled with an exponential function,
$3 \, c/\omega _{\mathrm {p}}$
. Qualitatively, the distributions are best modelled with an exponential function,
![]() $\exp (-w\omega _{\mathrm {p}}/c)$
. The width distribution does not greatly vary over time.
$\exp (-w\omega _{\mathrm {p}}/c)$
. The width distribution does not greatly vary over time.
In figure 6, we visualize the length distribution of our current sheets,
![]() $P_{\ell }(\ell )$
, and similarly to the width distribution, we find that the distribution remains roughly constant over time. The distribution can be modelled as a power-law distribution with an index,
$P_{\ell }(\ell )$
, and similarly to the width distribution, we find that the distribution remains roughly constant over time. The distribution can be modelled as a power-law distribution with an index,
![]() $\alpha = 2.5$
. The distribution peaks at
$\alpha = 2.5$
. The distribution peaks at
![]() $5 c/\omega _{\mathrm {p}}$
, and extends to
$5 c/\omega _{\mathrm {p}}$
, and extends to
![]() $\sim \!100 \, c/\omega _{\mathrm {p}}$
; i.e., close to the initial energy-carrying scale
$\sim \!100 \, c/\omega _{\mathrm {p}}$
; i.e., close to the initial energy-carrying scale
![]() $l_0$
of the simulation.
$l_0$
of the simulation.
Next, in figure 7, we visualize the curvature distribution
![]() $P_{r_c}(r_c)$
(although we omit structures with
$P_{r_c}(r_c)$
(although we omit structures with
![]() $\ell \lt 7.5 c/\omega _{\mathrm {p}}$
because the curvature measurement becomes unreliable for very short structures). The distribution is a clear power-law with an index
$\ell \lt 7.5 c/\omega _{\mathrm {p}}$
because the curvature measurement becomes unreliable for very short structures). The distribution is a clear power-law with an index
![]() $\alpha = 2.0$
. The distribution peaks at
$\alpha = 2.0$
. The distribution peaks at
![]() $3 \, c/\omega _{\mathrm {p}}$
, and extends to approximately
$3 \, c/\omega _{\mathrm {p}}$
, and extends to approximately
![]() $1000 \, c/\omega _{\mathrm {p}}$
. The distribution is steady in time, with no significant evolution.
$1000 \, c/\omega _{\mathrm {p}}$
. The distribution is steady in time, with no significant evolution.
Furthermore, we study the 2-D joint distributions of the width and length,
![]() $P_{w, \ell }(w,\ell )$
, in figure 8. We find no clear scaling between the two quantities. The distribution is bounded such that the upper limits of the distribution are fit by
$P_{w, \ell }(w,\ell )$
, in figure 8. We find no clear scaling between the two quantities. The distribution is bounded such that the upper limits of the distribution are fit by
![]() $w \propto \ell ^{\alpha }$
, where
$w \propto \ell ^{\alpha }$
, where
![]() $\alpha = 1.0$
. We fit
$\alpha = 1.0$
. We fit
![]() $2\log _{10}(\ell )$
for the lower bound.
$2\log _{10}(\ell )$
for the lower bound.

Figure 8. The 2-D histogram correlating the average width and length distributions for simulations with initial
![]() $\sigma _0 = 1, 10$
. The power law index fits the distributions shown in the legend.
$\sigma _0 = 1, 10$
. The power law index fits the distributions shown in the legend.

Figure 9. The 2-D histogram correlating the radius of curvature and length distributions for simulations with initial
![]() $\sigma _0 = 1, 10$
. The power law index fits the distributions shown in the legend.
$\sigma _0 = 1, 10$
. The power law index fits the distributions shown in the legend.

Figure 10. The 2-D histogram correlating the width and radius of curvature distributions for simulations with initial
![]() $\sigma _0 = 1, 10$
. The power law index fits the distributions shown in the legend.
$\sigma _0 = 1, 10$
. The power law index fits the distributions shown in the legend.
Similarly, in figure 9, we visualize the 2-D distributions of the curvature and length,
![]() $P_{r_c, \ell }(r_c,\ell )$
. The mean value of the sheets linearly scales with
$P_{r_c, \ell }(r_c,\ell )$
. The mean value of the sheets linearly scales with
![]() $\ell$
(dark orange line). This suggests that the relative curvature to size is the same for all
$\ell$
(dark orange line). This suggests that the relative curvature to size is the same for all
![]() $\ell$
. Additionally, we find that the distribution can be traced with
$\ell$
. Additionally, we find that the distribution can be traced with
![]() $r_{c} \propto \ell /\pi$
. We also show a fit that corresponds to
$r_{c} \propto \ell /\pi$
. We also show a fit that corresponds to
![]() $r_{c} \propto \ell ^{\alpha }/2$
, where
$r_{c} \propto \ell ^{\alpha }/2$
, where
![]() $\alpha = 1$
. One final note is that at
$\alpha = 1$
. One final note is that at
![]() $\ell \lt 7 c/\omega _{\mathrm {p}}$
the curvature measurement becomes unreliable and one can see a small ‘cluster’ of points at
$\ell \lt 7 c/\omega _{\mathrm {p}}$
the curvature measurement becomes unreliable and one can see a small ‘cluster’ of points at
![]() $r_c \approx 100 c/\omega _{\mathrm {p}}$
and
$r_c \approx 100 c/\omega _{\mathrm {p}}$
and
![]() $r_c \approx 300c/\omega _{\mathrm {p}} - 400 c/\omega _{\mathrm {p}}$
.
$r_c \approx 300c/\omega _{\mathrm {p}} - 400 c/\omega _{\mathrm {p}}$
.
Finally, in figure 10, we visualize the 2-D distribution of the width and curvature,
![]() $P_{w, r_c}(w,r_c)$
. Here, no strong correlation is seen. The upper end of the distribution is traced with
$P_{w, r_c}(w,r_c)$
. Here, no strong correlation is seen. The upper end of the distribution is traced with
![]() $w \propto \ell ^{\alpha }$
, where
$w \propto \ell ^{\alpha }$
, where
![]() $\alpha = 1$
. Since the structures have widths close to the dissipation scale, it seems reasonable that they are independent of the curvature, which is more likely sensitive to MHD-scale fluctuations.
$\alpha = 1$
. Since the structures have widths close to the dissipation scale, it seems reasonable that they are independent of the curvature, which is more likely sensitive to MHD-scale fluctuations.
5. Discussion
We have analysed various length statistics of tens of thousands of current sheets found in freely evolving (decaying) plasma turbulence. In particular, we have found the following.
-
(i) The current sheet length distribution has a power law tail with index
 $\alpha = 3.3$
; it is shallower (
$\alpha = 3.3$
; it is shallower (
 $\alpha \approx 2$
) at small lengths (
$\alpha \approx 2$
) at small lengths (
 $\ell \lesssim 30 \, c/\omega _{\mathrm {p}}$
).
$\ell \lesssim 30 \, c/\omega _{\mathrm {p}}$
). -
(ii) The width distribution is sharply peaked at
 $w \sim 3\, c/\omega _{\mathrm {p}}$
; it resembles an exponential decay at higher
$w \sim 3\, c/\omega _{\mathrm {p}}$
; it resembles an exponential decay at higher
 $w$
. There is a slight logarithmic increase of
$w$
. There is a slight logarithmic increase of
 $w$
as a function of
$w$
as a function of
 $\ell$
.
$\ell$
. -
(iii) The characteristic curvature radius is
 $r_c \sim \ell /2$
, hence the sheets are slightly curved. However, we find that short (
$r_c \sim \ell /2$
, hence the sheets are slightly curved. However, we find that short (
 $\ell \sim 10\, c/\omega _{\mathrm {p}}$
) sheets are often flatter (larger
$\ell \sim 10\, c/\omega _{\mathrm {p}}$
) sheets are often flatter (larger
 $r_{c}$
); hence, the curvature distribution is a shallower distribution than the length distribution (as seen by the 1-D histogram indices), with
$r_{c}$
); hence, the curvature distribution is a shallower distribution than the length distribution (as seen by the 1-D histogram indices), with
 $\alpha = 2.0$
.
$\alpha = 2.0$
. -
(iv) All distributions have weak (or no) time dependence as the turbulence evolves during the studied period of fully developed turbulence.
-
(v) All distributions have weak (or no) magnetization dependency in the considered range
 $1 \leqslant \sigma _0 \leqslant 10$
.
$1 \leqslant \sigma _0 \leqslant 10$
. -
(vi) In addition, we calibrated the machine-learning-based identification algorithm of Bussov & Nättilä (Reference Bussov and Nättilä2021) against the thresholding method. We found that the filling fraction of current sheets in our algorithm matches the thresholding method at a value of
 $J_{{thr}}/J_{{rms}} = 3$
.
$J_{{thr}}/J_{{rms}} = 3$
.
The limitations of our study are mainly due to our algorithm being 2-D. This is a simplification since, in this case, the sheets have a simpler topology to characterize. In three dimensions, the current sheets can have much more complex shapes. Ultimately, however, the analysis must be generalized to full three dimensions to obtain physically realistic sheet distributions.
Many possible extensions of the work can also be devised. For example, it is possible to measure plasma parameters (e.g., plasma-
![]() $\beta$
, real magnetization
$\beta$
, real magnetization
![]() $\sigma$
, temperature
$\sigma$
, temperature
![]() $T$
, the ratio of reversing field to guide field
$T$
, the ratio of reversing field to guide field
![]() $\delta B/B_{0}$
, etc.) upstream from the current sheet using the SCE algorithm, as done in Nurisso et al. (Reference Nurisso, Celotti, Mignone and Bodo2023), to gather information about the particle acceleration conditions. The sheet statistics should also be studied in different parameter regimes by varying, e.g., the initial amplitude
$\delta B/B_{0}$
, etc.) upstream from the current sheet using the SCE algorithm, as done in Nurisso et al. (Reference Nurisso, Celotti, Mignone and Bodo2023), to gather information about the particle acceleration conditions. The sheet statistics should also be studied in different parameter regimes by varying, e.g., the initial amplitude
![]() $\delta B/B$
, helicity and plasma composition (e.g., using an electron–ion rather than pair plasma composition). In addition, different driving methods should be explored, such as via wave collisions or purely compressive/solenoidal driving. These are expected to change the turbulence intermittency and affect the sheet statistics. The presented work is, therefore, only the first step in this direction. The differences between the non-relativistic (
$\delta B/B$
, helicity and plasma composition (e.g., using an electron–ion rather than pair plasma composition). In addition, different driving methods should be explored, such as via wave collisions or purely compressive/solenoidal driving. These are expected to change the turbulence intermittency and affect the sheet statistics. The presented work is, therefore, only the first step in this direction. The differences between the non-relativistic (
![]() $\sigma _0 \ll 1$
) and ultrarelativistic (
$\sigma _0 \ll 1$
) and ultrarelativistic (
![]() $\sigma _0 \gg 1$
) regimes are not obvious and will require more parameter studies.
$\sigma _0 \gg 1$
) regimes are not obvious and will require more parameter studies.
Our findings are relevant to a broad range of astrophysical systems because kinetic/MHD turbulence is also ubiquitous in those systems. Some problems where intermittency of kinetic/MHD turbulence plays a crucial role are as follows.
-
(i) Black hole accretion flows and jets in low luminosity active galactic nuclei. Their environments are expected to be magnetized and turbulent (e.g., Nättilä Reference Nättilä2024). Most of the current efforts in supermassive black-hole accretion flow modelling employ general relativistic MHD simulations (Event Horizon Telescope Collaboration et al. 2019). However, ideal fluid simulations cannot self-consistently model the temperature of electrons so the electron temperature profile is often ‘painted on’ via postprocessing (e.g., Mościbrodzka et al. (Reference Mościbrodzka, Falcke and Shiokawa2016); however, see Galishnikova et al. (Reference Galishnikova, Philippov, Quataert, Bacchini, Parfrey and Ripperda2023) for a recent fully kinetic general relativistic PIC simulations with realistic electron plasma physics). Alternatively, some general relativistic MHD simulations employ a variety of subgrid models to compute the electron and ion temperatures based on local PIC simulations of magnetic reconnection (Ball, Sironi & Özel Reference Ball, Sironi and Özel2018; Werner et al. Reference Werner, Uzdensky, Begelman, Cerutti and Nalewajko2018) or kinetic/MHD turbulent heating based models (Howes Reference Howes2010; Kawazura, Barnes & Schekochihin Reference Kawazura, Barnes and Schekochihin2019; Meringolo et al. Reference Meringolo, Cruz-Osorio, Rezzolla and Servidio2023).
-
(ii) The Crab pulsar wind nebula (PWN) is another example of a highly magnetized
 $(\sigma _0 \gtrsim 1)$
environment that can accelerate particles to very high energies (Rees & Gunn Reference Rees and Gunn1974; Kennel & Coroniti Reference Kennel and Coroniti1984
Reference Kennel and Coronitia
,
Reference Kennel and Coronitib
; Atoyan Reference Atoyan1999). Recently, in an attempt to resolve observational discrepancies of the Crab PWN with theoretical models, Luo et al. (Reference Luo, Lyutikov, Temim and Comisso2020) proposed a turbulent origin of the non-thermal emission in the Crab PWN.
$(\sigma _0 \gtrsim 1)$
environment that can accelerate particles to very high energies (Rees & Gunn Reference Rees and Gunn1974; Kennel & Coroniti Reference Kennel and Coroniti1984
Reference Kennel and Coronitia
,
Reference Kennel and Coronitib
; Atoyan Reference Atoyan1999). Recently, in an attempt to resolve observational discrepancies of the Crab PWN with theoretical models, Luo et al. (Reference Luo, Lyutikov, Temim and Comisso2020) proposed a turbulent origin of the non-thermal emission in the Crab PWN. -
(iii) Cosmic ray diffusion in galactic environments, such as interstellar and intercluster mediums, strongly depends on the turbulence physics (Ruszkowski & Pfrommer Reference Ruszkowski and Pfrommer2023). It is still not understood what exactly scatters the cosmic rays. However, one hypothesis is the intermittent structures in the turbulence (Kempski et al. Reference Kempski, Fielding, Quataert, Galishnikova, Kunz, Philippov and Ripperda2023; Lemoine Reference Lemoine2023).
In summary, we have obtained the scaling distributions for the geometric properties of current sheets, including the length, width and radius of curvature. We find that the length and radius of curvature distributions are well-approximated as power-law distributions and the width distribution with an exponential function. This information can be used to develop realistic subgrid models for turbulent heating in the accretion flows of compact objects and other turbulent environments.
Acknowledgments
The authors thank the anonymous reviewers for their comments, which improved the quality of the manuscript. The authors also thank L. Sironi and T. Ha for their helpful discussions. R.S. is also thankful to Stack Overflow user (Scott), and the Flatiron Institute for Guest Researcher appointment.
Funding
This work is supported by an ERC grant (ILLUMINATOR, 101114623). V.Z. acknowledges support from NSF grant PHY-2409316. J.N. and V.Z. acknowledge support from a Flatiron Research Fellowship at the Flatiron Institute. Research at the Flatiron Institute is supported by the Simons Foundation.
Declaration of interests
The authors report that they do not have a conflict of interest.
Appendix A. Transformation to local coordinate frame
In this appendix, we describe the local coordinate system constructed for presenting example current sheets in figure 3 and for measuring the width. This coordinate system is defined individually for each structure.
For each current sheet, we first need the perimeter points of the polygon,
![]() $(x_i, y_i)$
with
$(x_i, y_i)$
with
![]() $i \in \{ 1, \ldots, N_p \}$
, where
$i \in \{ 1, \ldots, N_p \}$
, where
![]() $N_p$
is the number of perimeter points identified by the SOM algorithm.Footnote
4
First, we identify the left-hand (or right-hand) edges of the polygon by finding the index
$N_p$
is the number of perimeter points identified by the SOM algorithm.Footnote
4
First, we identify the left-hand (or right-hand) edges of the polygon by finding the index
![]() $ i_{\textrm {L}}$
(or
$ i_{\textrm {L}}$
(or
![]() $i_{\textrm {R}}$
) at which
$i_{\textrm {R}}$
) at which
![]() $x_i$
takes a minimal (or maximal) value in the set
$x_i$
takes a minimal (or maximal) value in the set
![]() $\{ x_i \}$
; we denote the (Euclidean) distance between these points by
$\{ x_i \}$
; we denote the (Euclidean) distance between these points by
![]() $r_x = [(x_{i_{\textrm {R}}}-x_{i_{\textrm {L}}})^2 + (y_{i_{\textrm {R}}}-y_{i_{\textrm {L}}})^2]^{1/2}$
. Likewise, we identify the bottom (or top) edge of the polygon by finding the index
$r_x = [(x_{i_{\textrm {R}}}-x_{i_{\textrm {L}}})^2 + (y_{i_{\textrm {R}}}-y_{i_{\textrm {L}}})^2]^{1/2}$
. Likewise, we identify the bottom (or top) edge of the polygon by finding the index
![]() $i_{\textrm {B}}$
(or
$i_{\textrm {B}}$
(or
![]() $i_{\textrm {T}}$
) at which
$i_{\textrm {T}}$
) at which
![]() $y_i$
takes a minimal (or maximal) value in the set
$y_i$
takes a minimal (or maximal) value in the set
![]() $\{ y_i \}$
; we denote the distance between these points by
$\{ y_i \}$
; we denote the distance between these points by
![]() $r_y = [(x_{i_{\textrm {T}}}-x_{i_{\textrm {B}}})^2+(y_{i_{\textrm {T}}}-y_{i_{\textrm {B}}})^2]^{1/2}$
. The ‘major axis’ is then defined by the larger of
$r_y = [(x_{i_{\textrm {T}}}-x_{i_{\textrm {B}}})^2+(y_{i_{\textrm {T}}}-y_{i_{\textrm {B}}})^2]^{1/2}$
. The ‘major axis’ is then defined by the larger of
![]() $r_x$
and
$r_x$
and
![]() $r_y$
.Footnote
5
$r_y$
.Footnote
5
Next, we transform to a new coordinate system
![]() $(x',y')$
such that the centre of the polygon and the major axis is along the
$(x',y')$
such that the centre of the polygon and the major axis is along the
![]() $x'$
-axis. To achieve this, we define a vector
$x'$
-axis. To achieve this, we define a vector
![]() $\boldsymbol{D}$
that is oriented along the major axis,
$\boldsymbol{D}$
that is oriented along the major axis,
 \begin{align} \boldsymbol{D} = \begin{cases} \frac {(x_{i_{\textrm {R}}} - x_{i_{\textrm {L}}}, y_{i_{\textrm {R}}} - y_{i_{\textrm {L}}})}{r_x} \, & \, r_x \gt r_y \\[4pt] \frac {(x_{i_{\textrm {T}}} - x_{i_{\textrm {B}}}, y_{i_{\textrm {T}}} - y_{i_{\textrm {B}}})}{r_y} \, & \, \mathrm {otherwise}\\ \end{cases} \end{align}
\begin{align} \boldsymbol{D} = \begin{cases} \frac {(x_{i_{\textrm {R}}} - x_{i_{\textrm {L}}}, y_{i_{\textrm {R}}} - y_{i_{\textrm {L}}})}{r_x} \, & \, r_x \gt r_y \\[4pt] \frac {(x_{i_{\textrm {T}}} - x_{i_{\textrm {B}}}, y_{i_{\textrm {T}}} - y_{i_{\textrm {B}}})}{r_y} \, & \, \mathrm {otherwise}\\ \end{cases} \end{align}
and a rotation matrix
To transform to the new coordinates
![]() $(x',y')$
for each structure, we multiply the original coordinates
$(x',y')$
for each structure, we multiply the original coordinates
![]() $(x,y)$
by the rotation matrix
$(x,y)$
by the rotation matrix
![]() $M$
and then subtract the structure’s ‘average’ location from its position coordinates,
$M$
and then subtract the structure’s ‘average’ location from its position coordinates,
where
![]() $\langle x_i \rangle$
and
$\langle x_i \rangle$
and
![]() $\langle y_i \rangle$
are the mean location values from the sets
$\langle y_i \rangle$
are the mean location values from the sets
![]() $x_i$
, and
$x_i$
, and
![]() $y_{i}$
, respectively.
$y_{i}$
, respectively.
Appendix B. Algorithm for measuring the sheet width
Continuing the calculation from appendix A, we are now in the local coordinate frame
![]() $(x'_i, y'_i)$
. In this frame, we calculate the width of each current sheet. First, we must reidentify the left-hand (or right-hand) edges of the polygon in the local coordinate frame;
$(x'_i, y'_i)$
. In this frame, we calculate the width of each current sheet. First, we must reidentify the left-hand (or right-hand) edges of the polygon in the local coordinate frame;
![]() $i'_{\textrm {L}}$
(or
$i'_{\textrm {L}}$
(or
![]() $i'_{\textrm {R}}$
) at which
$i'_{\textrm {R}}$
) at which
![]() $x'_i$
takes a minimal (or maximal) value in the set
$x'_i$
takes a minimal (or maximal) value in the set
![]() $\{ x'_i \}$
of points on the structure’s perimeter. Likewise, we reidentify the bottom (or top) edge of the polygon by finding the index
$\{ x'_i \}$
of points on the structure’s perimeter. Likewise, we reidentify the bottom (or top) edge of the polygon by finding the index
![]() $i'_{\textrm {B}}$
(or
$i'_{\textrm {B}}$
(or
![]() $i'_{\textrm {T}}$
) at which
$i'_{\textrm {T}}$
) at which
![]() $y'_i$
takes a minimal (or maximal) value in the set
$y'_i$
takes a minimal (or maximal) value in the set
![]() $\{ y'_i \}$
.
$\{ y'_i \}$
.
One simple method to calculate the width would be to take the (Euclidean) distance between the points
![]() $(x'_{i'_{\textrm {T}}}, y'_{i'_{\textrm {T}}})$
and
$(x'_{i'_{\textrm {T}}}, y'_{i'_{\textrm {T}}})$
and
![]() $(x'_{i'_{\textrm {B}}}, y'_{i'_{\textrm {B}}})$
. However, this definition may not represent the overall structure if the current sheet’s width varies along its length.
$(x'_{i'_{\textrm {B}}}, y'_{i'_{\textrm {B}}})$
. However, this definition may not represent the overall structure if the current sheet’s width varies along its length.
Therefore, to define a better representation of the overall width, we take the additional step of breaking each current sheet into vertical strips and averaging the width across the strips. The first step is to divide each sheet into a ‘top’ half and ‘bottom’ half along the direction parallel to
![]() $x'_i$
. We begin from
$x'_i$
. We begin from
![]() $x'_{i'_{\textrm {L}}}$
, and find its
$x'_{i'_{\textrm {L}}}$
, and find its
![]() $y'$
-coordinate
$y'$
-coordinate
![]() $y'_{i'_{\textrm {L}}}$
, and similarly, we take
$y'_{i'_{\textrm {L}}}$
, and similarly, we take
![]() $x'_{i'_{\textrm {R}}}$
and find it’s
$x'_{i'_{\textrm {R}}}$
and find it’s
![]() $y'$
-coordinate pair
$y'$
-coordinate pair
![]() $y'_{i'_{\textrm {R}}}$
. Next, we begin sorting the
$y'_{i'_{\textrm {R}}}$
. Next, we begin sorting the
![]() $y'$
-coordinate pairs into two new arrays,
$y'$
-coordinate pairs into two new arrays,
![]() $y_{\mathrm {i, top}}$
and
$y_{\mathrm {i, top}}$
and
![]() $y_{\mathrm {i, bot}}$
in the following manner. We begin from
$y_{\mathrm {i, bot}}$
in the following manner. We begin from
![]() $x'_{i}$
at
$x'_{i}$
at
![]() $i=1$
and begin looping through
$i=1$
and begin looping through
![]() $i$
until
$i$
until
![]() $x'_{i'_{\textrm {L}}} = x'_{i}$
, or
$x'_{i'_{\textrm {L}}} = x'_{i}$
, or
![]() $x'_{i'_{\textrm {R}}} = x'_{i}$
. In the former case, we append the values of
$x'_{i'_{\textrm {R}}} = x'_{i}$
. In the former case, we append the values of
![]() $y'_{i}$
to
$y'_{i}$
to
![]() $y_{\mathrm {i, top}}(x'_{i})$
, and in the later case we append
$y_{\mathrm {i, top}}(x'_{i})$
, and in the later case we append
![]() $y'_{i}$
to
$y'_{i}$
to
![]() $y_{\mathrm {i, bot}}(x'_{i})$
. This process iterates until we reach
$y_{\mathrm {i, bot}}(x'_{i})$
. This process iterates until we reach
![]() $i = N_{p}$
.
$i = N_{p}$
.
Next, we use the `scipy.interpolate’ subpackage (Virtanen et al. Reference Virtanen2020) to interpolate between
![]() $y'_{\mathrm {i, top}}(x'_{i})$
and
$y'_{\mathrm {i, top}}(x'_{i})$
and
![]() $y'_{\mathrm {i, bot}}(x'_{i})$
using an array of points linearly spaced between
$y'_{\mathrm {i, bot}}(x'_{i})$
using an array of points linearly spaced between
![]() $x'_{i'_{\textrm {L}}}$
and
$x'_{i'_{\textrm {L}}}$
and
![]() $x'_{i'_{\textrm {R}}}$
, thus creating two new arrays
$x'_{i'_{\textrm {R}}}$
, thus creating two new arrays
![]() $y''_{\mathrm {top}}(x'_{i})$
and
$y''_{\mathrm {top}}(x'_{i})$
and
![]() $y''_{\mathrm {bot}}(x'_{i})$
of the
$y''_{\mathrm {bot}}(x'_{i})$
of the
![]() $y'$
coordinates corresponding to
$y'$
coordinates corresponding to
![]() $\{x'_i\}$
. This allows us to create vertical slices (along the
$\{x'_i\}$
. This allows us to create vertical slices (along the
![]() $y'$
-axis), and then we average over the sum of the slices to obtain our width,
$y'$
-axis), and then we average over the sum of the slices to obtain our width,
 \begin{align} w = \frac {1}{N_x} \sum _{i = 1}^{N_p} \left |\, y''_{{top}}(x'_{i}) - y''_{{bot}}(x'_{i}) \,\right |, \end{align}
\begin{align} w = \frac {1}{N_x} \sum _{i = 1}^{N_p} \left |\, y''_{{top}}(x'_{i}) - y''_{{bot}}(x'_{i}) \,\right |, \end{align}
where
![]() $N_x = 50$
is the number of points we use to generate the interpolator. We have found this method to yield a more robust estimate of
$N_x = 50$
is the number of points we use to generate the interpolator. We have found this method to yield a more robust estimate of
![]() $w$
in comparison with just using a slice (e.g.,
$w$
in comparison with just using a slice (e.g.,
![]() $w \approx |y''_{\mathrm {top}}(x'_s) - y''_{\mathrm {bot}}(x'_s)|$
at location
$w \approx |y''_{\mathrm {top}}(x'_s) - y''_{\mathrm {bot}}(x'_s)|$
at location
![]() $x'_s = \frac {1}{2}| x'_{i_{\textrm {L}}} - x'_{i_{\textrm {R}}}|$
) or averaging using the number of available pixels only. The reason for that is that the width of the sheet can vary along the length.
$x'_s = \frac {1}{2}| x'_{i_{\textrm {L}}} - x'_{i_{\textrm {R}}}|$
) or averaging using the number of available pixels only. The reason for that is that the width of the sheet can vary along the length.
Appendix C. Algorithm for calculating the parameters of a circle fitted through three points
Here, we summarize the algorithm that we use to calculate the radius of curvature of a given current sheet and the centre of the circle. The algorithm is based on the curve fitting algorithms listed in Umbach & Jones (Reference Umbach and Jones2003). More sophisticated methods, using more than three points, could also be used to obtain a ‘best fit’ circle instead.
We begin by choosing three points in our current sheet; the first two are
![]() $x'_{i_{L}}$
and
$x'_{i_{L}}$
and
![]() $x'_{i_{R}}$
described above, and the third point is obtained by first calculating the half width at the centre of the sheet using (B1); i.e.,
$x'_{i_{R}}$
described above, and the third point is obtained by first calculating the half width at the centre of the sheet using (B1); i.e.,
![]() $ y_{h} = 1/2|y''_{{top}}(x'_s) - y''_{{bot}}(x'_s)|$
at location
$ y_{h} = 1/2|y''_{{top}}(x'_s) - y''_{{bot}}(x'_s)|$
at location
![]() $x'_s = \frac {1}{2}| x'_{i_{\textrm {L}}} - x'_{i_{\textrm {R}}}|$
. Then we obtain the midpoint
$x'_s = \frac {1}{2}| x'_{i_{\textrm {L}}} - x'_{i_{\textrm {R}}}|$
. Then we obtain the midpoint
![]() $y_{m} = y_{h} + y''_{{bot}}(x'_s)$
. These points are marked by red dots in figure 3. Next we map the three points into the complex numbers
$y_{m} = y_{h} + y''_{{bot}}(x'_s)$
. These points are marked by red dots in figure 3. Next we map the three points into the complex numbers
![]() $(z'_{1}, z'_{2}, z'_{3})$
; using the definition
$(z'_{1}, z'_{2}, z'_{3})$
; using the definition
![]() $z' = x' + \sqrt {-1} y'$
.
$z' = x' + \sqrt {-1} y'$
.
We then apply a linear transformation to
![]() $(z'_{1}, z'_{2}, z'_{3})$
; i.e.,
$(z'_{1}, z'_{2}, z'_{3})$
; i.e.,
 \begin{align} z'_{j} \rightarrow \frac {z'_{j} - z'_{1}}{z'_{2}- z'_{1}}, \end{align}
\begin{align} z'_{j} \rightarrow \frac {z'_{j} - z'_{1}}{z'_{2}- z'_{1}}, \end{align}
which results in
![]() $z'_1 \rightarrow 0$
,
$z'_1 \rightarrow 0$
,
![]() $z'_2 \rightarrow 1$
and
$z'_2 \rightarrow 1$
and
![]() $z'_3 \rightarrow (z'_{3} - z'_{1})/(z'_{2}- z'_{1}) \equiv u$
. Here
$z'_3 \rightarrow (z'_{3} - z'_{1})/(z'_{2}- z'_{1}) \equiv u$
. Here
![]() $z'_1$
is the left-hand point of the structure,
$z'_1$
is the left-hand point of the structure,
![]() $z'_2$
is the right-hand point of the structure and finally,
$z'_2$
is the right-hand point of the structure and finally,
![]() $z'_3$
is the middle point in the structure.
$z'_3$
is the middle point in the structure.
We can then use the relationship
![]() $|z'_{j} - C| = r_{c}$
(where
$|z'_{j} - C| = r_{c}$
(where
![]() $r_{c}$
is the radius of curvature of the circle fit,
$r_{c}$
is the radius of curvature of the circle fit,
![]() $C$
is the coordinates of the circle’s centre, and
$C$
is the coordinates of the circle’s centre, and
![]() $j \in \{ 1,2,3 \})$
to obtain the following system of equations:
$j \in \{ 1,2,3 \})$
to obtain the following system of equations:
We solve
![]() $C$
from (C2)–(C4). The centre of the circle is then
$C$
from (C2)–(C4). The centre of the circle is then
Finally, we undo the linear transformation, which yields the centre of the circle in our original coordinates,
Therefore, we now have
![]() $C$
, and using (C2), we obtain the radius of curvature,
$C$
, and using (C2), we obtain the radius of curvature,
![]() $r_{c}$
.
$r_{c}$
.