1. INTRODUCTION
This paper is an extension of my contribution to the Pioneers Session at the ECLIM conference in Madrid, Spain, June 11–16, 2006 (Velarde & Santamaria, 2006; Hora, 2005a). I have included additional general remarks by Cartridge (2006) about the developments in fusion energy (Kaw & Burkhard, 2005), in view of the developments in fusion energy presented during the weeks of this conference. These developments require some general considerations about fusion energy, and about the achievements of particle beam driven fusion in the joint European torus (JET) experiment in relation to the ITER project. The main lines of developments in laser driven ICF are then summarized, and results are listed along the lines of discussions during the Pioneer Session.
The broad stream of research in fast igniter (Tabak et al., 1994) led to the scheme of laser driven very intense relativistic electron beams (Nuckolls & Wood, 2002) to ignite rather modestly compressed DT fuel. This is similar to the ignition by very intense sub-relativistic ion beams (Osman et al., 2004; Hora et al., 2005), where the observation of the very anomalous laser-plasma interaction of ps-TW laser pulses (Zhang et al., 1998; Badziak et al., 1999), by avoiding relativistic self-focusing (Sauerbrey, 1996) could be explained as a skin layer process (Hora et al., 2002; Hora, 2003, 2005a or 2005b; Badziak et al., 2003, 2004, 2005a, 2005b).
Due to personal reasons, my paper was presented at the ECLIM Conference by Professor Milan Kalal, Technical University Prague, whose kind endeavors are acknowledged with great thanks.
2. FUSION ENERGY
One of the leading experts on environment problems is James Lovelock, who played a key role in detecting the damage to the atmosphere by fluoric hydrocarbon emission and succeeded in their worldwide ban. He was listed by the magazine “Prospect” in 2005 as being one of the hundred most influential intellectuals in the world. In an interview with Ulli Kulke for the German newspaper, Lovelock (Lovelock & Kulke, 2006) pointed out that all of the separate observations of the environmental problems need to be combined, and then there may be 60 meter rising at ocean levels during the next dozens years. These catastrophic developments are irreversibly on the way and it is now too late to stop them, only a delay of the catastrophe may be possible. Under the banner “Das ist doch grüner Unsinn” (This definitely is green nonsense), Lovelock stated that he favored nuclear energy, and very interestingly, he mentioned fusion energy as being a part of the future.
In Tasmania, the fact that the environmental red line has been passed, can be seen from an evaluation of the rings in a more than 1000 year-old huon pines tree (Cook et al., 1991; Hora, 1998). Since the statistical variation of the thickness of the rings is always within 21%, well reflecting the 10.4 years periodicity with fluctuating maxima of solar radiation, and other influences. However, since 1950, the rings increased continuously up to 42%. This clearly confirms the conclusions of Loevelock that the manmade emission of carbon dioxide to the atmosphere was tolerable until 1950, and the increase since then by a factor of four caused the irreversible damage. Carbon dioxide emission has to be reduced to 20% of the today's level!! The results of hoping for sustainable energy sources like wind mills, solar cells, or the few percents from Kyoto Protocol are not only ridiculous, it is rather dangerous, or a kind of crime, if these vague hopes alienate us from our most urgent commitment to fight much more energetically against this catastrophe, not to mention how much of the taxpayers' money is wasted by ridiculous attempts (see Wetzel, 2006). The only positive example and splendid demonstration for having achieved a solution is in France, where 85% of the electric power is produced by nuclear fission. Though this energy production has been demonstrated to be completely safe and the energy costs are considerably lower than all other energy sources, further improvements are possible as the absolute safe scheme of a thorium breeding reactor imbedded in rocks 100 meter below the surface as proposed by Teller (2005).
While this fission energy option including breeding may be an energy source for the next time, it will not last for more than a few hundred years. The only clean, safe, long term and everywhere available low cost energy source will be the energy produced in the same way as on the sun, and all the myriads of stars: fusion of hydrogen isotopes or other light nuclei. After the very first uncontrolled exothermic fusion reaction succeeded in 1951 (Teller, 2001), an enormous amount of investments have gone into the research for a controlled fusion reaction to be used in power stations. The problems are difficult because the reactions of nuclei for fusion need temperatures of at least a few million degrees centigrade. Needing very high energy for such an ignition, much more energy should be gained form the reactions as the generated plasma cools down. The temperature needed for fusion is a real exception in nature, since the usual nuclear reactions need temperatures of several billion degrees. The discovery of the exception goes back to the time of the very first fusion reaction discovered (Oliphant et al., 1934; see Hora, 2004).
3. MAGNETIC CONFINEMENT: JET AND ITER
While irradiations of 100 keV deuterium ions on solid target are well suited for producing fusion reactions, it was realized (Hora, 2004) that controlled exothermic energy production is not possible because the electrons in the solid target will absorb much more of the 100 keV ion energy than fusion reactions are produced. The conclusion was that electrons and ions need to have the necessary temperature and fusion plasma need to be confined at this temperature by magnetic fields. This conclusion is correct in linear physics only while nonlinear physics permits beam fusion with cold targets, that is, using laser beams, I will address this point later in this paper.
Research on magnetic confinement fusion (MCF) needed to solve numerous unexpected problems, and it took dozens of years from the first measurements of fusion reactions to arrive now at the nearly energy break-even point (Kaw & Burkhard, 2005). At present, the decision to building an international thermonuclear experimental reactor (ITER) at the cost of $13 Billion Dollars (Cartridge, 2006) is ready to be ratified by the end of 2007 by China, the European Union, Japan, Russia, South Korea, and the USA.
As to the value of ITER, the following facts need to be taken into account. This most favored project is scheduled to go into operation in 2016, where the energy gain is still rather modest: 500 MW electricity input should produce 500 MW fusion power during 500 s, such that after conversion by 30% efficiency in an electric generator, a gain of 150 MW can result as reported by Tran to the UN-Energy conference, September 2004 in Sydney (Tran, 2004). The best measurement of MCF was with the JET (Keilhacker 1999), where a magnetically confined plasma torus for 2 s produced 16 MW fusion power by irradiation of 21 MW neutral beam power, and 3 MW heating by electromagnetic radiation. To this fusion gain of 0.66 MW, one had to ignore the 100 MW electricity that was needed to run the torus. If one takes the operation of JET into account, the gain of fusion energy is 0.129 MW, and with 30% conversion to electricity, the total gain is 0.042 MW. It has to be understood that this experiment, by producing 16 MW fusions from 21 MW neutral beams, and 3 MW irradiation, is a beam fusion experiment in some contradiction, that beam fusion should be excluded. Nevertheless it is the best result yet with magnetic confined plasmas.
Taking the result of JET into account, ITER should then produce an increase in energy by a factor of 7.4. It is argued that the aim is not the high gain, but to explore the conditions for a self-ignition of the plasma in ITER. For this very important and ambitious task, it is difficult to elaborate a prediction based on the usual knowledge of plasma properties. A more optimistic situation is for the prediction of whether a block of directed plasma (piston) would be able to ignite solid-state dense DT (Hora et al., 2005, 2006), where it is realized that the mechanisms of interpenetration of hot into cold plasma, the modification of the collision frequency by quantum effects, inhibition of thermal conduction due to electric double layers, reduced stopping power due to collective effects, and other processes have to be fully understood and included into the analysis.
In view of this important research problem, both for MCF as well as for ICF, it may be asked whether a combination of JET and ITER could indicate with a separation of steps, expense saving, and a much more efficient modification of ITER experiments following the first of a two-year study at JET. If a comparably small part of the budget could be used for a quick installation of a number of neutral beam injectors at JET, for which the blueprint is on the shelf, and where the costs of the injectors in a series production could be reduced, then a repetition of the 1999 experiments (Keilhacker 1999) could result in a very much higher energy gain than mentioned above. A rather simple measurement of the scaling on growing parameters may disclose properties for ignition and perhaps would arrive at a full scale ignition. If with this knowledge, the experiments at ITER could then be modified, this may lead to a very important progress, and a much higher efficient investment of the present efforts.
4. LASER FUSION
It was understood at the discovery of the laser, that the use of radiation ignition for fusion reactions may be considered when applying laser radiation as envisaged by Nuckolls (2005). From his knowledge about radiation driven reactions, he noted that the laser intensity for 1017 W/cm2 is the same intensity of the Planck radiation for a temperature of 1 keV (11 Million degrees). I will now summarize some developments to these aims which will develop along three different lines and finally merging in schemes for mutual support.
4.1. Volume ignition
This line of research mostly follows the use of the self-similarity model (Hora, 1991 Sect. 5), as it was used at the very beginning in the computations by Basov and Krokhin and by Dawson, Engelhard, and Hora (see Hora, 1991, p. 339). If an energy, Eo, is uniformly deposited into a volume, Vo (of radius, Ro) of DT, with an initial density, no, related to the solid-state density, ns, and a break-even energy, EBE, at an initial zero expansion velocity, and an optimum temperature of 17 keV, the subsequent adiabatic expansion results in a fusion gain (DT fusion energy per Eo with a break-even energy of 6 MJ)
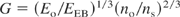
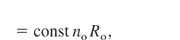
where Eq. (1) is based on computations published by Hora and Pfirsch (1970) and Eq. (2) is based on computations published by Kidder (1974). When these computations included the alpha self-heat, X-ray re-absorption, and fuel depletion, the volume ignition was discovered (Hora & Ray, 1978), resulting in very high gains, up to 2000, and low ignition temperatures, down to keV, and less at compressions to higher than 1000 times the solid-state density (Hora et al., 1998; Amendt et al., 2005). This volume ignition was later confirmed by Kirkpatrick and Wheeler (1981), Lackner et al. (1994), and others.
Initial experiments (Engelhardt et al., 1970) clearly showed that laser interaction with irradiated solid spheres, indicated (apart from a nonlinear (ponderomotive) force driven fast plasma ablation) that most of the laser energy went into a spherical core fully following the self-similarity expansion. It is remarkable that the much later measured highest DT neutron generation, at direct laser drive, exactly followed the self-similarity model (Hora et al., 1998), where any shock generation had to be avoided, as known from the fast pusher where the gains were much lower. The highest gain reactions followed volume burn on the way to volume ignition, where the physics is rather “robust” based on the ideal adiabatic dynamics as it was explained by Lackner et al. (1994). This fact leads to the rather realistic expectation that lasers with ns pulses like the national ignition facility (NIF) at the Lawrence Livermore Laboratory, with 5 MJ pulses and fuel compression to a few 1000 times the solid state should produce at least 500 MJ fusion energy in a most conservative way (Miley et al., 2005).
4.2. Radiation ignition and spark ignition
The motivation for these lines may have come from two arguments. First, it was the enthusiasm that laser irradiation may arrive at similar conditions for radiation ignition in solids or moderately compressed DT fuel as envisaged by Nuckolls (2005), based on the radiation ignition or propagating thermonuclear burn as known form the uncontrolled reactions. The second argument was that the gains of Eq. (1) were terribly low before the very high gains at volume ignition were discovered (Hora & Ray, 1978; Hora et al., 1998). The ingenious approach to solving both questions was the introduction of the spark scheme (Lindl, 2005).
The question of directly igniting solid DT by a laser pulse was answered negatively by Bobin (1974), when computations indicated that the fusion flame need to have an energy flux density of
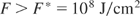
or irradiation corresponding to an ion current density
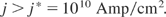
The condition for beam fusion (Eq. (4)) was by more than five orders of magnitude out of possibilities for using particle beams as drivers. For achieving Eq. (3), Nuckolls deduced the spark or central core ignition, where the laser radiation (or after conversion into X-rays as “indirect drive,” see Lindl, 2005), compressed the DT in such a very sophisticated way, producing isobaric, a very hot but low density central core, whose fusion reaction ignited into the surrounding low temperature, high density mantle, a very high gain fusion detonation wave (Hora et al., 1998, Fig. 4). The reaction in the core was shown to be an ideal volume ignition and energy flux density for driving the fusion detonation wave in the range of F = 7 × 108 J/cm2, fulfilling Eq. (3). The detailed computation based on otherwise known realistic conditions arrived at generation of 1000 MJ fusion energy produced by a laser pulse of 10 MJ (Storm et al., 1988). The problems consist of how to achieve such an exclusive temperature and density profile against the Ryleigh–Taylor instabilities and irradiation asymmetries.
4.3. Fast ignition
When spherical laser irradiation compressed polyethylene-like polymers to 2000 times the solid-state density (Azechi et al., 1991), only a temperature of about 300 eV was measured. In order to reach fusion conditions, it was proposed by Tabak et al. (1994) to add a laser pulse of PW power and ps duration to the center of the compressed plasma, where pulses were just becoming available by chirped pulse amplification (CPA), or by the Schäfer technique (see Sauerbrey, 1996). When performing the first experiments with these pulses, it was surprising that all kinds of relativistic effects appeared, as generation of 100 MeV electrons, up to GeV ions, 20 MeV gammas with subsequent nuclear reactions, but just not the desired deposition of the pulse energy to the center of the 1000 times solid pre-compressed plasma for spark ignition.
It must be understood that the rather low temperatures, by 2000 times compression, are not the end of laser fusion. Based on volume ignition, it was evaluated by Miley et al. (2005), that this very robust and experimentally proved method should produce high gain laser fusion using MJ-ns laser pulses, and compression to a 1000 times the solid density where the ignition temperature is less than keV, such that the reaction can take place in one step of ns pulse irradiation without any additional ps laser pulse. This is at least a feasible option for laser fusion with lasers of the NIF generation, where the engineering reduction of size and costs is not limited by physical principles as understood in Section 4.1.
Modifications of the fast igniter line were developed, of which the generation of 5 MeV intense proton beams was mentioned (Roth et al., 2005), for depositing energy into the center of pre-compressed DT fuel with the aim of achieving spark ignition.
Another modification opens the possibility for the initial aim on how to ignite nearly uncompressed solid DT fuel. Based on PW-ps laser pulses hitting 1000 times the pre-compressed plasma, Nuckolls and Wood (2002) expected that 5 MeV electron beams could be generated with such an extreme intensity, that 100 MJ fusion energy could be produced by 10 kJ laser pulses (see Teller, 2005, p. 13). The requirement to produce fusion gains above 10000 in a fully controlled way is then fulfilled by using “large mass of low density DT compressed fuel.” The advantage of using pre-compression up to 12 times the solid-state DT fuel is only explained by Nuckolls and Wood (2002), and how even lower pre-compression is of advantage.
5. CONTRIBUTIONS OF NONLINEARITIES, RELATIVISTIC, AND QUANTUM EFFECTS
The author has been involved in laser fusion research since 1962 as the main part of his activities. The main points of his achievements are listed under the following topics:
(1) Optical constants for plasma: Spitzer's collision frequency arrives at the same values as QED or kinetic theory. First dielectric response and absorption for super dense plasma was calculated (Hora, 1991, Sec. 6.4).
(2) Explanation of nonlinear laser-plasma interaction: The measured 10 keV ions, with linear energy dependence on the ion charge number Z, at interaction of laser pulses with more than a few MW power, did not follow the thermal generation at lower powers, with ion energies of less than a few dozens eV. The explanation was based on the acceleration of the nonlinear (ponderomotive) force, which had to be derived in general terms (Hora, 1969) for the non-transient (Hora, 1985) and for the transient interaction, arriving at the general formula for the force density in plasma. Derivation of the first quantitative ponderomotive self focusing of laser beams in plasma (Hora, 1969a), explained the 1 MW threshold above which nonlinear interaction begins. Complete derivation of the electrodynamic force (nonlinear force) of laser-plasma interaction in contrast to five approximative transient theories was based on symmetry relations (Hora, 1985). Its proof of completeness of the derived formula was based on Lorentz and gauge invariance by Terence Rowlands (2006).
(3) Relativistic studies: The second paper about pair production in laser fields was published by Hora (1973) following the work by Prokhorov and Bunkin (1969) leading to black hole problems (Stait-Gardner & Castillo, 2006). This led to the nonlinear and relativistic formulation of the optical constants in plasmas. As a consequence, the first generally valid theory of relativistic self-focusing was derived in 1974 with many further evaluations (Hora, 1975).
(4) First derivation of longitudinal fields' components of laser beams in a vacuum as needed for a correct theory of the lateral emission of electrons from laser beams (Boreham & Hora, 1979; Cicchitelli et al., 1990). A consequence is that exact nonlinear results can change a result in linear physics from fully right to fully wrong (Hora, 2000). This opens a basically new dimension in physics research for exact deriving completely unexpected phenomena.
(5) Quantum correction of collision frequency (Hora, 1991, Sec. 2.6). For the electron–ion collision frequency, there is not only a quantum mechanical change in the Coulomb logarithm of the Spitzer–Härm formula, but for the whole quantity for a quantitative explanation of anomalous resistivity. Several clear examples were shown for this quantum modification of the collision frequency at higher temperatures defined by the square of the fine structure constant, that is why the diffusion of deuterons in stellarators are 20 times faster across the magnetic field than classical. For the correct use in numerical codes of the genuine two-fluids hydrodynamics see Glowacz et al. (2006). Another example is seen from the proof that GeV ions emitted from ps laser pulse interaction follow the Gitomer hot electron model and not the relativistic self-focusing (Hora, 2003).
(6) Genuine two-fluid hydrodynamics for deriving electric double layers and internal dynamic electric fields in inhomogeneous plasmas with new resonance, punching and second harmonics generation: Very high amplitude Langmuir oscillations by lasers were calculated (Lalousis & Hora, 1983), and electron acceleration (Eliezer & Hora, 1989) in these internal fields of inhomogeneous plasmas (Hora et al., 1984), and a resonance at perpendicular incidence derived (Hora & Ghatak, 1985).
(7) Against enormous controversy: Acceleration of electrons by lasers in a vacuum is possible due to nonlinear interaction (Hora, 1988).
(8) After numerical discovery of von-Laue density rippling (Hora,1974): explanation of 20-ps pulsating interaction and suppression by laser beam smoothing (Hora & Aydin, 1992; Hora, 2006).
(9) First paper on volume ignition for laser fusion (Hora & Ray, 1978) in agreement with highest measured fusion gains for volume burn (Hora et al., 1998), see Section 4.1 in this paper.
(10) Clarification that the very anomalous observations (Sauerbrey, 1996; Zhang et al., 1998; Badziak et al., 1999) can be explained by a nonlinear-force skin-layer mechanism with suppression of relativistic self-focusing at very high contrast ratio (Hora et al., 2002; Hora, 2003) with consequences for modified fast ignition with generation of plasma blocks (pistons) with extreme ion current densities for fusion (see the following sections).
6. NEW INTERACTION EFFECT WITHOUT SELF-FOCUSING
After conceptually opening the line for igniting nearly solid-state density DT by PW-ps laser driven electron beams for controlled fusion with gains of 10000 (Nuckolls & Wood, 2002), this type of laser pulses may open a similar line for laser driven ion beams in space charge neutral plasma. This involves a basically new phenomenon of ion beams and is based on the few exceptionally anomalous interaction measurements by avoiding relativistic self-focusing in contrast to the usual experiments, where self-focusing results in all kinds of relativistic effects as 100 MeV electron or GeV ion beams, 20 MeV gamma bursts, exotic nuclear reactions, pair production etc..
In contrast to these relativistic interaction processes, it is a well pronounced anomaly in the experiments by Zhang et al. (1998) where the usually irradiated TW-ps laser pulses did not produce the always observed very intense X-ray emission. Another anomaly was the fact (Badziak et al., 1999) that the ions emitted from targets did not have the usually observed ion energies (22 MeV expected from the always involved relativistic self-focusing), but showing maximum energies of half MeV. Though it has to be realized in retrospect, there are the measurements of emitted directed plasma fronts which were rather uniform and showed very high values of acceleration (Sauerbrey, 1996). The later experiments where indeed exceptional where TW sub-ps laser pulses were generated in a very intriguing way by the technique of Schäfer, with excimer lasers having an extremely high quality with a contrast ratio better than 108 (ratio of suppression of prepulses). Following a discussion with one of his co-authors, Lang Wong (Zhang et al., 1998), it became evident that all these very unusual anomalous observations could be explained by nonlinear-force-driven skin-layer acceleration (Hora et al., 2002; Hora, 2003).
Summarizing the essential aspects of the new anomaly and related recent results since its confirmation, the key question is whether there are conditions that the interaction of a focused laser beam at the surface of a solid target in a vacuum is following the conditions of a plane wave interaction described preferably in one dimension, or whether the laser beam, as in most of the usual cases, produces a pre-generated plasma in front of the target, performing self-focusing and undergoing a shrinking of the laser beam by relativistic self focusing (Hora, 1975), to less than a wavelength diameter from where the nonlinear forces accelerate the highly charged ions from MeV to GeV energy in all directions, causing all the mentioned relativistic effects with TW-ps laser pulses.
The plane wave interaction was studied by hydrodynamic computations including nearly all realistic and general plasma properties, of which one of the numerous cases is shown in Figure 1. Within about ps interaction of a 1018 W/cm2 neodymium glass laser pulse on a deuterium target, with an initially very low reflection (bi-Rayleigh) density profile, the nonlinear force is generating blocks of deuterium plasma of about 15 vacuum wavelengths thickness, moving with velocities exceeding 109 cm/s against the laser light and a similar block moving into the target interior.
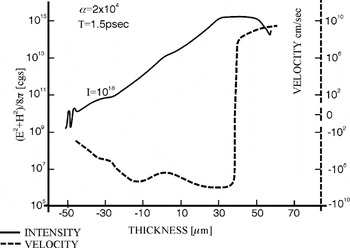
Generation of blocks of deuterium plasma moving against the neodymium glass laser light (positive velocities v to the right) and moving into the plasma interior (negative velocities) at irradiation by a neodymium glass laser of 1018 W/cm2 intensity onto an initially 100 eV hot and 100 μm thick bi-Rayleigh profile (Hora, 1991, Fig. 10.17). The electromagnetic energy density (E2 + H2)/(8π) is shown at the same time of 1.5 ps after begin of the constant irradiation from V.F. Lawrence PhD thesis UNSW 1978.
It was many years later that these plane geometry conditions were available in experiments, showing such velocities gained by irradiation of similar excimer laser intensities at less than a ps duration, measured in all details from the Doppler shift by Sauerbrey (1996). The resulting accelerations of 1020 cm/s2 were in full agreement with the expectation from the nonlinear (ponderomotive) force interaction (Hora, 1969, 1985), determined by the force density with the electric and magnetic laser fields E and H from the gradients of the electromagnetic energy density (nonlinear ponderomotive force)
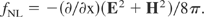
Sauerbrey (1996) confirmed in retrospect that his 350 fs TW laser pulses were sufficiently clean. The pulses were produced by the Schäfer-method with amplifying one of his discovered 350 fs dye-laser-pulses through an activated KrF laser medium, not needing gratings or pulse compression as with Mourou's chirped pulse amplification CPA. Sauerbrey (1996) measured an acceleration A in a carbon plasma front by Doppler effect moving against the laser being produced by the 350 fs TW KrF laser pulse at 3.5 × 1017 W/cm2 of
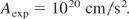
This corresponds to an electric field E2 = 2.9 × 1015 erg/cm3 and a density ni mi for the accelerated plasma layer of 5.4 × 10−3 g/cm3 at the critical density ni = 1.6 × 1021 cm−3 for C+6 ions. The nonlinear force for the simplified plane geometry is
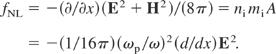
Assuming for simplification, dx = Δx = 10 μm and a swelling S = 2 (the experiments (Badziak et al., 2003, 2005, 2005a, 2005b) for ps pulses resulted in S = 3), we find the theoretical value
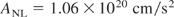
are in agreement with measurements.
This result was confirmed and elaborated in retrospect with the help of Sauerbrey. The initial consideration was initiated at the summit on plasma physics in Islamabad, organized by Hamid Saleem, February 2001, in discussions with Long Wang, putting attention on the results of Zhang et al. (1998). Under the leadership of Jie Zhang, the TW-ps laser pulses at the Institute of Physics of the Chinese Academy of Science in Beijing, were extremely clean with a contrast ratio higher than 108. When they fired a half ps-TW laser pulse at a target, the X-ray emission was terribly low compared with all the numerous usual TW interaction experiments. What has happened? Jie Zhang was clever enough to pre-irradiate a few percent of the main laser pulse of about 30 wavelength diameter interaction area within times t before the main pulse arrived at the target. At t for 10 ps to 50 ps nothing changed with the low X-ray emission. But at t = 70 ps, the very high X-rays appeared in the same way as known from the numerous other experiments around. The time of 70 ps was just sufficient to produce plasma in front of the target about two times deeper than the focus diameter was. This was just sufficient (Hora, 1975), that the laser beam was shrinking by relativistic self-focusing within the generated plasma plume to one wavelength diameter, and producing then the extremely high beam intensities in the target for the enormous X-ray emission.
This result was the starting point for understanding the most anomalous ion emission measured by Badziak et al. (1999). Being aware of the different mechanisms for ion emission from laser produced plasmas, including ponderomotive and relativistic self-focusing from the beginning (Hora, 1975), or the hot electron ambipolar acceleration Hora, 2003), and thermo-kinetic mechanisms, the result of Badziak et al. (1999) could not be explained by any of them. The fact that these measurements showed a constant number for the energetic ions when varying the laser power by a factor of 30, led to a crucial hint that there is the same importance of the prepulse as in the experiments as in the X-ray measurements by Zhang et al. (1998). This was the basis to understand the experiments of Badziak et al. (1999): it was again the very good beam quality with very high contrast ratio preventing self-focusing and permitting an acceleration of the nearly constant plasma volume in the skin depth. It has to be appreciated that it was the special merit of the editor of Optics Communications, Wolfgang Schleich, Ulm, Germany, who overruled an unqualified referees' reports, such that our conclusion was published (Hora et al., 2002), followed by very detailed experimental confirmations (Badziak et al., 2003, 2004, 2005a, 2005b). This was seen from the expected highly directed ion beam against the laser light in contrast to the wide angle ion emission measured under similarly conditions with longer pulses including self-focusing. The recoil of the nonlinear force driven plasma block results in a block (piston) of plasma (Fig. 1), moving into the target, as has been confirmed by measurements at irradiating very thin foils. From comparisons with irradiating targets and heavy or light nuclei with ps or ns pulses, and from the emitted X-ray spectrum, it could be clearly evaluated that the laser intensity had a swelling by a factor of about 3.5, within the plasma corona where the effective laser wavelength was then again three times the vacuum value, and the energetic fast plasma blocks were several vacuum wavelength thick (Cang et al., 2005; Badziak et al., 2004), similar to the computations in Figure 1.
Taking into account the cut-off density of 1021 electrons/cm3 in the blocks and the velocity of more than 108 cm/s for the blocks, deuterium ion current densities of
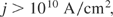
of nonlinear force driven highly directed space charge neutral ion beams are verified, which can then be used as pistons for fulfilling Eq. (4) for igniting a fusion flame in solid-state density DT according to Bobin (1974). The fact that the measurements of plasma blocks (pistons) are generated, and no plasma jets can be seen from the agreement of genuine two-fluid computations (Cang et al., 2005; Glowacz et al., 2006), of the nonlinear (ponderomotive) force acceleration of the skin layer, and the generation of a plasma block moving into the target with ion current densities of Eq. (8) and higher.
Another important result from the experiments of Zhang et al. (1998) and Badziak et al. (1999) together with that of Sauerbrey (1996), that it is possible to produce very wide nonlinear force driven plane layers (blocks) instead of jets for laser compression of plasmas. The importance of beam smoothing was underlined by Hora (2006) and it now clarified that the lasers beams need to have a very high contrast ratio for direct drive. This is especially importance for compressing plasmas under NIF-conditions and was recently studied (Kyrala et al., 2005; Blue et al., 2005). The question is whether the emitted plasma beam was a block (piston, Esirkepov et al., 2004; Klimo & Limpouch, 2006) or whether this was a jet as known from self focusing as produced under similar wide focusing irradiation (Kasperczuk et al., 2006), in which case self-focusing could be concluded instead of plane plasma block generation.
7. ASPECTS FOR LASER FUSION FROM BLOCK (PISTON) IGNITION
The result (Eq. (4)) that plasma block (piston) represents a fully directed space charge neutral DT beam of more than 1010 Amps/cm2 with preferably 80 keV ion energy, provides a necessary condition for ignition of a fusion flame in uncompressed solid DT (Bobin, 1974). For Eq. (3) of the energy flux density of the block, it was estimated that the conditions even for the pessimistic values of Bobin (1974) should be reached (Hora, 2005b, Fig. 6). The question is whether sufficient thermonuclear energy is produced to ignite the DT and whether the piston has not a too low mass per area that it will blow apart before enough thermonuclear energy is generated. The question is how to correlate the results with that of ignition for 12 times solid-state density DT by the relativistic electron beam from a 10 PW-ps laser pulse (Nuckolls & Wood, 2002, see Sect. 4.3), and how a lower DT density may be possible.
Taking the case of Storm et al. (1988) for spark ignition (Hora et al., 1998), the evaluation arrived at the volume ignition of the plasma core for a temperature of 12 keV and 200 times the solid-state density, containing 430 kJ to ignite a fusion flame into the surrounding high density mantle at a value of 7 g/cm2, for producing a gain of 100 of fusion energy per input total laser energy. A mechanism for a sufficiently thick plasma block to avoid blowing apart the piston (Esirkepov et al., 2004), may be reached by using a spherical irradiation geometry (Badziak et al., 2005a, Fig. 6). This aim was first to improve the proton fast ignition scheme of Roth et al. (2005) by a factor of 1000, by using the plasma block generation, but the same geometry can be used also for generation of a thicker piston. When the first compressing DT layer is produced, that is, of 10 vacuum wavelength thicknesses (Badziak et al., 2005a, Fig. 6, red arrows), and when this moves spherically to the center, its low thermal energy will cause an expansion of the thickness of the layer. In order to keep or even to increase the density in the directed high ion energy of block motion, the concentric moving block layer increases the density while the block is getting thicker.
For generating the fusion flame (Bobin, 1974), it has to be evaluated how the interpenetration process of the energetic directed block ions into the cold DT fuel is improving the conditions on which the energy flux density, Eq. (3), is based. At least a reduction by a factor of 20 was shown (Hora, 1983), due to the interpenetration process. What more has to be included into these studies is the increase of the electron-ion collision (anomalous resistivity as clarified by a quantum modification), the inhibition of thermal conduction as explained by a double layer mechanism (Eliezer & Hora, 1989), the increase of the stopping length of the nuclear reaction products by collective effects, and a stochastic analysis of the interpenetration. All these processes are involved also in the studies of the ignition process in magnetically confined plasmas, the reason why is shown in Section 3, a mutual interest exists between ICF and research on neutral beam injection in JET, in order to improve the conditions and efficiency for designing ITER experiments. Indeed there is no question that a block (piston) ignition of uncompressed DT without any pre-compression would enormously simplify a fusion reactor for very low cost energy production (Hora et al., 2006).
While these ambitious aims for a direct laser ignition of uncompressed solid DT fuel need further extensive studies, it should be noted that the fast igniter scheme using 5 MeV proton of DT beams for a spark ignition of a thousand times solid pre-compressed DT sphere (Roth et al., 2005), will be strongly improved by the nonlinear force driven skin layer acceleration. Thousand time's higher ion current densities can be expected than by the preceding methods (Badziak et al., 2006).



