INTRODUCTION
During spring 2009, a novel H1N1 virus strain caused the first influenza pandemic of the 21st century. When the spring wave in the USA subsided, there was speculation about the early autumn return of pandemic virus and about what prevention and control measures could be put in place. There was keen interest in whether communities affected in spring would be spared if a second wave occurred in early autumn when schools reopened so that vaccine and other control measures could be appropriately targeted. In theory, herd immunity derived from a disease outbreak should be effective in reducing subsequent transmission. Based on previous research [Reference Barry, Viboud and Simonsen1], some theorized that geographical areas with high spring incidence would not be affected in early autumn, or if disease did occur, it would occur later in those areas than in areas that were not affected in spring [Reference Hartocollis and McNeill2]. We evaluated whether areas that had extensive influenza activity during the spring wave also had extensive influenza activity during the early autumn wave. This evaluation dealt with the relative effect of spring incidence by region, not with the spring wave impact on the overall autumn wave disease burden.
We examined this hypothesis using data from the U.S. Outpatient Influenza-Like Illness Surveillance Network (ILINet), a collaborative effort among the Centers for Disease Control and Prevention (CDC), local and state health departments, and primary healthcare providers. For the unit of spatial data aggregation, we used the U.S. Office of Management and Budget's core-based statistical area (CBSA), widely used for analysis of national statistics [3]. The CBSA designation includes both metropolitan (population >50 000) and micropolitan (population between 10 000 and 50 000) areas. Initially we developed an analysis strategy to evaluate changes in morbidity over time at the metropolitan and micropolitan levels. This strategy was then used to evaluate differences in morbidity in communities during the spring and early autumn time periods to determine whether areas affected by the H1N1 virus in spring were protected from illness in early autumn.
MATERIALS AND METHODS
ILINet description
The ILINet participant base includes over 3300 healthcare providers representing all 50 states, the District of Columbia, and the U.S. Virgin Islands. Enrolled providers use the internet or fax to send weekly reports to CDC. These reports give the total number of patients seen for any reason and, for each of a fixed set of age groups (0–4, 5–24, 25–49, 50–64, ⩾65 years), the number of those patients with influenza-like illness (ILI). Case definition for ILI is fever (patient temperature of 37·8 °C) with a cough and/or sore throat in the absence of a known cause other than influenza.
An ILINet data provider may be a physician practice, a health centre, or as large as a group of hospital emergency departments. These participating units reported total visit counts averaging from 10 to >10 000 per week. In 2009, the median total weekly reported visit count was nearly 650 000 and during the height of the pandemic exceeded 850 000. Thus, while coverage is national, data are somewhat heterogeneous and subject to large local fluctuations in representation. Until summer 2009, CDC conducted surveillance with ILINet data at the regional level because of the fluctuating, heterogeneous provider base. The nine-division census partition of states shown in Table 1 [4] was used for this purpose. Each of these divisions includes more than 300 data providers.
Table 1. Nine US census divisions used for ILINet baseline calculations

Determination of baseline ILI rates at the regional level
For each of the nine census divisions, the statistic used to determine excess ILI rates for a region was:
The observed ILI ratio is the current week's number of reported ILI cases divided by the total number of visits. The baseline ILI ratio is the proportion during weeks from the past three influenza seasons [October of one year to mid-May of the following year (weeks 40 to 20)] when virological data indicate that influenza activity is at a minimum [defined as weeks during which fewer than 10% of laboratory tests reported to the 80 U.S. World Health Organization (WHO) affiliated laboratories and 70 National Respiratory and Enteric Virus Surveillance System (NREVSS) laboratories for influenza had positive results for the region of interest]. Figure 1 illustrates the selection of baseline weeks at the national level. The dotted curve shows weekly proportions of laboratory influenza tests that gave positive results, and baseline weeks are those during influenza seasons for which the curve is below the thick 10% line. Weeks for the baseline calculation are chosen similarly for each region. Observed and baseline ratios are weighted by the state population for both regional and national aggregation to avoid using ratios skewed by unrepresentative participation among states. In view of the data heterogeneity, anomalies are presented as the number of standard deviations above the baseline mean without assuming a fixed probability distribution [5].

Fig. 1. Weekly counts (–––) of ILINet data providers shown with weekly ratios (- - -) of WHO/NREVSS positive laboratory tests for influenza. Baseline weeks are those, from weeks 40 of one year to week 20 of the next (shown within bold parentheses), for which <10% of influenza laboratory tests have positive results.
Determination of baseline ILI rates at the CBSA level
Since understanding of disease transmission patterns at the local level is important for effective public health response, analysis of ILINet data at finer spatial resolution was needed. We adjusted the regional estimation approach to calculate baseline rates at the CBSA level, including both metropolitan and micropolitan areas. A CBSA is an ‘area containing a substantial population nucleus, together with adjacent communities having a high degree of economic and social integration with that core’ [Reference Hartocollis and McNeill2]. Providers of recent ILINet data represent approximately 450 of the total 935 CBSAs in the nation.
The CBSA estimation approach adjusts for weekly variations in reporting by sentinel providers within a CBSA and also for the increase in the number of participating providers observed. The first step is to estimate provider-specific baseline ratios. These were estimated by either a trusted provider method or a provider-type method. Trusted providers were defined as those with substantial reporting over the past three influenza seasons, where the substantial reporting criterion was that the provider's data included non-zero ILI counts for at least 10 weeks during the previous year. This criterion was derived empirically, based on the mix of trusted and non-established providers and on the classification of some providers whose usual reporting was known. For each trusted provider, we estimated the baseline mean ILI ratio as the mean over the past three influenza seasons of weekly ratios of ILI counts to total visits for that provider, restricted to weeks when the ILI count was positive. Among the hundreds of data providers, zero reports could occur because a provider might consider ILI activity negligible or for reasons related to various reporting system operations. Inclusion of all weeks with zero reports yielded test statistics that were volatile even during baseline weeks.
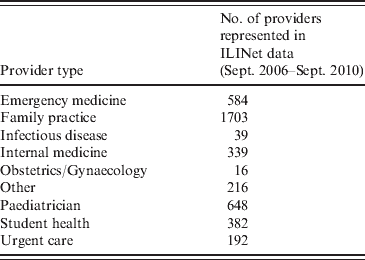
For providers whose ILI counts did not meet the 10-week criterion, we estimated the baseline mean ratio using the provider type. These types are listed in Table 2. Distinct differences between provider types were found in baseline ILI ratios, ranging from <1% for a miscellaneous category to 2·6% for paediatric providers. Therefore provider-type-specific baseline mean ratios were computed using data from all trusted providers of each type. We assigned to non-established providers, including many enrollees that began participating during the pandemic, the baseline mean ratios of their respective practice types.
Table 2. Distribution of ILINet provider types for 4119 data providers
For each week and each CBSA, the baseline ratio is a weighted sum of the baseline ratios for providers within that CBSA. Each provider ratio is weighted by the fraction of the current-week total visits from that provider in the CBSA in the current week. For example, assume that a CBSA has two participating data providers, a paediatric practice with a baseline ILI ratio of 0·025, and a community clinic with a baseline ratio of 0·010. In the current week, if the paediatric practice reports 1000 total cases and the community clinic reports 300 total cases, then the CBSA baseline ratio for this week is:
We calculated the CBSA baseline standard deviation by taking the standard deviation of the binomial distribution centred at the baseline ratio [Reference Lindgren6]. The CBSA baseline mean and standard deviation estimates were then combined with observed CBSA ILI ratios as in equation (1) to obtain the test statistic. This procedure adjusts for growth in the number of providers and for weekly reporting variability.
We tested the impact of test statistic modifications in several ways for both metropolitan and micropolitan CBSAs. We examined the number of CBSAs whose statistic was 2, 2·5, …, 5 standard deviations (s.d.) above the baseline value for endemic periods back to 2006 and found stable behaviour even for the smaller CBSAs with less than 200 total visits per week. In comparisons with/without the provider adjustment, the adjustment significantly reduced the number of CBSAs above each threshold during non-epidemic periods. Provider counts and baselines within individual CBSAs were examined to verify the effect of this adjustment. Statistical behaviour during known seasonal influenza epidemics and the spring 2009 H1N1 wave indicated sensitivity and timely increases at the tested thresholds. Figure 2 shows greyscale values of the provider-adjusted ILINet statistic at four stages of the 2009 pandemic.

Fig. 2. Greyscale maps of provider-adjusted ILINet statistic by core-based statistical area (CBSA) at four stages of the novel H1N1 pandemic.
Estimation of incidence in CBSAs for spring and early autumn influenza waves
We analysed 2009 CBSA-level ILINet data during the first emergence of novel H1N1 in spring (weeks 13–26, 29 March–4 July) and for the early autumn wave (weeks 31–39, 2 August–3 October). The analysis stopped weeks before the autumn wave peak because we were mainly interested in determining the effect of high spring incidence on the occurrence and relative timing of the onset of increased influenza activity during the early autumn wave of the pandemic. Figure 3 plots nationwide weekly ILI ratios during these intervals, with the spring and early autumn time periods indicated by solid shading in the curve. For the basic scenario, we classified each CBSA as ‘in exceedance’, a surrogate for high incidence, if its weekly ILI ratio was at least 3 s.d. above baseline for ⩾2 consecutive weeks. This requirement was imposed to reduce the effect of worried ill on ILINet data, for example because heightened media coverage could have caused more people to seek medical care with minor ILI symptoms.

Fig. 3. Plot of nationwide influenza-like illness (ILI) ratios illustrating weeks chosen to measure spring and autumn H1N1 incidence. Weeks 13–26 and 31–39 were initially chosen for spring and autumn, respectively, with endpoints of alternate intervals.
Regarding CBSA threshold exceedance during the spring weeks as group exposure, we computed the odds of early autumn exceedance with/without this exposure. Because the autumn and spring measurements are regarded not as matched observations but as exposure and outcome indicators, we used a conventional odds ratio rather than a matched-pairs design. The contingency table for the odds ratio calculation is given explicitly in Table 3.
Table 3. Contingency table formats for CBSA counts

CBSA, Core-based statistical area.
Pooling the test statistics for represented CBSAs, we used the following formula to calculate the odds of ILI levels in early autumn being in exceedance:
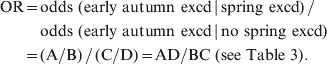 $$\eqalign{ \hskip-2pt {\rm OR} \equals \tab {\rm odds}{\rm \ \lpar early \ autumn\ excd} \, {\rm\vert \, spring\ excd\rpar \, \sol} \ \cr \tab {\rm odds\ \lpar early \ autumn\ excd \, \vert \, no\ spring\ excd\rpar } \cr \equals \tab \lpar {\rm A}\sol {\rm B}\rpar \, \sol \, \lpar {\rm C}\sol {\rm D}\rpar \equals {\rm AD}\sol {\rm BC \ \lpar see\ Table\ 3\rpar }{\rm.} \cr} \hskip-1pt$$
$$\eqalign{ \hskip-2pt {\rm OR} \equals \tab {\rm odds}{\rm \ \lpar early \ autumn\ excd} \, {\rm\vert \, spring\ excd\rpar \, \sol} \ \cr \tab {\rm odds\ \lpar early \ autumn\ excd \, \vert \, no\ spring\ excd\rpar } \cr \equals \tab \lpar {\rm A}\sol {\rm B}\rpar \, \sol \, \lpar {\rm C}\sol {\rm D}\rpar \equals {\rm AD}\sol {\rm BC \ \lpar see\ Table\ 3\rpar }{\rm.} \cr} \hskip-1pt$$where OR = odds ratio, and excd = exceedance.
We calculated 95% confidence intervals for each odds ratio using the Woolf method [Reference Woolf7] for computing the odds ratio standard deviation. A protective effect in early autumn from spring exceedance would be indicated by a statistically significant odds ratio <1.
Sensitivity analysis: alternate scenarios
To check the robustness of this calculation, we varied both the definition of exceedance and the weeks chosen for comparison for the spring and early autumn seasons. The exceedance definition was varied to comprise 12 combinations: 1, 2, 3, and 4 s.d. above the mean applied at minimum consecutive intervals of 1, 2, and 3 weeks. Each combination was applied to the following spring/early autumn interval definitions:
Spring weeks 13–26, early autumn weeks 31–39 (used for Fig. 4),
Spring weeks 17–26, early autumn weeks 31–36,
Spring weeks 17–26, early autumn weeks 31–39,
Spring weeks 17–26, early autumn weeks 31–42.

Fig. 4. Scatter plot of maximum ILINet statistic during spring (x-axis) and autumn (y-axis) 2009 intervals for 433 core-based statistical areas (CBSAs), with threshold lines indicating 3 s.d. above the expected influenza-like illness (ILI) ratio. The statistic is the normalized difference of the observed and baseline ILI ratios.
We chose the three alternate sets of intervals to avoid the residual effects of the seasonal influenza epidemics and to include earlier and later effects of the widespread early autumn H1N1 outbreak. Figure 4 allows visualization of the odds ratio cell counts for the scenario of single-week, 3 s.d. exceedance with the original spring/early autumn intervals.
RESULTS
Descriptive data statistics
Approximately 60% of participating providers send data every week during the influenza season, some intermittently, and the provider base generally grows with occasional dropouts. The solid curve in Figure 1 shows weekly variation of the number of participating providers for >4 years beginning 2 October 2006. Note the seasonal participation, brief holiday drop-offs, and sustained participation resulting from the pandemic. For the last year of this interval, the median weekly reported visit count was just above 649 500 (range ∼431 000 to >864 000).
Evaluation of CBSA-based odds ratios for spring and early autumn wave analysis
Our calculated odds ratios provided quantitative measure of the effect of spring exceedance on early autumn exceedance. For the exceedance definition given in the previous section – an ILI ratio ⩾3 s.d. above its baseline ratio for 2 consecutive weeks – the cell counts for exceedance combinations of (a) neither spring nor early autumn interval, (b) early autumn only, (c) spring only, and (d) both spring and early autumn, were 282, 17, 101, and 33, respectively. The resultant odds ratio was
The 95% confidence interval for this calculation is 2·89–10·15. A protective effect from spring exceedance would be indicated by an odds ratio <1.
Figure 5 shows CBSAs whose ILI ratios satisfied this exceedance requirement for both spring and early autumn intervals, for spring weeks only, for early autumn weeks only, and for neither interval. Note that localities affected in spring are mainly urban metropolitan areas.

Fig. 5. Colour-coded map showing core-based statistical areas (CBSAs) in 50 US states in which the influenza-like illness (ILI) ratios met the exceedance criterion of 3 s.d. above baseline for two consecutive weeks during the designated spring and autumn intervals.
Alternate scenario findings
From applying the 12 exceedance definitions to the four sets of intervals, all resulting 48 odds ratios were >1, with a median 4·36 and a minimum 1·85. Figure 6 plots these ratios on a log scale with confidence intervals.

Fig. 6. Sensitivity analysis: Spring/autumn odds ratios with confidence limits for variations in statistic threshold, consecutive week limits, and chosen spring/autumn intervals. Table 4 contains additional details.
Confidence limits <1 were found for only five of the 48 alternate scenarios, and these five all had the more stringent exceedance requirement of 3 consecutive weeks with an ILI ratio above baseline. Full details including odds ratio cell counts are shown in Table 4.
Table 4. Details of odds ratio findings for 48 exceedance scenarios

OR, Odds ratio, CI, confidence interval; excd, exceedance; s.d., standard deviation.
Odds ratio visualization
The main scenario changed to exceedance based on single-week statistics allows graphic presentation of the odds ratio calculation. For this purpose, Figure 4 shows a scatter plot of the maximum provider-adjusted statistic for the 433 CBSAs with providers that supplied data in both spring and early autumn intervals. Each CBSA is represented by one marker, whose x value is the statistic maximum during 2009 spring weeks, and whose y value is the statistic maximum over early autumn weeks. The lower left quadrant markers indicate 214 CBSAs whose ILI ratios were not in exceedance in either spring or early early autumn interval. Markers in the lower right quadrant indicate the 25 CBSAs that experienced ⩾1 week in spring when ILI ratios were in exceedance, but none in early autumn. The upper left quadrant markers show the 137 CBSAs with ⩾1 week of exceedance in early autumn but none in spring. The upper right quadrant shows the 57 CBSAs that had ⩾1 week of elevated ILI ratios during both spring and early autumn. If a high spring incidence, as measured by elevated ratios for ILI-related visits, did indeed impart a protective effect, we would expect to see negative correlation between spring and early autumn visit ratios. However, a line fitted to the plotted points has a positive slope, with a Pearson correlation coefficient of 0·31 (P < 0·0001) between the spring and early autumn statistics. From scenario 7 of Table 4a, the odds ratio corresponding to this single-week scenario is 3·56, as opposed to the main-scenario odds ratio (scenario 8, Table 4a) of 5·42, and both scenarios have a lower confidence limit well above 1.
Effect of threshold on odds ratios
An additional sensitivity analysis held fixed the 2 consecutive-week exceedance definition in the original spring and early autumn intervals, and we computed odds ratios for thresholds ranging from 2 to 15 s.d. to examine the effect of the threshold on odds ratios. As seen in Figure 7, the odds ratio values increased monotonically with the threshold and remained statistically significant up to a threshold of 13. For higher thresholds, significance is lost because the Table 3 cell counts A and B for spring exceedance become too small, increasing the odds ratio variance.

Fig. 7. Odds ratios with confidence limits for statistic thresholds from 2 to 15 s.d. above baseline for at least 2 consecutive weeks. UCL, Upper confidence limit; LCL, lower confidence limit.
Sensitivity analysis for provider type
We conducted another sensitivity analysis to address the wide variation in provider type among CBSAs (Table 2). For more than half of the CBSAs, the data are obtained from only 1–2 providers. The concern was that some of these would have artificially reduced ILINet statistics during the H1N1 pandemic if they lacked representation of younger patients. For a more restrictive analysis, we considered only CBSAs whose data included providers classified as either ‘paediatrician’ or ‘student health’, and the 433 CBSAs supplying data in both seasons dropped to 237. For the exceedances ⩾3 s.d. for ⩾2 consecutive weeks, the Figure 4 cell counts became 131 for exceedance in neither spring nor early autumn, 12 for spring-only exceedance, 71 for early autumn only, and 23 for exceedance in both seasons. The odds ratio remained significant at 3·54 (95% CI 1·66–7·53). For this reduced number of CBSAs, we also repeated the odds ratio calculations for the rest of the 48 exceedance definitions. Odds ratios for all of these other combinations remained >1 with a median of 2·55, but more of the lower confidence limits for the stricter exceedance criteria fell to <1.
Effect of CBSA size and population density
We investigated the effect of CBSA size on this study by inspecting the week-by-week Pearson correlation of the test statistic with population and density across all CBSAs providing data. For this purpose the data interval was widened to January 2008 to February 2010. For the substantial 2007–2008 H3N2 epidemic, there was positive correlation with population size and density, although the weekly correlation coefficients never exceeded 0·2. Following that event, there was prolonged slight but consistently negative correlation of the test statistic with both population and density. We again found mild positive correlation for the milder 2009 H3 influenza season and then the 2009 spring wave of H1N1, but none for the early autumn wave.
DISCUSSION
We developed a method to monitor changes in ILI activity at the CBSA level. We used this method to examine the likelihood of high ILI activity in early autumn given high ILI activity in spring. Our results demonstrate that an outbreak of novel H1N1 in spring did not protect against the onset of an autumn wave at the CBSA level. In fact, a spring outbreak increased rather than decreased the probability of an early autumn outbreak. This finding was sustained in multiple sensitivity analyses. Altering the definitions of an exceedance and the chosen study weeks had only minor effects on these findings.
The association between local incidence levels during the two pandemic waves depends on multiple factors, including herd immunity, population dynamics, age structure, relationship to other population centres, and antigenic drift of the novel virus. Recent works by other authors have addressed these factors in context of 2009 pandemic transmission [Reference Kana8–Reference Katriel and Stone10]. For the current study, the CBSA is a plausible unit for studying the aggregation of these effects because of its definition as ‘a substantial population nucleus, together with adjacent communities having a high degree of economic and social integration’. Thus, the residence and workplace of a susceptible individual are likely to be in the same CBSA as those of most of his/her contacts. However, it is possible a given CBSA was too small (unaffected by the spring wave because of size) or too large (multiple subpopulations with varied experience) for group-level analysis.
The cross-wave protection hypothesis that motivated this study is natural in view of the widely accepted finding that naturally acquired immunity to H1N1 variants often lasts for more than 20 years [Reference Couch and Kasel11]. Authors have theorized [Reference Andreasen, Viboud and Simonsen12] and, more recently, investigated this hypothesis using 1918 pandemic data [Reference Barry, Viboud and Simonsen1]. A logical question is whether an initial epidemic wave affects enough of the population to provide some protection against subsequent waves or whether it only introduces a new endemic strain that can later reach more of the population when conditions of climate and population mixing are more conducive to transmission. An important feature of the investigation by Barry et al. [Reference Barry, Viboud and Simonsen1] was the substantial 11·8% overall attack rate among the closed populations whose first-wave data were examined. Data from closed populations with known denominators were not available for the current study, so attack rate estimates were difficult to quantify. Nevertheless, evidence of an overall relatively weak first wave in 2009 is ample: only ∼5% of the total 56 million cases had occurred up to July 2009 [Reference Shrestha13]. Another US study [Reference Brammer14] found only 1 week from 28 March until 22 August (weeks 12–33) during which the ILI percentage exceeded baseline levels nationally. Other authors have reported that the secondary attack rate and the effective reproductive number of the pandemic were low relative to past large epidemics (e.g. [Reference Jhung15]). Furthermore, studies both within [Reference Brammer14] and outside [Reference Correia, Queirós and Dias16, Reference Petrovic17] the USA cite the focal nature of the first wave as one of its defining characteristics; a study from Serbia [Reference Petrovic17] notes that ‘the most significant features of this epidemic [were] the rapid establishment … and abrupt cessation of community transmission’. Thus, many CBSA-level spring attack rates were probably small, and so our findings support a competing hypothesis that spring outbreaks were insufficient to provide protection at the CBSA level in the autumn. By this hypothesis, because a novel H1N1 virus was introduced late relative to the usual influenza season, it did not infect to population exhaustion and could persist until the next opportune outbreak season (early autumn) to resume transmission. Hence, the combination of susceptible individuals returning from vacation and climatic conditions favourable to virus-shedding may have provided a renewed spreading opportunity for the endemic strain introduced in spring. The effects of climatic factors on transmissibility have been quantified in detail [Reference Hanley and Borup18].
Study limitations include ILINet data quality issues which restricted the analysis methodology. Data providers gave ILI counts for each age group, but the total visit counts are not age-stratified, so only all-age ILI ratios may be directly calculated. The multiple types of care providers (Table 2) contributing ILINet data suggest heterogeneity in the covered patient base across CBSAs. This heterogeneity gives a broad basis of information but complicates comparisons between CBSAs with substantially different provider types. The sections above describe adjustments for this heterogeneity both in the test statistic and in the subsequent analysis. Effectiveness of these adjustments is difficult to quantify without years of labelled historical data, but anecdotal verification and the stability of the adjusted ILINet statistic during baseline weeks have been positive.
Although adjustments were made to baselines based on provider type, analysis of variance investigations revealed regional differences in rates within provider types, particularly among Emergency Departments and Urgent Care centres, that may have led to assignment of incorrect baseline levels and misclassification of CBSAs both for the early autumn and spring exceedance. However, we have no reason to suspect systematic estimation bias across time periods of interest. Therefore, we believe that misclassification had little effect on the odds ratio. Similarly, disregarding weeks of zero ILI case reports may have caused loss of sensitivity, although our testing indicated oversensitivity during non-epidemic weeks when these weeks were included, and our simple modification gave plausible results using historical data.
The study methodology is dichotomous in that the odds ratio requires classification of excessive or non-excessive ILI ratios relative to the computed CBSA baseline. As discussed above, we sought to avoid artifacts of this classification by repeating the analysis with several definitions of ILI ratio exceedance, our surrogate for high incidence. A more general logistic, hierarchical modelling approach is under development. Any such approach should account for the evolving set of data providers, the substantial variation among ILI ratios both within and between provider types, and the heterogeneity among CBSAs.
The second wave analysis was restricted to the early autumn cases with the idea that similar methodology might be used to aid public health decision-making in a future anticipated multi-wave scenario. This decision has both positive and negative implications for the validity of the findings. Negative effects are that early stages of an epidemic are associated with high variability [Reference Nishiura19], so restriction to the first 9 weeks (weeks 6–11 in sensitivity analysis) of the lengthy autumn wave may have been insufficient to avoid net odds ratio bias in the findings among the hundreds of CBSAs in the study. On the positive side, the restriction probably reduced odds ratio bias by improving the specificity of the ILI diagnoses. The positive predictive value (PPV) of symptoms approximating ILINet criteria for influenza has been reported at 79–87% in studies during influenza seasons [Reference Monto20, Reference Boivin21]. While the symptom PPV is reduced before the peak period of many seasonal epidemics [Reference Smieszek22], it was plausibly higher in the early weeks of the 2009 autumn wave, weeks in this year when ILINet reporting is usually low and before competing febrile respiratory infections are prevalent.
An intended objective of the current study and of similar analytical findings is to inform decision-makers responsible for preparedness and vaccine programme planning activities. Any such planning should also consider effects of external commuting patterns that may cause a highly variable degree of inter-area transmission among CBSAs. The importance of such factors has been modelled and documented [Reference Grais, Ellis and Glass23, Reference Brownstein, Wolfe and Mandl24]. However, these factors probably do not contradict our findings that high spring incidence was not generally protective against illness in early autumn at the community level.
In summary we developed an approach for assessing and monitoring influenza activity at the local level and used the method to determine that elevated influenza activity during the first wave of the 2009 pandemic was not generally protective of localities from subsequent disease in early autumn nor did it delay the onset of the autumn outbreak. The approach seeks epidemiological inference using a routinely collected dataset lacking individual patient detail. Both metropolitan and micropolitan areas are represented among CBSAs [Reference Hartocollis and McNeill2], and while it was not feasible to investigate contact patterns or vaccination rates in each CBSA, it is reasonable to expect some cancellation of these differences among hundreds of CBSAs. Richer analyses with patient-level data are required to address many important questions, but broad statements such as the claim of protection from an earlier wave are difficult to quantify on a population level by clinically detailed studies, and this study is an attempt at such quantification. The study approach, while not sufficiently detailed to directly measure herd immunity, may serve as an inexpensive, readily available tool to help assess the likelihood of localized subsequent wave disease occurrence using high-volume, pre-diagnostic data.
ACKNOWLEDGEMENTS
The authors are grateful to internal reviewers Dr Carolyn Bridges and Dr Jay Wenger and to two anonymous external reviewers for their careful attention and helpful suggestions and advice.
DECLARATION OF INTEREST
None.













