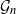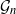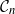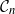1. Introduction
Gaussian graphical models (GGMs) [Reference Dempster10, Reference Lauritzen20] have become a standard technique to represent the conditional independence structure of a set of random variables. Given an undirected graph
![]() $G = (V, E)$
, the set of vertices
$G = (V, E)$
, the set of vertices
![]() $V=\{1,\ldots,n\}$
represents the random variables while the set of edges
$V=\{1,\ldots,n\}$
represents the random variables while the set of edges
![]() $E \subseteq \{(i,j) \in V \times V\colon i < j\}$
represents conditional dependencies between the variables. In the Bayesian literature, a latent graph G is often inferred by first specifying a prior p(G) on the space of graphs followed by a prior on the precision matrix K conditional on the graph,
$E \subseteq \{(i,j) \in V \times V\colon i < j\}$
represents conditional dependencies between the variables. In the Bayesian literature, a latent graph G is often inferred by first specifying a prior p(G) on the space of graphs followed by a prior on the precision matrix K conditional on the graph,
![]() $p(K \mid G)$
. Then posterior inference is performed through sampling algorithms such as Markov chain Monte Carlo (MCMC) (e.g. [Reference Giudici and Green15], [Reference Jones, Carvalho, Dobra, Hans, Carter and West18]) or sequential Monte Carlo (SMC) [Reference Tan, Jasra, De Iorio and Ebbels34, Reference Van den Boom, Jasra, De Iorio, Beskos and Eriksson36]. One of the main challenges in graph inference is that the number of graphs grows exponentially with the number of vertices since the size of the space
$p(K \mid G)$
. Then posterior inference is performed through sampling algorithms such as Markov chain Monte Carlo (MCMC) (e.g. [Reference Giudici and Green15], [Reference Jones, Carvalho, Dobra, Hans, Carter and West18]) or sequential Monte Carlo (SMC) [Reference Tan, Jasra, De Iorio and Ebbels34, Reference Van den Boom, Jasra, De Iorio, Beskos and Eriksson36]. One of the main challenges in graph inference is that the number of graphs grows exponentially with the number of vertices since the size of the space
![]() $\mathcal{G}_n$
of all graphs with n vertices is
$\mathcal{G}_n$
of all graphs with n vertices is
![]() $2^{n (n -1) / 2}$
.
$2^{n (n -1) / 2}$
.
There are two main lines of research addressing the computational difficulties associated with the size of graph space: (i) devising efficient sampling algorithms and (ii) considering particular subsets of
![]() $\mathcal{G}_n$
with desirable properties. This work explores novel subsets in light of this second direction. A particularly popular restriction of
$\mathcal{G}_n$
with desirable properties. This work explores novel subsets in light of this second direction. A particularly popular restriction of
![]() $\mathcal{G}_n$
consists of focusing on the set of decomposable graphs as it allows for exact posterior computation under the conjugate hyper-inverse Wishart prior; see e.g. [Reference Giudici14], [Reference Giudici and Green15], [Reference Green and Thomas16], [Reference Lauritzen20], [Reference Scott and Carvalho31], and [Reference Wang and Carvalho39]. However, the decomposability assumption is often restrictive in applications: suppose that the ‘true’ graph is non-decomposable. Niu et al. [Reference Niu, Pati and Mallick26] prove that as the number of observations goes to infinity, the posterior distribution concentrates at the minimal triangulations of the true graph. These triangulations can present
$\mathcal{G}_n$
consists of focusing on the set of decomposable graphs as it allows for exact posterior computation under the conjugate hyper-inverse Wishart prior; see e.g. [Reference Giudici14], [Reference Giudici and Green15], [Reference Green and Thomas16], [Reference Lauritzen20], [Reference Scott and Carvalho31], and [Reference Wang and Carvalho39]. However, the decomposability assumption is often restrictive in applications: suppose that the ‘true’ graph is non-decomposable. Niu et al. [Reference Niu, Pati and Mallick26] prove that as the number of observations goes to infinity, the posterior distribution concentrates at the minimal triangulations of the true graph. These triangulations can present
![]() ${\mathrm{O}}(n \log n)$
spurious edges [Reference Chung and Mumford8].
${\mathrm{O}}(n \log n)$
spurious edges [Reference Chung and Mumford8].
As an alternative to decomposable graphs, recent research effort has been devoted to considering the set of spanning trees
![]() $\mathcal{T}_n$
on the complete graph (i.e. the graph containing all possible edges), which is necessarily a subset of decomposable graphs as trees do not contain cycles. Højsgaard et al. [Reference Højsgaard, Edwards and Lauritzen17] propose a maximum a posteriori estimator of the latent spanning tree based on Kruskal’s [Reference Kruskal19] algorithm. Schwaller et al. [Reference Schwaller, Robin and Stumpf30] are able to derive the exact posterior distribution of each tree in
$\mathcal{T}_n$
on the complete graph (i.e. the graph containing all possible edges), which is necessarily a subset of decomposable graphs as trees do not contain cycles. Højsgaard et al. [Reference Højsgaard, Edwards and Lauritzen17] propose a maximum a posteriori estimator of the latent spanning tree based on Kruskal’s [Reference Kruskal19] algorithm. Schwaller et al. [Reference Schwaller, Robin and Stumpf30] are able to derive the exact posterior distribution of each tree in
![]() $\mathcal{T}_n$
given a set of observations by applying Kirchoff’s matrix tree theorem [Reference Chaiken and Kleitman7], while Duan and Dunson [Reference Duan and Dunson13] propose a Bayesian model for spanning trees where the likelihood function is built on a generative graph process and leads to an efficient Gibbs sampling algorithm. Although spanning trees provide computational advantages compared to considering all graphs, they only allow inference of the ‘backbone’ of the graph [Reference Duan and Dunson13], i.e. the minimum spanning tree of the data generating graph, at the cost of losing information about its global structures.
$\mathcal{T}_n$
given a set of observations by applying Kirchoff’s matrix tree theorem [Reference Chaiken and Kleitman7], while Duan and Dunson [Reference Duan and Dunson13] propose a Bayesian model for spanning trees where the likelihood function is built on a generative graph process and leads to an efficient Gibbs sampling algorithm. Although spanning trees provide computational advantages compared to considering all graphs, they only allow inference of the ‘backbone’ of the graph [Reference Duan and Dunson13], i.e. the minimum spanning tree of the data generating graph, at the cost of losing information about its global structures.
In this paper we investigate larger subsets of
![]() $\mathcal{G}_n$
arising from an algebraic perspective on graphs with the cycle space as the main concrete example. First, note that the set
$\mathcal{G}_n$
arising from an algebraic perspective on graphs with the cycle space as the main concrete example. First, note that the set
![]() $\mathcal{G}_n$
together with the edgewise modulo two addition
$\mathcal{G}_n$
together with the edgewise modulo two addition
![]() $\oplus$
and the trivial multiplication (both operations are defined in Section 2.3) forms a vector space on the finite field
$\oplus$
and the trivial multiplication (both operations are defined in Section 2.3) forms a vector space on the finite field
![]() $\mathbb{Z}_2$
, where the set of all edges in the complete graph forms the standard basis of
$\mathbb{Z}_2$
, where the set of all edges in the complete graph forms the standard basis of
![]() $\mathcal{G}_n$
. Definitions and preliminary results about the graph vector space are deferred to Section 2.
$\mathcal{G}_n$
. Definitions and preliminary results about the graph vector space are deferred to Section 2.
Our work builds on the fact that alternative bases for
![]() $\mathcal{G}_n$
exist. In particular, we consider the example of the space spanned by linear combinations of cycles on V which forms the cycle space
$\mathcal{G}_n$
exist. In particular, we consider the example of the space spanned by linear combinations of cycles on V which forms the cycle space
![]() $\mathcal{C}_n$
. The cycle space is a proper subspace of
$\mathcal{C}_n$
. The cycle space is a proper subspace of
![]() $\mathcal{G}_n$
which can be spanned using bases consisting of cycles [Reference Wallis38]. We investigate the theoretical properties of this space and of the prior distribution on graphs when the prior is specified through a prior on cycles, instead of the common practice of specifying a prior on the edges, as well as the implications for statistical inference of such a prior. We show that the cycle space
$\mathcal{G}_n$
which can be spanned using bases consisting of cycles [Reference Wallis38]. We investigate the theoretical properties of this space and of the prior distribution on graphs when the prior is specified through a prior on cycles, instead of the common practice of specifying a prior on the edges, as well as the implications for statistical inference of such a prior. We show that the cycle space
![]() $\mathcal{C}_n$
is a substantially smaller set than
$\mathcal{C}_n$
is a substantially smaller set than
![]() $\mathcal{G}_n$
, though this does not notably affect posterior inference such as edge inclusion probabilities in the concluding application.
$\mathcal{G}_n$
, though this does not notably affect posterior inference such as edge inclusion probabilities in the concluding application.
The paper is structured as follows. Section 2 reviews graphical modelling concepts, how
![]() $\mathcal{G}_n$
constitutes a vector space, cycle basis theory, and compares the cycle space with the set of decomposable graphs. Section 3 analyses the cycle basis prior. Section 4 contains simulation studies. In Section 5 we apply the proposed algorithm to gene expression data. Section 6 concludes the paper and discusses potential future directions. All proofs can be found in the Supplementary Material.
$\mathcal{G}_n$
constitutes a vector space, cycle basis theory, and compares the cycle space with the set of decomposable graphs. Section 3 analyses the cycle basis prior. Section 4 contains simulation studies. In Section 5 we apply the proposed algorithm to gene expression data. Section 6 concludes the paper and discusses potential future directions. All proofs can be found in the Supplementary Material.
2. Background
2.1. Graph preliminaries
We consider undirected graphs with no loops and no multi-edges, also called simple graphs. A path
![]() $\gamma_{\alpha,\beta}$
between two vertices
$\gamma_{\alpha,\beta}$
between two vertices
![]() $\alpha,\beta\in V$
is a sequence of edges
$\alpha,\beta\in V$
is a sequence of edges
![]() $(e_1, \ldots, e_m)$
such that
$(e_1, \ldots, e_m)$
such that
![]() $v_1 = \alpha$
,
$v_1 = \alpha$
,
![]() $v_{m+1} = \beta$
, and
$v_{m+1} = \beta$
, and
![]() $e_i = (v_i, v_{i+1})$
for all
$e_i = (v_i, v_{i+1})$
for all
![]() $i \in \{1, \ldots, m\}$
, where every vertex in the vertex sequence
$i \in \{1, \ldots, m\}$
, where every vertex in the vertex sequence
![]() $(v_1, \ldots, v_{m+1})$
is distinct. A circuit is a sequence of edges
$(v_1, \ldots, v_{m+1})$
is distinct. A circuit is a sequence of edges
![]() $(e_1, \ldots, e_m)$
where
$(e_1, \ldots, e_m)$
where
![]() $v_1 = v_{m+1}$
. A cycle is a circuit where every vertex in
$v_1 = v_{m+1}$
. A cycle is a circuit where every vertex in
![]() $(v_1, \ldots, v_m)$
is distinct. A graph is connected when a path
$(v_1, \ldots, v_m)$
is distinct. A graph is connected when a path
![]() $\gamma_{\alpha,\beta}$
exists for all
$\gamma_{\alpha,\beta}$
exists for all
![]() $\alpha, \beta \in V$
. A graph is complete if it contains all possible edges, i.e.
$\alpha, \beta \in V$
. A graph is complete if it contains all possible edges, i.e.
![]() $E = \{(i,j) \in V \times V\colon i < j\}$
. A tree is a graph where there is exactly one path between any pair of vertices. A spanning tree of a connected graph
$E = \{(i,j) \in V \times V\colon i < j\}$
. A tree is a graph where there is exactly one path between any pair of vertices. A spanning tree of a connected graph
![]() $G = (V, E)$
is a tree with vertex set V and an edge set which is a subset of E. A star tree T on the vertices
$G = (V, E)$
is a tree with vertex set V and an edge set which is a subset of E. A star tree T on the vertices
![]() $\{v_0, \ldots, v_{n-1}\}$
is the spanning tree whose edges are
$\{v_0, \ldots, v_{n-1}\}$
is the spanning tree whose edges are
![]() $(v_0, v_i)$
for
$(v_0, v_i)$
for
![]() $i = 1, \ldots, n-1$
. In this case,
$i = 1, \ldots, n-1$
. In this case,
![]() $v_0$
is the root of T. The degree of a vertex v is the number of edges incident to v.
$v_0$
is the root of T. The degree of a vertex v is the number of edges incident to v.
2.2. Bayesian inference of GGMs
In a GGM, a graph
![]() $G=(V,E)$
on n vertices models the zeros in the precision matrix K of the Gaussian distribution
$G=(V,E)$
on n vertices models the zeros in the precision matrix K of the Gaussian distribution
![]() $N(0, K^{-1})$
on the independent rows of the
$N(0, K^{-1})$
on the independent rows of the
![]() $N\times n$
data matrix X:
$N\times n$
data matrix X:
where
![]() $U = X^{{\top}} X$
and
$U = X^{{\top}} X$
and
![]() $\langle A, B\rangle = \mathrm{tr}(A^{{\top}} B)$
. Specifically,
$\langle A, B\rangle = \mathrm{tr}(A^{{\top}} B)$
. Specifically,
![]() $K_{ij}=0$
if
$K_{ij}=0$
if
![]() $(i,j) \notin E$
. For Bayesian inference, Dawid and Lauritzen [Reference Dawid and Lauritzen9] introduced the hyper-inverse Wishart prior, which is a conjugate prior
$(i,j) \notin E$
. For Bayesian inference, Dawid and Lauritzen [Reference Dawid and Lauritzen9] introduced the hyper-inverse Wishart prior, which is a conjugate prior
![]() $p(K \mid G)$
for decomposable graphs G. Giudici [Reference Giudici14] and Roverato [Reference Roverato28] generalise this idea to non-decomposable graphs, proposing the G-Wishart distribution
$p(K \mid G)$
for decomposable graphs G. Giudici [Reference Giudici14] and Roverato [Reference Roverato28] generalise this idea to non-decomposable graphs, proposing the G-Wishart distribution
![]() $W_G(\delta, D)$
with degrees of freedom
$W_G(\delta, D)$
with degrees of freedom
![]() $\delta>2$
and rate matrix D which has density
$\delta>2$
and rate matrix D which has density
with respect to the Lebesgue measure on the set of positive definite matrices with zeros imposed by G. Here,
![]() $I_G(\delta, D)$
is a normalising constant.
$I_G(\delta, D)$
is a normalising constant.
Combining the prior in (2) and the likelihood (1),
![]() $K\mid G,X \sim W_G (\delta + N, D + U)$
due to conjugacy. The likelihood for G with K marginalised out follows as (e.g. [Reference Atay-Kayis and Massam3])
$K\mid G,X \sim W_G (\delta + N, D + U)$
due to conjugacy. The likelihood for G with K marginalised out follows as (e.g. [Reference Atay-Kayis and Massam3])
Unfortunately, computing
![]() $I_G(\delta, D)$
for a general graph G, despite a recently derived recursive expression [Reference Uhler, Lenkoski and Richards35], is intractable. Monte Carlo [Reference Atay-Kayis and Massam3] and Laplace [Reference Lenkoski and Dobra21] approximations have thus been suggested, along with methods that avoid the normalising constant computation entirely [Reference Wang and Li40] using the exchange algorithm of Murray et al. [Reference Murray, Ghahramani and MacKay25]. Notably,
$I_G(\delta, D)$
for a general graph G, despite a recently derived recursive expression [Reference Uhler, Lenkoski and Richards35], is intractable. Monte Carlo [Reference Atay-Kayis and Massam3] and Laplace [Reference Lenkoski and Dobra21] approximations have thus been suggested, along with methods that avoid the normalising constant computation entirely [Reference Wang and Li40] using the exchange algorithm of Murray et al. [Reference Murray, Ghahramani and MacKay25]. Notably,
![]() $I_G(\delta, D)$
is computationally tractable for decomposable G, motivating the common restriction of the space of graphs
$I_G(\delta, D)$
is computationally tractable for decomposable G, motivating the common restriction of the space of graphs
![]() $\mathcal{G}_n$
to decomposable graphs.
$\mathcal{G}_n$
to decomposable graphs.
Having the marginal likelihood of the observations given a general graph, Bayesian inference is performed by defining a prior p(G) on
![]() $\mathcal{G}_n$
. Such prior distributions are usually constructed through the specification of edge inclusion probabilities. In the next section we define a prior distribution over graph space based on more complex substructures than edges.
$\mathcal{G}_n$
. Such prior distributions are usually constructed through the specification of edge inclusion probabilities. In the next section we define a prior distribution over graph space based on more complex substructures than edges.
2.3.
 $\mathcal{G}_{\boldsymbol{n}}$
as vector space and the cycle space
$\mathcal{G}_{\boldsymbol{n}}$
as vector space and the cycle space
The set
![]() $\mathcal{G}_n$
of all graphs with n vertices is part of a vector space over the finite field
$\mathcal{G}_n$
of all graphs with n vertices is part of a vector space over the finite field
![]() $\mathbb{Z}_2$
. Here,
$\mathbb{Z}_2$
. Here,
![]() $\mathbb{Z}_2$
is a field on the set
$\mathbb{Z}_2$
is a field on the set
![]() $\{0, 1\}$
, where addition is the modulo 2 addition (i.e.
$\{0, 1\}$
, where addition is the modulo 2 addition (i.e.
![]() $0 + 0 = 0$
,
$0 + 0 = 0$
,
![]() $1 + 0 = 0 + 1 = 1$
, and
$1 + 0 = 0 + 1 = 1$
, and
![]() $1 + 1 = 0$
) while multiplication is trivial (i.e.
$1 + 1 = 0$
) while multiplication is trivial (i.e.
![]() $0 \times x = 0$
and
$0 \times x = 0$
and
![]() $1 \times x = x$
for any
$1 \times x = x$
for any
![]() $x \in \{0, 1\}$
). The vector space is the triple
$x \in \{0, 1\}$
). The vector space is the triple
![]() $(\mathcal{G}_n, \oplus, \otimes)$
, where
$(\mathcal{G}_n, \oplus, \otimes)$
, where
![]() $\oplus$
is the modulo 2 addition of the edges and
$\oplus$
is the modulo 2 addition of the edges and
![]() $\otimes$
is the (trivial) multiplication such that
$\otimes$
is the (trivial) multiplication such that
![]() $0 \otimes G$
is the graph with no edges, and
$0 \otimes G$
is the graph with no edges, and
![]() $1 \otimes G = G$
. Note that the set of all edges in the complete graph forms one basis of this vector space, which we call the standard basis. Alternative bases exist for the same vector space, which can (i) be used as building components of a graph (in a similar way as with edges) and (ii) induce priors p(G) through the specification of a distribution on the elements of the basis. For illustration, Figure 1 considers three different bases of
$1 \otimes G = G$
. Note that the set of all edges in the complete graph forms one basis of this vector space, which we call the standard basis. Alternative bases exist for the same vector space, which can (i) be used as building components of a graph (in a similar way as with edges) and (ii) induce priors p(G) through the specification of a distribution on the elements of the basis. For illustration, Figure 1 considers three different bases of
![]() $\mathcal{G}_n$
with
$\mathcal{G}_n$
with
![]() $n=4$
vertices.
$n=4$
vertices.

Figure 1. The table (a) shows three different bases of the graph space
![]() $\mathcal{G}_n$
with
$\mathcal{G}_n$
with
![]() $n=4$
vertices. Consider the decomposition of the graph
$n=4$
vertices. Consider the decomposition of the graph
![]() $G\in \mathcal{G}_n$
(b) over each of the bases: with the standard basis,
$G\in \mathcal{G}_n$
(b) over each of the bases: with the standard basis,
![]() $G = {B1} + {B3} + {B4} + {B6}$
; with the cycle basis,
$G = {B1} + {B3} + {B4} + {B6}$
; with the cycle basis,
![]() $G = {B2} + {B3}$
; for the last basis,
$G = {B2} + {B3}$
; for the last basis,
![]() $G = {B1} + {B2} + {B5}$
.
$G = {B1} + {B2} + {B5}$
.
The basis of this work is restricting the graph space in GGMs by considering subspaces of
![]() $\mathcal{G}_n$
. A subspace of the graph vector space is a subset of
$\mathcal{G}_n$
. A subspace of the graph vector space is a subset of
![]() $\mathcal{G}_n$
that is closed under
$\mathcal{G}_n$
that is closed under
![]() $\oplus$
. Restricting graphs via an appropriate subspace is desirable in GGMs for two reasons. Firstly, it shrinks the search space to a subset of
$\oplus$
. Restricting graphs via an appropriate subspace is desirable in GGMs for two reasons. Firstly, it shrinks the search space to a subset of
![]() $\mathcal{G}_n$
. Secondly, being closed under addition, a subspace lends itself well to convenient Monte Carlo sampling steps, as algorithms that only propose states in the subspace are readily constructed. In this paper we focus on one particular subspace, namely the cycle space.
$\mathcal{G}_n$
. Secondly, being closed under addition, a subspace lends itself well to convenient Monte Carlo sampling steps, as algorithms that only propose states in the subspace are readily constructed. In this paper we focus on one particular subspace, namely the cycle space.
Definition 1. (Cycle space.) The cycle space
![]() $\mathcal{C}_n$
of graphs with n vertices is the set of linear combinations of cycles in
$\mathcal{C}_n$
of graphs with n vertices is the set of linear combinations of cycles in
![]() $\mathcal{G}_n$
.
$\mathcal{G}_n$
.
We now present some relevant properties of
![]() $\mathcal{C}_n$
. By its definition,
$\mathcal{C}_n$
. By its definition,
![]() $\mathcal{C}_n$
is closed under addition making it a proper vector space:
$\mathcal{C}_n$
is closed under addition making it a proper vector space:
-
P1. The cycle space
 $\mathcal{C}_n$
is a subspace of the vector space
$\mathcal{C}_n$
is a subspace of the vector space
 $(\mathcal{G}_n, \oplus, \otimes)$
[Reference Wallis38, Theorem 5.1].
$(\mathcal{G}_n, \oplus, \otimes)$
[Reference Wallis38, Theorem 5.1].
Whether a graph
![]() $G\in\mathcal{G}_{n}$
is in
$G\in\mathcal{G}_{n}$
is in
![]() $\mathcal{C}_n$
can be conveniently checked using Veblen’s theorem:
$\mathcal{C}_n$
can be conveniently checked using Veblen’s theorem:
-
P2. A graph
 $G\in\mathcal{G}_n$
is an element of
$G\in\mathcal{G}_n$
is an element of
 $\mathcal{C}_n$
if and only if every vertex has even degree in G, i.e. every vertex has an even number of neighbours [Reference Veblen37].
$\mathcal{C}_n$
if and only if every vertex has even degree in G, i.e. every vertex has an even number of neighbours [Reference Veblen37].
A more intuitive description of the graphs in
![]() $\mathcal{C}_n$
is that they are precisely those that are the union of edge-disjoint cycles [Reference Wallis38, Theorem 5.1]. Also, each connected component of a graph in
$\mathcal{C}_n$
is that they are precisely those that are the union of edge-disjoint cycles [Reference Wallis38, Theorem 5.1]. Also, each connected component of a graph in
![]() $\mathcal{C}_n$
is a circuit. Notably, the edge union of cycles with overlapping edges is not necessarily in
$\mathcal{C}_n$
is a circuit. Notably, the edge union of cycles with overlapping edges is not necessarily in
![]() $\mathcal{C}_n$
: the edge union of the cycles (1, 2, 3, 1) and (1, 2, 4, 1) in the example from Figure 1 results in a degree of three for vertices 1 and 2. Also, whether the complete graph is in
$\mathcal{C}_n$
: the edge union of the cycles (1, 2, 3, 1) and (1, 2, 4, 1) in the example from Figure 1 results in a degree of three for vertices 1 and 2. Also, whether the complete graph is in
![]() $\mathcal{C}_n$
depends on the parity of n by property .
$\mathcal{C}_n$
depends on the parity of n by property .
Bases of
![]() $\mathcal{C}_n$
can be readily found using fundamental systems of cycles.
$\mathcal{C}_n$
can be readily found using fundamental systems of cycles.
Definition 2. (Fundamental system of cycles.) Let
![]() $T = (V, E_T)$
be a spanning tree of the complete graph and let
$T = (V, E_T)$
be a spanning tree of the complete graph and let
![]() $\overline{T} = (V, E_{\overline{T}})$
be the complement of T. That is,
$\overline{T} = (V, E_{\overline{T}})$
be the complement of T. That is,
![]() $e\in E_{\overline{T}}$
if and only if
$e\in E_{\overline{T}}$
if and only if
![]() $e\notin E_{T}$
. The fundamental system of cycles with respect to T is the set of graphs obtained by taking each cycle formed by adding one edge in
$e\notin E_{T}$
. The fundamental system of cycles with respect to T is the set of graphs obtained by taking each cycle formed by adding one edge in
![]() $\overline{T}$
to T.
$\overline{T}$
to T.
(We constrain ourselves to spanning trees of the complete graph for simplicity, though note that the fundamental system of cycles is usually also defined for incomplete graphs.)
-
P3. Every fundamental system of cycles is a basis of
 $\mathcal{C}_n$
[Reference Wallis38, Theorem 5.5].
$\mathcal{C}_n$
[Reference Wallis38, Theorem 5.5].
Figure 2 visualises how to obtain the fundamental system of cycles that constitutes the cycle basis considered in Figure 1. In Figure 1, this basis, which spans
![]() $\mathcal{C}_n$
, is extended to span the whole of
$\mathcal{C}_n$
, is extended to span the whole of
![]() $\mathcal{G}_n$
. Such extensions exist for any basis spanning a subspace [Reference Axler4]. Since T has
$\mathcal{G}_n$
. Such extensions exist for any basis spanning a subspace [Reference Axler4]. Since T has
![]() $(n - 1)$
edges and the number of elements in the fundamental system of cycles equals the number of edges in
$(n - 1)$
edges and the number of elements in the fundamental system of cycles equals the number of edges in
![]() $\overline{T}$
, property implies the dimension of
$\overline{T}$
, property implies the dimension of
![]() $\mathcal{C}_n$
:
$\mathcal{C}_n$
:
-
P4. The number of elements in a cycle basis and thus the dimension of the vector space
 $\mathcal{C}_n$
is
$\mathcal{C}_n$
is
 $n(n-1)/2 - (n - 1) = (n-1)(n-2)/2$
.
$n(n-1)/2 - (n - 1) = (n-1)(n-2)/2$
.
As considered in Figure 1, the number of basis elements in a decomposition of a graph varies with the basis considered. The same is true when only considering cycle bases. Consider for instance Figure 3. The graph that is basis element B6 for the path graph involves not one but three basis elements for the cycle basis derived from the star tree (B1 + B2 + B5).

Figure 2. Illustration of a fundamental system of cycles. The graph (a) visualises the spanning tree T with solid lines and its complement
![]() $\overline{T}$
with dashed lines. The basis elements (b) are the cycles obtained by adding one of the dashed edges in
$\overline{T}$
with dashed lines. The basis elements (b) are the cycles obtained by adding one of the dashed edges in
![]() $\overline{T}$
to T.
$\overline{T}$
to T.

Figure 3. Illustration of two fundamental systems of cycles with
![]() $n=5$
vertices.
$n=5$
vertices.
2.4. Comparing the cycle space with the set of decomposable graphs
As discussed in Section 1, there have been efforts to limit the search space to a subset of
![]() $\mathcal{G}_n$
, most notably to the set of decomposable graphs. While this restriction has the advantage of allowing normalising factors to be computed exactly, there are drawbacks to this restriction especially in applications. Firstly, unlike the cycle space, the set of decomposable graphs is not known to be closed under any vector addition operation. As a result, more involved MCMC algorithms have been proposed to ensure that proposed graphs are decomposable via constraints on which edge to flip [Reference Giudici and Green15, Reference Stingo and Marchetti33] or by sampling from the larger set of junction trees, which correspond to decomposable graphs [Reference Green and Thomas16]. On the other hand, in the cycle space, we are able to propose moves that are guaranteed to be in
$\mathcal{G}_n$
, most notably to the set of decomposable graphs. While this restriction has the advantage of allowing normalising factors to be computed exactly, there are drawbacks to this restriction especially in applications. Firstly, unlike the cycle space, the set of decomposable graphs is not known to be closed under any vector addition operation. As a result, more involved MCMC algorithms have been proposed to ensure that proposed graphs are decomposable via constraints on which edge to flip [Reference Giudici and Green15, Reference Stingo and Marchetti33] or by sampling from the larger set of junction trees, which correspond to decomposable graphs [Reference Green and Thomas16]. On the other hand, in the cycle space, we are able to propose moves that are guaranteed to be in
![]() $\mathcal{C}_n$
by standard properties of vector spaces. Similarly, decomposability cannot be checked as easily as property , which determines membership of
$\mathcal{C}_n$
by standard properties of vector spaces. Similarly, decomposability cannot be checked as easily as property , which determines membership of
![]() $\mathcal{C}_n$
.
$\mathcal{C}_n$
.
Another, more important drawback of restricting inference to decomposable graphs is that in general decomposable graphs do not approximate other graphs well. For instance,
![]() ${\mathrm{O}}(n \log n)$
edges need to be added to a graph to make the resulting graph decomposable in general [Reference Chung and Mumford8]. This contrasts with the cycle space as any graph
${\mathrm{O}}(n \log n)$
edges need to be added to a graph to make the resulting graph decomposable in general [Reference Chung and Mumford8]. This contrasts with the cycle space as any graph
![]() $G\in\mathcal{G}_n$
is at most
$G\in\mathcal{G}_n$
is at most
![]() $n/2$
edges different from a graph in
$n/2$
edges different from a graph in
![]() $\mathcal{C}_n$
per the following result.
$\mathcal{C}_n$
per the following result.
Proposition 1.
Let k be the number of odd-degree vertices in
![]() $G\in\mathcal{G}_n$
. Then there exists a graph in
$G\in\mathcal{G}_n$
. Then there exists a graph in
![]() $ \mathcal{C}_n$
that differs from G by
$ \mathcal{C}_n$
that differs from G by
![]() $k/2$
edges while there exists no graph in
$k/2$
edges while there exists no graph in
![]() $ \mathcal{C}_n$
that differs from G by less than
$ \mathcal{C}_n$
that differs from G by less than
![]() $k/2$
edges.
$k/2$
edges.
The size of
![]() $\mathcal{C}_n$
is also larger than that of the set of decomposable graphs. Note that
$\mathcal{C}_n$
is also larger than that of the set of decomposable graphs. Note that
![]() $\mathcal{G}_n$
has
$\mathcal{G}_n$
has
![]() $2^{n (n-1)/ 2}$
elements since the standard basis is the edge set containing
$2^{n (n-1)/ 2}$
elements since the standard basis is the edge set containing
![]() $n (n-1)/ 2$
elements. By property , the cardinality of
$n (n-1)/ 2$
elements. By property , the cardinality of
![]() $\mathcal{C}_n$
is
$\mathcal{C}_n$
is
![]() $2^{(n-1) (n-2) / 2}$
. In contrast, the number of decomposable graphs on n vertices tends towards
$2^{(n-1) (n-2) / 2}$
. In contrast, the number of decomposable graphs on n vertices tends towards
![]() $2^{n^2/4 + {\mathrm{O}}(n \log n)}$
as
$2^{n^2/4 + {\mathrm{O}}(n \log n)}$
as
![]() $n\to\infty$
[Reference Bender, Richmond and Wormald5]. (For comparison, the number of spanning trees on the complete graph, which are decomposable, is
$n\to\infty$
[Reference Bender, Richmond and Wormald5]. (For comparison, the number of spanning trees on the complete graph, which are decomposable, is
![]() $|\mathcal{T}_n|=n^{n-2}$
by Cayley’s [Reference Cayley6] formula.) Thus, constraining graphs to the cycle space is substantially less restrictive than assuming decomposability with a clear upper bound to the difference between any true graph and
$|\mathcal{T}_n|=n^{n-2}$
by Cayley’s [Reference Cayley6] formula.) Thus, constraining graphs to the cycle space is substantially less restrictive than assuming decomposability with a clear upper bound to the difference between any true graph and
![]() $\mathcal{C}_n$
. Lastly, the set of decomposable graphs is not a subset of
$\mathcal{C}_n$
. Lastly, the set of decomposable graphs is not a subset of
![]() $\mathcal{C}_n$
. For instance, trees are not in
$\mathcal{C}_n$
. For instance, trees are not in
![]() $\mathcal{C}_n$
by property since their leaf vertices have degree one.
$\mathcal{C}_n$
by property since their leaf vertices have degree one.
3. Theoretical properties of cycle basis priors
A prior distribution on
![]() $\mathcal{C}_n$
can be induced by assigning a distribution to cycle basis elements. In this section we explore the theoretical properties of such priors. Here C denotes a basis of cycles for
$\mathcal{C}_n$
can be induced by assigning a distribution to cycle basis elements. In this section we explore the theoretical properties of such priors. Here C denotes a basis of cycles for
![]() $\mathcal{C}_n$
. Thus C is a set of
$\mathcal{C}_n$
. Thus C is a set of
![]() $(n-1)(n-2)/2$
cycles. The results hold for any fixed basis C unless otherwise noted. We begin by showing that it is possible to induce the uniform prior on
$(n-1)(n-2)/2$
cycles. The results hold for any fixed basis C unless otherwise noted. We begin by showing that it is possible to induce the uniform prior on
![]() $\mathcal{C}_n$
.
$\mathcal{C}_n$
.
A cycle basis prior can be defined in terms of cycle-inclusion probabilities. Similarly to the standard basis, when the cycle-inclusion probability is 0.5, we get the uniform prior on
![]() $\mathcal{C}_n$
.
$\mathcal{C}_n$
.
Proposition 2.
Let C be any cycle basis for the cycle space
![]() $\mathcal{C}_n$
. Suppose that the inclusion of each cycle in C is an independent Bernoulli random variable with probability
$\mathcal{C}_n$
. Suppose that the inclusion of each cycle in C is an independent Bernoulli random variable with probability
![]() $0.5$
. Then the induced distribution on
$0.5$
. Then the induced distribution on
![]() $\mathcal{C}_n$
is uniform and the marginal edge inclusion probabilities are equal to
$\mathcal{C}_n$
is uniform and the marginal edge inclusion probabilities are equal to
![]() $0.5$
.
$0.5$
.
This uniformity holds for any C and thus also for the distribution on
![]() $\mathcal{C}_n$
induced by a distribution on such bases C. The edge inclusions are not independent under the uniform distribution over
$\mathcal{C}_n$
induced by a distribution on such bases C. The edge inclusions are not independent under the uniform distribution over
![]() $\mathcal{C}_n$
: independent edges with probability
$\mathcal{C}_n$
: independent edges with probability
![]() $0.5$
yield the uniform distribution over
$0.5$
yield the uniform distribution over
![]() $\mathcal{G}_n$
. Instead, edge flips can only happen jointly on sets of edges that correspond to graphs in
$\mathcal{G}_n$
. Instead, edge flips can only happen jointly on sets of edges that correspond to graphs in
![]() $\mathcal{C}_n$
to stay in the cycle space, i.e. to continue to satisfy property .
$\mathcal{C}_n$
to stay in the cycle space, i.e. to continue to satisfy property .
Often there is interest in non-uniform distributions, for instance to induce sparsity. In general, the edge inclusion probabilities induced by inclusion probabilities of cycle basis elements depend on the choice of cycle basis, and hence on the choice of spanning tree used to generate this basis via the fundamental system of cycles (property ). Although a closed-form expression is not available, we propose an efficient algorithm to compute the edge inclusion probabilities from a cycle basis prior.
Proposition 3.
Let
![]() $e \in \{(i,j) \in V \times V\colon i < j\}$
be any edge. Let
$e \in \{(i,j) \in V \times V\colon i < j\}$
be any edge. Let
![]() $\{c_1, \ldots, c_r\}\subset C$
be the set of basis elements that contain e. Suppose that the inclusions of these elements are independent with inclusion probabilities
$\{c_1, \ldots, c_r\}\subset C$
be the set of basis elements that contain e. Suppose that the inclusions of these elements are independent with inclusion probabilities
![]() $\{p_1, \ldots, p_r\}$
. Define the polynomial
$\{p_1, \ldots, p_r\}$
. Define the polynomial
Then the induced marginal probability of inclusion of the edge e is the sum of the coefficients of the odd powers of x in f(x). This edge probability reduces to
![]() ${\{1 - (1-2p)^r\}/2}$
if the probabilities
${\{1 - (1-2p)^r\}/2}$
if the probabilities
![]() $\{p_1, \ldots, p_r\}$
are all equal to p.
$\{p_1, \ldots, p_r\}$
are all equal to p.
If the cycle basis is generated from a star tree with independent and equally probable inclusion of basis elements, then these probabilities simplify. (The fundamental system of cycles with respect to a star tree is the set of all cycles of three edges that are incident to its root.)
Corollary 1.
Let the basis C be defined as the fundamental system of cycles with respect to a star tree T on
![]() $n\geq 2$
vertices. Suppose that the cycle inclusions are independent Bernoulli random variables with probability p. Then the marginal edge inclusion probabilities are given by
$n\geq 2$
vertices. Suppose that the cycle inclusions are independent Bernoulli random variables with probability p. Then the marginal edge inclusion probabilities are given by
 \[ \mathbb{P}\{(i,j) \in E \mid T\} =\begin{cases} \{1-(1-2p)^{n-2}\}/2 & {\textit{i} or \textit{j} \textit{is the root of} \textit{T},} \\[5pt] p & \textit{otherwise.}\end{cases}\]
\[ \mathbb{P}\{(i,j) \in E \mid T\} =\begin{cases} \{1-(1-2p)^{n-2}\}/2 & {\textit{i} or \textit{j} \textit{is the root of} \textit{T},} \\[5pt] p & \textit{otherwise.}\end{cases}\]
Moreover, the distribution induced by the uniform distribution over all star trees has
![]() $\mathbb{P}\{(i,j) \in E\} = p + \{1-2p - (1-2p)^{n-2}\}/n$
.
$\mathbb{P}\{(i,j) \in E\} = p + \{1-2p - (1-2p)^{n-2}\}/n$
.
Polynomial multiplication can be performed efficiently using linear convolution based on a fast Fourier transform (FFT), making the computation of the probabilities in Proposition 3 efficient. For the sake of completeness, we also provide an algorithm to compute the joint distribution of edge inclusions induced by the cycle basis prior. This is useful in, for example, calculating the degree distribution of a vertex.
Proposition 4.
Let
![]() $v\in V$
be any vertex. Let
$v\in V$
be any vertex. Let
![]() $\{e_1, \ldots, e_m\}$
be the set of edges incident to v. Let
$\{e_1, \ldots, e_m\}$
be the set of edges incident to v. Let
![]() $\{c_1, \ldots, c_r\} \subset C$
be the set of cycles incident to v. Suppose that the cycle inclusions are independent with inclusion probabilities
$\{c_1, \ldots, c_r\} \subset C$
be the set of cycles incident to v. Suppose that the cycle inclusions are independent with inclusion probabilities
![]() $\{p_1, \ldots, p_r\}$
. For
$\{p_1, \ldots, p_r\}$
. For
![]() $i=1,\ldots,r$
, let
$i=1,\ldots,r$
, let
![]() $a(i), b(i) \in \{1, \ldots, m\}$
be such that
$a(i), b(i) \in \{1, \ldots, m\}$
be such that
![]() $e_{a(i)}, e_{b(i)}$
are the edges of
$e_{a(i)}, e_{b(i)}$
are the edges of
![]() $c_i$
that are incident to v. Define the polynomial
$c_i$
that are incident to v. Define the polynomial
Let g be the image of f in the polynomial ring
![]() $\mathbb{R}[x_1, \ldots, x_m]/ \langle x_1^2, \ldots, x_m^2 \rangle$
under the unique ring homomorphism satisfying
$\mathbb{R}[x_1, \ldots, x_m]/ \langle x_1^2, \ldots, x_m^2 \rangle$
under the unique ring homomorphism satisfying
![]() $t_i \mapsto x_{a(i)}x_{b(i)}$
. Then the probability of including any set of edges
$t_i \mapsto x_{a(i)}x_{b(i)}$
. Then the probability of including any set of edges
![]() $\{e_s\}_{s\in S}$
while excluding the other
$\{e_s\}_{s\in S}$
while excluding the other
![]() $m-|S|$
edges incident to v is given by the coefficient of
$m-|S|$
edges incident to v is given by the coefficient of
![]() $\prod_{s\in S} x_s$
in g.
$\prod_{s\in S} x_s$
in g.
The above proposition can be applied in practice by noting that g is equal to the product of the polynomials
![]() $1 - p_i + p_i x_{a(i)}x_{b(i)}$
in the ring
$1 - p_i + p_i x_{a(i)}x_{b(i)}$
in the ring
![]() $\mathbb{R}[x_1, \ldots, x_m]/\langle x_1^2, \ldots, x_m^2 \rangle$
. Multiplication of linear polynomials modulo squares is equivalent to a circular convolution. By the circulant convolution theorem, this can be efficiently performed using an FFT of length 2 in m dimensions.
$\mathbb{R}[x_1, \ldots, x_m]/\langle x_1^2, \ldots, x_m^2 \rangle$
. Multiplication of linear polynomials modulo squares is equivalent to a circular convolution. By the circulant convolution theorem, this can be efficiently performed using an FFT of length 2 in m dimensions.
Although the above algorithm can be used to calculate degree distributions in the general case, closed-form expressions may be computed when the spanning tree used to generate the cycle basis has a tractable structure as in the case of star trees.
Proposition 5.
Let the basis C be defined as the fundamental system of cycles with respect to the star tree on the vertices
![]() $\{v_0, \ldots, v_{n-1}\}$
,
$\{v_0, \ldots, v_{n-1}\}$
,
![]() $n\geq 2$
, rooted at
$n\geq 2$
, rooted at
![]() $v_0$
. Suppose that the cycle inclusions are independent Bernoulli random variables with probability p. Then the degree distribution for the vertices
$v_0$
. Suppose that the cycle inclusions are independent Bernoulli random variables with probability p. Then the degree distribution for the vertices
![]() $\{v_1, \ldots, v_{n-1}\}$
is given by
$\{v_1, \ldots, v_{n-1}\}$
is given by
 \[ \mathbb{P}\{\deg\!(v_i) = k\} =\begin{cases} (1-p)^{n-2} & k=0, \\[5pt] \sum_{j=k-1}^k\binom{n-2}{j}p^j (1-p)^{n-2-j} & {2 \leq k < n \, and \,{k} \, is \, even,} \\[5pt] 0 & \textit{otherwise.}\end{cases}\]
\[ \mathbb{P}\{\deg\!(v_i) = k\} =\begin{cases} (1-p)^{n-2} & k=0, \\[5pt] \sum_{j=k-1}^k\binom{n-2}{j}p^j (1-p)^{n-2-j} & {2 \leq k < n \, and \,{k} \, is \, even,} \\[5pt] 0 & \textit{otherwise.}\end{cases}\]
We now briefly discuss the sparsity of graphs in the cycle space. For a given probability p of independent basis element inclusions, Proposition 3 gives the edge probability
![]() $\{1 - (1-2p)^r\}/2$
, which is an increasing function of p for
$\{1 - (1-2p)^r\}/2$
, which is an increasing function of p for
![]() $p\leq 0.5$
and which involves the number r of elements in the basis C that include the edge. Thus, setting a smaller p yields shrinkage on the number of edges: the edge probability can be made arbitrarily small via p. This shrinkage depends on C via r. For instance, consider Figure 3 and edge (2, 3). There,
$p\leq 0.5$
and which involves the number r of elements in the basis C that include the edge. Thus, setting a smaller p yields shrinkage on the number of edges: the edge probability can be made arbitrarily small via p. This shrinkage depends on C via r. For instance, consider Figure 3 and edge (2, 3). There,
![]() $r=1$
for C generated by the star tree and
$r=1$
for C generated by the star tree and
![]() $r=5$
for C generated by the path graph. In general,
$r=5$
for C generated by the path graph. In general,
![]() $r=1$
for any edges in the complement
$r=1$
for any edges in the complement
![]() $\overline{T}$
of the spanning tree T that generated C. For edges in T, r varies with C.
$\overline{T}$
of the spanning tree T that generated C. For edges in T, r varies with C.
More generally, there is no simple relationship between the sparsity of a graph in terms of its cycle basis inclusions and the edge-sparsity of that graph. However, analytical results are available in the particular case that the cycle basis is generated from a star tree.
Proposition 6.
Let the basis C be defined as the fundamental system of cycles with respect to a star tree on n vertices. Define
![]() $m=\lfloor(n-1)/2\rfloor$
. Consider the graph
$m=\lfloor(n-1)/2\rfloor$
. Consider the graph
![]() $G = (V, E)$
formed by the inclusion of q basis elements from C. Then the number of edges
$G = (V, E)$
formed by the inclusion of q basis elements from C. Then the number of edges
![]() $|E|$
is bounded as
$|E|$
is bounded as
![]() $q \leq |E| \leq q + 2 \min\!(q ,\, m)$
. The upper bound is tight for
$q \leq |E| \leq q + 2 \min\!(q ,\, m)$
. The upper bound is tight for
![]() $q \leq m$
.
$q \leq m$
.
This implies that specifying a shrinkage prior on q leads to shrinkage on the number of included edges for cycle bases induced by a star tree. We also consider
![]() $|E|$
as a function of q empirically in Figure 4. The empirical results show that a number q implies a smaller range of
$|E|$
as a function of q empirically in Figure 4. The empirical results show that a number q implies a smaller range of
![]() $|E|$
than suggested by Proposition 6, especially for a large number of vertices. Simulation studies in Section 4 confirm that limiting q also results in lower posterior edge inclusion probabilities, as does lowering the prior basis element inclusion probability p.
$|E|$
than suggested by Proposition 6, especially for a large number of vertices. Simulation studies in Section 4 confirm that limiting q also results in lower posterior edge inclusion probabilities, as does lowering the prior basis element inclusion probability p.

Figure 4. Box plots of
![]() $|E|-q $
from 100 graphs G generated by sampling q elements from a basis C generated by a star tree without replacement. The dashed lines mark the bounds
$|E|-q $
from 100 graphs G generated by sampling q elements from a basis C generated by a star tree without replacement. The dashed lines mark the bounds
![]() $0 \leq |E|-q \leq 2 \min\!(q ,\, m)$
from Proposition 6.
$0 \leq |E|-q \leq 2 \min\!(q ,\, m)$
from Proposition 6.
Apart from the prior process on cycle bases, we also consider the prior induced by edge unions of spanning trees in the Supplementary Material. However, we find that computation of the induced prior p(G) is intractable since edge unions of spanning trees do not form a vector space. We propose an algorithm to compute p(G), specifically to count the number of decompositions of a graph into spanning trees, with complexity
![]() ${\mathrm{O}}(2^{|E|}\, n^3)$
, which is an improvement over the super-exponential complexity of the brute-force enumeration method. Further, we prove bounds to attempt an approximation of the prior ratio as appearing in a Metropolis–Hastings acceptance probability, but simulations shows that the bounds are too wide to be of use (see the Supplementary Material).
${\mathrm{O}}(2^{|E|}\, n^3)$
, which is an improvement over the super-exponential complexity of the brute-force enumeration method. Further, we prove bounds to attempt an approximation of the prior ratio as appearing in a Metropolis–Hastings acceptance probability, but simulations shows that the bounds are too wide to be of use (see the Supplementary Material).
4. Simulation studies with the cycle basis prior
We conduct simulation studies to better understand the effect of certain cycle basis priors on posterior inference. We do not apply these priors to the gene expression application in Section 5, as the decomposition of a graph into changing cycle bases in step 2b of Algorithm S1 in the Supplementary Material is too expensive with
![]() $n=93$
vertices. We simulate the
$n=93$
vertices. We simulate the
![]() $N\times n$
data matrix X from the model
$N\times n$
data matrix X from the model
![]() $p(X\mid K)$
in (1) with the
$p(X\mid K)$
in (1) with the
![]() $n\times n$
precision matrix K given by
$n\times n$
precision matrix K given by
![]() $K_{ii}=1$
for
$K_{ii}=1$
for
![]() $i=1,\ldots,n$
and
$i=1,\ldots,n$
and
![]() $K_{12}=K_{13}=K_{23}=K_{34}=K_{35}=K_{45}=0.3$
while all other upper-triangular elements of K are equal to zero. This fully defines K as it is a symmetric matrix. Thus the true underlying graph G corresponds to the union of the two cycles (1, 2, 3) and (3, 4, 5). We set
$K_{12}=K_{13}=K_{23}=K_{34}=K_{35}=K_{45}=0.3$
while all other upper-triangular elements of K are equal to zero. This fully defines K as it is a symmetric matrix. Thus the true underlying graph G corresponds to the union of the two cycles (1, 2, 3) and (3, 4, 5). We set
![]() $n=15$
as the number of vertices and
$n=15$
as the number of vertices and
![]() $N=150$
as the number of observations.
$N=150$
as the number of observations.
We consider six different priors on graphs. The first one is the edge basis prior with independent edge inclusions with probability
![]() $p=0.5$
. The next four priors are constrained to the cycle space
$p=0.5$
. The next four priors are constrained to the cycle space
![]() $\mathcal{C}_n$
as follows. The second prior is induced by the uniform prior p(T) over all spanning trees combined with the prior
$\mathcal{C}_n$
as follows. The second prior is induced by the uniform prior p(T) over all spanning trees combined with the prior
![]() $p(G\mid T)$
resulting from a priori independent basis element inclusions with probability
$p(G\mid T)$
resulting from a priori independent basis element inclusions with probability
![]() $p=0.5$
, where the cycle basis is generated by spanning tree T. The third prior uses the same uniform
$p=0.5$
, where the cycle basis is generated by spanning tree T. The third prior uses the same uniform
![]() $p(G\mid T)$
but with p(T) uniform over all star trees instead of the larger set of all spanning trees. The fourth prior is the same as the third prior but with a different
$p(G\mid T)$
but with p(T) uniform over all star trees instead of the larger set of all spanning trees. The fourth prior is the same as the third prior but with a different
![]() $p(G\mid T)$
, where the a priori basis element inclusion probability is
$p(G\mid T)$
, where the a priori basis element inclusion probability is
![]() $p=0.05$
instead of
$p=0.05$
instead of
![]() $0.5$
. The fifth prior is like the third prior but with
$0.5$
. The fifth prior is like the third prior but with
![]() $p(G\mid T)$
uniform over all graphs that consist of
$p(G\mid T)$
uniform over all graphs that consist of
![]() $q=3$
or fewer elements from the cycle basis generated by T. Finally, the last prior is uniform over all decomposable graphs.
$q=3$
or fewer elements from the cycle basis generated by T. Finally, the last prior is uniform over all decomposable graphs.
We compute the posterior for the first five priors using Algorithm S1 in the Supplementary Material, where we repeat step 1 nine times for each step 2. Step 2 involves sampling from p(T). For the uniform prior over all spanning trees (the second prior), we use the algorithm from [Reference Aldous1] to sample from p(T). Schild [Reference Schild29] provides a faster alternative. We set the total number of MCMC steps, i.e. executions of Algorithm S1, to
![]() $10^5$
of which
$10^5$
of which
![]() $10^4$
serve as burn-in. Posterior computation for the prior on decomposable graphs is as described in Section 5. Figure 5 visualises the resulting posterior edge inclusion probabilities. The probabilities are not notably different between the edge basis and the uniform prior over the cycle space
$10^4$
serve as burn-in. Posterior computation for the prior on decomposable graphs is as described in Section 5. Figure 5 visualises the resulting posterior edge inclusion probabilities. The probabilities are not notably different between the edge basis and the uniform prior over the cycle space
![]() $\mathcal{C}_n$
induced by considering all spanning trees or all star trees with
$\mathcal{C}_n$
induced by considering all spanning trees or all star trees with
![]() $p=0.5$
.
$p=0.5$
.

Figure 5. The posterior edge inclusion probabilities (upper triangle) and the median probability graph (lower triangle) resulting from the six different priors considered for the simulated data.
The median probability graphs of the first three priors plus the star tree prior with the number of basis elements q capped at three (
![]() $q\leq 3$
) have identical recovery of the true underlying graph with the cycle (3, 4, 5) and edge (1, 3) correctly detected, failure to detect (1, 2) and (2, 3), and no false positives. The extra prior regularisation in the fourth prior with
$q\leq 3$
) have identical recovery of the true underlying graph with the cycle (3, 4, 5) and edge (1, 3) correctly detected, failure to detect (1, 2) and (2, 3), and no false positives. The extra prior regularisation in the fourth prior with
![]() $p=0.05$
results in edge (1, 3) not being detected. The truncation
$p=0.05$
results in edge (1, 3) not being detected. The truncation
![]() $q\leq 3$
in the fifth prior results in lower inclusion probabilities: an average probability of
$q\leq 3$
in the fifth prior results in lower inclusion probabilities: an average probability of
![]() $0.054$
compared to
$0.054$
compared to
![]() $0.056$
for the third prior with
$0.056$
for the third prior with
![]() $p=0.5$
. The fourth prior with
$p=0.5$
. The fourth prior with
![]() $p=0.05$
yields an even lower average probability at
$p=0.05$
yields an even lower average probability at
![]() $0.033$
. The prior on decomposable graphs produces an average of 0.11 with notably non-zero probabilities also for edges with endpoints outside the first five nodes.
$0.033$
. The prior on decomposable graphs produces an average of 0.11 with notably non-zero probabilities also for edges with endpoints outside the first five nodes.

Figure 6. The posterior edge inclusion probabilities (upper triangle) and the median probability graph (lower triangle) resulting from the standard edge basis (a), cycle basis (b), and the set of decomposable graphs (c).

Figure 7. Graphs obtained by including edges whose posterior inclusion probability is larger than
![]() $0.95$
when using the standard edge basis (a) and the cycle basis (b). Graph (a) has 141 edges and graph (b) has 147 edges, 123 of which appear in both graphs.
$0.95$
when using the standard edge basis (a) and the cycle basis (b). Graph (a) has 141 edges and graph (b) has 147 edges, 123 of which appear in both graphs.
5. Application to gene expression data
In this section we restrict the graph space
![]() $\mathcal{G}_n$
to the cycle space
$\mathcal{G}_n$
to the cycle space
![]() $\mathcal{C}_n$
while inferring a gene expression network. The data are gene expression profiles taken from tumours of breast cancer patients obtained from the
$\mathcal{C}_n$
while inferring a gene expression network. The data are gene expression profiles taken from tumours of breast cancer patients obtained from the
![]() $\texttt{R}$
package
$\texttt{R}$
package
![]() $\texttt{gRbase}$
[Reference Dethlefsen and Højsgaard11] preprocessed following the procedure in [Reference Højsgaard, Edwards and Lauritzen17], which yields
$\texttt{gRbase}$
[Reference Dethlefsen and Højsgaard11] preprocessed following the procedure in [Reference Højsgaard, Edwards and Lauritzen17], which yields
![]() $n=93$
genes of interest from
$n=93$
genes of interest from
![]() $N=250$
patients. For a further description of the data collection, see [Reference Miller, Smeds, George, Vega, Vergara, Ploner, Pawitan, Hall, Klaar, Liu and Bergh23].
$N=250$
patients. For a further description of the data collection, see [Reference Miller, Smeds, George, Vega, Vergara, Ploner, Pawitan, Hall, Klaar, Liu and Bergh23].
For this application, we consider three priors on
![]() $\mathcal{G}_n$
: the uniform prior on
$\mathcal{G}_n$
: the uniform prior on
![]() $\mathcal{G}_n$
corresponding to the standard ‘edge’ basis, the uniform prior on
$\mathcal{G}_n$
corresponding to the standard ‘edge’ basis, the uniform prior on
![]() $\mathcal{C}_n$
such as arising from a cycle basis (e.g. Proposition 2) and a uniform prior over all decomposable graphs. We use a Metropolis–Hastings algorithm for posterior inference where the proposal is to flip the presence of one basis element in G where we use the edge basis also for the prior on decomposable graphs. For the cycle basis, this proposal is guaranteed to be in
$\mathcal{C}_n$
such as arising from a cycle basis (e.g. Proposition 2) and a uniform prior over all decomposable graphs. We use a Metropolis–Hastings algorithm for posterior inference where the proposal is to flip the presence of one basis element in G where we use the edge basis also for the prior on decomposable graphs. For the cycle basis, this proposal is guaranteed to be in
![]() $\mathcal{C}_n$
as a vector space is closed under addition. See Section S3.2 of the Supplementary Material for details of the MCMC. The computational cost is similar for the edge and cycle basis. Since the Metropolis–Hastings proposal that we use for decomposable graphs is not constrained to decomposable graphs, the rejection rate of that MCMC is high. We therefore run it for longer than the MCMC with the edge and cycle basis.
$\mathcal{C}_n$
as a vector space is closed under addition. See Section S3.2 of the Supplementary Material for details of the MCMC. The computational cost is similar for the edge and cycle basis. Since the Metropolis–Hastings proposal that we use for decomposable graphs is not constrained to decomposable graphs, the rejection rate of that MCMC is high. We therefore run it for longer than the MCMC with the edge and cycle basis.
Figures 6 and 7 and Table 1 summarise the resulting graph inference. There is no major difference between the posterior edge inclusion probabilities with the edge basis and the cycle basis. This is despite the cycle space restriction with the cycle basis. These results suggest that restricting inference to the cycle space
![]() $\mathcal{C}_n \subset \mathcal{G}_n$
does not substantially affect posterior inference from when the graph space
$\mathcal{C}_n \subset \mathcal{G}_n$
does not substantially affect posterior inference from when the graph space
![]() $\mathcal{G}_n$
is not restricted. This contrasts with the results for decomposable graphs, which are substantially different from both the edge and cycle basis results, reflecting that decomposability is a more severe restriction than the cycle space.
$\mathcal{G}_n$
is not restricted. This contrasts with the results for decomposable graphs, which are substantially different from both the edge and cycle basis results, reflecting that decomposability is a more severe restriction than the cycle space.
Table 1. Minimum, average and maximum absolute difference in posterior edge inclusion probabilities resulting from the cycle basis and the set of decomposable graphs relative to the standard edge basis.

6. Discussion
In this paper we introduce a generalisation of the edge inclusion prior based on vector spaces and, in particular, investigate the cycle subspace. We present theoretical results about the cycle space and their bases. While the results presented in Section 2 are not our own except for Proposition 1, to the extent of our knowledge, this is the first time the idea of restricting inference to the cycle space has been introduced in the graphical model literature.
We also study a novel prior based on assigning independent prior basis inclusion probabilities, proving its degree distribution and shrinkage properties. We implement an MCMC algorithm that samples from the cycle space. Our algorithm is more straightforward to implement when compared to methods for decomposable graphs [Reference Giudici and Green15, Reference Green and Thomas16, Reference Stingo and Marchetti33], by the fact that vector spaces are closed under addition. We show empirically that studying a smaller but dense subset of the graph space does not significantly affect inference of posterior edge inclusion probabilities.
Moreover, this paper opens up an opportunity to various extensions of existing methodologies by considering alternative graph vector spaces such as those induced by cycle bases as opposed to the edge basis. For example, the size-based prior of Armstrong et al. [Reference Armstrong, Carter, Wong and Kohn2] can be used to shrink to the number of basis elements. Also, a birth–death proposal on the basis elements can be used instead of the proposal used in this paper that randomly switches one basis element selected from a uniform distribution on all elements.
Lastly, in this paper we have only considered standard GGMs. However, it may be possible to extend this method to other types of graphical models such as multiple graphs [Reference Peterson, Stingo and Vannucci27, Reference Tan, Jasra, De Iorio and Ebbels34], Gaussian copulas [Reference Dobra and Lenkoski12, Reference Mohammadi and Wit24] and chain graphs [Reference Lu, De Iorio, Jasra and Rosner22, Reference Sonntag and Peña32].
Funding information
This work was supported by the Singapore Ministry of Education Academic Research Fund Tier 2 under grant MOE2019-T2-2-100.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
Data
The data related to the application in Section 5 can be found at https://github.com/ kristoforusbryant/cbmcmc/blob/main/breastcancer/data/breastcancer_data_93_250.csv.
Supplementary material
The Supplementary Material for this article can be found at http://doi.org/10.1017/jpr.2023.33.