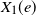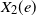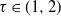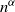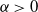1. Introduction and main results
First passage percolation (FPP) was introduced in [Reference Hammersley and Welsh20] as a model for the flow of fluid through random media, and has evolved into one of the fundamental models of random growth. The basic model for FPP on a graph is defined by assigning independent and identically distributed (i.i.d.) non-negative random weights to the edges, referred to as passage times and interpreted as the times or costs of traversing the edges. This induces a random metric on the vertex set where the distance between two vertices is the minimal cost-sum among all nearest-neighbor paths connecting the two vertices. Of primary interest is the asymptotic behavior of distances, balls and geodesics (time-minimizing paths) in the first passage metric. The classical example is when the underlying structure is taken to be the
![]() $\mathbb{Z}^d$
-lattice; see [Reference Auffinger, Damron and Hanson5] for a recent survey of results in this setting. The case with exponential passage times has received particular attention and is referred to as the Richardson model.
$\mathbb{Z}^d$
-lattice; see [Reference Auffinger, Damron and Hanson5] for a recent survey of results in this setting. The case with exponential passage times has received particular attention and is referred to as the Richardson model.
In [Reference Häggström and Pemantle18], the Richardson model (on
![]() $\mathbb{Z}^d$
) was extended to a two-type version that describes a competition between two infection types that evolve simultaneously using passage times with (potentially) different intensities. The event that both infection types occupy infinite parts of the lattice is referred to as infinite coexistence, and it is conjectured that this has positive probability if and only if the infections have the same intensity. The if-direction was proved in full generality independently in [Reference Garet and Marchand17] and [Reference Hoffman21]. The only-if-direction remains to be fully resolved, but partial results can be found in [Reference Häggström and Pemantle19]. We refer to [Reference Deijfen and Häggström15] for a survey and further references.
$\mathbb{Z}^d$
) was extended to a two-type version that describes a competition between two infection types that evolve simultaneously using passage times with (potentially) different intensities. The event that both infection types occupy infinite parts of the lattice is referred to as infinite coexistence, and it is conjectured that this has positive probability if and only if the infections have the same intensity. The if-direction was proved in full generality independently in [Reference Garet and Marchand17] and [Reference Hoffman21]. The only-if-direction remains to be fully resolved, but partial results can be found in [Reference Häggström and Pemantle19]. We refer to [Reference Deijfen and Häggström15] for a survey and further references.
The past few years have witnessed an explosion in the amount of empirical data on networks, showing that many networks exhibit similar properties. This has motivated the formulation of a large number of network models aiming at capturing and explaining these properties. One property that is observed in many real-world networks is that they display asymptotic power-law degree distributions, that is, the number of vertices with degree k decays asymptotically for large networks as well as large k as
![]() $k^{-\tau}$
for some exponent
$k^{-\tau}$
for some exponent
![]() $\tau\gt 1$
, which for a variety of empirical networks has been observed to range from just above 1 to a bit above 3; see [Reference Albert and Barabási3, Table II]. See also [Reference Voitalov, van der Hoorn, van der Hofstad and Krioukov32] for more recent estimates of power-law exponents, and [Reference Broido and Clauset14] for criticism on the prevailing suggestion that power laws are omnipresent. The regime
$\tau\gt 1$
, which for a variety of empirical networks has been observed to range from just above 1 to a bit above 3; see [Reference Albert and Barabási3, Table II]. See also [Reference Voitalov, van der Hoorn, van der Hofstad and Krioukov32] for more recent estimates of power-law exponents, and [Reference Broido and Clauset14] for criticism on the prevailing suggestion that power laws are omnipresent. The regime
![]() $\tau\gt 3$
corresponds to finite variance,
$\tau\gt 3$
corresponds to finite variance,
![]() $\tau \in (2,3)$
to finite mean but infinite variance, and
$\tau \in (2,3)$
to finite mean but infinite variance, and
![]() $\tau \in (1,2)$
to infinite mean. The standard model for generating graphs with a prescribed degree distribution is known as the configuration model, and is constructed by independently assigning half-edges to the vertices according to the desired distribution and then pairing the half-edges randomly. Its structure is well understood in all three power-law regimes mentioned above; see e.g. [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26], [Reference Van der Hofstad, Hooghiemstra and Van Mieghem29], [Reference Van der Hofstad, Hooghiemstra and Znamenski30], and [Reference Van der Hofstad, Hooghiemstra and Znamenski31]. FPP on the configuration model with
$\tau \in (1,2)$
to infinite mean. The standard model for generating graphs with a prescribed degree distribution is known as the configuration model, and is constructed by independently assigning half-edges to the vertices according to the desired distribution and then pairing the half-edges randomly. Its structure is well understood in all three power-law regimes mentioned above; see e.g. [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26], [Reference Van der Hofstad, Hooghiemstra and Van Mieghem29], [Reference Van der Hofstad, Hooghiemstra and Znamenski30], and [Reference Van der Hofstad, Hooghiemstra and Znamenski31]. FPP on the configuration model with
![]() $\tau\gt 2$
and exponential passage times was analyzed in [Reference Bhamidi, van der Hofstad and Hooghiemstra10] and the results for
$\tau\gt 2$
and exponential passage times was analyzed in [Reference Bhamidi, van der Hofstad and Hooghiemstra10] and the results for
![]() $\tau\gt 3$
were extended to all continuous passage-time distributions in [Reference Bhamidi, van der Hofstad and Hooghiemstra12]. For
$\tau\gt 3$
were extended to all continuous passage-time distributions in [Reference Bhamidi, van der Hofstad and Hooghiemstra12]. For
![]() $\tau \in (2,3)$
, FPP was studied in more detail in [Reference Baroni, van der Hofstad and Komjáthy7] and [Reference Baroni, van der Hofstad and Komjáthy8], and for
$\tau \in (2,3)$
, FPP was studied in more detail in [Reference Baroni, van der Hofstad and Komjáthy7] and [Reference Baroni, van der Hofstad and Komjáthy8], and for
![]() $\tau \in (1,2)$
in [Reference Bhamidi, van der Hofstad and Hooghiemstra11].
$\tau \in (1,2)$
in [Reference Bhamidi, van der Hofstad and Hooghiemstra11].
In competing FPP on the configuration model, two infection types compete to invade the vertices in the graph. Each edge is equipped with two independent non-negative random weights from two potentially different distributions, indicating the passage time for types 1 and 2, respectively. When a vertex is type i infected, the passage times on the incident edges are activated. Then a given neighbor that is uninfected when the type i passage time on the connecting edge has passed becomes type i infected at that time. Infected vertices become immune to the other type and stay infected forever. The growth is typically started from two uniformly chosen vertices. The model was analyzed for exponential passage times and constant degrees (leading to random regular graphs) in [Reference Antunovic, Dekel, Mossel and Peres4], where it was shown that the strongest type occupies all but a vanishing fraction of the vertices when the intensities are different, while both types occupy positive fractions of the vertices when they are equal (the analysis in [Reference Antunovic, Dekel, Mossel and Peres4] also included more general initial sets leading to modified results). For exponential passage times and degree exponent
![]() $\tau\gt 3$
, it was shown in [Reference Ahlberg, Deijfen and Janson1] that the behavior is the same as for constant degrees. The case with exponential passage times and
$\tau\gt 3$
, it was shown in [Reference Ahlberg, Deijfen and Janson1] that the behavior is the same as for constant degrees. The case with exponential passage times and
![]() $\tau\in(2,3)$
was considered in [Reference Deijfen and van der Hofstad16], where it was shown that one of the types then occupies all but a finite number of the vertices. Furthermore, both types have a positive probability of winning regardless of the intensities of the infections. The model has also been analyzed for constant passage times in the regime
$\tau\in(2,3)$
was considered in [Reference Deijfen and van der Hofstad16], where it was shown that one of the types then occupies all but a finite number of the vertices. Furthermore, both types have a positive probability of winning regardless of the intensities of the infections. The model has also been analyzed for constant passage times in the regime
![]() $\tau\in(2,3)$
in [Reference Baroni, van der Hofstad and Komjáthy6] and [Reference Van der Hofstad and Komjáthy28]. When the types have different (constant) passage times, the faster type occupies all but a vanishing fraction of the vertices [Reference Baroni, van der Hofstad and Komjáthy6], while in the symmetric case coexistence can occur depending on the choice of the two starting vertices [Reference Van der Hofstad and Komjáthy28].
$\tau\in(2,3)$
in [Reference Baroni, van der Hofstad and Komjáthy6] and [Reference Van der Hofstad and Komjáthy28]. When the types have different (constant) passage times, the faster type occupies all but a vanishing fraction of the vertices [Reference Baroni, van der Hofstad and Komjáthy6], while in the symmetric case coexistence can occur depending on the choice of the two starting vertices [Reference Van der Hofstad and Komjáthy28].
In this paper we analyze competing FPP on graphs generated by the configuration model with degree exponent
![]() $\tau\in(1,2)$
for a large class of passage-time distributions. Values of
$\tau\in(1,2)$
for a large class of passage-time distributions. Values of
![]() $\tau \in (1, 2)$
have been observed in social networks, such as email networks and collaboration networks, in technological networks, such as the link structure of the World Wide Web and networks of dependences between software packages, and in ecological networks; see [Reference Albert and Barabási3, Table II] and [Reference Newman25, Table II]. We show that with high probability as the number of vertices grows to infinity, one of the infection types occupies all vertices except for the starting point of the other type, leading to the most extreme ‘winner-takes-it-all’ phenomenon possible. Moreover, both types have a positive probability of winning, regardless of the passage-time distribution. For
$\tau \in (1, 2)$
have been observed in social networks, such as email networks and collaboration networks, in technological networks, such as the link structure of the World Wide Web and networks of dependences between software packages, and in ecological networks; see [Reference Albert and Barabási3, Table II] and [Reference Newman25, Table II]. We show that with high probability as the number of vertices grows to infinity, one of the infection types occupies all vertices except for the starting point of the other type, leading to the most extreme ‘winner-takes-it-all’ phenomenon possible. Moreover, both types have a positive probability of winning, regardless of the passage-time distribution. For
![]() $\tau\in(1,2)$
, the graph has a degenerate structure where all vertices are connected to a small number of giant-degree vertices with degrees comparable to the total degree in the graph. The competition is essentially won by the type that first makes it from its starting point to one of its (giant-degree) neighbors. After this happens, the infection type quickly invades all the other giant-degree vertices, thereby preventing the other type from making any progress at all. The behavior is explosive and the outcome of the competition is determined in finite time.
$\tau\in(1,2)$
, the graph has a degenerate structure where all vertices are connected to a small number of giant-degree vertices with degrees comparable to the total degree in the graph. The competition is essentially won by the type that first makes it from its starting point to one of its (giant-degree) neighbors. After this happens, the infection type quickly invades all the other giant-degree vertices, thereby preventing the other type from making any progress at all. The behavior is explosive and the outcome of the competition is determined in finite time.
1.1. Definition of the model
The configuration model takes n vertices and a probability distribution with support on non-negative integers as input. Let D be a random variable drawn from the given probability distribution and let
![]() $D_1, D_2, \ldots, D_n$
be i.i.d. copies. These represent the degrees of the vertices and we write
$D_1, D_2, \ldots, D_n$
be i.i.d. copies. These represent the degrees of the vertices and we write
![]() $L_n = \sum_{i=1}^n D_i$
for the total degree. To construct the graph, each vertex
$L_n = \sum_{i=1}^n D_i$
for the total degree. To construct the graph, each vertex
![]() $i\in \{1, \ldots, n\}=[n]$
is first assigned
$i\in \{1, \ldots, n\}=[n]$
is first assigned
![]() $D_i$
half-edges. The half-edges are then iteratively paired to form edges. Specifically, at each step we pick two half-edges uniformly at random from the set of half-edges that have not been paired yet, and connect them into an edge. If
$D_i$
half-edges. The half-edges are then iteratively paired to form edges. Specifically, at each step we pick two half-edges uniformly at random from the set of half-edges that have not been paired yet, and connect them into an edge. If
![]() $L_n$
is odd, so that only one half-edge remains in the last step, then we add one extra half-edge at a uniformly chosen vertex. To avoid trivial complications in the formulation of our results, we assume throughout that
$L_n$
is odd, so that only one half-edge remains in the last step, then we add one extra half-edge at a uniformly chosen vertex. To avoid trivial complications in the formulation of our results, we assume throughout that
![]() $D_i\geq 1$
, so that there are no isolated vertices in the graph.
$D_i\geq 1$
, so that there are no isolated vertices in the graph.
The probability mass function of the degree distribution is denoted by
and the distribution function is given by
 \begin{align*} F(x) = \mathbb{P} (D \leq x) = \sum_{j=1}^{\lfloor x \rfloor} f_j,\end{align*}
\begin{align*} F(x) = \mathbb{P} (D \leq x) = \sum_{j=1}^{\lfloor x \rfloor} f_j,\end{align*}
where
![]() $\lfloor x \rfloor$
indicates the largest integer smaller than or equal to x. Our main assumption is that
$\lfloor x \rfloor$
indicates the largest integer smaller than or equal to x. Our main assumption is that
where
![]() $\ell$
is a slowly varying function, that is, the degrees obey a power law with infinite mean. The notation
$\ell$
is a slowly varying function, that is, the degrees obey a power law with infinite mean. The notation
![]() $n\mapsto \ell(n)$
will refer throughout to a slowly varying function that might differ at different occurrences.
$n\mapsto \ell(n)$
will refer throughout to a slowly varying function that might differ at different occurrences.
To define the competition process, given the edge set E, we equip each edge
![]() $e \in E$
in the graph with two independent weights
$e \in E$
in the graph with two independent weights
![]() $X_1(e)$
and
$X_1(e)$
and
![]() $X_2(e)$
representing the passage time through the edge for type 1 and 2, respectively. We assume that
$X_2(e)$
representing the passage time through the edge for type 1 and 2, respectively. We assume that
![]() $(X_1(e))_{e \in E}$
is an i.i.d. sequence, and so is
$(X_1(e))_{e \in E}$
is an i.i.d. sequence, and so is
![]() $(X_2(e))_{e \in E}$
. The two sequences are independent of each other, but may have different distributions. At time 0, vertex 1 is infected with type 1 and vertex 2 is infected with type 2 while all other vertices are uninfected. Note that since vertices are exchangeable in the configuration model, this is equivalent to starting from two distinct vertices chosen uniformly at random. The infections then spread in the graph via nearest neighbors: the time it takes for the type 1 (resp. 2) infection to traverse an edge
$(X_2(e))_{e \in E}$
. The two sequences are independent of each other, but may have different distributions. At time 0, vertex 1 is infected with type 1 and vertex 2 is infected with type 2 while all other vertices are uninfected. Note that since vertices are exchangeable in the configuration model, this is equivalent to starting from two distinct vertices chosen uniformly at random. The infections then spread in the graph via nearest neighbors: the time it takes for the type 1 (resp. 2) infection to traverse an edge
![]() $e=\{u,v\}$
from u and reach the vertex v at the other end of the edge is given by
$e=\{u,v\}$
from u and reach the vertex v at the other end of the edge is given by
![]() $X_1(e)$
(resp.
$X_1(e)$
(resp.
![]() $X_2(e)$
). If v is still uninfected at that time, then it becomes type 1 (resp. 2) infected. An infected vertex remains infected with the same type forever and becomes immune to the other type.
$X_2(e)$
). If v is still uninfected at that time, then it becomes type 1 (resp. 2) infected. An infected vertex remains infected with the same type forever and becomes immune to the other type.
For a random variable Y, let supp(Y) denote the support of the distribution of Y. We work with a fairly large class of passage-time distributions, assuming only that
 \begin{equation}\begin{aligned} &\text{$X_1(e)$ and $ X_2(e)$ are continuous random variables}\\[5pt] & \text{with $\inf \operatorname{supp}\!(X_1(e))=\inf \operatorname{supp}\!(X_2(e))=0 $.}\end{aligned}\end{equation}
\begin{equation}\begin{aligned} &\text{$X_1(e)$ and $ X_2(e)$ are continuous random variables}\\[5pt] & \text{with $\inf \operatorname{supp}\!(X_1(e))=\inf \operatorname{supp}\!(X_2(e))=0 $.}\end{aligned}\end{equation}
1.2. Results and heuristics
It is well known that when
![]() $\tau \in (1,2)$
and
$\tau \in (1,2)$
and
![]() $D_i\geq 1$
, the graph generated by the configuration model contains a giant component that comprises almost all vertices, that is, the asymptotic fraction of vertices in the giant component converges to 1; see [Reference Aiello, Chung and Lu2] and [Reference Molloy and Reed23]. This means that almost all vertices will eventually be infected in the competition process described above. Recall that we are considering a graph with n vertices. Let
$D_i\geq 1$
, the graph generated by the configuration model contains a giant component that comprises almost all vertices, that is, the asymptotic fraction of vertices in the giant component converges to 1; see [Reference Aiello, Chung and Lu2] and [Reference Molloy and Reed23]. This means that almost all vertices will eventually be infected in the competition process described above. Recall that we are considering a graph with n vertices. Let
![]() $N_i(n)$
denote the number of vertices ultimately infected by type i
$N_i(n)$
denote the number of vertices ultimately infected by type i
![]() $(i=1,2)$
and define
$(i=1,2)$
and define
![]() ${N_{\mathrm{los}}}(n)=\min\{N_1(n),N_2(n)\}$
. Also write
${N_{\mathrm{los}}}(n)=\min\{N_1(n),N_2(n)\}$
. Also write
![]() $Z_i$
for the minimal passage time from the initial type i vertex to one of its neighbors, so that, assuming that i does not have any self-loops,
$Z_i$
for the minimal passage time from the initial type i vertex to one of its neighbors, so that, assuming that i does not have any self-loops,
![]() $Z_i \stackrel{d}{=} \min\{X_i(j)\colon j=1, \ldots, D_i\}$
, where
$Z_i \stackrel{d}{=} \min\{X_i(j)\colon j=1, \ldots, D_i\}$
, where
![]() $(X_i(j))_{j\geq 1}$
are i.i.d. random variables from the passage-time distribution, and with
$(X_i(j))_{j\geq 1}$
are i.i.d. random variables from the passage-time distribution, and with
![]() $Z_1$
and
$Z_1$
and
![]() $Z_2$
being independent. Note that
$Z_2$
being independent. Note that
![]() $Z_i = Z_i(n)$
, but for simplicity of notation we omit the dependence on n. Our main result states that one of the types overtakes the other by occupying all vertices except for the starting point of the other type. Furthermore, the winning type is the one that makes the first move in the process by infecting one of its neighbors.
$Z_i = Z_i(n)$
, but for simplicity of notation we omit the dependence on n. Our main result states that one of the types overtakes the other by occupying all vertices except for the starting point of the other type. Furthermore, the winning type is the one that makes the first move in the process by infecting one of its neighbors.
Theorem 1.1. (The winner takes it all but one.) Consider competing FPP on the configuration model satisfying (1.1) and (1.2). Then
![]() $\lim_{n\to\infty} {\mathbb{P}}({N_{\mathrm{los}}}(n)=1)=1$
. Furthermore,
$\lim_{n\to\infty} {\mathbb{P}}({N_{\mathrm{los}}}(n)=1)=1$
. Furthermore,
Note that it follows from (1.2) that the event
![]() $\{Z_1\gt Z_2\}$
has a non-trivial probability, implying that both types have a positive probability of winning the whole graph except for the other starting location.
$\{Z_1\gt Z_2\}$
has a non-trivial probability, implying that both types have a positive probability of winning the whole graph except for the other starting location.
To heuristically explain the result, note that for i.i.d. power-law random variables with exponent
![]() $\tau \in (1,2)$
, the sum
$\tau \in (1,2)$
, the sum
![]() $L_n$
is of order
$L_n$
is of order
![]() $n^{1/(\tau-1)+{\mathrm{o}}(1)}$
when (1.1) holds, which is also the scaling of the maximum degree. In terms of our configuration graph, this means that the bulk of the contribution to the total degree comes from a finite number of vertices with degrees of the same order as the total degree. We refer to these as giant-degree vertices or simply giants. A basic fact for the configuration model is that the number of connections between two sets of half-edges of sizes a and b is of order
$n^{1/(\tau-1)+{\mathrm{o}}(1)}$
when (1.1) holds, which is also the scaling of the maximum degree. In terms of our configuration graph, this means that the bulk of the contribution to the total degree comes from a finite number of vertices with degrees of the same order as the total degree. We refer to these as giant-degree vertices or simply giants. A basic fact for the configuration model is that the number of connections between two sets of half-edges of sizes a and b is of order
![]() $ab/L_n$
. This implies that since the giants have degree of order
$ab/L_n$
. This implies that since the giants have degree of order
![]() $n^{1/(\tau-1)+{\mathrm{o}}(1)}$
, they are all linked to each other, thus forming a tightly connected complete graph, with the number of multiple edges between two giants being of order
$n^{1/(\tau-1)+{\mathrm{o}}(1)}$
, they are all linked to each other, thus forming a tightly connected complete graph, with the number of multiple edges between two giants being of order
![]() $n^{1/(\tau-1)+{\mathrm{o}}(1)}$
. Furthermore, with high probability as
$n^{1/(\tau-1)+{\mathrm{o}}(1)}$
. Furthermore, with high probability as
![]() $n \to \infty$
, all other vertices are connected only to giants. We refer to [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26] for a more detailed description of the structure of the graph.
$n \to \infty$
, all other vertices are connected only to giants. We refer to [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26] for a more detailed description of the structure of the graph.
Theorem 1.1 is now explained in that all neighbors of the initially infected vertices are tightly connected giants, implying that the type that makes the first move by occupying one of these giants will quickly invade all other giants as well, thereby preventing the other type from making any progress at all. Indeed, the passage time between two giants is the minimum of
![]() $n^{1/(\tau-1)+{\mathrm{o}}(1)}$
(the number of multiple edges) i.i.d. edge passage times, which converges to 0 in probability under the assumption (1.2). The spread between giants is hence extremely fast, since there are many edges between giants.
$n^{1/(\tau-1)+{\mathrm{o}}(1)}$
(the number of multiple edges) i.i.d. edge passage times, which converges to 0 in probability under the assumption (1.2). The spread between giants is hence extremely fast, since there are many edges between giants.
Next, we investigate a more general scenario in which the competition starts from multiple vertices chosen uniformly at random. In our main result, for a process started from
![]() $k_i$
type i vertices, we denote the minimum passage time from the initial type i vertices to the set of neighbors of these vertices by
$k_i$
type i vertices, we denote the minimum passage time from the initial type i vertices to the set of neighbors of these vertices by
![]() $Z_{i,k_i} \stackrel{d}{=} \min\{X_i(j)\colon j=1, \ldots, \sum_{l=1}^{k_i} D_l\}$
, again with
$Z_{i,k_i} \stackrel{d}{=} \min\{X_i(j)\colon j=1, \ldots, \sum_{l=1}^{k_i} D_l\}$
, again with
![]() $Z_{1,k_1}$
and
$Z_{1,k_1}$
and
![]() $Z_{2,k_2}$
being independent.
$Z_{2,k_2}$
being independent.
Corollary 1.1. (Multiple starting points.) Consider competing FPP on the configuration model satisfying (1.1) and (1.2), and starting with
![]() $k_i$
type i vertices chosen uniformly at random, where
$k_i$
type i vertices chosen uniformly at random, where
![]() $k_i\geq 1$
is fixed
$k_i\geq 1$
is fixed
![]() $(i=1,2)$
. The number
$(i=1,2)$
. The number
![]() ${N_{\mathrm{los}}}(n)$
converges in distribution to a random variable W with
${N_{\mathrm{los}}}(n)$
converges in distribution to a random variable W with
![]() ${\mathbb{P}}(W=k_1)=1-{\mathbb{P}}(W=k_2)={\mathbb{P}}(Z_{1,k_1}\gt Z_{2,k_2})$
. More specifically,
${\mathbb{P}}(W=k_1)=1-{\mathbb{P}}(W=k_2)={\mathbb{P}}(Z_{1,k_1}\gt Z_{2,k_2})$
. More specifically,
If
![]() $k_1$
is fixed and
$k_1$
is fixed and
![]() $k_2=k_2(n)\to\infty$
as
$k_2=k_2(n)\to\infty$
as
![]() $n\to\infty$
, the conclusions remain valid with
$n\to\infty$
, the conclusions remain valid with
![]() $W\equiv k_1$
and
$W\equiv k_1$
and
![]() $\lim_{n\to\infty}{\mathbb{P}}(N_1(n)=k_1)=1$
. Similarly, if
$\lim_{n\to\infty}{\mathbb{P}}(N_1(n)=k_1)=1$
. Similarly, if
![]() $k_2$
is fixed and
$k_2$
is fixed and
![]() $k_1=k_1(n)\to\infty$
, then
$k_1=k_1(n)\to\infty$
, then
![]() $W\equiv k_2$
and
$W\equiv k_2$
and
![]() $\lim_{n\to\infty}{\mathbb{P}}(N_2(n)=k_2)=1$
.
$\lim_{n\to\infty}{\mathbb{P}}(N_2(n)=k_2)=1$
.
The result is again explained by the fact that the type that first reaches a neighbor of its initial set will soon thereafter occupy all giants in the graph, thereby preventing the other type from growing beyond its initial set. If both
![]() $k_1$
and
$k_1$
and
![]() $k_2$
are fixed, then
$k_2$
are fixed, then
![]() ${\mathbb{P}}(Z_{1,k_1}\gt Z_{2,k_2})\in(0,1)$
and both types have a positive probability of winning. If
${\mathbb{P}}(Z_{1,k_1}\gt Z_{2,k_2})\in(0,1)$
and both types have a positive probability of winning. If
![]() $k_1$
is fixed while
$k_1$
is fixed while
![]() $k_2$
grows with n, then
$k_2$
grows with n, then
![]() ${\mathbb{P}}(Z_{1,k_1}\gt Z_{2,k_2})\to 0$
, implying that the type 2 infection wins with high probability.
${\mathbb{P}}(Z_{1,k_1}\gt Z_{2,k_2})\to 0$
, implying that the type 2 infection wins with high probability.
The conditioned model. The maximum degree in our configuration graph is of order
![]() $n^{1/(\tau-1)+{\mathrm{o}}(1)}$
with
$n^{1/(\tau-1)+{\mathrm{o}}(1)}$
with
![]() $\tau\in(1,2)$
. In some situations these large degrees are artificial, and we may want to prevent this while keeping the same form of degree distribution. This may be the case, for instance, in certain types of communication networks and other networks where there are limitations on the capacity of the vertices. We therefore extend our results to the case when the degrees are conditioned to be smaller than
$\tau\in(1,2)$
. In some situations these large degrees are artificial, and we may want to prevent this while keeping the same form of degree distribution. This may be the case, for instance, in certain types of communication networks and other networks where there are limitations on the capacity of the vertices. We therefore extend our results to the case when the degrees are conditioned to be smaller than
![]() $n^{\alpha}$
for some
$n^{\alpha}$
for some
![]() $\alpha\gt 0$
. Specifically, we let the degrees be i.i.d copies of a random variable D(n), with probability mass function
$\alpha\gt 0$
. Specifically, we let the degrees be i.i.d copies of a random variable D(n), with probability mass function
Theorem 1.2. (Conditioned model.) Under assumptions (1.1) and (1.2), the conclusions of Theorem 1.1 and Corollary 1.1 are also valid for competing FPP on the configuration model with degree distribution (1.3) for any
![]() $\alpha\neq 1/(\tau +k)$
,
$\alpha\neq 1/(\tau +k)$
,
![]() $k\in\mathbb{N}$
.
$k\in\mathbb{N}$
.
When
![]() $\alpha\gt 1/(\tau-1)$
the conditioning has no effect on the graph, so the interesting regime is
$\alpha\gt 1/(\tau-1)$
the conditioning has no effect on the graph, so the interesting regime is
![]() $\alpha\lt 1/(\tau-1)$
. The maximum degree in the graph is then
$\alpha\lt 1/(\tau-1)$
. The maximum degree in the graph is then
![]() $n^\alpha$
and the total degree
$n^\alpha$
and the total degree
![]() $L_n=\sum_{i\in[n]} D_i(n)$
is of order
$L_n=\sum_{i\in[n]} D_i(n)$
is of order
![]() $n^{1+\alpha(2-\tau)}$
. This means that all vertices are still connected only to the vertices of maximal degree
$n^{1+\alpha(2-\tau)}$
. This means that all vertices are still connected only to the vertices of maximal degree
![]() $n^\alpha$
, which now play the role of the giants. In contrast to the unconditioned case, the number of giants grows to infinity with n, indicating that the time from when one giant is infected until all giants are infected may not vanish. We show, however, that the time until the infection reaches all (giant) neighbors of the type that failed to make the first move does vanish. For
$n^\alpha$
, which now play the role of the giants. In contrast to the unconditioned case, the number of giants grows to infinity with n, indicating that the time from when one giant is infected until all giants are infected may not vanish. We show, however, that the time until the infection reaches all (giant) neighbors of the type that failed to make the first move does vanish. For
![]() $\alpha\gt 1/\tau$
, this follows from the fact that the giants still form a complete graph with a large number of multiple edges between them. For
$\alpha\gt 1/\tau$
, this follows from the fact that the giants still form a complete graph with a large number of multiple edges between them. For
![]() $\alpha\lt 1/\tau$
, the giants no longer form a complete graph, but in [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26] it was shown that for
$\alpha\lt 1/\tau$
, the giants no longer form a complete graph, but in [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26] it was shown that for
![]() $\alpha\in(1/(\tau+k),1/(\tau+k-1))$
,
$\alpha\in(1/(\tau+k),1/(\tau+k-1))$
,
![]() $k \in \mathbb{N}$
, the graph distance between two giants is at most
$k \in \mathbb{N}$
, the graph distance between two giants is at most
![]() $k+1$
. This observation can be used to show that any two giants are with high probability connected by a large number of disjoint paths of bounded length. Assuming (1.2), this gives the desired conclusion, since the passage times of disjoint paths are independent and the sum of at most
$k+1$
. This observation can be used to show that any two giants are with high probability connected by a large number of disjoint paths of bounded length. Assuming (1.2), this gives the desired conclusion, since the passage times of disjoint paths are independent and the sum of at most
![]() $k+1$
i.i.d. passage times still has 0 as the infimum of its support. Our results do not cover the boundary cases
$k+1$
i.i.d. passage times still has 0 as the infimum of its support. Our results do not cover the boundary cases
![]() $\alpha = 1/(\tau + k)$
for
$\alpha = 1/(\tau + k)$
for
![]() $k \in \mathbb{N}$
, since the graph distance between two giants then potentially depends on the slowly varying function in (1.1); see [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26], where it is conjectured to be supported on at most two values.
$k \in \mathbb{N}$
, since the graph distance between two giants then potentially depends on the slowly varying function in (1.1); see [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26], where it is conjectured to be supported on at most two values.
The erased model. The configuration model allows for self-loops and multiple edges between vertices. Indeed, for
![]() $\tau\in(1,2)$
, these structures are abundant and the occurrence of multiple edges is one of the explanations for the behavior of the competition process. In some situations, however, self-loops and multiple edges are not desirable, for instance when modeling acquaintance networks or email networks where the multiplicity of a contact is not relevant, but one only cares about whether two individuals have contact at all. One option is then to first generate the graph and then delete all self-loops and merge all multiple edges. This is known as the erased configuration model.
$\tau\in(1,2)$
, these structures are abundant and the occurrence of multiple edges is one of the explanations for the behavior of the competition process. In some situations, however, self-loops and multiple edges are not desirable, for instance when modeling acquaintance networks or email networks where the multiplicity of a contact is not relevant, but one only cares about whether two individuals have contact at all. One option is then to first generate the graph and then delete all self-loops and merge all multiple edges. This is known as the erased configuration model.
The topology of a graph generated by the erased configuration model was studied in [Reference Bhamidi, van der Hofstad and Hooghiemstra11] under the slightly stronger assumption on F that there exists a constant
![]() $c>0$
such that
$c>0$
such that
As a result of the erasure, there are no longer multiple edges between vertices, but the set of neighbors of a given vertex remains the same. It was shown that the number of joint neighbors of two given giants, with degree of order
![]() $n^{1/(\tau-1)}$
before erasure, is of order n, so that two giants are hence connected by a large number of disjoint two-step paths. Hence (1.2) implies that the passage time between two giants is also vanishing in the erased model, giving rise to the same behavior for the competition process. The behavior persists also in the erased version of the conditioned model, since the disjoint paths constructed between giants in the proof of Theorem 1.2 do not rely on multiple edges.
$n^{1/(\tau-1)}$
before erasure, is of order n, so that two giants are hence connected by a large number of disjoint two-step paths. Hence (1.2) implies that the passage time between two giants is also vanishing in the erased model, giving rise to the same behavior for the competition process. The behavior persists also in the erased version of the conditioned model, since the disjoint paths constructed between giants in the proof of Theorem 1.2 do not rely on multiple edges.
Theorem 1.3. (Erased models.) The conclusions of Theorem 1.1 and Corollary 1.1 are also valid for competing FPP on the erased configuration model satisfying (1.2) and (1.4). Furthermore, under assumptions (1.1) and (1.2), the conclusions are valid for the erased version of the configuration model with conditioned degree distribution (1.3) for
![]() $\alpha\neq 1/(\tau +k)$
,
$\alpha\neq 1/(\tau +k)$
,
![]() $k\in\mathbb{N}$
.
$k\in\mathbb{N}$
.
The rest of the paper is organized so that Section 2 contains the proofs, followed by some suggestions for further work in Section 3.
2. Proofs
This section contains the proofs. We first give a more formal definition of giant-degree vertices and then show a key proposition stating that the passage time between two giants is vanishing in all three instances of the model (the original one, the conditioned model, and the erased model). With this at hand, all results follow without much further effort. We consider the case with two initial points and then briefly describe at the end of the section how the arguments can be generalized to larger initial sets.
We start by defining the giant-degree vertices as those with a degree of the same order as the maximal degree in the graph. To this end, let
![]() $\{u_n\}$
be a sequence satisfying
$\{u_n\}$
be a sequence satisfying
It follows from standard extreme value theory that
![]() $u_n$
is the scaling of the total degree
$u_n$
is the scaling of the total degree
![]() $L_n$
as well as the maximal degrees in the graph; see e.g. [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26, Lemma 2.1], where this is formulated in the context of the configuration model. Furthermore, it follows from (1.1) that
$L_n$
as well as the maximal degrees in the graph; see e.g. [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26, Lemma 2.1], where this is formulated in the context of the configuration model. Furthermore, it follows from (1.1) that
![]() $\ell(u_n) u_n^{-(\tau-1)} =(1+{\mathrm{o}}(1))/n$
and hence that there exists a slowly varying function
$\ell(u_n) u_n^{-(\tau-1)} =(1+{\mathrm{o}}(1))/n$
and hence that there exists a slowly varying function
![]() $n\mapsto l(n)$
such that
$n\mapsto l(n)$
such that
Definition 2.1. (Giant-degree vertices.) Fix a sequence
![]() $({\varepsilon}_n)$
such that
$({\varepsilon}_n)$
such that
![]() ${\varepsilon}_n \searrow 0$
arbitrarily slowly with
${\varepsilon}_n \searrow 0$
arbitrarily slowly with
![]() ${\varepsilon}_n^{-1}$
slowly varying. The set of giant-degree vertices (or giants) is given by
${\varepsilon}_n^{-1}$
slowly varying. The set of giant-degree vertices (or giants) is given by
![]() $\mathcal{H}_n = \{ h\colon D_h > {\varepsilon}_n u_n \}$
in the original and the erased model, and
$\mathcal{H}_n = \{ h\colon D_h > {\varepsilon}_n u_n \}$
in the original and the erased model, and
![]() $\mathcal{H}_n = \{ h\colon D_h(n) > {\varepsilon}_n n^\alpha \}$
in the conditioned model.
$\mathcal{H}_n = \{ h\colon D_h(n) > {\varepsilon}_n n^\alpha \}$
in the conditioned model.
Note that
![]() $D_h$
refers to the degree before erasure in the erased model and is hence the same as in the original model. Vertices in
$D_h$
refers to the degree before erasure in the erased model and is hence the same as in the original model. Vertices in
![]() $\mathcal{H}_n^c=[n]\setminus \mathcal{H}_n$
are referred to as normal vertices. An important consequence of the definition of giant-degree vertices is that other vertices are connected solely to them.
$\mathcal{H}_n^c=[n]\setminus \mathcal{H}_n$
are referred to as normal vertices. An important consequence of the definition of giant-degree vertices is that other vertices are connected solely to them.
Lemma 2.1. (Neighbors are giants.) Assume that (1.1) holds. A uniformly chosen vertex is with high probability only connected to giant-degree vertices.
Remark 2.1. For a set of uniformly chosen vertices, pick one of the vertices in proportion to its (erased) degree. It follows from the proof of the lemma that this vertex is with high probability only connected to giant-degree vertices. This observation will be used to establish Corollary 1.1.
Proof. The lemma is a consequence of the fact that the total degree of normal vertices is negligible compared to the total degree of the giants. This is proved in [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26, Lemmas 2.2 and 3.1] for the original and the erased model, respectively, but since the definitions of giant-degree vertices differ slightly from ours we give a brief sketch here.
Let
![]() $D_{\scriptscriptstyle (1)}\leq D_{\scriptscriptstyle (2)}\leq \cdots \leq D_{\scriptscriptstyle (n)}$
denote the order statistics of the degrees, so that
$D_{\scriptscriptstyle (1)}\leq D_{\scriptscriptstyle (2)}\leq \cdots \leq D_{\scriptscriptstyle (n)}$
denote the order statistics of the degrees, so that
![]() $D_{\scriptscriptstyle (1)}$
is the smallest degree,
$D_{\scriptscriptstyle (1)}$
is the smallest degree,
![]() $D_{\scriptscriptstyle (2)}$
the second smallest, and so on. Also, let
$D_{\scriptscriptstyle (2)}$
the second smallest, and so on. Also, let
![]() $K_n$
denote the total number of half-edges belonging to non-giants. It follows from [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26, Lemma 2.1] that
$K_n$
denote the total number of half-edges belonging to non-giants. It follows from [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26, Lemma 2.1] that
![]() ${\mathbb{P}}(D_{\scriptscriptstyle (n-k)}\geq {\varepsilon}_nu_n)\to 1$
for any k, and hence, with high probability,
${\mathbb{P}}(D_{\scriptscriptstyle (n-k)}\geq {\varepsilon}_nu_n)\to 1$
for any k, and hence, with high probability,
Also, by [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26, Lemma 2.1],
where
![]() $(\xi_i)_{i\geq 1}$
are almost surely finite and non-negative random variables such that
$(\xi_i)_{i\geq 1}$
are almost surely finite and non-negative random variables such that
![]() $\sum_{i=1}^\infty\xi_i<\infty$
. Since this holds for any k, we conclude that
$\sum_{i=1}^\infty\xi_i<\infty$
. Since this holds for any k, we conclude that
![]() $K_n/L_n\to 0$
in probability so that half-edges of a randomly chosen vertex in the original model are with high probability connected to half-edges of giant-degree vertices. Since giants in the erased model are defined based on the non-erased degree, we draw the same conclusion there.
$K_n/L_n\to 0$
in probability so that half-edges of a randomly chosen vertex in the original model are with high probability connected to half-edges of giant-degree vertices. Since giants in the erased model are defined based on the non-erased degree, we draw the same conclusion there.
To deal with the conditioned model, with degree distribution given by (1.3), write
![]() $M_n$
for the total degree in this case. Then
$M_n$
for the total degree in this case. Then
 \begin{equation*}{\mathbb{E}}[M_n]=\dfrac{n}{F(n^\alpha)}\sum_{j=1}^{n^\alpha}[{\mathbb{P}}(D>j)-{\mathbb{P}}(D>n^\alpha)].\end{equation*}
\begin{equation*}{\mathbb{E}}[M_n]=\dfrac{n}{F(n^\alpha)}\sum_{j=1}^{n^\alpha}[{\mathbb{P}}(D>j)-{\mathbb{P}}(D>n^\alpha)].\end{equation*}
Recall (1.1). By Karamata’s theorem [Reference Bingham, Goldie and Teugels13, Theorems 1.7.2 and 2.6.1],
 \begin{equation*} \sum_{j=1}^{n^\alpha}{\mathbb{P}}(D>j)=(1+{\mathrm{o}}(1)) \ell(n^\alpha) (2-\tau)^{-1} n^{\alpha(2-\tau)}, \end{equation*}
\begin{equation*} \sum_{j=1}^{n^\alpha}{\mathbb{P}}(D>j)=(1+{\mathrm{o}}(1)) \ell(n^\alpha) (2-\tau)^{-1} n^{\alpha(2-\tau)}, \end{equation*}
while
![]() $n^\alpha{\mathbb{P}}(D>n^\alpha)=\ell(n^\alpha)n^{\alpha(2-\tau)}$
. Thus
$n^\alpha{\mathbb{P}}(D>n^\alpha)=\ell(n^\alpha)n^{\alpha(2-\tau)}$
. Thus
Further,
since
![]() $\alpha\lt 1+\alpha(2-\tau)$
. In particular,
$\alpha\lt 1+\alpha(2-\tau)$
. In particular,
![]() $M_n/{\mathbb{E}}[M_n]\stackrel{{\mathbb P}}{\longrightarrow} 1.$
Similarly, with
$M_n/{\mathbb{E}}[M_n]\stackrel{{\mathbb P}}{\longrightarrow} 1.$
Similarly, with
![]() $K_n^\alpha$
denoting the total degree of non-giants,
$K_n^\alpha$
denoting the total degree of non-giants,
 \begin{equation*}{\mathbb{E}}[K_n^\alpha]\leq \dfrac{n}{F(n^\alpha)}\sum_{j=1}^{{\varepsilon}_n n^\alpha}{\mathbb{P}}(D>j)=(1+{\mathrm{o}}(1)) \ell({\varepsilon}_n n^\alpha) (2-\tau)^{-1} ({\varepsilon}_n n)^{\alpha(2-\tau)}={\mathrm{o}}({\mathbb{E}}[M_n]),\end{equation*}
\begin{equation*}{\mathbb{E}}[K_n^\alpha]\leq \dfrac{n}{F(n^\alpha)}\sum_{j=1}^{{\varepsilon}_n n^\alpha}{\mathbb{P}}(D>j)=(1+{\mathrm{o}}(1)) \ell({\varepsilon}_n n^\alpha) (2-\tau)^{-1} ({\varepsilon}_n n)^{\alpha(2-\tau)}={\mathrm{o}}({\mathbb{E}}[M_n]),\end{equation*}
since
![]() $\alpha\lt 1/(\tau-1)$
and since
$\alpha\lt 1/(\tau-1)$
and since
![]() $\ell({\varepsilon}_n n^\alpha)/\ell(n^\alpha)\leq c {\varepsilon}_n^{-\delta}$
for any
$\ell({\varepsilon}_n n^\alpha)/\ell(n^\alpha)\leq c {\varepsilon}_n^{-\delta}$
for any
![]() $\delta>0$
by Potter’s theorem [Reference Bingham, Goldie and Teugels13, Theorem 1.5.6]. Thus
$\delta>0$
by Potter’s theorem [Reference Bingham, Goldie and Teugels13, Theorem 1.5.6]. Thus
![]() $K^\alpha_n/M_n\stackrel{{\mathbb P}}{\longrightarrow} 0$
.
$K^\alpha_n/M_n\stackrel{{\mathbb P}}{\longrightarrow} 0$
.
For two given vertices u and v, write
![]() $T_i(u,v)$
for the first passage time between u and v in a one-type FPP process based on
$T_i(u,v)$
for the first passage time between u and v in a one-type FPP process based on
![]() $(X_i(e))_e$
, that is,
$(X_i(e))_e$
, that is,
 \begin{equation}T_i(u,v)=\inf\Biggl\{\sum_{e\in\Gamma}X_i(e)\colon \Gamma\ \text{is a path between} \textit{u} \, \text{and} \, \textit{v}\Biggr\}.\end{equation}
\begin{equation}T_i(u,v)=\inf\Biggl\{\sum_{e\in\Gamma}X_i(e)\colon \Gamma\ \text{is a path between} \textit{u} \, \text{and} \, \textit{v}\Biggr\}.\end{equation}
The following key result states that the first passage time between two giants is vanishing.
Proposition 2.1. (The infection spreads quickly between giants.) Consider a configuration model obtained from the original, the conditioned, the erased, or the conditioned
![]() $+$
erased model and let
$+$
erased model and let
![]() $h_i$
be a randomly chosen neighbor of vertex i
$h_i$
be a randomly chosen neighbor of vertex i
![]() $(i=1,2)$
. If (1.1) and (1.2) hold, then, for any
$(i=1,2)$
. If (1.1) and (1.2) hold, then, for any
![]() ${\varepsilon}\gt 0$
,
${\varepsilon}\gt 0$
,
Remark 2.2. By Lemma 2.1, with high probability,
![]() $h_1$
and
$h_1$
and
![]() $h_2$
are indeed giants. The conclusion of Proposition 2.1 is in fact valid for a wide choice of giant-degree vertices, but we formulate it for neighbors of vertices 1 and 2 since this is what we will apply it to. In establishing Corollary 1.1, we will instead of
$h_2$
are indeed giants. The conclusion of Proposition 2.1 is in fact valid for a wide choice of giant-degree vertices, but we formulate it for neighbors of vertices 1 and 2 since this is what we will apply it to. In establishing Corollary 1.1, we will instead of
![]() $h_1$
apply it to the vertex
$h_1$
apply it to the vertex
![]() $h'_{\!\!1}$
to which the edge with the smallest passage time among all edges incident to the
$h'_{\!\!1}$
to which the edge with the smallest passage time among all edges incident to the
![]() $k_1$
initial type 1 vertices is attached. By Remark 2.1, the vertex
$k_1$
initial type 1 vertices is attached. By Remark 2.1, the vertex
![]() $h'_{\!\!1}$
also has a giant degree.
$h'_{\!\!1}$
also has a giant degree.
Proof. We prove the claim separately for the four versions of the model, and end by treating the combination of the conditioned and the erased version. By Lemma 2.1, both
![]() $h_1$
and
$h_1$
and
![]() $h_2$
are with high probability giant-degree vertices. We will therefore assume throughout that their degrees are at least
$h_2$
are with high probability giant-degree vertices. We will therefore assume throughout that their degrees are at least
![]() ${\varepsilon}_n u_n$
in the original model and its erased version, and at least
${\varepsilon}_n u_n$
in the original model and its erased version, and at least
![]() ${\varepsilon}_n n^{\alpha}$
in the conditioned model and its erased version (recall that in the erased models giants are defined according to their degree before erasure).
${\varepsilon}_n n^{\alpha}$
in the conditioned model and its erased version (recall that in the erased models giants are defined according to their degree before erasure).
First consider the original configuration model and let
![]() $E(h_1,h_2)$
denote the number of edges between
$E(h_1,h_2)$
denote the number of edges between
![]() $h_1$
and
$h_1$
and
![]() $h_2$
. Since there are at least
$h_2$
. Since there are at least
![]() ${\varepsilon}_n u_n -1$
half-edges attached to each one of
${\varepsilon}_n u_n -1$
half-edges attached to each one of
![]() $h_1$
and
$h_1$
and
![]() $h_2$
, in addition to the ones that are used to connect to vertices 1 and 2, respectively, the variable
$h_2$
, in addition to the ones that are used to connect to vertices 1 and 2, respectively, the variable
![]() $E(h_1,h_2)$
is stochastically larger than a binomial variable with parameters
$E(h_1,h_2)$
is stochastically larger than a binomial variable with parameters
![]() $({\varepsilon}_nu_n-1)/2$
and
$({\varepsilon}_nu_n-1)/2$
and
![]() $({\varepsilon}_n u_n-1)/(2(L_n-2))$
. Indeed, when we go through the first half of the half-edges of
$({\varepsilon}_n u_n-1)/(2(L_n-2))$
. Indeed, when we go through the first half of the half-edges of
![]() $h_1$
and check if they are connected to a half-edge of
$h_1$
and check if they are connected to a half-edge of
![]() $h_2$
, the outcome is stochastically larger than a sequence of i.i.d. trials with the specified success probability, since there are then still at least
$h_2$
, the outcome is stochastically larger than a sequence of i.i.d. trials with the specified success probability, since there are then still at least
![]() $({\varepsilon}_nu_n-1)/2$
half-edges left to connect to at
$({\varepsilon}_nu_n-1)/2$
half-edges left to connect to at
![]() $h_2$
while the total number of available half-edges is at most
$h_2$
while the total number of available half-edges is at most
![]() $L_n-2$
. It follows from [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26, Lemma 2.1] that
$L_n-2$
. It follows from [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26, Lemma 2.1] that
![]() ${\mathbb{P}}(L_n<u_n^{1+\delta})\to 1$
as
${\mathbb{P}}(L_n<u_n^{1+\delta})\to 1$
as
![]() $n\to \infty$
for any
$n\to \infty$
for any
![]() $\delta>0$
. Let
$\delta>0$
. Let
![]() $Y_n$
denote a binomial random variable with parameters
$Y_n$
denote a binomial random variable with parameters
![]() ${\varepsilon}_nu_n/4$
and
${\varepsilon}_nu_n/4$
and
![]() ${\varepsilon}_nu_n/(4u_n^{1+\delta})$
. On the event
${\varepsilon}_nu_n/(4u_n^{1+\delta})$
. On the event
![]() $\{L_n<u_n^{1+\delta}\}$
, we then have that
$\{L_n<u_n^{1+\delta}\}$
, we then have that
![]() $E(h_1,h_2)$
is stochastically larger than
$E(h_1,h_2)$
is stochastically larger than
![]() $Y_n$
. Now recall Janson’s inequality for a binomial random variable
$Y_n$
. Now recall Janson’s inequality for a binomial random variable
![]() $Y_n$
stating that
$Y_n$
stating that
see [Reference Janson22, Theorem 1]. Picking
![]() $\delta \in (0,1)$
and defining
$\delta \in (0,1)$
and defining
it follows from Janson’s inequality with
![]() $t=f(n)$
that
$t=f(n)$
that
where
![]() $C>0$
is a constant. By recalling (2.1) and the fact that
$C>0$
is a constant. By recalling (2.1) and the fact that
![]() ${\varepsilon}_n^{-1}$
is slowly varying, we conclude that
${\varepsilon}_n^{-1}$
is slowly varying, we conclude that
![]() ${\mathbb{P}}(E(h_1,h_2) \leq f(n))\to 0$
as
${\mathbb{P}}(E(h_1,h_2) \leq f(n))\to 0$
as
![]() $n\to\infty$
, with
$n\to\infty$
, with
![]() $f(n)\to\infty$
. The passage time between
$f(n)\to\infty$
. The passage time between
![]() $h_1$
and
$h_1$
and
![]() $h_2$
is smaller than the minimum of the edge passage times of the direct edges between them, implying that
$h_2$
is smaller than the minimum of the edge passage times of the direct edges between them, implying that
The assumption (1.2) guarantees that the first term on the right-hand side tends to 0, which completes the proof for the original model.
Moving on to the (non-conditioned) erased model, we write N(u, v) for the number of joint neighbors of the vertices u and v. It was shown in [Reference Bhamidi, van der Hofstad and Hooghiemstra11, Lemma 6.7] that
![]() $N(h_1,h_2)/n\stackrel{d}{\to}Y$
as
$N(h_1,h_2)/n\stackrel{d}{\to}Y$
as
![]() $n\to\infty$
, where
$n\to\infty$
, where
![]() $h_1$
and
$h_1$
and
![]() $h_2$
are giant-degree vertices and Y a proper random variable. It follows that
$h_2$
are giant-degree vertices and Y a proper random variable. It follows that
![]() ${\mathbb{P}}(N(h_1,h_2) \leq n^\gamma)\to 0$
for any
${\mathbb{P}}(N(h_1,h_2) \leq n^\gamma)\to 0$
for any
![]() $\gamma<1$
. Giant vertices are hence connected to each other by a large number of (disjoint) two-step paths. For
$\gamma<1$
. Giant vertices are hence connected to each other by a large number of (disjoint) two-step paths. For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $X^{\scriptscriptstyle(2)}_i(j)\stackrel{d}{=}X_i(e)+X_i(\tilde{e})$
denote the total passage time of the jth such path. Then
$X^{\scriptscriptstyle(2)}_i(j)\stackrel{d}{=}X_i(e)+X_i(\tilde{e})$
denote the total passage time of the jth such path. Then
Here
![]() $(X^{\scriptscriptstyle(2)}_i(j))_{j\geq 1}$
are i.i.d. and inherit the property that inf supp
$(X^{\scriptscriptstyle(2)}_i(j))_{j\geq 1}$
are i.i.d. and inherit the property that inf supp
![]() $(X^{\scriptscriptstyle(2)}_i(j))=0$
from their summands, implying that the first term converges to 0 for any
$(X^{\scriptscriptstyle(2)}_i(j))=0$
from their summands, implying that the first term converges to 0 for any
![]() $\gamma>0$
. This proves the claim.
$\gamma>0$
. This proves the claim.
Next, consider the model where the degrees are conditioned to be at most
![]() $n^\alpha$
, with
$n^\alpha$
, with
![]() $\alpha\lt 1/(\tau-1)$
. For
$\alpha\lt 1/(\tau-1)$
. For
![]() $\alpha\gt 1/\tau$
the graph still has the same topology in the sense that the giants constitute a tightly connected complete graph, that is, the number of multiple edges between them grows to infinity with n. Let
$\alpha\gt 1/\tau$
the graph still has the same topology in the sense that the giants constitute a tightly connected complete graph, that is, the number of multiple edges between them grows to infinity with n. Let
![]() $E^\alpha(h_1,h_2)$
denote the number of edges connecting the two giants
$E^\alpha(h_1,h_2)$
denote the number of edges connecting the two giants
![]() $h_1$
and
$h_1$
and
![]() $h_2$
. In the same way as when dealing with the original model, the number
$h_2$
. In the same way as when dealing with the original model, the number
![]() $E^\alpha(h_1,h_2)$
can be stochastically bounded from below by a binomial random variable
$E^\alpha(h_1,h_2)$
can be stochastically bounded from below by a binomial random variable
![]() $Y^\alpha_n$
with parameters
$Y^\alpha_n$
with parameters
![]() ${\varepsilon}_nn^\alpha/4$
and
${\varepsilon}_nn^\alpha/4$
and
![]() ${\varepsilon}_nn^\alpha/(4n^{1+\alpha(2-\tau)+\delta})$
, and mean
${\varepsilon}_nn^\alpha/(4n^{1+\alpha(2-\tau)+\delta})$
, and mean
![]() ${\mathbb{E}}[Y^\alpha_n]={\varepsilon}_n^2 n^{\alpha\tau-1-\delta}/16$
. Picking
${\mathbb{E}}[Y^\alpha_n]={\varepsilon}_n^2 n^{\alpha\tau-1-\delta}/16$
. Picking
![]() $\delta\in (0,\alpha\tau-1)$
, the same argument as for the original model yields
$\delta\in (0,\alpha\tau-1)$
, the same argument as for the original model yields
![]() ${\mathbb{P}}(T_i(h_1,h_2) \geq {\varepsilon})\to 0$
.
${\mathbb{P}}(T_i(h_1,h_2) \geq {\varepsilon})\to 0$
.
For
![]() $\alpha\lt 1/\tau$
, we have to work slightly harder. Fix
$\alpha\lt 1/\tau$
, we have to work slightly harder. Fix
![]() $k\in\mathbb{N}$
. It was shown in [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26, Lemma 3.3] that when
$k\in\mathbb{N}$
. It was shown in [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski26, Lemma 3.3] that when
![]() $\alpha\in(1/(\tau+k),1/(\tau+k-1))$
, the graph distance between any two giant-degree vertices is with high probability at most
$\alpha\in(1/(\tau+k),1/(\tau+k-1))$
, the graph distance between any two giant-degree vertices is with high probability at most
![]() $k+1$
. We claim that in fact there is a large number of disjoint paths of length at most
$k+1$
. We claim that in fact there is a large number of disjoint paths of length at most
![]() $2(k+1)$
between two giants. To see this, first note that the number of giant-degree vertices is given by
$2(k+1)$
between two giants. To see this, first note that the number of giant-degree vertices is given by
![]() $|\mathcal{H}_n|=\sum_{v\in[n]}\textbf{1}_{\{D_v(n)>{\varepsilon}_n n^\alpha\}}$
, with
$|\mathcal{H}_n|=\sum_{v\in[n]}\textbf{1}_{\{D_v(n)>{\varepsilon}_n n^\alpha\}}$
, with
 \begin{align*} {\mathbb{E}}[|\mathcal{H}_n|] & = n \mathbb{P}(D(n) > {\varepsilon}_n n^{\alpha}) \\[5pt] & = n \dfrac{F(n^{\alpha}) - F({\varepsilon}_n n^{\alpha})}{F(n^{\alpha})}\\[5pt] & \geq n(F(n^{\alpha}) - F({\varepsilon}_n n^{\alpha})) \\[5pt]&= \ell(n)n^{1-\alpha(\tau-1)},\end{align*}
\begin{align*} {\mathbb{E}}[|\mathcal{H}_n|] & = n \mathbb{P}(D(n) > {\varepsilon}_n n^{\alpha}) \\[5pt] & = n \dfrac{F(n^{\alpha}) - F({\varepsilon}_n n^{\alpha})}{F(n^{\alpha})}\\[5pt] & \geq n(F(n^{\alpha}) - F({\varepsilon}_n n^{\alpha})) \\[5pt]&= \ell(n)n^{1-\alpha(\tau-1)},\end{align*}
where we have used that
![]() ${\varepsilon}_n^{-1}$
is slowly varying and where
${\varepsilon}_n^{-1}$
is slowly varying and where
![]() $n\mapsto \ell(n)$
denotes a slowly varying function (that may differ from previous occurrences). Since
$n\mapsto \ell(n)$
denotes a slowly varying function (that may differ from previous occurrences). Since
![]() $\alpha\lt 1/(\tau-1)$
, we have
$\alpha\lt 1/(\tau-1)$
, we have
![]() $1-\alpha(\tau-1)>0$
, and an application of Janson’s inequality (2.3) yields
$1-\alpha(\tau-1)>0$
, and an application of Janson’s inequality (2.3) yields
with high probability for
![]() $\gamma\in(0,1-\alpha(\tau-1))$
. The number of giant-degree vertices hence grows to infinity with n. With this observation at hand, we proceed to construct a growing number of paths between
$\gamma\in(0,1-\alpha(\tau-1))$
. The number of giant-degree vertices hence grows to infinity with n. With this observation at hand, we proceed to construct a growing number of paths between
![]() $h_1$
and
$h_1$
and
![]() $h_2$
that are with high probability disjoint.
$h_2$
that are with high probability disjoint.

Figure 1. Construction of the m disjoint paths of length at most
![]() $2(k+1)$
from
$2(k+1)$
from
![]() $h_1$
to
$h_1$
to
![]() $h_2$
, where
$h_2$
, where
![]() $m=m(n)$
grows to infinity with n.
$m=m(n)$
grows to infinity with n.
Let
![]() $\Gamma_1$
be a path from
$\Gamma_1$
be a path from
![]() $h_1$
to
$h_1$
to
![]() $h_2$
of length at most
$h_2$
of length at most
![]() $k+1$
. Pick a giant vertex
$k+1$
. Pick a giant vertex
![]() $x_2 \notin \Gamma_1$
; this is possible with high probability since the number of giant-degree vertices grows to infinity with n. Then there exist paths
$x_2 \notin \Gamma_1$
; this is possible with high probability since the number of giant-degree vertices grows to infinity with n. Then there exist paths
![]() $\Gamma'_{\!\!2}$
and
$\Gamma'_{\!\!2}$
and
![]() $\Gamma''_{\!\!\!2}$
of length at most
$\Gamma''_{\!\!\!2}$
of length at most
![]() $k+1$
connecting
$k+1$
connecting
![]() $x_2$
to
$x_2$
to
![]() $h_1$
and
$h_1$
and
![]() $h_2$
, respectively. Let
$h_2$
, respectively. Let
![]() $\Gamma_2 = \Gamma'_{\!\!2} \cup \Gamma''_{\!\!\!2}$
, where loops arising from common vertices in
$\Gamma_2 = \Gamma'_{\!\!2} \cup \Gamma''_{\!\!\!2}$
, where loops arising from common vertices in
![]() $\Gamma'_{\!\!2}$
and
$\Gamma'_{\!\!2}$
and
![]() $\Gamma''_{\!\!\!2}$
are removed. Then
$\Gamma''_{\!\!\!2}$
are removed. Then
![]() $\Gamma_2$
constitutes a path between
$\Gamma_2$
constitutes a path between
![]() $h_1$
and
$h_1$
and
![]() $h_2$
of length at most
$h_2$
of length at most
![]() $2(k+1)$
. We claim that with high probability as
$2(k+1)$
. We claim that with high probability as
![]() $n \to \infty$
, the paths
$n \to \infty$
, the paths
![]() $\Gamma_1$
and
$\Gamma_1$
and
![]() $\Gamma_2$
are disjoint, except for the first and last vertices
$\Gamma_2$
are disjoint, except for the first and last vertices
![]() $h_1$
and
$h_1$
and
![]() $h_2$
. Let
$h_2$
. Let
![]() $B_n=\{M_n>\ell(n)n^{1+\alpha(2-\tau)}\}$
and recall from the proof of Lemma 2.1 that
$B_n=\{M_n>\ell(n)n^{1+\alpha(2-\tau)}\}$
and recall from the proof of Lemma 2.1 that
![]() ${\mathbb{P}}(B_n)\to 1$
. Conditionally on all degrees, the probability that there is an edge between two vertices u and v is at most
${\mathbb{P}}(B_n)\to 1$
. Conditionally on all degrees, the probability that there is an edge between two vertices u and v is at most
![]() $D_u(n)D_{v}(n)/M_n$
. Using the fact that the degrees are at most
$D_u(n)D_{v}(n)/M_n$
. Using the fact that the degrees are at most
![]() $n^\alpha$
, and letting
$n^\alpha$
, and letting
![]() $u \leftrightarrow v$
denote the event that there is an edge between u and v, we obtain
$u \leftrightarrow v$
denote the event that there is an edge between u and v, we obtain
Note that if
![]() $\Gamma_1$
and
$\Gamma_1$
and
![]() $\Gamma_2$
are not disjoint, then there must exist a vertex in
$\Gamma_2$
are not disjoint, then there must exist a vertex in
![]() $\Gamma_1$
that is connected to a vertex in
$\Gamma_1$
that is connected to a vertex in
![]() $\Gamma_2$
. With
$\Gamma_2$
. With
![]() $A_2$
denoting the event that
$A_2$
denoting the event that
![]() $\Gamma_1$
and
$\Gamma_1$
and
![]() $\Gamma_2$
are disjoint, we hence have
$\Gamma_2$
are disjoint, we hence have
Next, pick a giant vertex
![]() $x_3 \notin \Gamma_1 \cup \Gamma_2$
connected to
$x_3 \notin \Gamma_1 \cup \Gamma_2$
connected to
![]() $h_1$
and
$h_1$
and
![]() $h_2$
by paths
$h_2$
by paths
![]() $\Gamma'_{\!\!3}$
and
$\Gamma'_{\!\!3}$
and
![]() $\Gamma''_{\!\!\!3}$
, respectively, of length at most
$\Gamma''_{\!\!\!3}$
, respectively, of length at most
![]() $k+1$
. Let
$k+1$
. Let
![]() $\Gamma_3 = \Gamma'_{\!\!3} \cup \Gamma''_{\!\!\!3}$
, again removing any loops. Then
$\Gamma_3 = \Gamma'_{\!\!3} \cup \Gamma''_{\!\!\!3}$
, again removing any loops. Then
![]() $\Gamma_3$
is a path from
$\Gamma_3$
is a path from
![]() $h_1$
to
$h_1$
to
![]() $h_2$
of length at most
$h_2$
of length at most
![]() $2(k+1)$
. Let
$2(k+1)$
. Let
![]() $A_3$
denote the event that
$A_3$
denote the event that
![]() $\Gamma_3$
and
$\Gamma_3$
and
![]() $\Gamma_1\cup \Gamma_2$
are disjoint. Since
$\Gamma_1\cup \Gamma_2$
are disjoint. Since
![]() $|\Gamma_1\cup \Gamma_2|\leq 3(k+1)$
, we obtain as above that
$|\Gamma_1\cup \Gamma_2|\leq 3(k+1)$
, we obtain as above that
Iterating this construction, in step m we pick a giant vertex
![]() $x_m$
connected to
$x_m$
connected to
![]() $h_1$
and
$h_1$
and
![]() $h_2$
by paths
$h_2$
by paths
![]() $\Gamma'_{\!\!m}$
and
$\Gamma'_{\!\!m}$
and
![]() $\Gamma''_{\!\!\!m}$
, respectively, of length at most
$\Gamma''_{\!\!\!m}$
, respectively, of length at most
![]() $k+1$
, and set
$k+1$
, and set
![]() $\Gamma_m=\Gamma'_{\!\!m}\cup \Gamma''_{\!\!\!m}$
with loops removed. See Figure 1 for the above construction. Define
$\Gamma_m=\Gamma'_{\!\!m}\cup \Gamma''_{\!\!\!m}$
with loops removed. See Figure 1 for the above construction. Define
Then, since
![]() $|\Gamma_m|\leq 2(k+1)$
and
$|\Gamma_m|\leq 2(k+1)$
and
![]() $|\Gamma_1\cup\cdots\cup\Gamma_{m-1}|\leq (2m-3)(k+1)$
, we can bound
$|\Gamma_1\cup\cdots\cup\Gamma_{m-1}|\leq (2m-3)(k+1)$
, we can bound
Let
![]() $\bar{A}_m=\cap_{j=2}^mA_j$
denote the event that there is no overlap between any of the paths that we have constructed. Then
$\bar{A}_m=\cap_{j=2}^mA_j$
denote the event that there is no overlap between any of the paths that we have constructed. Then
 \begin{align*} {\mathbb{P}}(\bar{A}_m\cap B_n) & = {\mathbb{P}}\Biggl(\bigcup_{j=2}^m A_j^c\cap B_n\Biggr) \\[5pt] &\leq \sum_{j=2}^m \mathbb{P}(A_j^c\cap B_n) \\[5pt]& \leq 2(k+1)^2 \ell(n)n^{\alpha \tau -1}\sum_{j=2}^m (2j-3) \\[5pt]&\leq 2(k+1)^2 m^2\ell(n)n^{\alpha \tau -1}.\end{align*}
\begin{align*} {\mathbb{P}}(\bar{A}_m\cap B_n) & = {\mathbb{P}}\Biggl(\bigcup_{j=2}^m A_j^c\cap B_n\Biggr) \\[5pt] &\leq \sum_{j=2}^m \mathbb{P}(A_j^c\cap B_n) \\[5pt]& \leq 2(k+1)^2 \ell(n)n^{\alpha \tau -1}\sum_{j=2}^m (2j-3) \\[5pt]&\leq 2(k+1)^2 m^2\ell(n)n^{\alpha \tau -1}.\end{align*}
Since
![]() $\alpha\lt 1/\tau$
, we have
$\alpha\lt 1/\tau$
, we have
![]() $\alpha\tau-1<0$
. Pick
$\alpha\tau-1<0$
. Pick
![]() $\delta\in(0,1-\alpha\tau)$
and take
$\delta\in(0,1-\alpha\tau)$
and take
![]() $m=m(n)=n^{\delta/2}$
so that
$m=m(n)=n^{\delta/2}$
so that
![]() ${\mathbb{P}}(\bar{A}_{m(n)})\to 0$
. Note that
${\mathbb{P}}(\bar{A}_{m(n)})\to 0$
. Note that
![]() $1-\alpha\tau\lt 1- \alpha(\tau-1)$
, implying that
$1-\alpha\tau\lt 1- \alpha(\tau-1)$
, implying that
![]() $|\mathcal{H}_n| > m$
with high probability.
$|\mathcal{H}_n| > m$
with high probability.
To complete the proof, for
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $X_i^{\scriptscriptstyle 2(k+1)}$
be a random variable with
$X_i^{\scriptscriptstyle 2(k+1)}$
be a random variable with
![]() $X_i^{\scriptscriptstyle 2(k+1)}\stackrel{d}{=}X_i(1)+\cdots +X_i(2(k+1))$
, that is,
$X_i^{\scriptscriptstyle 2(k+1)}\stackrel{d}{=}X_i(1)+\cdots +X_i(2(k+1))$
, that is,
![]() $X_i^{\scriptscriptstyle 2(k+1)}$
is distributed as the passage time of a given path of length
$X_i^{\scriptscriptstyle 2(k+1)}$
is distributed as the passage time of a given path of length
![]() $2(k+1)$
. On the event
$2(k+1)$
. On the event
![]() $\bar{A}_m$
that the m paths that we have constructed between
$\bar{A}_m$
that the m paths that we have constructed between
![]() $h_1$
and
$h_1$
and
![]() $h_2$
are disjoint, the passage time
$h_2$
are disjoint, the passage time
![]() $T_i(h_1,h_2)$
between
$T_i(h_1,h_2)$
between
![]() $h_1$
and
$h_1$
and
![]() $h_2$
is bounded from above by the minimum of m i.i.d. copies of
$h_2$
is bounded from above by the minimum of m i.i.d. copies of
![]() $X_i^{\scriptscriptstyle 2(k+1)}$
. Under the assumption (1.2), such a minimum converges to 0 in probability, since
$X_i^{\scriptscriptstyle 2(k+1)}$
. Under the assumption (1.2), such a minimum converges to 0 in probability, since
![]() $m(n)=n^\delta\to\infty$
. Let
$m(n)=n^\delta\to\infty$
. Let
![]() $\{X_i^{\scriptscriptstyle(2(k+1))}(j)\}_{j\geq 1}$
be the i.i.d. sequence. The proof is completed by noting that
$\{X_i^{\scriptscriptstyle(2(k+1))}(j)\}_{j\geq 1}$
be the i.i.d. sequence. The proof is completed by noting that
where all terms have been shown above to converge to 0.
Finally, consider the erased version of the conditioned model. For
![]() $\alpha\lt 1/\tau$
with
$\alpha\lt 1/\tau$
with
![]() $\alpha\neq 1/(\tau +k)$
for
$\alpha\neq 1/(\tau +k)$
for
![]() $k\in\mathbb{N}$
, the claim follows from the same construction as above, since the argument does not rely on the occurrence of multiple edges. For
$k\in\mathbb{N}$
, the claim follows from the same construction as above, since the argument does not rely on the occurrence of multiple edges. For
![]() $\alpha\in(1/\tau,1/(\tau-1))$
, the claim follows in the same way as in the non-conditioned erased model if we can argue that giant vertices are connected to each other by a large number of two-step paths in this regime of the conditioned model. First, note that after erasure the giants still form a complete graph (without multiple edges) with high probability. From the same argument as in the proof of Lemma 2.1, it follows that
$\alpha\in(1/\tau,1/(\tau-1))$
, the claim follows in the same way as in the non-conditioned erased model if we can argue that giant vertices are connected to each other by a large number of two-step paths in this regime of the conditioned model. First, note that after erasure the giants still form a complete graph (without multiple edges) with high probability. From the same argument as in the proof of Lemma 2.1, it follows that
![]() $M_n < \ell(n) n^{1+\alpha(2-\tau)}$
with high probability. Moreover, on the event
$M_n < \ell(n) n^{1+\alpha(2-\tau)}$
with high probability. Moreover, on the event
![]() $M_n < \ell(n) n^{1+\alpha(2-\tau)}$
and conditionally on the degrees, by [Reference Van der Hofstad27, Lemma 7.13] the probability that two giant vertices
$M_n < \ell(n) n^{1+\alpha(2-\tau)}$
and conditionally on the degrees, by [Reference Van der Hofstad27, Lemma 7.13] the probability that two giant vertices
![]() $u,v \in \mathcal{H}_n$
are not directly connected satisfies
$u,v \in \mathcal{H}_n$
are not directly connected satisfies
By applying the union bound, we obtain that the probability of the event G that the giants form a complete graph satisfies
where the last term tends to 1 as
![]() $n \to \infty$
, since
$n \to \infty$
, since
![]() ${\varepsilon}_n^{-1}$
is slowly varying and
${\varepsilon}_n^{-1}$
is slowly varying and
![]() $\alpha\gt 1/\tau$
. Note also that the number of giants grows to infinity with n. More precisely, from (2.5) with high probability
$\alpha\gt 1/\tau$
. Note also that the number of giants grows to infinity with n. More precisely, from (2.5) with high probability
![]() $|\mathcal{H}_n| \geq n^{\gamma}$
with
$|\mathcal{H}_n| \geq n^{\gamma}$
with
![]() $\gamma \in (0, 1-\alpha(\tau-1))$
. Hence, since the set of joint neighbors of the giant vertices
$\gamma \in (0, 1-\alpha(\tau-1))$
. Hence, since the set of joint neighbors of the giant vertices
![]() $h_1$
and
$h_1$
and
![]() $h_2$
includes at least all the remaining giants, it follows that
$h_2$
includes at least all the remaining giants, it follows that
![]() $N(h_1,h_2) \geq |\mathcal{H}_n|-2$
and then
$N(h_1,h_2) \geq |\mathcal{H}_n|-2$
and then
![]() ${\mathbb{P}}(N(h_1,h_2) < n^{\gamma/2}) \to 0$
, where
${\mathbb{P}}(N(h_1,h_2) < n^{\gamma/2}) \to 0$
, where
![]() $N(h_1,h_2)$
indicates the number of joint neighbors of
$N(h_1,h_2)$
indicates the number of joint neighbors of
![]() $h_1$
and
$h_1$
and
![]() $h_2$
. The proof is completed by using (2.4) in the same way as for the erased model without conditioning.
$h_2$
. The proof is completed by using (2.4) in the same way as for the erased model without conditioning.
Remark 2.3. (Avoiding the initial vertices.) Note from the proof that Proposition 2.1 remains true also when vertex 1 and 2 (or any finite set of vertices) are not allowed to be used to transfer the infection from
![]() $h_1$
to
$h_1$
to
![]() $h_2$
, that is, when the infimum in (2.2) is taken over all paths
$h_2$
, that is, when the infimum in (2.2) is taken over all paths
![]() $\Gamma$
that do not contain vertex 1 or 2. This will be relevant when applying the result to the competition model below.
$\Gamma$
that do not contain vertex 1 or 2. This will be relevant when applying the result to the competition model below.
With Lemma 2.1 and Proposition 2.1 in hand, we are ready to prove Theorems 1.1, 1.2, and 1.3 Given that Lemma 2.1 and Proposition 2.1 apply to all versions of the model, the proofs are identical and can be merged.
Proof of Theorems
1.1, 1.2, and 1.3. We show that for any
![]() $\delta>0$
there exists
$\delta>0$
there exists
![]() $n_\delta$
such that
$n_\delta$
such that
that is,
![]() ${\mathbb{P}}(N_2(n)=1\mid Z_1<Z_2)\to 1$
. That
${\mathbb{P}}(N_2(n)=1\mid Z_1<Z_2)\to 1$
. That
![]() ${\mathbb{P}}(N_1(n)=1\mid Z_1\gt Z_2)\to 1$
follows by symmetry.
${\mathbb{P}}(N_1(n)=1\mid Z_1\gt Z_2)\to 1$
follows by symmetry.
Let
![]() ${\mathcal{N}}_i$
denote the set of neighbors of vertex i. With high probability neither vertex 1 nor vertex 2 has a self-loop on it, and we therefore assume that
${\mathcal{N}}_i$
denote the set of neighbors of vertex i. With high probability neither vertex 1 nor vertex 2 has a self-loop on it, and we therefore assume that
![]() $i\not\in{\mathcal{N}}_i$
for
$i\not\in{\mathcal{N}}_i$
for
![]() $i=1,2$
. Write
$i=1,2$
. Write
![]() $h^*$
for the first vertex in
$h^*$
for the first vertex in
![]() ${\mathcal{N}}_1\cup {\mathcal{N}}_2$
that is infected. By definition, if
${\mathcal{N}}_1\cup {\mathcal{N}}_2$
that is infected. By definition, if
![]() $Z_1<Z_2$
, then
$Z_1<Z_2$
, then
![]() $h^*=h_1\in{\mathcal{N}}_1$
. Write
$h^*=h_1\in{\mathcal{N}}_1$
. Write
![]() $\widetilde{T}_i(h_1,h)$
for the type i first passage time between
$\widetilde{T}_i(h_1,h)$
for the type i first passage time between
![]() $h_1$
and h when vertices 1 and 2 are not allowed to be used. For any
$h_1$
and h when vertices 1 and 2 are not allowed to be used. For any
![]() ${\varepsilon}\gt 0$
, if all vertices in
${\varepsilon}\gt 0$
, if all vertices in
![]() ${\mathcal{N}}_2$
are reached by type 1 from
${\mathcal{N}}_2$
are reached by type 1 from
![]() $h_1$
within time
$h_1$
within time
![]() ${\varepsilon}$
, while the time that it takes for type 2 to reach any vertex in
${\varepsilon}$
, while the time that it takes for type 2 to reach any vertex in
![]() ${\mathcal{N}}_2$
is larger than
${\mathcal{N}}_2$
is larger than
![]() ${\varepsilon}$
, then type 2 is not able to make any progress at all, and thus ends up occupying only its initial site. Hence, conditionally on
${\varepsilon}$
, then type 2 is not able to make any progress at all, and thus ends up occupying only its initial site. Hence, conditionally on
![]() $Z_1<Z_2$
,
$Z_1<Z_2$
,
Now pick
![]() ${\varepsilon}$
small so that
${\varepsilon}$
small so that
![]() ${\mathbb{P}}(Z_2-Z_1\leq {\varepsilon}\mid Z_1<Z_2)<\delta/2$
. This is possible since
${\mathbb{P}}(Z_2-Z_1\leq {\varepsilon}\mid Z_1<Z_2)<\delta/2$
. This is possible since
![]() $Z_2-Z_1$
is a proper random variable with support on
$Z_2-Z_1$
is a proper random variable with support on
![]() $(0,\infty)$
. Also, fix d such that
$(0,\infty)$
. Also, fix d such that
![]() ${\mathbb{P}}(|{\mathcal{N}}_2|>d\mid Z_1<Z_2)<\delta/4$
and observe that
${\mathbb{P}}(|{\mathcal{N}}_2|>d\mid Z_1<Z_2)<\delta/4$
and observe that
 \begin{align*} &{\mathbb{P}}\biggl(\max_{h\in{\mathcal{N}}_2}\widetilde{T}_1(h_1,h) \geq {\varepsilon}\mid Z_1<Z_2\biggr) \\[5pt] &\quad \leq {\mathbb{P}}\biggl(\biggl\{\max_{h\in{\mathcal{N}}_2}\widetilde{T}_1(h_1,h)\geq {\varepsilon}\biggr\} \cap \, \{ |\mathcal{N}_2| \leq d\} \mid Z_1<Z_2\biggr) +\delta/4.\end{align*}
\begin{align*} &{\mathbb{P}}\biggl(\max_{h\in{\mathcal{N}}_2}\widetilde{T}_1(h_1,h) \geq {\varepsilon}\mid Z_1<Z_2\biggr) \\[5pt] &\quad \leq {\mathbb{P}}\biggl(\biggl\{\max_{h\in{\mathcal{N}}_2}\widetilde{T}_1(h_1,h)\geq {\varepsilon}\biggr\} \cap \, \{ |\mathcal{N}_2| \leq d\} \mid Z_1<Z_2\biggr) +\delta/4.\end{align*}
The event
![]() $Z_1<Z_2$
only contains information about vertex 1 and 2 and hence does not affect
$Z_1<Z_2$
only contains information about vertex 1 and 2 and hence does not affect
![]() $\widetilde{T}_1(h_1,h)$
for
$\widetilde{T}_1(h_1,h)$
for
![]() $h \in \mathcal{N}_2$
. Combining this with a union bound, we obtain
$h \in \mathcal{N}_2$
. Combining this with a union bound, we obtain
where
![]() $h_1$
and
$h_1$
and
![]() $h_2$
are randomly chosen neighbors of vertex 1 and 2, respectively. Here the right-hand side converges to 0 by Proposition 2.1 and Remark 2.3 and so can be made smaller than
$h_2$
are randomly chosen neighbors of vertex 1 and 2, respectively. Here the right-hand side converges to 0 by Proposition 2.1 and Remark 2.3 and so can be made smaller than
![]() $\delta/4$
by picking n large. This concludes the proof of (2.6).
$\delta/4$
by picking n large. This concludes the proof of (2.6).
Finally, we indicate how the above proof can be generalized to establish Corollary 1.1 and its counterparts for the erased and the conditioned model.
Proof of Corollary
1.1. Generalizing (2.6), we now need to show that for any
![]() $\delta>0$
there exists
$\delta>0$
there exists
![]() $n_\delta$
such that
$n_\delta$
such that
To this end, consider all edges attached to the
![]() $k_1$
initial type 1 vertices and let
$k_1$
initial type 1 vertices and let
![]() $h'_{\!\!1}$
be the other end point of the edge with the smallest passage time; this is the vertex that is infected when type 1 makes its first move. Note that (2.7) can be proved in a similar way as above by showing that for any
$h'_{\!\!1}$
be the other end point of the edge with the smallest passage time; this is the vertex that is infected when type 1 makes its first move. Note that (2.7) can be proved in a similar way as above by showing that for any
![]() ${\varepsilon}\gt 0$
, conditionally on
${\varepsilon}\gt 0$
, conditionally on
![]() $Z_{1,k_1}\lt Z_{2,k_2}$
,
$Z_{1,k_1}\lt Z_{2,k_2}$
,
where both events on the right-hand side have probability smaller than
![]() $\delta/2$
. Here, to bound the first term, we use Remark 2.2. We conclude that
$\delta/2$
. Here, to bound the first term, we use Remark 2.2. We conclude that
![]() ${\mathbb{P}}(N_2(n)=k_2 \mid Z_{1,k_1}\lt Z_{2,k_2})\to 1$
. If
${\mathbb{P}}(N_2(n)=k_2 \mid Z_{1,k_1}\lt Z_{2,k_2})\to 1$
. If
![]() $k_2$
is fixed while
$k_2$
is fixed while
![]() $k_1=k_1(n)\to\infty$
, then
$k_1=k_1(n)\to\infty$
, then
![]() ${\mathbb{P}}(Z_{1,k_1}\lt Z_{2,k_2})\to 1$
, implying that
${\mathbb{P}}(Z_{1,k_1}\lt Z_{2,k_2})\to 1$
, implying that
![]() ${\mathbb{P}}(N_2(n)=k_2)\to 1$
.
${\mathbb{P}}(N_2(n)=k_2)\to 1$
.
3. Further work
There are a number of aspects of the model treated here that deserve further attention. We give a few examples below.
Growing initial sets. When both initial sets grow with n, we believe that the outcome of the competition depends on the combination of growth rates of the initial sets and the passage-time distribution. For a growing initial set, the time until the corresponding infection type reaches a giant vertex should converge to 0 in probability, with the rate of convergence being determined by the growth of the set, as well as the behavior close to zero of the passage-time distribution. Also, the rate at which the first passage time between two giants converges to 0 depends on the passage-time distribution. We believe that there are setups where both types occupy a positive fraction of the vertices (starting from an initial set that does not grow linearly) as well as setups where one of the types occupies everything except for the initial set of the other type.
Other passage-time distributions. What happens for continuous passage-time distributions that do not fulfill our assumption (1.2)? We believe that the outcome of the competition may then depend not only on the infimum of the supports but also on other properties of the distributions. In general, if the passage-time distribution does not have support down to 0, then the first passage time between two giants for the corresponding type is not vanishing, implying that the other type is not cut off from the possibility of capturing vertices beyond its initial set. However, a type that does not have support down to 0 may still have the possibility of occupying all initially uninfected vertices. Suppose that type 1 has a passage time with support down to 0, while type 2 has a passage time with support down to
![]() $\eta>0$
. Suppose also that the support of the passage time of type 1 is larger than
$\eta>0$
. Suppose also that the support of the passage time of type 1 is larger than
![]() $2\eta$
. Then, with positive probability,
$2\eta$
. Then, with positive probability,
![]() $Z_1\gt 2(\eta+{\varepsilon})$
for some
$Z_1\gt 2(\eta+{\varepsilon})$
for some
![]() ${\varepsilon}\gt 0$
, while
${\varepsilon}\gt 0$
, while
![]() $Z_2\leq \eta+{\varepsilon}$
. As a result, from the giant neighbor that type 2 reaches at time
$Z_2\leq \eta+{\varepsilon}$
. As a result, from the giant neighbor that type 2 reaches at time
![]() $Z_2$
, with high probability conditionally on
$Z_2$
, with high probability conditionally on
![]() $Z_1\gt 2(\eta+{\varepsilon})$
and
$Z_1\gt 2(\eta+{\varepsilon})$
and
![]() $Z_2\leq 2(\eta+{\varepsilon})$
, all other giants are reached at time
$Z_2\leq 2(\eta+{\varepsilon})$
, all other giants are reached at time
![]() $2(\eta+{\varepsilon})$
by type 2, since the giant is connected to all other giants with an increasing number of edges so the passage time of type 2 is close to
$2(\eta+{\varepsilon})$
by type 2, since the giant is connected to all other giants with an increasing number of edges so the passage time of type 2 is close to
![]() $\eta$
. Since vertex 1 is only connected to giants, at time
$\eta$
. Since vertex 1 is only connected to giants, at time
![]() $2(\eta+{\varepsilon})$
it becomes isolated, even though the support of its passage times does go down to zero while the one for type 2 does not. We conclude that type 2 wins with positive probability but naturally also type 1 wins with positive probability. Working out what the exact winning probabilities are for each of the two types in cases where the supports do not go down to zero is quite interesting.
$2(\eta+{\varepsilon})$
it becomes isolated, even though the support of its passage times does go down to zero while the one for type 2 does not. We conclude that type 2 wins with positive probability but naturally also type 1 wins with positive probability. Working out what the exact winning probabilities are for each of the two types in cases where the supports do not go down to zero is quite interesting.
Another option that might seem natural is to consider discrete passage times. In order to be meaningful, however, this would presumably require some type of non-lattice condition guaranteeing that both types cannot arrive at a vertex at the same time. If both types arrive simultaneously at a vertex, then a tie-breaking rule is needed to decide the type that occupies the vertex, and due to the special structure of the graph for
![]() $\tau\in(1,2)$
it is likely that the choice of tie-breaker will in fact decide the competition. In less heavy-tailed regimes, the tie-breaker typically kicks in only when the competition is already decided and is thereby essentially irrelevant; see e.g. [Reference Baroni, van der Hofstad and Komjáthy6] and [Reference Van der Hofstad and Komjáthy28].
$\tau\in(1,2)$
it is likely that the choice of tie-breaker will in fact decide the competition. In less heavy-tailed regimes, the tie-breaker typically kicks in only when the competition is already decided and is thereby essentially irrelevant; see e.g. [Reference Baroni, van der Hofstad and Komjáthy6] and [Reference Van der Hofstad and Komjáthy28].
Conditioned model with stricter upper bound. In the conditioned model, the degrees are conditioned to be smaller than
![]() $n^\alpha$
for some
$n^\alpha$
for some
![]() $\alpha\gt 0$
. The upper bound could also be taken as a more general function
$\alpha\gt 0$
. The upper bound could also be taken as a more general function
![]() $a_n$
of n. When
$a_n$
of n. When
![]() $a_n$
grows more slowly with n, the conditioning has a larger impact on the structure of the graph. Specifically, when
$a_n$
grows more slowly with n, the conditioning has a larger impact on the structure of the graph. Specifically, when
![]() $a_n$
is sufficiently small, the graph may lose the property that any two vertices of maximal degree are within finite distance from each other. This would be interesting to study in its own right, but would also have implications for the competition process in that the first passage time between two giants is then no longer vanishing. We believe that for a certain class of natural passage-time distributions including the exponential and uniform distributions, the cut-off may be at
$a_n$
is sufficiently small, the graph may lose the property that any two vertices of maximal degree are within finite distance from each other. This would be interesting to study in its own right, but would also have implications for the competition process in that the first passage time between two giants is then no longer vanishing. We believe that for a certain class of natural passage-time distributions including the exponential and uniform distributions, the cut-off may be at
![]() $a_n\propto \log n$
. For other distributions having a thicker or thinner tail close to 0, we believe the cut-off to be at a different value of
$a_n\propto \log n$
. For other distributions having a thicker or thinner tail close to 0, we believe the cut-off to be at a different value of
![]() $a_n$
. We leave this for future research.
$a_n$
. We leave this for future research.
Funding information
The work of MD and MS is supported by the Swedish Research Council through grant number 2020-04479_VR. The work of RvdH is supported in part by the Netherlands Organisation for Scientific Research (NWO) through Gravitation grant NETWORKS-024.002.003.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.