1 INTRODUCTION
The link between massive progenitor star and the type of core-collapse event it produces at the end of its nuclear burning life is the fundamental piece of information that underpins our understanding of the physical processes involved in stellar explosions. (see Langer Reference Langer2012, for a recent theoretical overview). Since the end of the 1990’s, the supernova (SN) community has been extensively searching publicly available archives for high-resolution and deep images of nearby galaxies which host SN. The existence of these pre-explosion images has allowed direct identification of the progenitor stars of some of the nearest core-collapse SN (e.g. Van Dyk, Li, & Filippenko Reference Van Dyk, Li and Filippenko2003b; Smartt et al. Reference Smartt, Maund, Hendry, Tout, Gilmore, Mattila and Benn2004; Maund, Smartt, & Danziger Reference Maund, Smartt and Danziger2005; Li et al. Reference Li, Van Dyk, Filippenko, Cuillandre, Jha, Bloom, Riess and Livio2006). Many of these, as individual events, are quite compatible with stellar evolutionary model predictions. The fact that numerous red supergiants are now observed as the stellar end points that produce the most common class of type II SN is a validation of modern stellar structure theory. In 2009, the number of detections of progenitor stars had reached a point that analysis of samples was possible (Smartt et al. Reference Smartt, Eldridge, Crockett and Maund2009) and a review of what these constraints meant for the field in the broader sense was warranted (Smartt Reference Smartt2009). Since then, there has been further very significant progress and results which are more consequential than just an increase in sample size. This review will consider work done in the field since 2009, and review the results as a whole in the context of the SN population we observe in the Local Universe as quantified by, for example, Leaman et al. (Reference Leaman, Li, Chornock and Filippenko2011), and Li et al. (Reference Li2011). Some of the highlights in the last 5 years are the significant increase in the sample size, nine further detections of progenitors, evidence for the disappearance of progenitor stars many years after explosion, and detections of possible binary companions. There has also been active discussion in the literature concerning the analysis methods, particularly in the treatment of extinction toward progenitors and how that may affect the luminosity and mass estimates. There are even some progenitor stars with multi-epoch data that allow pre-explosion variability to be probed, and as data sets grow then lightcurve monitoring of progenitors may become more common place (e.g. Elias-Rosa et al. Reference Elias-Rosa2009; Szczygieł et al. Reference Szczygieł, Gerke, Kochanek and Stanek2012; Fraser et al. Reference Fraser2014).
In an attempt to set a well-defined sample, Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009) (and later Eldridge et al. Reference Eldridge, Fraser, Smartt, Maund and Crockett2013) defined criteria for selecting a time- and volume-limited sample of SNe for which searches for progenitors were feasible: all CCSNe in galaxies with recessional velocities V vir ⩽ 2000kms−1(corrected for Virgo infall, which corresponds to a distance of d ⩽ 28 Mpc for H 0 = 72kms−1 Mpc−1). This distance limit was imposed from practical experience of analysing Hubble Space Telescope (HST) archival image data and the difficulty in retrieving photometry of resolved individual massive stars beyond this distance. Additionally, as galaxy number count increases as the distance cubed, the relative number of galaxies with high-quality archival imaging rapidly decreases. Hence, the probability of finding coincidences of SN discoveries combined with existing pre-explosion images of the galaxies also falls off quickly. As we will see later in this review, the SN which yield the most restrictive information on their progenitor stars have tended to be significantly closer than 28 Mpc. Two groups have worked extensively in this area, a California-based team (who started their concerted search with HST in Van Dyk et al. Reference Van Dyk, Peng, Barth and Filippenko1999), and a UK-based group (initiated with their first paper: Smartt et al. Reference Smartt, Gilmore, Trentham, Tout and Frayn2001) but others have also made significant contributions (e.g. Gal-Yam et al. Reference Gal-Yam2007; Kochanek, Khan, & Dai Reference Kochanek, Khan and Dai2012; Prieto et al. Reference Prieto2008). The UK-based group have focused their attention on this volume- and time-limited survey to get high-resolution, deep imaging of all SN that have useful archival imaging so that the precise SN positions can be astrometrically placed on the pre-explosion images. The Van Dyk led team have also pursued a similar strategy and both teams have used combinations of HST imaging (e.g. Smartt et al. Reference Smartt, Maund, Hendry, Tout, Gilmore, Mattila and Benn2004; Elias-Rosa et al. Reference Elias-Rosa2011; Van Dyk et al. Reference Van Dyk2014) ground-based AO imaging (e.g. Fraser et al. Reference Fraser2011, Reference Fraser2012; Van Dyk et al. Reference Van Dyk2012a) or good image quality natural seeing images (e.g. Li et al. Reference Li, Van Dyk, Filippenko and Cuillandre2005; Fraser et al. Reference Fraser2014) to locate the SN positions to accuracies of ~ 30–50 milliarcsec on the pre-explosion frames.
2 VOLUME- AND TIME-LIMITED SURVEY DATA
The definition of a time- and volume-limited survey has significant advantages in determining the overall properties of SN progenitor systems as a function of initial mass. There have been some remarkable discoveries of individual stars before explosion, with tight physical constraints on their luminosity and temperature (Smartt et al. Reference Smartt, Maund, Hendry, Tout, Gilmore, Mattila and Benn2004; Van Dyk et al. Reference Van Dyk2012b) some of which have been shown to have disappeared (Van Dyk et al. Reference Van Dyk2013; Maund, Reilly, & Mattila Reference Maund, Reilly and Mattila2014b; Maund et al. Reference Maund, Reilly and Mattila2014b). However, the most interesting aspect of this area is now the statistical sample of more than a dozen unambiguous direct detections and many restrictive limits to produce a defined survey sample of 44 objects. Objects outside this distance limit have also contributed to our understanding, such as the massive progenitor of SN2005gl at 60 Mpc (Gal-Yam et al. Reference Gal-Yam2007) but the relative frequency of such an event needs to be put in context with the fixed volume sample.
This review extends the time- and volume-limited sample introduced by Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009) and Eldridge et al. (Reference Eldridge, Fraser, Smartt, Maund and Crockett2013) for the type II and Ibc progenitors to the end of 2013. The discussion is extended to include all other progenitors within this survey sample including the IIb and IIn types and some beyond. The closest SNe provide the best opportunity for studying their progenitors, carrying out multi-wavelength monitoring until very late times. It is likely that we are not missing a large fraction of SNe in galaxies closer than ~ 12 Mpc (Botticella et al. Reference Botticella, Smartt, Kennicutt, Cappellaro, Sereno and Lee2012) as the star formation rates of these galaxies are in quite good agreement with the measured SN rate for a a lower mass limit of 8 M⊙ for core-collapse (although Horiuchi et al. Reference Horiuchi, Beacom, Kochanek, Prieto, Stanek and Thompson2011, suggests that at higher redshift there is a discrepancy). These closest SNe offer the best opportunities for progenitor detection, but as we cannot influence the SN rate nor the discovery rate (assuming we are 70–80% complete) the only way to increase the progenitor discovery rate is through patience and time. The following sections discuss the results published to date for the different subtypes of progenitors and Section 3 presents a discussion of these empirical results in the context of massive stars, the initial mass function (IMF), and the local SN population.
2.1. Type II supernovae
As illustrated in Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009), the chance of having an image of a nearby galaxy with one of the three main imaging cameras onboard HST (WFPC2, ACS, or WF3) for any nearby SNe (within V vir < 2000kms−1) is about 25%. If multi-colour imaging is available, then these colours can be fit with either observed supergiant colours or model atmospheres to determine approximate spectral types or effective temperatures, bolometric corrections, and hence bolometric luminosity. An alternative, but equivalent approach is to use stellar evolutionary models that have associated model atmosphere spectral energy distributions (SEDs) for the surface characteristic T eff, and logL (or logg) and synthetic photometry calculated from these spectra. There have been variations on these two methods from the early days of the first red supergiant detection of the progenitor of SN2003dg (Van Dyk et al. Reference Van Dyk, Li and Filippenko2003b; Smartt et al. Reference Smartt, Maund, Hendry, Tout, Gilmore, Mattila and Benn2004) through to the latest which have extended spectral colours in the near-infrared (Fraser et al. Reference Fraser2012; Kochanek et al. Reference Kochanek, Khan and Dai2012; Van Dyk et al. Reference Van Dyk2012a). Detections of red supergiants in JHK-bands are quite powerful indicators of the bolometric flux, since extinction uncertainties are lower and the bolometric corrections are less uncertain (Levesque et al. Reference Levesque, Massey, Olsen, Plez, Meynet and Maeder2006). Deep enough near-infrared pre-explosions images of nearby SN are still the exception rather than common place (although limits can set restrictions on super-AGB progenitors for example; Eldridge, Mattila, & Smartt Reference Eldridge, Mattila and Smartt2007).
Early results indicated that the detections of the progenitors of II-P SNe were red supergiants, with estimated luminosities in the range 4.3 < logL/L⊙ < 5.0 (see review of results in Smartt Reference Smartt2009), which would mean zero age main-sequence (ZAMS) masses in the region 7–15 M⊙. Since then, improvement of the analysis methods have provided updated estimates of the stellar parameters both for previously published detections and new discoveries. Efforts have been made to systematically include the MARCs stellar models and consistently apply synthetic photometry to reduce comparative errors in colour corrections and homogenise the analysis (for more in depth discussion, see Fraser et al. Reference Fraser2011; Davies et al. Reference Davies2013). Observing the SN progenitor position 3–4 years after explosion to check that the identified stellar progenitor has disappeared now allows difference imaging techniques to be applied in order to improve the precision of the pre-explosion photometry. Maund et al. (Reference Maund, Mattila, Ramirez-Ruiz and Eldridge2014a, Reference Maund, Reilly and Mattila2014b) discuss this in detail and the case for the disappearance of the progenitor of SN2011dh is presented in Van Dyk et al. (Reference Van Dyk2013). The treatment of the extinction toward the progenitors has progressed and the paper of Kochanek et al. (Reference Kochanek, Khan and Dai2012) highlights the need to consider interstellar medium (ISM) and circumstellar medium (CSM) extinction separately and consistently. Groh et al. (Reference Groh, Meynet, Georgy and Ekström2013c) have considered rotating and non-rotating models showing that initial rotation of the progenitor introduces a further uncertainty on the progenitor mass estimate as the core luminosity changes. They suggest that any particular mass may be uncertain to within 4–5 M⊙ but the overall mass range derived for type II-P progenitors is quite similar to that originally derived in Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009). All of this work has put the estimates of stellar parameters on a firmer footing with some changes in the stellar T eff and logL for various progenitor stars. However, it is fair to say that the improved estimates of stellar luminosity (and hence mass) are not significantly different to the originally published work. The main result from the data up to 2009 (Smartt et al. Reference Smartt, Eldridge, Crockett and Maund2009) still holds : type II-P SN come from red supergiants for which the lowest mass estimated is around 8 M⊙ and the highest mass progenitor has a luminosity of L ≃ 5.0 L⊙ (corresponding to a ZAMS of 15–18 M⊙).
The most recent results, and in the opinion of the author, the most reliable estimates of the physical parameters of detected progenitors of type II SNe are listed in Table 1 with the references to the relevant papers. Where new and updated estimates are used, references to the original detections are provided with comments. This review will not discuss all the detections individually, and the differences between the measurement and analysis methods. However, two SNe are taken here as examples for a more in depth discussion as case studies. The issues either in updated stellar luminosities or the disagreement between analysis methods are discussed for SN2004A and SN2012aw.
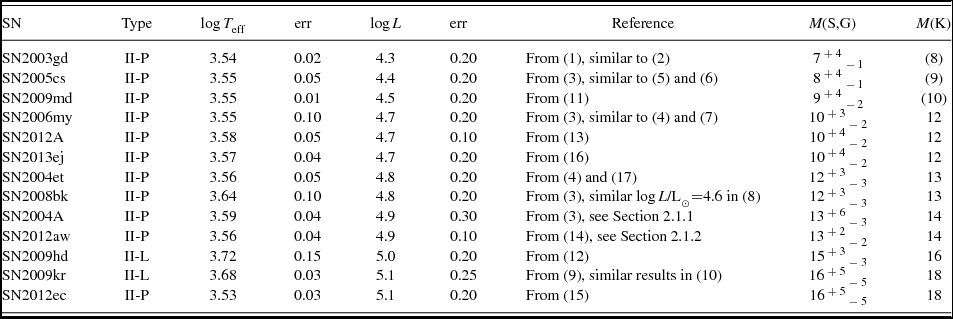
Table 1. List of detections of type II progenitors. The comments in the Reference column give guidance as to the source of the stellar progenitor data for the luminosities (logL/L⊙). The initial masses of model stars that end with these luminosities are given in the last two columns : M(S,G) are the masses (in M⊙) from the STARS and Geneva rotating models (which have similar final luminosities); M(K) are from the KEPLER models (see Section 3.1 for details). The values for the initial masses from KEPLER for 2003gd, 2005cs, and 2009md are uncertain since there are no KEPLER models evolved to end points at this mass and luminosity. They are based on extrapolation, and quoted in parentheses. The errors for M(K) can be assumed to be the same as those quote for M(S,G).

(1)Maund & Smartt (Reference Maund and Smartt2009); (2)Smartt et al. (Reference Smartt, Maund, Hendry, Tout, Gilmore, Mattila and Benn2004); (3)Maund et al. (Reference Maund, Reilly and Mattila2014b); (4)Crockett et al. (Reference Crockett, Smartt, Pastorello, Eldridge, Stephens, Maund and Mattila2011); (5)Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009); (6)Maund et al. (Reference Maund, Smartt and Danziger2005); (7)Li et al. (Reference Li, Wang, Van Dyk, Cuillandre, Foley and Filippenko2007); (8)Mattila et al. (Reference Mattila, Smartt, Eldridge, Maund, Crockett and Danziger2008); (9)Fraser et al. (Reference Fraser2010); (10)Elias-Rosa et al. (Reference Elias-Rosa2010); (11)Fraser et al. (Reference Fraser2011); (12)Elias-Rosa et al. (Reference Elias-Rosa2011): note the T eff and logL/L⊙values are upper limits. (13)Tomasella et al. (Reference Tomasella2013): note the T eff was an assumption, and not derived from multiple colours; (14)Kochanek et al. (Reference Kochanek, Khan and Dai2012); (15)Maund et al. (Reference Maund2013); (16)Fraser et al. (Reference Fraser2014): note the T eff was an assumption, and not derived from multiple colours; (17) M. Fraser et al. (in preparation).
The two SNe which fell on compact, and likely coeval clusters (SN2004dj and SN2004am) in NGC2403 and M82 are not considered here, although the turn-off mass estimated for both is in the regime of the moderate to low masses that are derived for II-P progenitors. Hence, their inclusion would support the results discussed below. SN1999ev is also not included as Maund et al. (Reference Maund, Reilly and Mattila2014b) showed that the progenitor object identified originally by Maund & Smartt (Reference Maund and Smartt2005) was likely a stellar cluster. Finally, SN2003ie, which was included in Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009) is no longer considered as with the higher extinction estimates used later in this analysis, the luminosity limit is neither useful nor restrictive in any way.
2.1.1. SN2004A
This SN progenitor is taken as an example were the original estimate of luminosity has a significant discrepancy with a new measurement. As the later measurement is based on new data after explosion, with difference imaging applied it is worth discussing as a an example how significantly results could change. Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009) and Hendry et al. (Reference Hendry2006) originally estimated a logL/L⊙ = 4.5 ± 0.3. With deep follow-up imaging, Maund et al. (Reference Maund, Reilly and Mattila2014b) showed the progenitor object identified has disappeared and suggested a significantly higher value of logL/L⊙ = 4.9 ± 0.3. The estimate of the magnitude of the progenitor in the HST F814W pre-explosion image is similar in Hendry et al. (Reference Hendry2006) and Maund et al. (Reference Maund, Reilly and Mattila2014b), illustrating the difference in final quoted luminosity arises in the analysis methods. The methods differ in that a higher extinction of E(B − V) = 0.16 was employed by Maund et al. (Reference Maund, Reilly and Mattila2014b), together with application of the MARCS model atmospheres. In his PhD thesis work, Fraser (Reference Fraser2011) undertook a re-analysis of the type II-P progenitor sample. As an experiment, he suggested that adding in extinction values that are seen toward the red supergiant population of local group galaxies M31, the Large Magellanic Cloud (LMC) and Small Magellanic Cloud (SMC) would be appropriate to test if the typical extinctions estimated for SN progenitors are systematically lower than those observed toward existing red supergiants. Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009) had also discussed this method for adding extra ad hoc extinction to those progenitors for which foreground estimates only where available. While Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009) had adopted an additional AV ≃ 0.3, Fraser (Reference Fraser2011) adopted an additional AV ≃ 0.53. Hence, there are three estimates of logL/L⊙=4.5, 4.8 and 4.9 from Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009), Fraser (Reference Fraser2011), and Maund et al. (Reference Maund, Reilly and Mattila2014b), each with an uncertainty of ± 0.3 dex. This is probably the most extreme case of a discrepant result due to different methods, although formally, the uncertainties overlap. The value of logL/L⊙ = 4.9 ± 0.3 is reported in Table 1, and it serves to illustrate the point made earlier that results from improved analysis methods should be adopted for individual objects were possible. However, it will be shown that the luminosity shifts do not affect the important overall trend of a lack of high-mass stars.
2.1.2. SN2012aw
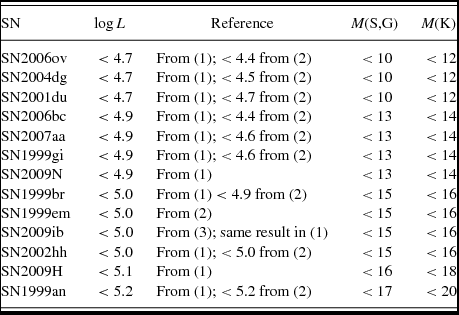
The second specific case study example is the progenitor of SN2012aw. This was a very well-studied type II-P SN in M95 (d = 10 Mpc) discovered within 1–2 days of explosion and followed well into the nebular phase (Bose et al. Reference Bose2013; Dall’Ora et al. Reference Dall’Ora2014). Van Dyk et al. (Reference Van Dyk2012a) and Fraser et al. (Reference Fraser2012) both identified the same progenitor object as the culprit star with detections in HST filters F555W, F814W, and in near-infrared ground-based images through filters J and K. The galaxy was also imaged by the SINGS (Kennicutt et al. Reference Kennicutt2003) Spitzer survey but no detection of a single point source was possible, as discussed in detail in Kochanek et al. (Reference Kochanek, Khan and Dai2012). Both Fraser et al. (Reference Fraser2012) and Van Dyk et al. (Reference Van Dyk2012a) carried out a similar analysis and suggested the progenitor star was quite luminous and relatively high mass in the range 14–26 M⊙ and 15–20 M⊙, respectively. They also suggested that the progenitor suffered significant reddening. Since the SN itself suffered low line of sight extinction, this was taken as evidence that the progenitor reddening was due to CSM dust which was destroyed in the explosion. Up to this point in the history of progenitor analysis, all treatments of reddening towards progenitors had assumed that applying interstellar laws and relations were applicable also to circumstellar dust. However, Kochanek et al. (Reference Kochanek, Khan and Dai2012) presented an alternative analysis in which they discussed the three consequences of such assumptions. Attempting to model CSM dust with ISM laws ignores dust emission in the near-IR, assumes (wrongly) that all scattered photons are lost to the observer and do not treat the (probable) dust composition correctly. In the case of SN2012aw, Kochanek et al. (Reference Kochanek, Khan and Dai2012) argued that Fraser et al. (Reference Fraser2012) and Van Dyk et al. (Reference Van Dyk2012a) had significantly overestimated the luminosity of the progenitor. Using the dusty code of Ivezic & Elitzur (Reference Ivezic and Elitzur1997) to compute how photons are scattered, absorbed and reemitted by a dusty region enclosing a stellar source, Kochanek et al. (Reference Kochanek, Khan and Dai2012) calculated a model to fit the detected magnitudes and the upper limits from the mid-IR (see Figure 1). They suggested a significantly lower luminosity progenitor, a stellar temperature of T eff ≃ 3600+300−200 K and an upper mass limit of M ZAMS < 15 M⊙. The amount of CSM gas, due to the progenitor’s stellar wind was also constrained by the x-ray and radio detections. The mass-loss estimate of ![]() $\dot{M} \lesssim10^{-5}$ M⊙ yr−1 is roughly consistent with a star of this temperature and luminosity.
$\dot{M} \lesssim10^{-5}$ M⊙ yr−1 is roughly consistent with a star of this temperature and luminosity.

Figure 1. Analysis of the progenitor of SN2012aw. Upper: The SED fit of a dusty model from Kochanek et al. (Reference Kochanek, Khan and Dai2012) to the detections in the optical and NIR filters presented in Fraser et al. (Reference Fraser2012), Van Dyk et al. (Reference Van Dyk2012a), and the mid-IR Spitzer limits. The black curves show the SED model which is made up of the three components of scattered photons, direct photons and dust emission radiation (the red-dashed curves from left to right respectively). The blue line is the unobscured SED of the star itself. This is for a dust temperature of T d = 1000 K and a graphitic dust composition (see the original reference for a similar silicate fit). Lower: Comparison of the luminosity estimates of the three studies - point with error bar from Van Dyk et al. (Reference Van Dyk2012a), dashed contours from Fraser et al. (Reference Fraser2012) and red locus from Kochanek et al. (Reference Kochanek, Khan and Dai2012), illustrating the importance of considering the treatment of both dust absorption and emission. As discussed in Section 2.1.2, the proper inclusion of dust treatment lowers the luminosity estimates substantially. Reproduced from Figures 5 and 6 in ‘On Absorption by Circumstellar Dust, with the Progenitor of SN 2012aw as a Case Study’ by Kochanek et al. Reference Kochanek, Khan and Dai2012, ApJ, 759, 20.
This progenitor is important as the discussion over the CSM reddening has implications for estimates of the most massive stars that can explode as bright SN, as we shall see in Section 3.
2.1.3. Upper luminosity limits
While Table 1 lists the 13 type II SN that have secure detections of their progenitors in the period from 1999 to 2013 (inclusive), there are a further 13 type II SNe which have pre-explosion HST data (or alternative high-quality ground-based images) in which no progenitor is detected. In these cases the progenitor falls below the detection limit of the images and no information on the colour and effective temperatures of the stars can be gained a priori. Any individual event does not therefore add a lot of new information or insights compared to the large number of detections now available. However, the statistical significance of the number of non-detections does provide a constraint on the mass and luminosity range of the progenitor population as discussed in Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009) and in Kochanek et al. (Reference Kochanek, Beacom, Kistler, Prieto, Stanek, Thompson and Yüksel2008). Since the Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009) study, there have been three more non-detections that can boost the statistical significance of the sample further. These are SN2009H (Li, Cenko, & Filippenko Reference Li, Cenko and Filippenko2009), SN2009N (Takáts et al. Reference Takáts2014), and SN2009ib (Takáts et al. Reference Takáts2015). As discussed in Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009) and previous papers such as Smartt et al. (Reference Smartt, Maund, Gilmore, Tout, Kilkenny and Benetti2003) and Van Dyk, Li, & Filippenko (Reference Van Dyk, Li and Filippenko2003a), if one assumes that the progenitors of these type II (mostly II-P) SNe are red supergiants then a luminosity limit can be calculated for this effective temperature regime. An I-band like filter sampling the wavelength region between 7 000 and 9 000 Å is particularly powerful since the stellar SED peaks in this region and the bolometric correction change means the luminosity limit is roughly constant across the K to M-type supergiant colours and temperatures. The major uncertainty is the extinction to adopt toward the progenitor and different methods have been proposed.
Initial work in this area simply adopted the estimated line-of-sight extinction toward the SN as appropriate to apply to the progenitor. The extinction could be estimated from the spectral slope of the SN (Smartt et al. Reference Smartt, Maund, Gilmore, Tout, Kilkenny and Benetti2003), the absorption of Na i lines (Poznanski et al. Reference Poznanski, Ganeshalingam, Silverman and Filippenko2011; Poznanski, Prochaska, & Bloom Reference Poznanski, Prochaska and Bloom2012), or from three colour photometry of the surrounding stellar population (Maund et al. Reference Maund, Reilly and Mattila2014b). There are problems with all of these estimates, but even more important is that this line-of-sight extinction may either not be directly applicable to the progenitor (as in the case of the surrounding stellar population) or may be simply a lower limit since it does not take into account circumstellar medium extinction in the locality of the progenitor star (see the discussion in Section 2.1.2). It is quite possible, and indeed probable that CSM dust (within a radius of approximately 10–100R ⋆, where R ⋆ is a typical red super giant (RSG) radius of 500–1 000 R⊙) is destroyed during the UV flash of the SN. The discovery of a dust enshrouded progenitor, and a relatively unobscured transient for SN2008S (Prieto et al. Reference Prieto2008; Botticella et al. Reference Botticella2009) illustrated this possibility, followed by the case of SN2012aw (Section 2.1.2). The upper limits suffer much more uncertainty than the direct detections as in the latter cases the extinction can be constrained by SED fits, at least for the cases with the largest wavelength coverage in the broad band colours. Nevertheless, under reasonable assumptions, the limits are a useful constraint. Approaches have been to adopt the best estimate of reddening toward the SN, to adopt an arbitrary extinction to represent the CSM, or to model it from theoretical assumptions. Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009) added an additional AV ≃ 0.3 for those progenitors which had only Milky Way foreground estimates (the value of 0.3 coming from comparisons between the SN sample and the red supergiant population of the LMC). Fraser (Reference Fraser2011) reanalysed this sample, using a better method of model star SEDs (MARCs models) and adopting extra extinction of AV ≃ 0.5 for all (again from comparing the M31, LMC and SMC populations of red supergiants). To be conservative the values for the luminosity limits in Table 2 are quoted from Fraser (Reference Fraser2011) with this higher, ad hoc (but physically plausible) extra extinction of AV ≃ 0.5. The results of the theoretical modelling of stellar mass-loss rates and dust production of Walmswell & Eldridge (Reference Walmswell and Eldridge2012) will be discussed further in Section 3.3.
Table 2. Upper limits for the luminosity of type II and type IIP SNe. Most of the limits quoted here were re-calculated by Fraser (Reference Fraser2011), based on the original published photometry limits and with an additional, but adhoc extinction of AV ≃ 0.5mag applied as a conservative estimate. The values for the initial mass of star which ends it life with that luminosity is given in the last two columns. As in Table 1, these are for the STARS and Geneva models M(S,G) and the KEPLER models M(K), as discussed in Section 3.1.

(1) Fraser (Reference Fraser2011); (2)Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009); (3) Takáts et al. (Reference Takáts2015).
2.2. Type IIb supernovae
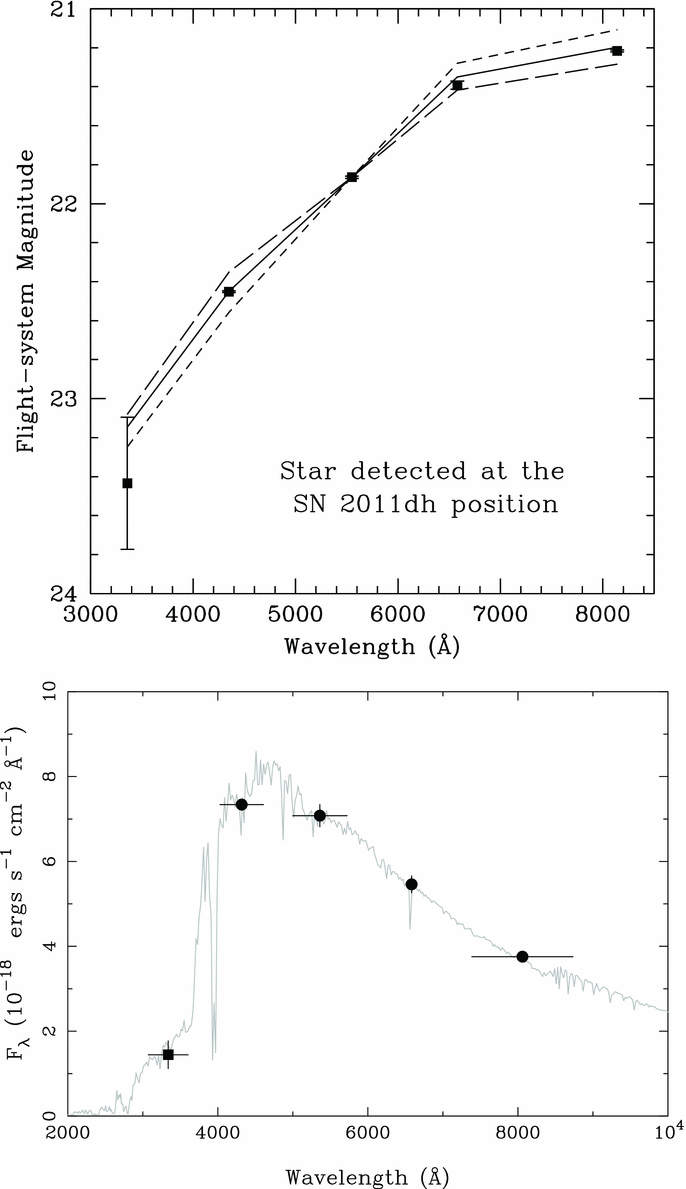
As discussed in the previous two sections, the pre-discovery images of type II-P SNe are often not deep enough to detect the progenitor stars. This is not surprising since for distance moduli of μ = 30–32 (10–25 Mpc) and the typical depth of HST images (m AB ~ 25m), the lowest luminosity red supergiants would go undetected. If the broad picture of core-collapse, neutron star formation and successful SNe occurring in stars above an initial mass of ~ 8 M⊙ is true, then the IMF must dictate that the bulk of CCSNe we detect are from the lower mass region. The IIb SNe are those which begin by resembling type II SNe with unmistakable H i Balmer lines and evolve to have H-weak and He-strong spectra (Filippenko Reference Filippenko1997), the prototype of which is SN1993J (Filippenko, Matheson, & Ho Reference Filippenko, Matheson and Ho1993; Matheson et al. Reference Matheson, Filippenko, Ho, Barth and Leonard2000). It is remarkable that the three IIb SNe in the 1999–2013 distance and time-limited survey which have high-quality imaging all have relatively bright progenitors (or progenitor systems) detected at the SN position. The detections of the progenitors of SN2008ax (Crockett et al. Reference Crockett2008), SN2011dh (Maund et al. Reference Maund2011; Van Dyk et al. Reference Van Dyk2011), and SN2013df (Van Dyk et al. Reference Van Dyk2014) are summarised in Table 3. The SED of the progenitor of SN2011dh is very well fit with a spectrum of a single star with T eff = 6000 K and logL = 4.9 L⊙ as shown in Figure 2. The progenitor of SN2013df is cooler, with Van Dyk et al. (Reference Van Dyk2014) finding T eff = 4250 K and remarking that the detected progenitor appears quite similar to that of SN1993J (Aldering, Humphreys, & Richmond Reference Aldering, Humphreys and Richmond1994). The progenitor of SN1993J was postulated, and shown to be, a binary system of a K-type supergiant and hotter companion. It too had a luminosity of logL = 5.2 ± 0.3 L⊙ (Van Dyk et al. Reference Van Dyk, Garnavich, Filippenko, Höflich, Kirshner, Kurucz and Challis2002; Maund et al. Reference Maund, Smartt, Kudritzki, Podsiadlowski and Gilmore2004; Fox et al. Reference Fox2014).
Table 3. Type IIb detections.

(1) Crockett et al. (Reference Crockett2008); (2) Maund et al. (Reference Maund2011); (3) Van Dyk et al. (Reference Van Dyk2011); (4) Van Dyk et al. (Reference Van Dyk2014).

Figure 2. The SED fit of the progenitor of the yellow supergiant progenitor of SN2011dh from two independent analyses of Van Dyk et al. (Reference Van Dyk2011) (upper) and Maund et al. (Reference Maund2011) (lower). The pre-explosion HST data points (solid black with errors) are impressively fit with a single stellar source and an ATLAS model atmosphere for T eff = 6000 K and logg = 1.0 in both analyses. Reproduced from Figure 3 in ‘The Progenitor of Supernova 2011dh/PTF11eon in Messier 51 by Van Dyk et al. Reference Van Dyk2011, ApJ, 741, L28 and Figure 2 in ‘The Yellow Supergiant Progenitor of the Type II Supernova 2011dh in M51’ by Maund et al. Reference Maund2011, ApJ, 739, L37.
The colours of the progenitor of SN2008ax could not be satisfactorily fit with a single stellar SED (Crockett et al. Reference Crockett2008) or with a plausible binary which led the authors to suggest it might be a single WR-type star or a system which has contaminated flux from a physically associated cluster or nearby stars. Crockett et al. found the absolute magnitude of the star coincident with the SN position to be M F606W = −7.4 ± 0.3, and if we assume a bolometric correction of − 0.6 (to cover possible supergiant stars from late B-type to early K-type), then this implies a stellar logL ~ 5.1 L⊙ but with quite large uncertainties due to the difficulty in fitting a single SED. Groh, Meynet, & Ekström (Reference Groh, Meynet and Ekström2013b) suggest that the progenitor could have been a rotating star of around 20 M⊙ that ends its nuclear burning life as a ‘compact LBV’ with a luminosity of around logL = 5.2–5.3 dex. Nevertheless, taken together the IIb progenitors tend to be brighter, more often detected, and of systematically higher luminosity than the bulk of the type II-P SNe.
The model of IIb SNe coming from extended supergiants which have had mass stripped due to a binary companion was supported initially by the detection of a progenitor companion in SN1993J (Podsiadlowski et al. Reference Podsiadlowski, Hsu, Joss and Ross1993; Nomoto et al. Reference Nomoto, Suzuki, Shigeyama, Kumagai, Yamaoka and Saio1993; Woosley et al. Reference Woosley, Eastman, Weaver and Pinto1994; Maund et al. Reference Maund, Smartt, Kudritzki, Podsiadlowski and Gilmore2004; Fox et al. Reference Fox2014) and recently also for SN2011dh. At the time of discovery of SN2011dh a yellow star dominated the SED of the progenitor system, and the community had split views on whether the yellow supergiant or its putative compact companion had exploded (e.g. Soderberg et al. Reference Soderberg2012). The disappearance of the bright yellow star (Van Dyk et al. Reference Van Dyk2013) and the detection of a UV source remaining at the SN position by Folatelli et al. (Reference Folatelli2014) is strong evidence that it was indeed the yellow supergiant that exploded and that it had a more compact companion (see the model in Benvenuto, Bersten, & Nomoto Reference Benvenuto, Bersten and Nomoto2013).
It remains to be seen if the existing, and follow-up data for SN2013df and SN2008ax also can be explained with binary models. However, it is certain that the progenitors all have luminosities around logL ≃ 5.0L⊙, albeit with the assumption that the bolometric correction for the SN2008ax progenitor is not unusually high. The stellar evolutionary models employed in the studies discussed in this section to explain the progenitor luminosities have ZAMS masses in the range 13–17 M⊙. It would appear that IIb progenitors are consistently among the highest luminosity (and hence highest mass) progenitors so far detected. There are few other upper limits, and with four cases of nearby IIb SNe all with bright, detected progenitors it seems reasonable to conclude that they are not produced by lower mass systems in the 8–12 M⊙ range. The physical reason for this is not determined and it will be interesting in the future to test quantitative models. One may speculate that it could be due to higher mass stars-forming closer binaries more easily or brighter progenitors being more extended and hence their envelopes more efficiently undergoing Roche lobe overflow when they reach the L1 point.
A spectrum of the light echo of Cas A showed this Milky Way SN to be of type IIb (Krause et al. Reference Krause, Tanaka, Usuda, Hattori, Goto, Birkmann and Nomoto2008; Rest et al. Reference Rest2008). There is no sign of an obvious companion star in the centre of the Cas A remnant, leading to the speculation that this was a high-mass single star that lost most of its hydrogen envelope through winds. However, the total amount of gas either ejected or residing in the CSM, and therefore recently ejected by the progenitor is not particularly high. The mass of the shocked and unshocked ejecta is estimated at 3–4 M⊙ (Hwang & Laming Reference Hwang and Laming2012) and the mass in the CSM which the blastwave has swept-up is around 8 M⊙ (Hwang & Laming Reference Hwang and Laming2009; Patnaude & Fesen Reference Patnaude and Fesen2009). Adding in ~ 2 M⊙ for a neutron star remnant, results in a total progenitor mass estimate of about 15 M⊙. The internal structure seen in the ejecta originate from turbulent mixing processes and plumes of 56Ni-rich material (Milisavljevic & Fesen Reference Milisavljevic and Fesen2015). These detailed constraints are in reasonable agreement with the results from the three IIb SNe with progenitors discussed above—originating from stars with initial masses in the range ~ 15 ± 3 M⊙. However, the puzzle remains for Cas A—if the star had no companion, and the initial mass was only ~ 15 M⊙, then how did it lose its envelope to become a IIb SN? One might speculate it was a high-mass, obscured star, although it seems the extinction toward Cas A is no more than AV ≃ 6-7mag (Eriksen et al. Reference Eriksen, Arnett, McCarthy and Young2009) and this is integrated along the Galactic line of sight rather than being local to the SN and the progenitor.
2.3. Type Ibc supernovae
There are two possible models for the progenitors of type Ibc SN. The first are Wolf–Rayet stars which are evolved, single massive stars that have lost their hydrogen envelopes (in the case of WN stars) and also helium layers (in the case of WC and WO stars) primarily through radiatively driven winds, (Kudritzki & Puls Reference Kudritzki and Puls2000; Vink & de Koter Reference Vink and de Koter2005) or episodic mass-loss (Smith & Owocki Reference Smith and Owocki2006) or through rapid rotation and chemical homogenous evolution (Yoon & Langer Reference Yoon and Langer2005). The observed Wolf–Rayet stars in our galaxy and the Magellanic clouds are observationally constrained to come from stars (either single or binary) above about 25–30 M⊙ from considerations of the turn-off masses in stellar clusters (e.g. see review of Crowther Reference Crowther2007). From a theoretical standpoint, the stellar winds of single stars below this mass are not strong enough alone to cause sufficient mass-loss to expose the He and CO cores. These stars are predominantly found in young stellar clusters and OB associations within the Local Group and turn-off masses for coeval stellar populations have provided estimates of mass and age (e.g. Massey et al. Reference Massey, Lang, Degioia-Eastwood and Garmany1995). The second alternative is lower mass stars in binary systems with initial masses lower than that required for single stars (Paczyński Reference Paczyński1967; Vanbeveren, De Loore, & Van Rensbergen Reference Vanbeveren, De Loore and Van Rensbergen1998; Nomoto, Iwamoto, & Suzuki Reference Nomoto, Iwamoto and Suzuki1995; Podsiadlowski, Joss, & Hsu Reference Podsiadlowski, Joss and Hsu1992; Eldridge, Izzard, & Tout Reference Eldridge, Izzard and Tout2008; Yoon, Woosley, & Langer Reference Yoon, Woosley and Langer2010). Theoretical stellar populations including binaries with reasonable distributions of stellar masses and separations can produce large number fractions of He stars with core masses large enough to undergo core-collapse (e.g. Eldridge et al. Reference Eldridge, Fraser, Smartt, Maund and Crockett2013). However one problem with these models is that the systems they predict are not observationally identified in the Milky Way.
As discussed in Section 2, the volume- and time-limited survey of Eldridge et al. (Reference Eldridge, Fraser, Smartt, Maund and Crockett2013) presented an extensive search for the progenitors of all type Ibc SNe in pre-discovery images (from 1998 to 2012.25). This paper described the compilation of literature data, and new analysis of images of the progenitors of a total of 12 type Ibc SNe. There are no detections of progenitors, or progenitor systems in any of these. The deepest limits in the typical BVR-bands were between − 4 and − 5 and, the authors compared these limits with the observed magnitudes of WR stars in the LMC. As WR stars, or stripped He stars in binary systems, have diverse temperatures and radii (and hence diverse colours, SEDs, and bolometric corrections), the quantitative fitting methods which have been successful for type II progenitors cannot be applied to the Ibc limits without major uncertainties in the results. Hence, a more empirical approach was applied which simply postulated that the observed WR star population of the LMC are plausible progenitor systems of Ibc SNe and then determined what was the statistical uncertainty that no detections were made. Since then, there have been two further Ibc SNe within the distance limit, also with no detections of progenitors SN2013dk (Elias-Rosa et al. Reference Elias-Rosa2013) and SN2012cw (Graur & Maoz Reference Graur and Maoz2012). Eldridge et al. (Reference Eldridge, Fraser, Smartt, Maund and Crockett2013) originally estimated the probability of not finding a progenitor system detection, if the LMC WR population are direct progenitors of Ibc SNe to be 16%, and with the inclusion of the limits of SN2013dk and SN2012cw this drops to ~ 12%. This is an interesting constraint but not in itself strong enough to rule out WR stars being the progenitors of the normal Ibc population we see in the local Universe. Several other authors have argued that the temperature and luminosity (which of course dictate optical and NIR fluxes) of the observed WR population are not applicable to WR stars at the point of collapse and that significant evolution to higher temperatures and fainter optical magnitudes occur in their models (Yoon et al. Reference Yoon, Gräfener, Vink, Kozyreva and Izzard2012; Groh et al. Reference Groh, Meynet, Georgy and Ekström2013c). These of course are dependent on the mass-loss rates and the time to core-collapse from where we observe them now. It is also possible that the extinction toward these progenitors, or CSM extinction, is systematically underestimated as discussed above for the type II-P progenitors and limits (in Section 2.1.3).
There are two other strong constraints on the progenitors of type Ibc SNe. The first is their relatively high rate which has been explained with binary population models (for example as discussed in Podsiadlowski et al. Reference Podsiadlowski, Joss and Hsu1992; Eldridge et al. Reference Eldridge, Izzard and Tout2008). More recently, Smith et al. (Reference Smith, Li, Filippenko and Chornock2011a) pointed out that the SN rates from the volume-limited Lick Observatory Supernova Search (LOSS) survey imply a rate (26% of all CC) that is a factor of ~ 2 too high for massive, single WR stars to be the sole producers just from simple IMF arguments. An IMF of single stars would produce a WR fraction (and hence a Ibc fraction) of 14–18% of all massive stars between 8 and 100 M⊙ if the minimum mass to produce a WR is 25–30 M⊙. Eldridge et al. (Reference Eldridge, Fraser, Smartt, Maund and Crockett2013) built on this with the Binary Population and Spectral Synthesis (bpass) code to calculate rates of progenitors in stellar population models including binaries. The rate of Ibc SNe within 28 Mpc (during 1998–2012.25) is also 26%, and Eldridge et al. (Reference Eldridge, Fraser, Smartt, Maund and Crockett2013) find that the rates can only be produced if a mixed population of single stars and binaries are used with one single star for every binary system and the mass ratio and initial separations are set such that approximately two thirds of the binaries interact. This value is compatible with the observed result of Sana et al. (Reference Sana2012) who showed that this fraction of massive binaries are likely to interact. These multiple and consistent observational constraints from relative SN rates and the binary fraction of massive stars are rather compelling arguments that binary systems are likely to produce the bulk, if not all of the Ibc SN progenitors. Eldridge et al. (Reference Eldridge, Fraser, Smartt, Maund and Crockett2013) points out that the reason that Galactic analogues may be difficult to identify is that stars in binaries with initial masses below 20 M⊙ tend to retain a low-mass hydrogen envelope until quite close to core-collapse, ≃ 104 yrs. Hence, they are not easily detectable as H-free compact helium stars.
The second additional argument for Ibc SNe coming from interacting binaries is that the ejecta masses calculated from lightcurve modelling are typically in the range 1–4 M⊙ (see Valenti et al. Reference Valenti2008; Drout et al. Reference Drout2011, the results of which are summarised in Eldridge et al. Reference Eldridge, Fraser, Smartt, Maund and Crockett2013). These final masses are somewhat low compared to the estimated masses of WR stars in the Local Group, which are typically in the range 8–20 M⊙ (from binary orbits, Figure 4 of Crowther Reference Crowther2007). The binary models of Eldridge et al. (Reference Eldridge, Fraser, Smartt, Maund and Crockett2013) produce helium stars that would have typical ejecta masses of 4.2 ± 2.4 M⊙, in agreement with those measured (also see Lyman et al. Reference Lyman, Bersier, James, Mazzali, Eldridge, Fraser and Pian2014).
Anderson et al. (Reference Anderson, Habergham, James and Hamuy2012) and Anderson & James (Reference Anderson and James2008) have matched the positions of nearby SNe to the Hα emission produced in star-forming regions. The SNe Ibc in their sample are more closely associated with the Hα emission than type II SNe in general. They interpret this as the SNe Ibc (and SN Ic in particular) arising from younger regions and hence coming from higher mass progenitors. Crowther (Reference Crowther2013) compared a much closer sample of CCSNe (⩽ 15 Mpc) with higher resolution images and also concluded that the association of Ibc with Hα regions was stronger than for type II SNe. However, the diagnostic power of this association in quantitatively determining the mass ranges was shown to be difficult to interpret. The Ibc progenitors do appear to come from younger populations than the bulk of the type II progenitors. However, the latter are dominated by stars in the 8–12 M⊙ regime, and a quantitative age and mass estimate for the Ibc progenitors has not yet been possible. Although they may on the whole be from more massive progenitors, the data cannot at present distinguish between WR stars and lower mass (say 12–20 M⊙) binaries.
2.3.1. PTF13bvn
Just after the publication of the Eldridge et al. (Reference Eldridge, Fraser, Smartt, Maund and Crockett2013) summary, the Palomar Transient Factory (PTF) discovered a nearby Ib SN in NGC5806 (d = 22 Mpc) and set a very restrictive time on the explosion epoch (Cao et al. Reference Cao2013). The non-detections indicate that the first detection was within 24 h of the shock breakout. The HST pre-explosion images of the site indicate a blue star at the position of the SN. Cao et al. (Reference Cao2013) noted that their alignment of a high-resolution ground-based image of the SN was close to, but not formally within the 1σ error circle of the alignment calculation. However, one cannot confidently reject a physical association unless there is a 3σ difference and the σ is correctly defined and measured. Subsequent alignment in Eldridge et al. (Reference Eldridge, Fraser, Maund and Smartt2015) with HST imaging again found a similar result but supported the suggestion by Cao et al. (Reference Cao2013) that this was likely the progenitor system and the first detection of a stellar progenitor of a Ibc SN. Cao et al. (Reference Cao2013) and Groh et al. (Reference Groh, Georgy and Ekström2013a) proposed that the broad-band magnitudes of the source in the HST images were similar to massive WR stars and a stellar model of initially M ZAMS ≃ 30 M⊙ evolved into a WN star with model parameters logL/Lodot = 5.6 and T eff = 46kK (producing a final CO star mass of 10 M⊙). A reassessment of the HST magnitudes of the progenitor led Eldridge et al. (Reference Eldridge, Fraser, Maund and Smartt2015) to argue that a binary system could explain the updated stellar magnitudes better. They found brighter magnitudes by about 0.5m; M F435W = −6.0 ± 0.4, M F555W = −6.0 ± 0.4, M F814W = −5.9 ± 0.4. These updated magnitudes do not rule out the single WR models of Groh et al. (Reference Groh, Georgy and Ekström2013a), but the model binary systems reproduce the measurements quite well.
Both Bersten et al. (Reference Bersten2014) and Eldridge et al. (Reference Eldridge, Fraser, Maund and Smartt2015) presented binary models as alternatives which have initial masses of either 20 + 19 M⊙ or 10 + 8 M⊙ components. These produce a stripped He-core with a final mass of Mfinal = 3–4 M⊙ and the combined flux from the binary systems can reproduce the progenitor magnitudes. The ejecta mass would then be of order 2 M⊙ in agreement with the estimate of Fremling et al. (Reference Fremling2014) from lightcurve modelling. While a single, massive WR star cannot be definitively ruled out, the progenitor magnitudes and ejecta mass estimates are quite well reproduced with a binary system (see Section 3.1 for a position on the Hertzsprung Russell Diagram [HRD]).
In a recent development in this area, Gal-Yam et al. (Reference Gal-Yam2014) took a spectrum of SN2013cu within the first day after explosion showing that it has spectral features similar to those seen in WR stars (specifically H i, He i, He ii, C iv and N iv seen in WN type stars). While this could be interpreted as evidence for a direct WR progenitor star, Gal-Yam et al. (Reference Gal-Yam2014) note that the inferred wind density and mass-loss rate are rather extreme when compared to typical WR stars. Groh (Reference Groh2014) applied a more detailed analysis code to suggest that a WR progenitor star, with a classical radiatively driven wind, is not likely and the precursor was possibly an Luminous Blue Variable (LBV)-type or yellow hypergiant with a recent eruptive phase. SN2013cu was a type IIb and the mass-loss event that produced the circumstellar mass illuminated in the wind could have plausibly occurred during mass-transfer in a binary or in an eruptive phase. The remarkable spectrum is similar to Galactic WR star spectra, although the emitting surface is likely a factor ~ 10 larger than the typical WR stellar radii and the narrow cores of the emission lines seen in SN2013cu are not typical of fast WR wind lines. As Smith et al. (Reference Smith2015) and Shivvers et al. (Reference Shivvers, Mauerhan, Leonard, Filippenko and Fox2014) point out, the spectrum of the early SN is not a direct indicator of the spectral type of the progenitor star before explosion, but it is a powerful measure of the recent mass-loss history of the progenitor. It shows that the CSM material within ~ 10 AU is similar in H and He composition to WN star winds, rather than the star definitely being a WR-type progenitor (Groh Reference Groh2014; Shivvers et al. Reference Shivvers, Mauerhan, Leonard, Filippenko and Fox2014; Smith et al. Reference Smith2015).
2.4. Type IIn progenitors: LBVs and SN2009ip
There are three SNe which have been proposed as core-collapse SNe of type IIn with either identified high-luminosity stellar progenitors detected or reasonably strong arguments in favour of high-mass progenitors (other work has suggested LBV-like progenitors from modulations in radio lightcurves or in optical spectral features; Kotak & Vink Reference Kotak and Vink2006; Trundle et al. Reference Trundle, Kotak, Vink and Meikle2008). The first discovered was the progenitor of SN2005gl which was a bright MV ≃ −10 progenitor detected at the surprisingly large distance of 60 Mpc (Gal-Yam et al. Reference Gal-Yam2007; Gal-Yam & Leonard Reference Gal-Yam and Leonard2009).
The type IIn SN2010jl has HST pre-explosion imaging of its host galaxy (at 50 Mpc) and Smith et al. (Reference Smith2011b) identified the site of the explosion. At this distance, the relatively crowded region of the explosion site prevents a confident detection of a resolved point source, but the blue flux coincident with the SN is likely to be either a very young cluster or a single massive star. Smith et al. (Reference Smith2011b) argued that either of these two cases suggest that the progenitor had an initial mass higher than M ZAMS > 30 M⊙. Both of these SNe occurred within the time limit of the survey defined by Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009) and Eldridge et al. (Reference Eldridge, Fraser, Smartt, Maund and Crockett2013) but are much more distant than the 28 Mpc limit.
The now infamous SN2009ip is a type IIn SN (Mauerhan et al. Reference Mauerhan2013) with a progenitor detected in outburst over many years. After the initial discovery of a non-terminal, but luminous (M ~ −14) outburst in 2009 (Maza et al. Reference Maza2009) at which point it was named SN2009ip, a luminous progenitor star (MV = −10) was detected in HST archival imaging taken in 1999 (Smith et al. Reference Smith2010; Foley et al. Reference Foley, Berger, Fox, Levesque, Challis, Ivans, Rhoads and Soderberg2011). Subsequent monitoring over the next three years, mostly by Pastorello et al. (Reference Pastorello2013) illustrated that the explosion in SN2009ip was part of a regular, but temporally sporadic, series of outbursts of a massive star which photometrically shared similarities with the LBVs of the Local Group. Indeed, it is not even clear if the detection in the HST imaging is the star in outburst or quiescence and hence attaching a bolometric luminosity to any of the data points is not easy to interpret with hydrostatic stellar evolutionary models. It may be that the luminosity is powered at all phases, including that in the archival HST images, by interaction (and the same could be true for SN2005gl).
In 2012, the star had a 30 day outburst that peaked at a luminosity similar to the brightest known LBV giant outbursts (the ‘2012a’ event; MV ≃ −15, logL = 41.5 erg s−1), which was followed by a 10 day rise to SN luminosities (the ‘2012b’ event; MV ≃ −18, logL = 43 erg s−1) (monitored by Pastorello et al. Reference Pastorello2013; Mauerhan et al. Reference Mauerhan2013; Prieto et al. Reference Prieto, Brimacombe, Drake and Howerton2013). The cause and nature of the two are still debated. Smith, Mauerhan, & Prieto (Reference Smith, Mauerhan and Prieto2014) fervently argue that core-collapse must have occurred to cause the bright 2012b peak, and indeed many observational characteristics of this explosion are similar or identical to type IIn SN. Mauerhan et al. (Reference Mauerhan2013) and Smith et al. (Reference Smith, Mauerhan and Prieto2014) propose that the fainter ‘2012a’ event was a non-terminal giant eruption, that core-collapse caused gas to be accelerated to velocities of > 10000kms−1 and the kinetic energy of this gas is efficiently converted to radiative energy in colliding with a dense, but possibly asymmetric CSM to produce a bright SN. Both Pastorello et al. (Reference Pastorello2013) and Fraser et al. (Reference Fraser2013a) argued that it is still possible that the last SN-like event in the history of SN2009ip was not due to core-collapse, but caused by the collisions of massive shells ejected from the star with a dense CSM. The energetics are plausible, although are disputed by Smith et al. (Reference Smith, Mauerhan and Prieto2014). Other papers on the topic (Graham et al. Reference Graham2014; Margutti et al. Reference Margutti2014) have also presented extensive data and analysis but none as yet have definitively proven the true nature. Ofek et al. (Reference Ofek2014) have suggested that at least 50% of type IIn SNe have outbursts within the last few years of their explosion. This seems plausible given the PTF discovery rate, the other discoveries of pre-explosion outbursts (Pastorello et al. Reference Pastorello2007; Fraser et al. Reference Fraser2013b) and the theoretical ideas of hydrodynamic instabilities discussed in Smith & Arnett (Reference Smith and Arnett2014). Whatever mechanism powers the bulk of IIn SNe it appears clear that eruptions in the few years before explosion are much more frequent that previously thought.
For the purposes of this review, the interesting question concerns the possibility that very massive stars produce successful SNe through the core-collapse mechanism. The faintest magnitude that the progenitor star of SN2009ip was observed at was MV = −10, and with a bolometric correction appropriate for a blue supergiant (−1.0 ≲ BC ≲ −0.5), this equates to logL/L⊙ = 6.0–6.3 dex, or an initial mass of 60–80 M⊙. The discussion that follows, will consider the possibility that SN2009ip has undergone a core-collapse and successful explosion.
Although it has been reasonable to link SN of types IIn to LBVs or very massive stars that have had violent recent mass-loss history, an alternative explanation was recently put forward by Mackey et al. (Reference Mackey, Mohamed, Gvaramadze, Kotak, Langer, Meyer, Moriya and Neilson2014). In this model, a red supergiant with a fairly standard mass-loss rate (such as Betelgeuse with ![]() $\dot{M}=1.2\times 10^{-6}$ M⊙ yr−1) produces a static shell of circumstellar material through pressure from photoionization by radiation from external sources. The steady wind gets confined into a static photoionization-confined shell which could contain up to 35 per cent of all mass lost during the red supergiant phase. This gas shell is confined close to the star, giving a possibility of a type IIn SN resulting from a moderate mass red supergiant with standard mass-loss.
$\dot{M}=1.2\times 10^{-6}$ M⊙ yr−1) produces a static shell of circumstellar material through pressure from photoionization by radiation from external sources. The steady wind gets confined into a static photoionization-confined shell which could contain up to 35 per cent of all mass lost during the red supergiant phase. This gas shell is confined close to the star, giving a possibility of a type IIn SN resulting from a moderate mass red supergiant with standard mass-loss.
3 DISCUSSION
3.1. The luminosity distribution of progenitors
A summary of the detected progenitors and their limits are illustrated in a Hertzsprung Russell Diagram in Figure 3, along with a set of theoretical stellar evolutionary models of Eldridge & Tout (Reference Eldridge and Tout2004). This represents a complete summary of the progenitors detected (and limits set) within the time and volume limit of Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009) and Eldridge et al. (Reference Eldridge, Fraser, Smartt, Maund and Crockett2013) (extended to all data published up to end of 2013) and hence the relative numbers and distribution of the stars in this plot are meaningful. The striking result is that there is a deficit of progenitors above an estimated luminosity of logL/L⊙ ≃ 5.1. There are 30 progenitors (type II detections, II limits, IIb, and Ib detections) below this luminosity limit. The final luminosity of a SN progenitor is determined by the He core mass and luminosity, and this luminosity equates to a slightly different mass depending on the stellar evolutionary models used. This logL/L⊙ ≃ 5.1 equates to 16 M⊙for the STARS models of Eldridge & Tout (Reference Eldridge and Tout2004); 16 M⊙ for the rotating Geneva models of Hirschi, Meynet, & Maeder (Reference Hirschi, Meynet and Maeder2004); 18 M⊙ for the Woosley & Heger (Reference Woosley and Heger2007) (see Figure 4) and other stellar evolutionary codes produce model progenitors that are broadly in this range.

Figure 3. The positions of the detected progenitors and upper limits to the type II SNe as discussed in Section 2. The stellar evolutionary tracks are from Eldridge & Tout (Reference Eldridge and Tout2004). The possible positions of the progenitor star of PTF13bvn is marked with two symbols, joined by the dotted line. These show the two positions of the progenitors proposed by Bersten et al. (Reference Bersten2014) and Eldridge et al. (Reference Eldridge, Fraser, Maund and Smartt2015) in their binary models. The position of the progenitor of SN2009ip is shown as the magenta symbol, as estimated from the faintest magnitude the LBV star was found at (see Section 2.4 for more details). The 14 Ibc progenitors with no detections are not quantitatively marked here. If they were WR stars, then one would expect to find them around the blue shaded area (although the box position is illustrative as some models predict progenitors outside this locus, e.g. Groh, Georgy, & Ekström Reference Groh, Georgy and Ekström2013a; Groh et al. Reference Groh, Meynet, Georgy and Ekström2013c) There are 30 progenitors below logL = 5.1, and only one (SN2009ip) above, if indeed SN2009ip is a genuine core-collapse SN.

Figure 4. A comparison of the final pre-SN luminosity as a function of stellar mass, from three sets of stellar evolution models, discussed in the text (Jerkstrand et al. Reference Jerkstrand, Smartt, Fraser, Fransson, Sollerman, Taddia and Kotak2014). The STARS and rotating Geneva models have very similar core masses throughout the mass range, whereas the KEPLER models are 0.1–0.2 dex less luminous at the same stellar mass. This would corresponds to difference in estimated progenitor mass of 2–3 M⊙ if the final luminosity is used as an initial mass tracer. The progenitor limits for the dusty model are those for SN2012aw, from and are discussed further in Section 3.5. Reproduced from Figure 5, in ‘The nebular spectra of SN 2012aw and constraints on stellar nucleosynthesis from oxygen emission lines’, Jerkstrand et al. Reference Jerkstrand, Smartt, Fraser, Fransson, Sollerman, Taddia and Kotak2014, MNRAS, 439, 3649.
For a Salpeter IMF with α = −2.35, 70% of stars between 8–100 M⊙ are in the 8–18 M⊙ range. Hence, with this number of stars (30) lying below the mass limit of 18 M⊙, one would expect to have found 13 higher mass progenitors with logL/L⊙ > 5.1 dex and M ZAMS > 18 M⊙.Footnote 1 There is possibly one (SN2009ip; Section 2.4), but the Poissonian probability of finding between 0 and 1, if the expectation value is 13 would be p = 3 × 10−5.
The number 13 is a very close match to the number of Ibc progenitors for which we have upper limits and one detection. One could argue that the bulk of stars above 18 M⊙ evolve into WR stars and evade detection due to them being too hot and faint at the point of core-collapse. And the numbers would match (almost too well). This is not strictly ruled out by any of the observational constraints to date but it appears to be unlikely. The three constraints of having no detected progenitors, the high relative rate of Ibc SNe, and the low ejecta masses estimated from lightcurve fitting (presented in Section 2.3) all suggest that the binary channel dominates the production of type Ibc SNe.
The missing high-mass stars clearly exist in substantial numbers in star-forming regions and we observe them following a Salpeter (or similar) IMF. Therefore, the question is, why are they not detected as SN progenitors? It does not appear likely that they are all WR stars that have evaded detection, given the arguments above. One argument put forward is a bias in detecting high-mass stellar progenitors as they may exist in denser, younger star-forming regions—dense clusters or associations. Thus, the surface brightness of these regions could make resolving individual stars more difficult. However, there are only three known SNe within the distance and time limit that fall on compact clusters. Two of them SN2004am and SN2004dj are relatively old clusters and very unlikely to host stars of M ZAMS > 20 M⊙ (Mattila et al. Reference Mattila, Fraser, Smartt, Meikle, Romero-Cañizales, Crockett and Stephens2013; Maíz-Apellániz et al. Reference Maíz-Apellániz, Bond, Siegel, Lipkin, Maoz, Ofek and Poznanski2004), and the other is SN1999ev which is also unlikely to be a very young cluster (Maund et al. Reference Maund, Reilly and Mattila2014b). It is also unlikely that these missing high-mass progenitors stars produce normal luminosity SNe that are systematically missed by nearby surveys because of surface brightness effects—since SN2004am was a relatively faint and reddened SN, recovered on top of a bright super star cluster in M82 (Singer, Pugh, & Li Reference Singer, Pugh and Li2004; Mattila et al. Reference Mattila, Fraser, Smartt, Meikle, Romero-Cañizales, Crockett and Stephens2013). And SN2004dj was also easily detected in amateur surveys (Nakano & Itagaki Reference Nakano and Itagaki2004). It would appear that the SN population we observe in the local Universe are not being produced, in large proportions, by stars with logL/L⊙ > 5.1 (M ZAMS ≳ 18 M⊙).
3.2. The mass function of progenitors
Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009) calculated the mass function of progenitors of type II SNe, assuming that there are no major biases in selecting the SNe with progenitor information from the broader local SN population. This paper used a consistent approach, employing the STARS models to attach an initial stellar mass to the luminosities and luminosity limits determined. They defined the ‘red supergiant problem’ which articulates the fact that while red supergiants are commonly found as direct progenitors of II-P SNe, there were no progenitors found above an estimated initial mass of around 17 M⊙, or logL/L⊙ ≃ 5.1. As discussed in Levesque et. al (Reference Levesque, Massey, Plez and Olsen2009), red supergiants are found up to luminosities of logL/L⊙ ≃ 5.5.
It is timely to review this in light of the discoveries made since 2009 and the increase in statistics now available and updated values using different methodologies. The luminosities compiled in this paper for detections and non-detections are used with three sets of models to estimate initial masses of the progenitor stars. The end points of three sets of models are plotted in Figure 4 showing the initial mass–final luminosity relation for the STARS models (Eldridge & Tout Reference Eldridge and Tout2004), the rotating Geneva models of Hirschi et al. (Reference Hirschi, Meynet and Maeder2004) and the KEPLER models of Woosley & Heger (Reference Woosley and Heger2007). The STARS and rotating Geneva models have quite similar final luminosities, hence we consider the results of these to be indistinguishable (at least at the level of accuracy possible for any individual SN progenitor). The KEPLER models are less luminous at their end points by between 0.1 and 0.2 dex which typically translates into a difference in mass of 1–2 M⊙. In Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009) and other work that employed one set of stellar models, the uncertainty in the theoretical models was taken into account by using luminosities at the end of the He burning. This was somewhat artificial and this review uses an alternative approach of taking the end points of three sets of evolutionary model grids.
The estimated initial masses of the progenitors are listed in Tables 1 and 2. The masses for the three lowest luminosity progenitors (SN2003gd, SN2005cs, and SN2009md) are uncertain in the KEPLER models, as this code does not yet have published end points for stars in the 8–10 M⊙ regime. This is a problematic regime in that second dredge-up may occur, pushing the progenitors to higher luminosities than their more massive counterparts as discussed in Eldridge et al. (Reference Eldridge, Mattila and Smartt2007), Smartt et al. (Reference Smartt, Gilmore, Tout and Hodgkin2002), and references there in. The quoted, but uncertain estimates from employing the KEPLER model are simply the extrapolated differences from the STARS estimates.
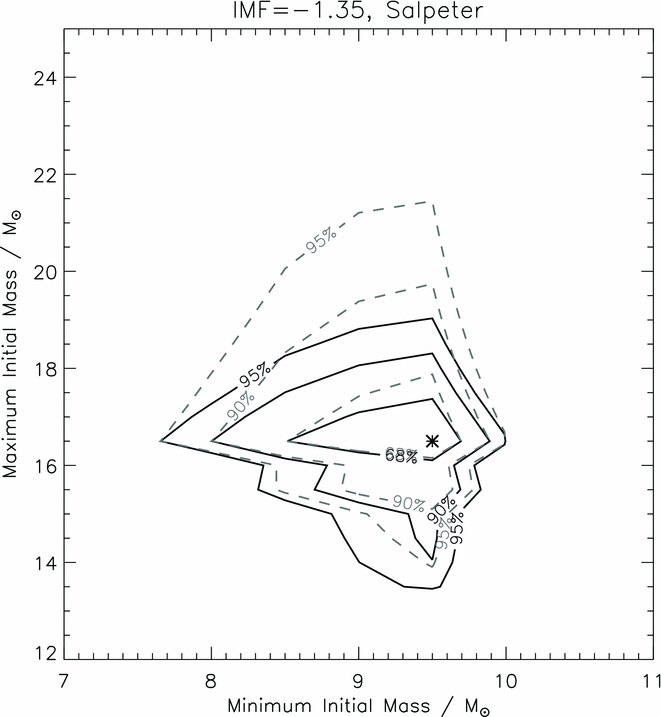
As in Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009), one can assume that the progenitors come from a mass function of some slope and take α = −2.35 as a reliable standard. A maximum likelihood calculation can produce an estimate of the most likely lower mass and upper mass of the distribution, assuming the masses follow a Salpeter function. For the masses estimated with the STARS (and rotating Geneva) models, the values determined (using the same idl routine as employed in Smartt et al. Reference Smartt, Eldridge, Crockett and Maund2009) are a minimum mass for the distribution of m min = 9.5+0.5−2 and a maximum mass of m max = 16.5+2.5−2.5 where the errors are the 95% confidence limits (see Figure 5). If we employ the KEPLER models, then the values are m min = 10+0.5−1.5 and a maximum mass of m max = 18.5+3−4 (again with 95% confidence limits). These results are illustrated further in Figure 6 where the masses are plotted with a Salpeter IMF (cumulative frequency function). The plots show that the mass distributions are comfortably reproduced with a standard IMF between the lower and upper mass limits from the maximum likelihood calculations, but they need to be truncated at the higher mass. If one allows the mass function to vary up to say 30 M⊙, then the mass distribution cannot be reproduced. This is the same basic result as shown in Figure 3—the population of progenitors is missing the high-mass end of the distribution, but this time the IMF is quantitatively considered. The maximum likelihood calculation is visualised in this cumulative frequency plot—given an IMF slope, the line fit should go through the error bars of the detections and not conflict with any of the upper limits.

Figure 5. The maximum likelihood of the minimum and maximum initial masses of the type II progenitor distribution, assuming the stars follow a Salpeter IMF. Originally calculated in Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009), and reproduced here with the updated and extended masses in this review. The dashed lines show the confidence contours (68, 90, and 95%) for the detections only and the solid lines show the confidence contours for the detections and upper limits combined. The star symbol marks the best fit, as described in Section 3.2, of m min = 9.5+0.5−2 and m max = 16.5+2.5−2.5. This is for the masses from the STARS and Geneva rotating models, the values for the KEPLER masses are given in the text.
The lower mass limit to produce a core-collapse SN was estimated in Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009) to be m min = 8.5+1.0−1.5 from the same method and the sample to that point. Smartt (Reference Smartt2009) reviewed the limits from the maximum masses of white dwarf progenitors, suggesting a convergence at m min = 8 ± 1. The two values estimated here slightly higher: the value from the STARS models is m min = 9.5+0.5−2 (integer mass models evolved through C-burning down to that mass have been calculated) which is not significantly different to that estimated previously given the errors. The value from the KEPLER models is higher again, at m min = 10+0.5−1.5. However, low-mass models (7–10 M⊙) are not available from KEPLER and the values in this luminosity range were estimated assuming the same differential in luminosity between KEPLER and STARS models exists between 7 and 10 M⊙ as at 11 M⊙ (Figure 4). This is uncertain and the lower mass from KEPLER should not be treated as a quantitative estimate: m min is critically dependent on the mass estimates for the three lowest luminosity progenitors and if these are adjusted down by ~ 1 M⊙then the value of m min = 9.5 would be reproduced. Some further quantitative modelling of stars in this interesting mass range is required to reproduce the stellar luminosities and produce either a Fe-core collapse or O–Mg–Ne core that collapses through electron capture. Despite this uncertainty at the lower end, the existence of a high-mass upper limit for type II SNe appears be secure. The value is model dependent of course, but the basic result is that type II progenitors are statistically lacking above a logL/L⊙ ≃ 5.1 dex. The final model luminosities at this value are stars with m max = 16.5 (19 M⊙ at 95% confidence) for the STARS and Geneva models and m max = 18.5 (21.5 M⊙ at 95% confidence) for the KEPLER models.
While Smartt et al. (Reference Smartt, Eldridge, Crockett and Maund2009) first discussed this as the ‘red supergiant problem’, the lack of detected high-mass progenitors is now a broader issue for all SN types. This broader issue of a lack of high-mass progenitors generally was discussed in Kochanek et al. (Reference Kochanek, Beacom, Kistler, Prieto, Stanek, Thompson and Yüksel2008), who took all historical and literature limits to that date. The fact that there are now three type IIb SNe in our sample with progenitor detections (Table 3) and these also have luminosities less than ~ 5.1 dex illustrates that the missing high-mass star problem is relevant for all type II SNe (type II-P, II-L, IIb). We address the issue of type IIn progenitors below.
Alternative methods of probing the mass function of SN progenitor stars have been recently advanced by Williams et al. (Reference Williams, Peterson, Murphy, Gilbert, Dalcanton, Dolphin and Jennings2014) and Jennings et al. (Reference Jennings, Williams, Murphy, Dalcanton, Gilbert, Dolphin, Weisz and Fouesneau2014). These use similar methods of quantifying the stellar population around historical SNe in galaxies closer than 8 Mpc and around SN remnants in M31 and M33. They use high-quality HST imaging and careful stellar photometric measurements to determine the luminosity and masses of stars within the immediate vicinity of SNe (typically within 50 pc). Jennings et al. (Reference Jennings, Williams, Murphy, Dalcanton, Gilbert, Dolphin, Weisz and Fouesneau2014) find that there is a lack of high-mass stars close to the SN remnants in M31 and M33, suggesting either the highest mass stars do not produce SNe, or that SNR surveys are biased against finding objects in the very youngest (< 10 Myr old) star-forming regions. Williams et al. (Reference Williams, Peterson, Murphy, Gilbert, Dalcanton, Dolphin and Jennings2014) also suggest that their results are compatible with progenitors all coming from masses M < 20 M⊙ although the uncertainties do not rule out the possibility of no upper-mass cut-off.
3.3. Possible explanations
The reasons for these missing high-mass progenitors are discussed as follows
3.3.1. Dust formation and circumstellar extinction
As discussed in Section 2.1.3, the extinction toward the progenitors is often estimated from the extinction toward the SN itself, or the nearby stellar population. The former estimates may not be directly applicable since the circumstellar dust around the progenitor stars can be destroyed in explosions—as in the case of SN2012aw and SN2008S.
Walmswell & Eldridge (Reference Walmswell and Eldridge2012) calculated the dust that could be produced in red supergiant winds and the extra extinction that this would produce. The idea is well motivated and valid, but Kochanek et al. (Reference Kochanek, Khan and Dai2012) showed that treating CSM extinction with a slab of ISM material is not physically consistent. As shown in Kochanek et al. (Reference Kochanek, Khan and Dai2012), the progenitor of SN2012aw was thought to be quite a high-mass star but correct treatment of radiative transfer in a spherical dust shell reduces the progenitor luminosity limit while comfortably fitting the optical, NIR, and MIR detections and limits. The major concern for this sample is that the objects with limits only are effectively unconstrained—one could propose that these are all high-mass objects enshrouded in dust and having no detection at any waveband does not allow meaningful constraints. However, there is another important constraint which comes from x-ray and radio observations of type II SNe.
Chevalier, Fransson, & Nymark (Reference Chevalier, Fransson and Nymark2006) considered a sample of six type II-P SNe with x-ray and radio observations. They estimated the mass-loss densities in the progenitor star’s stellar wind from the thermal x-ray and radio synchrotron flux which originates when the fast moving SN ejecta interact with a pre-existing, lower velocity stellar wind from the progenitor star. The results for these six SNe (which are in the compilation presented here, either in Table 1 or 2), were consistent with the mass-loss expected for progenitor red supergiants in the mass range ~ 8–20 M⊙. Dwarkadas (Reference Dwarkadas2014) has now compiled all the available literature x-ray detections for type II-P SNe and used the Chevalier & Fransson (Reference Chevalier, Fransson and Weiler2003) treatment of the free-free x-ray luminosity from the shocks produced by the SN ejecta and the stellar winds. Red supergiant stars have observed mass-loss rates that span a wide range of values from < 10−6 M⊙ yr−1 up to ~ 10−4 M⊙ yr−1 (Mauron & Josselin Reference Mauron and Josselin2011). The observed x-ray luminosity is ![]() $L_{\rm x\text{-}ray} \propto (\dot{M}/v)^2$ (where
$L_{\rm x\text{-}ray} \propto (\dot{M}/v)^2$ (where ![]() $\dot{M}$ is the stellar mass-loss rate and v is the stellar wind velocity; Chevalier & Fransson Reference Chevalier, Fransson and Weiler2003). With a wind velocity of around ~ 10kms−1, the x-ray luminosities imply mass-loss rates of less than
$\dot{M}$ is the stellar mass-loss rate and v is the stellar wind velocity; Chevalier & Fransson Reference Chevalier, Fransson and Weiler2003). With a wind velocity of around ~ 10kms−1, the x-ray luminosities imply mass-loss rates of less than ![]() $\dot{M} < 10^{-5}$ M⊙ yr−1. The mass-loss rates of red supergiants are correlated with stellar luminosities and Dwarkadas (Reference Dwarkadas2014) then used the Mauron & Josselin (Reference Mauron and Josselin2011) relations (
$\dot{M} < 10^{-5}$ M⊙ yr−1. The mass-loss rates of red supergiants are correlated with stellar luminosities and Dwarkadas (Reference Dwarkadas2014) then used the Mauron & Josselin (Reference Mauron and Josselin2011) relations (![]() $\dot{M} = 4.7\times 10^{-6}(L/10^{5})^{1.7}$) to illustrate that type II-P SNe do not have high enough x-ray luminosities to have had progenitors significantly greater than logL/L⊙ ≃ 5.2 dex or 19 M⊙. Similar arguments were used in Kochanek et al. (Reference Kochanek, Khan and Dai2012) specifically for the case of SN2012aw to show that the steady wind of
$\dot{M} = 4.7\times 10^{-6}(L/10^{5})^{1.7}$) to illustrate that type II-P SNe do not have high enough x-ray luminosities to have had progenitors significantly greater than logL/L⊙ ≃ 5.2 dex or 19 M⊙. Similar arguments were used in Kochanek et al. (Reference Kochanek, Khan and Dai2012) specifically for the case of SN2012aw to show that the steady wind of ![]() $\dot{M} \lesssim10^{-5.5}$ to 10−5 M⊙ yr−1 was consistent with the x-ray and radio fluxes measured. The existence of obscuring CSM dust cannot exist without CSM gas, in the form of stellar winds, with typical dust masses around ~ 0.5% that of the gas masses (from the typical opacties in Kochanek et al. Reference Kochanek, Khan and Dai2012). Therefore, an obscured progenitor should be brighter in x-ray and radio than the typical luminosities observed to date. Dwarkadas (Reference Dwarkadas2014) shows that the IIb and IIL SNe have typically higher x-ray luminosities than the II-P, with values around ~ 1039.5erg s−1 (also see Dwarkadas & Gruszko Reference Dwarkadas and Gruszko2012). This is consistent with their higher luminosity progenitors, in the range of logL/L⊙ ≃ 5.1−5.2 dex. As remarked upon by Dwarkadas (Reference Dwarkadas2014), the general agreement between the two independent methods is remarkably consistent. While dust obscuration should still be considered carefully for any progenitor and limit, it appears the sample as a whole is not significantly biased and there are no major discrepancies between the optical–NIR luminosity and mass estimates of progenitors and the SN x-ray and radio fluxes.
$\dot{M} \lesssim10^{-5.5}$ to 10−5 M⊙ yr−1 was consistent with the x-ray and radio fluxes measured. The existence of obscuring CSM dust cannot exist without CSM gas, in the form of stellar winds, with typical dust masses around ~ 0.5% that of the gas masses (from the typical opacties in Kochanek et al. Reference Kochanek, Khan and Dai2012). Therefore, an obscured progenitor should be brighter in x-ray and radio than the typical luminosities observed to date. Dwarkadas (Reference Dwarkadas2014) shows that the IIb and IIL SNe have typically higher x-ray luminosities than the II-P, with values around ~ 1039.5erg s−1 (also see Dwarkadas & Gruszko Reference Dwarkadas and Gruszko2012). This is consistent with their higher luminosity progenitors, in the range of logL/L⊙ ≃ 5.1−5.2 dex. As remarked upon by Dwarkadas (Reference Dwarkadas2014), the general agreement between the two independent methods is remarkably consistent. While dust obscuration should still be considered carefully for any progenitor and limit, it appears the sample as a whole is not significantly biased and there are no major discrepancies between the optical–NIR luminosity and mass estimates of progenitors and the SN x-ray and radio fluxes.
It is interesting to note that it is not just steady wind mass-loss that has been proposed to produce dense CSM shells, and potentially extra extinction, around progenitors. Shiode & Quataert (Reference Shiode and Quataert2014) have argued that after core neon burning, internal gravity waves can transport a super-Eddington energy flux out into the stellar envelope and cause a mass ejection of around 1 M⊙ of material. They suggest that this could occur preferentially in progenitors with M ZAMS ~ 20 M⊙ within a few months to a decade of core-collapse, with the most intense mass-loss preferentially occurring closer to core-collapse. This timescale is quite similar to the typical time differences between SN explosions and dates of progenitor detections. The dates of the observations of progenitors, or limits (for the SNe in Tables 1, 2, and 3) have a range of 2 months to 17 years before the SN discovery dates (which one can assume is close to the explosion date to within ~ weeks at worst). The median and standard deviation of the time of data being taken before SN discovery are 65 and 54 months. It is possible that these ejection episodes could create dust shells; however, the gas masses would be inconsistent with the x-ray and radio fluxes, as discussed for the steady mass-loss scenarios. There is no obvious correlation between probability of discovery and date of data taken, and some of the discoveries have images taken within 5–9 months before explosion (e.g. 2003gd, 2005cs, 2008bk).
3.3.2. Biased luminosity estimates and evolution to the blue
An argument could be made that the observed limit that we see for red supergiant progenitors of logL/L⊙ ≃ 5.1 dex is not significantly lower, than the highest luminosity red supergiants of logL/L⊙ ≃ 5.45 dex (Levesque et al. Reference Levesque, Massey, Plez and Olsen2009) and that uncertainties in the extinction and luminosity estimates from small numbers of broad-band fluxes are high enough to argue that this is not a discrepancy at all. Rather, this indicates broad and basic agreement (see Davies et al. Reference Davies2013, for a discussion on careful model atmosphere techniques). However, the increase in statistics now available, and the statistical and quantitative deficit of high-luminosity progenitors as calculated in Section 3.2 would suggest that this is not a satisfactory answer.
More broadly, the question then is—if there is no real ‘red supergiant problem’, then where in the HRD to these M ZAMS ≳ 18 M⊙ stars evolve to before the point of core-collapse and what SN do they produce ? They must end up with an iron core and, within the bounds of current theory, they must collapse. It does not appear that they can all produce WR stars and Ibc SNe for the reasons discussed in Section 2.3. The search for progenitors is not biased against any particular SN type, and the one II-L progenitor (SN2009kr), and the three IIb progenitors do not have luminosities higher than the observed limit of 5.1 dex. If high-mass stars (M > 18 M⊙) evolve to produce visible SN explosions, there is no obvious reason we should not detect both the SN and their progenitors, unless the SNe themselves are intrinsically faint and have evaded either detection or recognition.
The type IIn SNe have been suggested as a way out. High-mass stars, with high mass-loss rates produce high enough CSM gas masses that the SNe are observed to be IIn types. This is reasonable and indeed corroborated by two detections of likely high-mass progenitors for IIn SNe (Gal-Yam & Leonard Reference Gal-Yam and Leonard2009; Smith et al. Reference Smith2011b), but we have not systematically found enough of them to account for the missing mass range. Smith et al. (Reference Smith, Li, Filippenko and Chornock2011a) argue for quite a high relative rate of IIn SNe in the LOSS survey and that these would naturally have high-mass progenitor stars. It seems almost certain that SNe IIn do come from high-mass progenitors (see Section 2.4). Some have detected progenitors (as in SN2009ip and SN2005gl) and they tend to have the largest x-ray and radio fluxes that require mass-loss rates which cannot be realistically produced by low to moderate-mass stars (Dwarkadas Reference Dwarkadas2014, and references therein). However, the high relative rate estimated in Smith et al. (Reference Smith, Li, Filippenko and Chornock2011a) does not appear to hold at lower distances (see Eldridge et al. Reference Eldridge, Fraser, Smartt, Maund and Crockett2013, for a discussion on this topic). There is no reason why we should not detect them and no reason why they should not appear in Figure 3 other than there are not enough high-mass stars producing visible IIn SNe.
Other work has also hinted that there could be some systematic bias underlying the mass estimates from the direct detection of progenitors. Hydrodynamic modelling of type II-P SN lightcurves and velocity measurements has suggested a significant discrepancy between the SN ejected masses and the stellar masses of the progenitors. The detailed modelling of Utrobin & Chugai (Reference Utrobin and Chugai2008) and Utrobin & Chugai (Reference Utrobin and Chugai2009) for example has estimated ejecta masses for five type II SNe (1987A, 1999em, 2003Z, 2005cs, and 2004et) which would imply initial stellar masses a factor of ~ 2 higher than those estimated from the progenitor luminosity and stellar evolutionary tracks. Utrobin & Chugai (Reference Utrobin and Chugai2009) speculate that the hydrodynamics may be affected by asymmetry in the explosion and the lack of treatment of the multi-dimensional effects of Rayleigh–Taylor mixing between the helium core and the hydrogen envelope. However, Spiro et al. (Reference Spiro2014) used a different code (that of Pumo & Zampieri Reference Pumo and Zampieri2011) to find better agreement between the direct progenitor masses and hydrodynamic masses estimates. A major goal for the SN community is to reconcile these independent and complimentary estimates as they fundamentally link the progenitor, explosion mechanism, and SN observables. One would hope uniform agreement could be found that each method can inform the other of potential systematic errors.
3.4. Black hole formation and failed supernovae
On the basis of available data, the above two explanations are unlikely. Therefore, the reason for the lack of high-mass progenitors may be simply that they do not exist. In other words, the SN population that we observe does not, on the whole, come from stars with initial masses greater than M ZAMS ~ 18 M⊙. That these high-mass stars will evolve to carbon–oxygen cores and subsequently to an Fe core composition and collapse is inevitable. However, if black holes are formed, either directly or by fall back, and the neutrino energy deposition is not sufficient to drive the shock through the steeper density profiles of these progenitors, a failed SN is possible. It is plausible to postulate that the reason for the missing high-mass progenitors is that they produce failed SNe that have, so far gone undetected (or unrecognised) in all of our efforts to find and quantify transients in the local Universe. From a theoretical standpoint, this is not surprising at all, the issue of explodabilty of the most massive stars has been a question since the 1980s and 1990s. Fryer (Reference Fryer1999) explored black hole formation through direct collapse and fall back and already suggested then that stars above 20 M⊙ would produce black holes, possibly without an SN explosion.
The density profiles in stellar cores is a strong function of stellar mass, and recent work has revisited the idea that very massive stars may not produce detectable SNe. As discussed in the introduction in Sukhbold & Woosley (Reference Sukhbold and Woosley2014), the density gradient in more massive stars is relatively shallow, which will likely lead to higher accretion rates onto the compact object created at the point of collapse. It would also lead to higher ‘ram pressure’ which would need to be overcome by the shock (through the nuetrino energy deposition mechanism) to launch a successful explosion through the star. The difficulty in getting successful simulated explosions has reinvigorated the study of the explodability of stars and in particular, three independent analyses by O’Connor & Ott (Reference O’Connor and Ott2011), Ugliano et al. (Reference Ugliano, Janka, Marek and Arcones2012), and Sukhbold & Woosley (Reference Sukhbold and Woosley2014) and have used the compactness parameter (defined in O’Connor & Ott) which quantifies the core radius within which a certain amount of mass is confined in the final progenitor model ξ = M/R(M) where M is in solar masses and R(M) is in units of 1 000 km. Defining ξ2.5 for a value of 2.5 M⊙ has been proposed. All three of these studies suggest that the compactness parameter is not a monotonically increasing and simple function of initial stellar mass. It will depend critically on mass-loss rate, internal mixing mechanisms in the stellar model not to mention metallicity and rotation (and very likely mass-transfer in binaries will have similar effects to mass-loss). Figure 7 is from O’Connor & Ott (Reference O’Connor and Ott2011) showing the compactness ξ2.5 at bounce, as a function of M ZAMS. The three studies all suggest that at critical values of ξ2.5 > 0.2–0.3, successful explosions are difficult to achieve. The figure illustrates that the compactness is dependent on the mass-loss recipes used in the stellar models, and that below M ZAMS < 20 M⊙, the stars are relatively easy to explode. However, above that threshold, it becomes significantly more difficult to achieve explosions. There are what have been termed ‘islands of explodability’ such that at some masses, the combination of mass-loss and final core structure may make it easier or hard to explode. What is constant in all these three studies is that above M ZAMS > 20 M⊙, one would expect to have failed explosions and that there will be a tendency for stars not to produce visible SNe. It may be that there is not a one to one relation and there is no simple, single numerical mass threshold at which neutron star or black hole formation occurs. Overall though, model stars above this threshold have a tendency to produce failed SNe at the point of core-collapse whereas stars below it generally proceed to explosion. In the same spirit, Horiuchi et al. (Reference Horiuchi, Nakamura, Takiwaki, Kotake and Tanaka2014) have carried out an extensive series of simulations with more than 300 models and argue that a critical value of ξ2.5 ~ 0.2 is the likely divide between successful and failed explosions. This would result in stars in the initial mass range ~ 16–30 M⊙ not producing canonical SNe.

Figure 7. From O’Connor & Ott (Reference O’Connor and Ott2011). The upper plot shows the compactness parameter ξ2.55 of stellar cores as a function of ZAMS mass for different stellar evolutionary models. The lower plot shows the time to black hole formation, assuming no explosion has occurred. Reproduced from Figure 9 in ‘Black Hole Formation in Failing Core-Collapse SN’, by O’Connor & Ott Reference O’Connor and Ott2011, ApJ, 730, 70.
The observational constraints presented in this review can reasonably be explained, and in a quantitative manner, with this model framework. The search for progenitors has been more difficult than was first thought, with the dearth of high-mass and high-luminosity progenitors an inescapable fact. Arguments can be made concerning dust, bias, and evolution to very faint WR stars but these have been addressed above. The reasonable agreement between the explosion theories based on the core compactness and the progenitor constraints mean they should be considered to be physically linked. As first noted by Kochanek et al. (Reference Kochanek, Beacom, Kistler, Prieto, Stanek, Thompson and Yüksel2008), the prediction of this scenario is that many massive stars (a fraction as high as f = 20–30%) end their lives by disappearing without a visible SN. As the dynamical timescale of a star of red supergiant dimensions is of the order of a year, these failed SNe may give rise to faint, long-lived red transients as proposed by Lovegrove & Woosley (Reference Lovegrove and Woosley2013). However, Piro (Reference Piro2013) proposed that a short timescale optical transient (lasting 3–10 days) with a faint luminosity of ~ 1040–1041erg s−1 could be produced due to the breakout of a shock induced in the stellar envelope from neutrino losses in the core. Gerke, Kochanek, & Stanek (Reference Gerke, Kochanek and Stanek2015) have just presented the first results from their novel and ongoing survey for failed stars and this has turned up one plausible candidate that requires further investigation. One could reasonably argue that black-hole-forming cores and failed explosions are not controversial ideas, rather they are solid theoretical predictions that have been proposed for more than 15 years (e.g. Fryer Reference Fryer1999). Kochanek (Reference Kochanek2014) finds that the observed black hole mass function in the Galaxy can be modelled by assuming that black hole formation (and hence successful SN explosion) is determined by the core compactness parameter. All of this adds impetus to the searches of Gerke et al. (Reference Gerke, Kochanek and Stanek2014) and surveys for transients in the local Universe to identify the signatures that have been suggested by, for example, Lovegrove & Woosley (Reference Lovegrove and Woosley2013) and Piro (Reference Piro2013).
A final note on this topic of the explosion mechanism is the potential of recent work to compare the ejecta velocities in successful SNe to the progenitor mass estimates by Poznanski (Reference Poznanski2013). There appears to be a relation between the observed ejecta velocities, plateau duration, and progenitor mass which could be explained if the energy deposition (the kinetic energy observed in the ejected envelope) is proportional to the initial mass of the progenitor cubed (E∝M 3). If this analysis holds, then it could be telling us something about the efficiency of the deposition process in a neutrino-revived explosion. As noted by Poznanski (Reference Poznanski2013), the paucity of objects with low energy and large mass could support the idea of a population of failed SNe. This interesting correlation is worth pursuing further both from the observational gathering of larger samples and theoretical investigation of the explosion mechanisms.
3.5. Nebular spectra and nucelosynthesis
A potentially powerful method of testing stellar evolutionary modelling and explosive nucleosynthesis is by observing, and physically modelling SNe when they are in their nebular phase. As the ejecta expand and become optically thin, the inner regions of the progenitor star become visible and the elements synthesised within the He and CO cores during stellar evolution become visible. Nebular spectra allow the diagnosis of nucleosynthesis products. This becomes particularly interesting for SNe with detected progenitors, as the independent estimate of the main-sequence mass from nebular modelling can test the prediction from the progenitor luminosity. An evolutionary model should reproduce the pre-explosion stellar luminosity and the oxygen mass (for example) produced during helium and carbon burning. (as in Kozma & Fransson Reference Kozma and Fransson1998). Figure 8 visually illustrates the diagnostic power of combining these two methods. The progenitor star is detected, seen to disappear and the faint blue flux visible at the star’s position can be studied spectroscopically to determine element masses synthesised in the progenitor (e.g. the [O i] doublet at 6300,6364 is a useful diagnostic of the neutral oxygen mass). The key to this of course is having a reliable and sophisticated radiative transfer model that can reproduce the observed spectra and estimate element masses in the ejecta from the absolute and relative strengths of the emission lines. One of the leading codes for this has been developed by Jerkstrand (Reference Jerkstrand2011), Jerkstrand, Fransson, & Kozma (Reference Jerkstrand, Fransson and Kozma2011), and Jerkstrand et al. (Reference Jerkstrand, Fransson, Maguire, Smartt, Ergon and Spyromilio2012). There are others such as Dessart, Livne, & Waldman (Reference Dessart, Livne and Waldman2010) and Mazzali et al. (Reference Mazzali, Maurer, Valenti, Kotak and Hunter2010) which have been successfully applied. The Jerkstrand et al. code, developed in Stockholm, calculates the physical conditions in the expanding nebula and includes non-thermal heating, ionization, and excitation from the gamma-ray and positron energy deposition of 56Ni/56Co (and 57Co and 44Ti at later phases), and computes thermal and statistical equilibrium with the latest atomic data. It treats multi- line radiative transfer with a Monte Carlo technique and is being actively applied to those SNe with progenitor detections and limits (e.g. Jerkstrand et al. Reference Jerkstrand, Smartt, Fraser, Fransson, Sollerman, Taddia and Kotak2014, Reference Jerkstrand, Ergon, Smartt, Fransson, Sollerman, Taubenberger, Bersten and Spyromilio2015). These models can successfully reproduce the observed optical, near-IR and (when available) mid-IR spectra of type II SNe at late phases (see the results for SN2004et in Jerkstrand et al. Reference Jerkstrand, Fransson, Maguire, Smartt, Ergon and Spyromilio2012; Maguire et al. Reference Maguire2012).

Figure 8. Upper: The visually striking illustration of the disappearance of the red supergiant progenitor of SN2008bk, from Mattila et al. (Reference Mattila, Smartt, Maund, Benetti and Ergon2010). Panel A shows the VLT colour image of the progenitor (marked). Panel B shows the VLT NACO image of SN2008bk and the surrounding population at high resolution. Panel C shows an NTT colour image at approximately 940 days after explosion illustrating the disappearance of the red source. The quantitative mass estimates of the progenitor are in Maund et al. (Reference Maund, Mattila, Ramirez-Ruiz and Eldridge2014a). Middle and Lower: A spectrum of the faint blue source seen at 547 days after explosion from Maguire et al. (Reference Maguire2012), showing the nebular phase emission lines from the SN ejecta, with a model from Jerkstrand et al. (Reference Jerkstrand, Fransson, Maguire, Smartt, Ergon and Spyromilio2012). The model is from an exploded 12 M⊙ star, which is in good agreement with the updated progenitor mass estimate in Maund et al. (Reference Maund, Mattila, Ramirez-Ruiz and Eldridge2014a) and in the summary table here (see Table 1. Reproduced from Figure 13, in ‘Constraining the physical properties of Type II-Plateau supernovae using nebular phase spectra’, Maguire et al. Reference Maguire2012, MNRAS, 420, 3451.
In particular, the application to SN2012aw allows a self-consistent comparison of the progenitor luminosity and the oxygen produced. In a progenitor model, the stellar luminosity is determined by the He core luminosity. The He core size and burning rate dictates the oxygen production. Thus, a progenitor model which has been artificially exploded should be able to reproduce the oxygen line strengths and the final luminosity consistently. The physical sophistication of the Jerkstrand et al. (Reference Jerkstrand, Fransson and Kozma2011) code now allows this to be done to high accuracy. For SN2012aw, the nebular phase spectra are in good agreement with the ejecta from a KEPLER model of M ZAMS = 15 M⊙ progenitor star (Jerkstrand et al. Reference Jerkstrand, Smartt, Fraser, Fransson, Sollerman, Taddia and Kotak2014) and the forbidden neutral oxygen lines can be used to constrain the mass of oxygen to be less than < 1 M⊙(see Figure 9). This provides a physically consistent match to the progenitor luminosity of a KEPLER model of the same mass (14 M⊙ as in Table 1 and illustrated in Figure 4).

Figure 9. Upper panel: This shows the observed line luminosities for [O i], Mg i] and Na i for SN2012aw compared to the nebular models for 12–25 M⊙ stars (Jerkstrand et al. Reference Jerkstrand, Smartt, Fraser, Fransson, Sollerman, Taddia and Kotak2014). The line strengths support the mass estimate from direct detection of the progenitor star of around M ZAMS = 15 M⊙ and are much weaker than is predicted expect for exploding high-mass progenitor models of 20–25 M⊙. Reproduced from Figure 4, in ‘The nebular spectra of SN 2012aw and constraints on stellar nucleosynthesis from oxygen emission lines’, Jerkstrand et al. Reference Jerkstrand, Smartt, Fraser, Fransson, Sollerman, Taddia and Kotak2014, MNRAS, 439, 3649. Lower panel: A compilation of the [O i] line luminosities compared to the predictions of exploding models of 12, 15, 19 and 25 M⊙. This again illustrates that type II SNe (predominantly II-P) do not have the observational signatures expected from higher mass 19–25 M⊙progenitors. Reproduced from Figure 9, in ‘Supersolar Ni/Fe production in the Type IIP SN 2012ec’, Jerkstrand et al. Reference Jerkstrand, Ergon, Smartt, Fransson, Sollerman, Taubenberger, Bersten and Spyromilio2015, MNRAS, in press.
The [O i] line strengths (and also the Mg i and Na i fluxes) are strongly dependent on progenitor mass. The conclusion of Jerkstrand et al. (Reference Jerkstrand, Smartt, Fraser, Fransson, Sollerman, Taddia and Kotak2014) is that to date, there is no convincing example of a type II-P SN which displays the nucleosynthetic products expected from a M ZAMS > 20 M⊙ progenitor in its nebular spectra (see Figure 9). Jerkstrand et al. (Reference Jerkstrand, Ergon, Smartt, Fransson, Sollerman, Taubenberger, Bersten and Spyromilio2015) further modelled the nebular spectra of the IIb SNe 1993J, 2008ax and 2011dh and constrained the initial mass of the progenitors to be M ZAMS = 12–16 M⊙ from the line strengths of the oxygen lines. Together with progenitor detections, constraints on the mass-loss rates, these nebular spectra and the radiative transfer analysis there is a consistent picture that there are no type II SNe in the local Universe which come from high-mass progenitors. While the nebular spectral analysis provides the strong progenitor constraints useful for this review, it is becoming a powerful way to probe the enrichment of SNe and to allow quantitative checks on what role various SNe play in galactic chemical evolution models.
3.6. Nucleosynthesis and chemical evolution
If all stars above a certain main-sequence mass do form black holes, then they are not likely to eject the elements synthesised during stellar evolution. The important implications of this were recently studied by Brown & Woosley (Reference Brown and Woosley2013) who found that the solar abundance pattern (from oxygen to strontium, at A ≃ 90) are fit well if there is no cut-off assumed. This calculation had all stars up to 120 M⊙ produce successful SN and produce nucleosynthetic yields according to Woosley & Heger (Reference Woosley and Heger2007). If the limiting main sequence mass that produces a black hole and no SN (and therefore no enrichment) is reduced to M BH = 25 M⊙, then the solar elemental abundance pattern is still comfortably reproduced. However, there are unpalatable consequences if this mass limit is as low as M BH = 18 M⊙, for which there is some direct evidence as discussed earlier in this review. For this limit to be compatible with the observed abundance pattern, Brown & Woosley (Reference Brown and Woosley2013) show that the mass-loss rates should be lower than currently assumed (to keep the carbon abundance under control), and the reaction rate for 22Ne(α, n)Mg25 needs to near the experimental maximum rate in order to reproduce the s-process isotopes. In addition, the historical SN rate needs to be three times higher than that when no cut-off is assumed. The non-monotonic distribution of compactness discussed in Section 3.4 which results in some higher mass stars exploding in the islands of explodability would mitigate these problems. However, that would require significant numbers of successful explosions above about 22 M⊙. One way out is that if SN from the most massive stars (M > 20 M⊙) are successful in enrichment but are more often enshrouded in dust and invisible to current surveys. The discussion in Section 3.3 disfavours this scenario. Searches for SNe in very high star formation rate galaxies such as dusty luminous infra-red galaxies suggest that more than about 80% of expected core-collapse SNe are missed in optical and near-infrared searches (Mattila et al. Reference Mattila2012). For normal galaxies, the missing fraction is more likely to be 10–15% (again estimated in Mattila et al. Reference Mattila2012) and these missing SNe would need to be from the most massive stars to explain the deficit of high-mass progenitors and ease the tension on the elemental production budget. Further work on searches for SNe specifically in the radio and mid-IR searches would be required to tie this down securely.
4 CONCLUSION
Drawing together the observational results by the community over the period 1999–2013, together with the theoretical concepts on exploding stars, the following conclusions are proposed:
• There are 45 SN with either detected progenitors or upper limits in the volume-limited sample and either none (or one, if SN2009ip is included) has a progenitor above the luminosity limit of logL/L⊙ ≃ 5.1 (or an equivalent initial mass of M ≃ 18 M⊙). A Salpeter IMF would suggest there should be 13 objects and the probability of finding 0 or 1 is p = 3 × 10−5.
• The various possible biases that have been suggested to explain this deficit were explored in this review including circumstellar dust, selection bias, and luminosity analysis errors. It does not seem likely that they can explain the deficit.
• One possible explanation is that most, or nearly all, stars above M ≳ 18 M⊙ evolve into WR stars that are hot and faint at the point of core-collapse when they produce Ibc SNe. However, this ignores the growing evidence that the Ibc SN population are produced mostly by binary systems with masses in the range 8–20 M⊙.
• Explosion modelling by several theoretical groups actually predict that stars above the mass limit of M ≃ 18 M⊙ have a tendency to produce failed SNe and form black holes. Above this limit, there are islands of explodability that can produce neutron stars and successful explosions. There is no monotonic relationship between the core ‘compactness’ parameter (which will dictate the likelihood of a successful explosion) and initial mass. There is reasonable agreement between the observed limits for the luminosity of progenitors and the theory of explosions.
• The nebular spectra of core-collapse SNe which have identified progenitors is a new and powerful way to probe the progenitor mass range and nucleosynthesis in massive stars. The results to date support the idea that the progenitors discovered to date are in the 8–17 M⊙ range and illustrate that the SN from high-mass stars which are thought to produce the bulk of cosmic oxygen have not yet been found.
ACKNOWLEDGEMENTS
I thank Morgan Fraser, John Eldridge, Anders Jerkstrand for their initial comments and my collaborators over many years in this area, including Justyn Maund, Seppo Mattila, Mark Crockett, and Maggie Hendry. I also thank Dan Milisavljevic, Rob Fesen, Dan Patnaude, José Groh, Stan Woosley, Avishay Gal-Yam, Joe Anderson, Dovi Poznanski, Nolan Walborn, Edward Young for comments on the initial version and discussion. It is a pleasure to acknowledge funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC Grant agreement no. [291222] and STFC grants ST/I001123/1 and ST/L000709/1. I thank the organisers and participants of the 2014 CAASTRO Annual Scientific Conference ‘Supernovae in the Local Universe: celebrating 10 000 days of SN1987A’ for an immensely enjoyable meeting.