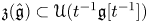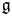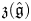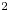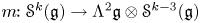Introduction
Let ![]() $G$ be a complex reductive group. Set
$G$ be a complex reductive group. Set ![]() $\mathfrak g=\mathrm {Lie\,} G$. As is well known, the algebra
$\mathfrak g=\mathrm {Lie\,} G$. As is well known, the algebra ![]() ${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ of symmetric
${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ of symmetric ![]() $\mathfrak g$-invariants and the centre
$\mathfrak g$-invariants and the centre ![]() ${\mathcal {Z}}(\mathfrak g)$ of the enveloping algebra
${\mathcal {Z}}(\mathfrak g)$ of the enveloping algebra ![]() ${{\mathcal {U}}}(\mathfrak g)$ are polynomial algebras with
${{\mathcal {U}}}(\mathfrak g)$ are polynomial algebras with ![]() $\mathrm {rk}\,\mathfrak g$ generators. Therefore there are several isomorphisms between them. Two of these isomorphisms can be distinguished, the one given by the symmetrisation map, which is a homomorphism of
$\mathrm {rk}\,\mathfrak g$ generators. Therefore there are several isomorphisms between them. Two of these isomorphisms can be distinguished, the one given by the symmetrisation map, which is a homomorphism of ![]() $\mathfrak g$-modules, and the Duflo isomorphism, which is a homomorphism of algebras. Both of them exist for any finite-dimensional complex Lie algebra.
$\mathfrak g$-modules, and the Duflo isomorphism, which is a homomorphism of algebras. Both of them exist for any finite-dimensional complex Lie algebra.
The symmetrisation map is defined in the infinite-dimensional case as well. However, no analogue of the Duflo isomorphism for Lie algebras ![]() $\mathfrak q$ with
$\mathfrak q$ with ![]() $\dim \mathfrak q=\infty$ is known. Furthermore, one may need to complete
$\dim \mathfrak q=\infty$ is known. Furthermore, one may need to complete ![]() ${{\mathcal {U}}}(\mathfrak q)$ in order to replace
${{\mathcal {U}}}(\mathfrak q)$ in order to replace ![]() ${\mathcal {Z}}(\mathfrak q)$ with an interesting related object, see e.g. [Reference KacKac84]. In this paper, we are dealing with the most notable class of infinite-dimensional Lie algebras, namely affine Kac–Moody algebras
${\mathcal {Z}}(\mathfrak q)$ with an interesting related object, see e.g. [Reference KacKac84]. In this paper, we are dealing with the most notable class of infinite-dimensional Lie algebras, namely affine Kac–Moody algebras ![]() ${{\hat {\mathfrak g}}}$, and the related centres at the critical level.
${{\hat {\mathfrak g}}}$, and the related centres at the critical level.
The Feigin–Frenkel centre ![]() $\mathfrak z(\hat {\mathfrak g})$ is a remarkable commutative subalgebra of the enveloping algebra
$\mathfrak z(\hat {\mathfrak g})$ is a remarkable commutative subalgebra of the enveloping algebra ![]() ${{\mathcal {U}}}(t^{-1}\mathfrak g[t^{-1}])$. The central elements of the completed enveloping algebra
${{\mathcal {U}}}(t^{-1}\mathfrak g[t^{-1}])$. The central elements of the completed enveloping algebra ![]() $\tilde {{{\mathcal {U}}}}_{\kappa }({{\hat {\mathfrak g}}})$ at the critical level
$\tilde {{{\mathcal {U}}}}_{\kappa }({{\hat {\mathfrak g}}})$ at the critical level ![]() $\kappa =-{\tt h}\!^{\vee }$ can be obtained from the elements of
$\kappa =-{\tt h}\!^{\vee }$ can be obtained from the elements of ![]() $\mathfrak z({{\hat {\mathfrak g}}})$ by employing the vertex algebra structure [Reference FrenkelFre07, § 4.3.2]. The structure of
$\mathfrak z({{\hat {\mathfrak g}}})$ by employing the vertex algebra structure [Reference FrenkelFre07, § 4.3.2]. The structure of ![]() $\mathfrak z(\hat {\mathfrak g})$ is described by a theorem of Feigin and Frenkel [Reference Feigin and FrenkelFF92], hence the name. This algebra provides a quantisation of the local Hitchin system [Reference Beilinson and DrinfeldBD, § 2]. Elements
$\mathfrak z(\hat {\mathfrak g})$ is described by a theorem of Feigin and Frenkel [Reference Feigin and FrenkelFF92], hence the name. This algebra provides a quantisation of the local Hitchin system [Reference Beilinson and DrinfeldBD, § 2]. Elements ![]() $S\in \mathfrak z({{\hat {\mathfrak g}}})$ give rise to higher Hamiltonians of the Gaudin model, which describes a completely integrable quantum spin chain [Reference Feigin, Frenkel and ReshetikhinFFR94].
$S\in \mathfrak z({{\hat {\mathfrak g}}})$ give rise to higher Hamiltonians of the Gaudin model, which describes a completely integrable quantum spin chain [Reference Feigin, Frenkel and ReshetikhinFFR94].
The classical counterpart of ![]() $\mathfrak z({{\hat {\mathfrak g}}})$ is the Poisson-commutative subalgebra of
$\mathfrak z({{\hat {\mathfrak g}}})$ is the Poisson-commutative subalgebra of ![]() $\mathfrak g[t]$-invariants in
$\mathfrak g[t]$-invariants in ![]() ${{\mathcal {S}}}(\mathfrak g[t,t^{-1}])/(\mathfrak g[t])\cong {{\mathcal {S}}}(t^{-1}\mathfrak g[t^{-1}])$, which is a polynomial ring with infinitely many generators according to a direct generalisation of a Raïs–Tauvel theorem [Reference Raïs and TauvelRT92]. Explicit formulas for the elements of
${{\mathcal {S}}}(\mathfrak g[t,t^{-1}])/(\mathfrak g[t])\cong {{\mathcal {S}}}(t^{-1}\mathfrak g[t^{-1}])$, which is a polynomial ring with infinitely many generators according to a direct generalisation of a Raïs–Tauvel theorem [Reference Raïs and TauvelRT92]. Explicit formulas for the elements of ![]() $\mathfrak z({{\hat {\mathfrak g}}})$ appeared first in type A [Reference Chervov and TalalaevCT06, Reference Chervov and MolevCM09] following Talalaev's discovery [Reference TalalaevTal06] of explicit higher Gaudin Hamiltonians. Then they were extended to all classical types in [Reference MolevMol13]. The construction of [Reference MolevMol13] relies on the Schur–Weyl duality involving the Brauer algebra. Type G
$\mathfrak z({{\hat {\mathfrak g}}})$ appeared first in type A [Reference Chervov and TalalaevCT06, Reference Chervov and MolevCM09] following Talalaev's discovery [Reference TalalaevTal06] of explicit higher Gaudin Hamiltonians. Then they were extended to all classical types in [Reference MolevMol13]. The construction of [Reference MolevMol13] relies on the Schur–Weyl duality involving the Brauer algebra. Type G![]() $_2$ is covered by [Reference Molev, Ragoucy and RozhkovskayaMRR16]. The subject is beautifully summarised in [Reference MolevMol18].
$_2$ is covered by [Reference Molev, Ragoucy and RozhkovskayaMRR16]. The subject is beautifully summarised in [Reference MolevMol18].
Unlike the finite-dimensional case, no natural isomorphism between the algebras ![]() ${{\mathcal {S}}}(t^{-1}\mathfrak g[t^{-1}])^{\mathfrak g[t]}$ and
${{\mathcal {S}}}(t^{-1}\mathfrak g[t^{-1}])^{\mathfrak g[t]}$ and ![]() $\mathfrak z({{\hat {\mathfrak g}}})$ is known. Also, generally speaking, an element of
$\mathfrak z({{\hat {\mathfrak g}}})$ is known. Also, generally speaking, an element of ![]() $\mathfrak z(\hat {\mathfrak g})$ cannot be obtained by the symmetrisation
$\mathfrak z(\hat {\mathfrak g})$ cannot be obtained by the symmetrisation ![]() $\varpi$ from a homogeneous
$\varpi$ from a homogeneous ![]() $\mathfrak g[t]$-invariant in
$\mathfrak g[t]$-invariant in ![]() ${{\mathcal {S}}}(t^{-1}\mathfrak g[t^{-1}])$. At the same time, some of the elements do come in this way, see Example 5.2, which is dealing with the Pfaffians of
${{\mathcal {S}}}(t^{-1}\mathfrak g[t^{-1}])$. At the same time, some of the elements do come in this way, see Example 5.2, which is dealing with the Pfaffians of ![]() $\mathfrak {so}_{2n}$. In this paper, we show that for all classical Lie algebras,
$\mathfrak {so}_{2n}$. In this paper, we show that for all classical Lie algebras, ![]() $\varpi$ can produce generators of
$\varpi$ can produce generators of ![]() $\mathfrak z({{\hat {\mathfrak g}}})$. The symmetrisation map is not a homomorphism of algebras. However, it is a homomorphism of
$\mathfrak z({{\hat {\mathfrak g}}})$. The symmetrisation map is not a homomorphism of algebras. However, it is a homomorphism of ![]() $\mathfrak g[t^{-1}]$-modules and it behaves well with respect to taking various limits.
$\mathfrak g[t^{-1}]$-modules and it behaves well with respect to taking various limits.
According to a striking result of Rybnikov [Reference RybnikovRyb08], ![]() $\mathfrak z({{\hat {\mathfrak g}}})$ is the centraliser in
$\mathfrak z({{\hat {\mathfrak g}}})$ is the centraliser in ![]() ${{\mathcal {U}}}(t^{-1}\mathfrak g[t^{-1}])$ of a single quadratic element
${{\mathcal {U}}}(t^{-1}\mathfrak g[t^{-1}])$ of a single quadratic element ![]() ${\mathcal {H}}[-1]$, see § 1.1. This fact is crucial for our considerations.
${\mathcal {H}}[-1]$, see § 1.1. This fact is crucial for our considerations.
Any ![]() ${\mathcal {Y}}\in {{\mathcal {U}}}(t^{-1}\mathfrak g[t^{-1}])$ can be expressed as a sum
${\mathcal {Y}}\in {{\mathcal {U}}}(t^{-1}\mathfrak g[t^{-1}])$ can be expressed as a sum
Here ![]() $Y_k=\mathrm {gr}({\mathcal {Y}})$ if
$Y_k=\mathrm {gr}({\mathcal {Y}})$ if ![]() $Y_k\ne 0$. Note that
$Y_k\ne 0$. Note that ![]() $\sum _{0\leqslant j\leqslant k}\varpi (Y_j)$ is a
$\sum _{0\leqslant j\leqslant k}\varpi (Y_j)$ is a ![]() $\mathfrak g$-invariant if and only if each
$\mathfrak g$-invariant if and only if each ![]() $Y_j$ is a
$Y_j$ is a ![]() $\mathfrak g$-invariant. In the following, we consider only elements with
$\mathfrak g$-invariant. In the following, we consider only elements with ![]() $Y_0=0$.
$Y_0=0$.
A polarisation of a ![]() $\mathfrak g$-invariant
$\mathfrak g$-invariant ![]() $F\in {{\mathcal {S}}}(\mathfrak g)$ is a
$F\in {{\mathcal {S}}}(\mathfrak g)$ is a ![]() $\mathfrak g$-invariant in
$\mathfrak g$-invariant in ![]() ${{\mathcal {S}}}(t^{-1}\mathfrak g[t^{-1}])$, see § 1.5 for the definition of a polarisation. However,
${{\mathcal {S}}}(t^{-1}\mathfrak g[t^{-1}])$, see § 1.5 for the definition of a polarisation. However, ![]() ${{\mathcal {S}}}(t^{-1}\mathfrak g[t^{-1}])^{\mathfrak g}$ is not generated by elements of this sort, see (3.7) for an example.
${{\mathcal {S}}}(t^{-1}\mathfrak g[t^{-1}])^{\mathfrak g}$ is not generated by elements of this sort, see (3.7) for an example.
There are finite sets of elements ![]() $\{S_1,\ldots,S_{\ell }\}\subset \mathfrak z({{\hat {\mathfrak g}}})$ with
$\{S_1,\ldots,S_{\ell }\}\subset \mathfrak z({{\hat {\mathfrak g}}})$ with ![]() $\ell =\mathrm {rk}\,\mathfrak g$, called complete sets of Segal–Sugawara vectors, see § 1.6 for the definition, that are of vital importance for the understanding of
$\ell =\mathrm {rk}\,\mathfrak g$, called complete sets of Segal–Sugawara vectors, see § 1.6 for the definition, that are of vital importance for the understanding of ![]() $\mathfrak z({{\hat {\mathfrak g}}})$. We prove that if
$\mathfrak z({{\hat {\mathfrak g}}})$. We prove that if ![]() $\mathfrak g$ is either a classical Lie algebra or an exceptional Lie algebra of type G
$\mathfrak g$ is either a classical Lie algebra or an exceptional Lie algebra of type G![]() $_2$, then there is a complete set
$_2$, then there is a complete set ![]() $\{S_k\}$ of Segal–Sugawara vectors such that all the terms
$\{S_k\}$ of Segal–Sugawara vectors such that all the terms ![]() $Y_j$ occurring in presentations (0.1) for
$Y_j$ occurring in presentations (0.1) for ![]() $S_k$ are polarisations of symmetric invariants of
$S_k$ are polarisations of symmetric invariants of ![]() $\mathfrak g$. The map m, defined in § 1.4, plays a crucial rôle in the selection of suitable
$\mathfrak g$. The map m, defined in § 1.4, plays a crucial rôle in the selection of suitable ![]() $\mathfrak g$-invariants. In particular, if
$\mathfrak g$-invariants. In particular, if ![]() $F[-1]\in {{\mathcal {S}}}^{k}(\mathfrak g t^{-1})$ is obtained from
$F[-1]\in {{\mathcal {S}}}^{k}(\mathfrak g t^{-1})$ is obtained from ![]() $F\in {{\mathcal {S}}}^{k}(\mathfrak g)^{\mathfrak g}$ using the canonical isomorphism
$F\in {{\mathcal {S}}}^{k}(\mathfrak g)^{\mathfrak g}$ using the canonical isomorphism ![]() $\mathfrak g t^{-1}\cong \mathfrak g$, then
$\mathfrak g t^{-1}\cong \mathfrak g$, then ![]() $\varpi (F[-1])\in \mathfrak z({{\hat {\mathfrak g}}})$ if and only if
$\varpi (F[-1])\in \mathfrak z({{\hat {\mathfrak g}}})$ if and only if ![]() ${\sf m}(F)=0$, see Theorem 3.5 and the remark after it. More generally, if
${\sf m}(F)=0$, see Theorem 3.5 and the remark after it. More generally, if ![]() $H\in {{\mathcal {S}}}^{k}(\mathfrak g)^{\mathfrak g}$ is such that
$H\in {{\mathcal {S}}}^{k}(\mathfrak g)^{\mathfrak g}$ is such that
then there is a way to produce an element of ![]() $\mathfrak z({{\hat {\mathfrak g}}})$ corresponding to
$\mathfrak z({{\hat {\mathfrak g}}})$ corresponding to ![]() $H$, see Theorem 3.11 and (2.4).
$H$, see Theorem 3.11 and (2.4).
First, for ![]() $F=\xi _1\ldots \xi _m\in {{\mathcal {S}}}^{m}(\mathfrak g)$ and
$F=\xi _1\ldots \xi _m\in {{\mathcal {S}}}^{m}(\mathfrak g)$ and ![]() $\bar a=(a_1,\ldots,a_m)\in {{\mathbb {Z}}}_{<0}^{m}$, set
$\bar a=(a_1,\ldots,a_m)\in {{\mathbb {Z}}}_{<0}^{m}$, set
then extend this notation to all elements ![]() $F\in {{\mathcal {S}}}^{m}(\mathfrak g)$ by linearity. According to Lemma 2.1,
$F\in {{\mathcal {S}}}^{m}(\mathfrak g)$ by linearity. According to Lemma 2.1, ![]() $\varpi (F)[\bar a]=\varpi (F[\bar a])$ for the
$\varpi (F)[\bar a]=\varpi (F[\bar a])$ for the ![]() $\bar a$-polarisation
$\bar a$-polarisation ![]() $F[\bar a]\in {{\mathcal {S}}}^{m}(t^{-1}\mathfrak g[t^{-1}])$ of
$F[\bar a]\in {{\mathcal {S}}}^{m}(t^{-1}\mathfrak g[t^{-1}])$ of ![]() $F$.
$F$.
The expression ![]() $\varpi (\tau ^{r} F[-1]){\cdot }1$ encodes a sum of
$\varpi (\tau ^{r} F[-1]){\cdot }1$ encodes a sum of ![]() $ ({1}/{(m+r)!}) c(r,\bar a) \varpi (F)[\bar a]$, where the vectors
$ ({1}/{(m+r)!}) c(r,\bar a) \varpi (F)[\bar a]$, where the vectors ![]() $\bar a\in {{\mathbb {Z}}}_{<0}^{m}$ are such that
$\bar a\in {{\mathbb {Z}}}_{<0}^{m}$ are such that ![]() $\sum _{j=1}^{m} a_j=-m-r$ and
$\sum _{j=1}^{m} a_j=-m-r$ and ![]() $c(r,\bar a)\in \mathbb {N}$ are certain combinatorially defined coefficients, which we do not compute explicitly. It is not clear whether any interesting combinatorial identity can be produced in this context.
$c(r,\bar a)\in \mathbb {N}$ are certain combinatorially defined coefficients, which we do not compute explicitly. It is not clear whether any interesting combinatorial identity can be produced in this context.
For each classical Lie algebra ![]() $\mathfrak g$, there is a set of generators
$\mathfrak g$, there is a set of generators ![]() $\{H_1,\ldots,H_\ell \}\subset {{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ such that
$\{H_1,\ldots,H_\ell \}\subset {{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ such that ![]() ${\sf m}(H_k)\in {{\mathbb {C}}}H_j$ for some
${\sf m}(H_k)\in {{\mathbb {C}}}H_j$ for some ![]() $j$ depending on
$j$ depending on ![]() $k$, see §§ 2, 4, 7 and in particular Propositions 2.3, 4.3, 7.5. In types
$k$, see §§ 2, 4, 7 and in particular Propositions 2.3, 4.3, 7.5. In types ![]() $\mathsf{A}$ and
$\mathsf{A}$ and ![]() $\mathsf{C}$, we are using the coefficients of the characteristic polynomial. In the orthogonal case, one has to work with
$\mathsf{C}$, we are using the coefficients of the characteristic polynomial. In the orthogonal case, one has to work with ![]() $\det (I_n-q(F_{ij}))^{-1}$ instead. In type
$\det (I_n-q(F_{ij}))^{-1}$ instead. In type ![]() $\mathsf{A}_{n-1}$,
$\mathsf{A}_{n-1}$,
in type C![]() $_n$,
$_n$,
and finally for ![]() $\mathfrak g=\mathfrak {so}_n$, we have
$\mathfrak g=\mathfrak {so}_n$, we have
This leads to the following complete sets of Segal–Sugawara vectors:
 \begin{align*} &\biggl\{\tilde S_{k-1}=\varpi(\tilde\Delta_k[-1]) + \sum_{1\le r<(k-1)/2} \binom{n-k+2r}{2r} \varpi(\tau^{2r} \tilde\Delta_{k-2r}[-1]){\cdot}1 \mid 2\le k\le n\biggr\}\ \text{ in type } {\sf A}_{n-1};\\ &\biggl\{S_k=\varpi(\Delta_{2k}[-1]) + \sum_{1\le r<k} \binom{2n-2k+2r+1}{2r}\varpi(\tau^{2r}\Delta_{2k-2r}[-1]){\cdot}1\mid 1\le k\le n\biggr\}\ \text { in type } {\sf C}_n;\\ &\biggl\{S_{k}=\varpi(\Phi_{2k}[-1]) +\!\sum_{1\le r<k} \binom{n+2k-2}{2r} \varpi(\tau^{2r} \Phi_{2k-2r}[-1]){\cdot 1} \mid 1 \le k <\ell \biggr\} \text{ for $\mathfrak {so}_n$ with $n=2\ell-1$} \end{align*}
\begin{align*} &\biggl\{\tilde S_{k-1}=\varpi(\tilde\Delta_k[-1]) + \sum_{1\le r<(k-1)/2} \binom{n-k+2r}{2r} \varpi(\tau^{2r} \tilde\Delta_{k-2r}[-1]){\cdot}1 \mid 2\le k\le n\biggr\}\ \text{ in type } {\sf A}_{n-1};\\ &\biggl\{S_k=\varpi(\Delta_{2k}[-1]) + \sum_{1\le r<k} \binom{2n-2k+2r+1}{2r}\varpi(\tau^{2r}\Delta_{2k-2r}[-1]){\cdot}1\mid 1\le k\le n\biggr\}\ \text { in type } {\sf C}_n;\\ &\biggl\{S_{k}=\varpi(\Phi_{2k}[-1]) +\!\sum_{1\le r<k} \binom{n+2k-2}{2r} \varpi(\tau^{2r} \Phi_{2k-2r}[-1]){\cdot 1} \mid 1 \le k <\ell \biggr\} \text{ for $\mathfrak {so}_n$ with $n=2\ell-1$} \end{align*}
with the addition of ![]() $S_{\ell }=\varpi ({\rm Pf}[-1])$ for
$S_{\ell }=\varpi ({\rm Pf}[-1])$ for ![]() $\mathfrak {so}_{n}$ with
$\mathfrak {so}_{n}$ with ![]() $n=2\ell$.
$n=2\ell$.
The result in type ![]() $\mathsf{A}$ is not new. It follows via a careful rewriting from the formulas of [Reference Chervov and TalalaevCT06, Reference Chervov and MolevCM09]. We are not giving a new proof. Quite the contrary, we use the statement in type A in order to extend the formula to other types.
$\mathsf{A}$ is not new. It follows via a careful rewriting from the formulas of [Reference Chervov and TalalaevCT06, Reference Chervov and MolevCM09]. We are not giving a new proof. Quite the contrary, we use the statement in type A in order to extend the formula to other types.
Our formulas for ![]() $\mathfrak {so}_n$ and
$\mathfrak {so}_n$ and ![]() $\mathfrak {sp}_{2n}$ describe the same elements as [Reference MolevMol13], for the case of the Pfaffian-type Segal–Sugawara vector, see § 5; a more general result is recently obtained in [Reference MolevMol21].
$\mathfrak {sp}_{2n}$ describe the same elements as [Reference MolevMol13], for the case of the Pfaffian-type Segal–Sugawara vector, see § 5; a more general result is recently obtained in [Reference MolevMol21].
The advantage of our method is that it reduces questions about elements of ![]() $\mathfrak z({{\hat {\mathfrak g}}})$ to questions on the structure of
$\mathfrak z({{\hat {\mathfrak g}}})$ to questions on the structure of ![]() ${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ in a type-free way. For example, it is possible to deal with type
${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ in a type-free way. For example, it is possible to deal with type ![]() ${\sf G}_2$ by hand unlike [Reference Molev, Ragoucy and RozhkovskayaMRR16], see (6.3). It is quite probable that other exceptional types can be handled on a computer. Conjecturally, each exceptional Lie algebra possesses a set
${\sf G}_2$ by hand unlike [Reference Molev, Ragoucy and RozhkovskayaMRR16], see (6.3). It is quite probable that other exceptional types can be handled on a computer. Conjecturally, each exceptional Lie algebra possesses a set ![]() $\{H_k\}$ of generating symmetric invariants such that each
$\{H_k\}$ of generating symmetric invariants such that each ![]() $H_k$ satisfies (0.2).
$H_k$ satisfies (0.2).
One of the significant applications of the Feigin–Frenkel centre is related to Vinberg's quantisation problem. The symmetric algebra ![]() ${{\mathcal {S}}}(\mathfrak g)$ carries a Poisson structure extended from the Lie bracket on
${{\mathcal {S}}}(\mathfrak g)$ carries a Poisson structure extended from the Lie bracket on ![]() $\mathfrak g$ by the Leibniz rule. To each
$\mathfrak g$ by the Leibniz rule. To each ![]() $\mu \in \mathfrak g^{*}\cong \mathfrak g$, one associates the Mishchenko–Fomenko subalgebra
$\mu \in \mathfrak g^{*}\cong \mathfrak g$, one associates the Mishchenko–Fomenko subalgebra ![]() ${{\mathcal {A}}}_\mu \subset {{\mathcal {S}}}(\mathfrak g)$, which is an extremely interesting Poisson-commutative subalgebra [Reference Mishchenko and FomenkoMF78]. In [Reference VinbergVin91], Vinberg proposed to find a commutative subalgebra
${{\mathcal {A}}}_\mu \subset {{\mathcal {S}}}(\mathfrak g)$, which is an extremely interesting Poisson-commutative subalgebra [Reference Mishchenko and FomenkoMF78]. In [Reference VinbergVin91], Vinberg proposed to find a commutative subalgebra ![]() ${\mathcal {C}}_\mu \subset {{\mathcal {U}}}(\mathfrak g)$ such that
${\mathcal {C}}_\mu \subset {{\mathcal {U}}}(\mathfrak g)$ such that ![]() $\mathrm {gr}({\mathcal {C}}_\mu )=\langle \mathrm {gr}(Y)\mid Y\in {\mathcal {C}}_\mu \rangle _{{{\mathbb {C}}}}$ coincides with
$\mathrm {gr}({\mathcal {C}}_\mu )=\langle \mathrm {gr}(Y)\mid Y\in {\mathcal {C}}_\mu \rangle _{{{\mathbb {C}}}}$ coincides with ![]() ${{\mathcal {A}}}_\mu$. Partial solutions to this problem are obtained in [Reference Nazarov and OlshanskiNO96, Reference TarasovTar00]. The breakthrough came in [Reference RybnikovRyb06], where a certain commutative subalgebra
${{\mathcal {A}}}_\mu$. Partial solutions to this problem are obtained in [Reference Nazarov and OlshanskiNO96, Reference TarasovTar00]. The breakthrough came in [Reference RybnikovRyb06], where a certain commutative subalgebra ![]() $\tilde {{\mathcal {A}}}_\mu \subset {{\mathcal {U}}}(\mathfrak g)$ is constructed as an image of
$\tilde {{\mathcal {A}}}_\mu \subset {{\mathcal {U}}}(\mathfrak g)$ is constructed as an image of ![]() $\mathfrak z({{\hat {\mathfrak g}}})$, cf. (8.1).
$\mathfrak z({{\hat {\mathfrak g}}})$, cf. (8.1).
In [Reference Molev and YakimovaMY19, § 3.3], sets of generators ![]() $\{H_k\mid 1\leqslant k\leqslant \ell \}$ of
$\{H_k\mid 1\leqslant k\leqslant \ell \}$ of ![]() ${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ such that
${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ such that ![]() $\tilde {{\mathcal {A}}}_\mu$ is generated by
$\tilde {{\mathcal {A}}}_\mu$ is generated by ![]() $\varpi (\partial _\mu ^{m} H_k)$, cf. (8.3), are exhibited in types B, C, and D. For the symplectic Lie algebra,
$\varpi (\partial _\mu ^{m} H_k)$, cf. (8.3), are exhibited in types B, C, and D. For the symplectic Lie algebra, ![]() $H_k=\Delta _{2k}$, in the orthogonal case
$H_k=\Delta _{2k}$, in the orthogonal case ![]() $H_k=\Phi _{2k}$ with the exception of
$H_k=\Phi _{2k}$ with the exception of ![]() $H_\ell ={\rm Pf}$ in type
$H_\ell ={\rm Pf}$ in type ![]() ${\sf D}_\ell$. Results of this paper provide a different proof for [Reference Molev and YakimovaMY19, Theorem 3.2]. We have pushed the symmetrisation map to the level of
${\sf D}_\ell$. Results of this paper provide a different proof for [Reference Molev and YakimovaMY19, Theorem 3.2]. We have pushed the symmetrisation map to the level of ![]() ${{\mathcal {U}}}(t^{-1}\mathfrak g[t^{-1}])$.
${{\mathcal {U}}}(t^{-1}\mathfrak g[t^{-1}])$.
In § 8.2, we briefly consider Gaudin algebras ![]() ${{\mathcal {G}}}$. If
${{\mathcal {G}}}$. If ![]() $\mathfrak g$ is a classical Lie algebra, then the two-points Gaudin subalgebra
$\mathfrak g$ is a classical Lie algebra, then the two-points Gaudin subalgebra ![]() ${{\mathcal {G}}}\subset {{\mathcal {U}}}(\mathfrak g \oplus \mathfrak g)$ is generated by the symmetrisations of certain bi-homogeneous
${{\mathcal {G}}}\subset {{\mathcal {U}}}(\mathfrak g \oplus \mathfrak g)$ is generated by the symmetrisations of certain bi-homogeneous ![]() $\mathfrak g$-invariants in
$\mathfrak g$-invariants in ![]() ${{\mathcal {S}}}(\mathfrak g \oplus \mathfrak g)$, see Theorem 8.4.
${{\mathcal {S}}}(\mathfrak g \oplus \mathfrak g)$, see Theorem 8.4.
1. Preliminaries and notation
Let ![]() $\mathfrak g=\mathrm {Lie\,} G$ be a non-Abelian complex reductive Lie algebra. The Feigin–Frenkel centre
$\mathfrak g=\mathrm {Lie\,} G$ be a non-Abelian complex reductive Lie algebra. The Feigin–Frenkel centre ![]() $\mathfrak z({{\hat {\mathfrak g}}})$ is the centre of the universal affine vertex algebra associated with the affine Kac–Moody algebra
$\mathfrak z({{\hat {\mathfrak g}}})$ is the centre of the universal affine vertex algebra associated with the affine Kac–Moody algebra ![]() ${{\hat {\mathfrak g}}}$ at the critical level [Reference Feigin and FrenkelFF92, Reference FrenkelFre07]. There is an injective homomorphism
${{\hat {\mathfrak g}}}$ at the critical level [Reference Feigin and FrenkelFF92, Reference FrenkelFre07]. There is an injective homomorphism ![]() $\mathfrak z({{\hat {\mathfrak g}}}) \hookrightarrow {{\mathcal {U}}}(t^{-1}\mathfrak {g}[t^{-1}])$ and
$\mathfrak z({{\hat {\mathfrak g}}}) \hookrightarrow {{\mathcal {U}}}(t^{-1}\mathfrak {g}[t^{-1}])$ and ![]() $\mathfrak z({{\hat {\mathfrak g}}})$ can be viewed as a commutative subalgebra of
$\mathfrak z({{\hat {\mathfrak g}}})$ can be viewed as a commutative subalgebra of ![]() ${{\mathcal {U}}}(t^{-1}\mathfrak {g}[t^{-1}])$ [Reference FrenkelFre07, § 3.3]. Each element of
${{\mathcal {U}}}(t^{-1}\mathfrak {g}[t^{-1}])$ [Reference FrenkelFre07, § 3.3]. Each element of ![]() $\mathfrak {z}(\hat {\mathfrak {g}})$ is annihilated by the adjoint action of
$\mathfrak {z}(\hat {\mathfrak {g}})$ is annihilated by the adjoint action of ![]() $\mathfrak g$, cf. [Reference MolevMol18, § 6.2.].
$\mathfrak g$, cf. [Reference MolevMol18, § 6.2.].
1.1 The Feigin–Frenkel centre as a centraliser
We set ![]() $\mathfrak g[b]:=\mathfrak g t^{b}$ and
$\mathfrak g[b]:=\mathfrak g t^{b}$ and ![]() $x[b]:=xt^{b}$ for
$x[b]:=xt^{b}$ for ![]() $x\in \mathfrak g$. Furthermore,
$x\in \mathfrak g$. Furthermore, ![]() $\hat {\mathfrak g}^-:= t^{-1}\mathfrak {g}[t^{-1}]$. According to [Reference RybnikovRyb08],
$\hat {\mathfrak g}^-:= t^{-1}\mathfrak {g}[t^{-1}]$. According to [Reference RybnikovRyb08], ![]() $\mathfrak {z}(\hat {\mathfrak {g}})$ is the centraliser in
$\mathfrak {z}(\hat {\mathfrak {g}})$ is the centraliser in ![]() ${{\mathcal {U}}}(\hat {\mathfrak g}^-)$ of the following quadratic element
${{\mathcal {U}}}(\hat {\mathfrak g}^-)$ of the following quadratic element
 \[ {\mathcal{H}}[-1]=\sum_{a=1}^{\dim\mathfrak g} x_a[-1]x_a[-1], \]
\[ {\mathcal{H}}[-1]=\sum_{a=1}^{\dim\mathfrak g} x_a[-1]x_a[-1], \]
where ![]() $\{x_1,\ldots,x_{\dim \mathfrak g}\}$ is any basis of
$\{x_1,\ldots,x_{\dim \mathfrak g}\}$ is any basis of ![]() $\mathfrak g$ that is orthonormal with respect to a fixed
$\mathfrak g$ that is orthonormal with respect to a fixed ![]() $\mathfrak g$-invariant non-degenerate scalar product
$\mathfrak g$-invariant non-degenerate scalar product ![]() $(\,\,,\,)$. In this paper, a scalar product is a symmetric bilinear form.
$(\,\,,\,)$. In this paper, a scalar product is a symmetric bilinear form.
1.2 The symmetrisation map
For any complex Lie algebra ![]() $\mathfrak q$, let
$\mathfrak q$, let ![]() $\varpi \!:{{\mathcal {S}}}^{k}(\mathfrak q)\to \mathfrak q^{\otimes k}$ be the canonical symmetrisation map. Following the usual convention, we let
$\varpi \!:{{\mathcal {S}}}^{k}(\mathfrak q)\to \mathfrak q^{\otimes k}$ be the canonical symmetrisation map. Following the usual convention, we let ![]() $\varpi$ stand also for the symmetrisation map from
$\varpi$ stand also for the symmetrisation map from ![]() ${{\mathcal {S}}}(\mathfrak q)$ to
${{\mathcal {S}}}(\mathfrak q)$ to ![]() ${{\mathcal {U}}}(\mathfrak q)$. Let
${{\mathcal {U}}}(\mathfrak q)$. Let ![]() $\mathrm {gr}(X)\in {{\mathcal {S}}}(\mathfrak q)$ be the symbol of
$\mathrm {gr}(X)\in {{\mathcal {S}}}(\mathfrak q)$ be the symbol of ![]() $X\in {{\mathcal {U}}}(\mathfrak q)$. Then
$X\in {{\mathcal {U}}}(\mathfrak q)$. Then ![]() $\mathrm {gr}(\varpi (Y))=Y$ for
$\mathrm {gr}(\varpi (Y))=Y$ for ![]() $Y\in {{\mathcal {S}}}^{k}(\mathfrak q)$ by the construction.
$Y\in {{\mathcal {S}}}^{k}(\mathfrak q)$ by the construction.
1.3 The antipode
Let us define the anti-involution ![]() $\omega$ on
$\omega$ on ![]() ${\mathcal {U}}(\hat {\mathfrak g}^-)$ to be the
${\mathcal {U}}(\hat {\mathfrak g}^-)$ to be the ![]() $\mathbb {C}$-linear map such that
$\mathbb {C}$-linear map such that ![]() $\omega (y[k])=-y[k]$ for each
$\omega (y[k])=-y[k]$ for each ![]() $y\in \mathfrak g$ and
$y\in \mathfrak g$ and
Let also ![]() $\omega$ be the analogues anti-involution on
$\omega$ be the analogues anti-involution on ![]() ${{\mathcal {U}}}(\mathfrak q)$ for any complex Lie algebra
${{\mathcal {U}}}(\mathfrak q)$ for any complex Lie algebra ![]() $\mathfrak q$.
$\mathfrak q$.
Clearly, ![]() $\omega ({\mathcal {H}}[-1])={\mathcal {H}}[-1]$. Therefore
$\omega ({\mathcal {H}}[-1])={\mathcal {H}}[-1]$. Therefore ![]() $\omega$ acts on
$\omega$ acts on ![]() $\mathfrak {z}(\hat {\mathfrak {g}})$. For
$\mathfrak {z}(\hat {\mathfrak {g}})$. For ![]() $Y_j\in {{\mathcal {S}}}^{j}({{\hat {\mathfrak g}}}^-)$, we have
$Y_j\in {{\mathcal {S}}}^{j}({{\hat {\mathfrak g}}}^-)$, we have ![]() $\omega (\varpi (Y_j))=(-1)^{j}\varpi (Y_j)$. A non-zero element
$\omega (\varpi (Y_j))=(-1)^{j}\varpi (Y_j)$. A non-zero element ![]() ${\mathcal {Y}}\in {{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)$ presented in the form (0.1) is an eigenvector of
${\mathcal {Y}}\in {{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)$ presented in the form (0.1) is an eigenvector of ![]() $\omega$ if and only if either all
$\omega$ if and only if either all ![]() $Y_j$ with even
$Y_j$ with even ![]() $j$ or all
$j$ or all ![]() $Y_j$ with odd
$Y_j$ with odd ![]() $j$ are zero.
$j$ are zero.
1.4 The map m
For ![]() $\mathfrak {gl}_N=\mathfrak {gl}_N({{\mathbb {C}}})={\rm End}({{\mathbb {C}}}^{N})$ and
$\mathfrak {gl}_N=\mathfrak {gl}_N({{\mathbb {C}}})={\rm End}({{\mathbb {C}}}^{N})$ and ![]() $1\leqslant r\leqslant k$, consider the linear map
$1\leqslant r\leqslant k$, consider the linear map
Note that clearly
Via the adjoint representation of ![]() $\mathfrak g$, the map
$\mathfrak g$, the map ![]() ${\sf m}_r$ leads to a map
${\sf m}_r$ leads to a map ![]() $\mathfrak g^{\otimes k}\to {\rm End}(\mathfrak g) \otimes \mathfrak g^{\otimes (k-r)}$, which we denote by the same symbol. Explicitly, the map
$\mathfrak g^{\otimes k}\to {\rm End}(\mathfrak g) \otimes \mathfrak g^{\otimes (k-r)}$, which we denote by the same symbol. Explicitly, the map
Observe that
where ![]() $\mathfrak {so}(\mathfrak g)=\{\xi \in {\rm End}(\mathfrak g)\mid (\xi (x),y)=-(x,\xi (y)) \, \forall x,y\in \mathfrak g\}$; the isomorphism
$\mathfrak {so}(\mathfrak g)=\{\xi \in {\rm End}(\mathfrak g)\mid (\xi (x),y)=-(x,\xi (y)) \, \forall x,y\in \mathfrak g\}$; the isomorphism ![]() $\Lambda ^{2}\mathfrak g\cong \mathfrak {so}(\mathfrak g)$ is given by
$\Lambda ^{2}\mathfrak g\cong \mathfrak {so}(\mathfrak g)$ is given by
for ![]() $y_1,y_2,x\in \mathfrak g$.
$y_1,y_2,x\in \mathfrak g$.
We embed ![]() ${{\mathcal {S}}}^{k}(\mathfrak g)$ in
${{\mathcal {S}}}^{k}(\mathfrak g)$ in ![]() $\mathfrak g^{\otimes k}$ via
$\mathfrak g^{\otimes k}$ via ![]() $\varpi$. Set
$\varpi$. Set ![]() ${\sf m}={\sf m}_3$. Then
${\sf m}={\sf m}_3$. Then ![]() ${\sf m}\!: {{\mathcal {S}}}^{k}(\mathfrak g)\to \Lambda ^{2}\mathfrak g \otimes {{\mathcal {S}}}^{k-3}(\mathfrak g)$. For example, if
${\sf m}\!: {{\mathcal {S}}}^{k}(\mathfrak g)\to \Lambda ^{2}\mathfrak g \otimes {{\mathcal {S}}}^{k-3}(\mathfrak g)$. For example, if ![]() $Y=y_1y_2y_3\in {{\mathcal {S}}}^{3}(\mathfrak g)$, then
$Y=y_1y_2y_3\in {{\mathcal {S}}}^{3}(\mathfrak g)$, then
Similarly one defines ![]() ${\sf m}_{2r+1}\!: {{\mathcal {S}}}^{k}(\mathfrak g)\to \Lambda ^{2}\mathfrak g \otimes {{\mathcal {S}}}^{(k-2r-1)}(\mathfrak g)$ for each odd
${\sf m}_{2r+1}\!: {{\mathcal {S}}}^{k}(\mathfrak g)\to \Lambda ^{2}\mathfrak g \otimes {{\mathcal {S}}}^{(k-2r-1)}(\mathfrak g)$ for each odd ![]() $2r+1\leqslant k$. Note that each
$2r+1\leqslant k$. Note that each ![]() ${\sf m}_{2r+1}$ is
${\sf m}_{2r+1}$ is ![]() $G$-equivariant. It is convenient to put
$G$-equivariant. It is convenient to put ![]() ${\sf m}({{\mathcal {S}}}^{k}(\mathfrak g))=0$ for
${\sf m}({{\mathcal {S}}}^{k}(\mathfrak g))=0$ for ![]() $k\leqslant 2$.
$k\leqslant 2$.
Suppose that ![]() $\mathfrak g$ is simple. There is a
$\mathfrak g$ is simple. There is a ![]() $G$-stable decomposition
$G$-stable decomposition ![]() $\Lambda ^{2}\mathfrak g=\mathfrak g\oplus V$. This
$\Lambda ^{2}\mathfrak g=\mathfrak g\oplus V$. This ![]() $V$ will be called the Cartan component of
$V$ will be called the Cartan component of ![]() $\Lambda ^{2}\mathfrak g$. If
$\Lambda ^{2}\mathfrak g$. If ![]() $\mathfrak g$ is not of type
$\mathfrak g$ is not of type ![]() $\mathsf{A}$, then
$\mathsf{A}$, then ![]() $V$ is irreducible. For certain elements
$V$ is irreducible. For certain elements ![]() $H\in {{\mathcal {S}}}^{k}(\mathfrak g)$, we have
$H\in {{\mathcal {S}}}^{k}(\mathfrak g)$, we have ![]() ${\sf m}(H)\in \mathfrak g\otimes {{\mathcal {S}}}^{k-3}(\mathfrak g)$. Note that the embedding
${\sf m}(H)\in \mathfrak g\otimes {{\mathcal {S}}}^{k-3}(\mathfrak g)$. Note that the embedding ![]() $\mathfrak g\hookrightarrow \mathfrak {so}(\mathfrak g)$ is canonical: it is given by the adjoint action of
$\mathfrak g\hookrightarrow \mathfrak {so}(\mathfrak g)$ is canonical: it is given by the adjoint action of ![]() $\mathfrak g$. If
$\mathfrak g$. If ![]() ${\sf m}(H)\in {{\mathcal {S}}}^{k-2}(\mathfrak g)$, then
${\sf m}(H)\in {{\mathcal {S}}}^{k-2}(\mathfrak g)$, then ![]() ${\sf m}_{2r+1}(H)={\sf m_{2r-1}} \circ {\sf m}(H)$, because of (1.1). Since
${\sf m}_{2r+1}(H)={\sf m_{2r-1}} \circ {\sf m}(H)$, because of (1.1). Since ![]() $(\Lambda ^{2}\mathfrak g)^{\mathfrak g}=0$, we have
$(\Lambda ^{2}\mathfrak g)^{\mathfrak g}=0$, we have ![]() ${\sf m}({{\mathcal {S}}}^{3}(\mathfrak g)^{\mathfrak g})=0$.
${\sf m}({{\mathcal {S}}}^{3}(\mathfrak g)^{\mathfrak g})=0$.
1.5 Polarisations and fully symmetrised elements
For elements ![]() $y_1,\ldots, y_m \in \mathfrak g$ and a vector
$y_1,\ldots, y_m \in \mathfrak g$ and a vector ![]() $\bar a=(a_1,\ldots,a_m)\in \mathbb {Z}_{<0}^{m}$, set
$\bar a=(a_1,\ldots,a_m)\in \mathbb {Z}_{<0}^{m}$, set ![]() $\Upsilon [\bar a]=\prod _{i=1}^{m} y_i[a_i]\in {{\mathcal {S}}}(\hat {\mathfrak g}^-)$. If we consider the product
$\Upsilon [\bar a]=\prod _{i=1}^{m} y_i[a_i]\in {{\mathcal {S}}}(\hat {\mathfrak g}^-)$. If we consider the product ![]() $Y=\prod _{i} y_i\in {{\mathcal {S}}}^{m}(\mathfrak g)$, then there is no uniquely defined sequence of factors
$Y=\prod _{i} y_i\in {{\mathcal {S}}}^{m}(\mathfrak g)$, then there is no uniquely defined sequence of factors ![]() $y_i$. However, the
$y_i$. However, the ![]() $\bar a$-polarisation
$\bar a$-polarisation ![]() $Y[\bar a]:= ({1}/{m!}) \sum _{\sigma \in {\tt S}_m} \Upsilon [\sigma (\bar a)]$ of
$Y[\bar a]:= ({1}/{m!}) \sum _{\sigma \in {\tt S}_m} \Upsilon [\sigma (\bar a)]$ of ![]() $Y$ is well defined. We extend this notion to all elements of
$Y$ is well defined. We extend this notion to all elements of ![]() ${{\mathcal {S}}}^{m}(\mathfrak g)$ by linearity. Linear combinations of the elements
${{\mathcal {S}}}^{m}(\mathfrak g)$ by linearity. Linear combinations of the elements
are said to be fully symmetrised. Note that ![]() $\varpi (H)$ is fully symmetrised if
$\varpi (H)$ is fully symmetrised if ![]() $H\in {{\mathcal {S}}}^{m}(\mathfrak g t^{-1})$. If
$H\in {{\mathcal {S}}}^{m}(\mathfrak g t^{-1})$. If ![]() $a_i=a$ for all
$a_i=a$ for all ![]() $i$, then
$i$, then ![]() $\Upsilon [\bar a]=Y[\bar a]$ and we denote it simply by
$\Upsilon [\bar a]=Y[\bar a]$ and we denote it simply by ![]() $Y[a]$.
$Y[a]$.
The evaluation ![]() ${\sf Ev}_1$ at
${\sf Ev}_1$ at ![]() $t=1$ defines an isomorphism
$t=1$ defines an isomorphism ![]() ${\sf Ev}_1\!: {{\mathcal {S}}}(\mathfrak g[a])\to {{\mathcal {S}}}(\mathfrak g)$ of
${\sf Ev}_1\!: {{\mathcal {S}}}(\mathfrak g[a])\to {{\mathcal {S}}}(\mathfrak g)$ of ![]() $\mathfrak g$-modules. For
$\mathfrak g$-modules. For ![]() $F\in {{\mathcal {S}}}(\mathfrak g)$, let
$F\in {{\mathcal {S}}}(\mathfrak g)$, let ![]() $F[a]$ stand for
$F[a]$ stand for ![]() ${\sf Ev}_1^{-1}(F)\in {{\mathcal {S}}}(\mathfrak g[a])$. Then
${\sf Ev}_1^{-1}(F)\in {{\mathcal {S}}}(\mathfrak g[a])$. Then ![]() $\varpi (F)[a]:=\varpi (F[a])$ is fully symmetrised.
$\varpi (F)[a]:=\varpi (F[a])$ is fully symmetrised.
1.6 Segal–Sugawara vectors
Set ![]() $\tau =-\partial _t$. According to [Reference Feigin and FrenkelFF92],
$\tau =-\partial _t$. According to [Reference Feigin and FrenkelFF92], ![]() $\mathfrak z(\hat {\mathfrak {g}})$ is a polynomial algebra in infinitely many variables with a distinguished set of ‘generators’
$\mathfrak z(\hat {\mathfrak {g}})$ is a polynomial algebra in infinitely many variables with a distinguished set of ‘generators’ ![]() $\{S_1,\ldots,S_{\ell }\}$ such that
$\{S_1,\ldots,S_{\ell }\}$ such that ![]() $\ell =\mathrm {rk}\,\mathfrak g$ and
$\ell =\mathrm {rk}\,\mathfrak g$ and
We have ![]() $\mathrm {gr}(S_k)=H_k[-1]$ with
$\mathrm {gr}(S_k)=H_k[-1]$ with ![]() $H_k\in {{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ and
$H_k\in {{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ and ![]() ${{\mathbb {C}}}[H_1,\ldots,H_\ell ]={{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$. The set
${{\mathbb {C}}}[H_1,\ldots,H_\ell ]={{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$. The set ![]() $\{S_k\}$ is said to be a complete set of Segal–Sugawara vectors. The symbols of
$\{S_k\}$ is said to be a complete set of Segal–Sugawara vectors. The symbols of ![]() $\tau ^{m}(S_k)$ generate
$\tau ^{m}(S_k)$ generate ![]() ${{\mathcal {S}}}({{\hat {\mathfrak g}}}^-)^{\mathfrak g[t]}$ in accordance with [Reference Raïs and TauvelRT92].
${{\mathcal {S}}}({{\hat {\mathfrak g}}}^-)^{\mathfrak g[t]}$ in accordance with [Reference Raïs and TauvelRT92].
Suppose that we have ![]() $\tilde S_k\in \mathfrak z({{\hat {\mathfrak g}}})$ with
$\tilde S_k\in \mathfrak z({{\hat {\mathfrak g}}})$ with ![]() $1\leqslant k\leqslant \ell$ and
$1\leqslant k\leqslant \ell$ and ![]() $\mathrm {gr}(S_k)=\tilde H_k[-1]$, where
$\mathrm {gr}(S_k)=\tilde H_k[-1]$, where ![]() $\tilde H_k\in {{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$, for each
$\tilde H_k\in {{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$, for each ![]() $k$. The structural properties of
$k$. The structural properties of ![]() $\mathfrak z({{\hat {\mathfrak g}}})$ imply that
$\mathfrak z({{\hat {\mathfrak g}}})$ imply that ![]() $\{\tilde S_k\}$ is a complete set of Segal–Sugawara vectors if and only if the set
$\{\tilde S_k\}$ is a complete set of Segal–Sugawara vectors if and only if the set ![]() $\{\tilde H_k\}$ generates
$\{\tilde H_k\}$ generates ![]() ${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$.
${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$.
1.7 Symmetric invariants
For a finite-dimensional Lie algebra ![]() $\mathfrak q$, we have
$\mathfrak q$, we have ![]() ${{\mathcal {S}}}(\mathfrak q)\cong {{\mathbb {C}}}[\mathfrak q^{*}]$. For any reductive Lie algebra, there is an isomorphism of
${{\mathcal {S}}}(\mathfrak q)\cong {{\mathbb {C}}}[\mathfrak q^{*}]$. For any reductive Lie algebra, there is an isomorphism of ![]() $\mathfrak g$-modules
$\mathfrak g$-modules ![]() $\mathfrak g\cong \mathfrak g^{*}$. For
$\mathfrak g\cong \mathfrak g^{*}$. For ![]() $\xi \in (\mathfrak {gl}_n)^{*}$, write
$\xi \in (\mathfrak {gl}_n)^{*}$, write
Then ![]() ${{\mathcal {S}}}(\mathfrak {gl}_n)^{\mathfrak {gl}_n}={{\mathbb {C}}}[\Delta _1,\ldots,\Delta _n]$.
${{\mathcal {S}}}(\mathfrak {gl}_n)^{\mathfrak {gl}_n}={{\mathbb {C}}}[\Delta _1,\ldots,\Delta _n]$.
Let ![]() $\mathfrak f\subset \mathfrak g$ be a reductive subalgebra. Then there is an
$\mathfrak f\subset \mathfrak g$ be a reductive subalgebra. Then there is an ![]() $\mathfrak f$-stable subspace
$\mathfrak f$-stable subspace ![]() $\mathfrak m\subset \mathfrak g$ such that
$\mathfrak m\subset \mathfrak g$ such that ![]() $\mathfrak g=\mathfrak f\oplus \mathfrak m$, whereby also
$\mathfrak g=\mathfrak f\oplus \mathfrak m$, whereby also ![]() $\mathfrak g^{*} \cong \mathfrak f^{*}\oplus \mathfrak m^{*}$. Identifying
$\mathfrak g^{*} \cong \mathfrak f^{*}\oplus \mathfrak m^{*}$. Identifying ![]() $\mathfrak f$ with
$\mathfrak f$ with ![]() $\mathfrak f^{*}$, one defines the restriction
$\mathfrak f^{*}$, one defines the restriction ![]() $H|_{\mathfrak f}$ of
$H|_{\mathfrak f}$ of ![]() $H\in {{\mathcal {S}}}(\mathfrak g)$ to
$H\in {{\mathcal {S}}}(\mathfrak g)$ to ![]() $\mathfrak f$. This is the image of
$\mathfrak f$. This is the image of ![]() $H$ in
$H$ in ![]() ${{\mathcal {S}}}(\mathfrak g)/\mathfrak m{{\mathcal {S}}}(\mathfrak g)\cong {{\mathcal {S}}}(\mathfrak f)$.
${{\mathcal {S}}}(\mathfrak g)/\mathfrak m{{\mathcal {S}}}(\mathfrak g)\cong {{\mathcal {S}}}(\mathfrak f)$.
In cases ![]() $n=2\ell$,
$n=2\ell$, ![]() $\mathfrak f=\mathfrak {sp}_{2\ell }$ and
$\mathfrak f=\mathfrak {sp}_{2\ell }$ and ![]() $n=2\ell +1$,
$n=2\ell +1$, ![]() $\mathfrak f=\mathfrak {so}_n$, the restrictions
$\mathfrak f=\mathfrak {so}_n$, the restrictions ![]() ${\Delta _{2k}}|_{\mathfrak f}$ with
${\Delta _{2k}}|_{\mathfrak f}$ with ![]() $1\leqslant k\leqslant \ell$ form a generating set in
$1\leqslant k\leqslant \ell$ form a generating set in ![]() ${{\mathcal {S}}}(\mathfrak f)^{\mathfrak f}$. In the case
${{\mathcal {S}}}(\mathfrak f)^{\mathfrak f}$. In the case ![]() $\mathfrak f=\mathfrak {so}_{n}$ with
$\mathfrak f=\mathfrak {so}_{n}$ with ![]() $n=2\ell$, the restriction of the determinant
$n=2\ell$, the restriction of the determinant ![]() $\Delta _{2\ell }$ is the square of the Pfaffian and has to be replaced by the Pfaffian in the generating set.
$\Delta _{2\ell }$ is the square of the Pfaffian and has to be replaced by the Pfaffian in the generating set.
Explicit formulas for basic symmetric invariants of the exceptional Lie algebras are less transparent.
Let ![]() $\mathfrak g$ be simple. The inclusions
$\mathfrak g$ be simple. The inclusions ![]() $\mathfrak g\subset {{\mathcal {S}}}(\mathfrak g)$ are ruled by the symmetric invariants. The key point here is that
$\mathfrak g\subset {{\mathcal {S}}}(\mathfrak g)$ are ruled by the symmetric invariants. The key point here is that ![]() ${{\mathcal {S}}}(\mathfrak g)$ is a free module over
${{\mathcal {S}}}(\mathfrak g)$ is a free module over ![]() ${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ [Reference KostantKos63]. If
${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ [Reference KostantKos63]. If ![]() $\{H_1,\ldots,H_\ell \}\subset {{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ is a generating set consisting of homogeneous elements and
$\{H_1,\ldots,H_\ell \}\subset {{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ is a generating set consisting of homogeneous elements and ![]() $\deg H_i=d_i+1$, then to each
$\deg H_i=d_i+1$, then to each ![]() $i$ corresponds a primitive copy of
$i$ corresponds a primitive copy of ![]() $\mathfrak g$ in
$\mathfrak g$ in ![]() ${{\mathcal {S}}}^{d_i}(\mathfrak g)$. The non-primitive copies are obtained as linear combinations of the primitive ones with coefficients from
${{\mathcal {S}}}^{d_i}(\mathfrak g)$. The non-primitive copies are obtained as linear combinations of the primitive ones with coefficients from ![]() ${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$.
${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$.
1.8 Miscellaneousness
Let ![]() $\mathfrak h\subset \mathfrak g$ be a Cartan subalgebra, we let
$\mathfrak h\subset \mathfrak g$ be a Cartan subalgebra, we let ![]() $\ell$ stand for
$\ell$ stand for ![]() $\dim \mathfrak h=\mathrm {rk}\,\mathfrak g$ and
$\dim \mathfrak h=\mathrm {rk}\,\mathfrak g$ and ![]() $W=W(\mathfrak g,\mathfrak h)$ stand for the Weyl group of
$W=W(\mathfrak g,\mathfrak h)$ stand for the Weyl group of ![]() $\mathfrak g$. The fundamental weights of a simple Lie algebra
$\mathfrak g$. The fundamental weights of a simple Lie algebra ![]() $\mathfrak g$ are
$\mathfrak g$ are ![]() $\pi _k$ with
$\pi _k$ with ![]() $1\leqslant k\leqslant \ell$ and
$1\leqslant k\leqslant \ell$ and ![]() $V(\lambda )$ stands for an irreducible finite-dimensional
$V(\lambda )$ stands for an irreducible finite-dimensional ![]() $\mathfrak g$-module with the highest weight
$\mathfrak g$-module with the highest weight ![]() $\lambda =\sum _{k=1}^{\ell } c_k \pi _k$. Please keep in mind that the Vinberg–Onishchik numbering [Reference Vinberg and OniwikVO88, Tables] of simple roots (and fundamental weights) is used. If
$\lambda =\sum _{k=1}^{\ell } c_k \pi _k$. Please keep in mind that the Vinberg–Onishchik numbering [Reference Vinberg and OniwikVO88, Tables] of simple roots (and fundamental weights) is used. If ![]() $\alpha \in \mathfrak h^{*}$ is a positive root, then
$\alpha \in \mathfrak h^{*}$ is a positive root, then ![]() $\{e_\alpha,h_\alpha,f_\alpha \}\subset \mathfrak g$ is an
$\{e_\alpha,h_\alpha,f_\alpha \}\subset \mathfrak g$ is an ![]() $\mathfrak {sl}_2$-triple associated with
$\mathfrak {sl}_2$-triple associated with ![]() $\alpha$.
$\alpha$.
An automorphism ![]() $\sigma \in {\rm Aut}(\mathfrak g)$ extends to
$\sigma \in {\rm Aut}(\mathfrak g)$ extends to ![]() $\mathfrak g[t^{-1}]$ by setting
$\mathfrak g[t^{-1}]$ by setting ![]() $\sigma (t^{-1})=t^{-1}$. In this context,
$\sigma (t^{-1})=t^{-1}$. In this context, ![]() $\sigma$ stands also for the corresponding automorphism of
$\sigma$ stands also for the corresponding automorphism of ![]() ${{\mathcal {S}}}(\mathfrak g[t^{-1}])$. If we take a
${{\mathcal {S}}}(\mathfrak g[t^{-1}])$. If we take a ![]() $\sigma$-invariant product
$\sigma$-invariant product ![]() $(\,\,,\,)$, then
$(\,\,,\,)$, then ![]() $\sigma ({\mathcal {H}}[-1])={\mathcal {H}}[-1]$. Therefore
$\sigma ({\mathcal {H}}[-1])={\mathcal {H}}[-1]$. Therefore ![]() $\sigma$ acts on
$\sigma$ acts on ![]() $\mathfrak z({{\hat {\mathfrak g}}})$.
$\mathfrak z({{\hat {\mathfrak g}}})$.
If ![]() $\sigma \in {\rm Aut}(\mathfrak g)$ is of finite order
$\sigma \in {\rm Aut}(\mathfrak g)$ is of finite order ![]() $m$, then it leads to a
$m$, then it leads to a ![]() ${{\mathbb {Z}}}/m{{\mathbb {Z}}}$-grading
${{\mathbb {Z}}}/m{{\mathbb {Z}}}$-grading ![]() $\mathfrak g=\mathfrak g_0\oplus \mathfrak g_1\oplus \ldots \oplus \mathfrak g_{m-1}$. In the case
$\mathfrak g=\mathfrak g_0\oplus \mathfrak g_1\oplus \ldots \oplus \mathfrak g_{m-1}$. In the case ![]() $m=2$, we have
$m=2$, we have ![]() $\mathfrak g_1=\{\xi \in \mathfrak g\mid \sigma (\xi )=-\xi \}$.
$\mathfrak g_1=\{\xi \in \mathfrak g\mid \sigma (\xi )=-\xi \}$.
Throughout the paper:
•
 $\{x_i\}$ is an orthonormal basis of
$\{x_i\}$ is an orthonormal basis of  $\mathfrak g$;
$\mathfrak g$;• in the sums
 $\sum _{i} x_i$ or
$\sum _{i} x_i$ or  $\sum _{i,j} x_i x_j$, the ranges are from
$\sum _{i,j} x_i x_j$, the ranges are from  $1$ to
$1$ to  $\dim \mathfrak g$ for
$\dim \mathfrak g$ for  $i$ and for
$i$ and for  $j$;
$j$;•
 $\bar b=(b_1,b_2)\in \mathbb {Z}_{<0}^{2}$ and
$\bar b=(b_1,b_2)\in \mathbb {Z}_{<0}^{2}$ and  ${\mathcal {H}}[\bar b]$ stands for
${\mathcal {H}}[\bar b]$ stands for  $\sum _{i} x_i[b_1]x_i[b_2]\in {{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)$ and also for the symbol of this sum (in the sense of § 1.2);
$\sum _{i} x_i[b_1]x_i[b_2]\in {{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)$ and also for the symbol of this sum (in the sense of § 1.2);•
 $G_\xi$ stands for the stabiliser of
$G_\xi$ stands for the stabiliser of  $\xi$ and it is always clear from the context, which
$\xi$ and it is always clear from the context, which  $G$-action is considered,
$G$-action is considered,  $\mathfrak g_\xi =\mathrm {Lie\,} G_\xi$;
$\mathfrak g_\xi =\mathrm {Lie\,} G_\xi$;•
 $\mathfrak q$ stands for an arbitrary unspecified complex Lie algebra;
$\mathfrak q$ stands for an arbitrary unspecified complex Lie algebra;• if
 ${{\mathcal {A}}}\subset {{\mathcal {U}}}(\mathfrak q)$ is a subalgebra, then
${{\mathcal {A}}}\subset {{\mathcal {U}}}(\mathfrak q)$ is a subalgebra, then  $\mathrm {gr}({{\mathcal {A}}}):=\langle \mathrm {gr}(x) \mid x\in {{\mathcal {A}}}\rangle _{{{\mathbb {C}}}}\subset {{\mathcal {S}}}(\mathfrak q)$.
$\mathrm {gr}({{\mathcal {A}}}):=\langle \mathrm {gr}(x) \mid x\in {{\mathcal {A}}}\rangle _{{{\mathbb {C}}}}\subset {{\mathcal {S}}}(\mathfrak q)$.
2. Explicit formulas in type  $\mathsf{A}$
$\mathsf{A}$
In type ![]() $\mathsf{A}$, there are several explicit formulas for the Segal–Sugawara vectors [Reference Chervov and TalalaevCT06, Reference Chervov and MolevCM09], see also [Reference MolevMol18, § 7.1]. One of them actually uses symmetrisation. One can form the matrix
$\mathsf{A}$, there are several explicit formulas for the Segal–Sugawara vectors [Reference Chervov and TalalaevCT06, Reference Chervov and MolevCM09], see also [Reference MolevMol18, § 7.1]. One of them actually uses symmetrisation. One can form the matrix
with ![]() $E_{ij}\in \mathfrak {gl}_n$ and calculate its column determinant and symmetrised determinant. Due to the fact that this matrix is Manin, see [Reference MolevMol18, Definition 3.1.1, p. 48, Lemma 7.1.2], the results are the same. The symmetrised version is more suitable for our purpose. The elements
$E_{ij}\in \mathfrak {gl}_n$ and calculate its column determinant and symmetrised determinant. Due to the fact that this matrix is Manin, see [Reference MolevMol18, Definition 3.1.1, p. 48, Lemma 7.1.2], the results are the same. The symmetrised version is more suitable for our purpose. The elements ![]() $S_j$ are coefficients of
$S_j$ are coefficients of ![]() $\tau ^{n-j}$ in
$\tau ^{n-j}$ in
Assume the conventions that
and ![]() $\tau {\cdot }1=0$. This leads for example to
$\tau {\cdot }1=0$. This leads for example to ![]() $\tau x[-1]{\cdot }1= x[-2]$. Note that
$\tau x[-1]{\cdot }1= x[-2]$. Note that ![]() $\varpi$ acts on the summands of
$\varpi$ acts on the summands of ![]() $\tau ^{n-k} \Delta _{k}[-1]$ as on products of
$\tau ^{n-k} \Delta _{k}[-1]$ as on products of ![]() $n$ factors. It permutes
$n$ factors. It permutes ![]() $\tau$ with elements of
$\tau$ with elements of ![]() $\mathfrak {gl}_n[-1]$.
$\mathfrak {gl}_n[-1]$.
Let ![]() $\theta$ be a Weyl involution of
$\theta$ be a Weyl involution of ![]() $\mathfrak g$, i.e. there is a
$\mathfrak g$, i.e. there is a ![]() $\theta$-stable Cartan subalgebra
$\theta$-stable Cartan subalgebra ![]() $\mathfrak h\subset \mathfrak g$ such that
$\mathfrak h\subset \mathfrak g$ such that ![]() $\theta |_{\mathfrak h}=-{{\rm id}}_{\mathfrak h}$. As is well known,
$\theta |_{\mathfrak h}=-{{\rm id}}_{\mathfrak h}$. As is well known, ![]() $\theta (\Delta _k)=(-1)^{k}\Delta _k$ if
$\theta (\Delta _k)=(-1)^{k}\Delta _k$ if ![]() $\mathfrak g=\mathfrak {gl}_n$. In particular,
$\mathfrak g=\mathfrak {gl}_n$. In particular, ![]() $\theta ({\mathcal {H}}[-1])={\mathcal {H}}[-1]$ and
$\theta ({\mathcal {H}}[-1])={\mathcal {H}}[-1]$ and ![]() $\theta$ acts on
$\theta$ acts on ![]() $\mathfrak z({{\hat {\mathfrak g}}})$. Hence one can always modify the Segal–Sugawara vectors in such a way that they become eigenvectors of
$\mathfrak z({{\hat {\mathfrak g}}})$. Hence one can always modify the Segal–Sugawara vectors in such a way that they become eigenvectors of ![]() $\theta$. The resulting simplified forms are
$\theta$. The resulting simplified forms are
 \begin{align} S_n&= \varpi(\Delta_n[-1])+\varpi(\tau^{2}\Delta_{n-2}[-1]){\cdot}1+\cdots + \varpi(\tau^{2r}\Delta_{n-2r}[-1]){\cdot 1}+ \cdots \nonumber\\ & \quad + \varpi(\tau^{n-u}\Delta_u[-1]){\cdot}1 \quad \text{with } u=n-2\bigg[\frac{n-1}{2}\bigg], \end{align}
\begin{align} S_n&= \varpi(\Delta_n[-1])+\varpi(\tau^{2}\Delta_{n-2}[-1]){\cdot}1+\cdots + \varpi(\tau^{2r}\Delta_{n-2r}[-1]){\cdot 1}+ \cdots \nonumber\\ & \quad + \varpi(\tau^{n-u}\Delta_u[-1]){\cdot}1 \quad \text{with } u=n-2\bigg[\frac{n-1}{2}\bigg], \end{align} \begin{align} S_k&=\varpi(\Delta_k[-1])+ \sum_{1\leqslant r< k/2} \binom{n-k+2r}{2r}\varpi(\tau^{2r}\Delta_{k-2r}[-1]){\cdot}1. \end{align}
\begin{align} S_k&=\varpi(\Delta_k[-1])+ \sum_{1\leqslant r< k/2} \binom{n-k+2r}{2r}\varpi(\tau^{2r}\Delta_{k-2r}[-1]){\cdot}1. \end{align} We will see that there is a direct connection with the symmetrisation and that one could have used ![]() $\omega$ instead of
$\omega$ instead of ![]() $\theta$ in order to simplify the formulas. The following two lemmas are valid for all Lie algebras.
$\theta$ in order to simplify the formulas. The following two lemmas are valid for all Lie algebras.
Lemma 2.1 Take ![]() $Y=y_1 \ldots y_m \in {{\mathcal {S}}}^{m}(\mathfrak g)$ and
$Y=y_1 \ldots y_m \in {{\mathcal {S}}}^{m}(\mathfrak g)$ and ![]() $\bar a=(a_1,\ldots,a_m)\in \mathbb {Z}_{<0}^{m}$. Then in
$\bar a=(a_1,\ldots,a_m)\in \mathbb {Z}_{<0}^{m}$. Then in ![]() ${{\mathcal {U}}}(\hat {\mathfrak g}^-)$, we have
${{\mathcal {U}}}(\hat {\mathfrak g}^-)$, we have
 \[ \mathbb{Y}[\bar a]:= \sum_{\sigma\in {\tt S}_m} y_{\sigma(1)}[a_1]\ldots y_{\sigma(m)}[a_m] =\varpi\biggl(\sum_{\sigma\in {\tt S}_m} y_{1}[a_{\sigma(1)}]\ldots y_{m}[a_{\sigma(m)}] \biggr) = m! \varpi(Y[\bar a]) \]
\[ \mathbb{Y}[\bar a]:= \sum_{\sigma\in {\tt S}_m} y_{\sigma(1)}[a_1]\ldots y_{\sigma(m)}[a_m] =\varpi\biggl(\sum_{\sigma\in {\tt S}_m} y_{1}[a_{\sigma(1)}]\ldots y_{m}[a_{\sigma(m)}] \biggr) = m! \varpi(Y[\bar a]) \]in the notation of § 1.5.
Proof. It suffices to show that ![]() $\mathbb {Y}[\bar a]$ is invariant under all
$\mathbb {Y}[\bar a]$ is invariant under all ![]() ${\tt t}_i=(i\,i+1)\in {\tt S}_m$ with
${\tt t}_i=(i\,i+1)\in {\tt S}_m$ with ![]() $1\leqslant i< m$. For each
$1\leqslant i< m$. For each ![]() $\sigma \in {\tt S}_m$, both monomials
$\sigma \in {\tt S}_m$, both monomials
appear in ![]() $\mathbb {Y}[\bar a]$ with the same coefficient
$\mathbb {Y}[\bar a]$ with the same coefficient ![]() $1$. Let
$1$. Let ![]() $s(\sigma,i)$ stand for their sum. Then
$s(\sigma,i)$ stand for their sum. Then
because ![]() $[y_{\sigma (i)}[a_i],y_{\sigma (i+1)}[a_{i+1}]]=[y_{\sigma (i)},y_{\sigma (i+1)}][a_i+ a_{i+1}]= - [y_{\sigma (i+1)}[a_{i}],y_{\sigma (i)}[a_{i+1}]]$. Since
$[y_{\sigma (i)}[a_i],y_{\sigma (i+1)}[a_{i+1}]]=[y_{\sigma (i)},y_{\sigma (i+1)}][a_i+ a_{i+1}]= - [y_{\sigma (i+1)}[a_{i}],y_{\sigma (i)}[a_{i+1}]]$. Since ![]() $\mathbb {Y}[\bar a]=\frac {1}{2}\sum _{\sigma } s(\sigma,i)$ for each
$\mathbb {Y}[\bar a]=\frac {1}{2}\sum _{\sigma } s(\sigma,i)$ for each ![]() $i$, we are done.
$i$, we are done.
Lemma 2.2 Take ![]() $F\in {{\mathcal {S}}}^{m}(\mathfrak g)$ and
$F\in {{\mathcal {S}}}^{m}(\mathfrak g)$ and ![]() $r\geqslant 1$. Then
$r\geqslant 1$. Then ![]() $\varpi (\tau ^{r} F[-1]){\cdot }1$ is fully symmetrised and therefore is an eigenvector of
$\varpi (\tau ^{r} F[-1]){\cdot }1$ is fully symmetrised and therefore is an eigenvector of ![]() $\omega$ corresponding to the eigenvalue
$\omega$ corresponding to the eigenvalue ![]() $(-1)^{m}$.
$(-1)^{m}$.
Proof. Notice that ![]() $\varpi (\tau ^{r} (F+F')[-1]){\cdot }1=\varpi (\tau ^{r} F[-1]){\cdot }1+ \varpi (\tau ^{r} F'[-1]){\cdot }1$ for any
$\varpi (\tau ^{r} (F+F')[-1]){\cdot }1=\varpi (\tau ^{r} F[-1]){\cdot }1+ \varpi (\tau ^{r} F'[-1]){\cdot }1$ for any ![]() $F'\in {{\mathcal {S}}}^{m}(\mathfrak g)$. Hence we may assume that
$F'\in {{\mathcal {S}}}^{m}(\mathfrak g)$. Hence we may assume that ![]() $F=y_1\ldots y_m$ with
$F=y_1\ldots y_m$ with ![]() $y_j\in \mathfrak g$. By the construction,
$y_j\in \mathfrak g$. By the construction, ![]() $\varpi (\tau ^{r} F[-1]){\cdot }1$ is the sum of terms
$\varpi (\tau ^{r} F[-1]){\cdot }1$ is the sum of terms
taken over all vectors ![]() $\bar a=(a_1,\ldots,a_m)\in {{\mathbb {Z}}}_{<0}^{m}$ such that
$\bar a=(a_1,\ldots,a_m)\in {{\mathbb {Z}}}_{<0}^{m}$ such that ![]() $\sum a_j=-(m+r)$. The scalars
$\sum a_j=-(m+r)$. The scalars ![]() $c(r,\bar a)$ depend on
$c(r,\bar a)$ depend on ![]() $(m,r,\bar a)$ in an elementary combinatorial way. Each summand here is a fully symmetrised element by Lemma 2.1. Hence the desired conclusion follows.
$(m,r,\bar a)$ in an elementary combinatorial way. Each summand here is a fully symmetrised element by Lemma 2.1. Hence the desired conclusion follows.
Let ![]() $z= ({1}/{n})I_n$ be a central element of
$z= ({1}/{n})I_n$ be a central element of ![]() $\mathfrak g=\mathfrak {gl}_n$ and let
$\mathfrak g=\mathfrak {gl}_n$ and let ![]() $\tilde \Delta _k\in {{\mathcal {S}}}^{k}(\mathfrak {sl}_n)$ denote the restriction of
$\tilde \Delta _k\in {{\mathcal {S}}}^{k}(\mathfrak {sl}_n)$ denote the restriction of ![]() $\Delta _k$ to
$\Delta _k$ to ![]() $\mathfrak {sl}_n$. Then
$\mathfrak {sl}_n$. Then
Fix ![]() $\mathfrak h=\langle E_{ii} \mid 1\leqslant i\leqslant n\rangle _{{{\mathbb {C}}}}$. Let
$\mathfrak h=\langle E_{ii} \mid 1\leqslant i\leqslant n\rangle _{{{\mathbb {C}}}}$. Let ![]() $\varepsilon _i\in \mathfrak h^{*}$ be a linear function such that
$\varepsilon _i\in \mathfrak h^{*}$ be a linear function such that ![]() $\varepsilon _i(E_{jj})=\delta _{i,j}$. For
$\varepsilon _i(E_{jj})=\delta _{i,j}$. For ![]() $E_{ii}\in \mathfrak g$, set
$E_{ii}\in \mathfrak g$, set ![]() $\tilde E_{ii}=E_{ii}-z$.
$\tilde E_{ii}=E_{ii}-z$.
Proposition 2.3 In type ![]() $\mathsf{A}$, we have
$\mathsf{A}$, we have
if ![]() $k-2r > 1$ and
$k-2r > 1$ and ![]() ${\sf m}(\tilde \Delta _3)={\sf m}(\Delta _3)=0$.
${\sf m}(\tilde \Delta _3)={\sf m}(\Delta _3)=0$.
Proof. Notice that the centre of ![]() $\mathfrak g$ plays a very specific rôle in m, since
$\mathfrak g$ plays a very specific rôle in m, since ![]() $\mathrm {ad}(z)=0$. In particular,
$\mathrm {ad}(z)=0$. In particular, ![]() ${\sf m}({{\mathcal {S}}}^{3}(\mathfrak {gl}_n))={\sf m}({{\mathcal {S}}}^{3}(\mathfrak {sl}_n))\subset \Lambda ^{2}\mathfrak {sl}_n$. Furthermore,
${\sf m}({{\mathcal {S}}}^{3}(\mathfrak {gl}_n))={\sf m}({{\mathcal {S}}}^{3}(\mathfrak {sl}_n))\subset \Lambda ^{2}\mathfrak {sl}_n$. Furthermore,
where one can use the multiplication in either ![]() ${\rm End}(\mathfrak {gl}_{n})$ or
${\rm End}(\mathfrak {gl}_{n})$ or ![]() ${\rm End}(\mathfrak {sl}_{n})$ for the definition of
${\rm End}(\mathfrak {sl}_{n})$ for the definition of ![]() ${\sf m}$. Therefore we can work either with
${\sf m}$. Therefore we can work either with ![]() $\mathfrak {sl}_n$ or with
$\mathfrak {sl}_n$ or with ![]() $\mathfrak {gl}_n$, whichever is more convenient.
$\mathfrak {gl}_n$, whichever is more convenient.
Suppose that ![]() $Y=E_{ij}E_{ls}E_{up}$ is a factor of a monomial of
$Y=E_{ij}E_{ls}E_{up}$ is a factor of a monomial of ![]() $\Delta _k$. Then
$\Delta _k$. Then
The ![]() $\mathfrak h$-weight of
$\mathfrak h$-weight of ![]() $Y$ cannot be equal to either
$Y$ cannot be equal to either ![]() $2\varepsilon _1-\varepsilon _n-\varepsilon _{n-1}$ or
$2\varepsilon _1-\varepsilon _n-\varepsilon _{n-1}$ or ![]() $\varepsilon _1+\varepsilon _2-2\varepsilon _n$. These are the highest weights of the Cartan component of
$\varepsilon _1+\varepsilon _2-2\varepsilon _n$. These are the highest weights of the Cartan component of ![]() $\Lambda ^{2}\mathfrak {sl}_n$. Hence
$\Lambda ^{2}\mathfrak {sl}_n$. Hence ![]() ${\sf m}(\Delta _k)\in (\mathfrak {sl}_n \otimes {{\mathcal {S}}}^{k-3}(\mathfrak g))^{\mathfrak g}$. The image in question is a polynomial function on
${\sf m}(\Delta _k)\in (\mathfrak {sl}_n \otimes {{\mathcal {S}}}^{k-3}(\mathfrak g))^{\mathfrak g}$. The image in question is a polynomial function on ![]() $(\mathfrak {sl}_n \oplus \mathfrak g)^{*}\cong \mathfrak {sl}_n\oplus \mathfrak g$ of degree
$(\mathfrak {sl}_n \oplus \mathfrak g)^{*}\cong \mathfrak {sl}_n\oplus \mathfrak g$ of degree ![]() $1$ in
$1$ in ![]() $\mathfrak {sl}_n$ and degree
$\mathfrak {sl}_n$ and degree ![]() $k-3$ in
$k-3$ in ![]() $\mathfrak g$. Note that
$\mathfrak g$. Note that ![]() ${\sf m}(\Delta _3)$ is a
${\sf m}(\Delta _3)$ is a ![]() $\mathfrak {gl}_n$-invariant in
$\mathfrak {gl}_n$-invariant in ![]() $\mathfrak {sl}_n$ and is thereby zero. Suppose that
$\mathfrak {sl}_n$ and is thereby zero. Suppose that ![]() $n\geqslant k>3$.
$n\geqslant k>3$.
Fortunately, ![]() $G(\mathfrak {sl}_n \oplus \mathfrak h)$ is a dense subset of
$G(\mathfrak {sl}_n \oplus \mathfrak h)$ is a dense subset of ![]() $\mathfrak {sl}_n \oplus \mathfrak g$. We calculate the restriction
$\mathfrak {sl}_n \oplus \mathfrak g$. We calculate the restriction
of ![]() ${\sf m}(\Delta _k)$ to
${\sf m}(\Delta _k)$ to ![]() $\mathfrak {sl}_n\oplus \mathfrak h$. Write
$\mathfrak {sl}_n\oplus \mathfrak h$. Write ![]() ${{\boldsymbol f}}=\sum _{\nu =1}^{L} \xi _\nu \otimes {{\boldsymbol H}}_\nu$ with
${{\boldsymbol f}}=\sum _{\nu =1}^{L} \xi _\nu \otimes {{\boldsymbol H}}_\nu$ with ![]() $\xi _\nu \in \mathfrak {sl}_n$ and pairwise different monomials
$\xi _\nu \in \mathfrak {sl}_n$ and pairwise different monomials ![]() ${{\boldsymbol H}}_\nu \in {{\mathcal {S}}}^{k-3}(\mathfrak h)$ in
${{\boldsymbol H}}_\nu \in {{\mathcal {S}}}^{k-3}(\mathfrak h)$ in ![]() $\{E_{ii}\}$. Since
$\{E_{ii}\}$. Since ![]() ${\sf m}(\Delta _k)$ is an element of
${\sf m}(\Delta _k)$ is an element of ![]() $\mathfrak h$-weight zero,
$\mathfrak h$-weight zero, ![]() $\xi _\nu \in \mathfrak h$ for each
$\xi _\nu \in \mathfrak h$ for each ![]() $\nu$. Thus one can say that
$\nu$. Thus one can say that ![]() ${{\boldsymbol f}}$ is an invariant of the Weyl group
${{\boldsymbol f}}$ is an invariant of the Weyl group ![]() $W(\mathfrak g,\mathfrak h)\cong {\tt S}_{n}$. Without loss of generality assume that
$W(\mathfrak g,\mathfrak h)\cong {\tt S}_{n}$. Without loss of generality assume that ![]() ${{\boldsymbol H}}_1= y_4\ldots y_k$ with
${{\boldsymbol H}}_1= y_4\ldots y_k$ with ![]() $y_s=E_{ss}$ for all
$y_s=E_{ss}$ for all ![]() $s\geqslant 4$. In order to understand
$s\geqslant 4$. In order to understand ![]() ${{\boldsymbol f}}$, it suffices to calculate
${{\boldsymbol f}}$, it suffices to calculate ![]() $\xi _1$. Let
$\xi _1$. Let ![]() $F$ be the polynomial obtained from
$F$ be the polynomial obtained from ![]() $\Delta _3$ by setting
$\Delta _3$ by setting ![]() $E_{ij}=0$ for all
$E_{ij}=0$ for all ![]() $(i,j)$ such that
$(i,j)$ such that ![]() $i$ or
$i$ or ![]() $j$ belongs to
$j$ belongs to ![]() $\{4,\ldots,k\}$. Then
$\{4,\ldots,k\}$. Then ![]() $\xi _1= ({3!(k-3)!}/{k!}) {\sf m}(F)$.
$\xi _1= ({3!(k-3)!}/{k!}) {\sf m}(F)$.
Now take ![]() $Y$ as above with
$Y$ as above with ![]() $\{i,l,u\}=\{j,s,p\}=\{1,2,3\}$. Then:
$\{i,l,u\}=\{j,s,p\}=\{1,2,3\}$. Then:
•
 ${\sf m}(Y)(E_{14})=0$ if
${\sf m}(Y)(E_{14})=0$ if  $i=j$ or
$i=j$ or  $l=s$ or
$l=s$ or  $u=p$;
$u=p$;•
 ${\sf m}(Y)(E_{14})=\frac {1}{6} E_{14}$ if
${\sf m}(Y)(E_{14})=\frac {1}{6} E_{14}$ if  $Y= E_{13} E_{32} E_{21}$;
$Y= E_{13} E_{32} E_{21}$;•
 ${\sf m}(Y)(E_{14})=\frac {1}{6} E_{14}$ if
${\sf m}(Y)(E_{14})=\frac {1}{6} E_{14}$ if  $Y= E_{12} E_{23} E_{31}$.
$Y= E_{12} E_{23} E_{31}$.
Besides, ![]() ${\sf m}(Y)(E_{vw})=0$ if
${\sf m}(Y)(E_{vw})=0$ if ![]() $v,w\geqslant 4$. In the self-explanatory notation,
$v,w\geqslant 4$. In the self-explanatory notation, ![]() $\eta ={\sf m}(\Delta _3^{(1,2,3)})$ is an invariant of
$\eta ={\sf m}(\Delta _3^{(1,2,3)})$ is an invariant of ![]() $(\mathfrak {gl}_3\oplus \mathfrak {gl}_{n-3})$ and
$(\mathfrak {gl}_3\oplus \mathfrak {gl}_{n-3})$ and ![]() $\eta$ acts on
$\eta$ acts on ![]() $\mathfrak {gl}_3=\langle E_{vw} \mid 1\leqslant v,w\leqslant 3\rangle _{{{\mathbb {C}}}}$ as zero. Since
$\mathfrak {gl}_3=\langle E_{vw} \mid 1\leqslant v,w\leqslant 3\rangle _{{{\mathbb {C}}}}$ as zero. Since ![]() $\Delta _3^{(1,2,3)}$ is a linear combination of
$\Delta _3^{(1,2,3)}$ is a linear combination of ![]() $Y=E_{ij}E_{ls}E_{up}$ with
$Y=E_{ij}E_{ls}E_{up}$ with ![]() $\{i,l,u\}=\{j,s,p\}=\{1,2,3\}$, the element
$\{i,l,u\}=\{j,s,p\}=\{1,2,3\}$, the element ![]() $\eta$ acts on
$\eta$ acts on ![]() $\mathfrak g$ as
$\mathfrak g$ as ![]() $\frac {1}{3}(E_{11}+E_{22}+E_{33})$. This implies that
$\frac {1}{3}(E_{11}+E_{22}+E_{33})$. This implies that ![]() $\eta =\frac {1}{3}(\tilde E_{11}+\tilde E_{22}+\tilde E_{33})$. By the construction of
$\eta =\frac {1}{3}(\tilde E_{11}+\tilde E_{22}+\tilde E_{33})$. By the construction of ![]() $F$, we now have
$F$, we now have ![]() ${\sf m}(F)=\binom {n-k+2}{2} \sum _{l\not \in \{4,\ldots,k\}} \frac {1}{3} \tilde E_{ll}$ and hence
${\sf m}(F)=\binom {n-k+2}{2} \sum _{l\not \in \{4,\ldots,k\}} \frac {1}{3} \tilde E_{ll}$ and hence
 \[ \xi_1\otimes{{\boldsymbol H}}_1=\frac{3!(k-3)!}{k!}\frac{1}{3}\binom{n-k+2}{2}\bigg(\sum_{l\not\in\{4,\ldots,k\}} \tilde E_{ll}\bigg) \otimes E_{44} \ldots E_{kk}. \]
\[ \xi_1\otimes{{\boldsymbol H}}_1=\frac{3!(k-3)!}{k!}\frac{1}{3}\binom{n-k+2}{2}\bigg(\sum_{l\not\in\{4,\ldots,k\}} \tilde E_{ll}\bigg) \otimes E_{44} \ldots E_{kk}. \]From this one deduces that up to the scalar
the restriction of ![]() ${\sf m}(\tilde \Delta _k)$ to
${\sf m}(\tilde \Delta _k)$ to ![]() $\mathfrak {sl}_n\oplus \mathfrak h$ coincides with the restriction
$\mathfrak {sl}_n\oplus \mathfrak h$ coincides with the restriction ![]() $\tilde \Delta _{k-2}|_{\mathfrak {sl}_n \oplus \mathfrak h}$, where we regard
$\tilde \Delta _{k-2}|_{\mathfrak {sl}_n \oplus \mathfrak h}$, where we regard ![]() $\tilde \Delta _{k-2}$ as an element of
$\tilde \Delta _{k-2}$ as an element of ![]() $\mathfrak {sl}_n \otimes {{\mathcal {S}}}^{k-3}(\mathfrak g)$. In particular,
$\mathfrak {sl}_n \otimes {{\mathcal {S}}}^{k-3}(\mathfrak g)$. In particular, ![]() ${\sf m}(\tilde \Delta _k)$ is a symmetric invariant. More explicitly,
${\sf m}(\tilde \Delta _k)$ is a symmetric invariant. More explicitly,
Iterating the map m, we obtain the result.
Remark Strictly speaking, ![]() ${\sf m}(\Delta _k)$ is not an element of
${\sf m}(\Delta _k)$ is not an element of ![]() ${{\mathcal {S}}}^{k-2}(\mathfrak {gl}_n)$. This is the reason for working with
${{\mathcal {S}}}^{k-2}(\mathfrak {gl}_n)$. This is the reason for working with ![]() $\mathfrak {sl}_n$.
$\mathfrak {sl}_n$.
Now we can exhibit formulas for Segal–Sugawara vectors of ![]() $t$-degree
$t$-degree ![]() $k$ that are independent of
$k$ that are independent of ![]() $n$, i.e. these formulas are valid for all
$n$, i.e. these formulas are valid for all ![]() $n\geqslant k$. First of all notice that in view of (2.3), Formula (2.2) produces an element of
$n\geqslant k$. First of all notice that in view of (2.3), Formula (2.2) produces an element of ![]() $\mathfrak z(\widehat {\mathfrak {sl}_n})$ if we replace each
$\mathfrak z(\widehat {\mathfrak {sl}_n})$ if we replace each ![]() $\Delta _{k-2r}$ with
$\Delta _{k-2r}$ with ![]() $\tilde \Delta _{k-2r}$. (This statement can be deduced from (2.1) as well.) Making use of Proposition 2.3, one obtains that for
$\tilde \Delta _{k-2r}$. (This statement can be deduced from (2.1) as well.) Making use of Proposition 2.3, one obtains that for ![]() $H=\tilde \Delta _k$,
$H=\tilde \Delta _k$,
 \begin{equation} \tilde S_{k-1}=\varpi(H[-1])+\sum_{1\leqslant r<(k-1)/2} \binom{k}{2r} \varpi(\tau^{2r} {\sf m}_{2r+1}(H)[-1]){\cdot}1 \end{equation}
\begin{equation} \tilde S_{k-1}=\varpi(H[-1])+\sum_{1\leqslant r<(k-1)/2} \binom{k}{2r} \varpi(\tau^{2r} {\sf m}_{2r+1}(H)[-1]){\cdot}1 \end{equation}is a Segal–Sugawara vector.
3. Commutators and Poisson brackets
In this section, we prove that Formula (2.4) is universal, i.e. that it is valid in all types, providing ![]() ${\sf m}_{2r+1}(H)$ is a symmetric invariant for each
${\sf m}_{2r+1}(H)$ is a symmetric invariant for each ![]() $r\geqslant 1$.
$r\geqslant 1$.
For ![]() $F\in {{\mathcal {S}}}^{m}(\mathfrak g)$, set
$F\in {{\mathcal {S}}}^{m}(\mathfrak g)$, set ![]() $\mathbb {X}_{F[-1]}:=[{\mathcal {H}}[-1], \varpi (F)[-1]]$ . Note that
$\mathbb {X}_{F[-1]}:=[{\mathcal {H}}[-1], \varpi (F)[-1]]$ . Note that
Hence ![]() $\omega$ multiplies
$\omega$ multiplies ![]() $\mathbb {X}_{F[-1]}$ with
$\mathbb {X}_{F[-1]}$ with ![]() $(-1)^{m+1}$. This implies that the symbol of
$(-1)^{m+1}$. This implies that the symbol of ![]() $\mathbb {X}_{F[-1]}$ has degree
$\mathbb {X}_{F[-1]}$ has degree ![]() $m+1-2d$ with
$m+1-2d$ with ![]() $d\geqslant 0$. Let
$d\geqslant 0$. Let ![]() ${\mathcal {H}}[-1]$ stand also for
${\mathcal {H}}[-1]$ stand also for ![]() $\sum _{i} x_i[-1]x_i[-1]\in {{\mathcal {S}}}^{2}(\mathfrak g[-1])$.
$\sum _{i} x_i[-1]x_i[-1]\in {{\mathcal {S}}}^{2}(\mathfrak g[-1])$.
The symmetric algebra ![]() ${{\mathcal {S}}}(\mathfrak q)$ of a Lie algebra
${{\mathcal {S}}}(\mathfrak q)$ of a Lie algebra ![]() $\mathfrak q$ is equipped with the standard Poisson bracket
$\mathfrak q$ is equipped with the standard Poisson bracket ![]() $\{\,\,,\,\}$ such that
$\{\,\,,\,\}$ such that ![]() $\{x,y\}=[x,y]$ for
$\{x,y\}=[x,y]$ for ![]() $x,y\in \mathfrak q$. Using the standard filtration on
$x,y\in \mathfrak q$. Using the standard filtration on ![]() ${{\mathcal {U}}}(\mathfrak q)$, one can state that
${{\mathcal {U}}}(\mathfrak q)$, one can state that
The fact that ![]() $\{{\mathcal {H}}[-1], F[-1]\}=0$ for
$\{{\mathcal {H}}[-1], F[-1]\}=0$ for ![]() $F\in {{\mathcal {S}}}^{m}(\mathfrak g)^{\mathfrak g}$ follows from [Reference Feigin and FrenkelFF92]. For convenience, we present a short proof here.
$F\in {{\mathcal {S}}}^{m}(\mathfrak g)^{\mathfrak g}$ follows from [Reference Feigin and FrenkelFF92]. For convenience, we present a short proof here.
Lemma 3.1 Take two arbitrary ![]() $\mathfrak g$-invariants
$\mathfrak g$-invariants ![]() $F,F'$ in
$F,F'$ in ![]() ${{\mathcal {S}}}(\mathfrak g)$. Then
${{\mathcal {S}}}(\mathfrak g)$. Then ![]() $\{F[-1],F'[-1]\}=0$.
$\{F[-1],F'[-1]\}=0$.
Proof. The Poisson bracket of two polynomial functions can be calculated by
In the case of ![]() $F[-1]$ and
$F[-1]$ and ![]() $F'[-1]$, the differentials
$F'[-1]$, the differentials ![]() $d_\gamma F[-1], d_\gamma F'[-1]$ at
$d_\gamma F[-1], d_\gamma F'[-1]$ at ![]() $\gamma$ depend only on the
$\gamma$ depend only on the ![]() $(-1)$-part of
$(-1)$-part of ![]() $\gamma$. More explicitly, if
$\gamma$. More explicitly, if ![]() $\gamma (x[-1])=\tilde \gamma (x)$ with
$\gamma (x[-1])=\tilde \gamma (x)$ with ![]() $\tilde \gamma \in \mathfrak g^{*}$, then
$\tilde \gamma \in \mathfrak g^{*}$, then ![]() $d_\gamma F[-1]=(d_{\tilde \gamma } F)[-1]$ and the same identity hods for
$d_\gamma F[-1]=(d_{\tilde \gamma } F)[-1]$ and the same identity hods for ![]() $F'$. We have
$F'$. We have ![]() $d_{\tilde \gamma } F,d_{\tilde \gamma }F'\in (\mathfrak g_\gamma )^{\mathfrak g_\gamma }$, since
$d_{\tilde \gamma } F,d_{\tilde \gamma }F'\in (\mathfrak g_\gamma )^{\mathfrak g_\gamma }$, since ![]() $F$ and
$F$ and ![]() $F'$ are
$F'$ are ![]() $\mathfrak g$-invariants. Hence
$\mathfrak g$-invariants. Hence ![]() $[d_{\tilde \gamma } F,d_{\tilde \gamma }F']=0$ and also
$[d_{\tilde \gamma } F,d_{\tilde \gamma }F']=0$ and also ![]() $[d_{\gamma }F[-1],d_{\gamma }F'[-1]]=0$ for any
$[d_{\gamma }F[-1],d_{\gamma }F'[-1]]=0$ for any ![]() $\gamma \in ({{\hat {\mathfrak g}}}^-)^{*}$.
$\gamma \in ({{\hat {\mathfrak g}}}^-)^{*}$.
If ![]() $[\mathfrak g,\mathfrak g]$ is not simple, then the following assumption on the choice of the scalar product on
$[\mathfrak g,\mathfrak g]$ is not simple, then the following assumption on the choice of the scalar product on ![]() $\mathfrak g$ is made in order to simplify the calculations.
$\mathfrak g$ is made in order to simplify the calculations.
(
 ${\blacklozenge}$) There is a constant
${\blacklozenge}$) There is a constant  $C\in {{\mathbb {C}}}$ such that
$C\in {{\mathbb {C}}}$ such that  $\sum _{i=1}^{\dim \mathfrak g} \mathrm {ad}(x_i)^{2}(\xi )=C\xi$ for each
$\sum _{i=1}^{\dim \mathfrak g} \mathrm {ad}(x_i)^{2}(\xi )=C\xi$ for each  $\xi \in [\mathfrak g,\mathfrak g]$.
$\xi \in [\mathfrak g,\mathfrak g]$.
The constant ![]() $C$ depends on the scalar product in question.
$C$ depends on the scalar product in question.
From now on, assume that ![]() $\mathfrak g$ is semisimple. As the next step we examine the difference
$\mathfrak g$ is semisimple. As the next step we examine the difference
and more general expressions, where the commutator is taken with ![]() ${\mathcal {H}}[\bar b]$. Our goal is to present
${\mathcal {H}}[\bar b]$. Our goal is to present ![]() $\mathbb {X}_{F[-1]}$ in the form (0.1). For any
$\mathbb {X}_{F[-1]}$ in the form (0.1). For any ![]() ${\mathcal {F}}_1,{\mathcal {F}}_2\in {{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)$, the symbol
${\mathcal {F}}_1,{\mathcal {F}}_2\in {{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)$, the symbol ![]() $\mathrm {gr}([{\mathcal {F}}_1,{\mathcal {F}}_2])$ is equal to the Poisson bracket
$\mathrm {gr}([{\mathcal {F}}_1,{\mathcal {F}}_2])$ is equal to the Poisson bracket ![]() $\{\mathrm {gr}({\mathcal {F}}_1),\mathrm {gr}({\mathcal {F}}_2)\}$ if this Poisson bracket is non-zero.
$\{\mathrm {gr}({\mathcal {F}}_1),\mathrm {gr}({\mathcal {F}}_2)\}$ if this Poisson bracket is non-zero.
3.1 Commutators, the first approximation
Fix ![]() $m\geqslant 1$. Then set
$m\geqslant 1$. Then set ![]() $\check {j}=m-j$ for
$\check {j}=m-j$ for ![]() $1\leqslant j< m$.
$1\leqslant j< m$.
Lemma 3.2 For ![]() $Y=\hat y_1\ldots \hat y_m\in {{\mathcal {S}}}({{\hat {\mathfrak g}}}^-)$ with
$Y=\hat y_1\ldots \hat y_m\in {{\mathcal {S}}}({{\hat {\mathfrak g}}}^-)$ with ![]() $\hat y_j=y_j[a_j]$, set
$\hat y_j=y_j[a_j]$, set
Then
 \begin{align*} &X_Y= \sum_{l=1}^{m}\sum_{\sigma\in \tilde{\tt S}_{m-1}}\sum_{j< p} \sum_{i,u} ({\sf m}(y_{\sigma(p)} \otimes y_{l} \otimes y_{\sigma(j)}) (x_i), x_{u}) \\ &\times (c_{2,3}(j,p) \hat y_{\sigma(1)}\ldots \hat y_{\sigma(j-1)} x_i[b_1+a_{\sigma(j)}] \hat y_{\sigma(j+1)}\ldots \hat y_{\sigma(p-1)} x_{u}[b_2+a_{l}+a_{\sigma(p)}] \hat y_{\sigma(p+1)} \ldots \hat y_{\sigma(m-1)} \\ &+c_{2,3}(j,p) \hat y_{\sigma(1)}\ldots \hat y_{\sigma(j-1)} x_i[b_2+a_{\sigma(j)}] \hat y_{\sigma(j+1)}\ldots \hat y_{\sigma(p-1)} x_{u}[b_1+a_{l}+a_{\sigma(p)}] \hat y_{\sigma(p+1)} \ldots \hat y_{\sigma(m-1)} \\ & + (-1) c_{3,2}(j,p) \hat y_{\sigma(1)}\ldots \hat y_{\sigma(j-1)} x_i[b_1+a_{\sigma(j)}+a_{l}] \hat y_{\sigma(j+1)}\ldots \hat y_{\sigma(p-1)} x_{u}[b_2+a_{\sigma(p)}] \hat y_{\sigma(p+1)} \ldots \hat y_{\sigma(m-1)} \\ & + (-1) c_{3,2}(j,p) \hat y_{\sigma(1)}\ldots \hat y_{\sigma(j-1)} x_i[b_2\!+a_{\sigma(j)}\!+a_{l}] \hat y_{\sigma(j+1)}\ldots \hat y_{\sigma(p-1)} x_{u}[b_1\!+a_{\sigma(p)}] \hat y_{\sigma(p+1)} \ldots \hat y_{\sigma(m-1)} ), \end{align*}
\begin{align*} &X_Y= \sum_{l=1}^{m}\sum_{\sigma\in \tilde{\tt S}_{m-1}}\sum_{j< p} \sum_{i,u} ({\sf m}(y_{\sigma(p)} \otimes y_{l} \otimes y_{\sigma(j)}) (x_i), x_{u}) \\ &\times (c_{2,3}(j,p) \hat y_{\sigma(1)}\ldots \hat y_{\sigma(j-1)} x_i[b_1+a_{\sigma(j)}] \hat y_{\sigma(j+1)}\ldots \hat y_{\sigma(p-1)} x_{u}[b_2+a_{l}+a_{\sigma(p)}] \hat y_{\sigma(p+1)} \ldots \hat y_{\sigma(m-1)} \\ &+c_{2,3}(j,p) \hat y_{\sigma(1)}\ldots \hat y_{\sigma(j-1)} x_i[b_2+a_{\sigma(j)}] \hat y_{\sigma(j+1)}\ldots \hat y_{\sigma(p-1)} x_{u}[b_1+a_{l}+a_{\sigma(p)}] \hat y_{\sigma(p+1)} \ldots \hat y_{\sigma(m-1)} \\ & + (-1) c_{3,2}(j,p) \hat y_{\sigma(1)}\ldots \hat y_{\sigma(j-1)} x_i[b_1+a_{\sigma(j)}+a_{l}] \hat y_{\sigma(j+1)}\ldots \hat y_{\sigma(p-1)} x_{u}[b_2+a_{\sigma(p)}] \hat y_{\sigma(p+1)} \ldots \hat y_{\sigma(m-1)} \\ & + (-1) c_{3,2}(j,p) \hat y_{\sigma(1)}\ldots \hat y_{\sigma(j-1)} x_i[b_2\!+a_{\sigma(j)}\!+a_{l}] \hat y_{\sigma(j+1)}\ldots \hat y_{\sigma(p-1)} x_{u}[b_1\!+a_{\sigma(p)}] \hat y_{\sigma(p+1)} \ldots \hat y_{\sigma(m-1)} ), \end{align*}
where ![]() $\tilde{\tt S}_{m-1}$ stands for the set of bijective maps from
$\tilde{\tt S}_{m-1}$ stands for the set of bijective maps from ![]() $\{1,\ldots,m-1\}$ to
$\{1,\ldots,m-1\}$ to ![]() $\{1,\ldots,m\}{\setminus} \{l\}$ and we have
$\{1,\ldots,m\}{\setminus} \{l\}$ and we have ![]() $1\leqslant j< p\leqslant m-1$. The constants
$1\leqslant j< p\leqslant m-1$. The constants ![]() $c_{2,3}(j,p)$,
$c_{2,3}(j,p)$, ![]() $c_{3,2}(j,p)\in \mathbb {Q}$ do not depend on
$c_{3,2}(j,p)\in \mathbb {Q}$ do not depend on ![]() $Y$, they depend only on
$Y$, they depend only on ![]() $m$. Besides,
$m$. Besides,
![]() $c_{2,3}(j,p)\leqslant 0$ for all
$c_{2,3}(j,p)\leqslant 0$ for all ![]() $j< p$, and
$j< p$, and ![]() $c_{2,3}(j,p)< 0$ if in addition
$c_{2,3}(j,p)< 0$ if in addition ![]() $\check {j}\geqslant p$.
$\check {j}\geqslant p$.
Proof. Set ![]() $\hat Y=\hat y_1\ldots \hat y_m\in {{\mathcal {U}}}(t^{-1}\mathfrak g[t^{-1}])$. Let
$\hat Y=\hat y_1\ldots \hat y_m\in {{\mathcal {U}}}(t^{-1}\mathfrak g[t^{-1}])$. Let ![]() $\hat x_i^{(1)}$ stand for
$\hat x_i^{(1)}$ stand for ![]() $x_i[b_1]$ and
$x_i[b_1]$ and ![]() $\hat x_i^{(2)}$ for
$\hat x_i^{(2)}$ for ![]() $x_i[b_2]$. Then
$x_i[b_2]$. Then
 \[ [{\mathcal{H}}[b_1,b_2],\hat Y]= \sum_{j=1,i=1}^{j=m,i=\dim\mathfrak g} (\hat y_1\ldots \hat y_{j-1} \hat x_i^{(1)} [\hat x_i^{(2)},\hat y_j] \hat y_{j+1}\ldots \hat y_m+ \hat y_1\ldots \hat y_{j-1} [\hat x_i^{(1)},\hat y_j] \hat x_i^{(2)} \hat y_{j+1}\ldots\hat y_m). \]
\[ [{\mathcal{H}}[b_1,b_2],\hat Y]= \sum_{j=1,i=1}^{j=m,i=\dim\mathfrak g} (\hat y_1\ldots \hat y_{j-1} \hat x_i^{(1)} [\hat x_i^{(2)},\hat y_j] \hat y_{j+1}\ldots \hat y_m+ \hat y_1\ldots \hat y_{j-1} [\hat x_i^{(1)},\hat y_j] \hat x_i^{(2)} \hat y_{j+1}\ldots\hat y_m). \]Furthermore,
Each summand of ![]() $[{\mathcal {H}}[b_1,b_2],\sigma (\hat Y)]$ we regard as a formal non-commutative product. The symmetrisation of
$[{\mathcal {H}}[b_1,b_2],\sigma (\hat Y)]$ we regard as a formal non-commutative product. The symmetrisation of ![]() $P_Y=\{{\mathcal {H}}[b_1,b_2], Y\}$ resembles (3.2), but with a rather significant difference: the factor
$P_Y=\{{\mathcal {H}}[b_1,b_2], Y\}$ resembles (3.2), but with a rather significant difference: the factor ![]() $\hat x_i^{(\upsilon )}$, which is not involved in
$\hat x_i^{(\upsilon )}$, which is not involved in ![]() $[\hat x_i^{(\nu )},\hat y_{\sigma (j)}]$, does not have to stay next to
$[\hat x_i^{(\nu )},\hat y_{\sigma (j)}]$, does not have to stay next to ![]() $[\hat x_i^{(\nu )},\hat y_{\sigma (j)}]$ (here we have
$[\hat x_i^{(\nu )},\hat y_{\sigma (j)}]$ (here we have ![]() $\{\nu,\upsilon \}=\{1,2\}$). The idea behind the computation of
$\{\nu,\upsilon \}=\{1,2\}$). The idea behind the computation of ![]() $X_Y$ is to modify each term of
$X_Y$ is to modify each term of ![]() $\varpi (P_Y)$ in such a way that the wayward factor
$\varpi (P_Y)$ in such a way that the wayward factor ![]() $\hat x_i^{(\upsilon )}$ gets back to its place as in
$\hat x_i^{(\upsilon )}$ gets back to its place as in ![]() $[{\mathcal {H}}[b_1,b_2],\varpi (Y)]$. In this process, other commutators
$[{\mathcal {H}}[b_1,b_2],\varpi (Y)]$. In this process, other commutators ![]() $\pm [\hat x_i^{(\upsilon )},\hat y_l]$ will appear. It is convenient to consider the differences
$\pm [\hat x_i^{(\upsilon )},\hat y_l]$ will appear. It is convenient to consider the differences
 \[ X_{\sigma(\hat Y)}= [{\mathcal{H}}[b_1,b_2],\sigma(\hat Y)] - \frac{1}{m+1}\sum_{j=1}^{m}\sum_{\upsilon=1}^{2} \overset{\underbrace{\phantom{1237719278}\hat x_i^{(\upsilon)}\ \text{at different places}\phantom{1733543293}}}{\hat y_{\sigma(1)}{\ldots}\hat y_{\sigma(j-1)} [\hat x_i^{(\nu)},\hat y_{\sigma(j)}] \hat y_{\sigma(j+1)}\ldots \hat y_{\sigma(m-1)}\hat y_{\sigma(m)}}, \]
\[ X_{\sigma(\hat Y)}= [{\mathcal{H}}[b_1,b_2],\sigma(\hat Y)] - \frac{1}{m+1}\sum_{j=1}^{m}\sum_{\upsilon=1}^{2} \overset{\underbrace{\phantom{1237719278}\hat x_i^{(\upsilon)}\ \text{at different places}\phantom{1733543293}}}{\hat y_{\sigma(1)}{\ldots}\hat y_{\sigma(j-1)} [\hat x_i^{(\nu)},\hat y_{\sigma(j)}] \hat y_{\sigma(j+1)}\ldots \hat y_{\sigma(m-1)}\hat y_{\sigma(m)}}, \]
where for each fixed ![]() $j$ and
$j$ and ![]() $\upsilon$, we add
$\upsilon$, we add ![]() $m+1$ different formal products with
$m+1$ different formal products with ![]() $\hat x_i^{(\upsilon )}$ standing in
$\hat x_i^{(\upsilon )}$ standing in ![]() $m+1$ different places. Then
$m+1$ different places. Then ![]() $X_Y= ({1}/{m!}) \sum _{\sigma \in {\tt S}_m} X_{\sigma (\hat Y)}$.
$X_Y= ({1}/{m!}) \sum _{\sigma \in {\tt S}_m} X_{\sigma (\hat Y)}$.
While modifying ![]() $\varpi (P_Y)$, one obtains products of the form
$\varpi (P_Y)$, one obtains products of the form
with some coefficients; one also has to commute ![]() $\hat x_i^{(\upsilon )}$ with
$\hat x_i^{(\upsilon )}$ with ![]() $[\hat x_i^{(\nu )},\hat y_j]$. The total sum of the products that correspond to
$[\hat x_i^{(\nu )},\hat y_j]$. The total sum of the products that correspond to ![]() $X_{\hat Y}$ and contain a double commutator
$X_{\hat Y}$ and contain a double commutator ![]() $[ \hat x_i^{(\upsilon )},[\hat x_i^{(\nu )},\hat y_j]]$ as a factor is
$[ \hat x_i^{(\upsilon )},[\hat x_i^{(\nu )},\hat y_j]]$ as a factor is
Observe that
Applying ![]() $\sigma$ to all
$\sigma$ to all ![]() $\hat y_p$ with
$\hat y_p$ with ![]() $1\leqslant p\leqslant m$, we obtain
$1\leqslant p\leqslant m$, we obtain ![]() $X_{{\rm dcom}}(\sigma,j,i)$ from
$X_{{\rm dcom}}(\sigma,j,i)$ from ![]() $X_{{\rm dcom}}({{\rm id}},j,i)$. Set
$X_{{\rm dcom}}({{\rm id}},j,i)$. Set ![]() $X_{{\rm dcom}}=\sum _{j=1}^{m}\sum _{\sigma \in {\tt S}_m}\sum _i X_{{\rm dcom}}(\sigma,j,i)$. We have
$X_{{\rm dcom}}=\sum _{j=1}^{m}\sum _{\sigma \in {\tt S}_m}\sum _i X_{{\rm dcom}}(\sigma,j,i)$. We have ![]() $\mathrm {gr}(X_{{\rm dcom}})=0$, since
$\mathrm {gr}(X_{{\rm dcom}})=0$, since
for the transposition ![]() $\vartheta =(j(m-j+1))$.
$\vartheta =(j(m-j+1))$.
Now consider expressions ![]() $[[\hat x_i^{(\upsilon )},[\hat x_i^{(\nu )},\hat y_j]],\hat y_l]$. In view of (
$[[\hat x_i^{(\upsilon )},[\hat x_i^{(\nu )},\hat y_j]],\hat y_l]$. In view of (![]() $\blacklozenge$),
$\blacklozenge$),
where ![]() $b=b_1+b_2$. This leads to
$b=b_1+b_2$. This leads to
Thus ![]() $\sum _i X_{{\rm dcom}}({{\rm id}},j,i)-\varpi (\mathrm {gr}(\sum _i X_{{\rm dcom}}({{\rm id}},j,i))) = C \sum _{l\ne j} c_{(j,l)} X_{{\rm dcom}}^{[j,l]}({{\rm id}})$, where
$\sum _i X_{{\rm dcom}}({{\rm id}},j,i)-\varpi (\mathrm {gr}(\sum _i X_{{\rm dcom}}({{\rm id}},j,i))) = C \sum _{l\ne j} c_{(j,l)} X_{{\rm dcom}}^{[j,l]}({{\rm id}})$, where
 \[ X_{{\rm dcom}}^{[j,l]}({{\rm id}})= \begin{cases} \hat y_1\ldots\hat y_{l-1} [y_j,y_l][a_j+a_l+b]\hat y_{l+1}\ldots\hat y_{j-1}\hat y_{j+1}\ldots\hat y_m & \text{if } l< j \\ \hat y_1\ldots\hat y_{j-1}\hat y_{j+1} \ldots\hat y_{l-1} [y_j,y_l][a_j+a_l+b]\hat y_{l+1}\ldots \hat y_m & \text{if } l>j; \end{cases} \]
\[ X_{{\rm dcom}}^{[j,l]}({{\rm id}})= \begin{cases} \hat y_1\ldots\hat y_{l-1} [y_j,y_l][a_j+a_l+b]\hat y_{l+1}\ldots\hat y_{j-1}\hat y_{j+1}\ldots\hat y_m & \text{if } l< j \\ \hat y_1\ldots\hat y_{j-1}\hat y_{j+1} \ldots\hat y_{l-1} [y_j,y_l][a_j+a_l+b]\hat y_{l+1}\ldots \hat y_m & \text{if } l>j; \end{cases} \]
furthermore ![]() $c_{(j,l)}\in \mathbb {Q}$. Set
$c_{(j,l)}\in \mathbb {Q}$. Set ![]() $\sigma =(j\,l)$. The difference
$\sigma =(j\,l)$. The difference
 \[ \sum_i X_{{\rm dcom}}(\sigma,j,i)-\varpi\biggl(\mathrm{gr}\biggl(\sum_i X_{{\rm dcom}}(\sigma,j,i)\biggr)\biggr) \]
\[ \sum_i X_{{\rm dcom}}(\sigma,j,i)-\varpi\biggl(\mathrm{gr}\biggl(\sum_i X_{{\rm dcom}}(\sigma,j,i)\biggr)\biggr) \]has a summand
This proves that ![]() $\sum _{\sigma \in {\tt S}_m,j,i} X_{{\rm dcom}}(\sigma,j,i)=0$, i.e. the expressions containing double commutators
$\sum _{\sigma \in {\tt S}_m,j,i} X_{{\rm dcom}}(\sigma,j,i)=0$, i.e. the expressions containing double commutators ![]() $[\hat x_i^{(\upsilon )},[\hat x_i^{(\nu )},\hat y_j]]$ as factors have no contribution to
$[\hat x_i^{(\upsilon )},[\hat x_i^{(\nu )},\hat y_j]]$ as factors have no contribution to ![]() $X_Y$.
$X_Y$.
In the modification of ![]() $(m+1)X_{\hat Y}$, a term
$(m+1)X_{\hat Y}$, a term
appears ![]() $j$ times with the coefficient
$j$ times with the coefficient ![]() $1$ (these are the instances, where
$1$ (these are the instances, where ![]() $\hat x_i^{(\upsilon )}$ is the wayward factor); it also appears
$\hat x_i^{(\upsilon )}$ is the wayward factor); it also appears ![]() $(m-l+1)$ times with the coefficient
$(m-l+1)$ times with the coefficient ![]() $(-1)$ from the instances, where
$(-1)$ from the instances, where ![]() $\hat x_i^{(\nu )}$ is the wayward factor. Thereby
$\hat x_i^{(\nu )}$ is the wayward factor. Thereby
 \[ X_{\sigma(\hat Y)}= \frac{1}{m+1} \sum_{j< l} \sum_{\upsilon} \sum_{i} (j+l-m-1) X(\sigma,i,\upsilon,\nu;j,l). \]
\[ X_{\sigma(\hat Y)}= \frac{1}{m+1} \sum_{j< l} \sum_{\upsilon} \sum_{i} (j+l-m-1) X(\sigma,i,\upsilon,\nu;j,l). \]
Set ![]() $j'=m-j+1$. Then
$j'=m-j+1$. Then ![]() $j+j'=m+1$. Assume that
$j+j'=m+1$. Assume that ![]() $l\ne j'$ and
$l\ne j'$ and ![]() $l>j$. For any
$l>j$. For any ![]() $\sigma \in {\tt S}_m$, the symbol of
$\sigma \in {\tt S}_m$, the symbol of ![]() $X(\sigma,i,\upsilon,\nu ;j,l)$ is the same as the symbol of
$X(\sigma,i,\upsilon,\nu ;j,l)$ is the same as the symbol of ![]() $X(\tilde \sigma,i,\upsilon,\nu ;l',j')$, where
$X(\tilde \sigma,i,\upsilon,\nu ;l',j')$, where
furthermore, these two expressions appear in ![]() $X_{Y}$ with opposite coefficients. This shows that
$X_{Y}$ with opposite coefficients. This shows that ![]() $X_{Y}\in {{\mathcal {U}}}_{m-1}(\hat {\mathfrak g}^-)$. In order to get a better understanding of
$X_{Y}\in {{\mathcal {U}}}_{m-1}(\hat {\mathfrak g}^-)$. In order to get a better understanding of ![]() $X_{Y}$, we modify the terms
$X_{Y}$, we modify the terms ![]() $X(\sigma,i,\upsilon,\nu ;j,l)$, which we consider as formal products.
$X(\sigma,i,\upsilon,\nu ;j,l)$, which we consider as formal products.
Each ![]() $X(\sigma,i,\upsilon,\nu ;j,l)$ has factors of two sorts: elements
$X(\sigma,i,\upsilon,\nu ;j,l)$ has factors of two sorts: elements ![]() $\hat y_p$ (depicted as points in the diagram below) and two commutators
$\hat y_p$ (depicted as points in the diagram below) and two commutators ![]() $[\hat x_i^{(\upsilon )},\hat y_{\sigma (j)}]$,
$[\hat x_i^{(\upsilon )},\hat y_{\sigma (j)}]$, ![]() $[\hat x_i^{(\upsilon )},\hat y_{\sigma (l)}]$, which are depicted as stars. We move the commutator that is closer to the middle point of the product until the expression obtains a central symmetry. In the case
$[\hat x_i^{(\upsilon )},\hat y_{\sigma (l)}]$, which are depicted as stars. We move the commutator that is closer to the middle point of the product until the expression obtains a central symmetry. In the case ![]() $l\leqslant {m}/{2}$, this looks as follows:
$l\leqslant {m}/{2}$, this looks as follows:
See also Example 3.3 below. The commutator ![]() $[\hat x_i^{(\upsilon )},\hat y_{\sigma (l)}]$ is moving if and only if
$[\hat x_i^{(\upsilon )},\hat y_{\sigma (l)}]$ is moving if and only if ![]() $l< j'$. After the modification, the products of
$l< j'$. After the modification, the products of ![]() $m$ factors annihilate each other and
$m$ factors annihilate each other and ![]() $X_Y$ is now a
$X_Y$ is now a ![]() $\mathbb {Q}$-linear combination of products of
$\mathbb {Q}$-linear combination of products of ![]() $m-1$ factors, where in each term,
$m-1$ factors, where in each term, ![]() $m-3$ factors are elements
$m-3$ factors are elements ![]() $\hat y_w$, one is a commutator
$\hat y_w$, one is a commutator ![]() $[\hat x_i^{(\upsilon )},\hat y_j]$, and another one is a commutator
$[\hat x_i^{(\upsilon )},\hat y_j]$, and another one is a commutator ![]() $[[\hat x_i^{(\nu )},\hat y_l],\hat y_p]$. A possible example in the case
$[[\hat x_i^{(\nu )},\hat y_l],\hat y_p]$. A possible example in the case ![]() $\sigma ={{\rm id}}$, is
$\sigma ={{\rm id}}$, is
It appears only if ![]() $l< j'$. First we deal with these expressions ‘qualitative’ and after that describe the coefficients.
$l< j'$. First we deal with these expressions ‘qualitative’ and after that describe the coefficients.
Observe that for ![]() $y\in \mathfrak g$ and
$y\in \mathfrak g$ and ![]() $a\in {{\mathbb {Z}}}_{<0}$, we have
$a\in {{\mathbb {Z}}}_{<0}$, we have ![]() $y[a]=\sum _{i} (x_i,y) x_i[a]$. Assume for simplicity that
$y[a]=\sum _{i} (x_i,y) x_i[a]$. Assume for simplicity that ![]() $\{j,p,l\}=\{1,2,3\}$, disregard for the moment the other factors, and ignore the
$\{j,p,l\}=\{1,2,3\}$, disregard for the moment the other factors, and ignore the ![]() $t$-degrees of the elements. Consider the sum
$t$-degrees of the elements. Consider the sum
 \begin{align} \sum_i [x_i,y_1] [y_3,[y_2,x_i]] &= \sum_{i,j,u} ([x_i,y_1],x_j)x_j ([y_3,[y_2,x_i]],x_u)x_u \nonumber\\ & = \sum_{i,j,u} (x_i,[ y_1,x_j] )x_j (x_i, \mathrm{ad}(y_2)\mathrm{ad}(y_3)(x_u))x_u \nonumber\\ & = \sum_{i,j,u} (( \mathrm{ad}(y_2)\mathrm{ad}(y_3)(x_u), x_i) x_i, [y_1,x_j]) x_j x_u \nonumber\\ & = \sum_{j,u} (\mathrm{ad}(y_2)\mathrm{ad}(y_3)(x_u),[y_1,x_j])x_jx_u \nonumber\\ &=\sum_{j,u}(\mathrm{ad}(y_3)\mathrm{ad}(y_2)\mathrm{ad}(y_1)(x_j), x_u)x_j x_u. \end{align}
\begin{align} \sum_i [x_i,y_1] [y_3,[y_2,x_i]] &= \sum_{i,j,u} ([x_i,y_1],x_j)x_j ([y_3,[y_2,x_i]],x_u)x_u \nonumber\\ & = \sum_{i,j,u} (x_i,[ y_1,x_j] )x_j (x_i, \mathrm{ad}(y_2)\mathrm{ad}(y_3)(x_u))x_u \nonumber\\ & = \sum_{i,j,u} (( \mathrm{ad}(y_2)\mathrm{ad}(y_3)(x_u), x_i) x_i, [y_1,x_j]) x_j x_u \nonumber\\ & = \sum_{j,u} (\mathrm{ad}(y_2)\mathrm{ad}(y_3)(x_u),[y_1,x_j])x_jx_u \nonumber\\ &=\sum_{j,u}(\mathrm{ad}(y_3)\mathrm{ad}(y_2)\mathrm{ad}(y_1)(x_j), x_u)x_j x_u. \end{align}
Note that ![]() $\mathrm {ad}(y_3)\mathrm {ad}(y_2)\mathrm {ad}(y_1)(x_j)={\sf m}(y_3\otimes y_2\otimes y_1)(x_j)$. If we recall the
$\mathrm {ad}(y_3)\mathrm {ad}(y_2)\mathrm {ad}(y_1)(x_j)={\sf m}(y_3\otimes y_2\otimes y_1)(x_j)$. If we recall the ![]() $t$-degrees, then the product
$t$-degrees, then the product ![]() $x_j x_u$ has to be replaced with
$x_j x_u$ has to be replaced with ![]() $x_j[b_\upsilon +a_1] x_u[b_\nu +a_2+a_3]$ in (3.4). The other factors
$x_j[b_\upsilon +a_1] x_u[b_\nu +a_2+a_3]$ in (3.4). The other factors ![]() $\hat y_w$ do not interfere with the transformations in (3.4).
$\hat y_w$ do not interfere with the transformations in (3.4).
In the process of changing the sequence of factors of ![]() $X({{\rm id}},i,\upsilon,\nu ;j,l)$ with
$X({{\rm id}},i,\upsilon,\nu ;j,l)$ with ![]() $j< l< j'$, the term
$j< l< j'$, the term ![]() $\cdots [\hat x_i^{(\upsilon )},\hat y_j]\cdots [[\hat x_i^{(\nu )},\hat y_l],\hat y_p]\cdots$ appears with the negative coefficient
$\cdots [\hat x_i^{(\upsilon )},\hat y_j]\cdots [[\hat x_i^{(\nu )},\hat y_l],\hat y_p]\cdots$ appears with the negative coefficient ![]() $(j+l-m-1)$ as long as
$(j+l-m-1)$ as long as ![]() $l< p\leqslant j'$. This shows that indeed the constants
$l< p\leqslant j'$. This shows that indeed the constants ![]() $c_{2,3}(j,p)$ do not depend on
$c_{2,3}(j,p)$ do not depend on ![]() $Y$, they depend only on
$Y$, they depend only on ![]() $m$. Moreover,
$m$. Moreover, ![]() $c_{2,3}(j,p)=0$ if
$c_{2,3}(j,p)=0$ if ![]() $p>\check {j}$ and
$p>\check {j}$ and ![]() $c_{2,3}(j,p)<0$ if
$c_{2,3}(j,p)<0$ if ![]() $p\leqslant \check {j}$.
$p\leqslant \check {j}$.
The symmetry ![]() $c_{2,3}(j,p)=c_{3,2}(\check {p},\check {j})$ is justified by the fact that
$c_{2,3}(j,p)=c_{3,2}(\check {p},\check {j})$ is justified by the fact that ![]() $\omega (X_Y)=(-1)^{m-1}X_Y$. A more direct way to see this, is to notice that if a factor
$\omega (X_Y)=(-1)^{m-1}X_Y$. A more direct way to see this, is to notice that if a factor ![]() $[\hat x_i^{(\nu )},\hat y_l]$ moves from a place
$[\hat x_i^{(\nu )},\hat y_l]$ moves from a place ![]() $v$ to
$v$ to ![]() $j'$ in some term, then
$j'$ in some term, then ![]() $j< v< j'$ and there is a term with the apposite coefficient, where
$j< v< j'$ and there is a term with the apposite coefficient, where ![]() $[\hat x_i^{(\nu )},\hat y_l]$ moves from
$[\hat x_i^{(\nu )},\hat y_l]$ moves from ![]() $v'$ to
$v'$ to ![]() $j$. The first type of moves produces
$j$. The first type of moves produces
and the second
We have ![]() $(x_i,{\sf m}(y_{\sigma (j)}\otimes y_l\otimes y_{\sigma (p)})(x_u))= - ({\sf m}(y_{\sigma (p)}\otimes y_l\otimes y_{\sigma (j)})(x_i),x_u)$ and the scalar product
$(x_i,{\sf m}(y_{\sigma (j)}\otimes y_l\otimes y_{\sigma (p)})(x_u))= - ({\sf m}(y_{\sigma (p)}\otimes y_l\otimes y_{\sigma (j)})(x_i),x_u)$ and the scalar product ![]() $(\,\,,\,)$ is symmetric. These facts confirm the symmetry of the constants and justifies the minus signs in front of
$(\,\,,\,)$ is symmetric. These facts confirm the symmetry of the constants and justifies the minus signs in front of ![]() $c_{3,2}(j,p)$ in the answer.
$c_{3,2}(j,p)$ in the answer.
Example 3.3 Consider the case ![]() $m=6$. One obtains that
$m=6$. One obtains that
 \begin{align*} X_Y&= \frac{1}{7!}\sum_{\sigma\in {\tt S}_6,i}( 4 X(\sigma,i,1,2;5,6) - 4 X(\sigma,i,1,2;1,2) + 3 X(\sigma,i,1,2;4,6) - 3 X(\sigma,i,1,2;1,3) \\ &\quad +2 X(\sigma,i,1,2;3,6) - 2 X(\sigma,i,1,2;1,4) + 2 X(\sigma,i,1,2;4,5) - 2 X(\sigma,i,1,2;2,3) \\ &\quad+ X(\sigma,i,1,2;2,6) - X(\sigma,i,1,2;1,5) + X(\sigma,i,1,2;3,5) - X(\sigma,i,1,2;2,4)) \\ &\quad+ (\text{the similar expression for } (\upsilon,\nu)=(2,1)). \end{align*}
\begin{align*} X_Y&= \frac{1}{7!}\sum_{\sigma\in {\tt S}_6,i}( 4 X(\sigma,i,1,2;5,6) - 4 X(\sigma,i,1,2;1,2) + 3 X(\sigma,i,1,2;4,6) - 3 X(\sigma,i,1,2;1,3) \\ &\quad +2 X(\sigma,i,1,2;3,6) - 2 X(\sigma,i,1,2;1,4) + 2 X(\sigma,i,1,2;4,5) - 2 X(\sigma,i,1,2;2,3) \\ &\quad+ X(\sigma,i,1,2;2,6) - X(\sigma,i,1,2;1,5) + X(\sigma,i,1,2;3,5) - X(\sigma,i,1,2;2,4)) \\ &\quad+ (\text{the similar expression for } (\upsilon,\nu)=(2,1)). \end{align*}
Take ![]() $\sigma ={{\rm id}}$. Performing the modification
$\sigma ={{\rm id}}$. Performing the modification
we move the factor ![]() $[\hat x_i^{(1)},\hat y_5]$ to the first place producing commutators with
$[\hat x_i^{(1)},\hat y_5]$ to the first place producing commutators with ![]() $\hat y_4$,
$\hat y_4$, ![]() $\hat y_3$,
$\hat y_3$, ![]() $\hat y_2$,
$\hat y_2$, ![]() $\hat y_1$ on the way. In the same manner,
$\hat y_1$ on the way. In the same manner,
and for ![]() $\tilde \sigma =(1\,5\,3)(2\,6\,4)$,
$\tilde \sigma =(1\,5\,3)(2\,6\,4)$,
Performing the modification
we move the factor ![]() $[\hat x_i^{(1)},\hat y_4]$ to the second place producing commutators with
$[\hat x_i^{(1)},\hat y_4]$ to the second place producing commutators with ![]() $\hat y_3$ and
$\hat y_3$ and ![]() $\hat y_2$. The non-zero constants
$\hat y_2$. The non-zero constants ![]() $c^-(j,p):=-c_{2,3}(j,p)$ are
$c^-(j,p):=-c_{2,3}(j,p)$ are
Instead of the usual symmetrisation map, one can consider a weighted ‘symmetrisation’ or rather shuffle, where each permutation is added with a scalar coefficient assigned by a certain function ![]() $\Psi$. We will need only a very particular case of this construction. Let
$\Psi$. We will need only a very particular case of this construction. Let ![]() $\Psi \!: {\tt S}_{k+2}\to \mathbb {Q}$ be a weight function, satisfying the following assumptions:
$\Psi \!: {\tt S}_{k+2}\to \mathbb {Q}$ be a weight function, satisfying the following assumptions:
(A)
 $\Psi (\sigma )$ depends only on
$\Psi (\sigma )$ depends only on  $j=\sigma (k+1)$ and
$j=\sigma (k+1)$ and  $p=\sigma (k+2)$, i.e.
$p=\sigma (k+2)$, i.e.  $\Psi (\sigma )=\Psi (j,p)$;
$\Psi (\sigma )=\Psi (j,p)$;(B)
 $\Psi (j,p)=\Psi (j',p')$ if
$\Psi (j,p)=\Psi (j',p')$ if  $j'=k+3-j$.
$j'=k+3-j$.
Then set
for ![]() $y_j\in \mathfrak q$. Let also
$y_j\in \mathfrak q$. Let also ![]() $\varpi _{\rm wt}$ stand for the corresponding map from
$\varpi _{\rm wt}$ stand for the corresponding map from ![]() ${{\mathcal {S}}}^{k}(\mathfrak q)\otimes \mathfrak q\otimes \mathfrak q$ to
${{\mathcal {S}}}^{k}(\mathfrak q)\otimes \mathfrak q\otimes \mathfrak q$ to ![]() ${{\mathcal {U}}}(\mathfrak q)$. Condition (B) guaranties that
${{\mathcal {U}}}(\mathfrak q)$. Condition (B) guaranties that ![]() $\omega (\varpi _{\rm wt}(F))=(-1)^{k} \varpi _{\rm wt}(F)$ for each
$\omega (\varpi _{\rm wt}(F))=(-1)^{k} \varpi _{\rm wt}(F)$ for each ![]() $F\in {{\mathcal {S}}}^{k}(\mathfrak q)\otimes \mathfrak q\otimes \mathfrak q$. In the case
$F\in {{\mathcal {S}}}^{k}(\mathfrak q)\otimes \mathfrak q\otimes \mathfrak q$. In the case ![]() $\Psi (\sigma )= {1}/{(k+2)!}$, the map
$\Psi (\sigma )= {1}/{(k+2)!}$, the map ![]() $\varpi _{\rm wt}$ coincides with
$\varpi _{\rm wt}$ coincides with ![]() $\varpi$. Keep in mind that each appearing
$\varpi$. Keep in mind that each appearing ![]() $\varpi _{\rm wt}$ may have its own weight function.
$\varpi _{\rm wt}$ may have its own weight function.
Suppose that ![]() $Y\in {{\mathcal {S}}}^{m}(\mathfrak g)$,
$Y\in {{\mathcal {S}}}^{m}(\mathfrak g)$, ![]() $\bar a\in \mathbb {Z}_{<0}^{m}$, and we want to merge them in order to obtain an element of
$\bar a\in \mathbb {Z}_{<0}^{m}$, and we want to merge them in order to obtain an element of ![]() ${{\mathcal {S}}}^{m}({{\hat {\mathfrak g}}}^-)$. The only canonical way to do so is to replace
${{\mathcal {S}}}^{m}({{\hat {\mathfrak g}}}^-)$. The only canonical way to do so is to replace ![]() $\bar a$ with the orbit
$\bar a$ with the orbit ![]() ${\tt S}_m\bar a$, add over this orbit, and divide by
${\tt S}_m\bar a$, add over this orbit, and divide by ![]() $|{\tt S}_m\bar a|$ as we have done in § 1.5. The result is the
$|{\tt S}_m\bar a|$ as we have done in § 1.5. The result is the ![]() $\bar a$-polarisation
$\bar a$-polarisation ![]() $Y[\bar a]$ of
$Y[\bar a]$ of ![]() $Y$. Set
$Y$. Set
For different numbers ![]() $u,v,l\in \{1,\ldots,m\}$, let
$u,v,l\in \{1,\ldots,m\}$, let ![]() $\bar a^{u,v,l}\in \mathbb {Z}_{<0}^{m-3}$ be the vector obtained from
$\bar a^{u,v,l}\in \mathbb {Z}_{<0}^{m-3}$ be the vector obtained from ![]() $\bar a$ by removing
$\bar a$ by removing ![]() $a_u$,
$a_u$, ![]() $a_v$, and
$a_v$, and ![]() $a_l$. Let
$a_l$. Let ![]() $\langle u,v,l\rangle$ be a triple such that
$\langle u,v,l\rangle$ be a triple such that ![]() $l< v$ and
$l< v$ and ![]() $u\ne l,v$. Write
$u\ne l,v$. Write ![]() ${\sf m}(Y)= \sum _{w=1}^{L} \xi _w \otimes R_w$ with
${\sf m}(Y)= \sum _{w=1}^{L} \xi _w \otimes R_w$ with ![]() $\xi _w \in \Lambda ^{2}\mathfrak g$,
$\xi _w \in \Lambda ^{2}\mathfrak g$, ![]() $R_w\in {{\mathcal {S}}}^{m-3}(\mathfrak g)$.
$R_w\in {{\mathcal {S}}}^{m-3}(\mathfrak g)$.
Proposition 3.4 The element ![]() $X_{Y[\bar a]}$ is equal to
$X_{Y[\bar a]}$ is equal to
where ![]() $\Psi (j,p)= 2c_{2,3}(j,p)$ if
$\Psi (j,p)= 2c_{2,3}(j,p)$ if ![]() $j< p$ and
$j< p$ and ![]() $\Psi (j,p)=2c_{3,2}(p,j)$ if
$\Psi (j,p)=2c_{3,2}(p,j)$ if ![]() $j>p$ for the weight function
$j>p$ for the weight function ![]() $\Psi$.
$\Psi$.
Proof. Using the linearity, we may assume that ![]() $Y=y_1\ldots y_m$. The symmetry in
$Y=y_1\ldots y_m$. The symmetry in ![]() $t$-degrees allows one to add the expressions appearing in the formulation of Lemma 3.2 over the triples
$t$-degrees allows one to add the expressions appearing in the formulation of Lemma 3.2 over the triples ![]() $(y_{e}[a_{\sigma (p)}], y_{f}[a_l], e_g[a_{\sigma (j)}])$ with
$(y_{e}[a_{\sigma (p)}], y_{f}[a_l], e_g[a_{\sigma (j)}])$ with ![]() $\{e,f,g\}=\{\sigma (p),l,\sigma (j)\}$ while keeping
$\{e,f,g\}=\{\sigma (p),l,\sigma (j)\}$ while keeping ![]() $x_i[b_\upsilon +a_{\sigma (j)}]$,
$x_i[b_\upsilon +a_{\sigma (j)}]$, ![]() $x_u[b_\nu +a_{l}+a_{\sigma (p)}]$ and
$x_u[b_\nu +a_{l}+a_{\sigma (p)}]$ and ![]() $x_i[b_\upsilon +a_{\sigma (j)}+a_l]$,
$x_i[b_\upsilon +a_{\sigma (j)}+a_l]$, ![]() $x_u[b_\nu +a_{\sigma (p)}]$ at their places. In this way the coefficient
$x_u[b_\nu +a_{\sigma (p)}]$ at their places. In this way the coefficient ![]() ${\sf m}(y_{\sigma (p)}\otimes y_l \otimes y_{\sigma (j)})$ is replaced with
${\sf m}(y_{\sigma (p)}\otimes y_l \otimes y_{\sigma (j)})$ is replaced with ![]() ${\sf m}(y_{\sigma (p)} y_l y_{\sigma (j)})$ and thereby
${\sf m}(y_{\sigma (p)} y_l y_{\sigma (j)})$ and thereby ![]() $\xi _w$ with
$\xi _w$ with ![]() ${1\leqslant w\leqslant L}$ come into play. It remains to count the scalars and describe the weight function.
${1\leqslant w\leqslant L}$ come into play. It remains to count the scalars and describe the weight function.
Suppose that ![]() $j< p$. Then
$j< p$. Then
and thereby ![]() $\Psi (j,p)=2c_{2,3}(j,p)$. Analogously,
$\Psi (j,p)=2c_{2,3}(j,p)$. Analogously, ![]() $\Psi (p,j)=2c_{3,2}(j,p)$.
$\Psi (p,j)=2c_{3,2}(j,p)$.
Theorem 3.5 For ![]() $F\in {{\mathcal {S}}}^{m}(\mathfrak g)^{\mathfrak g}$ with
$F\in {{\mathcal {S}}}^{m}(\mathfrak g)^{\mathfrak g}$ with ![]() $m\geqslant 4$, the symmetrisation
$m\geqslant 4$, the symmetrisation ![]() $\varpi (F)[-1]$ is an element of the Feigin–Frenkel centre if and only if
$\varpi (F)[-1]$ is an element of the Feigin–Frenkel centre if and only if ![]() ${\sf m}(F)=0$.
${\sf m}(F)=0$.
Proof. According to [Reference RybnikovRyb08], ![]() $\varpi (F)[-1]\in \mathfrak z({{\hat {\mathfrak g}}})$ if and only if it commutes with
$\varpi (F)[-1]\in \mathfrak z({{\hat {\mathfrak g}}})$ if and only if it commutes with ![]() ${\mathcal {H}}[-1]$. In view of Lemma 3.1, this is the case if and only if
${\mathcal {H}}[-1]$. In view of Lemma 3.1, this is the case if and only if ![]() $X_{F[-1]}=0$. Lemma 3.2 describes this element. It states that
$X_{F[-1]}=0$. Lemma 3.2 describes this element. It states that ![]() $c_{2,3}(j,p), c_{3,2}(j,p)\leqslant 0$ and
$c_{2,3}(j,p), c_{3,2}(j,p)\leqslant 0$ and ![]() $c_{2,3}(j,p)<0$ if
$c_{2,3}(j,p)<0$ if ![]() $p\leqslant \check {j}$ as well as
$p\leqslant \check {j}$ as well as ![]() $c_{3,2}(j,p)<0$ if
$c_{3,2}(j,p)<0$ if ![]() $\check {p}\leqslant j$. Since
$\check {p}\leqslant j$. Since ![]() $\varpi (F)[-1]$ is fully symmetrised, we can use Proposition 3.4. It immediately implies that if
$\varpi (F)[-1]$ is fully symmetrised, we can use Proposition 3.4. It immediately implies that if ![]() ${\sf m}(F)=0$, then
${\sf m}(F)=0$, then ![]() $X_{F[-1]}=0$.
$X_{F[-1]}=0$.
Suppose that ![]() ${\sf m}(F)\ne 0$. Write
${\sf m}(F)\ne 0$. Write ![]() ${\sf m}(F)= \sum _{w=1}^{L} \xi _w \otimes R_w$ with
${\sf m}(F)= \sum _{w=1}^{L} \xi _w \otimes R_w$ with ![]() $\xi _w \in \Lambda ^{2}\mathfrak g$ and linearly independent
$\xi _w \in \Lambda ^{2}\mathfrak g$ and linearly independent ![]() $R_w\in {{\mathcal {S}}}^{m-3}(\mathfrak g)$. If
$R_w\in {{\mathcal {S}}}^{m-3}(\mathfrak g)$. If ![]() $\xi \in \Lambda ^{2}\mathfrak g$ is non-zero, then there are
$\xi \in \Lambda ^{2}\mathfrak g$ is non-zero, then there are ![]() $i,j$ such that
$i,j$ such that ![]() ${(\xi (x_i),x_j)\ne 0}$.
${(\xi (x_i),x_j)\ne 0}$.
Set ![]() ${\boldsymbol c}=2\sum _{j< p} (c_{2,3}(j,p)+c_{3,2}(j,p))$. According to Lemma 3.2,
${\boldsymbol c}=2\sum _{j< p} (c_{2,3}(j,p)+c_{3,2}(j,p))$. According to Lemma 3.2, ![]() ${\boldsymbol c}<0$. Hence
${\boldsymbol c}<0$. Hence
 \[ \frac{m!}{(m-3)!} \, {\boldsymbol c} \sum_{w=1}^{w=L} \sum_{i,j}(\xi_w(x_i),x_j) x_i[-2]x_j[-3] R_w[-1] \]
\[ \frac{m!}{(m-3)!} \, {\boldsymbol c} \sum_{w=1}^{w=L} \sum_{i,j}(\xi_w(x_i),x_j) x_i[-2]x_j[-3] R_w[-1] \]
is a non-zero element of ![]() ${{\mathcal {S}}}({{\hat {\mathfrak g}}}^-)$. In view of the same lemma, this expression is equal to
${{\mathcal {S}}}({{\hat {\mathfrak g}}}^-)$. In view of the same lemma, this expression is equal to ![]() $\mathrm {gr}(X_{F[-1]})$. Thus
$\mathrm {gr}(X_{F[-1]})$. Thus ![]() $X_{F[-1]}\ne 0$. This completes the proof.
$X_{F[-1]}\ne 0$. This completes the proof.
Remark If ![]() $\mathfrak g$ is simple, then
$\mathfrak g$ is simple, then ![]() $\mathfrak g^{\mathfrak g}$ is equal to zero and
$\mathfrak g^{\mathfrak g}$ is equal to zero and ![]() ${{\mathcal {S}}}^{2}(\mathfrak g)^{\mathfrak g}$ is spanned by
${{\mathcal {S}}}^{2}(\mathfrak g)^{\mathfrak g}$ is spanned by ![]() ${\mathcal {H}}=\sum _{i} x_i^{2}$. By our convention,
${\mathcal {H}}=\sum _{i} x_i^{2}$. By our convention, ![]() ${\sf m}({{\mathcal {S}}}^{m}(\mathfrak g))=0$ if
${\sf m}({{\mathcal {S}}}^{m}(\mathfrak g))=0$ if ![]() $m\leqslant 2$. Furthermore,
$m\leqslant 2$. Furthermore, ![]() ${\sf m}({{\mathcal {S}}}^{3}(\mathfrak g)^{\mathfrak g})\subset (\Lambda ^{2}\mathfrak g)^{\mathfrak g}=0$. Therefore Theorem 3.5 holds for
${\sf m}({{\mathcal {S}}}^{3}(\mathfrak g)^{\mathfrak g})\subset (\Lambda ^{2}\mathfrak g)^{\mathfrak g}=0$. Therefore Theorem 3.5 holds for ![]() $m\leqslant 3$ as well.
$m\leqslant 3$ as well.
We will be using weighted shuffles ![]() $\varpi _{\rm wt}$ of Poisson half-brackets. If
$\varpi _{\rm wt}$ of Poisson half-brackets. If ![]() $Y=\hat y_1\ldots \hat y_m\in {{\mathcal {S}}}({{\hat {\mathfrak g}}}^-)$, then
$Y=\hat y_1\ldots \hat y_m\in {{\mathcal {S}}}({{\hat {\mathfrak g}}}^-)$, then
 \begin{equation} \varpi_{\rm wt}(Y, b_1,b_2):= \sum_{j=1,i=1}^{j=m,i=\dim\mathfrak g} \varpi_{\rm wt}(Y/\hat y_j \otimes x_i[b_1] \otimes [x_i[b_2],\hat y_j] ). \end{equation}
\begin{equation} \varpi_{\rm wt}(Y, b_1,b_2):= \sum_{j=1,i=1}^{j=m,i=\dim\mathfrak g} \varpi_{\rm wt}(Y/\hat y_j \otimes x_i[b_1] \otimes [x_i[b_2],\hat y_j] ). \end{equation}
Strictly speaking, here ![]() $\varpi _{\rm wt}$ is a linear map from
$\varpi _{\rm wt}$ is a linear map from ![]() ${{\mathcal {S}}}^{m}({{\hat {\mathfrak g}}}^-)$ in
${{\mathcal {S}}}^{m}({{\hat {\mathfrak g}}}^-)$ in ![]() ${{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)$ depending on
${{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)$ depending on ![]() $(b_1,b_2)$ and the choice of a weight function
$(b_1,b_2)$ and the choice of a weight function ![]() $\Psi$. The absence of
$\Psi$. The absence of ![]() ${\rm wt}$ in the lower index indicates that we are taking the usual symmetrisation.
${\rm wt}$ in the lower index indicates that we are taking the usual symmetrisation.
3.2 Iterated shuffling
Another general fact about Lie algebras ![]() $\mathfrak q$ will be needed. Suppose that
$\mathfrak q$ will be needed. Suppose that ![]() $Y=y_1\ldots y_m\in {{\mathcal {S}}}^{m}(\mathfrak q)$ and
$Y=y_1\ldots y_m\in {{\mathcal {S}}}^{m}(\mathfrak q)$ and ![]() $x\in \mathfrak q$. Write
$x\in \mathfrak q$. Write ![]() $Y=({1}/{m}) \sum _{1\leqslant j\leqslant m} y_j \otimes Y^{(j)}$ with
$Y=({1}/{m}) \sum _{1\leqslant j\leqslant m} y_j \otimes Y^{(j)}$ with ![]() $Y^{(j)}=Y/y_j$. Then
$Y^{(j)}=Y/y_j$. Then
Proposition 3.6 Let ![]() ${\mathcal {F}}[\check {\bar a}]=\varpi (F[\bar a])\in {{\mathcal {U}}}(\hat {\mathfrak g}^-)$ be a fully symmetrised element corresponding to a polynomial
${\mathcal {F}}[\check {\bar a}]=\varpi (F[\bar a])\in {{\mathcal {U}}}(\hat {\mathfrak g}^-)$ be a fully symmetrised element corresponding to a polynomial ![]() $F\in {{\mathcal {S}}}^{m}(\mathfrak g)$ and a vector
$F\in {{\mathcal {S}}}^{m}(\mathfrak g)$ and a vector ![]() $\bar a=(a_1,\ldots,a_m)\in \mathbb {Z}_{<0}^{m}$. Suppose that
$\bar a=(a_1,\ldots,a_m)\in \mathbb {Z}_{<0}^{m}$. Suppose that ![]() ${\sf m}_{2r+1}(F)\in {{\mathcal {S}}}^{m-2r}(\mathfrak g)$ for all
${\sf m}_{2r+1}(F)\in {{\mathcal {S}}}^{m-2r}(\mathfrak g)$ for all ![]() $m/2>r\geqslant 1$. Then:
$m/2>r\geqslant 1$. Then:
(i)
 $X_{F[\bar a]}=[{\mathcal {H}}[\bar b],{\mathcal {F}}[\check {\bar a}]] - \varpi (\{ {\mathcal {H}}[\bar b], F[\bar a]\})$ is a sum of weighted symmetrisations
where
$X_{F[\bar a]}=[{\mathcal {H}}[\bar b],{\mathcal {F}}[\check {\bar a}]] - \varpi (\{ {\mathcal {H}}[\bar b], F[\bar a]\})$ is a sum of weighted symmetrisations
where \[ \varpi_{\rm wt}({\sf m}(F)[\bar a^{l,j}], b_1+a_l,b_2+a_j), \quad \varpi_{\rm wt}({\sf m}(F)[\bar a^{l,j}], b_2+a_l,b_1+a_j), \]
\[ \varpi_{\rm wt}({\sf m}(F)[\bar a^{l,j}], b_1+a_l,b_2+a_j), \quad \varpi_{\rm wt}({\sf m}(F)[\bar a^{l,j}], b_2+a_l,b_1+a_j), \] $l\ne j$ and
$l\ne j$ and  $\bar a^{l,j}$ is obtained from
$\bar a^{l,j}$ is obtained from  $\bar a$ by removing
$\bar a$ by removing  $a_l$ and
$a_l$ and  $a_j$;
$a_j$;(ii) for every weight function
 $\Psi$, there is a constant
$\Psi$, there is a constant  $c\in \mathbb {Q}$, which is independent of
$c\in \mathbb {Q}$, which is independent of  $F$, such that
$F$, such that  ${\mathcal {P}}_{F[\bar a]}=\varpi _{\rm wt}(F[\bar a], b_1,b_2) - c\varpi (F[\bar a],b_1,b_2)$ is a sum of
${\mathcal {P}}_{F[\bar a]}=\varpi _{\rm wt}(F[\bar a], b_1,b_2) - c\varpi (F[\bar a],b_1,b_2)$ is a sum of  $\varpi _{\rm wt}({\sf m}(F)[\bar a^{(1)}], b_\upsilon +\gamma _\upsilon, b_\nu +\gamma _\nu )$ with different weight functions, whereby
$\varpi _{\rm wt}({\sf m}(F)[\bar a^{(1)}], b_\upsilon +\gamma _\upsilon, b_\nu +\gamma _\nu )$ with different weight functions, whereby  $\bar a^{(1)}$ is a subvector of
$\bar a^{(1)}$ is a subvector of  $\bar a$ with
$\bar a$ with  $m-2$ entries and
$m-2$ entries and  $\bar \gamma \in \mathbb {Z}_{<0}^{2}$ is constructed from the complement
$\bar \gamma \in \mathbb {Z}_{<0}^{2}$ is constructed from the complement  $\bar a{\setminus} \bar a^{(1)}$ of
$\bar a{\setminus} \bar a^{(1)}$ of  $\bar a^{(1)}$;
$\bar a^{(1)}$;(iii)
 $\mathbb {X}_{F[a]}=[{\mathcal {H}}[b_1,b_2],{\mathcal {F}}[\check {\bar a}]]$ is a sum of
where
$\mathbb {X}_{F[a]}=[{\mathcal {H}}[b_1,b_2],{\mathcal {F}}[\check {\bar a}]]$ is a sum of
where \[ C(\bar a^{(r)},\bar\gamma)\varpi({\sf m}_{2r+1}(F)[\bar a^{(r)}], b_\upsilon+\gamma_\upsilon, b_\nu+\gamma_{\nu}), \]
\[ C(\bar a^{(r)},\bar\gamma)\varpi({\sf m}_{2r+1}(F)[\bar a^{(r)}], b_\upsilon+\gamma_\upsilon, b_\nu+\gamma_{\nu}), \] $0\leqslant r< m/2$,
$0\leqslant r< m/2$,  $\bar a^{(r)}$ is a subvector of
$\bar a^{(r)}$ is a subvector of  $\bar a$ with
$\bar a$ with  $m-2r$ entries,
$m-2r$ entries,  $\bar \gamma \in \mathbb {Z}_{<0}^{2}$ is constructed from
$\bar \gamma \in \mathbb {Z}_{<0}^{2}$ is constructed from  $\bar a{\setminus} \bar a^{(r)}$, and the coefficients
$\bar a{\setminus} \bar a^{(r)}$, and the coefficients  $C(\bar a^{(r)},\bar \gamma )\in \mathbb {Q}$ are independent of
$C(\bar a^{(r)},\bar \gamma )\in \mathbb {Q}$ are independent of  $F$.
$F$.
Proof. Since we are working with a fully symmetrised element, Proposition 3.4 applies. In the same notation, write ![]() ${\sf m}(F)=\sum _{w=1}^{L} \xi _w \otimes R_w$. By our assumptions,
${\sf m}(F)=\sum _{w=1}^{L} \xi _w \otimes R_w$. By our assumptions, ![]() ${\sf m}(F)\in {{\mathcal {S}}}^{m-2}(\mathfrak g)$. In particular,
${\sf m}(F)\in {{\mathcal {S}}}^{m-2}(\mathfrak g)$. In particular, ![]() $\xi _w\in \mathfrak g$ for each
$\xi _w\in \mathfrak g$ for each ![]() $w$. Observe that
$w$. Observe that
Thereby part (i) follows from Proposition 3.4 in view of (3.6).
(ii) Note that ![]() $\omega ({\mathcal {P}}_{F[\bar a]})=(-1)^{m+1} {\mathcal {P}}_{F[\bar a]}$, because of the assumption (
$\omega ({\mathcal {P}}_{F[\bar a]})=(-1)^{m+1} {\mathcal {P}}_{F[\bar a]}$, because of the assumption (![]() $\mathsf{B}$) imposed on all weight functions. By the construction, the image of
$\mathsf{B}$) imposed on all weight functions. By the construction, the image of ![]() $\varpi _{\rm wt}(F[\bar a], b_1,b_2)$ in
$\varpi _{\rm wt}(F[\bar a], b_1,b_2)$ in ![]() ${{\mathcal {S}}}^{m+1}({{\hat {\mathfrak g}}}^-)$ is equal to
${{\mathcal {S}}}^{m+1}({{\hat {\mathfrak g}}}^-)$ is equal to ![]() $c \sum _{i} \{x_i[b_2],F[\bar a]\}x_i[b_1]$ for some
$c \sum _{i} \{x_i[b_2],F[\bar a]\}x_i[b_1]$ for some ![]() $c\in \mathbb {Q}$. This constant
$c\in \mathbb {Q}$. This constant ![]() $c$ depends only on the weight function
$c$ depends only on the weight function ![]() $\Psi$. For this
$\Psi$. For this ![]() $c$, we have
$c$, we have ![]() $\deg \mathrm {gr}({\mathcal {P}}_{F[\bar a]})\leqslant m$.
$\deg \mathrm {gr}({\mathcal {P}}_{F[\bar a]})\leqslant m$.
The element ![]() ${\mathcal {P}}_{F[\bar a]}$ is a linear combination of products, where each product contains
${\mathcal {P}}_{F[\bar a]}$ is a linear combination of products, where each product contains ![]() $m+1$ linear factors. Let us symmetrise the summands of
$m+1$ linear factors. Let us symmetrise the summands of ![]() ${\mathcal {P}}_{F[\bar a]}$ by changing the sequence of factors in them. Note that there is no need to commute factors
${\mathcal {P}}_{F[\bar a]}$ by changing the sequence of factors in them. Note that there is no need to commute factors ![]() $\hat y_j=y_j[a_{\sigma (j)}]$ and
$\hat y_j=y_j[a_{\sigma (j)}]$ and ![]() $\hat y_l=y_l[a_{\sigma (l)}]$, since
$\hat y_l=y_l[a_{\sigma (l)}]$, since ![]() ${\mathcal {P}}_{F[\bar a]}$ is symmetric in the
${\mathcal {P}}_{F[\bar a]}$ is symmetric in the ![]() $\hat y_{p}$. There is no sense in commuting
$\hat y_{p}$. There is no sense in commuting ![]() $\hat x_i^{(1)}$ and
$\hat x_i^{(1)}$ and ![]() $\hat x_i^{(2)}$ either. After this symmetrisation all products of
$\hat x_i^{(2)}$ either. After this symmetrisation all products of ![]() $m+1$ factors annihilate each other and
$m+1$ factors annihilate each other and ![]() ${\mathcal {P}}_{F[\bar a]}$ becomes a linear combination of products containing
${\mathcal {P}}_{F[\bar a]}$ becomes a linear combination of products containing ![]() $m$ factors. Now we symmetrise these new products. Because of the antipode symmetry, they disappear after the symmetrisation and now
$m$ factors. Now we symmetrise these new products. Because of the antipode symmetry, they disappear after the symmetrisation and now ![]() ${\mathcal {P}}_{F[\bar a]}$ is a linear combination of products containing
${\mathcal {P}}_{F[\bar a]}$ is a linear combination of products containing ![]() $m-1$ factors. Furthermore, each non-zero summand must contain certain factors according to one of the types listed below:
$m-1$ factors. Furthermore, each non-zero summand must contain certain factors according to one of the types listed below:
(1)
 $[\hat x_i^{(\nu )},y_j]$ and
$[\hat x_i^{(\nu )},y_j]$ and  $[[\hat x_i^{(\upsilon )},\hat y_l],\hat y_p]$;
$[[\hat x_i^{(\upsilon )},\hat y_l],\hat y_p]$;(2)
 $[\hat y_p,[\hat y_l,[\hat y_j,\hat x_i^{(\upsilon )}]]]=\mathrm {ad}(y_p)\mathrm {ad}(y_l)\mathrm {ad}(y_j)(x_i[b_\upsilon +a_{\sigma (p)}+a_{\sigma (l)}+a_{\sigma (j)}])$ and
$[\hat y_p,[\hat y_l,[\hat y_j,\hat x_i^{(\upsilon )}]]]=\mathrm {ad}(y_p)\mathrm {ad}(y_l)\mathrm {ad}(y_j)(x_i[b_\upsilon +a_{\sigma (p)}+a_{\sigma (l)}+a_{\sigma (j)}])$ and  $\hat x_i^{(\nu )}$;
$\hat x_i^{(\nu )}$;(3)
 $[[\hat y_p,\hat x_i^{(\upsilon )}], [\hat y_l,\hat x_i^{(\nu )}]]=[[y_p,x_i], [y_l,x_i]][a_{\sigma (p)}+ a_{\sigma (l)}+b_1+b_2]$;
$[[\hat y_p,\hat x_i^{(\upsilon )}], [\hat y_l,\hat x_i^{(\nu )}]]=[[y_p,x_i], [y_l,x_i]][a_{\sigma (p)}+ a_{\sigma (l)}+b_1+b_2]$;(4)
 $[\hat y_p,[\hat x_i^{(\upsilon )}, [\hat x_i^{(\nu )},\hat y_j]]]$;
$[\hat y_p,[\hat x_i^{(\upsilon )}, [\hat x_i^{(\nu )},\hat y_j]]]$;(5)
 $[\hat x_i^{(\upsilon )},[ \hat y_p, [\hat y_j,\hat x_i^{(\nu )}]]]=[[\hat x_i^{(\upsilon )},\hat y_p], [\hat y_j,\hat x_i^{(\nu )}]] - [\hat y_p, [\hat x_i^{(\upsilon )}, [\hat x_i^{(\nu )},\hat y_j]]]$.
$[\hat x_i^{(\upsilon )},[ \hat y_p, [\hat y_j,\hat x_i^{(\nu )}]]]=[[\hat x_i^{(\upsilon )},\hat y_p], [\hat y_j,\hat x_i^{(\nu )}]] - [\hat y_p, [\hat x_i^{(\upsilon )}, [\hat x_i^{(\nu )},\hat y_j]]]$.
The terms of type (4) disappear if we add over all ![]() $i$ and permute
$i$ and permute ![]() $p$ and
$p$ and ![]() $j$, because of the properties of
$j$, because of the properties of ![]() ${\mathcal {H}}[\bar b]$, cf. (3.3). The terms of type (3) disappear if we permute
${\mathcal {H}}[\bar b]$, cf. (3.3). The terms of type (3) disappear if we permute ![]() $l$ and
$l$ and ![]() $p$. Therefore the terms of type (5) disappear as well.
$p$. Therefore the terms of type (5) disappear as well.
One can deal with the terms of types (1) and (2) in the same way as in Lemma 3.2 and Proposition 3.4. They lead to ![]() $\gamma =(a_j,a_l)$ and
$\gamma =(a_j,a_l)$ and ![]() $\gamma =(a_j+a_l,0)$ as well as
$\gamma =(a_j+a_l,0)$ as well as ![]() $\gamma = (0,a_j+a_l)$. Note that the commutators of type (2) are easier to understand, since there is no need to permute the
$\gamma = (0,a_j+a_l)$. Note that the commutators of type (2) are easier to understand, since there is no need to permute the ![]() $t$-degrees, and at the same time they give rise to half-brackets.
$t$-degrees, and at the same time they give rise to half-brackets.
(iii) We are presenting ![]() $\mathbb {X}_{F[\bar a]}$ in the form (0.1) and can state at once that it has terms of degrees
$\mathbb {X}_{F[\bar a]}$ in the form (0.1) and can state at once that it has terms of degrees ![]() $m+1-2d$ only. Note that
$m+1-2d$ only. Note that ![]() $[{\mathcal {H}}[\bar b],{\mathcal {F}}[\check {\bar a}]]$ can be viewed as a weighted symmetrisation
$[{\mathcal {H}}[\bar b],{\mathcal {F}}[\check {\bar a}]]$ can be viewed as a weighted symmetrisation ![]() $\varpi _{\rm wt}(F[\bar a], b_1, b_2)$ if we choose
$\varpi _{\rm wt}(F[\bar a], b_1, b_2)$ if we choose ![]() $\Psi (j,j+1)=\Psi (j+1,j)=1$ and
$\Psi (j,j+1)=\Psi (j+1,j)=1$ and ![]() $\Psi (j,l)=0$ in the case
$\Psi (j,l)=0$ in the case ![]() $|l-j|>1$. The term of degree
$|l-j|>1$. The term of degree ![]() $m+1$ is the Poisson bracket
$m+1$ is the Poisson bracket ![]() $\{{\mathcal {H}}[\bar b],F[\bar a]\}$. Here
$\{{\mathcal {H}}[\bar b],F[\bar a]\}$. Here ![]() $r=0$ and
$r=0$ and ![]() $\bar \gamma =0$. In degree
$\bar \gamma =0$. In degree ![]() $m-1$, we obtain images in
$m-1$, we obtain images in ![]() ${{\mathcal {S}}}^{m-1}({{\hat {\mathfrak g}}}^-)$ of the weighted symmetrisations described in part (i). Further terms, which are of degrees
${{\mathcal {S}}}^{m-1}({{\hat {\mathfrak g}}}^-)$ of the weighted symmetrisations described in part (i). Further terms, which are of degrees ![]() $m-3,m-5,m-7$, and so on, are described by the iterated application of part (ii). At all steps, we obtain combinatorially defined rational coefficients, which are independent of
$m-3,m-5,m-7$, and so on, are described by the iterated application of part (ii). At all steps, we obtain combinatorially defined rational coefficients, which are independent of ![]() $F$.
$F$.
Example 3.7 Suppose that ![]() $F\in {{\mathcal {S}}}^{4}(\mathfrak g)^{\mathfrak g}$ and that
$F\in {{\mathcal {S}}}^{4}(\mathfrak g)^{\mathfrak g}$ and that ![]() $\mathfrak g$ is simple. Here we have
$\mathfrak g$ is simple. Here we have ![]() ${\sf m}(F)\in (\Lambda ^{2}\mathfrak g \otimes \mathfrak g)^{\mathfrak g}$ and
${\sf m}(F)\in (\Lambda ^{2}\mathfrak g \otimes \mathfrak g)^{\mathfrak g}$ and ![]() $\dim (\Lambda ^{2}\mathfrak g \otimes \mathfrak g)^{\mathfrak g}=1$. This subspace is spanned by
$\dim (\Lambda ^{2}\mathfrak g \otimes \mathfrak g)^{\mathfrak g}=1$. This subspace is spanned by ![]() ${\mathcal {H}}=\sum x_i^{2}$. Hence
${\mathcal {H}}=\sum x_i^{2}$. Hence ![]() ${\sf m}(F)={\mathcal {H}}$ up to a scalar. As we will proof in § 3.3,
${\sf m}(F)={\mathcal {H}}$ up to a scalar. As we will proof in § 3.3, ![]() $S=\varpi (F[-1])+6\varpi (\tau ^{2}{\sf m}(F)[-1]){\cdot }1$ is a Segal–Sugawara vector. Making use of the fact that
$S=\varpi (F[-1])+6\varpi (\tau ^{2}{\sf m}(F)[-1]){\cdot }1$ is a Segal–Sugawara vector. Making use of the fact that ![]() $\tau ^{2}({\mathcal {H}}[-1])\in \mathfrak z({{\hat {\mathfrak g}}})$, one can write
$\tau ^{2}({\mathcal {H}}[-1])\in \mathfrak z({{\hat {\mathfrak g}}})$, one can write ![]() $S$ as a sum
$S$ as a sum ![]() $\varpi (F[-1])+B{\mathcal {H}}[-2]$ for some scalar
$\varpi (F[-1])+B{\mathcal {H}}[-2]$ for some scalar ![]() $B\in \mathbb {{\mathbb {C}}}$.
$B\in \mathbb {{\mathbb {C}}}$.
The only possible vector ![]() $\bar \gamma$ that can appear in Proposition 3.6(iii) is
$\bar \gamma$ that can appear in Proposition 3.6(iii) is ![]() $(-1,-1)$. Therefore the commutator
$(-1,-1)$. Therefore the commutator ![]() $[{\mathcal {H}}[-1],\varpi (F[-1])]$ is equal to
$[{\mathcal {H}}[-1],\varpi (F[-1])]$ is equal to ![]() $B\varpi (\{{\mathcal {H}}[-2],{\mathcal {H}}[-1]\})=B[{\mathcal {H}}[-2],{\mathcal {H}}[-1]]$. In the orthonormal basis
$B\varpi (\{{\mathcal {H}}[-2],{\mathcal {H}}[-1]\})=B[{\mathcal {H}}[-2],{\mathcal {H}}[-1]]$. In the orthonormal basis ![]() $\{x_i\}$, we have
$\{x_i\}$, we have
3.3 Poisson (half-)brackets
Suppose that ![]() $\hat Y=\hat y_1\ldots \hat y_m\in {{\mathcal {S}}}^{m}({{\hat {\mathfrak g}}}^-)$ and
$\hat Y=\hat y_1\ldots \hat y_m\in {{\mathcal {S}}}^{m}({{\hat {\mathfrak g}}}^-)$ and ![]() $\hat y_j=y_j[a_j]$. Then
$\hat y_j=y_j[a_j]$. Then ![]() $P_{\hat Y}:= \{ {\mathcal {H}}[\bar b], \hat Y\} =P_{\hat Y}(b_1,b_2)+P_{\hat Y}(b_2,b_1)$, where
$P_{\hat Y}:= \{ {\mathcal {H}}[\bar b], \hat Y\} =P_{\hat Y}(b_1,b_2)+P_{\hat Y}(b_2,b_1)$, where
 \[ P_{\hat Y}(b_\upsilon,b_\nu)= \sum_{j=1,i=1}^{j=m,i=\dim\mathfrak g} [x_i[b_\nu],\hat y_j] x_i[b_\upsilon] \hat Y/\hat y_j = \sum_{j,i,u} ([x_u,x_i],y_j) x_u[b_\nu+a_j] x_i[b_\upsilon] \hat Y/\hat y_j. \]
\[ P_{\hat Y}(b_\upsilon,b_\nu)= \sum_{j=1,i=1}^{j=m,i=\dim\mathfrak g} [x_i[b_\nu],\hat y_j] x_i[b_\upsilon] \hat Y/\hat y_j = \sum_{j,i,u} ([x_u,x_i],y_j) x_u[b_\nu+a_j] x_i[b_\upsilon] \hat Y/\hat y_j. \]
Note that in the case ![]() $b_\nu +a_j=b_\upsilon$, each summand
$b_\nu +a_j=b_\upsilon$, each summand ![]() $([x_u,x_i],y_j) x_u[b_\nu +a_j] x_i[b_\upsilon ] \hat Y/\hat y_j$ is annihilated by
$([x_u,x_i],y_j) x_u[b_\nu +a_j] x_i[b_\upsilon ] \hat Y/\hat y_j$ is annihilated by ![]() $([x_i,x_u],y_j) x_i[b_\nu +a_j] x_u[b_\upsilon ] \hat Y/\hat y_j$. Hence
$([x_i,x_u],y_j) x_i[b_\nu +a_j] x_u[b_\upsilon ] \hat Y/\hat y_j$. Hence
The product ![]() $(\,\,,\,)$ extends to a non-degenerate
$(\,\,,\,)$ extends to a non-degenerate ![]() $\mathfrak g$-invariant scalar product on
$\mathfrak g$-invariant scalar product on ![]() ${{\mathcal {S}}}({{\hat {\mathfrak g}}}^-)$. We will assume that
${{\mathcal {S}}}({{\hat {\mathfrak g}}}^-)$. We will assume that ![]() $(\mathfrak g[a],\mathfrak g[d])=0$ for
$(\mathfrak g[a],\mathfrak g[d])=0$ for ![]() $a\ne d$, that
$a\ne d$, that ![]() $(x[a],y[a])=(x,y)$ for
$(x[a],y[a])=(x,y)$ for ![]() $x,y\in \mathfrak g$, and that
$x,y\in \mathfrak g$, and that
if ![]() $\xi _j,\eta _j\in {{\mathcal {S}}}({{\hat {\mathfrak g}}}^-)$,
$\xi _j,\eta _j\in {{\mathcal {S}}}({{\hat {\mathfrak g}}}^-)$, ![]() ${\boldsymbol m}\geqslant {\boldsymbol k}$. Let
${\boldsymbol m}\geqslant {\boldsymbol k}$. Let ![]() ${\mathcal {B}}$ be a monomial basis of
${\mathcal {B}}$ be a monomial basis of ![]() ${{\mathcal {S}}}({{\hat {\mathfrak g}}}^-)$ consisting of the elements
${{\mathcal {S}}}({{\hat {\mathfrak g}}}^-)$ consisting of the elements ![]() $\hat v_1\ldots \hat v_{\boldsymbol k}$, where
$\hat v_1\ldots \hat v_{\boldsymbol k}$, where ![]() $\hat v_j=v_j[d_j]$ and
$\hat v_j=v_j[d_j]$ and ![]() $v_j\in \{x_i\}$. Then
$v_j\in \{x_i\}$. Then ![]() ${\mathcal {B}}$ is an orthogonal, but not an orthonormal basis. For instance, if
${\mathcal {B}}$ is an orthogonal, but not an orthonormal basis. For instance, if ![]() $\Xi =x_1^{\gamma _1} \ldots x_{\boldsymbol k}^{\gamma _{\boldsymbol k}}$ with
$\Xi =x_1^{\gamma _1} \ldots x_{\boldsymbol k}^{\gamma _{\boldsymbol k}}$ with ![]() $\boldsymbol k\leqslant \dim \mathfrak g$, then
$\boldsymbol k\leqslant \dim \mathfrak g$, then ![]() $(\Xi,\Xi )=\gamma _1!\ldots \gamma _{\boldsymbol k}!$.
$(\Xi,\Xi )=\gamma _1!\ldots \gamma _{\boldsymbol k}!$.
Set ![]() $M:=m+1$,
$M:=m+1$, ![]() ${\mathcal {B}}(M):={\mathcal {B}}\cap {{\mathcal {S}}}^{M}({{\hat {\mathfrak g}}}^-)$, and write
${\mathcal {B}}(M):={\mathcal {B}}\cap {{\mathcal {S}}}^{M}({{\hat {\mathfrak g}}}^-)$, and write
expressing each ![]() $\hat Y/\hat y_j$ in the basis
$\hat Y/\hat y_j$ in the basis ![]() ${\mathcal {B}}$.
${\mathcal {B}}$.
Lemma 3.8 If ![]() $A(\mathbb {V})\ne 0$ and
$A(\mathbb {V})\ne 0$ and ![]() $\mathbb {V}=\hat v_1\ldots \hat v_M$, then
$\mathbb {V}=\hat v_1\ldots \hat v_M$, then ![]() ${\boldsymbol p}:=\{ p \mid d_p=b_1\}\ne \varnothing$. Furthermore,
${\boldsymbol p}:=\{ p \mid d_p=b_1\}\ne \varnothing$. Furthermore,
 \begin{equation} A(\mathbb{V}) = \sum_{p\in{\boldsymbol p}, l\not\in{\boldsymbol p}} (\mathbb{V},\mathbb{V})^{-1} \bigg(\hat Y, \frac{\mathbb{V}}{\hat v_l\hat v_p} [v_l,v_p][d_l-b_2]\bigg). \end{equation}
\begin{equation} A(\mathbb{V}) = \sum_{p\in{\boldsymbol p}, l\not\in{\boldsymbol p}} (\mathbb{V},\mathbb{V})^{-1} \bigg(\hat Y, \frac{\mathbb{V}}{\hat v_l\hat v_p} [v_l,v_p][d_l-b_2]\bigg). \end{equation}Proof. The first statement is clear, cf. (3.8). It remains to calculate the coefficient of ![]() $\mathbb {V}$ in
$\mathbb {V}$ in ![]() $P_{\hat Y}(b_1,b_2)$. Pick a pair
$P_{\hat Y}(b_1,b_2)$. Pick a pair ![]() $(p,l)$ with
$(p,l)$ with ![]() $p\in {\boldsymbol p}$ and
$p\in {\boldsymbol p}$ and ![]() $l\not \in {\boldsymbol p}$. If we take into account only those summands of
$l\not \in {\boldsymbol p}$. If we take into account only those summands of ![]() $P_{\hat Y}(b_1,b_2)$, where
$P_{\hat Y}(b_1,b_2)$, where ![]() $\mathbb {V}^{p,l}=\mathbb {V}/(\hat v_p\hat v_l)$ is a summand of
$\mathbb {V}^{p,l}=\mathbb {V}/(\hat v_p\hat v_l)$ is a summand of ![]() $\hat Y/\hat y_j$ for some
$\hat Y/\hat y_j$ for some ![]() $j$, the factor
$j$, the factor ![]() $\hat v_l$ is
$\hat v_l$ is ![]() $x_u[a_j+b_2]$, and
$x_u[a_j+b_2]$, and ![]() $\hat v_p$ appears as
$\hat v_p$ appears as ![]() $x_i[b_1]$, then the coefficient is
$x_i[b_1]$, then the coefficient is
 \[ \sum_{j=1}^{m} (\hat y_j,[v_l,v_p][d_l-b_2]) (\hat Y/\hat y_j, \mathbb{V}^{p,l}) (\mathbb{V}^{p,l},\mathbb{V}^{p,l})^{-1} = (\mathbb{V}^{p,l},\mathbb{V}^{p,l})^{-1} (\hat Y, \mathbb{V}^{p,l} [v_l,v_p][d_l-b_2]). \]
\[ \sum_{j=1}^{m} (\hat y_j,[v_l,v_p][d_l-b_2]) (\hat Y/\hat y_j, \mathbb{V}^{p,l}) (\mathbb{V}^{p,l},\mathbb{V}^{p,l})^{-1} = (\mathbb{V}^{p,l},\mathbb{V}^{p,l})^{-1} (\hat Y, \mathbb{V}^{p,l} [v_l,v_p][d_l-b_2]). \]
If one adds these expressions over the pairs ![]() $(p,l)$, then certain instances may be counted more than once. If
$(p,l)$, then certain instances may be counted more than once. If ![]() $\hat v_p=\hat v_{p'}$ for some
$\hat v_p=\hat v_{p'}$ for some ![]() $p'\ne p$ or
$p'\ne p$ or ![]() $\hat v_l=\hat v_{l'}$ for some
$\hat v_l=\hat v_{l'}$ for some ![]() $l'\ne l$, then
$l'\ne l$, then ![]() $(p,l')$ or
$(p,l')$ or ![]() $(p',l)$ has to be omitted from the summation. In other words, it is necessary to divide the contribution of
$(p',l)$ has to be omitted from the summation. In other words, it is necessary to divide the contribution of ![]() $(p,l)$ by the multiplicities
$(p,l)$ by the multiplicities ![]() $\gamma _p$ and
$\gamma _p$ and ![]() $\gamma _l$ of
$\gamma _l$ of ![]() $v_p[d_p]$,
$v_p[d_p]$, ![]() $v_l[d_l]$ in
$v_l[d_l]$ in ![]() $\mathbb {V}$. Since
$\mathbb {V}$. Since ![]() $(\mathbb {V},\mathbb {V})=\gamma _p\gamma _l (\mathbb {V}^{p,l},\mathbb {V}^{p,l})$, the result follows.
$(\mathbb {V},\mathbb {V})=\gamma _p\gamma _l (\mathbb {V}^{p,l},\mathbb {V}^{p,l})$, the result follows.
The Poisson bracket ![]() $P_{\hat Y}$ is not multi-homogeneous with respect to
$P_{\hat Y}$ is not multi-homogeneous with respect to ![]() ${{\hat {\mathfrak g}}}^-=\bigoplus _{d\leqslant -1} \mathfrak g[d]$. If
${{\hat {\mathfrak g}}}^-=\bigoplus _{d\leqslant -1} \mathfrak g[d]$. If ![]() $b_1\ne b_2$, then in general the ‘halves’ of
$b_1\ne b_2$, then in general the ‘halves’ of ![]() $P_{\hat Y}$ have different multi-degrees and neither of them has to be multi-homogeneous. We need to split
$P_{\hat Y}$ have different multi-degrees and neither of them has to be multi-homogeneous. We need to split ![]() $P_{\hat Y}(b_1,b_2)$ into smaller pieces. For
$P_{\hat Y}(b_1,b_2)$ into smaller pieces. For ![]() $\bar a\in {{\mathbb {Z}}}_{<0}^{m}$, set
$\bar a\in {{\mathbb {Z}}}_{<0}^{m}$, set ![]() ${{\mathcal {S}}}^{\bar a}({{\hat {\mathfrak g}}}^-)=\prod _{j=1}^{m} \mathfrak g[a_j]\subset {{\mathcal {S}}}({{\hat {\mathfrak g}}}^-)$.
${{\mathcal {S}}}^{\bar a}({{\hat {\mathfrak g}}}^-)=\prod _{j=1}^{m} \mathfrak g[a_j]\subset {{\mathcal {S}}}({{\hat {\mathfrak g}}}^-)$.
Let ![]() $\bar \alpha =\{\alpha _1^{r_1},\ldots,\alpha _s^{r_s}\}$ be a multi-set such that
$\bar \alpha =\{\alpha _1^{r_1},\ldots,\alpha _s^{r_s}\}$ be a multi-set such that ![]() $\alpha _i\ne \alpha _j$ for
$\alpha _i\ne \alpha _j$ for ![]() $i\ne j$,
$i\ne j$, ![]() $\alpha _j\in {{\mathbb {Z}}}_{<0}$ for all
$\alpha _j\in {{\mathbb {Z}}}_{<0}$ for all ![]() $1\leqslant j\leqslant s$,
$1\leqslant j\leqslant s$, ![]() $\sum _{j=1}^{s} r_j=M$, and
$\sum _{j=1}^{s} r_j=M$, and ![]() $r_j>0$ for all
$r_j>0$ for all ![]() $j$. Set
$j$. Set ![]() ${{\mathcal {S}}}^{\bar \alpha }({{\hat {\mathfrak g}}}^-):=\prod _{j=1}^{s} {{\mathcal {S}}}^{r_j}(\mathfrak g[\alpha _j])$,
${{\mathcal {S}}}^{\bar \alpha }({{\hat {\mathfrak g}}}^-):=\prod _{j=1}^{s} {{\mathcal {S}}}^{r_j}(\mathfrak g[\alpha _j])$, ![]() ${\mathcal {B}}(\bar \alpha ):={\mathcal {B}}\cap {{\mathcal {S}}}^{\bar \alpha }({{\hat {\mathfrak g}}}^-)$. Fix different
${\mathcal {B}}(\bar \alpha ):={\mathcal {B}}\cap {{\mathcal {S}}}^{\bar \alpha }({{\hat {\mathfrak g}}}^-)$. Fix different ![]() $i,j\in \{1,\ldots,s\}$. Assume that a monomial
$i,j\in \{1,\ldots,s\}$. Assume that a monomial ![]() $\mathbb {V}=\hat v_1\ldots \hat v_M\in {\mathcal {B}}(\bar \alpha )$ with
$\mathbb {V}=\hat v_1\ldots \hat v_M\in {\mathcal {B}}(\bar \alpha )$ with ![]() $\hat v_l=v_l[d_l]$ is written in such a way that
$\hat v_l=v_l[d_l]$ is written in such a way that ![]() $d_l=\alpha _i$ for
$d_l=\alpha _i$ for ![]() $1\leqslant l\leqslant r_i$ and
$1\leqslant l\leqslant r_i$ and ![]() $d_l=\alpha _j$ for
$d_l=\alpha _j$ for ![]() $r_i< l\leqslant r_i+r_j$. Finally suppose that
$r_i< l\leqslant r_i+r_j$. Finally suppose that ![]() $F\in {{\mathcal {S}}}^{m}(\mathfrak g)$. In this notation, set
$F\in {{\mathcal {S}}}^{m}(\mathfrak g)$. In this notation, set
 \begin{gather} \mathbb{W}[F, \bar\alpha, (i,j)] :=\sum_{{\mathbb{V}}\in{\mathcal{B}}(\bar\alpha)} A(\mathbb{V}) \mathbb{V}\quad \text{with} \nonumber\\ A(\hat v_1\ldots \hat v_M)= (\mathbb{V},\mathbb{V})^{-1} \sum_{\substack{1\leqslant l\leqslant r_i, \nonumber\\ r_i< p \leqslant r_i+r_j}} \bigg(F,[v_l,v_p] \prod_{u\ne p,l} v_u\bigg). \end{gather}
\begin{gather} \mathbb{W}[F, \bar\alpha, (i,j)] :=\sum_{{\mathbb{V}}\in{\mathcal{B}}(\bar\alpha)} A(\mathbb{V}) \mathbb{V}\quad \text{with} \nonumber\\ A(\hat v_1\ldots \hat v_M)= (\mathbb{V},\mathbb{V})^{-1} \sum_{\substack{1\leqslant l\leqslant r_i, \nonumber\\ r_i< p \leqslant r_i+r_j}} \bigg(F,[v_l,v_p] \prod_{u\ne p,l} v_u\bigg). \end{gather}
Clearly, ![]() $\mathbb {W}[F, \bar \alpha, (j,i)] = - \mathbb {W}[F, \bar \alpha, (i,j)]$.
$\mathbb {W}[F, \bar \alpha, (j,i)] = - \mathbb {W}[F, \bar \alpha, (i,j)]$.
Proposition 3.9 Let ![]() $F\in {{\mathcal {S}}}^{m}(\mathfrak g)^{\mathfrak g}$ be fixed. Then the elements
$F\in {{\mathcal {S}}}^{m}(\mathfrak g)^{\mathfrak g}$ be fixed. Then the elements ![]() $\mathbb {W}[\bar \alpha, (i,j)]=\mathbb {W}[F,\bar \alpha, (i,j)]$ satisfy the following ‘universal’ relations:
$\mathbb {W}[\bar \alpha, (i,j)]=\mathbb {W}[F,\bar \alpha, (i,j)]$ satisfy the following ‘universal’ relations:
These relations are independent of ![]() $F$.
$F$.
Proof. Follow the notation of (3.10). Note that for each ![]() $1\leqslant l \leqslant r_i$,
$1\leqslant l \leqslant r_i$,
 \[ \bigg(F, \sum_{w:\, w\ne l} [v_l,v_w] \prod_{u:\, u\ne l,w} v_u\bigg) =\bigg(\{F,v_l\}, \prod_{w:\, w\ne l} v_w\bigg)=0. \]
\[ \bigg(F, \sum_{w:\, w\ne l} [v_l,v_w] \prod_{u:\, u\ne l,w} v_u\bigg) =\bigg(\{F,v_l\}, \prod_{w:\, w\ne l} v_w\bigg)=0. \]
Of course, here we are adding also over the pairs ![]() $(l,w)$ with
$(l,w)$ with ![]() $\hat v_w\in \mathfrak g[\alpha _i]$ if
$\hat v_w\in \mathfrak g[\alpha _i]$ if ![]() $r_i>1$. However,
$r_i>1$. However, ![]() $[v_l,v_w]=-[v_w,v_l]$ and hence the coefficient of
$[v_l,v_w]=-[v_w,v_l]$ and hence the coefficient of ![]() $\mathbb {V}$ in
$\mathbb {V}$ in ![]() $\sum _{j\ne i} \mathbb {W}[\bar \alpha, (i,j)]$ is equal to
$\sum _{j\ne i} \mathbb {W}[\bar \alpha, (i,j)]$ is equal to
 \[ (\mathbb{V},\mathbb{V})^{-1} \sum_{1\leqslant l \leqslant r_i} \bigg(F, \sum_{w:\, w\ne l} [v_l,v_w] \prod_{u:\, u\ne l,w} v_u\bigg) = \sum_{1\leqslant l \leqslant r_i} 0 =0. \]
\[ (\mathbb{V},\mathbb{V})^{-1} \sum_{1\leqslant l \leqslant r_i} \bigg(F, \sum_{w:\, w\ne l} [v_l,v_w] \prod_{u:\, u\ne l,w} v_u\bigg) = \sum_{1\leqslant l \leqslant r_i} 0 =0. \]This completes the proof.
Proposition 3.10 For ![]() $Y[\bar a]$ with
$Y[\bar a]$ with ![]() $Y=y_1{\ldots } y_m\in {{\mathcal {S}}}^{m}(\mathfrak g)$ and
$Y=y_1{\ldots } y_m\in {{\mathcal {S}}}^{m}(\mathfrak g)$ and ![]() $\bar a\in \mathbb {Z}_{<0}^{m}$ (see § 1.5 for the notation), the rescaled Poisson half-bracket
$\bar a\in \mathbb {Z}_{<0}^{m}$ (see § 1.5 for the notation), the rescaled Poisson half-bracket
is equal to the sum of ![]() $\mathbb {W}[Y, \bar \alpha, (i,j)]$ with
$\mathbb {W}[Y, \bar \alpha, (i,j)]$ with ![]() $i< j$ over all multi-sets
$i< j$ over all multi-sets ![]() $\bar \alpha$ as above such that the multi-set
$\bar \alpha$ as above such that the multi-set ![]() $\{a_1,\ldots,a_m\}$ of entries of
$\{a_1,\ldots,a_m\}$ of entries of ![]() $\bar a$ can be obtained from
$\bar a$ can be obtained from ![]() $\bar \alpha$ by removing one
$\bar \alpha$ by removing one ![]() $\alpha _j=b_1$ and replacing one
$\alpha _j=b_1$ and replacing one ![]() $\alpha _i$ with
$\alpha _i$ with ![]() $\alpha _i-b_2$.
$\alpha _i-b_2$.
Proof. For each multi-homogeneous component of ![]() ${\boldsymbol P}[\bar a]$, the multi-set of
${\boldsymbol P}[\bar a]$, the multi-set of ![]() $t$-degrees is obtained from the entries of
$t$-degrees is obtained from the entries of ![]() $\bar a$ by appending
$\bar a$ by appending ![]() $b_1$ and replacing one
$b_1$ and replacing one ![]() $a_l$ with
$a_l$ with ![]() $a_l+b_2$. Moreover, here
$a_l+b_2$. Moreover, here ![]() $b_1\ne a_l+b_2$, cf. (3.8). This explains the restrictions on
$b_1\ne a_l+b_2$, cf. (3.8). This explains the restrictions on ![]() $\bar \alpha$.
$\bar \alpha$.
For ![]() $\bar \alpha$ and
$\bar \alpha$ and ![]() $(i,j)$ satisfying the assumptions of the proposition, we have to compare the coefficients
$(i,j)$ satisfying the assumptions of the proposition, we have to compare the coefficients ![]() $A(\mathbb {V})$ of
$A(\mathbb {V})$ of ![]() $\mathbb {V}\in {\mathcal {B}}(\bar \alpha )$ given by (3.10) and (3.9). The key point here is the observation that
$\mathbb {V}\in {\mathcal {B}}(\bar \alpha )$ given by (3.10) and (3.9). The key point here is the observation that ![]() $(Y[\bar a], \mathbb {V})=|{\tt S}_m \bar a|^{-1} (Y,v_1\ldots v_m)$ for any
$(Y[\bar a], \mathbb {V})=|{\tt S}_m \bar a|^{-1} (Y,v_1\ldots v_m)$ for any ![]() $\mathbb {V}=\hat v_1\ldots \hat v_m \in {\mathcal {B}}\cap {{\mathcal {S}}}^{\bar a}({{\hat {\mathfrak g}}}^-)$.
$\mathbb {V}=\hat v_1\ldots \hat v_m \in {\mathcal {B}}\cap {{\mathcal {S}}}^{\bar a}({{\hat {\mathfrak g}}}^-)$.
In a more relevant setup, suppose that a summand ![]() $(y_{\sigma (1)}, [v_l,v_p]) \prod _{w\ne 1,u\ne l,p} (y_{\sigma (w)},v_u)$ of the scalar product on the right hand side of (3.10) is non-zero for some
$(y_{\sigma (1)}, [v_l,v_p]) \prod _{w\ne 1,u\ne l,p} (y_{\sigma (w)},v_u)$ of the scalar product on the right hand side of (3.10) is non-zero for some ![]() $\sigma \in {\tt S}_m$ and some
$\sigma \in {\tt S}_m$ and some ![]() $l,p$. Then there is exactly one choice, prescribed by
$l,p$. Then there is exactly one choice, prescribed by ![]() $(d_1,\ldots,d_M)$, of the
$(d_1,\ldots,d_M)$, of the ![]() $t$-degrees for a monomial of
$t$-degrees for a monomial of ![]() $Y[\bar a]$ such that the corresponding summand
$Y[\bar a]$ such that the corresponding summand
of the scalar product on the right hand side of (3.9) is non-zero as well. By our assumptions on the scalar product, these summands are equal.
Theorem 3.11 Suppose that ![]() ${\sf m}_{2r+1}(H)$ with
${\sf m}_{2r+1}(H)$ with ![]() $H\in {{\mathcal {S}}}^{k}(\mathfrak g)^{\mathfrak g}$ is a symmetric invariant for each
$H\in {{\mathcal {S}}}^{k}(\mathfrak g)^{\mathfrak g}$ is a symmetric invariant for each ![]() $r\geqslant 1$. Then (2.4) provides a Segal–Sugawara vector
$r\geqslant 1$. Then (2.4) provides a Segal–Sugawara vector ![]() $S$ associated with
$S$ associated with ![]() $H$.
$H$.
Proof. Since ![]() ${\sf m}_{2l+1}(H)\in {{\mathcal {S}}}(\mathfrak g)$ for any
${\sf m}_{2l+1}(H)\in {{\mathcal {S}}}(\mathfrak g)$ for any ![]() $l$, we can say that
$l$, we can say that ![]() ${\sf m}_{2r+1}(H)={\sf m}^{r}(H)$, cf. (1.1). By Lemma 2.2, each
${\sf m}_{2r+1}(H)={\sf m}^{r}(H)$, cf. (1.1). By Lemma 2.2, each ![]() $\varpi (\tau ^{2r}{\sf m}^{r}(H)[-1]){\cdot }1$ is a fully symmetrised element. It can be written as a sum of
$\varpi (\tau ^{2r}{\sf m}^{r}(H)[-1]){\cdot }1$ is a fully symmetrised element. It can be written as a sum of ![]() $\tilde c(r,\bar a)\varpi ({\sf m}^{r}(H)[\bar a])$, where
$\tilde c(r,\bar a)\varpi ({\sf m}^{r}(H)[\bar a])$, where ![]() $\bar a\in {{\mathbb {Z}}}_{<0}^{k-2r}$ and the coefficients
$\bar a\in {{\mathbb {Z}}}_{<0}^{k-2r}$ and the coefficients ![]() $\tilde c(r,\bar a)\in \mathbb {Q}$ depend only on
$\tilde c(r,\bar a)\in \mathbb {Q}$ depend only on ![]() $k$,
$k$, ![]() $r$, and
$r$, and ![]() $\bar a$. The coefficients of (2.4) depend only on
$\bar a$. The coefficients of (2.4) depend only on ![]() $k$ and
$k$ and ![]() $r$. Combining this observation with Propositions 3.6(iii) and 3.10, we obtain that
$r$. Combining this observation with Propositions 3.6(iii) and 3.10, we obtain that
where again the coefficients ![]() $C(r,\bar \alpha,i,j)\in \mathbb {Q}$ do not depend on
$C(r,\bar \alpha,i,j)\in \mathbb {Q}$ do not depend on ![]() $H$. For a given degree
$H$. For a given degree ![]() $k$, one obtains a bunch of
$k$, one obtains a bunch of ![]() $(r,\bar \alpha )$, which depends only on
$(r,\bar \alpha )$, which depends only on ![]() $k$, and each appearing coefficient depends on
$k$, and each appearing coefficient depends on ![]() $k$,
$k$, ![]() $r$,
$r$, ![]() $\bar \alpha$, and
$\bar \alpha$, and ![]() $(i,j)$. In type
$(i,j)$. In type ![]() $\mathsf{A}$, for each
$\mathsf{A}$, for each ![]() $k\geqslant 2$, we find the invariant
$k\geqslant 2$, we find the invariant ![]() $\tilde \Delta _k$ such that the corresponding commutator
$\tilde \Delta _k$ such that the corresponding commutator ![]() $[{\mathcal {H}}[-1],\tilde S_{k-1}]$ vanishes, cf. (2.4).
$[{\mathcal {H}}[-1],\tilde S_{k-1}]$ vanishes, cf. (2.4).
For each ![]() $F\in {{\mathcal {S}}}^{m}(\mathfrak g)^{\mathfrak g}$, the elements
$F\in {{\mathcal {S}}}^{m}(\mathfrak g)^{\mathfrak g}$, the elements ![]() $\mathbb {W}[F,\bar \alpha, (i,j)]$ are linearly dependent. They satisfy the ‘universal’ relations, see Proposition 3.9. At the same time, for
$\mathbb {W}[F,\bar \alpha, (i,j)]$ are linearly dependent. They satisfy the ‘universal’ relations, see Proposition 3.9. At the same time, for ![]() $m=k-2r$, the coefficients
$m=k-2r$, the coefficients ![]() $C(r,\bar \alpha,i,j)$ provide a relation among
$C(r,\bar \alpha,i,j)$ provide a relation among ![]() $\mathbb {W}[\tilde \Delta _m,\bar \alpha, (i,j)]$. Our goal is to prove that this relation holds for
$\mathbb {W}[\tilde \Delta _m,\bar \alpha, (i,j)]$. Our goal is to prove that this relation holds for ![]() $\mathbb {W}[{\sf m}^{r}(H),\bar \alpha, (i,j)]$ as well. To this end, it suffices to show that the terms
$\mathbb {W}[{\sf m}^{r}(H),\bar \alpha, (i,j)]$ as well. To this end, it suffices to show that the terms ![]() $\mathbb {W}[\tilde \Delta _m,\bar \alpha, (i,j)]=\mathbb {W}[(i,j)]$ with fixed
$\mathbb {W}[\tilde \Delta _m,\bar \alpha, (i,j)]=\mathbb {W}[(i,j)]$ with fixed ![]() $m$ and fixed
$m$ and fixed ![]() $\bar \alpha$ do not satisfy any other linear relation, not spanned by the ‘universal’ ones.
$\bar \alpha$ do not satisfy any other linear relation, not spanned by the ‘universal’ ones.
We consider the complete simple graph with ![]() $s$ vertices
$s$ vertices ![]() $1,\ldots,s$ and identify pairs
$1,\ldots,s$ and identify pairs ![]() $(i,j)$ with the corresponding (oriented) edges. Now one can say that a linear relation among the polynomials
$(i,j)$ with the corresponding (oriented) edges. Now one can say that a linear relation among the polynomials ![]() $\mathbb {W}[(i,j)]$ is given by its coefficients on the edges. Note that if
$\mathbb {W}[(i,j)]$ is given by its coefficients on the edges. Note that if ![]() $s=2$, then
$s=2$, then ![]() $\mathbb {W}[F,\bar \alpha,(1,2)]=0$ for each
$\mathbb {W}[F,\bar \alpha,(1,2)]=0$ for each ![]() $F\in {{\mathcal {S}}}^{m}(\mathfrak g)^{\mathfrak g}$, cf. Example 3.12(i) below. Therefore assume that
$F\in {{\mathcal {S}}}^{m}(\mathfrak g)^{\mathfrak g}$, cf. Example 3.12(i) below. Therefore assume that ![]() $s\geqslant 3$.
$s\geqslant 3$.
Suppose there is a relation and that the coefficient of ![]() $\mathbb {W}[(i,j)]$ is non-zero. We work in the basis
$\mathbb {W}[(i,j)]$ is non-zero. We work in the basis
Choose ![]() $\hat y_1=E_{12}[\alpha _i]$,
$\hat y_1=E_{12}[\alpha _i]$, ![]() $\hat y_2=E_{21}[\alpha _j]$ and let all other factors
$\hat y_2=E_{21}[\alpha _j]$ and let all other factors ![]() $\hat y_l$ with
$\hat y_l$ with ![]() $2< l \leqslant M$ be elements of
$2< l \leqslant M$ be elements of ![]() $t^{-1}\mathfrak h[t^{-1}]$. Assume that
$t^{-1}\mathfrak h[t^{-1}]$. Assume that ![]() $\hat y_3=(E_{11}- E_{22})[\alpha _p]$ with
$\hat y_3=(E_{11}- E_{22})[\alpha _p]$ with ![]() $p\ne i,j$ and that
$p\ne i,j$ and that ![]() $(E_{11}-E_{22},y_l)=0$ for all
$(E_{11}-E_{22},y_l)=0$ for all ![]() $l>3$. Then the monomial
$l>3$. Then the monomial ![]() $\hat y_1\ldots \hat y_M$ appears with a non-zero coefficient only in
$\hat y_1\ldots \hat y_M$ appears with a non-zero coefficient only in ![]() $\mathbb {W}[(i,j)]$,
$\mathbb {W}[(i,j)]$, ![]() $\mathbb {W}[(i,p)]$, and
$\mathbb {W}[(i,p)]$, and ![]() $\mathbb {W}[(p,j)]$. This means that in the triangle
$\mathbb {W}[(p,j)]$. This means that in the triangle ![]() $(i,j,p)$ at least one of the edges
$(i,j,p)$ at least one of the edges ![]() $(i,p)$ and
$(i,p)$ and ![]() $(j,p)$ has a non-zero coefficient as well.
$(j,p)$ has a non-zero coefficient as well.
We erase all edges with zero coefficients on them. Now the task is to modify the relation or, equivalently, the graph, by adding scalar multiplies of the universal relations in such a way that all edges disappear.
If a vertex ![]() $l$ is connected with
$l$ is connected with ![]() $j$, remove the edge
$j$, remove the edge ![]() $(j,l)$ using the universal relation ‘at
$(j,l)$ using the universal relation ‘at ![]() $l$’. In this way
$l$’. In this way ![]() $j$ becomes isolated. This means that there is no edge left.
$j$ becomes isolated. This means that there is no edge left.
Example 3.12 Keep the assumption ![]() $F\in {{\mathcal {S}}}^{m}(\mathfrak g)^{\mathfrak g}$.
$F\in {{\mathcal {S}}}^{m}(\mathfrak g)^{\mathfrak g}$.
(i) Suppose that
 $s=2$. Then
$s=2$. Then  $\mathbb {W}(F,\bar \alpha, (1,2))=0$ according to the universal relation. This provides a different proof of Lemma 3.1.
$\mathbb {W}(F,\bar \alpha, (1,2))=0$ according to the universal relation. This provides a different proof of Lemma 3.1.Also in the case of
 $\bar a=(-3,(-1)^{m-1})$, we have
$\bar a=(-3,(-1)^{m-1})$, we have  $\{{\mathcal {H}}[-1],F[\bar a]\}\in \mathfrak g[-3]\mathfrak g[-2] {{\mathcal {S}}}^{m-1}(\mathfrak g[-1])$.
$\{{\mathcal {H}}[-1],F[\bar a]\}\in \mathfrak g[-3]\mathfrak g[-2] {{\mathcal {S}}}^{m-1}(\mathfrak g[-1])$.(ii) Now suppose that
 $s=3$. Then
$s=3$. Then  $\mathbb {W}(F,\bar \alpha, (1,2))=-\mathbb {W}(F,\bar \alpha, (1,3))=\mathbb {W}(F,\bar \alpha, (2,3))$.
$\mathbb {W}(F,\bar \alpha, (1,2))=-\mathbb {W}(F,\bar \alpha, (1,3))=\mathbb {W}(F,\bar \alpha, (2,3))$.
4. Type C
There is a very suitable matrix realisation, where ![]() $\mathfrak {sp}_{2n}\subset \mathfrak {gl}_{2n}$ is the linear span of the elements
$\mathfrak {sp}_{2n}\subset \mathfrak {gl}_{2n}$ is the linear span of the elements ![]() $F_{ij}$ with
$F_{ij}$ with ![]() $i,j\in \{1,\ldots,2n\}$ such that
$i,j\in \{1,\ldots,2n\}$ such that
with ![]() $i'=2n-i+1$ and
$i'=2n-i+1$ and ![]() $\epsilon _i=1$ for
$\epsilon _i=1$ for ![]() $i\leqslant n$,
$i\leqslant n$, ![]() $\epsilon _i=-1$ for
$\epsilon _i=-1$ for ![]() $i> n$. Of course,
$i> n$. Of course, ![]() $F_{ij}\!=\!\pm F_{j'i'}$. Set
$F_{ij}\!=\!\pm F_{j'i'}$. Set
The symmetric decomposition ![]() $\mathfrak {gl}_{2n}=\mathfrak {sp}_{2n}\oplus \mathfrak p$ leads to explicit formulas for symmetric invariants of
$\mathfrak {gl}_{2n}=\mathfrak {sp}_{2n}\oplus \mathfrak p$ leads to explicit formulas for symmetric invariants of ![]() $\mathfrak {sp}_{2n}$. One writes
$\mathfrak {sp}_{2n}$. One writes ![]() $E_{ij}=\frac {1}{2}F_{ij}+ \frac {1}{2}(E_{i j}+\epsilon _i\,\epsilon _j\, E_{j' i'})$, expands the coefficients
$E_{ij}=\frac {1}{2}F_{ij}+ \frac {1}{2}(E_{i j}+\epsilon _i\,\epsilon _j\, E_{j' i'})$, expands the coefficients ![]() $\Delta _k$ of (1.2) accordingly, and then sets
$\Delta _k$ of (1.2) accordingly, and then sets ![]() $(E_{i j}+\epsilon _i\,\epsilon _j\, E_{j' i'})=0$. Up to the multiplication with
$(E_{i j}+\epsilon _i\,\epsilon _j\, E_{j' i'})=0$. Up to the multiplication with ![]() $2^{k}$, this is equivalent to replacing each
$2^{k}$, this is equivalent to replacing each ![]() $E_{ij}$ with
$E_{ij}$ with ![]() $F_{ij}$ in the formulas for
$F_{ij}$ in the formulas for ![]() $\Delta _{k}\in {{\mathcal {S}}}(\mathfrak {gl}_{2n})$. As is well known, the restriction of
$\Delta _{k}\in {{\mathcal {S}}}(\mathfrak {gl}_{2n})$. As is well known, the restriction of ![]() $\Delta _{2k+1}$ to
$\Delta _{2k+1}$ to ![]() $\mathfrak {sp}_{2n}$ is equal to zero for each
$\mathfrak {sp}_{2n}$ is equal to zero for each ![]() $k$.
$k$.
Until the end of this section, ![]() $\Delta _{2k}$ stands for the symmetric invariant of
$\Delta _{2k}$ stands for the symmetric invariant of ![]() $\mathfrak g=\mathfrak {sp}_{2n}$ that is equal to the sum of the principal
$\mathfrak g=\mathfrak {sp}_{2n}$ that is equal to the sum of the principal ![]() $(2k\times2k)$-minors of the matrix
$(2k\times2k)$-minors of the matrix ![]() $(F_{ij})$.
$(F_{ij})$.
Lemma 4.1 For each ![]() $k\geqslant 2$, we have
$k\geqslant 2$, we have ![]() ${\sf m}(\Delta _{2k})\in (\mathfrak g\otimes {{\mathcal {S}}}^{k-3}(\mathfrak g))^{\mathfrak g}$.
${\sf m}(\Delta _{2k})\in (\mathfrak g\otimes {{\mathcal {S}}}^{k-3}(\mathfrak g))^{\mathfrak g}$.
Proof. Note that ![]() $\Lambda ^{2} \mathfrak g=V(2\pi _1+\pi _2)\oplus \mathfrak g$. In the standard notation [Reference Vinberg and OniwikVO88, Ref. Chapter, § 2], we have
$\Lambda ^{2} \mathfrak g=V(2\pi _1+\pi _2)\oplus \mathfrak g$. In the standard notation [Reference Vinberg and OniwikVO88, Ref. Chapter, § 2], we have ![]() $2\pi _1+\pi _2=3\varepsilon _1+\varepsilon _2$. Assume that
$2\pi _1+\pi _2=3\varepsilon _1+\varepsilon _2$. Assume that ![]() $y_1y_2y_3$ is a factor of a summand of
$y_1y_2y_3$ is a factor of a summand of ![]() $\Delta _{2k}$ of weight
$\Delta _{2k}$ of weight ![]() $3\varepsilon _1+\varepsilon _2$ and
$3\varepsilon _1+\varepsilon _2$ and ![]() $y_s\in \{F_{i j}\}$ for each
$y_s\in \{F_{i j}\}$ for each ![]() $s$. Then:
$s$. Then:
• either
 $F_{1(2n)}\in \{y_1,y_2,y_3\}$ and some
$F_{1(2n)}\in \{y_1,y_2,y_3\}$ and some  $y_j\ne F_{1(2n)}$ lies in the first row or the last column;
$y_j\ne F_{1(2n)}$ lies in the first row or the last column;• or all three elements
 $y_s$ must lie in the union of the first row and the last column.
$y_s$ must lie in the union of the first row and the last column.
Each of the two possibilities contradicts the definition of ![]() $\Delta _{2k}$. Thus,
$\Delta _{2k}$. Thus, ![]() ${\sf m}(\Delta _k)\in (\mathfrak g \otimes {{\mathcal {S}}}^{2k-3}(\mathfrak g))^{\mathfrak g}$.
${\sf m}(\Delta _k)\in (\mathfrak g \otimes {{\mathcal {S}}}^{2k-3}(\mathfrak g))^{\mathfrak g}$.
Lemma 4.2 We have:
(i)
 ${\sf m}(\Delta _{6})= ({(n-2)(2n-3)}/{15})\Delta _4$; and
${\sf m}(\Delta _{6})= ({(n-2)(2n-3)}/{15})\Delta _4$; and(ii)
 ${\sf m}(\partial _{F_{11}}\Delta _4)= \frac {-1}{3} (2n-1)(2n-2) F_{11}$.
${\sf m}(\partial _{F_{11}}\Delta _4)= \frac {-1}{3} (2n-1)(2n-2) F_{11}$.
Proof. According to Lemma 4.1, ![]() ${\sf m}(\Delta _6)\in (\mathfrak g \otimes {{\mathcal {S}}}^{3}(\mathfrak g))^{\mathfrak g}$. Observe that
${\sf m}(\Delta _6)\in (\mathfrak g \otimes {{\mathcal {S}}}^{3}(\mathfrak g))^{\mathfrak g}$. Observe that ![]() ${{\mathcal {S}}}^{3}(\mathfrak g)$ contains exactly two linearly independent copies of
${{\mathcal {S}}}^{3}(\mathfrak g)$ contains exactly two linearly independent copies of ![]() $\mathfrak g$: one is equal to
$\mathfrak g$: one is equal to ![]() $\{\xi \Delta _2 \mid \xi \in \mathfrak {sp}_{2n}\}$, the other is primitive. Therefore
$\{\xi \Delta _2 \mid \xi \in \mathfrak {sp}_{2n}\}$, the other is primitive. Therefore
By the construction, ![]() $\Delta _2^{2}$ contains the summand
$\Delta _2^{2}$ contains the summand ![]() $F_{11}^{4}$. Since
$F_{11}^{4}$. Since ![]() $F_{1 1}^{3}$ cannot be a factor of a summand of
$F_{1 1}^{3}$ cannot be a factor of a summand of ![]() $\Delta _6$, we conclude that
$\Delta _6$, we conclude that ![]() ${\sf m}(\Delta _6)$ is proportional to
${\sf m}(\Delta _6)$ is proportional to ![]() $\Delta _4$.
$\Delta _4$.
Let ![]() $y\otimes F_{11}^{2} F_{22}$ be a summand of
$y\otimes F_{11}^{2} F_{22}$ be a summand of ![]() ${\sf m}(\Delta _6)$. Then
${\sf m}(\Delta _6)$. Then ![]() $y\in {{\mathbb {C}}}F_{22}$. Also
$y\in {{\mathbb {C}}}F_{22}$. Also ![]() $y= ({-3!3!}/{6!}){\sf m}(\partial _{F_{22}} \Delta _4^{[1]})$, where
$y= ({-3!3!}/{6!}){\sf m}(\partial _{F_{22}} \Delta _4^{[1]})$, where ![]() $\Delta _4^{[1]}\in {{\mathcal {S}}}^{4}(\mathfrak {sp}_{2n-2})$ stands for
$\Delta _4^{[1]}\in {{\mathcal {S}}}^{4}(\mathfrak {sp}_{2n-2})$ stands for ![]() $\Delta _4$ of
$\Delta _4$ of ![]() $\mathfrak {sp}_{2n-2}\subset \mathfrak g_{F_{11}}$. Next we compute
$\mathfrak {sp}_{2n-2}\subset \mathfrak g_{F_{11}}$. Next we compute ![]() $\eta ={\sf m}(\partial _{F_{22}} \Delta _4^{[1]})(F_{12})$. This will settle part (ii). So far we have shown that
$\eta ={\sf m}(\partial _{F_{22}} \Delta _4^{[1]})(F_{12})$. This will settle part (ii). So far we have shown that
and part (ii) describes this constant ![]() $c$, which is to be computed.
$c$, which is to be computed.
Recall that ![]() $F_{12}=- F_{(2n-1) 2n}$. The terms of
$F_{12}=- F_{(2n-1) 2n}$. The terms of ![]() $\Delta _4^{[1]}$ have neither
$\Delta _4^{[1]}$ have neither ![]() $1$ nor
$1$ nor ![]() $2n$ in the indices. Therefore a non-zero action on
$2n$ in the indices. Therefore a non-zero action on ![]() $F_{12}$ comes only from the following summands of
$F_{12}$ comes only from the following summands of ![]() $\Delta _4^{[1]}$:
$\Delta _4^{[1]}$:
One easily computes that
 \[ {\sf m}(F_{(2n-1) j} F_{js} F_{s (2n-1)})(F_{12})= \begin{cases} \frac{1}{6} F_{12} & \text{if } j\ne s', \\[6pt] \frac{1}{3} F_{12} & \text{if } j = s', \text{ because } F_{s' s}=2E_{s' s}, \end{cases} \]
\[ {\sf m}(F_{(2n-1) j} F_{js} F_{s (2n-1)})(F_{12})= \begin{cases} \frac{1}{6} F_{12} & \text{if } j\ne s', \\[6pt] \frac{1}{3} F_{12} & \text{if } j = s', \text{ because } F_{s' s}=2E_{s' s}, \end{cases} \]
and that ![]() ${\sf m}(F_{(2n-1) s} F_{s' s'} F_{s (2n-1)})(F_{12})= -\frac {1}{6}F_{12}$. There are
${\sf m}(F_{(2n-1) s} F_{s' s'} F_{s (2n-1)})(F_{12})= -\frac {1}{6}F_{12}$. There are ![]() $2n-4$ choices for
$2n-4$ choices for ![]() $s$ in line (4.3). If
$s$ in line (4.3). If ![]() $s$ is fixed, then there are
$s$ is fixed, then there are ![]() $2n-5$ possibilities for
$2n-5$ possibilities for ![]() $j$, since
$j$, since ![]() $j\ne s$, but the choice
$j\ne s$, but the choice ![]() $j=s'$ has to be counted twice. Applying the symmetry
$j=s'$ has to be counted twice. Applying the symmetry ![]() $F_{uv}=\pm F_{v'u'}$, we see that the terms in line (4.4) are the same as in (4.3). Now
$F_{uv}=\pm F_{v'u'}$, we see that the terms in line (4.4) are the same as in (4.3). Now
Hence ![]() $y= ({(n-2)(2n-3)}/{30})F_{22}$. Since
$y= ({(n-2)(2n-3)}/{30})F_{22}$. Since ![]() $({(n-2)(2n-3)}/{30}) F_{11}\otimes F_{11}F_{22}^{2}$ is also a summand of
$({(n-2)(2n-3)}/{30}) F_{11}\otimes F_{11}F_{22}^{2}$ is also a summand of ![]() ${\sf m}(\Delta _6)$, we obtain
${\sf m}(\Delta _6)$, we obtain ![]() ${\sf m}(\Delta _6)= ({(n-2)(2n-3)}/{15})\Delta _4$.
${\sf m}(\Delta _6)= ({(n-2)(2n-3)}/{15})\Delta _4$.
Proposition 4.3 We have
Proof. First we have to show that ![]() ${\sf m}(\Delta _{2k})\in {{\mathcal {S}}}^{2k-2}(\mathfrak g)$. By Lemma 4.1,
${\sf m}(\Delta _{2k})\in {{\mathcal {S}}}^{2k-2}(\mathfrak g)$. By Lemma 4.1, ![]() ${\sf m}(\Delta _{2k})$ is a
${\sf m}(\Delta _{2k})$ is a ![]() $G$-invariant polynomial function on
$G$-invariant polynomial function on ![]() $\mathfrak g\oplus \mathfrak g$. We use again the fact that
$\mathfrak g\oplus \mathfrak g$. We use again the fact that ![]() $G(\mathfrak g\oplus \mathfrak h)$ is dense in
$G(\mathfrak g\oplus \mathfrak h)$ is dense in ![]() $\mathfrak g\oplus \mathfrak g$.
$\mathfrak g\oplus \mathfrak g$.
Examine first the summands of ![]() $\Delta _{2k}$ that lie in
$\Delta _{2k}$ that lie in ![]() ${{\mathcal {S}}}^{3}(\mathfrak g){{\mathcal {S}}}^{2k-3}(\mathfrak h)$. Such a summand has the form
${{\mathcal {S}}}^{3}(\mathfrak g){{\mathcal {S}}}^{2k-3}(\mathfrak h)$. Such a summand has the form ![]() $y_1y_2y_3 (F_{i_1 i_1}\ldots F_{i_s i_s})^{2} F_{j_1 j_1}\ldots F_{j_u j_u}$. Here
$y_1y_2y_3 (F_{i_1 i_1}\ldots F_{i_s i_s})^{2} F_{j_1 j_1}\ldots F_{j_u j_u}$. Here ![]() $j_a\ne j_b,j_b'$ if
$j_a\ne j_b,j_b'$ if ![]() $a\ne b$ and the product
$a\ne b$ and the product ![]() $y_1y_2y_3$ is an element of weight zero lying in
$y_1y_2y_3$ is an element of weight zero lying in ![]() ${{\mathcal {S}}}^{3}(\mathfrak f)$, where
${{\mathcal {S}}}^{3}(\mathfrak f)$, where ![]() $\mathfrak f$ is a subalgebra of
$\mathfrak f$ is a subalgebra of ![]() $\mathfrak g$ isomorphic either to
$\mathfrak g$ isomorphic either to ![]() $\mathfrak {sp}_6$ or
$\mathfrak {sp}_6$ or ![]() $\mathfrak {sp}_4$. Furthermore, the numbers
$\mathfrak {sp}_4$. Furthermore, the numbers ![]() $i_b, i_b'$ with
$i_b, i_b'$ with ![]() $1\leqslant b\leqslant s$ do not appear among the indices of the elements of
$1\leqslant b\leqslant s$ do not appear among the indices of the elements of ![]() $\mathfrak f$ and at most three different numbers
$\mathfrak f$ and at most three different numbers ![]() $j_b$ with
$j_b$ with ![]() $1\leqslant b\leqslant u$ can appear among the indices of the elements of
$1\leqslant b\leqslant u$ can appear among the indices of the elements of ![]() $\mathfrak f$.
$\mathfrak f$.
If ![]() $u>3$, we can change at least one
$u>3$, we can change at least one ![]() $F_{j_b j_b}$ to
$F_{j_b j_b}$ to ![]() $F_{j_b' j_b'}=-F_{j_b j_b}$ without altering the other factors and produce a different summand of
$F_{j_b' j_b'}=-F_{j_b j_b}$ without altering the other factors and produce a different summand of ![]() $\Delta _{2k}$. These two expressions annihilate each other. Therefore
$\Delta _{2k}$. These two expressions annihilate each other. Therefore ![]() $u=3$ or
$u=3$ or ![]() $u=1$. Suppose
$u=1$. Suppose ![]() $u=3$ and that there is no way to annihilate the term via
$u=3$ and that there is no way to annihilate the term via ![]() $F_{j_b j_b}\mapsto F_{j_b' j_b'}$. Then
$F_{j_b j_b}\mapsto F_{j_b' j_b'}$. Then ![]() $\mathfrak f\cong \mathfrak {sp}_6$ and
$\mathfrak f\cong \mathfrak {sp}_6$ and ![]() $y_1y_2y_3 F_{j_1 j_1} F_{j_2 j_2} F_{j_3 j_3}$ is a summand of the determinant
$y_1y_2y_3 F_{j_1 j_1} F_{j_2 j_2} F_{j_3 j_3}$ is a summand of the determinant ![]() $\Delta _6^{(\mathfrak f)}\in {{\mathcal {S}}}^{6}(\mathfrak f)$. Since
$\Delta _6^{(\mathfrak f)}\in {{\mathcal {S}}}^{6}(\mathfrak f)$. Since ![]() ${\sf m}(\Delta _6)$ is proportional to
${\sf m}(\Delta _6)$ is proportional to ![]() $\Delta _4$ by Lemma 4.2 and
$\Delta _4$ by Lemma 4.2 and ![]() $F_{j_1 j_1} F_{j_2 j_2} F_{j_3 j_3}$ cannot appear in
$F_{j_1 j_1} F_{j_2 j_2} F_{j_3 j_3}$ cannot appear in ![]() $\Delta _4$, we conclude that terms
$\Delta _4$, we conclude that terms ![]() $y\otimes (F_{i_1 i_1}\ldots F_{i_s i_s})^{2} F_{j_1 j_1}\ldots F_{j_u j_u}$ with
$y\otimes (F_{i_1 i_1}\ldots F_{i_s i_s})^{2} F_{j_1 j_1}\ldots F_{j_u j_u}$ with ![]() $u>1$ do not appear in
$u>1$ do not appear in ![]() ${\sf m}(\Delta _{2k})$.
${\sf m}(\Delta _{2k})$.
Fix an element ![]() ${{\boldsymbol H}}=F_{11}F_{22}^{2}\ldots F_{ll}^{2}$ with
${{\boldsymbol H}}=F_{11}F_{22}^{2}\ldots F_{ll}^{2}$ with ![]() $l=k-1$. We compute the coefficient of
$l=k-1$. We compute the coefficient of ![]() ${{\boldsymbol H}}$ in
${{\boldsymbol H}}$ in ![]() ${\sf m}(\Delta _{2k})$. This coefficient is equal to
${\sf m}(\Delta _{2k})$. This coefficient is equal to ![]() $(-1)^{k} ({3!(2k-3)!}/{(2k)!}) {\sf m}(\partial _{F_{11}} \Delta _{4}^{(l)})$, where
$(-1)^{k} ({3!(2k-3)!}/{(2k)!}) {\sf m}(\partial _{F_{11}} \Delta _{4}^{(l)})$, where ![]() $\Delta _4^{(l)}$ is
$\Delta _4^{(l)}$ is ![]() $\Delta _4$ of the
$\Delta _4$ of the ![]() $\mathfrak {sp}_{2n-2k+4}$-subalgebra generated by
$\mathfrak {sp}_{2n-2k+4}$-subalgebra generated by ![]() $F_{ij}$ with
$F_{ij}$ with ![]() $i,j\not \in \{2,2',\ldots,l,l'\}$. According to Lemma 4.2,
$i,j\not \in \{2,2',\ldots,l,l'\}$. According to Lemma 4.2, ![]() ${\sf m}(\partial _{F_{11}} \Delta _{4}^{(l)})= \frac {-1}{3} (2n-2k+3)(2n-2k+2) F_{11}$. Making use of the action of the Weyl group
${\sf m}(\partial _{F_{11}} \Delta _{4}^{(l)})= \frac {-1}{3} (2n-2k+3)(2n-2k+2) F_{11}$. Making use of the action of the Weyl group ![]() $W(\mathfrak g,\mathfrak h)$ on
$W(\mathfrak g,\mathfrak h)$ on ![]() $\mathfrak h\oplus \mathfrak h$, we conclude that
$\mathfrak h\oplus \mathfrak h$, we conclude that ![]() ${\sf m}(\Delta _{2k})$ is proportional to
${\sf m}(\Delta _{2k})$ is proportional to ![]() $\Delta _{2k-2}$, more explicitly
$\Delta _{2k-2}$, more explicitly
and with some simplifications
Iterating the map ![]() ${\sf m}$, one obtains the result.
${\sf m}$, one obtains the result.
Theorem 4.4 For ![]() $\mathfrak g=\mathfrak {sp}_{2n}$ and
$\mathfrak g=\mathfrak {sp}_{2n}$ and ![]() $1\leqslant k\leqslant n$,
$1\leqslant k\leqslant n$,
 \[ S_{k} = \varpi(\Delta_{2k}[-1]) + \sum_{1\leqslant r< k} \binom{2n-2k+2r+1}{2r}\varpi(\tau^{2r}\Delta_{2k-2r}[-1]){\cdot}1 \]
\[ S_{k} = \varpi(\Delta_{2k}[-1]) + \sum_{1\leqslant r< k} \binom{2n-2k+2r+1}{2r}\varpi(\tau^{2r}\Delta_{2k-2r}[-1]){\cdot}1 \]is a Segal–Sugawara vector.
5. Several exceptional examples
There are instances, where our methods work very well.
Example 5.1 Suppose that ![]() $\mathfrak g=\mathfrak {so}_8$. Then
$\mathfrak g=\mathfrak {so}_8$. Then ![]() ${\rm Aut}(\mathfrak g)/{\rm Inn}(\mathfrak g)={\tt S}_3$, where
${\rm Aut}(\mathfrak g)/{\rm Inn}(\mathfrak g)={\tt S}_3$, where ![]() ${\rm Inn}(\mathfrak g)$ is the group of inner automorphisms. There are two Segal–Sugawara vectors, say
${\rm Inn}(\mathfrak g)$ is the group of inner automorphisms. There are two Segal–Sugawara vectors, say ![]() $S_2$ and
$S_2$ and ![]() $S_3$, such that their symbols are
$S_3$, such that their symbols are ![]() $\mathfrak g$-invariants of degree
$\mathfrak g$-invariants of degree ![]() $4$ in
$4$ in ![]() ${{\mathcal {S}}}(\mathfrak g[-1])$. Assume that
${{\mathcal {S}}}(\mathfrak g[-1])$. Assume that ![]() $S_2$ and
$S_2$ and ![]() $S_3$ are fixed vectors of
$S_3$ are fixed vectors of ![]() $\omega$. Then each of them is a sum
$\omega$. Then each of them is a sum ![]() $\varpi (Y_4)+\varpi (Y_2)$, cf. (0.1). Each element in
$\varpi (Y_4)+\varpi (Y_2)$, cf. (0.1). Each element in ![]() ${{\mathcal {S}}}^{2}({{\hat {\mathfrak g}}}^-)^{\mathfrak g}$ is proportional to
${{\mathcal {S}}}^{2}({{\hat {\mathfrak g}}}^-)^{\mathfrak g}$ is proportional to ![]() ${\mathcal {H}}[\bar b]$ for some
${\mathcal {H}}[\bar b]$ for some ![]() $\bar b$. Hence it is also an invariant of
$\bar b$. Hence it is also an invariant of ![]() ${\tt S}_3$. Without loss of generality we may assume that the symbols of
${\tt S}_3$. Without loss of generality we may assume that the symbols of ![]() $S_2$ and
$S_2$ and ![]() $S_3$ are Pfaffians
$S_3$ are Pfaffians ![]() ${\rm Pf}_2[-1]$,
${\rm Pf}_2[-1]$, ![]() ${\rm Pf}_3[-1]$ related to different matrix realisations of
${\rm Pf}_3[-1]$ related to different matrix realisations of ![]() $\mathfrak {so}_8$. Then for each of them there is an involution
$\mathfrak {so}_8$. Then for each of them there is an involution ![]() $\sigma \in {\tt S}_3$ such that
$\sigma \in {\tt S}_3$ such that ![]() $\sigma (Y_4)=-Y_4$. Replacing
$\sigma (Y_4)=-Y_4$. Replacing ![]() $S_j$ with
$S_j$ with ![]() $S_j-\sigma (S_j)$, we see that
$S_j-\sigma (S_j)$, we see that ![]() $\tilde S_2=\varpi ({\rm Pf}_2[-1])$ and
$\tilde S_2=\varpi ({\rm Pf}_2[-1])$ and ![]() $\tilde S_3=\varpi ({\rm Pf}_3[-1])$ are also Segal–Sugawara vectors. In view of Theorem 3.5, this implies that
$\tilde S_3=\varpi ({\rm Pf}_3[-1])$ are also Segal–Sugawara vectors. In view of Theorem 3.5, this implies that ![]() ${\sf m}({\rm Pf}_2)={\sf m}({\rm Pf}_3)=0$.
${\sf m}({\rm Pf}_2)={\sf m}({\rm Pf}_3)=0$.
Automorphisms of ![]() $\mathfrak g$ make themselves extremely useful. We will see the full power of this devise in § 7, which deals with the orthogonal case. At the moment notice the following thing, any
$\mathfrak g$ make themselves extremely useful. We will see the full power of this devise in § 7, which deals with the orthogonal case. At the moment notice the following thing, any ![]() $\sigma \in {\rm Aut}(\mathfrak g)$ acts on
$\sigma \in {\rm Aut}(\mathfrak g)$ acts on ![]() ${{\mathcal {S}}}(\mathfrak g)$ in the natural way and induces a map
${{\mathcal {S}}}(\mathfrak g)$ in the natural way and induces a map ![]() $\sigma _{(m)}\!: {{\mathcal {S}}}^{m}(\mathfrak g)\to {{\mathcal {S}}}^{m}(\mathfrak g)$. Let
$\sigma _{(m)}\!: {{\mathcal {S}}}^{m}(\mathfrak g)\to {{\mathcal {S}}}^{m}(\mathfrak g)$. Let ![]() $\mathfrak v_m\otimes \mathfrak g$ be the isotypic component of
$\mathfrak v_m\otimes \mathfrak g$ be the isotypic component of ![]() ${{\mathcal {S}}}^{m}(\mathfrak g)$ corresponding to
${{\mathcal {S}}}^{m}(\mathfrak g)$ corresponding to ![]() $\mathfrak g$. Then
$\mathfrak g$. Then ![]() $\sigma$ acts on
$\sigma$ acts on ![]() $\mathfrak v_m$ and for this action, we have
$\mathfrak v_m$ and for this action, we have ![]() $\sigma (v)\otimes \sigma (x)=\sigma _{(m)}(v\otimes x)$, where
$\sigma (v)\otimes \sigma (x)=\sigma _{(m)}(v\otimes x)$, where ![]() $v\in \mathfrak v_m$,
$v\in \mathfrak v_m$, ![]() $x\in \mathfrak g$.
$x\in \mathfrak g$.
An interesting story is related to Pfaffians in higher ranks.
Example 5.2 (The Pfaffians)
Take ![]() $\mathfrak g=\mathfrak {so}_{2n}$. If
$\mathfrak g=\mathfrak {so}_{2n}$. If ![]() $n<4$, these algebras appear in type A. In the case
$n<4$, these algebras appear in type A. In the case ![]() $n=4$, the Pfaffian-like Segal–Sugawara vectors are examined in Example 5.1. Suppose that
$n=4$, the Pfaffian-like Segal–Sugawara vectors are examined in Example 5.1. Suppose that ![]() $n>4$ and that
$n>4$ and that ![]() $\mathfrak {so}_{2n}\subset \mathfrak {gl}_{2n}$ consists of the skew-symmetric with respect to the antidiagonal matrices. The highest weight of the Cartan component of
$\mathfrak {so}_{2n}\subset \mathfrak {gl}_{2n}$ consists of the skew-symmetric with respect to the antidiagonal matrices. The highest weight of the Cartan component of ![]() $\Lambda ^{2}\mathfrak g$ is
$\Lambda ^{2}\mathfrak g$ is ![]() $\pi _1+\pi _3=2\varepsilon _1+\varepsilon _2+\varepsilon _3$. Assume that
$\pi _1+\pi _3=2\varepsilon _1+\varepsilon _2+\varepsilon _3$. Assume that ![]() $\pi _1+\pi _3$ appears as the weight of a factor
$\pi _1+\pi _3$ appears as the weight of a factor ![]() $y_1y_2y_3$ for a summand
$y_1y_2y_3$ for a summand ![]() $y_1\ldots y_n$ of the Pfaffian
$y_1\ldots y_n$ of the Pfaffian ![]() ${\rm Pf}$. Then up to the change of indices, we must have
${\rm Pf}$. Then up to the change of indices, we must have
where ![]() $i'=2n+1-i$. If this is really the case, then the determinant
$i'=2n+1-i$. If this is really the case, then the determinant ![]() $\Delta _{2n}\in {{\mathcal {S}}}^{2n}(\mathfrak {gl}_{2n})$ has a summand
$\Delta _{2n}\in {{\mathcal {S}}}^{2n}(\mathfrak {gl}_{2n})$ has a summand ![]() $E_{1i}E_{1j}\ldots$, a contradiction.
$E_{1i}E_{1j}\ldots$, a contradiction.
Thus ![]() ${\sf m}({\rm Pf})\in (\mathfrak g\otimes {{\mathcal {S}}}^{n-3}(\mathfrak g))^{\mathfrak g}$. If
${\sf m}({\rm Pf})\in (\mathfrak g\otimes {{\mathcal {S}}}^{n-3}(\mathfrak g))^{\mathfrak g}$. If ![]() $n$ is odd, then there is no copy of
$n$ is odd, then there is no copy of ![]() $\mathfrak g$ in
$\mathfrak g$ in ![]() ${{\mathcal {S}}}^{n-3}(\mathfrak g)$ and we conclude at once that the image of the Pfaffian under m is zero.
${{\mathcal {S}}}^{n-3}(\mathfrak g)$ and we conclude at once that the image of the Pfaffian under m is zero.
Suppose that ![]() $n$ is even. Then we can rely on the fact that
$n$ is even. Then we can rely on the fact that ![]() $G(\mathfrak g\oplus \mathfrak h)$ is dense in
$G(\mathfrak g\oplus \mathfrak h)$ is dense in ![]() $\mathfrak g\oplus \mathfrak g$. Fix a factor
$\mathfrak g\oplus \mathfrak g$. Fix a factor ![]() ${\boldsymbol H}\in {{\mathcal {S}}}^{n-3}(\mathfrak h)$ of a summand of
${\boldsymbol H}\in {{\mathcal {S}}}^{n-3}(\mathfrak h)$ of a summand of ![]() ${\rm Pf}$. Without loss of generality assume that
${\rm Pf}$. Without loss of generality assume that ![]() ${\boldsymbol H}= \prod _{s>3} (E_{ss}-E_{s's'})$. Let
${\boldsymbol H}= \prod _{s>3} (E_{ss}-E_{s's'})$. Let ![]() ${\rm Pf}^{(3)}$ be the Pfaffian of the subalgebra spanned by
${\rm Pf}^{(3)}$ be the Pfaffian of the subalgebra spanned by
Since this subalgebra is isomorphic to ![]() $\mathfrak {so}_6\cong \mathfrak {sl}_4$ write also
$\mathfrak {so}_6\cong \mathfrak {sl}_4$ write also ![]() $\tilde \Delta _3^{(4)}$ for
$\tilde \Delta _3^{(4)}$ for ![]() ${\rm Pf}^{(3)}$. By the construction,
${\rm Pf}^{(3)}$. By the construction, ![]() $({3!(n-3)!}/{n!}){\sf m}({\rm Pf}^{(3)})\otimes {\boldsymbol H}$ is a summand of
$({3!(n-3)!}/{n!}){\sf m}({\rm Pf}^{(3)})\otimes {\boldsymbol H}$ is a summand of ![]() ${\sf m}({\rm Pf})$. For a Weyl involution
${\sf m}({\rm Pf})$. For a Weyl involution ![]() $\theta$ of
$\theta$ of ![]() $\mathfrak {sl}_4$, we have
$\mathfrak {sl}_4$, we have ![]() $\theta (\tilde \Delta _3^{(4)})=-\tilde \Delta _3^{(4)}$. Therefore
$\theta (\tilde \Delta _3^{(4)})=-\tilde \Delta _3^{(4)}$. Therefore ![]() $\varpi (\tilde \Delta _3^{(4)})$ acts as zero on any irreducible self-dual
$\varpi (\tilde \Delta _3^{(4)})$ acts as zero on any irreducible self-dual ![]() $\mathfrak {sl}_4$-module, in particular, on
$\mathfrak {sl}_4$-module, in particular, on ![]() $\mathfrak {sl}_4$ and on
$\mathfrak {sl}_4$ and on ![]() $\Lambda ^{2}{{\mathbb {C}}}^{4}={{\mathbb {C}}}^{6}$. Now we can conclude that
$\Lambda ^{2}{{\mathbb {C}}}^{4}={{\mathbb {C}}}^{6}$. Now we can conclude that ![]() ${\sf m}({\rm Pf}^{(3)})=0$ and hence
${\sf m}({\rm Pf}^{(3)})=0$ and hence ![]() ${\sf m}({\rm Pf})=0$. Thus
${\sf m}({\rm Pf})=0$. Thus ![]() $\varpi ({\rm Pf})[-1]$ is a Segal–Sugawara vector for each
$\varpi ({\rm Pf})[-1]$ is a Segal–Sugawara vector for each ![]() $n$.
$n$.
Keep the assumption that ![]() $n$ is even. Another way to see that
$n$ is even. Another way to see that ![]() ${\sf m}({\rm Pf})=0$ is to use an outer involution
${\sf m}({\rm Pf})=0$ is to use an outer involution ![]() $\sigma \in {\rm Aut}(\mathfrak {so}_{2n})$ such that
$\sigma \in {\rm Aut}(\mathfrak {so}_{2n})$ such that ![]() $\sigma ({\rm Pf})=-{\rm Pf}$. Here
$\sigma ({\rm Pf})=-{\rm Pf}$. Here ![]() $\sigma (v)=-v$ for
$\sigma (v)=-v$ for ![]() $v\in \mathfrak v_{n-1}$ such that
$v\in \mathfrak v_{n-1}$ such that ![]() $v\otimes \mathfrak g$ is the primitive copy of
$v\otimes \mathfrak g$ is the primitive copy of ![]() $\mathfrak g$ that gives rise to
$\mathfrak g$ that gives rise to ![]() ${\rm Pf}$ and also
${\rm Pf}$ and also ![]() $\sigma ({\sf m}({\rm Pf}))=-{\sf m}({\rm Pf})$. At the same time,
$\sigma ({\sf m}({\rm Pf}))=-{\sf m}({\rm Pf})$. At the same time, ![]() $\sigma$ acts as
$\sigma$ acts as ![]() ${{\rm id}}$ on
${{\rm id}}$ on ![]() $\mathfrak v_{n-3}$. Therefore
$\mathfrak v_{n-3}$. Therefore ![]() $\sigma$ acts as
$\sigma$ acts as ![]() ${{\rm id}}$ on
${{\rm id}}$ on ![]() $(\mathfrak g\otimes {{\mathcal {S}}}^{n-3}(\mathfrak g))^{\mathfrak g}$. Since
$(\mathfrak g\otimes {{\mathcal {S}}}^{n-3}(\mathfrak g))^{\mathfrak g}$. Since ![]() ${\sf m}({\rm Pf})\in (\mathfrak g\otimes {{\mathcal {S}}}^{n-3}(\mathfrak g))^{\mathfrak g}$, it must be zero.
${\sf m}({\rm Pf})\in (\mathfrak g\otimes {{\mathcal {S}}}^{n-3}(\mathfrak g))^{\mathfrak g}$, it must be zero.
Explicit formulas for the Pfaffian-type Segal–Sugawara vector ![]() ${\rm Pf} F[-1]\in {{\mathcal {U}}}(\mathfrak {so}_{2n}[t^{-1}])$ are given in [Reference MolevMol13, Reference RozhkovskayaRoz14]. In the basis
${\rm Pf} F[-1]\in {{\mathcal {U}}}(\mathfrak {so}_{2n}[t^{-1}])$ are given in [Reference MolevMol13, Reference RozhkovskayaRoz14]. In the basis ![]() $\{F_{ij}^{\circ }=E_{ij}-E_{ji}\mid 1\leqslant i< j\leqslant 2n\}$ for
$\{F_{ij}^{\circ }=E_{ij}-E_{ji}\mid 1\leqslant i< j\leqslant 2n\}$ for ![]() $\mathfrak {so}_{2n}$, the vector
$\mathfrak {so}_{2n}$, the vector ![]() ${\rm Pf} F[-1]$ is written as a sum of monomials with pairwise commuting factors, see [Reference MolevMol13] and [Reference MolevMol18, Equation (8.11)]. Hence it coincides with the symmetrisation of its symbol, in our notation,
${\rm Pf} F[-1]$ is written as a sum of monomials with pairwise commuting factors, see [Reference MolevMol13] and [Reference MolevMol18, Equation (8.11)]. Hence it coincides with the symmetrisation of its symbol, in our notation, ![]() ${\rm Pf} F[-1] = \varpi ({\rm Pf})[-1]$. Example 5.2 provides a different proof for [Reference MolevMol18, Proposistion 8.4].
${\rm Pf} F[-1] = \varpi ({\rm Pf})[-1]$. Example 5.2 provides a different proof for [Reference MolevMol18, Proposistion 8.4].
Another easy to understand instance is provided by the invariant of degree ![]() $5$ in type
$5$ in type ![]() ${\sf E}_6$.
${\sf E}_6$.
Example 5.3 Suppose that ![]() $\mathfrak g$ is a simple Lie algebra of type
$\mathfrak g$ is a simple Lie algebra of type ![]() ${\sf E}_6$. Let
${\sf E}_6$. Let ![]() $H\in {{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ be a homogeneous invariant of degree
$H\in {{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ be a homogeneous invariant of degree ![]() $5$. Then
$5$. Then ![]() ${\sf m}(H)\in (\Lambda ^{2}\mathfrak g\otimes {{\mathcal {S}}}^{2}(\mathfrak g))^{\mathfrak g}$. Here
${\sf m}(H)\in (\Lambda ^{2}\mathfrak g\otimes {{\mathcal {S}}}^{2}(\mathfrak g))^{\mathfrak g}$. Here ![]() $\Lambda ^{2}\mathfrak g=V(\pi _3)\oplus \mathfrak g$ and
$\Lambda ^{2}\mathfrak g=V(\pi _3)\oplus \mathfrak g$ and ![]() ${{\mathcal {S}}}^{2}(\mathfrak g)=V(2\pi _6)\oplus V(\pi _1+\pi _5)\oplus \mathbb {C}$. Therefore
${{\mathcal {S}}}^{2}(\mathfrak g)=V(2\pi _6)\oplus V(\pi _1+\pi _5)\oplus \mathbb {C}$. Therefore ![]() ${\sf m}(H)=0$.
${\sf m}(H)=0$.
Recall that we are considering only semisimple ![]() $\mathfrak g$ now and that
$\mathfrak g$ now and that ![]() $(\,\,,\,)$ is fixed in such a way that
$(\,\,,\,)$ is fixed in such a way that ![]() ${\mathcal {H}}\in {{\mathcal {U}}}(\mathfrak g)$ acts on
${\mathcal {H}}\in {{\mathcal {U}}}(\mathfrak g)$ acts on ![]() $\mathfrak g$ as
$\mathfrak g$ as ![]() $C{{\rm id}}_{\mathfrak g}$ for some
$C{{\rm id}}_{\mathfrak g}$ for some ![]() $C\in {{\mathbb {C}}}$.
$C\in {{\mathbb {C}}}$.
Lemma 5.4 There is ![]() $c_1\in {{\mathbb {C}}}$ depending on the scalar product
$c_1\in {{\mathbb {C}}}$ depending on the scalar product ![]() $(\,\,,\,)$ such that
$(\,\,,\,)$ such that ![]() $\sum _{i} x_i[\xi,x_i] = c_1 \xi$ in
$\sum _{i} x_i[\xi,x_i] = c_1 \xi$ in ![]() ${{\mathcal {U}}}(\mathfrak g)$ for any
${{\mathcal {U}}}(\mathfrak g)$ for any ![]() $\xi \in \mathfrak g$. Furthermore,
$\xi \in \mathfrak g$. Furthermore, ![]() ${\mathcal {H}}(\xi )=\sum _{i} \mathrm {ad}(x_i)^{2} (\xi )=-2c_1 \xi$, i.e.
${\mathcal {H}}(\xi )=\sum _{i} \mathrm {ad}(x_i)^{2} (\xi )=-2c_1 \xi$, i.e. ![]() $C=-2c_1$.
$C=-2c_1$.
Proof. For each ![]() $\xi \in \mathfrak g$, set
$\xi \in \mathfrak g$, set ![]() $\psi _1(\xi )=\sum _{i} x_i[\xi,x_i] = \sum _i x_i\xi x_i - {\mathcal {H}} \xi$. Since
$\psi _1(\xi )=\sum _{i} x_i[\xi,x_i] = \sum _i x_i\xi x_i - {\mathcal {H}} \xi$. Since ![]() $[{\mathcal {H}},\xi ]=0$, we have then
$[{\mathcal {H}},\xi ]=0$, we have then ![]() $\omega (\psi _1(\xi ))=-\psi _1(\xi )$. Note that
$\omega (\psi _1(\xi ))=-\psi _1(\xi )$. Note that
Thereby ![]() $2\psi _1(\xi )=-{\mathcal {H}}(\xi )=-C\xi$.
$2\psi _1(\xi )=-{\mathcal {H}}(\xi )=-C\xi$.
Lemma 5.5 Let ![]() $\mathfrak g$ be a simple Lie algebra of rank at least
$\mathfrak g$ be a simple Lie algebra of rank at least ![]() $2$. Then
$2$. Then ![]() ${\sf m}({\mathcal {H}}^{3})\not \in \mathfrak g\otimes {{\mathcal {S}}}^{3}(\mathfrak g)$.
${\sf m}({\mathcal {H}}^{3})\not \in \mathfrak g\otimes {{\mathcal {S}}}^{3}(\mathfrak g)$.
Proof. Choose an orthogonal basis of ![]() $\mathfrak h$ such that at least one element in it is equal to
$\mathfrak h$ such that at least one element in it is equal to ![]() $h_\alpha$ for a simple root
$h_\alpha$ for a simple root ![]() $\alpha$. If the root system of
$\alpha$. If the root system of ![]() $\mathfrak g$ is not simply laced, suppose that
$\mathfrak g$ is not simply laced, suppose that ![]() $\alpha$ is a long root. Suppose further that either
$\alpha$ is a long root. Suppose further that either ![]() $\alpha =\alpha _1$ or
$\alpha =\alpha _1$ or ![]() $\alpha =\alpha _\ell$. Changing the scalar product if necessary, we may assume that
$\alpha =\alpha _\ell$. Changing the scalar product if necessary, we may assume that ![]() $h_\alpha \in \{x_i\}$. Consider the summand
$h_\alpha \in \{x_i\}$. Consider the summand ![]() $\xi \otimes h_\alpha ^{3}$ of
$\xi \otimes h_\alpha ^{3}$ of ![]() ${\sf m}({\mathcal {H}}^{3})$. We have
${\sf m}({\mathcal {H}}^{3})$. We have
Set ![]() $\xi _0={\sf m}(h_\alpha {\mathcal {H}})$. Note that
$\xi _0={\sf m}(h_\alpha {\mathcal {H}})$. Note that ![]() $h_\alpha {\mathcal {H}}\in {{\mathcal {U}}}(\mathfrak g)$ acts on
$h_\alpha {\mathcal {H}}\in {{\mathcal {U}}}(\mathfrak g)$ acts on ![]() $\mathfrak g$ as a scalar multiple of
$\mathfrak g$ as a scalar multiple of ![]() $\mathrm {ad}(h_\alpha )$. In view of Lemma 5.4, the sum
$\mathrm {ad}(h_\alpha )$. In view of Lemma 5.4, the sum ![]() $\sum _{i} x_i h_\alpha x_i$ acts on
$\sum _{i} x_i h_\alpha x_i$ acts on ![]() $\mathfrak g$ as another multiple of
$\mathfrak g$ as another multiple of ![]() $\mathrm {ad}(h_\alpha )$. Hence
$\mathrm {ad}(h_\alpha )$. Hence ![]() $\xi _0\in \mathfrak g$.
$\xi _0\in \mathfrak g$.
It remains to show that ![]() $\eta =\mathrm {ad}(h_\alpha )^{3}$ is not an element of
$\eta =\mathrm {ad}(h_\alpha )^{3}$ is not an element of ![]() $\mathfrak g\subset \mathfrak {so}(\mathfrak g)$. Let
$\mathfrak g\subset \mathfrak {so}(\mathfrak g)$. Let ![]() $\alpha '$ be the unique simple root not orthogonal to
$\alpha '$ be the unique simple root not orthogonal to ![]() $\alpha$. Observe that
$\alpha$. Observe that ![]() $\eta (e_\alpha )=8 e_\alpha$ and
$\eta (e_\alpha )=8 e_\alpha$ and ![]() $\eta (e_{\alpha '})= - e_{\alpha '}$. Set
$\eta (e_{\alpha '})= - e_{\alpha '}$. Set ![]() $\gamma =\alpha +\alpha '$. Then
$\gamma =\alpha +\alpha '$. Then ![]() $e_\gamma \ne 0$ and
$e_\gamma \ne 0$ and ![]() $\eta (e_\gamma )=e_\gamma$. Since
$\eta (e_\gamma )=e_\gamma$. Since ![]() $1\ne 8-1$, we conclude that indeed
$1\ne 8-1$, we conclude that indeed ![]() $\eta \not \in \mathfrak g$.
$\eta \not \in \mathfrak g$.
Proposition 5.6 Let ![]() $\mathfrak g$ be an exceptional simple Lie algebra. Suppose that
$\mathfrak g$ be an exceptional simple Lie algebra. Suppose that ![]() $H\in {{\mathcal {S}}}^{6}(\mathfrak g)^{\mathfrak g}$. Then there is
$H\in {{\mathcal {S}}}^{6}(\mathfrak g)^{\mathfrak g}$. Then there is ![]() ${{\boldsymbol b}}\in \mathbb {C}$ such that
${{\boldsymbol b}}\in \mathbb {C}$ such that ![]() ${\sf m}(H-{{\boldsymbol b}}{\mathcal {H}}^{3})\in \mathbb {C} {\mathcal {H}}^{2}\subset {{\mathcal {S}}}^{4}(\mathfrak g)$.
${\sf m}(H-{{\boldsymbol b}}{\mathcal {H}}^{3})\in \mathbb {C} {\mathcal {H}}^{2}\subset {{\mathcal {S}}}^{4}(\mathfrak g)$.
Proof. Let ![]() $V$ be the Cartan component of
$V$ be the Cartan component of ![]() $\Lambda ^{2}\mathfrak g$. A straightforward calculation shows that
$\Lambda ^{2}\mathfrak g$. A straightforward calculation shows that ![]() $V$ appears in
$V$ appears in ![]() ${{\mathcal {S}}}^{3}(\mathfrak g)$ with multiplicity one as in the following table.
${{\mathcal {S}}}^{3}(\mathfrak g)$ with multiplicity one as in the following table.

We have ![]() ${\sf m}(H)\in (V\otimes {{\mathcal {S}}}^{3}(\mathfrak g))^{\mathfrak g}\oplus (\mathfrak g\otimes {{\mathcal {S}}}^{3}(\mathfrak g))^{\mathfrak g}$. The first summand here is one-dimensional. Since
${\sf m}(H)\in (V\otimes {{\mathcal {S}}}^{3}(\mathfrak g))^{\mathfrak g}\oplus (\mathfrak g\otimes {{\mathcal {S}}}^{3}(\mathfrak g))^{\mathfrak g}$. The first summand here is one-dimensional. Since ![]() ${\sf m}({\mathcal {H}}^{3})\not \in \mathfrak g\otimes {{\mathcal {S}}}^{3}(\mathfrak g)$ by Lemma 5.5, there is
${\sf m}({\mathcal {H}}^{3})\not \in \mathfrak g\otimes {{\mathcal {S}}}^{3}(\mathfrak g)$ by Lemma 5.5, there is ![]() ${{\boldsymbol b}}\in {{\mathbb {C}}}$ such that
${{\boldsymbol b}}\in {{\mathbb {C}}}$ such that ![]() ${\sf m}(\tilde H)\in \mathfrak g\otimes {{\mathcal {S}}}^{3}(\mathfrak g)$ for
${\sf m}(\tilde H)\in \mathfrak g\otimes {{\mathcal {S}}}^{3}(\mathfrak g)$ for ![]() $\tilde H=H-{{\boldsymbol b}}{\mathcal {H}}^{3}$.
$\tilde H=H-{{\boldsymbol b}}{\mathcal {H}}^{3}$.
The degrees of basic symmetric invariants ![]() $\{H_k\mid 1\leqslant k\leqslant l\}$ indicate that
$\{H_k\mid 1\leqslant k\leqslant l\}$ indicate that ![]() ${{\mathcal {S}}}^{3}(\mathfrak g)$ contains exactly one copy of
${{\mathcal {S}}}^{3}(\mathfrak g)$ contains exactly one copy of ![]() $\mathfrak g$. (This is also apparent in the table above.) Hence
$\mathfrak g$. (This is also apparent in the table above.) Hence ![]() $(\mathfrak g\otimes {{\mathcal {S}}}^{3}(\mathfrak g))^{\mathfrak g}= {{\mathcal {S}}}^{4}(\mathfrak g)^{\mathfrak g}={{\mathbb {C}}} {\mathcal {H}}^{2}$.
$(\mathfrak g\otimes {{\mathcal {S}}}^{3}(\mathfrak g))^{\mathfrak g}= {{\mathcal {S}}}^{4}(\mathfrak g)^{\mathfrak g}={{\mathbb {C}}} {\mathcal {H}}^{2}$.
Corollary 5.7 Keep the assumption that ![]() $\mathfrak g$ is exceptional. Then
$\mathfrak g$ is exceptional. Then ![]() $\tilde H=H-{{\boldsymbol b}}{\mathcal {H}}^{3}$ of Proposition 5.6 satisfies (0.2) and there are
$\tilde H=H-{{\boldsymbol b}}{\mathcal {H}}^{3}$ of Proposition 5.6 satisfies (0.2) and there are ![]() $R(1),R(2)\in {{\mathbb {C}}}$ such that
$R(1),R(2)\in {{\mathbb {C}}}$ such that
is an element of ![]() $\mathfrak z({{\hat {\mathfrak g}}})$.
$\mathfrak z({{\hat {\mathfrak g}}})$.
6. Type G $_2$
$_2$
Let ![]() $\mathfrak g$ be a simple Lie algebra of type G
$\mathfrak g$ be a simple Lie algebra of type G![]() $_2$. Then
$_2$. Then ![]() $\ell =2$. The algebra
$\ell =2$. The algebra ![]() ${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ has two generators,
${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ has two generators, ![]() ${\mathcal {H}}$ and
${\mathcal {H}}$ and ![]() $\Delta _6\in {{\mathcal {S}}}^{6}(\mathfrak g)$. In this section, we compute the constant
$\Delta _6\in {{\mathcal {S}}}^{6}(\mathfrak g)$. In this section, we compute the constant ![]() ${{\boldsymbol b}}$ of Proposition 5.6 for
${{\boldsymbol b}}$ of Proposition 5.6 for ![]() $H=\Delta _6$ and
$H=\Delta _6$ and ![]() $R(1), R(2)$ of (5.1). All our computations are done by hand. A computer-aided explicit formula for a Segal–Sugawara vector of
$R(1), R(2)$ of (5.1). All our computations are done by hand. A computer-aided explicit formula for a Segal–Sugawara vector of ![]() $t$-degree
$t$-degree ![]() $6$ is obtained in [Reference Molev, Ragoucy and RozhkovskayaMRR16].
$6$ is obtained in [Reference Molev, Ragoucy and RozhkovskayaMRR16].
First we choose a matrix realisation of ![]() $\mathfrak g\subset \mathfrak {so}_7$. The embedding
$\mathfrak g\subset \mathfrak {so}_7$. The embedding ![]() $\iota \!:\mathfrak {sl}_3\to \mathfrak {so}_7$ is fixed by
$\iota \!:\mathfrak {sl}_3\to \mathfrak {so}_7$ is fixed by
for ![]() $i\ne j$. We choose a basis of
$i\ne j$. We choose a basis of ![]() $\mathfrak h\subset \mathfrak {sl}_3$ as
$\mathfrak h\subset \mathfrak {sl}_3$ as ![]() $\{h_1,h_2\}$ with
$\{h_1,h_2\}$ with ![]() $h_1={{\rm diag}}(1,-1,0)$,
$h_1={{\rm diag}}(1,-1,0)$, ![]() $h_2={{\rm diag}}(1,1,-2)$ and extend it to a basis of
$h_2={{\rm diag}}(1,1,-2)$ and extend it to a basis of ![]() $\mathfrak {sl}_3$ by adding
$\mathfrak {sl}_3$ by adding ![]() $e_i,f_i$ with
$e_i,f_i$ with ![]() $1\leqslant i\leqslant 3$ in the semi-standard notation, e.g.
$1\leqslant i\leqslant 3$ in the semi-standard notation, e.g. ![]() $e_3=E_{13}$,
$e_3=E_{13}$, ![]() $f_1=E_{21}$,
$f_1=E_{21}$, ![]() $f_3=E_{31}$. Let
$f_3=E_{31}$. Let ![]() $\varepsilon _i\in \mathfrak h^{*}$ with
$\varepsilon _i\in \mathfrak h^{*}$ with ![]() $1\leqslant i\leqslant 3$ be the same as in § 2. Now it remains to describe the complement of
$1\leqslant i\leqslant 3$ be the same as in § 2. Now it remains to describe the complement of ![]() $\mathfrak {sl}_3 = (\mathfrak {so}_6 \cap \mathfrak g)$, which is isomorphic to
$\mathfrak {sl}_3 = (\mathfrak {so}_6 \cap \mathfrak g)$, which is isomorphic to ![]() ${{\mathbb {C}}}^{3}\oplus ({{\mathbb {C}}}^{3})^{*}$.
${{\mathbb {C}}}^{3}\oplus ({{\mathbb {C}}}^{3})^{*}$.
Matrix (6.1) presents an element of ![]() ${{\mathbb {C}}}^{3}\oplus ({{\mathbb {C}}}^{3})^{*}\subset \mathfrak {so}_7$:
${{\mathbb {C}}}^{3}\oplus ({{\mathbb {C}}}^{3})^{*}\subset \mathfrak {so}_7$:
 \begin{equation} \left(\begin{array}{cccccc|c} & & & -{{\tt \beta}} & {{\tt \gamma}} & 0 & \sqrt{2}{{\tt a}} \\ & & & {{\tt \alpha}} & 0 & -{{\tt \gamma}} & \sqrt{2}{{\tt b}} \\ & & & 0 & -\alpha & {{\tt \beta}} & \sqrt{2}{{\tt c}} \\ {{\tt b}} & -{{\tt a}} & 0 & & & & \sqrt{2}{{\tt \gamma}} \\ -{{\tt c}} & 0 & {{\tt a}} & & & & \sqrt{2}{{\tt \beta}} \\ 0 & {{\tt c}} & -{{\tt b}} & & & & \sqrt{2} {{\tt \alpha}} \\ \hline \vphantom{\frac{a^l_{1}}{a^l_{1}}}-\sqrt{2}{{\tt \alpha}} & -\sqrt{2}{{\tt \beta}} & -\sqrt{2}{{\tt \gamma}} & -\sqrt{2}{{\tt c}} & -\sqrt{2}{{\tt b}} & -\sqrt{2}{{\tt a}} & 0 \end{array}\right). \end{equation}
\begin{equation} \left(\begin{array}{cccccc|c} & & & -{{\tt \beta}} & {{\tt \gamma}} & 0 & \sqrt{2}{{\tt a}} \\ & & & {{\tt \alpha}} & 0 & -{{\tt \gamma}} & \sqrt{2}{{\tt b}} \\ & & & 0 & -\alpha & {{\tt \beta}} & \sqrt{2}{{\tt c}} \\ {{\tt b}} & -{{\tt a}} & 0 & & & & \sqrt{2}{{\tt \gamma}} \\ -{{\tt c}} & 0 & {{\tt a}} & & & & \sqrt{2}{{\tt \beta}} \\ 0 & {{\tt c}} & -{{\tt b}} & & & & \sqrt{2} {{\tt \alpha}} \\ \hline \vphantom{\frac{a^l_{1}}{a^l_{1}}}-\sqrt{2}{{\tt \alpha}} & -\sqrt{2}{{\tt \beta}} & -\sqrt{2}{{\tt \gamma}} & -\sqrt{2}{{\tt c}} & -\sqrt{2}{{\tt b}} & -\sqrt{2}{{\tt a}} & 0 \end{array}\right). \end{equation}With a certain abuse of notation, we denote the elements of the corresponding basis by the same symbols, for instance,
as a vector of ![]() ${{\mathbb {C}}}^{3}$.
${{\mathbb {C}}}^{3}$.
The scalar product ![]() $(\,\,,\,)$ is such that
$(\,\,,\,)$ is such that ![]() ${\mathcal {H}}=\Delta _2$ with
${\mathcal {H}}=\Delta _2$ with
The basic invariant of degree ![]() $6$,
$6$, ![]() $\Delta _6$, is chosen as the restriction to
$\Delta _6$, is chosen as the restriction to ![]() $\mathfrak g$ of the coefficient
$\mathfrak g$ of the coefficient ![]() $\Delta _6^{(7)}$ of degree 6 in (1.2) written for
$\Delta _6^{(7)}$ of degree 6 in (1.2) written for ![]() $\mathfrak {gl}_7$. In this case, the restriction of
$\mathfrak {gl}_7$. In this case, the restriction of ![]() $\Delta _6$ to
$\Delta _6$ to ![]() $\mathfrak {sl}_3$ is equal to
$\mathfrak {sl}_3$ is equal to ![]() $-\tilde \Delta _3^{2}$, where
$-\tilde \Delta _3^{2}$, where ![]() $\tilde \Delta _3$ is the determinant of
$\tilde \Delta _3$ is the determinant of ![]() $\mathfrak {sl}_3$. For future use, we record
$\mathfrak {sl}_3$. For future use, we record
The decomposition ![]() $\mathfrak g=({{\mathbb {C}}}^{3})^{*}\oplus \mathfrak g\oplus {{\mathbb {C}}}^{3}$ is a
$\mathfrak g=({{\mathbb {C}}}^{3})^{*}\oplus \mathfrak g\oplus {{\mathbb {C}}}^{3}$ is a ![]() ${{\mathbb {Z}}}/3{{\mathbb {Z}}}$-grading induced by an (inner) automorphism
${{\mathbb {Z}}}/3{{\mathbb {Z}}}$-grading induced by an (inner) automorphism ![]() $\sigma$ of
$\sigma$ of ![]() $\mathfrak g$. Note that our basis for
$\mathfrak g$. Note that our basis for ![]() $\mathfrak g$ consists of eigenvectors of
$\mathfrak g$ consists of eigenvectors of ![]() $\sigma$.
$\sigma$.
Recall that ![]() $S_2$ is given by (5.1) and that we are computing the constants occurring there. There is an easy part of the calculation. It concerns the projection of
$S_2$ is given by (5.1) and that we are computing the constants occurring there. There is an easy part of the calculation. It concerns the projection of ![]() ${\sf m}(\Delta _2^{3})$ on
${\sf m}(\Delta _2^{3})$ on ![]() $(V\otimes {{\mathcal {S}}}^{3}(\mathfrak g))^{\mathfrak g}$. As we already know, the highest weight of
$(V\otimes {{\mathcal {S}}}^{3}(\mathfrak g))^{\mathfrak g}$. As we already know, the highest weight of ![]() $V$ is
$V$ is ![]() $3\pi _1$. Next choose a monomial of weight
$3\pi _1$. Next choose a monomial of weight ![]() $3\pi _1$, for instance,
$3\pi _1$, for instance, ![]() $e_3^{2} f_1$.
$e_3^{2} f_1$.
Lemma 6.1 Let ![]() $\xi \otimes e_3^{2} f_1$ be a summand of
$\xi \otimes e_3^{2} f_1$ be a summand of ![]() ${\sf m}(\Delta _2^{3})$. Then
${\sf m}(\Delta _2^{3})$. Then ![]() $\xi (e_3)=\frac {6}{5} f_2$.
$\xi (e_3)=\frac {6}{5} f_2$.
Proof. Observe that in ![]() $\Delta _2^{3}$, the factor
$\Delta _2^{3}$, the factor ![]() $e_3^{2} f_1$ appears only in the summand
$e_3^{2} f_1$ appears only in the summand ![]() $24 e_3^{2} f_3^{2} e_1f_1$. By the construction, we have
$24 e_3^{2} f_3^{2} e_1f_1$. By the construction, we have
Note that ![]() $[e_1,e_3]=0$. Hence
$[e_1,e_3]=0$. Hence
 \begin{align*} \tfrac{5}{6}\xi(e_3)&=\tfrac{1}{6}(2\mathrm{ad}(e_1)\mathrm{ad}(f_3)^{2}+2\mathrm{ad}(f_3)\mathrm{ad}(e_1)\mathrm{ad}(f_3))(e_3)\\ & = \tfrac{1}{6}(-2\mathrm{ad}(f_2)\mathrm{ad}(f_3)-4\mathrm{ad}(f_3)\mathrm{ad}(f_2))(e_3)=-[f_2,[f_3,e_3]]=f_2 \end{align*}
\begin{align*} \tfrac{5}{6}\xi(e_3)&=\tfrac{1}{6}(2\mathrm{ad}(e_1)\mathrm{ad}(f_3)^{2}+2\mathrm{ad}(f_3)\mathrm{ad}(e_1)\mathrm{ad}(f_3))(e_3)\\ & = \tfrac{1}{6}(-2\mathrm{ad}(f_2)\mathrm{ad}(f_3)-4\mathrm{ad}(f_3)\mathrm{ad}(f_2))(e_3)=-[f_2,[f_3,e_3]]=f_2 \end{align*}and the result follows.
In the above computation, we did not see the projection of ![]() ${\sf m}(\Delta _2^{3})$ on
${\sf m}(\Delta _2^{3})$ on ![]() $(\mathfrak g\otimes {{\mathcal {S}}}^{3}(\mathfrak g))^{\mathfrak g}$, which is equally important. Set
$(\mathfrak g\otimes {{\mathcal {S}}}^{3}(\mathfrak g))^{\mathfrak g}$, which is equally important. Set ![]() $h_3=[e_3,f_3]$. Note that
$h_3=[e_3,f_3]$. Note that ![]() $\{f_3,h_3,e_3\}$ is an
$\{f_3,h_3,e_3\}$ is an ![]() $\mathfrak {sl}_2$-triple associated with the highest root of
$\mathfrak {sl}_2$-triple associated with the highest root of ![]() $\mathfrak g$. In the following lemma,
$\mathfrak g$. In the following lemma, ![]() $\mathfrak {sl}_2$ means
$\mathfrak {sl}_2$ means ![]() $\langle f_3,h_3,e_3\rangle _{{{\mathbb {C}}}}$.
$\langle f_3,h_3,e_3\rangle _{{{\mathbb {C}}}}$.
Lemma 6.2 Let ![]() $\eta \otimes e_3^{2}f_3$ be a summand of
$\eta \otimes e_3^{2}f_3$ be a summand of ![]() ${\sf m}(\Delta _2^{3})$. Then
${\sf m}(\Delta _2^{3})$. Then ![]() $\eta$ acts as
$\eta$ acts as ![]() $\frac {48}{5}\mathrm {ad}(f_3)$ on
$\frac {48}{5}\mathrm {ad}(f_3)$ on ![]() $\langle e_3,f_3,h_3\rangle _{{{\mathbb {C}}}}$ and as
$\langle e_3,f_3,h_3\rangle _{{{\mathbb {C}}}}$ and as ![]() $\frac {42}{5}\mathrm {ad}(f_3)$ on the
$\frac {42}{5}\mathrm {ad}(f_3)$ on the ![]() $11$-dimensional
$11$-dimensional ![]() $\mathfrak {sl}_2$-stable complement of this subspace.
$\mathfrak {sl}_2$-stable complement of this subspace.
Proof. In this case, one has to pay a special attention to the summand ![]() $8e_3^{3}f_3^{3}$ of
$8e_3^{3}f_3^{3}$ of ![]() $\Delta _2^{3}$. In the product
$\Delta _2^{3}$. In the product ![]() $(e_3f_3)(e_3f_3)(e_3f_3)$, there are six choices of
$(e_3f_3)(e_3f_3)(e_3f_3)$, there are six choices of ![]() $(e_3,e_3,f_3)$ such that
$(e_3,e_3,f_3)$ such that ![]() $f_3$ and one of the elements
$f_3$ and one of the elements ![]() $e_3$ belong to one and the same copy of
$e_3$ belong to one and the same copy of ![]() $\Delta _2$; there are also three other choices. These first six choices are absorbed in
$\Delta _2$; there are also three other choices. These first six choices are absorbed in ![]() $({3!3!}/{6!}) 24 {\sf m}(f_3\Delta _2)$. Note that
$({3!3!}/{6!}) 24 {\sf m}(f_3\Delta _2)$. Note that ![]() $ ({3!\times 3! \times 24}/{6!})=\frac {6}{5}$. The contribution to
$ ({3!\times 3! \times 24}/{6!})=\frac {6}{5}$. The contribution to ![]() $\eta$ of the three other choices is
$\eta$ of the three other choices is ![]() $({3!3!}/{6!}) 24 {\sf m}(e_3f_3^{2})$. Hence
$({3!3!}/{6!}) 24 {\sf m}(e_3f_3^{2})$. Hence ![]() $\eta =\frac {6}{5}({\sf m}(f_3\Delta _2)+{\sf m}(e_3f_3^{2}))$.
$\eta =\frac {6}{5}({\sf m}(f_3\Delta _2)+{\sf m}(e_3f_3^{2}))$.
The element ![]() $\varpi (\Delta _2)\in {{\mathcal {U}}}(\mathfrak g)$ acts on
$\varpi (\Delta _2)\in {{\mathcal {U}}}(\mathfrak g)$ acts on ![]() $\mathfrak g$ as a scalar. That scalar is
$\mathfrak g$ as a scalar. That scalar is ![]() $8$ in our case. According to Lemma 5.4, the sum
$8$ in our case. According to Lemma 5.4, the sum ![]() $\sum _{i} x_i f_3 x_i\in {{\mathcal {U}}}(\mathfrak g)$ is equal to
$\sum _{i} x_i f_3 x_i\in {{\mathcal {U}}}(\mathfrak g)$ is equal to ![]() ${\mathcal {H}}f_3 -4 f_3$. Thus,
${\mathcal {H}}f_3 -4 f_3$. Thus, ![]() ${\sf m}(f_3\Delta _2) = (8-\frac {4}{3})\mathrm {ad}(f_3)$ and
${\sf m}(f_3\Delta _2) = (8-\frac {4}{3})\mathrm {ad}(f_3)$ and ![]() $\frac {6}{5}{\sf m}(f_3\Delta _2)=8\mathrm {ad}(f_3)$.
$\frac {6}{5}{\sf m}(f_3\Delta _2)=8\mathrm {ad}(f_3)$.
Now consider ![]() $\eta _0=(e_3f_3^{2}+f_3^{2}e_3+f_3e_3f_3)\in {{\mathcal {U}}}(\mathfrak {sl}_2)$. Clearly,
$\eta _0=(e_3f_3^{2}+f_3^{2}e_3+f_3e_3f_3)\in {{\mathcal {U}}}(\mathfrak {sl}_2)$. Clearly, ![]() ${\eta }_0$ acts as zero on a trivial
${\eta }_0$ acts as zero on a trivial ![]() $\mathfrak {sl}_2$-module; for the defining representation on
$\mathfrak {sl}_2$-module; for the defining representation on ![]() ${{\mathbb {C}}}^{2}=\langle v_1,v_2\rangle _{{{\mathbb {C}}}}$ with
${{\mathbb {C}}}^{2}=\langle v_1,v_2\rangle _{{{\mathbb {C}}}}$ with ![]() $e_3v_1=0$, one obtains
$e_3v_1=0$, one obtains ![]() ${\eta }_0(v_1)=v_2$ and
${\eta }_0(v_1)=v_2$ and ![]() ${\eta }_0(v_2)=0$. This suffices to state that
${\eta }_0(v_2)=0$. This suffices to state that ![]() $\frac {6}{5}{\sf m}(e_3f_3^{2})$ acts as
$\frac {6}{5}{\sf m}(e_3f_3^{2})$ acts as ![]() $\frac {2}{5}\mathrm {ad}(f_3)$ on the
$\frac {2}{5}\mathrm {ad}(f_3)$ on the ![]() $\mathfrak {sl}_2$-stable complement of
$\mathfrak {sl}_2$-stable complement of ![]() $\langle f_3,h_3,e_3\rangle _{{{\mathbb {C}}}}$. Finally,
$\langle f_3,h_3,e_3\rangle _{{{\mathbb {C}}}}$. Finally, ![]() ${\eta }_0(f_3)=0$ by the obvious reasons,
${\eta }_0(f_3)=0$ by the obvious reasons, ![]() ${\eta }_0(e_3)=-2h_3-2h_3=4\mathrm {ad}(f_3)(e_3)$ and
${\eta }_0(e_3)=-2h_3-2h_3=4\mathrm {ad}(f_3)(e_3)$ and ![]() ${\eta }_0(h_3)=4\mathrm {ad}(f_3)(h_3)$ as well, since
${\eta }_0(h_3)=4\mathrm {ad}(f_3)(h_3)$ as well, since ![]() ${\eta }_0$ acts on
${\eta }_0$ acts on ![]() $\mathfrak g$ as an element of
$\mathfrak g$ as an element of ![]() $\mathfrak {so}(\mathfrak g)$. All computations are done now and the proof is finished.
$\mathfrak {so}(\mathfrak g)$. All computations are done now and the proof is finished.
Let ![]() ${\sf pr}\!:\mathfrak {so}_7\to \mathfrak g$ be the orthogonal projection. In order to work with
${\sf pr}\!:\mathfrak {so}_7\to \mathfrak g$ be the orthogonal projection. In order to work with ![]() $\Delta _6$, one needs to compute the images under
$\Delta _6$, one needs to compute the images under ![]() ${\sf pr}$ of
${\sf pr}$ of ![]() $F_{ij}=E_{ij}-E_{(8-j)(8-i)}\in \mathfrak {so}_7$. For the elements of
$F_{ij}=E_{ij}-E_{(8-j)(8-i)}\in \mathfrak {so}_7$. For the elements of ![]() $\mathfrak {gl}_3\subset \mathfrak {so}_6$, this is easy, the task reduces to
$\mathfrak {gl}_3\subset \mathfrak {so}_6$, this is easy, the task reduces to ![]() $F_{ii}$ with
$F_{ii}$ with ![]() $1\leqslant i\leqslant 3$, where we have
$1\leqslant i\leqslant 3$, where we have
The elements of ![]() $F_{ij}\in \mathfrak {so}_6$ with
$F_{ij}\in \mathfrak {so}_6$ with ![]() $1\leqslant i\leqslant 3$,
$1\leqslant i\leqslant 3$, ![]() $4\leqslant j\leqslant 6$ project with the coefficient
$4\leqslant j\leqslant 6$ project with the coefficient ![]() $\frac {1}{3}$ on the corresponding letters in (6.1), e.g,
$\frac {1}{3}$ on the corresponding letters in (6.1), e.g, ![]() ${\sf pr}(F_{14})=\frac {-1}{3}{{\tt \beta }}$,
${\sf pr}(F_{14})=\frac {-1}{3}{{\tt \beta }}$, ![]() ${\sf pr}(F_{15})=\frac {1}{3}{{\tt \gamma }}$, and so on. The elements
${\sf pr}(F_{15})=\frac {1}{3}{{\tt \gamma }}$, and so on. The elements ![]() $F_{i7}$ project with the coefficient
$F_{i7}$ project with the coefficient ![]() $\frac {\sqrt {2}}{3}$ on the corresponding letters, e.g,
$\frac {\sqrt {2}}{3}$ on the corresponding letters, e.g, ![]() ${\sf pr}(F_{17})=\frac {\sqrt {2}}{3}{{\tt a}}$. Finally, the elements
${\sf pr}(F_{17})=\frac {\sqrt {2}}{3}{{\tt a}}$. Finally, the elements ![]() $F_{7i}$ project with the coefficient
$F_{7i}$ project with the coefficient ![]() $\frac {-\sqrt {2}}{3}$ on the corresponding letters, e.g,
$\frac {-\sqrt {2}}{3}$ on the corresponding letters, e.g, ![]() ${\sf pr}(F_{71})=\frac {-\sqrt {2}}{3} {{\tt \alpha }}$. An explicit formula for
${\sf pr}(F_{71})=\frac {-\sqrt {2}}{3} {{\tt \alpha }}$. An explicit formula for ![]() $\Delta _6$ can be obtained by replacing first
$\Delta _6$ can be obtained by replacing first ![]() $E_{ij}$ with
$E_{ij}$ with ![]() $F_{ij}$ in
$F_{ij}$ in ![]() $\Delta _6^{(7)}\in {{\mathcal {S}}}^{6}(\mathfrak {gl}_7)$ and then replacing
$\Delta _6^{(7)}\in {{\mathcal {S}}}^{6}(\mathfrak {gl}_7)$ and then replacing ![]() $F_{ij}$ with
$F_{ij}$ with ![]() ${\sf pr}(F_{ij})$. We write down some of the terms of
${\sf pr}(F_{ij})$. We write down some of the terms of ![]() $\Delta _6$:
$\Delta _6$:
 \begin{align*} \Delta_6 &=-\tilde\Delta_3^{2} - \tfrac{4}{27} {{\tt c}}^{3}e_3^{2}f_1 - \tfrac{4}{9} {{\tt c}}{{\tt \beta}}f_3 e_3^{2} f_1 + \tfrac{2}{3} {{\tt c}} {{\tt \alpha}}f_2 e_3^{2} f_1 + \tfrac{1}{9} {{\tt c}}{{\tt \alpha}}h_1 f_3 e_3^{2} -\tfrac{1}{27} {{\tt c}} {{\tt \alpha}}h_2 f_3 e_3^{2}\\ &\quad - \tfrac{4}{9} {{\tt b}}{{\tt \alpha}}f_2f_3e_3^{2}+\cdots . \end{align*}
\begin{align*} \Delta_6 &=-\tilde\Delta_3^{2} - \tfrac{4}{27} {{\tt c}}^{3}e_3^{2}f_1 - \tfrac{4}{9} {{\tt c}}{{\tt \beta}}f_3 e_3^{2} f_1 + \tfrac{2}{3} {{\tt c}} {{\tt \alpha}}f_2 e_3^{2} f_1 + \tfrac{1}{9} {{\tt c}}{{\tt \alpha}}h_1 f_3 e_3^{2} -\tfrac{1}{27} {{\tt c}} {{\tt \alpha}}h_2 f_3 e_3^{2}\\ &\quad - \tfrac{4}{9} {{\tt b}}{{\tt \alpha}}f_2f_3e_3^{2}+\cdots . \end{align*}
With this knowledge we can attack the computation of ![]() ${\sf m}(\Delta _6)$. The first challenge is to understand the term
${\sf m}(\Delta _6)$. The first challenge is to understand the term ![]() $\tilde \xi \otimes e_3^{2} f_1$.
$\tilde \xi \otimes e_3^{2} f_1$.
Lemma 6.3 For ![]() $\tilde \xi$ as above, we have
$\tilde \xi$ as above, we have ![]() $\tilde {\xi }(e_3)=\frac {5}{18}f_2$.
$\tilde {\xi }(e_3)=\frac {5}{18}f_2$.
Proof. Once again, we rely on a direct computation. The terms of ![]() $\tilde \Delta _3$ containing
$\tilde \Delta _3$ containing ![]() $e_3$ as a factor are
$e_3$ as a factor are ![]() $e_3f_1f_2$ and
$e_3f_1f_2$ and ![]() $e_3f_3(\frac {1}{2}h_1-\frac {1}{6}h_2)$. Thereby the contribution of
$e_3f_3(\frac {1}{2}h_1-\frac {1}{6}h_2)$. Thereby the contribution of ![]() $-\tilde \Delta _3^{2}$ to
$-\tilde \Delta _3^{2}$ to ![]() $\tilde \xi$ is
$\tilde \xi$ is
and this element of ![]() ${\rm End}(\mathfrak g)$ maps
${\rm End}(\mathfrak g)$ maps ![]() $e_3$ to
$e_3$ to ![]() $\frac {3}{20} f_2$.
$\frac {3}{20} f_2$.
Since ![]() $\sigma (\Delta _6)=\Delta _6$, the summands of
$\sigma (\Delta _6)=\Delta _6$, the summands of ![]() $\Delta _6$ that contain
$\Delta _6$ that contain ![]() $e_3^{2} f_1$ as a factor are of tri-degrees
$e_3^{2} f_1$ as a factor are of tri-degrees ![]() $(3,3,0)$ or
$(3,3,0)$ or ![]() $(1,4,1)$ with respect to the
$(1,4,1)$ with respect to the ![]() ${{\mathbb {Z}}}/3{{\mathbb {Z}}}$-grading
${{\mathbb {Z}}}/3{{\mathbb {Z}}}$-grading ![]() $\mathfrak g=({{\mathbb {C}}}^{3})^{*}\oplus \mathfrak {sl}_3\oplus {{\mathbb {C}}}^{3}$. By the weight considerations, the first possibility occurs only for the monomial
$\mathfrak g=({{\mathbb {C}}}^{3})^{*}\oplus \mathfrak {sl}_3\oplus {{\mathbb {C}}}^{3}$. By the weight considerations, the first possibility occurs only for the monomial ![]() ${{\tt c}}^{3} e_3^{2} f_1$. Record that
${{\tt c}}^{3} e_3^{2} f_1$. Record that
The coefficient of ![]() ${{\tt c}}^{3} e_3^{2} f_1$ in
${{\tt c}}^{3} e_3^{2} f_1$ in ![]() $\Delta _6$ is equal to
$\Delta _6$ is equal to ![]() $\frac {-4}{27}$. The monomials of the tri-degree
$\frac {-4}{27}$. The monomials of the tri-degree ![]() $(1,4,1)$ are
$(1,4,1)$ are ![]() ${{\tt c}}{{\tt \beta }}f_3 e_3^{2} f_1$ and
${{\tt c}}{{\tt \beta }}f_3 e_3^{2} f_1$ and ![]() ${{\tt c}} {{\tt \alpha }}f_2 e_3^{2} f_1$. Their coefficients are
${{\tt c}} {{\tt \alpha }}f_2 e_3^{2} f_1$. Their coefficients are ![]() $\frac {-4}{9}$ and
$\frac {-4}{9}$ and ![]() $\frac {2}{3}$, respectively.
$\frac {2}{3}$, respectively.
Next
and
Summing up, we have
and we are done.
Corollary 6.4 We have ![]() ${{\boldsymbol b}}= \frac {25}{108}$ and the invariant
${{\boldsymbol b}}= \frac {25}{108}$ and the invariant ![]() $\tilde H$ of Proposition 5.6 is equal to
$\tilde H$ of Proposition 5.6 is equal to ![]() $\Delta _6 - \frac {25}{108} \Delta _2^{3}$.
$\Delta _6 - \frac {25}{108} \Delta _2^{3}$.
Proof. By the definition of ![]() ${{\boldsymbol b}}$, we must have
${{\boldsymbol b}}$, we must have ![]() $(\tilde \xi -{{\boldsymbol b}}\xi )(e_3)=0$. From Lemmas 6.1 and 6.3 we obtain that
$(\tilde \xi -{{\boldsymbol b}}\xi )(e_3)=0$. From Lemmas 6.1 and 6.3 we obtain that ![]() ${{\boldsymbol b}}=\frac {5}{18}\times \frac {5}{6}=\frac {25}{108}$.
${{\boldsymbol b}}=\frac {5}{18}\times \frac {5}{6}=\frac {25}{108}$.
Next we deal with ![]() $\tilde \eta$ for the summand
$\tilde \eta$ for the summand ![]() $\tilde \eta \otimes e_3^{2}f_3$ of
$\tilde \eta \otimes e_3^{2}f_3$ of ![]() ${\sf m}(\Delta _6)$.
${\sf m}(\Delta _6)$.
Lemma 6.5 For ![]() $\tilde \eta$ as above, we have
$\tilde \eta$ as above, we have
and
Proof. We go through the relevant summands of ![]() $\Delta _6$. In
$\Delta _6$. In ![]() $-\tilde \Delta _3^{2}$, these are
$-\tilde \Delta _3^{2}$, these are ![]() $\frac {-1}{36}e_3^{2}f_3^{2}(3h_1-h_2)^{2}$ and
$\frac {-1}{36}e_3^{2}f_3^{2}(3h_1-h_2)^{2}$ and ![]() $\frac {-1}{3} e_3^{2} f_1 f_2 f_3 (3h_1-h_2)$. The corresponding contributions to
$\frac {-1}{3} e_3^{2} f_1 f_2 f_3 (3h_1-h_2)$. The corresponding contributions to ![]() $\tilde \eta$ are
$\tilde \eta$ are
multiplied by ![]() $\frac {1}{20}$. We are going to keep the factor
$\frac {1}{20}$. We are going to keep the factor ![]() $\frac {1}{20}$ in the background. Note that
$\frac {1}{20}$ in the background. Note that ![]() ${\sf m}(f_3(3h_1-h_2)^{2})$ acts on
${\sf m}(f_3(3h_1-h_2)^{2})$ acts on ![]() ${{\tt a}}$ as
${{\tt a}}$ as ![]() $4\mathrm {ad}(f_3)$, and hence we add
$4\mathrm {ad}(f_3)$, and hence we add ![]() $\frac {-2}{9}$. Since
$\frac {-2}{9}$. Since ![]() $2-4+2=0$, the second of the above elements acts on
$2-4+2=0$, the second of the above elements acts on ![]() ${{\tt a}}$ as zero. If we consider the action on
${{\tt a}}$ as zero. If we consider the action on ![]() $h_3$ instead, then the contribution of the first term is zero and
$h_3$ instead, then the contribution of the first term is zero and ![]() ${\sf m}(f_1f_2(3h_1-h_2))$ acts as
${\sf m}(f_1f_2(3h_1-h_2))$ acts as ![]() $\mathrm {ad}([f_1,f_2])=-\mathrm {ad}(f_3)$.
$\mathrm {ad}([f_1,f_2])=-\mathrm {ad}(f_3)$.
On account of ![]() $\sigma$, the other relevant terms have tri-degrees
$\sigma$, the other relevant terms have tri-degrees ![]() $(3,3,0)$,
$(3,3,0)$, ![]() $(0,3,3)$,
$(0,3,3)$, ![]() $(1,4,1)$, where the former two possibilities occur for
$(1,4,1)$, where the former two possibilities occur for ![]() $\frac {4}{27} {{\tt c}}^{2}{{\tt b}}e_3^{2}f_3$ and
$\frac {4}{27} {{\tt c}}^{2}{{\tt b}}e_3^{2}f_3$ and ![]() $\frac {4}{27} {{\tt \alpha }}^{2}{{\tt \beta }}e_3^{2}f_3$. Here
$\frac {4}{27} {{\tt \alpha }}^{2}{{\tt \beta }}e_3^{2}f_3$. Here
 \begin{align*} {\sf m}({{\tt c}}^{2} {{\tt b}})(h_3)&=\tfrac{1}{3}(\mathrm{ad}({{\tt b}})\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt c}})+\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt b}})\mathrm{ad}({{\tt c}}))(h_3)\\ & = \tfrac{1}{3}(-2\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt c}})-4\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt \alpha}}))(h_3)=(-2\mathrm{ad}(f_3)-2\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt \alpha}}))(h_3). \end{align*}
\begin{align*} {\sf m}({{\tt c}}^{2} {{\tt b}})(h_3)&=\tfrac{1}{3}(\mathrm{ad}({{\tt b}})\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt c}})+\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt b}})\mathrm{ad}({{\tt c}}))(h_3)\\ & = \tfrac{1}{3}(-2\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt c}})-4\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt \alpha}}))(h_3)=(-2\mathrm{ad}(f_3)-2\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt \alpha}}))(h_3). \end{align*}
Since ![]() $[{{\tt \alpha }},h_3]={{\tt \alpha }}$ and
$[{{\tt \alpha }},h_3]={{\tt \alpha }}$ and ![]() $[{{\tt c}},{{\tt \alpha }}]=-3f_3$, the contribution in question is
$[{{\tt c}},{{\tt \alpha }}]=-3f_3$, the contribution in question is ![]() $\frac {4}{27}\mathrm {ad}(f_3)$. Similarly,
$\frac {4}{27}\mathrm {ad}(f_3)$. Similarly,
 \begin{align*} {\sf m}({{\tt \alpha}}^{2} {{\tt \beta}})(h_3)&=\tfrac{1}{3}(\mathrm{ad}({{\tt \beta}})\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt \alpha}})+\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt \beta}})\mathrm{ad}({{\tt \alpha}}))(h_3)\\ & = \tfrac{1}{3}(2\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt \alpha}})+4\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt c}}))(h_3)=(2\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt c}})-2\mathrm{ad}(f_3))(h_3). \end{align*}
\begin{align*} {\sf m}({{\tt \alpha}}^{2} {{\tt \beta}})(h_3)&=\tfrac{1}{3}(\mathrm{ad}({{\tt \beta}})\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt \alpha}})+\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt \beta}})\mathrm{ad}({{\tt \alpha}}))(h_3)\\ & = \tfrac{1}{3}(2\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt \alpha}})+4\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt c}}))(h_3)=(2\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt c}})-2\mathrm{ad}(f_3))(h_3). \end{align*}
Since ![]() $[{{\tt c}},h_3]={{\tt c}}$,
$[{{\tt c}},h_3]={{\tt c}}$, ![]() $[{{\tt \alpha }},{{\tt c}}]=3f_3$, we obtain again
$[{{\tt \alpha }},{{\tt c}}]=3f_3$, we obtain again ![]() $\frac {4}{27}\mathrm {ad}(f_3)$. A slightly different story happens at
$\frac {4}{27}\mathrm {ad}(f_3)$. A slightly different story happens at ![]() $a$, namely,
$a$, namely,
 \begin{align*} {\sf m}({{\tt c}}^{2} {{\tt b}})({{\tt a}})&=(-2\mathrm{ad}(f_3)-2\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt \alpha}}) +\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt b}}))({{\tt a}}) \\ & = (-2\mathrm{ad}(f_3) -2\mathrm{ad}(f_3)+ 4\mathrm{ad}(f_3))({{\tt a}})=(-4+4)\mathrm{ad}(f_3)({{\tt a}})=0, \\ {\sf m}({{\tt \alpha}}^{2} {{\tt \beta}})({{\tt a}})&=(2\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt c}}) -2\mathrm{ad}(f_3)+\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt \beta}}))({{\tt a}}) \\ & =(8-2-6)\mathrm{ad}(f_3) ({{\tt a}})=0. \end{align*}
\begin{align*} {\sf m}({{\tt c}}^{2} {{\tt b}})({{\tt a}})&=(-2\mathrm{ad}(f_3)-2\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt \alpha}}) +\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt b}}))({{\tt a}}) \\ & = (-2\mathrm{ad}(f_3) -2\mathrm{ad}(f_3)+ 4\mathrm{ad}(f_3))({{\tt a}})=(-4+4)\mathrm{ad}(f_3)({{\tt a}})=0, \\ {\sf m}({{\tt \alpha}}^{2} {{\tt \beta}})({{\tt a}})&=(2\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt c}}) -2\mathrm{ad}(f_3)+\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt \beta}}))({{\tt a}}) \\ & =(8-2-6)\mathrm{ad}(f_3) ({{\tt a}})=0. \end{align*} Now consider the terms of the tri-degree ![]() $(1,4,1)$. Let
$(1,4,1)$. Let ![]() $\varepsilon _i-\varepsilon _j$ be the weight of the fourth element from
$\varepsilon _i-\varepsilon _j$ be the weight of the fourth element from ![]() $\mathfrak {sl}_3$. Assume first that
$\mathfrak {sl}_3$. Assume first that ![]() $i\ne j$. Then
$i\ne j$. Then ![]() $\varepsilon _3-\varepsilon _1=(\varepsilon _i-\varepsilon _j)+\varepsilon _s-\varepsilon _l$ for some
$\varepsilon _3-\varepsilon _1=(\varepsilon _i-\varepsilon _j)+\varepsilon _s-\varepsilon _l$ for some ![]() $s$ and
$s$ and ![]() $l$. One of the possibilities is
$l$. One of the possibilities is ![]() $i=3, j=1$, and
$i=3, j=1$, and ![]() $s=l$. The other two come from the decomposition
$s=l$. The other two come from the decomposition ![]() $\varepsilon _1-\varepsilon _3=(\varepsilon _1-\varepsilon _2)+(\varepsilon _2-\varepsilon _3)$.
$\varepsilon _1-\varepsilon _3=(\varepsilon _1-\varepsilon _2)+(\varepsilon _2-\varepsilon _3)$.
In the case ![]() $s=l$, the relevant term is
$s=l$, the relevant term is ![]() $\frac {4}{9} e_3^{2}f_3^{2} {{\tt b}}{{\tt \beta }}$ and its contribution to
$\frac {4}{9} e_3^{2}f_3^{2} {{\tt b}}{{\tt \beta }}$ and its contribution to ![]() $\tilde \eta$ is
$\tilde \eta$ is ![]() $\frac {8}{9}{\sf m}(f_3 {{\tt b}}{{\tt \beta }})$. Since both
$\frac {8}{9}{\sf m}(f_3 {{\tt b}}{{\tt \beta }})$. Since both ![]() ${{\tt b}}$ and
${{\tt b}}$ and ![]() ${{\tt \beta }}$ commute with
${{\tt \beta }}$ commute with ![]() $f_3$ and
$f_3$ and ![]() $h_3$, we see that
$h_3$, we see that ![]() ${\sf m}(f_3 {{\tt b}}{{\tt \beta }})(h_3)=0$. Furthermore,
${\sf m}(f_3 {{\tt b}}{{\tt \beta }})(h_3)=0$. Furthermore,
In this way the summand ![]() $\frac {-28}{9}$ appears in the first formula of the lemma.
$\frac {-28}{9}$ appears in the first formula of the lemma.
In the case ![]() $s\ne l$, the relevant terms are
$s\ne l$, the relevant terms are ![]() $\frac {-4}{9} {{\tt b}}{{\tt \alpha }}f_2 f_3 e_3^{2}$ and
$\frac {-4}{9} {{\tt b}}{{\tt \alpha }}f_2 f_3 e_3^{2}$ and ![]() $\frac {-4}{9} {{\tt c}}{{\tt \beta }}f_1 f_3 e_3^{2}$. On
$\frac {-4}{9} {{\tt c}}{{\tt \beta }}f_1 f_3 e_3^{2}$. On ![]() $h_3$, each of the elements
$h_3$, each of the elements ![]() ${\sf m}({{\tt b}}{{\tt \alpha }}f_2)$,
${\sf m}({{\tt b}}{{\tt \alpha }}f_2)$, ![]() ${\sf m}({{\tt c}}{{\tt \beta }}f_1)$ acts as
${\sf m}({{\tt c}}{{\tt \beta }}f_1)$ acts as ![]() $\frac {-1}{2}\mathrm {ad}(f_3)$. Thus,
$\frac {-1}{2}\mathrm {ad}(f_3)$. Thus, ![]() $\frac {4}{9}$ appears in the second formula. Further,
$\frac {4}{9}$ appears in the second formula. Further,
 \begin{align*} {\sf m}({{\tt b}}{{\tt \alpha}}f_2)({{\tt a}})&=\tfrac{1}{6}(\mathrm{ad}(f_2)\mathrm{ad}({{\tt b}})\mathrm{ad}({{\tt \alpha}})+2\mathrm{ad}({{\tt \alpha}})\mathrm{ad}(f_2)\mathrm{ad}({{\tt b}}))({{\tt a}}) \\ &= \tfrac{1}{6}(\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt \alpha}})+2\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt c}}))({{\tt a}})= \tfrac{1}{2}\mathrm{ad}(f_3)({{\tt a}})+\mathrm{ad}(f_3)({{\tt a}})=\tfrac{3}{2}\mathrm{ad}(f_3)({{\tt a}}). \end{align*}
\begin{align*} {\sf m}({{\tt b}}{{\tt \alpha}}f_2)({{\tt a}})&=\tfrac{1}{6}(\mathrm{ad}(f_2)\mathrm{ad}({{\tt b}})\mathrm{ad}({{\tt \alpha}})+2\mathrm{ad}({{\tt \alpha}})\mathrm{ad}(f_2)\mathrm{ad}({{\tt b}}))({{\tt a}}) \\ &= \tfrac{1}{6}(\mathrm{ad}({{\tt c}})\mathrm{ad}({{\tt \alpha}})+2\mathrm{ad}({{\tt \alpha}})\mathrm{ad}({{\tt c}}))({{\tt a}})= \tfrac{1}{2}\mathrm{ad}(f_3)({{\tt a}})+\mathrm{ad}(f_3)({{\tt a}})=\tfrac{3}{2}\mathrm{ad}(f_3)({{\tt a}}). \end{align*}
In the same fashion ![]() ${\sf m}({{\tt c}}{{\tt \beta }}f_1)({{\tt a}})=\frac {3}{2}\mathrm {ad}(f_3)({{\tt a}})$. This justifies
${\sf m}({{\tt c}}{{\tt \beta }}f_1)({{\tt a}})=\frac {3}{2}\mathrm {ad}(f_3)({{\tt a}})$. This justifies ![]() $\frac {-4}{3}$ in the first formula.
$\frac {-4}{3}$ in the first formula.
The final term, which is ![]() $\frac {1}{27} {{\tt c}} {{\tt \alpha }} (3h_1-h_2) f_3 e_3^{2}$, fulfils the case
$\frac {1}{27} {{\tt c}} {{\tt \alpha }} (3h_1-h_2) f_3 e_3^{2}$, fulfils the case ![]() $i=j$,
$i=j$, ![]() $s=3$,
$s=3$, ![]() $l=1$. Here we have
$l=1$. Here we have ![]() ${\sf m}((3h_1-h_2){{\tt c}}{{\tt \alpha }})({{\tt a}})=6\mathrm {ad}(f_3)({{\tt a}})$, hence the last summand in the first formula is
${\sf m}((3h_1-h_2){{\tt c}}{{\tt \alpha }})({{\tt a}})=6\mathrm {ad}(f_3)({{\tt a}})$, hence the last summand in the first formula is ![]() $\frac {2}{9}$. Similarly,
$\frac {2}{9}$. Similarly,
This justifies ![]() $\frac {1}{27}$ in the second formula.
$\frac {1}{27}$ in the second formula.
Lemma 6.5 provides a different way to compute ![]() ${{\boldsymbol b}}$. Namely,
${{\boldsymbol b}}$. Namely, ![]() $\tilde \eta -{{\boldsymbol b}}\eta$ has to act on
$\tilde \eta -{{\boldsymbol b}}\eta$ has to act on ![]() $\mathfrak g$ as a scalar multiple of
$\mathfrak g$ as a scalar multiple of ![]() $\mathrm {ad}(f_3)$. Check
$\mathrm {ad}(f_3)$. Check
 $$\begin{gather} \bigg(\tilde\eta - \frac{25}{108}\eta\bigg)({{\tt a}})=\bigg(-\frac{2}{9}-\frac{25}{108}\times\frac{42}{5}\bigg) \mathrm{ad}(f_3)({{\tt a}}) = \frac{-13}{6}\mathrm{ad}(f_3)({{\tt a}}), \\ \bigg(\tilde\eta - \frac{25}{108}\eta\bigg)(h_3)=\bigg(\frac{1}{18}-\frac{5\times 48}{108}\bigg) \mathrm{ad}(f_3)(h_3) = \frac{-39}{18}\mathrm{ad}(f_3)(h_3) =\frac{-13}{6}\mathrm{ad}(f_3)(h_3). \nonumber \end{gather}$$
$$\begin{gather} \bigg(\tilde\eta - \frac{25}{108}\eta\bigg)({{\tt a}})=\bigg(-\frac{2}{9}-\frac{25}{108}\times\frac{42}{5}\bigg) \mathrm{ad}(f_3)({{\tt a}}) = \frac{-13}{6}\mathrm{ad}(f_3)({{\tt a}}), \\ \bigg(\tilde\eta - \frac{25}{108}\eta\bigg)(h_3)=\bigg(\frac{1}{18}-\frac{5\times 48}{108}\bigg) \mathrm{ad}(f_3)(h_3) = \frac{-39}{18}\mathrm{ad}(f_3)(h_3) =\frac{-13}{6}\mathrm{ad}(f_3)(h_3). \nonumber \end{gather}$$
In order to compute ![]() $R(1)$ and
$R(1)$ and ![]() $R(2)$, state first that according to (6.2),
$R(2)$, state first that according to (6.2), ![]() $\frac {-13}{6} \mathrm {ad}(f_3) \otimes e_3^{2} f_3$ is a summand of
$\frac {-13}{6} \mathrm {ad}(f_3) \otimes e_3^{2} f_3$ is a summand of ![]() ${\sf m}(\tilde H)$. This indicates that if
${\sf m}(\tilde H)$. This indicates that if ![]() ${\sf m}(\tilde H)$ is written as an element of
${\sf m}(\tilde H)$ is written as an element of ![]() ${{\mathcal {S}}}^{4}(\mathfrak g)$, then it has a term
${{\mathcal {S}}}^{4}(\mathfrak g)$, then it has a term ![]() $\frac {-13}{3} e_3^{2} f_3^{2}$, which is a summand of
$\frac {-13}{3} e_3^{2} f_3^{2}$, which is a summand of ![]() $\frac {-13}{12} \Delta _2^{2}$. Thus
$\frac {-13}{12} \Delta _2^{2}$. Thus ![]() ${\sf m}(\tilde H)=\frac {-13}{12} \Delta _2^{2}$. In terms of Lemma 5.4, we have
${\sf m}(\tilde H)=\frac {-13}{12} \Delta _2^{2}$. In terms of Lemma 5.4, we have
since ![]() $c_1=-4$ in our case. Making use of Theorem 3.11, we obtain the main result of this section:
$c_1=-4$ in our case. Making use of Theorem 3.11, we obtain the main result of this section:
is an element of ![]() $\mathfrak z({{\hat {\mathfrak g}}})$. Furthermore,
$\mathfrak z({{\hat {\mathfrak g}}})$. Furthermore, ![]() $S_1={\mathcal {H}}[-1]$ and
$S_1={\mathcal {H}}[-1]$ and ![]() $S_2$ form a complete set of Segal–Sugawara vectors for
$S_2$ form a complete set of Segal–Sugawara vectors for ![]() $\mathfrak g$.
$\mathfrak g$.
7. The orthogonal case
Now suppose that ![]() $\mathfrak g=\mathfrak {so}_n\subset \mathfrak {gl}_n$ with
$\mathfrak g=\mathfrak {so}_n\subset \mathfrak {gl}_n$ with ![]() $n\geqslant 7$. A suitable matrix realisation of
$n\geqslant 7$. A suitable matrix realisation of ![]() $\mathfrak g$ uses the elements
$\mathfrak g$ uses the elements ![]() $F_{i j}=E_{i j}-E_{j' i'}$ with
$F_{i j}=E_{i j}-E_{j' i'}$ with ![]() $i,j\in \{1,\ldots,n\}$,
$i,j\in \{1,\ldots,n\}$, ![]() $i'=n-i+1$. We will be working with the coefficients
$i'=n-i+1$. We will be working with the coefficients ![]() $\Phi _{2k}\in {{\mathcal {S}}}^{2k}(\mathfrak g)^{\mathfrak g}$ of
$\Phi _{2k}\in {{\mathcal {S}}}^{2k}(\mathfrak g)^{\mathfrak g}$ of
The generating invariants of this type appeared in [Reference Molev and YakimovaMY19, § 3] in connection with the symmetrisation map and they can be used in (2.4) as well. In [Reference MolevMol18, Reference Molev and YakimovaMY19], the elements ![]() $\Phi _{2k}$ are called permanents, but they are not the permanents of matrices in the usual sense. Set
$\Phi _{2k}$ are called permanents, but they are not the permanents of matrices in the usual sense. Set ![]() $\mathfrak h=\langle F_{jj} \mid 1\leqslant j\leqslant \ell \rangle _{{{\mathbb {C}}}}$.
$\mathfrak h=\langle F_{jj} \mid 1\leqslant j\leqslant \ell \rangle _{{{\mathbb {C}}}}$.
In general, ![]() $\det (I_n- qA)^{-1}=\det (I_n+qA+q^{2} A^{2}+\cdots )$ for
$\det (I_n- qA)^{-1}=\det (I_n+qA+q^{2} A^{2}+\cdots )$ for ![]() $A\in \mathfrak {gl}_n$. In particular,
$A\in \mathfrak {gl}_n$. In particular, ![]() ${\Phi _{2k}}|_{\mathfrak h}$ is equal to the homogeneous part of degree
${\Phi _{2k}}|_{\mathfrak h}$ is equal to the homogeneous part of degree ![]() $2k$ of
$2k$ of
 \[ \prod_{j=1}^{\ell} (1+ F_{jj}^{2}+ F_{jj}^{4}+ F_{jj}^{6} + \cdots) . \]
\[ \prod_{j=1}^{\ell} (1+ F_{jj}^{2}+ F_{jj}^{4}+ F_{jj}^{6} + \cdots) . \]
By the construction, ![]() ${\sf m}(\Phi _{2k})$ is a polynomial function on
${\sf m}(\Phi _{2k})$ is a polynomial function on ![]() $(\Lambda ^{2}\mathfrak g\oplus \mathfrak g)^{*}\cong \Lambda ^{2}\mathfrak g\oplus \mathfrak g$. Set
$(\Lambda ^{2}\mathfrak g\oplus \mathfrak g)^{*}\cong \Lambda ^{2}\mathfrak g\oplus \mathfrak g$. Set
 \[ {{\boldsymbol f}}={\sf m}(\Phi_{2k})|_{\Lambda^{2}\mathfrak g\oplus\mathfrak h} \quad \text{and write} \quad {{\boldsymbol f}}=\sum_{\nu}^{L} \xi_\nu\otimes {{\boldsymbol H}}_{\nu}, \]
\[ {{\boldsymbol f}}={\sf m}(\Phi_{2k})|_{\Lambda^{2}\mathfrak g\oplus\mathfrak h} \quad \text{and write} \quad {{\boldsymbol f}}=\sum_{\nu}^{L} \xi_\nu\otimes {{\boldsymbol H}}_{\nu}, \]
where ![]() ${{\boldsymbol H}}_{\nu }\in {{\mathcal {S}}}^{2k-3}(\mathfrak h)$ are linearly independent monomials in
${{\boldsymbol H}}_{\nu }\in {{\mathcal {S}}}^{2k-3}(\mathfrak h)$ are linearly independent monomials in ![]() $\{F_{jj}\}$ and
$\{F_{jj}\}$ and ![]() $\xi _\nu \in \Lambda ^{2}\mathfrak g$. Note that each
$\xi _\nu \in \Lambda ^{2}\mathfrak g$. Note that each ![]() $\Phi _{2k}$ is an invariant of
$\Phi _{2k}$ is an invariant of ![]() ${\rm Aut}(\mathfrak g)$. Since
${\rm Aut}(\mathfrak g)$. Since ![]() $\Phi _{2k}$ is an element of
$\Phi _{2k}$ is an element of ![]() $\mathfrak h$-weight zero, each
$\mathfrak h$-weight zero, each ![]() $\xi _\nu$ is also of weight zero. Hence one can say that
$\xi _\nu$ is also of weight zero. Hence one can say that ![]() ${{\boldsymbol f}}$ is an invariant of
${{\boldsymbol f}}$ is an invariant of ![]() $W(\mathfrak g,\mathfrak h)$.
$W(\mathfrak g,\mathfrak h)$.
Let ![]() $\sigma \in {\rm Aut}(\mathfrak g)$ be an involution such that
$\sigma \in {\rm Aut}(\mathfrak g)$ be an involution such that ![]() $\mathfrak g_0=\mathfrak g^{\sigma }\cong \mathfrak {so}_{n-1}$,
$\mathfrak g_0=\mathfrak g^{\sigma }\cong \mathfrak {so}_{n-1}$, ![]() $\sigma (F_{11})=-F_{11}$, i.e.
$\sigma (F_{11})=-F_{11}$, i.e. ![]() $F_{11}\in \mathfrak g_1$, and
$F_{11}\in \mathfrak g_1$, and ![]() $\sigma (F_{ss})=F_{ss}$ for
$\sigma (F_{ss})=F_{ss}$ for ![]() $\ell \geqslant s>1$. Then
$\ell \geqslant s>1$. Then ![]() $\mathfrak g_{0,F_{11}}:=(\mathfrak g_0)_{F_{11}}\cong \mathfrak {so}_{n-2}$. Such an involution
$\mathfrak g_{0,F_{11}}:=(\mathfrak g_0)_{F_{11}}\cong \mathfrak {so}_{n-2}$. Such an involution ![]() $\sigma$ is not unique and we fix it by assuming that
$\sigma$ is not unique and we fix it by assuming that
The centraliser ![]() $\mathfrak g_{1,F_{11}}$ of
$\mathfrak g_{1,F_{11}}$ of ![]() $F_{11}$ in
$F_{11}$ in ![]() $\mathfrak g_1$ is equal to
$\mathfrak g_1$ is equal to ![]() ${{\mathbb {C}}}F_{11}$. This property defines an involution of rank one. Set
${{\mathbb {C}}}F_{11}$. This property defines an involution of rank one. Set ![]() $\mathfrak h_0=\langle F_{ss} \mid \ell \geqslant s>1\rangle _{{{\mathbb {C}}}}$.
$\mathfrak h_0=\langle F_{ss} \mid \ell \geqslant s>1\rangle _{{{\mathbb {C}}}}$.
By the construction, the map ![]() ${\sf m}$ is
${\sf m}$ is ![]() ${\rm Aut}(\mathfrak g)$-equivariant. Here the group
${\rm Aut}(\mathfrak g)$-equivariant. Here the group ![]() ${\rm Aut}(\mathfrak g)\subset {{\rm GL}}(\mathfrak g)$ acts on
${\rm Aut}(\mathfrak g)\subset {{\rm GL}}(\mathfrak g)$ acts on ![]() $\mathfrak {so}(\mathfrak g)\subset \mathfrak {gl}(\mathfrak g)$ via conjugation. In particular,
$\mathfrak {so}(\mathfrak g)\subset \mathfrak {gl}(\mathfrak g)$ via conjugation. In particular, ![]() $\sigma$ acts as
$\sigma$ acts as ![]() $-{{\rm id}}$ on
$-{{\rm id}}$ on ![]() $\mathfrak g_0\wedge \mathfrak g_1\subset \mathfrak {so}(\mathfrak g)$ and as
$\mathfrak g_0\wedge \mathfrak g_1\subset \mathfrak {so}(\mathfrak g)$ and as ![]() ${{\rm id}}$ on the subspaces
${{\rm id}}$ on the subspaces ![]() $\Lambda ^{2}\mathfrak g_0$ and
$\Lambda ^{2}\mathfrak g_0$ and ![]() $\Lambda ^{2}\mathfrak g_1$. For the future use, record:
$\Lambda ^{2}\mathfrak g_1$. For the future use, record: ![]() ${\sf m}(F_{ii}^{3})=F_{ii}$ and if
${\sf m}(F_{ii}^{3})=F_{ii}$ and if ![]() $i\ne j,j'$, then
$i\ne j,j'$, then ![]() ${\sf m}(F_{ii}F_{jj}^{2})$ acts as
${\sf m}(F_{ii}F_{jj}^{2})$ acts as ![]() ${{\rm id}}$ on
${{\rm id}}$ on ![]() $F_{ij}=-F_{j'i'}$,
$F_{ij}=-F_{j'i'}$, ![]() $F_{ij'}=-F_{ji'}$, as
$F_{ij'}=-F_{ji'}$, as ![]() $-{{\rm id}}$ on
$-{{\rm id}}$ on ![]() $F_{ji}=-F_{i'j'}$,
$F_{ji}=-F_{i'j'}$, ![]() $F_{j'i}=-F_{i'j}$, and as zero on all other elements
$F_{j'i}=-F_{i'j}$, and as zero on all other elements ![]() $F_{uw}$. In particular,
$F_{uw}$. In particular, ![]() ${\sf m}(F_{ii}F_{jj}^{2})\not \in \mathfrak g$ if
${\sf m}(F_{ii}F_{jj}^{2})\not \in \mathfrak g$ if ![]() $i\not \in \{j,j'\}$.
$i\not \in \{j,j'\}$.
Lemma 7.1 Suppose that ![]() ${{\boldsymbol H}}_\nu =F_{11}^{\beta _1}\ldots F_{\ell \ell }^{\beta _\ell }$ and
${{\boldsymbol H}}_\nu =F_{11}^{\beta _1}\ldots F_{\ell \ell }^{\beta _\ell }$ and ![]() $\xi _\nu \ne 0$. Then there is exactly one odd
$\xi _\nu \ne 0$. Then there is exactly one odd ![]() $\beta _j$ with
$\beta _j$ with ![]() $1\leqslant j\leqslant \ell$. Furthermore, if
$1\leqslant j\leqslant \ell$. Furthermore, if ![]() $\beta _1$ is odd, then
$\beta _1$ is odd, then
Proof. Without loss of generality assume that ![]() $\beta _j$ is odd for
$\beta _j$ is odd for ![]() $j\leqslant u$ and is even for
$j\leqslant u$ and is even for ![]() $j>u$. Let
$j>u$. Let ![]() $\sigma _j\in {\rm Aut}(\mathfrak g)$ with
$\sigma _j\in {\rm Aut}(\mathfrak g)$ with ![]() $2\leqslant j\leqslant u$ be an involution of rank one such that
$2\leqslant j\leqslant u$ be an involution of rank one such that ![]() $\sigma _j(F_{jj})=-1$ and
$\sigma _j(F_{jj})=-1$ and ![]() $\sigma _j(F_{ss})=F_{ss}$ for
$\sigma _j(F_{ss})=F_{ss}$ for ![]() $s\ne j,j'$. Following the case of
$s\ne j,j'$. Following the case of ![]() $\sigma _1=\sigma$, fix
$\sigma _1=\sigma$, fix ![]() $\sigma _j$ by setting
$\sigma _j$ by setting
As we have already mentioned, ![]() $\sigma _j(\Phi _{2k})=\Phi _{2k}$ for each
$\sigma _j(\Phi _{2k})=\Phi _{2k}$ for each ![]() $j$. Thereby
$j$. Thereby ![]() ${\sf m}(\Phi _{2k})$ is a
${\sf m}(\Phi _{2k})$ is a ![]() $\sigma _j$-invariant as well. At the same time
$\sigma _j$-invariant as well. At the same time ![]() $\sigma _j({\boldsymbol H}_\nu )=-{\boldsymbol H}_{\nu }$ by the construction. Hence
$\sigma _j({\boldsymbol H}_\nu )=-{\boldsymbol H}_{\nu }$ by the construction. Hence ![]() $\sigma _j(\xi _\nu )=-\xi _\nu$ for each
$\sigma _j(\xi _\nu )=-\xi _\nu$ for each ![]() $1\leqslant j\leqslant u$.
$1\leqslant j\leqslant u$.
The above discussion has clarified, how involutions ![]() $\sigma _j$ act on
$\sigma _j$ act on ![]() $\Lambda ^{2}\mathfrak g={\sf m}({{\mathcal {S}}}^{3}(\mathfrak g))$. In particular, we must have
$\Lambda ^{2}\mathfrak g={\sf m}({{\mathcal {S}}}^{3}(\mathfrak g))$. In particular, we must have ![]() $\xi _\nu \in \mathfrak g_0 \wedge \mathfrak g_1$. We know also that
$\xi _\nu \in \mathfrak g_0 \wedge \mathfrak g_1$. We know also that ![]() $\xi _\nu$ is an element of
$\xi _\nu$ is an element of ![]() $\mathfrak h$-weight zero and that
$\mathfrak h$-weight zero and that ![]() $F_{11}\in \mathfrak h$. Recall that
$F_{11}\in \mathfrak h$. Recall that ![]() $\mathfrak g_{1,F_{11}}={{\mathbb {C}}}F_{11}$. The decomposition
$\mathfrak g_{1,F_{11}}={{\mathbb {C}}}F_{11}$. The decomposition ![]() $\mathfrak g_0=\mathfrak g_{0,F_{11}}\oplus [F_{11},\mathfrak g_1]$ indicates that
$\mathfrak g_0=\mathfrak g_{0,F_{11}}\oplus [F_{11},\mathfrak g_1]$ indicates that
Both summands here are ![]() $\mathfrak h$-stable. Furthermore,
$\mathfrak h$-stable. Furthermore, ![]() $( \mathfrak g_{0,F_{11}}\wedge F_{11})^{\mathfrak h}$ is spanned by
$( \mathfrak g_{0,F_{11}}\wedge F_{11})^{\mathfrak h}$ is spanned by ![]() $F_{ss}\wedge F_{11}$ with
$F_{ss}\wedge F_{11}$ with ![]() $\ell \geqslant s>1$.
$\ell \geqslant s>1$.
The subspace ![]() $[F_{11},\mathfrak g_1]$ is spanned by
$[F_{11},\mathfrak g_1]$ is spanned by ![]() $F_{1i}-F_{i'1}$, where
$F_{1i}-F_{i'1}$, where ![]() $1< i< n$. For each
$1< i< n$. For each ![]() $i$, the element of the opposite
$i$, the element of the opposite ![]() $\mathfrak h_0$-weight in
$\mathfrak h_0$-weight in ![]() $\mathfrak g_1$ is
$\mathfrak g_1$ is ![]() $F_{1i'}+F_{i1}$. Note that
$F_{1i'}+F_{i1}$. Note that ![]() $(F_{1i}+F_{i'1})\wedge (F_{1i'}-F_{i1})$ is an eigenvector of
$(F_{1i}+F_{i'1})\wedge (F_{1i'}-F_{i1})$ is an eigenvector of ![]() $F_{11}$ if and only if
$F_{11}$ if and only if ![]() $i=i'$. Thus,
$i=i'$. Thus, ![]() $([F_{11},\mathfrak g_1] \wedge \mathfrak g_1)^{\mathfrak h}$ is a linear span of
$([F_{11},\mathfrak g_1] \wedge \mathfrak g_1)^{\mathfrak h}$ is a linear span of
with ![]() $1< i\leqslant i'$.
$1< i\leqslant i'$.
If ![]() $u>1$, then
$u>1$, then ![]() $u\geqslant 3$. The involution
$u\geqslant 3$. The involution ![]() $\sigma _2$ acts on
$\sigma _2$ acts on ![]() $F_{1i}\pm F_{i'1}$ as
$F_{1i}\pm F_{i'1}$ as ![]() ${{\rm id}}$ if
${{\rm id}}$ if ![]() $2< i< n-1$. Therefore
$2< i< n-1$. Therefore ![]() $\xi _\nu$ has to be a linear combination of
$\xi _\nu$ has to be a linear combination of ![]() $F_{22} \wedge F_{11}$ and
$F_{22} \wedge F_{11}$ and ![]() $\Xi (2)$. At the same time,
$\Xi (2)$. At the same time, ![]() $\sigma _3$ acts as
$\sigma _3$ acts as ![]() ${{\rm id}}$ on both these vectors. This contradiction proves that
${{\rm id}}$ on both these vectors. This contradiction proves that ![]() $u=1$.
$u=1$.
Remark Lemma 7.1 is valid for any homogeneous ![]() $\Phi \in {{\mathcal {S}}}(\mathfrak g)^{{\rm Aut}(\mathfrak g)}$.
$\Phi \in {{\mathcal {S}}}(\mathfrak g)^{{\rm Aut}(\mathfrak g)}$.
Now fix ![]() ${\boldsymbol H}={{\boldsymbol H}}_\nu =F_{11}^{2b_1-1} F_{22}^{2b_2} \ldots F_{\ell \ell }^{2b_\ell }$ with
${\boldsymbol H}={{\boldsymbol H}}_\nu =F_{11}^{2b_1-1} F_{22}^{2b_2} \ldots F_{\ell \ell }^{2b_\ell }$ with ![]() $b_j\in {{\mathbb {Z}}}_{\geqslant 0}$ and
$b_j\in {{\mathbb {Z}}}_{\geqslant 0}$ and ![]() $b_1\geqslant 1$. The task is to compute
$b_1\geqslant 1$. The task is to compute ![]() $\xi =\xi _\nu$. Set
$\xi =\xi _\nu$. Set ![]() $b_{j'}=b_j$ for
$b_{j'}=b_j$ for ![]() $j\leqslant \ell$. In type B, set also
$j\leqslant \ell$. In type B, set also ![]() $b_{\ell +1}=0$. Below we list the terms
$b_{\ell +1}=0$. Below we list the terms ![]() $Y_3$ such that
$Y_3$ such that ![]() $Y_3 {{\boldsymbol H}}$ is a summand of
$Y_3 {{\boldsymbol H}}$ is a summand of ![]() $\Phi _{2k}$:
$\Phi _{2k}$:
 \begin{equation} \begin{gathered} F_{11}^{3}, \quad F_{11}F_{jj}^{2}, \quad 2(b_1+1)(b_j+1)F_{11} F_{1j} F_{j1}, \quad (b_i+1)(b_j+1)F_{11} F_{ij} F_{ji}, \\ 2b_1(b_j+1)F_{1j}F_{j1} F_{jj}, \quad 2b_1(b_i+1)(b_j+1)F_{1i} F_{ij} F_{j1}, \end{gathered} \end{equation}
\begin{equation} \begin{gathered} F_{11}^{3}, \quad F_{11}F_{jj}^{2}, \quad 2(b_1+1)(b_j+1)F_{11} F_{1j} F_{j1}, \quad (b_i+1)(b_j+1)F_{11} F_{ij} F_{ji}, \\ 2b_1(b_j+1)F_{1j}F_{j1} F_{jj}, \quad 2b_1(b_i+1)(b_j+1)F_{1i} F_{ij} F_{j1}, \end{gathered} \end{equation}
where ![]() $1< i,j< n$ and
$1< i,j< n$ and ![]() $i\not \in \{j,j'\}$, and also in
$i\not \in \{j,j'\}$, and also in ![]() $F_{jj}$ we have
$F_{jj}$ we have ![]() $1< j\leqslant \ell$. When computing
$1< j\leqslant \ell$. When computing ![]() ${\sf m}$, one has to take into account the additional coefficients appearing from the powers of
${\sf m}$, one has to take into account the additional coefficients appearing from the powers of ![]() $F_{ii}$. For instance, in the case of
$F_{ii}$. For instance, in the case of ![]() $F_{11}^{3}$, this coefficient is
$F_{11}^{3}$, this coefficient is ![]() $\binom {2b_1+2}{3}$, for
$\binom {2b_1+2}{3}$, for ![]() $2b_1(b_j+1)F_{1j}F_{j1} F_{jj}$, the additional scalar factor is
$2b_1(b_j+1)F_{1j}F_{j1} F_{jj}$, the additional scalar factor is ![]() $2b_j+1$.
$2b_j+1$.
We will show that ![]() $\xi$ acts on
$\xi$ acts on ![]() $F_{ij}$ as
$F_{ij}$ as ![]() $c(i,j)F_{11}$ for some constant
$c(i,j)F_{11}$ for some constant ![]() $c(i,j)\in {{\mathbb {C}}}$, compute these constants and see that all of them are equal. Note that
$c(i,j)\in {{\mathbb {C}}}$, compute these constants and see that all of them are equal. Note that ![]() $[F_{11},F_{ij}]=0$ if
$[F_{11},F_{ij}]=0$ if ![]() $i,j\not \in \{1,n\}$.
$i,j\not \in \{1,n\}$.
Lemma 7.2 We have ![]() $\xi (F_{11})=0$, furthermore
$\xi (F_{11})=0$, furthermore ![]() $\xi (F_{ij})=0$ if
$\xi (F_{ij})=0$ if ![]() $i,j\not \in \{1,n\}$.
$i,j\not \in \{1,n\}$.
Proof. By a direct computation, we show that indeed ![]() $\xi (F_{11})=0$. Some expressions in (7.2) act on
$\xi (F_{11})=0$. Some expressions in (7.2) act on ![]() $F_{11}$ as zero by obvious reasons. If one takes into account that
$F_{11}$ as zero by obvious reasons. If one takes into account that ![]() $F_{1j}F_{11}F_{j1}+F_{j1}F_{11}F_{1j}$ acts as
$F_{1j}F_{11}F_{j1}+F_{j1}F_{11}F_{1j}$ acts as ![]() $[F_{j1},F_{j1}]$, this covers the first line of (7.2). The same argument takes care of
$[F_{j1},F_{j1}]$, this covers the first line of (7.2). The same argument takes care of ![]() ${\sf m}(F_{jj}F_{1j}F_{j1})$. It remains to calculate
${\sf m}(F_{jj}F_{1j}F_{j1})$. It remains to calculate ![]() $\eta ={\sf m}(F_{1i}F_{ij}F_{j1})(F_{11})$. Here we have
$\eta ={\sf m}(F_{1i}F_{ij}F_{j1})(F_{11})$. Here we have ![]() $6\eta =(F_{11}-F_{ii}) + (F_{jj}-F_{11})$. If we switch
$6\eta =(F_{11}-F_{ii}) + (F_{jj}-F_{11})$. If we switch ![]() $i$ and
$i$ and ![]() $j$, then the total sum is zero.
$j$, then the total sum is zero.
Since ![]() $(F_{ss}\wedge F_{11})(F_{11})=F_{ss}$ up to a non-zero scalar, Lemma 7.1 now implies that
$(F_{ss}\wedge F_{11})(F_{11})=F_{ss}$ up to a non-zero scalar, Lemma 7.1 now implies that
Hence ![]() $\xi (F_{ij})=0$ if
$\xi (F_{ij})=0$ if ![]() $i,j\not \in \{1,n\}$.
$i,j\not \in \{1,n\}$.
Lemma 7.3 Suppose that ![]() $n=2\ell$. Assume that
$n=2\ell$. Assume that ![]() $1< u< n$. Then
$1< u< n$. Then
and ![]() $C(1)$ is equal to
$C(1)$ is equal to
 \[ \binom{2b_1+2}{3} +\frac{2}{3} b_1 \sum_{j=2}^{\ell} (2b_j+1)(b_j+1) + \frac{8}{3} b_1(b_1+1) \sum_{j=2}^{\ell} (b_j+1)+ \frac{8}{3} b_1 \sum_{1< i< j\leqslant\ell} (b_i+1)(b_j+1). \]
\[ \binom{2b_1+2}{3} +\frac{2}{3} b_1 \sum_{j=2}^{\ell} (2b_j+1)(b_j+1) + \frac{8}{3} b_1(b_1+1) \sum_{j=2}^{\ell} (b_j+1)+ \frac{8}{3} b_1 \sum_{1< i< j\leqslant\ell} (b_i+1)(b_j+1). \]Proof. Recall that ![]() ${\sf m}(F_{11}^{3})=F_{11}$. This leads to the summand
${\sf m}(F_{11}^{3})=F_{11}$. This leads to the summand ![]() $\binom {2b_1+2}{3}$ of
$\binom {2b_1+2}{3}$ of ![]() $C(1)$. Consider
$C(1)$. Consider
with ![]() $1< j\leqslant \ell$. Here
$1< j\leqslant \ell$. Here ![]() $\xi _1^{(j)}(F_{1u})= \frac {1}{3}F_{1u}$ for
$\xi _1^{(j)}(F_{1u})= \frac {1}{3}F_{1u}$ for ![]() $u\not \in \{j,j'\}$ and
$u\not \in \{j,j'\}$ and ![]() $\xi _1^{(j)}(F_{1j})=(1-\frac {2}{3})F_{1j}$ as well as
$\xi _1^{(j)}(F_{1j})=(1-\frac {2}{3})F_{1j}$ as well as ![]() $\xi _1^{(j)}(F_{1j'})=(1-\frac {2}{3})F_{1j'}$. In
$\xi _1^{(j)}(F_{1j'})=(1-\frac {2}{3})F_{1j'}$. In ![]() $C(1)$, we have to add
$C(1)$, we have to add ![]() $\frac {1}{3}$ with the coefficients
$\frac {1}{3}$ with the coefficients
The next terms are ![]() $\xi _2^{(j)}={\sf m}(F_{11} F_{1j} F_{j1})$ with
$\xi _2^{(j)}={\sf m}(F_{11} F_{1j} F_{j1})$ with ![]() $1< j< n$. Here
$1< j< n$. Here ![]() $\xi _2^{(j)}(F_{1u})=\frac {1}{3}F_{1u}$ for
$\xi _2^{(j)}(F_{1u})=\frac {1}{3}F_{1u}$ for ![]() $u\not \in \{j,j'\}$. Furthermore,
$u\not \in \{j,j'\}$. Furthermore, ![]() $\xi _2^{(j)}(F_{1j})=\frac {2}{3}F_{1j}$ and
$\xi _2^{(j)}(F_{1j})=\frac {2}{3}F_{1j}$ and ![]() $\xi _2^{(j)}(F_{1j'})=0$. Adding
$\xi _2^{(j)}(F_{1j'})=0$. Adding ![]() $\xi _2^{(j)}$ and
$\xi _2^{(j)}$ and ![]() $\xi _2^{(j')}$ with
$\xi _2^{(j')}$ with ![]() $j\leqslant \ell$ and recalling the coefficient of
$j\leqslant \ell$ and recalling the coefficient of ![]() $\xi _2^{(j)}$, we obtain the summands
$\xi _2^{(j)}$, we obtain the summands ![]() $\frac {8}{3}(b_1+1)b_1(b_j+1)$.
$\frac {8}{3}(b_1+1)b_1(b_j+1)$.
Fix ![]() $1< i,j < n$ with
$1< i,j < n$ with ![]() $i\not \in \{j,j'\}$ and consider
$i\not \in \{j,j'\}$ and consider
An easy observation is that ![]() $\xi _4^{i,j}(F_{1u})=0$ if
$\xi _4^{i,j}(F_{1u})=0$ if ![]() $u\not \in \{i,i',j,j'\}$. Also
$u\not \in \{i,i',j,j'\}$. Also ![]() $\xi _3^{i,j}(F_{1u})=\frac {1}{6} F_{1u}$ in this case. Furthermore,
$\xi _3^{i,j}(F_{1u})=\frac {1}{6} F_{1u}$ in this case. Furthermore, ![]() $\xi _4^{i,j}(F_{1i})=\frac {1}{2}F_{1i}$ and
$\xi _4^{i,j}(F_{1i})=\frac {1}{2}F_{1i}$ and ![]() $\xi _4^{i,j}(F_{1i'})=\frac {1}{2}F_{1i'}$. A more lengthy calculation brings
$\xi _4^{i,j}(F_{1i'})=\frac {1}{2}F_{1i'}$. A more lengthy calculation brings
 \begin{gather*} \xi_3^{i,j}(F_{1i})=\tfrac{1}{6}F_{1i} - \tfrac{1}{6}((\mathrm{ad}(F_{1i})\mathrm{ad}(F_{j1})+\mathrm{ad}(F_{j1})\mathrm{ad}(F_{1i}))(F_{1j})=\tfrac{1}{6}F_{1i}-\tfrac{1}{6}F_{1i}=0; \\ \xi_3^{i,j}(F_{1j})=\tfrac{1}{6}F_{1j} +\tfrac{1}{6} \mathrm{ad}(F_{ij})(F_{1i}) =0; \quad \xi_3^{i,j}(F_{1j'})= \tfrac{1}{6} \mathrm{ad}(F_{1i})\mathrm{ad}(F_{j1})(F_{1i'})=-\tfrac{1}{6}F_{1j'}; \\ \xi_3^{i,j}(F_{1i'})= \tfrac{1}{6} \mathrm{ad}(F_{ij})\mathrm{ad}(F_{1i})(F_{ji'}) =\tfrac{1}{6} \mathrm{ad}(F_{ij}) (F_{j n})=-\tfrac{1}{6} F_{1i'}. \end{gather*}
\begin{gather*} \xi_3^{i,j}(F_{1i})=\tfrac{1}{6}F_{1i} - \tfrac{1}{6}((\mathrm{ad}(F_{1i})\mathrm{ad}(F_{j1})+\mathrm{ad}(F_{j1})\mathrm{ad}(F_{1i}))(F_{1j})=\tfrac{1}{6}F_{1i}-\tfrac{1}{6}F_{1i}=0; \\ \xi_3^{i,j}(F_{1j})=\tfrac{1}{6}F_{1j} +\tfrac{1}{6} \mathrm{ad}(F_{ij})(F_{1i}) =0; \quad \xi_3^{i,j}(F_{1j'})= \tfrac{1}{6} \mathrm{ad}(F_{1i})\mathrm{ad}(F_{j1})(F_{1i'})=-\tfrac{1}{6}F_{1j'}; \\ \xi_3^{i,j}(F_{1i'})= \tfrac{1}{6} \mathrm{ad}(F_{ij})\mathrm{ad}(F_{1i})(F_{ji'}) =\tfrac{1}{6} \mathrm{ad}(F_{ij}) (F_{j n})=-\tfrac{1}{6} F_{1i'}. \end{gather*}
Note that ![]() $\xi _4^{i,j}=\xi _4^{j,i}=\xi _4^{i',j'}$. Now fix
$\xi _4^{i,j}=\xi _4^{j,i}=\xi _4^{i',j'}$. Now fix ![]() $1< i< j\leqslant \ell$ and consider
$1< i< j\leqslant \ell$ and consider
Here ![]() $2b_1(b_i+1)(b_j+1)\xi _5^{i,j}$ is a summand of
$2b_1(b_i+1)(b_j+1)\xi _5^{i,j}$ is a summand of ![]() $ ({(2k)!}/{3!(2k-3)!}) \xi$. Moreover,
$ ({(2k)!}/{3!(2k-3)!}) \xi$. Moreover, ![]() $\xi _5^{i,j}(F_{1s})=\frac {4}{3}F_{1s}$ for each
$\xi _5^{i,j}(F_{1s})=\frac {4}{3}F_{1s}$ for each ![]() $1< s< n$. This justifies the last summand of
$1< s< n$. This justifies the last summand of ![]() $C(1)$.
$C(1)$.
Rearranging the expression for ![]() $C(1)$, one obtains
$C(1)$, one obtains
 \begin{equation} C(1)=\frac{2}{3} b_1 \biggl(\sum_{j=1}^{\ell} (b_j+1)(2b_j+1) + 4\sum_{1\leqslant i< j\leqslant\ell} (b_i+1)(b_j+1) \biggr). \end{equation}
\begin{equation} C(1)=\frac{2}{3} b_1 \biggl(\sum_{j=1}^{\ell} (b_j+1)(2b_j+1) + 4\sum_{1\leqslant i< j\leqslant\ell} (b_i+1)(b_j+1) \biggr). \end{equation}Lemma 7.4 Suppose that ![]() $n=2\ell +1$. Assume that
$n=2\ell +1$. Assume that ![]() $1< u< n$. Then
$1< u< n$. Then
and ![]() $\tilde C(1)$ is equal to
$\tilde C(1)$ is equal to
 \[ C(1)+ \frac{4}{3}b_1(b_1+1) + \frac{4}{3}b_1\sum_{1< i\leqslant\ell}(b_i+1)=C(1)+ \frac{4}{3} b_1 \sum_{1\leqslant j\leqslant\ell} (b_j+1). \]
\[ C(1)+ \frac{4}{3}b_1(b_1+1) + \frac{4}{3}b_1\sum_{1< i\leqslant\ell}(b_i+1)=C(1)+ \frac{4}{3} b_1 \sum_{1\leqslant j\leqslant\ell} (b_j+1). \]Proof. We have to take care of the instances, where ![]() $j=\ell +1=j'$. Here
$j=\ell +1=j'$. Here ![]() $F_{jj}=0$, thereby also
$F_{jj}=0$, thereby also ![]() $\xi _1^{(j)}=0$. By a direct calculation,
$\xi _1^{(j)}=0$. By a direct calculation, ![]() $\xi _2^{(j)}(F_{1u})=\frac {1}{3}F_{1u}$ for each
$\xi _2^{(j)}(F_{1u})=\frac {1}{3}F_{1u}$ for each ![]() $u$. Recall that
$u$. Recall that ![]() $\xi _2^{(j)}$ corresponds to
$\xi _2^{(j)}$ corresponds to ![]() $Y_3=2(b_1+1)(b_j+1)F_{11}F_{1j}F_{j1}$ in (7.2) and that the additional scalar factor in this case is
$Y_3=2(b_1+1)(b_j+1)F_{11}F_{1j}F_{j1}$ in (7.2) and that the additional scalar factor in this case is ![]() $2b_1$. Since
$2b_1$. Since ![]() $b_{\ell +1}=0$, we have to add
$b_{\ell +1}=0$, we have to add ![]() $\frac {4}{3}b_1(b_1+1)$ to
$\frac {4}{3}b_1(b_1+1)$ to ![]() $C(1)$.
$C(1)$.
The calculations for ![]() $\xi _3^{i,j}, \xi _3^{j,i}$, and
$\xi _3^{i,j}, \xi _3^{j,i}$, and ![]() $\xi _4^{i,j}$ have to be altered. The modifications are:
$\xi _4^{i,j}$ have to be altered. The modifications are:
and ![]() $\xi _5^{i,j}$ with
$\xi _5^{i,j}$ with ![]() $1< i< j=l+1$ has a simpler form, here
$1< i< j=l+1$ has a simpler form, here
The coefficient of this ![]() $\xi _5^{i,j}$ in
$\xi _5^{i,j}$ in ![]() $({(2k)!}/{3!(2k-3)!}) \xi$ is
$({(2k)!}/{3!(2k-3)!}) \xi$ is ![]() $2b_1(b_i+1)$ and
$2b_1(b_i+1)$ and ![]() $\xi _5^{i,j}(F_{1u})=\frac {2}{3} F_{1u}$ for all
$\xi _5^{i,j}(F_{1u})=\frac {2}{3} F_{1u}$ for all ![]() $u$. This justifies the second additional summand.
$u$. This justifies the second additional summand.
Proposition 7.5 For ![]() $\mathfrak g=\mathfrak {so}_{n}$, we have
$\mathfrak g=\mathfrak {so}_{n}$, we have ![]() ${\sf m}(\Phi _{2k})=R(k) \Phi _{2k-2}$, where
${\sf m}(\Phi _{2k})=R(k) \Phi _{2k-2}$, where
Proof. According to Lemmas 7.3 and 7.4, there is ![]() $c(1)\in {{\mathbb {C}}}$ such that
$c(1)\in {{\mathbb {C}}}$ such that ![]() $\xi (F_{1u})=c(1)F_{1u}$ for each
$\xi (F_{1u})=c(1)F_{1u}$ for each ![]() $1< u< n$. Since
$1< u< n$. Since ![]() $\xi \in \mathfrak {so}(\mathfrak g)$, we have also
$\xi \in \mathfrak {so}(\mathfrak g)$, we have also ![]() $\xi (F_{u1})= -c(1) F_{u1}$. Taking into account Lemma 7.2, we conclude that
$\xi (F_{u1})= -c(1) F_{u1}$. Taking into account Lemma 7.2, we conclude that ![]() $\xi =c(1)F_{11}$.
$\xi =c(1)F_{11}$.
Simplifying (7.3) and using Lemma 7.4, we obtain that
 \begin{align*} c(1)&=\frac{2}{3}b_1\frac{3!(2k-3)!}{(2k)!} \bigg(2\bigg(\sum_{j=1}^{\ell} b_j\bigg)^{2} + (4\ell-1)\bigg(\sum_{j=1}^{\ell} b_j\bigg)+\ell+ 2\ell(\ell-1)\bigg) \\ &= \frac{b_1}{k(2k-1)(k-1)} (2(k-1)^{2}+(4\ell-1)(k-1)+\ell(2\ell-1) ) \end{align*}
\begin{align*} c(1)&=\frac{2}{3}b_1\frac{3!(2k-3)!}{(2k)!} \bigg(2\bigg(\sum_{j=1}^{\ell} b_j\bigg)^{2} + (4\ell-1)\bigg(\sum_{j=1}^{\ell} b_j\bigg)+\ell+ 2\ell(\ell-1)\bigg) \\ &= \frac{b_1}{k(2k-1)(k-1)} (2(k-1)^{2}+(4\ell-1)(k-1)+\ell(2\ell-1) ) \end{align*}in type D and that
in type B. In both cases, the scalars ![]() $c(1)/b_1$ depend only on
$c(1)/b_1$ depend only on ![]() $k$ and
$k$ and ![]() $\ell$. Making use of the action of
$\ell$. Making use of the action of ![]() $W(\mathfrak g,\mathfrak h)$, we can conclude now that
$W(\mathfrak g,\mathfrak h)$, we can conclude now that ![]() ${\sf m}(\Phi _{2k})$ is a symmetric invariant and that it is equal to
${\sf m}(\Phi _{2k})$ is a symmetric invariant and that it is equal to ![]() $R(k) \Phi _{2k-2}$ with
$R(k) \Phi _{2k-2}$ with ![]() $R(k)\in \mathbb {Q}$. More explicitly,
$R(k)\in \mathbb {Q}$. More explicitly, ![]() $R(k)$ is equal to
$R(k)$ is equal to ![]() $2(k-1) ({c(1)}/{2b_1})= ({(k-1)c(1)}/{b_1})$.
$2(k-1) ({c(1)}/{2b_1})= ({(k-1)c(1)}/{b_1})$.
In type D, we have ![]() $2(k-1)^{2}+(4\ell -1)(k-1) = 2n(k-1)+(k-1)(2k-3)$ and
$2(k-1)^{2}+(4\ell -1)(k-1) = 2n(k-1)+(k-1)(2k-3)$ and ![]() $\ell (2\ell -1)=\binom {n}{2}$. Quite similarly, in type B, we have
$\ell (2\ell -1)=\binom {n}{2}$. Quite similarly, in type B, we have ![]() $\ell (2\ell -1)+2\ell =\ell (2\ell +1)=\binom {n}{2}$ and
$\ell (2\ell -1)+2\ell =\ell (2\ell +1)=\binom {n}{2}$ and
Therefore multiplying ![]() $c(1)$ with
$c(1)$ with ![]() $(k-1)/b_1$ we obtain the desired formula for
$(k-1)/b_1$ we obtain the desired formula for ![]() $R(k)$.
$R(k)$.
We have
 \begin{align*} R(k)&=\frac{1}{k(2k-1)} \bigg(\binom{n}{2} + 2n(k-1) + (k-1)(2k-3) \bigg) \\ &=\frac{1}{k(2k-1)}\bigg((k-1)(n+2k-3)+\frac{n}{2}(2k-2+n-1)\bigg)\\ &=\frac{(n+2k-3)(n+2k-2)}{2k(2k-1)} \end{align*}
\begin{align*} R(k)&=\frac{1}{k(2k-1)} \bigg(\binom{n}{2} + 2n(k-1) + (k-1)(2k-3) \bigg) \\ &=\frac{1}{k(2k-1)}\bigg((k-1)(n+2k-3)+\frac{n}{2}(2k-2+n-1)\bigg)\\ &=\frac{(n+2k-3)(n+2k-2)}{2k(2k-1)} \end{align*}and then
 \[ \binom{2k}{2r} \prod_{u=0}^{r-1} R(k-u)=\binom{2k}{2r} \prod_{u=1}^{r} \frac{(n+2k-2u)(n+2k-2u-1)}{(2k-2u+2)(2k-2u+1)}=\binom{n+2k-2}{2r}. \]
\[ \binom{2k}{2r} \prod_{u=0}^{r-1} R(k-u)=\binom{2k}{2r} \prod_{u=1}^{r} \frac{(n+2k-2u)(n+2k-2u-1)}{(2k-2u+2)(2k-2u+1)}=\binom{n+2k-2}{2r}. \]
Iterating the map ![]() ${\sf m}$, sf. (2.4) and Theorem 3.11, we obtain the following result.
${\sf m}$, sf. (2.4) and Theorem 3.11, we obtain the following result.
Theorem 7.6 For any ![]() $k\geqslant 2$,
$k\geqslant 2$,
 \[ S_k=\varpi(\Phi_{2k})[-1]+\sum_{1\leqslant r< k} \binom{n+2k-2}{2r} \varpi(\tau^{2r} \Phi_{2k-2r}[-1])\cdot 1 \]
\[ S_k=\varpi(\Phi_{2k})[-1]+\sum_{1\leqslant r< k} \binom{n+2k-2}{2r} \varpi(\tau^{2r} \Phi_{2k-2r}[-1])\cdot 1 \]is a Segal–Sugawara vector.
8. Applications and open questions
The Feigin–Frenkel centre can be used in order to construct commutative subalgebras of the enveloping algebra in finite-dimensional cases. There are two most remarkable instances.
8.1 Quantum Mishchenko–Fomenko subalgebras
Recall the construction from [Reference RybnikovRyb06]. For any ![]() $\mu \in \mathfrak g^{*}$ and a non-zero
$\mu \in \mathfrak g^{*}$ and a non-zero ![]() $u\in \mathbb {C}$, the map
$u\in \mathbb {C}$, the map
defines a ![]() $G_\mu$-equivariant algebra homomorphism. The image of
$G_\mu$-equivariant algebra homomorphism. The image of ![]() $\mathfrak z(\hat {\mathfrak g})$ under
$\mathfrak z(\hat {\mathfrak g})$ under ![]() $\varrho _{\mu,u}$ is a commutative subalgebra
$\varrho _{\mu,u}$ is a commutative subalgebra ![]() $\tilde {{\mathcal {A}}}_{\mu }$ of
$\tilde {{\mathcal {A}}}_{\mu }$ of ![]() ${{\mathcal {U}}}(\mathfrak g)$, which does not depend on
${{\mathcal {U}}}(\mathfrak g)$, which does not depend on ![]() $u$ [Reference RybnikovRyb06, Reference Feigin, Frenkel and Toledano LaredoFFTL10]. Moreover,
$u$ [Reference RybnikovRyb06, Reference Feigin, Frenkel and Toledano LaredoFFTL10]. Moreover, ![]() $\mathrm {gr}(\tilde {{\mathcal {A}}}_\mu )$ contains the Mishchenko–Fomenko subalgebra
$\mathrm {gr}(\tilde {{\mathcal {A}}}_\mu )$ contains the Mishchenko–Fomenko subalgebra ![]() ${{\mathcal {A}}}_\mu \subset {{\mathcal {S}}}(\mathfrak g)$ associated with
${{\mathcal {A}}}_\mu \subset {{\mathcal {S}}}(\mathfrak g)$ associated with ![]() $\mu$, which is generated by all
$\mu$, which is generated by all ![]() $\mu$-shifts
$\mu$-shifts ![]() $\partial _\mu ^{m} H$ of the
$\partial _\mu ^{m} H$ of the ![]() $\mathfrak g$-invariants
$\mathfrak g$-invariants ![]() $H\in {{\mathcal {S}}}(\mathfrak g)$. The main property of
$H\in {{\mathcal {S}}}(\mathfrak g)$. The main property of ![]() ${{\mathcal {A}}}_\mu$ is that it is Poisson-commutative, i.e.
${{\mathcal {A}}}_\mu$ is that it is Poisson-commutative, i.e. ![]() $\{{{\mathcal {A}}}_\mu,{{\mathcal {A}}}_\mu \}=0$ [Reference Mishchenko and FomenkoMF78]. If
$\{{{\mathcal {A}}}_\mu,{{\mathcal {A}}}_\mu \}=0$ [Reference Mishchenko and FomenkoMF78]. If ![]() $\mu \in \mathfrak g^{*}\cong \mathfrak g$ is regular, i.e. if
$\mu \in \mathfrak g^{*}\cong \mathfrak g$ is regular, i.e. if ![]() $\dim \mathfrak g_\mu =\mathrm {rk}\,\mathfrak g$, then
$\dim \mathfrak g_\mu =\mathrm {rk}\,\mathfrak g$, then ![]() ${{\mathcal {A}}}_\mu$ is a maximal with respect to inclusion Poisson-commutative subalgebra of
${{\mathcal {A}}}_\mu$ is a maximal with respect to inclusion Poisson-commutative subalgebra of ![]() ${{\mathcal {S}}}(\mathfrak g)$ [Reference Panyushev and YakimovaPY08] and hence
${{\mathcal {S}}}(\mathfrak g)$ [Reference Panyushev and YakimovaPY08] and hence ![]() $\mathrm {gr}(\tilde {{\mathcal {A}}}_\mu )={{\mathcal {A}}}_\mu$. Several important properties and applications of (quantum) MF-subalgebras are discussed e.g. in [Reference VinbergVin91, Reference Feigin, Frenkel and RybnikovFFR10].
$\mathrm {gr}(\tilde {{\mathcal {A}}}_\mu )={{\mathcal {A}}}_\mu$. Several important properties and applications of (quantum) MF-subalgebras are discussed e.g. in [Reference VinbergVin91, Reference Feigin, Frenkel and RybnikovFFR10].
Mishchenko–Fomenko subalgebras were introduced in [Reference Mishchenko and FomenkoMF78], before the appearance of the Feigin–Frenkel centre. In [Reference VinbergVin91], Vinberg posed a problem of finding a quantisation of ![]() ${{\mathcal {A}}}_\mu$. A natural idea is to look for a solution given by the symmetrisation map
${{\mathcal {A}}}_\mu$. A natural idea is to look for a solution given by the symmetrisation map ![]() $\varpi$. For
$\varpi$. For ![]() $\mathfrak g=\mathfrak {gl}_n$, the elements
$\mathfrak g=\mathfrak {gl}_n$, the elements ![]() $\varpi (\partial _\mu ^{m}\Delta _k)\in {{\mathcal {U}}}(\mathfrak g)$ with
$\varpi (\partial _\mu ^{m}\Delta _k)\in {{\mathcal {U}}}(\mathfrak g)$ with ![]() $1\leqslant k\leqslant n$,
$1\leqslant k\leqslant n$, ![]() $0\leqslant m< k$ commute and therefore produce a solution to Vinberg's quantisation problem [Reference TarasovTar00, Reference Futorny and MolevFM15, Reference Molev and YakimovaMY19].
$0\leqslant m< k$ commute and therefore produce a solution to Vinberg's quantisation problem [Reference TarasovTar00, Reference Futorny and MolevFM15, Reference Molev and YakimovaMY19].
Consider ![]() ${\mathcal {F}}[\bar a]=\varpi (F)[\bar a]\in {{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)$ corresponding to
${\mathcal {F}}[\bar a]=\varpi (F)[\bar a]\in {{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)$ corresponding to ![]() $F\in {{\mathcal {S}}}^{m}(\mathfrak g)^{\mathfrak g}$ in the sense of (0.3). Set
$F\in {{\mathcal {S}}}^{m}(\mathfrak g)^{\mathfrak g}$ in the sense of (0.3). Set ![]() $p=|\{i \mid a_i=-1\}|$. Then
$p=|\{i \mid a_i=-1\}|$. Then
Combining (8.2) with (2.2), we conclude immediately that for ![]() $\mathfrak g=\mathfrak {gl}_n$, the algebra
$\mathfrak g=\mathfrak {gl}_n$, the algebra ![]() $\tilde {{\mathcal {A}}}_\mu$ is generated by
$\tilde {{\mathcal {A}}}_\mu$ is generated by ![]() $\varpi (\partial _\mu ^{m}\Delta _k)$. This observation is not new, see [Reference Molev and YakimovaMY19, § 3] and in particular § 3.2 there for a historical overview and a more elaborated proof.
$\varpi (\partial _\mu ^{m}\Delta _k)$. This observation is not new, see [Reference Molev and YakimovaMY19, § 3] and in particular § 3.2 there for a historical overview and a more elaborated proof.
In [Reference Molev and YakimovaMY19, § 3.3], sets of generators ![]() $\{H_i\mid 1\leqslant i\leqslant \ell \}$ of
$\{H_i\mid 1\leqslant i\leqslant \ell \}$ of ![]() ${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ such that
${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ such that
are exhibited in types ![]() $\mathsf{B}$,
$\mathsf{B}$, ![]() $\mathsf{C}$, and
$\mathsf{C}$, and ![]() $\mathsf{D}$. We rejoice to say that in type
$\mathsf{D}$. We rejoice to say that in type ![]() $\mathsf{C}$,
$\mathsf{C}$, ![]() $H_k=\Delta _{2k}$ in the notation of § 4. In the even orthogonal case, the set
$H_k=\Delta _{2k}$ in the notation of § 4. In the even orthogonal case, the set ![]() $\{H_i\}$ includes the Pfaffian. The other generators in types
$\{H_i\}$ includes the Pfaffian. The other generators in types ![]() $\mathsf{B}$ and
$\mathsf{B}$ and ![]() $\mathsf{D}$ are
$\mathsf{D}$ are ![]() $\Phi _{2k}$ of § 7. Thus Theorems 4.4 and 7.6 provide a new proof of [Reference Molev and YakimovaMY19, Theorem 3.2].
$\Phi _{2k}$ of § 7. Thus Theorems 4.4 and 7.6 provide a new proof of [Reference Molev and YakimovaMY19, Theorem 3.2].
In conclusion, we show that Proposition 5.6 confirms Conjecture 3.3 of [Reference Molev and YakimovaMY19] in type ![]() $\mathsf{G}_2$.
$\mathsf{G}_2$.
Proposition 8.1 Let ![]() $\mathfrak g$ be a simple Lie algebra of type
$\mathfrak g$ be a simple Lie algebra of type ![]() $\mathsf{G}_2$. Let
$\mathsf{G}_2$. Let ![]() $\tilde H\in {{\mathcal {S}}}^{6}(\mathfrak g)$ be a
$\tilde H\in {{\mathcal {S}}}^{6}(\mathfrak g)$ be a ![]() $\mathfrak g$-invariant satisfying (0.2), cf. Corollaries 5.7 and 6.4. Then
$\mathfrak g$-invariant satisfying (0.2), cf. Corollaries 5.7 and 6.4. Then ![]() $\tilde {{\mathcal {A}}}_\mu$ is generated by
$\tilde {{\mathcal {A}}}_\mu$ is generated by ![]() $\mu, {\mathcal {H}}$, and
$\mu, {\mathcal {H}}$, and ![]() $\varpi (\partial _\mu ^{m} \tilde H)$ with
$\varpi (\partial _\mu ^{m} \tilde H)$ with ![]() $0\leqslant m\leqslant 5$.
$0\leqslant m\leqslant 5$.
Proof. We work with ![]() $\mu$ as with an element of
$\mu$ as with an element of ![]() $\mathfrak g$. Clearly
$\mathfrak g$. Clearly ![]() $\partial _\mu {\mathcal {H}}=2 \sum (x_i,\mu ) x_i=2\mu$ and
$\partial _\mu {\mathcal {H}}=2 \sum (x_i,\mu ) x_i=2\mu$ and
Let ![]() $S_2$ be the Segal–Sugawara vector provided by (5.1) and (6.3). Set also
$S_2$ be the Segal–Sugawara vector provided by (5.1) and (6.3). Set also ![]() $S_1={\mathcal {H}}[-1]$. Then
$S_1={\mathcal {H}}[-1]$. Then ![]() $\{S_1,S_2\}$ is a complete set of Segal–Sugawara vectors. A general observation is that
$\{S_1,S_2\}$ is a complete set of Segal–Sugawara vectors. A general observation is that ![]() $\tilde {{\mathcal {A}}}_\mu$ is generated by
$\tilde {{\mathcal {A}}}_\mu$ is generated by ![]() $\{\varrho _{\mu,u}(S_\nu ) \mid u\in {{\mathbb {C}}}^{{}^\times}, \nu =1,2\}$ [Reference MolevMol18, Corollary 9.2.3]. We have already computed the images of
$\{\varrho _{\mu,u}(S_\nu ) \mid u\in {{\mathbb {C}}}^{{}^\times}, \nu =1,2\}$ [Reference MolevMol18, Corollary 9.2.3]. We have already computed the images of ![]() $S_1$ and also of
$S_1$ and also of ![]() $\varpi (\tau ^{4}{\mathcal {H}}[-1]){\cdot }1$. Similarly to (8.2), the images of
$\varpi (\tau ^{4}{\mathcal {H}}[-1]){\cdot }1$. Similarly to (8.2), the images of ![]() $\varpi (\tilde H)[-1]$ span
$\varpi (\tilde H)[-1]$ span ![]() $\langle \varpi (\partial _\mu ^{m} H)\rangle _{{{\mathbb {C}}}}$. It remains to deal with
$\langle \varpi (\partial _\mu ^{m} H)\rangle _{{{\mathbb {C}}}}$. It remains to deal with
Here ![]() ${\mathcal {Y}}_1$ is proportional to
${\mathcal {Y}}_1$ is proportional to ![]() $\mu$; the term
$\mu$; the term ![]() ${\mathcal {Y}}_2$ is a linear combination of
${\mathcal {Y}}_2$ is a linear combination of ![]() ${\mathcal {H}}$ and
${\mathcal {H}}$ and ![]() $\mu ^{2}$. Furthermore,
$\mu ^{2}$. Furthermore, ![]() ${\mathcal {Y}}_3$ is a linear combination of
${\mathcal {Y}}_3$ is a linear combination of ![]() $\mu {\mathcal {H}}$ and
$\mu {\mathcal {H}}$ and ![]() $\sum _{i} x_i\mu x_i$, therefore of
$\sum _{i} x_i\mu x_i$, therefore of ![]() $\mu {\mathcal {H}}$ and
$\mu {\mathcal {H}}$ and ![]() $\mu$, cf. Lemma 5.4. Finally,
$\mu$, cf. Lemma 5.4. Finally, ![]() ${\mathcal {Y}}_4$ is a linear combination of
${\mathcal {Y}}_4$ is a linear combination of ![]() ${\mathcal {H}}^{2}$ and
${\mathcal {H}}^{2}$ and ![]() $\sum _{i,j} x_i x_jx_j x_i=\sum _{i} x_i {\mathcal {H}} x_i={\mathcal {H}}^{2}$,
$\sum _{i,j} x_i x_jx_j x_i=\sum _{i} x_i {\mathcal {H}} x_i={\mathcal {H}}^{2}$,
This completes the proof.
8.2 Gaudin algebras
Recall that elements ![]() $S\in \mathfrak z({{\hat {\mathfrak g}}})$ give rise to higher Hamiltonians of the Gaudin models, which describe completely integrable quantum spin chains [Reference Feigin, Frenkel and ReshetikhinFFR94].
$S\in \mathfrak z({{\hat {\mathfrak g}}})$ give rise to higher Hamiltonians of the Gaudin models, which describe completely integrable quantum spin chains [Reference Feigin, Frenkel and ReshetikhinFFR94].
The underlying space of a Gaudin model is the direct sum of ![]() $n$-copies of
$n$-copies of ![]() $\mathfrak g$, and the Hamiltonians are the following sums
$\mathfrak g$, and the Hamiltonians are the following sums
 \[ {\mathcal{H}}_k=\sum_{j\ne k} \frac{\sum_i x_i^{(k)} x_i^{(j)}}{z_k-z_j} , \quad 1\leqslant k\leqslant n, \]
\[ {\mathcal{H}}_k=\sum_{j\ne k} \frac{\sum_i x_i^{(k)} x_i^{(j)}}{z_k-z_j} , \quad 1\leqslant k\leqslant n, \]
where ![]() $z_1,\ldots,z_n$ are pairwise different complex numbers. Here
$z_1,\ldots,z_n$ are pairwise different complex numbers. Here ![]() $\{x_i^{(k)}\mid 1\leqslant i\leqslant \dim \mathfrak g\}$ is an orthonormal basis for the
$\{x_i^{(k)}\mid 1\leqslant i\leqslant \dim \mathfrak g\}$ is an orthonormal basis for the ![]() $k$’th copy of
$k$’th copy of ![]() $\mathfrak g$. These Gaudin Hamiltonians can be regarded as elements of
$\mathfrak g$. These Gaudin Hamiltonians can be regarded as elements of ![]() ${{\mathcal {U}}}(\mathfrak g)^{\otimes n}$ or of
${{\mathcal {U}}}(\mathfrak g)^{\otimes n}$ or of ![]() ${{\mathcal {S}}}(\mathfrak g\oplus \cdots \oplus \mathfrak g)$. They commute (and hence Poisson-commute) with each other. Higher Gaudin Hamiltonians are elements of
${{\mathcal {S}}}(\mathfrak g\oplus \cdots \oplus \mathfrak g)$. They commute (and hence Poisson-commute) with each other. Higher Gaudin Hamiltonians are elements of ![]() ${{\mathcal {U}}}(\mathfrak g)^{\otimes n}$ that commute with all
${{\mathcal {U}}}(\mathfrak g)^{\otimes n}$ that commute with all ![]() ${\mathcal {H}}_k$.
${\mathcal {H}}_k$.
The construction of [Reference Feigin, Frenkel and ReshetikhinFFR94] produces a Gaudin subalgebra ![]() ${\mathcal {G}}$, which consists of Gaudin Hamiltonians and contains
${\mathcal {G}}$, which consists of Gaudin Hamiltonians and contains ![]() ${\mathcal {H}}_k$ for each
${\mathcal {H}}_k$ for each ![]() $k$. Let
$k$. Let ![]() $\Delta {{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)\cong {{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)$ be the diagonal of
$\Delta {{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)\cong {{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)$ be the diagonal of ![]() ${{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)^{\otimes n}$. Then a vector
${{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)^{\otimes n}$. Then a vector ![]() $\bar z=(z_1,\ldots,z_n)\in ({{\mathbb {C}}}^{{}^\times}\!)^{n}$ defines a natural homomorphism
$\bar z=(z_1,\ldots,z_n)\in ({{\mathbb {C}}}^{{}^\times}\!)^{n}$ defines a natural homomorphism ![]() $\rho _{\bar z}\!:\Delta {{\mathcal {U}}}({{\hat {\mathfrak g}}}^-) \to {{\mathcal {U}}}(\mathfrak g)^{\otimes n}$. In this notation,
$\rho _{\bar z}\!:\Delta {{\mathcal {U}}}({{\hat {\mathfrak g}}}^-) \to {{\mathcal {U}}}(\mathfrak g)^{\otimes n}$. In this notation, ![]() ${\mathcal {G}}={\mathcal {G}}(\bar z)$ is the image of
${\mathcal {G}}={\mathcal {G}}(\bar z)$ is the image of ![]() $\mathfrak z({{\hat {\mathfrak g}}})$ under
$\mathfrak z({{\hat {\mathfrak g}}})$ under ![]() $\rho _{\bar z}$. By the construction,
$\rho _{\bar z}$. By the construction, ![]() ${\mathcal {G}}\subset ({{\mathcal {U}}}(\mathfrak g)^{\otimes n})^{\mathfrak g}$. Since
${\mathcal {G}}\subset ({{\mathcal {U}}}(\mathfrak g)^{\otimes n})^{\mathfrak g}$. Since ![]() $\mathfrak z({{\hat {\mathfrak g}}})$ is homogeneous in
$\mathfrak z({{\hat {\mathfrak g}}})$ is homogeneous in ![]() $t$, it is clear that
$t$, it is clear that ![]() ${{\mathcal {G}}(\bar z)}={{\mathcal {G}}}(c\bar z)$ for any non-zero complex number
${{\mathcal {G}}(\bar z)}={{\mathcal {G}}}(c\bar z)$ for any non-zero complex number ![]() $c$.
$c$.
Gaudin subalgebras have attracted a great deal of attention, see e.g. [Reference Chervov, Falqui and RybnikovCFR10] and references therein. They are closely related to quantum Mishchenko–Fomenko subalgebras and share some of their properties. In particular, for a generic ![]() $\bar z$, the action of
$\bar z$, the action of ![]() ${{\mathcal {G}}(\bar z)}$ on an irreducible finite-dimensional
${{\mathcal {G}}(\bar z)}$ on an irreducible finite-dimensional ![]() $(\mathfrak g \oplus \cdots \oplus \mathfrak g)$-module
$(\mathfrak g \oplus \cdots \oplus \mathfrak g)$-module ![]() $V(\lambda _1)\otimes \cdots \otimes V(\lambda _n)$ is diagonalisable and has a simple spectrum on the subspace of highest weight vectors of the diagonal
$V(\lambda _1)\otimes \cdots \otimes V(\lambda _n)$ is diagonalisable and has a simple spectrum on the subspace of highest weight vectors of the diagonal ![]() $\mathfrak g$ [Reference RybnikovRyb20]. Applying
$\mathfrak g$ [Reference RybnikovRyb20]. Applying ![]() $\rho _{\bar z}$, one obtains explicit formulas for higher Gaudin Hamiltonians from explicit formulas for the generators of
$\rho _{\bar z}$, one obtains explicit formulas for higher Gaudin Hamiltonians from explicit formulas for the generators of ![]() $\mathfrak z({{\hat {\mathfrak g}}})$. In the following, we discuss which generators of
$\mathfrak z({{\hat {\mathfrak g}}})$. In the following, we discuss which generators of ![]() $\mathfrak z({{\hat {\mathfrak g}}})$ one has to consider.
$\mathfrak z({{\hat {\mathfrak g}}})$ one has to consider.
Let ![]() $\{S_1,\ldots,S_\ell \}$ with
$\{S_1,\ldots,S_\ell \}$ with ![]() $\mathrm {gr}(S_k)=H_k[-1]$ be a complete set of Segal–Sugawara vectors as in § 1.6. Set
$\mathrm {gr}(S_k)=H_k[-1]$ be a complete set of Segal–Sugawara vectors as in § 1.6. Set ![]() $\deg H_k=:d_k$. Assume that
$\deg H_k=:d_k$. Assume that ![]() $z_k\ne z_j$ for
$z_k\ne z_j$ for ![]() $k\ne j$ and that
$k\ne j$ and that ![]() $z_k\ne 0$ for all
$z_k\ne 0$ for all ![]() $k$. According to [Reference Chervov, Falqui and RybnikovCFR10, Proposition 1],
$k$. According to [Reference Chervov, Falqui and RybnikovCFR10, Proposition 1], ![]() ${\mathcal {G}}(\bar z)$ has a set of algebraically independent generators
${\mathcal {G}}(\bar z)$ has a set of algebraically independent generators ![]() $\{F_1,\ldots,F_{{{\boldsymbol B}}(n)}\}$, where
$\{F_1,\ldots,F_{{{\boldsymbol B}}(n)}\}$, where ![]() ${{\boldsymbol B}}(n):= ({n-1}/{2})(\dim \mathfrak g+\ell )+\ell$, see also [Reference RybnikovRyb06, Theorems 2&3]. Moreover, exactly
${{\boldsymbol B}}(n):= ({n-1}/{2})(\dim \mathfrak g+\ell )+\ell$, see also [Reference RybnikovRyb06, Theorems 2&3]. Moreover, exactly ![]() $(n-1)d_k +1$ elements among the
$(n-1)d_k +1$ elements among the ![]() $F_j$ belong to
$F_j$ belong to ![]() $\langle \rho _{\bar z}(\tau ^{m}(S_k)) \mid m\geqslant 0\rangle _{{{\mathbb {C}}}}$ [Reference Chervov, Falqui and RybnikovCFR10, Proposition 1]. Note that
$\langle \rho _{\bar z}(\tau ^{m}(S_k)) \mid m\geqslant 0\rangle _{{{\mathbb {C}}}}$ [Reference Chervov, Falqui and RybnikovCFR10, Proposition 1]. Note that ![]() $\sum _{k=1}^{\ell } d_k$ equals
$\sum _{k=1}^{\ell } d_k$ equals ![]() $(\dim \mathfrak g+\ell )/2$. Furthermore, the symbols
$(\dim \mathfrak g+\ell )/2$. Furthermore, the symbols ![]() $\mathrm {gr}(F_j)$ are algebraically independent as well and
$\mathrm {gr}(F_j)$ are algebraically independent as well and ![]() $\deg \mathrm {gr}(F_j)=d_k$ if
$\deg \mathrm {gr}(F_j)=d_k$ if ![]() $F_j\in \langle \rho _{\bar z}(\tau ^{m}(S_k)) \mid m\geqslant 0\rangle _{{{\mathbb {C}}}}$, see the proof of [Reference Chervov, Falqui and RybnikovCFR10, Proposition 1(2)] and [Reference RybnikovRyb06, § 4].
$F_j\in \langle \rho _{\bar z}(\tau ^{m}(S_k)) \mid m\geqslant 0\rangle _{{{\mathbb {C}}}}$, see the proof of [Reference Chervov, Falqui and RybnikovCFR10, Proposition 1(2)] and [Reference RybnikovRyb06, § 4].
Remark 8.2 If ![]() ${{\mathcal {A}}}\subset ({{\mathcal {S}}}(\mathfrak g)^{\otimes n})^{\mathfrak g}$ is a Poisson-commutative algebra, then
${{\mathcal {A}}}\subset ({{\mathcal {S}}}(\mathfrak g)^{\otimes n})^{\mathfrak g}$ is a Poisson-commutative algebra, then ![]() ${\rm tr.deg}\,{{\mathcal {A}}}\leqslant {{\boldsymbol B}}(n)$ by [Reference Molev and YakimovaMY19, Proposition 1.1]. Combining this with [Reference Borho and KraftBK76, Satz 5.7], we obtain that
${\rm tr.deg}\,{{\mathcal {A}}}\leqslant {{\boldsymbol B}}(n)$ by [Reference Molev and YakimovaMY19, Proposition 1.1]. Combining this with [Reference Borho and KraftBK76, Satz 5.7], we obtain that ![]() ${\rm tr.deg}\,\tilde {{\mathcal {A}}}\leqslant {{\boldsymbol B}}(n)$ for a commutative subalgebra
${\rm tr.deg}\,\tilde {{\mathcal {A}}}\leqslant {{\boldsymbol B}}(n)$ for a commutative subalgebra ![]() $\tilde {{\mathcal {A}}}\subset ({{\mathcal {U}}}(\mathfrak g)^{\otimes n})^{\mathfrak g}$. Thus
$\tilde {{\mathcal {A}}}\subset ({{\mathcal {U}}}(\mathfrak g)^{\otimes n})^{\mathfrak g}$. Thus ![]() ${{\mathcal {G}}}$ has the maximal possible transcendence degree. Arguing in the spirit of [Reference Panyushev and YakimovaPY08] and using the results of [Reference RybnikovRyb06], one can show that
${{\mathcal {G}}}$ has the maximal possible transcendence degree. Arguing in the spirit of [Reference Panyushev and YakimovaPY08] and using the results of [Reference RybnikovRyb06], one can show that ![]() ${{\mathcal {G}}}$ is also a maximal commutative subalgebra of
${{\mathcal {G}}}$ is also a maximal commutative subalgebra of ![]() $({{\mathcal {U}}}(\mathfrak g)^{\otimes n})^{\mathfrak g}$ with respect to inclusion.
$({{\mathcal {U}}}(\mathfrak g)^{\otimes n})^{\mathfrak g}$ with respect to inclusion.
In the case ![]() $n=2$, the application of our result looks particularly nice. Besides, this two points case has several features. Suppose that
$n=2$, the application of our result looks particularly nice. Besides, this two points case has several features. Suppose that ![]() $n=2$. Set
$n=2$. Set ![]() $\mathfrak l=\mathfrak g\oplus \mathfrak g$. For
$\mathfrak l=\mathfrak g\oplus \mathfrak g$. For ![]() $H\in {{\mathcal {S}}}^{d}(\mathfrak l)$,
$H\in {{\mathcal {S}}}^{d}(\mathfrak l)$, ![]() $\xi ^{(1)}$ in the first copy of
$\xi ^{(1)}$ in the first copy of ![]() $\mathfrak g$,
$\mathfrak g$, ![]() $\eta ^{(2)}$ in the second, and a non-zero
$\eta ^{(2)}$ in the second, and a non-zero ![]() $c\in {{\mathbb {C}}}$, write
$c\in {{\mathbb {C}}}$, write
 \begin{align} H(\xi^{(1)}+c\eta^{(2)})&=H_{d,0}(\xi^{(1)})+cH_{d-1,1}(\xi^{(1)},\eta^{(2)})+\cdots +c^{d-1}H_{1,d-1}(\xi^{(1)},\eta^{(2)})\nonumber\\ &\quad +c^{d}H_{0,d}(\eta^{(2)}). \end{align}
\begin{align} H(\xi^{(1)}+c\eta^{(2)})&=H_{d,0}(\xi^{(1)})+cH_{d-1,1}(\xi^{(1)},\eta^{(2)})+\cdots +c^{d-1}H_{1,d-1}(\xi^{(1)},\eta^{(2)})\nonumber\\ &\quad +c^{d}H_{0,d}(\eta^{(2)}). \end{align}
Here ![]() $H_{d,0}$ belongs to the symmetric algebra of the first copy of
$H_{d,0}$ belongs to the symmetric algebra of the first copy of ![]() $\mathfrak g$. The symbol of
$\mathfrak g$. The symbol of ![]() $\rho _{\bar z}(\tau ^{m}(S_k))$ lies in
$\rho _{\bar z}(\tau ^{m}(S_k))$ lies in ![]() $\langle (H_k)_{d_k-j,j} \mid 0\leqslant j\leqslant d_k\rangle _{{{\mathbb {C}}}}$. Since we must have
$\langle (H_k)_{d_k-j,j} \mid 0\leqslant j\leqslant d_k\rangle _{{{\mathbb {C}}}}$. Since we must have ![]() $d_k+1$ linearly independent elements among these symbols,
$d_k+1$ linearly independent elements among these symbols, ![]() $\mathrm {gr}({{\mathcal {G}}})$ is freely generated by
$\mathrm {gr}({{\mathcal {G}}})$ is freely generated by ![]() $(H_k)_{d_k-j,j}$ with
$(H_k)_{d_k-j,j}$ with ![]() $1\leqslant k\leqslant \ell$,
$1\leqslant k\leqslant \ell$, ![]() $0\leqslant j\leqslant d_k$.
$0\leqslant j\leqslant d_k$.
The Lie algebra ![]() $\mathfrak l$ has the following symmetric decomposition
$\mathfrak l$ has the following symmetric decomposition
and ![]() $\mathfrak l_0=\Delta \mathfrak g=\{(\xi,\xi )\mid \xi \in \mathfrak g\}$ is the diagonal. Similarly to (8.4), one polarises
$\mathfrak l_0=\Delta \mathfrak g=\{(\xi,\xi )\mid \xi \in \mathfrak g\}$ is the diagonal. Similarly to (8.4), one polarises ![]() $H\in {{\mathcal {S}}}^{d}(\mathfrak l)$ with respect to the decomposition (8.5). Let
$H\in {{\mathcal {S}}}^{d}(\mathfrak l)$ with respect to the decomposition (8.5). Let ![]() $H_{[j,d-j]}$ with
$H_{[j,d-j]}$ with ![]() $0\leqslant j\leqslant d$ be the arising components. Then
$0\leqslant j\leqslant d$ be the arising components. Then ![]() $\langle H_{j,d-j} \mid 0\leqslant j\leqslant d\rangle _{{{\mathbb {C}}}}= \langle H_{[j,d-j]} \mid 0\leqslant j\leqslant d\rangle _{{{\mathbb {C}}}}$.
$\langle H_{j,d-j} \mid 0\leqslant j\leqslant d\rangle _{{{\mathbb {C}}}}= \langle H_{[j,d-j]} \mid 0\leqslant j\leqslant d\rangle _{{{\mathbb {C}}}}$.
On the one side, the polynomials ![]() $(H_k)_{j,d_k-j}$ generate
$(H_k)_{j,d_k-j}$ generate ![]() $\mathrm {gr}({{\mathcal {G}}})$, on the other, the polynomials
$\mathrm {gr}({{\mathcal {G}}})$, on the other, the polynomials ![]() $(H_k)_{[j,d_k-j]}$ generate a Poisson-commutative subalgebra
$(H_k)_{[j,d_k-j]}$ generate a Poisson-commutative subalgebra ![]() ${\mathcal {Z}} \subset {{\mathcal {S}}}(\mathfrak l)$ related to the symmetric pair
${\mathcal {Z}} \subset {{\mathcal {S}}}(\mathfrak l)$ related to the symmetric pair ![]() $(\mathfrak l,\mathfrak l_0)$, which has many interesting properties [Reference Panyushev and YakimovaPY21]. Thus, our discussion results in the following statement.
$(\mathfrak l,\mathfrak l_0)$, which has many interesting properties [Reference Panyushev and YakimovaPY21]. Thus, our discussion results in the following statement.
Corollary 8.3 (cf. [Reference Panyushev and YakimovaPY21, Example 6.5])
The two-points Gaudin subalgebra ![]() ${{\mathcal {G}}}(z_1,z_2)$ is a quantisation of the Poisson-commutative subalgebra
${{\mathcal {G}}}(z_1,z_2)$ is a quantisation of the Poisson-commutative subalgebra ![]() ${\mathcal {Z}}$ associated with the symmetric pair
${\mathcal {Z}}$ associated with the symmetric pair ![]() $(\mathfrak g \oplus \mathfrak g,\Delta \mathfrak g)$.
$(\mathfrak g \oplus \mathfrak g,\Delta \mathfrak g)$.
Let us give more information on the issue of Corollary 8.3. Observe that ![]() ${{\mathcal {G}}}(z_1,z_2)={{\mathcal {G}}}(z_1-b,z_2-b)$ if
${{\mathcal {G}}}(z_1,z_2)={{\mathcal {G}}}(z_1-b,z_2-b)$ if ![]() $b\in {{\mathbb {C}}}{\setminus} \{z_1,z_2\}$, see [Reference Chervov, Falqui and RybnikovCFR10, Proposition 1]. Hence
$b\in {{\mathbb {C}}}{\setminus} \{z_1,z_2\}$, see [Reference Chervov, Falqui and RybnikovCFR10, Proposition 1]. Hence
For ![]() $\rho =\rho _{1,-1}$, we have
$\rho =\rho _{1,-1}$, we have ![]() $\rho (\xi t^{k})=\xi ^{(1)}+(-1)^{k} \xi ^{(2)}$, i.e.
$\rho (\xi t^{k})=\xi ^{(1)}+(-1)^{k} \xi ^{(2)}$, i.e. ![]() $\mathfrak g[-1]$, as well as any
$\mathfrak g[-1]$, as well as any ![]() $\mathfrak g[-2k-1]$, is mapped into
$\mathfrak g[-2k-1]$, is mapped into ![]() $\mathfrak l_1$ and each
$\mathfrak l_1$ and each ![]() $\mathfrak g[-2k]$ is mapped into
$\mathfrak g[-2k]$ is mapped into ![]() $\Delta \mathfrak g$. One can understand
$\Delta \mathfrak g$. One can understand ![]() $\rho$ as the map from
$\rho$ as the map from ![]() ${{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)$ to
${{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)$ to ![]() ${{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)/(t^{2}-1)\cong {{\mathcal {U}}}(\mathfrak l)$.
${{\mathcal {U}}}({{\hat {\mathfrak g}}}^-)/(t^{2}-1)\cong {{\mathcal {U}}}(\mathfrak l)$.
It is not difficult to see that ![]() $\mathrm {gr}(\rho (S_k))=(H_k)_{[0,d_k]}$,
$\mathrm {gr}(\rho (S_k))=(H_k)_{[0,d_k]}$, ![]() $\mathrm {gr}(\rho (\tau (S_k)))=(H_k)_{[1,d_k-1]}$, and in general
$\mathrm {gr}(\rho (\tau (S_k)))=(H_k)_{[1,d_k-1]}$, and in general
as long as ![]() $m\leqslant d_k$. This shows that indeed
$m\leqslant d_k$. This shows that indeed ![]() $\mathrm {gr}({{\mathcal {G}}})={\mathcal {Z}}$ and that
$\mathrm {gr}({{\mathcal {G}}})={\mathcal {Z}}$ and that
Suppose that ![]() $H_1,\ldots,H_\ell$ are homogeneous generators of
$H_1,\ldots,H_\ell$ are homogeneous generators of ![]() ${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ and for each
${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ and for each ![]() $k$ there is
$k$ there is ![]() $k'$ such that
$k'$ such that ![]() $0\leqslant k'< k$ and
$0\leqslant k'< k$ and ![]() ${\sf m}(H_{k})\in {{\mathbb {C}}}H_{k'}$, where
${\sf m}(H_{k})\in {{\mathbb {C}}}H_{k'}$, where ![]() $H_0=0$. If
$H_0=0$. If ![]() $\mathfrak g$ is simple and classical, then explicit descriptions of such sets are contained in §§ 2, 4, 7.
$\mathfrak g$ is simple and classical, then explicit descriptions of such sets are contained in §§ 2, 4, 7.
Theorem 8.4 If we keep the above assumption on the set ![]() $\{H_k\}$, then the two-points Gaudin subalgebra
$\{H_k\}$, then the two-points Gaudin subalgebra ![]() ${{\mathcal {G}}}\subset {{\mathcal {U}}}(\mathfrak l)$ is generated by
${{\mathcal {G}}}\subset {{\mathcal {U}}}(\mathfrak l)$ is generated by ![]() $\varpi ((H_k)_{d_k-j,j})$ with
$\varpi ((H_k)_{d_k-j,j})$ with ![]() $1\leqslant k\leqslant \ell$,
$1\leqslant k\leqslant \ell$, ![]() $0\leqslant j\leqslant d_k$.
$0\leqslant j\leqslant d_k$.
Proof. For each ![]() $k$, let
$k$, let ![]() $S_k$ be the Segal–Sugawara vector obtained from
$S_k$ be the Segal–Sugawara vector obtained from ![]() $H_k$ by (2.4). We will show that
$H_k$ by (2.4). We will show that ![]() $V_{\rm sym}:=\langle \varpi ((H_k)_{d_k-j,j}) \mid 1\leqslant k\leqslant \ell, \, 0\leqslant j\leqslant d_k\rangle _{{{\mathbb {C}}}}$ is equal to
$V_{\rm sym}:=\langle \varpi ((H_k)_{d_k-j,j}) \mid 1\leqslant k\leqslant \ell, \, 0\leqslant j\leqslant d_k\rangle _{{{\mathbb {C}}}}$ is equal to
Since ![]() $\dim V_{{{\mathcal {G}}}} =\dim V_{\rm sym}$, it suffices to prove the inclusion
$\dim V_{{{\mathcal {G}}}} =\dim V_{\rm sym}$, it suffices to prove the inclusion ![]() $V_{{{\mathcal {G}}}}\subset V_{\rm sym}$. We argue by induction on
$V_{{{\mathcal {G}}}}\subset V_{\rm sym}$. We argue by induction on ![]() $k$. If
$k$. If ![]() $k=1$, then
$k=1$, then ![]() $S_1=\varpi (H_1[-1])$. Hence
$S_1=\varpi (H_1[-1])$. Hence ![]() $\langle \rho (\tau ^{m}(S_1))\mid 0 \leqslant m \leqslant d_1\rangle _{{{\mathbb {C}}}}$ is equal to
$\langle \rho (\tau ^{m}(S_1))\mid 0 \leqslant m \leqslant d_1\rangle _{{{\mathbb {C}}}}$ is equal to
If ![]() $k\geqslant 2$ and
$k\geqslant 2$ and ![]() $m\leqslant d_k$, then according to the structure of (2.4) and our condition on
$m\leqslant d_k$, then according to the structure of (2.4) and our condition on ![]() $\{H_1,\ldots,H_\ell \}$, we have
$\{H_1,\ldots,H_\ell \}$, we have
where
Thus ![]() $\rho (\tau ^{m}(S_k))\in V_{\rm sym}$ and we are done.
$\rho (\tau ^{m}(S_k))\in V_{\rm sym}$ and we are done.
8.3 Further directions
For all classical types, we find families of generators ![]() $\{H_k\}$ that behave well in terms of (0.2). The general picture is not complete yet, since the following question remains open.
$\{H_k\}$ that behave well in terms of (0.2). The general picture is not complete yet, since the following question remains open.
Question 8.5 Does any exceptional Lie algebra ![]() $\mathfrak g$ poses a set of generators
$\mathfrak g$ poses a set of generators ![]() $\{H_k\}\subset {{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ such that each
$\{H_k\}\subset {{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ such that each ![]() $H_k$ satisfies (0.2)?
$H_k$ satisfies (0.2)?
Proposition 5.6 takes care of type ![]() ${\sf G}_2$. We have seen also some partial positive answers in other types.
${\sf G}_2$. We have seen also some partial positive answers in other types.
Question 8.6 Are there homogeneous generators ![]() $\{H_k\}$ of
$\{H_k\}$ of ![]() ${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ such that
${{\mathcal {S}}}(\mathfrak g)^{\mathfrak g}$ such that ![]() ${\sf m}(H_k)=0$ for each
${\sf m}(H_k)=0$ for each ![]() $k$?
$k$?
The calculations in § 6 prove that in type G![]() $_2$, the answer is negative. I would expect that the answer is negative in general.
$_2$, the answer is negative. I would expect that the answer is negative in general.
As Example 3.7 shows, a set of generators ![]() $\{H_k\}$, where each
$\{H_k\}$, where each ![]() $H_k$ satisfies (0.2), is not unique. For the classical Lie algebras, there is a freedom of choice in degree
$H_k$ satisfies (0.2), is not unique. For the classical Lie algebras, there is a freedom of choice in degree ![]() $4$ and there is also some freedom in degree
$4$ and there is also some freedom in degree ![]() $6$.
$6$.
It is quite possible that the condition (8.3) on the set ![]() $\{H_k\}$ is less restrictive than (0.2). However, we have no convincing evidence to this point.
$\{H_k\}$ is less restrictive than (0.2). However, we have no convincing evidence to this point.
Remark 8.7 Probably there are some intricate combinatorial identities hidden in (2.4). In order to reveal them, one has to understand the natural numbers ![]() $c(r,\bar a)$ appearing in the proof of Lemma 2.2, the rational constants
$c(r,\bar a)$ appearing in the proof of Lemma 2.2, the rational constants ![]() $c_{2,3}(j,p)$ of Lemma 3.2, as well as the scalars
$c_{2,3}(j,p)$ of Lemma 3.2, as well as the scalars ![]() $C(\bar a^{(r)},\bar \gamma )$ of Proposition 3.4.
$C(\bar a^{(r)},\bar \gamma )$ of Proposition 3.4.
Acknowledgements
I am grateful to Alexander Molev for his enlightening explanations on the subjects of Segal–Sugawara vectors and vertex algebras. A special thank you is due to Leonid Rybnikov for bringing Gaudin subalgebras to my attention.
Part of this work was done during my visit to the Mathematical Institute of Cologne University. It is a pleasure to thank Peter Littelmann for his hospitality and many inspiring conversations about mathematics in general as well as Kac–Moody algebras in particular.