Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-24T10:52:11.890Z Has data issue: false hasContentIssue false
  • English
  • Français

SCOTT SENTENCE COMPLEXITIES OF LINEAR ORDERINGS

Part of: Set theory Computability and recursion theory Model theory

Published online by Cambridge University Press:  13 December 2024

DAVID GONZALEZ Open the ORCID record for DAVID GONZALEZ [Opens in a new window]  and
DINO ROSSEGGER Open the ORCID record for DINO ROSSEGGER [Opens in a new window]
DAVID GONZALEZ*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF CALIFORNIA BERKELEY, 970 EVANS HALL BERKELEY, CA 94720 USA
DINO ROSSEGGER
Affiliation:
INSTITUTE OF DISCRETE MATHEMATICS AND GEOMETRY TECHNISCHE UNIVERSITÄT WIEN WIEDNER HAUPTSTRAßE 8–10/104 1040 WIEN AUSTRIA E-mail: [email protected]
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study possible Scott sentence complexities of linear orderings using two approaches. First, we investigate the effect of the Friedman–Stanley embedding on Scott sentence complexity and show that it only preserves 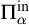$\Pi ^{\mathrm {in}}_{\alpha }$ complexities. We then take a more direct approach and exhibit linear orderings of all Scott sentence complexities except 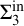$\Sigma ^{\mathrm {in}}_{3}$ and 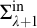$\Sigma ^{\mathrm {in}}_{\lambda +1}$ for 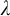$\lambda $ a limit ordinal. We show that the former cannot be the Scott sentence complexity of a linear ordering. In the process we develop new techniques which appear to be helpful to calculate the Scott sentence complexities of structures.

Keywords

Scott sentenceScott sentence complexityScott ranklinear orderslinear orderingstotal ordersinfinitary logiccomputable structures

MSC classification

Primary: 03C57: Effective and recursion-theoretic model theory 03C70: Logic on admissible sets 03E15: Descriptive set theory
Secondary: 03D45: Theory of numerations, effectively presented structures
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 30
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alvir, R., Greenberg, N., Harrison-Trainor, M., and Turetsky, D., Scott complexity of countable structures . The Journal of Symbolic Logic , vol. 86 (2021), no. 4, pp. 1706–1720.CrossRefGoogle Scholar
Alvir, R., Knight, J., and McCoy, C., Complexity of Scott sentences . Fundamenta Mathematicae , vol. 251 (2020), pp. 109–129.CrossRefGoogle Scholar
Alvir, R. and Rossegger, D., The complexity of Scott sentences of scattered linear orders . The Journal of Symbolic Logic , vol. 85 (2020), no. 3, pp. 1079–1101.CrossRefGoogle Scholar
Ash, C. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy , Stud. Logic Found. Math. , vol. 144. North-Holland Publishing Co., Amsterdam, 2000.Google Scholar
Ash, C. J., Recursive labelling systems and stability of recursive structures in hyperarithmetical degrees . Transactions of the American Mathematical Society , vol. 298 (1986), no. 2, pp. 497–514.CrossRefGoogle Scholar
Ash, C. J., A construction for recursive linear orderings . The Journal of Symbolic Logic , vol. 56 (1991), no. 2, pp. 673–683.CrossRefGoogle Scholar
Calvert, W., Goncharov, S. S., and Knight, J. F., Computable structures of Scott rank ${\omega}_1^{CK}$ in familiar classes . Advances in logic , vol. 425 (2007), pp. 49–66.Google Scholar
Friedman, H. and Stanley, L., A Borel reducibility theory for classes of countable structures . The Journal of Symbolic Logic , vol. 54 (1989), no. 03, pp. 894–914.CrossRefGoogle Scholar
Frolov, A., Kalimullin, I. S., Harizanov, V., Kudinov, O., and Miller, R., Spectra of $hig{h}_n$ and $non- lo{w}_n$ degrees . Journal of Logic and Computation , vol. 22 (2010), no. 4, pp. 755–777.CrossRefGoogle Scholar
Frolov, A. N., Effective categoricity of computable linear orderings . Algebra and Logic , vol. 54 (2015), no. 5, pp. 415–418.CrossRefGoogle Scholar
Gao, S., Some dichotomy theorems for isomorphism relations of countable models . The Journal of Symbolic Logic , vol. 66 (2001), no. 2, pp. 902–922.CrossRefGoogle Scholar
Gao, S., Invariant Descriptive Set Theory . CRC Press, Boca Raton, 2008.CrossRefGoogle Scholar
Goncharov, S., Harizanov, V., Knight, J., McCoy, C., Miller, R., and Solomon, R., Enumerations in computable structure theory . Annals of Pure and Applied Logic , vol. 136 (2005), no. 3, pp. 219–246.CrossRefGoogle Scholar
Gonzalez, D. and Montalbán, A., The $\omega$ -vaught’s conjecture. Trans. Amer. Math. Soc. , vol. 376 (2023), no. 8, pp. 5989–6008.Google Scholar
Harrison, J., Recursive pseudo-well-orderings . Transactions of the American Mathematical Society , vol. 131 (1968), no. 2, pp. 526–543.CrossRefGoogle Scholar
Harrison-Trainor, M. and Montalbán, A., The tree of tuples of a structure . The Journal of Symbolic Logic , vol. 87 (2022), no. 1, pp. 21–46.CrossRefGoogle Scholar
Knight, J. F., Soskova, A. A., and Vatev, S. V., Coding in graphs and linear orderings . The Journal of Symbolic Logic , vol. 85 (2020), no. 2, pp. 673–690.CrossRefGoogle Scholar
McCoy, C. F. D., ${\varDelta}_2^0$ - categoricity in Boolean algebras and linear orderings . Annals of Pure and Applied Logic , vol. 119 (2003), no. 1, pp. 85–120.CrossRefGoogle Scholar
Montalbán, A., A robuster Scott rank . Proceedings of the American Mathematical Society , vol. 143 (2015), no. 12, pp. 5427–5436.CrossRefGoogle Scholar
Montalbán, A., Classes of structures with no intermediate isomorphism problems . Journal of Symbolic Logic , vol. 81 (2016), no. 1, pp. 127–150.CrossRefGoogle Scholar
Montalbán, A., Computable Structure Theory: Within the Arithmetic , Perspectives in Logic, Cambridge University Press, Cambridge, 2021.CrossRefGoogle Scholar
Montalbán, A., Computable Structure Theory: Beyond the Arithmetic . 2022, https://math.berkeley.edu/~antonio/CSTpart2_DRAFT.pdf.CrossRefGoogle Scholar
Remmel, J. B., Recursively categorical linear orderings . Proceedings of the American Mathematical Society , vol. 83 (1981), no. 2, pp. 387–391.CrossRefGoogle Scholar
Richter, L. J., Degrees of structures . The Journal of Symbolic Logic , vol. 46 (1981), no. 4, pp. 723–731.CrossRefGoogle Scholar