Ill posedness in modelling two-dimensional morphodynamic problems: effects of bed slope and secondary flow

Abstract

A two-dimensional model describing river morphodynamic processes under mixed-size sediment conditions is analysed with respect to its well posedness. Well posedness guarantees the existence of a unique solution continuously depending on the problem data. When a model becomes ill posed, infinitesimal perturbations to a solution grow infinitely fast. Apart from the fact that this behaviour cannot represent a physical process, numerical simulations of an ill-posed model continue to change as the grid is refined. For this reason, ill-posed models cannot be used as predictive tools. One source of ill posedness is due to the simplified description of the processes related to vertical mixing of sediment. The current analysis reveals the existence of two additional mechanisms that lead to model ill posedness: secondary flow due to the flow curvature and the effect of gravity on the sediment transport direction. When parametrising secondary flow, accounting for diffusion in the transport of secondary flow intensity is a requirement for obtaining a well-posed model. When considering the theoretical amount of diffusion, the model predicts instability of perturbations that are incompatible with the shallow water assumption. The effect of gravity on the sediment transport direction is a necessary mechanism to yield a well-posed model, but not all closure relations to account for this mechanism are valid under mixed-size sediment conditions. Numerical simulations of idealised situations confirm the results of the stability analysis and highlight the consequences of ill posedness.

1 Introduction

Modelling of fluvial morphodynamic processes is a powerful tool not only to predict the future state of a river after, for instance, an intervention or a change in the discharge regime (Blom et al. 2017), but also as a source of understanding of the natural processes responsible for patterns such as dunes, meanders and bars (Callander 1969; Seminara 2006; Colombini & Stocchino 2012). A framework for modelling the morphodynamic development of alluvial rivers is composed of a system of partial differential equations for modelling the flow, change in bed elevation and change in the bed surface texture. The Saint-Venant (1871) equations account for conservation of water mass and momentum and enable modelling processes with a characteristic length scale significantly longer than the flow depth in one-dimensional cases. The shallow water equations describe the depth-averaged flow in two-dimensional cases. Conservation of unisize bed sediment is typically modelled using the Exner (1920) equation and, under mixed-size sediment conditions, the active layer model (Hirano 1971) accounts for mass conservation of bed sediment of each grain size.

Although widely successful in predicting river morphodynamics, a fundamental problem arises when using the above framework. Under certain conditions the description of the natural phenomena is not captured by the system of equations, which manifests as an ill-posed model. Models describe a simplified version of reality, which allows us to understand the key elements playing a major role in the dynamics of the system studied (Paola & Leeder 2011). Major simplifications such as reducing streamwise morphodynamic processes to a diffusion equation allow for insight into the creation of stratigraphic records and evolution on large spatial scales (Paola, Heller & Angevine 1992; Paola 2000; Paola & Leeder 2011). There is a difference between greatly simplified models and models that do not capture the physical processes. A simplified model reproduces a reduced-complexity version of reality (Murray 2007) and it is mathematically well posed, as a unique solution exists that depends continuously on the data (Hadamard 1923; Joseph & Saut 1990). An ill-posed model lacks crucial physical processes that cause the model to be unsuitable to capture the dynamics of the system (Fowler 1997). An ill-posed model is unrepresentative of a physical phenomenon, as the growth rate of infinitesimal perturbations to a solution (i.e. negligible noise from a physical perspective) tends to infinity (Kabanikhin 2008). This is different from chaotic systems, in which noise similarly causes the solution to diverge but not infinitely fast (Devaney 1989; Banks et al. 1992).

An example of an ill-posed model is the one describing the dynamics of granular flow. The continuum formulation of such a problem depends on deriving a model for the granular viscosity. Jop, Forterre & Pouliquen (2005, 2006) relate viscosity to a dimensionless shear rate. The model captures the dynamics of granular flows if the dimensionless shear rate is within a certain range, but otherwise the model is ill-posed and loses its predictive capabilities (Barker et al. 2015). A better representation of the physical processes guaranteeing that viscosity tends to 0 when the dimensionless shear rate tends to 0 extends the domain of well posedness (Barker & Gray 2017).

Under unisize sediment and one-dimensional flow conditions, the Saint-Venant–Exner model may be ill posed when the Froude number is larger than 6 (Cordier, Le & De Luna 2011). As most flows of interest are well below this limit, we can consider modelling of fluvial problems under unisize sediment conditions to be well posed. This is not the case when considering mixed-size sediment. Using the active layer model we assume that the bed can be discretised into two layers: the active layer and the substrate. The sediment transport rate depends on the grain size distribution of the active layer. A vertical flux of sediment occurs between the active layer and the substrate if the elevation of the interface between the active layer and the substrate changes. The active layer is well mixed, whereas the substrate can be stratified. The above simplification of the physical processes responsible for vertical mixing causes the active layer model to be ill posed (Ribberink 1987; Stecca, Siviglia & Blom 2014; Chavarrías, Stecca & Blom 2018). In particular, the active layer is prone to be ill posed under degradational conditions into a substrate finer than the active layer (i.e. an armoured bed (Parker & Sutherland 1990)) for any value of the Froude number.

Previous analyses of river morphodynamic models regarding their well posedness have been focused on conditions of one-dimensional flow (Ribberink 1987; Cordier et al. 2011; Stecca et al. 2014; Chavarrías et al. 2018). Our objective is to extend these analyses to conditions of two-dimensional flow. More specifically we include the secondary flow and the bed slope effect in the analysis of the well posedness of the system of equations.

As the flow is intrinsically three-dimensional, the depth-averaging procedure eliminates an important flow component: the secondary flow (Van Bendegom 1947; Rozovskii 1957). The secondary flow causes, for instance, an increase in the amplitude of meanders (Kitanidis & Kennedy 1984) and plays an important role in bar development (Olesen 1982). To understand the morphology of two-dimensional features, it is necessary to account for the fact that the sediment transport direction is affected by the gravitational pull when the bed slope in the transverse direction is significant (Dietrich & Smith 1984; Seminara 2006). This is usually done using a closure relation that sets the angle between the flow and the sediment transport directions as a function of the flow and sediment parameters (Van Bendegom 1947; Engelund 1974; Talmon, Struiksma & Mierlo 1995; Seminara, Solari & Parker 2002; Parker, Seminara & Solari 2003; Francalanci & Solari 2007, 2008; Baar et al. 2018).

In this paper we show that combining these two effects, secondary flow and sediment deflection by the bed slope, leads in some cases to an ill-posed system of equations. The paper is organised as follows. In § 2 we present the model equations describing the primary and secondary flow, as well as changes in bed elevation and surface texture. In § 3 we extend the explanation of ill posedness and relate it to growth of perturbations. We subsequently conduct a stability analysis of the equations, which indicates the conditions under which the secondary flow model and the closure relation for the bed slope effect yield an ill-posed model (§ 4). In § 5 we run numerical simulations of idealised cases to test the validity of the analytical results and study the consequences of ill posedness.

2 Mathematical model

In this section we present the two-dimensional mathematical model of flow, accounting for secondary flow, coupled to a morphodynamic model for mixed-size sediment. We subsequently introduce the equations describing the primary flow (§ 2.1), the secondary flow (§ 2.2) and morphodynamic change (§ 2.3). In § 2.4 we linearise the system of equations to study the stability of perturbations.

2.1 Primary flow equations

The primary flow is described using the depth-averaged shallow water equations (e.g. Vreugdenhil 1994):

(2.1) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}q_{x}}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}q_{y}}{\unicode[STIX]{x2202}y}=0, & & \displaystyle\end{eqnarray}$$

(2.2) $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}q_{x}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}(q_{x}^{2}/h+gh^{2}/2)}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}\left(\displaystyle \frac{q_{x}q_{y}}{h}\right)}{\unicode[STIX]{x2202}y}+gh\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}x}-F_{sx}\nonumber\\ \displaystyle & & \displaystyle \quad =2\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\unicode[STIX]{x1D708}h\frac{\unicode[STIX]{x2202}\left(\displaystyle \frac{q_{x}}{h}\right)}{\unicode[STIX]{x2202}x}\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left(\unicode[STIX]{x1D708}h\left(\displaystyle \frac{\unicode[STIX]{x2202}\left(\displaystyle \frac{q_{x}}{h}\right)}{\unicode[STIX]{x2202}y}+\frac{\unicode[STIX]{x2202}\left(\displaystyle \frac{q_{y}}{h}\right)}{\unicode[STIX]{x2202}x}\right)\right)-ghS_{fx},\end{eqnarray}$$

(2.3) $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}q_{y}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}(q_{y}^{2}/h+gh^{2}/2)}{\unicode[STIX]{x2202}y}+\frac{\unicode[STIX]{x2202}\left(\displaystyle \frac{q_{x}q_{y}}{h}\right)}{\unicode[STIX]{x2202}x}+gh\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}y}-F_{sy}\nonumber\\ \displaystyle & & \displaystyle \quad =2\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left(\unicode[STIX]{x1D708}h\frac{\unicode[STIX]{x2202}\left(\displaystyle \frac{q_{y}}{h}\right)}{\unicode[STIX]{x2202}y}\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\unicode[STIX]{x1D708}h\left(\frac{\unicode[STIX]{x2202}\left(\displaystyle \frac{q_{y}}{h}\right)}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}\left(\displaystyle \frac{q_{x}}{h}\right)}{\unicode[STIX]{x2202}y}\right)\right)-ghS_{fy},\end{eqnarray}$$

where $(x,y)$ (m) are Cartesian coordinates and $t$ (s) is the time coordinate. The variables $(q_{x},q_{y})=(uh,vh)$ ( $\text{m}^{2}~\text{s}^{-1}$ ) are the specific water discharges in the $x$ and $y$ direction, respectively, where $h$ (m) is the flow depth and $u$ ( $\text{m}~\text{s}^{-1}$ ) and $v$ ( $\text{m}~\text{s}^{-1}$ ) are the depth-averaged flow velocities. The variable $\unicode[STIX]{x1D702}$ (m) is the bed elevation and $g$ ( $\text{m}~\text{s}^{-2}$ ) the acceleration due to gravity. The friction slopes are $(S_{fx},S_{fy})$ ( $-$ ) and the diffusion coefficient $\unicode[STIX]{x1D708}$ ( $\text{m}^{2}~\text{s}^{-1}$ ) is the horizontal eddy viscosity. The depth-averaging procedure of the equations of motion introduces terms that originate from the difference between the actual velocity at a certain elevation in the water column and the depth-averaged velocity. We separate the contributions due to turbulent motion and secondary flow caused by the flow curvature. The contribution due to turbulent motion is accounted for by the diffusion coefficient. Elder (1959) derived an expression for the diffusion coefficient that accounts for the effect of turbulent motion on the depth-averaged flow assuming a logarithmic profile for the primary flow and negligible effect of molecular viscosity:

(2.4) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{E}={\textstyle \frac{1}{6}}\unicode[STIX]{x1D705}hu^{\ast }, & & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D705}=0.41$ ( $-$ ) is the von Kármán constant and $u^{\ast }=\sqrt{C_{f}}Q/h$ ( $\text{m}~\text{s}^{-1}$ ) is the friction velocity. Parameter $C_{f}$ ( $-$ ) is a non-dimensional friction coefficient, which we assume to be constant (Ikeda, Parker & Sawai 1981; Schielen, Doelman & De Swart 1993) and $Q=\sqrt{q_{x}^{2}+q_{y}^{2}}$ ( $\text{m}^{2}~\text{s}^{-1}$ ) is the module of the specific water discharge. In the numerical simulations we will assume the eddy viscosity to be a constant equal to the value given by $\unicode[STIX]{x1D708}_{E}$ in a reference state (e.g. Falconer 1980; Lien et al. 1999). Appendix A presents the limitations of the coefficient derived by Elder (1959).

The terms ( $F_{sx},F_{sy}$ ) ( $\text{m}^{2}~\text{s}^{-2}$ ) account for the effect of secondary flow. These terms are responsible for a transfer of momentum that shifts the maximum velocity to the outer bend (Kalkwijk & De Vriend 1980), as well as for a sink of energy in the secondary circulation (Flokstra 1977; Begnudelli, Valiani & Sanders 2010). We deal with these terms in § 2.2.

We assume a Chézy-type friction:

(2.5a,b ) $$\begin{eqnarray}\displaystyle S_{fx}=\frac{C_{f}q_{x}Q}{gh^{3}},\quad S_{fy}=\frac{C_{f}q_{y}Q}{gh^{3}}. & & \displaystyle\end{eqnarray}$$

One underlying assumption of the system of equations presented above is that the vertical length and velocity scales are negligible with respect to the horizontal ones. Another assumption is the fact that the concentration of sediment (the ratio between the solid and liquid discharge) is small (below $6\times 10^{-3}$ (Garegnani, Rosatti & Bonaventura 2011, 2013)), such that we apply the clear water approximation.

2.2 Secondary flow equations

This section describes the equations that model secondary flow (i.e. formulations for $F_{sx}$ and $F_{sy}$ in (2.2) and (2.3)). The secondary flow velocity profile $u^{s}$ ( $\text{m}~\text{s}^{-1}$ ) (i.e. the vertical profile of the velocity component perpendicular to the primary flow) is assumed to have a universal shape as a function of the relative elevation in the water column $\unicode[STIX]{x1D701}=(z-\unicode[STIX]{x1D702})/h$ ( $-$ ), where $z$ (m) is the vertical Cartesian coordinate perpendicular to $x$ and $y$ increasing in the upward direction (Rozovskii 1957; Engelund 1974; De Vriend 1977, 1981; Booij & Pennekamp 1984). Worded differently, the vertical profile of the secondary flow is parametrised by a single value representing the intensity of the secondary flow $I$ ( $\text{m}~\text{s}^{-1}$ ), such that $u^{s}=f(\unicode[STIX]{x1D701})I$ . The secondary flow intensity $I$ is the integral of the absolute value of the secondary flow velocity profile (De Vriend 1981). Among others, Rozovskii (1957), Engelund (1974) and De Vriend (1977), derive equilibrium profiles of the secondary flow that differ in the description of the eddy viscosity, vertical profile of the primary flow and the boundary condition of the flow at the bed. Following De Vriend (1977), we assume a logarithmic profile for the primary flow (i.e. a parabolic distribution of the eddy viscosity) and vanishing velocity close to the bed at $\unicode[STIX]{x1D701}=\exp (-1-1/\unicode[STIX]{x1D6FC})$ where $\unicode[STIX]{x1D6FC}=\sqrt{C_{f}}/\unicode[STIX]{x1D705}<0.5$ .

The depth-averaging procedure yields the integral value (along $z$ ) of the force per unit mass that the secondary flow exerts on the primary flow (De Vriend 1977; Kalkwijk & De Vriend 1980):

(2.6) $$\begin{eqnarray}\displaystyle & \displaystyle F_{sx}=\frac{\unicode[STIX]{x2202}T_{xx}}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}T_{xy}}{\unicode[STIX]{x2202}y}, & \displaystyle\end{eqnarray}$$

(2.7) $$\begin{eqnarray}\displaystyle & \displaystyle F_{sy}=\frac{\unicode[STIX]{x2202}T_{yx}}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}T_{yy}}{\unicode[STIX]{x2202}y}, & \displaystyle\end{eqnarray}$$

where $T_{lm}$ ( $\text{m}^{3}~\text{s}^{-2}$ ) is the integral shear stress per unit mass in the direction $l$ - $m$ . Assuming a large width-to-depth ratio (i.e. $B/h\gg 1$ , where $B$ (m) is the characteristic channel width) and a mild curvature (i.e. $h/R_{s}\ll 1$ , where $R_{s}$ (m) is the radius of curvature of the streamlines), the shear stress terms are:

(2.8) $$\begin{eqnarray}\displaystyle & \displaystyle T_{xx}=-2\frac{\unicode[STIX]{x1D6FD}^{\ast }I}{Q}q_{x}q_{y}, & \displaystyle\end{eqnarray}$$

(2.9) $$\begin{eqnarray}\displaystyle & \displaystyle T_{xy}=T_{yx}=\frac{\unicode[STIX]{x1D6FD}^{\ast }I}{Q}(q_{x}^{2}-q_{y}^{2}), & \displaystyle\end{eqnarray}$$

(2.10) $$\begin{eqnarray}\displaystyle & \displaystyle T_{yy}=T_{yy}=2\frac{\unicode[STIX]{x1D6FD}^{\ast }I}{Q}q_{x}q_{y}, & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D6FD}^{\ast }=5\unicode[STIX]{x1D6FC}-15.6\unicode[STIX]{x1D6FC}^{2}+37.5\unicode[STIX]{x1D6FC}^{3}$ .

The simplest strategy to account for secondary flow assumes that the secondary flow is fully developed. This is equivalent to saying that the secondary flow intensity is equal to the equilibrium value $I_{e}=Q/R_{s}$ ( $\text{m}~\text{s}^{-1}$ ) found in an infinitely long bend (Rozovskii 1957; Engelund 1974; De Vriend 1977, 1981; Booij & Pennekamp 1983). A change in channel curvature leads to the streamwise adaptation of secondary flow to the equilibrium value (De Vriend 1981; Ikeda & Nishimura 1986; Johannesson & Parker 1989; Seminara & Tubino 1989). Booij & Pennekamp (1984) and Kalkwijk & Booij (1986) not only account for the spatial adaptation but also the temporal adaptation of the secondary flow associated with a variable discharge or tides. Here we adopt the latter strategy, which has been applied, for instance, in modelling the morphodynamics of braided rivers (Javernick et al. 2016; Williams et al. 2016; Javernick, Redolfi & Bertoldi 2018). The spatial and temporal adaptation of secondary flow is expressed by (Jagers 2003):

(2.11) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}I}{\unicode[STIX]{x2202}t}+\frac{q_{x}}{h}\frac{\unicode[STIX]{x2202}I}{\unicode[STIX]{x2202}x}+\frac{q_{y}}{h}\frac{\unicode[STIX]{x2202}I}{\unicode[STIX]{x2202}y}-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\unicode[STIX]{x1D708}\frac{\unicode[STIX]{x2202}I}{\unicode[STIX]{x2202}x}\right)-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left(\unicode[STIX]{x1D708}\frac{\unicode[STIX]{x2202}I}{\unicode[STIX]{x2202}y}\right)=S_{s}, & & \displaystyle\end{eqnarray}$$

where $S_{s}$ ( $\text{m}~\text{s}^{-2}$ ) is a source term which depends on the difference between the local secondary flow intensity and its equilibrium value:

(2.12) $$\begin{eqnarray}\displaystyle S_{s}=-\frac{I-I_{e}}{T_{I}}, & & \displaystyle\end{eqnarray}$$

where $T_{I}$ (s) is the adaptation time scale of the secondary flow:

(2.13) $$\begin{eqnarray}\displaystyle T_{I}=\frac{L_{I}h}{Q}, & & \displaystyle\end{eqnarray}$$

where $L_{I}=L_{I}^{\ast }h$ (m) is the adaptation length scale of the secondary flow, which depends on the non-dimensional length scale $L_{I}^{\ast }=(1-2\unicode[STIX]{x1D6FC})/2\unicode[STIX]{x1D705}^{2}\unicode[STIX]{x1D6FC}$ (Kalkwijk & Booij 1986).

The radius of curvature of the streamlines is defined as (e.g. Legleiter & Kyriakidis 2006):

(2.14) $$\begin{eqnarray}\displaystyle \frac{1}{R_{s}}=\frac{\displaystyle \frac{\text{d}\hspace{1.0pt}x}{\text{d}t}\frac{\text{d}^{2}y}{\text{d}t^{2}}-\frac{\text{d}y}{\text{d}t}\frac{\text{d}^{2}x}{\text{d}t^{2}}}{\left(\left(\displaystyle \frac{\text{d}\hspace{1.0pt}x}{\text{d}t}\right)^{2}+\left(\displaystyle \frac{\text{d}y}{\text{d}t}\right)^{2}\right)^{3/2}}, & & \displaystyle\end{eqnarray}$$

assuming steady flow and in terms of water discharge we obtain:

(2.15) $$\begin{eqnarray}\displaystyle \frac{1}{R_{s}}=\frac{-q_{x}q_{y}\displaystyle \frac{\unicode[STIX]{x2202}q_{x}}{\unicode[STIX]{x2202}x}+q_{x}^{2}\frac{\unicode[STIX]{x2202}q_{y}}{\unicode[STIX]{x2202}x}-q_{y}^{2}\frac{\unicode[STIX]{x2202}q_{x}}{\unicode[STIX]{x2202}y}+q_{x}q_{y}\frac{\unicode[STIX]{x2202}q_{y}}{\unicode[STIX]{x2202}y}}{(q_{x}^{2}+q_{y}^{2})^{3/2}}. & & \displaystyle\end{eqnarray}$$

The secondary flow model described in this section closes the primary flow model described in § 2.1 given a certain bed elevation. In the following section we describe the model equations that describe changes in bed elevation as a function of the primary and secondary flow.

2.3 Morphodynamic equations

We consider an alluvial bed composed of an arbitrary number $N$ of non-cohesive sediment fractions characterised by a grain size $d_{k}$ (m), where the subscript $k$ denotes the grain size fraction in increasing order (i.e. $d_{1}<d_{2}<\cdots <d_{N}$ ). Bed elevation change depends on the divergence of the sediment transport rate (Exner 1920):

(2.16) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}q_{bx}}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}q_{by}}{\unicode[STIX]{x2202}y}=0, & & \displaystyle\end{eqnarray}$$

where $q_{bx}=\sum _{k=1}^{N}q_{bxk}$ ( $\text{m}^{2}~\text{s}^{-1}$ ) and $q_{by}=\sum _{k=1}^{N}q_{byk}$ ( $\text{m}^{2}~\text{s}^{-1}$ ) are the total specific (i.e. per unit of differential length) sediment transport rates including pores in the $x$ and $y$ direction, respectively. The variables $q_{bxk}$ ( $\text{m}^{2}~\text{s}^{-1}$ ) and $q_{byk}$ ( $\text{m}^{2}~\text{s}^{-1}$ ) are the specific sediment transport rates of size fraction $k$ including pores. For simplicity we assume a constant porosity and density of the bed sediment. The sediment transport rate is assumed to be locally at capacity, which implies that we do not model the temporal and spatial adaptation of the sediment transport rate to capacity conditions (Bell & Sutherland 1983; Phillips & Sutherland 1989; Jain 1992).

Changes in the bed surface grain size distribution are accounted for using the active layer model (Hirano 1971). For simplicity, we assume a constant active layer thickness $L_{a}$ (m). Conservation of sediment mass of size fraction $k$ in the active layer reads:

(2.17) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}M_{ak}}{\unicode[STIX]{x2202}t}+f_{k}^{I}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}q_{bxk}}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}q_{byk}}{\unicode[STIX]{x2202}y}=0\quad k\in \{1,N-1\}, & & \displaystyle\end{eqnarray}$$

and in the substrate (Chavarrías et al. 2018):

(2.18) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}M_{sk}}{\unicode[STIX]{x2202}t}-f_{k}^{I}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}t}=0\quad k\in \{1,N-1\}, & & \displaystyle\end{eqnarray}$$

where $M_{ak}=F_{ak}L_{a}$ (m) and $M_{sk}=\int _{\unicode[STIX]{x1D702}_{0}}^{\unicode[STIX]{x1D702}_{0}+\unicode[STIX]{x1D702}-L_{a}}f_{sk}(z)\,\text{d}z$ (m) are the volume of sediment of size fraction $k$ per unit of bed area in the active layer and the substrate, respectively. Parameter $\unicode[STIX]{x1D702}_{0}$ (m) is a datum for bed elevation. Parameters $F_{ak}\in [0,1]$ , $f_{sk}\in [0,1]$ and $f_{k}^{I}\in [0,1]$ are the volume fraction content of sediment of size fraction $k$ in the active layer, substrate and at the interface between the active layer and the substrate, respectively. By definition, the sum of the volume fraction content over all size fractions equals 1:

(2.19a-c ) $$\begin{eqnarray}\displaystyle \mathop{\sum }_{k=1}^{N}F_{ak}=1,\quad \mathop{\sum }_{k=1}^{N}f_{sk}(z)=1,\quad \mathop{\sum }_{k=1}^{N}f_{k}^{I}=1. & & \displaystyle\end{eqnarray}$$

Under degradational conditions, the volume fraction content of size fraction $k$ at the interface between the active layer and the substrate is equal to that at the top part of the substrate ( $f_{k}^{I}=f_{sk}(z=\unicode[STIX]{x1D702}-L_{a})$ for $\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}t<0$ ). This allows for modelling of arbitrarily abrupt changes in grain size due to erosion of previous deposits. Under aggradational conditions the sediment transferred to the substrate is a weighted mixture of the sediment in the active layer and the bed load (Parker 1991; Hoey & Ferguson 1994; Toro-Escobar, Paola & Parker 1996). Here we simplify the analysis and we assume that the contribution of the bed load to the depositional flux is negligible (i.e. $f_{k}^{I}=F_{ak}$ for $\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}t>0$ ) (Hirano 1971).

The magnitude of the sediment transport rate is assumed to be a function of the local bed shear stress. We apply the sediment transport relation by Engelund & Hansen (1967) in a fractional manner (Blom, Viparelli & Chavarrías 2016; Blom et al. 2017) as well as the one by Ashida & Michiue (1971) (appendix B).

The direction of the sediment transport ( $\unicode[STIX]{x1D711}_{sk}$ (rad)) is affected by the secondary flow and the bed slope (Van Bendegom 1947):

(2.20) $$\begin{eqnarray}\displaystyle \tan \unicode[STIX]{x1D711}_{sk}=\frac{\sin \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}-\displaystyle \frac{1}{g_{sk}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}y}}{\cos \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}-\displaystyle \frac{1}{g_{sk}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}x}}\quad k\in \{1,N\}, & & \displaystyle\end{eqnarray}$$

where $g_{sk}$ ( $-$ ) is a function that accounts for the influence of the bed slope on the sediment transport direction and $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}$ (rad) is the direction of the sediment transport accounting for the secondary flow only:

(2.21) $$\begin{eqnarray}\displaystyle \tan \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}=\frac{q_{y}-h\unicode[STIX]{x1D6FC}_{I}\displaystyle \frac{q_{x}}{Q}I}{q_{x}-h\unicode[STIX]{x1D6FC}_{I}\displaystyle \frac{q_{y}}{Q}I}. & & \displaystyle\end{eqnarray}$$

Assuming a mild curvature, uniform flow conditions and a logarithmic profile of the primary flow, the constant $\unicode[STIX]{x1D6FC}_{I}$ ( $-$ ) is (De Vriend 1977):

(2.22) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{I}=\frac{2}{\unicode[STIX]{x1D705}^{2}}(1-\unicode[STIX]{x1D6FC}). & & \displaystyle\end{eqnarray}$$

The effect of the bed slope on the sediment transport direction depends on the grain size (Parker & Andrews 1985). We account for this effect setting:

(2.23) $$\begin{eqnarray}\displaystyle g_{sk}=A_{s}\unicode[STIX]{x1D703}_{k}^{B_{s}}\quad k\in \{1,N\}, & & \displaystyle\end{eqnarray}$$

where $A_{s}$ ( $-$ ) and $B_{s}$ ( $-$ ) are non-dimensional parameters and $\unicode[STIX]{x1D703}_{k}$ ( $-$ ) is the Shields (1936) stress (appendix B). Different values of the coefficients $A_{s}$ and $B_{s}$ have been proposed (for a recent review, see Baar et al. (2018)). We consider two possibilities: (i) $A_{s}=1$ , $B_{s}=0$ (Schielen et al. 1993) and (ii) $A_{s}=1.70$ and $B_{s}=0.5$ (Talmon et al. 1995). In the first and simpler case, the bed slope effect is independent of the bed shear stress (Engelund & Skovgaard 1973; Engelund 1975). In the second, more complex, case, the bed slope effect is assumed to be dependent on the fluid drag force on the grains, which is assumed to depend on the Shields stress (Koch & Flokstra 1981).

2.4 Linearised system of equations

The system of equations describing the flow, change of bed level and change of the bed surface texture is highly nonlinear. Here we linearise the system of equations to provide insight on the fundamental properties of the model and to study the stability of perturbations. To this end we consider a reference state that is a solution to the system of equations. The reference state is a steady uniform straight flow in the $x$ direction over an inclined plane bed composed of an arbitrary number of size fractions. Mathematically: $h_{0}=\text{ct.}$ , $q_{x0}=\text{ct.}$ , $q_{y0}=0$ , $I_{0}=0$ , $\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}x=\text{ct.}=-C_{f}q_{x0}^{2}/gh_{0}^{3}$ , $\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}y=0$ , $M_{ak0}=\text{ct.}$ $\forall k\in \{1,N-1\}$ , where ct. denotes a constant different from 0 and subscript $0$ indicates the reference solution.

We add a small perturbation to the reference solution denoted by $^{\prime }$ and we linearise the resulting system of equations. After substituting the reference solution we obtain a system of equations of the perturbed variables:

(2.24) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{Q}^{\prime }}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D63F}_{\boldsymbol{x}\mathbf{0}}\frac{\unicode[STIX]{x2202}^{2}\boldsymbol{Q}^{\prime }}{\unicode[STIX]{x2202}x^{2}}+\unicode[STIX]{x1D63F}_{\boldsymbol{y}\mathbf{0}}\frac{\unicode[STIX]{x2202}^{2}\boldsymbol{Q}^{\prime }}{\unicode[STIX]{x2202}y^{2}}+\unicode[STIX]{x1D63C}_{\boldsymbol{x}\mathbf{0}}\frac{\unicode[STIX]{x2202}\boldsymbol{Q}^{\prime }}{\unicode[STIX]{x2202}x}+\unicode[STIX]{x1D63C}_{\boldsymbol{y}\mathbf{0}}\frac{\unicode[STIX]{x2202}\boldsymbol{Q}^{\prime }}{\unicode[STIX]{x2202}y}+\unicode[STIX]{x1D63D}_{\mathbf{0}}\boldsymbol{Q}^{\prime }=0, & & \displaystyle\end{eqnarray}$$

where the vector of dependent variables is:

(2.25) $$\begin{eqnarray}\displaystyle \boldsymbol{Q}^{\prime }=[h^{\prime },q_{x}^{\prime },q_{y}^{\prime },I^{\prime },\unicode[STIX]{x1D702}^{\prime },[M_{ak}^{\prime }]]^{\text{T}}, & & \displaystyle\end{eqnarray}$$

where the square bracket indicates the vector character.

The diffusive matrix in $x$ direction is:

(2.26)

where $\mathbb{0}$ denotes the zero matrix. The diffusive matrix in the $y$ direction is:

(2.27)

The advective matrix in the $x$ direction is:

(2.28)

The advective matrix in the $y$ direction is:

(2.29)

The matrix of linear terms is:

(2.30)

We assume that the perturbations can be represented as a Fourier series, which implies that they are piecewise smooth and bounded for $x=\pm \infty$ . Using this assumption the solution of the perturbed system is expressed in the form of normal modes:

(2.31) $$\begin{eqnarray}\displaystyle \boldsymbol{Q}^{\prime }=\text{Re}(\boldsymbol{V}\text{e}^{\text{i}(k_{wx}+k_{wy}-\unicode[STIX]{x1D714}t)}), & & \displaystyle\end{eqnarray}$$

where $\text{i}$ is the imaginary unit, $k_{wx}$ ( $\text{rad}~\text{m}^{-1}$ ) and $k_{wy}$ ( $\text{rad}~\text{m}^{-1}$ ) are the real wavenumbers in the $x$ and $y$ direction, respectively, $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{r}+\text{i}\unicode[STIX]{x1D714}_{i}$ ( $\text{rad}~\text{s}^{-1}$ ) is the complex angular frequency, $\boldsymbol{V}$ is the complex amplitude vector and Re denotes the real part of the solution (which we will omit in the subsequent steps). The variable $\unicode[STIX]{x1D714}_{r}$ is the angular frequency and $\unicode[STIX]{x1D714}_{i}$ the attenuation coefficient. A value of $\unicode[STIX]{x1D714}_{i}>0$ implies growth of perturbations and $\unicode[STIX]{x1D714}_{i}<0$ decay. Substitution of (2.31) in (2.24) yields:

(2.32) $$\begin{eqnarray}\displaystyle [\unicode[STIX]{x1D648}_{\mathbf{0}}-\unicode[STIX]{x1D714}\mathbb{1}]\boldsymbol{V}=0, & & \displaystyle\end{eqnarray}$$

where:

(2.33) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D648}_{\mathbf{0}}=\unicode[STIX]{x1D63F}_{\boldsymbol{x}\mathbf{0}}k_{wx}^{2}\text{i}+\unicode[STIX]{x1D63F}_{\boldsymbol{y}\mathbf{0}}k_{wy}^{2}\text{i}+\unicode[STIX]{x1D63C}_{\boldsymbol{x}\mathbf{0}}k_{wx}+\unicode[STIX]{x1D63C}_{\boldsymbol{y}\mathbf{0}}k_{wy}-\unicode[STIX]{x1D63D}_{\mathbf{0}}\text{i}, & & \displaystyle\end{eqnarray}$$

and $\mathbb{1}$ denotes the unit matrix. Equation (2.32) is an eigenvalue problem in which the eigenvalues of $\unicode[STIX]{x1D648}_{\mathbf{0}}$ (as a function of the wavenumber) are the values of $\unicode[STIX]{x1D714}$ satisfying (2.32).

The solution of the linear model provides information regarding the development of small amplitude oscillations only, but for an arbitrary wavenumber. For this reason the linear model is convenient for studying the well posedness of the model, which we will assess in the following section.

3 Instability, hyperbolicity and ill posedness

Ill posedness has been related to the system of governing equations losing its hyperbolic character. Stability analysis investigates growth and decay of perturbations of a base state. The two mathematical problems may seem unrelated but in fact they are strongly linked. In this section we clarify the terms unstable, hyperbolic and ill posed, and present the mathematical framework that we use to study the well posedness of the system of equations.

A system is stable if perturbations to an equilibrium state decay and the solution returns to its original state. This is equivalent to saying that all possible combinations of wavenumbers in the $x$ and $y$ directions yield a negative growth rate ( $\unicode[STIX]{x1D714}_{i}$ (2.31)). An example of a stable system in hydrodynamics is the inviscid shallow water equations (iSWE) for a Froude number smaller than 2 (Jeffreys 1925; Balmforth & Mandre 2004; Colombini & Stocchino 2005). In figure 1(a) we show the maximum growth rate of perturbations to a reference solution (Case I1, tables 1 and 2) of the iSWE on an inclined plane (i.e. the first three equations of the complete system (2.24), with neither secondary flow nor diffusion). The growth rate is obtained numerically by computing the eigenvalues of the reduced matrix $\unicode[STIX]{x1D648}_{\mathbf{0}}$ (the first three rows and columns in (2.33)) for wavenumbers between 0 and $250~\text{rad}~\text{m}^{-1}$ , which is equivalent to wavelengths ( $l_{wx}=2\unicode[STIX]{x03C0}/k_{wx}$ and equivalently for $y$ ) down to 1 cm. Figure 1(b) presents the same information as figure 1(a) in terms of wavelength rather than wavenumber to better illustrate the behaviour for large wavelengths. The growth rate is negative for all wavenumbers, which confirms that the iSWE for $Fr<2$ yield a stable solution.

Table 1. Reference state.

Table 2. Cases of a stable well-posed model (I1), an unstable well-posed model (B1) and an ill-posed model (I2). Case I2 has the same parameter values as Case I1 but for a mean flow velocity which is equal to $6.30~\text{m}~\text{s}^{-1}$ .

Figure 1. Growth rate of perturbations added to the reference case (tables 1 and 2) as a function of the wavenumber and the wavelength: (a–b) iSWE, $Fr<2$ (Case I1, well posed), (c–d) iSWE $+$ Exner (Case B1, well posed) and (e–f) iSWE, $Fr>2$ (Case I2, ill posed). The panels in the two columns show the same information but highlight the behaviour for large wavenumbers (left column) and for large wavelengths (right column). Red and green indicates growth and decay of perturbations, respectively.

A system is unstable when perturbations to an equilibrium state grow and the solution diverges from the initial equilibrium state. The growth of river bars is an example of an unstable system in river morphodynamics. A straight alluvial channel is stable if the width-to-depth ratio is sufficiently small and, above a certain threshold value, the channel becomes unstable and free alternate bars grow (Engelund & Skovgaard 1973; Fredsøe 1978; Colombini, Seminara & Tubino 1987; Schielen et al. 1993). Mathematically, an unstable system has a region, a domain in the wavenumber space, in which the growth rate of perturbations is positive. In figure 1(c,d) we present the growth rate of perturbations to a reference solution consisting of uniform flow (table 1) on an alluvial bed composed of unisize sediment with a characteristic grain size equal to 0.001 m (Case B1, table 2). The sediment transport rate is computed using the relation by Engelund & Hansen (1967) (B 4) and the effect of the bed slope on the sediment transport direction is accounted for using the simplest formulation, $g_{s}=1$ . Figure 1(d) confirms the classical result of linear bar theory: there exists a critical transverse wavelength ( $l_{wyc}$ ) below which all perturbations decay. In our particular case $l_{wyc}=40.2~\text{m}$ . Impermeable boundary conditions at the river banks limit the possible wavelengths to fractions of the channel width $B$ (m) such that $l_{wy}=2B/m$ for $m=1,2,\ldots$  (Callander 1969). As the most unstable mode is the first one (i.e. $m=1$ , alternate bars) (Colombini et al. 1987; Schielen et al. 1993), the minimum channel width above which perturbations grow is $B_{c}=l_{wyc}/2=20.1~\text{m}$ , which confirms the results of Schielen et al. (1993). Figure 1(c) highlights, as for Case I1, the decay of short waves.

A particular case of instability is that in which the domain of positive growth rate extends to infinitely large wavenumbers (i.e. short waves). Under this condition there is no cutoff wavenumber above which we can neglect the contribution of ever shorter waves with non-zero growth rates. For any unstable perturbation a shorter one can be found which is even more unstable. This implies that the growth rate of an infinitesimal perturbation (i.e. noise) tends to infinity. Such a system cannot represent a physical phenomenon, as the growth rate of any physical process in nature is bounded. A system in which the growth rate of infinitesimal perturbations tends to infinity does not have a unique solution depending continuously on the initial and boundary conditions, which implies that the system is ill posed (Hadamard 1923; Joseph & Saut 1990). An example of an ill-posed hydrodynamic model is the iSWE for flow with a Froude number larger than 2. In figure 1(e,f) we show the growth rate of perturbations to the reference solution of a case in which the Froude number is slightly larger than 2 (Case I2, table 2). The growth rate extends to infinitely large wavenumbers, which confirms that this case is ill posed. A model being ill posed is an indication that there is a relevant physical mechanism that has been neglected in the model derivation (Fowler 1997). Viscous forces regularise the iSWE (i.e. make the model well posed) and rather than ill posed, the viscous shallow water equations become simply unstable for a Froude number larger than 2, predicting the formation of roll waves (Balmforth & Mandre 2004; Balmforth & Vakil 2012; Rodrigues & Zumbrun 2016; Barker et al. 2017a , b ).

Chaotic models, just as ill-posed models, are sensitive to the initial and boundary conditions and lose their predictive capabilities in a deterministic sense (Lorenz 1963). Yet, there are two essential differences. First, chaotic systems lose their predictive capabilities after a certain time (Devaney 1989; Banks et al. 1992), yet there exists a finite time in which the dynamics is predictable. In ill-posed models infinitesimal perturbations to the initial condition cause a finite divergence in the solution in an arbitrarily (but fixed) short time. Second, while the dynamics of a chaotic model is not predictable in deterministic terms after a certain time, these continue to be predictable in statistical terms. For this reason, although being sensitive to the initial and boundary conditions, a model presenting chaotic properties can be used, for instance, to capture the essential dynamics and spatio-temporal features of river braiding (Murray & Paola 1994, 1997). On the contrary, the dynamics of an ill-posed model cannot be analysed in statistical terms.

The numerical solution of an ill-posed problem continues to change as the grid is refined because a smaller grid size resolves larger wavenumbers with faster growth rates (Joseph & Saut 1990; Kabanikhin 2008; Barker et al. 2015; Woodhouse et al. 2012). In other words, the numerical solution of an ill-posed problem does not converge when the grid cell size is reduced. This property emphasises the unrealistic nature of ill-posed problems and shows that ill-posed models cannot be applied in practice.

We present an example of grid dependence specifically related to river morphodynamics under conditions with mixed-size sediment. We consider a case of degradation into a substrate finer than the active layer, as this is a situation in which the active layer model is prone to be ill posed (§ 1). The reference state is the same as in Case B1, yet the sediment is a mixture of two sizes equal to 0.001 m and 0.010 m. The bed surface is composed of 10 % fine sediment. The active layer thickness is equal to 0.05 m, which in this case is representative of small dunes covering the bed (e.g. Deigaard & Fredsøe 1978; Armanini & di Silvio 1988; Blom 2008). Depending on the substrate composition, this situation yields an ill-posed model (Chavarrías et al. 2018). When the substrate is composed of 50 % fine sediment (Case H1, table 3), the problem is well posed and it is ill posed when the substrate is composed of 90 % fine sediment (Case H2, table 3).

We use the software package Delft3D (Lesser et al. 2004) to solve the system of equations. We stress that the problem of ill posedness is inherent to the system of equations and independent from the numerical solver. We have implemented a subroutine that assesses the well posedness of the system of equations at each node and time step. The domain is 100 m long and 10 m wide. The downstream water level is lowered at a rate of $0.01~\text{m}~\text{h}^{-1}$ to induce degradational conditions. The upstream sediment load is constant and equal to the equilibrium value of the reference state (Blom et al. 2017). The cells are square and we consider three different sizes (table 3). The time step varies between simulations to maintain a constant value of the CFL (Courant, Friedrichs & Lewy 1928) number.

Table 3. Cases showing the effect of grid cell size on the numerical solution of well-posed and ill-posed models.

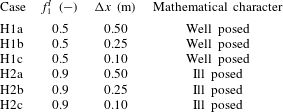
Figure 2 presents the bed elevation after 10 h. The result of the well-posed case (H1, left column) is grid independent. The result of the ill-posed case (H2, right column) changes as the grid is refined and presents an oscillatory pattern characteristic of ill-posed simulations (Joseph & Saut 1990; Woodhouse et al. 2012; Barker et al. 2015; Chavarrías et al. 2018). The bed seems to be flat in the ill-posed simulation with a coarser grid (figure 2 b). This is because oscillations grow slowly on a coarse grid and require more time to be perceptible. The waviness of the bed is seen in the result of the check routine, as it predicts ill posedness only at those locations where the bed degrades (the stoss face of the oscillations). The fact that the model is well posed in almost the entire domain in the ill-posed case solved using a cell size equal to 0.25 m (H2b, figure 2 d) and 0.10 m (H2c, figure 2 f) does not mean that the results are realistic. Non-physical oscillations have grown and vertically mixed the sediment such that the situation is well posed after 10 h (Chavarrías et al. 2018). We provide a movie of figure 2 in the online supplementary material available at https://doi.org/10.1017/jfm.2019.166.

Figure 2. Simulated bed elevation (surface) and mean grain size at the bed surface (colour) of a well-posed case (left column, H1, table 3) and an ill-posed case (right column, H2, table 3). In each row we present the results for varying cell size. The colour of the $x$ – $y$ plane shows the result of the routine that checks whether the conditions at each node yield a well-posed (green) or an ill-posed (red) model.

In the above idealised situations it is evident that the oscillations are non-physical and it is straightforward to do a converge test to clarify that the solution is grid dependent. In complex domains in which several processes play a role, it is more difficult to associate oscillations with ill posedness. Moreover, in long term applications the growth rate of perturbations may be fast compared to the frequency at which model results are assessed, which may hide the consequences of ill posedness. If one studies a process that covers months or years (and consequently analyses the results on a monthly basis) but perturbations due to ill posedness grow on an hourly scale, it may be difficult to identify that the problem is ill posed. Using poor numerical techniques to solve the system of equations also contributes to hiding the consequences of ill posedness as numerical diffusion dampens perturbations. These factors may explain why the problem of ill posedness in mixed-sediment river morphodynamics is not widely acknowledged.

In the river morphodynamics community, the term ellipticity has been used to refer to the ill posedness of the system of equations in contrast to hyperbolicity, which is associated with well posedness (Ribberink 1987; Mosselman 2005; Stecca et al. 2014; Siviglia, Stecca & Blom 2017; Chavarrías et al. 2018). In general the terms are equivalent, but not always. We consider a unit vector $\hat{\boldsymbol{n}}$ in the direction $(x,y)$ , $\hat{\boldsymbol{n}}=(\hat{n}_{x},\hat{n}_{y})$ . The system of equations (2.24) is hyperbolic if matrix $\unicode[STIX]{x1D63C}=\unicode[STIX]{x1D63C}_{\boldsymbol{x}\mathbf{0}}\hat{n}_{x}+\unicode[STIX]{x1D63C}_{\boldsymbol{y}\mathbf{0}}\hat{n}_{y}$ diagonalises with real eigenvalues $\forall \hat{n}$ (e.g. LeVeque 2004; Castro et al. 2009). Neglecting friction and diffusive processes (i.e. $\unicode[STIX]{x1D63D}_{\mathbf{0}}=\unicode[STIX]{x1D63F}_{\boldsymbol{x}\mathbf{0}}=\unicode[STIX]{x1D63F}_{\boldsymbol{y}\mathbf{0}}=\mathbb{0}$ ), hyperbolicity implies that the eigenvalues of $\unicode[STIX]{x1D648}_{\mathbf{0}}$ (2.33) are real. In this case, as the growth rate of perturbations (i.e. the imaginary part of the eigenvalues of $\unicode[STIX]{x1D648}_{\mathbf{0}}$ ) is equal to 0 regardless of the wavenumber, the system of equations is well posed. As the coefficients of $\unicode[STIX]{x1D63C}$ are real, complex eigenvalues appear in conjugate pairs. This means that if $\unicode[STIX]{x1D63C}$ has a complex eigenvalue (i.e. the problem is not hyperbolic), at least one wave will have a positive growth rate. Neglecting friction and diffusive processes, non-hyperbolicity implies that infinitely large wavenumbers have a positive growth rate. We conclude that, in the absence of diffusion and friction, lack of hyperbolicity implies ill posedness. Note that ellipticity (i.e. the eigenvalues of $\unicode[STIX]{x1D63C}$ are all complex) is not required for the problem to be ill posed, as it suffices that the problem is not hyperbolic. When considering diffusion and friction even when $\unicode[STIX]{x1D63C}$ has complex eigenvalues, the imaginary part of the eigenvalues of $\unicode[STIX]{x1D648}_{\mathbf{0}}$ may all be negative and the problem well posed.

Finally, well posedness and hyperbolicity are similar terms when dealing with problems arising from conservation laws and changes with time, as hyperbolicity guarantees the existence of wave solutions (Lax 1980; Courant & Hilbert 1989; Strikwerda 2004; Toro 2009; Dafermos 2010; Bressan 2011; Dafermos 2016). In communities such as materials science, it is the term hyperbolicity that is associated with ill posedness, as a smooth solution of, for instance the stress, requires that the system is elliptic (Knowles & Sternberg 1975, 1976; Veprek, Steiger & Witzigmann 2007).

4 Stability analysis

In this section we study the applicability of the system of equations to model two-dimensional river morphodynamics by means of a stability analysis of perturbations. We study the effects of the secondary flow model (§ 4.1) and the bed slope (§ 4.2) on model ill posedness.

4.1 Ill posedness due to secondary flow

In this section we study how the stability of the system of equations is affected by the secondary flow model. To gain insight we compare three cases. In the first case we omit secondary flow. In the second and third cases we include the secondary flow model with and without considering diffusion (table 4).

Table 4. Variations to the reference state (table 1) and results of the linear analysis with respect to secondary flow.

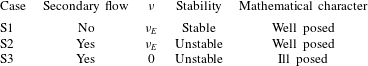
The first case is equivalent to I1 (table 2), yet the eddy viscosity is equal to the value derived by Elder ((2.4), $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{E}=0.0057~\text{m}^{2}~\text{s}^{-1}$ ). In figure 3(a,b) we plot the maximum growth rate of perturbations as a function of the wavenumber and the wavelength, respectively. Diffusion appears to significantly dampen perturbations (compare figure 1(a) in which diffusion is neglected to figure 3 a).

Figure 3. Growth rate of perturbations added to the reference case (tables 1 and 4) as a function of the wavenumber and the wavelength: (a,b) without secondary flow (Case S1, well posed), (c,d) accounting for secondary flow with diffusion (Case S2, well posed) and (e,f) accounting for secondary flow without diffusion (Case S3, ill posed). The panels in the two columns show the same information but highlight the behaviour for large wavenumbers (a,c,e) and for large wavelengths (b,d,f). Red and green indicate growth and decay of perturbations, respectively.

In the second case we repeat the analysis including the equation for advection and diffusion of the secondary flow intensity (i.e. the first four rows and columns of matrix $\unicode[STIX]{x1D648}_{\mathbf{0}}$ in (2.33), Case S2, table 4). We observe that accounting for secondary flow introduces an instability mechanism (figure 3 d). For the specific conditions of the case, a growth domain appears for wavelengths between 0.7 m and 39 m long and between 0.4 m and 19 m wide. The maximum growth corresponds to a wavelength in the $x$ and $y$ direction equal to 1.29 m and 0.74 m, respectively. This situation is well posed, as for large wavenumbers perturbations decay (figure 3 c). Yet, the model is unsuitable for reproducing such instability, as it predicts growth of perturbations with a length scale of the order of the flow depth and shorter, for which the shallow water equation model is not suited. Given the fact that we consider a depth-averaged formulation of the primary flow, processes that scale with the flow depth are not resolved by the model and consequently perturbations at that scale must decay to yield physically realistic results. Otherwise, scales of the order of the flow depth become relevant, which contradicts the assumptions of the depth-averaged formulation. To model processes that scale with the flow depth such as dune growth, it is necessary to account for non-depth-averaged flow formulations that consider, for instance, rotational flow (Colombini & Stocchino 2011, 2012), or non-hydrostatic pressure (Giri & Shimizu 2006; Shimizu et al. 2009).

In the third case we test the secondary flow model without accounting for diffusion in the system of equations ( $\unicode[STIX]{x1D708}=0$ , Case S3, table 4). We observe that the instability domain extends to infinitely large wavenumbers (figure 3 e), which implies that this model is ill posed (§ 3). We now aim to prove that the shallow water equations in combination with the secondary flow model without diffusion always yields an ill-posed model. To this end we obtain the characteristic polynomial of matrix  $\unicode[STIX]{x1D648}_{\mathbf{0}}$ (2.33). We compute the discriminant of the fourth-order characteristic polynomial and we find that for $k_{wx}<k_{wy}$ the growth rate of perturbations is positive (appendix C). The model is ill posed, as there always exists a domain of growth extending to infinitely large wavenumbers in the transverse direction.

We assess how the length scale of the instability related to the secondary flow model depends on the flow parameters. For this purpose we compute the shortest wave with positive growth for a varying diffusion coefficient and flow conditions (figure 4). We observe that, independently of the flow conditions, the theoretical value of the diffusion coefficient derived by Elder (1959) (2.4) is insufficient for dampening oscillations scaling with the flow depth. We conclude that if the diffusion coefficient is realistic, the treatment of the secondary flow yields an unrealistic model. It is necessary to use an unrealistically large value of the diffusion coefficient to obtain a realistic depth-averaged model in which perturbations scaling with the flow depth decay.

Figure 4. Wavelength of the shortest perturbation with positive growth rate ( $l_{wm}$ ) relative to the flow depth ( $h$ ) as a function of the Froude number ( $Fr$ ) and the diffusion coefficient ( $\unicode[STIX]{x1D708}$ ) relative to the diffusion coefficient according to Elder (1959) ( $\unicode[STIX]{x1D708}_{E}$ ). Different flow conditions are studied varying the flow depth between 0.2 m and 1.5 m from the reference case (table 1). The cyan markers indicate the conditions of three numerical simulations with different values of the diffusion coefficient (§ 5.1). The arrow next to the diamond marker indicates that the value lies outside the figure. Red (green) colour indicates that the shortest wavelength with positive growth rate are smaller (larger) than the flow depth.

4.2 Ill posedness due to bed slope effect

In this section we study the influence of considering the effect of the bed slope on model well posedness. To gain insight we compare five cases in which we consider unisize and mixed-size sediment, various sediment transport relations and various bed slope functions (table 5). We neglect secondary flow and diffusion to reduce the complexity of the problem (Parker 1976; Fredsøe 1978; Colombini et al. 1987; Schielen et al. 1993).

Our reference case is B1 (§ 3) which considers unisize sediment conditions, and the effect of the bed slope on the sediment transport direction is accounted for using the simplest formulation, $g_{s}=1$ . We have shown that this case is well posed. Neglecting the effect of the bed slope on the sediment transport direction (Case B2, table 5) makes the problem ill posed (figure 5 a). This illustrates that accounting for the effect of the bed slope is required for obtaining not only physically realistic but also mathematically well-posed results. We prove that the shallow water equations in combination with the Exner (1920) equation without considering the effect of the bed slope always yields an ill-posed model by studying the growth rate of perturbations in the limit as the wavenumber $k_{wy}$ tends to infinity (appendix D).

Figure 5. Growth rate of perturbations added to the reference case (tables 1 and 5) as a function of the wavenumber and the wavelength: (a,b) Case B2 (ill posed), (c,d) Case B3 (well posed), (e,f) Case B4 (ill posed) and (g,h) Case B5 (ill posed). The panels in the two columns show the same information but highlight the behaviour for large wavenumbers (a,c,e,g) and for large wavelengths (b,d,f,h). Red and green indicate growth and decay of perturbations, respectively.

Table 5. Variations to the reference state (table 1) and results of the linear analysis with respect to the effect of the bed slope on the sediment transport direction. EH and AM refer to the sediment transport relations by Engelund & Hansen (1967) and Ashida & Michiue (1971), respectively.

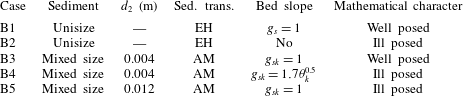
The fact that the bed slope effect dampens perturbations under unisize conditions is expected from the fact that the only diffusive term in the system of equations is $\unicode[STIX]{x2202}q_{by}/\unicode[STIX]{x2202}s_{y}$ (2.27), where $s_{y}=\unicode[STIX]{x2202}\unicode[STIX]{x1D702}/\unicode[STIX]{x2202}y$ . This term is negative and approximately equal to $-q_{b}/g_{s}$ for a small streamwise slope. When we consider more than one grain size, diffusive terms appear in each active layer equation. We find that these diffusive terms may be positive, which hints at the possibility of an antidiffusive behaviour, which may lead to ill posedness. To study this possibility we compute the growth rate of perturbations of a simplified case consisting of two sediment size fractions. In the limit for the wavenumbers tending to infinity, the maximum growth rate is:

(4.1) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}_{i}^{lim}=\unicode[STIX]{x1D6FC}_{1}(r_{y1}-d_{x1,1})^{2}+\unicode[STIX]{x1D6FC}_{2}(r_{y1}-d_{x1,1})+\unicode[STIX]{x1D6FC}_{3}, & & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D6FC}_{i}$ for $i=1,2,3$ are parameters relating the flow and the sediment transport rate (appendix E). The parameter $r_{y1}$ explains how the sediment transport rate of the fine fraction is affected by changes in the transverse bed slope:

(4.2) $$\begin{eqnarray}\displaystyle r_{y1}=\frac{\unicode[STIX]{x2202}q_{by1}/\unicode[STIX]{x2202}s_{y}}{\unicode[STIX]{x2202}q_{by}/\unicode[STIX]{x2202}s_{y}}, & & \displaystyle\end{eqnarray}$$

and the parameter $d_{x1,1}$ relates changes in the sediment transport rate to changes in the volume of sediment in the active layer:

(4.3) $$\begin{eqnarray}\displaystyle d_{x1,1}=\frac{\unicode[STIX]{x2202}q_{bx1}/\unicode[STIX]{x2202}M_{a1}}{\unicode[STIX]{x2202}q_{bx}/\unicode[STIX]{x2202}M_{a1}}. & & \displaystyle\end{eqnarray}$$

As $\unicode[STIX]{x1D6FC}_{1}>0$ (appendix E), there exists an interval $(r_{y1}-d_{x1,1})^{-}<(r_{y1}-d_{x1,1})<(r_{y1}-d_{x1,1})^{+}$ in which $\unicode[STIX]{x1D714}_{i}^{lim}<0$ and the model is well posed. Outside the interval, $\unicode[STIX]{x1D714}_{i}^{lim}>0$ and the problem is ill posed.

The physical interpretation of the limit values for obtaining a well-posed model is as follows. The effect of the transverse bed slope ( $r_{y1}$ ) needs to be balanced with respect to the effect of changes in surface texture ( $d_{x1,1}$ ) to obtain a well-posed model. For a given $d_{x1,1}$ , if parameter $r_{y1}$ is too small (i.e. the bed slope effect is not sufficiently strong) perturbations in the transverse direction are not dampened and the model is ill posed. On the other hand, for a given $r_{y1}$ , if parameter $d_{x1,1}$ is too small (e.g. due to relatively strong hiding or in conditions close to incipient motion) perturbations in the streamwise direction do not decay and the model is also ill posed. The critical values $r_{y1}^{\pm }$ that allow for a well-posed model are shown in appendix E.

In Cases B3–B5 we illustrate the possibility of ill posedness due to the bed slope closure relation (table 5). In Case B3 the sediment mixture consists of two grain size fractions with characteristic grain sizes equal to 0.001 m and 0.004 m. The volume fraction content of the fine sediment in the active layer and at the interface between the active layer and the substrate is equal to 0.5. The sediment transport rate is computed using the relation developed by Ashida & Michiue (1971). The other parameters are equal to the reference case (table 1). The system is well posed when the effect of the bed slope does not depend on the bed shear stress (figure 5 c). The situation is ill posed if the effect of the bed slope depends on the bed shear stress (Case B4, table 5, figure 5 e). The cause of the ill posedness is not found in the closure relation for the bed slope effect only but in the combination of the closure relation with the flow and bed surface conditions. A case equal to B3 except for the fact that the coarse grain size is equal to 0.012 m is ill posed (Case B5, table 5, figure 5 g).

We assess how the domain of ill posedness due to the bed slope effect depends on the model parameters. For given sediment sizes, flow and bed surface texture, parameter $B_{s}$ (2.23) controls the effect of the bed slope by modifying $r_{y1}$ only. The parameter $A_{s}$ (2.23) cancels in $r_{y1}$ and does not play a role. For this reason we study how $g_{s1}/A_{s}$ ( $-$ ) affects the domain of ill posedness for varying sediment properties, flow and bed surface grain size distribution (figure 6). We consider Case B3 and we vary $B_{s}$ between 0 and 0.5 to vary the bed slope effect. The sediment size of the coarse fraction varies between $d_{1}$ and 0.020 m. The mean flow velocity varies between $1~\text{m}~\text{s}^{-1}$ and $2.8~\text{m}~\text{s}^{-1}$ . The volume fraction content of fine sediment at the bed surface varies between 0 and 1. We aim to isolate the problem of ill posedness due to bed slope effect from the problem of ill posedness due to a different grain size distribution at the bed surface and at the interface between the bed surface and the substrate (Chavarrías et al. 2018). For this reason, in this analysis the volume fraction content of fine sediment at the interface is equal to the one at the bed surface. Under this condition the problem can be ill posed due to the effect of the bed slope only.

As we have shown analytically, under unisize conditions (i.e. $d_{1}/d_{2}=1$ or $F_{a1}=1$ or $F_{a1}=0$ ) the model is well posed (figure 6 a,c). For sufficiently different grain sizes ( $d_{1}/d_{2}\lessapprox 0.15$ ) the model is well posed regardless of the bed slope effect but for a small range of values ( $0.08\lessapprox d_{1}/d_{2}\lessapprox 0.1$ ). This small range of ill-posed values is associated with $r_{y1}$ increasing for decreasing values of $d_{1}/d_{2}$ and acquiring a value larger than $r_{y1}^{+}$ such that the model becomes ill posed for all values of the bed slope effect. A further decrease in $d_{1}/d_{2}$ increases the limit value $r_{y1}^{+}$ faster than $r_{y1}$ such that the model becomes well posed for all values of the bed slope effect.

An increase in the Froude number decreases the domain of well posedness, which is explained from the fact that an increase in Froude number decreases $r_{y1}$ while it does not modify $r_{y1}^{-}$ . We have assumed steady flow in deriving $\unicode[STIX]{x1D714}_{i}^{lim}$ to reduce the complexity of the model such that we can find an analytical solution (appendix E). This causes a physically unrealistic resonance phenomenon for $Fr\rightarrow 1$ (Colombini & Stocchino 2005). In reality we do not expect that for $Fr=1$ the model is always ill posed regardless of the bed slope effect. Apart from the limit values in which the problem becomes unisize, the surface volume fraction content does not significantly affect the domain of ill posedness (figure 6 c) as it rescales in more or less a similar way $r_{y1}^{\pm }$ and $r_{y1}$ .

While Case B4 is ill posed because the effect of the bed slope ( $r_{y1}$ ) is small, Case B5 is ill posed because parameter $d_{x1,1}$ is small. The different origin of ill posedness does not cause a significant difference in the growth rate of perturbations as a function of the wavenumber (figure 5 e–g). However, we will find out that the pattern resulting from the perturbations depends on the origin of the ill posedness.

Figure 6. Domain of ill posedness due to the bed slope effect under mixed-size sediment conditions: as a function of the ratio between fine and coarse sediment (a), the Froude number (b) and the volume fraction content of fine sediment in the active layer (c). The bed slope effect is measured by $g_{s1}/A_{s}$ and the range of parameters is obtained by varying $B_{s}$ (2.23). The range of values of $d_{1}/d_{2}$ is obtained by varying $d_{2}$ . The range of values of the Froude number is obtained by varying $u$ . The volume fraction content of fine sediment at the interface between the active layer and the substrate is kept equal to the volume fraction content of fine sediment in the active layer. The conditions represent unisize sediment when $d_{1}/d_{2}=1$ , $F_{a1}=0$ , or $F_{a1}=1$ .

5 Application

The results of the linear stability analysis (§ 4) neglect second-order terms and nonlinear interactions. In this section we study the effects of the terms neglected in the linear analysis and the development of perturbations by means of numerical simulations. We use the software package Delft3D (Lesser et al. 2004). This exercise provides information on the consequences of ill posedness in numerical simulations and clarifies the limitations of the current modelling approach. We study the effect of secondary flow (§ 5.1) and the bed slope effect (§ 5.2).

5.1 Secondary flow

We run five numerical simulations with a fixed bed (i.e. only the flow is computed) to study the roles of the secondary flow model and the diffusion coefficient in the ill posedness of the system of equations. The first three simulations reproduce the conditions of Cases S1, S2 and S3 (table 4). The domain is rectangular, 100 m long and 10 m wide. We use square cells with size equal to 0.1 m. The time step is equal to 0.01 s and we simulate 10 min of flow. We set a constant water discharge and the downstream water level remains constant with time. The initial condition represents normal flow for the values in table 1 (i.e. equilibrium conditions).

The simulation not accounting for secondary flow does not present growth of perturbations as predicted by the linear analysis and remains stable with time (figure 7 a). We observe growth of perturbations when we account for secondary flow with the diffusion coefficient derived by Elder (1959) (figure 7 b). The results are physically unrealistic as the flow depth presents variations of up to 7 % of the normal flow depth and the length scale of the perturbations is smaller than the flow depth. We have not introduced any perturbation in the initial or boundary conditions which implies that perturbations grow from numerical truncation errors. This supports the fact that the simulation is physically unrealistic. The case with a diffusion coefficient equal to 0 is ill posed and the solution presents unreasonably large oscillations (figure 7 c). These numerical results confirm the results of the linear stability analysis.

In the fourth simulation we set a diffusion coefficient 100 times larger than the one derived by Elder (1959) (figure 7 d). Under this condition the linear analysis predicts all short waves to decay (diamond in figure 4). These numerical results confirm the linear theory. The last simulation is equal to Case S2 except for the fact that we use a coarser grid ( $\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}y=1~\text{m}$ ). In this case the numerical grid is not sufficiently detailed to resolve the perturbations due to secondary flow and the simulation is stable (figure 7 e). This last case highlights an important limitation of a physically unrealistic model. Although Case S2 is mathematically well posed, the solution presents similarities with ill-posed cases in the sense that a refinement of the grid causes non-physical oscillations to appear.

Figure 7. Flow depth at the end of the simulations: (a) without accounting for secondary flow (Case S1), (b) setting $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{E}$ (Case S2), (c) setting $\unicode[STIX]{x1D708}=0$ (Case S3), (d) setting $\unicode[STIX]{x1D708}=100\unicode[STIX]{x1D708}_{E}$ and (e) setting $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{E}$ using a coarser numerical grid (Case S2). The colour map is adjusted for each case and centred on the initial and equilibrium values ( $h=1~\text{m}$ ).

5.2 Bed slope effect

In this section we focus on the consequences of accounting for the bed slope effect on the mathematical character of the model. To this end we run five more numerical simulations without accounting for secondary flow and updating the bed (i.e. accounting for morphodynamic change). The simulations reproduce Cases B1–B5 (table 5). We simulate 8 h using a time step $\unicode[STIX]{x0394}t=0.1~\text{s}$ .

We have proved that accounting for the effect of the bed slope makes a unisize simulation well posed (§ 4.2 and figure 1 c). The numerical solution of this case (B1, table 2) is stable and perturbations do not grow (figure 8 a). Moreover, no alternate bars appear as the channel width is below the critical value (§ 3). Perturbations grow when the effect of the bed slope is not taken into account (Case B2, figure 8 b), which confirms that this case is ill posed.

Figure 8. Flow depth at the end of the simulations of: (a) Case B1, (b) Case B2; and volume fraction content of fine sediment in the active layer: (c) Case B3, (d) Case B4, (e) Case B5. The colour map is adjusted for each case and centred on the initial and equilibrium values.

The mixed-size sediment conditions of Case B3 yield a well-posed model (figure 5 e) and the simulation is stable (figure 8 c). On the other hand, the ill-posed cases B4 and B5 present growth of unrealistic and non-physical perturbations (figure 8 d,e). While the growth of perturbations in Case B5 seems random, in Case B4 we observe a clear pattern. Moreover, oscillations have grown significantly faster in Case B5 than in Case B4. While after 8 h the changes in volume fraction content at the bed surface are of the order of $10^{-3}$ in Case B4, these are of order 1 in Case B5.

The fact that oscillations grow faster in Case B5 than in Case B4 is related to the different origin of ill posedness. While Case B4 is ill posed because the effect of the bed slope is not sufficiently strong (i.e. $r_{y1}<r_{y1}^{-}$ ), Case B5 is ill posed because changes in the sediment transport rate due to changes in the volume of fine sediment in the active layer are too small (i.e. $r_{y1}>r_{y1}^{+}$ ). The first case is closely linked to the lateral direction, in which sediment transport is initially zero. The fact that initially the lateral sediment transport rate is zero limits the rate at which lateral changes occur. In the second case perturbations are linked to the streamwise direction, in which the sediment transport rate initially is non-zero, which enhances the rate at which changes develop.

6 Discussion

The origin of the instability due to secondary flow is found in the source term ( $S_{s}$ in (2.11)). As the source term depends on the flow curvature, the source term is 0 in a straight flow. A small perturbation in the flow causes the flow to curve. The flow curvature causes a source of secondary flow intensity, which further increases the flow curvature, causing a positive feedback. The flow curvature is largest for the smallest perturbations, which explains why the model is ill posed if a dampening mechanism (i.e. diffusion) is not taken into account. This destabilising mechanism may seem plausible to explain secondary flow circulation observed in straight channels (Nikuradse 1930; Brundrett & Baines 1964; Nezu & Nakagawa 1984; Gavrilakis 1992). However, secondary flow in a straight channel can only be caused by anisotropy of turbulence (Einstein & Li 1958; Gessner & Jones 1965; Bradshaw 1987; Colombini 1993), which is not included in the model for secondary flow. For this reason, the secondary flow model must predict decay of secondary flow intensity in case of straight flow. Diffusion of secondary flow intensity causes decay of perturbations, but the theoretical diffusion coefficient derived by Elder (1959) appears to be insufficient to dampen perturbations.

The advection equation for the secondary flow intensity was initially derived for steady decaying secondary flow on a straight reach after a bend neglecting the effect of diffusion (De Vriend 1981). It is assumed that the same advective behaviour is valid for a varying curvature (De Vriend 1981; Olesen 1982) and in an unsteady situation (Booij & Pennekamp 1984). These assumptions have, to our knowledge, not been tested. Moreover, secondary flow affects the vertical profile of the primary flow. This feedback mechanism, which limits the development of secondary flow (Blanckaert & De Vriend 2004; Blanckaert 2009), is not included in the model. Blanckaert & De Vriend (2003), Blanckaert & Graf (2004) and Ottevanger et al. (2013) propose nonlinear models that take into consideration this mechanism. We expect that accounting for the feedback mechanism yields a well-posed model.

The feedback mechanism between the secondary and the primary flow may be seen as an increase of diffusivity, as it causes an enhanced momentum redistribution. For a situation in which the nonlinear model for the secondary flow appears to be excessively expensive in computational terms, a diffusion coefficient depending on the secondary flow intensity would (partially) account for the enhanced momentum redistribution and provide a well-posed and realistic model.

We have assumed that the diffusion coefficient is constant and equal in all directions, which is a crude approximation, as in the streamwise direction diffusion is larger than in the transverse direction (appendix A). It would be interesting to study the effect of anisotropic diffusion, however, we do not expect that this will significantly alter our results. This is because a larger diffusion coefficient in the streamwise direction will not alter the most unstable wavelength in the lateral direction. For this reason the shortest unstable waves remain of the order of the flow depth.

The nonlinear relation between the flow and the sediment transport rate causes the growth of perturbations in bed elevation. Worded differently, a deep flow attracts the flow and vice versa, which enhances the growth of perturbations. This mechanism is counteracted by the bed slope effect, which causes deep parts to fill in. In this sense, it seems logical that it is necessary to account for bed slope effects to obtain a well-posed model. This may be confirmed by the facts that Parker (1976), by not considering the bed slope effect, found that all streams tend to form bars and, similarly, Olesen (1982) concluded that ‘the stream will develop an infinite number of submerged bars’. From our point of view the fact that all streams seem to be unstable and develop an infinite number of submerged bars is a consequence of the model being ill posed. Our analysis shows that the bed slope effect is a crucial physical process in analysing two-dimensional morphodynamic processes.

Nevertheless, the numerical simulations by Qian et al. (2016) for bar development without accounting for the bed slope effect do not show unrealistic oscillatory behaviour as is characteristic of ill posedness. Yet, there is an essential difference between their model and the one we analyse here. We do not model the interaction between the sediment in the bed and the sediment in transport as we assume that the sediment transport rate adapts instantaneously to changes in the flow (i.e. the sediment transport rate depends on the flow variables only). Essentially, sediment in transport is not conserved and bed elevation and surface texture changes depend on the divergence of the sediment transport rate at capacity conditions. Qian et al. (2016) account for the conservation of mass of the sediment in transport and use an entrainment–deposition formulation for modelling bed elevation and surface texture changes (Parker, Paola & Leclair 2000). In this formulation changes depend on the difference between the rate at which sediment is entrained from the bed and at which it is deposited on the bed. The fact that their model does not show symptoms of ill posedness, while the effect of the bed slope is not taken into consideration, raises the question as to whether the entrainment–deposition formulation in combination with mass conservation of the sediment in transport is responsible, like the bed slope effect, for a mechanism that counteracts growth of perturbations in bed elevation. If the model used by Qian et al. (2016) is indeed well posed, the effect of the bed slope may be a crucial process only when mass conservation of the sediment in transport is not considered.

Lanzoni & Tubino (1999) investigated the development of alternate bars under mixed-size sediment conditions using a model similar to the one we apply here. They assumed secondary flow to be negligible and considered a different set of closure relations for friction, the sediment transport rate and the effect of the bed slope. Under the conditions they studied, they found that, similarly to the unisize case, growth of perturbations occurs if the width-to-depth ratio is above a critical value. This implies that they found that their model is well posed, as short wavelength perturbations decay. Given that the essence of the closure relations they considered is the same as that of the ones considered here and there is no fundamental difference, we suppose that their model may become ill posed if different conditions are studied (i.e. different flow or sediment parameters). This is because well posedness is not related to the model equations only, but also to the conditions in which the model is applied.

The bed slope effect (represented by the parameter $r_{y1}$ ) needs to be balanced with respect to the effect of changes in the bed surface grain size distribution (represented by $d_{x1,1}$ ) to yield a well-posed model. The balance depends on the flow and bed conditions. For this reason, a particular closure relation may yield an ill-posed model in some subdomain of a simulation and a well-posed model in some other subdomain. It is necessary to further study the development of the transverse bed slope under mixed-size sediment conditions (e.g. Baar et al. 2018) to obtain a universally applicable closure relation.

Overall, there are three causes of ill posedness of the model: (i) the secondary flow parametrisation, (ii) the closure relation for the bed slope effect and (iii) the representation of the vertical mixing processes when using the active layer model (Ribberink 1987; Chavarrías et al. 2018). We summarise all the conditions in which the model may become ill posed in figure 9.

Only in idealised simulations is it straightforward to relate the instability of the system of equations to ill posedness. We advocate for an a priori test of whether the system of equations is well posed or ill posed, especially when dealing with mixed-size sediment cases. If at some time a location in the model becomes ill posed, the model results should be carefully evaluated. The fact that some domain area has always been well posed does not guarantee a unique solution, as oscillations caused by upstream or downstream ill-posed areas propagate through the domain. Similarly, the fact that the entire domain is well posed at some time is no guarantee of a unique solution, as past oscillations due to ill posedness affect the present solution.

Figure 9. Conditions in which the flow model (a) and the morphodynamic model (b) is stable, unstable or ill posed. The code below the model type (e.g. S1) indicates an example case of such a situation. See tables 2–5 for an explanation of the cases S1-3, B1-4, H1-2 and I2; $^{\ast }$ parameter $\unicode[STIX]{x1D6FD}_{c}$ denotes the critical width-to-depth ratio (Engelund & Skovgaard 1973; Colombini et al. 1987; Schielen et al. 1993).

7 Conclusions

We have studied a two-dimensional system of equations used to model mixed-size river morphodynamics as regards to its well posedness. The model is based on the depth-averaged shallow water equations in combination with the Exner (1920) and active layer (Hirano 1971) equations to model bed elevation and surface texture changes, respectively. In particular we have focused on modelling of the secondary flow induced by flow curvature and the effect of the bed slope on the sediment transport direction, which causes particles to deviate from the direction of the bed shear stress.

By means of a linear stability analysis of the system of equations we find that:

• ∙ The parametrisation accounting for secondary flow yields an ill-posed model if diffusion is not accounted for.

• ∙ The theoretical amount of diffusion due to depth averaging the vertical profile of the primary flow (Elder 1959) yields a well-posed model but it predicts growth of perturbations that are incompatible with the shallow water assumption.

• ∙ The effect of the bed slope on the direction of the sediment transport is a necessary mechanism for the model being well posed. Yet, a different modelling strategy accounting for conservation of the sediment in transport and an entrainment–deposition formulation may yield a well-posed model without accounting for the effect of the bed slope.

• ∙ Not all closure relations accounting for the bed slope effect are valid under mixed-size sediment conditions. There needs to be a balance between the effect of the bed slope and the effect of the streamwise variation of grain size distribution on the sediment transport rate.

Numerical simulations of idealised cases confirm the above results of the linear stability analysis.