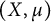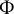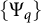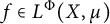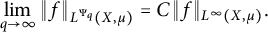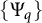Families of Young functions and limits of Orlicz norms

Abstract

Given a $\sigma $-finite measure space $(X,\mu )$, a Young function $\Phi $, and a one-parameter family of Young functions $\{\Psi _q\}$, we find necessary and sufficient conditions for the associated Orlicz norms of any function $f\in L^\Phi (X,\mu )$ to satisfy

$$\begin{align*}\lim_{q\rightarrow \infty}\|f\|_{L^{\Psi_q}(X,\mu)}=C\|f\|_{L^\infty(X,\mu)}. \end{align*}$$

The constant C is independent of f and depends only on the family $\{\Psi _q\}$. Several examples of one-parameter families of Young functions satisfying our conditions are given, along with counterexamples when our conditions fail.

1 Introduction

It is a well-known result in classical analysis (see, e.g., [5, 6]) that if $(X,\mu )$ is a measure space and if $f\in L^r(X,\mu )$ for some $r\geq 1$ , then

(1.1) $$ \begin{align} \lim_{p\rightarrow\infty}\|f\|_{L^p(X,\mu)}= \|f\|_{L^\infty(X,\mu)}. \end{align} $$

The authors of [2] investigated a similar limiting property of Orlicz norms associated with a one-parameter family of Young functions $\{\Psi _q\}$ which is defined by setting $\Psi _q(t)=t^p\log (e-1+t)^q$ , where $p\geq 1$ is fixed and q can be any positive real number. They showed that if f belongs to the Orlicz space $L^{\Psi _{q_0}}(X,\mu )$ for some $q_0>0,$ then

(1.2) $$ \begin{align} \lim_{q\rightarrow\infty}\|f\|_{L^{\Psi_q}(X,\mu)}=\|f\|_{L^\infty(X,\mu)}. \end{align} $$

Here, $\|f\|_{L^{\Psi _q}(X,\mu )}$ denotes the Luxembourg norm of f with respect to $\Psi _q$ given by

$$\begin{align*}\|f\|_{L^{\Psi_q}(X,\mu)}=\inf\bigg\{\lambda>0:\int_X\Psi_q\bigg(\frac{|f|}{\lambda}\bigg)~d\mu\leq1\bigg\}. \end{align*}$$

Modifying [110pt] the proof of [2, Theorem 1], we show that (1.2) holds for any family of Young functions $\{\Psi _q\}$ that satisfies Condition 1.1, which we call $\delta $ -admissibility. Like the authors of [2], our efforts were motivated by an application in partial differential equations, where we sought to employ a Moser iterative scheme in Orlicz spaces to study regularity of weak solutions to Poisson’s equation. Ultimately, those results were achieved using alternative techniques in [1].

Nevertheless, our main result Theorem 1.2 may be useful in the study of related problems. Furthermore, it illustrates a surprising relationship between Orlicz spaces defined with respect to $(X,\mu )$ , and the space $L^\infty (X,\mu )$ of essentially bounded functions on X.

Throughout this work, we assume that $(X,\mu )$ is a positive measure space with $\mu (X)>0$ . To state our main result concisely, we begin by defining $\delta $ -admissibility.

Condition 1.1 Given $\delta>0$ , a one-parameter family of Young functions $\{\Psi _q\}$ is said to be $\delta $ -admissible if $\displaystyle \lim _{q\rightarrow \infty } \Psi _q(t) = \infty $ for $t>\delta $ , and for $0<t<\delta ,$ one of the following holds:

1. (i) If $\mu (X)=\infty $ , then $\displaystyle \lim _{q\rightarrow \infty } \Psi _q(t) =0$ .

2. (ii) If $\mu (X)<\infty $ , then $\displaystyle \lim _{q\rightarrow \infty } \Psi _q(t)< \mu (X)^{-1}$ .

Perhaps the simplest $\delta $ -admissible family is the $1$ -admissible collection obtained by taking $\Psi _q(t)=t^q$ for $q\geq 1$ , and more examples of $\delta $ -admissible families are discussed in Section 3.

Now, we state our main result concerning these families of Young functions.

Theorem 1.2 Let $(X,\mu )$ be a $\sigma $ -finite measure space, and let $\{\Psi _q\}$ be a one-parameter family of Young functions. Let $\Phi $ be another Young function such that, for any $k>0$ , the composition

(1.3) $$ \begin{align} \frac{t}{\Psi_q^{-1}(\Phi(t))} \end{align} $$

is nondecreasing on the interval $[0,k]$ whenever q is sufficiently large. Then the identity

(1.4) $$ \begin{align} \lim_{q\rightarrow \infty} \|f\|_{L^{\Psi_q}(X,\mu)} =\frac{1}{\delta}\|f\|_{L^\infty(X,\mu)} \end{align} $$

holds for every $f\in L^\Phi (X,\mu )$ if and only if $\{\Psi _q\}$ is $\delta $ -admissible for some $0<\delta <\infty $ .

Remark 1.3

1. (1) We note that $\sigma $ -finiteness of $(X,\mu )$ is only required for the forward implication. Further, in many cases, (1.3) is nondecreasing on all of $[0,\infty )$ for large q. For example, if $\Psi _q(t)=t^q$ and $\Phi (t) = t^r$ for $r\geq 1$ , then (1.3) is nondecreasing on $[0,\infty )$ for $q\geq r$ .

2. (2) The distinction between cases (i) and (ii) in Condition 1.1 is needed to prove necessity of $\delta $ -admissibility for identity (1.4), but it is not needed for sufficiency. Indeed, if $\mu (X)<\infty $ and $0<t<\mu (X)^{-1}$ , then one cannot select sets of large enough $\mu $ -measure with which to compute the limit of $\Psi _q^{-1}(t)$ as $q\rightarrow \infty $ using (1.4). We also note that Condition 1.1 is weaker than the closely related sufficient condition where $\displaystyle \lim _{q\rightarrow \infty }\Psi _q(t)=0$ in (i) and (ii).

Usually it is difficult to find the inverse of a given Young function in closed form. To make (1.3) easier to verify for given examples of $\Phi $ and $\Psi _q$ , notice that (1.3) is nondecreasing on $[0,k]$ exactly when the following is nondecreasing on $[0,\Phi (k)]$ :

$$\begin{align*}\frac{\Phi^{-1}(t)}{\Psi_q^{-1}(t)}. \end{align*}$$

So, to check that the conditions of Theorem 1.2 hold for a Young function $\Phi $ and a given family $\{\Psi _q\}$ , it suffices to compute the inverse of $\Psi _q$ for each $q>0$ , and to know either $\Phi $ or $\Phi ^{-1}$ .

The theorem stated above implies the main result of [2], and we include a streamlined proof of this special case in Section 5. Furthermore, we observe that if $\Phi (t)=t$ , then (1.3) is nondecreasing whenever $\Psi _q$ is a Young function, and from Theorem 1.2, we obtain the following result that involves no growth condition.

Corollary 1.4 If $(X,\mu )$ is a $\sigma $ -finite measure space and if $\{\Psi _q\}$ is a $\delta $ -admissible family for $0<\delta <\infty $ , then (1.4) holds for every $f\in L^1(X,\mu )$ .

The remainder of this paper is organized as follows: In Section 2, we establish preliminary results for Young functions and Orlicz spaces, and in Section 3, we discuss several examples of $\delta $ -admissible families to show how Theorem 1.2 can be applied. Section 4 is then devoted to the proof of our main result, and Section 5 examines the special case of log-bumps. We conclude with Section 6, where we demonstrate that identity (1.4) can fail if the family $\{\Psi _q\}$ is not $\delta $ -admissible for any finite $\delta>0$ .

2 Preliminaries

This section contains a brief introduction to Young functions and Orlicz spaces. Our discussion is largely expository, and for a complete treatment, the reader is referred to [4]. To begin, a nonnegative function $\psi : [0,\infty )\rightarrow [0,\infty )$ is said to be a density if it is right continuous, nondecreasing, $\psi (t)=0$ exactly when $t=0$ , and $\psi (t) \rightarrow \infty $ as $t\rightarrow \infty $ . Given a density $\psi $ , the associated function $\Psi :[0,\infty )\rightarrow [0,\infty )$ defined by

$$\begin{align*}\Psi(t) = \int_0^t \psi(s)ds \end{align*}$$

is called a Young function. For our purposes, the important functional properties of $\Psi $ are that it is continuous, strictly increasing, and convex on $(0,\infty )$ . Moreover, it is clear that $\Psi (0)=0$ and that $\Psi (t)\rightarrow \infty $ as $t\rightarrow \infty $ . Since the function $\Psi (t)=t$ has constant density it is not a Young function according to the definition above, however for our purposes, it can often be treated as one.

Given a Young function $\Psi $ and a measure space $(X,\mu )$ , the Orlicz space $L^\Psi (X,\mu )$ is defined as the collection of $\mu $ -measurable functions $f:X\rightarrow \mathbb {R}$ for which the Luxembourg norm

$$\begin{align*}\|f\|_{L^{\Psi}(X,\mu)} = \inf\bigg\{\lambda>0: \int_X \Psi\left( \frac{|f|}{\lambda}\right)d\mu \leq 1\bigg\} \end{align*}$$

is finite. Equipped with this norm $L^\Psi (X,\mu )$ is a Banach space (see [6]). The Orlicz classes generalize the Lebesgue spaces, and it is easy to verify that $\|\cdot \|_{L^p(X,\mu )}=\|\cdot \|_{L^\Psi (X,\mu )}$ when $\Psi (t)=t^p$ for $p\geq 1$ . Orlicz spaces can also provide a finer scale of norms then $L^p(X,\mu )$ in the following sense: if $\mu (X)<\infty $ and $\Psi _q(t)=t^p(1+\log (1+t))^q$ for $p\geq 1$ and $q>0$ , then, for any $\varepsilon>0,$ we have

$$\begin{align*}L^{p+\varepsilon}(X,\mu)\subsetneq L^{\Psi_q}(X,\mu)\subsetneq L^p(X,\mu). \end{align*}$$

These inclusions can be verified using Hölder’s inequality, and their strictness follows from the examples constructed in [3].

In the sections that follow, we employ several properties of the Luxembourg norm which we now establish. The first is a version of Chebyshev’s inequality on the Orlicz scale. Henceforth, we use the notation $\chi _S$ to denote the indicator function of a set $S\subseteq X$ .

Theorem 2.1 (Chebyshev’s inequality)

For $\alpha \geq 0$ , a $\mu $ -measurable function ${f:X\rightarrow \mathbb {R}}$ , and a Young function $\Psi $ , the following inequality holds:

(2.1) $$ \begin{align} \alpha\Psi^{-1}(\mu(\{x\in X:|f(x)|\geq\alpha\})^{-1})^{-1}\leq\|f\|_{L^\Psi(X,\mu)}. \end{align} $$

Proof First, we establish a simpler form of (2.1) in the norm of $L^1(X,\mu )$ using a standard argument. Fix $\alpha>0$ and define $f_\alpha =\alpha \chi _{\{|f|\geq \alpha \}}$ so that $f_\alpha \leq |f|$ holds pointwise and

$$ \begin{align*} \mu(\{|f|\geq\alpha\})=\mu(\{x\in X:|f(x)|\geq\alpha\})&=\frac{1}{\alpha}\int_Xf_\alpha(x)d\mu\leq\frac{1}{\alpha}\int_X|f(x)|d\mu\\ &=\frac{1}{\alpha}\|f\|_{L^1(X,\mu)}. \end{align*} $$

Next, we replace $\alpha $ with $\beta =\alpha /\|f\|_\Psi $ . Using that $\Psi $ is strictly increasing, it follows from the inequality above that

$$ \begin{align*} \mu(\{|f|\geq\beta\|f\|_\Psi\})&=\mu\bigg(\bigg\{\Psi\bigg(\frac{|f|}{\|f\|_{L^\Psi(X,\mu)}}\bigg)\geq\Psi(\beta)\bigg\}\bigg)\\ &\leq\frac{1}{\Psi(\beta)}\int_X\Psi\bigg(\frac{|f|}{\|f\|_{L^\Psi(X,\mu)}}\bigg)d\mu. \end{align*} $$

It is a well-known property of the Luxembourg norm, established in many standard references (e.g., [4]), that $\int _X\Psi (|f|/\|f\|_{L^\Psi (X,\mu )})d\mu \leq 1$ . From this, it follows that $\mu (\{|f|\geq \beta \|f\|_{L^\Psi (X,\mu )}\})\leq \Psi (\beta )^{-1}$ , and since $\Psi ^{-1}$ is increasing, this implies that $\Psi ^{-1}(\mu (\{x\in X:|f|\geq \alpha \})^{-1})^{-1}\leq \beta ^{-1}$ . Writing $\beta $ in terms of $\alpha $ and f gives (2.1).

Equipped with this result, we can compute the Orlicz norms of indicator functions.

Corollary 2.2 If $S\subseteq X$ is $\mu $ -measurable, then $\|\chi _S\|_{L^\Psi (X,\mu )}=\Psi ^{-1}(\mu (S)^{-1})^{-1}.$

Proof The estimate $\Psi ^{-1}(\mu (S)^{-1})^{-1}\leq \|\chi _S\|_\Psi $ follows at once from Chebyshev’s inequality. For the reverse inequality, observe that

$$\begin{align*}\int_{X}\Psi\bigg(\frac{\chi_S}{\Psi^{-1}(\mu(S)^{-1})^{-1}}\bigg)d\mu=\int_S\Psi\bigg(\frac{1}{\Psi^{-1}(\mu(S)^{-1})^{-1}}\bigg)d\mu=\int_S\frac{1}{\mu(S)}d\mu=1. \end{align*}$$

By the definition of the Luxembourg norm, this implies that $\|\chi _S\|_\Psi \leq \Psi ^{-1}(\mu (S)^{-1})^{-1}$ .

In this paper, we work with limits of Orlicz norms that are defined by a one-parameter family of Young functions. Subject to appropriate growth conditions, these families have useful pointwise properties which we will exploit in the sections to follow. Our main condition on these families is the following generalization of Condition 1.1.

Condition 2.3 Given $\alpha \geq 0$ and $\beta \geq \alpha $ , a family of Young functions $\{\Psi _q\}$ is said to be $(\alpha ,\beta )$ -admissible if $\displaystyle \lim _{q\rightarrow \infty } \Psi _q(t) = \infty $ for $t>\beta $ , and for $0<t<\alpha ,$ one of the following holds:

1. (i) If $\mu (X)=\infty $ then $\displaystyle \lim _{q\rightarrow \infty } \Psi _q(t) =0$ .

2. (ii) If $\mu (X)<\infty $ then $\displaystyle \lim _{q\rightarrow \infty } \Psi _q(t) <\mu (X)^{-1}$ .

Proposition 2.4 Let $\{\Psi _q\}$ be an $(\alpha ,\beta )$ -admissible family. If $\mu (X)=\infty $ and $t>0$ , or if $\mu (X)<\infty $ and $t\geq \mu (X)^{-1}$ , then

(2.2) $$ \begin{align} \alpha\leq \liminf_{q\rightarrow\infty}\Psi_q^{-1}(t)\leq \limsup_{q\rightarrow\infty}\Psi_q^{-1}(t)\leq \beta. \end{align} $$

Proof If $\alpha =0,$ then the first inequality in (2.2) holds trivially, so we assume that $\alpha>0$ .

Fix $t>0,$ if $\mu (X)=\infty $ and $t\geq \mu (X)^{-1}$ if $\mu (X)<\infty $ , and assume toward a contradiction that there exists $\eta>0$ such that

$$\begin{align*}\liminf_{q\rightarrow\infty}\Psi_q^{-1}(t)\leq\alpha-\eta. \end{align*}$$

Given any $0<\varepsilon <\eta $ then, there exists an increasing sequence $\{q_j\}$ such that $q_j\rightarrow \infty $ and $j\rightarrow \infty $ and $\Psi _{q_j}^{-1}(t)< \alpha -\varepsilon $ for each j. Since each $\Psi _q$ is strictly increasing for all $q>0$ , we find that $t< \Psi _{q_j}(\alpha -\varepsilon )$ for each j. Taking the limit as $j\rightarrow \infty $ , we see from Condition 2.3 that $0<t\leq 0$ if $\mu (X)=\infty $ , and $\mu (X)^{-1}\leq t<\mu (X)^{-1}$ if $\mu (X)<\infty $ . In any case, this is a contradiction, meaning that

$$\begin{align*}\alpha-\eta<\liminf_{q\rightarrow\infty}\Psi_q^{-1}(t). \end{align*}$$

Since $\eta>0$ was arbitrary, we get the first inequality in (2.2). The estimates for the limit supremum in (2.2) follow in an identical fashion.

If $\alpha =\beta =\delta $ for some $\delta>0,$ then Condition 2.3 is the same as $\delta $ -admissibility, and Proposition 2.4 gives

$$\begin{align*}\lim_{q\rightarrow\infty} \Psi^{-1}_q(t)=\delta \end{align*}$$

for each $t>0$ when $\mu (X)=\infty $ , and for each $t\geq \mu (X)^{-1}$ when $0<\mu (X)<\infty $ . In fact, the limit identity above is equivalent to $\delta $ -admissibility.

Proposition 2.5 A family of Young functions $\{\Psi _q\}$ is $\delta $ -admissible if and only if

(2.3) $$ \begin{align} \lim_{q\rightarrow\infty}\Psi_q^{-1}(t)=\delta \end{align} $$

holds for all $t>0$ if $\mu (X)=\infty $ , and for all $t\geq \mu (X)^{-1}$ if $0<\mu (X)<\infty $ .

Proof Proposition 2.4 gives the forward implication, leaving us to prove that if (2.3) holds for t in the appropriate range then $\{\Psi _q\}$ is $\delta $ -admissible. Regardless of whether $\mu (X)$ is finite or infinite, if $\Psi _q(t)\leq M$ for some $M>0$ and large q, then $t\leq \Psi _q^{-1}(M)$ and (2.3) gives

$$\begin{align*}t\leq \lim_{q\rightarrow\infty}\Psi_q^{-1}(M)=\delta. \end{align*}$$

As M was arbitrary, it follows in the contrapositive that if $t>\delta $ , then $\displaystyle \lim _{q\rightarrow \infty }\Psi _q(t)=\infty $ .

Assume now that $0<\mu (X)<\infty $ and suppose (2.3) holds for all $t\geq \mu (X)^{-1}>0$ . If

$$\begin{align*}\lim_{q\rightarrow\infty}\Psi_q(t)\geq \mu(X)^{-1}, \end{align*}$$

then given $0<\varepsilon <1,$ we have $\Psi _q(t)> \mu (X)^{-1}(1-\varepsilon )$ whenever q is sufficiently large. By convexity of $\Psi _q$ , it follows that

$$\begin{align*}\mu(X)^{-1}\leq \frac{\Psi_q(t)}{1-\varepsilon}\leq \Psi_q\bigg(\frac{t}{1-\varepsilon}\bigg), \end{align*}$$

and so $t\geq (1-\varepsilon )\Psi _q^{-1}(\mu (X)^{-1})$ whenever q is sufficiently large. Using (2.3), we take the limit to find

$$\begin{align*}t\geq(1-\varepsilon)\lim_{q\rightarrow\infty}\Psi_q^{-1}(\mu(X)^{-1})=(1-\varepsilon)\delta. \end{align*}$$

Since $\varepsilon $ was arbitrary, we conclude that $t\geq \delta $ . Thus, $\displaystyle \lim _{q\rightarrow \infty }\Psi _q(t)<\mu (X)^{-1}$ when $t<\delta $ .

On the other hand, if $\mu (X)=\infty $ and (2.3) is satisfied for $t>0$ , and if $\Psi _q(t)\geq \varepsilon $ for some $\varepsilon>0$ and for all large q, then

$$\begin{align*}t\geq \lim_{q\rightarrow\infty}\Psi_q^{-1}(\varepsilon)=\delta. \end{align*}$$

Thus, if $t<\delta ,$ then $\displaystyle \lim _{q\rightarrow \infty }\Psi _q(t)\leq \varepsilon $ , and as $\varepsilon>0$ was arbitrary, we have ${\displaystyle \lim _{q\rightarrow \infty }\Psi _q(t)=0}$ .

3 Examples

There are many examples of $\delta $ -admissible families of Young functions, and moreover, they are often easy to construct. In this section, we showcase some families to illustrate the utility of our main result, Theorem 1.2.

Example 3.1 If $\Psi _q(t) = t^q$ and $\Phi (t) = t^r$ for some $r\geq 1$ , then (1.3) is nondecreasing for $t>0$ whenever $q\geq r$ . Moreover, the family $\{\Psi _q\}$ is 1-admissible, and an application of Theorem 1.2 gives the well-known identity (1.1).

Example 3.2 If $\Phi (t)=t^r$ for $r\geq 1$ and $\Psi _q(t)=t^p\log (e-1+t)^q$ for $p\geq 1$ , then

$$\begin{align*}\frac{\Phi^{-1}(\Psi_q(t))}{t}=\frac{t^{\frac{p}{r}}\log(e-1+t)^{\frac{q}{r}}}{t} \end{align*}$$

fails the growth condition of Theorem 1.2 when $r>p$ , and satisfies it when $r\leq p$ , regardless of the value of $q>0$ . In the latter case, Theorem 1.2 recovers identity (1.2) for $f\in L^r(X,\mu )$ .

Example 3.3 Given $N\in \mathbb {N}$ and $p\geq 1$ , consider the family of $N\mathrm {th}$ -order iterated log-bumps

$$\begin{align*}\Psi_{q}(t) = t^p\underbrace{\log\ldots\log}_{N\;\mathrm{times}}(c+t)^q, \end{align*}$$

where c is chosen independent of q so that $\Psi _q(1)=1$ . This family is $1$ -admissible, and a straightforward adaptation of the argument in Section 5 shows that (1.3) is nondecreasing on any interval of the form $[0,k]$ for $f\in L^{\Psi _{q_0}}(X,\mu )$ whenever ${q>q_0>0}$ is sufficiently large. Thus, Theorem 1.2 applies to the Orlicz norms characterized by the $N\mathrm {th}$ -order iterated log-bumps above, giving

$$\begin{align*}\lim_{q\rightarrow \infty} \|f\|_{L^{\Psi_q}(X,\mu)} =\|f\|_{L^\infty(X,\mu),} \end{align*}$$

whenever $f\in L^{\Psi _{q_0}}(X,\mu )$ for some $q_0>0$ . We emphasize that in this example, the convergence of the $\|f\|_{L^{\Psi _q}(X,\mu )}$ norms to $\|f\|_{L^{\infty }(X,\mu )}$ is independent of p. Thus, for identity (1.4) to hold when $\{\Psi _q\}$ is a family of iterated log-bumps, it is not necessary to assume that $f\in L^{p+\varepsilon }(X,\mu )$ for any $\varepsilon>0$ .

Example 3.4 For any fixed Young function $\Phi $ , one can obtain a $1$ -admissible family using the structure of $N\mathrm {th}$ -order iterated log-bumps by defining

$$\begin{align*}\Psi_q(t)=\Phi(t)\underbrace{\log\ldots\log}_{N\;\mathrm{times}}(c+t)^q, \end{align*}$$

where c is chosen so that $\Psi _q(1)=\Phi (1)$ for all q. Indeed, iterated log-bumps of the form

(3.1) $$ \begin{align} \Psi_q(t)=\bigg(t\prod_{j=1}^N\underbrace{\log\ldots\log}_{j\;\mathrm{times}}(c_j+t)\bigg)^p\underbrace{\log\ldots\log}_{N\;\mathrm{times}}(c_N+t)^q \end{align} $$

are of this type, for $p\geq 1$ , provided that the constants $c_1,\dots ,c_N$ are chosen so that the value of $\Psi _q(\delta )$ is independent of q for some $\delta>0$ . Once again Theorem 1.2 applies to this family, allowing us to reproduce the limit in [3, Theorem 6.1]. This result is proved in [3] by means of a modification of the techniques of [2], which rely on the properties of iterated logarithms.

As in the last example, a similar calculation to that employed in Section 5 shows that if $\Phi =\Psi _{q_0}$ for $\Psi _q$ as in (3.1), then (1.3) is nondecreasing on any bounded interval of the form $[0,k]$ for $k>0$ whenever $q>q_0$ is sufficiently large. Once again, we conclude that the $L^{\Psi _q}(X,\mu )$ norms of f converge to $\|f\|_{L^\infty (X,\mu )}$ , provided $f\in L^{\Psi _{q_0}}(X,\mu )$ for some $q_0>0$ .

There are many more families for which $\delta $ -admissibility can be established, and the interested reader is encouraged to construct their own examples.

4 Proof of Theorem 1.2

Every Orlicz norm used in this section is defined with respect to a fixed measure space $(X,\mu )$ , so we will always write $\|\cdot \|_{L^\Psi (X,\mu )}=\|\cdot \|_\Psi $ and $\|\cdot \|_{L^\infty (X,\mu )}=\|\cdot \|_\infty $ . Fix $\delta>0$ and suppose that $\{\Psi _q\}$ is a $\delta $ -admissible family of Young functions. Identity (1.4) is trivial if $f\equiv 0$ , and we will treat the case of unbounded f separately at the end. Thus, we begin by assuming that $0<\|f\|_\infty <\infty $ , and we note that it is enough to prove (1.4) when $\|f\|_\Phi =1$ . Since (1.3) is nondecreasing on $[0,\|f\|_\infty ]$ by hypothesis for q sufficiently large, we have

$$\begin{align*}\| f\|_{\Psi_q}=\left\| \Psi_q^{-1}(\Phi(|f|))\frac{|f|}{\Psi_q^{-1}(\Phi(|f|))}\right\|_{\Psi_q} \leq \left\| \Psi_q^{-1}(\Phi(|f|))\right\|_{\Psi_q}\frac{\|f\|_\infty}{\Psi_q^{-1}(\Phi(\|f\|_\infty))}. \end{align*}$$

Additionally, we see that $\| \Psi _q^{-1}(\Phi (|f|))\|_{\Psi _q}\leq 1$ since by definition of the Luxembourg norm,

$$\begin{align*}\int_X \Psi_q\left(\Psi_q^{-1}\left(\Phi(|f(x)|)\right)\right)d\mu=\int_X\Phi(|f|)d\mu\leq 1. \end{align*}$$

Moreover, in the case $0<\mu (X)<\infty ,$ we have that

$$\begin{align*}\Phi(\|f\|_\infty)\geq \mu(X)^{-1}\int_X \Phi(|f|)d\mu = \mu(X)^{-1}. \end{align*}$$

Equality holds above since $\|f\|_\Phi =1$ and since f is bounded by assumption (see, e.g., [7, Equation (3.13)]). Using these estimates, we find from Proposition 2.5 that

$$\begin{align*}\limsup_{q\rightarrow\infty}\|f\|_{\Psi_q}\leq\|f\|_\infty\lim_{q\rightarrow\infty}\Psi_q^{-1}(\Phi(\|f\|_\infty))^{-1}=\frac{\|f\|_\infty}{\delta}. \end{align*}$$

Next, suppose that $0<\varepsilon <\|f\|_\infty $ , and let $S=\{x\in \Omega :|f(x)|\geq \|f\|_\infty -\varepsilon \}$ . From the definition of the essential supremum and Chebyshev’s inequality, it follows at once that $0<\mu (S)\leq \Phi ((\|f\|_\infty -\varepsilon )^{-1})$ , meaning that $\mu (S)$ is finite and nonzero. Moreover, Chebyshev’s inequality with $\alpha = \|f\|_\infty -\varepsilon $ also shows that

$$\begin{align*}(\|f\|_\infty-\varepsilon)\Psi_q^{-1}(\mu(S)^{-1})^{-1}\leq \|f\|_{\Psi_q}. \end{align*}$$

From Proposition 2.5, it follows that $\Psi _q^{-1}(\mu (S)^{-1})^{-1}\rightarrow \delta ^{-1}$ as $q\rightarrow \infty $ , since $S\subseteq X$ and $\mu (S)^{-1}\geq \mu (X)^{-1}$ when $0<\mu (X)<\infty $ . As a result, we find that

$$\begin{align*}\frac{\|f\|_\infty-\varepsilon}{\delta}\leq \displaystyle\liminf_{q\rightarrow\infty}\|f\|_{\Psi_q}. \end{align*}$$

Since $\varepsilon>0$ was arbitrary, this gives $\displaystyle \delta ^{-1}\|f\|_\infty \leq \displaystyle \liminf _{q\rightarrow \infty }\|f\|_{\Psi _q}$ , proving that (1.4) holds.

In the case where $\|f\|_\infty = \infty $ , choose $N>1$ and set $f_N = \min \{|f|,N\}$ so that $\|f_N\|_\infty =N$ . Applying our work above, we see that

$$\begin{align*}\displaystyle\liminf_{q\rightarrow \infty} \|f\|_{\Psi_q} \geq \liminf_{q\rightarrow \infty} \|f_N\|_{\Psi_q}\geq \delta^{-1}\|f_N\|_\infty = \delta^{-1}N.\end{align*}$$

Since N may be chosen arbitrarily large, we find $\displaystyle \liminf _{q\rightarrow \infty } \|f\|_{\Psi _q}=\infty $ as required.

Now, we show that if (1.4) holds for all $f\in L^\Phi (X,\mu )$ , then the family $\{\Psi _q\}$ is $\delta $ -admissible. Specifically, we utilize the characterization of $\delta $ -admissible families given by Proposition 2.5 to recognize that it is enough to show that

$$\begin{align*}\lim_{q\rightarrow\infty} \Psi^{-1}_q(t) = \delta \end{align*}$$

for every $t>0$ when $\mu (X)=\infty $ , and for $t\geq \mu (X)^{-1}$ when $\mu (X)$ is finite and positive.

Suppose, first that $\mu (X)=\infty $ . Given $t>0$ , we use that $(X,\mu )$ is $\sigma $ -finite to select sets $S_1\subset X$ and $S_2\subset X$ of sufficiently large measure so that with $t_j = \mu (S_j)^{-1}$ we have $0<t_2<t_1<t$ . Using (1.4) with $f_j = \chi _{S_j}\in L^\Phi (X,\mu ),$ we find from Corollary 2.2 that

$$\begin{align*}\lim_{q\rightarrow \infty} \Psi_q^{-1}(t_j)=\lim_{q\rightarrow \infty} \|f_j\|_{L^{\Psi_q}(X,\mu)}^{-1} =\delta\|f_j\|_{L^\infty(X,\mu)}^{-1}=\delta. \end{align*}$$

Since we may choose $\lambda \in (0,1)$ so that $\lambda t_2+(1-\lambda )t = t_1$ , the concavity of $\Psi _q^{-1}$ gives

$$\begin{align*}\lambda\Psi_q^{-1}(t_2) + (1-\lambda)\Psi_q^{-1}(t) \leq \Psi_q^{-1}(t_1). \end{align*}$$

Letting $q\rightarrow \infty $ we find after taking a limit supremum and rearranging that

$$\begin{align*}\limsup_{q\rightarrow\infty}\Psi_q^{-1}(t) \leq \delta. \end{align*}$$

Moreover, since $\Psi _q^{-1}$ is increasing, $\delta \leq \displaystyle \liminf _{q\rightarrow \infty }\Psi _q^{-1}(t)$ . Thus, $\displaystyle \lim _{q\rightarrow \infty }\Psi _q^{-1}(t) = \delta $ for $t>0$ .

In the case that $0<\mu (X)<\infty $ , if $t>\mu (X)^{-1}$ , we may proceed exactly as above (see Remark 1.3). If $t=\mu (X)^{-1}$ , the required estimate follows at once by applying (1.4) to $f =\chi _X\in L^\Phi (X,\mu )$ . In any case, we have established that

$$\begin{align*}\displaystyle\lim_{q\rightarrow\infty}\Psi_q^{-1}(t) = \delta \end{align*}$$

for $t\geq \mu (X)^{-1}$ when $0<\mu (X)<\infty $ , and for $t>0$ when $\mu (X)=\infty $ . It follows from Proposition 2.5 that $\{\Psi _q\}$ is $\delta $ -admissible.

Remark 4.1 If we use the more general Condition 2.3 in place of Condition 1.1 in Theorem 1.2, simple modifications of the proof above show that one has the estimates

(4.1) $$ \begin{align} \frac{1}{\beta}\|f\|_\infty\leq \liminf_{q\rightarrow\infty}\|f\|_{\Psi_q}\leq \limsup_{q\rightarrow\infty}\|f\|_{\Psi_q}\leq \frac{1}{\alpha}\|f\|_\infty. \end{align} $$

It may be the case that the limit of the norms $\| f\|_{\Psi _q}$ does not exist for a family $\{\Psi _q\}$ which is $(\alpha ,\beta )$ -admissible, as we show with the following example. Let

$$\begin{align*}\Psi_q(t)=\begin{cases} \hfil\frac{1}{2}t^q, & 0\leq t\leq \frac{1}{2},\\ \frac{1}{2}(t^q+(2t-1)^{2+\sin q}), & \frac{1}{2}<t< 1,\\ \hfil\frac{1}{2}(t^q+(2t-1)^3), & \hfill t\geq1, \end{cases} \end{align*}$$

so that $\{\Psi _q\}$ is $(\frac {1}{2},1)$ -admissible. If $f=\chi _S$ for S with $2<\mu (S),$ then $\|f\|_\infty =1$ and

$$\begin{align*}1\leq \liminf_{q\rightarrow\infty}\|f\|_{\Psi_q}\leq \limsup_{q\rightarrow\infty}\|f\|_{\Psi_q}\leq 2. \end{align*}$$

On the other hand, we can show that $\displaystyle \lim _{q\rightarrow \infty }\Psi _q^{-1}(t)$ does not exist for $t\in (0,\frac {1}{2})$ , and thus

(4.2) $$ \begin{align} \lim_{q\rightarrow\infty}\|f\|_{\Psi_q}=\lim_{q\rightarrow\infty}\Psi_q^{-1}(\mu(S)^{-1})^{-1} \end{align} $$

does not exist. To see this, assume toward a contradiction that there is a $t\in (0,\frac {1}{2})$ such that $\displaystyle \lim _{q\rightarrow \infty }\Psi _q^{-1}(t)=d.$

First, we show that $d\in (\frac {1}{2},1)$ . Given $\varepsilon>0,$ we have for all large q that $d-\varepsilon <\Psi _q^{-1}(t)<d+\varepsilon $ and $\Psi _q(d-\varepsilon )<t<\Psi _q(d+\varepsilon )$ . If $d<\frac {1}{2}$ , then we can choose $\varepsilon $ small enough that $d+\varepsilon \leq \frac {1}{2}$ , meaning that $\Psi _q(d+\varepsilon )\rightarrow 0$ as $q\rightarrow \infty $ . Since $t<\Psi _q(d+\varepsilon )$ for all large $q,$ this gives a contradiction for large q. Likewise, if $d> 1,$ then we can choose $\varepsilon $ such that $d-\varepsilon \geq 1$ , meaning that $ \Psi _q(d-\varepsilon )\rightarrow \infty $ as $q\rightarrow \infty $ . Since $\Psi _q(d-\varepsilon )<t<\frac {1}{2}$ , this gives another contradiction, and it follows that $\frac {1}{2}\leq d\leq 1$ .

If $d=\frac {1}{2}$ , then $\frac {1}{2}<d+\varepsilon < 1$ when $\varepsilon $ is small and $\Psi _q(d+\varepsilon )=\frac {1}{2}((\frac {1}{2}+\varepsilon )^q+(2\varepsilon )^{2+\sin q})$ . Choosing $\varepsilon <\frac {1}{2}$ so small that $(2\varepsilon )^{2+\sin q}\leq 2\varepsilon \leq t$ and then taking q so large that $(\frac {1}{2}+\varepsilon )^q\leq t$ , we get $\Psi _q(d+\varepsilon )\leq t$ , a contradiction. Similarly, if $d=1,$ then $\frac {1}{2}<d-\varepsilon <1$ for small $\varepsilon $ and

$$\begin{align*}\Psi_q(d-\varepsilon)=\frac{(1-\varepsilon)^q+(1-2\varepsilon)^{2+\sin q}}{2}\geq \frac{(1-2\varepsilon)^{2+\sin q}}{2}\geq \frac{(1-2\varepsilon)^{3}}{2}. \end{align*}$$

Since $t<\frac {1}{2}$ , we can choose $\varepsilon $ sufficiently small that $\frac {(1-2\varepsilon )^{3}}{2}\geq t$ , another contradiction. It follows that $\frac {1}{2}<d<1$ and $\frac {1}{2}<d-\varepsilon <d+\varepsilon <1$ for small $\varepsilon $ . Consequently,

$$\begin{align*}\Psi_q(d\pm \varepsilon)=\frac{(d\pm\varepsilon)^q+(2(d\pm\varepsilon)-1)^{2+\sin q}}{2}. \end{align*}$$

Taking $q=\frac {\pi }{2}+k\pi $ for odd $k\in \mathbb {Z}$ gives $t>\Psi _q(d-\varepsilon )=\frac {1}{2}((d-\varepsilon )^q+2(d-\varepsilon )-1)$ , while using even k gives $t<\Psi _q(d+\varepsilon )=\frac {1}{2}((d+\varepsilon )^q+(2(d+\varepsilon )-1)^{3})$ . For $\varepsilon $ small and q large, we show that this is impossible. By convexity of the map $t\mapsto t^q$ for $q\geq 1,$ we have $(d+\varepsilon )^q<(d-\varepsilon )^q+(d+3\varepsilon )^q$ , and moreover, a straightforward calculation shows that

$$\begin{align*}(2(d+\varepsilon)-1)^{3}=4d(2d-1)(d-1)+4\varepsilon(2+6d^2-6d+6d\varepsilon+2\varepsilon^2-3\varepsilon)+(2d-2\varepsilon-1). \end{align*}$$

Note that $4d(2d-1)(d-1)<0$ when $\frac {1}{2}<d<1$ . From the estimates above, we get

$$ \begin{align*} (d+\varepsilon)^q+(2(d+\varepsilon)-1)^{3}&<(d-\varepsilon)^q+(d+3\varepsilon)^q+4d(2d-1)(d-1)\\&\quad +4\varepsilon(2+2\varepsilon^2+3\varepsilon)+(2d-2\varepsilon-1). \end{align*} $$

Taking $\varepsilon $ small and q large, we can ensure that

$$\begin{align*}(d+3\varepsilon)^q+4d(2d-1)(d-1)+4\varepsilon(2+2\varepsilon^2+3\varepsilon)\leq 0, \end{align*}$$

and doing this gives the following contradiction:

$$\begin{align*}2t<(d+\varepsilon)^q+(2(d+\varepsilon)-1)^{3}\leq (d-\varepsilon)^q+2(d-\varepsilon)-1)<2t. \end{align*}$$

Thus, the limit in (4.2) may not exist when the $\delta $ -admissibility condition fails.

5 Log-bump Orlicz norms

Here, we show that Theorem 1.2 implies [2, Theorem 1], which states that (1.4) holds with $\delta =1$ for a specific family of log-bump Young functions. Given $p\geq 1$ , the log-bumps are of the form $\Psi _q(t)=t^p\log (e-1+t)^q$ for $q>0$ , and the collection of all these bumps is a $1$ -admissible family. Thus, [2, Theorem 1] follows from Theorem 1.2, once we demonstrate that for $k>0,$ the function (1.3) is nondecreasing on $[0,k]$ when $\Phi (t) = \Psi _{q_0}(t)$ for some $q_0>0$ and when q is large. To do this, we first assume that $q>q_0$ and for $t>0,$ we define

$$\begin{align*}F(t)=\frac{t}{\Psi_q^{-1}(\Psi_{q_0}(t))}, \end{align*}$$

so that F satisfies the equation $\Psi _{q_0}(t)=\Psi _q(tF(t)^{-1})$ . Recalling the form of $\Psi _q$ , we get

(5.1) $$ \begin{align} F(t)^p\log(e-1+t)^{q_0}=\log\bigg(e-1+\frac{t}{F(t)}\bigg)^q \end{align} $$

for $t>0$ . It follows from the definition above that F is continuous on $(0,\infty )$ , and to extend F continuously to zero, we observe that

$$\begin{align*}\log(e-1)^{q_0}\lim_{t\rightarrow 0^+}F(t)^p=\log\bigg(e-1+\lim_{t\rightarrow 0^+}\Psi_q^{-1}(\Psi_{q_0}(t))\bigg)^q=\log(e-1)^q. \end{align*}$$

Setting $F(0)=\displaystyle \lim _{t\rightarrow 0^+}F(t)=\log (e-1)^{\frac {q-q_0}{p}}$ , thus ensures that F is continuous on $[0,\infty )$ .

Lemma 5.1 If $q>q_0$ , then $F(t)>F(0)$ for every $t>0$ .

Proof Observe that if $q>q_0$ , then $\Psi _q(t)\geq \Psi _{q_0}(t)$ when $t\geq 1$ , while $ \Psi _q(t)< \Psi _{q_0}(t)$ when $0<t<1$ . In the case $t\geq 1$ , we use that $\Psi _{q}^{-1}$ is strictly increasing to see that $t\geq \Psi _q^{-1}(\Psi _{q_0}(t))$ , which implies that $F(t)\geq 1>F(0)$ . Likewise, $0<t<1$ gives $F(t)<1,$ and by (5.1), we find

$$\begin{align*}\log(e-1+t)^q<\log\bigg(e-1+\frac{t}{F(t)}\bigg)^q=F(t)^p\log(e-1+t)^{q_0}. \end{align*}$$

Rearranging, we see that $F(t)>\log (e-1+t)^{\frac {q-q_0}{p}}>F(0)$ .

Now, fix $k>0$ , set $I=[0,k]$ , and let $M=\sup _IF$ . We show that F is injective on I when q is large enough. To this end, fix $t_1\in I$ , set $c=F(t_1)$ , and note that $F(t_1)=F(0)$ if and only if $t_1=0$ . On the other hand, if $t_1>0,$ then $c\in (F(0), M]$ by Lemma 5.1. Moreover, from (5.1), we see that $t_1$ is a fixed point of the map $T_c:[0,\infty )\rightarrow \mathbb {R}$ defined by

$$\begin{align*}T_c(t)=c\exp\big(c^{\frac{p}{q}}\log(e-1+t)^{\frac{q_0}{q}}\big)-c(e-1). \end{align*}$$

Since $F(0)< c$ , it is easy to see that $T_c(0)>0$ . Furthermore, a straightforward computation shows that $T_c"(t)<0$ if and only if

(5.2) $$ \begin{align} q_{0}c^{\frac{p}{q}}\log\left(e-1+t\right)^{\frac{q_{0}}{q}}<q\log\left(e-1+t\right)+q-q_{0}. \end{align} $$

For large q, this is achieved uniformly in $c\in [0,M]$ . To see why, choose $q\geq q_0$ so that

$$\begin{align*}M^p\leq \bigg(\frac{q}{q_0}\bigg)^q\log(e-1)^{q-q_0}. \end{align*}$$

Then $c^{\frac {p}{q}}\leq \frac {q}{q_0}\log (e-1)^{1-\frac {q_0}{q}}\leq \frac {q}{q_0}\log (e-1+1)^{1-\frac {q_0}{q}}$ for each $t\geq 0$ , and this shows that (5.2) holds for each $t\geq 0$ , and we see $T_c(t)$ is strictly concave on $(0,\infty )$ .

For q large as above, we find that $T_c(0)>0$ and $T_c$ is a continuous and strictly concave function on $(0,\infty )$ . Thus, $T_c(t)$ has a unique fixed point in $[0,\infty )$ and so it is $t_1$ . This gives F injective on I since $F(t_2)=c=F(t_1)$ shows that $t_1$ and $t_2$ are fixed points of $T_c(t)$ . Since F is a continuous, injective function on I, the Intermediate Value Theorem shows that F is strictly monotone on I. Lastly, since Lemma 5.1 shows that $F(0)<F(t)$ for $t\in I$ , we conclude that F is strictly increasing on I when q is sufficiently large. Thus, with the hypotheses of Theorem 1.2 verified, we have reproved [2, Theorem 1].

6 Necessity of admissibility conditions

Finally, we show that Conditions 1.1 and 2.3 are necessary for the norm limit to be related to the essential supremum of a function. This means that our admissibility conditions cannot be weakened in Theorem 1.2 or Remark 4.1.

Theorem 6.1 Let $\{\Psi _q\}$ be a family of Young functions, and let $\Phi $ be a Young function for which (1.3) is nondecreasing, and assume that there exists $f\in L^\Phi (X,\mu )\cap L^\infty (X,\mu )$ such that

(6.1) $$ \begin{align} 0<\liminf_{q\rightarrow\infty}\|f\|_{\Psi_q}\leq \limsup_{q\rightarrow\infty}\|f\|_{\Psi_q}<\infty. \end{align} $$

Then $\{\Psi _q\}$ is $(\alpha ,\beta )$ -admissible for some $\beta>0$ and $\alpha \geq 0$ .

Proof First, assume to the contrary that $\Psi _q(t)\rightarrow \infty $ as $q\rightarrow \infty $ for each fixed $t>0$ . Arguing as in the proof of Proposition 2.4, we conclude that $\Psi _q^{-1}(t)\rightarrow 0$ as $q\rightarrow \infty $ for each $t>0$ . Since the limit infimum in (6.1) is nonzero, we have $0<\|f\|_\infty $ , and as in the proof of Theorem 1.2, we can choose $\varepsilon <\|f\|_\infty $ to see that

$$\begin{align*}(\|f\|_\infty-\varepsilon)\liminf_{q\rightarrow\infty}\Psi_q^{-1}(\mu(\{x\in\Omega:|f(x)|\geq \|f\|_\infty-\varepsilon\})^{-1})^{-1}\leq \liminf_{q\rightarrow\infty}\|f\|_{\Psi_q}. \end{align*}$$

By definition of the essential supremum, $\mu (\{x\in \Omega :|f(x)|\geq \|f\|_\infty -\varepsilon \})>0$ , meaning that the limit on the left-hand side above diverges and $\|f\|_{\Psi _q}\rightarrow \infty $ as ${q\rightarrow \infty }$ , contradicting the right-hand limit of (6.1). Thus, there is a $t_0>0$ for which $\displaystyle \limsup _{q\rightarrow \infty }\Psi _q(t_0)<\infty $ , and therefore,

$$\begin{align*}\limsup_{q\rightarrow\infty}\Psi_q(t)<\infty \end{align*}$$

holds for every $0\leq t\leq t_0$ since each Young function is strictly increasing. This means that $(\alpha ,\beta )$ -admissibility holds for some $\alpha \geq 0$ and $\beta>0$ .

Similarly, suppose that $\Psi _q(t)\rightarrow 0$ as $q\rightarrow \infty $ for each $t>0$ , so that $\Psi _q^{-1}(t)\rightarrow \infty $ by the argument of Proposition 2.4. Arguing as in Section 4, we have

$$\begin{align*}\limsup_{q\rightarrow\infty}\|f\|_{\Psi_q}\leq\|f\|_\infty\limsup_{q\rightarrow\infty}\Psi_q^{-1}(\Phi(\|f\|_\infty))^{-1}=0, \end{align*}$$

and again this contradicts (6.1). Since each $\Psi _q$ is strictly increasing, we conclude that $\displaystyle \liminf _{q\rightarrow \infty }\Psi _q(t)>0$ for large $t>0$ . Thus, there exists $\alpha \leq \beta $ satisfying Condition 2.3.

In the case of $\delta $ -admissibility, where $\alpha =\beta =\delta $ , the argument above shows that Theorem 1.2 fails when $\delta $ is not both positive and finite.

Corollary 6.2 Let $\{\Psi _q\}$ be a family of Young functions such that for every $t>0$ ,

$$\begin{align*}\lim_{q\rightarrow\infty}\Psi_q(t)=\infty\qquad(\textrm{resp. }\lim_{q\rightarrow \infty} \Psi_q(t)=0). \end{align*}$$

If f satisfies the remaining hypotheses of Theorem 1.2, then regardless of the value of $\|f\|_\infty $ ,

$$\begin{align*}\lim_{q\rightarrow \infty} \|f\|_{L^{\Psi_q}(X,\mu)}=\infty\qquad(\textrm{resp. }\lim_{q\rightarrow \infty} \|f\|_{L^{\Psi_q}(X,\mu)}=0). \end{align*}$$

To illustrate, if $f=\chi _{[0,1]}$ and $\Psi _q(t) = t^p\log (e+t)^q$ , then Corollary 2.2 shows that $\|f\|_{L^{\Psi _q}(\mathbb {R},dx)}=\Psi _q^{-1}(1)^{-1}$ , but $\{\Psi _q\}$ is not $\delta $ -admissible for any $\delta>0$ . A straightforward calculation shows that

$$\begin{align*}\lim_{q\rightarrow\infty}\|f\|_{L^{\Psi_q}(\mathbb{R},dx)}\geq\liminf_{q\rightarrow\infty}\|f\|_{L^{\Psi_q}(\mathbb{R},dx)}=\liminf_{q\rightarrow\infty}\Psi_q^{-1}(1)^{-1}=\infty> \|f\|_{L^\infty(\mathbb{R},dx)}. \end{align*}$$

Thus, if Condition 1.1 fails, then the Orlicz norms may not converge to $\|f\|_{L^\infty (X,\mu )}$ .