Introduction
The polar regions are important components of the global environment. Antarctic ice, which contains 90% of the world’s total ice (70% of the freshwater ice), plays an active role in global climatic change, and estimating the glacier dynamics is essential for understanding the mass balance of the Antarctic ice sheet (Reference Gloersen and CampbellGloersen and Campbell, 1988; Reference MeirMeir, 1993; Reference Wingham, Ridout, Scharroo and ArthernWingham and others, 1998). Some 90% of the discharge from the Antarctic ice sheet is through a small number of ice streams and outlet glaciers. Understanding the complex dynamics of these drainage systems requires fundamental information, such as surface mass balance, depth and temperature of the ice, meteorological conditions, surface velocity vectors, strain rates, surface gradients and changes in surface elevation. Some of these important outlet glaciers have been studied (e.g. ice velocity observations on Potsdam Glacier (Reference Dietrich, Metzig and KorthDietrich and others, 1999; Reference Metzig, Dietrich, Korth, Perlt and HartmannMetzig and others, 2000; Reference Anschütz, Oerter and SteinhageAnschütz and others, 2007), Lambert Glacier (Reference Manson, Coleman and MorganManson and others, 2000; Reference Testut, Hurd, Coleman, Rémy and LegrésyTestut and others, 2003), the Amery Ice Shelf (Reference KingKing, 2001; Reference Bassis, Coleman and FrickerBassis and others, 2005; Reference Fricker, Young, Coleman and BassisFricker and others, 2005), Shirase Glacier (Reference Pattyn and NarusePattyn and Naruse, 2003), Pine Island Glacier (Reference Joughin, Rignot, Rosanova and LucchittaJoughin and others, 2003) and the Larsen B ice shelf (Reference Rignot, Casassa, Gogineni, Krabill and RiveraRignot and others, 2004). Schirmacher Glacier makes a major contribution to the drainage of coastal East Antarctica, being an important outlet glacier in central Dronning Maud Land.
Prior to the mid-1970s, ice flow velocities were measured using astronomical positioning techniques (e.g. Liebert and Leonhardt, 1973) and stake readings. With advances in airborne and space-borne geodetic techniques, it is now feasible to monitor glacier velocities and strain rates very precisely (Reference KingKing, 2004). There are several well-established space-borne geodetic techniques for this purpose, including global positioning system (GPS) (Reference LeickLeick, 1995), interferometric synthetic aperture radar (InSAR) (Reference Goldstein, Engelhardt and KambGoldstein and others, 1993) and the Ice, Cloud and land Elevation satellite (ICESat) (Reference ZwallyZwally and others, 2002). Amongst these, GPS remains an indispensable tool for a comprehensive understanding of ice kinematics. Reference Korth and DietrichKorth and Dietrich (1996), Reference Dietrich, Metzig and KorthDietrich and others (1999), Reference Metzig, Dietrich, Korth, Perlt and HartmannMetzig and others (2000) and M. Scheinert (unpublished information) outline a variety of geodetic observation techniques, which have been applied in investigations of geodynamic phenomena in the Schirmacher Oasis region. Here, we describe the velocity and strain-rate fields obtained during two GPS campaigns undertaken on Schirmacher Glacier during the summer seasons of 2003 and 2004.
Geodynamic Settings
Schirmacher Glacier in central Dronning Maud Land (Fig. 1) is part of the Antarctic rift system that has evolved in different stages since the Gondwanaland break-up in Jurassic time (Reference Lawver, Cahagan and CoffinLawver and others, 1992). It is located between an area south of the Lazarev Sea and Nivlisen ice shelf (Reference SenguptaSengupta, 1986; Reference HermichenHermichen, 1995; Reference HorwathHorwath and others, 2006) and north of Potsdam Glacier and the Wohlthat Mountains; Reference Anschütz, Oerter and SteinhageAnschütz and others 2007). The study region is bounded by latitudes 70°40′ S and 71°00′ S and longitudes 11° 10′ E and 12°10′ E. Mean annual air temperature is below –20°C (Reference Bormann and FritzscheBormann and Fritzsche, 1995). In general terms, the Schirmacher Glacier flow is blocked by the Schirmacher Oasis (a low-lying nunatak) located to the north.

Fig. 1. Location map of central Dronning Maud Land, East Antarctica, showing the study area of Schirmacher Glacier (rectangle) superimposed on a shaded relief map of GTOPO30 digital elevation model with 500 m elevation contour interval. Dotted line below the rectangle indicates the location of ground-penetrating radar (GPR) profiles by Anschutz and others (2007).
The study area is divided into three distinct topographic units: the southern continental ice sheet, elevated nunataks and, to the north, shelf ice which exhibits distinct surface undulations (Reference Ravindra, Chadurvedi and BegRavindra and others, 2002). The region is also characterized by gentle to steep gradient surface slopes with some subglacial highs and lows above mean sea level (Reference Damm and EisenburgerDamm and Eisenburger, 2005; Reference Meyer, Steinhage, Nixdorf and MillerMeyer and others, 2005), criss-cross fractures and crevasses close to the Schirmacher Oasis. To the north of Schirmacher Oasis there is shelf ice exhibiting pressure ridges. A large ablation area is located in the south-southeast, which extends to the Wohlthat Mountains (Reference Bormann and FritzscheBormann and Fritzsche, 1995).
Survey Description and Data Processing
The GPS network on Schirmacher Glacier consists of 21 sites with ∼5 km inter-station spacing (Fig. 4). At all sites in the network, GPS data were collected using dual-frequency (L1/ L2) geodetic Trimble 4000SSi receivers with choke ring antennae, during January to March in 2003 and 2004. In the second campaign, only 15 sites (out of 21) were reoccupied, as some were lost/untraced due to accumulation of fresh snow. Each antenna was fixed on a 1.5 cm diameter threaded steel bolt fixed on a wooden block of 0.5 m × 0.5 m, embedded to a depth of 0.75 m in the ice (Fig. 2a). All the sites were observed continuously for 48–72 hours with 30 s sampling interval and 15° elevation mask. The base station (MAIT) was set up on exposed bedrock near the Indian Antarctic Research Station, Maitri, which is ∼15km away from the survey region (Figs 2b and 4). The GPS receivers in the field were powered by specially sealed 12 V, 72 Ah charged batteries enclosed in non-conducting boxes.

Fig. 2. (a) GPS antenna mounted on wooden platform on the glacier. (b) Set-up of the GPS base station on bedrock.
The recorded GPS data, organized into 24 hour segments, covered a Universal Time Coordinated (UTC) day and were analyzed in three steps. In the first step, the GPS carrier phase data were processed with the precise ephemeris from the International GPS Service (IGS) stations to produce position estimates and an associated covariance matrix of loosely constrained daily solutions for station positions using GPS Analysis Massachusetts Institute of Technology (GAMIT) software (Reference King and BockKing and Bock, 2002). In the next step these loosely constrained regional solutions were combined with global solutions produced by the Scripps Orbit and Permanent Array Center, San Diego, California, USA, using the Global Kalman filter (GLOBK) program (Reference HerringHerring, 2002). The basic algorithms and a description of this technique are given by Reference Herring and KingHerring and King (1990), and its application to GPS data is given by Reference FeiglFeigl and others (1993). Station position and velocity vectors at each site were obtained from these combined quasiobservations (Reference Dong and HerringDong and others, 1998) in the third step. Since the velocity of the glaciers is very high compared to crustal movement, we consider only the MAIT base station and nearby global IGS stations, SYOG and VESL to constrain the glacier velocity solutions in International Terrestrial Reference Frame (ITRF2000) (Reference Altamimi and SillardAltamimi and others, 2002).
Base Station Repeatability
In GPS studies, the consistency/stability of the base station is very important, particularly in the Antarctic, where glacial load and ice flow can cause crustal deformation. The precision of the sites is assured provided the base station has high repeatability in the position coordinates. To improve the ambiguity resolution of the MAIT base station, data from the nearby IGS stations (OHI2, SYOG, VESL and MAW1) were imposed by putting tight constraints (3–5 mm in the horizontal, 5–10 mm in the vertical) on their a priori coordinate values in the ITRF2000 frame. At MAIT the coordinates were allowed to vary freely by way of very loose constraints (10 m) to avoid singularity in the normal matrix (Reference Dong and HerringDong and others, 1998). The short-term precision of the MAIT position is estimated from the daily solution repeatability (with corresponding rms) separately for the two campaigns.
To check the repeatability of the MAIT position, 44 days of data during 2003 (Julian days 31–74) and 39 days of data during 2004 (Julian days 33–71) have been used. The daily coordinates were obtained by considering wet tropospheric zenith delay (Reference VeyVey and others, 2002), ionospheric free-linear combination (Reference Davies and HartmannDavies and Hartmann, 1997), real valued carrier phase ambiguities, latitude-dependent variation (Reference King, Coleman and NguyenKing and others, 2003) and satellite and receiver clock errors. Due to the satellite constellation, the GPS-estimated vertical coordinates are less precise than the horizontal coordinates; here we focus only on the precise estimation of the horizontal component of the base station. Thus we estimate the horizontal repeatability of MAIT with rms limits of 1.80 and 2.03 mm for the first and second campaigns, respectively. Figure 3 shows the time-series plots of daily position variations (total horizontal component) for the base station during the two campaigns. As seen from Figure 3, the daily coordinates show neither a significant offset nor a change of trend. This indicates good stability and justifies the use of MAIT as the base station. For estimating ice velocities and positions, measurements were equally constrained with respect to MAIT and to the IGS stations by applying equal weights.

Fig. 3. Total horizontal component time series of base station (shown in Fig. 2b), for campaigns during (a) 2003 and (b) 2004.
Velocity and Glacier Flow
For a complete description of the flow field of a glacier, both the horizontal and vertical components of the velocity are required. However, as mentioned above, we confine our analysis to the horizontal velocity components. By imposing tight constraints (1 cm a–1) on the horizontal components of the base station and the IGS sites, and relaxed constraints on glacier points (100 ma−1), we obtained solutions for the horizontal velocity of Schirmacher Glacier. Table 1 gives the magnitude of the horizontal velocities (in ITRF2000 at epoch 2004.0) at various sites on Schirmacher Glacier.
Table 1. Geodetic coordinates of the GPS stations on Schirmacher Glacier with horizontal flow rates (in ITRF2000 at epoch 2004.0), azimuth and uncertainty. The dashed lines indicate absence of flow rates due to the inability to reoccupy stations during the second campaign
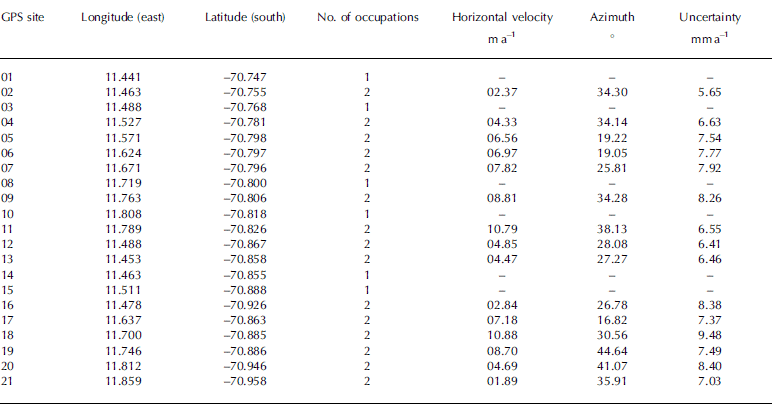
The velocity vectors shown in Figure 4 represent the spatial pattern of glacier movement across Schirmacher Glacier. The lowest velocity, 1.89 ± 0.01 ma−1, and highest, 10.88 ± 0.01 ma−1, were observed in the southeastern and northeastern parts of the study area, respectively, with an average velocity of 6.21 ± 0.01 ma−1 in the north-northeast direction, with error limits of 95% confidence. The resulting velocities show that the eastern part of the Schirmacher Oasis acts to funnel Schirmacher Glacier toward Nivlisen. The GPS sites 02, 04, 05, 06 and 07 (Fig. 4), which are located over the continental slope with maximum steepness, exhibit low velocities, i.e. the velocity distribution is such that it is lowest near the Schirmacher Oasis margin and highest near the eastern part where the blockage of Schirmacher Oasis is absent. Overall, the velocity distribution shows that velocities decrease away from Schirmacher Oasis and towards the continental ice.
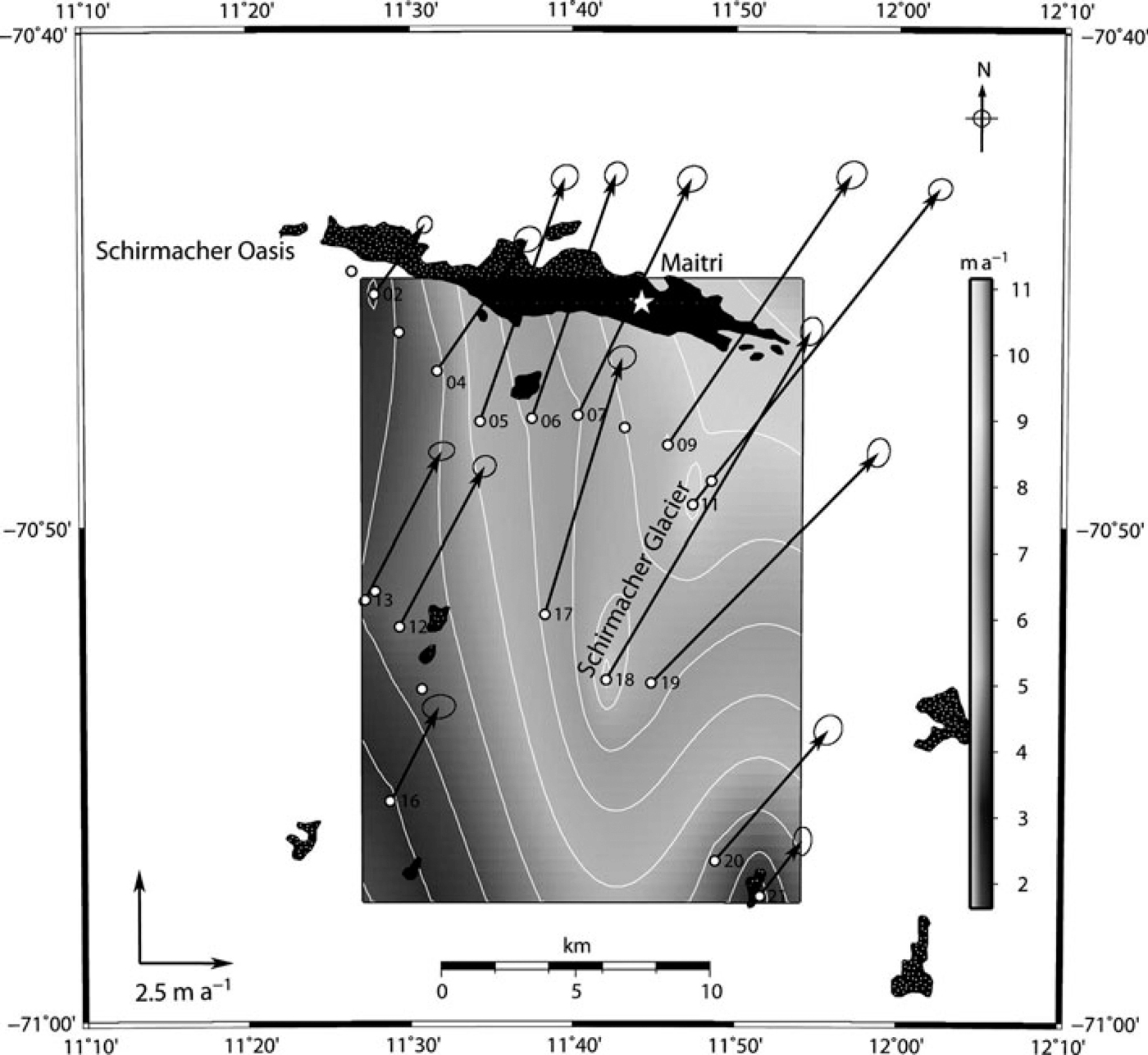
Fig. 4. Horizontal velocity vectors (with 95% confidence ellipses) for the GPS network on Schirmacher Glacier, superimposed on a shaded relief velocity-distribution map with 1 m contour interval obtained from the GPS velocity field. The scale represents the glacier flow rate corresponding to the velocity shaded relief (ma−1). The black patches indicate the Schirmacher Oasis and nunataks.
Strain-rate Analysis
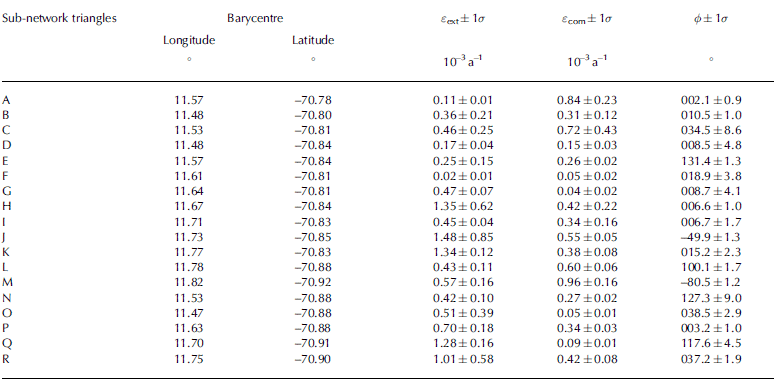
While station velocities display absolute motion with respect to the reference frame and provide information on the kinematics of the glacier surface, strain rates provide information on the physics of how the ice flows, i.e. on the deformational characteristics of the ice. Since triangulation techniques provide large spatial variability of the strain-rate pattern and are more sensitive to single station velocities and inter-site distances (Reference Serpelloni, Anzidei, Baldi and CasulaSerpelloni and others, 2005) we divided the Schirmacher Glacier network into 18 triangular subnetworks to study the strain-rate distribution. Using a standard least-squares procedure (Reference Feigl and KingFeigl and others, 1990) we computed the horizontal strain-rate tensor within each region. Further, we derived the rates of shortening and elongation in the direction of the principal strain axes. The triangular regions and computed horizontal principal strain-rate axes are shown in Figure 5.

Fig. 5. Spatial distribution of the principal strain rates for triangular regions. The outward and inward arrows display extension and contraction, respectively. Coordinates of the barycentres of these triangles are given in Table 2.
We computed the spatial distribution of the principal strain rate (ε) and the principal axis azimuth (ϕ) for the Schirmacher Glacier sites over a period of 1 year. The compressional strain rate (εcom ) ranges from (0.04 ± 0.01) × 10−3 (triangle G) to (0.96 ± 0.16) × 10−3 a−1, with high compressional strain rates of (0.84 ± 0.23) × 10−3, (0.72 ± 0.43) × 10−3 and (0.96 ± 0.16) × 10−3a−1 observed in triangular regions A, C and M respectively. The extensional strain rates (εext ) are in the range (0.02 ± 0.01) × 10−3 a−1 (triangle F) to (1.48 ± 0.85) × 10−3 a−1 (triangle J). The east-west to north-northeast trending maximum extensional strains occur in the triangular regions H, J, K, Q and R, which are located in the eastern part of the glacier, where velocities are high. Very small compressional and extensional strain rates are found in triangle F. This pattern is due to acceleration along divergent flowlines in the east of Schirmacher Glacier. The calculated principal strain rates with azimuth and 1σ uncertainties are listed in Table 2.
Table 2. Principal strain rates with 1σ uncertainties and azimuth angles computed in the triangular regions shown in Figure 5; ε ext and ε com are extension and contraction strain rates, respectively, and ϕ is the azimuth of ε com
Discussion
The velocity distribution map (Fig. 4) with velocity magnitude contour, prepared from the measured station velocities, shows the trend of the glacier flow towards the north-northeast into Nivlisen. The map shows lesser velocities in the southwestern part of the area and a gradual increase up to a maximum of ∼11 m a–1 in the ice-shelf area towards the northeastern part of the glacier. The high-velocity region shown on the map consists of GPS sites 09, 11,18 and 19. A gentle slope was observed in this region during the field survey and from the 30 arcsec global topographic (GTOPO30) digital elevation model; the maximum velocities seen in this part are due to the minimum blockage of the Schirmacher Oasis. At GPS sites 02, 04, 05, 06 and 07, despite their location over the steep elevation gradient region, the velocity is low; this is because of the resistance to flow due to the Schirmacher Oasis blockage. The results from this study agree with previous geodetic investigations (Reference Dietrich, Metzig and KorthDietrich and others, 1999; Reference Metzig, Dietrich, Korth, Perlt and HartmannMetzig and others, 2000; M. Scheinert, unpublished information) carried out near this area and show that the major outlet of Schirmacher Glacier towards Nivlisen is through the eastern end of the Schirmacher Oasis. However, the general trend of the velocity pattern shows that, away from the Schirmacher Oasis towards the continental ice, the velocity decreases due to the very gentle slope in the continental ice surface and the presence of nunataks. A ground-penetrating radar (GPR) study conducted south of our study area, on Potsdam Glacier (Fig. 1), shows evidence of subsurface undulations with an ablation area in the southeastern part of Schirmacher Glacier (Reference Anschütz, Oerter and SteinhageAnschütz and others, 2007); these also contribute to the reduction of velocity from north to south in the continental ice. Measured surface velocities for Schirmacher Glacier (with maximum velocity ∼11 m a–1) are much lower than the velocities of Shirase Glacier (2700 m a–1) which lies in a narrow trough less than 10 km wide (Reference Pattyn and DerauwPattyn and Derauw, 2002; Reference Pattyn and NarusePattyn and Naruse, 2003). However, they are closer to those of Lambert Glacier (10–25 m a–1) (Reference Manson, Coleman and MorganManson and others, 2000) and Potsdam Glacier (20–30 m a–1 at higher elevations and 70–80 ma–1 at lower elevations) (Reference Dietrich, Metzig and KorthDietrich and others, 1999; Reference Anschütz, Oerter and SteinhageAnschütz and others, 2007) which also flow into ice shelves and which have similar surface trends.
As seen in Figure 5, the compressional strain rate in triangles A and C indicates blockage of the flow by the Schirmacher Oasis and presence of a nunatak near sites 05 and 06. The highest compression, in triangle M, is due to the resistance of Pevikhornet nunatak (near site 21). The north–south-trending compressional strain axes clearly indicate the role of the Schirmacher Oasis and nunataks in defining the compressive regime in Schirmacher Glacier. The highest extensional strain rates occur in triangle regions H, J, K, Q and R, which show the occurrence and contribution of steep and shallow criss-cross fracture zones and crevasses in the high-velocity region. The east–west to north-northeast trend of the extensional strain rates also follows the divergence of Schirmacher Glacier towards Nivlisen.
Conclusions
The velocity and strain distribution of Schirmacher Glacier have been investigated during two GPS campaigns during January to March, 2003 and 2004. The glacier velocity results show that the magnitude of the horizontal velocity is in the range 1.89–10.88 m a–1 with an average of 6.21 m a–1, in the north-northeast direction. The distribution of velocity can be spatially correlated with topography, subsurface undulations, fractures/crevasses (coinciding with high velocities) and the influence of the blockage of Schirmacher Oasis. The surface strain analysis indicates that the region of extensional strain coincides with the surface gradient and crevasses, while the region of compressional strain is due to the blockage of Schirmacher Oasis and nunataks. The general trend to low (compared to other glaciers) velocities (∼11 ma–1) is primarily attributed to the fact that Schirmacher Glacier is located in a region of exposed nunataks which extend along the ice-shelf grounding line.
GPR measurements can facilitate the detection of changes in the flow field, subglacial topography and internal structure of the glacier. To model glacier dynamics and estimate mass-balance change, a comprehensive knowledge of glacier geometry, boundary conditions, ice deformation and basal components of the glacier velocity is required. For studying the seasonal changes in velocity pattern, we propose to install continuous-recording GPS (with meteorological package) at selected sites on Schirmacher Glacier.
Acknowledgements
We thank A. Bhattacharyya (Director, Indian Institute of Geomagnetism) and R. Ravindra (Director, National Centre for Antarctic and Ocean Research, India) for encouragement and support to carry out this study. We are grateful to A. Hanchinal, M. Doiphode, C. Selvaraj and P. Elango for support in the deployment of the GPS receivers under hostile climatic conditions. The continued interest and assistance provided by K. Kachroo, A. Dharwadkar, R. Asthana and S. Saini is gratefully acknowledged. We thank R. King for making GAMIT/GLOBK GPS data analysis software available and P. Wessel and W.H.F. Smith for GMT software. Finally we thank R. Coleman, M. King, M. Pandit and an anonymous reviewer for valuable comments and suggestions which significantly improved the manuscript.









