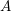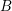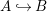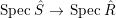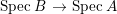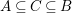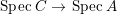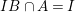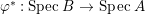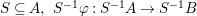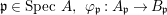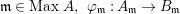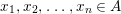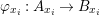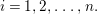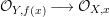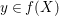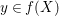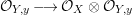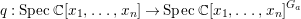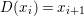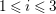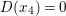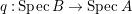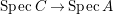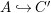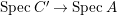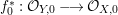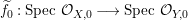0 Introduction
Let 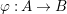 ${\it\varphi}:A\rightarrow B$ be a homomorphism of commutative rings. We say that
${\it\varphi}:A\rightarrow B$ be a homomorphism of commutative rings. We say that ![]() ${\it\varphi}$ is a pure homomorphism, or pure embedding, or pure extension if the canonical homomorphism
${\it\varphi}$ is a pure homomorphism, or pure embedding, or pure extension if the canonical homomorphism 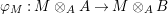 ${\it\varphi}_{M}:M\otimes _{A}A\rightarrow M\otimes _{A}B$ is injective, for any
${\it\varphi}_{M}:M\otimes _{A}A\rightarrow M\otimes _{A}B$ is injective, for any ![]() $A$-module
$A$-module ![]() $M$. This condition implies that
$M$. This condition implies that ![]() ${\it\varphi}$ is injective. Therefore, identifying
${\it\varphi}$ is injective. Therefore, identifying ![]() $A$ with
$A$ with ![]() ${\it\varphi}(A)$, we often say that
${\it\varphi}(A)$, we often say that ![]() $A$ is a pure subring of
$A$ is a pure subring of ![]() $B$, or that
$B$, or that ![]() $B$ is a pure extension of
$B$ is a pure extension of ![]() $A$. The notion of purity was first raised by Warfield [Reference Warfield15]. The associated morphism
$A$. The notion of purity was first raised by Warfield [Reference Warfield15]. The associated morphism 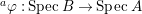 $^{a}{\it\varphi}:\text{Spec}\,B\rightarrow \text{Spec}\,A$ is also called a pure morphism of affine schemes.
$^{a}{\it\varphi}:\text{Spec}\,B\rightarrow \text{Spec}\,A$ is also called a pure morphism of affine schemes.
A morphism of schemes 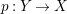 $p:Y\rightarrow X$ is called a pure morphism if
$p:Y\rightarrow X$ is called a pure morphism if ![]() $p$ is an affine morphism, and there exists an affine open covering
$p$ is an affine morphism, and there exists an affine open covering ![]() $\{U_{i}\}_{i\in I}$ of
$\{U_{i}\}_{i\in I}$ of ![]() $X$, such that
$X$, such that 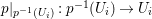 $p|_{p^{-1}(U_{i})}:p^{-1}(U_{i})\rightarrow U_{i}$ is a pure morphism for every
$p|_{p^{-1}(U_{i})}:p^{-1}(U_{i})\rightarrow U_{i}$ is a pure morphism for every ![]() $i\in I$. The formal properties of pure subalgebras and pure morphisms are summarized in Section 1.
$i\in I$. The formal properties of pure subalgebras and pure morphisms are summarized in Section 1.
In this paper, we are interested in pure subalgebras of an affine or local domain. The underlying field ![]() $k$, unless otherwise specified, is always assumed to be algebraically closed and of characteristic
$k$, unless otherwise specified, is always assumed to be algebraically closed and of characteristic ![]() $0$. Sometimes we also assume
$0$. Sometimes we also assume ![]() $k$ to be the field of complex numbers
$k$ to be the field of complex numbers ![]() $\mathbb{C}$ to apply results of local analytic algebras. Let
$\mathbb{C}$ to apply results of local analytic algebras. Let ![]() $A$ be a pure
$A$ be a pure ![]() $k$-subalgebra of an affine domain
$k$-subalgebra of an affine domain ![]() $B$. Then, by [Reference Hashimoto5],
$B$. Then, by [Reference Hashimoto5], ![]() $A$ itself is affine. Furthermore, if
$A$ itself is affine. Furthermore, if ![]() $B$ is normal then
$B$ is normal then ![]() $A$ is also normal, and the associated morphism
$A$ is also normal, and the associated morphism 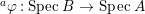 $^{a}{\it\varphi}:\text{Spec}\,B~\rightarrow ~\text{Spec}\,A$ is surjective by Lemma 1.1 below.
$^{a}{\it\varphi}:\text{Spec}\,B~\rightarrow ~\text{Spec}\,A$ is surjective by Lemma 1.1 below.
It is easy to see that a faithfully flat extension of commutative rings is pure (Lemma 1.7). There are many important results about flat extensions of commutative rings by J. Frisch, A. Grothendieck, L. Gruson, M. Raynaud, and others.
The fibers of a flat morphism are all equidimensional, but the converse is not true in general. Interestingly, for a morphism between normal varieties, equidimensionality of fibers implies purity of the morphism (Lemma 2.7). Unfortunately, in general, fibers of a pure morphism do not have correct dimension. Rings of invariants of reductive group actions on a polynomial ring provide plenty of examples of pure subrings such that the corresponding quotient morphisms do not have equidimensional fibers. This fact is one of the underlying reasons why invariant theory is such a fascinating subject.
It is the authors’ impression that there are not many papers about pure extensions. We use some important results due to M. Hochster about pure extensions (Section 1). In this paper we prove several new results about pure extensions, and give many examples to indicate the subtlety of the notion of purity.
We study the following questions.
Question 1. If ![]() $R\subseteq S$ is a pure extension of algebraic local rings, is the induced map of completions
$R\subseteq S$ is a pure extension of algebraic local rings, is the induced map of completions ![]() $\hat{R}~\rightarrow ~{\hat{S}}$ also a pure homomorphism?
$\hat{R}~\rightarrow ~{\hat{S}}$ also a pure homomorphism?
Question 2. If ![]() $R\subseteq S$ is an extension of algebraic local rings such that the associated map
$R\subseteq S$ is an extension of algebraic local rings such that the associated map 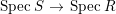 $\text{Spec}\,S~\rightarrow ~\text{Spec}\,R$ is surjective, is the induced map
$\text{Spec}\,S~\rightarrow ~\text{Spec}\,R$ is surjective, is the induced map 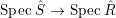 $\text{Spec}\,{\hat{S}}~\rightarrow ~\text{Spec}\,\hat{R}$ also surjective?
$\text{Spec}\,{\hat{S}}~\rightarrow ~\text{Spec}\,\hat{R}$ also surjective?
Closely related to these is another question.
Question 3. Let ![]() $R\subseteq S$ be a pure extension of analytic local rings, corresponding to germs of complex spaces
$R\subseteq S$ be a pure extension of analytic local rings, corresponding to germs of complex spaces 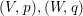 $(V,p),(W,q)$. Is it true that the image of a neighborhood of
$(V,p),(W,q)$. Is it true that the image of a neighborhood of ![]() $q$ in
$q$ in ![]() $W$ contains a neighborhood of
$W$ contains a neighborhood of ![]() $p$ in
$p$ in ![]() $V$?
$V$?
We show that all of these questions have affirmative answers with mild restrictions on ![]() $R$ and
$R$ and ![]() $S$.
$S$.
We now state the main results proved in this paper.
(1) Let
 $R\subseteq S$ be algebraic local rings. Assume that this is a pure extension. If
$R\subseteq S$ be algebraic local rings. Assume that this is a pure extension. If  $R$ is either reduced, or Gorenstein, then the induced map of completions
$R$ is either reduced, or Gorenstein, then the induced map of completions  $\hat{R}\subseteq {\hat{S}}$ is also pure (Corollary 3.2.1).
$\hat{R}\subseteq {\hat{S}}$ is also pure (Corollary 3.2.1).(2) Let
 $R\subseteq S$ be algebraic local rings such that
$R\subseteq S$ be algebraic local rings such that  $\hat{R}$ is an integral domain. If the morphism
$\hat{R}$ is an integral domain. If the morphism  $\text{Spec}\,S~\rightarrow ~\text{Spec}\,R$ is a surjection, then
$\text{Spec}\,S~\rightarrow ~\text{Spec}\,R$ is a surjection, then  $\text{Spec}\,{\hat{S}}~\rightarrow ~\text{Spec}\,\hat{R}$ is also a surjection (Theorem 3.4).
$\text{Spec}\,{\hat{S}}~\rightarrow ~\text{Spec}\,\hat{R}$ is also a surjection (Theorem 3.4).(3) Let
 $R\subseteq S$ be a pure extension of analytic local rings over
$R\subseteq S$ be a pure extension of analytic local rings over  $\mathbb{C}$ such that
$\mathbb{C}$ such that  $R$ is an integral domain. Then the image of a Euclidean neighborhood of the closed point of
$R$ is an integral domain. Then the image of a Euclidean neighborhood of the closed point of  $\text{Spec}\,S$ contains a Euclidean neighborhood of the closed point of
$\text{Spec}\,S$ contains a Euclidean neighborhood of the closed point of  $~\text{Spec}\,R$ (Theorem 3.5).
$~\text{Spec}\,R$ (Theorem 3.5).(4) Let
 $A\subseteq B$ be an inclusion of normal affine domains over a field
$A\subseteq B$ be an inclusion of normal affine domains over a field  $k$ such that the morphism
$k$ such that the morphism  $\text{Spec}\,B~\rightarrow ~\text{Spec}\,A$ is generically finite and surjective. Then there exists a normal affine domain
$\text{Spec}\,B~\rightarrow ~\text{Spec}\,A$ is generically finite and surjective. Then there exists a normal affine domain  $C/k$ such that
$C/k$ such that  $A\subseteq C\subseteq B$, the morphism
$A\subseteq C\subseteq B$, the morphism  $\text{Spec}\,C~\rightarrow ~\text{Spec}\,A$ is quasi-finite and surjective, and
$\text{Spec}\,C~\rightarrow ~\text{Spec}\,A$ is quasi-finite and surjective, and  $C$ is the largest affine subring of
$C$ is the largest affine subring of  $B$ containing
$B$ containing  $A$ with these properties. Further,
$A$ with these properties. Further,  $C$ is a pure extension of
$C$ is a pure extension of  $A$ (Theorem 4.4).
$A$ (Theorem 4.4).
The proofs of Theorems 3.4 and 3.5 are rather nontrivial. For the proof of Theorem 3.4 we need ideas from Artin’s approximation theorem.
The following question arises in this context, and we discuss it later.
Question.
Let ![]() $A$ be a two-dimensional pure subalgebra of
$A$ be a two-dimensional pure subalgebra of ![]() $k[x,y]$. Is the associated morphism
$k[x,y]$. Is the associated morphism 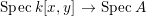 $\text{Spec}\,k[x,y]~\rightarrow ~\text{Spec}\,A$ quasi-finite?
$\text{Spec}\,k[x,y]~\rightarrow ~\text{Spec}\,A$ quasi-finite?
We give a counterexample to this question. However, if ![]() $A$ is a graded subring of
$A$ is a graded subring of ![]() $k[x,y]$ then we do not yet know if the answer is affirmative.
$k[x,y]$ then we do not yet know if the answer is affirmative.
A faithfully flat extension is pure. In general, the fibers of a pure morphism can have variable dimensions. In Section 5 we give several examples, and also some positive results, which illustrate the subtlety of the notion of pure extensions, and which shed more light on this important notion.
We raise several open problems whose solution, we believe, is valuable for algebraic geometry and commutative algebra.
We are indebted to M. Hashimoto for motivating us to study the present subject. In fact, the announcement of his result [Reference Hashimoto5] at a workshop in Oberwolfach in 2005 initiated our study of pure subalgebras of polynomial rings.
1 Preliminaries
We recall some of the standard properties of pure extensions which are frequently used in the paper. Some of these are trivial consequences of the definitions. For the rest, appropriate references are mentioned.
For a commutative ring ![]() $A$, let
$A$, let ![]() $\text{Spec}\,A$ and Max
$\text{Spec}\,A$ and Max![]() $~A$ denote the sets of prime ideals and maximal ideals of
$~A$ denote the sets of prime ideals and maximal ideals of ![]() $A$ respectively.
$A$ respectively.
Let ![]() $A\subseteq B$ be commutative rings. If
$A\subseteq B$ be commutative rings. If ![]() $A$ is a direct summand of
$A$ is a direct summand of ![]() $B$ (as an
$B$ (as an ![]() $A$-module), it follows from the definition that
$A$-module), it follows from the definition that ![]() $A$ is a pure subring of
$A$ is a pure subring of ![]() $B$. This fact is implicitly used in this paper. Later, we will see two important instances when this happens:
$B$. This fact is implicitly used in this paper. Later, we will see two important instances when this happens:
(a) if
 $A$ is normal, and
$A$ is normal, and  $B$ is a finite module over
$B$ is a finite module over  $A$; or
$A$; or(b) if
 $A$ is a complete local ring, and
$A$ is a complete local ring, and  $A\subseteq B$ is pure.
$A\subseteq B$ is pure.
By an algebraic local ring we mean a localization of an affine algebra over a field ![]() $k$ at a maximal ideal.
$k$ at a maximal ideal.
Lemma 1.1. Let 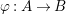 ${\it\varphi}:A\rightarrow B$ be a pure embedding. Then the following assertions hold.
${\it\varphi}:A\rightarrow B$ be a pure embedding. Then the following assertions hold.
(1) Suppose that
 ${\it\varphi}$ splits as
${\it\varphi}$ splits as
Then
 ${\it\varphi}_{1}$ is a pure embedding. If
${\it\varphi}_{1}$ is a pure embedding. If  ${\it\varphi}_{1}$ and
${\it\varphi}_{1}$ and  ${\it\varphi}_{2}$ are pure embeddings, then so is
${\it\varphi}_{2}$ are pure embeddings, then so is  ${\it\varphi}$, that is, pure extension is transitive.
${\it\varphi}$, that is, pure extension is transitive.(2) For any ideal
 $I$ of
$I$ of  $A$, we have
$A$, we have  $IB\cap A=I$. In particular, if
$IB\cap A=I$. In particular, if  $B$ is Noetherian, so is
$B$ is Noetherian, so is  $A$.
$A$.(3) The associated morphism
 ${\it\varphi}^{\ast }:\text{Spec}\,B~\rightarrow ~\text{Spec}\,A$ is surjective.
${\it\varphi}^{\ast }:\text{Spec}\,B~\rightarrow ~\text{Spec}\,A$ is surjective.
Lemma 1.2. A ring homomorphism 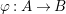 ${\it\varphi}:A\rightarrow B$ is pure if and only if
${\it\varphi}:A\rightarrow B$ is pure if and only if 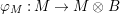 ${\it\varphi}_{M}:M\rightarrow M\otimes B$ is injective for any finitely generated
${\it\varphi}_{M}:M\rightarrow M\otimes B$ is injective for any finitely generated ![]() $A$-module
$A$-module ![]() $M$.
$M$.
Lemma 1.3. (Local criteria for purity)
If 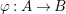 ${\it\varphi}:A\rightarrow B$ is a ring homomorphism, then the following are equivalent.
${\it\varphi}:A\rightarrow B$ is a ring homomorphism, then the following are equivalent.
(1) The homomorphism
 ${\it\varphi}$ is pure.
${\it\varphi}$ is pure.(2) For any multiplicatively closed set
 $S\subseteq A,~S^{-1}{\it\varphi}:S^{-1}A\rightarrow S^{-1}B$ is pure.
$S\subseteq A,~S^{-1}{\it\varphi}:S^{-1}A\rightarrow S^{-1}B$ is pure.(3) For any
 $\mathfrak{p}\in \text{Spec}~A,~{\it\varphi}_{\mathfrak{p}}:A_{\mathfrak{p}}\rightarrow B_{\mathfrak{p}}$ is pure.
$\mathfrak{p}\in \text{Spec}~A,~{\it\varphi}_{\mathfrak{p}}:A_{\mathfrak{p}}\rightarrow B_{\mathfrak{p}}$ is pure.(4) For any
 $\mathfrak{m}\in \text{Max}~A,~{\it\varphi}_{\mathfrak{m}}:A_{\mathfrak{m}}\rightarrow B_{\mathfrak{m}}$ is pure.
$\mathfrak{m}\in \text{Max}~A,~{\it\varphi}_{\mathfrak{m}}:A_{\mathfrak{m}}\rightarrow B_{\mathfrak{m}}$ is pure.(5) There exist
 $x_{1},x_{2},\ldots ,x_{n}\in A$, generating the unit ideal, such that
$x_{1},x_{2},\ldots ,x_{n}\in A$, generating the unit ideal, such that  ${\it\varphi}_{x_{i}}:A_{x_{i}}\rightarrow B_{x_{i}}$ is pure for each
${\it\varphi}_{x_{i}}:A_{x_{i}}\rightarrow B_{x_{i}}$ is pure for each  $i=1,2,\ldots ,n.$
$i=1,2,\ldots ,n.$
Lemma 1.4. (Extension of scalars)
If ![]() $A{\hookrightarrow}B$ is a pure extension of commutative rings, for any
$A{\hookrightarrow}B$ is a pure extension of commutative rings, for any ![]() $A$-algebra
$A$-algebra ![]() $C$,
$C$, 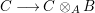 $C\longrightarrow C\otimes _{A}B$ is pure.
$C\longrightarrow C\otimes _{A}B$ is pure.
Corollary 1.4.1. Given any two pure ![]() $A$-algebras
$A$-algebras ![]() $B$ and
$B$ and ![]() $C$,
$C$, 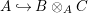 $~A{\hookrightarrow}B\otimes _{A}C$ is a pure extension.
$~A{\hookrightarrow}B\otimes _{A}C$ is a pure extension.
A ring homomorphism 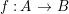 $f:A~\rightarrow ~B$ is called cyclically pure if, for any ideal
$f:A~\rightarrow ~B$ is called cyclically pure if, for any ideal ![]() $I\subseteq B$,
$I\subseteq B$, 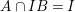 $A\cap IB=I$, or, equivalently, if any ideal in
$A\cap IB=I$, or, equivalently, if any ideal in ![]() $A$ is contracted from some ideal in
$A$ is contracted from some ideal in ![]() $B$. Note that analogues of Lemma 1.1 hold for cyclically pure extensions.
$B$. Note that analogues of Lemma 1.1 hold for cyclically pure extensions.
The following important result from [Reference Hochster6, Theorem 1.7] is often used in this paper. We state a special case which is sufficient for our purposes.
Lemma 1.5. Let ![]() $A$ be a Noetherian excellent ring, and let
$A$ be a Noetherian excellent ring, and let 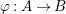 ${\it\varphi}:A\rightarrow B$ be an embedding. Then the following assertion holds.
${\it\varphi}:A\rightarrow B$ be an embedding. Then the following assertion holds.
If ![]() $A$ is reduced, or Gorenstein, or a local Cohen–Macaulay ring of dimension
$A$ is reduced, or Gorenstein, or a local Cohen–Macaulay ring of dimension ![]() ${\geqslant}2$, then
${\geqslant}2$, then ![]() ${\it\varphi}$ is a pure embedding if and only if it is cyclically pure.
${\it\varphi}$ is a pure embedding if and only if it is cyclically pure.
The following result is proved in [Reference Hochster9].
Lemma 1.6. Let ![]() $A\subseteq B$ be affine domains over a field of characteristic
$A\subseteq B$ be affine domains over a field of characteristic ![]() $0$. If
$0$. If ![]() $A$ is normal, and the induced morphism
$A$ is normal, and the induced morphism 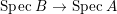 $\text{Spec}\,B~\rightarrow ~\text{Spec}\,A$ is quasi-finite and surjective, then
$\text{Spec}\,B~\rightarrow ~\text{Spec}\,A$ is quasi-finite and surjective, then ![]() ${\it\varphi}$ is a pure embedding.
${\it\varphi}$ is a pure embedding.
Lemma 1.6 immediately implies that if ![]() $A$ is a normal affine subalgebra of
$A$ is a normal affine subalgebra of 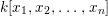 $k[x_{1},x_{2},\ldots ,x_{n}]$, such that the extension is integral, then this is a pure extension.
$k[x_{1},x_{2},\ldots ,x_{n}]$, such that the extension is integral, then this is a pure extension.
Lemma 1.7. If ![]() $A$ is a subring of
$A$ is a subring of ![]() $B$, such that
$B$, such that ![]() $B$ is a faithfully flat
$B$ is a faithfully flat ![]() $A$-module, then the extension is pure.
$A$-module, then the extension is pure.
Proof. See [Reference Matsumura11, Theorem 7.5]. ◻
The following criterion of purity can be found in [Reference Hochster and Roberts8, Corollary 5.3].
Lemma 1.8. Let ![]() $A$ be a Noetherian ring, which is a subring of
$A$ be a Noetherian ring, which is a subring of ![]() $B$. Then
$B$. Then ![]() $A$ is a pure subring of
$A$ is a pure subring of ![]() $B$ if and only if
$B$ if and only if ![]() $A$ is a direct summand, as an
$A$ is a direct summand, as an ![]() $A$-module, of each finitely generated
$A$-module, of each finitely generated ![]() $A$-submodule of
$A$-submodule of ![]() $B$. In particular, if
$B$. In particular, if ![]() $B$ is a finitely generated
$B$ is a finitely generated ![]() $A$-module,
$A$-module, ![]() $A{\hookrightarrow}B$ is a pure embedding if and only if
$A{\hookrightarrow}B$ is a pure embedding if and only if ![]() $A$ is a direct summand of
$A$ is a direct summand of ![]() $B$ as an
$B$ as an ![]() $A$-module.
$A$-module.
The following result and its proof were shown to us by C. Huneke to whom we are very thankful.
Lemma 1.9. Let ![]() $A$ be a pure subring of
$A$ be a pure subring of ![]() $B$. Assume that
$B$. Assume that ![]() $A$ is a Noetherian complete local domain. Then
$A$ is a Noetherian complete local domain. Then ![]() $A$ is a direct summand of
$A$ is a direct summand of ![]() $B$ as an
$B$ as an ![]() $A$-module.
$A$-module.
Proof. Let ![]() $E$ be the injective hull of the residue field of
$E$ be the injective hull of the residue field of ![]() $A$. The hypothesis that
$A$. The hypothesis that ![]() $A$ is a pure subalgebra of
$A$ is a pure subalgebra of ![]() $B$ implies that the map
$B$ implies that the map  $E\rightarrow E\otimes _{A}B$ is injective. Hence, the dual map
$E\rightarrow E\otimes _{A}B$ is injective. Hence, the dual map 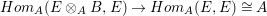 $Hom_{A}(E\otimes _{A}B,E)\rightarrow Hom_{A}(E,E)\cong A$ is surjective, where the last isomorphism follows since
$Hom_{A}(E\otimes _{A}B,E)\rightarrow Hom_{A}(E,E)\cong A$ is surjective, where the last isomorphism follows since ![]() $A$ is complete. However,
$A$ is complete. However, 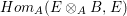 $Hom_{A}(E\otimes _{A}B,E)$ is isomorphic to
$Hom_{A}(E\otimes _{A}B,E)$ is isomorphic to 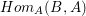 $Hom_{A}(B,A)$, and the surjective map from this module to
$Hom_{A}(B,A)$, and the surjective map from this module to ![]() $A$ just sends a homomorphism
$A$ just sends a homomorphism ![]() $f$ to
$f$ to ![]() $f(1)$. Thus, there exists an
$f(1)$. Thus, there exists an ![]() $A$-module homomorphism
$A$-module homomorphism 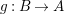 $g:B\rightarrow A$, and consequently
$g:B\rightarrow A$, and consequently ![]() $A$ is a direct summand of
$A$ is a direct summand of ![]() $B$.◻
$B$.◻
2 Some new observations
We use the following terminologies in this paper.
Let 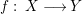 $f:~X\longrightarrow Y$ be a dominant morphism of affine algebraic varieties. Then we have the following.
$f:~X\longrightarrow Y$ be a dominant morphism of affine algebraic varieties. Then we have the following.
(1) The morphism
 $f$ is called
$f$ is called  $\mathbf{pure}$ if the induced morphism
$\mathbf{pure}$ if the induced morphism  $f^{\ast }:{\mathcal{O}}_{Y}\longrightarrow {\mathcal{O}}_{X}$ is pure.
$f^{\ast }:{\mathcal{O}}_{Y}\longrightarrow {\mathcal{O}}_{X}$ is pure.(2) A point
 $x\in X$ is called
$x\in X$ is called  $\mathbf{pure}$ if
$\mathbf{pure}$ if  ${\mathcal{O}}_{Y,f(x)}\longrightarrow {\mathcal{O}}_{X,x}$ is pure. We call
${\mathcal{O}}_{Y,f(x)}\longrightarrow {\mathcal{O}}_{X,x}$ is pure. We call  $f$
$f$ $\mathbf{strongly~pure}$ if each
$\mathbf{strongly~pure}$ if each  $x\in X$ is pure.
$x\in X$ is pure.(3) A point
 $y\in f(X)$ is called
$y\in f(X)$ is called  $\mathbf{completely~pure}$ if each point in
$\mathbf{completely~pure}$ if each point in  $f^{-1}(y)$ is pure.
$f^{-1}(y)$ is pure.(4) A point
 $y\in Y$ is called
$y\in Y$ is called  $\mathbf{partially~pure}$ if some point in
$\mathbf{partially~pure}$ if some point in  $f^{-1}(y)$ is pure.
$f^{-1}(y)$ is pure.(5) A point
 $y\in f(X)$ is called
$y\in f(X)$ is called  $\mathbf{pure}$ if
$\mathbf{pure}$ if  ${\mathcal{O}}_{Y,y}\longrightarrow {\mathcal{O}}_{X}\otimes {\mathcal{O}}_{Y,y}$ is pure.
${\mathcal{O}}_{Y,y}\longrightarrow {\mathcal{O}}_{X}\otimes {\mathcal{O}}_{Y,y}$ is pure.
Note. An algebraic variety is always assumed to be irreducible unless otherwise specified.
Since given any 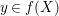 $y\in f(X)$ and some
$y\in f(X)$ and some 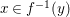 $x\in f^{-1}(y)$, we have a natural factorization
$x\in f^{-1}(y)$, we have a natural factorization
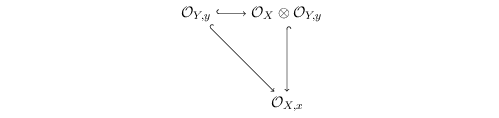
it is easy to see that any completely pure point is partially pure, which, in turn, is pure.
Let ![]() $A{\hookrightarrow}B$ be a pure extension. Suppose that there is an element
$A{\hookrightarrow}B$ be a pure extension. Suppose that there is an element ![]() $x$ of
$x$ of ![]() $B$ satisfying a relation
$B$ satisfying a relation
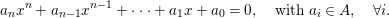 $$\begin{eqnarray}a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}=0,\quad \text{with}~a_{i}\in A,\quad \forall i.\end{eqnarray}$$
$$\begin{eqnarray}a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}=0,\quad \text{with}~a_{i}\in A,\quad \forall i.\end{eqnarray}$$ Then, as an easy corollary of Lemma 1.5, it follows that ![]() $a_{0}$ is contained in the ideal generated by
$a_{0}$ is contained in the ideal generated by 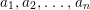 $a_{1},a_{2},\ldots ,a_{n}$ in
$a_{1},a_{2},\ldots ,a_{n}$ in ![]() $A$. A partial converse of this fact holds under special conditions.
$A$. A partial converse of this fact holds under special conditions.
Lemma 2.1. Let A be a Dedekind domain. Then, for any polynomial
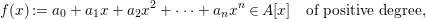 $$\begin{eqnarray}f(x):=a_{0}+a_{1}x+a_{2}x^{2}+\cdots +a_{n}x^{n}\in A[x]\quad \text{of positive degree,}\end{eqnarray}$$
$$\begin{eqnarray}f(x):=a_{0}+a_{1}x+a_{2}x^{2}+\cdots +a_{n}x^{n}\in A[x]\quad \text{of positive degree,}\end{eqnarray}$$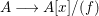 $A\longrightarrow A[x]/(f)$ is pure if
$A\longrightarrow A[x]/(f)$ is pure if ![]() $a_{0}$ is contained in the ideal generated by
$a_{0}$ is contained in the ideal generated by 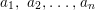 $a_{1},~a_{2},\ldots ,a_{n}$ in
$a_{1},~a_{2},\ldots ,a_{n}$ in ![]() $A$.
$A$.
Proof. In view of the local criteria for purity as in Lemma 1.3, after localizing the extension at a maximal ideal of ![]() $A$, we may assume that
$A$, we may assume that ![]() $A$ is a discrete valuation ring. First, we observe that, if B is a (cyclically) pure A-algebra, for any A-algebra C,
$A$ is a discrete valuation ring. First, we observe that, if B is a (cyclically) pure A-algebra, for any A-algebra C, ![]() $B\oplus C$ is also a (cyclically) pure A-algebra.
$B\oplus C$ is also a (cyclically) pure A-algebra.
Now, coming to the proof, if ![]() $a_{0}=0$, there exists
$a_{0}=0$, there exists ![]() $m>0$ such that
$m>0$ such that ![]() $x^{m}|f$ but
$x^{m}|f$ but ![]() $x^{m+1}$ does not divide
$x^{m+1}$ does not divide ![]() $f$. Since
$f$. Since ![]() $A[x]$ is a unique factorization domain, and
$A[x]$ is a unique factorization domain, and 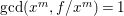 $\gcd (x^{m},f/x^{m})=1$, we have
$\gcd (x^{m},f/x^{m})=1$, we have
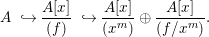 $$\begin{eqnarray}A~{\hookrightarrow}\frac{A[x]}{(f)}~{\hookrightarrow}\frac{A[x]}{(x^{m})}\oplus \frac{A[x]}{(f/x^{m})}.\end{eqnarray}$$
$$\begin{eqnarray}A~{\hookrightarrow}\frac{A[x]}{(f)}~{\hookrightarrow}\frac{A[x]}{(x^{m})}\oplus \frac{A[x]}{(f/x^{m})}.\end{eqnarray}$$ Now, 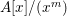 $A[x]/(x^{m})$, being a free module over A, is pure. Hence, by the above observation,
$A[x]/(x^{m})$, being a free module over A, is pure. Hence, by the above observation,
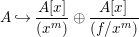 $$\begin{eqnarray}A{\hookrightarrow}\frac{A[x]}{(x^{m})}\oplus \frac{A[x]}{(f/x^{m})}\end{eqnarray}$$
$$\begin{eqnarray}A{\hookrightarrow}\frac{A[x]}{(x^{m})}\oplus \frac{A[x]}{(f/x^{m})}\end{eqnarray}$$ is also pure, and consequently so is 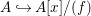 $A{\hookrightarrow}A[x]/(f)$.
$A{\hookrightarrow}A[x]/(f)$.
Otherwise, if ![]() $a_{0}\neq 0$, then
$a_{0}\neq 0$, then ![]() $f$ can be factored as
$f$ can be factored as ![]() $f=ag$, where
$f=ag$, where 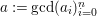 $a:=\gcd (a_{i})_{i=0}^{n}$, and
$a:=\gcd (a_{i})_{i=0}^{n}$, and ![]() $g$ is a primitive polynomial. Therefore, we have
$g$ is a primitive polynomial. Therefore, we have
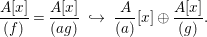 $$\begin{eqnarray}\frac{A[x]}{(f)}=\frac{A[x]}{(ag)}~{\hookrightarrow}~\frac{A}{(a)}[x]\oplus \frac{A[x]}{(g)}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{A[x]}{(f)}=\frac{A[x]}{(ag)}~{\hookrightarrow}~\frac{A}{(a)}[x]\oplus \frac{A[x]}{(g)}.\end{eqnarray}$$ However, then, by [Reference Nagata14], 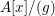 $A[x]/(g)$ is a faithfully flat A-algebra. Therefore, the above observation, together with Lemma 1.7, implies that
$A[x]/(g)$ is a faithfully flat A-algebra. Therefore, the above observation, together with Lemma 1.7, implies that
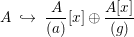 $$\begin{eqnarray}A~{\hookrightarrow}~\frac{A}{(a)}[x]\oplus \frac{A[x]}{(g)}\end{eqnarray}$$
$$\begin{eqnarray}A~{\hookrightarrow}~\frac{A}{(a)}[x]\oplus \frac{A[x]}{(g)}\end{eqnarray}$$ is pure, and consequently so is 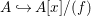 $A{\hookrightarrow}A[x]/(f)$.◻
$A{\hookrightarrow}A[x]/(f)$.◻
The following lemma is in the same spirit, which shows that for Dedekind domains, the question of purity boils down to the question of surjectivity of the associated morphism of schemes.
Lemma 2.2. Let ![]() $A\subseteq B$ be integral domains. Suppose that a height
$A\subseteq B$ be integral domains. Suppose that a height ![]() $1$ prime
$1$ prime ![]() $\mathfrak{p}$ in
$\mathfrak{p}$ in ![]() $A$ is contracted from
$A$ is contracted from ![]() $B$, and that
$B$, and that ![]() $A_{\mathfrak{p}}$ is a DVR. Then any
$A_{\mathfrak{p}}$ is a DVR. Then any ![]() $\mathfrak{p}$-primary ideal in
$\mathfrak{p}$-primary ideal in ![]() $A$ is contracted from some ideal in
$A$ is contracted from some ideal in ![]() $B$.
$B$.
Proof. We have the following commutative diagram:

Since ![]() $\mathfrak{p}$-primary ideals in
$\mathfrak{p}$-primary ideals in ![]() $A$ are in one-to-one correspondence with the
$A$ are in one-to-one correspondence with the ![]() $\mathfrak{p}A_{\mathfrak{p}}$-primary ideals of
$\mathfrak{p}A_{\mathfrak{p}}$-primary ideals of ![]() $A_{\mathfrak{p}}$, it is sufficient to prove that any
$A_{\mathfrak{p}}$, it is sufficient to prove that any ![]() $\mathfrak{p}A_{\mathfrak{p}}$-primary ideal is contracted from some ideal in
$\mathfrak{p}A_{\mathfrak{p}}$-primary ideal is contracted from some ideal in ![]() $B_{\mathfrak{p}}$. This is a special case of the following lemma.
$B_{\mathfrak{p}}$. This is a special case of the following lemma.
Lemma 2.3. Let ![]() $A\subseteq B$ be integral domains, with
$A\subseteq B$ be integral domains, with ![]() $A$ being a UFD. If any height
$A$ being a UFD. If any height ![]() $1$ prime in
$1$ prime in ![]() $A$ is contracted from some ideal in
$A$ is contracted from some ideal in ![]() $B$, then any principal ideal in
$B$, then any principal ideal in ![]() $A$ is a contracted ideal.
$A$ is a contracted ideal.
Proof. Let ![]() $a$ be any nonzero, nonunit element in
$a$ be any nonzero, nonunit element in ![]() $A$ with a prime factorization (up to a unit)
$A$ with a prime factorization (up to a unit)
 $$\begin{eqnarray}a=\mathop{\prod }_{i=1}^{r}p_{i}^{e_{i}},\quad \text{with distinct primes}~p_{i}~\text{and positive integers}~e_{i}.\end{eqnarray}$$
$$\begin{eqnarray}a=\mathop{\prod }_{i=1}^{r}p_{i}^{e_{i}},\quad \text{with distinct primes}~p_{i}~\text{and positive integers}~e_{i}.\end{eqnarray}$$ If possible, let 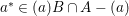 $a^{\ast }\in (a)B\cap A-(a)$. Then
$a^{\ast }\in (a)B\cap A-(a)$. Then ![]() $a^{\ast }$ can be written as
$a^{\ast }$ can be written as
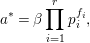 $$\begin{eqnarray}a^{\ast }={\it\beta}\mathop{\prod }_{i=1}^{r}p_{i}^{f_{i}},\end{eqnarray}$$
$$\begin{eqnarray}a^{\ast }={\it\beta}\mathop{\prod }_{i=1}^{r}p_{i}^{f_{i}},\end{eqnarray}$$ where the ![]() $f_{i}$ are nonnegative integers, and
$f_{i}$ are nonnegative integers, and 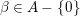 ${\it\beta}\in A-\{0\}$ is relatively prime to
${\it\beta}\in A-\{0\}$ is relatively prime to ![]() $p_{i}$, for each
$p_{i}$, for each ![]() $i$. Since
$i$. Since 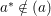 $a^{\ast }\notin (a)$, there exists some
$a^{\ast }\notin (a)$, there exists some ![]() $i$ for which
$i$ for which ![]() $f_{i}<e_{i}$. Again,
$f_{i}<e_{i}$. Again, 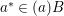 $a^{\ast }\in (a)B$ implies that there exists some
$a^{\ast }\in (a)B$ implies that there exists some ![]() $b\in B$ such that
$b\in B$ such that ![]() $a^{\ast }=ab$, implying that
$a^{\ast }=ab$, implying that 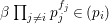 ${\it\beta}\prod _{j\neq i}p_{j}^{f_{j}}\in (p_{i})$, leading to a contradiction.◻
${\it\beta}\prod _{j\neq i}p_{j}^{f_{j}}\in (p_{i})$, leading to a contradiction.◻
We have the following corollaries of Lemma 2.2 (using Lemma 1.5).
Corollary 2.3.1. If ![]() $A\subseteq B$ are integral domains, with
$A\subseteq B$ are integral domains, with ![]() $A$ being a Noetherian normal domain, such that every height 1 prime in
$A$ being a Noetherian normal domain, such that every height 1 prime in ![]() $A$ is contracted, then any unmixed ideal of height 1 in
$A$ is contracted, then any unmixed ideal of height 1 in ![]() $A$ is also a contracted ideal.
$A$ is also a contracted ideal.
Corollary 2.3.2. Any surjective morphism from an affine variety to a smooth curve is pure.
This also follows easily since such a morphism is faithfully flat (and Lemma 1.7).
The following corollary extends a cyclically pure version of Lemma 2.1 to the formal power series case.
Corollary 2.3.3. Let ![]() $A$ be a Dedekind domain, and let
$A$ be a Dedekind domain, and let 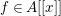 $f\in A[[x]]$ be a nonconstant formal power series. Then
$f\in A[[x]]$ be a nonconstant formal power series. Then
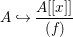 $$\begin{eqnarray}A{\hookrightarrow}\frac{A[[x]]}{(f)}\end{eqnarray}$$
$$\begin{eqnarray}A{\hookrightarrow}\frac{A[[x]]}{(f)}\end{eqnarray}$$ is cyclically pure if ![]() $f_{0}$ lies in the ideal generated by
$f_{0}$ lies in the ideal generated by 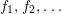 $f_{1},f_{2},\ldots$
, where
$f_{1},f_{2},\ldots$
, where 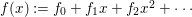 $f(x):=f_{0}+f_{1}x+f_{2}x^{2}+\cdots \,$.
$f(x):=f_{0}+f_{1}x+f_{2}x^{2}+\cdots \,$.
Proof. The proof follows almost the same lines as the proof of Lemma 2.1. However, instead of using Nagata’s criteria for faithful flatness, we take a prime factorization of ![]() $f$ and apply Corollary 2.3.1.◻
$f$ and apply Corollary 2.3.1.◻
The following lemma is a special case of Lemma 1.1(1). We write it down in this particular form for the sake of future reference.
Lemma 2.4. (Square diagram for purity)
If
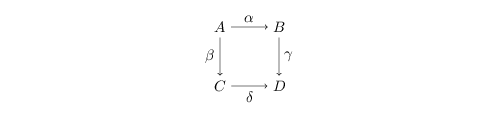
is a commutative diagram of commutative rings, then ![]() ${\it\beta},{\it\gamma},{\it\delta}$ are (cyclically) pure implies that
${\it\beta},{\it\gamma},{\it\delta}$ are (cyclically) pure implies that ![]() ${\it\alpha}$ is also (cyclically) pure.
${\it\alpha}$ is also (cyclically) pure.
Proof. The proof follows directly from the definitions. ◻
Lemma 2.5. Let ![]() $A\subseteq B$ be integral domains, with
$A\subseteq B$ be integral domains, with ![]() $A$ being a Noetherian normal domain. If the image of
$A$ being a Noetherian normal domain. If the image of ![]() $\text{Spec}~B$ contains all height 1 primes of
$\text{Spec}~B$ contains all height 1 primes of ![]() $\text{Spec}~A$, then any element
$\text{Spec}~A$, then any element ![]() ${\it\xi}$ of the quotient field of A, which is integral over
${\it\xi}$ of the quotient field of A, which is integral over ![]() $B$, is an element of
$B$, is an element of ![]() $A$. In particular, the result is true for pure extensions, as the morphism of schemes associated to any pure morphism is surjective.
$A$. In particular, the result is true for pure extensions, as the morphism of schemes associated to any pure morphism is surjective.
Proof. Since ![]() $A$ is normal, it suffices to show that
$A$ is normal, it suffices to show that ![]() ${\it\xi}$ is in every localization of
${\it\xi}$ is in every localization of ![]() $A$ at a height
$A$ at a height ![]() $1$ prime ideal
$1$ prime ideal ![]() $\mathfrak{p}$. Suppose that this is not true for some
$\mathfrak{p}$. Suppose that this is not true for some ![]() $\mathfrak{p}$. Then
$\mathfrak{p}$. Then ![]() ${\it\xi}^{-1}$ must lie in the maximal ideal
${\it\xi}^{-1}$ must lie in the maximal ideal ![]() $\mathfrak{p}A_{\mathfrak{p}}$, that is,
$\mathfrak{p}A_{\mathfrak{p}}$, that is, 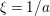 ${\it\xi}=1/a$ for some
${\it\xi}=1/a$ for some ![]() $a\in \mathfrak{p}A_{\mathfrak{p}}$. Since
$a\in \mathfrak{p}A_{\mathfrak{p}}$. Since ![]() ${\it\xi}$ is integral over
${\it\xi}$ is integral over ![]() $B$,
$B$, ![]() ${\it\xi}$ satisfies an integral equation
${\it\xi}$ satisfies an integral equation 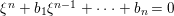 ${\it\xi}^{n}+b_{1}{\it\xi}^{n-1}+\cdots +b_{n}=0$, with
${\it\xi}^{n}+b_{1}{\it\xi}^{n-1}+\cdots +b_{n}=0$, with ![]() $b_{i}\in B$. By replacing
$b_{i}\in B$. By replacing ![]() ${\it\xi}$ by
${\it\xi}$ by ![]() $1/a$, and clearing the denominator in the equation, we obtain
$1/a$, and clearing the denominator in the equation, we obtain
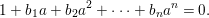 $$\begin{eqnarray}1+b_{1}a+b_{2}a^{2}+\cdots +b_{n}a^{n}=0.\end{eqnarray}$$
$$\begin{eqnarray}1+b_{1}a+b_{2}a^{2}+\cdots +b_{n}a^{n}=0.\end{eqnarray}$$ Therefore, ![]() $a$ is a unit in
$a$ is a unit in ![]() $B$. However, by the given condition, there exists
$B$. However, by the given condition, there exists 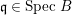 $\mathfrak{q}\in \text{Spec}~B$ such that
$\mathfrak{q}\in \text{Spec}~B$ such that 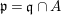 $\mathfrak{p}=\mathfrak{q}\cap A$, which implies that
$\mathfrak{p}=\mathfrak{q}\cap A$, which implies that ![]() $a\in \mathfrak{q}$, leading to a contradiction.◻
$a\in \mathfrak{q}$, leading to a contradiction.◻
Lemma 2.6. Let ![]() $A$ be an affine
$A$ be an affine ![]() $k$-domain, and let
$k$-domain, and let ![]() $A{\hookrightarrow}B$ be a pure embedding. Let
$A{\hookrightarrow}B$ be a pure embedding. Let ![]() $I$ be a radical ideal of
$I$ be a radical ideal of ![]() $A$, let
$A$, let 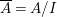 $\overline{A}=A/I$, and let
$\overline{A}=A/I$, and let 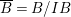 $\overline{B}=B/IB$. Then
$\overline{B}=B/IB$. Then ![]() $\overline{A}{\hookrightarrow}\overline{B}$ is a pure embedding.
$\overline{A}{\hookrightarrow}\overline{B}$ is a pure embedding.
More generally, if ![]() $I$ is any ideal in
$I$ is any ideal in ![]() $A$ such that
$A$ such that ![]() $\overline{A}$ is Gorenstein, then
$\overline{A}$ is Gorenstein, then ![]() $\overline{A}{\hookrightarrow}\overline{B}$ is a pure embedding.
$\overline{A}{\hookrightarrow}\overline{B}$ is a pure embedding.
Proof. It is a special case of the base change property of pure extensions, as stated in Lemma 1.4. ◻
Lemma 2.7. Let 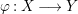 ${\it\varphi}:X\longrightarrow Y$ be a dominant morphism of affine varieties, with dim
${\it\varphi}:X\longrightarrow Y$ be a dominant morphism of affine varieties, with dim ![]() $X=m$ and dim
$X=m$ and dim ![]() $Y=n$. Assume that
$Y=n$. Assume that ![]() $Y$ is normal. Let
$Y$ is normal. Let ![]() $x\in X$ be such that any irreducible component of
$x\in X$ be such that any irreducible component of 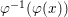 $~{\it\varphi}^{-1}({\it\varphi}(x))$, which contains
$~{\it\varphi}^{-1}({\it\varphi}(x))$, which contains ![]() $x$, has dimension equal to
$x$, has dimension equal to ![]() $m-n$. Then the induced local morphism
$m-n$. Then the induced local morphism
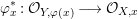 $$\begin{eqnarray}{\it\varphi}_{x}^{\ast }:{\mathcal{O}}_{Y,{\it\varphi}(x)}\longrightarrow {\mathcal{O}}_{X,x}\end{eqnarray}$$
$$\begin{eqnarray}{\it\varphi}_{x}^{\ast }:{\mathcal{O}}_{Y,{\it\varphi}(x)}\longrightarrow {\mathcal{O}}_{X,x}\end{eqnarray}$$is pure.
Proof. We indicate a proof when 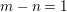 $m-n=1$. The general case is proved similarly by taking repeated hyperplane sections. Let
$m-n=1$. The general case is proved similarly by taking repeated hyperplane sections. Let ![]() $H$ be a general hyperplane section of
$H$ be a general hyperplane section of ![]() $X$ through
$X$ through ![]() $x$. Then
$x$. Then 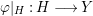 ${\it\varphi}|_{H}:H\longrightarrow Y$ is quasi-finite. Hence, the induced morphism of complete local rings
${\it\varphi}|_{H}:H\longrightarrow Y$ is quasi-finite. Hence, the induced morphism of complete local rings 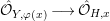 $\hat{{\mathcal{O}}}_{Y,{\it\varphi}(x)}\longrightarrow \hat{{\mathcal{O}}}_{H,x}$ is finite. By Lemma 1.8, this is a pure embedding; in fact this is a direct summand. Since there is a surjection
$\hat{{\mathcal{O}}}_{Y,{\it\varphi}(x)}\longrightarrow \hat{{\mathcal{O}}}_{H,x}$ is finite. By Lemma 1.8, this is a pure embedding; in fact this is a direct summand. Since there is a surjection 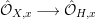 $\hat{{\mathcal{O}}}_{X,x}\longrightarrow \hat{{\mathcal{O}}}_{H,x}$, we deduce that
$\hat{{\mathcal{O}}}_{X,x}\longrightarrow \hat{{\mathcal{O}}}_{H,x}$, we deduce that 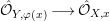 $\hat{{\mathcal{O}}}_{Y,{\it\varphi}(x)}\longrightarrow \hat{{\mathcal{O}}}_{X,x}$ is also a direct summand, hence a pure extension. This, together with Lemmas 2.4 and 1.7, implies that
$\hat{{\mathcal{O}}}_{Y,{\it\varphi}(x)}\longrightarrow \hat{{\mathcal{O}}}_{X,x}$ is also a direct summand, hence a pure extension. This, together with Lemmas 2.4 and 1.7, implies that 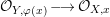 ${\mathcal{O}}_{Y,{\it\varphi}(x)}\longrightarrow {\mathcal{O}}_{X,x}$ is a pure extension.◻
${\mathcal{O}}_{Y,{\it\varphi}(x)}\longrightarrow {\mathcal{O}}_{X,x}$ is a pure extension.◻
Remark.
In Section 5.10 we give an example where the set of completely pure points is not open in ![]() $Y$.
$Y$.
We add here the following remark.
Let ![]() $G$ be a reductive algebraic group acting on an affine regular
$G$ be a reductive algebraic group acting on an affine regular ![]() $\mathbb{C}$-domain
$\mathbb{C}$-domain ![]() $A$. Then by Hochster–Roberts [Reference Hochster and Roberts7], the ring
$A$. Then by Hochster–Roberts [Reference Hochster and Roberts7], the ring ![]() $A^{G}$ of
$A^{G}$ of ![]() $G$-invariants is a pure subalgebra of
$G$-invariants is a pure subalgebra of ![]() $A$. In a similar context, we can ask whether the ring of invariants of a
$A$. In a similar context, we can ask whether the ring of invariants of a ![]() $G_{a}$-action on a polynomial ring
$G_{a}$-action on a polynomial ring 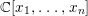 $\mathbb{C}[x_{1},\ldots ,x_{n}]$ is a pure subring of
$\mathbb{C}[x_{1},\ldots ,x_{n}]$ is a pure subring of 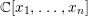 $\mathbb{C}[x_{1},\ldots ,x_{n}]$. The answer is positive if
$\mathbb{C}[x_{1},\ldots ,x_{n}]$. The answer is positive if ![]() $n\leqslant 3$ but negative for
$n\leqslant 3$ but negative for ![]() $n\geqslant 4$. There are three crucial points to prove in the case
$n\geqslant 4$. There are three crucial points to prove in the case ![]() $n\leqslant 3$. Namely, we have the following.
$n\leqslant 3$. Namely, we have the following.
(1) The ring of invariants is regular.
(2) The quotient morphism
is surjective. $$\begin{eqnarray}q:\text{Spec}\,\mathbb{C}[x_{1},\ldots ,x_{n}]\rightarrow \text{Spec}\,\mathbb{C}[x_{1},\ldots ,x_{n}]^{G_{a}}\end{eqnarray}$$
$$\begin{eqnarray}q:\text{Spec}\,\mathbb{C}[x_{1},\ldots ,x_{n}]\rightarrow \text{Spec}\,\mathbb{C}[x_{1},\ldots ,x_{n}]^{G_{a}}\end{eqnarray}$$(3) The fibers of the quotient morphism
 $q$ are all of dimension one.
$q$ are all of dimension one.
In fact, with all three conditions satisfied, ![]() $q$ is a faithfully flat morphism, and hence pure by Lemma 1.7. In the study of pure extensions, the surjectivity of the morphism
$q$ is a faithfully flat morphism, and hence pure by Lemma 1.7. In the study of pure extensions, the surjectivity of the morphism 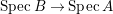 $\text{Spec}\,B\rightarrow \text{Spec}\,A$ is always a key point. Bonnet [Reference Bonnet3] and later Kaliman [Reference Kaliman10] proved via topological arguments that if
$\text{Spec}\,B\rightarrow \text{Spec}\,A$ is always a key point. Bonnet [Reference Bonnet3] and later Kaliman [Reference Kaliman10] proved via topological arguments that if ![]() $n=3$, the quotient morphism
$n=3$, the quotient morphism ![]() $q$ is surjective. This is a fairly significant result in understanding the subalgebras of a polynomial ring, and it is desirable to give a proof which may elucidate the algebro-geometric background.
$q$ is surjective. This is a fairly significant result in understanding the subalgebras of a polynomial ring, and it is desirable to give a proof which may elucidate the algebro-geometric background.
Proposition 2.8. Let 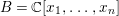 $B=\mathbb{C}[x_{1},\ldots ,x_{n}]$ be a polynomial ring with a nontrivial action of the additive group
$B=\mathbb{C}[x_{1},\ldots ,x_{n}]$ be a polynomial ring with a nontrivial action of the additive group ![]() $G_{a}$, let
$G_{a}$, let ![]() $D$ be the associated locally nilpotent derivation, and let
$D$ be the associated locally nilpotent derivation, and let ![]() $A$ be the kernel of
$A$ be the kernel of ![]() $D$. Then we have the following assertions.
$D$. Then we have the following assertions.
(1) If
 $n\leqslant 3$, the inclusion
$n\leqslant 3$, the inclusion  $A{\hookrightarrow}B$ is a pure embedding.
$A{\hookrightarrow}B$ is a pure embedding.(2) Suppose
 $n=4$. Define the Weitzenböck derivation by
$n=4$. Define the Weitzenböck derivation by  $D(x_{i})=x_{i+1}$ for
$D(x_{i})=x_{i+1}$ for  $1\leqslant i\leqslant 3$ and
$1\leqslant i\leqslant 3$ and  $D(x_{4})=0$. Then the quotient morphism
$D(x_{4})=0$. Then the quotient morphism  $q:\text{Spec}\,B\rightarrow \text{Spec}\,A$ is neither surjective nor flat. Hence, the inclusion
$q:\text{Spec}\,B\rightarrow \text{Spec}\,A$ is neither surjective nor flat. Hence, the inclusion  $A{\hookrightarrow}B$ is not a pure embedding.
$A{\hookrightarrow}B$ is not a pure embedding.
Proof. (1) If ![]() $n\leqslant 3$, we show that
$n\leqslant 3$, we show that ![]() $B$ is faithfully flat over
$B$ is faithfully flat over ![]() $A$, whence
$A$, whence ![]() $A{\hookrightarrow}B$ is a pure embedding by Lemma 1.7. We only consider the case
$A{\hookrightarrow}B$ is a pure embedding by Lemma 1.7. We only consider the case ![]() $n=3$. It is known that
$n=3$. It is known that ![]() $A$ is a polynomial ring in two variables, and
$A$ is a polynomial ring in two variables, and ![]() $q$ is equidimensional of dimension one (cf. [Reference Miyanishi12]). Hence,
$q$ is equidimensional of dimension one (cf. [Reference Miyanishi12]). Hence, ![]() $B$ is flat over
$B$ is flat over ![]() $A$. On the other hand, the surjectivity of
$A$. On the other hand, the surjectivity of ![]() $q$ is proved by [Reference Bonnet3] and [Reference Kaliman10]. Hence,
$q$ is proved by [Reference Bonnet3] and [Reference Kaliman10]. Hence, ![]() $B$ is faithfully flat over
$B$ is faithfully flat over ![]() $A$.
$A$.
(2) The ring ![]() $A$ is generated over
$A$ is generated over ![]() $\mathbb{C}$ by the following four elements:
$\mathbb{C}$ by the following four elements:
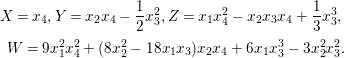 $$\begin{eqnarray}\displaystyle X=x_{4},Y=x_{2}x_{4}-\frac{1}{2}x_{3}^{2},Z=x_{1}x_{4}^{2}-x_{2}x_{3}x_{4}+\frac{1}{3}x_{3}^{3}, & & \displaystyle \nonumber\\ \displaystyle W=9x_{1}^{2}x_{4}^{2}+(8x_{2}^{2}-18x_{1}x_{3})x_{2}x_{4}+6x_{1}x_{3}^{3}-3x_{2}^{2}x_{3}^{2}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X=x_{4},Y=x_{2}x_{4}-\frac{1}{2}x_{3}^{2},Z=x_{1}x_{4}^{2}-x_{2}x_{3}x_{4}+\frac{1}{3}x_{3}^{3}, & & \displaystyle \nonumber\\ \displaystyle W=9x_{1}^{2}x_{4}^{2}+(8x_{2}^{2}-18x_{1}x_{3})x_{2}x_{4}+6x_{1}x_{3}^{3}-3x_{2}^{2}x_{3}^{2}. & & \displaystyle \nonumber\end{eqnarray}$$ Hence, ![]() $\text{Spec}\,A$ is a hypersurface
$\text{Spec}\,A$ is a hypersurface 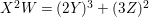 $X^{2}W=(2Y)^{3}+(3Z)^{2}$ in
$X^{2}W=(2Y)^{3}+(3Z)^{2}$ in ![]() $\mathbb{A}^{4}$. We show that the set
$\mathbb{A}^{4}$. We show that the set 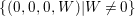 $\{(0,0,0,W)|W\neq 0\}$ is not in the image of
$\{(0,0,0,W)|W\neq 0\}$ is not in the image of ![]() $q$. In fact, for a closed point of
$q$. In fact, for a closed point of ![]() $\text{Spec}\,A$ with
$\text{Spec}\,A$ with 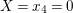 $X=x_{4}=0$, we have
$X=x_{4}=0$, we have  $Y=-\frac{1}{2}x_{3}^{2}$ and
$Y=-\frac{1}{2}x_{3}^{2}$ and 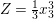 $Z=\frac{1}{3}x_{3}^{3}$. If
$Z=\frac{1}{3}x_{3}^{3}$. If ![]() $x_{3}$ moves, the point
$x_{3}$ moves, the point 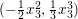 $(-\frac{1}{2}x_{3}^{2},\frac{1}{3}x_{3}^{3})$ covers the curve
$(-\frac{1}{2}x_{3}^{2},\frac{1}{3}x_{3}^{3})$ covers the curve  $(2Y)^{3}+(3Z)^{2}=0$ in the
$(2Y)^{3}+(3Z)^{2}=0$ in the ![]() $(Y,Z)$-plane. If
$(Y,Z)$-plane. If ![]() $x_{3}\neq 0$, we can find
$x_{3}\neq 0$, we can find ![]() $x_{1},x_{2}$ so that
$x_{1},x_{2}$ so that 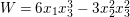 $W=6x_{1}x_{3}^{3}-3x_{2}^{2}x_{3}^{2}$ takes an arbitrary value. If
$W=6x_{1}x_{3}^{3}-3x_{2}^{2}x_{3}^{2}$ takes an arbitrary value. If ![]() $x_{3}=0$, then
$x_{3}=0$, then ![]() $W=0$. Hence,
$W=0$. Hence, 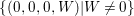 $\{(0,0,0,W)|W\neq 0\}$ is not in the image of
$\{(0,0,0,W)|W\neq 0\}$ is not in the image of ![]() $q$.
$q$.
As for the flatness of ![]() $B$ over
$B$ over ![]() $A$, it suffices to show that
$A$, it suffices to show that ![]() $q$ is not equidimensional. It is clear that the general fibers of
$q$ is not equidimensional. It is clear that the general fibers of ![]() $q$ have dimension one. However, over the point
$q$ have dimension one. However, over the point  $(0,0,0,0)$, the fiber is given by
$(0,0,0,0)$, the fiber is given by 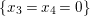 $\{x_{3}=x_{4}=0\}$, which is a plane. Therefore, we have shown that
$\{x_{3}=x_{4}=0\}$, which is a plane. Therefore, we have shown that ![]() $A{\hookrightarrow}B$ is not a pure embedding.
$A{\hookrightarrow}B$ is not a pure embedding.
A more straightforward way to see that ![]() $A{\hookrightarrow}B$ is not a pure embedding is to use that
$A{\hookrightarrow}B$ is not a pure embedding is to use that 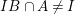 $IB\cap A\neq I$, for
$IB\cap A\neq I$, for 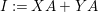 $I:=XA+YA$. In fact,
$I:=XA+YA$. In fact, ![]() $IB$ contains
$IB$ contains 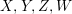 $X,Y,Z,W$, but
$X,Y,Z,W$, but 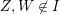 $Z,W\not \in I$.
$Z,W\not \in I$.
We note that Bonnet [Reference Bonnet3] constructed an example of ![]() $G_{a}$-action on
$G_{a}$-action on ![]() $\mathbb{A}^{4}$ whose quotient morphism is not surjective.◻
$\mathbb{A}^{4}$ whose quotient morphism is not surjective.◻
3 Purity and surjectivity
In this section we study the relationship between the notions of purity and surjectivity of the induced morphism 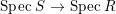 $\text{Spec}\,S~\rightarrow ~\text{Spec}\,R$ for an inclusion of rings
$\text{Spec}\,S~\rightarrow ~\text{Spec}\,R$ for an inclusion of rings 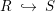 $R~{\hookrightarrow}~S$. Of particular interest will be the cases when
$R~{\hookrightarrow}~S$. Of particular interest will be the cases when ![]() $R,S$ are analytic local rings, or complete local rings.
$R,S$ are analytic local rings, or complete local rings.
We now answer the questions raised in the introduction.
Let ![]() $R\subseteq S$ be algebraic local rings.
$R\subseteq S$ be algebraic local rings.
By Lemma 1.7, faithful flatness implies purity. Therefore, in answering Question 3, we have a generalization of the well-known result that flat maps are open.
We believe that this is a new result about pure morphisms. The proof of this result is quite nontrivial.
As a first step in relating purity to surjectivity we record the following easy consequence of Chevalley’s theorem, as in [Reference Matsumura11, Theorem 6], which tells us that the surjectivity of the ![]() $\text{Spec}\,$ map, associated to a local morphism, actually translates into the local surjectivity in Zariski-topology.
$\text{Spec}\,$ map, associated to a local morphism, actually translates into the local surjectivity in Zariski-topology.
Theorem 3.1. Let ![]() $A\subseteq B$ be Noetherian rings of finite krull dimension, such that
$A\subseteq B$ be Noetherian rings of finite krull dimension, such that ![]() $A$ is an integral domain, and
$A$ is an integral domain, and ![]() $B$ is a finitely generated algebra over
$B$ is a finitely generated algebra over ![]() $A$. Suppose that, for some
$A$. Suppose that, for some 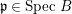 $\mathfrak{p}\in \text{Spec}~B$, the induced morphism of schemes
$\mathfrak{p}\in \text{Spec}~B$, the induced morphism of schemes
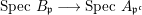 $$\begin{eqnarray}\text{Spec}~B_{\mathfrak{p}}\longrightarrow \text{Spec}~A_{\mathfrak{p^{c}}}\end{eqnarray}$$
$$\begin{eqnarray}\text{Spec}~B_{\mathfrak{p}}\longrightarrow \text{Spec}~A_{\mathfrak{p^{c}}}\end{eqnarray}$$ is surjective. Then there exists an open set 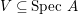 $V\subseteq \text{Spec}~A$, such that
$V\subseteq \text{Spec}~A$, such that 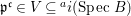 $\mathfrak{p^{c}}\in V\subseteq ^{a}i(\text{Spec}~B)$, where
$\mathfrak{p^{c}}\in V\subseteq ^{a}i(\text{Spec}~B)$, where 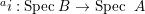 $^{a}i:\text{Spec}\,B~\rightarrow ~\text{Spec}\,~A$ is induced by the natural inclusion
$^{a}i:\text{Spec}\,B~\rightarrow ~\text{Spec}\,~A$ is induced by the natural inclusion 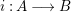 $i:A\longrightarrow B$.
$i:A\longrightarrow B$.
Corollary 3.1.1. Let 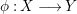 ${\it\phi}:X\longrightarrow Y$ be a morphism of affine algebraic sets, with
${\it\phi}:X\longrightarrow Y$ be a morphism of affine algebraic sets, with ![]() $Y$ being irreducible. If
$Y$ being irreducible. If ![]() $x\in X$ is such that
$x\in X$ is such that
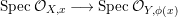 $$\begin{eqnarray}\displaystyle \text{Spec}\,{\mathcal{O}}_{X,x}\longrightarrow \text{Spec}\,{\mathcal{O}}_{Y,{\it\phi}(x)} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Spec}\,{\mathcal{O}}_{X,x}\longrightarrow \text{Spec}\,{\mathcal{O}}_{Y,{\it\phi}(x)} & & \displaystyle \nonumber\end{eqnarray}$$ is surjective, then there exists an open set ![]() $V\subseteq Y$, satisfying
$V\subseteq Y$, satisfying 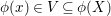 ${\it\phi}(x)\in V\subseteq {\it\phi}(X)$. In particular, the result is true when
${\it\phi}(x)\in V\subseteq {\it\phi}(X)$. In particular, the result is true when ![]() $x\in X$ is pure.
$x\in X$ is pure.
The next result shows that purity carries over to completion.
Theorem 3.2. Let 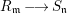 $R_{\mathfrak{m}}\longrightarrow S_{\mathfrak{n}}$ be a cyclically pure extension of algebraic local rings. Then the induced map
$R_{\mathfrak{m}}\longrightarrow S_{\mathfrak{n}}$ be a cyclically pure extension of algebraic local rings. Then the induced map 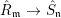 $\hat{R}_{\mathfrak{m}}~\rightarrow ~{\hat{S}}_{\mathfrak{n}}$ is also cyclically pure. (Note that cyclic purity implies that the morphism is local.)
$\hat{R}_{\mathfrak{m}}~\rightarrow ~{\hat{S}}_{\mathfrak{n}}$ is also cyclically pure. (Note that cyclic purity implies that the morphism is local.)
Proof. If 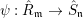 ${\it\psi}:\hat{R}_{\mathfrak{m}}~\rightarrow ~{\hat{S}}_{\mathfrak{n}}$ is the induced natural map, then we get the following commutative diagram:
${\it\psi}:\hat{R}_{\mathfrak{m}}~\rightarrow ~{\hat{S}}_{\mathfrak{n}}$ is the induced natural map, then we get the following commutative diagram:

Given any ideal ![]() $\hat{I}$ of
$\hat{I}$ of ![]() $\hat{R}_{\mathfrak{m}}$, by Krull’s intersection theorem, we have
$\hat{R}_{\mathfrak{m}}$, by Krull’s intersection theorem, we have
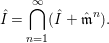 $$\begin{eqnarray}\hat{I} =\mathop{\bigcap }_{n=1}^{\infty }(\hat{I} +\hat{\mathfrak{m}}^{n}).\end{eqnarray}$$
$$\begin{eqnarray}\hat{I} =\mathop{\bigcap }_{n=1}^{\infty }(\hat{I} +\hat{\mathfrak{m}}^{n}).\end{eqnarray}$$ Since the ideal ![]() $\hat{I} +\hat{\mathfrak{m}}^{n}$ is
$\hat{I} +\hat{\mathfrak{m}}^{n}$ is ![]() $\hat{\mathfrak{m}}$-primary for each
$\hat{\mathfrak{m}}$-primary for each ![]() $n$, it is sufficient to show that any
$n$, it is sufficient to show that any ![]() $\hat{\mathfrak{m}}$-primary ideal is contracted from some ideal in
$\hat{\mathfrak{m}}$-primary ideal is contracted from some ideal in ![]() ${\hat{S}}_{\mathfrak{n}}$. If
${\hat{S}}_{\mathfrak{n}}$. If ![]() $\hat{\mathfrak{q}}$ is any
$\hat{\mathfrak{q}}$ is any ![]() $\hat{\mathfrak{m}}$-primary ideal in
$\hat{\mathfrak{m}}$-primary ideal in ![]() $\hat{R}_{\mathfrak{m}}$, then there exists an
$\hat{R}_{\mathfrak{m}}$, then there exists an ![]() $\mathfrak{m}$-primary ideal
$\mathfrak{m}$-primary ideal ![]() $\mathfrak{q}$ in
$\mathfrak{q}$ in ![]() $R_{\mathfrak{m}}$ such that
$R_{\mathfrak{m}}$ such that 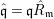 $\hat{\mathfrak{q}}=\mathfrak{q}\hat{R}_{\mathfrak{m}}$. Now,
$\hat{\mathfrak{q}}=\mathfrak{q}\hat{R}_{\mathfrak{m}}$. Now, 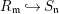 $R_{\mathfrak{m}}{\hookrightarrow}S_{\mathfrak{n}}$ being pure, there exists an ideal
$R_{\mathfrak{m}}{\hookrightarrow}S_{\mathfrak{n}}$ being pure, there exists an ideal ![]() $\mathfrak{p}\in S_{\mathfrak{n}}$ satisfying
$\mathfrak{p}\in S_{\mathfrak{n}}$ satisfying 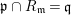 $\mathfrak{p}\cap R_{\mathfrak{m}}=\mathfrak{q}$. Since completion is faithfully flat and hence pure by Lemma 1.7, there exists an ideal
$\mathfrak{p}\cap R_{\mathfrak{m}}=\mathfrak{q}$. Since completion is faithfully flat and hence pure by Lemma 1.7, there exists an ideal ![]() $\hat{\mathfrak{p}}\in \hat{S_{\mathfrak{n}}}$ such that
$\hat{\mathfrak{p}}\in \hat{S_{\mathfrak{n}}}$ such that  $\hat{\mathfrak{p}}\cap S_{\mathfrak{n}}=\mathfrak{p}$. The diagram being commutative,
$\hat{\mathfrak{p}}\cap S_{\mathfrak{n}}=\mathfrak{p}$. The diagram being commutative,  ${\it\psi}^{-1}(\hat{\mathfrak{p}})\cap R_{\mathfrak{m}}=\mathfrak{q}$. Therefore,
${\it\psi}^{-1}(\hat{\mathfrak{p}})\cap R_{\mathfrak{m}}=\mathfrak{q}$. Therefore, ![]() ${\it\psi}^{-1}(\hat{\mathfrak{p}})$ is also
${\it\psi}^{-1}(\hat{\mathfrak{p}})$ is also ![]() $\hat{\mathfrak{m}}$-primary, and consequently an extended ideal. Hence,
$\hat{\mathfrak{m}}$-primary, and consequently an extended ideal. Hence,  ${\it\psi}^{-1}(\hat{\mathfrak{p}})=\hat{\mathfrak{q}}$, as the extended ideals are in one-to-one correspondence with the contracted ideals. Therefore,
${\it\psi}^{-1}(\hat{\mathfrak{p}})=\hat{\mathfrak{q}}$, as the extended ideals are in one-to-one correspondence with the contracted ideals. Therefore, ${\it\psi}:\hat{R}_{\mathfrak{m}}~\rightarrow ~{\hat{S}}_{\mathfrak{n}}$ is cyclically pure.
${\it\psi}:\hat{R}_{\mathfrak{m}}~\rightarrow ~{\hat{S}}_{\mathfrak{n}}$ is cyclically pure.
As a corollary, we get an affirmative answer to Question 1. This also follows from [Reference Hochster and Roberts7, Proposition 6.11], but we have given a direct elementary proof. ◻
Corollary 3.2.1. Let ![]() $R\subseteq S$ be a pure extension of algebraic local rings. If
$R\subseteq S$ be a pure extension of algebraic local rings. If ![]() $R$ is either reduced or Gorenstein, then the induced map
$R$ is either reduced or Gorenstein, then the induced map ![]() $\hat{R}~\rightarrow ~{\hat{S}}$ is also a pure extension. Similarly, the extension of the associated analytic local rings
$\hat{R}~\rightarrow ~{\hat{S}}$ is also a pure extension. Similarly, the extension of the associated analytic local rings 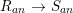 $R_{an}~\rightarrow ~S_{an}$ is also a pure extension.
$R_{an}~\rightarrow ~S_{an}$ is also a pure extension.
Proof. The proof follows from Lemma 1.5.
Since ![]() $\hat{R}$ is the completion of
$\hat{R}$ is the completion of ![]() $R_{an}$, we deduce the result that the extension of the associated analytic local rings
$R_{an}$, we deduce the result that the extension of the associated analytic local rings 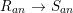 $R_{an}~\rightarrow ~S_{an}$ is also a pure extension.◻
$R_{an}~\rightarrow ~S_{an}$ is also a pure extension.◻
Next, for Question 2, we begin by recalling a simple fact in commutative algebra.
Lemma 3.3. If ![]() $~\mathfrak{p}$ is a prime ideal in a Noetherian ring
$~\mathfrak{p}$ is a prime ideal in a Noetherian ring ![]() $R$, such that
$R$, such that 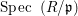 $\text{Spec}\,~(R/\mathfrak{p})$ is infinite, then
$\text{Spec}\,~(R/\mathfrak{p})$ is infinite, then
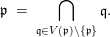 $$\begin{eqnarray}\mathfrak{p}~=~\mathop{\bigcap }_{\mathfrak{q}\in V(\mathfrak{p})\setminus \{\mathfrak{p}\}}\mathfrak{q}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{p}~=~\mathop{\bigcap }_{\mathfrak{q}\in V(\mathfrak{p})\setminus \{\mathfrak{p}\}}\mathfrak{q}.\end{eqnarray}$$Proof. The proof follows from the prime avoidance theorem. ◻
Now, let ![]() $R$ be an algebraic local domain of dimension
$R$ be an algebraic local domain of dimension ![]() ${>}1$. Then, by a standard result in commutative algebra,
${>}1$. Then, by a standard result in commutative algebra, ![]() $\hat{R}$ is a reduced ring. Therefore, in this case Lemma 3.3 has the following corollaries.
$\hat{R}$ is a reduced ring. Therefore, in this case Lemma 3.3 has the following corollaries.
Corollary 3.3.1. With the above hypothesis for ![]() $R$, the intersection of all nonzero prime ideals is
$R$, the intersection of all nonzero prime ideals is ![]() $(0)$ in
$(0)$ in ![]() $R$ as well as in
$R$ as well as in ![]() $\hat{R}$.
$\hat{R}$.
Corollary 3.3.2. If dim ![]() $\hat{R}=d$, then any prime ideal
$\hat{R}=d$, then any prime ideal ![]() $\mathfrak{p}$ of height smaller than
$\mathfrak{p}$ of height smaller than ![]() $d$ is the intersection of all prime ideals of height
$d$ is the intersection of all prime ideals of height ![]() $d-1$ containing
$d-1$ containing ![]() $\mathfrak{p}$. (Geometrically, this means that every irreducible germ of an algebroid variety is the union of all the algebroid curves in it.)
$\mathfrak{p}$. (Geometrically, this means that every irreducible germ of an algebroid variety is the union of all the algebroid curves in it.)
Theorem 3.4. Let  $(R,\mathfrak{m})\subset (S,\mathfrak{n})$ be algebraic local domains such that
$(R,\mathfrak{m})\subset (S,\mathfrak{n})$ be algebraic local domains such that ![]() $\hat{R}$ is an integral domain. Suppose that the morphism
$\hat{R}$ is an integral domain. Suppose that the morphism 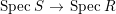 $\text{Spec}\,S~\rightarrow ~\text{Spec}\,R$ is surjective. Then the morphism
$\text{Spec}\,S~\rightarrow ~\text{Spec}\,R$ is surjective. Then the morphism 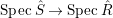 $\text{Spec}\,{\hat{S}}\rightarrow \text{Spec}\,\hat{R}$ is also surjective.
$\text{Spec}\,{\hat{S}}\rightarrow \text{Spec}\,\hat{R}$ is also surjective.
Proof. By [Reference Abhyankar1, Chapter 3, (10.14)], we have an injection ![]() $\hat{R}~\rightarrow ~{\hat{S}}$.
$\hat{R}~\rightarrow ~{\hat{S}}$.
Consider first the case when ![]() $\mathfrak{m}S$ is primary for
$\mathfrak{m}S$ is primary for ![]() $\mathfrak{n}$. Then it is easy to see that
$\mathfrak{n}$. Then it is easy to see that ![]() ${\hat{S}}$ is integral over
${\hat{S}}$ is integral over ![]() $\hat{R}$. In this case the result is well known.
$\hat{R}$. In this case the result is well known.
So we assume that ![]() $\mathfrak{m}S$ is not primary for
$\mathfrak{m}S$ is not primary for ![]() $\mathfrak{n}$. Let
$\mathfrak{n}$. Let ![]() $d:=$ dim
$d:=$ dim![]() $~R$. We further assume that
$~R$. We further assume that ![]() $d>1$, since the result is trivial for
$d>1$, since the result is trivial for ![]() $d=1$.
$d=1$.
We claim that it suffices to prove that given any prime ideal ![]() $\hat{\mathfrak{p}}\subset \hat{R}$ such that height
$\hat{\mathfrak{p}}\subset \hat{R}$ such that height 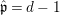 $\hat{\mathfrak{p}}=d-1$, there is a prime ideal
$\hat{\mathfrak{p}}=d-1$, there is a prime ideal ![]() $\hat{\mathfrak{q}}\subset {\hat{S}}$ such that
$\hat{\mathfrak{q}}\subset {\hat{S}}$ such that 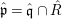 $\hat{\mathfrak{p}}=\hat{\mathfrak{q}}\cap \hat{R}$.
$\hat{\mathfrak{p}}=\hat{\mathfrak{q}}\cap \hat{R}$.
For, assuming this, if 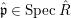 $\hat{\mathfrak{p}}\in \text{Spec}\,\hat{R}$ is of height less than
$\hat{\mathfrak{p}}\in \text{Spec}\,\hat{R}$ is of height less than ![]() $d-1$, then, by Corollary 3.3.2, there exists an ideal
$d-1$, then, by Corollary 3.3.2, there exists an ideal ![]() $I$ in
$I$ in ![]() ${\hat{S}}$ contracting to
${\hat{S}}$ contracting to ![]() $\hat{\mathfrak{p}}$. However, any maximal element of the set
$\hat{\mathfrak{p}}$. However, any maximal element of the set 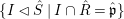 $\{I{\vartriangleleft}{\hat{S}}\mid I\cap \hat{R}=\hat{\mathfrak{p}}\}$ is a prime ideal in
$\{I{\vartriangleleft}{\hat{S}}\mid I\cap \hat{R}=\hat{\mathfrak{p}}\}$ is a prime ideal in ![]() $S$, and hence
$S$, and hence ![]() $\hat{\mathfrak{p}}$ must be in the image of
$\hat{\mathfrak{p}}$ must be in the image of ![]() $\text{Spec}\,{\hat{S}}$.
$\text{Spec}\,{\hat{S}}$.
Let 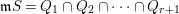 $\mathfrak{m}S=Q_{1}\cap Q_{2}\cap \cdots \cap Q_{r+1}$, where
$\mathfrak{m}S=Q_{1}\cap Q_{2}\cap \cdots \cap Q_{r+1}$, where ![]() $Q_{i}$ are primary for prime ideals
$Q_{i}$ are primary for prime ideals ![]() $\mathfrak{p_{i}}$ strictly smaller than
$\mathfrak{p_{i}}$ strictly smaller than ![]() $\mathfrak{n}$ for
$\mathfrak{n}$ for 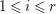 $1\leqslant i\leqslant r$, and
$1\leqslant i\leqslant r$, and ![]() $Q_{r+1}$ (if it occurs in a minimal primary decomposition) is primary for
$Q_{r+1}$ (if it occurs in a minimal primary decomposition) is primary for ![]() $\mathfrak{n}$. Suppose that
$\mathfrak{n}$. Suppose that ![]() $\hat{\mathfrak{p}}$ is not of the form
$\hat{\mathfrak{p}}$ is not of the form ![]() $\hat{\mathfrak{q}}\cap \hat{R}$ for any prime ideal of
$\hat{\mathfrak{q}}\cap \hat{R}$ for any prime ideal of ![]() $\hat{\mathfrak{q}}$ in
$\hat{\mathfrak{q}}$ in ![]() $S$. Then
$S$. Then 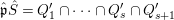 $\hat{\mathfrak{p}}{\hat{S}}=Q_{1}^{\prime }\cap \cdots \cap Q_{s}^{\prime }\cap Q_{s+1}^{\prime }$, where
$\hat{\mathfrak{p}}{\hat{S}}=Q_{1}^{\prime }\cap \cdots \cap Q_{s}^{\prime }\cap Q_{s+1}^{\prime }$, where ![]() $Q_{j}^{\prime }$ is primary for a prime ideal
$Q_{j}^{\prime }$ is primary for a prime ideal ![]() $\mathfrak{p}_{j}^{\prime }$ which contracts to some
$\mathfrak{p}_{j}^{\prime }$ which contracts to some ![]() $\mathfrak{p}_{j_{i}}$ for
$\mathfrak{p}_{j_{i}}$ for 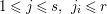 $1\leqslant j\leqslant s,~j_{i}\leqslant r$, and
$1\leqslant j\leqslant s,~j_{i}\leqslant r$, and ![]() $Q_{s+1}^{\prime }$ is primary for
$Q_{s+1}^{\prime }$ is primary for ![]() $\hat{\mathfrak{n}}$. Clearly,
$\hat{\mathfrak{n}}$. Clearly, ![]() $s\geqslant 1$.
$s\geqslant 1$.
We write 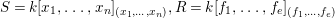 $S=k[x_{1},\ldots ,x_{n}]_{(x_{1},\ldots ,x_{n})},R=k[f_{1},\ldots ,f_{e}]_{(f_{1},\ldots ,f_{e})}$. It follows that
$S=k[x_{1},\ldots ,x_{n}]_{(x_{1},\ldots ,x_{n})},R=k[f_{1},\ldots ,f_{e}]_{(f_{1},\ldots ,f_{e})}$. It follows that ![]() $f_{l}\in \mathfrak{p}_{i}$ for each
$f_{l}\in \mathfrak{p}_{i}$ for each ![]() $l$, and
$l$, and 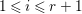 $1\leqslant i\leqslant r+1$, where
$1\leqslant i\leqslant r+1$, where 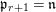 $\mathfrak{p}_{r+1}=\mathfrak{n}$. Let
$\mathfrak{p}_{r+1}=\mathfrak{n}$. Let 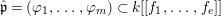 $\hat{\mathfrak{p}}=({\it\varphi}_{1},\ldots ,{\it\varphi}_{m})\subset k[[f_{1},\ldots ,f_{e}]]$. Then
$\hat{\mathfrak{p}}=({\it\varphi}_{1},\ldots ,{\it\varphi}_{m})\subset k[[f_{1},\ldots ,f_{e}]]$. Then ![]() ${\it\varphi}_{j}\in \mathfrak{p}_{{\it\beta}}^{\prime }$ for each
${\it\varphi}_{j}\in \mathfrak{p}_{{\it\beta}}^{\prime }$ for each ![]() $j$, and
$j$, and 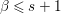 ${\it\beta}\leqslant s+1$. Each
${\it\beta}\leqslant s+1$. Each ![]() $\mathfrak{p}_{{\it\beta}}^{\prime }$ contains some
$\mathfrak{p}_{{\it\beta}}^{\prime }$ contains some ![]() $\mathfrak{p}_{{\it\beta}_{i}}$. Hence, each
$\mathfrak{p}_{{\it\beta}_{i}}$. Hence, each ![]() $f_{{\it\alpha}}$ is contained in each
$f_{{\it\alpha}}$ is contained in each ![]() $\mathfrak{p}_{{\it\beta}}^{\prime }$ for
$\mathfrak{p}_{{\it\beta}}^{\prime }$ for 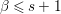 ${\it\beta}\leqslant s+1$. Thus,
${\it\beta}\leqslant s+1$. Thus, 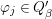 ${\it\varphi}_{j}\in Q_{{\it\beta}}^{\prime }$ for each
${\it\varphi}_{j}\in Q_{{\it\beta}}^{\prime }$ for each ![]() $j$, and
$j$, and 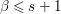 ${\it\beta}\leqslant s+1$.
${\it\beta}\leqslant s+1$.
There exists ![]() $N>0$ such that
$N>0$ such that 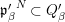 ${\mathfrak{p}_{{\it\beta}}^{\prime }}^{N}\subset Q_{{\it\beta}}^{\prime }$ for each
${\mathfrak{p}_{{\it\beta}}^{\prime }}^{N}\subset Q_{{\it\beta}}^{\prime }$ for each ![]() ${\it\beta}$. Hence, we can write
${\it\beta}$. Hence, we can write
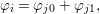 $$\begin{eqnarray}{\it\varphi}_{i}={\it\varphi}_{j0}+{\it\varphi}_{j1},\end{eqnarray}$$
$$\begin{eqnarray}{\it\varphi}_{i}={\it\varphi}_{j0}+{\it\varphi}_{j1},\end{eqnarray}$$ where each ![]() ${\it\varphi}_{j0}$ is a polynomial in
${\it\varphi}_{j0}$ is a polynomial in 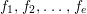 $f_{1},f_{2},\ldots ,f_{e}$, and
$f_{1},f_{2},\ldots ,f_{e}$, and 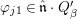 ${\it\varphi}_{j1}\in \hat{\mathfrak{n}}\cdot Q_{{\it\beta}}^{\prime }$. It follows that the ideal
${\it\varphi}_{j1}\in \hat{\mathfrak{n}}\cdot Q_{{\it\beta}}^{\prime }$. It follows that the ideal 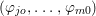 $({\it\varphi}_{jo},\ldots ,{\it\varphi}_{m0})$ generates
$({\it\varphi}_{jo},\ldots ,{\it\varphi}_{m0})$ generates 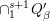 $\cap _{1}^{s+1}Q_{{\it\beta}}^{\prime }$ mod
$\cap _{1}^{s+1}Q_{{\it\beta}}^{\prime }$ mod 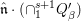 $\hat{\mathfrak{n}}\cdot (\cap _{1}^{s+1}Q_{{\it\beta}}^{\prime })$. By Nakayama’s lemma, this implies that
$\hat{\mathfrak{n}}\cdot (\cap _{1}^{s+1}Q_{{\it\beta}}^{\prime })$. By Nakayama’s lemma, this implies that 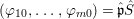 $({\it\varphi}_{10},\ldots ,{\it\varphi}_{m0})=\hat{\mathfrak{p}}{\hat{S}}$.
$({\it\varphi}_{10},\ldots ,{\it\varphi}_{m0})=\hat{\mathfrak{p}}{\hat{S}}$.
By [Reference Artin2, pages 32–33], we can assume that 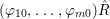 $({\it\varphi}_{10},\ldots ,{\it\varphi}_{m0})\hat{R}$ is of height
$({\it\varphi}_{10},\ldots ,{\it\varphi}_{m0})\hat{R}$ is of height ![]() $d-1$. Let
$d-1$. Let  $I=({\it\varphi}_{10},\ldots ,{\it\varphi}_{m0})\subset R$.
$I=({\it\varphi}_{10},\ldots ,{\it\varphi}_{m0})\subset R$.
Claim.
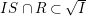 $IS\cap R\subset \sqrt{I}$.
$IS\cap R\subset \sqrt{I}$.
To see this, we write the primary decomposition of ![]() $I$ as
$I$ as ![]() $I=\cap J_{i}$, where the
$I=\cap J_{i}$, where the ![]() $J_{i}$ are primary for distinct prime ideals
$J_{i}$ are primary for distinct prime ideals ![]() $\widetilde{J_{i}}$. Since
$\widetilde{J_{i}}$. Since 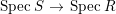 $\text{Spec}\,S~\rightarrow ~\text{Spec}\,R$ is surjective, we have
$\text{Spec}\,S~\rightarrow ~\text{Spec}\,R$ is surjective, we have 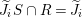 $\widetilde{J_{i}}S\cap R=\widetilde{J_{i}}$. It follows that
$\widetilde{J_{i}}S\cap R=\widetilde{J_{i}}$. It follows that 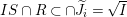 $IS\cap R\subset \cap \widetilde{J_{i}}=\sqrt{I}$.
$IS\cap R\subset \cap \widetilde{J_{i}}=\sqrt{I}$.
Now, 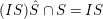 $(IS){\hat{S}}\cap S=IS$, since
$(IS){\hat{S}}\cap S=IS$, since ![]() ${\hat{S}}$ is a faithfully flat extension of
${\hat{S}}$ is a faithfully flat extension of ![]() $S$. It follows that
$S$. It follows that 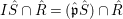 $I{\hat{S}}\cap \hat{R}=(\hat{\mathfrak{p}}{\hat{S}})\cap \hat{R}$ is an ideal, which contracts to an ideal contained in
$I{\hat{S}}\cap \hat{R}=(\hat{\mathfrak{p}}{\hat{S}})\cap \hat{R}$ is an ideal, which contracts to an ideal contained in ![]() $\sqrt{I}$. Hence,
$\sqrt{I}$. Hence, ![]() $\hat{\mathfrak{p}}{\hat{S}}$ cannot contract to an ideal which is primary for
$\hat{\mathfrak{p}}{\hat{S}}$ cannot contract to an ideal which is primary for ![]() $\hat{\mathfrak{n}}$.
$\hat{\mathfrak{n}}$.
This contradiction shows that ![]() $\hat{\mathfrak{p}}$ is contracted from
$\hat{\mathfrak{p}}$ is contracted from ![]() ${\hat{S}}$. This completes the proof of Theorem 3.4.◻
${\hat{S}}$. This completes the proof of Theorem 3.4.◻
Remark.
With the notation and assumptions of Theorem 3.4, we deduce easily that the morphism 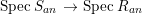 $\text{Spec}\,S_{an}~\rightarrow ~\text{Spec}\,R_{an}$ is also surjective.
$\text{Spec}\,S_{an}~\rightarrow ~\text{Spec}\,R_{an}$ is also surjective.
The next result gives an affirmative answer to Question 3 for morphisms of complex analytic varieties. This generalizes the well-known result that a flat morphism is open.
We need the following well-known result from complex analysis.
Rouché’s theorem.
Let 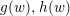 $g(w),h(w)$ be holomorphic functions of one variable
$g(w),h(w)$ be holomorphic functions of one variable ![]() $w$ in a simply connected open set
$w$ in a simply connected open set ![]() $U\subseteq \mathbb{C}$. Let
$U\subseteq \mathbb{C}$. Let ![]() ${\rm\Gamma}$ be a simple closed curve in
${\rm\Gamma}$ be a simple closed curve in ![]() $U$. If
$U$. If 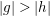 $|g|>|h|$ on
$|g|>|h|$ on ![]() ${\rm\Gamma}$, then
${\rm\Gamma}$, then ![]() $g$ and
$g$ and ![]() $g+h$ have the same number of zeros counted with multiplicity inside
$g+h$ have the same number of zeros counted with multiplicity inside ![]() ${\rm\Gamma}$.
${\rm\Gamma}$.
We use this as follows.
Let ![]() $g(z,w)$ be holomorphic in variables
$g(z,w)$ be holomorphic in variables 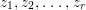 $z_{1},z_{2},\ldots ,z_{r}$ and one variable
$z_{1},z_{2},\ldots ,z_{r}$ and one variable ![]() $w$ in an open neighborhood
$w$ in an open neighborhood ![]() $U$ of
$U$ of ![]() $(0,0)$ in
$(0,0)$ in ![]() $\mathbb{C}^{r+1}$. Suppose that
$\mathbb{C}^{r+1}$. Suppose that 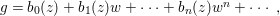 $g=b_{0}(z)+b_{1}(z)w+\cdots +b_{n}(z)w^{n}+\cdots \,,$ where
$g=b_{0}(z)+b_{1}(z)w+\cdots +b_{n}(z)w^{n}+\cdots \,,$ where ![]() $n$ is the smallest positive integer such that
$n$ is the smallest positive integer such that ![]() $b_{n}$ is a unit in the convergent power series ring
$b_{n}$ is a unit in the convergent power series ring ![]() $\mathbb{C}\{z\}$. Assume for simplicity that
$\mathbb{C}\{z\}$. Assume for simplicity that 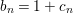 $b_{n}=1+c_{n}$, where
$b_{n}=1+c_{n}$, where ![]() $c_{n}(z)$ is a nonunit.
$c_{n}(z)$ is a nonunit.
Claim.
There exist open sets ![]() $U_{1},U_{2}$ in
$U_{1},U_{2}$ in ![]() $\mathbb{C}^{r},\mathbb{C}$ respectively such that
$\mathbb{C}^{r},\mathbb{C}$ respectively such that 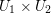 $U_{1}\times U_{2}$ is contained in
$U_{1}\times U_{2}$ is contained in ![]() $U$, and such that for any fixed
$U$, and such that for any fixed 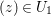 $(z)\in U_{1}$, we have
$(z)\in U_{1}$, we have  $|b_{0}+b_{1}w+\cdots +w^{n}|>|c_{n}w^{n}+b_{n+1}w^{n+1}+\cdots |$ on the boundary of
$|b_{0}+b_{1}w+\cdots +w^{n}|>|c_{n}w^{n}+b_{n+1}w^{n+1}+\cdots |$ on the boundary of ![]() $U_{2}$.
$U_{2}$.
To see this, suppose 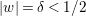 $|w|={\it\delta}<1/2$. Since
$|w|={\it\delta}<1/2$. Since 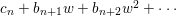 $c_{n}+b_{n+1}w+b_{n+2}w^{2}+\cdots \,$ vanishes at the origin in
$c_{n}+b_{n+1}w+b_{n+2}w^{2}+\cdots \,$ vanishes at the origin in ![]() $\mathbb{C}^{r+1}$, by continuity we can assume that
$\mathbb{C}^{r+1}$, by continuity we can assume that ![]() ${\it\delta}_{1},{\it\delta}$ are so small that
${\it\delta}_{1},{\it\delta}$ are so small that 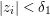 $|z_{i}|<{\it\delta}_{1}$ in
$|z_{i}|<{\it\delta}_{1}$ in ![]() $N_{1}$,
$N_{1}$, ![]() $|w|<{\it\delta}$ in
$|w|<{\it\delta}$ in ![]() $U_{2}$, and
$U_{2}$, and 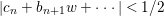 $|c_{n}+b_{n+1}w+\cdots |<1/2$ in
$|c_{n}+b_{n+1}w+\cdots |<1/2$ in  $N_{1}\times U_{2}$. Since
$N_{1}\times U_{2}$. Since 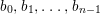 $b_{0},b_{1},\ldots ,b_{n-1}$ are nonunits, we can find an open neighborhood
$b_{0},b_{1},\ldots ,b_{n-1}$ are nonunits, we can find an open neighborhood ![]() $N_{1}^{\prime }$ of
$N_{1}^{\prime }$ of ![]() $0\in C^{r}$ such that
$0\in C^{r}$ such that 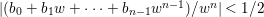 $|(b_{0}+b_{1}w+\cdots +b_{n-1}w^{n-1})/w^{n}|<1/2$ for all
$|(b_{0}+b_{1}w+\cdots +b_{n-1}w^{n-1})/w^{n}|<1/2$ for all 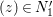 $(z)\in N_{1}^{\prime }$ and
$(z)\in N_{1}^{\prime }$ and ![]() $|w|={\it\delta}$. Taking
$|w|={\it\delta}$. Taking 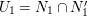 $U_{1}=N_{1}\cap N_{1}^{\prime }$, we get the required result.
$U_{1}=N_{1}\cap N_{1}^{\prime }$, we get the required result.
Now by Rouché’s theorem, for any fixed 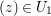 $(z)\in U_{1}$, the numbers of zeroes of
$(z)\in U_{1}$, the numbers of zeroes of 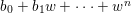 $b_{0}+b_{1}w+\cdots +w^{n}$ and
$b_{0}+b_{1}w+\cdots +w^{n}$ and ![]() $g$ in
$g$ in ![]() $U_{2}$ are the same. Clearly, by shrinking
$U_{2}$ are the same. Clearly, by shrinking ![]() $U_{1}$ if necessary, for any
$U_{1}$ if necessary, for any 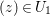 $(z)\in U_{1}$ the equation
$(z)\in U_{1}$ the equation 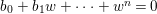 $b_{0}+b_{1}w+\cdots +w^{n}=0$ has
$b_{0}+b_{1}w+\cdots +w^{n}=0$ has ![]() $n$ zeroes in
$n$ zeroes in ![]() $U_{2}$. Hence, this is also true for
$U_{2}$. Hence, this is also true for ![]() $g$ inside
$g$ inside ![]() $U_{2}$. This proves that the image of any neighborhood of
$U_{2}$. This proves that the image of any neighborhood of ![]() $(0,0)$ in
$(0,0)$ in ![]() $\{g=0\}$ under the map
$\{g=0\}$ under the map 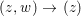 $(z,w)~\rightarrow ~(z)$ contains a neighborhood of
$(z,w)~\rightarrow ~(z)$ contains a neighborhood of ![]() $0$ in
$0$ in ![]() $\mathbb{C}^{r}$.
$\mathbb{C}^{r}$.
In the application of the above ideas in the proof of Theorem 3.5 when dim ![]() $V>1$, we have
$V>1$, we have 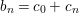 $b_{n}=c_{0}+c_{n}$, where
$b_{n}=c_{0}+c_{n}$, where ![]() $c_{0}\in \mathbb{C}$, with
$c_{0}\in \mathbb{C}$, with 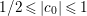 $1/2\leqslant |c_{0}|\leqslant 1$, and
$1/2\leqslant |c_{0}|\leqslant 1$, and ![]() $c_{n}$ is a nonunit. Then the rest of the above argument can be changed to get an upper bound on
$c_{n}$ is a nonunit. Then the rest of the above argument can be changed to get an upper bound on ![]() $|w|$ which is a root of
$|w|$ which is a root of ![]() $g=0$.
$g=0$.
Theorem 3.5. Let 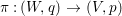 ${\it\pi}:(W,q)~\rightarrow ~(V,p)$ be a morphism of complex analytic germs. Assume that
${\it\pi}:(W,q)~\rightarrow ~(V,p)$ be a morphism of complex analytic germs. Assume that ![]() $V$ is reduced and irreducible (but
$V$ is reduced and irreducible (but ![]() $W$ may be reducible or nonreduced). If the induced map on the local rings
$W$ may be reducible or nonreduced). If the induced map on the local rings 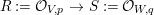 $R:={\mathcal{O}}_{V,p}~\rightarrow ~S:={\mathcal{O}}_{W,q}$ is pure, then for any Euclidean neighborhood
$R:={\mathcal{O}}_{V,p}~\rightarrow ~S:={\mathcal{O}}_{W,q}$ is pure, then for any Euclidean neighborhood ![]() $U$ of
$U$ of ![]() $q$ in
$q$ in ![]() $W$ the image
$W$ the image ![]() ${\it\pi}(U)$ contains a Euclidean neighborhood of
${\it\pi}(U)$ contains a Euclidean neighborhood of ![]() $p$ in
$p$ in ![]() $V$.
$V$.
Proof. We prove the result using suitable induction on dim ![]() $V$ and the number
$V$ and the number ![]() $r+m$ defined below for
$r+m$ defined below for ![]() $W$.◻
$W$.◻
We implicitly use the following observation. If ![]() $I\subseteq R$ is an ideal such that one of the conditions of Lemma 1.5 is satisfied for the inclusion
$I\subseteq R$ is an ideal such that one of the conditions of Lemma 1.5 is satisfied for the inclusion 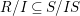 $R/I\subseteq S/IS$, then this is also a pure embedding.
$R/I\subseteq S/IS$, then this is also a pure embedding.
We assume that ![]() $p,q$ are the origins in
$p,q$ are the origins in 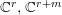 $\mathbb{C}^{r},\mathbb{C}^{r+m}$ respectively.
$\mathbb{C}^{r},\mathbb{C}^{r+m}$ respectively.
Let 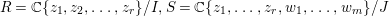 $R=\mathbb{C}\{z_{1},z_{2},\ldots ,z_{r}\}/I,S=\mathbb{C}\{z_{1},\ldots ,z_{r},w_{1},\ldots ,w_{m}\}/J$. Here,
$R=\mathbb{C}\{z_{1},z_{2},\ldots ,z_{r}\}/I,S=\mathbb{C}\{z_{1},\ldots ,z_{r},w_{1},\ldots ,w_{m}\}/J$. Here, ![]() $r+m$ may be larger than the embedding dimension of
$r+m$ may be larger than the embedding dimension of ![]() $S$. Let
$S$. Let 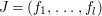 $J=(f_{1},\ldots ,f_{l})$.
$J=(f_{1},\ldots ,f_{l})$.
Write 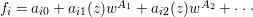 $f_{i}=a_{i0}+a_{i1}(z)w^{A_{1}}+a_{i2}(z)w^{A_{2}}+\cdots \,$, where each
$f_{i}=a_{i0}+a_{i1}(z)w^{A_{1}}+a_{i2}(z)w^{A_{2}}+\cdots \,$, where each ![]() $A_{j}$ is a multi-index
$A_{j}$ is a multi-index 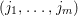 $(j_{1},\ldots ,j_{m})$, and
$(j_{1},\ldots ,j_{m})$, and 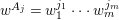 $w^{A_{j}}=w_{1}^{j_{1}}\cdots w_{m}^{j_{m}}$, etc. For any multi-index
$w^{A_{j}}=w_{1}^{j_{1}}\cdots w_{m}^{j_{m}}$, etc. For any multi-index ![]() $A_{j}$, we denote
$A_{j}$, we denote 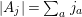 $|A_{j}|=\sum _{a}j_{a}$.
$|A_{j}|=\sum _{a}j_{a}$.
Let ![]() $U$ be the set of points in
$U$ be the set of points in ![]() $\mathbb{C}^{r+m}$ such that
$\mathbb{C}^{r+m}$ such that  $|z_{i}|\leqslant {\it\delta}_{0},|w|\leqslant {\it\delta}_{0}<1/2$ for a suitable
$|z_{i}|\leqslant {\it\delta}_{0},|w|\leqslant {\it\delta}_{0}<1/2$ for a suitable ![]() ${\it\delta}_{0}$.
${\it\delta}_{0}$.
Case 1. Suppose that, for some ![]() $f_{i}$, one of the coefficients
$f_{i}$, one of the coefficients ![]() $a_{i{\it\alpha}}$ is a unit in
$a_{i{\it\alpha}}$ is a unit in ![]() $R$. (This includes the case when
$R$. (This includes the case when ![]() $W$ is a product of
$W$ is a product of ![]() $V$ and another variety.)
$V$ and another variety.)
By making a unitary (linear) change of coordinates involving only 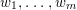 $w_{1},\ldots ,w_{m}$ (so that Euclidean distances are preserved), we can assume that the monomial corresponding to
$w_{1},\ldots ,w_{m}$ (so that Euclidean distances are preserved), we can assume that the monomial corresponding to ![]() $a_{i{\it\alpha}}$ is
$a_{i{\it\alpha}}$ is ![]() $w_{m}^{j_{m}}$ for some
$w_{m}^{j_{m}}$ for some ![]() $j_{m}$. By the Weierstrass preparation theorem, we can write
$j_{m}$. By the Weierstrass preparation theorem, we can write 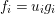 $f_{i}=u_{i}g_{i}$, where
$f_{i}=u_{i}g_{i}$, where ![]() $u_{i}$ is a unit in
$u_{i}$ is a unit in 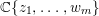 $\mathbb{C}\{z_{1},\ldots ,w_{m}\}$, and
$\mathbb{C}\{z_{1},\ldots ,w_{m}\}$, and 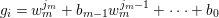 $g_{i}=w_{m}^{j_{m}}+b_{m-1}w_{m}^{j_{m}-1}+\cdots +b_{0}$. The coefficients
$g_{i}=w_{m}^{j_{m}}+b_{m-1}w_{m}^{j_{m}-1}+\cdots +b_{0}$. The coefficients 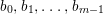 $b_{0},b_{1},\ldots ,b_{m-1}$ are nonunits in
$b_{0},b_{1},\ldots ,b_{m-1}$ are nonunits in 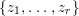 $\{z_{1},\ldots ,z_{r}\}$. It follows that
$\{z_{1},\ldots ,z_{r}\}$. It follows that ![]() $S$ is integral over a subring
$S$ is integral over a subring ![]() $S_{1}$ such that
$S_{1}$ such that 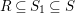 $R\subseteq S_{1}\subseteq S$ and
$R\subseteq S_{1}\subseteq S$ and 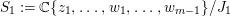 $S_{1}:=\mathbb{C}\{z_{1},\ldots ,w_{1},\ldots ,w_{m-1}\}/J_{1}$. Let
$S_{1}:=\mathbb{C}\{z_{1},\ldots ,w_{1},\ldots ,w_{m-1}\}/J_{1}$. Let ![]() $W_{1}$ be the germ in
$W_{1}$ be the germ in 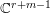 $\mathbb{C}^{r+m-1}$ corresponding to
$\mathbb{C}^{r+m-1}$ corresponding to ![]() $J_{1}$. Then the image of any neighborhood of
$J_{1}$. Then the image of any neighborhood of  $(0,0)\in W$ under the map
$(0,0)\in W$ under the map 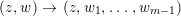 $(z,w)~\rightarrow ~(z,w_{1},\ldots ,w_{m-1})$ contains a neighborhood of the origin in
$(z,w)~\rightarrow ~(z,w_{1},\ldots ,w_{m-1})$ contains a neighborhood of the origin in ![]() $W_{1}$. Any such point in
$W_{1}$. Any such point in ![]() $W$ is contained in
$W$ is contained in  $\{f_{i}=0\}$.
$\{f_{i}=0\}$.
Now we are in a position to use Rouché’s theorem. By the discussion above, we can find open neighborhoods ![]() $U_{1},U_{2}$ of the origins in
$U_{1},U_{2}$ of the origins in 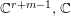 $\mathbb{C}^{r+m-1},\mathbb{C}$ respectively such that over any point in
$\mathbb{C}^{r+m-1},\mathbb{C}$ respectively such that over any point in 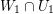 $W_{1}\cap U_{1}$ there are exactly
$W_{1}\cap U_{1}$ there are exactly ![]() $j_{m}$ points in
$j_{m}$ points in 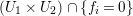 $(U_{1}\times U_{2})\cap \{f_{i}=0\}$, one of which lies in
$(U_{1}\times U_{2})\cap \{f_{i}=0\}$, one of which lies in ![]() $W$.
$W$.
Since ![]() $R~\rightarrow ~S$ is pure, so is
$R~\rightarrow ~S$ is pure, so is 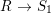 $R~\rightarrow ~S_{1}$. By induction, the result is true for
$R~\rightarrow ~S_{1}$. By induction, the result is true for 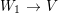 $W_{1}~\rightarrow ~V$. Hence, it is also true for
$W_{1}~\rightarrow ~V$. Hence, it is also true for 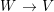 $W~\rightarrow ~V$.
$W~\rightarrow ~V$.
To complete the induction for Case 1, we must prove the result for ![]() $m=1$.
$m=1$.
However, the same argument as above shows that in this case the morphism ![]() ${\it\pi}$ satisfies the assertion of the theorem.
${\it\pi}$ satisfies the assertion of the theorem.
Case 2. Now we can assume that for each ![]() $i$ every
$i$ every ![]() $a_{i{\it\alpha}}$ is a nonunit in
$a_{i{\it\alpha}}$ is a nonunit in ![]() $R$.
$R$.
Case 2.1. Suppose first that dim ![]() $R=1$ and
$R=1$ and 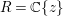 $R=\mathbb{C}\{z\}$. The proof of this case is the crucial point of the proof of the general case.
$R=\mathbb{C}\{z\}$. The proof of this case is the crucial point of the proof of the general case.
Since ![]() ${\it\pi}$ is nonconstant, using the well-known result in
${\it\pi}$ is nonconstant, using the well-known result in ![]() $1$-variable complex analysis that a nonconstant holomorphic map is open, we can easily deduce the result. However, we must prove a uniform statement for all
$1$-variable complex analysis that a nonconstant holomorphic map is open, we can easily deduce the result. However, we must prove a uniform statement for all ![]() $1$-dimensional sections of
$1$-dimensional sections of ![]() $V$ obtained by intersecting with linear subspaces when dim
$V$ obtained by intersecting with linear subspaces when dim ![]() $V>1$ and their scheme-theoretic inverse images in
$V>1$ and their scheme-theoretic inverse images in ![]() $W$. We consider a neighborhood
$W$. We consider a neighborhood ![]() $U$ of
$U$ of ![]() $p$ in
$p$ in ![]() $V$ defined by points
$V$ defined by points ![]() $p^{\prime }$ with
$p^{\prime }$ with ![]() $|z_{k}|\leqslant {\it\delta}$ for a suitable
$|z_{k}|\leqslant {\it\delta}$ for a suitable ![]() ${\it\delta}<1$, which we will choose later, and
${\it\delta}<1$, which we will choose later, and ![]() $k$ varies over the set
$k$ varies over the set 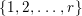 $\{1,2,\ldots ,r\}$.
$\{1,2,\ldots ,r\}$.
Now, each ![]() $a_{i{\it\alpha}}$ is a power series in one variable
$a_{i{\it\alpha}}$ is a power series in one variable ![]() $z$ vanishing at the origin. For any element
$z$ vanishing at the origin. For any element ![]() $f\in J$ let
$f\in J$ let ![]() $z^{e}$ be the largest power of
$z^{e}$ be the largest power of ![]() $z$ which divides all
$z$ which divides all ![]() $a_{{\it\alpha}}$, where
$a_{{\it\alpha}}$, where 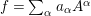 $f=\sum _{{\it\alpha}}a_{{\it\alpha}}A^{{\it\alpha}}$. Let
$f=\sum _{{\it\alpha}}a_{{\it\alpha}}A^{{\it\alpha}}$. Let ![]() $J^{\prime }$ be the ideal generated by all
$J^{\prime }$ be the ideal generated by all ![]() $f/z^{e}$ as
$f/z^{e}$ as ![]() $f$ varies over elements in
$f$ varies over elements in ![]() $J$. Then
$J$. Then ![]() $W$ is locally the union of
$W$ is locally the union of ![]() $\{z=0\}$ and the variety
$\{z=0\}$ and the variety ![]() $W^{\prime }$ defined by
$W^{\prime }$ defined by ![]() $J^{\prime }$.
$J^{\prime }$.
For simplicity, assume that ![]() $J^{\prime }$ is generated by
$J^{\prime }$ is generated by 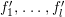 $f_{1}^{\prime },\ldots ,f_{l}^{\prime }$, and
$f_{1}^{\prime },\ldots ,f_{l}^{\prime }$, and 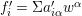 $f_{i}^{\prime }={\rm\Sigma}a_{i{\it\alpha}}^{\prime }w^{{\it\alpha}}$, where
$f_{i}^{\prime }={\rm\Sigma}a_{i{\it\alpha}}^{\prime }w^{{\it\alpha}}$, where 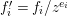 $f_{i}^{\prime }=f_{i}/z^{e_{i}}$. No
$f_{i}^{\prime }=f_{i}/z^{e_{i}}$. No ![]() $a_{i0}^{\prime }$ can be a unit in
$a_{i0}^{\prime }$ can be a unit in ![]() $R$, for otherwise
$R$, for otherwise ![]() $J^{\prime }$ is the unit ideal and
$J^{\prime }$ is the unit ideal and ![]() $W^{\prime }={\it\phi}$. This implies that
$W^{\prime }={\it\phi}$. This implies that ![]() ${\it\pi}$ is constant near
${\it\pi}$ is constant near ![]() $q$. This contradicts the hypothesis that
$q$. This contradicts the hypothesis that ![]() $R~\rightarrow ~S$ is pure (hence injective). However, by construction for each
$R~\rightarrow ~S$ is pure (hence injective). However, by construction for each ![]() $i$, some
$i$, some ![]() $a_{i{\it\alpha}}^{\prime }$ with
$a_{i{\it\alpha}}^{\prime }$ with ![]() $|{\it\alpha}|>0$ is a unit. Arguing as above, we can reduce to the case
$|{\it\alpha}|>0$ is a unit. Arguing as above, we can reduce to the case ![]() $m=1$, in which case we get the required result.
$m=1$, in which case we get the required result.
Since we need to prove this result for all ![]() $1$-dimensional sections of
$1$-dimensional sections of ![]() $V$ when dim
$V$ when dim ![]() $V>1$, we must prove a quantitative statement involving an upper bound on
$V>1$, we must prove a quantitative statement involving an upper bound on ![]() $|a_{ij}|$.
$|a_{ij}|$.
Again, let ![]() $f:=f_{1}$, and let
$f:=f_{1}$, and let  $f=a_{0}+a_{1}w+\cdots \,$.
$f=a_{0}+a_{1}w+\cdots \,$.
Let 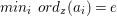 $min_{i}~ord_{z}(a_{i})=e$. Let
$min_{i}~ord_{z}(a_{i})=e$. Let 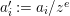 $a_{i}^{\prime }:=a_{i}/z^{e}$. Our equation is of the form
$a_{i}^{\prime }:=a_{i}/z^{e}$. Our equation is of the form  $a_{0}^{\prime }(z)+a_{1}^{\prime }(z)+\cdots +a_{n}^{\prime }(z)w^{n}+a_{n+1}^{\prime }(z)w^{n+1}+\cdots =0$, such that all the
$a_{0}^{\prime }(z)+a_{1}^{\prime }(z)+\cdots +a_{n}^{\prime }(z)w^{n}+a_{n+1}^{\prime }(z)w^{n+1}+\cdots =0$, such that all the ![]() $a_{i}^{\prime }$ are nonunits for
$a_{i}^{\prime }$ are nonunits for ![]() $i<n$, and
$i<n$, and ![]() $a_{n}^{\prime }$ is a unit. By the application of Rouché’s theorem discussed earlier we deduce the result in this case.
$a_{n}^{\prime }$ is a unit. By the application of Rouché’s theorem discussed earlier we deduce the result in this case.
This completes the proof of Case 2.1 when dim  $R=1,m=1$ and
$R=1,m=1$ and ![]() $V$ is smooth.
$V$ is smooth.
Case 2.2. Now we consider the case when dim 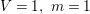 $V=1,~m=1$, and
$V=1,~m=1$, and ![]() $V$ is a singular curve.
$V$ is a singular curve.
The normalization of ![]() ${\mathcal{O}}_{V,p}$ in its quotient field is isomorphic to
${\mathcal{O}}_{V,p}$ in its quotient field is isomorphic to ![]() $\mathbb{C}\{z\}$. Let
$\mathbb{C}\{z\}$. Let 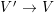 $V^{\prime }~\rightarrow ~V$ be the normalization. Let
$V^{\prime }~\rightarrow ~V$ be the normalization. Let ![]() $W^{\prime }$ be the fiber product
$W^{\prime }$ be the fiber product  $W\times _{V}V^{\prime }$. Both the morphisms
$W\times _{V}V^{\prime }$. Both the morphisms  $V^{\prime }~\rightarrow ~V,~W^{\prime }~\rightarrow ~W$ are finite, and
$V^{\prime }~\rightarrow ~V,~W^{\prime }~\rightarrow ~W$ are finite, and 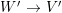 $W^{\prime }~\rightarrow ~V^{\prime }$ is pure by Lemma 1.4. By taking small open neighborhoods of points in
$W^{\prime }~\rightarrow ~V^{\prime }$ is pure by Lemma 1.4. By taking small open neighborhoods of points in ![]() $V^{\prime }$ lying over
$V^{\prime }$ lying over ![]() $p$ we are reduced to the previous case.
$p$ we are reduced to the previous case.
Case 3. Now assume that dim ![]() $V\geqslant 2$.
$V\geqslant 2$.
Case 3.1. To explain the main idea we first assume that ![]() $V$ is smooth of dimension
$V$ is smooth of dimension ![]() $2$.
$2$.
First, we prove two technical results which are useful in the arguments below.
Let 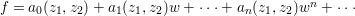 $f=a_{0}(z_{1},z_{2})+a_{1}(z_{1},z_{2})w+\cdots +a_{n}(z_{1},z_{2})w^{n}+\cdots \,$ be a convergent power series in variables
$f=a_{0}(z_{1},z_{2})+a_{1}(z_{1},z_{2})w+\cdots +a_{n}(z_{1},z_{2})w^{n}+\cdots \,$ be a convergent power series in variables  $z_{1},z_{2},w$, such that
$z_{1},z_{2},w$, such that 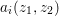 $a_{i}(z_{1},z_{2})$ is a nonunit in
$a_{i}(z_{1},z_{2})$ is a nonunit in 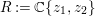 $R:=\mathbb{C}\{z_{1},z_{2}\}$ for every
$R:=\mathbb{C}\{z_{1},z_{2}\}$ for every ![]() $i$. For any linear homogeneous polynomial
$i$. For any linear homogeneous polynomial 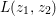 $L(z_{1},z_{2})$, consider the ring
$L(z_{1},z_{2})$, consider the ring 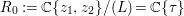 $R_{0}:=\mathbb{C}\{z_{1},z_{2}\}/(L)=\mathbb{C}\{{\it\tau}\}$. Clearly, we can take
$R_{0}:=\mathbb{C}\{z_{1},z_{2}\}/(L)=\mathbb{C}\{{\it\tau}\}$. Clearly, we can take ![]() $\overline{z_{1}}$ or
$\overline{z_{1}}$ or ![]() $\overline{z_{2}}$ as
$\overline{z_{2}}$ as ![]() ${\it\tau}$. Assume that
${\it\tau}$. Assume that ![]() $\overline{z_{1}}={\it\tau}$. Let
$\overline{z_{1}}={\it\tau}$. Let ![]() $\overline{a_{i}}$ be the image of
$\overline{a_{i}}$ be the image of ![]() $a_{i}$ in
$a_{i}$ in ![]() $R_{0}$. Then
$R_{0}$. Then ![]() $\overline{a_{i}}$ is a nonunit. Let
$\overline{a_{i}}$ is a nonunit. Let ![]() $e_{i}>0$ be the
$e_{i}>0$ be the ![]() ${\it\tau}$-order of
${\it\tau}$-order of ![]() $\overline{a_{i}}$. Consider the set of integers
$\overline{a_{i}}$. Consider the set of integers 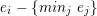 $e_{i}-\{min_{j}~e_{j}\}$. We assume that for any
$e_{i}-\{min_{j}~e_{j}\}$. We assume that for any ![]() $L$ we have
$L$ we have 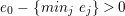 $e_{0}-\{min_{j}~e_{j}\}>0$. Let
$e_{0}-\{min_{j}~e_{j}\}>0$. Let ![]() $n_{L}$ be the smallest integer
$n_{L}$ be the smallest integer ![]() $i$ (depending on
$i$ (depending on ![]() $L$) such that
$L$) such that 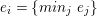 $e_{i}=\{min_{j}~e_{j}\}$.
$e_{i}=\{min_{j}~e_{j}\}$.
Lemma 3.5.1. The integers 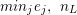 $min_{j}e_{j},~n_{L}$ are bounded as
$min_{j}e_{j},~n_{L}$ are bounded as ![]() $L$ varies over the set of all linear homogeneous polynomials, so that at least one
$L$ varies over the set of all linear homogeneous polynomials, so that at least one ![]() $\overline{a_{i}}$ is nonzero in
$\overline{a_{i}}$ is nonzero in ![]() $R_{0}$.
$R_{0}$.
Proof. We consider the ideal 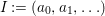 $I:=(a_{0},a_{1},\ldots )$. Since
$I:=(a_{0},a_{1},\ldots )$. Since ![]() $I$ is finitely generated, it follows that
$I$ is finitely generated, it follows that ![]() $min_{j}e_{j}$ is bounded as
$min_{j}e_{j}$ is bounded as ![]() $L$ varies, such that at least one
$L$ varies, such that at least one ![]() $\overline{a_{i}}$ is nonzero in
$\overline{a_{i}}$ is nonzero in ![]() $R_{0}$. Similarly,
$R_{0}$. Similarly, ![]() $n_{L}$ is bounded above.◻
$n_{L}$ is bounded above.◻
The next result concerns upper bounds on the coefficients of the terms occurring in the application of Rouché’s theorem as the linear homogeneous polynomials ![]() $L$ vary.
$L$ vary.
As above, let 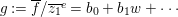 $g:=\overline{f}/\overline{z_{1}}^{e}=b_{0}+b_{1}w+\cdots \,$ be a nonunit in
$g:=\overline{f}/\overline{z_{1}}^{e}=b_{0}+b_{1}w+\cdots \,$ be a nonunit in 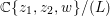 $\mathbb{C}\{z_{1},z_{2},w\}/(L)$, with
$\mathbb{C}\{z_{1},z_{2},w\}/(L)$, with ![]() $f\in J$, such that for some
$f\in J$, such that for some ![]() $n$ there is a term in
$n$ there is a term in ![]() $g$ of the form
$g$ of the form ![]() $b_{n}w^{n}$, where
$b_{n}w^{n}$, where ![]() $b_{n}$ is a unit in
$b_{n}$ is a unit in ![]() $R$. To start with, by making a suitable unitary (linear) change of coordinates involving
$R$. To start with, by making a suitable unitary (linear) change of coordinates involving ![]() $z_{1},z_{2}$, we can assume that
$z_{1},z_{2}$, we can assume that  $b_{n}=c_{0}+c_{n}$, where
$b_{n}=c_{0}+c_{n}$, where ![]() $c_{0}$ is a constant, with
$c_{0}$ is a constant, with  $1/2\leqslant |c_{0}|\leqslant 1$, and
$1/2\leqslant |c_{0}|\leqslant 1$, and ![]() $c_{n}$ is a nonunit. In order not to complicate the notation, we assume that
$c_{n}$ is a nonunit. In order not to complicate the notation, we assume that ![]() $c_{0}=1$. We also assume that
$c_{0}=1$. We also assume that ![]() $n_{L}$ is the smallest such integer. Then
$n_{L}$ is the smallest such integer. Then ![]() $n_{L}>0$ for all
$n_{L}>0$ for all ![]() $L$ such that
$L$ such that ![]() $L$ does not divide
$L$ does not divide ![]() $f$. For a fixed
$f$. For a fixed ![]() $f$, the set of integers
$f$, the set of integers ![]() $n_{L}$ is bounded above. Hence, for simplicity of exposition, we assume that
$n_{L}$ is bounded above. Hence, for simplicity of exposition, we assume that ![]() $n_{L}$ is a constant
$n_{L}$ is a constant ![]() $n\geqslant 1$.
$n\geqslant 1$.
We can assume that there are suitable  ${\it\delta}_{1}>0,{\it\delta}_{2}>0$ such that
${\it\delta}_{1}>0,{\it\delta}_{2}>0$ such that 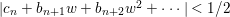 $|c_{n}+b_{n+1}w+b_{n+2}w^{2}+\cdots |<1/2$ if
$|c_{n}+b_{n+1}w+b_{n+2}w^{2}+\cdots |<1/2$ if 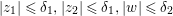 $|z_{1}|\leqslant {\it\delta}_{1},|z_{2}|\leqslant {\it\delta}_{1},|w|\leqslant {\it\delta}_{2}$.
$|z_{1}|\leqslant {\it\delta}_{1},|z_{2}|\leqslant {\it\delta}_{1},|w|\leqslant {\it\delta}_{2}$.
Since ![]() $b_{i}$ is a nonunit for
$b_{i}$ is a nonunit for ![]() $i<n$, we can assume that
$i<n$, we can assume that ![]() ${\it\delta}_{1}$ is such that
${\it\delta}_{1}$ is such that 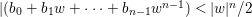 $|(b_{0}+b_{1}w+\cdots +b_{n-1}w^{n-1})<|w|^{n}/2$ when
$|(b_{0}+b_{1}w+\cdots +b_{n-1}w^{n-1})<|w|^{n}/2$ when 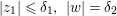 $|z_{1}|\leqslant {\it\delta}_{1},~|w|={\it\delta}_{2}$. Now, it follows that
$|z_{1}|\leqslant {\it\delta}_{1},~|w|={\it\delta}_{2}$. Now, it follows that 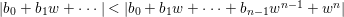 $|b_{0}+b_{1}w+\cdots |<|b_{0}+b_{1}w+\cdots +b_{n-1}w^{n-1}+w^{n}|$ when
$|b_{0}+b_{1}w+\cdots |<|b_{0}+b_{1}w+\cdots +b_{n-1}w^{n-1}+w^{n}|$ when 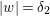 $|w|={\it\delta}_{2}$. By Roché’s theorem, for any
$|w|={\it\delta}_{2}$. By Roché’s theorem, for any 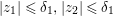 $|z_{1}|\leqslant {\it\delta}_{1},|z_{2}|\leqslant {\it\delta}_{1}$, the numbers of zeros of the equations
$|z_{1}|\leqslant {\it\delta}_{1},|z_{2}|\leqslant {\it\delta}_{1}$, the numbers of zeros of the equations 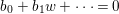 $b_{0}+b_{1}w+\cdots =0$ and
$b_{0}+b_{1}w+\cdots =0$ and 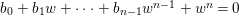 $b_{0}+b_{1}w+\cdots +b_{n-1}w^{n-1}+w^{n}=0$ inside
$b_{0}+b_{1}w+\cdots +b_{n-1}w^{n-1}+w^{n}=0$ inside  $|w|<{\it\delta}_{2}$ are the same. As in the discussion above, this number can be assumed to be
$|w|<{\it\delta}_{2}$ are the same. As in the discussion above, this number can be assumed to be ![]() $n$.
$n$.
We must show that the numbers ![]() ${\it\delta}_{1},{\it\delta}_{2}$ can be chosen independent of
${\it\delta}_{1},{\it\delta}_{2}$ can be chosen independent of ![]() $L$.
$L$.
This can be seen as follows.
Any line ![]() $L$ in
$L$ in ![]() $\mathbb{C}^{2}$ has the equation
$\mathbb{C}^{2}$ has the equation 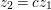 $z_{2}=cz_{1}$ for some constant
$z_{2}=cz_{1}$ for some constant ![]() $c$, or
$c$, or ![]() $z_{1}=0$. We give the argument assuming that
$z_{1}=0$. We give the argument assuming that ![]() $|c|\leqslant 1$, since if
$|c|\leqslant 1$, since if ![]() $|c|>1$ then we can take
$|c|>1$ then we can take ![]() $\overline{z_{2}}={\it\tau}$.
$\overline{z_{2}}={\it\tau}$.
We need to analyze the power series  $f(z_{1},cz_{1},w)$ more carefully. If some monomial
$f(z_{1},cz_{1},w)$ more carefully. If some monomial ![]() ${\it\gamma}z_{1}^{a}z_{2}^{b}$ occurs in
${\it\gamma}z_{1}^{a}z_{2}^{b}$ occurs in ![]() $f$ with
$f$ with ![]() ${\it\gamma}\in \mathbb{C}$ a nonzero constant, then there is a term
${\it\gamma}\in \mathbb{C}$ a nonzero constant, then there is a term ![]() ${\it\gamma}c^{b}z_{1}^{a+b}$ in
${\it\gamma}c^{b}z_{1}^{a+b}$ in 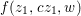 $f(z_{1},cz_{1},w)$. The maximum possible number of monomials of total degree
$f(z_{1},cz_{1},w)$. The maximum possible number of monomials of total degree ![]() $a+b$ in
$a+b$ in ![]() $z_{1},z_{2}$ is
$z_{1},z_{2}$ is 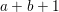 $a+b+1$. For terms
$a+b+1$. For terms ![]() $b_{i}$ with
$b_{i}$ with ![]() $i<n$, if
$i<n$, if 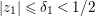 $|z_{1}|\leqslant {\it\delta}_{1}<1/2$, then
$|z_{1}|\leqslant {\it\delta}_{1}<1/2$, then 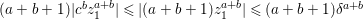 $(a+b+1)|c^{b}z_{1}^{a+b}|\leqslant |(a+b+1)z_{1}^{a+b}|\leqslant (a+b+1){\it\delta}^{a+b}$. Since
$(a+b+1)|c^{b}z_{1}^{a+b}|\leqslant |(a+b+1)z_{1}^{a+b}|\leqslant (a+b+1){\it\delta}^{a+b}$. Since ![]() $n$ is bounded, there are at most
$n$ is bounded, there are at most 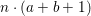 $n\cdot (a+b+1)$ terms containing
$n\cdot (a+b+1)$ terms containing ![]() $z_{1}^{a+b}$ for
$z_{1}^{a+b}$ for ![]() $i<n$. Collecting all the terms with the same monomial
$i<n$. Collecting all the terms with the same monomial ![]() $z_{1}^{a+b}$, we get
$z_{1}^{a+b}$, we get ![]() $n$ convergent power series of the form
$n$ convergent power series of the form ![]() $\sum _{l}{\it\gamma}_{l}{\it\delta}^{l}$, which tend to
$\sum _{l}{\it\gamma}_{l}{\it\delta}^{l}$, which tend to ![]() $0$ as
$0$ as ![]() ${\it\delta}_{1}$ tends to
${\it\delta}_{1}$ tends to ![]() $0$. Hence,
$0$. Hence, ![]() ${\it\delta}_{1}$ and
${\it\delta}_{1}$ and ![]() ${\it\delta}_{2}<1$ can be chosen small and independent of
${\it\delta}_{2}<1$ can be chosen small and independent of ![]() $L$. The argument for the series
$L$. The argument for the series 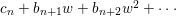 $c_{n}+b_{n+1}w+b_{n+2}w^{2}+\cdots \,$ is similar but more complicated. In this case we get a convergent power series in variables
$c_{n}+b_{n+1}w+b_{n+2}w^{2}+\cdots \,$ is similar but more complicated. In this case we get a convergent power series in variables ![]() ${\it\delta}_{1},{\it\delta}_{2}$ of the form
${\it\delta}_{1},{\it\delta}_{2}$ of the form 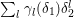 $\sum _{l}{\it\gamma}_{l}({\it\delta}_{1}){\it\delta}_{2}^{l}$, where
$\sum _{l}{\it\gamma}_{l}({\it\delta}_{1}){\it\delta}_{2}^{l}$, where ![]() ${\it\gamma}_{l}$ is a convergent power series in
${\it\gamma}_{l}$ is a convergent power series in ![]() ${\it\delta}_{1}$. Hence, a similar argument shows that
${\it\delta}_{1}$. Hence, a similar argument shows that 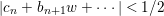 $|c_{n}+b_{n+1}w+\cdots |<1/2$ when
$|c_{n}+b_{n+1}w+\cdots |<1/2$ when 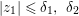 $|z_{1}|\leqslant {\it\delta}_{1},~{\it\delta}_{2}$ are sufficiently small (independent of
$|z_{1}|\leqslant {\it\delta}_{1},~{\it\delta}_{2}$ are sufficiently small (independent of ![]() $L$).
$L$).
Now, as in the proof when dim ![]() $V=1$, we prove that the image of any Euclidean neighborhood of
$V=1$, we prove that the image of any Euclidean neighborhood of ![]() $O$ in
$O$ in ![]() $W$ contains a Euclidean neighborhood of
$W$ contains a Euclidean neighborhood of ![]() $O$ in
$O$ in ![]() $V$.
$V$.
As before, let 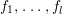 $f_{1},\ldots ,f_{l}$ be the equations defining
$f_{1},\ldots ,f_{l}$ be the equations defining ![]() $W$.
$W$.
Let ![]() $J_{i}$ be the ideal generated by all the
$J_{i}$ be the ideal generated by all the ![]() $a_{i{\it\alpha}}$ in
$a_{i{\it\alpha}}$ in ![]() ${\mathcal{O}}_{V,p}$. We consider a prime ideal
${\mathcal{O}}_{V,p}$. We consider a prime ideal ![]() $\mathfrak{p}$ which defines an irreducible curve
$\mathfrak{p}$ which defines an irreducible curve ![]() $C$ in
$C$ in ![]() $V$ which is an irreducible component of a hyperplane section of
$V$ which is an irreducible component of a hyperplane section of ![]() $V$. It suffices to show that there is an
$V$. It suffices to show that there is an ![]() ${\it\epsilon}>0$ such that for every such curve
${\it\epsilon}>0$ such that for every such curve ![]() $C$ there is an
$C$ there is an ![]() ${\it\epsilon}$-neighborhood of
${\it\epsilon}$-neighborhood of ![]() $p$ in
$p$ in ![]() $C$ which is contained in the image of
$C$ which is contained in the image of ![]() ${\it\pi}$.
${\it\pi}$.
For the application of Rouché’s theorem, we use ![]() $f:=f_{1}$ below, write
$f:=f_{1}$ below, write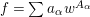 $f=\sum a_{{\it\alpha}}w^{A_{{\it\alpha}}}$, and assume that
$f=\sum a_{{\it\alpha}}w^{A_{{\it\alpha}}}$, and assume that ![]() $f|_{L}$ is not identically zero for every
$f|_{L}$ is not identically zero for every ![]() $L$.
$L$.
By Lemma 1.3, the extension 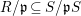 $R/\mathfrak{p}\subseteq S/\mathfrak{p}S$ is also pure.
$R/\mathfrak{p}\subseteq S/\mathfrak{p}S$ is also pure.
Again, first consider the case when ![]() $R/\mathfrak{p}$ is smooth. As before, we can assume that
$R/\mathfrak{p}$ is smooth. As before, we can assume that 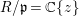 $R/\mathfrak{p}=\mathbb{C}\{z\}$.
$R/\mathfrak{p}=\mathbb{C}\{z\}$.
The functions ![]() $|a_{i{\it\alpha}}|_{C}$ have the same upper bound as
$|a_{i{\it\alpha}}|_{C}$ have the same upper bound as ![]() $|a_{i{\it\alpha}}|$ on
$|a_{i{\it\alpha}}|$ on ![]() $V$. It is possible that for some such
$V$. It is possible that for some such ![]() $C$ and an
$C$ and an ![]() $i$ all
$i$ all ![]() $a_{i{\it\alpha}}\in \mathfrak{p}$. Such an
$a_{i{\it\alpha}}\in \mathfrak{p}$. Such an ![]() $f_{i}$ can be ignored for the consideration that follows.
$f_{i}$ can be ignored for the consideration that follows.
We now consider only those ![]() $C$ for which
$C$ for which ![]() $a_{i{\it\alpha}}|_{C}$ are not all identically zero.
$a_{i{\it\alpha}}|_{C}$ are not all identically zero.
Now, ![]() $J_{i}\not \subset \mathfrak{p}$. As above, let
$J_{i}\not \subset \mathfrak{p}$. As above, let ![]() $e_{i}$ be the
$e_{i}$ be the ![]() $z$-order of
$z$-order of ![]() $\overline{f_{i}}$.
$\overline{f_{i}}$.
Claim. For any ![]() $\mathfrak{p}$ such that
$\mathfrak{p}$ such that ![]() $J_{i}\not \subset \mathfrak{p}$, the set of integers
$J_{i}\not \subset \mathfrak{p}$, the set of integers ![]() $e_{i}$ as
$e_{i}$ as ![]() $L$ varies is finite.
$L$ varies is finite.
This follows using the primary decomposition of ![]() $J_{i}$, and the hypothesis that dim
$J_{i}$, and the hypothesis that dim ![]() $V=2$.
$V=2$.
Now, 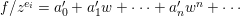 $f/z^{e_{i}}=a_{0}^{\prime }+a_{1}^{\prime }w+\cdots +a_{n}^{\prime }w^{n}+\cdots \,$, where
$f/z^{e_{i}}=a_{0}^{\prime }+a_{1}^{\prime }w+\cdots +a_{n}^{\prime }w^{n}+\cdots \,$, where ![]() $a_{n}^{\prime }$ is a unit, and no
$a_{n}^{\prime }$ is a unit, and no ![]() $a_{i}^{\prime }$ is a unit for
$a_{i}^{\prime }$ is a unit for ![]() $i<n$. The set of integers
$i<n$. The set of integers ![]() $e_{i},n_{L}$ is bounded above.
$e_{i},n_{L}$ is bounded above.
Hence, given any ![]() ${\it\eta}>0$, we can find a
${\it\eta}>0$, we can find a ![]() ${\it\delta}$ such that whenever
${\it\delta}$ such that whenever ![]() $|z_{i}|\leqslant {\it\delta}$, we have
$|z_{i}|\leqslant {\it\delta}$, we have 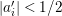 $|a_{i}^{\prime }|<1/2$ for
$|a_{i}^{\prime }|<1/2$ for ![]() $i<n$, and this for all
$i<n$, and this for all ![]() $L$. Similarly,
$L$. Similarly, 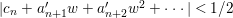 $|c_{n}+a_{n+1}^{\prime }w+a_{n+2}^{\prime }w^{2}+\cdots |<1/2$ if
$|c_{n}+a_{n+1}^{\prime }w+a_{n+2}^{\prime }w^{2}+\cdots |<1/2$ if 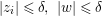 $|z_{i}|\leqslant {\it\delta},~|w|\leqslant {\it\delta}$ for all
$|z_{i}|\leqslant {\it\delta},~|w|\leqslant {\it\delta}$ for all ![]() $L$. Therefore, in the application of Rouché’s theorem there is a uniform upper bound on the absolute value of at least one
$L$. Therefore, in the application of Rouché’s theorem there is a uniform upper bound on the absolute value of at least one ![]() $w$ corresponding to any
$w$ corresponding to any  $(z)\in U_{1}$.
$(z)\in U_{1}$.
Now the proof is similar to the case when dim ![]() $R=1$, and
$R=1$, and ![]() $R$ is smooth.
$R$ is smooth.
A similar proof to that above works when dim  $R/\mathfrak{p}=1$, and
$R/\mathfrak{p}=1$, and ![]() $R/\mathfrak{p}$ is singular.
$R/\mathfrak{p}$ is singular.
Case 3.2. Now, let dim ![]() $V>2$.
$V>2$.
We again consider the ideals ![]() $J_{i}$ and irreducible components
$J_{i}$ and irreducible components ![]() $C$ of
$C$ of ![]() $1$-dimensional sections of
$1$-dimensional sections of ![]() $V$ with corresponding local ring
$V$ with corresponding local ring ![]() $R/\mathfrak{p}$. If some
$R/\mathfrak{p}$. If some ![]() $f_{i}\in \mathfrak{p}$, with the notation above, then such an
$f_{i}\in \mathfrak{p}$, with the notation above, then such an ![]() $f_{i}$ can be ignored for the consideration that follows. If there is a
$f_{i}$ can be ignored for the consideration that follows. If there is a ![]() $\mathfrak{p}$ which contains all
$\mathfrak{p}$ which contains all ![]() $J_{i}$, then every point in the curve
$J_{i}$, then every point in the curve ![]() $C$ is in the image of
$C$ is in the image of ![]() ${\it\pi}$.
${\it\pi}$.
Now, assume that not all ![]() $f_{i}\in \mathfrak{p}$. The proof is the same as in the two-dimensional case. (The proof of the claim is also not difficult.)
$f_{i}\in \mathfrak{p}$. The proof is the same as in the two-dimensional case. (The proof of the claim is also not difficult.)
We leave the details to the reader.
This completes the proof of Theorem 3.5.
Remark.
In Section 5, we give an example of a graded morphism  $\mathbb{C}^{2}~\rightarrow ~\mathbb{C}^{2}$, such that the image of any neighborhood of the origin in the domain contains a neighborhood of the origin in the range (which easily implies the surjectivity of the induced map at germ level), but the morphism is not pure. This shows that the converse of Theorem 3.5 is false.
$\mathbb{C}^{2}~\rightarrow ~\mathbb{C}^{2}$, such that the image of any neighborhood of the origin in the domain contains a neighborhood of the origin in the range (which easily implies the surjectivity of the induced map at germ level), but the morphism is not pure. This shows that the converse of Theorem 3.5 is false.
Theorem 3.5 has an interesting corollary. There exist convergent power series 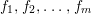 $f_{1},f_{2},\ldots ,f_{m}$ in variables
$f_{1},f_{2},\ldots ,f_{m}$ in variables 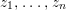 $z_{1},\ldots ,z_{n}$ with
$z_{1},\ldots ,z_{n}$ with ![]() $m>n$ such that there is no convergent power series relation between the
$m>n$ such that there is no convergent power series relation between the ![]() $f_{i}$, but there is a formal power series relation between them [Reference Gabrièlov4]. This gives an inclusion
$f_{i}$, but there is a formal power series relation between them [Reference Gabrièlov4]. This gives an inclusion 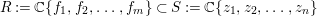 $R:=\mathbb{C}\{f_{1},f_{2},\ldots ,f_{m}\}\subset S:=\mathbb{C}\{z_{1},z_{2},\ldots ,z_{n}\}$.
$R:=\mathbb{C}\{f_{1},f_{2},\ldots ,f_{m}\}\subset S:=\mathbb{C}\{z_{1},z_{2},\ldots ,z_{n}\}$.
Corollary 3.5.2. Any inclusion ![]() $R\subseteq S$ of local analytic domains such that dim
$R\subseteq S$ of local analytic domains such that dim![]() $~R>$ dim
$~R>$ dim![]() $~S$ is not pure.
$~S$ is not pure.
Proof. Suppose that this is a pure extension. By Theorem 3.5, the image of the corresponding analytic map, say 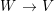 $W~\rightarrow ~V$, contains a nonempty open subset
$W~\rightarrow ~V$, contains a nonempty open subset ![]() $U$ of
$U$ of ![]() $V$. By Sard’s theorem, the inverse image of a general point of
$V$. By Sard’s theorem, the inverse image of a general point of ![]() $U$ is a nonempty smooth subvariety of
$U$ is a nonempty smooth subvariety of ![]() $W$. This is a contradiction, since dim
$W$. This is a contradiction, since dim ![]() $W<$ dim
$W<$ dim ![]() $V$.◻
$V$.◻
4 Some positive results in special cases
Coming back to the quasi-finiteness question raised in Section 1, we will see in Section 5 that even a pure morphism of affine planes need not be quasi-finite. However, the result is true for subalgebras generated by monomials.
Theorem 4.1. Let ![]() $A$ be a subring of
$A$ be a subring of 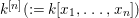 $k^{[n]}(:=k[x_{1},\ldots ,x_{n}])$, generated by the monomials
$k^{[n]}(:=k[x_{1},\ldots ,x_{n}])$, generated by the monomials 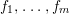 $f_{1},\ldots ,f_{m}$. Suppose that the induced morphism
$f_{1},\ldots ,f_{m}$. Suppose that the induced morphism 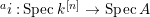 $^{a}i:\text{Spec}\,k^{[n]}~\rightarrow ~\text{Spec}\,A$ is generically quasi-finite. Then
$^{a}i:\text{Spec}\,k^{[n]}~\rightarrow ~\text{Spec}\,A$ is generically quasi-finite. Then 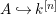 $A{\hookrightarrow}k^{[n]}$ is pure if and only if
$A{\hookrightarrow}k^{[n]}$ is pure if and only if ![]() $A$ is normal, and the powers
$A$ is normal, and the powers 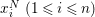 $x_{i}^{N}~(1\leqslant i\leqslant n)$ are contained in
$x_{i}^{N}~(1\leqslant i\leqslant n)$ are contained in ![]() $A$ for some integer
$A$ for some integer ![]() $N>0$. In particular,
$N>0$. In particular, ![]() $k^{[n]}$ is integral over
$k^{[n]}$ is integral over ![]() $A$ if
$A$ if 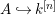 $A{\hookrightarrow}k^{[n]}$ is a pure embedding.
$A{\hookrightarrow}k^{[n]}$ is a pure embedding.
Proof. First, suppose that  $A{\hookrightarrow}k^{[n]}$ is a pure embedding. Then
$A{\hookrightarrow}k^{[n]}$ is a pure embedding. Then ![]() $A$ is also a normal domain. Let
$A$ is also a normal domain. Let 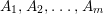 $A_{1},A_{2},\ldots ,A_{m}$ be the
$A_{1},A_{2},\ldots ,A_{m}$ be the ![]() $n$-tuples of exponents corresponding to
$n$-tuples of exponents corresponding to 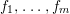 $f_{1},\ldots ,f_{m}$; namely,
$f_{1},\ldots ,f_{m}$; namely, 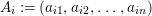 $A_{i}:=(a_{i1},a_{i2},\ldots ,a_{in})$ when
$A_{i}:=(a_{i1},a_{i2},\ldots ,a_{in})$ when 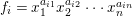 $f_{i}=x_{1}^{a_{i1}}x_{2}^{a_{i2}}\cdots x_{n}^{a_{in}}$. Since
$f_{i}=x_{1}^{a_{i1}}x_{2}^{a_{i2}}\cdots x_{n}^{a_{in}}$. Since ![]() $^{a}i$ is generically quasi-finite, the
$^{a}i$ is generically quasi-finite, the ![]() $m\times n$-matrix
$m\times n$-matrix ![]() $A$, whose row vectors are
$A$, whose row vectors are  $A_{1},\ldots ,A_{m}$, has rank
$A_{1},\ldots ,A_{m}$, has rank ![]() $n$. After reindexing, if required, we may assume that
$n$. After reindexing, if required, we may assume that  $A_{1},\ldots ,A_{n}$ are
$A_{1},\ldots ,A_{n}$ are ![]() $Q$-independent. Hence, they have maximal rank in the
$Q$-independent. Hence, they have maximal rank in the ![]() $Q$-vector space generated by
$Q$-vector space generated by 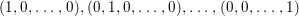 $(1,0,\ldots ,0),(0,1,0,\ldots ,0),\ldots ,(0,0,\ldots ,1)$. Then, for some integer
$(1,0,\ldots ,0),(0,1,0,\ldots ,0),\ldots ,(0,0,\ldots ,1)$. Then, for some integer ![]() $r>0$,
$r>0$, 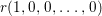 $r(1,0,0,\ldots ,0)$ lies in the abelian subgroup generated by
$r(1,0,0,\ldots ,0)$ lies in the abelian subgroup generated by 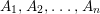 $A_{1},A_{2},\ldots ,A_{n}$. After a change of indices, we can write
$A_{1},A_{2},\ldots ,A_{n}$. After a change of indices, we can write
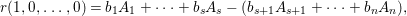 $$\begin{eqnarray}r(1,0,\ldots ,0)=b_{1}A_{1}+\cdots +b_{s}A_{s}-(b_{s+1}A_{s+1}+\cdots +b_{n}A_{n}),\end{eqnarray}$$
$$\begin{eqnarray}r(1,0,\ldots ,0)=b_{1}A_{1}+\cdots +b_{s}A_{s}-(b_{s+1}A_{s+1}+\cdots +b_{n}A_{n}),\end{eqnarray}$$ where each ![]() $b_{i}$ is nonnegative. This means that
$b_{i}$ is nonnegative. This means that
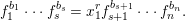 $$\begin{eqnarray}f_{1}^{b_{1}}\cdots f_{s}^{b_{s}}=x_{1}^{r}f_{s+1}^{b_{s+1}}\cdots f_{n}^{b_{n}}.\end{eqnarray}$$
$$\begin{eqnarray}f_{1}^{b_{1}}\cdots f_{s}^{b_{s}}=x_{1}^{r}f_{s+1}^{b_{s+1}}\cdots f_{n}^{b_{n}}.\end{eqnarray}$$ Since ![]() $A$ is a pure subring of the integral domain
$A$ is a pure subring of the integral domain ![]() $k^{[n]}$, it follows from Lemma 1.1(2) that
$k^{[n]}$, it follows from Lemma 1.1(2) that ![]() $x_{1}^{r}\in A$, and similarly for
$x_{1}^{r}\in A$, and similarly for 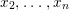 $x_{2},\ldots ,x_{n}$. Hence, the powers
$x_{2},\ldots ,x_{n}$. Hence, the powers ![]() $x_{i}^{N}$ are in
$x_{i}^{N}$ are in ![]() $A$ for some
$A$ for some ![]() $N>0$.
$N>0$.
The converse follows from Lemma 1.6. ◻
Generalizing Theorem 4.1, we can then ask whether the following conditions are equivalent.
Question 4.2. Let ![]() $A$ be a subring of
$A$ be a subring of ![]() $k^{[n]}$, generated by the homogeneous polynomials
$k^{[n]}$, generated by the homogeneous polynomials 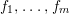 $f_{1},\ldots ,f_{m}$. Suppose that
$f_{1},\ldots ,f_{m}$. Suppose that ![]() $A$ is normal, and the induced morphism
$A$ is normal, and the induced morphism 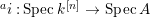 $^{a}i:\text{Spec}\,k^{[n]}~\rightarrow ~\text{Spec}\,A$ is generically quasi-finite. We want to investigate the equivalence of the following three statements.
$^{a}i:\text{Spec}\,k^{[n]}~\rightarrow ~\text{Spec}\,A$ is generically quasi-finite. We want to investigate the equivalence of the following three statements.
(1)
 $A{\hookrightarrow}k^{[n]}$ is a pure embedding.
$A{\hookrightarrow}k^{[n]}$ is a pure embedding.(2) The morphism
 $^{a}i$ is quasi-finite and surjective.
$^{a}i$ is quasi-finite and surjective.(3) The polynomial ring
 $k^{[n]}$ is integral over
$k^{[n]}$ is integral over  $A$.
$A$.
We know that any finite morphism is quasi-finite and surjective. Since ![]() $A$ is normal, by Lemma 1.6, any surjective and quasi-finite morphism must be pure. Again, it is not difficult to see that any quasi-finite, graded morphism is actually finite. Therefore, the question that remains open is whether a polynomial ring is quasi-finite over a graded, pure subring of the same dimension with induced grading.
$A$ is normal, by Lemma 1.6, any surjective and quasi-finite morphism must be pure. Again, it is not difficult to see that any quasi-finite, graded morphism is actually finite. Therefore, the question that remains open is whether a polynomial ring is quasi-finite over a graded, pure subring of the same dimension with induced grading.
Let ![]() $A{\hookrightarrow}B$ be an inclusion of affine domains over
$A{\hookrightarrow}B$ be an inclusion of affine domains over ![]() $k$. In order to approach the question of quasi-finiteness raised in the introduction, we construct the unique subalgebra
$k$. In order to approach the question of quasi-finiteness raised in the introduction, we construct the unique subalgebra ![]() $C$ of
$C$ of ![]() $B$, containing
$B$, containing ![]() $A$, and satisfying the following properties.
$A$, and satisfying the following properties.
(1) The morphism
 $\text{Spec}\,C\rightarrow \text{Spec}\,A$, induced by the inclusion
$\text{Spec}\,C\rightarrow \text{Spec}\,A$, induced by the inclusion  $A{\hookrightarrow}C$, is a quasi-finite surjective morphism.
$A{\hookrightarrow}C$, is a quasi-finite surjective morphism.(2)
 $C$ is an affine domain over
$C$ is an affine domain over  $k$.
$k$.(3) If
 $C^{\prime }\subset B$ is an affine domain over
$C^{\prime }\subset B$ is an affine domain over  $k$ such that
$k$ such that  $A{\hookrightarrow}C^{\prime }$, and the induced morphism
$A{\hookrightarrow}C^{\prime }$, and the induced morphism  $\text{Spec}\,C^{\prime }\rightarrow \text{Spec}\,A$ is quasi-finite and surjective, then
$\text{Spec}\,C^{\prime }\rightarrow \text{Spec}\,A$ is quasi-finite and surjective, then  $C^{\prime }\subseteq C$.
$C^{\prime }\subseteq C$.
We call ![]() $C$ the quasi-finite closure of
$C$ the quasi-finite closure of ![]() $A$ in
$A$ in ![]() $B$.
$B$.
Theorem 4.3. Suppose that ![]() $\mathbb{Q}(B)$ is an algebraic extension of
$\mathbb{Q}(B)$ is an algebraic extension of ![]() $\mathbb{Q}(A)$, and that the morphism
$\mathbb{Q}(A)$, and that the morphism 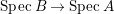 $\text{Spec}\,B\rightarrow \text{Spec}\,A$ is surjective. Further, assume that
$\text{Spec}\,B\rightarrow \text{Spec}\,A$ is surjective. Further, assume that ![]() $A,B$ are normal. Then the quasi-finite closure
$A,B$ are normal. Then the quasi-finite closure ![]() $C$ of
$C$ of ![]() $A$ in
$A$ in ![]() $B$ exists, and satisfies the following properties.
$B$ exists, and satisfies the following properties.
(1)
 $C$ is an integrally closed domain which is birationally equivalent to
$C$ is an integrally closed domain which is birationally equivalent to  $B$.
$B$.(2)
 $C$ is a pure extension of
$C$ is a pure extension of  $A$.
$A$.
Proof. (1) Let ![]() $C_{1}$ and
$C_{1}$ and ![]() $C_{2}$ be finitely generated
$C_{2}$ be finitely generated ![]() $k$-subalgebras of
$k$-subalgebras of ![]() $B$ containing
$B$ containing ![]() $A$, such that Spec
$A$, such that Spec ![]() $C_{i}\rightarrow$ Spec
$C_{i}\rightarrow$ Spec ![]() $A$ is quasi-finite and surjective for
$A$ is quasi-finite and surjective for ![]() $i=1,2$. Let
$i=1,2$. Let ![]() $C_{1}C_{2}$ be the
$C_{1}C_{2}$ be the ![]() $k$-subalgebra of
$k$-subalgebra of ![]() $B$ generated over
$B$ generated over ![]() $C_{1}$ by
$C_{1}$ by ![]() $C_{2}$. Any maximal ideal of
$C_{2}$. Any maximal ideal of ![]() $C_{1}C_{2}$ is generated by a pair of maximal ideals of
$C_{1}C_{2}$ is generated by a pair of maximal ideals of ![]() $C_{1},C_{2}$. This implies that
$C_{1},C_{2}$. This implies that 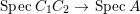 $\text{Spec}\,C_{1}C_{2}~\rightarrow ~\text{Spec}\,A$ is quasi-finite. It is also surjective since
$\text{Spec}\,C_{1}C_{2}~\rightarrow ~\text{Spec}\,A$ is quasi-finite. It is also surjective since  $\text{Spec}\,B~\rightarrow ~\text{Spec}\,A$ is surjective.
$\text{Spec}\,B~\rightarrow ~\text{Spec}\,A$ is surjective.
Now, let ![]() $C$ be the
$C$ be the ![]() $k$-subalgebra of
$k$-subalgebra of ![]() $B$ generated by all finitely generated
$B$ generated by all finitely generated ![]() $k$-subalgebras
$k$-subalgebras ![]() $C_{i}$ of
$C_{i}$ of ![]() $B$ containing
$B$ containing ![]() $A$, such that
$A$, such that 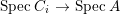 $\text{Spec}\,C_{i}~\rightarrow ~\text{Spec}\,A$ is a quasi-finite, surjective morphism.
$\text{Spec}\,C_{i}~\rightarrow ~\text{Spec}\,A$ is a quasi-finite, surjective morphism.
Since the degree of the field extension  $\mathbb{Q}(B)/\mathbb{Q}(A)$ is finite, say
$\mathbb{Q}(B)/\mathbb{Q}(A)$ is finite, say ![]() $d$, the degree of the extension
$d$, the degree of the extension 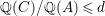 $\mathbb{Q}(C)/\mathbb{Q}(A)\leqslant d$. Since the normalization of
$\mathbb{Q}(C)/\mathbb{Q}(A)\leqslant d$. Since the normalization of ![]() $C_{i}$ in the quotient field of
$C_{i}$ in the quotient field of ![]() $B$ is finite and surjective over
$B$ is finite and surjective over ![]() $C_{i}$, we can assume that each
$C_{i}$, we can assume that each ![]() $C_{i}$ is normal and birational with
$C_{i}$ is normal and birational with ![]() $B$. By considering the rings
$B$. By considering the rings  $C_{1},C_{1}\cdot C_{2},C_{1}\cdot C_{2}\cdot C_{3},\ldots$ and their normalizations in their quotient field
$C_{1},C_{1}\cdot C_{2},C_{1}\cdot C_{2}\cdot C_{3},\ldots$ and their normalizations in their quotient field ![]() $\mathbb{Q}(B)$, we can assume that
$\mathbb{Q}(B)$, we can assume that  $C_{1}\subseteq C_{2}\subseteq C_{3}\subseteq \cdots \,$ are all quasi-finite extensions. This gives an increasing union of normal birational affine domains
$C_{1}\subseteq C_{2}\subseteq C_{3}\subseteq \cdots \,$ are all quasi-finite extensions. This gives an increasing union of normal birational affine domains  $R_{1}\subseteq R_{2}\subseteq \cdots \,$, which are quasi-finite extensions of
$R_{1}\subseteq R_{2}\subseteq \cdots \,$, which are quasi-finite extensions of ![]() $A$. It follows that every
$A$. It follows that every 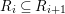 $R_{i}\subseteq R_{i+1}$ is also quasi-finite. By Zariski’s main theorem, these inclusions induce open embeddings of corresponding affine schemes. Each
$R_{i}\subseteq R_{i+1}$ is also quasi-finite. By Zariski’s main theorem, these inclusions induce open embeddings of corresponding affine schemes. Each ![]() $R_{i}\subseteq B$ is birational. Therefore, we can find a suitable hypersurface section
$R_{i}\subseteq B$ is birational. Therefore, we can find a suitable hypersurface section ![]() $H$ of
$H$ of ![]() $\text{Spec}\,B$ defined by
$\text{Spec}\,B$ defined by ![]() $\{h=0\}$ such that
$\{h=0\}$ such that 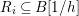 $R_{i}\subseteq B[1/h]$ for each
$R_{i}\subseteq B[1/h]$ for each ![]() $i$ (this is obvious), and
$i$ (this is obvious), and  $\text{Spec}\,B\setminus H$ is an affine variety contained in each
$\text{Spec}\,B\setminus H$ is an affine variety contained in each  $\text{Spec}\,R_{i}$. This implies that the sequence
$\text{Spec}\,R_{i}$. This implies that the sequence  $\text{Spec}\,R_{i}$ is constant for
$\text{Spec}\,R_{i}$ is constant for ![]() $i\gg 0$. This proves that
$i\gg 0$. This proves that ![]() $C$ is an affine domain.
$C$ is an affine domain.
Let ![]() $b$ be any element of
$b$ be any element of ![]() $B$. Since
$B$. Since ![]() $\mathbb{Q}(B)$ is algebraic over
$\mathbb{Q}(B)$ is algebraic over ![]() $\mathbb{Q}(A)$, there exists a nonzero element
$\mathbb{Q}(A)$, there exists a nonzero element ![]() $a\in A$ such that
$a\in A$ such that ![]() $ab$ is integral over
$ab$ is integral over ![]() $A$. Then
$A$. Then ![]() $A[ab]$, which is a
$A[ab]$, which is a ![]() $k$-subalgebra generated by
$k$-subalgebra generated by ![]() $ab$ over
$ab$ over ![]() $A$, is contained in
$A$, is contained in ![]() $C$ because
$C$ because 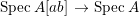 $\text{Spec}\,A[ab]~\rightarrow ~\text{Spec}\,A$ is a finite morphism. Hence,
$\text{Spec}\,A[ab]~\rightarrow ~\text{Spec}\,A$ is a finite morphism. Hence, 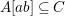 $A[ab]\subseteq C$. This implies that
$A[ab]\subseteq C$. This implies that 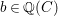 $b\in \mathbb{Q}(C)$, and hence
$b\in \mathbb{Q}(C)$, and hence 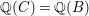 $\mathbb{Q}(C)=\mathbb{Q}(B)$. If
$\mathbb{Q}(C)=\mathbb{Q}(B)$. If ![]() $b$ is an integral element of
$b$ is an integral element of ![]() $B$ over
$B$ over ![]() $C$, then
$C$, then ![]() $C[b]$ is a
$C[b]$ is a ![]() $k$-subalgebra of
$k$-subalgebra of ![]() $B$, such that
$B$, such that 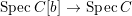 $\text{Spec}\,C[b]~\rightarrow ~\text{Spec}\,C$ is a finite morphism. Hence,
$\text{Spec}\,C[b]~\rightarrow ~\text{Spec}\,C$ is a finite morphism. Hence, 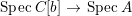 $\text{Spec}\,C[b]~\rightarrow ~\text{Spec}\,A$ is a quasi-finite surjective morphism. Hence,
$\text{Spec}\,C[b]~\rightarrow ~\text{Spec}\,A$ is a quasi-finite surjective morphism. Hence,  $C[b]=C$, implying that
$C[b]=C$, implying that ![]() $b\in C$.
$b\in C$.
(2) This follows from the quasi-finiteness of 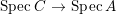 $\text{Spec}\,C~\rightarrow ~\text{Spec}\,A$.◻
$\text{Spec}\,C~\rightarrow ~\text{Spec}\,A$.◻
With the notation as in Theorem 4.3, set ![]() $Y:=$ Spec
$Y:=$ Spec 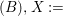 $(B),X:=$ Spec
$(B),X:=$ Spec ![]() $(A)$, and
$(A)$, and 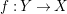 $f:Y\rightarrow X$ is the morphism induced by the inclusion
$f:Y\rightarrow X$ is the morphism induced by the inclusion ![]() $A{\hookrightarrow}B$. We assume that
$A{\hookrightarrow}B$. We assume that ![]() $A$ and
$A$ and ![]() $B$ are normal. Let
$B$ are normal. Let ![]() $F$ be the closed set of
$F$ be the closed set of ![]() $X$ consisting of the points
$X$ consisting of the points ![]() $x$, such that
$x$, such that ![]() $f^{-1}(x)$ contains an irreducible component of positive dimension. Let
$f^{-1}(x)$ contains an irreducible component of positive dimension. Let ![]() ${\rm\Delta}$ be the union of all irreducible components of codimension one in
${\rm\Delta}$ be the union of all irreducible components of codimension one in ![]() $f^{-1}(F)$, and let
$f^{-1}(F)$, and let 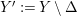 $Y^{\prime }:=Y\setminus {\rm\Delta}$. Then
$Y^{\prime }:=Y\setminus {\rm\Delta}$. Then ![]() $Y^{\prime }$ is an affine scheme
$Y^{\prime }$ is an affine scheme 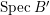 $\text{Spec}\,B^{\prime }$, where
$\text{Spec}\,B^{\prime }$, where ![]() $B^{\prime }$ is the ideal quotient
$B^{\prime }$ is the ideal quotient 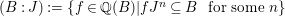 $(B:J):=\{f\in \mathbb{Q}(B)|fJ^{n}\subseteq B~\text{ for some }n\}$, where
$(B:J):=\{f\in \mathbb{Q}(B)|fJ^{n}\subseteq B~\text{ for some }n\}$, where ![]() $J$ is the defining ideal of
$J$ is the defining ideal of ![]() ${\rm\Delta}$. In fact, since
${\rm\Delta}$. In fact, since ![]() $B$ is normal,
$B$ is normal, ![]() $B^{\prime }$ is the intersection of
$B^{\prime }$ is the intersection of ![]() $B_{\mathfrak{q}}$, where
$B_{\mathfrak{q}}$, where ![]() $\mathfrak{q}$ ranges over all prime ideals of height one of
$\mathfrak{q}$ ranges over all prime ideals of height one of ![]() $B$ such that
$B$ such that 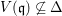 $V(\mathfrak{q})\not \subseteq {\rm\Delta}$. We prove the following result.
$V(\mathfrak{q})\not \subseteq {\rm\Delta}$. We prove the following result.
Theorem 4.4. Let the notations and assumptions be the same as in Theorem 4.3 and as above. Suppose that ![]() $C$ is finitely generated over
$C$ is finitely generated over ![]() $k$. Then
$k$. Then ![]() $Y^{\prime }$ is an open set of
$Y^{\prime }$ is an open set of ![]() $\text{Spec}\,C$, and the restriction
$\text{Spec}\,C$, and the restriction 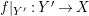 $f|_{Y^{\prime }}:Y^{\prime }\rightarrow X$ is almost surjective, that is, the image
$f|_{Y^{\prime }}:Y^{\prime }\rightarrow X$ is almost surjective, that is, the image ![]() $f(Y^{\prime })$ contains all codimension one points of
$f(Y^{\prime })$ contains all codimension one points of ![]() $X$.
$X$.
Proof. Let ![]() $\mathfrak{p}$ be a prime ideal of height 1 of
$\mathfrak{p}$ be a prime ideal of height 1 of ![]() $A$. Since
$A$. Since 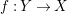 $f:Y\rightarrow X$ is surjective, there exists a prime ideal
$f:Y\rightarrow X$ is surjective, there exists a prime ideal ![]() $\mathfrak{q}$ of
$\mathfrak{q}$ of ![]() $B$ such that
$B$ such that 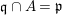 $\mathfrak{q}\cap A=\mathfrak{p}$. Then
$\mathfrak{q}\cap A=\mathfrak{p}$. Then ![]() $\mathfrak{q}$ has height 1. In fact, let
$\mathfrak{q}$ has height 1. In fact, let 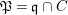 $\mathfrak{P}=\mathfrak{q}\cap C$. Since Spec
$\mathfrak{P}=\mathfrak{q}\cap C$. Since Spec ![]() $(C)\rightarrow$ Spec
$(C)\rightarrow$ Spec ![]() $(A)$ is a quasi-finite morphism,
$(A)$ is a quasi-finite morphism, ![]() $\mathfrak{P}$ has height 1. Note that
$\mathfrak{P}$ has height 1. Note that ![]() $B$ and
$B$ and ![]() $C$ are birational, and
$C$ are birational, and ![]() $B_{\mathfrak{q}}$ dominates
$B_{\mathfrak{q}}$ dominates ![]() $C_{\mathfrak{P}}$. Since
$C_{\mathfrak{P}}$. Since ![]() $C_{\mathfrak{P}}$ is a discrete valuation ring, we have
$C_{\mathfrak{P}}$ is a discrete valuation ring, we have 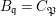 $B_{\mathfrak{q}}=C_{\mathfrak{P}}$. Note that, if
$B_{\mathfrak{q}}=C_{\mathfrak{P}}$. Note that, if ![]() $\mathfrak{p}$ ranges over all prime ideals of height 1 in
$\mathfrak{p}$ ranges over all prime ideals of height 1 in ![]() $A$, then
$A$, then ![]() $\mathfrak{q}$, lying over
$\mathfrak{q}$, lying over ![]() $\mathfrak{p}$, will range over all prime ideals of height 1 in
$\mathfrak{p}$, will range over all prime ideals of height 1 in ![]() $B$ such that
$B$ such that 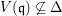 $V(\mathfrak{q})\not \subseteq {\rm\Delta}$. Therefore, the open set
$V(\mathfrak{q})\not \subseteq {\rm\Delta}$. Therefore, the open set ![]() $Y^{\prime }$ is contained in Spec
$Y^{\prime }$ is contained in Spec ![]() $(C)$. The above argument shows that
$(C)$. The above argument shows that ![]() $f|_{Y^{\prime }}$ is almost surjective.◻
$f|_{Y^{\prime }}$ is almost surjective.◻
Let ![]() $S$ be the polynomial ring in
$S$ be the polynomial ring in ![]() $n$-variables over
$n$-variables over ![]() $k$, and let
$k$, and let ![]() $G$ be a reductive algebraic subgroup of
$G$ be a reductive algebraic subgroup of 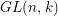 $GL(n,k)$, acting naturally on
$GL(n,k)$, acting naturally on ![]() $S$. Then the ring of invariants
$S$. Then the ring of invariants 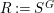 $R:=S^{G}$ is a graded subring of
$R:=S^{G}$ is a graded subring of ![]() $S$. Let
$S$. Let ![]() $\mathfrak{m},\mathfrak{n}$ be the irrelevant maximal ideals of
$\mathfrak{m},\mathfrak{n}$ be the irrelevant maximal ideals of ![]() $R,S$ respectively.
$R,S$ respectively.
The next result may be well known to the experts.
Proposition 4.5. ![]() $R_{\mathfrak{m}}$ is a pure subring of
$R_{\mathfrak{m}}$ is a pure subring of ![]() $S_{\mathfrak{n}}$.
$S_{\mathfrak{n}}$.
Proof. The Reynold’s operator sends ![]() $f\in S$ to
$f\in S$ to ![]() $f_{0}\in R$ by a suitable integration over a maximal compact subgroup
$f_{0}\in R$ by a suitable integration over a maximal compact subgroup ![]() $K$ of
$K$ of ![]() $G$. An element
$G$. An element ![]() $f\in S$ vanishes at the origin if and only if
$f\in S$ vanishes at the origin if and only if ![]() $f_{0}$ vanishes at the vertex in
$f_{0}$ vanishes at the vertex in ![]() $\text{Spec}\,R$. Any element in
$\text{Spec}\,R$. Any element in ![]() $S_{\mathfrak{n}}$ is of the form
$S_{\mathfrak{n}}$ is of the form ![]() $f/g$, where
$f/g$, where ![]() $f,g$ have no common factor, and
$f,g$ have no common factor, and ![]() $g$ does not vanish at the origin. Since
$g$ does not vanish at the origin. Since ![]() $S$ has no nonconstant units, such a representation of an element of
$S$ has no nonconstant units, such a representation of an element of ![]() $S_{\mathfrak{n}}$ is unique up to a nonzero constant. Therefore, the Reynold’s operator can be uniquely extended to an
$S_{\mathfrak{n}}$ is unique up to a nonzero constant. Therefore, the Reynold’s operator can be uniquely extended to an ![]() $R_{\mathfrak{m}}$-module homomorphism of
$R_{\mathfrak{m}}$-module homomorphism of ![]() $S_{\mathfrak{n}}$ to
$S_{\mathfrak{n}}$ to ![]() $R_{\mathfrak{m}}$ by sending
$R_{\mathfrak{m}}$ by sending ![]() $f/g$ to
$f/g$ to ![]() $f_{0}/g_{0}$. This shows that
$f_{0}/g_{0}$. This shows that ![]() $R_{\mathfrak{m}}$ is a direct summand of
$R_{\mathfrak{m}}$ is a direct summand of ![]() $S_{\mathfrak{n}}$, and hence a pure subring.◻
$S_{\mathfrak{n}}$, and hence a pure subring.◻
5 Examples, and more observations on pure extensions
To start with, let us consider the following two morphisms of affine domains, which manifest the subtlety of pure extensions.
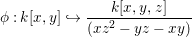 $$\begin{eqnarray}{\it\phi}:k[x,y]{\hookrightarrow}\frac{k[x,y,z]}{(xz^{2}-yz-xy)}\end{eqnarray}$$
$$\begin{eqnarray}{\it\phi}:k[x,y]{\hookrightarrow}\frac{k[x,y,z]}{(xz^{2}-yz-xy)}\end{eqnarray}$$and
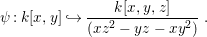 $$\begin{eqnarray}{\it\psi}:k[x,y]{\hookrightarrow}\frac{k[x,y,z]}{(xz^{2}-yz-xy^{2})}~.\end{eqnarray}$$
$$\begin{eqnarray}{\it\psi}:k[x,y]{\hookrightarrow}\frac{k[x,y,z]}{(xz^{2}-yz-xy^{2})}~.\end{eqnarray}$$ Then ![]() ${\it\phi}$ is not pure, but
${\it\phi}$ is not pure, but ![]() ${\it\psi}$ is pure.
${\it\psi}$ is pure.
Proof. To show that ![]() ${\it\phi}$ is not pure, look at the ideal
${\it\phi}$ is not pure, look at the ideal 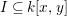 $I\subseteq k[x,y]$, generated by
$I\subseteq k[x,y]$, generated by ![]() $x^{4}$ and
$x^{4}$ and 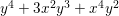 $y^{4}+3x^{2}y^{3}+x^{4}y^{2}$. Then
$y^{4}+3x^{2}y^{3}+x^{4}y^{2}$. Then 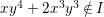 $xy^{4}+2x^{3}y^{3}\notin I$, whereas
$xy^{4}+2x^{3}y^{3}\notin I$, whereas 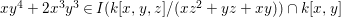 $xy^{4}+2x^{3}y^{3}\in I(k[x,y,z]/(xz^{2}+yz+xy))\cap k[x,y]$ because of the relation
$xy^{4}+2x^{3}y^{3}\in I(k[x,y,z]/(xz^{2}+yz+xy))\cap k[x,y]$ because of the relation
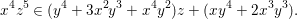 $$\begin{eqnarray}x^{4}z^{5}\in (y^{4}+3x^{2}y^{3}+x^{4}y^{2})z+(xy^{4}+2x^{3}y^{3}).\end{eqnarray}$$
$$\begin{eqnarray}x^{4}z^{5}\in (y^{4}+3x^{2}y^{3}+x^{4}y^{2})z+(xy^{4}+2x^{3}y^{3}).\end{eqnarray}$$ The relation is obtained by successive substitution 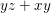 $yz+xy$ for
$yz+xy$ for ![]() $xz^{2}$. The purity of
$xz^{2}$. The purity of ![]() ${\it\psi}$, on the other hand, is a consequence of the following lemma.
${\it\psi}$, on the other hand, is a consequence of the following lemma.
Lemma 5.2. Let ![]() $f$ be a polynomial in
$f$ be a polynomial in ![]() $k[x,y]$, divisible by
$k[x,y]$, divisible by ![]() $y^{2}$. Then the map
$y^{2}$. Then the map
 $$\begin{eqnarray}{\rm\Psi}:k[x,y]\longrightarrow \frac{k[x,y,z]}{(xz^{2}+yz+f)}\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Psi}:k[x,y]\longrightarrow \frac{k[x,y,z]}{(xz^{2}+yz+f)}\end{eqnarray}$$is pure.
Proof. First, note that the associated morphism of schemes is surjective, since it is surjective on the closed points. Therefore, by local criteria for purity as in Lemma 1.3, it is sufficient to check that the induced local morphism over the origin
 $$\begin{eqnarray}{\rm\Psi}_{0}:k[x,y]_{(x,y)}\longrightarrow \frac{k[x,y,z]}{(xz^{2}+yz+f)}\otimes k[x,y]_{(x,y)}\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Psi}_{0}:k[x,y]_{(x,y)}\longrightarrow \frac{k[x,y,z]}{(xz^{2}+yz+f)}\otimes k[x,y]_{(x,y)}\end{eqnarray}$$is pure, as, over any point other than the origin, the morphism is quasi-finite, and hence is pure by Lemma 1.6. Again, in view of the observation that any partially pure point is pure, it suffices if we can show that the induced map
 $$\begin{eqnarray}{\rm\Psi}_{0}^{\prime }:k[x,y]_{(x,y)}\longrightarrow \Big(\frac{k[x,y,z]}{(xz^{2}+yz+f)}\Big)_{(x,y,z)}\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Psi}_{0}^{\prime }:k[x,y]_{(x,y)}\longrightarrow \Big(\frac{k[x,y,z]}{(xz^{2}+yz+f)}\Big)_{(x,y,z)}\end{eqnarray}$$ is pure. However, the polynomial  $xz^{2}+yz+f$, as a polynomial in
$xz^{2}+yz+f$, as a polynomial in ![]() $z$, has roots in
$z$, has roots in ![]() $k[[x,y]]$ since
$k[[x,y]]$ since ![]() $y^{2}|f$. Therefore, the corresponding map of completions
$y^{2}|f$. Therefore, the corresponding map of completions
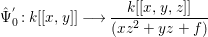 $$\begin{eqnarray}\hat{{\rm\Psi}}_{0}^{^{\prime }}:k[[x,y]]\longrightarrow \frac{k[[x,y,z]]}{(xz^{2}+yz+f)}\end{eqnarray}$$
$$\begin{eqnarray}\hat{{\rm\Psi}}_{0}^{^{\prime }}:k[[x,y]]\longrightarrow \frac{k[[x,y,z]]}{(xz^{2}+yz+f)}\end{eqnarray}$$is pure. Consequently, in view of the commutative diagram,
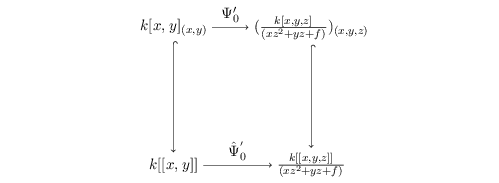
Lemma 2.4 implies that ![]() ${\rm\Psi}_{0}^{\prime }$ is pure. Hence,
${\rm\Psi}_{0}^{\prime }$ is pure. Hence, ![]() ${\rm\Psi}$ is pure. This completes the proof of Lemma 5.2 and shows that
${\rm\Psi}$ is pure. This completes the proof of Lemma 5.2 and shows that ![]() ${\it\psi}$ is a pure morphism.◻
${\it\psi}$ is a pure morphism.◻
The notion of pure morphism generalizes the ring of invariants of a polynomial ring under some group actions. If a finite group ![]() $G$ acts on
$G$ acts on  $A:=k[x_{1},~x_{2},\ldots ,~x_{n}]$, then
$A:=k[x_{1},~x_{2},\ldots ,~x_{n}]$, then ![]() $A$ is finite over the ring of invariants
$A$ is finite over the ring of invariants ![]() $A^{G}$. However, in the case of a pure extension of normal, affine domains of same dimension, the map may not even be quasi-finite.
$A^{G}$. However, in the case of a pure extension of normal, affine domains of same dimension, the map may not even be quasi-finite.
Example 5.3. (A pure morphism of affine surfaces need not be quasi-finite)
Let us consider the affine morphism
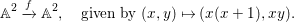
It is easy to see that ![]() $f$ is surjective. Moreover, it is quasi-finite outside the origin, and the fiber over the origin is the union of the line
$f$ is surjective. Moreover, it is quasi-finite outside the origin, and the fiber over the origin is the union of the line  $L:=\{(x,y)\in \mathbb{A}^{2}~|~x=0\}$ and the point
$L:=\{(x,y)\in \mathbb{A}^{2}~|~x=0\}$ and the point ![]() $(-1,0)$. Therefore, removing
$(-1,0)$. Therefore, removing ![]() $L$, we get a morphism, say
$L$, we get a morphism, say ![]() $\widetilde{f}$, between normal affine varieties, which is quasi-finite and surjective.
$\widetilde{f}$, between normal affine varieties, which is quasi-finite and surjective.
By Lemma 1.6, the morphism ![]() $\widetilde{f}$ is a pure morphism of affine normal varieties. Hence,
$\widetilde{f}$ is a pure morphism of affine normal varieties. Hence, ![]() $f$ is a pure morphism by Lemma 1.1(1). However,
$f$ is a pure morphism by Lemma 1.1(1). However, ![]() $f$ is not quasi-finite.
$f$ is not quasi-finite.
Remark.
In the following commutative diagram:

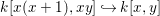 $k[x(x+1),xy]{\hookrightarrow}k[x,y]$ is pure, and hence, by Lemma 1.1,
$k[x(x+1),xy]{\hookrightarrow}k[x,y]$ is pure, and hence, by Lemma 1.1, 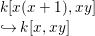 $k[x(x+1),xy]{\hookrightarrow}k[x,xy]$ is also pure. However, since
$k[x(x+1),xy]{\hookrightarrow}k[x,xy]$ is also pure. However, since ![]() $k[x,xy]$ is birational to
$k[x,xy]$ is birational to ![]() $k[x,y]$, Corollary 2.3.1 implies that
$k[x,y]$, Corollary 2.3.1 implies that 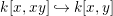 $k[x,xy]{\hookrightarrow}k[x,y]$ cannot be pure. This should be contrasted with Lemma 2.5.
$k[x,xy]{\hookrightarrow}k[x,y]$ cannot be pure. This should be contrasted with Lemma 2.5.
We saw in Example 5.3 that the local morphism at the origin is pure in spite of the fiber over it containing a line. However, in this case, the fiber also contains an isolated point, i.e., a component of “correct” dimension. Therefore, it is natural to ask whether the purity is due to the presence of the “correct” dimensional component in the fiber. Therefore, we pose the following question.
Question.
Let 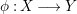 ${\it\phi}:X\longrightarrow Y$ be a morphism of normal affine varieties. Suppose that
${\it\phi}:X\longrightarrow Y$ be a morphism of normal affine varieties. Suppose that ![]() $y\in Y$ is pure. Is it true that
$y\in Y$ is pure. Is it true that ![]() ${\it\phi}^{-1}(y)$ must contain a component of “correct” dimension, i.e., of dimension equal to dim
${\it\phi}^{-1}(y)$ must contain a component of “correct” dimension, i.e., of dimension equal to dim ![]() $X-$dim
$X-$dim ![]() $Y$?
$Y$?
Unfortunately, this question has a negative answer, as the following example shows.
Example 5.4. Let the multiplicative group ![]() $\mathbb{C}^{\ast }$ act on the polynomial ring
$\mathbb{C}^{\ast }$ act on the polynomial ring  $S:=\mathbb{C}[X,Y,Z,W]$ by
$S:=\mathbb{C}[X,Y,Z,W]$ by  ${\it\rho}_{{\it\lambda}}(X,Y,Z,W)=({\it\lambda}X,{\it\lambda}Y,{\it\lambda}^{-1}Z,{\it\lambda}^{-1}W)$. By the use of Reynold’s operator, it is well known that the ring of invariants
${\it\rho}_{{\it\lambda}}(X,Y,Z,W)=({\it\lambda}X,{\it\lambda}Y,{\it\lambda}^{-1}Z,{\it\lambda}^{-1}W)$. By the use of Reynold’s operator, it is well known that the ring of invariants 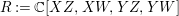 $R:=\mathbb{C}[XZ,XW,YZ,YW]$ is a direct summand of
$R:=\mathbb{C}[XZ,XW,YZ,YW]$ is a direct summand of ![]() $S$, and hence
$S$, and hence ![]() $R\subset S$ is a pure extension. The inverse image of the
$R\subset S$ is a pure extension. The inverse image of the ![]() $vertex$ of
$vertex$ of ![]() $\text{Spec}\,R$ in
$\text{Spec}\,R$ in ![]() $\text{Spec}\,S$ is the union of two linear subvarieties
$\text{Spec}\,S$ is the union of two linear subvarieties 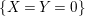 $\{X=Y=0\}$ and
$\{X=Y=0\}$ and 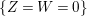 $\{Z=W=0\}$, each having dimension
$\{Z=W=0\}$, each having dimension ![]() $2$, which is larger than dim
$2$, which is larger than dim ![]() $S-$ dim
$S-$ dim ![]() $R=1$.
$R=1$.
Example 5.5. (The pure locus is not open in general)
Consider the affine morphism
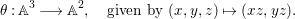 $$\begin{eqnarray}\mathbb{{\it\theta}}:\mathbb{A}^{3}\longrightarrow \mathbb{A}^{2},\quad \text{given by}~(x,y,z)\mapsto (xz,yz).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{{\it\theta}}:\mathbb{A}^{3}\longrightarrow \mathbb{A}^{2},\quad \text{given by}~(x,y,z)\mapsto (xz,yz).\end{eqnarray}$$ The fiber over 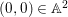 $(0,0)\in \mathbb{A}^{2}$ is the union of the line
$(0,0)\in \mathbb{A}^{2}$ is the union of the line 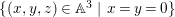 $\{(x,y,z)\in \mathbb{A}^{3}~|~x=y=0\}$ and the plane
$\{(x,y,z)\in \mathbb{A}^{3}~|~x=y=0\}$ and the plane 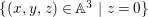 $\{(x,y,z)\in \mathbb{A}^{3}~|~z=0\}$. Now
$\{(x,y,z)\in \mathbb{A}^{3}~|~z=0\}$. Now 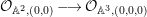 ${\mathcal{O}}_{\mathbb{A}^{2},(0,0)}\longrightarrow {\mathcal{O}}_{\mathbb{A}^{3},(0,0,0)}$ is pure by Proposition 4.5, since
${\mathcal{O}}_{\mathbb{A}^{2},(0,0)}\longrightarrow {\mathcal{O}}_{\mathbb{A}^{3},(0,0,0)}$ is pure by Proposition 4.5, since 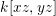 $k[xz,yz]$ is the ring of invariants of
$k[xz,yz]$ is the ring of invariants of 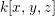 $k[x,y,z]$ under the action of
$k[x,y,z]$ under the action of ![]() $k^{\ast }$, given by
$k^{\ast }$, given by 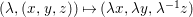 $({\it\lambda},(x,y,z))\mapsto ({\it\lambda}x,{\it\lambda}y,{\it\lambda}^{-1}z)$. However, it follows from the following Theorem 5.6 that there exist points in
$({\it\lambda},(x,y,z))\mapsto ({\it\lambda}x,{\it\lambda}y,{\it\lambda}^{-1}z)$. However, it follows from the following Theorem 5.6 that there exist points in ![]() $\mathbb{A}^{3}$, arbitrarily close to the origin, such that
$\mathbb{A}^{3}$, arbitrarily close to the origin, such that 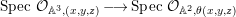 $\text{Spec}~{\mathcal{O}}_{\mathbb{A}^{3},(x,y,z)}\longrightarrow \text{Spec}~{\mathcal{O}}_{\mathbb{A}^{2},{\it\theta}(x,y,z)}$ is not surjective, and consequently
$\text{Spec}~{\mathcal{O}}_{\mathbb{A}^{3},(x,y,z)}\longrightarrow \text{Spec}~{\mathcal{O}}_{\mathbb{A}^{2},{\it\theta}(x,y,z)}$ is not surjective, and consequently 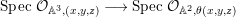 $\text{Spec}~{\mathcal{O}}_{\mathbb{A}^{3},(x,y,z)}\longrightarrow \text{Spec}~{\mathcal{O}}_{\mathbb{A}^{2},{\it\theta}(x,y,z)}$ is not pure.
$\text{Spec}~{\mathcal{O}}_{\mathbb{A}^{3},(x,y,z)}\longrightarrow \text{Spec}~{\mathcal{O}}_{\mathbb{A}^{2},{\it\theta}(x,y,z)}$ is not pure.
Theorem 5.6. Let 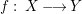 $f:~X\longrightarrow Y$ be a morphism of affine varieties, with
$f:~X\longrightarrow Y$ be a morphism of affine varieties, with ![]() $y\in Y$, such that dim
$y\in Y$, such that dim  $f^{-1}(y)~>$ dim
$f^{-1}(y)~>$ dim ![]() $X~-$ dim
$X~-$ dim ![]() $Y$. Then, for any irreducible component of highest dimension, say
$Y$. Then, for any irreducible component of highest dimension, say ![]() $Z$, of
$Z$, of ![]() $f^{-1}(y)$, there exists a nonempty Zariski-open set
$f^{-1}(y)$, there exists a nonempty Zariski-open set ![]() $U\subseteq Z$, such that for all
$U\subseteq Z$, such that for all ![]() $x\in U$, the induced morphism
$x\in U$, the induced morphism 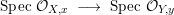 $\text{Spec}~{\mathcal{O}}_{X,x}~\longrightarrow ~\text{Spec}~{\mathcal{O}}_{Y,y}$ is not surjective.
$\text{Spec}~{\mathcal{O}}_{X,x}~\longrightarrow ~\text{Spec}~{\mathcal{O}}_{Y,y}$ is not surjective.
Proof. The proof is left to the reader as an exercise. ◻
Theorem 5.6 has the following two interesting corollaries.
Corollary 5.6.1. Any strongly pure morphism of affine algebraic varieties is equidimensional.
Corollary 5.6.2. The nonequidimensional pure extension
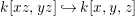 $$\begin{eqnarray}k[xz,yz]{\hookrightarrow}k[x,y,z]\end{eqnarray}$$
$$\begin{eqnarray}k[xz,yz]{\hookrightarrow}k[x,y,z]\end{eqnarray}$$shows that a pure morphism need not be strongly pure.
Note. If we choose the underlying field to be the field of complex numbers ![]() $\mathbb{C}$, then the above proof also tells us that the pure locus is not even open in Euclidean topology, as any nonempty Zariski-open set in a variety is dense in the Euclidean topology.
$\mathbb{C}$, then the above proof also tells us that the pure locus is not even open in Euclidean topology, as any nonempty Zariski-open set in a variety is dense in the Euclidean topology.
5.7. The set of completely pure points may not be open.
Let 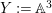 $Y:=\mathbb{A}^{3}$,
$Y:=\mathbb{A}^{3}$, 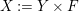 $X:=Y\times F$, where
$X:=Y\times F$, where ![]() $F\cong \mathbb{A}^{3}$. Let
$F\cong \mathbb{A}^{3}$. Let ![]() $L\in Y$ be a line, and let
$L\in Y$ be a line, and let  $L^{\prime }:=L\times \{0\}\subset X$, which maps isomorphically onto
$L^{\prime }:=L\times \{0\}\subset X$, which maps isomorphically onto ![]() $L$. Let
$L$. Let 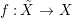 $f:\tilde{X}~\rightarrow ~X$ be the blow-up with center
$f:\tilde{X}~\rightarrow ~X$ be the blow-up with center ![]() $L^{\prime }$, and let
$L^{\prime }$, and let 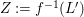 $Z:=f^{-1}(L^{\prime })$. Then,
$Z:=f^{-1}(L^{\prime })$. Then,  $Z\cong L^{\prime }\times \mathbb{P}^{4}$. Every fiber of the composite morphism
$Z\cong L^{\prime }\times \mathbb{P}^{4}$. Every fiber of the composite morphism  $\tilde{X}~\rightarrow ~Y$ for a point
$\tilde{X}~\rightarrow ~Y$ for a point ![]() $y$ in
$y$ in ![]() $L$ is a union of the proper transform of
$L$ is a union of the proper transform of ![]() $F_{y}$ and a variety
$F_{y}$ and a variety ![]() $V_{y}$ isomorphic to
$V_{y}$ isomorphic to ![]() $\mathbb{P}^{4}$, where
$\mathbb{P}^{4}$, where ![]() $F_{y}$ is the fiber over
$F_{y}$ is the fiber over ![]() $y$ of the morphism
$y$ of the morphism  $X~\rightarrow ~Y$. Let
$X~\rightarrow ~Y$. Let 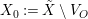 $X_{0}:=\tilde{X}\setminus V_{O}$, where
$X_{0}:=\tilde{X}\setminus V_{O}$, where ![]() $O\in Y$ is the origin. Now, the natural morphism
$O\in Y$ is the origin. Now, the natural morphism 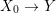 $X_{0}~\rightarrow ~Y$ has the property that the fiber over
$X_{0}~\rightarrow ~Y$ has the property that the fiber over ![]() $O$ has dimension
$O$ has dimension ![]() $3$, and for any
$3$, and for any ![]() $y\in Y$ with
$y\in Y$ with ![]() $y\neq O$, the fiber over
$y\neq O$, the fiber over ![]() $y$ contains an irreducible component of dimension
$y$ contains an irreducible component of dimension ![]() $4$. The point
$4$. The point ![]() $O\in Y$ is completely pure for the morphism
$O\in Y$ is completely pure for the morphism 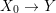 $X_{0}~\rightarrow ~Y$, but other points in
$X_{0}~\rightarrow ~Y$, but other points in ![]() $L$ are not pure for this morphism. This shows that the set of completely pure points may not be open.
$L$ are not pure for this morphism. This shows that the set of completely pure points may not be open.
Remark.
The above example also shows that in Grothendieck’s theorem on generic flatness, for a morphism 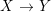 $X~\rightarrow ~Y$, the set of points
$X~\rightarrow ~Y$, the set of points ![]() $y$ in
$y$ in ![]() $Y$ such that the morphism is flat over
$Y$ such that the morphism is flat over ![]() $y$ may not be open. It also shows that the dimension of a fiber may not be an upper-semicontinuous function on
$y$ may not be open. It also shows that the dimension of a fiber may not be an upper-semicontinuous function on ![]() $Y$.
$Y$.
In Section 1, we saw that pure extensions are preserved under tensor products. However, as the following example shows, this fails to hold true for the composite of subalgebras.
Example 5.8. Let 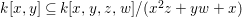 $k[x,y]\subseteq k[x,y,z,w]/(x^{2}z+yw+x)$. Now consider the two
$k[x,y]\subseteq k[x,y,z,w]/(x^{2}z+yw+x)$. Now consider the two ![]() $k[x,y]$-subalgebras
$k[x,y]$-subalgebras  $B_{1}:=k[x,y,z]~\text{and}~B_{2}:=k[x,y,w]$. Then, each
$B_{1}:=k[x,y,z]~\text{and}~B_{2}:=k[x,y,w]$. Then, each ![]() $B_{i}$ is a pure extension of
$B_{i}$ is a pure extension of ![]() $k[x,y]$. However,
$k[x,y]$. However,  $k[x,y,z,w]/(x^{2}z+yw+x)=B_{1}B_{2}$ is not a pure extension of
$k[x,y,z,w]/(x^{2}z+yw+x)=B_{1}B_{2}$ is not a pure extension of ![]() $k[x,y]$.
$k[x,y]$.
Proof. If ![]() $I$ is defined to be the ideal generated by
$I$ is defined to be the ideal generated by ![]() $x^{2}$ and
$x^{2}$ and ![]() $y$ in
$y$ in ![]() $k[x,y]$, then
$k[x,y]$, then
 $$\begin{eqnarray}x\in I\Big(\frac{k[x,y,z,w]}{(x^{2}z+yw+x)}\Big)\cap k[x,y]\setminus I.\end{eqnarray}$$
$$\begin{eqnarray}x\in I\Big(\frac{k[x,y,z,w]}{(x^{2}z+yw+x)}\Big)\cap k[x,y]\setminus I.\end{eqnarray}$$Remark.
If ![]() $A\subseteq B$ are commutative rings, then a simple application of Zorn’s lemma shows that there exist maximal (cyclically) pure extensions of
$A\subseteq B$ are commutative rings, then a simple application of Zorn’s lemma shows that there exist maximal (cyclically) pure extensions of ![]() $A$ in
$A$ in ![]() $B$. However, the above example shows that there may be several such maximal extensions, with none being ‘the maximum’ one. Consequently, any attempt to define notions like (cyclically) pure closure proves futile.
$B$. However, the above example shows that there may be several such maximal extensions, with none being ‘the maximum’ one. Consequently, any attempt to define notions like (cyclically) pure closure proves futile.
Lemma 1.9 tells us that, if ![]() $A$ is a Noetherian complete local ring, then a ring extension
$A$ is a Noetherian complete local ring, then a ring extension ![]() $A\subseteq B$ is pure if and only if
$A\subseteq B$ is pure if and only if ![]() $A$ is a direct summand of
$A$ is a direct summand of ![]() $B$. The next example shows that a pure extension of Noetherian rings, in general, need not be a direct summand.
$B$. The next example shows that a pure extension of Noetherian rings, in general, need not be a direct summand.
Lemma 5.9. Let ![]() $A$ be an integral domain, and let
$A$ be an integral domain, and let ![]() $A[x,y]$ be the polynomial ring in two variables over
$A[x,y]$ be the polynomial ring in two variables over ![]() $A$. Then,
$A$. Then,
 $$\begin{eqnarray}A[x]{\hookrightarrow}\frac{A[x,y]}{(xy^{2}-y+1)}\end{eqnarray}$$
$$\begin{eqnarray}A[x]{\hookrightarrow}\frac{A[x,y]}{(xy^{2}-y+1)}\end{eqnarray}$$is faithfully flat by Nagata’s criteria of faithful flatness [Reference Nagata14], and hence pure by Lemma 1.7. However, this extension is not a direct summand.
Proof. If possible, let
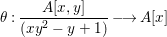 $$\begin{eqnarray}{\it\theta}:\frac{A[x,y]}{(xy^{2}-y+1)}\longrightarrow A[x]\end{eqnarray}$$
$$\begin{eqnarray}{\it\theta}:\frac{A[x,y]}{(xy^{2}-y+1)}\longrightarrow A[x]\end{eqnarray}$$ be an ![]() $A[x]$-linear map, and denote the image of
$A[x]$-linear map, and denote the image of ![]() ${\it\theta}(Y^{n})$ by
${\it\theta}(Y^{n})$ by ![]() ${\it\theta}_{n}$. Then, for any
${\it\theta}_{n}$. Then, for any ![]() $n\geqslant 0$, we have
$n\geqslant 0$, we have
 $$\begin{eqnarray}x{\it\theta}_{n+2}={\it\theta}_{n+1}-{\it\theta}_{n}.\end{eqnarray}$$
$$\begin{eqnarray}x{\it\theta}_{n+2}={\it\theta}_{n+1}-{\it\theta}_{n}.\end{eqnarray}$$ First, note that ![]() ${\it\theta}_{1}$ must have a positive degree, as otherwise either
${\it\theta}_{1}$ must have a positive degree, as otherwise either ![]() ${\it\theta}_{2}$ or
${\it\theta}_{2}$ or ![]() ${\it\theta}_{3}$ is not solvable. Again, deg
${\it\theta}_{3}$ is not solvable. Again, deg ![]() ${\it\theta}_{2}=$ deg
${\it\theta}_{2}=$ deg ![]() ${\it\theta}_{3}=$ deg
${\it\theta}_{3}=$ deg ![]() ${\it\theta}_{1}-1$. A routine inductive argument shows that, for any
${\it\theta}_{1}-1$. A routine inductive argument shows that, for any ![]() $n\geqslant 1$,
$n\geqslant 1$,
 $$\begin{eqnarray}\text{deg}\,{\it\theta}_{2n}\leqslant \text{deg}\,{\it\theta}_{1}-n,\text{ as well as }\text{deg}\,{\it\theta}_{2n+1}\leqslant \text{deg}\,{\it\theta}_{1}-n.\end{eqnarray}$$
$$\begin{eqnarray}\text{deg}\,{\it\theta}_{2n}\leqslant \text{deg}\,{\it\theta}_{1}-n,\text{ as well as }\text{deg}\,{\it\theta}_{2n+1}\leqslant \text{deg}\,{\it\theta}_{1}-n.\end{eqnarray}$$ Since the degree of any nonzero polynomial is always nonnegative, the ![]() ${\it\theta}_{n}$ will eventually be
${\it\theta}_{n}$ will eventually be ![]() $0$ for all
$0$ for all ![]() $n\gg 0$. Let
$n\gg 0$. Let ![]() $n_{0}$ be a positive integer such that
$n_{0}$ be a positive integer such that  ${\it\theta}_{n_{0}-1}\neq 0$ and
${\it\theta}_{n_{0}-1}\neq 0$ and ![]() ${\it\theta}_{n}=0$ for all
${\it\theta}_{n}=0$ for all ![]() $n\geqslant n_{0}$. Then,
$n\geqslant n_{0}$. Then,
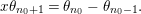 $$\begin{eqnarray}x{\it\theta}_{n_{0}+1}={\it\theta}_{n_{0}}-{\it\theta}_{n_{0}-1}.\end{eqnarray}$$
$$\begin{eqnarray}x{\it\theta}_{n_{0}+1}={\it\theta}_{n_{0}}-{\it\theta}_{n_{0}-1}.\end{eqnarray}$$This is a contradiction. ◻
The following example shows that we can even get a pure embedding of algebraic local domains which is not a direct summand.
Example 5.10. Let ![]() $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic ![]() $0$. Let us consider the following example:
$0$. Let us consider the following example:
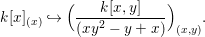 $$\begin{eqnarray}k[x]_{(x)}{\hookrightarrow}\Big(\frac{k[x,y]}{(xy^{2}-y+x)}\Big)_{(x,y)}.\end{eqnarray}$$
$$\begin{eqnarray}k[x]_{(x)}{\hookrightarrow}\Big(\frac{k[x,y]}{(xy^{2}-y+x)}\Big)_{(x,y)}.\end{eqnarray}$$The extension is faithfully flat by Nagata’s criteria of faithful flatness [Reference Nagata14], and hence pure by Lemma 1.7. However, as we will see, it is not a direct summand.
Proof. The polynomial 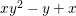 $xy^{2}-y+x$, as a polynomial in
$xy^{2}-y+x$, as a polynomial in ![]() $y$ over
$y$ over ![]() $k[x]$, splits in
$k[x]$, splits in ![]() $k[[x]]$, with the roots being
$k[[x]]$, with the roots being
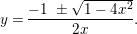 $$\begin{eqnarray}y=\frac{-1~\pm \sqrt{1-4x^{2}}}{2x}.\end{eqnarray}$$
$$\begin{eqnarray}y=\frac{-1~\pm \sqrt{1-4x^{2}}}{2x}.\end{eqnarray}$$ Therefore, taking the ‘![]() $-$’ sign, we get a root, say
$-$’ sign, we get a root, say ![]() $xy_{0}$, with
$xy_{0}$, with 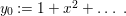 $y_{0}:=1+x^{2}+\ldots \,.$ If possible, let
$y_{0}:=1+x^{2}+\ldots \,.$ If possible, let
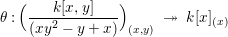 $$\begin{eqnarray}{\it\theta}:\Big(\frac{k[x,y]}{(xy^{2}-y+x)}\Big)_{(x,y)}~{\twoheadrightarrow}~k[x]_{(x)}\end{eqnarray}$$
$$\begin{eqnarray}{\it\theta}:\Big(\frac{k[x,y]}{(xy^{2}-y+x)}\Big)_{(x,y)}~{\twoheadrightarrow}~k[x]_{(x)}\end{eqnarray}$$ be a ![]() $k[x]_{(x)}$-linear map. A moment’s reflection will convince the reader that
$k[x]_{(x)}$-linear map. A moment’s reflection will convince the reader that 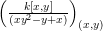 $\Big(\frac{k[x,y]}{(xy^{2}-y+x)}\Big)_{(x,y)}$ is a DVR, and
$\Big(\frac{k[x,y]}{(xy^{2}-y+x)}\Big)_{(x,y)}$ is a DVR, and
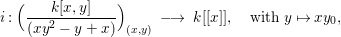 $$\begin{eqnarray}i:\Big(\frac{k[x,y]}{(xy^{2}-y+x)}\Big)_{(x,y)}~\longrightarrow ~k[[x]],\quad \text{with }y\mapsto xy_{0},\end{eqnarray}$$
$$\begin{eqnarray}i:\Big(\frac{k[x,y]}{(xy^{2}-y+x)}\Big)_{(x,y)}~\longrightarrow ~k[[x]],\quad \text{with }y\mapsto xy_{0},\end{eqnarray}$$ is an embedding of local rings. Let ![]() $B_{\mathfrak{n}}$ be the image of
$B_{\mathfrak{n}}$ be the image of 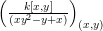 $\Big(\frac{k[x,y]}{(xy^{2}-y+x)}\Big)_{(x,y)}$ under
$\Big(\frac{k[x,y]}{(xy^{2}-y+x)}\Big)_{(x,y)}$ under ![]() $i$. Then,
$i$. Then,
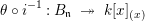 $$\begin{eqnarray}{\it\theta}\circ i^{-1}:B_{\mathfrak{ n}}~{\twoheadrightarrow}~k[x]_{(x)}\end{eqnarray}$$
$$\begin{eqnarray}{\it\theta}\circ i^{-1}:B_{\mathfrak{ n}}~{\twoheadrightarrow}~k[x]_{(x)}\end{eqnarray}$$ is also ![]() $k[x]_{(x)}$-linear. Note that the
$k[x]_{(x)}$-linear. Note that the ![]() $\mathfrak{n}B_{\mathfrak{n}}$-adic topology of
$\mathfrak{n}B_{\mathfrak{n}}$-adic topology of ![]() $B_{\mathfrak{n}}$ coincides with the topology induced by the
$B_{\mathfrak{n}}$ coincides with the topology induced by the ![]() $xk[[x]]$-adic topology of
$xk[[x]]$-adic topology of ![]() $k[[x]]$. Since
$k[[x]]$. Since ![]() $k[x]_{(x)}$ is dense in
$k[x]_{(x)}$ is dense in ![]() $k[[x]]$ with respect to the
$k[[x]]$ with respect to the ![]() $xk[[x]]$-adic topology, it follows that
$xk[[x]]$-adic topology, it follows that ![]() $k[x]_{(x)}$ is also dense in
$k[x]_{(x)}$ is also dense in ![]() $B_{\mathfrak{n}}$ with respect to the
$B_{\mathfrak{n}}$ with respect to the ![]() $\mathfrak{n}B_{\mathfrak{n}}$-adic topology. Moreover, any
$\mathfrak{n}B_{\mathfrak{n}}$-adic topology. Moreover, any ![]() $k[x]_{(x)}$-linear endomorphism of
$k[x]_{(x)}$-linear endomorphism of ![]() $B_{\mathfrak{n}}$ is continuous with respect to the
$B_{\mathfrak{n}}$ is continuous with respect to the ![]() $\mathfrak{n}B_{\mathfrak{n}}$-adic topology. So the
$\mathfrak{n}B_{\mathfrak{n}}$-adic topology. So the ![]() $k[x]_{(x)}$-linear map
$k[x]_{(x)}$-linear map ![]() ${\it\theta}\circ i^{-1}$, being identity on a dense subset
${\it\theta}\circ i^{-1}$, being identity on a dense subset ![]() $k[x]_{(x)}$, must be identity on
$k[x]_{(x)}$, must be identity on ![]() $B_{\mathfrak{n}}$. This is a contradiction since
$B_{\mathfrak{n}}$. This is a contradiction since  $xy_{0}\in B_{\mathfrak{n}}$ is not contained in
$xy_{0}\in B_{\mathfrak{n}}$ is not contained in ![]() $k[x]_{(x)}$.◻
$k[x]_{(x)}$.◻
In the final two examples, we deal with complex affine varieties. Suppose that ![]() $X$ and
$X$ and ![]() $Y$ are affine cones, i.e., affine varieties given by homogeneous prime ideals, of the same dimension, and
$Y$ are affine cones, i.e., affine varieties given by homogeneous prime ideals, of the same dimension, and  $f:X\longrightarrow Y$ is a surjective morphism given by homogeneous polynomials. In this set-up, the question of purity over the origin plays a key role in determining the purity of
$f:X\longrightarrow Y$ is a surjective morphism given by homogeneous polynomials. In this set-up, the question of purity over the origin plays a key role in determining the purity of ![]() $f$. Therefore, it is natural to ask how the following three properties are related.
$f$. Therefore, it is natural to ask how the following three properties are related.
(1) The induced local morphism at the origin
 $f_{0}^{\ast }:{\mathcal{O}}_{Y,0}\longrightarrow {\mathcal{O}}_{X,0}$ is pure.
$f_{0}^{\ast }:{\mathcal{O}}_{Y,0}\longrightarrow {\mathcal{O}}_{X,0}$ is pure.(2) Given any Euclidean open ball around the origin in
 $X$,
$X$,  $f(X)$ contains a Euclidean open ball around the origin in
$f(X)$ contains a Euclidean open ball around the origin in  $Y$.
$Y$.(3) The associated morphism of stalks at the origin
 $\widetilde{f}_{0}:\text{Spec}~{\mathcal{O}}_{X,0}\longrightarrow \text{Spec}~{\mathcal{O}}_{Y,0}$ is surjective.
$\widetilde{f}_{0}:\text{Spec}~{\mathcal{O}}_{X,0}\longrightarrow \text{Spec}~{\mathcal{O}}_{Y,0}$ is surjective.
By Lemma 1.1, purity implies local surjectivity of the corresponding morphism of schemes. By Theorem 3.5, (1) implies (2).
Since any nonempty Euclidean open set in a variety is dense in its Zariski-topology, it is easy to see that (2) implies (3). The last property, as one might expect, is indeed weaker than the other two. In the next example, we see that (3) does not imply either (1) or (2). Finally, the last example shows that, even if the image of any Euclidean ball at the origin contains an open set around the origin, the induced local morphism may not be pure.
Example 5.11. Let us consider a morphism of affine planes
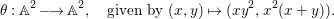 $$\begin{eqnarray}{\it\theta}:\mathbb{A}^{2}\longrightarrow \mathbb{A}^{2},\quad \text{given by}~(x,y)\mapsto (xy^{2},x^{2}(x+y)).\end{eqnarray}$$
$$\begin{eqnarray}{\it\theta}:\mathbb{A}^{2}\longrightarrow \mathbb{A}^{2},\quad \text{given by}~(x,y)\mapsto (xy^{2},x^{2}(x+y)).\end{eqnarray}$$ Clearly, ![]() ${\it\theta}$ is surjective. Considering the factorizations of polynomials in the variables
${\it\theta}$ is surjective. Considering the factorizations of polynomials in the variables ![]() $xy^{2}$ and
$xy^{2}$ and 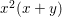 $x^{2}(x+y)$ in
$x^{2}(x+y)$ in ![]() $k[x,y]$, it is also not difficult to see that even
$k[x,y]$, it is also not difficult to see that even
 $$\begin{eqnarray}\text{Spec}~k[x,y]_{(x,y)}\longrightarrow \text{Spec}~k[xy^{2},x^{2}(x+y)]_{(xy^{2},x^{2}(x+y))}\end{eqnarray}$$
$$\begin{eqnarray}\text{Spec}~k[x,y]_{(x,y)}\longrightarrow \text{Spec}~k[xy^{2},x^{2}(x+y)]_{(xy^{2},x^{2}(x+y))}\end{eqnarray}$$is surjective, which, since the rings under consideration are two-dimensional, also implies that the going-down property holds for
 $$\begin{eqnarray}k[xy^{2},x^{2}(x+y)]_{(xy^{2},x^{2}(x+y))}{\hookrightarrow}k[x,y]_{(x,y)}.\end{eqnarray}$$
$$\begin{eqnarray}k[xy^{2},x^{2}(x+y)]_{(xy^{2},x^{2}(x+y))}{\hookrightarrow}k[x,y]_{(x,y)}.\end{eqnarray}$$ After a suitable change of variables, one can show that 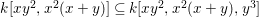 $k[xy^{2},x^{2}(x+y)]\subseteq k[xy^{2},x^{2}(x+y),y^{3}]$ is not pure, implying that
$k[xy^{2},x^{2}(x+y)]\subseteq k[xy^{2},x^{2}(x+y),y^{3}]$ is not pure, implying that 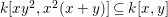 $k[xy^{2},x^{2}(x+y)]\subseteq k[x,y]$ is also not pure. Finally, to make sense of the second property, we confine ourselves to complex affine varieties. In order to show that
$k[xy^{2},x^{2}(x+y)]\subseteq k[x,y]$ is also not pure. Finally, to make sense of the second property, we confine ourselves to complex affine varieties. In order to show that ![]() ${\it\theta}$ does not satisfy
${\it\theta}$ does not satisfy ![]() $(2)$, first note that since the map is homogeneous, it is sufficient to prove that there exists an open ball, say
$(2)$, first note that since the map is homogeneous, it is sufficient to prove that there exists an open ball, say ![]() $\mathbb{B}$, around the origin such that
$\mathbb{B}$, around the origin such that ![]() ${\it\theta}(\mathbb{B})$ does not contain any open set around the origin.
${\it\theta}(\mathbb{B})$ does not contain any open set around the origin.
Therefore, let us define 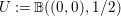 $U:=\mathbb{B}((0,0),1/2)$. If possible, let
$U:=\mathbb{B}((0,0),1/2)$. If possible, let ![]() $V$ be an open set around the origin contained in
$V$ be an open set around the origin contained in ![]() $f(U)$. Choose any
$f(U)$. Choose any 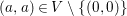 $(a,a)\in V\setminus \{(0,0)\}$. Then, a routine computation shows that for any sufficiently large
$(a,a)\in V\setminus \{(0,0)\}$. Then, a routine computation shows that for any sufficiently large ![]() $n$, the points of the form
$n$, the points of the form 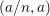 $(a/n,a)$ are not in the image of
$(a/n,a)$ are not in the image of ![]() $U$. Hence,
$U$. Hence, ![]() $f(U)$ does not contain any open set around the origin.
$f(U)$ does not contain any open set around the origin.
The last example shows that ![]() $(3)$ is actually weaker than
$(3)$ is actually weaker than ![]() $(1)$.
$(1)$.
Example 5.12. Let 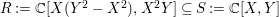 $R:=\mathbb{C}[X(Y^{2}-X^{2}),X^{2}Y]\subseteq S:=\mathbb{C}[X,Y]$. This gives a morphism
$R:=\mathbb{C}[X(Y^{2}-X^{2}),X^{2}Y]\subseteq S:=\mathbb{C}[X,Y]$. This gives a morphism  ${\it\pi}:\mathbb{C}^{2}~\rightarrow ~\mathbb{C}^{2}$. Since the line
${\it\pi}:\mathbb{C}^{2}~\rightarrow ~\mathbb{C}^{2}$. Since the line 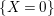 $\{X=0\}$ maps to the origin,
$\{X=0\}$ maps to the origin, ![]() ${\it\pi}$ is not quasi-finite. It is not difficult to show that the image of any neighborhood of the origin contains a neighborhood of the origin. However, the morphism is not pure.
${\it\pi}$ is not quasi-finite. It is not difficult to show that the image of any neighborhood of the origin contains a neighborhood of the origin. However, the morphism is not pure.
6 Open problems
In this section we gather together several questions about pure extensions for which the authors do not know answers.
Question 1. Let ![]() $A$ be an
$A$ be an ![]() $n$-dimensional affine graded
$n$-dimensional affine graded ![]() $k$-subalgebra of the polynomial ring
$k$-subalgebra of the polynomial ring 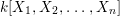 $k[X_{1},X_{2},\ldots ,X_{n}]$. If this is a pure extension, then is the corresponding morphism of schemes quasi-finite?
$k[X_{1},X_{2},\ldots ,X_{n}]$. If this is a pure extension, then is the corresponding morphism of schemes quasi-finite?
Question 2. Let 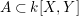 $A\subset k[X,Y]$ be a
$A\subset k[X,Y]$ be a ![]() $2$-dimensional
$2$-dimensional ![]() $k$-subalgebra of the polynomial ring
$k$-subalgebra of the polynomial ring ![]() $k[X,Y]$ such that
$k[X,Y]$ such that ![]() $A$ is a direct summand of
$A$ is a direct summand of ![]() $k[X,Y]$ as an
$k[X,Y]$ as an ![]() $A$-module. Is the corresponding morphism of schemes quasi-finite?
$A$-module. Is the corresponding morphism of schemes quasi-finite?
Question 3. Let ![]() $A\subset B$ be affine domains. Suppose that for some maximal ideal
$A\subset B$ be affine domains. Suppose that for some maximal ideal ![]() $\mathfrak{m}\subset A$ the extension
$\mathfrak{m}\subset A$ the extension 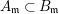 $A_{\mathfrak{m}}\subset B_{\mathfrak{m}}$ is pure. Is there a maximal ideal
$A_{\mathfrak{m}}\subset B_{\mathfrak{m}}$ is pure. Is there a maximal ideal ![]() $\mathfrak{n}\subset B$ lying over
$\mathfrak{n}\subset B$ lying over ![]() $\mathfrak{m}$ such that
$\mathfrak{m}$ such that 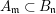 $A_{\mathfrak{m}}\subset B_{\mathfrak{n}}$ is pure?
$A_{\mathfrak{m}}\subset B_{\mathfrak{n}}$ is pure?
Question 4. Let ![]() $A\subset B$ be a pure extension of affine
$A\subset B$ be a pure extension of affine ![]() $k$-domains (or algebraic local domains) such that this is a pure extension. Assume that
$k$-domains (or algebraic local domains) such that this is a pure extension. Assume that ![]() $A$ is normal. Is the extension
$A$ is normal. Is the extension ![]() $A\subset \overline{B}$ also pure, where
$A\subset \overline{B}$ also pure, where ![]() $\overline{B}$ is the integral closure of
$\overline{B}$ is the integral closure of ![]() $B$ in its quotient field?
$B$ in its quotient field?
Question 5. Let ![]() $A\subset B$ be affine
$A\subset B$ be affine ![]() $k$-domains. Consider the set of prime ideals
$k$-domains. Consider the set of prime ideals ![]() $\mathfrak{p}\subset A$ such that
$\mathfrak{p}\subset A$ such that 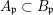 $A_{\mathfrak{p}}\subset B_{\mathfrak{p}}$ is a pure extension. Is this set open in
$A_{\mathfrak{p}}\subset B_{\mathfrak{p}}$ is a pure extension. Is this set open in ![]() $\text{Spec}\,A$?
$\text{Spec}\,A$?
Question 6. Let ![]() $A\subset B$, as in Question 5 above. Consider the set of prime ideals
$A\subset B$, as in Question 5 above. Consider the set of prime ideals ![]() $\mathfrak{p}\subset A$ such that for some prime ideal
$\mathfrak{p}\subset A$ such that for some prime ideal ![]() $\mathfrak{q}\subset B$ lying over
$\mathfrak{q}\subset B$ lying over ![]() $\mathfrak{p}$ the extension
$\mathfrak{p}$ the extension 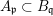 $A_{\mathfrak{p}}\subset B_{\mathfrak{q}}$ is pure. Is this set open in
$A_{\mathfrak{p}}\subset B_{\mathfrak{q}}$ is pure. Is this set open in ![]() $\text{Spec}\,A$?
$\text{Spec}\,A$?