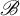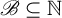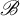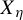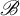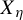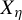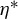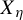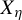1 Introduction
1.1 Background
Given
![]() $\mathscr {B}\subseteq {\mathbb {N}}$
, consider the corresponding set
$\mathscr {B}\subseteq {\mathbb {N}}$
, consider the corresponding set
![]() $\mathcal {M}_{\mathscr {B}}=\bigcup _{b\in \mathscr {B}}b{\mathbb {Z}}$
of the multiples of
$\mathcal {M}_{\mathscr {B}}=\bigcup _{b\in \mathscr {B}}b{\mathbb {Z}}$
of the multiples of
![]() $\mathscr {B}$
and its complement
$\mathscr {B}$
and its complement
![]() $\mathcal {F}_{\mathscr {B}}={\mathbb {Z}}\setminus \mathcal {M}_{\mathscr {B}}$
, that is, the set of
$\mathcal {F}_{\mathscr {B}}={\mathbb {Z}}\setminus \mathcal {M}_{\mathscr {B}}$
, that is, the set of
![]() $\mathscr {B}$
-free integers. We study the dynamics of
$\mathscr {B}$
-free integers. We study the dynamics of
![]() $\eta =\mathbf {1}_{\mathcal {F}_{\mathscr {B}}}\in \{0,1\}^{\mathbb {Z}}$
, that is, of the orbit closure
$\eta =\mathbf {1}_{\mathcal {F}_{\mathscr {B}}}\in \{0,1\}^{\mathbb {Z}}$
, that is, of the orbit closure
![]() $X_\eta $
of
$X_\eta $
of
![]() $\eta $
under the left shift
$\eta $
under the left shift
![]() $\sigma $
. The motivation for such studies goes back to the 1930s, when sets of multiples were investigated from the number-theoretic perspective by Besicovitch, Chowla, Erdős and others (see [Reference Hall12] and the references therein). In 2010, Sarnak [Reference Sarnak34] suggested to study the dynamics of the square-free system, i.e.
$\sigma $
. The motivation for such studies goes back to the 1930s, when sets of multiples were investigated from the number-theoretic perspective by Besicovitch, Chowla, Erdős and others (see [Reference Hall12] and the references therein). In 2010, Sarnak [Reference Sarnak34] suggested to study the dynamics of the square-free system, i.e.
![]() $X_\eta $
corresponding to
$X_\eta $
corresponding to
![]() $\mathscr {B}$
being the set of squares of all primes. In this case,
$\mathscr {B}$
being the set of squares of all primes. In this case,
![]() $\eta |_{\mathbb {N}}$
is the square of the Möbius function
$\eta |_{\mathbb {N}}$
is the square of the Möbius function
![]() $\mu $
, and the aim was to gain more knowledge about the Möbius function itself. Sarnak formulated a certain ‘program’ for
$\mu $
, and the aim was to gain more knowledge about the Möbius function itself. Sarnak formulated a certain ‘program’ for
![]() $\mu ^2$
and indicated how to prove the statements about
$\mu ^2$
and indicated how to prove the statements about
![]() $\mu ^2$
. Without going into details, there was a list of properties related both to measure-theoretic and topological dynamics of
$\mu ^2$
. Without going into details, there was a list of properties related both to measure-theoretic and topological dynamics of
![]() $X_{\mu ^2}$
. A natural question arose whether analogous results are true for other sets
$X_{\mu ^2}$
. A natural question arose whether analogous results are true for other sets
![]() $\mathscr {B}$
. The dynamics of
$\mathscr {B}$
. The dynamics of
![]() $X_\eta $
was studied systematically for the first time in [Reference El Abdalaoui, Lemańczyk and de la Rue9] in the Erdős case, that is, when
$X_\eta $
was studied systematically for the first time in [Reference El Abdalaoui, Lemańczyk and de la Rue9] in the Erdős case, that is, when
![]() $\mathscr {B}$
is infinite and pairwise coprime with
$\mathscr {B}$
is infinite and pairwise coprime with
![]() $\sum _{b\in \mathscr {B}}{1}/{b}<\infty $
. In this case, the properties of
$\sum _{b\in \mathscr {B}}{1}/{b}<\infty $
. In this case, the properties of
![]() $X_\eta $
resemble the properties of
$X_\eta $
resemble the properties of
![]() $X_{\mu ^2}$
. In particular,
$X_{\mu ^2}$
. In particular,
![]() $X_\eta $
is hereditary, that is, if
$X_\eta $
is hereditary, that is, if
![]() $x\in X_\eta $
and
$x\in X_\eta $
and
![]() $y\in \{0,1\}^{\mathbb {Z}}$
is such that
$y\in \{0,1\}^{\mathbb {Z}}$
is such that
![]() $y\leq x$
coordinatewise then
$y\leq x$
coordinatewise then
![]() $y\in X_\eta $
. In fact, we have
$y\in X_\eta $
. In fact, we have
(
![]() $X_{\mathscr {B}}$
is called the
$X_{\mathscr {B}}$
is called the
![]() $\mathscr {B}$
-admissible subshift). When we relax the assumptions on
$\mathscr {B}$
-admissible subshift). When we relax the assumptions on
![]() $\mathscr {B}$
, various things can happen to
$\mathscr {B}$
, various things can happen to
![]() $X_\eta $
, in particular, it may no longer be hereditary. Thus, one often looks at its hereditary closure
$X_\eta $
, in particular, it may no longer be hereditary. Thus, one often looks at its hereditary closure
![]() $\widetilde {X}_\eta $
, that is, the smallest hereditary subshift containing
$\widetilde {X}_\eta $
, that is, the smallest hereditary subshift containing
![]() $X_\eta $
. Such general
$X_\eta $
. Such general
![]() $\mathscr {B}$
-free systems were studied in [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7]. We may have
$\mathscr {B}$
-free systems were studied in [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7]. We may have
![]() $ X_\eta \subsetneq \widetilde {X}_\eta \subsetneq X_{\mathscr {B}} $
(see [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7] for various examples).
$ X_\eta \subsetneq \widetilde {X}_\eta \subsetneq X_{\mathscr {B}} $
(see [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7] for various examples).
In this paper, we concentrate on invariant measures on
![]() $X_\eta $
. Let us give now some more detailed background related to this. In the Erdős case,
$X_\eta $
. Let us give now some more detailed background related to this. In the Erdős case,
![]() $\eta $
turns out to be a generic point for the so-called Mirsky measure [Reference El Abdalaoui, Lemańczyk and de la Rue9] denoted by
$\eta $
turns out to be a generic point for the so-called Mirsky measure [Reference El Abdalaoui, Lemańczyk and de la Rue9] denoted by
![]() $\nu _\eta $
:
$\nu _\eta $
:
 $$ \begin{align*} \frac{1}{L}\sum_{\ell\leq L}\delta_{\sigma^\ell \eta} \to \nu_\eta \end{align*} $$
$$ \begin{align*} \frac{1}{L}\sum_{\ell\leq L}\delta_{\sigma^\ell \eta} \to \nu_\eta \end{align*} $$
(in this case, the above formula can be treated as the definition of
![]() $\nu _\eta $
). In other words, the frequencies of
$\nu _\eta $
). In other words, the frequencies of
![]() $0{-}1$
blocks on
$0{-}1$
blocks on
![]() $\eta $
exist (in the square-free case, they were first studied by Mirsky [Reference Mirsky30, Reference Mirsky31], hence the name). In general,
$\eta $
exist (in the square-free case, they were first studied by Mirsky [Reference Mirsky30, Reference Mirsky31], hence the name). In general,
![]() $\eta $
might not be a generic point. However, it is quasi-generic along any sequence
$\eta $
might not be a generic point. However, it is quasi-generic along any sequence
![]() $(\ell _i)$
realizing the lower density of
$(\ell _i)$
realizing the lower density of
![]() $\mathcal {M}_{\mathscr {B}}$
(that is, such that
$\mathcal {M}_{\mathscr {B}}$
(that is, such that
![]() $\lim _{i\to \infty }({1}/{\ell _i})|\mathcal {M}_{\mathscr {B}}\cap [1,\ell _i]|=\liminf _{L\to \infty }({1}/{L})|\mathcal {M}_{\mathscr {B}}\cap [1,L]| =: \underline {d}(\mathcal {M}_{\mathscr {B}})$
). This is a consequence of the deep number-theoretic result of Davenport and Erdős [Reference Davenport and Erdös3] that the logarithmic density of
$\lim _{i\to \infty }({1}/{\ell _i})|\mathcal {M}_{\mathscr {B}}\cap [1,\ell _i]|=\liminf _{L\to \infty }({1}/{L})|\mathcal {M}_{\mathscr {B}}\cap [1,L]| =: \underline {d}(\mathcal {M}_{\mathscr {B}})$
). This is a consequence of the deep number-theoretic result of Davenport and Erdős [Reference Davenport and Erdös3] that the logarithmic density of
![]() $\mathcal {M}_{\mathscr {B}}$
, that is,
$\mathcal {M}_{\mathscr {B}}$
, that is,
![]() $\boldsymbol {\delta }(\mathcal {M}_{\mathscr {B}})=\lim _{L\to \infty }({1}/{\ln L})\sum _{\ell \in \mathcal {M}_{\mathscr {B}}\cap [1,L]}({1}/{\ell })$
always exists and we have
$\boldsymbol {\delta }(\mathcal {M}_{\mathscr {B}})=\lim _{L\to \infty }({1}/{\ln L})\sum _{\ell \in \mathcal {M}_{\mathscr {B}}\cap [1,L]}({1}/{\ell })$
always exists and we have
(
![]() $d(A)$
for
$d(A)$
for
![]() $A\subseteq {\mathbb {Z}}$
stands for the natural density:
$A\subseteq {\mathbb {Z}}$
stands for the natural density:
![]() $d(A)=\lim _{L\to \infty }({1}/{L})|A\cap [1,L]|$
). Again, we call the resulting measure the Mirsky measure and denote it by
$d(A)=\lim _{L\to \infty }({1}/{L})|A\cap [1,L]|$
). Again, we call the resulting measure the Mirsky measure and denote it by
![]() $\nu _\eta $
:
$\nu _\eta $
:
 $$ \begin{align*} \lim_{i\to\infty}\frac{1}{\ell_i}\sum_{\ell\leq \ell_i}\delta_{\sigma^\ell \eta}= \nu_\eta, \end{align*} $$
$$ \begin{align*} \lim_{i\to\infty}\frac{1}{\ell_i}\sum_{\ell\leq \ell_i}\delta_{\sigma^\ell \eta}= \nu_\eta, \end{align*} $$
see [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7]. The following problems, already asked by Sarnak in the square-free case, arise.
-
• Give a description of the set
 $\mathcal {P}(X_\eta )$
of all invariant measures on
$\mathcal {P}(X_\eta )$
of all invariant measures on
 $X_\eta $
.
$X_\eta $
. -
• Compute the topological entropy
 $h(X_\eta )$
of
$h(X_\eta )$
of
 $X_\eta $
.
$X_\eta $
. -
• Determine whether
 $X_\eta $
is intrinsically ergodic, that is, whether it has only one measure of maximal entropy.
$X_\eta $
is intrinsically ergodic, that is, whether it has only one measure of maximal entropy.
The solution to the second problem and the positive answer to the third one in the square-free case were given by Peckner [Reference Peckner32]. However, the proof used the properties of the squares of primes and it was not clear if it can be extended to a more general setting. It turned out to be true:
This was proved in [Reference Kułaga-Przymus, Lemańczyk and Weiss22] in the Erdős case (where
![]() $X_\eta =\widetilde {X}_\eta $
) and then, in [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7], for all sets
$X_\eta =\widetilde {X}_\eta $
) and then, in [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7], for all sets
![]() ${\mathscr {B}\subseteq {\mathbb {N}}}$
. Moreover, the topological entropy
${\mathscr {B}\subseteq {\mathbb {N}}}$
. Moreover, the topological entropy
![]() $h(\widetilde {X}_\eta )$
of
$h(\widetilde {X}_\eta )$
of
![]() $\widetilde {X}_\eta $
is equal to the upper density of
$\widetilde {X}_\eta $
is equal to the upper density of
![]() $\mathcal {F}_{\mathscr {B}}$
:
$\mathcal {F}_{\mathscr {B}}$
:
and
where
![]() $B_{1/2,1/2}$
is the symmetric Bernoulli measure on
$B_{1/2,1/2}$
is the symmetric Bernoulli measure on
![]() $\{0,1\}^{\mathbb {Z}}$
and
$\{0,1\}^{\mathbb {Z}}$
and
![]() $M\colon (\{0,1\}^{\mathbb {Z}})^2\to \{0,1\}^{\mathbb {Z}}$
stands for the coordinatewise multiplication (in each case, the proofs were given in the corresponding paper covering the intrinsic ergodicity in the same class). We also have
$M\colon (\{0,1\}^{\mathbb {Z}})^2\to \{0,1\}^{\mathbb {Z}}$
stands for the coordinatewise multiplication (in each case, the proofs were given in the corresponding paper covering the intrinsic ergodicity in the same class). We also have
(this is true, in general, for hereditary subshifts; for a proof, see [Reference Kwietniak26]).
As for the set of invariant measures, it was shown in [Reference Kułaga-Przymus, Lemańczyk and Weiss22] that in the Erdős case,
where
![]() $\nu _\eta \vee \kappa $
stands for any joining of
$\nu _\eta \vee \kappa $
stands for any joining of
![]() $\nu _\eta $
and
$\nu _\eta $
and
![]() $\kappa $
, that is, any probability measure
$\kappa $
, that is, any probability measure
![]() $\rho $
on
$\rho $
on
![]() $(\{0,1\}^{\mathbb {Z}})^2$
invariant under
$(\{0,1\}^{\mathbb {Z}})^2$
invariant under
![]() $\sigma ^{\times 2}$
whose projection onto the first coordinate equals
$\sigma ^{\times 2}$
whose projection onto the first coordinate equals
![]() $\nu _\eta $
and the projection onto the second coordinate equals
$\nu _\eta $
and the projection onto the second coordinate equals
![]() $\kappa $
. Later, in [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7], this result was extended to any set
$\kappa $
. Later, in [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7], this result was extended to any set
![]() $\mathscr {B}\subseteq {\mathbb {N}}$
.
$\mathscr {B}\subseteq {\mathbb {N}}$
.
Recall that a central role in the theory of
![]() $\mathscr {B}$
-free systems is played by the notion of tautness [Reference Hall12]:
$\mathscr {B}$
-free systems is played by the notion of tautness [Reference Hall12]:
It was shown in [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7] (see Theorem C therein) that for any
![]() $\mathscr {B}\subseteq \mathbb {N}$
, there exists a unique taut set
$\mathscr {B}\subseteq \mathbb {N}$
, there exists a unique taut set
![]() $\mathscr {B}^{\prime }\subseteq {\mathbb {N}}$
with
$\mathscr {B}^{\prime }\subseteq {\mathbb {N}}$
with
![]() $\mathcal {M}_{\mathscr {B}}\subseteq \mathcal {M}_{\mathscr {B}^{\prime }}$
and
$\mathcal {M}_{\mathscr {B}}\subseteq \mathcal {M}_{\mathscr {B}^{\prime }}$
and
![]() $\nu _\eta =\nu _{\eta ^{\prime }}$
(for more details about
$\nu _\eta =\nu _{\eta ^{\prime }}$
(for more details about
![]() $\mathscr {B}^{\prime }$
, see §1.2.3). In fact, we have
$\mathscr {B}^{\prime }$
, see §1.2.3). In fact, we have
Moreover, in [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7] (see Corollaries 4.35 and 9.1 therein), the following combinatorial result on taut sets was proved. Fix
![]() $\mathscr {B}\subseteq \mathbb {N}$
and a taut set
$\mathscr {B}\subseteq \mathbb {N}$
and a taut set
![]() $\mathscr {C}\subseteq {\mathbb {N}}$
. Let
$\mathscr {C}\subseteq {\mathbb {N}}$
. Let
![]() $\eta _{\mathscr {C}}:=\mathbf {1}_{\mathcal {F}_{\mathscr {C}}}$
. Then the following are equivalent:
$\eta _{\mathscr {C}}:=\mathbf {1}_{\mathcal {F}_{\mathscr {C}}}$
. Then the following are equivalent:
 $$ \begin{align} \nonumber \text{for each } b\in\mathscr{B}, \text{there exists}\ c\in\mathscr{C}\ \text{such that}\ c\mid b {\iff} \eta_{\mathscr{C}}\leq \eta {\iff} \widetilde{X}_{\eta_{\mathscr{C}}}\subseteq \widetilde{X}_\eta\\ {\iff} \eta_{\mathscr{C}}\in\widetilde{X}_\eta {\iff} \nu_{\eta_{\mathscr{C}}}\in\mathcal{P}(\widetilde{X}_\eta) {\iff} \mathcal{P}(\widetilde{X}_{\eta_{\mathscr{C}}})\subseteq \mathcal{P}(\widetilde{X}_\eta). \end{align} $$
$$ \begin{align} \nonumber \text{for each } b\in\mathscr{B}, \text{there exists}\ c\in\mathscr{C}\ \text{such that}\ c\mid b {\iff} \eta_{\mathscr{C}}\leq \eta {\iff} \widetilde{X}_{\eta_{\mathscr{C}}}\subseteq \widetilde{X}_\eta\\ {\iff} \eta_{\mathscr{C}}\in\widetilde{X}_\eta {\iff} \nu_{\eta_{\mathscr{C}}}\in\mathcal{P}(\widetilde{X}_\eta) {\iff} \mathcal{P}(\widetilde{X}_{\eta_{\mathscr{C}}})\subseteq \mathcal{P}(\widetilde{X}_\eta). \end{align} $$
In particular, an immediate consequence of this result is a list of conditions equivalent to
![]() $\mathscr {B}=\mathscr {C}$
, whenever both
$\mathscr {B}=\mathscr {C}$
, whenever both
![]() $\mathscr {B}$
and
$\mathscr {B}$
and
![]() $\mathscr {C}$
are taut, see [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Theorem L].
$\mathscr {C}$
are taut, see [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Theorem L].
Last but not least, let us mention some results related to the subset
![]() $\mathcal {P}^e(\widetilde {X}_\eta )$
of the ergodic measures on
$\mathcal {P}^e(\widetilde {X}_\eta )$
of the ergodic measures on
![]() $\widetilde {X}_\eta $
. It was shown in [Reference Kułaga-Przymus, Lemańczyk, Weiss, Auslander, Johnson and Silva23] that
$\widetilde {X}_\eta $
. It was shown in [Reference Kułaga-Przymus, Lemańczyk, Weiss, Auslander, Johnson and Silva23] that
![]() $\mathcal {P}(\widetilde {X}_\eta )$
is a Poulsen simplex (that is, a non-trivial simplex with dense subset of ergodic measures with respect to the weak-star topology) whenever
$\mathcal {P}(\widetilde {X}_\eta )$
is a Poulsen simplex (that is, a non-trivial simplex with dense subset of ergodic measures with respect to the weak-star topology) whenever
![]() $h(\widetilde {X}_\eta )>0$
. Recall that the density of ergodic measures implies the arcwise connectedness of the set of invariant measures [Reference Lindenstrauss, Olsen and Sternfeld29] (the latter property was proved to hold in a hereditary setting wider than just
$h(\widetilde {X}_\eta )>0$
. Recall that the density of ergodic measures implies the arcwise connectedness of the set of invariant measures [Reference Lindenstrauss, Olsen and Sternfeld29] (the latter property was proved to hold in a hereditary setting wider than just
![]() $\mathscr {B}$
-free systems in [Reference Konieczny, Kupsa and Kwietniak20]). Recently, a yet stronger result was obtained by Konieczny, Kupsa and Kwietniak [Reference Konieczny, Kupsa and Kwietniak21]: namely,
$\mathscr {B}$
-free systems in [Reference Konieczny, Kupsa and Kwietniak20]). Recently, a yet stronger result was obtained by Konieczny, Kupsa and Kwietniak [Reference Konieczny, Kupsa and Kwietniak21]: namely,
that is, for any
![]() $\mu \in \mathcal {P}(\widetilde {X}_\eta )$
, there exist
$\mu \in \mathcal {P}(\widetilde {X}_\eta )$
, there exist
![]() $\mu _n\in \mathcal {P}^e(\widetilde {X}_\eta )$
such that
$\mu _n\in \mathcal {P}^e(\widetilde {X}_\eta )$
such that
![]() $\mu _n\to \mu $
weakly and the measure-theoretic entropies
$\mu _n\to \mu $
weakly and the measure-theoretic entropies
![]() $h(\widetilde {X}_\eta ,\sigma ,\mu _n)$
of
$h(\widetilde {X}_\eta ,\sigma ,\mu _n)$
of
![]() $(\widetilde {X}_\eta ,\sigma ,\mu _n)$
converge to the measure-theoretic entropy
$(\widetilde {X}_\eta ,\sigma ,\mu _n)$
converge to the measure-theoretic entropy
![]() $h(\widetilde {X}_\eta ,\sigma ,\mu )$
of
$h(\widetilde {X}_\eta ,\sigma ,\mu )$
of
![]() $(\widetilde {X}_\eta ,\sigma ,\mu )$
.
$(\widetilde {X}_\eta ,\sigma ,\mu )$
.
Clearly, if
![]() $X_\eta $
is hereditary, all of the above results apply to
$X_\eta $
is hereditary, all of the above results apply to
![]() $X_\eta =\widetilde {X}_\eta $
. We study analogous questions and prove the analogues of (2)–(9) for
$X_\eta =\widetilde {X}_\eta $
. We study analogous questions and prove the analogues of (2)–(9) for
![]() $X_\eta $
in the non-hereditary case. For a summary of our results, see §1.3.
$X_\eta $
in the non-hereditary case. For a summary of our results, see §1.3.
1.2 Notation and main objects
1.2.1 Dynamics
We say that
![]() $(X,T)$
is a topological dynamical system if T is a homeomorphism of a compact metric space X. We equip X with the Borel sigma-algebra. The set of all probability Borel T-invariant measures will be denoted by
$(X,T)$
is a topological dynamical system if T is a homeomorphism of a compact metric space X. We equip X with the Borel sigma-algebra. The set of all probability Borel T-invariant measures will be denoted by
![]() $\mathcal {P}(X,T)$
(or just
$\mathcal {P}(X,T)$
(or just
![]() $\mathcal {P}(X)$
if T is clear from the context). The subset of ergodic measures will be denoted by
$\mathcal {P}(X)$
if T is clear from the context). The subset of ergodic measures will be denoted by
![]() $\mathcal {P}^e(X,T)$
or
$\mathcal {P}^e(X,T)$
or
![]() $\mathcal {P}^e(X)$
. For each choice of
$\mathcal {P}^e(X)$
. For each choice of
![]() $\mu \in \mathcal {P}(X)$
, the triple
$\mu \in \mathcal {P}(X)$
, the triple
![]() $(X,T,\mu )$
is called a measure-theoretic dynamical system. Given two measure-theoretic dynamical systems
$(X,T,\mu )$
is called a measure-theoretic dynamical system. Given two measure-theoretic dynamical systems
![]() $(X,T,\mu )$
and
$(X,T,\mu )$
and
![]() $(Y,S,\nu )$
, we say that
$(Y,S,\nu )$
, we say that
![]() $(Y,S,\nu )$
is a factor of
$(Y,S,\nu )$
is a factor of
![]() $(X,T,\mu )$
whenever there exists a measurable map
$(X,T,\mu )$
whenever there exists a measurable map
![]() $\pi \colon X\to Y$
(defined
$\pi \colon X\to Y$
(defined
![]() $\mu $
-almost everywhere (a.e.)) such that the image
$\mu $
-almost everywhere (a.e.)) such that the image
![]() $\pi _\ast (\mu )$
of
$\pi _\ast (\mu )$
of
![]() $\mu $
via
$\mu $
via
![]() $\pi $
equals
$\pi $
equals
![]() $\nu $
and
$\nu $
and
![]() $\pi \circ T=S\circ \pi $
$\pi \circ T=S\circ \pi $
![]() $\mu $
-a.e.
$\mu $
-a.e.
Both in the measure-theoretic and in the topological setting, there is a notion of entropy that describes the complexity of a given system. The measure-theoretic entropy of
![]() $(X,T,\mu )$
is denoted by
$(X,T,\mu )$
is denoted by
![]() $h(X,T,\mu )$
. We skip its lengthy definition and refer the reader, for example, to [Reference Downarowicz5]. For a topological dynamical system
$h(X,T,\mu )$
. We skip its lengthy definition and refer the reader, for example, to [Reference Downarowicz5]. For a topological dynamical system
![]() $(X,T)$
, the topological entropy is denoted by
$(X,T)$
, the topological entropy is denoted by
![]() $h(X)$
or
$h(X)$
or
![]() $h(X,T)$
. We will mostly deal with
$h(X,T)$
. We will mostly deal with
![]() $0$
–
$0$
–
![]() $1$
subshifts, that is,
$1$
subshifts, that is,
![]() $(X,\sigma )$
, where
$(X,\sigma )$
, where
![]() $X\subseteq \{0,1\}^{\mathbb {Z}}$
is closed and invariant under the left shift
$X\subseteq \{0,1\}^{\mathbb {Z}}$
is closed and invariant under the left shift
![]() $\sigma \colon \{0,1\}^{\mathbb {Z}}\to \{0,1\}^{\mathbb {Z}}$
. In this case, the topological entropy is easy to define: if
$\sigma \colon \{0,1\}^{\mathbb {Z}}\to \{0,1\}^{\mathbb {Z}}$
. In this case, the topological entropy is easy to define: if
![]() $p_n(X)$
is the number of distinct blocks of length n appearing on X, then
$p_n(X)$
is the number of distinct blocks of length n appearing on X, then
![]() $h(X)=\lim _{n\to \infty }({1}/{n})\log _2 p_n(X)$
. If X is the orbit closure of
$h(X)=\lim _{n\to \infty }({1}/{n})\log _2 p_n(X)$
. If X is the orbit closure of
![]() $x\in \{0,1\}^{\mathbb {Z}}$
, we will write
$x\in \{0,1\}^{\mathbb {Z}}$
, we will write
![]() $p_n(x)$
instead of
$p_n(x)$
instead of
![]() $p_n(X)$
. There is the following variational principle (valid in general, not only for subshifts):
$p_n(X)$
. There is the following variational principle (valid in general, not only for subshifts):
![]() $h(X,T)=\sup _{\mu \in \mathcal {P}(X,T)}h(X,T,\mu )$
. In the case of subshifts, there is always at least one measure
$h(X,T)=\sup _{\mu \in \mathcal {P}(X,T)}h(X,T,\mu )$
. In the case of subshifts, there is always at least one measure
![]() $\mu $
realizing the supremum from the variational principle. If this measure is unique, we say that X is intrinsically ergodic.
$\mu $
realizing the supremum from the variational principle. If this measure is unique, we say that X is intrinsically ergodic.
Given a topological dynamical system
![]() $(X,T)$
and a point
$(X,T)$
and a point
![]() $x\in X$
, we say that x is a generic point for
$x\in X$
, we say that x is a generic point for
![]() $\mu \in \mathcal {P}(X,T)$
if
$\mu \in \mathcal {P}(X,T)$
if
![]() $({1}/{L})\sum _{\ell \leq L}\delta _{T^\ell x}\to \mu $
weakly. We say that
$({1}/{L})\sum _{\ell \leq L}\delta _{T^\ell x}\to \mu $
weakly. We say that
![]() $x\in X$
is quasi-generic for
$x\in X$
is quasi-generic for
![]() $\mu $
along
$\mu $
along
![]() $(\ell _i)$
if
$(\ell _i)$
if
![]() $({1}/{\ell _i})\sum _{\ell \leq \ell _i}\delta _{T^\ell x}\to \mu $
weakly.
$({1}/{\ell _i})\sum _{\ell \leq \ell _i}\delta _{T^\ell x}\to \mu $
weakly.
Given two measure-theoretic dynamical systems
![]() $(X_i,T_i,\mu _i)$
,
$(X_i,T_i,\mu _i)$
,
![]() $i=1,2$
, we say that
$i=1,2$
, we say that
![]() $\rho \in \mathcal {P}(X_1\times X_2,T_1\times T_2)$
(with
$\rho \in \mathcal {P}(X_1\times X_2,T_1\times T_2)$
(with
![]() $X_1\times X_2$
equipped with the product sigma-algebra) is a joining of
$X_1\times X_2$
equipped with the product sigma-algebra) is a joining of
![]() $(X_1,T_1,\mu _1)$
and
$(X_1,T_1,\mu _1)$
and
![]() $(X_2,T_2,\mu _2)$
, whenever
$(X_2,T_2,\mu _2)$
, whenever
![]() $\mu _i=(\pi _i)_\ast (\rho )$
for
$\mu _i=(\pi _i)_\ast (\rho )$
for
![]() $i=1,2$
(
$i=1,2$
(
![]() $\pi _i$
will always denote the projection onto the ith coordinate, we will also use similar notation for projections onto more than one coordinate). We write then
$\pi _i$
will always denote the projection onto the ith coordinate, we will also use similar notation for projections onto more than one coordinate). We write then
![]() $\rho =\mu _1\vee \mu _2$
or
$\rho =\mu _1\vee \mu _2$
or
![]() ${\rho \in J((X_1,T_1,\mu _1),(X_2,T_2,\mu _2))}$
. We always have
${\rho \in J((X_1,T_1,\mu _1),(X_2,T_2,\mu _2))}$
. We always have
![]() $\mu _1\otimes \mu _2\in J((X_1,T_1,\mu _1),(X_2,T_2,\mu _2))$
. In fact, if
$\mu _1\otimes \mu _2\in J((X_1,T_1,\mu _1),(X_2,T_2,\mu _2))$
. In fact, if
![]() $(Y_i,S_i,\nu _i)$
is a factor of
$(Y_i,S_i,\nu _i)$
is a factor of
![]() $(X_i,T_i,\mu _i)$
via a factor map
$(X_i,T_i,\mu _i)$
via a factor map
![]() $F_i$
,
$F_i$
,
![]() $i=1,2$
and
$i=1,2$
and
![]() $\rho = \nu _1\vee \nu _2$
, then there exists
$\rho = \nu _1\vee \nu _2$
, then there exists
![]() $\hat {\rho }\in J((X_1,T_1,\mu _1),(X_2,T_2,\mu _2))$
such that
$\hat {\rho }\in J((X_1,T_1,\mu _1),(X_2,T_2,\mu _2))$
such that
![]() $(Y_1\times Y_2,S_1\times S_2,\rho )$
is a factor of
$(Y_1\times Y_2,S_1\times S_2,\rho )$
is a factor of
![]() $(X_1\times X_2,T_1\times T_2,\hat {\rho })$
via
$(X_1\times X_2,T_1\times T_2,\hat {\rho })$
via
![]() $F_1\times F_2$
(for example, the so-called relatively independent extension of
$F_1\times F_2$
(for example, the so-called relatively independent extension of
![]() $\rho $
has such a property). Last but not least, for
$\rho $
has such a property). Last but not least, for
![]() $S\colon (X_1,T_1,\mu _1)\to (X_2,T_2,\mu _2)$
, we will denote by
$S\colon (X_1,T_1,\mu _1)\to (X_2,T_2,\mu _2)$
, we will denote by
![]() $\triangle _S$
the graph joining of
$\triangle _S$
the graph joining of
![]() $(X_2,T_2,\mu _2)$
and
$(X_2,T_2,\mu _2)$
and
![]() $(X_1,T_1,\mu _1)$
given by
$(X_1,T_1,\mu _1)$
given by
![]() $\triangle _S(A_2\times A_1)=\mu _1(S^{-1}A_2\cap A_1)$
for any measurable
$\triangle _S(A_2\times A_1)=\mu _1(S^{-1}A_2\cap A_1)$
for any measurable
![]() $A_1\subseteq X_1$
,
$A_1\subseteq X_1$
,
![]() $A_2\subseteq X_2$
. (Note that usually
$A_2\subseteq X_2$
. (Note that usually
![]() $\triangle _S$
stands for the joining of
$\triangle _S$
stands for the joining of
![]() $T_1$
and
$T_1$
and
![]() $T_2$
where the coordinates are written in the opposite order.) For more information on joinings, we refer the reader to [Reference Glasner11].
$T_2$
where the coordinates are written in the opposite order.) For more information on joinings, we refer the reader to [Reference Glasner11].
1.2.2 Toeplitz systems
A sequence
![]() $x\in \{0,1\}^{\mathbb {Z}}$
is called Toeplitz if for each
$x\in \{0,1\}^{\mathbb {Z}}$
is called Toeplitz if for each
![]() $i\in {\mathbb {Z}}$
, there exists
$i\in {\mathbb {Z}}$
, there exists
![]() $s\in {\mathbb {N}}$
such that
$s\in {\mathbb {N}}$
such that
![]() $x(i+sk)=x(i)$
for all
$x(i+sk)=x(i)$
for all
![]() $k\in {\mathbb {Z}}$
. A Toeplitz subshift is the orbit closure of a Toeplitz sequence under the left shift. Any Toeplitz subshift is minimal [Reference Williams35] (the orbit of each point is dense). For each symbol
$k\in {\mathbb {Z}}$
. A Toeplitz subshift is the orbit closure of a Toeplitz sequence under the left shift. Any Toeplitz subshift is minimal [Reference Williams35] (the orbit of each point is dense). For each symbol
![]() $a\in \{0,1\}$
and any
$a\in \{0,1\}$
and any
![]() $s\in {\mathbb {N}}$
, we set
$s\in {\mathbb {N}}$
, we set
The s-periodic part of x is defined to be the set of positions
A Toeplitz sequence x is called regular if
 $$ \begin{align*} \lim_{r\to \infty}d\bigg(\bigcup_{s\leq r}\operatorname{Per}(x,s)\bigg)=1. \end{align*} $$
$$ \begin{align*} \lim_{r\to \infty}d\bigg(\bigcup_{s\leq r}\operatorname{Per}(x,s)\bigg)=1. \end{align*} $$
(Notice that this is equivalent to the usual definition via the so-called period structure.) The remaining Toeplitz sequences are called irregular. For any regular Toeplitz sequence, the corresponding Toeplitz subshift is uniquely ergodic, see [Reference Jacobs and Keane13, Theorem 5]. For more information on Toeplitz sequences, we refer the reader, for example, to the survey [Reference Downarowicz, Kolyada, Manin and Ward4].
1.2.3
 $\mathscr {B}$
-free systems
$\mathscr {B}$
-free systems
Since the notation differs a bit between various papers related to
![]() $\mathscr {B}$
-free systems that are crucial for this work, we need to make certain adjustments.
$\mathscr {B}$
-free systems that are crucial for this work, we need to make certain adjustments.
Subshifts
First, let us recall the main subshifts that are of our interest. Given
![]() $\mathscr {B}\subseteq {\mathbb {N}}$
, we consider
$\mathscr {B}\subseteq {\mathbb {N}}$
, we consider
where
![]() $\text {supp }x=\{n\in {\mathbb {Z}} : x( n ) =1\}$
stands for the support of x. They are called the
$\text {supp }x=\{n\in {\mathbb {Z}} : x( n ) =1\}$
stands for the support of x. They are called the
![]() $\mathscr {B}$
-free subshift
$\mathscr {B}$
-free subshift
![]() $ X_{\eta } $
and the
$ X_{\eta } $
and the
![]() $\mathscr {B}$
-admissible subshift
$\mathscr {B}$
-admissible subshift
![]() $ X_{{\mathscr {B}}} $
corresponding to the set
$ X_{{\mathscr {B}}} $
corresponding to the set
![]() $\mathscr {B}$
. Moreover, the so-called hereditary closure
$\mathscr {B}$
. Moreover, the so-called hereditary closure
![]() $\widetilde {X}_\eta $
of
$\widetilde {X}_\eta $
of
![]() $X_\eta $
is given by
$X_\eta $
is given by
![]() $\widetilde {X}_\eta =M(X_\eta \times \{0,1\}^{\mathbb {Z}})$
, where
$\widetilde {X}_\eta =M(X_\eta \times \{0,1\}^{\mathbb {Z}})$
, where
![]() $M\colon (\{0,1\}^{\mathbb {Z}})^2\to \{0,1\}^{\mathbb {Z}}$
stands for the coordinatewise multiplication of sequences (this is equivalent to defining
$M\colon (\{0,1\}^{\mathbb {Z}})^2\to \{0,1\}^{\mathbb {Z}}$
stands for the coordinatewise multiplication of sequences (this is equivalent to defining
![]() $\widetilde {X}_\eta $
as the smallest hereditary subshift containing
$\widetilde {X}_\eta $
as the smallest hereditary subshift containing
![]() $X_\eta $
). Since
$X_\eta $
). Since
![]() $X_{\mathscr {B}}$
is hereditary, we have
$X_{\mathscr {B}}$
is hereditary, we have
Usually, we will assume that
![]() $\mathscr {B}$
is primitive, that is, for any
$\mathscr {B}$
is primitive, that is, for any
![]() $b,b^{\prime }\in \mathscr {B}$
, if
$b,b^{\prime }\in \mathscr {B}$
, if
![]() $b\mid b^{\prime }$
, then
$b\mid b^{\prime }$
, then
![]() $b=b^{\prime }$
. This assumption has no influence on the studied dynamics since
$b=b^{\prime }$
. This assumption has no influence on the studied dynamics since
![]() $\mathcal {M}_{\mathscr {B}}=\mathcal {M}_{\mathscr {B}^{\mathrm {prim}}}$
, where by
$\mathcal {M}_{\mathscr {B}}=\mathcal {M}_{\mathscr {B}^{\mathrm {prim}}}$
, where by
![]() $\mathscr {B}^{\mathrm {prim}}$
, we will denote the maximal primitive subset of
$\mathscr {B}^{\mathrm {prim}}$
, we will denote the maximal primitive subset of
![]() $\mathscr {B}$
.
$\mathscr {B}$
.
In fact, there are also some other interesting subshifts of
![]() $X_{\mathscr {B}}$
that we will discuss in a later paragraph. Let us now give an overview of the most important classes of sets
$X_{\mathscr {B}}$
that we will discuss in a later paragraph. Let us now give an overview of the most important classes of sets
![]() $\mathscr {B}$
appearing in the literature. We say that
$\mathscr {B}$
appearing in the literature. We say that
![]() $\mathscr {B}\subseteq {\mathbb {N}}$
is:
$\mathscr {B}\subseteq {\mathbb {N}}$
is:
-
• Erdős if
 $\mathscr {B}$
is infinite, pairwise coprime and
$\mathscr {B}$
is infinite, pairwise coprime and
 $\sum _{b\in \mathscr {B}}({1}/{b})<\infty $
;
$\sum _{b\in \mathscr {B}}({1}/{b})<\infty $
; -
• Besicovitch if
 $d(\mathcal {M}_{\mathscr {B}})$
exists;
$d(\mathcal {M}_{\mathscr {B}})$
exists; -
• taut if for every
 $b\in \mathscr {B}$
, we have
$b\in \mathscr {B}$
, we have
 $\boldsymbol {\delta }(\mathcal {M}_{\mathscr {B}\setminus \{b\}})<\boldsymbol {\delta }(\mathcal {M}_{\mathscr {B}})$
;
$\boldsymbol {\delta }(\mathcal {M}_{\mathscr {B}\setminus \{b\}})<\boldsymbol {\delta }(\mathcal {M}_{\mathscr {B}})$
; -
• Behrend if
 $\boldsymbol {\delta }(\mathcal {M}_{\mathscr {B}})=1$
.
$\boldsymbol {\delta }(\mathcal {M}_{\mathscr {B}})=1$
.
Recall (see [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Theorem 3.7]) that any non-trivial Behrend set contains an infinite pairwise coprime subset. Moreover,
![]() $\mathscr {B}$
is taut if and only if
$\mathscr {B}$
is taut if and only if
![]() $c\mathcal {A}\not \subseteq \mathscr {B}$
for any Behrend set
$c\mathcal {A}\not \subseteq \mathscr {B}$
for any Behrend set
![]() $\mathcal {A}$
and any
$\mathcal {A}$
and any
![]() $ c \in {\mathbb {N}} $
, see [Reference Hall12].
$ c \in {\mathbb {N}} $
, see [Reference Hall12].
Given
![]() $\mathscr {B}\subseteq \mathbb {N}$
, we can now define the following.
$\mathscr {B}\subseteq \mathbb {N}$
, we can now define the following.
-
•
 $\mathscr {B}^{\prime }:=(\mathscr {B}\cup C)^{\mathrm {prim}}$
, where The set
$\mathscr {B}^{\prime }:=(\mathscr {B}\cup C)^{\mathrm {prim}}$
, where The set $$ \begin{align*} C=\{c\in{\mathbb{N}} : c\mathcal{A}\subseteq \mathscr{B}\text{ for some Behrend set }\mathcal{A}\}. \end{align*} $$
$$ \begin{align*} C=\{c\in{\mathbb{N}} : c\mathcal{A}\subseteq \mathscr{B}\text{ for some Behrend set }\mathcal{A}\}. \end{align*} $$
 $\mathscr {B}^{\prime }$
is called the tautification of
$\mathscr {B}^{\prime }$
is called the tautification of
 $\mathscr {B}$
, and it is the unique taut set such that
$\mathscr {B}$
, and it is the unique taut set such that
 $\nu _\eta =\nu _{\eta ^{\prime }}$
(see [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Reference Dymek, Kasjan and Kułaga-Przymus6] for more details about
$\nu _\eta =\nu _{\eta ^{\prime }}$
(see [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Reference Dymek, Kasjan and Kułaga-Przymus6] for more details about
 $\mathscr {B}^{\prime }$
).
$\mathscr {B}^{\prime }$
).
-
•
 $\mathscr {B}^{*}:=(\mathscr {B}\cup D)^{\mathrm {prim}}$
, where The set
$\mathscr {B}^{*}:=(\mathscr {B}\cup D)^{\mathrm {prim}}$
, where The set $$ \begin{align*} D=\{d\in {\mathbb{N}} : d\mathcal{A}\subseteq\mathscr{B}\text{ for some infinite pairwise coprime set }\mathcal{A}\}. \end{align*} $$
$$ \begin{align*} D=\{d\in {\mathbb{N}} : d\mathcal{A}\subseteq\mathscr{B}\text{ for some infinite pairwise coprime set }\mathcal{A}\}. \end{align*} $$
 $\mathscr {B}^{*}$
corresponds to the unique minimal subshift
$\mathscr {B}^{*}$
corresponds to the unique minimal subshift
 $X_{\eta ^{*}}$
of
$X_{\eta ^{*}}$
of
 $X_\eta $
(see [Reference Keller17, Corollary 5]). By [Reference Keller17, Lemma 3(c)],
$X_\eta $
(see [Reference Keller17, Corollary 5]). By [Reference Keller17, Lemma 3(c)],
 $\mathscr {B}^{*}$
does not contain a scaled copy of an infinite pairwise coprime subset. Thus,
$\mathscr {B}^{*}$
does not contain a scaled copy of an infinite pairwise coprime subset. Thus,
 $\mathscr {B}^{*}$
does not contain a scaled copy of a Behrend set and, hence,
$\mathscr {B}^{*}$
does not contain a scaled copy of a Behrend set and, hence,
 $\mathscr {B}^{*}$
is taut (for another proof, see [Reference Kasjan, Keller and Lemańczyk14, Lemma 3.7]). Moreover,
$\mathscr {B}^{*}$
is taut (for another proof, see [Reference Kasjan, Keller and Lemańczyk14, Lemma 3.7]). Moreover,
 $\eta ^{*}$
is a Toeplitz sequence (see [Reference Kasjan, Keller and Lemańczyk14, Theorem B]) with a subsequence of
$\eta ^{*}$
is a Toeplitz sequence (see [Reference Kasjan, Keller and Lemańczyk14, Theorem B]) with a subsequence of
 $(\operatorname {\mathrm {lcm}}(\mathscr {B}^{*}_K))_{K\geq 1}$
being its period structure, which in particular means that
$(\operatorname {\mathrm {lcm}}(\mathscr {B}^{*}_K))_{K\geq 1}$
being its period structure, which in particular means that
 $\eta ^{*}$
is a regular Toeplitz sequence if and only if (10)(We will not need the notion of a period structure of a Toeplitz sequence, so let us skip it here and refer the reader to [Reference Downarowicz, Kolyada, Manin and Ward4].)
$\eta ^{*}$
is a regular Toeplitz sequence if and only if (10)(We will not need the notion of a period structure of a Toeplitz sequence, so let us skip it here and refer the reader to [Reference Downarowicz, Kolyada, Manin and Ward4].) $$ \begin{align} \lim_{ K \to \infty }{d}( {\mathbb{Z}} \setminus \operatorname{Per}( \eta^{*} ,\operatorname{\mathrm{lcm}}( \mathscr{B}^{*}_{K} ) ) = 0. \end{align} $$
$$ \begin{align} \lim_{ K \to \infty }{d}( {\mathbb{Z}} \setminus \operatorname{Per}( \eta^{*} ,\operatorname{\mathrm{lcm}}( \mathscr{B}^{*}_{K} ) ) = 0. \end{align} $$
We have
see [Reference Dymek, Kasjan and Kułaga-Przymus6, Remark 3.22] for the first inclusion, and [Reference Kułaga-Przymus and Lemańczyk24, (27)] for the second one. Note also that it was shown earlier that
![]() $X_{\eta ^{*}}\subseteq X_\eta $
, see [Reference Keller17, Corollary 1.5]. We have
$X_{\eta ^{*}}\subseteq X_\eta $
, see [Reference Keller17, Corollary 1.5]. We have
Indeed,
![]() $X_{(\eta ^{\prime })^{*}}$
is the unique minimal subshift of
$X_{(\eta ^{\prime })^{*}}$
is the unique minimal subshift of
![]() $X_{\eta ^{\prime }}$
, while
$X_{\eta ^{\prime }}$
, while
![]() $X_{\eta ^{*}}$
is the unique minimal subshift of
$X_{\eta ^{*}}$
is the unique minimal subshift of
![]() $X_\eta $
. Hence, since
$X_\eta $
. Hence, since
![]() $X_{\eta ^{\prime }}\subseteq X_\eta $
, it follows that
$X_{\eta ^{\prime }}\subseteq X_\eta $
, it follows that
![]() $X_{(\eta ^{\prime })^{*}}=X_{\eta ^{*}}$
. This is equivalent to (12) by [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Theorem L], cf. (8).
$X_{(\eta ^{\prime })^{*}}=X_{\eta ^{*}}$
. This is equivalent to (12) by [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Theorem L], cf. (8).
Basic algebraic objects
There are also certain important objects of algebraic nature related to
![]() $\mathscr {B}$
:
$\mathscr {B}$
:
-
• the product group
 $G:=\prod _{b\in \mathscr {B}}{\mathbb {Z}}/b{\mathbb {Z}}$
;
$G:=\prod _{b\in \mathscr {B}}{\mathbb {Z}}/b{\mathbb {Z}}$
; -
• the canonical embedding
 $\Delta \colon {\mathbb {Z}} \to G$
given by
$\Delta \colon {\mathbb {Z}} \to G$
given by
 $\Delta (n)=(n,n,\ldots )$
;
$\Delta (n)=(n,n,\ldots )$
; -
• the subgroup
 $H:=\overline {\Delta ({\mathbb {Z}})}$
;
$H:=\overline {\Delta ({\mathbb {Z}})}$
; -
• the rotation
 $R=R_{\Delta (1)}\colon H\to H$
given by
$R=R_{\Delta (1)}\colon H\to H$
given by
 $R(h)=h+\Delta (1)$
;
$R(h)=h+\Delta (1)$
; -
• the window associated to
 $\mathscr {B}$
, given by
$\mathscr {B}$
, given by
 $ W:=\{h\in H : h_b\neq 0 \text { for each }b\in \mathscr {B}\} $
, and the closure of its interior, which we denote by
$ W:=\{h\in H : h_b\neq 0 \text { for each }b\in \mathscr {B}\} $
, and the closure of its interior, which we denote by
 $ \underline {W} := \overline {\text {int}(W)} $
;
$ \underline {W} := \overline {\text {int}(W)} $
; -
• the coding function
 $\varphi _A\colon H\to \{0,1\}^{\mathbb {Z}}$
for
$\varphi _A\colon H\to \{0,1\}^{\mathbb {Z}}$
for
 $A\subseteq H$
, given by
$A\subseteq H$
, given by
 $\varphi _A(h)(n)=1{\iff} h+\Delta (n)\in A$
; note that
$\varphi _A(h)(n)=1{\iff} h+\Delta (n)\in A$
; note that
 $\varphi _A\circ R=\sigma \circ \varphi _A$
; in particular, we will use note that
$\varphi _A\circ R=\sigma \circ \varphi _A$
; in particular, we will use note that $$ \begin{align*} \varphi:=\varphi_W\quad \text{and}\quad\underline{\varphi}:=\varphi_{\underline{W}}; \end{align*} $$
$$ \begin{align*} \varphi:=\varphi_W\quad \text{and}\quad\underline{\varphi}:=\varphi_{\underline{W}}; \end{align*} $$
 $\eta =\varphi (\Delta (0))$
;
$\eta =\varphi (\Delta (0))$
;
-
• the subset of admissible sequences with only one residue class mod each
 $b\in \mathscr {B}$
missing:
$b\in \mathscr {B}$
missing:  $$ \begin{align*} Y:=\{x\in\{0,1\}^Z : |\text{supp }x \bmod b|=b-1 \text{ for each }b\in\mathscr{B}\}\subseteq X_{\mathscr{B}}; \end{align*} $$
$$ \begin{align*} Y:=\{x\in\{0,1\}^Z : |\text{supp }x \bmod b|=b-1 \text{ for each }b\in\mathscr{B}\}\subseteq X_{\mathscr{B}}; \end{align*} $$
-
• the function
 $\theta \colon Y\to G$
‘reading’ the (unique) missing residue class mod each
$\theta \colon Y\to G$
‘reading’ the (unique) missing residue class mod each
 $b\in \mathscr {B}$
, which is given by
$b\in \mathscr {B}$
, which is given by
 $\theta (y)=h{\iff} \text {supp }y\cap (b{\mathbb {Z}}-h_b)=\emptyset $
for
$\theta (y)=h{\iff} \text {supp }y\cap (b{\mathbb {Z}}-h_b)=\emptyset $
for
 $b\in \mathscr {B}$
.
$b\in \mathscr {B}$
.
All these objects can be defined just as well for
![]() $\mathscr {B}^{\prime }$
and
$\mathscr {B}^{\prime }$
and
![]() $\mathscr {B}^{*}$
. We will use the superscripts
$\mathscr {B}^{*}$
. We will use the superscripts
![]() $^{\prime }$
and
$^{\prime }$
and
![]() ${}^{*}$
to indicate which of them we mean. For example, we have
${}^{*}$
to indicate which of them we mean. For example, we have
![]() $H^{\prime }=\overline {\Delta ^{\prime }({\mathbb {Z}})}$
where
$H^{\prime }=\overline {\Delta ^{\prime }({\mathbb {Z}})}$
where
![]() $\Delta ^{\prime }\colon {\mathbb {Z}} \to G^{\prime }$
and similarly
$\Delta ^{\prime }\colon {\mathbb {Z}} \to G^{\prime }$
and similarly
Also, we will write
![]() $\varphi ^{\prime }$
for
$\varphi ^{\prime }$
for
![]() $\varphi ^{\prime }_{W^{\prime }}$
and
$\varphi ^{\prime }_{W^{\prime }}$
and
![]() $\underline {\varphi ^{\prime }}$
for
$\underline {\varphi ^{\prime }}$
for
![]() $\varphi ^{\prime }_{\underline {W^{\prime }}}$
.
$\varphi ^{\prime }_{\underline {W^{\prime }}}$
.
Remark 1.1. Notice that the meaning of
![]() $W^{\prime }$
differs from the one used in [Reference Keller17]: Keller used
$W^{\prime }$
differs from the one used in [Reference Keller17]: Keller used
![]() $W^{\prime }$
for
$W^{\prime }$
for
![]() $\overline {\text {int}(W)}$
, which we denote as
$\overline {\text {int}(W)}$
, which we denote as
![]() $\underline {W}$
.
$\underline {W}$
.
Group homomorphisms
By [Reference Keller17, Lemma 1.2], there is a continuous surjective group homomorphism
given by the unique continuous extension of the map
![]() $ \Delta (n) \mapsto \Delta ^{*}(n) $
to
$ \Delta (n) \mapsto \Delta ^{*}(n) $
to
![]() $ H $
. In fact, the following lemma provides a direct formula for
$ H $
. In fact, the following lemma provides a direct formula for
![]() $\Gamma _{H,H^{*}}$
(by the definition of
$\Gamma _{H,H^{*}}$
(by the definition of
![]() $\mathscr {B}^{*}$
, for each
$\mathscr {B}^{*}$
, for each
![]() $b^{*}$
, there exists
$b^{*}$
, there exists
![]() $b\in \mathscr {B}$
such that
$b\in \mathscr {B}$
such that
![]() $b^{*}\mid b$
).
$b^{*}\mid b$
).
Lemma 1.2. Let
![]() $h\in H$
. Then
$h\in H$
. Then
![]() $\Gamma _{H,H^{*}}(h)_{b^{*}}=h_b\bmod b^{*}$
for any
$\Gamma _{H,H^{*}}(h)_{b^{*}}=h_b\bmod b^{*}$
for any
![]() $b\in {\mathscr {B}}$
and any
$b\in {\mathscr {B}}$
and any
![]() $b^{*}\in {\mathscr {B}}^{*}$
such that
$b^{*}\in {\mathscr {B}}^{*}$
such that
![]() $b^{*}\mid b$
. In particular,
$b^{*}\mid b$
. In particular,
![]() $\Gamma _{H,H^{*}}(h)_b=h_b$
for any
$\Gamma _{H,H^{*}}(h)_b=h_b$
for any
![]() $b\in {\mathscr {B}}\cap {\mathscr {B}}^{*}$
.
$b\in {\mathscr {B}}\cap {\mathscr {B}}^{*}$
.
Proof. Let
![]() $(n_k)_{k\geq 1}$
be such that
$(n_k)_{k\geq 1}$
be such that
![]() $\lim _{k\to \infty }\Delta (n_k) = h$
. Fix
$\lim _{k\to \infty }\Delta (n_k) = h$
. Fix
![]() $ b \in {\mathscr {B}} $
. Then
$ b \in {\mathscr {B}} $
. Then
![]() $ n_k\bmod b = h_b $
for sufficiently large
$ n_k\bmod b = h_b $
for sufficiently large
![]() $k\geq 1$
. Therefore,
$k\geq 1$
. Therefore,
![]() $n_k\bmod b^{*} = h_b\bmod b^{*} $
for any
$n_k\bmod b^{*} = h_b\bmod b^{*} $
for any
![]() $b^{*}$
such that
$b^{*}$
such that
![]() $b^{*}\mid b$
. The assertion follows by the continuity of
$b^{*}\mid b$
. The assertion follows by the continuity of
![]() $\Gamma _{H,H^{*}}$
.
$\Gamma _{H,H^{*}}$
.
Moreover, it was shown in [Reference Keller17, Lemma 1.4] that
It follows that
Indeed,
![]() $ \varphi ^{*}(\Gamma _{H,H^{*}}(h))( n ) \kern1.3pt{=}\kern1.3pt 1 $
if and only if
$ \varphi ^{*}(\Gamma _{H,H^{*}}(h))( n ) \kern1.3pt{=}\kern1.3pt 1 $
if and only if
![]() $ {\Gamma _{H,H^{*}}( h ) + \Delta ^{*}(n) \kern1.3pt{=}\kern1.3pt \Gamma _{H,H^{*}}( h + \Delta (n) ) \kern1.3pt{\in}\kern1.3pt W^{*} }$
, which is equivalent to
$ {\Gamma _{H,H^{*}}( h ) + \Delta ^{*}(n) \kern1.3pt{=}\kern1.3pt \Gamma _{H,H^{*}}( h + \Delta (n) ) \kern1.3pt{\in}\kern1.3pt W^{*} }$
, which is equivalent to
![]() $ h + \Delta (n) \in \underline {W} $
due to (13).
$ h + \Delta (n) \in \underline {W} $
due to (13).
More subshifts
We will also need:
and
The subshift
![]() $X_\varphi $
first appeared in [Reference Keller and Richard19] (under the name
$X_\varphi $
first appeared in [Reference Keller and Richard19] (under the name
![]() $\mathcal {M}_W^G$
) and was later studied in [Reference Kasjan, Keller and Lemańczyk14]. The set
$\mathcal {M}_W^G$
) and was later studied in [Reference Kasjan, Keller and Lemańczyk14]. The set
![]() $[\underline {\varphi },\varphi ]$
that may not be a subshift (it is
$[\underline {\varphi },\varphi ]$
that may not be a subshift (it is
![]() $\sigma $
-invariant, but is not necessarily closed) was introduced in [Reference Keller17]. If
$\sigma $
-invariant, but is not necessarily closed) was introduced in [Reference Keller17]. If
![]() $\mathscr {B}$
is primitive, then
$\mathscr {B}$
is primitive, then
![]() $\varphi (H)\subseteq [\underline {\varphi },\varphi ]\subseteq X_\varphi $
by [Reference Keller17, Theorem 1.1], so in particular,
$\varphi (H)\subseteq [\underline {\varphi },\varphi ]\subseteq X_\varphi $
by [Reference Keller17, Theorem 1.1], so in particular,
Moreover, if
![]() $\mathscr {B}$
is taut, then by [Reference Keller17, Corollary 1.2], we have
$\mathscr {B}$
is taut, then by [Reference Keller17, Corollary 1.2], we have
Similar notation to that in (15) will be used for sequences. Given
![]() ${w,x\in \{0,1\}^{\mathbb {Z}}}$
, we set
${w,x\in \{0,1\}^{\mathbb {Z}}}$
, we set
Again, this may not be a subshift; one can consider its closure
![]() $\overline {[w,x]}$
if necessary.
$\overline {[w,x]}$
if necessary.
Remark 1.3. Let us comment here on the codomain of
![]() $\theta $
. Since
$\theta $
. Since
![]() $\theta $
is defined on whole Y, in general, we cannot say much more than that
$\theta $
is defined on whole Y, in general, we cannot say much more than that
![]() $\theta (y)\in G$
. It was shown in [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Remark 2.45] that
$\theta (y)\in G$
. It was shown in [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Remark 2.45] that
![]() $\theta (Y\cap \widetilde {X}_\eta )\subseteq H$
. However, this is not sufficient for us: we need to think of
$\theta (Y\cap \widetilde {X}_\eta )\subseteq H$
. However, this is not sufficient for us: we need to think of
![]() $\theta $
as of a function from (at least)
$\theta $
as of a function from (at least)
![]() $Y\cap [\underline {\varphi },\varphi ]$
to H. We will show that
$Y\cap [\underline {\varphi },\varphi ]$
to H. We will show that
In the first equality, ‘
![]() $ \supseteq $
’ follows from
$ \supseteq $
’ follows from
![]() $ \widetilde {X}_\varphi \supseteq X_{\varphi } $
. For the converse inclusion, consider
$ \widetilde {X}_\varphi \supseteq X_{\varphi } $
. For the converse inclusion, consider
![]() $ {y \in Y \cap \widetilde {X}_{\varphi } }$
and
$ {y \in Y \cap \widetilde {X}_{\varphi } }$
and
![]() $ x \in X_{\varphi } = \overline {\varphi (H)} $
with
$ x \in X_{\varphi } = \overline {\varphi (H)} $
with
![]() $ y \leq x $
. Notice that
$ y \leq x $
. Notice that
![]() $ \overline {\varphi (H)} \subseteq X_{{\mathscr {B}}} $
since
$ \overline {\varphi (H)} \subseteq X_{{\mathscr {B}}} $
since
![]() $ \operatorname {\mathrm {supp}} \varphi ( h ) $
misses the residue class
$ \operatorname {\mathrm {supp}} \varphi ( h ) $
misses the residue class
![]() $-h_{b}$
modulo
$-h_{b}$
modulo
![]() $ b $
for each
$ b $
for each
![]() $b\in \mathscr {B}$
and
$b\in \mathscr {B}$
and
![]() $ X_{{\mathscr {B}}} $
is closed. Thus,
$ X_{{\mathscr {B}}} $
is closed. Thus,
![]() $ \operatorname {\mathrm {supp}} x $
misses at least one residue class for each
$ \operatorname {\mathrm {supp}} x $
misses at least one residue class for each
![]() $ b \in {\mathscr {B}} $
. Due to
$ b \in {\mathscr {B}} $
. Due to
![]() $ y \in Y $
and
$ y \in Y $
and
![]() $ y \leq x $
, the support of
$ y \leq x $
, the support of
![]() $ x $
misses exactly one residue class for each
$ x $
misses exactly one residue class for each
![]() $ b $
, namely the same as
$ b $
, namely the same as
![]() $ \operatorname {\mathrm {supp}} y $
. This yields
$ \operatorname {\mathrm {supp}} y $
. This yields
![]() $ \theta (y) = \theta ( x ) \in \theta ( Y \cap X_{\varphi } ) $
.
$ \theta (y) = \theta ( x ) \in \theta ( Y \cap X_{\varphi } ) $
.
To see
![]() $ \theta ( Y \cap X_{\varphi } ) \subseteq H $
, we fix
$ \theta ( Y \cap X_{\varphi } ) \subseteq H $
, we fix
![]() $ b \in {\mathscr {B}} $
and
$ b \in {\mathscr {B}} $
and
![]() $ x \in X_{ \varphi } = \overline { \varphi ( H ) } $
. Then there exists a sequence
$ x \in X_{ \varphi } = \overline { \varphi ( H ) } $
. Then there exists a sequence
![]() $ ( \varphi (h_{n}) ) $
which converges to
$ ( \varphi (h_{n}) ) $
which converges to
![]() $ x $
, and (by definition) we have
$ x $
, and (by definition) we have
![]() $ \varphi (h_{n}) |_{ -(h_{n})_{b} + b {\mathbb {Z}} } = 0 $
. Since
$ \varphi (h_{n}) |_{ -(h_{n})_{b} + b {\mathbb {Z}} } = 0 $
. Since
![]() $ H $
is compact, we can assume that
$ H $
is compact, we can assume that
![]() $ (h_{n}) $
has a limit
$ (h_{n}) $
has a limit
![]() $ h \in H $
. In particular, there exists
$ h \in H $
. In particular, there exists
![]() $ n_{0} \in {\mathbb {N}} $
with
$ n_{0} \in {\mathbb {N}} $
with
![]() $ (h_{n})_{b} = h_{b} $
for all
$ (h_{n})_{b} = h_{b} $
for all
![]() $ n \geq n_{0} $
. This yields
$ n \geq n_{0} $
. This yields
![]() $ \varphi (h_{n}) |_{ -h_{b} + b {\mathbb {Z}} } = 0 $
for all
$ \varphi (h_{n}) |_{ -h_{b} + b {\mathbb {Z}} } = 0 $
for all
![]() $ n \geq n_{0} $
and thus
$ n \geq n_{0} $
and thus
![]() $ x |_{ -h_{b} + b {\mathbb {Z}} } = 0 $
. For
$ x |_{ -h_{b} + b {\mathbb {Z}} } = 0 $
. For
![]() $ x \in Y \cap X_{ \varphi } $
, it follows that
$ x \in Y \cap X_{ \varphi } $
, it follows that
![]() $ -h_{b} $
is the unique residue class modulo
$ -h_{b} $
is the unique residue class modulo
![]() $ b $
that
$ b $
that
![]() $ \operatorname {\mathrm {supp}} x $
misses. Since
$ \operatorname {\mathrm {supp}} x $
misses. Since
![]() $ b \in {\mathscr {B}} $
was arbitrary, we obtain
$ b \in {\mathscr {B}} $
was arbitrary, we obtain
![]() $ \theta ( x ) = h \in H $
.
$ \theta ( x ) = h \in H $
.
1.2.4 Dynamical diagrams
The aim of this section is to introduce a certain language related to diagrams involving dynamical systems and factoring maps between them. It will allow us to summarize some of our results on diagrams, which, in turn, can help to understand the structure of some more complicated proofs since the diagrams are easier to ‘glue together’ than the assertions written in the form of sentences. We will use the language of category theory. Namely, we consider the category where:
-
• the objects are triples of the form
 $(X,T,\mathcal {P}_X)$
, where
$(X,T,\mathcal {P}_X)$
, where
 $(X,T)$
is a topological dynamical system and
$(X,T)$
is a topological dynamical system and
 $\emptyset \neq \mathcal {P}_X\subseteq \mathcal {P}(X)$
; if
$\emptyset \neq \mathcal {P}_X\subseteq \mathcal {P}(X)$
; if
 $\mathcal {P}_X=\mathcal {P}(X)$
, we skip it and write
$\mathcal {P}_X=\mathcal {P}(X)$
, we skip it and write
 $(X,T)$
instead of
$(X,T)$
instead of
 $(X,T,\mathcal {P}(X))$
;
$(X,T,\mathcal {P}(X))$
; -
• a morphism from
 $(X,T,\mathcal {P}_X)$
to
$(X,T,\mathcal {P}_X)$
to
 $(Y,S,\mathcal {P}_Y)$
is a map
$(Y,S,\mathcal {P}_Y)$
is a map
 $f\colon (X,T,\mathcal {P}_X)\to (Y,S,\mathcal {P}_Y)$
such that there exist
$f\colon (X,T,\mathcal {P}_X)\to (Y,S,\mathcal {P}_Y)$
such that there exist
 $X_0\subseteq X$
where
$X_0\subseteq X$
where
 $X_0$
is
$X_0$
is
 $T$
-invariant with
$T$
-invariant with
 $\mu (X_0)=1$
for any
$\mu (X_0)=1$
for any
 $\mu \in \mathcal {P}_X$
,
$\mu \in \mathcal {P}_X$
,
 $f\colon X_0\to Y$
,
$f\colon X_0\to Y$
,
 $f_\ast (\mathcal {P}_X)\subseteq \mathcal {P}_Y$
and
$f_\ast (\mathcal {P}_X)\subseteq \mathcal {P}_Y$
and
 $S\circ f=f\circ T$
on
$S\circ f=f\circ T$
on
 $X_0$
.
$X_0$
.
Any graph whose vertices are the above-defined objects and whose arrows denote morphisms is called a dynamical diagram.
Remark 1.4. We identify two morphisms
![]() $f,g\colon (X,T,\mathcal {P}_X)\to (Y,S,\mathcal {P}_Y)$
, whenever f and g agree on a subset
$f,g\colon (X,T,\mathcal {P}_X)\to (Y,S,\mathcal {P}_Y)$
, whenever f and g agree on a subset
![]() $X_0\subseteq X$
that is of full measure for every measure
$X_0\subseteq X$
that is of full measure for every measure
![]() $\mu \in \mathcal {P}_X$
.
$\mu \in \mathcal {P}_X$
.
Definition 1.5. We define the composition of morphisms
![]() $f\colon (X,T,\mathcal {P}_X)\to (Y,S,\mathcal {P}_Y)$
and
$f\colon (X,T,\mathcal {P}_X)\to (Y,S,\mathcal {P}_Y)$
and
![]() $g\colon (Y,S,\mathcal {P}_Y)\to (Z,R,\mathcal {P}_Z)$
as the composition
$g\colon (Y,S,\mathcal {P}_Y)\to (Z,R,\mathcal {P}_Z)$
as the composition
![]() $g\circ f$
. Notice that such a definition is correct in view of Remark 1.4. Indeed, let
$g\circ f$
. Notice that such a definition is correct in view of Remark 1.4. Indeed, let
![]() $f\colon X_0\to Y$
and
$f\colon X_0\to Y$
and
![]() $g\colon Y_0\to Z$
, where
$g\colon Y_0\to Z$
, where
![]() $\mu (X_0)=1$
for every
$\mu (X_0)=1$
for every
![]() $\mu \in \mathcal {P}_X$
and
$\mu \in \mathcal {P}_X$
and
![]() $\nu (Y_0)=1$
for every
$\nu (Y_0)=1$
for every
![]() $\nu \in \mathcal {P}_Y$
. Then the composition
$\nu \in \mathcal {P}_Y$
. Then the composition
![]() $g\circ f$
is defined on
$g\circ f$
is defined on
![]() $X_0\cap f^{-1}(Y_0)$
and
$X_0\cap f^{-1}(Y_0)$
and
![]() $\mu (X_0\cap f^{-1}(Y_0))=1$
for any
$\mu (X_0\cap f^{-1}(Y_0))=1$
for any
![]() $\mu \in \mathcal {P}_X$
.
$\mu \in \mathcal {P}_X$
.
Definition 1.6. We will say that a dynamical diagram commutes if for any choice of
![]() $(X,T,\mathcal {P}_X)$
and
$(X,T,\mathcal {P}_X)$
and
![]() $(Y,S,\mathcal {P}_Y)$
in this diagram, the composition of morphisms along any path connecting
$(Y,S,\mathcal {P}_Y)$
in this diagram, the composition of morphisms along any path connecting
![]() $(X,T,\mathcal {P}_X)$
with
$(X,T,\mathcal {P}_X)$
with
![]() $(Y,S,\mathcal {P}_Y)$
does not depend on the choice of the path, including the trivial (zero) path.
$(Y,S,\mathcal {P}_Y)$
does not depend on the choice of the path, including the trivial (zero) path.
Remark 1.7. In the definition of commutativity, we implicitly assume that our diagram includes, for each vertex
![]() $(X,T,\mathcal {P}_X)$
, the identity map
$(X,T,\mathcal {P}_X)$
, the identity map
![]() $\text {id}\colon (X,T,\mathcal {P}_X)\to (X,T,\mathcal {P}_X)$
. To increase the readability of the diagrams, we will skip the corresponding arrow in our figures. Notice that this means in particular that whenever a dynamical diagram of the form
$\text {id}\colon (X,T,\mathcal {P}_X)\to (X,T,\mathcal {P}_X)$
. To increase the readability of the diagrams, we will skip the corresponding arrow in our figures. Notice that this means in particular that whenever a dynamical diagram of the form
 $$ \begin{align*} (X,T,\mathcal{P}_X)\mathrel{\mathop{\rightleftarrows}^{f}_{g}}(Y,S,\mathcal{P}_Y) \end{align*} $$
$$ \begin{align*} (X,T,\mathcal{P}_X)\mathrel{\mathop{\rightleftarrows}^{f}_{g}}(Y,S,\mathcal{P}_Y) \end{align*} $$
is commutative, then
![]() $g\circ f=\text {id}_X$
a.e. with respect to any
$g\circ f=\text {id}_X$
a.e. with respect to any
![]() $\mu \in \mathcal {P}_X$
and
$\mu \in \mathcal {P}_X$
and
![]() $f\circ g=\text {id}_Y$
a.e. with respect to any
$f\circ g=\text {id}_Y$
a.e. with respect to any
![]() $\nu \in \mathcal {P}_Y$
. Note that usually, diagrams with loops do not appear in the context of commutative diagrams in category theory—they will however appear in the present paper.
$\nu \in \mathcal {P}_Y$
. Note that usually, diagrams with loops do not appear in the context of commutative diagrams in category theory—they will however appear in the present paper.
Remark 1.8. In a commutative diagram for any pair of its vertices
![]() $(X,T,\mathcal {P}_X)$
,
$(X,T,\mathcal {P}_X)$
,
![]() $(Y,S,\mathcal {P}_Y)$
, there is at most one morphism
$(Y,S,\mathcal {P}_Y)$
, there is at most one morphism
![]() $f\colon (X,T,\mathcal {P}_X)\to (Y,S,\mathcal {P}_Y)$
. Notice also that any linear dynamical diagram is automatically commutative (by a linear diagram, we mean any diagram whose underlying undirected graph consists of vertices arranged in a line). The same applies to any dynamical diagram that is of the form of a directed tree (a graph whose underlying undirected graph is a tree, that is, a connected acyclic undirected graph).
$f\colon (X,T,\mathcal {P}_X)\to (Y,S,\mathcal {P}_Y)$
. Notice also that any linear dynamical diagram is automatically commutative (by a linear diagram, we mean any diagram whose underlying undirected graph consists of vertices arranged in a line). The same applies to any dynamical diagram that is of the form of a directed tree (a graph whose underlying undirected graph is a tree, that is, a connected acyclic undirected graph).
Definition 1.9. We will say that a morphism
![]() $f\colon (X,T,\mathcal {P}_X) \to (Y,S,\mathcal {P}_Y)$
is surjective if
$f\colon (X,T,\mathcal {P}_X) \to (Y,S,\mathcal {P}_Y)$
is surjective if
![]() $f_\ast (\mathcal {P}_X)=\mathcal {P}_Y$
. We will say that a dynamical diagram is surjective if every morphism in this diagram is surjective. If
$f_\ast (\mathcal {P}_X)=\mathcal {P}_Y$
. We will say that a dynamical diagram is surjective if every morphism in this diagram is surjective. If
![]() $(X,T,\mathcal {P}_X)\xrightarrow {f} (Y,S,\mathcal {P}_Y)$
is surjective, we will sometimes just say that (the morphism) f is surjective. Notice that this notion is not the same as the surjectivity of the map
$(X,T,\mathcal {P}_X)\xrightarrow {f} (Y,S,\mathcal {P}_Y)$
is surjective, we will sometimes just say that (the morphism) f is surjective. Notice that this notion is not the same as the surjectivity of the map
![]() $f\colon X\to Y$
.
$f\colon X\to Y$
.
Remark 1.10. (Cf. Remark 1.7)
Any commutative dynamical diagram that is a loop is automatically surjective. For example, if
 $$ \begin{align*} (X,T,\mathcal{P}_X)\mathrel{\mathop{\rightleftarrows}^{f}_{g}}(Y,S,\mathcal{P}_Y) \end{align*} $$
$$ \begin{align*} (X,T,\mathcal{P}_X)\mathrel{\mathop{\rightleftarrows}^{f}_{g}}(Y,S,\mathcal{P}_Y) \end{align*} $$
is a commutative dynamical diagram, then it is surjective. Indeed,
![]() $\mathcal {P}_X=\text {id}_\ast (\mathcal {P}_X)=g_\ast (f_\ast (\mathcal {P}_X))\subseteq g_\ast (\mathcal {P}_Y)\subseteq \mathcal {P}_X$
, so, in fact,
$\mathcal {P}_X=\text {id}_\ast (\mathcal {P}_X)=g_\ast (f_\ast (\mathcal {P}_X))\subseteq g_\ast (\mathcal {P}_Y)\subseteq \mathcal {P}_X$
, so, in fact,
![]() $\mathcal {P}_X=g_\ast (\mathcal {P}_Y)$
. By the same token,
$\mathcal {P}_X=g_\ast (\mathcal {P}_Y)$
. By the same token,
![]() ${\mathcal {P}_Y=f_\ast (\mathcal {P}_X)}$
.
${\mathcal {P}_Y=f_\ast (\mathcal {P}_X)}$
.
Example 1.11
-
(1) Suppose that
 $\mathscr {B}\subseteq \mathbb {N}$
is taut. Then
$\mathscr {B}\subseteq \mathbb {N}$
is taut. Then
 $\nu _\eta \in \mathcal {P}(X_\eta \cap Y)$
by [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Theorem H], so
$\nu _\eta \in \mathcal {P}(X_\eta \cap Y)$
by [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Theorem H], so
 $\mathcal {P}(X_\eta \cap Y)\neq \emptyset $
. Thus, is a dynamical diagram. Its subdiagram
$\mathcal {P}(X_\eta \cap Y)\neq \emptyset $
. Thus, is a dynamical diagram. Its subdiagram $$ \begin{align*} (X_\eta\cap Y,\sigma)\xrightarrow{\theta}(H,R)\xrightarrow{\varphi}(X_\eta,\sigma) \end{align*} $$
$$ \begin{align*} (X_\eta\cap Y,\sigma)\xrightarrow{\theta}(H,R)\xrightarrow{\varphi}(X_\eta,\sigma) \end{align*} $$
 $(X_\eta \cap Y,\sigma )\xrightarrow {\theta }(H,R)$
is surjective (by the unique ergodicity of
$(X_\eta \cap Y,\sigma )\xrightarrow {\theta }(H,R)$
is surjective (by the unique ergodicity of
 $(H,R)$
, we have
$(H,R)$
, we have
 $\theta _\ast (\nu )=m_H\in \mathcal {P}(H)$
for any
$\theta _\ast (\nu )=m_H\in \mathcal {P}(H)$
for any
 ${\nu \in \mathcal {P}(X_\eta \cap Y)}$
), while
${\nu \in \mathcal {P}(X_\eta \cap Y)}$
), while
 $(H,R)\xrightarrow {\varphi }(X_\eta ,\sigma )$
is not surjective unless
$(H,R)\xrightarrow {\varphi }(X_\eta ,\sigma )$
is not surjective unless
 $X_\eta $
is uniquely ergodic (cf. Corollary G in §1.3.1).
$X_\eta $
is uniquely ergodic (cf. Corollary G in §1.3.1).
-
(2) The dynamical diagram
does not commute: indeed, $$ \begin{align*} (\{0,1\}^{\mathbb{Z}},\sigma)\mathrel{\mathop{\rightleftarrows}^{\sigma}_{\sigma}} (\{0,1\}^{\mathbb{Z}},\sigma) \end{align*} $$
$$ \begin{align*} (\{0,1\}^{\mathbb{Z}},\sigma)\mathrel{\mathop{\rightleftarrows}^{\sigma}_{\sigma}} (\{0,1\}^{\mathbb{Z}},\sigma) \end{align*} $$
 $\sigma \circ \sigma \neq \text {id}$
(except at the four fixed points of
$\sigma \circ \sigma \neq \text {id}$
(except at the four fixed points of
 $\sigma ^2$
). Notice, however, that if we equip each vertex with
$\sigma ^2$
). Notice, however, that if we equip each vertex with
 $\emptyset \neq \mathcal {P}\subseteq \{\delta _{\mathbf {0}},\tfrac 12(\delta _{\ldots 1 0 1 0 1\ldots }+\delta _{\ldots 0 1 0 1 0\ldots }),\delta _{\mathbf {1}}\})$
, then becomes a commutative dynamical diagram (and thus it is surjective by Remark 1.10).
$\emptyset \neq \mathcal {P}\subseteq \{\delta _{\mathbf {0}},\tfrac 12(\delta _{\ldots 1 0 1 0 1\ldots }+\delta _{\ldots 0 1 0 1 0\ldots }),\delta _{\mathbf {1}}\})$
, then becomes a commutative dynamical diagram (and thus it is surjective by Remark 1.10). $$ \begin{align*} (\{0,1\}^{\mathbb{Z}},\sigma,\mathcal{P})\mathrel{\mathop{\rightleftarrows}^{\sigma}_{\sigma}} (\{0,1\}^{\mathbb{Z}},\sigma,\mathcal{P}) \end{align*} $$
$$ \begin{align*} (\{0,1\}^{\mathbb{Z}},\sigma,\mathcal{P})\mathrel{\mathop{\rightleftarrows}^{\sigma}_{\sigma}} (\{0,1\}^{\mathbb{Z}},\sigma,\mathcal{P}) \end{align*} $$
-
(3) If
 $\mathscr {B}\subseteq {\mathbb {N}}$
is taut, then is a commutative dynamical diagram (and thus it is surjective by Remark 1.10). Indeed,
$\mathscr {B}\subseteq {\mathbb {N}}$
is taut, then is a commutative dynamical diagram (and thus it is surjective by Remark 1.10). Indeed, $$ \begin{align*} (X_\eta,\sigma,\{\nu_\eta\})\mathrel{\mathop{\rightleftarrows}^{\varphi^{-1}}_{\varphi}}(H,R) \end{align*} $$
$$ \begin{align*} (X_\eta,\sigma,\{\nu_\eta\})\mathrel{\mathop{\rightleftarrows}^{\varphi^{-1}}_{\varphi}}(H,R) \end{align*} $$
 $\varphi \colon (H,R,m_H)\to (X_\eta ,\sigma ,\nu _\eta )$
is a measure-theoretic isomorphism, see [Reference El Abdalaoui, Lemańczyk and de la Rue9] for the Erdős case and [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Theorem F] for the taut case. The map
$\varphi \colon (H,R,m_H)\to (X_\eta ,\sigma ,\nu _\eta )$
is a measure-theoretic isomorphism, see [Reference El Abdalaoui, Lemańczyk and de la Rue9] for the Erdős case and [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Theorem F] for the taut case. The map
 $\varphi ^{-1}$
can be replaced with
$\varphi ^{-1}$
can be replaced with
 $\theta $
(recall that for taut
$\theta $
(recall that for taut
 $\mathscr {B}$
, we have
$\mathscr {B}$
, we have
 $\nu _\eta (X_\eta \cap Y)=1$
, so
$\nu _\eta (X_\eta \cap Y)=1$
, so
 $\theta $
is well defined
$\theta $
is well defined
 $\nu _\eta $
-a.e. on
$\nu _\eta $
-a.e. on
 $X_\eta $
).
$X_\eta $
).
-
(4) The diagram
is clearly a dynamical diagram (as $$ \begin{align*} ((\{0,1\}^{\mathbb{Z}})^2,\sigma^{\times 2},\{\nu_\eta\vee\kappa : \kappa\in \mathcal{P}(\{0,1\}^{\mathbb{Z}})\})\xrightarrow{M} (\widetilde{X}_\eta,\sigma) \end{align*} $$
$$ \begin{align*} ((\{0,1\}^{\mathbb{Z}})^2,\sigma^{\times 2},\{\nu_\eta\vee\kappa : \kappa\in \mathcal{P}(\{0,1\}^{\mathbb{Z}})\})\xrightarrow{M} (\widetilde{X}_\eta,\sigma) \end{align*} $$
 $M\circ (\sigma \times \sigma )=\sigma \circ M$
everywhere). It is linear, hence commutative. Moreover, it is surjective by (6).
$M\circ (\sigma \times \sigma )=\sigma \circ M$
everywhere). It is linear, hence commutative. Moreover, it is surjective by (6).
1.3 Summary
In this section, we present our main results. They are divided into three groups:
-
• results about invariant measures;
-
• combinatorial results related to the notion of tautness;
-
• entropy results.
We also discuss how to interpret some of them in terms of dynamical diagrams and indicate the main steps in their proofs.
1.3.1 Main results: invariant measures
In [Reference Keller17], Keller formulated a conjecture on the form of
![]() $\mathcal {P}(X_\eta )$
. Let us restate it using our notation.
$\mathcal {P}(X_\eta )$
. Let us restate it using our notation.
Conjecture 1. [Reference Keller17, Conjecture 1]
Let
![]() $\mathscr {B}\subseteq {\mathbb {N}}$
be such that
$\mathscr {B}\subseteq {\mathbb {N}}$
be such that
![]() $\eta ^{*}$
is a regular Toeplitz sequence. Then for any
$\eta ^{*}$
is a regular Toeplitz sequence. Then for any
![]() $\nu \in \mathcal {P}(X_\varphi )$
, there exists
$\nu \in \mathcal {P}(X_\varphi )$
, there exists
![]() $\rho \in \mathcal {P}(H\times \{0,1\}^{\mathbb {Z}},R\times \sigma )$
such that for any measurable
$\rho \in \mathcal {P}(H\times \{0,1\}^{\mathbb {Z}},R\times \sigma )$
such that for any measurable
![]() $A\subseteq X_\varphi $
,
$A\subseteq X_\varphi $
,
 $$ \begin{align*} \nu(A)=\int_{H\times \{0,1\}^{\mathbb{Z}}}\mathbf{1}_A(\underline{\varphi}(h)+ x\cdot(\varphi(h)-\underline{\varphi}(h)))\,d\rho(h,x). \end{align*} $$
$$ \begin{align*} \nu(A)=\int_{H\times \{0,1\}^{\mathbb{Z}}}\mathbf{1}_A(\underline{\varphi}(h)+ x\cdot(\varphi(h)-\underline{\varphi}(h)))\,d\rho(h,x). \end{align*} $$
In other words, for each
![]() $\nu \in \mathcal {P}(X_\varphi )$
, we have
$\nu \in \mathcal {P}(X_\varphi )$
, we have
![]() $\nu =(M_H)_\ast (\rho )$
for some
$\nu =(M_H)_\ast (\rho )$
for some
![]() $\rho \in \mathcal {P}(H\times \{0,1\}^{\mathbb {Z}}, R\times \sigma )$
, where
$\rho \in \mathcal {P}(H\times \{0,1\}^{\mathbb {Z}}, R\times \sigma )$
, where
![]() $M_H\colon H\times \{0,1\}^{\mathbb {Z}}\to [\underline {\varphi },\varphi ]$
is given by
$M_H\colon H\times \{0,1\}^{\mathbb {Z}}\to [\underline {\varphi },\varphi ]$
is given by
Notice that each
![]() $\rho \in \mathcal {P}(H\times \{0,1\}^{\mathbb {Z}},R\times \sigma )$
is a joining of
$\rho \in \mathcal {P}(H\times \{0,1\}^{\mathbb {Z}},R\times \sigma )$
is a joining of
![]() $m_H$
with some measure
$m_H$
with some measure
![]() $\kappa \in \mathcal {P}(\{0,1\}^{\mathbb {Z}})$
, that is,
$\kappa \in \mathcal {P}(\{0,1\}^{\mathbb {Z}})$
, that is,
![]() $\rho =m_H\vee \kappa $
. Our motivation for writing this paper was to prove the above conjecture. In fact, we will prove not only that all
$\rho =m_H\vee \kappa $
. Our motivation for writing this paper was to prove the above conjecture. In fact, we will prove not only that all
![]() $\sigma $
-invariant measures on
$\sigma $
-invariant measures on
![]() $X_\varphi $
are of the form
$X_\varphi $
are of the form
![]() $(M_H)_\ast (m_H\vee \kappa )$
, but also that the opposite inclusion holds and that
$(M_H)_\ast (m_H\vee \kappa )$
, but also that the opposite inclusion holds and that
![]() $\mathcal {P}(X_\eta )=\mathcal {P}(X_\varphi )$
. Thus, we not only settle Keller’s conjecture, but also answer his question from [Reference Keller17] about the existence of invariant measures supported on
$\mathcal {P}(X_\eta )=\mathcal {P}(X_\varphi )$
. Thus, we not only settle Keller’s conjecture, but also answer his question from [Reference Keller17] about the existence of invariant measures supported on
![]() $X_{\varphi }\setminus X_\eta $
(there are no such measures). The following theorem that captures all of this is our main result.
$X_{\varphi }\setminus X_\eta $
(there are no such measures). The following theorem that captures all of this is our main result.
Theorem A. For any
![]() $\mathscr {B}\subseteq {\mathbb {N}}$
such that
$\mathscr {B}\subseteq {\mathbb {N}}$
such that
![]() $\eta ^{*}$
is a regular Toeplitz sequence, we have
$\eta ^{*}$
is a regular Toeplitz sequence, we have
An auxiliary result, used to prove Theorem A, but also interesting on its own, is another description of the set
![]() $\mathcal {P}(X_\eta )=\mathcal {P}(X_\varphi )$
.
$\mathcal {P}(X_\eta )=\mathcal {P}(X_\varphi )$
.
Theorem B. (Cf. (6))
For any
![]() $\mathscr {B}\subseteq {\mathbb {N}}$
such that
$\mathscr {B}\subseteq {\mathbb {N}}$
such that
![]() $\eta ^{*}$
is a regular Toeplitz sequence, we have
$\eta ^{*}$
is a regular Toeplitz sequence, we have
where
![]() $N\colon (\{0,1\}^{{\mathbb {Z}}})^3\to \{0,1\}^{{\mathbb {Z}}}$
is the map given by
$N\colon (\{0,1\}^{{\mathbb {Z}}})^3\to \{0,1\}^{{\mathbb {Z}}}$
is the map given by
![]() $N(w,x,y)=w+y\cdot (x-w)$
and
$N(w,x,y)=w+y\cdot (x-w)$
and
![]() $\nu _{\eta ^{*}}\triangle \nu _\eta $
is the joining of
$\nu _{\eta ^{*}}\triangle \nu _\eta $
is the joining of
![]() $\nu _{\eta ^{*}}$
with
$\nu _{\eta ^{*}}$
with
![]() $\nu _\eta $
for which the pair
$\nu _\eta $
for which the pair
![]() $(\eta ^{*},\eta )$
is quasi-generic along any sequence
$(\eta ^{*},\eta )$
is quasi-generic along any sequence
![]() $(\ell _i)$
realizing the lower density of
$(\ell _i)$
realizing the lower density of
![]() $\mathcal {M}_{\mathscr {B}}$
.
$\mathcal {M}_{\mathscr {B}}$
.
Remark 1.12. Note that it is non-trivial that
![]() $(\eta ^{*},\eta )$
is quasi-generic under
$(\eta ^{*},\eta )$
is quasi-generic under
![]() $\sigma \times \sigma $
along
$\sigma \times \sigma $
along
![]() $(\ell _i)$
realizing the lower density of
$(\ell _i)$
realizing the lower density of
![]() $\mathcal {M}_{\mathscr {B}}$
—this will be shown in course of the proof of Theorem B. In fact, we will describe the limit measure, see Lemma 2.3. Notice also that once a pair
$\mathcal {M}_{\mathscr {B}}$
—this will be shown in course of the proof of Theorem B. In fact, we will describe the limit measure, see Lemma 2.3. Notice also that once a pair
![]() $(x,y)\in \{0,1\}^{\mathbb {Z}}$
is quasi-generic under
$(x,y)\in \{0,1\}^{\mathbb {Z}}$
is quasi-generic under
![]() $\sigma \times \sigma $
for some measure
$\sigma \times \sigma $
for some measure
![]() $\rho $
, then
$\rho $
, then
![]() $\rho $
is
$\rho $
is
![]() $(\sigma \times \sigma )$
-invariant. Moreover, x and y are quasi-generic (along the same subsequence) for the marginals of
$(\sigma \times \sigma )$
-invariant. Moreover, x and y are quasi-generic (along the same subsequence) for the marginals of
![]() $\rho $
and thus,
$\rho $
and thus,
![]() $\rho $
is a joining of its marginals.
$\rho $
is a joining of its marginals.
1.3.2 Main results: tautness and combinatorics
Proposition D. (Cf. (8))
Let
![]() $\mathscr {B}\subseteq \mathbb {N}$
. Suppose that
$\mathscr {B}\subseteq \mathbb {N}$
. Suppose that
![]() $\mathscr {C}\subseteq {\mathbb {N}}$
is taut. Then the following are equivalent:
$\mathscr {C}\subseteq {\mathbb {N}}$
is taut. Then the following are equivalent:

Given
![]() $\mathscr {B}\subseteq \mathbb {N}$
, let
$\mathscr {B}\subseteq \mathbb {N}$
, let
Consider the following partial order
![]() $\prec $
on
$\prec $
on
![]() $Taut(\mathscr {B})$
:
$Taut(\mathscr {B})$
:
Clearly,
![]() $\mathscr {B}^{\prime },\mathscr {B}^{*}\in Taut(\mathscr {B})$
. Moreover,
$\mathscr {B}^{\prime },\mathscr {B}^{*}\in Taut(\mathscr {B})$
. Moreover,
![]() $\mathscr {B}^{*}$
is the smallest element of
$\mathscr {B}^{*}$
is the smallest element of
![]() $Taut(\mathscr {B})$
. Indeed, if
$Taut(\mathscr {B})$
. Indeed, if
![]() $\mathscr {C}\in Taut(\mathscr {B})$
, then
$\mathscr {C}\in Taut(\mathscr {B})$
, then
![]() $X_{\eta ^{*}}\subseteq X_{\eta _{\mathscr {C}}}$
since
$X_{\eta ^{*}}\subseteq X_{\eta _{\mathscr {C}}}$
since
![]() $X_{\eta ^{*}}$
is the unique minimal subset of
$X_{\eta ^{*}}$
is the unique minimal subset of
![]() $X_\eta $
. As an immediate consequence of Proposition D (more precisely, by
$X_\eta $
. As an immediate consequence of Proposition D (more precisely, by
![]() $(c){\iff} (c^{\prime })$
), we obtain the following.
$(c){\iff} (c^{\prime })$
), we obtain the following.
Corollary E. For any
![]() $\mathscr {B}\subseteq \mathbb {N}$
,
$\mathscr {B}\subseteq \mathbb {N}$
,
![]() $\mathscr {B}^{\prime }$
is the largest element of
$\mathscr {B}^{\prime }$
is the largest element of
![]() $Taut(\mathscr {B})$
with respect to
$Taut(\mathscr {B})$
with respect to
![]() $\prec $
.
$\prec $
.
1.3.3 Main results: entropy
Last, but not least, we prove some results on the entropy of
![]() $\mathscr {B}$
-free systems.
$\mathscr {B}$
-free systems.
Theorem F. (Cf. (3))
For any
![]() $\mathscr {B}\subseteq {\mathbb {N}}$
, we have
$\mathscr {B}\subseteq {\mathbb {N}}$
, we have
![]() $h(X_\eta )\geq \overline {d}-\overline {d}^{*}$
, where
$h(X_\eta )\geq \overline {d}-\overline {d}^{*}$
, where
![]() $\overline {d}=\overline {d}(\mathcal {F}_{\mathscr {B}})$
and
$\overline {d}=\overline {d}(\mathcal {F}_{\mathscr {B}})$
and
![]() $\overline {d}^{*}=\overline {d}(\mathcal {F}_{\mathscr {B}^{*}})$
. If additionally
$\overline {d}^{*}=\overline {d}(\mathcal {F}_{\mathscr {B}^{*}})$
. If additionally
![]() $X_{\eta ^{*}}$
is uniquely ergodic (in particular, if
$X_{\eta ^{*}}$
is uniquely ergodic (in particular, if
![]() $\eta ^{*}$
is a regular Toeplitz sequence), then
$\eta ^{*}$
is a regular Toeplitz sequence), then
![]() $h(X_\eta )=\overline {d}-d^{*}$
, where
$h(X_\eta )=\overline {d}-d^{*}$
, where
![]() $d^{*}=d(\mathcal {F}_{\mathscr {B}^{*}})$
.
$d^{*}=d(\mathcal {F}_{\mathscr {B}^{*}})$
.
Corollary G. (Cf. (5))
For any
![]() $\mathscr {B}\subseteq {\mathbb {N}}$
such that
$\mathscr {B}\subseteq {\mathbb {N}}$
such that
![]() $\eta ^{*}$
is a regular Toeplitz sequence, we have
$\eta ^{*}$
is a regular Toeplitz sequence, we have
(note that if the above holds, then
![]() $\nu _{\eta }=\nu _{\eta ^{*}}$
).
$\nu _{\eta }=\nu _{\eta ^{*}}$
).
Remark 1.13. In Corollary G, the second equivalence is true without any assumption on
![]() $\eta ^{*}$
. It seems open whether there exists
$\eta ^{*}$
. It seems open whether there exists
![]() $\mathscr {B}$
such that
$\mathscr {B}$
such that
![]() $\eta ^{*}$
is an irregular Toeplitz sequence with
$\eta ^{*}$
is an irregular Toeplitz sequence with
![]() $h(X_{\eta })=0$
and
$h(X_{\eta })=0$
and
![]() $\mathcal {P}(X_\eta )$
being not a singleton, cf. Remark 1.14 below.
$\mathcal {P}(X_\eta )$
being not a singleton, cf. Remark 1.14 below.
Theorem H. (Cf. (2) and (4))
For any
![]() $\mathscr {B}\subseteq {\mathbb {N}}$
such that
$\mathscr {B}\subseteq {\mathbb {N}}$
such that
![]() $\eta ^{*}$
is a regular Toeplitz sequence, the subshift
$\eta ^{*}$
is a regular Toeplitz sequence, the subshift
![]() $X_\eta $
is intrinsically ergodic. The measure of maximal entropy equals
$X_\eta $
is intrinsically ergodic. The measure of maximal entropy equals
![]() $N_\ast ((\nu _{\eta ^{*}}\triangle \nu _{\eta })\otimes B_{1/2,1/2})$
.
$N_\ast ((\nu _{\eta ^{*}}\triangle \nu _{\eta })\otimes B_{1/2,1/2})$
.
Theorem I. (Cf. (9))
For any
![]() $\mathscr {B}\subseteq {\mathbb {N}}$
such that
$\mathscr {B}\subseteq {\mathbb {N}}$
such that
![]() $\eta ^{*}$
is a regular Toeplitz sequence, the ergodic measures are entropy-dense in
$\eta ^{*}$
is a regular Toeplitz sequence, the ergodic measures are entropy-dense in
![]() $\mathcal {P}(X_\eta )$
.
$\mathcal {P}(X_\eta )$
.
1.3.4 Dynamical diagrams viewpoint
In this section, we present a dynamical diagrams viewpoint on Theorems B, C, A and H. The first three of these results can be formulated in terms of dynamical diagrams and the structure of the proofs also relies on this notion. As for Theorem H, the dynamical diagrams serve as a tool in the proof.
On Theorems B and C
These two results can be proved separately (Theorem C is then a consequence of Theorem B); however, there is a nice way to treat them together, which has the additional advantage of slightly shortening the proofs. Recall that by (11), (16) and (17), we have
Moreover, under the extra assumption that
![]() $\eta ^{*}$
is a regular Toeplitz sequence, by [Reference Keller17, Remark 1.4] and observing (12), we have
$\eta ^{*}$
is a regular Toeplitz sequence, by [Reference Keller17, Remark 1.4] and observing (12), we have
Remark 1.14. The first equality in (18) is actually the main reason for the extra assumption on
![]() $\eta ^{*}$
in Keller’s conjecture from [Reference Keller17] (see Remark 1.4 therein). In fact, this goes deeper. If
$\eta ^{*}$
in Keller’s conjecture from [Reference Keller17] (see Remark 1.4 therein). In fact, this goes deeper. If
![]() $\eta ^{*}$
is a regular Toeplitz sequence, then
$\eta ^{*}$
is a regular Toeplitz sequence, then
![]() $\mathcal {P}(X_{\eta ^{*}})=\{\nu _{\eta ^{*}}\}$
, while when we drop the assumption on
$\mathcal {P}(X_{\eta ^{*}})=\{\nu _{\eta ^{*}}\}$
, while when we drop the assumption on
![]() $\eta ^{*}$
, various things can happen to
$\eta ^{*}$
, various things can happen to
![]() $\mathcal {P}(X_{\eta ^{*}})$
: it can be a singleton consisting only of
$\mathcal {P}(X_{\eta ^{*}})$
: it can be a singleton consisting only of
![]() $\nu _{\eta ^{*}}$
, see [Reference Keller18, Theorem 2] (even if
$\nu _{\eta ^{*}}$
, see [Reference Keller18, Theorem 2] (even if
![]() $\eta ^{*}$
is an irregular Toeplitz sequence!), but it can also contain some positive entropy measure, see [Reference Keller18, Theorem 1]. Thus, since
$\eta ^{*}$
is an irregular Toeplitz sequence!), but it can also contain some positive entropy measure, see [Reference Keller18, Theorem 1]. Thus, since
![]() $X_{\eta ^{*}}\subseteq X_\eta $
, we cannot expect to obtain a consistent description of
$X_{\eta ^{*}}\subseteq X_\eta $
, we cannot expect to obtain a consistent description of
![]() $\mathcal {P}(X_\eta )$
without imposing any restrictions on
$\mathcal {P}(X_\eta )$
without imposing any restrictions on
![]() $\eta ^{*}$
. We will use the fact that the Toeplitz sequence
$\eta ^{*}$
. We will use the fact that the Toeplitz sequence
![]() $\eta ^{*}$
is regular very frequently in our proofs.
$\eta ^{*}$
is regular very frequently in our proofs.
Continuing our argument from (18), we obtain for a regular Toeplitz sequences
![]() $ \eta ^{*} $
that
$ \eta ^{*} $
that
 $$ \begin{align} &\mathcal{P}([\underline{\varphi^{\prime}},\varphi^{\prime}])=\mathcal{P}(\overline{[\underline{\varphi^{\prime}},\varphi^{\prime}]})=\mathcal{P}(X_{\varphi^{\prime}})=\mathcal{P}(X_{\eta^{\prime}}) \nonumber\\ &\quad\subseteq \mathcal{P}(X_\eta) \subseteq \mathcal{P}(X_\varphi) =\mathcal{P}(\overline{[\underline{\varphi},\varphi]})=\mathcal{P}([\underline{\varphi},\varphi]). \end{align} $$
$$ \begin{align} &\mathcal{P}([\underline{\varphi^{\prime}},\varphi^{\prime}])=\mathcal{P}(\overline{[\underline{\varphi^{\prime}},\varphi^{\prime}]})=\mathcal{P}(X_{\varphi^{\prime}})=\mathcal{P}(X_{\eta^{\prime}}) \nonumber\\ &\quad\subseteq \mathcal{P}(X_\eta) \subseteq \mathcal{P}(X_\varphi) =\mathcal{P}(\overline{[\underline{\varphi},\varphi]})=\mathcal{P}([\underline{\varphi},\varphi]). \end{align} $$
Therefore, the assertions of Theorems B and C are equivalent to the following two inclusions:
Consider the following diagram:

and notice that the assertions of Theorems B and C are equivalent to ( D B,C ) being a surjective commutative dynamical diagram. Indeed:
-
• ( D B,C ) is a dynamical diagram if and only if the maps N and id are morphisms, which implies the second inclusion in (20) holds.
Notice that by (19), the map id is a morphism if and only if
![]() $\mathcal {P}([\underline {\varphi },\varphi ])=\mathcal {P}(X_{\varphi ^{\prime }})$
. Therefore, id is then automatically surjective.
$\mathcal {P}([\underline {\varphi },\varphi ])=\mathcal {P}(X_{\varphi ^{\prime }})$
. Therefore, id is then automatically surjective.
-
• ( D B,C ) is in addition surjective if and only if the morphism N is surjective, which implies the first inclusion in equation (20) holds.
Moreover, if both inclusions in (20) hold, then by (19), we obtain the equality
![]() $ \{N_\ast ((\nu _{\eta ^{*}}\triangle \nu _\eta ) \vee \kappa ) : \kappa \in \mathcal {P}(\{0,1\}^{\mathbb {Z}})\} = \mathcal {P}([\underline {\varphi },\varphi ]) = \mathcal {P}(X_{\varphi ^{\prime }}) $
, which implies that
$ \{N_\ast ((\nu _{\eta ^{*}}\triangle \nu _\eta ) \vee \kappa ) : \kappa \in \mathcal {P}(\{0,1\}^{\mathbb {Z}})\} = \mathcal {P}([\underline {\varphi },\varphi ]) = \mathcal {P}(X_{\varphi ^{\prime }}) $
, which implies that
![]() $ N $
and id are surjective morphisms.
$ N $
and id are surjective morphisms.
On Theorem A
Having proved Theorem B first, to prove Theorem A, we will only need to show that
Let
![]() $\underline {\varphi }\otimes \varphi \colon H\to (\{0,1\}^{\mathbb {Z}})^2$
and
$\underline {\varphi }\otimes \varphi \colon H\to (\{0,1\}^{\mathbb {Z}})^2$
and
![]() $(\underline {\varphi }\otimes \varphi )(h)=(\underline {\varphi }(h),\varphi (h))$
. Consider the following diagram:
$(\underline {\varphi }\otimes \varphi )(h)=(\underline {\varphi }(h),\varphi (h))$
. Consider the following diagram:

Then:
-
• if ( D A ) is a commutative diagram, then
(indeed, by the commutativity, ‘travelling’ via $$ \begin{align*} \{(M_H)_\ast(m_H\vee\kappa):\kappa\in \mathcal{P}(\{0,1\}^{\mathbb{Z}})\}\subseteq \{N_\ast((\nu_{\eta*}\triangle\nu_\eta)\vee\kappa) : \kappa\in\mathcal{P}(\{0,1\}^{{\mathbb{Z}}})\} \end{align*} $$
$$ \begin{align*} \{(M_H)_\ast(m_H\vee\kappa):\kappa\in \mathcal{P}(\{0,1\}^{\mathbb{Z}})\}\subseteq \{N_\ast((\nu_{\eta*}\triangle\nu_\eta)\vee\kappa) : \kappa\in\mathcal{P}(\{0,1\}^{{\mathbb{Z}}})\} \end{align*} $$
 $M_H$
is the same as ‘travelling’ first via
$M_H$
is the same as ‘travelling’ first via
 $(\underline {\varphi }\otimes \varphi )\times \text {id}$
and then via N);
$(\underline {\varphi }\otimes \varphi )\times \text {id}$
and then via N);
-
• if ( D A ) is surjective, then
(indeed, we can travel up from $$ \begin{align*} \{ N_\ast((\nu_{\eta*}\triangle\nu_\eta)\vee\kappa) : \kappa\in\mathcal{P}(\{0,1\}^{{\mathbb{Z}}}) \}\subseteq \{ (M_H)_\ast(m_H\vee\kappa):\kappa\in \mathcal{P}(\{0,1\}^{\mathbb{Z}})\} \end{align*} $$
$$ \begin{align*} \{ N_\ast((\nu_{\eta*}\triangle\nu_\eta)\vee\kappa) : \kappa\in\mathcal{P}(\{0,1\}^{{\mathbb{Z}}}) \}\subseteq \{ (M_H)_\ast(m_H\vee\kappa):\kappa\in \mathcal{P}(\{0,1\}^{\mathbb{Z}})\} \end{align*} $$
 $N_\ast ((\nu _{\eta *}\triangle \nu _\eta )\vee \kappa )$
to
$N_\ast ((\nu _{\eta *}\triangle \nu _\eta )\vee \kappa )$
to
 $(\nu _{\eta *}\triangle \nu _\eta )\vee \kappa $
via N, then again up by
$(\nu _{\eta *}\triangle \nu _\eta )\vee \kappa $
via N, then again up by
 $(\underline {\varphi }\otimes \varphi )\times \text {id}$
, that is, use the surjectivity of
$(\underline {\varphi }\otimes \varphi )\times \text {id}$
, that is, use the surjectivity of
 $(\underline {\varphi }\otimes \varphi )\times \text {id}$
and finally use that
$(\underline {\varphi }\otimes \varphi )\times \text {id}$
and finally use that
 $M_H=N\circ ((\underline {\varphi }\otimes \varphi )\times \text {id})$
as (
D
A
) commutes).
$M_H=N\circ ((\underline {\varphi }\otimes \varphi )\times \text {id})$
as (
D
A
) commutes).
In other words, the assertion of Theorem A follows from Theorem B and the commutativity and the surjectivity of ( D A ).
In fact, Theorems A, B and C can be summarized using a single diagram, namely:

Notice that if we prove that the above diagram is a commutative and surjective dynamical diagram, then indeed we get:
-
•
 $\mathcal {P}(X_{\varphi ^{\prime }})=\mathcal {P}(X_{\eta ^{\prime }})=\mathcal {P}(X_\eta )=\mathcal {P}([\underline {\varphi },\varphi ])$
;
$\mathcal {P}(X_{\varphi ^{\prime }})=\mathcal {P}(X_{\eta ^{\prime }})=\mathcal {P}(X_\eta )=\mathcal {P}([\underline {\varphi },\varphi ])$
; -
•
 $\mathcal {P}(X_\eta )=\{N_\ast ((\nu _{\eta ^{*}}\triangle \nu _\eta )\vee \kappa ):\kappa \in \mathcal {P} (\{0,1\}^{\mathbb {Z}})\}\\ =\{(M_H)_\ast (m_H\vee \kappa ) :\kappa \in \mathcal {P}(\{0,1\}^{\mathbb {Z}} ) \}$
.
$\mathcal {P}(X_\eta )=\{N_\ast ((\nu _{\eta ^{*}}\triangle \nu _\eta )\vee \kappa ):\kappa \in \mathcal {P} (\{0,1\}^{\mathbb {Z}})\}\\ =\{(M_H)_\ast (m_H\vee \kappa ) :\kappa \in \mathcal {P}(\{0,1\}^{\mathbb {Z}} ) \}$
.
On Theorem H
The main idea of the proof of Theorem H is to equip the diagram
(which is surjective by Theorem A) with an ‘intermediate’ vertex:
where
![]() $\widetilde {R}$
is a certain skew product over
$\widetilde {R}$
is a certain skew product over
![]() $R\colon H\to H$
and the maps
$R\colon H\to H$
and the maps
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
are morphisms defined later. We prove then that
$\Psi $
are morphisms defined later. We prove then that
![]() $h(H\times \{0,1\}^{\mathbb {Z}},\widetilde {R})=\overline {d}-d^{*}$
(which equals to
$h(H\times \{0,1\}^{\mathbb {Z}},\widetilde {R})=\overline {d}-d^{*}$
(which equals to
![]() $h(X_\eta )$
by Theorem F) and prove the intrinsic ergodicity of
$h(X_\eta )$
by Theorem F) and prove the intrinsic ergodicity of
![]() $(H\times \{0,1\}^{\mathbb {Z}},\widetilde {R})$
. For the details, see §4.2.
$(H\times \{0,1\}^{\mathbb {Z}},\widetilde {R})$
. For the details, see §4.2.
2 Invariant measures
Before we begin working on the description of
![]() $\mathcal {P}(X_\eta )$
, let us concentrate on
$\mathcal {P}(X_\eta )$
, let us concentrate on
![]() $X_\eta $
itself. Keller [Reference Keller17] proved that for any taut set
$X_\eta $
itself. Keller [Reference Keller17] proved that for any taut set
![]() $\mathscr {B}$
, the subshift
$\mathscr {B}$
, the subshift
![]() $X_\eta $
is in a way ‘hereditary’. We rephrase his result in the following way.
$X_\eta $
is in a way ‘hereditary’. We rephrase his result in the following way.
Proposition 2.1. For any
![]() $\mathscr {B}\subseteq \mathbb {N}$
, we have
$\mathscr {B}\subseteq \mathbb {N}$
, we have
![]() $ X_\eta \subseteq \overline {[\eta ^{*},\eta ]}\subseteq X_\varphi. $
In particular, if
$ X_\eta \subseteq \overline {[\eta ^{*},\eta ]}\subseteq X_\varphi. $
In particular, if
![]() $\mathscr {B}$
is taut,
$\mathscr {B}$
is taut,
![]() $X_\eta =\overline {[\eta ^{*},\eta ]}=X_\varphi $
.
$X_\eta =\overline {[\eta ^{*},\eta ]}=X_\varphi $
.
Proof. Clearly,
![]() $\varphi (\Delta (0))=\eta \in [\eta ^{*},\eta ]$
. Moreover, by [Reference Keller17, Corollary 1.4], we have
$\varphi (\Delta (0))=\eta \in [\eta ^{*},\eta ]$
. Moreover, by [Reference Keller17, Corollary 1.4], we have
![]() ${\eta ^{*}=\underline {\varphi }(\Delta (0))}$
. Thus,
${\eta ^{*}=\underline {\varphi }(\Delta (0))}$
. Thus,
![]() $[\eta ^{*},\eta ]\subseteq [\underline {\varphi },\varphi ]$
. This yields
$[\eta ^{*},\eta ]\subseteq [\underline {\varphi },\varphi ]$
. This yields
By [Reference Keller17, Corollary 1.2], if
![]() $\mathscr {B}$
is taut, we have
$\mathscr {B}$
is taut, we have
![]() $X_\eta =X_\varphi $
, which completes the proof.
$X_\eta =X_\varphi $
, which completes the proof.
2.1 Proof of Theorems B and C
2.1.1 ( D B,C ) is a (commutative) dynamical diagram
We will need a certain lemma from [Reference Bergelson, Downarowicz and Vandehey2] about ‘lifting’ quasi-generic points to joinings. We formulate it here for
![]() ${\mathbb {Z}}$
-actions, while the original version is more general (the result is true for actions of countable cancellative semigroups and arbitrary Følner sequences).
${\mathbb {Z}}$
-actions, while the original version is more general (the result is true for actions of countable cancellative semigroups and arbitrary Følner sequences).
Theorem 2.2. [Reference Bergelson, Downarowicz and Vandehey2, Theorem 5.16]
Let
![]() $\mathcal {A}_1,\mathcal {A}_2$
be finite alphabets. If
$\mathcal {A}_1,\mathcal {A}_2$
be finite alphabets. If
![]() $x\in \mathcal {A}_1^{\mathbb {Z}}$
is quasi-generic for
$x\in \mathcal {A}_1^{\mathbb {Z}}$
is quasi-generic for
![]() $\nu $
along
$\nu $
along
![]() $ (\ell _{i}) $
and
$ (\ell _{i}) $
and
![]() $\nu \vee \kappa \in \mathcal {P}(\mathcal {A}_1^{\mathbb {Z}}\times \mathcal {A}_2^{\mathbb {Z}},\sigma \times \sigma )$
, then there exists
$\nu \vee \kappa \in \mathcal {P}(\mathcal {A}_1^{\mathbb {Z}}\times \mathcal {A}_2^{\mathbb {Z}},\sigma \times \sigma )$
, then there exists
![]() $y\in \mathcal {A}_2^{\mathbb {Z}}$
such that the pair
$y\in \mathcal {A}_2^{\mathbb {Z}}$
such that the pair
![]() $(x,y)$
is quasi-generic for
$(x,y)$
is quasi-generic for
![]() $\nu \vee \kappa $
along some subsequence of
$\nu \vee \kappa $
along some subsequence of
![]() $ (\ell _{i}) $
.
$ (\ell _{i}) $
.
Let
![]() $(\ell _i)$
be a sequence realizing the lower density of
$(\ell _i)$
be a sequence realizing the lower density of
![]() $\mathcal {M}_{\mathscr {B}}$
and suppose that
$\mathcal {M}_{\mathscr {B}}$
and suppose that
![]() $X_{\eta ^{*}}$
is uniquely ergodic (in particular, this happens if
$X_{\eta ^{*}}$
is uniquely ergodic (in particular, this happens if
![]() $\eta ^{*}$
is a regular Toeplitz sequence). If the pair
$\eta ^{*}$
is a regular Toeplitz sequence). If the pair
![]() $(\eta ^{*},\eta )$
is quasi-generic along a subsequence
$(\eta ^{*},\eta )$
is quasi-generic along a subsequence
![]() $(\ell _{i_j})$
of
$(\ell _{i_j})$
of
![]() $(\ell _i)$
for some measure, then this limit measure must be a joining of
$(\ell _i)$
for some measure, then this limit measure must be a joining of
![]() $\nu _{\eta ^{*}}$
and
$\nu _{\eta ^{*}}$
and
![]() $\nu _\eta $
. In fact, we have the following lemma which we will prove in a moment.
$\nu _\eta $
. In fact, we have the following lemma which we will prove in a moment.
Lemma 2.3. Let
![]() $\mathscr {B}\subseteq \mathbb {N}$
be such that
$\mathscr {B}\subseteq \mathbb {N}$
be such that
![]() $X_{\eta ^{*}}$
is uniquely ergodic. Let
$X_{\eta ^{*}}$
is uniquely ergodic. Let
![]() $(\ell _i)$
be any sequence realizing the lower density of
$(\ell _i)$
be any sequence realizing the lower density of
![]() $\mathcal {M}_{\mathscr {B}}$
. Then the point
$\mathcal {M}_{\mathscr {B}}$
. Then the point
![]() $(\eta ^{*},\eta )$
is quasi-generic along
$(\eta ^{*},\eta )$
is quasi-generic along
![]() $(\ell _i)$
for
$(\ell _i)$
for
![]() $(\underline {\varphi }\otimes \varphi )_\ast (m_H)$
.
$(\underline {\varphi }\otimes \varphi )_\ast (m_H)$
.
Remark 2.4. Instead of
![]() $(\underline {\varphi }\otimes \varphi )_\ast (m_H)$
, we will usually write
$(\underline {\varphi }\otimes \varphi )_\ast (m_H)$
, we will usually write
![]() $\nu _{\eta ^{*}}\triangle \nu _{\eta }$
. In this subsection, we will only use that
$\nu _{\eta ^{*}}\triangle \nu _{\eta }$
. In this subsection, we will only use that
![]() $(\eta ^{*},\eta )$
is quasi-generic along
$(\eta ^{*},\eta )$
is quasi-generic along
![]() $(\ell _i)$
, while the specific form of the limit measure will be used later. Let us justify here our notation
$(\ell _i)$
, while the specific form of the limit measure will be used later. Let us justify here our notation
![]() $\nu _{\eta ^{*}}\triangle \nu _\eta $
and show that this is a certain off-diagonal joining with marginals
$\nu _{\eta ^{*}}\triangle \nu _\eta $
and show that this is a certain off-diagonal joining with marginals
![]() $\nu _{\eta ^{*}}$
and
$\nu _{\eta ^{*}}$
and
![]() $\nu _\eta $
. Indeed, by (14), we have
$\nu _\eta $
. Indeed, by (14), we have
Notice that
is a factoring map. Moreover, for any measurable sets
![]() $A,B\subseteq \{0,1\}^{\mathbb {Z}}$
, we have
$A,B\subseteq \{0,1\}^{\mathbb {Z}}$
, we have
 $$ \begin{align*} \triangle_S(A\times B)&=\nu_\eta((\varphi^{*}\circ \Gamma_{H,H^{*}}\circ \varphi^{-1})^{-1}(A)\cap B)\\ &=m_H((\varphi^{*}\circ \Gamma_{H,H^{*}})^{-1}(A)\cap \varphi^{-1}(B))=((\varphi^{*}\circ \Gamma_{H,H^{*}})\otimes \varphi)_\ast(m_H)(A\times B)\\ &=\nu_{\eta^{*}}\triangle \nu_\eta(A\times B). \end{align*} $$
$$ \begin{align*} \triangle_S(A\times B)&=\nu_\eta((\varphi^{*}\circ \Gamma_{H,H^{*}}\circ \varphi^{-1})^{-1}(A)\cap B)\\ &=m_H((\varphi^{*}\circ \Gamma_{H,H^{*}})^{-1}(A)\cap \varphi^{-1}(B))=((\varphi^{*}\circ \Gamma_{H,H^{*}})\otimes \varphi)_\ast(m_H)(A\times B)\\ &=\nu_{\eta^{*}}\triangle \nu_\eta(A\times B). \end{align*} $$
Recall also that it was shown in [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7] that
where
![]() $(\ell _i)_{i\geq 1}$
is any sequence realizing the lower density of
$(\ell _i)_{i\geq 1}$
is any sequence realizing the lower density of
![]() $\mathcal {M}_{\mathscr {B}^{\prime }}$
. Moreover (see the proof of [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Lemma 4.11]), any sequence
$\mathcal {M}_{\mathscr {B}^{\prime }}$
. Moreover (see the proof of [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Lemma 4.11]), any sequence
![]() $(\ell _i)$
realizing the lower density of
$(\ell _i)$
realizing the lower density of
![]() $\mathcal {M}_{\mathscr {B}^{\prime }}$
is also realizing the lower density of
$\mathcal {M}_{\mathscr {B}^{\prime }}$
is also realizing the lower density of
![]() $\mathcal {M}_{\mathscr {B}}$
. For any such
$\mathcal {M}_{\mathscr {B}}$
. For any such
![]() $(\ell _i)_{i\geq 1}$
, also
$(\ell _i)_{i\geq 1}$
, also
whenever
![]() $X_{\eta ^{*}}$
is uniquely ergodic.
$X_{\eta ^{*}}$
is uniquely ergodic.
Let us now prove that (
D
B,C
) is indeed a dynamical diagram (and since it is linear, it is then commutative by Remark 1.8). Notice that it suffices to show that for any measure of the form
![]() $N_\ast (\rho )$
, where
$N_\ast (\rho )$
, where
![]() $\rho =(\nu _{\eta ^{*}}\triangle \nu _\eta )\vee \kappa $
with
$\rho =(\nu _{\eta ^{*}}\triangle \nu _\eta )\vee \kappa $
with
![]() $\kappa \in \mathcal {P}(\{0,1\}^{\mathbb {Z}})$
, we have
$\kappa \in \mathcal {P}(\{0,1\}^{\mathbb {Z}})$
, we have
![]() $N_\ast (\rho )(X_{\varphi ^{\prime }})=1$
. To see that this is indeed the case, fix such a measure
$N_\ast (\rho )(X_{\varphi ^{\prime }})=1$
. To see that this is indeed the case, fix such a measure
![]() $\rho $
. It follows by Theorem 2.2 and by (22) that
$\rho $
. It follows by Theorem 2.2 and by (22) that
![]() $\rho $
has a quasi-generic point of the form
$\rho $
has a quasi-generic point of the form
![]() $(\eta ^{*},\eta ^{\prime },y)$
with
$(\eta ^{*},\eta ^{\prime },y)$
with
![]() $y\in \{0,1\}^{\mathbb {Z}}$
. Therefore,
$y\in \{0,1\}^{\mathbb {Z}}$
. Therefore,
![]() $z:=N(\eta ^{*},\eta ^{\prime },y)$
is quasi-generic for
$z:=N(\eta ^{*},\eta ^{\prime },y)$
is quasi-generic for
![]() $N_\ast (\rho )$
and thus
$N_\ast (\rho )$
and thus
![]() $N_\ast (\rho )(X_z)=1$
. It remains to notice that
$N_\ast (\rho )(X_z)=1$
. It remains to notice that
![]() $\eta ^{*}\leq z\leq \eta ^{\prime }$
. Thus,
$\eta ^{*}\leq z\leq \eta ^{\prime }$
. Thus,
where the last equality follows from Proposition 2.1.
Proof of Lemma 2.3
Fix
![]() $(\ell _i)$
which realizes the lower density of
$(\ell _i)$
which realizes the lower density of
![]() $\mathcal {M}_{\mathscr {B}}$
. By a pure measure theory argument (see the proof of [Reference El Abdalaoui, Lemańczyk and de la Rue9, Theorem 4.1]), we only need to prove that
$\mathcal {M}_{\mathscr {B}}$
. By a pure measure theory argument (see the proof of [Reference El Abdalaoui, Lemańczyk and de la Rue9, Theorem 4.1]), we only need to prove that
 $$ \begin{align*} \frac{1}{\ell_i} \sum_{n\leq \ell_i} \delta_{ ( \sigma^n\underline{\varphi}(\Delta(0)),\sigma^n\varphi(\Delta(0)))}(\underline{A}\times A) \to (\underline{\varphi}\otimes \varphi)_\ast(m_H)(\underline{A}\times A) \end{align*} $$
$$ \begin{align*} \frac{1}{\ell_i} \sum_{n\leq \ell_i} \delta_{ ( \sigma^n\underline{\varphi}(\Delta(0)),\sigma^n\varphi(\Delta(0)))}(\underline{A}\times A) \to (\underline{\varphi}\otimes \varphi)_\ast(m_H)(\underline{A}\times A) \end{align*} $$
for
with
![]() $\underline {S},S\subseteq {\mathbb {Z}}$
being arbitrary finite sets. By
$\underline {S},S\subseteq {\mathbb {Z}}$
being arbitrary finite sets. By
![]() $\sigma \circ \underline {\varphi }=\underline {\varphi }\circ R$
and
$\sigma \circ \underline {\varphi }=\underline {\varphi }\circ R$
and
![]() $\sigma \circ \varphi =\varphi \circ R$
, this is equivalent to proving that
$\sigma \circ \varphi =\varphi \circ R$
, this is equivalent to proving that
 $$ \begin{align*} \lim_{i\to\infty}\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\underline{\varphi}^{-1}(\underline{A})\times \varphi^{-1}(A)}(R^n (\Delta(0)),R^n (\Delta(0)))=(\underline{\varphi}\otimes \varphi)_\ast(m_H)(\underline{A}\times A). \end{align*} $$
$$ \begin{align*} \lim_{i\to\infty}\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\underline{\varphi}^{-1}(\underline{A})\times \varphi^{-1}(A)}(R^n (\Delta(0)),R^n (\Delta(0)))=(\underline{\varphi}\otimes \varphi)_\ast(m_H)(\underline{A}\times A). \end{align*} $$
The main underlying idea is to approximate
![]() $\underline {\varphi }^{-1}(\underline {A})$
and
$\underline {\varphi }^{-1}(\underline {A})$
and
![]() $\varphi ^{-1}(A)$
by clopen sets, so that we can use the ergodicity properties of rotations. We will begin with the right-hand side, as it is easier (the approximation of the left-hand side requires the use of the Davenport–Erdős theorem, i.e. (1)).
$\varphi ^{-1}(A)$
by clopen sets, so that we can use the ergodicity properties of rotations. We will begin with the right-hand side, as it is easier (the approximation of the left-hand side requires the use of the Davenport–Erdős theorem, i.e. (1)).
Approximation of the right-hand side. We have
Let, for
![]() $K\geq 1$
,
$K\geq 1$
,
Let
Each
![]() $W_K$
is clopen and
$W_K$
is clopen and
![]() $W_K \searrow W$
when
$W_K \searrow W$
when
![]() $K\to \infty $
. Thus, given
$K\to \infty $
. Thus, given
![]() $\varepsilon>0$
, for K large enough, we have
$\varepsilon>0$
, for K large enough, we have
Recall from (14) that
![]() $\underline {\varphi }=\varphi ^{*}\circ \Gamma _{H,H^{*}}$
and let
$\underline {\varphi }=\varphi ^{*}\circ \Gamma _{H,H^{*}}$
and let
 $$ \begin{align*} \underline{C}\kern1.3pt{:=}\kern1.3pt\underline{\varphi}^{-1}(\underline{A})\kern1.3pt{=}\kern1.3pt\Gamma_{H,H^{*}}^{-1}((\varphi^{*})^{-1}(\underline{A}))\kern1.3pt{=}\kern1.3pt \Gamma_{H,H^{*}}^{-1} \bigcap_{s\in\underline{S}}(R^{*})^{-s}(W^{*})^c\kern1.3pt{=}\kern1.3pt\bigcap_{s\in\underline{S}}\Gamma_{H,H^{*}}^{-1}(R^{*})^{-s}(W^{*})^c. \end{align*} $$
$$ \begin{align*} \underline{C}\kern1.3pt{:=}\kern1.3pt\underline{\varphi}^{-1}(\underline{A})\kern1.3pt{=}\kern1.3pt\Gamma_{H,H^{*}}^{-1}((\varphi^{*})^{-1}(\underline{A}))\kern1.3pt{=}\kern1.3pt \Gamma_{H,H^{*}}^{-1} \bigcap_{s\in\underline{S}}(R^{*})^{-s}(W^{*})^c\kern1.3pt{=}\kern1.3pt\bigcap_{s\in\underline{S}}\Gamma_{H,H^{*}}^{-1}(R^{*})^{-s}(W^{*})^c. \end{align*} $$
Define
![]() $W_K^{*}$
in a similar way as
$W_K^{*}$
in a similar way as
![]() $W_K$
:
$W_K$
:
Finally, let
 $$ \begin{align} \underline{C}_K:=\bigcap_{s\in\underline{S}}\Gamma_{H,H^{*}}^{-1}(R^{*})^{-s}(W_{K}^{*})^c. \end{align} $$
$$ \begin{align} \underline{C}_K:=\bigcap_{s\in\underline{S}}\Gamma_{H,H^{*}}^{-1}(R^{*})^{-s}(W_{K}^{*})^c. \end{align} $$
Then, for K large enough,
Notice that
Thus, it follows by (24) and (26) that
for K sufficiently large.
Approximation of the left-hand side. Let
![]() $(\ell _i)_{i\geq 1}$
be a sequence realizing the lower density of
$(\ell _i)_{i\geq 1}$
be a sequence realizing the lower density of
![]() $\mathcal {M}_{\mathscr {B}}$
. By definition,
$\mathcal {M}_{\mathscr {B}}$
. By definition,
 $$ \begin{align*} \frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\underline{A}\times A}(\underline{\varphi}(R^n (\Delta(0))),\varphi(R^n (\Delta(0))))=\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\underline{C}}(R^n(\Delta(0)))\mathbf{1}_{C}(R^n(\Delta(0))). \end{align*} $$
$$ \begin{align*} \frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\underline{A}\times A}(\underline{\varphi}(R^n (\Delta(0))),\varphi(R^n (\Delta(0))))=\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\underline{C}}(R^n(\Delta(0)))\mathbf{1}_{C}(R^n(\Delta(0))). \end{align*} $$
Moreover, for K large enough,
 $$ \begin{align*} \lim_{i\to\infty}&\bigg|\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\underline{C}}(R^n(\Delta(0)))\mathbf{1}_{C}(R^n(\Delta(0)))-\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\underline{C}}(R^n(\Delta(0)))\mathbf{1}_{C_K}(R^n(\Delta(0)))\bigg|\\ &\leq \lim_{i\to\infty}\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{C\setminus C_K}(R^n(\Delta(0))) \leq \lim_{i\to\infty}\sum_{s\in S}\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{W^c\setminus W_K^c}(R^{n+s}(\Delta(0)))\\ &=|S| \cdot \lim_{i\to\infty} \frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{W^c\setminus W_K^c}(R^{n} (\Delta(0))) = |S| \cdot \lim_{i\to\infty} \frac{1}{\ell_{i}} |[1,\ell_i]\cap (\mathcal{M}_{\mathscr{B}}\setminus \mathcal{M}_{\mathscr{B}_K})|<\varepsilon, \end{align*} $$
$$ \begin{align*} \lim_{i\to\infty}&\bigg|\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\underline{C}}(R^n(\Delta(0)))\mathbf{1}_{C}(R^n(\Delta(0)))-\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\underline{C}}(R^n(\Delta(0)))\mathbf{1}_{C_K}(R^n(\Delta(0)))\bigg|\\ &\leq \lim_{i\to\infty}\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{C\setminus C_K}(R^n(\Delta(0))) \leq \lim_{i\to\infty}\sum_{s\in S}\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{W^c\setminus W_K^c}(R^{n+s}(\Delta(0)))\\ &=|S| \cdot \lim_{i\to\infty} \frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{W^c\setminus W_K^c}(R^{n} (\Delta(0))) = |S| \cdot \lim_{i\to\infty} \frac{1}{\ell_{i}} |[1,\ell_i]\cap (\mathcal{M}_{\mathscr{B}}\setminus \mathcal{M}_{\mathscr{B}_K})|<\varepsilon, \end{align*} $$
where the second inequality follows from
the last equality from
and the last inequality is a consequence of the Davenport–Erdős theorem (i.e. (1))—we use that
![]() $(\ell _i)_{i\geq 1}$
is a specific sequence and that K is large only for this last inequality.
$(\ell _i)_{i\geq 1}$
is a specific sequence and that K is large only for this last inequality.
We will now use similar arguments for
![]() $ C_{K} $
and
$ C_{K} $
and
![]() $ \underline {C}_{K} $
instead of
$ \underline {C}_{K} $
instead of
![]() $ C $
and
$ C $
and
![]() $ \underline {C} $
. We have
$ \underline {C} $
. We have
 $$ \begin{align*} \lim_{i\to\infty}&\bigg|\frac{1}{\ell_i}\sum_{n\leq \ell_i} \mathbf{1}_{\underline{C}}(R^n(\Delta(0)))\mathbf{1}_{C_K}(R^n(\Delta(0)))- \frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\underline{C}_K}(R^n(\Delta(0)))\mathbf{1}_{C_K}(R^n(\Delta(0))) \bigg|\\ &\leq \lim_{k\to\infty}\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\underline{C}\setminus \underline{C}_K}(R^n(\Delta(0)))\\ &\leq |\underline{S}|\cdot \lim_{i\to \infty}\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\Gamma_{H,H^{*}}^{-1}((W^{*})^c\setminus (W_K^{*})^c)}(R^n(\Delta(0)))\\ &=|\underline{S}|\cdot \lim_{i\to\infty}\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{(W^{*})^c\setminus (W_K^{*})^c}((R^{*})^n(\Delta^{*}(0)))\\ &=|\underline{S}|\cdot d(\mathcal{M}_{\mathscr{B}^{*}}\setminus \mathcal{M}_{\mathscr{B}^{*}_K})<\varepsilon, \end{align*} $$
$$ \begin{align*} \lim_{i\to\infty}&\bigg|\frac{1}{\ell_i}\sum_{n\leq \ell_i} \mathbf{1}_{\underline{C}}(R^n(\Delta(0)))\mathbf{1}_{C_K}(R^n(\Delta(0)))- \frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\underline{C}_K}(R^n(\Delta(0)))\mathbf{1}_{C_K}(R^n(\Delta(0))) \bigg|\\ &\leq \lim_{k\to\infty}\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\underline{C}\setminus \underline{C}_K}(R^n(\Delta(0)))\\ &\leq |\underline{S}|\cdot \lim_{i\to \infty}\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\Gamma_{H,H^{*}}^{-1}((W^{*})^c\setminus (W_K^{*})^c)}(R^n(\Delta(0)))\\ &=|\underline{S}|\cdot \lim_{i\to\infty}\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{(W^{*})^c\setminus (W_K^{*})^c}((R^{*})^n(\Delta^{*}(0)))\\ &=|\underline{S}|\cdot d(\mathcal{M}_{\mathscr{B}^{*}}\setminus \mathcal{M}_{\mathscr{B}^{*}_K})<\varepsilon, \end{align*} $$
where in the second inequality, we used
 $$ \begin{align*} \underline{C}\setminus \underline{C}_K \subseteq \bigcup_{s\in\underline{S}} R^{-s}\Gamma_{H,H^{*}}^{-1}((W^{*})^c\setminus (W_K^{*})^c), \end{align*} $$
$$ \begin{align*} \underline{C}\setminus \underline{C}_K \subseteq \bigcup_{s\in\underline{S}} R^{-s}\Gamma_{H,H^{*}}^{-1}((W^{*})^c\setminus (W_K^{*})^c), \end{align*} $$
the first equality follows from
![]() $\Gamma _{H,H^{*}}(R^n\Delta (0))=(R^{*})^n \Gamma _{H,H^{*}}(\Delta (0))=(R^{*})^n(\Delta ^{*}(0))$
, the second equality is a consequence of
$\Gamma _{H,H^{*}}(R^n\Delta (0))=(R^{*})^n \Gamma _{H,H^{*}}(\Delta (0))=(R^{*})^n(\Delta ^{*}(0))$
, the second equality is a consequence of
and the last inequality follows by (1), i.e. the Davenport–Erdős theorem (notice that we use here that
![]() $X_{\eta ^{*}}$
is uniquely ergodic, so, in particular,
$X_{\eta ^{*}}$
is uniquely ergodic, so, in particular,
![]() $\mathscr {B}^{*}$
is Besicovitch and thus the density of
$\mathscr {B}^{*}$
is Besicovitch and thus the density of
![]() $\mathcal {M}_{\mathscr {B}^{*}}$
along
$\mathcal {M}_{\mathscr {B}^{*}}$
along
![]() $(\ell _i)$
is just its natural density).
$(\ell _i)$
is just its natural density).
Convergence for clopen sets. After the above reductions, it remains to prove that
 $$ \begin{align*} \lim_{i\to\infty}\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\underline{C}_K}(R^n(\Delta(0)))\mathbf{1}_{C_K}(R^n(\Delta(0)))=m_H(\underline{C}_K\cap C_K). \end{align*} $$
$$ \begin{align*} \lim_{i\to\infty}\frac{1}{\ell_i}\sum_{n\leq \ell_i}\mathbf{1}_{\underline{C}_K}(R^n(\Delta(0)))\mathbf{1}_{C_K}(R^n(\Delta(0)))=m_H(\underline{C}_K\cap C_K). \end{align*} $$
However, both
![]() $C_K$
and
$C_K$
and
![]() $\underline {C}_K$
are clopen (recall (23) and (25)) and thus the claim follows directly by the unique ergodicity of R.
$\underline {C}_K$
are clopen (recall (23) and (25)) and thus the claim follows directly by the unique ergodicity of R.
2.1.2 ( D B,C ) is surjective
This part of the proof relies mostly on certain natural periodic approximations of
![]() $\eta $
and
$\eta $
and
![]() $\eta ^{*}$
. More precisely, we will need a periodic approximation of
$\eta ^{*}$
. More precisely, we will need a periodic approximation of
![]() $\eta $
from above and of
$\eta $
from above and of
![]() $\eta ^{*}$
from below.
$\eta ^{*}$
from below.
For each
![]() $K\geq 1$
, we set
$K\geq 1$
, we set
![]() ${\mathscr {B}}_K:=\{b\in \mathscr {B} : b\leq K\}$
and
${\mathscr {B}}_K:=\{b\in \mathscr {B} : b\leq K\}$
and
![]() ${\mathscr {B}}_K^{*}=\{b^{*}\in {\mathscr {B}}^{*} : b^{*}\leq K\}$
. We define
${\mathscr {B}}_K^{*}=\{b^{*}\in {\mathscr {B}}^{*} : b^{*}\leq K\}$
. We define
![]() $\varphi _K\colon H \to \{0,1\}^{\mathbb {Z}}$
by
$\varphi _K\colon H \to \{0,1\}^{\mathbb {Z}}$
by
Recall that there is a continuous group homomorphism
![]() $ \Gamma _{H,H^{*}}\colon H \to H^{*} $
with
$ \Gamma _{H,H^{*}}\colon H \to H^{*} $
with
![]() ${\underline {\varphi }(h)=\varphi ^{*}(\Gamma _{H,H^{*}}(h))}$
, see (14). We define
${\underline {\varphi }(h)=\varphi ^{*}(\Gamma _{H,H^{*}}(h))}$
, see (14). We define
![]() $\underline {\varphi }_K\colon H\to \{0,1\}^{\mathbb {Z}}$
by
$\underline {\varphi }_K\colon H\to \{0,1\}^{\mathbb {Z}}$
by
 $$ \begin{align*} \underline{\varphi}_K(h)(n)&=\begin{cases} \underline{\varphi}(h)(n)& \text{if }n\in \text{Per}(\underline{\varphi}(h),\operatorname{\mathrm{lcm}}({\mathscr{B}}_K^{*})),\\ 0& \text{otherwise},\end{cases}\\ &= \begin{cases} 1 & \text{if }n\in \text{Per}(\varphi^{*}(\Gamma_{H,H^{*}}(h)), 1 , \operatorname{\mathrm{lcm}}({\mathscr{B}}_K^{*})),\\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \underline{\varphi}_K(h)(n)&=\begin{cases} \underline{\varphi}(h)(n)& \text{if }n\in \text{Per}(\underline{\varphi}(h),\operatorname{\mathrm{lcm}}({\mathscr{B}}_K^{*})),\\ 0& \text{otherwise},\end{cases}\\ &= \begin{cases} 1 & \text{if }n\in \text{Per}(\varphi^{*}(\Gamma_{H,H^{*}}(h)), 1 , \operatorname{\mathrm{lcm}}({\mathscr{B}}_K^{*})),\\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
Note that for every
![]() $h\in H$
, we have
$h\in H$
, we have
Lemma 2.5. For any
![]() $K\geq 1$
, the functions
$K\geq 1$
, the functions
![]() $\varphi _K$
and
$\varphi _K$
and
![]() $\underline {\varphi }_K$
depend on a finite number of coordinates. In particular, they are continuous.
$\underline {\varphi }_K$
depend on a finite number of coordinates. In particular, they are continuous.
Proof. For
![]() $\varphi _K$
, the assertion is clear by the very definition. Let us now turn to
$\varphi _K$
, the assertion is clear by the very definition. Let us now turn to
![]() $\underline {\varphi }_K$
. To shorten notation, we will write
$\underline {\varphi }_K$
. To shorten notation, we will write
![]() $ h^{*}=\Gamma _{H,H^{*}}(h) $
and
$ h^{*}=\Gamma _{H,H^{*}}(h) $
and
![]() $s^{*}=\operatorname {\mathrm {lcm}}({\mathscr {B}}_K^{*})$
. We will show that
$s^{*}=\operatorname {\mathrm {lcm}}({\mathscr {B}}_K^{*})$
. We will show that
![]() $ \text {Per}(\varphi ^{*}(h^{*}_{1}), 1 , s^{*}) = \text {Per}(\varphi ^{*}(h^{*}_{2}), 1 , s^{*}) $
whenever
$ \text {Per}(\varphi ^{*}(h^{*}_{1}), 1 , s^{*}) = \text {Per}(\varphi ^{*}(h^{*}_{2}), 1 , s^{*}) $
whenever
![]() $ h^{*}_{1} $
and
$ h^{*}_{1} $
and
![]() $ h^{*}_{2} $
agree on
$ h^{*}_{2} $
agree on
![]() $ {\mathscr {B}}_{K}^{*} $
. Since there exists
$ {\mathscr {B}}_{K}^{*} $
. Since there exists
![]() $ L \in {\mathbb {N}} $
such that every
$ L \in {\mathbb {N}} $
such that every
![]() $ b^{*} \in {\mathscr {B}}^{*}_{K} $
divides some
$ b^{*} \in {\mathscr {B}}^{*}_{K} $
divides some
![]() $ b \in {\mathscr {B}}_{L} $
, by Lemma 1.2, it then follows that
$ b \in {\mathscr {B}}_{L} $
, by Lemma 1.2, it then follows that
![]() $\underline {\varphi }_{K}( h )$
is determined by
$\underline {\varphi }_{K}( h )$
is determined by
![]() $ ( h_{b} )_{b \in \mathscr {B}_{L}} $
. To see that
$ ( h_{b} )_{b \in \mathscr {B}_{L}} $
. To see that
![]() $ \text {Per}(\varphi ^{*}(h^{*}), 1 , s^{*}) $
depends only on
$ \text {Per}(\varphi ^{*}(h^{*}), 1 , s^{*}) $
depends only on
![]() $ {\mathscr {B}}_{K}^{*} $
, take
$ {\mathscr {B}}_{K}^{*} $
, take
![]() $ h_{1}^{*} , h_{2}^{*} \in H^{*} = \overline {\Delta ^{*}( {\mathbb {Z}} )} $
with
$ h_{1}^{*} , h_{2}^{*} \in H^{*} = \overline {\Delta ^{*}( {\mathbb {Z}} )} $
with
![]() $ ( h_{2}^{*} - h_{1}^{*} )_{b^{*}} = 0 $
for all
$ ( h_{2}^{*} - h_{1}^{*} )_{b^{*}} = 0 $
for all
![]() $ b^{*} \in {\mathscr {B}}_{K}^{*} $
. Then there exists a sequence
$ b^{*} \in {\mathscr {B}}_{K}^{*} $
. Then there exists a sequence
![]() $ (n_{k}) $
with
$ (n_{k}) $
with
![]() $ \Delta ^{*}( n_{k} ) \to h_{2}^{*} - h_{1}^{*} $
and
$ \Delta ^{*}( n_{k} ) \to h_{2}^{*} - h_{1}^{*} $
and
![]() $ \operatorname {\mathrm {lcm}}( {\mathscr {B}}^{*}_{K} ) = s^{*} \mid n_{k} $
. We notice that
$ \operatorname {\mathrm {lcm}}( {\mathscr {B}}^{*}_{K} ) = s^{*} \mid n_{k} $
. We notice that
 $$ \begin{align*} \text{Per}(\varphi^{*}( h^{*}_{1} + \Delta^{*}( n_{k} ) ), 1 , s^{*}) &= \text{Per}( \sigma^{n_{k}} \varphi^{*}( h^{*}_{1} ), 1 , s^{*}) = \text{Per}(\varphi^{*}(h^{*}_{1} ), 1 , s^{*}) - n_{k} \\ &= \text{Per}(\varphi^{*}( h^{*}_{1} ), 1 , s^{*}) , \end{align*} $$
$$ \begin{align*} \text{Per}(\varphi^{*}( h^{*}_{1} + \Delta^{*}( n_{k} ) ), 1 , s^{*}) &= \text{Per}( \sigma^{n_{k}} \varphi^{*}( h^{*}_{1} ), 1 , s^{*}) = \text{Per}(\varphi^{*}(h^{*}_{1} ), 1 , s^{*}) - n_{k} \\ &= \text{Per}(\varphi^{*}( h^{*}_{1} ), 1 , s^{*}) , \end{align*} $$
since
![]() $ \text {Per}(\varphi ^{*}( h^{*}_{1} ), 1 , s^{*}) $
is an
$ \text {Per}(\varphi ^{*}( h^{*}_{1} ), 1 , s^{*}) $
is an
![]() $ s^{*} $
-periodic set. In particular, for every
$ s^{*} $
-periodic set. In particular, for every
![]() $ j \kern1.3pt{\in}\kern1.3pt \text {Per}(\varphi ^{*}( h^{*}_{1} ), 1 , s^{*}) $
, we get
$ j \kern1.3pt{\in}\kern1.3pt \text {Per}(\varphi ^{*}( h^{*}_{1} ), 1 , s^{*}) $
, we get
![]() $ \varphi ^{*}( h^{*}_{1} + \Delta ^{*}( n_{k} ) )( j ) = 1 $
for all
$ \varphi ^{*}( h^{*}_{1} + \Delta ^{*}( n_{k} ) )( j ) = 1 $
for all
![]() $ k $
. Since
$ k $
. Since
![]() $ h^{*}_{1} + \Delta ^{*}( n_{k} ) $
converges to
$ h^{*}_{1} + \Delta ^{*}( n_{k} ) $
converges to
![]() $ h_{2}^{*} $
, and
$ h_{2}^{*} $
, and
![]() $ \varphi ^{*} $
is coordinatewise upper semicontinuous, this yields
$ \varphi ^{*} $
is coordinatewise upper semicontinuous, this yields
![]() $ \varphi ^{*}( h^{*}_{2} )( j ) = 1 $
for all
$ \varphi ^{*}( h^{*}_{2} )( j ) = 1 $
for all
![]() $ {j \in \text {Per}(\varphi ^{*}( h^{*}_{1} ), 1 , s^{*}) }$
and hence
$ {j \in \text {Per}(\varphi ^{*}( h^{*}_{1} ), 1 , s^{*}) }$
and hence
![]() $ \text {Per}(\varphi ^{*}( h^{*}_{1} ), 1 , s^{*}) \subseteq \text {Per}(\varphi ^{*}( h^{*}_{2} ), 1 , s^{*}) $
. By the symmetry between
$ \text {Per}(\varphi ^{*}( h^{*}_{1} ), 1 , s^{*}) \subseteq \text {Per}(\varphi ^{*}( h^{*}_{2} ), 1 , s^{*}) $
. By the symmetry between
![]() $ h^{*}_{1} $
and
$ h^{*}_{1} $
and
![]() $ h^{*}_{2} $
, the converse inclusion follows from the same argument, thus proving the claim.
$ h^{*}_{2} $
, the converse inclusion follows from the same argument, thus proving the claim.
Similar to
![]() $ [\underline {\varphi } ,\varphi ] $
, we define
$ [\underline {\varphi } ,\varphi ] $
, we define
![]() $ [\underline {\varphi }_K,\varphi _K] :=\{x\in \{0,1\}^Z : \underline {\varphi }_K(h)\leq x\leq \varphi _K(h)\text { for some } h\in H\} $
.
$ [\underline {\varphi }_K,\varphi _K] :=\{x\in \{0,1\}^Z : \underline {\varphi }_K(h)\leq x\leq \varphi _K(h)\text { for some } h\in H\} $
.
Lemma 2.6. The set
![]() $ [\underline {\varphi }_K,\varphi _K] \subseteq \{ 0 , 1 \}^{{\mathbb {Z}}} $
is a subshift.
$ [\underline {\varphi }_K,\varphi _K] \subseteq \{ 0 , 1 \}^{{\mathbb {Z}}} $
is a subshift.
Proof. That
![]() $ [\underline {\varphi }_K,\varphi _K] $
is closed follows immediately from the continuity of
$ [\underline {\varphi }_K,\varphi _K] $
is closed follows immediately from the continuity of
![]() $\varphi _K$
and
$\varphi _K$
and
![]() $\underline {\varphi }_K$
. In addition, it is
$\underline {\varphi }_K$
. In addition, it is
![]() $\sigma $
-invariant as
$\sigma $
-invariant as
Indeed, the first equality holds as
![]() $\varphi _K$
is a coding of orbits of points in H with respect to
$\varphi _K$
is a coding of orbits of points in H with respect to
![]() $\{h\in H : h_{b}\neq 0 \text { for all }b\in {\mathscr {B}}_K\}$
. The second equality follows from the definition of
$\{h\in H : h_{b}\neq 0 \text { for all }b\in {\mathscr {B}}_K\}$
. The second equality follows from the definition of
![]() $ \underline {\varphi }_{K} $
in terms of
$ \underline {\varphi }_{K} $
in terms of
![]() $\underline {\varphi }$
, the equality
$\underline {\varphi }$
, the equality
![]() $\underline {\varphi }\circ R\kern1.3pt{=}\kern1.3pt\sigma \circ \underline {\varphi }$
(since
$\underline {\varphi }\circ R\kern1.3pt{=}\kern1.3pt\sigma \circ \underline {\varphi }$
(since
![]() $\underline {\varphi }$
is a coding) and
$\underline {\varphi }$
is a coding) and
![]() $\operatorname {Per}\nolimits (\sigma x,s)\kern1.3pt{=}\kern1.3pt\operatorname {Per}\nolimits (x,s)\kern1.3pt{-}\kern1.3pt1$
for x in the orbit closure of a Toeplitz sequence.
$\operatorname {Per}\nolimits (\sigma x,s)\kern1.3pt{=}\kern1.3pt\operatorname {Per}\nolimits (x,s)\kern1.3pt{-}\kern1.3pt1$
for x in the orbit closure of a Toeplitz sequence.
We set
![]() $ \eta _K := \varphi _{K}(\Delta (0))=\mathbf {1}_{\mathcal {F}_{\mathscr {B}_K}}$
and
$ \eta _K := \varphi _{K}(\Delta (0))=\mathbf {1}_{\mathcal {F}_{\mathscr {B}_K}}$
and
![]() $ \underline {\eta }_K := \underline {\varphi }_K(\Delta (0)) $
. Then
$ \underline {\eta }_K := \underline {\varphi }_K(\Delta (0)) $
. Then
![]() $\underline {\eta }_K\leq \eta ^{*}\leq \eta \leq \eta _K$
(this is a special case of (27) for
$\underline {\eta }_K\leq \eta ^{*}\leq \eta \leq \eta _K$
(this is a special case of (27) for
![]() $h = \Delta (0)$
).
$h = \Delta (0)$
).
Lemma 2.7. Let
![]() $\mathscr {B}\subseteq {\mathbb {N}}$
and suppose that
$\mathscr {B}\subseteq {\mathbb {N}}$
and suppose that
![]() $\eta ^{*}$
is a regular Toeplitz sequence. Let
$\eta ^{*}$
is a regular Toeplitz sequence. Let
![]() $(\ell _{i})$
be a sequence realizing the lower density of
$(\ell _{i})$
be a sequence realizing the lower density of
![]() $\mathcal {M}_{\mathscr {B}}$
. Then
$\mathcal {M}_{\mathscr {B}}$
. Then
Proof. It suffices to notice that
and
The first assertion follows by the Davenport–Erdős theorem (that is, by (1)). For the second, notice that
![]() $\underline {\eta }_K(n)\neq \eta ^{*}(n)$
implies that
$\underline {\eta }_K(n)\neq \eta ^{*}(n)$
implies that
![]() $n\not \in \operatorname {Per}(\eta ^{*},\operatorname {\mathrm {lcm}}(\mathscr {B}_K^{*}))$
. Thus,
$n\not \in \operatorname {Per}(\eta ^{*},\operatorname {\mathrm {lcm}}(\mathscr {B}_K^{*}))$
. Thus,
as
![]() $\eta ^{*}$
is a regular Toeplitz sequence, cf. (10).
$\eta ^{*}$
is a regular Toeplitz sequence, cf. (10).
We will also need the following well-known fact related to quasi-generic points and the corresponding invariant measures (we skip its proof and refer the reader e.g. to [Reference Lemańczyk28, Appendix C], see also [Reference Kwietniak, Łącka and Oprocha27]).
Proposition 2.8. Let
![]() $\mathcal {A}$
be a finite alphabet and suppose that
$\mathcal {A}$
be a finite alphabet and suppose that
![]() $(\ell _{i}) \subseteq {\mathbb {N}}$
is an increasing sequence and that
$(\ell _{i}) \subseteq {\mathbb {N}}$
is an increasing sequence and that
![]() $x_K\in \mathcal {A}^{\mathbb {Z}}$
for
$x_K\in \mathcal {A}^{\mathbb {Z}}$
for
![]() $K\geq 1$
and
$K\geq 1$
and
![]() $x\in \mathcal {A}^{\mathbb {Z}}$
are such that
$x\in \mathcal {A}^{\mathbb {Z}}$
are such that
Suppose additionally that
![]() $x_K$
,
$x_K$
,
![]() $K\geq 1$
, and x are quasi-generic along
$K\geq 1$
, and x are quasi-generic along
![]() $(\ell _{i})$
for measures
$(\ell _{i})$
for measures
![]() $\nu _K$
,
$\nu _K$
,
![]() $K\geq 1$
, and
$K\geq 1$
, and
![]() $\nu $
, respectively. Then
$\nu $
, respectively. Then
![]() $\nu _K \to \nu $
in the weak topology.
$\nu _K \to \nu $
in the weak topology.
Last but not least, we will need the following result to pass from the description of ergodic measures to that of all invariant measures on
![]() $X_\eta $
.
$X_\eta $
.
Proposition 2.9. Suppose that for a subshift
![]() $X\subseteq \{0,1\}^{\mathbb {Z}}$
, we have
$X\subseteq \{0,1\}^{\mathbb {Z}}$
, we have
![]() $\mathcal {P}^e(X)\subseteq \{N_\ast ((\nu _{\eta ^{*}}\triangle \nu _\eta )\vee \kappa ) : \kappa \kern1.2pt{\in}\kern1.2pt \mathcal {P}(\{0,1\}^{\mathbb {Z}})\}.$
Then
$\mathcal {P}^e(X)\subseteq \{N_\ast ((\nu _{\eta ^{*}}\triangle \nu _\eta )\vee \kappa ) : \kappa \kern1.2pt{\in}\kern1.2pt \mathcal {P}(\{0,1\}^{\mathbb {Z}})\}.$
Then
![]() $\mathcal {P}(X)\kern1.2pt{\subseteq}\kern1.2pt \{N_\ast ((\nu _{\eta ^{*}}\triangle \nu _\eta )\vee \kappa ) : \kappa \kern1.2pt{\in}\kern1.2pt \mathcal {P}(\{0,1\}^{\mathbb {Z}})\}.$
$\mathcal {P}(X)\kern1.2pt{\subseteq}\kern1.2pt \{N_\ast ((\nu _{\eta ^{*}}\triangle \nu _\eta )\vee \kappa ) : \kappa \kern1.2pt{\in}\kern1.2pt \mathcal {P}(\{0,1\}^{\mathbb {Z}})\}.$
We skip the proof—it is a repetition (with obvious changes such as replacing the map M by N and the Mirsky measure
![]() $\nu _\eta $
by the joining
$\nu _\eta $
by the joining
![]() $\nu _{\eta ^{*}}\triangle \nu _\eta $
) of the proof of an analogous part of [Reference Lemańczyk28, Theorem 4.1.23] (more specifically, see p. 66 therein). The main tool there is the ergodic decomposition and the Arsenin–Kunungui theorem on measurable selection (see, e.g. [Reference Kechris15, Theorem 18.18]). A more general result (with a shorter proof) will be published in [Reference Kułaga-Przymus, Lemańczyk and Rams25].
$\nu _{\eta ^{*}}\triangle \nu _\eta $
) of the proof of an analogous part of [Reference Lemańczyk28, Theorem 4.1.23] (more specifically, see p. 66 therein). The main tool there is the ergodic decomposition and the Arsenin–Kunungui theorem on measurable selection (see, e.g. [Reference Kechris15, Theorem 18.18]). A more general result (with a shorter proof) will be published in [Reference Kułaga-Przymus, Lemańczyk and Rams25].
Now, fix
![]() $\nu \in \mathcal {P}^{e}(\overline {[\underline {\varphi },\varphi ]}) = \mathcal {P}^e([\underline {\varphi },\varphi ])$
, see (18). Since
$\nu \in \mathcal {P}^{e}(\overline {[\underline {\varphi },\varphi ]}) = \mathcal {P}^e([\underline {\varphi },\varphi ])$
, see (18). Since
![]() $\nu $
is ergodic, since
$\nu $
is ergodic, since
![]() $[ \underline {\varphi } , \varphi ]\subseteq [\underline {\varphi }_K,\varphi _K]$
and the latter set is a subshift by Lemma 2.6, there exists a generic point
$[ \underline {\varphi } , \varphi ]\subseteq [\underline {\varphi }_K,\varphi _K]$
and the latter set is a subshift by Lemma 2.6, there exists a generic point
![]() $u_K\in [\underline {\varphi }_K,\varphi _K]$
for
$u_K\in [\underline {\varphi }_K,\varphi _K]$
for
![]() $\nu $
. Without loss of generality, we can assume
$\nu $
. Without loss of generality, we can assume
(Indeed, since
![]() $u_K\in [\underline {\varphi }_K,\varphi _K]$
, there exists
$u_K\in [\underline {\varphi }_K,\varphi _K]$
, there exists
![]() $ h \in H $
with
$ h \in H $
with
![]() $ \underline {\varphi }_K(h)\leq u_K\leq \varphi _K(h) $
. If
$ \underline {\varphi }_K(h)\leq u_K\leq \varphi _K(h) $
. If
![]() $j\in {\mathbb {N}}$
is such that
$j\in {\mathbb {N}}$
is such that
![]() $h_{b}+j=0 \bmod \ b$
for all b in a sufficiently large, finite subset of
$h_{b}+j=0 \bmod \ b$
for all b in a sufficiently large, finite subset of
![]() ${\mathscr {B}}$
, then Lemma 2.5 shows
${\mathscr {B}}$
, then Lemma 2.5 shows
![]() $ \underline {\varphi }_K(\Delta (0)) \leq \sigma ^ju_K\leq \varphi _K( \Delta (0) ) $
, where
$ \underline {\varphi }_K(\Delta (0)) \leq \sigma ^ju_K\leq \varphi _K( \Delta (0) ) $
, where
![]() $\sigma ^ju_K$
is generic for
$\sigma ^ju_K$
is generic for
![]() $\nu $
.) Thus, there exits
$\nu $
.) Thus, there exits
![]() $ y_{K} \in \{ 0,1 \}^{{\mathbb {Z}}} $
such that
$ y_{K} \in \{ 0,1 \}^{{\mathbb {Z}}} $
such that
![]() $ u_K=N(\underline {\eta }_K,\eta _K,y_K) $
. Notice that
$ u_K=N(\underline {\eta }_K,\eta _K,y_K) $
. Notice that
![]() $ (\underline {\eta }_K,\eta _K,y_K) $
is quasi-generic for some measure
$ (\underline {\eta }_K,\eta _K,y_K) $
is quasi-generic for some measure
![]() $ \rho _K $
. Using the periodicity of
$ \rho _K $
. Using the periodicity of
![]() $ \underline {\eta }_{K} $
and
$ \underline {\eta }_{K} $
and
![]() $ \eta _K $
, we hence obtain that
$ \eta _K $
, we hence obtain that
![]() $(\underline {\eta }_K,\eta _K)$
is generic for
$(\underline {\eta }_K,\eta _K)$
is generic for
![]() $(\pi _{1,2})_\ast (\rho _K)$
. In addition,
$(\pi _{1,2})_\ast (\rho _K)$
. In addition,
![]() $ ( \eta ^{*} , \eta ) $
is quasi-generic along
$ ( \eta ^{*} , \eta ) $
is quasi-generic along
![]() $ (\ell _{i}) $
for
$ (\ell _{i}) $
for
![]() $ \nu _{\eta ^{*}}\triangle \nu _\eta $
by (21) and (22). Thus, Proposition 2.8 and Lemma 2.7 yield
$ \nu _{\eta ^{*}}\triangle \nu _\eta $
by (21) and (22). Thus, Proposition 2.8 and Lemma 2.7 yield
If
![]() $ \rho $
is a limit of
$ \rho $
is a limit of
![]() $ \rho _{K} $
, it follows that
$ \rho _{K} $
, it follows that
![]() $(\pi _{1,2})_\ast (\rho ) = \nu _{\eta ^{*}}\triangle \nu _\eta $
, so
$(\pi _{1,2})_\ast (\rho ) = \nu _{\eta ^{*}}\triangle \nu _\eta $
, so
![]() $ \rho $
is of the form
$ \rho $
is of the form
![]() $ {\rho = (\nu _{\eta ^{*}}\triangle \nu _\eta ) \vee \kappa} $
for some
$ {\rho = (\nu _{\eta ^{*}}\triangle \nu _\eta ) \vee \kappa} $
for some
![]() $ \kappa \in \mathcal {P}( \{ 0 , 1 \}^{{\mathbb {Z}}} ) $
. Finally, since
$ \kappa \in \mathcal {P}( \{ 0 , 1 \}^{{\mathbb {Z}}} ) $
. Finally, since
![]() $ (\underline {\eta }_K,\eta _K,y_K) $
is quasi-generic for
$ (\underline {\eta }_K,\eta _K,y_K) $
is quasi-generic for
![]() $ \rho _K $
, it follows that
$ \rho _K $
, it follows that
![]() $ u_K=N(\underline {\eta }_K,\eta _K,y_K) $
is quasi-generic for
$ u_K=N(\underline {\eta }_K,\eta _K,y_K) $
is quasi-generic for
![]() $ N_{*} (\rho _K) $
. However, by assumption,
$ N_{*} (\rho _K) $
. However, by assumption,
![]() $ u_{K} $
is also generic for
$ u_{K} $
is also generic for
![]() $ \nu $
, which yields
$ \nu $
, which yields
![]() $\nu = N_{*} (\rho _K) $
for all
$\nu = N_{*} (\rho _K) $
for all
![]() $ K \in {\mathbb {N}} $
, and thus
$ K \in {\mathbb {N}} $
, and thus
![]() $\nu = N_{*}(\rho ) \in \{ N_{\ast }( (\nu _{\eta ^{*}} \triangle \nu _{\eta }) \vee \kappa ) : \kappa \in \mathcal {P}( \{ 0 , 1 \}^{{\mathbb {Z}}} ) \} $
. This proves
$\nu = N_{*}(\rho ) \in \{ N_{\ast }( (\nu _{\eta ^{*}} \triangle \nu _{\eta }) \vee \kappa ) : \kappa \in \mathcal {P}( \{ 0 , 1 \}^{{\mathbb {Z}}} ) \} $
. This proves
![]() $ \mathcal {P}^e([\underline {\varphi },\varphi ]) \subseteq \{ N_{\ast }( (\nu _{\eta ^{*}} \triangle \nu _{\eta }) \vee \kappa ) : \kappa \in \mathcal {P}( \{ 0 , 1 \}^{{\mathbb {Z}}} ) \} $
. To complete the proof of the surjectivity of
D
B,C
, we use Proposition 2.9.
$ \mathcal {P}^e([\underline {\varphi },\varphi ]) \subseteq \{ N_{\ast }( (\nu _{\eta ^{*}} \triangle \nu _{\eta }) \vee \kappa ) : \kappa \in \mathcal {P}( \{ 0 , 1 \}^{{\mathbb {Z}}} ) \} $
. To complete the proof of the surjectivity of
D
B,C
, we use Proposition 2.9.
2.2 Proof of Theorem A
2.2.1 ( D A ) is a commutative dynamical diagram
The proof that ( D A ) is a commutative dynamical diagram uses two ingredients. The first of them is that the following is a dynamical diagram:

which is a consequence of Lemma 2.3.
The second ingredient that we need to prove the commutativity of ( D A ) is the following equality (that holds everywhere):
which can be checked in a direct one-line calculation.
2.2.2 ( D A ) is surjective
Recall that by (19) and by the surjectivity of ( D B,C ), the diagram

is surjective. Thus (using also the commutativity of ( D A )), to prove the surjectivity of ( D A ), it suffices to prove that

is surjective. However, by Lemma 2.3 (cf. Remark 2.4),
![]() $((\{0,1\}^{\mathbb {Z}})^2,\sigma ^{\times 2},\nu _{\eta ^{*}}\triangle \nu _\eta )$
is a factor of
$((\{0,1\}^{\mathbb {Z}})^2,\sigma ^{\times 2},\nu _{\eta ^{*}}\triangle \nu _\eta )$
is a factor of
![]() $(H,R,m_H)$
via
$(H,R,m_H)$
via
![]() $\underline {\varphi }\otimes \varphi $
, so given any joining
$\underline {\varphi }\otimes \varphi $
, so given any joining
![]() $(\nu _{\eta ^{*}}\triangle \nu _\eta )\vee \kappa $
, it suffices to take its relatively independent extension to a joining of
$(\nu _{\eta ^{*}}\triangle \nu _\eta )\vee \kappa $
, it suffices to take its relatively independent extension to a joining of
![]() $m_H$
with
$m_H$
with
![]() $\kappa $
to conclude that (29) is surjective.
$\kappa $
to conclude that (29) is surjective.
3 Tautness and combinatorics
Proof of Proposition D
We first show that the conditions (a
![]() $^{\prime }$
)–(f
$^{\prime }$
)–(f
![]() $^{\prime }$
) are all equivalent. We then pass to proving that, in fact, they are also equivalent to each of conditions (a)–(f).
$^{\prime }$
) are all equivalent. We then pass to proving that, in fact, they are also equivalent to each of conditions (a)–(f).
Note that the implications (d
![]() $^{\prime }$
)
$^{\prime }$
)
![]() $ {\implies} $
(c
$ {\implies} $
(c
![]() $^{\prime }$
)
$^{\prime }$
)
![]() $ {\implies} $
(f
$ {\implies} $
(f
![]() $^{\prime }$
)
$^{\prime }$
)
![]() $ {\implies} $
(e
$ {\implies} $
(e
![]() $^{\prime }$
) are immediate. Next we show (e
$^{\prime }$
) are immediate. Next we show (e
![]() $^{\prime }$
)
$^{\prime }$
)
![]() $ {\implies} $
(a
$ {\implies} $
(a
![]() $^{\prime }$
). It was shown in [Reference Keller16] that for taut sets, the corresponding Mirsky measure is of full support in the corresponding
$^{\prime }$
). It was shown in [Reference Keller16] that for taut sets, the corresponding Mirsky measure is of full support in the corresponding
![]() $\mathscr {B}$
-free subshift. Applying this to
$\mathscr {B}$
-free subshift. Applying this to
![]() $\mathscr {C}$
, we conclude that each block that appears on
$\mathscr {C}$
, we conclude that each block that appears on
![]() $X_{\eta _{\mathscr {C}}}$
is of positive
$X_{\eta _{\mathscr {C}}}$
is of positive
![]() $\nu _{\eta _{\mathscr {C}}}$
-measure. Thus, it follows from condition (e
$\nu _{\eta _{\mathscr {C}}}$
-measure. Thus, it follows from condition (e
![]() $^{\prime }$
) that
$^{\prime }$
) that
![]() $X_{\eta _{\mathscr {C}}}\subseteq X_{\eta ^{\prime }}$
, and hence
$X_{\eta _{\mathscr {C}}}\subseteq X_{\eta ^{\prime }}$
, and hence
![]() $\widetilde {X}_{\eta _{\mathscr {C}}} \subseteq \widetilde {X}_{\eta ^{\prime }}$
. Using (8), we obtain that
$\widetilde {X}_{\eta _{\mathscr {C}}} \subseteq \widetilde {X}_{\eta ^{\prime }}$
. Using (8), we obtain that
![]() $ \forall _{b^{\prime }\in \mathscr {B}^{\prime }} \exists _{c\in \mathscr {C}}\, c\mid b^{\prime }$
. Moreover
$ \forall _{b^{\prime }\in \mathscr {B}^{\prime }} \exists _{c\in \mathscr {C}}\, c\mid b^{\prime }$
. Moreover
![]() $X_{\eta _{\mathscr {C}}}\subseteq X_\eta $
implies
$X_{\eta _{\mathscr {C}}}\subseteq X_\eta $
implies
![]() $X_{\eta ^{*}}\subseteq X_{\eta _{\mathscr {C}}}$
, since
$X_{\eta ^{*}}\subseteq X_{\eta _{\mathscr {C}}}$
, since
![]() $X_{\eta ^{*}}$
is the unique minimal subset of
$X_{\eta ^{*}}$
is the unique minimal subset of
![]() $X_\eta $
. This yields
$X_\eta $
. This yields
![]() $\widetilde {X}_{\eta ^{*}}\subseteq \widetilde {X}_{\eta _{\mathscr {C}}}$
. Using (8) again, we obtain that
$\widetilde {X}_{\eta ^{*}}\subseteq \widetilde {X}_{\eta _{\mathscr {C}}}$
. Using (8) again, we obtain that
![]() $\forall _{c\in \mathscr {C}}\,\exists _{b^{*}\in \mathscr {B}^{*}}\ b^{*}\mid c$
, which proves condition (a
$\forall _{c\in \mathscr {C}}\,\exists _{b^{*}\in \mathscr {B}^{*}}\ b^{*}\mid c$
, which proves condition (a
![]() $^{\prime }$
). Next we note that (a
$^{\prime }$
). Next we note that (a
![]() $^{\prime }$
)
$^{\prime }$
)
![]() $ {\implies} $
(b
$ {\implies} $
(b
![]() $^{\prime }$
) by the very definition of
$^{\prime }$
) by the very definition of
![]() $\eta ^{\prime },\eta _{\mathscr {C}}$
and
$\eta ^{\prime },\eta _{\mathscr {C}}$
and
![]() $\eta ^{*}$
. To finish the first part, it only remains to notice that by Proposition 2.1 and tautness of
$\eta ^{*}$
. To finish the first part, it only remains to notice that by Proposition 2.1 and tautness of
![]() $ \mathscr {B}^{\prime } $
, it follows that
$ \mathscr {B}^{\prime } $
, it follows that
![]() $X_{\eta ^{\prime }}=\overline { [\eta ^{*},\eta ^{\prime }] } $
, which yields (b
$X_{\eta ^{\prime }}=\overline { [\eta ^{*},\eta ^{\prime }] } $
, which yields (b
![]() $^{\prime }$
)
$^{\prime }$
)
![]() $ \implies $
(d
$ \implies $
(d
![]() $^{\prime }$
).
$^{\prime }$
).
Since the proof of (b
![]() $^{\prime }$
)
$^{\prime }$
)
![]() $ \implies $
(d
$ \implies $
(d
![]() $^{\prime }$
) was the only place where we used the tautness of
$^{\prime }$
) was the only place where we used the tautness of
![]() $ \mathscr {B}^{\prime } $
, the same arguments as above show also that (d)
$ \mathscr {B}^{\prime } $
, the same arguments as above show also that (d)
![]() $ {\implies} $
(c)
$ {\implies} $
(c)
![]() $ {\implies} $
(f)
$ {\implies} $
(f)
![]() $ {\implies} $
(e)
$ {\implies} $
(e)
![]() ${\implies \text {(a)} { \implies } \text {(b)}}$
. We now prove (b)
${\implies \text {(a)} { \implies } \text {(b)}}$
. We now prove (b)
![]() $ \implies $
(b
$ \implies $
(b
![]() $^{\prime }$
). As (b
$^{\prime }$
). As (b
![]() $^{\prime }$
)
$^{\prime }$
)
![]() $ \implies $
(d
$ \implies $
(d
![]() $^{\prime }$
) was already shown, and as
$^{\prime }$
) was already shown, and as
![]() $(\text {d}^{\prime }) { \implies } \text {(d)}$
follows directly from
$(\text {d}^{\prime }) { \implies } \text {(d)}$
follows directly from
![]() $ X_{ \eta ^{\prime } } \subseteq X_{\eta } $
, this will finish the proof. Thus, suppose that
$ X_{ \eta ^{\prime } } \subseteq X_{\eta } $
, this will finish the proof. Thus, suppose that
![]() $\eta _{\mathscr {C}}\leq \eta $
. It follows then by (8) that
$\eta _{\mathscr {C}}\leq \eta $
. It follows then by (8) that
![]() $\nu _{\eta _{\mathscr {C}}}\in \mathcal {P}(\widetilde {X}_\eta )=\mathcal {P}(\widetilde {X}_{\eta ^{\prime }})$
. Applying again (8), we obtain
$\nu _{\eta _{\mathscr {C}}}\in \mathcal {P}(\widetilde {X}_\eta )=\mathcal {P}(\widetilde {X}_{\eta ^{\prime }})$
. Applying again (8), we obtain
![]() $\eta _{\mathscr {C}}\leq \eta ^{\prime }$
, and hence condition (b
$\eta _{\mathscr {C}}\leq \eta ^{\prime }$
, and hence condition (b
![]() $^{\prime }$
).
$^{\prime }$
).
4 Entropy
4.1 Entropy of
 $X_\eta $
: proof of Theorem F and of Corollary G
$X_\eta $
: proof of Theorem F and of Corollary G
Remark 4.1. If
![]() $X_\eta $
is uniquely ergodic, then the Mirsky measure
$X_\eta $
is uniquely ergodic, then the Mirsky measure
![]() $\nu _\eta $
(whose entropy is zero) is the unique invariant measure and it follows immediately by the variational principle that
$\nu _\eta $
(whose entropy is zero) is the unique invariant measure and it follows immediately by the variational principle that
![]() $h(X_\eta )=0$
.
$h(X_\eta )=0$
.
Proof of Theorem F
To show the inequality
![]() $ h(X_{\eta }) \geq \overline {d}-\overline {d}^{*}$
, we first assume that
$ h(X_{\eta }) \geq \overline {d}-\overline {d}^{*}$
, we first assume that
![]() $ {\mathscr {B}} $
is taut and consider the following block:
$ {\mathscr {B}} $
is taut and consider the following block:
![]() $B=\eta [1,n]\in \{0,1\}^n$
. Then
$B=\eta [1,n]\in \{0,1\}^n$
. Then
![]() $B(\ell )=0$
for any
$B(\ell )=0$
for any
![]() ${\ell \in {\cal M}_{\mathscr {B}}\cap [1,n]}$
and
${\ell \in {\cal M}_{\mathscr {B}}\cap [1,n]}$
and
![]() $B(\ell )=1$
for any
$B(\ell )=1$
for any
![]() $\ell \in \mathcal {F}_{{\mathscr {B}}}\cap [1,n]$
(so, in particular, for any
$\ell \in \mathcal {F}_{{\mathscr {B}}}\cap [1,n]$
(so, in particular, for any
![]() $\ell \in \mathcal {F}_{{\mathscr {B}}^{*}}\cap [1,n]$
). It follows by Proposition 2.1 that any block
$\ell \in \mathcal {F}_{{\mathscr {B}}^{*}}\cap [1,n]$
). It follows by Proposition 2.1 that any block
![]() $C\in \{0,1\}^n$
that agrees with B on the positions belonging to
$C\in \{0,1\}^n$
that agrees with B on the positions belonging to
![]() $\mathcal {M}_{\mathscr {B}}\cup \mathcal {F}_{\mathscr {B}^{*}}$
also appears in
$\mathcal {M}_{\mathscr {B}}\cup \mathcal {F}_{\mathscr {B}^{*}}$
also appears in
![]() $X_\eta $
. There are
$X_\eta $
. There are
such blocks C (they are pairwise distinct). Thus,
It follows that
 $$ \begin{align} \overline{d}-\overline{d}^{*}&=\limsup_{n\to\infty}\frac{|\mathcal{F}_{\mathscr{B}}\cap[1,n]|}{n}-\limsup_{n\to\infty} \frac{|\mathcal{F}_{{\mathscr{B}}^{*}}\cap[1,n]|}{n} \nonumber\\ &\leq\limsup_{n\to\infty}\frac{|\mathcal{F}_{\mathscr{B}}\cap[1,n]|-|\mathcal{F}_{{\mathscr{B}}^{*}}\cap[1,n]|}{n}\leq \lim_{n\to\infty}\frac{\log_2 p_n(\eta)}{n}=h(X_\eta). \end{align} $$
$$ \begin{align} \overline{d}-\overline{d}^{*}&=\limsup_{n\to\infty}\frac{|\mathcal{F}_{\mathscr{B}}\cap[1,n]|}{n}-\limsup_{n\to\infty} \frac{|\mathcal{F}_{{\mathscr{B}}^{*}}\cap[1,n]|}{n} \nonumber\\ &\leq\limsup_{n\to\infty}\frac{|\mathcal{F}_{\mathscr{B}}\cap[1,n]|-|\mathcal{F}_{{\mathscr{B}}^{*}}\cap[1,n]|}{n}\leq \lim_{n\to\infty}\frac{\log_2 p_n(\eta)}{n}=h(X_\eta). \end{align} $$
For general (not necessarily taut)
![]() $ {\mathscr {B}} $
, we apply (30) to the tautification
$ {\mathscr {B}} $
, we apply (30) to the tautification
![]() $ {\mathscr {B}}^{\prime } $
. We use
$ {\mathscr {B}}^{\prime } $
. We use
![]() $ X_{\eta ^{\prime }} \subseteq X_{\eta } $
,
$ X_{\eta ^{\prime }} \subseteq X_{\eta } $
,
![]() $ ({\mathscr {B}}^{\prime })^{*} = {\mathscr {B}}^{*} $
and
$ ({\mathscr {B}}^{\prime })^{*} = {\mathscr {B}}^{*} $
and
![]() $ \overline {d}^{\prime } = \overline {d} $
(see (11), (12) and (21), respectively) to obtain
$ \overline {d}^{\prime } = \overline {d} $
(see (11), (12) and (21), respectively) to obtain
Now, assume additionally that
![]() $X_{\eta ^{*}}$
is uniquely ergodic. Fix
$X_{\eta ^{*}}$
is uniquely ergodic. Fix
![]() $K\geq 1$
and let
$K\geq 1$
and let
![]() ${n\in (\prod _{b\in {\mathscr {B}}_K}b){\mathbb {N}}}$
. Since
${n\in (\prod _{b\in {\mathscr {B}}_K}b){\mathbb {N}}}$
. Since
![]() $\eta ^{*}\leq \eta \leq \eta _K$
, it follows that
$\eta ^{*}\leq \eta \leq \eta _K$
, it follows that
For any block
![]() $B\in \{0,1\}^n$
which appears in
$B\in \{0,1\}^n$
which appears in
![]() $\overline {[\eta ^{*},\eta _K]}$
, there exists
$\overline {[\eta ^{*},\eta _K]}$
, there exists
![]() $M\in {\mathbb {Z}}$
such that
$M\in {\mathbb {Z}}$
such that
Clearly, if
![]() $\eta ^{*}( M+\ell )=1$
, then
$\eta ^{*}( M+\ell )=1$
, then
![]() $B(\ell )=1$
and there are
$B(\ell )=1$
and there are
such ‘mandatory’
![]() $1$
s on B coming from
$1$
s on B coming from
![]() $\eta ^{*}$
. Moreover, if
$\eta ^{*}$
. Moreover, if
![]() $\eta _K(M+\ell )=0$
, then also
$\eta _K(M+\ell )=0$
, then also
![]() ${B(\ell )=0}$
and there are
${B(\ell )=0}$
and there are
such ‘mandatory’
![]() $0$
s on B coming from
$0$
s on B coming from
![]() $\eta _K$
. All the other positions on B can be altered arbitrarily, without loosing the property that B appears in
$\eta _K$
. All the other positions on B can be altered arbitrarily, without loosing the property that B appears in
![]() $\overline {[\eta ^{*},\eta _K]}$
. The number of such ‘free’ positions equals
$\overline {[\eta ^{*},\eta _K]}$
. The number of such ‘free’ positions equals
Each choice of
![]() $0$
s and
$0$
s and
![]() $1$
s on the ‘free’ positions yields a different block of length n from
$1$
s on the ‘free’ positions yields a different block of length n from
![]() $\overline {[\eta ^{*},\eta _K]}$
. Thus, for each choice of M, we obtain
$\overline {[\eta ^{*},\eta _K]}$
. Thus, for each choice of M, we obtain
blocks and it follows that
Since
![]() $\eta _K$
is
$\eta _K$
is
![]() $\operatorname {\mathrm {lcm}}({\mathscr {B}}_K)$
-periodic and
$\operatorname {\mathrm {lcm}}({\mathscr {B}}_K)$
-periodic and
![]() $\operatorname {\mathrm {lcm}}({\mathscr {B}}_K)\mid n$
, we have
$\operatorname {\mathrm {lcm}}({\mathscr {B}}_K)\mid n$
, we have
By the uniform ergodicity of
![]() $X_{\eta ^{*}}$
, for any
$X_{\eta ^{*}}$
, for any
![]() $\varepsilon>0$
and for large enough n, we have
$\varepsilon>0$
and for large enough n, we have
for every
![]() $M\in {\mathbb {Z}}$
. Using (31), (32) and (33), we conclude that
$M\in {\mathbb {Z}}$
. Using (31), (32) and (33), we conclude that
Hence,
By Remark 4.1, we have
![]() $h(X_{\eta ^{*}})=0$
and
$h(X_{\eta ^{*}})=0$
and
![]() $h(X_{\eta _K})=0$
since
$h(X_{\eta _K})=0$
since
![]() $\eta _K$
is periodic. Recall also that by the Davenport–Erdős theorem (i.e. (1)),
$\eta _K$
is periodic. Recall also that by the Davenport–Erdős theorem (i.e. (1)),
![]() $\lim _{K\to \infty }d(\mathcal {F}_{{\mathscr {B}}_K})=\overline {d}$
. This yields
$\lim _{K\to \infty }d(\mathcal {F}_{{\mathscr {B}}_K})=\overline {d}$
. This yields
which completes the proof of Theorem F.
For the proof of Corollary G, we will need the following lemma.
Lemma 4.2. For any
![]() $\mathscr {B}\subseteq {\mathbb {N}}$
such that
$\mathscr {B}\subseteq {\mathbb {N}}$
such that
![]() $\eta ^{\prime }\neq \eta ^{*}$
, we have
$\eta ^{\prime }\neq \eta ^{*}$
, we have
![]() $\overline {d}>\overline {d}^{*}$
.
$\overline {d}>\overline {d}^{*}$
.
Proof. Since
![]() $\overline {d}=\overline {d}^{\prime }:=\overline {d}(\mathcal {F}_{\mathscr {B}^{\prime }})$
, we can assume without loss of generality that
$\overline {d}=\overline {d}^{\prime }:=\overline {d}(\mathcal {F}_{\mathscr {B}^{\prime }})$
, we can assume without loss of generality that
![]() $\mathscr {B}$
is taut. Let
$\mathscr {B}$
is taut. Let
![]() $(\ell _i)$
be a sequence realizing the lower density of
$(\ell _i)$
be a sequence realizing the lower density of
![]() $\mathcal {M}_{\mathscr {B}^{*}}$
. It follows by the result of Davenport and Erdős (that is, by (1)) that
$\mathcal {M}_{\mathscr {B}^{*}}$
. It follows by the result of Davenport and Erdős (that is, by (1)) that
 $$ \begin{align*} \overline{d}^{*}&=\overline{d}(\mathcal{F}_{\mathscr{B}^{*}})=\lim_{i\to \infty}\frac{1}{\ell_i}|\mathcal{F}_{\mathscr{B}^{*}}\cap [1,\ell_i]|=\liminf_{i\to \infty}\frac{1}{\ell_i}|\mathcal{F}_{\mathscr{B}^{*}}\cap [1,\ell_i]| \\ &\leq\liminf_{i\to\infty}\frac{1}{\ell_i}|\mathcal{F}_{\mathscr{B}}\cap [1,\ell_i]|\leq \limsup_{i\to\infty}\frac{1}{\ell_i}|\mathcal{F}_{\mathscr{B}}\cap [1,\ell_i]|\leq \overline{d}(\mathcal{F}_{\mathscr{B}})=\overline{d}. \end{align*} $$
$$ \begin{align*} \overline{d}^{*}&=\overline{d}(\mathcal{F}_{\mathscr{B}^{*}})=\lim_{i\to \infty}\frac{1}{\ell_i}|\mathcal{F}_{\mathscr{B}^{*}}\cap [1,\ell_i]|=\liminf_{i\to \infty}\frac{1}{\ell_i}|\mathcal{F}_{\mathscr{B}^{*}}\cap [1,\ell_i]| \\ &\leq\liminf_{i\to\infty}\frac{1}{\ell_i}|\mathcal{F}_{\mathscr{B}}\cap [1,\ell_i]|\leq \limsup_{i\to\infty}\frac{1}{\ell_i}|\mathcal{F}_{\mathscr{B}}\cap [1,\ell_i]|\leq \overline{d}(\mathcal{F}_{\mathscr{B}})=\overline{d}. \end{align*} $$
If
![]() $\overline {d}=\overline {d}^{*}$
, then all inequalities in the above formula become equalities. In particular,
$\overline {d}=\overline {d}^{*}$
, then all inequalities in the above formula become equalities. In particular,
so that
![]() $\eta $
is generic along
$\eta $
is generic along
![]() $(\ell _i)$
for
$(\ell _i)$
for
![]() $\nu _\eta $
. Since
$\nu _\eta $
. Since
![]() $\eta ^{*}\leq \eta $
(by the construction of
$\eta ^{*}\leq \eta $
(by the construction of
![]() $\mathscr {B}^{*}$
), it follows that
$\mathscr {B}^{*}$
), it follows that
![]() $({1}/{\ell _i})|\{n\in [1,\ell _i]:\eta ( n ) \neq \eta ^{*}( n ) \}| \to 0$
. Thus, since
$({1}/{\ell _i})|\{n\in [1,\ell _i]:\eta ( n ) \neq \eta ^{*}( n ) \}| \to 0$
. Thus, since
![]() $\eta ^{*}$
is generic along
$\eta ^{*}$
is generic along
![]() $(\ell _i)$
for
$(\ell _i)$
for
![]() $\nu _{\eta ^{*}}$
, it follows immediately that
$\nu _{\eta ^{*}}$
, it follows immediately that
![]() $\eta $
has to be generic along
$\eta $
has to be generic along
![]() $(\ell _i)$
for the very same measure, that is,
$(\ell _i)$
for the very same measure, that is,
![]() $\nu _{\eta ^{*}}$
. However, we know that the Mirsky measure
$\nu _{\eta ^{*}}$
. However, we know that the Mirsky measure
![]() $\nu _\eta $
is the unique measure of maximal density, that is, the invariant measure of the greatest value for the cylinder
$\nu _\eta $
is the unique measure of maximal density, that is, the invariant measure of the greatest value for the cylinder
![]() $\{x\in X_\eta : x(0)=1\}$
, in each
$\{x\in X_\eta : x(0)=1\}$
, in each
![]() $\mathscr {B}$
-free subshift (see, e.g. [Reference Keller and Richard19, Theorem 4 and Corollary 4], cf. also [Reference Baake and Grimm1, Ch. 7]), which gives us
$\mathscr {B}$
-free subshift (see, e.g. [Reference Keller and Richard19, Theorem 4 and Corollary 4], cf. also [Reference Baake and Grimm1, Ch. 7]), which gives us
![]() $\nu _\eta =\nu _{\eta ^{*}}$
. Now it suffices to use [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Corollary 9.2] which says (in particular) that the latter condition is equivalent to
$\nu _\eta =\nu _{\eta ^{*}}$
. Now it suffices to use [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Corollary 9.2] which says (in particular) that the latter condition is equivalent to
![]() $\eta =\eta ^{*}$
(cf. (8)).
$\eta =\eta ^{*}$
(cf. (8)).
Proof of Corollary G
By Remark 4.1, if
![]() $X_\eta $
is uniquely ergodic, then
$X_\eta $
is uniquely ergodic, then
![]() $h(X_\eta )=0$
.
$h(X_\eta )=0$
.
Suppose that
![]() $h(X_\eta )=0$
. Then, by Theorem F, we have
$h(X_\eta )=0$
. Then, by Theorem F, we have
![]() $\overline {d}=d^{*}$
which implies
$\overline {d}=d^{*}$
which implies
![]() $\eta ^{\prime }=\eta ^{*}$
by Lemma 4.2. The latter condition is equivalent to
$\eta ^{\prime }=\eta ^{*}$
by Lemma 4.2. The latter condition is equivalent to
![]() $\mathscr {B}^{\prime }=\mathscr {B}^{*}$
by [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Theorem L], as both
$\mathscr {B}^{\prime }=\mathscr {B}^{*}$
by [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7, Theorem L], as both
![]() $\mathscr {B}^{\prime }$
and
$\mathscr {B}^{\prime }$
and
![]() $\mathscr {B}^{*}$
are taut (cf. (8)). It follows immediately that
$\mathscr {B}^{*}$
are taut (cf. (8)). It follows immediately that
![]() $X_{\eta ^{\prime }}$
must be uniquely ergodic as it is equal to
$X_{\eta ^{\prime }}$
must be uniquely ergodic as it is equal to
![]() $X_{\eta ^{*}}$
and the latter subshift is uniquely ergodic since
$X_{\eta ^{*}}$
and the latter subshift is uniquely ergodic since
![]() $\eta ^{*}$
is assumed to be a regular Toeplitz sequence. It suffices to use Theorem C to complete the proof.
$\eta ^{*}$
is assumed to be a regular Toeplitz sequence. It suffices to use Theorem C to complete the proof.
4.2 Intrinsic ergodicity of
 $X_\eta $
: proof of Theorem H
$X_\eta $
: proof of Theorem H
Consider first the case when
![]() ${\eta ^{\prime }=\eta ^{*}}$
. It follows by Theorem C that
${\eta ^{\prime }=\eta ^{*}}$
. It follows by Theorem C that
Thus, if
![]() $X_{\eta ^{*}}$
is uniquely ergodic, then
$X_{\eta ^{*}}$
is uniquely ergodic, then
![]() $X_\eta $
is also uniquely ergodic. Moreover, the pair
$X_\eta $
is also uniquely ergodic. Moreover, the pair
![]() $(\eta ^{*},\eta )$
is quasi-generic for
$(\eta ^{*},\eta )$
is quasi-generic for
![]() $ \nu _{\eta ^{*}}\triangle \nu _\eta $
along
$ \nu _{\eta ^{*}}\triangle \nu _\eta $
along
![]() $(\ell _i)$
realizing the lower density of
$(\ell _i)$
realizing the lower density of
![]() $\mathcal {M}_{\mathscr {B}}$
. It follows by Remark 4.1 that
$\mathcal {M}_{\mathscr {B}}$
. It follows by Remark 4.1 that
Thus,
![]() $\nu _{\eta ^{*}}\triangle \nu _\eta $
is the diagonal joining of two copies of
$\nu _{\eta ^{*}}\triangle \nu _\eta $
is the diagonal joining of two copies of
![]() $\nu _\eta $
. Let
$\nu _\eta $
. Let
![]() $(x,x,y)$
be a generic point for
$(x,x,y)$
be a generic point for
![]() $(\nu _{\eta ^{*}}\triangle \nu _\eta )\otimes B_{1/2, 1/2}$
. Then
$(\nu _{\eta ^{*}}\triangle \nu _\eta )\otimes B_{1/2, 1/2}$
. Then
![]() $N(x,x,y)=x$
is a generic point for
$N(x,x,y)=x$
is a generic point for
![]() $ N_\ast ((\nu _{\eta ^{*}}\triangle \nu _\eta )\otimes B_{1/2, 1/2}). $
It follows immediately that
$ N_\ast ((\nu _{\eta ^{*}}\triangle \nu _\eta )\otimes B_{1/2, 1/2}). $
It follows immediately that
![]() $ N_\ast ((\nu _{\eta ^{*}}\triangle \nu _\eta )\otimes B_{1/2, 1/2})=\nu _\eta $
.
$ N_\ast ((\nu _{\eta ^{*}}\triangle \nu _\eta )\otimes B_{1/2, 1/2})=\nu _\eta $
.
Assume now that
![]() $\eta ^{\prime }\neq \eta ^{*}$
. We will study the following diagram:
$\eta ^{\prime }\neq \eta ^{*}$
. We will study the following diagram:

Let us now introduce all maps appearing in this diagram. We define
![]() $\widetilde {R}\colon H\times \{0,1\}^{\mathbb {Z}} \to H\times \{0,1\}^{\mathbb {Z}}$
by
$\widetilde {R}\colon H\times \{0,1\}^{\mathbb {Z}} \to H\times \{0,1\}^{\mathbb {Z}}$
by
 $$ \begin{align*} \widetilde{R}(h,x)=\begin{cases} (Rh,x) & \text{ if } \underline{\varphi}(h)(0)=\varphi(h)(0),\\ (Rh,\sigma x) & \text{ if } 0=\underline{\varphi}(h)(0)<\varphi(h)(0)=1. \end{cases} \end{align*} $$
$$ \begin{align*} \widetilde{R}(h,x)=\begin{cases} (Rh,x) & \text{ if } \underline{\varphi}(h)(0)=\varphi(h)(0),\\ (Rh,\sigma x) & \text{ if } 0=\underline{\varphi}(h)(0)<\varphi(h)(0)=1. \end{cases} \end{align*} $$
Let
Given
![]() $x\in \{0,1\}^{\mathbb {Z}}$
and
$x\in \{0,1\}^{\mathbb {Z}}$
and
![]() $z\in Z_\infty $
, let
$z\in Z_\infty $
, let
![]() $\hat {x}_z$
be the sequence obtained by reading consecutive coordinates of x which are in the support of z and such that
$\hat {x}_z$
be the sequence obtained by reading consecutive coordinates of x which are in the support of z and such that
Now, let
and define
![]() $\Psi \colon H_\infty \times \{0,1\}^{\mathbb {Z}}\to H_\infty \times \{0,1\}^{\mathbb {Z}}$
by
$\Psi \colon H_\infty \times \{0,1\}^{\mathbb {Z}}\to H_\infty \times \{0,1\}^{\mathbb {Z}}$
by
(notice that
![]() $\varphi (h)(n)-\underline {\varphi }(h)(n)=1 {\iff} R^nh\in W\setminus \underline {W}$
, so for
$\varphi (h)(n)-\underline {\varphi }(h)(n)=1 {\iff} R^nh\in W\setminus \underline {W}$
, so for
![]() $h\in H_\infty $
, we have
$h\in H_\infty $
, we have
![]() ${\varphi (h)-\underline {\varphi }(h)\in Z_\infty }$
). It remains to define
${\varphi (h)-\underline {\varphi }(h)\in Z_\infty }$
). It remains to define
![]() $\Phi $
. Let
$\Phi $
. Let
![]() $\Phi \colon H_\infty \times \{0,1\}^{\mathbb {Z}}\to [\underline {\varphi },\varphi ]$
be defined by mapping
$\Phi \colon H_\infty \times \{0,1\}^{\mathbb {Z}}\to [\underline {\varphi },\varphi ]$
be defined by mapping
![]() $ (h , x) $
to the unique element in
$ (h , x) $
to the unique element in
![]() $[\underline {\varphi },\varphi ]$
such that
$[\underline {\varphi },\varphi ]$
such that
We will show that the diagram in (34) commutes (it will then follow by Theorem A that the maps
![]() $M_H$
and
$M_H$
and
![]() $\Phi $
are surjective morphisms).
$\Phi $
are surjective morphisms).
Lemma 4.3. For any
![]() $\mathscr {B}\subseteq {\mathbb {N}}$
, we have
$\mathscr {B}\subseteq {\mathbb {N}}$
, we have
![]() $m_H(W\setminus \underline {W})=\overline {d}-\overline {d}^{*}$
. Moreover, if
$m_H(W\setminus \underline {W})=\overline {d}-\overline {d}^{*}$
. Moreover, if
![]() $\eta ^{\prime }\neq \eta ^{*}$
, we have
$\eta ^{\prime }\neq \eta ^{*}$
, we have
![]() $m_H(W\setminus \underline {W})>0$
.
$m_H(W\setminus \underline {W})>0$
.
Before we begin the proof of this lemma, recall some results from [Reference Keller17] that we already mentioned in the introduction: there is a continuous surjective group homomorphism
![]() $\Gamma _{H,H^{*}} \colon H \to H^{*} $
, which maps
$\Gamma _{H,H^{*}} \colon H \to H^{*} $
, which maps
![]() $ \Delta (n) $
to
$ \Delta (n) $
to
![]() $ \Delta ^{*}(n) $
. In addition, it has the following property, see (13):
$ \Delta ^{*}(n) $
. In addition, it has the following property, see (13):
Recall also that it was shown in [Reference Kasjan, Keller and Lemańczyk14, Lemma 4.1] that
Proof of Lemma 4.3
We have
 $$ \begin{align*} m_H(W\setminus \underline{W})&=m_H(W)-m_H(\underline{W})\\ &=m_H(W)-m_H(\Gamma_{H,H^{*}}^{-1}(W^{*}))\\ &=m_H(W)-(\Gamma_{H,H^{*}})_{\ast}(m_H)(W^{*})\\ &=m_H(W)-m_{H^{*}}(W^{*}) \end{align*} $$
$$ \begin{align*} m_H(W\setminus \underline{W})&=m_H(W)-m_H(\underline{W})\\ &=m_H(W)-m_H(\Gamma_{H,H^{*}}^{-1}(W^{*}))\\ &=m_H(W)-(\Gamma_{H,H^{*}})_{\ast}(m_H)(W^{*})\\ &=m_H(W)-m_{H^{*}}(W^{*}) \end{align*} $$
(the second equality follows from (13) and the fourth equality follows by the unique ergodicity of
![]() $R^{*}$
). It remains to use (35) to deduce that
$R^{*}$
). It remains to use (35) to deduce that
![]() $m_H(W\setminus \underline {W})=\overline {d}-\overline {d}^{*}$
and Lemma 4.2 to conclude that
$m_H(W\setminus \underline {W})=\overline {d}-\overline {d}^{*}$
and Lemma 4.2 to conclude that
![]() $m_H(W\setminus \underline {W})>0$
whenever
$m_H(W\setminus \underline {W})>0$
whenever
![]() $\eta ^{\prime }\neq \eta ^{*}$
.
$\eta ^{\prime }\neq \eta ^{*}$
.
It follows now from Lemma 4.3 and from the ergodicity of
![]() $(H,R,m_H)$
that
$(H,R,m_H)$
that
![]() ${m_H(H_\infty )=1}$
. Thus, to conclude that (34) commutes, it remains to check whether for every
${m_H(H_\infty )=1}$
. Thus, to conclude that (34) commutes, it remains to check whether for every
![]() $h\in H_\infty $
and every
$h\in H_\infty $
and every
![]() $x\in \{0,1\}^{\mathbb {Z}}$
, we have the commutativity relations
$x\in \{0,1\}^{\mathbb {Z}}$
, we have the commutativity relations
 $$ \begin{align} \begin{split}M_H(h,x) &= (\Phi \circ \Psi)(h,x) , \\ (\widetilde{R}\circ\Psi)(h,x) &= (\Psi\circ(R\times \sigma))(h,x) ,\\ (\sigma\circ\Phi)(h,x) &= (\Phi\circ \widetilde{R})(h,x). \end{split} \end{align} $$
$$ \begin{align} \begin{split}M_H(h,x) &= (\Phi \circ \Psi)(h,x) , \\ (\widetilde{R}\circ\Psi)(h,x) &= (\Psi\circ(R\times \sigma))(h,x) ,\\ (\sigma\circ\Phi)(h,x) &= (\Phi\circ \widetilde{R})(h,x). \end{split} \end{align} $$
The first equality in (36) is immediate by the definition of the maps, while the second and third follow from
 $$ \begin{align} \widehat{\sigma x}_{\sigma z}=\begin{cases} \hat{x}_z& \text{ if }z(0)=0,\\ \sigma\hat{x}_z&\text{ if }z(0)=1, \end{cases} \end{align} $$
$$ \begin{align} \widehat{\sigma x}_{\sigma z}=\begin{cases} \hat{x}_z& \text{ if }z(0)=0,\\ \sigma\hat{x}_z&\text{ if }z(0)=1, \end{cases} \end{align} $$
(the proof of (37) consists of a straightforward but lengthy calculation; an analogous property is proved in [Reference Kułaga-Przymus, Lemańczyk and Weiss22]).
Notice that it follows by Theorem A that the morphism
![]() $M_H$
is surjective. Thus, the morphism
$M_H$
is surjective. Thus, the morphism
![]() $\Phi $
is also surjective.
$\Phi $
is also surjective.
Now, we are ready to complete the proof of the intrinsic ergodicity of
![]() $X_\eta $
. The main ideas come from [Reference Kułaga-Przymus, Lemańczyk and Weiss22]. We will present the sketch of the proof only (similarly as in [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7] for
$X_\eta $
. The main ideas come from [Reference Kułaga-Przymus, Lemańczyk and Weiss22]. We will present the sketch of the proof only (similarly as in [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk7] for
![]() $\widetilde {X}_\eta $
). Clearly, any point from
$\widetilde {X}_\eta $
). Clearly, any point from
![]() $H_\infty \cap (W\setminus \underline {W})$
returns to
$H_\infty \cap (W\setminus \underline {W})$
returns to
![]() $W\setminus \underline {W}$
infinitely often under R and
$W\setminus \underline {W}$
infinitely often under R and
![]() $m_H(H_\infty \cap (W\setminus \underline {W}))=m_H(W\setminus \underline {W})$
. Recall that
$m_H(H_\infty \cap (W\setminus \underline {W}))=m_H(W\setminus \underline {W})$
. Recall that
 $$ \begin{align*} \widetilde{R}(h,x)=\begin{cases} (Rh,x)& \text{ if } \underline{\varphi}(h)(0)=\varphi(h)(0),\\ (Rh,\sigma x)& \text{ if } 0=\underline{\varphi}(h)(0)<\varphi(h)(0)=1. \end{cases} \end{align*} $$
$$ \begin{align*} \widetilde{R}(h,x)=\begin{cases} (Rh,x)& \text{ if } \underline{\varphi}(h)(0)=\varphi(h)(0),\\ (Rh,\sigma x)& \text{ if } 0=\underline{\varphi}(h)(0)<\varphi(h)(0)=1. \end{cases} \end{align*} $$
Then every point from
![]() $(H_\infty \cap (W\setminus \underline {W}))\times \{0,1\}^{\mathbb {Z}}$
returns to
$(H_\infty \cap (W\setminus \underline {W}))\times \{0,1\}^{\mathbb {Z}}$
returns to
![]() $(W\setminus \underline {W})\times \{0,1\}^{\mathbb {Z}}$
infinitely often under
$(W\setminus \underline {W})\times \{0,1\}^{\mathbb {Z}}$
infinitely often under
![]() $\widetilde {R}$
and
$\widetilde {R}$
and
![]() $\nu ((H_\infty \cap (W\setminus \underline {W}))\times \{0,1\}^{\mathbb {Z}})=\nu ((W\setminus \underline {W})\times \{0,1\}^{\mathbb {Z}})$
for every
$\nu ((H_\infty \cap (W\setminus \underline {W}))\times \{0,1\}^{\mathbb {Z}})=\nu ((W\setminus \underline {W})\times \{0,1\}^{\mathbb {Z}})$
for every
![]() $\nu \in \mathcal {P}(H\times \{0,1\}^{\mathbb {Z}},\widetilde {R})$
. Thus, the induced transformation
$\nu \in \mathcal {P}(H\times \{0,1\}^{\mathbb {Z}},\widetilde {R})$
. Thus, the induced transformation
![]() $\widetilde {R}_{{(W\setminus \underline {W})}\times \{0,1\}^{\mathbb {Z}}}$
is well defined, that is,
$\widetilde {R}_{{(W\setminus \underline {W})}\times \{0,1\}^{\mathbb {Z}}}$
is well defined, that is,
![]() $\widetilde {R}_{{(W\setminus \underline {W})}\times \{0,1\}^{\mathbb {Z}}}(h,x)=\widetilde {R}^{n(h,x)}(h,x)$
for
$\widetilde {R}_{{(W\setminus \underline {W})}\times \{0,1\}^{\mathbb {Z}}}(h,x)=\widetilde {R}^{n(h,x)}(h,x)$
for
![]() $\nu $
-almost every
$\nu $
-almost every
![]() $(h,x)\in (W\setminus \underline {W})\times \{0,1\}^{\mathbb {Z}}$
, where
$(h,x)\in (W\setminus \underline {W})\times \{0,1\}^{\mathbb {Z}}$
, where
![]() $n(h,x):=\min \{n\geq 1: \ \widetilde {R}^n(h,x)\in (W\setminus \underline {W})\times \{0,1\}^{\mathbb {Z}}\}$
. It follows that
$n(h,x):=\min \{n\geq 1: \ \widetilde {R}^n(h,x)\in (W\setminus \underline {W})\times \{0,1\}^{\mathbb {Z}}\}$
. It follows that
![]() $\widetilde {R}_{(W\setminus \underline {W})\times \{0,1\}^{\mathbb {Z}}}=R_{(W\setminus \underline {W})}\times \sigma $
a.e. for any
$\widetilde {R}_{(W\setminus \underline {W})\times \{0,1\}^{\mathbb {Z}}}=R_{(W\setminus \underline {W})}\times \sigma $
a.e. for any
![]() $\widetilde {R}$
-invariant measure.
$\widetilde {R}$
-invariant measure.
We will show now that
![]() $\widetilde {R}$
has a unique measure of maximal (measure-theoretic) entropy. Since
$\widetilde {R}$
has a unique measure of maximal (measure-theoretic) entropy. Since
![]() $m_H(W\setminus \underline {W})>0$
whenever
$m_H(W\setminus \underline {W})>0$
whenever
![]() $\eta ^{\prime }\neq \eta ^{*}$
(see Lemma 4.3) and since
$\eta ^{\prime }\neq \eta ^{*}$
(see Lemma 4.3) and since
![]() ${\kappa (W\setminus \underline {W}\times \{0,1\}^{\mathbb {Z}})=m_H(W\setminus \underline {W})>0}$
for any
${\kappa (W\setminus \underline {W}\times \{0,1\}^{\mathbb {Z}})=m_H(W\setminus \underline {W})>0}$
for any
![]() $R_{W\setminus \underline {W}}\times \sigma $
-invariant probability measure
$R_{W\setminus \underline {W}}\times \sigma $
-invariant probability measure
![]() $\kappa $
, in view of the Abramov formula, it suffices to show that
$\kappa $
, in view of the Abramov formula, it suffices to show that
![]() $\widetilde {R}_{(W\setminus \underline {W})\times \{0,1\}^{\mathbb {Z}}}=R_{(W\setminus \underline {W})}\times \sigma $
has a unique measure of maximal entropy. For any
$\widetilde {R}_{(W\setminus \underline {W})\times \{0,1\}^{\mathbb {Z}}}=R_{(W\setminus \underline {W})}\times \sigma $
has a unique measure of maximal entropy. For any
![]() $R_{(W\setminus \underline {W})}\times \sigma $
-invariant measure
$R_{(W\setminus \underline {W})}\times \sigma $
-invariant measure
![]() $\kappa $
, by the Pinsker formula, we have
$\kappa $
, by the Pinsker formula, we have
 $$ \begin{align*} \begin{split} &h(\{0,1\}^{\mathbb{Z}},\sigma,(\pi_2)_\ast(\kappa))\leq h( (W\setminus \underline{W})\times \{0,1\}^{\mathbb{Z}},R_{W\setminus \underline{W}}\times \sigma,\kappa )\\ &\ \!\leq\! h(W\setminus \underline{W}, R_{W\setminus \underline{W}},(\pi_1)_\ast(\kappa)|_{(W\setminus \underline{W})}) +h(\{0,1\}^{\mathbb{Z}},\sigma,(\pi_2)_\ast(\kappa))\!=\!h(\{0,1\}^{\mathbb{Z}},\sigma,(\pi_2)_\ast(\kappa)), \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} &h(\{0,1\}^{\mathbb{Z}},\sigma,(\pi_2)_\ast(\kappa))\leq h( (W\setminus \underline{W})\times \{0,1\}^{\mathbb{Z}},R_{W\setminus \underline{W}}\times \sigma,\kappa )\\ &\ \!\leq\! h(W\setminus \underline{W}, R_{W\setminus \underline{W}},(\pi_1)_\ast(\kappa)|_{(W\setminus \underline{W})}) +h(\{0,1\}^{\mathbb{Z}},\sigma,(\pi_2)_\ast(\kappa))\!=\!h(\{0,1\}^{\mathbb{Z}},\sigma,(\pi_2)_\ast(\kappa)), \end{split} \end{align*} $$
where
![]() $h(W\setminus \underline {W}, R_{W\setminus \underline {W}},(\pi _1)_\ast (\kappa )|_{(W\setminus \underline {W})})$
vanishes by the Abramov formula as
$h(W\setminus \underline {W}, R_{W\setminus \underline {W}},(\pi _1)_\ast (\kappa )|_{(W\setminus \underline {W})})$
vanishes by the Abramov formula as
![]() $R_{W\setminus \underline {W}}$
is an induced map coming from a rotation. Since
$R_{W\setminus \underline {W}}$
is an induced map coming from a rotation. Since
![]() $(\pi _2)_\ast (\kappa )$
can be arbitrary, it follows that a measure
$(\pi _2)_\ast (\kappa )$
can be arbitrary, it follows that a measure
![]() $\kappa $
has the maximal entropy among all
$\kappa $
has the maximal entropy among all
![]() $R_{W\setminus \underline {W}}\times \sigma $
-invariant measures if and only if
$R_{W\setminus \underline {W}}\times \sigma $
-invariant measures if and only if
![]() $h((W\setminus \underline {W})\times \{0,1\}^{{\mathbb {Z}}}, R_{W\setminus \underline {W}}\times \sigma ,\kappa )=h(\{0,1\}^{\mathbb {Z}},\sigma )$
. Moreover,
$h((W\setminus \underline {W})\times \{0,1\}^{{\mathbb {Z}}}, R_{W\setminus \underline {W}}\times \sigma ,\kappa )=h(\{0,1\}^{\mathbb {Z}},\sigma )$
. Moreover,
![]() $\kappa $
is a measure of maximal entropy for
$\kappa $
is a measure of maximal entropy for
![]() $R_{W\setminus \underline {W}}\times \sigma $
if and only if
$R_{W\setminus \underline {W}}\times \sigma $
if and only if
![]() $(\pi _2)_\ast (\kappa )$
is the measure of maximal entropy for
$(\pi _2)_\ast (\kappa )$
is the measure of maximal entropy for
![]() $\sigma $
, that is, when
$\sigma $
, that is, when
![]() $(\pi _2)_\ast (\kappa )$
is the Bernoulli measure
$(\pi _2)_\ast (\kappa )$
is the Bernoulli measure
![]() $B_{1/2, 1/2}$
, that is, when
$B_{1/2, 1/2}$
, that is, when
![]() $\kappa $
is a joining of the unique invariant measure for
$\kappa $
is a joining of the unique invariant measure for
![]() $R_{W\setminus \underline {W}}$
and
$R_{W\setminus \underline {W}}$
and
![]() $B_{1/2, 1/2}$
. Since the unique invariant measure for
$B_{1/2, 1/2}$
. Since the unique invariant measure for
![]() $R_{W\setminus \underline {W}}$
is of zero entropy, it follows from the disjointness of K-automorphisms with zero entropy automorphisms [Reference Furstenberg10] that
$R_{W\setminus \underline {W}}$
is of zero entropy, it follows from the disjointness of K-automorphisms with zero entropy automorphisms [Reference Furstenberg10] that
![]() $\kappa $
is the product measure. In particular,
$\kappa $
is the product measure. In particular,
![]() $\kappa $
is unique.
$\kappa $
is unique.
The last step to conclude the intrinsic ergodicity of
![]() $X_\eta $
is to show that
$X_\eta $
is to show that
Let us justify each of the equalities above. By the variational principle, by the Abramov formula and by the Pinsker formula, we have
 $$ \begin{align*} h(H\times \{0,1\}^{\mathbb{Z}}, \widetilde{R})&=\sup_\rho\{h(H\times \{0,1\}^{\mathbb{Z}}, \widetilde{R},\rho) \}\\ &=m_H(W\setminus\underline{W})\cdot\sup_\rho\{h((W\setminus \underline{W})\times \{0,1\}^{\mathbb{Z}},R_{W\setminus\underline{W}}\times\sigma,\rho)\}\\ &=m_H(W\setminus \underline{W})\cdot \sup_\rho \{h(\{0,1\}^{\mathbb{Z}},\rho)\}=m_H(W\setminus\underline{W}), \end{align*} $$
$$ \begin{align*} h(H\times \{0,1\}^{\mathbb{Z}}, \widetilde{R})&=\sup_\rho\{h(H\times \{0,1\}^{\mathbb{Z}}, \widetilde{R},\rho) \}\\ &=m_H(W\setminus\underline{W})\cdot\sup_\rho\{h((W\setminus \underline{W})\times \{0,1\}^{\mathbb{Z}},R_{W\setminus\underline{W}}\times\sigma,\rho)\}\\ &=m_H(W\setminus \underline{W})\cdot \sup_\rho \{h(\{0,1\}^{\mathbb{Z}},\rho)\}=m_H(W\setminus\underline{W}), \end{align*} $$
where the suprema are taken over all Borel probability invariant measures for the corresponding maps. This yields the first equality in (38). Moreover, the middle equality in (38) follows by Lemma 4.3, while the last one follows by Theorem F.
4.3 Entropy density of
 $X_\eta $
: proof of Theorem I
$X_\eta $
: proof of Theorem I
The idea of the proof of Theorem I is the same as that of the analogous result for
![]() $\widetilde {X}_\eta $
in [Reference Konieczny, Kupsa and Kwietniak21]. Let us introduce the necessary tools and notation. Given
$\widetilde {X}_\eta $
in [Reference Konieczny, Kupsa and Kwietniak21]. Let us introduce the necessary tools and notation. Given
![]() $x,y\in \{0,1\}^{\mathbb {Z}}$
, consider the following premetric:
$x,y\in \{0,1\}^{\mathbb {Z}}$
, consider the following premetric:
(being a premetric means that
![]() $\underline {d}$
is a real-valued, non-negative, symmetric function on
$\underline {d}$
is a real-valued, non-negative, symmetric function on
![]() $(\{0,1\}^{\mathbb {Z}})^2$
vanishing on the diagonal; the triangle inequality for
$(\{0,1\}^{\mathbb {Z}})^2$
vanishing on the diagonal; the triangle inequality for
![]() $\underline {d}$
fails). As a premetric,
$\underline {d}$
fails). As a premetric,
![]() $\underline {d}$
induces a Hausdorff pseudometric
$\underline {d}$
induces a Hausdorff pseudometric
![]() $\underline {d}^H$
on the space of all non-empty subsets of
$\underline {d}^H$
on the space of all non-empty subsets of
![]() $\{0,1\}^{\mathbb {Z}}$
in the following way:
$\{0,1\}^{\mathbb {Z}}$
in the following way:
for any
![]() $\emptyset \neq X, Y\subseteq \{0,1\}^{\mathbb {Z}}$
and
$\emptyset \neq X, Y\subseteq \{0,1\}^{\mathbb {Z}}$
and
![]() $x\in X,y\in Y$
.
$x\in X,y\in Y$
.
Let us now recall some results from [Reference Konieczny, Kupsa and Kwietniak21] (we formulate them for
![]() $0$
–
$0$
–
![]() $1$
shifts, however, they are valid for shifts over any finite alphabet).
$1$
shifts, however, they are valid for shifts over any finite alphabet).
Proposition 4.4. [Reference Konieczny, Kupsa and Kwietniak21, Proposition 26]
Let
![]() $x\in \{0,1\}^{\mathbb {Z}}$
be a periodic point under
$x\in \{0,1\}^{\mathbb {Z}}$
be a periodic point under
![]() $\sigma $
. Then the hereditary closure of the orbit of x is a transitive sofic shift.
$\sigma $
. Then the hereditary closure of the orbit of x is a transitive sofic shift.
Remark 4.5. We skip here the definition of a sofic shift as it is quite technical and this notion serves here as a tool only. Namely, in any sofic transitive shift, the ergodic measures are entropy dense (more general results are known, see [Reference Eizenberg, Kifer and Weiss8, Reference Pfister and Sullivan33]). The following modification of Proposition 4.4 holds. Let
![]() $w, x\in \{0,1\}^{\mathbb {Z}}$
be periodic, such that
$w, x\in \{0,1\}^{\mathbb {Z}}$
be periodic, such that
![]() $w\leq x$
. Then
$w\leq x$
. Then
![]() $[w,x]$
is a transitive sofic shift. The proof is a straightforward adjustment of the proof of [Reference Konieczny, Kupsa and Kwietniak21, Proposition 26].
$[w,x]$
is a transitive sofic shift. The proof is a straightforward adjustment of the proof of [Reference Konieczny, Kupsa and Kwietniak21, Proposition 26].
Proposition 4.6. [Reference Konieczny, Kupsa and Kwietniak21, Corollary 20]
Let
![]() $(X_K)_{K\geq 1}\subseteq \{0,1\}^{\mathbb {Z}}$
be a sequence of transitive sofic shifts. If
$(X_K)_{K\geq 1}\subseteq \{0,1\}^{\mathbb {Z}}$
be a sequence of transitive sofic shifts. If
![]() $X\subseteq \{0,1\}^{\mathbb {Z}}$
is a subshift such that
$X\subseteq \{0,1\}^{\mathbb {Z}}$
is a subshift such that
![]() $\underline {d}^H(X_K,X)\to 0$
, then ergodic measures are entropy-dense in
$\underline {d}^H(X_K,X)\to 0$
, then ergodic measures are entropy-dense in
![]() $\mathcal {P}(X)$
.
$\mathcal {P}(X)$
.
Proof of Theorem I
Since
![]() $\mathcal {P}(X_\eta )=\mathcal {P}(X_{\eta ^{\prime }})$
by Theorem C, we can assume without loss of generality that
$\mathcal {P}(X_\eta )=\mathcal {P}(X_{\eta ^{\prime }})$
by Theorem C, we can assume without loss of generality that
![]() $\mathscr {B}$
is taut. Hence,
$\mathscr {B}$
is taut. Hence,
![]() $ X_{\eta } = \overline {[ \eta ^{*} , \eta ]} $
by Proposition 2.1, and in view of Remark 4.5 and Proposition 4.6, it suffices to prove that
$ X_{\eta } = \overline {[ \eta ^{*} , \eta ]} $
by Proposition 2.1, and in view of Remark 4.5 and Proposition 4.6, it suffices to prove that
![]() $ \underline {d}^{H}( [\underline {\eta }_{K} , \eta _{K} ] , \overline {[ \eta ^{*} , \eta ]} ) \to 0 $
. To do so, we show that
$ \underline {d}^{H}( [\underline {\eta }_{K} , \eta _{K} ] , \overline {[ \eta ^{*} , \eta ]} ) \to 0 $
. To do so, we show that
where the right-hand side tends to zero by the regularity of
![]() $\eta ^{*}$
(cf. (28)) and the Davenport–Erdős theorem (i.e. (1)). Fix now
$\eta ^{*}$
(cf. (28)) and the Davenport–Erdős theorem (i.e. (1)). Fix now
![]() $K\geq 1$
. We claim that for
$K\geq 1$
. We claim that for
![]() $ \underline {\eta }_{K} \leq x \leq \eta _{K} $
, there exists
$ \underline {\eta }_{K} \leq x \leq \eta _{K} $
, there exists
![]() $ y \in [ \eta ^{*} , \eta ] $
with
$ y \in [ \eta ^{*} , \eta ] $
with
Indeed, set
![]() $ y := N( \eta ^{*} , \eta , x ) = \eta ^{*} + x( \eta - \eta ^{*} ) $
. Then
$ y := N( \eta ^{*} , \eta , x ) = \eta ^{*} + x( \eta - \eta ^{*} ) $
. Then
![]() $ y(n) \neq x(n) $
implies that
$ y(n) \neq x(n) $
implies that
![]() $ {\eta ^{*}( n ) = \eta ( n ) }$
and
$ {\eta ^{*}( n ) = \eta ( n ) }$
and
![]() $ \underline {\eta }_{K}( n ) \neq \eta _{K}( n ) $
(recall that
$ \underline {\eta }_{K}( n ) \neq \eta _{K}( n ) $
(recall that
![]() $ \underline {\eta }_{K} \leq \eta ^{*} \leq \eta \leq \eta _{K} $
). Thus, for every
$ \underline {\eta }_{K} \leq \eta ^{*} \leq \eta \leq \eta _{K} $
). Thus, for every
![]() $ n \in {\mathbb {Z}} $
with
$ n \in {\mathbb {Z}} $
with
![]() $ y(n) \neq x(n) $
, we have either that
$ y(n) \neq x(n) $
, we have either that
![]() $ \underline {\eta }_{K}( n ) \neq \eta ^{*}( n ) $
or that
$ \underline {\eta }_{K}( n ) \neq \eta ^{*}( n ) $
or that
![]() $ \eta ( n ) \neq \eta _{K}( n ) $
, that is,
$ \eta ( n ) \neq \eta _{K}( n ) $
, that is,
This yields (39). To finish the proof, note that for every
![]() $ x \in [\underline {\eta }_{K} , \eta _{K} ] $
, there exists
$ x \in [\underline {\eta }_{K} , \eta _{K} ] $
, there exists
![]() $ m \in {\mathbb {Z}} $
such that
$ m \in {\mathbb {Z}} $
such that
![]() $ \underline {\eta }_{K} \leq \sigma ^{m} x \leq \eta _{K} $
. By the above construction, for every
$ \underline {\eta }_{K} \leq \sigma ^{m} x \leq \eta _{K} $
. By the above construction, for every
![]() $ x \in [\underline {\eta }_{K} , \eta _{K} ] $
, there exists therefore
$ x \in [\underline {\eta }_{K} , \eta _{K} ] $
, there exists therefore
![]() $ y \in [ \eta ^{*} , \eta ] $
with
$ y \in [ \eta ^{*} , \eta ] $
with
![]() $ \underline {d}( x , y ) \leq \underline {d}( \underline {\eta }_{K} , \eta ^{*} ) + \underline {d}( \eta , \eta _{K} ) $
. In addition, we have
$ \underline {d}( x , y ) \leq \underline {d}( \underline {\eta }_{K} , \eta ^{*} ) + \underline {d}( \eta , \eta _{K} ) $
. In addition, we have
![]() $ \overline {[ \eta ^{*} , \eta ]} \subseteq [\underline {\eta }_{K} , \eta _{K} ] $
.
$ \overline {[ \eta ^{*} , \eta ]} \subseteq [\underline {\eta }_{K} , \eta _{K} ] $
.
Acknowledgements
We are indebted to Stanisław Kasjan and Mariusz Lemańczyk for helpful discussions, in particular on category theory notation. Research of A.D. and J.K.-P. is supported by Narodowe Centrum Nauki grant UMO-2019/33/B/ST1/00364. Research of D.S. is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Projektnummer 454053022.