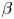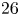Nomenclature
- $a$

linear size of the plasma
- $A_{\phi }$

toroidal component of the magnetic potential vector
- $b$

${k_f(1+{1}/{Q})}/{2(1+w)}$

- $B$

intensity of the magnetic field
- $B_N$

${{\rm \pi} B_e R_c}/{\mu _{0} I}$

- $\boldsymbol {B}$

magnetic field
- $B_e$

vertical magnetic field due to external coils
- $B_{\phi }$

toroidal component of the magnetic field
- $ECRH$

electron cyclotron radiofrequency heating
- $F$

${B_{\phi }}/{r}$

- $I$

electric current flowing in the internal coil
- $k_f$

proportionality constant between the density of fusion power and $p^2$

- $MCF$

fusion with magnetic confinement
- $n$

particle density
- $n_{\max }$

maximum value of $n$
 compatible with stability
compatible with stability- $N$

total number of particles
- $NBI$

neutral beam injection
- $p$

plasma pressure
- $p_{\max }$

maximum plasma pressure
- $p_{*}$

$\lambda p^2$

- $P_{a}$

non-fusion heating power
- $P_{c}$

power lost through conduction
- $P_{f}$

fusion heating power
- $P_{r}$

power lost through radiation
- $Q$

${P_f}/{P_a}$

- $r$

radial coordinate
- $R_c$

radius of the internal coil at $z = 0$

- $R_p$

value of $r$
 where $p = p_{\max }$
where $p = p_{\max }$ at $z = 0$
at $z = 0$
- $R_w$

radius of the internal wall at $z = 0$

- $T$

temperature
- $T_e$

electron temperature
- $T_i$

ion temperature
- $T_{\rm opt}$

optimum temperature
- $u$

internal energy density
- $v$

${{\rm d} V}/{{\rm d} \psi }$

- $V$

volume contained within a $\psi = {\rm const.}$
 surface
surface- $w$

${P_r}/{P_c}$

- $W_{\rm int}$

internal energy
- $W_{m}$

magnetic energy
- $W_{n}$

energy of neutrons
- $W_{\alpha }$

energy of $\alpha$
 particles
particles- $z$

vertical coordinate
Greek Symbols
- $\beta$

ratio of plasma pressure and magnetic pressure
- $\gamma$

specific heat ratio
- $\eta$

stability parameter
- $\lambda$

Lagrange multiplier
- $\mu _0$

$4 {\rm \pi}\cdot 10^{-7}\ {\rm T} \cdot {\rm A}^{-1} \cdot {\rm m}$

- $\tau _E$

energy confinement time
- $\tau _*$

threshold on $\tau _E$

- $\phi$

toroidal coordinate
- $\psi$

$(2 {\rm \pi})^{-1} \cdot$
 poloidal flux
poloidal flux- $\psi _{\max }$

maximum value of $\psi$

- $\psi _{\min }$

minimum value of $\psi$

1. The problem
Magnetic confinement of a toroidal axisymmetric plasma with vanishing toroidal magnetic field and dipole-like poloidal field is a decade-old idea in the controlled fusion research with magnetically confined plasmas (MCFs) (Lehnert Reference Lehnert1958, Reference Lehnert1968a,Reference Lehnertb; Hasegawa Reference Hasegawa1987). This plasma is the terrestrial analogue of the ionospheric plasma which is confined by the dipole magnetic field of the Earth. The field is produced by a toroidal loop of current; this current flows across a circular, toroidal coil.
In spite of decades spent in MCF research since the proposal of Lehnert (Reference Lehnert1958), research on fusion-relevant dipole-confined plasmas is somehow still in its infancy. To start with, the main toroidal coil whose current sustains the confining magnetic field is internal to the plasma, rather than external to it; this fact provides the basis for excellent MHD stability (Freidberg Reference Freidberg2014) but then applications on Earth (unlike applications to space propulsion Teller et al. Reference Teller, Glass, Fowler, Hasegawa and Santarius1992) require a reliable coil support system. In an early experiment, a copper coil was kept in place by retractile supports and then allowed to fall for $0.02$![]() s, a time interval during which experiments were performed (Anderson et al. Reference Anderson, Birdsall, Hartman, Lauer and Furth1968). If unmagnetized rods and wires support a superconducting coil, then losses towards the supports are far from negligible (Freeman et al. Reference Freeman, Okabayashi, Pacher and Yoshikawa1969); this remains true also if a toroidal field is added (Breton & Ya'akobi Reference Breton and Ya'akobi1973). In the proposal of Hasegawa (Reference Hasegawa1987), the coil is superconducting, and levitates magnetically in an external field. A superconducting coil has been successfully levitated for time intervals ${\approx }O(10^4 s)$
s, a time interval during which experiments were performed (Anderson et al. Reference Anderson, Birdsall, Hartman, Lauer and Furth1968). If unmagnetized rods and wires support a superconducting coil, then losses towards the supports are far from negligible (Freeman et al. Reference Freeman, Okabayashi, Pacher and Yoshikawa1969); this remains true also if a toroidal field is added (Breton & Ya'akobi Reference Breton and Ya'akobi1973). In the proposal of Hasegawa (Reference Hasegawa1987), the coil is superconducting, and levitates magnetically in an external field. A superconducting coil has been successfully levitated for time intervals ${\approx }O(10^4 s)$![]() and an electric current ${\approx }O(10^6 A)$
and an electric current ${\approx }O(10^6 A)$![]() has been induced in such a coil in the experiments Levitron (Skellett Reference Skellett1975), RT-1 (Saitoh et al. Reference Saitoh2010) and LDX (Garnier et al. Reference Garnier2006; Kesner & Mauel Reference Kesner and Mauel2013). An alternative layout, where the toroidal coil is in contact with material leads which are screened against the impinging plasma particles by the very magnetic field flowing across them, has been proposed in Lehnert (Reference Lehnert1958, Reference Lehnert1968a,Reference Lehnertb) and has never been tested to date, to the best of the author's knowledge at least. Moreover, the formidable technological issues involved in the close proximity of a thermonuclear plasma to the main toroidal coil nudged public funding towards allegedly less technologically demanding approaches, like e.g. the tokamak. As a consequence, today (2024) the performances of dipole-confined plasmas are far from being of thermonuclear interest, and order-of-magnitude worse than the corresponding results of much more investigated devices like tokamaks: peak electron density $10^{18}\ {\rm m}^{-3}$
has been induced in such a coil in the experiments Levitron (Skellett Reference Skellett1975), RT-1 (Saitoh et al. Reference Saitoh2010) and LDX (Garnier et al. Reference Garnier2006; Kesner & Mauel Reference Kesner and Mauel2013). An alternative layout, where the toroidal coil is in contact with material leads which are screened against the impinging plasma particles by the very magnetic field flowing across them, has been proposed in Lehnert (Reference Lehnert1958, Reference Lehnert1968a,Reference Lehnertb) and has never been tested to date, to the best of the author's knowledge at least. Moreover, the formidable technological issues involved in the close proximity of a thermonuclear plasma to the main toroidal coil nudged public funding towards allegedly less technologically demanding approaches, like e.g. the tokamak. As a consequence, today (2024) the performances of dipole-confined plasmas are far from being of thermonuclear interest, and order-of-magnitude worse than the corresponding results of much more investigated devices like tokamaks: peak electron density $10^{18}\ {\rm m}^{-3}$![]() , peak electron temperature $0.5$
, peak electron temperature $0.5$![]() KeV, energy confinement time $0.028$
KeV, energy confinement time $0.028$![]() s (Kesner & Mauel Reference Kesner and Mauel2013) (even if much better results have been claimed Yoshida et al. Reference Yoshida, Saitoh, Yano, Mikami, Kasaoka, Sakamoto, Morikawa, Furukawa and Mahajan2013).
s (Kesner & Mauel Reference Kesner and Mauel2013) (even if much better results have been claimed Yoshida et al. Reference Yoshida, Saitoh, Yano, Mikami, Kasaoka, Sakamoto, Morikawa, Furukawa and Mahajan2013).
The potential advantages of the dipole approach to MCF are nevertheless relevant, and the results of both theory and experiments are quite promising. For example, dipole-confined plasmas enjoy excellent MHD stability. The internal coil of the dipole acts as the internal, rigid current-carrying conductor of a toroidal hardcore Z-pinch, which is MHD stable and achieves values of $\beta$![]() much larger than in tokamaks (Freidberg Reference Freidberg2014), i.e. up to $26$
much larger than in tokamaks (Freidberg Reference Freidberg2014), i.e. up to $26$![]() % (Mauel Reference Mauel2008). Qualitatively at least, the dipole can be thought of as a toroidal mirror, much more similar to the Earth's field than the linear system in a traditional magnetic mirror trap (Dolan Reference Dolan1982). Particles in the toroidal area around the outside of the central magnet that move up or down see increasing magnetic density and tend to move back towards the equator area again. This gives the system some level of natural stability. Particles with higher energy, the ones that would escape a traditional mirror trap, instead follow the field lines through the hollow centre of the magnet, recirculating back into the equatorial area again. The poloidal current density vanishes everywhere; then, the only destabilizing term in the extended energy principle of MHD (Freidberg Reference Freidberg2014) arises from the curvature of the magnetic field lines and can be compensated either by raising $B$
% (Mauel Reference Mauel2008). Qualitatively at least, the dipole can be thought of as a toroidal mirror, much more similar to the Earth's field than the linear system in a traditional magnetic mirror trap (Dolan Reference Dolan1982). Particles in the toroidal area around the outside of the central magnet that move up or down see increasing magnetic density and tend to move back towards the equator area again. This gives the system some level of natural stability. Particles with higher energy, the ones that would escape a traditional mirror trap, instead follow the field lines through the hollow centre of the magnet, recirculating back into the equatorial area again. The poloidal current density vanishes everywhere; then, the only destabilizing term in the extended energy principle of MHD (Freidberg Reference Freidberg2014) arises from the curvature of the magnetic field lines and can be compensated either by raising $B$![]() or by making the system larger (thus reducing the curvature), ensuring stability against both interchange and ballooning modes (Garnier, Kesner & Mauel Reference Garnier, Kesner and Mauel1999; Krashenninikov, Catto & Hazeltine Reference Krashenninikov, Catto and Hazeltine1999; Simakov Reference Simakov2001).
or by making the system larger (thus reducing the curvature), ensuring stability against both interchange and ballooning modes (Garnier, Kesner & Mauel Reference Garnier, Kesner and Mauel1999; Krashenninikov, Catto & Hazeltine Reference Krashenninikov, Catto and Hazeltine1999; Simakov Reference Simakov2001).
Moreover, the magnetic geometry is quite simple, an important technological advantage. For a given amount of fusion power, the simpler dipole is expected to be much less massive than a tokamak of comparable power and therefore able to produce greater specific power (Teller et al. Reference Teller, Glass, Fowler, Hasegawa and Santarius1992). Additional toroidal coils – external to the plasma – may help in shaping the plasma at MHD equilibrium, e.g. by providing separatrices for impurity control. The simplicity of the coil set and its lack of interlocking coils allows easy access to the coils for routine maintenance. Large values of $\beta$![]() and lack of toroidal field allow a dramatic reduction of mechanical stresses for given volume-averaged pressure of the confined plasma. The fact that the plasma is confined outside of the coil allows for very good field usage and mitigates issues related to heat dissipation in the divertor since the geometry allows for a large, cooling expansion of magnetic flux.
and lack of toroidal field allow a dramatic reduction of mechanical stresses for given volume-averaged pressure of the confined plasma. The fact that the plasma is confined outside of the coil allows for very good field usage and mitigates issues related to heat dissipation in the divertor since the geometry allows for a large, cooling expansion of magnetic flux.
Furthermore, unfavourable scaling laws notoriously plague MCF research. Undesired diffusion of energy and particles far from the high-pressure regions where fusion occurs hampers the achievement of a favourable energy balance. For example, tokamak plasmas have a ‘neoclassical’ degradation of transport that derives from the drifts of particles off of the flux surfaces. In a dipole the drifts are toroidal and define the flux surfaces; the plasma carries only a diamagnetic, toroidal current, and is created with the help of auxiliary heating (typically electron cyclotron radiofrequency heating, or ECRH) rather than through ohmic heating (Kesner & Mauel Reference Kesner and Mauel1997), and is not prone to major disruptions. Steady states have been experimentally sustained up to 20 s through ECRH (Kesner & Mauel Reference Kesner and Mauel2013). The Lorentz force due to the diamagnetic current and the poloidal field counteracts the pressure gradient and confines the plasma. Then, only cross-field transport occurs as far as contact with the unscreened material wall is prevented. In tokamaks, the energy confinement time degrades with increasing auxiliary heating. In a dipole, no such degradation occurs (Kesner & Mauel Reference Kesner and Mauel2013), the particle confinement time is 3–10 times smaller than the value predicted by classical diffusion but with the same favourable scaling with ${B^2 \sqrt {T}}/{n}$![]() and particle transport can be reduced through control of the magnetic shear, just like in other MCF devices (Edlington et al. Reference Edlington, Fletcher, Riviere and Todd1980).
and particle transport can be reduced through control of the magnetic shear, just like in other MCF devices (Edlington et al. Reference Edlington, Fletcher, Riviere and Todd1980).
Finally, in other MCF experiments small fluctuations can cause significant energy loss. In a dipolar magnetic field fluctuations tend to compress the plasma, without energy loss. The spontaneous peaking (Kobayashi, Rogers & Dorland Reference Kobayashi, Rogers and Dorland2010) of particle density and pressure (in opposition to the usual direction of diffusion) near the axis, where the dipole field lines followed by the particles are densely packed, is dubbed ‘turbulent pinch’ (Boxer et al. Reference Boxer, Bergmann, Ellsworth, Garnier, Kesner, Mauel and Woskov2010). These peaked profiles keep the plasma far from the material walls and raise the fusion power density locally, potentially facilitating the achievement of breakeven and ignition.
Thus, in today's climate of renewed widespread interest in nuclear fusion, a start-up, OpenStar, puts forward the proposal of a levitating superconducting coil made of the newest high temperature superconductors (Berry, Mataira-Cole & Simpson Reference Berry, Mataira-Cole and Simpson2023), also used in RT-1. Another start-up, Deutelio, follows the alternative strategy (Lehnert Reference Lehnert1968b) of magnetically isolated material leads sustaining a water-cooled coil made of copper and puts forward the proposal of a dedicated experiment, the POLOMAC (Elio Reference Elio2014).
Information on the prospect of success of these (or similar future) proposals is highly desirable. Admittedly, no data concerning the behaviour of dipole-confined plasmas near breakeven are available – yet. Moreover, our knowledge of energy transport across the plasma is incomplete, to say the least; this makes any independent reliable prediction impossible. The aim of the present work is to write down a necessary condition for the achievement of breakeven in dipole fusion. Our goal is more modest than a prediction; correspondingly, we need fewer assumptions.
We assume steady-state, non-rotating, axisymmetric MHD equilibrium with zero toroidal field. We limit ourselves to a two-species plasma in the MHD approximation, neglect plasma rotation, assume the temperatures of all species to be equal (unless stated otherwise), invoke no assumption concerning the actual physical mechanism ruling non-fusion plasma heating and energy transport in the plasma, assume that the same peaked profiles of particle density and pressure observed so far occur also at breakeven, make the customary assumption (Dolan Reference Dolan1982) that the fusion heating power of the plasma is proportional to the square of the pressure, assume that the pressure is isotropic and neglect the impact of non-Maxwellian particles. Admittedly, the latter assumption is well satisfied for levitated coils only (Saitoh et al. Reference Saitoh2010; Kesner & Mauel Reference Kesner and Mauel2013; Berry et al. Reference Berry, Mataira-Cole and Simpson2023); contact with material leads has been associated with non-thermal particles and degraded confinement (Mauel Reference Mauel2008). Thus, our discussion applies to POLOMAC, where material leads are in contact with the central coil (Elio Reference Elio2014), only if the prediction of screening due to the magnetic field generated by the currents flowing in the leads themselves turns out to be correct (Lehnert Reference Lehnert1968b). Finally, our discussion does not apply to another plasma with vanishing toroidal field, the field reversed configuration (FRC) with both neutral beam injection (NBI) and a confinement barrier sustained by radial electric fields (Binderbauer et al. Reference Binderbauer2015), because the stability of this FRC relies on fast particles due to NBI, which our discussion neglects.
We present a short review of the properties of the peaked profiles of density and pressure hinted at above in § 2, as these properties play a crucial role in the following discussion. Section 3 displays the relevant balances of momentum and energy. We show in § 4 that self-consistency between such balances under the assumptions listed above leads to a necessary condition on the energy confinement time, which can be more stringent than the familiar Lawson criterion because of the constraint of zero toroidal field. We derive useful expressions for this condition in a dipole-confined plasma in § 5 and obtain numerical results in § 6. Conclusions are drawn in § 7. SI units are used, unless stated otherwise.
2. Invariant profiles
Spontaneous relaxation towards well-peaked profiles of pressure $p$![]() and particle density $n$
and particle density $n$![]() has been predicted (Hasegawa Reference Hasegawa1987; Kobayashi et al. Reference Kobayashi, Rogers and Dorland2010) and experimentally confirmed (Saitoh et al. Reference Saitoh2011; Kesner & Mauel Reference Kesner and Mauel2013; Yoshida et al. Reference Yoshida, Saitoh, Yano, Mikami, Kasaoka, Sakamoto, Morikawa, Furukawa and Mahajan2013) when the superconducting current loop is levitated (so that particle losses along the field lines are negligible); for a thermodynamic description of the relaxation, see the Appendix. The relaxed profile of $p$
has been predicted (Hasegawa Reference Hasegawa1987; Kobayashi et al. Reference Kobayashi, Rogers and Dorland2010) and experimentally confirmed (Saitoh et al. Reference Saitoh2011; Kesner & Mauel Reference Kesner and Mauel2013; Yoshida et al. Reference Yoshida, Saitoh, Yano, Mikami, Kasaoka, Sakamoto, Morikawa, Furukawa and Mahajan2013) when the superconducting current loop is levitated (so that particle losses along the field lines are negligible); for a thermodynamic description of the relaxation, see the Appendix. The relaxed profile of $p$![]() is marginally stable against the ideal MHD interchange mode, i.e. any interchange of position between adjacent tubes in this profile induces a perturbation in the pressure profile which satisfies
is marginally stable against the ideal MHD interchange mode, i.e. any interchange of position between adjacent tubes in this profile induces a perturbation in the pressure profile which satisfies
where $\gamma = \frac {5}{3}$![]() for three-dimensional motion, $v = {{\rm d} V}/{{\rm d} \psi }, \psi$
for three-dimensional motion, $v = {{\rm d} V}/{{\rm d} \psi }, \psi$![]() being the poloidal flux. Interchange motion leaves the (‘invariant’) pressure profile unaffected; as (2.1) holds, the value of $p v ^ \gamma$
being the poloidal flux. Interchange motion leaves the (‘invariant’) pressure profile unaffected; as (2.1) holds, the value of $p v ^ \gamma$![]() is the same for all flux tubes. Analogously, if each flux tube contains the same number of particles
is the same for all flux tubes. Analogously, if each flux tube contains the same number of particles
$($![]() we assume temperature $T \propto {p}/{n}$
we assume temperature $T \propto {p}/{n}$![]() ) then the profile of $n$
) then the profile of $n$![]() is invariant. Remarkably, invariant profiles have flat gradients in magnetic-flux space, not real space. Flattening of such gradients is highly beneficial to plasma stability and transport. In principle, the plasma may still be unstable to both pressure gradient driven MHD modes, and density or temperature gradient driven drift modes. Theoretical studies have shown that stability to the MHD interchange mode is sufficient for stability to MHD ballooning modes (Simakov et al. Reference Simakov, Catto, Krashenninikov and Ramos2000). Studies of drift modes (Kesner Reference Kesner1997; Kesner & Hastie Reference Kesner and Hastie2002) have shown that the critical parameter for stability is $\eta = {{\rm d} \ln T}/{{\rm d} \ln n} = \gamma - 1$
is invariant. Remarkably, invariant profiles have flat gradients in magnetic-flux space, not real space. Flattening of such gradients is highly beneficial to plasma stability and transport. In principle, the plasma may still be unstable to both pressure gradient driven MHD modes, and density or temperature gradient driven drift modes. Theoretical studies have shown that stability to the MHD interchange mode is sufficient for stability to MHD ballooning modes (Simakov et al. Reference Simakov, Catto, Krashenninikov and Ramos2000). Studies of drift modes (Kesner Reference Kesner1997; Kesner & Hastie Reference Kesner and Hastie2002) have shown that the critical parameter for stability is $\eta = {{\rm d} \ln T}/{{\rm d} \ln n} = \gamma - 1$![]() , and the most stable operating point is $\eta = \frac {2}{3}$
, and the most stable operating point is $\eta = \frac {2}{3}$![]() , which, combined with (2.1), corresponds to the invariant profiles of $p$
, which, combined with (2.1), corresponds to the invariant profiles of $p$![]() and $n$
and $n$![]() .
.
Invariant profiles are tantalizing because flat gradients in the magnetic-flux space are extremely peaked in real space, for a dipole at least. Let $N = \int n \, {\rm d} V \propto n r^3$![]() be the total number of particles. In a dipole field $\psi \propto {1}/{r}$
be the total number of particles. In a dipole field $\psi \propto {1}/{r}$![]() at large $r$
at large $r$![]() . (This scaling is exact at $\beta = 0$
. (This scaling is exact at $\beta = 0$![]() and is a common tool in dipole research. If $\beta > 0$
and is a common tool in dipole research. If $\beta > 0$![]() , the profile $\psi \propto {1}/{r}$
, the profile $\psi \propto {1}/{r}$![]() approximately becomes $\psi \propto r^{-1+{502 \beta }/{1001}}$
approximately becomes $\psi \propto r^{-1+{502 \beta }/{1001}}$![]() Krashenninikov et al. Reference Krashenninikov, Catto and Hazeltine1999.) Then, (2.2) implies $n r^3 \propto \int n v \, {\rm d} \psi = n v \int {\rm d} \psi = {\rm const.} \int {\rm d} \psi \propto \psi \propto {1}/{r}$
Krashenninikov et al. Reference Krashenninikov, Catto and Hazeltine1999.) Then, (2.2) implies $n r^3 \propto \int n v \, {\rm d} \psi = n v \int {\rm d} \psi = {\rm const.} \int {\rm d} \psi \propto \psi \propto {1}/{r}$![]() , i.e. $n \propto {1}/{r^4}$
, i.e. $n \propto {1}/{r^4}$![]() ; as (2.2) gives $n v = {\rm const.}$
; as (2.2) gives $n v = {\rm const.}$![]() , we get $v \propto {1}/{n} \propto r^4 \propto \psi ^{-4}$
, we get $v \propto {1}/{n} \propto r^4 \propto \psi ^{-4}$![]() , and (2.1) gives $p \propto {1}/{r^{4 \gamma }} \propto \psi ^{4\gamma }$
, and (2.1) gives $p \propto {1}/{r^{4 \gamma }} \propto \psi ^{4\gamma }$![]() . Peaked profiles make nuclear fusion easier at low $r$
. Peaked profiles make nuclear fusion easier at low $r$![]() while limiting the heat load on the material wall, as the fusion power density is quadratic in $n$
while limiting the heat load on the material wall, as the fusion power density is quadratic in $n$![]() and is a strongly increasing function of temperature $T \propto {p}/{n} \propto {1}/{r^{4 (\gamma - 1)}}$
and is a strongly increasing function of temperature $T \propto {p}/{n} \propto {1}/{r^{4 (\gamma - 1)}}$![]() . Moreover, the ratios of peak $p$
. Moreover, the ratios of peak $p$![]() to the scrape-off layer (SOL) value $p$
to the scrape-off layer (SOL) value $p$![]() , peak $n$
, peak $n$![]() to the SOL $n$
to the SOL $n$![]() and peak $T$
and peak $T$![]() to the SOL $T$
to the SOL $T$![]() are $({R_w}/{R_p})^{4 \gamma } , ({R_w}/{R_p})^4$
are $({R_w}/{R_p})^{4 \gamma } , ({R_w}/{R_p})^4$![]() and $({R_w}/{R_p})^{4 (\gamma - 1)}$
and $({R_w}/{R_p})^{4 (\gamma - 1)}$![]() respectively, where $R_w$
respectively, where $R_w$![]() and $R_p$
and $R_p$![]() are the radial coordinates of the wall and the peak of $p \propto nT$
are the radial coordinates of the wall and the peak of $p \propto nT$![]() , respectively. Thus, the basic design for a dipole reactor has a small coil levitated inside a large vacuum chamber.
, respectively. Thus, the basic design for a dipole reactor has a small coil levitated inside a large vacuum chamber.
3. Balances of energy and momentum
The balance of Lorenz force $({1}/{\mu _0}) (\boldsymbol {\nabla } \wedge \boldsymbol {B}) \wedge \boldsymbol {B}$![]() and pressure gradient $\boldsymbol {\nabla } p$
and pressure gradient $\boldsymbol {\nabla } p$![]() allows mechanical equilibrium in magnetically confined plasmas described by MHD ($\mu _{0} = 4 {\rm \pi}\cdot 10^{-7}\ {\rm T} \cdot {\rm A}^{-1} \cdot {\rm m}, \boldsymbol {B}$
allows mechanical equilibrium in magnetically confined plasmas described by MHD ($\mu _{0} = 4 {\rm \pi}\cdot 10^{-7}\ {\rm T} \cdot {\rm A}^{-1} \cdot {\rm m}, \boldsymbol {B}$![]() magnetic field). The Grad–Shafranov equation
magnetic field). The Grad–Shafranov equation
describes such equilibrium in cylindrical coordinates $(r, \phi, z)$![]() . Here, $\psi = \psi (r, z)$
. Here, $\psi = \psi (r, z)$![]() is $(2{\rm \pi} )^{-1}$
is $(2{\rm \pi} )^{-1}$![]() times the poloidal flux and is such that the radial and the vertical component of the poloidal magnetic field are $- ({1}/{r}) ({\partial \psi }/{\partial z})$
times the poloidal flux and is such that the radial and the vertical component of the poloidal magnetic field are $- ({1}/{r}) ({\partial \psi }/{\partial z})$![]() and $({1}/{r}) ({\partial \psi }/{\partial r})$
and $({1}/{r}) ({\partial \psi }/{\partial r})$![]() respectively. Moreover, $p = p (\psi ), F = F ( \psi ) \equiv {B_{\phi }}/{r}$
respectively. Moreover, $p = p (\psi ), F = F ( \psi ) \equiv {B_{\phi }}/{r}$![]() and $B_{\phi }$
and $B_{\phi }$![]() is the toroidal component of $\boldsymbol {B}$
is the toroidal component of $\boldsymbol {B}$![]() .
.
We focus on problems where $\psi$![]() is fixed at the plasma boundary here and below. Then, (3.1) is the Euler–Lagrange equation in $\psi$
is fixed at the plasma boundary here and below. Then, (3.1) is the Euler–Lagrange equation in $\psi$![]() of the variational principle (Lao, Hirshman & Wieland Reference Lao, Hirshman and Wieland1981)
of the variational principle (Lao, Hirshman & Wieland Reference Lao, Hirshman and Wieland1981)
where the domain of integration and ${\rm d} V$![]() are the plasma volume $\propto O ( r^3 )$
are the plasma volume $\propto O ( r^3 )$![]() and the volume element respectively. (We specify if the extremum is a minimum or a maximum below.) In particular, if $B_{\phi } \equiv 0$
and the volume element respectively. (We specify if the extremum is a minimum or a maximum below.) In particular, if $B_{\phi } \equiv 0$![]() then
then
and (3.2) simplifies to
As for the energy balance, plasma heating compensates for energy losses in steady state, hence
where $P_f , P_a , P_c$![]() and $P_r$
and $P_r$![]() are the fusion plasma heating power, the non-fusion plasma heating power (ohmic, RF$\ldots$
are the fusion plasma heating power, the non-fusion plasma heating power (ohmic, RF$\ldots$![]() ), the power lost through conduction and the power lost through radiation, respectively.
), the power lost through conduction and the power lost through radiation, respectively.
As for $P_f$![]() , we neglect the impact of fast, non-Maxwellian particles, follow the well-known, approximate treatment of Maxwellian-averaged fusion cross-section of section 2D of Dolan (Reference Dolan1982) and write $P_f = \int k_f p^2 \,{\rm d} V$
, we neglect the impact of fast, non-Maxwellian particles, follow the well-known, approximate treatment of Maxwellian-averaged fusion cross-section of section 2D of Dolan (Reference Dolan1982) and write $P_f = \int k_f p^2 \,{\rm d} V$![]() .
.
As for $P_a$![]() , we write $P_a = {P_f}/{Q}, Q$
, we write $P_a = {P_f}/{Q}, Q$![]() being the fusion plasma heating power; $Q = 1$
being the fusion plasma heating power; $Q = 1$![]() at breakeven. In the following, our results rely on no detailed description of the actual mechanism underlying auxiliary heating.
at breakeven. In the following, our results rely on no detailed description of the actual mechanism underlying auxiliary heating.
As for $P_c$![]() , we write $P_l = {W_{\rm int}}/{\tau _E}$
, we write $P_l = {W_{\rm int}}/{\tau _E}$![]() , with $\tau _E , u = \frac {3}{2} p$
, with $\tau _E , u = \frac {3}{2} p$![]() and $W_{\rm int} \equiv \int u \, {\rm d} V$
and $W_{\rm int} \equiv \int u \, {\rm d} V$![]() energy confinement time, internal energy density and internal energy of the plasma, respectively.
energy confinement time, internal energy density and internal energy of the plasma, respectively.
As for $P_r$![]() , for our purposes it is useful to define the dimensionless quantity $w \equiv {P_r}/{P_c}$
, for our purposes it is useful to define the dimensionless quantity $w \equiv {P_r}/{P_c}$![]() ; we are going to discuss cases with different values of $w$
; we are going to discuss cases with different values of $w$![]() in the following.
in the following.
4. A necessary condition
If we want to assess the feasibility of a steady-state, $B_{\phi } = 0$![]() , axisymmetric plasma at breakeven (dubbed ‘our plasma’, below), then the usual approach needs computing of $\tau _E$
, axisymmetric plasma at breakeven (dubbed ‘our plasma’, below), then the usual approach needs computing of $\tau _E$![]() starting either from first principles or from dimensional analysis or both, a far-from-trivial task because the available models of plasma energy transport are far from achieving general consensus.
starting either from first principles or from dimensional analysis or both, a far-from-trivial task because the available models of plasma energy transport are far from achieving general consensus.
Here, we adopt an alternative strategy: firstly, we postulate that our plasma exists, then we derive the minimum value $\tau _*$![]() that $\tau _E$
that $\tau _E$![]() must have in our plasma in order to achieve fusion at a given $Q$
must have in our plasma in order to achieve fusion at a given $Q$![]() . Here, we focus on breakeven; we drop this assumption below. If $\tau _E < \tau _*$
. Here, we focus on breakeven; we drop this assumption below. If $\tau _E < \tau _*$![]() , then the energy confinement is unable to sustain steady-state fusion; this inequality $\tau _E < \tau _*$
, then the energy confinement is unable to sustain steady-state fusion; this inequality $\tau _E < \tau _*$![]() is a sufficient condition for failure and describes implicitly a range of parameters to be avoided. Thus, its violation
is a sufficient condition for failure and describes implicitly a range of parameters to be avoided. Thus, its violation
is the necessary condition for achieving fusion at a given $Q$![]() . If it turns out that $\tau _*$
. If it turns out that $\tau _*$![]() is unrealistically high (say, $1000$
is unrealistically high (say, $1000$![]() s), then fusion is definitely impossible. Generally speaking, it is desirable to lower $\tau _*$
s), then fusion is definitely impossible. Generally speaking, it is desirable to lower $\tau _*$![]() as much as possible.
as much as possible.
We are going to compute $\tau _*$![]() with the help of three physically independent conditions - namely, (3.1), (3.3) and (3.5) for $\tau _E = \tau _*$
with the help of three physically independent conditions - namely, (3.1), (3.3) and (3.5) for $\tau _E = \tau _*$![]()

for three quantities $\psi, F$![]() and $p$
and $p$![]() in dipole fusion devices; $b \rightarrow k_f$
in dipole fusion devices; $b \rightarrow k_f$![]() for $Q = 1$
for $Q = 1$![]() and $w = 0$
and $w = 0$![]() (negligible $P_r$
(negligible $P_r$![]() ). Our plasma satisfies both momentum and energy balance simultaneously, i.e. it solves the extremum problem (3.4) with the constraint (4.2a,b). Accordingly, we write
). Our plasma satisfies both momentum and energy balance simultaneously, i.e. it solves the extremum problem (3.4) with the constraint (4.2a,b). Accordingly, we write
with $\lambda$![]() the Lagrange multiplier. Remarkably, ${\lambda }/{b}$
the Lagrange multiplier. Remarkably, ${\lambda }/{b}$![]() is a time. But there is only one physically meaningful quantity with the dimension of a time in a system described by (3.1), (3.3) and (4.2a,b), namely $\tau _*$
is a time. But there is only one physically meaningful quantity with the dimension of a time in a system described by (3.1), (3.3) and (4.2a,b), namely $\tau _*$![]() . Self-consistency requires that we solve this conundrum; to this purpose, we invoke the fact that any rescaling of the Lagrange multiplier leaves the solution of the problem unaffected. (A well-known example is the thermodynamic equilibrium in Gibbs’ statistical mechanics. Such an equilibrium, indeed, corresponds to a maximum of entropy constrained by a given amount of total energy with ${1}/{T}$
. Self-consistency requires that we solve this conundrum; to this purpose, we invoke the fact that any rescaling of the Lagrange multiplier leaves the solution of the problem unaffected. (A well-known example is the thermodynamic equilibrium in Gibbs’ statistical mechanics. Such an equilibrium, indeed, corresponds to a maximum of entropy constrained by a given amount of total energy with ${1}/{T}$![]() as the Lagrange multiplier; of course, its nature does not change if we rescale $T$
as the Lagrange multiplier; of course, its nature does not change if we rescale $T$![]() , e.g. by changing the scale of the thermometer.) Analogously, the nature of a steady state remains unaffected if we rescale time.
, e.g. by changing the scale of the thermometer.) Analogously, the nature of a steady state remains unaffected if we rescale time.
Below, we justify the following choice of time rescaling:
Then, (4.3) reduces to
where $p_* (\psi ) \equiv \lambda p^2 (\psi )$![]() . With the rescaling (4.4), it is clear that the extremum in (3.2)–(4.5) is a minimum. In this case, indeed, the facts that $B = {\vert \boldsymbol {\nabla } \psi \vert }/{r}$
. With the rescaling (4.4), it is clear that the extremum in (3.2)–(4.5) is a minimum. In this case, indeed, the facts that $B = {\vert \boldsymbol {\nabla } \psi \vert }/{r}$![]() and $\int {\rm d} V p_* \propto \int {\rm d} V p^2 \propto P_f$
and $\int {\rm d} V p_* \propto \int {\rm d} V p^2 \propto P_f$![]() imply that solving (4.5) means finding a minimum of magnetic energy $W_m \equiv \int {\rm d} V ({B^2}/{2 \mu _0})$
imply that solving (4.5) means finding a minimum of magnetic energy $W_m \equiv \int {\rm d} V ({B^2}/{2 \mu _0})$![]() for a given $P_f$
for a given $P_f$![]() . But this is equivalent to finding a maximum of $P_f$
. But this is equivalent to finding a maximum of $P_f$![]() for a given $W_m$
for a given $W_m$![]() , according to a lemma of variational calculus, the reciprocity principle for isoperimetric problems (Elsgolts Reference Elsgolts1981). In particular, if $W_m = 0$
, according to a lemma of variational calculus, the reciprocity principle for isoperimetric problems (Elsgolts Reference Elsgolts1981). In particular, if $W_m = 0$![]() (i.e. if there is no confining magnetic field) then the maximum allowable value of $P_f$
(i.e. if there is no confining magnetic field) then the maximum allowable value of $P_f$![]() is zero (i.e. no fusion occurs, as expected). Now, maximization of $P_f$
is zero (i.e. no fusion occurs, as expected). Now, maximization of $P_f$![]() for a given $W_m$
for a given $W_m$![]() implies minimization of ${W_m}/{P_f} = {(Q+1)W_m}/{Q (P_f+P_a)} = {(Q+1)W_m}/{Q (P_c+P_r)} $
implies minimization of ${W_m}/{P_f} = {(Q+1)W_m}/{Q (P_f+P_a)} = {(Q+1)W_m}/{Q (P_c+P_r)} $![]() $= {(Q+1)W_{\rm int}}/{Q \beta (P_c+P_r)} = ({Q+1})/{Q \beta (1+w)}\tau _E$
$= {(Q+1)W_{\rm int}}/{Q \beta (P_c+P_r)} = ({Q+1})/{Q \beta (1+w)}\tau _E$![]() , hence of $\tau _E$
, hence of $\tau _E$![]() for plasmas with given values of $Q , w$
for plasmas with given values of $Q , w$![]() and $\beta$
and $\beta$![]() . In other words, (4.4) allows the value of $\tau _*$
. In other words, (4.4) allows the value of $\tau _*$![]() in (4.5) to be precisely the required lower bound on the values of $\tau _E$
in (4.5) to be precisely the required lower bound on the values of $\tau _E$![]() compatible with fusion. This is why we adopt the rescaling (4.4).
compatible with fusion. This is why we adopt the rescaling (4.4).
Comparison of (3.4) and (4.5) shows that the inclusion of the energy balance constraint (4.2a,b) in the momentum balance of our plasma leads back to the familiar, unconstrained momentum balance of our plasma with the rescaling $p \rightarrow p_*$![]() ; i.e. $p_*$
; i.e. $p_*$![]() is the pressure field which solves (3.1)–(3.3) in our plasma where $\tau _E = \tau _*$
is the pressure field which solves (3.1)–(3.3) in our plasma where $\tau _E = \tau _*$![]() .
.
The definition of $p_*$![]() and (4.2a,b) give $p = \sqrt {{p_*}/{\lambda }}$
and (4.2a,b) give $p = \sqrt {{p_*}/{\lambda }}$![]() and $\lambda = {\int p \, {\rm d} V}/{\int p^2 \, {\rm d} V}$
and $\lambda = {\int p \, {\rm d} V}/{\int p^2 \, {\rm d} V}$![]() respectively. Then, $\lambda = ({\int \sqrt {p_*} \, {\rm d} V}/{\int p_* \, {\rm d} V})^2$
respectively. Then, $\lambda = ({\int \sqrt {p_*} \, {\rm d} V}/{\int p_* \, {\rm d} V})^2$![]() , (4.1) and the definition of $\lambda$
, (4.1) and the definition of $\lambda$![]() provide us with the following necessary condition for our plasma to achieve fusion at a given $Q$
provide us with the following necessary condition for our plasma to achieve fusion at a given $Q$![]() :
:

5. Thresholds
In order to apply (4.6) to dipole fusion, we drop the subscript $_{*}$![]() below and recall that ${\rm d} V = v \, {\rm d} \psi, v = v_0 \psi ^{-4} , \gamma = \frac {5}{3}$
below and recall that ${\rm d} V = v \, {\rm d} \psi, v = v_0 \psi ^{-4} , \gamma = \frac {5}{3}$![]() and $p = p_{0} \psi ^{4 \gamma }$
and $p = p_{0} \psi ^{4 \gamma }$![]() in present experiments, where $v_0$
in present experiments, where $v_0$![]() and $p_{0}$
and $p_{0}$![]() are positive proportionality constant quantities. With no loss of generality we assume also that $\psi _{\min } \leq \psi \leq \psi _{\max }$
are positive proportionality constant quantities. With no loss of generality we assume also that $\psi _{\min } \leq \psi \leq \psi _{\max }$![]() with $\psi _{\min } \ll \psi _{\max }$
with $\psi _{\min } \ll \psi _{\max }$![]() . Then, (4.6) gives
. Then, (4.6) gives
where $p_{\max } = p (\psi = \psi _{\max }), p_0= p_0(p_{\max})$![]() and $v_0$
and $v_0$![]() cancels out. In turn, if $p = p_{\max }$
cancels out. In turn, if $p = p_{\max }$![]() at a radial position $R_p$
at a radial position $R_p$![]() and is minimum near the wall located at $r = R_w$
and is minimum near the wall located at $r = R_w$![]() then for an invariant profile $p \propto \psi ^{4 \gamma } \propto r^{-{20}/{3}}$
then for an invariant profile $p \propto \psi ^{4 \gamma } \propto r^{-{20}/{3}}$![]() we write $p = p_{\max } ({R_p}/{r})^{{20}/{3}}$
we write $p = p_{\max } ({R_p}/{r})^{{20}/{3}}$![]() and the volume average of $p$
and the volume average of $p$![]() is $\langle \,p \rangle = {\int _{R_p} ^{R_w} 4 {\rm \pi}p r^2 \, {\rm d} r }/{\frac {4}{3} {\rm \pi}( R_w^3 -R_p^3)} \approx \frac {9}{11} p_{\max } ({R_p}/{R_w})^3$
is $\langle \,p \rangle = {\int _{R_p} ^{R_w} 4 {\rm \pi}p r^2 \, {\rm d} r }/{\frac {4}{3} {\rm \pi}( R_w^3 -R_p^3)} \approx \frac {9}{11} p_{\max } ({R_p}/{R_w})^3$![]() for $R_p \ll R_w$
for $R_p \ll R_w$![]() , i.e. $p_{\max } = \frac {11}{9} ({R_w}/{R_p})^3 \langle \,p \rangle$
, i.e. $p_{\max } = \frac {11}{9} ({R_w}/{R_p})^3 \langle \,p \rangle$![]() . Substitution in (5.1) gives the main result of this paper
. Substitution in (5.1) gives the main result of this paper
as $({R_c}/{R_w})({R_p}/{R_c}) = {R_p}/{R_w}$![]() , where $R_c$
, where $R_c$![]() is the radius of the toroidal coil internal to the plasma. The smaller $b$
is the radius of the toroidal coil internal to the plasma. The smaller $b$![]() is, the larger $\tau _*$
is, the larger $\tau _*$![]() is, the more likely the violation of (4.1) is. Just as expected, if there is no fusion then $b \rightarrow 0 , \tau _* \rightarrow \infty$
is, the more likely the violation of (4.1) is. Just as expected, if there is no fusion then $b \rightarrow 0 , \tau _* \rightarrow \infty$![]() and (4.1) is always violated; we may also raise $\tau _*$
and (4.1) is always violated; we may also raise $\tau _*$![]() by increasing $w$
by increasing $w$![]() (i.e. in case of larger radiation losses) and ignition $(Q = \infty )$
(i.e. in case of larger radiation losses) and ignition $(Q = \infty )$![]() corresponds to a larger $\tau _*$
corresponds to a larger $\tau _*$![]() than breakeven $(Q = 1)$
than breakeven $(Q = 1)$![]() .
.
Qualitatively speaking, we may reasonably say that the fact that (4.6) – which (5.2) is based upon – is an additional constraint on $\tau _E$![]() beyond Lawson's criterion itself corresponds to the fact that (3.3) is an additional restriction on MHD equilibrium, which forces the steady state to give up the beneficial stabilizing effect of the toroidal field. By the way, we may note that, in his original paper, Lawson assumed that the conduction loss is zero (Lawson Reference Lawson1957); this seems to agree with the fact that the necessary condition (5.2) is physically independent of Lawson's criterion.
beyond Lawson's criterion itself corresponds to the fact that (3.3) is an additional restriction on MHD equilibrium, which forces the steady state to give up the beneficial stabilizing effect of the toroidal field. By the way, we may note that, in his original paper, Lawson assumed that the conduction loss is zero (Lawson Reference Lawson1957); this seems to agree with the fact that the necessary condition (5.2) is physically independent of Lawson's criterion.
The fact that $\tau _* \propto {1}/{b\langle \,p \rangle }$![]() has an intuitive physical meaning. It has been shown (Taylor Reference Taylor1997) that the picture of a plasma with linear size $a$
has an intuitive physical meaning. It has been shown (Taylor Reference Taylor1997) that the picture of a plasma with linear size $a$![]() made of filamentary tube fluxes continuously swapping their mutual position while leaving the global profiles of $n$
made of filamentary tube fluxes continuously swapping their mutual position while leaving the global profiles of $n$![]() and $T$
and $T$![]() unaffected, i.e. – in the dipole slang – of a plasma with invariant profiles, leads to the so-called ‘Bohm scaling’ $\tau _E \propto {Ba^2}/{T}$
unaffected, i.e. – in the dipole slang – of a plasma with invariant profiles, leads to the so-called ‘Bohm scaling’ $\tau _E \propto {Ba^2}/{T}$![]() (Connor & Taylor Reference Connor and Taylor1977). This scaling is often observed in turbulent plasmas, like the central, turbulent pinch region near the axis of a dipole plasma (Boxer et al. Reference Boxer, Bergmann, Ellsworth, Garnier, Kesner, Mauel and Woskov2010) where density peaking occurs and nuclear fusion reactions are more likely to occur; it is also routinely observed in tokamaks (Perkins et al. Reference Perkins1993) and is a common tool in the design of future experiments (Romanelli & Orsitto Reference Romanelli and Orsitto2021). As $p \propto nT$
(Connor & Taylor Reference Connor and Taylor1977). This scaling is often observed in turbulent plasmas, like the central, turbulent pinch region near the axis of a dipole plasma (Boxer et al. Reference Boxer, Bergmann, Ellsworth, Garnier, Kesner, Mauel and Woskov2010) where density peaking occurs and nuclear fusion reactions are more likely to occur; it is also routinely observed in tokamaks (Perkins et al. Reference Perkins1993) and is a common tool in the design of future experiments (Romanelli & Orsitto Reference Romanelli and Orsitto2021). As $p \propto nT$![]() , we rewrite Bohm scaling as $\tau _E \propto {nBa^2}/{p}$
, we rewrite Bohm scaling as $\tau _E \propto {nBa^2}/{p}$![]() . Now, when solving (4.5) we aim at finding a maximum value $P_{\max }$
. Now, when solving (4.5) we aim at finding a maximum value $P_{\max }$![]() for $P_f$
for $P_f$![]() in stable equilibrium; accordingly, we write $\tau _* = (\tau _{E})_{P_f = P_{\max }}$
in stable equilibrium; accordingly, we write $\tau _* = (\tau _{E})_{P_f = P_{\max }}$![]() . We obtain the maximum of $P_f$
. We obtain the maximum of $P_f$![]() at an optimal temperature $T_{\rm opt}$
at an optimal temperature $T_{\rm opt}$![]() dictated by Lawson's criterion and at the maximum value $n_{\max }$
dictated by Lawson's criterion and at the maximum value $n_{\max }$![]() of $n$
of $n$![]() compatible with the stability of a toroidal plasma. Conservatively, we assume that $n_{\max } \propto {I}/{a^2} \propto {B}/{a}$
compatible with the stability of a toroidal plasma. Conservatively, we assume that $n_{\max } \propto {I}/{a^2} \propto {B}/{a}$![]() (Greenwald Reference Greenwald2002) where $I \propto aB$
(Greenwald Reference Greenwald2002) where $I \propto aB$![]() has the dimension of an electric current. Accordingly, $P_{\max } \propto b n_{\max }^2 T_{\rm opt}^2 a^3$
has the dimension of an electric current. Accordingly, $P_{\max } \propto b n_{\max }^2 T_{\rm opt}^2 a^3$![]() and $\tau _* = (\tau _{E})_{n = n_{\max }, T = T_{\rm opt}}$
and $\tau _* = (\tau _{E})_{n = n_{\max }, T = T_{\rm opt}}$![]() . Bohm scaling gives therefore: $\tau _* \propto a^2 ({n_{\max }B}/{p}) \propto {n_{\max }^2 a^3}/{p} = {bn_{\max }^2 T_{\rm opt}^2 a^3}/{bp T_{\rm opt}^2} = ({1}/{bp}) ({P_{\max }}/{T_{\rm opt}^2})$
. Bohm scaling gives therefore: $\tau _* \propto a^2 ({n_{\max }B}/{p}) \propto {n_{\max }^2 a^3}/{p} = {bn_{\max }^2 T_{\rm opt}^2 a^3}/{bp T_{\rm opt}^2} = ({1}/{bp}) ({P_{\max }}/{T_{\rm opt}^2})$![]() . Since both $P_{\max }$
. Since both $P_{\max }$![]() and $T_{\rm opt}$
and $T_{\rm opt}$![]() are fixed, we obtain $\tau _* \propto {1}/{bp}$
are fixed, we obtain $\tau _* \propto {1}/{bp}$![]() , as in (5.2).
, as in (5.2).
As for breakeven, Bohm scaling is a more pessimistic model of energy transport than both the classical diffusion assumed in Kesner & Mauel (Reference Kesner and Mauel1997) and the scaling experimentally observed in levitating dipoles (Edlington et al. Reference Edlington, Fletcher, Riviere and Todd1980). Since fusion reactions occur mainly where $p$![]() is maximum, i.e. not too far from the $r = 0$
is maximum, i.e. not too far from the $r = 0$![]() axis where the turbulent pinch is located, it is a conservative but reasonable assumption that Bohm scaling applies in such a region. On the other hand, it is only natural to invoke a pessimistic scaling for energy confinement, Bohm scaling, when estimating a lower bound on the values of $\tau _E$
axis where the turbulent pinch is located, it is a conservative but reasonable assumption that Bohm scaling applies in such a region. On the other hand, it is only natural to invoke a pessimistic scaling for energy confinement, Bohm scaling, when estimating a lower bound on the values of $\tau _E$![]() allowed for breakeven to occur.
allowed for breakeven to occur.
The fact that $\tau _* \propto ({R_p}/{R_w})^3$![]() reflects the positive impact of peaked profiles of $p$
reflects the positive impact of peaked profiles of $p$![]() , as $\tau _*$
, as $\tau _*$![]() shrinks as $R_p \ll R_w$
shrinks as $R_p \ll R_w$![]() . Moreover, (5.2) shows the advantage in having $R_c \ll R_w$
. Moreover, (5.2) shows the advantage in having $R_c \ll R_w$![]() , i.e. a vacuum chamber much larger than the internal coil. It remains to compute ${R_p}/{R_c}$
, i.e. a vacuum chamber much larger than the internal coil. It remains to compute ${R_p}/{R_c}$![]() . To this purpose, we recall that $p = p_{\max }$
. To this purpose, we recall that $p = p_{\max }$![]() , where $\psi = \psi _{\max }$
, where $\psi = \psi _{\max }$![]() and that $\psi = r A_{\phi }$
and that $\psi = r A_{\phi }$![]() with $A_{\phi }$
with $A_{\phi }$![]() being the toroidal component of the magnetic potential vector (Freidberg Reference Freidberg2014), focus on the horizontal symmetry plane $z = 0$
being the toroidal component of the magnetic potential vector (Freidberg Reference Freidberg2014), focus on the horizontal symmetry plane $z = 0$![]() , follow the $\beta = 0$
, follow the $\beta = 0$![]() analytical approximation of Kesner & Mauel (Reference Kesner and Mauel1997) in vacuum (i.e. as $R_w \rightarrow \infty$
analytical approximation of Kesner & Mauel (Reference Kesner and Mauel1997) in vacuum (i.e. as $R_w \rightarrow \infty$![]() for a conducting wall) including the contribution of coils external to the plasma and compute $R_p$
for a conducting wall) including the contribution of coils external to the plasma and compute $R_p$![]() as the solution of
as the solution of


where $I$![]() is the current flowing in the coil internal to the plasma, $K$
is the current flowing in the coil internal to the plasma, $K$![]() and $E$
and $E$![]() are complete elliptic integrals of the first and second kind respectively, and $B_e$
are complete elliptic integrals of the first and second kind respectively, and $B_e$![]() is an additional, vertical magnetic field due to additional toroidal coils external to the plasma, which can give birth to magnetic separatrices (Kesner & Mauel Reference Kesner and Mauel1997). It turns out that ${R_p}/{R_c}$
is an additional, vertical magnetic field due to additional toroidal coils external to the plasma, which can give birth to magnetic separatrices (Kesner & Mauel Reference Kesner and Mauel1997). It turns out that ${R_p}/{R_c}$![]() is a decreasing function of the dimensionless parameter $B_N \equiv {{\rm \pi} B_e R_c}/{\mu _0 I}$
is a decreasing function of the dimensionless parameter $B_N \equiv {{\rm \pi} B_e R_c}/{\mu _0 I}$![]() – see figure 1. For given values of $R_c , R_w$
– see figure 1. For given values of $R_c , R_w$![]() and $I$
and $I$![]() , therefore, the necessary condition (5.2) reduces to a lower bound on the external vertical field. If ${R_p}/{R_c} < 1 ( > 1)$
, therefore, the necessary condition (5.2) reduces to a lower bound on the external vertical field. If ${R_p}/{R_c} < 1 ( > 1)$![]() then the peak of pressure lies inside (outside) the coil internal to the plasma. Not surprisingly, external coils help in compressing the plasma towards $r = 0$
then the peak of pressure lies inside (outside) the coil internal to the plasma. Not surprisingly, external coils help in compressing the plasma towards $r = 0$![]() . Of course, a description of $\psi$
. Of course, a description of $\psi$![]() more detailed than (5.3) should take into account either the presence of a conductive wall at finite $R_w$
more detailed than (5.3) should take into account either the presence of a conductive wall at finite $R_w$![]() or the fact that $\beta > 0$
or the fact that $\beta > 0$![]() ; the former and the latter (Krashenninikov et al. Reference Krashenninikov, Catto and Hazeltine1999) may provide lower and larger values of ${R_p}/{R_c}$
; the former and the latter (Krashenninikov et al. Reference Krashenninikov, Catto and Hazeltine1999) may provide lower and larger values of ${R_p}/{R_c}$![]() respectively.
respectively.

Figure 1. Value of ${R_p}/{R_c}$![]() vs. normalized vertical field $B_N \equiv {{\rm \pi} B_e R_c}/{\mu _0 I}$
vs. normalized vertical field $B_N \equiv {{\rm \pi} B_e R_c}/{\mu _0 I}$![]() .
.
6. Numerical results
Our discussion has referred to no particular nuclear fusion reaction up to this point. In order to obtain numerical results, however, we must specify the value of $k_f$![]() , which in turn depends on the reaction of interest. Let us start with DT fusion, where (Dolan Reference Dolan1982) $k_f = 2.9 \cdot 10^{-5} \cdot ({W_{\alpha }}/({W_{\alpha }+W_n})) \cdot (1+{T_e}/{T_i})^{-2}\ {\rm W} \cdot {\rm m}^{-3} \cdot {\rm Pa}^{-2}$
, which in turn depends on the reaction of interest. Let us start with DT fusion, where (Dolan Reference Dolan1982) $k_f = 2.9 \cdot 10^{-5} \cdot ({W_{\alpha }}/({W_{\alpha }+W_n})) \cdot (1+{T_e}/{T_i})^{-2}\ {\rm W} \cdot {\rm m}^{-3} \cdot {\rm Pa}^{-2}$![]() $= 5.8 \cdot 10^{-6} \cdot (1+{T_e}/{T_i})^{-2}\ {\rm W} \cdot {\rm m}^{-3} \cdot {\rm Pa}^{-2}$
$= 5.8 \cdot 10^{-6} \cdot (1+{T_e}/{T_i})^{-2}\ {\rm W} \cdot {\rm m}^{-3} \cdot {\rm Pa}^{-2}$![]() , with $T_e$
, with $T_e$![]() the electron temperature, $T_i$
the electron temperature, $T_i$![]() the ion temperature, $W_{\alpha } = 3.52$
the ion temperature, $W_{\alpha } = 3.52$![]() MeV and $W_{n} = 14.06$
MeV and $W_{n} = 14.06$![]() MeV the energy of the $\alpha$
MeV the energy of the $\alpha$![]() 's and of the neutrons produced by the reaction, respectively. We assume ${T_e}/{T_i} =1$
's and of the neutrons produced by the reaction, respectively. We assume ${T_e}/{T_i} =1$![]() is uniform across the plasma for simplicity.
is uniform across the plasma for simplicity.
A typical value for $\langle \,p \rangle$![]() in a DT reactor for $n = 10^{20}\ {\rm m}^{-3}$
in a DT reactor for $n = 10^{20}\ {\rm m}^{-3}$![]() , $T = 10$
, $T = 10$![]() KeV is $1.6 \cdot 10^5$
KeV is $1.6 \cdot 10^5$![]() Pa. Correspondingly, Lawson's criterion requires $\tau _E \approx 3$
Pa. Correspondingly, Lawson's criterion requires $\tau _E \approx 3$![]() s. As for $\tau _*$
s. As for $\tau _*$![]() , let us start with $Q = 1$
, let us start with $Q = 1$![]() and negligible $P_r ( w = 0 )$
and negligible $P_r ( w = 0 )$![]() ; we shall drop both assumptions below. Then, $\tau _* = (6.8 \cdot {R_p}/{R_w})^3$
; we shall drop both assumptions below. Then, $\tau _* = (6.8 \cdot {R_p}/{R_w})^3$![]() in (5.2). Breakeven is achievable if $\tau _* \leq \tau _E$
in (5.2). Breakeven is achievable if $\tau _* \leq \tau _E$![]() , i.e. for ${R_p}/{R_w} \leq 0.2$
, i.e. for ${R_p}/{R_w} \leq 0.2$![]() . For example, in POLOMAC, $R_w = 7.9$
. For example, in POLOMAC, $R_w = 7.9$![]() m and $R_c = 5.4$
m and $R_c = 5.4$![]() m. Then, ${R_p}/{R_c} = ({R_p}/{R_w}) ({R_w}/{R_c}) \leq 0.2 \cdot ({R_w}/{R_c}) = 0.2 \cdot ({7.9}/{5.4}) 1.46 = 0.29$
m. Then, ${R_p}/{R_c} = ({R_p}/{R_w}) ({R_w}/{R_c}) \leq 0.2 \cdot ({R_w}/{R_c}) = 0.2 \cdot ({7.9}/{5.4}) 1.46 = 0.29$![]() , corresponding to $B_N \geq 1.5$
, corresponding to $B_N \geq 1.5$![]() . A more detailed analysis which takes into account both the actual shape of a conducting wall at finite distance from the internal coil on one hand and the impact of $\beta > 0$
. A more detailed analysis which takes into account both the actual shape of a conducting wall at finite distance from the internal coil on one hand and the impact of $\beta > 0$![]() on the other hand is likely to modify this lower bound somehow, as the magnetic surfaces are likely to be bent towards $r = 0$
on the other hand is likely to modify this lower bound somehow, as the magnetic surfaces are likely to be bent towards $r = 0$![]() by the wall while a finite $\beta$
by the wall while a finite $\beta$![]() hints at a deformation of the same surfaces outwards, i.e. away from $r = 0$
hints at a deformation of the same surfaces outwards, i.e. away from $r = 0$![]() .
.
The cubic dependence of $\tau _*$![]() on ${R_c}/{R_w}$
on ${R_c}/{R_w}$![]() is due to the peakedness of the invariant profile of $p$
is due to the peakedness of the invariant profile of $p$![]() and has relevant consequence when removing the assumptions $Q = 1$
and has relevant consequence when removing the assumptions $Q = 1$![]() and $w = 0$
and $w = 0$![]() . If we require ignition rather than breakeven, i.e. if we replace $Q = 1$
. If we require ignition rather than breakeven, i.e. if we replace $Q = 1$![]() with $Q = \infty$
with $Q = \infty$![]() , then $b$
, then $b$![]() gets halved; the same occurs if we drop the assumption $w = 0$
gets halved; the same occurs if we drop the assumption $w = 0$![]() of negligible radiation losses and replace it with the more pessimistic assumption $P_r = P_c$
of negligible radiation losses and replace it with the more pessimistic assumption $P_r = P_c$![]() , i.e. $w = 1$
, i.e. $w = 1$![]() . In both cases (5.2) leads to ${R_p}/{R_c} \leq 0.29$
. In both cases (5.2) leads to ${R_p}/{R_c} \leq 0.29$![]() so that $B_N \geq 1.6$
so that $B_N \geq 1.6$![]() . As for $P_f$
. As for $P_f$![]() , our results depend on $Q$
, our results depend on $Q$![]() only weakly: basically, if a dipole is able to attain breakeven it is also likely to be able to attain ignition. As for $P_r$
only weakly: basically, if a dipole is able to attain breakeven it is also likely to be able to attain ignition. As for $P_r$![]() , our results agree with the fact that both plasma temperature and particle density are particularly low near the wall (where radiation processes are dominant) for the very peaked, invariant profiles of a dipole-confined plasma.
, our results agree with the fact that both plasma temperature and particle density are particularly low near the wall (where radiation processes are dominant) for the very peaked, invariant profiles of a dipole-confined plasma.
When it comes to catalysed DD fusion, according to Kesner et al. (Reference Kesner, Garnier, Hansen, Mauel and Bromberg2004), approximately 94 % of the power is generated in energetic ions and a substantial fraction of the plasma energy leaves the plasma as bremsstrahlung radiation. Then, we write (Dolan Reference Dolan1982) $k_f = \frac {94}{100} \cdot 6.9 \cdot 10^{-7} \cdot (1+{T_e}/{T_i})^{-2} \sqrt {{30}/{T_i ({\rm KeV})}}\ {\rm W} \cdot {\rm m}^{-3} \cdot {\rm Pa}^{-2}$![]() . We assume ${T_e}/{T_i}$
. We assume ${T_e}/{T_i}$![]() uniform across the plasma for simplicity.
uniform across the plasma for simplicity.
Kesner et al. (Reference Kesner, Garnier, Hansen, Mauel and Bromberg2004) discusses two scenarios of ignition in catalysed DD fusion: A ($P_a = 0, P_{f} = 610$![]() MW, $P_{r} = 430$
MW, $P_{r} = 430$![]() MW, $p_{\max } = 5.4 \cdot 10^6$
MW, $p_{\max } = 5.4 \cdot 10^6$![]() Pa, $T_i = 41$
Pa, $T_i = 41$![]() KeV, $T_e = 30$
KeV, $T_e = 30$![]() KeV) and B ($P_a = 0 , P_{f} = 384$
KeV) and B ($P_a = 0 , P_{f} = 384$![]() MW, $P_{r} = 362$
MW, $P_{r} = 362$![]() MW , $p_{\max } = 4.1 \cdot 10^6$
MW , $p_{\max } = 4.1 \cdot 10^6$![]() Pa, $T_i = 37$
Pa, $T_i = 37$![]() KeV, $T_e = 30$
KeV, $T_e = 30$![]() KeV). The values of $w = {P_r}/{P_c} = {P_r}/{(P_f - P_r)} , b$
KeV). The values of $w = {P_r}/{P_c} = {P_r}/{(P_f - P_r)} , b$![]() and $\tau _*$
and $\tau _*$![]() in A and B are $w = {430}/({610-430}) = 2.4$
in A and B are $w = {430}/({610-430}) = 2.4$![]() , $b = 2.7 \cdot 10^{-8}\ {\rm W} \cdot {\rm m}^{-3} \cdot {\rm Pa}^{-2}$
, $b = 2.7 \cdot 10^{-8}\ {\rm W} \cdot {\rm m}^{-3} \cdot {\rm Pa}^{-2}$![]() , $\tau _* = 622$
, $\tau _* = 622$![]() s and $w = {362}/({384-362}) = 16.5 , b = 5.0 \cdot 10^{-9} \ {\rm W} \cdot {\rm m}^{-3} \cdot {\rm Pa}^{-2}$
s and $w = {362}/({384-362}) = 16.5 , b = 5.0 \cdot 10^{-9} \ {\rm W} \cdot {\rm m}^{-3} \cdot {\rm Pa}^{-2}$![]() and $\tau _* = 4426$
and $\tau _* = 4426$![]() s, respectively. As for $\tau _E$
s, respectively. As for $\tau _E$![]() , according to Kesner et al. (Reference Kesner, Garnier, Hansen, Mauel and Bromberg2004) (and in agreement with Lawson's criterion for ignition in this range of temperatures) $\tau _E = 5.1$
, according to Kesner et al. (Reference Kesner, Garnier, Hansen, Mauel and Bromberg2004) (and in agreement with Lawson's criterion for ignition in this range of temperatures) $\tau _E = 5.1$![]() s. Then (5.1) tells us that both A and B are too optimistic. (It is possible to show that a similar conclusion holds also for the DT ignition scenario outlined in Kesner et al. Reference Kesner, Garnier, Hansen, Mauel and Bromberg2004.) Remarkably, and in contrast with Kesner et al. (Reference Kesner, Garnier, Hansen, Mauel and Bromberg2004), our results do not rely on the assumption that turbulent transport does not substantially degrade confinement.
s. Then (5.1) tells us that both A and B are too optimistic. (It is possible to show that a similar conclusion holds also for the DT ignition scenario outlined in Kesner et al. Reference Kesner, Garnier, Hansen, Mauel and Bromberg2004.) Remarkably, and in contrast with Kesner et al. (Reference Kesner, Garnier, Hansen, Mauel and Bromberg2004), our results do not rely on the assumption that turbulent transport does not substantially degrade confinement.
However, the peakedness of the pressure profile – and, in particular, the fact that $p_{\max } = \frac {11}{9} ({R_w}/{R_p})^3 \langle \,p \rangle$![]() – suggests that we may still achieve ignition in catalysed DD fusion – e.g. in scenario A – by raising ${R_w}/{R_p}$
– suggests that we may still achieve ignition in catalysed DD fusion – e.g. in scenario A – by raising ${R_w}/{R_p}$![]() by a factor $(\frac {622}{5.1})^{{1}/{3}} \approx 5$
by a factor $(\frac {622}{5.1})^{{1}/{3}} \approx 5$![]() while leaving $\langle \,p \rangle$
while leaving $\langle \,p \rangle$![]() unaffected. A detailed discussion lies outside the scope of the present work; all the same, our discussion highlights the beneficial role played by the peaked profiles of pressure, which provide us with a wide choice of available operational parameters for a reactor. As far as these profiles are invariant (Davis Reference Davis2013), moreover, if larger values of $p$
unaffected. A detailed discussion lies outside the scope of the present work; all the same, our discussion highlights the beneficial role played by the peaked profiles of pressure, which provide us with a wide choice of available operational parameters for a reactor. As far as these profiles are invariant (Davis Reference Davis2013), moreover, if larger values of $p$![]() at the SOL near the wall are allowed then larger values of $\langle \,p \rangle$
at the SOL near the wall are allowed then larger values of $\langle \,p \rangle$![]() can be obtained, thus facilitating the achievement of large values of $Q$
can be obtained, thus facilitating the achievement of large values of $Q$![]() .
.
7. Conclusions
After years of neglect, and in spite of considerable technological issues arising in a reactor-relevant environment, the excellent MHD stability properties and the promising scaling laws for energy confinement have aroused new, significant interest (Elio Reference Elio2014; Berry et al. Reference Berry, Mataira-Cole and Simpson2023) in the approach to controlled nuclear fusion based on plasmas confined by a dipole magnetic field (Lehnert Reference Lehnert1958, Reference Lehnert1968a,Reference Lehnertb; Hasegawa Reference Hasegawa1987; Teller et al. Reference Teller, Glass, Fowler, Hasegawa and Santarius1992).
The profiles of both particle density and pressure in a dipole-confined plasma can be well peaked, as a result of a spontaneous relaxation process (Hasegawa Reference Hasegawa1987; Kobayashi et al. Reference Kobayashi, Rogers and Dorland2010; Davis Reference Davis2013; Yoshida et al. Reference Yoshida, Saitoh, Yano, Mikami, Kasaoka, Sakamoto, Morikawa, Furukawa and Mahajan2013). Relaxation leads to a spontaneous raise of density and pressure near the axis of the dipole, the so-called ‘turbulent pinch’ (Boxer et al. Reference Boxer, Bergmann, Ellsworth, Garnier, Kesner, Mauel and Woskov2010), where the fusion rate is maximum. As a whole, moreover, the relaxed dipole-confined plasma enjoys excellent MHD stability, is inherently steady state, achieves high values of $\beta$![]() , is intrinsically free from disruptions, satisfies promising scaling laws as for the particle confinement time, shows no degradation of the energy confinement time with increasing ECRH power sustaining the plasma and is confined by toroidal coils with very simple geometry (Kesner & Mauel Reference Kesner and Mauel2013). Crucially, however, one of these coils is internal to the plasma itself. The resulting technological issues have been coped with to date through levitation of a superconducting coil with no contact with material leads and supports (Skellett Reference Skellett1975; Hasegawa Reference Hasegawa1987). Admittedly, this approach – with its lack of any umbilical connection to the dipole coil – may be considered fragile. In the years following the shutdown of the major experiment on dipole fusion – LDX (Kesner & Mauel Reference Kesner and Mauel2013) – in 2011, the topic has been basically neglected almost completely. An experimental campaign with high-temperature superconductors (Saitoh et al. Reference Saitoh2010) triggered the proposal of an experiment equipped with such superconductors and focussed on a reactor regime (Berry et al. Reference Berry, Mataira-Cole and Simpson2023). An alternative (and older) approach is to allow contact between the coil and material leads, provided that the latter are magnetically screened (Lehnert Reference Lehnert1968a,Reference Lehnertb). This is the rationale of the proposal of a new experiment with a dipole-confined plasma, POLOMAC (Elio Reference Elio2014).
, is intrinsically free from disruptions, satisfies promising scaling laws as for the particle confinement time, shows no degradation of the energy confinement time with increasing ECRH power sustaining the plasma and is confined by toroidal coils with very simple geometry (Kesner & Mauel Reference Kesner and Mauel2013). Crucially, however, one of these coils is internal to the plasma itself. The resulting technological issues have been coped with to date through levitation of a superconducting coil with no contact with material leads and supports (Skellett Reference Skellett1975; Hasegawa Reference Hasegawa1987). Admittedly, this approach – with its lack of any umbilical connection to the dipole coil – may be considered fragile. In the years following the shutdown of the major experiment on dipole fusion – LDX (Kesner & Mauel Reference Kesner and Mauel2013) – in 2011, the topic has been basically neglected almost completely. An experimental campaign with high-temperature superconductors (Saitoh et al. Reference Saitoh2010) triggered the proposal of an experiment equipped with such superconductors and focussed on a reactor regime (Berry et al. Reference Berry, Mataira-Cole and Simpson2023). An alternative (and older) approach is to allow contact between the coil and material leads, provided that the latter are magnetically screened (Lehnert Reference Lehnert1968a,Reference Lehnertb). This is the rationale of the proposal of a new experiment with a dipole-confined plasma, POLOMAC (Elio Reference Elio2014).
Admittedly, when assessing the prospects of these recent proposals (Elio Reference Elio2014; Berry et al. Reference Berry, Mataira-Cole and Simpson2023) from the point of view of net energy production both insufficient available data and incomplete knowledge of physical processes ruling energy transport in plasmas still make any independent extrapolation of present performances (Saitoh et al. Reference Saitoh2010; Kesner & Mauel Reference Kesner and Mauel2013) to a reactor scarcely reliable.
We have written down a necessary condition for the achievement of breakeven in dipole fusion. This necessary condition is distinct from and more stringent than the Lawson criterion; this is justified by the fact that, in dipole-confined plasmas, we are subject to the constraint of zero toroidal magnetic field, and we are therefore bound to give up the stabilizing impact of this field on the plasma. Our goal is more modest than a prediction; correspondingly, we need fewer assumptions, and rely on no detailed model of energy transport across the plasma.
We describe our dipole-confined plasma as an axisymmetric, non-rotating, steady-state plasma with no fast particles, isotropic pressure and zero toroidal magnetic field at breakeven. We make also the customary assumption (Dolan Reference Dolan1982) that the fusion heating power of the plasma is proportional to the square of the pressure. (The fact that we rule out fast particles prevents us from applying the present discussion to NBI-assisted FRCs; Binderbauer et al. Reference Binderbauer2015.) Both the Grad–Shafranov equation and the energy balance depend crucially on the same pressure profile, which must satisfy both of them simultaneously. When looking for such a profile, we may cast the two equations in the form of a constrained variational principle. This principle takes a particularly simple form when the toroidal magnetic field is zero. The Lagrange multiplier of the latter is proportional to a time constant. But the only time constant relevant to the system is the energy confinement time, which rules power losses in the energy balance and appears explicitly in the variational principle. We remove this apparent contradiction just by taking advantage of the fact that no rescaling of time may ever affect the physics of steady states. We choose therefore that rescaling which makes the pressure profile identified by the variational principle to provide us with the minimum value of the energy confinement time compatible with the assumptions. Remarkably, the rationale of this lower bound relies on no particular assumption concerning power losses – like e.g. the relevance of bremsstrahlung radiation in the proof of Lawson criterion. The existence of this minimum value acts therefore as a new, independent condition, due to the vanishing of the stabilizing toroidal field. Breakeven is therefore only possible if this minimum value is equal or smaller than the value required by Lawson criterion. If this is not true, then breakeven is impossible.
Together, the necessary condition on breakeven hinted at above and the relaxed profiles of a dipole-confined plasma link the ratio between the radius of the vacuum vessel and the radius of the main toroidal coil on one hand and the (suitably adimensionalized) ratio between the vertical field provided by external shaping coils and the current flowing across the toroidal coil internal to the plasma on the other hand. For breakeven to be possible, once one of these ratios is given the other cannot be too small. As for DT fusion, numerical values are not unreasonably far from those available in recent proposals (Elio Reference Elio2014). A constraint is also obtained on ignition in catalysed DD fusion (Kesner et al. Reference Kesner, Garnier, Hansen, Mauel and Bromberg2004).
Remarkably, our results rely on no assumption on energy transport; on the contrary, it turns out that the scaling law which fits our results in the most natural way is Bohm scaling. This fact makes sense in the turbulent pinch near the dipole axis at least, but strongly suggests that our estimates are likely to be too conservative. Despite this, we conclude therefore that a dipole-confined plasma contained in a vacuum vessel with given radius and with a given current flowing across the toroidal coil internal to the plasma may achieve breakeven in DT fusion provided that we suitably choose both the radius of the internal coil and the value of the external vertical field.
Of course, this conclusion does not mean that this plasma will actually achieve the breakeven: such prediction is impossible without a detailed model of energy transport across the plasma, all the more so because the crucial issue of the interaction between the thermonuclear plasma and the toroidal coil internal to this plasma remains unanswered to date. Our conclusion says only that the energy transport does not prevent the plasma from achieving breakeven provided that enough auxiliary heating of the plasma is available (e.g. via ECRH), that the internal coil withstands the proximity with the thermonuclear plasma, etc.
Generalization of this discussion to ignition is straightforward. Our results depend on the fusion gain factor only weakly: in other words, if a dipole is able to attain breakeven it is also likely to be able to attain ignition.
Admittedly, our discussion is rather qualitative. A rigorous discussion requires a detailed computation of MHD equilibria in a realistic geometry. All the same, it seems worthwhile to stress the point that the attractiveness of dipole confinement as a roadmap to steady-state nuclear fusion in a reactor with relatively simple layout stems out from a minimum set of physical assumptions, well grounded in both theory and experiments.
Acknowledgements
Motivation and encouragement of Dr F. Elio of DEUTELIO, Gavirate, Italy are gratefully acknowledged.
Editor Cary Forest thanks the referees for their advice in evaluating this article.
Declaration of interest
The authors report no conflict of interest.
Funding
This research received no specific grant from any funding agency, commercial or not-for-profit sectors.
Appendix
As suggested in Yoshida et al. (Reference Yoshida, Saitoh, Yano, Mikami, Kasaoka, Sakamoto, Morikawa, Furukawa and Mahajan2013) – where a maximization of entropy is postulated with no further justification – the stability of the relaxed state allows thermodynamic interpretation. Experiments (Garnier et al. Reference Garnier, Boxer, Ellsworth, Kesner and Mauel2009; Davis Reference Davis2013; Kesner & Mauel Reference Kesner and Mauel2013) show that the levitation of the coil corresponds to a reduced fraction of non-thermal electrons (due e.g. to the interaction of the electrons with ECRH waves Davis Reference Davis2013). In this case, (15) and (16) of Rogister & Li (Reference Rogister and Li1992) – a consequence of the Fokker–Planck equation – show that the typical time scales of thermalization (= relaxation to a Maxwellian distribution function) of ions and electrons in a weakly collisional, axisymmetric, toroidal, low-$\beta$![]() turbulent plasma region between adjacent magnetic surfaces are $\ll$
turbulent plasma region between adjacent magnetic surfaces are $\ll$![]() the typical time scales of particle and energy transport in the direction parallel to $\boldsymbol {\nabla } \psi$
the typical time scales of particle and energy transport in the direction parallel to $\boldsymbol {\nabla } \psi$![]() . This constraint holds at all times during the plasma lifetime even for weakly collisional plasmas and regardless of the detailed mechanism underlying transport; thus, it implies that we may safely assume that the distribution function of ions and electrons are locally Maxwellian, where by ‘locally’ we mean: ‘as far as we are interested in phenomena occurring between adjacent magnetic surfaces on a time scale $\ll$
. This constraint holds at all times during the plasma lifetime even for weakly collisional plasmas and regardless of the detailed mechanism underlying transport; thus, it implies that we may safely assume that the distribution function of ions and electrons are locally Maxwellian, where by ‘locally’ we mean: ‘as far as we are interested in phenomena occurring between adjacent magnetic surfaces on a time scale $\ll$![]() the typical time scales related to the transport of energy and particles’. If the distribution function is locally Maxwellian then the familiar thermodynamical relationships apply and we may identify the $p v^\gamma = {\rm const.}$
the typical time scales related to the transport of energy and particles’. If the distribution function is locally Maxwellian then the familiar thermodynamical relationships apply and we may identify the $p v^\gamma = {\rm const.}$![]() condition equivalent to (2.1) with the condition of constant entropy inside the flux tube. In other words, if the profile of $p$
condition equivalent to (2.1) with the condition of constant entropy inside the flux tube. In other words, if the profile of $p$![]() is invariant then no net amount of entropy is ever produced inside the flux tube. Note that entropy is actually always produced in the bulk of a non-ideal plasma – e.g. by Joule dissipation of the electric currents induced during the interchange motion of flux tubes; it is just carried away by transport in steady state. In a stable steady state this entropy production is a minimum, regardless of the detailed mechanism of heating (e.g. fusion); as for Joule dissipation, this is a property clearly described by Kirchhoff (Hermann Reference Hermann1986). Its role in the self-organization of plasmas (Yoshida et al. Reference Yoshida, Saitoh, Yano, Mikami, Kasaoka, Sakamoto, Morikawa, Furukawa and Mahajan2013) is discussed in Di Vita (Reference Di Vita2022). In particular, in the framework of Hall MHD (which is likely to hold in the outer regions where the particle density is lower and the ion collisionless skin depth correspondingly larger) Saitoh et al. (Reference Saitoh2011) describes relaxed high-$\beta$
is invariant then no net amount of entropy is ever produced inside the flux tube. Note that entropy is actually always produced in the bulk of a non-ideal plasma – e.g. by Joule dissipation of the electric currents induced during the interchange motion of flux tubes; it is just carried away by transport in steady state. In a stable steady state this entropy production is a minimum, regardless of the detailed mechanism of heating (e.g. fusion); as for Joule dissipation, this is a property clearly described by Kirchhoff (Hermann Reference Hermann1986). Its role in the self-organization of plasmas (Yoshida et al. Reference Yoshida, Saitoh, Yano, Mikami, Kasaoka, Sakamoto, Morikawa, Furukawa and Mahajan2013) is discussed in Di Vita (Reference Di Vita2022). In particular, in the framework of Hall MHD (which is likely to hold in the outer regions where the particle density is lower and the ion collisionless skin depth correspondingly larger) Saitoh et al. (Reference Saitoh2011) describes relaxed high-$\beta$![]() dipole-confined plasmas as double Beltrami states; the latter states are also the outcome of the minimization of entropy production in the plasma bulk (Di Vita Reference Di Vita2009).
dipole-confined plasmas as double Beltrami states; the latter states are also the outcome of the minimization of entropy production in the plasma bulk (Di Vita Reference Di Vita2009).