Multiscale tip asymptotics for a deflating hydraulic fracture with leak-off

Abstract

This paper deals with the construction of the tip asymptotes for a hydraulic fracture deflating in a permeable elastic medium. Specifically, the paper describes the changing nature of the asymptotic fields during the arrest and recession phases following propagation of the fracture after fluid injection has ended. It shows that as the fracture deflates in the arrest phase, the region of dominance of the linear elastic fracture mechanics tip asymptote $w\sim x^{1/2}$ of the fracture aperture $w$ with distance $x$ from the front shrinks to the benefit of an intermediate asymptote $w\sim x^{3/4}$. Hence only the velocity-independent $3/4$ asymptote is left at the arrest–recession transition. Furthermore, with increasing receding velocity of the front, a linear asymptote $w\sim x$ develops progressively at the fracture tip, with $w\sim x^{3/4}$ again becoming an intermediate asymptote. These universal multiscale asymptotes for the arrest and recession phases are key to determining, in combination with a computational algorithm that can simulate the evolution of a finite fracture, the decaying stress intensity factor during arrest, the time at which the fracture transitions from arrest to recession, and the negative front velocity during recession.

1. Introduction

A large body of research in the last 10 years has demonstrated unequivocally that the construction of accurate and efficient numerical models of hydraulic fractures benefits from embedding the tip asymptotic behaviour, which is appropriate for the discretization length of the computational grid (Adachi & Detournay 2008; Peirce & Detournay 2008; Lecampion et al. 2013; Peirce 2015, 2016). Hitherto, research has focused on the simulation of a propagating fracture. Nonetheless, there is considerable interest in modelling the deflation of hydraulic fractures once injection has ceased, as they evolve through successive phases of arrest and recession following propagation. The main motivation for this work is to provide a more rigorous framework to interpret the decline of the borehole pressure during deflation of the fracture, either to determine the leak-off coefficient (Nolte 1979, 1986) or to estimate accurately the minimum in situ stress (Zoback et al. 1977; Haimson 1989; Hayashi & Haimson 1991; Plahn et al. 1997; Sano et al. 2005; Fjær et al. 2008; Lakirouhani, Detournay & Bunger 2016).

In this paper, we describe the construction of multiscale tip asymptotes for deflating fractures in permeable elastic media, when the front is either at rest or receding. When combined with an algorithm to simulate an evolving hydraulic fracture, these asymptotes make it possible to compute accurately not only the stress intensity factor as it declines when the front is at rest until it eventually vanishes at the transition between arrest and recession, but also the negative front velocity during recession. The asymptotes are derived by analysing the stationary solution of a semi-infinite hydraulic fracture either at rest or steadily receding, using an approach similar to the one used to construct the tip asymptotes for a propagating fracture (Desroches et al. 1994; Lenoach 1995; Garagash & Detournay 2000; Garagash, Detournay & Adachi 2011; Dontsov & Peirce 2015; Dontsov 2016; Dontsov & Kresse 2018; Moukhtari & Lecampion 2018; Lecampion & Zia 2019).

The paper is structured as follows. First, the governing equations are summarized within the context of a semi-infinite fracture. Salient features of the tip asymptotics near the end of the propagation phase are then reviewed. Next, we determine successively, through a local eigenvalue analysis, the singular asymptotes that develop closest to the fracture tip during arrest, at the transition between arrest and recession, and during recession. We then construct the multiscale asymptotes that control the development of singular boundary layers at the tip, either at the end of the arrest phase or at the beginning of recession. Implementation of these multiscale asymptotes in a numerical code is briefly discussed. Finally, an argument based on the tip asymptotics, about the inability of a fracture to recede in an impermeable medium, is described in Appendix A.

2. Governing equations for a semi-infinite hydraulic fracture

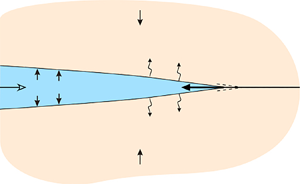
Here, we consider the problem of a semi-infinite hydraulic fracture that is either travelling at a constant velocity $V$ or at rest in an infinite permeable elastic medium; see figure 1. The velocity $V$ is taken as positive if the fracture is advancing and thus creating new solid surfaces, and negative if the fracture is receding, thus closing previously created solid surfaces at the tip. There is a far-field uniform compressive stress $\sigma _{0}$ normal to the fracture. Fluid is leaking from the fracture into the solid medium. The solution to this idealized problem can actually be understood as capturing the asymptotics in the vicinity of the crack front of a finite hydraulic fracture.

Figure 1. Receding tip of a deflating hydraulic fracture.

Although the tip asymptotics are critically dependent on the nature of the leak-off in propagating fractures, it is not the case for fractures that are either at rest or receding. Indeed, leak-off can be singular at the tip of an advancing fracture only under conditions of linear flow, when a Carter-type leak-off prevails (Lenoach 1995; Garagash et al. 2011); otherwise, leak-off is a regular function of position and time, and does not affect the singularity of the stress field at the fracture tip.

Let $x$ denote a moving coordinate centred on the tip with the $x$-axis pointing inside the fracture. Let $w(x,t)$, $p(x,t)$ and $q(x,t)$ denote the fracture aperture, net pressure and flux, all functions of position $x$ and time $t$. The problem is formulated in terms of the net pressure defined as $p=p_{f}-\sigma _{0}$ instead of the fluid pressure $p_{f}(x,t)$, recognizing that $\sigma _{0}$ introduces only a shift to the fluid pressure $p_{f}(x,t)$ when the crack is completely filled by the fracturing fluid. By convention, the flux $q$ is taken as positive when directed opposite to the $x$-axis; thus flux $q$ and tip velocity $V$ have the same sign convention. The equations governing $w(x,t)$, $p(x,t)$ and $q(x,t)$ depend on, besides $V$: Young's modulus $E$, Poisson's ratio $\nu$, and toughness $K_{Ic}$ of the solid; viscosity $\mu$ of the fluid; and also Carter's leak-off coefficient $C_{L}$ (as in the fracture propagating phase) or more generally on a known regular leak-off function $g(x,t)$. However, the equations are formulated here in terms of the alternative parameters

(2.1a–d)\begin{equation} E'=\frac{E}{1-\nu^{2}},\quad K'=4\left(\frac{2}{\rm \pi} \right)^{1/2}K_{Ic},\quad \mu'=12\mu,\quad C'=2C_{L},\end{equation}

which are introduced to keep the equations uncluttered by numerical factors, noting also that $E'$ is the plane strain modulus. These alternative parameters will simply be referred to as the elastic modulus ($E'$), toughness ($K'$), viscosity ($\mu '$) and leak-off coefficient ($C'$).

The elasticity integral equation for a semi-infinite crack under plane strain conditions reads (Bilby & Eshelby 1968)

(2.2)\begin{equation} p=\frac{E'}{4{\rm \pi}}\int_{0}^{\infty}\frac{{\partial} w}{\partial\xi}\,\frac{\mathrm{d}\xi}{x-\xi}.\end{equation}

This equation represents asymptotically the elasticity equation in the tip region of a finite planar crack at distances from the crack front that are small compared to its radius of curvature (Peirce & Detournay 2008). For the singular integral in (2.2) to converge, it is sufficient that: (i) $w\overset {x\rightarrow \infty }{\sim }x^{\lambda }$ with $\lambda \in (0,1)$; (ii) $\lim _{x\rightarrow 0}w=0$; and (iii) $w$ is a monotonically increasing function of $x$.

Under the approximation of lubrication theory, the viscous flow in the crack is governed by Poiseuille's law,

(2.3)\begin{equation} q=\frac{w^{3}}{\mu'}\,\frac{\partial p}{\partial x},\end{equation}

and by the continuity equation

(2.4)\begin{equation} \frac{\partial w}{\partial t}+V\,\frac{\partial w}{\partial x}- \frac{\partial q}{\partial x}+g=0.\end{equation}

According to Carter's law (Carter 1957), the leak-off rate $g(x,t)$ is given by

(2.5)\begin{equation} g=\frac{C'}{\sqrt{t-t_{0}(x,t)}},\end{equation}

where $t_{0}(x,t)$ denotes the time of first exposure to the fracturing fluid of a fixed point on the fracture wall that is located at $x$ at time $t$. The leak-off term has a square root singularity at the tip if $V>0$, but is finite if $V\le 0$. Indeed, $t-t_{0}(x,t)\overset {x\rightarrow 0}{\sim }x/V$ if $V>0$, implying that $g\overset {x\rightarrow 0}{\sim }C'(V/x)^{1/2}$ in that case. However, as stated earlier, the assumption of Carter leak-off is relaxed when $V\le 0$, with $g(x,t)$ simply assumed to be a known regular function.

The aperture at the fracture tip must satisfy the condition

(2.6)\begin{equation} \lim_{x\rightarrow0}\frac{w(x)}{x^{1/2}}=\frac{K'}{E'}\,h(V),\end{equation}

where $h(V)$ is a set-valued function defined as

(2.7)\begin{equation} h(V)=\begin{cases} 1, & V>0,\\ [0,1], & V=0,\\ 0, & V<0. \end{cases}\end{equation}

Equation (2.6) is equivalent to stating that: (i) the stress intensity factor $K_{I}$ is equal to toughness $K_{Ic}$ if the fracture propagates ($V>0$) – the classical expression for the linear elastic fracture mechanics (LEFM) propagation criterion; (ii) $0< K_{I}< K_{Ic}$ if the fracture is at rest ($V=0$); and (iii) $K_{I}=0$ if the fracture is receding ($V<0$). In particular, the condition (2.6) for $V<0$ implies that the power-law index ${{\lambda }}>1/2$ if $w\sim x^{\lambda }$ as $x\rightarrow 0$, and the fracture is closed, $w(x)=0$, for $x<0$.

3. General considerations about tip asymptotes

We are now considering asymptotic solutions for $w(x,t)$ of the form

(3.1)\begin{equation} w(x,t)=A(t)\,x^{\lambda},\end{equation}

with the power-law index $\lambda$ constrained to the range

(3.2)\begin{equation} \tfrac{1}{2}\le\lambda\le1.\end{equation}

The lower-bound restriction on $\lambda$ stems from the requirement for the elastic energy release rate at the crack tip to be finite (Rice 1968), while the upper-bound limit results from an inability to satisfy simultaneously the elasticity and the lubrication equations if $\lambda >1$, as will become clear in § 5.2.

By invoking the elasticity equation (2.2) and Poiseuille's law (2.3), the asymptotic behaviour of $q(x,t)$, consistent with (3.1), can be derived. The asymptotics of $w(x,t)$ and $q(x,t)$ can then be used, in conjunction with the continuity equation (2.3), to identify the power-law index $\lambda$ corresponding to different dominant balances in the continuity equation. Different values of the index $\lambda$ can thus be related to different phases in the evolution of the hydraulic fracture.

The solution of the elasticity equation (2.2), for an aperture $w$ varying as the power law (3.1), is given by (Oberhettinger 1970)

(3.3)\begin{equation} p=AE'\,\frac{\lambda}{4}\cot({\rm \pi}\lambda)\,x^{\lambda-1}, \quad 0<\lambda<1,\end{equation}

noting that the restriction on $\lambda$ also defines the conditions for which the aperture (3.1) is an eigenfunction of the integral operator in (2.2). However, $\lambda$ is necessarily restricted to $\lambda \ge \frac {1}{2}$ in the context of elasticity, as $\lambda$ in the range $(0,\frac {1}{2})$ is associated with an infinite energy release rate.

We note that for the near-tip asymptotic behaviour $w\overset {x\rightarrow 0}{\sim }Ax$,

(3.4)\begin{equation} p\overset{x\rightarrow0}{\sim}\frac{AE'}{4{\rm \pi}}\ln x.\end{equation}

This asymptotic expression for the net pressure for the case $\lambda =1$ can be obtained by considering the dominant term of the solution near the tip of a finite fracture (Adachi & Detournay 2002; Peirce & Detournay 2022b).

Differentiating Poiseuille's law (2.3) with aperture $w$ given by (3.1), and net pressure $p$ given by (3.3) if $1/2<\lambda <1$ or by (3.4) if $\lambda =1$, yields

(3.5)$$\begin{gather} \frac{{\mathrm{d}}q}{{\mathrm{d}}\kern0.06em x}=\lambda(\lambda-1)\left(\lambda- \frac{1}{2}\right)\cot({\rm \pi}\lambda)\,\frac{A^{4}E'}{\mu'}\,x^{4\lambda-3}, \quad\frac{1}{2}<\lambda<1, \end{gather}$$

(3.6)$$\begin{gather}\frac{{\mathrm{d}}q}{{\mathrm{d}}\kern0.06em x}=\frac{A^{4}E'}{2{\rm \pi}\mu'}\,x, \quad\lambda=1, \end{gather}$$

keeping in mind that (3.5) and (3.6) apply only asymptotically for $x\rightarrow 0$.

In order to determine ${\mathrm {d}}q/{\mathrm {d}}\kern0.06em x$ in the particular case $\lambda =\tfrac {1}{2}$, we need to account for the next-order term in the asymptotic expansion of $w$, as $w\sim x^{1/2}$ is strictly compatible only with an inviscid fluid or a fluid at rest in the context of an hydraulic fracture after noting that (3.3) reduces to $p=0$ if $\lambda =\tfrac {1}{2}$. The next-order term depends, however, on whether the fracture is at rest or propagating, and on whether the medium is permeable or impermeable (Garagash et al. 2011). The case of a deflating fracture at rest is analysed in § 5, while the case of a hydraulic fracture propagating in an elastic medium with toughness is summarized next.

4. Tip asymptotics near the end of the propagation phase

The tip asymptotics for a hydraulic fracture propagating in a permeable elastic medium has been constructed using the device of a semi-infinite fracture moving steadily at velocity $V$ under the condition of plane strain (Lenoach 1995; Adachi & Detournay 2008; Garagash et al. 2011). This asymptotic solution has a multiscale nature characterized by two length scales, $\ell _{\tilde {m}k'}$ and $\ell _{m\tilde {m}}$:

(4.1a,b)\begin{equation} \ell_{\tilde{m}k'}=\frac{K^{\prime8}}{4E^{\prime6} C^{\prime2}\mu^{\prime2}V},\quad\ell_{m\tilde{m}}= \frac{2^{6}C^{\prime6}E^{\prime2}}{\mu^{\prime2}V^{5}}.\end{equation}

The structure of the solution depends on the number $\chi$ defined in terms of the length scale ratio as Garagash et al. (2011)

(4.2)\begin{equation} {\chi}={\left(\frac{\ell_{m\tilde{m}}}{\ell_{\tilde{m}k'}}\right)^{1/8}} ={\frac{2C^{\prime}E^{\prime}}{K^{\prime}V^{1/2}}}.\end{equation}

If $\chi$ is $O(100)$ or larger, then the crack aperture behaves as $x^{1/2}$ in the near field, $x^{5/8}$ at intermediate distance, and $x^{2/3}$ in the far field. In particular, the LEFM asymptote $w=(K'/E')x^{1/2}$ applies approximately to the region $0< x\lesssim 10^{-7}\ell _{\tilde {m}k'}$ for large $\chi$.

Noting that $\ell _{\tilde {m}k'}\sim V^{-1}$ and $\chi \sim V^{-1/2}$, the near-tip region of a finite hydraulic fracture is dominated by the LEFM asymptote near the end of the propagation phase after fluid injection has stopped. In this region of LEFM dominance, the pressure gradient is given by (Garagash et al. 2011)

(4.3)\begin{equation} \frac{\mathrm{d}p}{\mathrm{d}\kern0.06em x}=\frac{2C'\mu'E'^{3}V^{1/2}}{K'^{3}x}, \end{equation}

implying that the flux is $q\sim x^{1/2}$. Thus the three dominant terms $V\,\partial w/\partial x$, $\partial q/\partial x$ and $g$ in the continuity equation (2.4) have the same singularity $x^{-1/2}$ at the fracture tip. As will be shown below, the dominant balance in the continuity equation changes during deflation of the fracture.

5. Near-field tip asymptotics during fracture arrest and recession

After the fracture stops propagating, it is in a state of arrest that lasts as long as the stress intensity factor $0< K< K'$. The arrest phase is then followed by recession of the tip until the fracture closes completely. In this section, we study the near-field tip asymptotics during the phases of arrest and recession, as well at the transition between arrest and recession, while relaxing the assumption of Carter's leak-off. We refer to these solutions as vertex solutions.

5.1. Arrest ($K>0$, $V=0$)

During the arrest phase ($V=0$), the stress intensity factor $K$ decreases steadily from $K^{\prime }$ to $0$. The near-tip asymptote is thus given by LEFM:

(5.1a,b)\begin{equation} w\stackrel{x\rightarrow0}{\sim}\ell_{k}^{1/2}x^{1/2},\quad \ell_{k}=\left(\frac{K}{E^{\prime}}\right)^{2},\end{equation}

with $\ell _{k}$ a decreasing function of time. We refer to (5.1a,b) as the $k$-asymptote. Once the fracture stops propagating, the leak-off $g(x,t)$ is no longer singular at the crack tip, and to first order, it is assumed to be spatially uniform in the asymptotic tip region. To acknowledge this approximation, leak-off is now denoted by $g_{0}(t)$, a regular function of time.

Considering the continuity equation (2.4), which can now be written as

(5.2)\begin{equation} \frac{\partial w}{\partial t}-\frac{\partial q}{\partial x}+g_{0}=0,\end{equation}

and the aperture asymptote (5.1a,b), it is evident that the rate term $\partial w/\partial t$ in (5.2) is subdominant, and that the leak-off $g_{0}$ can be balanced only by the divergence of the flux as $x\rightarrow 0$. Hence integrating the dominant terms in (5.2) with the condition $q(0)=0$ yields

(5.3)\begin{equation} q=g_{0}x,\quad x\rightarrow0.\end{equation}

Further integrating Poiseuille's law, while taking into account (5.1a,b) and (5.3), leads to the non-singular pressure field in the tip region

(5.4)\begin{equation} p=p_{0}+\frac{2\mu^{\prime}g_{0}}{\ell_{k}^{3/2}}\,x^{1/2}, \quad x\rightarrow0, \end{equation}

where the finite tip pressure $p_{o}$ and the length sale $\ell _{k}$ are both functions of time.

5.2. Arrest–recession transition ($K=0$, $V=0$)

At the end of the arrest phase, $K=0$ and $V=0$. Although the passage from arrest to recession is instantaneous, the transition is accompanied by a switch in the near-field asymptote, as shown next.

To construct the tip asymptote at the arrest–recession transition, we assume that $w(x)\sim x^{\lambda }$ as $x\rightarrow 0$, and again neglect the rate term $\partial w/\partial t$ in (5.2), since it is subdominant compared to $g_{0}$ as $x\rightarrow 0.$ Thus the continuity equation at the arrest–recession transition is again given asymptotically by (5.3). We further note that the power-law index $\lambda$ is necessarily in the range $1/2<\lambda <1$. Indeed, $\lambda >1/2$ since $K=0$; also, $\lambda <1$, because the flux divergence deduced from elasticity and Poiseuille's law would be subdominant to $g_{0}$ for $\lambda \ge 1$, in contradiction to (5.3).

Combining the elastic eigensolution (3.1) and (3.3), and Poiseuille's law (2.3), yields

(5.5)\begin{equation} q=\lambda(\lambda-1)\cot({\rm \pi}\lambda)\,\frac{A^{4}E^{\prime}}{4 \mu^{\prime}}\,x^{4\lambda-2},\quad x\rightarrow0.\end{equation}

Then after inserting (5.3) in (5.5), identifying the power-law index $\lambda$ so as to remove the dependence of the equation on $x$, and finally solving the remaining algebraic equation for $A$, leads to

(5.6a,b)\begin{equation} \lambda=\tfrac{3}{4},\quad A=\beta_{g}\ell_{g}^{1/4},\end{equation}

with the coefficient $\beta _{g}$ and the length scale $\ell _{g}$ given by

(5.7a,b)\begin{equation} \beta_{g}=\left(\frac{64}{3}\right)^{1/4}\simeq2.149,\quad \ell_{g}=\frac{\mu^{\prime}g_{0}}{E^{\prime}}.\end{equation}

Hence the asymptotic expressions for the aperture and the net pressure at the arrest–recession transition read

(5.8a,b)\begin{equation} w\stackrel{x\rightarrow0}{\sim}\beta_{g}\ell_{g}^{1/4}x^{3/4},\quad \frac{p}{E^{\prime}}\stackrel{x\rightarrow0}{\sim}- \frac{3\beta_{g}}{16}\left(\frac{\ell_{g}}{x}\right)^{1/4}.\end{equation}

We refer to this asymptote as the $g$-asymptote.

5.3. Recession ($K=0$, $V<0$)

We again search for an asymptotic expression of the form $w(x)\sim x^{\lambda }$ as $x\rightarrow 0$, where, for the reasons outlined above, the power-law index $\lambda$ is in the range $1/2<\lambda \le 1$. However, in contrast to the arrest and transition cases, the full continuity equation (2.4) needs to be considered when the fracture is receding.

It can be shown readily that the continuity equation (2.4) can be satisfied only if $\lambda =1$. Indeed, with $\lambda =1$, leak-off at the tip is balanced during recession by the advective term $|V|\,\partial w/\partial x$ rather than the flux divergence $\partial q/\partial x$ as is the case during arrest, while the two other terms are subdominant as $\partial w/\partial t,\partial q/\partial x\sim x$. Hence the leading-order match yields

(5.9)\begin{equation} -V\,\frac{\partial w}{\partial x}=g_{0},\end{equation}

while matching the next order yields

(5.10)\begin{equation} \frac{\partial w}{\partial t}=\frac{\partial q}{\partial x}, \quad x\rightarrow0,\end{equation}

noting again that $g_{0}$ is not singular as in the arrest phase. (A power-law index ${\lambda =2/3}$ could in principle balance $\partial w/\partial x$ and $\partial q/\partial x$, but the two terms cannot balance algebraically because of the sign mismatch.)

The dominant balance (5.9) yields a positive aperture factor $A=-g_{0}/V=g_{0}/|V|$, hence

(5.11a,b)\begin{equation} w=\frac{g_{0}}{|V|}\,x,\quad p=\frac{g_{0}E'}{4{\rm \pi}\,|V|}\ln x, \quad x\rightarrow0,\end{equation}

which will be referred as the $r$-asymptote. It will be convenient, when constructing the recession multiscale asymptote, to define the length scale $\ell _{r}$ as

(5.12)\begin{equation} \ell_{r}=\frac{\mu^{\prime}\,|V|}{E^{\prime}}.\end{equation}

Integrating (3.6) with $q(0)=0$ shows that $q>0$ in the tip region, thus implying that the fluid is flowing towards the tip, even though the crack is receding. Furthermore, we deduce from (5.10) that $\partial w/\partial t>0$, since $\partial q/\partial x>0$ according to (3.6). In other words, the asymptotic aperture at a fixed distance from the moving tip is increasing with respect to time. However, it can be shown that in a fixed coordinate system, $Dw/Dt=\partial w/\partial t+V\,\partial w/\partial x<0$ as $x\rightarrow 0$, since $\partial w/\partial t\sim x$ and is subdominant to $V\,\partial w/\partial x$, which is a negative $x$-independent quantity.

6. Multiscale tip asymptotics during fracture arrest and recession

6.1. The connection problem

Changes in the power-law index of the tip aperture $w\sim x^{\lambda }$, as the fracture evolves during the arrest and recession phases ($\lambda =1/2$ for $K>0$ and $V=0$, $\lambda =3/4$ for $K=0$ and $V=0$, and $\lambda =1$ for $K=0$ and $V<0$), suggest the existence of multiscale asymptotes in the progressive transition between these two phases. Specifically, we envision that the region of dominance of the $k$-asymptote shrinks in favour of the far-field $g$-asymptote, as the length scale $\ell _{k}$ decreases with diminishing $K$ during arrest. At the ephemeral arrest–recession transition, the $g$-asymptote fully characterizes the tip region. However, this asymptote is replaced progressively in the near field by the $r$-asymptote as the magnitude $|V|$ of the receding tip velocity increases. It is therefore expected that for a finite hydraulic fracture, the $g$-asymptote acts as an intermediate asymptote near the arrest–recession transition.

Thus the multiscale $kg$-asymptote applies when the fracture is arrested, and the $rg$-asymptote when it is receding. Construction of the asymptotes, referred to as edge solutions, involves connecting the vertex solutions that are present in the tip boundary layer. Following the approach described by Dontsov & Peirce (2015), this connection problem is formulated as a nonlinear non-singular integral equation for the aperture, which can be solved using simple quadratures. This integral equation is obtained as follows. First, (2.2) is inverted (provided that $p\overset {x\rightarrow \infty }{\sim }O(x^{-a})$ for $a>0$) to yield an expression for $w(x)$ in terms of an integral operator acting on $p$ (Garagash & Detournay 2000). After an integration by parts, this integral equation reads

(6.1)\begin{equation} w(x)=\frac{K}{E^{\prime}}\,x^{1/2}+\frac{4}{{\rm \pi} E^{\prime}} x^{1/2}\int_{0}^{\infty}s^{1/2}\,G\left(\frac{s^{1/2}}{x^{1/2}}\right) \frac{\mathrm{d}p(s)}{\mathrm{d}s}\,\mathrm{d}s.\end{equation}

Here, $K$ is the scaled stress intensity factor, and $G(t)$ is a non-singular kernel given by

(6.2)\begin{equation} G(t)=\frac{1-t^{2}}{t}\ln\left|\frac{1+t}{1-t}\right|+2,\end{equation}

with

(6.3a,b)\begin{equation} G(t)=4,\ t\rightarrow0,\quad \mathrm{and}\quad G(t)\sim\frac{4}{3t^{2}},\ t\rightarrow\infty. \end{equation}

A nonlinear Fredholm integral equation of the second kind for $w(x)$ is finally deduced by replacing the pressure gradient in (6.1) by its expression from the lubrication equation. The dominant balance in the lubrication equation depends, however, on whether the fracture is at rest or receding, as shown earlier.

6.2. $kg$-edge solution

A universal description of the $kg$-asymptote, independent of any physical parameter, can be achieved by selecting appropriately the scales for length ($\ell _{kg}$), aperture ($w_{kg}$), flux ($q_{kg}$) and pressure ($p_{kg}$). This is done by defining length scale $\ell _{kg}$ as the distance from the fracture tip at which the $k$- and $g$-asymptotes yield approximately the same aperture $w_{kg}$; thus $w_{kg}\sim \ell _{k}^{1/2}\ell _{kg}^{1/2}\sim \ell _{g}^{1/4}\ell _{kg}^{3/4}$. In view of (5.1a,b) and (5.8a,b), both scales $\ell _{kg}$ and $w_{kg}$ can be expressed in terms of $\ell _{k}$ and $\ell _{g}$ according to

(6.4a,b)\begin{equation} \ell_{kg}=\frac{\ell_{k}^{2}}{\ell_{g}},\quad w_{kg}=\frac{\ell_{k}^{3/2}}{\ell_{g}^{1/2}}.\end{equation}

From Poiseuille's law (2.3) and the continuity equation (5.3), we further deduce the scales $q_{kg}$ and $p_{kg}$:

(6.5a,b)\begin{equation} q_{kg}=g_{0}\ell_{kg},\quad p_{kg}=E'\,\frac{w_{kg}}{\ell_{kg}}.\end{equation}

After introducing the dimensionless variables $\hat {x}=x/\ell _{kg}$, $\hat {w}=w/w_{kg}$, $\hat {p}=p/p_{kg}$, ${\hat{q}=q/q_{kg}}$, and accounting for $V=0$, the lubrication equation (2.3) and (5.3) combine to give

(6.6)\begin{equation} \frac{\mathrm{d}\hat{p}}{\mathrm{d}\hat{x}}= \frac{\hat{x}}{\hat{w}^{3}}.\end{equation}

Scaling the elastic integral equation (6.1) and combining it with (6.6) yields

(6.7)\begin{equation} \hat{w}(\hat{x})=\hat{x}^{1/2}\left[1+\frac{4}{\rm \pi} \int_{0}^{\infty}G\left(\frac{\hat{s}^{1/2}}{\hat{x}^{1/2}} \right)\frac{\hat{s}^{3/2}}{\hat{w}(\hat{s})^{3}}\, \mathrm{d}\hat{s}\right],\end{equation}

noting also that $\hat {w}=\hat {x}^{1/2}$ if $\hat {x}\ll 1$, and $\hat {w}=\beta _{g}\hat {x}^{3/4}$ if $\hat {x}\gg 1$. The universal $kg$-asymptote $\hat {w}({{\hat {x}}})$ is the solution of the Fredholm integral equation (6.7).

To solve for $\hat {w}(\hat {x})$, the integral equation (6.7) is reformulated as (Dontsov & Peirce 2015)

(6.8)\begin{equation} \hat{\omega}(\hat{\xi})=1+\frac{8}{\rm \pi}\int_{0}^{\infty}G \left(\frac{\hat{\eta}}{\hat{\xi}}\right)\frac{\hat{\eta}\, \mathrm{d}\hat{\eta}}{\hat{\omega}(\hat{\eta})^{3}},\end{equation}

where the variables $\hat {\omega }$, $\hat {\xi }$ and $\hat {\eta }$ are defined as

(6.9a–c)\begin{equation} \hat{\omega}=\frac{\hat{w}}{\hat{x}^{1/2}},\quad \hat{\xi}=\hat{x}^{1/2},\quad \hat{\eta} =\hat{s}^{1/2}.\end{equation}

Under this transformation, the $k$- and $g$-asymptotes transform to $\hat {\omega }(0)=1$ and $\hat {\omega }=\beta _{g}\hat {\xi }^{1/2}$ as $\hat {\xi }\rightarrow \infty$, respectively. These asymptotic behaviours can actually be recovered directly from the transformed integral equation (6.8) by assessing the integral in the limits $\hat {\xi }=0$ and $\hat {\xi }\rightarrow \infty$, and taking into account the asymptotic behaviours (6.3a,b) of the function $G(t)$, and the result (Dontsov & Peirce 2015)

(6.10)\begin{equation} \int_{0}^{\infty}\frac{G(t)}{t^{\gamma}}\,\mathrm{d}t= \frac{2{\rm \pi}}{\gamma(2-\gamma)}\tan\left(\frac{\rm \pi}{2}\gamma \right).\end{equation}

Since the integrand in (6.8) is positive and non-singular, a numerical solution of $\hat {\omega }(\hat {\xi })$ can be obtained by solving a system of nonlinear algebraic equations formulated by discretizing the integral using the trapezoidal rule. To capture correctly the complete $kg$-asymptote, the grid points should be spaced uniformly on a logarithmic scale.

As in Dontsov & Peirce (2015), it is possible to obtain an approximate $kg$-edge solution, which in this case has relative error less than $3\,\%$, by differentiating (6.8) and assuming a power-law behaviour for $\hat {\omega }$ to obtain a separable ordinary differential equation, whose solution, along with the condition $\hat {\omega }(0)=1$, yields

(6.11)\begin{equation} \hat{\omega}\approx(1+\beta_{g}^{4}\hat{\xi}^{2})^{1/4}\quad \text{or}\quad\hat{w}\approx\hat{x}^{1/2}(1+\beta_{g}^{4} \hat{x})^{1/4}.\end{equation}

In figure 2, we plot $\hat {x}^{1/2}/\hat {w}$ versus $\hat {x}$ (or equivalently $1/\hat {\omega }$ versus $\hat {\xi }^{2}$). We have chosen to plot the reciprocal of $\hat {\omega }$ as this emphasizes the variation in $\hat {\omega }$, with respect to the scaled variables, between the small- and large-$\hat {\xi }$ asymptotic behaviours. The solid curve in this figure represents the numerical solution of (6.8), and the dashed curve the approximate solution (6.11).

Figure 2. The $kg$-asymptote plotted as $\hat {x}^{1/2}/\hat {w}$ versus $\hat {x}$ (or equivalently $1/\hat {\omega }$ versus $\hat {\xi }^{2}$): numerical solution (continuous line) and approximate closed-form solution (dashed line).

6.3. $rg$-edge solution

For the multiscale tip asymptote applicable to the recession phase, we proceed in a manner similar to the construction of the $kg$-transition. Now the $r$-asymptote (instead of the $k$-asymptote) dominates the near-tip region, $x\ll \ell _{rg}$, and the $g$-asymptote applies in the far-tip region, $x\gg \ell _{rg}$, where $\ell _{rg}$ is the transition length scale of the $rg$-asymptote.

The scales $\ell _{rg}$ and $w_{rg}$ are deduced from the $r$- and $g$-asymptotes by determining the distance from the tip at which both asymptotes yield approximately the same aperture:

(6.12a,b)\begin{equation} \ell_{rg}=\frac{\ell_{r}^{4}}{\ell_{g}^{3}},\quad w_{rg}=\frac{\ell_{r}^{3}}{\ell_{g}^{2}}. \end{equation}

Hence $\tilde {w}=\tilde {x}$ if $\tilde {x}\ll 1$, and $\tilde {w}=\beta _{g}\tilde {x}^{3/4}$ if $\tilde {x}\gg 1$, with $\tilde {x}=x/\ell _{rg}$ and $\tilde {w}=w/w_{rg}$. Moreover, from the continuity equation (2.4) and Poiseuille's law (2.3), we deduce the flux scale $q_{rg}$ and the pressure scale $p_{rg}$:

(6.13a,b)\begin{equation} q_{rg}=|V|\,w_{rg},\quad p_{rg}=E'\,\frac{w_{rg}}{\ell_{rg}}. \end{equation}

In the early stage of the recession, when the tip is under the $rg$-asymptotic umbrella, we can again neglect the rate term $\partial w/\partial t$ in the continuity equation (2.4), which, after scaling and integration and noting that $V<0$ in (2.4), now reads

(6.14)\begin{equation} \tilde{q}=\tilde{x}-\tilde{w}.\end{equation}

Hence the lubrication equation simplifies to

(6.15)\begin{equation} \frac{\mathrm{d}\tilde{p}}{\mathrm{d}\tilde{x}}= \frac{\tilde{x}-\tilde{w}}{\tilde{w}^{3}},\end{equation}

where the tilde denotes a dimensionless variable in the $rg$-scaling.

For the $rg$-transition, the elasticity equation (6.1) becomes

(6.16)\begin{equation} \tilde{w}(\tilde{x})=\frac{4\tilde{x}^{1/2}}{\rm \pi} \int_{0}^{\infty}\tilde{s}^{1/2}\,G \left(\frac{\tilde{s}^{1/2}}{\tilde{x}^{1/2}}\right) \frac{\tilde{s}-\tilde{w}}{\tilde{w}^{3}}\,\mathrm{d}\tilde{s},\end{equation}

after dropping the inhomogeneous term $\tilde {x}^{1/2}$ since $K=0$, and replacing the pressure gradient by its expression derived from the lubrication equation (6.15). We note, however, that $\tilde {w}=\tilde {s}$ is in the null space of the integral operator (6.16). Moreover, $\tilde {w}\sim \tilde {s}$ is the near-tip asymptote valid for $\tilde {s}\ll 1$. We therefore define the function $\tilde {\omega }(\tilde {x})$ as a perturbation of the near-tip asymptote, i.e.

(6.17)\begin{equation} \tilde{\omega}(\tilde{x})=\frac{\tilde{w}(\tilde{x})}{\tilde{x}}-1,\end{equation}

such that $\tilde {\omega }(0)=0$ and $\tilde {\omega }(\infty )=-1$

The integral equation can then be rewritten as

(6.18)\begin{equation} \tilde{\omega}(\tilde{x})={-}1-\frac{4}{{\rm \pi}\tilde{x}^{1/2}} \int_{0}^{\infty}G\left(\frac{\tilde{s}^{1/2}}{\tilde{x}^{1/2}}\right) \frac{\tilde{\omega}(\tilde{s})}{\tilde{s}^{3/2}(1+ \tilde{\omega}(s))^{3}}\,\mathrm{d}\tilde{s}.\end{equation}

In view of the limiting behaviours (6.3a,b) of the function $G(t)$, the above integral converges if $\tilde {\omega }(\tilde {x})\sim \tilde {x}^{\gamma }$ as $\tilde {x}\rightarrow 0$, provided that $\gamma >\text {\ensuremath {1/2}}$.

Figure 3 shows $\tilde {w}(\tilde {x})/\tilde {x}$ as a function of the scaled distance to the fracture tip, $\tilde {x}$. We have chosen to plot the shifted perturbation $1+\tilde {\omega }$ as it varies from $0$ to $1$, noting that the perturbation $\tilde {\omega }$ is bounded above by the asymptote $\tilde {\omega }\overset {\tilde {x}\rightarrow 0}{\rightarrow }0$ associated with the $r$-vertex solution, and bounded below by the asymptote $\tilde {\omega }\overset {\tilde {x}\rightarrow \infty }{\rightarrow }-1+\beta _{g}\tilde {x}^{-1/4}$ associated with the $g$-vertex solution. The solid black curve in figure 3 represents the numerical solution of (6.18).

Figure 3. The $rg$-asymptote plotted as $\tilde {w}(\tilde {x})/\tilde {x}$ versus $\tilde {x}$.

6.4. Application of the $kg$- and $rg$-asymptotes during deflation

Here, we outline briefly the determination of the stress intensity factor $K$ during the arrest phase of a deflating fracture, using the $kg$-asymptote within the framework of a numerical hydraulic fracturing simulator. This methodology is inspired by procedures developed for implementing multiscale tip asymptotics in numerical codes to simulate propagating hydraulic fractures (Peirce 2015, 2016; Dontsov & Peirce 2017).

The methodology relies on the ability to compute the fracture aperture at a grid point, away from the tip but still inside the asymptotic region, by solving numerically the system of equations governing the response of a hydraulic fracture during deflation. Assume that at a certain time $t$, the aperture $w_{n}^{(k)}$ at node $n$ located at distance $\ell _{n}$ from the tip has been calculated iteratively, with superscript $(k)$ denoting the current iteration count at time $t$. The pair ($\ell _{n},w_{n}^{(k)}$) is forced to be mapped onto the $kg$-asymptotic solution $\hat {w}(\hat {x})$ by selecting the appropriate stress intensity factor $K$. However, this new value of $K$ impacts the asymptotic aperture of the fracture behind node $n$, which in turn affects the aperture at node $n$ through the elasticity and the lubrication equation. An iterative procedure is thus needed to determine the arrest solution at a given time $t$ to correctly identify $K$. It is important to point out that the distance $\ell _{n}$ should be constrained by $\ell _{n}\lesssim 10^{6}\ell _{kg}$ so that the node is outside the region of dominance of the $g$-asymptote, as all information about $K$ would otherwise be lost since

(6.19)\begin{equation} w\overset{x\rightarrow\infty}{\sim}w_{kg}\beta_{g} \left(\frac{x}{\ell_{kg}}\right)^{3/4}= \beta_{g}\ell_{g}^{1/4}x^{3/4}. \end{equation}

A similar approach is used to determine the recession velocity $V$ using the $rg$-asymptote. Again, the nodal point must not be inside the $g$-asymptotic region, i.e. $\ell _{n}\lesssim 10^{9}\ell _{rg}$, noting that

(6.20)\begin{equation} w\overset{x\rightarrow\infty}{\sim}w_{rg}\beta_{g} \left(\frac{x}{\ell_{rg}}\right)^{3/4}=\beta_{g}\ell_{g}^{1/4}x^{3/4}, \end{equation}

which shows that the asymptote is agnostic about the tip velocity when $x\gg \ell _{rg.}$ The $rg$-edge solution is used until the point at which there is a negligible difference between the value of $|V|$ determined from the $rg$-edge solution and that given by the linear asymptote in (5.11a,b).

The detailed procedure for applying the $kg$- and $rg$-asymptotes to the numerical modelling of a deflating fracture is described elsewhere (Peirce 2022; Peirce & Detournay 2022b).

7. Concluding remarks

This paper describes the construction of two multiscale tip asymptotes for a hydraulic fracture deflating in a permeable elastic medium, the $kg$-asymptote when the fracture is at rest, and the $rg$-asymptote when the fracture is receding. The asymptotes were obtained by solving a Fredholm integral equation of the second kind, formulated in terms of the aperture for a semi-infinite deflating fracture that is either at rest or steadily receding. The arrest $kg$-asymptote is characterized in the near field by the classic LEFM asymptote $w\sim x^{1/2}$ as $x\rightarrow 0$, while the receding asymptote behaves as $w\sim x$ as $x\rightarrow 0$; however, both asymptotes share the same power law $w\sim x^{3/4}$ as $x\rightarrow \infty$. Thus the fluid pressure is regular when the fracture is at rest, but has a logarithmic singularity during recession.

The scaled tip asymptotes are universal since they do not depend on any parameter. Scaling indicates that: during arrest, the region of dominance of the $1/2$ asymptote shrinks to the benefit of the intermediate $3/4$ asymptote as the fracture deflates; and during recession, a linear $1/1$ asymptote develops progressively at the fracture tip with increasing receding velocity, with the $3/4$ becoming again an intermediate asymptote. Hence only the fleeting $3/4$ asymptote remains at the arrest–recession transition point. It is worth noting that the multiscale receding asymptote has an unusual structure in that the power-law index is larger in the near field than in the far field. This ordering is dictated by the nature of the $3/4$ asymptote, which cannot exist with a non-zero velocity and is thus agnostic about the velocity, hence is unable to balance the leak-off as $x\rightarrow 0$ during recession. Finally, note that the asymptotes for a deflating fracture can be extended to cases where the criterion for fracture closure is more generally described by $w=w_0$. Here, $w_0$ is a residual aperture associated, for example, with the presence of proppant in the fracture. The tip asymptotes then apply to the difference aperture field $w-w_0$.

These universal multiscale asymptotes are key to determining the decaying stress intensity factor during arrest, the time at which the fracture transitions from arrest to recession, and the negative front velocity during recession when simulating the deflation of a hydraulic fracture in a permeable elastic medium. The dependence of the tip asymptotic response on time is thus only indirect, via the stress intensity factor if the fracture is arrested, or via the tip velocity if receding. It further requires combining consideration of the finite fracture and of the tip asymptotes.

The arrest and recession asymptotes are instrumental both for implementing robust algorithms for simulating deflating fractures (Peirce 2022; Peirce & Detournay 2022a) and for constructing closed-form solutions for radial and plane strain fractures in the latest stage of closure (Peirce & Detournay 2022b). Such ‘sunset’ solutions can be used to interpret the leak-off coefficient or the in situ stress from measurements collected during shut-in.

It has been assumed in this work that the permeable solid has toughness $K' > 0$. Consideration of the case $K'=0$ would require analysing the evolution of the asymptotics during the direct transition from propagation to recession, as there is no arrest phase in this particular case. The case $K'>0$ for an impermeable solid is treated in Appendix A, where it is shown that a deflating hydraulic fracture in an impermeable medium cannot recede even if it is bleeding fluid back to the borehole.