Climate sensitivity and mass-balance evolution of Gran Campo Nevado ice cap, southwest Patagonia

Abstract

A degree-day model extended for surface mass-balance calculations has been applied to derive the sensitivity of Gran Campo Nevado ice cap (GCN), southwest Patagonia, to climate change. Seasonal sensitivity characteristics were computed using automatic weather station data gathered in the period 2000–05. Results indicate pronounced mass-balance sensitivity to temperature during the summer, with monthly values of –0.27±0.01mw.e. K^–1. Monthly sensitivity to a 10% precipitation perturbation fluctuates around +0.03mw.e The sensitivity characteristics obtained were used to model the surface mass-balance evolution of GCN during the 20th and 21 st centuries based on monthly means of air temperature and precipitation derived from bias-corrected weather station data and statistically downscaled re-analysis and general climate model data. Surface mass balance shows a persistently negative trend ranging from around +1mw.e. a^–1 at the beginning of the 20th century down to almost –1.5mw.e. a^–1 during the first years of the 21st century, with only a few positive years occurring occasionally during the second half of the 20th century. The scenario for the end of the 21 st century totals approximately –4.5mw.e. a^–1, i.e. an estimated ice volume loss for GCN of 59 km³ during 1900–2099.

Introduction

The southern part of South America features one of the most pronounced climate divides of the entire Earth. It forms the only continental land mass between 48˚ S and 55˚ S, and the north–south-striking southern Andes are one of the very few mountain ranges located in these latitudes. Hence, they form a very effective barrier for the Southern Hemispheric westerlies. This results in a precipitation increase from ~2000–4000mma^–1 on the windward Pacific coast to >10 000mma^–1 in the summit regions due to orographic effects. The leeward side, in contrast, is characterized by <500mma^–1 (Aceituno and others, 1993; Cerveny, 1998; Schneider and others, 2003). These extreme precipitation sums provide for the existence of Gran Campo Nevado ice cap (GCN; Fig. 1) despite its location at comparatively low altitudes of up to 1700ma.s.l. and the moderate mean annual air temperature of +5.7˚C at sea level (Schneider and others, 2003).

Fig. 1. Location of GCN and terrain surface classification of the research area. Contour spacing is 200 m. Coordinates correspond to Universal Transverse Mercator (UTM) zone 18S. AWS is the automatic weather station located at Puerto Bahamondes at 28 ma.s.l.

Located in this extreme climate setting, the glaciated areas of Patagonia have been subject to intensive research during the past decade (e.g. Casassa and others, 2002b; Rivera and others, 2002). Most of the glaciological and climatological studies have been focused on the large icefields Hielo Patagónico Norte (HPN; northern Patagonia icefield) and Hielo Patagónico Sur (HPS; southern Patagonia icefield; HPS). However, since 2000 GCN (Fig. 1) has also been subject to intensive research (e.g. Casassa and others, 2002a; Koch and Kilian, 2005; Kilian and others, 2007; Möller and others, 2007; Schneider and others, 2007a). With 199.5 km² (Schneider and others, 2007b), GCN is the largest ice mass in Patagonia outside HPN and HPS north of the Strait of Magellan (Casassa, 1995).

Accordingly, recession of Patagonian glaciers during the 20th century is well documented in terms of both historical length fluctuations (e.g. Casassa and others, 1997; Warren and others, 1997; Raymond and others, 2005) and area or volume changes (e.g. Rignot and others, 2003; Rivera and others, 2005, 2007). However, long-term surface mass-balance (SMB) time series are rare around Patagonia and even the whole of southern South America. Naruse and others (1997) modelled an ablation time series of Glaciar Perito Moreno, HPS, from temperature records of the nearby Argentine weather station Calafate for the period 1962–94. Stuefer and others (2007) presented a complete mass-balance time series of the same glacier for the second half of the 20th century. However, up to now no continuous 20th-century SMB time series has been created for any ice cap or glacier in Patagonia, nor has a simulation of future SMB variations in response to global climate change been assessed.

In this study, an SMB model based on the degree-day method is used to compute ablation and accumulation employing a digital terrain model (DTM) representing the glacier surface elevations in 2000 within the glacier surface extent of 1998 (Möller and others, 2007). By driving this model with daily automatic weather station (AWS) data, the seasonal sensitivity characteristics of GCN were computed according to Oerlemans and Reichert (2000). The resulting seasonal sensitivity matrix (SSM) was used to perform the SMB reconstruction by employing a method presented by Oerlemans (2001).

The aim of this study is to analyze the sensitivity of GCN to climate change and to derive a continuous SMB time series of GCN for the 20th and 21st centuries and an estimate of the associated volume loss.

Data

Several datasets covering different, partly overlapping time periods had to be used for this study. A dataset obtained from an AWS (AWS GCN Puerto Bahamondes; Fig. 1) that was operated about 3.5 km from the ice margin of GCN at 28ma.s.l. (Schneider and others, 2003) served as input for the SSM computation and as a local reference for statistical downscaling of the synoptic-scale climate data. It provides continuous daily air-temperature and precipitation records covering the period September 2000–August 2005 (Fig. 2). Air temperature was measured with a combined air-temperature and air-humidity sensor at a precision of <0.1 K and precipitation with a tipping-gauge rain bucket at a precision of at least ±20% (Schneider and others, 2003).

Fig. 2. Monthly mean air-temperature and precipitation sums of the AWS Puerto Bahamondes (Fig. 1) for the period September 2000– August 2005.

SMB reconstruction for the first half of the 20th century employs a subset of the 1900–2001 temperature and precipitation records from the weather station Faro Evange-listas (WSFE), which is operated by the Chilean Navy on a coastal island at 52^˚24^' S, 75^˚06^'W (~50ma.s.l.; Fig. 3).

Fig. 3. Location of NCEP/NCAR and HadCM3 gridpoints and of the WS Faro Evangelistas (FE) operated by the Chilean Navy. Gridpoint numbers correspond to numbers used in Table 1 and in transfer equations (Equations (3a) and (3b)). Prediction (NCEP)/US National Center for Atmospheric Research (NCAR) re-analysis (NNR) project (Kalnay and others, 1996) covering the period 1948–2006. Data were provided by the National Oceanic and Atmospheric Administration–Cooperative Institute for Research in Environmental Sciences (NOAA–CIRES) Climate Diagnostics Center, Boulder, CO, USA (http://www.cdc.noaa.gov/).

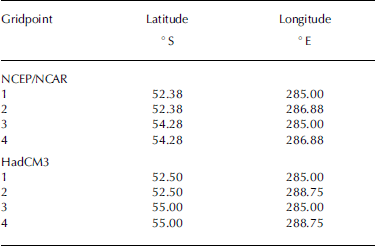
Table 1. Coordinates of NCEP/NCAR and HadCM3 gridpoints used in this study. Gridpoint names correspond to labels used in transfer equations. Numbering corresponds to gridpoint numbers used in Figure 2

For reconstruction of the SMB time series covering the second half of the 20th century, we used gridded monthly mean 2 m air temperatures and monthly mean precipitation rate data from the US National Centers for Environmental

The estimate of the 21st-century SMB time series is based on monthly mean 2 m surface air-temperature and monthly precipitation sum grids (J.A. Lowe, http://cera-www.dkrz.de/WDCC/ui /Compact. jsp ? acronym=UKMO_HadCM3_ SRESA2_1) of the third UK Meteorological Office Hadley Centre coupled ocean–atmosphere general circulation model (GCM) (HadCM3) provided by the UK Meteorological Office Hadley Centre (Crown copyright 2005). Representing scenario A2 of the Intergovernmental Panel on Climate Change (IPCC) Fourth Assessment Report (Solomon and others, 2007), these datasets could be regarded as worst-case climate forcing for glacier change.

From both gridded datasets (NNR and HadCM3) we used subsets consisting of the four gridpoints located closest to GCN. An overview of their geographical coordinates and locations is shown in Table 1 and Figure 3.

Methods

Downscaling of climate data

The gridded NNR and GCM datasets were statistically downscaled to fit local conditions at GCN by employing the ‘local scaling’ method (Widmann and others, 2003; Salathé, 2005; Radić and Hock, 2006) and multiple regression analysis. The WSFE dataset was fitted to local conditions at GCN only by local scaling.

Local scaling can be regarded as an adjustment of the synoptic-scale mean seasonal cycle to that of the local-scale cycle. In a first step, both datasets were detrended to remove the linear part of the inherent long-term trends. Then the mean seasonal cycles (Fig. 4) were calculated by employing the entire datasets in case of the synoptic-scale data. Regarding the local-scale data (AWS), the record of the first year was omitted for calculation of the mean seasonal cycle (Fig. 4) to perform downscaling over the same period as the calculation of the SSM. Afterwards, data were corrected according to the biases between the monthly values of the seasonal cycles of synoptic-scale air temperature and precipitation data and the respective monthly values of the seasonal cycles of measurements at the AWS and Thus the data were locally scaled. The various downscaled air-temperature time series were calculated by adding monthly differences to the synoptic-scale data (Salathé, 2005), while the various downscaled precipitation time series were calculated by multiplying the synoptic-scale data with monthly proportions (Widmann and others, 2003) according to

(1)

and

(2)

Fig. 4. (a, c) Mean seasonal cycles of air temperature (a) and precipitation (c) of the NNR and HadCM3 gridpoints (Fig. 3; Table 1) before downscaling. (b, d) Mean seasonal cycles of air temperature (b) and precipitation (d) of NNR and HadCM3 data after downscaling but before retrending.

and

with Ti _{, ds(} n ₎ and Pi _{, ds(} n ₎ representing downscaled air temperature and precipitation for the ith month of the time series of gridpoint n (Table 1; Fig. 3). Ti _{, syn,m} and P_{i , syn,m} represent the respective synoptic-scale air temperature and precipitation, while the subscript m refers to the mth month within the respective mean annual cycle.

Four-year subsets equivalent to the period of the AWS record utilized were created from these locally scaled four NNR or HadCM3 gridpoints, which surround GCN (Table 1; Fig. 3). Based on these subsets, a multiple regression analysis was performed to achieve the best-fit combinations between the local scaled data of the gridpoints and the detrended record of the AWS. The resulting transfer functions in general are given by

(3a)

(3b)

with T_{i , ds} and P_{i , ds} being the result of the regression analysis. The coefficients (a_T , . . ., e_T and a_P , . . ., e_P ) for both NNR and HadCM3 data are presented in Table 2. The transfer functions (Equations (3a) and (3b)) were then applied to the entire locally scaled NNR or HadCM3 time series of the four gridpoints. Afterwards, the resulting time series for air temperature and precipitation were retrended to the mean of the original trends inherent in the respective unchanged synoptic-scale datasets to obtain the final downscaled NNR or HadCM3 time series (Fig. 5) used for SMB modelling (NNR_ds or HadCM3_ds).

Table 2. Regression constants and coefficients of the transfer functions (Equations (3a) and (3b)) used for downscaling of NNR and HadCM3 data

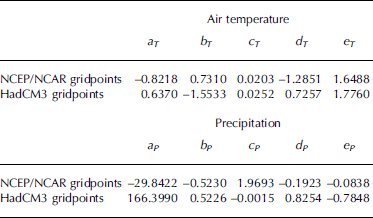
Fig. 5. Downscaled mean annual air temperature (a) and precipitation sum (b) from WSFE data (1900–47), NNR data (1948–2006) and HadCM3 data (2007–99). Annual means of the AWS Puerto Bahamondes (Fig. 1) are additionally printed as solid circles.

A local scaling to adjust the detrended WSFE record to the detrended NNR_ds time series was performed to fit the WSFE record to local conditions at GCN. A subsequent retrending as likewise done in case of the synoptic-scale data yielded the final locally scaled WSFE time series (Fig. 5) used for SMB modelling (WSFE_ls). The data period used for calculation of the biases between the two annual cycles needed for local scaling is limited to 1948–79, as the WSFE record features extensive data gaps and a conspicuous positive offset within the precipitation data in the 1980s. An adjustment using the AWS record as a reference for local scaling was therefore inhibited by the lack of an overlapping period. The period 1948–79 is also characterized by various data gaps within the precipitation record. Since the local scaling method is based on mean seasonal cycles the various resulting locally scaled temperature and precipitation time series (Fig. 5) were nevertheless considered to be suitable for SMB modelling.

Surface mass-balance model

The SMB model is based on a degree-day model (DDM; e.g. Ohmura, 2001; Hock, 2003) that is extended to compute SMB by employing a DTM (Braithwaite and Zhang, 2000; Möller and others, 2007). It calculates the ablation (M) and the accumulation (S) at a specific altitude (a) of the glacier surface (A) based on the positive mean daily air temperature (T_i ), the daily solid precipitation sum (P_i ), degree-day factors (F) for snow and for ice surfaces and a stochastic term ( x_i = 0mmd^–1) according to Braithwaite (1981) as

(4a)

and

(4b)

To obtain the specific mass balance at each specific altitude, the calculated ablation is subtracted from accumulation. The differences are integrated over the whole set of terrain elevations given by the DTM to obtain the overall volume change (ΔV) and the SMB according to

(5a)

and

(5b)

For computation of ablation, F is set to 7.0 mmK^-1 d^-1 in the case of an ice surface (F_ice ) and 3.5 mmK^-1 d^-1 in the case of a snow surface (F_snow ) according to ablation stake measurements carried out on an easterly outlet glacier of GCN, Glaciar Lengua, in the period 2000–03 (Möller and others, 2007; Schneider and others, 2007b). The temperature lapse rate (0.63 K (100 m)^-1) and the increase in precipitation with altitude (5% (100 m)^-1) are estimated from AWS measurements at different altitudes during the same period (Schneider and others, 2003). A specific pattern of remaining snow cover from the previous winter that starts with 0mm thickness at 300ma.s.l. and rises to 500mm thickness at 700 ma.s.l. is used as the starting condition for the model. The transition from rainfall to solid precipitation at temperatures between 0 and +2˚C is modelled using a smoothing function. All parameters of this SMB model are described in detail in Möller and others (2007).

Climate sensitivity characteristics

The climate sensitivity of GCN was assessed using a method presented by Oerlemans and Reichert (2000). The sensitivity of the SMB to changes in air-temperature and precipitation regimes in terms of monthly values was computed from the 5 year record of the AWS Puerto Bahamondes, omitting the first year as a period of model initialization. The resulting 2 by 12 SSM (Fig. 6) consists of coefficients C_{T , k} and C_{P , k} for each month k that represent the change of the mean SMB due to perturbations of temperature (C_{T , k} ) and precipitation (CP,k). According to Oerlemans and Reichert (2000), the seasonal sensitivity coefficients are calculated as

(6a)

Fig. 6. Seasonal sensitivity matrix for GCN according to Oerlemans and Reichert (2000) computed from the September 2000–August 2005 AWS record. Error bars reflect the combined uncertainties of SMB sensitivity due to variations of T _off and P _off and possible uncertainties inherent in the degree-day factors.

and

(6b)

with B the mean SMB, T _ref and P _ref a reference temperature and precipitation time series belonging to a zero mean SMB, T _off = 1 K a fixed temperature offset and P _off = 10% a fixed precipitation offset. The reference temperature time series T _ref leading to a zero mean SMB of GCN was achieved by adding a systematic offset of –0.648 K to the original air-temperature time series.

Modelling of SMB

According to Oerlemans (2001), the SSM described can be used to model the SMB of a specific year (B _m) from the zero reference SMB (B _ref ) achieved from the T _ref and P _ref reference temperature and precipitation time series and the deviations of the actual SMB from B _ref (ΔB _m) using monthly temperature and precipitation anomalies as

(7)

with

(8)

Thus, the yearly values of ΔB _m needed for SMB reconstruction are obtained by summing up the respective monthly values. The associated annual volume changes are calculated by integrating B _m over the whole 1998 glacier surface area.

Error Considerations

Seasonal sensitivity matrix

For assessment of the errors inherent in the method used, the uncertainties of the SSM have first to be considered. To do so, the coefficients C_{T , k} and C_{P , k} were computed using (1) varying temperature and precipitation perturbations during matrix calculation and (2) varying degree-day factors in the SMB model to analyze the impact of uncertainties in model calibration.

(1) Sensitivity characteristics were computed additionally with values for T _off of ±0.5 K and ±1.5 K and values for P _off of ±5% and ±15%, with the respective results being converted to ±1 K and ±10% equivalents for comparison with the original SSM. This yielded maximum monthly changes of 3.4% for temperature and 0.7% for precipitation sensitivity (Fig. 6). The absolute annual error range for temperature sensitivity thus amounts to ±0.03mw.e. K^–1 a^–1, while the absolute error range of precipitation sensitivity proved to be completely negligible.

(2) Furthermore, the entire SSM was computed using degree-day factors F _ice = 6.0 and 8.0mmK^–1 d^–1 and degree-day factors F _snow = 3.0 and 4.0 mmK^–1 d^–1. The results yielded a maximal monthly change in temperature sensitivity of 9.8%, while monthly precipitation sensitivity changed by not more than 4.2% (Fig. 6). This added to absolute annual error ranges of ±0.17mw.e. K^–1 a^–1 for temperature sensitivity and ±0.01mw.e. a^–1 per 10% precipitation perturbation for precipitation sensitivity.

According to these findings, the resulting overall annual error range relevant for SMB modelling depends on the difference between the climate conditions in the modelled year and the annual reference climate used for calculation of the SSM. Hence, an air-temperature-induced error range of ±0.20mw.e. K^–1 difference and a precipitation-induced error range of ±0.01mw.e. (10%)^–1 difference must be taken into consideration.

Downscaling of climate data

To derive the accuracy and quality of the statistical downscaling process and thus the climate data used for SMB modelling, two time series (NNR_ds and HadCM3_ds) were compared with the measured air-temperature and precipitation record from the AWS (Fig. 2), and one time series (WSFE_ls) was compared with NNR_ds. Correlations and explained variances were calculated and tested on significance. The reduction of the significance levels due to autocorrelation was taken into account. The results (Table 3; Fig. 4) indicate very good performance for the downscaling method, as, for example, the various downscaled air-temperature time series show explained variances of up to 94% (NNR_ds) and even the synthetically generated precipitation time series of the HadCM3 accounts for an explained variance of 19% after the downscaling. Moreover, all correlations are highly significant on the 99.5% level so that all climate data used (Fig. 5) could be regarded as a suitable basis for SMB time-series modelling.

Table 3. Error analysis of the results of climate data downscaling

Modelled SMB

According to the three different time periods of climate data (Fig. 5), the error analysis regarding the modelled SMB time series has to consider three different SMB time series, each modelled using the method described by Oerlemans and Reichert (2000). The first (SMB_NNR,ds) is based on the NNR_ds dataset, the second (SMB_HadCM3,ds) on the HadCM3_ds dataset and the third (SMB_WSFE,ls) on the WSFE_ls dataset.

To obtain uncertainties and error ranges of SMB_NNR,ds and SMB_HadCM3,ds, these two time series were compared with a reference SMB time series (SMB_ref) obtained by directly driving the SMB model with the daily records of the AWS for the period September 2000–August 2005 (Fig. 7). However, the first year of SMB_ref was omitted as a period of model initialization. For assessment of uncertainty and error range of SMB_WSFE,ls a comparison with SMB_ref was not possible due to lack of overlapping data. Hence, the comparison was performed with SMB_NNR,ds. During error analysis, correlations and explained variances were calculated and tested on significance, accounting for reduction due to autocorrelation. Results (Table 4) indicate good performance for the modelling procedure, with highly significant correlations of up to r = 0.92 equalling explained variances of up to 85%. The associated annual rms errors (Table 4) were taken as error ranges of the modelled SMB time series. The small systematic offsets, which appear between the two NNR_ds- and HadCM3_ds-based SMB time series and SMB_ref as well as between the WSFE_ls-based time series and SMB_NNR,ds (Table 4), were taken as additional error ranges of the modelled SMB time series.

Table 4. Error analysis of the results of SMB modelling. The annual rms error is based on annual SMB sums of all complete years within each period

Fig. 7. Comparison between monthly SMB_NNR,ds, SMB_HadCM3,ds and SMB_ref in the period September 2000–August 2005.

The overall annual error range (Fig. 8) is composed by the annual rms error, the annual mean offset and the climate-dependent error range (e _cd) induced by the uncertainties of the SSM. It amounts to 2.49 +e _cdmw.e. (1900–47), 1.44+ e _cdmw.e. (1948–2006) and 1.25 +e _cdmw.e. (2007–99).

Fig. 8. Modelled SMB time series according to WSFE_ls, NNR_ds and HadCM3_ds. SMB values obtained by directly driving the SMB model with AWS data are printed as solid circles.

Results and Discussion

Climate sensitivity

Generally, there are two aspects of the analysis of the climate sensitivity of SMB to be considered. The first is the variations of SMB induced by temperature and/or precipitation change that were obtained by SMB modelling as presented in Möller and others (2007). The second comprises the seasonal differences of climate sensitivity that are analyzed using seasonal sensitivity characteristics (Oerlemans and Reichert, 2000).

Findings by Möller and others (2007) show that the temperature sensitivity of GCN is much stronger/higher than precipitation sensitivity, as indicated by the steep gradient of the SMB deviations for different temperature and precipitation offsets (Fig. 9). To achieve the same change in SMB as induced by a small temperature perturbation of ±0.5 K, precipitation would have to vary by about ±25%. The SMB values associated with such changes are presented in Table 5. A temperature increase of +0.5 K would alter the September 2000–August 2005 mean annual SMB of GCN (–0.50±0.15mw.e. a^–1) to a value of –1.54mw.e. a^–1, whereas a minor precipitation change of –5% would only shift this value to –0.69mw.e. a^–1 (Table 5). From Figure 9 it can be seen that the dominance of the temperature sensitivity of GCN would increase in a warmer, more humid climate and would decrease in colder, drier climate settings. Therefore, the dominance of temperature sensitivity will increase whatever precipitation trend evolves during the oncoming decades because of the persistently positive temperature trend shown in Figure 5 (Solomon and others, 2007). Thus, even any possible future increase in precipitation in the summit regions due to enhanced westerly airflow (Marshall and others, 2004; Möller and others, 2007), which would lead to an increase in orographically induced precipitation, would not be sufficient to counteract the negative effect caused by ongoing climate warming.

Table 5. SMB estimates according to given temperature and precipitation offsets. Changes are computed in mm w.e. a^–1 by adding constant temperature and precipitation offsets to the AWS records according to Möller and others (2007)

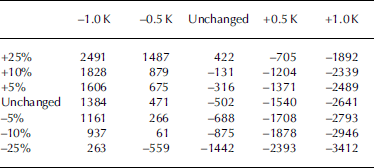
Fig. 9. Deviations of SMB from September 2000–August 2005 mean annual SMB (–502mmw.e. a^–1) induced by the given climate-change forcing. Presented deviations were calculated in mmw.e. a^–1 by adding the given temperature and precipitation offsets to the September 2000–August 2005 AWS record serving as input for SMB modelling (altered from Möller and others, 2007).

The results underline the extreme climate setting of GCN. Braithwaite and Zhang (1999) obtained SMB change rates for 37 glaciers from all over the world between 0.10 and 1.30mw.e. a^–1 K^–1, and Yongijan and others (1999) derived a comparable mean SMB change rate of 0.80mw.e. a^–1 K^–1 from measurements at 40 different glaciers. In contrast, GCN shows a SMB change rate of up to 2.10mw.e. a^–1 K^–1.

These findings are supported by the SSM obtained for GCN (Fig. 6) based on the AWS record from September 2001 to August 2005. The maximal monthly sensitivity of SMB to temperature perturbations is almost seven times higher than the maximal monthly sensitivity of SMB to precipitation perturbations. Maximum temperature sensitivity is reached during summer (–0.27±0.01mw.e. K^–1 in January), with a further occurrence of maximum values extending through early autumn. Sensitivity to ±10% precipitation perturbation shows no pronounced annual cycle and never amounts to more than +0.04mw.e. (November). Even if the strong/high temperature sensitivity should partly be due to the fact that a degree-day-method-based SMB model was used for computation of the SSM, the prevailing sensitivity to temperature is still obvious.

The absolute values characterizing the maximum temperature sensitivity of GCN during the summer months exceed, for example, comparable values for the strongly maritime Franz Josef Glacier (FJG), New Zealand, by approximately 50%, while winter minimum values are not even as high as those of FJG (Oerlemans and Reichert, 2000). Thus, the annual cycle of temperature sensitivity at GCN is distinctly more pronounced than the cycle at FJG. This, and the fact that during the winter months considerable temperature sensitivity exists at all, documents the highly maritime climate setting of GCN. The balanced precipitation sensitivity testifies the year-round high precipitation sums along the west coast of the southernmost Andes (Schneider and others, 2003).

SMB evolution

Climate data of the WS Faro Evangelistas, NNR and HadCM3 runs were used to reconstruct the past SMB evolution of GCN and to predict its future evolution. The changeover dates between the three underlying SMB time series were set to 1947/48 and 2006/07, respectively, thus using the highest-quality (Table 4) SMB time series (SMB_NNR,ds) as long as possible. The results indicate a persistently negative general trend in the evolution of SMB of GCN during the period 1900–2099 (Fig. 8).

During the first three decades of the 20th century, the SMB time series starts with positive SMB values of up to +1.6±1.9mw.e. a^–1, with an interim decrease to slightly negative values at around 1915. Afterwards, the SMB time series starts to tend downwards persistently, leaving the positive region and the period of mass gain in the 1930s (Fig. 8). However, in the 1950s and during the last 15 years of the century, a few slightly positive SMB years do still occur. The positive SMB values prevailing during the first part of the 20th century lead to a persistent growth in the ice volume of GCN while showing decreasing growth rates with time. SMB becomes prevailingly negative after 1930, and the volumetric evolution of GCN turns to a consistent mass loss. With a continuing negative SMB trend, the former mass gain finally disappeared by around 1960 (Fig. 10). During the first years of the 21st century, the SMB of GCN is roughly the opposite of the conditions present around 100 years earlier, as by this time SMB values decreased to a mean of –1.0±1.0mw.e. a^–1 (Fig. 8).

Fig. 10. Cumulated ice-volume changes in km³ of GCN calculated from the SMB time series and its associated error range presented in Figure 8.

Moraine dating by Koch and Kilian (2005) and a glacier inventory by Schneider and others (2007b) using airborne photography taken in 1942 show that up to now the outlet glaciers of GCN have retreated considerably from the latest terminal moraines, which formed in 1941 according to Koch and Kilian (2005). These findings coincide with the highly positive SMB values that occurred until the mid-1920s (Fig. 8), when the response time estimate of 15±10 years obtained for GCN by Schneider and others (2007b) is included. However, the SMB calculations performed in this study are based on the fixed 1998 glacier surface extent (Fig. 1) of 199.5 km² (Schneider and others, 2007b) and thus neglect the effects of any decline in the ice-covered area during the 20th century. Therefore, it must be taken into account that the reconstructed SMB values of past decades tend to overestimate SMB because their calculation does not include vast areas of glacier surface located within the ablation zone, and thus large amounts of ablation.

In the 21st century a climate forcing according to scenario A2 of the IPCC Fourth Assessment Report (Solomon and others, 2007) would intensify the negative trend. Consequently, for the last decade of the 21st century a mean SMB of –4.3±1.4mw.e. a^–1 with single values even exceeding –5.0±1.5mw.e. a^–1 (Fig. 8) is predicted. This implies that by 2099, taking 1900 as a reference, GCN would have lost about 58.7±56.9km³ of its ice masses (Fig. 10). The estimate of sea-level rise associated with this mass loss amounts to 0.16±0.16 mm.

Since the glacier area will definitely become smaller during the 21st century as suggested by the positive future temperature trend predicted by the IPCC (Solomon and others, 2007), the estimation of SMB during future decades tends to underestimate SMB due to the inclusion of high ablation values at low-altitude glacier surfaces that actually will already have vanished by that time. This effect might be partly compensated by the fact that climate warming will most probably increase the sensitivity of the SMB of GCN to temperature perturbations. This in turn would lead to increased overall ablation. The uncertainty induced by these two factors is not exactly quantifiable unless a fully dynamic SMB model is used. At this stage, it can only be concluded that the SMB values have to be regarded as an upper limit of SMB in the past and a lower limit of SMB in the future. The employment of GCM output representing a future climate forcing according to IPCC scenario A2 (Solomon and others, 2007) for SMB modelling adds to this conclusion. As this scenario describes a worst-case future for the perpetual existence of glaciers, the actual future SMB evolution of GCN might also show a less negative trend. Accordingly, the SMB trend obtained must probably be corrected towards a smaller temporal gradient.

Conclusion

The sensitivity of GCN to climate change proves to be very high (Fig. 6) even when compared to other maritime glaciers (Oerlemans and Reichert, 2000). This underlines the highly maritime climate setting of the ice cap. Present temperature sensitivity proves to be as high as –0.27±0.01mw.e. K^–1 during the summer and shows a high seasonality, with distinctly lower values throughout the winter months. Precipitation sensitivity shows no pronounced annual cycle. Values fluctuate around approximately +0.03mw.e. per 10% precipitation perturbation. This documents constantly humid conditions throughout the year. As the dominance of the temperature sensitivity of GCN over its precipitation sensitivity tends to increase with climate warming (Fig. 9), it will most probably consolidate or even increase in the future. Thus it can be stated that the recession of the outlet glaciers of GCN already observable during the 20th century will most probably accelerate during the 21st century even if the precipitation regime shows increasing snowfall in the accumulation area.

The persistently negative SMB trend shows annual values decreasing from up to +1.6±1.9mw.e. at the beginning of the 20th century to –1.0±1.0mw.e. in recent years and down to distinctly less than –4.0±1.4mw.e. at the end of the 21st century (Fig. 8). At the end of the period 1900–2099, GCN will thus have lost an ice volume of 58.7±56.9km³ (Fig. 10).

However, it must be borne in mind that the results obtained overestimate SMB values in the past and underestimate them in the future. The scenario for the 21st century presented in this study should be regarded as the greatest possible glacier change and thus as the very lowest limits of probable future SMB and ice mass evolution of GCN.

Future work will have to include glacier area change in the modelling scheme, in order to include past and probable future changes in the ice-covered area to account for the overestimation of future losses in ice volume. Additionally, different climate forcing aside from scenario A2 will have to be considered for modelling the possible range of future SMB.