Article contents
Aristotle's Unmoved Movers
Published online by Cambridge University Press: 17 July 2017
Extract
According to Aristotle all heavenly movement is ultimately due to the activity of forty-seven (or fifty-five) ‘unmoved movers'. This doctrine is highly remarkable in itself and has exercised an enormous historical influence. It forms part of a world-picture the outlines of which are as follows. The universe consists of concentric spheres, revolving in circles. The outermost of these bears the fixed stars. The other either bear planets or, insofar as they do not, contribute indirectly to the movements of the latter. Each sphere is moved by the one immediately surrounding it, but also possesses a movement of its own, due to its mover, an unmoved, incorporeal being. (It was these beings which the schoolmen designated as the intelligentiae separatae.) The seemingly irregular movements of the planets are thus viewed as resulting from the combination of regular circular revolutions. The earth does not move and occupies the centre of the universe. Such was Aristotle's astronomic system, essential parts of which were almost universally adopted by the Arabic, Jewish, and Christian philosophers of the Middle Ages.
- Type
- Articles
- Information
- Copyright
- Copyright © 1946 by Cosmopolitan Science & Art Service Co., Inc.
References
1 I am indebted to the late Professor H. Gomperz for reading this paper in manuscript, for aiding me in bringing it into its present form, and for contributing by some of his criticisms to its content also.Google Scholar
2 Two further assumptions, however, also formed part of this system: spheres and stars were supposed to consist of ether, and the latter were viewed as living beings. See my paper ‘Ein Simplikios-Zitat bei Pseudo-Alexandros und ein Plotinos-Zitat bei Simplikios,’ in Rheinisches Museum 84 (1935) 154–160 (cf. Duhem, P., Le système du monde IV [Paris 1916] 422–428); my review of Walzer, R., Aristotelis dialogorum fragmenta, in Philologische Wochenschrift 58 (1938) 65–69, and W. K. C. Guthrie in Aristotle, On the Heavens (The Loeb Classical Library, London 1939) xv ff.Google Scholar
3 On the importance of this system see, e.g. P. H. Wicksteed in Aristotle, The Physics (Loeb Class. Libr. London 1929) lxxi; Wicksteed, P. H., The Reactions Between Dogma and Philosophy (London 1920) 33f.Google Scholar
4 1073a 14–1074b 14. In Physics Θ 6 it is hardly more than alluded to.Google Scholar
5 Metaph. A 8, 1074a 31–38.Google Scholar
6 At least according to the rather generally accepted interpretation of Aristotle. But cf. n. 46 infra. Google Scholar
7 Cf. Metaph. N 2, 1088b 14–28.Google Scholar
8 Cf. Jaeger, W., Aristotle (London 1934) 354. Jaeger's solution is as follows: (1) The whole of ch. 8 is a later addition. Originally, the entire book was based on the assumption that there is one unmoved mover only. (2) Later, Aristotle adopted the conception of 47 movers in order to adjust his metaphysics to the views of contemporary science. He thereby involved himself in difficulties from which he was unable to extricate himself, chiefly because a plurality of immaterial movers is inconceivable, according to Aristotelian principles. But the philosopher himself became aware of this impossibility and brooded over it. Section 1074a 31–38 contains his meditations on the problem. It was originally written on a loose ‘sheet’ and was incorporated into the text by the editors of the Metaphysics. The passage flatly contradicts the doctrine of a plurality of movers and is obviously foreign to the context of ch. 8, and is indeed destructive of its argument.—Jaeger's interpretation has been almost universally adopted. Only, it has often been assumed that 1074a 31–38 was not inserted later but presents a remnant of an earlier and more consistently monotheistic phase of Aristotle's development. Cf. Guthrie, W. K. C., ‘The Development of Aristotle's Theology,’ Classical Quarterly 1934, pp. 90–98 and esp. 91 n. 1; Mugnier, R., La théorie de premier moteur et l'évolution de la pensée aristotelicienne (Paris 1930). For criticism see Mansion, A., ‘La genèse de l'oeuvre d'Aristote d'après les travaux recents,’ Revue néo-scolastique de philosophie 1927, pp. 307–341, esp. 338f.; Mansion, A., ‘Autour des éthiques d'Aristote,’ ibid. 1931, pp. 232–234; Paulus, J., ‘La théorie du premier moteur chez Aristote,’ Revue de philosophie 1933, pp. 259–294; 394–424 (with many of whose conclusions I agree—see esp. 414ff.—though his main conclusion, viz. that the First Mover in the Physics means Soul, in the Metaphysics ‘intelligentia separata’, seems to be untenable); Ross, W. D., Aristotle's Physics (Oxford 1936) 94–102. Unavailable to me was Dockx, J., ‘De Theorie von den Onbewogen Beweger bij Aristoteles,’ Tijdschrift voor Philosophie 1 (1939) 747–800.Google Scholar
9 According to Jaeger, Aristotle implicitly assigned three different meanings to the term ‘first philosophy’ in three successive stages of his development. In the first phase, it is conceived as Theology and, as such, as the knowledge of but one, the highest departement of being, this phase being represented best by Metaph. A. In the second stage—that of transition—it means something like metaphysical logic; the knowledge of being as being (Metaph. Γ and E). In the third and final stage (which, however, was never fully and consistently worked out) it means knowledge of the Supersensible based on, and including, that of the Sensible (the latter also being a legitimate object of metaphysics); and it is this final view which underlies the discussion of Metaph. Z, H, Θ (in which εἲδος is conceived as imbedded in matter) and M 1–9 (where a new metaphysical approach is launched).—For criticism see Cherniss, H. F. in The American Journal of Philology 56 (1935) 261–271, esp. 265. It is at any rate metaphysics as theology, whether representing a particular stage or only a particular aspect of Aristotle's philosophy, that we must here consider.Google Scholar
10 It must be emphasized that the question, to what extent Aristotle's account of Plato's philosophy is correct, may be entirely disregarded for the purposes of the following discussion, for we are here concerned solely with Aristotle's self-interpretation by means of his interpretation—right or wrong—of Plato.Google Scholar
11 Metaph. A 6, 987b 14: ἒτι δὲ παρὰ τὰ αἰσθητὰ καὶ τὰ εἲδη τὰ μαθηματικὰ τῶν πραυμάτων εἲναι ϕησὶ (scil. Plato).Google Scholar
12 Metaph. Γ 2, 1004a 2: τοσαῦτα μέρη ϕιλοσοϕίας … ὂσαιπερ αἱ οὐσίαι. Cf. E 1, 1026a 6–20; K7, 1064b 1; De an. I 1, 403b 10; also Jaeger, , op. cit. 216; Ross, W. D., Aristotle's Metaphysics (London 1924) lxxviii. In Phys. B 2, 193b 22–36 and 194b 14 the distinction of these three ‘philosophies’ is likewise presupposed. On the history of this famous trichotomy see Mariétan, J., Problème de la classification des sciences d'Aristote à St.-Thomas (St.-Maurice and Paris 1901) and L. Baur in Dominicus Gundissalinus, De divisione philosophiae (Beiträge zur Geschichte der Philosophie des Mittelalters 4, Münster 1903) 194–204 and 325–397; a modern interpretation of it in Maritain, J., The Degrees of Knowledge (London 1937) 44–46. Cf. also Zeller, E., Die Philosophie der Griechen II 2 (4th ed. Leipzig 1921) 181 n. 3. To the Platonic root of this tripartite division no sufficient attention seems to be paid; I intend to return to this topic and to the question of how ‘degrees of being’ became gradually transformed into ‘degrees of knowledge’. Cf. Phys. B 7, 198a 29 and St. Thomas' commentary ad loc. with n. 24.Google Scholar
12a Metaph. Z 11, 1037a 14; A 1, 1069b 1; M 1, 1076a 9; 9, 1086a 21. Cf. Jaeger, , op. cit. 206f. 220ff.; Ross, W. D., Aristotle (3rd ed. London 1937) 69.Google Scholar
13 Metaph. E 1, 1026a 18; K 1, 1059b 2; 7, 1064b 1.Google Scholar
14 These characteristics they have in common with the objects of mathematics, from which, however, they differ in so far as there can be many mathematical objects (e.g. similar triangles) in one and the same class, whereas only one Form corresponds to any entire class. Metaph. A 6, 987b 16; B 6, 1002b 14.Google Scholar
15 Metaph. E 1, 1026a 10; K 7, 1064a 33.Google Scholar
16 Metaph. A 992b 15; B 1, 995b 16; 2, 997b 1 and 12; 998a 7; 6, 1002b 12 (particularly remarkable because Aristotle—ex hypothesi—supports the theory of Forms by arguments of his own); Z 2, 1028b 20; H 1, 1042a 11 and 22; K 1, 1059a 38; A 1, 1069a 33; M 1, 1076a 8; 6, 1080b 11; 9, 1086a 11 and 26.Google Scholar
17 Metaph. Z 2, 1028b 19; M 1, 1076a 21.Google Scholar
18 Metaph. K 1, 1059b 2 and 13; M 2, 1077b 23; N 3, 1090a 29.Google Scholar
19 Metaph. A 1, 1069a 33; cf. 6, 1071b 3.Google Scholar
20 Xenocr. fr. 5 Heinze and pp. 3ff. and 75 Heinze. Cf. Ross, , Arist. Metaph. lxxv n. 2; also Theophrastus', Metaphysics ed. Ross, and Fobes, (London 1929) 56f. Incidentally, it is worth noting that it is, virtually, impossible to tell whether in Rep. VI 13, 500c, Plato is speaking of ideas or else of celestial bodies. Cf. Arist. Metaph. K 6, 1063a 16; Γ 5, 1009a 30 and 1010a 30; Cherniss, H., Aristotle's Criticism of Plato and the Academy I (Baltimore 1944) 199 n. 117.Google Scholar
21 The expression ἐν τῷ οὐρανῷ for αἰσθητά occurs in Aristotle, e.g. Metaph. B 2, 997b 7; cf. A 8, 990a 5; De caelo I 9, 278b 19–21.Google Scholar
22 That the Sensible can be an object of ‘philosophy’, therefore true knowledge, seems to be a doctrine peculiar to Aristotle. But see Solmsen, F., Plato's Theology (Ithaca 1942) 82f.Google Scholar
23 Cf. Joachim, H. H. in his edition of Aristotle's, De gen. et corr. (Oxford 1922) xix and xxii; Ross, , Aristotle 3 70; Metaph. A 8, 989b 34; E 1, 1026a 27.Google Scholar
24 In Phys. B 7, 198a 29 we read: διό τρεῖς αἱ πραγματεῖαι, and expect to find physics, mathematics, theology, but find actually 17 ἡ μὲν περὶ ἀκινήτων, ἡ δὲ περὶ κινουμὲνων μὲν ἀϕθάρτων δὲ, ἡ δὲ περὶ τὰ ϕθαρτά. The second division obviously designates astronomy. Cf. n. 12 i.f.Google Scholar
25 Metaph. A 6, 987b 23; 9, 991b 9 and 22; A 8, 1073a 18; M 6, 1080b 13; 7, 1081a 7; 8, 1083a 18; 9, 1086a 5 and 12; N 3, 1090a 17; 4, 1092a 8.—For all problems referring to the identification of Ideas and Numbers cf. Ross. Arist. Metaph. lxiv ff.; Becker, O., ‘Die diairetische Erzeugung der Platonischen Idealzahlen,’ Quellen und Studien …, Abt. B I (1931), 464–501.—Shorey, P. (e.g. in Plato, , The Republic, Loeb Class. Libr. II, pp. xx and 164f.) denies emphatically the existence of such a doctrine in Plato's writings and is obviously very much inclined to deny its existence in Plato's teachings at all. The motive seems to be his conviction that both the identification of Ideas with Numbers and the distinction of ideal from mathematical numbers are ‘silly’ and could be maintained only by ‘uncritical students of the Academy’. Shorey's attitude towards Aristotle's reports on Plato reminds one of Natorp. At any rate, for our present purposes, the historic correctness of Aristotle's report is of no importance. Cf. now also Cherniss, H., The Riddle of the Early Academy (Berkeley-Los Angeles 1945) 17–30; 60.Google Scholar
26 Cf. Metaph. M 8, 1084a 12; Phys. Γ 6, 206b 32.Google Scholar
27 Metaph. A 8, 1073a 14–22. Cf. Ross, , Arist. Metaph. lxix f.; Jaeger, , op. cit. 220 n. 3.Google Scholar
28 This explains why as early as ch. 6 (1071b 21) a plurality of eternal οὐσίαι is assumed as a matter of course. Cf. n. 53 infra and Cherniss, , Aristotle's Criticism I 220; 458 n. 406.Google Scholar
29 Metaph. A 8, 989b 23.Google Scholar
30 Metaph. Γ 8, 1017b 10; Z 2, 1028b 8; H 1, 1042a 8.Google Scholar
31 Metaph. A 8, 989b 24; B 1, 995b 11–18; 2, 997a 15–18; 34; 997b 1; Γ 2, 1004a 4; 3, 1005b 1; 5, 1009a 38; E 1, 1026a 28–30; B 2, 1028b 10; 21–34; 11, 1037a 11–17; H 1, 1042a 5–13; K 1, 1059a 27; 1059b 1–2; 7, 1064a 35; 1064b 10–14; A 1, 1069a 30–1069b 2; 6, 1071b 4; 10, 1075b 38; M 1, 1076a 17–24; 9, 1086a 24; N 1, 1087a 29. Cherniss, , op. cit. 364, suggests ‘reality’.Google Scholar
32 The use of this term was suggested to me by the late Prof. Gomperz.Google Scholar
33 Cf. Lagrange, J., ‘Comment s'est transformée la pensée religieuse d' Aristote,’ Revue thomiste 1926, pp. 285–329, esp. 310ff.Google Scholar
34 It has been repeated so often how great an artist Plato was when compared with Aristotle that I beg leave to call to mind that even as a myth the Timaeus is often ugly or almost ridiculous. Suffice it to mention the little pegs used by the gods in order to keep man together (43a).Google Scholar
35 Cf. Guthrie, , Class. Quart. 1934, pp. 92 and 98.Google Scholar
36 Cf. Frank, E., Plato und die sogenannten Pythagoreer (Halle 1923) 133f.Google Scholar
37 Plato's, Ideal Numbers do not lack matter altogether; the Great-and-Small function as such. Cf. Metaph. A 6, 987b 21 and 35; N 1, 1087b 7; cf. 2, 1088b 20. But this is evidently not matter as a principium individuationis. It would be absurd to maintain that the Great-and-Small, i.e. the Indefinite Quantity which is turned into a definite Quantity by the number Two was another Great-and-Small than that to which definiteness is imparted by the number Three.Google Scholar
38 Metaph. M 6, 1080a 17; 8, 1083a 34; cf. Robin, L., La théorie platonicienne des Idées et des Nombres d' après Aristote (Paris 1908) 289; Ross, , Arist. Metaph. p. liii and II 427.Google Scholar
39 On this explanation see Ross, , op. cit. cxix and cxxxix. Actually, it is not specifically Thomistic since it was already known to Albertus Magnus: Metaph. XI, II, 10: ‘coelestes … circuli habent animas sed praeter animas sunt intelligentiae separatae et has intelligentias Angelos vocant …’; XI, II, 28: ‘omnes substantiae separatae differunt ab invicem specie … Sicut loco sphaerarum una est superior altera, ita etiam dignitate una substantia differt ab altera.’ But his own opinion expressed in Summa theol. II, II, q. 7 reads: ‘frivolum est dicere quod intelligentia movens aliquid corporum coelestium sit Angelus.’—The subjects of Albertus' vocant are, of course, philosophers like Avicenna, Averroës, Maimonides (on whose interpretation of the unmoved movers see Wolfson, H. A., Crescas' Critique of Aristotle [Cambridge 1929] 108f. 666f.). On the whole question of angelology cf. Cl. Baeumker, , Witelo (Münster 1908) 523–606, esp. 537 and 545; Wicksteed, , The Reactions (n. 3 supra) 73–86; Sharp, D. E., Franciscan Philosophy at Oxford in the Thirteenth Century (London 1930) 263f. Both doctrines (movers are angels differing from one another specifically) are in al-Farabi: see Madkour, I., La place d'al Fârâbî dans l'école philosophique musulmane (Paris 1934) 82, 84, 85 n. 2, 88, 98; Alfārābis philosophische Abhandlungen übers. von Fr. Dieterici (Leiden 1892) 98; Horten, M., Das Buch der Ringsteine Farabis (Münster 1906), 200f.; Duhem, , op. cit. (n. 2 supra) IV 442.Google Scholar
40 See e.g. Summa theol. I 50, 3–4: ‘proprius effectus separatarum substantiarum videtur esse motus corporum coelestium … Si ergo angeli non sunt compositi ex materia et forma … sequitur quod impossibile sit esse duos angelos unius speciei … Magis et minus … secundum quod causantur ex formis diversarum graduum … diversificant speciem … et hoc modo angeli diversificantur secundum magis et minus.’ De subst. sep. 2 (I 76 Mand.): ‘… sunt intellectuales substantiae coelestibus corporibus unitae. Harum autem numerum Aristoteles investigare conatur secundum numerum coelestium corporum.’ Op. cit. 6 (I 93 Mand.): ‘… invenitur in formis diversitas secundum quemdam ordinem perfectionis et imperfectionis.’ De nat. mat. c. 3 (V 201 Mand.): ‘… in eis (scil. formis separatis) tot sunt species quot sunt individua.’ De ente et essentia c. 5 (I 156f. Mand.): ‘non oportet quod inveniantur plura individua unius speciei in illis (scil. sine materia) substantiis: sed quot-quot sunt individua tot sunt species ut Avicenna dicit expresse.’ Cf. Duhem, , op. cit. V (Paris 1917) 539–559; Syrianus in Metaph. B 1, 996a 1 (9, 30 Kroll).—For the relation between stars and angels cf. also Stimson, D., The Gradual Acceptance of the Copernican Theory of the Universe (New York 1917) 18 n. 2, quoting Philastrius, , De haer. c. 133 (PL 12, 1265A) and Fabricius' note ad loc. reprinted in Migne; also Scotus, Ioannes, De div. nat. II 23 (PL 122, 574B).Google Scholar
41 Cf. Ross, , Arist. Metaph. cxl; Metaph. Δ 28,1024b 8; Z 12,1038a 6; I 8, 1058a 23; Cherniss, , op. cit. (n. 20 supra) 174 n. 98.Google Scholar
42 Metaph. B 3, 999a 6; Eth. Nic. A 6, 1096a 17; Eth. Eud. A 8, 1218a 1; Pol. Γ 1, 1275a 34; De an. B 3, 414b 21. See also Ross, , op. cit. I 237 and (on the significance of the doctrine for Plato) Gomperz, H., ‘Plato's Parmenides,’ The Personalist 1941, p. 258 n. 7. In a passage like Metaph. Δ 28, 1024a 36, where ἐπίπεδθν and στερεόν are termed γὲνος in relation to the different ἐπίπεδα and σπερεά Aristotle seems to think of qualitative differences (rectilinear, curvilinear) as forming the differentiae specificae .Google Scholar
43 Metaph. Δ 11, 1019a 1. Cf. Phys. Θ 7, 260b 18 and Robin, , op. cit. (n. 38 supra) 612–626.Google Scholar
44 Metaph. A 8, 1073b 1: ὅτι μὲν οὒν εἰσὶν οὐσίαι (scil. the unmoved movers) καὶ τούτων τὶς πρώτη καὶ δευτὲρα κατὰ τὴν αὐτὴν τάξιν ταῖς ϕοραῖς τῶν ἂστρων, ϕανερόν .Google Scholar
45 Do species ordered hierarchically form a genus?—this is one of the crucial questions in Adler, M. J., Problems for Thomists (New York 1940), and in his ‘Solution of the Problem of Species,’ The Thomist 3 (1941) 279–379 (available to me through courtesy of the author). It would seem that by raising this question, Adler unwittingly revives the problem underlying the logical views of Plato and Aristotle discussed above.Google Scholar
46 It seems that this interpretation is akin to that given by Thomas Aquinas and Ps. Duns Scotus. The latter writes in his commentary on Aristotle's Metaphysics (XII, II, c. V); 'Posset enim forsan aliquis dicere, quod sunt plures alii mundi, in quorum quolibet sunt plures, et tot sphaerae et motus, sicut et in isto et ideo oportet ponere plures immateriales substantias. Hoc ergo excludens dicit: “Quod autem sit unum coelum tantum manifestum est. Si enim essent plures coeli”, supple numero et in eadem specie, “ut” sunt plures “homines”, sequitur quod “principium”, supple primum et immobile, quod esset “circa unumquodque” primum coelum, fieret “unum specie, numero vero multa”, ita quod essent plura prima principia secundum numerum communicantia in una specie, quod ostendit esse impossibile dicens: “Sed quaecunque sunt multa numero”, et supple unum specie, “habent materiam”. … ‘St. Thomas’ commentary ad loc. (2593–5 Catala2) is almost identical; an additional note in Ps. Duns Scotus is, therefore, all the more interesting: Aliqui pervertentes sensum literae, he says, maintain based on this Aristotelian passage that matter is causa individuationis. The aliqui refers, of course, to St. Thomas and the note is another contribution to the controversy matter vs. haecceitas as the principle of individuation. Cf. Duns Scotus in his commentary in II sent. dist. 3, q. 7; also Sharp, , op. cit. (n. 39) 380f.Google Scholar
47 From the viewpoint of context, likewise the passage 1074a 31–38 connects smoothly and unobjectionably with what precedes: τὲλος … πάσης ϕορᾶς τῶν ϕερομένων τι θείων σωμάτων κατὰ τὸν οὐρανόν. ὅτι δὲ εἲς οὐρανός, ϕανερόν .Google Scholar
48 It is highly significant that this criticism of traditional mythology takes exception at its anthropomorphism, but not at all at its polytheism. Even St. Thomas ad loc. (2597 Catala2) seems to be not quite sure of Aristotle's monotheism.Google Scholar
49 Apart, of course, from the well known error committed by Aristotle in reckoning the number of the spheres.Google Scholar
60 On the whole solution, cf. Arnim, H. v., ‘Die Entstehung der Gotteslehre des Aristoteles,’ Sitzungsberichte der Akademie der Wissenschaften in Wien, Phil.-hist. Klasse 212 (1931) 72ff. Arnim's objections against an interpretation that would resemble the one given in this paper are hardly convincing.Google Scholar
51 Ἐπεὶ δ' ἢσαν τρεῖς οὐσίαι, δύο μὲν αἱ ϕυσικαί, μία δ' ἡ ἀκίνητος, περὶ ταύτης λεκτέον ὅτι ἀνάγκη εἲναι ἀΐδιόν τινα οὒσίαν ἀκίνητον. Because ούσίαι πρῶται τῶν ὄντων, καὶ εἰ πᾶσαι ϕθαρταί, πάντα ϕθαρτά. But ἀδύνατον κίνησιν … ϕθαρῆναι (up to this point Aristotle has proved that an eternal entity must exist). Furthermore οὐδὲν ὄϕελος … ἐὰν οὐσίας ποιήσωμεν ἀϊδίους, ὥσπερ οἱ τὰ εἴδη, εἰ μή τις δυναμένη ἐνέσται ὰρχὴ μεταεάλλειν … Οὐ τοίνυν ούδ' αὕτη (scil. οὐσία = εἴδη) ἱκανή, οὐδ' ἄλλη οὐσία (e.g. the mathematical) παρὰ τὰ εἴδη … εἰ μὴ ἐνεργήσει … Ἔτι οὐδ' εἰ ἐνεργήσει, ἡ δ' οὐσία (essence) αὐτῆς (of the eternal entity searched for) δύναμις. Δεῖ ἄρα εἴναι ἀρχὴν τοιαύτην ἤς ἡ οὐσία (essence) ἐνέργεια .Google Scholar
52
ἔτι τοίνυν ταύτας δεῖ τὰς οὐσίας (plural !) ![]() (cf. Ross' apparatus) ἄρα. Cf. n. 53.Google Scholar
(cf. Ross' apparatus) ἄρα. Cf. n. 53.Google Scholar
52a What is the ἄλλη οὐσία παρὰ τὰ εἴδη? The soul? Mathematical? On this problem. see Cherniss, , op. cit. 391 n. 311. To me, the plural οὐσίας in 1071b 21 seems to prove that the latter are meant.Google Scholar
53 Such a plurality seems to be envisaged (at least as possible) also in Δ 5, 1015b 14, and, particularly, in E 1, 1026a 16: Theology deals with χωριστὰ καὶ ἀκίνητα and ἀΐδια (plural !) and ταῦτα … αἴτια τοῖς ϕανεροῖς τῶν θείων (heavenly bodies). In order to maintain his ‘monotheistic’ interpretation, Arnim (op. cit. 59) is compelled to declare the whole sentence from Ἐνέργειαι ἄρα (cf. n. 52) spurious. Cf. v. Arnim, , ‘Eudemische Ethik und Metaphysik,’ Sitzungsber. Akad. Wien, Phil.-hist. Kl. 207 (1928) 36; Jaeger, , op. cit. 217; Cherniss, , op. cit. 593–95.Google Scholar
54 Ross, , op. cit. II 371. If this interpretation is correct, the passage would seem to imply that Aristotle recognized at least two different principles of motion: one responsible for the movement of the First Heaven, the other for the movement of the sun. It may be worth while to note that Plato's distinction between two types of motion (Tim. 36c)—one characterized by Sameness and related to the motion of the outermost heaven, the other characterized by Otherness and referred to the motion of the planets—forms a remarkable counterpart to Aristotle's words. Another explanation of the Aristotelian passage is to be found in v. Arnim, , ‘Die Entstehung …’ 59–62; ‘Eudemische Ethik …’ 43–47.Google Scholar
55 De caelo I 9, 279a 18 (Oxford translation, slightly modified).Google Scholar
56 Eth. Nic. X 8, 1178b 7 (Oxford translation). Here, where ‘God’ and ‘gods’ alternate, nothing indicates that Aristotle was less enthusiastic about the life of many than about the contemplative life of the one God.Google Scholar
57 The words ἀμερὴς καὶ ἀδιαίρετος (1073a 6) certainly do not imply this in any way. When someone contends that ‘the soul’ is essentially simple and indivisible he does not mean to imply that there is but one soul in existence. His meaning is that these properties may be predicated of any and every soul. And in the same way the contention that the ‘unmoved entity’ is without parts and indivisible is far from implying any assertion regarding the number of such entities (Prof. Gomperz' remark).Google Scholar
58 Blass, F.—it may be worth noting—in ‘Aristotelisches,’ Rheinisches Museum 30 (1875) 481ff. esp. 486f. and 493, maintained, indeed, that the entire section 1073a 3–1074b 14 was a later addition, inserted by Aristotle himself, but originally forming part of another dissertation. Thus, the οὀτοι in 1074b 3 had a definite reference in its original context whereas it now seems to float in the air. In addition, however, the inserted section was itself interrupted by another insertion: 1073b 38–1074a 38 (the section correcting Eudoxus' figures). Blass based his theory on his observation of hiatus. There is no hiatus in 1073a 3-b 38 whereas they abound in 1073b 38–1074a 38, to disappear again in 1074a 38-b 14. Now, even according to this theory, the ‘monotheistic’ passage 1074a 31–38 would have formed part of the larger section 1073a 3–1074b 14 before this was incorporated with Metaph. A and consequently could not have been written for the purpose of criticizing the plurality of movers. But even if it could be proved that it is, after all, a later addition, it could only have been inserted for the purpose of supplementing and completing the proof that the number of unmoved movers cannot be greater than 47 or 55—a proof which otherwise would have remained incomplete.Google Scholar
59 πρῶτον applies equally well to one mover and to several; the point is merely that the First cannot arise from contraries.Google Scholar
60 Εἰ δ' ἔσται τὰ εἴδη ἢ (or explicativum) ἀριθμοί mss. omnes Εἰ δ' ἔσται τὰ εἴδη ἢ (or explicativum) ἀριθμοί mss. omnes .Google Scholar
61 Criticisms 3, 4, 5, 6, 7, 8, 10, 11, 16, 18 refer partly to non-Platonic views, partly to Platonic (not just Plato's) doctrines having but little to do with the present investigation.Google Scholar
62 On this ἀναγωγή see e.g. Metaph. Γ 2, 1004b 33; K 2, 1061a 10.Google Scholar
63
Metaph. A 4, 1070a 31; 1070b 9–22; 26–30; 5, 1071a 3–11; 19–24 (principles common per analogiam). The further case of common principles (what is principle of an ![]() is also principle of its accidents): 5, 1070b 36–1071a 3; 1071a 34.Google Scholar
is also principle of its accidents): 5, 1070b 36–1071a 3; 1071a 34.Google Scholar
64 Metaph. A 4, 1070b 34f.; 5, 1071a 36.Google Scholar
65 Metaph. A 10, 1075b 22; N 2, 1088b 14–28.Google Scholar
66 Cf. Metaph. B 1, 995b 8; Γ 2, 1003b 17.Google Scholar
67 Metaph. A 1, 982b 9.Google Scholar
68 Metaph. A 8, 982b 24–990a 7. Cf. n. 11 supra .Google Scholar
69 Metaph. A 6, 987b 18f.Google Scholar
70 On the equation, elements = principles = causes, see Diels, H., Elementum (Leipzig 1899) 22, 31, 34f. On the difference see Metaph. Λ 4, 1070b 22: every στοιχεῖον is ἀρχή and αἴτών, but, since it is always an immanent ἀρχή or αἴτιον (an ἐνυπάρχον), the στοιχεῖον can never be an ἀρχή or αἴτιον in the sense of a κινοῦν. Δ 1, 1013a 21 and b 18 and Δ c. 3 are irrelevant in the present context. Plato's contraries, i.e. the Great-and-Small, are described not only as στοιχεῖα but also as ἀρχαί and αἴτια; Metaph. A 9, 992b 18–993a 10; A 4, 1070a 34; 1070b 1–35; 5, 1071a 24 and 30; M 9, 1086a 28; 10, 1086b 20; N 2, 1088b 15; 28f.; 34; N 4, 1091a 31; b 3; 21; 24; 31; 1092a 7.Google Scholar
71 Metaph. A 6, 987b 14–988a 15. Plato παρὰ τὰ αἰσθητὰ καὶ τὰ εἴδη τὰ μαθηματικὰ τῶν πραγμάτων εἶναί ϕησι μεταξύ … Ἐπεὶ δ' αἲτια τὰ εἲδη τοῖς ἄλλοις, τἀκείνων στοιχεῖα πάντων ὠῄθη τῶν ὄντων εἶναι στοιχεῖα. Ὡς μὲν οὖν ὕλην τὸ μέγα καὶ τὸ μικρὸν εἶναι ἀρχάς, ὡς δ' οὐσίαν τὸ ἕν … Ἔτι … τὴν τοῦ εὖ καὶ κακῶς αἰτίαν τοῖς στοιχεῖοις ἀπέδωκεν. Cf. A 9, 992a 10 (οὐσίας ἀνάγειν εἰς τάς ἀρχάς); B 1, 996a 2; B 4, 100a 5 and 20.Google Scholar
72 E.g. all the arguments assailing the recognition of subsistent forms and/or mathematical objects lack significance in the present context and so do those that refer to the issue whether the principles (elements, causes) of the forms are concrete or general. For the relation between A and N cf. Jaeger, , op. cit . 223ff.Google Scholar
73 Why just these two are named will be seen below.Google Scholar
74 Metaph. N 1, 1087a 29-b 4 (cf. supra p. 19, criticism 1).Google Scholar
75 Metaph N 1, 1087b 4–33 (cf. criticism 2).Google Scholar
76 Metaph. N 1, 1087b 33–1088a 8.Google Scholar
77 Metaph. N 2, 1088b 14–28 (cf. criticism 19).Google Scholar
78 Cf. criticisms 10 and 11, and Phys. A 3, 187a 7.Google Scholar
79 Metaph. N 2, 1088b 35–1089a 6. Cf. criticisms 10 and 11.Google Scholar
79a Metaph. N 2, 1089a 7.Google Scholar
80 Metaph. N 2, 1090a 4–15 (οὐθενὸς … οὔτε ϕησὶν ὁ λέγων αὐτὸν [scil. μαθηματικὸν ἀριθμόν] <αἴτιον with Jaeger> εἶναι).+εἶναι).>Google Scholar
81 Metaph. N 3, 1090a 25–28.Google Scholar
82 Metaph. N 3, 1090b 16–20 (cf. supra, criticism 21). A comparison of this passage with Z 2, 1028b 21 and A 10, 1076a 1 makes it clear that it is Speusippus who is assailed in the three passages. On Speusippus' spheres of being see Frank, , op. cit. (n. 36 supra) 245–261.Google Scholar
83 Cf. Metaph. A 9, 991b 29; N 3, 1090b 30–32.Google Scholar
84 Cf. Metaph. M 9, 1085a 9–14; 31–35; N 3, 1090b 37. In the realm of spatial magnitudes the Long-and-Short, the Broad-and-Narrow, and the High-and-Low represent specific forms of the Great-and-Small; the One, in this realm, is represented by the point.Google Scholar
85 Metaph. N 3, 1090b 32–1091a 5.Google Scholar
86 Metaph. M 1, 1076a 19; 9, 1086a 26; N 1, 1087a 30; 2, 1090a 4–3, 1090a 19; 3, 1090b 20.Google Scholar
87 Metaph. M 9, 1086a 26.Google Scholar
88 Metaph. N 2, 1088b 14.Google Scholar
89 Duhem, , op. cit. V 355. Albert the Great and Henry of Ghent, at any rate, saw Aristotle's polytheism clearly; see Talamo, S., L'aristotelismo della scolastica (3rd ed. Siena 1881) 162ff.; cf. Boehner, Ph., ‘Der Aristotelismus im Mittelalter,’ Franziskanische Studien 22 (1935) 338–347, esp. 340 n. 4. Ps. Duns Scotus, in his commentary in Metaph. (loc. cit.), says: ‘Philosophus videtur aperte consentire opinioni, quae dicebat omnes substantias immateriales esse Deos …’ For St. Thomas see n. 48 supra .Google Scholar
90 Duhem, , op. cit. V 548.Google Scholar
90a Cf. De gen. et. corr. II 10, 337a 20–22.Google Scholar
91 Cf. Renan, E., Averroës et l'Averroisme (4th ed. Paris 1882) 118.Google Scholar
92 And in this respect his position seems but to reflect the general attitude of the Greek mind. I am indebted to Prof. Gomperz for the following quotation from Meyer, E., Geschichte des Altertums II (Stuttgart 1893) 769: ‘In Griechenland spielt die Frage bezüglich eines oder mehrerer Götter kaum irgend eine Rolle. Ob die göttliche Macht als eine Einheit oder Mehrheit gedacht wird, ist belanglos im Vergleiche zu der Frage, ob sie überhaupt existiert und wie ihre Natur und Beziehung zur Welt verstanden werden muss.’ Exceptions are, of course, always possible. One of them is represented by Philodemus, who (De pietate 17–19, pp. 84–86 Gomp.) maintains that monotheism is godless and only the polytheistic view really pious. Much later Celsus (Orig. c. Celsum VIII 11; 25) will assail the godlessness of the Jewish monotheism. It has been said by W. Jaeger (‘Greeks and Jews,’ The Journal of Religion 18 [1938] 127–143) that Hecataeus of Abdera, the first Greek author to mention the Jews, must have been attracted by their monotheism; and that Theophrastus must have appreciated the Jews as a philosophic nation because of their monotheism. But even if we do not assume with Bidez, J. and Cumont, F., Les mages hellenisés (Paris 1938) 240–242, that Hecataeus, indebted to Democritus or Leucippus, was entirely an esprit libre, we must allow the possibility that he was, perhaps, more shocked than attracted by Jewish monotheism. For the Mosaic ἀπάνθρωπος and μισόζενος way of living (FGrHist. 1 F 6) he has but little sympathy.Google Scholar
93 Phys. Θ 6, 259a 6–20.Google Scholar
94 Fr. 80 Mullach (p. 105, 5 Spengel) : δείξς πρώτων, ὅτι ἔστι κίνησις ἀεί … εἶτα ἐϕεξῆς, δείξας, ὅτι τὸ πρώτως κινοῦν “καθ' ἑκάστην κίνησιν”, ὡς ὁ Eὔδημος προστίθησιν, άκίνητον εἶναι χρὴ καὶ καθ' αὑτὸ καὶ κατὰ συμβεβηκός… Google Scholar
95 Μία in passages like 259a 19 obviously means μία καὶ ἡ αὐτή (one and the same), not ‘the only one’. Cf. Phys. 9 7, 260a 26.Google Scholar
96 Op. cit. 357–367.Google Scholar
97 Phys. Θ 6, 259b 25: ἀκίνητον καὶ [μὴ] κατά συμβεβηκός. Google Scholar
98 Cf. Guthrie, , ‘The Development’ (n. 8 supra) p. 91 n.: ‘In so far as the possibility of more than one unmoved mover has occurred to Aristotle [scil. in Phys. Θ 6], it has presented itself in the form of a succession of movers, not a coexistent plurality like that described in Metaph. A. The argument for unity which is based on the continuity of motion could only be valid against the conception of a series of movers succeeding one another in time …’ Google Scholar
99
For the sake of convenience I shall quote the decisive passages of that chapter, including between double brackets the words that are, according to Jaeger, a later insertion: 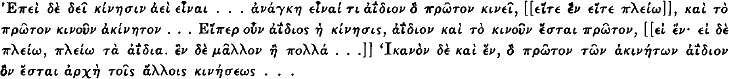 Google Scholar
Google Scholar

The following describes souls as (relatively) unmoved movers; they are moved κατὰ συμβεβηκός. Accordingly, the movement of their bodies is discontinuous. But: Eἴπερ ἀνάγκη συνεχῶς εἶναι κίνησιν, εἶναί τι δεῖ τὸ πρῶτον κινοῦν ἀκίνητον, καὶ [μὴ] κατὰ συμβεβηκός … [[Οὐκ ἔστι δὲ τὸ αὐτὸ τὸ κινεῖσθαι κατὰ συμβεβηκὸς ὑϕ' αὑτοῦ, καὶ ὑϕ' ἑτέρου. τὸ μὲν γάρ ὑϕ' ἑτέρου ὑπάρχει καὶ τῶν ὐν οὐρανῷ ἐνίαις ἀρχαῖς, ὅσα πλείους ϕέρεται ϕοράς, θάτερον δέ τοῖς ϕθαρτοῖς μόνον.]] According to Ross, , Physics 102. only the last passage is a later addition.Google Scholar
100 To the writer it has been a profound satisfaction to find that his evaluation of Aristotle's alleged monotheism, though based exclusively oil philological considerations, is in complete agreement with the view expressed by Gilson, É., L'esprit de la philosophie médiévale I (Paris 1932), esp. pp. 48f. 53, 226 n. 6, and 230 n. 13. Gilson shows convincingly that it would be idle to look for explicit monotheism in Aristotle and that his theology represents, at best, a semi-conscious step in the direction of this doctrine. de Corte, M., ‘La définition aristotélicienne de l' âme,’ Revue thomiste 1939, pp. 460–508, advocates a solution more or less like that propounded by Zeller: movers are souls and, hence, differ necessarily from the first mover who is not a soul. Is this not an interpretation presupposing rather than proving Aristotle's monotheism? Google Scholar
101 On Plato's monotheism see Ross, , Arist. Physics 100f.; Cornford, F. M., ‘The “Polytheism” of Plato,’ Mind 47 (1938) 321–330; Taylor, A. E., ‘The “Polytheism” of Plato,’ ibid. 180–199; Solmsen, , op. cit. (n. 22) 70.Google Scholar
102 It is worth noting that Hack, R. K., God in Greek Philosophy to the Time of Plato (Princeton 1931), esp. p. 149, also arrived at the concept of an un-anthropomorphic polytheism.Google Scholar
103 Two attempts at linking Aristotle's political to his theological theories should be mentioned: Peterson, Erik, Der Monotheismus als politisches Problem (Leipzig 1935) 14f.; Kelsen, Hans, ‘The Philosophy of Aristotle and the Hellenic-Macedonian Policy,’ International Journal of Ethics 47 (1937) 1–64.Google Scholar
- 7
- Cited by


