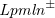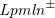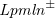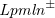1 Introduction
Answer set programming (ASP) (Reference LifschitzLifschitz (2002)) offers a rich knowledge representation language along with a powerful solving technology. While the paradigm has developed further, several probabilisitic extensions of ASP have been proposed, among them Lpmln (Reference Lee and WangLee and Wang, 2016), ProbLog (Reference Raedt, Kimmig and ToivonenRaedt et al., 2007), and P-log (Reference Baral, Gelfond and RushtonBaral et al., 2009).
In this work, we present an extension of the ASP system clingo, called plingo, which features various probabilistic reasoning modes. Plingo is centered on
![]() $\textit{Lpmln}^{\pm }$
, a simple variant of the probabilistic language Lpmln, which is based upon a weighted scheme from Markov logic (Reference Richardson and DomingosRichardson and Domingos, 2006). Lpmln has already proven to be useful in several settings (Reference Lee and WangLee and Wang, 2018; Reference Ahmadi, Lee, Papotti and SaeedAhmadi et al., 2019) and it serves us also as a middle-ground formalism connecting to other probabilistic modeling languages. We rely on translations from ProbLog and P-log to Lpmln (Reference Lee and WangLee and Wang, 2016; Reference Lee and YangLee and Yang, 2017), respectively, to capture these approaches as well. In fact, Lpmln has already been implemented in the system lpmln2asp (Reference Lee, Talsania and WangLee et al., 2017) by mapping Lpmln-based reasoning into reasoning modes in clingo (viz., optimization and enumeration of stable models). As such, the core of plingo can be seen as a re-implementation of lpmln2asp that is well integrated with clingo by using its multi-shot and theory reasoning functionalities.
$\textit{Lpmln}^{\pm }$
, a simple variant of the probabilistic language Lpmln, which is based upon a weighted scheme from Markov logic (Reference Richardson and DomingosRichardson and Domingos, 2006). Lpmln has already proven to be useful in several settings (Reference Lee and WangLee and Wang, 2018; Reference Ahmadi, Lee, Papotti and SaeedAhmadi et al., 2019) and it serves us also as a middle-ground formalism connecting to other probabilistic modeling languages. We rely on translations from ProbLog and P-log to Lpmln (Reference Lee and WangLee and Wang, 2016; Reference Lee and YangLee and Yang, 2017), respectively, to capture these approaches as well. In fact, Lpmln has already been implemented in the system lpmln2asp (Reference Lee, Talsania and WangLee et al., 2017) by mapping Lpmln-based reasoning into reasoning modes in clingo (viz., optimization and enumeration of stable models). As such, the core of plingo can be seen as a re-implementation of lpmln2asp that is well integrated with clingo by using its multi-shot and theory reasoning functionalities.
In more detail, the language
![]() $\textit{Lpmln}^{\pm }$
constitutes a subset of Lpmln restricting the form of weight rules while being extended with ASP’s regular weak constraints. This restriction allows us to partition logic programs into two independent parts: a hard part generating optimal stable models and a soft part determining the probabilities of these optimal stable models. Arguably, this separation yields a simpler semantics that leads in turn to an easier way of modeling probabilistic logic programs. Nonetheless, it turns out that this variant is still general enough to capture full Lpmln.
$\textit{Lpmln}^{\pm }$
constitutes a subset of Lpmln restricting the form of weight rules while being extended with ASP’s regular weak constraints. This restriction allows us to partition logic programs into two independent parts: a hard part generating optimal stable models and a soft part determining the probabilities of these optimal stable models. Arguably, this separation yields a simpler semantics that leads in turn to an easier way of modeling probabilistic logic programs. Nonetheless, it turns out that this variant is still general enough to capture full Lpmln.
The system plingo implements the language
![]() $\textit{Lpmln}^{\pm }$
within the input language of clingo. The idea is to describe the hard part in terms of normal rules and weak constraints at priority levels different from
$\textit{Lpmln}^{\pm }$
within the input language of clingo. The idea is to describe the hard part in terms of normal rules and weak constraints at priority levels different from
![]() $0$
and the soft part via weak constraints at priority level
$0$
and the soft part via weak constraints at priority level
![]() $0$
. This fits well with the semantics of clingo, which considers higher priority levels more important. On top of this, plingo offers three alternative frontends for Lpmln, P-log, and ProbLog, respectively, featuring dedicated language constructs that are in turn translated into the format described above. The frontends rely on the translations from ProbLog and P-log to Lpmln from Reference Lee and WangLee and Wang (2016) and Reference Lee and YangLee and Yang (2017), respectively, and on our translation from Lpmln to
$0$
. This fits well with the semantics of clingo, which considers higher priority levels more important. On top of this, plingo offers three alternative frontends for Lpmln, P-log, and ProbLog, respectively, featuring dedicated language constructs that are in turn translated into the format described above. The frontends rely on the translations from ProbLog and P-log to Lpmln from Reference Lee and WangLee and Wang (2016) and Reference Lee and YangLee and Yang (2017), respectively, and on our translation from Lpmln to
![]() $\textit{Lpmln}^{\pm }$
. For solving, the basic algorithm of plingo follows the approach of lpmln2asp by reducing probabilistic reasoning to clingo’s regular optimization and enumeration modes. This is complemented by two additional solving methods. The first is an approximation algorithm that calculates probabilities using only the most probable
$\textit{Lpmln}^{\pm }$
. For solving, the basic algorithm of plingo follows the approach of lpmln2asp by reducing probabilistic reasoning to clingo’s regular optimization and enumeration modes. This is complemented by two additional solving methods. The first is an approximation algorithm that calculates probabilities using only the most probable
![]() $k$
stable models given an input parameter
$k$
stable models given an input parameter
![]() $k$
. This algorithm takes advantage of a new improved implementation of the task of ASEO (Reference Pajunen and JanhunenPajunen and Janhunen (2021)). The second method is based on a novel translation from
$k$
. This algorithm takes advantage of a new improved implementation of the task of ASEO (Reference Pajunen and JanhunenPajunen and Janhunen (2021)). The second method is based on a novel translation from
![]() $\textit{Lpmln}^{\pm }$
to ProbLog, which we introduce in this paper. The method translates the input program into a ProbLog program and then runs the system problog 2.2 (Reference Fierens, den Broeck, Renkens, Shterionov, Gutmann, Thon, Janssens and RaedtFierens et al., 2015) on that program. Naturally, this approach benefits from the current and future developments of ProbLog solvers. Interestingly, the solving techniques of problog 2.2 are quite mature, and they are different to the ones implemented in plingo, making the approach a good complement to the system.
$\textit{Lpmln}^{\pm }$
to ProbLog, which we introduce in this paper. The method translates the input program into a ProbLog program and then runs the system problog 2.2 (Reference Fierens, den Broeck, Renkens, Shterionov, Gutmann, Thon, Janssens and RaedtFierens et al., 2015) on that program. Naturally, this approach benefits from the current and future developments of ProbLog solvers. Interestingly, the solving techniques of problog 2.2 are quite mature, and they are different to the ones implemented in plingo, making the approach a good complement to the system.
We have empirically evaluated plingo’s performance by comparing its different solving methods and by contrasting them to original implementations of Lpmln, ProbLog, and P-log. The results show that the different solving approaches of plingo are indeed complementary and that plingo performs at the same level as other probabilistic reasoning systems.
There are many other probabilistic extensions of logic programming. For a recent review about them, we refer the reader to Reference Cozman and MauáCozman and Mauá (2020) and the references therein. Among the latest work most relevant to us, from the knowledge representation perspective, the credal semantics (Reference Cozman and MauáCozman and Mauá, 2020) and SMProblog (Reference Totis, Kimmig and RaedtTotis et al., 2021) can be seen as two different generalizations of ProbLog to normal logic programs under stable models semantics. From the implementation perspective, Reference Eiter, Hecher and KieselEiter et al. (2021) present a method for algebraic answer set counting, implemented in the system aspmc, and show promising results on its application to probabilistic inference under stable model semantics.
The paper is organized as follows. In Section 2, we review the necessary background material about Lpmln and ProbLog. In Section 3, we define our language
![]() $\textit{Lpmln}^{\pm }$
and introduce the translations from Lpmln to
$\textit{Lpmln}^{\pm }$
and introduce the translations from Lpmln to
![]() $\textit{Lpmln}^{\pm }$
and from
$\textit{Lpmln}^{\pm }$
and from
![]() $\textit{Lpmln}^{\pm }$
to ProbLog. We continue in Section 4 with the description of the language of the system plingo. There, we also present the frontends of Lpmln, P-log, and ProbLog, going through various examples. Section 5 is devoted to the description of the implementation of plingo, and Section 6 describes the experimental evaluation. We conclude in Section 7. The proofs of the theoretical results are available in the Appendix.
$\textit{Lpmln}^{\pm }$
to ProbLog. We continue in Section 4 with the description of the language of the system plingo. There, we also present the frontends of Lpmln, P-log, and ProbLog, going through various examples. Section 5 is devoted to the description of the implementation of plingo, and Section 6 describes the experimental evaluation. We conclude in Section 7. The proofs of the theoretical results are available in the Appendix.
This article extends the conference paper presented in Reference Hahn, Janhunen, Kaminski, Romero, Rühling and SchaubHahn et al. (2022). It includes many new examples to illustrate the formal definitions and the proofs of the formal results. Most notably, this extended version introduces the translation from
![]() $\textit{Lpmln}^{\pm }$
to ProbLog, its implementation in plingo, and its experimental evaluation using problog 2.2. The comparison with problog of Reference Hahn, Janhunen, Kaminski, Romero, Rühling and SchaubHahn et al. (2022) had shown us that problog could be much faster that plingo and the other ASP-based probabilistic systems. This extension basically turns that handicap into an opportunity for plingo.
$\textit{Lpmln}^{\pm }$
to ProbLog, its implementation in plingo, and its experimental evaluation using problog 2.2. The comparison with problog of Reference Hahn, Janhunen, Kaminski, Romero, Rühling and SchaubHahn et al. (2022) had shown us that problog could be much faster that plingo and the other ASP-based probabilistic systems. This extension basically turns that handicap into an opportunity for plingo.
2 Background
A logic program is a set of propositional formulas. A rule is a propositional formula of the form
![]() $H \leftarrow B$
where the head
$H \leftarrow B$
where the head
![]() $H$
is a disjunction of literals and the body
$H$
is a disjunction of literals and the body
![]() $B$
is either
$B$
is either
![]() $\top$
or a conjunction of literals. A rule is normal if
$\top$
or a conjunction of literals. A rule is normal if
![]() $H$
is an atom
$H$
is an atom
![]() $a$
, and it is a choice rule if
$a$
, and it is a choice rule if
![]() $H$
is a disjunction
$H$
is a disjunction
![]() $a \vee \neg a$
for some atom
$a \vee \neg a$
for some atom
![]() $a$
. If
$a$
. If
![]() $B$
is
$B$
is
![]() $\top$
, we write simply
$\top$
, we write simply
![]() $H$
, and if the rule is normal, we call it a fact. We often identify a set of facts with the corresponding set of atoms. A normal logic program is a set of normal rules. An interpretation is a set of propositional atoms. An interpretation
$H$
, and if the rule is normal, we call it a fact. We often identify a set of facts with the corresponding set of atoms. A normal logic program is a set of normal rules. An interpretation is a set of propositional atoms. An interpretation
![]() $X$
is a stable model of a logic program
$X$
is a stable model of a logic program
![]() $\Pi$
if it is a subset minimal model of the program that results from replacing in
$\Pi$
if it is a subset minimal model of the program that results from replacing in
![]() $\Pi$
every maximal subformula that is not satisfied by
$\Pi$
every maximal subformula that is not satisfied by
![]() $X$
by
$X$
by
![]() $\bot$
(Reference FerrarisFerraris, 2005). The set of stable models of a logic program
$\bot$
(Reference FerrarisFerraris, 2005). The set of stable models of a logic program
![]() $\Pi$
is denoted by
$\Pi$
is denoted by
![]() $\mathit{SM}(\Pi )$
. A logic program with weak constraints is a set
$\mathit{SM}(\Pi )$
. A logic program with weak constraints is a set
![]() $\Pi _1 \cup \Pi _2$
where
$\Pi _1 \cup \Pi _2$
where
![]() $\Pi _1$
is a logic program and
$\Pi _1$
is a logic program and
![]() $\Pi _2$
is a set of weak constraints of the form
$\Pi _2$
is a set of weak constraints of the form
![]() $ :\sim \, F[\mathit{w}, \mathit{l}]$
where
$ :\sim \, F[\mathit{w}, \mathit{l}]$
where
![]() $F$
is a formula,
$F$
is a formula,
![]() $\mathit{w}$
is a real number weight, and
$\mathit{w}$
is a real number weight, and
![]() $\mathit{l}$
is a nonnegative integer. The cost of a stable model
$\mathit{l}$
is a nonnegative integer. The cost of a stable model
![]() $X$
of
$X$
of
![]() $\Pi _1$
at some nonnegative integer level
$\Pi _1$
at some nonnegative integer level
![]() $l$
is the sum of the costs
$l$
is the sum of the costs
![]() $w$
of the weak constraints
$w$
of the weak constraints
![]() $:\sim \, F[\mathit{w}, \mathit{l}]$
from
$:\sim \, F[\mathit{w}, \mathit{l}]$
from
![]() $\Pi _1$
whose formula
$\Pi _1$
whose formula
![]() $F$
is satisfied by
$F$
is satisfied by
![]() $X$
. Given two stable models
$X$
. Given two stable models
![]() $X$
and
$X$
and
![]() $Y$
of
$Y$
of
![]() $\Pi _1$
,
$\Pi _1$
,
![]() $X$
is preferred to
$X$
is preferred to
![]() $Y$
wrt.
$Y$
wrt.
![]() $\Pi _2$
if there is some nonnegative integer
$\Pi _2$
if there is some nonnegative integer
![]() $l$
such that the cost of
$l$
such that the cost of
![]() $X$
at
$X$
at
![]() $l$
is smaller than the cost of
$l$
is smaller than the cost of
![]() $Y$
at
$Y$
at
![]() $l$
, and for all
$l$
, and for all
![]() $l^{\prime} \gt l$
, the costs of
$l^{\prime} \gt l$
, the costs of
![]() $X$
and
$X$
and
![]() $Y$
at
$Y$
at
![]() $l^{\prime}$
are the same.
$l^{\prime}$
are the same.
![]() $X$
is an optimal model of
$X$
is an optimal model of
![]() $\Pi _1 \cup \Pi _2$
if it is a stable model of
$\Pi _1 \cup \Pi _2$
if it is a stable model of
![]() $\Pi _1$
and there is no stable model
$\Pi _1$
and there is no stable model
![]() $Y$
of
$Y$
of
![]() $\Pi _1$
such that
$\Pi _1$
such that
![]() $Y$
is preferred to
$Y$
is preferred to
![]() $X$
wrt.
$X$
wrt.
![]() $\Pi _2$
(Reference Buccafurri, Leone and RulloBuccafurri et al., 2000).
$\Pi _2$
(Reference Buccafurri, Leone and RulloBuccafurri et al., 2000).
We review the definition of Lpmln from Reference Lee and WangLee and Wang (2016). An Lpmln program
![]() $\Pi$
is a finite set of weighted formulas
$\Pi$
is a finite set of weighted formulas
![]() $w : F$
where
$w : F$
where
![]() $F$
is a propositional formula and
$F$
is a propositional formula and
![]() $w$
is either a real number (in which case, the weighted formula is called soft) or
$w$
is either a real number (in which case, the weighted formula is called soft) or
![]() $\alpha$
for denoting the infinite weight (in which case, the weighted formula is called hard). If
$\alpha$
for denoting the infinite weight (in which case, the weighted formula is called hard). If
![]() $\Pi$
is an Lpmln program, by
$\Pi$
is an Lpmln program, by
![]() $\Pi ^{\mathit{soft}}$
and
$\Pi ^{\mathit{soft}}$
and
![]() $\Pi ^{\mathit{hard}}$
we denote the set of soft and hard formulas of
$\Pi ^{\mathit{hard}}$
we denote the set of soft and hard formulas of
![]() $\Pi$
, respectively. For any Lpmln program
$\Pi$
, respectively. For any Lpmln program
![]() $\Pi$
and any set
$\Pi$
and any set
![]() $X$
of atoms,
$X$
of atoms,
![]() ${\overline{\Pi }}$
denotes the set of (unweighted) formulas obtained from
${\overline{\Pi }}$
denotes the set of (unweighted) formulas obtained from
![]() $\Pi$
by dropping the weights, and
$\Pi$
by dropping the weights, and
![]() $\Pi _X$
denotes the set of weighted formulas
$\Pi _X$
denotes the set of weighted formulas
![]() $w : F$
in
$w : F$
in
![]() $\Pi$
such that
$\Pi$
such that
![]() $X \models F$
. Given an Lpmln program
$X \models F$
. Given an Lpmln program
![]() $\Pi$
,
$\Pi$
,
![]() $\mathit{SSM}(\Pi )$
denotes the set of soft stable models
$\mathit{SSM}(\Pi )$
denotes the set of soft stable models
![]() $ \{X \mid X \textrm{ is a stable model of }{{\overline{\Pi _X}}} \}.$
The total weight of
$ \{X \mid X \textrm{ is a stable model of }{{\overline{\Pi _X}}} \}.$
The total weight of
![]() $\Pi$
, written
$\Pi$
, written
![]() $\mathit{TW}(\Pi )$
, is defined as
$\mathit{TW}(\Pi )$
, is defined as
![]() $\mathit{exp}(\sum _{w:F \in \Pi }w)$
.
$\mathit{exp}(\sum _{w:F \in \Pi }w)$
.
The weight
![]() $W_{\Pi }(X)$
of an interpretation and its probability
$W_{\Pi }(X)$
of an interpretation and its probability
![]() $P_{\Pi }(X)$
are defined, respectively, as
$P_{\Pi }(X)$
are defined, respectively, as
 \begin{align*}{W_{\Pi }(X)} & = \begin{cases}{\mathit{TW}(\Pi _X)} & \textrm{ if } X \in{\mathit{SSM}(\Pi )} \\ 0 & \textrm{ otherwise } \end{cases} \\ \textrm{ and } \\{P_{\Pi }(X)} & = \lim _{\alpha \rightarrow \infty } \frac{{W_{\Pi }(X)}}{\sum _{Y \in{\mathit{SSM}(\Pi )}}{W_{\Pi }(Y)}} \, . \end{align*}
\begin{align*}{W_{\Pi }(X)} & = \begin{cases}{\mathit{TW}(\Pi _X)} & \textrm{ if } X \in{\mathit{SSM}(\Pi )} \\ 0 & \textrm{ otherwise } \end{cases} \\ \textrm{ and } \\{P_{\Pi }(X)} & = \lim _{\alpha \rightarrow \infty } \frac{{W_{\Pi }(X)}}{\sum _{Y \in{\mathit{SSM}(\Pi )}}{W_{\Pi }(Y)}} \, . \end{align*}
An interpretation
![]() $X$
is called a probabilistic stable model of
$X$
is called a probabilistic stable model of
![]() $\Pi$
if
$\Pi$
if
![]() ${P_{\Pi }(X)} \neq 0$
.
${P_{\Pi }(X)} \neq 0$
.
Example 1. Let
![]() $\Pi _1$
be the Lpmln program that consists of the following formulas:
$\Pi _1$
be the Lpmln program that consists of the following formulas:
The soft stable models of
![]() $\Pi _1$
are
$\Pi _1$
are
![]() $\emptyset$
,
$\emptyset$
,
![]() $\{a\}$
,
$\{a\}$
,
![]() $\{b\}$
, and
$\{b\}$
, and
![]() $\{a,b\}$
. Their weights and probabilities are as follows:
$\{a,b\}$
. Their weights and probabilities are as follows:
To calculate the probabilities, we first determine the denominator
For the soft stable model
![]() $\{b\}$
, we get
$\{b\}$
, we get
If we apply
![]() $\lim _{\alpha \rightarrow \infty }$
, we see that the denominator tends to infinity, while the numerator is a constant. Therefore, the whole expression tends to
$\lim _{\alpha \rightarrow \infty }$
, we see that the denominator tends to infinity, while the numerator is a constant. Therefore, the whole expression tends to
![]() $0$
as
$0$
as
![]() $\alpha$
approaches infinity. In the same way, we can simplify the denominator by removing the
$\alpha$
approaches infinity. In the same way, we can simplify the denominator by removing the
![]() $\mathit{exp}(1)$
as it will always be dominated by the other terms containing
$\mathit{exp}(1)$
as it will always be dominated by the other terms containing
![]() $\mathit{exp}(\alpha )$
. For the soft stable models
$\mathit{exp}(\alpha )$
. For the soft stable models
![]() $\{a\}$
and
$\{a\}$
and
![]() $\{a,b\}$
we then get the exact probabilities
$\{a,b\}$
we then get the exact probabilities
![]() ${P_{\Pi _1}(\{a\})} = 1 / (1+e)$
and
${P_{\Pi _1}(\{a\})} = 1 / (1+e)$
and
![]() ${P_{\Pi _1}(\{a,b\})} = e / (1+e)$
whose approximate values we showed above. For the soft stable model
${P_{\Pi _1}(\{a,b\})} = e / (1+e)$
whose approximate values we showed above. For the soft stable model
![]() $\{ \emptyset \}$
, the probability is
$\{ \emptyset \}$
, the probability is
![]() $0$
since the weight is
$0$
since the weight is
![]() $0$
.
$0$
.
Let
![]() $\Pi _2=\Pi _1 \cup \{\alpha : \neg a\}$
. The soft stable models of
$\Pi _2=\Pi _1 \cup \{\alpha : \neg a\}$
. The soft stable models of
![]() $\Pi _2$
are the same as those of
$\Pi _2$
are the same as those of
![]() $\Pi _1$
, but their weights and probabilities are different:
$\Pi _1$
, but their weights and probabilities are different:
Let
![]() $\Pi _3$
and
$\Pi _3$
and
![]() $\Pi _4$
replace the formula
$\Pi _4$
replace the formula
![]() $1: b$
by the two formulas
$1: b$
by the two formulas
![]() $\alpha : b \vee \neg b$
and
$\alpha : b \vee \neg b$
and
![]() $1 : \neg \neg b$
in
$1 : \neg \neg b$
in
![]() $\Pi _1$
and
$\Pi _1$
and
![]() $\Pi _2$
, respectively, i.e.,
$\Pi _2$
, respectively, i.e.,
![]() $\Pi _3 = \{ \alpha : a, \, \alpha : b \vee \neg b, \, 1 : \neg \neg b \}$
and
$\Pi _3 = \{ \alpha : a, \, \alpha : b \vee \neg b, \, 1 : \neg \neg b \}$
and
![]() $\Pi _4=\Pi _3 \cup \{\alpha : \neg a\}$
. The soft stable models of
$\Pi _4=\Pi _3 \cup \{\alpha : \neg a\}$
. The soft stable models of
![]() $\Pi _3$
are the same as those of
$\Pi _3$
are the same as those of
![]() $\Pi _1$
, their weights are the same as in
$\Pi _1$
, their weights are the same as in
![]() $\Pi _1$
but incremented by
$\Pi _1$
but incremented by
![]() $\alpha$
, since all of them satisfy the new choice rule
$\alpha$
, since all of them satisfy the new choice rule
![]() $\alpha : b \vee \neg b$
, and their probabilities are the same as in
$\alpha : b \vee \neg b$
, and their probabilities are the same as in
![]() $\Pi _1$
. The same relation holds between the soft stable models of
$\Pi _1$
. The same relation holds between the soft stable models of
![]() $\Pi _4$
and
$\Pi _4$
and
![]() $\Pi _2$
.
$\Pi _2$
.
Besides the standard definition, we consider also an alternative definition for Lpmln from Reference Lee and WangLee and Wang (2016), where soft stable models must satisfy all hard formulas of
![]() $\Pi$
. In this case, we have
$\Pi$
. In this case, we have
while the weight
![]() $W_{\Pi }^{\mathit{alt}}(X)$
of an interpretation and its probability
$W_{\Pi }^{\mathit{alt}}(X)$
of an interpretation and its probability
![]() $P_{\Pi }^{\mathit{alt}}(X)$
are defined, respectively, as
$P_{\Pi }^{\mathit{alt}}(X)$
are defined, respectively, as
 \begin{align*}{W_{\Pi }^{\mathit{alt}}(X)} & = \begin{cases}{\mathit{TW}({\Pi ^{\mathit{soft}}}_X)} & \textrm{ if } X \in{\mathit{SSM}^{\mathit{alt}}(\Pi )} \\[3pt] 0 & \textrm{ otherwise } \end{cases} \\ \textrm{ and } \\{P_{\Pi }^{\mathit{alt}}(X)} & = \frac{{W_{\Pi }^{\mathit{alt}}(X)}}{\sum _{Y \in{\mathit{SSM}^{\mathit{alt}}(\Pi )}}{W_{\Pi }^{\mathit{alt}}(Y)}} \, . \end{align*}
\begin{align*}{W_{\Pi }^{\mathit{alt}}(X)} & = \begin{cases}{\mathit{TW}({\Pi ^{\mathit{soft}}}_X)} & \textrm{ if } X \in{\mathit{SSM}^{\mathit{alt}}(\Pi )} \\[3pt] 0 & \textrm{ otherwise } \end{cases} \\ \textrm{ and } \\{P_{\Pi }^{\mathit{alt}}(X)} & = \frac{{W_{\Pi }^{\mathit{alt}}(X)}}{\sum _{Y \in{\mathit{SSM}^{\mathit{alt}}(\Pi )}}{W_{\Pi }^{\mathit{alt}}(Y)}} \, . \end{align*}
The set
![]() $\mathit{SSM}^{\mathit{alt}}(\Pi )$
may be empty if there is no soft stable model that satisfies all hard formulas of
$\mathit{SSM}^{\mathit{alt}}(\Pi )$
may be empty if there is no soft stable model that satisfies all hard formulas of
![]() $\Pi$
, in which case
$\Pi$
, in which case
![]() $P_{\Pi }^{\mathit{alt}}(X)$
is not defined. On the other hand, if
$P_{\Pi }^{\mathit{alt}}(X)$
is not defined. On the other hand, if
![]() $\mathit{SSM}^{\mathit{alt}}(\Pi )$
is not empty, then for every interpretation
$\mathit{SSM}^{\mathit{alt}}(\Pi )$
is not empty, then for every interpretation
![]() $X$
, the values of
$X$
, the values of
![]() $P_{\Pi }^{\mathit{alt}}(X)$
and
$P_{\Pi }^{\mathit{alt}}(X)$
and
![]() $P_{\Pi }(X)$
are the same (cf. Proposition2 from Reference Lee and WangLee and Wang (2016)).
$P_{\Pi }(X)$
are the same (cf. Proposition2 from Reference Lee and WangLee and Wang (2016)).
Example 2. According to the alternative definition of Lpmln, the soft stable models of both
![]() $\Pi _1$
and
$\Pi _1$
and
![]() $\Pi _3$
are
$\Pi _3$
are
![]() $\{a\}$
and
$\{a\}$
and
![]() $\{a,b\}$
. Their weights with respect to
$\{a,b\}$
. Their weights with respect to
![]() $\Pi _1$
are
$\Pi _1$
are
![]() $\mathit{exp}(0)$
and
$\mathit{exp}(0)$
and
![]() $\mathit{exp}(1)$
, respectively, and they are also
$\mathit{exp}(1)$
, respectively, and they are also
![]() $\mathit{exp}(0)$
and
$\mathit{exp}(0)$
and
![]() $\mathit{exp}(1)$
with respect to
$\mathit{exp}(1)$
with respect to
![]() $\Pi _3$
. The denominator is thus
$\Pi _3$
. The denominator is thus
![]() $1+e$
in both cases, and therefore, their probabilities are
$1+e$
in both cases, and therefore, their probabilities are
![]() $1/(1+e)$
and
$1/(1+e)$
and
![]() $e/(1+e)$
, the same as under the the standard definition. In turn, programs
$e/(1+e)$
, the same as under the the standard definition. In turn, programs
![]() $\Pi _2$
and
$\Pi _2$
and
![]() $\Pi _4$
have no soft stable models with the alternative semantics, and for this reason, the probabilities of all of their interpretations are undefined.
$\Pi _4$
have no soft stable models with the alternative semantics, and for this reason, the probabilities of all of their interpretations are undefined.
In the next paragraphs, we adapt the definition of ProbLog from Reference Fierens, den Broeck, Renkens, Shterionov, Gutmann, Thon, Janssens and RaedtFierens et al. (2015) to our notation. A basic ProbLog program
![]() $\Pi$
consists of two parts: a set
$\Pi$
consists of two parts: a set
![]() ${{\Pi }^{\mathit{normal}}}$
of normal rules and a set
${{\Pi }^{\mathit{normal}}}$
of normal rules and a set
![]() ${{\Pi }^{\mathit{probs}}}$
of probabilistic facts of the form
${{\Pi }^{\mathit{probs}}}$
of probabilistic facts of the form
![]() $p :: a$
for some probability
$p :: a$
for some probability
![]() $p$
and some atom
$p$
and some atom
![]() $a$
. Without loss of generality, we consider that
$a$
. Without loss of generality, we consider that
![]() $p$
is strictly between
$p$
is strictly between
![]() $0$
and
$0$
and
![]() $1$
. By
$1$
. By
![]() ${{\mathit{choices}(\Pi )}}$
, we denote the set
${{\mathit{choices}(\Pi )}}$
, we denote the set
![]() $\{ a \mid p :: a \in{{{\Pi }^{\mathit{probs}}}}\}$
of atoms occurring in the probabilistic facts of such a program. We say that a basic ProbLog program is valid if it satisfies these conditions:
$\{ a \mid p :: a \in{{{\Pi }^{\mathit{probs}}}}\}$
of atoms occurring in the probabilistic facts of such a program. We say that a basic ProbLog program is valid if it satisfies these conditions:
-
1. The probabilistic atoms
 $a \in{{{\mathit{choices}(\Pi )}}}$
must not occur in any head
$a \in{{{\mathit{choices}(\Pi )}}}$
must not occur in any head
 $H$
of any rule
$H$
of any rule
 $H \leftarrow B$
from
$H \leftarrow B$
from
 ${\Pi }^{\mathit{normal}}$
.
${\Pi }^{\mathit{normal}}$
. -
2. For every set
 $X \subseteq{{{\mathit{choices}(\Pi )}}}$
, the well-founded model (Reference Van Gelder, Ross and SchlipfVan Gelder et al., 1991) of
$X \subseteq{{{\mathit{choices}(\Pi )}}}$
, the well-founded model (Reference Van Gelder, Ross and SchlipfVan Gelder et al., 1991) of
 ${{{\Pi }^{\mathit{normal}}}}\cup X$
must be total.
${{{\Pi }^{\mathit{normal}}}}\cup X$
must be total.
The second condition holds, in particular, if
![]() ${{\Pi }^{\mathit{normal}}}$
is positive or stratified (Reference Van Gelder, Ross and SchlipfVan Gelder et al., 1991). Note also that if the second condition holds, then the program
${{\Pi }^{\mathit{normal}}}$
is positive or stratified (Reference Van Gelder, Ross and SchlipfVan Gelder et al., 1991). Note also that if the second condition holds, then the program
![]() ${{{\Pi }^{\mathit{normal}}}}\cup X$
has a unique stable model that coincides with the true atoms of its well-founded model. Following Reference Fierens, den Broeck, Renkens, Shterionov, Gutmann, Thon, Janssens and RaedtFierens et al. (2015), we consider only basic ProbLog programs that are valid.
${{{\Pi }^{\mathit{normal}}}}\cup X$
has a unique stable model that coincides with the true atoms of its well-founded model. Following Reference Fierens, den Broeck, Renkens, Shterionov, Gutmann, Thon, Janssens and RaedtFierens et al. (2015), we consider only basic ProbLog programs that are valid.
Given a basic ProbLog program
![]() $\Pi$
, the probability
$\Pi$
, the probability
![]() $P_{\Pi }(X)$
of an interpretation
$P_{\Pi }(X)$
of an interpretation
![]() $X$
is defined as follows:
$X$
is defined as follows:
-
• If
 $X$
is the (unique) stable model of
$X$
is the (unique) stable model of
 ${{{\Pi }^{\mathit{normal}}}}\cup (X \cap{{{\mathit{choices}(\Pi )}}})$
, then
${{{\Pi }^{\mathit{normal}}}}\cup (X \cap{{{\mathit{choices}(\Pi )}}})$
, then
 $P_{\Pi }(X)$
is the product of the products
$P_{\Pi }(X)$
is the product of the products \begin{align*} \prod _{\substack{\phantom{a}p :: a \in{{{\Pi }^{\mathit{probs}}}} \\ a \in X}}p \textrm{ and } \prod _{\substack{\phantom{a}p :: a \in{{{\Pi }^{\mathit{probs}}}} \\ a \notin X}}1 - p. \end{align*}
\begin{align*} \prod _{\substack{\phantom{a}p :: a \in{{{\Pi }^{\mathit{probs}}}} \\ a \in X}}p \textrm{ and } \prod _{\substack{\phantom{a}p :: a \in{{{\Pi }^{\mathit{probs}}}} \\ a \notin X}}1 - p. \end{align*}
-
• Otherwise,
 $P_{\Pi }(X)$
is
$P_{\Pi }(X)$
is
 $0$
.
$0$
.
Example 3. Let
![]() $\Pi _6$
be the ProbLog program that consists of the following elements:
$\Pi _6$
be the ProbLog program that consists of the following elements:
We have that
![]() ${{{\Pi }_{6}^{\mathit{probs}}}}=\{ 0.4 :: a\}$
, and
${{{\Pi }_{6}^{\mathit{probs}}}}=\{ 0.4 :: a\}$
, and
![]() ${{{\Pi }_{6}^{\mathit{normal}}}}=\{ b \leftarrow \neg a\}$
,
${{{\Pi }_{6}^{\mathit{normal}}}}=\{ b \leftarrow \neg a\}$
,
![]() ${{{\mathit{choices}(\Pi _6)}}}=\{a\}$
. Program
${{{\mathit{choices}(\Pi _6)}}}=\{a\}$
. Program
![]() $\Pi _6$
is valid because it satisfies both condition 1, since the unique atom
$\Pi _6$
is valid because it satisfies both condition 1, since the unique atom
![]() $a \in{{{\mathit{choices}(\Pi _6)}}}$
does not occur in the head of the unique rule of
$a \in{{{\mathit{choices}(\Pi _6)}}}$
does not occur in the head of the unique rule of
![]() ${{\Pi }_{6}^{\mathit{normal}}}$
, and condition 2, since the program
${{\Pi }_{6}^{\mathit{normal}}}$
, and condition 2, since the program
![]() ${{\Pi }_{6}^{\mathit{normal}}}$
is stratified. The interpretations
${{\Pi }_{6}^{\mathit{normal}}}$
is stratified. The interpretations
![]() $\{a\}$
and
$\{a\}$
and
![]() $\{b\}$
have probability
$\{b\}$
have probability
![]() $0.4$
and
$0.4$
and
![]() $0.6$
, respectively, and the others have probability
$0.6$
, respectively, and the others have probability
![]() $0$
.
$0$
.
In Reference Fierens, den Broeck, Renkens, Shterionov, Gutmann, Thon, Janssens and RaedtFierens et al. (2015), the definition of an inference task may include the specification of some evidence. Here, to simplify the presentation, it is convenient to include the evidence as part of a ProbLog program. To do this, we represent this evidence by formulas of the form
![]() $\neg a$
or
$\neg a$
or
![]() $\neg \neg a$
for some atom
$\neg \neg a$
for some atom
![]() $a$
, which we call evidence literals. We use evidence literals of the form
$a$
, which we call evidence literals. We use evidence literals of the form
![]() $\neg \neg a$
, instead of normal atoms of the form
$\neg \neg a$
, instead of normal atoms of the form
![]() $a$
, to distinguish them clearly from normal facts and to simplify our presentation later. Then, we consider extended ProbLog programs that contain a set
$a$
, to distinguish them clearly from normal facts and to simplify our presentation later. Then, we consider extended ProbLog programs that contain a set
![]() ${{\Pi }^{\mathit{evidence}}}$
of evidence literals in addition to normal rules and probabilistic facts. Both the notation and the definition of validity that we introduced above carry over naturally to ProbLog programs of this extended form. Just like before, we consider only valid extended ProbLog programs. Next, let
${{\Pi }^{\mathit{evidence}}}$
of evidence literals in addition to normal rules and probabilistic facts. Both the notation and the definition of validity that we introduced above carry over naturally to ProbLog programs of this extended form. Just like before, we consider only valid extended ProbLog programs. Next, let
![]() $\Pi$
be an extended ProbLog program. If
$\Pi$
be an extended ProbLog program. If
![]() $X$
is an interpretation, by
$X$
is an interpretation, by
![]() $P^{\mathit{basic}}_{\Pi }(X)$
we denote the probability
$P^{\mathit{basic}}_{\Pi }(X)$
we denote the probability
![]() $P_{{{{\Pi }^{\mathit{normal}}}}\cup{{{\Pi }^{\mathit{probs}}}}}(X)$
of the corresponding basic ProbLog program. Then, the probability of the evidence of
$P_{{{{\Pi }^{\mathit{normal}}}}\cup{{{\Pi }^{\mathit{probs}}}}}(X)$
of the corresponding basic ProbLog program. Then, the probability of the evidence of
![]() $\Pi$
is the sum of the basic probabilities
$\Pi$
is the sum of the basic probabilities
![]() $P^{\mathit{basic}}_{\Pi }(X)$
of the interpretations
$P^{\mathit{basic}}_{\Pi }(X)$
of the interpretations
![]() $X$
that satisfy all evidence literals in
$X$
that satisfy all evidence literals in
![]() ${{\Pi }^{\mathit{evidence}}}$
. Finally, given an extended ProbLog program
${{\Pi }^{\mathit{evidence}}}$
. Finally, given an extended ProbLog program
![]() $\Pi$
, the probability
$\Pi$
, the probability
![]() $P_{\Pi }(X)$
of an interpretation
$P_{\Pi }(X)$
of an interpretation
![]() $X$
is
$X$
is
-
• undefined if the probability of the evidence of
 $\Pi$
is zero, otherwise
$\Pi$
is zero, otherwise -
• it is
 $0$
if
$0$
if
 $X$
does not satisfy all evidence literals in
$X$
does not satisfy all evidence literals in
 ${{\Pi }^{\mathit{evidence}}}$
, and otherwise
${{\Pi }^{\mathit{evidence}}}$
, and otherwise -
• it is the quotient between
 $P^{\mathit{basic}}_{\Pi }(X)$
and the probability of the evidence of
$P^{\mathit{basic}}_{\Pi }(X)$
and the probability of the evidence of
 $\Pi$
.
$\Pi$
.
Basic ProbLog programs are a special case of extended ProbLog programs where
![]() ${{\Pi }^{\mathit{evidence}}}$
is empty. From now on, we refer to extended ProbLog programs simply as ProbLog programs.
${{\Pi }^{\mathit{evidence}}}$
is empty. From now on, we refer to extended ProbLog programs simply as ProbLog programs.
Example 4. Let
![]() $\Pi _7=\Pi _6\cup \{\neg b\}$
be the ProbLog program that extends
$\Pi _7=\Pi _6\cup \{\neg b\}$
be the ProbLog program that extends
![]() $\Pi _6$
by the evidence literal
$\Pi _6$
by the evidence literal
![]() $\neg b$
. It holds that
$\neg b$
. It holds that
![]() $P^{\mathit{basic}}_{\Pi _7}(X)$
is the same as
$P^{\mathit{basic}}_{\Pi _7}(X)$
is the same as
![]() $P_{\Pi _6}(X)$
for all interpretations
$P_{\Pi _6}(X)$
for all interpretations
![]() $X$
. Given this, the only interpretation of
$X$
. Given this, the only interpretation of
![]() $\Pi _7$
with basic probability greater than
$\Pi _7$
with basic probability greater than
![]() $0$
that satisfies the evidence literal
$0$
that satisfies the evidence literal
![]() $\neg b$
is
$\neg b$
is
![]() $\{a\}$
, whose basic probability is
$\{a\}$
, whose basic probability is
![]() $0.4$
. Hence, the probability of the evidence of
$0.4$
. Hence, the probability of the evidence of
![]() $\Pi _7$
is
$\Pi _7$
is
![]() $0.4$
. Then, the probability of the interpretation
$0.4$
. Then, the probability of the interpretation
![]() $\{a\}$
is
$\{a\}$
is
![]() $1$
, and it is
$1$
, and it is
![]() $0$
for all other interpretations. If we replace the evidence literal
$0$
for all other interpretations. If we replace the evidence literal
![]() $\neg b$
by
$\neg b$
by
![]() $\neg \neg b$
, then it is
$\neg \neg b$
, then it is
![]() $\{b\}$
who has probability
$\{b\}$
who has probability
![]() $1$
, and the others have probability
$1$
, and the others have probability
![]() $0$
. And if we add both
$0$
. And if we add both
![]() $\neg b$
and
$\neg b$
and
![]() $\neg \neg b$
at the same time, then the probabilities of all interpretations become undefined.
$\neg \neg b$
at the same time, then the probabilities of all interpretations become undefined.
We close this section with the definition of the probability of a query atom
![]() $q$
that is similar in both versions of Lpmln and in ProbLog: it is undefined if the probability of the interpretations of the corresponding program is undefined, which cannot happen with the standard definition of Lpmln, and otherwise it is the sum of the probabilities of the interpretations that contain the query atom.
$q$
that is similar in both versions of Lpmln and in ProbLog: it is undefined if the probability of the interpretations of the corresponding program is undefined, which cannot happen with the standard definition of Lpmln, and otherwise it is the sum of the probabilities of the interpretations that contain the query atom.
3 The language
 $\textit{Lpmln}^{\pm }$
$\textit{Lpmln}^{\pm }$
In this section, we introduce the language
![]() $\textit{Lpmln}^{\pm }$
and present translations from Lpmln to
$\textit{Lpmln}^{\pm }$
and present translations from Lpmln to
![]() $\textit{Lpmln}^{\pm }$
, and from
$\textit{Lpmln}^{\pm }$
, and from
![]() $\textit{Lpmln}^{\pm }$
to ProbLog. The former are used in the frontends of Lpmln, ProbLog and P-log, combined with the translations from ProbLog and P-log to Lpmln from Reference Lee and WangLee and Wang (2016) and Reference Lee and YangLee and Yang (2017), respectively. The latter is used in the solving component of plingo to translate from
$\textit{Lpmln}^{\pm }$
to ProbLog. The former are used in the frontends of Lpmln, ProbLog and P-log, combined with the translations from ProbLog and P-log to Lpmln from Reference Lee and WangLee and Wang (2016) and Reference Lee and YangLee and Yang (2017), respectively. The latter is used in the solving component of plingo to translate from
![]() $\textit{Lpmln}^{\pm }$
to ProbLog and run a problog solver.
$\textit{Lpmln}^{\pm }$
to ProbLog and run a problog solver.
The language
![]() $\textit{Lpmln}^{\pm }$
is based on Lpmln under the alternative semantics. The superscript
$\textit{Lpmln}^{\pm }$
is based on Lpmln under the alternative semantics. The superscript
![]() $\pm$
in the name indicates that the new language both extends and restricts Lpmln. The extension simply consists in adding weak constraints to the language. This is a natural extension that allows us to capture the whole Lpmln language under both the alternative and the standard semantics. On the other hand, the restriction limits the form of soft formulas to soft integrity constraints of the form
$\pm$
in the name indicates that the new language both extends and restricts Lpmln. The extension simply consists in adding weak constraints to the language. This is a natural extension that allows us to capture the whole Lpmln language under both the alternative and the standard semantics. On the other hand, the restriction limits the form of soft formulas to soft integrity constraints of the form
![]() $w : \neg F$
for some propositional formula
$w : \neg F$
for some propositional formula
![]() $F$
. This is attractive because it allows us to provide a definition of the semantics that is arguably very simple and intuitive. Interestingly, the translations from ProbLog and P-log (Reference Lee and WangLee and Wang, 2016; Reference Lee and YangLee and Yang, 2017) fall into this fragment of Lpmln. Recall that in ASP, integrity constraints of the form
$F$
. This is attractive because it allows us to provide a definition of the semantics that is arguably very simple and intuitive. Interestingly, the translations from ProbLog and P-log (Reference Lee and WangLee and Wang, 2016; Reference Lee and YangLee and Yang, 2017) fall into this fragment of Lpmln. Recall that in ASP, integrity constraints of the form
![]() $\neg F$
do not affect the generation of stable models, but they can only eliminate some of the stable models generated by the rest of the program. In Lpmln, soft integrity constraints parallel that role, since they do not affect the generation of soft stable models, but they can only affect the probabilistic weights of the soft stable models generated by the rest of the program. More precisely, it holds that the soft stable models of an Lpmln program
$\neg F$
do not affect the generation of stable models, but they can only eliminate some of the stable models generated by the rest of the program. In Lpmln, soft integrity constraints parallel that role, since they do not affect the generation of soft stable models, but they can only affect the probabilistic weights of the soft stable models generated by the rest of the program. More precisely, it holds that the soft stable models of an Lpmln program
![]() $\Pi$
remain the same if we remove from
$\Pi$
remain the same if we remove from
![]() $\Pi$
all its soft integrity constraints. The reader can check that this is the case in our example programs
$\Pi$
all its soft integrity constraints. The reader can check that this is the case in our example programs
![]() $\Pi _3$
and
$\Pi _3$
and
![]() $\Pi _4$
if we remove their soft integrity constraint
$\Pi _4$
if we remove their soft integrity constraint
![]() $1 : \neg \neg b$
. This observation leads us to the following proposition.
$1 : \neg \neg b$
. This observation leads us to the following proposition.
Proposition 1.
If
![]() $\Pi$
is an Lpmln program such that
$\Pi$
is an Lpmln program such that
![]() $\Pi ^{\mathit{soft}}$
contains only soft integrity constraints, then
$\Pi ^{\mathit{soft}}$
contains only soft integrity constraints, then
![]() ${\mathit{SSM}^{\mathit{alt}}(\Pi )}={\mathit{SM}({{\overline{{\Pi ^{\mathit{hard}}}}}})}$
.
${\mathit{SSM}^{\mathit{alt}}(\Pi )}={\mathit{SM}({{\overline{{\Pi ^{\mathit{hard}}}}}})}$
.
This allows us to leave aside the notion of soft stable models and simply replace in
![]() $W_{\Pi }^{\mathit{alt}}(X)$
and
$W_{\Pi }^{\mathit{alt}}(X)$
and
![]() $P_{\Pi }^{\mathit{alt}}(X)$
the set
$P_{\Pi }^{\mathit{alt}}(X)$
the set
![]() $\mathit{SSM}^{\mathit{alt}}(\Pi )$
by
$\mathit{SSM}^{\mathit{alt}}(\Pi )$
by
![]() $\mathit{SM}({{\overline{{\Pi ^{\mathit{hard}}}}}})$
. From this perspective, an Lpmln program of this restricted form has two separated parts:
$\mathit{SM}({{\overline{{\Pi ^{\mathit{hard}}}}}})$
. From this perspective, an Lpmln program of this restricted form has two separated parts:
![]() $\Pi ^{\mathit{hard}}$
, which generates stable models, and
$\Pi ^{\mathit{hard}}$
, which generates stable models, and
![]() $\Pi ^{\mathit{soft}}$
, which determines the weights of the stable models, from which their probabilities can be calculated.
$\Pi ^{\mathit{soft}}$
, which determines the weights of the stable models, from which their probabilities can be calculated.
With these ideas, we can define the syntax and semantics of
![]() $\textit{Lpmln}^{\pm }$
programs. Formally, an
$\textit{Lpmln}^{\pm }$
programs. Formally, an
![]() $\textit{Lpmln}^{\pm }$
program
$\textit{Lpmln}^{\pm }$
program
![]() $\Pi$
is a set of hard formulas, soft integrity constraints, and weak constraints, denoted, respectively, by
$\Pi$
is a set of hard formulas, soft integrity constraints, and weak constraints, denoted, respectively, by
![]() $\Pi ^{\mathit{hard}}$
,
$\Pi ^{\mathit{hard}}$
,
![]() $\Pi ^{\mathit{soft}}$
, and
$\Pi ^{\mathit{soft}}$
, and
![]() $\Pi ^{\mathit{weak}}$
. In what follows, we may identify a hard formula or a set of them with their corresponding unweighted versions. We say that
$\Pi ^{\mathit{weak}}$
. In what follows, we may identify a hard formula or a set of them with their corresponding unweighted versions. We say that
![]() $\Pi$
is normal if
$\Pi$
is normal if
![]() $\Pi ^{\mathit{hard}}$
is normal. By
$\Pi ^{\mathit{hard}}$
is normal. By
![]() $\mathit{OPT}^{{\pm }}(\Pi )$
we denote the optimal stable models of
$\mathit{OPT}^{{\pm }}(\Pi )$
we denote the optimal stable models of
![]() ${{\overline{{\Pi ^{\mathit{hard}}}}}} \cup{\Pi ^{\mathit{weak}}}$
. Then, the weight and the probability of an interpretation
${{\overline{{\Pi ^{\mathit{hard}}}}}} \cup{\Pi ^{\mathit{weak}}}$
. Then, the weight and the probability of an interpretation
![]() $X$
, written
$X$
, written
![]() $W_{\Pi }^{{\pm }}(X)$
and
$W_{\Pi }^{{\pm }}(X)$
and
![]() $P_{\Pi }^{{\pm }}(X)$
, are defined as
$P_{\Pi }^{{\pm }}(X)$
, are defined as
 \begin{align*}{W_{\Pi }^{{\pm }}(X)} & = \begin{cases}{\mathit{TW}({\Pi ^{\mathit{soft}}}_X)} & \textrm{ if } X \in{\mathit{OPT}^{{\pm }}(\Pi )} \\[3pt] 0 & \textrm{ otherwise } \end{cases} \\ \textrm{ and } \\{P_{\Pi }^{{\pm }}(X)} & = \frac{{W_{\Pi }^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}(\Pi )}}{W_{\Pi }^{{\pm }}(Y)}} \, . \end{align*}
\begin{align*}{W_{\Pi }^{{\pm }}(X)} & = \begin{cases}{\mathit{TW}({\Pi ^{\mathit{soft}}}_X)} & \textrm{ if } X \in{\mathit{OPT}^{{\pm }}(\Pi )} \\[3pt] 0 & \textrm{ otherwise } \end{cases} \\ \textrm{ and } \\{P_{\Pi }^{{\pm }}(X)} & = \frac{{W_{\Pi }^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}(\Pi )}}{W_{\Pi }^{{\pm }}(Y)}} \, . \end{align*}
Note that, as before,
![]() $\mathit{OPT}^{{\pm }}(\Pi )$
may be empty, in which case
$\mathit{OPT}^{{\pm }}(\Pi )$
may be empty, in which case
![]() $P_{\Pi }^{{\pm }}(X)$
is not defined. Naturally, when
$P_{\Pi }^{{\pm }}(X)$
is not defined. Naturally, when
![]() $\Pi ^{\mathit{weak}}$
is empty the semantics coincide with the alternative semantics for Lpmln. In this case,
$\Pi ^{\mathit{weak}}$
is empty the semantics coincide with the alternative semantics for Lpmln. In this case,
![]() $\mathit{OPT}^{{\pm }}(\Pi )$
is equal to
$\mathit{OPT}^{{\pm }}(\Pi )$
is equal to
![]() $\mathit{SM}({{\overline{{\Pi ^{\mathit{hard}}}}}})$
, which by Proposition1 is equal to
$\mathit{SM}({{\overline{{\Pi ^{\mathit{hard}}}}}})$
, which by Proposition1 is equal to
![]() $\mathit{SSM}^{\mathit{alt}}(\Pi )$
, and both definitions are the same.
$\mathit{SSM}^{\mathit{alt}}(\Pi )$
, and both definitions are the same.
Example 5. Programs
![]() $\Pi _1$
and
$\Pi _1$
and
![]() $\Pi _2$
are not
$\Pi _2$
are not
![]() $\textit{Lpmln}^{\pm }$
programs because they contain the soft formula
$\textit{Lpmln}^{\pm }$
programs because they contain the soft formula
![]() $1 : b$
. On the other hand,
$1 : b$
. On the other hand,
![]() $\Pi _3$
and
$\Pi _3$
and
![]() $\Pi _4$
are
$\Pi _4$
are
![]() $\textit{Lpmln}^{\pm }$
programs, and they define the same probabilities as under the alternative semantics of Lpmln. Let us introduce the
$\textit{Lpmln}^{\pm }$
programs, and they define the same probabilities as under the alternative semantics of Lpmln. Let us introduce the
![]() $\textit{Lpmln}^{\pm }$
program
$\textit{Lpmln}^{\pm }$
program
![]() $\Pi _5$
that replaces in
$\Pi _5$
that replaces in
![]() $\Pi _3$
the formula
$\Pi _3$
the formula
![]() $\alpha : a$
by the formulas
$\alpha : a$
by the formulas
![]() $\alpha : a \vee \neg a$
and
$\alpha : a \vee \neg a$
and
![]() $:\sim \, a [-1,1]$
, that is
$:\sim \, a [-1,1]$
, that is
![]() $\Pi _5 = \{ \alpha : a \vee \neg a, \, :\sim \, a [-1,1], \, \alpha : b \vee \neg b, \, 1 : \neg \neg b \}$
. The set
$\Pi _5 = \{ \alpha : a \vee \neg a, \, :\sim \, a [-1,1], \, \alpha : b \vee \neg b, \, 1 : \neg \neg b \}$
. The set
![]() $\mathit{OPT}^{{\pm }}(\Pi _5)$
consists of the models
$\mathit{OPT}^{{\pm }}(\Pi _5)$
consists of the models
![]() $\{a\}$
and
$\{a\}$
and
![]() $\{a,b\}$
, whose weights are
$\{a,b\}$
, whose weights are
![]() $\mathit{exp}(0)$
and
$\mathit{exp}(0)$
and
![]() $\mathit{exp}(1)$
, respectively, and whose probabilities are the same as in
$\mathit{exp}(1)$
, respectively, and whose probabilities are the same as in
![]() $\Pi _3$
.
$\Pi _3$
.
3.1 From Lpmln to
 $\textit{Lpmln}^{\pm }$
$\textit{Lpmln}^{\pm }$
We translate Lpmln programs to
![]() $\textit{Lpmln}^{\pm }$
programs following the idea of the translation lpmln2wc from Reference Lee and YangLee and Yang (2017). An Lpmln program
$\textit{Lpmln}^{\pm }$
programs following the idea of the translation lpmln2wc from Reference Lee and YangLee and Yang (2017). An Lpmln program
![]() $\Pi$
under the standard semantics is captured by the
$\Pi$
under the standard semantics is captured by the
![]() $\textit{Lpmln}^{\pm }$
program
$\textit{Lpmln}^{\pm }$
program
![]() $\mathit{standard}(\Pi )$
that contains
$\mathit{standard}(\Pi )$
that contains
-
• the hard formulas
 $ \{ \alpha : F \vee \neg F \mid w:F \in \Pi \}$
,
$ \{ \alpha : F \vee \neg F \mid w:F \in \Pi \}$
, -
• the soft formulas
 $\{ w : \neg \neg F \mid w :F \in \Pi, w \neq \alpha \}$
, and
$\{ w : \neg \neg F \mid w :F \in \Pi, w \neq \alpha \}$
, and -
• the weak constraints
 $\{ :\sim \, F [-1,1] \mid w : F \in \Pi, w = \alpha \}$
.
$\{ :\sim \, F [-1,1] \mid w : F \in \Pi, w = \alpha \}$
.
The hard formulas generate the soft stable models of
![]() $\Pi$
, the weak constraints select those which satisfy most of the hard formulas of
$\Pi$
, the weak constraints select those which satisfy most of the hard formulas of
![]() $\Pi$
, while the soft formulas attach the right weight to each of them, without interfering in their generation. The alternative semantics is captured by the translation
$\Pi$
, while the soft formulas attach the right weight to each of them, without interfering in their generation. The alternative semantics is captured by the translation
![]() $\mathit{alternative}(\Pi )$
that contains
$\mathit{alternative}(\Pi )$
that contains
-
• the hard formulas
 $\{ \alpha : F \mid w:F \in \Pi, w = \alpha \} \cup \{ \alpha : F \vee \neg F \mid w:F \in \Pi, w \neq \alpha \}$
,
$\{ \alpha : F \mid w:F \in \Pi, w = \alpha \} \cup \{ \alpha : F \vee \neg F \mid w:F \in \Pi, w \neq \alpha \}$
, -
• the same soft formulas as in
 $\mathit{standard}(\Pi )$
, and
$\mathit{standard}(\Pi )$
, and -
• no weak constraints.
The first hard formulas enforce that the hard formulas of
![]() $\Pi$
must be satisfied, while the latter is the same as in
$\Pi$
must be satisfied, while the latter is the same as in
![]() $\mathit{standard}(\Pi )$
, but only for the soft formulas of
$\mathit{standard}(\Pi )$
, but only for the soft formulas of
![]() $\Pi$
. The weak constraints are not needed anymore.
$\Pi$
. The weak constraints are not needed anymore.
Proposition 2.
Let
![]() $\Pi$
be an Lpmln program. For every interpretation
$\Pi$
be an Lpmln program. For every interpretation
![]() $X$
, it holds that
$X$
, it holds that
 \begin{align*} &{P_{\Pi }(X)} ={P_{{\mathit{standard}(\Pi )}}^{{\pm }}(X)} \quad \textrm{ and } \\ &{P_{\Pi }^{\mathit{alt}}(X)} ={P_{{\mathit{alternative}(\Pi )}}^{{\pm }}(X)} \, . \end{align*}
\begin{align*} &{P_{\Pi }(X)} ={P_{{\mathit{standard}(\Pi )}}^{{\pm }}(X)} \quad \textrm{ and } \\ &{P_{\Pi }^{\mathit{alt}}(X)} ={P_{{\mathit{alternative}(\Pi )}}^{{\pm }}(X)} \, . \end{align*}
Example 6. The
![]() $\textit{Lpmln}^{\pm }$
programs
$\textit{Lpmln}^{\pm }$
programs
![]() $\Pi _3$
,
$\Pi _3$
,
![]() $\Pi _4$
, and
$\Pi _4$
, and
![]() $\Pi _5$
of our examples are the result of applying the previous translations to the Lpmln programs
$\Pi _5$
of our examples are the result of applying the previous translations to the Lpmln programs
![]() $\Pi _1$
and
$\Pi _1$
and
![]() $\Pi _2$
. Namely,
$\Pi _2$
. Namely,
![]() $\Pi _3$
is
$\Pi _3$
is
![]() $\mathit{alternative}(\Pi _1)$
,
$\mathit{alternative}(\Pi _1)$
,
![]() $\Pi _4$
is
$\Pi _4$
is
![]() $\mathit{alternative}(\Pi _2)$
, and
$\mathit{alternative}(\Pi _2)$
, and
![]() $\Pi _5$
is
$\Pi _5$
is
![]() $\mathit{standard}(\Pi _1)$
. Accordingly, for all interpretations
$\mathit{standard}(\Pi _1)$
. Accordingly, for all interpretations
![]() $X$
, it holds that
$X$
, it holds that
![]() ${P_{\Pi _1}^{\mathit{alt}}(X)}={P_{\Pi _3}^{{\pm }}(X)}$
,
${P_{\Pi _1}^{\mathit{alt}}(X)}={P_{\Pi _3}^{{\pm }}(X)}$
,
![]() ${P_{\Pi _2}^{\mathit{alt}}(X)}={P_{\Pi _4}^{{\pm }}(X)}$
, and
${P_{\Pi _2}^{\mathit{alt}}(X)}={P_{\Pi _4}^{{\pm }}(X)}$
, and
![]() ${P_{\Pi _1}(X)}={P_{\Pi _5}^{{\pm }}(X)}$
. The program
${P_{\Pi _1}(X)}={P_{\Pi _5}^{{\pm }}(X)}$
. The program
![]() $\mathit{standard}(\Pi _2)$
is
$\mathit{standard}(\Pi _2)$
is
![]() $\Pi _5\cup \{\alpha : \neg a \vee \neg \neg a, \, :\sim \, \neg a [-1,1]\}$
.
$\Pi _5\cup \{\alpha : \neg a \vee \neg \neg a, \, :\sim \, \neg a [-1,1]\}$
.
As noted in Reference Lee, Talsania and WangLee et al. (2017), these kinds of translations can be troublesome when applied to logic programs with variables in the input language of clingo (Reference Calimeri, Faber, Gebser, Ianni, Kaminski, Krennwallner, Leone, Maratea, Ricca and SchaubCalimeri et al., 2020). This is the case of the Lpmln frontend in plingo, where the rules at the input can be seen as safe implications
![]() $H \leftarrow B$
where
$H \leftarrow B$
where
![]() $H$
is a disjunction and
$H$
is a disjunction and
![]() $B$
a conjunction of first-order atoms. It is hard to see how to apply the previous translations in such a way that the resulting soft formulas and weak constraints belong to the input language of clingo, since the result has to safisfy clingo’s safety conditions. For instance, if we try to apply the
$B$
a conjunction of first-order atoms. It is hard to see how to apply the previous translations in such a way that the resulting soft formulas and weak constraints belong to the input language of clingo, since the result has to safisfy clingo’s safety conditions. For instance, if we try to apply the
![]() $\mathit{standard}$
translation to the hard rule a(X) :- b(X)., a possible approach could generate the two weak constraints : a(X). [-1,X] and : not b(X). [-1,X], but the second of them is not safe and will not be accepted by clingo. To overcome this problem, we can use the negative versions of the previous translations, based on the translation lpmln2wc
$\mathit{standard}$
translation to the hard rule a(X) :- b(X)., a possible approach could generate the two weak constraints : a(X). [-1,X] and : not b(X). [-1,X], but the second of them is not safe and will not be accepted by clingo. To overcome this problem, we can use the negative versions of the previous translations, based on the translation lpmln2wc
![]() $^{pnt}$
from Reference Lee and YangLee and Yang (2017), where the soft formulas for both translations are
$^{pnt}$
from Reference Lee and YangLee and Yang (2017), where the soft formulas for both translations are
and the weak constraints for the standard semantics are
Observe that now
![]() $F$
always occurs under one negation. In this case, when
$F$
always occurs under one negation. In this case, when
![]() $F$
has the form
$F$
has the form
![]() $H \leftarrow B$
, the formulas
$H \leftarrow B$
, the formulas
![]() $\neg F$
can be simply written as
$\neg F$
can be simply written as
![]() $\neg H \wedge B$
, and this formulation can be easily incorporated into clingo. For instance, a(X) :- b(X). is translated in this way to : not a(X), b(X). [1,X], which is safe and accepted by clingo. These negative versions are the result of applying to
$\neg H \wedge B$
, and this formulation can be easily incorporated into clingo. For instance, a(X) :- b(X). is translated in this way to : not a(X), b(X). [1,X], which is safe and accepted by clingo. These negative versions are the result of applying to
![]() $\mathit{standard}(\Pi )$
and
$\mathit{standard}(\Pi )$
and
![]() $\mathit{alternative}(\Pi )$
the translation of the following proposition, and then simplifying the soft formulas of the form
$\mathit{alternative}(\Pi )$
the translation of the following proposition, and then simplifying the soft formulas of the form
![]() $-w : \neg \neg \neg F$
to
$-w : \neg \neg \neg F$
to
![]() $-w : \neg F$
.
$-w : \neg F$
.
Proposition 3.
Given an
![]() $\textit{Lpmln}^{\pm }$
program
$\textit{Lpmln}^{\pm }$
program
![]() $\Pi$
, let
$\Pi$
, let
![]() $\mathit{negative}(\Pi )$
be the program
$\mathit{negative}(\Pi )$
be the program
For every interpretation
![]() $X$
, it holds that
$X$
, it holds that
![]() $P_{\Pi }^{{\pm }}(X)$
and
$P_{\Pi }^{{\pm }}(X)$
and
![]() $P_{{\mathit{negative}(\Pi )}}^{{\pm }}(X)$
coincide.
$P_{{\mathit{negative}(\Pi )}}^{{\pm }}(X)$
coincide.
This proposition is closely related to Corollary 1 from Reference Lee and YangLee and Yang (2017).
Example 7. The program
![]() $\mathit{negative}(\Pi _5)$
is
$\mathit{negative}(\Pi _5)$
is
![]() $\{ \alpha : a \vee \neg a, \, :\sim \, \neg a [1,1], \, \alpha : b \vee \neg b, \, -1 : \neg \neg \neg b \}$
. Its last formula can be simplified to
$\{ \alpha : a \vee \neg a, \, :\sim \, \neg a [1,1], \, \alpha : b \vee \neg b, \, -1 : \neg \neg \neg b \}$
. Its last formula can be simplified to
![]() $-1 : \neg b$
. The optimal stable models of this program are
$-1 : \neg b$
. The optimal stable models of this program are
![]() $\{a\}$
and
$\{a\}$
and
![]() $\{a,b\}$
, their weights are
$\{a,b\}$
, their weights are
![]() $\mathit{exp}(-1)$
and
$\mathit{exp}(-1)$
and
![]() $\mathit{exp}(0)$
, respectively, and their probabilities are the same as in
$\mathit{exp}(0)$
, respectively, and their probabilities are the same as in
![]() $\Pi _5$
.
$\Pi _5$
.
3.2 From ProbLog to
 $\textit{Lpmln}^{\pm }$
and back
$\textit{Lpmln}^{\pm }$
and back
Reference Lee and WangLee and Wang (2016) show how to translate ProbLog programs to Lpmln. We obtain a translation from ProbLog to
![]() $\textit{Lpmln}^{\pm }$
by combining that translation with our
$\textit{Lpmln}^{\pm }$
by combining that translation with our
![]() $\mathit{alternative}$
translation from Lpmln to
$\mathit{alternative}$
translation from Lpmln to
![]() $\textit{Lpmln}^{\pm }$
. Recall that we may identify a hard formula or a set of them by their corresponding unweighted versions. Let
$\textit{Lpmln}^{\pm }$
. Recall that we may identify a hard formula or a set of them by their corresponding unweighted versions. Let
![]() $\Pi$
be a ProbLog program, then the
$\Pi$
be a ProbLog program, then the
![]() $\textit{Lpmln}^{\pm }$
program
$\textit{Lpmln}^{\pm }$
program
![]() ${{\mathit{problog2lpmln}(\Pi )}}$
is:Footnote
1
${{\mathit{problog2lpmln}(\Pi )}}$
is:Footnote
1
Proposition 4.
Let
![]() $\Pi$
be a ProbLog program. For every interpretation
$\Pi$
be a ProbLog program. For every interpretation
![]() $X$
, it holds that
$X$
, it holds that
![]() $P_{\Pi }(X)$
and
$P_{\Pi }(X)$
and
![]() $P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
are the same.
$P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
are the same.
Example 8. Given our previous ProbLog program
![]() $\Pi _7=\{ b \leftarrow \neg a, \, \neg b, \, 0.4 :: a \}$
, the
$\Pi _7=\{ b \leftarrow \neg a, \, \neg b, \, 0.4 :: a \}$
, the
![]() $\textit{Lpmln}^{\pm }$
program
$\textit{Lpmln}^{\pm }$
program
![]() ${{\mathit{problog2lpmln}(\Pi _7)}}$
consists of the following formulas:
${{\mathit{problog2lpmln}(\Pi _7)}}$
consists of the following formulas:
where
![]() $-0.405$
is the result of
$-0.405$
is the result of
![]() $\mathit{ln}(0.4/(1-0.4))$
. It holds that
$\mathit{ln}(0.4/(1-0.4))$
. It holds that
![]() $P_{{{{\mathit{problog2lpmln}(\Pi _7)}}}}^{{\pm }}(X)$
is
$P_{{{{\mathit{problog2lpmln}(\Pi _7)}}}}^{{\pm }}(X)$
is
![]() $1$
when
$1$
when
![]() $X=\{a\}$
, and it is
$X=\{a\}$
, and it is
![]() $0$
otherwise, which is the same as
$0$
otherwise, which is the same as
![]() $P_{\Pi _7}(X)$
.
$P_{\Pi _7}(X)$
.
In the remainder of this section, we present a translation in the other direction, from
![]() $\textit{Lpmln}^{\pm }$
to ProbLog. The translation applies to non-disjunctive
$\textit{Lpmln}^{\pm }$
to ProbLog. The translation applies to non-disjunctive
![]() $\textit{Lpmln}^{\pm }$
programs without weak constraints. At first sight, it may seem counterintuitive that such a translation is possible, since ProbLog is based on the well-founded semantics, and the second condition for valid ProbLog programs severely restricts the form of their normal part. However, a closer look reveals that this restriction can be compensated by the other components of ProbLog’s programs: probabilistic facts and evidence literals. As we will see, they can fulfill the role of choice rules and integrity constraints in ASP, respectively. Under this view, ProbLog programs resemble logic programs that follow the Generate, Define and Test methodology (Reference LifschitzLifschitz, 2002) where probabilistic facts generate possible solutions, normal rules define additional predicates, and evidence literals filter the actual solutions. This relation makes the existence of a translation more intuitive. We make it precise in the next paragraphs.
$\textit{Lpmln}^{\pm }$
programs without weak constraints. At first sight, it may seem counterintuitive that such a translation is possible, since ProbLog is based on the well-founded semantics, and the second condition for valid ProbLog programs severely restricts the form of their normal part. However, a closer look reveals that this restriction can be compensated by the other components of ProbLog’s programs: probabilistic facts and evidence literals. As we will see, they can fulfill the role of choice rules and integrity constraints in ASP, respectively. Under this view, ProbLog programs resemble logic programs that follow the Generate, Define and Test methodology (Reference LifschitzLifschitz, 2002) where probabilistic facts generate possible solutions, normal rules define additional predicates, and evidence literals filter the actual solutions. This relation makes the existence of a translation more intuitive. We make it precise in the next paragraphs.
We present the translation for a normal
![]() $\textit{Lpmln}^{\pm }$
program
$\textit{Lpmln}^{\pm }$
program
![]() $\Pi$
without weak constraints, whose soft formulas have the form
$\Pi$
without weak constraints, whose soft formulas have the form
![]() $w : \neg \neg a$
for some atom
$w : \neg \neg a$
for some atom
![]() $a$
. We assume that in
$a$
. We assume that in
![]() $\Pi$
there are no different soft formulas
$\Pi$
there are no different soft formulas
![]() $w_1 : \neg \neg a$
and
$w_1 : \neg \neg a$
and
![]() $w_2 : \neg \neg a$
for the same atom
$w_2 : \neg \neg a$
for the same atom
![]() $a$
. Using well-known translations, it is easy to extend the results to more general types of
$a$
. Using well-known translations, it is easy to extend the results to more general types of
![]() $\textit{Lpmln}^{\pm }$
programs, as long as the complexity of deciding the satisfiability of the hard part remains in
$\textit{Lpmln}^{\pm }$
programs, as long as the complexity of deciding the satisfiability of the hard part remains in
![]() $\mathit{NP}$
, and the programs contain no weak constraints. In fact, the implementation of this translation in our system plingo works for non-disjunctive clingo programs (Reference Calimeri, Faber, Gebser, Ianni, Kaminski, Krennwallner, Leone, Maratea, Ricca and SchaubCalimeri et al., 2020).
$\mathit{NP}$
, and the programs contain no weak constraints. In fact, the implementation of this translation in our system plingo works for non-disjunctive clingo programs (Reference Calimeri, Faber, Gebser, Ianni, Kaminski, Krennwallner, Leone, Maratea, Ricca and SchaubCalimeri et al., 2020).
We modify
![]() $\Pi$
in four steps until we have a
$\Pi$
in four steps until we have a
![]() $\textit{Lpmln}^{\pm }$
program that, in step 5, we can easily turn into a ProbLog program by inverting the translation
$\textit{Lpmln}^{\pm }$
program that, in step 5, we can easily turn into a ProbLog program by inverting the translation
![]() ${{\mathit{problog2lpmln}}}$
. We take as our running example the following
${{\mathit{problog2lpmln}}}$
. We take as our running example the following
![]() $\textit{Lpmln}^{\pm }$
program
$\textit{Lpmln}^{\pm }$
program
![]() $\Pi _8$
that is the result of applying to
$\Pi _8$
that is the result of applying to
![]() $\Pi _3$
the usual translation from choice rules to normal rules:
$\Pi _3$
the usual translation from choice rules to normal rules:
The (optimal) stable models of
![]() $\Pi _8$
are
$\Pi _8$
are
![]() $\{a,\mathit{nb}\}$
and
$\{a,\mathit{nb}\}$
and
![]() $\{a,b\}$
. Their probabilities are
$\{a,b\}$
. Their probabilities are
![]() $0.269$
and
$0.269$
and
![]() $0.731$
, respectively, just like those of
$0.731$
, respectively, just like those of
![]() $\{a\}$
and
$\{a\}$
and
![]() $\{a,b\}$
with respect to
$\{a,b\}$
with respect to
![]() $\Pi _3$
.
$\Pi _3$
.
Step 1. We assume that the atom
![]() $\mathit{bot}$
does not occur in
$\mathit{bot}$
does not occur in
![]() $\Pi$
, and we add the literal
$\Pi$
, and we add the literal
![]() $\neg{\mathit{bot}}$
to
$\neg{\mathit{bot}}$
to
![]() $\Pi$
. In the end, this will be the unique evidence literal in the resulting ProbLog program. Integrity constraints
$\Pi$
. In the end, this will be the unique evidence literal in the resulting ProbLog program. Integrity constraints
![]() $\bot \leftarrow B$
are not allowed in ProbLog, but once we have the evidence literal
$\bot \leftarrow B$
are not allowed in ProbLog, but once we have the evidence literal
![]() $\neg{\mathit{bot}}$
, we can represent them simply by
$\neg{\mathit{bot}}$
, we can represent them simply by
![]() ${\mathit{bot}} \leftarrow B$
. This shows how evidence literals fulfill the role of integrity constraints.
${\mathit{bot}} \leftarrow B$
. This shows how evidence literals fulfill the role of integrity constraints.
Step 2. For every atom
![]() $a$
occurring in
$a$
occurring in
![]() $\Pi$
, we add the following rules introducing a new atom
$\Pi$
, we add the following rules introducing a new atom
![]() $a^{\prime}$
that works as a copy of
$a^{\prime}$
that works as a copy of
![]() $a$
:
$a$
:
The choice rule selects a truth value for
![]() $a^{\prime}$
, while the other rules act as integrity constraints that enforce the truth values of
$a^{\prime}$
, while the other rules act as integrity constraints that enforce the truth values of
![]() $a$
and
$a$
and
![]() $a^{\prime}$
to be the same. After adding
$a^{\prime}$
to be the same. After adding
![]() $\neg{\mathit{bot}}$
and these rules to
$\neg{\mathit{bot}}$
and these rules to
![]() $\Pi$
, the resulting
$\Pi$
, the resulting
![]() $\textit{Lpmln}^{\pm }$
program has the same stable models as before, but for every atom
$\textit{Lpmln}^{\pm }$
program has the same stable models as before, but for every atom
![]() $a$
in a stable model, we also have its copy
$a$
in a stable model, we also have its copy
![]() $a^{\prime}$
. Apart from this, the probabilities of the stable models remain the same. In our example, we add to
$a^{\prime}$
. Apart from this, the probabilities of the stable models remain the same. In our example, we add to
![]() $\Pi _8$
the literal
$\Pi _8$
the literal
![]() $\neg{\mathit{bot}}$
, as well as the formulas (1) for the three atoms
$\neg{\mathit{bot}}$
, as well as the formulas (1) for the three atoms
![]() $a$
,
$a$
,
![]() $b$
, and
$b$
, and
![]() $\mathit{nb}$
occurring in
$\mathit{nb}$
occurring in
![]() $\Pi _8$
. The stable models are now
$\Pi _8$
. The stable models are now
![]() $\{a,{a^{\prime}},\mathit{nb},{\mathit{nb}^{\prime}}\}$
and
$\{a,{a^{\prime}},\mathit{nb},{\mathit{nb}^{\prime}}\}$
and
![]() $\{a,{a^{\prime}},\mathit{b},{\mathit{b}^{\prime}}\}$
, and their probabilities are, as before,
$\{a,{a^{\prime}},\mathit{b},{\mathit{b}^{\prime}}\}$
, and their probabilities are, as before,
![]() $0.269$
and
$0.269$
and
![]() $0.731$
.
$0.731$
.
Step 3. To be able to satisfy condition 2 of valid ProbLog programs, we turn the set of normal rules of the original program into a set of stratified rules, by replacing every negative literal
![]() $\neg a$
occurring in them by
$\neg a$
occurring in them by
![]() $\neg{a^{\prime}}$
. That is, we replace every normal rule
$\neg{a^{\prime}}$
. That is, we replace every normal rule
![]() $r$
in the original program of the form:
$r$
in the original program of the form:
by the normal rule
![]() ${\mathit{stratify}}(r)$
:
${\mathit{stratify}}(r)$
:
This replacement does not affect the stable models of the program, given that
![]() $a$
and
$a$
and
![]() $a^{\prime}$
are equivalent and the replacement only happens in negative literals. If we also replaced the atoms
$a^{\prime}$
are equivalent and the replacement only happens in negative literals. If we also replaced the atoms
![]() $a_1$
to
$a_1$
to
![]() $a_m$
by
$a_m$
by
![]() ${a^{\prime}}_1$
to
${a^{\prime}}_1$
to
![]() ${a^{\prime}}_m$
, then the resulting program would represent the supported models of the original program instead of the stable ones. It is easy to see that the resulting set of rules is stratified because the atoms
${a^{\prime}}_m$
, then the resulting program would represent the supported models of the original program instead of the stable ones. It is easy to see that the resulting set of rules is stratified because the atoms
![]() $a^{\prime}$
occurring in the negative literals do not occur in any head. In our example, the three normal rules of
$a^{\prime}$
occurring in the negative literals do not occur in any head. In our example, the three normal rules of
![]() $\Pi _8$
are replaced by these ones:
$\Pi _8$
are replaced by these ones:
Step 4. To invert the translation
![]() ${\mathit{problog2lpmln}}$
, we have to translate every pair of a choice rule and a soft formula of our current
${\mathit{problog2lpmln}}$
, we have to translate every pair of a choice rule and a soft formula of our current
![]() $\textit{Lpmln}^{\pm }$
program into a probabilistic fact., for doing this, we need such a pairing between choice rules and soft formulas. We achieve it as follows. We replace every soft formula of the form
$\textit{Lpmln}^{\pm }$
program into a probabilistic fact., for doing this, we need such a pairing between choice rules and soft formulas. We achieve it as follows. We replace every soft formula of the form
![]() $w : \neg \neg a$
by
$w : \neg \neg a$
by
![]() $w : \neg \neg{a^{\prime}}$
. This does not change the probabilities of the stable models, since
$w : \neg \neg{a^{\prime}}$
. This does not change the probabilities of the stable models, since
![]() $a$
and
$a$
and
![]() $a^{\prime}$
are equivalent. Additionally, for the atoms
$a^{\prime}$
are equivalent. Additionally, for the atoms
![]() $a$
not occurring in the soft formulas, we add the trivial formula
$a$
not occurring in the soft formulas, we add the trivial formula
![]() $0 : \neg \neg{a^{\prime}}$
. Clearly, this does not affect the probabilities of the stable models. At this point, for every choice rule
$0 : \neg \neg{a^{\prime}}$
. Clearly, this does not affect the probabilities of the stable models. At this point, for every choice rule
![]() ${a^{\prime}} \vee \neg{a^{\prime}}$
in our
${a^{\prime}} \vee \neg{a^{\prime}}$
in our
![]() $\textit{Lpmln}^{\pm }$
program there is one soft formula
$\textit{Lpmln}^{\pm }$
program there is one soft formula
![]() $w : \neg \neg{a^{\prime}}$
, and vice versa. In our example, the previous soft formula
$w : \neg \neg{a^{\prime}}$
, and vice versa. In our example, the previous soft formula
![]() $1 : \neg \neg b$
is replaced by these ones:
$1 : \neg \neg b$
is replaced by these ones:
Step 5. To finalize, we just have to invert the translation
![]() ${{\mathit{problog2lpmln}}}$
. We do it by replacing every pair of a choice rule
${{\mathit{problog2lpmln}}}$
. We do it by replacing every pair of a choice rule
![]() ${a^{\prime}} \vee \neg{a^{\prime}}$
and a soft formula
${a^{\prime}} \vee \neg{a^{\prime}}$
and a soft formula
![]() $w : \neg \neg{a^{\prime}}$
by the probabilistic fact
$w : \neg \neg{a^{\prime}}$
by the probabilistic fact
![]() $e^w / (e^w + 1) ::{a^{\prime}}$
. The function from
$e^w / (e^w + 1) ::{a^{\prime}}$
. The function from
![]() $w$
to
$w$
to
![]() $e^w / (e^w + 1)$
to calculate the probabilities is simply the inverse of the function from
$e^w / (e^w + 1)$
to calculate the probabilities is simply the inverse of the function from
![]() $p$
to
$p$
to
![]() $\mathit{ln}(p/(1-p))$
to calculate the weights in
$\mathit{ln}(p/(1-p))$
to calculate the weights in
![]() ${{\mathit{problog2lpmln}}}$
. In particular, for
${{\mathit{problog2lpmln}}}$
. In particular, for
![]() $w=0$
, it leads to the probability
$w=0$
, it leads to the probability
![]() $0.5$
. Note how probabilistic facts fulfill the role of the choice rules, and at the same time, they stand for the soft formulas. In our example, the choice rules from (1) and the previous soft formulas are replaced by the following probabilistic facts:
$0.5$
. Note how probabilistic facts fulfill the role of the choice rules, and at the same time, they stand for the soft formulas. In our example, the choice rules from (1) and the previous soft formulas are replaced by the following probabilistic facts:
In the resulting ProbLog program, the interpretations
![]() $\{a,{a^{\prime}},\mathit{nb},{\mathit{nb}^{\prime}}\}$
and
$\{a,{a^{\prime}},\mathit{nb},{\mathit{nb}^{\prime}}\}$
and
![]() $\{a,{a^{\prime}},\mathit{b},{\mathit{b}^{\prime}}\}$
have probabilities
$\{a,{a^{\prime}},\mathit{b},{\mathit{b}^{\prime}}\}$
have probabilities
![]() $0.269$
and
$0.269$
and
![]() $0.731$
, respectively, and the other interpretations have probability
$0.731$
, respectively, and the other interpretations have probability
![]() $0$
. This is the same as in
$0$
. This is the same as in
![]() $\Pi _8$
, once we eliminate the additional atoms
$\Pi _8$
, once we eliminate the additional atoms
![]() $a^{\prime}$
,
$a^{\prime}$
,
![]() $b^{\prime}$
, and
$b^{\prime}$
, and
![]() $\mathit{nb}^{\prime}$
.
$\mathit{nb}^{\prime}$
.
Finally, we can put all the steps of the translation together. Let
![]() $\Pi$
be our original program, let
$\Pi$
be our original program, let
![]() $\mathit{atoms}(\Pi )$
denote the set of atoms of
$\mathit{atoms}(\Pi )$
denote the set of atoms of
![]() $\Pi$
, and
$\Pi$
, and
![]() $\mathit{soft}(\Pi )$
denote the set of atoms
$\mathit{soft}(\Pi )$
denote the set of atoms
![]() $\{a \mid w : \neg \neg a \in{\Pi ^{\mathit{soft}}}\}$
occurring in the soft formulas of
$\{a \mid w : \neg \neg a \in{\Pi ^{\mathit{soft}}}\}$
occurring in the soft formulas of
![]() $\Pi$
. Then, the ProbLog program
$\Pi$
. Then, the ProbLog program
![]() ${{\mathit{lpmln2problog}(\Pi )}}$
consists of:
${{\mathit{lpmln2problog}(\Pi )}}$
consists of:
-
• the normal rules
 \begin{align*} \{{\mathit{bot}} \leftarrow a \wedge \neg{a^{\prime}} & \mid a \in{\mathit{atoms}(\Pi )}\} \, \cup \\ \{{\mathit{bot}} \leftarrow \neg a \wedge{a^{\prime}} & \mid a \in{\mathit{atoms}(\Pi )}\} \, \cup \\ \{{{\mathit{stratify}}(r)} & \mid r \in{\Pi ^{\mathit{hard}}}\}, \end{align*}
\begin{align*} \{{\mathit{bot}} \leftarrow a \wedge \neg{a^{\prime}} & \mid a \in{\mathit{atoms}(\Pi )}\} \, \cup \\ \{{\mathit{bot}} \leftarrow \neg a \wedge{a^{\prime}} & \mid a \in{\mathit{atoms}(\Pi )}\} \, \cup \\ \{{{\mathit{stratify}}(r)} & \mid r \in{\Pi ^{\mathit{hard}}}\}, \end{align*}
-
• the probabilistic facts
 \begin{align*} \{ e^w / (e^w + 1) ::{a^{\prime}} \mid w : \neg \neg a \in{\Pi ^{\mathit{soft}}} \} & \, \cup \\ \{ 0.5 ::{a^{\prime}} \mid a \in{\mathit{atoms}(\Pi )}\setminus{\mathit{soft}(\Pi )}\} &, \end{align*}
\begin{align*} \{ e^w / (e^w + 1) ::{a^{\prime}} \mid w : \neg \neg a \in{\Pi ^{\mathit{soft}}} \} & \, \cup \\ \{ 0.5 ::{a^{\prime}} \mid a \in{\mathit{atoms}(\Pi )}\setminus{\mathit{soft}(\Pi )}\} &, \end{align*}
-
• and the evidence literals
 $\{\neg{\mathit{bot}}\}.$
$\{\neg{\mathit{bot}}\}.$
Observe that this is a valid ProbLog program. Condition 1 of validity is satisfied because the atoms
![]() $a^{\prime}$
occurring in the probabilistic facts do not occur in any head of the normal rules, and condition 2 is satisfied because the normal rules are stratified. The following proposition states the correctness of the translation.
$a^{\prime}$
occurring in the probabilistic facts do not occur in any head of the normal rules, and condition 2 is satisfied because the normal rules are stratified. The following proposition states the correctness of the translation.
Proposition 5.
Let
![]() $\Pi$
be a normal
$\Pi$
be a normal
![]() $\textit{Lpmln}^{\pm }$
program
$\textit{Lpmln}^{\pm }$
program
![]() $\Pi$
without weak constraints, whose soft formulas have the form
$\Pi$
without weak constraints, whose soft formulas have the form
![]() $w : \neg \neg a$
for some atom
$w : \neg \neg a$
for some atom
![]() $a$
that has at most one formula of that form. For every interpretation
$a$
that has at most one formula of that form. For every interpretation
![]() $X$
disjoint from
$X$
disjoint from
![]() $\{{a^{\prime}}\mid a \in{\mathit{atoms}(\Pi )}\}$
it holds that
$\{{a^{\prime}}\mid a \in{\mathit{atoms}(\Pi )}\}$
it holds that
![]() $P_{\Pi }^{{\pm }}(X)$
and
$P_{\Pi }^{{\pm }}(X)$
and
![]() $P_{{{{\mathit{lpmln2problog}(\Pi )}}}}(X\cup \{{a^{\prime}}\mid a \in X\})$
are the same.
$P_{{{{\mathit{lpmln2problog}(\Pi )}}}}(X\cup \{{a^{\prime}}\mid a \in X\})$
are the same.
4 The language of plingo and its frontends
In this section, we first describe the core language of plingo that basically re-interprets the language of clingo in terms of the semantics of
![]() $\textit{Lpmln}^{\pm }$
. After that, we illustrate the frontends of plingo with examples, showing in each case what is the result of the translation to the core language of plingo.
$\textit{Lpmln}^{\pm }$
. After that, we illustrate the frontends of plingo with examples, showing in each case what is the result of the translation to the core language of plingo.
The main idea of plingo is to keep the input language of clingo, and re-interpret weak constraints at priority level
![]() $0$
as soft integrity constraints. As explained above, these constraints are not considered to determine the optimal stable models, but instead are used to determine the weights of those models, from which their probabilities are calculated. For programs in the input language of plingo (or of clingo, i.e., the same) we can in fact provide a general definition that relies on the definitions used for clingo (Reference Calimeri, Faber, Gebser, Ianni, Kaminski, Krennwallner, Leone, Maratea, Ricca and SchaubCalimeri et al., 2020), and that therefore covers its whole language. We define a plingo program
$0$
as soft integrity constraints. As explained above, these constraints are not considered to determine the optimal stable models, but instead are used to determine the weights of those models, from which their probabilities are calculated. For programs in the input language of plingo (or of clingo, i.e., the same) we can in fact provide a general definition that relies on the definitions used for clingo (Reference Calimeri, Faber, Gebser, Ianni, Kaminski, Krennwallner, Leone, Maratea, Ricca and SchaubCalimeri et al., 2020), and that therefore covers its whole language. We define a plingo program
![]() $\Pi$
as a logic program in the language of clingo, and we let
$\Pi$
as a logic program in the language of clingo, and we let
![]() $\mathit{OSM}^{\mathit{plingo}}(\Pi )$
denote the optimal stable models of
$\mathit{OSM}^{\mathit{plingo}}(\Pi )$
denote the optimal stable models of
![]() $\Pi$
without considering weak constraints at level
$\Pi$
without considering weak constraints at level
![]() $0$
, and
$0$
, and
![]() $\mathit{Cost}_{\Pi }(X,0)$
denote the cost of the interpretation
$\mathit{Cost}_{\Pi }(X,0)$
denote the cost of the interpretation
![]() $X$
at priority level
$X$
at priority level
![]() $0$
, according to the definitions of Reference Calimeri, Faber, Gebser, Ianni, Kaminski, Krennwallner, Leone, Maratea, Ricca and SchaubCalimeri et al. (2020). Then, the weight and the probability of an interpretation
$0$
, according to the definitions of Reference Calimeri, Faber, Gebser, Ianni, Kaminski, Krennwallner, Leone, Maratea, Ricca and SchaubCalimeri et al. (2020). Then, the weight and the probability of an interpretation
![]() $X$
, written
$X$
, written
![]() $W_{\Pi }^{\mathit{plingo}}(X)$
and
$W_{\Pi }^{\mathit{plingo}}(X)$
and
![]() $P_{\Pi }^{\mathit{plingo}}(X)$
, respectively, are analogous to
$P_{\Pi }^{\mathit{plingo}}(X)$
, respectively, are analogous to
![]() $W_{\Pi }^{\mathit{alt}}(X)$
and
$W_{\Pi }^{\mathit{alt}}(X)$
and
![]() $P_{\Pi }^{\mathit{alt}}(X)$
, but replacing the set
$P_{\Pi }^{\mathit{alt}}(X)$
, but replacing the set
![]() $\mathit{SSM}^{\mathit{alt}}(\Pi )$
by
$\mathit{SSM}^{\mathit{alt}}(\Pi )$
by
![]() $\mathit{OSM}^{\mathit{plingo}}(\Pi )$
:
$\mathit{OSM}^{\mathit{plingo}}(\Pi )$
:
 \begin{align*}{W_{\Pi }^{\mathit{plingo}}(X)} & = \begin{cases} \mathit{exp}({\mathit{Cost}_{\Pi }(X,0)}) & \textrm{ if } X \in{\mathit{OSM}^{\mathit{plingo}}(\Pi )} \\ 0 & \textrm{ otherwise } \end{cases} \\ \textrm{ and } \\{P_{\Pi }^{\mathit{plingo}}(X)} & = \frac{{W_{\Pi }^{\mathit{plingo}}(X)}}{\sum _{Y \in{\mathit{OSM}^{\mathit{plingo}}(\Pi )}}{W_{\Pi }^{\mathit{plingo}}(Y)}} & \, . \end{align*}
\begin{align*}{W_{\Pi }^{\mathit{plingo}}(X)} & = \begin{cases} \mathit{exp}({\mathit{Cost}_{\Pi }(X,0)}) & \textrm{ if } X \in{\mathit{OSM}^{\mathit{plingo}}(\Pi )} \\ 0 & \textrm{ otherwise } \end{cases} \\ \textrm{ and } \\{P_{\Pi }^{\mathit{plingo}}(X)} & = \frac{{W_{\Pi }^{\mathit{plingo}}(X)}}{\sum _{Y \in{\mathit{OSM}^{\mathit{plingo}}(\Pi )}}{W_{\Pi }^{\mathit{plingo}}(Y)}} & \, . \end{align*}
4.1 The frontend of lpmln
Listing 1 shows the birds example from Reference Lee and WangLee and Wang (2016) using the frontend of Lpmln. To start with, there is some general knowledge about birds: both resident birds and migratory birds are birds, and a bird cannot be both resident and migratory. This is represented by the hard rules in Lines 1-3 that are written as common clingo rules. Additionally, from one source of information, we have the fact that
![]() $\texttt{jo}$
is a resident bird, while from another, we have that
$\texttt{jo}$
is a resident bird, while from another, we have that
![]() $\texttt{jo}$
is a migratory bird. For some reason, we hold the first source to be more trustworthy than the second. This information is represented by the soft rules in Lines 4 and 5 where the weights are expressed by the (integer) arguments of their &weight/1 atoms in the body. The first soft rule corresponds to the weighted formula
$\texttt{jo}$
is a migratory bird. For some reason, we hold the first source to be more trustworthy than the second. This information is represented by the soft rules in Lines 4 and 5 where the weights are expressed by the (integer) arguments of their &weight/1 atoms in the body. The first soft rule corresponds to the weighted formula
![]() $2 : resident(jo)$
and the second to
$2 : resident(jo)$
and the second to
![]() $1 : migratory(jo)$
. Under both the standard and the alternative semantics, this program has three probabilistic stable models:
$1 : migratory(jo)$
. Under both the standard and the alternative semantics, this program has three probabilistic stable models:
![]() $\{\}$
,
$\{\}$
,
![]() $\{{resident(jo)},{bird(jo)}\}$
, and
$\{{resident(jo)},{bird(jo)}\}$
, and
![]() $\{{migratory(jo)},{bird(jo)}\}$
, whose probabilities are
$\{{migratory(jo)},{bird(jo)}\}$
, whose probabilities are
![]() $0.09$
,
$0.09$
,
![]() $0.67$
, and
$0.67$
, and
![]() $0.24$
, respectively. They can be computed by plingo, running the command plingo –mode=lpmln birds.plp for the standard semantics, and using the option –mode=lpmln-alt for the alternative semantics.
$0.24$
, respectively. They can be computed by plingo, running the command plingo –mode=lpmln birds.plp for the standard semantics, and using the option –mode=lpmln-alt for the alternative semantics.
Listing 1. Lpmln birds example (birds.plp).

Listing 2. Translation of the birds example.

Plingo translates Lpmln programs using the negative versions of the
![]() $\mathit{standard}$
and
$\mathit{standard}$
and
![]() $\mathit{alternative}$
translations from Section 3.1. Considering first the alternative semantics, the hard rules remain the same, while the soft ones are translated as shown in Listing 2. According to the negative version of the
$\mathit{alternative}$
translations from Section 3.1. Considering first the alternative semantics, the hard rules remain the same, while the soft ones are translated as shown in Listing 2. According to the negative version of the
![]() $\mathit{alternative}$
translation, the soft formula
$\mathit{alternative}$
translation, the soft formula
![]() $2 : resident(jo)$
becomes the hard formula
$2 : resident(jo)$
becomes the hard formula
![]() $\alpha : resident(jo) \vee \neg resident(jo)$
and the soft formula
$\alpha : resident(jo) \vee \neg resident(jo)$
and the soft formula
![]() $-2 : \neg resident(jo)$
. In plingo, the first is written as the choice rule in Line 1 and the second as the weak constraint at level
$-2 : \neg resident(jo)$
. In plingo, the first is written as the choice rule in Line 1 and the second as the weak constraint at level
![]() $0$
of Line 2. The translation of the other soft fact is similar. Considering now the standard semantics, the first rule of Listing 1 becomes the choice rule bird(X) :- resident(X) together with the weak constraint : not bird(X), resident(X).[-1@1,X]. The second rule is translated similarly. The third one becomes simply : resident(X), migratory(X). [-1@1,X], since the additional choice rule is a tautology and can be skipped. Observe that both weak constraints use the variable X in the expression [-1@1,X]. This ensures that stable models obtain a weight of -1 for every ground instantiation of the corresponding body that they satisfy.
$0$
of Line 2. The translation of the other soft fact is similar. Considering now the standard semantics, the first rule of Listing 1 becomes the choice rule bird(X) :- resident(X) together with the weak constraint : not bird(X), resident(X).[-1@1,X]. The second rule is translated similarly. The third one becomes simply : resident(X), migratory(X). [-1@1,X], since the additional choice rule is a tautology and can be skipped. Observe that both weak constraints use the variable X in the expression [-1@1,X]. This ensures that stable models obtain a weight of -1 for every ground instantiation of the corresponding body that they satisfy.
4.2 The frontend of ProbLog
We illustrate the frontend of ProbLog with an example where we toss two biased coins whose probability of turning up heads is
![]() $0.6$
. We would like to know what is the probability of the first coin turning up heads, given some evidence against the case that both coins turn up heads. The representation in plingo is shown in Listing 3. The first rule represents the toss of the coins. Its ground instantiation leads to two probabilistic facts, one for each coin, whose associated probabilities are specified by the &problog/1 atom in the body. The argument of &problog/1 atoms is a string that contains either a float number or an expression, for example
$0.6$
. We would like to know what is the probability of the first coin turning up heads, given some evidence against the case that both coins turn up heads. The representation in plingo is shown in Listing 3. The first rule represents the toss of the coins. Its ground instantiation leads to two probabilistic facts, one for each coin, whose associated probabilities are specified by the &problog/1 atom in the body. The argument of &problog/1 atoms is a string that contains either a float number or an expression, for example
![]() $``\texttt{3/5}"$
. Since the argument is a probability, the string must either contain or evaluate to a real number between
$``\texttt{3/5}"$
. Since the argument is a probability, the string must either contain or evaluate to a real number between
![]() $0$
and
$0$
and
![]() $1$
. The next line poses the query about the probability of the first coin turning up heads, using the theory atom &query/1, whose unique argument is an atom. Finally, Lines 3 and 4 add the available evidence, using the theory atom &evidence/2, whose arguments are an atom and a truth value (true or false). In ProbLog, the probabilistic facts alone lead to four possible worlds:
$1$
. The next line poses the query about the probability of the first coin turning up heads, using the theory atom &query/1, whose unique argument is an atom. Finally, Lines 3 and 4 add the available evidence, using the theory atom &evidence/2, whose arguments are an atom and a truth value (true or false). In ProbLog, the probabilistic facts alone lead to four possible worlds:
![]() $\{\}$
with probability
$\{\}$
with probability
![]() $0.4*0.4=0.16$
,
$0.4*0.4=0.16$
,
![]() $\{\texttt{heads(1)}\}$
and
$\{\texttt{heads(1)}\}$
and
![]() $\{\texttt{heads(2)}\}$
with probability
$\{\texttt{heads(2)}\}$
with probability
![]() $0.6*0.4=0.24$
each, and
$0.6*0.4=0.24$
each, and
![]() $\{\texttt{heads(1)}, \texttt{heads(2)}\}$
with probability
$\{\texttt{heads(1)}, \texttt{heads(2)}\}$
with probability
![]() $0.6*0.6=0.36$
. The last possible world is eliminated by the evidence, and we are left with three possible worlds. Then, the probability of
$0.6*0.6=0.36$
. The last possible world is eliminated by the evidence, and we are left with three possible worlds. Then, the probability of
![]() $\texttt{heads(1)}$
is the result of dividing the probability of
$\texttt{heads(1)}$
is the result of dividing the probability of
![]() $\{\texttt{heads(1)}\}$
by the sum of the probabilities of the three possible worlds, that is
$\{\texttt{heads(1)}\}$
by the sum of the probabilities of the three possible worlds, that is
![]() $\frac{0.24}{0.16+0.24+0.24}=0.375$
. This is the result that we obtain running the command plingo –mode=problog coins.plp.
$\frac{0.24}{0.16+0.24+0.24}=0.375$
. This is the result that we obtain running the command plingo –mode=problog coins.plp.
Plingo translates ProbLog programs using the translation
![]() ${{\mathit{problog2lpmln}}}$
from Section 3.2. The result in this case is shown in Listing 4. In the propositional case, the probabilistic ProbLog fact
${{\mathit{problog2lpmln}}}$
from Section 3.2. The result in this case is shown in Listing 4. In the propositional case, the probabilistic ProbLog fact
![]() $0.6 :: heads(1)$
is translated to the weighted fact
$0.6 :: heads(1)$
is translated to the weighted fact
![]() $w: heads(1)$
, where
$w: heads(1)$
, where
![]() $w=ln(0.6/(1-0.6))\approx 0.40546$
Footnote
2
that in
$w=ln(0.6/(1-0.6))\approx 0.40546$
Footnote
2
that in
![]() $\textit{Lpmln}^{\pm }$
becomes the hard formula
$\textit{Lpmln}^{\pm }$
becomes the hard formula
![]() $\alpha : heads(1) \vee \neg heads(1)$
together with the soft integrity constraint
$\alpha : heads(1) \vee \neg heads(1)$
together with the soft integrity constraint
![]() $w : \neg \neg heads(1)$
. The translation for the other probabilistic fact is similar. In plingo, for
C = 1..2, the hard formula is written as the choice rule of Line 1, and the soft one is written as a weak constraint at level
$w : \neg \neg heads(1)$
. The translation for the other probabilistic fact is similar. In plingo, for
C = 1..2, the hard formula is written as the choice rule of Line 1, and the soft one is written as a weak constraint at level
![]() $0$
in the next line, after simplifying away the double negation, where @f(X) is an external function that returns the natural logarithm of X/(1-X). Going back to the original program, the &query/1 atom is stored by the system to determine what reasoning task to perform, the normal rule in Line 3 is kept intact, and the &evidence/1 atom is translated to the integrity constraint of Line 4, which excludes the possibility of both coins turning up heads.
$0$
in the next line, after simplifying away the double negation, where @f(X) is an external function that returns the natural logarithm of X/(1-X). Going back to the original program, the &query/1 atom is stored by the system to determine what reasoning task to perform, the normal rule in Line 3 is kept intact, and the &evidence/1 atom is translated to the integrity constraint of Line 4, which excludes the possibility of both coins turning up heads.
Listing 3. ProbLog tossing coins example (coins.plp).

Listing 4. Translation of the coins example.

4.3 The frontend of P-log
We illustrate the frontend of P-log with a simplified version of the dice example from Reference Baral, Gelfond and RushtonBaral et al. (2009), where there are two dice of six faces. The first dice is fair, while the second one is biased to roll
![]() $6$
half of the times. We roll both dice and observe that the first rolls a
$6$
half of the times. We roll both dice and observe that the first rolls a
![]() $1$
. We would like to know what is the probability of the second dice rolling another
$1$
. We would like to know what is the probability of the second dice rolling another
![]() $1$
. The representation in plingo using the P-log frontend is shown in Listing 5. Given that the original language P-log is sorted, a representation in that language would contain the sorts
$1$
. The representation in plingo using the P-log frontend is shown in Listing 5. Given that the original language P-log is sorted, a representation in that language would contain the sorts
![]() $\mathit{dice}=\{\texttt{d1},\texttt{d2}\}$
and
$\mathit{dice}=\{\texttt{d1},\texttt{d2}\}$
and
![]() $\mathit{score}=\{\texttt{1}, \ldots, \texttt{6}\}$
, and the attribute
$\mathit{score}=\{\texttt{1}, \ldots, \texttt{6}\}$
, and the attribute
![]() $\mathit{roll}: \mathit{dice} \to \mathit{score}$
. In plingo there are no attributes, and the sorts are represented by normal atoms, like in the first two lines of Listing 5. Then, for example, to assert that the result of rolling dice d2 is 6, in P-log one would write an assignment roll(d2) = 6 stating that the attribute roll(d2) has the value 6, while in plingo one would use a normal atom of the form roll(d2,6). Going back to the encoding, Line 3 contains a random selection rule that describes the experiments of rolling every dice D. Each of these experiments selects at random one of the scores of the dice, unless this value is fixed by a deliberate action of the form &do(A), which does not occur in our example. Line 3 contains a probabilistic atom stating that the probability of dice d2 rolling a 6 is
$\mathit{roll}: \mathit{dice} \to \mathit{score}$
. In plingo there are no attributes, and the sorts are represented by normal atoms, like in the first two lines of Listing 5. Then, for example, to assert that the result of rolling dice d2 is 6, in P-log one would write an assignment roll(d2) = 6 stating that the attribute roll(d2) has the value 6, while in plingo one would use a normal atom of the form roll(d2,6). Going back to the encoding, Line 3 contains a random selection rule that describes the experiments of rolling every dice D. Each of these experiments selects at random one of the scores of the dice, unless this value is fixed by a deliberate action of the form &do(A), which does not occur in our example. Line 3 contains a probabilistic atom stating that the probability of dice d2 rolling a 6 is
![]() $1/2$
. By the principle of indifference, embodied in the semantics of P-log, the probability of each of the
$1/2$
. By the principle of indifference, embodied in the semantics of P-log, the probability of each of the
![]() $5$
other faces of d2 is
$5$
other faces of d2 is
![]() $(1-1/2)/5=0.1$
, while the probability of each face of d1 is
$(1-1/2)/5=0.1$
, while the probability of each face of d1 is
![]() $1/6$
. Line 5 represents the observation of the first dice rolling a
$1/6$
. Line 5 represents the observation of the first dice rolling a
![]() $1$
, and the last line states the query about the probability of the second dice rolling another
$1$
, and the last line states the query about the probability of the second dice rolling another
![]() $1$
. Running the command plingo –mode=plog dice.plp, we obtain that this probability is, as expected,
$1$
. Running the command plingo –mode=plog dice.plp, we obtain that this probability is, as expected,
![]() $0.1$
. If we replace the query by &query(roll(d1,1)), then we obtain a probability of
$0.1$
. If we replace the query by &query(roll(d1,1)), then we obtain a probability of
![]() $1$
, and not of
$1$
, and not of
![]() $1/6$
, because the observation in Line 5 is only consistent with the first dice rolling a
$1/6$
, because the observation in Line 5 is only consistent with the first dice rolling a
![]() $1$
.
$1$
.
Listing 5. P-log dice example (dice.plp).

Listing 6. Translation of the dice example.

Plingo translates P-log programs by combining the translation from Reference Lee, Talsania and WangLee et al. (2017) to Lpmln with the
![]() $\mathit{alternative}$
translation from Section 3.1. Given the input file dice.plp, plingo copies the normal rules of Lines 1–2, translates the rules specific to P-log into the Listing 6, stores internally the information about the &query atom, and adds the general meta-encoding of Listing 7. In Listing 6, Line 5 defines for every dice D one random experiment, identified by the term roll(D), which may select for the attribute roll(D) one possible score X. The atoms defined that way are fed to the first rule of the meta-encoding to choose exactly one of those assignments, represented in this case by n special predicate h/1 (standing for ”holds”), which is made equivalent to the predicate roll/2 in Lines 5–6 of Listing 7. Those lines are the interface between the specific input program and the general meta-encoding. They allow the latter to refer to the atoms of the former using the predicate h/1. Next, Line 2 of Listing 6 defines the probability of the second dice rolling a 6 in the experiment identified by the term roll(d2). This is used in Line 6 of the meta-encoding, where @f1(P) returns the logarithm of P, to add that weight whenever the following conditions hold: the attribute A has the value V, this value has not been fixed by a deliberate action, and some probabilistic atom gives the probability P. If there is no such probabilistic atom, then the rule of Line 9 derives that the assignment chosen in the experiment E receives the default probability, calculated in Lines 11–14 following the principle of indifference mentioned above, where @f2(Y) returns the logarithm of 1-Y, and @f3(M) returns the logarithm of 1/M. The idea of this calculation is as follows. For some experiment E, the number Y accounts for the sum of the probabilities of the probabilistic atoms related to E, and M is the number of outcomes of the experiment E for which there are no probabilistic atoms. Then, the probability of each outcome of the experiment E for which there is no probabilistic atom is (1-Y)*(1/M). Instead of multiplying those probabilities 1-Y and 1/M, the encoding adds their logarithms, and it does so in two steps: one in each of the last two weak constraints. Finally, the observation fact generated in Line 3 of Listing 6 is handled by Lines 3-4 of Listing 7, and the possible deliberate actions, represented by atoms of the form do(A), are handled in Line 6 of the meta-encoding.
$\mathit{alternative}$
translation from Section 3.1. Given the input file dice.plp, plingo copies the normal rules of Lines 1–2, translates the rules specific to P-log into the Listing 6, stores internally the information about the &query atom, and adds the general meta-encoding of Listing 7. In Listing 6, Line 5 defines for every dice D one random experiment, identified by the term roll(D), which may select for the attribute roll(D) one possible score X. The atoms defined that way are fed to the first rule of the meta-encoding to choose exactly one of those assignments, represented in this case by n special predicate h/1 (standing for ”holds”), which is made equivalent to the predicate roll/2 in Lines 5–6 of Listing 7. Those lines are the interface between the specific input program and the general meta-encoding. They allow the latter to refer to the atoms of the former using the predicate h/1. Next, Line 2 of Listing 6 defines the probability of the second dice rolling a 6 in the experiment identified by the term roll(d2). This is used in Line 6 of the meta-encoding, where @f1(P) returns the logarithm of P, to add that weight whenever the following conditions hold: the attribute A has the value V, this value has not been fixed by a deliberate action, and some probabilistic atom gives the probability P. If there is no such probabilistic atom, then the rule of Line 9 derives that the assignment chosen in the experiment E receives the default probability, calculated in Lines 11–14 following the principle of indifference mentioned above, where @f2(Y) returns the logarithm of 1-Y, and @f3(M) returns the logarithm of 1/M. The idea of this calculation is as follows. For some experiment E, the number Y accounts for the sum of the probabilities of the probabilistic atoms related to E, and M is the number of outcomes of the experiment E for which there are no probabilistic atoms. Then, the probability of each outcome of the experiment E for which there is no probabilistic atom is (1-Y)*(1/M). Instead of multiplying those probabilities 1-Y and 1/M, the encoding adds their logarithms, and it does so in two steps: one in each of the last two weak constraints. Finally, the observation fact generated in Line 3 of Listing 6 is handled by Lines 3-4 of Listing 7, and the possible deliberate actions, represented by atoms of the form do(A), are handled in Line 6 of the meta-encoding.
Listing 7. Meta-encoding for the frontend of P-log.

5 The system plingo
The implementation of plingo is based on clingo and its Python API (v5.5, Reference Gebser, Kaminski, Kaufmann, Ostrowski, Schaub and WankoGebser et al. (2016)). The system architecture is described in Figure 1. The input is a logic program written in some probabilistic language:
![]() $\textit{Lpmln}^{\pm }$
, Lpmln, ProbLog or P-log. For
$\textit{Lpmln}^{\pm }$
, Lpmln, ProbLog or P-log. For
![]() $\textit{Lpmln}^{\pm }$
, the input language (orange element of Figure 1) is the same as the input language of clingo, except for the fact that the weights of the weak constraints can be strings representing real numbers. For the other languages, the system uses the corresponding frontends that translate the input logic programs (yellow elements of Figure 1) to the input language of plingo using the Transformer module, as illustrated by the examples in Section 4. Among other things, this involves converting the theory atoms (preceeded by “&”) to normal atoms. The only exception to this is &query atoms that are eliminated from the program and stored internally. For P-log, the frontend also appends the meta-encoding (Listing 7) to the translation of the input program.
$\textit{Lpmln}^{\pm }$
, the input language (orange element of Figure 1) is the same as the input language of clingo, except for the fact that the weights of the weak constraints can be strings representing real numbers. For the other languages, the system uses the corresponding frontends that translate the input logic programs (yellow elements of Figure 1) to the input language of plingo using the Transformer module, as illustrated by the examples in Section 4. Among other things, this involves converting the theory atoms (preceeded by “&”) to normal atoms. The only exception to this is &query atoms that are eliminated from the program and stored internally. For P-log, the frontend also appends the meta-encoding (Listing 7) to the translation of the input program.

Fig 1. System architecture of plingo. The frontends are colored in yellow. Modules of the system are gray boxes. The green flow corresponds to most probable explanation (MPE) inference, the blue one to exact marginal inference, and the red one to approximate inference, all of them using plingo’s internal solving algorithms. The purple flow corresponds to MPE and marginal inference using problog.
Plingo can be used to solve two reasoning tasks: most probable explanation (MPE) inference and marginal inference. MPE inference corresponds to the task of finding the most probable stable model of a probabilistic logic program.Footnote
3
Following the approach of Reference Lee, Talsania and WangLee et al. (2017), this task is reduced in plingo to finding one optimal stable model of the input program using clingo’s built-in optimization methods. The only changes that have to be made concern handling the strings that may occur as weights of weak constraints, and switching the sign of such weights, since otherwise clingo would compute a least probable stable model. Regarding marginal inference, it can be either applied in general or with respect to a query. In the first case, the task is to find all stable models and their probabilities. In the second case, the task is to find the probability of some query atom, which is undefined if the input program has no stable models, and otherwise it is the sum of the probabilities of the stable models that contain that atom. The basic algorithm of plingo for both cases is the same. First, the system enumerates all optimal stable models of the input program excluding the weak constraints at level
![]() $0$
. Afterward, those optimal stable models are passed, together with their costs at level
$0$
. Afterward, those optimal stable models are passed, together with their costs at level
![]() $0$
, to the Probability module, which calculates the required probabilities.
$0$
, to the Probability module, which calculates the required probabilities.
In addition to this exact method (represented by the upper blue arrows in Figure 1), plingo implements an approximation method (red arrows in Figure 1) based on the approach presented in Reference Pajunen and JanhunenPajunen and Janhunen (2021). The idea is to simplify the solving process by computing just a subset of the stable models and using this smaller set to approximate the actual probabilities. Formally, in the definitions of
![]() $W_{\Pi }^{\mathit{plingo}}(X)$
and
$W_{\Pi }^{\mathit{plingo}}(X)$
and
![]() $P_{\Pi }^{\mathit{plingo}}(X)$
, this implies replacing the set
$P_{\Pi }^{\mathit{plingo}}(X)$
, this implies replacing the set
![]() $\mathit{OSM}^{\mathit{plingo}}(\Pi )$
by one of its subsets. In the implementation, the modularity of this change is reflected by the fact that the Probability module is agnostic to whether the stable models that it receives as input are all or just some subset of them. For marginal inference in general, this smaller subset consists of
$\mathit{OSM}^{\mathit{plingo}}(\Pi )$
by one of its subsets. In the implementation, the modularity of this change is reflected by the fact that the Probability module is agnostic to whether the stable models that it receives as input are all or just some subset of them. For marginal inference in general, this smaller subset consists of
![]() $k$
stable models with the highest possible probability, given some positive integer
$k$
stable models with the highest possible probability, given some positive integer
![]() $k$
that is part of the input. To compute this subset, the Solver module of plingo uses a new implementation for the task of answer set enumeration in the order of optimality (ASEO) presented in Reference Pajunen and JanhunenPajunen and Janhunen (2021). Given some positive integer
$k$
that is part of the input. To compute this subset, the Solver module of plingo uses a new implementation for the task of answer set enumeration in the order of optimality (ASEO) presented in Reference Pajunen and JanhunenPajunen and Janhunen (2021). Given some positive integer
![]() $k$
, the implementation first computes the stable models of the smallest cost, then, among the remaining stable models, computes the ones of the smallest cost, and so on until
$k$
, the implementation first computes the stable models of the smallest cost, then, among the remaining stable models, computes the ones of the smallest cost, and so on until
![]() $k$
stable models (if they exist) have been computed.Footnote
4
For marginal inference with respect to a query, the smaller subset consists of
$k$
stable models (if they exist) have been computed.Footnote
4
For marginal inference with respect to a query, the smaller subset consists of
![]() $k$
stable models containing the query of the highest possible probability and another
$k$
stable models containing the query of the highest possible probability and another
![]() $k$
stable models without the query of the highest possible probability. In this case, the algorithm for ASEO is set to compute
$k$
stable models without the query of the highest possible probability. In this case, the algorithm for ASEO is set to compute
![]() $2\times k$
stable models in total. But once it has computed
$2\times k$
stable models in total. But once it has computed
![]() $k$
stable models that contain the query, or
$k$
stable models that contain the query, or
![]() $k$
stable models that do not contain the query, whichever happens first, it adds a constraint enforcing that the remaining stable models fall into the opposite case.
$k$
stable models that do not contain the query, whichever happens first, it adds a constraint enforcing that the remaining stable models fall into the opposite case.
Plingo offers a third solving method that generates a ProbLog program using the translation
![]() ${{\mathit{lpmln2problog}}}$
and afterward runs a problog solver. This method can be used for both MPE and marginal inference. In fact, it can leverage all solving modes and options of a ProbLog solver. In Figure 1, it is represented by the purple arrow. The Translator component takes as input a
${{\mathit{lpmln2problog}}}$
and afterward runs a problog solver. This method can be used for both MPE and marginal inference. In fact, it can leverage all solving modes and options of a ProbLog solver. In Figure 1, it is represented by the purple arrow. The Translator component takes as input a
![]() $\textit{Lpmln}^{\pm }$
program and uses the meta-programming option –output=reify of clingo (Reference Kaminski, Romero, Schaub and WankoKaminski et al., 2023) to ground and reify that program into a list of facts. Then, in our first approach, we just combined those facts with a ProbLog meta-encoding implementing the translation
$\textit{Lpmln}^{\pm }$
program and uses the meta-programming option –output=reify of clingo (Reference Kaminski, Romero, Schaub and WankoKaminski et al., 2023) to ground and reify that program into a list of facts. Then, in our first approach, we just combined those facts with a ProbLog meta-encoding implementing the translation
![]() ${{\mathit{lpmln2problog}}}$
. While this approach was very elegant, it turned out to be inefficient, because problog 2.2 needed too much time to ground the meta-encoding. Perhaps a more experienced ProbLog programmer could develop a more performant meta-encoding.Footnote
5
In our case, we decided to move the grounding efforts to clingo. We developed a meta-encoding that implements the translation
${{\mathit{lpmln2problog}}}$
. While this approach was very elegant, it turned out to be inefficient, because problog 2.2 needed too much time to ground the meta-encoding. Perhaps a more experienced ProbLog programmer could develop a more performant meta-encoding.Footnote
5
In our case, we decided to move the grounding efforts to clingo. We developed a meta-encoding that implements the translation
![]() ${{\mathit{lpmln2problog}}}$
, but replaces the ProbLog’s probabilistic facts of the form
${{\mathit{lpmln2problog}}}$
, but replaces the ProbLog’s probabilistic facts of the form
![]() $p :: a$
by ASP facts of the form
$p :: a$
by ASP facts of the form
![]() $prob(p,a)$
. This meta-encoding, together with the reified program, is grounded by clingo using option –text, resulting in a ground normal logic program. The final ProbLog program is the combination of this program with a small ProbLog meta-encoding that creates the corresponding probabilistic facts given the atoms
$prob(p,a)$
. This meta-encoding, together with the reified program, is grounded by clingo using option –text, resulting in a ground normal logic program. The final ProbLog program is the combination of this program with a small ProbLog meta-encoding that creates the corresponding probabilistic facts given the atoms
![]() $\mathit{prob}(p,a)$
. This is the approach that is actually implemented in plingo. We would like to highlight that, although in Section 3.2 we have defined the translation
$\mathit{prob}(p,a)$
. This is the approach that is actually implemented in plingo. We would like to highlight that, although in Section 3.2 we have defined the translation
![]() ${{\mathit{lpmln2problog}}}$
only for normal logic programs, the actual implementation in plingo covers the whole non-disjunctive part of the clingo language (Reference Calimeri, Faber, Gebser, Ianni, Kaminski, Krennwallner, Leone, Maratea, Ricca and SchaubCalimeri et al., 2020). Furthermore, the meta-encoding has been optimized to minimize the number of new atoms that it introduces. For example, for programs that follow the Generate, Define, and Test methodology (Reference LifschitzLifschitz, 2002) of ASP, the meta-encoding only introduces the atoms
${{\mathit{lpmln2problog}}}$
only for normal logic programs, the actual implementation in plingo covers the whole non-disjunctive part of the clingo language (Reference Calimeri, Faber, Gebser, Ianni, Kaminski, Krennwallner, Leone, Maratea, Ricca and SchaubCalimeri et al., 2020). Furthermore, the meta-encoding has been optimized to minimize the number of new atoms that it introduces. For example, for programs that follow the Generate, Define, and Test methodology (Reference LifschitzLifschitz, 2002) of ASP, the meta-encoding only introduces the atoms
![]() $a^{\prime}$
of the translation for those original atoms
$a^{\prime}$
of the translation for those original atoms
![]() $a$
that are not generated by the choice rules and do occur in soft formulas.
$a$
that are not generated by the choice rules and do occur in soft formulas.
6 Experiments
In this section, we experimentally evaluate the three solving methods of plingo version 1.1 and compare them to native implementations of Lpmln, ProbLog, and P-log.Footnote
6
For Lpmln, we evaluate the system lpmln2asp (Reference Lee, Talsania and WangLee et al., 2017) that is the foundation of the basic implementation of plingo. For ProbLog, we consider the problog system version 2.2.2 (Reference Fierens, den Broeck, Renkens, Shterionov, Gutmann, Thon, Janssens and RaedtFierens et al., 2015) that implements various methods for probabilistic reasoning. In the experiments, we use one of those methods that is designed specifically to answer probabilistic queries. It converts the input program to a weighted Boolean formula and then applies a knowledge compilation method for weighted model counting. For P-log, we evaluate two implementations, which we call plog-naive and plog-dco (Reference BalaiiBalaii, 2017). While the former works like plingo and lpmln2asp by enumerating stable models, the latter implements a different algorithm that builds a computation tree specific to the input query. All benchmarks were run on an Intel
![]() $^{\textrm{{TM}}}$
Xeon E5-2650v4 under Debian GNU/Linux 10, with 24 GB of memory and a timeout of 1200s per instance.
$^{\textrm{{TM}}}$
Xeon E5-2650v4 under Debian GNU/Linux 10, with 24 GB of memory and a timeout of 1200s per instance.
We have performed three experiments. In the first one, our goal is to evaluate the performance of the three solving methods of plingo and compare it to the performance of all the other systems on the same domain. In particular, we want to analyze the solving time and the accuracy of the approximation method for different values of the input parameter
![]() $k$
, and we want to compare the problog-based method of plingo with the system problog running an original ProbLog encoding. In the second experiment, our goal is to compare plingo with the implementations of P-log on domains that are specific to this language. Finally, the goal of the third experiment is to compare plingo and lpmln2asp on the task of MPE inference. In particular, in this case, the basic implementation of plingo and the implementation of lpmln2asp are very similar and boil down to a single call to clingo. Here, we would like to evaluate if in this situation there is any difference in performance between both approaches.
$k$
, and we want to compare the problog-based method of plingo with the system problog running an original ProbLog encoding. In the second experiment, our goal is to compare plingo with the implementations of P-log on domains that are specific to this language. Finally, the goal of the third experiment is to compare plingo and lpmln2asp on the task of MPE inference. In particular, in this case, the basic implementation of plingo and the implementation of lpmln2asp are very similar and boil down to a single call to clingo. Here, we would like to evaluate if in this situation there is any difference in performance between both approaches.
In the first experiment, we compare all systems on the task of marginal inference with respect to a query in a probabilistic Grid domain from Reference ZhuZhu (2012),which appeared in a slightly different form in Reference Fierens, den Broeck, Renkens, Shterionov, Gutmann, Thon, Janssens and RaedtFierens et al. (2015). We have chosen this domain because it can be easily and similarly represented in all these probabilistic languages, which is required if we want to compare all systems in terms of a single benchmark. In this domain, there is a grid of size
![]() $m \times n$
, where each node
$m \times n$
, where each node
![]() $(i,j)$
passes information to the nodes
$(i,j)$
passes information to the nodes
![]() $(i+1,j)$
and
$(i+1,j)$
and
![]() $(i,j+1)$
if
$(i,j+1)$
if
![]() $(i,j)$
is not faulty, and each node in the grid can be faulty with probability
$(i,j)$
is not faulty, and each node in the grid can be faulty with probability
![]() $0.1$
. The task poses the following question: what is the probability that node
$0.1$
. The task poses the following question: what is the probability that node
![]() $(m,n)$
receives information from node
$(m,n)$
receives information from node
![]() $(1,1)$
? To answer this, we run exact marginal inference with all approaches, and approximate marginal inference with plingo for different values of
$(1,1)$
? To answer this, we run exact marginal inference with all approaches, and approximate marginal inference with plingo for different values of
![]() $k$
:
$k$
:
![]() $10^1$
,
$10^1$
,
![]() $10^2$
, …, and
$10^2$
, …, and
![]() $10^6$
. The results are shown in Figure 2. On the left side, there is a cactus plot representing how many instances were solved within a given runtime. The dashed lines represent the runtimes of approximate marginal inference in plingo for
$10^6$
. The results are shown in Figure 2. On the left side, there is a cactus plot representing how many instances were solved within a given runtime. The dashed lines represent the runtimes of approximate marginal inference in plingo for
![]() $k=10^5$
and
$k=10^5$
and
![]() $k=10^6$
. Among the exact implementations, problog and the problog-based method of plingo are the clear winners. Their solving times are almost the same, showing that in this case the translation generated by plingo does not incur in any additional overhead. The specific algorithm of problog for answering queries is much faster than the other exact systems that either have to enumerate all stable models or, in the case of plog-dco, may have to explore its whole solution tree. The runtimes among the rest of the exact systems are comparable, but plingo is a bit faster than the others. For the approximation method, on the right side of Figure 2, for every value of
$k=10^6$
. Among the exact implementations, problog and the problog-based method of plingo are the clear winners. Their solving times are almost the same, showing that in this case the translation generated by plingo does not incur in any additional overhead. The specific algorithm of problog for answering queries is much faster than the other exact systems that either have to enumerate all stable models or, in the case of plog-dco, may have to explore its whole solution tree. The runtimes among the rest of the exact systems are comparable, but plingo is a bit faster than the others. For the approximation method, on the right side of Figure 2, for every value of
![]() $k$
and every instance, there is a dot whose coordinates represent the probability calculated by the approximation method and the true probability (calculated by problog). This is complemented by Table 1 that shows the average absolute error and the maximal absolute error for each value of
$k$
and every instance, there is a dot whose coordinates represent the probability calculated by the approximation method and the true probability (calculated by problog). This is complemented by Table 1 that shows the average absolute error and the maximal absolute error for each value of
![]() $k$
in
$k$
in
![]() $\%$
, where the absolute error for some instance and some
$\%$
, where the absolute error for some instance and some
![]() $k$
in
$k$
in
![]() $\%$
is defined as the absolute value of the difference between the calculated probability and the true probability for that instance, multiplied by
$\%$
is defined as the absolute value of the difference between the calculated probability and the true probability for that instance, multiplied by
![]() $100$
. We can see that, as the value of
$100$
. We can see that, as the value of
![]() $k$
increases, the performance of the approximation method deteriorates, while the quality of the approximated probabilities increases. A good compromise is found for
$k$
increases, the performance of the approximation method deteriorates, while the quality of the approximated probabilities increases. A good compromise is found for
![]() $k=10^5$
, where the runtime is better than problog, and the average error is below
$k=10^5$
, where the runtime is better than problog, and the average error is below
![]() $1\%$
.
$1\%$
.
Table 1. Average and maximal error (in
![]() $\%$
) of the approximation method on the Grid domain for different values of
$\%$
) of the approximation method on the Grid domain for different values of
![]() $k$
$k$


Fig 2. Runtimes of all systems and quality of the approximation method on the Grid domain.
In the second experiment, we compare the performance of the two exact methods of plingo using the P-log frontend with the two native implementations of that language, on tasks of marginal inference with respect to a query in three different domains: NASA, Blocks, and Squirrel. The NASA domain (Reference BalaiiBalaii, 2017) involves logical and probabilistic reasoning about the faults of a control system. For this domain, there are only three instances. All of them are solved by basic plingo in about a second, while problog-based plingo takes between
![]() $1$
and
$1$
and
![]() $80$
s, plog-naive between
$80$
s, plog-naive between
![]() $1$
and
$1$
and
![]() $5$
s, and plog-dco between
$5$
s, and plog-dco between
![]() $40$
and
$40$
and
![]() $100$
se. The Blocks domain (Reference ZhuZhu, 2012) starts with a grid and a set of
$100$
se. The Blocks domain (Reference ZhuZhu, 2012) starts with a grid and a set of
![]() $n$
blocks and asks what is the probability that two locations are still connected after the
$n$
blocks and asks what is the probability that two locations are still connected after the
![]() $n$
blocks have been randomly placed on the grid. In the experiments, we use a single map of
$n$
blocks have been randomly placed on the grid. In the experiments, we use a single map of
![]() $20$
locations and vary
$20$
locations and vary
![]() $n$
between
$n$
between
![]() $1$
and
$1$
and
![]() $5$
. The results are shown in Figure 3, where we can see a similar pattern as in the NASA domain: basic plingo and plog-naive solve all instances in just a few seconds, while plog-dco needs much more time for the bigger instances, and plingo combined with problog times out in all instances. The Squirrel domain (Reference Baral, Gelfond and RushtonBaral et al., 2009; Reference BalaiiBalaii, 2017) is an example of Bayesian learning, where the task is to update the probability of a squirrel finding some food in a patch on day
$5$
. The results are shown in Figure 3, where we can see a similar pattern as in the NASA domain: basic plingo and plog-naive solve all instances in just a few seconds, while plog-dco needs much more time for the bigger instances, and plingo combined with problog times out in all instances. The Squirrel domain (Reference Baral, Gelfond and RushtonBaral et al., 2009; Reference BalaiiBalaii, 2017) is an example of Bayesian learning, where the task is to update the probability of a squirrel finding some food in a patch on day
![]() $n$
after failing to find it on the first day. In the experiments we vary the number of days
$n$
after failing to find it on the first day. In the experiments we vary the number of days
![]() $n$
between
$n$
between
![]() $1$
and
$1$
and
![]() $27$
. The results are shown in Figure 3. In this domain, problog-based plingo can solve instances for up to
$27$
. The results are shown in Figure 3. In this domain, problog-based plingo can solve instances for up to
![]() $16$
days, while plog-naive can solve instances for up to
$16$
days, while plog-naive can solve instances for up to
![]() $23$
days, and plingo and plog-dco can solve instances for up to
$23$
days, and plingo and plog-dco can solve instances for up to
![]() $27$
days. To interpret the results, recall that the underlying algorithms of plog-naive and plingo are very similar. Hence, we conjecture that the better performance of plingo is due to details of the implementation. On the other hand, plog-dco uses a completely different algorithm. According to the authors (Balaii, Reference Balaii2017), this algorithm should be faster than plog-naive when the value of the query can be determined from a partial assignment of the atoms of the program. This may be what is happening in the Squirrel domain, where it is on par with plingo, while it does not seem to be the case for the other domains. We hoped that the problog-based method would allow plingo to solve faster the P-log benchmarks, but the results are in the opposite direction. In these domains, clingo generates relatively big ground programs in a short time, and then ProbLog’s solving components take a long time to reason about those programs.
$27$
days. To interpret the results, recall that the underlying algorithms of plog-naive and plingo are very similar. Hence, we conjecture that the better performance of plingo is due to details of the implementation. On the other hand, plog-dco uses a completely different algorithm. According to the authors (Balaii, Reference Balaii2017), this algorithm should be faster than plog-naive when the value of the query can be determined from a partial assignment of the atoms of the program. This may be what is happening in the Squirrel domain, where it is on par with plingo, while it does not seem to be the case for the other domains. We hoped that the problog-based method would allow plingo to solve faster the P-log benchmarks, but the results are in the opposite direction. In these domains, clingo generates relatively big ground programs in a short time, and then ProbLog’s solving components take a long time to reason about those programs.

Fig 3. Runtimes of plingo, plog-naive and plog-dco on the P-log domains.
In the third experiment, we compare the performance of the exact methods of plingo using the Lpmln frontend with the system lpmln2asp on tasks of MPE inference in two domains: Alzheimer and Smokers. The goal in the Alzheimer domain (Reference Raedt, Kimmig and ToivonenRaedt et al., 2007) is to determine the probability that two edges are connected in a directed probabilistic graph based on a real-world biological dataset of Alzheimer genes (Shterionov, Reference Shterionov2015).Footnote
7
The data consists of a directed probabilistic graph with 11530 edges and 5220 nodes. In the experiments we select different subgraphs of this larger graph, varying the number of nodes from
![]() $100$
to
$100$
to
![]() $2800$
. The results are shown in Figure 4, where we observe that problog-based plingo is slower than the other two methods, which behave similarly except on some instances of middle size and which can be solved by lpmln2asp but not by basic plingo. The Smokers domain involves probabilistic reasoning about a network of friends. Originally it was presented in Reference Domingos, Kok, Lowd, Poon, Richardson and SinglaDomingos et al. (2008), but we use a slightly simplified version from (Reference Lee, Talsania and WangLee et al., 2017). In the experiments we vary the number of friends in the network. In Figure 4, we can observe that basic plingo is the fastest, followed by lpmln2asp and then by problog-based plingo. Given that the underlying algorithms of basic plingo and lpmln2asp are similar, we expected them to have a similar performance. Looking at the results, we have no specific explanation for the differences in some instances of the Alzheimer domain, and we conjecture that they are due to the usual variations in solver performance. On the Smokers domain, the worse performance of lpmln2asp seems to be due to the usage of an external parser that increases a lot the preprocessing time for the bigger instances. With respect to problog-based plingo, in both domains, it spends most of its time grounding the translation with clingo, which seems to explain its worse performance.
$2800$
. The results are shown in Figure 4, where we observe that problog-based plingo is slower than the other two methods, which behave similarly except on some instances of middle size and which can be solved by lpmln2asp but not by basic plingo. The Smokers domain involves probabilistic reasoning about a network of friends. Originally it was presented in Reference Domingos, Kok, Lowd, Poon, Richardson and SinglaDomingos et al. (2008), but we use a slightly simplified version from (Reference Lee, Talsania and WangLee et al., 2017). In the experiments we vary the number of friends in the network. In Figure 4, we can observe that basic plingo is the fastest, followed by lpmln2asp and then by problog-based plingo. Given that the underlying algorithms of basic plingo and lpmln2asp are similar, we expected them to have a similar performance. Looking at the results, we have no specific explanation for the differences in some instances of the Alzheimer domain, and we conjecture that they are due to the usual variations in solver performance. On the Smokers domain, the worse performance of lpmln2asp seems to be due to the usage of an external parser that increases a lot the preprocessing time for the bigger instances. With respect to problog-based plingo, in both domains, it spends most of its time grounding the translation with clingo, which seems to explain its worse performance.

Fig 4. Runtimes of plingo and lpmln2asp on the Lpmln domains.
7 Conclusion
We have presented plingo, an extension of the ASP system clingo with various probabilistic reasoning modes. Although based on Lpmln, it also supports P-log and ProbLog. While the basic syntax of plingo is the same as the one of clingo, its semantics relies on re-interpreting the cost of a stable model at priority level
![]() $0$
as a measure of its probability. Solving exploits the relation between most probable stable models and optimal stable models (Reference Lee and YangLee and Yang, 2017); it relies on clingo’s optimization and enumeration modes, as well as an approximation method based on answer set enumeration in the order of optimality (Reference Pajunen and JanhunenPajunen and Janhunen, 2021). This is complemented by another method that is based on a novel translation to ProbLog. Our empirical evaluation has shown that plingo is at eye height with other ASP-based probabilistic systems and that the different solving methods implemented in the system are complementary. Notably, the approximation method produced low runtimes and low error rates (below
$0$
as a measure of its probability. Solving exploits the relation between most probable stable models and optimal stable models (Reference Lee and YangLee and Yang, 2017); it relies on clingo’s optimization and enumeration modes, as well as an approximation method based on answer set enumeration in the order of optimality (Reference Pajunen and JanhunenPajunen and Janhunen, 2021). This is complemented by another method that is based on a novel translation to ProbLog. Our empirical evaluation has shown that plingo is at eye height with other ASP-based probabilistic systems and that the different solving methods implemented in the system are complementary. Notably, the approximation method produced low runtimes and low error rates (below
![]() $1\%$
) on the Grid domain. Plingo is freely available at https://github.com/potassco/plingo.
$1\%$
) on the Grid domain. Plingo is freely available at https://github.com/potassco/plingo.
Acknowledgments
This work was supported by DFG grant SCHA 550/15. T. Janhunen was partially supported by the Academy of Finland under grant 345633 (XAILOG).
Appendix A Proofs
Proof of Proposition 1. We fix an interpretation
![]() $X$
. First, note that since
$X$
. First, note that since
![]() $\Pi ^{\mathit{soft}}$
contains only soft integrity constraints,
$\Pi ^{\mathit{soft}}$
contains only soft integrity constraints,
![]() ${\overline{{\Pi ^{\mathit{soft}}}}}$
contains only (unweighted) integrity constraints. Per definition, those integrity constraints which are not satisfied by
${\overline{{\Pi ^{\mathit{soft}}}}}$
contains only (unweighted) integrity constraints. Per definition, those integrity constraints which are not satisfied by
![]() $X$
are not included in
$X$
are not included in
![]() ${\overline{\Pi _X}}$
. The other integrity constraints are satisfied by
${\overline{\Pi _X}}$
. The other integrity constraints are satisfied by
![]() $X$
and thus do not have any effect on the generation (soft) stable models, that is
$X$
and thus do not have any effect on the generation (soft) stable models, that is
![]() $\text{SM}({{\overline{\Pi _X}}}) = \text{SM}({{\overline{\Pi _X^{hard}}}})$
. Therefore, we have that
$\text{SM}({{\overline{\Pi _X}}}) = \text{SM}({{\overline{\Pi _X^{hard}}}})$
. Therefore, we have that
 \begin{align*}{\mathit{SSM}^{\mathit{alt}}(\Pi )} & = \left \{X \mid X \textrm{ is a (standard) stable model of }{{\overline{\Pi _X}}} \textrm{ that satisfies }{{\overline{{\Pi ^{\mathit{hard}}}}}} \right \} \\[3pt] & = \left \{X \mid X \textrm{ is a (standard) stable model of }{{\overline{\Pi _X^{hard}}}} \textrm{ that satisfies }{{\overline{{\Pi ^{\mathit{hard}}}}}} \right \} \\[3pt] & = {\mathit{SSM}^{\mathit{alt}}(\Pi ^{hard})} \, \end{align*}
\begin{align*}{\mathit{SSM}^{\mathit{alt}}(\Pi )} & = \left \{X \mid X \textrm{ is a (standard) stable model of }{{\overline{\Pi _X}}} \textrm{ that satisfies }{{\overline{{\Pi ^{\mathit{hard}}}}}} \right \} \\[3pt] & = \left \{X \mid X \textrm{ is a (standard) stable model of }{{\overline{\Pi _X^{hard}}}} \textrm{ that satisfies }{{\overline{{\Pi ^{\mathit{hard}}}}}} \right \} \\[3pt] & = {\mathit{SSM}^{\mathit{alt}}(\Pi ^{hard})} \, \end{align*}
Next we prove that
-
 $X$
is a stable model of
$X$
is a stable model of
 ${\overline{\Pi _X^{hard}}}$
that satisfies
${\overline{\Pi _X^{hard}}}$
that satisfies
 ${\overline{{\Pi ^{\mathit{hard}}}}}$
iff
${\overline{{\Pi ^{\mathit{hard}}}}}$
iff -
 $X$
is a stable model of
$X$
is a stable model of
 ${\overline{\Pi ^{hard}}}$
${\overline{\Pi ^{hard}}}$
From the first to the second, if
![]() $X$
satisfies
$X$
satisfies
![]() ${\overline{{\Pi ^{\mathit{hard}}}}}$
, then
${\overline{{\Pi ^{\mathit{hard}}}}}$
, then
![]() ${{\overline{\Pi _X^{hard}}}} ={{\overline{\Pi ^{hard}}}}$
, and so the second follows. From the second to the first, if
${{\overline{\Pi _X^{hard}}}} ={{\overline{\Pi ^{hard}}}}$
, and so the second follows. From the second to the first, if
![]() $X$
is a stable model of
$X$
is a stable model of
![]() ${\overline{\Pi ^{hard}}}$
, then it satisfies
${\overline{\Pi ^{hard}}}$
, then it satisfies
![]() ${\overline{{\Pi ^{\mathit{hard}}}}}$
and again
${\overline{{\Pi ^{\mathit{hard}}}}}$
and again
![]() ${{\overline{\Pi _X^{hard}}}} ={{\overline{\Pi ^{hard}}}}$
and the first follows. Using this, we can simplify the definition of
${{\overline{\Pi _X^{hard}}}} ={{\overline{\Pi ^{hard}}}}$
and the first follows. Using this, we can simplify the definition of
![]() $\mathit{SSM}^{\mathit{alt}}(\Pi ^{hard})$
as follows:
$\mathit{SSM}^{\mathit{alt}}(\Pi ^{hard})$
as follows:
 \begin{align*}{\mathit{SSM}^{\mathit{alt}}(\Pi ^{hard})} & = \left\{ X \mid X \text{ is a (standard) stable model of }{{\overline{\Pi ^{hard}}}} \right \} \\[3pt] & = \text{SM}({{\overline{\Pi ^{hard}}}}) \end{align*}
\begin{align*}{\mathit{SSM}^{\mathit{alt}}(\Pi ^{hard})} & = \left\{ X \mid X \text{ is a (standard) stable model of }{{\overline{\Pi ^{hard}}}} \right \} \\[3pt] & = \text{SM}({{\overline{\Pi ^{hard}}}}) \end{align*}
This gives us the desired result.
Lemma 1.
Let
![]() $\Pi$
be an Lpmln program. The optimal stable models of
$\Pi$
be an Lpmln program. The optimal stable models of
![]() $\mathit{standard}(\Pi )$
are a subset of the soft stable models of
$\mathit{standard}(\Pi )$
are a subset of the soft stable models of
![]() $\Pi$
$\Pi$
Proof of Lemma 1. Let
![]() $X \in{\mathit{OPT}^{{\pm }}({\mathit{standard}(\Pi )})}$
. Then
$X \in{\mathit{OPT}^{{\pm }}({\mathit{standard}(\Pi )})}$
. Then
![]() $X$
is an optimal stable model of
$X$
is an optimal stable model of
![]() $ \{ F \vee \neg F \mid w:F \in \Pi \}$
, and the weak constraints
$ \{ F \vee \neg F \mid w:F \in \Pi \}$
, and the weak constraints
![]() $\{ :\sim \, F [-1,1] \mid w : F \in \Pi, w = \alpha \}$
. So it is a (standard) stable model of
$\{ :\sim \, F [-1,1] \mid w : F \in \Pi, w = \alpha \}$
. So it is a (standard) stable model of
![]() $ \{ F \vee \neg F \mid w:F \in \Pi \}$
. Then
$ \{ F \vee \neg F \mid w:F \in \Pi \}$
. Then
![]() $X$
is also a stable model of
$X$
is also a stable model of
![]() $\{ F \mid w : F \in \Pi, X \models F \}$
. But this is just
$\{ F \mid w : F \in \Pi, X \models F \}$
. But this is just
![]() ${\overline{\Pi _X}}$
and thus
${\overline{\Pi _X}}$
and thus
![]() $X \in{\mathit{SSM}(\Pi )}$
.
$X \in{\mathit{SSM}(\Pi )}$
.
Lemma 2.
Let
![]() $\Pi$
be an Lpmln program. If there is at least one interpretation
$\Pi$
be an Lpmln program. If there is at least one interpretation
![]() $X$
, which satisfies all hard rules in
$X$
, which satisfies all hard rules in
![]() $\Pi$
, then
$\Pi$
, then
Proof of Lemma 2. Note that
![]() $\mathit{alternative}(\Pi )$
and
$\mathit{alternative}(\Pi )$
and
![]() $\mathit{standard}(\Pi )$
differ only in their hard rules and that
$\mathit{standard}(\Pi )$
differ only in their hard rules and that
![]() $\mathit{alternative}(\Pi )$
does not have weak constraints (the hard rules have to be satisfied anyways). More specifically the rules in the set
$\mathit{alternative}(\Pi )$
does not have weak constraints (the hard rules have to be satisfied anyways). More specifically the rules in the set
![]() $\{ \alpha : F \mid w:F \in \Pi, w = \alpha \}$
in
$\{ \alpha : F \mid w:F \in \Pi, w = \alpha \}$
in
![]() $\mathit{alternative}(\Pi )$
, are replaced by a set of choice rules
$\mathit{alternative}(\Pi )$
, are replaced by a set of choice rules
![]() $\{ \alpha : F \vee \neg F \mid w:F \in \Pi, w = \alpha \}$
in
$\{ \alpha : F \vee \neg F \mid w:F \in \Pi, w = \alpha \}$
in
![]() $\mathit{standard}(\Pi )$
. Since there is at least one interpretation
$\mathit{standard}(\Pi )$
. Since there is at least one interpretation
![]() $X$
satisfying all hard rules in
$X$
satisfying all hard rules in
![]() $\Pi$
, we know that
$\Pi$
, we know that
![]() $\mathit{OPT}^{{\pm }}({\mathit{alternative}(\Pi )})$
is not empty.
$\mathit{OPT}^{{\pm }}({\mathit{alternative}(\Pi )})$
is not empty.
Further the weak constraints
![]() $\{ :\sim \, F [-1,1] \mid w : F \in \Pi, w = \alpha \}$
in
$\{ :\sim \, F [-1,1] \mid w : F \in \Pi, w = \alpha \}$
in
![]() $\mathit{standard}(\Pi )$
guarantee that all optimal stable model of
$\mathit{standard}(\Pi )$
guarantee that all optimal stable model of
![]() $\mathit{standard}(\Pi )$
satisfy all hard rules. Thus
$\mathit{standard}(\Pi )$
satisfy all hard rules. Thus
![]() ${\mathit{OPT}^{{\pm }}({\mathit{alternative}(\Pi )})} ={\mathit{OPT}^{{\pm }}({\mathit{standard}(\Pi )})}$
. The soft rules in both translations are the same so it follows that
${\mathit{OPT}^{{\pm }}({\mathit{alternative}(\Pi )})} ={\mathit{OPT}^{{\pm }}({\mathit{standard}(\Pi )})}$
. The soft rules in both translations are the same so it follows that
![]() ${W_{{\mathit{alternative}(\Pi )}}^{{\pm }}(X)} ={W_{{\mathit{standard}(\Pi )}}^{{\pm }}(X)}$
and
${W_{{\mathit{alternative}(\Pi )}}^{{\pm }}(X)} ={W_{{\mathit{standard}(\Pi )}}^{{\pm }}(X)}$
and
![]() ${P_{{\mathit{alternative}(\Pi )}}^{{\pm }}(X)} ={P_{{\mathit{standard}(\Pi )}}^{{\pm }}(X)}$
.
${P_{{\mathit{alternative}(\Pi )}}^{{\pm }}(X)} ={P_{{\mathit{standard}(\Pi )}}^{{\pm }}(X)}$
.
Proof of Proposition 2. We first prove the equation for the standard semantics.
For any interpretation
![]() $X$
under the Lpmln semantics, we have per definition:
$X$
under the Lpmln semantics, we have per definition:
Using Lemma1, we can split up the sum in the denominator as follows:
where
![]() ${\mathit{OS}^{{\pm }}(\Pi )} ={\mathit{OPT}^{{\pm }}({\mathit{standard}(\Pi )})}$
,
${\mathit{OS}^{{\pm }}(\Pi )} ={\mathit{OPT}^{{\pm }}({\mathit{standard}(\Pi )})}$
,
![]() ${\mathit{NOS}^{{\pm }}(\Pi )} ={\mathit{SSM}(\Pi )} \setminus{\mathit{OPT}^{{\pm }}({\mathit{standard}(\Pi )})}$
and the left sum contains only those interpretations which satisfy some maximal number of hard rules
${\mathit{NOS}^{{\pm }}(\Pi )} ={\mathit{SSM}(\Pi )} \setminus{\mathit{OPT}^{{\pm }}({\mathit{standard}(\Pi )})}$
and the left sum contains only those interpretations which satisfy some maximal number of hard rules
![]() $m$
. The right sum contains interpretations which satisfy strictly less than
$m$
. The right sum contains interpretations which satisfy strictly less than
![]() $m$
hard rules. We can thus also rewrite the weights in the denominator as follows:
$m$
hard rules. We can thus also rewrite the weights in the denominator as follows:
and
with
![]() $n(Y) = |{\Pi ^{\mathit{hard}}} \cap \Pi _Y|$
.
$n(Y) = |{\Pi ^{\mathit{hard}}} \cap \Pi _Y|$
.
Case 1:
![]() $X \in{\mathit{OS}^{{\pm }}(\Pi )}$
. If
$X \in{\mathit{OS}^{{\pm }}(\Pi )}$
. If
![]() $X$
is an optimal stable model of
$X$
is an optimal stable model of
![]() $\mathit{standard}(\Pi )$
it satisfies some maximal number
$\mathit{standard}(\Pi )$
it satisfies some maximal number
![]() $m$
of hard rules. We can rewrite its weight as
$m$
of hard rules. We can rewrite its weight as
So the probability becomes
We divide both the numerator and denominator by
![]() $\mathit{exp}(m \alpha )$
:
$\mathit{exp}(m \alpha )$
:
Since
![]() $n(Y) \lt m$
, we conclude that the right sum in the denominator approaches
$n(Y) \lt m$
, we conclude that the right sum in the denominator approaches
![]() $0$
when
$0$
when
![]() $\alpha$
tends to infinity:
$\alpha$
tends to infinity:
Next, observe that
![]() ${\Pi ^{\mathit{soft}}}_X$
contains all soft rules
${\Pi ^{\mathit{soft}}}_X$
contains all soft rules
![]() $w : F$
satisfied by
$w : F$
satisfied by
![]() $X$
. If
$X$
. If
![]() $X$
satisfies
$X$
satisfies
![]() $w : F$
, then it also satisfies
$w : F$
, then it also satisfies
![]() $w : \neg \neg F$
and vice versa; therefore,
$w : \neg \neg F$
and vice versa; therefore,
![]() ${\Pi ^{\mathit{soft}}}_X ={{\mathit{standard}(\Pi )}_X^{\mathit{soft}}}$
and
${\Pi ^{\mathit{soft}}}_X ={{\mathit{standard}(\Pi )}_X^{\mathit{soft}}}$
and
![]() ${\mathit{TW}({\Pi ^{\mathit{soft}}}_X)} ={\mathit{TW}({{\mathit{standard}(\Pi )}_X^{\mathit{soft}}})}$
. This means we can replace the corresponding expressions in the above equation and obtain the desired result:
${\mathit{TW}({\Pi ^{\mathit{soft}}}_X)} ={\mathit{TW}({{\mathit{standard}(\Pi )}_X^{\mathit{soft}}})}$
. This means we can replace the corresponding expressions in the above equation and obtain the desired result:
 \begin{align*}{P_{\Pi }(X)} & = \frac{{\mathit{TW}({\Pi ^{\mathit{soft}}}_X)}}{\sum _{Y \in{\mathit{OS}^{{\pm }}(\Pi )}}{\mathit{TW}({\Pi ^{\mathit{soft}}}_Y)}} \\[0.8em] & = \frac{{\mathit{TW}({{\mathit{standard}(\Pi )}_X^{\mathit{soft}}})}}{\sum _{Y \in{\mathit{OS}^{{\pm }}(\Pi )}}{\mathit{TW}({{\mathit{standard}(\Pi )}_X^{\mathit{soft}}})}} ={P_{{\mathit{standard}(\Pi )}}^{{\pm }}(X)} \, . \end{align*}
\begin{align*}{P_{\Pi }(X)} & = \frac{{\mathit{TW}({\Pi ^{\mathit{soft}}}_X)}}{\sum _{Y \in{\mathit{OS}^{{\pm }}(\Pi )}}{\mathit{TW}({\Pi ^{\mathit{soft}}}_Y)}} \\[0.8em] & = \frac{{\mathit{TW}({{\mathit{standard}(\Pi )}_X^{\mathit{soft}}})}}{\sum _{Y \in{\mathit{OS}^{{\pm }}(\Pi )}}{\mathit{TW}({{\mathit{standard}(\Pi )}_X^{\mathit{soft}}})}} ={P_{{\mathit{standard}(\Pi )}}^{{\pm }}(X)} \, . \end{align*}
Case 2:
![]() $X \in{\mathit{NOS}^{{\pm }}(\Pi )}$
. If
$X \in{\mathit{NOS}^{{\pm }}(\Pi )}$
. If
![]() $X$
is not an optimal stable model of
$X$
is not an optimal stable model of
![]() $\mathit{standard}(\Pi )$
but it is a soft stable model of
$\mathit{standard}(\Pi )$
but it is a soft stable model of
![]() $\Pi$
, per definition its weight and thus its probability are zero under
$\Pi$
, per definition its weight and thus its probability are zero under
![]() $\textit{Lpmln}^{\pm }$
semantics. Under Lpmln semantics its probability is similar as above, only we need to replace
$\textit{Lpmln}^{\pm }$
semantics. Under Lpmln semantics its probability is similar as above, only we need to replace
![]() $m$
in the numerator by
$m$
in the numerator by
![]() $n(X) = |{\Pi ^{\mathit{hard}}} \cap \Pi _X|$
:
$n(X) = |{\Pi ^{\mathit{hard}}} \cap \Pi _X|$
:
 \begin{align*}{P_{\Pi }(X)} & = \lim _{\alpha \rightarrow \infty } \frac{\mathit{exp}(n(X) \alpha ) \cdot{\mathit{TW}({\Pi ^{\mathit{soft}}}_X)}}{\sum _{Y \in{\mathit{OS}^{{\pm }}(\Pi )}} \mathit{exp}(m \alpha ) \cdot{\mathit{TW}({\Pi ^{\mathit{soft}}}_Y)} + \sum _{Y \in{\mathit{NOS}^{{\pm }}(\Pi )}} \mathit{exp}(n(Y) \cdot \alpha ) \cdot{\mathit{TW}({\Pi ^{\mathit{soft}}}_Y)}} \\[0.8em] & \leq \lim _{\alpha \rightarrow \infty } \frac{\mathit{exp}(n(X) \cdot \alpha )}{\mathit{exp}(m \alpha )} \cdot \frac{{\mathit{TW}({\Pi ^{\mathit{soft}}}_X)}}{\sum _{Y \in{\mathit{OS}^{{\pm }}(\Pi )}}{\mathit{TW}({\Pi ^{\mathit{soft}}}_Y)}} \, . \end{align*}
\begin{align*}{P_{\Pi }(X)} & = \lim _{\alpha \rightarrow \infty } \frac{\mathit{exp}(n(X) \alpha ) \cdot{\mathit{TW}({\Pi ^{\mathit{soft}}}_X)}}{\sum _{Y \in{\mathit{OS}^{{\pm }}(\Pi )}} \mathit{exp}(m \alpha ) \cdot{\mathit{TW}({\Pi ^{\mathit{soft}}}_Y)} + \sum _{Y \in{\mathit{NOS}^{{\pm }}(\Pi )}} \mathit{exp}(n(Y) \cdot \alpha ) \cdot{\mathit{TW}({\Pi ^{\mathit{soft}}}_Y)}} \\[0.8em] & \leq \lim _{\alpha \rightarrow \infty } \frac{\mathit{exp}(n(X) \cdot \alpha )}{\mathit{exp}(m \alpha )} \cdot \frac{{\mathit{TW}({\Pi ^{\mathit{soft}}}_X)}}{\sum _{Y \in{\mathit{OS}^{{\pm }}(\Pi )}}{\mathit{TW}({\Pi ^{\mathit{soft}}}_Y)}} \, . \end{align*}
We can remove the second sum in the denominator since we know that it is always greater or equal than 0. Now similar as above we know that
![]() $n(X) \lt m$
, so the whole expression approaches
$n(X) \lt m$
, so the whole expression approaches
![]() $0$
. It follows
$0$
. It follows
Since we know that
![]() ${P_{\Pi }(X)} \geq 0$
, we have the desired result.
${P_{\Pi }(X)} \geq 0$
, we have the desired result.
Case 3:
![]() $X \notin{\mathit{SSM}(\Pi )}$
. If
$X \notin{\mathit{SSM}(\Pi )}$
. If
![]() $X$
is not a soft stable model, it is neither an optimal stable model. Per definition, the weight of
$X$
is not a soft stable model, it is neither an optimal stable model. Per definition, the weight of
![]() $X$
is zero under both semantics, and thus
$X$
is zero under both semantics, and thus
![]() ${P_{\Pi }(X)} ={P_{{\mathit{standard}(\Pi )}}^{{\pm }}(X)}$
.
${P_{\Pi }(X)} ={P_{{\mathit{standard}(\Pi )}}^{{\pm }}(X)}$
.
Next, we prove the equation for the alternative semantics. If there is no interpretation
![]() $X$
that satisfies all hard rules in
$X$
that satisfies all hard rules in
![]() $\Pi$
, then
$\Pi$
, then
![]() $P_{\Pi }^{\mathit{alt}}(X)$
is not defined. In that case
$P_{\Pi }^{\mathit{alt}}(X)$
is not defined. In that case
![]() $\mathit{OPT}^{{\pm }}({\mathit{alternative}(\Pi )})$
is also empty, since
$\mathit{OPT}^{{\pm }}({\mathit{alternative}(\Pi )})$
is also empty, since
Thus
![]() $P_{{\mathit{alternative}(\Pi )}}^{{\pm }}(X)$
is also not defined. If
$P_{{\mathit{alternative}(\Pi )}}^{{\pm }}(X)$
is also not defined. If
![]() $\mathit{SSM}^{\mathit{alt}}(\Pi )$
is not empty, then it holds that
$\mathit{SSM}^{\mathit{alt}}(\Pi )$
is not empty, then it holds that
![]() ${P_{\Pi }^{\mathit{alt}}(X)} ={P_{\Pi }(X)}$
for every interpretation
${P_{\Pi }^{\mathit{alt}}(X)} ={P_{\Pi }(X)}$
for every interpretation
![]() $X$
(cf. Proposition2 from Lee and Wang (Reference Lee and Wang2016)). Combining this with Lemma2 gives the desired result
$X$
(cf. Proposition2 from Lee and Wang (Reference Lee and Wang2016)). Combining this with Lemma2 gives the desired result
Proof of Proposition 3. The proof goes analogously to the proofs of Corollary 1 from Reference Lee and YangLee and Yang (2017) and Theorem 1 from Reference Lee, Talsania and WangLee et al. (2017).
First of all, we show that
![]() ${\mathit{OPT}^{{\pm }}(\Pi )} ={\mathit{OPT}^{{\pm }}({\mathit{negative}(\Pi )})}$
. It is easy to see that
${\mathit{OPT}^{{\pm }}(\Pi )} ={\mathit{OPT}^{{\pm }}({\mathit{negative}(\Pi )})}$
. It is easy to see that
![]() ${\mathit{SM}(\Pi )} ={\mathit{SM}({\mathit{negative}(\Pi )})}$
. It remains to prove that optimality is preserved as well. Let
${\mathit{SM}(\Pi )} ={\mathit{SM}({\mathit{negative}(\Pi )})}$
. It remains to prove that optimality is preserved as well. Let
![]() $\mathit{Cost}_{\Pi }(l)$
be the total weak constraint cost at priority level
$\mathit{Cost}_{\Pi }(l)$
be the total weak constraint cost at priority level
![]() $l$
for program
$l$
for program
![]() $\Pi$
and
$\Pi$
and
![]() $\mathit{Cost}_{\Pi }(X,l)$
be the cost of interpretation
$\mathit{Cost}_{\Pi }(X,l)$
be the cost of interpretation
![]() $X$
at priority level
$X$
at priority level
![]() $l$
. If we negate the formulas and flip the weights in the weak constraints (as proposed in the proposition), it holds that
$l$
. If we negate the formulas and flip the weights in the weak constraints (as proposed in the proposition), it holds that
This means that if
![]() $\mathit{Cost}_{\Pi }(X,l)$
is minimal in
$\mathit{Cost}_{\Pi }(X,l)$
is minimal in
![]() $\Pi$
for some level
$\Pi$
for some level
![]() $l$
,
$l$
,
![]() $\mathit{Cost}_{{\mathit{negative}(\Pi )}}(X,l)$
is minimal in
$\mathit{Cost}_{{\mathit{negative}(\Pi )}}(X,l)$
is minimal in
![]() $\mathit{negative}(\Pi )$
at that level and so optimality is preserved.
$\mathit{negative}(\Pi )$
at that level and so optimality is preserved.
Second, we show that
![]() ${W_{\Pi }^{{\pm }}(X)} ={\mathit{TW}({\Pi ^{\mathit{soft}}})} \cdot{W_{{\mathit{negative}(\Pi )}}^{{\pm }}(X)}$
. When
${W_{\Pi }^{{\pm }}(X)} ={\mathit{TW}({\Pi ^{\mathit{soft}}})} \cdot{W_{{\mathit{negative}(\Pi )}}^{{\pm }}(X)}$
. When
![]() $X$
is not an optimal stable model of
$X$
is not an optimal stable model of
![]() $\Pi$
this is obvious. When
$\Pi$
this is obvious. When
![]() $X \in{\mathit{OPT}^{{\pm }}(\Pi )}$
, we have
$X \in{\mathit{OPT}^{{\pm }}(\Pi )}$
, we have
 \begin{align*}{W_{\Pi }^{{\pm }}(X)} & ={\mathit{TW}({\Pi _X^{\mathit{soft}}})} \\ & = \mathit{exp} ( \sum _{w:F \in{\Pi ^{\mathit{soft}}} \text{ and } X \models F} w ) \\ & = \mathit{exp} ( \sum _{w:F \in{\Pi ^{\mathit{soft}}}} w - \sum _{w:F \in{\Pi ^{\mathit{soft}}} \text{ and } X \nvDash F} w) \\ & = \mathit{exp} ( \sum _{w:F \in{\Pi ^{\mathit{soft}}}} w ) \cdot \mathit{exp} ( - \sum _{w:F \in{\Pi ^{\mathit{soft}}} \text{ and } X \nvDash F} w) \\ & ={\mathit{TW}({\Pi ^{\mathit{soft}}})} \cdot \mathit{exp} (\sum _{w:F \in{{\mathit{negative}(\Pi )}^{\mathit{soft}}} \text{ and } X \models F} w ) \\ & ={\mathit{TW}({\Pi ^{\mathit{soft}}})} \cdot{\mathit{TW}({{\mathit{negative}(\Pi )}_X^{\mathit{soft}}})} \\ & ={\mathit{TW}({\Pi ^{\mathit{soft}}})} \cdot{W_{{\mathit{negative}(\Pi )}}^{{\pm }}(X)} \, . \end{align*}
\begin{align*}{W_{\Pi }^{{\pm }}(X)} & ={\mathit{TW}({\Pi _X^{\mathit{soft}}})} \\ & = \mathit{exp} ( \sum _{w:F \in{\Pi ^{\mathit{soft}}} \text{ and } X \models F} w ) \\ & = \mathit{exp} ( \sum _{w:F \in{\Pi ^{\mathit{soft}}}} w - \sum _{w:F \in{\Pi ^{\mathit{soft}}} \text{ and } X \nvDash F} w) \\ & = \mathit{exp} ( \sum _{w:F \in{\Pi ^{\mathit{soft}}}} w ) \cdot \mathit{exp} ( - \sum _{w:F \in{\Pi ^{\mathit{soft}}} \text{ and } X \nvDash F} w) \\ & ={\mathit{TW}({\Pi ^{\mathit{soft}}})} \cdot \mathit{exp} (\sum _{w:F \in{{\mathit{negative}(\Pi )}^{\mathit{soft}}} \text{ and } X \models F} w ) \\ & ={\mathit{TW}({\Pi ^{\mathit{soft}}})} \cdot{\mathit{TW}({{\mathit{negative}(\Pi )}_X^{\mathit{soft}}})} \\ & ={\mathit{TW}({\Pi ^{\mathit{soft}}})} \cdot{W_{{\mathit{negative}(\Pi )}}^{{\pm }}(X)} \, . \end{align*}
Combining the two results above
 \begin{align*}{P_{\Pi }^{{\pm }}(X)} & = \frac{{W_{\Pi }^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}(\Pi )}}{W_{\Pi }^{{\pm }}(Y)}} \\ & = \frac{{W_{\Pi }^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({\mathit{negative}(\Pi )})}}{W_{\Pi }^{{\pm }}(Y)}} \\ & = \frac{{\mathit{TW}({\Pi ^{\mathit{soft}}})} \cdot{W_{{\mathit{negative}(\Pi )}}^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({\mathit{negative}(\Pi )})}}{\mathit{TW}({\Pi ^{\mathit{soft}}})} \cdot{W_{{\mathit{negative}(\Pi )}}^{{\pm }}(Y)}} \\ & = \frac{{W_{{\mathit{negative}(\Pi )}}^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({\mathit{negative}(\Pi )})}}{W_{{\mathit{negative}(\Pi )}}^{{\pm }}(Y)}} \cdot \frac{{\mathit{TW}({\Pi ^{\mathit{soft}}})}}{{\mathit{TW}({\Pi ^{\mathit{soft}}})}} \\ & = \frac{{W_{{\mathit{negative}(\Pi )}}^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({\mathit{negative}(\Pi )})}}{W_{{\mathit{negative}(\Pi )}}^{{\pm }}(Y)}} \\ & ={P_{{\mathit{negative}(\Pi )}}^{{\pm }}(X)} \, . \end{align*}
\begin{align*}{P_{\Pi }^{{\pm }}(X)} & = \frac{{W_{\Pi }^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}(\Pi )}}{W_{\Pi }^{{\pm }}(Y)}} \\ & = \frac{{W_{\Pi }^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({\mathit{negative}(\Pi )})}}{W_{\Pi }^{{\pm }}(Y)}} \\ & = \frac{{\mathit{TW}({\Pi ^{\mathit{soft}}})} \cdot{W_{{\mathit{negative}(\Pi )}}^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({\mathit{negative}(\Pi )})}}{\mathit{TW}({\Pi ^{\mathit{soft}}})} \cdot{W_{{\mathit{negative}(\Pi )}}^{{\pm }}(Y)}} \\ & = \frac{{W_{{\mathit{negative}(\Pi )}}^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({\mathit{negative}(\Pi )})}}{W_{{\mathit{negative}(\Pi )}}^{{\pm }}(Y)}} \cdot \frac{{\mathit{TW}({\Pi ^{\mathit{soft}}})}}{{\mathit{TW}({\Pi ^{\mathit{soft}}})}} \\ & = \frac{{W_{{\mathit{negative}(\Pi )}}^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({\mathit{negative}(\Pi )})}}{W_{{\mathit{negative}(\Pi )}}^{{\pm }}(Y)}} \\ & ={P_{{\mathit{negative}(\Pi )}}^{{\pm }}(X)} \, . \end{align*}
Proof of Proposition 4. We consider first the basic case where
![]() ${{\Pi }^{\mathit{evidence}}}$
is empty.
${{\Pi }^{\mathit{evidence}}}$
is empty.
Basic case:
![]() ${{\Pi }^{\mathit{evidence}}}$
is empty.
${{\Pi }^{\mathit{evidence}}}$
is empty.
Let
![]() $\Pi _1$
be the
$\Pi _1$
be the
![]() $\textit{Lpmln}^{\pm }$
program:
$\textit{Lpmln}^{\pm }$
program:
By Theorem 4 from Reference Lee and WangLee and Wang (2016), and Proposition2 from this paper, for every interpretation
![]() $X$
, it holds that
$X$
, it holds that
![]() $P_{\Pi }(X)$
and
$P_{\Pi }(X)$
and
![]() $P_{\Pi _1}^{{\pm }}(X)$
are the same. We prove next that
$P_{\Pi _1}^{{\pm }}(X)$
are the same. We prove next that
![]() $P_{\Pi _1}^{{\pm }}(X)$
and
$P_{\Pi _1}^{{\pm }}(X)$
and
![]() $P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
are the same. This allows us to infer that
$P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
are the same. This allows us to infer that
![]() $P_{\Pi }(X)$
and
$P_{\Pi }(X)$
and
![]() $P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
are the same and prove this basic case.
$P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
are the same and prove this basic case.
Take any atom
![]() $a$
such that
$a$
such that
![]() $p :: a \in{{{\Pi }^{\mathit{probs}}}}$
. Let
$p :: a \in{{{\Pi }^{\mathit{probs}}}}$
. Let
![]() $\Pi _2$
be the
$\Pi _2$
be the
![]() $\textit{Lpmln}^{\pm }$
program that results from replacing in
$\textit{Lpmln}^{\pm }$
program that results from replacing in
![]() $\Pi _1$
the pair of formulas
$\Pi _1$
the pair of formulas
![]() $\mathit{ln}(p) : \neg \neg a$
and
$\mathit{ln}(p) : \neg \neg a$
and
![]() $\mathit{ln}(1-p) : \neg a$
by the single formula
$\mathit{ln}(1-p) : \neg a$
by the single formula
![]() $\mathit{ln}(p/ (1-p)) : \neg \neg a$
. We show next that the probabilities defined by
$\mathit{ln}(p/ (1-p)) : \neg \neg a$
. We show next that the probabilities defined by
![]() $\Pi _1$
and
$\Pi _1$
and
![]() $\Pi _2$
are the same. Since applying this replacement in a sequence to all atoms occurring in probabilistic facts we obtain our program
$\Pi _2$
are the same. Since applying this replacement in a sequence to all atoms occurring in probabilistic facts we obtain our program
![]() ${{\mathit{problog2lpmln}(\Pi )}}$
, this gives us that
${{\mathit{problog2lpmln}(\Pi )}}$
, this gives us that
![]() $P_{\Pi _1}^{{\pm }}(X)$
and
$P_{\Pi _1}^{{\pm }}(X)$
and
![]() $P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
are the same.
$P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
are the same.
We show that for all interpretations
![]() $X$
it holds that
$X$
it holds that
Given that
![]() $\Pi _1$
and
$\Pi _1$
and
![]() $\Pi _2$
only differ in their soft formulas, it holds that
$\Pi _2$
only differ in their soft formulas, it holds that
![]() $\mathit{OPT}^{{\pm }}(\Pi _1)$
and
$\mathit{OPT}^{{\pm }}(\Pi _1)$
and
![]() $\mathit{OPT}^{{\pm }}(\Pi _2)$
are the same. Then, if
$\mathit{OPT}^{{\pm }}(\Pi _2)$
are the same. Then, if
![]() $X \not \in{\mathit{OPT}^{{\pm }}(\Pi _1)}$
, we have that
$X \not \in{\mathit{OPT}^{{\pm }}(\Pi _1)}$
, we have that
![]() $X \not \in{\mathit{OPT}^{{\pm }}(\Pi _2)}$
; therefore,
$X \not \in{\mathit{OPT}^{{\pm }}(\Pi _2)}$
; therefore,
![]() ${W_{\Pi _1}^{{\pm }}(X)} ={W_{\Pi _2}^{{\pm }}(X)} = 0$
, and equation (A1) holds. Otherwise, if
${W_{\Pi _1}^{{\pm }}(X)} ={W_{\Pi _2}^{{\pm }}(X)} = 0$
, and equation (A1) holds. Otherwise, if
![]() $X \in{\mathit{OPT}^{{\pm }}(\Pi _1)}$
, we consider two cases. In the first case,
$X \in{\mathit{OPT}^{{\pm }}(\Pi _1)}$
, we consider two cases. In the first case,
![]() $a \in X$
. Since the weight of
$a \in X$
. Since the weight of
![]() $\neg \neg a$
is
$\neg \neg a$
is
![]() $\mathit{ln}(p)$
, we can represent the value of
$\mathit{ln}(p)$
, we can represent the value of
![]() $W_{\Pi _1}^{{\pm }}(X)$
as
$W_{\Pi _1}^{{\pm }}(X)$
as
![]() $\mathit{exp}(\mathit{ln}(p) + \alpha )$
for some integer
$\mathit{exp}(\mathit{ln}(p) + \alpha )$
for some integer
![]() $\alpha$
. Furthermore, given that
$\alpha$
. Furthermore, given that
![]() $\Pi _2$
only replaces in
$\Pi _2$
only replaces in
![]() $\Pi _1$
the soft formulas for the atom
$\Pi _1$
the soft formulas for the atom
![]() $a$
, we can also represent the value
$a$
, we can also represent the value
![]() $W_{\Pi _2}^{{\pm }}(X)$
as
$W_{\Pi _2}^{{\pm }}(X)$
as
![]() $\mathit{exp}(\mathit{ln}(p/(1-p)) + \alpha )$
. Then, equation (A1) follows from the next equalities:
$\mathit{exp}(\mathit{ln}(p/(1-p)) + \alpha )$
. Then, equation (A1) follows from the next equalities:
 \begin{align*}{W_{\Pi _2}^{{\pm }}(X)} & = \mathit{exp}(\mathit{ln}(p/(1-p)) + \alpha ) \\ & = \mathit{exp}(\mathit{ln}(p/(1-p))) \cdot \mathit{exp}(\alpha ) \\ & = \mathit{exp}(\mathit{ln}(p))/(1-p) \cdot \mathit{exp}(\alpha ) \\ & = \mathit{exp}(\mathit{ln}(p)+ \alpha )/(1-p) \\ & ={W_{\Pi _1}^{{\pm }}(X)}/(1-p). \end{align*}
\begin{align*}{W_{\Pi _2}^{{\pm }}(X)} & = \mathit{exp}(\mathit{ln}(p/(1-p)) + \alpha ) \\ & = \mathit{exp}(\mathit{ln}(p/(1-p))) \cdot \mathit{exp}(\alpha ) \\ & = \mathit{exp}(\mathit{ln}(p))/(1-p) \cdot \mathit{exp}(\alpha ) \\ & = \mathit{exp}(\mathit{ln}(p)+ \alpha )/(1-p) \\ & ={W_{\Pi _1}^{{\pm }}(X)}/(1-p). \end{align*}
In the second case, where
![]() $a \notin X$
, we can represent
$a \notin X$
, we can represent
![]() $W_{\Pi _1}^{{\pm }}(X)$
as
$W_{\Pi _1}^{{\pm }}(X)$
as
![]() $\mathit{exp}(\mathit{ln}(1-p) + \beta )$
, and
$\mathit{exp}(\mathit{ln}(1-p) + \beta )$
, and
![]() $W_{\Pi _2}^{{\pm }}(X)$
as
$W_{\Pi _2}^{{\pm }}(X)$
as
![]() $\mathit{exp}(\beta )$
for some integer
$\mathit{exp}(\beta )$
for some integer
![]() $\beta$
. Then, equation (A1) follows:
$\beta$
. Then, equation (A1) follows:
 \begin{align*}{W_{\Pi _2}^{{\pm }}(X)} & = \mathit{exp}(\beta ) \\ & = \mathit{exp}(\mathit{ln}(1-p) + \beta - \mathit{ln}(1-p)) \\ & = \mathit{exp}(\mathit{ln}(1-p) + \beta ) / \mathit{exp}(\mathit{ln}(1-p)) \\ & = \mathit{exp}(\mathit{ln}(1-p) + \beta ) / (1-p) \\ & ={W_{\Pi _1}^{{\pm }}(X)}/(1-p). \end{align*}
\begin{align*}{W_{\Pi _2}^{{\pm }}(X)} & = \mathit{exp}(\beta ) \\ & = \mathit{exp}(\mathit{ln}(1-p) + \beta - \mathit{ln}(1-p)) \\ & = \mathit{exp}(\mathit{ln}(1-p) + \beta ) / \mathit{exp}(\mathit{ln}(1-p)) \\ & = \mathit{exp}(\mathit{ln}(1-p) + \beta ) / (1-p) \\ & ={W_{\Pi _1}^{{\pm }}(X)}/(1-p). \end{align*}
With this, we finish the proof for the case where
![]() ${{\Pi }^{\mathit{evidence}}}$
is empty by showing that the probabilities defined by
${{\Pi }^{\mathit{evidence}}}$
is empty by showing that the probabilities defined by
![]() $\Pi _1$
and
$\Pi _1$
and
![]() $\Pi _2$
are the same. Take any interpretation
$\Pi _2$
are the same. Take any interpretation
![]() $X$
, and recall that
$X$
, and recall that
![]() $\mathit{OPT}^{{\pm }}(\Pi _1)$
and
$\mathit{OPT}^{{\pm }}(\Pi _1)$
and
![]() $\mathit{OPT}^{{\pm }}(\Pi _2)$
are the same. If
$\mathit{OPT}^{{\pm }}(\Pi _2)$
are the same. If
![]() $\mathit{OPT}^{{\pm }}(\Pi _1)$
is empty, then clearly
$\mathit{OPT}^{{\pm }}(\Pi _1)$
is empty, then clearly
![]() ${P_{\Pi _1}^{{\pm }}(X)}$
and
${P_{\Pi _1}^{{\pm }}(X)}$
and
![]() $P_{\Pi _1}^{{\pm }}(X)$
are undefined. Otherwise, we have that
$P_{\Pi _1}^{{\pm }}(X)$
are undefined. Otherwise, we have that
 \begin{align*}& = \frac{{W_{\Pi _1}^{{\pm }}(X)}/(1-p)}{\sum _{Y \in{\mathit{OPT}^{{\pm }}(\Pi _1)}} \big ({W_{\Pi _1}^{{\pm }}(Y)}/(1-p)\big )} \\ & = \frac{{W_{\Pi _1}^{{\pm }}(X)}/(1-p)}{\big (\sum _{Y \in{\mathit{OPT}^{{\pm }}(\Pi _1)}}{W_{\Pi _1}^{{\pm }}(Y)}\big )/(1-p)} \\ & = \frac{{W_{\Pi _1}^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}(\Pi _1)}}{W_{\Pi _1}^{{\pm }}(Y)}} \\ & ={P_{\Pi _1}^{{\pm }}(X)} \end{align*}
\begin{align*}& = \frac{{W_{\Pi _1}^{{\pm }}(X)}/(1-p)}{\sum _{Y \in{\mathit{OPT}^{{\pm }}(\Pi _1)}} \big ({W_{\Pi _1}^{{\pm }}(Y)}/(1-p)\big )} \\ & = \frac{{W_{\Pi _1}^{{\pm }}(X)}/(1-p)}{\big (\sum _{Y \in{\mathit{OPT}^{{\pm }}(\Pi _1)}}{W_{\Pi _1}^{{\pm }}(Y)}\big )/(1-p)} \\ & = \frac{{W_{\Pi _1}^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}(\Pi _1)}}{W_{\Pi _1}^{{\pm }}(Y)}} \\ & ={P_{\Pi _1}^{{\pm }}(X)} \end{align*}
General case.
Given a ProbLog program
![]() $\Pi$
, by
$\Pi$
, by
![]() $\mathit{models}(\Pi )$
we denote the set of interpretations
$\mathit{models}(\Pi )$
we denote the set of interpretations
![]() $X$
such that
$X$
such that
![]() $P_{\Pi }(X)$
is greater than
$P_{\Pi }(X)$
is greater than
![]() $0$
. We show that
$0$
. We show that
We consider first the program without evidence
![]() $\Pi \setminus{{{\Pi }^{\mathit{evidence}}}}$
. Take any interpretation
$\Pi \setminus{{{\Pi }^{\mathit{evidence}}}}$
. Take any interpretation
![]() $X$
, and consider two cases.
$X$
, and consider two cases.
In the first case,
![]() $X$
belongs to
$X$
belongs to
![]() $\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}})$
. The probability
$\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}})$
. The probability
![]() $P_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(X)$
is a fraction whose numerator is the exponential of some number and whose denominator is greater or equal than the numerator. Hence,
$P_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(X)$
is a fraction whose numerator is the exponential of some number and whose denominator is greater or equal than the numerator. Hence,
![]() ${P_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(X)} \gt 0$
. Given the basic case that we proved above, this implies that
${P_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(X)} \gt 0$
. Given the basic case that we proved above, this implies that
![]() ${P_{\Pi \setminus{{{\Pi }^{\mathit{evidence}}}}}(X)} \gt 0$
, and therefore,
${P_{\Pi \setminus{{{\Pi }^{\mathit{evidence}}}}}(X)} \gt 0$
, and therefore,
![]() $X$
belongs to
$X$
belongs to
![]() $\mathit{models}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})$
.
$\mathit{models}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})$
.
In the second case,
![]() $X$
does not belong to
$X$
does not belong to
![]() $\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}})$
. Hence,
$\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}})$
. Hence,
![]() $P_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(X)$
is
$P_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(X)$
is
![]() $0$
or undefined. Given the basic case that we proved above, this implies that
$0$
or undefined. Given the basic case that we proved above, this implies that
![]() $P_{\Pi \setminus{{{\Pi }^{\mathit{evidence}}}}}(X)$
cannot be greater than
$P_{\Pi \setminus{{{\Pi }^{\mathit{evidence}}}}}(X)$
cannot be greater than
![]() $0$
, and therefore,
$0$
, and therefore,
![]() $X$
does not belong to
$X$
does not belong to
![]() $\mathit{models}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})$
.
$\mathit{models}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})$
.
Both cases together prove equation (A2) for program
![]() $\Pi \setminus{{{\Pi }^{\mathit{evidence}}}}$
. The result for program
$\Pi \setminus{{{\Pi }^{\mathit{evidence}}}}$
. The result for program
![]() $\Pi$
in general follows from this, given that
$\Pi$
in general follows from this, given that
-
•
 ${\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}})}={\mathit{models}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}$
,
${\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}})}={\mathit{models}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}$
, -
•
 $\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})$
is the subset of
$\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})$
is the subset of
 $\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}})$
that satisfies all literals in
$\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}})$
that satisfies all literals in
 ${{\Pi }^{\mathit{evidence}}}$
, and
${{\Pi }^{\mathit{evidence}}}$
, and -
•
 ${\mathit{models}(\Pi )}$
is the subset of
${\mathit{models}(\Pi )}$
is the subset of
 $\mathit{models}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})$
that satisfies all literals in
$\mathit{models}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})$
that satisfies all literals in
 ${{\Pi }^{\mathit{evidence}}}$
.
${{\Pi }^{\mathit{evidence}}}$
.
Once equation (A2) is proved, we can approach the general case of this proposition.
We consider first the case where
![]() $\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})$
is empty. On the one side, this implies that
$\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})$
is empty. On the one side, this implies that
![]() $P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
is undefined for every interpretation
$P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
is undefined for every interpretation
![]() $X$
. On the other side,
$X$
. On the other side,
![]() $\mathit{models}(\Pi )$
is also empty by equation (A2), and therefore,
$\mathit{models}(\Pi )$
is also empty by equation (A2), and therefore,
![]() $P_{\Pi }(X)$
is also undefined for every interpretation
$P_{\Pi }(X)$
is also undefined for every interpretation
![]() $X$
.
$X$
.
Now, we consider the case where
![]() $\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})$
is not empty. Note that this implies that the probabilities of
$\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})$
is not empty. Note that this implies that the probabilities of
![]() $\Pi$
and
$\Pi$
and
![]() ${{\mathit{problog2lpmln}(\Pi )}}$
are all defined. Take any interpretation
${{\mathit{problog2lpmln}(\Pi )}}$
are all defined. Take any interpretation
![]() $X$
. If
$X$
. If
![]() $P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
is
$P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
is
![]() $0$
, then
$0$
, then
![]() $X$
does not belong to
$X$
does not belong to
![]() $\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})$
. Hence,
$\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})$
. Hence,
![]() $X$
does not belong to
$X$
does not belong to
![]() $\mathit{models}(\Pi )$
by equation (A2), and
$\mathit{models}(\Pi )$
by equation (A2), and
![]() $P_{\Pi }(X)$
is also
$P_{\Pi }(X)$
is also
![]() $0$
. We prove the case where
$0$
. We prove the case where
![]() $P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
is greater than
$P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
is greater than
![]() $0$
by the equalities below. Note that this case implies that
$0$
by the equalities below. Note that this case implies that
![]() $X$
belongs to
$X$
belongs to
![]() $\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})$
. By
$\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})$
. By
![]() $\mathit{sum}(\Pi )$
, we denote the sum
$\mathit{sum}(\Pi )$
, we denote the sum
 \begin{align*} {P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)} = \frac{{W_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})}}{W_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(Y)}} \end{align*}
\begin{align*} {P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)} = \frac{{W_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})}}{W_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(Y)}} \end{align*}
 \begin{align*} & = \frac{{W_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)} /{\mathit{sum}(\Pi )}}{\big (\ \sum _{Y \in{\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})}}{W_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(Y)}\big ) /{\mathit{sum}(\Pi )}} \\[3pt] & = \frac{{W_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)} /{\mathit{sum}(\Pi )}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})}} \big ({W_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(Y)} /{\mathit{sum}(\Pi )}\big )} \\[3pt] & = \frac{{W_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(X)} /{\mathit{sum}(\Pi )}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})}} \big ({W_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(Y)} /{\mathit{sum}(\Pi )}\big )} \\[3pt] & = \frac{{P_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})}}{P_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(Y)}} \\[3pt] & = \frac{{P_{\Pi \setminus{{{\Pi }^{\mathit{evidence}}}}}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})}}{P_{\Pi \setminus{{{\Pi }^{\mathit{evidence}}}}}(Y)}} \\[3pt] & = \frac{{P^{\mathit{basic}}_{\Pi }(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})}}{P^{\mathit{basic}}_{\Pi }(Y)}} \\[3pt] & = \frac{{P^{\mathit{basic}}_{\Pi }(X)}}{\sum _{Y \in{\mathit{models}(\Pi )}}{P^{\mathit{basic}}_{\Pi }(Y)}} \\[3pt] & ={P_{\Pi }(X)} \end{align*}
\begin{align*} & = \frac{{W_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)} /{\mathit{sum}(\Pi )}}{\big (\ \sum _{Y \in{\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})}}{W_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(Y)}\big ) /{\mathit{sum}(\Pi )}} \\[3pt] & = \frac{{W_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)} /{\mathit{sum}(\Pi )}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})}} \big ({W_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(Y)} /{\mathit{sum}(\Pi )}\big )} \\[3pt] & = \frac{{W_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(X)} /{\mathit{sum}(\Pi )}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})}} \big ({W_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(Y)} /{\mathit{sum}(\Pi )}\big )} \\[3pt] & = \frac{{P_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})}}{P_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(Y)}} \\[3pt] & = \frac{{P_{\Pi \setminus{{{\Pi }^{\mathit{evidence}}}}}(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})}}{P_{\Pi \setminus{{{\Pi }^{\mathit{evidence}}}}}(Y)}} \\[3pt] & = \frac{{P^{\mathit{basic}}_{\Pi }(X)}}{\sum _{Y \in{\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})}}{P^{\mathit{basic}}_{\Pi }(Y)}} \\[3pt] & = \frac{{P^{\mathit{basic}}_{\Pi }(X)}}{\sum _{Y \in{\mathit{models}(\Pi )}}{P^{\mathit{basic}}_{\Pi }(Y)}} \\[3pt] & ={P_{\Pi }(X)} \end{align*}
The first equality holds by definition of
![]() $P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
. The second is the result of dividing both sides of the fraction by
$P_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
. The second is the result of dividing both sides of the fraction by
![]() $\mathit{sum}(\Pi )$
. The third rearranges the formulas in the denominator. The fourth replaces
$\mathit{sum}(\Pi )$
. The third rearranges the formulas in the denominator. The fourth replaces
![]() $W_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
by
$W_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(X)$
by
![]() $W_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(X)$
and
$W_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(X)$
and
![]() $W_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(Y)$
by
$W_{{{{\mathit{problog2lpmln}(\Pi )}}}}^{{\pm }}(Y)$
by
![]() $W_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(Y)$
. This replacement is sound given that
$W_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(Y)$
. This replacement is sound given that
![]() $X$
and the
$X$
and the
![]() $Y$
’s belong to
$Y$
’s belong to
![]() $\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})$
, and in this case, the subtraction of
$\mathit{OPT}^{{\pm }}({{{\mathit{problog2lpmln}(\Pi )}}})$
, and in this case, the subtraction of
![]() ${{\Pi }^{\mathit{evidence}}}$
does not affect their corresponding weights. The fifth equation holds by definition of
${{\Pi }^{\mathit{evidence}}}$
does not affect their corresponding weights. The fifth equation holds by definition of
![]() $P_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(X)$
. The sixth holds by the basic case that we proved above. The seventh holds by definition of
$P_{{{{\mathit{problog2lpmln}(\Pi \setminus{{{\Pi }^{\mathit{evidence}}}})}}}}^{{\pm }}(X)$
. The sixth holds by the basic case that we proved above. The seventh holds by definition of
![]() $P^{\mathit{basic}}_{\Pi }(X)$
. The eighth holds by equation (A2). Finally, the ninth equation holds by definition of
$P^{\mathit{basic}}_{\Pi }(X)$
. The eighth holds by equation (A2). Finally, the ninth equation holds by definition of
![]() $P_{\Pi }(X)$
.
$P_{\Pi }(X)$
.
Proof of Proposition 5. We show that the probabilities remain the same through the steps of the translations of Section 3.2. We start at step 2. Given a set
![]() $Y$
, by
$Y$
, by
![]() $Y^{\prime}$
we denote its extension with copy atoms
$Y^{\prime}$
we denote its extension with copy atoms
![]() $Y \cup \{{a^{\prime}}\mid a \in Y\}$
.
$Y \cup \{{a^{\prime}}\mid a \in Y\}$
.
Step 2. Let
![]() $\Gamma$
be the union of
$\Gamma$
be the union of
![]() $\{\neg{\mathit{bot}}\}$
with the set of rules (1) for every atom
$\{\neg{\mathit{bot}}\}$
with the set of rules (1) for every atom
![]() $a \in{\mathit{atoms}(\Pi )}$
and
$a \in{\mathit{atoms}(\Pi )}$
and
![]() $\Pi _2$
be
$\Pi _2$
be
![]() $\Pi \cup \Gamma$
(we jump program
$\Pi \cup \Gamma$
(we jump program
![]() $\Pi _1$
). We focus now on the hard part of
$\Pi _1$
). We focus now on the hard part of
![]() $\Pi _2$
. By the Splitting Set Theorem for propositional formulas (Reference FerrarisFerraris, 2011),
$\Pi _2$
. By the Splitting Set Theorem for propositional formulas (Reference FerrarisFerraris, 2011),
![]() $\Pi _2^{\mathit{hard}}$
can be splitted into
$\Pi _2^{\mathit{hard}}$
can be splitted into
![]() $\Pi ^{\mathit{hard}}$
and
$\Pi ^{\mathit{hard}}$
and
![]() $\Gamma$
. Then,
$\Gamma$
. Then,
![]() $Y$
is a stable model of
$Y$
is a stable model of
![]() $\Pi _2^{\mathit{hard}}$
iff
$\Pi _2^{\mathit{hard}}$
iff
![]() $Y$
is a stable model of
$Y$
is a stable model of
![]() $\Gamma \cup Z$
for some stable model
$\Gamma \cup Z$
for some stable model
![]() $Z$
of
$Z$
of
![]() $\Pi ^{\mathit{hard}}$
. The stable models
$\Pi ^{\mathit{hard}}$
. The stable models
![]() $Y$
of
$Y$
of
![]() $\Gamma \cup Z$
are exactly the sets
$\Gamma \cup Z$
are exactly the sets
![]() $Z\cup Z^{\prime}$
. To see this, observe that
$Z\cup Z^{\prime}$
. To see this, observe that
-
• The set of atoms occurring in the heads of the rules of
 $\Gamma \cup Z$
is
$\Gamma \cup Z$
is
 $Z\cup \{{a^{\prime}}\mid a \in{\mathit{atoms}(\Pi )}\}$
.Footnote
8
Hence,
$Z\cup \{{a^{\prime}}\mid a \in{\mathit{atoms}(\Pi )}\}$
.Footnote
8
Hence,
 $Y \subseteq Z\cup \{{a^{\prime}}\mid a \in{\mathit{atoms}(\Pi )}\}$
.
$Y \subseteq Z\cup \{{a^{\prime}}\mid a \in{\mathit{atoms}(\Pi )}\}$
. -
• The formulas in
 $\Gamma \cup Z$
classically entail the facts
$\Gamma \cup Z$
classically entail the facts
 $Z$
, and they also entail that
$Z$
, and they also entail that
 $a \equiv{a^{\prime}}$
for every atom
$a \equiv{a^{\prime}}$
for every atom
 $a \in{\mathit{atoms}(\Pi )}$
. This, together with the previous item, implies that
$a \in{\mathit{atoms}(\Pi )}$
. This, together with the previous item, implies that
 $Y$
must have the form
$Y$
must have the form
 $Z\cup Z^{\prime}$
.
$Z\cup Z^{\prime}$
. -
• Every atom in
 $Z\cup Z^{\prime}$
is justified, either by a fact in
$Z\cup Z^{\prime}$
is justified, either by a fact in
 $Z$
or by a choice rule in
$Z$
or by a choice rule in
 $\Gamma$
.
$\Gamma$
.
Given the previous statements, it follows that the set of stable models of
![]() $\Pi _2^{\mathit{hard}}$
is
$\Pi _2^{\mathit{hard}}$
is
![]() $\{Z \cup Z^{\prime} \mid Z \mathrm{ is a stable model of }{\Pi ^{\mathit{hard}}}\}$
. Since
$\{Z \cup Z^{\prime} \mid Z \mathrm{ is a stable model of }{\Pi ^{\mathit{hard}}}\}$
. Since
![]() $\Pi ^{\mathit{weak}}$
and
$\Pi ^{\mathit{weak}}$
and
![]() $\Pi _2^{\mathit{weak}}$
are empty, the sets
$\Pi _2^{\mathit{weak}}$
are empty, the sets
![]() $\mathit{OPT}^{{\pm }}(\Pi )$
and
$\mathit{OPT}^{{\pm }}(\Pi )$
and
![]() $\mathit{OPT}^{{\pm }}(\Pi _2)$
consist of the sets of stable models of
$\mathit{OPT}^{{\pm }}(\Pi _2)$
consist of the sets of stable models of
![]() $\Pi ^{\mathit{hard}}$
and
$\Pi ^{\mathit{hard}}$
and
![]() $\Pi _2^{\mathit{hard}}$
, respectively. Then, it follows that the set
$\Pi _2^{\mathit{hard}}$
, respectively. Then, it follows that the set
![]() $\mathit{OPT}^{{\pm }}(\Pi _2)$
is
$\mathit{OPT}^{{\pm }}(\Pi _2)$
is
![]() $\{Z \cup Z^{\prime} \mid Z \in{\mathit{OPT}^{{\pm }}(\Pi )}\}$
. Finally, since the soft formulas of
$\{Z \cup Z^{\prime} \mid Z \in{\mathit{OPT}^{{\pm }}(\Pi )}\}$
. Finally, since the soft formulas of
![]() $\Pi _2$
are the same as those of
$\Pi _2$
are the same as those of
![]() $\Pi$
, and they refer only to the atoms in
$\Pi$
, and they refer only to the atoms in
![]() $\mathit{atoms}(\Pi )$
, we can conclude that for every interpretation
$\mathit{atoms}(\Pi )$
, we can conclude that for every interpretation
![]() $X$
, disjoint from
$X$
, disjoint from
![]() $\{{a^{\prime}}\mid a \in{\mathit{atoms}(\Pi )}\}$
, it holds that
$\{{a^{\prime}}\mid a \in{\mathit{atoms}(\Pi )}\}$
, it holds that
![]() ${W_{\Pi _2}^{{\pm }}(X \cup X^{\prime})} ={W_{\Pi }^{{\pm }}(X)}$
and
${W_{\Pi _2}^{{\pm }}(X \cup X^{\prime})} ={W_{\Pi }^{{\pm }}(X)}$
and
![]() ${P_{\Pi _2}^{{\pm }}(X \cup X^{\prime})} ={P_{\Pi }^{{\pm }}(X)}$
.
${P_{\Pi _2}^{{\pm }}(X \cup X^{\prime})} ={P_{\Pi }^{{\pm }}(X)}$
.
Step 3. Let
![]() ${\mathit{stratify}}(\Pi )$
be the set of rules
${\mathit{stratify}}(\Pi )$
be the set of rules
![]() $\{{{\mathit{stratify}}(r)}\mid r \in{\Pi ^{\mathit{hard}}}\}$
and
$\{{{\mathit{stratify}}(r)}\mid r \in{\Pi ^{\mathit{hard}}}\}$
and
![]() $\Pi _3$
be the program
$\Pi _3$
be the program
![]() $(\Pi _2 \setminus{\Pi ^{\mathit{hard}}}) \cup{{\mathit{stratify}}(\Pi )}$
. Program
$(\Pi _2 \setminus{\Pi ^{\mathit{hard}}}) \cup{{\mathit{stratify}}(\Pi )}$
. Program
![]() $\Pi _3$
can also be represented as
$\Pi _3$
can also be represented as
![]() ${{\mathit{stratify}}(\Pi )}\cup \Gamma \cup{\Pi ^{\mathit{soft}}}$
. We show below that the stable models of
${{\mathit{stratify}}(\Pi )}\cup \Gamma \cup{\Pi ^{\mathit{soft}}}$
. We show below that the stable models of
![]() $\Pi _2^{\mathit{hard}}$
and
$\Pi _2^{\mathit{hard}}$
and
![]() $\Pi _3^{\mathit{hard}}$
are the same. Then, given that the soft formulas of both programs do not change, we can conclude that
$\Pi _3^{\mathit{hard}}$
are the same. Then, given that the soft formulas of both programs do not change, we can conclude that
![]() ${W_{\Pi _3}^{{\pm }}(X \cup X^{\prime})} ={W_{\Pi _2}^{{\pm }}(X \cup X^{\prime})} ={W_{\Pi }^{{\pm }}(X)}$
and
${W_{\Pi _3}^{{\pm }}(X \cup X^{\prime})} ={W_{\Pi _2}^{{\pm }}(X \cup X^{\prime})} ={W_{\Pi }^{{\pm }}(X)}$
and
![]() ${P_{\Pi _3}^{{\pm }}(X \cup X^{\prime})} ={P_{\Pi _2}^{{\pm }}(X \cup X^{\prime})} ={P_{\Pi }^{{\pm }}(X)}$
for every interpretation
${P_{\Pi _3}^{{\pm }}(X \cup X^{\prime})} ={P_{\Pi _2}^{{\pm }}(X \cup X^{\prime})} ={P_{\Pi }^{{\pm }}(X)}$
for every interpretation
![]() $X$
disjoint from
$X$
disjoint from
![]() $\{{a^{\prime}}\mid a \in{\mathit{atoms}(\Pi )}\}$
.
$\{{a^{\prime}}\mid a \in{\mathit{atoms}(\Pi )}\}$
.
For similar reasons as in step 2, the stable models of
![]() $\Pi _3^{\mathit{hard}}$
must have the form
$\Pi _3^{\mathit{hard}}$
must have the form
![]() $Z \cup Z^{\prime}$
for some set
$Z \cup Z^{\prime}$
for some set
![]() $Z \subseteq{\mathit{atoms}(\Pi )}$
. The same holds for the stable models of
$Z \subseteq{\mathit{atoms}(\Pi )}$
. The same holds for the stable models of
![]() $\Pi _2^{\mathit{hard}}$
. Hence, we can consider only interpretations of that form. We say that those interpretations are valid. We prove that the stable models of
$\Pi _2^{\mathit{hard}}$
. Hence, we can consider only interpretations of that form. We say that those interpretations are valid. We prove that the stable models of
![]() $\Pi _2^{\mathit{hard}}$
and
$\Pi _2^{\mathit{hard}}$
and
![]() $\Pi _3^{\mathit{hard}}$
are the same by showing that for every valid interpretation
$\Pi _3^{\mathit{hard}}$
are the same by showing that for every valid interpretation
![]() $X$
the reduct of
$X$
the reduct of
![]() $\Pi _2^{\mathit{hard}}$
with respect to
$\Pi _2^{\mathit{hard}}$
with respect to
![]() $X$
is the same program as the reduct of
$X$
is the same program as the reduct of
![]() $\Pi _3^{\mathit{hard}}$
with respect to
$\Pi _3^{\mathit{hard}}$
with respect to
![]() $X$
. Recall that the reduct of a program with respect to an interpretation is the result of replacing in that program every maximal subformula that is not satisfied by
$X$
. Recall that the reduct of a program with respect to an interpretation is the result of replacing in that program every maximal subformula that is not satisfied by
![]() $X$
by
$X$
by
![]() $\bot$
. The rules in
$\bot$
. The rules in
![]() $\Gamma$
are the same in
$\Gamma$
are the same in
![]() $\Pi _2^{\mathit{hard}}$
and
$\Pi _2^{\mathit{hard}}$
and
![]() $\Pi _3^{\mathit{hard}}$
; hence, their reduct is also the same in both programs. Then, we only have to consider the rules
$\Pi _3^{\mathit{hard}}$
; hence, their reduct is also the same in both programs. Then, we only have to consider the rules
![]() $r \in{\Pi ^{\mathit{hard}}}$
of the form:
$r \in{\Pi ^{\mathit{hard}}}$
of the form:
and their translation
![]() ${{\mathit{stratify}}(r)} \in{{\mathit{stratify}}(\Pi )}$
:
${{\mathit{stratify}}(r)} \in{{\mathit{stratify}}(\Pi )}$
:
Let
![]() $B(r)$
denote the body of
$B(r)$
denote the body of
![]() $r$
, and
$r$
, and
![]() $B({{\mathit{stratify}}(r)})$
denote the body of
$B({{\mathit{stratify}}(r)})$
denote the body of
![]() ${\mathit{stratify}}(r)$
. Note that since
${\mathit{stratify}}(r)$
. Note that since
![]() $X$
is valid, it satisfies any literal in
$X$
is valid, it satisfies any literal in
![]() $r$
iff it satisfies the corresponding literal in
$r$
iff it satisfies the corresponding literal in
![]() ${\mathit{stratify}}(r)$
. This also implies that
${\mathit{stratify}}(r)$
. This also implies that
![]() $X$
satisfies
$X$
satisfies
![]() $B(r)$
iff
$B(r)$
iff
![]() $X$
satisfies
$X$
satisfies
![]() $B({{\mathit{stratify}}(r)})$
. We consider four cases and show that for each of them the reducts of
$B({{\mathit{stratify}}(r)})$
. We consider four cases and show that for each of them the reducts of
![]() $r$
and
$r$
and
![]() ${\mathit{stratify}}(r)$
are the same:
${\mathit{stratify}}(r)$
are the same:
-
•
 $X$
neither satisfies
$X$
neither satisfies
 $a_0$
nor
$a_0$
nor
 $B(r)$
: then
$B(r)$
: then
 $X$
does not satisfy
$X$
does not satisfy
 $B({{\mathit{stratify}}(r)})$
, and the reduct of both
$B({{\mathit{stratify}}(r)})$
, and the reduct of both
 $r$
and
$r$
and
 ${\mathit{stratify}}(r)$
wrt.
${\mathit{stratify}}(r)$
wrt.
 $X$
is
$X$
is
 $\bot \leftarrow \bot$
;
$\bot \leftarrow \bot$
; -
•
 $X$
does not satisfy
$X$
does not satisfy
 $a_0$
, but it satisfies
$a_0$
, but it satisfies
 $B(r)$
: then
$B(r)$
: then
 $X$
satisfies
$X$
satisfies
 $B({{\mathit{stratify}}(r)})$
, and the reduct of both
$B({{\mathit{stratify}}(r)})$
, and the reduct of both
 $r$
and
$r$
and
 ${\mathit{stratify}}(r)$
wrt.
${\mathit{stratify}}(r)$
wrt.
 $X$
is
$X$
is
 $\bot \leftarrow a_1 \wedge \ldots \wedge a_m$
;
$\bot \leftarrow a_1 \wedge \ldots \wedge a_m$
; -
•
 $X$
satisfies
$X$
satisfies
 $a_0$
but does not satisfy
$a_0$
but does not satisfy
 $B(r)$
: then
$B(r)$
: then
 $X$
does not satisfy
$X$
does not satisfy
 $B({{\mathit{stratify}}(r)})$
, and the reduct of both
$B({{\mathit{stratify}}(r)})$
, and the reduct of both
 $r$
and
$r$
and
 ${\mathit{stratify}}(r)$
wrt.
${\mathit{stratify}}(r)$
wrt.
 $X$
is
$X$
is
 $a_0 \leftarrow \bot$
;
$a_0 \leftarrow \bot$
; -
•
 $X$
satisfies
$X$
satisfies
 $a_0$
and
$a_0$
and
 $B(r)$
: then
$B(r)$
: then
 $X$
satisfies
$X$
satisfies
 $B({{\mathit{stratify}}(r)})$
, and the reduct of both
$B({{\mathit{stratify}}(r)})$
, and the reduct of both
 $r$
and
$r$
and
 ${\mathit{stratify}}(r)$
wrt.
${\mathit{stratify}}(r)$
wrt.
 $X$
is
$X$
is
 $a_0 \leftarrow a_1 \wedge \ldots \wedge a_m$
.
$a_0 \leftarrow a_1 \wedge \ldots \wedge a_m$
.
Step 4. Let
![]() $\Pi _4$
the union of
$\Pi _4$
the union of
![]() $\Pi _3^{\mathit{hard}}$
and the following soft formulas:
$\Pi _3^{\mathit{hard}}$
and the following soft formulas:
which replace the soft formulas
![]() $w : \neg \neg a$
from
$w : \neg \neg a$
from
![]() $\Pi _3^{\mathit{soft}}$
. The sets
$\Pi _3^{\mathit{soft}}$
. The sets
![]() $\mathit{OPT}^{{\pm }}(\Pi _3)$
and
$\mathit{OPT}^{{\pm }}(\Pi _3)$
and
![]() $\mathit{OPT}^{{\pm }}(\Pi _4)$
are the same given that
$\mathit{OPT}^{{\pm }}(\Pi _4)$
are the same given that
![]() $\Pi _3$
and
$\Pi _3$
and
![]() $\Pi _4$
only differ in their soft formulas. This implies that if
$\Pi _4$
only differ in their soft formulas. This implies that if
![]() $X$
belongs to
$X$
belongs to
![]() $\mathit{OPT}^{{\pm }}(\Pi _4)$
, then
$\mathit{OPT}^{{\pm }}(\Pi _4)$
, then
![]() $X$
is valid. Given such a valid
$X$
is valid. Given such a valid
![]() $X$
, let
$X$
, let
![]() $\Omega _3$
and
$\Omega _3$
and
![]() $\Omega _4$
denote the set of soft formulas
$\Omega _4$
denote the set of soft formulas
![]() ${\alpha ^{\mathit{soft}}}_{X}$
for
${\alpha ^{\mathit{soft}}}_{X}$
for
![]() $\alpha =\Pi _3$
and
$\alpha =\Pi _3$
and
![]() $\alpha =\Pi _4$
, respectively. The following equivalences show that
$\alpha =\Pi _4$
, respectively. The following equivalences show that
![]() $\mathit{TW}(\Omega _3)$
is the same as
$\mathit{TW}(\Omega _3)$
is the same as
![]() $\mathit{TW}(\Omega _4)$
:
$\mathit{TW}(\Omega _4)$
:
 \begin{align*}{\mathit{TW}(\Omega _3)} & = \mathit{exp}(\sum _{\{w : \neg \neg a \in \Pi _3 \, \mid \, X \textrm{ satisfies }\neg \neg a\}}w) \\ & = \mathit{exp}(\sum _{\{w : \neg \neg a \in \Pi _3 \, \mid \, X \textrm{ satisfies }\neg \neg{a^{\prime}}\}}w) \\ & = \mathit{exp}(\sum _{\{w : \neg \neg{a^{\prime}} \in \Pi _4 \, \mid \, X \textrm{ satisfies }\neg \neg{a^{\prime}}\}}w) \\ & ={\mathit{TW}(\Omega _4)} \end{align*}
\begin{align*}{\mathit{TW}(\Omega _3)} & = \mathit{exp}(\sum _{\{w : \neg \neg a \in \Pi _3 \, \mid \, X \textrm{ satisfies }\neg \neg a\}}w) \\ & = \mathit{exp}(\sum _{\{w : \neg \neg a \in \Pi _3 \, \mid \, X \textrm{ satisfies }\neg \neg{a^{\prime}}\}}w) \\ & = \mathit{exp}(\sum _{\{w : \neg \neg{a^{\prime}} \in \Pi _4 \, \mid \, X \textrm{ satisfies }\neg \neg{a^{\prime}}\}}w) \\ & ={\mathit{TW}(\Omega _4)} \end{align*}
The first equality holds by definition of
![]() $\mathit{TW}(\Omega _3)$
; the second holds given that
$\mathit{TW}(\Omega _3)$
; the second holds given that
![]() $X$
is valid; the third one holds given that
$X$
is valid; the third one holds given that
![]() $w : \neg \neg a \in \Pi _3$
implies that
$w : \neg \neg a \in \Pi _3$
implies that
![]() $w : \neg \neg{a^{\prime}} \in \Pi _4$
, and the remaining soft formulas of
$w : \neg \neg{a^{\prime}} \in \Pi _4$
, and the remaining soft formulas of
![]() $\Pi _4$
have weight
$\Pi _4$
have weight
![]() $0$
; and the fourth equality holds by definition of
$0$
; and the fourth equality holds by definition of
![]() $\mathit{TW}(\Omega _4)$
.
$\mathit{TW}(\Omega _4)$
.
All in all, we have that the sets
![]() $\mathit{OPT}^{{\pm }}(\Pi _3)$
and
$\mathit{OPT}^{{\pm }}(\Pi _3)$
and
![]() $\mathit{OPT}^{{\pm }}(\Pi _4)$
are the same, and for every
$\mathit{OPT}^{{\pm }}(\Pi _4)$
are the same, and for every
![]() $X$
that belongs to them, it holds that
$X$
that belongs to them, it holds that
![]() ${\mathit{TW}(\Omega _3)}={\mathit{TW}(\Omega _4)}$
. From this, we conclude that
${\mathit{TW}(\Omega _3)}={\mathit{TW}(\Omega _4)}$
. From this, we conclude that
![]() ${W_{\Pi _4}^{{\pm }}(X \cup X^{\prime})} ={W_{\Pi _3}^{{\pm }}(X \cup X^{\prime})} ={W_{\Pi }^{{\pm }}(X)}$
and
${W_{\Pi _4}^{{\pm }}(X \cup X^{\prime})} ={W_{\Pi _3}^{{\pm }}(X \cup X^{\prime})} ={W_{\Pi }^{{\pm }}(X)}$
and
![]() ${P_{\Pi _4}^{{\pm }}(X \cup X^{\prime})} ={P_{\Pi _3}^{{\pm }}(X \cup X^{\prime})} ={P_{\Pi }^{{\pm }}(X)}$
for every interpretation
${P_{\Pi _4}^{{\pm }}(X \cup X^{\prime})} ={P_{\Pi _3}^{{\pm }}(X \cup X^{\prime})} ={P_{\Pi }^{{\pm }}(X)}$
for every interpretation
![]() $X$
disjoint from
$X$
disjoint from
![]() $\{{a^{\prime}}\mid a \in{\mathit{atoms}(\Pi )}\}$
.
$\{{a^{\prime}}\mid a \in{\mathit{atoms}(\Pi )}\}$
.
Step 5. We consider the ProbLog program
![]() ${{\mathit{lpmln2problog}(\Pi )}}$
, which is the result of replacing in
${{\mathit{lpmln2problog}(\Pi )}}$
, which is the result of replacing in
![]() $\Pi _4$
the choice rules
$\Pi _4$
the choice rules
and the soft formulas
by the probabilistic facts
In turn, the program
![]() ${{\mathit{problog2lpmln}({{{\mathit{lpmln2problog}(\Pi )}}})}}$
is the result of replacing in
${{\mathit{problog2lpmln}({{{\mathit{lpmln2problog}(\Pi )}}})}}$
is the result of replacing in
![]() ${{\mathit{lpmln2problog}(\Pi )}}$
those probabilistic facts by the choice rules
${{\mathit{lpmln2problog}(\Pi )}}$
those probabilistic facts by the choice rules
and the soft formulas
 \begin{align*} \left\{ \mathit{ln}\left( \frac{ \frac{e^w}{e^w + 1} }{ 1-\frac{e^w}{e^w + 1}} \right) ::{a^{\prime}} \mid w : \neg \neg a \in{\Pi ^{\mathit{soft}}} \right\} & \, \cup \\ \left\{ \mathit{ln}\left(\frac{0.5}{1-0.5}\right) ::{a^{\prime}} \mid a \in{\mathit{atoms}(\Pi )}\setminus{\mathit{soft}(\Pi )}\right\} & . \end{align*}
\begin{align*} \left\{ \mathit{ln}\left( \frac{ \frac{e^w}{e^w + 1} }{ 1-\frac{e^w}{e^w + 1}} \right) ::{a^{\prime}} \mid w : \neg \neg a \in{\Pi ^{\mathit{soft}}} \right\} & \, \cup \\ \left\{ \mathit{ln}\left(\frac{0.5}{1-0.5}\right) ::{a^{\prime}} \mid a \in{\mathit{atoms}(\Pi )}\setminus{\mathit{soft}(\Pi )}\right\} & . \end{align*}
This program
![]() ${\mathit{problog2lpmln}({{{\mathit{lpmln2problog}(\Pi )}}})}$
is the same as
${\mathit{problog2lpmln}({{{\mathit{lpmln2problog}(\Pi )}}})}$
is the same as
![]() $\Pi _4$
, once we simplify the weights of the soft formulas. The choice rules are the same, given that the first set of choice rules can also be represented as
$\Pi _4$
, once we simplify the weights of the soft formulas. The choice rules are the same, given that the first set of choice rules can also be represented as
![]() $\{{a^{\prime}} \vee \neg{a^{\prime}} \mid a \in{\mathit{soft}(\Pi )} \}$
and
$\{{a^{\prime}} \vee \neg{a^{\prime}} \mid a \in{\mathit{soft}(\Pi )} \}$
and
![]() ${\mathit{atoms}(\Pi )}={\mathit{soft}(\Pi )}\cup ({\mathit{atoms}(\Pi )}\setminus{\mathit{soft}(\Pi )})$
. The soft formulas are the same because
${\mathit{atoms}(\Pi )}={\mathit{soft}(\Pi )}\cup ({\mathit{atoms}(\Pi )}\setminus{\mathit{soft}(\Pi )})$
. The soft formulas are the same because
 \begin{equation*} \mathit {ln}\left( \frac { \frac {e^w}{e^w + 1} }{ 1-\frac {e^w}{e^w + 1}} \right) = \mathit {ln}\left( \frac { \frac {e^w}{e^w + 1} }{ \frac {e^w + 1 - e^w}{e^w + 1}} \right) = \mathit {ln}\left( \frac { \frac {e^w}{e^w + 1} }{ \frac {1}{e^w + 1}} \right) = \mathit {ln}\left( \frac { e^w }{ 1 } \right) = w \end{equation*}
\begin{equation*} \mathit {ln}\left( \frac { \frac {e^w}{e^w + 1} }{ 1-\frac {e^w}{e^w + 1}} \right) = \mathit {ln}\left( \frac { \frac {e^w}{e^w + 1} }{ \frac {e^w + 1 - e^w}{e^w + 1}} \right) = \mathit {ln}\left( \frac { \frac {e^w}{e^w + 1} }{ \frac {1}{e^w + 1}} \right) = \mathit {ln}\left( \frac { e^w }{ 1 } \right) = w \end{equation*}
and
From Proposition4, for every interpretation
![]() $X$
, the probabilities
$X$
, the probabilities
![]() $P_{{{{\mathit{lpmln2problog}(\Pi )}}}}(X)$
and
$P_{{{{\mathit{lpmln2problog}(\Pi )}}}}(X)$
and
![]() $P_{{{{\mathit{problog2lpmln}({{{\mathit{lpmln2problog}(\Pi )}}})}}}}^{{\pm }}(X)$
are the same. Since
$P_{{{{\mathit{problog2lpmln}({{{\mathit{lpmln2problog}(\Pi )}}})}}}}^{{\pm }}(X)$
are the same. Since
![]() ${{\mathit{problog2lpmln}({{{\mathit{lpmln2problog}(\Pi )}}})}}$
is the same as
${{\mathit{problog2lpmln}({{{\mathit{lpmln2problog}(\Pi )}}})}}$
is the same as
![]() $\Pi _4$
, the probabilities
$\Pi _4$
, the probabilities
![]() $P_{{{{\mathit{lpmln2problog}(\Pi )}}}}(X)$
and
$P_{{{{\mathit{lpmln2problog}(\Pi )}}}}(X)$
and
![]() $P_{\Pi _4}^{{\pm }}(X)$
are also the same. Given this and the results of step 4, we can conclude that
$P_{\Pi _4}^{{\pm }}(X)$
are also the same. Given this and the results of step 4, we can conclude that
![]() ${P_{{{{\mathit{lpmln2problog}(\Pi )}}}}(X \cup X^{\prime})} ={P_{\Pi _4}^{{\pm }}(X \cup X^{\prime})} ={P_{\Pi }^{{\pm }}(X)}$
for every interpretation
${P_{{{{\mathit{lpmln2problog}(\Pi )}}}}(X \cup X^{\prime})} ={P_{\Pi _4}^{{\pm }}(X \cup X^{\prime})} ={P_{\Pi }^{{\pm }}(X)}$
for every interpretation
![]() $X$
disjoint from
$X$
disjoint from
![]() $\{{a^{\prime}}\mid a \in{\mathit{atoms}(\Pi )}\}$
and finish the proof.
$\{{a^{\prime}}\mid a \in{\mathit{atoms}(\Pi )}\}$
and finish the proof.