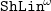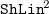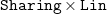1 Introduction
In the field of static analysis of logic programs, sharing information is one of the most interesting and widely used property. The goal of sharing analysis is to detect sets of variables which share a common variable. For instance, in the substitution
![]() $\{x/f(z,a),y/g(z) \}$
, the variables
$\{x/f(z,a),y/g(z) \}$
, the variables
![]() $x$
and
$x$
and
![]() $y$
share the common variable
$y$
share the common variable
![]() $z$
. Sharing may also track and infer groundness in the same way as the Def domain (de la Banda and Hermenegildo, Reference de la Banda and Hermenegildo1993; Armstrong et al., Reference Armstrong, Marriott, Schachte and Søndergaard1998). Typical applications of sharing analysis are in the fields of optimization of unification (Søndergaard, Reference Søndergaard1986) and parallelization of logic programs (Hermenegildo and Rossi, Reference Hermenegildo and Rossi1995).
$z$
. Sharing may also track and infer groundness in the same way as the Def domain (de la Banda and Hermenegildo, Reference de la Banda and Hermenegildo1993; Armstrong et al., Reference Armstrong, Marriott, Schachte and Søndergaard1998). Typical applications of sharing analysis are in the fields of optimization of unification (Søndergaard, Reference Søndergaard1986) and parallelization of logic programs (Hermenegildo and Rossi, Reference Hermenegildo and Rossi1995).
It is widely recognized that the pioneering abstract domain
![]() $\mathtt{Sharing}$
(Langen, Reference Langen1990; Jacobs and Langen, 1992) is not very precise, so it is often combined with other domains for tracking freeness, linearity, groundness, or structural information (see Bagnara et al. (Reference Bagnara, Zaffanella and Hill2005); Codish et al. (Reference Codish, Mulkers, Bruynooghe, de la Banda and Hermenegildo1995) for comparative evaluations).
$\mathtt{Sharing}$
(Langen, Reference Langen1990; Jacobs and Langen, 1992) is not very precise, so it is often combined with other domains for tracking freeness, linearity, groundness, or structural information (see Bagnara et al. (Reference Bagnara, Zaffanella and Hill2005); Codish et al. (Reference Codish, Mulkers, Bruynooghe, de la Banda and Hermenegildo1995) for comparative evaluations).
Any domain for static analysis of logic programs must be equipped with four standard operators: renaming, projection, union, and unification. The theory of abstract interpretation (Cousot and Cousot, Reference Cousot and Cousot1979, Reference Cousot and Cousot1992a) ensures the existence of the optimal (best correct) abstract operator for each concrete operator. Nevertheless, while finding optimal operators for renaming, projection, and union is trivial most of the time, devising an optimal abstract unification is much harder.
Amato and Scozzari (Reference Amato and Scozzari2010, Reference Amato and Scozzari2014) have proposed a new (infinite) domain
![]() $\mathtt{ShLin}^{\omega }$
that precisely represents the interaction between sharing and linearity properties, while discharging other structural, irrelevant information. All the abstract operators for
$\mathtt{ShLin}^{\omega }$
that precisely represents the interaction between sharing and linearity properties, while discharging other structural, irrelevant information. All the abstract operators for
![]() $\mathtt{ShLin}^{\omega }$
are shown to be optimal. From
$\mathtt{ShLin}^{\omega }$
are shown to be optimal. From
![]() $\mathtt{ShLin}^{\omega }$
, the authors derive, for the first time, optimal abstract unification for well-known domains combining sharing and linearity, such as
$\mathtt{ShLin}^{\omega }$
, the authors derive, for the first time, optimal abstract unification for well-known domains combining sharing and linearity, such as
![]() $\mathtt{ShLin}^2$
(King, Reference King1994) and
$\mathtt{ShLin}^2$
(King, Reference King1994) and
![]() $\mathtt{Sharing} \times \mathtt{Lin}$
(Muthukumar and Hermenegildo, Reference Muthukumar and Hermenegildo1992).
$\mathtt{Sharing} \times \mathtt{Lin}$
(Muthukumar and Hermenegildo, Reference Muthukumar and Hermenegildo1992).
In this paper, we extend the
![]() $\mathtt{ShLin}^{\omega }$
framework to the case of goal-dependent analysis. In this setting, the unification operator is used twice (see Figure 1):
$\mathtt{ShLin}^{\omega }$
framework to the case of goal-dependent analysis. In this setting, the unification operator is used twice (see Figure 1):
-
forward unification: performs parameter passing by unifying the goal and the call substitution with the head of the chosen clause. The result is called entry substitution.
-
backward unification: propagates back to the goal the exit substitution (i.e., the result of the sub-computation), obtaining the answer substitution.Footnote 1

Fig. 1. The role of forward and backward unification in goal-dependent analysis.
Despite its name, backward unification may be implemented through matching, exploiting the property that the exit substitution is always more instantiated than the call substitution. Analyses with matching are strictly more precise than analyses which do not use matching (see Bruynooghe (Reference Bruynooghe1991) and Amato and Scozzari (Reference Amato and Scozzari2009) for a thorough discussion of the problem). This idea has been implemented in real abstract interpreters such as GAIA (Le Charlier and Van Hentenryck, Reference Le Charlier and Van Hentenryck1994) and PLAI (Muthukumar and Hermenegildo, Reference Muthukumar and Hermenegildo1992).
However, except for Amato and Scozzari (Reference Amato and Scozzari2009), none of the papers that are based on matching (Bruynooghe, Reference Bruynooghe1991; Hans and Winkler, Reference Hans and Winkler1992; Muthukumar and Hermenegildo, Reference Muthukumar and Hermenegildo1992; Le Charlier and Van Hentenryck, Reference Le Charlier and Van Hentenryck1994; King and Longley, Reference King and Longley1995) has ever proved optimality of the proposed abstract operators. In particular, there is no known optimal matching operator for any domain combining sharing and linearity.
The lack of optimal operators brings two kinds of disadvantages: first, the analysis obviously loses precision when using suboptimal abstract operators; second, computing approximated abstract objects can lead to a speed down of the analysis. The latter is typical of sharing analysis, where abstract domains are usually defined in such a way that the less information we have, the more abstract objects are complex. This is not the case for other kinds of analyses, such as groundness analysis, where the complexity of abstract objects may grow according to the amount of groundness information they encode. Moreover, knowing the optimal abstract operator, even if we do not plan to implement it, is useful to understand the potentiality and limits of the abstract domain in use and to guide the search for a more precise (or more efficient) domain.
For this reason, in this paper, we define a matching operator for
![]() $\mathtt{ShLin}^{\omega }$
and prove its optimality. Moreover, from this operator, we derive, for the first time, optimal matching operators for domains combining sharing and linearity information, such as
$\mathtt{ShLin}^{\omega }$
and prove its optimality. Moreover, from this operator, we derive, for the first time, optimal matching operators for domains combining sharing and linearity information, such as
![]() $\mathtt{ShLin}^2$
and
$\mathtt{ShLin}^2$
and
![]() $\mathtt{Sharing} \times \mathtt{Lin}$
.
$\mathtt{Sharing} \times \mathtt{Lin}$
.
2 Notations
We fix a first order signature that includes a constant symbol and a function symbol of arity at least two; otherwise, every term has at most one variable, and the structure of terms is trivial (we need this assumption in the proofs of optimality). The signature also includes a denumerable set of variables
![]() $\mathcal{V}$
. Given a term or other syntactic object
$\mathcal{V}$
. Given a term or other syntactic object
![]() $o$
, we denote by
$o$
, we denote by
![]() $\mathrm{vars}(o)$
the set of variables occurring in
$\mathrm{vars}(o)$
the set of variables occurring in
![]() $o$
. Given a set
$o$
. Given a set
![]() $A$
, we denote by
$A$
, we denote by
![]() $\mathscr{P}(A)$
the powerset of
$\mathscr{P}(A)$
the powerset of
![]() $A$
and by
$A$
and by
![]() $\mathscr{P}_f(A)$
the set of finite subsets of
$\mathscr{P}_f(A)$
the set of finite subsets of
![]() $A$
.
$A$
.
2.1 Multisets
A multiset is a set where repetitions are allowed. We denote by
![]() $\{\!\!\{ x_1, \ldots, x_m \}\!\!\}$
a multiset, where
$\{\!\!\{ x_1, \ldots, x_m \}\!\!\}$
a multiset, where
![]() $x_1, \ldots, x_m$
is a sequence with (possible) repetitions, and by
$x_1, \ldots, x_m$
is a sequence with (possible) repetitions, and by
![]() $\{\!\!\{ \}\!\!\}$
the empty multiset. We will often use the polynomial notation
$\{\!\!\{ \}\!\!\}$
the empty multiset. We will often use the polynomial notation
![]() $v_1^{i_1} \ldots v_n^{i_n}$
, where
$v_1^{i_1} \ldots v_n^{i_n}$
, where
![]() $v_1, \ldots, v_n$
is a sequence without repetitions, to denote a multiset
$v_1, \ldots, v_n$
is a sequence without repetitions, to denote a multiset
![]() $A$
whose element
$A$
whose element
![]() $v_j$
appears
$v_j$
appears
![]() $i_j$
times. The set
$i_j$
times. The set
![]() $\{v_j \mid i_j \gt 0\}$
is called the support of
$\{v_j \mid i_j \gt 0\}$
is called the support of
![]() $A$
and is denoted by
$A$
and is denoted by
![]() $\lfloor \!\lfloor A \rfloor \!\rfloor$
. We also use the functional notation
$\lfloor \!\lfloor A \rfloor \!\rfloor$
. We also use the functional notation
![]() $A: \{v_1, \ldots, v_n\} \rightarrow \mathbb{N}$
, where
$A: \{v_1, \ldots, v_n\} \rightarrow \mathbb{N}$
, where
![]() $A(v_j)=i_j$
.
$A(v_j)=i_j$
.
In this paper, we only consider multisets whose support is finite. We denote with
![]() $\mathscr{P}_m(X)$
the set of all the multisets whose support is any finite subset of
$\mathscr{P}_m(X)$
the set of all the multisets whose support is any finite subset of
![]() $X$
. For example,
$X$
. For example,
![]() $a^3c^5$
and
$a^3c^5$
and
![]() $a^3b^2c^1$
are elements of
$a^3b^2c^1$
are elements of
![]() $\mathscr{P}_m(\{a,b,c\})$
. The fundamental operation for multisets is the sum, defined as
$\mathscr{P}_m(\{a,b,c\})$
. The fundamental operation for multisets is the sum, defined as
Note that we also use
![]() $\uplus$
to denote disjoint union for standard sets. The context will allow us to discern the proper meaning of
$\uplus$
to denote disjoint union for standard sets. The context will allow us to discern the proper meaning of
![]() $\uplus$
. Given a multiset
$\uplus$
. Given a multiset
![]() $A$
and
$A$
and
![]() $X \subseteq \lfloor \!\lfloor A \rfloor \!\rfloor$
, the restriction of
$X \subseteq \lfloor \!\lfloor A \rfloor \!\rfloor$
, the restriction of
![]() $A$
over
$A$
over
![]() $X$
, denoted by
$X$
, denoted by
![]() $A_{|X}$
, is the only multiset
$A_{|X}$
, is the only multiset
![]() $B$
such that
$B$
such that
![]() $\lfloor \!\lfloor B \rfloor \!\rfloor =X$
and
$\lfloor \!\lfloor B \rfloor \!\rfloor =X$
and
![]() $B(v)=A(v)$
for each
$B(v)=A(v)$
for each
![]() $v \in X$
.
$v \in X$
.
2.2 The domain of existential substitutions
We work in the framework of existential substitutions (Amato and Scozzari, Reference Amato and Scozzari2009), which allows us to simplify those semantic definitions which are heavily based on renaming apart objects and to avoid variable clashes. In this framework, all the details concerning renamings are moved to the inner level of the semantic domain, where they are more easily manageable. We briefly recall the basic definitions of the domain.
The set of substitutions, idempotent substitutions, and renamings are denoted by
![]() $\mathit{Subst}$
,
$\mathit{Subst}$
,
![]() $\mathit{ISubst}$
, and
$\mathit{ISubst}$
, and
![]() $\mathit{Ren}$
, respectively. Given
$\mathit{Ren}$
, respectively. Given
![]() $\theta _1, \theta _2 \in \mathit{Subst}$
and
$\theta _1, \theta _2 \in \mathit{Subst}$
and
![]() $U \in \mathscr{P}_f({\mathcal{V}})$
, the preorder
$U \in \mathscr{P}_f({\mathcal{V}})$
, the preorder
![]() $\preceq _U$
is defined as follows:
$\preceq _U$
is defined as follows:
The notation
![]() $\theta _1 \preceq _U \theta _2$
states that
$\theta _1 \preceq _U \theta _2$
states that
![]() $\theta _1$
is an instance of
$\theta _1$
is an instance of
![]() $\theta _2$
w.r.t. the variables in
$\theta _2$
w.r.t. the variables in
![]() $U$
. The equivalence relation induced by the preorder
$U$
. The equivalence relation induced by the preorder
![]() $\preceq _U$
is given by
$\preceq _U$
is given by
Let
![]() $\mathit{ISubst}_{\sim _U}$
be the quotient set of
$\mathit{ISubst}_{\sim _U}$
be the quotient set of
![]() $\mathit{ISubst}$
w.r.t.
$\mathit{ISubst}$
w.r.t.
![]() $\sim _U$
. The domain
$\sim _U$
. The domain
![]() $\mathit{ISubst}_\sim$
of existential substitutions is defined as the disjoint union of all the
$\mathit{ISubst}_\sim$
of existential substitutions is defined as the disjoint union of all the
![]() $\mathit{ISubst}_{\sim _U}$
for
$\mathit{ISubst}_{\sim _U}$
for
![]() $U\in \mathscr{P}_f({\mathcal{V}})$
, namely:
$U\in \mathscr{P}_f({\mathcal{V}})$
, namely:
In the following, we write
![]() $[\theta ]_{U}$
for the equivalence class of
$[\theta ]_{U}$
for the equivalence class of
![]() $\theta$
w.r.t.
$\theta$
w.r.t.
![]() $\sim _U$
. The partial order
$\sim _U$
. The partial order
![]() $\preceq$
over
$\preceq$
over
![]() $\mathit{ISubst}_\sim$
is given by
$\mathit{ISubst}_\sim$
is given by
Intuitively,
![]() $[\theta ]_U \preceq [\theta ^{\prime}]_V$
means that
$[\theta ]_U \preceq [\theta ^{\prime}]_V$
means that
![]() $\theta$
is an instance of
$\theta$
is an instance of
![]() $\theta ^{\prime}$
w.r.t. the variables in
$\theta ^{\prime}$
w.r.t. the variables in
![]() $V$
, provided that they are all variables of interest of
$V$
, provided that they are all variables of interest of
![]() $\theta$
.
$\theta$
.
To ease notation, we often omit braces from the sets of variables of interest when they are given extensionally. So we write
![]() $[\theta ]_{x,y}$
or
$[\theta ]_{x,y}$
or
![]() $[\theta ]_{xy}$
instead of
$[\theta ]_{xy}$
instead of
![]() $[\theta ]_{\{x,y\}}$
and
$[\theta ]_{\{x,y\}}$
and
![]() $\sim _{x,y,z}$
instead of
$\sim _{x,y,z}$
instead of
![]() $\sim _{\{x,y,z\}}$
. When the set of variables of interest is clear from the context or when it is not relevant, it will be omitted. Finally, we omit the braces that enclose the bindings of a substitution when the latter occurs inside an equivalence class; that is, we write
$\sim _{\{x,y,z\}}$
. When the set of variables of interest is clear from the context or when it is not relevant, it will be omitted. Finally, we omit the braces that enclose the bindings of a substitution when the latter occurs inside an equivalence class; that is, we write
![]() $[x/y]_U$
instead of
$[x/y]_U$
instead of
![]() $[\{x/y\}]_U$
.
$[\{x/y\}]_U$
.
2.2.1 Unification
Given
![]() $U,V \in \mathscr{P}_f({\mathcal{V}})$
,
$U,V \in \mathscr{P}_f({\mathcal{V}})$
,
![]() $[\theta _1]_U, [\theta _2]_V \in \mathit{ISubst}_{\sim }$
, the most general unifier between these two classes is defined as the mgu of suitably chosen representatives, where variables not of interest are renamed apart. In formulas:
$[\theta _1]_U, [\theta _2]_V \in \mathit{ISubst}_{\sim }$
, the most general unifier between these two classes is defined as the mgu of suitably chosen representatives, where variables not of interest are renamed apart. In formulas:
where
![]() $\theta _1 \sim _U \theta ^{\prime}_1 \in \mathit{ISubst}$
,
$\theta _1 \sim _U \theta ^{\prime}_1 \in \mathit{ISubst}$
,
![]() $\theta _2 \sim _V \theta ^{\prime}_2 \in \mathit{ISubst}$
, and
$\theta _2 \sim _V \theta ^{\prime}_2 \in \mathit{ISubst}$
, and
![]() $(U \cup \mathrm{vars}(\theta ^{\prime}_1)) \cap (V \cup \mathrm{vars}(\theta ^{\prime}_2)) \subseteq U \cap V$
. The last condition is needed to avoid variable clashes between the chosen representatives
$(U \cup \mathrm{vars}(\theta ^{\prime}_1)) \cap (V \cup \mathrm{vars}(\theta ^{\prime}_2)) \subseteq U \cap V$
. The last condition is needed to avoid variable clashes between the chosen representatives
![]() $\theta ^{\prime}_1$
and
$\theta ^{\prime}_1$
and
![]() $\theta ^{\prime}_2$
. It turns out that
$\theta ^{\prime}_2$
. It turns out that
![]() $\mathsf{mgu}$
is the greatest lower bound of
$\mathsf{mgu}$
is the greatest lower bound of
![]() $\mathit{ISubst}_{\sim }$
ordered by
$\mathit{ISubst}_{\sim }$
ordered by
![]() $\preceq$
.
$\preceq$
.
A different version of unification is obtained when one of the two arguments is an existential substitution and the other one is a standard substitution. In this case, the latter argument may be viewed as an existential substitution where all the variables are of interest:
Note that deriving the general unification in (1) from the special case in (2) is not possible. This is because there are elements in
![]() $\mathit{ISubst}_\sim$
, which cannot be obtained as
$\mathit{ISubst}_\sim$
, which cannot be obtained as
![]() $[\delta ]_{\mathrm{vars}(\delta )}$
for any
$[\delta ]_{\mathrm{vars}(\delta )}$
for any
![]() $\delta \in \mathit{ISubst}$
.
$\delta \in \mathit{ISubst}$
.
This is the form of unification that is better suited for analysis of logic programs, where existential substitutions are the denotations of programs while standard substitutions are the result of unification between goals and heads of clauses. Devising optimal abstract operators for (2) in different abstract domains is the topic of Amato and Scozzari (Reference Amato and Scozzari2010).
2.2.2 Matching
Given
![]() $U_1,U_2 \in \mathscr{P}_f({\mathcal{V}})$
,
$U_1,U_2 \in \mathscr{P}_f({\mathcal{V}})$
,
![]() $[\theta _1]_{U_1} \in \mathit{ISubst}_{\sim }$
, and
$[\theta _1]_{U_1} \in \mathit{ISubst}_{\sim }$
, and
![]() $[\theta _2]_{U_2} \in \mathit{ISubst}$
, the matching of
$[\theta _2]_{U_2} \in \mathit{ISubst}$
, the matching of
![]() $[\theta _1]_{U_1}$
with
$[\theta _1]_{U_1}$
with
![]() $[\theta _2]_{U_2}$
(Amato and Scozzari, Reference Amato and Scozzari2009) is defined in the same way as unification, as soon as none of the variables in
$[\theta _2]_{U_2}$
(Amato and Scozzari, Reference Amato and Scozzari2009) is defined in the same way as unification, as soon as none of the variables in
![]() $U_1$
get instantiated in the result. If this is not the case, the matching is undefined.
$U_1$
get instantiated in the result. If this is not the case, the matching is undefined.
Definition 2.1 (Matching). Given
![]() $[\theta _1]_{U_1}, [\theta _2]_{U_2} \in \mathit{ISubst}_{\sim }$
, we have that
$[\theta _1]_{U_1}, [\theta _2]_{U_2} \in \mathit{ISubst}_{\sim }$
, we have that
 \begin{align} \mathsf{match}([\theta _1]_{U_1},[\theta _2]_{U_2})=\begin{cases} \mathsf{mgu}([\theta _1]_{U_1},[\theta _2]_{U_2}) & \text{if } \theta _1 \preceq _{U_1 \cap U_2} \theta _2, \\[3pt] \text{undefined} & \text{otherwise.} \end{cases} \end{align}
\begin{align} \mathsf{match}([\theta _1]_{U_1},[\theta _2]_{U_2})=\begin{cases} \mathsf{mgu}([\theta _1]_{U_1},[\theta _2]_{U_2}) & \text{if } \theta _1 \preceq _{U_1 \cap U_2} \theta _2, \\[3pt] \text{undefined} & \text{otherwise.} \end{cases} \end{align}
Note that the condition
![]() $\theta _1 \preceq _{U_1 \cap U_2} \theta _2$
is equivalent to
$\theta _1 \preceq _{U_1 \cap U_2} \theta _2$
is equivalent to
![]() $[\theta _1]_{U_1}= \mathsf{mgu}([\theta _1]_{U_1},[\theta _2]_{U_2})_{|U_1}$
(Amato and Scozzari, Reference Amato and Scozzari2009).
$[\theta _1]_{U_1}= \mathsf{mgu}([\theta _1]_{U_1},[\theta _2]_{U_2})_{|U_1}$
(Amato and Scozzari, Reference Amato and Scozzari2009).
Example 2.2. If we unify
![]() $[\theta _1]_{x,y}=[x/a, y/b]_{x,y}$
with
$[\theta _1]_{x,y}=[x/a, y/b]_{x,y}$
with
![]() $[\theta _2]_{y,z}=[z/r(y)]_{y,z}$
, we obtain
$[\theta _2]_{y,z}=[z/r(y)]_{y,z}$
, we obtain
![]() $[\theta _3]_{x,y,z}=[x/a, y/b, z/r(b)]_{x,y,z}$
. Note that the variables
$[\theta _3]_{x,y,z}=[x/a, y/b, z/r(b)]_{x,y,z}$
. Note that the variables
![]() $y$
and
$y$
and
![]() $z$
in
$z$
in
![]() $\theta _3$
are instantiated w.r.t.
$\theta _3$
are instantiated w.r.t.
![]() $\theta _2$
; therefore,
$\theta _2$
; therefore,
![]() $\mathsf{match}([\theta _2]_{y,z}, [\theta _1]_{x,y})$
is undefined. However,
$\mathsf{match}([\theta _2]_{y,z}, [\theta _1]_{x,y})$
is undefined. However,
![]() $x$
and
$x$
and
![]() $y$
in
$y$
in
![]() $\theta _3$
are not instantiated w.r.t.
$\theta _3$
are not instantiated w.r.t.
![]() $\theta _1$
; therefore,
$\theta _1$
; therefore,
![]() $\mathsf{match}([\theta _1]_{x,y},[\theta _2]_{y,z})=[\theta _3]_{x,y,z}$
.
$\mathsf{match}([\theta _1]_{x,y},[\theta _2]_{y,z})=[\theta _3]_{x,y,z}$
.
Most of the time, when matching is applied in goal-dependent analysis of logic programs, we have that
![]() $U_1 \subseteq U_2$
. This is because
$U_1 \subseteq U_2$
. This is because
![]() $U_1$
is the set of variables in a clause, while
$U_1$
is the set of variables in a clause, while
![]() $U_2$
contains both the variables in the clause and in the call substitution. Nonetheless, we study here the general case so that it can be applied in any framework.
$U_2$
contains both the variables in the clause and in the call substitution. Nonetheless, we study here the general case so that it can be applied in any framework.
2.2.3 Other operations
Given
![]() $V \in \mathscr{P}_f({\mathcal{V}})$
and
$V \in \mathscr{P}_f({\mathcal{V}})$
and
![]() $[\theta ]_{U} \in \mathit{ISubst}_\sim$
, we denote by
$[\theta ]_{U} \in \mathit{ISubst}_\sim$
, we denote by
![]() $([\theta ]_U)_{|V}$
the projection of
$([\theta ]_U)_{|V}$
the projection of
![]() $[\theta ]_U$
on the set of variables
$[\theta ]_U$
on the set of variables
![]() $V$
, defined as:
$V$
, defined as:
2.3 Abstract interpretation
Given two sets
![]() $C$
and
$C$
and
![]() $A$
of concrete and abstract objects, respectively, an abstract interpretation (Cousot and Cousot, Reference Cousot and Cousot1992b) is given by an approximation relation
$A$
of concrete and abstract objects, respectively, an abstract interpretation (Cousot and Cousot, Reference Cousot and Cousot1992b) is given by an approximation relation
![]() $\triangleright \subseteq A \times C$
. When
$\triangleright \subseteq A \times C$
. When
![]() $a \triangleright c$
holds, this means that
$a \triangleright c$
holds, this means that
![]() $a$
is a correct abstraction of
$a$
is a correct abstraction of
![]() $c$
. We are interested in the case when
$c$
. We are interested in the case when
![]() $(A,\leq _A)$
is a poset and
$(A,\leq _A)$
is a poset and
![]() $a \leq _A a^{\prime}$
means that
$a \leq _A a^{\prime}$
means that
![]() $a$
is more precise than
$a$
is more precise than
![]() $a^{\prime}$
. In this case, we require that if
$a^{\prime}$
. In this case, we require that if
![]() $a \triangleright c$
and
$a \triangleright c$
and
![]() $a \leq _A a^{\prime}$
, then
$a \leq _A a^{\prime}$
, then
![]() $a^{\prime} \triangleright c$
, too. In more detail, we require what Cousot and Cousot (Reference Cousot and Cousot1992b) call the existence of the best abstract approximation assumption; that is, the existence of a map
$a^{\prime} \triangleright c$
, too. In more detail, we require what Cousot and Cousot (Reference Cousot and Cousot1992b) call the existence of the best abstract approximation assumption; that is, the existence of a map
![]() $\alpha : C \rightarrow A$
such that for all
$\alpha : C \rightarrow A$
such that for all
![]() $a \in A, c \in C$
, it holds that
$a \in A, c \in C$
, it holds that
![]() $a \triangleright c \iff \alpha (c) \leq _A a$
. The map
$a \triangleright c \iff \alpha (c) \leq _A a$
. The map
![]() $\alpha$
is called the abstraction function and maps each
$\alpha$
is called the abstraction function and maps each
![]() $c$
to its best approximation in
$c$
to its best approximation in
![]() $A$
.
$A$
.
Given a (possibly partial) function
![]() $f: C \rightarrow C$
, we say that
$f: C \rightarrow C$
, we say that
![]() $\tilde{f}: A \rightarrow A$
is a correct abstraction of
$\tilde{f}: A \rightarrow A$
is a correct abstraction of
![]() $f$
, and write
$f$
, and write
![]() $\tilde{f} \triangleright f$
, whenever
$\tilde{f} \triangleright f$
, whenever
assuming that
![]() $\tilde{f}(a) \triangleright f(c)$
is true whenever
$\tilde{f}(a) \triangleright f(c)$
is true whenever
![]() $f(c)$
is not defined. We say that
$f(c)$
is not defined. We say that
![]() $\tilde{f}: A \rightarrow A$
is the optimal abstraction of
$\tilde{f}: A \rightarrow A$
is the optimal abstraction of
![]() $f$
when it is the best correct approximation of
$f$
when it is the best correct approximation of
![]() $f$
, that is, when
$f$
, that is, when
![]() $\tilde{f} \triangleright f$
and
$\tilde{f} \triangleright f$
and
In some cases, we prefer to deal with a stronger framework, in which the domain
![]() $C$
is also endowed with a partial order
$C$
is also endowed with a partial order
![]() $\leq _C$
and
$\leq _C$
and
![]() $\alpha : C \rightarrow A$
is a left adjoint to
$\alpha : C \rightarrow A$
is a left adjoint to
![]() $\gamma : A \rightarrow C$
, that is,
$\gamma : A \rightarrow C$
, that is,
The pair
![]() $\langle \alpha, \gamma \rangle$
is called a Galois connection. In particular, we will only consider the case of Galois insertions, which are Galois connections such that
$\langle \alpha, \gamma \rangle$
is called a Galois connection. In particular, we will only consider the case of Galois insertions, which are Galois connections such that
![]() $\alpha \circ \gamma$
is the identity map. If
$\alpha \circ \gamma$
is the identity map. If
![]() $\langle \alpha, \gamma \rangle$
is a Galois insertion and
$\langle \alpha, \gamma \rangle$
is a Galois insertion and
![]() $f: C \rightarrow C$
is a monotone map, the optimal abstraction
$f: C \rightarrow C$
is a monotone map, the optimal abstraction
![]() $\tilde{f}$
always exists, and it is definable as
$\tilde{f}$
always exists, and it is definable as
![]() $\tilde{f}= \alpha \circ f \circ \gamma$
.
$\tilde{f}= \alpha \circ f \circ \gamma$
.
3 Abstract matching over
 $\mathtt{ShLin}^{\omega }$
$\mathtt{ShLin}^{\omega }$
The domain
![]() $\mathtt{ShLin}^{\omega }$
(Amato and Scozzari, Reference Amato and Scozzari2010) generalizes
$\mathtt{ShLin}^{\omega }$
(Amato and Scozzari, Reference Amato and Scozzari2010) generalizes
![]() $\mathtt{Sharing}$
by recording multiplicity of variables in sharing groups. For example, the substitution
$\mathtt{Sharing}$
by recording multiplicity of variables in sharing groups. For example, the substitution
![]() $\theta =\{x/s(u,v), y/g(u,u,u), z/v\}$
is abstracted on
$\theta =\{x/s(u,v), y/g(u,u,u), z/v\}$
is abstracted on
![]() $\mathtt{Sharing}$
into
$\mathtt{Sharing}$
into
![]() $\{uxy,vxz\}$
, where the sharing group
$\{uxy,vxz\}$
, where the sharing group
![]() $uxy$
means that
$uxy$
means that
![]() $\theta (u)$
,
$\theta (u)$
,
![]() $\theta (x)$
, and
$\theta (x)$
, and
![]() $\theta (y)$
share a common variable, namely
$\theta (y)$
share a common variable, namely
![]() $u$
. In
$u$
. In
![]() $\mathtt{ShLin}^{\omega }$
the same substitution would be abstracted as
$\mathtt{ShLin}^{\omega }$
the same substitution would be abstracted as
![]() $\{uxy^3,vxz\}$
, with the additional information that the variable
$\{uxy^3,vxz\}$
, with the additional information that the variable
![]() $u$
occurs three times in
$u$
occurs three times in
![]() $\theta (y)$
. For the sake of completeness, in the following section, we recall the basic definitions.
$\theta (y)$
. For the sake of completeness, in the following section, we recall the basic definitions.
3.1
The domain
 $\mathtt{ShLin}^{\omega }$
$\mathtt{ShLin}^{\omega }$
We call
![]() $\omega$
-sharing group a multiset of variables, that is, an element of
$\omega$
-sharing group a multiset of variables, that is, an element of
![]() $\mathscr{P}_m({\mathcal{V}})$
. Given a substitution
$\mathscr{P}_m({\mathcal{V}})$
. Given a substitution
![]() $\theta$
and a variable
$\theta$
and a variable
![]() $v \in{\mathcal{V}}$
, we denote by
$v \in{\mathcal{V}}$
, we denote by
![]() $\theta ^{-1}(v)$
the
$\theta ^{-1}(v)$
the
![]() $\omega$
-sharing group
$\omega$
-sharing group
![]() $\lambda w \in{\mathcal{V}}. \mathit{occ}(v,\theta (w))$
, which maps each variable
$\lambda w \in{\mathcal{V}}. \mathit{occ}(v,\theta (w))$
, which maps each variable
![]() $w$
to the number of occurrences of
$w$
to the number of occurrences of
![]() $v$
in
$v$
in
![]() $\theta (w)$
.
$\theta (w)$
.
Given a set of variables
![]() $U$
and a set of
$U$
and a set of
![]() $\omega$
-sharing groups
$\omega$
-sharing groups
![]() $S \subseteq \mathscr{P}_m(U)$
, we say that
$S \subseteq \mathscr{P}_m(U)$
, we say that
![]() $[S]_U$
correctly approximates a substitution
$[S]_U$
correctly approximates a substitution
![]() $[\theta ]_W$
if
$[\theta ]_W$
if
![]() $U=W$
and, for each
$U=W$
and, for each
![]() $v \in{\mathcal{V}}$
,
$v \in{\mathcal{V}}$
,
![]() $\theta ^{-1}(v)_{|U} \in S$
. We write
$\theta ^{-1}(v)_{|U} \in S$
. We write
![]() $[S]_U \triangleright [\theta ]_W$
to mean that
$[S]_U \triangleright [\theta ]_W$
to mean that
![]() $[S]_U$
correctly approximates
$[S]_U$
correctly approximates
![]() $[\theta ]_W$
. Therefore,
$[\theta ]_W$
. Therefore,
![]() $[S]_U \triangleright [\theta ]_U$
when
$[S]_U \triangleright [\theta ]_U$
when
![]() $S$
contains all the
$S$
contains all the
![]() $\omega$
-sharing groups in
$\omega$
-sharing groups in
![]() $\theta$
, restricted to the variables in
$\theta$
, restricted to the variables in
![]() $U$
.
$U$
.
Definition 3.1 (
![]() $\mathtt{ShLin}^{\omega }$
). The domain
$\mathtt{ShLin}^{\omega }$
). The domain
![]() $\mathtt{ShLin}^{\omega }$
is defined as
$\mathtt{ShLin}^{\omega }$
is defined as
and ordered by
![]() $[S_1]_{U_1} \leq _\omega [S_2]_{U_2}$
iff
$[S_1]_{U_1} \leq _\omega [S_2]_{U_2}$
iff
![]() $U_1=U_2$
and
$U_1=U_2$
and
![]() $S_1 \subseteq S_2$
.
$S_1 \subseteq S_2$
.
The existence of the empty multiset, when
![]() $S$
is not empty, is required in order to have a surjective abstraction function.
$S$
is not empty, is required in order to have a surjective abstraction function.
In order to ease the notation, we write
![]() $[\{\{\!\!\{ \}\!\!\}, B_1,\ldots, B_n\}]_U$
as
$[\{\{\!\!\{ \}\!\!\}, B_1,\ldots, B_n\}]_U$
as
![]() $[B_1,\ldots, B_n]_U$
by omitting the braces and the empty multiset, and variables in each
$[B_1,\ldots, B_n]_U$
by omitting the braces and the empty multiset, and variables in each
![]() $\omega$
-sharing group are sorted lexicographically. Moreover, if
$\omega$
-sharing group are sorted lexicographically. Moreover, if
![]() $X \in{\mathtt{ShLin}^{\omega }}$
, we write
$X \in{\mathtt{ShLin}^{\omega }}$
, we write
![]() $B \in X$
in place of
$B \in X$
in place of
![]() $X=[S]_U \wedge B \in S$
. Analogously, if
$X=[S]_U \wedge B \in S$
. Analogously, if
![]() $S^{\prime} \in{\mathtt{ShLin}^{\omega }}$
, we write
$S^{\prime} \in{\mathtt{ShLin}^{\omega }}$
, we write
![]() $S^{\prime} \subseteq X$
in place of
$S^{\prime} \subseteq X$
in place of
![]() $X=[S]_U \wedge S^{\prime} \subseteq S$
. The best correct abstraction of a substitution
$X=[S]_U \wedge S^{\prime} \subseteq S$
. The best correct abstraction of a substitution
![]() $[\theta ]_U$
is
$[\theta ]_U$
is
Example 3.2. Given
![]() $\theta =\{x/s(y,u,y), z/s(u,u), v/u\}$
and
$\theta =\{x/s(y,u,y), z/s(u,u), v/u\}$
and
![]() $U=\{w,x,y,z\}$
, we have
$U=\{w,x,y,z\}$
, we have
![]() $\theta ^{-1}(u)=uvxz^2$
,
$\theta ^{-1}(u)=uvxz^2$
,
![]() $\theta ^{-1}(y)= x^2y$
,
$\theta ^{-1}(y)= x^2y$
,
![]() $\theta ^{-1}(z)=\theta ^{-1}(v)=\theta ^{-1}(x)=\{\!\!\{ \}\!\!\}$
, and
$\theta ^{-1}(z)=\theta ^{-1}(v)=\theta ^{-1}(x)=\{\!\!\{ \}\!\!\}$
, and
![]() $\theta ^{-1}(o)=o$
for all the other variables (
$\theta ^{-1}(o)=o$
for all the other variables (
![]() $w$
included). Projecting over
$w$
included). Projecting over
![]() $U$
, we obtain
$U$
, we obtain
![]() $\alpha _\omega ([\theta ]_U)=[x^2y,xz^2,w]_U$
.
$\alpha _\omega ([\theta ]_U)=[x^2y,xz^2,w]_U$
.
3.2 Matching operator
In the matching operation, when
![]() $[\theta _1]_{U_1}$
is matched with
$[\theta _1]_{U_1}$
is matched with
![]() $[\theta _2]_{U_2}$
, sharing groups in
$[\theta _2]_{U_2}$
, sharing groups in
![]() $\theta _1$
and
$\theta _1$
and
![]() $\theta _2$
are joined together in the resulting substitution. However, not all combinations are allowed. Assume
$\theta _2$
are joined together in the resulting substitution. However, not all combinations are allowed. Assume
![]() $\alpha _{\mathrm{\omega }}([\theta _i]_{U_i})=[S_i]_{U_i}$
for
$\alpha _{\mathrm{\omega }}([\theta _i]_{U_i})=[S_i]_{U_i}$
for
![]() $i \in \{1,2\}$
. If
$i \in \{1,2\}$
. If
![]() $\mathsf{match}([\theta _1]_{U_1},[\theta _2]_{U_2})$
is defined,
$\mathsf{match}([\theta _1]_{U_1},[\theta _2]_{U_2})$
is defined,
![]() $\theta _1$
will not be further instantiated and thus
$\theta _1$
will not be further instantiated and thus
![]() $\alpha _{\mathrm{\omega }}(\mathsf{match}([\theta _1]_{U_1}, [\theta _2]_{U_2})_{|U_1} ) \subseteq S_1$
. Moreover, the sharing groups in
$\alpha _{\mathrm{\omega }}(\mathsf{match}([\theta _1]_{U_1}, [\theta _2]_{U_2})_{|U_1} ) \subseteq S_1$
. Moreover, the sharing groups in
![]() $S_2$
which do not contain any variable in
$S_2$
which do not contain any variable in
![]() $U_1$
are not affected by the unification, since the corresponding existential variable does not appear in
$U_1$
are not affected by the unification, since the corresponding existential variable does not appear in
![]() $\theta _2(v)$
for any
$\theta _2(v)$
for any
![]() $v \in U_1$
.
$v \in U_1$
.
Example 3.3. Let
![]() $\theta _1 = \{ x/r(w_1,w_2,w_2,w_3,w_3), y/a, z/r(w_1) \}$
with
$\theta _1 = \{ x/r(w_1,w_2,w_2,w_3,w_3), y/a, z/r(w_1) \}$
with
![]() $U_1=\{x,y,z\}$
and
$U_1=\{x,y,z\}$
and
![]() $\theta _2 = \{ x/r(w_4, w_5, w_6,w_8,w_8), u/r(w_4,w_7), v/r(w_7,w_8)\}$
with
$\theta _2 = \{ x/r(w_4, w_5, w_6,w_8,w_8), u/r(w_4,w_7), v/r(w_7,w_8)\}$
with
![]() $U_2=\{u,v,x\}$
. We have that
$U_2=\{u,v,x\}$
. We have that
with
![]() $U=\{u,v,x,y,z\}$
. At the abstract level, we have
$U=\{u,v,x,y,z\}$
. At the abstract level, we have
![]() $[S_1]_{U_1}= \alpha _{\mathrm{\omega }}([\theta _1]_{U_1})= [x^2, xz]_{U_1}$
,
$[S_1]_{U_1}= \alpha _{\mathrm{\omega }}([\theta _1]_{U_1})= [x^2, xz]_{U_1}$
,
![]() $[S_2]_{U_2}= \alpha _{\mathrm{\omega }}([\theta _2]_{U_2})= [uv,ux,vx^2,x]_{U_2}$
, and
$[S_2]_{U_2}= \alpha _{\mathrm{\omega }}([\theta _2]_{U_2})= [uv,ux,vx^2,x]_{U_2}$
, and
![]() $[S]_U = \alpha _{\mathrm{\omega }}([\theta ]_U)= [uv, uxz, vx^2, x^2]_U$
.
$[S]_U = \alpha _{\mathrm{\omega }}([\theta ]_U)= [uv, uxz, vx^2, x^2]_U$
.
Note that the new sharing group
![]() $uxz$
has the property that its restriction to
$uxz$
has the property that its restriction to
![]() $U_1$
is in
$U_1$
is in
![]() $S_1$
. More generally, if we abstract
$S_1$
. More generally, if we abstract
![]() $\theta _1$
w.r.t. the variables in
$\theta _1$
w.r.t. the variables in
![]() $U_1$
, we get
$U_1$
, we get
![]() $\alpha _{\mathrm{\omega }}([\theta ]_{U_1}) = [x^2, xz]_{U_1}$
. This is equal to
$\alpha _{\mathrm{\omega }}([\theta ]_{U_1}) = [x^2, xz]_{U_1}$
. This is equal to
![]() $[S_1]_{U_1}$
, showing that no new sharing group has been introduced by the matching operation relative to the variables in
$[S_1]_{U_1}$
, showing that no new sharing group has been introduced by the matching operation relative to the variables in
![]() $U_1$
. Moreover, the sharing group
$U_1$
. Moreover, the sharing group
![]() $uv$
, which does not contain variables in
$uv$
, which does not contain variables in
![]() $U_1$
, is brought unchanged from
$U_1$
, is brought unchanged from
![]() $S_2$
to
$S_2$
to
![]() $S$
.
$S$
.
Following the idea presented above, we may design an abstract matching operation for the domain
![]() $\mathtt{ShLin}^{\omega }$
.
$\mathtt{ShLin}^{\omega }$
.
Definition 3.4 (Matching over
![]() $\mathtt{ShLin}^{\omega }$
). Given
$\mathtt{ShLin}^{\omega }$
). Given
![]() $[S_1]_{U_1}, [S_2]_{U_2} \in{\mathtt{ShLin}^{\omega }}$
, we define
$[S_1]_{U_1}, [S_2]_{U_2} \in{\mathtt{ShLin}^{\omega }}$
, we define
where
We now show an example of computing the matching over
![]() $\mathtt{ShLin}^{\omega }$
.
$\mathtt{ShLin}^{\omega }$
.
Example 3.5. Consider
![]() $[S_1]_{U_1}=[x^2, xz]_{xyz}$
and
$[S_1]_{U_1}=[x^2, xz]_{xyz}$
and
![]() $[S_2]_{U_2}=[uv,ux,vx^2,x]_{uvx}$
as in Example 3.3. We show that from the definition of
$[S_2]_{U_2}=[uv,ux,vx^2,x]_{uvx}$
as in Example 3.3. We show that from the definition of
![]() $\mathsf{match}_{\mathrm{\omega }}$
, it holds
$\mathsf{match}_{\mathrm{\omega }}$
, it holds
First, we have that
![]() $S^{\prime}_2 = \{uv\}$
and
$S^{\prime}_2 = \{uv\}$
and
![]() $S^{\prime\prime}_2 = \{ux, vx^2, x\}$
. Apart from
$S^{\prime\prime}_2 = \{ux, vx^2, x\}$
. Apart from
![]() $uv$
, which directly comes from
$uv$
, which directly comes from
![]() $S^{\prime}_2$
, all the other
$S^{\prime}_2$
, all the other
![]() $\omega$
-sharing groups in the result may be obtained by choosing a multiset
$\omega$
-sharing groups in the result may be obtained by choosing a multiset
![]() $\mathcal{M}$
of sharing groups in
$\mathcal{M}$
of sharing groups in
![]() $S^{\prime\prime}_2$
and summing them together, obtaining
$S^{\prime\prime}_2$
and summing them together, obtaining
![]() $\uplus \mathcal{M}$
. Then, we consider if it is possible to add to
$\uplus \mathcal{M}$
. Then, we consider if it is possible to add to
![]() $\uplus \mathcal{M}$
some occurrences of the variables
$\uplus \mathcal{M}$
some occurrences of the variables
![]() $y$
and
$y$
and
![]() $z$
, for instance,
$z$
, for instance,
![]() $n$
occurrences of
$n$
occurrences of
![]() $y$
and
$y$
and
![]() $m$
of
$m$
of
![]() $z$
, in such a way that
$z$
, in such a way that
![]() $(\uplus \mathcal{M}) \uplus \{\!\!\{ y^{n} z^{m} \}\!\!\}$
restricted to
$(\uplus \mathcal{M}) \uplus \{\!\!\{ y^{n} z^{m} \}\!\!\}$
restricted to
![]() $U_1$
is a sharing group in
$U_1$
is a sharing group in
![]() $S_1$
.
$S_1$
.
We start by considering
![]() $\mathcal{M}$
with a single
$\mathcal{M}$
with a single
![]() $\omega$
-sharing group.
$\omega$
-sharing group.
-
• If
 $\mathcal{M} = \{\!\!\{ ux \}\!\!\}$
, then
$\mathcal{M} = \{\!\!\{ ux \}\!\!\}$
, then
 $\uplus \mathcal{M} = ux$
but
$\uplus \mathcal{M} = ux$
but
 $(\uplus \mathcal{X})|_{U_1} = x \notin S_1$
. However, we can add the variable
$(\uplus \mathcal{X})|_{U_1} = x \notin S_1$
. However, we can add the variable
 $z$
to get
$z$
to get
 $uxz \in S_1$
; hence
$uxz \in S_1$
; hence
 $uxz$
is an
$uxz$
is an
 $\omega$
-sharing group in the result of
$\omega$
-sharing group in the result of
 $\mathsf{match}_{\mathrm{\omega }}$
.
$\mathsf{match}_{\mathrm{\omega }}$
. -
• If
 $\mathcal{M} = \{\!\!\{ vx^2 \}\!\!\}$
, then
$\mathcal{M} = \{\!\!\{ vx^2 \}\!\!\}$
, then
 $\uplus \mathcal{M} = vx^2$
and
$\uplus \mathcal{M} = vx^2$
and
 $(\uplus \mathcal{M})|_{U_1} = x^2$
, which is already an element of
$(\uplus \mathcal{M})|_{U_1} = x^2$
, which is already an element of
 $S_1$
. Therefore,
$S_1$
. Therefore,
 $vx^2$
is in the result of
$vx^2$
is in the result of
 $\mathsf{match}_{\mathrm{\omega }}$
.
$\mathsf{match}_{\mathrm{\omega }}$
. -
• If
 $\mathcal{M} = \{\!\!\{ x \}\!\!\}$
, then
$\mathcal{M} = \{\!\!\{ x \}\!\!\}$
, then
 $\uplus \mathcal{M} = x$
, but
$\uplus \mathcal{M} = x$
, but
 $(\uplus \mathcal{M})|_{U_1} = x \notin S_1$
. However, we can add the variable
$(\uplus \mathcal{M})|_{U_1} = x \notin S_1$
. However, we can add the variable
 $z$
to get
$z$
to get
 $xz \in S_1$
; hence
$xz \in S_1$
; hence
 $xz$
is in the result of
$xz$
is in the result of
 $\mathsf{match}_{\mathrm{\omega }}$
.
$\mathsf{match}_{\mathrm{\omega }}$
.
We now consider the cases when
![]() $\mathcal{M}$
has two (possibly equal) elements. Note that if
$\mathcal{M}$
has two (possibly equal) elements. Note that if
![]() $\mathcal{M}$
contains
$\mathcal{M}$
contains
![]() $vx^2$
, it cannot contain anything else; otherwise,
$vx^2$
, it cannot contain anything else; otherwise,
![]() $\uplus \mathcal{M}$
would contain at least three occurrences of
$\uplus \mathcal{M}$
would contain at least three occurrences of
![]() $x$
, and no sharing group in
$x$
, and no sharing group in
![]() $S_1$
could be matched. Therefore, the only choices are
$S_1$
could be matched. Therefore, the only choices are
-
• if
 $\mathcal{M} = \{\!\!\{ ux, ux \}\!\!\}$
, then
$\mathcal{M} = \{\!\!\{ ux, ux \}\!\!\}$
, then
 $\uplus \mathcal{M} = u^2x^2$
and
$\uplus \mathcal{M} = u^2x^2$
and
 $(\uplus \mathcal{M})|_{U_1} = x^2$
, which is already in
$(\uplus \mathcal{M})|_{U_1} = x^2$
, which is already in
 $S_1$
; hence
$S_1$
; hence
 $u^2x^2$
is in the result of
$u^2x^2$
is in the result of
 $\mathsf{match}_{\mathrm{\omega }}$
;
$\mathsf{match}_{\mathrm{\omega }}$
; -
• if
 $\mathcal{M} = \{\!\!\{ x, x \}\!\!\}$
, then
$\mathcal{M} = \{\!\!\{ x, x \}\!\!\}$
, then
 $\uplus \mathcal{M} = x^2$
and
$\uplus \mathcal{M} = x^2$
and
 $(\uplus \mathcal{M})|_{U_1} = x^2$
, which is already in
$(\uplus \mathcal{M})|_{U_1} = x^2$
, which is already in
 $S_1$
; hence
$S_1$
; hence
 $x^2$
is in the result of
$x^2$
is in the result of
 $\mathsf{match}_{\mathrm{\omega }}$
;
$\mathsf{match}_{\mathrm{\omega }}$
; -
• if
 $\mathcal{M} = \{\!\!\{ ux, x \}\!\!\}$
, then
$\mathcal{M} = \{\!\!\{ ux, x \}\!\!\}$
, then
 $\uplus \mathcal{M} = ux^2$
and
$\uplus \mathcal{M} = ux^2$
and
 $(\uplus \mathcal{M})|_{U_1} = x^2$
, which is already in
$(\uplus \mathcal{M})|_{U_1} = x^2$
, which is already in
 $S_1$
; hence
$S_1$
; hence
 $ux^2$
is in the result of
$ux^2$
is in the result of
 $\mathsf{match}_{\mathrm{\omega }}$
.
$\mathsf{match}_{\mathrm{\omega }}$
.
In theory, we should also consider the case when
![]() $\mathcal{M}$
has more than two elements, but in the example, this would not lead to new results, for the same reason why
$\mathcal{M}$
has more than two elements, but in the example, this would not lead to new results, for the same reason why
![]() $vx^2$
may only be used alone.
$vx^2$
may only be used alone.
We will prove that
![]() $\mathsf{match}_{\mathrm{\omega }}$
is correct and therefore comes as no surprise that
$\mathsf{match}_{\mathrm{\omega }}$
is correct and therefore comes as no surprise that
The lack of equality means that
![]() $\mathsf{match}_{\mathrm{\omega }}$
is not (
$\mathsf{match}_{\mathrm{\omega }}$
is not (
![]() $\alpha$
-)complete (Giacobazzi et al., Reference Giacobazzi, Ranzato and Scozzari2000; Amato and Scozzari, Reference Amato and Scozzari2011). We will show later that it is optimal.
$\alpha$
-)complete (Giacobazzi et al., Reference Giacobazzi, Ranzato and Scozzari2000; Amato and Scozzari, Reference Amato and Scozzari2011). We will show later that it is optimal.
We try to give the intuition behind the definition of
![]() $\mathsf{match}$
, especially in the context of the backward unification. First note that the operator is additive on the first argument, namely:
$\mathsf{match}$
, especially in the context of the backward unification. First note that the operator is additive on the first argument, namely:
 \begin{align*}\mathsf {match}_{\mathrm {\omega }}([S_1]_{U_1},[S_2]_{U_2}) = \left [\bigcup _{B\in S_1} \mathsf {match}_{\mathrm {\omega }}([\{B\}]_{U_1},[S_2]_{U_2}) \right ]_{U_1\cup U_2}\end{align*}
\begin{align*}\mathsf {match}_{\mathrm {\omega }}([S_1]_{U_1},[S_2]_{U_2}) = \left [\bigcup _{B\in S_1} \mathsf {match}_{\mathrm {\omega }}([\{B\}]_{U_1},[S_2]_{U_2}) \right ]_{U_1\cup U_2}\end{align*}
This immediately implies that we can reason on matching considering one sharing group at a time. Given a sharing group
![]() $B\in S_1$
, which represents the exit substitution from a sub-computation, we try to guess which of the sharing groups in
$B\in S_1$
, which represents the exit substitution from a sub-computation, we try to guess which of the sharing groups in
![]() $S_2$
are part of the entry substitution that has generated the sub-computation ending with
$S_2$
are part of the entry substitution that has generated the sub-computation ending with
![]() $B$
. In the simple case, when
$B$
. In the simple case, when
![]() $U_1 \supseteq U_2$
, we simply check that
$U_1 \supseteq U_2$
, we simply check that
![]() $B$
can be generated by the sharing groups in
$B$
can be generated by the sharing groups in
![]() $S_2$
; that is, there exists
$S_2$
; that is, there exists
![]() $\mathcal{S} \in \mathscr{P}_m(S_2)$
such that
$\mathcal{S} \in \mathscr{P}_m(S_2)$
such that
![]() $B_{|U_2} = \uplus \mathcal{S}$
.
$B_{|U_2} = \uplus \mathcal{S}$
.
The difficult case is when
![]() $U_2$
contains some variables that are not in
$U_2$
contains some variables that are not in
![]() $U_1$
. These variables come from the call substitution; they are removed from the abstraction before entering the sub-computation and now should be re-introduced as precisely as possible. In this case, we build a new sharing group
$U_1$
. These variables come from the call substitution; they are removed from the abstraction before entering the sub-computation and now should be re-introduced as precisely as possible. In this case, we build a new sharing group
![]() $X$
such that
$X$
such that
![]() $X_{|U_1}$
coincides with
$X_{|U_1}$
coincides with
![]() $B$
and
$B$
and
![]() $X_{|U_2}$
is generated by
$X_{|U_2}$
is generated by
![]() $S_2$
; namely, there exists
$S_2$
; namely, there exists
![]() $\mathcal{S} \in \mathscr{P}_m(S_2)$
such that
$\mathcal{S} \in \mathscr{P}_m(S_2)$
such that
![]() $X_{|U_2} = \uplus \mathcal{S}$
. This condition ensures that we pair each exit substitution
$X_{|U_2} = \uplus \mathcal{S}$
. This condition ensures that we pair each exit substitution
![]() $\theta _1$
(in the concretization of
$\theta _1$
(in the concretization of
![]() $B$
) with some entry substitution
$B$
) with some entry substitution
![]() $\theta _2$
(in the concretization of
$\theta _2$
(in the concretization of
![]() $\mathcal{S}$
), which is less instantiated than
$\mathcal{S}$
), which is less instantiated than
![]() $\theta _1$
.
$\theta _1$
.
Note that, although the abstract unification operator
![]() $\mathsf{mgu}_{\mathrm{\omega }}$
defined in Amato and Scozzari (Reference Amato and Scozzari2010) takes an abstract object and a substitution as inputs, the operator
$\mathsf{mgu}_{\mathrm{\omega }}$
defined in Amato and Scozzari (Reference Amato and Scozzari2010) takes an abstract object and a substitution as inputs, the operator
![]() $\mathsf{match}_{\mathrm{\omega }}$
is designed in such a way that both the arguments are abstract objects. The reason for this choice is that these are the variants needed for static analysis of logic programs. However, it would be possible to devise a variant of
$\mathsf{match}_{\mathrm{\omega }}$
is designed in such a way that both the arguments are abstract objects. The reason for this choice is that these are the variants needed for static analysis of logic programs. However, it would be possible to devise a variant of
![]() $\mathsf{mgu}_{\mathrm{\omega }}$
with two abstract arguments and variants of
$\mathsf{mgu}_{\mathrm{\omega }}$
with two abstract arguments and variants of
![]() $\mathsf{match}_{\mathrm{\omega }}$
with one abstract argument and a concrete one.
$\mathsf{match}_{\mathrm{\omega }}$
with one abstract argument and a concrete one.
In order to prove the correctness of
![]() $\mathsf{match}_{\mathrm{\omega }}$
, we first extend the definition of
$\mathsf{match}_{\mathrm{\omega }}$
, we first extend the definition of
![]() $\theta ^{-1}$
to the case when it is applied to a sharing group
$\theta ^{-1}$
to the case when it is applied to a sharing group
![]() $B$
, elementwise as
$B$
, elementwise as
It turns out that
a result that has been proved in Amato and Scozzari (Reference Amato and Scozzari2010).
Example 3.6. Given
![]() $\eta =\{x/s(y,u,y), z/s(u,u), v/u\}$
and
$\eta =\{x/s(y,u,y), z/s(u,u), v/u\}$
and
![]() $\theta = \{ v/a, w/s(x, x) \}$
, we have
$\theta = \{ v/a, w/s(x, x) \}$
, we have
![]() $\eta \circ \theta = \{ v/a, w/s(s(y,u,y), s(y,u,y)), x/s(y,u,y), z/s(u,u))\}$
and
$\eta \circ \theta = \{ v/a, w/s(s(y,u,y), s(y,u,y)), x/s(y,u,y), z/s(u,u))\}$
and
![]() $(\eta \circ \theta )^{-1}(u) = uw^2xz^2$
. The same result may be obtained as
$(\eta \circ \theta )^{-1}(u) = uw^2xz^2$
. The same result may be obtained as
![]() $\theta ^{-1}(\eta ^{-1}(u))$
since
$\theta ^{-1}(\eta ^{-1}(u))$
since
![]() $\eta ^{-1}(u) = uvxz^2$
and
$\eta ^{-1}(u) = uvxz^2$
and
Theorem 3.7 (Correctness of
![]() $\mathsf{match}_{\mathrm{\omega }}$
).
$\mathsf{match}_{\mathrm{\omega }}$
).
![]() $\mathsf{match}_{\mathrm{\omega }}$
is correct w.r.t.
$\mathsf{match}_{\mathrm{\omega }}$
is correct w.r.t.
![]() $\mathsf{match}$
.
$\mathsf{match}$
.
Proof Given
![]() $[S_1]_{U_1} \triangleright [\theta _1]_{U_1}$
and
$[S_1]_{U_1} \triangleright [\theta _1]_{U_1}$
and
![]() $[S_2]_{U_2} \triangleright [\theta _2]_{U_2}$
such that
$[S_2]_{U_2} \triangleright [\theta _2]_{U_2}$
such that
![]() $\mathsf{match}([\theta _1]_{U_1},[\theta _2]_{U_2})$
is defined, we need to prove that
$\mathsf{match}([\theta _1]_{U_1},[\theta _2]_{U_2})$
is defined, we need to prove that
Assume without loss of generality that
![]() $\mathrm{dom}(\theta _1)=U_1$
,
$\mathrm{dom}(\theta _1)=U_1$
,
![]() $\mathrm{dom}(\theta _2)=U_2$
, and
$\mathrm{dom}(\theta _2)=U_2$
, and
![]() $\mathrm{vars}(\theta _1) \cap \mathrm{vars}(\theta _2) \subseteq U_1 \cap U_2$
. In particular, this implies
$\mathrm{vars}(\theta _1) \cap \mathrm{vars}(\theta _2) \subseteq U_1 \cap U_2$
. In particular, this implies
![]() $\mathrm{rng}(\theta _1) \cap \mathrm{rng}(\theta _2)=\emptyset$
. By hypothesis
$\mathrm{rng}(\theta _1) \cap \mathrm{rng}(\theta _2)=\emptyset$
. By hypothesis
![]() $\theta _1 \preceq _{U_1 \cap U_2} \theta _2$
, that is, there exists
$\theta _1 \preceq _{U_1 \cap U_2} \theta _2$
, that is, there exists
![]() $\delta \in \mathit{ISubst}$
such that
$\delta \in \mathit{ISubst}$
such that
![]() $\theta _1(x)= \delta (\theta _2(x))$
for each
$\theta _1(x)= \delta (\theta _2(x))$
for each
![]() $x \in U_1 \cap U_2$
,
$x \in U_1 \cap U_2$
,
![]() $\mathrm{dom}(\delta )=\mathrm{vars}(\theta _2(U_1 \cap U_2))$
and
$\mathrm{dom}(\delta )=\mathrm{vars}(\theta _2(U_1 \cap U_2))$
and
![]() $\mathrm{rng}(\delta )=\mathrm{vars}(\theta _1(U_1 \cap U_2))$
. We have
$\mathrm{rng}(\delta )=\mathrm{vars}(\theta _1(U_1 \cap U_2))$
. We have
 \begin{eqnarray*} &&\mathsf{mgu}(\theta _1,\theta _2)\\ &=&\mathsf{mgu}(\{ \theta _2(x)=\theta _2(\theta _1(x)) \mid x \in U_1 \}) \circ \theta _2\\ &&\quad \text{[by assumptions on the $\theta _i$'s]}\\ &=&\mathsf{mgu}(\{ \theta _2(x)=\theta _1(x) \mid x \in U_1 \}) \circ \theta _2\\ &=&\mathsf{mgu}(\{ \theta _2(x)=\theta _1(x) \mid x \in U_1 \cap U_2 \}) \circ (\theta _1)_{|U_1 \setminus U_2} \circ \theta _2\\ &&\quad \text{[since $\mathrm{vars}(\theta _2) \cap \mathrm{vars}((\theta _1)_{U_1 \setminus U_2})=\emptyset ]$}\\ &=&\mathsf{mgu}(\{ \theta _2(x)=\delta (\theta _2(x)) \mid x \in U_1 \cap U_2\}) \circ ((\theta _1)_{|U_1 \setminus U_2} \uplus \theta _2)\\ &=&\delta \circ ((\theta _1)_{|U_1 \setminus U_2} \uplus \theta _2)\\ &&\quad \text{[since $\mathrm{dom}(\delta ) \cap \mathrm{vars}((\theta _1)_{U_1 \setminus U_2})=\emptyset ]$}\\ &=&(\theta _1)_{|U_1 \setminus U_2} \uplus (\delta \circ \theta _2) \enspace . \end{eqnarray*}
\begin{eqnarray*} &&\mathsf{mgu}(\theta _1,\theta _2)\\ &=&\mathsf{mgu}(\{ \theta _2(x)=\theta _2(\theta _1(x)) \mid x \in U_1 \}) \circ \theta _2\\ &&\quad \text{[by assumptions on the $\theta _i$'s]}\\ &=&\mathsf{mgu}(\{ \theta _2(x)=\theta _1(x) \mid x \in U_1 \}) \circ \theta _2\\ &=&\mathsf{mgu}(\{ \theta _2(x)=\theta _1(x) \mid x \in U_1 \cap U_2 \}) \circ (\theta _1)_{|U_1 \setminus U_2} \circ \theta _2\\ &&\quad \text{[since $\mathrm{vars}(\theta _2) \cap \mathrm{vars}((\theta _1)_{U_1 \setminus U_2})=\emptyset ]$}\\ &=&\mathsf{mgu}(\{ \theta _2(x)=\delta (\theta _2(x)) \mid x \in U_1 \cap U_2\}) \circ ((\theta _1)_{|U_1 \setminus U_2} \uplus \theta _2)\\ &=&\delta \circ ((\theta _1)_{|U_1 \setminus U_2} \uplus \theta _2)\\ &&\quad \text{[since $\mathrm{dom}(\delta ) \cap \mathrm{vars}((\theta _1)_{U_1 \setminus U_2})=\emptyset ]$}\\ &=&(\theta _1)_{|U_1 \setminus U_2} \uplus (\delta \circ \theta _2) \enspace . \end{eqnarray*}
With an analogous derivation, we obtain
Now, if
![]() $\eta =\mathsf{mgu}(\theta _1,\theta _2)$
, we need to prove that for each
$\eta =\mathsf{mgu}(\theta _1,\theta _2)$
, we need to prove that for each
![]() $v \in{\mathcal{V}}$
,
$v \in{\mathcal{V}}$
,
![]() $\eta ^{-1}(v)_{|U_1 \cup U_2} \in \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2})$
. We distinguish several cases.
$\eta ^{-1}(v)_{|U_1 \cup U_2} \in \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2})$
. We distinguish several cases.
-
•
 $v \notin \mathrm{rng}(\theta _1)$
and
$v \notin \mathrm{rng}(\theta _1)$
and
 $v \notin \mathrm{rng}(\theta _2)$
. In this case
$v \notin \mathrm{rng}(\theta _2)$
. In this case
 $v \notin \mathrm{vars}(\delta )$
and
$v \notin \mathrm{vars}(\delta )$
and
 $\eta ^{-1}(v)_{|U_1 \cup U_2}=\{\!\!\{ \}\!\!\} \in \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2})$
.
$\eta ^{-1}(v)_{|U_1 \cup U_2}=\{\!\!\{ \}\!\!\} \in \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2})$
. -
•
 $v \in \mathrm{rng}(\theta _1)$
and
$v \in \mathrm{rng}(\theta _1)$
and
 $v \notin \mathrm{vars}(\theta _1(U_2))$
. In this case
$v \notin \mathrm{vars}(\theta _1(U_2))$
. In this case
 $v \notin \mathrm{rng}(\theta _2)$
and
$v \notin \mathrm{rng}(\theta _2)$
and
 $v \notin \mathrm{vars}(\delta )$
. We have
$v \notin \mathrm{vars}(\delta )$
. We have
 $\eta ^{-1}(v)_{|U_1 \cup U_2} = \theta _1^{-1}(v)_{|U_1} \in S_1 \subseteq \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2})$
.
$\eta ^{-1}(v)_{|U_1 \cup U_2} = \theta _1^{-1}(v)_{|U_1} \in S_1 \subseteq \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2})$
. -
•
 $v \in \mathrm{rng}(\theta _2)$
and
$v \in \mathrm{rng}(\theta _2)$
and
 $v \notin \mathrm{vars}(\theta _2(U_1))$
. In this case
$v \notin \mathrm{vars}(\theta _2(U_1))$
. In this case
 $v \notin \mathrm{rng}(\theta _1)$
and
$v \notin \mathrm{rng}(\theta _1)$
and
 $v \notin \mathrm{vars}(\delta )$
. We have
$v \notin \mathrm{vars}(\delta )$
. We have
 $\eta ^{-1}(v)_{|U_1 \cup U_2} = \theta _2^{-1}(v)_{|U_2} \in S_2$
. Since
$\eta ^{-1}(v)_{|U_1 \cup U_2} = \theta _2^{-1}(v)_{|U_2} \in S_2$
. Since
 $v \notin \mathrm{vars}(\theta _2(U_1))$
, then
$v \notin \mathrm{vars}(\theta _2(U_1))$
, then
 $\theta _2^{-1}(v)_{|U_2} \in S^{\prime}_2 \subseteq \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2})$
.
$\theta _2^{-1}(v)_{|U_2} \in S^{\prime}_2 \subseteq \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2})$
. -
•
 $v \in \mathrm{vars}(\theta _2(U_1 \cap U_2))$
. In this case
$v \in \mathrm{vars}(\theta _2(U_1 \cap U_2))$
. In this case
 $v \notin \mathrm{rng}(\theta _1)$
and
$v \notin \mathrm{rng}(\theta _1)$
and
 $v \in \mathrm{dom}(\delta )$
; therefore,
$v \in \mathrm{dom}(\delta )$
; therefore,
 $\eta ^{-1}(v)_{|U_1 \cup U_2}=\{\!\!\{ \}\!\!\}$
.
$\eta ^{-1}(v)_{|U_1 \cup U_2}=\{\!\!\{ \}\!\!\}$
. -
•
 $v \in \mathrm{vars}(\theta _1(U_1 \cap U_2))$
. Now,
$v \in \mathrm{vars}(\theta _1(U_1 \cap U_2))$
. Now,
 $v \in \mathrm{rng}(\delta )$
and
$v \in \mathrm{rng}(\delta )$
and
 $\eta ^{-1}(v)_{|U_2}=\theta _2^{-1}( \delta ^{-1}(v))_{|U_2}=\biguplus X$
, where
$\eta ^{-1}(v)_{|U_2}=\theta _2^{-1}( \delta ^{-1}(v))_{|U_2}=\biguplus X$
, where
 $X \in \mathscr{P}_m(S_2)$
and each sharing group
$X \in \mathscr{P}_m(S_2)$
and each sharing group
 $B \in X$
is of the form
$B \in X$
is of the form
 $\theta _2^{-1}(w)_{|U_2}$
for some
$\theta _2^{-1}(w)_{|U_2}$
for some
 $w \in \lfloor \!\lfloor \delta ^{-1}(v) \rfloor \!\rfloor$
. Note that every such
$w \in \lfloor \!\lfloor \delta ^{-1}(v) \rfloor \!\rfloor$
. Note that every such
 $w$
is an element of
$w$
is an element of
 $\mathrm{vars}(\theta _2(U_1 \cap U_2))$
; therefore,
$\mathrm{vars}(\theta _2(U_1 \cap U_2))$
; therefore,
 $\theta _2^{-1}(w)_{|U_2} \in S^{\prime\prime}_2$
,
$\theta _2^{-1}(w)_{|U_2} \in S^{\prime\prime}_2$
,
 $X \in \mathscr{P}_m(S^{\prime\prime}_2)$
, and
$X \in \mathscr{P}_m(S^{\prime\prime}_2)$
, and
 $\biguplus X \in (S_2^{\prime\prime})^*$
. On the other side, since
$\biguplus X \in (S_2^{\prime\prime})^*$
. On the other side, since
 $\eta =\theta _1 \uplus (\delta \circ (\theta _2)_{|U_2 \setminus U_1})$
, we have
$\eta =\theta _1 \uplus (\delta \circ (\theta _2)_{|U_2 \setminus U_1})$
, we have
 $\eta ^{-1}(v)_{|U_1}=\theta _1^{-1}(v)_{|U_1} \in S_1$
. Hence,
$\eta ^{-1}(v)_{|U_1}=\theta _1^{-1}(v)_{|U_1} \in S_1$
. Hence,
 $\eta ^{-1}(v)_{|U_1 \cup U_2} \in \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2})$
.
$\eta ^{-1}(v)_{|U_1 \cup U_2} \in \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2})$
.
This concludes the proof.
Now, we may prove the optimality of
![]() $\mathsf{match}_{\mathrm{\omega }}$
. Actually, we prove a stronger property, a sort of weak completeness of
$\mathsf{match}_{\mathrm{\omega }}$
. Actually, we prove a stronger property, a sort of weak completeness of
![]() $\mathsf{match}_{\mathrm{\omega }}$
, which will be used later to derive optimality.
$\mathsf{match}_{\mathrm{\omega }}$
, which will be used later to derive optimality.
Example 3.8. Consider again the substitutions and sharing groups in Examples 3.3 and 3.5. Recall that
![]() $U_1 = \{x, y, z\}$
and
$U_1 = \{x, y, z\}$
and
![]() $U_2 = \{ u, v, x \}$
. We have seen that, although the sharing groups
$U_2 = \{ u, v, x \}$
. We have seen that, although the sharing groups
![]() $xz$
,
$xz$
,
![]() $u^2x^2$
, and
$u^2x^2$
, and
![]() $ux^2$
are in
$ux^2$
are in
![]() $\mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2})$
, they are not in
$\mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2})$
, they are not in
![]() $\alpha _{\mathrm{\omega }}(\mathsf{match}([\theta _1]_{U_1}, [\theta _2]_{U_2}))$
. If
$\alpha _{\mathrm{\omega }}(\mathsf{match}([\theta _1]_{U_1}, [\theta _2]_{U_2}))$
. If
![]() $\mathsf{match}_{\mathrm{\omega }}$
were optimal, we should be able to find, for each
$\mathsf{match}_{\mathrm{\omega }}$
were optimal, we should be able to find, for each
![]() $B \in \{xz, u^2x^2, ux^2\}$
, a pair of substitutions
$B \in \{xz, u^2x^2, ux^2\}$
, a pair of substitutions
![]() $\theta _3$
and
$\theta _3$
and
![]() $\theta _4$
such that
$\theta _4$
such that
![]() $[S_1]_{U_1} \triangleright [\theta _3]_{U_1}$
,
$[S_1]_{U_1} \triangleright [\theta _3]_{U_1}$
,
![]() $[S_2]_{U_2} \triangleright [\theta _4]_{U_2}$
, and
$[S_2]_{U_2} \triangleright [\theta _4]_{U_2}$
, and
![]() $B \in \alpha _{\mathrm{\omega }}(\mathsf{match}([\theta _3]_{U_1}, [\theta _4]_{U_2})$
. Actually, we can do better, keep
$B \in \alpha _{\mathrm{\omega }}(\mathsf{match}([\theta _3]_{U_1}, [\theta _4]_{U_2})$
. Actually, we can do better, keep
![]() $\theta _4=\theta _2$
fixed, and only change
$\theta _4=\theta _2$
fixed, and only change
![]() $\theta _3$
for different sharing groups.
$\theta _3$
for different sharing groups.
Consider
![]() $B=xz$
. Note that
$B=xz$
. Note that
![]() $B_{|U_1}=xz$
and
$B_{|U_1}=xz$
and
![]() $B_{|U_2}= x = \biguplus \mathcal{X}$
, with
$B_{|U_2}= x = \biguplus \mathcal{X}$
, with
![]() $\mathcal{X}= \{\!\!\{ x \}\!\!\}$
. The sharing group
$\mathcal{X}= \{\!\!\{ x \}\!\!\}$
. The sharing group
![]() $x$
in
$x$
in
![]() $\theta _2$
is generated by the variables
$\theta _2$
is generated by the variables
![]() $w_5$
and
$w_5$
and
![]() $w_6$
. Consider the substitution
$w_6$
. Consider the substitution
![]() $\theta _3 = \{ x/r(a, w, a, a, a), y/a, z/w \}$
where
$\theta _3 = \{ x/r(a, w, a, a, a), y/a, z/w \}$
where
-
• the binding
 $x/r(a,w,a, a, a)$
is obtained by the corresponding binding in
$x/r(a,w,a, a, a)$
is obtained by the corresponding binding in
 $\theta _2$
replacing
$\theta _2$
replacing
 $w_5$
with a fresh variable
$w_5$
with a fresh variable
 $w$
and all the other variables in the range with the constant symbol
$w$
and all the other variables in the range with the constant symbol
 $a$
;
$a$
; -
• the bindings
 $\{ y/a, z/w \}$
are chosen according to
$\{ y/a, z/w \}$
are chosen according to
 $B_{|U_1 \setminus U_2}=z$
.
$B_{|U_1 \setminus U_2}=z$
.
It is immediate to show that
![]() $xz \in \alpha _{\mathrm{\omega }}(\mathsf{mgu}([\theta _3]_{U_1}, [\theta _2]_{U_2}))$
and
$xz \in \alpha _{\mathrm{\omega }}(\mathsf{mgu}([\theta _3]_{U_1}, [\theta _2]_{U_2}))$
and
![]() $[S_1]_{U_1} \triangleright [\theta _3]_{U_1}$
.
$[S_1]_{U_1} \triangleright [\theta _3]_{U_1}$
.
As another example, let us consider
![]() $B=u^2x^2$
. In this case,
$B=u^2x^2$
. In this case,
![]() $B_{|U_1}=x^2 \in S_1$
and
$B_{|U_1}=x^2 \in S_1$
and
![]() $B_{|U_2} = u^2x^2 = \biguplus \{\!\!\{ ux, ux \}\!\!\}$
. The variable that generates the sharing group
$B_{|U_2} = u^2x^2 = \biguplus \{\!\!\{ ux, ux \}\!\!\}$
. The variable that generates the sharing group
![]() $ux$
is
$ux$
is
![]() $w_4$
. We proceed as before and obtain
$w_4$
. We proceed as before and obtain
![]() $\theta _3 = \{ x/r(r(w,w),a,a,a,a), y/a, z/a\}$
. Note that
$\theta _3 = \{ x/r(r(w,w),a,a,a,a), y/a, z/a\}$
. Note that
![]() $w_4$
has been replaced with
$w_4$
has been replaced with
![]() $r(w,w)$
since two copies of
$r(w,w)$
since two copies of
![]() $ux$
are needed to obtain
$ux$
are needed to obtain
![]() $u^2x^2$
. Again
$u^2x^2$
. Again
![]() $[S_1]_{U_1} \triangleright [\theta _3]_{U_1}$
and
$[S_1]_{U_1} \triangleright [\theta _3]_{U_1}$
and
![]() $u^2x^2 \in \alpha _{\mathrm{\omega }}(\mathsf{mgu}([\theta _3]_{U_1}, [\theta _2]_{U_2}))$
.
$u^2x^2 \in \alpha _{\mathrm{\omega }}(\mathsf{mgu}([\theta _3]_{U_1}, [\theta _2]_{U_2}))$
.
We distill the idea presented above in the following result.
Lemma 3.9 (Completeness on the second argument). Given
![]() $[S_1]_{U_1} \in{\mathtt{ShLin}^{\omega }}$
and
$[S_1]_{U_1} \in{\mathtt{ShLin}^{\omega }}$
and
![]() $[\theta _2]_{U_2} \in \mathit{ISubst}_\sim$
, there exist
$[\theta _2]_{U_2} \in \mathit{ISubst}_\sim$
, there exist
![]() $\delta _1,\dots, \delta _n \in \mathit{ISubst}_\sim$
such that for all
$\delta _1,\dots, \delta _n \in \mathit{ISubst}_\sim$
such that for all
![]() $i\in \{1,\dots, n\}$
,
$i\in \{1,\dots, n\}$
,
![]() $[S_1]_{U_1} \triangleright [\delta _i]_{U_1}$
and
$[S_1]_{U_1} \triangleright [\delta _i]_{U_1}$
and
 \begin{align*}\mathsf {match}_{\mathrm {\omega }}([S_1]_{U_1}, \alpha _{\mathrm {\omega }}([\theta _2]_{U_2}))= \left [\bigcup _ {i\in \{1,\ldots, n\}} \alpha _\omega (\mathsf {match}([\delta _i]_{U_1}, [\theta _2]_{U_2}))\right ]_{U_1\cup U_2} \end{align*}
\begin{align*}\mathsf {match}_{\mathrm {\omega }}([S_1]_{U_1}, \alpha _{\mathrm {\omega }}([\theta _2]_{U_2}))= \left [\bigcup _ {i\in \{1,\ldots, n\}} \alpha _\omega (\mathsf {match}([\delta _i]_{U_1}, [\theta _2]_{U_2}))\right ]_{U_1\cup U_2} \end{align*}
Proof Since we already know that
![]() $\mathsf{match}_{\mathrm{\omega }}$
is a correct abstraction of
$\mathsf{match}_{\mathrm{\omega }}$
is a correct abstraction of
![]() $\mathsf{match}$
, we only need to prove that, given
$\mathsf{match}$
, we only need to prove that, given
![]() $[S_1]_{U_1} \in{\mathtt{ShLin}^{\omega }}$
and
$[S_1]_{U_1} \in{\mathtt{ShLin}^{\omega }}$
and
![]() $[\theta _2]_{U_2} \in \mathit{ISubst}_\sim$
, for any sharing group
$[\theta _2]_{U_2} \in \mathit{ISubst}_\sim$
, for any sharing group
![]() $B \in \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1}, \alpha _{\mathrm{\omega }}([\theta _2]_{U_2}))$
, there exists
$B \in \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1}, \alpha _{\mathrm{\omega }}([\theta _2]_{U_2}))$
, there exists
![]() $[\theta _1]_{U_1} \in \mathit{ISubst}_\sim$
such that
$[\theta _1]_{U_1} \in \mathit{ISubst}_\sim$
such that
![]() $[S_1]_{U_1} \triangleright [\theta _1]_{U_1}$
and
$[S_1]_{U_1} \triangleright [\theta _1]_{U_1}$
and
![]() $B \in \alpha _{\mathrm{\omega }}(\mathsf{match}([\theta _1]_{U_1}, [\theta _2]_{U_2}))$
.
$B \in \alpha _{\mathrm{\omega }}(\mathsf{match}([\theta _1]_{U_1}, [\theta _2]_{U_2}))$
.
In order to ease notation, let
![]() $U=U_1 \cup U_2$
,
$U=U_1 \cup U_2$
,
![]() $[S_2]_{U_2}=\alpha _{\mathrm{\omega }}([\theta _2]_{U_2})$
, and
$[S_2]_{U_2}=\alpha _{\mathrm{\omega }}([\theta _2]_{U_2})$
, and
![]() $[S]_U=\mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1}, [S_2]_{U_2})$
. We may choose
$[S]_U=\mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1}, [S_2]_{U_2})$
. We may choose
![]() $\theta _2$
such that
$\theta _2$
such that
![]() $\mathrm{dom}(\theta _2)=U_2$
without loss of generality. Moreover,
$\mathrm{dom}(\theta _2)=U_2$
without loss of generality. Moreover,
![]() $S^{\prime}_2$
and
$S^{\prime}_2$
and
![]() $S^{\prime\prime}_2$
are given as in the definition of abstract matching. We distinguish two cases.
$S^{\prime\prime}_2$
are given as in the definition of abstract matching. We distinguish two cases.
-
first case) If
 $B \in S^{\prime}_2$
, there exists
$B \in S^{\prime}_2$
, there exists
 $v \in{\mathcal{V}}$
such that
$v \in{\mathcal{V}}$
such that
 $\theta _2^{-1}(v)_{|U_2}=B$
. Let
$\theta _2^{-1}(v)_{|U_2}=B$
. Let
 $X=\mathrm{vars}(\theta _2(U_1 \cap U_2))$
and take
$X=\mathrm{vars}(\theta _2(U_1 \cap U_2))$
and take
 $\delta =\{ x/a \mid x \in X \}$
. Then
$\delta =\{ x/a \mid x \in X \}$
. Then
 $\theta _1=(\delta \circ \theta _2)_{|U_1} \uplus \{ x/a \mid x \in U_1 \setminus U_2\}$
is such that
$\theta _1=(\delta \circ \theta _2)_{|U_1} \uplus \{ x/a \mid x \in U_1 \setminus U_2\}$
is such that
 $\theta _1^{-1}(v)_{|U_1}= \{\!\!\{ \}\!\!\}$
for each
$\theta _1^{-1}(v)_{|U_1}= \{\!\!\{ \}\!\!\}$
for each
 $v \in{\mathcal{V}}$
, therefore
$v \in{\mathcal{V}}$
, therefore
 $[S_1]_{U_1} \triangleright [\theta _1]_{U_1}$
. Moreover, since
$[S_1]_{U_1} \triangleright [\theta _1]_{U_1}$
. Moreover, since
 $\theta _1 \preceq _{U_1 \cap U_2} \theta _2$
, we have that
$\theta _1 \preceq _{U_1 \cap U_2} \theta _2$
, we have that
 $\mathsf{match}_{\mathrm{\omega }}([\theta _1]_{U_1}, [\theta _2]_{U_2})$
is defined equal to
$\mathsf{match}_{\mathrm{\omega }}([\theta _1]_{U_1}, [\theta _2]_{U_2})$
is defined equal to
 $\mathsf{mgu}([\theta _1]_{U_1}, [\theta _2]_{U_2})$
and
$\mathsf{mgu}([\theta _1]_{U_1}, [\theta _2]_{U_2})$
and
 $\mathsf{mgu}([\theta _1]_{U_1}, [\theta _2]_{U_2})=[\mathsf{mgu}(\theta _1,\theta _2)]_U$
since
$\mathsf{mgu}([\theta _1]_{U_1}, [\theta _2]_{U_2})=[\mathsf{mgu}(\theta _1,\theta _2)]_U$
since
 $\mathrm{vars}(\theta _1)\cap \mathrm{vars}(\theta _2) \subseteq U_1 \cap U_2$
. By the proof of Theorem3.7, we have that
$\mathrm{vars}(\theta _1)\cap \mathrm{vars}(\theta _2) \subseteq U_1 \cap U_2$
. By the proof of Theorem3.7, we have that
 $\mathsf{mgu}(\theta _1,\theta _2)=(\theta _1)_{|U_1 \setminus U_2} \uplus (\delta \circ \theta _2)$
. Since
$\mathsf{mgu}(\theta _1,\theta _2)=(\theta _1)_{|U_1 \setminus U_2} \uplus (\delta \circ \theta _2)$
. Since
 $B_{|U_1}=\{\!\!\{ \}\!\!\}$
, then
$B_{|U_1}=\{\!\!\{ \}\!\!\}$
, then
 $v \notin X=\mathrm{vars}(\delta )$
, and therefore,
$v \notin X=\mathrm{vars}(\delta )$
, and therefore,
 $\mathsf{mgu}(\theta _1,\theta _2)^{-1}(v)_{|U}=\theta _2^{-1}(v)_{|U}=B$
. Hence,
$\mathsf{mgu}(\theta _1,\theta _2)^{-1}(v)_{|U}=\theta _2^{-1}(v)_{|U}=B$
. Hence,
 $B$
is an
$B$
is an
 $\omega$
-sharing group in
$\omega$
-sharing group in
 $\alpha _{\mathrm{\omega }}(\mathsf{match}([\theta _1]_{U_1}, [\theta _2]_{U_2}))$
, which is what we wanted to prove.
$\alpha _{\mathrm{\omega }}(\mathsf{match}([\theta _1]_{U_1}, [\theta _2]_{U_2}))$
, which is what we wanted to prove.
-
second case) We now assume
 $B_{|U_1} \in S_1$
and
$B_{|U_1} \in S_1$
and
 $B_{|U_2}=\biguplus X$
with
$B_{|U_2}=\biguplus X$
with
 $\mathcal{X} \in \mathscr{P}_m(S^{\prime\prime}_2)$
. Then, for each
$\mathcal{X} \in \mathscr{P}_m(S^{\prime\prime}_2)$
. Then, for each
 $H \in \lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor$
, there exists
$H \in \lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor$
, there exists
 $v_H \in{\mathcal{V}}$
such that
$v_H \in{\mathcal{V}}$
such that
 $\theta _2^{-1}(v_H)_{|U_2}=H$
. Since
$\theta _2^{-1}(v_H)_{|U_2}=H$
. Since
 $H \cap U_1 \neq \{\!\!\{ \}\!\!\}$
for each
$H \cap U_1 \neq \{\!\!\{ \}\!\!\}$
for each
 $H \in \lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor$
, then
$H \in \lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor$
, then
 $v_H \in Y=\mathrm{vars}(\theta _2(U_1 \cap U_2))$
. Consider the substitutionsfor a fresh variable
$v_H \in Y=\mathrm{vars}(\theta _2(U_1 \cap U_2))$
. Consider the substitutionsfor a fresh variable \begin{align*} \delta & =\{ v_H/t(\underbrace{v,\ldots, v}_{\text{$\mathcal{X}(H)$ times}}) \mid H \in \lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor \} \uplus \{ y/a \mid y \in Y \text{ and } \forall H \in \lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor . y \neq v_H\} \enspace, \\ \eta & =\{ w/t(\underbrace{v, \ldots, v}_{\text{$B(w)$ times}}) \mid w \in U_1 \setminus U_2 \} \enspace, \end{align*}
\begin{align*} \delta & =\{ v_H/t(\underbrace{v,\ldots, v}_{\text{$\mathcal{X}(H)$ times}}) \mid H \in \lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor \} \uplus \{ y/a \mid y \in Y \text{ and } \forall H \in \lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor . y \neq v_H\} \enspace, \\ \eta & =\{ w/t(\underbrace{v, \ldots, v}_{\text{$B(w)$ times}}) \mid w \in U_1 \setminus U_2 \} \enspace, \end{align*}
 $v$
. Let us define
$v$
. Let us define
 $\theta _1=\eta \uplus (\delta \circ \theta _2)_{|U_1}$
. We want to prove that
$\theta _1=\eta \uplus (\delta \circ \theta _2)_{|U_1}$
. We want to prove that
 $[S_1]_{U_1} \triangleright [\theta _1]_{U_1}$
. Note that
$[S_1]_{U_1} \triangleright [\theta _1]_{U_1}$
. Note that
 $\mathrm{vars}(\theta _1(U_1))=\{v\}$
, hence we only need to check that
$\mathrm{vars}(\theta _1(U_1))=\{v\}$
, hence we only need to check that
 $\theta ^{-1}_1(v)_{|U_1} \in S_1$
. We have that
$\theta ^{-1}_1(v)_{|U_1} \in S_1$
. We have that
 $\theta ^{-1}(v)_{|U_1}=\eta ^{-1}(v)_{|U_1} \uplus (\theta _2^{-1}\delta ^{-1}(v))_{|U_1} = \eta ^{-1}(v)_{|U_1} \uplus \theta _2^{-1}( \{\!\!\{ v_{H}^{X(H)} \mid H \in \lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor \}\!\!\})_{|U_1}=B_{|U_1 \setminus U_2} \uplus (\biguplus \mathcal{X})_{|U_1 \cap U_2}=B_{|U_1} \uplus B_{|U_1 \cap U_2}=B_{|U_1}$
which, we know, is an element of
$\theta ^{-1}(v)_{|U_1}=\eta ^{-1}(v)_{|U_1} \uplus (\theta _2^{-1}\delta ^{-1}(v))_{|U_1} = \eta ^{-1}(v)_{|U_1} \uplus \theta _2^{-1}( \{\!\!\{ v_{H}^{X(H)} \mid H \in \lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor \}\!\!\})_{|U_1}=B_{|U_1 \setminus U_2} \uplus (\biguplus \mathcal{X})_{|U_1 \cap U_2}=B_{|U_1} \uplus B_{|U_1 \cap U_2}=B_{|U_1}$
which, we know, is an element of
 $S_1$
. Moreover, since
$S_1$
. Moreover, since
 $\theta _1 \preceq _{U_1 \cap U_2} \theta _2$
and
$\theta _1 \preceq _{U_1 \cap U_2} \theta _2$
and
 $\mathrm{vars}(\theta _1) \cap \mathrm{vars}(\theta _2) \subseteq U_1 \cap U_2$
, we have that
$\mathrm{vars}(\theta _1) \cap \mathrm{vars}(\theta _2) \subseteq U_1 \cap U_2$
, we have that
 $\mathsf{match}_{\mathrm{\omega }}([\theta _1]_{U_1},[\theta _2]_{U_2})= [\mathsf{mgu}(\theta _1,\theta _2)]_U$
. If we define
$\mathsf{match}_{\mathrm{\omega }}([\theta _1]_{U_1},[\theta _2]_{U_2})= [\mathsf{mgu}(\theta _1,\theta _2)]_U$
. If we define
 $\theta =\mathsf{mgu}(\theta _1, \theta _2)$
, by looking at the proof of Theorem3.7, we have that
$\theta =\mathsf{mgu}(\theta _1, \theta _2)$
, by looking at the proof of Theorem3.7, we have that
 $\theta =\theta _1 \uplus (\delta \circ (\theta _2)_{|U_2 \setminus U_1})$
and
$\theta =\theta _1 \uplus (\delta \circ (\theta _2)_{|U_2 \setminus U_1})$
and
 $\theta =(\theta _1)_{|U_1 \setminus U_2} \uplus (\delta \circ \theta _2)$
. By the first equality, it is immediate to check that
$\theta =(\theta _1)_{|U_1 \setminus U_2} \uplus (\delta \circ \theta _2)$
. By the first equality, it is immediate to check that
 $\theta ^{-1}(v)_{|U_1} = \theta _1^{-1}(v)_{|U_1}= B_{|U_1}$
. By the second equality,
$\theta ^{-1}(v)_{|U_1} = \theta _1^{-1}(v)_{|U_1}= B_{|U_1}$
. By the second equality,
 $\theta ^{-1}(v)_{|U_2}= \theta _2^{-1}(\{\!\!\{ v_{H}^{\mathcal{X}(H)} \mid H \in \lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor \}\!\!\})_{|U_2} = \biguplus \mathcal{X} =B_{|U_2}$
. Therefore,
$\theta ^{-1}(v)_{|U_2}= \theta _2^{-1}(\{\!\!\{ v_{H}^{\mathcal{X}(H)} \mid H \in \lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor \}\!\!\})_{|U_2} = \biguplus \mathcal{X} =B_{|U_2}$
. Therefore,
 $\theta ^{-1}(v)_{|U}=B$
.
$\theta ^{-1}(v)_{|U}=B$
.
It is worth noting that, although this proof uses a function symbol of arbitrary arity, it may be easily rewritten using only one constant symbol and one function symbol of arity at least two, as required at the beginning of Section 2.1.
Theorem 3.10 (Optimality of
![]() $\mathsf{match}_{\mathrm{\omega }}$
). The operation
$\mathsf{match}_{\mathrm{\omega }}$
). The operation
![]() $\mathsf{match}_{\mathrm{\omega }}$
is optimal w.r.t.
$\mathsf{match}_{\mathrm{\omega }}$
is optimal w.r.t.
![]() $\mathsf{match}$
.
$\mathsf{match}$
.
Proof It is enough to prove that for each
![]() $[S_1]_{U_1}, [S_2]_{U_2} \in{\mathtt{ShLin}^{\omega }}$
and
$[S_1]_{U_1}, [S_2]_{U_2} \in{\mathtt{ShLin}^{\omega }}$
and
![]() $B \in \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2})$
, there are substitutions
$B \in \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2})$
, there are substitutions
![]() $\theta _1$
,
$\theta _1$
,
![]() $\theta _2$
such that
$\theta _2$
such that
![]() $[S_1]_{U_1} \triangleright [\theta _1]_{U_1}$
,
$[S_1]_{U_1} \triangleright [\theta _1]_{U_1}$
,
![]() $[S_2]_{U_21} \triangleright [\theta _2]_{U_2}$
and
$[S_2]_{U_21} \triangleright [\theta _2]_{U_2}$
and
![]() $B \in \alpha _{\mathrm{\omega }}(\mathsf{match}([\theta _1]_{U_1}, [\theta _2]_{U_2})$
. Assume
$B \in \alpha _{\mathrm{\omega }}(\mathsf{match}([\theta _1]_{U_1}, [\theta _2]_{U_2})$
. Assume
![]() $B_{|U_2}=\biguplus \mathcal{X}$
where
$B_{|U_2}=\biguplus \mathcal{X}$
where
![]() $\mathcal{X} \in \mathscr{P}_m(S^{\prime\prime}_2)$
. Consider a substitution
$\mathcal{X} \in \mathscr{P}_m(S^{\prime\prime}_2)$
. Consider a substitution
![]() $[\theta _2]_{U_2}$
such that
$[\theta _2]_{U_2}$
such that
![]() $[\lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor ]_{U_2} \leq \alpha _{\mathrm{\omega }}([\theta _2]_{U_2}) \leq [S_2]_{U_2}$
. It means that, for each
$[\lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor ]_{U_2} \leq \alpha _{\mathrm{\omega }}([\theta _2]_{U_2}) \leq [S_2]_{U_2}$
. It means that, for each
![]() $H \in \lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor$
, there is
$H \in \lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor$
, there is
![]() $v_H \in{\mathcal{V}}$
such that
$v_H \in{\mathcal{V}}$
such that
![]() $\theta _2^{-1}(v_H)_{|U_2}=H$
. If
$\theta _2^{-1}(v_H)_{|U_2}=H$
. If
![]() $\lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor =\{ H_1, \ldots, H_n \}$
, we may define
$\lfloor \!\lfloor \mathcal{X} \rfloor \!\rfloor =\{ H_1, \ldots, H_n \}$
, we may define
![]() $\theta _2$
as the substitution with
$\theta _2$
as the substitution with
![]() $\mathrm{dom}(\theta _2)=U_2$
and, for each
$\mathrm{dom}(\theta _2)=U_2$
and, for each
![]() $u \in U_2$
,
$u \in U_2$
,
By Lemma 3.9, there exists
![]() $[\theta _1]_{U_1}$
, such that
$[\theta _1]_{U_1}$
, such that
![]() $[S_1]_{U_1} \triangleright [\theta _1]_{U_1}$
and
$[S_1]_{U_1} \triangleright [\theta _1]_{U_1}$
and
![]() $B \in \alpha _{\mathrm{\omega }}(\mathsf{match}([\theta _1]_{U_1}, [\theta _2]_{U_2}))$
. Therefore,
$B \in \alpha _{\mathrm{\omega }}(\mathsf{match}([\theta _1]_{U_1}, [\theta _2]_{U_2}))$
. Therefore,
![]() $\mathsf{match}_{\mathrm{\omega }}$
is the optimal approximation of
$\mathsf{match}_{\mathrm{\omega }}$
is the optimal approximation of
![]() $\mathsf{match}$
.
$\mathsf{match}$
.
4 Abstract matching over
 $\mathtt{ShLin}^2$
$\mathtt{ShLin}^2$
The domain
![]() $\mathtt{ShLin}^{\omega }$
has been inspired by the domain
$\mathtt{ShLin}^{\omega }$
has been inspired by the domain
![]() $\mathtt{ShLin}^2$
, which appeared for the first time in King (Reference King1994). The novelty of
$\mathtt{ShLin}^2$
, which appeared for the first time in King (Reference King1994). The novelty of
![]() $\mathtt{ShLin}^2$
was to embed linearity information inside the sharing groups, instead of keeping them separate like it was in
$\mathtt{ShLin}^2$
was to embed linearity information inside the sharing groups, instead of keeping them separate like it was in
![]() $\mathtt{Sharing} \times \mathtt{Lin}$
.
$\mathtt{Sharing} \times \mathtt{Lin}$
.
4.1
The domain
 $\mathtt{ShLin}^2$
$\mathtt{ShLin}^2$
Here we recall the main definitions for the domain
![]() $\mathtt{ShLin}^2$
, viewed as an abstraction of
$\mathtt{ShLin}^2$
, viewed as an abstraction of
![]() $\mathtt{ShLin}^{\omega }$
, following the presentation given in Amato and Scozzari (Reference Amato and Scozzari2010).
$\mathtt{ShLin}^{\omega }$
, following the presentation given in Amato and Scozzari (Reference Amato and Scozzari2010).
The idea is to simplify the domain
![]() $\mathtt{ShLin}^{\omega }$
by only recording whether a variable in a sharing group is linear or not, but forgetting its actual multiplicity. Intuitively, we abstract an
$\mathtt{ShLin}^{\omega }$
by only recording whether a variable in a sharing group is linear or not, but forgetting its actual multiplicity. Intuitively, we abstract an
![]() $\omega$
-sharing group by replacing any exponent equal to or greater than
$\omega$
-sharing group by replacing any exponent equal to or greater than
![]() $2$
with a new symbol
$2$
with a new symbol
![]() $\infty$
.
$\infty$
.
A 2-sharing group is a map
![]() $o:{\mathcal{V}} \rightarrow \{0,1,\infty \}$
such that its support
$o:{\mathcal{V}} \rightarrow \{0,1,\infty \}$
such that its support
![]() $\lfloor \!\lfloor o \rfloor \!\rfloor =\{ v \in{\mathcal{V}} \mid o(v) \neq 0\}$
is finite. We use a polynomial notation for 2-sharing groups as for
$\lfloor \!\lfloor o \rfloor \!\rfloor =\{ v \in{\mathcal{V}} \mid o(v) \neq 0\}$
is finite. We use a polynomial notation for 2-sharing groups as for
![]() $\omega$
-sharing groups. For instance,
$\omega$
-sharing groups. For instance,
![]() $o=xy^\infty z$
denotes the 2-sharing group whose support is
$o=xy^\infty z$
denotes the 2-sharing group whose support is
![]() $\lfloor \!\lfloor o \rfloor \!\rfloor =\{x,y,z\}$
, such that
$\lfloor \!\lfloor o \rfloor \!\rfloor =\{x,y,z\}$
, such that
![]() $o(x)=o(z)=1$
and
$o(x)=o(z)=1$
and
![]() $o(y)=\infty$
. We denote with
$o(y)=\infty$
. We denote with
![]() $\emptyset$
the 2-sharing group with empty support and by
$\emptyset$
the 2-sharing group with empty support and by
![]() ${\mathit{Sg}^2}(V)$
the set of 2-sharing groups whose support is a subset of
${\mathit{Sg}^2}(V)$
the set of 2-sharing groups whose support is a subset of
![]() $V$
. Note that in King (Reference King1994) the number
$V$
. Note that in King (Reference King1994) the number
![]() $2$
is used as an exponent instead of
$2$
is used as an exponent instead of
![]() $\infty$
, but we prefer our notation to be coherent with
$\infty$
, but we prefer our notation to be coherent with
![]() $\omega$
-sharing groups.
$\omega$
-sharing groups.
An
![]() $\omega$
-sharing group
$\omega$
-sharing group
![]() $B$
may be abstracted into the 2-sharing group
$B$
may be abstracted into the 2-sharing group
![]() $\alpha _{\mathrm{2}}(B)$
given by
$\alpha _{\mathrm{2}}(B)$
given by
 \begin{align} \alpha _{\mathrm{2}}(B)=\lambda v\in{\mathcal{V}} . \begin{cases} B(v) & \text{if $B(v)\leq 1$,} \\[3pt] \infty & \text{otherwise.} \end{cases} \end{align}
\begin{align} \alpha _{\mathrm{2}}(B)=\lambda v\in{\mathcal{V}} . \begin{cases} B(v) & \text{if $B(v)\leq 1$,} \\[3pt] \infty & \text{otherwise.} \end{cases} \end{align}
For instance, the
![]() $\omega$
-sharing groups
$\omega$
-sharing groups
![]() $xy^{2} z,xy^{3} z,xy^{4} z,xy^{5} z,\ldots$
are all abstracted into
$xy^{2} z,xy^{3} z,xy^{4} z,xy^{5} z,\ldots$
are all abstracted into
![]() $xy^\infty z$
.
$xy^\infty z$
.
There are operations on 2-sharing groups that correspond to variable projection and multiset union. For projection
 \begin{align} o_{|V} = \lambda v \in{\mathcal{V}}. \begin{cases} o(V) & \text{if $v \in V$,} \\[3pt] 0 & \text{otherwise,} \end{cases} \end{align}
\begin{align} o_{|V} = \lambda v \in{\mathcal{V}}. \begin{cases} o(V) & \text{if $v \in V$,} \\[3pt] 0 & \text{otherwise,} \end{cases} \end{align}
while for multiset union
where
![]() $0 \oplus x= x \oplus 0=x$
and
$0 \oplus x= x \oplus 0=x$
and
![]() $\infty \oplus x=x \oplus \infty =1 \oplus 1= \infty$
. We will use
$\infty \oplus x=x \oplus \infty =1 \oplus 1= \infty$
. We will use
![]() $\biguplus \{\!\!\{ o_1, \ldots, o_n \}\!\!\}$
for
$\biguplus \{\!\!\{ o_1, \ldots, o_n \}\!\!\}$
for
![]() $o_1 \uplus \cdots \uplus o_n$
. Given a sharing group
$o_1 \uplus \cdots \uplus o_n$
. Given a sharing group
![]() $o$
, we also define the delinearization operator:
$o$
, we also define the delinearization operator:
This operator is extended pointwise to sets and multisets. The next proposition shows some properties of these operators.
Proposition 4.1
Given an
![]() $\mathrm{\omega }$
-sharing group
$\mathrm{\omega }$
-sharing group
![]() $B$
, a set of variables
$B$
, a set of variables
![]() $V$
, and multiset of
$V$
, and multiset of
![]() $\omega$
-sharing groups
$\omega$
-sharing groups
![]() $\mathcal{X}$
, the following properties hold:
$\mathcal{X}$
, the following properties hold:
-
1.
 $\lfloor \!\lfloor B \rfloor \!\rfloor = \lfloor \!\lfloor \alpha _{\mathrm{2}}(B) \rfloor \!\rfloor$
$\lfloor \!\lfloor B \rfloor \!\rfloor = \lfloor \!\lfloor \alpha _{\mathrm{2}}(B) \rfloor \!\rfloor$
-
2.
 $\alpha _{\mathrm{2}}(B_{|V})= \alpha _{\mathrm{2}}(B)_{|V}$
$\alpha _{\mathrm{2}}(B_{|V})= \alpha _{\mathrm{2}}(B)_{|V}$
-
3.
 $\alpha _{\mathrm{2}}(\biguplus \mathcal{X})= \biguplus \alpha _{\mathrm{2}}(\mathcal{X})$
$\alpha _{\mathrm{2}}(\biguplus \mathcal{X})= \biguplus \alpha _{\mathrm{2}}(\mathcal{X})$
-
4.
 $\alpha _{\mathrm{2}}(B \uplus B) = \alpha _{\mathrm{2}}(B)^2$
$\alpha _{\mathrm{2}}(B \uplus B) = \alpha _{\mathrm{2}}(B)^2$
where
![]() $\alpha _{\mathrm{2}}(\mathcal{X})$
is just the elementwise extension of
$\alpha _{\mathrm{2}}(\mathcal{X})$
is just the elementwise extension of
![]() $\alpha _{\mathrm{2}}$
to a multiset of
$\alpha _{\mathrm{2}}$
to a multiset of
![]() $\omega$
-sharing groups.
$\omega$
-sharing groups.
Proof Given the
![]() $\omega$
-sharing group
$\omega$
-sharing group
![]() $B$
, we have
$B$
, we have
![]() $\lfloor \!\lfloor \alpha _{\mathrm{2}}(B) \rfloor \!\rfloor = \{ x \in{\mathcal{V}} \mid \alpha _{\mathrm{2}}(B) \neq 0 \} = \{ x \in{\mathcal{V}} \mid B(x) \neq 0 \} = \lfloor \!\lfloor B \rfloor \!\rfloor$
, which proves Property 1. For Property 2, given
$\lfloor \!\lfloor \alpha _{\mathrm{2}}(B) \rfloor \!\rfloor = \{ x \in{\mathcal{V}} \mid \alpha _{\mathrm{2}}(B) \neq 0 \} = \{ x \in{\mathcal{V}} \mid B(x) \neq 0 \} = \lfloor \!\lfloor B \rfloor \!\rfloor$
, which proves Property 1. For Property 2, given
![]() $V \subseteq{\mathcal{V}}$
, we want to prove that
$V \subseteq{\mathcal{V}}$
, we want to prove that
![]() $\alpha _{\mathrm{2}}(B_{|V})(v)= (\alpha _{\mathrm{2}}(B)_{|V})(v)$
for each
$\alpha _{\mathrm{2}}(B_{|V})(v)= (\alpha _{\mathrm{2}}(B)_{|V})(v)$
for each
![]() $v \in{\mathcal{V}}$
. The property is easily proved considering the three cases
$v \in{\mathcal{V}}$
. The property is easily proved considering the three cases
![]() $v \notin V$
,
$v \notin V$
,
![]() $v \in V \setminus \lfloor \!\lfloor B \rfloor \!\rfloor$
, and
$v \in V \setminus \lfloor \!\lfloor B \rfloor \!\rfloor$
, and
![]() $v \in V \cap \lfloor \!\lfloor B \rfloor \!\rfloor$
. Property 3 has been proved in Amato and Scozzari (Reference Amato and Scozzari2010). Property 4 is a trivial consequence of Property 3.
$v \in V \cap \lfloor \!\lfloor B \rfloor \!\rfloor$
. Property 3 has been proved in Amato and Scozzari (Reference Amato and Scozzari2010). Property 4 is a trivial consequence of Property 3.
Since we do not want to represent definite nonlinearity, we introduce an order relation over sharing groups as follows:
and we restrict our attention to downward closed sets of sharing groups. The domain we are interested in is the following:
where
![]() $\mathscr{P}_{{\mathop{\downarrow }}}({\mathit{Sg}^2}(U))$
is the powerset of downward closed subsets of
$\mathscr{P}_{{\mathop{\downarrow }}}({\mathit{Sg}^2}(U))$
is the powerset of downward closed subsets of
![]() ${\mathit{Sg}^2}(U)$
according to
${\mathit{Sg}^2}(U)$
according to
![]() $\leq$
and
$\leq$
and
![]() $[T_1]_{U_1} \leq _{\mathrm{2}} [T_2]_{U_2}$
iff
$[T_1]_{U_1} \leq _{\mathrm{2}} [T_2]_{U_2}$
iff
![]() $U_1=U_2$
and
$U_1=U_2$
and
![]() $T_1 \subseteq T_2$
. For instance, the set
$T_1 \subseteq T_2$
. For instance, the set
![]() $\{xy^\infty z\}$
is not downward closed, while
$\{xy^\infty z\}$
is not downward closed, while
![]() $\{xyz,xy^\infty z\}$
is downward closed. There is a Galois insertion of
$\{xyz,xy^\infty z\}$
is downward closed. There is a Galois insertion of
![]() $\mathtt{ShLin}^2$
into
$\mathtt{ShLin}^2$
into
![]() $\mathtt{ShLin}^{\omega }$
given by the pair of adjoint maps
$\mathtt{ShLin}^{\omega }$
given by the pair of adjoint maps
![]() $\gamma _{\mathrm{2}}:{\mathtt{ShLin}^2} \rightarrow{\mathtt{ShLin}^{\omega }}$
and
$\gamma _{\mathrm{2}}:{\mathtt{ShLin}^2} \rightarrow{\mathtt{ShLin}^{\omega }}$
and
![]() $\alpha _{\mathrm{2}}:{\mathtt{ShLin}^{\omega }} \rightarrow{\mathtt{ShLin}^2}$
:
$\alpha _{\mathrm{2}}:{\mathtt{ShLin}^{\omega }} \rightarrow{\mathtt{ShLin}^2}$
:
where
![]() ${\mathop{\downarrow }} T = \{o \mid o^{\prime} \in T, o \leq o^{\prime}\}$
is the downward closure of
${\mathop{\downarrow }} T = \{o \mid o^{\prime} \in T, o \leq o^{\prime}\}$
is the downward closure of
![]() $T$
. With an abuse of notation, we also apply
$T$
. With an abuse of notation, we also apply
![]() $\gamma _{\mathrm{2}}$
and
$\gamma _{\mathrm{2}}$
and
![]() $\alpha _{\mathrm{2}}$
to subsets of
$\alpha _{\mathrm{2}}$
to subsets of
![]() $\omega$
-sharing groups and 2-sharing groups, respectively, by ignoring the set of variables of interest. For instance,
$\omega$
-sharing groups and 2-sharing groups, respectively, by ignoring the set of variables of interest. For instance,
![]() $\gamma _{\mathrm{2}}([\emptyset, xyz,xy^\infty z]_{x,y,z})= [ \{\!\!\{\}\!\!\}, xyz, xy^{2} z,xy^{3} z,xy^{4} z,xy^{5} z,\ldots ]_{x,y,z}$
. Moreover, we write
$\gamma _{\mathrm{2}}([\emptyset, xyz,xy^\infty z]_{x,y,z})= [ \{\!\!\{\}\!\!\}, xyz, xy^{2} z,xy^{3} z,xy^{4} z,xy^{5} z,\ldots ]_{x,y,z}$
. Moreover, we write
![]() ${\mathop{\downarrow }} [S]_U$
as an alternative form for
${\mathop{\downarrow }} [S]_U$
as an alternative form for
![]() $[{\mathop{\downarrow }} S]_U$
.
$[{\mathop{\downarrow }} S]_U$
.
Example 4.2. Consider the substitution
![]() $[\theta ]_U = [\{x/s(y,u,y), z/s(u,u), v/u \}]_{w,x,y,z}$
in Example 3.2. Its abstraction in
$[\theta ]_U = [\{x/s(y,u,y), z/s(u,u), v/u \}]_{w,x,y,z}$
in Example 3.2. Its abstraction in
![]() $\mathtt{ShLin}^2$
is given by
$\mathtt{ShLin}^2$
is given by
Analogously, substitutions
![]() $[\theta _1]_{U_1} = [\{ x/r(w_1,w_2,w_2,w_3,w_3), y/a, z/r(w_1) \}]_{x,y,z}$
and
$[\theta _1]_{U_1} = [\{ x/r(w_1,w_2,w_2,w_3,w_3), y/a, z/r(w_1) \}]_{x,y,z}$
and
![]() $[\theta _2]_{U_2} = [\{ x/r(w_4, w_5, w_6, w_8, w_8), u/r(w_4,w_7), v/r(w_7,w_8)\}]_{u,v,x}$
from Example 3.3 are abstracted into
$[\theta _2]_{U_2} = [\{ x/r(w_4, w_5, w_6, w_8, w_8), u/r(w_4,w_7), v/r(w_7,w_8)\}]_{u,v,x}$
from Example 3.3 are abstracted into
![]() $[T_1]_{U_1}={\mathop{\downarrow }}[x^\infty, xz]_{U_1}$
and
$[T_1]_{U_1}={\mathop{\downarrow }}[x^\infty, xz]_{U_1}$
and
![]() $[T_2]_{U_2} ={\mathop{\downarrow }}[uv, ux, vx^\infty, x]_{U_2}$
, respectively.
$[T_2]_{U_2} ={\mathop{\downarrow }}[uv, ux, vx^\infty, x]_{U_2}$
, respectively.
4.2 Matching operator
By composition,
![]() $\alpha _{\mathrm{2}} \circ \alpha _{\mathrm{\omega }}$
is an abstraction from
$\alpha _{\mathrm{2}} \circ \alpha _{\mathrm{\omega }}$
is an abstraction from
![]() $\mathit{ISubst}_\sim$
to
$\mathit{ISubst}_\sim$
to
![]() $\mathtt{ShLin}^2$
. Properties of the Galois connection
$\mathtt{ShLin}^2$
. Properties of the Galois connection
![]() $\langle \alpha _{\mathrm{2}}, \gamma _{\mathrm{2}} \rangle$
may be lifted to properties of
$\langle \alpha _{\mathrm{2}}, \gamma _{\mathrm{2}} \rangle$
may be lifted to properties of
![]() $\alpha _{\mathrm{2}} \circ \alpha _{\mathrm{\omega }}$
. In our case, we need to define an abstract matching
$\alpha _{\mathrm{2}} \circ \alpha _{\mathrm{\omega }}$
. In our case, we need to define an abstract matching
![]() $\mathsf{match}_{\mathrm{2}}$
over
$\mathsf{match}_{\mathrm{2}}$
over
![]() $\mathtt{ShLin}^2$
, which is an optimal w.r.t.
$\mathtt{ShLin}^2$
, which is an optimal w.r.t.
![]() $\mathsf{match}$
. However, optimality of
$\mathsf{match}$
. However, optimality of
![]() $\mathsf{match}_{\mathrm{2}}$
w.r.t.
$\mathsf{match}_{\mathrm{2}}$
w.r.t.
![]() $\mathsf{match}$
is immediately derived by optimality w.r.t.
$\mathsf{match}$
is immediately derived by optimality w.r.t.
![]() $\mathsf{match}_{\mathrm{\omega }}$
. Since the correspondence between
$\mathsf{match}_{\mathrm{\omega }}$
. Since the correspondence between
![]() $\mathtt{ShLin}^{\omega }$
and
$\mathtt{ShLin}^{\omega }$
and
![]() $\mathtt{ShLin}^2$
is straightforward, the same happens for
$\mathtt{ShLin}^2$
is straightforward, the same happens for
![]() $\mathsf{match}_{\mathrm{\omega }}$
and
$\mathsf{match}_{\mathrm{\omega }}$
and
![]() $\mathsf{match}_{\mathrm{2}}$
.
$\mathsf{match}_{\mathrm{2}}$
.
Definition 4.3 (Matching over
![]() $\mathtt{ShLin}^2$
). Given
$\mathtt{ShLin}^2$
). Given
![]() $[T_1]_{U_1}, [T_2]_{U_2} \in{\mathtt{ShLin}^2}$
, we define
$[T_1]_{U_1}, [T_2]_{U_2} \in{\mathtt{ShLin}^2}$
, we define
where
![]() $T^{\prime}_2=\{ B \in T_2 \mid B_{|U_1} = \emptyset \}$
,
$T^{\prime}_2=\{ B \in T_2 \mid B_{|U_1} = \emptyset \}$
,
![]() $T^{\prime\prime}_2 = T_2 \setminus T^{\prime}_2$
and
$T^{\prime\prime}_2 = T_2 \setminus T^{\prime}_2$
and
![]() $T^* = \{ \biguplus X \mid X \subseteq T \cup T^2 \}$
.
$T^* = \{ \biguplus X \mid X \subseteq T \cup T^2 \}$
.
Example 4.4. Under the hypothesis of Examples 3.5 and 4.2, and according to the definition of
![]() $\mathsf{match}_{\mathrm{2}}$
, we have that
$\mathsf{match}_{\mathrm{2}}$
, we have that
![]() $T^{\prime}_2 = \{ uv \}$
,
$T^{\prime}_2 = \{ uv \}$
,
![]() $T^{\prime\prime}_2 = \{ ux, vx, vx^\infty, x \}$
and
$T^{\prime\prime}_2 = \{ ux, vx, vx^\infty, x \}$
and
Note that
This is consistent with the fact that
![]() $\mathsf{match}_{\mathrm{2}}$
is correct w.r.t.
$\mathsf{match}_{\mathrm{2}}$
is correct w.r.t.
![]() $\mathsf{match}_{\mathrm{\omega }}$
. The 2-sharing groups
$\mathsf{match}_{\mathrm{\omega }}$
. The 2-sharing groups
![]() $u^\infty v^\infty x^\infty$
,
$u^\infty v^\infty x^\infty$
,
![]() $v^\infty x^\infty$
and
$v^\infty x^\infty$
and
![]() $vxz$
do not appear in
$vxz$
do not appear in
![]() $\alpha _{\mathrm{2}}(\mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2}))$
since
$\alpha _{\mathrm{2}}(\mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2}))$
since
![]() $\mathsf{match}_{\mathrm{2}}$
is not complete w.r.t.
$\mathsf{match}_{\mathrm{2}}$
is not complete w.r.t.
![]() $\mathsf{match}_{\mathrm{\omega }}$
$\mathsf{match}_{\mathrm{\omega }}$
As anticipated before, we prove the optimality of
![]() $\mathsf{match}_{\mathrm{2}}$
w.r.t.
$\mathsf{match}_{\mathrm{2}}$
w.r.t.
![]() $\mathsf{match}_{\mathrm{\omega }}$
, which automatically entails optimality w.r.t.
$\mathsf{match}_{\mathrm{\omega }}$
, which automatically entails optimality w.r.t.
![]() $\mathsf{match}$
.
$\mathsf{match}$
.
Theorem 4.5 (Correctness and optimality of
![]() $\mathsf{match}_{\mathrm{2}}$
). The operator
$\mathsf{match}_{\mathrm{2}}$
). The operator
![]() $\mathsf{match}_{\mathrm{2}}$
is correct and optimal w.r.t.
$\mathsf{match}_{\mathrm{2}}$
is correct and optimal w.r.t.
![]() $\mathsf{match}_{\mathrm{\omega }}$
.
$\mathsf{match}_{\mathrm{\omega }}$
.
Proof We need to prove that, for each
![]() $[T_1]_{U_1}, [T_2]_{U_2} \in{\mathtt{ShLin}^2}$
,
$[T_1]_{U_1}, [T_2]_{U_2} \in{\mathtt{ShLin}^2}$
,
To ease notation, we denote
![]() $\gamma _{\mathrm{2}}([T_1]_{U_1})$
and
$\gamma _{\mathrm{2}}([T_1]_{U_1})$
and
![]() $\gamma _{\mathrm{2}}([T_2]_{U_2})$
by
$\gamma _{\mathrm{2}}([T_2]_{U_2})$
by
![]() $[S_1]_{U_1}$
and
$[S_1]_{U_1}$
and
![]() $[S_2]_{U_2}$
, respectively. Moreover, we denote with
$[S_2]_{U_2}$
, respectively. Moreover, we denote with
![]() $S^{\prime}_2$
,
$S^{\prime}_2$
,
![]() $S^{\prime\prime}_2$
,
$S^{\prime\prime}_2$
,
![]() $T^{\prime}_2$
, and
$T^{\prime}_2$
, and
![]() $T^{\prime\prime}_2$
the subsets of
$T^{\prime\prime}_2$
the subsets of
![]() $S_2$
and
$S_2$
and
![]() $T_2$
given accordingly to Definitions 3.4 and 4.3. Since
$T_2$
given accordingly to Definitions 3.4 and 4.3. Since
![]() $\lfloor \!\lfloor B \rfloor \!\rfloor =\lfloor \!\lfloor \alpha _{\mathrm{2}}(B) \rfloor \!\rfloor$
, given
$\lfloor \!\lfloor B \rfloor \!\rfloor =\lfloor \!\lfloor \alpha _{\mathrm{2}}(B) \rfloor \!\rfloor$
, given
![]() $B \in S_2$
, we have that
$B \in S_2$
, we have that
![]() $B \in S_2^{\prime}$
iff
$B \in S_2^{\prime}$
iff
![]() $\alpha _{\mathrm{2}}(B) \in T_2^{\prime}$
.
$\alpha _{\mathrm{2}}(B) \in T_2^{\prime}$
.
Let
![]() $o \in \mathsf{match}_{\mathrm{2}}([T_1]_{U_1},[T_2]_{U_2})$
. If
$o \in \mathsf{match}_{\mathrm{2}}([T_1]_{U_1},[T_2]_{U_2})$
. If
![]() $o \in T^{\prime}_2$
, consider any
$o \in T^{\prime}_2$
, consider any
![]() $B \in \alpha ^{-1}_{\mathrm{2}}(o) \subseteq S_2$
. Then,
$B \in \alpha ^{-1}_{\mathrm{2}}(o) \subseteq S_2$
. Then,
![]() $B \in S^{\prime}_2 \subseteq \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2})$
. Therefore,
$B \in S^{\prime}_2 \subseteq \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1},[S_2]_{U_2})$
. Therefore,
![]() $o = \alpha _{\mathrm{2}}(B)$
is in the right-hand side of (13). If
$o = \alpha _{\mathrm{2}}(B)$
is in the right-hand side of (13). If
![]() $o \notin T^{\prime}_2$
, then
$o \notin T^{\prime}_2$
, then
![]() $o \leq o^{\prime}$
where
$o \leq o^{\prime}$
where
![]() $o^{\prime}_{|U_1} \in T_1$
and
$o^{\prime}_{|U_1} \in T_1$
and
![]() $o^{\prime}_{|U_2} \in (T^{\prime\prime}_2)^*$
; that is, there is
$o^{\prime}_{|U_2} \in (T^{\prime\prime}_2)^*$
; that is, there is
![]() $X \subseteq T^{\prime\prime}_2 \cup (T^{\prime\prime}_2)^2$
such that
$X \subseteq T^{\prime\prime}_2 \cup (T^{\prime\prime}_2)^2$
such that
![]() $o^{\prime}_{|U_2}=\biguplus X$
. For each
$o^{\prime}_{|U_2}=\biguplus X$
. For each
![]() $o^{\prime\prime} \in X \cap T_2$
, let
$o^{\prime\prime} \in X \cap T_2$
, let
![]() $B_{o^{\prime\prime}} \in \alpha ^{-1}_{\mathrm{2}}(o^{\prime\prime})$
. For each
$B_{o^{\prime\prime}} \in \alpha ^{-1}_{\mathrm{2}}(o^{\prime\prime})$
. For each
![]() $o^{\prime\prime} \in X \setminus T_2$
, we have
$o^{\prime\prime} \in X \setminus T_2$
, we have
![]() $o^{\prime\prime} = (o^{\prime\prime\prime})^2$
for some
$o^{\prime\prime} = (o^{\prime\prime\prime})^2$
for some
![]() $o^{\prime\prime\prime} \in T_2$
, and let
$o^{\prime\prime\prime} \in T_2$
, and let
![]() $B_{o^{\prime\prime}} \in \alpha ^{-1}_{\mathrm{2}}(o^{\prime\prime\prime})$
. Let
$B_{o^{\prime\prime}} \in \alpha ^{-1}_{\mathrm{2}}(o^{\prime\prime\prime})$
. Let
![]() $\mathcal{X}$
be a multiset containing a single copy of each
$\mathcal{X}$
be a multiset containing a single copy of each
![]() $B^{\prime\prime}_o$
for
$B^{\prime\prime}_o$
for
![]() $o \in X \cap T_2$
and two copies of
$o \in X \cap T_2$
and two copies of
![]() $B^{\prime\prime}_o$
for each
$B^{\prime\prime}_o$
for each
![]() $o \in X \setminus T_2$
, for example,
$o \in X \setminus T_2$
, for example,
![]() $\mathcal{X} = \{\!\!\{ B_{o^{\prime\prime}} \mid o^{\prime\prime} \in X \cap T_2 \}\!\!\} \uplus \biguplus \{\!\!\{ \{\!\!\{ B_{o^{\prime\prime}}, B_{o^{\prime\prime}} \}\!\!\} \mid o^{\prime\prime} \in X \setminus T_2 \}\!\!\})$
. Note that
$\mathcal{X} = \{\!\!\{ B_{o^{\prime\prime}} \mid o^{\prime\prime} \in X \cap T_2 \}\!\!\} \uplus \biguplus \{\!\!\{ \{\!\!\{ B_{o^{\prime\prime}}, B_{o^{\prime\prime}} \}\!\!\} \mid o^{\prime\prime} \in X \setminus T_2 \}\!\!\})$
. Note that
![]() $\alpha _{\mathrm{2}}(\biguplus \mathcal{X})=\biguplus \alpha _2(X)=o^{\prime}_{|U_2}$
by (3) of Proposition 4.1. Then, consider the
$\alpha _{\mathrm{2}}(\biguplus \mathcal{X})=\biguplus \alpha _2(X)=o^{\prime}_{|U_2}$
by (3) of Proposition 4.1. Then, consider the
![]() $\omega$
-sharing group
$\omega$
-sharing group
![]() $C$
such that
$C$
such that
 \begin{align*} C(v)=\begin {cases} (\biguplus \mathcal {X})(v) & \text {for $v \in U_2$,} \\[3pt] o^{\prime}(v) & \text {if $v \in U_1 \setminus U_2$ and $o(v)\leq 1$,} \\[3pt] 2 & \text {otherwise}. \end {cases} \end{align*}
\begin{align*} C(v)=\begin {cases} (\biguplus \mathcal {X})(v) & \text {for $v \in U_2$,} \\[3pt] o^{\prime}(v) & \text {if $v \in U_1 \setminus U_2$ and $o(v)\leq 1$,} \\[3pt] 2 & \text {otherwise}. \end {cases} \end{align*}
It is clear that
![]() $\alpha _{\mathrm{2}}(C_{|U_1})= o^{\prime}_{|U_1}$
, hence
$\alpha _{\mathrm{2}}(C_{|U_1})= o^{\prime}_{|U_1}$
, hence
![]() $C_{|U_1} \in S_1$
. Moreover,
$C_{|U_1} \in S_1$
. Moreover,
![]() $C_{|U_2} = \biguplus X$
with
$C_{|U_2} = \biguplus X$
with
![]() $\mathcal{X} \in \mathscr{P}_m(S_2^{\prime\prime})$
. Therefore, we have
$\mathcal{X} \in \mathscr{P}_m(S_2^{\prime\prime})$
. Therefore, we have
![]() $C \in \mathsf{match}_{\mathrm{\omega }}([T_1]_{U_1}, [T_2]_{U_2})$
and
$C \in \mathsf{match}_{\mathrm{\omega }}([T_1]_{U_1}, [T_2]_{U_2})$
and
![]() $\alpha _{\mathrm{2}}(C)=o^{\prime}$
is in the right-hand side of (13). The same holds for
$\alpha _{\mathrm{2}}(C)=o^{\prime}$
is in the right-hand side of (13). The same holds for
![]() $o$
by downward closure of
$o$
by downward closure of
![]() $\alpha _{\mathrm{2}}$
.
$\alpha _{\mathrm{2}}$
.
Conversely, let
![]() $o \in \alpha _{\mathrm{2}}(\mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1}, [S_2]_{U_2}))$
. As a consequence, there exists
$o \in \alpha _{\mathrm{2}}(\mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1}, [S_2]_{U_2}))$
. As a consequence, there exists
![]() $B \in \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1}, [S_2]_{U_2})$
such that
$B \in \mathsf{match}_{\mathrm{\omega }}([S_1]_{U_1}, [S_2]_{U_2})$
such that
![]() $o \leq o^{\prime}$
and
$o \leq o^{\prime}$
and
![]() $o^{\prime} = \alpha _{\mathrm{2}}(B)$
. It is enough to prove that
$o^{\prime} = \alpha _{\mathrm{2}}(B)$
. It is enough to prove that
![]() $o^{\prime} \in \mathsf{match}_{\mathrm{2}}([T_1]_{U_1},[T_2]_{U_2})$
. If
$o^{\prime} \in \mathsf{match}_{\mathrm{2}}([T_1]_{U_1},[T_2]_{U_2})$
. If
![]() $B \in S^{\prime}_2$
then
$B \in S^{\prime}_2$
then
![]() $o^{\prime} \in T^{\prime}_2$
, hence
$o^{\prime} \in T^{\prime}_2$
, hence
![]() $o^{\prime} \in \mathsf{match}_{\mathrm{2}}([T_1]_{U_1},[T_2]_{U_2})$
. If
$o^{\prime} \in \mathsf{match}_{\mathrm{2}}([T_1]_{U_1},[T_2]_{U_2})$
. If
![]() $B \notin S^{\prime}_2$
, then
$B \notin S^{\prime}_2$
, then
![]() $B_{|U_1} \in S_1$
and
$B_{|U_1} \in S_1$
and
![]() $B_{|U_2} = \biguplus \mathcal{X}$
, where
$B_{|U_2} = \biguplus \mathcal{X}$
, where
![]() $\mathcal{X} \in \mathscr{P}_m(S^{\prime\prime}_2)$
. By
$\mathcal{X} \in \mathscr{P}_m(S^{\prime\prime}_2)$
. By
![]() $B_{|U_1} \in S_1$
, we have
$B_{|U_1} \in S_1$
, we have
![]() $o^{\prime}_{|U_1} = \alpha _{\mathrm{2}}(B_{|U_1}) \in T_1$
. For each
$o^{\prime}_{|U_1} = \alpha _{\mathrm{2}}(B_{|U_1}) \in T_1$
. For each
![]() $C \in \mathcal{X}$
with
$C \in \mathcal{X}$
with
![]() $\mathcal{X}(C)=1$
, we define
$\mathcal{X}(C)=1$
, we define
![]() $o_{C}=\alpha _{\mathrm{2}}(C) \in T^{\prime\prime}_2$
, while for each
$o_{C}=\alpha _{\mathrm{2}}(C) \in T^{\prime\prime}_2$
, while for each
![]() $C$
with
$C$
with
![]() $\mathcal{X}(C)\gt 1$
, we define
$\mathcal{X}(C)\gt 1$
, we define
![]() $o_{C}=\alpha _{\mathrm{2}}(C)^2 \in (T^{\prime\prime}_2)^2$
. We have that
$o_{C}=\alpha _{\mathrm{2}}(C)^2 \in (T^{\prime\prime}_2)^2$
. We have that
![]() $o^{\prime\prime}_{|U_2} = \alpha _{\mathrm{2}}(B)_{|U_2} = \alpha _{\mathrm{2}}(B_{|U_2})=\alpha _{\mathrm{2}}(\biguplus \mathcal{X})=\biguplus X$
where
$o^{\prime\prime}_{|U_2} = \alpha _{\mathrm{2}}(B)_{|U_2} = \alpha _{\mathrm{2}}(B_{|U_2})=\alpha _{\mathrm{2}}(\biguplus \mathcal{X})=\biguplus X$
where
![]() $X = \{ o_C \mid C \in \mathcal{X}\}$
is an element of
$X = \{ o_C \mid C \in \mathcal{X}\}$
is an element of
![]() $\mathscr{P}(T^{\prime\prime}_2 \cup (T^{\prime\prime}_2)^2)$
. This means that
$\mathscr{P}(T^{\prime\prime}_2 \cup (T^{\prime\prime}_2)^2)$
. This means that
![]() $o^{\prime} \in \mathsf{match}_{\mathrm{2}}([T_1]_{U_1},[T_2]_{U_2})$
.
$o^{\prime} \in \mathsf{match}_{\mathrm{2}}([T_1]_{U_1},[T_2]_{U_2})$
.
Although
![]() $\mathsf{match}_{\mathrm{2}}$
is not complete w.r.t. either
$\mathsf{match}_{\mathrm{2}}$
is not complete w.r.t. either
![]() $\mathsf{match}_{\mathrm{\omega }}$
or
$\mathsf{match}_{\mathrm{\omega }}$
or
![]() $\mathsf{match}$
, we claim it enjoys a property analogous to the one in Lemma 3.9.
$\mathsf{match}$
, we claim it enjoys a property analogous to the one in Lemma 3.9.
4.3 Optimization
In a real implementation, we would like to encode an element of
![]() $\mathtt{ShLin}^2$
with the set of its maximal elements. This works well only if we may compute
$\mathtt{ShLin}^2$
with the set of its maximal elements. This works well only if we may compute
![]() $\mathsf{match}_{\mathrm{2}}$
starting from its maximal elements, without implicitly computing the downward closure. We would also like
$\mathsf{match}_{\mathrm{2}}$
starting from its maximal elements, without implicitly computing the downward closure. We would also like
![]() $\mathsf{match}_{\mathrm{2}}$
to compute as few non-maximal elements as possible. We provide a new algorithm for
$\mathsf{match}_{\mathrm{2}}$
to compute as few non-maximal elements as possible. We provide a new algorithm for
![]() $\mathsf{match}_{\mathrm{2}}$
following this approach.
$\mathsf{match}_{\mathrm{2}}$
following this approach.
Definition 4.6. Given
![]() $T_1, T_2$
sets of
$T_1, T_2$
sets of
![]() $2$
-sharing groups and
$2$
-sharing groups and
![]() $U_1, U_2 \subseteq{\mathcal{V}}$
, we define
$U_1, U_2 \subseteq{\mathcal{V}}$
, we define
where
with
![]() $T^{\prime}_2$
and
$T^{\prime}_2$
and
![]() $T^{\prime\prime}_2$
as in Definition 4.3,
$T^{\prime\prime}_2$
as in Definition 4.3,
![]() $\mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu = \{ o^{\prime} \in T^{\prime\prime}_2 \mid \forall v \in o^{\prime} \cap U_1, o(v)=\infty \}$
and
$\mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu = \{ o^{\prime} \in T^{\prime\prime}_2 \mid \forall v \in o^{\prime} \cap U_1, o(v)=\infty \}$
and
 \begin{align*} o \wedge o^{\prime}= \lambda v.\begin {cases} o(v) & \text {if $v \in U_1 \setminus U_2$}, \\ min(o(v), o^{\prime}(v)) & \text {if $v \in U_1 \cap U_2$,} \\ o^{\prime}(v) & \text {otherwise.} \end {cases} \end{align*}
\begin{align*} o \wedge o^{\prime}= \lambda v.\begin {cases} o(v) & \text {if $v \in U_1 \setminus U_2$}, \\ min(o(v), o^{\prime}(v)) & \text {if $v \in U_1 \cap U_2$,} \\ o^{\prime}(v) & \text {otherwise.} \end {cases} \end{align*}
The operator
![]() $\mathsf{match}^{\prime}_{\mathrm{2}}$
aims at computing the set of maximal
$\mathsf{match}^{\prime}_{\mathrm{2}}$
aims at computing the set of maximal
![]() $2$
-sharing groups in
$2$
-sharing groups in
![]() $\mathsf{match}_{\mathrm{2}}([{\mathop{\downarrow }} T_1]_{U_1},[{\mathop{\downarrow }} T_2]_{U_2})$
. It works by considering one sharing group
$\mathsf{match}_{\mathrm{2}}([{\mathop{\downarrow }} T_1]_{U_1},[{\mathop{\downarrow }} T_2]_{U_2})$
. It works by considering one sharing group
![]() $o \in T_1$
at a time and calling an auxiliary operator that computes the maximal
$o \in T_1$
at a time and calling an auxiliary operator that computes the maximal
![]() $2$
-sharing groups compatible with
$2$
-sharing groups compatible with
![]() $o$
. A
$o$
. A
![]() $2$
-sharing group
$2$
-sharing group
![]() $o^{\prime}$
is compatible with
$o^{\prime}$
is compatible with
![]() $o$
if
$o$
if
![]() $\lfloor \!\lfloor o^{\prime} \rfloor \!\rfloor \cap U_1 = \lfloor \!\lfloor o \rfloor \!\rfloor \cap U_1$
.
$\lfloor \!\lfloor o^{\prime} \rfloor \!\rfloor \cap U_1 = \lfloor \!\lfloor o \rfloor \!\rfloor \cap U_1$
.
When computing the auxiliary operator
![]() $\mathsf{match}^{\prime}_{\mathrm{2}}(o)$
we choose a subset
$\mathsf{match}^{\prime}_{\mathrm{2}}(o)$
we choose a subset
![]() $X$
of
$X$
of
![]() $T^{\prime\prime}_2$
. Given
$T^{\prime\prime}_2$
. Given
![]() $o^{\prime} \in X$
, note that
$o^{\prime} \in X$
, note that
![]() $\lfloor \!\lfloor o^{\prime} \rfloor \!\rfloor$
may be viewed as a
$\lfloor \!\lfloor o^{\prime} \rfloor \!\rfloor$
may be viewed as a
![]() $2$
-sharing group which is the linearized version of
$2$
-sharing group which is the linearized version of
![]() $o^{\prime}$
: it has the same support as
$o^{\prime}$
: it has the same support as
![]() $o^{\prime}$
, but all variables are linear. If
$o^{\prime}$
, but all variables are linear. If
![]() $o^{\prime} \in T^{\prime\prime}_2$
, its linearization is in
$o^{\prime} \in T^{\prime\prime}_2$
, its linearization is in
![]() ${\mathop{\downarrow }} T_2$
. The choice of
${\mathop{\downarrow }} T_2$
. The choice of
![]() $X$
is valid if the multiset sum of all its linearizations is smaller than
$X$
is valid if the multiset sum of all its linearizations is smaller than
![]() $o$
for all the variables in
$o$
for all the variables in
![]() $U_1 \cap U_2$
. Once established that
$U_1 \cap U_2$
. Once established that
![]() $X$
is a valid choice, we do not take directly
$X$
is a valid choice, we do not take directly
![]() $\biguplus \lfloor \!\lfloor X \rfloor \!\rfloor$
as the resulting
$\biguplus \lfloor \!\lfloor X \rfloor \!\rfloor$
as the resulting
![]() $2$
-sharing group, but we try to find an
$2$
-sharing group, but we try to find an
![]() $o^{\prime\prime} \geq \biguplus X$
.
$o^{\prime\prime} \geq \biguplus X$
.
To this purpose, we observe that, given
![]() $o^{\prime} \in X$
, if
$o^{\prime} \in X$
, if
![]() $o(v)=\infty$
for each
$o(v)=\infty$
for each
![]() $v \in \lfloor \!\lfloor o^{\prime} \rfloor \!\rfloor \cap U_1$
, then we may take
$v \in \lfloor \!\lfloor o^{\prime} \rfloor \!\rfloor \cap U_1$
, then we may take
![]() $o^{\prime}$
twice. We denote with
$o^{\prime}$
twice. We denote with
![]() $\mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu$
the set of all the sharing groups in
$\mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu$
the set of all the sharing groups in
![]() $T^{\prime\prime}_2$
, which is such a property, and we unconditionally add to the result the sharing groups in
$T^{\prime\prime}_2$
, which is such a property, and we unconditionally add to the result the sharing groups in
![]() $X \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu$
so that all these sharing groups are taken twice. Therefore, the biggest element compatible with
$X \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu$
so that all these sharing groups are taken twice. Therefore, the biggest element compatible with
![]() $o$
is
$o$
is
![]() $(o \wedge \biguplus X) \uplus \biguplus (X \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu)$
.
$(o \wedge \biguplus X) \uplus \biguplus (X \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu)$
.
Example 4.7. Under the hypothesis of Examples 3.5 and 4.2, let us define
![]() $T_1=\{x^\infty, xz\}$
and
$T_1=\{x^\infty, xz\}$
and
![]() $T_2 = \{ uv, ux, vx^\infty, x \}$
. We have
$T_2 = \{ uv, ux, vx^\infty, x \}$
. We have
![]() $T^{\prime}_2 = \{uv\}$
and
$T^{\prime}_2 = \{uv\}$
and
![]() $T^{\prime\prime}_2 = \{ux, vx^\infty, x \}$
.
$T^{\prime\prime}_2 = \{ux, vx^\infty, x \}$
.
Let us compute
![]() $\mathsf{match}^{\prime}_{\mathrm{2}}(x^\infty )$
. We have
$\mathsf{match}^{\prime}_{\mathrm{2}}(x^\infty )$
. We have
![]() $\mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu = T^{\prime\prime}_2$
. If we take
$\mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu = T^{\prime\prime}_2$
. If we take
![]() $X=\{ux, xv^\infty \}$
, we have
$X=\{ux, xv^\infty \}$
, we have
![]() $\left (\biguplus \lfloor \!\lfloor X \rfloor \!\rfloor \right )_{|U_1} = x^\infty$
, hence the choice is valid. The corresponding result is
$\left (\biguplus \lfloor \!\lfloor X \rfloor \!\rfloor \right )_{|U_1} = x^\infty$
, hence the choice is valid. The corresponding result is
![]() $(x^\infty \wedge \biguplus X) \uplus \biguplus X = uv^\infty x^\infty \uplus uv^\infty x^\infty = u^\infty v^\infty x^\infty$
. Overall, we have
$(x^\infty \wedge \biguplus X) \uplus \biguplus X = uv^\infty x^\infty \uplus uv^\infty x^\infty = u^\infty v^\infty x^\infty$
. Overall, we have
![]() $\mathsf{match}^{\prime}_{\mathrm{2}}(x^\infty )= \{ u^\infty x^\infty, v^\infty x^\infty, x^\infty, u^\infty x^\infty v^\infty \}$
. Note that some results are computed by different choices of
$\mathsf{match}^{\prime}_{\mathrm{2}}(x^\infty )= \{ u^\infty x^\infty, v^\infty x^\infty, x^\infty, u^\infty x^\infty v^\infty \}$
. Note that some results are computed by different choices of
![]() $X$
. For example, both
$X$
. For example, both
![]() $\{ux, x\}$
and
$\{ux, x\}$
and
![]() $\{ux\}$
generates
$\{ux\}$
generates
![]() $u^\infty x^\infty$
.
$u^\infty x^\infty$
.
Let us compute
![]() $\mathsf{match}^{\prime}_{\mathrm{2}}(xz)$
and take
$\mathsf{match}^{\prime}_{\mathrm{2}}(xz)$
and take
![]() $X=\{ v x^\infty \}$
. We have that
$X=\{ v x^\infty \}$
. We have that
![]() $\left (\biguplus \lfloor \!\lfloor X \rfloor \!\rfloor \right )_{|U_1} = x = xz_{|U_2}$
. In this case,
$\left (\biguplus \lfloor \!\lfloor X \rfloor \!\rfloor \right )_{|U_1} = x = xz_{|U_2}$
. In this case,
![]() $\mkern 1.5mu\overline{\mkern -1.5muT^{\prime\prime}_2\mkern -1.5mu}\mkern 1.5mu = \emptyset$
. Therefore, the result is
$\mkern 1.5mu\overline{\mkern -1.5muT^{\prime\prime}_2\mkern -1.5mu}\mkern 1.5mu = \emptyset$
. Therefore, the result is
![]() $x \wedge vx^\infty = vx$
. Note that if we take
$x \wedge vx^\infty = vx$
. Note that if we take
![]() $X= \{xz, x\}$
, then
$X= \{xz, x\}$
, then
![]() $\left (\biguplus \lfloor \!\lfloor X \rfloor \!\rfloor \right )_{|U_1} = x \uplus x= x^\infty$
, and the choice is not valid. This shows that, due to the downward closure, choosing in
$\left (\biguplus \lfloor \!\lfloor X \rfloor \!\rfloor \right )_{|U_1} = x \uplus x= x^\infty$
, and the choice is not valid. This shows that, due to the downward closure, choosing in
![]() $X$
a sharing group with a nonlinear variable is very different from choosing the same variable twice. At the end, we have
$X$
a sharing group with a nonlinear variable is very different from choosing the same variable twice. At the end, we have
![]() $\mathsf{match}^{\prime}_{\mathrm{2}}(xz) = \{ uxz, vxz, xz \}$
. Finally,
$\mathsf{match}^{\prime}_{\mathrm{2}}(xz) = \{ uxz, vxz, xz \}$
. Finally,
This is exactly the set of maximal elements in
![]() $\mathsf{match}_{\mathrm{2}}([{\mathop{\downarrow }} T_1]_{U_1}, [{\mathop{\downarrow }} T_2]_{U_2})$
.
$\mathsf{match}_{\mathrm{2}}([{\mathop{\downarrow }} T_1]_{U_1}, [{\mathop{\downarrow }} T_2]_{U_2})$
.
We can show that the correspondence between
![]() $\mathsf{match}_{\mathrm{2}}$
and
$\mathsf{match}_{\mathrm{2}}$
and
![]() $\mathsf{match}^{\prime}_{\mathrm{2}}$
in the previous example was not by chance, proving the following:
$\mathsf{match}^{\prime}_{\mathrm{2}}$
in the previous example was not by chance, proving the following:
Theorem 4.8. Given
![]() $T_1, T_2$
sets of
$T_1, T_2$
sets of
![]() $2$
-sharing groups such that
$2$
-sharing groups such that
![]() ${\mathop{\downarrow }} [T_1]_{U_1},{\mathop{\downarrow }} [T_2]_{U_2} \in{\mathtt{ShLin}^2}$
, we have
${\mathop{\downarrow }} [T_1]_{U_1},{\mathop{\downarrow }} [T_2]_{U_2} \in{\mathtt{ShLin}^2}$
, we have
Proof We start by proving that if
![]() $o$
is an element in
$o$
is an element in
![]() $\mathsf{match}_{\mathrm{2}}({\mathop{\downarrow }}[T_1]_{U_1},{\mathop{\downarrow }} [T_2]_{U_2})$
, then
$\mathsf{match}_{\mathrm{2}}({\mathop{\downarrow }}[T_1]_{U_1},{\mathop{\downarrow }} [T_2]_{U_2})$
, then
![]() $o \in{\mathop{\downarrow }} \mathsf{match}^{\prime}_{\mathrm{2}}(T_1,U_1,T_2,U_2)$
. If
$o \in{\mathop{\downarrow }} \mathsf{match}^{\prime}_{\mathrm{2}}(T_1,U_1,T_2,U_2)$
. If
![]() $o \in{\mathop{\downarrow }} T^{\prime}_2$
, this is trivial since
$o \in{\mathop{\downarrow }} T^{\prime}_2$
, this is trivial since
![]() $T^{\prime}_2 \subseteq \mathsf{match}^{\prime}_{\mathrm{2}}(T_1,U_1,T_2,U_2)$
. Otherwise,
$T^{\prime}_2 \subseteq \mathsf{match}^{\prime}_{\mathrm{2}}(T_1,U_1,T_2,U_2)$
. Otherwise,
![]() $o_{|U_1} \in{\mathop{\downarrow }} T_1$
and
$o_{|U_1} \in{\mathop{\downarrow }} T_1$
and
![]() $o_{|U_2} \in ({\mathop{\downarrow }} T^{\prime\prime}_2)^*$
, according to Definition 4.3. Let
$o_{|U_2} \in ({\mathop{\downarrow }} T^{\prime\prime}_2)^*$
, according to Definition 4.3. Let
![]() $o_1 \in T_1$
such that
$o_1 \in T_1$
such that
![]() $o_1 \geq o_{|U_1}$
, we want to prove that there exists
$o_1 \geq o_{|U_1}$
, we want to prove that there exists
![]() $\bar o \in \mathsf{match}^{\prime}_{\mathrm{2}}(o_1)$
such that
$\bar o \in \mathsf{match}^{\prime}_{\mathrm{2}}(o_1)$
such that
![]() $o \leq \bar o$
.
$o \leq \bar o$
.
Since
![]() $o_{|U_2} \in ({\mathop{\downarrow }} T^{\prime\prime}_2)^*$
, there are
$o_{|U_2} \in ({\mathop{\downarrow }} T^{\prime\prime}_2)^*$
, there are
![]() $X_a \subseteq{\mathop{\downarrow }} T^{\prime\prime}_2$
and
$X_a \subseteq{\mathop{\downarrow }} T^{\prime\prime}_2$
and
![]() $X_b \subseteq ({\mathop{\downarrow }} T^{\prime\prime}_2)^2$
such that
$X_b \subseteq ({\mathop{\downarrow }} T^{\prime\prime}_2)^2$
such that
![]() $o_{|U_2} = \biguplus X_a \uplus \biguplus X_b$
. For each
$o_{|U_2} = \biguplus X_a \uplus \biguplus X_b$
. For each
![]() $o_a \in X_a$
, consider
$o_a \in X_a$
, consider
![]() $o^{\prime}_a \in T^{\prime\prime}_2$
such that
$o^{\prime}_a \in T^{\prime\prime}_2$
such that
![]() $o^{\prime}_a \geq o_a \in T^{\prime\prime}_2$
. Let
$o^{\prime}_a \geq o_a \in T^{\prime\prime}_2$
. Let
![]() $Y_a$
be the set of all those
$Y_a$
be the set of all those
![]() $o^{\prime}_a$
. For each
$o^{\prime}_a$
. For each
![]() $o_b \in X_b$
, consider an
$o_b \in X_b$
, consider an
![]() $o^{\prime}_b \in T^{\prime\prime}_2$
such that
$o^{\prime}_b \in T^{\prime\prime}_2$
such that
![]() $(o^{\prime}_b)^2 = o_b$
. Let
$(o^{\prime}_b)^2 = o_b$
. Let
![]() $Y_b$
be the set of all those
$Y_b$
be the set of all those
![]() $o^{\prime}_b$
. By construction
$o^{\prime}_b$
. By construction
![]() $\biguplus Y_a \geq \biguplus X_a \geq \biguplus \lfloor \!\lfloor Y_a \rfloor \!\rfloor$
and
$\biguplus Y_a \geq \biguplus X_a \geq \biguplus \lfloor \!\lfloor Y_a \rfloor \!\rfloor$
and
![]() $\biguplus Y_b \uplus \biguplus Y_b = \biguplus \lfloor \!\lfloor Y_b \rfloor \!\rfloor \uplus \biguplus \lfloor \!\lfloor Y_b \rfloor \!\rfloor = \biguplus X_b$
.
$\biguplus Y_b \uplus \biguplus Y_b = \biguplus \lfloor \!\lfloor Y_b \rfloor \!\rfloor \uplus \biguplus \lfloor \!\lfloor Y_b \rfloor \!\rfloor = \biguplus X_b$
.
Let
![]() $Y= Y_a \cup Y_b$
. Obviously
$Y= Y_a \cup Y_b$
. Obviously
![]() $Y \subseteq T^{\prime\prime}_2$
and
$Y \subseteq T^{\prime\prime}_2$
and
![]() $(\biguplus \lfloor \!\lfloor Y \rfloor \!\rfloor )_{|U_1} = \biguplus \lfloor \!\lfloor Y_a \rfloor \!\rfloor \uplus \biguplus \lfloor \!\lfloor Y_b \rfloor \!\rfloor \leq (\biguplus X_a \uplus \biguplus X_b)_{|U_1} = (o_{|U_2})_{|U_1} = (o_{|U_1})_{|U_2} \leq (o_1)_{|U_2}$
. Therefore,
$(\biguplus \lfloor \!\lfloor Y \rfloor \!\rfloor )_{|U_1} = \biguplus \lfloor \!\lfloor Y_a \rfloor \!\rfloor \uplus \biguplus \lfloor \!\lfloor Y_b \rfloor \!\rfloor \leq (\biguplus X_a \uplus \biguplus X_b)_{|U_1} = (o_{|U_2})_{|U_1} = (o_{|U_1})_{|U_2} \leq (o_1)_{|U_2}$
. Therefore,
![]() $\bar o = (o_1 \wedge \biguplus Y) \uplus \biguplus (Y \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu) \in \mathsf{match}_{\mathrm{2}}^{\prime}(o_1)$
. We now prove that
$\bar o = (o_1 \wedge \biguplus Y) \uplus \biguplus (Y \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu) \in \mathsf{match}_{\mathrm{2}}^{\prime}(o_1)$
. We now prove that
![]() $o \leq \bar o$
.
$o \leq \bar o$
.
Given any
![]() $o_b \in X_b$
, we have that
$o_b \in X_b$
, we have that
![]() $o_1(v) = o_b(v)=\infty$
for each
$o_1(v) = o_b(v)=\infty$
for each
![]() $v \in o_b \cap U_1$
. This implies that
$v \in o_b \cap U_1$
. This implies that
![]() $Y_b \subseteq \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu$
. Therefore,
$Y_b \subseteq \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu$
. Therefore,
![]() $\bar o \geq (o_1 \wedge \biguplus Y_a \uplus \biguplus Y_b) \uplus \biguplus Y_b = (o_1 \wedge \biguplus Y_a) \uplus \biguplus Y_b \uplus \biguplus Y_b \geq (o_1 \wedge \biguplus X_a) \uplus \biguplus X_b = o_1 \wedge (\biguplus X_a \uplus \biguplus X_b) = o_1 \wedge o_{|U_2}$
. Now, if
$\bar o \geq (o_1 \wedge \biguplus Y_a \uplus \biguplus Y_b) \uplus \biguplus Y_b = (o_1 \wedge \biguplus Y_a) \uplus \biguplus Y_b \uplus \biguplus Y_b \geq (o_1 \wedge \biguplus X_a) \uplus \biguplus X_b = o_1 \wedge (\biguplus X_a \uplus \biguplus X_b) = o_1 \wedge o_{|U_2}$
. Now, if
![]() $v \in U_1 \setminus U_2$
, we have
$v \in U_1 \setminus U_2$
, we have
![]() $\bar o(v)= o_1(v) \geq o(v)$
. If
$\bar o(v)= o_1(v) \geq o(v)$
. If
![]() $v \in U_2 \setminus U_1$
, we have
$v \in U_2 \setminus U_1$
, we have
![]() $\bar o(v) \geq o_{|U_2}(v) = o(v)$
. Finally, if
$\bar o(v) \geq o_{|U_2}(v) = o(v)$
. Finally, if
![]() $v \in U_1 \cap U_2$
, then
$v \in U_1 \cap U_2$
, then
![]() $o_1(v) \geq o_{|U_1}(v) = o_{|U_2}(v)=o(v)$
, hence
$o_1(v) \geq o_{|U_1}(v) = o_{|U_2}(v)=o(v)$
, hence
![]() $\bar o(v) \geq o(v)$
. This concludes one side of the proof.
$\bar o(v) \geq o(v)$
. This concludes one side of the proof.
For the other side of the equality, assume
![]() $o \in \mathsf{match}^{\prime}_2(T_1, U_1, T_2, U_2)$
and prove
$o \in \mathsf{match}^{\prime}_2(T_1, U_1, T_2, U_2)$
and prove
![]() $o \in \mathsf{match}_{\mathrm{2}}({\mathop{\downarrow }}[T_1]_{U_1},{\mathop{\downarrow }} [T_2]_{U_2})$
. If
$o \in \mathsf{match}_{\mathrm{2}}({\mathop{\downarrow }}[T_1]_{U_1},{\mathop{\downarrow }} [T_2]_{U_2})$
. If
![]() $o \in T^{\prime}_2$
, this is trivial since
$o \in T^{\prime}_2$
, this is trivial since
![]() $\mathsf{match}_{\mathrm{2}}({\mathop{\downarrow }}[T_1]_{U_1},{\mathop{\downarrow }} [T_2]_{U_2}) \supseteq{\mathop{\downarrow }} T^{\prime}_2$
. Otherwise,
$\mathsf{match}_{\mathrm{2}}({\mathop{\downarrow }}[T_1]_{U_1},{\mathop{\downarrow }} [T_2]_{U_2}) \supseteq{\mathop{\downarrow }} T^{\prime}_2$
. Otherwise,
![]() $o = (o_1 \wedge \biguplus X) \uplus \biguplus (X \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu)$
for some
$o = (o_1 \wedge \biguplus X) \uplus \biguplus (X \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu)$
for some
![]() $o_1 \in T_1$
and
$o_1 \in T_1$
and
![]() $X \subseteq T^{\prime\prime}_2$
satisfying the properties of Definition 4.6. Consider
$X \subseteq T^{\prime\prime}_2$
satisfying the properties of Definition 4.6. Consider
![]() $Y=(X \setminus \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu) \cup (X \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu)^2$
, which is an element of
$Y=(X \setminus \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu) \cup (X \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu)^2$
, which is an element of
![]() $T^{\prime\prime}_2 \cup (T^{\prime\prime}_2)^2$
such that
$T^{\prime\prime}_2 \cup (T^{\prime\prime}_2)^2$
such that
![]() $\biguplus Y = \biguplus X \uplus \biguplus (X \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu) \in (T^{\prime\prime}_2)^*$
. It is enough to prove that
$\biguplus Y = \biguplus X \uplus \biguplus (X \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu) \in (T^{\prime\prime}_2)^*$
. It is enough to prove that
![]() $o_{|U_1}=o_1$
and
$o_{|U_1}=o_1$
and
![]() $o_{|U_2}= \biguplus Y$
. If
$o_{|U_2}= \biguplus Y$
. If
![]() $v \in U_1 \setminus U_2$
, we have
$v \in U_1 \setminus U_2$
, we have
![]() $o(v)=o_1(v)$
. Note that if
$o(v)=o_1(v)$
. Note that if
![]() $\bar o \in X \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu$
and
$\bar o \in X \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu$
and
![]() $v \in \bar o \cap U_1$
, then
$v \in \bar o \cap U_1$
, then
![]() $o_1(v)=\infty$
. Therefore, for each
$o_1(v)=\infty$
. Therefore, for each
![]() $v \in U_1 \cap U_2$
, we have
$v \in U_1 \cap U_2$
, we have
![]() $o(v)=o_1(v)$
. Finally, if
$o(v)=o_1(v)$
. Finally, if
![]() $v \in U_2$
, we have
$v \in U_2$
, we have
![]() $o(v)=\biguplus X \uplus \biguplus (X \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu)= \biguplus Y$
.
$o(v)=\biguplus X \uplus \biguplus (X \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu)= \biguplus Y$
.
5 Abstract matching over
 $\mathtt{Sharing} \times \mathtt{Lin}$
$\mathtt{Sharing} \times \mathtt{Lin}$
The reduced product
![]() $\mathtt{ShLin}=\mathtt{Sharing} \times \mathtt{Lin}$
has been used for a long time in the analysis of aliasing properties since it was recognized quite early that the precision of these analyses could be greatly improved by keeping track of the linear variables. In the following, we briefly recall the definition of the abstract domain following the presentation in Amato and Scozzari (Reference Amato and Scozzari2010).
$\mathtt{ShLin}=\mathtt{Sharing} \times \mathtt{Lin}$
has been used for a long time in the analysis of aliasing properties since it was recognized quite early that the precision of these analyses could be greatly improved by keeping track of the linear variables. In the following, we briefly recall the definition of the abstract domain following the presentation in Amato and Scozzari (Reference Amato and Scozzari2010).
5.1
The domain
 $\mathtt{ShLin}$
$\mathtt{ShLin}$
The domain
![]() $\mathtt{ShLin}$
couples an object of
$\mathtt{ShLin}$
couples an object of
![]() $\mathtt{Sharing}$
with the set of variables known to be linear. Each element of
$\mathtt{Sharing}$
with the set of variables known to be linear. Each element of
![]() $\mathtt{ShLin}$
is therefore a triple: the first component is an object of
$\mathtt{ShLin}$
is therefore a triple: the first component is an object of
![]() $\mathtt{Sharing}$
; the second component is an object of
$\mathtt{Sharing}$
; the second component is an object of
![]() $\mathtt{Lin}$
, that is, the set of variables that are linear in all the sharing groups of the first component; and the third component is the set of variables of interest. It is immediate that
$\mathtt{Lin}$
, that is, the set of variables that are linear in all the sharing groups of the first component; and the third component is the set of variables of interest. It is immediate that
![]() $\mathtt{ShLin}$
is an abstraction of
$\mathtt{ShLin}$
is an abstraction of
![]() $\mathtt{ShLin}^2$
(and thus of
$\mathtt{ShLin}^2$
(and thus of
![]() $\mathtt{ShLin}^{\omega }$
).
$\mathtt{ShLin}^{\omega }$
).
with the approximation relation
![]() $\leq _{\mathit{sl}}$
defined as
$\leq _{\mathit{sl}}$
defined as
![]() $[S,L,U] \leq _{\mathit{sl}} [S^{\prime},L^{\prime},U^{\prime}]$
iff
$[S,L,U] \leq _{\mathit{sl}} [S^{\prime},L^{\prime},U^{\prime}]$
iff
![]() $U=U^{\prime}$
,
$U=U^{\prime}$
,
![]() $S \subseteq S^{\prime}$
,
$S \subseteq S^{\prime}$
,
![]() $L \supseteq L^{\prime}$
. There is a Galois insertion of
$L \supseteq L^{\prime}$
. There is a Galois insertion of
![]() $\mathtt{ShLin}$
into
$\mathtt{ShLin}$
into
![]() $\mathtt{ShLin}^2$
given by the pair of maps:
$\mathtt{ShLin}^2$
given by the pair of maps:
where
![]() $B_L$
is the 2-sharing group that has the same support of
$B_L$
is the 2-sharing group that has the same support of
![]() $B$
, with linear variables dictated by the set
$B$
, with linear variables dictated by the set
![]() $L$
:
$L$
:
 \begin{align*} B_L & =\lambda v \in{\mathcal{V}}. \begin{cases} \infty & \text{if $v \in B \setminus L$,} \\ 1 & \text{if $v \in B \cap L$,} \\ 0 & \text{otherwise.} \end{cases} \end{align*}
\begin{align*} B_L & =\lambda v \in{\mathcal{V}}. \begin{cases} \infty & \text{if $v \in B \setminus L$,} \\ 1 & \text{if $v \in B \cap L$,} \\ 0 & \text{otherwise.} \end{cases} \end{align*}
The functional composition of
![]() $\alpha _{\mathrm{\omega }}$
,
$\alpha _{\mathrm{\omega }}$
,
![]() $\alpha _{\mathrm{2}}$
, and
$\alpha _{\mathrm{2}}$
, and
![]() $\alpha _{\mathit{sl}}$
gives the standard abstraction map from substitutions to
$\alpha _{\mathit{sl}}$
gives the standard abstraction map from substitutions to
![]() $\mathtt{ShLin}$
. We still use the polynomial notation to represent sharing groups, but now all the exponents are fixed to one. Note that the last component
$\mathtt{ShLin}$
. We still use the polynomial notation to represent sharing groups, but now all the exponents are fixed to one. Note that the last component
![]() $U$
in
$U$
in
![]() $[S,L,U]$
is redundant since it can be retrieved as
$[S,L,U]$
is redundant since it can be retrieved as
![]() $L \cup \mathrm{vars}(S)$
. This is because the set
$L \cup \mathrm{vars}(S)$
. This is because the set
![]() $L$
contains all the ground variables.
$L$
contains all the ground variables.
Example 5.1. Consider the substitution
![]() $[\theta ]_U = [\{x/s(y,u,y), z/s(u,u), v/u \}]_{w,x,y,z}$
in Example 3.2. Its abstraction in
$[\theta ]_U = [\{x/s(y,u,y), z/s(u,u), v/u \}]_{w,x,y,z}$
in Example 3.2. Its abstraction in
![]() $\mathtt{ShLin}$
is given by
$\mathtt{ShLin}$
is given by
Analogously, substitutions
![]() $[\theta _1]_{U_1} = [\{ x/r(w_1,w_2,w_2,w_3,w_3), y/a, z/r(w_1) \}]_{x,y,z}$
and
$[\theta _1]_{U_1} = [\{ x/r(w_1,w_2,w_2,w_3,w_3), y/a, z/r(w_1) \}]_{x,y,z}$
and
![]() $[\theta _2]_{U_2} = [\{ x/r(w_4, w_5, w_6, w_8, w_8), u/r(w_4,w_7), v/r(w_7,w_8)\}]_{u,v,x}$
from Example 3.3 are abstracted into
$[\theta _2]_{U_2} = [\{ x/r(w_4, w_5, w_6, w_8, w_8), u/r(w_4,w_7), v/r(w_7,w_8)\}]_{u,v,x}$
from Example 3.3 are abstracted into
![]() $[S_1,L_1,U_1]=[\{x, xz\},\{y, z\}, U_1]$
and
$[S_1,L_1,U_1]=[\{x, xz\},\{y, z\}, U_1]$
and
![]() $[S_2, L_2, U_2] = [\{ uv, ux, vx, x\}, \{u,v\}, U_2]$
, respectively.
$[S_2, L_2, U_2] = [\{ uv, ux, vx, x\}, \{u,v\}, U_2]$
, respectively.
5.2 Matching operator
We want to provide an optimal abstract matching operator for
![]() $\mathtt{ShLin}$
. We may effectively compute
$\mathtt{ShLin}$
. We may effectively compute
![]() $\mathsf{match}_{\mathit{sl}}$
by composing
$\mathsf{match}_{\mathit{sl}}$
by composing
![]() $\gamma _{\mathit{sl}}$
,
$\gamma _{\mathit{sl}}$
,
![]() $\mathsf{match}_{\mathrm{2}}$
, and
$\mathsf{match}_{\mathrm{2}}$
, and
![]() $\alpha _{\mathit{sl}}$
. However, we provide a more direct characterization of
$\alpha _{\mathit{sl}}$
. However, we provide a more direct characterization of
![]() $\mathsf{match}_{\mathit{sl}}$
, which may potentially improve performance.
$\mathsf{match}_{\mathit{sl}}$
, which may potentially improve performance.
First, we define the auxiliary function
![]() $nl: \mathscr{P}(\mathscr{P}({\mathcal{V}})) \rightarrow \mathscr{P}({\mathcal{V}})$
which takes a set
$nl: \mathscr{P}(\mathscr{P}({\mathcal{V}})) \rightarrow \mathscr{P}({\mathcal{V}})$
which takes a set
![]() $X$
of sharing groups and returns the set of variables that appear in
$X$
of sharing groups and returns the set of variables that appear in
![]() $X$
more than once. In formulas:
$X$
more than once. In formulas:
The name
![]() $nl$
stands for nonlinear since it is used to recover those variables that, after joining sharing groups in
$nl$
stands for nonlinear since it is used to recover those variables that, after joining sharing groups in
![]() $X$
, are definitively not linear.
$X$
, are definitively not linear.
Definition 5.2 (Matching over
![]() $\mathtt{ShLin}$
). Given
$\mathtt{ShLin}$
). Given
![]() $[S_1,L_1,U_1]$
and
$[S_1,L_1,U_1]$
and
![]() $[S_2,L_2,U_2] \in \mathtt{ShLin}$
, we define
$[S_2,L_2,U_2] \in \mathtt{ShLin}$
, we define
where
![]() $U=U_1 \cup U_2$
,
$U=U_1 \cup U_2$
,
![]() $S^{\prime}_2=\{ B \in S_2 \mid B \cap U_1 = \emptyset \}$
,
$S^{\prime}_2=\{ B \in S_2 \mid B \cap U_1 = \emptyset \}$
,
![]() $S^{\prime\prime}_2=S_2 \setminus S^{\prime}_2$
,
$S^{\prime\prime}_2=S_2 \setminus S^{\prime}_2$
,
![]() $\mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu = \{B \in S^{\prime\prime}_2 \mid B \cap L_1 = \emptyset \}$
and
$\mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu = \{B \in S^{\prime\prime}_2 \mid B \cap L_1 = \emptyset \}$
and
 \begin{align*} S^{\prime}_0 & = \bigl \{ \langle B, L_2 \rangle \mid B \in S^{\prime}_2 \bigr \}, \\ S^{\prime\prime}_0 & = \Big \{ \left \langle B \cup \bigcup X, L_2 \setminus nl(X) \setminus \bigcup (X \cap \mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu) \right \rangle \Bigm | B \in S_1, \\ & \qquad X \subseteq S^{\prime\prime}_2, B \cap U_2 = \left (\bigcup X\right ) \cap U_1, L_1 \cap nl(X)=\emptyset \Big \}, \end{align*}
\begin{align*} S^{\prime}_0 & = \bigl \{ \langle B, L_2 \rangle \mid B \in S^{\prime}_2 \bigr \}, \\ S^{\prime\prime}_0 & = \Big \{ \left \langle B \cup \bigcup X, L_2 \setminus nl(X) \setminus \bigcup (X \cap \mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu) \right \rangle \Bigm | B \in S_1, \\ & \qquad X \subseteq S^{\prime\prime}_2, B \cap U_2 = \left (\bigcup X\right ) \cap U_1, L_1 \cap nl(X)=\emptyset \Big \}, \end{align*}
 \begin{align*} s(H) & = \left \{ B \mid \langle B, L \rangle \in H \right \}, \\ l(H) & = \bigcap \left \{ L_1 \cup L \cup (U \setminus B) \mid \langle B,L \rangle \in H \right \}. \end{align*}
\begin{align*} s(H) & = \left \{ B \mid \langle B, L \rangle \in H \right \}, \\ l(H) & = \bigcap \left \{ L_1 \cup L \cup (U \setminus B) \mid \langle B,L \rangle \in H \right \}. \end{align*}
This operator is more complex than previous ones because linearity information is not connected to sharing groups and needs to be handled separately. In view of this and a similar situation that happens for unification (Amato and Scozzari, Reference Amato and Scozzari2010), it seems that the idea of embedding linearity within sharing groups from King (Reference King1994) was particularly insightful.
We give an intuitive explanation of
![]() $\mathsf{match}_{\mathit{sl}}$
. It essentially works by simulating the optimized version of
$\mathsf{match}_{\mathit{sl}}$
. It essentially works by simulating the optimized version of
![]() $\mathsf{match}_{\mathrm{2}}$
starting from
$\mathsf{match}_{\mathrm{2}}$
starting from
![]() $[T_1]_{U_1}=\gamma _{\mathrm{2}}([S_1,L_1,U_1])$
and
$[T_1]_{U_1}=\gamma _{\mathrm{2}}([S_1,L_1,U_1])$
and
![]() $[T_2]_{U_2}=\gamma _{\mathrm{2}}([S_2, L_2, U_2])$
. The sets
$[T_2]_{U_2}=\gamma _{\mathrm{2}}([S_2, L_2, U_2])$
. The sets
![]() $S^{\prime}_2$
and
$S^{\prime}_2$
and
![]() $S^{\prime\prime}_2$
are defined as for the other matching operators. Each element of
$S^{\prime\prime}_2$
are defined as for the other matching operators. Each element of
![]() $H$
,
$H$
,
![]() $S^{\prime}_0$
, or
$S^{\prime}_0$
, or
![]() $S^{\prime\prime}_0$
is a pair
$S^{\prime\prime}_0$
is a pair
![]() $\langle B, L \rangle$
that corresponds to the
$\langle B, L \rangle$
that corresponds to the
![]() $2$
-sharing group
$2$
-sharing group
![]() $B_{L \cup L_1}$
in
$B_{L \cup L_1}$
in
![]() $\mathsf{match}_{\mathrm{2}}([T_1]_{U_1}, [T_2]_{U_2})$
. The component
$\mathsf{match}_{\mathrm{2}}([T_1]_{U_1}, [T_2]_{U_2})$
. The component
![]() $B$
is the support of the
$B$
is the support of the
![]() $2$
-sharing group, while
$2$
-sharing group, while
![]() $L$
is the set of linear variables. We only record a subset of the linear variables, since those in
$L$
is the set of linear variables. We only record a subset of the linear variables, since those in
![]() $L_1$
are always linear.
$L_1$
are always linear.
The set
![]() $S^{\prime}_0$
encodes all the maximal
$S^{\prime}_0$
encodes all the maximal
![]() $2$
-sharing groups derived from
$2$
-sharing groups derived from
![]() $S^{\prime}_2$
. The set
$S^{\prime}_2$
. The set
![]() $S^{\prime\prime}_0$
encodes
$S^{\prime\prime}_0$
encodes
![]() $2$
-sharing groups which may be generated by gluing the sharing groups in
$2$
-sharing groups which may be generated by gluing the sharing groups in
![]() $S^{\prime\prime}_2$
in a way which is compatible with
$S^{\prime\prime}_2$
in a way which is compatible with
![]() $S_1$
. A given choice of
$S_1$
. A given choice of
![]() $X \subseteq T^{\prime\prime}_2$
is compatible with a sharing group
$X \subseteq T^{\prime\prime}_2$
is compatible with a sharing group
![]() $B \in S_1$
only if
$B \in S_1$
only if
![]() $\bigcup X$
and
$\bigcup X$
and
![]() $B$
have the same support on the common variables
$B$
have the same support on the common variables
![]() $U_1 \cap U_2$
and if
$U_1 \cap U_2$
and if
![]() $X$
does not conflict with the linearity of variables given by
$X$
does not conflict with the linearity of variables given by
![]() $L_1$
. This means that we cannot use a variable in
$L_1$
. This means that we cannot use a variable in
![]() $L_1$
more than once; therefore,
$L_1$
more than once; therefore,
![]() $L_1 \cap nl(X)=\emptyset$
. Note that we may use a variable
$L_1 \cap nl(X)=\emptyset$
. Note that we may use a variable
![]() $v \in L_1 \setminus L_2$
since
$v \in L_1 \setminus L_2$
since
![]() $v \notin L_2$
means that
$v \notin L_2$
means that
![]() $v$
is possibly, but not definitively, nonlinear. On the contrary, if
$v$
is possibly, but not definitively, nonlinear. On the contrary, if
![]() $v \in nl(X)$
, then
$v \in nl(X)$
, then
![]() $v$
is definitively nonlinear in the resultant sharing group. Once established that
$v$
is definitively nonlinear in the resultant sharing group. Once established that
![]() $X$
is compatible with
$X$
is compatible with
![]() $B$
, the set
$B$
, the set
![]() $\mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu$
plays the same role of
$\mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu$
plays the same role of
![]() $\mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu$
in Definition 4.6: we may join another copy of the sharing groups in
$\mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu$
in Definition 4.6: we may join another copy of the sharing groups in
![]() $X \cap \mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu$
, making all their variables nonlinear.
$X \cap \mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu$
, making all their variables nonlinear.
Finally, the maps
![]() $s$
and
$s$
and
![]() $l$
extract from
$l$
extract from
![]() $S^{\prime}_0$
and
$S^{\prime}_0$
and
![]() $S^{\prime\prime}_0$
, the set of all the sharing groups and the set of variables that are linear in all the sharing groups.
$S^{\prime\prime}_0$
, the set of all the sharing groups and the set of variables that are linear in all the sharing groups.
Example 5.3. Consider the substitutions in Example 5.1. According to the definition of
![]() $\mathsf{match}_{\mathit{sl}}$
, we have
$\mathsf{match}_{\mathit{sl}}$
, we have
![]() $S^{\prime}_2 = \{uv\}$
,
$S^{\prime}_2 = \{uv\}$
,
![]() $S^{\prime\prime}_2 = \mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu = \{ux, vx, x \}$
,
$S^{\prime\prime}_2 = \mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu = \{ux, vx, x \}$
,
![]() $S^{\prime}_0 = \{ \langle uv, \{ u,v \} \rangle \}$
, and
$S^{\prime}_0 = \{ \langle uv, \{ u,v \} \rangle \}$
, and
![]() $S^{\prime\prime}_0 = \{ \langle ux, \emptyset \rangle, \langle vx, \emptyset \rangle, \langle x, \emptyset \rangle, \langle uvx, \emptyset \rangle, \langle uxz, \emptyset \rangle, \langle vxz, \emptyset \rangle, \langle xz, \emptyset \rangle, \langle uvxz, \emptyset \rangle \}$
. The final result is
$S^{\prime\prime}_0 = \{ \langle ux, \emptyset \rangle, \langle vx, \emptyset \rangle, \langle x, \emptyset \rangle, \langle uvx, \emptyset \rangle, \langle uxz, \emptyset \rangle, \langle vxz, \emptyset \rangle, \langle xz, \emptyset \rangle, \langle uvxz, \emptyset \rangle \}$
. The final result is
Considering the results for
![]() $\mathsf{match}_{\mathrm{2}}$
in Example 4.4, we have
$\mathsf{match}_{\mathrm{2}}$
in Example 4.4, we have
 \begin{align*} &\alpha _{\mathit{sl}}(\mathsf{match}_{\mathrm{2}}([T_1]_{U_1},[T_2]_{U_2}))\\ &= \alpha _{\mathit{sl}}({\mathop{\downarrow }} [ uv, u^\infty v^\infty x^\infty, uxz, u^\infty x^\infty, v^\infty x^\infty, vxz, x^\infty, xz ]_{u,v,x,y,z} )\\ &= [\{ uv, uvx, uxz, ux, vx, vxz, x, xz\}, \{ y,z\},\{u,v,x,y,z\}] \end{align*}
\begin{align*} &\alpha _{\mathit{sl}}(\mathsf{match}_{\mathrm{2}}([T_1]_{U_1},[T_2]_{U_2}))\\ &= \alpha _{\mathit{sl}}({\mathop{\downarrow }} [ uv, u^\infty v^\infty x^\infty, uxz, u^\infty x^\infty, v^\infty x^\infty, vxz, x^\infty, xz ]_{u,v,x,y,z} )\\ &= [\{ uv, uvx, uxz, ux, vx, vxz, x, xz\}, \{ y,z\},\{u,v,x,y,z\}] \end{align*}
and
![]() $\mathsf{match}_{\mathit{sl}}([S_1,L_1,U_1],[S_2,L_2,U_2]) \gt \alpha _{\mathit{sl}}(\mathsf{match}_{\mathrm{2}}([T_1]_{U_1},[T_2]_{U_2}))$
. In particular, the sharing group
$\mathsf{match}_{\mathit{sl}}([S_1,L_1,U_1],[S_2,L_2,U_2]) \gt \alpha _{\mathit{sl}}(\mathsf{match}_{\mathrm{2}}([T_1]_{U_1},[T_2]_{U_2}))$
. In particular, the sharing group
![]() $uvxz$
does not appear in
$uvxz$
does not appear in
![]() $\alpha _{\mathit{sl}}(\mathsf{match}_{\mathrm{2}}([T_1]_{U_1},[T_2]_{U_2}))$
which proves that
$\alpha _{\mathit{sl}}(\mathsf{match}_{\mathrm{2}}([T_1]_{U_1},[T_2]_{U_2}))$
which proves that
![]() $\mathsf{match}_{\mathit{sl}}$
is not a complete abstraction of
$\mathsf{match}_{\mathit{sl}}$
is not a complete abstraction of
![]() $\mathsf{match}_{\mathrm{2}}$
. However, the next theorem shows that
$\mathsf{match}_{\mathrm{2}}$
. However, the next theorem shows that
![]() $\mathsf{match}_{\mathit{sl}}$
is optimal w.r.t.
$\mathsf{match}_{\mathit{sl}}$
is optimal w.r.t.
![]() $\mathsf{match}_{\mathrm{2}}$
and by composition also w.r.t.
$\mathsf{match}_{\mathrm{2}}$
and by composition also w.r.t.
![]() $\mathsf{match}_{\mathrm{\omega }}$
and
$\mathsf{match}_{\mathrm{\omega }}$
and
![]() $\mathsf{match}$
.
$\mathsf{match}$
.
Theorem 5.4 (Optimality of
![]() $\mathsf{match}_{\mathit{sl}}$
). The operator
$\mathsf{match}_{\mathit{sl}}$
). The operator
![]() $\mathsf{match}_{\mathit{sl}}$
is correct and optimal w.r.t.
$\mathsf{match}_{\mathit{sl}}$
is correct and optimal w.r.t.
![]() $\mathsf{match}_{\mathrm{2}}$
.
$\mathsf{match}_{\mathrm{2}}$
.
Proof We prove that, given
![]() $[S_1, L_1, U_1]$
and
$[S_1, L_1, U_1]$
and
![]() $[S_2, L_2, U_2] \in \mathtt{ShLin}$
, we have
$[S_2, L_2, U_2] \in \mathtt{ShLin}$
, we have
where
![]() $T_i = \{B_{L_i} \mid B \in S_i\}$
is the set of maximal elements of
$T_i = \{B_{L_i} \mid B \in S_i\}$
is the set of maximal elements of
![]() $\gamma _{\mathit{sl}}([S_i, L_i, U_i])$
and
$\gamma _{\mathit{sl}}([S_i, L_i, U_i])$
and
![]() $U=U_1 \cup U_2$
.
$U=U_1 \cup U_2$
.
Let us define the function
![]() $\gamma _0$
which maps a pair
$\gamma _0$
which maps a pair
![]() $\langle B, L \rangle$
with
$\langle B, L \rangle$
with
![]() $B, L \in \mathscr{P}({\mathcal{V}})$
to the
$B, L \in \mathscr{P}({\mathcal{V}})$
to the
![]() $2$
-sharing group
$2$
-sharing group
![]() $B_{L \cup L_1}$
. We show that, given
$B_{L \cup L_1}$
. We show that, given
![]() $H \subseteq \mathscr{P}({\mathcal{V}}) \times \mathscr{P}({\mathcal{V}})$
, we have
$H \subseteq \mathscr{P}({\mathcal{V}}) \times \mathscr{P}({\mathcal{V}})$
, we have
![]() $\alpha _{\mathit{sl}}([{\mathop{\downarrow }} \gamma _0(H)]_U) = [s(H), l(H), U]$
. Assume
$\alpha _{\mathit{sl}}([{\mathop{\downarrow }} \gamma _0(H)]_U) = [s(H), l(H), U]$
. Assume
![]() $\alpha _{\mathit{sl}}([{\mathop{\downarrow }} \gamma _0(S)]_U])=[R,V,U]$
. We have
$\alpha _{\mathit{sl}}([{\mathop{\downarrow }} \gamma _0(S)]_U])=[R,V,U]$
. We have
![]() $R= \{\lfloor \!\lfloor o \rfloor \!\rfloor \mid o \in{\mathop{\downarrow }} \gamma _0(S)\}= \{\lfloor \!\lfloor o \rfloor \!\rfloor \mid o \in \gamma _0(S)\}=\{ \lfloor \!\lfloor \gamma _o(\langle B,L \rangle ) \rfloor \!\rfloor \mid \langle B,L \rangle \in S \}=\{ B \mid \langle B,L \rangle \in S \} = s(S)$
and
$R= \{\lfloor \!\lfloor o \rfloor \!\rfloor \mid o \in{\mathop{\downarrow }} \gamma _0(S)\}= \{\lfloor \!\lfloor o \rfloor \!\rfloor \mid o \in \gamma _0(S)\}=\{ \lfloor \!\lfloor \gamma _o(\langle B,L \rangle ) \rfloor \!\rfloor \mid \langle B,L \rangle \in S \}=\{ B \mid \langle B,L \rangle \in S \} = s(S)$
and
![]() $V=\{ x\in U \mid \forall o \in{\mathop{\downarrow }} \gamma _0(S), o(x) \leq 1\} = \{ x \in U \mid \forall o \in \gamma _0(S), o(x) \leq 1\} = \{ x \in U \mid \forall \langle B, L \rangle \in S, B_{L \cup L_1}(x) \leq 1\} \} = \{ x \in U \mid \forall \langle B, L \rangle \in S, x \in L_1 \cup L \cup (U \setminus B) \} = \bigcap \{ L_1 \cup L \cup (U \setminus B) \mid \langle B, L \rangle \in S \} = l(S)$
.
$V=\{ x\in U \mid \forall o \in{\mathop{\downarrow }} \gamma _0(S), o(x) \leq 1\} = \{ x \in U \mid \forall o \in \gamma _0(S), o(x) \leq 1\} = \{ x \in U \mid \forall \langle B, L \rangle \in S, B_{L \cup L_1}(x) \leq 1\} \} = \{ x \in U \mid \forall \langle B, L \rangle \in S, x \in L_1 \cup L \cup (U \setminus B) \} = \bigcap \{ L_1 \cup L \cup (U \setminus B) \mid \langle B, L \rangle \in S \} = l(S)$
.
Therefore, if we prove that
![]() $\gamma _0(S^{\prime}_0 \cup S^{\prime\prime}_0) = \mathsf{match}^{\prime}_{\mathrm{2}}(T_1, U_1, T_2, U_2)$
, then we have
$\gamma _0(S^{\prime}_0 \cup S^{\prime\prime}_0) = \mathsf{match}^{\prime}_{\mathrm{2}}(T_1, U_1, T_2, U_2)$
, then we have
![]() $\mathsf{match}_{\mathit{sl}}([S_1,T_1,U_1],[S_2,T_2,U_2])= [s(S^{\prime}_0 \cup S^{\prime\prime}_0), l(S^{\prime}_0 \cup S^{\prime\prime}_0), U] = \alpha _{\mathit{sl}}([{\mathop{\downarrow }} \gamma _0(S^{\prime}_0 \cup S^{\prime\prime}_0)]_U]) = \alpha _{\mathit{sl}}({\mathop{\downarrow }} [\mathsf{match}^{\prime}_{\mathrm{2}}(T_1, U_1, T_2, U_2)]_{U}))$
.
$\mathsf{match}_{\mathit{sl}}([S_1,T_1,U_1],[S_2,T_2,U_2])= [s(S^{\prime}_0 \cup S^{\prime\prime}_0), l(S^{\prime}_0 \cup S^{\prime\prime}_0), U] = \alpha _{\mathit{sl}}([{\mathop{\downarrow }} \gamma _0(S^{\prime}_0 \cup S^{\prime\prime}_0)]_U]) = \alpha _{\mathit{sl}}({\mathop{\downarrow }} [\mathsf{match}^{\prime}_{\mathrm{2}}(T_1, U_1, T_2, U_2)]_{U}))$
.
Let us take
![]() $o \in \gamma _0(S^{\prime}_0 \cup S^{\prime\prime}_0)$
and prove
$o \in \gamma _0(S^{\prime}_0 \cup S^{\prime\prime}_0)$
and prove
![]() $o \in \mathsf{match}^{\prime}_{\mathrm{2}}(T_1, U_1, T_2, U_2)$
. If
$o \in \mathsf{match}^{\prime}_{\mathrm{2}}(T_1, U_1, T_2, U_2)$
. If
![]() $o=B_{L \cup L_1}$
for some
$o=B_{L \cup L_1}$
for some
![]() $\langle B,L \rangle \in S^{\prime}_0$
, then
$\langle B,L \rangle \in S^{\prime}_0$
, then
![]() $B \in S^{\prime}_2$
and
$B \in S^{\prime}_2$
and
![]() $L=L_2$
. Therefore,
$L=L_2$
. Therefore,
![]() $B_{L \cup L_1} = B_{L_2 \cup L_1} = B_{L_2} \in T_2$
since
$B_{L \cup L_1} = B_{L_2 \cup L_1} = B_{L_2} \in T_2$
since
![]() $B \cap U_1 = \emptyset$
. In particular,
$B \cap U_1 = \emptyset$
. In particular,
![]() $B_{L_2} \in T^{\prime}_2$
, hence
$B_{L_2} \in T^{\prime}_2$
, hence
![]() $B_{L_2} \in \mathsf{match}^{\prime}_{\mathrm{2}}(T_1, U_1, T_2, U_2)$
. Otherwise,
$B_{L_2} \in \mathsf{match}^{\prime}_{\mathrm{2}}(T_1, U_1, T_2, U_2)$
. Otherwise,
![]() $o= \gamma _0(\langle C, L \rangle )$
for
$o= \gamma _0(\langle C, L \rangle )$
for
![]() $\langle C, L \rangle \in S^{\prime\prime}_0$
, where
$\langle C, L \rangle \in S^{\prime\prime}_0$
, where
![]() $C = B \cup \bigcup X$
and
$C = B \cup \bigcup X$
and
![]() $L=L_2 \setminus nl(X) \setminus \bigcup (X \cap \mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu)$
according to Definition 5.2. For each sharing group
$L=L_2 \setminus nl(X) \setminus \bigcup (X \cap \mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu)$
according to Definition 5.2. For each sharing group
![]() $B^{\prime} \in X$
, consider the
$B^{\prime} \in X$
, consider the
![]() $2$
-sharing group
$2$
-sharing group
![]() $B^{\prime}_{L_2} \in T^{\prime\prime}_2$
, and let
$B^{\prime}_{L_2} \in T^{\prime\prime}_2$
, and let
![]() $Y$
be the set of all those
$Y$
be the set of all those
![]() $2$
-sharing groups. We want to prove that
$2$
-sharing groups. We want to prove that
![]() $o$
is generated by
$o$
is generated by
![]() $B_{L_1} \in T_1$
and
$B_{L_1} \in T_1$
and
![]() $Y \subseteq T^{\prime\prime}_2$
, according to Definition 4.6. First, note that
$Y \subseteq T^{\prime\prime}_2$
, according to Definition 4.6. First, note that
![]() $\lfloor \!\lfloor (\biguplus \lfloor \!\lfloor Y \rfloor \!\rfloor )_{|U_1} \rfloor \!\rfloor =\lfloor \!\lfloor (\biguplus X)_{|U_1} \rfloor \!\rfloor = (\bigcup X) \cap U_1 = B \cap U_2 = \lfloor \!\lfloor (B_{L_1})_{|U_2} \rfloor \!\rfloor$
. Now, assume
$\lfloor \!\lfloor (\biguplus \lfloor \!\lfloor Y \rfloor \!\rfloor )_{|U_1} \rfloor \!\rfloor =\lfloor \!\lfloor (\biguplus X)_{|U_1} \rfloor \!\rfloor = (\bigcup X) \cap U_1 = B \cap U_2 = \lfloor \!\lfloor (B_{L_1})_{|U_2} \rfloor \!\rfloor$
. Now, assume
![]() $v \in \lfloor \!\lfloor (B_{L_1})_{|U_2} \rfloor \!\rfloor$
. If
$v \in \lfloor \!\lfloor (B_{L_1})_{|U_2} \rfloor \!\rfloor$
. If
![]() $v$
is linear in
$v$
is linear in
![]() $(B_{L_1})_{|U_2}$
, then
$(B_{L_1})_{|U_2}$
, then
![]() $v \in L_1$
, hence
$v \in L_1$
, hence
![]() $v \notin nl(X)$
and
$v \notin nl(X)$
and
![]() $v$
is linear in
$v$
is linear in
![]() $(\biguplus X)_{|U_1}=(\biguplus \lfloor \!\lfloor Y \rfloor \!\rfloor )_{|U_1}$
. Therefore,
$(\biguplus X)_{|U_1}=(\biguplus \lfloor \!\lfloor Y \rfloor \!\rfloor )_{|U_1}$
. Therefore,
![]() $Y$
is a valid choice for
$Y$
is a valid choice for
![]() $\mathsf{match}_{\mathrm{2}}^{\prime}$
and
$\mathsf{match}_{\mathrm{2}}^{\prime}$
and
![]() $\mathsf{match}^{\prime}_{\mathrm{2}}(B)$
generates
$\mathsf{match}^{\prime}_{\mathrm{2}}(B)$
generates
![]() $o^{\prime}=(B_{L_1} \wedge \biguplus Y) \uplus \biguplus (Y \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu)$
. We prove
$o^{\prime}=(B_{L_1} \wedge \biguplus Y) \uplus \biguplus (Y \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu)$
. We prove
![]() $o^{\prime}=o$
.
$o^{\prime}=o$
.
First, we prove that
![]() $B^{\prime} \in \mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu$
iff
$B^{\prime} \in \mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu$
iff
![]() $B^{\prime}_{L_2} \in \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu$
. We have
$B^{\prime}_{L_2} \in \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu$
. We have
![]() $B^{\prime}_{L_2} \in \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu$
iff
$B^{\prime}_{L_2} \in \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu$
iff
![]() $B^{\prime}_{L_2} \in T^{\prime\prime}_2$
and
$B^{\prime}_{L_2} \in T^{\prime\prime}_2$
and
![]() $\forall v \in \lfloor \!\lfloor B^{\prime}_{L_2} \rfloor \!\rfloor \cap U_1, B^{\prime}_{L_1}(v)=\infty$
, iff
$\forall v \in \lfloor \!\lfloor B^{\prime}_{L_2} \rfloor \!\rfloor \cap U_1, B^{\prime}_{L_1}(v)=\infty$
, iff
![]() $B^{\prime} \in S^{\prime\prime}_2$
and
$B^{\prime} \in S^{\prime\prime}_2$
and
![]() $\forall v \in B^{\prime} \cap U_1$
,
$\forall v \in B^{\prime} \cap U_1$
,
![]() $v \notin L_1$
iff
$v \notin L_1$
iff
![]() $B^{\prime} \cap L_1 = \emptyset$
iff
$B^{\prime} \cap L_1 = \emptyset$
iff
![]() $B^{\prime} \in S^{\prime\prime}_2$
and
$B^{\prime} \in S^{\prime\prime}_2$
and
![]() $B^{\prime} \cap L_1=\emptyset$
iff
$B^{\prime} \cap L_1=\emptyset$
iff
![]() $B \in S$
.
$B \in S$
.
Now, it is immediate to check that,
![]() $\lfloor \!\lfloor o \rfloor \!\rfloor = B \cup \bigcup X =\lfloor \!\lfloor o^{\prime} \rfloor \!\rfloor$
. Then, consider
$\lfloor \!\lfloor o \rfloor \!\rfloor = B \cup \bigcup X =\lfloor \!\lfloor o^{\prime} \rfloor \!\rfloor$
. Then, consider
![]() $v \in \lfloor \!\lfloor o^{\prime} \rfloor \!\rfloor$
. We have that
$v \in \lfloor \!\lfloor o^{\prime} \rfloor \!\rfloor$
. We have that
 \begin{align*} & o^{\prime}(v)=1 \Leftrightarrow \\ & (B_{L_1}(v)=1 \vee \left (\biguplus Y\right )(v)=1) \wedge \left (\biguplus (Y \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu)\right )=0 \Leftrightarrow \\ & (v \in L_1 \vee (v \in L_2 \setminus nl(X))) \wedge v \notin \bigcup (X \cap \mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu) \Leftrightarrow \\ & v \in L_1 \vee (v \in L_2 \setminus nl(X) \setminus \bigcup (X \cap \mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu) \Leftrightarrow \\ & v \in L_1 \vee v \in L \Leftrightarrow \\ & B_{L \cup L_1}(v) = o(v)=1 \end{align*}
\begin{align*} & o^{\prime}(v)=1 \Leftrightarrow \\ & (B_{L_1}(v)=1 \vee \left (\biguplus Y\right )(v)=1) \wedge \left (\biguplus (Y \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu)\right )=0 \Leftrightarrow \\ & (v \in L_1 \vee (v \in L_2 \setminus nl(X))) \wedge v \notin \bigcup (X \cap \mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu) \Leftrightarrow \\ & v \in L_1 \vee (v \in L_2 \setminus nl(X) \setminus \bigcup (X \cap \mkern 1.5mu\overline{\mkern -1.5muS\mkern -1.5mu}\mkern 1.5mu) \Leftrightarrow \\ & v \in L_1 \vee v \in L \Leftrightarrow \\ & B_{L \cup L_1}(v) = o(v)=1 \end{align*}
It remains to prove that given
![]() $o \in \mathsf{match}^{\prime}_{\mathrm{2}}(T_1, U_1, T_2, U_2)$
, we have
$o \in \mathsf{match}^{\prime}_{\mathrm{2}}(T_1, U_1, T_2, U_2)$
, we have
![]() $o \in \gamma _0(S^{\prime}_0 \cup S^{\prime\prime}_0)$
. If
$o \in \gamma _0(S^{\prime}_0 \cup S^{\prime\prime}_0)$
. If
![]() $o \in T^{\prime}_2$
, then
$o \in T^{\prime}_2$
, then
![]() $o=B_{L_2}$
with
$o=B_{L_2}$
with
![]() $B \in S^{\prime}_2$
. Therefore,
$B \in S^{\prime}_2$
. Therefore,
![]() $\langle B, L_2 \rangle \in S^{\prime}_0$
and
$\langle B, L_2 \rangle \in S^{\prime}_0$
and
![]() $o= \gamma _0(\langle B,L_2 \rangle )$
. Otherwise,
$o= \gamma _0(\langle B,L_2 \rangle )$
. Otherwise,
![]() $o=(o^{\prime} \wedge \biguplus Y) \uplus \biguplus (Y \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu)$
. We know
$o=(o^{\prime} \wedge \biguplus Y) \uplus \biguplus (Y \cap \mkern 1.5mu\overline{\mkern -1.5muT\mkern -1.5mu}\mkern 1.5mu)$
. We know
![]() $o^{\prime}=B^{\prime}_{L_1}$
with
$o^{\prime}=B^{\prime}_{L_1}$
with
![]() $B^{\prime} \in S_1$
and let
$B^{\prime} \in S_1$
and let
![]() $X=\{ \lfloor \!\lfloor o^{\prime\prime} \rfloor \!\rfloor \mid o^{\prime\prime} \in Y \}$
. By Definition 4.6,
$X=\{ \lfloor \!\lfloor o^{\prime\prime} \rfloor \!\rfloor \mid o^{\prime\prime} \in Y \}$
. By Definition 4.6,
![]() $\bigcup X \cap U_1 = \lfloor \!\lfloor \uplus Y \rfloor \!\rfloor \cap U_1 = \lfloor \!\lfloor o^{\prime} \rfloor \!\rfloor \cap U_2 = B^{\prime} \cap U_2$
. Moreover, if
$\bigcup X \cap U_1 = \lfloor \!\lfloor \uplus Y \rfloor \!\rfloor \cap U_1 = \lfloor \!\lfloor o^{\prime} \rfloor \!\rfloor \cap U_2 = B^{\prime} \cap U_2$
. Moreover, if
![]() $v \in L_1$
, then
$v \in L_1$
, then
![]() $o^{\prime}(v) \leq 1$
, and therefore,
$o^{\prime}(v) \leq 1$
, and therefore,
![]() $v$
cannot appear twice in
$v$
cannot appear twice in
![]() $Y$
, which means
$Y$
, which means
![]() $v \notin nl(X)$
; hence
$v \notin nl(X)$
; hence
![]() $L_1 \cap nl(X) = \emptyset$
. Therefore,
$L_1 \cap nl(X) = \emptyset$
. Therefore,
![]() $B^{\prime}$
and
$B^{\prime}$
and
![]() $X$
make a valid choice for
$X$
make a valid choice for
![]() $\mathsf{match}_{\mathit{sl}}$
and generate the pair
$\mathsf{match}_{\mathit{sl}}$
and generate the pair
Using the first half of the proof, it is easy to check that
![]() $B_{L \cup L^{\prime}} = o$
, which terminates the proof.
$B_{L \cup L^{\prime}} = o$
, which terminates the proof.
6 Evaluation of matching in goal-dependent analysis
We now show two examples, in the context of goal-dependent analysis, where the newly introduced matching operators improve the precision w.r.t. what is attainable using only the mgu operators in Amato and Scozzari (Reference Amato and Scozzari2010).
6.1 Matching and backward unification
First, we show with a simple example how the matching operator strictly improves the result of a standard goal-dependent analysis using forward and backward unification. Consider the goal
![]() $p(x,f(x,z),z)$
with the (abstract) call substitution
$p(x,f(x,z),z)$
with the (abstract) call substitution
![]() $[x,z]_{xz}$
and the trivial program with just one clause:
$[x,z]_{xz}$
and the trivial program with just one clause:
![]() $p(u,v,w).$
$p(u,v,w).$
In order to analyze the goal, we first need to perform the forward unification between the call substitution
![]() $[x,z]_{xz}$
, the goal
$[x,z]_{xz}$
, the goal
![]() $p(x,f(x,z),z)$
, and the head of the clause
$p(x,f(x,z),z)$
, and the head of the clause
![]() $p(u,v,w)$
, and then project the result on the variables of the clause. In order to keep the notation simple, we do not perform renaming, unless necessary. This amounts to computing:
$p(u,v,w)$
, and then project the result on the variables of the clause. In order to keep the notation simple, we do not perform renaming, unless necessary. This amounts to computing:
By projecting the result on the variables of the clause, we obtain the entry substitution
![]() $[uv, vw]_{uvw}$
. Since the clause has no body, it is immediate to see that the exit substitution coincides with the entry substitution.
$[uv, vw]_{uvw}$
. Since the clause has no body, it is immediate to see that the exit substitution coincides with the entry substitution.
We now need to compute the backward unification of the exit substitution
![]() $[uv, vw]_{uvw}$
, the call substitution
$[uv, vw]_{uvw}$
, the call substitution
![]() $[x, z]_{xz}$
and
$[x, z]_{xz}$
and
![]() $\theta =\{u/x, v/f(x,z), w/z\}$
. If we implement this operator with the aid of matching, we may first unify
$\theta =\{u/x, v/f(x,z), w/z\}$
. If we implement this operator with the aid of matching, we may first unify
![]() $[x, z]_{xz}$
with
$[x, z]_{xz}$
with
![]() $\theta$
, obtaining
$\theta$
, obtaining
![]() $[uvx, vwz]_{uvwxz}$
as above, and then apply the matching with the exit substitution
$[uvx, vwz]_{uvwxz}$
as above, and then apply the matching with the exit substitution
![]() $[uv, vw]_{uvw}$
obtaining
$[uv, vw]_{uvw}$
obtaining
By projecting the result on the variables of the goal, we obtain the result
![]() $[x, z]_{xz}$
, which proves that
$[x, z]_{xz}$
, which proves that
![]() $x$
and
$x$
and
![]() $z$
do not share.
$z$
do not share.
On the contrary, if we avoid matching, the backward-unification operator must unify
![]() $[x, z]_{xz}$
with
$[x, z]_{xz}$
with
![]() $[uv, vw]_{uvw}$
and
$[uv, vw]_{uvw}$
and
![]() $\theta$
in any order it deems fit. However, this means that the operator must correctly approximate the mgu of any substitution
$\theta$
in any order it deems fit. However, this means that the operator must correctly approximate the mgu of any substitution
![]() $\theta _1$
in the concretization of the call substitution
$\theta _1$
in the concretization of the call substitution
![]() $[x,z]_{xz}$
, with any substitution
$[x,z]_{xz}$
, with any substitution
![]() $\theta _2$
in the concretization of the exit substitution
$\theta _2$
in the concretization of the exit substitution
![]() $[uv, vw]_{uvw}$
and
$[uv, vw]_{uvw}$
and
![]() $\theta =\{u/x, v/f(x,z), w/z\}$
. If we choose
$\theta =\{u/x, v/f(x,z), w/z\}$
. If we choose
![]() $\theta _1 = \epsilon$
and
$\theta _1 = \epsilon$
and
![]() $\theta _2 = \{v/f(w,u)\}$
, we obtain that the unification of
$\theta _2 = \{v/f(w,u)\}$
, we obtain that the unification of
![]() $\theta _1$
,
$\theta _1$
,
![]() $\theta _2$
, and
$\theta _2$
, and
![]() $\theta$
is
$\theta$
is
which is not in the concretization of
![]() $[uvx, vwz]_{uvwxz}$
since
$[uvx, vwz]_{uvwxz}$
since
![]() $u$
,
$u$
,
![]() $v$
, and
$v$
, and
![]() $w$
share a common variable. Moreover, in this substitution,
$w$
share a common variable. Moreover, in this substitution,
![]() $x$
and
$x$
and
![]() $z$
share. This means that, after the projection on the variables of the goals
$z$
share. This means that, after the projection on the variables of the goals
![]() $x$
and
$x$
and
![]() $z$
, the result will always include the
$z$
, the result will always include the
![]() $\omega$
-sharing group
$\omega$
-sharing group
![]() $xz$
. Note that this consideration holds for any correct abstract unification operator that avoids matching.
$xz$
. Note that this consideration holds for any correct abstract unification operator that avoids matching.
It is worth noting that the above example, with minimal changes, also works for
![]() $\mathtt{ShLin}^2$
and
$\mathtt{ShLin}^2$
and
![]() $\mathtt{ShLin}$
: also in these cases, matching improves the precision of the analysis.
$\mathtt{ShLin}$
: also in these cases, matching improves the precision of the analysis.
6.2 Example on a nontrivial program
Consider a program implementing the
![]() $\mathit{member}$
predicate. Using the Prolog notation for lists, we have
$\mathit{member}$
predicate. Using the Prolog notation for lists, we have
![]() $\mathit{member}(u, [u|v]).$
$\mathit{member}(u, [u|v]).$
![]() $\mathit{member}(u, [v|w]) \leftarrow \mathit{member}(u, w).$
$\mathit{member}(u, [v|w]) \leftarrow \mathit{member}(u, w).$
We want to analyze the goal
![]() $\mathit{member}(x,[y])$
in the domain
$\mathit{member}(x,[y])$
in the domain
![]() $\mathtt{ShLin}^2$
using the call substitution
$\mathtt{ShLin}^2$
using the call substitution
![]() $[xy, xz]_{xyz}$
.
$[xy, xz]_{xyz}$
.
We start by considering the first clause of
![]() $\mathit{member}$
. The concrete unification of the goal
$\mathit{member}$
. The concrete unification of the goal
![]() $\mathit{member}(x,[y])$
and the head of the clause
$\mathit{member}(x,[y])$
and the head of the clause
![]() $\mathit{member}(u, [u|v])$
yields the most general unifier
$\mathit{member}(u, [u|v])$
yields the most general unifier
![]() $\theta = \{ x/u, y/u, v/[] \}$
. Forward unification computes the entry substitution as the abstract mgu between the call substitution
$\theta = \{ x/u, y/u, v/[] \}$
. Forward unification computes the entry substitution as the abstract mgu between the call substitution
![]() $[xy, xz]_{xyz}$
and
$[xy, xz]_{xyz}$
and
![]() $\theta$
. Proceeding one binding at a time, we have
$\theta$
. Proceeding one binding at a time, we have
-
•
 $\mathsf{mgu}_{\mathrm{2}}([xy, xz]_{xyz}, \{x/u\}) = [uxy, uxz]_{uxyz}$
;
$\mathsf{mgu}_{\mathrm{2}}([xy, xz]_{xyz}, \{x/u\}) = [uxy, uxz]_{uxyz}$
; -
•
 $\mathsf{mgu}_{\mathrm{2}}([uxy, uxz]_{uxyz}, \{y/u\}) ={\mathop{\downarrow }} [u^\infty x^\infty y^\infty ]_{uxyz}$
;
$\mathsf{mgu}_{\mathrm{2}}([uxy, uxz]_{uxyz}, \{y/u\}) ={\mathop{\downarrow }} [u^\infty x^\infty y^\infty ]_{uxyz}$
; -
•
 $\mathsf{mgu}_{\mathrm{2}}({\mathop{\downarrow }} [u^\infty x^\infty y^\infty ]_{uxyz}, \{v/[]\} ) ={\mathop{\downarrow }} [u^\infty x^\infty y^\infty ]_{uvxyz}$
.
$\mathsf{mgu}_{\mathrm{2}}({\mathop{\downarrow }} [u^\infty x^\infty y^\infty ]_{uxyz}, \{v/[]\} ) ={\mathop{\downarrow }} [u^\infty x^\infty y^\infty ]_{uvxyz}$
.
Projecting over the variables of the clause, we get the entry substitution
![]() ${\mathop{\downarrow }} [u^\infty ]_{uv}$
. Since this clause has no body, the entry substitution is equal to the exit substitution, and we may proceed to compute the answer substitution through backward unification.
${\mathop{\downarrow }} [u^\infty ]_{uv}$
. Since this clause has no body, the entry substitution is equal to the exit substitution, and we may proceed to compute the answer substitution through backward unification.
First, we consider the case when the backward unification is performed using the standard
![]() $\mathsf{mgu}_{\mathrm{2}}$
operator. We need to unify the call substitution
$\mathsf{mgu}_{\mathrm{2}}$
operator. We need to unify the call substitution
![]() $[xy, xz]_{xyz}$
, the exit substitution
$[xy, xz]_{xyz}$
, the exit substitution
![]() ${\mathop{\downarrow }} [u^\infty ]_{uv}$
, and the concrete substitution
${\mathop{\downarrow }} [u^\infty ]_{uv}$
, and the concrete substitution
![]() $\theta$
(the same as before). Unifying call and exit substitution is immediate since they are relative to disjoint variables of interest: the result is
$\theta$
(the same as before). Unifying call and exit substitution is immediate since they are relative to disjoint variables of interest: the result is
![]() ${\mathop{\downarrow }} [u^\infty, xy, xz]_{uvxyz}$
, obtained by collecting all sharing groups together. This should be unified with
${\mathop{\downarrow }} [u^\infty, xy, xz]_{uvxyz}$
, obtained by collecting all sharing groups together. This should be unified with
![]() $\theta$
. Proceeding one binding at a time, and omitting the set of variables of interest since it does not change, we have
$\theta$
. Proceeding one binding at a time, and omitting the set of variables of interest since it does not change, we have
-
•
 $\mathsf{mgu}_{\mathrm{2}}({\mathop{\downarrow }} [u^\infty, xy, xz], \{x/u\}) ={\mathop{\downarrow }} [u^\infty x^\infty y^\infty, u^\infty x^\infty y^\infty z^\infty, u^\infty x^\infty z^\infty ]$
;
$\mathsf{mgu}_{\mathrm{2}}({\mathop{\downarrow }} [u^\infty, xy, xz], \{x/u\}) ={\mathop{\downarrow }} [u^\infty x^\infty y^\infty, u^\infty x^\infty y^\infty z^\infty, u^\infty x^\infty z^\infty ]$
; -
•
 $\mathsf{mgu}_{\mathrm{2}}({\mathop{\downarrow }} [u^\infty x^\infty y^\infty, u^\infty x^\infty y^\infty z^\infty, u^\infty x^\infty z^\infty ], \{y/u\}) ={\mathop{\downarrow }} [u^\infty x^\infty y^\infty, u^\infty x^\infty y^\infty z^\infty ]$
;
$\mathsf{mgu}_{\mathrm{2}}({\mathop{\downarrow }} [u^\infty x^\infty y^\infty, u^\infty x^\infty y^\infty z^\infty, u^\infty x^\infty z^\infty ], \{y/u\}) ={\mathop{\downarrow }} [u^\infty x^\infty y^\infty, u^\infty x^\infty y^\infty z^\infty ]$
; -
•
 $\mathsf{mgu}_{\mathrm{2}}({\mathop{\downarrow }} [u^\infty x^\infty y^\infty, u^\infty x^\infty y^\infty z^\infty ],\{v/[]\})={\mathop{\downarrow }} [u^\infty x^\infty y^\infty, u^\infty x^\infty y^\infty z^\infty ]$
.
$\mathsf{mgu}_{\mathrm{2}}({\mathop{\downarrow }} [u^\infty x^\infty y^\infty, u^\infty x^\infty y^\infty z^\infty ],\{v/[]\})={\mathop{\downarrow }} [u^\infty x^\infty y^\infty, u^\infty x^\infty y^\infty z^\infty ]$
.
Projecting over the set of variables in the goal, we get
![]() ${\mathop{\downarrow }} [x^\infty y^\infty, x^\infty y^\infty z^\infty ]_{xyz}$
.
${\mathop{\downarrow }} [x^\infty y^\infty, x^\infty y^\infty z^\infty ]_{xyz}$
.
On the contrary, if we perform backward unification using the matching operation, we need to compute the matching of the exit substitution
![]() $[u^\infty ]_{uv}$
with the entry substitution before variable projection
$[u^\infty ]_{uv}$
with the entry substitution before variable projection
![]() $[u^\infty x^\infty y^\infty ]_{uvxyz}$
, namely:
$[u^\infty x^\infty y^\infty ]_{uvxyz}$
, namely:
Projecting over the variables of the goal, we get
![]() ${\mathop{\downarrow }} [x^\infty y^\infty ]_{xyz}$
: using matching we can prove that
${\mathop{\downarrow }} [x^\infty y^\infty ]_{xyz}$
: using matching we can prove that
![]() $z$
is ground in the answer substitution.
$z$
is ground in the answer substitution.
However, we still need to check what happens when we analyze the second clause of the
![]() $\mathit{member}$
predicate. In this case, the concrete unification between
$\mathit{member}$
predicate. In this case, the concrete unification between
![]() $\mathit{member}(x, [y])$
and
$\mathit{member}(x, [y])$
and
![]() $\mathit{member}(u, [v|w])$
gives the substitution
$\mathit{member}(u, [v|w])$
gives the substitution
![]() $\theta = \{x/u, y/v, w/[]\}$
. Then, forward unification between the call substitution and
$\theta = \{x/u, y/v, w/[]\}$
. Then, forward unification between the call substitution and
![]() $\theta$
gives
$\theta$
gives
-
•
 $\mathsf{mgu}_{\mathrm{2}}([xy, xz]_{xyz}, \{x/u\}) = [uxy, uxz]_{uxyz}$
;
$\mathsf{mgu}_{\mathrm{2}}([xy, xz]_{xyz}, \{x/u\}) = [uxy, uxz]_{uxyz}$
; -
•
 $\mathsf{mgu}_{\mathrm{2}}([uxy, uxz]_{uxyz}, \{y/v\}) = [uvxy, uxz]_{uvxyz}$
;
$\mathsf{mgu}_{\mathrm{2}}([uxy, uxz]_{uxyz}, \{y/v\}) = [uvxy, uxz]_{uvxyz}$
; -
•
 $\mathsf{mgu}_{\mathrm{2}}([uvxy, uxz]_{uvxyz}, \{w/[]\}) = [uvxy, uxz]_{uvwxyz}$
.
$\mathsf{mgu}_{\mathrm{2}}([uvxy, uxz]_{uvxyz}, \{w/[]\}) = [uvxy, uxz]_{uvwxyz}$
.
Projecting over the variables of the clause, we get the entry substitution
![]() $[uv, v]_{uvw}$
.
$[uv, v]_{uvw}$
.
Now we should compute the answer substitution of the body
![]() $\mathit{member}(u, w)$
under the call substitution
$\mathit{member}(u, w)$
under the call substitution
![]() $[uv, u]_{uvw}$
. We could proceed by showing all the details, but we try to be more concise. In the abstract substitution
$[uv, u]_{uvw}$
. We could proceed by showing all the details, but we try to be more concise. In the abstract substitution
![]() $[uv, w]_{uvw}$
, the variable
$[uv, w]_{uvw}$
, the variable
![]() $w$
is known to be ground. When
$w$
is known to be ground. When
![]() $\mathit{member}$
is called with its second argument ground, the first argument becomes ground too. This property is easily captured by
$\mathit{member}$
is called with its second argument ground, the first argument becomes ground too. This property is easily captured by
![]() $\mathtt{Sharing}$
and more precise domains, independently of the fact that we use matching or not for the backward unification. Therefore, we can conclude that the answer substitution for the goal
$\mathtt{Sharing}$
and more precise domains, independently of the fact that we use matching or not for the backward unification. Therefore, we can conclude that the answer substitution for the goal
![]() $\mathit{member}(u, w)$
under the entry substitution
$\mathit{member}(u, w)$
under the entry substitution
![]() $[uv, u]_{uvw}$
is
$[uv, u]_{uvw}$
is
![]() $[\emptyset ]_{uvw}$
. Although we do not generally write the empty
$[\emptyset ]_{uvw}$
. Although we do not generally write the empty
![]() $\mathrm{2}$
-sharing group
$\mathrm{2}$
-sharing group
![]() $\emptyset$
in an element of
$\emptyset$
in an element of
![]() $\mathtt{ShLin}^2$
, in this case, it is important to write it in order to distinguish
$\mathtt{ShLin}^2$
, in this case, it is important to write it in order to distinguish
![]() $[\emptyset ]_{uvw}$
, denoting those substitutions in which
$[\emptyset ]_{uvw}$
, denoting those substitutions in which
![]() $u, v, w$
are ground, from
$u, v, w$
are ground, from
![]() $[]_{uvw}$
, denoting a non-succeeding derivation.
$[]_{uvw}$
, denoting a non-succeeding derivation.
Performing the backward unification of
![]() $[\emptyset ]_{uvw}$
, we get the answer substitution
$[\emptyset ]_{uvw}$
, we get the answer substitution
![]() $[\emptyset ]_{xyz}$
, independently of the use of matching.
$[\emptyset ]_{xyz}$
, independently of the use of matching.
Putting together the results we got for analyzing the goal
![]() $\mathit{member}(x, [y])$
according to the two clauses of the program, we have shown that using matching, we get
$\mathit{member}(x, [y])$
according to the two clauses of the program, we have shown that using matching, we get
![]() $[x^\infty y^\infty ]_{xyz}$
, while using standard unification, we get
$[x^\infty y^\infty ]_{xyz}$
, while using standard unification, we get
![]() $[x^\infty y^\infty, x^\infty y^\infty z^\infty ]_{xyz}$
, and we are not able to prove that
$[x^\infty y^\infty, x^\infty y^\infty z^\infty ]_{xyz}$
, and we are not able to prove that
![]() $z$
is ground after the goal returns.
$z$
is ground after the goal returns.
7 Conclusion
In this paper, we have extended the domain
![]() $\mathtt{ShLin}^{\omega }$
(Amato and Scozzari, Reference Amato and Scozzari2010) to goal-dependent analysis, by introducing a matching operator, and proved its optimality. From this operator, we have derived the optimal matching operators for the well-known
$\mathtt{ShLin}^{\omega }$
(Amato and Scozzari, Reference Amato and Scozzari2010) to goal-dependent analysis, by introducing a matching operator, and proved its optimality. From this operator, we have derived the optimal matching operators for the well-known
![]() $\mathtt{ShLin}^2$
(King, Reference King1994) and
$\mathtt{ShLin}^2$
(King, Reference King1994) and
![]() $\mathtt{Sharing} \times \mathtt{Lin}$
(Muthukumar and Hermenegildo, Reference Muthukumar and Hermenegildo1992) abstract domains.
$\mathtt{Sharing} \times \mathtt{Lin}$
(Muthukumar and Hermenegildo, Reference Muthukumar and Hermenegildo1992) abstract domains.
As far as we know, this is the first paper that shows matching optimality results for domains combining sharing and linearity information. In particular, the matching operators presented in Hans and Winkler (Reference Hans and Winkler1992) and King (Reference King2000) for the domain SFL, which combines set-sharing, linearity, and freeness information, are not optimal, as shown by Amato and Scozzari (Reference Amato and Scozzari2009).
Recently logic programming has been used as an intermediate representation for the analysis of imperative or object-oriented programs and services (see, e.g., Peralta et al. (Reference Peralta, Gallagher and Sağlam1998); Henriksen and Gallagher (Reference Henriksen and Gallagher2006); Benton and Fischer (Reference Benton and Fischer2007); Méndez-Lojo et al., (2008); Spoto et al. (Reference Spoto, Mesnard and Payet2010); Albert et al. (Reference Albert, Arenas, Genaim, Puebla and Zanardini2012); Ivanović et al., (Reference Ivanović, Carro and Hermenegildo2013); Gange et al. (Reference Gange, Navas, Schachte, Søndergaard and Stuckey2015); De Angelis et al. (Reference De Angelis, Fioravanti, Gallagher, Hermenegildo, Pettorossi and Proietti2021)). Since many of these approaches use existing logic program analysis on the transformed program, we believe that they can benefit from more precise logic program analysis.
Acknowledgements
We acknowledge the support of the PNRR project FAIR - Future AI Research (PE00000013), Spoke 9 - Green-aware AI, under the NRRP MUR program funded by the NextGenerationEU.
Competing interests
The authors declare none.