Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-04T19:02:26.221Z Has data issue: false hasContentIssue false
  • English
  • Français

On the cooperation of the constraint domains ℋ, ℛ, and ℱ in CFLP

Published online by Cambridge University Press:  01 July 2009

S. ESTÉVEZ-MARTÍN ,
T. HORTALÁ-GONZÁLEZ ,
M. RODRÍGUEZ-ARTALEJO ,
R. DEL VADO-VÍRSEDA ,
F. SÁENZ-PÉREZ  and
A. J. FERNÁNDEZ
S. ESTÉVEZ-MARTÍN
Affiliation:
Dpto. de Sistemas Informáticos y Computación, Universidad Complutense de Madrid, Spain (e-mail: [email protected], [email protected], [email protected], [email protected])
T. HORTALÁ-GONZÁLEZ
Affiliation:
Dpto. de Sistemas Informáticos y Computación, Universidad Complutense de Madrid, Spain (e-mail: [email protected], [email protected], [email protected], [email protected])
M. RODRÍGUEZ-ARTALEJO
Affiliation:
Dpto. de Sistemas Informáticos y Computación, Universidad Complutense de Madrid, Spain (e-mail: [email protected], [email protected], [email protected], [email protected])
R. DEL VADO-VÍRSEDA
Affiliation:
Dpto. de Sistemas Informáticos y Computación, Universidad Complutense de Madrid, Spain (e-mail: [email protected], [email protected], [email protected], [email protected])
F. SÁENZ-PÉREZ
Affiliation:
Dpto. de Ingeniería del Software e Inteligencia Artificial, Universidad Complutense de Madrid, Spain (e-mail: [email protected])
A. J. FERNÁNDEZ
Affiliation:
Dpto. de Lenguajes y Ciencias de la Computación, Universidad de Málaga, Spain (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper presents a computational model for the cooperation of constraint domains and an implementation for a particular case of practical importance. The computational model supports declarative programming with lazy and possibly higher-order functions, predicates, and the cooperation of different constraint domains equipped with their respective solvers, relying on a so-called constraint functional logic programming (CFLP) scheme. The implementation has been developed on top of the CFLP system 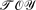, supporting the cooperation of the three domains ℋ, ℛ, and ℱ 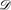, which supply equality and disequality constraints over symbolic terms, arithmetic constraints over the real numbers, and finite domain constraints over the integers, respectively. The computational model has been proved sound and complete w.r.t. the declarative semantics provided by the CFLP scheme, while the implemented system has been tested with a set of benchmarks and shown to behave quite efficiently in comparison to the closest related approach we are aware of.

Keywords

cooperating constraint domainsconstraint functional logic programmingconstrained lazy narrowingimplementation
Type
Regular Papers
Information
Theory and Practice of Logic Programming , Volume 9 , Issue 4 , July 2009 , pp. 415 - 527
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antoy, S., Echahed, R. and Hanus, M. 1994. A needed narrowing strategy. In Proc. POPL'94. ACM Press, 268–279.CrossRefGoogle Scholar
Antoy, S., Echahed, R. and Hanus, M. 2000. A needed narrowing strategy. Journal of the ACM 74, 4, 776–822.CrossRefGoogle Scholar
Antoy, S. and Hanus, M. 2000. Compiling multi-paradigm declarative programs into Prolog. In FroCoS. LNCS, vol. 1794. Springer, 171–185.Google Scholar
Arbab, F. and Monfroy, E. 1998. Using coordination for cooperative constraint solving. In SAC. 139–148.CrossRefGoogle Scholar
Arenas, P., Estévez, S., Fernández, A., Gil, A., López-Fraguas, F., Rodríguez-Artalejo, M. and Sáenz-Pérez, F. 2007. : A Multiparadigm Declarative Language (Version 2.3.1). Technical Report. R. Caballero and J. Sánchez, Eds. Available at http://toy.sourceforge.net.Google Scholar
Arenas, P., Gil, A. and López-Fraguas, F. 1994. Combining lazy narrowing with disequality constraints. In PLILP'94. LNCS, vol. 844. Springer, 385–399.Google Scholar
Baader, F. and Nipkow, T. 1998. Term Rewriting and All That. Cambridge University Press.CrossRefGoogle Scholar
Baader, F. and Schulz, K. 1995. On the combination of symbolic constraints, solution domains and constraints solvers. In CP'95. LNCS, vol. 976. Springer, 380–397.Google Scholar
Baader, F. and Schulz, K. 1996. Unification in the union of disjoint equational theories: combining decision procedures. Journal of Symbolic Computation 21, 2, 211–243.CrossRefGoogle Scholar
Baader, F. and Schulz, K. 1998. Combination of constraint solvers for free and quasi-free structures. TCS 192, 1, 107–161.CrossRefGoogle Scholar
Benhamou, F. 1996. Heterogeneous constraint solving. In ALP'96. LNCS, vol. 1139. Springer, 62–76.Google Scholar
Benhamou, F., Goualard, F. and Granvilliers, L. 1997. Programming with the declic language. In 2nd International Workshop on Interval Constraints. Port-Jefferson, New York, 1–13.Google Scholar
Benhamou, F., Goualard, F., Granvilliers, L. and Puget, J.-F. 1999. Revising hull and box consistency. In ICLP'99. The MIT Press, 230–244.Google Scholar
Benhamou, F. and Older, W. 1997. Applying interval arithmetic to real, integer and Boolean constraints. The Journal of Logic Programming 32, 1, 1–24.CrossRefGoogle Scholar
Beringer, H. and Backer, B. D. 1995. Combinatorial problem solving in constraint logic programming with cooperating solvers. In Logic Programming: Formal Methods and Practical Applications. Elsevier Science B.V., North-Holland, 245–272.Google Scholar
Bockmayr, A. and Kasper, T. 2000. Branch and infer: a unifying framework for integer and finite domain constraint programming. INFORMS Journal of Computing 10, 3, 287.Google Scholar
Buntine, W. L. and Bürckert, H. J. 1994. On solving equations and disequations. Journal of the ACM 41, 4, 591–629.CrossRefGoogle Scholar
Castro, C. and Monfroy, E. 2004. Designing hybrid cooperations with a component language for solving optimisation problems. In AIMSA 2004. LNCS, vol. 3192. Springer, 447–458.Google Scholar
Castro, C., Moossen, M. and Riff, M.-C. 2004. A cooperative framework based on local search and constraint programming for solving discrete global optimisation. In SBIA'04. LNCS, vol. 3171. Springer, 93–102.Google Scholar
Chiu, C.-K. and Lee, J. H.-M. 2002. Efficient interval linear equality solving in constraint logic programming. Reliable Computing 8, 2, 139–174.CrossRefGoogle Scholar
Colmerauer, A. 1984. Equations and inequations on finite and infinite trees. In Proc. of the 2nd International Conference on Fifth Generation Computer Systems, Clark, K.-L. and Tarnlund, S.-A., Eds. Tokyo, 85–99.Google Scholar
Colmerauer, A. 1990. An introduction to PROLOG III. Communications of the ACM (CACM) 33, 7, 69–90.CrossRefGoogle Scholar
Comon, H. 1991. Disunification: a survey. In Computational Logic—Essays in Honor of Alan Robinson. MIT Press, 322–359.Google Scholar
Comon, H. and Lescanne, P. 1989. Equational problems and disunification. Journal of Symbolic Computation 7, 371–425.CrossRefGoogle Scholar
Damas, L. and Milner, R. 1982. Principal type-schemes for functional programs. In POPL'82. ACM Press, 207–212.CrossRefGoogle Scholar
de la Banda, M., Jeffery, D., Marriott, K., Nethercote, N., Stuckey, P. and Holzbaur, C. 2001. Building constraint solvers with HAL. In ICLP'01. LNCS, vol. 2237. Springer, 90–104.Google Scholar
del Vado-Vírseda, R. 2003. A demand-driven narrowing calculus with overlapping definitional trees. In PPDP'03. ACM Press, 213–227.Google Scholar
del Vado-Vírseda, R. 2005. Declarative constraint programming with definitional trees. In Proc. FroCoS'05. LNAI, vol. 3717. Springer, 184–199.Google Scholar
del Vado-Vírseda, R. 2007. A higher-order demand-driven narrowing calculus with definitional trees. In ICTAC'07. LNCS, vol. 4711. Springer, 165–179.Google Scholar
Durfee, E., Lesser, V. and Corkill, D. 1989. Cooperative distributed problem solving. In The Handbook of Artificial Intelligence, Vol. IV, Feigenbaum, E., Barr, A. and Cohen, P., Eds. Addison-Wesley, 83–147.Google Scholar
Estévez-Martín, S., Fernández, A., Hortalá-González, T., Rodríguez-Artalejo, M., Sáenz-Pérez, F. and del Vado-Vírseda, R. 2007a. A proposal for the cooperation of solvers in constraint functional logic programming. ENTCS 188, 37–51.Google Scholar
Estévez-Martín, S., Fernández, A. and Sáenz-Pérez, F. 2006. Implementing TOY: A Constraint Functional Logic Programming with Solver Cooperation. Research Report LCC ITI 06-8, Universidad de Málaga.Google Scholar
Estévez-Martín, S., Fernández, A. J., Hortalá-González, M. T., Rodríguez-Artalejo, M. and del Vado Vírseda, R. 2007b. A fully sound goal solving calculus for the cooperation of solvers in the CFLP scheme. ENTCS 177, 235–252.Google Scholar
Estévez-Martín, S., Fernández, A. J., Hortalá-González, M. T., Rodríguez-Artalejo, M. and del Vado Vírseda, R. 2008a. Cooperation of constraint domains in the toy system. In PPDP'08. ACM Press, 258–268.CrossRefGoogle Scholar
Estévez-Martín, S., Fernández, A. J. and Sáenz-Pérez, F. 2007c. About implementing a constraint functional logic programming system with solver cooperation. In Proc. of CICLOPS'07. 57–71.Google Scholar
Estévez-Martín, S., Fernández, A. J. and Sáenz-Pérez, F. 2008b. Playing with OY: constraints and domain cooperation. In Proc. ESOP'08. LNCS, vol. 4960. Springer, 112–115.Google Scholar
Fernández, A. J. and Hill, P. M. 2004. An interval constraint system for lattice domains. ACM Transactions on Programming Languages and Systems 26, 1, 1–46.CrossRefGoogle Scholar
Fernández, A. J. and Hill, P. M. 2006. An interval constraint branching scheme for lattice domains. Journal of Universal Computer Science 12, 11, 1466–1499.Google Scholar
Fernandez, M. 1992. Narrowing based procedures for equational disunification. Applicable Algebra in Engineering, Communication and Computing 3, 1, 1–26.CrossRefGoogle Scholar
Frank, S., Hofstedt, P. and Mai, P. R. 2003a. A flexible meta-solver framework for constraint solver collaboration. In Proc. KI 2003. LNCS, vol. 2821. Springer, 520–534.Google Scholar
Frank, S., Hofstedt, P. and Mai, P. R. 2003b. Meta-s: a strategy-oriented meta-solver framework. In Proc. FLAIRS. AAAI Press, 177–181.Google Scholar
Frank, S., Hofstedt, P., Pepper, P. and Reckmann, D. 2007. Solution strategies for multi-domain constraint logic programs. In 6th International Andrei Ershov Memorial Conference on Perspectives of Systems Informatics (PSI 2006), Virbitskaite, I. and Voronkov, A., Eds. LNCS, vol. 4378. Springer, Novosibirsk, Russia, 209–222. Revised Papers.Google Scholar
Frank, S., Hofstedt, P. and Reckman, D. 2005. Meta-s—combining solver cooperation and programming languages. In Proc. W(C)LP 2005. Ulmer Informatik-Berichte 2005-01, 159–162.Google Scholar
Frank, S. and Mai, P. R. 2002. Strategies for Cooperating Constraint Solvers. Diploma Thesis, University of Technology, Berlin.Google Scholar
Frühwirth, T. 1998. Theory and practice of constraint handling rules. Journal of Logic Programming, Special Issue on Constraint Logic Programming 37, 1–3, 95–138.Google Scholar
Gervet, C. 1997. Interval propagation to reason about sets: definition and implementation of a practical language. Constraints 1, 3, 191–244.CrossRefGoogle Scholar
González-Moreno, J., Hortalá-González, M., López-Fraguas, F. and Rodríguez-Artalejo, M. 1996. A rewriting logic for declarative programming. In Proc. ESOP'96. LNCS, vol. 1058. Springer, 156–172.Google Scholar
González-Moreno, J., Hortalá-González, M., López-Fraguas, F. and Rodríguez-Artalejo, M. 1999. An approach to declarative programming based on a rewriting logic. Journal of Logic Programming 40, 47–87.CrossRefGoogle Scholar
González-Moreno, J. C., Hortalá-González, M. T. and Rodríguez-Artalejo, M. 2001. Polymorphic types in functional logic programming. Journal of Functional and Logic Programming 1, 1–71.Google Scholar
Goualard, F. 2001. Component programming and interoperatibility in constraint solver design. In ERCIM Workshop on Constraints. The Computing Research Repository (CoRR).Google Scholar
Goualard, F., Benhamou, F. and Granvilliers, L. 1999. An extension of the WAM for hybrid interval solvers. The Journal of Functional and Logic Programming 1, 1–36.Google Scholar
Granvilliers, L. 2001. On the combination of interval constraint solvers. Reliable Computing 7, 6, 467–483.CrossRefGoogle Scholar
Granvilliers, L., Monfroy, E. and Benhamou, F. 2001. Cooperative solvers in constraint programming: a short introduction. ALP Newsletter 14, 2.Google Scholar
Hanus, M. 2006. Curry: An Integrated Functional Logic Language (Version 0.8.2 of March 28, 2006). Technical Report. Available at http://www.informatik.uni-kiel.de/~mh/curry/.Google Scholar
Harjunkoski, Jain V. and Grossmann, I. 2000. Hybrid mixed-integer/constraint logic programming strategies for solving scheduling and combinatorial optimization problems. Computers and Chemical Engineering 24, 337–343.CrossRefGoogle Scholar
Hindley, R. 1969. The principal type-scheme of an object in combinatory logic. Transactions of the American Mathematical Society 146, 29–60.Google Scholar
Hofstedt, P. 2000a. Better communication for tighter cooperation. In 1st International Conference on Computational Logic (CL'2000). LNCS, vol. 1861. Springer, 342–357.CrossRefGoogle Scholar
Hofstedt, P. 2000b. Cooperating constraint solvers. In CP'2000. LNCS, vol. 1894. Springer, 520–524.Google Scholar
Hofstedt, P. 2001. Cooperation and Coordination of Constraint Solvers. Ph.D. Thesis, Technischen Universität Dresden, Fakultät Informatik.Google Scholar
Hofstedt, P. and Pepper, P. 2007. Integration of declarative and constraint programming. Theory and Practice of Logic Programming 7, 1–2, 93–121.CrossRefGoogle Scholar
Hong, H. 1994. Confluency of Cooperative Constraint Solving. Technical Report 94-08, Johannes Kepler University, Austria.Google Scholar
Hooker, J. 2000. Logic-based methods for optimization, combining optimization and constraint satisfaction. In Discrete Mathematics and Optimization. John Wiley & Sons, New York.Google Scholar
Jaffar, J. and Lassez, J. 1987. Constraint logic programming. In Proc. POPL'87. ACM Press, 111–119.CrossRefGoogle Scholar
Jaffar, J. and Maher, M. 1994. Constraint logic programming: a survey. Journal of Logic Programming 19–20, 503–581.Google Scholar
Jaffar, J., Maher, M., Marriott, K. and Stuckey, P. 1998. Semantics of constraints logic programs. Journal of Logic Programming 37, 1–3, 1–46.CrossRefGoogle Scholar
Jaffar, J., Michaylov, S., Stuckey, P. and Yap, R. 1992. The CLP(R) language and system. ACM Transactions on Programming Languages and Systems 14, 3, 339–395.CrossRefGoogle Scholar
Kepser, S. and Richts, J. 1999. Optimisation techniques for combining constraint solvers. In FroCoS'98. 193–210.Google Scholar
Khedro, T. and Genesereth, M. 1994. Modeling multiagent cooperation as distributed constraint satisfaction problem solving. In ECAI'94, Cohn, A., Ed. John Wiley & Sons, 249–253.Google Scholar
Kirchner, H. and Ringeissen, C. 1992. A constraint solver in finite algebras and its combination with unification algorithms. In Proc. of the Joint International Conference and Symposium on Logic Programming(JICSLP'92), Apt, K. R., Ed. MIT Press, 225–239.Google Scholar
Kirchner, H. and Ringeissen, C. 1994. Combining symbolic constraint solvers on algebraic domains. Journal of Symbolic Computation 18, 2, 113–155.CrossRefGoogle Scholar
Kobayashi, N. 2003. Study of an Open Equational Solving System. Ph.D. Thesis, Institute of Information Sciences and Electronics, University of Tsukuba, Japan.Google Scholar
Kobayashi, N., Marin, M. and Ida, T. 2001. Collaborative constraint functional logic programming in an open environment. In The Second Asian Workshop on Programming Languages and Systems (APLAS'01). Korea, 49–59.Google Scholar
Kobayashi, N., Marin, M. and Ida, T. 2003. Collaborative constraint functional logic programming system in an open environment. IEICE Transactions on Information and Systems E86-D, 1, 63–70.Google Scholar
Kobayashi, N., Marin, M., Ida, T. and Che, Z. 2002. Open CFLP: an open system for collaborative constraint functional logic programming. In 11th International Workshop on Functional and (Constraint) Logic Programming (WFLP'02). Grado, Italy, 229–232.Google Scholar
Krzikalla, O. 1997. Constraint solver für lineare constraints über reellen zahlen. Großer Beleg, Technische Universität Dresden.Google Scholar
Lassez, J., Maher, M. and Marriot, K. 1988. Unification revisited. In Foundations of logic and functional programming. LNCS, vol. 306. Springer, 67–113.CrossRefGoogle Scholar
Loogen, R., López-Fraguas, F. and Rodríguez-Artalejo, M. 1993. A demand driven computation strategy for lazy narrowing. In Proc. PLILP'93. LNCS, vol. 714. Springer, 184–200.Google Scholar
López-Fraguas, F., Rodríguez-Artalejo, M. and del Vado-Virseda, R. 2004. A lazy narrowing calculus for declarative constraint programming. In PPDP'04. ACM Press, 43–54.CrossRefGoogle Scholar
López-Fraguas, F., Rodríguez-Artalejo, M. and del Vado Vírseda, R. 2007. A new generic scheme for functional logic programming with constraints. Higher-Order and Symbolic Computation 20, 1–2, 73–122.CrossRefGoogle Scholar
Maher, M. J. 1988. Complete axiomatizations of the algebras of finite, rational and infinite trees. In LICS'88. IEEE Computer Society, 348–357.Google Scholar
Marin, M. 2000. Functional Logic Programming with Distributed Constraint Solving. Ph.D. Thesis, Johannes Kepler Universität Linz.Google Scholar
Marin, M., Ida, T. and Schreiner, W. 2001. CFLP: a Mathematica implementation of a distributed constraint solving system. In IMS'99, vol. 8. WIT Press, 287–300.Google Scholar
Marti, P. and Rueher, M. 1995. A distributed cooperating constraints solving system. International Journal of Artificial Intelligence Tools 4, 1–2, 93–113.Google Scholar
Milner, R. 1978. A theory of type polymorphism in programming. Journal of Computer and Systems Sciences 17, 348–375.CrossRefGoogle Scholar
Monfroy, E. 1996. Solver Collaboration for Constraint Logic Programming. Ph.D. Thesis, Centre de Recherche en Informatique de Nancy.Google Scholar
Monfroy, E. 1998. A solver collaboration in BALI. In Proc. of JCSLP'98. MIT Press, 349–350.Google Scholar
Monfroy, E. and Castro, C. 2004. A component language for hybrid solver cooperations. In ADVIS'04. LNCS, vol. 3261. Springer, 192–202.Google Scholar
Monfroy, E. and Ringeissen, C. 1999. An open automated framework for constraint solver extension: the solex approach. Fundamenta Informaticae 39, 1–2, 167–187.CrossRefGoogle Scholar
Monfroy, E., Rusinowitch, M. and Schott, R. 1995. Implementing Non-linear Constraints with Cooperative Solvers. Research Report 2747, CRI Nancy.CrossRefGoogle Scholar
N'Dong, S. 1997. Prolog IV ou la programmation par contraintes selon PrologIA. In JFPLC'97. Edition HERMES, 235–238.Google Scholar
Nelson, G. and Oppen, D. 1979. Simplification by cooperating decision procedures. ACM Transactions on Programming Languages and Systems 1, 2, 245–257.CrossRefGoogle Scholar
Pajot, B. and Monfroy, E. 2003. Separating search and strategy in solver cooperations. In Proc. PSI'03. LNCS, vol. 2890. Springer, 401–414.Google Scholar
Peyton-Jones, S. 2002. Haskell 98 Language and Libraries: The Revised Report. Technical Report. Avilable at: http://www.haskell.org/onlinereport/.Google Scholar
Rodosěk, R., Wallace, M. and Hajian, M. 1997. A new approach to integrating mixed integer programming and constraint logic programming. In Annals of Operations Research, vol. 86. 63–87.CrossRefGoogle Scholar
Rodríguez-Artalejo, M. 2001. Functional and constraint logic programming. In Constraints in Computational Logics: Theory and Applications. LNCS, vol. 2002. Springer, 202–270.CrossRefGoogle Scholar
Rueher, M. and Solnon, C. 1997. Concurrent cooperating solvers over reals. Reliable Computing 3, 3, 325–333.CrossRefGoogle Scholar
Sáenz-Pérez, F. 2007. ACIDE: an integrated development environment configurable for LaTeX. The PracTeX Journal 3, 1–17.Google Scholar
Saraswat, V. 1992. The category of constraint systems is cartesian closed. In Proc. of the 7th Annual IEEE Symposium on Logic in Computer Science. IEEE Press, 341–345.Google Scholar
SICStus Prolog. 2007. Available at http://www.sics.se/isl/sicstus.Google Scholar
Thorsteinsson, E. 2001. Branch-and-check: a hybrid framework integrating mixed integer programming and constraint logic programming. In CP 2001, Walsh, T., Ed. LNCS, vol. 2239. Springer, 16–30.Google Scholar
van Hentenryck, P., Saraswat, V. and Deville, Y. 1998. Design, implementation and evaluation of the constraint language cc(FD). Journal of Logic Programming 37, 139–164.CrossRefGoogle Scholar
vanHentenryck, P. Hentenryck, P., Simonis, H. and Dincbas, M. 1994. Constraint satisfaction using constraint logic programming. Artificial Intelligence 58, 113–159.Google Scholar
van Hoeve, W. 2000. Towards the Integration of Constraint Logic Programming and Mathematical Programming. Master's Thesis, University of Twente, The Netherlands.Google Scholar
Vandecasteele, H. and Rodosěk, . 1998. Modelling combinatorial problems for CLP(FD+R). In Proc. of the Benelux Workshop on Logic Programming. 1–9.Google Scholar
Zhou, J. 2000. Introduction to the constraint language NCL. The Journal of Logic Programming 45, 1-3, 71–103.CrossRefGoogle Scholar
Zoeteweij, P. 2003. Coordination-based distributed constraint solving in DICE. In ACM Symposium on Applied Computing (SAC'03). ACM, Melbourne, FL, 360–366.Google Scholar