No CrossRef data available.
Article contents
Elaboration Tolerant Representation of Markov Decision Process via Decision-Theoretic Extension of Probabilistic Action Language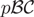 
$p{\cal BC}$+
Published online by Cambridge University Press: 23 December 2020
Abstract
We extend probabilistic action language 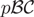$p{\cal BC}$+ with the notion of utility in decision theory. The semantics of the extended 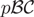$p{\cal BC}$+ can be defined as a shorthand notation for a decision-theoretic extension of the probabilistic answer set programming language LPMLN. Alternatively, the semantics of 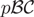$p{\cal BC}$+ can also be defined in terms of Markov decision process (MDP), which in turn allows for representing MDP in a succinct and elaboration tolerant way as well as leveraging an MDP solver to compute a $p{\cal BC}$+ action description. The idea led to the design of the system pbcplus2mdp, which can find an optimal policy of a $p{\cal BC}$+ action description using an MDP solver.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
Footnotes
We are grateful to the anonymous referees for their useful comments and to Siddharth Srivastava, Zhun Yang, and Yu Zhang for helpful discussions. This work was partially supported by the National Science Foundation under Grant IIS-1815337.
References
Babb, J. and Lee, J. 2015. Action language 
${\cal BC}$+. Journal of Logic and Computation, exv062.Google Scholar
${\cal BC}$+. Journal of Logic and Computation, exv062.Google ScholarBaral, C., Gelfond, M. and Rushton, J. N. 2009. Probabilistic reasoning with answer sets. Theory and Practice of Logic Programming 9, 1, 57–144.CrossRefGoogle Scholar
Bellman, R. 1957. A Markovian decision process. Indiana University Mathematics Journal 6, 679–684.CrossRefGoogle Scholar
Boutilier, C., Reiter, R. and Price, B. 2001. Symbolic dynamic programming for first-order MDPs. In Proceedings of the 17th International Joint Conference on Artificial Intelligence - Volume 1. IJCAI01, 690–697.Google Scholar
Broeck, G. V. d., Thon, I., Otterlo, M. v. and Raedt, L. D. 2010. DTProblog: A decision-theoretic probabilistic prolog. In Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence. AAAI’10. AAAI Press, 1217–1222.Google Scholar
Erdem, E., Gelfond, M. and Leone, N. 2016. Applications of answer set programming. AI Magazine 37, 3, 53–68.CrossRefGoogle Scholar
Faber, W., Leone, N. and Pfeifer, G. 2004. Recursive aggregates in disjunctive logic programs: Semantics and complexity. In Proceedings of European Conference on Logics in Artificial Intelligence (JELIA).CrossRefGoogle Scholar
Ferraris, P. 2005. Answer sets for propositional theories. In Proceedings of International Conference on Logic Programming and Nonmonotonic Reasoning (LPNMR), 119–131.Google Scholar
Ferreira, L. A., Bianchi, R. A. C., Santos, P. E. and de Mantaras, R. L. 2017. Answer set programming for non-stationary markov decision processes. Applied Intelligence 47, 4, 993–1007.CrossRefGoogle Scholar
Gelfond, M. and Lifschitz, V. 1993. Representing action and change by logic programs. Journal of Logic Programming 17, 301–322.CrossRefGoogle Scholar
Gelfond, M. and Lifschitz, V. 1998. Action languages. Electronic Transactions on Artificial Intelligence 3, 195–210. http://www.ep.liu.se/ea/cis/1998/016/.Google Scholar
Giunchiglia, E., Lee, J., Lifschitz, V., McCain, N. and Turner, H. 2004. Nonmonotonic causal theories. Artificial Intelligence 153, 1–2, 49–104.CrossRefGoogle Scholar
Kautz, H. and Selman, B. 1998. A general stochastic approach to solving problems with hard and soft constraints. In The Satisfiability Problem: Theory and Applications.Google Scholar
Lee, J. and Lifschitz, V. 2003. Loop formulas for disjunctive logic programs. In Proceedings of International Conference on Logic Programming (ICLP), 451–465.Google Scholar
Lee, J., Lifschitz, V. and Yang, F. 2013. Action language ${\cal BC}$: Preliminary report. In Proceedings of International Joint Conference on Artificial Intelligence (IJCAI).Google Scholar
${\cal BC}$: Preliminary report. In Proceedings of International Joint Conference on Artificial Intelligence (IJCAI).Google ScholarLee, J., Talsania, S. and Wang, Y. 2017. Computing LPMLN using ASP and MLN solvers. Theory and Practice of Logic Programming 17, 5–6, 942–960.CrossRefGoogle Scholar
Lee, J. and Wang, Y. 2016. Weighted rules under the stable model semantics. In Proceedings of International Conference on Principles of Knowledge Representation and Reasoning (KR), 145–154.Google Scholar
Lee, J. and Wang, Y. 2018. A probabilistic extension of action language BC+. Theory and Practice of Logic Programming 18, 3–4, 607–622.CrossRefGoogle Scholar
Leonetti, M., Iocchi, L. and Stone, P. 2016. A synthesis of automated planning and reinforcement learning for efficient, robust decision-making. Artificial Intelligence 241, 103–130.CrossRefGoogle Scholar
McCarthy, J. 1963. Situations, actions, and causal laws. Tech. rep., Stanford University CA Department of Computer Science.Google Scholar
Niemelä, I. and Simons, P. 2000. Extending the Smodels system with cardinality and weight constraints. In Logic-Based Artificial Intelligence, Minker, J., Ed. Kluwer, 491–521.CrossRefGoogle Scholar
Pelov, N., Denecker, M. and Bruynooghe, M. 2007. Well-Founded and stable semantics of logic programs with aggregates. Theory and Practice of Logic Programming 7, 3, 301–353.CrossRefGoogle Scholar
Poole, D. 2008. The independent choice logic and beyond. In Probabilistic Inductive Logic Programming. Springer, 222–243.CrossRefGoogle Scholar
Poole, D. 2013. A framework for decision-theoretic planning I: Combining the situation calculus, conditional plans, probability and utility. arXiv preprint arXiv:1302.3597.Google Scholar
Sanner, S. 2010. Relational dynamic influence diagram language (RDDL): Language description. Unpublished ms. Australian National University, 32.Google Scholar
Sanner, S. and Boutilier, C. 2009. Practical solution techniques for first-order MDPs. Artificial Intelligence 173, 5, 748–788. Advances in Automated Plan Generation.CrossRefGoogle Scholar
Son, T. C., Pontelli, E. and Tu, P. H. 2006. Answer sets for logic programs with arbitrary abstract constraint atoms. In Proceedings, The Twenty-First National Conference on Artificial Intelligence (AAAI).CrossRefGoogle Scholar
Sridharan, M., Gelfond, M., Zhang, S. and Wyatt, J. 2019. REBA: A refinement-based architecture for knowledge representation and reasoning in robotics. Journal of Artificial Intelligence Research 65, 1, 87–180.CrossRefGoogle Scholar
Wang, C., Joshi, S. and Khardon, R. 2008. First order decision diagrams for relational MDPs. Journal of Artificial Intelligence Research 31, 431–472.CrossRefGoogle Scholar
Wang, Y. and Lee, J. 2019. Elaboration tolerant representation of markov decision process via decision theoretic extension of action language pbc+. In Proceedings of the 15th International Conference on Logic Programming and Nonmonotonic Reasoning (LPNMR 2019).Google Scholar
Watkins, C. J. C. H. 1989. Learning from Delayed Rewards. Ph.D. thesis, King’s College, Cambridge, UK.Google Scholar
Yang, F., Lyu, D., Liu, B. and Gustafson, S. 2018. PEORL: Integrating symbolic planning and hierarchical reinforcement learning for robust decision-making. In IJCAI, 4860–4866.Google Scholar
Yoon, S., Fern, A. and Givan, R. 2002. Inductive policy selection for first-order MDPs. In Proceedings of the Eighteenth Conference on Uncertainty in Artificial Intelligence. UAI02. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 568–576.Google Scholar
Younes, H. L. and Littman, M. L. 2004. PPDDL1.0: An extension to PDDL for expressing planning domains with probabilistic effects. Techn. Rep. CMU-CS-04-162.Google Scholar
Zhang, S. and Stone, P. 2015. CORPP: Commonsense reasoning and probabilistic planning, as applied to dialog with a mobile robot. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence. AAAI’15. AAAI Press, 1394–1400.Google Scholar
Wang and Lee Supplementary Materials
Wang and Lee Supplementary Materials
PDF
387.9 KB