Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-19T02:21:55.407Z Has data issue: false hasContentIssue false
  • English
  • Français

A common view on strong, uniform, and other notions of equivalence in answer-set programming*

Published online by Cambridge University Press:  01 March 2008

STEFAN WOLTRAN
STEFAN WOLTRAN*
Affiliation:
Technische Universität Wien, Institut für Informationssysteme 184/2, Favoritenstrasse 9-11, A-1040 Vienna, Austria (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Logic programming under the answer-set semantics nowadays deals with numerous different notions of program equivalence. This is due to the fact that equivalence for substitution (known as strong equivalence) and ordinary equivalence are different concepts. The former holds, given programs P and Q, iff P can be faithfully replaced by Q within any context R, while the latter holds iff P and Q provide the same output, that is, they have the same answer sets. Notions in between strong and ordinary equivalence have been introduced as theoretical tools to compare incomplete programs and are defined by either restricting the syntactic structure of the considered context programs R or by bounding the set 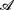of atoms allowed to occur in R (relativized equivalence). For the latter approach, different 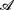yield properly different equivalence notions, in general. For the former approach, however, it turned out that any “reasonable” syntactic restriction to R coincides with either ordinary, strong, or uniform equivalence (for uniform equivalence, the context ranges over arbitrary sets of facts, rather than program rules). In this paper, we propose a parameterization for equivalence notions which takes care of both such kinds of restrictions simultaneously by bounding, on the one hand, the atoms which are allowed to occur in the rule heads of the context and, on the other hand, the atoms which are allowed to occur in the rule bodies of the context. We introduce a general semantical characterization which includes known ones as SE-models (for strong equivalence) or UE-models (for uniform equivalence) as special cases. Moreover, we provide complexity bounds for the problem in question and sketch a possible implementation method making use of dedicated systems for checking ordinary equivalence.

Keywords

Answer-set programmingStrong equivalenceRelativized equivalence
Type
Technical Note
Information
Theory and Practice of Logic Programming , Volume 8 , Issue 2 , March 2008 , pp. 217 - 234
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bonatti, P. 2001. Reasoning with open logic programs. In Proc. of the 6th International Conference on Logic Programming and Nonmonotonic Reasoning (LPNMR'01), Eiter, T., Faber, W., & Truszczynski, M., Eds. LNCS, vol. 2173. Springer, Berlin Heidelberg, New York, 147–159.Google Scholar
Eiter, T. & Fink, M. 2003. Uniform equivalence of logic programs under the stable model semantics. In Proc. of the 19th International Conference on Logic Programming (ICLP'03), Palamidessi, C., Ed. Number 2916 in LNCS. Springer, Berlin Heidelberg, New York, 224–238.Google Scholar
Eiter, T., Fink, M., Tompits, H. & Woltran, S. 2004. Simplifying Logic Programs Under Uniform and Strong Equivalence. In Proc. of the 7th International Conference on Logic Programming and Nonmonotonic Reasoning (LPNMR'04), Lifschitz, V. & Niemelä, I., Eds. LNCS, vol. 2923. Springer, Berlin Heidelberg, New York, 87–99.Google Scholar
Eiter, T., Fink, M. & Woltran, S. 2007. Semantical characterizations and complexity of equivalences in stable logic programming. ACM Transactions on Computational Logic 8, 3.CrossRefGoogle Scholar
Eiter, T., Tompits, H., & Woltran, S. 2005. On solution correspondences in answer set programming. In Proc. of the 19th International Joint Conference on Artificial Intelligence (IJCAI'05), Kaelbling, L. P. & Saffiotti, A., Eds. Professional Book Center, Denver, Colorado, 97–102.Google Scholar
Gelfond, M. & Lifschitz, V. 1991. Classical negation in logic programs and disjunctive databases. New Generation Computing 9, 365–385.CrossRefGoogle Scholar
Lifschitz, V., Pearce, D. & Valverde, A. 2001. Strongly equivalent logic programs. ACM Transactions on Computational Logic 2, 4, 526–541.CrossRefGoogle Scholar
Lifschitz, V. & Turner, H. 1994. Splitting a logic program. In Proc. of the 11th International Conference on Logic Programming (ICLP'94), Hentenryck, P. Van, Ed. MIT Press, Cambridge, 23–37.Google Scholar
Oetsch, J., Tompits, H. & Woltran, S. 2007. Facts do not cease to exist because they are ignored: Relativised uniform equivalence with answer-set projection. In Proc. of the 22nd National Conference on Artificial Intelligence (AAAI'07). AAAI Press, Menlo Park, California, 458–464.Google Scholar
Oikarinen, E. & Janhunen, T. 2004. Verifying the equivalence of logic programs in the disjunctive case. In Proc. of the 7th International Conference on Logic Programming and Nonmonotonic Reasoning (LPNMR'04), Lifschitz, V. & Niemelä, I., Eds. LNCS, vol. 2923. Springer, Berlin Heidelberg, New York, 180–193.Google Scholar
Oikarinen, E. & Janhunen, T. 2006. Modular equivalence for normal logic programs. In Proc. of the 17th European Conference on Artificial Intelligence (ECAI 2006), Brewka, G., Coradeschi, S., Perini, A., & Traverso, P., Eds. IOS Press, Amsterdam, 412–416.Google Scholar
Pearce, D., Tompits, H. & Woltran, S. 2007. Relativised equivalence in equilibrium logic and its applications to prediction and explanation: Preliminary report. In Proc. of the 1st Workshop Correspondence and Equivalence for Nonmonotonic Theories (CENT'07), Pearce, D., Polleres, A., Valverde, A., & Woltran, S., Eds. CEUR Workshop Proceedings, vol. 265. CEUR-WS.org, 37–48.Google Scholar
Pearce, D. & Valverde, A. 2004. Uniform equivalence for equilibrium logic and logic programs. In Proc. of the 7th International Conference on Logic Programming and Nonmonotonic Reasoning (LPNMR'04), Lifschitz, V. & Niemelä, I., Eds. LNCS, vol. 2923. Springer, Berlin Heidelberg, New York, 194–206.Google Scholar
Sagiv, Y. 1988. Optimizing datalog programs. In Foundations of Deductive Databases and Logic Programming, Minker, J., Ed. Morgan Kaufmann, 659–698.CrossRefGoogle Scholar
Turner, H. 2003. Strong equivalence made Easy: Nested expressions and weight constraints. Theory and Practice of Logic Programming 3, 4–5, 602–622.CrossRefGoogle Scholar
Woltran, S. 2004. Characterizations for relativized notions of equivalence in answer set programming. In Logics in Artificial Intelligence, 9th European Conference, JELIA'04, Proceedings, Alferes, J. J. & Leite, J. A., Eds. LNCS, vol. 3229. Springer, Berlin Heidelberg, New York, 161–173.Google Scholar