Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-16T11:19:47.617Z Has data issue: false hasContentIssue false
  • English
  • Français

atalog: A logic language for expressing search and optimization problems

Published online by Cambridge University Press:  18 January 2010

SERGIO GRECO ,
CRISTIAN MOLINARO ,
IRINA TRUBITSYNA  and
ESTER ZUMPANO
SERGIO GRECO
Affiliation:
Dipartimento di Elettronica Informatica e Sistemistica (DEIS), Università della Calabria, 87036 Rende, Italy (e-mail: [email protected], [email protected], [email protected], [email protected])
CRISTIAN MOLINARO
Affiliation:
Dipartimento di Elettronica Informatica e Sistemistica (DEIS), Università della Calabria, 87036 Rende, Italy (e-mail: [email protected], [email protected], [email protected], [email protected])
IRINA TRUBITSYNA
Affiliation:
Dipartimento di Elettronica Informatica e Sistemistica (DEIS), Università della Calabria, 87036 Rende, Italy (e-mail: [email protected], [email protected], [email protected], [email protected])
ESTER ZUMPANO
Affiliation:
Dipartimento di Elettronica Informatica e Sistemistica (DEIS), Università della Calabria, 87036 Rende, Italy (e-mail: [email protected], [email protected], [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper presents a logic language for expressing 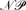search and optimization problems. Specifically, first a language obtained by extending (positive) DATALOG with intuitive and efficient constructs (namely, stratified negation, constraints, and exclusive disjunction) is introduced. Next, a further restricted language only using a restricted form of disjunction to define (nondeterministically) subsets (or partitions) of relations is investigated. This language, called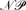 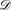atalog, captures the power of DATALOG¬ in expressing search and optimization problems. A system prototype implementing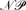 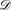atalog is presented. The system translates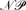 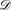atalog queries into Optimization Programming Language (OPL) programs which are executed by the ILOG OPL Development Studio. Our proposal combines easy formulation of problems, expressed by means of a declarative logic language, with the efficiency of the ILOG System. Several experiments show the effectiveness of this approach.

Keywords

logic languagesstable model semanticsconstraint programmingexpressivity and complexity of declarative query languages
Type
Regular Papers
Information
Theory and Practice of Logic Programming , Volume 10 , Issue 2 , March 2010 , pp. 125 - 166
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abiteboul, S., Hull, R. and Vianu, V. 1995. Foundations of Databases. Addison-Wesley.Google Scholar
Balduccini, M., Gelfond, M. and Nogueira, M. 2000. A-Prolog as a tool for declarative programming. In Proc. of the International Conference on Software Engineering and Knowledge Engineering 63–72.Google Scholar
Baral, C. 2003. Knowledge Representation Reasoning and Declarative Problem Solving. Cambridge University Press.CrossRefGoogle Scholar
Cadoli, M., Ianni, G., Palopoli, L., Schaerf, A. and Vasile, D. 2000. NP-SPEC: An executable specification language for solving all problems in NP. Computer Languages 26 (2–4), 165–195.CrossRefGoogle Scholar
Cadoli, M. and Schaerf, A. 2005. Compiling problem specifications into SAT. Artificial Intelligence 162 (1–2), 89–120.CrossRefGoogle Scholar
Cholewinski, P., Marek, V. W. and Truszczynski, M. 1996. Default reasoning system DeReS. In Proc. of the International Conference on Principles of Knowledge Representation and Reasoning, Aiello, L. C. et al. , Eds. Morgan Kaufmann, 518–528.Google Scholar
Denecker, M. 2000. Extending classical logic with inductive definitions. In Proc. of the International Conference on Computational Logic, Lloyd, J. W. et al. , Eds. LNCS, vol. 1861. Springer, 703–717.Google Scholar
East, D. and Truszczynski, M. 2000. DATALOG with constraints – An answer-set programming system. In Proc. of the National Conference on Artificial Intelligence, AAAI Press/The MIT Press, 163–168.Google Scholar
East, D. and Truszczynski, M. 2006. Predicate-calculus based logics for modeling and solving search problems. ACM Transaction on Computational Logic 7 (1), 38–83.CrossRefGoogle Scholar
Eiter, T., Leone, N., Mateis, C., Pfeifer, G. and Scarcello, F. 1997. A deductive system for non-monotonic reasoning. In Proc. of the International Conference on Logic Programming and Nonmonotonic Reasoning, Dix, J. et al. , Eds. LNCS, vol. 1265. Springer, 363–374.CrossRefGoogle Scholar
Fagin, R. 1974. Generalized first-order spectra and polynomial-time recognizable sets. In Complexity of Computation, Karp, R., Ed. SIAM-AMS Proc., vol. 7, 43–73.Google Scholar
Finkel, R. A., Marek, V. W. and Truszczynski, M. 2004. Constraint Lingo: Towards high-level constraint programming. Software Practice and Experience 34 (15), 1481–1504.CrossRefGoogle Scholar
Gebser, M., Kaufmann, B., Neumann, A. and Schaub, T. 2007. Conflict-driven answer set solving. In Proc. of the International Joint Conference on Artificial Intelligence, Veloso, M. M., Ed., 386–392.Google Scholar
Gelfond, M. and Lifschitz, V. 1988. The stable model semantics for logic programming. In Proc. of the International Conference on Logic Programming, Kowalski, R. A. and Bowen, K. A., Eds. The MIT Press, 1070–1080.Google Scholar
Gelfond, M. 2002. Representing knowledge in a-prolog. Computational Logic: Logic Programming and Beyond, Kakas, A. C. and Sadri, F., Eds. LNCS, vol. 2408. Springer, 413–451.CrossRefGoogle Scholar
Greco, S. 1999. Dynamic programming in datalog with aggregates. IEEE Transactions on Knowledge and Data Engineering 11 (2), 265–283.CrossRefGoogle Scholar
Greco, S. and Saccà, D. 2002. Search and optimization problems in datalog. Computational Logic: Logic Programming and Beyond, Kakas, A. C. and Sadri, F., Eds. LNCS, vol. 2408. Springer, 61–82.CrossRefGoogle Scholar
Greco, S. and Saccà, D. 1997. NP optimization problems in datalog. In Symposium on Logic Programming, Maluszynski, J., Ed. The MIT Press, 181–195.Google Scholar
Greco, S., Saccà, D. and Zaniolo, C. 1995. Datalog with stratified negation and choice: from P to DP. In Proc. of the International Conference on Database Theory, Gottlob, G. and Vardi, M. Y., Eds. LNCS, vol. 893. Springer, 574–589.Google Scholar
Greco, S. and Zaniolo, C. 2001. Greedy algorithms in datalog. Theory and Practice of Logic Programming 1 (4), 381–407.CrossRefGoogle Scholar
Jaffar, J., Michaylov, S., Stuckey, P.J. and Yap, R. 1992. The CLP(R) language and system. ACM Transaction on Programming Languages and Systems 14 (3), 339–395.CrossRefGoogle Scholar
Johnson, D. S. 1990. A Catalog of Complexity Classes. In Handbook of Theoretical Computer Science, Vol. 1, van Leewen, J., Ed. North-Holland, 67–161.Google Scholar
Kluzniak, F. and Milkowska, M. 1997. Spill – A logic language for writing testable requirements specifications. Science of Computer Programming 28 (2–3), 193–223.CrossRefGoogle Scholar
Kolaitis, P. and Papadimitriou, C. 1991. Why not negation by fixpoint? Journal of Computer and System Sciences 43 (1), 125–144.CrossRefGoogle Scholar
Kolaitis, P. G. and Thakur, M. N. 1995. Approximation properties of NP minimization classes. Journal of Computer and System Sciences 50 (3), 391–411.CrossRefGoogle Scholar
Leone, N., Pfeifer, G., Faber, W., Eiter, T., Gottlob, G., Perri, S. and Scarcello, F. 2006. The DLV System for knowledge representation and reasoning. ACM Transactions on Computational Logics 7 (3), 499–562.CrossRefGoogle Scholar
Lierler, Y. 2005. Disjunctive answer set programming via satisfiability. In Proc. of the International Workshop on Answer Set Programming, De Vos, M. and Provetti, A., Eds. CEUR Workshop Proceedings 142, 85–97.Google Scholar
Lierler, Y. 2005. Cmodels – SAT-based disjunctive answer set solver. In Proc. of the International Conference on Logic Programming and Nonmonotonic Reasoning, Baral, C. et al. , Eds. LNCS, vol. 3662. Springer, 447–451.CrossRefGoogle Scholar
Lin, F. and Zhao, Y. 2004. ASSAT: Computing answer sets of a logic program by SAT solvers. Artificial Intelligence 157 (1–2), 115–137.CrossRefGoogle Scholar
Marek, W. and Truszczynski, M. 1991. Autoepistemic logic. Journal of the ACM 38 (3), 588–619.CrossRefGoogle Scholar
Marien, M., Gilis, D. and Denecker, M. 2004. On the relation between ID-logic and answer set programming. Logics in Artificial Intelligence, Alferes, J. J. and Leite, J. A., Eds. LNCS, vol. 3229. Springer, 108–120.CrossRefGoogle Scholar
Marriott, K. and Stuckey, P. J. 1998. Programming with Constraints: An Introduction. MIT Press.CrossRefGoogle Scholar
Niemela, I., Simons, P. and Soininen, T. 1999. Stable model semantics of weight constraint rules. In Proc. of the International Conference on Logic Programming and Nonmonotonic Reasoning, Gelfond, M. et al. , Eds. LNCS, vol. 1730. Springer, 317–331.CrossRefGoogle Scholar
Papadimitriou, C. H. and Steiglitz, K. 1982. Combinatorial Optimization – Algorithms and Complexity. Prentice-Hall.Google Scholar
Papadimitriou, C. H. and Yannakakis, M. 1991. Optimization, approximation, and complexity classes. Journal Computer and System Sciences 43 (3), 425–440.CrossRefGoogle Scholar
Papadimitriou, C. H. 1994. Computational Complexity. Addison-Wesley.Google Scholar
Rao, P., Sagonas, K. F., Swift, T., Warren, D. S. and Freire, J. 1997. XSB: A system for effciently computing WFS. In Proc. of the International Conference on Logic Programming and Nonmonotonic Reasoning, Dix, J. et al. , Eds. LNCS, vol. 1265. Springer, 431–441.Google Scholar
Saccà, D. 1997. The expressive powers of stable models for bound and unbound queries. Journal of Computer and System Sciences 54 (3), 441–464.CrossRefGoogle Scholar
Schlipf, J. S. 1995. The expressive powers of the logic programming semantics. Journal of Computer and System Sciences 51 (1), 64–86.CrossRefGoogle Scholar
Smith, D. R. 1990. KIDS: A semiautomatic program development system. IEEE Transaction on Software Engineering 16 (9), 1024–1043.CrossRefGoogle Scholar
Simons, P., Niemela, I. and Soininen, T. 2002. Extending and implementing the stable model semantics. Artificial Intelligence 138 (1–2), 181–234.CrossRefGoogle Scholar
Ullman, J. K. 1988. Principles of Data and Knowledge-Base Systems, Vol. 1. Computer Science Press, New York.Google Scholar
Van Gelder, A., Ross, K. A. and Schlipf, J. S. 1991. The well-founded semantics for general logic programs. Journal of ACM 38 (3), 620–650.CrossRefGoogle Scholar
Van Hentenryck, P. 1988. The OPL Optimization Programming Language. MIT Press.Google Scholar
Van Hentenryck, P., Michel, L., Perron, L. and Regin, J. C. 1999. Constraint programming in OPL. In Proc. of the International Conference on Principles and Practice of Declarative Programming, Nadathur, G., Ed. LNCS, vol. 1702. Springer, 98–116.Google Scholar
Van Roy, P. 1999. Logic programming in Oz with Mozart. In Proc. of the International Conference on Logic Programming, De Schreye, D., Ed. The MIT Press, 38–51.Google Scholar
Wallace, M. and Schimpf, J. 1999. ECLiPSe: declarative specification and scaleable implementation. In Proc. of the International Workshop on Practical Aspects of Declarative Languages, Gupta, G., Ed. LNCS, vol. 1551. Springer, 365–366.Google Scholar
Zhou, N. 2002. Implementing constraint solvers in B-prolog. Intelligent Information Processing, Musen, M. A. et al. , Eds. IFIP Conference Proceedings, 249–260.CrossRefGoogle Scholar
Zumpano, E., Greco, S., Trubitsyna, I. and Veltri, P. 2004. On the semantics and expressive power of Datalog-like languages for NP search and optimization problems. In Proc. of the ACM Symppsium on Applied Computing, Haddad, H. et al. , Eds. ACM, 692–697.Google Scholar