Article contents
ASP (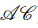 $\mathcal A \mathcal C$): Answer Set Programming with Algebraic Constraints
$\mathcal A \mathcal C$): Answer Set Programming with Algebraic Constraints
Published online by Cambridge University Press: 22 September 2020
Abstract
Weighted Logic is a powerful tool for the specification of calculations over semirings that depend on qualitative information. Using a novel combination of Weighted Logic and Here-and-There (HT) Logic, in which this dependence is based on intuitionistic grounds, we introduce Answer Set Programming with Algebraic Constraints (ASP(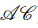 $\mathcal A \mathcal C$)), where rules may contain constraints that compare semiring values to weighted formula evaluations. Such constraints provide streamlined access to a manifold of constructs available in ASP, like aggregates, choice constraints, and arithmetic operators. They extend some of them and provide a generic framework for defining programs with algebraic computation, which can be fruitfully used e.g. for provenance semantics of datalog programs. While undecidable in general, expressive fragments of ASP(
$\mathcal A \mathcal C$)), where rules may contain constraints that compare semiring values to weighted formula evaluations. Such constraints provide streamlined access to a manifold of constructs available in ASP, like aggregates, choice constraints, and arithmetic operators. They extend some of them and provide a generic framework for defining programs with algebraic computation, which can be fruitfully used e.g. for provenance semantics of datalog programs. While undecidable in general, expressive fragments of ASP(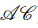 $\mathcal A \mathcal C$) can be exploited for effective problem solving in a rich framework.
$\mathcal A \mathcal C$) can be exploited for effective problem solving in a rich framework.
- Type
- Original Article
- Information
- Theory and Practice of Logic Programming , Volume 20 , Issue 6: 36th International Conference on Logic Programming Special Issue II , November 2020 , pp. 895 - 910
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 4
- Cited by



