Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Giordano, Laura
and
Theseider Dupré, Daniele
2020.
An ASP approach for reasoning in a concept-aware multipreferential lightweight DL.
Theory and Practice of Logic Programming,
Vol. 20,
Issue. 5,
p.
751.
Giordano, Laura
and
Theseider Dupré, Daniele
2021.
Logics in Artificial Intelligence.
Vol. 12678,
Issue. ,
p.
225.
Giordano, Laura
2021.
Symbolic and Quantitative Approaches to Reasoning with Uncertainty.
Vol. 12897,
Issue. ,
p.
557.
BOZZATO, LORIS
EITER, THOMAS
and
KIESEL, RAFAEL
2021.
Reasoning on Multirelational Contextual Hierarchies via Answer Set Programming with Algebraic Measures.
Theory and Practice of Logic Programming,
Vol. 21,
Issue. 5,
p.
593.
Giordano, Laura
Gliozzi, Valentina
and
Theseider DuprÉ, Daniele
2022.
A conditional, a fuzzy and a probabilistic interpretation of self-organizing maps.
Journal of Logic and Computation,
Vol. 32,
Issue. 2,
p.
178.
GIORDANO, LAURA
and
THESEIDER DUPRÉ, DANIELE
2022.
An ASP Approach for Reasoning on Neural Networks under a Finitely Many-Valued Semantics for Weighted Conditional Knowledge Bases.
Theory and Practice of Logic Programming,
Vol. 22,
Issue. 4,
p.
589.
Brewka, Gerhard
Delgrande, James
Romero, Javier
and
Schaub, Torsten
2023.
A general framework for preferences in answer set programming.
Artificial Intelligence,
Vol. 325,
Issue. ,
p.
104023.
Alviano, Mario
Giordano, Laura
and
Theseider Dupré, Daniele
2023.
Proceedings 39th International Conference on Logic Programming.
Electronic Proceedings in Theoretical Computer Science,
Vol. 385,
Issue. ,
p.
9.
Alviano, Mario
Bartoli, Francesco
Botta, Marco
Esposito, Roberto
Giordano, Laura
and
Theseider Dupré, Daniele
2024.
A preferential interpretation of MultiLayer Perceptrons in a conditional logic with typicality.
International Journal of Approximate Reasoning,
Vol. 164,
Issue. ,
p.
109065.
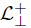 $\mathcal L_ \bot ^ + $.
$\mathcal L_ \bot ^ + $.