Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T04:59:54.241Z Has data issue: false hasContentIssue false
  • English
  • Français

Description, Implementation, and Evaluation of a Generic Design for Tabled CLP

Published online by Cambridge University Press:  18 January 2019

JOAQUÍN ARIAS  and
MANUEL CARRO
JOAQUÍN ARIAS*
Affiliation:
IMDEA Software Institute, Madrid, Spain Universidad Politécnica de Madrid, Madrid, Spain (e-mails: [email protected], [email protected], [email protected])
MANUEL CARRO
Affiliation:
IMDEA Software Institute, Madrid, Spain Universidad Politécnica de Madrid, Madrid, Spain (e-mails: [email protected], [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Logic programming with tabling and constraints (TCLP, tabled constraint logic programming) has been shown to be more expressive and in some cases more efficient than LP, CLP, or LP + tabling. Previous designs of TCLP systems did not fully use entailment to determine call/answer subsumption and did not provide a simple and well-documented interface to facilitate the integration of constraint solvers in existing tabling systems. We study the role of projection and entailment in the termination, soundness, and completeness of TCLP systems and present the design and an experimental evaluation of Mod TCLP, a framework that eases the integration of additional constraint solvers. Mod TCLP views constraint solvers as clients of the tabling system, which is generic w.r.t. the solver and only requires a clear interface from the latter. We validate our design by integrating four constraint solvers: a previously existing constraint solver for difference constraints, written in C; the standard versions of Holzbaur’s 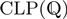and 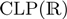, written in Prolog; and a new constraint solver for equations over finite lattices. We evaluate the performance of our framework in several benchmarks using the aforementioned solvers. Mod TCLP is developed in Ciao Prolog, a robust, mature, next-generation Prolog system.

Keywords

constraintstablingprologinterfaceimplementation
Type
Original Article
Information
Theory and Practice of Logic Programming , Volume 19 , Issue 3 , May 2019 , pp. 412 - 448
Copyright
Copyright © Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Carlson, B., Carlsson, M., and Diaz, D. 1994. Entailment of finite domain constraints. In International Conference on Logic Programming (ICLP’94), Santa Marherita Ligure, Italy, 13–18 Jun. 1994, Van Hentenryck, P. Ed. The MIT Press.Google Scholar
Charatonik, W., Mukhopadhyay, S. and Podelski, A. 2002. Constraint-based infinite model checking and tabulation for stratified CLP. In ICLP’02, Copenhagen, Denmark, 29 Jul.–1 Aug. 2002, Stuckey, P. J., Ed. Lecture Notes in Computer Science, vol. 2401. Springer, 115–129.Google Scholar
Chen, W. and Warren, D. S. 1996. Tabled evaluation with delaying for general logic programs. Journal of the ACM 43, 1 (January), 20–74.CrossRefGoogle Scholar
Chico de Guzmán, P., Carro, M., Hermenegildo, M. V. and Stuckey, P. 2012. A general implementation framework for tabled CLP. In FLOPS’12, Kobe, Japan, 23–25 May 2012, Schrijvers, T., and Thiemann, P., Eds. Lecture Notes in Computer Science, vol. 7294. Springer Verlag, 104–119.Google Scholar
Cousot, P. and Cousot, R. 1977. Abstract interpretation: A unified lattice model for static analysis of programs by construction or approximation of fixpoints. In ACM Symposium on Principles of Programming Languages (POPL’77), Los Angeles, CA. Jan. 1977, Graham, R. M., Harrison, M. A., and Sethi, R., Eds. ACM Press, 238–252.Google Scholar
Cui, B. and Warren, D. S. 2000. A system for Tabled Constraint Logic Programming. In International Conference on Computational Logic, London, UK, 24–28 Jul. 2000, Lloyd, J. W., Dahl, V., Furbach, U., Kerber, M., Lau, K.-K., Palamidessi, C., Moniz Pereira, L., Sagiv, Y., and Stuckey, P. J., Eds. Lecture Notes in Computer Science, vol. 1861. Springer Verlag, 478–492.Google Scholar
Dawson, S., Ramakrishnan, C. R. and Warren, D. S. 1996. Practical program analysis using general purpose logic programming systems– A case study. In Proc. of the ACM SIGPLAN’96 Conference on Programming Language Design and Implementation, Philadephia, PA, 21–24 May, 1996, Fischer, C. N., Ed. ACM Press, New York, USA, 117–126.Google Scholar
Daz, D. and Codognet, P. 1993. A minimal extension of the WAM for clp(fd). In Proc. of the Tenth International Conference on Logic Programming, Budapest, Hungary, 21–25 Jun. 1993, Warren, D. S., Ed. MIT Press, 774–790.Google Scholar
Dincbas, M., Hentenryck, P. V., Simonis, H. and Aggoun, A. 1988. The constraint logic programming language CHIP. In Proc. of the 2nd International Conference on Fifth Generation Computer Systems, Tokyo, Japan, 28 Nov.–2 Dec. 1988, ICOT Ed. 249–264.Google Scholar
Falaschi, M., Levi, G., Martelli, M. and Palamidessi, C. 1989. Declarative modeling of the operational behaviour of logic programs. Theoretical Computer Science 69, 289–318.CrossRefGoogle Scholar
Frigioni, D., Marchetti-Spaccamela, A. and Nanni, U. 1998. Fully dynamic shortest paths and negative cycles detection on digraphs with arbitrary arc weights. In ESA, Venice, Italy, 24–26 Aug. 1998, Bilardi, G., Italiano, G. F., Pietracaprina, A., and Pucci, G., Eds. Springer, 320–331.Google Scholar
Gange, G., Navas, J. A., Schachte, P., Søndergaard, H. and Stuckey, P. J. 2013. Failure tabled constraint logic programming by interpolation. TPLP 13, 4–5, 593–607.Google Scholar
Genaim, S., Codish, M. and Howe, J. 2001. Worst-case groundness analysis using definite Boolean functions. Theory and Practice of Logic Programming 1, 5, 611–615.CrossRefGoogle Scholar
Hermenegildo, M. V., Bueno, F., Carro, M., López, P., Mera, E., Morales, J. and Puebla, G. 2012. An overview of ciao and its design philosophy. Theory and Practice of Logic Programming 12, 1–2 (January), 219-252. URL: http://arxiv.org/abs/1102.5497. [Accessed on December 28, 2018].CrossRefGoogle Scholar
Holzbaur, C. 1995. OFAI CLP(Q, R) Manual, Edition 1.3.3. Tech. Rep. TR-95-09, Austrian Research Institute for Artificial Intelligence, OFAI, Vienna, Austria.Google Scholar
Jaffar, J. and Maher, M. 1994. Constraint logic programming: A survey. Journal of Logic Programming 19/20, 503–581.CrossRefGoogle Scholar
Kanellakis, P. C., Kuper, G. M. and Revesz, P. Z. 1995. Constraint query languages. Journal of Computer and System Sciences 51, 1, 26–52.CrossRefGoogle Scholar
Knuth, D. E. 1991. Textbook examples of recursion. In Artificial Intelligence and Mathematical Theory of Computation: Papers in Honor of John McCarthy, 207–230.CrossRefGoogle Scholar
Marriott, K. and Stuckey, P. J. 1998. Programming with Constraints: An Introduction. MIT Press.CrossRefGoogle Scholar
Ramakrishna, Y., Ramakrishnan, C., Ramakrishnan, I., Smolka, S., Swift, T. and Warren, D. 1997. Efficient model checking using tabled resolution. In Computer Aided Verification, Haifa, Israel, 22–25 Jun. 1997, Ramakrishna, Y. S., Ramakrishnan, C. R., Ramakrishnan, I. V., Smolka, S. A., Swift, T., and Warren, D. S., Eds. Lecture Notes in Computer Science, vol. 1254. Springer Verlag, 143–154.CrossRefGoogle Scholar
Ramakrishnan, I., Rao, P., Sagonas, K., Swift, T. and Warren, D. 1995. Efficient tabling mechanisms for logic programs. In ICLP’95, Tokyo, Japan, 13–16 Jun. 1995, Sterling, L., Ed. MIT Press, 697–711.Google Scholar
Schrijvers, T., Demoen, B. and Warren, D. S. 2008. TCHR: A framework for tabled CLP. Theory and Practice of Logic Programming 4, July, 491–526.CrossRefGoogle Scholar
Swift, T. and Warren, D. S. 2010. Tabling with answer subsumption: Implementation, applications and performance. In Logics in Artificial Intelligence, vol. 6341, Helsinki, Finland, 13–15 Sep. 2010, Janhunen, T., and Niemelä, I., Eds. Springer Verlag, 300–312.CrossRefGoogle Scholar
Swift, T. and Warren, D. S. 2012. XSB: Extending prolog with tabled logic programming. Theory and Practice of Logic Programming 1–2, January, 157–187.CrossRefGoogle Scholar
Tamaki, H. and Sato, M. 1986. OLD resolution with tabulation. In Third International Conference on Logic Programming, 14–18 Jul. 1986, Shapiro, E., Ed. Lecture Notes in Computer Science, Springer-Verlag, London, 84–98.CrossRefGoogle Scholar
Toman, D. 1997a. Constraint databases and program analysis using abstract interpretation. In Constraint Databases and Their Applications, Cambridge, MA, 19 Aug. 1996, Gaede, V., Brodsky, A., Günther, O., Srivastava, D., Vianu, V., and Wallace, M., Eds. Lecture Notes in Computer Science, vol. 1191, 246–262.CrossRefGoogle Scholar
Toman, D. 1997b. Memoing evaluation for constraint extensions of datalog. Constraints 2, 3/4, 337–359.CrossRefGoogle Scholar
Van Hentenryck, P. 1989. Constraint Satisfaction in Logic Programming. MIT Press.Google Scholar
Warren, D. S. 1992. Memoing for logic programs. Communications of the ACM 35, 3, 93–111.CrossRefGoogle Scholar
Warren, R., Hermenegildo, M. and Debray, S. K. 1988. On the practicality of global flow analysis of logic programs. In Fifth International Conference and Symposium on Logic Programming, Seattle, Washington, 15–19 Aug. 1988, Kowalski, R. A., and Bowen, K. A., Eds. MIT Press, 684–699.Google Scholar
Zou, Y., Finin, T. and Chen, H. 2005. F-OWL: An inference engine for semantic web. In Formal Approaches to Agent-Based Systems, Greenbelt, MD, 26–27 Apr. 2004, Hinchey, M. G., Rash, J. L., Truszkowski, W., and Rouff, C. A., Eds. Lecture Notes in Computer Science, vol. 3228. Springer Verlag, 238–248.CrossRefGoogle Scholar
Supplementary material: PDF

Arias and Carro supplementary material

Appendices A-C

Download Arias and Carro supplementary material(PDF)
PDF 327.2 KB