Rheological modelling of complex fluids. I. The concept of effective volume fraction revisited

Abstract

Number of complex fluids (as slurries, drilling muds, paints and coatings, many foods, cosmetics, biofluids...) can approximately be described as concentrated dispersions of Structural Units (SUs). Due to shear forces, SUs are assumed to be approximately spherical in shape and uniform in size under steady flow conditions, so that a complex fluid can be considered as a roughly monodisperse dispersion of roughly spherical SUs (with a shear-dependent mean radius), what allows to generalize hard sphere models of monodisperse suspensions to complex fluids. 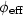A rheological model of such dispersions of SUs is based on the concept of the effective volume fraction, $\rm \phi_{eff}$ which depends on flow conditions. Indeed, in competition with particle interactions, hydrodynamic forces can modify (i) S, the number fraction of particles that all SUs contain, (ii) both SUs arrangements and their internal structure, especially the SU's compactness, φ. As a structural variable, S is governed by a kinetic equation. Through the shear-dependent kinetic rates involved in the latter, the general solution S depends on Γ, a dimensionless shear variable, leading to $\rm \phi_{eff}$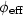(t, Γ; φ). 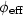The structural modelling is achieved by introducing this expression of $\rm \phi_{eff}$ into a well-established viscosity model of hard sphere suspensions. Using the steady state solution of the kinetic equation, S_eq(Γ), allows to model non-Newtonian behaviors of complex fluids under steady shear conditions, as pseudo-plastic, plastic, dilatant ... ones. In this model, the ratio of high shear to low shear limiting viscosities appears as a key variable. Different examples of application will be discussed.