Observer effects and heritability of childhood attention-deficit hyperactivity disorder symptoms

Abstract

Background

Twin studies have found that childhood attention-deficit hyperactivity disorder (ADHD) has a strong genetic component. Estimates of heritability the extent of non-additive genetic effects and of ‘sibling contrast’ effects vary between different studies.

Aims

To use multiple informants to assess the extent to which observer effects influence such estimates in an epidemiological sample of twins.

Method

Questionnaire packs were sent to the families and teachers of twins aged 5–16 years in the Bro Taf region of South Wales. The twins were ascertained from community paediatric registers.

Results

Both parent— and teacher-rated data showed a high degree of heritability for ADHD measured as a symptom dimension, but the correlation between the two types of rater was modest. Bivariate analyses suggested that parent and teacher ratings reflect the effects of different genes. Self-report data from twins aged 11–16 years showed no evidence of genetic effects.

Conclusions

Although ADHD is shown to be highly heritable by both parent— and teacher-rated data, the underlying genotypes may be substantially different. This has implications for study designs aiming to find genes that contribute to the disorder.

Twin studies have shown that attention-deficit hyperactivity disorder (ADHD) is highly heritable, as are dimensions based upon ADHD symptom scores (Thapar et al, 1999). Recent estimates of ‘broad’ heritability for ADHD from twin studies range between approximately 70% and 80% (Stevenson, 1992; Thapar et al, 1995; Faraone, 1996; Gjone et al, 1996; Eaves et al, 1997; Simonoff et al, 1998). Although these estimates are reasonably similar, findings on factors contributing to the variance are less consistent. Some studies have found only a combination of additive genetic factors and non-shared environmental influences (Stevenson, 1992; Faraone, 1996; Gjone et al, 1996). However, sibling interaction effects (contrast or competition) (Carey, 1986; Thapar et al, 1995; Simonoff et al, 1998) and shared environment (Sherman et al, 1997) have also been implicated.

A reason for these differences may be the choice of rater used in each study. For example, it was found from a sample of male twins that teachers and mothers may rate differently (Shermanet al, 1997). Results from both raters suggested that ADHD was highly heritable, estimated at 89% for mothers and 73% for teachers. It has also been found that what appears to be sibling interaction contributes to heritability in maternal and paternal estimates, but not in teacher estimates (Eaves et al, 1997).

Differences between these ratings may be due to the environment in which the observations are made. The parents are more likely to compare twins with each other, and so may exaggerate differences and similarities. Teachers, on the other hand, can compare each twin with a large number of children of similar age, so ratings may be more objective. Twin confusion may also be a factor, in that a teacher might attribute behaviour to the wrong twin whereas parents would seldom mis-report their own children (Simonoff et al, 1998). Moreover, the twins might behave in a different manner at home and at school (perhaps owing to different situational manifestations of ADHD) so that the raters would truly be observing different behaviours. This suggests that evidence from either rater alone cannot be interpreted as conclusive.

In this study we assess the extent to which there is overlap between the parent-and teacher-rated observations using the same questionnaires, and compare both with results for self-report data in the subset of children aged 11-16 years.

METHOD

Sample

An epidemiologically ascertained sample of twin births in the Cardiff area of South Wales had been set up previously (Thapar et al, 1995) using the Cardiff Birth Survey, a register of all births in the country of South Glamorgan, and was extended and updated using community child health databases to include all births of twins aged 5-16 years at 1 July 1997 in the Bro Taf Health District (formerly South and Mid Glamorgan) of South Wales. The full database was managed using Microsoft Access (Microsoft, 1995) and the response data managed using SPSS for Windows (SPSS, 1999).

An initial total of 3152 individual records were found, this was reduced to 2380 useable records after excluding those aged over 16 years, twins living apart, triplets or quadruplets, or where we were unable to trace the family. This yielded 1190 twin pairs, of whom 20 pairs were used for a pilot study to test the suitability of the questionnaire package. From the 1170 packages sent out in the first mailing, 61 were returned as wrongly addressed and thus 1109 families were left for the main study.

Measures

A six-item twin similarity questionnaire of demonstrated validity (Thapar et al, 1995) was used to assign zygosity to each twin pair. This approach has been shown to have good agreement with zygosity tests using blood groups or other genetic markers (McGuffin et al, 1994) and was used in the previous Cardiff twin study (Thapar & McGuffin, 1994). A short questionnaire adapted from Loehlin & Nichols (1976) was included to assess environmental sharing.

Symptoms of ADHD were measured using the abbreviated Conners scale (Conners, 1973) and the Strengths and Difficulties Questionnaire (SDQ) hyperactivity sub-scale (Goodman, 1997), and ratings were obtained from parents — usually mothers — and teachers. For the SDQ scale, self-reports were also collected in the adolescent sample (those aged 11-16 years).

Analyses

Exploratory analysis of the data was performed using SPSS (SPSS, 1999). The raw scores for both measures of ADHD were skewed with a ‘floor’ effect, whereby a high proportion of the sample have low scores. To achieve a closer approximation to normality, the data were transformed by taking square roots.

Variance—covariance matrices were obtained from the transformed data for monozygotic (MZ) and dizygotic (DZ) twins separately. These matrices were then used in the Mx package (Neale, 1997) to perform model-fitting.

First, univariate genetic models were tested for each type of rater (parent, teacher and adolescent) and for each of the ADHD measures. These analyses provided estimates of broad sense heritability and the extent of contributions from genetic and environmental effects. Next, bivariate modelling was performed to investigate to what extent phenotypes based on the observations of parents and teachers were influenced by the same factors or by different factors. In all cases, the full ‘ACE’ model was fitted to the data first: this tests for additive genetic effects (A), common environmental effects (C) and non-shared environmental effects (E). Models lacking one or more of these parameters are then fitted to see whether or not they can explain the data equally well. Where C can be dropped, it is then possible to test for non-additive genetic effects (D) in the models. As sibling interaction (i) has been found to be a contributing factor to the variance in ADHD in previous studies (Thapar et al, 1995; Silberg et al, 1996; Eaves et al, 1997; Nadder et al, 1998), it was also explored here. Nested models were compared using chi-squared differences and Akaike's information criterion (AIC), where AIC=χ²-(2 × d.f.) (Neale & Cardon, 1992).

RESULTS

Response rates

Questionnaires were received from 682 of the 1109 families (61%) ¹ . Of these, 561 (82%) gave consent to contact the twins' teachers. From these teachers, 443 replies were received, giving a teacher response rate of 79%. Of the 1109 families, 570 had twins over the age of 11 years. Of these adolescents, 286 complete pairs (50%) responded.

Zygosity, age and gender

The distribution of zygosity and gender in the study population is shown in Table 1. In total there were 278 MZ pairs (42%), 378 DZ pairs (56%) and 14 pairs in whom zygosity could not be assigned (2%). There were 223 pairs of male twins, of whom 124 pairs were MZ and 99 DZ; 235 female pairs of whom 154 pairs were MZ and 81 DZ; and 198 male/female pairs. This means there were 654 boys (49%) and 686 girls (51%).

Table 1 Participating twin pairs separated by zygosity and gender

Zygosity	Gender	Number of pairs	Proportion of sample (%)
Dizygotic	Male/female	198	29.6
Dizygotic	Male/male	99	14.8
Dizygotic	Female/female	81	12.1
Monozygotic	Male/male	124	18.5
Monozygotic	Female/female	154	23.0
Ambiguous or unassigned		14	2.

Tests were carried out to explore whether zygosity had an effect on the mean or variance of the scores. It appeared not to have any effect on mean scores (Mann—Whitney MZ v. DZ, Z=-1.416,P=0.157 for parent-rated Conners data, Z=-0.079,P=0.937 for parent-rated SDQ data, tests also performed separately for males only and females only) and a Kruskal—Wallis one-way analysis of variance (ANOVA) showed that variance is also unaffected by zygosity (χ²=2.006, P=0.157, MZ variance 31.710, DZ 39.952 for parent-rated Conners data, and χ²=0.006, P=0.937, MZ variance 6.362, DZ 8.087 for parent-rated SDQ data).

As mentioned above, self-report data were collected from twins aged 11 years and over. These data were compared with parent and teacher ratings on the same sample to determine whether any age effects existed. When the mean scores were compared differences were found (Z=-3.102,P=0.002, and Z=-7.244, P<0.001, respectively). This suggests that the adolescents rate themselves as having more symptoms of hyperactivity than do their parents or teachers.

Age effects were further explored using regression analysis. The results showed that there was no significant relationship between age and SDQ hyperactivity score (β=-0.071, P=0.011) but there was a modest, significant inverse relationship between age and Conners scores (β=-0.114, P<0.001). This may account for some of the differences between the self-report data and the parent and teacher data.

Environmental sharing

Environmental sharing was statistically significantly greater in MZ than DZ twins (t=10.398, P<0.001, d.f.=618). Consequently, in order to test whether greater environmental sharing in MZ than in DZ pairs was likely to invalidate the ‘equal environments’ assumption, a regression analysis was performed separately on the Conners scale and SDQ sub-scale hyperactivity scores (both parent-rated). For the Conners scale, the variance in difference in scores between twin 1 and twin 2 of each pair explained by environmental sharing (r ²) was −0.002, and the standardised regression coefficient (β) was −0.014 (P=0.731). For the SDQ sub-scale r ² was −0.002, and standardised β was −0.006 (P=0.886). In both cases the effects are small and not statistically significant, so that differences in environmental sharing between MZ and DZ pairs (at least as reflected by this particular measure) are unlikely to perturb the assumption of equal environments in subsequent model-fitting on the data obtained from the Conners and SDQ questionnaires.

Univariate model-fitting

The results of univariate model-fitting on the parent-rated ADHD measures are summarised in Table 2. The correlations at the top of each section of the table show that the MZ correlation (r _MZ) is more than twice that of DZ (r _DZ) pairs for both SDQ and Conners data. This suggests that the best-fitting model will include additive and non-additive genetic factors, or sibling interaction effects.

Table 2 Univariate models on parent-rated data

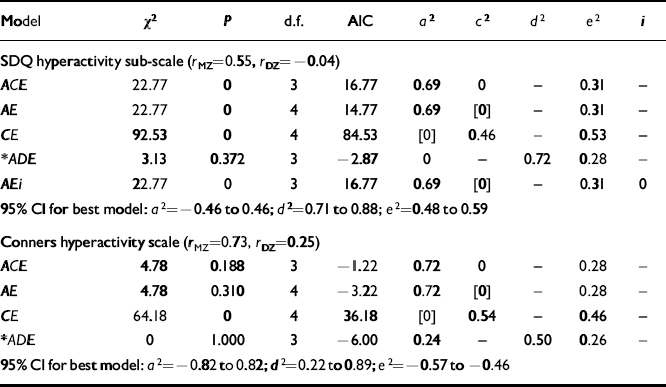
Model	χ 2	P	d.f.	AIC	a 2	c 2	d 2	e2	i
SDQ hyperactivity sub-scale (r MZ=0.55,r DZ=-0.04)
ACE	22.77	0	3	16.77	0.69	0	—	0.31	—
AE	22.77	0	4	14.77	0.69	[0]	—	0.31	—
CE	92.53	0	4	84.53	[0]	0.46	—	0.53	—
* ADE	3.13	0.372	3	-2.87	0	—	0.72	0.28	—
AEi	22.77	0	3	16.77	0.69	[0]	—	0.31	0
95% CI for best model: a 2=-0.46 to 0.46;d 2=0.71 to 0.88; e2=0.48 to 0.59
Conners hyperactivity scale (r MZ=0.73,r DZ=0.25)
ACE	4.78	0.188	3	-1.22	0.72	0	—	0.28	—
AE	4.78	0.310	4	-3.22	0.72	[0]	—	0.28	—
CE	64.18	0	4	36.18	[0]	0.54	—	0.46	—
* ADE	0	1.000	3	-6.00	0.24	—	0.50	0.26	—
95% CI for best model: a 2=-0.82 to 0.82;d 2=0.22 to 0.89; e2=-0.57 to −0.46

In keeping with this, the fit of the SDQ models containing only additive genetic effects (ACE or AE) is poor. The fit of theADE model, in contrast, is satisfactory (χ²=3.127,P=0.372) but the additive genetic component was estimated at its lower boundary value of zero. However, it is unlikely in nature that non-additive genetic factors occur in the absence of additive factors. Next, a test for sibling inter-action effects was carried out as denoted by the parameter i. This brought no change in χ² compared with the AE model and i was estimated at zero. Therefore on grounds of parsimony and goodness of fit, the ADE model offers the best explanation of the data. Since additive effects were estimated at zero we could go on to drop these from the model and achieve even greaterstatistical parsimony; however, it could be argued that such a model is biologically implausible. We therefore accept an estimate of broad sense heritability of 72% with no common environment effects.

For the Conners scale scores the ACE model gives an acceptable fit (χ²=4.783, AIC=-1.217, d.f.=3, P=0.188), the shared environment (c ²) being estimated at zero. Consequently, dropping C from the model results in the same χ², and, because there is one more degree of freedom, a lower AIC, but droppingA to give a CE model (no genetic transmission) results in a significant deterioration in fit (difference in χ²=37.393 for 1 d.f. when compared with the ACE model). Next, the presence of dominance was tested for and an ADE model was fitted. The AE model is a sub-model of ADE so a direct comparison can be made between the two. The ADE is a better fit (difference in χ ²=4.783 for 1 d.f., AIC better by 2.783). A model with sibling interaction cannot be fitted as the model would be unidentified (i.e. we would be trying to estimate too many parameters from the given data). On grounds of parsimony and goodness of fit, the ADE is accepted as the best fit, showing the broad sense heritability to be 74% and consisting of both additive genetic effects (24%) and non-additive genetic effects (50%).

The results of the univariate model-fitting on the teacher-rated data are summarised in Table 3.

Table 3 Univariate models on teacher-rated data

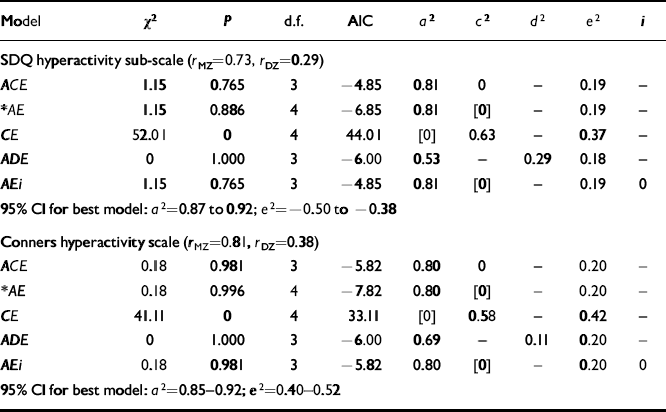
Model	χ 2	P	d.f.	AIC	a 2	c 2	d 2	e2	i
SDQ hyperactivity sub-scale (r MZ=0.73,r DZ=0.29)
ACE	1.15	0.765	3	-4.85	0.81	0	—	0.19	—
* AE	1.15	0.886	4	-6.85	0.81	[0]	—	0.19	—
CE	52.01	0	4	44.01	[0]	0.63	—	0.37	—
ADE	0	1.000	3	-6.00	0.53	—	0.29	0.18	—
AEi	1.15	0.765	3	-4.85	0.81	[0]	—	0.19	0
95% CI for best model: a 2=0.87 to 0.92; e2=-0.50 to −0.38
Conners hyperactivity scale (r MZ=0.81,r DZ=0.38)
ACE	0.18	0.981	3	-5.82	0.80	0	—	0.20	—
* AE	0.18	0.996	4	-7.82	0.80	[0]	—	0.20	—
CE	41.11	0	4	33.11	[0]	0.58	—	0.42	—
ADE	0	1.000	3	-6.00	0.69	—	0.11	0.20	—
AEi	0.18	0.981	3	-5.82	0.80	[0]	—	0.20	0
95% CI for best model: a 2=0.85-0.92; e2=0.40-0.52

From the teacher ratings there is less suggestion of non-additive effects than for the parent ratings, in that the DZ correlations are just under half of the size of the MZ correlations. For the SDQ data, the ACE model fits well (χ²=1.150, d.f.=3, AIC=-4.850, P=0.765) butC is estimated at zero. Dropping C from the model gives a better fit (AIC decreased by 2) and a simpler model. Removing A for the CE model gives a significant deterioration in fit (for 1 d.f., χ ² increased by 50.823, AIC increases by 48.863). In contrast, adding either dominance or sibling interaction effects produced no significant change in χ², which means that the AE model is accepted as the best explanation of the data.

For the Conners data, the pattern is identical with the AE model being accepted (χ²=0.178, AIC=-7.822, P=0.996), giving a heritability of 80%.

The results of the univariate model-fitting on the adolescent self-report data are summarised in Table 4.

Table 4 Univariate models on adolescent self-report scores (r _MZ=0.29, r _DZ=0.29)

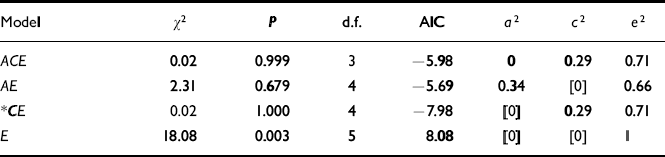
Model	χ 2	P	d.f.	AIC	a 2	c 2	e2
ACE	0.02	0.999	3	-5.98	0	0.29	0.71
AE	2.31	0.679	4	-5.69	0.34	[0]	0.66
* CE	0.02	1.000	4	-7.98	[0]	0.29	0.71
E	18.08	0.003	5	8.08	[0]	[0]	1

Looking at the correlations for the adolescent data, a model with common environment would be expected to fit best. The ACE model gives a good fit (χ²=0.016, AIC=-5.984, P=0.999) and additive genetic factors are estimated at zero. To test for additive genetic effects,C was dropped. This resulted in a small worsening of fit (both AIC and χ² increased). The CE model was then fitted which gave a superior fit in terms of AIC, but a change of only 2.292 in χ ². Finally, a ‘no transmission’ (E only) model was tested. This resulted in a much worse fit, and the CE model is accepted on the grounds of having the lowest AIC. This gives a variance of 29% due to shared environment.

Bivariate model-fitting

Before fitting the models, a test was performed to compare teacher-rated scores with parent-rated ones. The differences in mean scores are larger than you would expect by chance alone for both Conners and SDQ ratings (for Conners, Z=-9.414, P<0.001; for SDQ, Z=-4.419,P<0.001). This suggests either that there are differences in the way parents and teachers rate the children, with parents tending to report more symptoms, or that the children are behaving differently in school and home settings. Alternatively, a selection bias in the teacher data might result from only the parents of children with low scores giving permission to contact teachers. This was explored using a Mann—Whitney test between scores from parents who had allowed us to contact teachers, and those who had not. No significant difference in the means were found (for Conners,Z=-0.938, P=0.348; for SDQ, Z=-0.587,P=0.557), suggesting that such a selection bias is not present.

The results of bivariate model-fitting on the parent-rated and teacher-rated ADHD measures are summarised in Table 5. The model-fitting was carried out using the psychometric or ‘common pathway’ model (Neale & Cardon, 1992). Here it is assumed that both parent and teacher ratings are measuring the same latent phenotype (Fig. 1).

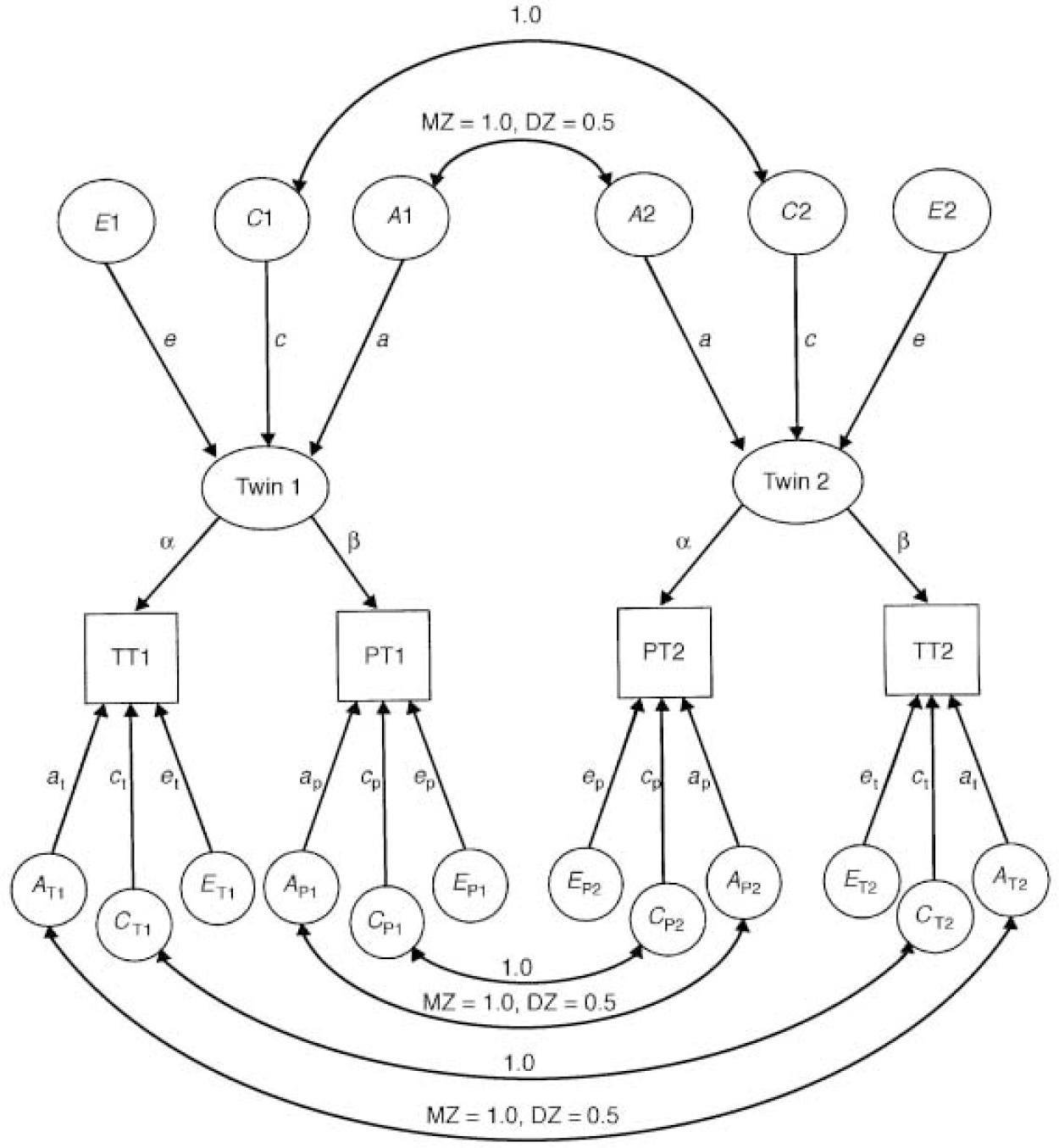
Fig. 1 The psychometric pathway model for parent (PT) and teacher ratings (TT).A, additive genetic effects; C, common environmental effects; E, non-shared environmental effects; DZ, dizygotic, MZ, monozygotic, x _T, specific teacher rating effect;x _P, specific parent rating effect.

Table 5 Bivariate analysis of parent-rated and teacher-rated scores

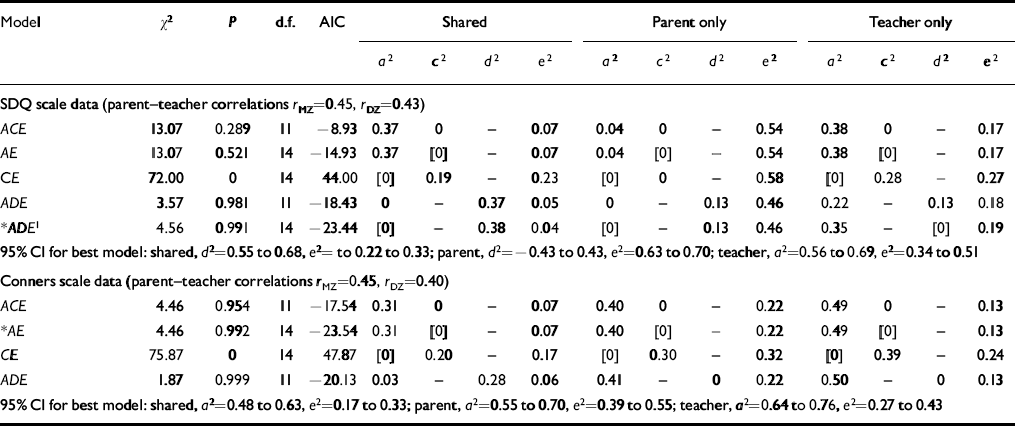
Model	χ 2	P	d.f.	AIC	Shared				Parent only				Teacher only
					a 2	c 2	d 2	e2	a 2	c 2	d 2	e2	a 2	c 2	d 2	e2
SDQ scale data (parent—teacher correlationsr MZ=0.45, r DZ=0.43)
ACE	13.07	0.289	11	-8.93	0.37	0	—	0.07	0.04	0	—	0.54	0.38	0	—	0.17
AE	13.07	0.521	14	— 14.93	0.37	[0]	—	0.07	0.04	[0]	—	0.54	0.38	[0]	—	0.17
CE	72.00	0	14	44.00	[0]	0.19	—	0.23	[0]	0	—	0.58	[0]	0.28	—	0.27
ADE	3.57	0.981	11	— 18.43	0	—	0.37	0.05	0	—	0.13	0.46	0.22	—	0.13	0.18
* ADE 1	4.56	0.991	14	— 23.44	[0]	—	0.38	0.04	[0]	—	0.13	0.46	0.35	—	[0]	0.19
95% Cl for best model: shared, d 2=0.55 to 0.68, e2=to 0.22 to 0.33; parent, d 2= — 0.43 to 0.43, e2=0.63 to 0.70; teacher, a 2=0.56 to 0.69, e2=0.34 to 0.51
Conners scale data (parent—teacher correlationsr MZ=0.45, r DZ=0.40)
ACE	4.46	0.954	11	— 17.54	0.31	0	—	0.07	0.40	0	—	0.22	0.49	0	—	0.13
* AE	4.46	0.992	14	— 23.54	0.31	[0]	—	0.07	0.40	[0]	—	0.22	0.49	[0]	—	0.13
CE	75.87	0	14	47.87	[0]	0.20	—	0.17	[0]	0.30	—	0.32	[0]	0.39	—	0.24
ADE	1.87	0.999	11	— 20.13	0.03	—	0.28	0.06	0.41	—	0	0.22	0.50	—	0	0.13
95% Cl for best model: shared, a 2=0.48 to 0.63, e2=0.17 to 0.33; parent, a 2=0.55 to 0.70, e2=0.39 to 0.55; teacher, a 2=0.64 to 0.76, e2=0.27 to 0.43

For the Conners data, the ACE model gives a good fit (χ²=4.464, AIC=-17.536, P=0.954), but C is estimated at zero and consequently dropping it from this model results in no change in fit and a lower AIC (χ²=4.464, AIC=-23.536,P=0.992). However, dropping A gives rise to a serious deterioration in fit (χ²=75.871, AIC=47.871,P=0.0001). The full ADE model when tested gave a little improvement in the fit and an increase in the AIC. Therefore the AE model provides the most acceptable explanation of the data, with parent and teacher ratings being explained by the same additive genetic factors accounting for 31% of variance. However, there were specific additive genetic effects of 41% for parent ratings and 50% for teachers. This suggests that despite both the teacher— and parent-observed phenotypes being strongly influenced by genetic factors, these to a substantial extent involve different genes.

From the SDQ data, the overall fit of models is similar to that for the Conners data, but a modified ADE model turns out to be the most satisfactory (χ²=4.56, AIC=-23.44, P=0.991). This variance of 38% is explained by shared non-additive genetic factors. For parent ratings there is a specific 13% of variance due to non-additive genetic factors, and for teacher ratings a specific 35% due to additive genetic effects.

In addition to the fitting shown in Table 5, models were fitted for both sets of data but with the shared additive genetic effect fixed at 1 (meaning that all covariation is due to common genetic factors). Both these tests failed, however, giving χ² values of over 10 000. These results again imply that what the parents and teachers observe with respect to SDQ hyperactivity items is influenced to a significant extent by different genes.

A previous study (Simonoff et al, 1998) found correlational differences between twins rated by the same teacher or by different teachers. In the present sample only 39 pairs (9.2%) of the teacher reports were made by a different teacher for each twin, hence this has not been explored.

DISCUSSION

Support for heritability

The results of the univariate analyses on parent— and teacher-rated measures support the findings of previous studies (Stevenson, 1992; Thapar et al, 1995; Faraone, 1996; Gjone et al, 1996; Eaves et al, 1997; Simonoff et al, 1998) that ADHD symptoms are strongly influenced by genes, with a broad sense heritability of 70-81%. However, the extent and nature of contributing factors differed depending on the rater. From parent-rated scores, on both the Conners and SDQ scales, we found significant non-additive genetic effects, whereas using the teacher ratings both scales produced a pattern of correlations that could be explained entirely by additive genetic variance. Essentially, the evidence for dominance effects in the parent ratings comes from having MZ correlations that are more than double the DZ correlations. Such a pattern might also arise from rater contrast effects (Simonoff et al, 1998); for example, parents who tend to look upon one member of a twin pair as ‘usually restless’ will tend to rate the other twin as ‘usually still’. If this were to affect DZ more than MZ pairs, it would result both in an inflated difference between MZ and DZ correlations and in an increase in the variance of DZ twin scores. A similar pattern could occur because of sibling interaction — that is, the twins themselves reacting to each other and tending to take on opposite types of behaviour. A previous study (Thapar et al, 1995) using a proportion of the present sample rated on an earlier occasion (304 individuals), found evidence of sibling interaction or contrast effects, whereas this study did not. Others have suggested on the basis of comparing parent and teacher ratings (Simonoff et al, 1998) that systematic biases in parent ratings probably do exist, resulting in contrasts rather than true sibling interaction effects. Certainly our findings support the proposition that observer effects are considerable.

Observer effects

The most striking difference in our results based on simple univariate model-fitting was between those from the adolescent twins' own ratings and those from parent or teacher ratings. Self-rated scores from adolescents resulted in equal correlations in MZ and DZ twins and the most acceptable model was one that had zero heritability. It could be argued that ADHD is an ‘externalising’ disorder and that therefore its symptoms would be more accurately reported by others rather than by subjects themselves. However, this seems unlikely on its own to account for the absence of genetic effects, since another externalising trait, mild antisocial behaviour, has been found to be heritable in adolescents in an earlier twin sample from South Wales (McGuffin & Thapar, 1997).

Our other major finding on observer effects comes from the bivariate analyses where we applied a model with the assumption that both parents and teachers are rating the same underlying phenotype. Each type of measure can then be thought of as a reflection of one latent variable. In fact we did find evidence of commonality, with the same genetic factors explaining some of the variance in parent and teacher ratings (31% using the Conners scale, 38% with the SDQ scale), but there were also sizeable specific genetic components for parents and teachers, suggesting that although both types of report result in high heritabilities there may be different sets of genes underlying what is observed. Unfortunately, the limitation of sample size precluded a trivariate analysis attempting to further explore ratings by parent, teacher and self-report.

Implications for genetic studies

This finding of observer effects has serious implications for molecular studies attempting to find causative genes for ADHD. Given the same population, if a study selected one sample for quantitative trait locus analysis purely on the basis of teacher-rated scores, and another study selected a sample for analysis based on only parent-rated scores, the results might be very different. The two studies might both detect a gene or genes contributing to the shared 31% of heritability, in which case it would be reasonably safe to accept the quantitative trait locus as being associated with ADHD. On the other hand, the studies might detect different genes involved in the specific or non-overlapping portions of the heritability, but neither group would be able to replicate the other's results and so both loci would be rejected and regarded as false positives. Thus, different definitions of what is apparently the same phenotype complicate the task of finding the causative genes.

The findings of the present study must be seen in the light of rater bias described in previous studies (Eaves et al, 1997; Simonoff et al, 1998). The results may indicate that although both raters are observing the same phenotype, they are scoring it differently because of their own particular biases. Another possible explanation is that the children are truly behaving differently at home from the way they do at school. This means that the raters would be scoring phenotypes for which the differences are ‘real’ to an extent. To date, most studies attempting to find genetic marker associations in ADHD have focused on categorical clinical samples, but most of the justification for performing such studies has come from research on general population samples, mainly using dimensional measures. Future studies aimed at finding genes involved in ADHD should incorporate multiple informants, and dimensional as well as clinical diagnostic measures in their design.

Clinical Implications and Limitations

CLINICAL IMPLICATIONS

1. • Symptoms of attention-deficit hyperactivity disorder (ADHD) as observed by parents and teachers are highly heritable, but self-report of ADHD symptoms in adolescents is not.

2. • The correlation between parent and teacher reports is modest, and bivariate analysis suggests they may be observing the effects of different genes.

3. • Multiple informants plus self-reports are desirable in the clinical assessment of ADHD.

LIMITATIONS

1. • Although based on an initial study group of 1170 twin pairs, this is a comparatively small sample by current standards.

2. • The parent response rate of 60% further reduced power and might also have introduced selection bias into the sample.

3. • Problems of self-report data on externalising measures are well documented.