BACKGROUND
More quantitative genetic research (family, twin and adoption studies) has been reported for cognitive abilities than for any other domain of science (Reference Plomin, DeFries and McClearnPlomin et al, 2001). Tests of cognitive abilities are related in a hierarchical manner in which specific tests (such as vocabulary and verbal fluency) intercorrelate to create group factors (e.g. verbal ability) which are called ‘specific cognitive abilities’ (Reference CarrollCarroll, 1993). Diverse specific cognitive abilities such as verbal and spatial abilities, processing speed and memory intercorrelate at about 0.4. This intercorrelation among specific cognitive abilities is known as general cognitive ability (g), a key factor in learning and memory (Reference JensenJensen, 1998). General cognitive ability, commonly called intelligence, is best conceptualised as a general factor (first unrotated principal component) among diverse tests of cognitive ability. Because most tests correlate moderately on a general factor, g is also indexed by total scores on diverse unit-weighted tests, as in IQ tests. A new direction for genetic research on g is to investigate other less direct measures such as information processing (Reference Neubauer, Spinath and RiemannNeubauer et al, 2001) and measures of brain function such as evoked potentials, positron emission tomography (PET) scans and functional magnetic resonance imaging (fMRI) (Reference VernonVernon, 1993; Reference Kosslyn, Plomin, Dougherty, Rauch and RosenbaumKosslyn & Plomin, 2000).
Multivariate genetic research
One of the most interesting yet little-known findings about cognitive abilities has emerged from multivariate genetic research, which examines the covariance among specific cognitive abilities rather than the variance of each cognitive ability considered separately. Specific cognitive abilities show substantial genetic influence, although less than for g (Reference Plomin and DeFriesPlomin & DeFries, 1998). The surprising finding from multivariate genetic research is that the same genetic factors largely influence different abilities (Reference PetrillPetrill, 1997). In other words, the genetic basis of cognitive abilities is g. What this finding means concretely is that if a specific gene were found that was associated with verbal ability, it would also be expected to be associated with spatial ability and other specific cognitive abilities. Conversely, g should be the best target for attempts to identify genes associated with cognitive abilities because genetic effects are general rather than specific. This finding is surprising because it goes against the tide of the popular modular theory of cognitive neuroscience, which assumes that cognitive processes are specific and independent and that genes work from the ‘bottom up’; that is, genes are assumed to be specific to elementary processes, with these modular effects then indirectly affecting more complex cognitive processes. However, multivariate genetic results are consistent with the opposite hypothesis of a ‘top down’ model, in which genes have their primary influence on g and these genetic effects trickle down to affect other cognitive processes.
Genetic influence on g
Clearly, g runs in families. Correlations for first-degree relatives living together average 0.43 for more than 8000 parent-offspring pairs and 0.47 for more than 25 000 pairs of siblings. However, g might run in families for reasons of nurture or of nature. In studies involving more than 10 000 pairs of twins, the average g correlations are 0.85 for identical twins and 0.60 for same-sex fraternal twins (Reference Plomin, Fulker and CorleyPlomin et al, 1997). These twin data suggest a genetic effect size (heritability) that explains about half of the total variance in g scores. Although heritability could differ in different cultures, moderate heritability of g has been found in twin studies not only in North America and western European countries, but also in Moscow, former East Germany, rural India, urban India and Japan. Adoption studies also yield estimates of substantial heritability. For example, identical twins reared apart are almost as similar for g as are identical twins reared together, with an average correlation of 0.78 for 93 such pairs (Reference Bouchard, Lykken and McGueBouchard et al, 1990). Adoption studies of other first-degree relatives also indicate substantial heritability, as illustrated by results from the longitudinal 25-year Colorado Adoption Project (Reference Plomin, Fulker and CorleyPlomin et al, 1997).
Model-fitting meta-analyses based on dozens of adoption and twin studies estimate that about half of the total variance can be attributed to genetic factors. Most of these studies involved children. Research during the 1990s has shown that the heritability of g increases steadily from infancy (20%) to childhood (40%), to adulthood (60%). For example, a study of twins aged 80 years and older reported a heritability of about 60% (Reference McClearn, Johansson and BergMcClearn et al, 1997). Studies of identical twins reared apart suggest that heritability may be as high as 80% in adulthood. Why does heritability of g increase during the life span? It is possible that fluctuating environmental differences are evened out as life goes by so that genetic differences appear to be relatively more important. It is also possible that completely new genes come to affect g as more sophisticated cognitive processes come on line. A possibility we favour is that relatively small genetic effects early in life snowball during development, creating larger and larger phenotypic effects, perhaps as individuals select or create environments that foster their genetic propensities. During the 1990s genetic research has shown substantial evidence for such genotype-environment correlation, in the sense that associations between environmental measures and cognitive development are mediated genetically (Reference PlominPlomin, 1994).
Environmental influences on g
The same genetic research on g that provides evidence for the important contribution of genetics also provides the best available evidence for the importance of the environment. If the heritability of g is 50%, this means that the rest of the reliable variance can be attributed to environmental factors. Moreover, genetic research has shown that the way the environment affects g is different from our theories of socialisation. Shared family environments, which makes siblings similar, are important only until adolescence. In the long run, environmental influences on g, whatever they may be, make two children growing up in the same family different from one another: this is the ‘non-shared environment’ (Reference Plomin and PetrillPlomin & Petrill, 1997). One direction for research is to begin to identify specific environmental factors responsible for non-shared environmental influences on cognitive development (Reference Chipuer and PlominChipuer & Plomin, 1992), especially in the context of genetically sensitive designs that control for genotype-environment correlation.
Identifying genes associated with g
Another exciting direction for research is to identify specific genes responsible for the substantial heritability of g. Heritability of complex dimensions such as g seems likely to be due to multiple genes of varying, but small, effect size rather than one or a few genes with major effect. In such multiplegene systems each gene is called a ‘quantitative trait locus’ (QTL) (Reference Plomin, Owen and McGuffinPlomin et al, 1994). Unlike single-gene effects, such as phenylketonuria, which are necessary and sufficient for the development of a disorder, QTLs contribute interchangeably and additively, analogous to probabilistic risk factors. If there are multiple genes that affect a trait, it is likely that the trait is distributed quantitatively as a dimension rather than qualitatively as a disorder; this was the essence of Fisher's classic 1918 paper on quantitative genetics (Reference FisherFisher, 1918). From a QTL perspective, there are no disorders, just the extremes of quantitative traits caused by the same genetic and environmental factors responsible for variation throughout the dimension. In other words, the QTL perspective predicts that genes found to be associated with complex disorders will also be associated with normal variation and vice versa.
Traditional methods for identifying single-gene effects are unlikely to succeed in identifying QTLs because the effect sizes of individual QTLs are likely to be small. For a single-gene trait, the traditional large-pedigree linkage design is guaranteed to find the chromosomal location of a gene by tracking co-transmission of markers with a disorder. However, it does not have the statistical power needed to detect QTLs for quantitative traits influenced by multiple genes of varying, but relatively small, effect size - as well as by multiple environmental factors. Moreover, traditional linkage approaches assume that a disorder is indeed co-transmitted in families with the ‘disease’ gene. Quantitative traits do not fit this mould unless one arbitrarily divides the quantitative dimensions and pretends that one part is qualitatively distinct, which is what has been done with many presumed disorders. Newer linkage designs such as the affected sib-pair design (Reference Suarez and Van EerdeweghSuarez & Van Eerdewegh, 1984; Reference Blackwelder and ElstonBlackwelder & Elston, 1985) are more compatible with a QTL perspective because the selected sibs can be viewed as being at the extreme of a quantitative dimension. Sib-pair QTL linkage explicitly assumes a quantitative dimension rather than a qualitative disorder (Reference Fulker and ChernyFulker & Cherny, 1996). This type of linkage was first successfully applied to reading disability, identifying a significant QTL linkage on the short arm of chromosome 6 (6p21) (Reference Cardon, Smith and FulkerCardon et al, 1994), a linkage that has been consistently confirmed in three subsequent studies (Reference Grigorenko, Wood and MeyerGrigorenko et al, 1997; Reference Fisher, Marlow and LambFisher, S. E., et al, 1999; Reference Gayán, Smith and ChernyGayán et al, 1999).
Linkage is systematic but not powerful. With just 350 markers (i.e. at 10 cM intervals - roughly one in every 10 million base pairs throughout the 3.5 billion in the genome), it is possible to search the genome for linkage because each marker can scan millions of base pairs for a gene of large effect. However, linkage cannot detect genes of small effect. Even sib-pair QTL linkage with reasonable sample size cannot detect genes that account for less than 10% of the variance. In other words, linkage is ‘far-sighted’ in that it can detect distant mountains, but it cannot see nearby hills. The other major approach for identifying genes, allelic association, sometimes confusingly called ‘linkage disequilibrium’, looks for correlation between marker alleles and the trait in the population, rather than within families. Allelic association is powerful for detecting QTLs of small effect (Reference Risch and MerikangasRisch & Merikangas, 1996). Although allelic association is simplest when functional polymorphisms in candidate genes are used as markers, it is also possible to detect QTLs employing non-functional DNA markers that are close enough to remain associated with the QTL for many generations. In contrast to linkage, allelic association is powerful but not systematic; it is ‘short-sighted’, detecting nearby hills, but not distant mountains. In the population, recombination breaks up alleles for a marker and a QTL that happen to be close together on the same chromosome unless the marker and the QTL are very close, essentially in the same gene.
In this sense, linkage and association are complementary, but because of the power of allelic association to detect genes of small effect size, association has become increasingly popular in the search for QTLs for complex traits such as behaviour (Reference Plomin, Owen and McGuffinPlomin et al, 1994; Reference Risch and MerikangasRisch & Merikangas, 1996). Unlike linkage, association is as easily applied to the study of quantitative dimensions as it is to qualitative disorders. However, because it is short-sighted, allelic association can only be found for markers that are very close to the QTL. For this reason, most association studies focus on markers in ‘candidate’ genes and, especially, markers that are themselves ‘functional’ in the sense that they result in a coding difference in amino acid sequences or show a physiological effect. For example, we investigated 100 DNA markers in or near genes relevant to the nervous system, but found no replicated QTL associations with g (Reference Plomin, McClearn and SmithPlomin et al, 1995).
This approach does not help much to make association systematic, because all of the 30 000 genes expressed in the brain could be considered to be candidate genes for g. In order to scan the genome systematically for allelic association in the same way as scans for linkage, thousands of markers would be needed, which would seem to be an impossible task. For example, with 200 subjects in a high g group and 200 subjects in a control group, each marker would require 400 genotypings, which means that 3500 markers needed for a 1 cM scan of the genome would require 1.4 million genotypings.
Work in progress
We attempted a preliminary search of this type for DNA markers associated with g on the long arm of chromosome 6 (Reference Chorney, Chorney and SeeseChorney et al, 1998). For one marker, the frequency of one of its alleles was twice as high in two groups of children with high g compared with two groups of children with average g (frequencies of about 30% versus 15%, respectively). Both samples yielded a significant difference in the same direction and combining these results yielded a highly significant result (χ2 = 12.41, P<0.004). The DNA marker happened to be in the 3′ untranslated region of the gene for insulin-like growth factor receptor-2 (IGF2R), which has recently been shown to be especially active in brain regions most involved in learning and memory (Reference WickelgrenWickelgren, 1998).
Pooling DNA from subjects within each group and comparing the pooled DNA across groups for a dense map of DNA markers offers a solution to the conundrum that linkage is systematic but not powerful, whereas allelic association is powerful but not systematic. Pooling can be used to screen thousands of DNA markers for QTL associations by creating pools of DNA for cases and controls. For example, only 7000 rather than 1.4 million genotypings would be needed in the previous example to screen 3500 markers for two groups. An approach to DNA pooling has been developed as part of our project on g comparing the allele image patterns (AIPs) from an automated DNA sequencer for two pools of DNA (Reference Daniels, Holmans and PlominDaniels et al, 1998). The DNA pooling method has been shown to be a reasonably accurate screening tool to detect the largest allelic frequency differences between two groups. We use a three-stage design in which pooled DNA is compared in an original sample and tested in a replication sample, and then surviving markers are individually genotyped and tested using conventional statistics.
The goal of this programme of research is to identify some (but certainly not all) QTLs associated with g. We hope to identify some of the oldest and largest QTLs, knowing that we will miss QTLs with complicated linkage disequilibrium histories, QTLs whose effect sizes are too small, and QTLs too far away from our markers. The premise of our approach is that it is reasonable to begin by identifying some QTLs of largest effect size using a reasonably dense map that can be made even denser as more markers become available. Pooling is a screening device that greatly reduces the amount of genotyping needed to conduct a genome scan for allelic association using a dense marker map. We have reported results for chromosomes 4 (Reference Fisher, Turic and McGuffinFisher, P. J., et al, 1999) and 22 (Reference Hill, Craig and BallHill et al, 1999) and at the time of writing are nearly halfway through a scan of the entire genome.
METHOD
A fuller description of the method is given by P. J. Fisher et al (Reference Fisher, Turic and McGuffin1999) and Hill et al (Reference Hill, Craig and Ball1999).
The sample groups of US children were restricted to non-Hispanic children of European descent so that differences in marker allele frequencies between the groups were less likely to be due to ethnic differences. The original high-g and control samples were selected from children living in a six-county area around Cleveland, Ohio, who were aged 6-15 years. General cognitive ability was assessed by a widely used IQ test, the Wechsler Intelligence Scale for Children - Revised (Reference WechslerWechsler, 1974). The high-g sample included 51 children (mean IQ 136; s.d.=9.3) and the control group included 51 children of average g (mean IQ 103; s.d.=5.6). A replication high-g group was obtained from the Study of Mathematically Precocious Youth (SMPY) in the USA, which began in the 1970s as a study of mathematical talent but since the late 1970s has put an equal emphasis on verbal talent (Reference Lubinski, Benbow, Subotnik and ArnoldLubinski & Benbow, 1994). The highest-scoring SMPY individuals were selected from the more than 1 million seventh- and eighth-graders (i.e. aged 12-14 years) who performed in the top 3% on a standardised test administered in their schools and were invited to take the Scholastic Aptitude Test (SAT) college entrance examination 4 years early, before the age of 13 years. The SAT correlates highly with g and with standard IQ tests in the normal range, for example, 0.84 for the mathematical part (SAT-M) and 0.89 for the verbal test (SAT-V) corrected for unreliability (Reference Brodnick and ReeBrodnick & Ree, 1995); using the SAT at age 13 years instead of the usual age of 17 years makes it possible to estimate IQ scores even though standard IQ tests do not cover scores as high as these. Fifty of the highest-scoring individuals were targeted for the high-replication sample. These participants earned scores of at least SAT-V≥630 and SAT-M≥630, or SAT-V≥550 and SAT-M≥700. They were required to have ‘flat’ SAT profiles in the sense that their SAT-V and SAT-M scores were required to be within 1 standard deviation of each other. These participants represent a selection intensity of about 1 in 30 000 as indicated by scores 4 s.d. above the mean (equivalent to an IQ score of 160), estimated from their composite (V+M) SAT scores. A replication control group consisting of 50 individuals (mean IQ 101; s.d.=7.2) was selected in the same manner (same geographical area, same age) as the original control group. Informed consent was obtained from all participants.
Three-stage replication design
A three-stage strategy was used in order to provide a balance between false-positive and false-negative results by permitting a lenient criterion for significance in the first stage (which does not correct for multiple testing but reduces false negatives) and then removing false positives in the second and third stages. In the first stage, differences in allele image patterns (see below) were compared for the two groups (high and average g) in the original sample for 213 markers across chromosomes 4 and 22. In the second stage, markers that yielded significant differences in allele-image patterns and a significant allele-specific difference (see below) in the first stage were replicated in independent pooled samples by testing an allele-specific directional hypothesis derived from the original sample. In the third stage, markers that were significant in the two DNA-pooling stages were genotyped individually for all subjects in order to confirm the results of DNA pooling using conventional statistics.
DNA pooling
The DNA pooling technique is described by Daniels et al (Reference Daniels, Holmans and Plomin1998). The DNA was obtained from permanent cell lines derived from lymphocytes in blood using a standard protocol. Each individual DNA sample was diluted to 8 ng/μl. Quantification of DNA prior to pooling was performed in triplicate using a Fluoroskan Ascent fluorometer (Dynex Laboratory Systems, Ashford, Middlesex, UK). Three replicate DNA pools were constructed for individuals in each of the two original groups (the high-g group and the average-g control group) and in each of the two replication groups.
Primer selection
Markers containing di-, tri- and tetranucleotide repeats at roughly 1 cM intervals (which means that a QTL is no more than 0.5 cM from a marker) were selected for chromosomes 4 and 22 from databases on the internet. Primers with fluorescent 5′ ends were purchased from MWG-Biotech (Ebersberg, Germany). An average density of 1.2 cM was obtained for the successfully amplified 147 markers on chromosome 4 and 66 markers on chromosome 22.
PCR amplification of pooled DNA samples
Rather than optimising each primer pair, a touchdown polymerase chain reaction (PCR) protocol was used to amplify pooled DNA for each marker. Markers that were not successfully amplified using these standard conditions were submitted to a second amplification protocol, and markers that continued to fail to amplify were replaced with other markers in the region. Each of the three DNA pools for each group was amplified twice, resulting in six PCR products for each group.
Gel electrophoresis using an automated DNA sequencer
Allele image patterns were generated on an ABI 377 DNA sequencer (Applied Biosystems, Foster City, CA, USA) for each pool's six PCR products for each marker. Up to four fluorescently labelled markers with distinct ranges of allele sizes underwent electrophoresis in each gel lane.
Analysis of AIPs
Other approaches to DNA pooling have attempted to estimate absolute allelic frequencies, which requires adjustments for technical problems such as differential amplification and stutter banding (Reference LeDuc, Miller and LichterLeDuc et al, 1995; Reference Perlin, Lancia and NgPerlin et al, 1995; Reference Barcellos, Klitz and FieldBarcellos et al, 1997). The essence of our approach to DNA pooling is that comparison of two groups only requires an estimate of relative allelic frequencies, which largely eliminates such artefactual differences between the two groups. That is, any perturbations to allele patterns due to such artefacts will be reproducible under standard conditions in both groups, thus allowing comparative differences between the groups to be identified. We focus on the difference in AIPs (ΔAIP) for the two groups seen when their AIPs are overlaid (Reference Daniels, Holmans and PlominDaniels et al, 1998). The six unmodified AIPs for each marker for each group were overlaid using Applied Biosystems' GENOTYPER software and imported into DeBabelizer (Equilibrium Technologies, Sausolito, CA, USA). The consensus AIP was taken to represent the relative allele frequencies. Markers were tested for significant differences in allele patterns between groups using a programme that simulates allele patterns from ΔAIP scores, heights of the peaks and the number of peaks. For markers yielding significant Δ AIPs in the original sample, the allele with the largest difference between the high-g and control group in the original sample was tested in order to establish an allele-specific directional hypothesis to be tested in the replication sample. The height of the allele's peak for each group was converted to a percentage of the total of all the peak heights for the group, and tested for significance using Pearson χ2 comparing that peak against all others. Markers can yield significant Δ AIPs because small differences between groups emerge for several alleles, or because a relatively large difference occurs for a specific allele. Unless a marker shows a significant difference for a specific allele in the original sample, it is unlikely that the allele-specific directional test will be significant in the replication sample. For this reason, we limit replication to markers that meet two criteria in the original sample: a significant ΔAIP and a significant specific allele difference between the two groups.
Individual genotyping
For markers with significant ΔAIPs in the original sample and significant χ2 for the allele-specific directional test in the replication sample, all subjects were genotyped individually. The PCR procedure was performed using a standard protocol with 30 ng of an individual's DNA used per PCR. For the original sample, the significance of the differences between the two groups was estimated for all of a marker's alleles using the CLUMP program, which is based on Monte Carlo simulations (Reference Vallada, Curtis and ShamVallada et al, 1995). For the replication sample, the allele-specific directional hypothesis derived from the original sample was tested for significance using Pearson χ2 comparing that allele against all others.
RESULTS
Figure 1 illustrates DNA pooling results in the first stage for one of the markers (D4S2943) that showed significant ΔAIPs. Because the DNA is pooled, the AIPs generated by the DNA sequencer show all six alleles for D4S2943 rather than just one or two alleles which would be seen in individual genotyping. The relative height of each allele is taken as a measure of its frequency. The overlaid AIPs for the original high-g group and the original control group indicate that differences between the AIPs for the two groups are due primarily to the fourth allele.
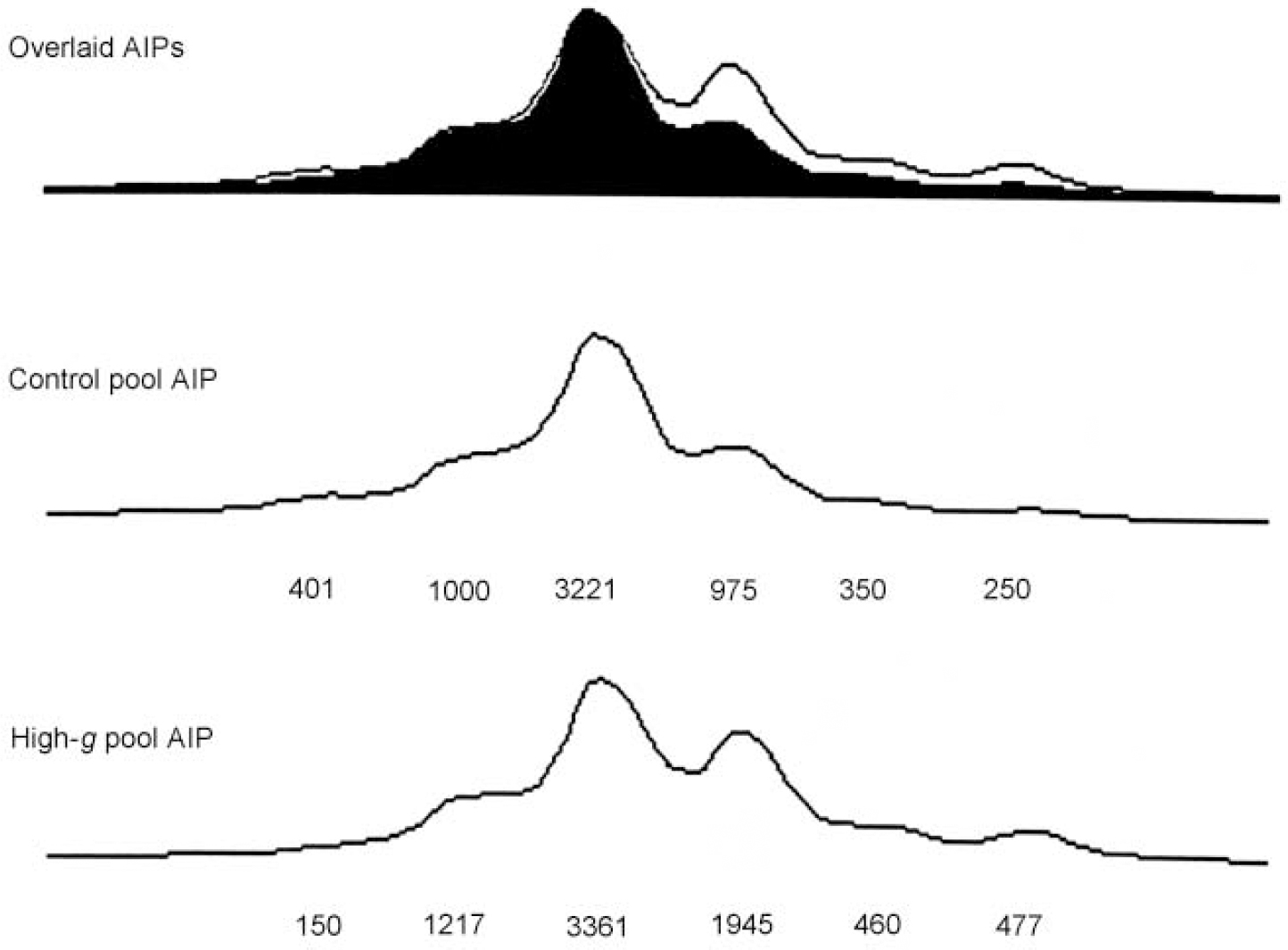
Fig. 1 Allele image patterns (AIPs) for D4S2943, showing the overlaid images (top), and separate patterns for the original control group (middle) and the original high-g group (bottom). The numbers represent peak heights expressed in fluorescence units. Although fluorescence units differ between the two groups because of polymerase chain reaction differences in the amount of amplification and differences in loading the wells for the sequencer, the overlaid AIPs calibrate the AIPs for the two groups by equating their peak heights.
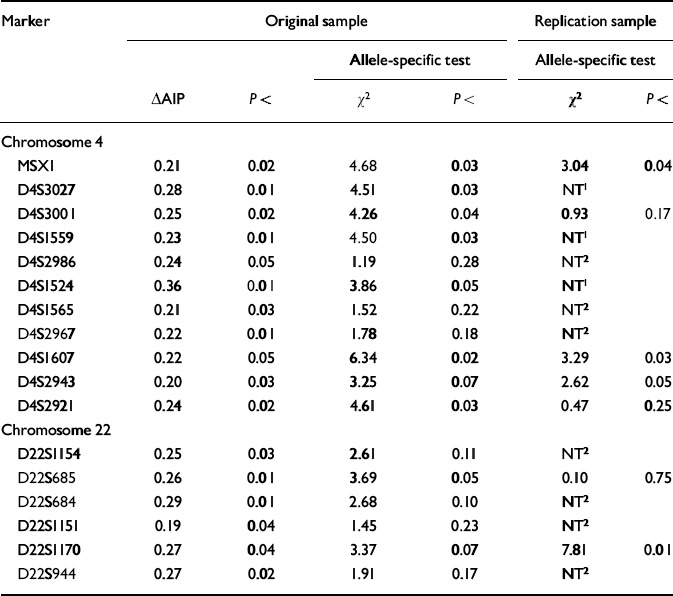
Seventeen of the 213 markers on chromosomes 4 and 22 yielded significant (P<0.05) ΔAIPs for the high-g and control groups in the original sample. With P set at <0.05, only 10 markers were expected to be significant by chance alone. The ΔAIPs and P values for these 17 markers are listed in Table 1, together with the χ2 and P values for the allele-specific test in the original sample. Of the 17 markers with significant ΔAIPs in the original sample, eight showed a significant difference for a specific allele. In addition, D4S2943 and D22S1170 showed trends (P<0.07) that together with their significant ΔAIPs warranted further exploration in the replication sample.
Table 1 Markers yielding significant (P < 0.05) differences in allele image patterns (ΔAIPs) in the original sample based on DNA pooling of 213 markers for high-g and control groups. These markers were also tested in the original sample for the significance of a specific allele showing the greatest frequency difference between the high-g and control groups. Significant allele-specific differences in the original sample were used as hypotheses to be tested in the replication sample
| Marker | Original sample | Replication sample | ||||
|---|---|---|---|---|---|---|
| Allele-specific test | Allele-specific test | |||||
| Δ AIP | P< | χ2 | P< | χ2 | P< | |
| Chromosome 4 | ||||||
| MSXI | 0.21 | 0.02 | 4.68 | 0.03 | 3.04 | 0.04 |
| D4S3027 | 0.28 | 0.01 | 4.51 | 0.03 | NT1 | |
| D4S3001 | 0.25 | 0.02 | 4.26 | 0.04 | 0.93 | 0.17 |
| D4S1559 | 0.23 | 0.01 | 4.50 | 0.03 | NT1 | |
| D4S2986 | 0.24 | 0.05 | 1.19 | 0.28 | NT2 | |
| D4S1524 | 0.36 | 0.01 | 3.86 | 0.05 | NT1 | |
| D4S1565 | 0.21 | 0.03 | 1.52 | 0.22 | NT2 | |
| D4S2967 | 0.22 | 0.01 | 1.78 | 0.18 | NT2 | |
| D4S1607 | 0.22 | 0.05 | 6.34 | 0.02 | 3.29 | 0.03 |
| D4S2943 | 0.20 | 0.03 | 3.25 | 0.07 | 2.62 | 0.05 |
| D4S2921 | 0.24 | 0.02 | 4.61 | 0.03 | 0.47 | 0.25 |
| Chromosome 22 | ||||||
| D22S1154 | 0.25 | 0.03 | 2.61 | 0.11 | NT2 | |
| D22S685 | 0.26 | 0.01 | 3.69 | 0.05 | 0.10 | 0.75 |
| D22S684 | 0.29 | 0.01 | 2.68 | 0.10 | NT2 | |
| D22S1151 | 0.19 | 0.04 | 1.45 | 0.23 | NT2 | |
| D22S1170 | 0.27 | 0.04 | 3.37 | 0.07 | 7.81 | 0.01 |
| D22S944 | 0.27 | 0.02 | 1.91 | 0.17 | NT2 | |
These 10 markers were tested for replication in stage 2 DNA pooling — where none of the markers would be expected to be significant by chance alone. Four of the 10 markers yielded a significant allele-specific difference in the replication sample that was in the same direction as the original sample (see Table 1).
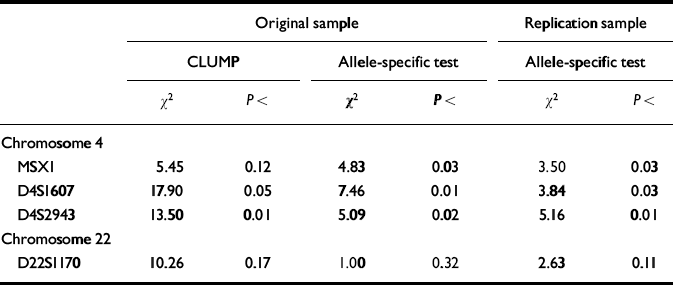
These four markers were therefore selected for the third stage of the design, in which each high-g and control individual was genotyped separately. Results for the individual genotyping are summarised in Table 2. Individual genotyping confirmed the DNA pooling observations for two markers (D4S1607, D4S2943) using CLUMP analysis to test all allelic differences between the two groups simultaneously. The other two markers nominated by DNA pooling yielded trends in the CLUMP analysis (MSX1 and D22S1170). The allele-specific directional test for individual genotyping results showed even stronger confirmation of DNA pooling. Three of the four markers showed significant differences between the groups in the original sample for the same alleles in the same direction as identified by DNA pooling. For three markers (MSX1, D4S1607, D4S2943), the individual genotyping allele-specific directional test reached significance in the original sample. All three markers were also significant in the replication sample for the allele-specific directional test.
Table 2 Results for individual genotyping of markers screened by DNA pooling as significant in the original sample (significant difference in allele image patterns (ΔAIP) plus significant allele-specific test) and in the replication sample (allele-specific directional test).
| Original sample | Replication sample | |||||
|---|---|---|---|---|---|---|
| CLUMP | Allele-specific test | Allele-specific test | ||||
| χ2 | P< | χ2 | P< | χ2 | P< | |
| Chromosome 4 | ||||||
| MSXI | 5.45 | 0.12 | 4.83 | 0.03 | 3.50 | 0.03 |
| D4S1607 | 17.90 | 0.05 | 7.46 | 0.01 | 3.84 | 0.03 |
| D4S2943 | 13.50 | 0.01 | 5.09 | 0.02 | 5.16 | 0.01 |
| Chromosome 22 | ||||||
| D22S1170 | 10.26 | 0.17 | 1.00 | 0.32 | 2.63 | 0.11 |
In summary, one marker (D4S1607) met all of the criteria for a significant QTL: stage 1 DNA pooling significance in the original sample for both Δ AIP and the allele-specific test; stage 2 DNA pooling significance in the replication sample for the allele-specific test; and stage 3 individual genotyping significance for the CLUMP test comparing all alleles, as well as for the allele-specific directional test in the original sample and for the allele-specific test in the replication sample. Two other markers just missed the criterion of P<0.05 for one of these six hurdles: MSX1 (where P<0.12 for the CLUMP test in stage 3) and D4S2943 (where P<0.07 for the allele-specific test in stage 1). Because the ultimate test of the allele-specific hypothesis using individual genotyping was significant for all three of these markers in both the original sample and replication sample, we nominate all three markers as QTLs for g (Reference Fisher, Turic and McGuffinFisher, P. J., et al, 1999). We have subsequently doubled our sample sizes and will look again with greater power at other markers that show replicable trends, such as D22S1170.
CONCLUSION
This first application of DNA pooling to screen for allelic association in a systematic genome scan at 1 cM marker density yielded one QTL (D4S1607) that met all six criteria for significance in our multistage replication design. Two other QTLs (MSX1 and D4S2943) met five of the six criteria and just missed the sixth criterion. We conclude that DNA pooling for association using a dense map of markers can identify some, although certainly not all, QTLs for g, one of the most heritable dimensions of behaviour and of greatest relevance to cognitive neuroscience. Although none of these QTLs individually is expected to account for a large portion of the genetic variance for g, we expect that a systematic genome scan will yield QTLs that together account for a substantial portion of the variance.
Allelic association based on linkage disequilibrium (that is, the presence of specific alleles at marker loci contiguous to QTLs at higher frequencies than expected by chance) is inherently limited to detecting mutations that occurred many generations ago very near the QTL and which have not been randomised in their association with the QTL through recombination as they spread through the population. The power of association analysis to detect a QTL depends not only on the magnitude of the effect of the QTL on the trait, but also on the magnitude of linkage disequilibrium between the QTL and a marker. The latter issue is complicated because drift, mutation, selection and migration may operate in different ways to determine the levels of linkage disequilibrium in different populations (Reference GuoGuo, 1997). More powerful approaches based on haplotypes across markers are being developed that will improve this situation (Reference Schork, Cardon and XuSchork et al, 1998).
A specific limitation of case-control association studies is the possibility that spurious associations can be caused by ethnic differences within the sample. Our approach is to find associations using case-control comparisons that exclude ethnic minority groups in order to minimise the possibility of ethnic stratification, and then to test for association using within-family designs which remove possibility of ethnic differences. We are currently collecting DNA from parents of the high-g children in order to test for within-family association (Reference Ewens and SpielmanEwens & Spielman, 1995; Sham & Curtis, Reference Sham and Curtis1995a ,Reference Sham and Curtis b ) which will also provide an additional test of replication.
Although denser maps are desirable, an interval of 1 cM (which means that a QTL is within 0.5 cM of a marker) appears to be a reasonable starting point for a genome screen, although it is generally accepted that a density at least 10 times greater would be needed to ensure linkage disequilibrium. We estimate that 75% of the genome is currently covered with a map density of 1 cM or greater and this coverage is increasing rapidly, especially for single nucleotide polymorphisms (SNPs). The goal of a 1 cM density will be a reality in the near future (Reference Collins, Euyer and ChakravartiCollins et al, 1997), and intense effort to identify several hundred thousand SNPs will facilitate a density of 0.1 cM or greater.
Our current 1 cM average density for the regions identified can be considered a framework for subsequent research that adds markers to fill in the map. In addition, we intend to test more markers in close proximity to those that yielded positive results. The distribution of QTL effect sizes is not known for any complex trait (Reference TanksleyTanksley, 1993). Although it is possible that there are one or two large effects, we assume that there is a continuous distribution of effect sizes skewed towards large effects with a long tail going out to infinitesimally small, undetectable effects. A systematic scan of the genome using allelic association will address this issue empirically. A reasonable goal for allelic association designs is to detect QTL associations that account for 1% of the variance in an unselected population. Although our present sample sizes are modest, they provide experimental power by selecting high-g subjects at the extreme of the distribution (Reference Van Gestel, Houwing-Duistermaat and AdolfssonVan Gestel et al, 2000). We are currently doubling our sample sizes in order to reach our goal of detecting effects that account for 1% of the variance. We are also obtaining large unselected samples of subjects assessed on g in order to test the hypothesis that QTLs identified at the high extreme of the distribution have similar effects throughout the distribution. One of these unselected samples involves older subjects, which will make it possible to test the hypothesis that the magnitude of genetic effects on g increases throughout the life span.
Identifying QTLs associated with g will provide discrete windows through which to view brain pathways between genes and learning and memory. In a few years, when the entire DNA sequence and its variants are known, we predict that we will be awash with QTLs for complex traits, including QTLs for cognitive abilities and disabilities. Research will increasingly be directed towards understanding the function of such QTLs. Although attention is focused now on finding genes associated with behaviour, few behavioural scientists are likely to join the hunt for genes, because it is difficult and expensive. However, once genes are identified, it is easy and inexpensive to use them to ask questions at the behavioural level of analysis (Reference Plomin and RutterPlomin & Rutter, 1998). The term ‘functional genomics’ usually connotes ‘bottom-up’ molecular biological research that identifies gene products and investigates their function at a cellular level. However, other higher levels of analysis will also be profitable in understanding the pathways between genes and behaviour. For example, cognitive neuroscience represents a middleway level of analysis that would benefit enormously from identification of QTLs for g. The ‘top-down’ behavioural level of analysis represented by psychology is also likely to make important contributions towards understanding the functions of QTLs. In order to highlight this top-down level of analyses, the term ‘behavioural genomics’ has been suggested (Reference Plomin and CrabbePlomin & Crabbe, 2000). Knowledge of specific genes related to cognitive abilities will greatly improve our ability to ask more refined and powerful questions about development, heterogeneity and comorbidity, and gene-environment interplay (Reference Plomin and RutterPlomin & Rutter, 1998). Do the effects of genes change during development? Do the genes correlate with some aspects of a trait but not others (heterogeneity), or do their effects extend across several traits (comorbidity)? Are genes for disorders also associated with normal dimensions, and vice versa? Do the genetic effects interact or correlate with the environment? The answers will open up new scientific horizons of immense potential for the behavioural sciences.
As is the case with most important advances in human genetics, identifying genes for g will confirm some people's worst fears about DNA, especially in relation to g (Reference Newson and WilliamsonNewson & Williamson, 1999). They fear that finding out about genetic risk when no prevention or cure is available will label people in ways that might lead to discrimination for insurance and employment, without being able to help them. Knowing about genetic risk might also become a self-fulfilling prophecy, for example if a child is labelled as at risk of learning disorders. Parents using in vitro fertilisation might select embryos with fewer genetic risks and more genetic strengths. These are serious problems, but some of the fears derive from misunderstandings about what genetics can and cannot do (Reference Rutter and PlominRutter & Plomin, 1997; Reference Sherman, DeFries and GottesmanSherman et al, 1997). The main misunderstanding is to think that genes determine outcomes in a hard-wired, there-is-nothing-we-can-do-about-it way. For thousands of rare single-gene disorders, such as the gene on chromosome 4 that causes Huntington's disease, genes do determine outcomes in this hard-wired way, but such knowledge may also enable therapeutic intervention, as is the case for phenylketonuria. However, behavioural disorders and dimensions are complex traits influenced by many genes as well as by many environmental factors. For complex traits, genetic factors operate like risk factors rather than determining outcomes. For these reasons, it is crucial that behavioural scientists should not be afraid of molecular genetics and that they should take advantage of the exciting developments in this field. Students in the behavioural sciences must be taught about genetics in order to prepare them for the future. Otherwise, the opportunity will slip away by default to geneticists — and genetics is much too important a topic to be left to geneticists!
ACKNOWLEDGEMENTS
This work was supported by a grant from the US National Institute of Child Health and Human Development (Grant HD27694) with R.P. as Principal Investigator and with co-investigators Philip Asherson, David Ball, Michael J. Chorney, Ian Craig, David Lubinski, Peter McGuffin and Michael J. Owen.






eLetters
No eLetters have been published for this article.