Article contents
Topology of the Negative Energy-Manifold of the Kepler Motion
Published online by Cambridge University Press: 14 August 2015
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The motion of a particle of mass m according to the central force of Newton, is denoted by
where K is a constant. x=0 corresponds to singular points of this equations. The domain of (1), denoted by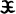 
= (R3 −{0})×R3, is called the phase space of the Kepler motion. In the sequel we set m=K=1 for simplicity and also transform the independent variable from t to s by dt =|x|ds (x≠0), then the Kepler motion in the phase space 
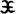is written as
Further, we shall confine the following discussion to the case of the negative energy value, except the preliminary discussion.
- Type
- Part I: Stability, N- and 3-Body Problems, Variable Mass
- Information
- Symposium - International Astronomical Union , Volume 81: Dynamics of the Solar System , 1979 , pp. 45 - 48
- Copyright
- Copyright © Reidel 1979
References
1.
Moser, J.: Regularization of Kepler's Problem and the Averaging Method on a Manifold. Comm. Pure Apple. Math.
23 (1970), 609–636.Google Scholar
2.
Kustaanheimo, P. and Stiefel, E.: Perturbation Theory of Kepler Motion Based on Spinor Regularization. J. Reine Angew. Math.
218 (1965), 204–219.Google Scholar
3.
Stiefel, E.L. and Scheifele, G.: Linear and Regular Celestial Mechanics, Springer-Verlag, Berlin
1971, Chap. II, III, and XI.Google Scholar
You have
Access
- 1
- Cited by
